| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322379 | |
| Published online | 14 March 2014 | |
Online material
Appendix A: The Johnson-Cousins UBVRI System
One of the most common and frequently used standard broad-band photometric systems is the photoelectric UBV system. Usually, the Johnson-Cousins UBVRI refers to the combined Johnson-Cousins UBV system (Johnson & Morgan 1953) and its red optical extension of the Cousins RI system (Cousins 1976). In this system the V-band represents an approximate measure of the visual photographic magnitude, whereas the B-band was defined to give a measure for the uncorrected photographic magnitude. In addition, the U-band probes the interesting window between the atmospheric cutoff and the B-band. However, the combination of the UBV system of having a cutoff defined by the atmosphere at low wavelengths (plus the original 1P21 glass optics) and a limit by the detector at long wavelengths (λλ ≈ 6320 ≈ VRcut) implicated that the U-band filter is sensitive to the atmospheric extinction. The original B and V bands of the UBV system could be well reproduced with current more sentitive (redder) CCD detectors (e.g., Buser 1978; Bessel 1986, for the U-band; Bessel 1990, for UBVRI). However, the characteristics of the U-band were more difficult to realise with current detector technologies, mainly because of short wavelength cutoff due to the atmosphere and the impact of temperature dependencies (Bessel et al. 1998).
In the photometric Johnson system the A0V star α Lyr (Vega) is defined to have V = 0.03 mag, whereas all other colours of Vega are equal to zero. The absolute flux of Vega can be calibrated using empirical relations (e.g., Bessel 1979, 1990), or some calibration standard stars (Landolt 1992).
For the present work, we have adopted the original 1953 UJ-Johnson filter (λc = 3499, WHM = 699, hereafter U-band) that has been reconstructed in the USA (Johnson & Morgan 1953). The original filter name is referred as Corning 9863 and was initially used in photoelectric observations. For an unreddened A0V star with V = 0.00, the U-Johnson filter gives a total flux of 3.98 × 10-9 erg cm-2 s-1 Å-1 (Lamla 1982). Our choice is primarily driven by the high filter response in the blue wavelength range compared to other U-band filters used in the literature. Because of its high sensitivity in the blue, the U-Johnson filter allow us to directly probe the luminous, hot and blue OB stars and SF associations in the stellar content of galaxies and therefore acts as a proxy for SF, although it is affected by dust extinction. However, using a combination of GALEX NUV and FUV IR colours, we demonstrate in Sect. 4.3 that we are able to perform a robust separation into red quiescent, blue star-forming galaxies as well as dust-obscured red galaxies with or without SF. Similar approaches adopting a pseudo-continuum U280 filter to split quiescent from star-forming galaxies have been used, for example, in moderate redshift clusters (Wolf et al. 2009) and for field galaxies (Nicol et al. 2011).
 |
Fig. A.1
Filter transmission curve for different popular U-band filters in the literature. The U-Johnson (dashed blue), used in VIPERS, is compared to the UBessel VVDS filter (red solid), U3 Buser filter (green), UBessel1990 (dotted cyan), u SDSS (black), u∗ CFHT MegaCam (pink), and the u⋆ CFHT MegaCam SAGEM filter (dot-dashed magenta line). |
| Open with DEXTER | |
Figure A.1 shows the filter transmission curve for the U-Johnson filter compared to other frequently used U-band filters in the literature. The U-Johnson (blue dashed) is compared to the UJKC Bessel filter (red solid), U3 Buser filter (green), UBessel 1990 (cyan dotted), u SDSS (black), u∗CFHT MegaCam (pink), and the u⋆ CFHT MegaCam SAGEM filter (dot-dashed magenta line), which is used in ALF, whereas for the SED modelling we adopt U-Johnson filter. Note that the Johnson filter has a quite different efficiency curve from the standard UJKC-Johnson-Kron-Cousins filter in the VVDS, or the U3 Buser filter as adopted in the PEGASE filter library (see Table 1 of Buser & Kurucz 1978) or in the Bruzual & Charlot (2003) models (record 12). The U-Johnson has a higher blue sensitivity than any other U-band filter and allows to obtain redder colours for red galaxies with a more prominent separation between blue and red galaxies with a minimum at (U − B) ~ 1.2 (AB). Moreover, the whole filter remains below 4000 Å and therefore is a good proxy for the 4000 Å break. The U3 filter is extended at larger wavelengths and therefore produces bluer colours compared to the U-Johnson filter and a minimum at (U3 − B) ~ 1.0 (AB).
For the BJKC filter we adopt the B3 Buser filter (Buser 1978) as commonly used in PEGASE (B3BK78) and the Bruzual & Charlot (2003) models (record 14). As the VJKC filter we define the V Buser (corresponding to VBK78 in PEGASE and record 15 in the Bruzual & Charlot (2003) models). Both the B3 and V Buser filters are also used in the Millennium simulation by De Lucia & Blaizot (2007). Table A.1 compares the main filter characteristics used in this work (U,B3,V) to the U3 filter.
Basic characteristics of different UBV filters.
We adopt the following transformation from the UJ-Johnson filter
passband to the rest-frame UJKC system (in AB):
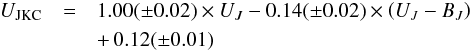 (A.1)The transformation from AB to Vega system
was performed using MJKC(AB) = MJKC(Vega) + cX(AB),
where the individual colour terms cX(AB) for each
filter were derived through the SED fitting procedure.
(A.1)The transformation from AB to Vega system
was performed using MJKC(AB) = MJKC(Vega) + cX(AB),
where the individual colour terms cX(AB) for each
filter were derived through the SED fitting procedure.
Among the literature the interpretation and application of the UBV-Johnson-Morgan-Cousins system is often inhomogeneous and ambiguous. For example, Cooper et al. (2010) used the U3 (Buser 1978) filter, whereas the B and V-band are not the corresponding Buser filters but the B2 and V filters by Asuzienis & Straizys (1969). More popular are the usage of the UBVJKC Johnson-Cousins definitions, like for the VVDS (Franzetti et al. 2007) or in the zCOSMOS survey (Cucciati et al. 2010). It is beyond the scope of the current investigation to reproduce the exact filter definitions used among works in the literature. We emphasize that that for comparisons with literature data one should always be precise and clearly describe which photometry and filter transmission curves are adopted.
Appendix B: Completeness test
In Fig. 10 we observe a change of the evolution of the RS intercept from z = 0.9 to z = 1.3. This change in the number of red galaxies could be either due to a real evolution or to sample incompleteness. To test the completeness of red galaxies in the highest redshift bin 1.0 < z < 1.3, we construct different samples of red galaxies in the lower redshift bin 0.9 < z < 1.0 (hereafter simulated samples) to verify whether the observed properties of the sample at 1.0 < z < 1.3 (hereafter real sample) are consistent with the properties of their counterparts at 0.9 < z < 1.0. Red galaxies in VIPERS are defined as those galaxies classified by SED type class 1 (see Sect. 2.4). We assume that the average observed (U − V) rest-frame distribution is the same for red galaxies at all redshifts. Because the reddest galaxies have the faintest ultra-violet magnitudes, a possible incompleteness bias would be apparent in the observed i′-band magnitude distribution with the reddest galaxies being absent.
We have computed the observed (U − V) rest-frame distribution of randomly selected red samples in the redshift bin 0.9 < z < 1.0, which were extracted from the observed (U − V) rest-frame distribution of all red galaxies within the same redshift interval. The real and randomly selected red galaxy samples at 0.9 < z < 1.0 share the same properties and the randomly selected (hence simulated) samples are always a sub-set of the total red galaxy sample. These simulated samples have the same number of galaxies as the sample at 1.0 < z < 1.3 and therefore should mimic the properties of the observed red galaxy sample at the highest redshift bin, assuming the latter is complete. We take a random set of two simulated samples at 0.9 < z < 1.0, referred to simulated 1 and simulated 2, to understand their variance and possible spread in properties. We assume the redshift bin 0.9 < z < 1.0 to be complete for all types of (red, green and blue) galaxies and we are mainly interested in possible incompleteness effects in the RS evolution at z > 1. For each galaxy in the simulated samples we derive the observed i′-band (AB) magnitudes.
For the real galaxy sample, we took the observed (U − V) rest-frame distribution of all red galaxies in the high-redshift bin 1.0 < z < 1.3 and computed for each galaxy separately the observed i′-band magnitudes. Finally, we corrected for the redshift evolution of each object as Δ(Mcorr) = Δ(Mi′)/0.3 × (zspec − 1), where Mi′ is the evolution correction from z = 1.3 to z = 0.9 derived from the LF of the VVDS (Ilbert et al. 2005) and zspec is the spectroscopic redshift of each single galaxy.
A comparison of the real and simulated red galaxy samples is shown in Fig. B.1. Two representative simulated samples of red galaxies (simulated 1 and simulated 2) are shown in blue and green, respectively. The red histogram shows the real red sample at 1.0 < z < 1.3, which was transformed to redshift 0.9 < z < 1.0. Table B.1 compares the median, first and third quartile, and the 1 σ Gaussian values of the distribution for the real and randomly selected simulated samples. The histograms display similar shapes and show consistent statistics. We therefore conclude that our red galaxy sample at z > 1 does not show any significant incompleteness of bright galaxies and that our sample is also highly complete at fainter magnitudes.
 |
Fig. B.1
Completeness test for red galaxies in the VIPERS PDR-1. The red histogram displays the observed real red galaxies at 1.0 < z < 1.3 transformed to 0.9 < z < 1.0, whereas the simulated samples are two representations of red galaxy samples at 0.9 < z < 1.0. The properties of the real sample are consistent with the properties of their simulated counterparts. |
| Open with DEXTER | |
Statistical properties of real and simulated red galaxy samples.
Appendix C: Cosmic variance
 |
Fig. C.1
Cosmic variance for the VIPERS PDR-1 sample and other surveys from the literature. Symbols denote data from AGES (Cool et al. 2012, red crosses), COMBO-17 (Bell et al. 2004b, black circles), COSMOS (Scoville et al. 2007, grey polygons), DEEP1 (Im et al. 2002, cyan stars), DEEP2 (Faber et al. 2007, orange triangles), NDWFS (Brown et al. 2007, magenta stars), and VVDS (Le Fèvre et al. 2005, 2013, green squares). |
| Open with DEXTER | |
Statistical measurements based on number counts such as the luminosity function or mass function are subjected to field-to-field variations of the number density that originate from the clustering of a particular galaxy population and from variations imprinted by the scale of the probed survey volume.
For a probability distribution function PN(V)
that denotes the probability of counting N objects within a volume V, the relative cosmic
variance is defined as  (C.1)where ⟨ N⟩ and
⟨ N2⟩ are the mean and variance of
the galaxy number counts (Somerville et al.
2004).
(C.1)where ⟨ N⟩ and
⟨ N2⟩ are the mean and variance of
the galaxy number counts (Somerville et al.
2004).
To test the impact of cosmic variance on our results, we have computed the uncertainty of cosmic variance for the VIPERS survey using the public code getcv (Moster et al. 2011). Figure C.1 shows the relative cosmic variance uncertainty in VIPERS (blue filled circles) divided into different mass ranges probed by the survey. For reference purposes, we also show the results of several other surveys taken from the literature.
For RS galaxies between 0.4 < z < 1.3, the uncertainties arising from cosmic variance vary in the range 0.04 < log (M⋆/M⊙) < 0.07, with a median of ⟨log (M⋆/M⊙)⟩ = 0.05. Note that the effective area of VIPERS is 10.32 deg2, which is about 4 deg2 larger than any other survey at intermediate redshifts (e.g., NDWFS, AGES). Figure C.1 shows that independent of the mass probed, the cosmic variance effects on VIPERS are a factor of two lower than AGES and 20% lower than NDWFS. Compared to all the other surveys, VIPERS is a factor of 4 or more less affected to cosmic variance effects. In particular, compared to DEEP2 and COMBO-17, the VIPERS data offers a huge improvement. Recent surveys like NDWFS or AGES cannot compete either with VIPERS. We emphasize that AGES has an average sampling rate of 20% in I and K-bands (Cool et al. 2012), which is a factor of two lower than the median sampling rate of VIPERS. We therefore conclude that the impact of cosmic variance has a negligible effect on our results.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


