| Issue |
A&A
Volume 562, February 2014
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 19 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201322001 | |
| Published online | 13 February 2014 | |
Kepler-91b: a planet at the end of its life
Planet and giant host star properties via light-curve variations⋆,⋆⋆
1 Departamento de Astrofísica, Centro de Astrobiología (CSIC-INTA), ESAC Campus, 28691 Villanueva de la Cañada, Madrid, Spain
e-mail: Jorge.Lillo@cab.inta-csic.es
2 Centro Astronómico Hispano-Alemán (CAHA), Calar Alto Observatory, c/ Jesús Durbán Remón 2-2, 04004 Almería, Spain
3 Institut d’Astrophysique et Géophysique de l’Université de Liège, Allée du six Août, 17 B-4000 Liège, Belgium
4 Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
5 European Southern Observatory, Alonso de Córdova 3107, Vitacura, Santiago, Chile
6 Osservatorio Astronomico di Padova, Vicolo Osservatorio 5, 35122 Padova, Italy
7 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
8 Dpto. de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
Received: 31 May 2013
Accepted: 5 December 2013
Context. The evolution of planetary systems is intimately linked to the evolution of their host stars. Our understanding of the whole planetary evolution process is based on the wide planet diversity observed so far. Only a few tens of planets have been discovered orbiting stars ascending the red giant branch. Although several theories have been proposed, the question of how planets die remains open owing to the small number statistics, making it clear that the sample of planets around post-main sequence stars needs to be enlarged.
Aims. In this work we study the giant star Kepler-91 (KOI-2133) in order to determine the nature of a transiting companion. This system was detected by the Kepler Space Telescope, which identified small dims in its light curve with a period of 6.246580 ± 0.000082 days. However, its planetary confirmation is needed due to the large pixel size of the Kepler camera, which can hide other stellar configurations able to mimic planet-like transit events.
Methods. We analysed Kepler photometry to 1) re-calculate transit parameters; 2) study the light-curve modulations; and 3) to perform an asteroseismic analysis (accurate stellar parameter determination) by identifying solar-like oscillations on the periodogram. We also used a high-resolution and high signal-to-noise ratio spectrum obtained with the Calar Alto Fiber-fed Échelle spectrograph (CAFE) to measure stellar properties. Additionally, false-positive scenarios were rejected by obtaining high-resolution images with the AstraLux lucky imaging camera on the 2.2 m telescope at the Calar Alto Observatory.
Results. We confirm the planetary nature of the object transiting the star Kepler-91 by deriving a mass of Mp=0.88+0.17-0.33 MJup and a planetary radius of Rp=1.384+0.011-0.054 RJup. Asteroseismic analysis produces a stellar radius of R⋆ = 6.30 ± 0.16 R⊙ and a mass of M⋆ = 1.31 ± 0.10 M⊙. We find that its eccentric orbit (e=0.066+0.013-0.017) is just 1.32+0.07-0.22 R⋆ away from the stellar atmosphere at the pericentre. We also detected three small dims in the phase-folded light curve. The combination of two of them agrees with the theoretical characteristics expected for secondary eclipse.
Conclusions. Kepler-91b could be the previous stage of the planet engulfment, which has recently been detected for BD+48 740. Our estimations show that Kepler-91b will be swallowed by its host star in less than 55 Myr. Among the confirmed planets around giant stars, this is the closest to its host star. At pericentre, the star subtends an angle of 48°, covering around 10% of the sky as seen from the planet. The planetary atmosphere seems to be inflated probably due to the high stellar irradiation.
Key words: planets and satellites: fundamental parameters / planets and satellites: detection / stars: oscillations / planets and satellites: dynamical evolution and stability / asteroseismology
Based on observations collected at the German-Spanish Astronomical Center, Calar Alto, jointly operated by the Max-Planck-Institut fur Astronomie (Heidelberg) and the Instituto de Astrofísica de Andalucía (IAA-CSIC, Granada).
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
From a theoretical point of view, giant planets around red giant stars have been extensively studied in recent years (Burkert & Ida 2007; Villaver & Livio 2009; Kunitomo et al. 2011; Passy et al. 2012). Observationally, a few tens of exoplanets have been found so far to be orbiting these evolved stars (e.g. Johnson et al. 2007; Adamów et al. 2012; Jones et al. 2013). In particular, the discovery of planets around K and G giants is crucial for planet formation theories. These stars evolved from F- and A-type main-sequence stars, for which accurate radial velocity studies are difficult (owing to the small number of absorption lines present in their spectrum), so that confirming planet candidates becomes hard. Since, as a result of this, very few planets have been found orbiting F and A parent stars, K and G giants (with deeper absorption lines) can help to better constrain the demography of planets around early-type stars.
In addition, there is a paucity of planets with short periods around stars ascending the red giant branch (RGB, Johnson et al. 2007). This desert has been theoretically studied by Villaver & Livio (2009), who conclude that it can be explained by planet disruption/engulfment during the ascent along the RGB (although other mechanisms are possible). However, as they state, these results are based on a limited sample of confirmed exoplanets around RGB stars. Therefore the detection of extremely close-in planets around post main-sequence (giant) stars can then constrain theoretical models about how planets are destroyed by their hosts.
In this context, we present the confirmation of the planetary nature of the Kepler object of interest KOI-2133b (KIC 8219268 and hereafter Kepler-91b), a close-in planet orbiting a K3 star in the giant branch. We achieve this confirmation by exploiting the high-precision photometry provided by the Kepler mission (Borucki et al. 2010) and complementary data. The accuracy of the Kepler light curve allows us to detect small variations (of tens of parts per million) in the out-of transit signal of the host star. Whenever a companion is present, the photometric modulation is known to be caused by the combination of three main factors: reflected/emitted light from the planet, ellipsoidal variations (or tidal distortions) induced by the planet on the star, and Doppler beaming due to the reflex motion of the star induced by the presence of a massive companion. These effects have been recently used to confirm a handful of transiting planets such as KOI-13 (Shporer et al. 2011; Mazeh et al. 2012; Mislis & Hodgkin 2012), HAT-P-7b (Borucki et al. 2009; Welsh et al. 2010), and Kepler-41b (Quintana et al. 2013). It is only possible to detect close-in giant planets with this method thanks to the subtle induced modulations. Other physical processes, such as stellar activity or pulsation, can also modulate the stellar light curve. Besides, even if the modulation is indeed produced by a companion, this technique does not provide the absolute value for its mass but instead the companion-to-host mass ratio. Thus, it is crucial to obtain the most accurate parameters for the host star. This is achieved (when possible) using the asteroseismology (see, for instance, Aerts et al. 2010; Mathur et al. 2012). The launch of space-borne, high-accuracy photometers, such as CoRoT (Baglin et al. 2006) and Kepler, has permitted obtaining long-term, very accurate photometry for several hundred thousand stars, which has led the rapid growth of this discipline.
A recent paper by Esteves et al. (2013) discards Kepler-91b (previously KOI-2133.01) as a planet candidate due to their finding a large albedo corresponding to a self-luminous object. In this paper we analysed all the public data and our own observations, and we firmly conclude that the transiting object is actually a very close-in hot-Jupiter planet in a stage previous to be engulfed by its host star.
The paper is organized as follows. In Sect. 2, we explain all the observational data available for this object, including our high-resolution images (Sect. 2.1) and our high-resolution and high signal-to-noise ratio spectrum (Sect. 2.2). We perform an exhaustive analysis of the host star properties in Sect. 3, comprising spectral energy distribution (Sect. 3.3), high-resolution spectrum (Sect. 3.4), and an asteroseismic study of the object (Sect. 3.5). We then analyse the signals induced by the planet candidate into the stellar light curve in Sect. 4, including a new primary transit fit (Sect. 4.1) and a detailed fitting of the light-curve modulations (Sect. 4.2). Other aspects of the light curve, such as the possible secondary eclipses, are discussed in Sect. 4.3, and the final discussion and conclusions of the paper are presented in Sect. 5. Throught out this paper we refer to the host star as Kepler-91, and add “b” when talking about the planet candidate.
2. Observations and data reduction
2.1. High spatial resolution: lucky imaging with CAHA/AstraLux
We applied the lucky imaging technique to the planet host candidate Kepler-91 to search for a possible stellar companion by achieving diffraction-limited resolution images. Owing to the large pixel size of the Kepler camera (3.98 arcsec/pixel) and the much larger aperture (6−10 arcsec), high-resolution imaging is crucial for discarding other possible stellar configurations mimicking the planetary transit (see, for example, Daemgen et al. 2009; Lillo-Box et al. 2012; Adams et al. 2013).
We used the AstraLux North instrument mounted on the 2.2 m telescope at the Calar Alto Observatory (CAHA, Almería, Spain). The observations were performed on May 25, 2012, with a mean seeing of 0.8 arcsec. We obtained 30 000 images of 50 ms exposure time in the full CCD array of the camera (24 × 24 arcsec2). Data cube images were reduced using the online pipeline of the instrument (Hormuth 2007), which performs basic cosmetic and preparatory tasks, selects the highest quality images, combines the best 1.0%, 2.5%, 5.0%, and 10% frames with the highest Strehl ratios (Strehl 1902), calculates the shifts between the single frames, performs the stacking, and resamples the final image to half the pixel size (i.e. from 0.0466′′/pixel to 0.0233′′/pixel).
In Fig. 1 we show the sensitivity map for the 10% selection rate image. According to our experience with the instrument, this rate provides the greatest image quality (regarding the interplay between magnitude difference and angular resolution). We refer the reader to Lillo-Box et al. (2012) for a detailed explanation about how the signal-to-noise ratio (S/N) was determined for each pair of angular separation and magnitude difference. Table 1 shows the sensitivity limits for the four selection rate images within 1.5 arcsec angular separation from the target star.
 |
Fig. 1 Contrast map of our high-resolution image taken with the 2.2 m telescope plus AstraLux at Calar Alto Observatory. Colour code corresponds to the S/N with which we would detect a theoretical source with a magnitude difference Δmi (y-axis) at the corresponding angular separation (x-axis). The two dotted lines represent the 3σ (lower line) and 5σ (upper line) contours. |
Sensitivity limits (in magnitude difference between the target and a theoretical companion) achieved in the iSDSS band of the Calar Alto 2.2 m/AstraLux high-resolution images for 4 selection rates.
2.2. High spectral resolution: échelle data with CAHA/CAFE
We have obtained a high-resolution, high S/N spectrum of Kepler-91 by using the Calar Alto Fiber-feb Échelle spectrograph (CAFE, Aceituno et al. 2013) on the 2.2 m telescope. This instrument consists of a high dispersion spectrograph (R = 62 000) located in an isolated, controlled chamber and fed with a 2.0 arcsec diameter fibre. The stability of the instrument has been proven in Aceituno et al. (2013) where the authors reproduce the expected radial velocity curve of the planet TrEs-3b (V = 12.5 mag) with the data collected during commissioning.
The data were reduced using the improved pipeline1 provided by the observatory that delivers a fully reduced spectrum (see details in Aceituno et al. 2013). A narrow range of the spectrum is shown in Fig. 2.
 |
Fig. 2 Narrow range of the high-resolution, high signal-to-noise (S/N = 123 at 5800 Å) spectrum of KOI-2133 obtained with the CAFE échelle spectrograph at Calar Alto Observatory. We show the part of the spectrum used in determining the stellar metallicity (see Sect. 3.4.1) and mark with dotted lines the doublets used to estimate the effective temperature (see Sect. 3.4.2). The spectrum has been shifted to the rest frame by correcting for the barycentric velocity. |
2.3. Kepler photometry: data handling
The Kepler telescope was almost continuously collecting data from the same field of view between March 2009 and April 2013. Its individual exposure time is 6.02 s with a 0.52 s readout time (Gilliland et al. 2010). For long-cadence targets (which is our case), the telescope integrates over 270 exposures resulting in a total time resolution of 29.4 min per datapoint. Time series are publicly available through the Kepler MAST (Mikulski Archive for Space Telescopes) webpage2.
Taking advantage of the large number of photometric points (around 52 000), we decided not to remove possible outliers or de-trend the Pre-search Data Conditioning Simple Aperture Photometry flux (PDCSAP, Smith et al. 2012; Stumpe et al. 2012) given the unknown nature of these possible trends. However, in order to compare how de-trending could improve the quality of our data, we applied an iterative rejection process. First, the entire dataset has been split into continuous sections (i.e. regions without temporal gaps). Each section was then fitted with a fifth-degree polynomial. Typical duration of the different sections are around 25−30 days (roughly one third of one Kepler quarter). Then, we divided our data by this fitted model and removed data points above 3σ. We iterated this process until no further outliers were detected. While the standard deviation of the raw PDCSAP flux (≈1152 days) is σraw = 400 ppm, the resulting cleaned light curve yields σcorrected = 380 ppm. Since the improvement is below 5%, we preferred not to apply any correction to the PDCSAP flux to prevent possible artificially added trends.
3. Properties of the host star
In the characterization of exoplanet properties, it is crucial to obtain the most accurate host-star parameters (radius, mass, effective temperature, age, etc.). The inference of both orbital and physical properties of the planet strongly depends on how well the stellar parameters are known (Seager & Mallén-Ornelas 2003). We have used our wealth of data on Kepler-91 to accurately determine these physical parameters following independent methods: model fit to the spectral energy distribution (SED), model fitting the high S/N spectrum, individual characterization of particular spectral lines, asteroseismology and comparison with isochrones and evolutionary tracks. Table 2 provides a summary of all stellar parameters derived by these methods. Descriptions of each of them follows.
3.1. Ancillary data and previous parameter estimations
The stellar parameters of Kepler-91 have been previously estimated by several methods that yield quite different results as shown in Table 2 and summarized hereafter.
The Kepler Input Catalog (KIC, Kepler Team 2009) provided photometric parameters for the whole sample of KOIs based on u, g, r, i, z, J, H, and Ks magnitudes obtained by Latham et al. (2005). Their estimations are: Teff = 4712 K, log g = 2.852 [cgs], [Fe/H] = 0.509, and E(B − V) = 0.137 mag or AV = 0.425 mag for RV = 3.1 (no errors are provided in this catalogue).
Pinsonneault et al. (2012) presented effective temperature corrections for the Kepler targets using SDSS colours and reported a value of Teff = 4837 ± 96 K for Kepler-91 (assuming a metallicity of [Fe/H] = −0.2). Surface gravity corrections were applied in that work to account for the evolved state of this target. We note that within the small sample of giants with spectroscopic information in the Kepler catalogue, the discrepancies between the SDSS temperature and the spectroscopic temperature range between −100 K and +400 K.
In Batalha et al. (2013), KIC effective temperature and log g are used as initial values for a parameter search using the Yonsei-Yale stellar evolution models, yielding refined values for the stellar mass and radius. For the latter one, the authors reported R⋆ = 9.30 R⊙, which, together with the surface gravity, yields M⋆ = 2.25 M⊙ (no errors provided), implying a mean stellar density of ρ⋆ = 3.9 kg/m3.
Finally, since the power spectrum of the Kepler light curve of Kepler-91 presents the typical set of frequency peaks generated by giant stars (see Fig. 3), an asteroseismic analysis was performed by Huber et al. (2013). Their results provided a mean density of ρ⋆ = 6.81 ± 0.32 kg/m3. Together with the spectroscopically derived effective temperature (Teff = 4605 ± 97 K) and asteroseismic relations (i.e. Kjeldsen & Bedding 1995, see also Sect. 3.5.1), they derived R⋆ = 6.528 ± 0.352 R⊙, M⋆ = 1.344 ± 0.169 M⊙, which translates into a surface gravity of log g = 2.94 ± 0.17. By analysing three high-resolution spectra with the stellar parameter classification technique (SPF, Buchhave et al. 2012), the authors also estimated a vsini = 3.2 ± 0.5 km s-1, and a metallicity of [Fe/H] = 0.29 ± 0.16. However, we must take into account that these asteroseismic relations (called scaling relations, see details in Sect. 3.5) have been obtained by mainly comparing stars with solar abundances, and the impact of a very different internal metallicity is not fully understood. Owing to the over-solar metallicity obtained by Huber et al. (2013), a more detailed work on the fit of the oscillating frequencies is needed to obtain more accurate values of these parameters. In Sect. 3.5.3, we perform an individual frequency modelling to obtain the most accurate stellar parameters possible with the current data.
 |
Fig. 3 Power spectrum of the light curve, in a region centred on the maximum of the oscillations. The upper part of the figure shows the various modes identified for increasing value of n: in red the modes with l = 0, green l = 2, blue l = 1. We also show the calculated global parameters of the lower spectrum. |
We used a complete set of available data for this object (photometry, Kepler light curve, and our own high-S/N spectrum) to compute self-consistent values for the stellar and orbital parameters. In Sects. 3.2−3.5 we give the details of these determinations.
3.2. Multiplicity and projection effects study based on high spatial resolution observations
We used our AstraLux high-resolution image to calculate the chance-aligned probability of a non-resolved eclipsing binary in our high-resolution image as a function of angular separation (α) and magnitude depth (Δm). We determined the density of stars ϱ at a given galactic latitude b and magnitude difference with the target, ϱ = ϱ(b,mi,mi + Δm). The number of possible chance-aligned sources within this angular separation is thus N = πα2ϱ. We calculated the density ϱ by following the scheme explained in Morton & Johnson (2011). In particular, we used the online tool TRILEGAL3 to compute the number of expected stars with a limiting magnitude within five degrees-squared centred on the galactic latitude of Kepler-91. We can then integrated N over a certain angular separation (each of which has a particular limiting magnitude in our AstraLux image, see Fig. 1) to compute the total probability of an undetected background source. We found that the background source probability for Kepler-91 is below 2.7% for our 10% selection rate AstraLux image. Before our high-resolution image, this probability was (assuming observations and resolutions by the Sloan Digital Survey, SDSS) greater than 7%.
On the other hand, we can calculate the probability that a given background source is actually an eclipsing binary able to mimic the signal of a planetary transit. This probability can be calculated with the correlation explained in Eq. (14) of Morton & Johnson (2011), and it provides a value of 0.03% for our target. In conclusion,multiplying the probability of a non-detected background source (2.7%) by the probability of such a source being an appropriate binary (0.03%), we have a 0.0008% chance for there being a non-detected appropriate eclipsing binary.
Although our analysis has reduced the background source probability down to 2.7%, we have to deal with the possibility of an undetected blended star. We can measure how an undetected source with a magnitude difference greater that the 3σ detection limit in the AstraLux image would affect the planet properties (in particular, the planetary radius). By removing the light contribution of a hypothetical undetected stellar companion of magnitude difference Δm, the depth of the transit (and thus the planetary radius) would be increased by the factor given in Eq. (6) of Lillo-Box et al. (2012). For instance, a Δm = 6 mag source at 0.5 arcsec would not have been detected by our high-resolution image (see Fig. 1). As a consequence, the actual transit depth would increase by a factor of 1.0039 (0.39%) as computed by the aforementioned expression. The last column in Table 1 shows the result of this calculation for each angular separation at a 3σ detection limit for the 10% selection-rate image.
The only relevant configuration that could mimic a planetary transit and cannot be rejected by our high-resolution images is a diluted binary in a triple system. However, Morton & Johnson (2011) provide an estimation of the probability for a given transit depth, period, and primary mass that such eclipse is produced by a hierarchical triple system. The authors conclude, for a given system with a one solar-mass primary star and a ten-day orbital period (similar to our system) that the probability of such an appropriate hierarchical triple system is of the order of 0.001% for diluted eclipse depths in the range 102 − 2 × 104 ppm.
Thus, with these considerations, we assume here that Kepler-91 is isolated, and its light curve is not affected by a close companion or any other object along its line of sight.
3.3. Spectral energy distribution analysis
A zero-order estimate for the stellar parameters of Kepler-91 was obtained using the Virtual Observatory SED Analyzer (VOSA4, Bayo et al. 2008). Its latest version (Bayo et al. 2013) uses Bayesian inference to compute the expected values for the effective temperature, surface gravity, metallicity, and interstellar extinction. We have used every photometric datapoint available in the literature (to our knowledge) to build and fit the SED from Kepler-91. In particular, we used the KIC photometry in the g, r, i, z filters (Brown et al. 2011), the 2MASS JHKs photometry (Cutri et al. 2003), WISE (Wide-field Infrared Survey) bands W1 to W4 (Wright et al. 2010), the Kepler band (Borucki et al. 2010), and UBV photometry from Everett et al. (2012). Table 3 summarizes this information.
The Bayesian analysis from VOSA reveals that Kepler-91 has an effective temperature of Teff = 4790 ± 110 K with metallicity being slightly oversolar [Fe/H] = 0.4 ± 0.2 (see summary in Table 2). We have set the extinction range to AV = [0.0,1.0] mag. The output expectance and variance from the Bayesian probabilities is AV = 0.43 ± 0.15 mag. The surface gravity, however, is not very well constrained, but the probability distribution function seems to indicate that log g < 3.5. These values are in good agreement to the ones obtained by the KIC study (Brown et al. 2011) and Huber et al. (2013).
3.4. Analysis of the high-resolution spectrum
We used the high-resolution and high-S/N spectrum obtained with CAFE to constrain stellar parameters better and to validate previous values from the SED analysis. In particular, we centred our study in the metallicity and effective temperature values that will be crucial for better constraining the parameter space in our own asteroseismic modelling. A previous inspection of the spectrum shows the lack of lithium at 6707.8 Å, indicating the evolved stage of the host star.
3.4.1. Metallicity
Instead of performing a general fit to the high-S/N spectrum (which would imply a large number of free parameters), we performed a focussed analysis of the metallicity of the star. The purely photometric analysis (see Sect. 3.3) provided a value of [Fe/H] = 0.4 ± 0.2, an over-solar abundance already determined by previous works.
We followed the giant stars specific prescriptions described by Gray et al. (2002) to obtain an independent value. This scheme uses a small part of the spectrum (from 6219.0 Å to 6261.5 Å) that was verified to mainly depend on the stellar metallicity. The method uses the percentage of stellar continuum absorbed by the atmospheric elements of the star. This percentage is what the authors call line absorption (LA). After masking specific lines that strongly depend on the effective temperature, they were able to fit a second-order polynomial that provides the value of [Fe/H] for the star as a function of the LA. Since the authors do not provide the coefficients of this polynomial, we used the results in their Table 4 to perform our own fit. It is important to note the clear difference between stars with Teff above and below 4830 K (although the physical reason is unknown, as the authors claim in their work). We divided the calibration sample into two groups according to this separation (hot for Teff > 4830 K and cold for Teff < 4830) and fit two different polynomials of the form [Fe/H] = a0 + a1x + a2x2 with x being the masked line absorption in %. Coefficients for the fit of both groups are reported in Table 4. In the left-hand panel of Fig. 4 we have plotted these polynomials together with the tested giant stars in Gray et al. (2002), with stars hotter than 4830 K in red and cooler in blue.
 |
Fig. 4 Left: determination of the stellar metallicity of KOI-2133 (see Sect. 3.4.1). We show data from giants compiled by Gray et al. (2002) to parametrize the line absorption parameter (LA) with the iron abundance [Fe/H]. Two samples are shown: giants with Teff > 4830 K (red) and giants with Teff < 4830 K (blue). Solid lines represent the fitted second-order polynomials to the test data. The dotted vertical line shows the obtained LA for KOI-2133 and the black circle its determined position in the diagram. Right: effective temperature versus LA showing that KOI-2133 should be considered in the cool group of giants regarding the left panel segregation. The red circles show the position of the test giants, and the dashed line represents an estimated empirical limit to the temperature for each LA. |
We measured the masked LA for our spectrum finding that 12.8 ± 0.7% of the light coming from the star is absorbed by chemical elements. Owing to the non-negligible segregation in temperature, we investigated the dependence of the LA with this parameter. The right-hand panel of Fig. 4 shows the values for the test giants. There is a clear lack of such objects in the upper right region of the figure (high temperatures and high LA values). It is clear from this figure that for the measured LA of Kepler-91, the effective temperature is not expected to lie above 4830 K. We therefore used the coefficients corresponding to the cool polynomial to compute the metallicity. The uncertainty has been calculated by a quadratic sum of the error of the LA parameter and the standard deviation of the residuals of the test giants with respect to the fitted polynomial5. Our final estimation is [Fe/H] = 0.11 ± 0.07, which agrees within the errors with the one obtained by Huber et al. (2013), [Fe/H] = 0.29 ± 0.16.
3.4.2. Effective temperature
We have used four line pairs in the spectrum to estimate the stellar effective temperature. The line depth ratios of these pairs are used in Gray & Brown (2001) to obtain temperatures giventhat one of the lines is temperature insensitive, while the second one strongly depends on it. We used the pairs Nii/Vi at 6223.99/6224.51 Å, Fei/Vi at 6232.65/6233.20 Å, Vi/Fei at 6251.83/6252.57 Å, and Fei/Vi at 6255.95/6256.89 Å. As a first step, to estimate the rotational velocity, we synthesized a grid of models using the ATLAS096 software for metallicities [Fe/H] = 0.0 − 0.2, effective temperatures in the range 4400−4800 K (50 K step), surface gravities from 2.5 to 3.5, and rotational velocities from 1.0 to 12.0 km s-1 in steps of 0.1 km s-1 (turbulence velocity fixed to 2.0 km s-1). A global fit to the spectrum provides a posterior distribution for the vsini parameter with a expectance and variance values of vsini = 6.8 ± 0.2 km s-1. By setting the rotational velocity in the calculated range, considering three values for the surface gravity (log g = 2.5, 3.0, and 3.5), and building a finer grid of temperatures with 25 K step, we proceeded to a least-square analysis of the four line pairs. A Bayesian analysis provides the next expectance and variance values for the different gravity values: 4600 ± 46 K for log g = 2.5, 4550 ± 47 K for log g = 3.0, and 4500 ± 50 K for log g = 3.5. As a compromise between these values we adopt an effective temperature of Teff = 4550 ± 75 K, whose central value nearly corresponds to the surface gravity determined by the asteroseismology (Huber et al. 2013, and our own calculations in the next section).
3.5. Asteroseismology
3.5.1. Scaling relations
Cool stars with a convective envelope may show solar-like oscillations, that is, pressure oscillation modes stochastically excited by turbulent motions. Their power spectra present a regular pattern modulated by a Gaussian shape and are characterized by two global parameters: the frequency at maximum power (thereafter νmax) and the frequency separation (Δν) between consecutive radial order (n) modes with the same angular degree (ℓ). These quantities are linked via scaling relations (Δν ∝ ρ1/2, 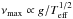 ) to global stellar parameters such as total mass, radius, and effective temperature (Ulrich 1986; Brown et al. 1991; Kjeldsen & Bedding 1995; Belkacem et al. 2011). These relations read as
) to global stellar parameters such as total mass, radius, and effective temperature (Ulrich 1986; Brown et al. 1991; Kjeldsen & Bedding 1995; Belkacem et al. 2011). These relations read as
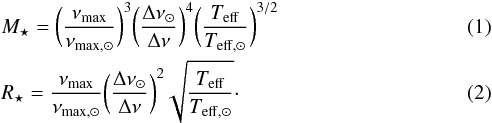 These equations allow us to derive mass and radius (once we have an estimate of the effective temperature) independently of the chemical composition and of stellar modelling. They are, however, approximate relations and must be calibrated. The validity of Δν ∝ ρ1/2 can be tested with predictions from models, as done by White et al. (2011), Miglio et al. (2013a), and Mosser et al. (2013). The second relation cannot be tested with models, and only a theoretical justification has been proposed by Belkacem et al. (2011). Nevertheless, comparisons between global parameters derived from seismology and those obtained from interferometry and spectroscopy of solar-like pulsators indicate that νmax is a very good proxy of the surface gravity and stellar radius (Miglio et al. 2012; Morel & Miglio 2012; White et al. 2013; Huber et al. 2012). These studies suggest that, in the analysed domain, Eqs. (1) and (2) can provide stellar radius and mass with an uncertainty of 4% and 10%, respectively (Huber et al. 2013, and references therein), and that is a significant improvement over the classical spectroscopic/photometric approach.
These equations allow us to derive mass and radius (once we have an estimate of the effective temperature) independently of the chemical composition and of stellar modelling. They are, however, approximate relations and must be calibrated. The validity of Δν ∝ ρ1/2 can be tested with predictions from models, as done by White et al. (2011), Miglio et al. (2013a), and Mosser et al. (2013). The second relation cannot be tested with models, and only a theoretical justification has been proposed by Belkacem et al. (2011). Nevertheless, comparisons between global parameters derived from seismology and those obtained from interferometry and spectroscopy of solar-like pulsators indicate that νmax is a very good proxy of the surface gravity and stellar radius (Miglio et al. 2012; Morel & Miglio 2012; White et al. 2013; Huber et al. 2012). These studies suggest that, in the analysed domain, Eqs. (1) and (2) can provide stellar radius and mass with an uncertainty of 4% and 10%, respectively (Huber et al. 2013, and references therein), and that is a significant improvement over the classical spectroscopic/photometric approach.
Pulsating modes observed for KOI-2133 ordered by frequency.
These scaling relations are being extensively used in the framework of stellar population studies (Miglio et al. 2009, 2013b; Mosser et al. 2010, 2011; Hekker et al. 2009, 2011) and of exoplanet parameter determination (see review by Moya 2011) to characterize dwarfs and red giant solar-like pulsators detected by CoRoT and Kepler. In particular, scaling relations have been recently applied to derive the stellar parameters of 66 Kepler planet-host candidates presenting solar-like oscillations (Huber et al. 2013). Although the information from global parameters Δν and νmax is extremely valuable for studying planetary systems, better and additional constraints (for instance stellar age) can be expected from individual frequencies.
For the particular case of Kepler-91, Huber et al. (2013) derived the global parameters of the power spectrum from the Kepler light curve: Δν = 9.39 ± 0.22 μHz and νmax = 108.9 ± 3.0 μHz. We used the A2Z pipeline (Mathur et al. 2010) to determine these values again, obtaining Δν = 9.48 ± 0.88 μHz and νmax = 109.4 ± 6.1 μHz, in good agreement at the 1σ level with the previous study, and leading to a mean density around 2% higher than that reported in Huber et al. (2013). The updated scaling relation suggested by Mosser et al. (2013) implies an additional increase in the density of 2% with respect to what is obtained with Eqs. (1) and (2). According to Mosser et al. (2013), these equations should be corrected by a factor of (1 − 4ζ) and (1 − 2ζ) respectively (with ζ = 0.038 for red giants), and the reference values for the Sun should be changed to ν⊙ = 3104 μHz and Δν⊙ = 138.8 μHz. By using these updated scaling relations and effective temperature (Tteff = 4550 ± 75 K), we derive the following stellar mass, radius, and mean density: 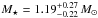 ,
, 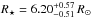 , and ρ⋆ = 7.04 ± 0.44 kg/m3 (errors have been calculated by performing Monte Carlo Markov Chain simulations). The corresponding stellar luminosity and surface gravity are: log g = 2.93 ± 0.17, and
, and ρ⋆ = 7.04 ± 0.44 kg/m3 (errors have been calculated by performing Monte Carlo Markov Chain simulations). The corresponding stellar luminosity and surface gravity are: log g = 2.93 ± 0.17, and 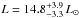 .
.
Actually, the high S/N of Kepler-91 power spectrum allows to detect 38 individual frequencies. In the next sections we try to use them with the spectroscopic results to better constrain the properties of this planetary system.
3.5.2. Determination of the individual frequencies
The individual frequencies of Kepler-91 were obtained by fitting the power spectrum of the signal to a model. For solar-like oscillations, the power spectrum shows a χ2 statistic distribution with two degrees of freedom. Then, a maximum likelihood estimation (MLE) is applied, a method widely used in determining p-mode parameters in the Sun and solar-like stars. Following Anderson et al. (1990), the likelihood function used for the MLE is ![\begin{equation} S = \sum \left[M_i + {O_i \over M_i}\right] \end{equation}](/articles/aa/full_html/2014/02/aa22001-13/aa22001-13-eq214.png) (3)where Oi are the data and Mi is the model, composed of Lorentzian profiles:
(3)where Oi are the data and Mi is the model, composed of Lorentzian profiles: ![\begin{equation} M_i = \sum {A_i (\Gamma_i /2)^2 \over [({\nu-\nu_i})^2 + (\Gamma_i /2)^2]} + N(\nu), \end{equation}](/articles/aa/full_html/2014/02/aa22001-13/aa22001-13-eq217.png) (4)being νi the oscillation frequency, Γi the linewidth, Ai the amplitude of each Lorentzian profile, and N(ν) the noise. Here, N(ν) is fitted using two components: constant white noise modelling the photon noise (W), and one Harvey-like profile (Harvey 1985), which reproduces the convective contribution to the background, typically granulation:
(4)being νi the oscillation frequency, Γi the linewidth, Ai the amplitude of each Lorentzian profile, and N(ν) the noise. Here, N(ν) is fitted using two components: constant white noise modelling the photon noise (W), and one Harvey-like profile (Harvey 1985), which reproduces the convective contribution to the background, typically granulation: ![\begin{equation} N(\nu) = {A \over [1 + ({\nu /B})^{\alpha}]} + W \end{equation}](/articles/aa/full_html/2014/02/aa22001-13/aa22001-13-eq223.png) (5)where A is related with the amplitude of the granulation, B has its characteristic timescale, and α is a positive parameter characterizing the slope of the decay.
(5)where A is related with the amplitude of the granulation, B has its characteristic timescale, and α is a positive parameter characterizing the slope of the decay.
The background was fitted prior to extracting the modes parameters and then held as a fixed value. For fitting the modes, all the parameters were allowed to be free with no bond among them. The entire spectrum was fitted at once between 65 and 145 μHz. The initial values for the p-mode parameters were extracted from the observed spectrum. The formal uncertainties were obtained from the Hessian matrix in the MLE procedure.
The results are given in Table 5 and plotted in Fig. 5 in an échelle diagram.
 |
Fig. 5 Left: échelle diagram of the power spectrum of the data with the fitted modes overplotted. Circles for l = 0, triangles for l = 1, and squares for l = 2. The power spectrum is fitted using maximum likelihood estimation (see Sect. 3.5.2). Right: comparison between observational (black solid dots and white symbols in the left panel) and theoretical (open symbols) frequencies in the échelle diagram for a typical good fitting of radial and non-radial modes. Circles correspond to radial modes, squares to dipole modes, and triangles to quadrupole ones. The size of the theoretical symbols is an indication of the expected amplitude based on the value of the inertia mode (Houdek et al. 1999). The asymptotic period spacing for this model is 76 s. |
3.5.3. Individual frequency modelling
The detailed properties of the oscillation modes depend on the stellar structure. In red giant stars, because of the contraction of the inert He core and the expansion of the hydrogen rich envelope, modes with frequencies in the solar-like domain can propagate in the gravity and acoustic cavities (internal and external regions respectively), thus presenting a mixed gravity-pressure character (Dziembowski et al. 2001; Christensen-Dalsgaard 2004; Dupret et al. 2009; Montalbán et al. 2010). While the solar-like spectra of main sequence pulsators are mainly made of a moderate number of acoustic modes for each angular degree, those of red giants can present a large number of non-radial g-p mixed modes in addition to radial modes.
As summarized in Table 5, the oscillation spectrum of Kepler-91 presents seven radial modes, seven quadrupole modes, and 23 ℓ = 1 modes. The arrangement of ℓ = 2 and ℓ = 0 modes on well defined vertical ridges in the échelle diagram (Fig. 5, right panel) suggests that the observed ℓ = 2 modes are trapped well in the acoustic cavity and behave as pure pressure modes. Therefore, from individual ℓ = 0 and ℓ = 2 frequencies, we can derive quantities, such as the large and small frequency separations, and try to use them as observational constrains in our analysis (Montalbán et al. 2010; Bedding et al. 2010; Huber et al. 2010). We have computed the mean large frequency separation for radial modes directly from frequencies (Δν(n,ℓ) = νn,ℓ − νn − 1,ℓ), and by fitting the asymptotic relation νnℓ ≈ (n + ℓ/2 + ϵ)Δν (Vandakurov 1967; Gough 1986; Tassoul 1980). In the first case we got ⟨ Δν0 ⟩ = 9.434 μHz with a standard deviation 0.1 μHz, and Δν = 9.37 ± 0.02 μHz in the second one. Dipole modes, given their p-g mixed character, do not follow the asymptotic relations for pressure modes, a certain regularity is expected, however, in the period spacing between consecutive radial orders (Beck et al. 2011; Bedding et al. 2011; Mosser et al. 2011), for similarity with the asymptotic behaviour of pure gravity modes (Tassoul 1980). From the detected dipole modes we got a mean value of the period spacing of mixed modes (ΔPobs) of the order of 53 s. This quantity is smaller than the asymptotic period spacing (Bedding et al. 2011; Mosser et al. 2011; Christensen-Dalsgaard 2012; Mosser et al. 2012; Montalbán et al. 2013) which, according to the Mosser et al. (2012) estimation for a RGB star with Δν ≈ 9.5 μHz, should be slightly lower than 80 s.
In our fit we also included the spectroscopic constraints, that is, Teff = 4550 ± 75 K and [Fe/H]= 0.11 ± 0.07. When taking different solar mixtures and the uncertainties in metallicity determination into account, the constraint used in our fit is then Z/X = 0.019 ± 0.005. (Z and X are the metal and hydrogen mass fractions, respectively.)
We used the stellar evolution code ATON (Ventura et al. 2008) to compute a grid of stellar models with masses between 1.0 and 1.6 M⊙ in steps of 0.02 M⊙, helium mass fraction of Y = 0.26 − 0.32 in steps of 0.01, metal mass fractions of Z = 0.01, 0.015, 0.0175, 0.020, and 0.025, and mixing length parameter αMLT =1.9, 2.05 and 2.2. The step in radius between consecutive models in the evolutionary tracks is of the order of 5 × 10-3 R⊙. For each model with a large frequency separation (from scaling law) within 10% of the observed value, we computed the adiabatic oscillation frequencies for ℓ = 0, 1, 2 modes using LOSC (Scuflaire et al. 2008; Montalbán et al. 2010). We also derived the theoretical values of ⟨ Δν0 ⟩ and ⟨ δν02 ⟩.
The theoretical values of the frequencies and frequency separations differ in general from the observational ones, because of the so-called near-surface effects. The model frequencies were therefore corrected using the method described in Kjeldsen et al. (2008). The power-law correction was applied to radial and non-radial modes. To take the different sensitivity of non-radial modes to surface layers into account, the surface correction of non-radial modes was multiplied by a factor 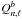 , where Qn,ℓ corresponds to the ratio of the mode inertia to the inertia of the closest radial mode (Aerts et al. 2010, Chap. 7). We considered several values of the exponent b in the surface-correction law: b = 5,6,7,8.
, where Qn,ℓ corresponds to the ratio of the mode inertia to the inertia of the closest radial mode (Aerts et al. 2010, Chap. 7). We considered several values of the exponent b in the surface-correction law: b = 5,6,7,8.
For the individual frequency fitting, we evaluated the agreement between models and observations by using different merit functions (reduced χ2, 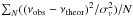 , including or not the dipole modes). The merit function for radial and quadrupole modes leads to a mean density of ρ = 7.3 ± 0.1 kg/m3. This value does not significantly depend on the assumed b parameter in the surface-effects correction. The mean density derived from frequency fitting is therefore 5.8% higher than derived from the classic scaling relations (1 and 2), and 3.7% higher than that provided by their updated version (Mosser et al. 2013). This discrepancy between both methods agrees with other studies (see for instance Fig. 4 in Belkacem et al. 2013).
, including or not the dipole modes). The merit function for radial and quadrupole modes leads to a mean density of ρ = 7.3 ± 0.1 kg/m3. This value does not significantly depend on the assumed b parameter in the surface-effects correction. The mean density derived from frequency fitting is therefore 5.8% higher than derived from the classic scaling relations (1 and 2), and 3.7% higher than that provided by their updated version (Mosser et al. 2013). This discrepancy between both methods agrees with other studies (see for instance Fig. 4 in Belkacem et al. 2013).
We have also evaluated the fit of the dipole modes in two different ways: one taking only the most trapped modes into account, those with lowest inertia between two radial modes (the largest symbols in the right panel of Fig. 5) and another taking all the dipole mixed modes into account. The results obtained by these two methods are consistent and provide two different minima in the stellar mass-radius domain: one around 1.25 M⊙ and the second around 1.45 M⊙. Excluding solutions with effective temperature deviating by more than 3σ reduces the space of parameters to M⋆ = 1.31 ± 0.10M⊙, R⋆ = 6.30 ± 0.16R⊙, log g = 2.953 ± 0.007, and an age of 4.86 ± 2.13 Gyr.
The frequencies of radial modes vary as ρ1/2. Given the steps used in stellar radius and mass, we can expect a typical change in frequencies between different models of the order of 0.8%, that is, 0.9 μHz. That value is much more than the intrinsic precision of the observational frequencies. The computation of non radial frequencies for such as evolved object is very time consuming. Moreover, given the uncertainties linked to the surface effects and its correction (see i.e. Gruberbauer et al. 2012), a denser grid of models is not worth it.
We used the theoretical isochrones from Girardi et al. (2002) to check the self-consistency of the asteroseismicly and spectroscopically determined parameters. We conclude that the results are fully compatible.
Results for the analysis of the primary transit and the light-curve modulations and comparison with the values obtained by Tenenbaum et al. (2012) in the second column.
4. Light curve analysis: planetary system parameters
In this section we revisit the Kepler photometric data and analyse the effects on the stellar light curve of the object orbiting Kepler-91. In particular, we revise previous solutions and investigate the possibility of a non-circular orbit. We then produce a new transit fitting with the inclusion of the eccentricity (e) and the argument of the periastron (ω) as new free parameters. Finally, we also study other signatures present in the light curve due to the presence of a close companion.
For this analysis, we phase-folded the whole light curve according to the recently published transit ephemeris and orbital period obtained by Tenenbaum et al. (2012). Then, we binned the light curve to nine minutes (around 52 original points) with a 3σ clipping rejection algorithm. No relevant improvement is found when performing a zero-order cleaning of the solar-like oscillations of the star filtering the high frequencies (explained in Sect. 3.5) in Fourier space. Since we work with more than 200 folded and binned transits, we estimate that these oscillations will be partially masked out so will not play a relevant role.
4.1. Revisiting transit parameters
The transit of this system has already been previously fitted in the TCE (threshold crossing events) analysis by Tenenbaum et al. (2012). The orbital and physical parameters calculated in that paper are summarized in the second column of Table 6. However, as shown in Sect. 3, the physical parameters of the host star are now determined much better. In particular, effective temperature, surface gravity, and metallicity are quite different from what is assumed by TCE. The dependency of these parameters on the transit shape comes from the limb darkening coefficients. By trilinearly interpolating the Claret & Bloemen (2011) tabulated values of the four quadratic limb darkening coefficients, we find that the relative differences between adopting the TCE stellar parameters and our determined parameters are of the order of 17%, 40%, 20%, and 7%, respectively. Thus, a new transit fitting is needed for this system.
In TCE, the authors assumed zero eccentricity for the orbit. The effect of a non-zero eccentricity in the shape of the transit is known to be tight for low values of e. It would produce asymmetries in the ingress and egress slopes since the planet-to-star distance at both orbital positions would be different. To test this possibility and due to the subtleness of this effect, we have carried out a Kolmogorov-Smirnov test between both sides of the transit. The results show a 70% probability that the ingress is equal to the egress. Several binnings were tested yielding similar results. Since the magnitude of the asymmetries could be very small and given that there is a non-negligible probability of 30% that the ingress is different from the egress, we find it justified to try fitting the transit with a non-zero eccentricity.
By allowing a non-circular orbit, the transit shape depends on six free parameters: planet-to-star radius (Rp/R∗), orbital eccentricity (e), argument of the periastron (ω), semi-major axis (a/R∗), orbital inclination from the plane of the sky perpendicular to our line of sight (i), and phase offset (φoffset) . This sixth parameter is included to account for possible deviations in the measured time of the mid-transit (T0). Limb darkening coefficients are fixed to the central values of the Teff, log g, and [Fe/H] since we have checked that, under their confident limits, the quadratic coefficients just vary below 4%, 6%, 3%, and 1%. Monte Carlo Markov Chain (MCMC) simulations show that these changes are inside the error bars of the final fitted parameters.
We used a genetic algorithm to model-fit our data (see Appendix A). The large amount of free parameters led us to note that the solution is multi-valuated. Different sets of solutions fit the data equally, having χ2 values inside the 99% of confidence (i.e. presenting differences in the χ2 value lower than 16.812 with respect to the 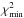 ). Although from statistics we cannot choose a particular set of parameters, we selected the one with the smallest relative errors in all parameters. The parameters of this model are shown in the fourth column of Table 6. Errors have been estimated by using 99% confident contours in χ2 maps for each pair of parameters. The largest upper and lower errors for all pairs have been used. Interestingly, the selected model has a non-zero eccentricity of e = 0.13 ± 0.12. But, other models inside the 99% of confidence provide a variety of eccentricities (e < 0.28), planet-to-star radius (Rp/R⋆ϵ [0.021,0.023]), semi-major axis (a/R⋆ϵ [2.2,2.8], correlated with the inclination parameter), and inclination (iϵ [65°,73°]). It is important to note that, for the calculated stellar radius, all solutions restrict the planet radius to 1.3 − 1.4 RJup. The χ2 value for the adopted eccentric model is
). Although from statistics we cannot choose a particular set of parameters, we selected the one with the smallest relative errors in all parameters. The parameters of this model are shown in the fourth column of Table 6. Errors have been estimated by using 99% confident contours in χ2 maps for each pair of parameters. The largest upper and lower errors for all pairs have been used. Interestingly, the selected model has a non-zero eccentricity of e = 0.13 ± 0.12. But, other models inside the 99% of confidence provide a variety of eccentricities (e < 0.28), planet-to-star radius (Rp/R⋆ϵ [0.021,0.023]), semi-major axis (a/R⋆ϵ [2.2,2.8], correlated with the inclination parameter), and inclination (iϵ [65°,73°]). It is important to note that, for the calculated stellar radius, all solutions restrict the planet radius to 1.3 − 1.4 RJup. The χ2 value for the adopted eccentric model is 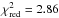 .
.
We have also run our genetic algorithm by assuming zero eccentricity, which leaves only four free parameters for the system. In this case, the least relative error solution provides a 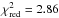 , and all statistically possible solutions provide parameters within the error bars of this model.
, and all statistically possible solutions provide parameters within the error bars of this model.
For comparison purposes, we have also reproduced the model fitted by TCE with their limb darkening coefficients and orbital and physical parameters. This model produces 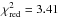 . All three models (TCE, e = 0, and e ≠ 0) are plotted in Fig. 6. Both quantitatively (by comparing the χ2 value) and qualitatively (by inspecting the aforementioned figure), our e = 0 (fixed) solution improves the quality of the fit from that of TCE. However, to evaluate whether including the eccentricity as a free parameter improves the fit of the transit or not, we have used the Bayesian information criterion (BIC, see for example, Schwarz 1978; Smith et al. 2009). For a given model solution, the BIC value is calculated as
. All three models (TCE, e = 0, and e ≠ 0) are plotted in Fig. 6. Both quantitatively (by comparing the χ2 value) and qualitatively (by inspecting the aforementioned figure), our e = 0 (fixed) solution improves the quality of the fit from that of TCE. However, to evaluate whether including the eccentricity as a free parameter improves the fit of the transit or not, we have used the Bayesian information criterion (BIC, see for example, Schwarz 1978; Smith et al. 2009). For a given model solution, the BIC value is calculated as 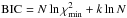 , where N is the number of observed points, and k is the number of free parameters. A difference greater than 2 in the BIC values of both models indicates positive evidence against the higher BIC value, and a difference greater than 6 indicates strong evidence. Since BIC(e = 0,fixed) = 624 and BIC(e = free) = 633, the eccentric case is not favoured over the zero eccentricity scenario. This means that we do not need the eccentricity to correctly fit the observed transit. However, we have proved that there is a combination of e,ω that also reproduces the transit with similar (inside confident limits) values for the Rp/R⋆, a/R⋆, and inclination parameters. Then, we can conclude that the primary transit fitting itself is not enough to determine whether the orbit of the transiting object is eccentric or not.
, where N is the number of observed points, and k is the number of free parameters. A difference greater than 2 in the BIC values of both models indicates positive evidence against the higher BIC value, and a difference greater than 6 indicates strong evidence. Since BIC(e = 0,fixed) = 624 and BIC(e = free) = 633, the eccentric case is not favoured over the zero eccentricity scenario. This means that we do not need the eccentricity to correctly fit the observed transit. However, we have proved that there is a combination of e,ω that also reproduces the transit with similar (inside confident limits) values for the Rp/R⋆, a/R⋆, and inclination parameters. Then, we can conclude that the primary transit fitting itself is not enough to determine whether the orbit of the transiting object is eccentric or not.
 |
Fig. 6 Best-fit solutions for the transit fitting according to different model schemes: assuming parameters from Tenenbaum et al. (2012) (dot-dashed blue line), assuming zero eccentricity (dashed black line), and leaving the eccentricity as a free parameter (solid red line). Residuals for the fixed e = 0 model are presented in the lower panel. |
4.2. Light-curve modulations: confirmation of a planetary-mass companion
4.2.1. Definitions and formulation
When inspecting the out-of-transit region of the folded light curve (LC) of Kepler-91, a clear double-peaked modulation is apparent (see Fig. 7). This light curve variation is known to be caused by the combination of three main factors in closely packed planetary systems: light coming from the planet (either reflected from the star or emitted by the planet), ellipsoidal variations (or tidal distortions) induced by the planet on the star, and Doppler beaming due to the reflex motion of the star induced by the presence of a massive companion. From now on, we refer to these LC variations as REB modulations (reflection, ellipsoidal, and beaming). In this section we show the equations and assumptions adopted for the REB fitting in this paper and obtain the solution for the mass of the companion body.
 |
Fig. 7 Best-fitted model to the REB modulations for an assumed circular orbit (dashed blue line) and the best model for a non-circular orbit (solid black line). Red circles show the folded light curve assuming the period obtained by the Kepler team and binned to 29.4 min intervals (similar to the real cadence of observations. In the small panel we show the individual contributions of ellipsoidal (red dotted-dashed line), reflection (blue dashed line), and Doppler beaming (green dotted line). The lower panel shows the residuals after substracting the non-circular model to the observed data. The three shadowed regions marked as A, B, and C represent the three detected dims (see Sect. 4.3). The theoretical location of the secondary eclipse according to the architecture of the system is marked with vertical grey dashed lines in the upper panel. By removing the contribution of the planet reflection in this region, we obtain the dotted black line. |
Regarding the tidal effect, as stated by Faigler & Mazeh (2011), the characterization of the ellipsoidal modulations in non circular orbits is still poorly understood for the case of very low-mass companions orbiting close to the primary star. However, Pfahl et al. (2008) provides an analytic formula for the excited oscillation modes of the primary component due to a less massive companion. According to it, for systems with null or small eccentricities, the tidal modulation could be modelled by only using the first harmonic (l = 2) of such oscillations. This harmonic includes a multiplying factor (a/r)3, with r being the planet-star distance given by 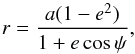 (6)
(6)
where ψ represents the true anomaly. For orbits not aligned with the line of sight, this factor implies different amplitudes at quarter phases. Thus, ellipsoidal variations can serve to constrain the eccentricity (e) and the argument of the periastron (ω) of the orbit. The light curve of Kepler-91 shows a small difference in the amplitudes at quarter phases, confirming a small non-zero eccentricity for this system.
According to these considerations, the analytic functions used to fit the observed REB modulations are
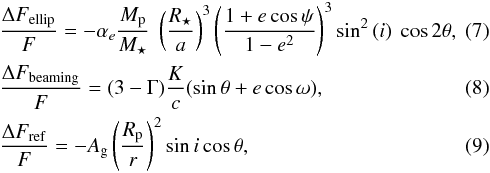 where θ represents the angle between the line of sight and the star-planet direction. Its value at each planet position can be obtained from the orbital phase (φ) for a given orbit with eccentricy e and argument of the periastron (ω) by solving the Kepler equations (see Eqs. (3.1.27) to (3.1.34) in Kallrath & Milone 2009).
where θ represents the angle between the line of sight and the star-planet direction. Its value at each planet position can be obtained from the orbital phase (φ) for a given orbit with eccentricy e and argument of the periastron (ω) by solving the Kepler equations (see Eqs. (3.1.27) to (3.1.34) in Kallrath & Milone 2009).
In Eq. (7), the αe factor depends on the linear limb darkening coefficients (obtained from trilinear interpolation of the tables provided by Claret & Bloemen 2011) by the expression introduced by Morris (1985): 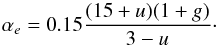 (10)In the beaming effect, the Γ factor is provided in Loeb & Gaudi (2003):
(10)In the beaming effect, the Γ factor is provided in Loeb & Gaudi (2003): 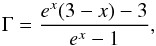 (11)where x = hc/kBλTeff, where we used λeff = 5750 Å for the Kepler band.
(11)where x = hc/kBλTeff, where we used λeff = 5750 Å for the Kepler band.
The parameter K represents the amplitude of the radial velocity, which can be written as 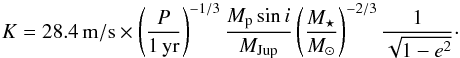 (12)In the reflection term, the Ag factor represents the geometric albedo of the planet, which was formulated by Kane & Gelino (2010) as
(12)In the reflection term, the Ag factor represents the geometric albedo of the planet, which was formulated by Kane & Gelino (2010) as 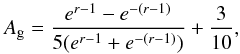 (13)where r is the planet-star distance.
(13)where r is the planet-star distance.
The total light curve modulation can thus be modelled by the sum of all three contributions: 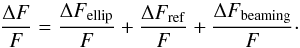 (14)While the first two contributions were commonly known from the study of stellar binary systems, the Doppler beaming was first detected by Faigler & Mazeh (2011) (although it was also barely detected by Maxted et al. 2000). In the era of the high-precision space photometers like Kepler or CoRoT, these three effects can contribute significantly to the confirmation and characterization of planet candidates. For example, Quintana et al. (2013) used observations from Kepler to independently confirm the hot Jupiter Kepler-41b via the detection of the REB modulations.
(14)While the first two contributions were commonly known from the study of stellar binary systems, the Doppler beaming was first detected by Faigler & Mazeh (2011) (although it was also barely detected by Maxted et al. 2000). In the era of the high-precision space photometers like Kepler or CoRoT, these three effects can contribute significantly to the confirmation and characterization of planet candidates. For example, Quintana et al. (2013) used observations from Kepler to independently confirm the hot Jupiter Kepler-41b via the detection of the REB modulations.
4.2.2. Fitting the REB modulations
Some of the whole set of parameters involved in Eqs. (7) to (13) can be fixed based on previous sections (see Table 7 for a summary of the adopted values). We then have six free parameters to fit: eccentricity (e), longitude of periastron (ω), planet mass (Mp), semi-major axis to stellar radius (a/R⋆), inclination (i), and phase offset (φoffset). In the lower part of Table 7, we have constrained the physical limits to the free parameters to restrict the fitting process.
Input parameters for the ellipsoidal and reflection modulations fitting.
By inspecting the shape of the observed modulation in Fig. 7, key features can be distinguished. The different amplitudes at φ = 0.75 could be produced by two causes: either the planet is very massive to produce a large Doppler beaming, or the orbit is actually eccentric and so ellipsoidal variations may not have the same amplitude at quarter phases (as far as ω ≠ 90° and ω ≠ 270°). Since the former effect has its maximum at φ = 0.25 and our observations show the maximum just in the opposite peak, we conclude that the difference must be caused by a non-circular orbit.
Since the amplitude of the REB modulations is quite small (100−150 ppm), we have used a larger bin size in this analysis (60 min with a 3σ rejection algorithm). The region where a possible occultation is located has been masked out (φ = [0.66,0.72]). We used our genetic algorithm to model fit the free parameters, obtaining 4000 convergence solutions (see detailed explanations about systematic error estimations and the method in Appendix A). To account for the errors introduced by non-fitted parameters (such as Teff, log g, Rp/R⋆, etc.), we have run MCMC simulations, allowing these parameters to vary inside their confidence limits. Posterior distributions provide the 1σ errors, which have been quadratically added to the systematic errors obtained by the genetic algorithm to produce the final parameter errors.
Since six free parameters are fitted, we cannot statistically disentangle sets of convergence solutions with a difference in the measured χ2-value of 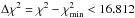 . However, we can choose the model that minimizes the relative errors among the sample of solutions. In particular, this model is also the one that minimizes the error in the companion’s mass, a key parameter for confirming its planetary nature. This solution is shown in the last column of Table 6. Most importantly, most of the aforementioned possible solutions are contained within the confident limits of these parameters. In Fig. 8, we show the location of all possible solutions in two-dimensional diagrams marking the location of the final adopted value ad the median value for all solutions. All common parameters with the transit analysis agree within the error bars, thus providing a self-consistent solution for the orbital and physical parameters. For comparisson purposes, we have estimated a mean amplitude for each modulation, assuming the star-planet distance equal to the semi-major axis 7. Our derived parameters provide the next peak-to-peak amplitudes:
. However, we can choose the model that minimizes the relative errors among the sample of solutions. In particular, this model is also the one that minimizes the error in the companion’s mass, a key parameter for confirming its planetary nature. This solution is shown in the last column of Table 6. Most importantly, most of the aforementioned possible solutions are contained within the confident limits of these parameters. In Fig. 8, we show the location of all possible solutions in two-dimensional diagrams marking the location of the final adopted value ad the median value for all solutions. All common parameters with the transit analysis agree within the error bars, thus providing a self-consistent solution for the orbital and physical parameters. For comparisson purposes, we have estimated a mean amplitude for each modulation, assuming the star-planet distance equal to the semi-major axis 7. Our derived parameters provide the next peak-to-peak amplitudes: 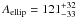 ppm,
ppm, 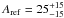 ppm, and
ppm, and 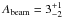 ppm. As expected, the most relevant effect in this system is the ellipsoidal modulation, given the small separation between the planet and the star.
ppm. As expected, the most relevant effect in this system is the ellipsoidal modulation, given the small separation between the planet and the star.
 |
Fig. 8 Possible solutions for the REB modulation fitting (see Sect. 4.2). Each grey open circle (and its correspondent error bars) represents a possible solution for the REB modulations whose χ2 value is statistically valid as compared to the minimum χ2 obtained with the genetic algorithm. We have marked the adopted model in black, being the one that presents the least relative errors. The red symbol corresponds to the most repeated value (and standard deviation deviation) for each parameter in the whole set of statistically acceptable solutions. |
We also ran the fitting algorithm by assuming zero eccentricity. The best-fit model is shown in Fig. 7. In this case, the improvement in the fit by accounting for non-zero eccentricity becomes clear and could be quantitatively measured by comparing the BIC values of both models: BICe = 0 − BICe ≠ 0 = 59. This difference is largely greater than six, which indicates that the REB modulations are clearly described better by an eccentric model.
The detection of this ellipsoidal modulation confirms the presence of a physically bound planetary-mass companion to Kepler-91 without the need for a radial velocity study. It is important to note that all statistically possible solutions mentioned before fit the data with companion masses between 0.5 MJup and 1.1 MJup, confirming the planetary nature of the object orbiting Kepler-91. Future radial velocity studies will help constrain the planet and orbital parameters better.
We find it unlikely that there could be a blended eclipsing binary (not detected by our AstraLux image) as the cause of the ellipsoidal variations measured here. This would require that the background binary orbits the centre of masses with the same period as needed for the planet to orbit the parent star. Also, our high-resolution image implied a probability below 2.7% for a non-detected blended binary, and much less for an eclipsing binary with the specific characteristics needed to mimic these modulations.
4.3. Detection of other small transits/eclipses
Since the orbital parameters have been constrained in previous sections, we can use the Wallenquist (1950) equation to determine the location of the secondary eclipse: 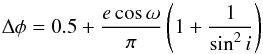 (15)where Δφ = φsec − φpri is the phase difference between primary and secondary eclipses. By doing so and using the orbital parameters from the REB analysis, we find that the secondary eclipse should be centred at φsec = 0.53. The duration of the secondary eclipse is expected to be similar to that of the primary due to the small eccentricity of the orbit (i.e. around 10−11 h). The theoretical locus of the secondary eclipse is marked in Fig. 7.
(15)where Δφ = φsec − φpri is the phase difference between primary and secondary eclipses. By doing so and using the orbital parameters from the REB analysis, we find that the secondary eclipse should be centred at φsec = 0.53. The duration of the secondary eclipse is expected to be similar to that of the primary due to the small eccentricity of the orbit (i.e. around 10−11 h). The theoretical locus of the secondary eclipse is marked in Fig. 7.
Final adopted values for the host star properties, planet, and orbit of the planetary system Kepler-91.
After removing the signal produced by the REB variations, three clear dims in the light curve can be detected (see Fig. 7). The first one is located at the mid orbital period (φA ≈ 0.5, labelled as A in Fig. 7). Its duration of dA ≈ 4.5 − 6.0 h is shorter than the primary transit, which prevents this from being the secondary eclipse. Secondly, another small dim (labelled as B) is found φB = 0.54. However, its duration of only 5−6 h, combined with its low S/N, also prevents us from confirming this as the secondary eclipse.
A third dim (C) is found at φ ≈ 0.68. In this case, the duration of the possible occultation is close to the primary transit’s duration (dC ≈ 11 − 12 h). However, the position of this dim prevents this from being the secondary eclipse of the confirmed planet Kepler-91b. Finally, although this is not as clear (in shape and location) as the previously analysed dims, there are two more occultations at φ ≈ 0.17 and φ ≈ 0.35. Similar reasons to those stated for the previous dims discard these other possibilities as the secondary occultation of Kepler-91b.
According to this analysis, we can conclude that none of the previously discussed dims agree with the expected location and duration of the occultation of this system. The contribution of the planet reflection at such orbital phases would yield a theoretical depth of Dsec = 25 ± 15 ppm for the secondary eclipse. Interestingly, this coincides with the depth of the observed dim labelled as B in Fig. 7. However, the theoretical location of the secondary eclipse encompasses both A and B dims. Thus, although observationally we do not detect a clear secondary eclipse accomplishing all theoretical constraints, we can set an upper limit of 40 ppm for the depth of such eclipse. This would agree with the depth of the two minima labelled as A and B. In other words, the combined position and duration of both dims make plausible, with caveats, the identification of the secondary eclipse. However, more work is needed to unveil the origin of such dims and to confirm the detection of the secondary eclipse.
In any case, the explanation for the three individual dims is beyond the scope of this paper and should be addressed by future work on this planetary system. We have already shown that A and B could be part of the secondary eclipse. Some explanations for the dim labelled as C that should be studied more in detail by future works are listed here:
-
The presence of a large trojan planet (located in the same orbit asKepler-91b) as the large bodies detected in the L4and L5 Lagrangian points of Jupiter (althoughstability studies are needed to confirm this possibility),
-
An outer resonant and transiting planet. This possibility implies non-coplanar orbits since for the measured inclination of i ≈ 66°, planets in wider orbits would not transit the parent star.
-
A large exomoon blocking the reflected light from the planet’s day side. This configuration would require that the moon’s period were an integer number of the planet’s period around the host star. Again, this possibility would need an exhaustive stability study.
-
Subtle effects of the Kepler reduction pipeline, combined with some activity effect on the stellar surface.
Accurate radial velocity measurements for this system would help determine the planet and orbital parameters more accurately which could feed theoretical studies of the stability of the possible explanations for these dims.
5. Discussion: the planet in context
5.1. Solution for star-planet and orbital parameters
By considering the whole analysis, we report in Table 8 the parameters calculated for the Kepler-91 system, and discuss here the most controversial ones.
Regarding stellar parameters, from all determinations of the effective temperature and metallicity, we have chosen our spectroscopically calculations since they are the most precise ones and lie within the uncertainty limits of other studies. Thanks to its high precision as compared to other methods, asteroseismology determinations of the rest of the stellar parameters have been assumed. According to both asteroseismology and the analysis of the isochrones and evolutionary tracks, we estimate a stellar age of 2.7 − 7.0 Gyr. Given the calculated stellar parameters (stellar radius, effective temperature, and extinction), we can estimate a distance to Kepler-91 by assuming the bolometric corrections polynomials defined by Flower (1996) and re-calculated by Torres (2010). The calculations provide a value of 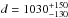 pc. In Fig. 9, we compare the properties of Kepler-91 to other known stars hosting planetary systems.
pc. In Fig. 9, we compare the properties of Kepler-91 to other known stars hosting planetary systems.
 |
Fig. 9 Stellar properties of KOI-2133 compared to other confirmed planetary systems as of July 16, 2013 (black circles). We have marked the location of this system with a yellow star-like symbol according to the properties obtained in Sect. 3. |
When it comes to the orbital parameters, we have demonstrated that an eccentric orbit is required to describe the REB modulations better. Thus, this parameter (together with the argument of the periastron) is better constrained by this technique rather than by the transit fitting. Both studies agree on the high inclination of the orbit and provide similar values. We thus use the REB modulation analysis value due to its higher precision.
Finally, given the planetary mass and radius obtained by the REB modulation and transit fitting studies, respectively, we can derive a mean density of 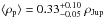 , placing Kepler-91b in the giant gaseous planet locus of the mass-radius diagram of known exoplanets (Fortney et al. 2007). As for HD 209458b, Kepler-91b seems to have an inflated atmosphere probably due to the strong stellar irradiation of its host star.
, placing Kepler-91b in the giant gaseous planet locus of the mass-radius diagram of known exoplanets (Fortney et al. 2007). As for HD 209458b, Kepler-91b seems to have an inflated atmosphere probably due to the strong stellar irradiation of its host star.
5.2. Comparison to previous works on Kepler-91
Our results clearly differ with the results from the recently published paper by Esteves et al. (2013) where the planetary nature of Kepler-91b is put in question. The authors base this conclusion on their determination of a geometric albedo as greater than 1.0 (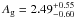 ), corresponding to a self-luminous object, hence a false positive. They use four key parameters to determine this value: their fit to the secondary eclipse, their orbital distance value of
), corresponding to a self-luminous object, hence a false positive. They use four key parameters to determine this value: their fit to the secondary eclipse, their orbital distance value of 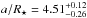 , the planet-to-stellar radius of
, the planet-to-stellar radius of 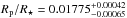 (both coming from the transit fitting), and the assumption of negligible contribution of the thermal emission of the planet. As we have seen, our fits provide quite different values for both parameters, became their semi-major-axis to stellar radius is more than twice our value. Since the geometric albedo depends on these parameters in the form
(both coming from the transit fitting), and the assumption of negligible contribution of the thermal emission of the planet. As we have seen, our fits provide quite different values for both parameters, became their semi-major-axis to stellar radius is more than twice our value. Since the geometric albedo depends on these parameters in the form  (16)where Fecl is related to the secondary eclipse depth, we find that the factor multiplying Fecl is more than seven times lower with our determined parameters than for their calculated values. Even assuming that the depth of the secondary eclipse is perfectly fitted (which we have shown to be unclear in Sect. 4.3), the geometric albedo would then be reduced by a factor of 5.4, placing it below 1 and thus eliminating the self-luminous scenario for Kepler-91b. Indeed, the upper limit for the secondary eclipse depth of 40 ppm calculated in Sect. 4.3 implies an upper limit for the geometric albedo of Ag < 0.5. Also, if we assume that the theoretical eclipse corresponds to a real detection of the observed eclipse, the calculated depth of Dsec = 25 ± 15 ppm would yield a geometric albedo of
(16)where Fecl is related to the secondary eclipse depth, we find that the factor multiplying Fecl is more than seven times lower with our determined parameters than for their calculated values. Even assuming that the depth of the secondary eclipse is perfectly fitted (which we have shown to be unclear in Sect. 4.3), the geometric albedo would then be reduced by a factor of 5.4, placing it below 1 and thus eliminating the self-luminous scenario for Kepler-91b. Indeed, the upper limit for the secondary eclipse depth of 40 ppm calculated in Sect. 4.3 implies an upper limit for the geometric albedo of Ag < 0.5. Also, if we assume that the theoretical eclipse corresponds to a real detection of the observed eclipse, the calculated depth of Dsec = 25 ± 15 ppm would yield a geometric albedo of 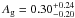 for this planet. The important differences in the physical and orbital parameters are probably due to the almost edge-on orbit calculated by Esteves et al. (2013). We performed an exhaustive fitting of this parameter exploring the whole parameter space and we found a lower value for the inclination of i = 68.5° to fit both the transit and REB modulations better (see Sects. 4.1 and 4.2.2). We note that such an inclination and small orbital distance agrees with the calculations by Tenenbaum et al. (2012).
for this planet. The important differences in the physical and orbital parameters are probably due to the almost edge-on orbit calculated by Esteves et al. (2013). We performed an exhaustive fitting of this parameter exploring the whole parameter space and we found a lower value for the inclination of i = 68.5° to fit both the transit and REB modulations better (see Sects. 4.1 and 4.2.2). We note that such an inclination and small orbital distance agrees with the calculations by Tenenbaum et al. (2012).
We can also estimate the stellar density (perfectly constrained from asteroseismology to be ρ⋆ = 7.3 ± 0.1 kg/m3) directly from photometric observations and fitting as proposed by Seager & Mallén-Ornelas (2003) and Sozzetti et al. (2007): 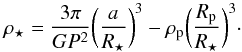 (17)Although the second term has a negligible influence, we can keep it since we have all the information available.
(17)Although the second term has a negligible influence, we can keep it since we have all the information available.
If we use the transit fitting results from Esteves et al. (2013) and their derived planet parameters, we get ρ⋆ = 44.5 ± 5.8 kg/m3, a much higher value than the asteroseismic one. However, our derived parameters from transit and REB modulation fittings provide a much closer estimation of 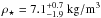 , which agrees with the asteroseismic result, within the confident limits. It is important to note that the above expression was derived under the assumption of circular orbit. Thus the result in our case must be taken only as a zero-order estimation and serve only as a comparison to the value computed with the Esteves et al. (2013) derived parameters.
, which agrees with the asteroseismic result, within the confident limits. It is important to note that the above expression was derived under the assumption of circular orbit. Thus the result in our case must be taken only as a zero-order estimation and serve only as a comparison to the value computed with the Esteves et al. (2013) derived parameters.
All these considerations, together with the fact that they use the photometrically derived stellar parameters by Batalha et al. (2013), led Esteves et al. to compute a companion’s mass of 5.92 MJup, if real. Our study uses the more accurate asteroseismic and spectroscopic analysis to determine the stellar parameters, yielding a planetary mass of 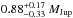 in our final fitting. According to all this information, we conclude that Kepler-91b is actually a hot Jupiter planet and that the self-luminous nature proposed by Esteves et al. (2013) is neither clear nor conclusive.
in our final fitting. According to all this information, we conclude that Kepler-91b is actually a hot Jupiter planet and that the self-luminous nature proposed by Esteves et al. (2013) is neither clear nor conclusive.
5.3. Stellar irradiation on the planet
The extremely close-in orbit of Kepler-91b and the large size of its host mean that stellar irradiation on the planet’s atmosphere should have been playing an important role in the evolution of this planetary system. The equilibrium temperature of the planet is given by López-Morales & Seager (2007): ![\begin{equation} T_{\rm eq}=T_{\star}\left(\frac{R_{\star}}{a} \right)^{1/2} [f(1-A_{\rm B})]^{1/4} \end{equation}](/articles/aa/full_html/2014/02/aa22001-13/aa22001-13-eq419.png) (18)
(18)
where 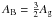 is the Bond albedo if we assume Lambert’s law. According to Eq. (13), the geometric albedo for the calculated parameters is Ag = 0.154. The f parameter describes the redistribution of the incident stellar flux in the planet’s atmosphere and goes from f = 1/4, when the energy is instantaneously redistributed in the atmosphere, to f = 2/3, when the energy is instantaneously re-radiated to space. The equilibrium temperature in both extreme cases would be
is the Bond albedo if we assume Lambert’s law. According to Eq. (13), the geometric albedo for the calculated parameters is Ag = 0.154. The f parameter describes the redistribution of the incident stellar flux in the planet’s atmosphere and goes from f = 1/4, when the energy is instantaneously redistributed in the atmosphere, to f = 2/3, when the energy is instantaneously re-radiated to space. The equilibrium temperature in both extreme cases would be 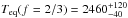 K and
K and 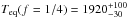 K. Neither Esteves et al. (2013) nor us have considered the effect on the planet equilibrium temperature of the actual fraction illuminated by the host star, as discussed in Guillot (2010). Given the calculated stellar and orbital parameters, we obtain that around 70% of the planet atmosphere would be illuminated by the host star (in contrast to the approximately 50% illuminated for planets on wider orbits). The extra angle illuminated of the planet as counted from the perpendicular axis to the orbital plane is, at the periastron (apastron) of the orbit,
K. Neither Esteves et al. (2013) nor us have considered the effect on the planet equilibrium temperature of the actual fraction illuminated by the host star, as discussed in Guillot (2010). Given the calculated stellar and orbital parameters, we obtain that around 70% of the planet atmosphere would be illuminated by the host star (in contrast to the approximately 50% illuminated for planets on wider orbits). The extra angle illuminated of the planet as counted from the perpendicular axis to the orbital plane is, at the periastron (apastron) of the orbit, 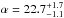 (
(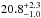 ) degrees (see Fig. 10). The angular size of the star as seen from the planet is given by tan(β/2) = R⋆/a so that, for this system, we obtain
) degrees (see Fig. 10). The angular size of the star as seen from the planet is given by tan(β/2) = R⋆/a so that, for this system, we obtain 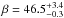 degrees at pericentre passage. This value is well above the rest of the known planetary systems (β < 10°). The implications of this effect on any determination of the planet and orbital parameters must be investigated by future works.
degrees at pericentre passage. This value is well above the rest of the known planetary systems (β < 10°). The implications of this effect on any determination of the planet and orbital parameters must be investigated by future works.
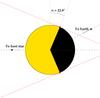 |
Fig. 10 Diagram illustrating the irradiation of the host star onto the planet surface at mid-transit. The red lines represent the boundaries of the stellar irradiation that hits the planet surface. The yellow part represents the dayside according to our best solution for the system. The black part represents the night side, and the red one is the extra region illuminated due to the close-in orbit and the large stellar radii. |
 |
Fig. 11 Properties of the Kepler-91 system from a comparative perspective. We plot the semi-major axis of all confirmed planets (grey circles) against the stellar radius (left) and the surface gravity (right). In the left panel, the red point marks the position of Kepler-91 and the solid line is the location of the stellar radius (1:1 line), showing that, among giant stars, this is the closest planet to the stellar surface. In the right panel, we can check that Kepler-91 lies below the solid line marking the empirical limit suggested by Nowak et al. (2013). Together with the intriguing case of HIP 13044, Kepler-91 is the only planet that goes through this line. |
5.4. A giant planet at the end of its life
According to the derived host star properties in Sect. 3 and orbital parameters of the planet in Sects. 4.1 and 4.2, Fig. 11 highlights the singular location of this system. We plot the semi-major axis of all confirmed planets against the stellar radius and the surface gravity. On the left, twe mark the position of Kepler-91b and the location of the stellar radius (1:1 line), showing that this is the closest planet to its host star among giant stars. The cases of HD 102956b (Johnson et al. 2010) and HIP 13044b (Klement et al. 2011) are marked as a reference. On the right, we can check that Kepler-91b lies below the line marking the empirical limit suggested by Nowak et al. (2013). Together with the intriguing case of HIP 13044, Kepler-91 is the only planet that goes below this line.
We used evolutionary tracks from Girardi et al. (2002) and assumed the effective temperature, metallicity, stellar radius, and mass from our spectroscopic and asteroseismic studies to compute the time that the radius of the star Kepler-91 will reach the current planet’s orbital pericenter. If we only take this evolutive constraint into account, we conclude that Kepler-91b will be engulfed by the stellar atmosphere in less than 55 Myr. It is important to note that other non-negligible effects inducing instabilities on the planetary orbit could speed up the planet engulfment. As a result, this result can be considered as an upper limit to the planet’s life. The first clear evidence of planet engulfment was published by Adamów et al. (2012). The authors showed the signs of a post-planet engulfment scenario for BD+48 740, where the presence of a highly eccentric (e = 0.67) secondary planet and an overabundance of lithium in the stellar spectrum could be caused by the previous engulfment of an inner planet. With a similar stellar mass, Kepler-91 could be in the immediately previous stage of BD+48 740, the scenario before the planet engulfment.
The planet-to-star distance measured in this paper (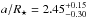 equivalent to
equivalent to 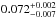 AU if we assume the calculated stellar radius) places Kepler-91b as the closest planet to a host giant star. From the sample of confirmed exoplanets8, none of them is closer than a/R⋆ = 3.0. Our derived orbital distance implies that more than 8% of the sky as seen from the planet is covered by the star (compared to the 0.0005% covered by the Sun from the Earth). This reinforces the idea that the planet under study is at the end of its life, with its host star rapidly inflating while ascending the RGB. Since we have found no overabundance of lithium in the spectrum of the host star, we conclude that the planet is still not being evaporated (at least the material has not been incorporated into the stellar atmosphere) and that no previous engulfment seems to have happened.
AU if we assume the calculated stellar radius) places Kepler-91b as the closest planet to a host giant star. From the sample of confirmed exoplanets8, none of them is closer than a/R⋆ = 3.0. Our derived orbital distance implies that more than 8% of the sky as seen from the planet is covered by the star (compared to the 0.0005% covered by the Sun from the Earth). This reinforces the idea that the planet under study is at the end of its life, with its host star rapidly inflating while ascending the RGB. Since we have found no overabundance of lithium in the spectrum of the host star, we conclude that the planet is still not being evaporated (at least the material has not been incorporated into the stellar atmosphere) and that no previous engulfment seems to have happened.
The non-zero eccentricity for such close-in planet is intriguing. Several effects can produce eccentric orbits of relatively close-in planets (e.g. other non-detected objects, tidal interactions, or instabilities due to the mass-loss in the transition from the main-sequence to the giant stage of the host, Debes & Sigurdsson 2002). Thus, a deeper study in this line is needed to unveil the origin of the eccentric orbit of this planet.
6. Conclusions
In this paper we have proved the planetary nature of the object orbiting the K3 giant star Kepler-91 (R⋆ = 6.30 ± 0.16 R⊙, M⋆ = 1.31 ± 0.10 M⊙). Modelling of the transit signal and light-curve modulations allowed us to measure a planetary mass and radius of 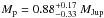 and
and 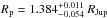 . The planet encompasses its host star in a very close-in eccentric orbit (
. The planet encompasses its host star in a very close-in eccentric orbit (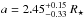 ,
, 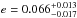 ).
).
We have determined that the expansion of the outer atmospheric layers of the giant star will reach the pericentre of the orbit in less than 55 Myr. The strong stellar irradiation induced by the close star is probably the cause of the inflated atmosphere presented by Kepler-91b and reflected in its low density (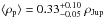 ). The combination of a large stellar radius and a very close-in orbit implies that more than 36% of the day sky of the planet is covered by the star. This combination also implies that around the 70% of the planet atmosphere is illuminated by the host stars. Detecting such additional illumination represents a challenge for current and future high-precision photometers.
). The combination of a large stellar radius and a very close-in orbit implies that more than 36% of the day sky of the planet is covered by the star. This combination also implies that around the 70% of the planet atmosphere is illuminated by the host stars. Detecting such additional illumination represents a challenge for current and future high-precision photometers.
Online material
Appendix A: Genetic algorithm
A correct sampling for a model depending on a large number of free parameters would yield a huge (unmanageable) grid of models. For instance, in a case where observations could be modelled with six parameters, by sampling each parameter with 15 values, which would generate 615 different sets of parameters. Depending on the time employed by a computer to calculate each model, the amount of time could last for weeks for a good sampling. Instead, a clever way to select the particular set of parameters to be tested can save us a lot of time. This is actually the main goal of the so-called genetic algorithms (GA).
We have written a genetic algorithm (IDL-based) to explore the whole parameter space without the need of creating a model grid. Basically, a range (minimum and maximum) for each parameter must be supplied, and optionally a prior (initial guessed) value for each parameter. The program performs the following steps:
-
1.
If provided, it uses the prior values as parents for the zero-agegeneration of individuals (i.e. sets of parameters).
-
2.
It generates a random population of N individuals within the range limits set by the user and based on the parents in step 1, modifying their values from −20% to 20% of the total range, with a given probability (also provided by the user but typically 10−30%). This allows some of the parameters to change while other maintain the same values.
-
3.
It generates the N models with the corresponding parameters. To get these models, the user has to provide the function to this end. For instance, in the case of transit fitting, one should provide a function that calculates the Mandel & Agol (2002) model for a given set of parameters or individuals.
-
4.
It obtains the χ2 value for each individual by comparing the models calculated in (3) to the provided datapoints.
-
5.
It selects the best 10% individuals and used them as parents for the new generation to be created in step (1).
The process is reiteratively repeated until a stable point is reached. This occurs when, after a specified number of generations, the best χ2 does not change more than 1% with respect to the best value of the previous generation. At this point, a random population of 10 × N new individuals is added to destabilize the minimum achieved to avoid local minima. If the stable point remains, we start again steps (1)−(5) until we reach again a stable point. The process is then repeated ten times. The final value has thus remained stable during more than 100 generations, with ten inclusions of 10 × N random points in the whole parameter space.
Once the final value has been obtained, we proceed to obtain the errors. We use generated χ2 maps for each pair of parameters centred on the best-fit parameters obtained by the GA. We slightly modify the GA values of each pair while keeping the others with the best-fit values. Then we measure the goodness of the fit (χ2). Finally, we compute χ2 contours for each pair for values 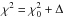 , where Δ is a tabulated value depending on the number of free parameters and the confidence limits to be achieved. We use 99% confident limits to ensure a good determination of the uncertainties in our parameters. Finally, if no correlation between parameters is found (the so-called banana-shaped contours), we select the upper and lower errors for each parameter as the largest ones obtained for all pairs.
, where Δ is a tabulated value depending on the number of free parameters and the confidence limits to be achieved. We use 99% confident limits to ensure a good determination of the uncertainties in our parameters. Finally, if no correlation between parameters is found (the so-called banana-shaped contours), we select the upper and lower errors for each parameter as the largest ones obtained for all pairs.
See Appendix on http://www.caha.es/CAHA/Instruments/CAFE/cafe/CAFE.pdf
Acknowledgments
This research has been funded by Spanish grants AYA 2010-21161-C02-02, AYA2012-38897-C02-01, and PRICIT-S2009/ESP-1496. J. Lillo-Box thanks the CSIC JAE-predoc programme for the PhD fellowship. We also thank Calar Alto Observatory, both the open TAC and Spanish GTO panel, for allocating our observing runs, and the CAHA staff for providing very useful information about the new échelle spectrograph. This publication made use of VOSA, developed under the Spanish Virtual Observatory project supported from the Spanish MICINN through grant AyA2008-02156. A. Bayo ackowledges funding and support from the Marie Curie Actions of the European Commission FP7-COFUND. B. Montesinos is supported by Spanish grant AYA2011-26202. J. Montalbán acknowledges financial support from Belspo for contract PRODEX-CoRoT. The authors acknowledge the two referees (experts on asteroseismology and exoplanets) for their useful comments and interesting suggestions that have improved the quality of the paper.
References
- Aceituno, J., Sánchez, S. F., Grupp, F., et al. 2013, A&A, 552, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adamów, M., Niedzielski, A., Villaver, E., Nowak, G., & Wolszczan, A. 2012, ApJ, 754, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, E. R., Dupree, A. K., Kulesa, C., & McCarthy, D. 2013, AJ, 146, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer Science + Business Media) [Google Scholar]
- Anderson, E. R., Duvall, Jr., T. L., & Jefferies, S. M. 1990, ApJ, 364, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006, in ESA SP 1306, eds. M. Fridlund, A. Baglin, J. Lochard, & L. Conroy, 33 [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2013, A&A, submitted [Google Scholar]
- Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bedding, T. R., Huber, D., Stello, D., et al. 2010, ApJ, 713, L176 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Belkacem, K., Goupil, M. J., Dupret, M. A., et al. 2011, A&A, 530, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Samadi, R., Mosser, B., Goupil, M. J., & Ludwig, H.-G. 2013, ASP Conf. Proc. (San Francisco: ASP), 479, 61 [Google Scholar]
- Borucki, W. J., Koch, D., Jenkins, J., et al. 2009, Science, 325, 709 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Latham, D. W., Everett, M. E., & Esquerdo, G. A. 2011, AJ, 142, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Burkert, A., & Ida, S. 2007, ApJ, 660, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2004, Sol. Phys., 220, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2012, Astron. Nachr., 333, 914 [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Daemgen, S., Hormuth, F., Brandner, W., et al. 2009, A&A, 498, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Debes, J. H., & Sigurdsson, S. 2002, ApJ, 572, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M.-A., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dziembowski, W. A., Gough, D. O., Houdek, G., & Sienkiewicz, R. 2001, MNRAS, 328, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Esteves, L. J., De Mooij, E. J. W., & Jayawardhana, R. 2013, ApJ, 772, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Everett, M. E., Howell, S. B., & Kinemuchi, K. 2012, PASP, 124, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Faigler, S., & Mazeh, T. 2011, MNRAS, 415, 3921 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L., Jenkins, J. M., Borucki, W. J., et al. 2010, ApJ, 713, L160 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gough, D. O. 1986, in Hydrodynamic and Magnetodynamic Problems in the Sun and Stars, Proc. Workshop, Tokyo, ed. Y. Osaki, 117 [Google Scholar]
- Gray, D. F., & Brown, K. 2001, PASP, 113, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F., Scott, H. R., & Postma, J. E. 2002, PASP, 114, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Gruberbauer, M., Guenther, D. B., & Kallinger, T. 2012, ApJ, 749, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2010, A&A, 520, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harvey, J. 1985, in Future Missions in Solar Heliospheric and Space Plasma Physics, eds. E. Rolfe, & B. Battrick, 99 [Google Scholar]
- Hekker, S., Kallinger, T., Baudin, F., et al. 2009, A&A, 506, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hekker, S., Gilliland, R. L., Elsworth, Y., et al. 2011, MNRAS, 414, 2594 [Google Scholar]
- Hormuth, F. 2007, Master’s thesis, University of Heidelberg [Google Scholar]
- Houdek, G., Balmforth, N. J., Christensen-Dalsgaard, J., & Gough, D. O. 1999, A&A, 351, 582 [NASA ADS] [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2010, ApJ, 723, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Ireland, M. J., Bedding, T. R., et al. 2012, ApJ, 760, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Chaplin, W. J., Christensen-Dalsgaard, J., et al. 2013, ApJ, 767, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Fischer, D. A., Marcy, G. W., et al. 2007, ApJ, 665, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Bowler, B. P., Howard, A. W., et al. 2010, ApJ, 721, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, M. I., Jenkins, J. S., Rojo, P., Melo, C. H. F., & Bluhm, P. 2013, A&A, 556, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallrath, J., & Milone, E. F. 2009, Eclipsing Binary Stars: Modeling and Analysis (Springer) [Google Scholar]
- Kane, S. R., & Gelino, D. M. 2010, ApJ, 724, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., & Christensen-Dalsgaard, J. 2008, ApJ, 683, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Klement, R. J., Setiawan, J., Henning, T., et al. 2011, in IAU Symp. 276, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 121 [Google Scholar]
- Kunitomo, M., Ikoma, M., Sato, B., Katsuta, Y., & Ida, S. 2011, ApJ, 737, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Latham, D. W., Brown, T. M., Monet, D. G., et al. 2005, BAAS, 37, 1340 [Google Scholar]
- Lillo-Box, J., Barrado, D., & Bouy, H. 2012, A&A, 546, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loeb, A., & Gaudi, B. S. 2003, ApJ, 588, L117 [NASA ADS] [CrossRef] [Google Scholar]
- López-Morales, M., & Seager, S. 2007, ApJ, 667, L191 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., García, R. A., Régulo, C., et al. 2010, A&A, 511, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Metcalfe, T. S., Woitaszek, M., et al. 2012, ApJ, 749, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Marsh, T. R., & North, R. C. 2000, MNRAS, 317, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Mazeh, T., Nachmani, G., Sokol, G., Faigler, S., & Zucker, S. 2012, A&A, 541, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Montalbán, J., Baudin, F., et al. 2009, A&A, 503, L21 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Miglio, A., Brogaard, K., Stello, D., et al. 2012, MNRAS, 419, 2077 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Chiappini, C., Morel, T., et al. 2013a, in EPJ Web Conf., 43, 3004 [Google Scholar]
- Miglio, A., Chiappini, C., Morel, T., et al. 2013b, MNRAS, 429, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Mislis, D., & Hodgkin, S. 2012, MNRAS, 422, 1512 [NASA ADS] [CrossRef] [Google Scholar]
- Montalbán, J., Miglio, A., Noels, A., Scuflaire, R., & Ventura, P. 2010, ApJ, 721, L182 [NASA ADS] [CrossRef] [Google Scholar]
- Montalbán, J., Miglio, A., Noels, A., et al. 2013, ApJ, 766, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, T., & Miglio, A. 2012, MNRAS, 419, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, S. L. 1985, ApJ, 295, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, T. D., & Johnson, J. A. 2011, ApJ, 738, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Belkacem, K., Goupil, M.-J., et al. 2010, A&A, 517, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Barban, C., Montalbán, J., et al. 2011, A&A, 532, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Michel, E., Belkacem, K., et al. 2013, A&A, 550, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moya, A. 2011 [arXiv:1111.2274] [Google Scholar]
- Nowak, G., Niedzielski, A., Wolszczan, A., Adamów, M., & Maciejewski, G. 2013, ApJ, 770, 53 [Google Scholar]
- Passy, J.-C., Mac Low, M.-M., & De Marco, O. 2012, ApJ, 759, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Pfahl, E., Arras, P., & Paxton, B. 2008, ApJ, 679, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., An, D., Molenda-Żakowicz, J., et al. 2012, ApJS, 199, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Quintana, E. V., Rowe, J. F., Barclay, T., et al. 2013, ApJ, 767, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Scuflaire, R., Montalbán, J., Théado, S., et al. 2008, Ap&SS, 316, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Shporer, A., Jenkins, J. M., Rowe, J. F., et al. 2011, AJ, 142, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R., Churcher, L. J., Wyatt, M. C., Moerchen, M. M., & Telesco, C. M. 2009, A&A, 493, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, J. C., Stumpe, M. C., Van Cleve, J. E., et al. 2012, PASP, 124, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Sozzetti, A., Torres, G., Charbonneau, D., et al. 2007, ApJ, 664, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Strehl, K. 1902, Astron. Nachr., 158, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Stumpe, M. C., Smith, J. C., Van Cleve, J. E., et al. 2012, PASP, 124, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Tenenbaum, P., Jenkins, J. M., Seader, S., et al. 2012, ApJS, submitted [arXiv:1212.2915] [Google Scholar]
- Torres, G. 2010, AJ, 140, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, R. K. 1986, ApJ, 306, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Vandakurov, Y. V. 1967, AZh, 44, 786 [NASA ADS] [Google Scholar]
- Ventura, P., D’Antona, F., & Mazzitelli, I. 2008, Ap&SS, 316, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Villaver, E., & Livio, M. 2009, ApJ, 705, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Wallenquist, Å. 1950, Arkiv for Astronomi, 1, 59 [Google Scholar]
- Welsh, W. F., Orosz, J. A., Seager, S., et al. 2010, ApJ, 713, L145 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 161 [NASA ADS] [CrossRef] [Google Scholar]
- White, T. R., Huber, D., Maestro, V., et al. 2013, MNRAS, 433, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Sensitivity limits (in magnitude difference between the target and a theoretical companion) achieved in the iSDSS band of the Calar Alto 2.2 m/AstraLux high-resolution images for 4 selection rates.
Results for the analysis of the primary transit and the light-curve modulations and comparison with the values obtained by Tenenbaum et al. (2012) in the second column.
Final adopted values for the host star properties, planet, and orbit of the planetary system Kepler-91.
All Figures
 |
Fig. 1 Contrast map of our high-resolution image taken with the 2.2 m telescope plus AstraLux at Calar Alto Observatory. Colour code corresponds to the S/N with which we would detect a theoretical source with a magnitude difference Δmi (y-axis) at the corresponding angular separation (x-axis). The two dotted lines represent the 3σ (lower line) and 5σ (upper line) contours. |
| In the text | |
 |
Fig. 2 Narrow range of the high-resolution, high signal-to-noise (S/N = 123 at 5800 Å) spectrum of KOI-2133 obtained with the CAFE échelle spectrograph at Calar Alto Observatory. We show the part of the spectrum used in determining the stellar metallicity (see Sect. 3.4.1) and mark with dotted lines the doublets used to estimate the effective temperature (see Sect. 3.4.2). The spectrum has been shifted to the rest frame by correcting for the barycentric velocity. |
| In the text | |
 |
Fig. 3 Power spectrum of the light curve, in a region centred on the maximum of the oscillations. The upper part of the figure shows the various modes identified for increasing value of n: in red the modes with l = 0, green l = 2, blue l = 1. We also show the calculated global parameters of the lower spectrum. |
| In the text | |
 |
Fig. 4 Left: determination of the stellar metallicity of KOI-2133 (see Sect. 3.4.1). We show data from giants compiled by Gray et al. (2002) to parametrize the line absorption parameter (LA) with the iron abundance [Fe/H]. Two samples are shown: giants with Teff > 4830 K (red) and giants with Teff < 4830 K (blue). Solid lines represent the fitted second-order polynomials to the test data. The dotted vertical line shows the obtained LA for KOI-2133 and the black circle its determined position in the diagram. Right: effective temperature versus LA showing that KOI-2133 should be considered in the cool group of giants regarding the left panel segregation. The red circles show the position of the test giants, and the dashed line represents an estimated empirical limit to the temperature for each LA. |
| In the text | |
 |
Fig. 5 Left: échelle diagram of the power spectrum of the data with the fitted modes overplotted. Circles for l = 0, triangles for l = 1, and squares for l = 2. The power spectrum is fitted using maximum likelihood estimation (see Sect. 3.5.2). Right: comparison between observational (black solid dots and white symbols in the left panel) and theoretical (open symbols) frequencies in the échelle diagram for a typical good fitting of radial and non-radial modes. Circles correspond to radial modes, squares to dipole modes, and triangles to quadrupole ones. The size of the theoretical symbols is an indication of the expected amplitude based on the value of the inertia mode (Houdek et al. 1999). The asymptotic period spacing for this model is 76 s. |
| In the text | |
 |
Fig. 6 Best-fit solutions for the transit fitting according to different model schemes: assuming parameters from Tenenbaum et al. (2012) (dot-dashed blue line), assuming zero eccentricity (dashed black line), and leaving the eccentricity as a free parameter (solid red line). Residuals for the fixed e = 0 model are presented in the lower panel. |
| In the text | |
 |
Fig. 7 Best-fitted model to the REB modulations for an assumed circular orbit (dashed blue line) and the best model for a non-circular orbit (solid black line). Red circles show the folded light curve assuming the period obtained by the Kepler team and binned to 29.4 min intervals (similar to the real cadence of observations. In the small panel we show the individual contributions of ellipsoidal (red dotted-dashed line), reflection (blue dashed line), and Doppler beaming (green dotted line). The lower panel shows the residuals after substracting the non-circular model to the observed data. The three shadowed regions marked as A, B, and C represent the three detected dims (see Sect. 4.3). The theoretical location of the secondary eclipse according to the architecture of the system is marked with vertical grey dashed lines in the upper panel. By removing the contribution of the planet reflection in this region, we obtain the dotted black line. |
| In the text | |
 |
Fig. 8 Possible solutions for the REB modulation fitting (see Sect. 4.2). Each grey open circle (and its correspondent error bars) represents a possible solution for the REB modulations whose χ2 value is statistically valid as compared to the minimum χ2 obtained with the genetic algorithm. We have marked the adopted model in black, being the one that presents the least relative errors. The red symbol corresponds to the most repeated value (and standard deviation deviation) for each parameter in the whole set of statistically acceptable solutions. |
| In the text | |
 |
Fig. 9 Stellar properties of KOI-2133 compared to other confirmed planetary systems as of July 16, 2013 (black circles). We have marked the location of this system with a yellow star-like symbol according to the properties obtained in Sect. 3. |
| In the text | |
 |
Fig. 10 Diagram illustrating the irradiation of the host star onto the planet surface at mid-transit. The red lines represent the boundaries of the stellar irradiation that hits the planet surface. The yellow part represents the dayside according to our best solution for the system. The black part represents the night side, and the red one is the extra region illuminated due to the close-in orbit and the large stellar radii. |
| In the text | |
 |
Fig. 11 Properties of the Kepler-91 system from a comparative perspective. We plot the semi-major axis of all confirmed planets (grey circles) against the stellar radius (left) and the surface gravity (right). In the left panel, the red point marks the position of Kepler-91 and the solid line is the location of the stellar radius (1:1 line), showing that, among giant stars, this is the closest planet to the stellar surface. In the right panel, we can check that Kepler-91 lies below the solid line marking the empirical limit suggested by Nowak et al. (2013). Together with the intriguing case of HIP 13044, Kepler-91 is the only planet that goes through this line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


