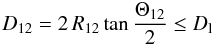| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322793 | |
| Published online | 03 January 2014 | |
Assessing the reliability of friends-of-friends groups on the future Javalambre Physics of the Accelerating Universe Astrophysical Survey
1 Instituto de Astronomía Teórica y Experimental, IATE, CONICET, Laprida 854, X5000BGR Córdoba, Argentina
e-mail: arielz77@gmail.com
2 Observatorio Astronómico, Universidad Nacional de Córdoba, Laprida 854, X5000 BGR Córdoba, Argentina
3 Instituto de Astronomía, Geofísica e Ciencias Atmosfericas, IAG, USP, 1226 rua do Matão, São Paulo, Brazil
4 Instituto de Astrofisica de Andalucía (CSIC), Apdo. 3044, 18008 Granada, Spain
5 University of Michigan, Ann Arbor MI 48109, USA; Eureka Scientific Inc., Oakland CA 94602-3017, USA
6 Observatório Nacional, rua Gal. José Cristino, 20921-400 Rio de Janeiro, Brazil
7 Department of Physics and Astronomy, University of Alabama, Box 870324, Tuscaloosa AL 35487, USA
Received: 4 October 2013
Accepted: 4 November 2013
Aims. We have performed a detailed analysis of the ability of the friends-of-friends algorithm to identify real galaxy systems in deep surveys such as the future Javalambre Physics of the Accelerating Universe Astrophysical Survey. Our approach was twofold: assessing the reliability of the algorithm in real and in redshift space. In the latter, our intention was also to determine the degree of accuracy that could be achieved when using spectroscopic or photometric-redshift determinations as a distance indicator.
Methods. We built a light-cone mock catalogue using synthetic galaxies constructed from the Millennium Run Simulation I plus a semi-analytical model of galaxy formation. We explored different ways to define the proper linking length parameters of the algorithm to identify the best-suited galaxy groups in each case.
Results. We found that when one identifies systems in redshift space using spectroscopic information, the linking lengths should take into account the variation of the luminosity function with redshift as well as the linear redshift dependence of the radial fiducial velocity in the line-of-sight direction. When we tested the purity and completeness of the group samples, we found that the best resulting group sample reaches values of ~40% and ~70% of systems with high levels of purity and completeness, when spectroscopic information was used. To identify systems using photometric redshifts, we adopted a probabilistic approach to link galaxies in the line-of-sight direction. Our result suggests that it is possible to identify a sample of groups with fewer than ~40% false identifications at the same time as we recover around 60% of the true groups.
Conclusions. This modified version of the algorithm can be applied to deep surveys provided that the linking lengths are selected appropriately for the science to be made with the data.
Key words: methods: numerical / methods: statistical / galaxies: groups: general
© ESO, 2014
1. Introduction
The study of galaxy systems is one of the most important topics of extragalactic astronomy because the history of galaxy formation and evolution is encrypted in these density peaks. Analysing the properties of galaxies in groups at different times directly probes the way the local environment shapes the galaxies inside of them, offering a direct insight into the physics that has occurred within the haloes.
To use these great laboratories to improve our understanding of the Universe, it is crucial to define them properly. To do this, it is necessary to implement an identification criterion to define galaxy systems. Throughout the decades, defining the proper algorithm for identifying galaxy systems has challenged scientists. Many attempts have been carried out in the search of the most suitable method for identifying galaxy systems using optical properties (see Gal 2006 for a review of different identification methods). Among these attempts, we highlight the following: methods that use positional information of galaxies to detect density peaks over a background density (e.g. Couch et al. 1991; Dalton et al. 1997; Ramella et al. 2001; Merchán & Zandivarez 2002; Trevese et al. 2007; Gillis & Hudson 2011; Farrens et al. 2011); methods that include some observational restrictions for a given type of galaxy, such as their colours, magnitudes, and their membership to a red sequence (e.g. Gladders & Yee 2000; Goto et al. 2002; Miller et al. 2005; Koester et al. 2007); and finally, methods that model cluster properties such as luminosity and density profiles through different probability approaches (e.g. Shectman 1985; Postman et al. 1996; Kepner et al. 1999; Gal et al. 2000; Milkeraitis et al. 2010; Ascaso et al. 2012).
Among all these different methods, those based only on the geometric positional information of galaxies have the advantage that they do not bin the data or impose constraints on the physical properties of the systems to avoid selection biases. The most extensively used finding algorithm that follows this criterion is the friends-of-friends (FoF) technique, which detects density enhancements in three dimensions by searching galaxy pairs that are closer than a given separation. When applied to an observational catalogue, the FoF algorithm makes use of the angular coordinates and the spectroscopic redshifts of the galaxies. Nevertheless, to identify groups in redshift space one has to deal with certain difficulties. One of them is the fact that in most cases the observational samples are flux limited, for which the observed decreasing galaxy number density as a function of redshift should be taken into account. Another important problem are the peculiar velocities of galaxies in groups, since they elongate groups in the redshift (line-of-sight) direction, making them harder to detect, and may cause group members to be linked with field galaxies or even to merge into another group. Although the FoF technique has been widely used to find groups and clusters in galaxy surveys, it has not been tested properly at intermediate and high redshifts. Therefore, it is very important to test the method in great detail to clearly determine its capability of recovering real systems.
In the past years, several medium-band photometric surveys (e.g., COMBO-17: Wolf et al. 2004; COSMOS 21: Ilbert et al. 2009; ALHAMBRA Survey: Moles et al. 2008; Molino et al. 2013; SHARDs: Pérez-González et al. 2013) have become available. These surveys provide ~1% photometric-redshift resolution and very valuable datasets for identifying galaxy concentrations. Future surveys will provide hundreds of millions of galaxies with this photo-z resolution, which makes it particularly important to study and develop the application of FoF algorithms to photometric-redshift datasets. This is no straightforward task, because of the pronounced blurring of galaxy systems in redshift space and the sometimes complex shape of the photometric-redshift error distributions. Several authors have proposed a modified FoF algorithm to be applied to photometric surveys (e.g. Botzler et al. 2004; Liu et al. 2008; Li & Yee 2008; van Breukelen & Clewley 2009). Beyond the chosen method, all the parameters and scaling relations of an algorithm should be carefully tested to apply one of these methods to a given deep photometric survey.
One of the most promising international projects with the aim of building a wide-field photometric survey is the Javalambre Physics of the Accelerating Universe Astrophysical Survey (J-PAS1, Benítez et al. 2009 and in prep.), which will cover more than 8000 square degrees in 54 narrow bands and 5 broad bands in the optical-frequency range. The survey, which is an international collaboration mainly between Spain and Brazil, will be carried out using two telescopes of 2.5 m and 0.8 m apertures, which are being built at Sierra de Javalambre in Spain (Benítez et al. 2009; Moles et al. 2010). The catalogue is planned to be assembled in 4−5 years and is expected to map 8000 deg2 down to an apparent magnitude of iAB ~ 23.
The advent of deep photometric surveys with reliable estimates of photometric redshifts, such as the future J-PAS, will demand a well-tailored set of tools to perform different statistical studies. Among them, the availability of different algorithms for extracting reliable samples of galaxy systems is quite important. However, to test the different observational restrictions in the identification procedure, we must use reliable mock galaxy catalogues built from cosmological numerical simulation with entire 3D positional information. One of the largest cosmological numerical simulations is the Millennium Simulation (Springel et al. 2005). When combined with semi-analytic models of galaxy formation, this simulation constitutes a very useful tool for mimicking the observational constraints of a given catalogue under study. The several snapshots available for this numerical simulation at different times can allow the construction of very detailed light-cone mock catalogues that include the corresponding effects of galaxy evolution up to redshift values similar to those expected to be achieved with the future J-PAS (z ~ 1).
The aim of this work is performing a detailed analysis of the capability of a modified FoF algorithm to identify galaxy systems in a deep photometric-redshift survey such as the future J-PAS. The adopted modified FoF algorithm is the one developed by Liu et al. (2008), known as probability FoF. This method uses a probability distribution function to model the photometric-redshift uncertainties, obtaining a very realistic way of dealing with the radial linking length without introducing artificial slices in the survey. Our work involves testing each observational restriction to separate possible problems introduced in the identification process. This task is performed on a J-PAS light-cone mock galaxy catalogue constructed using the semi-analytical galaxies extracted from the Millennium Simulation (Guo et al. 2011). Our study intends to determine the purity and completeness of a resulting galaxy group sample obtained from a group identification algorithm that only uses 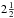 (angular coordinates+redshifts) positional galaxy information and the usefulness of this sample to become an input catalogue for further refinements adding other observational properties.
(angular coordinates+redshifts) positional galaxy information and the usefulness of this sample to become an input catalogue for further refinements adding other observational properties.
The layout of this paper is as follows: in Sect. 2, we describe the N-body simulation and the semi-analytic model of galaxy formation used to build the mock catalogue. In Sect. 3 we describe the implementation of the FoF algorithm and the modifications needed to identify groups in deep redshift surveys as well as photometric ones. We also include in this section the percentage of purity and completeness of the resulting finder algorithm as a function of redshift. Finally, in Sect. 4 we summarise our results and discuss the statistical implications of using this type of algorithm in deep photometric surveys.
2. Mock catalogue
We built a light-cone mock catalogue using a simulated set of galaxies extracted from the Guo et al. (2011) semi-analytical model of galaxy formation applied on top of the Millennium Run Simulation I.
2.1. N-body simulation
The Millennium Simulation is a cosmological tree-particle-mesh (Xu 1995) N-body simulation (Springel et al. 2005), that evolves 10 billion (21603) dark matter particles in a 500 h-1 Mpc periodic box, using a comoving softening length of 5 h-1 kpc. The cosmological parameters of this simulation are consistent with WMAP1 data (Spergel et al. 2003), that is, a flat cosmological model with a non-vanishing cosmological constant (ΛCDM): Ωm = 0.25, Ωb = 0.045, ΩΛ = 0.75, σ8 = 0.9, n = 1, and h = 0.73. The simulation was started at z = 127, with the particles initially positioned in a glass-like distribution according to the ΛCDM primordial density fluctuation power spectrum. The 1010 particles of mass 8.6 × 108 h-1 M⊙ were then advanced with the TPM code, using 11 000 internal time-steps, on a 512-processor supercomputer. The full particle data (positions and velocities) between z = 20 and z = 0 were stored at 60 output times spaced in expansion factor according to log (1 + zi) = i(i + 35)/4200. Additional outputs were added at z = 30, 50, 80, 127 to produce a total of 64 snapshots in all.
2.2. Semi-analytical model
To obtain a simulated galaxy set we adopted the Guo et al. (2011) semi-analytical model, in which several open problems present in some of its predecessors have been solved. For instance, the authors increased the efficiency of supernova feedback by introducing a direct dependence of the amount of gas reheated and ejected on the virial mass of the host halo. Although the resulting model fits the stellar mass function of galaxies well at low redshifts, it still overproduces low-mass galaxies at z > 1. Guo et al. (2011) also introduced a more realistic treatment of satellite galaxy evolution and of mergers, allowing satellites to continue forming stars for a longer period of time and reducing the excessive rapid reddening of the satellites. The model also includes a treatment of the tidal disruption of satellite galaxies.
This model produces a complete sample when considering galaxies with rest frame absolute magnitude in the SDSS i-band brighter than −16.4, which implies galaxies with stellar masses larger than ~108 h-1 M⊙.
Since different cosmological parameters have been found from WMAP7 (Komatsu et al. 2011), one may argue that the studies carried out in the present simulation may produce results that disagree with the current cosmological model. However, Guo et al. (2013) have demonstrated that the abundance and clustering of dark haloes and galaxy properties, including clustering, in WMAP7 are very similar to those found in WMAP1 for z ≤ 3, which is the redshift range of interest in this work (see Sect. 2.3).
2.3. Mock catalogue construction
 |
Fig. 1 Illustration of the process of galaxies when they are included twice or not at all in the mock catalogue for two consecutive snapshots. Upper panels: the case when a galaxy is counted twice when constructing a light-cone using different snapshots. The grey region shows the snapshot under consideration. The right panel shows the galaxy j at a previous time, inside the i + 1th shell, showing the direction of movement of the galaxy. Due to this direction of movement and the width of the shell, the galaxy j will appear also inside the ith shell at an earlier time (left panel), and consequently, it is included twice. Lower panels: the case when a galaxy is missing when constructing a light-cone. The right panel shows the galaxy j in a previous time, outside the i + 1th shell, and showing its direction of movement. Due to this situation, galaxy j will also appear outside the ith shell at an earlier time (left panel), resulting in a missing galaxy in both shells. |
 |
Fig. 2 Upper panel: a pie plot projection showing, in a thin slice, the distribution of the mock galaxies as a function of redshift. Lower panel: redshift distribution of galaxies with iSDSS ≤ 23 in the selected light-cone with an angular coverage of 17.6 deg2. The maximum redshift of the sample is ~1.5. |
We present mock observations of the artificial Universe constructed from the Millennium Simulation, by positioning a virtual observer at zero redshift and finding the galaxies that lie on the observer’s backward light-cone. To do this, we built a mock sample of galaxies within an octant (solid angle = π/2 sr), consisting of shells taken from different snapshots corresponding to the epoch of the lookback time at their corresponding distance. This method is commonly used to construct mock galaxy catalogues and it takes into account gravitational evolution as well as the evolution of the astrophysical properties (Díaz-Giménez 2002; Blaizot et al. 2005; Kitzbichler & White 2007; Henriques et al. 2012; Wang & White 2012). We used the last 27 snapshots, which reach a maximum redshift of z = 1.5. Given that the simulation box is only 500 h-1 Mpc on a side, it is necessary to use the periodicity of the simulation box and build a super-box to reach a greater distance, which is by construction several simulations put together side by side. The cosmological redshift (or redshift in real space) is obtained from the comoving distance of the galaxies in the super-box by using 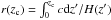 , where r is the comoving distance and
, where r is the comoving distance and 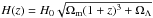 .
.
To mimic the observations, we introduce the distorted or spectroscopic redshift, zs, by considering the peculiar velocities of the galaxies in the radial direction, therefore: 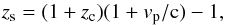 (1)where zc is the cosmological redshift and vp = v·r/ | r | is the peculiar velocity, with r the comoving coordinate within the super-box (see Peacock 1999; Mo et al. 2010).
(1)where zc is the cosmological redshift and vp = v·r/ | r | is the peculiar velocity, with r the comoving coordinate within the super-box (see Peacock 1999; Mo et al. 2010).
Given that the method used to construct the light-cone uses shells at different snapshots, it introduces differences when compared with the observed Universe:
-
1.
The first problem arises because all galaxies at a given shellhave the same evolutionary stage corresponding to the outputsimulation time. Therefore, the mock galaxies show a discretemagnitude evolution that is found to be more abrupt at higher red-shifts (since the snapshots are spaced logarithmically with time).However, observationally, the properties of the galaxies varycontinuously with redshift. This problem introduces a bias in thegalaxy density distribution of the resulting mock catalogue. Theclustering of galaxies also changes from snapshot to snapshotbecause of their proper movements: the larger the time-spacingbetween subsequent snapshots, the stronger the variation in the structures.
-
2.
The second problem arises because at the edges of the imaginary shells, galaxies come from two different evolutionary stages. Just considering the movement in the simulation box, if the spacing among outputs is too large, the positions of the galaxies could have changed dramatically from one output to the next, which means that a galaxy is observed either twice or not at all, depending on the direction of its motion (see Fig. 1).
To remedy these problems we introduced the following corrections during the mock construction procedure:
-
1.
Positions and velocities were interpolated between the outputsin the i and (i + 1) shells, according to their distance to the shell edges. We recomputed the rest-frame absolute magnitudes Mi of the galaxies within a given shell at cosmic time, ti, by interpolating linearly between the values corresponding to the current shell and the previous snapshot at ti + 1 (early time), but using the previously interpolated galaxy position inside the ith shell. It has been argued in previous works that using interpolated positions and velocities might produce dynamically incorrect velocities and might diffuse structures (Kitzbichler & White 2007). In Appendix A we show that using a mock catalogue with interpolated galaxy positions and velocities does not introduce a particular bias in the results that we have obtained in this work.
-
2.
We considered two possible cases. First, the repeated galaxies case, where galaxies near the low-redshift side of the (i + 1)th shell are moving towards lower redshifts (top right panel of Fig. 1) also appear in the ith shell (top left panel of Fig. 1). Second, the missing galaxies case, where galaxies close to the low-redshift side of the (i + 1)th shell, below the boundary, are moving towards higher redshifts (bottom right panel of Fig. 1), and do not appear in the ith shell either (bottom left panel of the Fig. 1). In the first case we just discarded the galaxy positioned at the ith shell, since it will appear at the consecutive shell. In the second case, we reassigned the position of the galaxy in the ith shell with the interpolated position of the galaxy in the (i + 1)th shell.
As previously stated, to reach the desired depth of the catalogue we filled the space with a required number of replications of the fundamental volume, leading us to obvious artefacts if the simulation is viewed along one of its preferred axes. Although we cannot avoid this behaviour in the octant light-cone, we could minimise this kaleidoscopic effect in a smaller light-cone by orienting the survey field appropriately following the procedure described by Kitzbichler & White (2007). According to that work, if we select an observational field defined by the lines of sight to the four points with Cartesian coordinates given by ((n ± 0.5/m)Lbox,(m ± 0.5/n)Lbox,nmLbox) where Lbox is the side of the cube, and n and m are arbitrary numbers, we obtain a nearly rectangular light-cone survey of angular size 1/m2n × 1/n2m sr with the first duplicate point at comoving distance s(zclean) ~ mnLbox. In this way, we selected the parameters to obtain a light-cone with a solid angle of 17.6 deg2 and without repetitions out to z ~ 1.02.
The volume-limited sample with absolute magnitudes brighter than − 16.4 contained in the selected light-cone comprises 6 756 097 galaxies up to z = 1.5. Finally, we computed the observer-frame galaxy apparent magnitudes from the publicly available rest-frame absolute magnitudes provided by the semi-analytic model: m = M + 25 + 5log (s(1 + zs)) − kcorr(zs), where s is the comoving distance computed from the spectroscopic redshift. The k-corrections were obtained as a byproduct of the method that computes the photometric redshifts (see Sect. 2.4). We set an observer-frame apparent magnitude limit of ilim = 23.
The final spectroscopic mock catalogue (sp-mock) comprises 793 559 galaxies with a median redshift of 0.72 within a solid angle of 17.6 deg2. In Fig. 2 we show an illustration of the galaxy distribution as a function of redshift (upper panel) and the redshift distribution of galaxies with iSDSS ≤ 23 in the selected light-cone (lower panel).
2.4. Photometric-redshift assignment
We assigned photometric redshifts to the mock catalogue previously built. To do this, we first obtained spectral types from the original rest-frame photometry and spectroscopic redshifts by running the Bayesian photometric-redshift package (BPZ, Benítez 2000) with the ONLY_TYPE yes option. Then, we transformed the given photometry in the mock catalogue to the photometry of the J-PAS. This transformation uses the filter curve response and the spectral types obtained. Finally, we ran BPZ again on this new photometry, obtaining the photometric redshift associated with the new photometry. As a byproduct of this method, we computed the observer-frame apparent magnitudes of the mock galaxies (and therefore, their corresponding k-corrections). All the details can be found in Ascaso et al. (in prep.).
3. Friends-of-friends algorithm and the tuning of the linking length parameters
The FoF algorithm was initially developed to identify galaxy systems in redshift space considering a flux-limited catalogue (Huchra & Geller 1982). Since then, several adaptations of this percolation algorithm have been used (Merchán & Zandivarez 2002; Eke et al. 2004; Knobel et al. 2009) or modified to identify haloes in 3D from simulations (Davis et al. 1985) − for a compilation of algorithms see Knebe et al. (2011)) − or identifying groups through photometric redshifts (Botzler et al. 2004; Li & Yee 2008; Liu et al. 2008).
The FoF algorithm links galaxies that share common neighbours (friends). It starts looking for the friends of an initial galaxy that have separations lower than a given threshold. Groups are defined as sets of galaxies that are connected by one or more friendship relation, that is, FoF. For each galaxy not assigned to a group, the algorithm searches around it for companions with projected separation from the first galaxy:
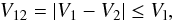 where Θ is the angular separation among a pair of galaxies, V1 and V2 refer to their radial velocities (or redshifts), and R12 = (R1 + R2)/2 is the mean of their comoving distances. All friends of a galaxy are added to the list of group members. The surroundings of each friend are then examined. This process is repeated until no more neighbours are found.
where Θ is the angular separation among a pair of galaxies, V1 and V2 refer to their radial velocities (or redshifts), and R12 = (R1 + R2)/2 is the mean of their comoving distances. All friends of a galaxy are added to the list of group members. The surroundings of each friend are then examined. This process is repeated until no more neighbours are found.
When working with observational samples, there are two main characteristics inherent to the observations that make the group-finding difficult. One of them is the flux limit of the catalogue, and the other is the redshift space distortion. To adopt the best linking length parameters, Dl and Vl, the two problems must be treated separately.
3.1. Reference sample: volume-limited sample in real space
We defined a sample of galaxies without these two problems, that is, we created a volume-limited sample of galaxies in real space. This sample is complete down to absolute magnitude MiSDSS = −16.4. Avoiding the observational constraints, the identification of groups in this sample can be performed straightforwardly. The linking length parameters are defined as follows:
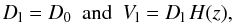 where H(z) is the Hubble constant as a function of redshift and D0 takes into account the overdensity of virialised structures in the Universe at a given time:
where H(z) is the Hubble constant as a function of redshift and D0 takes into account the overdensity of virialised structures in the Universe at a given time: ![\begin{equation} \label{d0} D_0(z)= \left[ \frac{4\pi}{3} \left( \frac{\delta \rho}{\rho} (z) + 1 \right) \int^{M_{\rm lim}}_{-\infty} \phi(z,M) {\rm d}M \right] ^{-1/3} , \end{equation}](/articles/aa/full_html/2014/01/aa22793-13/aa22793-13-eq77.png) (2)where φ(z,M) is the luminosity function (LF), and
(2)where φ(z,M) is the luminosity function (LF), and 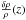 is the contour overdensity contrast. Similar to other authors in previous works (see for instance, Snaith et al. 2011), to model the
is the contour overdensity contrast. Similar to other authors in previous works (see for instance, Snaith et al. 2011), to model the 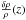 , we assumed that galaxies are unbiased mass tracers. Analysing the mass function of haloes identified with FoF algorithms, Courtin et al. (2011) found deviations from universality in the mass function due to the use of halo parameters not adjusted for different virialisation overdensities in different cosmologies and redshifts. More et al. (2011) showed that the boundary of FoF haloes does not correspond to a single local overdensity, but rather to a range of overdensities, and that the enclosed overdensities of the FoF haloes are significantly larger than commonly thought. Courtin et al. (2011) showed that deviations from universality are not random, but are correlated with the nonlinear virialisation overdensity, Δvir, expected from the spherical collapse model for a given cosmology and redshift. In particular, they showed that the linking length required to minimise deviations of the FoF mass function from universal form for a given cosmology and redshift is correlated with the corresponding Δvir as
, we assumed that galaxies are unbiased mass tracers. Analysing the mass function of haloes identified with FoF algorithms, Courtin et al. (2011) found deviations from universality in the mass function due to the use of halo parameters not adjusted for different virialisation overdensities in different cosmologies and redshifts. More et al. (2011) showed that the boundary of FoF haloes does not correspond to a single local overdensity, but rather to a range of overdensities, and that the enclosed overdensities of the FoF haloes are significantly larger than commonly thought. Courtin et al. (2011) showed that deviations from universality are not random, but are correlated with the nonlinear virialisation overdensity, Δvir, expected from the spherical collapse model for a given cosmology and redshift. In particular, they showed that the linking length required to minimise deviations of the FoF mass function from universal form for a given cosmology and redshift is correlated with the corresponding Δvir as
 |
Fig. 3 Best-fit parameters of a double Schechter luminosity function in the iSDSS band as a function of redshift. These parameters are obtained by fitting the luminosity distributions of the semi-analytic galaxies (Guo et al. 2011) down to an absolute magnitude of − 16.4 at different snapshots of the Millennium Simulation. |
 |
Fig. 4 Variation of the linking length parameters as a function of redshift. The left panel shows the transversely linking length for volume-limited samples, D0, the middle panel shows the scale factor Rs, while the right panel shows the transverse linking length for flux-limited samples, Dl (see equations in Sect. 3.2). The solid blue lines show the parameters using a LF that varies with redshift (see Fig. 3) while dashed red lines show the parameters when a fixed LF at redshift close to zero is adopted. |
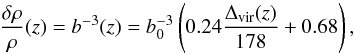 (3)where b0 is the linking length parameter commonly used for identifying dark matter haloes and is set to a value of 0.2. From Weinberg & Kamionkowski (2003), the enclosed overdensity of virialised haloes is
(3)where b0 is the linking length parameter commonly used for identifying dark matter haloes and is set to a value of 0.2. From Weinberg & Kamionkowski (2003), the enclosed overdensity of virialised haloes is
![$$ \Delta_{\rm vir} (z) = 18 \pi^2 \left[ 1 + 0.399\left( \frac{1} {\Omega_{\rm m}(z)} - 1 \right)^{0.941}\right] $$](/articles/aa/full_html/2014/01/aa22793-13/aa22793-13-eq86.png) with
with 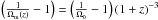 . For a Universe with cosmological parameters (0.3, 0.7), the last equation leads to the known value of an enclosed overdensity of virialised haloes at z = 0 of ~330. We recall that for the Millennium Simulation the cosmological parameters are (0.25, 0.75), which implies that the virialised overdensity at z = 0 is ~376.
. For a Universe with cosmological parameters (0.3, 0.7), the last equation leads to the known value of an enclosed overdensity of virialised haloes at z = 0 of ~330. We recall that for the Millennium Simulation the cosmological parameters are (0.25, 0.75), which implies that the virialised overdensity at z = 0 is ~376.
Even though we adopted a redshift-dependent contour overdensity contrast for our algorithm, it is worth noting that for the cosmology of the Millennium Simulation, the empirical relation produces a variation of b(z) of only ~8% in the whole redshift range under study. On the other hand, in Appendix B we introduce a variation in Eq. (3) to investigate the effect in our results of using a higher contour overdensity contrast, as expected from the analyses of galaxy group density profiles.
Before applying the identifier, it is necessary to compute the luminosity function of the galaxies in the catalogue. To this end, we made use of the information from the semi-analytic model, and computed the LF for every snapshot of the simulation. Then, we fitted double-Schechter functions to the distributions of rest-frame iSDSS absolute magnitudes:
![$$ \phi(L)=\frac{1}{L^*} \exp \left(-\frac{L}{L^*}\right) \, \left[ \phi_1 \left(\frac{ L}{ L^*} \right)^{\alpha_1} + \phi_2 \left(\frac{ L}{ L^*} \right)^{\alpha_2} \right]\cdot $$](/articles/aa/full_html/2014/01/aa22793-13/aa22793-13-eq90.png) The best-fit parameters are shown in Fig. 3 as a function of the redshift.
The best-fit parameters are shown in Fig. 3 as a function of the redshift.
The variation of D0 used in this section as a function of redshift can be seen as the solid line in the left panel of Fig. 4.
This algorithm produces a sample of 201 032 groups with four or more galaxy members within a solid angle of 17.6 deg2 up to redshift 1.5 (see Table 1). These groups constitute the reference sample that was used for testing the algorithm against as we introduce the observational constraints in the mock catalogue.
We also selected from the reference groups those that have four or more members with observer-frame magnitude iSDSS brighter than 23, that is, those groups that could be identified in the flux-limited catalogue. We refer to this subsample of reference groups as restricted-reference group sample, which comprises 14 347 groups (see Table 1).
Groups identified in different mock galaxy samples.
3.2. Flux-limited sample in real space
We first tested the algorithm against a flux-limited sample. Now, both linking lengths have to take into account the flux limit of the catalogue, therefore in addition to being related to the overdensity contrast they have to include the variation of the sampling of the luminosity function produced by the different distances of the groups to the observers, which is introduced, following Huchra & Geller (1982), by the scale factor2Rs: 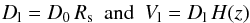 with
with ![\begin{equation} \label{rs} R_{\rm s} (z) = \left[ \frac{\int^{M_{12}}_{-\infty} \phi(z,M){\rm d}M}{\int^{M_{\rm lim}}_{-\infty} \phi(z,M){\rm d}M} \right]^{-1/3} , \end{equation}](/articles/aa/full_html/2014/01/aa22793-13/aa22793-13-eq106.png) (4)where Mlim = −16.4, and M12 = ilim − 25 − 5log (dL12), with dL12 the mean luminosity distance for the galaxy pair.
(4)where Mlim = −16.4, and M12 = ilim − 25 − 5log (dL12), with dL12 the mean luminosity distance for the galaxy pair.
Typically, for low-redshift samples, the luminosity function of galaxies included in the Rs factor is computed for the whole sample, and it is assumed that there is no evolution in the luminosities up to the maximum depth of the catalogue. Since we intend to reach higher-redshift groups, we introduced the evolution of the luminosities of the catalogued galaxies. To do this, we computed the luminosity function of the galaxies in bins of redshifts, as we did in the previous section, to account for the variation of the density of galaxies as well as their internal luminosity evolution. However, in this section we also select a sample of groups without using the luminosity evolution of galaxies, that is, by using a fixed luminosity function determined at redshift zero to assess the importance that it could have in the resulting sample. In Fig. 4, the variation of D0, Rs and the linking length Dl are shown as a function of redshift. Solid lines correspond to the values obtained from a LF that varies with redshift, while dashed lines correspond to a fixed luminosity function.
We used an observer-frame apparent magnitude 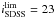 to limit our mock galaxies. The number of groups with four or more members identified with a fixed LF is 20 055, while it is 17 297 when varying the LF with redshift (see Table 1).
to limit our mock galaxies. The number of groups with four or more members identified with a fixed LF is 20 055, while it is 17 297 when varying the LF with redshift (see Table 1).
To compare the sample of groups identified in this flux-limited catalogue with the reference sample, we used the restricted-reference sample to analyse the purity and completeness of the flux-limited groups.
We defined purity and completeness based on a member-to-member comparison. As purity, we considered the fraction of members in the flux-limited groups that belongs to any restricted-reference group, that is, we quantified how good the identified groups are. As completeness we considered the fraction of members in the restricted-reference groups that are part of the flux-limited groups, this quantity intends to indicate the fraction of the true groups that we are able to identify.
Regarding the purity of the flux-limited sample, in the upper panels of Fig. 5 we show the fraction of galaxies belonging to a flux-limited group that are associated to one restricted-reference group that possesses the highest matching rate (solid lines) and the fraction of flux-limited group galaxy members that are not associated to any restricted-reference group (interlopers, dashed lines) each as a function of their real-space redshifts. The left boxes correspond to the flux-limited sample identified with a fixed LF, while the right boxes correspond to the sample identified with a variable LF. From these plots, it is clear that the effect of assuming no evolution in the luminosities leads to a more contaminated sample towards higher redshifts. It can be seen that when one consideres the evolution in the luminosity function, the purity of our flux-limited groups is high, or in other words, the fraction of interlopers is really low (lower than 20%).
 |
Fig. 5 Purity and completeness as a function of redshift for groups identified in a flux-limited sample in real space. Left boxes show the purity (upper panels) and completeness (lower panels) when a fixed LF is used in the linking length parameters, while right boxes show the trends when a LF varying with redshift is used to compute the linking length parameters. In the upper boxes (purity), the top panels show the fraction of identified galaxies (Glxs) associated with the group with the highest matching rate in the corresponding control sample (solid lines), and the fraction of galaxies that are classified as interlopers (dashed lines). In the lower boxes (completeness), the top panels show the fraction of galaxies in the control sample that are associated with the group with the highest matching rate in the identified sample (solid lines), and the fraction of galaxies that are classified as missing galaxies (dashed lines). The bottom panels in each plot show the trends observed for the fraction of groups (Grps) within the six categories of purity or completeness (see text for description). The short-dashed magenta lines correspond to the complement of P6 and C6. |
Total percentages of purity and completeness of groups (with z = 0 − 1.2) identified in different mock galaxy samples.
However, quantifying the fraction of member galaxies in a flux-limited group that belong to some restricted-reference group is not enough to understand the real nature of the identified groups. For instance, one single flux-limited group could be formed by members that originally belonged to more than one restricted-reference group. To separate the different galaxy contributions to a given galaxy group, six group categories were defined when we compared two samples of groups:  and ℬ.
and ℬ.
-
1.
P1 (perfect match): groups in sample
 with 100% of their members associated with only one group in control sample ℬ (solid red lines).
with 100% of their members associated with only one group in control sample ℬ (solid red lines). -
2.
P2 (quasi-perfect match): groups in sample
 with between 70% and 100% of their members associated with only one group in control sample ℬ, and the remaining galaxies are interlopers (0% < interlopers < 30%) (long-dashed blue lines).
with between 70% and 100% of their members associated with only one group in control sample ℬ, and the remaining galaxies are interlopers (0% < interlopers < 30%) (long-dashed blue lines). -
3.
P3 (merging): groups in sample
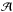 with between 70% and 100% (inclusive) of their members associated with more than one group in control sample ℬ. This category may accept interlopers (0% ≤ interlopers < 30%) (dot-and-short-dashed green lines).
with between 70% and 100% (inclusive) of their members associated with more than one group in control sample ℬ. This category may accept interlopers (0% ≤ interlopers < 30%) (dot-and-short-dashed green lines). -
4.
P4 (group+interlopers): groups in sample
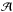 with fewer than 70% of their members belonging to only one group in control sample ℬ. The remaining members are interlopers (interlopers >30%) (dot-and-long-dashed cyan lines).
with fewer than 70% of their members belonging to only one group in control sample ℬ. The remaining members are interlopers (interlopers >30%) (dot-and-long-dashed cyan lines). -
5.
P5 (merging+interlopers): groups in sample
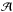 with fewer than 70% of their members belonging to more than one group in control sample ℬ, the remaining galaxies are interlopers (short-and-long-dashed brown lines).
with fewer than 70% of their members belonging to more than one group in control sample ℬ, the remaining galaxies are interlopers (short-and-long-dashed brown lines). -
6.
P6 (false): groups in sample
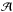 with 100% of their members not belonging to any group in control sample ℬ (100% interlopers) (dotted black lines).
with 100% of their members not belonging to any group in control sample ℬ (100% interlopers) (dotted black lines).
In this case, to examine the purity of the flux-limited groups, they were split into the six categories defined above taking the sample 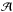 as the flux-limited sample, while control sample ℬ is the restricted-reference sample.
as the flux-limited sample, while control sample ℬ is the restricted-reference sample.
The fractions of flux-limited groups within each category of purity per redshift bin are shown in the bottom panels of the upper boxes of Fig. 5. The perfect match between flux-limited and restricted-reference groups are those in the P1, in which all the group members of the flux-limited sample belong to a unique restricted-reference group (still, the restricted-reference group might have more extra members). As expected, the higher the redshifts, the lower the fraction of perfectly matched groups. Even though this behaviour is common for both identifications, the P1 sample when using a variable LF has a higher percentage of groups along the whole redshift range than the corresponding values for the fixed LF. The P2 sample includes quasi-perfectly matched groups. The fraction of these groups is similar in both identifications.
The green dotted short dashed lines (P3) involve flux-limited groups that are the result of merging true groups plus few interlopers. For both identifications, this category is almost nonexistent.
P4 and P5 contain parts of real groups, but the interlopers are also an important fraction of the galaxies in these groups. In both identifications they add up to less than ~10% in the whole redshift range.
The least desired category is P6; these are completely false groups. It can be seen that identifying with a fixed LF produces a higher percentage of false groups at higher redshifts. The magenta short dashed lines are the complement of the P6 class, which means that they represent all other groups except the least desirable class, P6, or in other words, groups that contain at least part of the true groups.
In Table 2 we quote the percentage of groups in each of these classes for the whole samples. Clearly, the sample of flux-limited groups obtained from a variable LF contains a higher percentage (+ 15%) of P1 groups, lower percentage (− 11%) of P6, and very similar percentages of the remaining classes than those obtained when identifying groups with a fixed LF.
Regarding the completeness of the sample, the lower plots of Fig. 5 show the results as a function of redshift for both samples, fixed LF (left panels) and variable LF (right panels). To define completeness, we quantified the number of identified restricted-reference groups in the flux-limited sample. From the upper panels of the completeness plots, it can be seen that more than 95% of the members of the reference-sample are included in a given group of the flux-limited samples.
Following a similar procedure as used for the purity analysis, we split groups into six completeness categories:
-
1.
C1 (perfect match): groups in control sample
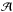 with 100% of their members identified within only one group in sample ℬ (solid red lines).
with 100% of their members identified within only one group in sample ℬ (solid red lines). -
2.
C2 (quasi-perfect match): groups in control sample
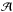 with between 70% and 100% of their members identified within only one group in sample ℬ, and the remaining galaxies are missing in the new identification (0% < missing < 30%, long-dashed blue lines).
with between 70% and 100% of their members identified within only one group in sample ℬ, and the remaining galaxies are missing in the new identification (0% < missing < 30%, long-dashed blue lines). -
3.
C3 (split): groups in control sample
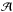 with between 70% and 100% (inclusive) of their members identified within more than one group in sample ℬ. This category may accept missing galaxies (0% ≤ missing < 30%, dot-and-short-dashed green lines).
with between 70% and 100% (inclusive) of their members identified within more than one group in sample ℬ. This category may accept missing galaxies (0% ≤ missing < 30%, dot-and-short-dashed green lines). -
4.
C4 (group+missing galaxies): groups in control sample
 with fewer than 70% of their members identified within only one group in sample ℬ. The remaining members are not identified in any group in the new identification (missing >30%, dot-and-long-dashed cyan lines).
with fewer than 70% of their members identified within only one group in sample ℬ. The remaining members are not identified in any group in the new identification (missing >30%, dot-and-long-dashed cyan lines). -
5.
C5 (split+missing galaxies): groups in control sample
 with fewer than 70% of their members identified within more than one group in sample ℬ, the remaining galaxies are lost (short-and-long-dashed brown lines).
with fewer than 70% of their members identified within more than one group in sample ℬ, the remaining galaxies are lost (short-and-long-dashed brown lines). -
6.
C6 (missing group): groups in control sample
 with 100% of their members not identified in any group in sample ℬ (100% missing galaxies, dotted black lines).
with 100% of their members not identified in any group in sample ℬ (100% missing galaxies, dotted black lines).
In this case, control sample  is the restricted-reference sample, while sample ℬ is the flux-limited group sample. The completeness as a function of redshifts based on the different categories is shown in the lower plots of the bottom boxes of Fig. 5. We found that both algorithms are able to identify most of the members of the restricted-reference sample, that is, the C1 and C2 categories are dominant at all redshifts. We observed that the variable LF identification shows a more pronounced decay of the fractions of C1 groups to higher redshift than those observed for the fixed LF case, but, this behaviour is almost fully compensated by an increasing fraction of C2 groups. The fraction of groups in the other categories is almost negligible, with a slight increase of C6 groups towards higher redshifts in the variable LF identification, which is lower than 20% at the highest redshifts.
is the restricted-reference sample, while sample ℬ is the flux-limited group sample. The completeness as a function of redshifts based on the different categories is shown in the lower plots of the bottom boxes of Fig. 5. We found that both algorithms are able to identify most of the members of the restricted-reference sample, that is, the C1 and C2 categories are dominant at all redshifts. We observed that the variable LF identification shows a more pronounced decay of the fractions of C1 groups to higher redshift than those observed for the fixed LF case, but, this behaviour is almost fully compensated by an increasing fraction of C2 groups. The fraction of groups in the other categories is almost negligible, with a slight increase of C6 groups towards higher redshifts in the variable LF identification, which is lower than 20% at the highest redshifts.
In Table 2 we quote the total percentages of the restricted-reference groups that belong to each of the completeness categories. The C1 class is lower by 7% and the C2 is higher by 4% in the variable LF identification than in the fixed LF identification, while the C6 class are quite similar in both. One might be tempted to think that the identification with fixed LF produced a better result since the fraction of C1 groups in this identification is slightly higher and the fraction of C6 slightly lower than when using a variable LF. However, it is not worth recovering most of the true group members if the identified groups will be contaminated by a larger number of interlopers that could change the intrinsic properties of the groups or including many false groups. Therefore, it is important to analyse the combination of purity and completeness. Categories 1 and 2 represent the highly pure and complete samples. Analysing Table 2, the percentages of highly complete groups of both identifications are quite similar (94% vs. 97%), while the percentage of highly pure groups when identified with LF variable is higher by 13%. Moreover, the fixed LF produces 30% of false groups compared with 19% for the variable LF. Therefore, using a variable LF to identify groups is the most appropriate procedure to recover as best as possible most of the restricted-reference group sample.
3.3. Redshift distortions: volume-limited sample in spectroscopic-redshift space
The other observational constraint that needs to be addressed to choose the best linking length parameters is the redshift space distortion. It is necessary to modify the radial linking length Vl when working in redshift space, since the structures seem elongated along the line of sight because of the infall of galaxies in virialised galaxy groups. These elongated structures are commonly called fingers of god. Therefore, we built a volume-limited sample complete down to iSDSS absolute magnitude − 16.4, just like the reference sample, but in this case the positions of galaxies are distorted according to Eq. (1). The linking length parameters are
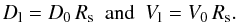 The value of D0 is defined above for the reference sample, the value Rs is taken equal to 1, since there is no flux limit, while here we investigate different options for the value of V0. Typically, V0 is defined as a constant for low-redshift samples that is tuned to produce the more reliable sample of groups in terms of purity and/or completeness.
The value of D0 is defined above for the reference sample, the value Rs is taken equal to 1, since there is no flux limit, while here we investigate different options for the value of V0. Typically, V0 is defined as a constant for low-redshift samples that is tuned to produce the more reliable sample of groups in terms of purity and/or completeness.
To determine the best value of V0 in this work, we analysed the sample of reference groups and computed the velocity differences in redshift space along the line of sight among the group members. Our goal is to find the most appropriate value that satisfies the requirement of being the lowest velocity value needed to link most of the galaxy members of a given group in redshift space. Therefore, for each group we searched for the maximum velocity difference of the members in the line of sight to their closest neighbours. These highest values are shown in the left upper panel of Fig. 6. Dots represent the median values per bin of redshifts while the error bars are their semi-interquartile ranges. The maximum velocity difference to the closest neighbour is increasing towards higher redshifts. In the left lower panel, we divided the y-axis by (1 + z). The medians of these points determine a roughly constant value of 130 km s-1 (solid line). Hence, we tested the identification algorithm against using a constant value of 130 km s-1 and a value that varies with redshift as 130(1 + z) km s-1. Moreover, to test the influence of the choice of V0, we also examined a second value. Instead of looking for the maximum of the velocity differences to the closest neighbours, we also investigated the second maximum of these differences. The results are shown in the right panels of Fig. 6. In this case, the values of V0 to be analysed are 70 km s-1 and 70(1 + z) km s-1. This second approach, with a lower value for V0, was made to test whether a lower value could improve the resulting group sample in both purity and completeness.
 |
Fig. 6 Left upper panel: scatter plot of the maximum velocity difference of the members in the line of sight to their closest neighbours. Right upper panel: the same as the right panel, but using the second maximum. In the lower panels we divided the upper panels by (1 + z). |
Therefore, we performed four different identifications. We found 183 717 groups with more than four members when using V0 = 130 km s-1, and when V0 = 130(1 + z) km s-1, we found 250 532. With the shorter linking length, we identified 106 920 and 197 290 groups, with V0 = 70 km s-1 and V0 = 70(1 + z) km s-1, respectively (see Table 1).
As in the previous subsection, we analysed and compared the purity and completeness of these samples to choose the best radial linking length parameter. The purity was defined considering the members of the new redshift-space identified groups (four samples  ) in comparison with the reference sample (control sample ℬ); while completeness was defined taking the members in the reference sample (control sample
) in comparison with the reference sample (control sample ℬ); while completeness was defined taking the members in the reference sample (control sample  ) and searching for their counterparts in the redshift-space groups (four samples ℬ). The results as a function of redshift are shown in Figs. 7 and 8.
) and searching for their counterparts in the redshift-space groups (four samples ℬ). The results as a function of redshift are shown in Figs. 7 and 8.
The effect of using either a constant or variable value of V0 can be seen by comparing the left with the right boxes of these figures. First, analysing the purity in Fig. 7, it can be seen that the purity of the groups is little affected, that is, modulating the linking length by (1 + z) or keeping it constant produces similar results as a function of redshift. We observe that roughly ~80% of galaxies are associated with the group in the reference sample with the highest matching rate, while ~20% of galaxies are interlopers. From the six-category analysis, we found ~40% and ~20% of P1 and P2 groups for the two identifications. When using a constant V0, ~20% of the groups are misidentified (P6) for any redshift, while this percentage is slightly higher when using a variable V0.
 |
Fig. 7 Same as Fig. 5, but for the samples of groups identified in a volume-limited sample in redshift space using V0 = 130 km s-1 (left boxes) or V0 = 130 (1 + z) km s-1 (right boxes). |
 |
Fig. 8 Same as Fig.5, but for the samples of groups identified in volume-limited sample in redshift space using V0 = 70 km s-1 (left boxes) or V0 = 70 (1 + z) km s-1 (right boxes). |
 |
Fig. 9 Purity and completeness as a function of redshift for groups identified in a flux-limited sample in redshift space. The left box shows the purity while the right box shows the completeness when an LF varying with redshift and V0 = 130(1 + z) km s-1 is used to compute the linking length parameters. In the left box (purity), the top panels show the fraction of galaxies identified that can be associated with galaxies of the group with the highest matching rate in the corresponding control sample (solid lines), and the fraction of galaxies that are classified as interlopers (dashed lines). In the right box (completeness), the top panels show the fraction of galaxies in the control sample that can be associated with galaxies identified in the spectroscopic group with the highest matching rate (solid lines), and the fraction of galaxies from the control sample that are classified as missing (dashed lines). The bottom panels show the trends observed for the fraction of groups within the six categories of purity or completeness (see text for description). The short-dashed magenta lines correspond to the complement of P6 and C6. |
Now, when including the completeness analysis for both identifications, remarkable differences arise. For the constant V0 = 130 km s-1, the fraction of galaxies in the reference sample associated with the group in the redshift-space sample with the highest matching rate drastically dropping as a function of redshift, declining to as low as 40% at higher redshifts (top panels of left bottom box of Fig. 7). Also at high redshifts, the C6 groups (completely missing) reach 40% and the contribution of C4 is ~20% in the whole redshift range. On the other hand, when analysing the completeness of the sample identified with variable V0, we observe that more than ~80% of galaxies in the reference sample are recovered at all redshifts, with only 15% galaxies missing (top panels of right bottom box). Moreover, the completeness is highly improved, obtaining ~50% of C1 groups and more than ~20% of the C2 groups, and fewer than 20% of the missing groups at all redshifts.
From Table 2, based on the combined percentages of classes 1 and 2, it can be seen that while the percentage of highly pure groups for the identification performed with V0 variable is lower by ~7%, the percentage of highly complete groups of this sample is significantly higher (+ 43%). Therefore, the best choice for the radial linking length is such that it varies with redshift.
By comparing Figs. 7 and 8, the effect of the amplitude of V0 can be seen. Using fixed or variable V0 with 70 km s-1, all the fractions observed in the purity analysis are slightly higher than those observed and described above when using 130 km s-1. Therefore, a shorter radial linking length (Fig. 8) seems better in terms of purity, that is, it is able to identify more groups whose members belong to some reference group (~7% higher in the total percentage of P1 class for both constant or variable V0, see Table 2). However, the results from the completeness analysis help choosing the appropriate value. For both of the 70-identifications, the resulting samples are highly incomplete regardless of the redshift. In the best scenario (considering variable V0), the fraction of reference members that are included in the redshift-space groups reaches only 50%. This result implies that shortening the size of the radial linking length causes the algorithm to identify fewer of the true groups, resulting in a completeness for the sample that is quite low. This result is clearer when inspecting the total percentages of classes 1 + 2 in Table 2. By analysing the identification with variable V0, it can be seen that the percentage of C1 + C2 groups drastically drops from the 73% obtained for 130(1 + z) to 35% for 70(1 + z). Even more, the resulting group samples obtained when using 70 km s-1 are not only incomplete, but are dominated by groups of category C6, the least desired.
It has also been corroborated that using a value higher than 130, which not only has no physical motivation, but increases the completeness of the sample at the cost of the purity, which becomes lower than 50%.
Therefore, our choice for the radial linking length in redshift space catalogues is V0 = 130(1 + z) (right plots of Fig. 7). The redshift space distortions make it difficult to recover perfectly matched groups (P1 and C1), although they are the most common categories that we identify at all redshifts, followed by P2 and C2. There are 30% of false groups, while the algorithm is not able to recover only 10% of the true groups. All in all, the resulting sample has more than 50% of highly pure groups while we are able to identify 73% of the highly complete groups.
3.4. Spectroscopic sample: flux-limited sample in spectroscopic-redshift space
After chosening the best linking length parameters, we identified groups in the mock galaxy catalogue described in Sect. 2.3. The identification was performed with the following linking lengths:
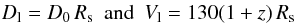 with D0 and Rs defined in Eqs. (2) and (4), respectively, and using a variable luminosity function.
with D0 and Rs defined in Eqs. (2) and (4), respectively, and using a variable luminosity function.
The algorithm produces a sample of 23 183 mock groups with four or more members (see Table 1). The purity and completeness as a function of redshifts for this sample are shown in Fig. 9. Both statistics were computed using the restricted-reference groups as control sample. The combined effect of these two observational constraints, the flux limit and the redshift space distortions, is evident. Regarding the purity, the fraction of members in the spectroscopic groups that also belong to the restricted-reference group with the highest matching rate (top panels in the left box) drastically decreases towards higher redshifts, ranging from ~80% to ~0%. When analysing the six categories of groups defined above, an increase in false identification (P6 groups) can be seen towards higher redshifts, with the sample at redshifts higher than z = 0.8 being dominated by these false groups. The perfectly matched groups (P1) and quasi-perfectly matched groups (P2) are more frequent in the other categories. Groups associated with a single real group plus more than 30% of interlopers (P4) represent ~10% at all redshifts.
From the completeness analysis (right box), the fraction of members in the restricted-reference sample that we were able to identify in the spectroscopic group with highest matching rate (top panels) decreases with redshift, that is, it is more likely to lose some of the true members at high redshift.
The perfectly recovered groups (C1) are dominant at all redshifts, followed by the groups where only a few members are missing (C2). The fraction of completely missing groups is almost constant at ~10% up to z = 0.8, and then increases towards higher redshifts.
To deepen our study, we analysed the purity of the spectroscopic groups by splitting the sample into low (<10) and high (≥10) membership groups. The results are shown in Fig.10. The low-membership groups are more prone to include false identifications (P6), while this category is almost non-existent at low redshifts among the high-membership groups, and it increases towards higher redshifts. The perfectly-matched groups are scarce in the high-membership groups, but this sample is dominated by the quasi-perfectly-matched groups until z = 0.7, and groups with more than 30% of interlopers (P4). The P3 groups (merging) are ~20% at all redshifts. These results indicate that the low-membership group sample is highly contaminated, and we strongly recommend not to use it for statistical purposes.
Analysing the total percentages within each of the purity and completeness classes (Table 2), we find that the spectroscopic group catalogue has 41% of groups of high-quality purity (P1 + P2), while the 69% of the restricted-reference sample is well recovered (C1 + C2). The false groups (P6) add up to ~43%, mainly because of low-membership false groups, while we completely loose ~12% of the true groups (C6). A closer inspection of the lower panels of Fig. 10 reveals that at low redshifts the percentage of false groups is lower than 40% for low-membership groups, while it is negligible for high-membership groups, which means that our choices of the linking lengths produce similar results to those that were found in low-redshift catalogues by Merchán & Zandivarez (2002).
 |
Fig. 10 Purity as a function of redshift for groups identified in a spectroscopic catalogue using an LF varying with redshift and V0 = 130(1 + z) km s-1 to compute the linking length parameters. Left panels correspond to low-membership groups while right panels are the high membership ones. The top panels show the fraction of galaxies identified that can be associated with galaxies of the group with the highest matching rate in the corresponding control sample (solid lines), and the fraction of galaxies that are classified as interlopers (dashed lines). The bottom panels show the trends observed for the fraction of groups within the six categories of purity (see text for description). The key for colours and line types is the same as in the previous figure. |
3.5. Photometric sample: flux-limited sample in photometric-redshift space
In this section we perform a similar analysis as in the previous section, but focus on observational catalogues with distances calculated using only photometric information, that is, by means of photometric redshifts.
3.5.1. Probability friend-of-friends: PFOF
To take into account the uncertainties of using photometric redshifts, we modified the identification algorithm in the line-of-sight direction using the method developed by Liu et al. (2008).
Instead of just computing the module difference among the velocities of a galaxy pair (|V2 − V1|) and restricting it to be smaller than Vl, the definition of a galaxy pair has to take into account the probabilistic nature of the photometric redshifts, and therefore the algorithm has to compute the probability of the distance between two galaxies to be shorter than the linking length, and then restrict this probability with an artificial threshold. Therefore, following Liu et al. (2008), the probability of two galaxies being closer than VL is 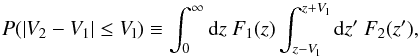 (5)where F1 and F2 are the probability distribution functions for the two galaxies in the line-of-sight direction. Therefore, the line-of-sight criterion to determine that two galaxies are physically associated is
(5)where F1 and F2 are the probability distribution functions for the two galaxies in the line-of-sight direction. Therefore, the line-of-sight criterion to determine that two galaxies are physically associated is
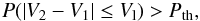 where Pth is an appropriate probability threshold. This threshold is determined in the sections below to obtain a sample of groups with a suitable balance between purity and completeness.
where Pth is an appropriate probability threshold. This threshold is determined in the sections below to obtain a sample of groups with a suitable balance between purity and completeness.
3.5.2. Testing the PFOF algorithm
To apply this modification to our algorithm, we adopted a probability distribution for the photometric redshifts.
The most common model used in the literature when working with photometric redshifts is a Gaussian probability distribution (Liu et al. 2008; Ascaso et al. 2012). Therefore, we followed that approach and modelled the probability distribution function associated with each galaxy by a Gaussian function, that is,
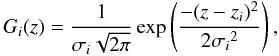 where zi is the photometric redshift and σi the photometric-redshift error of galaxy i.
where zi is the photometric redshift and σi the photometric-redshift error of galaxy i.
 |
Fig. 11 Left panels: scatter plots between the spectroscopic redshift (zs) and the photometric redshift (zp). Right panels: close-up of the distribution of the redshift differences zp − zs for | zp − zs | < 0.03. The grey colour is used when the photometric redshifts are computed using the BPZ code, while the black colour is used when the photometric redshifts are assigned randomly. In the upper panels the random photometric redshifts are assigned using a Gaussian probability distribution with the spectroscopic redshift as the centre and 0.0025 as the Gaussian width. In the lower panels the random photometric redshifts are assigned using a Lorentzian probability distribution, with a width of 0.00244 (see text for full description). |
But we also adopted a different probability distribution, a Lorentzian function, and tested the behaviour of the method against different distributions. A Lorentzian function is given by
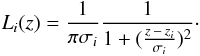 First, we tested the PFOF algorithm in the case where the galaxy redshifts have small uncertainties, as is true in the case of spectroscopic redshifts. We adopted σi = 30 km s-1 (the typical error in SDSS) and applied the PFOF to the mock galaxy catalogue described in Sect. 2.3 using a Gaussian probability distribution in Eq. (5). We identified 23 239 groups with four or more members using a probability threshold of 99%. Choosing as control sample the groups identified in Sect. 3.4, the analyses of completeness and purity revealed that the new identification is 99% pure and 99% complete, considering just the combined fractions P1 + P2 and C1 + C2, defined in the previous sections. This means that in the limit of small uncertainties, the PFOF algorithm behaves as the original FOF algorithm.
First, we tested the PFOF algorithm in the case where the galaxy redshifts have small uncertainties, as is true in the case of spectroscopic redshifts. We adopted σi = 30 km s-1 (the typical error in SDSS) and applied the PFOF to the mock galaxy catalogue described in Sect. 2.3 using a Gaussian probability distribution in Eq. (5). We identified 23 239 groups with four or more members using a probability threshold of 99%. Choosing as control sample the groups identified in Sect. 3.4, the analyses of completeness and purity revealed that the new identification is 99% pure and 99% complete, considering just the combined fractions P1 + P2 and C1 + C2, defined in the previous sections. This means that in the limit of small uncertainties, the PFOF algorithm behaves as the original FOF algorithm.
Groups identified in different galaxy samples in photometric-redshift space.
As a second test, the value of σi was adopted to mimic the difference between the BPZ photometric redshifts and the spectroscopic redshifts shown in the upper right panel of Fig. 11 (grey histogram). Choosing a Gaussian function to fit the differences, we adopted as the best-fit3 redshift error σi = 0.0025(1 + zs) for all galaxies. We also adopted a Lorentzian probability distribution to fit the differences. The best-fit redshift error for the Lorentzian function is σi = 0.00244(1 + zs).
Then, we modified the redshifts of the galaxies in the mock catalogue by randomly shifting the spectroscopic redshifts according to the previously fitted probability distributions: we generated a sample with the Gaussian distribution and a sample with the Lorentzian distribution. The distribution of differences for the resulting random samples are shown in Fig. 11. The sample generated with the Gaussian distribution is shown as the black histogram in the upper right panel. This distribution reproduces the mean of that obtained from a more realistic determination of photometric redshifts (BPZ). However, it is not possible to reproduce the tails of the realistic distribution when using a simple Gaussian function. The resulting redshift differences for the random Lorentzian sample are shown as a black histogram in the lower right panel of Fig. 11. In this case, the mean and the tails of the original distribution are well recovered.
We tested the PFOF algorithm on both samples, one with photometric redshifts generated from a Gaussian function, and the other where the photometric redshifts come from a Lorentzian function. The application of the PFOF is straightforward, one just uses for each galaxy the input distribution from which their redshifts have been generated to compute the probability of Eq. (5).
We tested different probability thresholds to identify the different samples. These thresholds are defined as being a percentage (99, 95, 90, 80, 70, 60, and 30%) of the maximum probability obtained from Eq. (5). The effect of choosing different thresholds is described in the analyses of purity and completeness of the resulting group samples.
The number of groups identified in each sample is shown in Table 3.
 |
Fig. 12 Percentages of false groups (solid blue line) and missing groups (dashed red line) as a function of the probability threshold used in the group identification algorithm. Top panel (bottom panel) corresponds to the identifications performed using a Gaussian (Lorentzian) function in the PFOF algorithm and in the assignment of random photometric redshifts. |
 |
Fig. 13 Percentages of false groups (solid blue line) and missing groups (dashed red line) as a function of the probability threshold used in the group identification algorithm. Top panel (bottom panel) corresponds to the identifications performed using a Gaussian (Lorentzian) function in the PFOF algorithm. The photometric redshifts were assigned using the BPZ code. |
We analysed the purity and completeness of these samples of groups by taking as control sample the restricted-reference group sample, defined in Sect. 3.1. In Fig. 12 we show the percentage of groups identified with PFOF that are classified to have purity P6 (blue solid lines), and the percentage of groups of the restricted-reference sample that have been lost by the PFOF algorithm (C6, red dashed lines), both as a function of the probability threshold. We show here only these categories since they show how poor the identification was. In this figure, the top panel corresponds to the identifications performed on samples of galaxies with photometric redshifts assigned randomly according to a Gaussian distribution, while the bottom panel shows the results for the samples where the photometric redshifts come from a Lorentzian distribution. The percentage of false identifications decreases towards higher probability thresholds, while the opposite happens with the percentage of the missing groups. An appropriate choice of the probability threshold would be the value where both trends overlap, that is, Pth = 91% for the Gaussian distributions, and Pth = 82% for the Lorentzian distribution. Having chosen the probability threshold, in both samples the false groups add up to 35%, which is also true of the missing groups.
3.5.3. Application of PFOF to mock galaxies with BPZ photometric redshift
We now tested the PFOF algorithm when applied to mock galaxies whose photometric redshifts were computed in a realistic way (see Sect. 2.4). We identified two samples of groups: (i) the algorithm works with a probability Gaussian function with σi = 0.0025(1 + zp), and (ii) the algorithm works with a probability Lorentzian function with σi = 0.00244(1 + zp)
The numbers of groups identified for the different probability thresholds are shown in Table 3. To determine the purity and completeness of these samples, we took as control sample the restricted-reference sample of groups. In Fig. 13, the percentages of false groups (P6) and the missing groups (C6) are shown as a function of the probability thresholds. The global behaviour of the trends are similar to what we found when the photometric redshifts were assigned randomly. There is little difference in the identifications when using a Gaussian function to describe the distribution of the photometric redshifts or a Lorentzian function, although the Lorentzian distribution is a better description for the data in a wider range (Fig. 11). The appropriate probability thresholds are Pth = 67 when using Gaussian functions in the algorithm, and Pth = 70 when using Lorentzian functions. The percentages of false and missing groups are ~40%.
The total percentages of purity and completeness within each category for the different probability threshold when using a Lorentzian function in the PFOF algorithm are quoted in Table 4. Pth = 70% is the best compromise to obtain higher percentages of purity and completeness (or lower fractions of false and missing groups).
Total percentages of purity and completeness of groups identified a mock galaxy catalogue with realistic photometric redshifts.
We also investigated the variation of the fraction of groups within each of the six categories of purity and completeness as a function of redshifts. We chose as our main sample that obtained when using a Lorentzian function in the PFOF algorithm and a probability threshold of Pth = 70. The resulting trends are shown in Fig. 14.
Regarding the purity (top panel), the resulting sample of groups is dominated by false groups (P6) at all redshifts, followed by groups with fewer than 70% of galaxies that belong to one true group (P4). Perfect or quasi-perfectly matched groups are less than 20% in the whole redshift range, which is expected because of the probabilistic nature of the identification. In this figure the short-dashed magenta line represents the sum of all the categories except for P6, which resembles groups that contain at least part of the true groups. At redshifts lower than 0.85 the contribution of all these categories together is higher than the contribution of the false groups, while this behaviour reverses at higher redshifts.
The analysis of the completeness is shown in the bottom panel of Fig. 14. Most of the true groups are missing at redshifts higher than 0.8, which is shown with the black dotted line (C6). At lower redshifts, groups with fewer than 70% of their members identified in the photometric sample are dominant. The contribution of all true groups whose members have been included entirely or partially in any photometric group (the sum of all categories except for C6) is higher than 60% at redshifts lower than 0.8.
We also split the sample of photometric groups into low and high-membership groups (for groups with 4 ≤ N < 10 and N ≥ 10, respectively). The six-category analysis of purity for low and high-membership groups is shown in Fig. 15. The top panel of this figure shows that the low-membership groups are responsible for the high contamination by false groups (P6) in the sample in the whole redshift range. There are fewer than 10% high-membership false groups at all redshifts, indicating that groups that contain at least part of the true groups add up to roughly 90%. Therefore, we suggest that the low-membership sample identified with this algorithm is not used to perform statistical studies.
 |
Fig. 14 Top panel: percentage of photometric groups split into the six categories of purity as a function of redshift. Bottom panel: percentage of restricted-reference split into the six categories of completeness as a function of redshifts. |
 |
Fig. 15 Purity of groups identified in a realistic photometric mock galaxy sample. Top panel: percentage of low-membership photometric groups split into the six categories of purity as a function of redshift. Bottom panel: percentage of high-membership photometric groups split into the six categories of purity as a function of redshift. |
4. Summary
We have performed a detailed analysis to assess the reliability of a FoF algorithm in obtaining real galaxy systems in deep spectroscopic/photometric-redshift surveys. To achieve this goal, we constructed a synthetic galaxy catalogue using one of the largest simulated galaxy samples available at the present, the semi-analytical galaxies built by Guo et al. (2011) on top of the Millennium Simulation I. We note that adopting a specific semi-analytical model could introduce a dependence of the results on the particular set of parameters and physical processes that were used in the model construction. But, analysing the differences caused by using different semi-analytical models is beyond the scope of this work.
To build a light-cone mock catalogue we used the information available at different evolutionary stages to reproduce temporal galaxy evolution. We applied several recipes in the mock catalogue construction procedure to avoid different problems that arise from the construction technique, such as missing/duplicate galaxies and repetition of structures in the survey. The mock catalogue was tailored to the future J-PAS apparent magnitude limit and photometric band. The technique of computing photometric redshifts for each mock galaxy is also the same as the one that will be applied to that future photometric all-sky survey. The resulting light-cone mock catalogue comprised roughly 800 000 galaxies down to an observer-frame apparent magnitude of 23 in the SDSS i-band, with a median redshift of 0.72 and a maximum of 1.5 within a solid angle of 17.6 deg2.
First, we sought the proper linking lengths to apply in a FoF algorithm to identify galaxy groups in a deep spectroscopic redshift survey. We analysed completeness and purity of the sample on the basis of a comparison member-to-member between the identified groups and a reference sample. The analyses of completeness and purity of the resulting sample revealed that the best identification is obtained when the algorithm takes into account the variation of the galaxy luminosity function with redshift, as well as a linear redshift dependence of the radial fiducial velocity in the line-of-sight direction. The best choice of the linking lengths is the one that leads to a compromise between the completeness and the purity of the resulting sample. In the best scenario, we were able to identify a galaxy group sample in the spectroscopic catalogue that contains more than 40% of highly pure groups (completely pure or with a few interlopers), at the same time we were able to recover 70% of highly complete groups (completely recovered or with only a few missing galaxies). The percentage of groups that contained at least part of a true group is 57% (in other words, 43% of the groups are completely false identifications), while 88% of the true groups were recovered in the identification process either in one or several groups (only 12% of the true groups were completely lost).
Second, using the procedure developed by Liu et al. (2008), we adapted the FoF algorithm in the line-of-sight direction to a probabilistic algorithm (PFOF) to work with photometric redshifts as distance estimators. Our analyses were performed to determine the proper probability distribution function that best describes the data and leads to the most reliable group identification. On the other hand, we determined the best probability threshold that produces the most complete and pure sample of groups. By comparing the spectroscopic and photometric information of the mock galaxies, we observed that a Lorentzian probability distribution function performs better than a Gaussian function in quantifying the discrepancies between the photometric and spectroscopic redshifts. However, after using both distribution functions in the identification procedure for different probability thresholds, we observed that the percentages of completely false and missing groups show little differences as a function of the adopted distribution function. Adopting a compromise between the completeness and purity of the resulting sample, we determined that the best identification is obtained for a probability threshold of 70% of the highest value. The resulting sample included fewer than 40% of false identifications while it was able to recover around 60% of the true groups.
We also observed that regardless of whether the redshifts are spectroscopic or photometric, the group samples were strongly improved (in terms of purity) when using only groups with more than ten galaxy members.
This work may be used to predict the number of groups that the algorithm described in this paper might find when applied to the future J-PAS survey. Taking into account the survey geometry, we expect to obtain a sample of ~6 000 000 groups with low membership (4 ≤ N < 10) and ~1 000 000 groups with high membership (N ≥ 10) when applying the PFOF algorithm with a Lorentzian probability function, an overdensity contrast that resembles the one used for DM haloes, and a probability threshold of 70%, out to z = 1.2. On the other hand, if we adopt a higher contour overdensity contrast assuming that galaxies are more concentrated than dark matter, we would obtain a galaxy group sample for the future J-PAS survey of ~4 000 000 low-membership groups and ~650 000 groups with high membership when applying the PFOF algorithm with a Lorentzian probability function and a probability threshold of 60%, out to z = 1.2 (see Appendix B for details).
However, we note that the choice of the probability threshold should be made according to the final purpose of the group sample: if the obtained groups will be used as proxies for other group-searching algorithms, one may choose a low-probability threshold, which would imply a sample with a high completeness level (low purity); if the groups will be used for performing analyses of group properties, it is better to choose a high-probability threshold, which would imply a high purity level (low completeness).
Finally, because our criteria to define purity and completeness of groups are very detailed and restrictive, we were able to assess the different types of groups that contribute to the resulting identified sample. Using more relaxed criteria to define pure and complete groups, as well as different reference samples, could lead to higher percentages than those found in this work.
During the latest stages of this work, we have become aware of the existence of the recently submitted work by Jian et al. (2013). In that work, the authors have performed a similar analysis to the one presented here, that is, using the Liu et al. (2008) adaptation of the FoF algorithm to identify galaxy groups, but in the Pan-STARRS1 Medium Deep Surveys. Even though both works pursued similar objectives about assessing the reliability of galaxy group identification in photometric-redshift surveys, the approaches adopted in the two works are quite different. For instance, the semi-analytical galaxies, the procedures for determining the proper linking length parameters, the reference samples, the criteria for computing purity and completeness of identified groups as well as the way to compute the photometric redshifts in mock catalogues are some of the points where the two works clearly differ. Although it is difficult to compare the two works fairly, we note that our values of purity and completeness are overall consistent with those obtained by Jian et al.
We kept the notation introduced by Huchra & Geller (1982) although the parameters in this work also depend on the redshifts.
Acknowledgments
We thank Manuel Merchán, Mario Sgró and Raúl Angulo for useful discussions and suggestions. The Millennium Simulation databases used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory (GAVO). We thank Qi Guo for allowing public access to the outputs of her very impressive semi-analytical model of galaxy formation. This work has been partially supported by Consejo Nacional de Investigaciones Científicas y Técnicas de la República Argentina (CONICET, PIP2011/2013 11220100100336), Secretaría de Ciencia y Tecnología de la Universidad de Córdoba (SeCyT) and Fundação de Amparo à Pesquisa do Estado do São Paulo (FAPESP), through grants 2011/50471-4 and 2011/50002-4. C.M.d.O. acknowleges support of FAPESP (grant #2006/56213-9) and Conselho Nacional de Pesquisas (CNPq). A.Z. and E.D.G. wish to thank the IAG staff for their hospitality during the extended visit, when part of this work was done.
References
- Ascaso, B., Wittman, D., & Benítez, N. 2012, MNRAS, 420, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N. 2000, ApJ, 536, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N., Gaztañaga, E., Miquel, R., et al. 2009, ApJ, 691, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., Frieman, J., Weinberg, D. H., et al. 2006, ApJS, 167, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Blaizot, J., Wadadekar, Y., Guiderdoni, B., et al. 2005, MNRAS, 360, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Botzler, C. S., Snigula, J., Bender, R., & Hopp, U. 2004, MNRAS, 349, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Couch, W. J., Ellis, R. S., MacLaren, I., & Malin, D. F. 1991, MNRAS, 249, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Courtin, J., Rasera, Y., Alimi, J.-M., et al. 2011, MNRAS, 410, 1911 [NASA ADS] [Google Scholar]
- Dalton, G. B., Maddox, S. J., Sutherland, W. J., & Efstathiou, G. 1997, MNRAS, 289, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Efstathiou, G., Frenk, C. S., & White, S. D. M. 1985, ApJ, 292, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Giménez, E. 2002, Master’s thesis, FaMAF, Universidad Nacional de Córdoba, Argentina [Google Scholar]
- Eke, V. R., Baugh, C. M., Cole, S., et al. 2004, MNRAS, 348, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Farrens, S., Abdalla, F. B., Cypriano, E. S., Sabiu, C., & Blake, C. 2011, MNRAS, 417, 1402 [NASA ADS] [CrossRef] [Google Scholar]
- Gal, R. R. 2006 [arXiv:astro-ph/0601195] [Google Scholar]
- Gal, R. R., de Carvalho, R. R., Odewahn, S. C., Djorgovski, S. G., & Margoniner, V. E. 2000, AJ, 119, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Geller, M. J., & Huchra, J. P. 1983, ApJS, 52, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Gillis, B. R., & Hudson, M. J. 2011, MNRAS, 410, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Gladders, M. D., & Yee, H. K. C. 2000, AJ, 120, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T., Sekiguchi, M., Nichol, R. C., et al. 2002, AJ, 123, 1807 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Boylan-Kolchin, M., et al. 2011, MNRAS, 413, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Angulo, R. E., et al. 2013, MNRAS, 428, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Henriques, B., White, S., Lemson, G., et al. 2012, MNRAS, 421, 2904 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., & Geller, M. J. 1982, ApJ, 257, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Jian, H.-Y., Lin, L., Chiueh, T., et al. 2013, ApJ, submitted [arXiv:1305.1891] [Google Scholar]
- Kepner, J., Fan, X., Bahcall, N., et al. 1999, ApJ, 517, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzbichler, M. G., & White, S. D. M. 2007, MNRAS, 376, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Knebe, A., Knollmann, S. R., Muldrew, S. I., et al. 2011, MNRAS, 415, 2293 [NASA ADS] [CrossRef] [Google Scholar]
- Knebe, A., Pearce, F. R., Lux, H., et al. 2013, MNRAS, 435, 1618 [NASA ADS] [CrossRef] [Google Scholar]
- Knobel, C., Lilly, S. J., Iovino, A., et al. 2009, ApJ, 697, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Li, I. H., & Yee, H. K. C. 2008, AJ, 135, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. B., Hsieh, B. C., Ho, P. T. P., Lin, L., & Yan, R. 2008, ApJ, 681, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Merchán, M., & Zandivarez, A. 2002, MNRAS, 335, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Merchán, M. E., & Zandivarez, A. 2005, ApJ, 630, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Milkeraitis, M., van Waerbeke, L., Heymans, C., et al. 2010, MNRAS, 406, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, C. J., Nichol, R. C., Reichart, D., et al. 2005, AJ, 130, 968 [Google Scholar]
- Mo, H., van den Bosch, F. C., & White, S. 2010, Galaxy Formation and Evolution (Cambridge: Cambridge University press) [Google Scholar]
- Moles, M., Benítez, N., Aguerri, J. A. L., et al. 2008, AJ, 136, 1325 [Google Scholar]
- Moles, M., Sánchez, S. F., Lamadrid, J. L., et al. 2010, PASP, 122, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Molino, A., Benítez, N., Moles, M., et al. 2013 [arXiv:1306.4968] [Google Scholar]
- More, S., Kravtsov, A. V., Dalal, N., & Gottlöber, S. 2011, ApJS, 195, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A. 1999, Cosmological Physics (Cambridge: Cambridge University press) [Google Scholar]
- Pérez-González, P. G., Cava, A., Barro, G., et al. 2013, ApJ, 762, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Postman, M., Lubin, L. M., Gunn, J. E., et al. 1996, AJ, 111, 615 [Google Scholar]
- Ramella, M., Geller, M. J., & Huchra, J. P. 1989, ApJ, 344, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Ramella, M., Boschin, W., Fadda, D., & Nonino, M. 2001, A&A, 368, 776 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shectman, S. A. 1985, ApJS, 57, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Snaith, O. N., Gibson, B. K., Brook, C. B., et al. 2011, MNRAS, 415, 2798 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Trevese, D., Castellano, M., Fontana, A., & Giallongo, E. 2007, A&A, 463, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Breukelen, C., & Clewley, L. 2009, MNRAS, 395, 1845 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, W., & White, S. D. M. 2012, MNRAS, 424, 2574 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, N. N., & Kamionkowski, M. 2003, MNRAS, 341, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Meisenheimer, K., Kleinheinrich, M., et al. 2004, A&A, 421, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, G. 1995, ApJS, 98, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Zandivarez, A., & Martínez, H. J. 2011, MNRAS, 415, 2553 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Testing the mock catalogue: non-interpolated galaxy positions and velocities
We performed an additional test using a different galaxy lightcone mock catalogue constructed using the original galaxy positions and peculiar velocities obtained from each simulation snapshot (hereafter, non-interpolated positions and velocities, NIPV).
The new mock catalogue comprises 6 756 931 galaxies with absolute magnitudes brighter than − 16.4 up to z = 1.5, that is, 0.01% more galaxies than in the interpolated positions and velocities (hereafter, IPV) mock catalogue.
Following the procedure described in Sect. 3.1, we identified a new reference sample for the NIPV mock catalogue. A comparison between the resulting group sample for the NIPV mock catalogue and the original IPV mock catalogue is shown in Table A.1.
From the Table, it can be seen that the new reference group sample is only 2.5% larger than the IPV group sample, and comprises 3.7% more galaxies. To investigate intrinsic differences among the groups of both reference samples we performed a comparison member by member. Using the IPV group sample as reference, our comparison shows that the 95% of the NIPV groups are directly correlated with the IPV group sample, while only 5% of NIPV groups are intrinsically different. On the other hand, using the NIPV group sample as reference, 98% of the IPV groups are directly correlated with the NIPV groups sample, while only 2% of IPV groups are missing in the NIPV group sample. Therefore, from this two-way comparison, we conclude that both reference samples show a high level of statistical agreement.
Reference group samples identified in the IPV and NIPV mock catalogues.
Nevertheless, small differences in the positions/velocities of galaxies in both mock catalogues could still have an impact on the resulting computations of purity and completeness of different group identifications carried out in this work. Hence, we performed a second test to quantify the impact of using an NIPV mock catalogue on the results obtained in our work. On the NIPV mock catalogue, we performed the same procedure as described in Sect. 3.3. First, we used the NIPV group reference sample and computed the maximum (and second maximum) velocity difference of the members in the line of sight to their closest neighbours. As expected from the very good statistical agreement among the reference samples, the values previously obtained in Sect. 3.3 are also the best values for the NIPV group sample, that is, V0 = 130(1 + z) km s-1 and V0 = 70(1 + z) km s-1. Second, we reproduced the test previously performed on the volume-limited IPV mock catalogue to analyse the effect of distortions in redshift space, by performing an identification of groups in redshift space on the volume-limited NIPV mock catalogue using four different linking length parameters in the line-of-sight direction: 130, 130(1 + z), 70 and 70(1 + z). The percentages of purity and completeness of groups split into six categories obtained for the NIPV group samples are shown in Table A.2. For a direct comparison, we also included the previous findings associated with the IPV samples.
Total percentages of purity and completeness of groups identified in the IPV/NIPV mock catalogues.
From the comparison with the values obtained for the IPV group samples, it is quite clear that identifying groups on an NIPV mock catalogue does not introduce statistically significant differences in the corresponding percentages of purity and completeness of groups. Therefore, we conclude that the adopted IPV mock catalogue used throughout our work does not introduce a particular bias in our results.
Appendix B: Groups identified with higher contour overdensity contrast
Properties of groups of galaxies depend sensitively on the algorithm for group selection. In the past, groups of galaxies have been identified in observational catalogues with FoF linking lengths corresponding to different contour overdensity contrasts: 20 (Geller & Huchra 1983), 80 (Ramella et al. 1989; Merchán & Zandivarez 2002, 2005), 200 (Zandivarez & Martínez 2011), or 365 (Berlind et al. 2006). According to Knebe et al. (2013), it must be stressed that there is no right or wrong way; users of halo-finder catalogues just need to be aware that several alternative definitions exist and which one of these has been used, especially when computing masses and other group properties.
In this section we apply a different contour overdensity contrast to identify groups in the mock galaxy catalogues. Some authors argued that since galaxies are more concentrated than dark matter, a higher contour overdensity contrast should be used (Eke et al. 2004; Berlind et al. 2006). Therefore, using these works, we modified the empirical contour overdensity contrast of Courtin et al. (2011), shown in Eq. (3), by lowering the original linking length parameter b0 from 0.2 to 0.14. Note that at redshift z = 0, this formula leads to δρ/ρ = 433 compared with δρ/ρ = 148 that has been used in the main body of this work. As stated in Sect. 3.1, we recall that the redshift dependence only introduces a variation of the linking length parameter of ~8% in the whole redshift range.
With the aim of analysing the effect of a different overdensity in the performance of the group finder, we repeated all the stages of this work for this new identification. The new reference sample identified in real space comprises 164 580 groups with more than four members. This sample has 18% fewer groups than the sample identified with a lower contour overdensity contrast.
Total percentages of purity and completeness of groups (with z = 0 − 1.2) identified in different mock galaxy samples.
Total percentages of purity and completeness of groups identified in a mock galaxy catalogue with realistic photometric redshifts.
 |
Fig. B.1 Top panel: percentage of photometric groups split into the six categories of purity as a function of redshift. Bottom panel: percentage of restricted-reference split into the six categories of completeness as a function of redshifts. |
 |
Fig. B.2 Purity of groups identified in a realistic photometric mock galaxy sample. Top panel: percentage of low-membership photometric groups split into the six categories of purity as a function of redshift. Bottom panel: percentage of high-membership photometric groups split into the six categories of purity as a function of redshift. |
We performed the tests of the FoF algorithm against redshift space distortions and flux limit. The appropriate linking length in the line-of-sight direction was determined in the same way as before: by measuring the maximum separation in the distorted radial direction to the closest neighbour (and second-closest neighbour). We found no differences in the result. In Table B.1, we quote the percentages of groups split into the different categories of purity and completeness. Comparing this with Table 2, it can be seen that there is no change in the behaviour of the group finder. The samples obtained with a higher contour overdensity contrast exhibit the same purity and completeness as the sample obtained with a lower overdensity contrast. The final spectroscopic sample of galaxy groups comprises 16 336 groups with more than four members, that is, it has 30% fewer groups than the sample obtained with the higher overdensity.
We also tested the algorithm in photometric-redshift space and determined the best-probability threshold in terms of purity and completeness. Table B.2 shows the percentage of groups in the different categories of purity and completeness for different probability thresholds. The best compromise between purity and completeness is reached when a probability threshold is adopted that is lower than in the identification with lower overdensity contrast. In this case, the best choice in terms of purity and completeness is Pth = 60%, which produces a sample of 10 740 groups with more than four members, which has 31% fewer groups than the best sample identified with the higher overdensity contrast and Pth = 70%. In this sample, the percentage of false groups is 41%, while the percentage of missing groups is 44%.
In Fig. B.1 we show the variation of the six categories of purity and completeness for the sample identified with Pth = 60% as a function of redshift. This figure can be directly compared with Fig. 14 to observe that changing the contour overdensity contrast does not introduce major differences in the purity/completeness of the resulting sample, provided the probability threshold is also changed.
Finally, in Fig. B.2 we also show the behaviour of the purity of the sample when groups, identified with Pth = 60%, are split into low (9323 groups) and high (1417 groups) membership. The low-membership sample introduces the highest percentage of false identifications (P6), and therefore we recommend to avoid using these groups when performing statistical analyses of the properties of groups. This result is very similar to the one previously shown in Fig. 15 using a lower overdensity contrast in the identification process.
All Tables
Total percentages of purity and completeness of groups (with z = 0 − 1.2) identified in different mock galaxy samples.
Total percentages of purity and completeness of groups identified a mock galaxy catalogue with realistic photometric redshifts.
Total percentages of purity and completeness of groups identified in the IPV/NIPV mock catalogues.
Total percentages of purity and completeness of groups (with z = 0 − 1.2) identified in different mock galaxy samples.
Total percentages of purity and completeness of groups identified in a mock galaxy catalogue with realistic photometric redshifts.
All Figures
 |
Fig. 1 Illustration of the process of galaxies when they are included twice or not at all in the mock catalogue for two consecutive snapshots. Upper panels: the case when a galaxy is counted twice when constructing a light-cone using different snapshots. The grey region shows the snapshot under consideration. The right panel shows the galaxy j at a previous time, inside the i + 1th shell, showing the direction of movement of the galaxy. Due to this direction of movement and the width of the shell, the galaxy j will appear also inside the ith shell at an earlier time (left panel), and consequently, it is included twice. Lower panels: the case when a galaxy is missing when constructing a light-cone. The right panel shows the galaxy j in a previous time, outside the i + 1th shell, and showing its direction of movement. Due to this situation, galaxy j will also appear outside the ith shell at an earlier time (left panel), resulting in a missing galaxy in both shells. |
| In the text | |
 |
Fig. 2 Upper panel: a pie plot projection showing, in a thin slice, the distribution of the mock galaxies as a function of redshift. Lower panel: redshift distribution of galaxies with iSDSS ≤ 23 in the selected light-cone with an angular coverage of 17.6 deg2. The maximum redshift of the sample is ~1.5. |
| In the text | |
 |
Fig. 3 Best-fit parameters of a double Schechter luminosity function in the iSDSS band as a function of redshift. These parameters are obtained by fitting the luminosity distributions of the semi-analytic galaxies (Guo et al. 2011) down to an absolute magnitude of − 16.4 at different snapshots of the Millennium Simulation. |
| In the text | |
 |
Fig. 4 Variation of the linking length parameters as a function of redshift. The left panel shows the transversely linking length for volume-limited samples, D0, the middle panel shows the scale factor Rs, while the right panel shows the transverse linking length for flux-limited samples, Dl (see equations in Sect. 3.2). The solid blue lines show the parameters using a LF that varies with redshift (see Fig. 3) while dashed red lines show the parameters when a fixed LF at redshift close to zero is adopted. |
| In the text | |
 |
Fig. 5 Purity and completeness as a function of redshift for groups identified in a flux-limited sample in real space. Left boxes show the purity (upper panels) and completeness (lower panels) when a fixed LF is used in the linking length parameters, while right boxes show the trends when a LF varying with redshift is used to compute the linking length parameters. In the upper boxes (purity), the top panels show the fraction of identified galaxies (Glxs) associated with the group with the highest matching rate in the corresponding control sample (solid lines), and the fraction of galaxies that are classified as interlopers (dashed lines). In the lower boxes (completeness), the top panels show the fraction of galaxies in the control sample that are associated with the group with the highest matching rate in the identified sample (solid lines), and the fraction of galaxies that are classified as missing galaxies (dashed lines). The bottom panels in each plot show the trends observed for the fraction of groups (Grps) within the six categories of purity or completeness (see text for description). The short-dashed magenta lines correspond to the complement of P6 and C6. |
| In the text | |
 |
Fig. 6 Left upper panel: scatter plot of the maximum velocity difference of the members in the line of sight to their closest neighbours. Right upper panel: the same as the right panel, but using the second maximum. In the lower panels we divided the upper panels by (1 + z). |
| In the text | |
 |
Fig. 7 Same as Fig. 5, but for the samples of groups identified in a volume-limited sample in redshift space using V0 = 130 km s-1 (left boxes) or V0 = 130 (1 + z) km s-1 (right boxes). |
| In the text | |
 |
Fig. 8 Same as Fig.5, but for the samples of groups identified in volume-limited sample in redshift space using V0 = 70 km s-1 (left boxes) or V0 = 70 (1 + z) km s-1 (right boxes). |
| In the text | |
 |
Fig. 9 Purity and completeness as a function of redshift for groups identified in a flux-limited sample in redshift space. The left box shows the purity while the right box shows the completeness when an LF varying with redshift and V0 = 130(1 + z) km s-1 is used to compute the linking length parameters. In the left box (purity), the top panels show the fraction of galaxies identified that can be associated with galaxies of the group with the highest matching rate in the corresponding control sample (solid lines), and the fraction of galaxies that are classified as interlopers (dashed lines). In the right box (completeness), the top panels show the fraction of galaxies in the control sample that can be associated with galaxies identified in the spectroscopic group with the highest matching rate (solid lines), and the fraction of galaxies from the control sample that are classified as missing (dashed lines). The bottom panels show the trends observed for the fraction of groups within the six categories of purity or completeness (see text for description). The short-dashed magenta lines correspond to the complement of P6 and C6. |
| In the text | |
 |
Fig. 10 Purity as a function of redshift for groups identified in a spectroscopic catalogue using an LF varying with redshift and V0 = 130(1 + z) km s-1 to compute the linking length parameters. Left panels correspond to low-membership groups while right panels are the high membership ones. The top panels show the fraction of galaxies identified that can be associated with galaxies of the group with the highest matching rate in the corresponding control sample (solid lines), and the fraction of galaxies that are classified as interlopers (dashed lines). The bottom panels show the trends observed for the fraction of groups within the six categories of purity (see text for description). The key for colours and line types is the same as in the previous figure. |
| In the text | |
 |
Fig. 11 Left panels: scatter plots between the spectroscopic redshift (zs) and the photometric redshift (zp). Right panels: close-up of the distribution of the redshift differences zp − zs for | zp − zs | < 0.03. The grey colour is used when the photometric redshifts are computed using the BPZ code, while the black colour is used when the photometric redshifts are assigned randomly. In the upper panels the random photometric redshifts are assigned using a Gaussian probability distribution with the spectroscopic redshift as the centre and 0.0025 as the Gaussian width. In the lower panels the random photometric redshifts are assigned using a Lorentzian probability distribution, with a width of 0.00244 (see text for full description). |
| In the text | |
 |
Fig. 12 Percentages of false groups (solid blue line) and missing groups (dashed red line) as a function of the probability threshold used in the group identification algorithm. Top panel (bottom panel) corresponds to the identifications performed using a Gaussian (Lorentzian) function in the PFOF algorithm and in the assignment of random photometric redshifts. |
| In the text | |
 |
Fig. 13 Percentages of false groups (solid blue line) and missing groups (dashed red line) as a function of the probability threshold used in the group identification algorithm. Top panel (bottom panel) corresponds to the identifications performed using a Gaussian (Lorentzian) function in the PFOF algorithm. The photometric redshifts were assigned using the BPZ code. |
| In the text | |
 |
Fig. 14 Top panel: percentage of photometric groups split into the six categories of purity as a function of redshift. Bottom panel: percentage of restricted-reference split into the six categories of completeness as a function of redshifts. |
| In the text | |
 |
Fig. 15 Purity of groups identified in a realistic photometric mock galaxy sample. Top panel: percentage of low-membership photometric groups split into the six categories of purity as a function of redshift. Bottom panel: percentage of high-membership photometric groups split into the six categories of purity as a function of redshift. |
| In the text | |
 |
Fig. B.1 Top panel: percentage of photometric groups split into the six categories of purity as a function of redshift. Bottom panel: percentage of restricted-reference split into the six categories of completeness as a function of redshifts. |
| In the text | |
 |
Fig. B.2 Purity of groups identified in a realistic photometric mock galaxy sample. Top panel: percentage of low-membership photometric groups split into the six categories of purity as a function of redshift. Bottom panel: percentage of high-membership photometric groups split into the six categories of purity as a function of redshift. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.