| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322739 | |
| Published online | 23 December 2013 | |
ALMA observations of cool dust in a low-metallicity starburst, SBS 0335−052⋆,⋆⋆
1
INAF − Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5,
50125
Firenze,
Italy
e-mail:
hunt@arcetri.astro.it
2
ESO, Karl Schwarzschild str. 2, 85748
Garching bei München,
Germany
3
INAF − Istituto di Radioastronomia & Italian ALMA
Regional Centre, via Gobetti 101, 40129
Bologna,
Italy
4
Observatorio Astronómico Nacional (OAN)-Observatorio de Madrid,
Alfonso XII 3,
28014
Madrid,
Spain
5
Observatoire de Paris, LERMA (CNRS:UMR8112), 61 Av. de
l’Observatoire, 75014
Paris,
France
6
Universidad Andrés Bello, Deparamento de Ciencias Físicas, República 252,
8370134
Santiago,
Chile
7
School of Physics and Astronomy, University of Leeds,
Leeds
LS2 9JT,
UK
8
Max-Planck-Institut für Radioastronomie,
auf dem Hügel 69,
53121
Bonn,
Germany
9 Astronomy Department, King Abdulaziz University, PO Box
80203, Jeddah, Saudia Arabia
10
Cavendish Laboratory, University of Cambridge,
19 J.J. Thomson
avenue, Cambridge
CB3 0HE,
UK
11
CEA, Laboratoire AIM, Irfu/SAp, Orme des Merisiers, 91191
Gif-sur-Yvette,
France
Received:
23
September
2013
Accepted:
21
November
2013
We present Atacama Large Millimeter/submillimeter Array (ALMA) Cycle 0 Band 7 observations of an extremely metal-poor dwarf starburst galaxy in the Local Universe, SBS 0335−052 (12 + log (O/H) ~ 7.2). With these observations, dust is detected at 870 μm (ALMA Band 7), but 87% of the flux in this band is due to free-free emission from the starburst. We have compiled a spectral energy distribution (SED) of SBS 0335−052 that spans almost 6 orders of magnitude in wavelength and fit it with a spherical dust shell heated by a single-age stellar population; the best-fit model gives a dust mass of (3.8 ± 0.6) × 104 M⊙. We have also constructed a SED including Herschel archival data for I Zw 18, another low-metallicity dwarf starburst (12 + log (O/H) ~ 7.17), and fit it with a similar model to obtain a dust mass of (3.4 ± 1.0) × 102 M⊙. It appears that for such low-metallicity dwarf galaxies, the ratio of their stellar mass to their dust mass is within the range of values found for spirals and other star-forming galaxies. However, compared with their atomic gas mass, the dust mass of SBS 0335−052 far exceeds the prediction of a linear trend of dust-to-gas mass ratio with metallicity, while I Zw 18 falls far below. We use gas scaling relations to assess a putative missing gas component in both galaxies and find that the missing, possibly molecular, gas in SBS 0335−052 is a factor of 6 times higher than the value inferred from the observed Hi column density; in I Zw 18 the missing component is much smaller. Finally, we constrain the H2 surface density conversion factor αCO with our upper limit for CO J = 3−2 line in SBS 0335−052, and find that this is consistent with a linear or even super-linear trend of increasing αCO with decreasing metallicity. Ultimately, despite their similarly low metallicity, the differences in gas and dust column densities in SBS 0335−052 and I Zw 18 suggest that metal abundance does not uniquely define star-formation processes. At some level, self-shielding and the survival of molecules may depend just as much on gas and dust column density as on metallicity. The effects of low metallicity may at least be partially compensated for by large column densities in the interstellar medium.
Key words: galaxies: starburst / galaxies: dwarf / galaxies: star formation / galaxies: ISM / galaxies: individual: SBS0335-052 / galaxies: individual: IZw18
Based on observations carried out with ALMA in Cycle 0; the Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.
Reduced ALMA data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/561/A49
© ESO, 2013
1. Introduction
First IRAS and ISO, then SCUBA, COBE, and most recently Spitzer and Herschel have convincingly shown that most of the star formation in the universe is enshrouded in dust. Large populations of infrared-luminous galaxies are major contributors to the far-infrared and sub-millimeter backgrounds, and are probably responsible for most of the star-formation activity at high redshifts (e.g., Chary & Elbaz 2001; Dole et al. 2006; Gruppioni et al. 2010). Indeed, half the energy and most of the photons in the universe come from the infrared spectral region (e.g., Hauser & Dwek 2001; Franceschini et al. 2008).
That dust is so prominent in the high-redshift universe may appear surprising, since it has been assumed that dust would be absent in primordial, metal-poor environments. However, the presence of large amounts of dust (and molecular gas) in z ~ 6 quasars (e.g., Wang et al. 2008) has been attributed to supernovae and asymptotic giant branch stars which evolve in a metal-free interstellar medium (ISM; e.g., Todini & Ferrara 2001; Schneider et al. 2004; Nozawa et al. 2007; Valiante et al. 2009). Dust at such high redshifts suggests that early star formation episodes must be very intense and relatively brief. However, exactly how these massive starbursts occur and evolve is not yet clear. The short interval in which star formation and the ensuing chemical enrichment and dust formation convert a dust-free metal-free environment to a dusty metal-rich one by redshift z ~ 6 is as yet unobserved, and studies of such transitions remain a major observational challenge.
The Local Universe is home to star-forming dwarf galaxies that are much more metal poor than galaxies observed thus far at high redshift. Only a handful of blue compact dwarf (BCD) galaxies have been discovered so far with 12 + log (O/H) ~ 7.2 (e.g., Izotov et al. 2007). Even at these extremely low metallicities, BCD spectral energy distributions (SEDs) can be dominated by infrared dust emission resulting from reprocessing of UV radiation from young massive stars (e.g., SBS 0335−052 and I Zw 18: Houck et al. 2004a; Wu et al. 2007). Because such galaxies are chemically unevolved, they can provide a window on primordial galaxy formation and evolution. This is, in some sense, a “local” approach to a cosmological problem. If we can study the properties of a metal-poor ISM and its constituents locally, we may be able to better understand the high-redshift transition from metal-free Population III stars to the chemically evolved massive galaxies typical of the current epoch.
In this paper, we present Atacama Large Millimeter/submillimeter Array (ALMA) Cycle 0 Band 7 (346.21 GHz) observations of an extremely low-metallicity starburst in the Local Universe, SBS 0335−052. We also compare it with a nearby similarly metal-poor dwarf galaxy, I Zw 18.
1.1. SBS0335−052
SBS 0335−052 (more properly, the eastern component, SBS 0335−052 E) is embedded together
with a western component, SBS 0335−052 W, in a giant Hi cloud roughly 4.2 arcmin
across, or 66 kpc at SBS 0335−052’s distance (Pustilnik et
al. 2001; Ekta et al. 2009).
SBS 0335−052 W, although physically related to SBS 0335−052 E because of their common
Hi envelope, is 22 kpc (1.4 arcmin) distant from SBS 0335−052 E. Both galaxies
are very metal-poor: 12 + log (O/H) ~ 7.2 for SBS 0335−052 E and 7.12 for SBS 0335−052 W,
similar to the “prototype” BCD, I Zw 18 with 12 + log (O/H) = 7.17 (Izotov et al. 1999, 2005).
SBS 0335−052 E hosts six super star clusters (SSCs), distributed (end-to-end) over roughly
2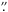 6 (~700 pc),
with most of the star formation activity taking place in the two brightest ones (SSC 1, 2)
to the southeast (Hunt et al. 2001; Dale et al. 2001). There are more than 10 000 O stars
within these two clusters, unresolved at Hubble Space Telescope (HST)
resolution (Thuan et al. 1997b; Reines et al. 2008). The stars in SBS 0335−052 are
mostly confined to the six SSCs, with a total mass of
~6 × 106 M⊙ (Reines et al. 2008). However, there is a faint underlying stellar component with
a mass comparable to the sum of the SSCs; Papaderos et al.
(1998) estimate a total mass including the diffuse populations of
3.1 × 106 M⊙, roughly half of that given by
Reines et al. for the clusters alone. Hence, in this paper we adopt the more massive
estimate of Reines et al. (2008).
6 (~700 pc),
with most of the star formation activity taking place in the two brightest ones (SSC 1, 2)
to the southeast (Hunt et al. 2001; Dale et al. 2001). There are more than 10 000 O stars
within these two clusters, unresolved at Hubble Space Telescope (HST)
resolution (Thuan et al. 1997b; Reines et al. 2008). The stars in SBS 0335−052 are
mostly confined to the six SSCs, with a total mass of
~6 × 106 M⊙ (Reines et al. 2008). However, there is a faint underlying stellar component with
a mass comparable to the sum of the SSCs; Papaderos et al.
(1998) estimate a total mass including the diffuse populations of
3.1 × 106 M⊙, roughly half of that given by
Reines et al. for the clusters alone. Hence, in this paper we adopt the more massive
estimate of Reines et al. (2008).
The total amount of Hi, ~4.3 × 108 M⊙ in SBS 0335−052 E makes it extremely gas rich, even without a, as yet undetected, H2 component (Ekta et al. 2009). The global radio continuum shows a non-thermal slope (Hunt et al. 2004), but with significant free-free absorption (i.e., by dense gas) which is even more prominent at high spatial resolution. Compact rising-spectrum (optically thick) thermal radio sources are found in the vicinity of SSCs 1 and 2 (Johnson et al. 2009), together with Paα (Reines et al. 2008). Even the optical spectrum implies elevated ionized gas densities ≳500 cm-3 (Izotov et al. 1999). In the relation between star-formation rate (SFR) surface density ΣSFR, and gas surface density (the Schmidt-Kennicutt law), SBS 0335−052 E is the equivalent of a massive starburst, with SFR = 1.2 M⊙ yr-1 occurring in a region of <500 pc in diameter. Because of their physical and apparent separation, hereafter we refer to the eastern component, SBS 0335−052 E, as SBS 0335−052 without the explicit “E” suffix. Table 1 shows the basic parameters for SBS 0335−052. At the assumed distance of ~54.1 Mpc, 1′′ = 262 pc.
1.2. Another metal-poor compact dwarf galaxy, I Zw 18
In order to place SBS 0335−052 in context, in this paper we compare its dust and gas properties with another very low-metallicity star-forming dwarf galaxy, I Zw 18.
I Zw 18 is closer than SBS 0335−052, at a distance of ~18 Mpc, and like SBS 0335−052, is embedded together with a faint companion, the “C” component, in a massive Hi envelope, although smaller in extent than that of SBS 0335−052 (~16 kpc, Lelli et al. 2012). Also like SBS 0335−052, I Zw 18 is extremely gas-rich, with ~108 M⊙ of atomic gas. Star formation in I Zw 18 takes place in two massive star clusters, which together host ~1900 massive stars. These clusters are more extended than those in SBS 0335−0521 (~150−200 pc in diameter), similar to concentrations of normal OB associations in the Milky Way and the Large Magellanic Cloud (Hunter & Thronson 1995)2. The mass of stars in I Zw 18, ~1.3 × 106 M⊙ (Fumagalli et al. 2010), is about 4 times lower than in SBS 0335−052, and I Zw 18’s SFR, estimated from radio free-free emission (Hunt et al. 2005b) is 0.17 M⊙ yr-1, about 5 times lower than in SBS 0335−052. The SFR surface density ΣSFR is more than 30 times lower than in SBS 0335−052. Unlike SBS 0335−052, there is no evidence for self-absorption in the radio spectrum of I Zw 18 (Hunt et al. 2005b; Cannon et al. 2005), implying the absence of dense gas.
Both SBS 0335−052 and I Zw 18 are thought to be interacting systems, embedded within their common Hi envelope (e.g., Ekta et al. 2008). This could foster star formation in massive central star clusters as modeled by Bekki (2008), perhaps causing age gradients in the stellar populations as observed (e.g., Thuan et al. 1997b; Reines et al. 2008; Contreras Ramos et al. 2011).
1.3. Constraining cool dust in SBS0335−052
Although Balmer lines suggest that the extinction AV in SBS 0335−052 is ~0.5 mag (Thuan et al. 1997b; Vanzi et al. 2000), the near-infrared Brackett line ratios (Brγ/Brα) imply AV ~ 12 mag (Hunt et al. 2001). The form of the infrared (IR) SED also indicates high values (AV ~ 15 mag, Houck et al. 2004a), but detailed studies of the optical SEDs of the individual SSCs show that the dust must be highly clumped (Reines et al. 2008). Up to now, the total dust mass was highly uncertain (Plante & Sauvage 2002; Hunt et al. 2005a), mainly because the SED peaks at ~30 μm (Houck et al. 2004a), and there were no data available to constrain the mass in the cooler dust expected to dominate at longer wavelengths. Cool dust constitutes the largest contribution to the dust mass budget, so observations at wavelengths well longward of the peak of the SED are crucial for reliable estimates of dust mass.
In this paper, we add this critical information via observations of the 870 μm continuum emission in this low-metallicity BCD. In Sect. 2, we present the data we have acquired and compiled in order to better constrain the dust mass and gas content in SBS 0335−052. We then estimate the free-free contribution to the SED, and fit the corrected multi-wavelength SED in Sect. 3 in order to estimate the total dust mass. In Sect. 4, we fit the SED of I Zw 18 in the same way as for SBS 0335−052, and derive the dust mass and compare it with the gas content of I Zw 18 and with SBS 0335−052. Finally, in Sect. 5 we discuss the implied dust-to-gas ratio in SBS 0335−052 and I Zw 18 and compare them with other low-metallicity dwarfs and spiral galaxies. We also constrain the CO-to-H2 conversion factor and infer limits to molecular gas mass from gas scaling relations. Our conclusions are given in Sect. 6.
Basic data for SBS 0335−052.
2. Data for SBS0335−052
We have acquired Band 7 images with ALMA in Cycle 0 and also retrieved data from the Herschel archive, and combined them with data from the literature to compile a SED for SBS 0335−052 that spans almost 6 orders of magnitude in wavelength.
2.1. ALMA observations
The observations were carried out in five separate sessions from Jul. 30 through Aug. 14, 2012 with the ALMA observatory as part of Early Science Cycle 0. The average number of antennas was 24 and the array was in the Early Science extended configuration providing baselines up to 400 m. SBS 0335−052 was observed with Band 7, simultaneously in the continuum and in the 12CO(3−2) transition, with a rest frequency of 345.79599 GHz. The central sky frequencies of the upper and lower sidebands were ~352 GHz and ~340 GHz, respectively. The observations were done as 6 executions of the same scheduling block. The unresolved extragalactic source J0339−017 was used for complex gain calibration, while Callisto or Uranus were used as flux calibrators. The measured fluxes of J0339−017 during the various observing sessions were consistently found to be ~0.98 Jy and ~0.95 Jy at 340 GHz and 352 GHz, respectively. The flux density scale accuracy is expected to be better than 5%.
The full width at half maximum of the ALMA antennas’ primary beam at the observing
frequency is ~17 arcsec. The galaxy was observed in dual polarization mode with 1.875 GHz
total bandwidth per baseband, and a velocity resolution of ~0.9 km s-1. The
spectra were then smoothed to 10 km s-1 to build channel maps. The original
plan was to use the line free part of the band to measure continuum emission. As no
emission was detected in the CO(3−2) line, in the end, the full 7.5 GHz bandwidth per
polarization was used to obtain a continuum measurement centered at the average frequency
of ~346 GHz. The data were reduced, calibrated and imaged with the CASA software (v3.4,
McMullin et al. 2007). The final maps have a beam
size of 0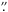 7 ×
0
7 ×
0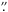 45 and PA of
79°, with a 1σ rms of 0.035 mJy/beam in the continuum.
45 and PA of
79°, with a 1σ rms of 0.035 mJy/beam in the continuum.
 |
Fig. 1 ALMA 870 μm continuum map of SBS 0335−052 shown as white contours overlaying the HST/ACS F555M image taken from Reines et al. (2008). Band 7 contours range from 1 to 2σ (σ = 0.035 mJy/beam). Black contours (ranging from 3 to 9σ, σ = 0.012 mJy/beam) give the high-resolution VLA map at 3.6 cm taken from Johnson et al. (2009). The radio and dust emission is associated with the two brightest SSCs (1, 2) toward the southeast. Beam sizes of the two contoured images are shown in the lower left corner. At the distance of SBS 0335−052, 1′′ corresponds to 262 pc. |
No CO(3−2) emission was detected. Our ALMA measurement gives a 1σ limit
of 0.8 mJy/beam in 10 km s-1 channels, which translates to 23.5 mK. Assuming
the CO line width in SBS 0335−052 is the same as that for Hi
(~50 km s-1), we obtain a 3σ upper limit on the CO(3−2) flux
of 1.58 K km s-1. Assuming an area of 1 arcsec2 subtended by the
source (see Sect. 5.1), and a CO(3−2)/CO(1−0) flux
ratio of 0.6 (see Sect. 5.2), this would give a
3σ limit of the luminosity in the CO(1−0) line
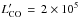 K km s-1 pc-2.
K km s-1 pc-2.
 |
Fig. 2 PACS images of SBS 0335−052 superimposed as contours on the F555M HST/ACS image shown with false colors (see also Fig. 1). From left to right are PACS 70, 100, and 160 μm maps. Contours start at 3σ and run to 22σ for PACS 70, to 20σ for PACS 100, and for PACS 160 to 8σ. These σ values correspond to the correlated noise measured from the images, which are roughly 4× smaller than the true noise (see PACS documentation and text). PACS beam sizes are shown as shaded ellipses in the upper portion of each panel. For display purposes, the PACS images have been rebinned to smaller pixel sizes. |
Figure 1 shows the ALMA Band 7 continuum map, with white contours superimposed on the HST/ACS F555M image from Reines et al. (2008). The black contours show the X-band Very Large Array (VLA) image (3.6 cm) taken from Johnson et al. (2009). The 870 μm Band 7 emission is elongated in the east-west direction, and is slightly resolved (there is a possible noise excess to the northwest). The elliptical beam shape precludes a definitive analysis of the orientation and extent of the emission. In any case, like the cm-emission, the Band 7 emission is associated with the two brightest SSCs to the southeast. The peak of the ALMA continuum lies closer to SSC 1 (the southernmost cluster) than SSC 2, although slightly offset from its optical peak.
We could be missing some diffuse low-surface brightness emission in SBS 0335−052 because of the angular-size limitations of the extended ALMA configuration. The field-of-view of our map is 17′′ (only a subset of the image is shown in Fig. 1), ~5 kpc, so clearly covers the entire galaxy and even some extended Hi emission outside the optical confines. Nevertheless, the nature of the ALMA interferometric measurement means that emission at angular scales ≳3′′ could be missed; such a spatial scale would be roughly the size of Fig. 1 or larger. Although we feel that this is unlikely in SBS 0335−052, additional flux at 870 μm would increase the dust mass we infer in Sect. 3.
2.2. Free-free emission at 870 μm in SBS 0335−052
870 μm emission can contain contributions from different physical processes: cool dust, thermal free-free emission (or bremsstrahlung) from ionized gas, and synchrotron emission from supernova remnants and their diffused non-thermal emission after longer timescales. In SBS 0335−052, synchrotron emission contributes a significant fraction of the total at long cm wavelengths and low spatial resolution (Hunt et al. 2004), but not at the highest radio frequencies observed (43 GHz, Johnson et al. 2009). Extrapolating from the 1.3 cm flux of ~0.52 mJy (Hunt et al. 2004; Johnson et al. 2009), we estimate a free-free flux at 870 μm of 0.40 ± 0.07 mJy. We can also infer the free-free emission from the Brα flux (Hunt et al. 2001), although there may be some contribution from optically-thick winds in this line (Hunt et al. 2004; Johnson et al. 2009). From Brα, we obtain a similar ALMA Band 7 flux, 0.42 ± 0.05 mJy. Taking the average of these, 0.41 mJy, we attribute ~0.06 mJy of the total ALMA Band 7 flux (0.47 mJy) to cool dust in SBS 0335−052. By adding in quadrature the uncertainties in the Band 7 continuum level and in the radio free-free flux, we obtain the uncertainty in this dust-only 870 μm flux, ~0.07 mJy, implying a very marginal detection. Nevertheless, it gives us an idea of what to expect in the SED fitting discussed in Sect. 3. Taken at face value, in SBS 0335−052 at 870 μm, there is a factor of 7 between the luminosity of the total emission including free-free, and that of the dust; ≳87% of the 870 μm emission is attributed to thermal free-free radiation.
2.3. Herschel observations
We retrieved from the Herschel Science Archive3 PACS (Photodetector Array Camera & Spectrometer4) images of SBS 0335−052, acquired in guaranteed time with proposal KPGT_smadde01_1 (ObsID 1342202302, 134220303, 134220304, 134220305, 1342237748, 134223749). PACS (Poglitsch et al. 2010) observed SBS 0335−052 at 70, 100, and 160 μm, in large-scan mode during two visits. In the first visit, observations were acquired with 10 legs in each scan map, of 3′ length, separated by 4′′, repetition factor 1 which gives a total on-source exposure time of 60 sec. In the second visit, observations were acquired with scan legs of 2′ length, repetition factor 19, for a total integration time of 1140 s. In both visits at each wavelength, in order to mitigate instrumental artefacts, two different maps were acquired at 110° and 70°, as recommended by the PACS instrument team. We reduced the observations with HIPE v.10.0 (Ott 2010), starting from the pipeline reprocessed Level 0.5 data. The “deep survey point-source" option was used, with masking performed on the images themselves before combining the repetitions and orthogonal scans into a single map. In the end, for the final maps at 100 and 160 μm, we used only the observations of the second visit, because of their superior signal-to-noise ratio; 70 μm maps were obtained only in the first visit. Figure 2 shows the three PACS maps superimposed on the HST/ACS F555M image as in Fig. 1.
We performed photometry in apertures between radius 10′′ and 14′′, and found that the flux remains stable to within a few percent in the largest apertures; however, the noise grows with aperture size, so we used the values at the 10′′ radius. Following the PACS calibration guidelines5, we adjusted the photometry for the appropriate aperture correction, and corrected the uncertainty estimates for correlated noise. Color corrections are of order unity, and within the uncertainties, so we neglected them. Uncertainties on the photometry are estimated to be ~8−9% for PACS 70 and PACS 100, including calibration and uncertainties on the sky subtraction; the source is clearly detected at 70 and 100 μm. At 160 μm, the detection is roughly at 2.9σ. Our photometry is slightly higher than, but compatible within the errors to that reported by Rémy-Ruyer et al. (2013).
In order to search for extended emission, we also reduced each of the PACS images with scanamorphos (Roussel 2013), starting from the pipeline reprocessed Level 0.5 data. The photometry of the resulting images gave in fact slightly lower fluxes with larger uncertainty, perhaps because of the slightly larger reconstructed beams. Hence, we adopt the photometry as described above, and are fairly confident that the reduction technique did not miss any extended emission at any of the PACS wavelengths.
2.4. Other multi-wavelength data
The broadband optical, near-, and mid-infrared portions of the SED were taken from the literature (Papaderos et al. 1998; Vanzi et al. 2000; Dale et al. 2001), including data from Spitzer/IRAC (InfraRed Array Camera, Fazio et al. 2004), Spitzer/IRS (InfraRed Spectrograph, Houck et al. 2004b), and Spitzer/MIPS (Multiband Imaging Photometer, Rieke et al. 2004), taken from Houck et al. (2004a) and Engelbracht et al. (2008). For use in the SED fitting, emission features (fine-structure lines) were subtracted from the Spitzer/IRS spectrum (Houck et al. 2004a), and the spectrum was then averaged over 0.5 μm bins.
Photometry from 1 to 10 μm was corrected for nebular continuum emission based on the SFR, as described in Hunt et al. (2012). The SFR was converted to free-free emission by first using the conversion factor of Kennicutt (1998) to estimate Hα luminosity, then with the coefficients in Osterbrock & Ferland (2006) to Brα and free-free and free-bound continuum levels. We compared this method based on the SFR with the directly observed Brα flux (Hunt et al. 2001) and the high-frequency radio emission (Hunt et al. 2004; Johnson et al. 2009) and obtain consistent results. This is an important correction since the free-free contribution at 2 μm is 55%, and ~20% at 3.6 and 4.5 μm. We also included in the SED the cm-wavelength radio data from Hunt et al. (2004) and from Johnson et al. (2009). Table 2 reports the photometry described above, corrected for nebular continuum where noted.
Global photometry for SBS 0335−052.
3. The spectral energy distribution of SBS0335−052
We have used the multi-wavelength dataset in Table 2 to estimate the dust mass in SBS 0335−052 by fitting a spherical DUSTY model (Ivezic & Elitzur 1997). Before fitting the SED, photometry was corrected for Galactic extinction assuming AV = 0.155 mag (taken from the NASA Extragalactic Database, NED6), and using the interstellar extinction curve by Cardelli et al. (1989). Because of the relatively large size of the IR beams (Spitzer, Herschel), we have considered the global photometry rather than that for only SSCs 1 + 2; although the optical HST data would have allowed such a separation (e.g., Reines et al. 2008), in the IR such a separation would be virtually impossible.
The DUSTY formalism solves analytically the radiative transfer problem of a spherical dust
shell heated by a point-like heating source whose immediate vicinity is devoid of dust.
Thus, our model consists of two SED components: the stellar heating spectrum and a DUSTY
spherical shell surrounding the internal radiation source. The dust re-processes a certain
fraction of the incident radiation into the IR regime, and produces the blackbody-like peak
in the total SED. The total SED is thus modeled as 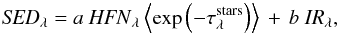 (1)where the total
SED, the heating function HFN, and the IR emission are wavelength-dependent. The stars
comprising the HFN will have different obscuring τ(V)
toward them, so we use the average of a mix of stars and dust:
(1)where the total
SED, the heating function HFN, and the IR emission are wavelength-dependent. The stars
comprising the HFN will have different obscuring τ(V)
toward them, so we use the average of a mix of stars and dust:
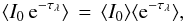 (2)where
(2)where
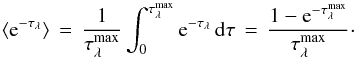 (3)The stellar
component is thus attenuated by a foreground screen of this average
(V-band) optical depth
(3)The stellar
component is thus attenuated by a foreground screen of this average
(V-band) optical depth 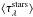 , not necessarily the same as
that of the dust itself.
, not necessarily the same as
that of the dust itself.
aand b are independently determined scales for the two components of the total SED, such that together they maximize the likelihood of the model fitting the observations. The reason behind two different normalizations is that DUSTY assumes a uniform dust cloud with a filling factor of unity. Hence, in our fits, the same DUSTY template is used to fit both stars and dust, but the relative normalization is allowed to vary in order to accommodate non-unity values of the fraction of dust that intercepts stellar light. The optical depth of the dust that reprocesses stellar radiation can be different from the optical depth of the dust that emits directly because dust may be clumpy, with the clumps having a higher opacity than the (possibly more diffuse) dust that absorbs stellar light. Once the best-fit parameters are defined, the shapes of all SED components are known, and the normalization can be found analytically (Nikutta 2012).
The optical regime of the DUSTY models requires three parameters: dust optical depth
(defined in the V band) for the stars, stellar age and metallicity. The
input parameters for the IR portion of the DUSTY models are: the temperature at the inner
part of the dust shell, Tin; the ratio of the outer shell radius
to that of the inner shell boundary,
Y ≡ Rout/Rin;
the power law index p of the dust distribution
∝R−p; and the V-band dust
optical depth 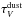 . The DUSTY
template library includes HFNs modeled as the single stellar population models of Bruzual & Charlot (2003) at three different
metallicities (0.02 Z⊙, 0.1 Z⊙, and
Z⊙) and 12 different ages from 1 Myr to 10 Gyr, assuming a
Chabrier (2003) Initial Mass Function. Also
included in the library are three different dust grain populations: Milky-Way dust (Draine & Li 2007), dust in the Small Magellanic
Cloud (SMC; Weingartner & Draine 2001), and
chemically unevolved dust in primordial supernovae (SNe; Bianchi & Schneider 2007).
. The DUSTY
template library includes HFNs modeled as the single stellar population models of Bruzual & Charlot (2003) at three different
metallicities (0.02 Z⊙, 0.1 Z⊙, and
Z⊙) and 12 different ages from 1 Myr to 10 Gyr, assuming a
Chabrier (2003) Initial Mass Function. Also
included in the library are three different dust grain populations: Milky-Way dust (Draine & Li 2007), dust in the Small Magellanic
Cloud (SMC; Weingartner & Draine 2001), and
chemically unevolved dust in primordial supernovae (SNe; Bianchi & Schneider 2007).
We find the best fits and the range of model parameter values compatible with the data via exploration of the seven-dimensional (7D) parameter space with an efficient Markov chain Monte Carlo code7. The three different dust-grain populations are fitted separately, and results are compared a posteriori. The HFNs and IR SEDs are tabulated on a 7D-rectilinear parameter grid, then interpolated for the specific trial parameters using the implementation from Nikutta (2012). We calculate the likelihood of each model assuming Gaussian flux errors on the measurements. The absolute normalization of the total posterior is irrelevant for the parameter estimation problem.
For most of the parameters to be fit, we assumed uniform prior probability density functions. However, we constrained the metallicity to be close to that measured by Izotov et al. (1999), 0.0347 ± 0.014 Z⊙. We imposed a truncated Gaussian as a prior, centered at 0.0347 M⊙, with a width equal to the 1σ uncertainty (truncated at the 1σ limits). The final fit gives the best-fit parameters (the normalized marginalized posteriors) and their confidence intervals.
3.1. SED-fitting results
Figure 3 shows the best-fit DUSTY model for the SED of SBS 0335−052. The radio emission has been approximated using a spectral index of α = −0.1, appropriate for pure thermal emission. The radio emission is generally well fit by such a spectrum, although at low frequencies the spectrum is self-absorbed by the dense gas in the radio nebulae and the synchrotron component begins to be significant (Hunt et al. 2004; Johnson et al. 2009).
 |
Fig. 3 SED of SBS 0335−052, together with best-fit DUSTY model overlaid. The two large (red) circles show the total ALMA Band 7 emission; the dust-only emission, estimated as described in the text, is indicated by the open (red) circle. The black curve represents the DUSTY fit, and the dotted (red) curve, only the dust; the long-dashed (blue) curve shows the stars. The radio slope is pure free-free, ∝ν-0.1, and the pure radio component is shown by a short-dashed (purple) line (longward of 250 μm). DUSTY models only extend to 1 mm, so the excess above the dust-only emission is the extrapolation of the radio. When not evident, the error bars are masked by the size of the symbols. |
The SED of SBS 0335−052 is very warm; as already noted by Houck et al. (2004a), the SED peaks between 20 and 30 μm, even
more extreme than the 60 μm-peaker galaxy population discovered with the
Infrared Astronomical Satellite (IRAS; Vader et al.
1993). The temperature at the inner radius of the shell is
497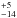 K;
this relatively high temperature is necessary to fit the rapidly-rising mid-infrared
portion of the spectrum. This short-wavelength peak combined with the intense star-forming
event makes it difficult to detect the cool dust in the SEDs of metal-poor dwarf
starbursts.
K;
this relatively high temperature is necessary to fit the rapidly-rising mid-infrared
portion of the spectrum. This short-wavelength peak combined with the intense star-forming
event makes it difficult to detect the cool dust in the SEDs of metal-poor dwarf
starbursts.
 |
Fig. 4 Modified single-temperature blackbody fits with fixed β of SBS 0335−052 (left panel) and I Zw 18 (right panel). The blue + signs show unfitted points; the upper limit at 850 μm for I Zw 18 was not fit either. In the right panel, the MIPS and PACS 70 μm points are so close in wavelength and measured flux that they are virtually indistinguishable. Details for I Zw 18 are given in Sect. 4. |
The best-fit stellar population age is 13.1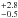 Myr,
at the lowest metallicity sampled (2% Z⊙). This age is
consistent with the oldest of the SSC ages estimated by Reines et al. (2008). In fact, there is an age gradient in the clusters that
could be as large as 25 Myr from the oldest (toward the northwest) to the youngest (in the
southeast, Thuan et al. 1997b), or even larger
(Papaderos et al. 1998). Thus, an age of 13 Myr
seems like a reasonable compromise for our global photometry which is a
luminosity-weighted average. The stars themselves suffer from a total extinction
Myr,
at the lowest metallicity sampled (2% Z⊙). This age is
consistent with the oldest of the SSC ages estimated by Reines et al. (2008). In fact, there is an age gradient in the clusters that
could be as large as 25 Myr from the oldest (toward the northwest) to the youngest (in the
southeast, Thuan et al. 1997b), or even larger
(Papaderos et al. 1998). Thus, an age of 13 Myr
seems like a reasonable compromise for our global photometry which is a
luminosity-weighted average. The stars themselves suffer from a total extinction
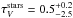 ,
significantly smaller than the optical depth of the dust clouds (see below). The stellar
mass can be inferred from the DUSTY fit, and we find
Mstar = 2.35 × 107 M⊙,
from the V-band luminosity of
5.6 × 108 L⊙ (corrected for extinction) and
assuming a V-band mass-to-light ratio (M/LV) of 0.04 (Bruzual & Charlot 2003), appropriate for a
13 Myr stellar population. This is 4 times greater than the mass given by Reines et al. (2008), obtained by fitting broadband
optical-near-infrared SEDs of the 6 individual SSCs with single stellar population models
(see also Fumagalli et al. 2010). However, the age
found by DUSTY corresponds to the oldest cluster, which would have a M/LV ratio
4 times larger than a 4 Myr population. When we impose a prior on the stellar age (in the
range of 3 to 6 Myr), the DUSTY fit returns a best-fit age of 4 Myr and a
V-band luminosity of
6.8 × 108 L⊙ (also corrected for extinction).
With M/LV = 0.01,
appropriate for 4 Myr, we find a stellar mass of
6.8 × 106 M⊙, only 20% more than the Reines et
al. value. We thus conclude that the DUSTY stellar mass is roughly consistent with earlier
estimates.
,
significantly smaller than the optical depth of the dust clouds (see below). The stellar
mass can be inferred from the DUSTY fit, and we find
Mstar = 2.35 × 107 M⊙,
from the V-band luminosity of
5.6 × 108 L⊙ (corrected for extinction) and
assuming a V-band mass-to-light ratio (M/LV) of 0.04 (Bruzual & Charlot 2003), appropriate for a
13 Myr stellar population. This is 4 times greater than the mass given by Reines et al. (2008), obtained by fitting broadband
optical-near-infrared SEDs of the 6 individual SSCs with single stellar population models
(see also Fumagalli et al. 2010). However, the age
found by DUSTY corresponds to the oldest cluster, which would have a M/LV ratio
4 times larger than a 4 Myr population. When we impose a prior on the stellar age (in the
range of 3 to 6 Myr), the DUSTY fit returns a best-fit age of 4 Myr and a
V-band luminosity of
6.8 × 108 L⊙ (also corrected for extinction).
With M/LV = 0.01,
appropriate for 4 Myr, we find a stellar mass of
6.8 × 106 M⊙, only 20% more than the Reines et
al. value. We thus conclude that the DUSTY stellar mass is roughly consistent with earlier
estimates.
Because there is a clear silicate absorption feature at 9.7 μm (Houck et al. 2004a), the dust must contain silicates;
SMC dust is the grain population that provides the best fit. To reproduce this feature in
absorption, it is necessary to have a relatively large quantity of cool dust in front of
the massive stars heating the dust. This is naturally achieved in DUSTY through a large
dust optical depth, τdust, with a relatively thick shell and a
large power-law index. In the case of SBS 0335−052, the best-fit
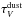 = 11.8
= 11.8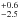 ;
the shell relative thickness
Y = Rout/Rin
is 605
;
the shell relative thickness
Y = Rout/Rin
is 605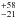 ,
and the power-law index of the radial dust distribution
(∝R−p),
,
and the power-law index of the radial dust distribution
(∝R−p),
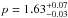 .
With a thinner shell and a less steep (more uniform) radial dust distribution, the
silicate feature would emerge in emission rather than in absorption.
.
With a thinner shell and a less steep (more uniform) radial dust distribution, the
silicate feature would emerge in emission rather than in absorption.
From the best-fit DUSTY model we obtain the dust mass, since the geometry of the dust and
the optical properties of the grains are known. We find that there are
(3.8 ± 0.6) × 104 M⊙ of dust in
SBS 0335−052. The normalization of the DUSTY models also gives the diameter of the
dust-emitting region, 2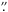 4 or ~660 pc,
comparable to the region (~2
4 or ~660 pc,
comparable to the region (~2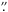 1) emitting
faint Paα (Reines et al. 2008).
1) emitting
faint Paα (Reines et al. 2008).
We performed two “sanity checks” for the derived dust mass: first, we performed a single-temperature modified blackbody fit (MBB) with variable emissivity, Fν ∝ νβ B(T,ν), where B(T,ν) is the Planck function. The MBB fitting was performed by fixing β to 2 because otherwise dust mass estimates are unreliable due to the dust opacities which are calibrated with roughly this value (Bianchi 2013). Allowed temperatures ranged from 5 K to 100 K because color corrections for PACS and MIPS are well defined only over this temperature range (e.g., Aniano et al. 2012). This fit8, shown in Fig. 4, results in a temperature T = 59 ± 1 K. Using this fit at 100 μm and assuming the SMC emissivity, we find a dust mass of 3.4 × 103 M⊙, a factor of 10 lower than the DUSTY value. However, Fig. 4 shows that the single-T MBB fit misses a large fraction of the warmer dust, and does not pass through the ALMA point so it is very likely that a significant fraction of cooler dust is also missing. We thus conclude that the DUSTY value is not unreasonable.
As a second check, we compared the DUSTY mass with that inferred from the dust optical depth at 870 μm. Assuming the mean dust temperature of ~59 K given by the MBB fit, and a mass coefficient at 870 μm for SMC dust of κν = 4.5 m2 kg-1 (Weingartner & Draine 2001), we obtain a dust mass surface density of Σdust = 0.45 M⊙ pc-2. The integrated area of the region with ALMA Band 7 emission ≥3σ is ~1 arcsec2. We would thus estimate a total dust mass of 3.1 × 104 M⊙, well within the uncertainties of the total dust mass given by the DUSTY fit. The dust mass surface density of ~0.75 M⊙ pc-2 inferred from the silicate optical depth τ9.7 (~0.46, Houck et al. 2004a) is higher than that from the 870 μm dust emission. This is perhaps not surprising because the dust traced at 9.7 μm in absorption is expected to be more concentrated (e.g., Dale et al. 2001).
 |
Fig. 5 Ratios of dust mass to stellar mass plotted against stellar mass (Mstar, left panel) and specific SFR (yr-1, right). SBS 0335−052 and I Zw 18 are plotted as filled (blue) circles. Data for KINGFISH galaxies, taken from Kennicutt et al. (2011), are also shown: × (for late Hubble types T ≥ 8), filled (green) triangles (0 < T < 8), and filled (red) circles (for early Hubble types T ≤ 0). The horizontal lines give the mean dust/stellar mass ratio for the KINGFISH sample, and the 1σ standard deviation. Given as open (magenta) squares are the passive spirals studied by Rowlands et al. (2012) and as filled (magenta) squares their early-type galaxies. |
Our estimate of the dust mass in SBS 0335−052 is more than 40 times higher than the value
of 800 M⊙ given by Rémy-Ruyer
et al. (2013). There are several reasons for this. The first, most obvious one,
is that they use an emissivity at 100 μm
κν = 4.5 m2 kg-1,
~30% higher than the best-fit SMC dust with
κν = 3.47 m2 kg-1
(Weingartner & Draine 2001). With this
emissivity, Rémy-Ruyer et al. (2013) would have
obtained 1037 M⊙, rather than
800 M⊙. Second, they included the 24 μm
point in their single-temperature MBB fit which skews fitted temperatures to higher
values, thus lowering the inferred dust mass. Indeed, if we repeat our MBB fit to the
fluxes in Table 2 letting β vary
and including the 24 μm point, we obtain
T = 87.5 K, β = 1.2, similar to
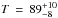 K
and
K
and 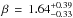 given by Rémy-Ruyer et al. (2013). Our MBB fit
including the 24 μm point would correspond to a dust mass of
1.4 × 103 M⊙, only 35% higher than the value of
Rémy-Ruyer et al. (2013) with the SMC emissivity,
but less than half the value we obtain without including the 24 μm point.
The inclusion of the 24 μm point leads to lower dust masses because of
the invalidity of the assumption of a single temperature (e.g., Dale et al. 2012). In the radial temperature profile given by the DUSTY
fit of SBS 0335−052, dust temperatures fall to ~20 K in the regions farthest from the
radiation source even though the innermost dust is very warm, ~500 K.
given by Rémy-Ruyer et al. (2013). Our MBB fit
including the 24 μm point would correspond to a dust mass of
1.4 × 103 M⊙, only 35% higher than the value of
Rémy-Ruyer et al. (2013) with the SMC emissivity,
but less than half the value we obtain without including the 24 μm point.
The inclusion of the 24 μm point leads to lower dust masses because of
the invalidity of the assumption of a single temperature (e.g., Dale et al. 2012). In the radial temperature profile given by the DUSTY
fit of SBS 0335−052, dust temperatures fall to ~20 K in the regions farthest from the
radiation source even though the innermost dust is very warm, ~500 K.
A third reason for the difference in dust masses is that the dust in SBS 0335−052 is not optically thin at short wavelengths, as implicitly assumed in the use of MBB fits. The clear silicate absorption feature and the behavior of the SED as modeled by DUSTY are signatures of the optical thickness of the dust radiation and the importance of radiative transfer. A fourth reason is that by letting β vary in the MBB fits as done by Rémy-Ruyer et al. (2013), long-wavelength constraints become important. When we fix β to 1.6 as in Rémy-Ruyer et al. (2013), we obtain roughly the same value of dust mass as for β = 1.2 (our best-fit β value, see above). When we let β vary in the MBB fitting, our data result in a flatter β slope because of the added constraint of 870 μm. On the other hand, when β is fixed, the need to accommodate longer-wavelength constraints with steeper (larger values of) β will lead to lower temperatures and consequently larger dust masses (e.g., Bianchi 2013).
The dust mass from the best-fit DUSTY model, 3.8 × 104 M⊙, gives a dust-to-stellar mass ratio of ~0.007 (assuming the stellar mass from Reines et al. 2008, see above). Ratios of dust-to-stellar mass for SBS 0335−052 are compared in Fig. 5 to the KINGFISH (Kennicutt et al. 2011) sample of galaxies and to passive spirals and early-type galaxies from H-ATLAS/GAMA (Rowlands et al. 2012). Also shown is I Zw 18 (see Sect. 4). H-ATLAS/GAMA values are derived from optical-infrared SED fitting. For KINGFISH, stellar parameters are taken from Kennicutt et al. (2011), or when not available, from Skibba et al. (2011) rescaled to the correct distances; dust masses are derived by Bianchi (2013). Since in these galaxies dust is usually spatially coincident with the stars, we have used global values for both sets of masses. Figure 5 shows that there is considerable scatter at low stellar masses, Mstar, but for more massive galaxies with Mstar≳ 1010 M⊙, dust-to-stellar mass ratios tend to be lower than at the low-mass end. The ratio for SBS 0335−052 is within the range of the KINGFISH galaxies (see also Cortese et al. 2012).
The right panel of Fig. 5 shows the dust-to-stellar mass ratios plotted against specific SFR, the ratio of SFR to Mstar (sSFR). As found by da Cunha et al. (2010), these two quantities are well correlated. Such a correlation would be expected if dust is broadly tracing the ISM content (i.e., mostly gas with approximately the same dust-to-gas ratio, see for example Eales et al. 2012). Galaxies with higher sSFR would be in earlier evolutionary stages with a higher ISM fraction. SBS 0335−052 has a sSFR ~ 100 times higher than the highest sSFR in the KINGFISH sample which implies that it is in a very early phase of its evolution. The comparison with the KINGFISH and H-ATLAS/GAMA samples shows that the galaxies with the highest sSFRs, including SBS 0335−052, generally have high dust-to-stellar mass ratios. While it would be tempting to draw a regression line between dust-to-stellar mass ratios and sSFR, models suggest that for sSFR ≳ 10-9 yr-1, the dust content falls (e.g., Calura et al. 2008; da Cunha et al. 2010). The early evolutionary stages implied by high sSFRs would presumably be in the dust-formation phase of the ISM, implying that the overall dust content is lower relative to later more evolved stages of evolution.
Figure 6 plots dust-to-stellar mass ratios vs. nebular oxygen abundance, 12 + log (O/H)9. The mass ratios are less well correlated with metallicity than with stellar mass or sSFR. SBS 0335−052 and I Zw 18 (see next section) have a similarly low metallicity, being among the most metal-poor star-forming galaxies in the Local Universe, but their dust-to-stellar ratios differ dramatically; however both galaxies have ratios that are similar to those of galaxies more than 30 times more metal-rich. Metallicity may be less important than other parameters for driving star-formation processes (e.g., Hunt et al. 2012).
 |
Fig. 6 Ratios of dust mass to stellar mass plotted against nebular 12 + log (O/H). SBS 0335−052 and I Zw 18 are plotted as filled (blue) circles. As in Fig. 5, data for KINGFISH galaxies (see text) are also shown: × (for Hubble type T ≥ 8), filled (green) triangles (0 < T < 8), and filled (red) circles (T ≤ 0). The horizontal lines give the mean dust/stellar mass ratio for the KINGFISH sample, and the 1σ standard deviation. |
4. Comparison with I Zw 18
As outlined in the Introduction, we wish to compare SBS 0335−052 with another very low-metallicity star-forming dwarf galaxy, I Zw 18. Here we describe the data we have assembled for the SED of I Zw 18, and the results from fitting it with the same DUSTY algorithm used for SBS 0335−052.
4.1. Herschel data for I Zw 18
We acquired from the Herschel Science Archive images of I Zw 18, acquired in guaranteed time with proposal KPGT_smadde01_1 (ObsID 1342209354, 1342209355, 1342209356, 1342209357) and in open time with proposal OT2_dfisher_1 (ObsID 1342245936, 1342245937). For 100 and 160 μm, we used only the latter observations as including also the former did not improve the noise characteristics of the final images. The data were reduced to Level 1 with HIPE v.10.0 (Ott 2010), starting from the pipeline reprocessed Level 0.5 data, but because of the need for conserving extended emission, we used scanamorphos (Roussel 2013) to create the final images shown in Fig. 7.
 |
Fig. 7 PACS images of I Zw 18 superimposed as contours on the F606W HST/ACS image shown with false colors. From left to right are PACS 70, 100, and 160 μm. Contours start at 3σ, and run to 7σ for PACS 70, to 16σ for PACS 100, and for PACS 160 to 2σ. As in Fig. 2, these σ values correspond to the correlated noise measured from the images, which are smaller than the true noise (see text). |
4.2. I Zw 18 photometry
We also downloaded the Spitzer/MIPS 24, 70, and 160 μm datasets, and combined the individual images into mosaics with MOPEX (Makovoz & Marleau 2005). The emission in the 24 μm image extended to radii of 12−13′′, which dictated the apertures we used for photometry. We used the 24 μm photometry to check if the IRS spectrum was missing flux because of the ~11′′ widths of the long-wavelength slits. After applying the MIPS aperture correction of 1.15, the measured flux of 6.3 mJy agrees very well with the 24 μm flux of 6.1−6.5 mJy measured by IRS.
The MIPS and PACS photometry was performed over apertures of radius 13′′, 1.6
times the optical radius (~8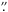 1). As for
SBS 0335−052, we corrected the PACS photometry and uncertainties for the aperture
correction and correlated noise because of non-independent pixels. Color corrections are
of order unity, so as for SBS 0335−052, we did not apply them. Uncertainties on the
photometry are estimated to be 6−7% for PACS 70 and ~4% for PACS 100, including
calibration and uncertainties of the sky subtraction. For MIPS photometry, we applied
aperture and color corrections as described in the MIPS data reduction guide. Final
uncertainties for MIPS including sky and calibration uncertainties are estimated to be
~11% at 24 μm, and ~14% at 70 μm, slightly higher than
those quoted by Engelbracht et al. (2008) and Herrera-Camus et al. (2012), respectively. Our
photometry agrees very well with these previous estimates.
1). As for
SBS 0335−052, we corrected the PACS photometry and uncertainties for the aperture
correction and correlated noise because of non-independent pixels. Color corrections are
of order unity, so as for SBS 0335−052, we did not apply them. Uncertainties on the
photometry are estimated to be 6−7% for PACS 70 and ~4% for PACS 100, including
calibration and uncertainties of the sky subtraction. For MIPS photometry, we applied
aperture and color corrections as described in the MIPS data reduction guide. Final
uncertainties for MIPS including sky and calibration uncertainties are estimated to be
~11% at 24 μm, and ~14% at 70 μm, slightly higher than
those quoted by Engelbracht et al. (2008) and Herrera-Camus et al. (2012), respectively. Our
photometry agrees very well with these previous estimates.
I Zw 18 is clearly detected at 70 (MIPS, PACS) and 100 μm (PACS). At 160 μm with PACS, the detection is marginal, ~2.4σ (see Fig. 7). Our photometry is consistent with that reported by Rémy-Ruyer et al. (2013) for 70 and 100 μm. Using shallower images, both Rémy-Ruyer et al. (2013) and Herrera-Camus et al. (2012) report non-detections at 160 μm: the former give a 5σ upper limit of 11 mJy, and the latter a 3σ limit of 27.2 mJy, both consistent with our measurement based on deeper data.
Basic data for I Zw 18 are reported in Table 3, and the compiled SED data are given in Table 4. At the assumed distance of 18.2 Mpc, 1′′ = 88 pc.
4.3. Fitting the SED of I Zw 18
As for SBS 0335−052, before fitting the SED, it was necessary to correct the photometry
from 1−10 μm for nebular emission. Based on I Zw 18’s
SFR = 0.17 M⊙ yr-1 (Hunt et al. 2005b, scaled to
D = 18.2 Mpc), this turns out to be an important correction: ~50% of the
3.6 μm and 4.5 μm emission is from nebular continuum +
Brα. I Zw 18 is extended at short IRS wavelengths (see Wu et al. 2007), and judging from the IRAC global
photometry, the 3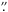 6 aperture for
the IRS short-low spectral range misses 50% or more of the emission. Hence, the free-free
subtraction resulted in unrealistically low fluxes, so we did not consider in the SED
fitting the short-wavelength IRS fluxes ≲10 μm. The 2.6 mm flux observed
by Leroy et al. (2007) is also contaminated by
free-free emission; extrapolating from the thermal fraction (47%) of the 8.4 GHz radio
continuum (Hunt et al. 2005b; Cannon et al. 2005) gives a free-free component at 115 GHz of 0.37 mJy.
Leroy et al. (2007) estimate that the free-free
flux at 115 GHz is between 0.36 and 0.51 mJy, which means that from 35% to 48% of the
observed flux [(1.06 ± 0.35) mJy] is bremsstrahlung.
6 aperture for
the IRS short-low spectral range misses 50% or more of the emission. Hence, the free-free
subtraction resulted in unrealistically low fluxes, so we did not consider in the SED
fitting the short-wavelength IRS fluxes ≲10 μm. The 2.6 mm flux observed
by Leroy et al. (2007) is also contaminated by
free-free emission; extrapolating from the thermal fraction (47%) of the 8.4 GHz radio
continuum (Hunt et al. 2005b; Cannon et al. 2005) gives a free-free component at 115 GHz of 0.37 mJy.
Leroy et al. (2007) estimate that the free-free
flux at 115 GHz is between 0.36 and 0.51 mJy, which means that from 35% to 48% of the
observed flux [(1.06 ± 0.35) mJy] is bremsstrahlung.
The Spitzer/IRS spectrum (not included in Table 4) is taken from Wu et al. (2007), and it was averaged over 1 μm bins after subtracting emission lines. As for SBS 0335−052, to fit the SED we imposed only a prior on metallicity. The result of the SED fitting is shown in Fig. 8. The radio emission is approximated by a radio spectral index of α = −0.25, slightly steeper than pure thermal emission because of a global synchrotron component (Hunt et al. 2005b).
Basic data for I Zw 18.
Global photometry for I Zw 18.
 |
Fig. 8 SED of I Zw 18, together with best-fit DUSTY model overlaid. The large open (red) circle shows the dust-only emission taken from Leroy et al. (2007), while the small filled (blue) circle above it shows the total 2.6 mm emission. The black curve represents the DUSTY fit, and the dotted (red) curve, only the dust; the long-dashed (blue) curve shows the stars. The error bars are masked by the size of the symbols. As in Fig. 3, DUSTY models only extend to 1 mm, so the excess above the dust-only emission is the extrapolation of the radio with a spectral index of −0.25 (see text). The pure radio component is shown by a short-dashed (purple) line (longward of 250 μm). |
Like the SED of SBS 0335−052, I Zw 18’s SED is warm; it peaks between 50 and
60 μm. The DUSTY fit fails to fit the estimated dust-only emission at
2.6 mm, and the prediction of the fit is such that dust would be impossible to detect at
this relatively long wavelength10. The temperature
at the inner radius of the shell is 850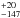 K,
warmer than in SBS 0335−052; this temperature is the maximum probed by our DUSTY template
library, so perhaps it is even a lower limit. The shell is about 5 times thinner than for
SBS 0335−052,
Y ≡ Rout/Rin
132
K,
warmer than in SBS 0335−052; this temperature is the maximum probed by our DUSTY template
library, so perhaps it is even a lower limit. The shell is about 5 times thinner than for
SBS 0335−052,
Y ≡ Rout/Rin
132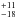 vs. Y ~ 600. Unlike SBS 0335−052, there is no signature of silicate
absorption in the SED of I Zw 18; in fact the best-fitting dust is that produced by
primordial Population III SNe (Bianchi & Schneider
2007) rather than the SMC dust that gave the best fit for SBS 0335−052. It was
impossible to fit the SED of I Zw 18 with either the Milky Way dust or the SMC dust as
given by Weingartner & Draine (2001); this
could be because of an intrinsic low silicate abundance in I Zw 18 since the SNe dust used
in our models (Bianchi & Schneider 2007)
contains no silicate grains.
vs. Y ~ 600. Unlike SBS 0335−052, there is no signature of silicate
absorption in the SED of I Zw 18; in fact the best-fitting dust is that produced by
primordial Population III SNe (Bianchi & Schneider
2007) rather than the SMC dust that gave the best fit for SBS 0335−052. It was
impossible to fit the SED of I Zw 18 with either the Milky Way dust or the SMC dust as
given by Weingartner & Draine (2001); this
could be because of an intrinsic low silicate abundance in I Zw 18 since the SNe dust used
in our models (Bianchi & Schneider 2007)
contains no silicate grains.
The best-fit stellar age is 18.3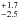 Myr,
≈2% solar metallicity, and with no measurable extinction. This age is compatible with the
mix of ages obtained from fitting the global optical+NIR photometry (Hunt et al. 2003). The implied stellar mass given by the
V-band luminosity of
6.56 × 107 L⊙, and
M/LV = 0.028 (for a
stellar population 18 Myr old, Bruzual & Charlot
2003) is 1.82 × 106 M⊙, roughly consistent
with the stellar mass of 1.34 × 106 M⊙ found by
Fumagalli et al. (2010) using broad-band colors.
The V-band dust optical depth
Myr,
≈2% solar metallicity, and with no measurable extinction. This age is compatible with the
mix of ages obtained from fitting the global optical+NIR photometry (Hunt et al. 2003). The implied stellar mass given by the
V-band luminosity of
6.56 × 107 L⊙, and
M/LV = 0.028 (for a
stellar population 18 Myr old, Bruzual & Charlot
2003) is 1.82 × 106 M⊙, roughly consistent
with the stellar mass of 1.34 × 106 M⊙ found by
Fumagalli et al. (2010) using broad-band colors.
The V-band dust optical depth 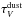 given by
the DUSTY fit is 72
given by
the DUSTY fit is 72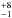 ,
quite high, typical of thick clouds. However, the relative normalizations of the two DUSTY
components (see Eq. (1)) implies that only
3% of the dust intercepts the stellar emission. Hence, the dust must be highly clumped.
,
quite high, typical of thick clouds. However, the relative normalizations of the two DUSTY
components (see Eq. (1)) implies that only
3% of the dust intercepts the stellar emission. Hence, the dust must be highly clumped.
The total dust mass in I Zw 18 given by the DUSTY fit is (3.4 ± 1.0) × 102 M⊙, an extremely small value. However, it is roughly consistent with what would be expected compared with SBS 0335−052. The IR luminosity of I Zw 18 (2.0 × 107 L⊙) is about 80 times lower than that of SBS 0335−052 (1.6 × 109 L⊙, see Tables 1 and 3). This means for the same dust mass-to-light (M/L) ratio (i.e., for the same mean dust temperature), I Zw 18 should have ~1/80 of the dust mass of SBS 0335−052, ~475 M⊙. Since I Zw 18 has a hotter temperature as inferred from the higher value of Tin from the DUSTY fit (and as discussed in the following), the dust mass would be even lower (because of the reduced dust M/L), thus consistent with the ~340 M⊙ of dust we obtain from the DUSTY fit.
Again, as a “sanity” check, we performed a single-temperature MBB fit11 of the SED, as shown in the right panel of Fig. 4. As for SBS 0335−052, fixing β = 2 and letting T vary between 5 K and 100 K in order to apply MIPS and PACS color corrections, we obtain a best-fit temperature of I Zw 18 of T = 67 ± 2.4 K, warmer than SBS 0335−052 (T = 59 ± 1.0 K). With the SNe dust emissivity at 100 μm (a clear detection), we would estimate dust mass of ~130 M⊙, a factor of ~3 lower than the DUSTY value. Judging from Fig. 4, unlike in SBS 0335−052, the single-T MBB fit for I Zw 18 is missing a small fraction of dust; in fact, this fit slightly overshoots the IRS portion of the SED. Nevertheless, both the MBB and DUSTY fits may be missing some cool dust mass because of the lack of constraints at longer wavelengths (≳300 μm).
There is some degeneracy in the I Zw 18 DUSTY fits, in the sense that large Y (Rout/Rin) and small τdust12 give a similar SED to small Y and large τdust (which is the best-fit model). Such a degeneracy is only possible in the case of featureless SNe dust, because any dust with significant silicates would produce a deep absorption feature at ~10 μm with large τdust. The large Y-small τdust fits of I Zw 18 give a factor of 3 less dust (~100 M⊙) than small Y-large τdust. The quality assessment of the small Y-large τdust fit of I Zw 18 shows that it is statistically superior, so the larger dust mass seems more probable. Nevertheless, there is significant uncertainty in the dust mass for I Zw 18.
Our value of Mdust for I Zw 18 is roughly consistent with the measurement by Fisher et al. (2013), given their range of acceptable values and the difference in dust emissivity for the Milky Way used by them (Draine & Li 2007) relative to the best-fit SNe dust. At 100 μm κν for the Milky Way is ~40% lower than for the best-fit SNe dust, causing their lower limit of 450 M⊙ to become 326 M⊙, close to our value of 342 M⊙.
5. Dust and gas in low-metallicity starbursts
We have found ~4 × 104 M⊙ of dust in SBS 0335−052, and an amount of dust more than 100 times lower in I Zw 18. Such a result is unexpected because both BCDs have roughly the same metallicity and are equally rich in gas. The ratio of Hi to stellar mass in SBS 0335−052 is 76 and 75 for I Zw 18. This means that the baryonic mass is dominated by atomic hydrogen; Hi comprises ~99% of the total baryonic mass (without considering a potential molecular gas component), and will potentially provide a vast amount of fuel for future star formation.
5.1. Dust-to-gas ratios
The dust-to-gas mass ratio,  ,
is a measure of the metals bound up in dust grains.
,
is a measure of the metals bound up in dust grains.
 should follow the balance of dust formation processes and grain destruction from SNe
explosions and other violent events in the ISM. If the interstellar abundances of heavy
elements were proportional to the gas-phase oxygen abundance O/H, we would expect a trend
of
should follow the balance of dust formation processes and grain destruction from SNe
explosions and other violent events in the ISM. If the interstellar abundances of heavy
elements were proportional to the gas-phase oxygen abundance O/H, we would expect a trend
of  with 12 + log (O/H), under the assumption that the fraction of metals in dust does not
vary from galaxy to galaxy. Such a correlation has been shown to hold in local galaxies
(e.g., Draine et al. 2007; Galametz et al. 2011; Leroy et al.
2011) and at high redshift (e.g., Santini et al.
2010; Magdis et al. 2011).
with 12 + log (O/H), under the assumption that the fraction of metals in dust does not
vary from galaxy to galaxy. Such a correlation has been shown to hold in local galaxies
(e.g., Draine et al. 2007; Galametz et al. 2011; Leroy et al.
2011) and at high redshift (e.g., Santini et al.
2010; Magdis et al. 2011).
 |
Fig. 9 Dust-to-gas mass ratios |
While measurements of dust-to-gas ratios at low metallicity are becoming more frequent
(e.g., Chen et al. 2013), up to now there have been
no reliable estimates of dust masses at 12 + log (O/H) ≲ 8 (Draine et al. 2007; Galametz et al.
2011). Here we add SBS 0335−052 and I Zw 18 to the available datasets, and test
whether the correlation between  and O/H extends to these low abundances. The main problem with such a test is that the
total gas mass estimate is missing the molecular component; this point will be discussed
further in Sect. 5.2. If we take the total
Hi mass in SBS 0335−052 from Ekta et al.
(2009), integrated over a region ≳2.5 kpc2 (several
4 × 3 arcsec2 beams, see Table 1), we
obtain
and O/H extends to these low abundances. The main problem with such a test is that the
total gas mass estimate is missing the molecular component; this point will be discussed
further in Sect. 5.2. If we take the total
Hi mass in SBS 0335−052 from Ekta et al.
(2009), integrated over a region ≳2.5 kpc2 (several
4 × 3 arcsec2 beams, see Table 1), we
obtain 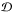 = 8.9 × 10-5,
which would be well below the linear trend of
= 8.9 × 10-5,
which would be well below the linear trend of 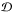 with O/H. However, as noticed by Draine et al.
(2007), it is important to consider the gas mass in the same region as the dust;
otherwise
with O/H. However, as noticed by Draine et al.
(2007), it is important to consider the gas mass in the same region as the dust;
otherwise 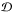 will be unfairly underestimated. Therefore, to calculate the gas mass we relied on column
densities rather than the total Hi masses given in Tables 1 and 3. The dust in SBS 0335−052
subtends an area of ~1 arcsec2, and the Hi column density (measured in
UV absorption) in a 2 × 2 arcsec2 aperture is
~56 M⊙ pc-2 (Thuan & Izotov 1997a). Hence, the total Hi mass in the region
where dust coexists is 3.85 × 106 M⊙, and
will be unfairly underestimated. Therefore, to calculate the gas mass we relied on column
densities rather than the total Hi masses given in Tables 1 and 3. The dust in SBS 0335−052
subtends an area of ~1 arcsec2, and the Hi column density (measured in
UV absorption) in a 2 × 2 arcsec2 aperture is
~56 M⊙ pc-2 (Thuan & Izotov 1997a). Hence, the total Hi mass in the region
where dust coexists is 3.85 × 106 M⊙, and
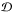 = 0.0099.
This gives the same
= 0.0099.
This gives the same 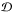 as dividing the dust column density (0.55 M⊙ pc-2)
by the Hi column (56 M⊙ pc-2). Applying
the same reasoning to I Zw 18, we find
as dividing the dust column density (0.55 M⊙ pc-2)
by the Hi column (56 M⊙ pc-2). Applying
the same reasoning to I Zw 18, we find 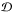 = 3.4 × 10-6,
assuming that both dust and gas subtend a circular region 8′′ (700 pc) in
radius. We would obtain the same value if we divided the total dust mass
(3.4 × 102 M⊙) by the total Hi mass
(1 × 108 M⊙), implying mean dust and Hi
column densities in I Zw 18 of
2.2 × 10-4 M⊙ pc-2 and
64 M⊙ pc-2, respectively.
= 3.4 × 10-6,
assuming that both dust and gas subtend a circular region 8′′ (700 pc) in
radius. We would obtain the same value if we divided the total dust mass
(3.4 × 102 M⊙) by the total Hi mass
(1 × 108 M⊙), implying mean dust and Hi
column densities in I Zw 18 of
2.2 × 10-4 M⊙ pc-2 and
64 M⊙ pc-2, respectively.
Figure 9 plots dust-to-gas mass ratios for four samples of galaxies taken from the literature, together with our new estimates for SBS 0335−052 and I Zw 18. The linear trend by Draine et al. (2007) shown as a short-dashed line fits the metal-rich data quite well. However, with Hi alone (shown as open blue circles in Fig. 9), SBS 0335−052 exceeds the trend by a factor of 30 or more, but I Zw 18 lies almost a factor of 100 below the trend. If our estimate of dust mass in I Zw 18 is correct, at low metallicity the trend of abundance and dust-to-gas ratios changes drastically, and in different ways according to some other parameter, for example SFR surface density or column densities of dust and ionized gas.
Our ALMA observations did not detect CO(3−2) in SBS 0335−052, but either the expected
linearity in 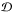 is incorrect, or there is a large fraction of missing molecular gas. We can use gas
scaling relations to estimate the total gas content in SBS 0335−052 and check whether we
are also missing a molecular component in I Zw 18. If the SF in SBS 0335−052 occurs in the
roughly same area as the ALMA emission (~1 arcsec2), we would find
ΣSFR ~ 18 M⊙ kpc-2. However, if we
conservatively consider a larger area of diameter 550 pc
(~2
is incorrect, or there is a large fraction of missing molecular gas. We can use gas
scaling relations to estimate the total gas content in SBS 0335−052 and check whether we
are also missing a molecular component in I Zw 18. If the SF in SBS 0335−052 occurs in the
roughly same area as the ALMA emission (~1 arcsec2), we would find
ΣSFR ~ 18 M⊙ kpc-2. However, if we
conservatively consider a larger area of diameter 550 pc
(~2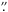 1), comparable
to the region emitting faint Paα (Reines
et al. 2008), we obtain ΣSFR ~
5 M⊙ kpc-2. The SF in I Zw 18 takes place in a
region of diameter ~1 kpc (Cannon et al. 2002,
2005), and we find ΣSFR ~
0.15 M⊙ kpc-2. These spatial scales are
sufficiently large that the gas scaling relations are not expected to have broken down
(e.g., Verley et al. 2010; Onodera et al. 2010). Figure 10
shows SFR surface density plotted against gas surface density; the figure is taken from
Daddi et al. (2010). SBS 0335−052 (the upper
point) and I Zw 18 (the lower one) correspond to filled blue circles, and the arrows
indicate how much gas would be needed to bring SBS 0335−052 to the starburst sequence and
I Zw 18 to the sequence of disks. At SBS 0335−052’s SFR surface density, the starburst
sequence of the SFR-gas scaling would require a total gas surface density of
~400 M⊙ pc-2. I Zw 18 already has too much
Hi to fall on the starburst sequence; if, on the other hand, it were to fall on
the disk sequence, it would need a total gas surface density of
~158 M⊙ pc-2. The missing gas mass, which we take
as the missing molecular component, is ~342 M⊙ pc-2
for SBS 0335−052, and ~94 M⊙ pc-2 for I Zw 18,
assuming for the latter the mean Hi column density of
64 M⊙ pc-2 (see Tables 1 and 3). However, if I Zw 18
falls on the starburst sequence, similarly to what we hypothesize for SBS 0335−052, it
would be missing no molecular mass; indeed, additional gas would move I Zw 18 farther from
what we might expect. In any case, these estimates of missing molecular gas for both
galaxies are highly uncertain, and should be taken as a basis for discussion, rather than
conclusive determinations.
1), comparable
to the region emitting faint Paα (Reines
et al. 2008), we obtain ΣSFR ~
5 M⊙ kpc-2. The SF in I Zw 18 takes place in a
region of diameter ~1 kpc (Cannon et al. 2002,
2005), and we find ΣSFR ~
0.15 M⊙ kpc-2. These spatial scales are
sufficiently large that the gas scaling relations are not expected to have broken down
(e.g., Verley et al. 2010; Onodera et al. 2010). Figure 10
shows SFR surface density plotted against gas surface density; the figure is taken from
Daddi et al. (2010). SBS 0335−052 (the upper
point) and I Zw 18 (the lower one) correspond to filled blue circles, and the arrows
indicate how much gas would be needed to bring SBS 0335−052 to the starburst sequence and
I Zw 18 to the sequence of disks. At SBS 0335−052’s SFR surface density, the starburst
sequence of the SFR-gas scaling would require a total gas surface density of
~400 M⊙ pc-2. I Zw 18 already has too much
Hi to fall on the starburst sequence; if, on the other hand, it were to fall on
the disk sequence, it would need a total gas surface density of
~158 M⊙ pc-2. The missing gas mass, which we take
as the missing molecular component, is ~342 M⊙ pc-2
for SBS 0335−052, and ~94 M⊙ pc-2 for I Zw 18,
assuming for the latter the mean Hi column density of
64 M⊙ pc-2 (see Tables 1 and 3). However, if I Zw 18
falls on the starburst sequence, similarly to what we hypothesize for SBS 0335−052, it
would be missing no molecular mass; indeed, additional gas would move I Zw 18 farther from
what we might expect. In any case, these estimates of missing molecular gas for both
galaxies are highly uncertain, and should be taken as a basis for discussion, rather than
conclusive determinations.
 |
Fig. 10 SBS 0335−052 (upper filled blue circle) and I Zw 18 (lower filled blue circle) on the gas scaling relations given by Daddi et al. (2010). Only Hi mass density is considered for the BCDs studied here; the arrows correspond to the missing gas mass surface density that would transport SBS 0335−052 to the “starburst sequence” and I Zw 18 to the “sequence of disks”. SFR surface density is plotted as a function of the gas (atomic and molecular) surface density for z ~ 0.5 disks (shown as red filled circles and triangles; brown crosses indicate z = 1−2.3 normal galaxies, and empty squares correspond to sub-millimeter galaxies. The shaded regions and filled triangles are local spiral galaxies, and small crosses are starbursts and ultra-luminous galaxies. References for these data are given in Daddi et al. (2010). |
Adding the (putative) missing molecular gas gives a total gas mass that corresponds to
the filled circles in the dust-to-gas mass ratios plotted in Fig. 9. The missing molecular component would be ~1.5 times the Hi
mass in I Zw 18 but a factor of 6 times the Hi mass in SBS 0335−052 (missing
342 M⊙ pc-2 vs.
56 M⊙ pc-2 in Hi). SBS 0335−052 would be
moved closer to, and possibly consistently with, the linear trend of
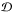 with metallicity, while I Zw 18 would be moved farther away.
with metallicity, while I Zw 18 would be moved farther away.
We therefore tentatively conclude that there is a large component of missing molecular
gas in SBS 0335−052; in I Zw 18 such a conclusion seems more remote, though possible.
Krumholz (2012) argues that at low metallicities
(perhaps lower than in these galaxies), star formation will occur in the cold atomic phase
of the ISM rather than necessarily in a molecular phase. This could be the case in
SBS 0335−052 and I Zw 18 since in both galaxies star formation is taking place in a very
Hi-rich medium. Nevertheless, the total gas fractions could be even higher in
SBS 0335−052; if SBS 0335−052 is to fall on the linear trend of
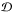 with O/H, it would be missing a yet unmeasured gas component. We discuss such a gas
component in the next section.
with O/H, it would be missing a yet unmeasured gas component. We discuss such a gas
component in the next section.
5.2. Constraints on molecular gas conversion factors in SBS 0335−052 and I Zw 18
Previous attempts to detect 12CO(1−0) and 12CO(2−1)13 in SBS 0335−052 were carried out by Dale et al. (2001) at Owens Valley. After 20.6 h of on-source integration time at 3 mm and 6.6 h of good integration time at 1mm, they achieved 3σ upper limits of 1.2 Jykm s-1 and 3.0 Jykm s-1, respectively. Converting these to brightness temperatures gives 3σ flux upper limits of 5.6 K km s-1 for CO(1−0) and 12.2 K km s-1 for CO(2−1). We can use these limits to constrain values for αCO, the factor to convert observed CO intensity ICO to H2 column density. In order to account for the “missing” molecular gas density of 342 M⊙ pc-2 in SBS 0335−052, αCO would be ≳61 M⊙ pc-2 (K km s-1)-1 for CO(1−0), 10−12 times higher than typical values for the Milky Way (e.g., Bolatto et al. 2013), but lower than would be expected (~30 times higher) for a linear trend of αCO with metallicity (e.g., Draine et al. 2007). Assuming a CO(2−1)/CO(1−0) ratio of 0.7 (Leroy et al. 2011), we would obtain αCO ≳ 40 M⊙ pc-2 (K km s-1)-1 for CO(2−1).
More stringent lower limits can be achieved if we use to estimate αCO the 3σ CO(3−2) upper limit for SBS 0335−052 (1.58 K km s-1) given in Sect. 2. Because ΣH2 = αCOICO(1−0), we need first to convert the CO(3−2) limit to one on CO(1−0). For a sample of dwarf starbursts, Meier et al. (2001) found an error-weighted mean CO(3−2)/CO(1−0) flux ratio of 0.6 ± 0.06, roughly consistent with the median value of 0.7 obtained by Mao et al. (2010). Converting CO(3−2) to CO(1−0) using the range in these ratios, to accommodate the “missing” 342 M⊙ pc-2 gas density in SBS 0335−052, αCO ≳ 130−152 M⊙ pc-2 (K km s-1)-1.
The same exercise can be performed for I Zw 18, using the 3σ CO(1−0) limit of 0.75 K km s-1 given by Leroy et al. (2007)14. From Fig. 10, we estimate that I Zw 18 is missing ~94 M⊙ pc-2 of gas density; hence αCO ≳ 125 M⊙ pc-2 (K km s-1)-1. The two lower limits for SBS 0335−052 and I Zw 18 are similar, but this is merely fortuitous, since it depends on the sensitivity of the CO observations, the missing gas, and the flux ratio of CO(3−2)/CO(1−0) in the case of SBS 0335−052. In the case of SBS 0335−052, the most conservative hypothesis would be that more gas is needed to bring it onto the starburst sequence of gas scaling relations (rather than the quiescent sequence). However, I Zw 18 is already on the starburst sequence with only Hi; putative missing gas would be needed to move this galaxy onto the more quiescent sequence of disks. If no molecular gas component were needed for I Zw 18 in the gas scaling relations (i.e., if it really should be on the starburst sequence), αCO for I Zw 18 would be undefined.
 |
Fig. 11 αCO vs. 12 + log (O/H) for nearby galaxies. The lower limits for SBS 0335−052 and I Zw 18 are shown as filled blue circles; data from Leroy et al. (2011) and Bolatto et al. (2008) are shown as filled squares and ×, respectively. The steeper regression, indicated by a dashed line, has a slope of −1.3 (Genzel et al. 2012) and the shallower one, shown by a dotted line, a slope of −0.9 (Sargent et al. 2013). |
Figure 11 shows the αCO lower limits for SBS 0335−052 and I Zw 18, together with measured αCO conversion factors for two samples of nearby galaxies (Bolatto et al. 2008; Leroy et al. 2011). The steeper of the two regressions (slope −1.3) is given by Genzel et al. (2012), and the shallower one (slope −0.9) by Sargent et al. (2013). Our lower limits on αCO for SBS 0335−052 and I Zw 18 lie slightly above the shallower regression, which would imply that the slope is closer to linear, or even super-linear as found by Genzel et al. (2012). To better constrain the low-metallicity end of the αCO conversion factor, deeper observations are needed. Even non-detections, but at a fainter intensity level, will help understand the fate of molecular gas and its tracers at low metallicity.
6. Summary and conclusions
We have presented our first ALMA results for SBS 0335−052, one of the most metal-poor
star-forming dwarf galaxies in the Local Universe. The ALMA Band 7 continuum observations at
870 μm allow us to reach an unprecedented spatial resolution of 90 pc,
even with the Cycle 0 capabilities. Extrapolating from high-resolution high-frequency radio
observations, we find that 85% of the Band 7 flux in SBS 0335−052 can be attributed to
free-free emission. The remainder is attributed to dust, and we use this new constraint to
estimate the dust mass in SBS 0335−052 by fitting its SED with a DUSTY model. The ratio of
the resulting dust mass of 3.8 × 104 M⊙ in
SBS 0335−052 and its stellar mass falls within the range of normal galaxies. However,
comparing the dust with Hi mass and surface density, we find that SBS 0335−052 far
exceeds the linear trend of dust-to-gas mass ratio  with oxygen abundance.
with oxygen abundance.
We have compared the results for SBS 0335−052 to another dwarf galaxy at similarly low
metallicity, I Zw 18. With data from the literature, and Herschel archival
observations, we have estimated the dust mass in I Zw 18 by fitting a DUSTY model, and find
3.4 × 102 M⊙ of dust. Compared with its Hi
mass and column density, unlike SBS 0335−052, I Zw 18 falls far below the expected scatter
of the linear trend of  with O/H. Finally, we have used the CO non-detections for both galaxies to constrain the
integrated CO(1−0) intensity to H2 surface density conversion factor,
αCO, and find that the lower limits are consistent with a
linear, or perhaps even super-linear trend with metallicity.
with O/H. Finally, we have used the CO non-detections for both galaxies to constrain the
integrated CO(1−0) intensity to H2 surface density conversion factor,
αCO, and find that the lower limits are consistent with a
linear, or perhaps even super-linear trend with metallicity.
Perhaps the most significant of our findings is that metallicity does not uniquely define star-formation processes. Considering only Hi gas, I Zw 18 falls roughly on the starburst sequence of gas scaling relations, but SBS 0335−052 is a clear outlier; a gas surface density 6 times higher than that from Hi alone would be required to bring it onto the sequence of starbursts (see Fig. 10).
Although specific SFRs (SFR/Mstar) are similar for both galaxies (~10-7 yr-1), the surface densities of SF are very different. SF in SBS 0335−052 occurs mainly in two luminous compact super-star clusters, while that in I Zw 18 originates in more diffuse ones; the SFR surface densities differ by more than an order of magnitude. This is probably the reason for the extreme short-wavelength peak in SBS 0335−052’s SED (~20−30 μm) and implies that physical conditions are extreme in this galaxy. Considering also the large volume densities of ionized gas implied by its self-absorbed thermal radio spectrum (Hunt et al. 2004; Johnson et al. 2009), the star formation activity in SBS 0335−052 must be occurring in very warm, dense regions. The physical conditions in I Zw 18 are less extreme; the radio spectrum is not self-absorbed, and electron densities are lower.
Ultimately, the influence of metallicity may not be as clear cut as commonly thought. At some level, self-shielding and the survival of molecules may depend just as much on gas and dust column density as on metallicity. The effects of low metallicity may at least be partially compensated for by large column densities in the ISM. More observations of extreme metal-poor galaxies are needed to judge whether this is generally true, and to better understand the degree to which such galaxies can serve as proxies for galaxy formation at high redshift.
The conclusions of Hunter & Thronson (1995) are still valid even with the updated distance of I Zw 18.
PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain).
We based it on the PyMC package: http://pymc-devs.github.io/pymc/
These are the Pilyugin & Thuan (2005) calibrations from Kennicutt et al. (2011), in order to be more comparable with the direct method used for SBS 0335−052 and I Zw 18 based on electron temperature.
The gradient in the radio spectral index makes the thermal/non-thermal separation in I Zw 18 problematic (Hunt et al. 2005b).
This is really 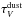 , as
defined in Sect. 3.
, as
defined in Sect. 3.
Acknowledgments
We appreciate the prompt review and careful comments of the referee which improved the clarity of the paper. We warmly thank Bruce Draine for constructive comments and suggestions, and Emanuele Daddi for interesting discussions. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00039.S (PI Hunt). ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. We are grateful to the Italian Alma Regional Center for assistance with data handling and analysis, and to the International Space Science Institute for hospitality during the conception of the paper. L.K.H. acknowledges support from PRIN-INAF 2012/13. We made use of the NASA/IPAC Extragalactic Database (NED).
References
- Aloisi, A., Clementini, G., Tosi, M., et al. 2007, ApJ, 667, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Aniano, G., Draine, B. T., Calzetti, D., et al. 2012, ApJ, 756, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bekki, K. 2008, MNRAS, 388, L10 [Google Scholar]
- Bianchi, S. 2013, A&A, 552, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., & Schneider, R. 2007, MNRAS, 378, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Leroy, A. K., Rosolowsky, E., Walter, F., & Blitz, L. 2008, ApJ, 686, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., Pipino, A., & Matteucci, F. 2008, A&A, 479, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cannon, J. M., Skillman, E. D., Garnett, D. R., & Dufour, R. J. 2002, ApJ, 565, 931 [CrossRef] [Google Scholar]
- Cannon, J. M., Walter, F., Skillman, E. D., & van Zee, L. 2005, ApJ, 621, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, B., Dai, X., Kochanek, C. S., & Chartas, G. 2013, ApJ, submitted [arXiv:1306.0008] [Google Scholar]
- ContrerasRamos, R., Annibali, F., Fiorentino, G., et al. 2011, ApJ, 739, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Cortese, L., Ciesla, L., Boselli, A., et al. 2012, A&A, 540, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- da Cunha, E., Eminian, C., Charlot, S., & Blaizot, J. 2010, MNRAS, 403, 1894 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., et al. 2010, ApJ, 714, L118 [Google Scholar]
- Dale, D. A., Helou, G., Neugebauer, G., et al. 2001, AJ, 122, 1736 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Aniano, G., Engelbracht, C. W., et al. 2012, ApJ, 745, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Dole, H., Lagache, G., Puget, J.-L., et al. 2006, A&A, 451, 417 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Eales, S., Smith, M. W. L., Auld, R., et al. 2012, ApJ, 761, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Ekta,Chengalur, J. N., & Pustilnik, S. A. 2008, MNRAS, 391, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Ekta, B., Pustilnik, S. A., & Chengalur, J. N. 2009, MNRAS, 397, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Rieke, G. H., Gordon, K. D., et al. 2008, ApJ, 678, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., Bolatto, A. D., Herrera-Camus, R., et al. 2013, Nature, in press [arXiv:1310.4842] [Google Scholar]
- Franceschini, A., Rodighiero, G., & Vaccari, M. 2008, A&A, 487, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fumagalli, M., Krumholz, M. R., & Hunt, L. K. 2010, ApJ, 722, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Galametz, M., Madden, S. C., Galliano, F., et al. 2011, A&A, 532, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Genzel, R., Tacconi, L. J., Combes, F., et al. 2012, ApJ, 746, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Madore, B. F., & Pevunova, O. 2003, ApJS, 147, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Gruppioni, C., Pozzi, F., Andreani, P., et al. 2010, A&A, 518, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilloteau, S., Lucas, R. 2000, Imaging at Radio through Submillimeter Wavelengths, ASP Conf. Ser., 217, 299 [NASA ADS] [Google Scholar]
- Hauser, M. G., & Dwek, E. 2001, ARA&A, 39, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera-Camus, R., Fisher, D. B., Bolatto, A. D., et al. 2012, ApJ, 752, 112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirashita, H., Tajiri, Y. Y., & Kamaya, H. 2002, A&A, 388, 439 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houck, J. R., Charmandaris, V., Brandl, B. R., et al. 2004a, ApJS, 154, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004b, ApJS, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., & Thronson, H. A., Jr. 1995, ApJ, 452, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Vanzi, L., & Thuan, T. X. 2001, A&A, 377, 66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Thuan, T. X., & Izotov, Y. I. 2003, ApJ, 588, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Dyer, K. K., Thuan, T. X., & Ulvestad, J. S. 2004, ApJ, 606, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L., Bianchi, S., & Maiolino, R. 2005a, A&A, 434, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Dyer, K. K., & Thuan, T. X. 2005b, A&A, 436, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L., Magrini, L., Galli, D., et al. 2012, MNRAS, 427, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezic, Z., & Elitzur, M. 1997, MNRAS, 287, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Chaffee, F. H., Foltz, C. B., et al. 1999, ApJ, 527, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Guseva, N. G. 2005, ApJ, 632, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
- James, A., Dunne, L., Eales, S., & Edmunds, M. G. 2002, MNRAS, 335, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, K. E., Hunt, L. K., & Reines, A. E. 2009, AJ, 137, 3788 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R. 2012, ApJ, 759, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., Verheijen, M., Fraternali, F., & Sancisi, R. 2012, A&A, 537, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leroy, A., Cannon, J., Walter, F., Bolatto, A., & Weiss, A. 2007, ApJ, 663, 990 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Magdis, G. E., Daddi, E., Elbaz, D., et al. 2011, ApJ, 740, L15 [Google Scholar]
- Makovoz, D., & Marleau, F. R. 2005, PASP, 117, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, R.-Q., Schulz, A., Henkel, C., et al. 2010, ApJ, 724, 1336 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., Golap, K. 2007, Astronomical Data Analysis Software and Systems XVI, ASP Conf. Ser., 376, 127 [NASA ADS] [Google Scholar]
- Meier, D. S., Turner, J. L., Crosthwaite, L. P., & Beck, S. C. 2001, AJ, 121, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Nikutta, R. 2012, Ph.D. Thesis, University of Kentucky, USA, http://uknowledge.uky.edu/physastron_etds/8/ [Google Scholar]
- Nozawa, T., Kozasa, T., Habe, A., et al. 2007, ApJ, 666, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Onodera, S., Kuno, N., Tosaki, T., et al. 2010, ApJ, 722, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei, 2nd edn. (Sausalito, CA: University Science Books) [Google Scholar]
- Ott, S. 2010, ASP Conf. Ser., 434, 139 [Google Scholar]
- Papaderos, P., Izotov, Y. I., Fricke, K. J., Thuan, T. X., & Guseva, N. G. 1998, A&A, 338, 43 [NASA ADS] [Google Scholar]
- Papaderos, P., Izotov, Y. I., Thuan, T. X., et al. 2002, A&A, 393, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S., & Thuan, T. X. 2005, ApJ, 631, 231 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Plante, S., & Sauvage, M. 2002, AJ, 124, 1995 [NASA ADS] [CrossRef] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pustilnik, S. A., Brinks, E., Thuan, T. X., Lipovetsky, V. A., & Izotov, Y. I. 2001, AJ, 121, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Reines, A. E., Johnson, K. E., & Hunt, L. K. 2008, AJ, 136, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2013, A&A, 557, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieke, G. H., Young, E. T., Engelbracht, C. W., et al. 2004, ApJS, 154, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Rowlands, K., Dunne, L., Maddox, S., et al. 2012, MNRAS, 419, 2545 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Maiolino, R., Magnelli, B., et al. 2010, A&A, 518, L154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sargent, M. T., Daddi, E., Béthermin, M., et al. 2013, ApJ, submitted [arXiv:1303.4392] [Google Scholar]
- Schneider, R., Ferrara, A., & Salvaterra, R. 2004, MNRAS, 351, 1379 [NASA ADS] [CrossRef] [Google Scholar]
- Skibba, R. A., Engelbracht, C. W., Dale, D., et al. 2011, ApJ, 738, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., & Izotov, Y. I. 1997a, ApJ, 489, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Thuan, T. X., Izotov, Y. I., & Lipovetsky, V. A. 1997b, ApJ, 477, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Todini, P., & Ferrara, A. 2001, MNRAS, 325, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Vader, J. P., Frogel, J. A., Terndrup, D. M., & Heisler, C. A. 1993, AJ, 106, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Valiante, R., Schneider, R., Bianchi, S., & Andersen, A. C. 2009, MNRAS, 397, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzi, L., Hunt, L. K., Thuan, T. X., & Izotov, Y. I. 2000, A&A, 363, 493 [NASA ADS] [Google Scholar]
- Verley, S., Corbelli, E., Giovanardi, C., & Hunt, L. K. 2010, A&A, 510, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, R., Carilli, C. L., Wagg, J., et al. 2008, ApJ, 687, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Charmandaris, V., Hunt, L. K., et al. 2007, ApJ, 662, 952 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 ALMA 870 μm continuum map of SBS 0335−052 shown as white contours overlaying the HST/ACS F555M image taken from Reines et al. (2008). Band 7 contours range from 1 to 2σ (σ = 0.035 mJy/beam). Black contours (ranging from 3 to 9σ, σ = 0.012 mJy/beam) give the high-resolution VLA map at 3.6 cm taken from Johnson et al. (2009). The radio and dust emission is associated with the two brightest SSCs (1, 2) toward the southeast. Beam sizes of the two contoured images are shown in the lower left corner. At the distance of SBS 0335−052, 1′′ corresponds to 262 pc. |
| In the text | |
 |
Fig. 2 PACS images of SBS 0335−052 superimposed as contours on the F555M HST/ACS image shown with false colors (see also Fig. 1). From left to right are PACS 70, 100, and 160 μm maps. Contours start at 3σ and run to 22σ for PACS 70, to 20σ for PACS 100, and for PACS 160 to 8σ. These σ values correspond to the correlated noise measured from the images, which are roughly 4× smaller than the true noise (see PACS documentation and text). PACS beam sizes are shown as shaded ellipses in the upper portion of each panel. For display purposes, the PACS images have been rebinned to smaller pixel sizes. |
| In the text | |
 |
Fig. 3 SED of SBS 0335−052, together with best-fit DUSTY model overlaid. The two large (red) circles show the total ALMA Band 7 emission; the dust-only emission, estimated as described in the text, is indicated by the open (red) circle. The black curve represents the DUSTY fit, and the dotted (red) curve, only the dust; the long-dashed (blue) curve shows the stars. The radio slope is pure free-free, ∝ν-0.1, and the pure radio component is shown by a short-dashed (purple) line (longward of 250 μm). DUSTY models only extend to 1 mm, so the excess above the dust-only emission is the extrapolation of the radio. When not evident, the error bars are masked by the size of the symbols. |
| In the text | |
 |
Fig. 4 Modified single-temperature blackbody fits with fixed β of SBS 0335−052 (left panel) and I Zw 18 (right panel). The blue + signs show unfitted points; the upper limit at 850 μm for I Zw 18 was not fit either. In the right panel, the MIPS and PACS 70 μm points are so close in wavelength and measured flux that they are virtually indistinguishable. Details for I Zw 18 are given in Sect. 4. |
| In the text | |
 |
Fig. 5 Ratios of dust mass to stellar mass plotted against stellar mass (Mstar, left panel) and specific SFR (yr-1, right). SBS 0335−052 and I Zw 18 are plotted as filled (blue) circles. Data for KINGFISH galaxies, taken from Kennicutt et al. (2011), are also shown: × (for late Hubble types T ≥ 8), filled (green) triangles (0 < T < 8), and filled (red) circles (for early Hubble types T ≤ 0). The horizontal lines give the mean dust/stellar mass ratio for the KINGFISH sample, and the 1σ standard deviation. Given as open (magenta) squares are the passive spirals studied by Rowlands et al. (2012) and as filled (magenta) squares their early-type galaxies. |
| In the text | |
 |
Fig. 6 Ratios of dust mass to stellar mass plotted against nebular 12 + log (O/H). SBS 0335−052 and I Zw 18 are plotted as filled (blue) circles. As in Fig. 5, data for KINGFISH galaxies (see text) are also shown: × (for Hubble type T ≥ 8), filled (green) triangles (0 < T < 8), and filled (red) circles (T ≤ 0). The horizontal lines give the mean dust/stellar mass ratio for the KINGFISH sample, and the 1σ standard deviation. |
| In the text | |
 |
Fig. 7 PACS images of I Zw 18 superimposed as contours on the F606W HST/ACS image shown with false colors. From left to right are PACS 70, 100, and 160 μm. Contours start at 3σ, and run to 7σ for PACS 70, to 16σ for PACS 100, and for PACS 160 to 2σ. As in Fig. 2, these σ values correspond to the correlated noise measured from the images, which are smaller than the true noise (see text). |
| In the text | |
 |
Fig. 8 SED of I Zw 18, together with best-fit DUSTY model overlaid. The large open (red) circle shows the dust-only emission taken from Leroy et al. (2007), while the small filled (blue) circle above it shows the total 2.6 mm emission. The black curve represents the DUSTY fit, and the dotted (red) curve, only the dust; the long-dashed (blue) curve shows the stars. The error bars are masked by the size of the symbols. As in Fig. 3, DUSTY models only extend to 1 mm, so the excess above the dust-only emission is the extrapolation of the radio with a spectral index of −0.25 (see text). The pure radio component is shown by a short-dashed (purple) line (longward of 250 μm). |
| In the text | |
 |
Fig. 9 Dust-to-gas mass ratios |
| In the text | |
 |
Fig. 10 SBS 0335−052 (upper filled blue circle) and I Zw 18 (lower filled blue circle) on the gas scaling relations given by Daddi et al. (2010). Only Hi mass density is considered for the BCDs studied here; the arrows correspond to the missing gas mass surface density that would transport SBS 0335−052 to the “starburst sequence” and I Zw 18 to the “sequence of disks”. SFR surface density is plotted as a function of the gas (atomic and molecular) surface density for z ~ 0.5 disks (shown as red filled circles and triangles; brown crosses indicate z = 1−2.3 normal galaxies, and empty squares correspond to sub-millimeter galaxies. The shaded regions and filled triangles are local spiral galaxies, and small crosses are starbursts and ultra-luminous galaxies. References for these data are given in Daddi et al. (2010). |
| In the text | |
 |
Fig. 11 αCO vs. 12 + log (O/H) for nearby galaxies. The lower limits for SBS 0335−052 and I Zw 18 are shown as filled blue circles; data from Leroy et al. (2011) and Bolatto et al. (2008) are shown as filled squares and ×, respectively. The steeper regression, indicated by a dashed line, has a slope of −1.3 (Genzel et al. 2012) and the shallower one, shown by a dotted line, a slope of −0.9 (Sargent et al. 2013). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.