| Issue |
A&A
Volume 560, December 2013
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321697 | |
| Published online | 03 December 2013 | |
Analytical representations of unified equations of state for neutron-star matter⋆
1 Centre de Recherche Astrophysique de Lyon, Université de Lyon, Université Lyon 1, Observatoire de Lyon, École Normale Supérieure de Lyon, CNRS, UMR 5574, 9 avenue Charles André, 69230 Saint-Genis Laval, France
e-mail: palex@astro.ioffe.ru
2 Ioffe Physical-Technical Institute, Politekhnicheskaya 26, 194021 St. Petersburg, Russia
3 Isaac Newton Institute of Chile, St. Petersburg Branch, 198504 St. Petersburg, Russia
4 Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, CP-226, 1050 Brussels, Belgium
5 Département de Physique, Université de Montréal, Montréal ( Québec ) H3C 3J7, Canada
Received: 15 April 2013
Accepted: 23 September 2013
Context. An equation of state (EoS) of dense nuclear matter is a prerequisite for studies of the structure and evolution of compact stars. A unified EoS should describe the crust and the core of a neutron star using the same physical model. The Brussels-Montreal group has recently derived a family of such EoSs based on the nuclear energy-density functional theory with generalized Skyrme effective forces that have been fitted with great precision to essentially all the available mass data. At the same time, these forces were constrained to reproduce microscopic calculations of homogeneous neutron matter based on realistic two- and three-nucleon forces.
Aims. We represent basic physical characteristics of the latest Brussels-Montreal EoS models by analytical expressions to facilitate their inclusion in astrophysical simulations.
Methods. We consider three EoS models, which significantly differ by stiffness: BSk19, BSk20, and BSk21. For each of them we constructed two versions of the EoS parametrization. In the first version, pressure P and gravitational mass density ρ are given as functions of the baryon number density nb. In the second version, P, ρ, and nb are given as functions of pseudo-enthalpy, which is useful for two-dimensional calculations of stationary rotating configurations of neutron stars. In addition to the EoS, we derived analytical expressions for several related quantities that are required in neutron-star simulations: number fractions of electrons and muons in the stellar core, nucleon numbers per nucleus in the inner crust, and equivalent radii and shape parameters of the nuclei in the inner crust.
Results. We obtain analytical representations for the basic characteristics of the models of cold dense matter, which are most important for studies of neutron stars. We demonstrate the usability of our results by applying them to calculations of neutron-star mass-radius relations, maximum and minimum masses, thresholds of direct Urca processes, and the electron conductivity in the neutron-star crust.
Key words: dense matter / equation of state / stars: neutron
Our analytical fitting expressions have been implemented in Fortran subroutines that are publicly available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/560/A48 or at http://www.ioffe.ru/astro/NSG/BSk/
© ESO, 2013
1. Introduction
The equation of state (EoS) of dense matter is crucial as input for neutron-star structure calculations. Usually, neutron-star matter is strongly degenerate, and therefore the EoS is barotropic (i.e., the pressure is temperature-independent), except for the outermost envelopes (a few meters thick).
A unified EoS is based on a single effective nuclear Hamiltonian and is valid in all regions of the neutron-star interior. For unified EoSs, the transitions between the outer crust and the inner crust, and between the inner and the core are treated consistently using the same physical model (e.g., Douchin & Haensel 2000; Pearson et al. 2012). Other (nonunified) EoSs consist of crust and core segments obtained using different models. The crust-core interface there has no physical meaning, and both segments are joined using an ad hoc matching procedure. This generally leads to thermodynamic inconsistencies, which can manifest themselves by the occurrence of spurious instabilities in neutron-star dynamical simulations. Even if the transitions are treated using a unified approach, instabilities might still arise due to numerical errors. In addition, realistic EoSs are generally calculated only for specific densities and/or pressures. These limitations can be circumvented by using analytical representations of the EoSs. In this paper we construct analytical representations of three recent unified EoSs for cold catalysed nuclear matter developed by the Brussels-Montreal group: BSk19, BSk20, and BSk21 (Goriely et al. 2010; Pearson et al. 2011, 2012).
We follow the approach developed by Haensel & Potekhin (2004), who constructed analytical representations for the previous unified EoS models FPS (Pandharipande & Ravenhall 1989) and SLy4 (Douchin & Haensel 2001). In addition, we present analytical parametrizations of the composition of the crust and number fractions of leptons and nucleons in the core of a neutron star. We adopt the “minimal model” (e.g., Haensel et al. 2007), which means we assume the nucleon-lepton matter without exotic particles.
The composition of the neutron-star crust can depend on its formation history. For example, if the star experienced accretion, then the crust could be formed by the nuclear transformations that accompany gradual density increase under the weight of the newly accreted matter (Haensel & Zdunik 1990). It differs from the matter in β-equilibrium (cold catalysed matter) that constitutes the crust soon after the birth of a neutron star. Moreover, the nonequilibrium composition of an accreted crust can also depend on the composition of the ashes of accretion-induced thermonuclear burning (Haensel & Zdunik 2003). Here, however, we do not consider these complications, but focus on the cold catalysed matter.
In Sect. 2 we briefly review the nuclear models used to construct the Brussels-Montreal EoSs, including a discussion of constraints coming from nuclear physics experiments and many-body calculations. In Sect. 3 we present a set of fully analytical approximations to the EoSs in the crust and the core of a neutron star. This set includes pressure P and baryon number density nb as functions of gravitational mass density ρ, the inverse function ρ(nb), and a fit of ρ as a function of the pseudo-enthalpy, which is a particularly convenient independent variable for simulations of rapidly rotating neutron stars (Bonazzola et al. 1993). In Sect. 4 we give analytical approximations to number fractions of electrons and muons in the core and the inner crust of a neutron star as functions of nb. Based on the one-dimensional approximation of the nuclear shapes suggested by Onsi et al. (2008), we describe the shapes of the nuclei in the inner crust as fully analytical functions of two arguments, the radial coordinate in a Wigner-Seitz cell r and the mean baryon density nb. We also present effective proton and neutron sizes of the nuclei in the inner crust as analytical functions of nb. In Sect. 5 we consider an application of the results to the calculation of electron conductivity in the stellar crust. The impact of the analytical representation of the EoSs on neutron-star structure is studied in Sect. 6. Concluding remarks are given in Sect. 7.
2. The unified Brussels-Montreal EoSs
The unified Brussels-Montreal EoSs that we consider here are based on the nuclear energy-density functionals (EDFs), labeled BSk19, BSk20, and BSk21, respectively. These EDFs were derived from generalized Skyrme interactions, supplemented with microscopic contact pairing interactions, a phenomenological Wigner term and correction terms for the collective energy (Goriely et al. 2010; Chamel 2010). Calculating the nuclear energy with the Hartree-Fock-Bogoliubov (HFB) method, the EDFs were fitted to the 2149 measured masses of atomic nuclei with proton number Z ≥ 8 and neutron number N ≥ 8 from the 2003 Atomic Mass Evaluation (Audi et al. 2003) with a root mean square (rms) deviation as low as 0.58 MeV. In making these fits the Skyrme part of the EDFs were simultaneously constrained to fit the zero-temperature EoS of homogeneous neutron matter (NeuM), as determined by many-body calculations with realistic two- and three-nucleon forces. Actually, several realistic calculations of the EoS of NeuM have been made, and while they all agree fairly closely at nuclear and subnuclear densities, at the much higher densities that can be encountered towards the center of neutron stars they differ greatly in their stiffness, and there are very few data, either observational or experimental, to distinguish between the different possibilities. It is in this way that the three different functionals were constructed, as follows. The BSk19 EDF was constrained to the soft Friedman & Pandharipande (1981) EoS obtained from the realistic Urbana v14 nucleon-nucleon force with the three-body force TNI, the BSk20 EDF was fitted to the Akmal et al. (1998) EoS labeled “A18 + δv + UIX”, and the BSk21 EDF was adjusted to the stiff EoS labeled “V18” in Li & Schulze (2008).
These NeuM constraints make the EDFs BSk19–21 suitable for application to the neutron-rich environments encountered in many different astrophysical situations, and our making three different such EDFs available reflects the current lack of knowledge of the high-density behavior of dense matter. In addition, these three EDFs were also constrained to reproduce several other properties of homogeneous nuclear matter as obtained from many-body calculations using realistic two- and three-nucleon interactions; among those, the ratio of the isoscalar effective mass 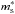 to bare nucleon mass m in symmetric nuclear matter at saturation was set to the realistic value of 0.8, and all three EDFs predict a neutron effective mass that is higher than the proton effective mass in neutron-rich matter, as found both experimentally and from microscopic calculations. Various properties of the BSk19, BSk20, and BSk21 EDFs are summarized in Table 1 (Goriely et al. 2010), namely: the rms deviations to the 2149 measured atomic masses σ(matom) and to the 782 measured charge radii σ(Rch), the energy per nucleon of symmetric nuclear matter at saturation density av, the baryon number density at saturation nb,0, the incompressibility of symmetric nuclear matter at saturation Kv (which was required to fall in the experimental range 240 ± 10 MeV, according to Colò et al. 2004), the symmetry energy coefficient J and its slope L, the isospin compressibility Kτ, the isoscalar and isovector effective masses
to bare nucleon mass m in symmetric nuclear matter at saturation was set to the realistic value of 0.8, and all three EDFs predict a neutron effective mass that is higher than the proton effective mass in neutron-rich matter, as found both experimentally and from microscopic calculations. Various properties of the BSk19, BSk20, and BSk21 EDFs are summarized in Table 1 (Goriely et al. 2010), namely: the rms deviations to the 2149 measured atomic masses σ(matom) and to the 782 measured charge radii σ(Rch), the energy per nucleon of symmetric nuclear matter at saturation density av, the baryon number density at saturation nb,0, the incompressibility of symmetric nuclear matter at saturation Kv (which was required to fall in the experimental range 240 ± 10 MeV, according to Colò et al. 2004), the symmetry energy coefficient J and its slope L, the isospin compressibility Kτ, the isoscalar and isovector effective masses 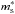 and
and 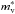 relative to the bare nucleon mass m, and the limiting baryonic density ncaus after which the EoSs of neutron-star matter violate causality. The last line indicates the NeuM EoS to which each EDF was fitted.
relative to the bare nucleon mass m, and the limiting baryonic density ncaus after which the EoSs of neutron-star matter violate causality. The last line indicates the NeuM EoS to which each EDF was fitted.
Properties of the Skyrme forces BSk19, BSk20, and BSk21 (Goriely et al. 2010). See text for details.
The Brussels-Montreal EDFs BSk19, BSk20, and BSk21 were used to compute the EoS of all regions of a neutron star. Following the BPS model (Baym et al. 1971), the outer crust was assumed to consist of fully ionized atoms arranged in a body-centered cubic lattice at zero temperature. The EoSs of the outer crust were calculated using either experimental atomic masses when available or theoretical masses obtained from the HFB mass models constructed with the BSk19, BSk20, and BSk21 EDFs, as appropriate (see Pearson et al. 2011, for details). For the inner crust, where neutron-proton clusters coexist with free neutrons, the kinetic-energy part of the appropriate EDF was calculated using the semi-classical extended Thomas-Fermi method with proton quantum shell corrections added via the Strutinsky integral theorem; neutron shell effects, which are known to be much smaller, were neglected (see Pearson et al. 2012, for details). This method is a computationally very fast approximation to the full Hartree-Fock equations. In order to further reduce the computations, nuclear clusters were assumed to be spherical, and parametrized nucleon distributions were introduced. Finally, the electrostatic energy was calculated using the Wigner-Seitz approximation, and pairing effects were neglected. The overall resulting errors in the EoS of the inner crust were found to be about 5% at the neutron-drip point. The EoSs of the core, assumed to consist of homogeneous β-equilibrated matter made of nucleons and leptons (electrons and muons), were calculated essentially analytically from the adopted EDF (Goriely et al. 2010).
In a recent paper, Dutra et al. (2012) analyzed 240 Skyrme parametrizations, including BSk EDFs, by comparing their predicted properties of symmetric nuclear matter and pure NeuM to some empirical constraints. On this basis, these authors rejected BSk19–21 EDFs (along with all but five of the 240 parametrizations that they considered). We now argue that this rejection is unjustified. In the first place, BSk19–21 EDFs are claimed to be incompatible with the constraint labeled “SM3” by Dutra et al. (2012), a constraint on the EoS of symmetric nuclear matter obtained from the analysis of particle-flow measurements in Au-Au collisions (Danielewicz et al. 2002) that can be represented by a band in the plot of pressure vs. density. Now the pressures calculated with the EDFs BSk19−21 fall within this band over 80% of the density range and never deviate by more than about 20% from those inferred by Danielewicz et al. (2002) (see, e.g., Fig. 3 of Chamel et al. 2011). Nevertheless, Dutra et al. (2012) reject these functionals on the grounds that the calculated EoSs do not fall within the band of Danielewicz et al. (2002) over 95% of the density range. This criterion is quite arbitrary, and without any sound statistical foundation. In addition, it has to be noted that the interpretation by Danielewicz et al. (2002) of the raw experimental data is subject to uncertainties of two different kinds of model dependence: i) the transport model that determines the particle flow in a given collision experiment; ii) extrapolation from the charge-asymmetric Au + Au system ((N − Z)/A ≈ 20%) to symmetric nuclear matter. As demonstrated by Gale et al. (1990), the flow is generated during the early nonequilibrium stages of the collision, whereas the interpretation in terms of the EoS by Danielewicz et al. (2002) is an equilibrium version of a simplified momentum-dependent interaction. Viewed in this light, the deviations of the pressures obtained with BSk19–21 from the values of Danielewicz et al. (2002) are altogether insignificant.
The EDFs BSk19-21 are also found to violate the NeuM constraint “PNM2” by Dutra et al. (2012). However, this constraint was actually obtained by Danielewicz et al. (2002) from the symmetric nuclear matter constraint “SM3” using a simple parametrization for the symmetry energy. For this reason, the constraint “PNM2” is even less meaningful than the constraint “SM3”.
Dutra et al. (2012) also studied the density dependence of the symmetry energy. In particular, they found that the coefficient L obtained with BSk19 and BSk20 EDFs falls outside the range of empirical values determined by Chen et al. (2010) thus violating the constraints labeled “MIX2” and “MIX5”. However, the situation regarding the symmetry energy still remains a matter of debate, different experiments and/or theoretical calculations leading to different and sometimes contradicting predictions, as shown e.g. in Fig. 12 of Lattimer (2012; see also Tsang et al. 2012; Goriely et al. 2010, Sect. IIIB). Different Skyrme EDFs can thus be selected depending on the experiments or many-body calculations. For example, the values of L obtained with BSk19–21 EDFs are all compatible with the range of values L = 55 ± 25 MeV deduced by Centelles et al. (2009) and Warda et al. (2009) from measurements of the neutron-skin thickness in nuclei. The L coefficients obtained with BSk20 and BSk21 are also in agreement with the values 36 MeV< L < 55 MeV found by Steiner & Gandolfi (2012) combining quantum Monte Carlo calculations with neutron-star mass and radius measurements. Incidentally, this latter constraint would rule out three of the only five functionals that survive the analysis of Dutra et al. (2012). Various other constraints on J and L obtained from the analysis of different experiments (Tsang et al. 2012; Lattimer & Lim 2012) have been summarized in Fig. 1. The figure shows the constraint deduced by Tsang et al. (2009) from heavy-ion collisions (HIC), that derived by Chen et al. (2010) from measurement of the neutron skin thickness in tin isotopes, and that obtained from the analysis of giant dipole resonance (GDR; Trippa et al. 2008; Lattimer & Lim 2012) and the electric dipole polarizability (Piekarewicz et al. 2012) in 208Pb. For comparison, the constraint obtained from our HFB nuclear mass models BSk9−26 (Goriely et al. 2013; Pearson et al. 2009, and references therein) as well as unpublished ones are also shown. Values of J and L have also been extracted from pygmy dipole resonances (Carbone et al. 2010) and isobaric analogue states (Danielewicz & Lee 2009). However, we have not included them in the figure because of large experimental and theoretical uncertainties (see, e.g., Reinhard & Nazarewicz 2010; Daoutidis & Goriely 2011). The HFB mass model not only agrees with GDR, neutron skin and dipole polarizability data, but also provides relatively strict constraints on the J an L values.
 |
Fig. 1 Experimental constraints on the symmetry energy parameters (see text for details), taken from Lattimer & Lim (2012). The dashed line represents the constraint obtained from fitting experimental nuclear masses using the Brussels-Montreal HFB models with a root-mean-square deviation below 0.84 MeV (best fits are for J = 30 MeV). Star symbols correspond to the models BSk19, BSk20, and BSk21. |
Dutra et al. (2012) also point out that the values of Kτ obtained for the EDFs BSk19, BSk20, and BSk21 are incompatible with the range − 760 MeV < Kτ < − 372 MeV that they extract from experimental data using a liquid-drop like approach (the constraint labeled “MIX3”). On the other hand, the values of Kτ obtained with BSk19, BSk20, and BSk21 are all compatible with the range of values − 370 ± 120 MeV inferred from isospin diffusion in heavy-ion collisions by Chen et al. (2009). Just as for the L coefficient, the uncertainties in Kτ still remain very large (see e.g. Sect. IIIC in Goriely et al. 2010, for a thorough discussion).
Thus the rejection of BSk19–21 EDFs by Dutra et al. (2012) is ungrounded. On the contrary, these EDFs are well adapted to a unified treatment of all parts of neutron stars: the outer crust, the inner crust and the core. The relevance of these EDFs to the core of neutron stars arises not only from their fit to the EoS of NeuM but also from the good agreement between their predicted EoS of symmetric nuclear matter and realistic calculations, which implies that they take correct account of the presence of protons. Since these EDFs were fitted to nuclear masses, they also take account of inhomogeneities, and thus are appropriate for the calculation of the inner crust of neutron stars. As for the outer crust, its properties are determined entirely by the mass tables that have been generated for the appropriate EDFs by Pearson et al. (2011).
3. Analytical representations of the EoS
3.1. Preliminary remarks
The first law of thermodynamics for a barotropic EoS implies the relation (see, e.g., Haensel & Proszynski 1982) 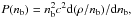 which can be also used in the integral forms:
which can be also used in the integral forms: 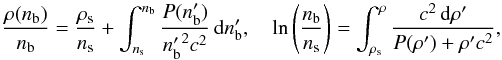 (1)where ρs and ns are the values of ρ and nb at the neutron-star surface. In the present paper we put ρs equal to the density of 56Fe at zero pressure and zero temperature, ρs = 7.86 g cm-3. One of the advantages of an analytical representation of the EoS is that it allows one to fulfill the relations (1) precisely.
(1)where ρs and ns are the values of ρ and nb at the neutron-star surface. In the present paper we put ρs equal to the density of 56Fe at zero pressure and zero temperature, ρs = 7.86 g cm-3. One of the advantages of an analytical representation of the EoS is that it allows one to fulfill the relations (1) precisely.
There are three qualitatively different domains of the interior of a neutron star: the outer crust, which consists of electrons and atomic nuclei; the inner crust, which consists of electrons, neutron-proton clusters, and “free” neutrons; and the core, which contains electrons, neutrons, protons, muons, and possibly other particles (see, e.g., Haensel et al. 2007, for review and references). In addition, there can be density discontinuities at the interfaces between layers containing different nuclei in the crust. An approximation of the EoS by a fully analytical function neglects these small discontinuities. However, the different character of the EoS in the three major domains is reflected by the complexity of our fit, which consists of several fractional-polynomial parts, matched together with the use of the function (ex + 1)-1.
For ρ < 106 g cm-3 the BSk EoSs are inadequate, primarily because atoms are not completely ionized, and thermal effects become non-negligible. The temperature dependence can be roughly described as (Haensel & Potekhin 2004) P = Pfit + P0, where Pfit is given by the fitting function presented below, and P0 = A(T) ρ provides a low-density continuation. For example, if the outer envelope consists of fully ionized iron, then A(T) ≈ 4 × 107 T K-1 (cm/s)2. Partial ionization decreases A(T): for example, at T = 107 K the best interpolation to the OPAL EoS (Rogers et al. 1996) is given by A = 3.5 × 1014 (cm/s)2 (that is, 14% smaller than for the fully ionized ideal gas).
We constructed analytical parametrizations for pressure P, gravitational mass density ρ, and baryon number density nb as functions of ρ, nb, or pseudo-enthalpy 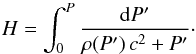 (2)The latter quantity is a convenient variable for models of rotating stars in General Relativity (see Stergioulas 2003, for review).
(2)The latter quantity is a convenient variable for models of rotating stars in General Relativity (see Stergioulas 2003, for review).
3.2. Pressure as a function of density
We introduce the variables ξ = log (ρ/gcm-3) and ζ = log (P/dyncm-2). Here and hereafter, log denotes log 10, while the natural logarithm is denoted by ln. Our parametrization of P(ρ) reads ![\begin{eqnarray} \zeta &=& \frac{a_1+a_2\xi+a_3\xi^3}{1+a_4\,\xi}\, \left\{\exp\left[a_5(\xi-a_6)\right]+1\right\}^{-1} \nonumber\\&& + (a_7+a_8\xi)\, \left\{\exp\left[a_9(a_6-\xi)\right]+1\right\}^{-1} \nonumber\\&& + (a_{10}+a_{11}\xi)\, \left\{\exp\left[a_{12}(a_{13}-\xi)\right]+1\right\}^{-1} \nonumber\\&& + (a_{14}+a_{15}\xi)\, \left\{\exp\left[a_{16}(a_{17}-\xi)\right]+1\right\}^{-1} \nonumber\\&& + \frac{a_{18}}{1+ [a_{19}\,(\xi-a_{20})]^2} + \frac{a_{21}}{1+ [a_{22}\,(\xi-a_{23})]^2}\cdot\label{fit.P} \end{eqnarray}](/articles/aa/full_html/2013/12/aa21697-13/aa21697-13-eq68.png) (3)The parameters ai are given in Table 2. The typical fit error of P is ≈1% for ξ ≳ 6. The maximum error is 3.7% at ξ = 9.51; it is determined by the jumps at the interfaces between layers containing different nuclides in the tabulated EoS. The fit (3) smoothly interpolates across these jumps.
(3)The parameters ai are given in Table 2. The typical fit error of P is ≈1% for ξ ≳ 6. The maximum error is 3.7% at ξ = 9.51; it is determined by the jumps at the interfaces between layers containing different nuclides in the tabulated EoS. The fit (3) smoothly interpolates across these jumps.
Compared to Eq. (14) of Haensel & Potekhin (2004), Eq. (3) contains additional terms in the last line with coefficients a18–a23. These terms improve the fit near the boundaries between the outer and inner crust and between the crust and the core, where the slope of P(ρ) sharply changes. In SLy4 the analogous changes were less abrupt. In the case of BSk models, however, the residuals of the fit without these additional terms may reach about 10% (Fantina et al. 2012).
 |
Fig. 2 Comparison of the data and fits for the pressure as a function of mass density for the EoS models BSk19, BSk20, and BSk21. Upper panel: rarefied tabular data (symbols) and the fit (3) (lines); lower panel: relative difference between the data and fit. Filled dots and dashed lines: BSk19; open circles and dot-dashed lines: BSk20; filled triangles and solid lines: BSk21. For comparison, the dotted line in the upper panel reproduces the fit to the EoS SLy4 (Haensel & Potekhin 2004). |
In Fig. 2 we compare the EoSs BSk19, BSk20, and BSk21 with their analytical representations. Symbols on the upper panel show the data, and lines show the fit. For comparison, the additional dotted line represents SLy4 EoS according to the fit of Haensel & Potekhin (2004). In order to make the differences between different EoSs visible, we plot the function ζ − 1.4ξ (cf. Fig. 4 of Haensel & Potekhin 2004). The data points in the figure are rarefied, i.e., we show only a small fraction of all numerical data used for the fitting. The lower panel of Fig. 2 shows the difference between the tabulated and fitted EoSs and thus illustrates the accuracy of Eq. (3).
3.3. Mass density versus number density
In some applications, it may be convenient to use nb as independent variable, and treat ρ and P as functions of nb. For this purpose we construct a fit to the deviation from the linear law ρ = nbmu, where mu = 1.66 × 10-24 g is the atomic mass unit: 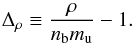 (4)In view of the relation (see, e.g., Haensel & Potekhin 2004)
(4)In view of the relation (see, e.g., Haensel & Potekhin 2004) 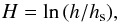 (5)where h = (ρc2 + P)/nb is the zero-T enthalpy per baryon and hs is the value of h at the stellar surface, Δρ must be consistent with Eq. (3). In order to fulfill Eq. (5) as closely as possible, we first calculate H(ρ) using Eqs. (2) and (3), and then refine the values of nb using Eq. (5). Our fit to the result is
(5)where h = (ρc2 + P)/nb is the zero-T enthalpy per baryon and hs is the value of h at the stellar surface, Δρ must be consistent with Eq. (3). In order to fulfill Eq. (5) as closely as possible, we first calculate H(ρ) using Eqs. (2) and (3), and then refine the values of nb using Eq. (5). Our fit to the result is 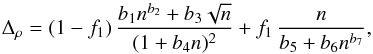 (6)where f1 ≡ [exp(1.1log n + b8) + 1]-1, n = nb/fm-3, and parameters bi are given in Table 3. The typical error of Eq. (6) for Δρ is (1–2)%, and the maximum relative error of 4.2% is at the low end of the fitted density range, min(ρ) = 106 g cm-3 (but at such low densities Δρ is itself negligible).
(6)where f1 ≡ [exp(1.1log n + b8) + 1]-1, n = nb/fm-3, and parameters bi are given in Table 3. The typical error of Eq. (6) for Δρ is (1–2)%, and the maximum relative error of 4.2% is at the low end of the fitted density range, min(ρ) = 106 g cm-3 (but at such low densities Δρ is itself negligible).
The inverse fit nb(ρ) is given by the formula 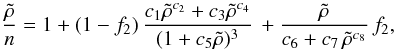 (7)where f2 ≡ [exp(ξ − c9) + 1]-1, the dimensionless argument is defined as
(7)where f2 ≡ [exp(ξ − c9) + 1]-1, the dimensionless argument is defined as 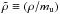 fm3 = ρ/(1.66 × 1015 gcm-3), and parameters ci are given in Table 4. As well as Eq. (6), the fit (7) also minimizes Δρ, and its residuals are similar: the average error is less than 2%, and the maximum relative error is 3.8% at the lower end of the fitted density range.
fm3 = ρ/(1.66 × 1015 gcm-3), and parameters ci are given in Table 4. As well as Eq. (6), the fit (7) also minimizes Δρ, and its residuals are similar: the average error is less than 2%, and the maximum relative error is 3.8% at the lower end of the fitted density range.
3.4. Density as a function of pseudo-enthalpy
As noted in Sect. 3.1, analytical expressions of ρ and P as functions of the pseudo-enthalpy H are expected to be useful for numerical simulations of rotating stars. In order to achieve the maximal consistency of our parametrizations, we first calculate H(ρ) using Eqs. (2) and (3), and then parametrize the result (cf. Sect. 3.3). The best fit reads ![\begin{eqnarray} \xi &=& \left[ 2.367+ \frac{21.84\,\eta^{0.1843}}{1+0.7\eta} \right] f_3 \nonumber\\&& + \frac{d_1+d_2\log\eta+(d_3+d_4\log\eta)(d_5\eta)^{d_{10}} }{ 1+d_6\eta+(d_5\eta)^{d_{10}}}\,(1-f_3) \nonumber\\&& + d_7\,\left\{\exp\left[d_8 (d_9-\log\eta)\right]+1\right\}^{-1}\!, \label{fit.rho-h} \end{eqnarray}](/articles/aa/full_html/2013/12/aa21697-13/aa21697-13-eq114.png) (8)where η ≡ eH − 1, f3 ≡ [exp (84log η + 167.2) + 1]-1, and the parameters di are given in Table 5.
(8)where η ≡ eH − 1, f3 ≡ [exp (84log η + 167.2) + 1]-1, and the parameters di are given in Table 5.
A comparison of the fit and the data is presented in Fig. 3. The typical fit error of ρ is about 1% in the interval 6 × 10-5 ≲ η ≲ 4, which corresponds to the considered mass density range 106 gcm-3 ≲ ρ ≲ 1016 g cm-3. The maximum fit errors of (3−5)% occur, as expected, near physical discontinuities, where the slope of the function ξ(η) quickly changes: at η ~ 0.01, where the fit goes smoothly through a break at the neutron-drip point, and at η ~ 0.03 − 0.1, near the crust-core interface.
4. Particle number fractions and density distributions
The physical input for numerical simulations of neutron-star thermal evolution includes the heat capacity, neutrino emissivity, and thermal conductivity tensors in the crust and the core (see Yakovlev & Pethick 2004; Page et al. 2006, for reviews). The evolution of the magnetic field is coupled to the thermal evolution and depends on the electrical conductivity tensor (e.g., Pons et al. 2009, and references therein). For calculation of these quantities, it is important to know the nucleon distributions in the crust and the composition of the core.
4.1. Nucleons and leptons in the core
 |
Fig. 3 Mass density as a function of pseudo-enthalpy. Upper panel: rarefied data to be fitted, calculated by integration according to Eqs. (2) and (3) (symbols), compared with the fit (8) (lines). Lower panel: fractional difference between the data and fit. The symbols and line styles for BSk19, BSk20, and BSk21 are the same as in Fig. 2. |
The core of a neutron star contains free neutrons, protons, electrons, and muons, whose number fractions relative to the total number of nucleons are, respectively, 1 − Yp, Yp, Ye, and Yμ. The condition of electric neutrality requires that Yp = Ye + Yμ. For Ye and Yμ, shown in Fig. 4, we obtained the following fitting expression: 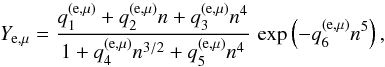 (9)where n = nb/fm-3, and parameters
(9)where n = nb/fm-3, and parameters 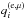 are given in Table 6. Whenever Eq. (9) gives a negative value, it must be replaced by zero. At the densities in the core, this can occur for muons, when the muon chemical potential is smaller than the electron rest energy. The fit residuals are typically (1−3) × 10-4 with a maximum of 7 × 10-4. Here, unlike in the preceding section, we quote absolute (not fractional) errors, because the fractional error loses its sense for a quantity that may be zero, as Yμ. The deviations of the fit from the data are displayed in the bottom panel of Fig. 4.
are given in Table 6. Whenever Eq. (9) gives a negative value, it must be replaced by zero. At the densities in the core, this can occur for muons, when the muon chemical potential is smaller than the electron rest energy. The fit residuals are typically (1−3) × 10-4 with a maximum of 7 × 10-4. Here, unlike in the preceding section, we quote absolute (not fractional) errors, because the fractional error loses its sense for a quantity that may be zero, as Yμ. The deviations of the fit from the data are displayed in the bottom panel of Fig. 4.
As well known, fractional abundances of leptons in the neutron-star core directly affect the thermal evolution of a neutron star at the neutrino cooling stage (e.g., Yakovlev & Pethick 2004; Page et al. 2006). In the region of a neutron-star core where the Fermi momenta of protons (pFp), neutrons (pFn), and electrons (pFe) satisfy the triangle inequality | pFp − pFe | < pFn < pFp + pFe, the direct Urca (durca) process of neutrino emission overpowers the more common modified Urca process and greatly accelerates the cooling of the star (Lattimer et al. 1991; Haensel 1995). As discussed by Chamel et al. (2011), the triangle inequality is never satisfied in the BSk19 model, but the models BSk20 and BSk21 allow it at sufficiently high densities nb > ndurca. The fitting expressions (9) allow us to reproduce the thresholds ndurca = 1.49 fm-3 for BSk20 and ndurca = 0.45 fm-3 for BSk21 (Chamel et al. 2011) with discrepancies of 0.08% and 0.3%, respectively.
4.2. Nucleon numbers in the crust
The outer crust consists of separate shells of different isotopes. The nuclear mass numbers A and charge numbers Z are constant within each shell and differ from one shell to another. The nuclei are embedded in the sea of degenerate electrons. Layers of diffusive mixing between adjacent shells are very narrow (see Hameury et al. 1983) and, therefore, unimportant for most applications. In particular, Pearson et al. (2011) have presented tables of Z and A in the outer crust for the models BSk19, BSk20, and BSk21.
 |
Fig. 4 Upper panel: number fractions of electrons Ye (solid lines) and muons Yμ (dashed lines) in the core of a neutron star, relative to the number of nucleons, as functions of nucleon number density nb for the three EoSs indicated near the curves. Lower panel: differences between the fit (9) and numerically computed tables for Ye and Yμ, plotted against nb. The vertical dotted lines show the position of the boundary between the crust and the core (ncc in Table 7). |
In the case of the inner crust, the EoS of Pearson et al. (2012) is based on the TETFSI (temperature-dependent extended Thomas-Fermi Strutinsky integral) method of Onsi et al. (2008). This is a semi-classical approximation to the HFB method, with proton shell corrections added perturbatively. A spherical Wigner-Seitz cell is assumed, with the neutron and proton density distributions parametrized according to 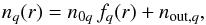 (10)where r is the distance to the center of the Wigner-Seitz cell, q =n for neutrons and q =p for protons, nout,q represents a constant background term, while fq(r) is a damped version of the usual Fermi profile. Specifically, we write it as
(10)where r is the distance to the center of the Wigner-Seitz cell, q =n for neutrons and q =p for protons, nout,q represents a constant background term, while fq(r) is a damped version of the usual Fermi profile. Specifically, we write it as ![\begin{equation} f_q(r) = \left[1+D_q(r)\,\exp\left(\frac{r-C_q}{a_q}\right) \right]^{-1}, \label{nucform} \end{equation}](/articles/aa/full_html/2013/12/aa21697-13/aa21697-13-eq153.png) (11)where Cq is the width of fq(r) at half maximum and aq is the diffuseness parameter, while Dq(r) is a damping factor given by
(11)where Cq is the width of fq(r) at half maximum and aq is the diffuseness parameter, while Dq(r) is a damping factor given by 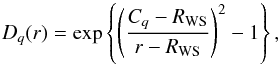 (12)where RWS is the Wigner-Seitz cell radius The purpose of this factor is to ensure that fq(r) and all its derivatives will vanish at the surface of the cell, a necessary condition for the validity of the semi-classical approximations that underlie the TETFSI method.
(12)where RWS is the Wigner-Seitz cell radius The purpose of this factor is to ensure that fq(r) and all its derivatives will vanish at the surface of the cell, a necessary condition for the validity of the semi-classical approximations that underlie the TETFSI method.
But whether we include this damping factor, or set it equal to unity, leaving us with a simple Fermi profile, the parametrization of Eq. (10) eliminates an arbitrary separation into liquid and gaseous phases within the Wigner-Seitz cell, and, strictly speaking, makes it illegitimate to draw a distinction between a “neutron gas” and “nuclei”. Nevertheless, if we denote by N′ the total number of neutrons in the cell at a given density, it is convenient to define the number of cluster neutrons as 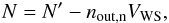 (13)where
(13)where 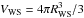 is the volume of the Wigner-Seitz cell, with a similar expression for the number of cluster protons Z. Actually, almost everywhere in the inner crust nout,p = 0, so that Z = Z′, the total number of protons in the cell. However, near the transition to the core some protons tend to spread over the entire cell, so that Z < Z′. This spreading corresponds to a smooth (second or higher order) phase transition between the crust and the core suggested by Pearson et al. (2012).
is the volume of the Wigner-Seitz cell, with a similar expression for the number of cluster protons Z. Actually, almost everywhere in the inner crust nout,p = 0, so that Z = Z′, the total number of protons in the cell. However, near the transition to the core some protons tend to spread over the entire cell, so that Z < Z′. This spreading corresponds to a smooth (second or higher order) phase transition between the crust and the core suggested by Pearson et al. (2012).
It turns out that for all three models considered here the number of protons Z′ in the Wigner-Seitz cell is equal to 40 for all densities. However, the number of neutrons N′ in the cell varies considerably with density, and, in fact, will be nonintegral in general since it is taken in the TETFSI method as one of the variables with respect to which the energy is minimized. The notion of a fractional number of neutrons per cell corresponds to the physical reality of delocalized neutrons. On the other hand, since the TETFSI method calculates proton (but not neutron) shell effects, Z′ cannot be allowed to become nonintegral, even when the protons become delocalized.
With N, Z, and A′ = N′ + Z′ varying smoothly with nb, we obtained the following parametrizations over the inner crust (note that Z′ = 40 everywhere): ![\begin{eqnarray} A-Z &=& \frac{ p_1 + p_2 \log x + (p_3 \log x)^{3.5} }{ 1 + (p_4 \log x)^{p_5}} \big[1-(\nb/\nc)^{p_0}\big],~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \label{fit.A} \\ Z &=& Z'\,\exp\left( -(\nb/\nc)^{p''_1} \right) \big[1-(\nb/\nc)^{p''_0}\big], \label{fit.Z} \\ A' &=& \frac{ p'_1 + p'_2 \log x +p'_3 (\log x)^2 }{ 1 + (p'_4 \log x)^4 } (1 + p'_5 x) \left[1-(p'_6 x)^2\right], \label{fit.A1} \end{eqnarray}](/articles/aa/full_html/2013/12/aa21697-13/aa21697-13-eq169.png) Here, x = nb/nd, nd is the baryon number density at the neutron-drip point, and ncc is the density of the transition to the homogeneous core. The parameters pi,
Here, x = nb/nd, nd is the baryon number density at the neutron-drip point, and ncc is the density of the transition to the homogeneous core. The parameters pi, 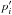 ,
, 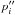 are listed in Table 7 along with the densities nd and ncc. The square brackets with the large power indices p0 in Eq. (14) and
are listed in Table 7 along with the densities nd and ncc. The square brackets with the large power indices p0 in Eq. (14) and 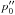 in Eq. (15) ensure the quick decrease of A and Z to zero in a narrow density interval at the transition from the crust to the core; they almost do not affect the fits in the bulk of the crust.
in Eq. (15) ensure the quick decrease of A and Z to zero in a narrow density interval at the transition from the crust to the core; they almost do not affect the fits in the bulk of the crust.
 |
Fig. 5 Effective nuclear parameters in the neutron-star crust, according to different models, as functions of baryon number density nb in the crust of a neutron star. Top panel: nuclear mass number A (the middle group of curves), the number of protons in a cluster Z (the lower curves), and the effective Wigner-Seitz cell mass number A′ (the upper curves). Bottom panel: rms charge radius of the nucleus. The results are shown for the models BSk19 (dashed lines and filled dots), BSk20 (dot-dashed lines and open circles), BSk21 (solid lines and filled triangles), and, for comparison, the smooth-composition model (the dotted curves). The left vertical dotted line shows the position of the boundary between the inner and outer crust, nb = nd (to the left of this line A′ = A). The right vertical dotted lines mark ncc, the interface between the crust and the core, in the BSk models. Between these boundaries, the curves represent analytical fits, and the symbols show some of the numerical data. |
In the upper panel of Fig. 5 we show the numbers A′, A, and Z as functions of nb in the outer and inner crust of a neutron star. In the lower panel we show the rms radius of the charge distribution, Rch. The values obtained in the models BSk19, BSk20, and BSk21 are compared with the smooth-composition (SC) model (Appendix B.2 of Haensel et al. 2007; see the next section). The vertical dotted lines mark the position of the neutron-drip point, which separates the inner and outer crust, and the transition from the crust to the core. In the inner crust, the fitted values (lines) are compared with the numerical results (symbols) for the BSk models. The numerical data are rarefied, in order to avoid crowding of the symbols. The agreement between the data and the fits are typically within a fraction of percent, except for a vicinity of the boundary with the core. Near the latter boundary, at 0.065 fm-3 ≲ nb < ncc, the neutron and proton distributions become rather flat (see Fig. 6 below), which hampers an accurate determination of the shape parameters. Therefore the numerical data suffer a significant scatter in this density interval, but the fits show an acceptable qualitative agreement with them. In the outer crust (at nb < nd) we use the elemental composition A and Z from Pearson et al. (2011) and Rch from bruslib1. From Fig. 5 we see that the SC model predicts a considerable jump of A′ at the neutron-drip point, while in the BSk models A′ is almost continuous. The latter continuity is equivalent to the equality of RWS at both sides of the drip boundary.
4.3. Nuclear shapes and sizes in the crust
In applications one sometimes needs a more detailed information about microscopic distributions of nucleons than given by the numbers A, A′, Z, and Z′ considered in Sect. 4.2. For example, cross sections of scattering of charged particles depend on the charge distribution in a nucleus. Previous calculations of neutrino bremsstrahlung (e.g., Kaminker et al. 1999) and electron heat conduction (e.g., Gnedin et al. 2001) in the crust of a neutron star employed nuclear form factors provided by the SC model based on the parametrization (10) with fq(r) = [1 − (r/rmax,q)bq] 3 (Oyamatsu 1993). Note that nout,p is effectively zero, and nout,n = (A′ − A)/VWS. Kaminker et al. (1999) fitted RWS, n0q, rmax,q, and bq as functions of nb by interpolating the Oyamatsu (1993) values of these parameters through the inner crust and making use of the Haensel & Pichon (1994) data for the outer crust.
 |
Fig. 6 Neutron (nn) and proton (np) density profiles at the values of the average baryon density nb = 3 × 10-4 fm-3 (near the top of the inner crust), 0.01 fm-3, 0.06 fm-3, and 0.075 fm-3 (near the bottom of the inner crust), according to the models BSk19, BSk20, and BSk21. The SC model (Haensel et al. 2007) is also shown for comparison. |
In Fig. 6 we show neutron and proton density distributions near the center of a Wigner-Seitz cell as given by Pearson et al. (2012), i.e., as described by Eqs. (11) and (12) for the models BSk19, BSk20, and BSk21. The four panels correspond to four different values of the mean baryon density nb in the inner crust. The neutron and proton density profiles predicted by the SC model are also shown for comparison. We present the parameters Cq, aq, and n0q that enter Eqs. (10) and (11) as functions of n = nb/fm-3, 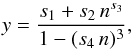 (17)where y = Cp, ap, Cn, or an, with numerical parameters si listed in Table 8. The decreasing denominator ensures the accelerated increase of the size and diffuseness of the nuclei when the density approaches that of the uniform nuclear matter near the crust-core interface. The values of n0q are related to the other fitted parameters via
(17)where y = Cp, ap, Cn, or an, with numerical parameters si listed in Table 8. The decreasing denominator ensures the accelerated increase of the size and diffuseness of the nuclei when the density approaches that of the uniform nuclear matter near the crust-core interface. The values of n0q are related to the other fitted parameters via 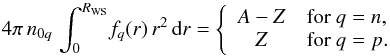 (18)Nevertheless we find it convenient for applications to have separate simple fits
(18)Nevertheless we find it convenient for applications to have separate simple fits ![\begin{eqnarray} n_{0p} &=& \left( q^\mathrm{(p)}_1 - \frac{q^\mathrm{(p)}_2 \, n }{ q^\mathrm{(p)}_3 + n^{q^\mathrm{(p)}_4}} \right)\, \left[ 1-(\nb/\nc)^9 \right], \label{fitn0p} \\ n_{0n} &=& \left( q^\mathrm{(n)}_1 + q^\mathrm{(n)}_2 \sqrt{n} - q^\mathrm{(n)}_3\,n \right)\, \left[ 1-(\nb/\nc)^{16} \right], \label{fitn0n} \end{eqnarray}](/articles/aa/full_html/2013/12/aa21697-13/aa21697-13-eq205.png) with parameters
with parameters 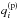 and
and 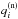 listed in Table 9. The agreement between the data and the fits are typically ~1% or better, except for a bottom crust layer, as explained in the previous section.
listed in Table 9. The agreement between the data and the fits are typically ~1% or better, except for a bottom crust layer, as explained in the previous section.
5. Conductivity in the neutron-star crust
As an example of application of our fitting formulae, we consider the electron conductivities in the crust of a neutron star. Practical formulae for calculation of the electron electrical and thermal conductivities of fully ionized plasmas have been developed by Potekhin et al. (1999) in the approximation of pointlike nuclei (see references therein for earlier works) and extended by Gnedin et al. (2001) to the case where the finite nuclear size cannot be neglected. The latter authors considered different nuclear shape models and concluded that their effect on electrical conductivity σ is mainly governed by the ratio xnuc = Reff/RWS, where 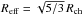 is the effective radius of the uniformly charged sphere that has the same rms radius of the charge distribution, Rch, as the considered nucleus. The same parameter xnuc determines the effect of nuclear form factors on the thermal conductivity κ, except at low temperatures where quantum lattice effects violate the Wiedemann-Franz relation in a nontrivial way (Gnedin et al. 2001). Under the assumption that the charge distribution is proportional to the proton distribution,
is the effective radius of the uniformly charged sphere that has the same rms radius of the charge distribution, Rch, as the considered nucleus. The same parameter xnuc determines the effect of nuclear form factors on the thermal conductivity κ, except at low temperatures where quantum lattice effects violate the Wiedemann-Franz relation in a nontrivial way (Gnedin et al. 2001). Under the assumption that the charge distribution is proportional to the proton distribution, 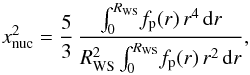 (21)we obtained a direct fit to this quantity, which facilitates calculation of the conductivities. In addition, we calculated and fitted the analogous size parameter xnuc,n = Reff,n/RWS for the neutron distribution fn(r). The fitting was done for the quantities obtained from Eqs. (21) and (11) with calculated (not fitted) values of Cq, aq, and RWS at each density. The fits have the form of Eq. (17) with the parameters listed in Table 10. The residuals are similar, with maxima of several percent near the end of the nb range and an order of magnitude smaller typical values.
(21)we obtained a direct fit to this quantity, which facilitates calculation of the conductivities. In addition, we calculated and fitted the analogous size parameter xnuc,n = Reff,n/RWS for the neutron distribution fn(r). The fitting was done for the quantities obtained from Eqs. (21) and (11) with calculated (not fitted) values of Cq, aq, and RWS at each density. The fits have the form of Eq. (17) with the parameters listed in Table 10. The residuals are similar, with maxima of several percent near the end of the nb range and an order of magnitude smaller typical values.
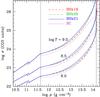 |
Fig. 7 Electrical conductivity σ of the neutron-star crust with nuclear parameters given by the models BSk19 (dashed lines), BSk20 (dot-dashed lines), BSk21 (solid lines), and the smooth-composition (SC) model (dotted curves) as functions of mass density ρ for T = 108 K, 108.5 K, and 109 K. The vertical dotted lines show the boundaries nd and ncc of the inner crust according to the three BSk models (Table 7). |
Figure 7 displays electrical conductivities σ calculated with the fitted A′, A, Z, and xnuc at temperatures and densities characteristic of the outer and inner crusts of neutron stars. Here, the calculations are performed for a body-centered cubic lattice of the nuclei without impurities. The crystalline structure of the crust is favored by recent results of molecular-dynamics simulations (Hughto et a. 2011) and supported by comparison of observations of X-ray transients in quiescence with simulations of the cooling of their crust (Shternin et al. 2007; Cackett et al. 2010). We have removed switching from Umklapp to normal processes of electron-phonon scattering at low T from the previously developed code (Gnedin et al. 2001), since Chugunov (2012) has shown that the normal processes have no effect under the conditions in a neutron-star crust. Figure 7 shows that the BSk models predict typically 1.5−2 times higher conductivity σ in the inner crust, than the SC model. On the other hand, this difference in σ can be removed by allowing a modest impurity parameter Zimp = ⟨ (Z − ⟨ Z ⟩ )2 ⟩ 1/2 ~ 3. The difference between the BSk and SC models increases near the bottom of the crust, where the BSk models (unlike SC) provide a continuous transition to the uniform nuclear matter in the stellar core. The conductivity is also almost continuous at the neutron drip density in the BSk models, at contrast to the SC model where it abruptly decreases at the drip point.
Similarly, we have used the analytical fits for calculating thermal conductivity κ. It has to be noted that electron conduction is probably the main mechanism of heat transport in the entire neutron-star crust despite the existence of competing transport channels. Radiative conduction is negligible at the crust densities (Potekhin & Yakovlev 2001; Pérez-Azorin et al. 2006), the heat transport by phonons is generally weaker than the electron transport (Pérez-Azorin et al. 2006; Chugunov & Haensel 2007), and the heat transport by superfluid neutrons in the inner crust (Bisnovatyi-Kogan & Romanova 1982; Aguilera et al. 2009) may be suppressed because of the strong coupling of the neutron superfluid to the nuclei due to nondissipative entrainment effects (Chamel 2012). We have found that the difference between the BSk and SC models for the electron heat conductivity κ is smaller than the corresponding difference for σ. The smaller difference is explained by the large contribution of the electron-electron scattering into the thermal resistivity of the inner crust (Shternin & Yakovlev 2006).
6. Neutron star configurations
 |
Fig. 8 Top rows: gravitational mass (in solar masses) versus circumferential radius of nonrotating neutron stars for the EoSs BSk19-20-21 (dots) and their analytical representations from Eq. (3) (lines). The solid and dotted parts of the lines correspond to the hydrostatically stable and unstable configurations, respectively. The dashed segment in the middle panel corresponds to superluminal EoS at the stellar center. The crosses mark the threshold beyond which the EoS becomes superluminal. The middle and bottom rows show respectively a zoom around the maximum neutron-star mass and the low mass region where the discrepancies are the largest. |
 |
Fig. 9 Top panels: gravitational mass (in solar masses) versus circumferential radius of rotating neutron stars (rotation frequency 716 Hz) for the EoSs BSk19-20-21 (dots) and their analytical representations from Eq. (8) (solid lines). The middle and bottom panels show respectively a zoom around the maximum neutron-star mass and the low mass region where the discrepancies are the largest. |
In order to estimate the errors introduced in the fitting formulae described in Sect. 3 on global neutron-star properties, we have computed the mass and radius of a neutron star from the tabulated EoSs and their analytical representations. For a nonrotating neutron star, we integrated the Tolman-Oppenheimer-Volkoff (TOV) equation from the center, with the central mass density ρc as a free parameter, outward to ρs, using the fourth-order Runge-Kutta method with an adaptive step and controlled accuracy. We avoided an affixment of an integration step to the calculated points using either linear or cubic spline interpolation in the tabulated EoSs. The neutron-star masses M obtained using these two types of interpolation agree to ~10-4 M⊙. The radii R agree typically to ~0.1%, if M ≳ 0.3 M⊙.
Figure 8 shows the mass-radius relation of nonrotating neutron stars for the EoSs BSk19, BSk20, and BSk21. The neutron-star configurations obtained with the original EoSs and with their analytical representations are drawn as dots and lines respectively. The maximum neutron-star masses are Mmax = 1.86 M⊙ at ρc = 3.48 × 1015 g cm-3 for BSk19, Mmax = 2.16 M⊙ at ρc = 2.69 × 1015 g cm-3 for BSk20, and Mmax = 2.27 M⊙ at ρc = 2.27 × 1015 g cm-3 for BSk21, in close agreement with Chamel et al. (2011) and Fantina et al. (2012). The differences between Mmax obtained using the original data and the fit are about 0.09%, 0.09%, and 0.17%, and the differences for corresponding ρc values are about 0.03%, 0.02%, and 0.7%, respectively. At higher ρc the condition of hydrostatic stability dM/dρc is violated; the unstable configurations are shown by the dotted parts of the curves to the left of the maxima in Fig. 8. The crosses in Fig. 8 correspond to the largest values of ρc for which dP/dρ < c2 (2.18 × 1015 g cm-3 for BSk19 and BSk20, and 2.73 × 1015 g cm-3 for BSk21). At higher densities the EoS becomes superluminal. The fit (3) and its first derivative determine these densities with accuracies within 2%. The corresponding stellar masses determined from the fit and from the tables agree to ~0.1%. Note that the EoS BSk20 becomes superluminal before the limit of hydrostatic stability is reached. Configurations with higher ρc, corresponding to 2.14 M⊙ < M < Mmax and shown by the dashed curve in Fig. 8, cannot be fully trusted (see, e.g., Haensel et al. 2007, Sect. 5.15, for a discussion)
The minimum neutron-star masses are 0.093 M⊙, 0.090 M⊙, and 0.087 M⊙ for the models BSk19, BSk20, and BSk21, with discrepancies between the original data and the fit ~0.7%, 0.1%, and 0.03%, respectively. The radii of neutron stars with the mass of 1.4 M⊙ are R = 10.74 km, 11.74 km, and 12.57 km, with discrepancies between the original data and the fit of ~0.1%, ~0.02%, and ~0.2%. The discrepancies in the circumferential radii (R = 11.5 km, 11.9 km, and 12.4 km) of neutron stars with M = 0.5 M⊙ are also smaller than 0.2% for all three EoSs.
As mentioned in Sect. 4.1 the triangle condition for the durca processes can be fulfilled for BSk20 and BSk21 models at nb > ndurca. The threshold ndurca cannot be reached in a stable neutron star in frames of the model BSk20, but it is reached for neutron stars with M > 1.59 M⊙ in the model BSk21. The latter mass value, first obtained by Chamel et al. (2011), is reproduced by the present fit with a discrepancy of 0.3%. Chamel et al. (2011) noted that all three EoSs are compatible with the constraint that no durca process should occur in neutron stars with masses 1−1.5 M⊙ (Klähn et al. 2006). On the other hand, according to the analysis of Yakovlev et al. (2008), the situation where the most massive neutron stars with nucleon superfluidity in the core experience enhanced cooling due to the durca processes appears in a better agreement with observations than the complete absence of such processes in any stars. Thus the model BSk21 may bring the cooling theory in a better agreement with observations than the other models. The fitting formulae presented above facilitate the checks of this kind. In this respect, it is worth noting that the effective nucleon masses 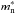 and
and 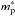 , which are needed for cooling simulations, are readily obtained in analytical form from Eq. (A.10) of Chamel et al. (2009), using the appropriate parameter set given in Goriely et al. (2010).
, which are needed for cooling simulations, are readily obtained in analytical form from Eq. (A.10) of Chamel et al. (2009), using the appropriate parameter set given in Goriely et al. (2010).
Similarly, we have analyzed the structure of a neutron star rotating at a frequency of 716 Hz, equal to the frequency of PSR J1748−2446ad, the fastest-spinning pulsar known (Hessels et al. 2006). For this purpose we used the Lorene/Codes/Nrotstar/nrotstar code from the public library lorene2. We have generated tables of the analytical EoSs from Eq. (8) and used them as an input in the nrotstar code. The results obtained using the original EoSs and their analytical representations are shown in Fig. 9. Here we plot only the stable stellar configurations that are described by subluminal EoSs. The relative differences in the maximum neutron-star masses are of similar magnitudes to those found for static neutron stars, namely ~0.03%, ~0.08% and ~0.2% for the EoSs BSk19, BSk20, and BSk21. The errors in the radii of 1 M⊙ neutron stars are ~0.1%, ~0.09%, and ~0.5%, respectively.
All in all, the discrepancies lie far below the observational uncertainties and therefore they do not affect the comparison with observational data. In computing the neutron star configurations, we have checked the violations of the general-relativistic virial identities GRV2 (Bonazzola 1973; Bonazzola & Gourgoulhon 1994) and GRV3 (Gourgoulhon & Bonazzola 1994). The absolute deviations lie between 10-3 and 10-6 thus confirming the high precision of the analytical representation of the EoSs.
7. Conclusions
We constructed analytical representations, in terms of the continuous and differentiable functions of a single chosen variable, of three recently developed equations of state BSk19, BSk20, and BSk21 (Pearson et al. 2011, 2012). We considered two choices of the independent variable. The first one is the mass density ρ. Then Eq. (3) gives function P(ρ), which fits the numerical EoS tables at 106 gcm-3 < ρ ≲ 2 × 1016 gcm-3 with a typical error of ~1%. The baryon number density nb can be calculated from Eq. (1) to satisfy exactly the first law of thermodynamics. Alternatively, nb can be evaluated using our fit (7). A variant is to choose nb as an independent variable and calculate ρ(nb) from the fit (6) and P(ρ(nb)) from Eq. (3). Then, if necessary, ρ can be corrected using the first integral relation in Eq. (1).
Differentiation of P(ρ) then yields analytical representations of the adiabatic index ![\begin{equation} \Gamma=\frac{\nb}{P}\,\frac{\dd P}{\dd \nb} = \left[ 1+ \frac{P}{\rho c^2} \right] \frac{\rho}{P}\frac{\dd P}{\dd\rho}, \end{equation}](/articles/aa/full_html/2013/12/aa21697-13/aa21697-13-eq263.png) (22)which is included in the computer code that realizes the fit. Different regions of neutron-star interior are characterized by distinct behavior of Γ as discussed, e.g., in Haensel & Potekhin (2004). This behavior remains qualitatively the same for different EoSs, but quantitative differences can be significant, as illustrated in Fig. 10.
(22)which is included in the computer code that realizes the fit. Different regions of neutron-star interior are characterized by distinct behavior of Γ as discussed, e.g., in Haensel & Potekhin (2004). This behavior remains qualitatively the same for different EoSs, but quantitative differences can be significant, as illustrated in Fig. 10.
 |
Fig. 10 Adiabatic index Γ for SLy4 and BSk EoSs. |
The other choice of the independent variable is the pseudo-enthalpy H, Eq. (2). This choice is particularly advantageous for simulations of neutron-star dynamics. We represented the EoSs by the continuous and differentiable functions P(H), ρ(H), and n(H), where ρ(H) is given by Eq. (8) with typical accuracy ~1%, while P(H) and nb(H) are calculated from the functions P(ρ) and nb(ρ), respectively.
We also obtained analytical representations of number fractions of neutrons, protons, electrons and muons in the inner crust and the core, and nuclear shape parameters in the inner crust of a neutron star as functions of nb. These results can be used, e.g., for neutron-star cooling simulations. As an application, we calculate electron conductivities in the crust with the use of the BSk models. Compared to the results of the smooth-composition model (Gnedin et al. 2001), we find that the BSk models yield appreciably higher electrical conductivities in the inner crust of a neutron star.
Finally, we estimated the errors introduced in the fitting formulae on global neutron-star properties and showed that they lie far below the observational uncertainties and therefore they do not affect the comparison of theoretical models with observational data.
The present work is mainly aimed at astrophysicists as they do not have to perform nuclear physics calculations for simulations of neutron-star structure and evolution. When required, the same method of constructing analytical approximations can be applied to other EoSs (see, e.g., Haensel et al. 2007 and Lattimer 2012, for references).
The Brussels Nuclear Library for Astrophysics Application, http://www.astro.ulb.ac.be/bruslib/
Langage Objet pour la Relativité Numérique, http://www.lorene.obspm.fr/
Acknowledgments
The work of A.Y.P. was partially supported by the Ministry of Education and Science of the Russian Federation (Agreement No. 8409, 2012), the Russian Foundation for Basic Research (RFBR grant 11-02-00253-a), the Russian Leading Scientific Schools program (grant NSh-4025.2012.2), and the Programme National de Physique Stellaire (CNRS/INSU, France). The work of A.F.F., N.C. and S.G. was supported by FNRS (Belgium). The work of J.M.P. was supported by the NSERC (Canada).
References
- Aguilera, D. N., Cirigliano, V., Pons, J. A., Reddy, S., & Sharma, R. 2009, Phys. Rev. Lett., 102, 091101 [NASA ADS] [CrossRef] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G., 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Audi, G., Wapstra, A. H., & Thibault, C. 2003, Nucl. Phys. A, 729, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., Pethick, C., & Sutherland, P. 1971, ApJ, 170, 299 [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Romanova, M. M. 1982, Sov. Phys. JETP, 56, 243 [Google Scholar]
- Bonazzola, S. 1973, ApJ, 182, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Bonazzola, S., & Gourgoulhon, E. 1994, Class. Quant. Grav., 11, 1775 [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., Salgado, M., & Marck, J. A. 1993, A&A, 278, 421 [NASA ADS] [Google Scholar]
- Cackett, E. M., Brown, E. F., Cumming, A., et al. 2010, ApJ, 722, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Carbone, A., Colò, G., Bracco, A., et al. 2010, Phys. Rev. C, 81, 041301 [Google Scholar]
- Centelles, M., Roca-Maza, X., Viñas, X., & Warda, M. 2009, Phys. Rev. Lett., 102, 122502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chamel, N. 2010, Phys. Rev. C, 82, 014313 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2012, Phys. Rev. C, 85, 035801 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Goriely, S., & Pearson, J. M. 2009, Phys. Rev. C, 80, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Fantina, A. F., Pearson, J. M., & Goriely, S. 2011, Phys. Rev. C, 84, 062802(R) [NASA ADS] [CrossRef] [Google Scholar]
- Chen, L.-W., Cai, B.-J., Ko, C. M., et al. 2009, Phys. Rev. C, 80, 014322 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, L.-W., Ko, C. M., Li, B.-A., & Xu, J. 2010, Phys. Rev. C, 82, 024321 [NASA ADS] [CrossRef] [Google Scholar]
- Chugunov, A. I. 2012, Astron. Lett., 38, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Chugunov, A. I., & Haensel, P. 2007, MNRAS, 381, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Colò, G., van Giai, N., Meyer, J., Bennaceur, K., & Bonche, P. 2004, Phys. Rev. C, 70, 024307 [NASA ADS] [CrossRef] [Google Scholar]
- Danielewicz, P., & Lee, J. 2009, Int. J. Mod. Phys. E, 18, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Danielewicz, P., Lacey, R., & Lynch, W. G. 2002, Science, 298, 1592 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Daoutidis, I., & Goriely, S. 2011, Phys. Rev. C, 84, 027301 [NASA ADS] [CrossRef] [Google Scholar]
- Douchin, F., & Haensel, P. 2000, Phys. Lett. B, 485, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutra, M., Lourenço, O., Sá Martins, J. S., et al. 2012, Phys. Rev. C, 85, 035201 [NASA ADS] [CrossRef] [Google Scholar]
- Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2012, J. Phys. Conf. Ser., 342, 012003 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, B., & Pandharipande, V. R. 1981, Nucl. Phys. A, 361, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Gale, C., Welke, G. M., Prakash, M., Lee, S. J., & Das Gupta, S. 1990, Phys. Rev. C, 41, 1545 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, O. Y., Yakovlev, D. G., & Potekhin, A. Y. 2001, MNRAS, 324, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2010, Phys. Rev. C, 82, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2013, Phys. Rev. C, 88, 024308 [NASA ADS] [CrossRef] [Google Scholar]
- Gourgoulhon, E., & Bonazzola, S. 1994, Class. Quant. Grav., 11, 443 [Google Scholar]
- Haensel, P. 1995, Space Sci. Rev., 74, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Pichon, 1994, A&A, 283, 313 [NASA ADS] [Google Scholar]
- Haensel, P., & Potekhin, A. Y. 2004, A&A, 498, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., & Proszynski, M. 1982, ApJ, 258, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990, A&A, 229, 117 [NASA ADS] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2003, A&A, 404, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1: Equation of State and Structure (New York: Springer) [Google Scholar]
- Hameury, J. M., Heyvaerts, J., & Bonazzola, S. 1983, A&A, 121, 259 [NASA ADS] [Google Scholar]
- Hessels, J. W. T., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hughto, J., Schneider, A. S., Horowitz, C. J., & Berry, D. K. 2011, Phys. Rev. E, 84, 016401 [NASA ADS] [CrossRef] [Google Scholar]
- Kaminker, A. D., Pethick, C. J., Potekhin, A. Y., Thorsson, V., & Yakovlev, D. G. 1999, A&A, 343, 1009 [NASA ADS] [Google Scholar]
- Klähn, T., Blaschke, D., Typel, S., et al. 2006, Phys. Rev. C, 74, 035802 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M. 2012, Annu. Rev. Nucl. Particle Sci., 62, 485 [Google Scholar]
- Lattimer, J. M., & Lim, Y. 2013, A&A, 771, 51 [Google Scholar]
- Lattimer, J. M., Pethick, C. J., Prakash, M., & Haensel, P. 1991, Phys. Rev. Lett., 66, 2701 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Li, Z. H., & Schulze, H. J. 2008, Phys. Rev. C, 78, 028801 [NASA ADS] [CrossRef] [Google Scholar]
- Onsi, M., Dutta, A. K., Chatri, H., et al. 2008, Phys. Rev. C, 77, 065805 [Google Scholar]
- Oyamatsu, K. 1993, Nucl. Phys. A, 561, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Geppert, U., & Weber, F. 2006, Nucl. Phys. A, 777, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Pandharipande, V. R., & Ravenhall, D. G. 1989, in Nuclear matter and heavy ion collisions, NATO ADS Ser., B205, eds. M. Soyeur, H. Flocard, B. Tamain, et al. (Dordrecht: Reidel), 103 [Google Scholar]
- Pearson, J. M., Goriely, S., Chamel, N., Samyn, M., & Onsi, M. 2009, in Bulk Nuclear Properties, ed. P. Danielewicz, AIP Conf. Proc., 1128, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., Goriely, S., & Chamel, N. 2011, Phys. Rev. C, 83, 065810 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., Chamel, N., Goriely, S., & Ducoin, C. 2012, Phys. Rev. C, 85, 065803 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Azorin, J. F., Miralles, J. A., & Pons, J. A. 2006, A&A, 451, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piekarewicz, J., Agrawal, B. K., Colò, G., et al. 2012, Phys. Rev. C, 85, 041302 [NASA ADS] [CrossRef] [Google Scholar]
- Pons, J. A., Miralles, J. A., & Geppert, U. 2009, A&A, 496, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., & Yakovlev, D. G. 2001, A&A, 374, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., Baiko, D. A., Haensel, P., & Yakovlev, D. G. 1999, A&A, 346, 345 [NASA ADS] [Google Scholar]
- Reinhard, P. G., & Nazarewicz, W. 2010, Phys. Rev. C, 81, 051303 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Shternin, P. S., & Yakovlev, D. G. 2006, Phys. Rev. D, 74, 043004 [NASA ADS] [CrossRef] [Google Scholar]
- Shternin, P. S., Yakovlev, D. G., Haensel, P., & Potekhin, A. Y. 2007, MNRAS, 382, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., & Gandolfi, S. 2012, Phys. Rev. Lett., 108, 081102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stergioulas, N. 2003, Living Rev. Relativity, 6, 3, http://www.livingreviews.org/lrr-2003-3/ [Google Scholar]
- Trippa, L., Colò, G., & Vigezzi, E. 2008, Phys. Rev. C, 77, 061304 [NASA ADS] [CrossRef] [Google Scholar]
- Tsang, M. B., Zhang, Y., Danielewicz, P., et al. 2009, Phys. Rev. Lett., 102, 122701 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tsang, M. B., Stone, J. R., Camera, F., et al. 2012, Phys. Rev. C, 86, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Yakovlev, D. G., Gnedin, O. Y., Kaminker, A. D., & Potekhin, A. Y. 2008, in 40 Years of Pulsars: Millisecond pulsars, magnetars and more, eds. C. Bassa, Z. Wang, A. Cumming, et al., AIP Conf. Proc., 983, 379 [Google Scholar]
- Warda, M., Viñas, X., Roca-Maza, X., & Centelles, M. 2009, Phys. Rev. C, 80, 024316 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Properties of the Skyrme forces BSk19, BSk20, and BSk21 (Goriely et al. 2010). See text for details.
All Figures
 |
Fig. 1 Experimental constraints on the symmetry energy parameters (see text for details), taken from Lattimer & Lim (2012). The dashed line represents the constraint obtained from fitting experimental nuclear masses using the Brussels-Montreal HFB models with a root-mean-square deviation below 0.84 MeV (best fits are for J = 30 MeV). Star symbols correspond to the models BSk19, BSk20, and BSk21. |
| In the text | |
 |
Fig. 2 Comparison of the data and fits for the pressure as a function of mass density for the EoS models BSk19, BSk20, and BSk21. Upper panel: rarefied tabular data (symbols) and the fit (3) (lines); lower panel: relative difference between the data and fit. Filled dots and dashed lines: BSk19; open circles and dot-dashed lines: BSk20; filled triangles and solid lines: BSk21. For comparison, the dotted line in the upper panel reproduces the fit to the EoS SLy4 (Haensel & Potekhin 2004). |
| In the text | |
 |
Fig. 3 Mass density as a function of pseudo-enthalpy. Upper panel: rarefied data to be fitted, calculated by integration according to Eqs. (2) and (3) (symbols), compared with the fit (8) (lines). Lower panel: fractional difference between the data and fit. The symbols and line styles for BSk19, BSk20, and BSk21 are the same as in Fig. 2. |
| In the text | |
 |
Fig. 4 Upper panel: number fractions of electrons Ye (solid lines) and muons Yμ (dashed lines) in the core of a neutron star, relative to the number of nucleons, as functions of nucleon number density nb for the three EoSs indicated near the curves. Lower panel: differences between the fit (9) and numerically computed tables for Ye and Yμ, plotted against nb. The vertical dotted lines show the position of the boundary between the crust and the core (ncc in Table 7). |
| In the text | |
 |
Fig. 5 Effective nuclear parameters in the neutron-star crust, according to different models, as functions of baryon number density nb in the crust of a neutron star. Top panel: nuclear mass number A (the middle group of curves), the number of protons in a cluster Z (the lower curves), and the effective Wigner-Seitz cell mass number A′ (the upper curves). Bottom panel: rms charge radius of the nucleus. The results are shown for the models BSk19 (dashed lines and filled dots), BSk20 (dot-dashed lines and open circles), BSk21 (solid lines and filled triangles), and, for comparison, the smooth-composition model (the dotted curves). The left vertical dotted line shows the position of the boundary between the inner and outer crust, nb = nd (to the left of this line A′ = A). The right vertical dotted lines mark ncc, the interface between the crust and the core, in the BSk models. Between these boundaries, the curves represent analytical fits, and the symbols show some of the numerical data. |
| In the text | |
 |
Fig. 6 Neutron (nn) and proton (np) density profiles at the values of the average baryon density nb = 3 × 10-4 fm-3 (near the top of the inner crust), 0.01 fm-3, 0.06 fm-3, and 0.075 fm-3 (near the bottom of the inner crust), according to the models BSk19, BSk20, and BSk21. The SC model (Haensel et al. 2007) is also shown for comparison. |
| In the text | |
 |
Fig. 7 Electrical conductivity σ of the neutron-star crust with nuclear parameters given by the models BSk19 (dashed lines), BSk20 (dot-dashed lines), BSk21 (solid lines), and the smooth-composition (SC) model (dotted curves) as functions of mass density ρ for T = 108 K, 108.5 K, and 109 K. The vertical dotted lines show the boundaries nd and ncc of the inner crust according to the three BSk models (Table 7). |
| In the text | |
 |
Fig. 8 Top rows: gravitational mass (in solar masses) versus circumferential radius of nonrotating neutron stars for the EoSs BSk19-20-21 (dots) and their analytical representations from Eq. (3) (lines). The solid and dotted parts of the lines correspond to the hydrostatically stable and unstable configurations, respectively. The dashed segment in the middle panel corresponds to superluminal EoS at the stellar center. The crosses mark the threshold beyond which the EoS becomes superluminal. The middle and bottom rows show respectively a zoom around the maximum neutron-star mass and the low mass region where the discrepancies are the largest. |
| In the text | |
 |
Fig. 9 Top panels: gravitational mass (in solar masses) versus circumferential radius of rotating neutron stars (rotation frequency 716 Hz) for the EoSs BSk19-20-21 (dots) and their analytical representations from Eq. (8) (solid lines). The middle and bottom panels show respectively a zoom around the maximum neutron-star mass and the low mass region where the discrepancies are the largest. |
| In the text | |
 |
Fig. 10 Adiabatic index Γ for SLy4 and BSk EoSs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


