| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202243715 | |
| Published online | 12 September 2022 | |
Accreting neutron stars from the nuclear energy-density functional theory
II. Equation of state and global properties⋆
1
Grand Accélérateur National d’Ions Lourds (GANIL), CEA/DRF – CNRS/IN2P3, Boulevard Henri Becquerel, 14076 Caen, France
e-mail: anthea.fantina@ganil.fr
2
Institut d’Astronomie et d’Astrophysique, CP-226, Université Libre de Bruxelles, 1050 Brussels, Belgium
3
N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
4
Dept. de Physique, Université de Montréal, Montréal, Québec H3C 3J7, Canada
5
Laboratoire Univers et Théories, Observatoire de Paris, Université PSL, Université Paris Cité, CNRS, 92190 Meudon, France
Received:
5
April
2022
Accepted:
2
July
2022
Context. The accretion of matter onto the surface of a neutron star in a low-mass X-ray binary triggers X-ray bursts, whose ashes are buried and further processed thus altering the composition and the properties of the stellar crust.
Aims. In this second paper of a series, the impact of accretion on the equation of state and on the global properties of neutron stars is studied in the framework of the nuclear energy-density functional theory.
Methods. Considering ashes made of 56Fe, we calculated the equations of state using the same Brussels-Montreal nuclear energy-density functionals BSk19, BSk20, and BSk21, as those already employed for determining the crustal heating in our previous study for the same ashes. All regions of accreting neutron stars were treated in a unified and thermodynamically consistent way. With these equations of state, we determined the mass, radius, moment of inertia, and tidal deformability of accreted neutron stars and compared with catalyzed neutron stars for which unified equations of state based on the same functionals are available.
Results. The equation of state of accreted neutron stars is found to be significantly stiffer than that of catalyzed matter, with an adiabatic index Γ ≈ 4/3 throughout the crust. For this reason, accreting neutron stars have larger radii. However, their crustal moment of inertia and their tidal deformability are hardly changed provided density discontinuities at the interface between adjacent crustal layers are properly taken into account.
Conclusions. The enhancement of the stiffness of the equation of state of accreting neutron stars is mainly a consequence of nuclear shell effects, thus confirming the importance of a quantum treatment as stressed in our first study. With our previous calculations of crustal heating using the same functionals, we have thus obtained consistent microscopic inputs for simulations of accreting neutron stars.
Key words: dense matter / equation of state / stars: neutron / accretion, accretion disks / nuclear reactions, nucleosynthesis, abundances
The tables of the equations of state are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/665/A74
© A. F. Fantina et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
The accretion of matter onto a neutron star (NS) in a low-mass X-ray binary induces thermonuclear explosions with total energies 1039 − 1040 erg observed as X-ray bursts lasting a few tens of seconds and with a typical recurrence time of hours to days (see e.g., Strohmayer & Bildsten 2006 for a review and Galloway et al. 2020 for a recent compilation of observations). The unstable carbon burning in deeper layers is thought to power less frequent superbursts with energies ∼1042 erg. On a longer timescale, the ashes from X-ray bursts may be further reprocessed by electron captures, neutron emissions, and neutron captures, and possibly pycnonuclear fusion reactions as they slowly sink inside the NS (see, e.g., Meisel et al. 2018 for a recent review). Depending on the duration of accretion episodes, the original crust of the NS can be partially or fully replaced (Tauris et al. 2012; see also the discussion in Fantina et al. 2018) and this may radically change its properties, as first shown by Haensel & Zdunik (1990a).
Simulations of accreting NSs usually rely on the equation of state (EoS) of Haensel & Zdunik (1990b) for the accreting crust together with the heat sources obtained by Haensel & Zdunik (1990a; or the more recent calculations of Haensel & Zdunik 2003, 2008). These results, which are based on the liquid-drop model, are then combined with some EoS for the deepest layers of the inner crust and for the core. However, significant errors on the global structure of the NS and on its tidal deformability may arise from the use of thermodynamically inconsistent EoSs (Fortin et al. 2016; Ferreira & Providência 2020; Suleiman et al. 2021).
In our previous study, we calculated the heat released in accreting NS crusts and the location of the heat sources using accurately calibrated Brussels-Montreal nuclear energy-density functionals (EDFs) taking into account nuclear shell effects perturbatively (Fantina et al. 2018). We found that the composition of the crust of an accreted NS can differ substantially from that of an isolated NS made of cold catalyzed matter. In this second paper, we present the corresponding EoSs. Both the outer and inner regions of accreted NS crusts are treated consistently within the same microscopic framework using the same EDFs as in Fantina et al. (2018). Together with the EoSs of the liquid core previously calculated in Goriely et al. (2010), unified EoSs describing all regions of accreted NSs with the same EDFs are constructed.
After briefly recalling the main features of the microscopic model of accreted NS crusts and of the adopted EDFs in Sect. 2, the calculated EoSs are presented in Sect. 3. The global properties of accreted NSs are discussed in Sect. 4 and conclusions are given in Sect. 5.
2. Model of accreted neutron-star crusts
2.1. Main assumptions
We recall here the main assumptions on how we model the crust of an accreting NS, by which we mean the region of the NS below the envelope and whose density is higher than 106 g cm−3. Because of the relatively low temperatures generally prevailing in accreting NS crusts, namely T < 109 K (see e.g., Chamel & Haensel 2008), the thermal contributions to the thermodynamic potentials can be neglected. For such temperatures, except for the shallowest regions, the innermost layers are expected to be in the solid state (Fantina et al. 2020; Carreau et al. 2020). The composition and structure of each layer were determined in the one-component plasma approximation: at each pressure P, matter is fully described by the proton number Z and the total nucleon number Acell in a single Wigner-Seitz (WS) cell. In the outer crust, Acell reduces to the mass number A of the corresponding nuclei, while in the inner crust Acell also accounts for free neutrons. Unlike cold catalyzed matter, accreting NS crusts are not in full thermodynamic equilibrium and reactions can thus occur. The compression of the ashes from X-ray bursts may trigger a series of electron captures, by which the nucleus (A, Z) transforms into a nucleus (A, Z − 1) with the emission of an electron neutrino. The one-component plasma approach induces discontinuities in the neutron density and the neutron chemical potential, while in fact the onset of neutron emission occurs at lower density and pressure than those predicted by the mean-nucleus approximation (see Chamel et al. 2015 for details). However, we did not consider neutron diffusion (Shchechilin & Chugunov 2019; Chugunov & Shchechilin 2020; Gusakov & Chugunov 2020), for consistency with our previous calculations of the heating (Fantina et al. 2018). With increasing density and decreasing proton number, neighbouring nuclei may overcome their Coulomb barrier and fuse. However, large uncertainties reside in the determination of the rates of these pycnonuclear reactions (see e.g., Yakovlev et al. 2006). We thus simply assumed that these processes occur whenever Z reaches the minimum value Zmin = 8 (see also the discussion in Sect. 3.2 in Fantina et al. 2018). As in Fantina et al. (2018), we supposed that the crust is fully accreted.
2.2. Brussels-Montreal nuclear energy-density functionals
Our models of accreted NS crusts are based on the nuclear EDF theory (Bender et al. 2003; Stone & Reinhard 2007), which has proved successful in describing finite nuclei, such as those encountered in the outer crust of a NS (Chamel et al. 2020), but also provides a consistent treatment of the inner crust, where neutron-proton clusters coexist with a neutron liquid. In this quantum mechanical approach, bound and unbound neutrons are consistently calculated. They do not need to be considered separately as in the liquid-drop treatment of Haensel & Zdunik (1990a,b, 2003, 2008). Moreover, the EDF approach is suitable to describe homogeneous matter, thus allowing for a unified description of all regions of a NS. Here, we employ the same Brussels-Montreal EDFs labelled BSk19, BSk20, and BSk21 (Goriely et al. 2010) as in Fantina et al. (2018).
The Brussels-Montreal EDFs BSk19, BSk20, and BSk21 are based on generalised Skyrme effective nucleon-nucleon interactions (Chamel et al. 2009; Goriely et al. 2010), supplemented with a microscopic contact pairing interaction (Chamel 2010). These EDFs were fitted to the 2149 measured masses of nuclei with neutron and proton numbers, N, Z ≥ 8, given in the 2003 Atomic Mass Evaluation (AME; Audi et al. 2003), with a root-mean square (rms) deviation as low as 0.58 MeV for the three functionals, while ensuring at the same time an optimal fit to charge radii. Incidentally, these models also yield an equally good fit to the experimental masses of nuclei with N, Z ≥ 8 given in the latest AME (Huang et al. 2021; Wang et al. 2021). The masses of bound nuclei were obtained by adding to the Hartree-Fock-Bogoliubov (HFB) energy a phenomenological Wigner term and correction term for the collective energy.
The BSk19, BSk20, and BSk21 EDFs were simultaneously constrained to reproduce various properties of homogeneous nuclear matter as obtained from many-body calculations using realistic two- and three- nucleon interactions. Specifically, these EDFs were fitted to three different neutron-matter EoSs, reflecting the current uncertainties of the high-density behaviour of dense matter. BSk19 was adjusted to the ‘soft’ EoS of neutron matter of Friedman & Pandharipande (1981) obtained from the realistic Urbana v14 nucleon-nucleon force with the three-body force TNI, BSk20 was fitted to the EoS of Akmal et al. (1998) labelled “A18 + δv + UIX”, whereas BSk21 was constrained to reproduce the ‘stiff’ EoS labelled “V18” from Li & Schulze (2008). All three neutron-matter EoSs are consistent at the low densities prevailing in nuclei and in NS crusts and are compatible with the more recent calculations based on auxiliary field diffusion Monte Carlo method and chiral effective field theory (see Fantina et al. 2014 and Fig. 13 in Fantina et al. 2018).
Furthermore: (i) the symmetry energy coefficient was set to J = 30 MeV for the three functionals (see e.g., Goriely et al. 2010; Tsang et al. 2012; Baldo & Burgio 2016; Tews et al. 2017; Burgio & Fantina 2018, for a discussion of experimental and theoretical estimates of J), (ii) the incompressibility Kv of symmetric nuclear matter at saturation was required to fall in the experimental range 240 ± 10 MeV (Colò et al. 2004; Stone et al. 2014), (iii) the ratio of the isoscalar effective mass to bare nucleon mass in symmetric nuclear matter at saturation was set to the realistic value of 0.8 (Goriely et al. 2003), (iv) the isovector effective mass was found to be smaller than the isoscalar effective mass, in agreement with both experiments and many-body calculations (see Goriely et al. 2010, for a discussion), (v) a qualitatively realistic distribution of the potential energy among the four spin-isospin channels in nuclear matter was obtained, and (vi) spurious spin and spin-isospin instabilities in nuclear matter that generally plagued earlier Skyrme functionals were eliminated for all densities prevailing in NSs (Chamel et al. 2009; Chamel & Goriely 2010). Finally, all these functionals are consistent with constraints on the EoS of symmetric nuclear matter inferred from heavy-ion collisions (Danielewicz et al. 2002; Lynch et al. 2009).
The BSk19-21 EDFs have been already applied to calculate the structure, the composition, and the EoS of non-accreted NSs under the cold catalyzed matter hypothesis (Pearson et al. 2011, 2012) and analytical representations of these EoSs have also been obtained by Potekhin et al. (2013). Even though the EoS based on the BSk19 EDF fails to explain the existence of the most massive observed NSs (Chamel et al. 2011; see also Fantina et al. 2013 for a discussion of various astrophysical constraints), such a soft EoS seems to be favoured by the analyses of K+ production (Fuchs et al. 2001; Sturm et al. 2001; Hartnack et al. 2006) and π−/π+ production ratio (Xiao et al. 2009) in heavy-ion collisions. This EoS also appears to be supported by the LIGO-Virgo data from the gravitational-wave signal GW170817 emitted by the merger of intermediate mass NSs (Perot et al. 2019). We have thus employed these three EDFs to calculate the EoS of all regions of accreted NSs, as described in the following, and we have studied their impact on NS properties.
2.3. Outer crust
We assumed that the outer crust is made of fully ionised atoms embedded in a charge-neutralising degenerate electron background. Since in hydrostatic equilibrium the pressure P varies continuously throughout the star, the suitable thermodynamic potential for determining the equilibrium structure of the crust is the Gibbs free energy per nucleon g(A, Z, P). The composition and EoS in each layer of pressure P were thus found by minimising g, given by
ℰ = ρc2 being the internal energy density and n the average baryon number density, keeping the mass number A fixed (recalling that in the outer crust the number of nucleons in the cell is equal to the nucleus mass number, i.e. Acell = A).
For the specific expressions of ℰ and P, we followed Pearson et al. (2011). To recall the main points, the internal energy per nucleon ℰ/n in the WS cell is given by
where M′(A, Z) is the nuclear mass, c is the speed of light, and ℰL is the lattice energy density,
with e the elementary charge, and we adopted the WS estimate C = −1.4508 for the lattice constant (Salpeter 1961). The last term in Eq. (2), ℰe, is the energy density of electrons, which accounts for the energy density of a free uniform electron gas of number density ne (see Weiss et al. 2004 for complete expressions), including the exchange and polarisation contributions, for which we used Eqs. (1), (6), and (8) in Chamel & Fantina (2016). We therefore neglected the electron correlation correction, as well as the finite-size and zero-point contributions, which were shown to be negligible (Pearson et al. 2011). The electron number density is related to the baryon number density by ne = (Z/A)n to ensure electric charge neutrality.
Similarly, for the pressure we have
with Pe the pressure of the electron (including exchange and charge-polarisation corrections) and PL = ℰL/3 the lattice pressure, the nuclei exerting no pressure in cold matter.
The only microscopic inputs of this model are the nuclear masses M′(A, Z), that were obtained from the atomic masses M(A, Z) after subtracting out the binding energy of atomic electrons (see Eq. (A4) in Lunney et al. 2003). For consistency with our previous study (Fantina et al. 2018), we made use of the experimental atomic masses from the 2016 AME (Wang et al. 2017), whenever available1, complemented with the Brussels-Montreal HFB atomic masses from the corresponding functional, also available from the BRUSLIB database (Xu et al. 2013).
With increasing pressure, Z remains unchanged until P reaches the threshold pressure Pβ for the onset of electron captures and such that g(A, Z, Pβ)=g(A, Z − 1, Pβ). Accurate analytical formulae for Pβ and the corresponding density ρβ were obtained by Chamel & Fantina (2015, 2016). The daughter nucleus (A, Z − 1) is generally unstable and further electron captures occur until the proton number reaches some value Z0 < Z such that g(A, Z0, Pβ)< g(A, Z0 − 1, Pβ), which corresponds to a local minimum of the Gibbs free energy per nucleon at pressure Pβ.
The onset of neutron drip was determined as in Chamel et al. (2015), thus ensuring the thermodynamic consistency across the boundary between the outer and inner crusts: the proton number of the dripping nucleus is given by the highest value of Z (below that of the initial ashes) for which the ΔN neutron separation energy is negative, i.e.
mn being the neutron mass. The properties of the accreted crust at the neutron-drip transition are summarised in Table 1, where we list, for the considered models, the proton number Z of the dripping nucleus, the number ΔN of emitted neutrons, the mass-energy density ρdrip, and the corresponding pressure Pdrip.
Neutron-drip transition in the crust of fully accreted NSs, as predicted by HFB-19, HFB-20, and HFB-21 nuclear mass models for 56Fe ashes: atomic number Z of the dripping nucleus, number ΔN of emitted neutrons, mass-energy density ρdrip and corresponding pressure Pdrip.
2.4. Inner crust
For the inner crust, we calculated the EoS using the 4th order Extended Thomas-Fermi (ETF) approach, with proton shell corrections added perturbatively via the Strutinsky integral (SI) theorem (see Onsi et al. 2008; Pearson et al. 2012 for details). Neutron shell corrections, which are expected to be much smaller than proton shell corrections (Pearson & Chamel 2022), were neglected. This so-called ETFSI approach is a computationally high-speed approximation of the fully self-consistent HFB method. We employed the same EDFs as those underlying the HFB nuclear mass models used for the outer crust, thus ensuring a consistent description of both the outer and the inner regions of the crust.
We further assumed that nuclear clusters remain spherical and we calculated the Coulomb energy in the WS approximation. Indeed, the presence of so-called nuclear ‘pasta’ has recently been found to be marginal within the ETFSI approach (Pearson & Chamel 2022). In order to further reduce the computation time, the nucleon density distributions in the WS cell were parametrised as nq(r)=nBq + nΛqfq(r), where q = n, p for neutrons and protons respectively, r is the radial distance from the centre of the spherical cell, nBq is the background density, and the second term accounts for the presence of inhomogeneities, with nΛq a constant term and fq(r) a damped Fermi function ensuring that density derivatives vanish at the surface of the cell, thus providing a smooth matching of the nucleon distributions between adjacent cells (Onsi et al. 2008).
Before the onset of pycnonuclear reactions, Acell remains unchanged with increasing pressure whereas Z can decrease if electron captures occur. The EoS can in principle be determined by minimising the baryon chemical potential, which is equal to the Gibbs free energy per nucleon g, with respect to all the parameters of the WS cell keeping Acell fixed. We note that, because of the presence of the free neutron gas, Acell > A with the number A of nucleons in clusters defined by
with Rcell the WS cell radius. However, this procedure would be computationally very costly. Instead, we proceeded as follows: (1) We first minimised the internal energy ℰ/n per nucleon at constant average baryon number density n, for given values of the proton number Z and nucleon number Acell (see Pearson et al. 2012, for details); (2) For this set of parameters (n, Z, Acell), we calculated the corresponding pressure P and the Gibbs free energy per nucleon g; (3) We repeated the calculations for different values of n and Z, thus allowing us to construct g as a function of Z and P for the given (fixed) value of Acell.
3. EoS for accreted neutron-star crusts
We calculated the composition and the EoSs of fully accreted NS crusts for the EDFs BSk19, BSk20, and BSk21, considering X-ray burst ashes made of 56Fe as in our previous study (Fantina et al. 2018).
3.1. Pressure-density relation
Results are plotted in Fig. 1. The EoS tables containing the number density n, the mass-energy density ρ, and the pressure P for the three EDFs are available at the CDS. As we can see from the left panel of Fig. 1, the three EoSs exhibit a similar behaviour, with steps associated to changes in the composition induced by electron captures and/or pycnonuclear reactions (Fantina et al. 2018). On the other hand, remarkable differences are observed between the EoS of accreted and catalyzed crusts, the former being notably stiffer than the latter, particularly in the density region between the neutron drip and ≈1013 g cm−3. This is clearly seen from the right panel of Fig. 1, where the EoS based on the BSk19 EDF is shown for both catalyzed (blue dashed line) and accreted (red solid line) crusts, as an illustrative example (the other EDFs yielding qualitatively similar results). One can also notice that, at higher densities, ρ ≳ 1013 g cm−3 (corresponding to P ≳ 5 × 1031 dyn cm−2), the two EoSs merge. The global properties of accreted NSs can thus be fairly accurately calculated by combining the EoS of accreted crust with that of catalyzed matter for densities beyond ρ ≳ 1013 g cm−3 (deep inner crust and core, see Sect. 4).
 |
Fig. 1. Pressure versus mass-energy density (in cgs units) in the NS crust. Left panel: predictions from the models based on the BSk19, BSk20, and BSk21 EDFs in accreted NS crust. Right panel: predictions from the models based on the BSk19 EDF comparing two different treatments for the inner crust: ETFSI and ETF. For comparison, results for the catalyzed crust are also shown. See text for details. |
These calculations assumed that the crust is fully accreted and stationary. This assumption is valid if the star has accreted for a long enough time, approximately given by (Suleiman et al. 2022)
where P31 is the pressure in 1031 dyn cm−2 at the crust-core transition, Ṁ−10 is the accretion rate in 10−10 M⊙ yr−1 (M⊙ being the mass of our Sun), and R6 = R/(10 km). Setting P31 = 60 (Pearson et al. 2012), M = 1.4 M⊙, and R = 12 km, we find τacc ∼ 430 Myr/Ṁ−10. On longer timescales, the EoS remains unchanged with further accretion and is therefore well defined. On the other hand, on a shorter accretion timescale, the NS crust is only partially replaced by the accreted material and a different treatment is required (Suleiman et al. 2022).
To assess the importance of shell effects on the EoS, we also display the results obtained using the ETF approach (black solid line in the right panel of Fig. 1). As previously discussed in Fantina et al. (2018), the compressed matter element undergoes in this case successive electron captures until the proton number is low enough to allow for pycnonuclear reactions to occur. As a consequence, variations of Z are more continuous and jumps in density are much smaller with respect to those obtained with the full ETFSI treatment. Even though the composition was found to be radically different, we showed that the proton fractions Z/Acell are comparable (see Fig. 4 in Fantina et al. 2018). Since the pressure is mainly determined by electrons and ρ ≈ nemuAcell/Z, with mu the unified atomic mass unit (recalling that ne = nZ/Acell due to electric charge neutrality), the EoS of accreted NS crusts is thus expected to be very similar to that of catalyzed crusts when shell corrections are neglected, as can be seen in Fig. 1. This shows that nuclear shell effects are important not only for determining the composition but also for the EoS of accreted crusts.
3.2. Adiabatic index
To better see the differences between the EoS of accreted and catalyzed crusts, we calculated the adiabatic index,
Results are plotted in Fig. 2 for models based on the BSk19 EDF. We focus on pressures around P ≈ 1030 − 1031 dyn cm−2 (or, equivalently, ρ ≈ 1012 − 1013 g cm−3) corresponding to the largest deviations in Fig. 1.
 |
Fig. 2. Adiabatic index Γ = dlog(P)/dlog(n) versus pressure (in cgs units) for the EoS based on the BSk19 EDF, presented in the right panel of Fig. 1. |
Assuming that the pressure in the shallow layers of the inner crust remains mainly determined by electrons, we have P ≈ P(ne)=P(nZ/Acell). The adiabatic index can thus be expressed as
where in the last equality we have considered the pressure of an ultrarelativistic electron Fermi gas
ℏ being the Dirac-Planck constant. In catalyzed crusts, Z/Acell decreases continuously with increasing n so that d(Z/Acell)/dlog(n) < 0, see e.g., Fig. 4 in Fantina et al. (2018). After the onset of neutron drip, Z/Acell falls rapidly leading to a sharp drop of Γ, as shown by the blue dashed line in Fig. 2. In accreted crusts, both Z and Acell remain unchanged until electrons are captured by clusters or pycnonuclear fusion occurs. Therefore, the second term in Eq. (9) vanishes beyond the neutron-drip point and Γ remains equal to 4/3 as in the densest layers of the outer crust. For the same reason, the adiabatic indices obtained within the ETF (black solid line) and ETFSI (red solid line) approaches are comparable. With further increase of the density, the neutron contribution to the pressure can no longer be ignored and Γ ≳ 4/3. This shows that the polytropic approximation according to which Γ is replaced by a constant is much more accurate for accreted crusts than for catalyzed crusts.
4. Neutron-star properties
4.1. Global structure of neutron stars
The structure of a non-rotating NS is determined by the well-known Tolman-Oppenheimer-Volkoff (TOV) equations (Tolman 1939; Oppenheimer & Volkoff 1939)
and
The numerical solution of the TOV Eqs. (11) and (12) is found by integrating from the centre of the star at r = 0 up to the surface at (circumferential) radius r = R such that P(R)=0. The gravitational mass of the star is then given by M ≡ ℳ(R). In practice, the TOV equations were integrated down to the density ρ = 106 g cm−3.
Numerical results are shown in Fig. 3 for both accreted and catalyzed NSs for the EoSs based on the EDFs BSk19, BSk20, and BSk21. We checked that the approximation proposed by Zdunik et al. (2017) for determining the mass-radius relation from the core EoS only remains equally accurate for the EoSs calculated here. As can be seen in Fig. 3, accreted NSs (solid lines) have larger radii than their non-accreted relatives made of catalyzed matter (dashed lines). This stems from the fact that the EoS of accreted NSs is stiffer, as discussed in Sect. 3. The differences in the radii is approximately given by Zdunik et al. (2017)
 |
Fig. 3. Mass-radius relation for accreted and catalyzed NSs for the EoSs based on the BSk19, BSk20, and BSk21 EDFs. Results obtained from Eq. (13) are indistinguishable from the exact ones. The coloured areas represent the recent mass-radius measurements (at 1σ) from NICER of PSR J0030+0451 and PSR J0740+6620. The analyses of Riley et al. (2019, 2021) are shown in green and those of Miller et al. (2019, 2021) in blue. See text for details. |
where R is the radius of the catalyzed NS and Qtot is the total energy per nucleon released in accreted crust.
For comparison, we show in Fig. 3 the recent mass and radius estimates from NICER observations of PSR J0030+0451 (Miller et al. 2019; Riley et al. 2019) and PSR J0740+6620 (Miller et al. 2021; Riley et al. 2021). Contours for the source PSR J0740+6620 include XMM-Newton priors on the mass. The contours taken from Miller et al. (2019) include both the two and three oval-spot analyses of the signal. PSR J0030+0451 and PSR J0740+6620 are two millisecond pulsars and are therefore expected to have been recycled by accretion from a companion in their past evolution. The EoS of accreted NSs should thus be more realistic than that of catalyzed matter. However, the deviations δR remain much smaller than the current observational uncertainties on the radii. Still, these observations clearly favour the EoSs based on the BSk20 and BSk21 EDFs. Incidentally, the latter is the one that was previously found to be in best agreement with nuclear data (Goriely et al. 2010) and various other astrophysical observations (Fantina et al. 2013). Even though the EoS based on the BSk19 EDF fails to reproduce the mass and radius of the very massive pulsar PSR J0740+6620, it remains compatible with those of the less massive pulsar PSR J0030+0451. This comparison is consistent with the analysis of GW170817.
4.2. Moment of inertia
The moments of inertia I of accreted and catalyzed NSs were calculated in the slow rigid rotation approximation (Hartle 1967), as implemented in Haensel & Prószyński (1982) 2:
where 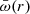 is the local spin frequency as measured in a local inertial frame, j(r) represents the contribution from the sphere of radius r to the stellar angular momentum J = j(R), Ω is the (uniform) angular frequency of the star expressible as
is the local spin frequency as measured in a local inertial frame, j(r) represents the contribution from the sphere of radius r to the stellar angular momentum J = j(R), Ω is the (uniform) angular frequency of the star expressible as
and we have introduced the metric function Φ(r) defined by
Results for the BSk21 EDF are shown in the top left panel of Fig. 4 for different NS masses. The differences ΔI in the moment of inertia between accreted and catalyzed NSs are indistinguishable and are of the order of ΔI ∼ 10−7I.
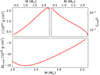 |
Fig. 4. Moment of inertia of accreted NSs. Top panels: total moment of inertia I (left panel) and fractional moment of inertia of the crust Icrust/I (right panel) in cgs units as a function of the NS mass. Results with accreted or catalyzed crust are indistiguishable. Bottom panel: difference ΔIcrust of the crustal moment of inertia between accreted and catalyzed NSs. Calculations were performed for the EoS based on the BSk21 EDF. |
Of particular interest for the analysis of pulsar frequency glitches (Andersson et al. 2012; Chamel 2013) is the fractional moment of inertia of the crust Icrust/I, with
rcc denoting the radial coordinate at the crust-core boundary determined by the pressure Pcc = 4.294 × 1032 dyn cm−2 (Pearson et al. 2012). Results are shown in the top right panel of Fig. 4. Whether the crust is accreted or not hardly changes the crustal moment of inertia. The deviations ΔIcrust plotted in the bottom panel of Fig. 4 amount to 0.1% of Icrust at most.
4.3. Tidal deformability
To assess the importance of accretion on the tidal deformability of a NS, we calculated the tidal deformability function:
with the tidal Love number function k2(r) given by (Hinderer 2008; Hinderer et al. 2010)
where we have introduced the dimensionless compactness parameter
and the function y(r) is obtained by integrating the following differential equation with the boundary condition y(0)=2 (Postnikov et al. 2010):
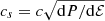 denoting the sound speed. Results for the functions y(r) and λ(r) for a NS with a gravitational mass M = 1.4 M⊙ are plotted in Figs. 5 and 6 respectively, focussing on the outer region where the EoS of accreted NSs differs from that of catalyzed NSs. Calculations were made for the EoS based on the BSk21 EDF. Accreted NSs are found to have a slightly smaller tidal deformability than catalyzed NSs. However, the deviations almost completely disappear when density discontinuities at the interfaces between adjacent crustal layers are properly taken into account following the prescription of Damour & Nagar (2009), as can be seen by comparing the solid lines and the dashed lines.
denoting the sound speed. Results for the functions y(r) and λ(r) for a NS with a gravitational mass M = 1.4 M⊙ are plotted in Figs. 5 and 6 respectively, focussing on the outer region where the EoS of accreted NSs differs from that of catalyzed NSs. Calculations were made for the EoS based on the BSk21 EDF. Accreted NSs are found to have a slightly smaller tidal deformability than catalyzed NSs. However, the deviations almost completely disappear when density discontinuities at the interfaces between adjacent crustal layers are properly taken into account following the prescription of Damour & Nagar (2009), as can be seen by comparing the solid lines and the dashed lines.
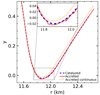 |
Fig. 5. Function y(r) characterising the tidal deformability of a 1.4 M⊙ NS for values of the radial coordinate r corresponding to the outer region of the star. For accreted NS, two approaches are presented: (1) treating y(r) as a continuous function (dotted line) and (2) taking into account discontinuities (solid line). Results are compared to those obtained for catalyzed NS (dashed line). Calculations were performed for the EoS based on the BSk21 EDF. |
The (observable) tidal deformability of the star given by Λ = λ(R) is displayed in the left panel of Fig. 7 for different NS masses using the EoS based on the BSk21 EDF. Results for accreted and catalyzed NSs are indistinguishable. The relative deviations are shown in the right panel. They are of the same order 10−5 − 10−6 as the precision of the calculations with the prescription of Damour & Nagar (2009). The Love numbers and tidal deformability coefficients previously calculated for catalyzed matter with the EoSs based on the BSk19, BSk20, and BSk21 EDFs as well as the comparison with the LIGO/Virgo measurement of GW170817 (Perot et al. 2019) therefore remain valid for accreted NSs. Ignoring density discontinuities leads to errors of the order of a few % (below 2% for NSs with masses M ≳ M⊙); although these errors remain rather small, they are larger than the relative contribution of the crust to Λ (Perot et al. 2020). A proper treatment of discontinuities is therefore necessary to correctly assess the role of the crust.
 |
Fig. 7. Tidal deformability of accreted NSs. Left panel: tidal deformability Λ as a function of the NS mass. Right panel: relative deviation between the value of Λ for accreted and catalyzed NSs with (solid line) and without (dotted line) a proper treatment of density discontinuities. Calculations were performed for the EoS based on the BSk21 EDF. |
5. Conclusions
In this paper, we presented the EoSs for accreted NSs, calculated employing the Brussels-Montreal EDFs BSk19, BSk20, and BSk21, and we evaluated their impact on global NS properties. Both the outer and inner crusts and the core were described with the same functional, thus ensuring a unified and thermodynamically consistent treatment. The EoS of accreted NS crusts is found to be remarkably different from that of catalyzed crusts, the former being notably stiffer than the latter, particularly in the density region between the neutron drip and ≈1013 g cm−3. This reflects in the adiabatic index, whose value ≈4/3 remains rather constant throughout the accreted crust, implying that the polytropic approximation is much more accurate for accreted crusts than for catalyzed ones.
The different stiffness between accreted and catalyzed EoSs also impacts the global NS structure. Indeed, accreted NSs with low and intermediate masses have larger radii than the non-accreted counterparts. However, the deviations remain smaller than current observational uncertainties on the radii. Likewise, the crustal moment of inertia and the tidal deformability of accreted NSs are almost indistinguishable from those of non-accreted NSs, provided density discontinuities at the interface between adjacent crustal layers are properly taken into account.
Although we considered here three specific models, to a good approximation the EoSs calculated for catalyzed matter remain applicable to compute the global properties of NSs, since they are mainly determined by the core. However, the composition of accreted crust, the heat sources, and their location may change depending on the chosen nuclear model. The BSk19, BSk20, and BSk21 EDFs were fitted to different realistic neutron-matter EoSs but were all constrained to yield the same symmetry energy coefficient J. The influence of varying this nuclear-matter parameter in accreted NSs has only been investigated on the boundary between the outer and inner crust in Fantina et al. (2016). The role of the symmetry energy in the crustal heating is left for future studies.
The results presented in this work complement our calculations of unified EoSs of catalyzed matter (Pearson et al. 2011, 2012; Fantina et al. 2013; Potekhin et al. 2013), of tidal deformability of NSs (Perot et al. 2019, 2020; Perot & Chamel 2021), and of the crustal heating in accreted NSs (Fantina et al. 2018), thus providing consistent microscopic inputs based on the same EDFs for simulations of both accreting and non-accreted NSs. In our calculations, we did not consider neutron diffusion in the inner crust of accreting NSs (Shchechilin & Chugunov 2019; Chugunov & Shchechilin 2020; Gusakov & Chugunov 2020). Its inclusion within the microscopic approach adopted here is left for future studies.
We note that in the second-to-last expression of Eq. (13) in Haensel & Prószyński (1982) a factor 6 is missing.
Acknowledgments
This work was partially supported by the Polish National Science Centre (NCN) grant no. 2018/29/B/ST9/02013, the CNRS PICS07889, the CNRS International Research Project (IRP) “Origine des éléments lourds dans l’univers: Astres Compacts et Nucléosynthèse (ACNu)”, the Fonds de la Recherche Scientifique (Belgium) under Grant No. IISN 4.4502.19, and the European Cooperation in Science and Technology (COST) action CA16214. S.G. and N.C. are F.R.S.-FNRS senior research associates.
References
- Andersson, N., Glampedakis, K., Ho, W. C. G., & Espinoza, C. M. 2012, Phys. Rev. Lett., 109, 241103 [NASA ADS] [CrossRef] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [Google Scholar]
- Audi, G., Wapstra, A. H., & Thibault, C. 2003, Nucl. Phys. A, 729, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Baldo, M., & Burgio, G. F. 2016, Prog. Part. Nucl. Phys., 91, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, M., Heenen, P.-H., & Reinhard, P.-G. 2003, Rev. Mod. Phys., 75, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Burgio, G. F., & Fantina, A. F. 2018, Astrophys. Space Sci. Lib., 457, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Carreau, T., Gulminelli, F., Chamel, N., Fantina, A. F., & Pearson, J. M. 2020, A&A, 635, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chamel, N. 2010, Phys. Rev. C, 82, 061307 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2013, Phys. Rev. Lett., 110, 011101 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Fantina, A. F. 2015, Phys. Rev. D, 92, 023008 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Fantina, A. F. 2016, Phys. Rev. D, 93, 063001 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Goriely, S. 2010, Phys. Rev. C, 82, 045804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Haensel, P. 2008, Liv. Rev. Rel., 11, 10 [Google Scholar]
- Chamel, N., Goriely, S., & Pearson, J. M. 2009, Phys. Rev. C, 80, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Fantina, A. F., Pearson, J. M., & Goriely, S. 2011, Phys. Rev. C, 84, 062802(R) [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Fantina, A. F., Zdunik, J. L., & Haensel, P. 2015, Phys. Rev. C, 91, 055803 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Fantina, A. F., Zdunik, J. L., & Haensel, P. 2020, Phys. Rev. C, 102, 015804 [CrossRef] [Google Scholar]
- Chugunov, A. I., & Shchechilin, N. N. 2020, MNRAS, 495, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Colò, G., van Giai, N., Meyer, J., Bennaceur, K., & Bonche, P. 2004, Phys. Rev. C, 70, 024307 [CrossRef] [Google Scholar]
- Damour, T., & Nagar, A. 2009, Phys. Rev D, 80, 084035 [NASA ADS] [CrossRef] [Google Scholar]
- Danielewicz, P., Lacey, R., & Lynch, W. G. 2002, Science, 298, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2013, A&A, 559, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2014, EPJ Web Conf., 66, 07005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fantina, A. F., Chamel, N., Mutafchieva, Y. D., et al. 2016, Phys. Rev. C, 93, 015801 [NASA ADS] [CrossRef] [Google Scholar]
- Fantina, A. F., Zdunik, J. L., Chamel, N., et al. 2018, A&A, 620, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fantina, A. F., De Ridder, S., Chamel, N., & Gulminelli, F. 2020, A&A, 633, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferreira, M., & Providência, C. 2020, Universe, 6, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Fortin, M., Providência, C., Raduta, Ad. R., et al. 2016, Phys. Rev. C, 94, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, B., & Pandharipande, V. R. 1981, Nucl. Phys. A, 361, 502 [Google Scholar]
- Fuchs, C., Faessler, A., Zabrodin, E., & Zheng, Y.-M. 2001, Phys. Rev. Lett., 86, 1974 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., in’t Zand, J., Chenevez, J., et al. 2020, ApJS, 249, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Samyn, M., Bender, M., & Pearson, J. M. 2003, Phys. Rev. C, 68, 054325 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2010, Phys. Rev. C, 82, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Gusakov, M. E., & Chugunov, A. I. 2020, Phys. Rev. Lett., 124, 191101 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Prószyński, M. 1982, ApJ, 258, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990a, A&A, 227, 431 [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990b, A&A, 229, 117 [NASA ADS] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2003, A&A, 404, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2008, A&A, 480, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartle, J. B. 1967, ApJ, 150, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Hartnack, C., Oeschler, H., & Aichelin, J. 2006, Phys. Rev. Lett., 96, 012302 [NASA ADS] [CrossRef] [Google Scholar]
- Hinderer, T. 2008, ApJ, 677, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Hinderer, T., Lackey, B. D., Lang, R. N., & Read, J. S. 2010, Phys. Rev. D, 81, 123016 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, W. J., Wang, M., Kondev, F. G., Audi, G., & Naimi, S. 2021, Chin. Phys. C, 45, 030002 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z. H., & Schulze, H.-J. 2008, Phys. Rev. C, 78, 028801 [Google Scholar]
- Lunney, D., Pearson, J. M., & Thibault, C. 2003, Rev. Mod. Phys., 75, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, W. G., Tsang, M. B., Zhang, Y., et al. 2009, Prog. Part. Nucl. Phys., 62, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Meisel, Z., Deibel, A., Keek, L., Shternin, P., & Elfritz, J. 2018, J. Phys. G, 45, 093001 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2019, ApJ, 887, L24 [Google Scholar]
- Miller, M. C., Lamb, F. K., Dittmann, A. J., et al. 2021, ApJ, 918, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Onsi, M., Dutta, A. K., Chatri, H., et al. 2008, Phys. Rev. C, 77, 065805 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, J. R., & Volkoff, G. M. 1939, Phys. Rev., 55, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., & Chamel, N. 2022, Phys. Rev. C, 105, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., Goriely, S., & Chamel, N. 2011, Phys. Rev. C, 83, 065810 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., Chamel, N., Goriely, S., & Ducoin, C. 2012, Phys. Rev. C, 85, 065803 [NASA ADS] [CrossRef] [Google Scholar]
- Perot, L., & Chamel, N. 2021, Phys. Rev. C, 103, 025801 [NASA ADS] [CrossRef] [Google Scholar]
- Perot, L., Chamel, N., & Sourie, A. 2019, Phys. Rev. C, 100, 035801 [NASA ADS] [CrossRef] [Google Scholar]
- Perot, L., Chamel, N., & Sourie, A. 2020, Phys. Rev. C, 101, 015806 [NASA ADS] [CrossRef] [Google Scholar]
- Postnikov, S., Prakash, M., & Lattimer, J. M. 2010, Phys. Rev. D, 82, 024016 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2013, A&A, 560, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riley, T. E., Watts, A. L., Bogdanov, S., et al. 2019, ApJ, 887, L21 [Google Scholar]
- Riley, T. E., Watts, A. L., Ray, P. S., et al. 2021, ApJ, 918, L27 [CrossRef] [Google Scholar]
- Salpeter, E. E. 1961, ApJ, 134, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Shchechilin, N. N., & Chugunov, A. I. 2019, MNRAS, 490, 3454 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. R., & Reinhard, P.-G. 2007, Prog. Part. Nucl. Phys., 58, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. R., Stone, N. J., & Moszkowski, S. A. 2014, Phys. Rev. C., 89, 044316 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T., & Bildsten, L. 2006, Compact stellar X-ray sources (Cambridge University Press), 113 [CrossRef] [Google Scholar]
- Sturm, C., Böttcher, I., Dȩbowski, M., et al. 2001, Phys. Rev. Lett., 86, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Suleiman, L., Fortin, M., Zdunik, J. L., & Haensel, P. 2021, Phys. Rev. C, 104, 015801 [NASA ADS] [CrossRef] [Google Scholar]
- Suleiman, L., Zdunik, J. L., Haensel, P., & Fortin, M. 2022, A&A, 662, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tauris, T. M., Langer, N., & Kramer, M. 2012, MNRAS, 425, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Tews, I., Lattimer, J. M., Ohnishi, A., & Kolomeitsev, E. E. 2017, ApJ, 848, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Tolman, R. C. 1939, Phys. Rev., 55, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Tsang, M. B., Stone, J. R., Camera, F., et al. 2012, Phys. Rev. C, 86, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, M., Audi, G., Kondev, F. G., et al. 2017, Chin. Phys. C, 41, 030003 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, M., Huang, W. J., Kondev, F. G., Audi, G., & Naimi, S. 2021, Chin. Phys. C, 45, 030003 [CrossRef] [Google Scholar]
- Weiss, A., Hillebrandt, W., Thomas, H.-C., & Ritter, H. 2004, Cox and Giuli’s Principles of Stellar Structure, 2nd edn. (Cambridge: Cambridge Scientific Publishers) [Google Scholar]
- Xiao, Z., Li, B.-A., Chen, L.-W., Yong, G.-C., & Zhang, M. 2009, Phys. Rev. Lett., 102, 062502 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Goriely, S., Jorissen, A., Chen, G. L., & Arnould, M. 2013, A&A, 549, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yakovlev, D. G., Gasques, L., & Wiescher, M. 2006, MNRAS, 371, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Zdunik, J. L., Fortin, M., & Haensel, P. 2017, A&A, 599, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Neutron-drip transition in the crust of fully accreted NSs, as predicted by HFB-19, HFB-20, and HFB-21 nuclear mass models for 56Fe ashes: atomic number Z of the dripping nucleus, number ΔN of emitted neutrons, mass-energy density ρdrip and corresponding pressure Pdrip.
All Figures
 |
Fig. 1. Pressure versus mass-energy density (in cgs units) in the NS crust. Left panel: predictions from the models based on the BSk19, BSk20, and BSk21 EDFs in accreted NS crust. Right panel: predictions from the models based on the BSk19 EDF comparing two different treatments for the inner crust: ETFSI and ETF. For comparison, results for the catalyzed crust are also shown. See text for details. |
| In the text | |
 |
Fig. 2. Adiabatic index Γ = dlog(P)/dlog(n) versus pressure (in cgs units) for the EoS based on the BSk19 EDF, presented in the right panel of Fig. 1. |
| In the text | |
 |
Fig. 3. Mass-radius relation for accreted and catalyzed NSs for the EoSs based on the BSk19, BSk20, and BSk21 EDFs. Results obtained from Eq. (13) are indistinguishable from the exact ones. The coloured areas represent the recent mass-radius measurements (at 1σ) from NICER of PSR J0030+0451 and PSR J0740+6620. The analyses of Riley et al. (2019, 2021) are shown in green and those of Miller et al. (2019, 2021) in blue. See text for details. |
| In the text | |
 |
Fig. 4. Moment of inertia of accreted NSs. Top panels: total moment of inertia I (left panel) and fractional moment of inertia of the crust Icrust/I (right panel) in cgs units as a function of the NS mass. Results with accreted or catalyzed crust are indistiguishable. Bottom panel: difference ΔIcrust of the crustal moment of inertia between accreted and catalyzed NSs. Calculations were performed for the EoS based on the BSk21 EDF. |
| In the text | |
 |
Fig. 5. Function y(r) characterising the tidal deformability of a 1.4 M⊙ NS for values of the radial coordinate r corresponding to the outer region of the star. For accreted NS, two approaches are presented: (1) treating y(r) as a continuous function (dotted line) and (2) taking into account discontinuities (solid line). Results are compared to those obtained for catalyzed NS (dashed line). Calculations were performed for the EoS based on the BSk21 EDF. |
| In the text | |
 |
Fig. 6. Same as Fig. 5 for the tidal deformability function λ(r). |
| In the text | |
 |
Fig. 7. Tidal deformability of accreted NSs. Left panel: tidal deformability Λ as a function of the NS mass. Right panel: relative deviation between the value of Λ for accreted and catalyzed NSs with (solid line) and without (dotted line) a proper treatment of density discontinuities. Calculations were performed for the EoS based on the BSk21 EDF. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



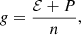
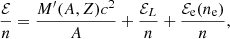
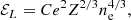
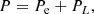
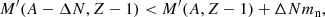
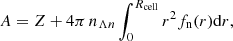
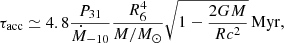
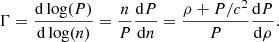
![$$ \begin{aligned}&\Gamma \approx \frac{\partial \log (P)}{\partial \log (n)}\biggr \vert _{Z/A_{\rm cell}} +\frac{\partial \log (P)}{\partial \log (Z/A_{\rm cell})}\biggr \vert _{n} \frac{ \mathrm{d} \log (Z/A_{\rm cell})}{ \mathrm{d} \log (n)} \nonumber \\&\ \ \approx \frac{4}{3}\biggl [1+\frac{ \mathrm{d} \log (Z/A_{\rm cell})}{ \mathrm{d} \log (n)}\biggr ], \end{aligned} $$](/articles/aa/full_html/2022/09/aa43715-22/aa43715-22-eq9.gif)
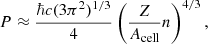
![$$ \begin{aligned}&\frac{\mathrm{d}P(r)}{\mathrm{d}r} = -\frac{G\rho (r)\mathcal{M} (r)}{r^2} \biggl [1+\frac{P(r)}{c^2\rho (r)}\biggr ] \nonumber \\&\qquad \quad \times \biggl [1+\frac{4\pi P(r)r^3}{c^2\mathcal{M} (r)}\biggr ]\biggl [1-\frac{2G\mathcal{M} (r)}{c^2 r}\biggr ]^{-1} \end{aligned} $$](/articles/aa/full_html/2022/09/aa43715-22/aa43715-22-eq11.gif)
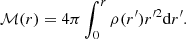
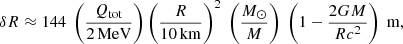
![$$ \begin{aligned} I&=\frac{8\pi }{3}\int _0^R\mathrm{d}r\, r^4\biggl [\rho (r)+\frac{P(r)}{c^2}\biggr ]e^{-\Phi (r)}\nonumber \\&\quad \times \left(\sqrt{1-\frac{2G\mathcal{M} (r)}{c^2 r} }\right)^{-1} \frac{\bar{\omega }(r)}{\Omega },\end{aligned} $$](/articles/aa/full_html/2022/09/aa43715-22/aa43715-22-eq14.gif)
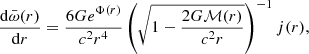
![$$ \begin{aligned} \frac{\mathrm{d}j(r)}{\mathrm{d}r}&= \frac{8\pi }{3} r^4\biggl [\rho (r)+\frac{P(r)}{c^2}\biggr ]e^{-\Phi (r)}\left(\sqrt{1-\frac{2G\mathcal{M} (r)}{c^2 r} }\right)^{-1} \bar{\omega }, \end{aligned} $$](/articles/aa/full_html/2022/09/aa43715-22/aa43715-22-eq16.gif)
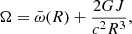
![$$ \begin{aligned} \frac{\mathrm{d}\Phi }{\mathrm{d}r}=-\frac{1}{\rho (r) c^2}\frac{\mathrm{d}P}{\mathrm{d}r}\biggl [1+\frac{P(r)}{\rho (r) c^2}\biggr ]^{-1}. \end{aligned} $$](/articles/aa/full_html/2022/09/aa43715-22/aa43715-22-eq19.gif)
![$$ \begin{aligned}&I_{\rm crust}=\frac{8\pi }{3}\int _{r_{\rm cc}}^R\mathrm{d}r\, r^4\biggl [\rho (r)+\frac{P(r)}{c^2}\biggr ]e^{-\Phi (r)}\nonumber \\&\qquad \times \left(\sqrt{1-\frac{2G\mathcal{M} (r)}{c^2 r} }\right)^{-1} \frac{\bar{\omega }(r)}{\Omega }, \end{aligned} $$](/articles/aa/full_html/2022/09/aa43715-22/aa43715-22-eq20.gif)
![$$ \begin{aligned} \lambda (r) = \frac{2}{3} k_2(r) \left[\frac{rc^2}{G\mathcal{M} (r)}\right]^5 , \end{aligned} $$](/articles/aa/full_html/2022/09/aa43715-22/aa43715-22-eq21.gif)
![$$ \begin{aligned}&k_2 = \,\frac{8C^5}{5}(1-2C)^2\big [2+2C({ y}-1)-{ y}\big ]\nonumber \\&\ \quad \times \Big \{2C\big [6-3{ y}+3C(5{ y}-8)\big ] \nonumber \\&\ \quad + 4C^3\big [13-11{ y}+C(3{ y}-2)+2C^2(1+{ y})\big ] \nonumber \\&\ \quad + 3(1-2C)^2\big [2-{ y}+2C({ y}-1)\big ] \ln (1-2C) \Big \}^{-1}, \end{aligned} $$](/articles/aa/full_html/2022/09/aa43715-22/aa43715-22-eq22.gif)
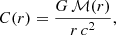
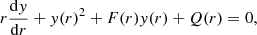
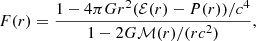
![$$ \begin{aligned}&Q(r)=\frac{4 \pi G r^2/c^4}{1-2G\mathcal{M} (r)/(r c^2)}\Biggl [5\mathcal{E} (r)+9P(r)\nonumber \\&\qquad \ +\frac{\mathcal{E} (r)+P(r)}{c_s(r)^2} c^2-\frac{6\, c^4}{4\pi r^2 G}\Biggr ] \nonumber \\&\qquad \ -4\Biggl [ \frac{G(\mathcal{M} (r)/(r c^2)+4\pi r^2 P(r)/c^4)}{1-2G\mathcal{M} (r)/(r c^2)}\Biggr ]^2 , \end{aligned} $$](/articles/aa/full_html/2022/09/aa43715-22/aa43715-22-eq26.gif)