| Issue |
A&A
Volume 558, October 2013
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 13 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321348 | |
| Published online | 14 October 2013 | |
Injection of thermal and suprathermal seed particles into coronal shocks of varying obliquity ⋆
1
Department of Physics and AstronomyUniversity of Turku,
20014
Turku,
Finland
e-mail:
markus.battarbee@utu.fi
2
Department of Physics, University of Helsinki,
00014
Helsinki,
Finland
3 Jeremiah Horrocks Institute, University of Central
Lancashire, Lancashire PR/2, UK
4
The Blackett Laboratory, Imperial College, London
SW7 2AZ,
UK
Received:
22
February
2013
Accepted:
30
August
2013
Context. Diffusive shock acceleration in the solar corona can accelerate solar energetic particles to very high energies. Acceleration efficiency is increased by entrapment through self-generated waves, which is highly dependent on the amount of accelerated particles. This, in turn, is determined by the efficiency of particle injection into the acceleration process.
Aims. We present an analysis of the injection efficiency at coronal shocks of varying obliquity. We assessed injection through reflection and downstream scattering, including the effect of a cross-shock potential. Both quasi-thermal and suprathermal seed populations were analysed. We present results on the effect of cross-field diffusion downstream of the shock on the injection efficiency.
Methods. Using analytical methods, we present applicable injection speed thresholds that were compared with both semi-analytical flux integration and Monte Carlo simulations, which do not resort to binary thresholds. Shock-normal angle θBn and shock-normal velocity Vs were varied to assess the injection efficiency with respect to these parameters.
Results. We present evidence of a significant bias of thermal seed particle injection at small shock-normal angles. We show that downstream isotropisation methods affect the θBn-dependence of this result. We show a non-negligible effect caused by the cross-shock potential, and that the effect of downstream cross-field diffusion is highly dependent on boundary definitions.
Conclusions. Our results show that for Monte Carlo simulations of coronal shock acceleration a full distribution function assessment with downstream isotropisation through scatterings is necessary to realistically model particle injection. Based on our results, seed particle injection at quasi-parallel coronal shocks can result in significant acceleration efficiency, especially when combined with varying field-line geometry.
Key words: acceleration of particles / shock waves / Sun: coronal mass ejections (CMEs)
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The majority of energetic particles in the near-Earth space environment are generated by energetic processes at the Sun (Reames 1999). Coronal or interplanetary shocks driven by coronal mass ejections (CMEs) play a major role in accelerating seed particles to high energies through a process of repeated shock encounters. This process of diffusive shock acceleration (DSA) was initially described by Axford et al. (1977), Krymskii (1977), Blandford & Ostriker (1978), and Bell (1978). Repeated shock encounters are assumed to occur due to trapping by upstream Alfvénic turbulence generated by the accelerated particles themselves (Lee 1983), and scattering of particles in the turbulent downstream medium.
For ambient solar wind particles to take part in the DSA process, they have to return to the upstream after encountering the propagating coronal shock for the first time. This process of injection is straightforward to understand assuming the seed particles have kinetic energies well in excess of the mean upstream incident ram energy. However, quantitative understanding of injection into DSA at low energies remains a challenge. A comprehensive understanding of the injection efficiency is especially important when particle entrapment in DSA is attributed to self-generated waves (see, e.g., Ng & Reames 1994; Vainio 2003; Lee 2005; Ng & Reames 2008; Vainio & Laitinen 2007, 2008). This is because self-generated wave intensity is scaled by the absolute level of resonant particle intensity. Thus, from the particle point of view, the theory is non-linear.
In this paper, we investigate seed particle injection using a simplified shock model, suitable for implementation in self-consistent Monte Carlo simulations of DSA (see, e.g., Battarbee et al. 2011). We present injection probabilities for quasi-thermal and non-thermal particle populations. We study only the injection of particles to the upstream after their first interaction with the shock front, not the subsequent energising process through consecutive crossings.
The bulk of the solar wind consists of thermal, cool particles. Much research has been done to link shock acceleration with non-thermal seed populations, which could be remnants from previous energetic eruptions (see, e.g., Mason et al. 1999; Tylka et al. 2001, 2005; Tylka & Lee 2006; Sandroos & Vainio 2007). It is uncertain whether energetic remnant seed populations are capable of supplying the required particle flux to generate efficient turbulent trapping in front of the shock, especially considering the high energies attained (van Nes et al. 1984). Given the speeds at which coronal shocks propagate, only a small fraction of thermal ions are likely to be injected into the acceleration process.
In this paper, we study the injection of thermal and suprathermal particles into the shock acceleration process. The quasi-thermal and non-thermal populations are described using κ-distributions. We used a simplified one-dimensional model to analyse the reflection and transmission of incident particles at the shock front. Comparisons of work presented by Kirk & Heavens (1989) and Ostrowski (1991) suggest that the one-dimensional adiabatic approximation is sufficient for our model. Particle transmission uses the scatter-free approximation (see, e.g., Decker 1988). However, we propagated the particles in the downstream until they were isotropised through pitch-angle scattering before applying analytical return-probability estimates.
The angle θBn between the shock normal and the upstream magnetic field, with values θBn = 0°...90°, was varied to assess the coupling of shock-normal angle θBn and particle injection probability. The electric cross-shock potential was assessed along with its effect on injection and reflection of incident particles. It should be noted that our analysis considers only the adiabatic approximation of shock-drift acceleration and does not take into account the effects of shock surfing.
Modification of shock-velocity profiles due to particle acceleration, as presented for instance in Ellison et al. (1996), is not expected to play a major role in interplanetary shocks with low Alfvénic Mach numbers (see, e.g., Terasawa et al. 2006). Therefore we adopted the test-particle approximation.
At supercritical shocks (see, e.g., Bemporad & Mancuso 2011), specularly reflected ions, ion beams, and upstream waves can interact and cause shock reformation (Leroy 1984; Burgess 1989; Scholer & Burgess 1992) and can also affect the energy dissipation. Because specular reflection requires full-orbit simulations, we did not consider the effect of shock reformation on particle injection.
2. Particle injection
In previous studies of shock acceleration, particle injection has been modelled through simplifications such as mono-energetic (e.g., Li et al. 2012) or power-law (e.g., Sandroos & Vainio 2007; Ng & Reames 2008) seed populations, or by using a thermostat model (Malkov & Völk 1995, 1998). Neergaard Parker & Zank (2012) employed a κ-distribution, using an ad-hoc minimum injection energy. A classical approximation for minimum particle injection speed is v > u1 (see, e.g., Lee 1983; le Roux & Webb 2009), where v is the particle speed and u1 is the plasma flow speed along the upstream magnetic field line. We show that this threshold speed is not always a good approximation.
Particle injection at oblique shocks has been simulated through Monte Carlo methods for instance by Ostrowski (1991), Baring et al. (1993), and Ellison et al. (1995). In the context of DSA at coronal shocks, we limit our analysis to a single shock encounter instead of propagating particles, for example, until they reach a threshold energy (see, e.g., Baring et al. 1994).
Highly variable magnetic fields and their effect on particle injection have been studied among others by Giacalone (2005) and Giacalone & Jokipii (2006). At large shock-normal angles (θBn ≳ 85°), such as at the quasi-perpendicular termination shock, cross-field diffusion via field-line random walk across the shock plays a major role, and the approximations presented here may not be applicable.
3. Shock geometry
Shocks launched from the solar corona travel outwards in the heliosphere, where the background magnetic field is described as the Parker spiral. A propagating shock can intersect magnetic field lines with a multitude of shock-normal angles θBn, especially during expansion within the complex coronal field. The specifics of shock expansion in the coronal magnetic field have been detailed for instance by Sandroos & Vainio (2006), Sandroos & Vainio (2009), and Pomoell et al. (2011). In this paper, we fixed the shock-normal propagation velocity Vs (measured in the inertial frame) and the solar wind parameters. We varied the angle θBn between the propagation direction of the shock and the mean magnetic field to assess injection efficiency at different points of a curved shock front.
We considered different shock-normal angles θBn as distinct test cases, ranging from θBn = 0° to θBn = 60°. This means that our results only apply to quasi-parallel and oblique portions of coronal or interplanetary shocks, but not to quasi-perpendicular shocks. We also neglected changes to the upstream shock-normal angle caused for example by upstream wave growth (see, e.g., Scholer 1993) or field-line meandering, and limited our cases to constant values of θBn. However, our results for each shock-normal angle can be applied as short intervals of locally constant θBn, as part of an evolving, propagating shock front.
We examined plasma flows at the shock in the de Hoffmann-Teller frame, where the mean magnetic field and mean plasma flow direction are parallel to each other in both the upstream and the downstream of the shock. Using the Rankine-Hugoniot equations, we solved the gas and magnetic compression ratios rg and rB at the shock front.
In our notation, de Hoffmann-Teller frame upstream quantities are sub-scripted with a 1 and downstream quantities with a 2. Positive pitch-angle cosines μ indicate propagation towards the upstream, whereas negative values indicate propagation towards the downstream. Quantities given in the upstream plasma frame are bare, and in the downstream plasma frame primed. The downstream plasma frame quantities are of most use when assessing return probabilities, and only upstream plasma frame quantities are initially given. The solar wind flows radially outward with velocity usw along the radial magnetic field. The plasma flow velocity u1 is given parallel to the magnetic field, with u1 = VssecθBn − usw.
Our radial solar wind model, introduced in Battarbee et al.
(2010), satisfies required continuities of mass flux and magnetic flux. Our choice
of heliocentric distance r = 3.17 R⊙ results
in a high Alfvén speed vA. Upstream parameters include the
plasma density ρ = 3.48 × 105 cm-3, background
magnetic field flux density B1 ≈ 0.19 G, temperature
T ≈ 2.0 × 106 K, sound speed
cs ≈ 2.34 × 107 cm s-1, Alfvén speed
vA ≈ 6.97 × 107 cm s-1, the plasma
beta 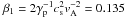 , solar wind speed
usw ≈ 9.98 × 106 cm s-1, and the
wave group speed
V = usw + vA ≈ 7.97 × 107 cm s-1.
Here γp = 5/3 is the ratio of specific heats.
For calculations and simulations, we used two different shock-normal velocities of
Vs = 1500 km s-1 and
Vs = 2000 km s-1 with shock-normal angles
ranging from θBn = 0° to
θBn = 60°.
, solar wind speed
usw ≈ 9.98 × 106 cm s-1, and the
wave group speed
V = usw + vA ≈ 7.97 × 107 cm s-1.
Here γp = 5/3 is the ratio of specific heats.
For calculations and simulations, we used two different shock-normal velocities of
Vs = 1500 km s-1 and
Vs = 2000 km s-1 with shock-normal angles
ranging from θBn = 0° to
θBn = 60°.
In Table 1, we present values for the upstream flow speed u1, the Alfvénic Mach number MA, the gas compression ratio rg, the magnetic compression ratio rB, and the downstream shock-normal angle θBn,2 for the cases studied in this paper. The shock compression ratio was solved parametrically as presented in Vainio & Schlickeiser (1999), with the case θBn = 0 solved for upstream angle 0.03°, to make certain that the shock is a fast-mode shock.
Shock-normal velocity, angle, and shock parameters solved with Rankine-Hugoniot equations.
3.1. Cross-shock potential
The solar wind consists of ions and electrons in suitable quantities to achieve
macroscopic plasma neutrality. An ion-to-electron imbalance at kinetic scales forms an
electrostatic field across the shock profile, resulting in the cross-shock potential. As
presented for instance in Hull et al. (2000), this
cross-shock potential can be approximated by various methods. Although we focused on
coronal shocks, we used the estimates found from observing the bow shock of the Earth,
where the potential jump is set to 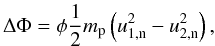 (1)which
is proportional to the change of the normal component of proton ram energy. Here
φ = 0.12 is an observational parameter (Hull et al. 2000) and mp is the proton mass.
(1)which
is proportional to the change of the normal component of proton ram energy. Here
φ = 0.12 is an observational parameter (Hull et al. 2000) and mp is the proton mass.
Although the significance of this electric potential has been investigated previously (see, e.g., Gedalin 1996; Zank et al. 2001; Zuo et al. 2013), its effect on particle acceleration efficiency is still largely ignored. Unless otherwise stated, the cross-shock potential is always accounted for in our calculations.
4. Seed particle populations
The bulk of the ambient solar wind consists of protons and electrons. Although most
particles encountered by a coronal shock have left the surface of the Sun in a thermalised
state (as depicted by a Maxwellian velocity distribution), the ambient plasma contains an
additional suprathermal halo. As the corona exists in a collisionless state, this halo
remains unthermalised during expansion to interplanetary scales. We describe particle
distributions using a κ-distribution (Vasyliunas 1968), where κ is a model parameter defining the
strength of the suprathermal tail. The representative speed parameter 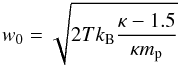 (2)is
based on the ion temperature T, where kB is the
Boltzmann constant. The particle distribution function is
(2)is
based on the ion temperature T, where kB is the
Boltzmann constant. The particle distribution function is ![\begin{equation} f(v) = \frac{ n(r) \Gamma(\kappa+1) }{ w_{0}^{3}\pi^{3/2}\kappa^{3/2}\Gamma(\kappa-1/2) } \left[1+ \frac{v^2}{\kappa w_{0}^{2}}\right]^{-\kappa-1} \label{eq:kappa}, \end{equation}](/articles/aa/full_html/2013/10/aa21348-13/aa21348-13-eq48.png) (3)where
Γ(x) denotes the gamma function. We compared the injection efficiency for
a distribution with a strong suprathermal tail (κ = 2) and for a
near-Maxwellian distribution (κ = 15). These populations along with a
Maxwellian distribution are shown in Fig. 1.
(3)where
Γ(x) denotes the gamma function. We compared the injection efficiency for
a distribution with a strong suprathermal tail (κ = 2) and for a
near-Maxwellian distribution (κ = 15). These populations along with a
Maxwellian distribution are shown in Fig. 1.
 |
Fig. 1 Particle distribution functions fth(v), fnth(v) and a Maxwellian distribution at T ≈ 2.0 × 106 K. |
4.1. Equation of motion
The equation of motion for a system of particles undergoing elastic pitch-angle
scattering in the frame of flowing plasma can be simplified, considering motion within a
flux tube extending from the shock (x1 = 0) to the far
upstream (x1 → ∞). The plasma speed
u1 is assumed constant and aligned with the constant
upstream magnetic field. In a steady state, the particle distribution function obeys
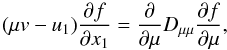 (4)where
x1 is the distance measured along the field lines in the
shock frame. f is taken to be a function of mixed coordinates in the
frame of the scattering centres (v,μ) and the shock
(x1).
(4)where
x1 is the distance measured along the field lines in the
shock frame. f is taken to be a function of mixed coordinates in the
frame of the scattering centres (v,μ) and the shock
(x1).
4.2. Flux conservation
When modelling the injection of strongly suprathermal particles at a coronal shock, information of the approaching shock can propagate into the upstream and alter the incident particle population. To maintain the flux conservation, the incident particle pitch-angle distribution should be adjusted. A full description of the steps taken is included in Appendix A.
According to Liouville’s theorem, the shock-incident particle phase-space distribution
f(x,p,t)
is conserved along particle orbits. Conservation of mass implies that the shock-normal
integrated particle flux 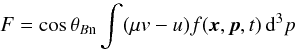 is
conserved.
is
conserved.
4.3. Downstream population isotropy
Particles transmitted to the downstream region of the shock scatter off turbulence and
isotropise. A portion of the isotropised particles, if energetic enough, can return to the
shock and be injected into the upstream. Jones &
Ellison (1991) gave the return probability for an isotropised particle as
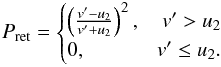 (5)This
probability is the ratio of particle fluxes towards and away from the shock at a plane in
the downstream, assuming isotropic particle distributions and a downstream of infinite
extent. We applied this equation to the guiding centre motion of a particle along the
magnetic field and, thus, the speed u2 in Eq. (5) is measured in the de Hoffmann-Teller frame.
(5)This
probability is the ratio of particle fluxes towards and away from the shock at a plane in
the downstream, assuming isotropic particle distributions and a downstream of infinite
extent. We applied this equation to the guiding centre motion of a particle along the
magnetic field and, thus, the speed u2 in Eq. (5) is measured in the de Hoffmann-Teller frame.
The method for estimating the downstream scattering of particles can have a significant
effect on the injection probability. Assessing downstream isotropisation methods and their
connection to injection efficiency are the primary focus of this paper. One method is
deducing the temperature of the transmitted population and choosing injection energies
based on the downstream gas temperature (see, e.g., Malkov
& Völk 1995; Zank et al. 2007).
Another is to assume that particles retain their plasma frame speed and achieve isotropy
through elastic small- or large-angle scattering in the plasma frame (Jones & Ellison 1991). This can be either Monte
Carlo-simulated or assumed to take place instantaneously. In Sect. 7, we present Monte Carlo simulations in which we varied the simulation
parameters to find the difference between assuming instant isotropy and letting particles
scatter until they have travelled a pre-chosen distance. For simplicity, we employed an
isotropic small-angle scattering process with pitch-angle diffusion coefficient
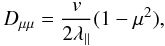 (6)where
λ∥ is the mean free path of particles undergoing scattering.
The field-parallel diffusion coefficient is
κ∥ = v′λ∥/3.
(6)where
λ∥ is the mean free path of particles undergoing scattering.
The field-parallel diffusion coefficient is
κ∥ = v′λ∥/3.
4.4. Cross-field diffusion
Owing to the presumably strong scattering in the downstream, particles are no longer
locked to a single magnetic field line (see, e.g., Jones
et al. 1993; Baring et al. 1995). A
strongly turbulent downstream field could be described by field-line random walk, which
presents challenges related to a field line potentially intersecting the shock multiple
times. A simplification suitable for DSA simulations is to describe the downstream
cross-field propagation of a particle as perpendicular diffusion across the mean magnetic
field. We describe downstream cross-field diffusion with a pitch-angle-dependent
perpendicular diffusion coefficient
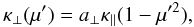 (7)where
a⊥ is a cross-field diffusion strength parameter and the
term (1 − μ′2) scales motion according to the Larmor radius
(7)where
a⊥ is a cross-field diffusion strength parameter and the
term (1 − μ′2) scales motion according to the Larmor radius
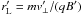 .
.
5. Analytical injection thresholds
In this section, we present analytical solutions of particle-speed thresholds, which allow either reflection at a shock front or injection following transmission to the downstream. We transmitted particles across the infinitesimally thin shock using the adiabatic guiding centre approximation and scatter-free approximation, similar to Decker (1988). However, we extended the formulation to include the cross-shock electric potential ΔΦ, solving the particle downstream plasma frame speed v′ using only shock- and upstream-flow parameters.
5.1. Particle reflection by the shock structure
The equations for adiabatic scatter-free particle transmission can be used to assess
changes in particle motion because it is transmitted across the shock front. A particle is
reflected at the shock front if the decrease of its parallel kinetic energy generated by
magnetic compression and the cross-shock potential exceeds its initial upstream parallel
kinetic energy. Assuming the conservation of magnetic moment and energy in the
shock-crossing of a particle, the downstream (shock frame) parallel velocity can be
derived as 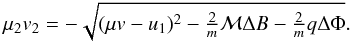 (8)For a reflected particle,
the term under the root sign is negative. Here
ΔB = B2 − B1,
q is the charge and m is the mass of the particle and
(8)For a reflected particle,
the term under the root sign is negative. Here
ΔB = B2 − B1,
q is the charge and m is the mass of the particle and
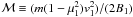 . Thus,
using the magnetic compression ratio
rB = B2/B1,
any particle for which
. Thus,
using the magnetic compression ratio
rB = B2/B1,
any particle for which 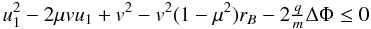 (9)holds true is
reflected at the shock. As the particle travels across the shock front, the parallel
kinetic energy reaches zero and the electrostatic potential and the magnetic gradient
cause the particle to be deflected in such a way that it is returned to the upstream. The
details of reflection-threshold velocities are examined in more detail in Appendix B, and speed thresholds for reflection, described in
Eqs. (B.3)and (B.4), are shown in Fig. 2.
(9)holds true is
reflected at the shock. As the particle travels across the shock front, the parallel
kinetic energy reaches zero and the electrostatic potential and the magnetic gradient
cause the particle to be deflected in such a way that it is returned to the upstream. The
details of reflection-threshold velocities are examined in more detail in Appendix B, and speed thresholds for reflection, described in
Eqs. (B.3)and (B.4), are shown in Fig. 2.
5.2. Particle transmission across the shock
Assuming particle injection after transmission occurs through isotropisation (see Sect. 4.3 and Eq. (5)), the primary parameter that defines the injection probability for a transmitted particle is the downstream plasma frame speed v′.
We find the particle downstream perpendicular velocity as 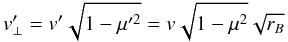 (10)and
the particle downstream plasma frame parallel velocity as
(10)and
the particle downstream plasma frame parallel velocity as 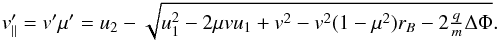 (11)These can be used to
solve the downstream plasma frame particle speed v′ and
pitch-angle μ′. The equations for
v′ and μ′ can be further
analysed to study whether a particle transmitted to the downstream can return to the
upstream. We discuss and derive analytical expressions for the threshold velocities for
this return in Appendix B. Speed thresholds for
injection through reflection or downstream scatterings are shown in Fig. 3 for a shock of velocity
Vs = 1500 kms-1.
(11)These can be used to
solve the downstream plasma frame particle speed v′ and
pitch-angle μ′. The equations for
v′ and μ′ can be further
analysed to study whether a particle transmitted to the downstream can return to the
upstream. We discuss and derive analytical expressions for the threshold velocities for
this return in Appendix B. Speed thresholds for
injection through reflection or downstream scatterings are shown in Fig. 3 for a shock of velocity
Vs = 1500 kms-1.
 |
Fig. 2 Reflection threshold speeds for Vs = 1500 km s-1: within the shaded area, protons may be reflected at the shock. Threshold #1 (v > vR1, v > u1/rB) is defined with Eq. (B.3)and threshold #2 (v > vR2, v < u1/rB) with Eq. (B.4). |
6. Numerical flux analysis
Although analytical methods can give information on threshold velocities for seed particle
injection, they cannot be used directly to estimate the injection efficiency. To do this, we
need to evaluate the proportion of the incoming particle flux, with a given upstream
distribution function, that is returned to the upstream after its first encounter with the
shock, that is, injected. We used a semi-analytical method, where the incident flux is found
by integrating the flux-weighted upstream seed particle distribution as
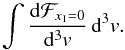 (12)The distributions used in
our model are described in Eqs. (A.3)and
(A.6). The reflected flux is found by
integrating over all cells where the requirements for reflection are fulfilled. The
transmitted portion of the distribution function is conserved according to Liouville’s
theorem, with new downstream values v′ and
μ′ given by Eqs. (10)and (11). The downstream flux
is then found by integrating over the whole downstream distribution. We integrated the
distribution with v∥ ,1 and
v∥ ,2 spanning up to
10u1 and v⊥ ,1
and v⊥ ,2 spanning up to
5u1. Conservation of the shock-normal component of particle
flux is confirmed.
(12)The distributions used in
our model are described in Eqs. (A.3)and
(A.6). The reflected flux is found by
integrating over all cells where the requirements for reflection are fulfilled. The
transmitted portion of the distribution function is conserved according to Liouville’s
theorem, with new downstream values v′ and
μ′ given by Eqs. (10)and (11). The downstream flux
is then found by integrating over the whole downstream distribution. We integrated the
distribution with v∥ ,1 and
v∥ ,2 spanning up to
10u1 and v⊥ ,1
and v⊥ ,2 spanning up to
5u1. Conservation of the shock-normal component of particle
flux is confirmed.
In Figs. 4 and 5, we present visualisations of quasi-thermal and non-thermal particle populations at two different shock-normal velocities and a selection of shock-normal angles. In the figures, velocities are measured in the frame of the shock. The shown quantity is the two-dimensional flux density dℱ/(dv∥ dv⊥), with contour boundaries at one-magnitude intervals.
The transmitted portion of the incident flux is shown as blue filled contours. The threshold curve of reflection at the shock is shown as a black and green dashed line and the reflected flux is shown as red filled contours moving away from the shock in the upstream direction. The transmitted flux, modified by the shock passage as given by Eqs. (10)and (11), is shown as red contours at one-magnitude intervals. The downstream velocities of the transmitted particle flux can then be assessed for its injection probability according to Eq. (5). The black dashed semicircle depicts the speed u2 in the downstream medium, representing the lowest particle speed for a possible injection. A guideline representing the speed at which the statistical return probability for an isotropic population in an infinite downstream is 25% (v′ = 3u2) is shown as a black dotted semicircle.
 |
Fig. 3 Injection threshold speeds for Vs = 1500 km s-1: the classical threshold u1 (solid curve) versus our reflection threshold (dashed) and the threshold for injection after downstream scatterings (dotted, v > vTμ−). Protons within the shaded areas have nonzero injection probability; the different shading represents the injection possibility through reflection, downstream scatterings, or both. The classical threshold overestimates the lowest injection speeds, especially at small shock-normal angles. |
 |
Fig. 4 Visualised transfer of quasi-thermal (left, κ = 15) and non-thermal (right, κ = 2) particle flux densities dℱ/(dv∥ dv⊥) across a shock of velocity Vs = 1500 km s-1 with four different shock-normal angles. Blue contours depict the incident transmitting flux, red contours depict the reflected flux, and red solid contours the downstream transmitted flux at one magnitude intensity intervals. The black semicircles depict downstream speed thresholds for statistical return probabilities of 0% (dashed) and 25% (dotted), and the black-green dashed curve represents the reflection threshold. |
 |
Fig. 5 Visualised transfer of quasi-thermal (left, κ = 15) and non-thermal (right, κ = 2) particle flux densities dℱ/(dv∥ dv⊥) across a shock of velocity Vs = 2000 km s-1 with four different shock-normal angles. Blue contours depict the incident transmitting flux, red contours depict the reflected flux, and red solid contours the transmitted downstream flux at one magnitude intensity intervals. The black semicircles depict downstream speed thresholds for statistical return probabilities of 0% (dashed) and 25% (dotted), and the black-green dashed curve represents the reflection threshold. |
7. Monte Carlo simulations
In this section, we describe Monte Carlo simulations that allow us to investigate the effect of downstream isotropisation and cross-field diffusion on the injection efficiency. A large number of particles were picked from the κ-distribution based on the flux conservation calculations presented in Sect. 4 and Appendix A. The upstream velocity and pitch-angle were randomised using Eqs. (3), (A.11)and (A.14). Owing to simulation run time constraints, the amount of simulated quasi-thermal particles was scaled down because the injection probability decreased with increasing shock-normal angle θBn.
As discussed in Sect. 4.3, scatter-free transmission across the shock results in the downstream population being anisotropic. To study the effect of anisotropy in the downstream, we present four sets of simulations. In the first set, particles are assumed to achieve instant isotropy without scattering or propagation. In sets two through four, particles isotropise through propagation and scattering in the downstream. In set two, downstream cross-field diffusion is suppressed. In sets three and four it is active, with a⊥ = 0.1. In set three, downstream cross-field diffusion can scatter the particle up to the vicinity of the shock, but not across it. In set four, the boundary condition at the shock allows particles with μ2 > 0 to propagate across the shock front to the upstream.
For simplicity, all our Monte Carlo simulations assumed a downstream of infinite extent. We propagated and scattered particles in the downstream within a region xn,2 ∈ (−ℬ,0) where ℬ is a boundary (parallel to the shock front) at which particles are considered to have isotropised (see also Ellison et al. 1996).
For set one (no downstream scattering), we set ℬ = 0. For sets two through four, we used
the diffusion equation
ux∂xn = ∂xκx∂xn
to define the downstream return boundary at three times the diffusion distance
κx/ux
from the shock. The shock-normal diffusion coefficient
κx = ⟨ (Δx)2 ⟩ /(2Δt)
can be split into field-parallel and field-perpendicular components with
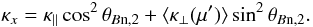 The average downstream
cross-field diffusion coefficient ⟨ κ⊥ ⟩ can be solved as
The average downstream
cross-field diffusion coefficient ⟨ κ⊥ ⟩ can be solved as
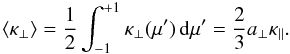 Because the true
pitch-angle distribution in the downstream is unknown, a cautious choice is instead to use
the highest value. Using
κ⊥|max = a⊥κ∥
and
κ∥ = v′λ∥/3,
we found the position of the downstream return boundary to be
Because the true
pitch-angle distribution in the downstream is unknown, a cautious choice is instead to use
the highest value. Using
κ⊥|max = a⊥κ∥
and
κ∥ = v′λ∥/3,
we found the position of the downstream return boundary to be
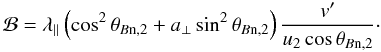 (13)We defined the downstream
cross-field diffusion strengths as a⊥ = 0 (set two) and
a⊥ = 0.1 (sets three and four).
(13)We defined the downstream
cross-field diffusion strengths as a⊥ = 0 (set two) and
a⊥ = 0.1 (sets three and four).
In the downstream, the field-parallel particle motion is
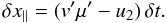 The diffusive step across
the mean field is solved using the stochastic differential equation method, as described in
Gardiner (1985). Thus, the particle is propagated
with
The diffusive step across
the mean field is solved using the stochastic differential equation method, as described in
Gardiner (1985). Thus, the particle is propagated
with 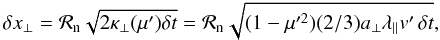 where ℛn is a
normal distributed random number with unit variance and zero mean. We additionally
constrained the field-perpendicular motion to
where ℛn is a
normal distributed random number with unit variance and zero mean. We additionally
constrained the field-perpendicular motion to 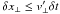 , which implies that we cut
off the tail of the normal distribution of ℛn at
, which implies that we cut
off the tail of the normal distribution of ℛn at
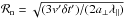 .
Combining δx∥ and
δx⊥, the motion normal to the shock front is
.
Combining δx∥ and
δx⊥, the motion normal to the shock front is
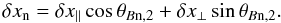 Particles encountering the
boundary xn = −ℬ because of the field-parallel motion were
considered isotropic, and the return probability Pret from Eq.
(5)was applied. The particle was then sent
back towards the shock from the distance of xn = −ℬ with a
randomised flux-weighted shock-bound pitch-angle. In sets 2...4, particles
propagated and experienced small-angle scattering in the downstream and are possibly again
convected to xn = −ℬ. Each time this occurred, Eq. (5)was applied, which resulted in the cumulative
return probability
Particles encountering the
boundary xn = −ℬ because of the field-parallel motion were
considered isotropic, and the return probability Pret from Eq.
(5)was applied. The particle was then sent
back towards the shock from the distance of xn = −ℬ with a
randomised flux-weighted shock-bound pitch-angle. In sets 2...4, particles
propagated and experienced small-angle scattering in the downstream and are possibly again
convected to xn = −ℬ. Each time this occurred, Eq. (5)was applied, which resulted in the cumulative
return probability 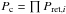 .
Downstream propagation continued until the particle either returned to the shock or the
cumulative return probability dropped below 10-6, at which point the particle was
considered to be not injected. If the particle returned to the shock, the successful
particle was injected with the assigned probability Pc.
.
Downstream propagation continued until the particle either returned to the shock or the
cumulative return probability dropped below 10-6, at which point the particle was
considered to be not injected. If the particle returned to the shock, the successful
particle was injected with the assigned probability Pc.
Because the rejection of uninjected particles may result in significantly reduced statistics for the injected flux, we used the minimum-variance unbiased estimator (see, e.g., Lehmann & Casella 1998) to improve the statistical accuracy of the injection probability. The method is described in Appendix C.
For downstream cross-field diffusion, we had to specify the terminating conditions for the trajectories that tried to cross boundaries at xn = −ℬ or xn = 0. We note that for cross-field diffusion across the downstream return boundary, there should be an equivalent, symmetric cross-field-diffusion flux backwards if the particle density is constant. We maintained this symmetry by cancelling out all steps δx⊥ that would result in a particle crossing the downstream return boundary.
We assumed that the perpendicular mean free path in the upstream region is zero, which means that no particles can propagate into the upstream by perpendicular diffusion. Thus, we needed to specify a terminating condition for the trajectories that tried to enter the upstream region via cross-field diffusion. We modelled two different boundary conditions at the shock front. In set three, we prevented particle propagation into the upstream through cross-field diffusion by reflecting all perpendicular steps δx⊥ at the shock front. In set four, we modified the boundary condition to allow cross-field jumps where the particle parallel motion is towards the upstream (i.e. where μ2 > 0) to inject the particle. The method of set four is intended to model the way in which cross-field diffusion brings the particle close to the shock, after which it is free to propagate along the field into the upstream.
8. Results and discussion
8.1. Velocity thresholds and shock obliquity
In Fig. 2, we show the analytical threshold velocity for reflection as a function of shock obliquity for a shock with Vs = 1500 km s-1. As can be seen, reflection is only possible for particles with initial speeds higher than ~930 km s-1, with the threshold increasing with shock-normal angle. For Vs = 2000 km s-1, we found a similar behaviour, with the threshold starting at ~1260 km s-1. Thus, through reflection, our fast shocks are capable of injecting only suprathermal particles.
The threshold for transmitted particle return to the upstream is not so straightforward, because for some shocks, particles of all velocities can be returned to upstream. In Fig. 3, we show that injection for transmitted particles of negligible upstream plasma frame speed (v = 0) is possible with shock-normal angles θBn ≤ 6° when Vs = 1500 km s-1. For Vs = 2000 km s-1 the requirement is θBn ≤ 14°. Because the bulk of the seed particles is thermal and thus relatively slow, these analytical results suggest a significant effect relating the efficiency of shock acceleration with the shock-normal angle θBn. For comparison, in addition to the lowest injection speed of transmitted particles, Fig. 3 shows the classical injection speed threshold u1 and speed thresholds for reflection. The classical model of v > u1 overestimates the lowest injection speeds by several hundred km s-1.
The semi-analytical flux transmission visualisations presented in Figs. 4 and 5 confirm that an increasing shock-normal angle θBn results in a decreasing injection probability for the core thermal population. In the parallel case (θBn = 0°), the core is found to be close to the 25% injection probability threshold. For Vs = 1500 km s-1, the threshold of no injection for a shock-normal angle of θBn = 5° approaches the thermal core, and a shock-normal angle of θBn = 15° results in the highest three magnitudes of flux density falling within the zone of no return. For Vs = 2000 km s-1, a similar effect is seen at slightly larger shock-normal angles. At θBn = 15°, the thermal core is intersected by the threshold of no return, and θBn = 30° sees the highest six flux density magnitudes within the zone of no return.
 |
Fig. 6 Particle fluxes at the shock: curves represent numerical integration results, data points are results of Monte Carlo simulations. Vs = 1500 km s-1 (left) and Vs = 2000 km s-1 (right). Simulations without downstream propagation of particles are designated with ℬ = 0, whereas simulations where particles isotropise through downstream scatterings are designated with ℬ > 0. The flux differences for the reflected particles in the Monte Carlo simulations (⋄ , +) are due to statistical uncertainties. For comparison, we show the integrated flux of all particles that are faster than the classical injection threshold v > u1 as a dash-dotted line. For κ = 15, reflected particle fluxes and the classical comparison are too low to be visible. |
Our main results are shown in Fig. 6, where we compare the results of Monte Carlo simulations with semi-analytical results. We calculated injected fluxes for particles both reflected at the shock and injected through downstream scatterings. For the semi-analytical flux analysis, this was achieved by integrating the selected κ-distribution over the whole velocity space, accounting for reflection or return probability. The classical threshold result was found by integrating the population for all particles that fulfil v > u1. When reflection dominates, this comparison is quite close to our results, but it should be noted that injection of all particles with v > u1 is unrealistic, with the difference compensated for because our model is able to also reflect particles of upstream speeds v < u1. For Monte Carlo simulations, the representative weight of all injected (reflected or returned) particle packages was compared with the total weight of all tested particles.
We found that Monte Carlo simulations without downstream propagation yield injection probabilities in line with semi-analytical results. As the shock-normal angle θBn increases, a threshold effect begins to prevent the abundant, slow-core particle population from being injected. For Vs = 1500 km s-1, an injection efficiency decrease of two orders of magnitude is seen as the shock-normal angle θBn increases from 0 to 7.5°. For Vs = 2000 km s-1, a similar decrease is observed as θBn increases from 0 to 15°. We note that this effect is greater than the one reported by Ellison et al. (1995), spanning several orders of magnitude. However, our work does not retain a constant gas compression ratio, but keeps Vs constant, thus allowing the compression ratio to decrease as obliquity increases.
For the non-thermal distribution (κ = 2), the reflected particle flux becomes higher than the flux of transmitted and subsequently injected particles when θBn ≥ 13° (Vs = 1500 km s-1) or when θBn ≥ 21° (Vs = 2000 km s-1). For the quasi-thermal distribution (κ = 15), the reflected particle flux is negligible and the injection probability continues to decrease as θBn increases. Injection of a quasi-thermal distribution is found to be negligible at θBn ≥ 25°.
We also studied the case of shock-normal velocity Vs = 1000 km s-1, which did not show a strong correlation between injection efficiency and shock-normal angle. With such a low shock-normal velocity, we found the injection of the thermal core to be improbable, regardless of the shock-normal angle θBn. This is mostly due to the small gas compression ratio for such a low Mach number shock.
8.2. Isotropisation in the downstream
In Fig. 6, we show how downstream isotropisation
methods affect our Monte Carlo simulations. We show that at small (large) shock-normal
angles, the assumption of instant downstream isotropy results in a higher (lower)
injection probability than the one actually needed to allow the population to achieve
isotropy through downstream scattering. This occurs because with velocities
v′ > u2,
the average parallel velocity in the downstream plasma frame
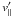 for
transmitted particles is negative (positive) at small (large) shock-normal angles.
Additionally, the thermal population exclusion is seen to be activated at smaller
shock-normal angles if isotropisation takes place through simulated scatterings. For
example, at Vs = 1500 km s-1 and
θBn = 10°, accounting for
downstream scattering decreases the returning flux of transmitted particles by well over
three orders of magnitude. At Vs = 2000 km s-1
and θBn = 10°, the decrease is
approximately two orders of magnitude. At parallel
(θBn = 0°) shocks, the
returning flux was found to decrease by 33%
(Vs = 1500 km s-1) or by 35%
(Vs = 2000 km s-1) compared with the values
found by assuming instant downstream isotropy.
for
transmitted particles is negative (positive) at small (large) shock-normal angles.
Additionally, the thermal population exclusion is seen to be activated at smaller
shock-normal angles if isotropisation takes place through simulated scatterings. For
example, at Vs = 1500 km s-1 and
θBn = 10°, accounting for
downstream scattering decreases the returning flux of transmitted particles by well over
three orders of magnitude. At Vs = 2000 km s-1
and θBn = 10°, the decrease is
approximately two orders of magnitude. At parallel
(θBn = 0°) shocks, the
returning flux was found to decrease by 33%
(Vs = 1500 km s-1) or by 35%
(Vs = 2000 km s-1) compared with the values
found by assuming instant downstream isotropy.
Thus, it is evident that the effects of transmitted population anisotropy cannot be ignored when gauging the injection efficiency at a propagating coronal shock.
8.3. Cross-field diffusion
In Fig. 7, we show comparisons between the simulation sets 2...4, which shows that accounting for the downstream cross-field diffusion affects the injection efficiency. At very low values of θBn, the cross-field diffusion in the downstream, acting as if it were boosting the isotropisation speed, increases the injection efficiency, but by a small margin. As the downstream shock-normal angle θBn,2 increases, downstream cross-field diffusion begins to play a larger role, and the choice of boundary conditions at the shock becomes very important. Allowing downstream cross-field diffusion to take place, but preventing jumps of particles with μ2 > 0 to the upstream, acts like rapid isotropisation, and the injection efficiency approaches the ℬ = 0 case. However, allowing downstream cross-field diffusion to inject particles with μ2 > 0 increases the injection by a factor of up to ~50%. At large shock-normal angles reflection remains the dominant injection mechanism.
 |
Fig. 7 Effect of downstream cross-field diffusion strength a⊥ = 0.1 on the injection efficiency for Vs = 1500 km s-1, κ = 2, and different shock-normal angles. Curves (from numerical integration results) and results from simulations without cross-field diffusion (squares) are the same as in Fig. 6. Results for the two types of downstream cross-field diffusion (sets three and four) are shown as triangles and diamonds. |
 |
Fig. 8 Ratios of total injected particle fluxes with active (FCSP) or inactive (FnoCSP) cross-shock potential. We show results for semi-analytical integration (curves) and Monte Carlo simulations (symbols). Presented shock-normal velocities are Vs = 1500 km s-1 (left) and Vs = 2000 km s-1 (right). Simulations without downstream propagation of particles are designated with ℬ = 0, whereas simulations where particles isotropise through downstream scatterings are designated with ℬ > 0. The flux differences for reflected particles in the Monte Carlo simulations (⋄ , +) are due to statistical uncertainties. For κ = 15, reflected particle fluxes are too low to be visible. |
8.4. Cross-shock potential effect on injection
In the presence of a cross-shock electric potential, particles are more likely to be reflected from the shock, and transmitted particles experience a decrease in parallel velocity. Thus, the expectation is for transmitted particles to be less likely to experience injection. Injected particles do, however, receive an additional speed boost when returning to the upstream. Injection efficiency ratios with active or inactive cross-shock potential are presented in Fig. 8. Results are shown only when the flux in question is not lower than 10-6 of the incoming flux. Reflection at small shock-normal angles in the absence of a cross-shock potential is very unlikely, which results in the large statistical uncertainty in Monte Carlo simulations.
Both the semi-analytical approach and Monte Carlo simulations confirm the increase in
reflection probability and decrease in transmitted particle injection probability. As
θBn increases, and injection of reflected
particles is possible only for the non-thermal tail of the κ = 2
population, the effect of the cross-shock potential on the injection diminishes.
Interestingly, accounting for downstream scattering causes the diminishing of thermal
particle injection to occur at significantly smaller shock-normal angles than if assuming
instant downstream isotropy. This is because the average parallel velocity in the
downstream plasma frame 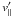 for
transmitted particles (with velocities
v′ > u2)
changes direction.
for
transmitted particles (with velocities
v′ > u2)
changes direction.
As the shock-normal angle θBn increases, the magnetic reflection probability of particles increases, and the relative magnitude of the effect caused by the cross-shock potential decreases. For Vs = 1500 km s-1, the increase of reflected particles at θBn = 5° is approximately 65%. For Vs = 2000 km s-1, the increase of reflected particles at θBn = 5° is approximately 270%. Both cases see the increase drop to approximately 30% when θBn approaches 25°.
As mentioned in Sect. 8.1, reflection overtakes downstream scattering as a source of injected particles when θBn ≥ 14° (Vs = 1500 km s-1), or when θBn ≥ 21° (Vs = 2000 km s-1). Subsequently, at small (large) shock-normal angles, the net injection effect of a cross-shock potential is negative (positive).
9. Conclusions
We have presented analytical and numerical results that indicate that quasi-parallel coronal shocks are capable of injecting a significant portion of the cold core of thermal particle when the shock-normal velocity Vs is sufficiently high. Requiring injected particles to fulfil the classical injection threshold u1 = VssecθBn − usw is unlikely to accurately describe particle injection.
With the assistance of Monte Carlo simulations, we showed the θBn-dependence of the injection efficiency to be highly sensitive to a proper assessment of transmitted particle flux anisotropy. Using an assumption of instant downstream isotropy can overestimate the injection probability by a factor of 3 to 3000. Allowing for downstream cross-field diffusion to take place can either increase or decrease the injection efficiency of particles, depending on chosen boundary conditions. However, cross-field diffusion in the downstream has a negligible effect at small shock-normal angles, where thermal particles can be injected. At large shock-normal angles, reflection remains the dominant injection method. Note, however, that our model assumed that cross-field diffusion is limited to the downstream region, indicating that this transport process can only bring the particle back to the shock, but not across it. If cross-field diffusion in the upstream region were added, its role in the injection process would most probably increase.
The DSA at coronal shocks is strongly dependent on the strength of self-generated turbulence, and thus, the amount of seed particles taking part in the acceleration process. The results presented in this paper suggest that fast quasi-parallel coronal shocks are capable of efficiently injecting the thermal core of the solar wind. A short, finite interval of parallel shock propagation could be efficient in boosting a significant portion of the thermal particle population to suprathermal energies, resulting in an injection hot-spot, after which they could be efficiently accelerated by either a quasi-parallel or an oblique shock front.
Additionally, we showed that a cross-shock potential has a significant effect in increasing the probability of reflection for incident particles and in decreasing the injection probability of thermal particles. For suprathermal particle populations, and by extension, oblique shocks, the cross-shock potential was shown to be of little significance.
Online material
Appendix A: Flux weighting
Appendix A.1: Upstream conservation of flux
The flux of particles through a given cross-sectional area of the flux tube towards
the shock is given as 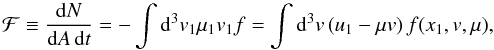 (A.1)which satisfies the
steady state requirement of
(A.1)which satisfies the
steady state requirement of 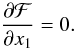 It is
noteworthy that although the mean direction of particles is in the negative
x-axis direction, we defined the total net flux across the shock as
being positive. We considered the shock to be an absorbing boundary, that is, the
distributions and fluxes represent particles that have yet to encounter the shock. The
particle flux, which is constant regardless of position
x1, is easily evaluated far from the shock, where only the
scattering process affects the angular distribution of the particles. The distribution
is assumed to be isotropic in the local plasma frame. Thus, sufficiently far upstream,
the flux is given by the form
It is
noteworthy that although the mean direction of particles is in the negative
x-axis direction, we defined the total net flux across the shock as
being positive. We considered the shock to be an absorbing boundary, that is, the
distributions and fluxes represent particles that have yet to encounter the shock. The
particle flux, which is constant regardless of position
x1, is easily evaluated far from the shock, where only the
scattering process affects the angular distribution of the particles. The distribution
is assumed to be isotropic in the local plasma frame. Thus, sufficiently far upstream,
the flux is given by the form
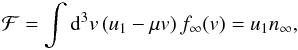 (A.2)where
n∞ is the particle density and
f∞ the particle distribution at infinity.
(A.2)where
n∞ is the particle density and
f∞ the particle distribution at infinity.
At velocities
v < u1, all
particles travel towards the shock, and thus, information of the shock at
x1 = 0 cannot propagate into the upstream. The
distribution remains isotropic in the local plasma frame, and the differential flux
impacting the shock is simply 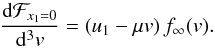 (A.3)Considering
particles with speeds
v > u1, the
picture becomes more complicated. Information of the shock can propagate against the
flow of plasma, because μv − u1 can be
positive. This means that the angular distribution of particles that have not yet
interacted with the shock becomes anisotropic, as the distribution
f(x1 = 0,v,μ) = 0 for
μv > u1, due to
the absorbing boundary at the shock. However, at a distance of
x1 = 2λ, for instance, we can still
assume isotropy and take
f(2λ,v,μ) ≈ f∞(v),
so that
(A.3)Considering
particles with speeds
v > u1, the
picture becomes more complicated. Information of the shock can propagate against the
flow of plasma, because μv − u1 can be
positive. This means that the angular distribution of particles that have not yet
interacted with the shock becomes anisotropic, as the distribution
f(x1 = 0,v,μ) = 0 for
μv > u1, due to
the absorbing boundary at the shock. However, at a distance of
x1 = 2λ, for instance, we can still
assume isotropy and take
f(2λ,v,μ) ≈ f∞(v),
so that 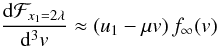 (A.4)is valid for
all velocities including
v > u1. In this
flux, particles with
μv > u1 cause a
negative contribution to the net flux, because they propagate outwards across the flux
tube cross-section surface at x1 = 2λ.
(A.4)is valid for
all velocities including
v > u1. In this
flux, particles with
μv > u1 cause a
negative contribution to the net flux, because they propagate outwards across the flux
tube cross-section surface at x1 = 2λ.
For the purpose of constructing a semi-analytical model of particle injection at high
particle speeds, we simplified the anisotropies of the particle distribution at the
shock. We assigned the modified differential flux of particles with
v > u1 at the
shock as 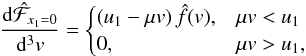 (A.5)where
(A.5)where
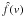 is a scaled distribution function yielding the correct total net flux, that is,
is a scaled distribution function yielding the correct total net flux, that is,
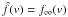 for v < u1, but
for v > u1,
for v < u1, but
for v > u1,
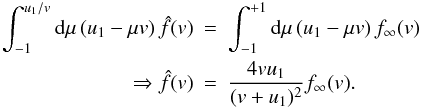 Thus,
for the particles that have not yet interacted with the shock, we find
Thus,
for the particles that have not yet interacted with the shock, we find 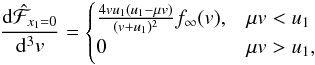 (A.6)valid
for particles of speed
v > u1. This
accounts for the absorbing boundary at the shock whilst maintaining the conservation
of total flux at a given particle speed v.
(A.6)valid
for particles of speed
v > u1. This
accounts for the absorbing boundary at the shock whilst maintaining the conservation
of total flux at a given particle speed v.
For Monte Carlo simulations, the same consideration of flux conservation must be
made. The flux, that is, the total amount of particles encountered by the shock within
time dt, is formulated as
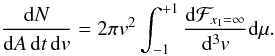 (A.7)For
particles of speeds
v < u1, the
whole population is advected towards the shock, meaning that no information of the
approaching shock can reach the particle distribution before impact. Thus, for these
particles, the differential flux, extended to encompass all pitch-angles, can be
written as
(A.7)For
particles of speeds
v < u1, the
whole population is advected towards the shock, meaning that no information of the
approaching shock can reach the particle distribution before impact. Thus, for these
particles, the differential flux, extended to encompass all pitch-angles, can be
written as 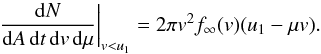 (A.8)Thus,
the probability of a particle with speed v exhibiting pitch-angle
μ when impacting the shock is given as
(A.8)Thus,
the probability of a particle with speed v exhibiting pitch-angle
μ when impacting the shock is given as
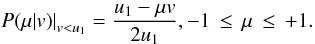 (A.9)This
can be integrated to find the cumulative distribution function for a value of
μ as
(A.9)This
can be integrated to find the cumulative distribution function for a value of
μ as 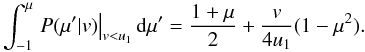 (A.10)From
this, the Monte Carlo randomisation formula for μ can be solved as
(A.10)From
this, the Monte Carlo randomisation formula for μ can be solved as
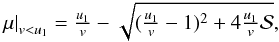 (A.11)where
μ receives values from the range
−1 < μ ≤ + 1 and
(A.11)where
μ receives values from the range
−1 < μ ≤ + 1 and
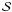 is a uniformly distributed random number in the range [0,1).
is a uniformly distributed random number in the range [0,1).
For particles with speeds v > u1, information of the propagating shock can extend into the upstream, affecting the incident particle pitch-angle distribution. Thus, we initialised the particle distribution in the upstream of the shock at a distance of x1 = 2λ, and allowed particles to convect towards the shock. This resulted in a realistic pitch-angle distribution at x1 = 0+, without having to resort to flux modification (Eq. (A.6)).
This pre-propagation is limited to the region x1 ∈ [0,2λ] with particles initialised isotropically at values μ < u1/v. As the total population is advected towards the shock, all particles that escape to x1 > 2λ will eventually return to the initialisation boundary of x1 = 2λ, isotropised in the fluid frame. Thus, particles escaping to the upstream can be simply re-initialised at that position.
The distribution of pitch-angles μ for a given speed
v, limiting the valid pitch-angle range to values
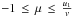 and normalising the total probability to 1, is
and normalising the total probability to 1, is 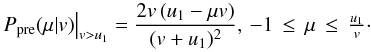 (A.12)This
will result in the shock-incident flux
(A.12)This
will result in the shock-incident flux
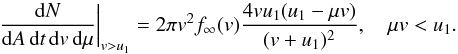 (A.13)Using Eq.
(A.12), the Monte Carlo
randomisation formula for μ can be solved (similar to Eq. (A.10)) as
(A.13)Using Eq.
(A.12), the Monte Carlo
randomisation formula for μ can be solved (similar to Eq. (A.10)) as 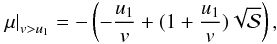 (A.14)where
μ receives values from the range
(A.14)where
μ receives values from the range
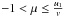 .
.
Appendix B: Analytical injection thresholds
Appendix B.1: Reflection threshold
In attempting to determine particle injection, we can solve certain seed particle
speed thresholds. A particle is reflected (see Eq. (9)), and thus, injected, if 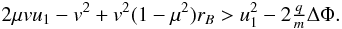 (B.1)The right-hand side
(RHS) of the equation is constant. Through roots of derivatives of the left-hand side
(LHS), we can find LHS maxima at
(B.1)The right-hand side
(RHS) of the equation is constant. Through roots of derivatives of the left-hand side
(LHS), we can find LHS maxima at 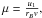 if
if
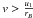 ,
or μ = 1, if
,
or μ = 1, if 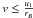 .
Thus, if
.
Thus, if 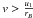 ,
the LHS maximum is given as
,
the LHS maximum is given as 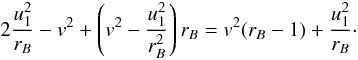 (B.2)This results
in no possibility of reflection, if
u1/rB < v < vR1,
where
(B.2)This results
in no possibility of reflection, if
u1/rB < v < vR1,
where 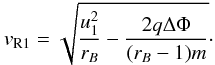 (B.3)If
(B.3)If
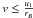 ,
the LHS has a maximum value of
2vu1 − v2.
This results in no possibility of reflection, if
v < vR2, where
,
the LHS has a maximum value of
2vu1 − v2.
This results in no possibility of reflection, if
v < vR2, where
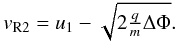 (B.4)The LHS minimum is
found at μ = −1. With these shock and solar wind parameters, there
exists no valid speed v for which this value of the LHS would be
positive. Under these circumstances, no seed particle speed v results
in certain reflection, regardless of pitch-angle μ.
(B.4)The LHS minimum is
found at μ = −1. With these shock and solar wind parameters, there
exists no valid speed v for which this value of the LHS would be
positive. Under these circumstances, no seed particle speed v results
in certain reflection, regardless of pitch-angle μ.
Appendix B.2: Threshold for return from the downstream
To split the transmitted particle population into portions with either possible or
impossible injection, we examined Eqs. (10)and (11)to find
![\appendix \setcounter{section}{2} \begin{eqnarray} v'^{2} &=& v'^{2}_\perp+v'^{2}_\parallel = v^{2}\left(1-\mu^{2}\right)r_{B} \nonumber \\ &+& \left[u_{2}-\sqrt{u_{1}^{2}-2\mu vu_{1}+v^{2}-v^{2}(1-\mu^{2})r_{B}-2\tfrac{q}{m}\Delta\Phi}\right]^{2}. \label{eq:downstreamvelocity} \end{eqnarray}](/articles/aa/full_html/2013/10/aa21348-13/aa21348-13-eq212.png) (B.5)We
found the maxima of downstream speed v′ for a given
v, because this can result in an injection velocity threshold.
Maxima for v′ can be found at μ = −1
and μ = + 1 or by solving the roots of the derivative of
v′(μ). Assigning
(B.5)We
found the maxima of downstream speed v′ for a given
v, because this can result in an injection velocity threshold.
Maxima for v′ can be found at μ = −1
and μ = + 1 or by solving the roots of the derivative of
v′(μ). Assigning
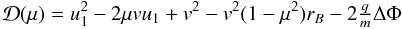 (B.6)and finding
the first derivative for v′2 gives
(B.6)and finding
the first derivative for v′2 gives ![\appendix \setcounter{section}{2} \begin{eqnarray} \frac{\partial v'^{2}}{\partial\mu} & = & \frac{\partial}{\partial\mu}\left[u_{2}-\sqrt{\mathcal{D}(\mu)}\right]^{2}-2\mu v^{2}r_{B}\\ & = & \frac{2(u_{1}-\mu vr_{B})vu_{2}}{\sqrt{\mathcal{D}(\mu)}}-2vu_{1}. \label{eq:middleextrema} \end{eqnarray}](/articles/aa/full_html/2013/10/aa21348-13/aa21348-13-eq217.png) Solving
the roots provides an extremum, if μ ∈ (−1, + 1)
and if
Solving
the roots provides an extremum, if μ ∈ (−1, + 1)
and if 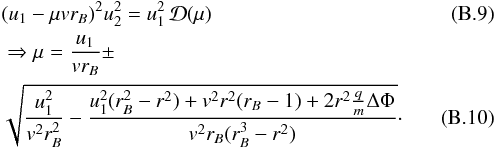 If
If
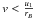 holds true, only the solution with the minus sign is of interest. These, in addition
to the possible extrema at μ = −1 and μ = + 1,
result in several possible threshold velocities.
holds true, only the solution with the minus sign is of interest. These, in addition
to the possible extrema at μ = −1 and μ = + 1,
result in several possible threshold velocities.
Appendix B.2.1: Extrema at μ =-1 and μ = + 1
The possible downstream velocity extrema at μ = −1 and
μ = + 1 can be solved by refining Eq. (B.5). Formulating this as the threshold
for no injection results in
![\appendix \setcounter{section}{2} \begin{equation} v'^{2}=\left[u_{2}-\sqrt{(u_{1}\mp v)^{2}-2\tfrac{q}{m}\Delta\Phi}\right]^{2} < u_{2}^{2}, \end{equation}](/articles/aa/full_html/2013/10/aa21348-13/aa21348-13-eq223.png) (B.11)where the term
inside the square root is positive for all transmitted particles. Thus, a
transmitted particle can return to the upstream only if
(B.11)where the term
inside the square root is positive for all transmitted particles. Thus, a
transmitted particle can return to the upstream only if
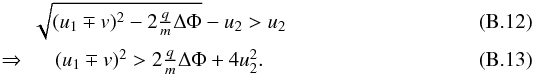 For
particles with
v > u1,
injection is always possible. For particles with
v < u1, we
found the additional requirements of
For
particles with
v > u1,
injection is always possible. For particles with
v < u1, we
found the additional requirements of 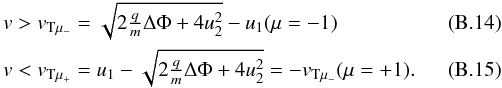 For
our parameters, only vTμ−
provides a valid condition for injection.
For
our parameters, only vTμ−
provides a valid condition for injection.
Appendix B.2.2: Extrema at μ ≠ ± 1
Solving the thresholds speeds for the one or two extrema given in Eq. (B.8)in an analytical fashion does not result in easily applicable equations. However, solving the velocity thresholds for these extrema in a numerical fashion revealed valid extrema only at shock-normal angles θBn ≤ 4°. At these shock-normal angles, the existing extrema at μ = ± 1 already allow theoretical return of particles regardless of their speed. Thus, these extrema do not affect the found particle return speed thresholds. However, in a more general case, they cannot be ignored.
Appendix C: Statistical handling of uninjected particles
In Sect. 7, we presented a method for estimating
the capability of a shock to inject particles using Monte Carlo simulations. In our
method, we propagated the particle in the downstream until it was either injected into
the upstream, or the cumulative probability of return at the downstream boundary fell
below 10-6 and it was removed from the simulation as an uninjected particle.
For some shock parameters, however, this method will result in very low statistics for
the injected particles. To improve the statistical accuracy, we used the fact that
successes and failures – injections and non-injections – are distributed according to a
negative binomial distribution. When the numbers of successes, ℛ, and failures,
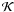 ,
are known, the probability for success
,
are known, the probability for success 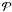 can be evaluated using the minimum-variance unbiased estimator (see, e.g., Lehmann & Casella 1998), which gives
can be evaluated using the minimum-variance unbiased estimator (see, e.g., Lehmann & Casella 1998), which gives
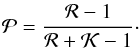 (C.1)It should be
noted, however, that the actual probability of injection for a particle is
(C.1)It should be
noted, however, that the actual probability of injection for a particle is
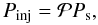 (C.2)
(C.2)
where Ps is the injection probability associated with the last encountered success.
To evaluate the unbiased estimator, we randomised particles in groups. For each
particle within the group, the newly randomised values of v and
μ were used to test the particle for reflection, as explained in
Sect. 5.1. Reflected particles were considered
successes and have Ps = 1. Non-reflected particles are
transmitted to the downstream, with v′ and
μ′ calculated according to Eqs. (10)and (11). They were then followed in the downstream, as described in
Sect. 7, until they were either injected,
incrementing ℛ, or considered uninjected, incrementing
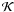 .
This was continued until ℛ = 5. The last particle of the group was then injected with
the probability Pinj.
.
This was continued until ℛ = 5. The last particle of the group was then injected with
the probability Pinj.
As a precaution against excessively low success probabilities, the group size was
limited to 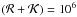 .
If this limit was reached and at least two successes were encountered, the values of
ℛi and
.
If this limit was reached and at least two successes were encountered, the values of
ℛi and 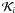 associated with the last encountered success were used to calculate
associated with the last encountered success were used to calculate
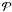 .
If the tests resulted in only 0 or 1 success, the group was considered to result in no
injection.
.
If the tests resulted in only 0 or 1 success, the group was considered to result in no
injection.
With these methods, the injected weight of the Monte Carlo particle was found to be Winj = WseedPinj, where Wseed is the representative weight of upstream seed particles assigned to this group, and was found based on the plasma density. The total injected weight was then used to calculate the particle flux.
Acknowledgments
The calculations presented were performed using the Finnish Grid Infrastructure (FGI) project (Turku, Finland). The authors would like to thank the Academy of Finland (AF) for financial support of projects 133723 and 259227. T.L. acknowledges support from the UK Science and Technology Facilities Council (STFC) (grant ST/J001341/1). The research leading to these results has received funding from the European Union’s Seventh Framework Programme (FP7/2007-2013) under grant agreement No 262773 (SEPServer). The authors gratefully acknowledge the important comments and suggestions provided by the anonymous referee.
References
- Axford, W. I., Leer, E., & Skadron, G. 1977, in International Cosmic Ray Conf., 11, 132 [Google Scholar]
- Baring, M. G., Ellison, D. C., & Jones, F. C. 1993, ApJ, 409, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Baring, M. G., Ellison, D. C., & Jones, F. C. 1994, ApJS, 90, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Baring, M. G., Ellison, D. C., & Jones, F. C. 1995, Adv. Space Res., 15, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Battarbee, M., Laitinen, T., Vainio, R., & Agueda, N. 2010, Twelfth International Solar Wind Conf., 1216, 84 [NASA ADS] [Google Scholar]
- Battarbee, M., Laitinen, T., & Vainio, R. 2011, A&A, 535, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Bemporad, A., & Mancuso, S. 2011, ApJ, 739, L64 [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Burgess, D. 1989, Geophys. Res. Lett., 16, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B. 1988, Space Sci. Rev., 48, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., Baring, M. G., & Jones, F. C. 1995, ApJ, 453, 873 [Google Scholar]
- Ellison, D. C., Baring, M. G., & Jones, F. C. 1996, ApJ, 473, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Gardiner, C. 1985, Handbook of stochastic methods for physics, chemistry, and the natural sciences, Springer series in synergetics (Springer-Verlag) [Google Scholar]
- Gedalin, M. 1996, J. Geophys. Res., 101, 4871 [NASA ADS] [CrossRef] [Google Scholar]
- Giacalone, J. 2005, ApJ, 624, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 2006, J. Phys. Conf. Ser., 47, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Hull, A. J., Scudder, J. D., Fitzenreiter, R. J., et al. 2000, J. Geophys. Res., 105, 20957 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, F. C., & Ellison, D. C. 1991, Space Sci. Rev., 58, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, F. C., Baring, M. G., & Ellison, D. C. 1993, in International Cosmic Ray Conf., 2, 243 [Google Scholar]
- Kirk, J. G., & Heavens, A. F. 1989, MNRAS, 239, 995 [NASA ADS] [Google Scholar]
- Krymskii, G. F. 1977, Akademiia Nauk SSSR Doklady, 234, 1306 [NASA ADS] [Google Scholar]
- le Roux, J. A., & Webb, G. M. 2009, ApJ, 693, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. A. 1983, J. Geophys. Res., 88, 6109 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. A. 2005, ApJS, 158, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, E., & Casella, G. 1998, Theory of Point Estimation, Springer Texts in Statistics (Springer) [Google Scholar]
- Leroy, M. M. 1984, Adv. Space Res., 4, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G., Shalchi, A., Ao, X., Zank, G., & Verkhoglyadova, O. P. 2012, Adv. Space Res., 49, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Malkov, M. A., & Völk, H. J. 1995, A&A, 300, 605 [NASA ADS] [Google Scholar]
- Malkov, M. A., & Völk, H. J. 1998, Adv. Space Res., 21, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, G. M., Mazur, J. E., & Dwyer, J. R. 1999, ApJ, 525, L133 [Google Scholar]
- Neergaard Parker, L., & Zank, G. P. 2012, ApJ, 757, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C. K., & Reames, D. V. 1994, ApJ, 424, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C. K., & Reames, D. V. 2008, ApJ, 686, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Ostrowski, M. 1991, MNRAS, 249, 551 [NASA ADS] [Google Scholar]
- Pomoell, J., Vainio, R., & Kissmann, R. 2011, Astrophys. Space Sci. Trans., 7, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Reames, D. V. 1999, Space Sci. Rev., 90, 413 [Google Scholar]
- Sandroos, A., & Vainio, R. 2006, A&A, 455, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandroos, A., & Vainio, R. 2007, ApJ, 662, L127 [Google Scholar]
- Sandroos, A., & Vainio, R. 2009, A&A, 507, L21 [CrossRef] [EDP Sciences] [Google Scholar]
- Scholer, M. 1993, J. Geophys. Res., 98, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Scholer, M., & Burgess, D. 1992, J. Geophys. Res., 97, 8319 [NASA ADS] [CrossRef] [Google Scholar]
- Terasawa, T., Oka, M., Nakata, K., et al. 2006, Adv. Space Res., 37, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Tylka, A. J., & Lee, M. A. 2006, ApJ, 646, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Tylka, A. J., Cohen, C. M. S., Dietrich, W. F., et al. 2001, ApJ, 558, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Tylka, A. J., Cohen, C. M. S., Dietrich, W. F., et al. 2005, ApJ, 625, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Vainio, R. 2003, A&A, 406, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vainio, R., & Laitinen, T. 2007, ApJ, 658, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Vainio, R., & Laitinen, T. 2008, J. Atmos. Sol.-Terr. Phys., 70, 467 [Google Scholar]
- Vainio, R., & Schlickeiser, R. 1999, A&A, 343, 303 [NASA ADS] [Google Scholar]
- van Nes, P., Reinhard, R., Sanderson, T. R., Wenzel, K.-P., & Zwickl, R. D. 1984, J. Geophys. Res., 89, 2122 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyliunas, V. M. 1968, J. Geophys. Res., 73, 2839 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Rice, W. K. M., Le Roux, J. A., Cairns, I. H., & Webb, G. M. 2001, Phys. Plasmas, 8, 4560 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Li, G., & Verkhoglyadova, O. 2007, Space Sci. Rev., 130, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Zuo, P., Zhang, M., & Rassoul, H. K. 2013, ApJ, 767, 6 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Shock-normal velocity, angle, and shock parameters solved with Rankine-Hugoniot equations.
All Figures
 |
Fig. 1 Particle distribution functions fth(v), fnth(v) and a Maxwellian distribution at T ≈ 2.0 × 106 K. |
| In the text | |
 |
Fig. 2 Reflection threshold speeds for Vs = 1500 km s-1: within the shaded area, protons may be reflected at the shock. Threshold #1 (v > vR1, v > u1/rB) is defined with Eq. (B.3)and threshold #2 (v > vR2, v < u1/rB) with Eq. (B.4). |
| In the text | |
 |
Fig. 3 Injection threshold speeds for Vs = 1500 km s-1: the classical threshold u1 (solid curve) versus our reflection threshold (dashed) and the threshold for injection after downstream scatterings (dotted, v > vTμ−). Protons within the shaded areas have nonzero injection probability; the different shading represents the injection possibility through reflection, downstream scatterings, or both. The classical threshold overestimates the lowest injection speeds, especially at small shock-normal angles. |
| In the text | |
 |
Fig. 4 Visualised transfer of quasi-thermal (left, κ = 15) and non-thermal (right, κ = 2) particle flux densities dℱ/(dv∥ dv⊥) across a shock of velocity Vs = 1500 km s-1 with four different shock-normal angles. Blue contours depict the incident transmitting flux, red contours depict the reflected flux, and red solid contours the downstream transmitted flux at one magnitude intensity intervals. The black semicircles depict downstream speed thresholds for statistical return probabilities of 0% (dashed) and 25% (dotted), and the black-green dashed curve represents the reflection threshold. |
| In the text | |
 |
Fig. 5 Visualised transfer of quasi-thermal (left, κ = 15) and non-thermal (right, κ = 2) particle flux densities dℱ/(dv∥ dv⊥) across a shock of velocity Vs = 2000 km s-1 with four different shock-normal angles. Blue contours depict the incident transmitting flux, red contours depict the reflected flux, and red solid contours the transmitted downstream flux at one magnitude intensity intervals. The black semicircles depict downstream speed thresholds for statistical return probabilities of 0% (dashed) and 25% (dotted), and the black-green dashed curve represents the reflection threshold. |
| In the text | |
 |
Fig. 6 Particle fluxes at the shock: curves represent numerical integration results, data points are results of Monte Carlo simulations. Vs = 1500 km s-1 (left) and Vs = 2000 km s-1 (right). Simulations without downstream propagation of particles are designated with ℬ = 0, whereas simulations where particles isotropise through downstream scatterings are designated with ℬ > 0. The flux differences for the reflected particles in the Monte Carlo simulations (⋄ , +) are due to statistical uncertainties. For comparison, we show the integrated flux of all particles that are faster than the classical injection threshold v > u1 as a dash-dotted line. For κ = 15, reflected particle fluxes and the classical comparison are too low to be visible. |
| In the text | |
 |
Fig. 7 Effect of downstream cross-field diffusion strength a⊥ = 0.1 on the injection efficiency for Vs = 1500 km s-1, κ = 2, and different shock-normal angles. Curves (from numerical integration results) and results from simulations without cross-field diffusion (squares) are the same as in Fig. 6. Results for the two types of downstream cross-field diffusion (sets three and four) are shown as triangles and diamonds. |
| In the text | |
 |
Fig. 8 Ratios of total injected particle fluxes with active (FCSP) or inactive (FnoCSP) cross-shock potential. We show results for semi-analytical integration (curves) and Monte Carlo simulations (symbols). Presented shock-normal velocities are Vs = 1500 km s-1 (left) and Vs = 2000 km s-1 (right). Simulations without downstream propagation of particles are designated with ℬ = 0, whereas simulations where particles isotropise through downstream scatterings are designated with ℬ > 0. The flux differences for reflected particles in the Monte Carlo simulations (⋄ , +) are due to statistical uncertainties. For κ = 15, reflected particle fluxes are too low to be visible. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


