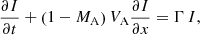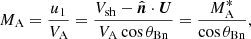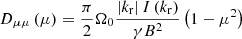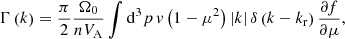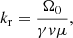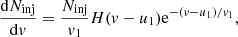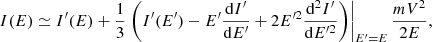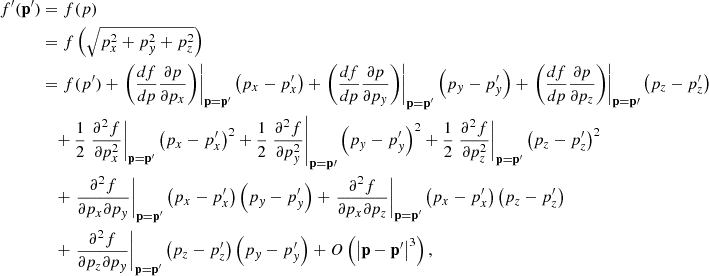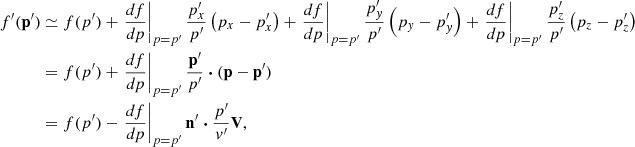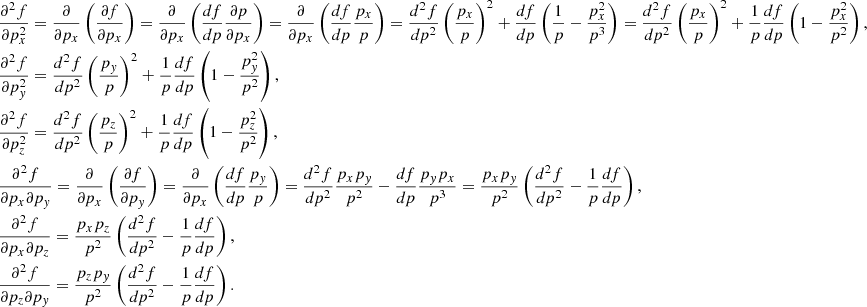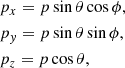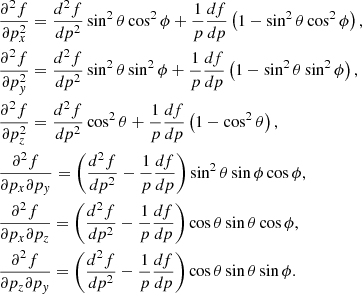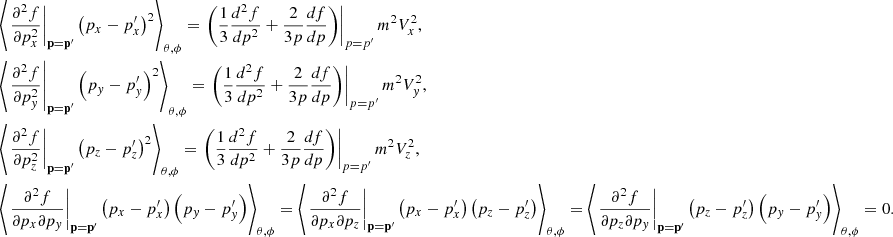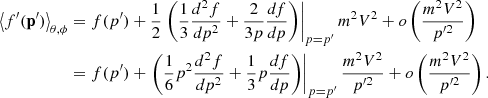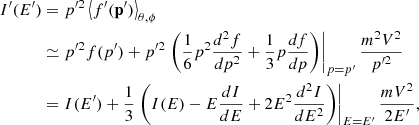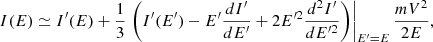EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 679 (November 2023) A&A, 679 (2023) A111 Full HTML
Open Access
Issue
A&A
Volume 679, November 2023
Article Number A111
Number of page(s) 10
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202346220
Published online 29 November 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Shock waves driven by coronal mass ejections are considered to be the source of the so-called gradual solar energetic particle (SEP) events, in which ions can achieve high energies (tens to hundreds of MeV/nuc; e.g., Reames 2017). Although the general mechanism by which ions can be accelerated to such energies – diffusive shock acceleration (DSA; Axford et al. 1977; Krymskii 1977; Bell 1978; Blandford & Ostriker 1978) – is widely accepted, the detailed acceleration process is still under investigation.

One open question concerns the origin of the turbulent magnetic fluctuations upstream of the shock, which are required by DSA. Estimations of the DSA efficiency, at least for coronal shocks, suggest that magnetic turbulence should be substantially enhanced close to the shock compared to its level as derived for the ambient solar wind (Ng & Reames 2008). A rather prevalent understanding is that this turbulence is self-generated, that is, excited by the accelerated particles themselves (mainly protons) via the streaming instability (e.g., Lee 1983; Zank et al. 2000; Ng & Reames 1994; Vainio 2003). This mechanism, however, requires the flux of streaming particles to exceed some threshold in order to be efficient (Vainio 2003). This has raised doubts regarding the self-generated turbulence resonant with high-energy protons (hundreds of MeV) being able to develop since proton energy spectra in shocks are expected to be steep (Kocharov et al. 2013, 2015).

The above argument is used to support another possible scenario, in which intense turbulence is inherent to the solar wind, being present in some magnetic flux tubes and absent in others (Kocharov et al. 2013, 2015). When a shock travels through such a structured solar wind, particles in turbulent flux tubes are efficiently trapped near the shock and accelerated via DSA, whereas particles in quiet tubes are able to escape from the shock vicinity into the ambient solar wind; in this scenario, the cross-field transport delivers accelerated particles from turbulent tubes to quiet ones.

Although a variety of models of ion acceleration in shocks that include self-generated (Alfvénic) turbulence exist (e.g., Bell 1978; Lee 1983, 2005; Gordon et al. 1999; Zank et al. 2000; Vainio & Laitinen 2007; Ng & Reames 2008; Afanasiev et al. 2015; Berezhko & Taneev 2016; Li et al. 2022), it is difficult to evaluate how well they reflect reality, especially at early times, when the shock is still in the corona. In this respect, it is important to note that they are based on the quasi-linear theory of wave–particle interactions1. However, one can attempt to get a better understanding of this problem by studying the so-called energetic storm particle (ESP) events, particle intensity enhancements associated with passages of interplanetary (IP) shocks over observing spacecraft (see, e.g., a review by Desai & Giacalone 2016, and references therein). Particle intensity measurements in the immediate vicinity of the shock and shock in situ measurements are available during such events. Therefore, ESP events can be used for more accurate tests to validate existing models of particle acceleration in shocks.

There are different types of ESP events (e.g., Lario et al. 2003). The so-called classic ESP events are characterized by a gradual increase in particle intensity, typically starting a few hours prior to the arrival of the shock at the spacecraft. Such ESP events are qualitatively consistent with the predictions of DSA (e.g., Giacalone 2012).

Attempts to compare DSA modeling that includes self-generated Alfvénic turbulence with classic ESP events were made by Kennel et al. (1986) and more recently by Berezhko & Taneev (2016) and Taneev et al. (2018). Kennel et al. (1986) tested the early analytical model from Lee (1983), which describes particle acceleration using Parker’s equation and, thus, is based on the assumption that the condition of spatial diffusion (the strong scattering condition) is satisfied everywhere in the shock upstream. Although Kennel et al. (1986) considered the theory predictions for accelerated particles rather successful, one can see that, for example, the measured particle intensities tend to fall off with increasing distance from the shock following a power law, rather than exponentially as predicted by the model (see their Fig. 1). Notably, the Vainio & Laitinen (2007) model predicts a ∼1/(1 + x/x0) dependence for the particle intensity versus distance, x, from the (parallel) shock upstream (x > 0, and x0 is the energy-dependent length scale), in agreement with Bell (1978).

thumbnail Fig. 1.

Omnidirectional particle intensities vs. time measured in different energy channels by the SEPT (top panel) and Low-Energy Telescope (LET; bottom panel) instruments on board the STEREO-A spacecraft, showing the SEP event associated with the modeled ESP event of November 10, 2012. The vertical dashed line marks the time of shock arrival at the spacecraft.

The Berezhko & Taneev (2016) model is a modification of the analytical treatment by Gordon et al. (1999), which, in turn, is an improvement to the Lee (1983) model. Berezhko & Taneev (2016) simplified the expression for the Alfvén wave growth rate derived by Gordon et al. (1999), using an approximate wave–particle resonance condition (omitting the pitch-angle cosine). On the other hand, they included an additional ad hoc factor (on the order of 0.1) in their expression of the growth rate in order to fit the model results to observations.

The difficulties faced by quasi-linear models that involve self-generated turbulence in accurately describing ESP events have motivated the search for particle acceleration models other than quasi-linear ones. One such model implements anomalous (super-diffusive) particle transport (e.g., Zimbardo & Perri 2013; Trotta et al. 2019; Perri et al. 2022). The super-diffusive transport results in a power-law dependence of the particle intensities versus time in the shock upstream.

Detailed comparisons of different physical models (quasi-linear or anomalous transport-based) with observed ESP events are needed in order to understand which scenario takes place in a given event. In this work, we present simulations of the ESP event of November 10, 2012, as observed by the Solar TErrestrial RElations Observatory A (STEREO-A) spacecraft, using the SOlar Particle Acceleration in Coronal Shocks (SOLPACS) Monte Carlo code (Afanasiev et al. 2015), which has been upgraded to allow simulations of oblique shocks (i.e., shocks for which the shock normal and the upstream magnetic field are not aligned). SOLPACS is based on the quasi-linear theory of wave–particle interactions. In contrast to the Berezhko & Taneev (2016) model, SOLPACS simulates particle pitch-angle diffusion instead of spatial diffusion and uses the exact gyro-resonance condition of wave–particle interactions.

The paper is organized as follows. In Sect. 2 details of the SOLPACS simulation code are provided. Section 3 describes the observations of the ESP event and the relevant data analysis. Section 4 presents and discusses the simulation results. Finally, Sect. 5 contains our conclusions.

2. Simulation code

SOLPACS is a Monte Carlo simulation code designed to model acceleration of protons in a shock, including the generation of Alfvén waves in the upstream region by the accelerated particles themselves. Here, we provide only the key points of the code and details concerning the implementation of oblique shocks; more details can be found in Afanasiev & Vainio (2013; see also Afanasiev et al. 2015). The code is based on a spatially one-dimensional (1D) local formulation, namely, particles and waves are traced under the guiding-center approximation along a single open magnetic field line, and the ambient plasma parameters in the 1D spatial simulation box along the magnetic field line (the plasma density n, the magnetic field magnitude B, and the bulk plasma speed U) as well as the shock parameters (e.g., the shock speed Vsh, the shock-normal angle θBn, etc.) are taken to be constant. The spatial simulation box is placed in the upstream of the shock and limited by the magnetohydrodynamic shock on one side, while on the other side of the box a free-escape boundary for particles is assumed.

The equations that SOLPACS solves can be given in the following form:

(1)

(2)

where Eq. (1) describes the evolution of the gyro-averaged distribution function f(x, v, μ, t) of particles, and Eq. (2) describes the evolution of the Alfvén wave intensity I(x, k, t). Here t is time, x is the spatial coordinate measured along the magnetic field line with respect to the shock (x > 0 upstream), k is the wavenumber, v and μ are the particle speed and the pitch-angle cosine as measured in the rest frame of Alfvén waves propagating at speed VA with respect to the ambient plasma, and MA is the Alfvénic Mach number of the shock. The MA is defined here as the ratio of the upstream bulk plasma speed, u1, in the de Hoffmann–Teller (HT) frame2 to the Alfvén speed:

(3)

where Vsh is the shock speed (measured along the shock normal 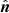) and U is the bulk plasma velocity, both measured in the spacecraft frame, and 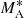is the conventional Alfvénic Mach number. Equation (1) represents the spatially 1D quasi-linear transport equation (e.g., Skilling 1975) written in the shock frame, assuming homogeneous magnetic field and plasma conditions; it describes the particle transport upstream of the shock. In this equation, the second term on the left-hand side describes particle streaming with respect to the shock, and the right-hand side term provides the pitch-angle scattering of particles. In Eq. (2), the second term on the left-hand side describes the wave advection toward the shock, and the term on the right-hand side describes the wave growth. The coefficients Dμμ(μ) and Γ(k) are the quasi-linear pitch-angle diffusion coefficient (Jokipii 1966) and wave growth rate (Vainio 2003), respectively:

(4)

(5)

where Ω0 is the proton cyclotron frequency, γ is the relativistic Lorentz factor, kr is the resonant wavenumber given by the resonance condition

and I(kr) is the resonant wave intensity. In Eq. (5), δ(⋅) is the Dirac delta-function, and the integration is performed over the particle momentum space.

We assumed the plasma turbulence in the box to be due to outward-propagating (if considered in the solar wind frame) Alfvén waves, with the initial spectral form ∝k−q0, where q0 is the spectral index. The initial level of turbulence was chosen to provide a prescribed value of the initial mean free path λ0 for 100 keV protons.

The process of seed particle injection into the acceleration process due to their interaction with the shock is not modeled in SOLPACS. In order to address this self-consistently, one has to resort to a kinetic description of the shock (see, e.g., Caprioli & Spitkovsky 2014; Trotta et al. 2021, and reference therein). In SOLPACS, we prescribe a suprathermal proton population being injected at the shock to the upstream throughout the simulation. This population is characterized by the following (shock-frame) velocity spectrum:

(6)

where Ninj = ϵinjnu1tsim is the total number of suprathermal particles injected into the acceleration process per unit cross section of the magnetic flux tube during the whole simulation of duration tsim, v1 is a parameter characterizing the extension of the exponential “tail” of the distribution, and H(⋅) is the Heaviside step function. The parameter ϵinj, therefore, characterizes the injection efficiency of the shock. It is one of the key SOLPACS parameters controlling the particle acceleration process, since appreciable wave growth at a given point in space requires a finite number of particles to pass through that point (Vainio 2003; Vainio & Laitinen 2007).

Interaction of injected particles with the magnetohydrodynamic shock is treated in the scatter-free approximation and assuming conservation of particle’s energy and magnetic moment (in the shock HT frame of reference). Interacted particles can be reflected back to the upstream or transmitted to the downstream region (see, e.g., Battarbee et al. 2013). The reflection–transmission condition is determined by the magnetic compression ratio of the shock, which (like the gas compression ratio) is calculated based on Rankine–Hugoniot conditions. Instead of tracing particles in the shock downstream, we employed a probability of return from the downstream region (Jones & Ellison 1991; Vainio & Laitinen 2007).

To run a SOLPACS simulation, the input of five main physical parameters is required: the Alfvén speed (VA) and density (n) of the ambient plasma, the Alfvénic Mach number of the shock (MA), the shock-normal angle (θBn), and the particle injection efficiency of the shock (ϵinj)3. All but the last parameter can be derived from in situ plasma measurements.

3. Observations

We used the STEREO IP shock list4 to look for clearly visible classic ESP events. From those, we selected an ESP event that occurred on November 10, 2012, for the simulation modeling with SOLPACS. This ESP event is associated with a preceding SEP event (Fig. 1) and has clear intensity enhancements peaking at the shock arrival time at energies up to ∼1 MeV (Fig. 2). One can see that the pronounced increases in the particle intensities measured by the Solar Electron and Proton Telescope (SEPT) start at least four hours before the shock arrival.

thumbnail Fig. 2.

Zoomed-in view around the shock arrival time at STEREO-A, showing (from top to bottom) the particle time-intensity profiles measured by the SEPT and LET instruments, the magnetic field vector measured by the In-situ Measurements of Particles And CME Transients MAGnetometer (IMPACT/MAG) instrument, and the plasma density and the bulk solar wind speed measured by the PLasma And Supra-Thermal Ion Composition investigation (PLASTIC) instrument.

We used the IP shock database5 of the University of Helsinki to get values for the in situ plasma and shock parameters needed to specify the SOLPACS input parameters. These are presented (together with error estimates) in Table 1. A large error is obtained for the shock-normal angle θBn. Besides, the STEREO IP shock list gives for θBn a value of 61.5°. The large error and the large difference between the values for θBn motivated us to conduct more detailed analysis of the magnetic field time series and calculations of θBn.

Table 1.

Upstream plasma and shock parameters provided in the IP shock database of the University of Helsinki and used in the SOLPACS simulations.

The magnetic field time series analysis indicates that there are multiple heliospheric current sheet crossings during the 30 min preceding the shock arrival at the spacecraft (Fig. 3). The downstream is even more complex, and the large number of data points with |B|∼0 nT indicate that the shock has been propagating through the current sheet for a while. Naturally, the frequent sign flips of BR and instances of near-zero field magnitudes make the shock parameter estimation particularly challenging, due to the high sensitivity to the choice of upstream/downstream averaging time window. This motivated us to look at distribution of θBn obtained for a variety of averaging window lengths, by applying the systematic window variation approach described in Trotta et al. (2022).

thumbnail Fig. 3.

Magnetic field magnitude and components, solar wind speed, proton number density, and proton temperature vs. time in the 3-h time window centered at the shock arrival time. The shock arrival time (∼22:30 UT) is marked by the dashed magenta line. The red and blue shaded areas denote the shortest (dark) and largest (light) averaging windows used for the shock parameter estimation upstream and downstream, respectively.

Earlier, Giacalone (2012) obtained for a number of ESP events an estimate of the proton acceleration time from some low (injection) energy even to ∼50 keV to be on the order of an hour. This implies that small averaging windows (on the order of several minutes) should not be relevant. In computations of distributions of θBn, we used averaging time windows varying in length from 30 min to 1 h with with a systematic increment Δt of 1 min, as highlighted in Fig. 3. Figure 4 shows the probability density functions (PDFs) for computed θBn values obtained by different methods to calculate the shock-normal vector, namely the magnetic coplanarity (MC) method and the three mixed-mode methods (MX1, MX2, and MX3; Trotta et al. 2022). The MC method uses only the data on the upstream and downstream magnetic field vectors, whereas the MX methods process the bulk flow velocity data together with the magnetic field vector data (for details, see Paschmann & Schwartz 2000). The left panel of Fig. 4 shows the PDF obtained with the MC method. All the values of θBn in this case are less than ∼30° with a clear peak at ∼8° and ⟨θBn⟩∼14°. We note that smaller values of θBn result from larger averaging windows. The right panel of Fig. 4 includes PDFs resulting from the MX1-2-3 methods. The PDFs obtained with MX2 and MX3 are quite narrow with ⟨θBn⟩∼32° and ∼34° correspondingly, but the PDF resulting from MX1 is much wider, with ⟨θBn⟩∼50° and without a pronounced peak. One can see that all the methods provide quite different results (although three of the four methods favor the quasi-parallel shock). We note that the upstream plasma bulk speed in Fig. 3 shows rather large variations seemingly associated with the current sheet crossings. This and the significant disagreement between some versions of the MX method suggest that MX methods may be less reliable compared to the MC method for the current event. Therefore, for our simulations we still took θBn = 16° as indicated in the IP shock database of the University of Helsinki, which is slightly larger than ⟨θBn⟩ given by the MC method.

thumbnail Fig. 4.

Results of computations of θBn via the MC and various mixed-mode methods and using averaging windows varying in length from 30 min to 1 h with Δt = 1 min.

For comparison with simulations, presented in the next section, we obtained from the particle data (Fig. 2) the particle energy spectrum at the shock and the (omnidirectional) particle intensity versus distance along the magnetic field in the shock upstream in different energy channels. The spectrum was derived by taking the omnidirectional intensities measured at the second minute after the shock crossing time. The particle intensities versus distance (distance-intensity profiles) were derived from the time-intensity profiles by converting the time to the distance from the shock x by applying x = Vsc(t − tsh), where tsh is the shock arrival time at the spacecraft and Vsc is the spacecraft speed along the upstream magnetic field relative to the shock. The latter quantity was calculated as Vsc = Vsh/cos θBn, where Vsh = 547 km s−1 as indicated in the IP shock database of the University of Helsinki.

4. Results and discussion

The SOLPACS main input parameter values (and of the plasma beta) are given in Table 1. The other physical parameters specifying the initial state of the system are the following: the initial mean free path λ0 for 100 keV protons is 0.23 au, the power-law index of the initial Alfvén wave spectrum q0 is 1.5, the parameter v1 of the seed proton spectrum given by Eq. (6) is taken to be 375 km s−1. It should be noted that the initial mean free path in the simulations depends on the particle energy as E(2 − q0)/2, which results from the quasi-linear theory. Specifically, for the prescribed q0 = 1.5, we obtain λ0 ∝ E1/4. The simulation box size is equal to 0.33 au.

The initial mean free path reference value chosen in our simulations is consistent with the values considered in SEP transport simulation studies for the ambient solar wind. For instance, in Wijsen et al. (2022) the mean free path of 0.1 au for 88 keV protons was chosen, whereas our choice of values gives ∼0.2 au at this energy.

It should be noted that, if the effect of self-generated waves dominates in the system (which is the case in our simulations), the influence of the exact initial mean free path is negligible. Similarly, under such conditions, the initial wave spectral form has no impact (i.e., we could take the Kolmogorov initial spectrum with q0 = 5/3).

To constrain the last parameter of the SOLPACS input parameter list, namely the particle injection efficiency of the shock, ϵinj, we ran simulations for different values of this parameter and compared the simulated particle energy spectra at shock with the one derived from the observations. For an accurate comparison, we transformed the output simulated spectra, computed in the upstream bulk plasma frame, to the spacecraft frame by applying a nonrelativistic Compton-Getting correction of the omnidirectional intensity, in which second-order terms in V/v are taken into account (cf. Forman 1970):

(7)

where 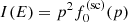is the omnidirectional particle intensity in the spacecraft frame as a function of energy E = mv2/2, p is the particle momentum magnitude, 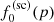is the isotropic part of the distribution function in this frame, I′(E′) is the omnidirectional intensity in a different (e.g., upstream plasma) frame, and V is the relative speed of one frame with respect to the other one. The derivation is presented in the appendix. It is easy to see that the omnidirectional intensity is invariant to first order in V/v (Forman 1970).

We applied the above correction, using an estimation for the relative frame speed (between the upstream plasma frame and the spacecraft frame), V ≈ Vsh − u1 = Vsh − MAVA = 334 km s−1, neglecting the small nonalignment of the ambient magnetic field, ambient solar wind and shock normal vectors. The correction is small at the observed energies and can be neglected at E > 200 keV.

The left panel of Fig. 5 shows the time evolution of the spectrum in the simulation for ϵinj = 6 × 10−3 superposed on the observed spectrum. Also shown is the injected seed particle spectrum in the shock frame and in the spacecraft frame. The latter spectrum was computed using Eq. (7) with V = Vsh = 547 km s−1. We note that all the spacecraft-frame spectra are shown only at those energies where V/v ≲ 0.3. One can see that the evolving spectrum arrives to a steady state at energies below the rollover energy, which matches well with the observed spectrum. We should note that the obtained value of ϵinj is close to a few percent of the solar wind protons reflected by quasi-parallel shocks as reported in previous studies (see, e.g., Ng & Reames 2008).

thumbnail Fig. 5.

Comparison of simulations with observations. Left panel: time evolution of the proton energy spectrum at the shock in the simulation for ϵinj = 6 × 10−3 (colored lines) superposed on the spectrum obtained from the observations (crosses). The indicated simulation times are in arbitrary units. Also shown is the seed particle spectrum as computed in the shock frame (black dashed line) and in the spacecraft frame (solid black line). See the main text for further details. Right panel: simulated proton distributions along the magnetic field line at tsim = 16 [arbitrary units] (solid lines) vs. the distributions obtained from the observations (dotted lines).

Having fixed ϵinj as described above, we computed the particle distance-intensity profiles in this simulation and compared those with the profiles derived from the observations (Fig. 5, right panel). One can see an excellent match at those energies where the spectra match as well. This result – the correspondence obtained simultaneously for both the energy spectrum and the distance-intensity profiles of protons for the same set of values of the input parameters – strongly suggests that it is the process of self-generation of Alfvén waves that controls the proton energization and mean free path in the upstream near the shock in this ESP event, rather than, for example, super-diffusive transport of particles.

At the same time, it can be seen that there is no match between the simulations and observations at the highest energy channel 875–982 keV, in which one can still see an enhancement in intensity (Fig. 2). However, the particle population at these (and higher) energies is not in a steady state by the end of the simulation, but it will tend to increase, if the simulation is continued. We note in this connection that the simulation times, tsim, given in Fig. 5 in arbitrary units could be given in physical units, for example hours. However, since the initial state of the modeled system in the simulations is characterized by a very low turbulence level, the acceleration time to a certain energy in the simulations is incomparably longer than the acceleration time estimated from the observed time-intensity profiles in ESP events, using classical DSA theory (for estimates of the acceleration times from ESP event observations, see, e.g., Giacalone 2012). This is because such estimates are done under the assumption of steady particle diffusion coefficients, while in the simulation it takes additional time for the accelerated particles to amplify the waves at resonant frequencies and bring them to a steady state. Taking that into consideration, the time in our simulations in the context of ESP event modeling is a parameter rather than the physical time. This makes it difficult to conclude whether the insufficient simulation time is the reason for the mismatch.

Another possible reason for that may be the spatial locality of the simulation (constant plasma and shock parameters). It may take ∼10 h to accelerate protons up to 1 MeV (extrapolating the acceleration times plotted in Fig. 10 in Giacalone 2012), so the constancy of the parameters can be quite a limiting approximation for high-energy particles. We note that the time-intensity profiles at energies > 1.8 MeV (Fig. 2) do not peak at the shock, but show a quasi-plateau-like shape with a smeared maximum before the shock arrival. This indicates that the shock does not accelerate particles at these energies at the time of passage of the spacecraft, but it did so earlier, so the shock was stronger at shorter heliocentric distances.

5. Conclusions and outlook

In this study, we have addressed the question of how well the modeling of particle (proton) acceleration in shocks, based on a self-consistent quasi-linear description of wave–particle interactions, can reproduce actual observations. To answer this question, we simulated the ESP event of November 10, 2012, observed by STEREO-A, with the SOLPACS code (Afanasiev et al. 2015) upgraded to be applicable to oblique shocks. We compared the proton energy spectrum at the shock and proton intensity distributions upstream obtained in the simulations with those derived from the observations. We find an excellent correspondence for the simulation input parameters fixed by the in situ plasma measurements at the spacecraft, at the energies at which the simulated system comes to a steady state by the end of the simulation. The mismatch at higher energies (at which the system is not in a steady state by the end of a simulation) may be due to a too short simulation time or the spatial locality of SOLPACS. Nevertheless, our study strongly supports the idea that the wave growth due to streaming particles is involved in the particle acceleration process in shocks. It also supports the quasi-linear description of wave–particle interactions, which are at the core of many self-consistent models of particle acceleration in shocks, and validates the SOLPACS code. It is of interest to model ESP events measured closer to the Sun. We are currently simulating several ESP events observed by the Solar Orbiter spacecraft at heliocentric distances < 1 au. At the current preliminary stage, we are finding a good correspondence between the simulations and the observations. This will be addressed in detail in a separate study. Another possibility that will be explored is modeling the particle injection spectrum as not only a supra-thermal component but also an energetic component in order to mimic the preceding SEP event. This may lead to a better match with observations at energies above the spectral rollover.

1

Here we are not concerned with self-consistent kinetic models, which are small-scale models in terms of the simulated time and spatial extent of the system.

2

The velocity transformation to the HT frame can be done directly from the spacecraft frame (Paschmann & Daly 1998) or from the normal incidence shock-rest frame (e.g., Kivelson & Russell 1995). The latter approach is implied in Eq. (3). In this case the shock speed needs to be determined first, which can be done by assuming conservation of the mass flux across the shock.

3

In fact, the upstream plasma beta parameter is needed to be specified in order to calculate the gas compression ratio of the shock based on Rankine–Hugoniot conditions. However, since it often has quite large uncertainty in the observations, we did not consider it as the main input parameter of the code.

Acknowledgments

This research has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreements No. 870405 (EUHFORIA 2.0) and 101004159 (SERPENTINE). The work in the University of Turku is performed under the umbrella of Finnish Centre of Excellence in Research of Sustainable Space (FORESAIL) funded by the Academy of Finland (grant No. 336809). N.D. is grateful for support by the Academy of Finland (SHOCKSEE, grant No. 346902). We also acknowledge the computer resources of the Finnish IT Center for Science (CSC) and the FGCI project (Finland).

References

  1. Afanasiev, A., & Vainio, R. 2013, ApJS, 207, 29 [NASA ADS] [CrossRef] [Google Scholar]
  2. Afanasiev, A., Battarbee, M., & Vainio, R. 2015, A&A, 584, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Axford, W. I., Leer, E., & Skadron, G. 1977, Int. Cosm. Ray Conf., 11, 132 [Google Scholar]
  4. Battarbee, M., Vainio, R., Laitinen, T., & Hietala, H. 2013, A&A, 558, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bell, A. R. 1978, MNRAS, 182, 147 [Google Scholar]
  6. Berezhko, E. G., & Taneev, S. N. 2016, Astron. Lett., 42, 126 [CrossRef] [Google Scholar]
  7. Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
  8. Caprioli, D., & Spitkovsky, A. 2014, ApJ, 783, 91 [CrossRef] [Google Scholar]
  9. Desai, M., & Giacalone, J. 2016, Liv. Rev. Sol. Phys., 13, 3 [NASA ADS] [CrossRef] [Google Scholar]
  10. Forman, M. A. 1970, Planet. Space Sci., 18, 25 [Google Scholar]
  11. Giacalone, J. 2012, ApJ, 761, 28 [NASA ADS] [CrossRef] [Google Scholar]
  12. Gordon, B. E., Lee, M. A., Möbius, E., & Trattner, K. J. 1999, J. Geophys. Res., 104, 28263 [NASA ADS] [CrossRef] [Google Scholar]
  13. Jokipii, J. R. 1966, ApJ, 146, 480 [Google Scholar]
  14. Jones, F. C., & Ellison, D. C. 1991, Space Sci. Rev., 58, 259 [Google Scholar]
  15. Kennel, C. F., Coroniti, F. V., Scarf, F. L., et al. 1986, J. Geophys. Res., 91, 11917 [CrossRef] [Google Scholar]
  16. Kivelson, M. G., & Russell, C. T. 1995, Introduction to Space Physics (Cambridge, UK: Cambridge University Press), 586 [Google Scholar]
  17. Kocharov, L., Laitinen, T., & Vainio, R. 2013, ApJ, 778, L5 [CrossRef] [Google Scholar]
  18. Kocharov, L., Laitinen, T., Vainio, R., et al. 2015, ApJ, 806, 80 [NASA ADS] [CrossRef] [Google Scholar]
  19. Krymskii, G. F. 1977, Dokl. Akad. Nauk SSSR, 234, 1306 [NASA ADS] [Google Scholar]
  20. Lario, D., Ho, G. C., Decker, R. B., et al. 2003, in Solar Wind Ten, eds. M. Velli, R. Bruno, F. Malara, B. Bucci, et al., AIP Conf. Ser., 679, 640 [NASA ADS] [CrossRef] [Google Scholar]
  21. Lee, M. A. 1983, J. Geophys. Res., 88, 6109 [NASA ADS] [CrossRef] [Google Scholar]
  22. Lee, M. A. 2005, ApJS, 158, 38 [NASA ADS] [CrossRef] [Google Scholar]
  23. Li, G., Bruno, A., Lee, M. A., et al. 2022, ApJ, 936, 91 [NASA ADS] [CrossRef] [Google Scholar]
  24. Ng, C. K., & Reames, D. V. 1994, ApJ, 424, 1032 [NASA ADS] [CrossRef] [Google Scholar]
  25. Ng, C. K., & Reames, D. V. 2008, ApJ, 686, L123 [NASA ADS] [CrossRef] [Google Scholar]
  26. Paschmann, G., & Daly, P. W. 1998, ISSI Sci. Rep. Ser., 1 [Google Scholar]
  27. Paschmann, G., & Schwartz, S. J. 2000, in Cluster-II Workshop Multiscale Multipoint Plasma Measurements, eds. R. A. Harris, ESA SP, 449, 99 [NASA ADS] [Google Scholar]
  28. Perri, S., Bykov, A., Fahr, H., Fichtner, H., & Giacalone, J. 2022, Space Sci. Rev., 218, 26 [NASA ADS] [CrossRef] [Google Scholar]
  29. Reames, D. V. 2017, Solar Energetic Particles: A Modern Primer on Understanding Sources, Acceleration and Propagation. Lecture Notes in Physics (Springer), 932 [CrossRef] [Google Scholar]
  30. Skilling, J. 1975, MNRAS, 172, 557 [CrossRef] [Google Scholar]
  31. Taneev, S. N., Starodubtsev, S. A., & Berezhko, E. G. 2018, J. Exp. Theor. Phys., 126, 636 [NASA ADS] [CrossRef] [Google Scholar]
  32. Trotta, D., Burgess, D., Prete, G., Perri, S., & Zimbardo, G. 2019, MNRAS, 491, 580 [Google Scholar]
  33. Trotta, D., Valentini, F., Burgess, D., & Servidio, S. 2021, Proc. Natl. Acad. Sci., 118, e2026764118 [NASA ADS] [CrossRef] [Google Scholar]
  34. Trotta, D., Vuorinen, L., Hietala, H., et al. 2022, Front. Astron. Space Sci., 9, 1005672 [NASA ADS] [CrossRef] [Google Scholar]
  35. Vainio, R. 2003, A&A, 406, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Vainio, R., & Laitinen, T. 2007, ApJ, 658, 622 [NASA ADS] [CrossRef] [Google Scholar]
  37. Wijsen, N., Aran, A., Scolini, C., et al. 2022, A&A, 659, A187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Zank, G. P., Rice, W. K. M., & Wu, C. C. 2000, J. Geophys. Res., 105, 25079 [NASA ADS] [CrossRef] [Google Scholar]
  39. Zimbardo, G., & Perri, S. 2013, ApJ, 778, 35 [CrossRef] [Google Scholar]

Appendix A: Second-order Compton-Getting correction of the particle omnidirectional intensity

In this section we denote the particle six-dimensional phase-space distribution function in the observer’s (primed) frame as f′ and assume the distribution in the unprimed frame, f, to be isotropic. We also assume that the unprimed frame moves with respect to the primed one (the observer) with velocity V. Then, due to the Lorentz-invariance of the distribution function (Forman 1970), we can write

where p and p′ denote the particle momentum in the respective frame, and we make use of Cartesian coordinates in the momentum space. Neglecting for the moment the second- and higher order terms, we obtain

where we used p − p′= − mV (i.e., nonrelativistic consideration), and n′=p′/p′ is a unit vector in the direction of the particle’s momentum. Thus, we reproduce Forman’s (1970) result.

The second-order terms are

Introducing the spherical coordinates

the second-order terms can be given as

Averaging the second-order terms over angles, we get

Taking Vx = Vy = 0 and Vz = V, we obtain for the isotropic part of the distribution function in the observer’s frame

Neglecting terms higher than m2V2/p′2, we obtain for the omnidirectional differential intensity in the observer’s frame, I′(E′)

where I(E) is the omnidirectional intensity in the unprimed frame, being a function of energy E.

To ease the notation in the main body of this paper, we can swap the primed and unprimed quantities in the resulting expression to get

which matches Eq. (7).

All Tables

Table 1.

Upstream plasma and shock parameters provided in the IP shock database of the University of Helsinki and used in the SOLPACS simulations.

In the text

All Figures

thumbnail Fig. 1.

Omnidirectional particle intensities vs. time measured in different energy channels by the SEPT (top panel) and Low-Energy Telescope (LET; bottom panel) instruments on board the STEREO-A spacecraft, showing the SEP event associated with the modeled ESP event of November 10, 2012. The vertical dashed line marks the time of shock arrival at the spacecraft.
In the text
thumbnail Fig. 2.

Zoomed-in view around the shock arrival time at STEREO-A, showing (from top to bottom) the particle time-intensity profiles measured by the SEPT and LET instruments, the magnetic field vector measured by the In-situ Measurements of Particles And CME Transients MAGnetometer (IMPACT/MAG) instrument, and the plasma density and the bulk solar wind speed measured by the PLasma And Supra-Thermal Ion Composition investigation (PLASTIC) instrument.
In the text
thumbnail Fig. 3.

Magnetic field magnitude and components, solar wind speed, proton number density, and proton temperature vs. time in the 3-h time window centered at the shock arrival time. The shock arrival time (∼22:30 UT) is marked by the dashed magenta line. The red and blue shaded areas denote the shortest (dark) and largest (light) averaging windows used for the shock parameter estimation upstream and downstream, respectively.
In the text
thumbnail Fig. 4.

Results of computations of θBn via the MC and various mixed-mode methods and using averaging windows varying in length from 30 min to 1 h with Δt = 1 min.
In the text
thumbnail Fig. 5.

Comparison of simulations with observations. Left panel: time evolution of the proton energy spectrum at the shock in the simulation for ϵinj = 6 × 10−3 (colored lines) superposed on the spectrum obtained from the observations (crosses). The indicated simulation times are in arbitrary units. Also shown is the seed particle spectrum as computed in the shock frame (black dashed line) and in the spacecraft frame (solid black line). See the main text for further details. Right panel: simulated proton distributions along the magnetic field line at tsim = 16 [arbitrary units] (solid lines) vs. the distributions obtained from the observations (dotted lines).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.