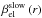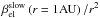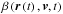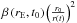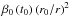| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 26 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201321700 | |
| Published online | 28 August 2013 | |
Modulation of neutral interstellar He, Ne, O in the heliosphere. Survival probabilities and abundances at IBEX⋆
1
Space Research Centre of the Polish Academy of Sciences,
00-716
Warsaw,
Poland
e-mail:
bzowski@cbk.waw.pl
2
Space Science Center and Department of Physics, University of New
Hampshire, Durham
NH,
USA
Received:
15
April
2013
Accepted:
14
June
2013
Context. Direct sampling of neutral interstellar (NIS) atoms by the Interstellar Boundary Explorer (IBEX) can potentially provide a complementary method for studying element abundances in the Local Interstellar Cloud (LIC) and processes in the heliosphere interface.
Aims. We set the stage for abundance-aimed in-depth analysis of measurements of NIS He, Ne, and O by IBEX and determine systematic differences between abundances derived from various calculation methods and their uncertainties.
Methods. Using a model of ionization rates of the NIS species in the heliosphere, based on independent measurements of the solar wind and solar EUV radiation, we developed a time-dependent method of calculating the survival probabilities of NIS atoms from the termination shock (TS) of the solar wind to IBEX. With them, we calculated densities of these species along the Earth’s orbit and simulated the fluxes of NIS species as observed by IBEX. We studied pairwise ratios of survival probabilities, densities, and fluxes of NIS species at IBEX to calculate correction factors for inferring the abundances at TS.
Results. The analytic method of calculating the survival probabilities gives acceptable results only for He and Ne during low solar activity. For the remaining portions of the solar cycle, and at all times for O, a fully time-dependent model should be used. Electron-impact ionization is surprisingly important for NIS O. Interpreting the IBEX observations using the time-dependent model yields the LIC Ne/O abundance of 0.16 ± 40%. The uncertainty is mostly due to uncertainties in the ionization rates and in the NIS gas flow vector.
Conclusions. The Ne/He, O/He, and Ne/O ratios for survival probabilities, local densities, and fluxes scaled to TS systematically differ and thus an analysis based only on survival probabilities or densities is not recommended, except the Ne/O abundance for observations at low solar activity.
Key words: ISM: abundances / Sun: heliosphere / Sun: UV radiation / ISM: atoms / solar wind / local insterstellar matter
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The abundance of interstellar Ne relative to O and He has important astrophysical implications (Slavin & Frisch 2007) since it provides insight into the processes shaping the Local Interstellar Cloud (LIC), in which the Sun is embedded (Redfield & Linsky 2008; Bzowski et al. 2012; Möbius et al. 2012). However, it cannot be directly measured in the LIC using traditional astrophysical methods because Ne is not visible in the absorption lines. Also, determining other abundances in the LIC is challenging because of the ambiguity of the components of the absorption lines observed in the spectra of nearby stars. The problem is how to reliably find the component from the LIC among components from other clouds filling the line of sight. A complementary method of inferring the abundances in the interstellar gas in the solar immediate neighborhood is therefore welcome.
Such a method has recently become available with the launch of the Interstellar Boundary Explorer (IBEX) satellite McComas et al. (2009), which owing to its time of flight (TOF) mass spectrometer IBEX-Lo (Fuselier et al. 2009), is able to sample neutral interstellar (NIS) H, He, Ne, and O at Earth’s orbit (Möbius et al. 2009; Bochsler et al. 2012).
Neutral interstellar species enter the heliosphere freely from the LIC and flow towards the Sun. While direct sampling of NIS atoms at Earth’s orbit is ideologically simple, interpreting the measurements to infer the abundances in the LIC requires taking ionization losses and modifications of the flux by solar gravitational accretion into account. This is usually referred to as the heliospheric filtration. As discussed by a number of authors (Izmodenov et al. 2004; Müller & Zank 2004), this filtration is a complex, two-step, species-dependent process. The first step is the filtration through the heliospheric interface region, the second is extinction due to the ionization inside the termination shock (TS), i.e., within the supersonic solar wind.
Upon entry into the heliospheric interface region, neutral interstellar gas first passes through the outer heliosheath (OHS) just outside the heliopause, which may be regarded as a bow wave in the interstellar gas. Until recently, it was believed that due to the supersonic speed of the heliosphere in the LIC the outer boundary of this region is a bow shock, but recent findings by Bzowski et al. (2012) and Möbius et al. (2012) suggest that this velocity is significantly lower, which prompted McComas et al. (2012) to propose that the bow wave is not a shock, and its exact nature depends on a number of parameters whose values are not precisely known.
Regardless of the exact properties of the heliospheric bow wave, however, the plasma flow decouples from the neutral component flow in the OHS. Consequently, charge-exchange reactions between the neutral interstellar atoms and ions in this region lead to the creation of another population of neutral atoms, the so-called secondary population (Izmodenov et al. 2001). This is in significant portions at the expense of the primary population of NIS atoms, which is depleted. This depletion is the first step in the filtration of neutral interstellar atoms on entry into the heliosphere. The filtration factor, defined as the ratio of post- to pre-OHS densities, depends on the species. Review of the filtration through heliospheric boundary based on models available in the literature has recently been presented by Bochsler et al. (2012), but one has to realize that the filtration of NIS species through the outer heliosheath without a bow shock has not been modeled yet.
The second step in heliospheric filtration of NIS species is the topic of this paper. Once inside the heliopause, NIS gas is subject to ionization processes due to the interaction with the heliospheric environment. The gas is collisionless, and the atoms follow individual hyperbolic trajectories in the solar gravitational potential. Some of them get ionized and are eliminated from the sample. Thus ionization acts as another filtration process for the NIS flux. The magnitude of this filtration depends on the species, location in the heliosphere, and time because the intensity of the ionization processes depends on time and solar distance.
In effect, the count number registered by a spacecraft traveling with Earth and observing the neutral species is proportional to the exposure time and the local atom flux. The flux varies along the orbit because of the combination of time- and space-variations of the local NIS flux. This variation must be appropriately taken into account when determining the abundance of NIS species at the inner boundary of the heliospheric interface region.
In the following sections of the paper, we briefly discuss ionization processes relevant to NIS He, Ne, and O as a function of time and heliocentric distance based on independently measured solar EUV and solar wind output. With the ionization rates on hand, we investigate the survival probabilities of NIS He, Ne, and O atoms from TS to Earth’s orbit and comment on the accuracy of various methods used to assess them. Next, we present calculated densities of NIS He, Ne, and O in the ecliptic plane and their variation in time during IBEX observations. In particular, we dwell on the evolution of these densities at Earth and on the change of the abundances relative to the values at TS. Finally, we discuss the evolution of the NIS Ne and O fluxes that enter the IBEX-Lo aperture and derive their abundance. We close with comments on the Ne/O abundance in the LIC, mostly repeating the approach of Bochsler et al. (2012), but using the assessment of the differential filtration of He, Ne, and O derived in this paper.
2. Ionization rates for neutral He, Ne, and O in the inner heliosphere
Ionization processes for neutral He, Ne, and O in the heliosphere include photoionization
by solar EUV radiation, charge exchange with solar wind ions, and ionization by the impacts
of solar wind electrons. The total ionization rate 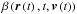 for
an atom traveling with velocity
for
an atom traveling with velocity 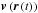 at
a time t and location
at
a time t and location 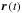 in the heliosphere is given by a sum of the rates of photoionization
βph, charge exchange βcx, and
electron impact βel:
in the heliosphere is given by a sum of the rates of photoionization
βph, charge exchange βcx, and
electron impact βel: 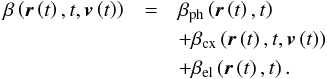 (1)In
the following, we present ionization rates at 1 AU from the Sun, calculated as Carrington
period averages centered at each of the halves of Carrington rotations, which are nodes of
the time grid used in the simulations discussed in later parts of the paper.
(1)In
the following, we present ionization rates at 1 AU from the Sun, calculated as Carrington
period averages centered at each of the halves of Carrington rotations, which are nodes of
the time grid used in the simulations discussed in later parts of the paper.
 |
Fig. 1 Time series of ionization rates of neutral He, Ne, and O used in this study. Shown are total ionization rates at 1 AU from the Sun, as well as photoionization, electron-impact, and charge exchange rates for all relevant reactions. The lower-right panel shows the total ionization rates of He, Ne, and O on a common scale. For comparison, the ionization rate of H (Bzowski et al. 2013) is added. |
2.1. Photoionization
Photoionization is the dominant reaction for all three species in question. It features a modulation with the solar activity cycle, as well as variations on shorter time scales. The amplitude of solar cycle modulation of the photoionization rates is approximately 2 (see Fig. A.1) and the maximum rates occur during the intervals of high solar activity. The intensity of photoionization goes down with the square of solar distance, just as the solar EUV flux does. Photoionization rates are predicted to feature some latitudinal anisotropy (Auchère et al. 2005) that evolves weakly during the solar cycle and features some north-south asymmetry. Since in this paper we focus on NIS gas in the ecliptic plane and mostly out of the focusing cones, we have adopted photoionization rates that evolve as indicated in Fig. A.1 and feature a fixed pole-to-equator flattening of 0.8 (for details, see Eq. (3) in Bzowski 2008).
We have developed a time series of photoionization rates of H, He, Ne, and O on a common time grid covering the time interval from 1948 until the present (Fig. A.1). The construction is based on direct measurements of the solar spectrum from TIMED/SEE (Woods et al. 2005) and a hierarchy of proxies. Details are presented in the Appendix.
2.2. Charge exchange
Charge exchange is the second most important ionization reaction for oxygen, but it is practically negligible for the noble gases He and Ne (see Fig. 1), being at a level of 1% of the total rate, which is much less than the uncertainty in the photoionization rate. Details of the physics of this reaction and of the reaction products have been extensively discussed in the past and will not be repeated here (see, e.g., Bzowski et al. 2013). The charge exchange rate also features a decrease with the square of solar distance and does not show a clear periodic modulation, but does show a latitudinal modulation with the phase of solar activity.
For O, the only relevant charge exchange reaction is
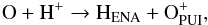 where
H+ is a solar wind proton and O an NIS O atom. Other ions in the solar wind
are not abundant enough to have a non-negligible effect (Zurbuchen et al. 2002). The cross section for this reaction was taken from Lindsay & Stebbings (2005), who conservatively
assess its accuracy in the energy range relevant for our applications at 25%.
where
H+ is a solar wind proton and O an NIS O atom. Other ions in the solar wind
are not abundant enough to have a non-negligible effect (Zurbuchen et al. 2002). The cross section for this reaction was taken from Lindsay & Stebbings (2005), who conservatively
assess its accuracy in the energy range relevant for our applications at 25%.
Similarly for neon, the only potentially important reaction is
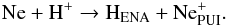 The
cross section for this reaction was adopted from Nakai et
al. (1987), with the rms error quoted at 20%.
The
cross section for this reaction was adopted from Nakai et
al. (1987), with the rms error quoted at 20%.
For He the situation is different. There are three potentially important reactions,
namely: 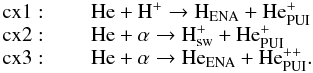 This
is because the cross sections for charge exchange between He atoms and alpha particles are
orders of magnitude larger than for charge exchange between He atoms and protons (Fig.
A.7; Barnett et al.
1990), and the abundance of solar wind alphas is quite large – about 4% (Kasper et al. 2012). The accuracy of the fits of the
cross section formula to data is quoted at rms = 10%.
This
is because the cross sections for charge exchange between He atoms and alpha particles are
orders of magnitude larger than for charge exchange between He atoms and protons (Fig.
A.7; Barnett et al.
1990), and the abundance of solar wind alphas is quite large – about 4% (Kasper et al. 2012). The accuracy of the fits of the
cross section formula to data is quoted at rms = 10%.
Because of the similarity in the first ionization potential of O and H, the charge exchange reaction for oxygen has a quasi-resonant character and is quite intense. During the past solar cycles, it was the dominant loss process for O; nowadays, however, because of the overall drop in the solar wind flux, which began in 1990s, the charge exchange rate is lower than the photoionization rate (see Fig. 1).
In the modeling presented in the paper, we calculate the charge exchange rates based on the in-ecliptic time series of solar wind speed and density known as the OMNI-2 time series (King & Papitashvili 2005) for the equatorial rates and on a compilation of the evolution of latitudinal structure of the solar wind speed and density by Sokół et al. (2013). This compilation is based on both remote-sensing observations of interplanetary scintillation (Tokumaru et al. 2010) and in situ Ulysses measurements (McComas et al. 2002, 2008). The densities and speeds are calculated on a uniform grid in time and heliolatitude with nodes at halves of Carrington rotations and at full tens degrees of heliolatitude. It is further assumed that density falls off with r2, and speed is independent of distance.
 |
Fig. 2 Comparison of the radial dependence of electron impact ionization adopted in this
paper with the 1/r2-dependence for
He, Ne, and O. Solid lines indicate the radial profiles calculated using
|
The charge exchange for a given species, location in space, and time moment is calculated “on the fly” during calculations based on the local density of solar wind and the computed relative speed between the local solar wind and the neutral atom in question (Bzowski et al. 2013). The evolution of the charge exchange rates in the ecliptic plane at 1 AU from the Sun in the stationary atom approximation is presented in Fig. 1. Details of the calculation scheme are available in the Appendix.
2.3. Electron impact ionization
The electron impact ionization rates are the poorest known among the ionization processes in the heliosphere. Electron ionization is special in the sense that its radial dependence differs significantly from 1/r2 (see Fig. 2). This is because the distribution function of solar wind electrons is complex, with a Maxwellian-like core and a halo (elevated wings) approximated by the Maxwellian or kappa-like function (Pilipp et al. 1987; Maksimovic et al. 1997). The abundance of the halo population relative to the core varies with heliocentric distance. Also the cooling rates of the two populations are different and change with solar distance. Neither of them is adiabatic. Details of processes modifying the electron distribution function have been poorly investigated. A review of the evolution of solar wind electron distribution function with solar distance and during the solar cycle has recently been provided by Issautier (2009).
It is worth mentioning that outside 1 AU only a very small portion of the core population electrons have enough energy to ionize He and Ne. A slightly higher portion of the core electrons can ionize O. The peak energies of the two electron populations at 1 AU are marked in the drawing that illustrates the energy dependence of the electron ionization cross sections, shown in Fig. A.6 in the Appendix. Thus, electron ionization outside 1 AU from the Sun is approximately as much by the core as by halo populations. The formulae used to approximate the electron rate with coefficients specific to the species in question are presented in the Appendix (Eqs. (A.9)–(A.11)).
The radial profiles of the electron ionization are steeper than 1/r2 (Fig. 2), so the relative contribution of this reaction to the total ionization rate rapidly decreases with solar distance. Beyond ~5 AU from the Sun, the electron rate for all species in question becomes negligible, as is easily inferred from Fig. 2. The evolution of the electron rate in time at 1 AU in the slow solar wind is presented in Fig. 1. It also does not show a clear time modulation with solar activity cycle, but does show a secular downward trend due to the drop of solar wind density, arrested in ~2005 (McComas et al. 2008).
The model we adopted is parametrized by time and heliolatitiude variations in solar-wind proton density (tied with the local electron density by the quasi-neutrality condition and taking the contribution from solar wind alphas into account). Its heliocentric distance dependence is based on radial profiles of electron temperatures measured by Ulysses during the previous solar cycle. They do not have to be exactly the same nowadays, but in lack of newer measurements we assume they have not changed. Consequently, we attribute large error bars to the electron ionization rates, as detailed in the error estimate section.
3. Survival probabilities of NIS He, Ne, and O
3.1. Calculation of survival probabilities
Survival probabilities are inherent elements of any approach to obtaining abundances of NIS species at TS based on in-situ observations performed in the inner heliosphere. Therefore in this section we elaborate on this subject in greater detail.
The theory of survival probabilities for neutral atoms on Keplerian trajectories under
time-constant solar conditions was developed by Blum
& Fahr (1970) and Axford (1972),
and for the time-dependent ionization rates by Ruciński et
al. (2003, see their Eq. (4)). In essence,
to calculate the survival probability of an atom on a given trajectory between two
selected points in space one has to compute the exponent of the ionization exposure
function ϵ, ![\begin{equation} w=\mathrm{exp}\left[ \epsilon \right], \label{eq:surPro} \end{equation}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq23.png) (2)where the ionization
exposure function is defined as
(2)where the ionization
exposure function is defined as 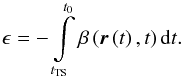 (3)Here
(3)Here
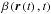 is the
instantaneous total ionization rate at time t in the location
is the
instantaneous total ionization rate at time t in the location
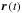 on the trajectory. The trajectory starts at a time tTS and
ends at t0;
tTS < t0.
The instantaneous ionization rate varies because of the changes in the heliocentric
distance
on the trajectory. The trajectory starts at a time tTS and
ends at t0;
tTS < t0.
The instantaneous ionization rate varies because of the changes in the heliocentric
distance 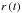 (the spatial effect) and the evolution in time of the ionizing factors (the time effect).
Since the probability value is between 0 and 1, the exposure function value must be
negative.
(the spatial effect) and the evolution in time of the ionizing factors (the time effect).
Since the probability value is between 0 and 1, the exposure function value must be
negative.
 |
Fig. 3 Integrand function in Eq. (3) for an
O atom on the orbit whose perihelion is at the location of the Earth at the time
corresponding to IBEX Orbit 16 in 2009 (λE = 130°). The
red line is the |
For the special, idealized case of an invariable ionization rate falling off with the
square of heliocentric distance, this formula can be evaluated analytically (Lee et al. 2012): 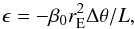 (4)where
β0 is the total ionization rate at a distance
rE from the Sun, L is the angular momentum
of the atom, and Δθ the angle swept by the atom on its orbit between the
infinity and the local point at its orbit.
(4)where
β0 is the total ionization rate at a distance
rE from the Sun, L is the angular momentum
of the atom, and Δθ the angle swept by the atom on its orbit between the
infinity and the local point at its orbit.
In reality, however, the simplification of stationary ionization rate falling off with 1/r2 works relatively well only for He and only for epochs of prolonged low solar activity, as experienced recently, but it is not reliable for species featuring higher ionization rates, as Ne and O, even for the relatively low activity conditions.
The reason for this lack of reliability is illustrated in Fig. 3, which shows the ionization rate experienced by an O atom observed in
its perihelion by IBEX on Orbit 16. This integrand function
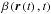 in Eq.
(3) is compared with the ionization rate
taken for the same trajectory assuming that the rate is constant in time, falling off
strictly as 1/r2 and equal to the rate at
the moment of detection in the perihelion of the trajectory. Insets in the figure show the
evolution of the heliocentric distance along the atom’s orbit in time and the ratio of the
actual ionization rate to the constant rate taken for the moment of detection.
in Eq.
(3) is compared with the ionization rate
taken for the same trajectory assuming that the rate is constant in time, falling off
strictly as 1/r2 and equal to the rate at
the moment of detection in the perihelion of the trajectory. Insets in the figure show the
evolution of the heliocentric distance along the atom’s orbit in time and the ratio of the
actual ionization rate to the constant rate taken for the moment of detection.
The differences between the survival probabilities calculated analytically and numerically using the time-dependent model are due to the actual evolution of the solar ionizing factors in time (i.e., due to the time variability of the photoionization rate, solar wind speed and density) and the contribution from electron ionization, not following the 1/r2 relation. It is clear that the integral of the function given by the red line in Fig. 3 will differ from the integral of the function drawn with the blue line. The actual ionization rate differs from the idealized case by a varying factor, up to 80%. Even the mean value of the variable integrand function differs from the idealized case, which results in different survival probabilities obtained from the analytical and realistic formulations.
The upper panel of Fig. 4 shows the time series of survival probabilities of the He, Ne, and O atoms that reach perihelia at ecliptic longitude 130° during a time interval spanning more than one solar cycle. The ratio of maximum to minimum values of survival probabilities during the solar cycle is the lowest for He – 1.9 but distinctly increases for Ne, reaching 7.7, and even stronger for O, up to 12.4. It is also worth noticing that the probabilities for the three species discussed feature similar departures from the mean during solar maximum, but definitely different for solar minimum. This is illustrated in the lower panel of Fig. 4.
 |
Fig. 4 Upper panel: survival probabilities for He, Ne, and O atoms on the trajectory reaching Earth in the perihelion in 2009 at 130° ecliptic longitude. Solid lines are for the velocity vector at infinity corresponding to the bulk flow of the gas as established by Bzowski et al. (2012) based on IBEX measurements, the broken lines illustrate the sensitivity of survival probabilities to the inflow parameters: they correspond to survival probabilities calculated for the NIS inflow vector as found by Witte (2004) based on GAS/Ulysses observations. Lower panel: ratios of survival probabilities to their mean values calculated from an 11-year interval ending at the detection time. |
 |
Fig. 5 Relative differences between survival probabilities of He (upper panel), Ne (middle panel), and O (lower panel) calculated using the analytical and the full time-dependent models. The time-dependent model is identical as used in Fig. 4, the analytical models were calculated using stationary ionization rates following the 1/r2 solar distance dependence, with the rates for 1 AU calculated as average values over intervals ending at the detection moment and spanning backward in time 1, 3, or 13 Carrington rotation periods. The relative differences do not average to 0. This effect is most visible for O, for the entire time interval shown in the figure. The systematic upward departure of the mean values from 0 is due to electron impact. |
Since the analytical formulae for survival probabilities under the conventional assumption of stationarity of the ionization rate and its 1/r2 dependence on the solar distance are so simple, many researchers use them in the analysis. We tried to find a recipe for the treatment of the actual solar ionizing factors to make such an approach reliable – and we failed. The idea was to find an interval to average the ionizing factors backward in time and to use the analytical models with the parameters obtained from the averaging. The result of this attempt is shown in Fig. 5. The figure shows relative differences between survival probabilities calculated using the analytical model with the ionization rate as averaged by time intervals of 1, 3, and 13 Carrington rotation periods before the detection time at 1 AU.
The relative differences for He and Ne are flat during low solar activity (from ~2005 to ~2009) and average slightly above 0. This is because the electron rate does not follow the 1/r2 dependence. Otherwise, however, the analytic approach is quite satisfactory for He and Ne because variations in the ionization rate are mild. But when the solar activity changes, as before 2005 and after 2009, the analytic model starts to differ from the time dependent one and none of the averaging intervals tested seems to be satisfactory.
Another feature visible in Fig. 5 is the systematic difference between the full and analytic models before 2003: the relative differences for He and Ne average above 0. This is due to a stronger contribution to the total ionization rate from electron ionization, caused by the higher solar wind density in that epoch than it is nowadays (McComas et al. 2008).
The ionization losses for O are so strong that even the mild variation in the ionization rate during low solar activity make it impossible to reconcile with the analytic model. Each of the lines in the lower panel of Fig. 5 shows a sawtooth behavior with an amplitude of ~20% throughout the time interval shown. The amplitude is higher during high solar activity. Additionally, the relatively strong contribution from electron ionization causes the persistent and systematic deviation of the relative difference upward from 0.
Thus, the simplified formula can be used for the times of prolonged low solar activity for He (as between ~2005 and ~2011) and to a lesser extent for Ne (between ~2005 and ~2009), but it is clearly less accurate when the activity is changing. The simplified approach cannot, however, be used for O for any times at all if the accuracy goal is better than 20%. Therefore we recommend not using the simplified analytic approach to calculate the survival probabilities of NIS species in the heliosphere.
The results of this study may raise concern if developing the time-dependent model of ionization losses based on the 27.28-day (Carrington rotation) averages of the ionization rate is not too crude since it is known that both solar wind and solar EUV output feature significant variations on time scales from minutes to weeks. This may be important because the survival probability for He at 27.28 days before detection is equal to ~0.73 and it goes down to ~0.66 for the moment of detection. For O the change is even stronger, the survival probability changes from ~0.09 to ~0.03.
Ideally, one would be willing to take the variations in a very fine resolution. The problem is that only point measurements at Earth are available and the NIS atoms close to Earth’s orbit, especially those observed by IBEX at their perihelia, travel just before detection (when the ionization is the strongest) with angular velocities almost twice higher than the angular velocity of the Earth and are running against the direction of the Earth’s motion. This means we do not have credible information on the actual ionization rates experienced by those atoms that is accurate enough to justify building the ionization rate models on a finer time grid.
Adoption of Carrington-rotation averaging is an attempt to find a balance between the global character of the ionization rate data, on one hand, and to account for actual time variations, on the other. The unavoidable imperfection of this approach is reflected in the relatively large uncertainties of survival probabilities, which we discuss in the following section of this paper.
3.2. Uncertainties of survival probabilities and contributions from different ionization reactions
There are two major sources of uncertainties on survival probabilities: (1) uncertainties of the ionization rates and (2) uncertainty in the velocity vector of the inflow of neutral interstellar gas on the heliosphere.
Uncertainties resulting from the uncertainty in the NIS gas velocity vector are illustrated in the upper panel of Fig. 4. In addition to survival probabilities calculated for the NIS gas velocity vector obtained by Bzowski et al. (2012) based on observations from IBEX, the probabilities calculated for the velocity vector obtained by Witte (2004) based on observations from GAS/Ulysses are also shown. The two velocity vectors differ by ~4 km s-1 in speed and ~4° in direction. The survival probability differences are systematic in character: for a faster speed, the exposure to ionization is lower, so the survival probabilities are higher, consistently for all species and all phases of solar activity. The influence of the LIC velocity vector of the gas on survival probabilities and their ratios is illustrated further in Fig. 8 and is discussed in a later part of this section.
Uncertainties of survival probabilities due to the uncertainties in the ionization rates are presented in greater detail below, as, to our knowledge, they have not been discussed in the literature. In the following, we will derive the uncertainties of the exposures to photoionization, charge exchange, and electron-impact losses and use them to calculate the overall uncertainty of survival probability.
The exposures to the three ionization reactions for a species X,
introduced in Eq. (3), are defined as
follows. For photoionization: 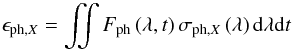 (5)where
Fph(λ,t)
is the solar spectral flux for a wavelength λ at a time
t as seen from a location
r(t), and
σph,X the photoionization cross section
for species X. For charge exchange,
(5)where
Fph(λ,t)
is the solar spectral flux for a wavelength λ at a time
t as seen from a location
r(t), and
σph,X the photoionization cross section
for species X. For charge exchange, 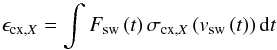 (6)where
(6)where
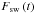 is the solar wind flux for time t in a location
r(t) and
σcx,X the cross section for charge
exchange for species X for relative speed between the reaction partners
approximated by the solar wind speed vsw. For electron impact,
is the solar wind flux for time t in a location
r(t) and
σcx,X the cross section for charge
exchange for species X for relative speed between the reaction partners
approximated by the solar wind speed vsw. For electron impact,
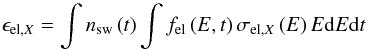 (7)where
(7)where
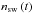 is solar wind proton density,
σel,X the
electron-impact ionization cross section for energy E, and
fel(E,t)
the solar wind electron distribution function in the location
r(t). This function depends on electron
energy and time and is defined so that
is solar wind proton density,
σel,X the
electron-impact ionization cross section for energy E, and
fel(E,t)
the solar wind electron distribution function in the location
r(t). This function depends on electron
energy and time and is defined so that 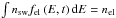 , and due to
quasi-neutrality, nel is approximately equal to the local
proton density plus twice the local solar wind alpha density.
, and due to
quasi-neutrality, nel is approximately equal to the local
proton density plus twice the local solar wind alpha density.
All the parameters pi affecting the
exposures are known from measurements. In the following discussion, we approximate the
uncertainties Δpi of these parameters by
their relative errors δpi,
so that 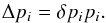 (8)The uncertainty
of the exposure
ϵ(p1,...,pi,...,pn)
is calculated from the general formula:
(8)The uncertainty
of the exposure
ϵ(p1,...,pi,...,pn)
is calculated from the general formula: ![\begin{equation} \Delta \epsilon=\left[ \sum_{i\,=\,1}^{n}{\left( \frac{\partial \epsilon}{\partial p_i}\Delta p_i \right)^2} \right]^{1/2} > 0. \label{eq:errorDef} \end{equation}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq65.png) (9)The uncertainty range
of survival probability of species X against a given reaction
proc is defined by the inequality:
(9)The uncertainty range
of survival probability of species X against a given reaction
proc is defined by the inequality: ![\begin{equation} \mathrm{exp}\!\left[ \epsilon_{\mathrm{proc,}X} \!-\! \Delta \epsilon_{\mathrm{proc,}X}\! \right] \!<\! w_{\mathrm{proc,}X} \!=\! \mathrm{exp}\left[\epsilon_{\mathrm{proc,}X} \!\right]\! <\! \mathrm{exp}\!\left[\! \epsilon_{\mathrm{proc,}X}\!+\!\Delta \epsilon_{\mathrm{proc,}X}\!\right]\!. \label{eq:epsErrorRange} \end{equation}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq66.png) (10)From the
application of formula in Eq. (9) to Eq.
(5), also using Eq. (8), we have the following formula for the
uncertainty of exposure to photoionization:
(10)From the
application of formula in Eq. (9) to Eq.
(5), also using Eq. (8), we have the following formula for the
uncertainty of exposure to photoionization: 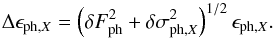 (11)The formula for
uncertainty of the charge exchange exposure is
(11)The formula for
uncertainty of the charge exchange exposure is 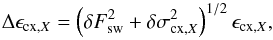 (12)and for the
uncertainty of the exposure to electron impact the following:
(12)and for the
uncertainty of the exposure to electron impact the following: 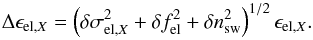 (13)The uncertainties
of exposure to individual ionization processes are expressed as products of the exposures
themselves and terms composed of relative errors of the measured quantities. These
uncertainties are collected in Table 1.
(13)The uncertainties
of exposure to individual ionization processes are expressed as products of the exposures
themselves and terms composed of relative errors of the measured quantities. These
uncertainties are collected in Table 1.
Relative uncertainties of parameters adopted for estimates of survival probability uncertainties
Survival probability against all ionization reactions can be calculated from the sum of
exposures to individual reactions, ![\begin{equation} w_{{X}} = \mathrm{exp}\left[ \epsilon _{{X}} \right] = \mathrm{exp}\left[ \epsilon_{\mathrm{ph,}X} + \epsilon_{\mathrm{cx,}X} + \epsilon_{\mathrm{el,}X} \right], \label{eq:surProFromProc} \end{equation}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq77.png) (14)and the
uncertainty ΔϵX of the total exposure
ϵX can be obtained from the general Eq.
(9). This uncertainty is then inserted
into Eq. (10) to assess the uncertainty
range of survival probabilities against all ionization processes.
(14)and the
uncertainty ΔϵX of the total exposure
ϵX can be obtained from the general Eq.
(9). This uncertainty is then inserted
into Eq. (10) to assess the uncertainty
range of survival probabilities against all ionization processes.
The history of total survival probability of NIS He, Ne, and O, as well as the breakdown of the probabilities into portions due to individual ionization reactions, is shown in Fig. 6. An additional source of uncertainty, as mentioned above, is due to the uncertainty of the inflow velocity vector. The magnitude of this effect is illustrated in Fig. 4. For all species, this uncertainty is less than the uncertainty owing to the inaccuracy of the ionization rates.
As evident in Fig. 6 (see also Fig. 1), practically all the ionization losses of He are due to photoionization. Electron impact eliminates fewer than 10% of the atoms from the original population, and charge exchange is practically negligible, eliminating just ~1% of the atoms, i.e., far below the uncertainty of the losses. For Ne, photoionization dominates and charge exchange is negligible, but the role of electron impact is greater: it eliminates ~10% of the original population.
For oxygen, the situation is quite different. The ionization losses of O are the strongest: only ~0.3% of the atoms survive to Earth’s orbit during high solar activity and up to ~3% during low activity. The main loss source is photoionization, with the charge exchange with solar wind protons a close second. A little surprising, and up to now unrecognized, important source of ionization is electron impact. This reaction eliminates as much as ~25% of the original NIS O population. Thus, this reaction cannot be neglected for O and Ne in the abundance studies. Neglecting electron impact for O causes an underestimation of the losses by ~25%, which may be mistaken for a deficit of NIS O in the interstellar medium surrounding the heliosphere.
 |
Fig. 6 Total survival probabilities (red) and survival probabilities against charge exchange (gray), photoionization (blue), and electron impact ionization (pale blue). The solid lines mark the most probable values, the broken lines mark the uncertainty ranges calculated from Eqs. (11)−(13) and (9). The scale for oxygen (bottom panel) is logarithmic. |
The uncertainties of survival probabilities are substantial. The main source are uncertainties in the reaction cross sections. An exception is the electron impact ionization. Here, on top of the substantial cross section uncertainty, the main source is the uncertainty of the electron distribution function. The model we use is certainly a broad approximation, based on the limited set of available observations. A discussion of the approximations made will be provided elsewhere (Sokół et al., in prep.).
3.3. Ratios of survival probabilities and application to abundance studies
Using ratios of analytically derived survival probabilities of Ne and O to assess the
Ne/O abundance at TS and then in the LIC (Bochsler et al.
2012) is equivalent to adopting the so-called cold-gas approximation (Blum & Fahr 1970; Axford 1972). In the cold-gas model, the NIS gas far away from the Sun has
density nTS and is composed of individual atoms that all have
identical velocity vectors, equal to the NIS gas inflow velocity
vB. The Sun modifies this homogeneous density
distribution by gravitational accretion and ionization. The local density
ncold(r,vB)
is due to atoms that follow two different hyperbolic trajectories intersecting at
r and asymptotically parallel far away from the Sun. The
local density is thus an algebraic sum of contributions from the so-called direct and
indirect trajectories:
ncold(r,vB) = ndir(r,vB) + nindir(r,vB),
where the local densities of the direct and indirect components are products of the
accretion factors
a(r,vB),
squares of the respective angular momenta
pdir(r,vB),
pindir(r,vB),
and survival probabilities
wdir(r,vB),
windir(r,vB):
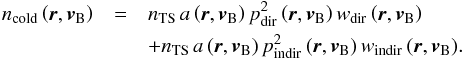 (15)For
a non-moving observer at r, the image of the NIS atoms flux
will be two point sources (except exactly at the downwind line, where the model has
singularity), and the flux will be
(15)For
a non-moving observer at r, the image of the NIS atoms flux
will be two point sources (except exactly at the downwind line, where the model has
singularity), and the flux will be 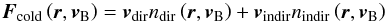 (16)where
vdir,
vindir are velocity vectors at
r of the direct and indirect components, respectively.
For a given solar distance r = |r |,
the directions of these vectors depend on vB and
on the angle between the bulk velocity vB and
r, but the magnitudes of velocities are equal and depend
solely on
vB = |vB |
and r due to the conservation of energy. The survival probabilities
wdir, windir are related to each
other by the respective angular momenta pdir,
pindir and by the angles swept by the atoms
on the direct and indirect orbits. The survival probabilities for indirect atoms are
typically much less than for direct ones, but an exception is the cone region, where they
become comparable.
(16)where
vdir,
vindir are velocity vectors at
r of the direct and indirect components, respectively.
For a given solar distance r = |r |,
the directions of these vectors depend on vB and
on the angle between the bulk velocity vB and
r, but the magnitudes of velocities are equal and depend
solely on
vB = |vB |
and r due to the conservation of energy. The survival probabilities
wdir, windir are related to each
other by the respective angular momenta pdir,
pindir and by the angles swept by the atoms
on the direct and indirect orbits. The survival probabilities for indirect atoms are
typically much less than for direct ones, but an exception is the cone region, where they
become comparable.
IBEX is able to observe NIS atoms close to their perihelia, and thus it can only catch
the direct population. The flux observed by IBEX
Fcold,IBEX will be amplified
by the proper velocity of IBEX relative to the inflowing beam of NIS gas: 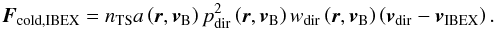 (17)In the approximation
that only the atoms at their perihelia can be observed, this equation is only valid for
the IBEX orbits for which the Earth’s velocity is directed dead against the velocity
vector of the direct population:
(17)In the approximation
that only the atoms at their perihelia can be observed, this equation is only valid for
the IBEX orbits for which the Earth’s velocity is directed dead against the velocity
vector of the direct population: 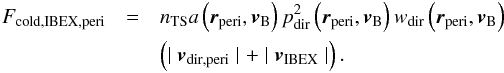 (18)This
equation can be evaluated for any NIS species observed by IBEX. Assuming that all species
have identical bulk velocity vectors, one immediately notices that the only two terms in
Eq. (18) that differ between the species
are nTS and wdir. When the total
counts at IBEX and survival probabilities are known, the abundance
ξdens,TS,X/Y = nTS,X/nTS,Y
of two species X,Y at TS is immediately calculated from
the formula:
(18)This
equation can be evaluated for any NIS species observed by IBEX. Assuming that all species
have identical bulk velocity vectors, one immediately notices that the only two terms in
Eq. (18) that differ between the species
are nTS and wdir. When the total
counts at IBEX and survival probabilities are known, the abundance
ξdens,TS,X/Y = nTS,X/nTS,Y
of two species X,Y at TS is immediately calculated from
the formula: 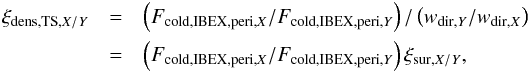 (19)which
can be directly applied to observations. The quotient
(19)which
can be directly applied to observations. The quotient 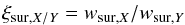 (20)can
be used to assess the X/Y species abundance at TS once
the ratio of registered counts of respective species is retrieved from the data. In Tables
2 and 3 we
list these factors for the bulk flow vectors obtained by Bzowski et al. (2012) and Witte (2004),
respectively, for the Earth ecliptic longitudes for which the maxima of NIS flux were
registered. Derivation of the ratios and their uncertainties, as well as their evolution
in time, are discussed in the following subsection.
(20)can
be used to assess the X/Y species abundance at TS once
the ratio of registered counts of respective species is retrieved from the data. In Tables
2 and 3 we
list these factors for the bulk flow vectors obtained by Bzowski et al. (2012) and Witte (2004),
respectively, for the Earth ecliptic longitudes for which the maxima of NIS flux were
registered. Derivation of the ratios and their uncertainties, as well as their evolution
in time, are discussed in the following subsection.
3.4. Time evolution of ratios of survival probabilities and their uncertainties
While the formula in Eq. (20) for the
ratio of survival probabilities is simple, we rewrite it in a more elaborate form to
better assess the uncertainties. The reason is that some of the uncertainty contributors
are independent between the species, while others are related to each other and this ought
to be taken into account in the calculation of the total uncertainty of
ξsur,X/Y:
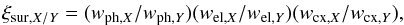 (21)which
is equivalent to
(21)which
is equivalent to ![\begin{eqnarray} \xi_{\mathrm{sur},X/Y}=\mathrm{exp} [ ( \epsilon_{\mathrm{ph,}X} - \epsilon_{\mathrm{ph,}Y} ) + ( \epsilon_{\mathrm{el,}X} - \epsilon_{\mathrm{el,}Y} ) + ( \epsilon_{\mathrm{cx,}X} - \epsilon_{\mathrm{cx,}Y} ) ]. \label{eq:xiSurProc} \end{eqnarray}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq112.png) (22)The
term in the exponent can be expressed by a sum of the exposure difference functions
ϵX/Y for each of the three ionization
processes:
(22)The
term in the exponent can be expressed by a sum of the exposure difference functions
ϵX/Y for each of the three ionization
processes: 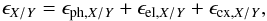 (23)where
ϵproc,X/Y
corresponds to the exposure difference for reaction proc.
(23)where
ϵproc,X/Y
corresponds to the exposure difference for reaction proc.
We do not repeat the derivation of formulae for uncertainties for all three reactions. We
illustrate the issue of uncertainty correlations on an example of charge exchange. The
exposure difference for charge exchange is equal to 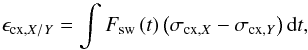 (24)which is a function
of three variables: Fsw,
σcx,X, and
σcx,Y. Based on Eq. (9) and the earlier derivation for the exposure
to charge exchange (Eq. (12)), we then
have the uncertainty of
ϵcx,X/Y
equal to
(24)which is a function
of three variables: Fsw,
σcx,X, and
σcx,Y. Based on Eq. (9) and the earlier derivation for the exposure
to charge exchange (Eq. (12)), we then
have the uncertainty of
ϵcx,X/Y
equal to ![\begin{eqnarray} \label{eq:epsCxXYError} \Delta \epsilon_{\mathrm{cx,}X/Y} &= & \left[ \left( \delta F_{\mathrm{sw}}^2+\delta \sigma_{\mathrm{cx,}X}^2 \right) \epsilon_{\mathrm{cx,}X}^2 + \left( \delta F_{\mathrm{sw}}^2 + \delta \sigma_{\mathrm{cx,}Y}^2\right)\epsilon_{\mathrm{cx,}Y}^2 \right. \nonumber\\ && \left. +\left( \delta F_{\mathrm{sw}} \epsilon_{\mathrm{cx,}X/Y} \right)^2 \right]^{1/2}. \end{eqnarray}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq121.png) (25)Similarly,
the uncertainties of the exposure differences for photoionization is given by
(25)Similarly,
the uncertainties of the exposure differences for photoionization is given by
![\begin{equation} \ \Delta \epsilon_{\mathrm{ph,}X/Y}= \left[ \left( \delta \sigma_{\mathrm{ph,}X} \epsilon_{\mathrm{ph,}X} \right)^2+ \left( \delta \sigma_{\mathrm{ph,}Y} \epsilon_{\mathrm{ph,}Y}\right)^2 + \left( \delta F_{\mathrm{ph}} \epsilon_{\mathrm{ph,}X/Y} \right)^2 \right]^{1/2}, \label{eq:epsPhXYError} \end{equation}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq122.png) (26)and the exposure
difference for electron impact by
(26)and the exposure
difference for electron impact by ![\begin{equation} \ \Delta \epsilon_{\mathrm{el,}X/Y}= \left[ \left( \delta \sigma_{\mathrm{el,}X} \epsilon_{\mathrm{el,}X} \right)^2 \!+ \! \left( \delta \sigma_{\mathrm{el,}Y} \epsilon_{\mathrm{el,}Y}\right)^2 \!+\! \left( \delta f_{\mathrm{el}}^2 \!+\!\delta n_{\mathrm{sw}}^2 \right) \epsilon_{\mathrm{el,}X/Y}^2 \right]^{1/2}. \label{eq:epsElXYError} \end{equation}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq123.png) (27)The total uncertainty of
the exposure difference is given by
(27)The total uncertainty of
the exposure difference is given by ![\begin{equation} \ \Delta \epsilon_{\mathrm{el,}X/Y}= \left[ \Delta \epsilon_{\mathrm{ph,}X/Y}^2 + \Delta \epsilon_{\mathrm{cx,}X/Y}^2 + \Delta \epsilon_{\mathrm{el,}X/Y}^2 \right]^{1/2}, \label{eq:epsXYError} \end{equation}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq124.png) (28)and the lower
(28)and the lower
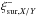 and upper
and upper
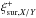 uncertainty
ranges for the ratio of survival probabilities
ξsur,X/Y
are given by
uncertainty
ranges for the ratio of survival probabilities
ξsur,X/Y
are given by ![\begin{eqnarray} \label{eq:xiSurRange} \xi^{-}_{\mathrm{sur,}X/Y} &=& \mathrm{exp}\left[ \epsilon_{ {X/Y}} - \Delta \epsilon_{ {X/Y}} \right] < \xi_{\mathrm{sur,}X/Y} \nonumber \\ & &< \mathrm{exp}\left[ \epsilon_{ {X/Y}} + \Delta \epsilon_{ {X/Y}} \right] = \xi^{+}_{\mathrm{sur,}X/Y}. \end{eqnarray}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq127.png) (29)The
history of survival probability ratios for the Ne/He, O/He, and Ne/O pairs is shown in
Fig. 7. The mean values of the ratios starkly differ
among the three pairs of species, which is understandable given the very different typical
ionization rates for the three species. All three ratios of survival probabilities feature
significant modulation during the solar cycle, but the character of the modulation differs
among the pairs. This is because the proportions between the ionization rates due to the
three relevant ionization reactions differ among the species.
(29)The
history of survival probability ratios for the Ne/He, O/He, and Ne/O pairs is shown in
Fig. 7. The mean values of the ratios starkly differ
among the three pairs of species, which is understandable given the very different typical
ionization rates for the three species. All three ratios of survival probabilities feature
significant modulation during the solar cycle, but the character of the modulation differs
among the pairs. This is because the proportions between the ionization rates due to the
three relevant ionization reactions differ among the species.
The dominant ionization reactions for He and Ne is photoionization, with some addition from electron impact, which is greater in the case of Ne. Since the photoionization rate features a clear modulation as a function of the solar cycle phase and since the magnitude of photoionization is larger for Ne than for He, the modulation of the ξsur,Ne/He ratio follows the solar cycle modulation of photoionization in antiphase. The amplitude of the modulation is relatively mild: 0.1 < ξsur,Ne/He < 0.4.
 |
Fig. 7 Modulation of the ratios of survival probabilities for the Ne/He, O/He and Ne/O species pairs, drawn with solid lines. The broken lines mark the uncertainties calculated using Eqs. (25)–(29). |
Oxygen is ionized much more strongly than helium, and among the contributing reactions only photoionization features a quasi-periodic solar cycle behavior (cf Fig. 1). The contribution to the losses from electron ionization and charge exchange are (jointly) comparable to the contribution from photoionization, and they are not periodical: they show a drop (and thus an increase in survival probability) since the previous maximum, which seems to have leveled off about 2008. Thus, ξsur,O/He has increased since the previous maximum of solar activity and shows a superimposed modulation in antiphase with the solar cycle. Since the total ionization rates for O are much higher than for He, the ξsur,O/He ratio is an order of magnitude less than ξsur,Ne/He, and it varies during the solar cycle almost by an order of magnitude, between ~0.006 and ~0.04.
The ξsur,Ne/O ratio (where, by the way, ξsur,Ne/O = ξsur,Ne/He/ξsur,O/He) varies during the solar cycle, but the quasi-periodic modulation is hidden by the solar wind-related effects discussed earlier. Between 1999 and 2012, it varied between 8.3 and 13 and during the time after IBEX launch remained relatively stable.
The uncertainties of the survival probability ratios are considerable. They vary in time, but typically are approximately ± 15% for ξsur,Ne/He, (−35%, + 50%) for ξsur,O/He, and ± 30% for ξsur,Ne/O. This estimate is obtained by taking solely the uncertainties of the ionization rates into account. In reality, as indicated earlier, they are also affected by uncertainties in the gas inflow vector parameters. Differences between the survival probabilities in time for two sets of the (speed, direction) pairs are illustrated in Fig. 4, where w for ecliptic longitudes and speeds of NIS He inferred by Bzowski et al. (2012) and by Witte (2004) are shown (respectively, (v = 22.8 km s-1,λ = 259.2°) and (v = 26.3 km s-1,λ = 255.4°)). In the following, we assess the magnitude of this additional uncertainty and the total uncertainty due to the uncertainties in the ionization rate and inflow parameters together.
 |
Fig. 8 Ratios of survival probabilities for Ne/He, O/He, and Ne/O, equivalent to the quotients ξsur,X/Y defined in Eq. (20), for various combinations of the flow vector of the NIS gas in the LIC. The solid lines indicate the acceptable parameter region established by Bzowski et al. (2012) for the NIS gas flow parameters based on IBEX observations. |
IBEX showed that acceptable solutions for the inflow parameters are correlated (Bzowski et al. 2012; Möbius et al. 2012). These correlation lines are drawn in Fig. 8. For our assessment of the uncertainty of ξsur,X/Y, we thus take two ξsur,X/Y values for the parameters at the black lines in Fig. 8: one for the inflow parameters obtained from IBEX (i.e., the nominal case discussed in the paper up to now: λ = 259.2°), and the other one corresponding to the longitude of inflow direction as obtained by Witte (2004) from GAS/Ulysses (i.e., λ = 255.4°). The additional uncertainty is assessed from the ξsur,X/Y values obtained from Fig. 8 for these two parameter sets. We denote the two ξ values as ξ0 and ξ1, respectively.
 |
Fig. 9 Relative densities (scaled to the values at TS, Eq. (32)) for NIS He, Ne, and O for the four IBEX sampling seasons, calculated for the apogee times of IBEX orbits for the inflow parameters obtained by Bzowski et al. (2012) from IBEX NIS He observations. The vertical bars mark the longitudes of IBEX apogees in 2009, the horizontal bars marks the relative density levels for this time and location in space. |
 |
Fig. 10 Relative change in the season-integrated flux (solid lines), density at the ecliptic longitude where the NIS gas flow intersects the Earth’s orbit (broken lines), and time-dependent survival probabilities of the NIS atoms reaching IBEX at this location (dotted lines). All quantities are shown as ratios to the respective values in 2009. The relative change in the flux is equivalent to the change of total counts per orbit. The color code for species is indicated in the panel. |
 |
Fig. 11 Heliospheric abundance quotients calculated from the relative densities shown in Fig. 9 using Eq. (32) for the times and locations as for Fig. 9. |
To assess the uncertainty range of
ξsur,X/Y,
we calculate the exposure differences:  (30)The total uncertainty of
the exposure difference, resulting from both the uncertainty of the ionization rate and
uncertainty of the inflow parameters, will be given by
(30)The total uncertainty of
the exposure difference, resulting from both the uncertainty of the ionization rate and
uncertainty of the inflow parameters, will be given by ![\begin{equation} \ \Delta \epsilon_{{X/Y,\rm tot}}=\left[ \Delta \epsilon_{{X/Y}}^2 + \left( \epsilon_{{X/Y,0}} - \epsilon_{ {X/Y,1}} \right)^2 \right]^{1/2},\label{eq:epsDiffTot} \end{equation}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq147.png) (31)and the uncertainty is
calculated by inserting this value to Eq. (29). The increase in the uncertainties is relatively small: the full
uncertainties are equal to ±20% for
δξsur,Ne/He,
(−40%, + 60%) for
δξsur,O/He,
±35% for
δξsur,Ne/O.
(31)and the uncertainty is
calculated by inserting this value to Eq. (29). The increase in the uncertainties is relatively small: the full
uncertainties are equal to ±20% for
δξsur,Ne/He,
(−40%, + 60%) for
δξsur,O/He,
±35% for
δξsur,Ne/O.
In reality, however, the cold gas approximation is not fully adequate for the abundance
studies because the thermal velocities of the NIS species
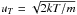 (where T is temperature, k the Boltzmann constant, and
m atomic mass) are not 0, and thus the velocities of individual atoms
in the LIC are neither identical nor parallel. Indeed, the temperature of the gas is
finite and the thermal spread of velocities of individual atoms in the LIC is substantial
when compared with the bulk flow speed. For T = ~6000 K, the thermal
speed is equal to 4.9 km s-1 for He, 2.5 km s-1 for O, and
2.2 km s-1 for Ne. Our calculations showed that the directions of velocity
vectors of the atoms actually observed by IBEX vary in the LIC by more than 15°.
Combinations of speeds and velocity directions of atoms in the LIC cover practically the
whole range of parameters shown in Fig. 8.
(where T is temperature, k the Boltzmann constant, and
m atomic mass) are not 0, and thus the velocities of individual atoms
in the LIC are neither identical nor parallel. Indeed, the temperature of the gas is
finite and the thermal spread of velocities of individual atoms in the LIC is substantial
when compared with the bulk flow speed. For T = ~6000 K, the thermal
speed is equal to 4.9 km s-1 for He, 2.5 km s-1 for O, and
2.2 km s-1 for Ne. Our calculations showed that the directions of velocity
vectors of the atoms actually observed by IBEX vary in the LIC by more than 15°.
Combinations of speeds and velocity directions of atoms in the LIC cover practically the
whole range of parameters shown in Fig. 8.
The survival probabilities depend not only on the details of the ionizing factors but also on details of the trajectories, which are governed by their velocity vectors in the LIC. The ratio of survival probabilities of species X and Y is a function of the velocity vectors in the LIC, as illustrated in Fig. 8. In this figure, we illustrate the values of ξsur,X/Y pairwise for He, Ne, and O at 1 AU from the Sun at the ecliptic longitude 130°, corresponding to the peak flux registered by IBEX in 2009, for various combinations of speed and ecliptic longitude of the inflow direction.
The range of ξsur,X/Y values for various combinations of speed and inflow direction is quite substantial. This indicates that studies of NIS abundances by direct sampling at 1 AU from the Sun require accurate knowledge of the gas inflow speed and direction, but also raises concern whether the ratios of survival probabilities calculated as presented above credibly represent the true change in the NIS abundances between TS and 1 AU from the Sun. This is verified in the next two sections.
4. Evolution of densities of NIS He, Ne, and O at Earth
To assess the quality of approximating the local abundance of NIS species by ratios of survival probabilities for the atoms on the special orbits, we calculate the local densities of NIS species along the Earth’s positions in space and their change from year to year during the IBEX observations of NIS gas. To calculate the local NIS densities, we use a time-dependent calculation scheme extensively discussed by Ruciński et al. (2003), with the ionization rates from the present paper linearly interpolated between the nodes of the time and heliolatitude grid. The calculations were performed using the most recent version of the Warsaw test particle model, successfully employed by Bzowski et al. (2012) to analyze IBEX observations of NIS He gas. This model is an extension of the model used by Ruciński et al. (2003) to model NIS He density evolution during the solar cycle, by Tarnopolski & Bzowski (2009) for modeling of NIS H, and by Tarnopolski & Bzowski (2008) and Kubiak et al. (2013) for NIS D.
We believe that our calculations of NIS He, Ne, and O in the inner heliosphere – carried out using realistic, measurement-based ionization rates and sophisticated test-particle models of NIS gas distribution in the heliosphere – is the first in the literature. Ruciński et al. (2003) discussed the time variations in NIS He gas in the inner heliosphere, but they neglected the electron ionization and assumed a simplified, sinusoidal evolution of the photoionization rate, even though the absolute values and extremes of their ionization model featured values are close to ours.
For the abundance study, the most relevant is not the absolute density
nX(r,t)
of a given species X, but the magnitude of change in density due to the
interaction with inner heliosphere, defined as the ratio of local density to the density at
TS: 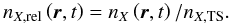 (32)We refer to these
quantities as relative densities. The ratio of relative densities of two species
X, Y at a given time moment and location in space,
(32)We refer to these
quantities as relative densities. The ratio of relative densities of two species
X, Y at a given time moment and location in space,
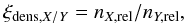 (33)is the change in the
absolute abundance of the two species due to the interaction with the heliosphere. We refer
to the ξdens factors as the abundance change quotients.
(33)is the change in the
absolute abundance of the two species due to the interaction with the heliosphere. We refer
to the ξdens factors as the abundance change quotients.
To facilitate comparison with IBEX, we calculated the relative densities of NIS He, Ne, and O along the Earth orbit during the IBEX observation seasons from 2009 to 2012, as shown in Fig. 9, and additionally pairwise the abundance change quotients ξdens,X/Y (i.e., ratios of relative densities Ne/O, Ne/He, and O/He), shown in Fig. 11.
The densities of NIS He, Ne, and O along the Earth orbit where the IBEX observations are carried out show different patterns between the species. While NIS He, which is weakly ionized in the heliosphere and has the highest thermal speed of ~5 km s-1, features a steady decrease in relative densities with ecliptic longitude when going away from the cone region, NIS Ne, which has an intermediate ionization rate and more than twice lower thermal speed, shows an almost constant density after the Earth leaves the cone region. Owing to its strongest ionization of the three species considered, NIS O features a moderate drop immediately past the cone and afterwards a relatively sharp increase with increasing longitude.
The densities of all three species varied relatively weakly from year to year during 2009, 2010, and 2011, but in 2012 they were appreciably reduced because of the increased ionization rate due to the increase in solar activity. This behavior of densities is a good explanation of the pattern of abundance changes along the Earth orbit in Fig. 11.
The relative year-to-year change in densities at the ecliptic longitude of Earth during the
IBEX peak orbits 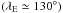 is shown in
Fig. 10. It is evident that the percentage change in
density relative to the density in 2009 (shown for Ne, He, and O) very closely follows the
relative change in the survival probabilities, calculated using the time-dependent approach.
Discrepancies are typically on a level of a few percent and are smallest for Ne, which has
the highest atomic mass from the three species discussed in this paper, hence the lowest
thermal spread. The discrepancies increase a little for O and reach a ~5% level for He in
2012, after a time interval of increasing ionization. It is a combination of these
conditions – a relatively high thermal spread (the highest from the three species in
question) and strongly time-varying ionization rate – that causes this discrepancy.
is shown in
Fig. 10. It is evident that the percentage change in
density relative to the density in 2009 (shown for Ne, He, and O) very closely follows the
relative change in the survival probabilities, calculated using the time-dependent approach.
Discrepancies are typically on a level of a few percent and are smallest for Ne, which has
the highest atomic mass from the three species discussed in this paper, hence the lowest
thermal spread. The discrepancies increase a little for O and reach a ~5% level for He in
2012, after a time interval of increasing ionization. It is a combination of these
conditions – a relatively high thermal spread (the highest from the three species in
question) and strongly time-varying ionization rate – that causes this discrepancy.
A conclusion from this part of the study is that during the first four years of IBEX operation, the percentage change of densities at the location on Earth orbit where the peak of NIS gas flux occurs closely follows the percentage change in survival probabilities of the NIS species, but the survival probabilities must be calculated taking the actual history of the ionization rates into account.
The Ne/He and O/He abundances increase with increasing ecliptic longitude, but from year to year they gradually go down with the increasing solar activity. In 2012, this overall decrease is expected to be much stronger than before, especially for the Ne/He abundance, because of the sharp reduction in the local O and Ne density. But the Ne/O abundance shows just the opposite behavior: it decreases with increasing ecliptic longitude and slightly increases from year to year (see Fig. 15). The Ne/He abundance at 1 AU is reduced by a factor of ~3 relative to the abundance at TS. The drop in the O/He abundance is stronger by an order of magnitude. By contrast, the Ne/O abundance at 1 AU is increased by a factor of ~10 where IBEX samples the atoms, and even stronger in the cone region. This is partly due to the higher ionization of O and partly to stronger focusing of Ne than O because of the lower thermal speed of Ne.
As can be seen from this comparison, the abundance change is similar, but not identical to the ratios of survival probabilities for the atoms that IBEX potentially can see, as discussed in the previous section. The reason is that analysis of survival probabilities of individual atoms cannot take into account that because of the finite temperature of the NIS gas in the LIC the atoms reaching a given space location at a given time moment (e.g., IBEX) have various velocity vectors in the LIC and thus have various survival probabilities. Typically, they do not reach this given region exactly at the perihelia of their orbits. Therefore studies of survival probabilities of individual atoms can provide only limited insight into the change in NIS species abundances in the inner heliosphere.
Because of the differences in the thermal velocities uT in the LIC, the widths of the focusing cones of NIS He, Ne, and O are quite different, and the big differences in the ionization rates are responsible for different density profiles at the remaining portions of Earth’s orbit. Because of the differences in relative densities of the NIS species, the abundances also vary strongly along the Earth orbit. Overall, however, the increase in the Ne/O abundance due to the interaction with the inner heliosphere is lower by ~10% than suggested by analysis of survival probabilities of the atoms that IBEX can see, presented in the former section.
The ratios of survival probabilities ξsur,X/Y and relative densities ξdens,X/Y are different for respective pairs of species (cf. Tables 2 and 4 and Fig. 16). In addition to the mixing of atoms with different velocity vectors in the LIC, the ξsur,X/Y factor does not consider the local change in density due to gravitational focusing of the gas and thus is not recommended as a measure of the local abundance of NIS species at 1 AU from the Sun. An exception is the ξdens,Ne/O ratio, which can be approximated by the easier-to-calculate ξsur,Ne/O within a few percent.
5. Evolution of NIS He, Ne, and O fluxes and their ratios at IBEX
IBEX samples individual atoms, and with the tallies of atoms of different species, the local abundances can be inferred. Since the tallies of directly sampled atoms are proportional to the fluxes of the direct population atoms relative the IBEX detectors, integrated over relevant intervals of time, the measured ratios of NIS atoms represent the local ratios of NIS atom fluxes averaged over the times of observations and the positions of Earth on its orbit around the Sun.
IBEX is a spin-stabilized spacecraft whose rotation axis was originally reoriented once per orbit and maintained within 7° of the Sun. In the middle of 2011, the IBEX orbit was raised (McComas et al. 2011) and thus the orbital period increased. To maintain the field of view sufficiently far from the Sun, a scheme of reorienting of the spin axis twice per orbit was implemented. The IBEX operations during the yearly NIS sampling campaigns were discussed by Möbius et al. (2012), and details of the spin axis orientation and discussion of its uncertainty were presented in detail by Hłond et al. (2012).
 |
Fig. 12 Daily fluxes of NIS He, Ne, and O scaled by respective density values at TS for the 2009 and 2012 observation seasons (Eq. (34)). The vertical bars mark the boundaries of orbital arcs, when the spin axis of the IBEX spacecraft was reoriented. The fluxes calculated assuming the NIS gas flow parameters obtained from IBEX analysis (Bzowski et al. 2012). |
The aperture of the IBEX-Lo detector, dedicated to observing NIS species, scans a great circle ~15° strip on the sky (the equivalent width due to the collimator transmission function is about 7°). The strip does not change between the spin axis reorientations. Since the spacecraft is traveling with Earth around the Sun approximately 1° per day, the beam of NIS atoms is moving across the field of view (FOV) and can be observed at its peak intensity during only one IBEX orbit each year. Thus the flux actually registered is expected to considerably vary both during individual orbits and from orbit to orbit.
 |
Fig. 13 Orbit-averaged scaled fluxes for the conditions as for Fig. 12 for He, Ne, and O, simulated for the first four NIS gas observation seasons by IBEX. The sawtooth features are due to IBEX spin axis reorientation. |
 |
Fig. 14 Flux abundance quotients ξflux,X/Y for the Ne/He, O/He, and Ne/O pairs calculated from the scaled fluxes integrated over IBEX spin phase and averaged over the orbits for the first four years of IBEX observations. |
To investigate the flux abundance of NIS species at IBEX, we simulated the fluxes at IBEX
(i.e., in the IBEX-inertial frame) for each day of the four seasons of NIS gas observations
following Eqs. (1)−(3) in Bzowski et al. (2012). The
fluxes are scaled to the density at TS; we refer to these quantities as the scaled flux
Fscaled,X: 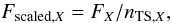 (34)where
FX is the absolute flux in the
IBEX-inertial frame for species X. From these, we calculated the fluxes
integrated over spin phase and averaged over the high altitude science operations (HASO)
times for each orbit.
(34)where
FX is the absolute flux in the
IBEX-inertial frame for species X. From these, we calculated the fluxes
integrated over spin phase and averaged over the high altitude science operations (HASO)
times for each orbit.
The time series of daily scaled fluxes for NIS He, Ne, and O at IBEX, integrated over the FOV, spin axis, and each day of the IBEX NIS gas campaigns in 2009 and 2012, are shown in Fig. 12. They illustrate the characteristic features of the observed flux. Because of the motion of IBEX with Earth around the Sun the beam of NIS gas wanders through the fixed FOV of IBEX-Lo. In this way, the daily counts registered by the instrument during the HASO times at a specific orbit systematically change. First, they decrease from one day to the next, until the spin axis of the spacecraft is changed and the NIS beam is realigned with the FOV. This sequence repeats until Earth passes ecliptic longitude of about 130°, when the FOV is aligned with the peak of the beam. During this one specific orbit, the daily counts change very little. Those are the orbits when the total counts registered are maximum.
After the peak, the orbital sequence of daily counts reverses: low at the beginning of the orbit and gradually increasing, until the spin axis is realigned to avoid sunlight in the aperture. This behavior of the flux, presented in simulation, has actually been observed by Saul et al. (2012) for H and He and by Möbius et al. (2012) and Bzowski et al. (2012) for He.
The reader will observe a few characteristic features in Fig. 12. The daily changes in the total flux appear to be approximately linear on log scale as a function of the ecliptic longitude of Earth. The slopes of the daily sequences vary from orbit to orbit and between the species even though the flow parameters in the LIC were assumed identical. This is because of the different masses of the atoms, which result in different thermal speeds for the same temperature. A combination of different natural widths of the beams with different ionization rates and some selection effects in the ionization losses (slower atoms attenuated more strongly than the faster ones) result in different slopes between the species and asymmetry of the orbit-averaged flux relative to the peak.
Differences between the spin-axis-pointing readjustments between seasons also affect the daily fluxes, hence the orbit-averaged fluxes. The change in the spin-axis reorientation scheme in 2011 affected the data collection. The daily fluxes for two seasons with different spin axis readjustment policies can be compared in the two panels of Fig. 12.
In Fig. 13 we show orbit-averaged fluxes of NIS He, Ne, O at IBEX during the four observation seasons, scaled to respective densities at TS according to Eq. (34). The quantities shown in this figure are directly proportional to the expected numbers of counts on specific orbits divided by the densities of respective species at TS.
The change in the total count numbers for given species between 2009 and 2010 are small, especially for Ne and He (see Table 5 and Fig. 10). This is because of the small year to year differences in the total ionization rates and relatively weak overall ionization losses. In 2011, one observes that a drop in the total counts starts, and it becomes clearly evident for all species in 2012. Another interesting feature is the shift towards larger longitudes of the increasing branch of the flux (the portion to the left of the peak in Fig. 13). This effect, as we have verified, is related to the change of IBEX orbit and to the resulting change in the spin axis reorientation strategy after the 2011 season.
The year-to-year changes in the count numbers do not track the changes in survival probability and local density (Fig. 10). This is because in addition to the varying ionization rate, details of the observation process (i.e., the history of field of view changes and details of the observation times, which in general do not cover the whole time interval on a given orbit) also strongly affect the averaged count numbers. Therefore, assessing the expected year-to-year changes in the counts requires carrying out detailed simulations of the observations. The predictions or conclusions drawn from analysis of survival probabilities, which are relatively easy to calculate, are not credible, and the errors become particularly large in the conditions of rapidly changing solar activity.
Taking the quantities shown in Fig. 13 pairwise and
calculating their quotients between species, one obtains ratios
ξflux,X/Y
of fluxes scaled to the values at TS: 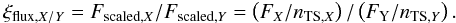 (35)They are similar to the
quantities shown in Fig. 11, i.e., to the modification
of the abundances of NIS species relative to their respective values at TS. We show them in
Fig. 14 and in Table 5 for Ne/He, O/He, and Ne/O ratios. These quantities, multiplied by respective
count ratios actually retrieved from IBEX data, would return the abundances of NIS species
at TS. In addition to the
ξflux,X/Y
quotients for the fluxes integrated over entire seasons, in Table 5 we present the quotients
(35)They are similar to the
quantities shown in Fig. 11, i.e., to the modification
of the abundances of NIS species relative to their respective values at TS. We show them in
Fig. 14 and in Table 5 for Ne/He, O/He, and Ne/O ratios. These quantities, multiplied by respective
count ratios actually retrieved from IBEX data, would return the abundances of NIS species
at TS. In addition to the
ξflux,X/Y
quotients for the fluxes integrated over entire seasons, in Table 5 we present the quotients  for the
“peak orbits” (i.e., for the orbits on which the observed NIS flux was maximum: 16, 64, 112,
154).
for the
“peak orbits” (i.e., for the orbits on which the observed NIS flux was maximum: 16, 64, 112,
154).
Survival probabilities w of He, Ne, and O atoms reaching their perihelia at ~130° ecliptic longitude, and respective heliospheric abundance quotients ξX/Y calculated from respective survival probabilities, for the velocity vector of the atoms in the LIC as established by Bzowski et al. (2012) from IBEX observations.
Same as Table 2, but for the velocity vectors in the LIC as established for He by Witte et al. (2004).
Same as Table 5, but for the inflow parameters of the gas as from Witte (2004).
 |
Fig. 15 Relative change of the ξ quotients for the season-integrated flux (solid lines), densities at the ecliptic longitude where the NIS gas flow intersects the Earth’s orbit (broken lines), and time-dependent survival probabilities of the NIS atoms reaching IBEX at this location (dotted lines). All quantities are shown as ratios to the respective values in 2009. The color code for species pairs is indicated in the panel. |
The time series of abundance quotients ξflux for the Ne/He and O/He have peaks at ecliptic longitudes greater than the longitude of maximum of the He flux. This behavior is consistent among all four observation seasons. The quotient for the Ne/O abundance, on the other hand, peaks before the longitude of the peak He flux.
The abundances obtained from the fluxes averaged over each complete season are listed in Table 5, and the evolution of the quotient relative to the value from 2009 is illustrated in Fig. 15. They feature a monotonic decrease between 2009 and 2012 for Ne/He and O/He, which can be explained by the increase in ionization losses because of the increase in solar activity. An exception is the Ne/O quotient, which increases from 2009 to 2011 and starts to decrease in 2012.
The evolution of the ξflux,X/Y quotients differs from the evolution of the survival probabilities quotients ξsur,X/Y, which is not surprising when one remembers that the flux evolution already did not agree too well with the evolution of w.
 |
Fig. 16 Abundance quotients calculated from various quantities discussed in the paper, divided by the flux quotient for the 2009 season, for all three pairs of NIS gas species. The figure illustrates the temporal evolution of the abundance quotients and differences between the quotients calculated using different definitions. Solid lines mark the NIS gas flow parameters obtained from IBEX (Bzowski et al. 2012), the broken line marks the flux quotient calculated for the gas inflow parameters obtained by Witte (2004) from GAS/Ulysses observations. |
The total count numbers from given orbits are sums of daily counts, but in reality it frequently happens that some time intervals are not suitable for analysis, and the actually observed sequence of orbit-integrated counts consequently deviates from a model with full time coverage. Therefore, the analysis above must be regarded as qualitative. For comparison with actual IBEX measurements, the actual observation times must be taken into account, as well as calibration and instrument setting details that we omitted from this analysis.
 |
Fig. 17 The Ne/O abundance in the LIC calculated from Eq. (20) for various combinations of NIS gas inflow longitude and speed, based on filtration factors and the Ne/O flux ratio measured at IBEX by Bochsler et al. (2012). The LIC abundances are listed at the line that is the correlation between the inflow longitude and speed obtained by Bzowski et al. (2012) from analysis of NIS He observations by IBEX-Lo. For the best-fit parameters obtained by Bzowski et al. (2012), the LIC abundance is 0.16, for the flow parameters obtained by Witte et al. (2004) from analysis of NIS He observations by GAS/Ulysses the abundance is 0.18. |
6. Summary and conclusions
We were mostly interested in the modification of the abundances of NIS species He, Ne, and O in the heliosphere due to solar accretion and ionization losses. We have carefully investigated the change in abundance of NIS gas species at 1 AU relative to the abundance at TS of the solar wind caused by the interaction of NIS gas with the Sun. All three NIS gas species investigated have identical bulk speed vectors and temperatures in the LIC. Equal temperatures imply different thermal velocities. Together with different ionization losses, this results in differences in the transmission of NIS species through the inner heliosphere and changes in the abundances relative to the respective abundances at TS.
We have analyzed the history of ionization rates of He, Ne, and O during the years of NIS species observation seasons by IBEX. The weakest ionization is for He, the strongest for O. The main ionization reaction for all three species is photoionization, whose rate varies during the solar cycle by a factor of ~2. For O, as well important is the charge exchange with solar wind protons. For Ne and He, this charge exchange is practically negligible. Electron impact ionization is of high significance, since it is responsible for the ionization of ~25% of NIS O atoms and of about 10% for Ne and He. However, electron impact ionization is the poorest known ionization process because of limited information on the evolution of the distribution function of solar wind electrons with the distance from the Sun.
The simplest way to assess the abundance change between TS and IBEX is to calculate the ratio of survival probabilities of individual atoms on orbits that reach perihelia at the detector. With the ionization rates on hand, we have investigated the quality of the approximation of the analytic model of the survival probabilities, where the ionization rate is assumed invariable with time and falling off with the square of solar distance with electron impact ionization excluded.
We showed that this approach is only acceptable for He and Ne during low solar activity (see Fig. 5), when discrepancies with the calculation performed using the full time-dependent ionization rate are within a few percent. For O the discrepancies are greater. Furthermore, we were unable to identify an averaging interval of the actual ionization rate that would guarantee reliable results from the analytical model at all times. The conclusion is that with the exception of NIS He during the low solar activity, calculating the survival probabilities of NIS species using the time dependent approach gives more reliable results.
The abundance change quotients ξsur calculated from survival probabilities for all four IBEX NIS gas sampling seasons are listed in Table 2. We also investigated the sensitivity of the ξsur to the inflow parameters of NIS gas (Fig. 8, Tables 2 and 3). The spread in the ratios for various inflow parameters is ~20% for O/He, ~12% for Ne/O, and ~7% for Ne/He. This suggests that the studies of NIS abundances in the LIC and of the NIS gas flow vector must go in parallel (see Figs. 8 and 17) because the results can potentially influence each other.
We performed a careful analysis of uncertainties of survival probabilities and their ratios. We took into account the uncertainties of the measurements of the solar quantities (solar wind and EUV fluxes) and of the reaction cross sections, and the NIS gas inflow velocity. The resulting uncertainties of the survival probabilities and their ratios vary between the pairs of species in question, from ~20% for Ne/He through ~35% for Ne/O to ~50% for O/He. We believe these uncertainties are also valid for the density and flux ratios.
We then investigated the evolution of densities of NIS species at the location on Earth’s orbit where IBEX sees the maximum of NIS flux. The relative variation in densities and survival probabilities of NIS species generally agree with each other, even though systematic differences do exist. This suggests that the changes in survival probabilities (calculated using the full time-dependent model) are sufficient to model the expected relative variations of NIS density, but not the absolute values of the densities, which should be evaluated using a time-dependent thermal (“hot”) model.
The most realistic, but also the most calculation-intensive approach to calculating the
abundance quotients is modeling based on a fully time-dependent model of the ionization
losses, where the local fluxes at IBEX are integrated over the field of view, spin phase,
and time. To infer the NIS gas abundance at TS, one can use either the flux quotients
ξflux calculated from the total counts of the NIS species
registered at IBEX during the whole observation season, or the quotient
 obtained
from counts registered on the peak orbit of each season. They are not identical (see Tables
5 and 6).
Using the latter method requires fewer calculations, but the former one potentially offers
more reliable statistics.
obtained
from counts registered on the peak orbit of each season. They are not identical (see Tables
5 and 6).
Using the latter method requires fewer calculations, but the former one potentially offers
more reliable statistics.
We studied differences between the local flux change quotients ξflux and density change quotients ξdens, which might potentially be useful for studies of NIS abundances. The patterns of the relative densities of NIS species at Earth are strong functions of ecliptic longitude. They are quite different between He, Ne, and O because of their different thermal speeds and different ionization rates (see Fig. 9). This results in different patterns of the density-change quotients for Ne/He, O/He, and Ne/O (Eq. (33), Fig. 11).
Generally, ξflux is greater by ~40% than
ξdens for Ne/He and O/He; in the case of Ne/O,
ξdens is greater than ξflux by
about 5% (Fig. 16). This is because the accretion
factors (Eqs. (15) and (16)) for Ne and O are very similar to each
other. See Table 4 and Fig. 16 for details. The differences between the abundance quotients
ξflux (Eq. (35)) and  are on the
order of 12% for Ne/He and O/He and a few percent for Ne/O (see Fig. 16 and Table 5). The quotients
ξflux and ξdens are also different
from ξsur (Eqs. (19) and (20), and the comparison
is shown in Fig. 16.
are on the
order of 12% for Ne/He and O/He and a few percent for Ne/O (see Fig. 16 and Table 5). The quotients
ξflux and ξdens are also different
from ξsur (Eqs. (19) and (20), and the comparison
is shown in Fig. 16.
For the 2009 season, ξflux,Ne/O quotient is ~9.52. Adopting the measured at IBEX Ne/O abundance and the filtration factors beyond TS from Bochsler et al. (2012), one immediately obtains the neutral Ne/O abundance at TS equal to 0.042 and 0.14 in the LIC. Using our estimate of the ξsur,Ne/O, the LIC Ne/O abundance equals 0.16 for the NIS gas inflow parameters from IBEX (Bzowski et al. 2012) and 0.18 for the inflow parameters from GAS/Ulysses (Witte 2004). Figure 17 presents the dependence of the NIS Ne/O abundance as a function of various inflow longitudes and speeds. The uncertainty of this result is approximately 40%. One has to realize, however, that this calculation does not take the actual time intervals into account that Bochsler et al. (2012) used in their analysis, so this estimate is approximate. A more thorough analysis of the NIS Ne/O abundance based on IBEX observations is ongoing and will be the subject of a future paper.
Online material
Appendix A: Modulation of the ionization rates of neutral He, Ne, O in the heliosphere
Appendix A.1: Photoionization rates of Ne, He, and O
The model of photoionization rates of NIS species used in this paper calculates Carrington rotation averages of H, He, O, Ne photoionization rates based on directly measured solar spectra from TIMED/SEE and CELIAS/SEM onboard SOHO and a hierarchy of solar EUV radiation proxies. The model of photoionization rates for hydrogen in the heliosphere was described by Bzowski et al. (2013), and here we focus on He, Ne, and O. Details of the derivation and discussion of instrumental and statistical uncertainties will be provided elsewhere (Sokół et al., in prep.; Bochsler et al., in prep.).
Basically, calculating the photoionization rate for a given species is simple. One
integrates the spectral flux of the Sun
F(λ,t) for
a wavelength λ and time t, multiplied by the cross
section 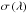 for a given species over an interval starting from 0 to the ionization threshold
wavelength λ0:
for a given species over an interval starting from 0 to the ionization threshold
wavelength λ0: 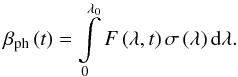 (A.1)For the cross
sections we adopted results from Verner et al.
(1996), see Fig. A.2.
(A.1)For the cross
sections we adopted results from Verner et al.
(1996), see Fig. A.2.
Regular measurements of the solar spectral flux are available only starting from 2002 owing to the TIMED experiment (Woods et al. 2005). Earlier, measurements in several spectral bands in the EUV above the ionization threshold of H, He, Ne, and O region (SEM/CELIAS/SOHO, Hovestadt et al. 1995) have been available since 1996. Fortunately, it has been demonstrated that the photoionization rates of many species are correlated with a number of other routinely measured quantities (proxies), including the MgII core-to-wing index (MgIIc/w, Heath & Schlesinger 1986; Viereck & Puga 1999), solar Lyman-α flux (Lyα, Woods et al. 1996, 2000), and the solar radio 10.7 cm flux (F10.7, Covington 1947; Tapping 1987). Thus, to infer a sufficiently long time series of photoionization rates of NIS species one can use proxies obtained from statistical analysis of the correlations.
The baseline of the model is the solar spectrum measured by TIMED/SEE (Woods et al. 2005) during a few years after launch, when the solar activity was going down from the maximum to minimum values and the absolute calibration of the instrument was the most reliable. These portions of the time series (calculated separately for each species) are shown in red in Fig. A.1. We used measurements of two-hours resolution in time and calculated the photoionization rates using Eq. (A.1). We filtered the results against flares and particle background and calculated Carrington rotation averages. Owing to suspected unaccounted degradation of the TIMED/SEE detector we decided to use only a few first years of the TIMED measurements, namely the first 27 Carrington rotations from 22 January 2002 for He and Ne, and 74 Carrington rotations for H and O. These data are shown in red in Fig. A.1.
For other times we developed a set of proxies by taking statistical correlation between the directly calculated values and the solar EUV radiation proxy. The hierarchical set of proxies is based on the chromospheric MgIIc/w index available from 1978 as released by LASP (Heath & Schlesinger 1986; Viereck & Puga 1999; Viereck et al. 2004), the F10.7 flux released by NOAA and DRAO (Tapping 1987) available from 1947, and the composite Lyman-α flux published by LASP (available from 1947, but based on actual UV observations from mid-1970-ties, with some gaps filled by proxies developed by the LASP team, see Woods et al. 2000). As the most reliable proxy we chose the CELIAS/SEM data (Hovestadt et al. 1995), which are measurements of the fragments of the solar spectrum responsible for most of the helium ionization.
The hierarchy of photoionization-rate retrieval we used was similar for He and Ne, since they show similar properties, and a different one for H and O, because they have the same ionization threshold energy (see photoionization cross sections in question in Fig. A.2).
The procedure for building the time series for the noble gases was as follows. In the first step we used the EUV flux in the two spectral bands measured by CELIAS/SEM onboard SOHO, which has been available since 1996. The first-order flux (26−34 nm, here referred to as Ch1) and the central order flux (0.1−50 nm, here referred to as Ch2) were considered. We found, for each species separately, a linear correlation between the daily time series of photoionization rates from the TIMED and SEM time series for the chosen time intervals from the TIMED data.
The general formula to calculate photoionization rate from SEM data (darker blue line
in Fig. A.1) is 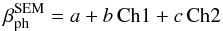 (A.2)with
the parameter values for He and Ne shown in Table A.1. From this formula we calculate daily photoionization rates, which are
further used to compute the Carrington-rotation averaged time series that we use as a
basis for further studies.
(A.2)with
the parameter values for He and Ne shown in Table A.1. From this formula we calculate daily photoionization rates, which are
further used to compute the Carrington-rotation averaged time series that we use as a
basis for further studies.
The time coverage of the SEM data is not quite long enough for modeling heliospheric ionization processes. The travel of NIS atoms from 150 AU takes about 30 years or more, even though most of the ionization losses occur inside ~10 AU from the Sun. Thus it is desirable to have a homogeneously prepared time history of the ionization rates in the heliosphere dating back as far as possible, so that one model can be used to analyze both present and past measurements, such as those obtained from Ulysses.
To extend the photoionization time series backwards we used the mentioned hierarchy of solar EUV radiation proxies (MgIIc/w, Lyman-α, and F10.7). We found the correlation between individual proxies or their combinations and Carrington-rotation averaged photoionization rates obtained using the aforementioned EUV measurements. We then used them to reproduce the historical record of photoionization rates of He, Ne, and O dating backward to 1948. The following formulae yield the photoionization rates with the highest correlation coefficients. The results of the goodness of those correlations are gathered in Figs. A.3 and A.4 for He and Ne, respectively, and in Fig. A.5 for O.
 |
Fig. A.1 Time series of Carrington period-averaged photoionization rates of H, He, Ne, and O at 1 AU from the Sun. The color code denotes the various sources of data and proxies used, as discussed in the text. |
 |
Fig. A.2 Cross sections for photoionization of neutral H, He, Ne, and O used in the calculations (Verner et al. 1996). The accuracy is at a ~5% level. Even though the ionization threshold energy for O and H are very similar, the cross section values for the low-energy portion, where the solar spectral flux is greatest, are substantially different. |
The formula to calculate the photoionization rate from the
MgIIc/w index and adjusted F10.7 index expressed in
the sfu units (i.e.,10-22 W m-2 Hz-1; darker green
line in Fig. A.1) is the following, with the
coefficients listed in Table A.2: 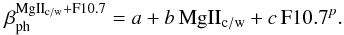 (A.3)The formula for
calculating the photoionization rate using only the F10.7 proxy is
(A.3)The formula for
calculating the photoionization rate using only the F10.7 proxy is 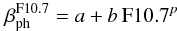 (A.4)with
the coefficients available in Table A.3. It is
drawn with the gray line in Fig. A.1. The
exponent in the F10.7 flux is close to 1/2, not 1, as was frequently adopted in the
past.
(A.4)with
the coefficients available in Table A.3. It is
drawn with the gray line in Fig. A.1. The
exponent in the F10.7 flux is close to 1/2, not 1, as was frequently adopted in the
past.
The procedure for oxygen is very similar to the procedure used for hydrogen,
described in Bzowski et al. (2013). The SEM
data are correlated with the TIMED/SEE observations and the Lyman-α
(Lyα) composite flux, according the formula using only
Carrington-rotation averaged time series (lighter blue line in Fig. A.1): 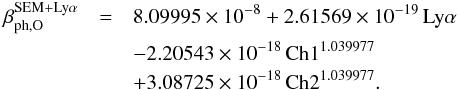 (A.5)When
the composite Lyman-α flux is not available, a formula with only the
Carrington-rotation averaged SEM data is used:
(A.5)When
the composite Lyman-α flux is not available, a formula with only the
Carrington-rotation averaged SEM data is used: 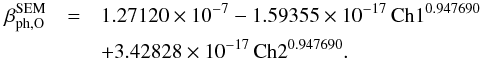 (A.6)When
SEM data are not available, we use a correlation of the Carrington-rotation averaged
TIMED/SEE flux and MgIIc/w index (lighter green line in
Fig. A.1):
(A.6)When
SEM data are not available, we use a correlation of the Carrington-rotation averaged
TIMED/SEE flux and MgIIc/w index (lighter green line in
Fig. A.1): 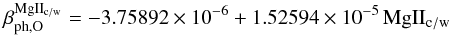 (A.7)
(A.7)
 |
Fig. A.3 Scatter plot of model vs. data for photoionization models for He defined in Eq. (A.2) (left column), Eq. (A.3) (middle column), and Eq. (A.4) (right column), fit residuals (middle row), and histograms of the residuals (lower row). The red y = x lines are eye guides. The statistical uncertainties of the models are indicated in insets in the histogram panels. |
 |
Fig. A.4 Scatter plot of model vs. data for photoionization models for Ne defined in Eq. (A.2) (left column), Eq. (A.3) (middle column) and Eq. (A.4) (right column), fit residuals (middle row), and histograms of the residuals (lower row). The red y = x lines are eye guides. The statistical uncertainties of the models are indicated in the insets in the histogram panels. |
 |
Fig. A.5 Scatter plot of model vs. data for photoionization models for O defined in Eq. (A.6) (top row), Eq. (A.7) (second row from the top), Eq. (A.7) (third row from the top), and Eq. (A.8) (bottom row); fit residuals (middle column); histograms of the residuals (right column). The red y = x lines are eye guides. The statistical uncertainties of the models are indicated in the insets in the histogram panels. |
and from 1948 until the beginning of the MgIIc/w time
series in 1978, the photoionization rates for O come from the correlation formula for
the F10.7 flux (gray line in Fig. A.1) based on
the comparison with Carrington-rotation averaged TIMED/SEE data: 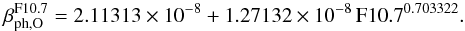 (A.8)This model
calculates Carrington rotation averages of the ionization rates. Extending the proxies
into sub-Carrington time scale requires further careful studies related to possible
limb darkening/brightening effects that may be present in some proxies but absent in
the EUV flux contributing to photoionization. Since in the present study we only need
Carrington-rotation averaged time series, we leave this aspect for future analysis.
(A.8)This model
calculates Carrington rotation averages of the ionization rates. Extending the proxies
into sub-Carrington time scale requires further careful studies related to possible
limb darkening/brightening effects that may be present in some proxies but absent in
the EUV flux contributing to photoionization. Since in the present study we only need
Carrington-rotation averaged time series, we leave this aspect for future analysis.
It is interesting to note that the photoionization rate for H and He are almost identical during solar maximum, but differ up to 40% during solar minimum. Also worth pointing out is the difference between the photoionization rates of H and O despite their almost identical ionization threshold. This is because of differences in the photoionization cross sections between these species.
Appendix A.2: Electron impact ionization of Ne, He, and O
The physical aspects of ionization of neutral heliospheric gas by solar wind electrons impacts were originally proposed by Ruciński & Fahr (1989, 1991) for He. Bzowski (2008) developed a model of electron ionization rate for H using measurements of electron distribution function from Ulysses (Salem et al. 2001; Issautier et al. 2001, 2008), carried out between ~1.5 and ~5.5 AU from the Sun, which were recently discussed by Bzowski et al. (2013). The distribution function is approximated by a bi-Maxwellian model that includes the dominating cool core and the secondary hot halo populations, with the abundance of the latter increasing towards increasing heliocentric distances. Under these assumptions, and also the assumption of the quasi-neutrality of solar wind, one can calculate a radial model of electron ionization rate for all species in question (Scime et al. 1994, Fig. 2).
The model values are proportional to solar wind density plus twice the alpha particle content, which approximate the solar wind electron densities and which are taken from the solar wind proton density model used to calculate the charge exchange rates. An extensive discussion of the background solar wind electron temperature model is presented in Bzowski (2008) and Bzowski et al. (2013).
In our calculation we follow the approach presented in these papers. We approximate the solar wind electron distribution function as bi-Maxwellian, with the dominating cool core and hot halo. The temperatures and relative densities of the core and halo populations evolve with the heliocentric distance, as measured by Ulysses (Scime et al. 1994). Calculating the electron ionization rate requires folding the local electron distribution function with the reaction cross section and integrating from the threshold ionization energy to infinity. In this paper we use only a model for the slow solar wind because the NIS atoms in question travel close to the ecliptic plane at all times. The reader is referred to Eqs. (A.9) in Bzowski (2008) for the adopted radial profiles of the core and halo temperatures and (A.11) for the evolution of the abundance of the halo population relative to the core.
 |
Fig. A.6 Cross sections of electron impact ionization for H, He, Ne, and O (Lotz 1967). The accuracies for H, He, and O are 10%, for Ne 15%. The vertical bars mark the energies corresponding to the temperatures of the core and halo solar wind electron populations in the slow solar wind at 1 AU from the Sun. The noble gases can only be ionized by a high-energy wing of the core population and mostly by the halo population. |
The cross sections were taken from Lotz (1967) and are presented in Fig. A.6. They seem accurate and reliable enough in the entire range of energies needed for our purposes and are consistent with more recent studies (Godunov &Ivanov 1999; Bartlett & Stelbovics 2004; Mattioli et al. 2007). The two vertical bars in this figure represent the energy equal to kTe for the temperatures of the core and halo populations at 1 AU from the Sun. They show that He and Ne are ionized predominantly by the halo population, with only the fastest wing of the core population being energetic enough to ionize, while H and O are ionized by both core and halo populations. The temperatures of both populations decrease with solar distance, and the farther from the Sun, the smaller the portion of the total electron population capable of ionizing the heliospheric species. The electron impact ionization contributes only ~10% to the total ionization rate at 1 AU from the Sun, and beyond ~5 AU from the Sun it becomes practically negligible. The electron impact rate is a linear function of the local electron density.
The ionization rate for the core and halo populations was tabulated as a function of
solar distance assuming nsw = 1 cm-3 and then
an analytic approximation formula was fitted separately for each species. Here we
present the resulting formulae to calculate the electron impact ionization in the slow
and fast solar wind regime. In the formulae below,
nsw(r,t)
is solar wind proton density at heliocentric distance r in AU, in
time t, the logarithms are natural: ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{eq:betaElSlow}&&\beta_{\mathrm{el}}^{\mathrm{slow}}\left( r, t \right) = n_{\mathrm{sw}}\left( r, t\right) \, \mathrm{exp} \left[ \frac{a+b\, \mathrm{ln}{r}+c\,\mathrm{ln}^2{r}}{d+e\,\mathrm{ln}{r}+f\,\mathrm{ln}^2{r}+g\,\mathrm{ln}^3{r}} \right] \quad\quad\quad\\ \label{eq:betaElFastHeNe}&&\beta_{\mathrm{el,He,Ne}}^{\mathrm{fast}} \left( r, t \right) = n_{\mathrm{sw}}\left( r, t\right) \, \mathrm{exp} \left[ \frac{a+b\, \mathrm{ln}{r}\!+\!c\,\mathrm{ln}^2{r}+d\,\mathrm{ln}^3{r}}{e\!+\!f\,\mathrm{ln}{r}+g\,\mathrm{ln}^2{r}^2+h\,\mathrm{ln}^3{r}} \right] \quad\quad\quad\\ \label{eq:betaElFastO}&&\beta_{\mathrm{el,O}}^{\mathrm{fast}} \left( r, t \right) \!=\! n_{\mathrm{sw}}\left( r, t\right) \mathrm{exp}\! \left[ \frac{a\!+\!b\,\mathrm{ln}{r}\!+\!c\,\mathrm{ln}^2{r}}{d\!\!+\!\!e\,\mathrm{ln}{r}\!+\!f\,\mathrm{ln}^2{r}\!+\!g\,\mathrm{ln}^3{r}\!+\!h\,\mathrm{ln}^5{r}} \right]\cdot \quad\quad\quad \end{eqnarray}](/articles/aa/full_html/2013/09/aa21700-13/aa21700-13-eq256.png) The
coefficients are gathered in Tables A.4 and
A.5. Throughout the paper we assume that the
solar wind proton density decreases with heliocentric distance as
1/r2. The
βel rate in our model is tied to the local solar wind
density
nsw(r,t)
and consequently it is calculated as a function of time, similarly to
nsw(r,t).
The
coefficients are gathered in Tables A.4 and
A.5. Throughout the paper we assume that the
solar wind proton density decreases with heliocentric distance as
1/r2. The
βel rate in our model is tied to the local solar wind
density
nsw(r,t)
and consequently it is calculated as a function of time, similarly to
nsw(r,t).
The ionization rates obtained using the presented model are consistent with the rates published by Arnaud & Rothenflug (1985), which for He0, Ne0, and O0 are based on the cross sections and approximation formulae from Lotz (1967).
Appendix A.3: Charge exchange rates for He, Ne, and O
In addition to the photoionization and electron impact rates discussed in the last section, the ionization processes relevant for neutral heliospheric species include charge exchange. The charge exchange reaction was recently discussed by Bzowski et al. (2013) for heliospheric H and most of the theory applies for O, Ne, and He.
The charge exchange cross sections for He and O used in the present paper come from Lindsay & Stebbings (2005) and for Ne from Nakai et al. (1987). Figure A.7 shows the product of the relative speed of the component of the reaction and cross section for charge exchange for the NIS species observed by IBEX. To obtain an instantaneous charge exchange rate, the value taken from the figure for a given speed must be multiplied by the local ion density, which is assumed to fall off with r2 and is a function of heliolatitude and time (Sokół et al. 2013). The figure explains the huge differences between the charge exchange rates for H and O, on one hand, and for the noble gases, on the other, and illustrates that charge exchange rates are not linear functions of the collision speed, as frequently approximated.
 |
Fig. A.7 Products of relative speeds of reaction components and charge exchange cross sections for these speeds for the charge exchange reactions listed in the text (see Sect. 2.2). To obtain the actual charge-exchange rate, one has to multiply a quantity read off from the figure for a given speed by the local density of the ionized reaction component (solar wind proton, alpha particle). The lower horizontal axis is scaled in km s-1, the upper axis in energy per nucleon in keV. |
The calculations were performed using Carrington-rotation averaged solar wind proton
densities and speeds from the formula Eq. (A.12). The values thus obtained are approximate because the atom speed is
assumed to be 0. In the simulations shown in the main text, we use the full formula
with | vrel| =
| vsw − vatom |
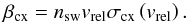 (A.12)vsw
and nsw were calculated for a given instant of time
t and heliolatitude φ from bilinear interpolation
between the grid nodes fixed at halves of Carrington rotations and full tens of
degrees heliolatitude (see Sokół et al. 2013).
For the dependence on heliocentric distance r, proton density
nsw was assumed to conform to the
1/r2 dependence and
vsw was assumed to be distance independent.
(A.12)vsw
and nsw were calculated for a given instant of time
t and heliolatitude φ from bilinear interpolation
between the grid nodes fixed at halves of Carrington rotations and full tens of
degrees heliolatitude (see Sokół et al. 2013).
For the dependence on heliocentric distance r, proton density
nsw was assumed to conform to the
1/r2 dependence and
vsw was assumed to be distance independent.
Appendix A.4: Total ionization rates for He, Ne, and O
The total ionization rates for NIS species are algebraic sums of rates of all relevant ionization processes. Figure 1 presents the total ionization rates of the contributing reactions for the NIS species observed by IBEX. For the noble gases, the main reaction is photoionization, and the next is electron impact ionization, which gives ~10% input to the total rate. The rate of charge exchange with solar wind protons (and alphas in the case of helium) is very low, most of the time much less than 1% of the total rate. The case of oxygen is more complex. During the previous minimum in 1996, the photoionization and charge exchange rates were comparable (~45% input each to the total rate), but since 1998 the input from charge exchange decreased (to ~35%) and photoionization became dominant (more than 50%).
The total ionization rates for He and Ne show a clear modulation with solar activity because they mainly depend on
photoionization, which varies quasi-periodically with the solar activity cycle. The ionization rate for O does not show a clear modulation with the solar activity cycle because it is a sum of a quasi-periodic component from photoionization and a time-dependent, but not periodic, component from charge exchange and electron impact. Owing to the similarity of the first ionization potential for H and O, it is usually assumed that the total ionization rates of these species should be very similar. Our analysis shows that it is true most of the time, but not always: the ionization rate for O was higher than for H for a couple of years during the previous solar maximum and it seems that this behavior is going to repeat during the forthcoming maximum as well. The ionization rate of H shown in Fig. 1 is taken from Bzowski et al. (2013) and shown here for comparison.
The uncertainties of the ionization rates used in this work will be the subject of separate paper (Sokół et al., in prep.). They arise from uncertainties in the reaction cross sections, from uncertainties of the measured quantities (the solar wind and solar EUV output), from the statistical uncertainties of the proxies used, and from simplifications used in the models. We estimate that the overall uncertainty in the total ionization rates is 15−20%. The statistical uncertainties of the proxy models are indicated in the figures of histograms (see Figs. A.3, A.4, A.5). The other uncertainties are listed in Table 1.
Acknowledgments
M.B. and J.M.S. would like to thank Peter Bochsler for exciting discussion and valuable remarks to a draft of the paper. The authors from SRC PAS were supported by grant N-N203-513-038 from the Polish Ministry for Science and Higher Education, managed by the Polish National Science Center. M.A.K was partly supported by a stipend from the START program of the Polish Science Foundation for 2012. The authors acknowledge the use of NASA/GSFC’s Space Physics Data Facility’s ftp service for Ulysses/SWOOPS and TIMED/SEE data, SOHO/CELIAS/SEM (http://www.usc.edu/dept/space_science/semdatafolder/long/daily_avg/), and OMNI2 data collection (ftp://nssdcftp.gsfc.nasa.gov/spacecraft_data/omni/). The F10.7 solar radio flux was provided by the NOAA and Pentincton Solar Radio Monitoring Programme operated jointly by the National Research Council and the Canadian Space Agency (ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/SOLAR_RADIO/FLUX/Penticton_Adjusted/ and ftp://ftp.geolab.nrcan.gc.ca/data/solar_flux/daily_flux_values/). The composite Lyman-α flux and MgIIc/w were obtained from LASP, accessed through the LISIRD Web page at (http://lasp.colorado.edu/lisird/lya/).
References
- Arnaud, M., & Rothenflug, R. 1985, ApJS, 60, 425 [Google Scholar]
- Auchère, F., Cook, J. W., Newmark, J. S., et al. 2005, ApJ, 625, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Axford, W. I. 1972, in The Solar Wind, eds. J. M. W. C. P. Sonnet, & P. J. Coleman, NASA Spec. Publ., 308, 609 [Google Scholar]
- Barnett, C. F., Hunter, H. T., Kirkpatrick, M. I., et al. 1990, Atomic data for fusion. Collisions of H, H2, He and Li atoms and ions with atoms and molecules, ORNL-6086/V1 (Oak Ridge, Tenn.: Oak Ridge National Laboratories) [Google Scholar]
- Bartlett, P. L., & Stelbovics, A. T. 2004, Atom. Data Nucl. Data Tables, 86, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, P., & Fahr, H. J. 1970, A&A, 4, 280 [NASA ADS] [Google Scholar]
- Bochsler, P., Petersen, L., Möbius, E., et al. 2012, ApJS, 198, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bzowski, M. 2008, A&A, 488, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bzowski, M., Kubiak, M. A., Möbius, E., et al. 2012, ApJS, 198, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Bzowski, M., Sokół, J. M., Tokumaru, M., et al. 2013, in ISSI Sci. Rep. 12, eds. R. Bonnet, E. Quémerais, & M. Snow, (Springer Science+Business Media), 13, 67 [Google Scholar]
- Covington, A. E. 1947, Nature, 159, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Fuselier, S. A., Bochsler, P., Chornay, D., et al. 2009, Space Sci. Rev., 146, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Godunov, A. L., & Ivanov, P. B. 1999, Phys. Sci., 59, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Heath, D. F., & Schlesinger, B. M. 1986, J. Geophys. Res., 91, 8672 [NASA ADS] [CrossRef] [Google Scholar]
- Hłond, M., Bzowski, M., Möbius, E., et al. 2012, ApJS, 198, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Hovestadt, D., Hilchenbach, M., Bürgi, A., et al. 1995, Sol. Phys., 162, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Issautier, K. 2009, in Turbulence in Space Plasmas, eds. P. Cargill, & L. Vlahos (Berlin: Springer Verlag), Lect. Notes Phys. 778, 223 [Google Scholar]
- Issautier, K., Skoug, R. M., Gosling, J. T., Gary, S. P., & McComas, D. J. 2001, J. Geophys. Res., 106, 15665 [NASA ADS] [CrossRef] [Google Scholar]
- Issautier, K., Le Chat, G., Meyer-Vernet, N., Moncuquet, M., et al. 2008, Geophys. Res. Lett., 35, L19101 [NASA ADS] [CrossRef] [Google Scholar]
- Izmodenov, V. V., Gruntman, M. A., & Malama, Y. G. 2001, J. Geophys. Res., 106, 10681 [NASA ADS] [CrossRef] [Google Scholar]
- Izmodenov, V., Malama, Y., Gloeckler, G., & Geiss, J. 2004, A&A, 414, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasper, J. C., Stevens, M. L., Korreck, K. E., et al. 2012, ApJ, 745, 162 [NASA ADS] [CrossRef] [Google Scholar]
- King, J. H., & Papitashvili, N. E. 2005, J. Geophys. Res., 110, 2104 [Google Scholar]
- Kubiak, M. A., Bzowski, M., Sokół, J. M., et al. 2013, A&A, 556, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. A., Möbius, E., Wu, X., & Bzowski, M. 2012, ApJS, 198, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsay, B. G., & Stebbings, R. F. 2005, J. Geophys. Res., 110, A12213 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, W. 1967, Z. Phys., 206, 205 [Google Scholar]
- Maksimovic, M., Pierrard, V., & Riley, P. 1997, Geophys. Res. Lett., 24, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Mattioli, M., Mazzitelli, G., Finkenthal, M., et al. 2007, J. Phys. B At. Mol. Phys., 40, 3569 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Elliott, H. A., Gosling, J. T., et al. 2002, Geophys. Res. Lett., 29, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Ebert, R. W., Elliot, H. A., et al. 2008, Geophys. Res. Lett., 35, L18103 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Allegrini, F., Bochsler, P., et al. 2009, Space Sci. Rev., 146, 11 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Carrico, J. P., Hautamaki, B., et al. 2011, Space Weather, 9, 11002 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Alexashov, D., Bzowski, M., et al. 2012, Science, 336, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Möbius, E., Bochsler, P., Bzowski, M., et al. 2009, Science, 326, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Möbius, E., Bochsler, P., Heirtzler, D., et al. 2012, ApJS, 198, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H.-R., & Zank, G. P. 2004, J. Geophys. Res., 109, A07104 [NASA ADS] [CrossRef] [Google Scholar]
- Nakai, Y., Shirai, T., Tabata, T., & Ito, R. 1987, Atom. Data Nucl. Data Tables, 37, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Pilipp, W. G., Muehlhaeuser, K.-H., Miggenrieder, H., Montgomery, M. D., & Rosenbauer, H. 1987, J. Geophys. Res., 92, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Redfield, S., & Linsky, J. L. 2008, ApJ, 673, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Ruciński, D., & Fahr, H. J. 1989, A&A, 224, 290 [NASA ADS] [Google Scholar]
- Ruciński, D., & Fahr, H. J. 1991, Ann. Geophys., 9, 102 [NASA ADS] [Google Scholar]
- Ruciński, D., Bzowski, M., & Fahr, H. J. 2003, Ann. Geophys., 21, 1315 [Google Scholar]
- Salem, C., Bosqued, J.-M., Larson, D. E., et al. 2001, J. Geophys. Res., 106, 21701 [NASA ADS] [CrossRef] [Google Scholar]
- Saul, L., Wurz, P., Möbius, E., et al. 2012, ApJS, 198, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Scime, E. E., Bame, S. J., Feldman, W. C., Gary, S. P., & Phillips, J. L. 1994, J. Geophys. Res., 99, 23401 [NASA ADS] [CrossRef] [Google Scholar]
- Slavin, J. D., & Frisch, P. C. 2007, Space Sci. Rev., 130, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Sokół, J. M., Bzowski, M., Tokumaru, M., Fujiki, K., & McComas, D. J. 2013, Sol. Phys., 285, 167 [Google Scholar]
- Tapping, K. F. 1987, J. Geophys. Res., 92, 829 [Google Scholar]
- Tarnopolski, S., & Bzowski, M. 2008, A&A, 483, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tarnopolski, S., & Bzowski, M. 2009, A&A, 493, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tokumaru, M., Kojima, M., & Fujiki, K. 2010, J. Geophys. Res., 115, A04102 [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, T. K., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Viereck, R. A., & Puga, L. C. 1999, J. Geophys. Res., 104, 9995 [NASA ADS] [CrossRef] [Google Scholar]
- Viereck, R., Floyd, L. E., Crane, P. C., et al. 2004, Space Weather, 2, S10005 [Google Scholar]
- Witte, M. 2004, A&A, 426, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Witte, M., Banaszkiewicz, M., Rosenbauer, H., & McMullin, D. 2004, Adv. Space Res., 34, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. N., Prinz, D. K., Rottman, G. J., et al. 1996, J. Geophys. Res., 101, 9541 [Google Scholar]
- Woods, T. N., Tobiska, W. K., Rottman, G. J., & Worden, J. R. 2000, J. Geophys. Res., 105, 27195 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. N., Eparvier, F. G., Bailey, S. M., et al. 2005, J. Geophys. Res., 110, A01312 [NASA ADS] [CrossRef] [Google Scholar]
- Zurbuchen, T. H., Fisk, L. A., Gloeckler, G., & von Steiger, R. 2002, Geophys. Res. Lett., 29, 090000 [Google Scholar]
All Tables
Relative uncertainties of parameters adopted for estimates of survival probability uncertainties
Survival probabilities w of He, Ne, and O atoms reaching their perihelia at ~130° ecliptic longitude, and respective heliospheric abundance quotients ξX/Y calculated from respective survival probabilities, for the velocity vector of the atoms in the LIC as established by Bzowski et al. (2012) from IBEX observations.
Same as Table 2, but for the velocity vectors in the LIC as established for He by Witte et al. (2004).
All Figures
 |
Fig. 1 Time series of ionization rates of neutral He, Ne, and O used in this study. Shown are total ionization rates at 1 AU from the Sun, as well as photoionization, electron-impact, and charge exchange rates for all relevant reactions. The lower-right panel shows the total ionization rates of He, Ne, and O on a common scale. For comparison, the ionization rate of H (Bzowski et al. 2013) is added. |
| In the text | |
 |
Fig. 2 Comparison of the radial dependence of electron impact ionization adopted in this
paper with the 1/r2-dependence for
He, Ne, and O. Solid lines indicate the radial profiles calculated using
|
| In the text | |
 |
Fig. 3 Integrand function in Eq. (3) for an
O atom on the orbit whose perihelion is at the location of the Earth at the time
corresponding to IBEX Orbit 16 in 2009 (λE = 130°). The
red line is the |
| In the text | |
 |
Fig. 4 Upper panel: survival probabilities for He, Ne, and O atoms on the trajectory reaching Earth in the perihelion in 2009 at 130° ecliptic longitude. Solid lines are for the velocity vector at infinity corresponding to the bulk flow of the gas as established by Bzowski et al. (2012) based on IBEX measurements, the broken lines illustrate the sensitivity of survival probabilities to the inflow parameters: they correspond to survival probabilities calculated for the NIS inflow vector as found by Witte (2004) based on GAS/Ulysses observations. Lower panel: ratios of survival probabilities to their mean values calculated from an 11-year interval ending at the detection time. |
| In the text | |
 |
Fig. 5 Relative differences between survival probabilities of He (upper panel), Ne (middle panel), and O (lower panel) calculated using the analytical and the full time-dependent models. The time-dependent model is identical as used in Fig. 4, the analytical models were calculated using stationary ionization rates following the 1/r2 solar distance dependence, with the rates for 1 AU calculated as average values over intervals ending at the detection moment and spanning backward in time 1, 3, or 13 Carrington rotation periods. The relative differences do not average to 0. This effect is most visible for O, for the entire time interval shown in the figure. The systematic upward departure of the mean values from 0 is due to electron impact. |
| In the text | |
 |
Fig. 6 Total survival probabilities (red) and survival probabilities against charge exchange (gray), photoionization (blue), and electron impact ionization (pale blue). The solid lines mark the most probable values, the broken lines mark the uncertainty ranges calculated from Eqs. (11)−(13) and (9). The scale for oxygen (bottom panel) is logarithmic. |
| In the text | |
 |
Fig. 7 Modulation of the ratios of survival probabilities for the Ne/He, O/He and Ne/O species pairs, drawn with solid lines. The broken lines mark the uncertainties calculated using Eqs. (25)–(29). |
| In the text | |
 |
Fig. 8 Ratios of survival probabilities for Ne/He, O/He, and Ne/O, equivalent to the quotients ξsur,X/Y defined in Eq. (20), for various combinations of the flow vector of the NIS gas in the LIC. The solid lines indicate the acceptable parameter region established by Bzowski et al. (2012) for the NIS gas flow parameters based on IBEX observations. |
| In the text | |
 |
Fig. 9 Relative densities (scaled to the values at TS, Eq. (32)) for NIS He, Ne, and O for the four IBEX sampling seasons, calculated for the apogee times of IBEX orbits for the inflow parameters obtained by Bzowski et al. (2012) from IBEX NIS He observations. The vertical bars mark the longitudes of IBEX apogees in 2009, the horizontal bars marks the relative density levels for this time and location in space. |
| In the text | |
 |
Fig. 10 Relative change in the season-integrated flux (solid lines), density at the ecliptic longitude where the NIS gas flow intersects the Earth’s orbit (broken lines), and time-dependent survival probabilities of the NIS atoms reaching IBEX at this location (dotted lines). All quantities are shown as ratios to the respective values in 2009. The relative change in the flux is equivalent to the change of total counts per orbit. The color code for species is indicated in the panel. |
| In the text | |
 |
Fig. 11 Heliospheric abundance quotients calculated from the relative densities shown in Fig. 9 using Eq. (32) for the times and locations as for Fig. 9. |
| In the text | |
 |
Fig. 12 Daily fluxes of NIS He, Ne, and O scaled by respective density values at TS for the 2009 and 2012 observation seasons (Eq. (34)). The vertical bars mark the boundaries of orbital arcs, when the spin axis of the IBEX spacecraft was reoriented. The fluxes calculated assuming the NIS gas flow parameters obtained from IBEX analysis (Bzowski et al. 2012). |
| In the text | |
 |
Fig. 13 Orbit-averaged scaled fluxes for the conditions as for Fig. 12 for He, Ne, and O, simulated for the first four NIS gas observation seasons by IBEX. The sawtooth features are due to IBEX spin axis reorientation. |
| In the text | |
 |
Fig. 14 Flux abundance quotients ξflux,X/Y for the Ne/He, O/He, and Ne/O pairs calculated from the scaled fluxes integrated over IBEX spin phase and averaged over the orbits for the first four years of IBEX observations. |
| In the text | |
 |
Fig. 15 Relative change of the ξ quotients for the season-integrated flux (solid lines), densities at the ecliptic longitude where the NIS gas flow intersects the Earth’s orbit (broken lines), and time-dependent survival probabilities of the NIS atoms reaching IBEX at this location (dotted lines). All quantities are shown as ratios to the respective values in 2009. The color code for species pairs is indicated in the panel. |
| In the text | |
 |
Fig. 16 Abundance quotients calculated from various quantities discussed in the paper, divided by the flux quotient for the 2009 season, for all three pairs of NIS gas species. The figure illustrates the temporal evolution of the abundance quotients and differences between the quotients calculated using different definitions. Solid lines mark the NIS gas flow parameters obtained from IBEX (Bzowski et al. 2012), the broken line marks the flux quotient calculated for the gas inflow parameters obtained by Witte (2004) from GAS/Ulysses observations. |
| In the text | |
 |
Fig. 17 The Ne/O abundance in the LIC calculated from Eq. (20) for various combinations of NIS gas inflow longitude and speed, based on filtration factors and the Ne/O flux ratio measured at IBEX by Bochsler et al. (2012). The LIC abundances are listed at the line that is the correlation between the inflow longitude and speed obtained by Bzowski et al. (2012) from analysis of NIS He observations by IBEX-Lo. For the best-fit parameters obtained by Bzowski et al. (2012), the LIC abundance is 0.16, for the flow parameters obtained by Witte et al. (2004) from analysis of NIS He observations by GAS/Ulysses the abundance is 0.18. |
| In the text | |
 |
Fig. A.1 Time series of Carrington period-averaged photoionization rates of H, He, Ne, and O at 1 AU from the Sun. The color code denotes the various sources of data and proxies used, as discussed in the text. |
| In the text | |
 |
Fig. A.2 Cross sections for photoionization of neutral H, He, Ne, and O used in the calculations (Verner et al. 1996). The accuracy is at a ~5% level. Even though the ionization threshold energy for O and H are very similar, the cross section values for the low-energy portion, where the solar spectral flux is greatest, are substantially different. |
| In the text | |
 |
Fig. A.3 Scatter plot of model vs. data for photoionization models for He defined in Eq. (A.2) (left column), Eq. (A.3) (middle column), and Eq. (A.4) (right column), fit residuals (middle row), and histograms of the residuals (lower row). The red y = x lines are eye guides. The statistical uncertainties of the models are indicated in insets in the histogram panels. |
| In the text | |
 |
Fig. A.4 Scatter plot of model vs. data for photoionization models for Ne defined in Eq. (A.2) (left column), Eq. (A.3) (middle column) and Eq. (A.4) (right column), fit residuals (middle row), and histograms of the residuals (lower row). The red y = x lines are eye guides. The statistical uncertainties of the models are indicated in the insets in the histogram panels. |
| In the text | |
 |
Fig. A.5 Scatter plot of model vs. data for photoionization models for O defined in Eq. (A.6) (top row), Eq. (A.7) (second row from the top), Eq. (A.7) (third row from the top), and Eq. (A.8) (bottom row); fit residuals (middle column); histograms of the residuals (right column). The red y = x lines are eye guides. The statistical uncertainties of the models are indicated in the insets in the histogram panels. |
| In the text | |
 |
Fig. A.6 Cross sections of electron impact ionization for H, He, Ne, and O (Lotz 1967). The accuracies for H, He, and O are 10%, for Ne 15%. The vertical bars mark the energies corresponding to the temperatures of the core and halo solar wind electron populations in the slow solar wind at 1 AU from the Sun. The noble gases can only be ionized by a high-energy wing of the core population and mostly by the halo population. |
| In the text | |
 |
Fig. A.7 Products of relative speeds of reaction components and charge exchange cross sections for these speeds for the charge exchange reactions listed in the text (see Sect. 2.2). To obtain the actual charge-exchange rate, one has to multiply a quantity read off from the figure for a given speed by the local density of the ionized reaction component (solar wind proton, alpha particle). The lower horizontal axis is scaled in km s-1, the upper axis in energy per nucleon in keV. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.