| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 26 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201321700 | |
| Published online | 28 August 2013 | |
Online material
Appendix A: Modulation of the ionization rates of neutral He, Ne, O in the heliosphere
Appendix A.1: Photoionization rates of Ne, He, and O
The model of photoionization rates of NIS species used in this paper calculates Carrington rotation averages of H, He, O, Ne photoionization rates based on directly measured solar spectra from TIMED/SEE and CELIAS/SEM onboard SOHO and a hierarchy of solar EUV radiation proxies. The model of photoionization rates for hydrogen in the heliosphere was described by Bzowski et al. (2013), and here we focus on He, Ne, and O. Details of the derivation and discussion of instrumental and statistical uncertainties will be provided elsewhere (Sokół et al., in prep.; Bochsler et al., in prep.).
Basically, calculating the photoionization rate for a given species is simple. One
integrates the spectral flux of the Sun
F(λ,t) for
a wavelength λ and time t, multiplied by the cross
section 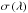 for a given species over an interval starting from 0 to the ionization threshold
wavelength λ0:
for a given species over an interval starting from 0 to the ionization threshold
wavelength λ0: 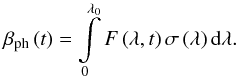 (A.1)For the cross
sections we adopted results from Verner et al.
(1996), see Fig. A.2.
(A.1)For the cross
sections we adopted results from Verner et al.
(1996), see Fig. A.2.
Regular measurements of the solar spectral flux are available only starting from 2002 owing to the TIMED experiment (Woods et al. 2005). Earlier, measurements in several spectral bands in the EUV above the ionization threshold of H, He, Ne, and O region (SEM/CELIAS/SOHO, Hovestadt et al. 1995) have been available since 1996. Fortunately, it has been demonstrated that the photoionization rates of many species are correlated with a number of other routinely measured quantities (proxies), including the MgII core-to-wing index (MgIIc/w, Heath & Schlesinger 1986; Viereck & Puga 1999), solar Lyman-α flux (Lyα, Woods et al. 1996, 2000), and the solar radio 10.7 cm flux (F10.7, Covington 1947; Tapping 1987). Thus, to infer a sufficiently long time series of photoionization rates of NIS species one can use proxies obtained from statistical analysis of the correlations.
The baseline of the model is the solar spectrum measured by TIMED/SEE (Woods et al. 2005) during a few years after launch, when the solar activity was going down from the maximum to minimum values and the absolute calibration of the instrument was the most reliable. These portions of the time series (calculated separately for each species) are shown in red in Fig. A.1. We used measurements of two-hours resolution in time and calculated the photoionization rates using Eq. (A.1). We filtered the results against flares and particle background and calculated Carrington rotation averages. Owing to suspected unaccounted degradation of the TIMED/SEE detector we decided to use only a few first years of the TIMED measurements, namely the first 27 Carrington rotations from 22 January 2002 for He and Ne, and 74 Carrington rotations for H and O. These data are shown in red in Fig. A.1.
For other times we developed a set of proxies by taking statistical correlation between the directly calculated values and the solar EUV radiation proxy. The hierarchical set of proxies is based on the chromospheric MgIIc/w index available from 1978 as released by LASP (Heath & Schlesinger 1986; Viereck & Puga 1999; Viereck et al. 2004), the F10.7 flux released by NOAA and DRAO (Tapping 1987) available from 1947, and the composite Lyman-α flux published by LASP (available from 1947, but based on actual UV observations from mid-1970-ties, with some gaps filled by proxies developed by the LASP team, see Woods et al. 2000). As the most reliable proxy we chose the CELIAS/SEM data (Hovestadt et al. 1995), which are measurements of the fragments of the solar spectrum responsible for most of the helium ionization.
The hierarchy of photoionization-rate retrieval we used was similar for He and Ne, since they show similar properties, and a different one for H and O, because they have the same ionization threshold energy (see photoionization cross sections in question in Fig. A.2).
The procedure for building the time series for the noble gases was as follows. In the first step we used the EUV flux in the two spectral bands measured by CELIAS/SEM onboard SOHO, which has been available since 1996. The first-order flux (26−34 nm, here referred to as Ch1) and the central order flux (0.1−50 nm, here referred to as Ch2) were considered. We found, for each species separately, a linear correlation between the daily time series of photoionization rates from the TIMED and SEM time series for the chosen time intervals from the TIMED data.
The general formula to calculate photoionization rate from SEM data (darker blue line
in Fig. A.1) is 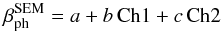 (A.2)with
the parameter values for He and Ne shown in Table A.1. From this formula we calculate daily photoionization rates, which are
further used to compute the Carrington-rotation averaged time series that we use as a
basis for further studies.
(A.2)with
the parameter values for He and Ne shown in Table A.1. From this formula we calculate daily photoionization rates, which are
further used to compute the Carrington-rotation averaged time series that we use as a
basis for further studies.
The time coverage of the SEM data is not quite long enough for modeling heliospheric ionization processes. The travel of NIS atoms from 150 AU takes about 30 years or more, even though most of the ionization losses occur inside ~10 AU from the Sun. Thus it is desirable to have a homogeneously prepared time history of the ionization rates in the heliosphere dating back as far as possible, so that one model can be used to analyze both present and past measurements, such as those obtained from Ulysses.
To extend the photoionization time series backwards we used the mentioned hierarchy of solar EUV radiation proxies (MgIIc/w, Lyman-α, and F10.7). We found the correlation between individual proxies or their combinations and Carrington-rotation averaged photoionization rates obtained using the aforementioned EUV measurements. We then used them to reproduce the historical record of photoionization rates of He, Ne, and O dating backward to 1948. The following formulae yield the photoionization rates with the highest correlation coefficients. The results of the goodness of those correlations are gathered in Figs. A.3 and A.4 for He and Ne, respectively, and in Fig. A.5 for O.
 |
Fig. A.1
Time series of Carrington period-averaged photoionization rates of H, He, Ne, and O at 1 AU from the Sun. The color code denotes the various sources of data and proxies used, as discussed in the text. |
| Open with DEXTER | |
 |
Fig. A.2
Cross sections for photoionization of neutral H, He, Ne, and O used in the calculations (Verner et al. 1996). The accuracy is at a ~5% level. Even though the ionization threshold energy for O and H are very similar, the cross section values for the low-energy portion, where the solar spectral flux is greatest, are substantially different. |
| Open with DEXTER | |
The formula to calculate the photoionization rate from the
MgIIc/w index and adjusted F10.7 index expressed in
the sfu units (i.e.,10-22 W m-2 Hz-1; darker green
line in Fig. A.1) is the following, with the
coefficients listed in Table A.2: 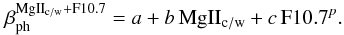 (A.3)The formula for
calculating the photoionization rate using only the F10.7 proxy is
(A.3)The formula for
calculating the photoionization rate using only the F10.7 proxy is 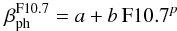 (A.4)with
the coefficients available in Table A.3. It is
drawn with the gray line in Fig. A.1. The
exponent in the F10.7 flux is close to 1/2, not 1, as was frequently adopted in the
past.
(A.4)with
the coefficients available in Table A.3. It is
drawn with the gray line in Fig. A.1. The
exponent in the F10.7 flux is close to 1/2, not 1, as was frequently adopted in the
past.
The procedure for oxygen is very similar to the procedure used for hydrogen,
described in Bzowski et al. (2013). The SEM
data are correlated with the TIMED/SEE observations and the Lyman-α
(Lyα) composite flux, according the formula using only
Carrington-rotation averaged time series (lighter blue line in Fig. A.1): 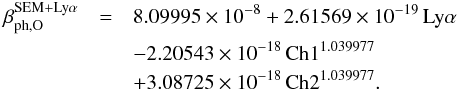 (A.5)When
the composite Lyman-α flux is not available, a formula with only the
Carrington-rotation averaged SEM data is used:
(A.5)When
the composite Lyman-α flux is not available, a formula with only the
Carrington-rotation averaged SEM data is used: 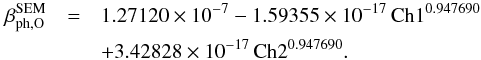 (A.6)When
SEM data are not available, we use a correlation of the Carrington-rotation averaged
TIMED/SEE flux and MgIIc/w index (lighter green line in
Fig. A.1):
(A.6)When
SEM data are not available, we use a correlation of the Carrington-rotation averaged
TIMED/SEE flux and MgIIc/w index (lighter green line in
Fig. A.1): 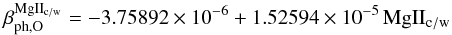 (A.7)
(A.7)
 |
Fig. A.3
Scatter plot of model vs. data for photoionization models for He defined in Eq. (A.2) (left column), Eq. (A.3) (middle column), and Eq. (A.4) (right column), fit residuals (middle row), and histograms of the residuals (lower row). The red y = x lines are eye guides. The statistical uncertainties of the models are indicated in insets in the histogram panels. |
| Open with DEXTER | |
 |
Fig. A.4
Scatter plot of model vs. data for photoionization models for Ne defined in Eq. (A.2) (left column), Eq. (A.3) (middle column) and Eq. (A.4) (right column), fit residuals (middle row), and histograms of the residuals (lower row). The red y = x lines are eye guides. The statistical uncertainties of the models are indicated in the insets in the histogram panels. |
| Open with DEXTER | |
 |
Fig. A.5
Scatter plot of model vs. data for photoionization models for O defined in Eq. (A.6) (top row), Eq. (A.7) (second row from the top), Eq. (A.7) (third row from the top), and Eq. (A.8) (bottom row); fit residuals (middle column); histograms of the residuals (right column). The red y = x lines are eye guides. The statistical uncertainties of the models are indicated in the insets in the histogram panels. |
| Open with DEXTER | |
and from 1948 until the beginning of the MgIIc/w time
series in 1978, the photoionization rates for O come from the correlation formula for
the F10.7 flux (gray line in Fig. A.1) based on
the comparison with Carrington-rotation averaged TIMED/SEE data: 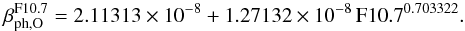 (A.8)This model
calculates Carrington rotation averages of the ionization rates. Extending the proxies
into sub-Carrington time scale requires further careful studies related to possible
limb darkening/brightening effects that may be present in some proxies but absent in
the EUV flux contributing to photoionization. Since in the present study we only need
Carrington-rotation averaged time series, we leave this aspect for future analysis.
(A.8)This model
calculates Carrington rotation averages of the ionization rates. Extending the proxies
into sub-Carrington time scale requires further careful studies related to possible
limb darkening/brightening effects that may be present in some proxies but absent in
the EUV flux contributing to photoionization. Since in the present study we only need
Carrington-rotation averaged time series, we leave this aspect for future analysis.
It is interesting to note that the photoionization rate for H and He are almost identical during solar maximum, but differ up to 40% during solar minimum. Also worth pointing out is the difference between the photoionization rates of H and O despite their almost identical ionization threshold. This is because of differences in the photoionization cross sections between these species.
Appendix A.2: Electron impact ionization of Ne, He, and O
The physical aspects of ionization of neutral heliospheric gas by solar wind electrons impacts were originally proposed by Ruciński & Fahr (1989, 1991) for He. Bzowski (2008) developed a model of electron ionization rate for H using measurements of electron distribution function from Ulysses (Salem et al. 2001; Issautier et al. 2001, 2008), carried out between ~1.5 and ~5.5 AU from the Sun, which were recently discussed by Bzowski et al. (2013). The distribution function is approximated by a bi-Maxwellian model that includes the dominating cool core and the secondary hot halo populations, with the abundance of the latter increasing towards increasing heliocentric distances. Under these assumptions, and also the assumption of the quasi-neutrality of solar wind, one can calculate a radial model of electron ionization rate for all species in question (Scime et al. 1994, Fig. 2).
The model values are proportional to solar wind density plus twice the alpha particle content, which approximate the solar wind electron densities and which are taken from the solar wind proton density model used to calculate the charge exchange rates. An extensive discussion of the background solar wind electron temperature model is presented in Bzowski (2008) and Bzowski et al. (2013).
In our calculation we follow the approach presented in these papers. We approximate the solar wind electron distribution function as bi-Maxwellian, with the dominating cool core and hot halo. The temperatures and relative densities of the core and halo populations evolve with the heliocentric distance, as measured by Ulysses (Scime et al. 1994). Calculating the electron ionization rate requires folding the local electron distribution function with the reaction cross section and integrating from the threshold ionization energy to infinity. In this paper we use only a model for the slow solar wind because the NIS atoms in question travel close to the ecliptic plane at all times. The reader is referred to Eqs. (A.9) in Bzowski (2008) for the adopted radial profiles of the core and halo temperatures and (A.11) for the evolution of the abundance of the halo population relative to the core.
 |
Fig. A.6
Cross sections of electron impact ionization for H, He, Ne, and O (Lotz 1967). The accuracies for H, He, and O are 10%, for Ne 15%. The vertical bars mark the energies corresponding to the temperatures of the core and halo solar wind electron populations in the slow solar wind at 1 AU from the Sun. The noble gases can only be ionized by a high-energy wing of the core population and mostly by the halo population. |
| Open with DEXTER | |
The cross sections were taken from Lotz (1967) and are presented in Fig. A.6. They seem accurate and reliable enough in the entire range of energies needed for our purposes and are consistent with more recent studies (Godunov &Ivanov 1999; Bartlett & Stelbovics 2004; Mattioli et al. 2007). The two vertical bars in this figure represent the energy equal to kTe for the temperatures of the core and halo populations at 1 AU from the Sun. They show that He and Ne are ionized predominantly by the halo population, with only the fastest wing of the core population being energetic enough to ionize, while H and O are ionized by both core and halo populations. The temperatures of both populations decrease with solar distance, and the farther from the Sun, the smaller the portion of the total electron population capable of ionizing the heliospheric species. The electron impact ionization contributes only ~10% to the total ionization rate at 1 AU from the Sun, and beyond ~5 AU from the Sun it becomes practically negligible. The electron impact rate is a linear function of the local electron density.
The ionization rate for the core and halo populations was tabulated as a function of
solar distance assuming nsw = 1 cm-3 and then
an analytic approximation formula was fitted separately for each species. Here we
present the resulting formulae to calculate the electron impact ionization in the slow
and fast solar wind regime. In the formulae below,
nsw(r,t)
is solar wind proton density at heliocentric distance r in AU, in
time t, the logarithms are natural: 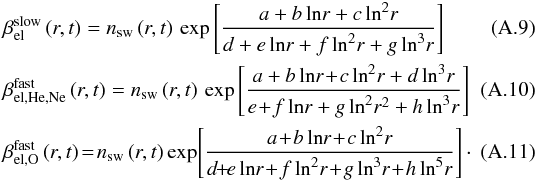 The
coefficients are gathered in Tables A.4 and
A.5. Throughout the paper we assume that the
solar wind proton density decreases with heliocentric distance as
1/r2. The
βel rate in our model is tied to the local solar wind
density
nsw(r,t)
and consequently it is calculated as a function of time, similarly to
nsw(r,t).
The
coefficients are gathered in Tables A.4 and
A.5. Throughout the paper we assume that the
solar wind proton density decreases with heliocentric distance as
1/r2. The
βel rate in our model is tied to the local solar wind
density
nsw(r,t)
and consequently it is calculated as a function of time, similarly to
nsw(r,t).
The ionization rates obtained using the presented model are consistent with the rates published by Arnaud & Rothenflug (1985), which for He0, Ne0, and O0 are based on the cross sections and approximation formulae from Lotz (1967).
Appendix A.3: Charge exchange rates for He, Ne, and O
In addition to the photoionization and electron impact rates discussed in the last section, the ionization processes relevant for neutral heliospheric species include charge exchange. The charge exchange reaction was recently discussed by Bzowski et al. (2013) for heliospheric H and most of the theory applies for O, Ne, and He.
The charge exchange cross sections for He and O used in the present paper come from Lindsay & Stebbings (2005) and for Ne from Nakai et al. (1987). Figure A.7 shows the product of the relative speed of the component of the reaction and cross section for charge exchange for the NIS species observed by IBEX. To obtain an instantaneous charge exchange rate, the value taken from the figure for a given speed must be multiplied by the local ion density, which is assumed to fall off with r2 and is a function of heliolatitude and time (Sokół et al. 2013). The figure explains the huge differences between the charge exchange rates for H and O, on one hand, and for the noble gases, on the other, and illustrates that charge exchange rates are not linear functions of the collision speed, as frequently approximated.
 |
Fig. A.7
Products of relative speeds of reaction components and charge exchange cross sections for these speeds for the charge exchange reactions listed in the text (see Sect. 2.2). To obtain the actual charge-exchange rate, one has to multiply a quantity read off from the figure for a given speed by the local density of the ionized reaction component (solar wind proton, alpha particle). The lower horizontal axis is scaled in km s-1, the upper axis in energy per nucleon in keV. |
| Open with DEXTER | |
The calculations were performed using Carrington-rotation averaged solar wind proton
densities and speeds from the formula Eq. (A.12). The values thus obtained are approximate because the atom speed is
assumed to be 0. In the simulations shown in the main text, we use the full formula
with | vrel| =
| vsw − vatom |
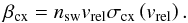 (A.12)vsw
and nsw were calculated for a given instant of time
t and heliolatitude φ from bilinear interpolation
between the grid nodes fixed at halves of Carrington rotations and full tens of
degrees heliolatitude (see Sokół et al. 2013).
For the dependence on heliocentric distance r, proton density
nsw was assumed to conform to the
1/r2 dependence and
vsw was assumed to be distance independent.
(A.12)vsw
and nsw were calculated for a given instant of time
t and heliolatitude φ from bilinear interpolation
between the grid nodes fixed at halves of Carrington rotations and full tens of
degrees heliolatitude (see Sokół et al. 2013).
For the dependence on heliocentric distance r, proton density
nsw was assumed to conform to the
1/r2 dependence and
vsw was assumed to be distance independent.
Appendix A.4: Total ionization rates for He, Ne, and O
The total ionization rates for NIS species are algebraic sums of rates of all relevant ionization processes. Figure 1 presents the total ionization rates of the contributing reactions for the NIS species observed by IBEX. For the noble gases, the main reaction is photoionization, and the next is electron impact ionization, which gives ~10% input to the total rate. The rate of charge exchange with solar wind protons (and alphas in the case of helium) is very low, most of the time much less than 1% of the total rate. The case of oxygen is more complex. During the previous minimum in 1996, the photoionization and charge exchange rates were comparable (~45% input each to the total rate), but since 1998 the input from charge exchange decreased (to ~35%) and photoionization became dominant (more than 50%).
The total ionization rates for He and Ne show a clear modulation with solar activity because they mainly depend on
photoionization, which varies quasi-periodically with the solar activity cycle. The ionization rate for O does not show a clear modulation with the solar activity cycle because it is a sum of a quasi-periodic component from photoionization and a time-dependent, but not periodic, component from charge exchange and electron impact. Owing to the similarity of the first ionization potential for H and O, it is usually assumed that the total ionization rates of these species should be very similar. Our analysis shows that it is true most of the time, but not always: the ionization rate for O was higher than for H for a couple of years during the previous solar maximum and it seems that this behavior is going to repeat during the forthcoming maximum as well. The ionization rate of H shown in Fig. 1 is taken from Bzowski et al. (2013) and shown here for comparison.
The uncertainties of the ionization rates used in this work will be the subject of separate paper (Sokół et al., in prep.). They arise from uncertainties in the reaction cross sections, from uncertainties of the measured quantities (the solar wind and solar EUV output), from the statistical uncertainties of the proxies used, and from simplifications used in the models. We estimate that the overall uncertainty in the total ionization rates is 15−20%. The statistical uncertainties of the proxy models are indicated in the figures of histograms (see Figs. A.3, A.4, A.5). The other uncertainties are listed in Table 1.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


