Integrand function in Eq. (3) for an O atom on the orbit whose perihelion is at the location of the Earth at the time corresponding to IBEX Orbit 16 in 2009 (λ_E = 130°). The red line is the 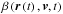from Eq. (1), taken along the orbit of the atom. The model used in 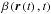is time dependent and has a component of electron impact rate, which does not follow the 1/r² dependence. The dark-blue line is the integrand function calculated for 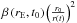, i.e., assuming that the ionization rate is equal to the ionization rate from our model calculated for the instant of detection t₀. The history of the radial distance of the atom from the Sun is shown in the lower right inset and is identical for the red and dark-blue lines. The upper-left inset presents the ratio of the actual ionization rate for atoms following this trajectory and the rate used in the analytical model 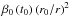. To obtain the survival probability, one must calculate the exponent of the time integral of the function drawn in red, see Eqs. (2) and (3). The analytic approximation is equivalent to taking the exponent of the integral of the function drawn with the blue line, i.e., to evaluating the exponent of the expression from Eqs. (2) and (4).