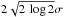| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 22 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321596 | |
| Published online | 11 September 2013 | |
Thermodynamic fluctuations in solar photospheric three-dimensional convection simulations and observations⋆
1
Instituto de Astrofísica de Canarias (IAC), Calle Vía Láctea s/n, 38205 La Laguna,
Tenerife, Spain
2
Departamento de Astrofísica, Universidad de La Laguna
(ULL), 38206,
La
Laguna, Tenerife,
Spain
3
National Solar Observatory (NSO), 3010 Coronal Loop, 88349
Sunspot, New Mexico, USA
e-mail:
cbeck@iac.es; damian@iac.es; fmi@iac.es
4
Leibniz-Institut für Astrophysik Potsdam (AIP) ,
An der Sternwarte
16, 14482
Potsdam,
Germany
e-mail:
kgp@aip.de
5
Kiepenheuer-Institut für Sonnenphysik (KIS),
Schöneckstr. 6,
79104
Freiburg,
Germany
e-mail:
rrezaei@kis.uni-freiburg.de
Received:
28
March
2013
Accepted:
23
June
2013
Context. Numerical three-dimensional (3D) radiative (magneto-)hydrodynamical [(M)HD] simulations of solar convection are nowadays used to understand the physical properties of the solar photosphere and convective envelope, and, in particular, to determine the Sun’s photospheric chemical abundances. To validate this approach, it is important to check that no excessive thermodynamic fluctuations arise as a consequence of the partially incomplete treatment of radiative transfer causing radiative damping that is too modest.
Aims. We investigate the realism of the thermodynamics in recent state-of-the-art 3D convection simulations of the solar atmosphere carried out with the Stagger code.
Methods. We compared the characteristic properties of several Fe i lines (557.6 nm, 630 nm, 1565 nm) and one Si i line at 1082.7 nm in solar disc-centre observations of different spatial resolution with spectra synthesized from 3D convection simulations. The observations were taken with ground-based (Echelle spectrograph, Göttingen Fabry-Pérot Interferometer (GFPI), POlarimetric LIttrow Spectrograph, Tenerife Infrared Polarimeter, all at the Vacuum Tower Telescope on Tenerife) and space-based instruments (Hinode/Spectropolarimeter). We degraded the synthetic spectra to the spatial resolution of the observations, based on the distribution of the continuum intensity Ic. We estimated the spectral degradation to be applied to the simulation results by comparing atlas spectra with averaged observed spectra. In addition to deriving a set of line parameters directly from the intensity profiles, we used the SIR (Stokes Inversion based on Response functions) code to invert the spectra.
Results. The spatial degradation kernels yield a similar generic spatial stray-light contamination of about 30% for all instruments. The spectral stray light inside the different spectrometers is found to be between 2% and 20%. Most of the line parameters from the observational data are matched by the degraded HD simulation spectra. The inversions predict a macroturbulent velocity vmac below 10 m s-1 for the HD simulation spectra at full spatial resolution, whereas they yield vmac ≲ 1000 m s-1 at a spatial resolution of 0.″3. The temperature fluctuations in the inversion of the degraded HD simulation spectra do not exceed those from the observational data (of the order of 100−200 K rms for −2 ⪅ log τ500 nm ⪅ −0.5). The comparison of line parameters in spatially averaged profiles with the averaged values of line parameters in spatially resolved profiles indicates a significant change in (average) line properties on a spatial scale between 0.″13 and 0.″3.
Conclusions. Up to a spatial resolution of 0.″3 (GFPI spectra), we find no indications of excessive thermodynamic fluctuations in the 3D HD simulation. To definitely confirm that simulations without spatial degradation contain fully realistic thermodynamic fluctuations requires observations at even higher spatial resolution (i.e. <0.″13).
Key words: Sun: photosphere / methods: data analysis / line: profiles
Appendices A and B are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The abundances of chemical elements in the solar atmosphere are crucial as a reference for chemical abundances throughout the universe, with a profound influence on planetary science, stellar evolution theory, or the interpretation of stellar spectra. Solar abundances are commonly derived from comparisons between observed spectral lines and theoretical spectra from atmospheric models with a varying degree of sophistication (see Asplund et al. 2005, and references therein). Such models range from static one-dimensional (1D) atmospheres treated in local thermal equilibrium (LTE) to dynamical three-dimensional (3D) atmospheres with a non-LTE treatment (e.g. Shchukina et al. 2012).
For static 1D solar atmosphere models, such as those of Holweger & Mueller (1974), Vernazza et al. (1981), Fontenla et al. (2006), and variations thereof, one must first adopt values for the solar abundance of the various chemical elements to derive a temperature stratification through the comparison of observed and synthetic spectra, using both the locations of bound-free edges, i.e. the limiting wavelength of relevant ionization transitions, and the shape of spectral lines. However, the retrieved temperature stratifications of the atmospheres are then used to derive the abundances by comparison of up to a few tens of resulting synthetic spectral lines to observations. This is therefore partly a case of circular reasoning, with the abundances as both input and output parameters.
Another problem of static 1D models is that the dynamical nature of the solar atmosphere cannot be consistently taken into account. Resolved or unresolved velocities can only be partly included in the static 1D models by using generic macroturbulent (vmac) and microturbulent (vmic) velocities. These are free parameters that show a certain degree of degeneracy when one tries to disentangle different contributions to the formation process of spectral lines (Allende Prieto et al. 2001).
The accuracy of the information about dynamical variations provided by observations is also always limited, since observed spectra suffer from the combined effects of limited spatial, spectral, and temporal resolution. The accurate retrieval of all thermodynamic parameters needed for an exact characterization of the dynamics, such as temperature, mass velocities, and mass densities, is therefore only partly possible on the observational side.
To obtain a realistic dynamical model of the solar atmosphere, one thus has to resort to numerical simulations. The growing available computing power has made it possible to run increasingly large-scale and higher-sampling multi-dimensional calculations solving the complex set of coupled differential equations necessary to model the relevant physics in the solar photosphere (e.g. Nordlund & Stein 1990; Steiner et al. 1998; Stein & Nordlund 1998). When one attempts, however, to extend such simulations to cover also the solar chromosphere, non-LTE effects appear that cannot be (fully) included in 3D numerical simulations that are of a sufficiently large scale while remaining computationally feasible (cf. Rammacher & Cuntz 1991; Skartlien 2000; Asplund et al. 2003; Leenaarts et al. 2007, 2009; Hayek et al. 2010; Wedemeyer-Böhm & Carlsson 2011; Carlsson & Leenaarts 2012; Leenaarts et al. 2012). Similarly, a possible problem of photospheric simulations is that radiative transfer through the atmosphere can only be included in an approximate way, commonly by using opacity binning (e.g. Nordlund 1982; Skartlien 2000; Vögler 2004; Vögler et al. 2004).
Nonetheless, the results of such numerical simulations are considered realistic enough to be used in approaches to determine solar abundances (e.g. Asplund et al. 2000). The advantages of these simulations are that they cover the dynamics of mass motions without the need to resort to ad-hoc parameters such as vmac or vmic. Furthermore, they directly contain all information, including especially the gas density, on an absolute geometrical height scale, while, e.g., spectral line inversions just provide information of physical parameters on an optical depth scale. The conversion to a geometrical height scale is in the latter case not straightforward, needing sophisticated methods and certain assumptions commonly in the form of a boundary condition on electron (or gas) pressure or density (e.g. Sánchez Almeida 2005; Puschmann et al. 2005, 2010; Beck 2011).
However, the use of 3D hydrodynamical (HD) simulations coupled with improved atomic data and differences in equivalent width measurements retrieved from observations resulted in the course of the last decade in a downward revision of the solar abundance of mainly C, N and O (Asplund et al. 2005, 2009), which significantly deteriorated the previous agreement between predicted and observed sound speeds in the solar interior derived from helioseismology (Bahcall et al. 2005). We note that, where available, non-LTE corrections (e.g. Fabbian et al. 2009a,b) were included in the abundance determination from simulations (cf. Asplund et al. 2009, and references therein). More recently, magnetic fields have been suggested as another source of appreciable uncertainty (Fabbian et al. 2010, 2012).
Kalkofen (2012) made an interesting comment about the use of simulation results as a reference. The atomic abundances are usually derived by matching the observed solar spectrum with the space- and/or time-averaged synthetic line profiles from the simulations. In the averaging process, the thermodynamic properties of the simulations are smeared out. Because of the simplified treatment of the radiative transfer in the simulations, an important damping factor could be missing. This could lead to unrealistic/excessive thermodynamic fluctuations both in temperature and mass motions. As a consequence of, e.g., too large velocity fluctuations, the average predicted profile would become too broad, thus leading to a downward revision of the solar abundance reference of a given chemical element, as derived by matching observational spectra. The argument by Kalkofen (2012) is based on the fact that the intrinsic thermodynamic parameters in simulations at full spatial resolution were investigated only partially up to now.
The agreement of synthetic and observed data was verified in terms of the contrast of continuum intensity, both at disc centre and for its centre-to-limb (CLV) variation (e.g. Asplund et al. 2000; Wedemeyer-Böhm & Rouppe van der Voort 2009; Asplund et al. 2009; Afram et al. 2011), as well as in terms of the match between average synthetic and observed profiles (e.g. Asplund et al. 2000). Spatially resolved profiles were later also studied for comparison purposes (Pereira et al. 2009c). All of these comparisons, however, have a clear limitation: the observations employed always have a lower spatial resolution than the original simulations,whose spatial grid size can be as small as several km. The good match with observations that was achieved in the aforementioned studies therefore proves that the simulations can be spatially and spectrally degraded to the properties of the observations, but it actually does not exclude excessively large thermodynamic fluctuations in the simulations themselves, as pointed out by Danilovic et al. (2008).
In this paper, we investigate the realism of the thermodynamics in numerical 3D convection simulations by comparing disc-centre observations in several spectral lines with the results from simulations. This shall serve as the first step in a thorough derivation of the solar oxygen abundance using the same set of simulations. In a subsequent study, we will turn to the CLV of selected spectral lines and in the continuum, which can allow one to calibrate the efficiency of H collisions in non-LTE calculations or to constrain the temperature stratification.
Instruments and data properties, and corresponding settings of the spectral synthesis for the simulations.
Sections 2 and 3, respectively, describe the observations and the modelling employed here. The data reduction and the analysis methods are explained in Sect. 4. Results are presented in Sect. 5 and are discussed in Sect. 6. Section 7 provides our conclusions. The Appendices contain the results for some of the spectral lines not discussed in the main text.
2. Observations
We used several quiet-Sun (QS) observations at disc centre taken with different instruments and telescopes (see Table 1). We introduce them here divided into three groups:
-
(a)
The infrared range. For all spectral lines in the (near)-infrared(IR) range (Si i 1082.7 nm,Fe i 1564.8 nm,Fe i 1565.2 nm), the Tener-ife Infrared Polarimeter (TIP; Martínez Pilletet al. 1999; Colladoset al. 2007) at the GermanVacuum Tower Telescope (VTT; Schröteret al. 1985) was em-ployed. The data in these lines were large-area scans.The data at 1083 nm were taken dur-ing a velocity calibration campaign of the CHROmo-spheric TELescope (CHROTEL; Bethgeet al. 2011) on 08 December2007 between UT 10:02:35 and 10:17:55. The data at 1565[en-tity!#x2009!]nm were taken on 21 May 2008 from UT 08:44:18until 08:51:43, in between the two long-integrated data setsused in Beck & Rezaei (2009), and cover thesame field of view (FOV) as the data presented in the latter article.Spatial and spectral sampling, total FOV, the integration timeand the approximate number of profiles in the FOV are listed inTable 1. The integration time denotes the totalexposure time that entered in a single measurement of the fullStokes vector at one wavelength position or one slit position.
-
(b)
The 630 nm lines. The data in the Fe i line at 630.25 nm, taken with the Göttingen Fabry-Pérot Interferometer (GFPI; Puschmann et al. 2006; Bello González & Kneer 2008) at the VTT on 07 June 2009, are described in detail in Puschmann & Beck (2011, PuB11). We use the same spectral scan as those authors, with data reduced on the one hand with the multi-object multi-frame blind deconvolution (MOMFBD; van Noort et al. 2005) method, and on the other hand only destretched to a reference image that was speckle-reconstructed with the method of Puschmann & Sailer (2006). The spectral line was sampled on 28 wavelength steps. The data at 630 nm from the POlarimetric LIttrow Spectrograph (POLIS; Beck et al. 2005a,b) were taken simultaneously to the TIP data in 1082.7 nm on 08 Dec. 2007. Bethge et al. (2012) discuss another example of data taken with this setup on the same day. The Hinode/Spectropolarimeter (SP; Kosugi et al. 2007; Tsuneta et al. 2008) map was taken during HOP 0190 on 05 Sep. 2011 between UT 07:34:50 and 07:59:03. The FOV was in this case located slightly off disc centre at a heliocentric angle of less than 10 degrees, which should, however, not have a strong impact on the spectra.
-
(c)
The 557 nm range. All the observations described so far provided Stokes vector measurements that allow one to locate any magnetic flux of sufficient strength inside the FOV and to determine the magnetic field properties. Data from a wavelength range around 557 nm were used in addition. They correspond to a part of the CLV observations that we collected as an ingredient to be used in the derivation of the solar oxygen abundance (Fabbian et al., in prep.), as a reappraisal of previous literature estimates (cf. Asplund et al. 2004; Meléndez & Asplund 2008; Pereira et al. 2009c,a). These spectra were obtained with the Echelle spectrograph of the VTT at high spectral resolution (λ/Δλ ~ 1 000 000), but without polarimetry. Additionally to an O i line at 557.7 nm, the spectral range encompassed also the strong Fe i line at 557.6 nm. We therefore included in the present study a disc-centre data set that we collected on 21 Nov. 09 between UT 08:50 and 09:05.
All ground-based observations profited from the real-time correction of seeing by the Kiepenheuer-Institut adaptive optics (AO) system (von der Lühe et al. 2003) at the VTT.
3. Convection simulations and spectral synthesis
The synthetic spectra used in our analysis are based on a set of 3D solar convection simulations obtained and described by Fabbian et al. (2010, 2012) that were carried out using the Stagger code (cf. Stein et al. 2011; Kritsuk et al. 2011; Beeck et al. 2012). The simulation box spanned approximately 6 × 6 Mm2 horizontally, covering ~15 granules at any given time, with 252 equidistant points in each direction, resulting in a horizontal grid spacing of ~24 km. The height range was covered by 126 grid points, reaching from ~0.5 Mm above the height corresponding to the optical depth unity (τ500 nm = 1) level down to ~2.0 Mm below it, with non-uniform vertical sampling having a finest spacing of about 15 km.
The Stagger code uses a sixth-order finite differences spatial scheme and a third-order Runge-Kutta temporal scheme to solve the equations for the conservation of mass, momentum and energy. At the same time, the radiative transfer equation is solved assuming LTE, in this instance along nine rays (one per octant, plus the vertical). Four opacity bins were employed to model the wavelength dependency of the radiation field. For more details on the opacity binning technique adopted in the code see Nordlund (1982), Collet et al. (2011) and Beeck et al. (2012).
The effective temperature in the simulation snapshots is controlled by the (fixed) entropy
density condition imposed on fluid flowing in from the bottom boundary. This parameter was
adjusted so that the resulting Teff in the atmospheric models
(about 5730 K) was within less than one percent of the solar effective temperature derived
from observations. Fabbian et al. (2012, their Fig.
2) have shown that the continuum intensity computed for the same series of
snapshots as employed here agrees reasonably well with literature data, albeit being
slightly ( 5%)
lower (cf. also the bottom left panel in Fig. 8 below).
The variation of the emerging radiative flux at the surface for the different
(magneto)-hydrodynamical [(M)HD] cases corresponds to an uncertainty on
Teff of the order of 0.2% only, i.e. about 10 K. The
simulation runs covered the field-free purely HD case and three MHD cases with a vertical
unipolar magnetic flux density of 50, 100, and 200 G, respectively.
5%)
lower (cf. also the bottom left panel in Fig. 8 below).
The variation of the emerging radiative flux at the surface for the different
(magneto)-hydrodynamical [(M)HD] cases corresponds to an uncertainty on
Teff of the order of 0.2% only, i.e. about 10 K. The
simulation runs covered the field-free purely HD case and three MHD cases with a vertical
unipolar magnetic flux density of 50, 100, and 200 G, respectively.
In the present investigation we selected only the last snapshot of the statistically stationary regime of each (M)HD run. The spectral synthesis was performed using the LTE code LILIA (Socas-Navarro 2001). For this step, the appropriate input data corresponding to the chosen snapshot were prepared by trimming the simulation results to a vertical extent ranging from ~+ 425 km above the average τ500 nm = 1 level to ~−475 km below it, and by interpolating to a grid of equidistant points over the new physical depth. Those heights correspond to an optical depth range from about log τ500 nm ≈ −4 to log τ500 nm ≈ + 2, but with some variation across the FOV. The final input data cube had 115 depth points with a constant, finer vertical grid spacing of ~7.8 km, which was better suited to our spectral synthesis purpose.
Finally, for the spectral synthesis we also reduced the horizontal sampling to only include
63 × 63 grid points (without binning or averaging of the corresponding physical values)
distributed over the same area as that of the original snapshot. Tests done for Fabbian et al. (2012) indicated that this approach does
not introduce any kind of bias in the resulting set of synthetic spectra, while still
providing a sufficiently large statistical base of about 4000 independent spectra. The final
spatial sampling then corresponded to 0 13, which is more
than twice better than the best spatial resolution in the observations (cf. Table 1).
13, which is more
than twice better than the best spatial resolution in the observations (cf. Table 1).
The spectral sampling for all synthetic lines was set to 0.5 pm. The synthetic spectra were computed using the Van der Waals broadening formula in the approximation of Unsöld (1955). The default solar abundance adopted by LILIA was used, i.e. the one given in Grevesse (1984), according to which the logarithmic solar abundance of iron is log (Fe) = 7.5 dex for the Sun, on the usual scale of 1012 atoms of hydrogen, i.e. log (H) = 12.0 dex.
The spectral lines considered in the present study form in the low to mid photosphere (cf. Cabrera Solana et al. 2005). All of them can be assumed to behave close to LTE except for the Si i line at 1082.7 nm, where the line core is sensitive to non-LTE effects and to a lesser amount sensitive to 3D effects (e.g. Wedemeyer2001; Shchukina & Trujillo Bueno2001; Shi et al.2008; Shchukina et al.2012; see also the corresponding sections in Asplund2005). The line core of the Si i line also forms in the uppermost layers of the simulation box (up to 0.5 Mm height; Bard & Carlsson 2008; Felipe et al. 2010) where the results of both the simulation and the spectral synthesis become less reliable.
4. Data reduction and analysis methods
4.1. Intensity normalization
For all observed or synthetic spectral lines up to 1.1 μm, we used the FTS atlas spectrum (Kurucz et al. 1984; Neckel 1999) as a reference. For spectra at longer wavelengths, data from the BASS20001 spectral database (Delbouille et al. 1973) were used. To correct for spectral intensity gradients in the observations (compare the blue-dotted and black curves in Fig. 1), we matched the continuum intensity of average observed spectra to the corresponding section of the atlas spectra in wavelength ranges outside (strong) spectral lines. Mismatches outside the wavelength range relevant for the derivation of the line parameters were ignored (e.g. the region at 630.07 nm in Fig. 1). The continuum intensity was normalized as in the case of the reference atlas spectra. The intensity normalization of all synthetic spectra from the simulations was always done fully analogously to the observations, i.e. with the atlas spectra as reference.
 |
Fig. 1 Example spectrum at 630 nm from POLIS. Blue-dotted line: average spectrum without correction for intensity gradients over the wavelength range. Black line: corrected spectrum. Red line: FTS atlas spectrum. The dashed vertical lines denote the “continuum” range, the solid vertical lines the range that was considered for determining the line parameters of Fe i 630.15 nm and Fe i 630.25 nm, respectively. The coloured horizontal lines inside the absorption profiles illustrate the method used to determine line properties at different line depression levels. |
 |
Fig. 2 Overview maps representative of the different observational data sets. Top to bottom: continuum intensity Ic, line-core intensity Icore and line-core velocity vcore. Left to right: SP, GFPI (MOMFBD), GPFI (destretched), POLIS, TIP@1083 nm, and TIP@1565 nm. Black/white in the velocity maps denotes motions towards/away from the observer. All images are scaled individually inside their full dynamical range. |
4.2. Line parameters used
To compare the thermodynamic properties of the observed and synthetic spectra, we used the following line parameters:
-
The line-core intensity Icore, i.e. the intensity at the deepest point of each absorption profile relative to the continuum intensity averaged over the full FOV.
-
The continuum intensity Ic in each profile.
-
The line depth, or, in other words, the difference Icore − Ic with both quantities evaluated for each spatially resolved profile.
-
The line-core velocity vcore, i.e. the velocity corresponding to the Doppler displacement of the location of minimal intensity relative to its average location in the FOV.
-
The relative line asymmetry, i.e. the relative difference of the areas enclosed between the line profile and the local continuum intensity level calculated on the blue or red side, respectively, of the line core. Calling those areas Ab and Ar, the relative line asymmetry is then given by
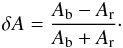 (1)
(1) -
The equivalent width, i.e. the total area of the absorption profile after its normalization to the average value of Ic.
-
The full-width at half-maximum (FWHM) of the line, i.e. the FWHM of a Gaussian fit to the intensity profile.
-
A few line properties at ten equidistant line depression levels (as illustrated in Fig. 1) between the local continuum and the line core, namely, the line width, the bisector velocity, and the intensity value of each of the ten depression levels (called “bisector intensity” in the following). The intensity levels Ij(x,y) (j = 1...10) were calculated by
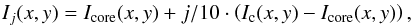 (2)where
x and y denote the pixel column and row inside
the FOV, respectively. This calculation retrieves bisector properties at a constant
line depth, which is assumed to correspond to layers of constant optical depth.
(2)where
x and y denote the pixel column and row inside
the FOV, respectively. This calculation retrieves bisector properties at a constant
line depth, which is assumed to correspond to layers of constant optical depth.
Figure 1 shows an example spectrum from the POLIS 630 nm data, with some of the relevant ranges and derived quantities. The continuum intensity was taken as the mean intensity inside the wavelength range limited by the two dashed lines. For the ground-based 630 nm data (POLIS, GFPI), we removed the telluric O2 blend at 630.27 nm by fitting a Gaussian to it that was subsequently subtracted. We applied the same routine to observational and synthetic spectra to compute the corresponding line parameters, with the wavelength ranges adapted for use with each of the target lines in the corresponding wavelength regime (557 nm, 630 nm, 1083 nm, 1565 nm).
Figure 2 shows maps of three of the line parameters (Ic, Icore, vcore) for the six observational data sets obtained with the SP, GFPI, POLIS, and TIP. To facilitate a direct comparison in the figure, we extracted an equal-sized area of about 30′′ by 46′′ from each observation. The two different approaches to reduce the GPFI data (MOMFBD and destretching, second and third column) have an identical FOV albeit at different spatial resolutions. The shown sections of the POLIS data at 630 nm and of the TIP data at 1082.7 nm (fourth and fifth column) have been roughly aligned with one another to pixel precision to again facilitate an easier visual comparison, i.e. by obtaining a common FOV. All other data are neither co-spatial nor co-temporal. The maps show a clear variation in spatial resolution that approximately decreases from left to right, showing increasingly smeared structures. The MOMFBD GFPI data have the highest spatial resolution, the Echelle data at 557 nm (not shown here, see Fig. 7 below) have a significantly lower spatial resolution because of the seeing conditions during this observation.
4.3. Spatial degradation
To match the spatial resolution of simulations and observations, we determined suitable
convolution kernels to degrade the simulations to the level of the observations (cf. Danilovic et al. 2008; Wedemeyer-Böhm & Rouppe van der Voort 2009; Pereira et al. 2009c; Hirzberger et al.
2010; Afram et al. 2011). We used a kernel
with two components, i.e. a Gaussian
KGauss(r,σ) that is assumed to mainly
reflect the spatial resolution and a Lorentzian
KLorentz(r,a) that should mimic the
stray-light contribution by means of its extended wings (e.g. Mattig 1983), where r denotes the radial distance from
a given pixel. σ is the variance of the Gaussian, and a
the parameter that regulates the shape of the Lorentzian. The final convolution kernel
Ktotal(r,σ,a) is then given by the
convolution of the two kernels: 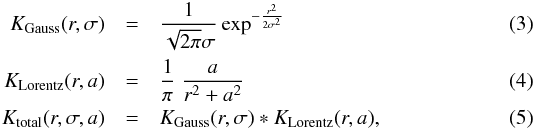 where
∗ denotes the convolution product.
where
∗ denotes the convolution product.
Top row: “best” degradation kernel parameters a and FWHM(σ) for each instrument. Second row: average spatial stray light level α corresponding to each of those “best” kernels. Bottom rows: width of “best” kernel at three percentage levels of maximum amplitude.
As discussed in, e.g., Pereira et al. (2009c), the
parameters (σ,a) of the two kernels cannot be chosen independently. To
prove that and to obtain a (semi-)automatic method for the derivation of the best
parameter values, we quantified the mismatch between observations and the convolved
simulations in the following way. We calculated histograms of the continuum intensity in
all pixels in the FOV of each observation and in the spatially degraded HD simulation
snapshot. Subsequently, we fitted Gaussian functions to all of the histograms (cf. Fig.
6 below for an example) from either the
observations (Gobs) or the degraded HD simulation
(Gdegr). The fitted Gaussian curves were always shifted to a
fixed reference central value and normalized by their maximum. The least-square value
χ2 to be minimized was then defined using two contributions,
one related to the deviation between the two Gaussian fits, and the other related to the
difference between root-mean-squared (rms) continuum intensity contrasts. For asymmetric
distributions the rms value and the width of the fitted Gaussian can differ significantly
because a Gaussian fit mainly reproduces the core of a distribution, whereas the estimator
of the rms takes also (far) outliers into account. We used a tenfold increased weighting
of the rms contrast to achieve a comparable magnitude for both contributions. The
χ2 was therefore set to 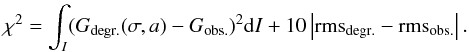 (6)The
χ2 was calculated for values of the FWHM of the
KGauss kernel (Eq. (2)) between
0
(6)The
χ2 was calculated for values of the FWHM of the
KGauss kernel (Eq. (2)) between
0 12 and
1.5′′ and for a in Eq. (3) between 0 and 2, using for
Gobs. and rmsobs. the different
observational data sets separately. The determination of the minimum of the resulting
χ2-surface turned out to be a degenerate problem: as
indicated by the blue/black coloured area in Fig. 3,
for (nearly) each value of σ a suitable value of a can
be found that yields a similarly small χ2. However, it is the
parameter σ that has the strongest influence on the resulting spatial
resolution. We therefore selected “best” kernels by choosing the σ value
that provided the closest match in spatial resolution when visually comparing the
observations and the degraded HD simulation (cf. Fig. 7 below). Having fixed σ, the minimum of the
χ2 function provides the corresponding a.
The white crosses in Fig. 3 denote the final choice
of (σ,a) for each observation (listed in the top row of Table 2).
12 and
1.5′′ and for a in Eq. (3) between 0 and 2, using for
Gobs. and rmsobs. the different
observational data sets separately. The determination of the minimum of the resulting
χ2-surface turned out to be a degenerate problem: as
indicated by the blue/black coloured area in Fig. 3,
for (nearly) each value of σ a suitable value of a can
be found that yields a similarly small χ2. However, it is the
parameter σ that has the strongest influence on the resulting spatial
resolution. We therefore selected “best” kernels by choosing the σ value
that provided the closest match in spatial resolution when visually comparing the
observations and the degraded HD simulation (cf. Fig. 7 below). Having fixed σ, the minimum of the
χ2 function provides the corresponding a.
The white crosses in Fig. 3 denote the final choice
of (σ,a) for each observation (listed in the top row of Table 2).
 |
Fig. 3 χ2 values as a function of FWHM
(= |
Figure 4 shows the final “best” kernels for matching the convolved HD simulation with the various observations. The shape of the kernels fits the expectations when considering the visual impression of the data properties (Fig. 2). Namely, the convolution kernels for the ground-based spectrograph data and the destretched GFPI spectra have broader cores and higher wings than the SP and MOMFBD GFPI data, which leads to the lower contrast and lower spatial resolution of the former. The GPFI MOMFBD kernel has the smallest core of all, in agreement with its intensity map in Fig. 2 that shows more small-scale fine-structure than any of our other observations.
The convolution kernels can be used to estimate the generic stray-light level in the
observations. We calculated the total spurious intensity introduced into the central pixel
of the simulation box from its surroundings (cf. Beck et
al. 2011, BE11, their Eq. (8)) as
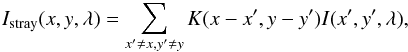 (7)where
I(x′,y′,λ)
are the synthetic spectra of the HD simulation at full resolution (HD-FR) and
x and y denote the pixel column and row inside the
FOV, respectively.
(7)where
I(x′,y′,λ)
are the synthetic spectra of the HD simulation at full resolution (HD-FR) and
x and y denote the pixel column and row inside the
FOV, respectively.
 |
Fig. 4 “Best” degradation kernels Ktotal for GFPI MOMFBD (black solid line), GFPI destretched (black crosses), Hinode/SP (thick red line), POLIS (thick blue line), TIP@1083 nm (orange line), TIP@1565 nm (purple line) and Echelle@557 nm (thick green line). |
The generic spatial stray-light level α is then given by the value of Istray(x,y,λ) in a continuum wavelength range. The second row of Table 2 lists the average stray-light level for the various instruments expected for QS conditions. All spectrograph data (SP, POLIS, TIP, Echelle) and the destretched GFPI data yield a value ≳30%, with little to no dependence on the spatial resolution. The only clear reduction of stray light is seen for the deconvolved GFPI spectra, where in the deconvolution process some inverse kernel was already applied. Our generic stray-light estimate encompasses both the effects of stray light from scattering on optics and from resolution effects caused by, e.g., the finite aperture size of the corresponding telescope (cf. for instance Danilovic et al. 2008). The contribution of resolution effects to stray light is present even for diffraction-limited observations and dominates the shape of the core of the kernel. For comparison, Wedemeyer-Böhm & Rouppe van der Voort (2009) determined an effective value of α of 33% for the blue channel of the SOT/BFI onboard Hinode, of which about 8% should be caused by stray light and the rest by resolution effects (cf. Wedemeyer-Böhm 2008). For the SP, Danilovic et al. (2008) required a stray-light level of about 5% in addition to the theoretical point spread function (PSF) from the resolution effects to match the continuum contrast of their simulations and SP observations. Stray-light estimates for POLIS are listed in BE11, with a lower limit of 10% in umbrae of sunspots and about 24% in QS.
The width of the kernels at three percentage levels of the maximum kernel amplitude is
listed in the lower rows of Table 2. The FWHM of
the convolution kernel (row labelled 50%) does not seem to be a good proxy for the spatial
resolution because its variation across the different data sets is clearly too small, with
a similar value of about 0 4 for all
instruments. Only at the lower two levels (25%, 10%) does the difference in quality become
prominent, with observations of lower spatial resolution showing significantly broader
kernels. For the ground-based slit-spectrograph data (TIP, POLIS, Echelle; cf. the fifth
row of Table 1 for the sampling-limited
resolution), we accordingly used the width at 25% of the maximum kernel amplitude as an
estimate of the spatial resolution.
4 for all
instruments. Only at the lower two levels (25%, 10%) does the difference in quality become
prominent, with observations of lower spatial resolution showing significantly broader
kernels. For the ground-based slit-spectrograph data (TIP, POLIS, Echelle; cf. the fifth
row of Table 1 for the sampling-limited
resolution), we accordingly used the width at 25% of the maximum kernel amplitude as an
estimate of the spatial resolution.
 |
Fig. 5 Estimates of the PSF for POLIS from the degradation of the HD simulation (thick black line), a measurement of a knife-edge function (red line) and a scan across the pinhole in F1 (blue/blue-dot-dashed lines: cuts along y/x). The inset at the upper left shows the intensity map of the pinhole scan. |
The derivation of the degradation kernel by a convolution of simulations is an indirect method that implicitly assumes that the simulation can be used as reference for the true spatial intensity distribution. In the case of ground-based observations, the actual degradation has three contributions (e.g. Mattig 1971, 1983): the degradation by seeing fluctuations, by the telescope optics, and by the (instrument) optics behind the focal plane of the telescope (F1). The latter part, the instrumental PSF, can also be directly measured by some methods, usually using some type of (artificial) occulting disc in the telescope focal plane (cf. Briand et al. 2006; Wedemeyer-Böhm 2008; Beck et al. 2011; Löfdahl & Scharmer 2012).
In the case of POLIS, we have an estimate of the PSF from an observation with a partly blocked FOV in F1 (BE11) and from a scan of a pinhole in F1 taken in April 2011. Figure 5 compares the convolution kernel derived for the HD simulation with the direct measurements of the PSF. The degradation of the HD simulation and the pinhole scan along the slit (y-axis) yield nearly identical kernels. The small oscillation around the simulations’ PSF likely represents the Airy pattern. The knife-edge measurement used in BE11 yields the same core, but has quite elevated wings compared to the other two methods. The cut in the scanning direction (x) yields a smaller kernel that drops to zero faster than the one for the cut in y, because only light that is scattered already in front of the spectrograph is detected. The observation of a pinhole seems to be a practical approach for an observational determination of the instrumental PSF (cf. Löfdahl & Scharmer 2012; Puschmann et al. 2012b), while the good match of the measured PSF with the one derived from degrading the simulation2 suggests the latter as method of choice to obtain a PSF estimate otherwise.
Figure 6 shows the quality in the reproduction of the observed intensities by the degradation of the simulations with the respective “best” kernels. The intensity histograms of the data with high spatial resolution are asymmetric, with an extended tail towards intensities above unity (SP and GFPI MOMFBD data in the top row of Fig. 6). The deviation of the average value from unity seen in some cases is caused by the intensity normalization of the spectra to the FTS atlas, because some of the chosen “continuum” wavelength ranges happened to fall in the far wings of strong lines (see Fig. 1). The rms contrasts were matched to ~0.3% (cf. Table 4 below) and the intensity histograms of the observations are matched adequately.
 |
Fig. 6 Intensity histograms for the observations (black lines), and (red lines) for the HD simulation spatially convolved with the corresponding “best” kernel. Instrument and wavelength are given at the top of each panel. The blue line in the panel corresponding to the POLIS data denotes the Gaussian fit to the observed intensity distribution. |
Parameters of the spectral degradation from FTS/BASS atlas to observations.
 |
Fig. 7 Comparison of observations (lower row in each panel) with the HD simulation (upper row in each panel) convolved using each observation’s “best” kernel. Top to bottom: Ic, v(50% line depression) and vcore. Left to right: SP, GFPI(MOMFBD), GFPI(destretched), POLIS, TIP@1083 nm, TIP@1565 nm and Echelle@557 nm. |
The general match between observations and simulation throughout a two-dimensional (2D) FOV is shown in Fig. 7. We cut out a 6 Mm × 6 Mm square from each observation for a visual comparison to the HD simulation convolved with the corresponding best kernel. The spatial patterns and the spatial resolution in Ic (top panel of Fig. 7), the velocity at 50% line depression (middle panel), and the line-core velocity (bottom panel) are well reproduced for all observations. Note, however, that the simulation data used for this comparison were already spectrally degraded as well (see the next section). Simulation data that were only spatially degraded showed some artifacts in the line-core velocity for all spectral lines except the low-forming Fe i lines at 1565 nm. In case of the GFPI MOMFBD data (second column in Fig. 7) it would be impossible to distinguish the observed and synthetic maps if the corresponding labels were absent. The spatial resolution and the rms contrast of the shown section of the 557 nm data is higher than throughout the rest of the observed FOV at this wavelength because the part presented in the figure belongs to the region around the AO lock point.
4.4. Spectral degradation
The spectral degradation was determined by matching FTS or BASS atlas spectra and average
observed profiles by adding a wavelength-independent stray-light offset β
to the atlas data and subsequently convolving them with a Gaussian G of
width σ′ (Allende Prieto et al.
2004; Cabrera Solana et al. 2007)
according to 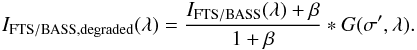 (8)The
value of β only refers to spectral stray light produced by scattering
inside the spectrometer, whereas the spatial stray light produced in front of the slit or
the instrument entrance does not contribute to the spectral degradation (BE11). The
squared deviation between the degraded FTS/BASS profile and the observed average profile
as a function of β and σ′ yields again a
matrix whose minimum indicates the best match of the profiles (e.g. Cabrera Solana et al. 2007, their Fig. A.1). We applied the procedure
to all strong observed spectral lines in the respective wavelength regimes, in addition to
those used for deriving the line parameters. The corresponding best-match parameters
β and σ′ are listed in Table 3. For the spectral degradation of the simulations in
those cases where multiple lines were observed with the same instrument and within the
same spectral region (e.g. 1564.8 nm and 1565.2 nm), we used the average values of
β and σ′. The spectral stray-light levels
range between ~2% (Echelle, SP) and 10% or more (TIP, POLIS). The velocity equivalents of
the spectral broadenings are about 1 km s-1 in most cases.
(8)The
value of β only refers to spectral stray light produced by scattering
inside the spectrometer, whereas the spatial stray light produced in front of the slit or
the instrument entrance does not contribute to the spectral degradation (BE11). The
squared deviation between the degraded FTS/BASS profile and the observed average profile
as a function of β and σ′ yields again a
matrix whose minimum indicates the best match of the profiles (e.g. Cabrera Solana et al. 2007, their Fig. A.1). We applied the procedure
to all strong observed spectral lines in the respective wavelength regimes, in addition to
those used for deriving the line parameters. The corresponding best-match parameters
β and σ′ are listed in Table 3. For the spectral degradation of the simulations in
those cases where multiple lines were observed with the same instrument and within the
same spectral region (e.g. 1564.8 nm and 1565.2 nm), we used the average values of
β and σ′. The spectral stray-light levels
range between ~2% (Echelle, SP) and 10% or more (TIP, POLIS). The velocity equivalents of
the spectral broadenings are about 1 km s-1 in most cases.
After applying the spatial degradation, or spatial and spectral degradation to the synthetic spectra of the HD simulation (denoted in the following by HD-SPAT and HD-SPAT-SPEC, respectively), we determined the line parameters, and inverted the spectra with the settings described in the next section. The noise level in the observed intensity spectra is of the order of 10-3 of Ic and should have a negligible impact on the analysis results as long as only Stokes I is involved. We therefore did not add noise to the synthetic spectra.
4.5. Inversion setup
Using the SIR code (Stokes Inversion based on Response functions; Ruiz Cobo & del Toro Iniesta 1992), we inverted the spectra of all observations (SP, GFPI, POLIS, TIP), as well as the synthetic 630 nm spectra in the HD-FR, HD-SPAT and HD-SPAT-SPEC. The spectral lines in our set of observations qualify as medium to strong lines and therefore provide information over an extended height range from the continuum forming layers up to log τ ≈ −1.5 to −2 (cf. Allende Prieto et al. 2001; Cabrera Solana et al. 2005). The inversion was done with a fixed generic spatial stray-light level α of 20% for all the observations and for the HD-SPAT and HD-SPAT-SPEC cases, whereas α was set to zero for the inversion of the synthetic profiles at full resolution. Only one component (filling factor 100%) was used in the inversion that was set to be either field-free or magnetic depending on whether the polarization degree in the spectra exceeded a specific threshold. This setup forced the inversion code to use just the temperature stratification to reproduce the observed Stokes I profile on each pixel, and hence the temperature in the horizontal plane also follows the spatial intensity variation.
 |
Fig. 8 Spatially averaged profiles of the 630 nm range (left top two rows), the 557 nm range (bottom left), and the near-IR wavelength ranges (right column). For the 630.15 nm line, the spectral sampling of the SP and POLIS is indicated by crosses. The thick purple curves show the spectra in the FTS or BASS atlas, depending on the wavelength range of interest. For 557.6 nm, 630.15 nm, 1564.8 nm and 1565.2 nm the profiles from the HD-SPAT-SPEC are over-plotted with dash-dotted lines. In the plot at 557.6 nm, absolute flux units are used and the normalization of the HD-FR spectra to the FTS was undone. |
 |
Fig. 9 Histograms of line parameters derived for HD-SPAT-SPEC and observations. Top left panel: line asymmetry. Top right panel: FWHM. Bottom left panel: equivalent width. Bottom right panel: line depth. The black line denotes the histogram of the relevant parameter for a given observational data set, the red line the one for the degraded simulation. Instrument and wavelength are denoted at the top of each panel. |
Inversion setups with a variable stray-light contribution or multiple inversion components do not reproduce the spatial variation of temperature well because of the interplay between temperature, stray-light contribution and/or filling factors (e.g. Martínez González et al. 2006). Effective magnetic filling factors are about 10% for ground-based observations at 1′′ resolution (e.g. Martínez González et al. 2008; Beck & Rezaei 2009) and reach 20% for SP data (Orozco Suárez et al. 2007). When using a variable stray-light contribution in a one-component inversion as the only factor taking the unresolved structure of the magnetic field into account, inversion codes will commonly tend to set it to unreasonably high (cf. Sect. 4.3) values of up to 80%, because under such an assumption this factor has to reproduce both the real stray light and the magnetic filling factor inside a pixel (but see also Lagg et al. 2010; Martínez González et al. 2012). Our choice of the inversion setup yields an acceptable fit to the Stokes I profiles (indicating a reasonable choice of α) while the polarization signal in Stokes QUV is less well reproduced because of our one-component assumption. This has no impact on the current study because we do not make use of the retrieved information on the magnetic field parameters.
We chose the Harvard Smithsonian Reference Atmosphere (HSRA; Gingerich et al. 1971) as initial temperature model. We used only two nodes (≡variation of the initial model by linear gradients) for the temperature stratification. From the inversion, we retrieved vmac, vmic and the temperature stratification T as characteristic thermodynamic parameters.
5. Results
5.1. Average line profiles of HD simulation and observations
Figure 8 shows the spatially averaged profiles from the observations and from the HD simulation, as well as the atlas profiles. The average spectra from the HD-FR are expected to reflect the average thermodynamic conditions in the QS (even if with some limitations), and should thus provide a good fit to the observed FTS spectrum. Possible sources of deviation are the lack of magnetic broadening, a somewhat inadequate choice of thermodynamic parameters in the simulation and the transition parameters and solar abundances used in the spectral synthesis.
The comparison of the FTS or BASS profiles (thick purple curves in Fig. 8) with the HD-FR spectra (red lines) shows a good match
for the 630.15 nm line, an acceptable match for 630.25 nm and from moderate to large
deviations for the rest of the spectral lines, mainly because at the corresponding
wavelengths (e.g. 557.6 nm, 1082.7 nm, 1565 nm), the HD-FR yields line profiles with
narrower wings than present in the atlas spectra. This is likely due to the collisional
broadening approximation employed in the spectral synthesis. For abundance determinations,
spectral synthesis codes such as NICOLE (Socas-Navarro et
al. 2000) can be employed that allow for the use of the more reliable collisional
treatment developed by Anstee, Barklem, and O’Mara (ABO; see Barklem et al. 2000) as well as for the inclusion of non-LTE effects.
The small deficiency ( 5%)
in continuum intensity caused by the slightly too low effective temperature of the
simulations (cf. Sect. 3) is demonstrated in the
bottom left panel of Fig. 8. The normalization of all
spectra to the atlas reference spectra removes it efficiently.
5%)
in continuum intensity caused by the slightly too low effective temperature of the
simulations (cf. Sect. 3) is demonstrated in the
bottom left panel of Fig. 8. The normalization of all
spectra to the atlas reference spectra removes it efficiently.
The spectral degradation determined in the previous section transforms the atlas spectra to the average profile of each observation. It therefore produces a good match of simulations and observations only when the spectra from the simulations at full resolution resemble the atlas spectra to start with. This is especially the case for the 630.15 nm line, but also for the rest of the lines the match between the degraded HD simulation and the observations is improved by the spectral degradation.
 |
Fig. 10 Histograms of line-core velocity in HD-SPAT-SPEC and observations. The black line denotes the histogram of the parameter in the observation and the red line that in the HD-SPAT-SPEC. Instrument and central wavelength of relevance are specified in the title of each sub-panel. |
Line parameters in observations and simulations.
5.2. Line parameters
The spatial resolution of the HD simulation and the observations was matched using the continuum intensity (Figs. 6 and 7), whereas the spectral degradation was determined comparing average observed and atlas profiles without using the simulations’ spectra. The comparison of the line parameters other than Ic therefore can reveal possible mismatches between the synthetic and observed spectra that can indicate shortcomings of either simulations or observations (or both). Figure 9 shows the histograms of the line asymmetry, FWHM, equivalent width and line depth for the HD-SPAT-SPEC and for the observations. We note that the size of the statistical sample for observations and simulations differs by about one order of magnitude (cf. the bottom row in Table 1). For all of the following histograms, always the full FOV of the observations with several ten thousand profiles was used, whereas the simulations only provide about 4000 profiles.
The line asymmetry (top left panel in Fig. 9) is seen to be sensitive to the spatial resolution, as also found by PuB11. The shape of the line asymmetry histogram in both observations and simulations changes from a roughly Gaussian distribution at the spatial resolution of the destretched GFPI data (second column, second row) to a broad, flatter distribution with a tail towards negative asymmetries at the resolution of the SP (top row). The line asymmetries in the observed POLIS spectra show a much broader histogram with significantly higher absolute values than the HD-SPAT-SPEC, which is also the case for most of the other line parameters from POLIS in Fig. 9 in one or both 630 nm lines. We suspect the presence of some spectral degradation effect that varies along the slit such as a varying spectral focus as a reason, because the average profiles matched very well (Fig. 8). The line depth in the data set used is also somewhat lower than for other POLIS observations (cf. Beck et al. 2005b, their Fig. 6). The line asymmetries of the near-IR lines at 1565 nm are smaller than those of all other lines because of the smaller formation height ranges of the former.
The shapes of the histograms of the FWHM (top right panel) and equivalent width (bottom left panel) are usually similar for the HD-SPAT-SPEC and the observations, but in some cases the histograms are (slightly) displaced from each other. There is a slight tendency for the HD-SPAT-SPEC to have a lower FWHM, but there are also reverse cases. A better match of the FWHM or equivalent width would require some fine-tuning in their determination (e.g. in the case of equivalent width measurements, accounting for line blends) and in the synthesis setup (e.g. abundances, line broadening). This issue, however, should not have a critical impact on the spatial distribution of the values caused by the thermodynamics. The line depth (bottom-right panel) shows a very good match for all lines, except for the Si i line at 1082.7 nm. All histograms share a common trend with increasing spatial resolution, i.e. they become more asymmetric/skewed rather than only becoming broader. Figure B.1 shows the corresponding histograms of the Fe i line at 557.6 nm for completeness.
The histograms of the line-core velocity are shown in Fig. 10 (see Fig. B.1 for 557.6 nm). The line-core velocity reflects the dynamics of the mass motions in the upper end of the respective formation heights of the various spectral lines. The match between the HD simulation and the observations is excellent, nearly as good as the one found for the continuum intensity distributions (Fig. 6) that we employed for the determination of the spatial degradation. For the SP data in 630.15 nm and the near-IR data in 1082.7 nm and 1565.2 nm, the line-core velocity histograms for the observational data show a peculiar shape, with a central plateau at low velocities, a steep decline at intermediate velocities and a low probability of finding velocities above about ±500 m s-1. This shape turns out to be reproduced surprisingly well by the HD-SPAT-SPEC and appears also in other convection simulations (e.g. Stein & Nordlund 1998; Beeck et al. 2012).
Table 4 lists the average and rms values of some line parameters for the observations, the HD-FR, the HD-SPAT and the HD-SPAT-SPEC. We also included the parameters of the 630.25 nm line in the MHD simulations with increasing average magnetic flux (50−200 G) at full resolution for comparison (lowermost three rows in Table 4).
The clearest trend in the observational values is the increase in all rms fluctuations with increasing spatial resolution, yielding a factor of about 1.5 between, e.g., POLIS and the SP in the rms velocities (fourth column of Table 4). The HD-FR shows rms velocities (compare the values with, e.g., Asplund et al. 2004, last column of their Table 1) higher by an additional factor of about two in comparison to SP and GFPI observations. Whereas the spatial degradation of the simulations always significantly decreases the corresponding rms fluctuations, the spectral degradation has in some cases the opposite effect of increasing the rms values, although only slightly (i.e. spectral degradation has a weaker impact than spatial degradation). The observed rms velocities are usually matched in the HD-SPAT-SPEC to within about ±50 m s-1. In the case of the line-core velocity vcore, the rms in the HD-SPAT-SPEC is lower than in the observations for all lines considered.
The line depth (sixth column of Table 4) of the HD simulation is usually reduced only slightly by the spatial degradation and more strongly by the spectral degradation, whereas the line-core intensity (seventh column of Table 4) naturally shows a corresponding increase. The factor with the biggest impact on the changes in line depth and line-core intensity is the stray-light offset β in the spectral degradation. The significant consequences of these changes in the line shape on the temperature stratifications retrieved by the inversion are discussed in Sect. 5.4 below.
The average line asymmetry (last-but-one column in Table 4) changes strongly with both the spatial or spectral degradation of the simulations, even including a change in sign. In most cases, the change from positive to negative asymmetry (or reverse) by the degradation is actually necessary to match the observed value (e.g. for 557.6 nm, for 630 nm in the SP and GFPI data, and for all near-IR lines). Assuming the same temperature structure in granules and intergranular lanes (IGLs), decelerating upflows (accelerating downflows) lead to a positive (negative) line asymmetry. The spatial average of the line asymmetry measures an intensity-weighted relative area filling factor of granules and small-scale IGLs, which, after the latter are largely suppressed by the spatial degradation process, yields mainly positive values.
Accounting for spatial degradation reduces the equivalent width (last column in Table 4) of the spectral lines by 0.02−0.09 pm, depending on the line, except for the destretched GFPI data at 630.25 nm, for which it increases the equivalent width by 0.13 pm. The increase in magnetic flux in the MHD-FR reduces the equivalent width of the 630.25 nm line by up to ~0.3 pm (HD-200 G). This effect is due to the warmer atmospheric temperature structure generally retrieved in the presence of magnetic fields that causes line-core weakening (line-gap; e.g. Stellmacher & Wiehr 1971; Chapman 1977; Hirzberger & Wiehr 2005). The corresponding decrease in equivalent width is the dominant effect of the presence of magnetic fields on iron lines in the visible wavelength range, even if they are also Zeeman-sensitive. At visible wavelengths, the Zeeman broadening is not sufficiently strong to counter the indirect effect on spectral lines due to the change in average temperature induced by magnetic flux (Fabbian et al. 2010). The spectral degradation tends to reduce the equivalent width by even larger amounts (up to several pm for the 1082.7 nm line), because the spectral stray-light offset β (cf. Table 3) directly scales the line depth, and hence also the total area of the absorption profile.
 |
Fig. 11 Top panel: spatially averaged bisector velocity (SABV) for the 630.25 nm line in the observations (solid lines), the HD-FR (solid black line) and the HD-SPAT-SPEC (dashed lines). Bottom panel: comparison between SABVs and bisector velocities of average profiles (BVAP) for the 630.25 nm line. Solid/dash-dotted black lines: SABV/BVAP in the HD-FR. Solid red/blue lines: SABV/BVAP for the SP data. Red/blue dashed lines: SABV/BVAP for the simulation degraded to SP resolution. The purple line gives the bisector in the FTS atlas profile. Positive velocities correspond to redshifts relative to the average velocity at 50% line depression. |
5.3. Line properties at different line depression levels
The bisector is defined as the curve connecting the central positions between left and right wing at different line depression levels throughout an absorption line. We determined the bisector position and the line width at ten different intensity levels throughout the absorption profiles. The variation of these properties in an individual spectral line profile traces the values of the corresponding thermodynamic stratification in the atmosphere and any possible gradients. A line depression of 0% denotes the continuum level, whereas 100% denotes the line core. We used the average bisector position at 50% line depression as zero point reference for the conversion to velocities.
The bisector positions at different line depression levels trace gradients of velocity with optical depth. For average spectra in QS granulation, the bisectors usually yield a C-shape throughout the different levels of line depression (e.g. Brandt & Schroeter 1982; Dravins 1982, 2008; Marquez et al. 1996; Puschmann et al. 1999; Hanslmeier et al. 2000; Asplund et al. 2000; Mikurda et al. 2006; Gray 2010; de la Cruz Rodríguez et al. 2011). The upper panel of Fig. 11 shows the spatial average of the bisector positions, converted to the corresponding velocities, for the 630.25 nm line in the observations and the HD simulation. A prominent difference is seen: the averaged bisector velocity of the HD-FR has a roughly inverse shape to that of all observations. The match between the velocity at different line depression levels in observed and synthetic spectra is, however, good for the spatially and spectrally degraded HD simulation, except for the lines at 557.6 nm and 1082.7 nm (Fig. A.1). For 557.6 nm, the deviations at line depression levels below 40% are presumably caused by the weak blends in its line wing. Note that the spatial average of the bisector velocities does not reflect the dynamical range of the vertical velocity fluctuations, but rather the average net vertical flow speed.
To determine the reason for the inversion of the bisector shape between observations and
the HD-FR, we reversed the order of the bisector determination and the spatial averaging
by calculating also bisectors for spatially averaged profiles. The lower panel of Fig.
11 compares the spatially averaged bisector
velocities (SABV) and the bisector velocities of average profiles (BVAP) for the 630.25 nm
line. We included the SP data, the HD-FR, the HD simulation spatially and spectrally
degraded to the SP data, and the profile of the FTS atlas. Applying the spatial averaging
to the spectra before determining the bisectors flips the shape of the bisector velocities
with respect to the HD-FR (compare the black solid and black dash-dotted lines in the
lower panel of Fig. 11). The similarity of the BVAP
for the simulation (black dash-dotted line) and the SABV for the HD simulation degraded to
SP resolution (red dashed line), or the SP data themselves (red solid line), indicates
that the change in the shape must be introduced by a small-scale averaging between the
full spatial sampling of the simulation (0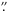 13 ~94 km) and the
resolution of the SP data (0
13 ~94 km) and the
resolution of the SP data (0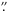 62 ~450 km). The
BVAP of the HD-FR also matches the bisector shape of the MOMFBD GFPI data (blue line in
the upper panel of Fig. 11), which puts an even
stricter upper limit to the spatial averaging effect of about
0
62 ~450 km). The
BVAP of the HD-FR also matches the bisector shape of the MOMFBD GFPI data (blue line in
the upper panel of Fig. 11), which puts an even
stricter upper limit to the spatial averaging effect of about
0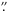 3 (~218 km). The
reversal of the shape of the bisector should also correspond to the sign change in the
line asymmetry by the spatial degradation that was found before (cf. Sect. 5.2 and Table 4)
and should be coupled to the relative area fraction of bright granules and dark
intergranular lanes.
3 (~218 km). The
reversal of the shape of the bisector should also correspond to the sign change in the
line asymmetry by the spatial degradation that was found before (cf. Sect. 5.2 and Table 4)
and should be coupled to the relative area fraction of bright granules and dark
intergranular lanes.
Compared to the small-scale spatial average caused already by the effective spatial resolution of the observations, any additional large-scale averaging done in the BVAP process adds only minor modifications. The SABV and BVAP of the SP data are similar (albeit not fully identical), and the bisector from the FTS atlas profile matches the BVAP from the SP data well for the 630.25 nm line. These two facts are indicative of two different subsequent averaging effects: on the one hand, the spatial averaging caused by the limited spatial resolution of all of our observations has already significantly changed the shape of the bisector velocity curve in comparison to the HD-FR. On the other hand, averaging over the full FOV (or a long time) leads to line profiles, and hence bisectors similar to FTS regardless of the spatial resolution of the input spectra. This second averaging step thus only produces minor variations of the bisector shape.
In contrast to the average position of the bisectors, the rms fluctuations of the bisector velocities do reflect the vertical velocity fluctuations caused by the dynamical evolution of the solar atmosphere. For the SP observations both at 630.25 nm (top panel of Fig. 12) and at 630.15 nm (Fig. A.4) and for the near-IR observations (Fig. A.4), an increase in the velocity rms is seen as one moves from the higher atmospheric levels towards the continuum formation layers in the lower atmosphere, i.e. for high bisector levels (line depression levels <40%). In the observed SP data at 630 nm, the velocity rms decreases monotonically with increasing line depression, like also in the HD-FR for all spectral lines. Towards low line depression levels (<40%) in most lines, the degraded HD simulation shows lower rms fluctuations than the observations, whereas the rms values are nearly identical near the line-core. The bisector velocity rms for the 557.6 nm line is shown in Fig. B.2 for completeness.
The decrease in the rms velocity fluctuations with height in the atmosphere indicates that the velocity formation heights for most of the spectral lines do not reach into the realm where propagating acoustic waves of increasing amplitude dominate the atmosphere making the rms velocities increase again strongly with height (e.g. Beck et al. 2009). The spectral lines used here therefore in general correspond to an height regime that is dominated by the convective velocity distribution as far as the line-of-sight (LOS) velocities are concerned.
The bisector intensity rms shows a different height dependence (e.g. middle panel of Fig. 12) than the bisector velocity rms. The relative (i.e. normalized by the average intensity) rms fluctuations of the intensity levels show increased fluctuations for line depression levels above about 70%. This indicates an increase in temperature fluctuations close to the line core, as expected for propagating acoustic waves with a steepening wave amplitude. This explanation stands at least for the HD simulation that is free of magnetic flux, whereas in the observations it could also in principle be related to the presence of magnetic fields, because the latter lead to brightenings in the line core (cf. Puschmann et al.2007, or Fig. 2, middle row: the brightenings in the lower left corner of the FOV for the GFPI data are of a magnetic origin (see PuB11)). The rms of the intensity in the observations generally exceeds the fluctuations in the HD-SPAT-SPEC.
The rms fluctuations in the line width at different line depression levels for 630.25 nm are shown in the bottom panel of Fig. 12. In this case, the rms fluctuations start to increase when reaching about 60% in line depression for the 630 nm lines (as well as for the 557.6 nm line, Fig. B.2) in the HD-FR, whereas all observations and the HD-SPAT-SPEC show a monotonic decrease in the rms with increasing line depression. The fluctuations of all parameters in the spatially degraded HD simulation generally are smaller than those in the observations besides for the low-forming 1565 nm lines, where the HD-SPAT-SPEC match the observations nearly perfectly (Fig. A.4). The average values of the bisector intensity and the line width at different line depression levels are shown in Figs. A.2 and A.3 for completeness.
 |
Fig. 12 Rms fluctuations in the line properties at different line depression levels for the 630.25 nm line in the observations (solid lines), in the HD-FR (solid black line) and in the HD-SPAT-SPEC (dashed lines). Top: bisector velocity. Middle: bisector intensity. Bottom: line width. |
 |
Fig. 13 Histograms of the macroturbulent (left column) and microturbulent velocity (right column) in the inversions. Top: inversions of observations. Middle: the same for the HD-SPAT simulation. Bottom: the same for the HD-SPAT-SPEC. Thin black lines in each panel: HD-FR. |
5.4. Inversion results
In the inversion, the macroturbulent velocity vmac is used to convolve the synthetic profiles with a Gaussian of variable width to match the observed spectra. The microturbulent velocity vmic is one of the contributions to the line width in a Lorentzian function that is used in the integration of the radiative transfer equation (see, e.g., Rutten 2003). The value of vmic could be specified to vary on the optical depth scale in the SIR code, but we set it to be constant at all τ values. The two ad hoc empirical parameters vmac and vmic encompass two different physical effects when observed spectra are inverted: the “real” macro/microturbulence caused by unresolved macro/microscopic velocities in the solar atmosphere and the spectral broadening caused by the characteristics of the respective spectrometer. While the former component should scale with the spatial resolution, the latter should be a constant characteristic of the spectrometer that in some inversion codes can be included by providing a measurement of the PSF such as those in Sect. 4.4. In the case of the simulations without any degradation, both effects are absent; for the spatially degraded simulations, only the broadening by unresolved velocities is included.
The top row of Fig. 13 shows the histograms of the macroturbulent (left column) and microturbulent (right column) velocities derived by applying the SIR code for the inversion of the different observed spectra. Only one value per wavelength range was derived. Even when multiple spectral lines were present in a given range, they were in fact inverted simultaneously. The middle and bottom row of Fig. 13 show the macroturbulent and microturbulent velocities retrieved from inverting the HD-SPAT and HD-SPAT-SPEC, respectively. The values from inverting the HD-FR are overplotted with black lines in each panel as reference.
Macroturbulent velocity
There is an offset in macroturbulent velocity between the observations at 630 nm (most vmac < 2 km s-1) and in the near-IR (most vmac > 2 km s-1) that is presumably caused by the lower spectral sampling and/or resolution of the near-IR observations with TIP (top left panel of Fig. 13). The distribution of vmac for the 1082.7 nm line is significantly broader than those obtained for any of the other observations. This was found to result from using only two nodes in the temperature stratification. An inversion of the observation in this line using three nodes yielded a distribution of vmac that was similar to that of all other observations, with a much smaller width and a roughly Gaussian shape. The Si i line at 1082.7 nm has an extended formation height and is sensitive to NLTE effects (cf. Shchukina et al. 2012, and references therein).
 |
Fig. 14 Temperature stratifications (top row), difference to the HSRA model (middle row), and rms fluctuations of temperature (bottom row) in the inversions. Left to right: observations, HD-SPAT and HD-SPAT-SPEC. The dotted vertical lines denote the approximate formation height range of the 630 nm lines, the dashed vertical line the upper end of the range for near-IR lines. Other labels are identical to Fig. 13. |
For all 630 nm observations, a slight trend with spatial resolution can be seen, with POLIS yielding the highest and the GFPI the lowest average vmac (1.7−1.9 km s-1, cf. Table 5). For the observational data, the spatial structuring in 2D maps of vmac roughly mirrored an inverse granulation pattern, with increased vmac in intergranular lanes, especially on all locations where polarization signal was also present. Such a characteristic resulting pattern is likely related to the one-component inversion setup, where the missing freedom in the magnetic fill factor forced the inversion code to emulate part of the Zeeman line broadening in intensity by an increased macroturbulence. The HD-FR exhibited a negligible macroturbulence, with vmac < 10 m s-1 on 90% of the pixels and an average vmac of 0.4 km s-1 on the remaining 10% of the FOV. The few pixels with increased vmac in the HD-FR were almost exclusively located inside intergranular lanes.
The macroturbulent velocity introduced into the synthetic spectra by the effect of
spatial degradation alone (left middle panel of Fig. 13) has average values increasing from 0.6 to 0.9 km s-1 with
decreasing spatial resolution (Table 5). The
value of vmac was significant on all pixels in the FOV of
the HD-SPAT. The macroturbulent velocity thus becomes significant between the spatial
sampling of the HD simulation of 0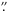 13 and the
highest spatial resolution in the observations of
0
13 and the
highest spatial resolution in the observations of
0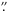 3. The spatial
structuring of vmac in the HD-SPAT resembled an inverse
granulation pattern, but only remotely.
3. The spatial
structuring of vmac in the HD-SPAT resembled an inverse
granulation pattern, but only remotely.
The inversion of the HD-SPAT-SPEC spectra (left bottom panel of Fig. 13) yielded an average
vmac lower by about 0.4−0.8 km s-1 than for the
observations. The final values from the inversion of the HD simulation agree well with
the quadratic addition of the two contributions from the spatial and spectral
degradation, indicating that the macroturbulent velocity retrieved by the inversion is a
rather “robust” quantity that reliably captures the different broadening contributions.
As an example, for the HD simulation degraded to SP resolution one has
⟨ vmac ⟩ = 1.03 km s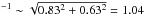 km s-1
(Tables 3 and 5), which nevertheless falls short of the value in the observations
(1.81 km s-1).
km s-1
(Tables 3 and 5), which nevertheless falls short of the value in the observations
(1.81 km s-1).
Microturbulent velocity
The microturbulent velocity vmic in the HD simulation and the observations behaved roughly opposite to vmac. The value of vmic stayed below 10 m s-1 on a large fraction of 50−85% of the FOV for all observations (Table 5, top part), contrary to vmac. It was instead significant on every pixel in the inversions of the synthetic HD-FR. The average microturbulent velocity for simulations with any type of degradation exceeded the value in the observation – again contrary to the behaviour of macroturbulent velocity. The spatial maps of vmic for the HD-FR spectra exhibited a granular pattern, whereas those of the observations resembled vmac of the HD-FR, i.e. for the observational data vmic was only significant in a few points in intergranular lanes. The HD-SPAT yielded a nearly identical average vmic of about 0.57 km s-1 regardless of the amount of spatial degradation. After the additional spectral degradation, vmic increases with decreasing spatial resolution (Table 5, bottom part) as for vmac.
Despite the effort in matching synthetic and observed spectra spatially and spectrally, the inversion with SIR retrieves a quite different behaviour with respect to vmac and vmic. The reason most likely is the usage of the Unsöld approximation by LILIA in the synthesis, whereas SIR used the ABO formalism in the inversion of the observed or synthetic spectra. In any case, this should not have had a significant influence on the temperature fluctuations retrieved by the inversion.
Temperature
The last indicators of thermodynamics provided by the inversion are the temperature stratifications T, and – more relevant for the current study – the rms fluctuations σT(τ) of the temperature at a given optical depth. Figure 14 shows the average temperature stratifications (top), their deviation from the HSRA model (middle), and their rms fluctuations (bottom) vs. optical depth for the observations (left column), the HD-SPAT (middle column), and the HD-SPAT-SPEC (right column).
The average temperature stratifications retrieved from the inversion of the
observations differ somewhat (top left panel), but overlap between them or with the HSRA
model within 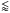 ± 100 K
in the range of log τ = 0 to −1 (left middle panel of Fig. 14). For
log τ < −1, they show a considerably larger
scatter between the different instruments and increasing temperature deviations. The
slope (from lower to higher optical depth) of the deviation from the HSRA changes from
being positive for the SP data to slightly negative for the GFPI data, and finally
becomes strongly negative for the POLIS data. The temperature stratification retrieved
by inverting the 630 nm spectra from the HD-FR would correspond roughly to the average
of all other stratifications derived from the observations. The deviation (from the HSRA
model) of the average temperature stratification retrieved from inverting the HD-FR
shows a slightly positive slope, with differences of ≲± 50 K.
± 100 K
in the range of log τ = 0 to −1 (left middle panel of Fig. 14). For
log τ < −1, they show a considerably larger
scatter between the different instruments and increasing temperature deviations. The
slope (from lower to higher optical depth) of the deviation from the HSRA changes from
being positive for the SP data to slightly negative for the GFPI data, and finally
becomes strongly negative for the POLIS data. The temperature stratification retrieved
by inverting the 630 nm spectra from the HD-FR would correspond roughly to the average
of all other stratifications derived from the observations. The deviation (from the HSRA
model) of the average temperature stratification retrieved from inverting the HD-FR
shows a slightly positive slope, with differences of ≲± 50 K.
We note that the trend in the slope of the deviation from HSRA (SP < GFPI < POLIS) in the case of the inversion of the observational data does not follow the spatial resolution trend of the latter (GFPI < SP < POLIS). A different suspect instead clearly comes to mind for which the trend is the same as for the slopes: namely, the stray-light offset inside the respective spectrometers (cf. Table 3). Whereas vmic and vmac can account for the spectral broadening in each instrument, the constant intensity offset β was not considered in the inversion. The hypothesis that the slope is related to the spectral stray-light offset is further confirmed when considering the inversions of the HD simulation degraded to GFPI resolution, where we have two cases with different spatial but identical spectral resolution. The deviations from HSRA after degrading the HD simulation only spatially to the spatial resolution of the MOMFBD or to the destretched GFPI spectra stay small and both slopes are almost identical (central panel, lines are overlapping) even if the spatial resolution is clearly different (Table 1 and Fig. 7). After the additional application of the spectral degradation to the spatially degraded HD simulation spectra, the slope of the deviation from HSRA increases significantly for the synthetic data at GFPI resolution (middle right panel), lying between that of the HD simulation at SP or POLIS resolution, but with again little difference between the two different spatial resolutions of the GFPI data (orange and blue line overlapping again). This indicates that, contrary to the spatial resolution, the spectral resolution has a strong effect on the deviation from HSRA, likely due to stray-light effects unaccounted for in the inversions.
The rms fluctuations of T are shown in the bottom row of Fig. 14. For the observations (bottom left panel), the values range from 100 to 200 K at log τ = 0, pass through a minimum of below 100 K rms between log τ ~ −0.7 and −1.2, and tend to increase to up to ~300 K at log τ ≲ −2.5. This agrees with the results obtained by Puschmann et al. (2003, 2005), who found a minimum temperature contrast between granules and IGLs at log τ = −1. The HD-FR yields about 100 K larger fluctuations in the lower atmosphere up to log τ = −1, but lower rms values than for instance the SP data above that height. The shape of the rms curve for the HD simulation is similar to that of the inversion of, e.g., the SP data, besides an offset in log τ of about 0.75 (compare the location of minimal rms in both curves). This offset could be caused by different values of gas (or electron) densities because for instance in the inversion with SIR the electron density at log τ = + 1.4 was fixed to the value in the HSRA as a boundary condition. After the spatial degradation of the HD simulation, the rms temperature fluctuations retrieved from the inversion with SIR match the observations in the lower photosphere from log τ = 0 to −1 well (compare the red/blue solid and red/blue-dotted curves in the bottom middle panel of Fig. 14), whereas they are smaller than the corresponding observed rms values for higher layers. The subsequent spectral degradation has no additional visible effect on the rms temperature fluctuations (bottom right panel), while it significantly changes the average temperature stratification, hence producing the difference to the HSRA (middle right panel).
The scatter of the average temperature stratifications retrieved from the HD-SPAT-SPEC becomes comparable to that between the different observations (top left and top right panels). The deviations between the average temperature stratification from the inversion of the HD-SPAT-SPEC and the HSRA (middle right panel) follow the same systematic trend as in the case of the observations (middle left panel), i.e. a decrease in the slope from SP to POLIS, but in this case starting already from a negative slope for the SP data. That the HD-SPAT-SPEC show the same trend as the observations – while the HD-SPAT (central panel) shows a basically zero slope – again confirms that the spectral degradation, and there mainly the stray-light offset, are responsible for the variation in the derived temperature stratifications. The stray-light offset changes mainly the line depth, and therefore compresses or expands the attributed optical depth scale in the inversion.
The deviations from the HSRA (or any other semi-empirical reference model) would be a concern for an abundance determination, but in the present study we are only interested in the behaviour of observations and simulations relative to each other when using the same analysis approach for both. In particular, we focus on the rms fluctuations rather than on the average values. In that respect, the rms temperature fluctuations as derived from the degraded HD simulation do not exceed the observed properties. Rather, they match them fairly well at layers of formation of photospheric spectral lines commonly used for abundance derivations, and actually are smaller than the observed ones at high layers.
5.5. Comparison of temperature fluctuations to other studies
The temperature fluctuations retrieved by the inversion of the degraded HD spectra do not exceed the observed values. To investigate whether this could be caused by the amplitude of fluctuations in our simulations being too small to start with, we compared the temperature fluctuations in our data (simulations and observations), with the values provided for other simulations (Fig. 15). All curves obtained from an inversion of 630 nm spectra were clipped at log τ = −2.5 because the formation height of the lines does not cover higher layers. To extend the height range covered from the observational side, we included the LTE inversion results of Ca ii H spectra from Beck et al. (2013a,b).
 |
Fig. 15 Relative temperature fluctuations vs. optical depth. Top panel: inversion results of SP (red line), GFPI (orange line) and Ca ii H data (blue line), and of the HD-FR simulation spectra (black-solid line). Overplotted are the relative temperature fluctuations in the HD-FR simulation box (black dashed-triple-dotted line) and the curve given in Hayek et al. (2010, HA10) for a simulation with continuum scattering (black-dashed line). Bottom panel: inversion results of SP/Ca ii H multiplied by two/five (red/blue lines), and the values from the simulations of Wedemeyer et al. (2004, WE04; black-dotted line), of HA10 with continuum scattering (black-dashed line) and of HA10 with continuum and line scattering (black-dash-dotted line). |
We compare our values with those given in Wedemeyer et al. (2004, WE04; their Fig. 9) and Hayek et al. (2010, HA10; their Fig. 10) because they correspond to different treatments of the radiative transfer in the simulations, i.e. grey atmosphere in LTE (WE04) and LTE with additional continuum and line scattering (HA10). Because these simulations were not spatially degraded, we overplotted the results for the inversion of the SP (Ca ii H) data multiplied by two (five) in the lower panel of Fig. 15. These factors roughly correspond to the ratio of continuum contrast between observations and simulations, e.g. for the SP (Ca ii H) one has an observed rms Ic = 7.2% (3.5%), whereas simulations predict about 15% (>20%; Hirzberger et al. 2010). We used the tabulated z − τ relation in the HSRA model to convert curves vs. geometrical height (HA10, HD-FR(z → τ) ) to an optical depth scale. This approach can slightly compress or stretch the curves, when the true density stratification differs from the one of the HSRA.
When comparing the curves of the temperature rms derived from observations and simulations, the best match is achieved between the one derived from Ca ii H, after scaling it up for the spatial resolution, and the results of HA10 including continuum and line scattering (lower panel of Fig. 15). The rms fluctuations in WE04 exceed all others above log τ = −1. The temperature fluctuations in the Stagger code simulations that we used closely match the HA10 case with only continuum scattering included. The rms fluctuations of all simulations are comparable up to about log τ = −2 with relative fluctuations between 5 and 7.5% at this optical depth, but increasingly deviate in higher layers with differences of up to 15% at log τ = −4 (≡up to 600 K difference in rms). From the comparison, we would exclude that the Stagger simulations that we analysed here are somehow biased towards an extraordinary low or high level of fluctuations in the photosphere up to log τ = −2, which is about the maximal height range where the spectral lines used here are fully reliable.
6. Summary and discussion
Numerical (M)HD simulations are increasingly used in the analysis or interpretation of observational data of the Sun (e.g. Khomenko et al. 2005; Shelyag et al. 2007; Carroll & Kopf 2008) and in particular also for the derivation of abundances (Asplund et al. 2004; Caffau et al. 2008; Pereira et al. 2009a; Fabbian et al. 2010, 2012). They are capable of predicting phenomena such as small-scale vortices (e.g. Stein & Nordlund 1998; Moll et al. 2011; Kitiashvili et al. 2011) that have been confirmed by observations only later on (Bonet et al. 2008; Steiner et al. 2010; Steiner & Rezaei 2012). The claim that a simulation is “realistic” is, however, often made solely based on the physics included in the numerical calculation, and not necessarily because the simulations were proven to correspond to the “real” Sun as far as can be determined from observations. Several different tests of the realism of simulations were performed in the past, but mainly concentrating on a few selected (average) parameters such as the continuum contrast (Wedemeyer-Böhm & Rouppe van der Voort 2009; Hirzberger et al. 2010), its CLV (Koesterke et al. 2008), average profiles (Asplund et al. 2000; Stein & Nordlund 2000; Allende Prieto et al. 2004) and their CLV (Asplund et al. 2004), or average temperature stratifications (e.g. Pereira et al. 2013). Only recently, spatially resolved properties of individual line profiles were also used for comparisons of simulations and observations (e.g. Pereira et al. 2009b,c). Additional cross-checks have recently been done between different simulation codes (e.g. Beeck et al. 2012), rather than between simulations and observations. Some of the plots in Beeck et al. (2012) can, however, be directly compared to those in the present study. We only point out one feature of the temperature rms vs. log τ (their Fig. 12), namely the location of minimum rms at about log τ ~ −0.7, compared to log τ ~ −1 in our inversions of the observed spectra, with a similar result also in the inversions of Puschmann et al. (2005).
All types of comparisons between simulations and observations usually share the same problem: the spatial resolution of the observations is not as good as that of the simulations, and thus it can only be shown that the simulations can be degraded sufficiently to match the observations, without the possibility to investigate if the original simulation results match the “real” Sun (cf. also Danilovic et al. 2008). Our present study demonstrated that to do this final step would require observational data with about three to four times better spatial resolution than currently available. Such data will be available soon with the upcoming telescope projects of the 1.5-m class such as the GREGOR solar telescope (e.g. Schmidt et al. 2012a,b) with the GREGOR Fabry-Perót Interferometer (e.g. Puschmann et al. 2012a,b,c) and the New Solar Telescope (Denker et al. 2006; Cao et al. 2010), or in the future with next generation solar telescopes of the 4-m class such as ATST (Wagner et al. 2008; Rimmele et al. 2010) or EST (Collados et al. 2010).
Our investigation shows that using 3D convection simulations as reference allows one to
derive an estimate of the spatial point spread function of instruments and telescopes that
can be used for an accurate stray-light correction and/or for a spatial deconvolution (BE11,
Löfdahl & Scharmer 2012). The good match to
a directly measured instrumental PSF (Fig. 5) implies
that the use of the simulations for this purpose is justified. The importance of knowing the
instrumental PSF should not be underestimated. The inversion of the HD-SPAT shows that the
spatial smearing introduces a significant broadening of spectral lines already at a
resolution of 0 3. Taking the PSF
explicitly into account in the analysis of data will thus yield more accurate solar
properties in an inversion of spectra not only for thermodynamic parameters, but also for
magnetic field properties. The PSF is commonly taken into account to correct for unpolarized
stray light only, but naturally applies as well to polarized stray light, where it has a
more profound impact on retrieved solar parameters, e.g. for all spectral lines in the
weak-field limit where the polarization amplitude is proportional to the total magnetic
flux, or wherever spatial resolution is critical because of solar fine-structure such as in
the penumbrae of sunspots (van Noort 2012).
3. Taking the PSF
explicitly into account in the analysis of data will thus yield more accurate solar
properties in an inversion of spectra not only for thermodynamic parameters, but also for
magnetic field properties. The PSF is commonly taken into account to correct for unpolarized
stray light only, but naturally applies as well to polarized stray light, where it has a
more profound impact on retrieved solar parameters, e.g. for all spectral lines in the
weak-field limit where the polarization amplitude is proportional to the total magnetic
flux, or wherever spatial resolution is critical because of solar fine-structure such as in
the penumbrae of sunspots (van Noort 2012).
The comparison of the HD-SPAT-SPEC data to the observations yielded a fair to very good
match for most line parameters. The HD-FR differs usually only by an increased amplitude of
the quantities, with the exception of the average bisector position (Fig. 11). For this parameter, we find that its average values
at different line depression levels trace a curve that for the HD-FR has a roughly reverse
shape compared to the one for the spatially degraded HD simulation and the ones
corresponding to the different observational data. This change thus has to happen on a
spatial scale between 0 13 and
0
13 and
0 3, close to the
photon mean free-path length in the solar photosphere. Given the corresponding
thermalization length, one does not expect significant spatial temperature variations in the
photosphere on spatial scales much smaller than 0
3, close to the
photon mean free-path length in the solar photosphere. Given the corresponding
thermalization length, one does not expect significant spatial temperature variations in the
photosphere on spatial scales much smaller than 0 13 (~100 km), but
this argument does not hold in the same way for spatial velocity variations. The presence of
Doppler shifts also enlarges the thermalization length (Skartlien 2000). The characteristic properties of the average bisector come from
an intensity-weighted spatial average of the corresponding velocities. The difference in
shape between the bisector derived from the HD-FR and those derived from any observed
spectra then presumably is caused by both mass flows and spatial temperature variations that
remain unresolved in the observations, while the spatial temperature variations should be
partially resolved or close to being resolved in our best observations.
13 (~100 km), but
this argument does not hold in the same way for spatial velocity variations. The presence of
Doppler shifts also enlarges the thermalization length (Skartlien 2000). The characteristic properties of the average bisector come from
an intensity-weighted spatial average of the corresponding velocities. The difference in
shape between the bisector derived from the HD-FR and those derived from any observed
spectra then presumably is caused by both mass flows and spatial temperature variations that
remain unresolved in the observations, while the spatial temperature variations should be
partially resolved or close to being resolved in our best observations.
The bisector flips to the observed shape with any large-scale averaging. Our finding therefore should have no impact on abundance determinations from averaged spectra. It, however, raises the warning that, since the characteristic properties of spatially averaged spectral line profiles derived from observations do not necessarily reflect those of spatially resolved profiles, achieving a match with the former is not fully sufficient to prove the realism of simulations. Many line parameters such as bisectors depend on the exact line shape caused by gradients of thermodynamic parameters. A spatial averaging can destroy the (non-linear) dependence of the profile shape on the thermodynamic parameters.
We point one peculiarity of the often used atlas spectra such as the FTS: the smearing of
these data due to spatial averaging and the corresponding amount of macroturbulent
broadening are practically unknown. Spatial smearing introduces a significant line
broadening of vmac ~ 1 km s-1 at a resolution of
0 3, as the
inversion of the HD-SPAT showed. In the case of spatially resolved observations, one can
estimate the characteristic macroturbulent line broadening of the data in the resolved and
averaged spectra. For the atlas spectra, this estimate cannot be done post-facto. The
commonly adopted implicit assumption that the broadening by macroturbulent velocities levels
off to a constant value at some degree of averaging should be investigated in more detail.
3, as the
inversion of the HD-SPAT showed. In the case of spatially resolved observations, one can
estimate the characteristic macroturbulent line broadening of the data in the resolved and
averaged spectra. For the atlas spectra, this estimate cannot be done post-facto. The
commonly adopted implicit assumption that the broadening by macroturbulent velocities levels
off to a constant value at some degree of averaging should be investigated in more detail.
The simulation box covered a height range up to more than 400 km above optical depth unity in the solar atmosphere, and the spectral lines used in this study – besides the Si i line at 1082.7 nm that is not fully reproduced – form in the low to mid photosphere. The variation of quantities with height, like for instance a monotonic decrease in rms velocities, indicates that the values retrieved from the spectral lines still belong to an atmospheric regime whose dynamics are governed by the convective energy transport. Any possible flaw of the numerical simulations because of the approximations used (namely, LTE and opacity binning treatment) for the radiative energy transfer and losses is thus less relevant in these layers because the directed mass motions control the energy balance. A similar study covering also (low) chromospheric layers, e.g. up to a height of 1 Mm, should, however, not be too difficult to achieve in the near future (cf. Wedemeyer et al. 2004; Leenaarts et al. 2007, 2009; Wedemeyer-Böhm & Carlsson 2011).
The inversion of the HD-SPAT yielded a small (≲± 50 K) spread in the resulting average
temperature stratifications even if the spatial resolution varied between
0 3 and about
1′′ (central panel of Fig. 14). The
spectral degradation, on the other hand, led to a strong variation in the retrieved
temperature stratifications, with a clear scaling by the constant wavelength-independent
stray-light offset β inside the spectrometer. This implies that for an
accurate derivation of temperatures from observed spectra the stray-light offset has to be
corrected before an inversion. On the positive side, the stray-light offset
β inside the SP spectrograph was found to be below 3% (see also Lites et al. 2013), which makes these data and data of
similar spectral quality well suited for a derivation of temperature stratifications in the
solar photosphere (e.g. Socas-Navarro 2011).
3 and about
1′′ (central panel of Fig. 14). The
spectral degradation, on the other hand, led to a strong variation in the retrieved
temperature stratifications, with a clear scaling by the constant wavelength-independent
stray-light offset β inside the spectrometer. This implies that for an
accurate derivation of temperatures from observed spectra the stray-light offset has to be
corrected before an inversion. On the positive side, the stray-light offset
β inside the SP spectrograph was found to be below 3% (see also Lites et al. 2013), which makes these data and data of
similar spectral quality well suited for a derivation of temperature stratifications in the
solar photosphere (e.g. Socas-Navarro 2011).
The size of the statistical samples of simulations and observations in our case are not identical. The FOV of the simulations of (6 Mm)2 covers only a small fraction of that of the observational data used. The close match between characteristic quantities indicates that any statistical effect should, however, not have a significant impact. The line properties change drastically with the spatial resolution, but in the same way in degraded simulations and observations. An inclusion of more simulation snapshots therefore is likely to confirm the close match between the statistics of line parameters from observations and degraded simulations. As a test, we compared the line profile resulting from averaging over one or over 21 snapshots covering the whole HD simulation series. The corresponding average profiles differed only slightly, maintaining similar differences towards FTS or the observed spectra as those seen in Fig. 8.
7. Conclusions
We find no indications that the thermodynamic fluctuations in a state-of-the-art numerical
hydrodynamical simulation exceed those in observations of the solar photosphere when the
simulation is spatially degraded to a resolution ≥ . For a final proof that the
initial properties of the simulation at full resolution do not exceed solar surface
properties, observations that resolve the photon mean free-path length
(<
. For a final proof that the
initial properties of the simulation at full resolution do not exceed solar surface
properties, observations that resolve the photon mean free-path length
(< ) are required. Solar telescopes
with free apertures of about 1.5 m and next-generation solar telescopes of the 4-m class are
designed to achieve this objective.
) are required. Solar telescopes
with free apertures of about 1.5 m and next-generation solar telescopes of the 4-m class are
designed to achieve this objective.
Online material
Appendix A: Line properties at different line depression levels
Appendix A.1: Average values
Figures A.1 to A.3 show the average values of the line properties at different line depression levels but for the average bisector velocity of the 630.25 nm line. The average bisector velocity of the 630.15 nm line is similar to that of 630.25 nm in Fig. 11. The two near-IR lines (bottom row of Fig. A.1) sample only low layers in the solar atmosphere. For the observations, the curves thus correspond to those from 10% line depression up to roughly the minimal bisector velocity of the 630 nm lines at 30% line depression. The results derived from the HD-FR spectra show nearly straight bisectors for the near-IR lines. For both the 557.6 nm and 1082.7 nm line, the line properties close to the continuum (<40% line depression) suffer from the presence of line blends (557.6 nm) or ill-defined line depression levels (1082.7 nm) because of the extended line wings. For the latter line, the limited extension of the simulation box is also likely to play a role. The HD-SPAT-SPEC actually gives smoother curves for these lines than the observations themselves. The average intensities at different line depression levels (Fig. A.2) provide little information in themselves because they basically only measure the line depth. The observations and the HD-SPAT-SPEC match well in most cases, with nearly identical values for instance for the 557.6 nm or 1565.2 nm lines. The average line widths at different line depression levels (Fig. A.3) show again that the near-IR line only sample the lower range of the atmosphere, with their curves corresponding to those of the 630 nm lines up to the inflection point at about the 50% line depression. The observations and the (degraded) HD simulation match well in the general shape of the curves here, whereas the absolute values of the line width slightly differ (cf. the red and red-dashed curves in Fig. A.3). This mismatch in line width was already seen in the average profiles (Fig. 8).
 |
Fig. A.1 Average velocities at different line depression levels for all lines but 630.25 nm in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). |
Appendix A.2: Rms fluctuations
 |
Fig. A.2 Average intensity at different line depression levels in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). |
 |
Fig. A.3 Average line width at different line depression levels in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). |
 |
Fig. A.4 Rms fluctuations in the line properties at different line depression levels for all lines but 630.25 nm and 557.6 nm in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). Top two rows: velocity. Middle two rows: intensity. Bottom two rows: line width. |
The rms fluctuations in the line properties at different line depression levels for all but the 630.25 nm and 557.6 nm lines are shown in Fig. A.4. The curves are all to some extent similar to the corresponding ones of the 630.25 nm line that are described in Sect. 5.3. The most noteworthy feature is that the fluctuations in the HD-SPAT-SPEC never significantly exceed the observed fluctuations in any of the parameters, but rather tend to show slightly lower values. Some parameters show a quite close match between observations and the degraded HD simulation, e.g. the rms velocities for all lines or the intensity rms for the near-IR lines.
Appendix B: Line parameters of 557.6 nm
 |
Fig. B.1 Histograms of the line parameters for the 557.6 nm line. Black lines: observations. Red lines: degraded HD simulation. |
 |
Fig. B.2 Rms fluctuations in the line properties at different line depression levels for the 557.6 nm line in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). Top: bisector velocity. Middle: bisector intensity. Bottom: line width. |
Figure B.1 shows histograms of all line parameters of the Fe i line at 557.6 nm for completeness. The 557 nm data were intended to be used for an abundance determination and were therefore recorded even under bad seeing conditions. This quite limits their usefulness for deriving spatial variations of line parameters because all observed spectra already represent some large-scale spatial average. The line is the only one in the sample with a Landé factor of zero, i.e. not sensitive to Zeeman broadening. It thus only reacts to the thermodynamic properties of the atmosphere and not directly to the magnetic field. The line parameters (Fig. B.1) show some deviation between the observations and the HD-SPAT-SPEC, especially the FWHM and the equivalent width. This is most likely related more to the settings in the spectral synthesis, i.e. the method for the inclusion of line broadening, than the thermodynamics themselves. The rms fluctuations in the line properties at different line depression levels (Fig. B.2) in observations and the HD-SPAT-SPEC are more similar than the histograms of line parameters. They show again lower fluctuations in the HD-SPAT-SPEC than in the observations. The 557.6 nm line will be most important in the comparison of the thermodynamic characteristics between the field-free, purely HD and the MHD simulations of increasing average magnetic flux. In the present context, this line shows no prominent deviations from the other Zeeman-sensitive lines in its behaviour.
Acknowledgments
The VTT is operated by the Kiepenheuer-Institut für Sonnenphysik (KIS) at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias (IAC). The POLIS instrument has been a joint development of the High Altitude Observatory (Boulder, USA) and the KIS. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway). C.B. acknowledges partial support by the Spanish Ministerio de Ciencia e Innovación through project AYA 2010-18029. R.R. acknowledges financial support by the DFG grant RE 3281/1-1. D.F. gratefully acknowledges financial support by the European Commission through the SOLAIRE Network (MTRN-CT-2006-035484) and by the Programa de Acceso a Grandes Instalaciones Científicas financed by the Spanish Ministerio de Ciencia e Innovación. The latter is also thanked by D.F. and F.M.-I. for providing funds through the related projects AYA2007-66502, CSD2007-00050, AYA2007-63881 and AYA2011-24808. The simulations were possible thanks to time awarded on the MareNostrum (BSC/CNS, Spain), the Danish Centre for Scientific Computing (DCSC-KU, Denmark), La Palma (IAC/RES, Spain) and the HRLS/DEISA (Germany) supercomputer installations. We thank A. Asensio Ramos and A. Lagg for their helpful comments on the present article.
References
- Afram, N., Unruh, Y. C., Solanki, S. K., et al. 2011, A&A, 526, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allende Prieto, C., Barklem, P. S., Asplund, M., & Ruiz Cobo, B. 2001, ApJ, 558, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Allende Prieto, C., Asplund, M., & Fabiani Bendicho, P. 2004, A&A, 423, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Nordlund, Å., Trampedach, R., Allen de Prieto, C., & Stein, R. F. 2000, A&A, 359, 729 [NASA ADS] [Google Scholar]
- Asplund, M., Carlsson, M., & Botnen, A. V. 2003, A&A, 399, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., Allen de Prieto, C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Basu, S., & Serenelli, A. M. 2005, ApJ, 631, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Bard, S., & Carlsson, M. 2008, ApJ, 682, 1376 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Beck, C. 2011, A&A, 525, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., & Rezaei, R. 2009, A&A, 502, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Schlichenmaier, R., Collados, M., Bellot Rubio, L., & Kentischer, T. 2005a, A&A, 443, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Schmidt, W., Kentischer, T., & Elmore, D. 2005b, A&A, 437, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Khomenko, E., Rezaei, R., & Collados, M. 2009, A&A, 507, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Fabbian, D. 2011, A&A, 535, A129 (BE11) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Puschmann, K. G. 2013a, A&A, 549, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Puschmann, K. G. 2013b, A&A, 553, A73 [NASA ADS] [EDP Sciences] [Google Scholar]
- Beeck, B., Collet, R., Steffen, M., et al. 2012, A&A, 539, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., & Kneer, F. 2008, A&A, 480, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bethge, C., Peter, H., Kentischer, T. J., et al. 2011, A&A, 534, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bethge, C., Beck, C., Peter, H., & Lagg, A. 2012, A&A, 537, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonet, J. A., Márquez, I., Sánchez Almeida, J., Cabello, I., & Domingo, V. 2008, ApJ, 687, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, P. N., & Schroeter, E. H. 1982, Sol. Phys., 79, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Briand, C., Mattig, W., Ceppatelli, G., & Mainella, G. 2006, Sol. Phys., 234, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera Solana, D., Bellot Rubio, L. R., & del Toro Iniesta, J. C. 2005, A&A, 439, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrera Solana, D., Bellot Rubio, L. R., Beck, C., & Del Toro Iniesta, J. C. 2007, A&A, 475, 1067 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Steffen, M., Ayres, T. R., et al. 2008, A&A, 488, 1031 [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, W., Gorceix, N., Coulter, R., Coulter, A., & Goode, P. R. 2010, in Ground-based and Airborne Telescopes III, eds. L. M. Stepp, G. R., & H. J. Hall, SPIE Conf. Ser., 7733 [Google Scholar]
- Carlsson, M., & Leenaarts, J. 2012, A&A, 539, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carroll, T. A., & Kopf, M. 2008, A&A, 481, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chapman, G. A. 1977, ApJS, 33, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Collados, M., Lagg, A., Díaz Garcí A, J. J., et al. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 611 [Google Scholar]
- Collados, M., Bettonvil, F., Cavaller, L., et al. 2010, in Ground-based and Airborne Telescopes III, eds. L. M. Stepp, G. R., & H. J. Hall, SPIE Conf. Ser., 7733 [Google Scholar]
- Collet, R., Hayek, W., Asplund, M., et al. 2011, A&A, 528, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Cruz Rodríguez, J., Kiselman, D., & Carlsson, M. 2011, A&A, 528, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delbouille, L., Roland, G., & Neven, L. 1973, Atlas photometrique DU spectre solaire de [lambda] 3000 a [lambda] 10000 (Liège: Université de Liège, Institut d’Astrophysique) [Google Scholar]
- Denker, C., Goode, P. R., Ren, D., et al. 2006, in Ground-based and Airborne Telescopes, ed. L. M. Stepp, SPIE Conf. Ser., 6267 [Google Scholar]
- Dravins, D. 1982, ARA&A, 20, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Dravins, D. 2008, A&A, 492, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabbian, D., Asplund, M., Barklem, P. S., Carlsson, M., & Kiselman, D. 2009a, A&A, 500, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabbian, D., Nissen, P. E., Asplund, M., Pettini, M., & Akerman, C. 2009b, A&A, 500, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabbian, D., Khomenko, E., Moreno-Insertis, F., & Nordlund, Å. 2010, ApJ, 724, 1536 [NASA ADS] [CrossRef] [Google Scholar]
- Fabbian, D., Moreno-Insertis, F., Khomenko, E., & Nordlund, Å. 2012, A&A, 548, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Felipe, T., Khomenko, E., Collados, M., & Beck, C. 2010, ApJ, 722, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Fontenla, J. M., Avrett, E., Thuillier, G., & Harder, J. 2006, ApJ, 639, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 2010, ApJ, 721, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N. 1984, Phys. Scr. T, 8, 49 [Google Scholar]
- Hanslmeier, A., Kučera, A., Rybák, J., Neunteufel, B., & Wöhl, H. 2000, A&A, 356, 308 [NASA ADS] [Google Scholar]
- Hayek, W., Asplund, M., Carlsson, M., et al. 2010, A&A, 517, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirzberger, J., & Wiehr, E. 2005, A&A, 438, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirzberger, J., Feller, A., Riethmüller, T. L., et al. 2010, ApJ, 723, L154 [NASA ADS] [CrossRef] [Google Scholar]
- Holweger, H., & Mueller, E. A. 1974, Sol. Phys., 39, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Kalkofen, W. 2012, Sol. Phys., 276, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E. V., Martínez González, M. J., Collados, M., et al. 2005, A&A, 436, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitiashvili, I. N., Kosovichev, A. G., Mansour, N. N., & Wray, A. A. 2011, ApJ, 727, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Koesterke, L., Allen de Prieto, C., & Lambert, L. 2008, ApJ, 680, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Nordlund, Å., Collins, D., et al. 2011, ApJ, 737, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm (National Solar Observatory, Sunspot, NM) [Google Scholar]
- Lagg, A., Solanki, S. K., Riethmüller, T. L., et al. 2010, ApJ, 723, L164 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Rutten, R. J. 2007, A&A, 473, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Rouppe van der Voort, L. 2009, ApJ, 694, L128 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2012, ApJ, 749, 136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W., Akin, D. L., Card, G., et al. 2013, Sol. Phys., 283, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Löfdahl, M. G., & Scharmer, G. B. 2012, A&A, 537, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marquez, I., Bonet, J. A., Vazquez, M., & Woehl, H. 1996, A&A, 305, 316 [NASA ADS] [Google Scholar]
- Martínez Pillet, V., Collados, M., Sánchez Almeida, J., et al. 1999, in High Resolution Solar Physics: Theory, Observations, and Techniques, ASP Conf. Ser., 183, 264 [Google Scholar]
- Martínez González, M. J., Collados, M., & Ruiz Cobo, B. 2006, A&A, 456, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez González, M. J., Collados, M., Ruiz Cobo, B., & Beck, C. 2008, A&A, 477, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez González, M. J., Bellot Rubio, L. R., Solanki, S. K., et al. 2012, ApJ, 758, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Mattig, W. 1971, Sol. Phys., 18, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Mattig, W. 1983, Sol. Phys., 87, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., & Asplund, M. 2008, A&A, 490, 817 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Mikurda, K., Tritschler, A., & Schmidt, W. 2006, A&A, 454, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moll, R., Cameron, R. H., & Schüssler, M. 2011, A&A, 533, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neckel, H. 1999, Sol. Phys., 184, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, A. 1982, A&A, 107, 1 [NASA ADS] [Google Scholar]
- Nordlund, Å., & Stein, R. F. 1990, Comp. Phys. Commun., 59, 119 [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C., et al. 2007, ApJ, 670, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira, T. M. D., Asplund, M., & Kiselman, D. 2009a, A&A, 508, 1403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Asplund, M., & Kiselman, D. 2009b, Mem. S.A. It., 75, 282 [Google Scholar]
- Pereira, T. M. D., Kiselman, D., & Asplund, M. 2009c, A&A, 507, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira, T. M. D., Asplund, M., Collet, R., et al. 2013, A&A, 554, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschmann, K. G., & Beck, C. 2011, A&A, 533, A21 (PuB11) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschmann, K. G., & Sailer, M. 2006, A&A, 454, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschmann, K., Hanslmeier, A., & Solanki, S. K. 1999, in Motions in the Solar Atmosphere, eds. A. Hanslmeier, & M. Messerotti, Astrophysics and Space Science Library, 239, 227 [Google Scholar]
- Puschmann, K., Vázquez, M., Bonet, J. A., Ruiz Cobo, B., & Hanslmeier, A. 2003, A&A, 408, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschmann, K. G., Ruiz Cobo, B., Vázquez, M., Bonet, J. A., & Hanslmeier, A. 2005, A&A, 441, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschmann, K. G., Kneer, F., Seelemann, T., & Wittmann, A. D. 2006, A&A, 451, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puschmann, K. G., Kneer, F., & Domínguez Cerdeña, I. 2007, in Modern solar facilities – advanced solar science, eds. F. Kneer, K. G. Puschmann, & A. D. Wittmann (Universitätsverlag Göttingen), 151 [Google Scholar]
- Puschmann, K. G., Ruiz Cobo, B., & Martínez Pillet, V. 2010, ApJ, 720, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Puschmann, K. G., Balthasar, H., Bauer, S.-M., et al. 2012a, in The Second ATST-EAST Meeting: Magnetic Fields from the Photosphere to the Corona, eds. T. R. Rimmele, A. Tritschler, F. Wöger, et al., ASP Conf. Ser., 463, 423 [Google Scholar]
- Puschmann, K. G., Balthasar, H., Beck, C., et al. 2012b, in Ground-based and Airborne Instrumentation for Astronomy IV, SPIE Conf. Ser., 8446, 79 [Google Scholar]
- Puschmann, K. G., Denker, C., Kneer, F., et al. 2012c, Astron. Nachr., 333, 880 [NASA ADS] [Google Scholar]
- Rammacher, W., & Cuntz, M. 1991, A&A, 250, 212 [NASA ADS] [Google Scholar]
- Rimmele, T. R., Wagner, J., Keil, S., et al. 2010, in Ground-based and Airborne Telescopes III, eds. L. M. Stepp, G. R., & H. J. Hall, SPIE Conf. Ser., 7733 [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. J. 2003, Radiative Transfer in Stellar Atmospheres, Lect. Notes Utrecht University [Google Scholar]
- Sánchez Almeida, J. 2005, ApJ, 622, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, W., von der Lühe, O., Volkmer, R., et al. 2012a, Astron. Nachr., 333, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, W., von der Lühe, O., Volkmer, R., et al. 2012b, in The Second ATST-EAST Meeting: Magnetic Fields from the Photosphere to the Corona, eds. T. R. Rimmele, A. Tritschler, F. Wöger, et al., ASP Conf. Ser., 463, 365 [Google Scholar]
- Schröter, E. H., Soltau, D., & Wiehr, E. 1985, Vist. Astron., 28, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Shchukina, N., & Trujillo Bueno, J. 2001, ApJ, 550, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Shchukina, N., Sukhorukov, A., & Trujillo Bueno, J. 2012, ApJ, 755, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Shelyag, S., Schüssler, M., Solanki, S. K., & Vögler, A. 2007, A&A, 469, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shi, J. R., Gehren, T., Butler, K., Mashonkina, L. I., & Zhao, G. 2008, A&A, 486, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skartlien, R. 2000, ApJ, 536, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H. 2001, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236, 487 [Google Scholar]
- Socas-Navarro, H. 2011, A&A, 529, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Socas-Navarro, H., Trujillo Bueno, J., & Ruiz Cobo, B. 2000, ApJ, 530, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, A. 1998, ApJ, 499, 914 [Google Scholar]
- Stein, R. F., & Nordlund, A. 2000, Sol. Phys., 192, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., Lagerfjärd, A., Nordlund, Å., & Georgobiani, D. 2011, Sol. Phys., 268, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, O., & Rezaei, R. 2012, in Fifth Hinode Science Meeting, eds. L. Golub, I. De Moortel, & T. Shimizu, ASP Conf. Ser., 456, 3 [Google Scholar]
- Steiner, O., Grossmann-Doerth, U., Knoelker, M., & Schuessler, M. 1998, ApJ, 495, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, O., Franz, M., Bello González, N., et al. 2010, ApJ, 723, L180 [NASA ADS] [CrossRef] [Google Scholar]
- Stellmacher, G., & Wiehr, E. 1971, Sol. Phys., 18, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Unsöld, A. 1955, Physik der Sternatmosphären, Mit besonderer Berücksichtigung der Sonne (Berlin: Springer, 2. Auflage) [Google Scholar]
- van Noort, M. 2012, A&A, 548, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Noort, M., Rouppe van der Voort, L., & Löfdahl, M. G. 2005, Sol. Phys., 228, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A. 2004, A&A, 421, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A., Bruls, J. H. M. J., & Schüssler, M. 2004, A&A, 421, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von der Lühe, O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics, eds. S. L. Keil, & S. V. Avakan, SPIE Conf. Ser., 4853, 187 [Google Scholar]
- Wagner, J., Rimmele, T. R., Keil, S., et al. 2008, in Ground-based and Airborne Telescopes II, eds. L. M. Stepp, & R. Gilmozzi, SPIE Conf. Ser., 7012 [Google Scholar]
- Wedemeyer, S. 2001, A&A, 373, 998 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., & Holweger, H. 2004, A&A, 414, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S. 2008, A&A, 487, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Carlsson, M. 2011, A&A, 528, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Instruments and data properties, and corresponding settings of the spectral synthesis for the simulations.
Top row: “best” degradation kernel parameters a and FWHM(σ) for each instrument. Second row: average spatial stray light level α corresponding to each of those “best” kernels. Bottom rows: width of “best” kernel at three percentage levels of maximum amplitude.
All Figures
 |
Fig. 1 Example spectrum at 630 nm from POLIS. Blue-dotted line: average spectrum without correction for intensity gradients over the wavelength range. Black line: corrected spectrum. Red line: FTS atlas spectrum. The dashed vertical lines denote the “continuum” range, the solid vertical lines the range that was considered for determining the line parameters of Fe i 630.15 nm and Fe i 630.25 nm, respectively. The coloured horizontal lines inside the absorption profiles illustrate the method used to determine line properties at different line depression levels. |
| In the text | |
 |
Fig. 2 Overview maps representative of the different observational data sets. Top to bottom: continuum intensity Ic, line-core intensity Icore and line-core velocity vcore. Left to right: SP, GFPI (MOMFBD), GPFI (destretched), POLIS, TIP@1083 nm, and TIP@1565 nm. Black/white in the velocity maps denotes motions towards/away from the observer. All images are scaled individually inside their full dynamical range. |
| In the text | |
 |
Fig. 3 χ2 values as a function of FWHM
(= |
| In the text | |
 |
Fig. 4 “Best” degradation kernels Ktotal for GFPI MOMFBD (black solid line), GFPI destretched (black crosses), Hinode/SP (thick red line), POLIS (thick blue line), TIP@1083 nm (orange line), TIP@1565 nm (purple line) and Echelle@557 nm (thick green line). |
| In the text | |
 |
Fig. 5 Estimates of the PSF for POLIS from the degradation of the HD simulation (thick black line), a measurement of a knife-edge function (red line) and a scan across the pinhole in F1 (blue/blue-dot-dashed lines: cuts along y/x). The inset at the upper left shows the intensity map of the pinhole scan. |
| In the text | |
 |
Fig. 6 Intensity histograms for the observations (black lines), and (red lines) for the HD simulation spatially convolved with the corresponding “best” kernel. Instrument and wavelength are given at the top of each panel. The blue line in the panel corresponding to the POLIS data denotes the Gaussian fit to the observed intensity distribution. |
| In the text | |
 |
Fig. 7 Comparison of observations (lower row in each panel) with the HD simulation (upper row in each panel) convolved using each observation’s “best” kernel. Top to bottom: Ic, v(50% line depression) and vcore. Left to right: SP, GFPI(MOMFBD), GFPI(destretched), POLIS, TIP@1083 nm, TIP@1565 nm and Echelle@557 nm. |
| In the text | |
 |
Fig. 8 Spatially averaged profiles of the 630 nm range (left top two rows), the 557 nm range (bottom left), and the near-IR wavelength ranges (right column). For the 630.15 nm line, the spectral sampling of the SP and POLIS is indicated by crosses. The thick purple curves show the spectra in the FTS or BASS atlas, depending on the wavelength range of interest. For 557.6 nm, 630.15 nm, 1564.8 nm and 1565.2 nm the profiles from the HD-SPAT-SPEC are over-plotted with dash-dotted lines. In the plot at 557.6 nm, absolute flux units are used and the normalization of the HD-FR spectra to the FTS was undone. |
| In the text | |
 |
Fig. 9 Histograms of line parameters derived for HD-SPAT-SPEC and observations. Top left panel: line asymmetry. Top right panel: FWHM. Bottom left panel: equivalent width. Bottom right panel: line depth. The black line denotes the histogram of the relevant parameter for a given observational data set, the red line the one for the degraded simulation. Instrument and wavelength are denoted at the top of each panel. |
| In the text | |
 |
Fig. 10 Histograms of line-core velocity in HD-SPAT-SPEC and observations. The black line denotes the histogram of the parameter in the observation and the red line that in the HD-SPAT-SPEC. Instrument and central wavelength of relevance are specified in the title of each sub-panel. |
| In the text | |
 |
Fig. 11 Top panel: spatially averaged bisector velocity (SABV) for the 630.25 nm line in the observations (solid lines), the HD-FR (solid black line) and the HD-SPAT-SPEC (dashed lines). Bottom panel: comparison between SABVs and bisector velocities of average profiles (BVAP) for the 630.25 nm line. Solid/dash-dotted black lines: SABV/BVAP in the HD-FR. Solid red/blue lines: SABV/BVAP for the SP data. Red/blue dashed lines: SABV/BVAP for the simulation degraded to SP resolution. The purple line gives the bisector in the FTS atlas profile. Positive velocities correspond to redshifts relative to the average velocity at 50% line depression. |
| In the text | |
 |
Fig. 12 Rms fluctuations in the line properties at different line depression levels for the 630.25 nm line in the observations (solid lines), in the HD-FR (solid black line) and in the HD-SPAT-SPEC (dashed lines). Top: bisector velocity. Middle: bisector intensity. Bottom: line width. |
| In the text | |
 |
Fig. 13 Histograms of the macroturbulent (left column) and microturbulent velocity (right column) in the inversions. Top: inversions of observations. Middle: the same for the HD-SPAT simulation. Bottom: the same for the HD-SPAT-SPEC. Thin black lines in each panel: HD-FR. |
| In the text | |
 |
Fig. 14 Temperature stratifications (top row), difference to the HSRA model (middle row), and rms fluctuations of temperature (bottom row) in the inversions. Left to right: observations, HD-SPAT and HD-SPAT-SPEC. The dotted vertical lines denote the approximate formation height range of the 630 nm lines, the dashed vertical line the upper end of the range for near-IR lines. Other labels are identical to Fig. 13. |
| In the text | |
 |
Fig. 15 Relative temperature fluctuations vs. optical depth. Top panel: inversion results of SP (red line), GFPI (orange line) and Ca ii H data (blue line), and of the HD-FR simulation spectra (black-solid line). Overplotted are the relative temperature fluctuations in the HD-FR simulation box (black dashed-triple-dotted line) and the curve given in Hayek et al. (2010, HA10) for a simulation with continuum scattering (black-dashed line). Bottom panel: inversion results of SP/Ca ii H multiplied by two/five (red/blue lines), and the values from the simulations of Wedemeyer et al. (2004, WE04; black-dotted line), of HA10 with continuum scattering (black-dashed line) and of HA10 with continuum and line scattering (black-dash-dotted line). |
| In the text | |
 |
Fig. A.1 Average velocities at different line depression levels for all lines but 630.25 nm in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). |
| In the text | |
 |
Fig. A.2 Average intensity at different line depression levels in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). |
| In the text | |
 |
Fig. A.3 Average line width at different line depression levels in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). |
| In the text | |
 |
Fig. A.4 Rms fluctuations in the line properties at different line depression levels for all lines but 630.25 nm and 557.6 nm in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). Top two rows: velocity. Middle two rows: intensity. Bottom two rows: line width. |
| In the text | |
 |
Fig. B.1 Histograms of the line parameters for the 557.6 nm line. Black lines: observations. Red lines: degraded HD simulation. |
| In the text | |
 |
Fig. B.2 Rms fluctuations in the line properties at different line depression levels for the 557.6 nm line in the observations (solid lines), the HD-SPAT-SPEC (dashed lines) and the HD-FR (solid black line). Top: bisector velocity. Middle: bisector intensity. Bottom: line width. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.