| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 8 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201321579 | |
| Published online | 16 September 2013 | |
On the statistical significance of the bulk flow measured by the Planck satellite
Física Teórica, Universidad de Salamanca, 37008 Salamanca, Spain
e-mail: atrio@usal.es
Received: 26 March 2013
Accepted: 4 August 2013
A recent analysis of data collected by the Planck satellite detected a net dipole at the location of X-ray selected galaxy clusters, corresponding to a large-scale bulk flow extending at least to z ~ 0.18, the median redshift of the cluster sample. The amplitude of this flow, as measured with Planck, is consistent with earlier findings based on data from the Wilkinson Microwave Anisotropy Probe (WMAP). However, the uncertainty assigned to the dipole by the Planck team is much larger than that found in the WMAP studies, leading the authors of the Planck study to conclude that the observed bulk flow is not statistically significant. Here, we show that two of the three implementations of random sampling used in the error analysis of the Planck study lead to systematic overestimates in the uncertainty of the measured dipole. Random simulations of the sky do not take into account that the actual realization of the sky leads to filtered data that have a 12% lower root-mean-square dispersion than the average simulation. Using rotations around the Galactic pole (the Z axis), increases the uncertainty of the X and Y components of the dipole and artificially reduces the significance of the dipole detection from 98−99% to less than 90% confidence. When either effect is taken into account, the corrected errors agree with those obtained using random distributions of clusters on Planck data, and the resulting statistical significance of the dipole measured by Planck is consistent with that of the WMAP results.
Key words: cosmology: observations / cosmic background radiation / large-scale structure of Universe / galaxies: clusters: general
© ESO, 2013
1. Introduction
The intrinsic difficulty of determining peculiar velocities from galaxy redshifts and distance indicators led Kashlinsky & Atrio-Barandela (2000) to propose an alternative method of probing the velocity field on large scales. Galaxy clusters leave an imprint on the cosmic microwave background (CMB) in the form of distortions in the CMB black-body spectrum caused by the Sunyaev-Zel’dovich (SZ) effect (Sunyaev & Zel’dovich 1970, 1972). Two different mechanisms contribute to the SZ effect: the thermal component (TSZ) is caused by the thermal motions of electrons in the potential wells of clusters, whereas the kinematic component (KSZ) is due to the motion of the cluster as a whole. We noted that any bulk flow of clusters would produce a dipole in the anisotropy temperature in the direction of clusters. Since this signal is small compared to the sampling variance of the intrinsic CMB dipole at the same positions, we proposed to use the statistical properties of the CMB data to filter out the dominant cosmological component, thereby increasing the signal-to-noise ratio of any contribution from a bulk-flow dipole.
In Atrio-Barandela et al. (2008) and Kashlinsky et al. (2008, 2009) we presented results of our application of this method to Wilkinson Microwave Anisotropy Probe (WMAP) 3-year data, later extended to WMAP 5-year and 7-year data (Kashlinsky et al. 2010, 2011). For a sample of ~700 X-ray-selected clusters, we detected a persistent dipole, measured at the cluster positions within apertures (of 25′ radius) that contain zero TSZ monopole. The dipole is roughly aligned with the CMB dipole and can be traced to cluster redshifts exceeding z ~ 0.2; its amplitude correlates with that of the monopole within apertures of 10′ radius. We interpreted this signal, associated exclusively with clusters, as evidence of a large-scale flow of amplitude ≃600−1000 km s-1 that could encompass the whole observable horizon. A “Dark Flow” of this amplitude, if real, would be equivalent to the all-sky CMB dipole being primarily of primordial origin, intrinsic to last scattering surface.
Our theoretical and numerical estimates indicated that our dipole detection is significant at the 99.4% confidence level. However, independent confirmation of this result is still lacking, and several studies have challenged our results. Keisler (2009) confirmed the existence of the dipole detected by us, but claimed that it was not statistically significant. It was shown though (Atrio-Barandela et al. 2010) that Keisler neglected to subtract the dipole outside the Galactic mask, causing the error bars of his measurement to be overestimated. More recently, Osborne et al. (2011) and Mody & Hajian (2012) did not find bulk flows in WMAP data using filtering schemes different from ours. However, both teams of authors implicitly assumed that clusters have the same angular extent in the original data as in the filtered maps, and that the electron pressure and the electron density in clusters follow the same radial profile. Both assumptions are incorrect and render these filters insensitive to bulk flows. In Atrio-Barandela et al. (2013) we demonstrated that correct implementation of either of these alternative filtering schemes leads to results that are consistent with ours. Two recent studies using galaxies, rather than clusters, to search for the KSZ signature of a large-scale bulk flow in CMB data have also challenged our findings. The CMB-galaxy cross-correlation study by Li et al. (2012) found a statistically anisotropic component in the CMB on scales out to z ~ 0.2, but ruled out the Dark Flow as its cause, due to the very high galaxy velocities implied by this interpretation. We note though that peculiar velocities in perfect agreement with our findings would result if their cross-correlation signal were dominated by cluster galaxies rather than field galaxies. Lavaux et al. (2013) aimed to use the KSZ effect from the plasma halo of galaxies to probe the peculiar velocity field and found results on small scales (< 50 h-1 Mpc) that are consistent with those obtained using galaxy distance indicators. On scales of ~ 500 h-1 Mpc, however, their analysis leads to an upper limit of 470 km s-1 (95% significance) for the bulk-flow velocity, in conflict with the Dark Flow amplitude measured by us. It should be noted though that these conclusions depend sensitively on the spatial distribution of ionized gas in and around galaxies, which is presently ill-constrained by observations.
A conclusive determination of the Dark Flow is expected to emerge from an authoritative study based on CMB data collected by the Planck satellite. With its higher resolution, better frequency coverage and lower noise levels Planck is much better suited for studies of the SZ effect than WMAP. A comparison between the dipole measurements from the two missions will also allow a much-needed consistency check, since differences between the instruments and scanning strategies result in data with different systematics. In this context, the Planck Collaboration has recently reported (Planck Collaboration 2013a,b) the aberration and modulation effects due to the motion of the Sun with respect to the CMB frame and found a significant agreement with the Doppler boosting of the CMB monopole. However, this measurement does not constrain the motion of the Local Group but the amplitude of its component in the direction of the solar motion. They have also reported the first Planck-based KSZ measurement of the peculiar motions of clusters (Planck Collaboration 2013a,b, hereafter PIR-13) using their own catalog of X-ray selected clusters (Piffaretti et al. 2011) and concluded that the Planck constraints on peculiar velocities were consistent with the concordance ΛCDM model.
In this paper we analyze and evaluate the error estimators employed by PIR-13. We begin by summarizing the PIR-13 results and methods in Sect. 2. Section 3 briefly reviews the formalism regarding error estimation developed by Atrio-Barandela et al. (2010), before we discuss in detail two problematic implementations of error estimation used in PIR-13, rotations and numerical simulations, in Sects. 4 and 5, respectively. We present our conclusions in Sect. 6.
2. Results and methods of the first Planck bulk-flow study
The PIR-13 results characterize the average peculiar velocities of clusters at different depths using three complementary diagnostics: the radial peculiar-velocity average, the root-mean-square (rms) velocity, and the bulk-flow velocity. The underlying analysis employs three different filtering schemes, including the one introduced by us (Kashlinsky et al. 2009). The study’s findings for all three diagnostics mentioned above are consistent with the very low ΛCDM predictions for the average peculiar velocities of galaxy clusters. Specifically, the PIR-13 abstract asserts that “there is no detection of [a] bulk flow as measured in any comoving sphere extending to the maximum redshift covered by the cluster sample”. To fully appreciate the nature and significance of this assertion, it is critical to understand that, when using our filtering scheme, PIR-13 detects the same dipole signal at cluster positions as previously found by us in WMAP data (PIR-13, Fig. 10). What renders their bulk-flow detection insignificant is thus not the absence of a dipole signal, but the uncertainty assigned to it. Before analyzing PIR-13 error estimates in more detail in the following section, we briefly discuss several key aspects of their work.
The PIR-13 study is based on the Meta Catalogue of X-ray detected Clusters of galaxies (MCXC; Piffaretti et al. 2011), a compilation of publicly available X-ray cluster samples drawn primarily from ROSAT All-Sky Survey projects, but also including mostly low-mass systems from serendipitous X-ray cluster surveys. Comprising 1750 clusters and rich galaxy groups, the MCXC is comparable in size to our proprietary catalog of 1558 X-ray selected clusters, but contains more low-luminosity systems and fewer very X-ray luminous clusters. By excluding MCXC entries close to bright point sources in any single-frequency Planck map, clusters lying in regions of high Galactic emission, and systems with estimated masses below 1013M⊙, the sample used by PIR-13 is reduced to 1405 clusters. PIR-13 conducted their analysis using a CMB map that is the weighted average of the single-frequency Planck maps. This so-called 2D Internal Linear Combination (2D-ILC) map introduces additional masking, resulting in a final sample of 1321 MCXC clusters. For comparison, our sample was limited to the 1205 clusters with X-ray luminosities LX [0.1−2.4 keV] ≥ 0.5 × 1044 erg s-1, and our results were obtained from 796 clusters that fall outside the extended KQ75 mask.
Comparing the WMAP and Planck cluster dipoles allows us to identify and account for previously undiagnosed systematic effects. First, differences in scanning strategy, angular resolution, foreground residuals and other systematics could give different error bars in WMAP and Planck even if the measured dipole values are the same. Second, a larger cluster catalog must improve the significance of the result if the cluster mass range is comparable. Third, the TSZ contribution can be determined and monitored much better with Planck data by comparing measurements at frequencies above and below the TSZ null at 217 GHz. Then, any correlation between the TSZ monopole within 10′ (radius) apertures and the KSZ dipole within 25′ apertures (Kashlinsky et al. 2010, 2011) can also be established better with Planck than with WMAP. Nevertheless, a direct comparison of the results could present some difficulties. In our WMAP-based analysis, the dipole signal was measured within discs of radius 25′ around each cluster, corresponding to the zero monopole aperture and, due to its higher resolution, the zero monopole aperture in Planck and in WMAP may be different. In addition, the correlation between the SZ monopole and dipole observed by us indicates that low-mass systems contribute little to the signal. A larger fraction of low-mass clusters in the MCXC could thus dilute the dipole, although we note in this paper the additional reasons for which PIR-13 failed to detect a significant cluster dipole, as we shall elaborate below.
PIR-13 applied several filtering schemes in Legendre space. While the actual filters differ from those previously used and described in the literature, the PIR-13 filter implementations share the drawbacks of the filters used by Osborne et al. (2011) and Mody & Hajian (2012). Specifically, the PIR-13 study assumes that clusters have the same size in the real as in the filtered data, and adopts isothermal cluster models to calibrate these filters. Both of these assumptions, however, render filters insensitive to bulk flows, as shown by Atrio-Barandela et al. (2013). In addition, PIR-13 uses the Aperture Photometry filter, first introduced in the context of bulk-flow measurements by Kashlinsky & Atrio-Barandela (2000). Contrary to other filters, the Aperture Photometry filter operates in real space: the intrinsic CMB signal is removed by subtracting the temperature averaged within an annulus (defined by radii θin,θout) from the temperature averaged within the inner disc of radius θin. While this process indeed removes the CMB, it also removes part of the SZ anisotropy of the cluster. In order to estimate the missing fraction, the profiles of the electron pressure and electron density need to be known for each cluster. Assuming clusters to be isothermal simplifies the task, but biases the result. If the electron density falls less rapidly than the electron pressure, then the KSZ component is removed more efficiently than the TSZ component, reducing the cluster dipole. In addition, all cluster annuli must have the same radii if the CMB is to be removed uniformly across the sky, but PIR-13 defines different radii for each cluster, causing the residual CMB to vary from cluster to cluster. A detailed discussion of the resulting complications will be given in a forthcoming paper.
Finally, and most importantly, the PIR-13 analysis uses three methods to estimate the uncertainties of their measurements: (1) dipole measurements performed on the filtered maps at randomized cluster positions, (2) dipole measurements performed on random realizations of the filtered data, but at the real cluster positions, and (3) dipole measurements performed by rotating the template of cluster positions on the real data. PIR-13 offers no discussion of these estimators’ relative efficiency or biases, which is surprising in view of the fact that the resulting error estimates differ greatly. When using (1), the significance of the KSZ dipole found by PIR-13 using Planck data is higher than the one found by us from WMAP data, but it is lower when using methods (2) and (3). A bias inherent in method (2) is well established and due to the power spectrum of the residual CMB component in the actual realization of the sky being about 12% smaller than that of the average random realization of the sky (Atrio-Barandela et al. 2010). In the following sections, we discuss key aspects of the error computation as well as the discrepancies of the error estimation methods (2) and (3) with method (1) in more detail.
3. On the error bars of the bulk flow measurement
Since clusters subtend a small solid angle on the sky, sampling variance is the largest source of uncertainty in the determination of bulk flows (Kashlinsky & Atrio-Barandela 2000). Random dipoles from the cosmological CMB component have much larger amplitude than any KSZ dipole caused by the bulk motion of a cluster sample. To suppress this noise term, we suggested to filter out the CMB signal using the statistical properties of the temperature anisotropy field. In addition, contributions from the Galaxy and point sources are removed by application of suitably defined masks. We assume use of the extended WMAP 7 yr mask (the KQ75 mask) in the following description of the convolution process that creates the filtered maps:
-
1.
Each CMB map is multiplied by the KQ75 mask. Monopole, dipole, and quadrupole are removed from the remaining pixels.
-
2.
The resulting CMB map is expanded into spherical harmonics with coefficients
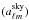 . The radiation power spectrum is
. The radiation power spectrum is 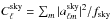 , where the division by fsky, the fraction of the sky outside the KQ75 mask, accounts for the power removed by the masking process.
, where the division by fsky, the fraction of the sky outside the KQ75 mask, accounts for the power removed by the masking process. -
3.
The power spectrum is filtered, and a Legendre transformation back to real space is applied:
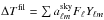 . We used the following Wiener-type filter:
. We used the following Wiener-type filter: ![\hbox{$F_\ell =[C_\ell^{\rm sky}-C_\ell^{\rm \Lambda CMB}B_\ell^2]/C_\ell^{\rm sky}$}](/articles/aa/full_html/2013/09/aa21579-13/aa21579-13-eq24.png) , where Bℓ is the antenna beam, and
, where Bℓ is the antenna beam, and 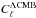 is the theoretical CMB radiation power spectrum of the concordance model that best fits the data.
is the theoretical CMB radiation power spectrum of the concordance model that best fits the data. -
4.
Finally, the filtered map ΔTfil is multiplied by the mask and any monopole and dipole introduced by the filtering process are removed from the remaining pixels.
In Atrio-Barandela et al. (2010) we presented a comprehensive discussion of the errors associated with our method and showed that the variance of the monopole and dipole components is 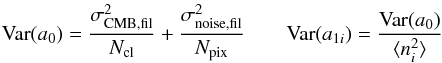 (1)with (ni) = (X,Y,Z) = (coslcosb,sinlcosb,sinb) being the direction cosines of the cluster positions on the sky. In this expression, σnoise,fil and σCMB,fil are the residual CMB and noise in the filtered maps. The noise is uncorrelated from pixel to pixel, whereas the correlation function of the residual CMB noise crosses zero at θ ~ 1°. Therefore, the sample variance of the contribution from the residual CMB scales approximately as the number of clusters Ncl, while the noise contribution scales with the number of pixels Npix.
(1)with (ni) = (X,Y,Z) = (coslcosb,sinlcosb,sinb) being the direction cosines of the cluster positions on the sky. In this expression, σnoise,fil and σCMB,fil are the residual CMB and noise in the filtered maps. The noise is uncorrelated from pixel to pixel, whereas the correlation function of the residual CMB noise crosses zero at θ ~ 1°. Therefore, the sample variance of the contribution from the residual CMB scales approximately as the number of clusters Ncl, while the noise contribution scales with the number of pixels Npix.
When estimating measurement uncertainties, we have to take into account (a) that clusters are not randomly distributed in the sky and that any anisotropy in their distribution could increase the errors, and (b) that, in addition to instrumental noise, filtered maps also contain unknown residuals of foreground emission and other systematics that cannot be precisely modeled. To take into account all sources of statistical uncertainty, error bars would have to be estimated using both the filtered data and the actual template of clusters in the sky. This is not possible (see also Sect. 4). However, errors computed using random templates on the filtered data showed a behavior very close to the prediction of Eq. (1), indicating that foreground residuals and other possible systematics can be safely neglected (Atrio-Barandela et al. 2010; Kashlinsky et al. 2012). To further explore item (a), the impact of anisotropies in the cluster distribution, here we consider two templates: T1, defined as the 796 clusters in our catalog with LX ≥ 0.5 × 1044 erg s-1 in the ROSAT broad band (0.1−2.4 keV), and T2, a subset of T1, comprising only the 327 most X-ray luminous clusters (LX ≥ 2.0 × 1044 erg s-1) at z ≤ 0.3.
We compute the dipole by assigning to all clusters the same angular radius of 25′, which roughly corresponds to the aperture within which the monopole vanishes in the filtered maps constructed with WMAP 7-year data. At Healpix resolution Nside = 512 (Gorski et al. 2005), samples T1 and T2 occupy 32 700 and 13 500 pixels, respectively (about 1% and 0.4% of the sky). Since gravitational instability drives low-mass systems towards the more massive clusters, we expect the distribution of the T1 sample to be less isotropic than that of the T2 template, offering the possibility to quantify the impact of anisotropies on the measurement errors. Using those templates and WMAP 7-year data from the W1 Differencing Assembly (DA), we find σCMB,fil ≈ 30 μk and σnoise,fil ≈ 75 μk. Given the relatively modest number of clusters in our samples T1 and T2, Eq. (1) then indicates that the residual CMB in the filtered map dominates the errors, as suggested independently by Keisler et al. (2009) and Kashlinsky et al. (2010). Simulations of filtered maps thus need to contain only the CMB, and can neglect noise, foreground residuals, and other systematics.
4. Error estimates from rotated cluster templates
As mentioned before, a rigorous computation of errors would require measuring dipoles at random locations in the filtered data, outside the cluster apertures, but using the same template that describes the real cluster positions used in the analysis. Because of the complex geometry of the mask, this is not possible. In Atrio-Barandela et al. (2010) we discussed the methods labeled (1) and (2) in Sect. 2: option (1) entails measuring dipoles in the filtered data, using random cluster templates that have no overlap with the real one, whereas option (2) measures dipoles in simulated data, but at the position of the real clusters. When applying method (1), we account for the contributions to the measurement error from foreground residuals and other systematics as far as they are known; with method (2), we account for the effect of anisotropic distribution of our cluster template on the sky as detailed later in this section. In our simulations we do not find any systematic differences between results obtained for real and simulated cluster templates beyond cosmic variance. This is understandable since clusters, at random or real positions, are, by design, selected outside the Galactic plane, and hence all templates share the large-scale inhomogeneity of the mask.
In PIR-13 a third method was introduced: (3) dipoles were measured in the filtered data at locations obtained by rotating the cluster template around the Z axis in steps of one degree. The Planck Collaboration expected this method to be optimal, since it includes all possible systematics of both the filtered data and the cluster template, including anisotropies and angular correlations. Unfortunately, this method is very inefficient and yields systematically larger errors than homogeneous random sampling. For one, the fixed step size of one degree allows only 359 different measurements and thus yields very few independent dipole estimates. In addition, a rotation does not move the clusters within the template alike. For instance, under rotation about the Z axis, the Coma cluster, located at b = 88°, never moves by more than four degrees from its initial position. Finally, for small rotation angles, nearby clusters that are very extended on the sky will continue to contribute to the random dipole, correlating the measurements. As a result, the space of all possible dipoles is poorly sampled; the measured random dipoles overpopulate the tail of the distribution, leading to overestimated uncertainties that dilute the significance of any real result.
In the following we discuss these systematic effects in more detail.
 |
Fig. 1 Monopole and dipole components evaluated at locations obtained by rotating the T1 cluster template about the Z axis. The dot-dashed (blue) line shown in the upper right panel marks the amplitude measured at zero rotation. The bottom two panels show the direction of the dipole measured for a given rotation angle. Note the pronounced inhomogeneities in the resulting sampling of all possible random dipoles, as well as the 120° periodicity in the amplitude of the monopole. |
4.1. Artificial correlations
Figure 1 shows the monopole, dipole, and angular direction of the dipole measured by rotating the T1 template (796 clusters) in the same manner as prescribed by PIR-13. We show results obtained with the W4 DA since it yields the largest dipole measured in the WMAP W-band, making it easier to identify any trends and biases. While, by design, all clusters in the unrotated T1 template fall outside the KQ75 mask, this is no longer the case after rotation1. The ensuing loss of clusters due to rotation (up to 10% of all pixels fall outside the mask for a given rotation angle) introduces additional variance in the measured dipoles.
Figure 1 illustrates several of the artifacts introduced by PIR-13’s rotation method. For instance, the measured monopole appears to repeat with a ~120° period, and the distribution of dipoles is similarly inhomogeneous. If a rotated template indeed sampled random dipoles, the angular directions of these dipoles would have to be distributed randomly. As shown by Fig. 1 this is clearly not the case; strong correlations are visible, especially for the Galactic longitude l of the dipole direction. Moreover, the amplitudes of the monopole and dipole are also correlated. For the T1 template, the correlation matrix of the dipole components is: 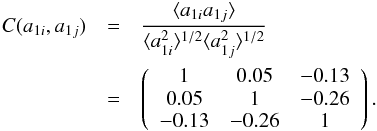 (2)In this expression, (i,j) = (X,Y,Z). Remarkably, the dipole component along the rotation axis, Z, correlates more strongly with the other two components than X and Y. These correlations are larger than the error bars estimated from method (1), which uses the real data and random cluster templates, and where for 400 dipoles the off-diagonal terms never exceed 7% of the diagonal terms (see Eq. (10.11) and Sect. 10.3.3 in Kashlinsky et al. 2012).
(2)In this expression, (i,j) = (X,Y,Z). Remarkably, the dipole component along the rotation axis, Z, correlates more strongly with the other two components than X and Y. These correlations are larger than the error bars estimated from method (1), which uses the real data and random cluster templates, and where for 400 dipoles the off-diagonal terms never exceed 7% of the diagonal terms (see Eq. (10.11) and Sect. 10.3.3 in Kashlinsky et al. 2012).
From the results shown in the top right panel of Fig. 1 we can immediately compute the significance of the dipole measurement. We find the dipole measured for the unrotated T1 template to be significant at the 92% confidence level; for the T2 subsample, the significance increases to 96%. Large variations in the significances thus derived are expected, owing to the small number of dipole measurements allowed by this method. Indeed, PIR-13 report yet another value (89%) when using our filter and their MCXC cluster template.
4.2. Increment of the uncertainties in the X and Y directions.
When the template is rotated, clusters do not move homogeneously on the celestial sphere. For rotations about the Z axis, the number of clusters at constant Galactic latitude, b, is fixed. Since clusters move more slowly close to the Galactic pole than they do near the Galactic plane, the Z component of the dipole is more heavily sampled than the X and Y components, resulting in smaller uncertainties for the former than for the latter. We can quantify this over- and under-sampling by using Eq. (1), which gives the error of each dipole component in units of the error of the monopole.
Relative uncertainty in the measurement of the three spatial components of the dipole, obtained with different error-estimation methods.
For clusters that are isotropically distributed on the sky the term 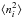 in Eq. (1) equals 1/3. This is the minimum variance estimator since the three quantities a1i are derived from the same data set as a0, and the error of each dipole component is given by
in Eq. (1) equals 1/3. This is the minimum variance estimator since the three quantities a1i are derived from the same data set as a0, and the error of each dipole component is given by 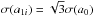 . In Table 1 we list, for all three error-estimation methods outlined before, the fractional increase of the errors caused by the anisotropy of both the cluster distribution and the sampling of the sky, relative to uniform sampling. Note that these error estimates only include the effect of the geometry of the cluster template, but not the additional variances introduced by the limited number of dipole estimates and from the systematics intrinsic to the data. Hence, the figures listed in Table 1 are the minimum error that can be achieved for a given cluster configuration.
. In Table 1 we list, for all three error-estimation methods outlined before, the fractional increase of the errors caused by the anisotropy of both the cluster distribution and the sampling of the sky, relative to uniform sampling. Note that these error estimates only include the effect of the geometry of the cluster template, but not the additional variances introduced by the limited number of dipole estimates and from the systematics intrinsic to the data. Hence, the figures listed in Table 1 are the minimum error that can be achieved for a given cluster configuration.
Note that, even for perfectly random sampling, i.e., method (1), the presence of the mask causes the error in the X and Y components to increase with respect to homogeneous sampling of the full celestial sphere, while the error in the Z component decreases. The same effect is evident for method (2) which results in slightly larger uncertainties due to the increased variance introduced by the anisotropy of the distribution of clusters in the sky. The by far largest deviations from uniform sampling, however, are induced by method (3) which employs rotations of the cluster template. Note (rightmost two columns in Table 1) that method (3) performs worst in the Y direction where it leads to a 15% increase in the uncertainty compared to method (2).
 |
Fig. 2 Stack of the T1 cluster template and its 359 rotations about the Z axis. The color is proportional to the number of clusters in a given pixel of the template stack. All clusters were assigned an angular size of 25′ (radius). |
Figure 2 shows a stack of the T1 template and its 359 one-degree rotations, illustrating the non-uniform sampling resulting from PIR-13’s rotation method. The observed banding, predominantly at high Galactic latitude, is a consequence of the differences in both the number of clusters for different values of b and in the angular displacement of clusters in Galactic longitude as a result of the rotation. The celestial sphere is sampled inhomogeneously, increasing the errors and resulting in dipoles that are strongly correlated (see also Eq. (2), and Fig. 1).
 |
Fig. 3 Significance of the dipole for the three error-estimation methods. For a given dipole amplitude, method (1) yields the smallest errors and thus the highest significance (red dot-dashed line), followed by method (2) (black solid line). Method (3), rotations of the actual cluster template, creates the by far largest uncertainties and thus assigns the lowest significance. Both method (1) and (2) were applied to 359 realizations of a random cluster template or a simulated CMB sky, respectively, in order to match the fixed statistics of 359 rotations provided by method (3). |
The uncertainties resulting from the three different error estimators (Table 1) can be translated into significances of detection for a dipole signal of given amplitude. Figure 3 shows these significances, based on 359 realizations for each of the three methods. A dipole of amplitude 3.8 μk would be significant at the 97% confidence level if the error estimate were obtained from 359 measurements of random dipoles that sample the celestial sphere perfectly uniformly. For methods (1), (2), and (3), applied outside the KQ75 mask, this number is 96%, 94% and less than 90%. In reality, the loss of significance caused by method (3) is even higher, due to the correlation between the dipole components, not accounted for in these theoretical estimates.
In summary, since it is the Y component of the dipole that dominates the Dark Flow signal (Kashlinsky et al. 2010) by increasing the error estimate on the Y-component, method (3) (sampling of the real CMB sky by rotating the cluster template about the Z axis) clearly and systematically degrades the significance of a dipole measurement compared to methods (1) and (2). Its sampling of the celestial sphere is the most inefficient and most anisotropic of the three estimators, and the method is especially insensitive to the Y-component of the dipole.
5. Error estimates from CMB simulations
Although method (3), rotation, is the most inefficient and biased error estimation technique discussed here, care also needs to be taken when interpreting the errors obtained from numerical simulations of the CMB sky, i.e., method (2). In general, simulated maps feature larger variances than the real sky and consequently lead to larger error estimates which, in turn, cause the significance of any real signal to be underestimated. We have identified three effects that contribute to this bias: (a) in the filtered data the power leaks from regions outside the mask and reduces the variance on pixels outside the mask compared with a simulated map (b) the power spectrum of the actual realization of the sky 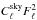 is smaller than the power spectrum of the theoretical ΛCDM concordance model
is smaller than the power spectrum of the theoretical ΛCDM concordance model 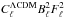 used to generate the simulated sky, and finally, (c) accidental sampling of a region with non-zero dipole, if the monopole and dipole were not removed from the region outside the KQ75 mask, prior to computing the dipole for a random sky.
used to generate the simulated sky, and finally, (c) accidental sampling of a region with non-zero dipole, if the monopole and dipole were not removed from the region outside the KQ75 mask, prior to computing the dipole for a random sky.
To quantify the impact of power leakage to the masked-out part of the sky we generated 1000 realizations of the CMB sky corresponding to the specifics of WMAP 7-year data W1 DA. Simulated maps were computed using Healpix Nside = 512 resolution, and multipoles were sampled up to ℓmax = 1024. The simulated (aℓm) coefficients were multiplied by the W1 beam before transformation to real space. Next, each map was multiplied by the mask, converted back into spherical harmonics, filtered, and transformed once more into real space as described in Sect. 3. For each realization, the Wiener-type filter used has the same functional form as specified in Sect. 3, but 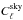 is now replaced by the power spectrum of the simulated “data”,
is now replaced by the power spectrum of the simulated “data”, 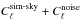 . Here
. Here 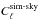 is the power spectrum of each simulated sky, corrected, if necessary, for the fraction of power removed by the mask, and
is the power spectrum of each simulated sky, corrected, if necessary, for the fraction of power removed by the mask, and 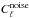 is the power spectrum of the noise. For each simulation we computed the rms of the filtered map inside and outside the mask. If in the initial data we do not multiply by the mask, the filtered map has an average power of σ = 30 ± 3 μk. If in the initial data we multiply by the KQ75 mask, then the power on the fraction of the mask outside the mask was σout = 28 ± 2 μk, while in the region excluded by the mask it was σin = 15 ± 3 μk. This effect of power leakage is illustrated in Fig. 4 for one of our simulations. We found the average fraction of power leaked to the mask to be 0.061 ± 0.016. Therefore, use of filtered maps generated using realizations of the filtered power spectra not taking onto account the effect of the mask will, on average, increase the errors by ~6%.
is the power spectrum of the noise. For each simulation we computed the rms of the filtered map inside and outside the mask. If in the initial data we do not multiply by the mask, the filtered map has an average power of σ = 30 ± 3 μk. If in the initial data we multiply by the KQ75 mask, then the power on the fraction of the mask outside the mask was σout = 28 ± 2 μk, while in the region excluded by the mask it was σin = 15 ± 3 μk. This effect of power leakage is illustrated in Fig. 4 for one of our simulations. We found the average fraction of power leaked to the mask to be 0.061 ± 0.016. Therefore, use of filtered maps generated using realizations of the filtered power spectra not taking onto account the effect of the mask will, on average, increase the errors by ~6%.
 |
Fig. 4 Residual power in a simulated map. We use the WMAP 7-year KQ75 mask. For clarity, the power outside the mask is set to zero and the plot is limited to the range [− 20,20] μk. Points above/below the specified range were given the value of the upper/lower bound. Note the power leaked to the masked-out region of the sky. |
 |
Fig. 5 Contribution to the rms dispersion of all multipoles up to ℓ (see Eq. (3)) for the WMAP W1 band. The thick solid (black) line corresponds to WMAP data, the thin solid (red) line to the best-fit concordance model |
The second effect contributing to the artificially high variance of the simulated CMB sky is illustrated in Fig. 5 where we plot the mean and rms dispersion of the filtered power spectrum of the simulations. We define the cumulative variance out to a given ℓ as 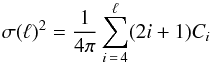 (3)where Ci is the filtered power spectrum. In Fig. 5 the solid black line represents the filtered power spectrum from the W1 DA data that contains both residual CMB and noise (solid black line), the thin red line represents
(3)where Ci is the filtered power spectrum. In Fig. 5 the solid black line represents the filtered power spectrum from the W1 DA data that contains both residual CMB and noise (solid black line), the thin red line represents 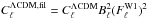 , where
, where 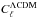 is the theoretical power spectrum of the ΛCDM cosmology and
is the theoretical power spectrum of the ΛCDM cosmology and 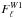 the filter constructed with the W1 data. Also shown is the filtered power spectrum, averaged over 1000 simulations, (dot-dashed blue line) and the rms dispersion around this mean (dashed blue lines). Let us remark that σ(ℓmax) is slightly larger than σCMB,fil of Eq. (1). We assign all clusters a radial extent of 25′, spatial scale that corresponds to ℓ ~ 400. Then, CMB residuals beyond ℓ ~ 400 do not contribute to the variance of the monopole and dipole measured within cluster apertures and σCMB,fil ≃ σ(ℓ ~ 300−400). As demonstrated in Atrio-Barandela et al. (2010), σCMB,fil is approximately 15−17 μk. Note that while in Fig. 5
the filter constructed with the W1 data. Also shown is the filtered power spectrum, averaged over 1000 simulations, (dot-dashed blue line) and the rms dispersion around this mean (dashed blue lines). Let us remark that σ(ℓmax) is slightly larger than σCMB,fil of Eq. (1). We assign all clusters a radial extent of 25′, spatial scale that corresponds to ℓ ~ 400. Then, CMB residuals beyond ℓ ~ 400 do not contribute to the variance of the monopole and dipole measured within cluster apertures and σCMB,fil ≃ σ(ℓ ~ 300−400). As demonstrated in Atrio-Barandela et al. (2010), σCMB,fil is approximately 15−17 μk. Note that while in Fig. 5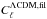 is very similar to the average power spectrum of one thousand simulated maps (filtered using the same pipeline as applied to the data), the power of the actual realization of the sky
is very similar to the average power spectrum of one thousand simulated maps (filtered using the same pipeline as applied to the data), the power of the actual realization of the sky 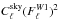 is about 10% smaller at ℓ = 300 (at larger ℓ’s, it is larger due to the noise contribution). Figure 5 shows that we live in a Universe were the residual CMB left in the data after filtering (solid black line) is smaller at ℓ = 300−400 than in the average sky (solid red line or dot-dashed blue line). Since the mean of the simulations is larger than our actual realization of the sky so will be the error bars computed from simulations and by the same amount. To properly compute the errors using simulations, care needs to be taken to generate simulations that, on average, reproduce the residual CMB left by the filter on the actual sky (solid black line). We thus reach the same conclusion as Atrio-Barandela et al. (2010); adding in quadrature the power leak due to the mask, simulations of filtered maps overestimate the errors on the monopole and the three dipole components by 12% with respect to the actual data.
is about 10% smaller at ℓ = 300 (at larger ℓ’s, it is larger due to the noise contribution). Figure 5 shows that we live in a Universe were the residual CMB left in the data after filtering (solid black line) is smaller at ℓ = 300−400 than in the average sky (solid red line or dot-dashed blue line). Since the mean of the simulations is larger than our actual realization of the sky so will be the error bars computed from simulations and by the same amount. To properly compute the errors using simulations, care needs to be taken to generate simulations that, on average, reproduce the residual CMB left by the filter on the actual sky (solid black line). We thus reach the same conclusion as Atrio-Barandela et al. (2010); adding in quadrature the power leak due to the mask, simulations of filtered maps overestimate the errors on the monopole and the three dipole components by 12% with respect to the actual data.
The third effect to consider when using simulated maps for the estimation of errors in the dipole measurement has already been mentioned in Sect. 3. For each of our thousand filtered maps, the dipole outside the KQ75 mask must be removed before computing the dipole at the cluster locations, just like for the real data. This step is essential to ensure that the random dipoles are computed for a zero-dipole sky. Keisler (2009) overlooked this crucial step, thereby artificially increasing his error bars. In Atrio-Barandela et al. (2010) we quantified that this omission leads to an increase in the error of the monopole close to 30%, of 15−20% for the X and Y components of the dipole, and of 2% for the Z component of the dipole.
To quantify the impact of the aforementioned biases on measurements of the statistical significance of the Dark Flow, we applied all three error estimation methods to W1 filtered data. To test the relevance of anisotropies in the cluster distribution, we conducted the analysis for the previously introduced T1 and T2 templates, but, for comparison, also for two randomly generated cluster templates S1 and S2 which comprise the same number of clusters as T1 and T2. We generated 10 simulated maps of the sky and, for each of them, computed the dipole for 100 random positions of each template, obtaining a total of 1000 dipoles. Before computing the dipole at the cluster locations, we removed the dipole outside the KQ75 mask. For simplicity, we did not include any noise or foreground residuals as they contribute negligibly to the final error budget. The initial power spectrum was 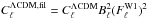 where
where 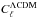 is the ΛCDM radiation power spectrum that best fits WMAP 7-year data, and
is the ΛCDM radiation power spectrum that best fits WMAP 7-year data, and 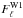 is the Kashlinsky et al. (2008) filter for the W1 band. To test method (3) we also computed 360 dipoles using one single map, by rotating the T1 and T2 templates in one-degree steps about the Z axis. We kept the KQ75 mask fixed during the rotation, so that pixels of the cluster templates were excised by the mask in the same way as the data.
is the Kashlinsky et al. (2008) filter for the W1 band. To test method (3) we also computed 360 dipoles using one single map, by rotating the T1 and T2 templates in one-degree steps about the Z axis. We kept the KQ75 mask fixed during the rotation, so that pixels of the cluster templates were excised by the mask in the same way as the data.
 |
Fig. 6 a) Histograms of 1000 dipoles measured from ten simulated filtered maps for the W1 DA. For each map, dipoles were computed placing the template at 100 random positions. The solid black and blue lines show the results obtained for the template of real clusters, T1, and for the simulated template of randomly positioned clusters, S1, respectively. For comparison, the solid red line shows the distribution of 360 dipoles computed by rotating the T1 template on a simulated map. b) As a) but focusing on the 3−5.5 μk range and showing the R1 renormalized to a total of 1000 to facilitate the comparison of the three error estimators. Panels c) and d) show the distribution of the dipole directions in Galactic coordinates. In all panels, the vertical dot-dashed line represents the measured dipole according to Kashlinsky et al. (2010). |
The results of this exercise are shown in Fig. 6 for the T1 and S1 cluster templates. Each method assigns different statistical significance to the dipole measured by Kashlinsky et al. (2010), namely 98.6%, 96.9% and 85.8% confidence level for method (1), using the random template S1, method (2), using the real cluster template T1, and method (3), using rotations of template T1. Once we correct our simulations to remove the excess of power in the simulated sky compared with the actual realization of the sky, as shown in Fig. 5, the significance increases to 99.6%, 98.4% and 90%, respectively, showing how strongly the rotation method dilutes the significance.
6. Conclusions
Using Planck data and the filtering scheme of Kashlinsky et al. (2010), the PIR-13 team has detected the same dipole signal reported by Kashlinsky et al. (2010, 2011) using WMAP data, but reaches a very different conclusion. Based on error estimates derived from simulations and rotations of the cluster template, the Planck Collaboration assigns the Dark Flow measurement a statistical significance below 90%.
In this paper we have analyzed the error-estimation methods used in PIR-13 and found biases that result in systematic overestimates of the uncertainty of the dipole measurement, and hence in a systematic underestimate of its significance. In particular the method of rotating the cluster template about the Z axis (devised by PIR-13 to account for angular correlations between clusters on the sky and all systematics present in the data) results in artificially inflated errors, due to several systematic flaws of the method: (1) since only 359 dipole measurements are possible, the resulting error estimate is not statistically robust; (2) the dipole components are strongly correlated with each other (see Figs. 1 and Eq. (2)); and (3) the sampling of the sky is highly anisotropic (see Fig. 1). Effects (2) and (3) result in errors for the X and Y components that are 5−15% larger than those obtained by the error-estimation methods discussed in Atrio-Barandela et al. (2010) and Kashlinsky et al. (2012) while decreasing the uncertainty of the Z component of the dipole. In addition, we have shown that numerical simulations, as implemented by PIR-13, also overestimate the uncertainty of the dipole measurement. Due to cosmic variance, the actual realization of the sky has less power at ℓ = 10−300 than the average of an ensemble of simulated skies (see Fig. 5) which leads to errors derived from simulated CMB maps that are too high by about 12%. When all biases are corrected for, the significance at the 90% confidence level reported by PIR-13 for the Dark Flow increases to ~99% in agreement with our previous estimates (Atrio-Barandela et al. 2010).
The strongest evidence that the measured dipole is genuinely associated with clusters was that it correlates with the TSZ signal measured at the cluster center as demonstrated in Kashlinsky et al. (2010). It is puzzling that this correlation was not observed by the Planck Collaboration. If the correlation is not there implies that either WMAP and Planck data are systematically different at the position of massive clusters or that the flow converges and does not reach as deep as the scale probed by the most massive clusters. Either possibility would be a very important result.
In principle the cluster template could of course be rotated about any axis but, due to the symmetry of the KQ75 mask with respect to the plane of the Galaxy, the choice of an axis other than the one through the Galactic poles would excise a much larger fraction of pixels for a rotated cluster template.
Acknowledgments
F.A.B. acknowledges financial support from the Spanish Ministerio de Educación y Ciencia (grants FIS2009-07238 and FIS2012-30926). Thanks are due to my collaborators A. Edge, A. Kashlinsky, D. Kocevski and particularly to H. Ebeling for a careful reading of this manuscript.
References
- Atrio-Barandela, F., Kashlinsky, A., Kocevski, D., & Ebeling, H. 2008, ApJ, 675, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Atrio-Barandela, F., Kashlinsky, A., Ebeling, H., Kocevski, D., & Edge, A. 2010, ApJ, 719, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Atrio-Barandela, F., Kashlinsky, A., Ebeling, H., & Kocevski, D., 2013, ApJ, submitted [arXiv:1211.4345] [Google Scholar]
- Gorski, K., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., & Atrio-Barandela, F. 2000, ApJ, 536, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., Kocevski, D., & Ebeling, H. 2008, ApJ, 686, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., Kocevski, D., & Ebeling, H. 2009, ApJ, 691, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., Ebeling, H., Edge, A., & Kocevski, D. 2010, ApJ, 712, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., & Ebeling, H. 2011, ApJ, 732, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., & Ebeling, H. 2012, Phys. Rep., submitted [arXiv:1202.0717] [Google Scholar]
- Keisler, R. 2009, ApJ, 707, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Lavaux, G., Hudson, M., & Afshordi, N. 2013, MNRAS, 430, 1617 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z., Zhang, P., & Chen, X. 2012, ApJ, 758, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Mody, K., & Hajian, A. 2012, ApJ, 758, 4 (MH) [NASA ADS] [CrossRef] [Google Scholar]
- Osborne, S. J., Mak, D. S. Y., Church, S. E., & Pierpaoli, E. 2011, ApJ, 737, 98 (OMCP) [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2013a, A&A, submitted [arXiv:1303.5090] [Google Scholar]
- Planck Collaboration 2013b, A&A, submitted [arXiv:1303.5087] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1970, ApSS, 7, 3 [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1972, CoASP, 4, 173 [Google Scholar]
All Tables
Relative uncertainty in the measurement of the three spatial components of the dipole, obtained with different error-estimation methods.
All Figures
 |
Fig. 1 Monopole and dipole components evaluated at locations obtained by rotating the T1 cluster template about the Z axis. The dot-dashed (blue) line shown in the upper right panel marks the amplitude measured at zero rotation. The bottom two panels show the direction of the dipole measured for a given rotation angle. Note the pronounced inhomogeneities in the resulting sampling of all possible random dipoles, as well as the 120° periodicity in the amplitude of the monopole. |
| In the text | |
 |
Fig. 2 Stack of the T1 cluster template and its 359 rotations about the Z axis. The color is proportional to the number of clusters in a given pixel of the template stack. All clusters were assigned an angular size of 25′ (radius). |
| In the text | |
 |
Fig. 3 Significance of the dipole for the three error-estimation methods. For a given dipole amplitude, method (1) yields the smallest errors and thus the highest significance (red dot-dashed line), followed by method (2) (black solid line). Method (3), rotations of the actual cluster template, creates the by far largest uncertainties and thus assigns the lowest significance. Both method (1) and (2) were applied to 359 realizations of a random cluster template or a simulated CMB sky, respectively, in order to match the fixed statistics of 359 rotations provided by method (3). |
| In the text | |
 |
Fig. 4 Residual power in a simulated map. We use the WMAP 7-year KQ75 mask. For clarity, the power outside the mask is set to zero and the plot is limited to the range [− 20,20] μk. Points above/below the specified range were given the value of the upper/lower bound. Note the power leaked to the masked-out region of the sky. |
| In the text | |
 |
Fig. 5 Contribution to the rms dispersion of all multipoles up to ℓ (see Eq. (3)) for the WMAP W1 band. The thick solid (black) line corresponds to WMAP data, the thin solid (red) line to the best-fit concordance model |
| In the text | |
 |
Fig. 6 a) Histograms of 1000 dipoles measured from ten simulated filtered maps for the W1 DA. For each map, dipoles were computed placing the template at 100 random positions. The solid black and blue lines show the results obtained for the template of real clusters, T1, and for the simulated template of randomly positioned clusters, S1, respectively. For comparison, the solid red line shows the distribution of 360 dipoles computed by rotating the T1 template on a simulated map. b) As a) but focusing on the 3−5.5 μk range and showing the R1 renormalized to a total of 1000 to facilitate the comparison of the three error estimators. Panels c) and d) show the distribution of the dipole directions in Galactic coordinates. In all panels, the vertical dot-dashed line represents the measured dipole according to Kashlinsky et al. (2010). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


