| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201321476 | |
| Published online | 14 August 2013 | |
The VIMOS Public Extragalactic Redshift Survey (VIPERS) ⋆
Luminosity and stellar mass dependence of galaxy clustering at 0.5 < z < 1.1
1 Dipartimento di Fisica e Astronomia – Università di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
e-mail: federico.marulli3@unibo.it
2 INAF – Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 INFN – Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
4 Dipartimento di Matematica e Fisica, Università degli Studi Roma Tre, via della Vasca Navale 84, 00146 Roma, Italy
5 INFN – Sezione di Roma Tre, via della Vasca Navale 84, 00146 Roma, Italy
6 INAF – Osservatorio Astronomico di Roma, via Frascati 33, 00040 Monte Porzio Catone (RM), Italy
7 SUPA – Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh, EH9 3HJ, UK
8 INAF – Osservatorio Astronomico di Brera, via Brera 28, 20122 Milano, via E. Bianchi 46, 23807 Merate, Italy
9 Dipartimento di Fisica, Università di Milano-Bicocca, P.zza della Scienza 3, 20126 Milano, Italy
10 Astronomical Observatory of the Jagiellonian University, Orla 171, 30-001 Cracow, Poland
11 National Centre for Nuclear Research, ul. Hoza 69, 00-681 Warszawa, Poland
12 INAF – Osservatorio Astronomico di Torino, 10025 Pino Torinese, Italy
13 Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
14 Canada–France-Hawaii Telescope, 65–1238 Mamalahoa Highway, Kamuela, HI 96743, USA
15 Centre de Physique Théorique, UMR 6207 CNRS-Université de Provence, Case 907, 13288 Marseille, France
16 INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica Milano, via Bassini 15, 20133 Milano, Italy
17 Laboratoire Lagrange, UMR 7293, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300 Nice, France
18 Institute of Astronomy and Astrophysics, Academia Sinica, PO Box 23–141, 10617 Taipei, Taiwan
19 INAF – Osservatorio Astronomico di Trieste, via G. B. Tiepolo 11, 34143 Trieste, Italy
20 Institute of Physics, Jan Kochanowski University, ul. Swietokrzyska 15, 25-406 Kielce, Poland
21 Department of Particle and Astrophysical Science, Nagoya University, Furo-cho, Chikusa-ku, 464-8602 Nagoya, Japan
22 Institute d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre et Marie Curie, 98bis Boulevard arago, 75014 Paris, France
23 Universitätssternwarte München, Ludwig-Maximillians Universität, Scheinerstr. 1, 81679 München, Germany
24 Max-Planck-Institut für Extraterrestrische Physik, 84571 Garching b. München, Germany
25 Institute of Cosmology and Gravitation, Dennis Sciama Building, University of Portsmouth, Burnaby Road, Portsmouth, PO1 3FX, UK
26 INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica Bologna, via Gobetti 101, 40129 Bologna, Italy
27 INAF – Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna, Italy
28 Università degli Studi di Milano, via G. Celoria 16, 20130 Milano, Italy
Received: 14 March 2013
Accepted: 30 May 2013
Aims. We investigate the dependence of galaxy clustering on luminosity and stellar mass in the redshift range 0.5 < z < 1.1, using the first ~ 55 000 redshifts from the VIMOS Public Extragalactic Redshift Survey (VIPERS).
Methods. We measured the redshift-space two-point correlation functions (2PCF), ξ(s) and ξ(rp,π) , and the projected correlation function, wp(rp), in samples covering different ranges of B-band absolute magnitudes and stellar masses. We considered both threshold and binned galaxy samples, with median B-band absolute magnitudes − 21.6 ≲ MB − 5log (h) ≲ − 19.5 and median stellar masses 9.8 ≲ log (M⋆ [h-2 M⊙]) ≲ 10.7. We assessed the real-space clustering in the data from the projected correlation function, which we model as a power law in the range 0.2 < rp [h-1 Mpc ] < 20. Finally, we estimated the galaxy bias as a function of luminosity, stellar mass, and redshift, assuming a flat Λ cold dark matter model to derive the dark matter 2PCF.
Results. We provide the best-fit parameters of the power-law model assumed for the real-space 2PCF – the correlation length, r0, and the slope, γ – as well as the linear bias parameter, as a function of the B-band absolute magnitude, stellar mass, and redshift. We confirm and provide the tightest constraints on the dependence of clustering on luminosity at 0.5 < z < 1.1. We prove the complexity of comparing the clustering dependence on stellar mass from samples that are originally flux-limited and discuss the possible origin of the observed discrepancies. Overall, our measurements provide stronger constraints on galaxy formation models, which are now required to match, in addition to local observations, the clustering evolution measured by VIPERS galaxies between z = 0.5 and z = 1.1 for a broad range of luminosities and stellar masses.
Key words: galaxies: distances and redshifts / galaxies: evolution / galaxies: statistics / cosmology: observations / large-scale structure of Universe
Based on observations collected at the European Southern Observatory, Paranal, Chile, under programmes 182.A-0886 (LP) at the Very Large Telescope, and also based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Science de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. The VIPERS web site is http://vipers.inaf.it/
© ESO, 2013
1. Introduction
The large scale structure (LSS) of the Universe contains fundamental information for investigating the nature of the dark matter (DM) and the origin of the accelerated expansion of the Universe. However, since the LSS is traced by galaxies, the relevant information can only be extracted after specifying the mapping between galaxies and DM (Kaiser 1984). The way galaxies trace the underlying density field, i.e. their biasing, can be understood through the mean occupation of galaxies in DM haloes, under the assumption that all DM mass in the Universe is in the form of haloes. This relation depends on the galaxy properties and the sample selection.
Indeed, it has been observationally established in the local Universe that the spatial distribution of galaxies significantly depends on their luminosity, stellar mass, colour, morphological, and spectral types, as well as on the environment (see e.g. Davis & Geller 1976; Giovanelli et al. 1986; Davis et al. 1988; Hamilton 1988; Einasto 1991; Maurogordato & Lachieze-Rey 1991; Loveday et al. 1995; Benoist et al. 1996; Guzzo et al. 1997, 2000; Willmer et al. 1998; Brown et al. 2000, 2003; Norberg et al. 2001, 2002; Zehavi et al. 2002, 2005; Madgwick et al. 2003; Abbas & Sheth 2006; Zehavi et al. 2011; Budavári et al. 2003; Li et al. 2006; Swanson et al. 2008; Loh et al. 2010; Ross et al. 2011; Guo et al. 2013a; Christodoulou et al. 2012). The general trend is that luminous and massive galaxies with bulge-dominated morphologies and red colours cluster more strongly than faint, less massive, blue, spiral galaxies, an effect that becomes particularly evident above the characteristic luminosity, L⋆, and stellar mass, M⋆, of the Schechter function. This is expected in the standard cosmological scenario of hierarchical growth of cosmic structures, where bright galaxies are hosted by massive, rare, and highly clustered DM haloes (Kaiser 1984; White et al. 1987).
Observations up to intermediate redshifts, z ~ 1, i.e. half way through the cosmic time from the microwave background to the present, show clustering trends similar to those observed in the local Universe, with the more luminous and massive galaxies being more clustered than the faint, less massive ones (see e.g. Coil et al. 2006, 2008; McCracken et al. 2008; Meneux et al. 2006, 2008, 2009; Pollo et al. 2006; Abbas et al. 2010; Coupon et al. 2012; Mostek et al. 2013). At higher redshifts, z > 1, observational constraints are generally weaker, suffering from a combination of many types of selection biases, but the measurements still show a luminosity and stellar mass segregation in galaxy clustering (see e.g. Daddi et al. 2003; Adelberger et al. 2005; Ouchi et al. 2005; Lee et al. 2006, 2009; Hildebrandt et al. 2009; Wake et al. 2011; Lin et al. 2012), with strong evidence of a steepening in the correlation function at r ≲ 1 h-1 Mpc with increasing luminosity.
It is possible to derive cosmological constraints from the spatial properties of galaxies using methods that do not explicitly depend on galaxy bias, such as by exploiting baryonic acoustic oscillations (see e.g. Eisenstein et al. 2005; Cole et al. 2005; Percival et al. 2007, 2010) or geometric clustering distortions (see e.g. Alcock & Paczynski 1979; Simpson & Peacock 2010; Marulli et al. 2012), or by combining the one- and two-point moments of the smoothed galaxy density distribution (Bel et al. 2013). However, to extract the full information encoded in the shape of the galaxy power spectrum and in its redshift-space distortions, the galaxy bias must be accounted for to some extent. Since the connection between baryons and DM can be significantly affected by non-linear phenomena, such as mergers, dynamical friction, cooling, feedback, etc., semi-analytic models or full hydrodynamic simulations provide useful tools for properly investigating how galaxies trace the DM distribution. Once a mathematical description of the galaxy bias has been obtained, cosmological constraints can be derived by marginalizing over the uncertain parameters that describe the bias. Alternatively, observational measurements of the galaxy bias, derived in a given cosmological framework, can be used to constrain the parameters of galaxy formation models.
In this paper, we focus on the dependence of galaxy clustering on luminosity and stellar mass, providing new observational constraints at redshift 0.5 < z < 1.1, from the first data release of the ongoing VIMOS Public Extragalactic Redshift Survey (VIPERS, Guzzo et al. 2013). The comparison between VIPERS clustering measurements with similar ones at lower and higher redshifts can constrain the cosmic evolution of the relationship between DM and galaxy properties, hence between gravity and cosmology on one side and processes associated with baryonic physics on the other side. The large number of objects with accurate spectroscopic redshifts and the large volume covered by the VIPERS survey give us the opportunity to measure the clustering of galaxies over a wide range of luminosities and stellar masses, back to the cosmic epoch when the Universe was still decelerating. In particular, we provide constraints on the projected correlation function, which we model as a single power law. This represents a reasonable, though not optimal, approximation at rp ≲ 20 h-1 Mpc , where rp is the direction perpendicular to the line-of-sight, and facilitates the comparison with previous studies. A more detailed interpretation of these data using halo occupation distribution (HOD) modelling is deferred to a future work (see also de la Torre et al. 2013).
The plan of this paper is as follows. In Sect. 2 we give a general overview of the VIPERS data, describing in detail the luminosity and stellar mass selections adopted in this work. We investigate the spatial distribution of VIPERS galaxies measuring the two-point correlation function (2PCF) in approximately volume-limited samples of different B-band absolute magnitudes and stellar masses. The methodology of this analysis is described in Sect. 3, where we also explain how we account for the incompleteness affecting our VIPERS samples. More technical details about the method to correct for the proximity effect and stellar mass incompleteness are provided in Appendix A. The results of our analysis are presented in Sect. 4. Finally, in Sect. 5 we summarize the main results of this work.
Throughout this paper, we assume a flat Λ cold dark matter (CDM) background cosmology, with mass density parameter ΩM = 0.25, both to convert the measured redshifts into comoving distances and to estimate the DM correlation used to assess the galaxy bias. Changing the value of ΩM in a reasonable range, given the current cosmological constraints, would only introduce small effects on our clustering measurements within their observational uncertainties (see e.g. Marulli et al. 2012). Galaxy magnitudes are quoted in the AB system. The dependence of observed quantities on the Hubble parameter is indicated as a function of h ≡ H0/100 km s-1 Mpc-1.
 |
Fig. 1 Luminosity and stellar mass selection as a function of redshift. The black dots show the W1 and W4 VIPERS galaxies. Yellow lines surround the selected sub-samples. Solid lines show the 90% completeness levels for the whole galaxy population (cyan lines) and for galaxies of four different photometric types: red E/Sa (red lines), early spiral (orange lines), late spiral (green lines), and irregular or starburst (blue lines). The B-band rest-frame magnitude limits in the left panel account for the average luminosity evolution of galaxies, as explained in the text. On the bottom axes, zeq,Λ ~ 0.44 is the redshift of DM-DE equality and zacc ~ 0.82 is the redshift when the Universe started accelerating, according to ΛCDM predictions with the set of cosmological parameters adopted in this work. |
2. The data
2.1. The VIPERS survey
We have used the data from the VIPERS Public Data Release 1 (PDR-1), which will be made publicly available in the fall of 2013. VIPERS is an ongoing Large Programme aimed at measuring redshifts for ~ 105 galaxies at 0.5 < z ≲ 1.2. One of the main goals of this survey is to characterize the galaxy spatial properties and growth rate of the LSS, measuring galaxy clustering and redshift-space distortions at an epoch when the Universe was about half its current age. Indeed, according to the standard ΛCDM scenario, the redshift range that VIPERS probes is previous to the dark energy (DE) dominated era, crossing the cosmic epoch when the Universe started accelerating (see the bottom labels in Fig. 1).
The galaxy target sample is selected from the Canada-France-Hawaii Telescope Legacy Survey Wide (CFHTLS-Wide) optical photometric catalogues (Mellier et al. 2008). VIPERS covers ~ 24 deg2 on the sky, divided over two areas within the W1 and W4 CFHTLS fields. Galaxies are selected down to a flux limit of iAB < 22.5, and a robust gri colour pre-selection is applied to effectively remove objects at z < 0.5. Coupled with an aggressive observing strategy (Scodeggio et al. 2009), this allows us to double the galaxy sampling rate in the redshift range of interest (~ 40%), with respect to a pure magnitude-limited sample. At the same time, the area and depth of the survey result in a fairly large volume, 5 × 107h-3 Mpc3 , analogous to that of the 2dFGRS at z ~ 0.1. Such a combination of sampling and depth is unique among current redshift surveys at z > 0.5. VIPERS is performed with the VIMOS multi-object spectrograph at the European Southern Observatory Very Large Telescope (Le Fèvre et al. 2002, 2003), at moderate resolution (R = 210), using the LR Red grism, providing a wavelength coverage of 5500–9500 Å and a typical radial velocity error of 140 km s-1. The full VIPERS area is covered through a mosaic of 288 VIMOS pointings (192 in the W1 area and 96 in the W4 area). A complete description of the VIPERS survey, from the definition of the target sample to the actual spectra and redshift measurements, is presented in the parallel survey description paper (Guzzo et al. 2013), while a discussion of the survey data reduction and management infrastructure can be found in Garilli et al. (2012).
The PDR-1 galaxy catalogue includes 53 608 redshifts and corresponds to the reduced data frozen in the VIPERS database at the end of the 2011/2012 observing campaign. The 2PCF of PDR-1 galaxies and the first constraints on the growth rate from redshift-space distortions are presented in a parallel paper (de la Torre et al. 2013). A measurement of ΩM using a novel clustering statistic is given in Bel et al. (2013). The galaxy stellar mass function is presented in Davidzon et al. (2013), while the luminosity function and the evolution of the colour bimodality is provided in Fritz et al. (2013). The PDR-1 galaxies are classified with a support vector machine algorithm in Malek et al. (2013), while an early subset of the spectra has been analysed and classified through a principal component analysis in Marchetti et al. (2013). Finally, the VIPERS redshift distribution has been used to measure the real-space galaxy power spectrum with colour-selected samples from the CFHTLS (Granett et al. 2012).
Properties of the selected VIPERS sub-samples in threshold luminosity bins.
Properties of the selected VIPERS sub-samples in binned luminosity bins.
2.2. Luminosity and mass selection
We consider galaxy samples selected in three redshift ranges: z ∈ [0.5,0.7], z ∈ [0.7,0.9] and z ∈ [0.9,1.1]. To investigate the luminosity and mass dependence of galaxy clustering, we use both threshold and binned sub-samples with different selections in B-band absolute magnitudes, MB, and stellar masses, M⋆. The latter quantities have been estimated with a spectral energy distribution (SED) fitting technique, using the HYPERZMASS code (Bolzonella et al. 2000, 2010). Absolute magnitudes are measured using the B Buser filter in the AB system. More details about the SED fitting procedure are given in Davidzon et al. (2013).
Figure 1 shows the sub-samples selected in this work. The B-band magnitude limits account for the average luminosity evolution of galaxies. Following Meneux et al. (2009), we model the average redshift evolution of galaxy magnitudes as MB(z) = MB(0) − z (Ilbert et al. 2005; Zucca et al. 2009). Instead, for the stellar mass-selected sub-samples, we adopt the more conservative and widely used flat thresholds, since the redshift evolution of M⋆ is negligible up to z ~ 1 (Pozzetti et al. 2007, 2010; Davidzon et al. 2013). The solid coloured lines represent the 90% completeness levels for the whole galaxy population and for galaxies of four different photometric types: red E/Sa, early spiral, late spiral and irregular or starburst (see Davidzon et al. 2013, for more details). We did not use these completeness limits to investigate the dependence of galaxy clustering on spectral type, which we defer to a future work. These lines are displayed here to show that our magnitude-selected samples are all volume-limited irrespective of their colours, with the exception of the last redshift bin, where our i band selection makes us start losing the reddest galaxy population. However, the mass-selected samples are affected by the incompleteness of red galaxies. We will come back to this point in Sect. 3.4 and Appendix A.
Finally, in the bottom axes of Fig. 1, we mark zeq,Λ, the redshift of DM-DE equality, and zacc, the redshift when the Universe started accelerating, according to ΛCDM predictions with the set of cosmological parameters adopted in this work. Clearly, the three redshift ranges considered for the present analysis probe different cosmic epochs, crossing the transition from deceleration to acceleration.
3. The two-point correlation function
In this section, we describe the methodology used to measure the galaxy 2PCF. In particular, we discuss our error estimates and sampling rate correction.
3.1. Clustering measurements
We quantify the spatial properties of the VIPERS galaxies using the 2PCF, ξ(r). This function is implicitly defined as dP = n2 [1 + ξ(r)] dV1dV2, where dP is the probability of finding a pair of galaxies in the comoving volumes dV1 and dV2, separated by a comoving distance r, and n is the galaxy average number density. In the following, we refer to real-space and redshift-space three-dimensional separations using the vectors r and s, respectively.
To measure the function ξ(s), we make use of the standard Landy & Szalay (1993) estimator: 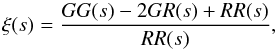 (1)where GG(s), GR(s), and RR(s) are the normalized galaxy–galaxy, galaxy-random, and random-random pairs, with spatial separation in the range [s − Δs/2,s + Δs/2], respectively.
(1)where GG(s), GR(s), and RR(s) are the normalized galaxy–galaxy, galaxy-random, and random-random pairs, with spatial separation in the range [s − Δs/2,s + Δs/2], respectively.
The random samples are generated in the right ascension-declination plane, adopting the same geometric mask of the real data. We set NR = 30 Ngal, where NR is the number of random objects and Ngal the number of galaxies in each sample. The latter set of values is reported in the fifth columns of Tables 1–4. The redshifts of the random objects are extracted from the smoothed radial distribution of the W1+W4 VIPERS galaxies, estimated in each luminosity and stellar mass sub-sample. Figure 2 shows the whole comoving radial distances distribution of the W1 and W4 VIPERS galaxies. To smooth the total W1+W4 radial distribution, we use the non-parametric Vmax method (see de la Torre et al. 2013, for more details). A similar result can be obtained by filtering the distribution with a Gaussian kernel of σ = 150 h-1 Mpc . The advantage of the Vmax method is that it does not require us to make assumptions about the kernel. We have verified that all the results presented in this paper do not vary significantly when changing the smoothing scheme adopted.
Properties of the selected VIPERS sub-samples in threshold stellar mass bins.
Properties of the selected VIPERS sub-samples in binned stellar mass bins.
3.2. Error estimate
The errors on the clustering measurements are estimated using a set of mock galaxy catalogues. For the luminosity-selected samples, we use data-calibrated HOD mocks, while for the stellar mass-selected samples, we consider galaxy mocks built from the stellar-to-halo mass relation (SHMR) of Moster et al. (2013). We use 26 independent HOD and SHMR mock catalogues, both constructed by assigning galaxies to DM haloes of the MultiDark simulation, a large N-body run in the ΛCDM framework (Prada et al. 2012). A novel technique has been used to repopulate the MultiDark simulation with haloes of mass below the resolution limit (de la Torre & Peacock 2012) and thus to be able to simulate the faintest and less massive galaxies observed in VIPERS. A detailed description of the method used to construct our mock galaxy catalogues can be found in de la Torre et al. (2013). The covariance error matrix is estimated from the dispersion among the mock catalogues: 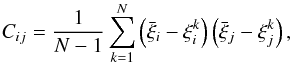 (2)where
(2)where 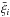 is the mean value of the 2PCF,
is the mean value of the 2PCF, 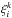 , measured in each mock catalogue. The errors on the 2PCF are then obtained from the square root of the diagonal values of the covariance matrix,
, measured in each mock catalogue. The errors on the 2PCF are then obtained from the square root of the diagonal values of the covariance matrix, 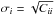 , which include both the Poissonian noise and the uncertainties due to the size of the volume explored, i.e. the sample variance. The luminosity and stellar mass dependence of the 2PCF errors is estimated by measuring the covariance matrix in mock sub-samples with the same luminosity and stellar mass selection used for the real data.
, which include both the Poissonian noise and the uncertainties due to the size of the volume explored, i.e. the sample variance. The luminosity and stellar mass dependence of the 2PCF errors is estimated by measuring the covariance matrix in mock sub-samples with the same luminosity and stellar mass selection used for the real data.
3.3. Weighting the galaxy pairs
To properly account for the effects of sampling rate and colour selection, each galaxy has been weighted according to its sky position and redshift, using the following weight function: 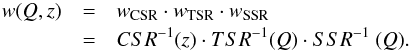 (3)All of the weights in Eq. (3) are derived directly from the data. The colour sampling rate, CSR, represents the completeness due to the colour selection. It mainly depends on redshift and can be modelled as CSR(z) = 0.5 [1 − erf(7.405 − 17.465·z)], where erf is the error function
(3)All of the weights in Eq. (3) are derived directly from the data. The colour sampling rate, CSR, represents the completeness due to the colour selection. It mainly depends on redshift and can be modelled as CSR(z) = 0.5 [1 − erf(7.405 − 17.465·z)], where erf is the error function 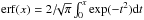 (Guzzo et al. 2013; Coupon et al. 2013). The target sampling rate, TSR, is defined as the fraction of galaxies in the photometric catalogue that have been spectroscopically targeted, TSR = Ngal(0 ≤ zflag ≤ 9.5)/Ntarget, where zflag is the quality flag of the spectroscopic redshift measurement (see Guzzo et al. 2013 for more details on zflag). In addition, we have a 3.2% stellar contamination in the target sample, but the effect on the TSR is negligible. Finally, the spectroscopic success rate, SSR, is defined as the fraction of the spectroscopically targeted galaxies for which a secure identification (i.e. high-quality flag) has been obtained, SSR = Ngal(2 ≤ zflag ≤ 9.5)/Ngal(0 ≤ zflag ≤ 9.5). Both the TSR and SSR depend on the VIMOS quadrant, Q, in which the galaxy has been observed. All the other possible dependencies, such as on redshift and magnitude, are comparatively smaller and can be neglected, as discussed in detail in de la Torre et al. (2013).
(Guzzo et al. 2013; Coupon et al. 2013). The target sampling rate, TSR, is defined as the fraction of galaxies in the photometric catalogue that have been spectroscopically targeted, TSR = Ngal(0 ≤ zflag ≤ 9.5)/Ntarget, where zflag is the quality flag of the spectroscopic redshift measurement (see Guzzo et al. 2013 for more details on zflag). In addition, we have a 3.2% stellar contamination in the target sample, but the effect on the TSR is negligible. Finally, the spectroscopic success rate, SSR, is defined as the fraction of the spectroscopically targeted galaxies for which a secure identification (i.e. high-quality flag) has been obtained, SSR = Ngal(2 ≤ zflag ≤ 9.5)/Ngal(0 ≤ zflag ≤ 9.5). Both the TSR and SSR depend on the VIMOS quadrant, Q, in which the galaxy has been observed. All the other possible dependencies, such as on redshift and magnitude, are comparatively smaller and can be neglected, as discussed in detail in de la Torre et al. (2013).
3.4. Proximity effects and mass incompleteness
The VIMOS multi-object spectrograph allows spectra for ~400 galaxies to be obtained in a single pointing (Bottini et al. 2005); however, it is not possible to target galaxies that are close to each other along the dispersion direction. Thus, the highest density regions are under-sampled, resulting in a systematic under-estimation of the correlation function, especially on small scales (Pollo et al. 2005; de la Torre et al. 2013). To estimate the impact of the proximity effect, we measured the mean ratio between the redshift-space 2PCF in two sets of mock catalogues with and without the slit mask target selection algorithm applied. A similar test has been applied by Coil et al. (2008). The mock catalogues used here are constructed with a semi-analytic model (De Lucia & Blaizot 2007) on top of the Millennium simulation (Springel et al. 2005). To obtain a smoothed version of this ratio, we modelled it with an error function (see Fig. A.2). Then, we multiplied the measured redshift-space 2PCF by this smoothed ratio. Since we find this correction to be almost independent of luminosity and stellar mass, we used the values obtained in our largest galaxy sample to correct all of our clustering measurements. At z ≲ 0.9, the under-estimation of the 2PCF due to the proximity effect is ~ 10% on scales r ≳ 1 h-1 Mpc, and increases slightly at smaller separations.
 |
Fig. 2 Comoving radial distance distribution of the W1 and W4 VIPERS galaxy samples, shown with the green and yellow histograms, respectively. The red and blue lines show the total W1+W4 smoothed distribution, obtained by filtering the observed distribution with a Gaussian kernel of σ = 150 h-1 Mpc and using the Vmax method, respectively. |
As shown in the right-hand panel of Fig. 1, our mass-selected galaxy samples are partially incomplete due to the limiting iAB < 22.5 flux cut of VIPERS, missing galaxies with high mass-to-light ratio. To correct for this effect, we would have to know what are the clustering properties of the galaxies that are missing in each of our samples. This can only be inferred using galaxy formation models both complete in mass and realistically describing the formation and evolution of faint galaxies.
Following what has already been done in previous studies (see e.g. Meneux et al. 2008, 2009), we implemented a correction method based on a strategy similar to the one described above for the proximity effect. Specifically, the correction is derived by measuring the ratio between the mean redshift-space 2PCF of two sets of mock catalogues, one complete in mass (down to ~ 108 M⊙) and the other one magnitude-limited at iAB < 22.5. According to the semi-analytic model considered here, the high mass-to-light ratio galaxies that are missed in our samples are faint red objects, which are predicted to be more clustered than the average population. As a result, the stellar mass incompleteness is expected to introduce a scale-dependent clustering suppression, up to ~50% on scales ≲1 h-1 Mpc , for the redshift-space 2PCF.
This correction assumes that different types of mock galaxies have clustering properties that match those of the real objects. However, this is only partially true. It is known that the model considered here overpredicts the abundance of faint and red galaxies. In addition, while the clustering of blue galaxies is well reproduced, the mock red galaxies appear more clustered than in real data (de la Torre et al. 2011; Cucciati et al. 2012). For the above reasons, such a model-dependent correction should be applied with caution. In the following, we show our clustering measurements without correcting for stellar mass incompleteness. Nevertheless, in Tables 3, 4, we provide our results obtained both with and without this correction, to directly show the expected effect according to the semi-analytic model considered. More details about these two corrections for the proximity effect and mass incompleteness are provided in Appendix A.
 |
Fig. 3 2PCF of VIPERS galaxies as a function of B-band absolute magnitude (upper panels) and stellar mass (bottom panels). The error bars are the square root of the diagonal values of the covariance matrix given by Eq. (2). Absolute magnitudes are given in the AB system. |
 |
Fig. 4 Projected correlation function of VIPERS galaxies as a function of B-band absolute magnitude (upper panels) and stellar mass (bottom panels). The solid lines show the best-fit power-law models, obtained by fitting the correlation functions in the interval 0.2 < rp [h-1 Mpc ] < 20. |
 |
Fig. 5 Best-fit values of the correlation length, r0, (left panels) and slope, γ, (right panels), as a function of B-band absolute magnitude (upper panels) and stellar mass (bottom panels). VIPERS costraints, obtained in threshold samples at z ∈ [0.5,0.7], z ∈ [0.7,0.9], and z ∈ [0.9,1.1] are shown, respectively, by blue squares, red diamonds, and green circles, as indicated by the labels. The remaining grey symbols refer to measurements based on data from other surveys, reported here for comparison: upper panels – DSS-DR7 data from Zehavi et al. (2011), 2dfGRS data from Norberg et al. (2002), VVDS-Deep data from Pollo et al. (2006) and DEEP2 data from Coil et al. (2006); lower panels – SDSS-DR2 data from Li et al. (2006), VVDS-Deep data from Meneux et al. (2008), zCOSMOS data from Meneux et al. (2009), NMBS data from Wake et al. (2011), DEEP2 data from Mostek et al. (2013) and BzK data from Lin et al. (2012). |
3.5. Projected and real-space correlations and galaxy bias
To correct for redshift-space distortions due to galaxy peculiar velocities and to derive the 2PCF in real space, ξ(r), we first measure the clustering as a function of the two distances perpendicular and parallel to the line-of-sight, ξ(rp,π), using the Landy & Szalay (1993) estimator. Then, we integrate along the line of sight, π, as 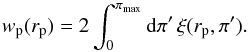 (4)The real-space 2PCF can then be estimated by deprojecting the function wp(rp) (Davis & Peebles 1983; Saunders et al. 1992):
(4)The real-space 2PCF can then be estimated by deprojecting the function wp(rp) (Davis & Peebles 1983; Saunders et al. 1992): 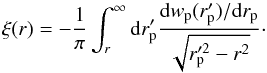 (5)To facilitate the comparison with previous studies, we do not use Eq. (5), but model the function ξ(r) as a single power law:
(5)To facilitate the comparison with previous studies, we do not use Eq. (5), but model the function ξ(r) as a single power law: 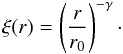 (6)With the above assumption, Eq. (4) can be solved analytically:
(6)With the above assumption, Eq. (4) can be solved analytically: 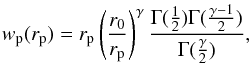 (7)where Γ is the Euler’s gamma function. Hence, a power-law fit to wp(rp) provides r0 and γ for the real-space correlation function ξ(r). Finally, the scale-dependent galaxy bias can be estimated as
(7)where Γ is the Euler’s gamma function. Hence, a power-law fit to wp(rp) provides r0 and γ for the real-space correlation function ξ(r). Finally, the scale-dependent galaxy bias can be estimated as 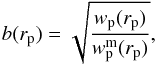 (8)where
(8)where 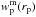 is the projected correlation function of matter. This is derived using the software CAMB (Lewis & Bridle 2002), which exploits the HALOFIT routine (Smith et al. 2003) to reproduce the non-linear evolution of the matter power spectrum.
is the projected correlation function of matter. This is derived using the software CAMB (Lewis & Bridle 2002), which exploits the HALOFIT routine (Smith et al. 2003) to reproduce the non-linear evolution of the matter power spectrum.
4. Results
In this section, we present our results for the luminosity and stellar-mass dependence of galaxy clustering and galaxy bias, and compare them with those of previous studies.
4.1. Redshift-space and projected 2PCF
Figure 3 shows the redshift-space 2PCF of VIPERS galaxies, ξ(s), as a function of B-band absolute magnitude (upper panels) and stellar mass (bottom panels), in the three redshift ranges z ∈ [0.5,0.7], z ∈ [0.7,0.9], and z ∈ [0.9,1.1]. The function ξ(s) has been estimated using Eq. (1), while the error bars are the square root of the diagonal values of the covariance matrix, given by Eq. (2).
To derive the real-space 2PCF and directly compare the VIPERS clustering with previous data, we estimate the projected correlation function using Eq. (4). We integrate ξ(rp,π) up to πmax = 30 h-1 Mpc . As we verified, this choice represents a convenient compromise between robustness and the need to exclude noisy bins at large separations. The projected 2PCF of VIPERS galaxies is shown in Fig. 4. The upper and lower panels show, respectively, the luminosity and stellar mass dependence of wp(rp), as indicated by the labels. The best-fit power-law models, given by Eq. (7), have been obtained by fitting the correlation functions in the interval 0.2 < rp [h-1 Mpc ] < 20. We can see in Fig. 4 that the power-law model does not describe the small-scale behaviour of wp(rp) well for the most massive galaxies. This steepening in the amplitude of the correlation function on scales below 1 h-1 Mpc can be interpreted in the framework of the halo model as due to the larger fraction of satellite galaxies in the massive haloes, creating a prominent one-halo term in the correlation function. Nevertheless, the results presented in this work are robust for the scale range used for the fit, given the estimated uncertainties.
We find a clear luminosity and stellar mass segregation in galaxy clustering at all redshifts considered. This result agrees with previous findings, as discussed in detail in the next section, and provides new strong constraints on galaxy formation models in the intermediate redshift Universe. The clustering measurements presented in Figs. 3 and 4 refer to threshold galaxy samples, as indicated by the labels. Our measurements on the galaxy clustering in both threshold and binned galaxy samples are given in Tables 1–4. Specifically, we provide the best-fit parameters of the power-law model: the correlation length r0 (sixth columns), and the slope γ (seventh columns). The errors on the best-fit parameters are derived from the scatter of the r0 and γ values among the 26 independent VIPERS mocks.
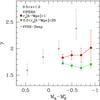 |
Fig. 6 Best-fit values of the VIPERS correlation slope, γ, as a function of luminosity. Green and red points show the VIPERS γ values obtained fitting wp(rp) in 0.2 < rp [h-1 Mpc ] < 20 and rp < 1 h-1 Mpc , respectively. Grey squares refer to the VVDS-Deep measurements. |
4.2. Comparison to previous studies
In Fig. 5, we compare our VIPERS measurements with previous results, at both low and high redshift. The upper panels show the best-fit values of r0 and γ as a function of the B-band magnitude. Following Pollo et al. (2006), we normalize the median magnitudes of each galaxy sample to the corresponding values of the characteristic magnitude of the Schechter luminosity function, 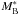 , obtained by fitting the values of
, obtained by fitting the values of 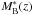 given by Ilbert et al. (2005). With this method, we can properly compare samples at different redshifts, taking the mean brightening of galaxies due to their evolution into account. A clear luminosity evolution of the clustering length, r0, is evident at all redshifts. We can see that r0 increases with time between z ~ 1 and z ~ 0.6. Moreover, there is some evidence that r0 grows faster for faint galaxies compared to the bright ones.
given by Ilbert et al. (2005). With this method, we can properly compare samples at different redshifts, taking the mean brightening of galaxies due to their evolution into account. A clear luminosity evolution of the clustering length, r0, is evident at all redshifts. We can see that r0 increases with time between z ~ 1 and z ~ 0.6. Moreover, there is some evidence that r0 grows faster for faint galaxies compared to the bright ones.
For the local Universe, we consider the data from Zehavi et al. (2011) and Norberg et al. (2002). Zehavi et al. (2011) measured the luminosity dependence of galaxy clustering using the Sloan Digital Sky Survey Seventh Data Release (SDSS-DR7), with volume-limited galaxy samples up to z = 0.25. Norberg et al. (2002) used the 2dF Galaxy Redshift Survey (2dFGRS) to measure the galaxy clustering up to z = 0.15. The VIMOS-VLT Deep Survey (VVDS) clustering measurements by Pollo et al. (2006) refer to the redshift ranges 0.1 < z < 0.5 and 0.5 < z < 1.2. Finally, the DEEP2 Galaxy Redshift Survey results have been obtained by Coil et al. (2006) at z ~ 1. The last two clustering measurements are at similar redshifts to VIPERS.
The bottom panels of Fig. 5 show the stellar mass dependence of r0 and γ. We compare our results to data from SDSS (Li et al. 2006), VVDS-Deep (Meneux et al. 2008), zCOSMOS (Meneux et al. 2009), NMBS (Wake et al. 2011), DEEP2 (Mostek et al. 2013) and BzK (Lin et al. 2012). The best-fit clustering lengths from SDSS-DR2 data in the local Universe (Li et al. 2006) have been fitted by Mostek et al. (2013). The measurements at intermediate redshifts similar to VIPERS are the VVDS-Deep results obtained at z ~ 0.85 by Meneux et al. (2008), the DEEP2 measurements at z ~ 1 from Mostek et al. (2013), the clustering measurements by Wake et al. (2011), using NMBS photometric redshifts in the range 0.9 < z < 1.3, obtained with a fixed slope γ = 1.6, and the zCOSMOS measurements by Meneux et al. (2009) at 0.5 < z < 1. The best-fit values of r0 and γ of zCOSMOS have been obtained by fitting the Meneux et al. (2009) data on the scales rp < 10 h-1 Mpc . All the remaining measurements refer to higher redshift data. The Wake et al. (2011) data have been taken at the two redshift ranges 1.2 < z < 1.75 and 1.6 < z < 2.2. Finally, the BzK r0 values have been estimated from the angular clustering analysis of star-forming galaxies at z ~ 2, for a fixed slope of γ = 1.8.
The general picture that emerges from these studies is that the clustering correlation length depends significantly on both luminosity and stellar mass, increasing monotonically from faint and low massive objects to luminous and massive ones, while the clustering slope remains fairly constant. Looking specifically to the luminosity dependence, it is interesting to note that for the intrinsically brightest samples, 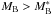 , the clustering amplitude r0 does not evolve significantly from the z ~ 1 measurements of VVDS and DEEP2 to the local references of 2dFGRS and SDSS. The same behaviour is seen in VIPERS: we find little evolution in the most luminous bin. Additionally, the VIPERS data allow us to track r0 with precision over a range of luminosities from z = 0.5–1.1, showing that the evolution becomes more significant at fainter luminosities. A simple qualitative interpretation of these observations is that low-luminosity galaxies follow the growth of structure approximately, without any substantial evolution in their bias factor. Conversely, luminous objects (
, the clustering amplitude r0 does not evolve significantly from the z ~ 1 measurements of VVDS and DEEP2 to the local references of 2dFGRS and SDSS. The same behaviour is seen in VIPERS: we find little evolution in the most luminous bin. Additionally, the VIPERS data allow us to track r0 with precision over a range of luminosities from z = 0.5–1.1, showing that the evolution becomes more significant at fainter luminosities. A simple qualitative interpretation of these observations is that low-luminosity galaxies follow the growth of structure approximately, without any substantial evolution in their bias factor. Conversely, luminous objects (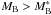 ) need to have a strong evolution of their bias factor from high to low redshifts, so as to apparently compensate for the growth of structure and produce the observed effect. These considerations are corroborated by the direct estimate of the bias factor for the different classes of galaxies, which we discuss in Sect. 4.3.
) need to have a strong evolution of their bias factor from high to low redshifts, so as to apparently compensate for the growth of structure and produce the observed effect. These considerations are corroborated by the direct estimate of the bias factor for the different classes of galaxies, which we discuss in Sect. 4.3.
On the other hand, when it comes to dependence of clustering on stellar mass, not all previous measurements are consistent. In particular, as noted in the bottom left-hand panel of Fig. 5, there is a big scatter between previous measurements, even when they probe similar redshift ranges. Clustering lengths at z ~ 1 found in the VVDS-Deep and DEEP2 surveys are significantly lower not only than the local measurements from the SDSS-DR7, but also than the values found by NMBS at 0.9 < z < 2.2, by the BzK at z ~ 2 and by zCOSMOS at 0.5 < z < 1. Our estimates of r0 are higher than the VVDS-Deep and DEEP2 ones, in the stellar mass range considered, while they agree fairly well with all the other data.
The differences are likely to arise from a combination of systematic effects. The surveys considered in Fig. 5 are characterized by different properties, such as the methods for mass estimation, the cosmological parameters adopted to assess the distances, and the selection criteria. The last certainly introduce the most relevant effects, as different surveys can be affected by stellar mass incompleteness to varying degrees. In particular, the VIPERS mass-selected samples contain, on average, much brighter galaxies than VVDS and DEEP2, owing to VIPERS higher flux selection cut.
Moreover, since the power-law model does not describe the data perfectly, measurements obtained from fitting over different ranges could produce different values of the fit parameters. This effect is especially significant for the most massive bins, where the shape of wp(rp) is the furthest from a power law and, thus, most sensitive to the range, binning, and choice of points used for fitting. Finally, the impact of sample variance has been estimated with different techniques, and it might be underestimated in some cases.
The VIPERS clustering slope is almost constant, considering the estimated errors, around γ ~ 1.7–1.8, with only tentative evidence of a slight luminosity and redshift evolution. This agrees overall with all previous data, except for the relation measured in VVDS-Deep. Using the data from the VVDS-Deep Survey, Pollo et al. (2006) found a significant steepening of the correlation slope from γ ~ 1.6 at ⟨ MB ⟩ = 19.6, to γ ~ 2.4 at ⟨ MB ⟩ = −21.3, fitting wp(rp) for separation <10 h-1 Mpc in their high-redshift range 0.5 < z < 1.2.
To directly compare these results with VVDS data, we measured the VIPERS 2PCF selecting all galaxies within the same redshift range used by Pollo et al. (2005), 0.5 < z < 1.2. In this way, any possible effect of the intrinsic evolution in the VVDS broad redshift slice should also be present in our measurements. We considered four volume-limited samples, with the following B-band magnitude thresholds MB(z = 1.2) − 5log (h) < − 21, − 21.25, − 21.5, − 21.75. The best-fit values of γ are shown in Fig. 6 and compared to the VVDS-Deep measurements in volume-limited samples. To investigate the scale dependence of the clustering slope, we compared the γ values obtained fitting wp(rp) in the interval 0.2 < rp [h-1 Mpc ] < 20, and considering only small scales, rp < 1 h-1 Mpc . The proximity effect caused by the one-pass strategy used in VIPERS is corrected with the method described in Sect. 3.3 and Appendix A. We are confident that the correction recovers the shape of the correlation function on small scales to within 5% (de la Torre et al. 2013).
 |
Fig. 7 Bias of VIPERS galaxies, averaged over the range [1–10] h-1 Mpc , as a function of B-band absolute magnitude (left panel) and stellar mass (right panel). The coloured symbols used for VIPERS measurements are the same as in Fig. 5. The black solid line in the left panel shows the fitted bias function by Zehavi et al. (2011). |
When the 2PCF is fitted on scales up to 20 h-1 Mpc , γ appears almost constant at the value ~ 1.7, as in Fig. 6, while if we fit only the small scales, γ results to be larger and slightly increasing, from γ ~ 1.8 at 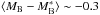 , to γ ~ 2 at
, to γ ~ 2 at 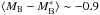 . The VIPERS clustering slope is still lower than the VVDS one at high luminosities, though the mismatch is not large (below 2σ significance).
. The VIPERS clustering slope is still lower than the VVDS one at high luminosities, though the mismatch is not large (below 2σ significance).
In conclusion, we find that the steepening of the slope in VVDS can be partly attributed to the range of scales used in the fit. Sample variance, if not fully recovered from the scatter between the mocks considered in these analyses, could explain the remaining discrepancy.
4.3. The galaxy bias
In this section, we present our estimates of the large-scale bias of VIPERS galaxies as a function of luminosity and stellar mass. We infer the scale-dependent bias, b(rp), using Eq. (8). Then, we average b(rp) in the range 1 < rp [h-1 Mpc ] < 10, where the galaxy bias is fairly constant. To estimate b(rp), we assume a flat ΛCDM model with the matter density parameter ΩM = 0.25, the baryon density parameter Ωb = 0.045, the scalar spectral index ns = 1, and the power spectrum normalization σ8 = 0.8. A full HOD formalism would be necessary to properly describe the bias relation between galaxies and DM on different scales. However, on large scales, the bias obtained from the ratio of the galaxy and matter correlation functions is consistent with those obtained using HOD modelling (see e.g. Zehavi et al. 2011).
In Fig. 7, we present the galaxy bias estimated in each threshold VIPERS sample, as a function of B-band absolute magnitude (left panel) and stellar mass (right panel). The error bars show the scatter among the bias values measured in the mock catalogues. The values of the bias and its error in each VIPERS sample are reported in Tables 1–4. The galaxy biasing estimated with Eq. (8) depends on the assumed cosmological model through both σ8 and ΩM. Its amplitude scales approximately as 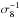 , since
, since 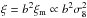 on large scales. The value of σ8 is known with an error of ~2%, so only just negligible when compared to uncertainties in our bias parameter (~4%). Uncertainties on ΩM, which is constrained in the interval ~ 0.22–0.28, also have an impact. Varying its input value in that range induces a ~2% shift in the estimated bias. On the other hand, relative bias between different galaxy types (e.g. the ratio between any two bias values reported in the tables), is almost model-independent.
on large scales. The value of σ8 is known with an error of ~2%, so only just negligible when compared to uncertainties in our bias parameter (~4%). Uncertainties on ΩM, which is constrained in the interval ~ 0.22–0.28, also have an impact. Varying its input value in that range induces a ~2% shift in the estimated bias. On the other hand, relative bias between different galaxy types (e.g. the ratio between any two bias values reported in the tables), is almost model-independent.
Figure 7 provides a compact view of the dependence of VIPERS clustering on luminosity and stellar mass. More luminous and massive galaxies appear more strongly biased than fainter and less massive ones at all redshifts considered. At fixed luminosity and stellar mass, the bias function increases with redshift, while the amplitude of the 2PCF decreases (see Fig. 5). In the left-hand panel of Fig. 7, we show the luminosity dependence of the galaxy bias in the local Universe, estimated by Zehavi et al. (2011) using the SDSS-DR7 data (see also Norberg et al. 2001; Tegmark et al. 2004, for similar results). We note that the normalization of the local bias is lower than our findings at intermediate redshifts, as predicted by evolution models (see e.g. Tegmark & Peebles 1998; Kauffmann et al. 1999; Blanton et al. 2000; Benson et al. 2001; Pillepich et al. 2010).
As already noted in the previous section, the VIPERS bias in low-mass-selected samples is biased toward high values compared to VVDS-Deep and DEEP2 measurements, as a consequence of the iAB < 22.5 selection. This has to be taken into account when comparing to theoretical predictions; i.e., the same flux selection has to be applied also in mock catalogues to introduce the same incompleteness of the VIPERS data.
A more detailed investigation on the scale dependence of the VIPERS galaxy bias derived with the deprojection method (see e.g. Marulli et al. 2012) and with a full HOD approach is deferred to a future work, while the non-linearity of the biasing function is presented in Di Porto et al. (in prep.).
4.4. Comparison to theoretical models
To provide a first theoretical interpretation of our measurements in a cosmological context, we compared the VIPERS clustering presented in previous sections with predictions of a standard galaxy formation model. The result is shown in Fig. 8, which compares the redshift-space 2PCF of VIPERS galaxies, measured in threshold samples of different luminosities (upper panels) and stellar masses (lower panels), with the theoretical predictions of the Munich semi-analytic model (De Lucia & Blaizot 2007). The VIPERS measurements and error bars are the same as in Fig. 3. The correlations in different sub-samples are offset by 0.5 dex, starting from the lower luminosity and stellar mass samples, for visual clarity. The Munich semi-analytic model, already introduced in Sect. 3.4 to calibrate the corrections for the proximity effect and stellar mass incompleteness, has been developed on the outputs of the Millennium run, a large N-body DM simulation of the ΛCDM cosmological framework (Springel et al. 2005). The area of the two galaxy mock catalogues used here is 10 × 3 deg2 each, slightly larger than the one of the complete VIPERS survey (~24 deg2). Only two independent mock catalogues of this volume can be extracted from the Millennium simulation. To estimate the sample variance, we therefore used our VIPERS HOD mocks, as in the previous sections. To directly compare our measurements with mock predictions, we introduced the VIPERS flux limit of iAB < 22.5 in the mock catalogues.
 |
Fig. 8 Redshift-space 2PCF of VIPERS galaxies compared to theoretical expectations as a function of B-band magnitude (upper panels) and stellar mass (bottom panels). The coloured symbols used for VIPERS measurements are the same as in Fig. 3. The grey shaded areas show the 2PCF measured in two large galaxy mock catalogues, constructed with the Munich semi-analytic model. The 2PCFs in different sub-samples are offset by 0.5 dex, starting from the lower luminosity and stellar mass samples, for visual clarity. |
As can be seen, our measurements are compatible with the expectations of the standard ΛCDM+semi-analytic framework. Both the luminosity and stellar mass dependence of VIPERS clustering appear in overall good agreement with theoretical expectations, though we note that the most luminous and massive VIPERS galaxies are slightly more clustered than the semi-analytic ones, especially at high redshift. We notice that the cosmological parameters of the Millennium simulation are based on first-year results from the Wilkinson Microwave Anisotropy Probe (WMAP1). In particular, the value of σ8 = 0.9 is significantly higher than the most recent estimates. If the Millennium predictions are properly rescaled to be consistent with the seven-year WMAP data (Guo et al. 2013b), galaxies at z ~ 1 are predicted to be slightly more clustered for M⋆ ≲ 1010.5 M⊙, while for lower masses the predicted clustering is almost coincident with the WMAP1 case. The differences are nevertheless quite small, given the uncertainties in current observational data, over the redshift range 0 < z < 3 (see Guo et al. 2013b, for more details). A thorough comparison between our measurements and theoretical predictions from different galaxy formation models is beyond the scope of the present paper, and will be fully pursued in a future work.
5. Summary and conclusions
In this work, we studied how galaxy clustering depends on luminosity and stellar mass in the redshift range 0.5 < z < 1.1, using the currently largest complete sample of galaxies with redshift measured in this range. To quantify the effect, we measured the redshift-space 2PCF of VIPERS galaxies in the first data release, PDR-1, and derived the real-space clustering and bias assuming a power-law form for the projected correlation function. Errors were estimated using a set of mock HOD and SHMR catalogues that mimick the characteristics and the observational selections of the VIPERS dataset.
The main results of this work can be summarized as follows.
-
We confirm with unprecedented precision at z = 0.5–1.1 a monotonic increase in the clustering length r0, both as a function of B-band magnitude and stellar mass, in all the three redshift ranges considered. In contrast, the clustering slope, γ, appears quite constant when derived in the range 0.2 < rp [h-1 Mpc ] < 20.
-
The dependence of the clustering length r0 on luminosity is stronger at high redshift. In terms of the evolution of r0 with redshift, we find that there is only a weak trend for the highest luminosity galaxies, while significant evolution in r0 is found in the lower luminosity samples.
-
The VIPERS measurements are generally consistent with previous studies, while establishing a bridge from the local references to the high-redshift Universe. This is particularly true for the dependence of clustering on luminosity. In terms of dependence on stellar mass, VIPERS is very consistent with results from surveys with comparable magnitude limit, such as zCOSMOS. However, there is a clear overall difference at the 2-σ level to previous measurements at z ~ 1 obtained from surveys with fainter flux limits, such as VVDS-Deep and DEEP2. A possible interpretation is that this is the result of two combined effects. First, VVDS-Deep and DEEP2 are about two magnitudes deeper than VIPERS; for this reason, a mass-selected sample is significantly more complete in mass than in the case of VIPERS or zCOSMOS, including a larger population of low-mass, plausibly less clustered galaxies. This would explain the lower value of r0 observed in the VVDS-Deep and DEEP2 samples with M⋆ ≲ 1011M⊙, that is, in the range of masses in which we know surveys like VIPERS or zCOSMOS are incomplete (see Fig. 1). However, this should not be the case above this value, and the correlation length measured in the fainter surveys should rapidly converge to the trend and amplitude indicated by VIPERS and the other “bright” surveys. In fact, this is not observed in Fig. 5. At least part of this could be the result of a different effect, that is, the much smaller volume of the deeper surveys compared to VIPERS or zCOSMOS. This is particularly severe for the VVDS-Deep sample, which is only 0.5 deg2 in area, against the ~11 deg2 effectively covered at the current stage by VIPERS, out of a footprint of ~15 deg2. This factor of ~20 between the sampled volumes for a given redshift range implies that the massive tail, populated by the most strongly clustered objects, is largely undersampled in the fainter surveys, compared to VIPERS, so biasing the measured clustering of the most massive objects toward lower values. This should be less severe for the DEEP2 survey, which is ~4 deg2 in area, thus larger than zCOSMOS. Still, at M⋆ ~ 1011 M⊙ the DEEP2 values of r0 remain significantly lower than the others.
-
We provide an estimate of galaxy bias, averaged over the range [1–10] h-1 Mpc , as a function of luminosity, stellar mass, and redshift, assuming a standard flat ΛCDM framework. The results are consistent with the predictions of hierarchical galaxy formation, although we will devote future work to testing evolution models in detail.
The measurements of the 2PCF presented here represent a considerable advance over past surveys at z ~ 1. The large volume of VIPERS ensures that sample variance is subdominant. Furthermore, we modelled the measurement covariance utilizing mock surveys that account for both astrophysical and observational effects in detail. The results constitute new, stringent constraints on the galaxy 2PCF over a broad range of luminosities and stellar mass to be used as references against which to test models of cosmology and galaxy formation at redshifts 0.5–1.1.
Acknowledgments
We warmly thank Simon D. M. White for helpful suggestions. We acknowledge the crucial contribution of the ESO staff for the management of service observations. In particular, we are deeply grateful to M. Hilker for his constant help and support of this programme. Italian participation in VIPERS has been funded by INAF through PRIN 2008 and 2010 programmes. L.G. acknowledges support of the European Research Council through the Darklight ERC Advanced Research Grant (#291521). O.L.F. acknowledges support of the European Research Council through the EARLY ERC Advanced Research Grant (#268107). Polish participants have been supported by the Polish Ministry of Science (grant N N203 51 29 38), the Polish-Swiss Astro Project (co-financed by a grant from Switzerland, through the Swiss Contribution to the enlarged European Union), the European Associated Laboratory Astrophysics Poland-France HECOLS, and a Japan Society for the Promotion of Science (JSPS) Postdoctoral Fellowship for Foreign Researchers (P11802). GDL acknowledges financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement No. 202781. W.J.P. and R.T. acknowledge financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement No. 202686. W.J.P. is also grateful for support from the UK Science and Technology Facilities Council through the grant ST/I001204/1. E.B., F.M. and L.M. acknowledge the support from grants ASI-INAF I/023/12/0 and PRIN MIUR 2010-2011. C.M. is grateful for support from specific project funding of the Institut Universitaire de France and the LABEX OCEVU. We would also like to thank the anonymous referee for useful comments and suggestions.
References
- Abbas, U., & Sheth, R. K. 2006, MNRAS, 372, 1749 [NASA ADS] [CrossRef] [Google Scholar]
- Abbas, U., de la Torre, S., Le Fèvre, O., et al. 2010, MNRAS, 406, 1306 [NASA ADS] [Google Scholar]
- Adelberger, K. L., Steidel, C. C., Pettini, M., et al. 2005, ApJ, 619, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., & Paczynski, B. 1979, Nature, 281, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Bel, J., Marinoni, C., Granett, B., et al. 2013, A&A, submitted [Google Scholar]
- Benoist, C., Maurogordato, S., da Costa, L. N., Cappi, A., & Schaeffer, R. 1996, ApJ, 472, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, A. J., Frenk, C. S., Baugh, C. M., Cole, S., & Lacey, C. G. 2001, MNRAS, 327, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Blaizot, J., Wadadekar, Y., Guiderdoni, B., et al. 2005, MNRAS, 360, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M., Cen, R., Ostriker, J. P., Strauss, M. A., & Tegmark, M. 2000, ApJ, 531, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
- Bolzonella, M., Kovač, K., Pozzetti, L., et al. 2010, A&A, 524, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bottini, D., Garilli, B., Maccagni, D., et al. 2005, PASP, 117, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. J. I., Webster, R. L., & Boyle, B. J. 2000, MNRAS, 317, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. J. I., Dey, A., Jannuzi, B. T., et al. 2003, ApJ, 597, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Budavári, T., Connolly, A. J., Szalay, A. S., et al. 2003, ApJ, 595, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Christodoulou, L., Eminian, C., Loveday, J., et al. 2012, MNRAS, 425, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Coil, A. L., Newman, J. A., Cooper, M. C., et al. 2006, ApJ, 644, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Coil, A. L., Newman, J. A., Croton, D., et al. 2008, ApJ, 672, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Percival, W. J., Peacock, J. A., et al. 2005, MNRAS, 362, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Kilbinger, M., McCracken, H. J., et al. 2012, A&A, 542, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coupon, J., Broadhurst, T., & Umetsu, K. 2013, ApJ, 772, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., De Lucia, G., Zucca, E., et al. 2012, A&A, 548, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Röttgering, H. J. A., Labbé, I., et al. 2003, ApJ, 588, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Davidzon, I., Bolzonella, M., Coupon, J., et al. 2013, A&A, submitted DOI: 10.1051/0004-6361/201321511 [Google Scholar]
- Davis, M., & Geller, M. J. 1976, ApJ, 208, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., & Peebles, P. J. E. 1983, ApJ, 267, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Meiksin, A., Strauss, M. A., da Costa, L. N., & Yahil, A. 1988, ApJ, 333, L9 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., & Peacock, J. A. 2012, MNRAS, submitted [arXiv:1212.3615] [Google Scholar]
- de la Torre, S., Meneux, B., De Lucia, G., et al. 2011, A&A, 525, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Torre, S., Guzzo, L., Peacock, J. A., et al. 2013, A&A, submitted DOI: 10.1051/0004-6361/201321463 [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M. 1991, MNRAS, 252, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Zehavi, I., Hogg, D. W., et al. 2005, ApJ, 633, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, A., Scodeggio, M., Ilbert, et al. 2013, A&A, submitted [Google Scholar]
- Garilli, B., Paioro, L., Scodeggio, M., et al. 2012, PASP, 124, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R., Haynes, M. P., & Chincarini, G. L. 1986, ApJ, 300, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Granett, B. R., Guzzo, L., Coupon, J., et al. 2012, MNRAS, 421, 251 [NASA ADS] [Google Scholar]
- Guo, H., Zehavi, I., Zheng, Z., et al. 2013a, ApJ, 767, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Angulo, R. E., et al. 2013b, MNRAS, 428, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Strauss, M. A., Fisher, K. B., Giovanelli, R., & Haynes, M. P. 1997, ApJ, 489, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., Bartlett, J. G., Cappi, A., et al. 2000, A&A, 355, 1 [NASA ADS] [Google Scholar]
- Guzzo, L., Scodeggio, M., Garilli, B., et al. 2013, A&A, submitted [arXiv:1303.2623] [Google Scholar]
- Hamilton, A. J. S. 1988, ApJ, 331, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Pielorz, J., Erben, T., et al. 2009, A&A, 498, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaiser, N. 1984, ApJ, 284, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Colberg, J. M., Diaferio, A., & White, S. D. M. 1999, MNRAS, 307, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Mancini, D., Saisse, M., et al. 2002, The Messenger, 109, 21 [NASA ADS] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in SPIE Conf. Ser. 4841, eds. M. Iye, & A. F. M. Moorwood, 1670 [Google Scholar]
- Lee, K.-S., Giavalisco, M., Gnedin, O. Y., et al. 2006, ApJ, 642, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, K.-S., Giavalisco, M., Conroy, C., et al. 2009, ApJ, 695, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., Kauffmann, G., Jing, Y. P., et al. 2006, MNRAS, 368, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, L., Dickinson, M., Jian, H.-Y., et al. 2012, ApJ, 756, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Loh, Y.-S., Rich, R. M., Heinis, S., et al. 2010, MNRAS, 407, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Loveday, J., Maddox, S. J., Efstathiou, G., & Peterson, B. A. 1995, ApJ, 442, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Madgwick, D. S., Hawkins, E., Lahav, O., et al. 2003, MNRAS, 344, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Malek, K., Solarz, A., Pollo, A., et al. 2013, A&A, 557, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchetti, A., Granett, B. R., Guzzo, L., et al. 2013, MNRAS, 428, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Marulli, F., Bianchi, D., Branchini, E., et al. 2012, MNRAS, 426, 2566 [NASA ADS] [CrossRef] [Google Scholar]
- Maurogordato, S., & Lachieze-Rey, M. 1991, ApJ, 369, 30 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Ilbert, O., Mellier, Y., et al. 2008, A&A, 479, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mellier, Y., Bertin, E., Hudelot, P., et al. 2008, http://terapix.iap.fr/cplt/oldSite/Descart/CFHTLS-T0005-Release.pdf [Google Scholar]
- Meneux, B., Le Fèvre, O., Guzzo, L., et al. 2006, A&A, 452, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneux, B., Guzzo, L., Garilli, B., et al. 2008, A&A, 478, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneux, B., Guzzo, L., de la Torre, S., et al. 2009, A&A, 505, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mostek, N., Coil, A. L., Cooper, M. C., et al. 2013, ApJ, 767, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Norberg, P., Baugh, C. M., Hawkins, E., et al. 2001, MNRAS, 328, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Norberg, P., Baugh, C. M., Hawkins, E., et al. 2002, MNRAS, 332, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Hamana, T., Shimasaku, K., et al. 2005, ApJ, 635, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, W. J., Cole, S., Eisenstein, D. J., et al. 2007, MNRAS, 381, 1053 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Percival, W. J., Reid, B. A., Eisenstein, D. J., et al. 2010, MNRAS, 401, 2148 [NASA ADS] [CrossRef] [Google Scholar]
- Pillepich, A., Porciani, C., & Hahn, O. 2010, MNRAS, 402, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Pollo, A., Meneux, B., Guzzo, L., et al. 2005, A&A, 439, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollo, A., Guzzo, L., Le Fèvre, O., et al. 2006, A&A, 451, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Lamareille, F., et al. 2007, A&A, 474, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prada, F., Klypin, A. A., Cuesta, A. J., Betancort-Rijo, J. E., & Primack, J. 2012, MNRAS, 423, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, A. J., Tojeiro, R., & Percival, W. J. 2011, MNRAS, 413, 2078 [NASA ADS] [CrossRef] [Google Scholar]
- Saunders, W., Rowan-Robinson, M., & Lawrence, A. 1992, MNRAS, 258, 134 [NASA ADS] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., Le Fèvre, O., & Guzzo, L. 2009, The Messenger, 135, 13 [NASA ADS] [Google Scholar]
- Simpson, F., & Peacock, J. A. 2010, Phys. Rev. D, 81, 043512 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. E., Peacock, J. A., Jenkins, A., et al. 2003, MNRAS, 341, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Swanson, M. E. C., Tegmark, M., Blanton, M., & Zehavi, I. 2008, MNRAS, 385, 1635 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., & Peebles, P. J. E. 1998, ApJ, 500, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Tegmark, M., Blanton, M. R., Strauss, M. A., et al. 2004, ApJ, 606, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Wake, D. A., Whitaker, K. E., Labbé, I., et al. 2011, ApJ, 728, 46 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., Frenk, C. S., Davis, M., & Efstathiou, G. 1987, ApJ, 313, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Willmer, C. N. A., da Costa, L. N., & Pellegrini, P. S. 1998, AJ, 115, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Blanton, M. R., Frieman, J. A., et al. 2002, ApJ, 571, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Eisenstein, D. J., Nichol, R. C., et al. 2005, ApJ, 621, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Zehavi, I., Zheng, Z., Weinberg, D. H., et al. 2011, ApJ, 736, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Bardelli, S., Bolzonella, M., et al. 2009, A&A, 508, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Correcting for stellar mass incompleteness and proximity effect
 |
Fig. A.1 Ratio between the redshift-space 2PCF as a function of mass, measured in flux-limited and complete semi-analytic mocks. The red dots show the clustering ratio averaged over the ten independent mock catalogues, while the error bars are the rms scatter. The black lines show the best-fit error function used to smooth these ratios. |
 |
Fig. A.2 Ratio between the redshift-space 2PCF measured in mock catalogues with and without the slit mask target selection algorithm applied. Symbols are the same as in Fig. A.1. |
A possible method for correcting the 2PCF measurements for stellar mass incompleteness is described in Sect. 3.4. We provide here more details on this procedure and quantify the impact on our measurements. The method consists in measuring the 2PCF in two sets of mock galaxy catalogues, one set complete in stellar masses, the other one with the same VIPERS iAB < 22.5 flux cut. We use mock catalogues constructed with the Munich semi-analytic galaxy formation model (De Lucia & Blaizot 2007), on top of the DM halo trees from the Millennium simulation (Springel et al. 2005). The MoMaF package has been used to produce the light-cones from which the VIPERS mock samples are extracted (Blaizot et al. 2005). These catalogues are complete in stellar masses down to ~108 M⊙. Figure A.1 shows the mean ratio between the 2PCF in flux-limited and complete mocks, averaged over ten independent catalogues, while the error bars are the rms scatter. The results refer to different redshift and stellar mass limits, as explicitly indicated by the labels. According to the Munich model, the mass incompleteness introduces a clear scale-dependent reduction of clustering, mainly significant on scales ≲1 h-1 Mpc . The best-fit error functions used to smooth these ratios represent the correction that we actually use to obtain the values of 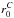 , γC and biasC reported in Tables 3, 4. Since the mock red and faint galaxies are significantly more clustered than the observed ones, this model-dependent correction should be taken with caution.
, γC and biasC reported in Tables 3, 4. Since the mock red and faint galaxies are significantly more clustered than the observed ones, this model-dependent correction should be taken with caution.
As discussed in Sect. 3.3, owing to our multi-object slit masks, it is not possible to observe galaxies that are too close to each other. This proximity effect introduces a further scale-dependent suppression in the 2PCF that we have to correct. We adopt the same strategy described above to correct for mass incompleteness; that is, we measure the ratio between the redshift-space 2PCF in mock catalogues with and without the slit mask target selection algorithm applied (also see Coil et al. 2008). As before, the mock galaxy catalogues used here are constructed with the Munich semi-analytic galaxy formation model. Figure A.2 shows the results of this method. This correction is almost independent of luminosity and stellar mass, similar to the results of Coil et al. (2006). Thus, we decided to use the correction calibrated in our largest galaxy sample to correct all our clustering measurements. We notice that the systematic clustering suppression due to the proximity effect becomes less severe going to high redshift. More details can be found in de la Torre et al. (2013).
All Tables
All Figures
 |
Fig. 1 Luminosity and stellar mass selection as a function of redshift. The black dots show the W1 and W4 VIPERS galaxies. Yellow lines surround the selected sub-samples. Solid lines show the 90% completeness levels for the whole galaxy population (cyan lines) and for galaxies of four different photometric types: red E/Sa (red lines), early spiral (orange lines), late spiral (green lines), and irregular or starburst (blue lines). The B-band rest-frame magnitude limits in the left panel account for the average luminosity evolution of galaxies, as explained in the text. On the bottom axes, zeq,Λ ~ 0.44 is the redshift of DM-DE equality and zacc ~ 0.82 is the redshift when the Universe started accelerating, according to ΛCDM predictions with the set of cosmological parameters adopted in this work. |
| In the text | |
 |
Fig. 2 Comoving radial distance distribution of the W1 and W4 VIPERS galaxy samples, shown with the green and yellow histograms, respectively. The red and blue lines show the total W1+W4 smoothed distribution, obtained by filtering the observed distribution with a Gaussian kernel of σ = 150 h-1 Mpc and using the Vmax method, respectively. |
| In the text | |
 |
Fig. 3 2PCF of VIPERS galaxies as a function of B-band absolute magnitude (upper panels) and stellar mass (bottom panels). The error bars are the square root of the diagonal values of the covariance matrix given by Eq. (2). Absolute magnitudes are given in the AB system. |
| In the text | |
 |
Fig. 4 Projected correlation function of VIPERS galaxies as a function of B-band absolute magnitude (upper panels) and stellar mass (bottom panels). The solid lines show the best-fit power-law models, obtained by fitting the correlation functions in the interval 0.2 < rp [h-1 Mpc ] < 20. |
| In the text | |
 |
Fig. 5 Best-fit values of the correlation length, r0, (left panels) and slope, γ, (right panels), as a function of B-band absolute magnitude (upper panels) and stellar mass (bottom panels). VIPERS costraints, obtained in threshold samples at z ∈ [0.5,0.7], z ∈ [0.7,0.9], and z ∈ [0.9,1.1] are shown, respectively, by blue squares, red diamonds, and green circles, as indicated by the labels. The remaining grey symbols refer to measurements based on data from other surveys, reported here for comparison: upper panels – DSS-DR7 data from Zehavi et al. (2011), 2dfGRS data from Norberg et al. (2002), VVDS-Deep data from Pollo et al. (2006) and DEEP2 data from Coil et al. (2006); lower panels – SDSS-DR2 data from Li et al. (2006), VVDS-Deep data from Meneux et al. (2008), zCOSMOS data from Meneux et al. (2009), NMBS data from Wake et al. (2011), DEEP2 data from Mostek et al. (2013) and BzK data from Lin et al. (2012). |
| In the text | |
 |
Fig. 6 Best-fit values of the VIPERS correlation slope, γ, as a function of luminosity. Green and red points show the VIPERS γ values obtained fitting wp(rp) in 0.2 < rp [h-1 Mpc ] < 20 and rp < 1 h-1 Mpc , respectively. Grey squares refer to the VVDS-Deep measurements. |
| In the text | |
 |
Fig. 7 Bias of VIPERS galaxies, averaged over the range [1–10] h-1 Mpc , as a function of B-band absolute magnitude (left panel) and stellar mass (right panel). The coloured symbols used for VIPERS measurements are the same as in Fig. 5. The black solid line in the left panel shows the fitted bias function by Zehavi et al. (2011). |
| In the text | |
 |
Fig. 8 Redshift-space 2PCF of VIPERS galaxies compared to theoretical expectations as a function of B-band magnitude (upper panels) and stellar mass (bottom panels). The coloured symbols used for VIPERS measurements are the same as in Fig. 3. The grey shaded areas show the 2PCF measured in two large galaxy mock catalogues, constructed with the Munich semi-analytic model. The 2PCFs in different sub-samples are offset by 0.5 dex, starting from the lower luminosity and stellar mass samples, for visual clarity. |
| In the text | |
 |
Fig. A.1 Ratio between the redshift-space 2PCF as a function of mass, measured in flux-limited and complete semi-analytic mocks. The red dots show the clustering ratio averaged over the ten independent mock catalogues, while the error bars are the rms scatter. The black lines show the best-fit error function used to smooth these ratios. |
| In the text | |
 |
Fig. A.2 Ratio between the redshift-space 2PCF measured in mock catalogues with and without the slit mask target selection algorithm applied. Symbols are the same as in Fig. A.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


