| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321145 | |
| Published online | 23 May 2013 | |
Modeling solar cycles 15 to 21 using a flux transport dynamo
1 Key Laboratory of Solar Activity, National Astronomical Observatories, Chinese Academy of Sciences, 100012 Beijing, PR China
e-mail: jiejiang@nao.cas.cn
2 Max-Planck-Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
3 Department of Physics, Faculty of Science & Letters, İstanbul Kültür University, Ataköy Campus, Bakırköy 34156 İstanbul, Turkey
Received: 22 January 2013
Accepted: 5 April 2013
Context. The Sun’s polar fields and open flux around the time of activity minima have been considered to be strongly correlated with the strength of the subsequent maximum of solar activity.
Aims. We aim to investigate the behavior of a Babcock-Leighton dynamo with a source poloidal term that is based on the observed sunspot areas and tilts. In particular, we investigate whether the toroidal fields at the base of convection zone from the model are correlated with the observed solar cycle activity maxima.
Methods. We used a flux transport dynamo model that includes convective pumping and a poloidal source term based on the historical record of sunspot group areas, locations, and tilt angles to simulate solar cycles 15 to 21.
Results. We find that the polar fields near minima and the toroidal flux at the base of the convection zone are both highly correlated with the subsequent maxima of solar activity levels (r = 0.85 and r = 0.93, respectively).
Conclusions. The Babcock-Leighton dynamo is consistent with the observationally inferred correlations.
Key words: magnetohydrodynamics (MHD) / Sun: dynamo / Sun: surface magnetism
© ESO, 2013
1. Introduction
The solar magnetic cycle is believed to be the result of a magnetohydrodynamic dynamo. One family of these dynamo models is the Babcock-Leighton (BL) model, which was first proposed by Babcock (1961) and further elaborated on by Leighton (1964). The essence of the BL mechanism is that the generation of the poloidal field comes from the decay of the tilt sunspot groups on the solar surface. BL models have been successful in reproducing some characteristics of the solar cycle (e.g., Choudhuri et al. 1995; Durney 1997; Choudhuri & Dikpati 1999; Dikpati & Charbonneau 1999; Nandy & Choudhuri 2002; Chatterjee et al. 2004; Rempel 2006; Guerrero & de Gouveia Dal Pino 2007; Yeates et al. 2008), including the solar cycle irregularities (e.g., Charbonneau & Dikpati 2000; Durney 2000; Charbonneau 2001; Karak 2010; Karak & Choudhuri 2011). Recent analyses of the long-term sunspot observations strengthen the idea that the dynamo is consistent with the BL mechanism (Dasi-Espuig et al.2010; Cameron et al.2010 [hereafter CJSS10]; Kitchatinov & Olemskoy2011).
The important ingredients in the BL dynamo model are (i) the generation of poloidal flux due to the emergence of tilted sunspot groups and the subsequent evolution of the surface magnetic flux; (ii) the transport of poloidal flux to the tachocline; (iii) the generation of toroidal magnetic flux due to the winding up of the poloidal field (the Ω-effect); and (iv) the subsequent formation and rise of flux loops through the convection zone until they emerge at the surface. This last process also includes the tilting of the flux tubes with respect to the equator. For more information about the models, see the review by Charbonneau (2010).
Some of these processes are directly observable, in particular, the surface evolution of the emerged magnetic field, part (i). Empirically the large-scale evolution is described well by the surface flux transport (SFT) model (e.g., Wang et al. 1989; Schrijver 2001; Mackay et al. 2002; Baumann et al. 2004; Jiang et al. 2010; Mackay & Yeates 2012). We previously (CJSS10) used the SFT model to reconstruct the surface field and open flux for the period 1913–1986. The observed sunspot longitudes, latitudes, areas, and cycle-averaged tilt angles were used to create the source term. The results of that model compare well with the open flux derived from geomagnetic indices (Lockwood 2003) and with the reversal times of the polar fields (Makarov et al. 2003).
The remaining processes (ii); (iii); and (iv) deal with the subsurface dynamics, which are currently poorly constrained by observations. These processes are not included in the SFT model but are described by the flux transport dynamo (FTD). The surface fields resulting from the two models are consistent, provided the FTD model has sufficient near-surface convective pumping (Cameron et al. 2012). The effect of pumping has been studied by Karak & Nandy (2012), who demonstrate that the effect of the convective pumping reduces the memory of the solar activity to one cycle. Other effects of the pumping on the BL dynamo have also been studied by, e.g., Käpylä et al. (2006), Guerrero & de Gouveia Dal Pino (2008), Do Cao & Brun (2011), and Kitchatinov & Olemskoy (2012).
Our approach is to study the Babcock-Leighton dynamo model using as many observational constraints as possible. We thus take the historical RGO/SOON sunspot record as the basis for constructing the source of poloidal flux, we employ boundary conditions where the magnetic field is vertical at photosphere, and we impose substantial downwards pumping near the surface (as required by observations, Cameron et al. 2012). The differential rotation (Schou et al. 1998), near-surface meridional flow, and near-surface turbulent diffusivity (see references in Cameron 2011) are observationally constrained and modeled in a similar way.
The diffusivity and pumping throughout the bulk of the convection zone, as well as the deeper structure of the meridional circulation remain observationally unconstrained. In this paper we first construct a reference case with intermediate choices (between the extremes of what can be considered as reasonable) for both the pumping and the diffusivity in the bulk of the convection zone. After presenting the results of the calculations for this reference case, we then consider the effect of varying these parameters. A more extensive study of the effect of the diffusivity and the meridional circulation in transporting the field is given by Yeates et al. (2008) for the case without magnetic pumping. The meridional circulation deep below the surface is controversial, with opposing views on such basic questions as whether there are one or two cells in the radial direction. For this paper we have assumed a one-cell structure.
Here we concentrate on processes (i), (ii), and (iii), using the FTD model to study the evolution of the toroidal flux when the source of poloidal flux, process (i), is based on the historical sunspot record. In a full BL dynamo model process (i), the appearance on the surface of tilted sunspot groups, is intimately connected with the formation and rise of flux loops from the bottom of the convection zone, i.e., process (iv). Since we are using the observed sunspot record for process (i), we can omit the formation and rise processes entirely. Ignoring processes (iv) means that we are solving a driven system rather than a self consistently driven dynamo. However, it allows us to address the question of whether the polar field strength at the minimum produced by a BL dynamo with a poloidal source term derived by observations of sunspot groups and cycle-average tilt angles is correlated with the observed strength of the following cycle. To be consistent with observations (e.g. see Wang & Sheeley 2009), a strong correlation should be present in the model.
The correlation between the minima of the open flux (which is closely related to the Sun’s axial magnetic dipole moment) and the strength of the subsequent maxima of solar activity (see Wang & Sheeley 2009; Jiang et al. 2011) implies processes (ii) and (iii) are – on average over a cycle – essentially linear. The argument is that a nonlinearity in going between the polar fields and the toroidal fields at the base of the convection zone would manifest itself in the number of sunspot groups that appear on the surface. Such a nonlinearity would then result in maxima of activity levels that are not strongly correlated with the polar fields. The maxima of the toroidal field at the base of the convection zone, which is determined by processes (i−iii), should therefore also be strongly correlated with the maxima of the activity level. This is an observationally inferred result, and it is therefore a test for the model.
There have been two previous efforts to relate the amount of toroidal flux produced by an FTD model and the observed sunspot record. The first effort, started by Dikpati & Gilman (2006), used the time evolution of the area coverage of sunspots (a measure of the amplitude of the solar cycle) as input. A very idealized model was used to convert this into the source of poloidal flux. In particular, their source term for cycle n requires knowing of the timing of the minimum between cycles n − 1 and n. Their finding was that the toroidal field at the base of the convection zone during any cycle n in the model was highly correlated with the actually observed strength of cycle n. An explanation for this correlation is suggested by Cameron & Schüssler (2007): incorporation of the timing of the minimum in the source term for the poloidal flux, in conjunction with the Waldmeier effect (Cameron & Schüssler 2008) introduces similar correlations even when the amplitudes are independent random realizations.
The second effort is that of Jiang et al. (2007). They found in the high-diffusivity regime that the poloidal flux is transported to the base of the convection zone at the same time as it is transported to the poles. The simultaneous transport of the field to the poles and to the base of the convection zone presented in this model offers an explanation for the observed correlation between the polar fields and the toroidal field at the base of the convection zone (see also Choudhuri et al. 2007). Jiang et al. (2007) then scaled the poloidal field at the end of each cycle so that the polar fields of the model had the same strength as those observed by the Wilcox Solar Observatory. The winding up of this poloidal field by differential rotation produces a toroidal field that is correlated with the polar fields. The high correlation between the toroidal fields of the model and the observed level of activity then follows from the previously reported correlation between the observed polar fields and the amplitude of the next cycle (Schatten et al. 1978). The exact nature of the sources in this model is irrelevant, since the field is rescaled, and this model says little about the causes of the cyclic amplitude variations.
These previous attempts were carried out before cycle-to-cycle tilt angle variations had been reported by Dasi-Espuig et al. (2010) and before it was recognized that a vertical field boundary condition at the photosphere and strong pumping are required to make the FTD model match the observations of the surface evolution of magnetic flux (Cameron et al. 2012). The question thus remains open as to what happens when we use the FTD model with these new constraints. Here we address this question using the FTD with pumping (Cameron et al. 2012) and sources based on as much information as is available (see CJSS10) to follow the evolution of the subsurface magnetic field over cycles 15 to 21.
The paper is organized as follows. The BL dynamo model is described in Sect. 2. The results for a reference-case set of parameters are presented in detail in Sect. 3. The influence of the observationally poorly constrained parameters describing the magnetic diffusivity and pumping in the bulk of the convection zone is studied in Sect. 4. The conclusions and discussion of our results are given in Sect. 5.
2. Flux transport dynamo model
The FTD model is based on the induction equation for an azimuthally symmetric field: ![\begin{eqnarray} \label{eq:At} \frac{\partial A}{\partial t}&=&\eta\left(\nabla^2-\frac{1}{s^2}\right)A-\frac{1}{s}(\boldsymbol{\upsilon'} \cdot\nabla)(sA)+S, \\ \label{eq:Bt} \frac{\partial B}{\partial t}&= &\eta\left(\nabla^2-\frac{1}{s^2}\right)B+\frac{1}{r}\frac{{\rm d}\eta}{{\rm d}r}\frac{\partial}{\partial r}(rB) \\ \nonumber &&-\frac{1}{r}\left[\frac{\partial}{\partial r}(r\upsilon'_rB)+\frac{\partial}{\partial\theta}(\upsilon'_\theta B)\right]+s(\boldsymbol{B}_{\rm p}\cdot\nabla)\Omega, \end{eqnarray}](/articles/aa/full_html/2013/05/aa21145-13/aa21145-13-eq7.png) where
where ![\begin{equation} \boldsymbol{B}=B(r,\theta)\boldsymbol{e_\phi} +\nabla\times[A(r,\theta)\boldsymbol{e_\phi}]. \end{equation}](/articles/aa/full_html/2013/05/aa21145-13/aa21145-13-eq8.png) (3)Here B(r,θ) is the toroidal component of the magnetic field and A(r,θ) the toroidal component of the vector potential, related to the poloidal component of the magnetic field by Bp = ∇ × (Aeφ); υ′ is the sum of the meridional velocity field υ(r,θ) and magnetic pumping γ = γ(r)er; Ω(r,θ) is the differential rotation profile; S(r,θ,t) is the source term for the poloidal field; η(r) is the magnetic diffusivity; and s = rsinθ.
(3)Here B(r,θ) is the toroidal component of the magnetic field and A(r,θ) the toroidal component of the vector potential, related to the poloidal component of the magnetic field by Bp = ∇ × (Aeφ); υ′ is the sum of the meridional velocity field υ(r,θ) and magnetic pumping γ = γ(r)er; Ω(r,θ) is the differential rotation profile; S(r,θ,t) is the source term for the poloidal field; η(r) is the magnetic diffusivity; and s = rsinθ.
The code used to solve the above problem was developed at the MPS. It has been checked against the benchmark dynamo of Jouve et al. (2008) and was previously used in Cameron et al. (2012). In essence it treats the advective term explicitly and an alternating direction implicit scheme for the diffusive terms. We use 181 × 71 grid cells in the latitudinal and radial directions, respectively, and a timestep of one day.
2.1. Boundary conditions
We carry out our calculations in a spherical shell (0.65 R⊙ ≤ r ≤ R⊙,0 ≤ θ ≤ π). At the poles (θ = 0, π), we have 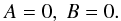 (4)The inner boundary matches a perfect conductor,
(4)The inner boundary matches a perfect conductor, 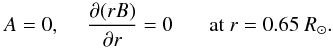 (5)As described in Cameron et al. (2012), the appropriate outer boundary is that the field is vertical there,
(5)As described in Cameron et al. (2012), the appropriate outer boundary is that the field is vertical there, 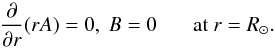 (6)The vertical outer boundary condition is also proposed by van Ballegooijen & Mackay (2007) and has previously been used in the BL dynamo models by, for example, Muñoz-Jaramillo et al. (2009) and Nandy et al. (2011).
(6)The vertical outer boundary condition is also proposed by van Ballegooijen & Mackay (2007) and has previously been used in the BL dynamo models by, for example, Muñoz-Jaramillo et al. (2009) and Nandy et al. (2011).
2.2. Flow field and turbulent diffusivity
We use the same profile for the differential rotation as was used in Cameron et al. (2012) and the references therein. We also use the same form for the meridional flow as given in that study, except that we have reduced the parameter v0 that determines the speed of the meridional flow so that the maximum speed at the surface is now 11 m/s instead of 15 m/s to be consistent with CJSS10.
We also follow Cameron et al. (2012) for the turbulent diffusivity profile ![\begin{eqnarray} \label{eq:eta} \eta(r)=\eta_{\rm rz} &+&\frac{\eta_{\rm cz}-\eta_{\rm rz}}{2}\left[1+\mathrm{erf}\left(\frac{r-r_{\rm rz}}{d}\right)\right] \nonumber \\ &+&\frac{\eta_{\rm s}-\eta_{\rm cz}}{2}\left[1+\mathrm{erf}\left(\frac{r-r_{\rm s}}{d}\right)\right], \end{eqnarray}](/articles/aa/full_html/2013/05/aa21145-13/aa21145-13-eq26.png) (7)where the subscript rz is for the radiative zone, cz is for the convection zone, and s is for the surface properties, ηrz = 0.1 km2 s-1, ηcz = 10 km2 s-1, ηs = 250 km2s-1, rcz = 0.7 R⊙, rs = 0.95 R⊙, and d = 0.02 R⊙. The argument for the choice of the surface diffusivity ηs is given in CJSS10 – it is near the middle of the range given by observations (see Table 6.2 of Schrijver & Zwaan 2000). This value for ηs is also consistent with the range found using comprehensive photospheric simulations (Cameron et al. 2011). The turbulent diffusivity in the convective zone ηcz is not directly constrained. The effect of different values for this parameter will be studied in Sect. 4.
(7)where the subscript rz is for the radiative zone, cz is for the convection zone, and s is for the surface properties, ηrz = 0.1 km2 s-1, ηcz = 10 km2 s-1, ηs = 250 km2s-1, rcz = 0.7 R⊙, rs = 0.95 R⊙, and d = 0.02 R⊙. The argument for the choice of the surface diffusivity ηs is given in CJSS10 – it is near the middle of the range given by observations (see Table 6.2 of Schrijver & Zwaan 2000). This value for ηs is also consistent with the range found using comprehensive photospheric simulations (Cameron et al. 2011). The turbulent diffusivity in the convective zone ηcz is not directly constrained. The effect of different values for this parameter will be studied in Sect. 4.
In Cameron et al. (2012), constraints were placed on the amount of magnetic pumping near the top of the convection zone. However, the strength of the pumping in the deeper layers is unconstrained. We assume here that the magnetic pumping extends to the base of the convection zone, albeit at a weaker level than in the near-surface layer. The radial dependence of the pumping is assumed to be ![\begin{eqnarray} \gamma(r)&=& \frac{\gamma_{\rm cz}}{2}\left[1+\mathrm{erf}\left(\frac{r-r_{\gamma}}{d}\right)\right] \nonumber \\ &&+\frac{\gamma_{\rm s}-\gamma_{\rm cz}}{2}\left[1+\mathrm{erf}\left(\frac{r-r_{\rm ns}}{d}\right)\right], \end{eqnarray}](/articles/aa/full_html/2013/05/aa21145-13/aa21145-13-eq37.png) (8)where γcz = −2 m s-1, γs = −20 m s-1, rns = 0.9 R⊙, and rγ = 0.7 R⊙. We assume here that the enhanced near surface pumping extends slightly deeper than the region of enhanced surface turbulent diffusivity (rns = 0.9 R⊙ rather than rs = 0.95 R⊙), below which its strength drops to 2 m/s. Since the value of the pumping in the convection zone and the depth at which pumping ceases (rγ) are unknown, we study the impact of varying these parameters in Sect. 4.
(8)where γcz = −2 m s-1, γs = −20 m s-1, rns = 0.9 R⊙, and rγ = 0.7 R⊙. We assume here that the enhanced near surface pumping extends slightly deeper than the region of enhanced surface turbulent diffusivity (rns = 0.9 R⊙ rather than rs = 0.95 R⊙), below which its strength drops to 2 m/s. Since the value of the pumping in the convection zone and the depth at which pumping ceases (rγ) are unknown, we study the impact of varying these parameters in Sect. 4.
 |
Fig. 1 Source term, S(r,θ,t)sin(θ) at r = R⊙ for the poloidal flux based on the RGO sunspot record. The factor of sinθ is included to make the figure proportional to the amount of signed flux. The red and blue colors indicate positive and negative signs of A, respectively. Data after 1977 is from the SOON network. |
 |
Fig. 2 Simulated variation of the magnetic field over cycle 19. The red and blue colors correspond to negative and positive toroidal fields, respectively. The solid (dashed) lines represent anti-clockwise (clockwise) orientated field lines of the poloidal field. The snapshots (A)−(F) cover cycle 19, corresponding to t = 1956, 1958, 1960, 1962, 1964, and 1966, respectively. |
2.3. Source term
The source of poloidal field in this model is based on the observed emergence of bipolar sunspot groups. We use the procedure of CJSS10 to convert the RGO sunspot group area observations into a change in the radial magnetic flux at the surface: the RGO sunspot area record is used to obtain sunspot group areas, longitudes, and latitudes. Tilt angles from the Mount Wilson and Kodaikanal observatories (Howard et al. 1984; Howard 1991; Sivaraman et al. 1993) are averaged over each cycle as in Dasi-Espuig et al. (2010) and CJSS10, and then used in conjunction with the RGO data for individual spot groups to determine the longitudinal and latitudinal separation between the two polarities in the bipolar group. The areas are converted into fluxes using the parameters in CJSS10 (also see the references therein). For each sunspot group we calculate the corresponding change in the radial field at the surface, ΔBr(R⊙,θ,φ,t).
The RGO data covers the period from 1874 to 1976. The tilt angles are known from 1906 to 1987, and the overlapped data (cycles 14 to 20) can be used to reconstruct the poloidal source term for cycles 15 to 21. The RGO sunspot records were replaced by results from the SOON network after this date, which used a different definition of what to include, and therefore introduces a number of cross-calibration issues. As pointed out in Cameron & Schüssler (2012) there are outstanding problems when the sunspot record is used in a non-linear way such as here (the sunspot areas affect the tilt, which is then multiplied by the area to get the poloidal source term). We thus restrict our calculation to the period from 1874 to 1981 (i.e., for the cycles for which the toroidal flux at the base of the convection zone is created from poloidal flux based on the RGO area data).
The tilt angle data is only available from 1906 onwards, so it can be used for the sources leading to cycles 15 to 21. For cycles 12 and 13, we use the linear relationship between the sunspot maxima and the cycle-averaged tilt angles reported by Dasi-Espuig et al. (2010). While we restrict our statistical analysis to cycles 15 to 21, simulating these early cycles makes us less sensitive to the initial condition.
To calculate the change in the azimuthal component of the vector potential A, we then use 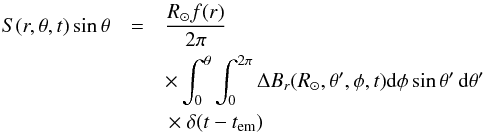 (9)where tem is the time at which the sunspot group was observed to emerge, and δ is the Dirac delta function. For the radial dependence of the source term we take
(9)where tem is the time at which the sunspot group was observed to emerge, and δ is the Dirac delta function. For the radial dependence of the source term we take ![\begin{equation} f(r)=\frac{1}{2}\left[1+\mathrm{erf}\left(\frac{r-0.9~R_\odot)}{d}\right)\right]\cdot \end{equation}](/articles/aa/full_html/2013/05/aa21145-13/aa21145-13-eq59.png) (10)The resulting sources at the surface are shown in Fig. 1. This procedure is conceptually related to the double-ring algorithm developed by Muñoz-Jaramillo et al. (2010).
(10)The resulting sources at the surface are shown in Fig. 1. This procedure is conceptually related to the double-ring algorithm developed by Muñoz-Jaramillo et al. (2010).
2.4. Initial conditions
Since we have neither direct measurements of the magnetic fields at the poles of the Sun in 1874 nor measurements of the toroidal field of the Sun at the base of the convection zone at any time, the appropriate initial condition for our model is not well known. The starting date for our simulations, May 1874, is however about three fifths of the way through cycle 11 (which ran from March 1867 to December 1878). This is close to the phase of the cycle where the axial-dipole field is weak, and given that the minimum of the open flux was low during this period (Wang & Sheeley 2009), A = 0 is a reasonable choice. The poloidal component of the initial condition is particularly important because the decay of the poloidal field is dominated by the rate at which it is removed from the surface. The process by which the removal takes place is diffusion across the equator, which is opposed at the surface by the poleward meridional flow. The resulting decay rate is about 4000 years (see CJSS10) in the absence of new sources, so the poloidal component of the initial condition affects the entire period studied in this paper.
The choice for the initial toroidal field is less critical because its diffusion rate is determined by diffusion across the equator at the base of the convection zone. Here the meridional flow is towards the equator, so it pushes the flux into a thin boundary layer where the field can easily diffuse across the equator. The pumping plays an important role here in that it keeps the meridional circulation from moving the flux upwards and back into the bulk of the convection zone. For this study we assumed B = 0 at the start of the simulation. This may not be adequate, but in view of the short decay time of the toroidal field it is sufficient to demonstrate that the Babcock-Leighton model has polar fields at the preceding minima and toroidal fields at maxima that are strongly correlated with the maxima of solar activity.
 |
Fig. 3 Radial component of the surface magnetic field for the reference case. The upper panel shows a time-latitude diagram. The lower panel gives the polar fields, defined as the average radial field strength beyond ± 70° latitude (black curve) and the sunspot numbers (red curve). The vertical line indicates the time until which RGO sunspot group area data are available. The correlation coefficient of the maxima of the polar fields and the subsequent maxima of sunspot number for cycles 15 to 21 is 0.85. |
 |
Fig. 4 Toroidal field at the base of the convection zone (r = 0.7 R⊙). The upper panel shows the evolution as a function of latitude and time. In the lower panel the average unsigned toroidal flux between ± 45° latitude corresponding to odd and even cycles is shown using dashed and solid curves, respectively. The correlation coefficient between the maxima of the toroidal field at the base of the convection zone and the maxima of the observed sunspot number for cycles 15−21 is 0.93. |
In summary, both the initial toroidal and the initial poloidal field are zero in our simulations. We use a poloidal source term constructed from the observed sunspot record rather than the self-consistent dynamo problem.
3. Results
The time evolution of the simulated magnetic field through cycle 19 is shown in Fig. 2 as an example. We see that throughout the cycle both the poloidal and toroidal fluxes have a simple form with no “conveyor belt” carrying flux from multiple cycles (cf. Dikpati & Gilman 2006) operating within the convection zone, which is consistent with Karak & Nandy (2012). Although we are in the “low-medium diffusivity” regime (cf. Yeates et al. 2008), the transport by convective pumping of poloidal flux from the surface to the tachocline occurs over the same time span as the flux is transported to the poles. The winding up of the field to produce toroidal flux due to the differential rotation takes place as the field is descending and after it reaches the base of the convection zone. The transport by downward pumping near the equator is opposed by the upward radial flow of the meridional circulation, together with the equatorward meridional flow, leading to a slower downward transport near the equator and a delayed reversal of the toroidal flux near the equator with respect to mid-latitudes.
The radial component of the field on the surface as a function of time for the entire period analyzed is shown in Fig. 3. The surface evolution of the field is similar to the one given by the surface flux transport model. Since with pumping the SFT and FTD models are consistent, and as we are using the same sources as in CJSS10, the correlation between the polar fields (here the average field from ± 70° latitude poleward) and the strength of the next cycle (the maxima of the yearly averaged sunspot number), based on cycles 15 to 21, is similar to the result in CJSS10 (correlation coefficient r = 0.85).
With our 2D dynamo model, we can now also consider the evolution of the toroidal field at the base of the convection zone, which could not be studied by the SFT model alone. Figure 4 shows the evolution of the toroidal flux at the base of the convection zone. The toroidal component of the magnetic field at r = 0.7 R⊙ is shown in the upper panel. In each hemisphere we see toroidal flux propagating equatorward at low latitudes. The reason for this propagation is, in part, the delayed reversal of the toroidal fields there as discussed above. The eruption of this flux will result in sunspot groups with an emergence latitude that migrates equatorward – that is, with properties similar to the observed butterfly diagram. There is also a high-latitude branch of toroidal magnetic field. We conjecture that this branch does not lead to sunspot emergence because, at latitudes above 75°, flux tubes at the bottom of the overshoot layer with field strengths of 6 × 104 G or more are stable with regard to the Parker instability (Ferriz-Mas & Schüssler 1995; Caligari et al. 1995). This flux thus remains hidden at the base of the convection zone. This explanation contrasts with those of Nandy & Choudhuri (2002) and Guerrero & Muñoz (2004), who show how a meridional flow that penetrates below the tachocline substantially weakens the high-latitude branch and pushes the toroidal flux below the tachocline. Flux emergence then can take place at low latitudes where the meridional circulation causes the flux to re-enter the convection zone.
 |
Fig. 5 Correlation coefficient between the maxima of the unsigned toroidal field corresponding to each cycle at the base of convection zone (r = 0.7 R⊙) and the observed maxima of the sunspot number for simulations with different values of the pumping (left panel), and the turbulent diffusivity (right panel) in the convection zone. The asterisk represents the actual numerical experiments which were performed. The square indicates the result for the reference case. |
The evolution of the unsigned toroidal field is shown in the lower panel of Fig. 4, taking proper account of the overlapping cycles at the base of the convection zone, at r = 0.7 R⊙ and averaged over latitudes −45° < λ < 45°. The maxima of the modeled activity levels are clearly related to the observed amplitude of the cycle, with the correlation coefficient calculated using cycles 15 to 21 being r = 0.93.
4. Effect of the pumping and diffusivity parameters in the bulk of the convection zone
The dynamics in the bulk of the convection zone and near the tachocline are much less well constrained by observations than are the near-surface dynamics. The strength of the pumping in the bulk of the convection zone (γcz) and the turbulent diffusivity in the convection zone (ηcz) are therefore free parameters of the model. The evolution of the surface field is largely independent of these choices, but the flux at the base of the convection zone is expected to be affected. To investigate this we performed simulations for which we varied these two parameters, one at a time. The effect on the correlation between the toroidal field at the base of the convection zone and the level of activity is shown in Fig. 5. The results show that the good correlation between the toroidal field at the base of the convection zone and the activity maxima is robust for convective pumping of 2 to 10 m/s and for diffusivities in the bulk of the convection zone of 20 km2 s-1 or less.
5. Conclusions
Our aim was to investigate whether the Babcock-Leighton model, with sources and parameters based on observations, is consistent with the correlations implied by the observations. We used a flux transport dynamo model with pumping and a poloidal source term based on the historical record of sunspot groups’ areas, locations, and tilt angles to study solar cycles 15 to 21, after starting the simulations during cycle 11.
Following Cameron et al. (2012), the inclusion of sufficient radial pumping of the magnetic field means that the surface field from the flux transport dynamo model, in particular the polar fields, is similar to the surface flux transport results in CJSS10. In the present work, we have also been able to study the evolution of the subsurface field, including the toroidal field at the base of the convection zone.
We found that the evolution corresponds to a particularly simple Babcock-Leighton type scenario: in each cycle the poloidal field from the surface is advected and diffused downwards so that by the end of a cycle, it completely replaces the previous poloidal flux. The toroidal field then results from the winding up of this poloidal field. The memory of the toroidal field is only one cycle (Karak & Nandy 2012). The decay time of the poloidal field is, in contrast about 4000 years. The equatorward propagation of the activity belt is reproduced. We find that the simulated toroidal flux at the base of the convection zone is highly correlated with the observed sunspot area observed during the same cycle, consistent with its being the source of the emerging sunspots. The simulated minimum of the polar fields between cycles n − 1 and n are highly correlated with the maximum activity of cycle n. The Babcock-Leighton model thus appears to be consistent with and able to explain the observationally inferred correlations.
Acknowledgments
We are grateful to the referee for very helpful comments on the paper. We gratefully acknowledge numerous fruitful discussions with Manfred Schüssler. J.J. acknowledges the financial support from the National Natural Science Foundations of China (11173033, 11178005, 11125314, 11221063, 41174153, 11125314, 2011CB811401) and the Knowledge Innovation Program of the CAS (KJCX2-EW-T07).
References
- Babcock, H. W. 1961, ApJ, 133, 572 [Google Scholar]
- Baumann, I., Schmitt, D., Schüssler, M., & Solanki, S. K. 2004, A&A, 426, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caligari, P., Moreno-Insertis, F., & Schüssler, M. 1995, ApJ, 441, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R., & Schüssler, M. 2007, ApJ, 659, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R., & Schüssler, M. 2008, ApJ, 685, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R., Vögler, A., & Schüssler, M. 2011, A&A, 533, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R. H. 2011, ASI Conf. Ser., 2, 143 [Google Scholar]
- Cameron, R. H., & Schüssler, M. 2012, A&A, 548, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R. H., Jiang, J., Schmitt, D., & Schüssler, M. 2010, ApJ, 719, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R. H., Schmitt, D., Jiang, J., & Işık, E. 2012, A&A, 542, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, P. 2001, Sol. Phys., 199, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 2010, Liv. Rev. Sol. Phys., 7, 3 [Google Scholar]
- Charbonneau, P., & Dikpati, M. 2000, ApJ, 543, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, P., Nandy, D., & Choudhuri, A. R. 2004, A&A, 427, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choudhuri, A. R., & Dikpati, M. 1999, Sol. Phys., 184, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Choudhuri, A. R., Schussler, M., & Dikpati, M. 1995, A&A, 303, L29 [NASA ADS] [Google Scholar]
- Choudhuri, A. R., Chatterjee, P., & Jiang, J. 2007, Phys. Rev. Lett., 98, 131103 [Google Scholar]
- Dasi-Espuig, M., Solanki, S. K., Krivova, N. A., Cameron, R., & Peñuela, T. 2010, A&A, 518, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dikpati, M., & Charbonneau, P. 1999, ApJ, 518, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Dikpati, M., & Gilman, P. A. 2006, ApJ, 649, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Do Cao, O., & Brun, A. S. 2011, Astron. Nachr., 332, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Durney, B. R. 1997, ApJ, 486, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Durney, B. R. 2000, Sol. Phys., 196, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Ferriz-Mas, A., & Schüssler, M. 1995, Geophys. and Astrophys. Fluid Dynamics, 81, 233 [Google Scholar]
- Guerrero, G. A., & Muñoz, J. D. 2004, MNRAS, 350, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Guerrero, G., & de Gouveia Dal Pino, E. M. 2007, A&A, 464, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guerrero, G., & de Gouveia Dal Pino, E. M. 2008, A&A, 485, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, R. F. 1991, Sol. Phys., 136, 251 [Google Scholar]
- Howard, R., Gilman, P. I., & Gilman, P. A. 1984, ApJ, 283, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Chatterjee, P., & Choudhuri, A. R. 2007, MNRAS, 381, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Cameron, R., Schmitt, D., & Schüssler, M. 2010, ApJ, 709, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2011, A&A, 528, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jouve, L., Brun, A. S., Arlt, R., et al. 2008, A&A, 483, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Käpylä, P. J., Korpi, M. J., & Tuominen, I. 2006, Astron. Nachr., 327, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Karak, B. B. 2010, ApJ, 724, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Karak, B. B., & Choudhuri, A. R. 2011, MNRAS, 410, 1503 [NASA ADS] [Google Scholar]
- Karak, B. B., & Nandy, D. 2012, ApJ, 761, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L. L., & Olemskoy, S. V. 2011, Astron. Lett., 37, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L. L., & Olemskoy, S. V. 2012, Sol. Phys., 276, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Leighton, R. B. 1964, ApJ, 140, 1547 [Google Scholar]
- Lockwood, M. 2003, J. Geophys. Res., 108, 1128 [Google Scholar]
- Mackay, D., & Yeates, A. 2012, Liv. Rev. Sol. Phys., 9, 6 [Google Scholar]
- Mackay, D. H., Priest, E. R., & Lockwood, M. 2002, Sol. Phys., 209, 287 [Google Scholar]
- Makarov, V. I., Tlatov, A. G., & Sivaraman, K. R. 2003, Sol. Phys., 214, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Jaramillo, A., Nandy, D., & Martens, P. C. H. 2009, ApJ, 698, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Jaramillo, A., Nandy, D., Martens, P. C. H., & Yeates, A. R. 2010, ApJ, 720, L20 [CrossRef] [Google Scholar]
- Nandy, D., & Choudhuri, A. R. 2002, Science, 296, 1671 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nandy, D., Muñoz-Jaramillo, A., & Martens, P. C. H. 2011, Nature, 471, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2006, ApJ, 647, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Schatten, K. H., Scherrer, P. H., Svalgaard, L., & Wilcox, J. M. 1978, Geophys. Res. Lett., 5, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J. 2001, ApJ, 547, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Zwaan, C. 2000, Solar and Stellar Magnetic Activity (Cambridge University Press) [Google Scholar]
- Sivaraman, K. R., Gupta, S. S., & Howard, R. F. 1993, Sol. Phys., 146, 27 [NASA ADS] [CrossRef] [Google Scholar]
- van Ballegooijen, A. A., & Mackay, D. H. 2007, ApJ, 659, 1713 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., & Sheeley, N. R. 2009, ApJ, 694, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., Nash, A. G., & Sheeley, N. R. 1989, Science, 245, 712 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Yeates, A. R., Nandy, D., & Mackay, D. H. 2008, ApJ, 673, 544 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Source term, S(r,θ,t)sin(θ) at r = R⊙ for the poloidal flux based on the RGO sunspot record. The factor of sinθ is included to make the figure proportional to the amount of signed flux. The red and blue colors indicate positive and negative signs of A, respectively. Data after 1977 is from the SOON network. |
| In the text | |
 |
Fig. 2 Simulated variation of the magnetic field over cycle 19. The red and blue colors correspond to negative and positive toroidal fields, respectively. The solid (dashed) lines represent anti-clockwise (clockwise) orientated field lines of the poloidal field. The snapshots (A)−(F) cover cycle 19, corresponding to t = 1956, 1958, 1960, 1962, 1964, and 1966, respectively. |
| In the text | |
 |
Fig. 3 Radial component of the surface magnetic field for the reference case. The upper panel shows a time-latitude diagram. The lower panel gives the polar fields, defined as the average radial field strength beyond ± 70° latitude (black curve) and the sunspot numbers (red curve). The vertical line indicates the time until which RGO sunspot group area data are available. The correlation coefficient of the maxima of the polar fields and the subsequent maxima of sunspot number for cycles 15 to 21 is 0.85. |
| In the text | |
 |
Fig. 4 Toroidal field at the base of the convection zone (r = 0.7 R⊙). The upper panel shows the evolution as a function of latitude and time. In the lower panel the average unsigned toroidal flux between ± 45° latitude corresponding to odd and even cycles is shown using dashed and solid curves, respectively. The correlation coefficient between the maxima of the toroidal field at the base of the convection zone and the maxima of the observed sunspot number for cycles 15−21 is 0.93. |
| In the text | |
 |
Fig. 5 Correlation coefficient between the maxima of the unsigned toroidal field corresponding to each cycle at the base of convection zone (r = 0.7 R⊙) and the observed maxima of the sunspot number for simulations with different values of the pumping (left panel), and the turbulent diffusivity (right panel) in the convection zone. The asterisk represents the actual numerical experiments which were performed. The square indicates the result for the reference case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


