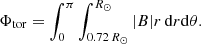| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202348201 | |
| Published online | 03 June 2024 | |
Modeling the effects of starspots on stellar magnetic cycles
1
School of Space and Environment, Beihang University, Beijing, PR China
e-mail: jiejiang@buaa.edu.cn
2
Key Laboratory of Space Environment Monitoring and Information Processing of MIIT, Beijing, PR China
3
Institute of Solar-Terrestrial Physics, Irkutsk, Russia
4
Pulkovo Astronomical Observatory, St. Petersburg, Russia
Received:
9
October
2023
Accepted:
28
February
2024
Context. Observations show that faster rotating stars tend to have stronger magnetic activity and shorter magnetic cycles. The cyclical magnetic activity of the Sun and stars is believed to be driven by the dynamo process. The success of the Babcock-Leighton (BL) dynamo in explaining the solar cycle suggests that starspots could play an important role in stellar magnetic cycles.
Aims. We aim to extend the BL mechanism to solar-mass stars with various rotation rates and explore the effects of emergence properties of starspots in latitudes and tilt angles on stellar magnetic cycles.
Methods. We adopt a kinematic BL-type dynamo model operating in the bulk of the convection zone. The profiles of the large-scale flow fields are from the mean-field hydrodynamical model for various rotators. The BL source term in the model is constructed based on the rotation dependence of starspot emergence; that is, faster rotators have starspots at higher latitudes with larger tilt angles.
Results. Faster rotators have poloidal flux appearing closer to about ±55° latitudes, where the toroidal field generation efficiency is the strongest because of the peak in the strength of the latitudinal differential rotation there. It takes a shorter time for faster rotators to transport the surface poloidal field from their emergence latitude to the ±55° latitudes of efficient Ω-effect, which shortens their magnetic cycles. The faster rotators operate in a more supercritical regime because of a stronger BL α-effect relating to the tilt angles, which leads to stronger saturated magnetic fields and makes the coupling of the poloidal field between two hemispheres more difficult. The magnetic field parity therefore shifts from the hemispherically asymmetric mixed mode to quadrupole, and further to dipole when a star spins down.
Conclusions. The emergence of starspots plays an essential role in the large-scale stellar dynamo.
Key words: dynamo / stars: activity / stars: magnetic field / stars: rotation / starspots
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The solar large-scale magnetic fields show the almost 11 year cyclic variations manifested by the sunspots (Hathaway 2015). Starspots and magnetic cycles are ubiquitous among cool stars (Strassmeier 2009; Boro Saikia et al. 2018). Progress in the study of solar magnetism is leading to advancements in our understanding of stellar activity (Brun et al. 2015).
The cyclical magnetic activity of stars is usually studied through the chromospheric emission; for example, Ca II H & K emission (Wilson 1978) or photospheric brightness variations (e.g., Reinhold et al. 2017; Montet et al. 2017). These studies show a general Prot − Pcyc relation; that is, the magnetic cycle period Pcyc tends to be longer for stars with a longer rotation period Prot (Noyes et al. 1984a). Some studies show that this relation has two branches, one active and one inactive, corresponding to high and low activity, respectively (Saar & Brandenburg 1999; Böhm-Vitense 2007; Wright et al. 2011), while the existence of the active branch is still controversial (Boro Saikia et al. 2018). Past efforts exploring stellar activity also reveal the dependence of magnetic activity amplitude on the rotation period, hereafter referred to as the Prot − Acyc relation. That is, younger and faster rotating stars tend to have higher magnetic activity amplitude Acyc. When rotators are sufficiently fast, magnetic activity amplitude tends to saturate at some level (Hempelmann et al. 1996; Güdel 2004; Wright & Drake 2016; Zhang et al. 2020).
The Prot − Pcyc relation of stellar magnetism provides an important observational test for dynamo models. In kinematic α − Ω mean-field dynamo, the decreasing trend of the cycle period along the rotation period is a general property, because the cycle period is determined by the dynamo number related to the rotation period (Tobias 1998). Over recent decades, the flux transport dynamo (FTD; Wang et al. 1991; Durney 1995; Choudhuri et al. 1995) has been treated as the paradigm in understanding the solar cycle. In the framework of the FTD, the cycle period is controlled by the rate of meridional flow (Dikpati & Charbonneau 1999; Jouve & Brun 2007). If extending the FTD model to stars, the Prot − Pcyc relation requires an increase in meridional flow as the rotation rate increases (Nandy 2004). However, magnetohydrodynamic (MHD) simulations show that the strength of meridional flow decreases as stars rotate faster (Brown et al. 2008; Augustson et al. 2012). Therefore, the faster rotators host longer magnetic cycles (Jouve et al. 2010; Karak et al. 2014a), which is contrary to what is observed. Kitchatinov (2022) suggests that the effective temperature is the most essential parameter in understanding stellar magnetic cycles. Hotter stars sustain shorter cycles and they rotate faster on average. Brun & Browning (2017) introduced muticell meridional flows to reconcile the discrepancy. Do Cao & Brun (2011) considered the effect of magnetic turbulent pumping, and found that the magnetic cycle shortens when the pumping effect becomes stronger with the increase in rotation rate. Pipin & Kosovichev (2016) include the dynamical quenching of magnetic buoyancy and magnetic helicity and Hazra et al. (2019) introduced near-surface pumping, assuming that faster rotators have a stronger BL source term. Both of these latter studies reproduce the relation between rotation period and magnetic cycle close to observations. MHD simulations report a weak relation between the rotation period and magnetic cycle with a negative slope (Warnecke 2018; Strugarek et al. 2017; Brun et al. 2022), while Guerrero et al. (2019) find a trend of increasing magnetic cycle with rotation period under some conditions.
The Prot − Acyc relation is another observational test for dynamo models. Faster rotators tend to form starspots with larger tilt angles, which could explain the Prot − Acyc relation in the framework of the BL mechanism. Sunspots are formed by the buoyant rise of subsurface toroidal flux (Parker 1955). The Coriolis force acts on the rising toroidal flux, leading to tilt angles of sunspot groups (Fan 2021). Starspots are expected to be formed by a similar process to that responsible for sunspots. The Coriolis force increases for faster rotators and could therefore lead to a larger tilt angle (Caligari et al. 1995; Işık et al. 2018). The tilt angles correspond to the strength of the BL source term, and so faster rotators sustain a stronger BL source term. Based on the assumption that faster rotators sustain a stronger BL source term due to larger tilt angles, the Pcyc − Acyc relation was reproduced by Karak et al. (2014a) and Hazra et al. (2019). Furthermore, Kitchatinov & Olemskoy (2015) considered a saturation of the BL mechanism for tilt angles approaching π/2 and reproduced the magnetic activity saturation for very fast rotators. Some MHD simulations have also been carried out to understand the scaling law between stellar magnetic activity and rotation period (Augustson et al. 2019; Brun et al. 2022).
Solar observations show that stronger cycles tend to have smaller tilt angles (Dasi-Espuig et al. 2010; Jiao et al. 2021), which influence the contribution of sunspots to the polar fields. The polar fields at cycle minimum are believed to be the source of the toroidal field of a new cycle, which determines the strength of the subsequent solar cycle (Muñoz-Jaramillo et al. 2013; Cameron & Schüssler 2015; Jiang et al. 2018). Therefore, the cycle-dependent tilt angles of sunspot emergence work as a nonlinear mechanism to modulate the amplitude of the solar cycle, which is called tilt quenching. Observations also show that stronger cycles tend to have sunspot emergence at higher latitudes (Li et al. 2003; Solanki et al. 2008; Jiang et al. 2011). The higher latitudes at which the sunspots emerge, the weaker their contribution to the build up of polar fields (Jiang et al. 2014a; Petrovay et al. 2020). This means that the cycle-dependent latitudes of sunspot emergence are another nonlinear feedback for the solar cycle, referred to as latitude quenching. Systematic studies on both forms of quenching have demonstrated that they play a crucial role in modulating the amplitude of the solar magnetic cycle (Jiang 2020; Karak 2020; Talafha et al. 2022). This raises an interesting question as to how starspot emergence latitudes and tilt angles influence stellar magnetic cycles.
Sunspots appear only at latitudes of lower than about 40°, but for starspots, the emergence latitudes could be distributed over the whole stellar disk (Strassmeier 2009). Observations also show that faster rotators tend to have starspots at higher latitudes and even at polar regions (Vogt & Penrod 1983; Strassmeier et al. 1991). Schuessler & Solanki (1992) were the first authors to propose a potential origin of the polar starspots, positing that they result from a dominance of the Coriolis force in the dynamics of magnetic-flux-tube emergence. Işık et al. (2018) calculated the emergence latitudes and tilt angles of starspots for various rotators, and then applied the surface flux transport model to understand the evolution of the large-scale field at stellar surfaces. These authors found that faster rotators with starspots at higher latitudes reverse the polarity of the polar field in a shorter time, which implies faster rotators have shorter magnetic cycles. This latter work also inspires us to explore the effects of the emergence properties of starspots on stellar magnetic cycles in the BL-type dynamo framework.
Zhang & Jiang (2022) recently developed a new version of the BL-type dynamo model that operates in the bulk of the convection zone rather than in the tachocline. The model establishes a global dipolar field connecting two solar poles. The configuration of the near-surface poloidal field is consistent with observations and differs from most other available dynamo models. The poloidal field is sheared by latitudinal differential rotation and generates a strong toroidal field in the bulk of the convection zone as the source of sunspots. The tachocline is not important in the model of Zhang & Jiang (2022), which is supported by stellar observations and MHD simulations that suggest that the dynamo process is more likely to operate in the bulk of the convection zone (Nelson et al. 2013; Yadav et al. 2015; Wright & Drake 2016).
The aim of the present work is to extend the solar dynamo model of Zhang & Jiang (2022) to stars with solar mass (M⊙) and rotation periods ranging from 10 to 25 days, and to explore the effect of starspot-emergence properties on magnetic cycles, and to further test whether or not the Prot − Pcyc and Prot − Acyc relations can be reproduced when properly considering starspot-emergence properties. On the other hand, our tests of stellar observations can also verify the solar dynamo model. We quantify the dependence of starspot-emergence properties – namely tilt angles and latitudes – on the rotation rate of stars based on observations.
The paper is organized as follows. The BL-type dynamo model is described in Sect. 2. We determine the critical dynamo number in Sect. 3.1.1. The effect of the emergence latitude of starspots on the magnetic cycle is explored in the linear regime in Sect. 3.1.2. The Pcyc − Acyc relation is studied in the nonlinear regime in Sect. 3.2. We summarize our results in Sect. 4.
2. Model
In this study, we adopt the kinematic dynamo model developed by Zhang & Jiang (2022), who deal with the evolution of axisymmetric large-scale magnetic field, ![$ \boldsymbol{B}(r,\theta,t)=B(r,\theta,t) \hat{\boldsymbol{e}}_\phi+ \nabla \times \left[A(r,\theta,t)\hat{\boldsymbol{e}}_\phi\right] $](/articles/aa/full_html/2024/06/aa48201-23/aa48201-23-eq1.gif) , with prescribed flow profiles in the standard spherical polar coordinates (r, θ, ϕ). The dynamo equations are expressed as
, with prescribed flow profiles in the standard spherical polar coordinates (r, θ, ϕ). The dynamo equations are expressed as
where η and γr represent the turbulent diffusivity and the radial pumping, respectively. Differential rotation and meridional flow are represented by Ω(r, θ) and 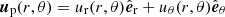 , respectively. The parameters are presented in the following subsections.
, respectively. The parameters are presented in the following subsections.
2.1. Differential rotation and meridional flow
The large-scale flows in 1 M⊙ stars rotating with different rates are specified with the method developed by Kitchatinov & Rüdiger (1999). The mean-field model based on this method (Kitchatinov & Olemskoy 2011, 2012) predicts the dependence of differential rotation on the spectral type and rotation rate in agreement with observations by Barnes et al. (2005) and Balona & Abedigamba (2016). Here, we applied the version of the differential rotation model by Kitchatinov & Nepomnyashchikh (2017a), which is adapted for use in dynamo simulations. The results have been adopted to understand properties of the stellar magnetic field (e.g., Hazra et al. 2014; Kitchatinov 2022). Observations indicate that faster rotators tend to have stronger torsional oscillations (Collier Cameron & Donati 2002) and more irregular stellar cycles (Baliunas et al. 1995; Boro Saikia et al. 2018). We therefore restrict our computations to slowly rotating 1 M⊙ stars with the rotation periods from 10 to 25 days.
Figures 1a and b show the profiles of differential rotation for stars with sidereal rotation periods of 25 and 13 days, respectively. The former value corresponds to the solar case and is close to that suggested by helioseismic results (Schou et al. 1998). With the increase in the rotation rate, the differential rotation changes toward a cylinder-shaped pattern. It is the latitudinal shear in the bulk of the convection zone that winds the poloidal field for the dynamo model we use. Figure 1c shows the latitudinal distribution of the latitudinal shear, 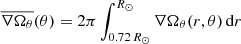 . With the increase in the rotation rate, the strength of latitudinal shear increases slightly, which is consistent with observations (Barnes et al. 2005). Similar to the Sun, all stars have the strongest latitudinal shear at about ±55° latitude, where the generation efficiency of the toroidal field is the strongest and corresponds to the seat of stellar dynamo processes (Zhang & Jiang 2022).
. With the increase in the rotation rate, the strength of latitudinal shear increases slightly, which is consistent with observations (Barnes et al. 2005). Similar to the Sun, all stars have the strongest latitudinal shear at about ±55° latitude, where the generation efficiency of the toroidal field is the strongest and corresponds to the seat of stellar dynamo processes (Zhang & Jiang 2022).
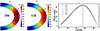 |
Fig. 1. Differential rotations of solar-mass stars. Panels a and b are the profiles of differential rotation for stars with rotation periods of 25 and 13 days, respectively. Panel c shows the latitudinal distribution of the radius-averaged latitudinal shear |
Figures 2a and b show the θ component of the meridional flow, uθ, for stars with rotation periods of 25 and 13 days, respectively. For all rotators, the flow has a single-cell structure in each hemisphere, and is poleward near the surface and equatorward at the bottom of the convection zone. Figure 2c shows the dependence of the equatorward return flow, 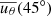 , on the rotation period. The radius-averaged return flow,
, on the rotation period. The radius-averaged return flow, 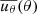 , is defined as
, is defined as 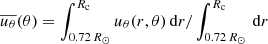 , where Rc is the depth at which the equatorward flow starts for different rotators. The strength of
, where Rc is the depth at which the equatorward flow starts for different rotators. The strength of 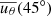 decreases from 3.15 m s−1 to 2.4 m s−1 with the decrease in the rotation period from 25 days to 10 days. This trend is consistent with 3D convective simulations (Brown et al. 2008; Augustson et al. 2012). The slower return flow for faster rotators is the reason why the FTD dynamo models failed to reproduce the observational Prot − Pcyc relation (Karak et al. 2014a).
decreases from 3.15 m s−1 to 2.4 m s−1 with the decrease in the rotation period from 25 days to 10 days. This trend is consistent with 3D convective simulations (Brown et al. 2008; Augustson et al. 2012). The slower return flow for faster rotators is the reason why the FTD dynamo models failed to reproduce the observational Prot − Pcyc relation (Karak et al. 2014a).
 |
Fig. 2. Meridional flows of solar-mass stars. Panels a and b are the latitudinal component of the meridional flow patterns for the stars with rotation periods of 25 and 13 days, respectively. Panel c shows the dependence of the averaged return flow at 45°, |
2.2. Turbulent pumping and diffusivity
A near-surface radial pumping γr is included in our model, the aim being to match the observed large-scale magnetic field evolution at the solar surface (Cameron et al. 2012; Jiang et al. 2013). We adopt its profile as
where rs = 0.9 R⊙ and ds = 0.01 R⊙, making sure that the pumping is confined near the surface and smoothly decreases to zero at 0.88 R⊙. A sufficiently large γ0 near the surface is used simply to prevent the diffusive escape of magnetic flux through the solar surface. Its amplitude and penetration depth are free parameters and have no effect on the cycle period of the dynamo model. Here we set γ0 = 20 m s−1 for all rotators.
Turbulent diffusivity η within the stellar convection zone is still poorly constrained. We assume that the turbulent convection dominates η in the convection zone and gets significantly reduced through the overshot layer. We adopt the following diffusivity profile
where rc = 0.7 R⊙ and dc = 0.03 R⊙ correspond to the center and thickness of the overshot layer. The turbulent diffusivity in the bulk of the convection zone ηcz is taken as 3.7 × 107 m2 s−1, which is closer to the value estimated by the mixing-length theory than most values used by FTD models (see Fig. 1 of Muñoz-Jaramillo et al. 2011). The diffusivity near the surface ηs is taken as the supergranular diffusivity 3.0 × 108 m2 s−1, which is within the range of values derived from observational studies summarized in Table 1 of Schrijver et al. (1996).
2.3. Babcock-Leighton source term
The Babcock-Leighton(BL)-type source term shown in Eq. (1) is the core of the model setup designed to achieve our main objective of exploring the influence of starspot-emergence characteristics on stellar magnetic cycles. It is defined as
The poloidal field is produced from the mean toroidal field 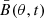 in the bulk of the convection zone from 0.72 R⊙ to 0.88 R⊙; that is,
in the bulk of the convection zone from 0.72 R⊙ to 0.88 R⊙; that is,
where 0.72 R⊙ and 0.88 R⊙ correspond to the inner boundary and penetration depth of the pumping, respectively.
The α-effect term can be written as
The radial dependence of the α-effect aims to constrain the BL process to work near the surface; it is rewritten in the form
where rα = 0.95 R⊙ and dα = 0.01 R⊙.
To explore how the latitudes of starspot emergence influence magnetic cycles, we designed the f(θ) term as
where cos θ reflects the latitude dependence of the tilt angles caused by the Coriolis force and Max[cos θsinnθ, θ ∈ (0, π)] keeps the maximum value of Eq. (9) the same for the various n values. The factor sinnθ reflects the dependence of the probability of toroidal flux emergence on latitude (Cameron & Schüssler 2017). We suppose a linear relation between the rotation period Prot of stars and the n value,
so that it is n = 1 for Prot = 10 days and n = 9.25 for Prot = 25 days. With the decrease in rotation rate, the n value increases and constrains the emergence of starspots to lower latitudes. Figure 3 shows latitudinal variations of Eq. (9) for various rotators. As stars rotate faster, n decreases and the maxima of the curves shift to higher latitudes. Moving from rotation periods of 25 days to 10 days, the latitude of maximum α changes from 18° to 45°.
 |
Fig. 3. Latitude variation of the α profiles determined by Eq. (9) for stars with different rotation periods. |
Note that Eq. (10) is formulated to mimic the observation of faster rotators displaying starspots at higher latitudes, which are nearer to ±55° latitudes. The trend is in agreement with the thin-flux-tube simulations by Işık et al. (2018), who used a surface flux transport model to investigate stellar brightness variations for different levels of magnetic activity and rotation rates. To date, neither observations nor numerical simulations have been able to determine the exact dependence of starspot latitudes on Prot. In Sect. 3.1, we also consider a quadratic relationship between n and Prot, that is n = 9.25(Prot/Psun)2, and independence of n from the rotation period, that is n = 1 in Eq. (10) as a contrast.
Another important parameter of the BL source term is its strength α0, which is dominated by tilt angles of starspots. The dynamo number, α0ΔΩR3/η2, is a key parameter in the dynamo process; it describes the efficiency of magnetic field generation versus decay caused by diffusion. A self-sustained dynamo process occurs when the dynamo number exceeds a critical value. Given a specific profile of diffusivity, differential rotation, and the source term of the poloidal field, the strength of the dynamo number is determined by the free parameter α0 in Eq. (7). This means that a nondecaying dynamo process occurs when α0 is greater than or equal to its critical value αc. In most previous dynamo models, α0 is determined arbitrarily. Kitchatinov & Nepomnyashchikh (2017b, hereafter KN17) suggest that α0 could be constrained based on observations.
KN17 assume that the upper bound Pmax on the rotation period of solar-type stars (van Saders et al. 2016) corresponds to near marginal dynamo excitation. In other words, the faster rotating stars tend to have a stronger α-effect and to operate in a more supercritical regime. For the BL mechanism, α0 is dominated by the tilt angles. The Coriolis force is stronger for faster rotators, leading to a larger tilt angle of starspots and then larger α0. The α0 − αc describes how supercritical the dynamo is. Motivated by KN17, we give α0 for a star with the rotation period Prot based on
where m is a free parameter constraining the amount of supercriticality. We take Pmax as 28 days for the solar-mass stars studied here.
The saturated unsigned toroidal flux within the convection zone is around 1023 Mx for the solar case (Cameron & Schüssler 2015). The flux puts a constraint on the m value, which is taken as m = 0.2. This entails that supercriticality varies from about 20% to 56% for rotators with Prot from 25 to 10 days.
2.4. Initial and boundary conditions
The configuration of large-scale magnetic fields in the Sun and stars can be classified as equatorially symmetric (quadrupolar) and anti-symmetric (dipolar) parity. The latter one is the dominant parity in the Sun, while some observations imply that fast rotators might have dominant quadrupolar fields (Kochukhov 2021). In the present work, we start the simulations with two kinds of seed magnetic fields, whereas the toroidal field is set to be
for dipolar parity, or
for quadrupolar parity. The poloidal field is set to be zero.
The outer boundary condition satisfies the vertical field condition based on the constraint by Cameron et al. (2012). Accordingly, we use ∂(rA)/∂r = 0, B = 0 at r = R⊙. The inner boundary matches a perfect conductor, which means that A = 0, ∂(rB)/∂r = 0 at r = 0.72 R⊙. At the poles, A = B = 0. The computational domain of our model is 0.72 R⊙ ≤ r ≤ R⊙, 0 ≤ θ ≤ π. Note again that our model does not include the tachocline.
Our model is calculated using a code that uses the Crank-Nicolson scheme and an approximate factorization technique (van der Houwen & Sommeijer 2001). The code developed at Beihang University was validated against the open-source Surya developed by A. R. Choudhuri and his colleagues (Chatterjee et al. 2004) and a dynamo benchmark (Jouve et al. 2008).
3. Results
For the onset of dynamo instability, controlling parameters should exceed a certain critical value. The α0 of Eq. (7) is the only variable parameter in our model, because other parameters involved in the dynamo number are given, that is, differential rotation and turbulent diffusivity. In Sect. 3.1, we first present an examination of αc for the dipolar and quadrupolar solutions and show how we analyzed the properties of the different symmetric solutions for different stars. In Sect. 3.2, we then show how we used the constrained α0 given by Eq. (11) to analyze the dynamo behaviors of different stars.
3.1. Linear model
3.1.1. Critical α-values, αc, for dipolar and quadrupolar modes
With the time-independent large-scale flows and α independent of the magnetic field, dynamo Eqs. (1) and (2) are fully linear. Therefore, both A and B have exponential time dependence in the form of eλt, with λ = σ + iω. The real part σ is a growth rate, and the imaginary part ω is an oscillation frequency satisfying 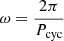 . The solution with zero linear growth rate (σ = 0) is the purely oscillatory one. The corresponding α0 is the critical value denoted αc. Usually, αc is derived as an eigenvalue problem of the linear system (e.g., Jiang & Wang 2006, 2007; Bonanno et al. 2002). Here, we solve the dynamo equations as an initial value problem. With a given initial condition, we try different α0 values. The larger the α0 value is, the faster the growth rate σ is. The αc can be constrained when |σ|< 10−3 as measured by the grow rate of the toroidal field integrated through the convection zone. In the linear system, the parity of fields is determined by the seed initial fields. For example, the seed fields with a pure dipolar parity can only excite a dipole-mode solution. We therefore use initial fields of dipolar (Eq. (12)) and quadrupolar (Eq. (13)) parity to find the critical values
. The solution with zero linear growth rate (σ = 0) is the purely oscillatory one. The corresponding α0 is the critical value denoted αc. Usually, αc is derived as an eigenvalue problem of the linear system (e.g., Jiang & Wang 2006, 2007; Bonanno et al. 2002). Here, we solve the dynamo equations as an initial value problem. With a given initial condition, we try different α0 values. The larger the α0 value is, the faster the growth rate σ is. The αc can be constrained when |σ|< 10−3 as measured by the grow rate of the toroidal field integrated through the convection zone. In the linear system, the parity of fields is determined by the seed initial fields. For example, the seed fields with a pure dipolar parity can only excite a dipole-mode solution. We therefore use initial fields of dipolar (Eq. (12)) and quadrupolar (Eq. (13)) parity to find the critical values 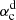 and
and 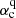 for dipolar and quadrupolar parity, respectively.
for dipolar and quadrupolar parity, respectively.
Figure 4 shows αc as a function of the stellar rotation period. For the Sun (sidereal rotation period of about 25 days), 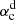 and
and 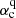 are 0.08 m s−1 and 0.18 m s−1, respectively. The solution of dipolar parity has the smallest αc, which means that the dipolar parity is easier to excite. This is consistent with the observed solar magnetic field, which is dominated by the dipolar field. Incidentally, αc for the kinetic helicity at the base of the solar convection zone is about 10 m s−1 based on the estimation of Charbonneau (2020). Furthermore, Fig. 4 shows that αc increases with the rotation rate. The increase rate of the dipolar solutions (in the solid curve) differs from the quadrupolar one (in the dashed curve). The rotation period of 18 days marks a turning point. The dipolar (quadrupolar) solution prevails when the stellar rotation period is longer (shorter) than 18 days. Larger αc indicates stronger diffusive annihilation of magnetic fields for a given system. In the following subsection, especially Fig. 5, we show that slower rotators have a simpler configuration of the magnetic field corresponding to lower order multipoles, which entails weaker diffusive annihilation (Wang & Sheeley 2002).
are 0.08 m s−1 and 0.18 m s−1, respectively. The solution of dipolar parity has the smallest αc, which means that the dipolar parity is easier to excite. This is consistent with the observed solar magnetic field, which is dominated by the dipolar field. Incidentally, αc for the kinetic helicity at the base of the solar convection zone is about 10 m s−1 based on the estimation of Charbonneau (2020). Furthermore, Fig. 4 shows that αc increases with the rotation rate. The increase rate of the dipolar solutions (in the solid curve) differs from the quadrupolar one (in the dashed curve). The rotation period of 18 days marks a turning point. The dipolar (quadrupolar) solution prevails when the stellar rotation period is longer (shorter) than 18 days. Larger αc indicates stronger diffusive annihilation of magnetic fields for a given system. In the following subsection, especially Fig. 5, we show that slower rotators have a simpler configuration of the magnetic field corresponding to lower order multipoles, which entails weaker diffusive annihilation (Wang & Sheeley 2002).
 |
Fig. 4. Critical α-value, αc, as a function of stellar rotation period (Prot). The solid (dashed) curve represents the dipolar (quadrupolar) parity solution. |
 |
Fig. 5. Snapshots of the magnetic field evolution during the interval of one-third of the magnetic cycle Pcyc/3. The first (third) row represents a rotation period of 10 days with dipolar (quadrupolar) fields. The second (forth) row represents a rotation period of 25 days with dipolar (quadrupolar) fields. The strength of magnetic field is arbitrary in a linear regime, and is normalized to a maximum of 1 here. The region in red (blue) represents toroidal fields and inward (outward). The solid (dashed) lines represent the poloidal field clockwise (anticlockwise). |
3.1.2. Prot–Pcyc relation and parity property
Figure 6 gives the relation between the rotation period and the magnetic cycle near marginal dynamo excitation. The solid (dashed) curve represents the dipolar (quadrupolar) solutions, both of which show that the magnetic cycle generally increases with the rotation period.
 |
Fig. 6. Relation between rotation period (Prot) and magnetic cycle (Pcyc). The solid (dashed) curve represents the dipolar (quadrupolar) parity solution. |
To understand what dominates the magnetic cycles in our model, we investigated the dependence of Pcyc on two parameters, the average speed of return meridional flow 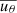 and the critical number αc. We find that
and the critical number αc. We find that 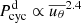 and
and 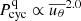 . When the meridional flow is faster, the magnetic cycle is longer. This indicates that our model is different from the FTD models, in which the relation between Pcyc and
. When the meridional flow is faster, the magnetic cycle is longer. This indicates that our model is different from the FTD models, in which the relation between Pcyc and 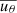 obeys
obeys 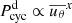 , where x = −0.89 as given by Dikpati & Charbonneau (1999) and x = −0.696 as given by Karak (2010). On the other hand, our findings suggest that
, where x = −0.89 as given by Dikpati & Charbonneau (1999) and x = −0.696 as given by Karak (2010). On the other hand, our findings suggest that 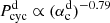 and
and 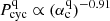 . The magnetic cycle decreases with αc and therefore with the dynamo number. Faster rotators have a dynamo process of higher efficiency, and then sustain a shorter magnetic cycle. In all simulations, we keep the pumping term the same. In models with turbulent pumping through the whole convection zone, the flux transport by pumping influences the cycle period (Guerrero & de Gouveia Dal Pino 2008; Hazra & Nandy 2016). The near-surface pumping introduced in our model only makes the surface part of the dynamo process consistent with observations (Cameron et al. 2012; Jiang et al. 2013); it does not affect the cycle period.
. The magnetic cycle decreases with αc and therefore with the dynamo number. Faster rotators have a dynamo process of higher efficiency, and then sustain a shorter magnetic cycle. In all simulations, we keep the pumping term the same. In models with turbulent pumping through the whole convection zone, the flux transport by pumping influences the cycle period (Guerrero & de Gouveia Dal Pino 2008; Hazra & Nandy 2016). The near-surface pumping introduced in our model only makes the surface part of the dynamo process consistent with observations (Cameron et al. 2012; Jiang et al. 2013); it does not affect the cycle period.
To further explore why faster rotators have a shorter magnetic cycle period, we plot the time evolution of dipolar and quadrupolar magnetic fields for Prot = 10 days in the first and third rows of Fig. 5, respectively. Figure 5a shows that the poloidal flux relating to starspot emergence first appears around ±55° latitudes, where the latitudinal shear is the strongest. Therefore, the newly generated poloidal flux could be sheared efficiently, generating the toroidal field for the subsequent cycle. The quick production of the toroidal field at high latitudes can be seen from Figs. 5b and c. Then, the toroidal field gives rise to the poloidal field, as illustrated by the dashed poloidal magnetic field lines in Fig. 5d. Therefore, a new magnetic cycle starts. The subsequent evolution of the poloidal field reverses the poloidal flux system of the old cycle. High-latitude starspot emergence shortens the dynamo process and therefore the magnetic cycle.
As a comparison, we show the corresponding results of the solar case with Prot = 25 days in the second row of Fig. 5. Figure 5e shows that the newly generated poloidal flux at the surface first appears around ±35° latitudes, which results from the setup of n = 9.25 in Eq. (9) to mimic the observation that sunspot emergence of each new cycle starts from about ±35°. The poloidal flux is then transported poleward, equatorward, and inward simultaneously. The surface turbulent diffusion leads to equatorward migration, so that the net flux of one polarity resulting from the tilt angle diffuses across the equator. Also, this helps to finally establish the global dipolar field as shown in Fig. 5g. The poleward meridional flow, along with the turbulent poleward diffusion, transports the net flux of the other polarity to higher and higher latitudes. After a time interval Δt1, the poloidal field is transported to around the ±55° latitudes, where the latitudinal shear is the strongest, and the poloidal field is transported to a deeper depth by the inward turbulent diffusion as well. This is how the toroidal field of a new cycle first appears around ±55° (see Fig. 5f). These toroidal fields could correspond to the ephemeral regions observed in the Sun (Zhang & Jiang 2022). The lower latitudes have a weaker latitudinal rotational shear, and therefore it takes more time to wind up the poloidal field to generate a sufficiently strong toroidal field for sunspot emergence of a new cycle. During the wind-up process, the newly generated weak toroidal field is transported to lower latitudes due to the effect of the equatorward return flows, which again requires more time to be wound up to generate a sufficiently strong toroidal field. So that the toroidal field of the new cycle is gradually built up at the lower latitudes as demonstrated by Figs. 5f–h. We denote the time delay caused by the latitude dependence of the latitudinal shear Δt2. Comparing with the case of Prot = 10 days, it takes more time, Δt1 + Δt2, to complete a dynamo loop for the case of Prot = 25 days, and therefore it has a longer cycle period.
In summary, the emergence latitude of starspots plays a crucial role in creating the observed relation between Prot and Pcyc. Faster rotators have starspots in closer proximity to the ±55° latitudes, where latitudinal differential rotation is the strongest and therefore toroidal field generation efficiency is the highest. The strongest latitudinal differential rotation around the ±55° latitudes has been confirmed on the Sun with helioseismological analysis. Slower rotators with starspots at lower latitudes require extra time to transport and wind up the poloidal flux, resulting in longer cycle periods. As long as the faster rotators have starspots located closer to latitudes of ±55°, the observed Prot − Pcyc relation is expected to be reproduced. To verify this deduction, we utilize the equation n = 9.25(Prot/Psun)2 to replace Eq. (10). As Prot ranges from 25 days to 10 days, the latitude of maximum α changes from 18° to 40°. The black curves in Fig. 7 indicate the simulated relation between Prot and Pcyc for dipolar (solid curve) and quadrupolar (dashed curve) solutions. The two solutions show similar results to those in Fig. 6. On the other hand, the blue curves in Fig. 7 show the results for n = 1 in Eq. (10), independent of Prot. There is a slight increase in Pcyc with the increase in Prot. This increase is too small to account for the observed property and is caused by variations in the meridional flow. Slow rotators have a greater return flow that can transport more toroidal flux towards lower latitudes. This leads to a decrease in the latitude of flux emergence and further a slight increase in the cycle period.
 |
Fig. 7. Relation between rotation period (Prot) and magnetic cycle (Pcyc) for cases of n = 1 (blue curve) and n = 9.25(prot/psun)2 (black curve). The solid (dashed) curve represents the dipolar (quadrupolar) parity solution. |
Figures 4 and 6 show that for fast rotators (Prot < 18 days), the dipolar and quadrupolar modes have similar cycle periods. Also, the quadrupolar mode has a smaller αc, and is therefore easier to excite. For slow rotators (Prot ≥ 18 days), the dipolar mode has the longer cycle period and is easier to excite than the quadrupolar mode. The time evolution of the quadrupolar field for the cases of Prot = 10 days and Prot = 25 days is shown in the third and the fourth rows of Fig. 5, respectively. For faster rotators, such as the case where Prot = 10 days, the surface poloidal field concentrates around mid to high latitudes. Most equatorward poloidal flux is canceled by the newly generated flux system of a new cycle, and the same is true for the toroidal flux. Therefore, the whole dynamo process operates locally and there is little coupling of magnetic fields between two hemispheres. The degree of coupling between the poloidal fields of the two hemispheres determines the parity dominating the dynamo process (Chatterjee et al. 2004; Hotta & Yokoyama 2010). For slower rotators, as in the case where Prot = 25 days, there is an across-equator cancelation of the toroidal field for the dipolar mode. These cancelations mean that a longer time is required for the poloidal flux generation of the new cycle to reverse that of the old cycle. The global dipolar mode has the slowest decay in the absence of sources (Cameron et al. 2010), and therefore has a smaller αc than the quadrupolar mode.
3.2. Prot–Acyc and Prot–Pcyc relations in the nonlinear regime
We investigated the dynamo process in the linear regime and found a dominant role of starspot-emergence latitude in determining the magnetic cycle. To explore the relation between the rotation period of a star Prot and the amplitude of its stellar activity Acyc, the dynamo model working in the nonlinear regime is required. We adopt the same algebraic quenching term as that in Zhang & Jiang (2022) as the nonlinear amplitude-limitation mechanism here. The initial condition can be any arbitrary linear combination of the dipolar and quadrupolar field presented by Eqs. (12) and (13), which do not affect the final magnetic field evolution. The strength of the BL source term α0 is prescribed by Eq. (11) depending on both αc and Prot, where αc is set to be the smaller one between 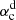 and
and 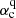 . Other ingredients of the dynamo model are the same as those in the linear regime.
. Other ingredients of the dynamo model are the same as those in the linear regime.
In a dynamo model using algebraic quenching, the saturated magnetic field depends on the value α0 − αc. In this work, we adopt the hypothesis from KN17 to determine α0 based on αc and Prot. Therefore, an increase in magnetic activity amplitude Acyc with rotation rate Prot is expected, which is demonstrated by Fig. 8. Here, magnetic activity amplitude Acyc is measured by cycle-averaged unsigned subsurface toroidal flux, Φtor,
 |
Fig. 8. Relation between rotation period (Prot) and magnetic activity amplitude (Acyc). The activity amplitude is measured by Φtor. Red dots, blue forks, and black inverted triangles represent the saturated magnetic fields with a dipolar, quadrupolar, and mixed parity, respectively. |
For the case of Prot = 25 days, Φtor is around 1023 Mx, which is consistent with observations (Cameron & Schüssler 2015). In contrast, Hazra et al. (2019) show a dip in their Prot − Acyc relation around Prot = 15 days. The dip results from the different ways to deal with the strength of the BL source term α0. These latter authors did not estimate αc for various rotators, and so the value of α0 − αc is not consistent with the expected trend of monotonic increase with the decrease in Prot based on gyrochronology.
Figure 9 shows the Prot − Pcyc relation in both the linear and nonlinear regimes. The magnetic cycles of the nonlinear solutions are slightly longer than those of the linear critical solutions, because algebraic quenching weakens the efficient dynamo number to its critical number as the toroidal field increases (Noyes et al. 1984b; Tobias 1998). We fit the simulated Prot − Pcyc relation in the nonlinear regime and obtain 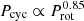 , which is close to the observed inactive branch. As demonstrated in the previous subsection, the rotation-dependent emergence latitude of starspots plays an essential role in our model to reproduce the Prot − Pcyc relation, while Hazra et al. (2019) suggested that different profiles of the BL source term have no effect on the Prot − Pcyc relation. The discrepancy here is caused by the difference in the dynamo models used. For Hazra et al. (2019), the toroidal field is mainly generated by the radial shear in the tachocline, which has the strongest value near the poles. Therefore, although Hazra et al. (2019) adopted two profiles of the BL source term, the surface poloidal field distributions are similar for the two cases they used because the strong toroidal field near the poles dominates the surface poloidal field distributions.
, which is close to the observed inactive branch. As demonstrated in the previous subsection, the rotation-dependent emergence latitude of starspots plays an essential role in our model to reproduce the Prot − Pcyc relation, while Hazra et al. (2019) suggested that different profiles of the BL source term have no effect on the Prot − Pcyc relation. The discrepancy here is caused by the difference in the dynamo models used. For Hazra et al. (2019), the toroidal field is mainly generated by the radial shear in the tachocline, which has the strongest value near the poles. Therefore, although Hazra et al. (2019) adopted two profiles of the BL source term, the surface poloidal field distributions are similar for the two cases they used because the strong toroidal field near the poles dominates the surface poloidal field distributions.
 |
Fig. 9. Relation between rotation period (Prot) and magnetic cycle (Pcyc). The solid and dashed lines represent the solution operating in the nonlinear regime and linear regime, respectively. |
Figure 4 shows that 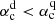 for the slow rotators with Prot > 18 days and
for the slow rotators with Prot > 18 days and 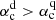 for the fast rotators with Prot < 18 days. These indicate that in the weakly nonlinear regime, slowly (fast-) rotating stars host dipolar (quadrupolar) global fields. For the case of Prot = 10 days, α0 is 56% above the critical value according to Eq. (11). The global fields host a mixed parity because the strong supercriticality could lead to the appearance of hemispherically asymmetric mixed-mode field (Jennings & Weiss 1991). Figure 10 shows the time-latitude diagram of subsurface toroidal flux (top panels) and surface radial field (bottom panels) for stars with rotation periods of 10, 15, and 25 days. For the case of Prot = 25 days, Figs. 10e and f clearly show the properties of the solar cycle, such as the dipolar field, regular polar field reversals approximately every 11 years, and latitudinal migration of the toroidal field. With the decrease in the rotation period from 25 days to 15 days, the surface poloidal field appears at higher latitudes. The magnetic cycle period becomes shorter, activity amplitude is stronger, and the global field shifts to the quadrupolar parity. For the case of Prot = 10 days, Figs. 10a and b show the mixed-mode solution. Besides the increase in the toroidal flux with the increase in the rotation rate, the amplitude of the polar field also increases with the rotation rate. The trend is consistent with the surface flux transport results given by Schrijver & Title (2001) and Işık et al. (2018). The polar field of several thousand Gauss could be responsible for the polar starspots in fast rotators.
for the fast rotators with Prot < 18 days. These indicate that in the weakly nonlinear regime, slowly (fast-) rotating stars host dipolar (quadrupolar) global fields. For the case of Prot = 10 days, α0 is 56% above the critical value according to Eq. (11). The global fields host a mixed parity because the strong supercriticality could lead to the appearance of hemispherically asymmetric mixed-mode field (Jennings & Weiss 1991). Figure 10 shows the time-latitude diagram of subsurface toroidal flux (top panels) and surface radial field (bottom panels) for stars with rotation periods of 10, 15, and 25 days. For the case of Prot = 25 days, Figs. 10e and f clearly show the properties of the solar cycle, such as the dipolar field, regular polar field reversals approximately every 11 years, and latitudinal migration of the toroidal field. With the decrease in the rotation period from 25 days to 15 days, the surface poloidal field appears at higher latitudes. The magnetic cycle period becomes shorter, activity amplitude is stronger, and the global field shifts to the quadrupolar parity. For the case of Prot = 10 days, Figs. 10a and b show the mixed-mode solution. Besides the increase in the toroidal flux with the increase in the rotation rate, the amplitude of the polar field also increases with the rotation rate. The trend is consistent with the surface flux transport results given by Schrijver & Title (2001) and Işık et al. (2018). The polar field of several thousand Gauss could be responsible for the polar starspots in fast rotators.
 |
Fig. 10. Time–latitude diagrams of subsurface toroidal flux (top) and surface radial field (bottom) for stars with rotation periods of 10, 15, and 25 days. |
4. Conclusion and discussion
We extended the BL mechanism to solar-mass stars and explored the effect of emergence properties of starspots on stellar magnetic cycles. The rotation-dependent emergence latitude and tilt angle of starspots are introduced in a BL-type dynamo working in the bulk of the convection zone developed by Zhang & Jiang (2022). Importantly, the model is able to account for the observed Prot − Pcyc and Prot − Acyc relations regarding stellar magnetic activity.
We are not the first to extend the BL mechanism developed based on solar observations to understand stellar magnetic cycles. Effort has previously been made in this direction (e.g., Jouve et al. 2010; Karak et al. 2014a; Kitchatinov & Olemskoy 2015; Vashishth et al. 2023). The past efforts mainly emphasized that the poloidal field results from the tilt angle of starspots and is generated near the stellar surface. The rotation-dependent tilt angle of starspots was considered by Hazra et al. (2019) and Kitchatinov (2022). To the best of our knowledge, we are the first to include the rotation-dependent emergence latitude in the BL mechanism to understand stellar cycles. We also demonstrate that without the rotation-dependent emergence latitude, the resulting Prot − Pcyc relation is inconsistent with the observation. The rotation-dependent emergence latitude of starspots is a property presented by observations of stellar magnetic activity. On the other hand, an essential role of the cycle-dependent emergence latitude of sunspots in modulating solar cycles (i.e., latitudinal quenching) was recently recognized (Jiang 2020; Karak 2020). This progress in our understanding of the solar cycle naturally extends to solar-type stars.
Also, some recent studies focused on the effects of the latitudinal distribution and tilt of starspots on stellar magnetic activity, such as brightness variations (Işık et al. 2018; Nèmec et al. 2023) and astrometric jitter (Sowmya et al. 2021), based on surface flux transport models (Baumann et al. 2004; Jiang et al. 2014b). The flux emergence properties in latitude and tilt are prescribed by a separate model. These studies assume that different rotators have the same cycle period as the solar magnetic cycle period – that is, 11 years. The observed Prot − Pcyc relation was not included.
In our BL-type dynamo model, the emergence latitudes of starspots play a crucial role in reproducing the Prot − Pcyc relation. Faster rotators have flux emergence closer to ±55° latitudes, where the latitudinal differential rotation and the toroidal field generation efficiency are the strongest. This entails a shorter cycle period. Slower rotators have flux emergence at lower latitudes. It takes some time for the surface poleward meridional flow and turbulent diffusion to transport the emergent poloidal field to around ±55° latitudes. The poloidal flux is transported inwards and equatorward simultaneously. It takes further time for the interior poloidal field at lower latitudes to be wound up to generate a sufficiently strong toroidal field because the lower latitudes have a weaker latitudinal shear. The extra time necessitated by the surface flux transport and the latitude dependence of the latitudinal shear in the interior leads to the longer cycle period Pcyc for slower rotators. There are no strict constraints on the relationship between the emergence latitude and rotation. As long as faster rotators have starspots closer to the ±55° latitudes, the observed Prot − Pcyc relation can be reproduced. Without the rotation dependence of the starspot-emergence latitudes, that is n = 1 in Eq. (10), the resulting Prot − Pcyc relation is inconsistent with the observed one. The latitude dependence of the latitudinal shear also contributes significantly to the equatorward migration of the toroidal field, which leads to the so-called butterfly diagram (Zhang et al. 2022).
The aforementioned explanations for the observed Prot − Pcyc relation based on our BL-type dynamo model distinguish our model developed by Zhang & Jiang (2022) from the flux transport dynamo models of Karak et al. (2014b), in which the equatorward return flow dominates the cycle period and the equatorward migration of the toroidal field. We will analyze the detailed physical ingredients of Zhang & Jiang (2022) accounting for the cycle period and butterfly diagram in a forthcoming paper.
In our BL-type dynamo models, the 55° latitude is regarded as the seat of the stellar dynamo; it is also key to understanding the Prot − Pcyc relation. The essential role of 55° latitude in our dynamo model results from the fact that the toroidal field is generated in the bulk of the convection zone by the latitudinal shear, rather than being generated in the tachocline, as is widely assumed. In the bulk of the convection zone, the 55° latitude has the strongest latitudinal shear. Although few dynamo models emphasize 55° latitude, the importance of 55° latitude in solar magnetism has been addressed by McIntosh et al. (2014, 2021) based on a wide variety of solar observations. The success of our model in reproducing the Prot − Pcyc relation of stellar activity adds a new piece of evidence supporting the important role of 55° latitude in stellar magnetism and consequently the idea that the stellar dynamo works in the bulk of the convection zone.
Being different from the Prot − Pcyc relation, the Prot − Acyc relation was not difficult to reproduce. For example, Karak et al. (2014a) and Kitchatinov & Olemskoy (2015) explained the relation by taking into account the rotation-dependent tilt angle of starspots in their dynamos. Inspired by KN17 and observations relevant to gyrochronology (Rengarajan 1984; van Saders et al. 2016), we assume that faster rotating stars operate in a more supercritical regime. The value α0 − αc, describing how supercritical the dynamo is, is larger for faster rotators. The critical value of the BL source term, αc, which corresponds to the marginal dynamo excitation, is calculated based on the linear models. The larger α0 − αc for faster rotators leads to a stronger saturated magnetic field, which explains the Prot − Acyc relation in the nonlinear regime. The large supercriticality corresponding to the strong nonlinearity for very fast rotators, for example with Prot = 10 days, could lead to fields with mixed parity. Higher latitude starspots for faster rotators make the coupling of poloidal flux between the two hemispheres more difficult, meaning that the dominated parity for faster rotators could be quadrupolar shifted from the dipolar parity for slower rotators. Hazra et al. (2019) already reported a change in magnetic field parity from dipolar to quadrupolar in rapidly rotating stars. Future stellar magnetic field measurements will help to verify the shift in magnetic field parity from mixed to quadrupolar, and further to dipolar when a star spins down with age because of the angular momentum loss.
Acknowledgments
Z.Z. and J.J. acknowledge financial support from the National Natural Science Foundation of China through grant Nos. 12173005 and 12350004, and the National Key R & D Program of China No. 2022YFF0503800. L.K. acknowledges financial support from the Ministry of Science and High Education of the Russian Federation.
References
- Augustson, K. C., Brown, B. P., Brun, A. S., Miesch, M. S., & Toomre, J. 2012, ApJ, 756, 169 [Google Scholar]
- Augustson, K. C., Brun, A. S., & Toomre, J. 2019, ApJ, 876, 83 [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [Google Scholar]
- Balona, L. A., & Abedigamba, O. P. 2016, MNRAS, 461, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. R., Collier Cameron, A., Donati, J. F., et al. 2005, MNRAS, 357, L1 [Google Scholar]
- Baumann, I., Schmitt, D., Schüssler, M., & Solanki, S. K. 2004, A&A, 426, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm-Vitense, E. 2007, ApJ, 657, 486 [CrossRef] [Google Scholar]
- Bonanno, A., Elstner, D., Rüdiger, G., & Belvedere, G. 2002, A&A, 390, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boro Saikia, S., Marvin, C. J., Jeffers, S. V., et al. 2018, A&A, 616, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, B. P., Browning, M. K., Brun, A. S., Miesch, M. S., & Toomre, J. 2008, ApJ, 689, 1354 [CrossRef] [Google Scholar]
- Brun, A. S., & Browning, M. K. 2017, Liv. Rev. Sol. Phys., 14, 4 [Google Scholar]
- Brun, A. S., García, R. A., Houdek, G., Nandy, D., & Pinsonneault, M. 2015, Space Sci. Rev., 196, 303 [Google Scholar]
- Brun, A. S., Strugarek, A., Noraz, Q., et al. 2022, ApJ, 926, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Caligari, P., Moreno-Insertis, F., & Schussler, M. 1995, ApJ, 441, 886 [Google Scholar]
- Cameron, R., & Schüssler, M. 2015, Science, 347, 1333 [Google Scholar]
- Cameron, R. H., & Schüssler, M. 2017, A&A, 599, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cameron, R. H., Jiang, J., Schmitt, D., & Schüssler, M. 2010, ApJ, 719, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, R. H., Schmitt, D., Jiang, J., & Işık, E. 2012, A&A, 542, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charbonneau, P. 2020, Liv. Rev. Sol. Phys., 17, 4 [Google Scholar]
- Chatterjee, P., Nandy, D., & Choudhuri, A. R. 2004, A&A, 427, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choudhuri, A. R., Schussler, M., & Dikpati, M. 1995, A&A, 303, L29 [NASA ADS] [Google Scholar]
- Collier Cameron, A., & Donati, J. F. 2002, MNRAS, 329, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Dasi-Espuig, M., Solanki, S. K., Krivova, N. A., Cameron, R., & Peñuela, T. 2010, A&A, 518, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dikpati, M., & Charbonneau, P. 1999, ApJ, 518, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Do Cao, O., & Brun, A. S. 2011, Astron. Nachr., 332, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Durney, B. R. 1995, Sol. Phys., 160, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y. 2021, Liv. Rev. Sol. Phys., 18, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Güdel, M. 2004, A&ARv, 12, 71 [CrossRef] [Google Scholar]
- Guerrero, G., & de Gouveia Dal Pino, E. M. 2008, A&A, 485, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guerrero, G., Zaire, B., Smolarkiewicz, P. K., et al. 2019, ApJ, 880, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H. 2015, Liv. Rev. Sol. Phys., 12, 4 [Google Scholar]
- Hazra, S., & Nandy, D. 2016, ApJ, 832, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Hazra, G., Karak, B. B., & Choudhuri, A. R. 2014, ApJ, 782, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Hazra, G., Jiang, J., Karak, B. B., & Kitchatinov, L. 2019, ApJ, 884, 35 [CrossRef] [Google Scholar]
- Hempelmann, A., Schmitt, J. H. M. M., & Stȩpień, K. 1996, A&A, 305, 284 [NASA ADS] [Google Scholar]
- Hotta, H., & Yokoyama, T. 2010, ApJ, 714, L308 [NASA ADS] [CrossRef] [Google Scholar]
- Işık, E., Solanki, S. K., Krivova, N. A., & Shapiro, A. I. 2018, A&A, 620, A177 [Google Scholar]
- Jennings, R. L., & Weiss, N. O. 1991, MNRAS, 252, 249 [Google Scholar]
- Jiang, J. 2020, ApJ, 900, 19 [Google Scholar]
- Jiang, J., & Wang, J.-X. 2006, Chin. J. Astron. Astrophys., 6, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, J., & Wang, J. X. 2007, MNRAS, 377, 711 [CrossRef] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Schüssler, M. 2011, A&A, 528, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, J., Cameron, R. H., Schmitt, D., & Işık, E. 2013, A&A, 553, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, J., Cameron, R. H., & Schüssler, M. 2014a, ApJ, 791, 5 [Google Scholar]
- Jiang, J., Hathaway, D. H., Cameron, R. H., et al. 2014b, Space Sci. Rev., 186, 491 [Google Scholar]
- Jiang, J., Wang, J.-X., Jiao, Q.-R., & Cao, J.-B. 2018, ApJ, 863, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Jiao, Q., Jiang, J., & Wang, Z.-F. 2021, A&A, 653, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jouve, L., & Brun, A. S. 2007, A&A, 474, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jouve, L., Brun, A. S., Arlt, R., et al. 2008, A&A, 483, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jouve, L., Brown, B. P., & Brun, A. S. 2010, A&A, 509, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karak, B. B. 2010, ApJ, 724, 1021 [CrossRef] [Google Scholar]
- Karak, B. B. 2020, ApJ, 901, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Karak, B. B., Kitchatinov, L. L., & Choudhuri, A. R. 2014a, ApJ, 791, 59 [CrossRef] [Google Scholar]
- Karak, B. B., Jiang, J., Miesch, M. S., Charbonneau, P., & Choudhuri, A. R. 2014b, Space Sci. Rev., 186, 561 [CrossRef] [Google Scholar]
- Kitchatinov, L. 2022, Res. Astron. Astrophys., 22, 125006 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L. L., & Nepomnyashchikh, A. A. 2017a, Astron. Lett., 43, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L., & Nepomnyashchikh, A. 2017b, MNRAS, 470, 3124 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L. L., & Olemskoy, S. V. 2011, MNRAS, 411, 1059 [CrossRef] [Google Scholar]
- Kitchatinov, L. L., & Olemskoy, S. V. 2012, MNRAS, 423, 3344 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchatinov, L. L., & Olemskoy, S. V. 2015, Res. Astron. Astrophys., 15, 1801 [Google Scholar]
- Kitchatinov, L. L., & Rüdiger, G. 1999, A&A, 344, 911 [NASA ADS] [Google Scholar]
- Kochukhov, O. 2021, A&ARv, 29, 1 [Google Scholar]
- Li, K. J., Wang, J. X., Zhan, L. S., et al. 2003, Sol. Phys., 215, 99 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, S. W., Wang, X., Leamon, R. J., et al. 2014, ApJ, 792, 12 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, S. W., Leamon, R. J., Egeland, R., et al. 2021, Sol. Phys., 296, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Montet, B. T., Tovar, G., & Foreman-Mackey, D. 2017, ApJ, 851, 116 [Google Scholar]
- Muñoz-Jaramillo, A., Nandy, D., & Martens, P. C. H. 2011, ApJ, 727, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Jaramillo, A., Dasi-Espuig, M., Balmaceda, L. A., & DeLuca, E. E. 2013, ApJ, 767, L25 [CrossRef] [Google Scholar]
- Nandy, D. 2004, Sol. Phys., 224, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, N. J., Brown, B. P., Brun, A. S., Miesch, M. S., & Toomre, J. 2013, ApJ, 762, 73 [Google Scholar]
- Nèmec, N. E., Shapiro, A. I., Işık, E., Solanki, S. K., & Reinhold, T. 2023, A&A, 672, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Weiss, N. O., & Vaughan, A. H. 1984a, ApJ, 287, 769 [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984b, ApJ, 279, 763 [Google Scholar]
- Parker, E. N. 1955, ApJ, 121, 491 [Google Scholar]
- Petrovay, K., Nagy, M., & Yeates, A. R. 2020, J. Space Weather Space Clim., 10, 50 [EDP Sciences] [Google Scholar]
- Pipin, V. V., & Kosovichev, A. G. 2016, ApJ, 823, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Reinhold, T., Cameron, R. H., & Gizon, L. 2017, A&A, 603, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rengarajan, T. N. 1984, ApJ, 283, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [Google Scholar]
- Schrijver, C. J., & Title, A. M. 2001, ApJ, 551, 1099 [Google Scholar]
- Schrijver, C. J., Shine, R. A., Hagenaar, H. J., et al. 1996, ApJ, 468, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Schuessler, M., & Solanki, S. K. 1992, A&A, 264, L13 [Google Scholar]
- Solanki, S. K., Wenzler, T., & Schmitt, D. 2008, A&A, 483, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sowmya, K., Nèmec, N. E., Shapiro, A. I., et al. 2021, ApJ, 919, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [Google Scholar]
- Strassmeier, K. G., Rice, J. B., Wehlau, W. H., et al. 1991, A&A, 247, 130 [NASA ADS] [Google Scholar]
- Strugarek, A., Beaudoin, P., Charbonneau, P., Brun, A. S., & do Nascimento, J. D. 2017, Science, 357, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Talafha, M., Nagy, M., Lemerle, A., & Petrovay, K. 2022, A&A, 660, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tobias, S. M. 1998, MNRAS, 296, 653 [CrossRef] [Google Scholar]
- van der Houwen, P. J., & Sommeijer, B. P. 2001, J. Comput. Appl. Math., 128, 447 [NASA ADS] [CrossRef] [Google Scholar]
- van Saders, J. L., Ceillier, T., Metcalfe, T. S., et al. 2016, Nature, 529, 181 [Google Scholar]
- Vashishth, V., Karak, B. B., & Kitchatinov, L. 2023, MNRAS, 522, 2601 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., & Penrod, G. D. 1983, PASP, 95, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y. M., & Sheeley, N. R. 2002, J. Geophys. Res.: Space Phys., 107, 1302 [NASA ADS] [Google Scholar]
- Wang, Y. M., Sheeley, N. R., & Nash, A. G. 1991, ApJ, 383, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Warnecke, J. 2018, A&A, 616, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, O. C. 1978, ApJ, 226, 379 [Google Scholar]
- Wright, N. J., & Drake, J. J. 2016, Nature, 535, 526 [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [Google Scholar]
- Yadav, R. K., Gastine, T., Christensen, U. R., & Reiners, A. 2015, A&A, 573, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Z., & Jiang, J. 2022, ApJ, 930, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Bi, S., Li, Y., et al. 2020, ApJS, 247, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Z., Jiang, J., & Zhang, H. 2022, ApJ, 941, L3 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Differential rotations of solar-mass stars. Panels a and b are the profiles of differential rotation for stars with rotation periods of 25 and 13 days, respectively. Panel c shows the latitudinal distribution of the radius-averaged latitudinal shear |
| In the text | |
 |
Fig. 2. Meridional flows of solar-mass stars. Panels a and b are the latitudinal component of the meridional flow patterns for the stars with rotation periods of 25 and 13 days, respectively. Panel c shows the dependence of the averaged return flow at 45°, |
| In the text | |
 |
Fig. 3. Latitude variation of the α profiles determined by Eq. (9) for stars with different rotation periods. |
| In the text | |
 |
Fig. 4. Critical α-value, αc, as a function of stellar rotation period (Prot). The solid (dashed) curve represents the dipolar (quadrupolar) parity solution. |
| In the text | |
 |
Fig. 5. Snapshots of the magnetic field evolution during the interval of one-third of the magnetic cycle Pcyc/3. The first (third) row represents a rotation period of 10 days with dipolar (quadrupolar) fields. The second (forth) row represents a rotation period of 25 days with dipolar (quadrupolar) fields. The strength of magnetic field is arbitrary in a linear regime, and is normalized to a maximum of 1 here. The region in red (blue) represents toroidal fields and inward (outward). The solid (dashed) lines represent the poloidal field clockwise (anticlockwise). |
| In the text | |
 |
Fig. 6. Relation between rotation period (Prot) and magnetic cycle (Pcyc). The solid (dashed) curve represents the dipolar (quadrupolar) parity solution. |
| In the text | |
 |
Fig. 7. Relation between rotation period (Prot) and magnetic cycle (Pcyc) for cases of n = 1 (blue curve) and n = 9.25(prot/psun)2 (black curve). The solid (dashed) curve represents the dipolar (quadrupolar) parity solution. |
| In the text | |
 |
Fig. 8. Relation between rotation period (Prot) and magnetic activity amplitude (Acyc). The activity amplitude is measured by Φtor. Red dots, blue forks, and black inverted triangles represent the saturated magnetic fields with a dipolar, quadrupolar, and mixed parity, respectively. |
| In the text | |
 |
Fig. 9. Relation between rotation period (Prot) and magnetic cycle (Pcyc). The solid and dashed lines represent the solution operating in the nonlinear regime and linear regime, respectively. |
| In the text | |
 |
Fig. 10. Time–latitude diagrams of subsurface toroidal flux (top) and surface radial field (bottom) for stars with rotation periods of 10, 15, and 25 days. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



 =\eta \left(\nabla ^{2}-\frac{1}{s^{2}}\right)A+{S\!}_{\rm BL}, \end{aligned} $$](/articles/aa/full_html/2024/06/aa48201-23/aa48201-23-eq2.gif)
![$$ \begin{aligned}&\frac{\partial B}{\partial t}+\frac{1}{r}\left[\frac{\partial (u_{\rm r}+\gamma _{\rm r})rB}{\partial r}+\frac{\partial (u_{\theta }B)}{\partial \theta }\right]=\eta \left(\nabla ^{2}-\frac{1}{s^2}\right)B+s(\boldsymbol{B}_{\rm p}\cdot \nabla \Omega ) \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad +\frac{1}{r}\frac{\mathrm{d}\eta }{\mathrm{d}r}\frac{\partial (rB)}{\partial r}, \end{aligned} $$](/articles/aa/full_html/2024/06/aa48201-23/aa48201-23-eq3.gif)
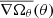
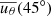
![$$ \begin{aligned} \gamma _{\rm r}(r) = -\frac{\gamma _{0}}{2}\left[1+\mathrm{erf}\left(\frac{r-r_{\rm s}}{d_{\rm s}}\right)\right], \end{aligned} $$](/articles/aa/full_html/2024/06/aa48201-23/aa48201-23-eq12.gif)
![$$ \begin{aligned} \eta =\frac{\eta _{\rm cz}}{2}\left[1+\mathrm{erf}\left(\frac{r-r_{\rm c}}{d_{\rm c}}\right)\right]+\frac{\eta _{\rm s}}{2}\left[1+\mathrm{erf}\left(\frac{r-r_{\rm s}}{d_{\rm s}}\right)\right], \end{aligned} $$](/articles/aa/full_html/2024/06/aa48201-23/aa48201-23-eq13.gif)
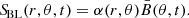
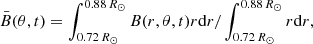
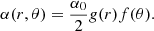
![$$ \begin{aligned} g(r)=\left[1+\mathrm{erf}\left(\frac{r-r_\alpha }{d_\alpha }\right)\right], \end{aligned} $$](/articles/aa/full_html/2024/06/aa48201-23/aa48201-23-eq18.gif)
![$$ \begin{aligned} f(\theta )=\dfrac{\cos \theta \sin ^{n}\theta }{\mathrm{Max}[\cos \theta \sin ^{n}\theta , \theta \in (0,\pi )]}, \end{aligned} $$](/articles/aa/full_html/2024/06/aa48201-23/aa48201-23-eq19.gif)
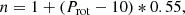
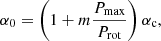
![$$ \begin{aligned} B(r, \theta )|_{t=0} = \sin (2\theta )\sin [\pi (r-0.72\,R_\odot )/0.28\,R_\odot ] \end{aligned} $$](/articles/aa/full_html/2024/06/aa48201-23/aa48201-23-eq22.gif)
![$$ \begin{aligned} B(r, \theta )|_{t=0} = \sin (\theta )\sin [\pi (r-0.72\,R_\odot )/0.28\,R_\odot ] \end{aligned} $$](/articles/aa/full_html/2024/06/aa48201-23/aa48201-23-eq23.gif)