| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 25 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220354 | |
| Published online | 06 May 2013 | |
Star-forming regions of the Aquila rift cloud complex
I. NH3 tracers of dense molecular cores⋆
1 Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
2 Ioffe Physical-Technical Institute, Polytekhnicheskaya Str. 26, 194021 St. Petersburg, Russia
e-mail: lev@astro.ioffe.rssi.ru
3 St. Petersburg Electrotechnical University “LETI”, Prof. Popov Str. 5, 197376 St. Petersburg, Russia
4 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
5 Astronomy Department, King Abdulaziz University, PO Box 80203, Jeddah 21589, Saudi Arabia
6 Purple Mountain Observatory, Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210008, PR China
Received: 10 September 2012
Accepted: 7 March 2013
Aims. The physics of star formation is an important part of Galactic evolution. Most stars are formed in high-density environments (n > 104 cm-3) and emit lines of diverse molecular transitions. In the present part of our survey we search for ammonia emitters in the Aquila rift complex, which trace the densest regions of molecular clouds.
Methods. From a CO survey carried out with the Delingha 14-m telescope we selected ~150 targets for observations in other molecular lines. Here we describe the mapping observations in the NH3(1, 1) and (2, 2) inversion lines of the first 49 sources performed with the Effelsberg 100-m telescope.
Results. The NH3(1, 1) emission lines are detected in 12 and the (2, 2) in 7 sources. Among the newly discovered NH3 sources, our sample includes the following well-known clouds: the starless core L694-2, the Serpens cloud cluster B, the Serpens dark cloudL572, the filamentary dark cloud L673, the isolated protostellar source B335, and the complex star-forming region Serpens South. Angular sizes between 40′′ and 80′′ (~0.04–0.08 pc) are observed for compact starless cores but can be as large as 9′ (~0.5 pc) for filamentary dark clouds. The measured kinetic temperatures of the clouds lie between 9 K and 18 K. From NH3 excitation temperatures of 3–8 K we determine H2 densities with typical values of ~ (0.4−4) × 104 cm-3. The masses of the mapped cores range between ~0.05 and ~ 0.5 M⊙. The relative ammonia abundance X = [NH3]/[H2] varies from 1 × 10-7 to 5 × 10-7 with the mean ⟨ X ⟩ = (2.7 ± 0.6) × 10-7 (estimated from spatially resolved cores assuming a filling factor of η = 1). In two clouds, we observe kinematically split NH3 profiles separated by ~1 km s-1. The splitting is most likely due to bipolar molecular outflows, for one of which we determine an acceleration of V ̇ ≲ 0.03 km s-1 yr-1. A starless core with significant rotational energy is found to have a higher kinetic temperature than the other ones, which is probably caused by magnetic energy dissipation.
Key words: ISM: clouds / ISM: molecules / ISM: kinematics and dynamics / radio lines: ISM / techniques: spectroscopic / line: profiles
Appendices and Table 2 are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
One of the central questions of stellar evolution concerns the processes that define the initial mass of a protostellar object. It is suggested that more than 70% of stars are formed in clusters embedded within giant molecular clouds (Lada & Lada 2003) and that the varying environment may affect the initial mass function (IMF).
In the present survey we search for the star-formation regions in the Aquila giant molecular cloud. Starting from Cygnus, in the direction of the Galactic center, the Milky Way appears to be split into two branches. The southern branch runs through Cygnus, Vulpecula, Sagitta, Aquila, and Scutum, entering the Galactic central bulge in Sagittarius. The northern branch crosses Vulpecula and Aquila and disappears in the northern part of the Serpens Cauda and Ophiuchus constellations. The separating dark band of obscuring dust is commonly called the Aquila rift, but absorbing clouds are found not only next to the Galactic plane: many dark clouds are located in areas extending up to latitudes of at least +10° and down to − 20° (e.g., Dame & Thaddeus 1985; Kawamura et al. 1999; Dobashi et al. 2005).
The distance to the Aquila rift was estimated from optical data and interstellar extinction as well as from parallax measurements. A sudden appearance of reddened stars is observed at D = 225 ± 55 pc, and the cloud distribution may have a thickness of ~80 pc (Straižys et al. 2003). This estimate is in line with the distance to the Serpens-Aquila region found from interstellar extinction by Knude (2011), D = 203 ± 7 pc, but significantly lower than the trigonometric parallax value 415 ± 25 pc deduced by Dzib et al. (2010) from the Very Long Baseline Array observations of the young stellar object EC 95 in the Serpens cloud. Since the discrepancy in the distance estimations may be caused by a projection effect, we used the weighted harmonic mean of the first two measurements, which are both based on large-size data sets, D = 203 ± 12 pc, if not otherwise specified. Thus, compared with other close molecular complexes, the distance to the Aquila rift is similar to that of the Perseus clouds (~250 pc; Rosolowsky et al. 2008) and lies between those of the Taurus and the Pipe Nebula (~140 pc; Rathborne et al. 2008) and the Auriga (~300 pc) molecular clouds (Heiderman et al. 2010; Cieza et al. 2012).
Recently, the Herschel Gould Belt Survey revealed a large number (≳500) of starless cores in the Aquila rift cloud complex (e.g., Bontemps et al. 2010; Könyves et al. 2010; Men’shchikov et al. 2010). We began our investigations of the Aquila clouds in 2010 with an extended survey of CO and extinction peaks using the Delingha 14-m telescope (Zuo et al. 2004). The targets were selected from the CO data of Kawamura et al. (1999, 2001) and from the optical data of Dobashi et al. (2005), limited in the latter case by the areas with Av > 6m. We observed and detected 23 Kawamura and 47 Dobashi clouds at λ ~ 3 mm. However, CO and 13CO trace not only the dense gas, but also outflows and low-density regions; in addition, CO may be saturation broadened. It is well known that the carbon-chain molecules disappear from the gas-phase in the central regions because of freeze-out onto dust grains (e.g., Tafalla et al. 2004), i.e., C-bearing molecules are usually distributed in the outer parts of the cores. That is why CO and 13CO are poor indicators for the dense molecular gas. In contrast, N-bearing molecules such as ammonia concentrate in the inner cores, where the gas density approaches 105 cm-3. Ammonia is still observable in the gas-phase since it resists depletion onto dust grains (e.g., Bergin & Langer 1997).
Based on the CO survey, we composed a list of ~150 targets where not only CO but also 13CO is quite strong, which indicates high column densities and hence promising conditions to detect dense cores. The objective of the current work, which was performed with the Effelsberg 100-m telescope, is to observe these targets in other molecular lines, in the first place in NH3, to confirm that the targets are indeed dense cores and to determine their physical properties.
In the present paper we describe the first 49 sources from our survey. Observations are described in Sect. 2. Individual molecular cores are considered in Sect. 3. The results obtained are summarized in Sect. 4, and computational methods are outlined in Appendix A. Appendix B contains NH3(1, 1) and (2, 2) spectra detected toward the ammonia peaks, tables with derived physical parameters, and maps showing distributions of these parameters within the three most prominent cores.
2. Observations
The ammonia observations were carried out with the Effelsberg 100-m telescope1 in four observing sessions between March 26 and 30, 2011, and in two sessions on January 12 and 13, 2012. The NH3 lines were measured with a K-band high-electron mobility transistor (HEMT) dual channel receiver, yielding spectra with a full-width at half power (FWHP) resolution of 40′′ in two orthogonally oriented linear polarizations at the rest frequency of the (J,K) = (1, 1) and (2, 2) lines (23 694.496 MHz and 23 722.631 MHz, respectively). Averaging the emission from both channels, the typical system temperature (receiver noise and atmosphere) is 100 K on a main beam brightness temperature scale.
In 2011, the measurements were obtained in frequency-switching mode using a frequency throw of ±2.5 MHz. The backend was an fast Fourier transform spectrometer (FFTS), operated with a bandwidth of 100 MHz, which simultaneously provided 16 384 channels for each polarization. For some offsets we also used the minimum bandwidth of 20 MHz for the NH3(1, 1) line. The resulting channel widths were 0.077 km s-1 and 0.015 km s-1. However, the true velocity resolution was about 1.6 times lower.
In 2012, the measurements were obtained with the backend eXtended bandwidth FFTS (XFFTS), operated with 100 MHz and 2 GHz bandwidths, which provides 32 768 channels for each polarization. The resulting channel widths were 0.038 km s-1 and 0.772 km s-1, but the true velocity resolution is 1.16 times lower (Klein et al. 2012).
The pointing was checked every hour by continuum cross-scans of nearby continuum sources. The pointing accuracy was better than 5′′. The spectral line data were calibrated by means of continuum sources with known flux density. We mainly used NGC7027 (Ott et al. 1994), 3C123 (Baars et al. 1977), and G29.96–0.02 (Churchwell et al. 1990). These calibration sources were used to establish a main beam brightness temperature scale, TMB. Since the main beam size (40′′) is smaller than most core radii (>50′′) of our Aquila objects, the ammonia emission couples well to the main beam and, thus, the TMB scale is appropriate. Compensations for differences in elevation between the calibrator and the source were ≲20% and have not been taken into account. Similar uncertainties of the main beam brightness temperature were found from a comparison of spectra toward the same position taken at different dates.
3. Results
The detected NH3 spectra were treated in the way described in Appendix A. The radial velocity VLSR, the linewidth Δv (FWHM), the optical depths τ11 and τ22, the integrated ammonia emission ∫TMBdv, and the kinetic temperature Tkin, are well determined physical parameters, whereas the excitation temperature Tex, the ammonia column density N(NH3), and the gas density n(H2) are less certain. The optical depth and kinetic temperature are parameters independent of calibration errors, since Tkin depends only on the intensity ratio of the simultaneously observed NH3(1, 1) and (2, 2) lines, and τ depends on the relative intensities of the various hyperfine (hf) components. On the other hand, the excitation temperature Tex depends on the ammonia line brightness and is sensitive to calibration errors (Lemme et al. 1996). In addition, Eq. (A.10) shows that Tex depends on the filling factor η, which is not known for unresolved cores.
Peak intensities of NH3(1, 1) line emission toward Aquila targets.
A typical error of the optical depth determined formally from the covariance matrix at the minimum of χ2 is 15−20% (Appendix A). The error of the integrated ammonia emission depends on the noise level, and for an rms ~0.2 K per 0.077 km s-1 channel it is ~0.3 K km s-1. The precision with which the Gaussian line center can be estimated is given by (e.g., Landman et al. 1982) 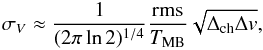 (1)where Δch and Δv are the channel and the line widths. At rms ~0.2 K and TMB ~ 2 K (see below) this gives σV ~ 0.005 km s-1 for our high-resolution settings. The same order of magnitude errors (i.e., from a few to ten m s-1) of the line centers and linewidths are obtained from the covariance matrix.
(1)where Δch and Δv are the channel and the line widths. At rms ~0.2 K and TMB ~ 2 K (see below) this gives σV ~ 0.005 km s-1 for our high-resolution settings. The same order of magnitude errors (i.e., from a few to ten m s-1) of the line centers and linewidths are obtained from the covariance matrix.
The results of our analysis are presented in Tables 1, 2 and B.1–B.4. Table 1 lists the regions where NH3 line emission was detected either in both (1, 1) and (2, 2) transitions or only in (1, 1). For non-detections (Table 2), the rms TMB values per channel width are given. In total, NH3 lines are detected in 12 sources out of 49 dense cores. In Table 1, we list the radial velocities VLSR, the observed linewidths Δv (FWHM), and the main-beam-brightness temperature TMB at the maximum of the main group of hf components. In Col. 2, different peaks resolved in the sources are labeled by Greek letters (α for the most intense NH3 emission), which are also indicated on color maps (Figs. 1–3, 5, and 7–10). The physical parameters calculated for each individual source are given in Table 1 and in the Appendix B, Tables B.1–B.4. The results obtained for the three most prominent sources Do279P6, Do279P12, and SS3 are additionly shown as maps (Figs. B.10–B.12). Below we describe the individual sources that were identified as dense molecular cores. We will report on statistical analysis of the full sample of Aquila cores after the survey is completed in 2013.
 |
Fig. 1 a) NH3(1, 1) intensity map (∫TMBdv) of Ka01. The starting point for the contour levels is 0.1 K km s-1, the increment is 0.7 K km s-1 between the first two and 0.8 K km s-1 between the other contour levels. The crosses mark measured positions. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 9.576 km s-1. The intensity peak is labeled as in Table 1. The Effelsberg beam size (HPBW) at 23.7 GHz is 40′′. |
3.1. Kawamura 01 (Ka01)
The starless cloud Kawamura 01 (Ka01, for short) belongs to the dark cloud L694 classified as opacity class 6 by Lynds (1962). This is an isolated dense core located in the sky close (~4°) to the protostar B335 (Sect. 3.6). No embedded IRAS luminosity source has been found (Harvey et al. 2002; Harvey et al. 2003a). Lee et al. (1999) found three dark spots L694–1, L694–2, and L694–3 in the Digital Sky Survey image of L694. The second spot is associated with Ka01. Using Wolf diagrams, Kawamura et al. (2001) determined the distance to L694-2 as D ≈ 230 pc.
We mapped Ka01 for the first time in the NH3(1, 1) and (2, 2) lines with a spacing of 40′′ at 29 positions marked by crosses in Fig. 1a. This shows that the NH3 emission arises from a very compact region. The fourth contour level in Fig. 1a corresponds to the half-peak of the integrated emission, ∫TMBdv. This allows us to calculate the apparent geometrical mean diameter (FWHP) 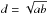 , where a ≈ 115′′ and b ≈ 65′′ (deconvolved) are the major and minor axes of this annulus, and a beam ammonia core size of approximately 0.08 pc – the typical value for dense molecular cores in the Taurus molecular cloud (e.g., Benson & Myers 1989).
, where a ≈ 115′′ and b ≈ 65′′ (deconvolved) are the major and minor axes of this annulus, and a beam ammonia core size of approximately 0.08 pc – the typical value for dense molecular cores in the Taurus molecular cloud (e.g., Benson & Myers 1989).
At the core center, we obtained two spectra with low (FWHM = 0.123 km s-1) and high (FWHM = 0.024 km s-1) spectral resolutions. The high-resolution spectra of the NH3(1, 1) and (2, 2) lines are shown in Fig. B.1 along with the synthetic spectra (red curves) calculated in the simultaneous fit of all hf components to the observed profiles (blue histograms). The residuals “observed data – model” are depicted beneath each NH3 spectrum in Fig. B.1.
The results of the fits to the low-resolution NH3 spectra obtained at different positions and the corresponding physical parameters are given in Table B.1. The estimate of the excitation temperature is made from the (1, 1) transition assuming a beam-filling factor η = 1 since both the major and minor axes of the core exceed the angular resolution. At two offsets (0′′,0′′) and (0′′, − 40′′), we calculated the rotational and kinetic temperatures from the two transitions (1, 1) and (2, 2), and from Eq. (A.21) we determine the gas densities nH2 ~ 1.2 × 104 and 2.5 × 104 cm-3 for a uniform cloud coverage (Col. 10 in Table B.1).
Assuming spherical geometry, we find a core mass M ~ 0.5 M⊙ (the mean molecular weight is 2.8). On the other hand, the virial mass (Eq. (A.26)) calculated from the linewidth Δv and the core radius r is Mvir ~ 1.0 M⊙. The observed difference in the masses could be due to deviations from a uniform gas density distribution and a core ellipticity.
The total ammonia column density of Ntot ~ 1.3 × 1015 cm-2 gives the abundance ratio [NH3]/[H2] ~ 2 × 10-7 at the core center (d ~ 0.08 pc), which is consistent with other sources (e.g., Dunham et al. 2011).
The high-resolution NH3 spectrum (Fig. B.1) can be used to estimate the input of the turbulent motions to the line broadening. The measured linewidth Δv = 0.27 km s-1 and the thermal width Δvth ~ 0.15 km s-1 at Tkin ~ 9 K (Table B.1) give σturb ~ 0.09 km s-1.
Figure 1b shows the NH3(1, 1) intensity (gray contours) and the radial velocity VLSR (color map) structure in L694-2. The radial velocities within the central 115′′ × 65′′ region do not show significant variation in both magnitude and direction, which suggests a simple solid-body rotation. The velocity gradient along the major axis (PA = 127°) is gradaV ≡ (V − ⟨ VLSR ⟩ )/0.5a ~ ± 1 km s-1 pc-1, and along the minor axis gradbV ≡ (V − ⟨ VLSR ⟩ )/0.5b ~ 0 and + 1 km s-1 pc-1. Toward the edges N-W (redshift) and S-E (blueshift), ~50′′ off the center, the radial velocity monotonically changes by ±0.06 km s-1. As they are attributed to cloud rotation, these systematic trends in VLSR correspond to an angular velocity 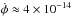 s-1.
s-1.
For a self-gravitating rigidly rotating sphere of constant density ρ, mass M, and radius r, the ratio of rotational to gravitational potential energy is 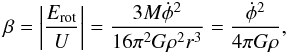 (2)or
(2)or 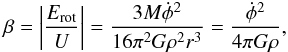 (3)where
(3)where 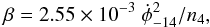 is the angular velocity in units of 10-14 s-1 and n4 is the gas density in units of 104 cm-3 (Menten et al. 1984).
is the angular velocity in units of 10-14 s-1 and n4 is the gas density in units of 104 cm-3 (Menten et al. 1984).
Equation (3) and the estimates of the angular velocity and the gas density obtained above show that β ≲ 0.016 and, hence, the rotation energy is a negligible fraction of the gravitational energy at this stage of evolution of the low-mass starless molecular core Ka01.
There is a different measure of the influence of cloud rotation upon cloud stability through the ratio between the rotational and combined thermal and non-thermal (turbulent) virial terms (e.g., Phillips 1999), 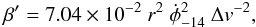 (4)where r is the cloud radius in pc and Δv the linewidth (FWHM) in km s-1. The influence of rotation and turbulence are comparable when the stability parameter β′(r) ≈ 1. For the core Ka01, β′ ≈ 0.02, which means that turbulence greatly exceeds the contribution due to rotation in determining cloud stability.
(4)where r is the cloud radius in pc and Δv the linewidth (FWHM) in km s-1. The influence of rotation and turbulence are comparable when the stability parameter β′(r) ≈ 1. For the core Ka01, β′ ≈ 0.02, which means that turbulence greatly exceeds the contribution due to rotation in determining cloud stability.
3.2. Dobashi 279 P6 (Do279 P6)
The source Dobashi 279 P6 (Do279P6, for short) shows a very complex structure in the NH3 emission (Fig. 2a) with many small clumps located along the main axis (PA = 56°, a ≈ 9′, or ~0.5 pc at D ~ 203 pc). We list the coordinates of five bright NH3 peaks, the peak temperatures TMB, their radial velocities VLSR, and the linewidths Δv in Table 1. The peaks are labeled from α to ε in Fig. 2b and in Table 1 according to decreasing main beam brightness temperature, TMB.
The location of Do279P6 coincides with a star formation region in the Serpens cloud, which is known under the name Cluster B (Harvey et al. 2006), or Ser G3-G6 (Cohen & Kuhi 1979), or Serpens NH3 (Djupvik et al. 2006). The area around Ser G3-G6 was mapped in the NH3(1, 1) emission line by Clark (1991), who found two ammonia condensations on each side of the complex, Ser G3-G6NE and Ser G3-G6SW (the map is not published; observations obtained with the Effelsberg 100-m telescope). The coordinates of these condensations coincide with the α and γ ammonia peaks, while the close group of G3-G6 stars lies in the field of the δ peak.
 |
Fig. 2 a) Same as Fig. 1a but for the source Do279P6. The starting point for the contour levels is 0.5 K km s-1, the increment is 0.5 K km s-1 between the first two and 1.0 K km s-1 between the other contour levels. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 7.986 km s-1. The intensity peaks are labeled as in Table 1. c) NH3(1, 1) intensity map as in panel a) and positions of YSO candidates observed with the Spitzer/IRAC in a star formation region Serpens cluster B (Harvey et al. 2006). Open circles of different colors mark Class I (red), intermediate type (yellow), and Class II (blue) YSOs. |
The Do279P6 cloud with identified YSO candidates is shown in Fig. 2c, in which open circles of different colors mark Class I (red), “flat” (yellow)2, and Class II (blue) candidates. Class II sources are more evolved and older than Class I and, thus, the NH3 core might be already more dispersed. So, what we observe at the S–W offset γ = ( − 160′′, − 80′′) is consistent with this expectation – only flat and Class II sources are located therein. On the other hand, all Class I sources (ID numbers B13 and B15–B18 as in Table 4 in Harvey et al. 2006) are detected in the vicinity of the core center α = (0′′,0′′), which has the highest gas density, nH2 ~ 2.3 × 104 cm-3, and the highest intensity of the ammonia emission TMB = 2.9 K (Table B.2). Source B18 lies within 8′′ off the NH3 peak, and B13 – the most distant – at ~80′′ along the N–W direction. Moreover, the angular size of the central condensation is two times smaller than that of the S–W clump, i.e., the region is probably less dispersed. The two other condensations with flat and Class II type sources are located at the offsets δ = ( − 120′′, − 40′′) with five and β = (40′′,40′′) with one embedded YSO(s). The only starless NH3 region detected at the ε condensation ε = (80′′,80′′) has the narrowest linewidth ΔV ≃ 0.4 km s-1 (Table 1) and the lowest kinetic temperature Tkin ≃ 10 K (Table B.2), which are comparable to Ka01 – the isolated dense core (Sect. 3.1).
Figure B.2 shows the high-resolution ammonia
spectra (channel spacing 0.015 km s-1) obtained at three NH3 peaks:
α, β, and γ. The corresponding
linewidths are Δv ≈ 0.75,0.63, and 0.96 km s-1. Given the
derived kinetic temperatures (Table B.2), we can
calculate the thermal contribution to the linewidth and the non-thermal velocity
component: 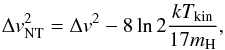 (5)where
(kTkin/17mH) is
the thermal broadening due to NH3, and mH is the
mass of the hydrogen atom.
(5)where
(kTkin/17mH) is
the thermal broadening due to NH3, and mH is the
mass of the hydrogen atom.
The calculated non-thermal velocity dispersion 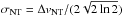 of about 0.3 km s-1 is comparable to the
large-scale motions observed in the cloud. Namely, the
N − E part is moving toward us (with respect to the
systemic velocity of the cloud, ⟨ VLSR ⟩ = 7.986 km
s-1) with a radial velocity VLSR ≈ −0.4 km
s-1 and the S–W part in the opposite direction with similar radial velocity
(Fig. 2b). In the middle of the cloud there is a
narrow zone along the cut Δα = −50′′ with positive
VLSR ≈ 0.3 km s-1, which is bracketed by two
zones with negative VLSR ≈ −0.3 km s-1. The whole
structure may be due to the differential rotation of different clumps distributed along
the main axis of the cloud.
of about 0.3 km s-1 is comparable to the
large-scale motions observed in the cloud. Namely, the
N − E part is moving toward us (with respect to the
systemic velocity of the cloud, ⟨ VLSR ⟩ = 7.986 km
s-1) with a radial velocity VLSR ≈ −0.4 km
s-1 and the S–W part in the opposite direction with similar radial velocity
(Fig. 2b). In the middle of the cloud there is a
narrow zone along the cut Δα = −50′′ with positive
VLSR ≈ 0.3 km s-1, which is bracketed by two
zones with negative VLSR ≈ −0.3 km s-1. The whole
structure may be due to the differential rotation of different clumps distributed along
the main axis of the cloud.
The central ammonia condensation consists of two clumps α and β separated by ~60′′. The position angle of the major axis of the brighter α clump is PA ~ 50°. The deconvolved diameters of the major and minor axes are a ≃ 130′′ and b ≃ 60′′ (FWHP). The angular sizes of the β clump are less certain because it is not completely resolved. The physical parameters were estimated assuming a filling factor η = 1 for both the α and β clumps and thus Tex, N(NH3), and n(H2), listed in Table B.2, correspond to their minimum values (for details, see Appendix A). With the mean diameter of ~90′′ (or 0.09 pc at D = 203 pc) the mass of this double clump is Mα,β ≳ 0.5 M⊙, and the ammonia abundance is [NH3]/[H2] ~ 2 × 10-7. The estimate through virial masses is less certain in this case because YSOs are embedded within the clumps.
Another double peak is formed by the γ and δ cores. The major axis of the brighter γ condensation (PA = 0°) is 113′′ and the minor axis is 69′′ (deconvolved, FWHP). The δ clump is not completely resolved, which gives, as for the previous pair, the lower bound on the mass Mγ,δ ≳ 0.4 M⊙ and the abundance ratio [NH3]/[H2] ~ 1 × 10-7.
The weakest peak, ε, separated by ~60′′ from β, is a completely unresolved ammonia clump with an angular size θ < 40′′. It shows the highest optical depth, τ11 ≃ 11, and the lowest kinetic temperature, Tkin ≃ 10 K (Table B.2). Other physical parameters listed in Table B.2 were calculated at η = 1, i.e., they are the minimum values. The filling factor η is restricted in this case between 0.2 and 1 (see Appendix A), which provides the following boundaries: 4 ≤ Tex < 10 K, 1.3 × 1015 ≤ N(NH3) < 3.2 × 1015 cm-2, and 0.8 × 104 ≤ n(H2) < 4.9 × 104 cm-3. The mass of the ε clump is less than 0.06 M⊙ if n(H2) ~ 3 × 104 cm-3 and its diameter d < 0.04 pc.
Of course, the derivation of relative ammonia abundances and masses is not very accurate and based on a number of model assumptions such as spherical geometry, homogeneous gas density, the distance to the target of 203 pc, etc. Nevertheless, the substellar mass of the ε clump may lie in the range of the lowest possible masses from which a brown dwarf can form: 0.03 − 0.08 M⊙ (e.g., Oliveira et al. 2009).
3.3. Dobashi 279 P8 (Do279 P8)
The molecular cloud Dobashi 279 P8 (Do279P8, for short) is an example of a starless core with no embedded IRAS point sources or a pre-main-sequence star. Our mapping reveals a slightly elongated structure of this core in the N − S direction (Fig. 3) with an FWHP angular size of ~45′′ × 57′′ (deconvolved), or ~0.04 × 0.06 pc2 linear size at D = 203 pc. The coordinates of the NH3 peak, the peak temperature TMB, its radial velocity VLSR, and the linewidth Δv (FWHM) are listed in Table 1. The NH3 spectrum is shown in Fig. B.3. We did not detect any emission at the expected position in the (2, 2) transition and, therefore, only an upper limit on the rotational temperature is given in Table B.1. The 1σ upper limit on Trot is very low, <10 K. A noticeable feature of the Do279P8 spectrum is a very narrow linewidth of the hfs transitions, Δv ≈ 0.26 km s-1. Another remarkable characteristic is the slow rotation of the cloud illustrated in Fig. 3b: at a radius of ~20′′ off the center (≈0.02 pc), the tangential velocity does not exceed ±0.04 km s-1, which leads to an angular velocity 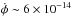 s-1. The axis of the velocity centroid is slightly tilted with respect to the main N − S axis of the NH3(1, 1) map.
s-1. The axis of the velocity centroid is slightly tilted with respect to the main N − S axis of the NH3(1, 1) map.
 |
Fig. 3 a) Same as Fig. 1a but for the source Do279P8. The contour levels start at 0.5 K km s-1 and increments are 0.5 K km s-1. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 8.553 km s-1. The intensity peak is labeled as in Table 1. |
The measured excitation temperatures at the offsets (0′′,0′′) and (0′′, − 40′′) are close to the upper limits on the rotational temperatures (see Table B.1). This may imply that the (1, 1) transition is almost thermalized and ammonia emission arises from an extended structure that fills the telescope beam homogeneously, η ≈ 1. At our angular resolution of 40′′, the NH3(1, 1) hfs components do not show any blueward or redward asymmetry that would indicate a contracting or expanding motions. Most probably, the core Do279P8 is in an early stage of evolution. According to Lee & Meyers (2011), the starless cores evolve from the static to the expanding and/or oscillating stages, and finally to the contracting cores. The suggestion that the core is in an initial stage of evolution is also supported by low values of β ≲ 0.1 and β′ ≈ 0.01. In this estimation, we used ngas ≳ 1 × 104 cm-3 ([NH3]/[H2] ~ 5 × 10-7) as a lower bound on the gas density. With the observed diameter d ~ 50′′ (deconvolved) and assuming spherical geometry, the lower limit on the mass of Do279P8 is M ~ 0.06 M⊙.
3.4. Dobashi 279 P12 (Do279 P12)
The source Dobashi 279 P12 (Do279P12, for short) is a dark cloud of the opacity class 4–5 according to Lynds (1962). The cloud is known as L572 (Lynds 1962), BDN 31.57+5.37 (Bernes 1977), or the Serpens dark cloud, which is a site of active star formation (Strom et al. 1974). Very many articles have been devoted to studying this cloud in all spectral ranges from radio to X-ray (for a review, see, e.g., Eiroa et al. 2008).
Single-dish ammonia observations of the Serpens dark cloud were begun by Little et al. (1980) and by Ho & Barrett (1980). Subsequently, Ungerechts & Güsten (1984) mapped an extended ammonia structure of this cloud with the Effelsberg 100-m telescope. Ammonia interferometric observations with the VLA by Torrelles et al. (1992) studied the embedded high-density molecular gas around the triple radio source Serpens FIRS 1 – a typical Class 0 protostar (Snell & Bally 1986; Rodrígues et al. 1980). Additional interferometric (VLA) and single dish (Haystack 37-m, Effelsberg 100-m) observations of FIRS 1 by Curiel et al. (1996) revealed high-velocity ammonia emission (up to ~30–40 km s-1 from the line center) aligned with the radio continuum jet.
The results of our Effelsberg observations are shown in Figs. 4–6. The NH3(1, 1) map (Fig. 4) exhibits a complex structure with three bright peaks, TMB ~ 3 K, located NW–SE at the offsets α = (160′′, − 40′′), β = (200′′, − 120′′), and γ = (40′′,40′′) (see Table 1 and Fig. 5, panel B). The α peak lies very close to the maximum of the NH3 emission detected by Little et al. (1980), while the β and γ peaks are spatially coincident with positions of the two peaks localized by Ho & Barrett (1980). The measured NH3 profiles show in this case a double structure in both the (1, 1) and (2, 2) transitions at four positions (Fig. B.4, Table B.3) and a split (1, 1) line at another three positions where the (2, 2) line was not detected. This multicomponent structure has not been resolved previously in the ammonia observations cited above. Since the splitting is also seen in the optically thin ammonia lines, the observed asymmetry of the NH3 profiles clearly has a kinematic origin.
 |
Fig. 4 a) Same as Fig. 1a but for the source Do279P12. The contour levels start at 0.5 K km s-1 and increments are 1.5 K km s-1. b) NH3(1, 1) intensity map as in panel a) and positions of IR sources. Open circles mark the Herbig-Haro objects (blue), far-infrared continuum sources (red and yellow) (Davis et al. 1999), submm-continuum sources (magenta) detected by SCUBA (Di Francesco et al. 2008), and the triple radio source FIRS 1 (cyan) (Snell & Bally 1986). |
 |
Fig. 5 NH3(1, 1) intensity (grey contours) and radial velocity (color map) structure in the source Do279P12. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 8.099 km s-1. The contour levels are the same as in Fig. 4a. Panels A) and B) represent the velocity maps for the components A and B in the NH3 profile, respectively (see Fig. B.4). The white crosses mark offsets where the splitting of the NH3 profiles is detected. The mean radial velocities of the components A and B are ⟨ VA ⟩ = 7.27 ± 0.11 km s-1 and ⟨ VB ⟩ = 8.54 ± 0.08 km s-1. In panel B), the intensity peaks are labeled as in Table 1. |
We used a two-component model, Eq. (A.7), to fit the data. The result is illustrated in Fig. B.4 by the red lines, the detected velocity subcomponents are labeled by letters A and B. The seven offsets with the split NH3 lines are marked by white crosses on the velocity maps shown in Fig. 5. The cluster of the white crosses at the SE part of Do279P12 outlines a small area of the bipolar outflow with an angular extent of ~40′′ × 80′′. Table B.3 displays the physical parameters estimated at different offsets. The mean radial velocities of the components A and B averaged over the seven offsets are ⟨ VA ⟩ = 7.27 ± 0.11 km s-1 and ⟨ VB ⟩ = 8.54 ± 0.08 km s-1, and the velocity difference is ΔVB − A = 1.3 ± 0.1 km s-1. Panel A in Fig. 5 shows that the gas surrounding the SE double component region predominantly has a negative radial velocity with respect to ⟨ VLSR ⟩, while the gas shown in panel B has a positive VLSR. The observed velocities converge on the mean ⟨ VLSR ⟩ at the cloud’s outskirts.
Figure 5 shows also a velocity gradient along the E–W direction around the isolated double component region at (80′′,0′′) with VA = 7.89 km s-1 and VB = 8.92 km s-1. The adjoining regions at (120′′,0′′) and (40′′,0′′) have intermediate velocities of VLSR = 8.14 and 8.42 km s-1, respectively, which become closer to the mean radial velocity of the cloud ⟨ VLSR ⟩ = 8.099 km s-1 at larger offsets: VLSR = 7.90 and 8.04 km s-1 at (280′′,0′′) and (− 40′′,0′′), respectively.
The measurement of the excitation temperatures reveals that Tex is essentially lower than Trot at all 23 offsets listed in Table B.3. As discussed above, this may indicate clumpiness of the ammonia distribution and η < 1. In Fig. 4b, we also show the Herbig-Haro (HH) objects and far-infrared continuum sources taken from Davis et al. (1999), the submm-continuum sources detected by SCUBA (Di Francesco et al. 2008), and the position of the triple radio source FIRS 1 (Snell & Bally 1986), which coincides with the brightest infrared object SMM1. The closest position of the split NH3 lines to the bipolar outflow in FIRS 1 is (80′′,0′′), which corresponds to a projected angular distance of θ = 45′′ from the SE knot of the radio source FIRS 1 (see also Fig. 13 in Snell & Bally 1986). All other splittings are located in the vicinity of the β peak, around the SMM2 and SMM11 sources.
The observed linewidths Δv of the split NH3 components are in the range between 0.62 km s-1 and 0.90 km s-1. However, larger linewidths (Δv ≳ 1.0 km s-1) measured at different offsets (Table B.3) may imply unresolved subcomponents of the ammonia lines due to the moderate spectral resolution of our database. Gas flows and jets usually accompany the mass accretion processes in YSOs and protostars. From this point of view the split and/or widened line profiles of NH3, – a tracer of the dense cores, – may indicate the first stages of the accretion processes in protostars, where jets of HH objects have not yet been formed.
 |
Fig. 6 Dots with 3σ error bars mark the differences between the radial velocities measured with the Effelsberg 100-m telescope in 1977–1981 (Ungerechts & Güsten 1984) and in the present dataset toward the same positions in Do279P12. The red points indicate deviations from zero that are larger than 3σ. At two offsets, (Δα,Δδ) = (80′′,0′′) and (160′′, − 120′′), we detected double NH3 profiles (see Fig. B.4). |
 |
Fig. 7 a) Same as Fig. 1a but for the source Do321P2. The contour levels start at 0.3 K km s-1 and increments are 1.0 K km s-1. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 6.905 km s-1. The intensity peaks are labeled as in Table 1. c) NH3(1, 1) intensity map as in panel a). Open circles of different colors mark Class I (red), intermediate type (yellow), Class II (blue), and Class III (cyan) YSOs taken from Tsitali et al. (2010). The SCUBA sources from Visser et al. (2002) are marked by magenta: SMM7 is a starless core, whereas SMM1 and SMM2 are protostars that coincide with IRAS 19180+1116 and IRAS 19180+1114. |
It may be instructive to compare our VLSR values with those measured with the same telescope and beam size in 1977–1981 (Ungerechts & Güsten 1984). In total, we have 29 overlapping positions shown in Fig. 6. The calculated differences ΔV = V1981 − V2011 are marked by dots with 3σ error bars. The red points indicate deviations from zero that are larger than 3σ. At two positions, (Δα,Δδ) = (80′′,0′′) and (160′′, − 120′′), we detected double NH3 profiles. Among these 29 positions, significant deviations from zero are revealed at six offsets, but other points show no variations over this timescale. The ammonia line splitting was not seen at (80′′,0′′) in 1981, although the linewidth was Δv1981 = 0.85 ± 0.20 km s-1, which is comparable to that given in Table B.3. However, at (160′′, − 120′′) the linewidth was Δv1981 = 1.68 ± 0.17 km s-1, i.e., two times larger than the value from Table B.3. We note that the weighted mean of the linewidth at the overlapping positions is ⟨ Δv ⟩ 1981 = 0.93 km s-1, and the dispersion of the sample is σΔv = 0.18 km s-1. The enhanced Δv(NH3) at (160′′, − 120′′) observed 30 years ago was probably caused by the unresolved structure of the ammonia lines. The highest deviation ΔVLSR ~ 1 km s-1 (Fig. 6) constrains the gas acceleration in an outflow at the level of 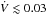 km s-1 yr-1. This means that the high-velocity ammonia emission up to ~30–40 km s-1 from the line center, observed, for example, in FIRS 1 (Curiel et al. 1996), could be reached in a period of ~1000 yr. This is comparable to the typical timescale of 103 yr – a scale for the episodic ejection of material from protostars (e.g., Ioannidis & Froebrich 2012). The mass of the protostar should be ≲0.3 M⊙, to eject the gas clump at the 40 AU radius with an acceleration of
km s-1 yr-1. This means that the high-velocity ammonia emission up to ~30–40 km s-1 from the line center, observed, for example, in FIRS 1 (Curiel et al. 1996), could be reached in a period of ~1000 yr. This is comparable to the typical timescale of 103 yr – a scale for the episodic ejection of material from protostars (e.g., Ioannidis & Froebrich 2012). The mass of the protostar should be ≲0.3 M⊙, to eject the gas clump at the 40 AU radius with an acceleration of 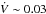 km s-1 yr-1.
km s-1 yr-1.
3.5. Dobashi 321 P2 (Do321 P2)
The source Dobashi 321 P2 (Do321P2, for short) is a filamentary dark cloud with the opacity class 6 according to Lynds (1962). The cloud is known under the names L673 (Lynds 1962), BDN 46.22-1.34 (Bernes 1977), or P77 (Parker 1988). Do321P2 was observed in ammonia lines by Anglada et al. (1997) and Tobin et al. (2011).
Our NH3 observations are shown in Fig. 7. The ammonia structure consists of five main subcondensations. Their reference positions are listed in Table 1. The brightest α and β peaks with TMB ~ 3 K are located near the sources IRAS 19180+1114 (SMM2) and IRAS 19180+1116 (SMM1). The ammonia peak detected by Anglada et al. has an offset (− 123′′,83′′) and is resolved into two clumps α and β in our observations (see Fig. 7). We also detected three weaker ammonia clumps γ, δ, and ε with TMB ~ 1.7,1.6, and 1.3 K. The γ and ε condensations, localized within the confines of the older map of Anglada et al. (1997), peak near the source IRAS 19181+1112, whereas the δ clump was not resolved by Anglada et al. (1977) because the angular resolution was too coarse.
Interferometric observations of a small region around SMM2 (~100′′ × 100′′) in lines of N2H+ and NH3 (Tobin et al. 2011; see Fig. 14) show a substantial amount of extended ammonia emission that closely traces the spacial distribution of N2H+. The measured NH3 radial velocity VLSR = 6.93 km s-1, the linewidth Δv = 0.50 km s-1, and the column density N(NH3) = 7.2 × 1014 cm-2 (Table 8 in Tobin et al.) agree well with our values for the α peak (Table 1): VLSR = 6.88 km s-1, Δv = 0.49 km s-1, and N(NH3) = 6 × 1014 cm-2. However, the estimates of the excitation temperature at this position contradict sharply: Tex = 33.3 K (Tobin et al.) and 6.8 K (our value from Table B.1). We detected NH3(1, 1) and (2, 2) at the α and β peaks (Fig. B.5). Their profiles are well described by a single-component model (red lines in Fig. B.5, model parameters are given in Table B.1). Both spectra show the same Tex, which is also consistent with the values measured in other dense molecular cores (see Tables B.2–B.4).
The NH3 velocity map (Fig. 7b) shows an irregular structure with distinct pockets of redshifted and blueshifted ammonia emission around the clusters of YSOs at the positions of SMM1 and SMM2 (Fig. 7c). The observed kinematics are caused by large-scale motions in this star-forming region that cannot be interpreted unambiguously.
The apparent diameters (beam-deconvolved) of the two NH3 condensations dα = 60′′ and dβ = 40′′ and the gas densities listed in Table B.1 allow us to estimate the masses of these clumps assuming spherical geometry: Mα ~ 0.3 M⊙, and Mβ ~ 0.1 M⊙. The relative ammonia abundance in both clumps is [NH3]/[H2] ~2 × 10-7. The corresponding virial masses of these clumps are considerably larger (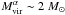 , and
, and 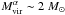 ) and are probably affected by the masses of YSOs embedded in the cloud.
) and are probably affected by the masses of YSOs embedded in the cloud.
3.6. Kawamura 05 (Ka05)
The source Kawamura 05 (Ka05, for short) is a Bok globule of the opacity class 6 (Lynds 1962). The cloud is known as B335 (Barnard 1927), L663 (Lynds 1962), or CB199 (Clemens & Barvainis 1988). Because it is the prototype of an isolated, star-forming dark cloud, B335 has been studied at many wavelengths.
Single-pointing ammonia observations toward B335 were carried out by Ho et al. (1977, 1978), Myers & Benson (1983), Benson & Myers (1989), and Levshakov et al. (2010). The first mapping of this core in the NH3(1, 1) and (2, 2) lines with the Effelsberg telescope revealed an elongated N-S structure (Menten et al. 1984, M 84 herein). The kinetic temperature measured at the four positions where the NH3(2, 2) line was observed is uniformly distributed across the core region, Tkin = 10–12 K.
We mapped the core Ka05 at nine offsets around the reference point α(J2000) = 19:37:01.3, δ(J2000) = +07:34:29.6, which is shifted off the center position in M 84 at (Δα,Δδ) = ( − 24.0′′, − 42.8′′). The results of our observations are shown in Fig. 8. Two positions (0′′,0′′) and (0′′, − 40′′) with TMB = 2.5 K and 2.1 K (Table 1) coincide with the offsets (20′′,40′′) with TMB = 3.4 K and (20′′,0′′) with TMB = 2.8 K in M 84. In between these positions, at (20′′,20′′), the brightness temperature was even higher, TMB = 4.1 K (M 84), but we did not observe this point with our larger step size of 40′′, nor the point (20′′,60′′) where TMB = 3.1 K. However, we measured NH3(1, 1) at (0′′,40′′) with TMB = 0.6 K, which corresponds to the point (20′′,80′′) not listed in Table 1 in M 84. The opposite marginal point (20′′, − 20′′) along the cut Δα = 20′′ in M 84 has TMB = 0.8 K. This indicates sharp drops of the brightness temperature at the edges of the disk-like envelope that surrounds the protostar.
 |
Fig. 8 a) Same as Fig. 1a but for the source Ka05. The contour levels start at 0.4 K km s-1 and increments are 1.0 K km s-1. The square indicates the position of the far-infrared source IRAS 19345+0727 coinciding with the 3.6 cm continuum source (Anglada et al. 1992). b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 8.390 km s-1. The intensity peak is labeled as in Table 1. |
The spectra with the measured (1, 1) and (2, 2) lines are shown in Fig. B.6. The radial velocities at two offsets (0′′,0′′) and (0′′, −40′′) are unchanged since 1982/83 (cf. Fig. 6, Sect. 3.4, where velocity shifts at some positions in the map of Do279P12 were detected for the same three decades). The linewidths (Table B.1) are also consistent with M 84. At these offsets, the measured kinetic temperatures, excitation temperatures, total optical depths, and column densities are in line with M 84.
The NH3(1, 1) velocity map is shown in Fig. 8b. The velocity distribution resembles a rigid-body rotation with the tangential velocity increasing from ≈− 0.040 km s-1 (NE) to ≈+ 0.040 km s-1 (SW) at cloud flanks. The radius of the NH3 disk-like envelope is about 40′′, which agrees with our and the M 84 maps. The distance to B335 was recently redetermined to be only D = 90 − 120 pc (Olofsson & Olofsson 2009). This gives us a radius r ~ 0.02 pc, and an angular velocity 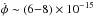 s-1 (β ≲ 0.001), which is close to the value of M 84,
s-1 (β ≲ 0.001), which is close to the value of M 84, 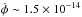 s-1. The corresponding stability parameter β′ ≈ 2 × 10-4. With the apparent diameter d ~ 0.04 pc, the relative abundance ratio is [NH3]/[H2] ~ 4 × 10-7.
s-1. The corresponding stability parameter β′ ≈ 2 × 10-4. With the apparent diameter d ~ 0.04 pc, the relative abundance ratio is [NH3]/[H2] ~ 4 × 10-7.
To compare our estimates with previous estimates of the mass of the gas that generates ammonia emission, we assumed spherical geometry and for the gas density nH2 ~ 2 × 104 cm-3 (Table B.1) obtained M ~ 0.05 M⊙ – 40 times lower than the value reported by Benson & Myers (1989), who used a core radius R = 0.11 pc (D = 250 pc) and a gas density nH2 ~ 6 × 103 cm-3.
If the centrifugal forces prevent the disk-like structure from collapse, then the mass of the center source is given within a factor of 2 by (e.g., Frerking & Langer 1982) 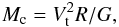 (6)where R is the distance of the material from the source and G is the gravitational constant. For Vt = 0.040 km s-1, this gives Mc ~ 0.03 M⊙. This estimate indicates that Ka05 is a low-mass protostellar source, which agrees with the measurement of the central source mass Mc ~ 0.04 M⊙ from SMA observations of the C18O(2–1) emission (Yen et al. 2010).
(6)where R is the distance of the material from the source and G is the gravitational constant. For Vt = 0.040 km s-1, this gives Mc ~ 0.03 M⊙. This estimate indicates that Ka05 is a low-mass protostellar source, which agrees with the measurement of the central source mass Mc ~ 0.04 M⊙ from SMA observations of the C18O(2–1) emission (Yen et al. 2010).
3.7. Dobashi 279 P7 (Do279 P7)
The dense molecular cloud Dobashi 279 P7 (Do279P7, for short) is the next example of a starless core from our list. This is a newly discovered dense clump that is little studied so far. No embedded IRAS sources or pre-main-sequence stars are known within 80′′ off the core center. The NH3(1, 1) intensity distribution shown in Fig. 9 has approximately circular symmetry. The half-power dimension of the core is 80′′ × 80′′, or, correcting for our beam, 70′′ × 70′′, i.e., the source is resolved in both right ascension and declination. Assuming a distance to the source of D ≈ 203 pc (see Sect. 1), its radius is about 0.03 pc. The parameters for the density peak at (− 80′′,40′′) are given in Table 1. The NH3 spectra are shown in Fig. B.7. We detected the (2, 2) transition at four positions, which allowed us to estimate Trot = 11.5 − 13.5 K and Tkin = 12.4 − 14.9 (Table B.1). These values slightly exceed the temperatures measured in the starless core Ka01, but the linewidths in Do279P7 are significantly larger than the linewidths in Ka01 and Do279P8 – another starless core but without detected (2, 2) transition (see Table B.1). The wider lines in Do279P7 indicate a higher level of turbulence in this core with the ratio of turbulent to thermal velocity dispersion of Δvturb/Δvth ≈ 5. The profiles of the NH3(1, 1) hfs components do not show any blueward or redward asymmetry that would indicate contracting or expanding motions. However, the NH3 intensity map shows a filament-like structure in the S-E direction (PA ≈ 135°) with VLSR ~ 0.8 km s-1 (Fig. 9).
The core exhibits a linear velocity gradient from the southern (VLSR ~ 0.0 km s-1) to the northern edge (VLSR ~ − 0.8 km s-1) that can be interpreted as rigid-body rotation around the axis Δδ ≈ 20′′, PA ≈ 90° (Fig. 9b). The measured tangential velocity of ± 0.4 km s-1 at r ≈ 0.03 pc leads to an angular velocity of 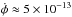 s-1. With nH2 ~ 1 × 104 cm-3 (Table B.1) and assuming spherical geometry, one obtains a core mass of M ~ 0.2 M⊙. The estimates of the angular velocity and the gas density give β ~ 6, which shows that the rotation energy is higher than or comparable to the gravitational energy of this starless core. The parameter β′ ≈ 0.3 is also rather high compared with other isolated cores Ka01, Do279P8, and Ka05, where β′ ≪ 1. The measured column density N ~ 6 × 1014 cm-2 and the linear size d ~ 0.06 pc indicate a relative ammonia abundance of [NH3]/[H2] ~ 3 × 10-7.
s-1. With nH2 ~ 1 × 104 cm-3 (Table B.1) and assuming spherical geometry, one obtains a core mass of M ~ 0.2 M⊙. The estimates of the angular velocity and the gas density give β ~ 6, which shows that the rotation energy is higher than or comparable to the gravitational energy of this starless core. The parameter β′ ≈ 0.3 is also rather high compared with other isolated cores Ka01, Do279P8, and Ka05, where β′ ≪ 1. The measured column density N ~ 6 × 1014 cm-2 and the linear size d ~ 0.06 pc indicate a relative ammonia abundance of [NH3]/[H2] ~ 3 × 10-7.
3.8. Serpens South 3 (SS3)
The source Serpens South 3 (SS3, for short) is a dense core located in an active star-forming region discovered by Gutermuth et al. (2008) in Spitzer IRAC mid-infrared imaging of the Serpens-Aquila rift. The central part of this region, near α = 18h30m03s, δ = −02°01′58.2′′ (J2000), which is called Serpens South, is composed of 37 Class I and 11 Class II sources at high mean surface density (>430 pc-2) and short median nearest-neighbor spacing (0.02 pc). The overall structure of the star-forming region exhibits a typical filamentary dense gas distribution elongated for about 14′ in the NW-SE direction.
For the first time, we mapped the core SS3 in the NH3(1, 1) and (2, 2) lines around the reference point α = 18h29m57.1s, δ = −02°00′10.0′′ (J2000) in the area Δα × Δδ = 160′′ × 360′′ (Fig. 10). The nominal center of the NH3 map is shifted by 2′29′′ (PA ≈ − 40°) with respect to the center of box 1 in the CO map of Nakamura et al. (2011, N11) and coincides with the intensity peak of the CO outflow lobe marked by R2 in N11. The angular size of the CO lobe within the 15 K km s-1 contour is about 70′′ × 60′′ (Figs. 9 and 15 in N11), and the whole region lies in the lowest NH3 intensity “valley” running in E–W direction along the cut Δδ = 0′′ in Fig. 10. To the south of this valley, at Δδ ≈ − 140′′, an intensity peak of NH3 (α peak in Table 1 and Fig. 10b) occurs at the northern part of another CO outflow lobe marked R3 in N11. These two redshifted lobes R2 and R3 appear to have the blueshifted counterparts B1 and B4 originating from a compact 3 mm source – a deeply embedded, extremely young Class 0 protostar (N11). It is interesting to note that the configuration of the NH3 valley just follows the lowest dust emission distribution on the 1.1 mm continuum image of this area shown in Fig. 15b in N11. To the north and south of the valley there are regions of relatively strong 1.1 mm emission, which are correlated with strong NH3 emission. The three NH3 peaks α,β, and γ listed in Table 1 and labeled in Fig. 10b have very high brightness temperatures TMB = 5.0, 3.1, and 3.0 K.
 |
Fig. 9 a) Same as Fig. 1a but for the source Do279P7. The contour levels start at 0.3 K km s-1 and increments are 0.6 K km s-1. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 6.715 km s-1. The intensity peak is labeled as in Table 1. |
Examples of the observed NH3(1, 1) and (2, 2) spectra are shown in Fig. B.8. Here again, as for the core Do279P12, we find split NH3 profiles. The apparent asymmetry of the ammonia lines is observed in optically thin hf components and, thus, cannot be due to radiative transfer effects (self-absorption). The components A and B, detected at two offsets (see Table B.4), have radial velocities of ⟨ VA ⟩ = 7.865 ± 0.005 km s-1 and ⟨ VB ⟩ = 6.856 ± 0.010 km s-1. The map of the velocity field is shown in Fig. 10b, where the positions of the split NH3 profiles are labeled by the white crosses. The closest Class 0 protostar to these positions is the MAMBO mm source MM10 (Maury et al. 2011) marked by the yellow circle in Fig. 10c at the offset (38′′, − 53′′). However, since the whole region is very complex, it is not clear which source drives this presumably bipolar molecular outflow that causes the observed splitting of the NH3 profiles.
 |
Fig. 10 a) Same as Fig. 1a but for the source SS3. The contour levels start at 0.0 K km s-1 and increments are 2.0 K km s-1. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 7.542 km s-1. The white crosses mark offsets where the splitting of the NH3 profiles is detected (see Fig. B.8). The mean radial velocities of the components A and B are ⟨ VA ⟩ = 7.865 ± 0.005 km s-1 and ⟨ VB ⟩ = 6.856 ± 0.010 km s-1. The intensity peaks are labeled as in Table 1. c) NH3 intensity map as in panel a) and positions of the MAMBO millimeter sources taken from Table 1 in Maury et al. (2011). Red and yellow open circles mark starless and YSO candidates, respectively. |
The measured linewidths listed in Table B.4 show that the values Δv ≳ 0.8 km s-1 are symmetrically distributed around the positions of the split NH3 profiles in the E–W strip of about 120′′ width, cut by the vertical edges of our map. The strip of enhanced linewidths (see Fig. B.12) may be associated with the E–W bipolar outflow, thus giving rise to the local redshifted and blueshifted patches of the velocity map shown in Fig. 10b.
Table B.4 shows that the values of the measured parameters fluctuate considerably from one position to another. Namely, the excitation temperature ranges from 3.3 K to 8.4 K, Trot – from 8.6 K to 14.8 K, Tkin – from 8.9 K to 16.8 K, the gas density nH2 – from 0.3 × 104 cm-3 to 4.2 × 104 cm-3, the total optical depth τ11 – from 1.5 to 20.0, and the column density N(NH3) – from 0.2 × 1015 cm-2 to 2.8 × 1015 cm-2. The highest gas density of nH2 ~ 4.2 × 104 cm-3 was measured at two positions where we observed the split NH3 lines profiles. The highest optical depths with 13.2 ≲ τ11 ≲ 20.0 are localized along the N–S cut Δα = 0′′ between Δδ = 80′′ and 200′′, which passes through the γ and β peaks in the region where three starless core candidates (red circles in Fig. 10c) were detected by Maury et al. (2011). The highest (16.6 K and 16.8 K) and lowest (8.9 K) kinetic temperatures are observed along the N−S cut at Δα = 80′′. The lowest kinetic temperature correlates with the lowest brightness temperature, TMB = 0.5 K, whereas TMB = 1.2 K at Tkin = 16.8 K (the foot of the α peak) and TMB = 5.0 K at Tkin = 16.6 K (the top of the α peak). This gradient of Tkin (8.9 − 16.8 K) is probably due to the two YSOs at the top and foot of the α peak shown in Fig. 10b.
3.9. Dobashi 243 P2, 279 P18, 279 P13, and 321 P1
The sources Do243P2, Do279P18, Do243P13, and Do321P1 (Table 1) were observed at their central positions and at 40′′ offsets toward the four cardinal directions. Only a weak NH3(1, 1) emission (TMB ≲ 1 K) is seen toward each of them. The corresponding spectra are depicted in Fig. B.9. For Do321P1, two possible detections of the ammonia emission are shown at the bottom panels, but the noise is high and the identification of the NH3(1, 1) line is not certain. The measured radial velocity of VLSR = 13.5 km s-1 for Do321P1 is somewhat higher than that measured for the other sources from Table 1, for which VLSR ranges between 6.0 km s-1 and 9.6 km s-1, but the 12CO(1–0) 115.3 GHz, 13CO(1–0) 110.2 GHz, and C18O(1–0) 109.8 GHz emission lines were also detected at VLSR ~ 13 km s-1 with the Delingha 14-m telescope (Wang, priv. comm.).
No submillimeter-continuum sources have been found within 2′ off the core centers of Do279P18, Do243P13, and Do321P1, but a SCUBA point-like source J180447.8-043208 (Di Francesco et al. 2008) lies in the field of Do243P2 at the angular distance θ = 41′′, PA = −30° from the nominal center (0′′,0′′).
3.10. Sources without detected NH3 emission
A list of 37 targets from our dataset with undetected NH3 emission is presented in Table 2. Columns 3 and 7 give the noise level per channel width of 0.077 km s-1 on a TMB scale and the mapped area. In the fields of some targets we found the following objects:
Do279P21: a point-like infrared source IRAS 18191-0310 (Cutri et al. 2003) at θ = 80′′, PA = −174°.
Do279P17: a point-like infrared source IRAS 18351+0010 (Cutri et al. 2003) at θ = 17′′, PA = 74°.
Do296P3: a point-like submillimeter-continuum source J185121.1-041714 (Di Francesco et al. 2008) at θ = 29′′, PA = −173°.
Ka15: a galaxy gJ194852.5-103056 (Skrutskie et al. 2006) at θ = 64′′, PA = 99°.
Ka17: a point-like infrared IRAS 19470-0630 (Porras et al. 2003) at θ = 57′′, PA = 162°.
4. Summary
We have used the Effelsberg 100-m telescope to observe the NH3(1, 1) and (2, 2) spectral lines in high-density molecular cores. The targets were preliminarily selected from the CO and 13CO survey of the Aquila rift cloud complex carried out with the Delingha 14-m telescope. We measured a minimum grid of five positions with 40′′ spacing centered upon the (0′′,0′′) position determined from the highest intensity of the CO maps. We mapped a larger area for sources where ammonia emission was detected to delineate the spatial distribution of NH3.
In total, we mapped the first 49 CO sources (from ~150 targets) and detected 12 NH3 emitters which amounts to overall detection rate of ~24 per cent, which is 3 times lower compared to the Pipe Nebula, which was observed with the GBT 100-m telescope (Rathborne et al. 2008) and which is not too far from the clouds studied here (see Sect. 1). The NH3 sources in our sample represent diverse populations of molecular clouds from isolated and homogeneous starless cores with suppressed turbulence to star formation regions with complex intrinsic motion and gas density fluctuations.
The starless cores Ka01, Do279P8, Do279P7, Do279P18, Do243P13, and a candidate – the clump εDo279P6 – have radial velocities VLSR ranging from 6.0 km s-1 to 9.6 km s-1 with the mean ⟨VLSR⟩ = 8.1 km s-1, and dispersion σ = 1.2 km s-1. The only starless core with VLSR beyond the 3σ interval around the mean is Do321P1, for which VLSR = 13.5 km s-1. Three cores – Ka01, Do279P8, and the clump εDo279P6 – demonstrate rather narrow linewidths, Δv ≲ 0.4 km s-1, whereas the others have Δv ~ 0.5 − 1 km s-1. The masses of the starless cores do not exceed a solar mass and are typically (0.1 − 0.5) M⊙, except for the cores εDo279P6, Do279P8, and Ka05, for which M < 0.1 M⊙. The measured ammonia abundance, X = [NH3]/[H2], ranges between 1 × 10-7 and 5 × 10-7 with the mean ⟨ X ⟩ = (2.7 ± 0.6) × 10-7.
For three cores – Ka01, Do279P8, and Ka05 – we measured low angular velocities (parameters β and β′ ≪ 1) and their rotation energies are lower than the gravitational energy, but Do279P7 – a fast rotator – yields a rotational energy comparable to the gravitational energy (β ≈ 6 and β′ ≈ 0.3). It also has a high ratio of the turbulent to thermal velocity.
Two isolated star-forming cores, Ka05 and Do243P2, were observed. The cores’ radial velocities are VLSR = 8.4 km s-1 and 7.0 km s-1, respectively, and therefore both of them belong to the same group of cores with VLSR ~ 8 km s-1. For the former core, we estimated a sub-solar mass and thus confirm that Ka05 is a low-mass protostellar source. Both cores exhibit narrow linewidths, Δv ~ 0.3 km s-1.
The most intense ammonia emission was observed toward four clouds with complex gas density and velocity structures that harbor numerous YSOs: Do279P6, Do279P12, Do321P2, and SS3. Each of them consists of a number of clumps with different angular sizes. The ⟨VLSR⟩ values show that the complex clouds have the same radial velocities as the starless cores and isolated star-forming clouds from our dataset. Only one cloud –Do279P12 – where the bulk motions dispersion has a comparable to the ammonia linewidths. The internal bulk motions in the other three clouds are less pronounced and show lower dispersions than the NH3 linewidths.
Kinematically split NH3 profiles were detected in Do279P12 and SS3. The velocity splitting is ~1 km s-1. In the former object, the splitting is most probably caused by bipolar molecular outflows observed in other molecular lines. This object has been observed in ammonia lines with the Effelsberg telescope three decades ago. We compared these observations with the current spectra and found velocity shifts at some positions that correspond to an acceleration of the gas flow of 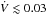 km s-1 yr-1.
km s-1 yr-1.
The measured kinetic temperatures lie between 9 K and 12 K for the starless and isolated star-forming sources, except for the fast rotator Do279P7, where Tkin ranges between 12 K and 15 K. An increased value of Tkin in this case may be due to magnetic energy dissipation since magnetic and non-thermal energy densities may be nearly equal in Do279P7: for n = 1.1 × 104 cm-3, v = 0.4 km s-1, and assuming B ~ 20 μG3 we obtained B2/8π ≈ ρv2/2 ~ 2 × 10-11 dyn cm-2. However, to what extent the magnetic energy dissipation contributes to the gas heating requires additional investigations.
For the complex filamentary dark clouds, Tkin varies between 9 K and 18 K and strongly fluctuates from point to point. We found no simple relationship between gas density and kinetic temperature. High-density condensations in the filamentary dark clouds have a broad range of temperatures, most probably determined by radiation from embedded stars and dust.
For the beam filling factor η = 1, we estimated the excitation temperature of an inversion doublet, the ammonia column densities, and H2 densities for those clouds where both the (1, 1) and (2, 2) transitions were detected. The typical values of Tex lie between 3 K and 8 K, the total NH3 column densities between 0.3 × 1015 cm-2 and 3 × 1015 cm-2, and H2 volume densities between 0.3 × 104 cm-3 and 4.2 × 104 cm-3.
The study of Aquila dense cores will be continued, with the remaining ~100 targets scheduled for observations at the Effelsberg 100-m telescope in 2013.
Online material
Molecular cores toward Aquila targets without detected NH3 emission in the (1, 1) and (2, 2) inversion transitions.
Appendix A: Analysis of NH3(1, 1) and (2, 2) spectra
In this appendix we discuss the methods used for calculating physical parameters from observations of the ammonia NH3 (J,K) = (1, 1) and (2, 2) transitions. We give a consistent summary of the basic formulae relevant to the study of cold molecular cores.
The recorded NH3 spectra were first converted into the TMB scale and a baseline was removed from each of them. The baseline was typically linear in the range covered by the ammonia hyperfine (hf) structure lines, but occasionally it was quadratic. After that the spectra of the same offset were co-added with weights inversely proportional to the mean variance of the noise per channel, rms-2, estimated from the channels without emission.
The NH3 spectra were fitted to determine the total optical depth τtot in the respective inversion transition, the LSR velocity of the line VLSR, the intrinsic full-width at half power linewidth Δv for an individual hf component, and the amplitude, 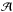 (e.g., Ungerechts et al. 1980):
(e.g., Ungerechts et al. 1980): ![\appendix \setcounter{section}{1} \begin{eqnarray} T(v) = {\cal A} \left[1 - {\rm e}^{-\tau(v)} \right]. \label{Eq1} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20354-12/aa20354-12-eq383.png) (A.1)The optical depth τ(v) at a given radial velocity v is defined by
(A.1)The optical depth τ(v) at a given radial velocity v is defined by ![\appendix \setcounter{section}{1} \begin{eqnarray} \tau(v) = \tau_{\rm tot} \sum^n_{i=1} r_i \exp \left\{ -2.77 \left[(v - V_{\rm LSR}) + v_i \right]^2 / (\Delta v)^2 \right\}. \label{Eq2} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20354-12/aa20354-12-eq385.png) (A.2)In this equation, the sum runs over the n hf components of the inversion transition (n = 18 and 21 for the NH3(1, 1) and (2, 2) inversion transitions), ri is the theoretical relative intensity of the ith hf line and vi is its velocity separation from the fiducial frequency. The values of these parameters are given in, e.g., Kukolich (1967) and Rydbeck et al. (1977).
(A.2)In this equation, the sum runs over the n hf components of the inversion transition (n = 18 and 21 for the NH3(1, 1) and (2, 2) inversion transitions), ri is the theoretical relative intensity of the ith hf line and vi is its velocity separation from the fiducial frequency. The values of these parameters are given in, e.g., Kukolich (1967) and Rydbeck et al. (1977).
In Eq.(A.2), the total optical depth τtot is the maximum optical depth that an unsplit (1, 1) or (2, 2) line would have at the central frequency if the hf levels were populated at the same excitation temperature for the two lines (1, 1) and (2, 2). Assuming that the line profile function has a Gaussian shape with width Δv (FWHM) and taking into account that the statistical weights of the upper and lower levels of an inversion transition are equal, one obtains 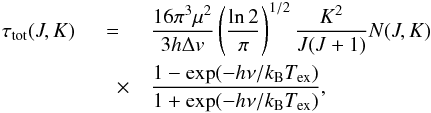 (A.3)where h and kB are Planck and Boltzmann constants, μ is the dipole moment, | μ | = 1.4719 Debye (JPL catalog4), N(J,K) is the inversion state column density – the sum of the column densities of the upper and lower levels of an inversion doublet, ν is the rest frequency of the inversion transition, and Tex is the excitation temperature that characterizes the NH3 population across the (J,K) inversion doublet.
(A.3)where h and kB are Planck and Boltzmann constants, μ is the dipole moment, | μ | = 1.4719 Debye (JPL catalog4), N(J,K) is the inversion state column density – the sum of the column densities of the upper and lower levels of an inversion doublet, ν is the rest frequency of the inversion transition, and Tex is the excitation temperature that characterizes the NH3 population across the (J,K) inversion doublet.
In Eq. (A.1), the amplitude 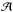 can be expressed in terms of the beam filling factor, η = Ωcloud/Ωbeam (solid angle Ω = πθ2/(4ln2), where θ is the angular diameter at FWHP), and the excitation temperature, Tex, as
can be expressed in terms of the beam filling factor, η = Ωcloud/Ωbeam (solid angle Ω = πθ2/(4ln2), where θ is the angular diameter at FWHP), and the excitation temperature, Tex, as ![\appendix \setcounter{section}{1} \begin{eqnarray} {\cal A} = \eta \left[ J_\nu(T_{\rm ex}) - J_\nu(T_{\rm bg}) \right], \label{Eq4} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20354-12/aa20354-12-eq403.png) (A.4)where Tbg = 2.7 K is the black-body background radiation temperature, and Jν(T) is defined by
(A.4)where Tbg = 2.7 K is the black-body background radiation temperature, and Jν(T) is defined by 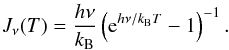 (A.5)For optically thin lines (e.g., τ11 ≪ 1), Eq. (A.1) degenerates into
(A.5)For optically thin lines (e.g., τ11 ≪ 1), Eq. (A.1) degenerates into ![\appendix \setcounter{section}{1} \begin{eqnarray} T(v) & =& {\cal A}\cdot\tau(v) \nonumber\\ & =& ({\cal A}\tau_{11}) \cdot \sum^n_{i=1} r_i \exp \left[ -2.77 (\Delta V_i / \Delta v)^2 \right], \label{Eq7} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20354-12/aa20354-12-eq408.png) (A.6)and it is not possible to determine
(A.6)and it is not possible to determine 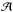 and τ11 separately. Here ΔVi = v − VLSR + vi.
and τ11 separately. Here ΔVi = v − VLSR + vi.
For some molecular cores we observe two-component NH3 profiles. The line parameters 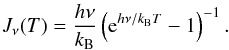 for the j = 1 and j = 2 components were determined in this case by fitting the function
for the j = 1 and j = 2 components were determined in this case by fitting the function 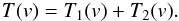 (A.7)This linear form assumes that two clouds in the beam have the same filling factor η and the same Tex for the lines (1, 1) and (2, 2).
(A.7)This linear form assumes that two clouds in the beam have the same filling factor η and the same Tex for the lines (1, 1) and (2, 2).
At low spectral resolutions, when the channel spacing Δch is near to the linewidth Δv, the derived line parameters are affected by the channel profile φ(v). In this case, the recorded spectrum, T′(v), was considered as a convolution of the true spectrum T(v) and φ(v) 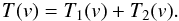 (A.8)We approximate φ(v) by a Gaussian function with the width FWHM defined by a particular back-end setting.
(A.8)We approximate φ(v) by a Gaussian function with the width FWHM defined by a particular back-end setting.
The calculated synthetic spectrum, which is defined as Tsyn(v) ≡ T(v) if Δch ≪ Δv, or Tsyn(v) ≡ T′(v) if Δch ~ Δv, was fitted to the observed spectrum Tobs(v) by minimizing the χ2 function ![\appendix \setcounter{section}{1} \begin{eqnarray} \chi^2 = \sum\, \left[ T_{\rm syn}(v) - T_{\rm obs}(v) \right]^2/{\rm rms}^2 \label{Eq10} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20354-12/aa20354-12-eq423.png) (A.9)in the five-dimensional space of the following model parameters:
(A.9)in the five-dimensional space of the following model parameters: 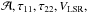 and Δv. Attempting to exclude at the 3σ level all noise-only channels in between the hf lines, the sum runs over the channels with observed NH3 emission from all hf components. The minimum of χ2 was computed using the simplex method (e.g., Press et al. 1992).
and Δv. Attempting to exclude at the 3σ level all noise-only channels in between the hf lines, the sum runs over the channels with observed NH3 emission from all hf components. The minimum of χ2 was computed using the simplex method (e.g., Press et al. 1992).
Equation (A.9) was also used to estimate the formal errors of the model parameters by calculating the covariance matrix at the minimum of χ2. Since the uncertainty in the amplitude scale calibration was ~15–20% (Sect. 2), and there were no noticeable correlations between the sequential channels in our datasets, we did not correct the calculated errors by an additional factor as described, e.g., in Rosolowsky et al. (2008).
Given the estimate of the amplitude 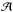 , the excitation temperature Tex can be calculated from Eq. (A.4)
, the excitation temperature Tex can be calculated from Eq. (A.4) ![\appendix \setcounter{section}{1} \begin{eqnarray} T_{\rm ex} = \frac{ T_0 } { \ln \left[ 1 + T_0 \eta / ( {\cal A} + \eta J_{\rm bg} ) \right] }, \label{Eq11} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20354-12/aa20354-12-eq426.png) (A.10)where T0 = hν/kB, and Jbg = Jν(Tbg). At Tbg = 2.725 K and NH3-inversion frequencies, we have Jbg = 2.20 K and T0 = 1.14 K.
(A.10)where T0 = hν/kB, and Jbg = Jν(Tbg). At Tbg = 2.725 K and NH3-inversion frequencies, we have Jbg = 2.20 K and T0 = 1.14 K.
In this equation the only unknown parameter is the filling factor η. If the source is completely resolved, then η = 1. Otherwise, Eq. (A.10) gives a lower bound on Tex corresponding to η = 1, whereas decreasing η drives Tex toward its upper bound at Tex = Tkin, which holds for LTE. For emission lines, the radiation temperature within the line is higher than the 2.7 K background and the excitation may be either radiative or collisional. At gas densities higher than the critical density5 and for optically thin lines, the local density of line photons is negligible compared to the background radiation field, and the lower metastable states in NH3 are mainly populated via collisions with molecular hydrogen6, i.e., the stimulated emission can be neglected. For low collisional excitation, ngas < ncr, the line radiation controls Tex for both optically thin and thick regimes (Kegel 1976). NH3(1, 1) emission usually arises from regions with ngas ≳ 104 cm-3 (e.g., Ho & Townes 1983). This means that the regime of low collisional excitation does not dominate. We also did not consider anomalous excitation (maser emission) that leads to Tex ≫ Tbg because masing is not observed in our data sample. Thus, using Tex = Tkin as a formal upper limit for the excitation temperature is legitimate. With this we can restrict the unknown filling factor for an unresolved source in the interval 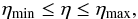 (A.11)and Tex within the boundaries
(A.11)and Tex within the boundaries 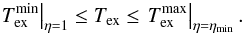 (A.12)From a separate analysis of the (1, 1) and (2, 2) lines with low noise level, we found that the two amplitudes
(A.12)From a separate analysis of the (1, 1) and (2, 2) lines with low noise level, we found that the two amplitudes 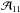 and
and 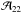 are equal within the observational errors, which implies that Tex(1, 1) ≈ Tex(2, 2). Albeit radiative transfer calculations show that the excitation temperatures Tex(1, 1) and Tex(2, 2) may differ by about 20% (Stutzki & Winnewisser 1985), assuming that they are equivalent seems to be sufficient in our case.
are equal within the observational errors, which implies that Tex(1, 1) ≈ Tex(2, 2). Albeit radiative transfer calculations show that the excitation temperatures Tex(1, 1) and Tex(2, 2) may differ by about 20% (Stutzki & Winnewisser 1985), assuming that they are equivalent seems to be sufficient in our case.
The second temperature, which describes the NH3 population, is the rotational temperature Trot, which characterizes the population of energy levels with different (J,K). As mentioned above, the population of the lower metastable inversion doublets is determined by collisions with H2 and, thus, is regulated by the kinetic temperature Tkin. The population ratio between the (1, 1) and (2, 2) states is defined as 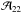 (A.13)Assuming that both transitions trace the same volume of gas and their linewidths Δv are equal, one finds from Eqs. (A.3) and (A.13) that
(A.13)Assuming that both transitions trace the same volume of gas and their linewidths Δv are equal, one finds from Eqs. (A.3) and (A.13) that 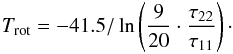 (A.14)We note that since radiative transitions between the different K-ladders of the (J,K) levels are forbidden and because the unknown filling factor η is canceled in the line intensity ratio of the NH3 (1, 1) and (2, 2) transitions, the estimate of the rotational temperature is more reliable than the excitation temperature.
(A.14)We note that since radiative transitions between the different K-ladders of the (J,K) levels are forbidden and because the unknown filling factor η is canceled in the line intensity ratio of the NH3 (1, 1) and (2, 2) transitions, the estimate of the rotational temperature is more reliable than the excitation temperature.
For a two-level system with a lower kinetic temperature than the energy gap between the (1, 1) and (2, 2) states (ΔE12 = 41.5 K), the rotational temperature can be related to the kinetic temperature through detailed balance arguments (e.g., Ragan et al. 2011): ![\appendix \setcounter{section}{1} \begin{eqnarray} T_{\rm kin} = T_{\rm rot} / \left[ 1 - \frac{ T_{\rm rot} }{ \Delta E_{12} }\cdot \ln \left(1 + 1.1\ {\rm e}^{-15.7/T_{\rm rot}}\right)\right]. \label{Eq18} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20354-12/aa20354-12-eq447.png) (A.15)The beam-averaged column density NJK (in cm-2) can be calculated from Eqs. (A.3) and (A.4) using the estimated values of the amplitude
(A.15)The beam-averaged column density NJK (in cm-2) can be calculated from Eqs. (A.3) and (A.4) using the estimated values of the amplitude 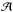 , the total optical depth τJK, and the linewidth Δv:
, the total optical depth τJK, and the linewidth Δv: 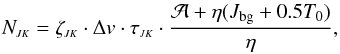 (A.16)where ζ11 = 1.3850 × 1013, ζ22 = 1.0375 × 1013, and Δv is in km s-1 (for details, see Ungerechts et al. 1980). As mentioned above,
(A.16)where ζ11 = 1.3850 × 1013, ζ22 = 1.0375 × 1013, and Δv is in km s-1 (for details, see Ungerechts et al. 1980). As mentioned above, 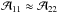 , and for both transitions T0 = 1.14 K and Jbg = 2.20 K. Substituting these numerical values in Eq. (A.16), one obtains
, and for both transitions T0 = 1.14 K and Jbg = 2.20 K. Substituting these numerical values in Eq. (A.16), one obtains 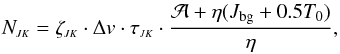 (A.17)This gives us lower and upper boundaries of N11 if η ∈ [ηmin,1]:
(A.17)This gives us lower and upper boundaries of N11 if η ∈ [ηmin,1]: 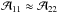 (A.18)The uncertainty interval
(A.18)The uncertainty interval 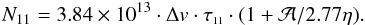 transforms directly into the estimate of the total NH3 column density:
transforms directly into the estimate of the total NH3 column density: ![\appendix \setcounter{section}{1} \begin{eqnarray} N({\rm NH}_3) & = & N_{11}\cdot [(1/3)\exp(23.2/T_{\rm rot}) + 1 + \nonumber\\ & & + (5/3)\exp(-41.5/T_{\rm rot}) \nonumber\\ & & + (14/3)\exp(-105.2/T_{\rm rot}) + \ldots ], \label{Eq16} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20354-12/aa20354-12-eq459.png) (A.19)which assumes that the relative population of all metastable levels of both ortho-NH3 (K = 3), which is not observable, and para-NH3 (K = 1,2) is governed by the rotational temperature of the system at thermal equilibrium (Winnewisser et al. 1979). Substituting
(A.19)which assumes that the relative population of all metastable levels of both ortho-NH3 (K = 3), which is not observable, and para-NH3 (K = 1,2) is governed by the rotational temperature of the system at thermal equilibrium (Winnewisser et al. 1979). Substituting 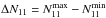 and
and 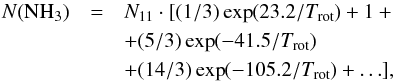 from (A.18) into (A.19), one finds:
from (A.18) into (A.19), one finds: 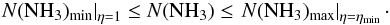 (A.20)The detailed balance calculations also provide a relation between the gas density, gas kinetic temperature, and the excitation temperature (e.g., Ho & Townes 1983):
(A.20)The detailed balance calculations also provide a relation between the gas density, gas kinetic temperature, and the excitation temperature (e.g., Ho & Townes 1983): ![\appendix \setcounter{section}{1} \begin{eqnarray} n({\rm H}_2) = \frac{A}{C} \left[ \frac{ J_\nu(T_{\rm ex}) - J_\nu(T_{\rm bg}) } { J_\nu(T_{\rm kin}) - J_\nu(T_{\rm ex}) } \right] \left[ 1 + \frac{J_\nu(T_{\rm kin})}{h\nu/k_{\rm B}} \right], \label{Eq19} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20354-12/aa20354-12-eq465.png) (A.21)where A is the Einstein A-coefficient and C is the rate coefficient for collisional de-excitation. For a typical kinetic temperature in the dense molecular cores of ~10–20 K, the collision coefficient is ~4 × 10-7 s-1 [n(H2)/104 cm-3]. The value of A for the inversion transition (1, 1) is 1.67 × 10-7 s-1. However, the gas density calculated using Eq. (A.21) may be significantly underestimated if the beam is not filled uniformly. Moreover, for Tex = Tkin, Eq. (A.21) is invalid and, hence, n(H2) needs to be calculated by different methods (see, e.g., Hildebrand 1983; Pandian et al. 2012). We used (A.21) just to set a lower bound on the gas density, n(H2)min, at η = 1.
(A.21)where A is the Einstein A-coefficient and C is the rate coefficient for collisional de-excitation. For a typical kinetic temperature in the dense molecular cores of ~10–20 K, the collision coefficient is ~4 × 10-7 s-1 [n(H2)/104 cm-3]. The value of A for the inversion transition (1, 1) is 1.67 × 10-7 s-1. However, the gas density calculated using Eq. (A.21) may be significantly underestimated if the beam is not filled uniformly. Moreover, for Tex = Tkin, Eq. (A.21) is invalid and, hence, n(H2) needs to be calculated by different methods (see, e.g., Hildebrand 1983; Pandian et al. 2012). We used (A.21) just to set a lower bound on the gas density, n(H2)min, at η = 1.
Given a fractional NH3 abundance, an upper bound on the gas density may be estimated from the deduced N(NH assuming that the ammonia emission traces the real distribution of the gas density7. If the source is unresolved, its diameter d and the beam filling factor are related as
assuming that the ammonia emission traces the real distribution of the gas density7. If the source is unresolved, its diameter d and the beam filling factor are related as 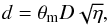 (A.22)where θm is the beam angular diameters (FWHP), and D the distance of the source. The highest gas density is obtained at the smallest diameter,
(A.22)where θm is the beam angular diameters (FWHP), and D the distance of the source. The highest gas density is obtained at the smallest diameter, 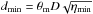 :
: 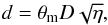 (A.23)where X = [NH3] / [H2] is a given abundance ratio. In this equation the unknown distance D can be found from the requirement that both values of the lowest gas densities calculated at η = 1 from Eq. (A.21) and from N(NH3)min at dmax = θmD be equal. This gives
(A.23)where X = [NH3] / [H2] is a given abundance ratio. In this equation the unknown distance D can be found from the requirement that both values of the lowest gas densities calculated at η = 1 from Eq. (A.21) and from N(NH3)min at dmax = θmD be equal. This gives 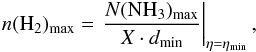 (A.24)For the unresolved source its axis – major, θa, or minor, θb – is less than θm, η < 1, and only limiting values can be obtained for Tex, NJK, N(NH3), and n(H2). If the source is resolved, i.e., θb > θm, then η = 1 and these physical parameters are directly defined. In the latter case we calculated the deconvolved values of θa and θb and their geometrical mean
(A.24)For the unresolved source its axis – major, θa, or minor, θb – is less than θm, η < 1, and only limiting values can be obtained for Tex, NJK, N(NH3), and n(H2). If the source is resolved, i.e., θb > θm, then η = 1 and these physical parameters are directly defined. In the latter case we calculated the deconvolved values of θa and θb and their geometrical mean 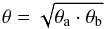 (A.25)which is used as a formal estimate of the source angular diameter.
(A.25)which is used as a formal estimate of the source angular diameter.
A similar procedure was applied to calculate the virial mass of the ammonia core through the linewidth, Δv. If the observed value Δv is of order of the spectral resolution Δsp (FWHM), then only an upper limit on Mvir is defined. Otherwise, if Δv> Δsp, then the deconvolved value of the linewidth, 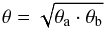 , and the core radius r give the virial mass (e.g., Lemme et al. 1996)
, and the core radius r give the virial mass (e.g., Lemme et al. 1996) 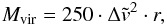 (A.26)where
(A.26)where 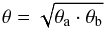 is in km s-1, r in pc, and Mvir in solar masses M⊙.
is in km s-1, r in pc, and Mvir in solar masses M⊙.
To conclude, we note that if Tkin varies slowly within an ammonia clump, the NH3 column density can be deduced from the (1, 1) line alone assuming the same average Tkin in the core as in the outskirts of a cloud. This allows us to extend the radial gas distribution to zones with unobservable (2, 2) emission (Morgan et al. 2013).
Appendix B: Ammonia spectra toward the Aquila rift cloud complex and derived physical parameters
The observed spectra of the NH3(1, 1) and (2, 2) transitions detected at the peak positions of ammonia emission toward each core are shown in Figs. B.1–B.9. The measured physical parameters are listed in Tables B.1–B.4. The distributions of the physical parameters for the three most abundant cores are presented in Figs. B.10–B.12. They demonstrate variations of the kinetic temperature Tkin, the excitation temperature Tex, the linewidth Δv (FWHM), the total optical depth τ11, the gas density nH2, and the total ammonia column density N(H2) across the mapped area of the core.
 |
Fig. B.1 Ammonia (1, 1) and (2, 2) spectra (blue) toward the source Ka01. The channel spacing is 0.015 km s-1, the spectral resolution FWHM = 0.024 km s-1. The red curves show the fit of a single-component Gaussian model to the original data. The residuals between the observed and model spectra are shown in black. |
 |
Fig. B.3 Same as Fig. B.1 but for the source Do279P8 and the channel spacing 0.077 km s-1 (FWHM = 0.123 km s-1). The red curves show the fit of a single-component Gaussian model to the NH3(1, 1) original data and the upper limit on NH3(2, 2). |
 |
Fig. B.4 Same as Fig. B.1 but for the source Do279P12. The ammonia spectra have a double structure. The upper panels show the high-resolution spectra (channel spacing 0.015 km s-1), and the other panels low-resolution spectra (channel spacing 0.077 km s-1). Two NH3 components are marked by ticks and labeled by letters A and B in the upper panels. |
 |
Fig. B.6 Same as Fig. B.1 but for the source Ka05 and the channel spacing 0.038 km s-1 (FWHM = 0.044 km s-1). |
 |
Fig. B.8 Same as Fig. B.1 but for the source SS3. The channel spacing is 0.77 km s-1 and 0.038 km s-1 in the two upper and three lower panels. The corresponding spectral resolutions are 0.895 km s-1 and 0.044 km s-1 (FWHM). The red curves show the fit of a single-component (two upper panels) and a double-component (three lower panels) Gaussian model to the original NH3 data. Two components of the NH3 emission are marked by ticks and labeled by letters A and B. |
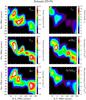 |
Fig. B.10 Spatial distributions of the physical parameters measured in Do279P6 from the ammonia inversion lines NH3(1, 1) and (2, 2). The corresponding numerical values are listed in Table B.2. |
 |
Fig. B.11 Spatial distributions of the physical parameters measured in Do279P12 from the ammonia inversion lines NH3(1, 1) and (2, 2). The corresponding numerical values are listed in Table B.3. |
 |
Fig. B.12 Spatial distributions of the physical parameters measured in SS3 from the ammonia inversion lines NH3(1, 1) and (2, 2). The corresponding numerical values are listed in Table B.4. |
Observed parameters of the NH3(1, 1) and (2, 2) lines and calculated model parameters for Kawamura 01 and 05, Dobashi 279 P7 and P8, and Dobashi 321 P2.
In cores, ambipolar diffusion leads to a mass to magnetic flux ratio, M/Φ = 7.6 × 10-21N(H2)/Btot, of M/Φ ~ 1 (e.g., Crutcher 2012). With the measured ammonia column density N ~ 6 × 1014 cm-2 and the abundance ratio [NH3]/[H2] ~ 3 × 10-7, one finds Btot ~ 20 μG.
The abundance ratio [H2]/[He] ~ 5 and the NH3-H2 collision rates are a factor of 3 higher than the NH3-He rates (Machin & Roueff 2005).
Ammonia and submillimeter maps of dense cores in Ophiuchus show a close correlation between the large-scale distributions of the NH3(1, 1) integrated intensity and the 850 μm continuum emission (Friesen et al. 2009).
Acknowledgments
We thank the staff of the Effelsberg 100-m telescope for the assistance in observations and acknowledge the help of Benjamin Winkel in preliminary data reduction. We also thank the anonymous referee and Malcolm Walmsley for suggestions that led to substantial improvements of the paper. We acknowledge Dima Shalybkov for valuable comments. S.A.L. is grateful for the kind hospitality of the Max-Planck-Institut für Radioastronomie, Hamburger Sternwarte and Shanghai Astronomical Observatory where this work has been prepared. This work was supported in part by the grant DFG Sonderforschungsbereich SFB 676 Teilprojekt C4, and by NSFC grants 10973040, 11127903, and 11233007.
References
- André, P., & Montmerle, T. 1994, ApJ, 420, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada, G., Sepúlveda, I., & Gómez, J. F. 1997, A&AS, 121, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anglada, G., Rodrǵuez, L. F., Cantó, J., Estalella, R., & Torrelles, J. M. 1992, ApJ, 395, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 99 [NASA ADS] [Google Scholar]
- Barnard, E. E. 1927, A photographic Atlas of selected regions of the Milky Way (Carnegie Inst. Washington D.C. Publ.) [Google Scholar]
- Benson, P. J., & Myers, P. C. 1989, ApJS, 71, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Langer, W. D. 1997, ApJ, 486, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Bernes, C. 1977, A&AS, 29, 65 [NASA ADS] [Google Scholar]
- Bontemps, S., André, Ph.,Könyves, V., et al. 2010, A&A, 518, L85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Churchwell, E., Walmsley, C. M., & Cesaroni, R. 1990, A&AS, 83, 119 [NASA ADS] [Google Scholar]
- Cieza, L. A., Schreiber, M. R., Romero, G. A., et al. 2012, ApJ, 750, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, F. O. 1991, ApJS, 75, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Clemens, D. P., & Barvainis, R. 1988, ApJS, 68, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., & Kuhi, L. V. 1979, ApJS, 41, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Curiel, S., Rodríguez, L. F., Gómez, J. F., et al. 1996, ApJ, 456, 677 [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog, II/246 [Google Scholar]
- Dame, T. M., & Thaddeus, P. 1985, ApJ, 197, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, C. J., Matthews, H. E., Ray, T. P., Dent, W. R. F., & Richer, J. S. 1999, MNRAS, 309, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Deharveng, L., Zavagno, A., Anderson, L. D., et al. 2012, A&A, 546, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Francesco, J., Johnstone, D., Kirk, H., MacKenzie, T., & Ledwosinska, E. 2008, ApJS, 175, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Djupvik, A. A., André, Ph., Bontemps, S., et al. 2006, A&A, 458, 789 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobashi, K., Uehara, H., Kandori, R., et al. 2005, PASJ, 57, 1 [Google Scholar]
- Dunham, M. K., Rosolowsky, E., Evans, N. J., II, Cyganowski, C., & Urquhart, J. S. 2011, ApJ, 741, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Dzib, S., Loinard, L., Mioduszewski, A. J., et al. 2010, ApJ, 718, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Eiroa, C., Djupvik, A. A., & Casali, M. M. 2008, in Handbook of Star Forming Regions, Volume II: The Southern Sky ASP Monograph Publications, ed. B. Reipurth, 5, 693 [Google Scholar]
- Frerking, M. A., & Langer, W. D. 1982, ApJ, 256, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Friesen, R. K., Di Francesco, J., Shirley, Y. L., & Myers, P. C. 2009, ApJ, 697, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, T. P., Wilking, B. A., André, P., Young, E. T., & Lada, C. J. 1994, ApJ, 434, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Gutermuth, R. A., Bourke, T. L., Allen, L. E., et al. 2008, ApJ, 673, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, D. W. A., Wilner, D. J., Di Francesco, J., et al. 2002, AJ, 123, 3325 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, D. W. A., Wilner, D. J., Lada, C. J., & Myers, P. C. 2003, ApJ, 598, 1112 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Chapman, N., Lai, S.-P., et al. 2006, ApJ, 644, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Heiderman, A., Evans, N. J., II, Allen, L. E., Huard, T., & Heyer, M. 2010, ApJ, 723, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Ho, P. T. P., & Barrett, A. H. 1980, ApJ, 237, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, P. T. P., Martin, R. N., Myers, P. C., & Barrett, A. H. 1977, ApJ, 215, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, P. T. P., Martin, R. N., & Barrett, A. H. 1978, ApJ, 221, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Ioannidis, G., & Froebrich, D. 2012, MNRAS, 425, 1380 [NASA ADS] [CrossRef] [Google Scholar]
- Kawamura, A., Onishi, T., Mizuno, A., Ogawa, H., & Fukui, Y. 1999, PASJ, 51, 851 [NASA ADS] [Google Scholar]
- Kawamura, A., Kun, M., Onishi, T., et al. 2001, PASJ, 53, 1097 [NASA ADS] [Google Scholar]
- Kegel, W. H. 1976, A&A, 50, 293 [NASA ADS] [Google Scholar]
- Könyves, V., André, Ph., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, B., Hochgürtel, S., Krämer, I., Bell, A., Meyer, K., & Güsten, R. 2012, 542, 3 [Google Scholar]
- Knude, J. 2011 [arXiv:1103.0455] [Google Scholar]
- Kukolich, S. G. 1967, Phys. Rev., 156, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Landman, D. A., Roussel-Dupré, R., & Tanigawa, G. 1982, ApJ, 261, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., & Myers, P. C. 1999, ApJS, 123, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., & Myers, P. C. 2011, ApJ, 734, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., Myers, P. C., & Tafalla, M. 1999, ApJ, 526, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Lemme, C., Wilson, T. L., Tieftrunk, A. R., & Henkel, C. 1996, A&A, 312, 585 [NASA ADS] [Google Scholar]
- Levshakov, S. A., Molaro, P., Lapinov, A. V., et al. 2010, A&A, 512, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Little, L. T., Brown, A. T., MacDonald, G. H., Riley, P. W., & Matheson, D. N. 1980, MNRAS, 193, 115 [NASA ADS] [Google Scholar]
- Lynds, B. T. 1962, ApJS, 7, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Machin, L., & Roueff, E. 2005, J. Phys. B: At. Mol. Phys., 38, 1519 [Google Scholar]
- Magnani, L., Blitz, L., & Mundy, L. 1985, ApJ, 295, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Faure, A., Scifoni, E., & Wiesenfeld, L. 2009, MNRAS, 399, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Maury, A. J., André, P., Men’shchikov, A., Könyves, V., & Bontemps, S. 2011, A&A, 535, A77 [Google Scholar]
- Men’shchikov, A., André, Ph., Didelon, P., et al. 2010, A&A, 518, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menten, K. M., Walmsley, C. M., Krügel, E., & Ungerechts, H. 1984, A&A, 137, 108 [NASA ADS] [Google Scholar]
- Morgan, L. K., Moore, T. J. T., Allsopp, J., & Eden, D. J. 2013, MNRAS, 428, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C., & Benson, P. J. 1983, ApJ 266, 309 [Google Scholar]
- Nakamura, F., Sugitani, K., Shimajiri, Y., et al. 2011, ApJ, 737, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Oliveira, J. M., Jeffries, R. D., & van Loon, J. Th. 2009, MNRAS, 392, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, S., & Olofsson, G. 2009, A&A, 498, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, M., Witzel, A., Quirrenbach, A., et al. 1994, A&A, 284, 331 [NASA ADS] [Google Scholar]
- Pandian, J. D., Wyrowski, F., & Menten, K. M. 2012, ApJ, 753, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, N. D. 1988, MNRAS, 235, 139 [NASA ADS] [Google Scholar]
- Phillips, J. P. 1999, A&AS, 134, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porras, A., Christopher, M., Allen, L., et al. 2003, AJ, 126, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C (Cambridge: Cambridge Uni. Press) [Google Scholar]
- Ragan, S. E., Bergin, E. A., & Wilner, D. 2011, ApJ, 736, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Lada, C. J., Muench, A. A., Alves, J. F., & Lombardi, M. 2008, ApJS, 174, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Rodrígues, L. F., Moran, J. M., Ho, P. T. P., & Gottlieb, E. W. 1980, ApJ, 235, 845 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E. W., Pineda, J. E., Foster, J. B., et al. 2008, ApJS, 175, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Rydbeck, O. E. H., Sume, A., Hjalmarson, Å, et al. 1977, ApJ, 215, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Snell, R. L., & Bally, J. 1986, ApJ, 303, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Straižys, V., Černis, K., & Bartašiūtė, S. 2003, A&A, 405, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strom, S. E., Grasdalen, G. L., & Strom, K. M. 1974, ApJ, 191, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Stutzki, J., & Winnewisser, G. 1985, A&A, 148, 254 [NASA ADS] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tobin, J. J., Hartmann, L., Chiang, H.-F., et al. 2011, ApJ, 740, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Torrelles, J. M., Gómez, J. F., Curiel, S., et al. 1992, ApJ, 384, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Tsitali, A. E., Bourke, T. L., Peterson, D. E., et al. 2010, ApJ, 725, 2461 [NASA ADS] [CrossRef] [Google Scholar]
- Ungerechts, H., & Güsten, R. 1984, A&A, 131, 177 [NASA ADS] [Google Scholar]
- Ungerechts, H., Walmsley, C. M., & Winnewisser, G. 1980, A&A, 88, 259 [NASA ADS] [Google Scholar]
- Visser, A. E., Richer, J. S., & Chandler, C. J. 2002, AJ, 124, 2756 [NASA ADS] [CrossRef] [Google Scholar]
- Winnewisser, G., Churchwell, E., & Walmsley, C. M. 1979, A&A, 72, 215 [NASA ADS] [Google Scholar]
- Yen, H.-W., Takakuwa, S., & Ohashi, N. 2010, ApJ, 710, 1786 [NASA ADS] [CrossRef] [Google Scholar]
- Zuo, Y.-X., Yang, J., Shi, S.C., et al. 2004, Chin. J. Astron. Astrophys., 4, 390 [Google Scholar]
All Tables
Molecular cores toward Aquila targets without detected NH3 emission in the (1, 1) and (2, 2) inversion transitions.
Observed parameters of the NH3(1, 1) and (2, 2) lines and calculated model parameters for Kawamura 01 and 05, Dobashi 279 P7 and P8, and Dobashi 321 P2.
All Figures
 |
Fig. 1 a) NH3(1, 1) intensity map (∫TMBdv) of Ka01. The starting point for the contour levels is 0.1 K km s-1, the increment is 0.7 K km s-1 between the first two and 0.8 K km s-1 between the other contour levels. The crosses mark measured positions. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 9.576 km s-1. The intensity peak is labeled as in Table 1. The Effelsberg beam size (HPBW) at 23.7 GHz is 40′′. |
| In the text | |
 |
Fig. 2 a) Same as Fig. 1a but for the source Do279P6. The starting point for the contour levels is 0.5 K km s-1, the increment is 0.5 K km s-1 between the first two and 1.0 K km s-1 between the other contour levels. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 7.986 km s-1. The intensity peaks are labeled as in Table 1. c) NH3(1, 1) intensity map as in panel a) and positions of YSO candidates observed with the Spitzer/IRAC in a star formation region Serpens cluster B (Harvey et al. 2006). Open circles of different colors mark Class I (red), intermediate type (yellow), and Class II (blue) YSOs. |
| In the text | |
 |
Fig. 3 a) Same as Fig. 1a but for the source Do279P8. The contour levels start at 0.5 K km s-1 and increments are 0.5 K km s-1. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 8.553 km s-1. The intensity peak is labeled as in Table 1. |
| In the text | |
 |
Fig. 4 a) Same as Fig. 1a but for the source Do279P12. The contour levels start at 0.5 K km s-1 and increments are 1.5 K km s-1. b) NH3(1, 1) intensity map as in panel a) and positions of IR sources. Open circles mark the Herbig-Haro objects (blue), far-infrared continuum sources (red and yellow) (Davis et al. 1999), submm-continuum sources (magenta) detected by SCUBA (Di Francesco et al. 2008), and the triple radio source FIRS 1 (cyan) (Snell & Bally 1986). |
| In the text | |
 |
Fig. 5 NH3(1, 1) intensity (grey contours) and radial velocity (color map) structure in the source Do279P12. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 8.099 km s-1. The contour levels are the same as in Fig. 4a. Panels A) and B) represent the velocity maps for the components A and B in the NH3 profile, respectively (see Fig. B.4). The white crosses mark offsets where the splitting of the NH3 profiles is detected. The mean radial velocities of the components A and B are ⟨ VA ⟩ = 7.27 ± 0.11 km s-1 and ⟨ VB ⟩ = 8.54 ± 0.08 km s-1. In panel B), the intensity peaks are labeled as in Table 1. |
| In the text | |
 |
Fig. 6 Dots with 3σ error bars mark the differences between the radial velocities measured with the Effelsberg 100-m telescope in 1977–1981 (Ungerechts & Güsten 1984) and in the present dataset toward the same positions in Do279P12. The red points indicate deviations from zero that are larger than 3σ. At two offsets, (Δα,Δδ) = (80′′,0′′) and (160′′, − 120′′), we detected double NH3 profiles (see Fig. B.4). |
| In the text | |
 |
Fig. 7 a) Same as Fig. 1a but for the source Do321P2. The contour levels start at 0.3 K km s-1 and increments are 1.0 K km s-1. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 6.905 km s-1. The intensity peaks are labeled as in Table 1. c) NH3(1, 1) intensity map as in panel a). Open circles of different colors mark Class I (red), intermediate type (yellow), Class II (blue), and Class III (cyan) YSOs taken from Tsitali et al. (2010). The SCUBA sources from Visser et al. (2002) are marked by magenta: SMM7 is a starless core, whereas SMM1 and SMM2 are protostars that coincide with IRAS 19180+1116 and IRAS 19180+1114. |
| In the text | |
 |
Fig. 8 a) Same as Fig. 1a but for the source Ka05. The contour levels start at 0.4 K km s-1 and increments are 1.0 K km s-1. The square indicates the position of the far-infrared source IRAS 19345+0727 coinciding with the 3.6 cm continuum source (Anglada et al. 1992). b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 8.390 km s-1. The intensity peak is labeled as in Table 1. |
| In the text | |
 |
Fig. 9 a) Same as Fig. 1a but for the source Do279P7. The contour levels start at 0.3 K km s-1 and increments are 0.6 K km s-1. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 6.715 km s-1. The intensity peak is labeled as in Table 1. |
| In the text | |
 |
Fig. 10 a) Same as Fig. 1a but for the source SS3. The contour levels start at 0.0 K km s-1 and increments are 2.0 K km s-1. b) NH3(1, 1) radial velocity (color map) structure. The velocity field is shown after subtracting the mean radial velocity ⟨ VLSR ⟩ = 7.542 km s-1. The white crosses mark offsets where the splitting of the NH3 profiles is detected (see Fig. B.8). The mean radial velocities of the components A and B are ⟨ VA ⟩ = 7.865 ± 0.005 km s-1 and ⟨ VB ⟩ = 6.856 ± 0.010 km s-1. The intensity peaks are labeled as in Table 1. c) NH3 intensity map as in panel a) and positions of the MAMBO millimeter sources taken from Table 1 in Maury et al. (2011). Red and yellow open circles mark starless and YSO candidates, respectively. |
| In the text | |
 |
Fig. B.1 Ammonia (1, 1) and (2, 2) spectra (blue) toward the source Ka01. The channel spacing is 0.015 km s-1, the spectral resolution FWHM = 0.024 km s-1. The red curves show the fit of a single-component Gaussian model to the original data. The residuals between the observed and model spectra are shown in black. |
| In the text | |
 |
Fig. B.3 Same as Fig. B.1 but for the source Do279P8 and the channel spacing 0.077 km s-1 (FWHM = 0.123 km s-1). The red curves show the fit of a single-component Gaussian model to the NH3(1, 1) original data and the upper limit on NH3(2, 2). |
| In the text | |
 |
Fig. B.4 Same as Fig. B.1 but for the source Do279P12. The ammonia spectra have a double structure. The upper panels show the high-resolution spectra (channel spacing 0.015 km s-1), and the other panels low-resolution spectra (channel spacing 0.077 km s-1). Two NH3 components are marked by ticks and labeled by letters A and B in the upper panels. |
| In the text | |
 |
Fig. B.6 Same as Fig. B.1 but for the source Ka05 and the channel spacing 0.038 km s-1 (FWHM = 0.044 km s-1). |
| In the text | |
 |
Fig. B.8 Same as Fig. B.1 but for the source SS3. The channel spacing is 0.77 km s-1 and 0.038 km s-1 in the two upper and three lower panels. The corresponding spectral resolutions are 0.895 km s-1 and 0.044 km s-1 (FWHM). The red curves show the fit of a single-component (two upper panels) and a double-component (three lower panels) Gaussian model to the original NH3 data. Two components of the NH3 emission are marked by ticks and labeled by letters A and B. |
| In the text | |
 |
Fig. B.10 Spatial distributions of the physical parameters measured in Do279P6 from the ammonia inversion lines NH3(1, 1) and (2, 2). The corresponding numerical values are listed in Table B.2. |
| In the text | |
 |
Fig. B.11 Spatial distributions of the physical parameters measured in Do279P12 from the ammonia inversion lines NH3(1, 1) and (2, 2). The corresponding numerical values are listed in Table B.3. |
| In the text | |
 |
Fig. B.12 Spatial distributions of the physical parameters measured in SS3 from the ammonia inversion lines NH3(1, 1) and (2, 2). The corresponding numerical values are listed in Table B.4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.






