| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 25 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220354 | |
| Published online | 06 May 2013 | |
Online material
Molecular cores toward Aquila targets without detected NH3 emission in the (1, 1) and (2, 2) inversion transitions.
Appendix A: Analysis of NH3(1, 1) and (2, 2) spectra
In this appendix we discuss the methods used for calculating physical parameters from observations of the ammonia NH3 (J,K) = (1, 1) and (2, 2) transitions. We give a consistent summary of the basic formulae relevant to the study of cold molecular cores.
The recorded NH3 spectra were first converted into the TMB scale and a baseline was removed from each of them. The baseline was typically linear in the range covered by the ammonia hyperfine (hf) structure lines, but occasionally it was quadratic. After that the spectra of the same offset were co-added with weights inversely proportional to the mean variance of the noise per channel, rms-2, estimated from the channels without emission.
The NH3 spectra were fitted to determine the total optical depth τtot in the respective inversion transition, the LSR velocity of the line VLSR, the intrinsic full-width at half power linewidth Δv for an individual hf component, and the amplitude, 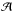 (e.g., Ungerechts et al. 1980):
(e.g., Ungerechts et al. 1980): 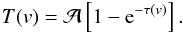 (A.1)The optical depth τ(v) at a given radial velocity v is defined by
(A.1)The optical depth τ(v) at a given radial velocity v is defined by 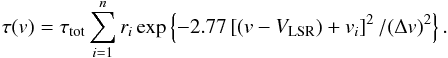 (A.2)In this equation, the sum runs over the n hf components of the inversion transition (n = 18 and 21 for the NH3(1, 1) and (2, 2) inversion transitions), ri is the theoretical relative intensity of the ith hf line and vi is its velocity separation from the fiducial frequency. The values of these parameters are given in, e.g., Kukolich (1967) and Rydbeck et al. (1977).
(A.2)In this equation, the sum runs over the n hf components of the inversion transition (n = 18 and 21 for the NH3(1, 1) and (2, 2) inversion transitions), ri is the theoretical relative intensity of the ith hf line and vi is its velocity separation from the fiducial frequency. The values of these parameters are given in, e.g., Kukolich (1967) and Rydbeck et al. (1977).
In Eq.(A.2), the total optical depth τtot is the maximum optical depth that an unsplit (1, 1) or (2, 2) line would have at the central frequency if the hf levels were populated at the same excitation temperature for the two lines (1, 1) and (2, 2). Assuming that the line profile function has a Gaussian shape with width Δv (FWHM) and taking into account that the statistical weights of the upper and lower levels of an inversion transition are equal, one obtains 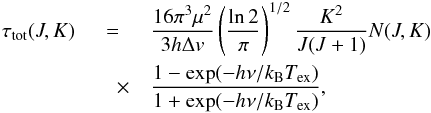 (A.3)where h and kB are Planck and Boltzmann constants, μ is the dipole moment, | μ | = 1.4719 Debye (JPL catalog4), N(J,K) is the inversion state column density – the sum of the column densities of the upper and lower levels of an inversion doublet, ν is the rest frequency of the inversion transition, and Tex is the excitation temperature that characterizes the NH3 population across the (J,K) inversion doublet.
(A.3)where h and kB are Planck and Boltzmann constants, μ is the dipole moment, | μ | = 1.4719 Debye (JPL catalog4), N(J,K) is the inversion state column density – the sum of the column densities of the upper and lower levels of an inversion doublet, ν is the rest frequency of the inversion transition, and Tex is the excitation temperature that characterizes the NH3 population across the (J,K) inversion doublet.
In Eq. (A.1), the amplitude 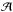 can be expressed in terms of the beam filling factor, η = Ωcloud/Ωbeam (solid angle Ω = πθ2/(4ln2), where θ is the angular diameter at FWHP), and the excitation temperature, Tex, as
can be expressed in terms of the beam filling factor, η = Ωcloud/Ωbeam (solid angle Ω = πθ2/(4ln2), where θ is the angular diameter at FWHP), and the excitation temperature, Tex, as 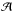 (A.4)where Tbg = 2.7 K is the black-body background radiation temperature, and Jν(T) is defined by
(A.4)where Tbg = 2.7 K is the black-body background radiation temperature, and Jν(T) is defined by 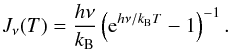 (A.5)For optically thin lines (e.g., τ11 ≪ 1), Eq. (A.1) degenerates into
(A.5)For optically thin lines (e.g., τ11 ≪ 1), Eq. (A.1) degenerates into 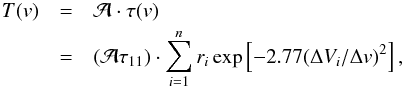 (A.6)and it is not possible to determine
(A.6)and it is not possible to determine  and τ11 separately. Here ΔVi = v − VLSR + vi.
and τ11 separately. Here ΔVi = v − VLSR + vi.
For some molecular cores we observe two-component NH3 profiles. The line parameters 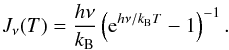 for the j = 1 and j = 2 components were determined in this case by fitting the function
for the j = 1 and j = 2 components were determined in this case by fitting the function 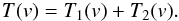 (A.7)This linear form assumes that two clouds in the beam have the same filling factor η and the same Tex for the lines (1, 1) and (2, 2).
(A.7)This linear form assumes that two clouds in the beam have the same filling factor η and the same Tex for the lines (1, 1) and (2, 2).
At low spectral resolutions, when the channel spacing Δch is near to the linewidth Δv, the derived line parameters are affected by the channel profile φ(v). In this case, the recorded spectrum, T′(v), was considered as a convolution of the true spectrum T(v) and φ(v) 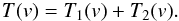 (A.8)We approximate φ(v) by a Gaussian function with the width FWHM defined by a particular back-end setting.
(A.8)We approximate φ(v) by a Gaussian function with the width FWHM defined by a particular back-end setting.
The calculated synthetic spectrum, which is defined as Tsyn(v) ≡ T(v) if Δch ≪ Δv, or Tsyn(v) ≡ T′(v) if Δch ~ Δv, was fitted to the observed spectrum Tobs(v) by minimizing the χ2 function 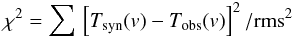 (A.9)in the five-dimensional space of the following model parameters:
(A.9)in the five-dimensional space of the following model parameters: 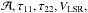 and Δv. Attempting to exclude at the 3σ level all noise-only channels in between the hf lines, the sum runs over the channels with observed NH3 emission from all hf components. The minimum of χ2 was computed using the simplex method (e.g., Press et al. 1992).
and Δv. Attempting to exclude at the 3σ level all noise-only channels in between the hf lines, the sum runs over the channels with observed NH3 emission from all hf components. The minimum of χ2 was computed using the simplex method (e.g., Press et al. 1992).
Equation (A.9) was also used to estimate the formal errors of the model parameters by calculating the covariance matrix at the minimum of χ2. Since the uncertainty in the amplitude scale calibration was ~15–20% (Sect. 2), and there were no noticeable correlations between the sequential channels in our datasets, we did not correct the calculated errors by an additional factor as described, e.g., in Rosolowsky et al. (2008).
Given the estimate of the amplitude 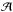 , the excitation temperature Tex can be calculated from Eq. (A.4)
, the excitation temperature Tex can be calculated from Eq. (A.4) 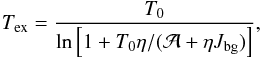 (A.10)where T0 = hν/kB, and Jbg = Jν(Tbg). At Tbg = 2.725 K and NH3-inversion frequencies, we have Jbg = 2.20 K and T0 = 1.14 K.
(A.10)where T0 = hν/kB, and Jbg = Jν(Tbg). At Tbg = 2.725 K and NH3-inversion frequencies, we have Jbg = 2.20 K and T0 = 1.14 K.
In this equation the only unknown parameter is the filling factor η. If the source is completely resolved, then η = 1. Otherwise, Eq. (A.10) gives a lower bound on Tex corresponding to η = 1, whereas decreasing η drives Tex toward its upper bound at Tex = Tkin, which holds for LTE. For emission lines, the radiation temperature within the line is higher than the 2.7 K background and the excitation may be either radiative or collisional. At gas densities higher than the critical density5 and for optically thin lines, the local density of line photons is negligible compared to the background radiation field, and the lower metastable states in NH3 are mainly populated via collisions with molecular hydrogen6, i.e., the stimulated emission can be neglected. For low collisional excitation, ngas < ncr, the line radiation controls Tex for both optically thin and thick regimes (Kegel 1976). NH3(1, 1) emission usually arises from regions with ngas ≳ 104 cm-3 (e.g., Ho & Townes 1983). This means that the regime of low collisional excitation does not dominate. We also did not consider anomalous excitation (maser emission) that leads to Tex ≫ Tbg because masing is not observed in our data sample. Thus, using Tex = Tkin as a formal upper limit for the excitation temperature is legitimate. With this we can restrict the unknown filling factor for an unresolved source in the interval 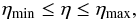 (A.11)and Tex within the boundaries
(A.11)and Tex within the boundaries 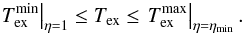 (A.12)From a separate analysis of the (1, 1) and (2, 2) lines with low noise level, we found that the two amplitudes
(A.12)From a separate analysis of the (1, 1) and (2, 2) lines with low noise level, we found that the two amplitudes 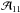 and
and 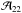 are equal within the observational errors, which implies that Tex(1, 1) ≈ Tex(2, 2). Albeit radiative transfer calculations show that the excitation temperatures Tex(1, 1) and Tex(2, 2) may differ by about 20% (Stutzki & Winnewisser 1985), assuming that they are equivalent seems to be sufficient in our case.
are equal within the observational errors, which implies that Tex(1, 1) ≈ Tex(2, 2). Albeit radiative transfer calculations show that the excitation temperatures Tex(1, 1) and Tex(2, 2) may differ by about 20% (Stutzki & Winnewisser 1985), assuming that they are equivalent seems to be sufficient in our case.
The second temperature, which describes the NH3 population, is the rotational temperature Trot, which characterizes the population of energy levels with different (J,K). As mentioned above, the population of the lower metastable inversion doublets is determined by collisions with H2 and, thus, is regulated by the kinetic temperature Tkin. The population ratio between the (1, 1) and (2, 2) states is defined as 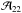 (A.13)Assuming that both transitions trace the same volume of gas and their linewidths Δv are equal, one finds from Eqs. (A.3) and (A.13) that
(A.13)Assuming that both transitions trace the same volume of gas and their linewidths Δv are equal, one finds from Eqs. (A.3) and (A.13) that 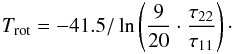 (A.14)We note that since radiative transitions between the different K-ladders of the (J,K) levels are forbidden and because the unknown filling factor η is canceled in the line intensity ratio of the NH3 (1, 1) and (2, 2) transitions, the estimate of the rotational temperature is more reliable than the excitation temperature.
(A.14)We note that since radiative transitions between the different K-ladders of the (J,K) levels are forbidden and because the unknown filling factor η is canceled in the line intensity ratio of the NH3 (1, 1) and (2, 2) transitions, the estimate of the rotational temperature is more reliable than the excitation temperature.
For a two-level system with a lower kinetic temperature than the energy gap between the (1, 1) and (2, 2) states (ΔE12 = 41.5 K), the rotational temperature can be related to the kinetic temperature through detailed balance arguments (e.g., Ragan et al. 2011): 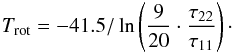 (A.15)The beam-averaged column density NJK (in cm-2) can be calculated from Eqs. (A.3) and (A.4) using the estimated values of the amplitude
(A.15)The beam-averaged column density NJK (in cm-2) can be calculated from Eqs. (A.3) and (A.4) using the estimated values of the amplitude 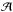 , the total optical depth τJK, and the linewidth Δv:
, the total optical depth τJK, and the linewidth Δv: 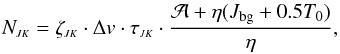 (A.16)where ζ11 = 1.3850 × 1013, ζ22 = 1.0375 × 1013, and Δv is in km s-1 (for details, see Ungerechts et al. 1980). As mentioned above,
(A.16)where ζ11 = 1.3850 × 1013, ζ22 = 1.0375 × 1013, and Δv is in km s-1 (for details, see Ungerechts et al. 1980). As mentioned above, 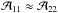 , and for both transitions T0 = 1.14 K and Jbg = 2.20 K. Substituting these numerical values in Eq. (A.16), one obtains
, and for both transitions T0 = 1.14 K and Jbg = 2.20 K. Substituting these numerical values in Eq. (A.16), one obtains 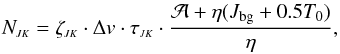 (A.17)This gives us lower and upper boundaries of N11 if η ∈ [ηmin,1]:
(A.17)This gives us lower and upper boundaries of N11 if η ∈ [ηmin,1]: 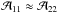 (A.18)The uncertainty interval
(A.18)The uncertainty interval 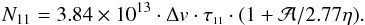 transforms directly into the estimate of the total NH3 column density:
transforms directly into the estimate of the total NH3 column density: 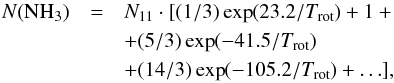 (A.19)which assumes that the relative population of all metastable levels of both ortho-NH3 (K = 3), which is not observable, and para-NH3 (K = 1,2) is governed by the rotational temperature of the system at thermal equilibrium (Winnewisser et al. 1979). Substituting
(A.19)which assumes that the relative population of all metastable levels of both ortho-NH3 (K = 3), which is not observable, and para-NH3 (K = 1,2) is governed by the rotational temperature of the system at thermal equilibrium (Winnewisser et al. 1979). Substituting 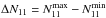 and
and 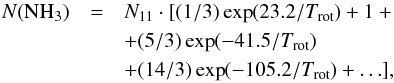 from (A.18) into (A.19), one finds:
from (A.18) into (A.19), one finds: 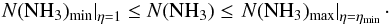 (A.20)The detailed balance calculations also provide a relation between the gas density, gas kinetic temperature, and the excitation temperature (e.g., Ho & Townes 1983):
(A.20)The detailed balance calculations also provide a relation between the gas density, gas kinetic temperature, and the excitation temperature (e.g., Ho & Townes 1983): 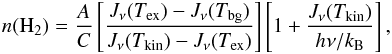 (A.21)where A is the Einstein A-coefficient and C is the rate coefficient for collisional de-excitation. For a typical kinetic temperature in the dense molecular cores of ~10–20 K, the collision coefficient is ~4 × 10-7 s-1 [n(H2)/104 cm-3]. The value of A for the inversion transition (1, 1) is 1.67 × 10-7 s-1. However, the gas density calculated using Eq. (A.21) may be significantly underestimated if the beam is not filled uniformly. Moreover, for Tex = Tkin, Eq. (A.21) is invalid and, hence, n(H2) needs to be calculated by different methods (see, e.g., Hildebrand 1983; Pandian et al. 2012). We used (A.21) just to set a lower bound on the gas density, n(H2)min, at η = 1.
(A.21)where A is the Einstein A-coefficient and C is the rate coefficient for collisional de-excitation. For a typical kinetic temperature in the dense molecular cores of ~10–20 K, the collision coefficient is ~4 × 10-7 s-1 [n(H2)/104 cm-3]. The value of A for the inversion transition (1, 1) is 1.67 × 10-7 s-1. However, the gas density calculated using Eq. (A.21) may be significantly underestimated if the beam is not filled uniformly. Moreover, for Tex = Tkin, Eq. (A.21) is invalid and, hence, n(H2) needs to be calculated by different methods (see, e.g., Hildebrand 1983; Pandian et al. 2012). We used (A.21) just to set a lower bound on the gas density, n(H2)min, at η = 1.
Given a fractional NH3 abundance, an upper bound on the gas density may be estimated from the deduced N(NH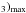 assuming that the ammonia emission traces the real distribution of the gas density7. If the source is unresolved, its diameter d and the beam filling factor are related as
assuming that the ammonia emission traces the real distribution of the gas density7. If the source is unresolved, its diameter d and the beam filling factor are related as 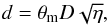 (A.22)where θm is the beam angular diameters (FWHP), and D the distance of the source. The highest gas density is obtained at the smallest diameter,
(A.22)where θm is the beam angular diameters (FWHP), and D the distance of the source. The highest gas density is obtained at the smallest diameter, 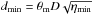 :
: 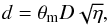 (A.23)where X = [NH3] / [H2] is a given abundance ratio. In this equation the unknown distance D can be found from the requirement that both values of the lowest gas densities calculated at η = 1 from Eq. (A.21) and from N(NH3)min at dmax = θmD be equal. This gives
(A.23)where X = [NH3] / [H2] is a given abundance ratio. In this equation the unknown distance D can be found from the requirement that both values of the lowest gas densities calculated at η = 1 from Eq. (A.21) and from N(NH3)min at dmax = θmD be equal. This gives 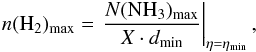 (A.24)For the unresolved source its axis – major, θa, or minor, θb – is less than θm, η < 1, and only limiting values can be obtained for Tex, NJK, N(NH3), and n(H2). If the source is resolved, i.e., θb > θm, then η = 1 and these physical parameters are directly defined. In the latter case we calculated the deconvolved values of θa and θb and their geometrical mean
(A.24)For the unresolved source its axis – major, θa, or minor, θb – is less than θm, η < 1, and only limiting values can be obtained for Tex, NJK, N(NH3), and n(H2). If the source is resolved, i.e., θb > θm, then η = 1 and these physical parameters are directly defined. In the latter case we calculated the deconvolved values of θa and θb and their geometrical mean 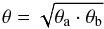 (A.25)which is used as a formal estimate of the source angular diameter.
(A.25)which is used as a formal estimate of the source angular diameter.
A similar procedure was applied to calculate the virial mass of the ammonia core through the linewidth, Δv. If the observed value Δv is of order of the spectral resolution Δsp (FWHM), then only an upper limit on Mvir is defined. Otherwise, if Δv> Δsp, then the deconvolved value of the linewidth, 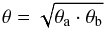 , and the core radius r give the virial mass (e.g., Lemme et al. 1996)
, and the core radius r give the virial mass (e.g., Lemme et al. 1996) 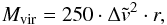 (A.26)where
(A.26)where 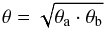 is in km s-1, r in pc, and Mvir in solar masses M⊙.
is in km s-1, r in pc, and Mvir in solar masses M⊙.
To conclude, we note that if Tkin varies slowly within an ammonia clump, the NH3 column density can be deduced from the (1, 1) line alone assuming the same average Tkin in the core as in the outskirts of a cloud. This allows us to extend the radial gas distribution to zones with unobservable (2, 2) emission (Morgan et al. 2013).
Appendix B: Ammonia spectra toward the Aquila rift cloud complex and derived physical parameters
The observed spectra of the NH3(1, 1) and (2, 2) transitions detected at the peak positions of ammonia emission toward each core are shown in Figs. B.1–B.9. The measured physical parameters are listed in Tables B.1–B.4. The distributions of the physical parameters for the three most abundant cores are presented in Figs. B.10–B.12. They demonstrate variations of the kinetic temperature Tkin, the excitation temperature Tex, the linewidth Δv (FWHM), the total optical depth τ11, the gas density nH2, and the total ammonia column density N(H2) across the mapped area of the core.
 |
Fig. B.1
Ammonia (1, 1) and (2, 2) spectra (blue) toward the source Ka01. The channel spacing is 0.015 km s-1, the spectral resolution FWHM = 0.024 km s-1. The red curves show the fit of a single-component Gaussian model to the original data. The residuals between the observed and model spectra are shown in black. |
| Open with DEXTER | |
 |
Fig. B.3
Same as Fig. B.1 but for the source Do279P8 and the channel spacing 0.077 km s-1 (FWHM = 0.123 km s-1). The red curves show the fit of a single-component Gaussian model to the NH3(1, 1) original data and the upper limit on NH3(2, 2). |
| Open with DEXTER | |
 |
Fig. B.4
Same as Fig. B.1 but for the source Do279P12. The ammonia spectra have a double structure. The upper panels show the high-resolution spectra (channel spacing 0.015 km s-1), and the other panels low-resolution spectra (channel spacing 0.077 km s-1). Two NH3 components are marked by ticks and labeled by letters A and B in the upper panels. |
| Open with DEXTER | |
 |
Fig. B.6
Same as Fig. B.1 but for the source Ka05 and the channel spacing 0.038 km s-1 (FWHM = 0.044 km s-1). |
| Open with DEXTER | |
 |
Fig. B.8
Same as Fig. B.1 but for the source SS3. The channel spacing is 0.77 km s-1 and 0.038 km s-1 in the two upper and three lower panels. The corresponding spectral resolutions are 0.895 km s-1 and 0.044 km s-1 (FWHM). The red curves show the fit of a single-component (two upper panels) and a double-component (three lower panels) Gaussian model to the original NH3 data. Two components of the NH3 emission are marked by ticks and labeled by letters A and B. |
| Open with DEXTER | |
 |
Fig. B.9
Same as Fig. B.3 but for the sources Do243P2, Do279P18, Do279P13, and Do321P1. |
| Open with DEXTER | |
 |
Fig. B.10
Spatial distributions of the physical parameters measured in Do279P6 from the ammonia inversion lines NH3(1, 1) and (2, 2). The corresponding numerical values are listed in Table B.2. |
| Open with DEXTER | |
 |
Fig. B.11
Spatial distributions of the physical parameters measured in Do279P12 from the ammonia inversion lines NH3(1, 1) and (2, 2). The corresponding numerical values are listed in Table B.3. |
| Open with DEXTER | |
 |
Fig. B.12
Spatial distributions of the physical parameters measured in SS3 from the ammonia inversion lines NH3(1, 1) and (2, 2). The corresponding numerical values are listed in Table B.4. |
| Open with DEXTER | |
Observed parameters of the NH3(1, 1) and (2, 2) lines and calculated model parameters for Kawamura 01 and 05, Dobashi 279 P7 and P8, and Dobashi 321 P2.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





