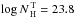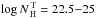EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 553 (May 2013) A&A, 553 (2013) A29 Full HTML
Free Access
Issue
A&A
Volume 553, May 2013
Article Number A29
Number of page(s) 9
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201220324
Published online 25 April 2013

© ESO, 2013

1. Introduction

There are two main observational signatures of reprocessed radiation in the X-ray spectra of active galactic nuclei (AGN): a Compton hump peaking around 30 keV and a fluorescent iron Kα line. While the Compton hump is produced only if the reprocessing material is Compton thick (CT, N H ≳ 1024 cm-2), the iron Kα line is also created in Compton-thin material (e.g., Matt et al. 2003). The iron Kα line is often observed as the superposition of two different components: a broad component and a narrow one. The broad component has a full width at half-maximum (FWHM) of  ≳30 000 km s and is thought to be created close to the black hole in the accretion disk (e.g., Fabian et al. 2000), or to be related to the presence of features created by partially covering warm absorbers in the line of sight (e.g., Turner & Miller 2009; Miyakawa et al. 2012). While the broad component is observed in only  ~35–45% of bright nearby AGN (e.g., de La Calle Pérez et al. 2010), the narrow (FWHM ~ 2000 km s, Shu et al. 2010) core of the iron line has been found to be almost ubiquitous (e.g., Nandra et al. 2007; Singh et al. 2011). This component peaks at 6.4 keV (e.g.,Yaqoob & Padmanabhan 2004), which points to the line being produced in cold neutral material. This material has often been identified as circumnuclear matter located at several thousand gravitational radii from the supermassive black hole, and it is likely related to the putative molecular torus (e.g., Nandra 2006), although a contribution of the outer part of the disk (e.g., Petrucci et al. 2002) or of the broad-line region (BLR, e.g., Bianchi et al. 2008) cannot be excluded. In a recent study, Shu et al. (2011) found that the weighted mean of the ratio between the FWHM of the narrow Fe Kα line and that of optical lines produced in the BLR is  ≃ 0.6. This implies that the size of the iron Kα-emitting region is on average about three times that of the BLR, indicating that most of the narrow iron Kα emission is produced in the putative molecular torus.

Table 1

Summary of the most recent studies (along with the original work of Iwasawa & Taniguchi 1993) of the X-ray Baldwin effect.

One of the most interesting characteristics of the narrow component of the iron Kα line is the inverse correlation between its equivalent width (EW) and the X-ray luminosity (e.g., Iwasawa & Taniguchi 1993). The existence of an anti-correlation between the EW of a line and the luminosity of the AGN continuum was found for the first time in the UV by Baldwin (1977) for the C IV λ1549 line and dubbed the Baldwin effect. A similar trend was later found for several other emission lines, such as Lyα, [C III] λ1908, Si IV λ1396, Mg II λ2798 (Dietrich et al. 2002), UV iron emission lines (Green et al. 2001), mid-infrared (mid-IR) lines such as [AR III] λ8.99 μm, [S IV] λ10.51 μm and [Ne II] λ12.81 μm (Hönig et al. 2008), and forbidden lines such as [O II] λ3727 and [Ne V] λ3426 (Croom et al. 2002). The slope of the Baldwin effect for most of these lines has been shown to be steeper for the lines originating from higher ionization species (e.g., Dietrich et al. 2002). The origin of the Baldwin effect is still unknown, although several possible explanations have been put forward, and might be different for lines originating in different regions of the AGN. For the lines produced in the BLR, the origin might be related to the lower ionization and photoelectric heating in the BLR gas of more luminous objects (e.g., Netzer et al. 1992).

Using Ginga observations of 37 AGN, Iwasawa & Taniguchi (1993) found in the X-rays the first evidence of an anti-correlation between the EW of the iron Kα line and the 2–10 keV luminosity (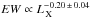). This trend is usually called the X-ray Baldwin effect or the Iwasawa-Taniguchi effect. Using ASCA observations, Nandra et al. (1997) confirmed the existence of such an anti-correlation and argued that most of the effect could be explained by variations of the broad component of the iron Kα line with the luminosity. The advent of XMM-Newton, Chandra, and Suzaku made clear however that most of the observed X-ray Baldwin effect is due to the narrow core of the iron Kα line (e.g., Page et al. 2004; Shu et al. 2010; Fukazawa et al. 2011). The significance of the effect was questioned by Jiménez-Bailón et al. (2005), who discussed the possible importance of contamination from radio-loud (RL) AGN, which have on average larger X-ray luminosities and smaller signatures of reprocessed radiation (e.g., Reeves & Turner 2000). However, Grandi et al. (2006), studying BeppoSAX observations of RL AGN, also found evidence of an X-ray Baldwin effect. This, together with the study of a large sample of radio-quiet (RQ) AGN carried out by Bianchi et al. (2007) using XMM-Newton data, showed that the X-ray Baldwin effect is not a mere artifact. Jiang et al. (2006) suggested that the X-ray Baldwin effect might be due to the delay between the variability of the AGN primary energy source and that of the reprocessing material located farther away. Using Chandra/HEG observations, Shu et al. (2010, 2012) confirmed the importance of variability, showing that averaging the values of EW obtained over multiple observations of individual sources would significantly attenuate the anti-correlation from 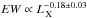to 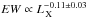. Chandra/HEG observations (Shu et al. 2010) have also shown that the normalization of the X-ray Baldwin effect is lower (i.e., the average EW of the narrow Fe Kα component is smaller) than that obtained by previous works performed using XMM-Newton. In Table 1 we report the values of the slope and the intercept obtained from the most recent XMM-Newton/EPIC and Chandra/HEG works, along with the original Ginga work of Iwasawa & Taniguchi (1993).

An intriguing possibility is that the X-ray Baldwin effect is related to the decrease of the covering factor of the torus with luminosity (e.g., Page et al. 2004; Zhou & Wang 2005) in the frame of the luminosity-dependent unification schemes. The EW of the iron Kα line is in fact expected to be proportional to the covering factor of the torus (e.g., Krolik et al. 1994, Ikeda et al. 2009), so that a covering factor of the torus decreasing with the luminosity might in principle be able to explain the X-ray Baldwin effect. Luminosity-dependent unification models have been proposed to explain the decrease of the fraction of obscured objects (fobs) with the increase of the AGN output power. The first suggestion of the existence of a relation between fobs and the luminosity was put forward about 30 years ago (Lawrence & Elvis 1982). Since then the idea that the covering factor of the obscuring material decreases with luminosity has been gaining observational evidence from radio (e.g., Grimes et al. 2004), infrared (e.g., Treister et al. 2008; Mor et al. 2009; Gandhi et al. 2009), optical (e.g., Simpson 2005), and X-ray (e.g., Ueda et al. 2003; Beckmann et al. 2009; Ueda et al. 2011) studies of AGN. Although luminosity-dependent unification models have long been suspected to play a major role in the X-ray Baldwin effect, no quantitative estimation of this effect has been performed so far.

thumbnail Fig. 1

Schematic representation of the torus geometry considered. The angle θ i is the inclination of the line of sight with respect to the torus axis, while θOA and are the half-opening angle and the equatorial column density of the molecular torus, respectively. H is the maximum height of the torus, while Rin and R are its inner and outer radius, respectively.

In this work we quantify for the first time the influence of the decrease of the covering factor of the torus with the luminosity on the EW of the iron Kα line. Using the Monte Carlo spectral simulations of a torus with a variable half-opening angle (θOA) (recently presented by Ikeda et al. 2009 and Brightman & Nandra 2011) together with the most recent and comprehensive observations in different energy bands of the decrease of fobs with the luminosity, we show that this mechanism is able to explain the X-ray Baldwin effect. The paper is organized as follows. In Sect. 2 we present in detail our spectral simulations, and in Sect. 3 we compare the slopes and intercepts obtained by our simulations with those measured by high-sensitivity Chandra/HEG observations, as they provide the best energy resolution available to date. In Sect. 4 we discuss our results, and in Sect. 5 we present our conclusions.

2. Simulations

2.1. The relation between θOA and L

As a proxy of the relationship between the half-opening angle of the molecular torus θOA (see Fig. 1) and the intrinsic X-ray luminosity of AGN, we used the variation of the fraction of obscured sources fobs with luminosity measured by the recent medium (2–10 keV) and hard (15–55 keV) X-ray surveys of Hasinger (2008) and Burlon et al. (2011). From a combination of surveys performed by HEAO-1, ASCA, BeppoSAX, XMM-Newton, and Chandra in the luminosity range 42 ≤ log LX ≤ 46, Hasinger (2008) found in the 2–10 keV band 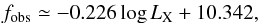(1)where LX is the luminosity in the 2–10 keV energy range. In the 15–55 keV band, using Swift/BAT to study AGN in the luminosity range 42 ≤ log LX ≤ 45 and fitting the data with 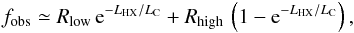(2)where LHX is the luminosity in the 15–55 keV band, Burlon et al. (2011) obtained Rlow = 0.8, Rhigh = 0.2, and LC = 1043.7 erg s. We also used the results of the IR work of Maiolino et al. (2007), who found an anti-correlation between the ratio λLλ(6.7 μm)/λLλ(5100 Å) and the [O III]λ5007 Å line luminosity. This trend was interpreted as an effect of the decrease of the covering factor of the circumnuclear dust as a function of luminosity, with fobs varying as 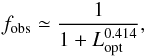(3)where Lopt = (λLλ(5100 Å))/1045.63. Following Maiolino et al. (2007), it is possible to rewrite Lopt as a function of the X-ray luminosity: .

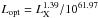thumbnail Fig. 2

Variation of the fraction of obscured sources (fobs) and of the half-opening angle of the torus (θOA) with the 2–10 keV luminosity for three of the most recent medium X-ray (2–10 keV, Hasinger 2008), hard X-ray (15–55 keV, Burlon et al. 2011), and IR (Maiolino et al. 2007) studies (Eqs. (1)–(3)).

The fraction of obscured sources at a given luminosity can be easily related to the half-opening angle of the torus using 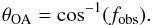(4)For Eq. (2) we converted the hard X-ray luminosity to the luminosity in the 2–10 keV band, assuming a photon index Γ = 1.9 (e.g., Beckmann et al. 2009). The three θOA − LX relationships used in this work are shown in Fig. 2.

2.2. Spectral simulations and fitting

Ikeda et al. (2009) recently presented Monte Carlo simulations of the reprocessed X-ray emission of an AGN surrounded by a three-dimensional spherical-toroidal structure. The simulations were performed using the ray-tracing method, taking into account Compton down-scattering and absorption. They are stored in tables, so that they can be used to perform spectral fitting. The free parameters of this model are the half-opening angle of the torus θOA, the line-of-sight inclination angle θ i, the torus equatorial column density , and the photon index Γ of the primary continuum. We note that should not be confused with the observed hydrogen column density N H. 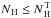In all objects, , with 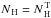 only if θ i = 90°. In Fig. 1 a schematic representation of the geometry considered is shown. The dependence of N H on the inclination angle is given by Eq. (3) of Ikeda et al. (2009). In the model of Ikeda et al. (2009), the ratio Rin/R is fixed to 0.01 and the inclination angle of the observer θi can vary between 1 and 89°, between 1022 and 1025 cm-2, while θOA spans the range between 10° and 70°. Because of the assumed dependence of the half-opening angle on the luminosity, the interval of values of θOA allowed by the model limits the range of luminosities we can probe. In the following we will consider luminosities above log LX = 42, because below this value few AGN are detected and several works point towards a possible disappearance of the molecular torus (e.g., Elitzur & Shlosman 2006). The upper-limit luminosity we can reach depends on the θOA − LX relationship used and, considering 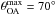, is log L max = 44.2 for Hasinger (2008), log L max = 43.8 for Burlon et al. (2011), and log L max = 45.0 for Maiolino et al. (2007). Due to its limitations in the values of θOA permitted, the model of Ikeda et al. (2009) restricts most of the simulations to the Seyfert regime ().

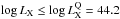thumbnail Fig. 3

Top panel: extract in the 5.5–7.5 keV region of a spectrum simulated using the model of Ikeda et al. (2009). The model has a torus with a half-opening angle of θOA = 46.2° (equivalent to log LX = 42.7, according to the relationship of Hasinger 2008), an equatorial column density of , and an inclination angle of θ i = 1°. The continuous line represents the fit to the simulated spectrum using for the continuum the same model we used for the simulations and a Gaussian line for the iron Kα fluorescent line. Bottom panel: contribution to the chi-squared for the best fit to the simulated spectrum.

To extend our study to the quasar regime (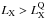), we simulated the X-ray Baldwin effect using the spectral model of Brightman & Nandra (2011). This model considers the same geometry as Ikeda et al. (2009) but has Rin = 0, a θ i-independent N H, and it allows different values of θOA (26° to 84°). The higher maximum half-opening angle permitted by this model allows to reach higher maximum luminosities in the simulations for the relationships of Hasinger (2008; log L max = 45.3) and Maiolino et al. (2007; log L max = 46.2), while that of Burlon et al. (2011) is flat (f obs ≃ 0.2) in the quasar regime. However, the lower boundary of θOA in the model of Brightman & Nandra (2011) limits the lower luminosity we can reach in the simulations, in particular log L min ≃ 43 for the relation of Maiolino et al. (2007). Thus, we used the model of Ikeda et al. (2009) to study the X-ray Baldwin effect in the Seyfert regime (42 ≤ log LX ≤ 44.2) and the model of Brightman & Nandra (2011) to probe the quasar regime (log LX > 44.2).

thumbnail Fig. 4

Equivalent width of the iron Kα line versus the X-ray luminosity obtained simulating a torus with an equatorial column density of and a covering factor decreasing with the luminosity. The θOA − LX relationship used here is that of Hasinger (2008; see Fig. 2). The relations of Bianchi et al. (2007, black dashed line) and Shu et al. (2012, blue line, obtained averaging different observations of the same source) are also shown for comparison (see also Table 1). The normalization of the relation of Bianchi et al. (2007) has been fixed to an arbitrary value for comparison.

thumbnail Fig. 5

Left panel: value of the slope (B) of the X-ray Baldwin effect obtained simulating the variation of the reprocessed X-ray radiation with the luminosity for tori with different values of the equatorial column density (in the range ) for the different θOA − LX relationships shown in Fig. 2 (Eqs. (1)–(3)) in the Seyfert regime (42 < log LX ≤ 44.2). The model used is that of Ikeda et al. (2009), and the simulated data were fitted with Eq. (5). The red line represents the value of the slope (B = − 0.12 ± 0.04) obtained by fitting in the Seyfert regime the data per source reported in Shu et al. (2010); the red shadowed area represents the 1σ contour of the slope. Right panel: same as left panel, but considering the intercept (A) of the X-ray Baldwin effect obtained by our simulations. The red line represents the value of the intercept (A = 1.64 ± 0.05) obtained by the fit to the Chandra/HEG data in the Seyfert regime, while the red shadowed area represents its 1σ error.

To estimate the influence of the decreasing covering factor of the torus on the EW of the iron line, we used the physical torus models to simulate a large number of spectra using the θOA − LX relationships reported in Eqs. (1)–(3). Using the three different θOA − LX relationships, we extrapolated the value of θOA for each luminosity bin (Δlog LX = 0.01). We fixed the equatorial column density of the torus to 26 different values, spanning 1022.5 cm-2 and 1025 cm-2, with a step of 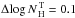. To simulate an unabsorbed population, similarly to what is usually used to determine the X-ray Baldwin effect, we considered inclination angles θ i between 1° and θOA for each value of L X and , with a binning of Δθ i = 3°. In XSPEC 12.7.1 (Arnaud 1996), we simulated spectra for each of the three θOA − LX relationships and for each bin of column density. For the continuum we used a power law with Γ = 1.9 (e.g., Beckmann et al. 2009). Our choice of the photon index does not significantly affect the simulations; by adding a scatter of ΔΓ = 0.3, we found EW − LX trends consistent with those obtained without scatter. The metallicity was set to the solar value in all our simulations, and the value of the normalization of the reflected component was fixed to that of the continuum.

We fitted the simulated spectra in the 0.3–10 keV band using the same model applied for the simulations, substituting the iron Kα line component with a Gaussian line. We obtained a good fit for all the simulations, with a reduced chi-squared of 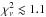. We show in Fig. 3 an example of a typical fit. The model used for the continuum fitting does not significantly affect the results, and the EW of the iron Kα line differs only  ~4% on average when using an alternative model like pexrav (Magdziarz & Zdziarski 1995). We evaluated the EW of the iron Kα line and studied its relationship with the luminosity. As an example, we show in Fig. 4 the simulated X-ray Baldwin effect obtained using the model of Ikeda et al. (2009) and the θOA − LX relationship of Hasinger (2008) for 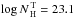, together with the fit to the X-ray Baldwin effect obtained by the recent works of Bianchi et al. (2007) and Shu et al. (2012). The spread in EW for a given luminosity is due to the range of values of θ i that we considered: larger values of EW usually correspond to lower values of θ i.

Most of the studies of the X-ray Baldwin effect performed in recent years have used a relationship of the type 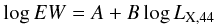(5)to fit the EW − LX trend, where LX,44 is the luminosity in units of 1044 erg s. In order to compare the simulated EW − LX trend with that observed in unabsorbed populations of AGN, we fitted the simulated data, for each value of , with Eq. (5) using the weighted least-square method, with weights of w = sinθ i. This makes it possible to account for the non-uniform probability of randomly observing an AGN within a certain solid angle from the polar axis.

3. The X-ray Baldwin effect

Most of the studies on the X-ray Baldwin effect have found, using Eq. (5), a slope of B ~ −0.2 (e.g., Iwasawa & Taniguchi 1993; Page et al. 2004; Bianchi et al. 2007). However, in all these works the values of EW and LX are obtained from individual observations of sources. As pointed out by Jiang et al. (2006) and confirmed by Shu et al. (2010, 2012), flux variability might play an important role in the observed X-ray Baldwin effect. Shu et al. (2012) recently found a clear anti-correlation between the EW of the iron Kα line and the luminosity for individual sources that had several Chandra/HEG observations. Using a sample of 32 RQ AGN, they also found that the fit per source (i.e., averaging different observations of the same object) results in a significantly flatter slope (B = −0.11 ± 0.03) than that done per observation (i.e., using all the available observations for every source of the sample; B = −0.18 ± 0.03).

To compare the slope obtained by the simulations in the two different luminosity bands with real data, we fitted the data per source (33 AGN) of Shu et al. (2010; obtained fixing σ = 1 eV) with Eq. (5) in the Seyfert and quasar regime. Consistent with what was done by Shu et al. (2010) we did not use the three AGN for which only upper limits of EW were obtained. Using the 28 AGN in the Seyfert regime, we found that the best fit to the X-ray Baldwin effect is given by A = 1.64 ± 0.05 and B = −0.12 ± 0.04. Chandra/HEG observations are available for only five objects in the quasar regime, and at these luminosities we obtained A = 1.5 ± 0.3 and B = −0.16 ± 0.22.

thumbnail Fig. 6

Left panel: value of the slope (B) of the X-ray Baldwin effect obtained simulating the variation of the reprocessed X-ray radiation with the luminosity for tori with different values of the equatorial column density for the different θOA − LX relationships shown in Fig. 2 (Eqs. (1)–(3)) in the quasar regime (log LX > 44.2). The model used is that of Brightman & Nandra (2011), and the simulated data were fitted with Eq. (5). The red line represents the value of the slope (B = −0.16 ± 0.22), which was obtained by fitting in the quasar regime the data per source reported in Shu et al. (2010); the red shadowed area represents the 1σ contour of the slope. Right panel: same as left panel, but considering the intercept (A) of the X-ray Baldwin effect obtained by our simulations. The red line represents the value of the intercept (A = 1.5 ± 0.3) obtained by the fit to the Chandra/HEG data in the quasar regime, while the red shadowed area represents its 1σ error.

3.1. Seyfert regime

Fitting the simulated data with Eq. (5) in the Seyfert regime, we found that the slope obtained becomes flatter for increasing values of the equatorial column density of the torus (Fig. 5, left panel). This is related to the fact that the iron Kα EW is tightly connected to both and θOA, so that EW is more strongly dependent on θOA (and thus on its variation) for low values of , which results in a steeper slope. On the other hand, the dependence on θOA becomes weaker and the slope flatter when increases. As shown in Fig. 5 (left panel), while the values of B obtained by the θOA − LX relationships of Burlon et al. (2011) and Hasinger (2008) are similar along the whole range of  considered, flatter slopes are obtained for that of Maiolino et al. (2007). In particular for the latter relationship the correlation becomes positive for .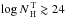

By combining the observations of the X-ray Baldwin effect with our simulations, we can extrapolate the average value of the equatorial column density of the torus of the unobscured AGN in the Chandra/HEG sample of Shu et al. (2010). A slope consistent within 1σ with our fit to the X-ray Baldwin effect in the Seyfert regime is obtained for 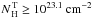for the θOA − LX relationship of Hasinger (2008), for 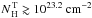for that of Burlon et al. (2011), and for 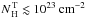for the relationship of Maiolino et al. (2007). Comparing the value of the intercept obtained by the simulations with that resulting from our fit of the X-ray Baldwin effect in the Seyfert regime, we found that only a narrow range of average equatorial column densities of the torus can reproduce the observations (right panel of Fig. 5). For the θOA − LX relationship of Maiolino et al. (2007), we found 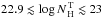, while for those of Burlon et al. (2011) and Hasinger (2008) we obtained 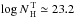. Using both the values of A and B, it is possible to extract the average values of  that can explain the X-ray Baldwin effect. As can be seen from the two figures for both the θOA − LX relationship of Hasinger (2008) and Burlon et al. (2011), the only value of column density consistent with both the observed intercept and slope is 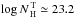. For the IR θOA − LX relationship of Maiolino et al. (2007) the values allowed are in the range 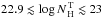. A similar result is obtained studying the A/B chi-squared contour plot of our fit to the Chandra/HEG data. Using the model of Brightman & Nandra (2011) to simulate the X-ray Baldwin effect in the Seyfert regime, we obtained a range of  consistent with that found using the model of Ikeda et al. (2009) (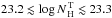). The lower values of  needed to explain the X-ray Baldwin effect using the relationship of Maiolino et al. (2007) are due to the larger values of fobs (and thus of θOA) predicted by Eq. (3). This is again due to the fact that EW depends on both and θOA, so that increasing the latter, one would obtain lower values of the former.

3.2. Quasar regime

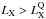To study the behavior of B in the quasar regime, we fitted the simulated data using Eq. (5) for each value of for luminosities . Our simulations show that EW decreases more steeply in the quasar regime than at lower luminosities for the θOA − LX relationships of Hasinger (2008) and Maiolino et al. (2007), with values of the slope of B ≲ −0.3 (left panel of Fig. 6). The slopes obtained by the simulations are consistent with those found by fitting Chandra/HEG data in the quasar regime for the θOA − LX relationship of Maiolino et al. (2007) for 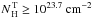. The values of the slope expected using the relationship of Hasinger (2008) are steeper than the observed value for the whole range of column densities considered, while the flattening of the relationship of Burlon et al. (2011) at high luminosities results in a slope of B ~ 0 along the whole range of , consistent within 1σ with the observations. The intercepts obtained using the relationship of Maiolino et al. (2007) are consistent with the observed value for 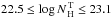(right panel of Fig. 6), with no overlap with the values of needed by the slope. We obtained intercepts that are consistent with the observations for 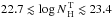and 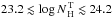 for the relation of Hasinger (2008) and Burlon et al. (2011), respectively. Thus only the hard X-ray θOA − LX relationship of Burlon et al. (2011) is able to explain (for 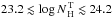) at the same time both the intercept and the slope of the X-ray Baldwin effect at high luminosities.

4. Discussion

Since its discovery about 20 years ago, the existence of the X-ray Baldwin effect has been confirmed by several works performed with the highest spectral resolution available in the X-ray band. So far, several explanations have been proposed. Jiang et al. (2006) argued that the observed anti-correlation could be related to the delay of the reprocessed radiation with respect to the primary continuum. The response of the circumnuclear material to the irradiated flux is not simultaneous, and one should always take this effect into account when performing studies of reprocessed features such as the iron Kα line or the Compton hump. Shu et al. (2010, 2012) have shown that averaging the values of LX and EW for all the observations of each source results in a significantly flattened anti-correlation. However, by itself variability fails to fully account for the observed correlation (Shu et al. 2012).

4.1. Explaining the X-ray Baldwin effect with a luminosity-dependent covering factor of the torus

A mechanism often invoked to explain the X-ray Baldwin effect is the decrease of the covering factor of the molecular torus with the luminosity (e.g., Page et al. 2004; Bianchi et al. 2007). The decrease of the fraction of obscured sources with the luminosity has been reported by several works performed at different wavelengths in the last decade, although some discordant results have been presented (e.g., Dwelly & Page 2006; Lawrence & Elvis 2010). In this work, we have shown that the covering factor–luminosity relationships obtained in the medium and hard X-ray band can explain well the X-ray Baldwin effect in the 1042−1044.2 erg s luminosity range. In particular, our simulations show that it is possible to reproduce the slope of the X-ray Baldwin effect with luminosity-dependent unification for average equatorial column densities of the torus of 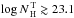, and both the slope and the intercept for 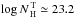(Fig. 5). In the same luminosity range, the θOA − LX IR relationship of Maiolino et al. (2007) can explain the X-ray Baldwin effect for .

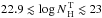thumbnail Fig. 7

Iron Kα EW versus X-ray luminosities and predicted trends obtained for different values of the equatorial column density of the torus. The points are the values of the EW of the iron Kα line reported by Shu et al. (2010) and obtained by averaging multiple Chandra/HEG observations of AGN. The two blue dash-dotted lines are the fits to our simulations of the X-ray Baldwin effect using the θOA − LX relationship of Hasinger (2008) for the Seyfert regime (log EW = 1.01−0.17log LX,44 for , and log EW = 2.05−0.08log LX,44 for ). The blue long-dashed lines represent the EW − LX relations obtained in the quasar regime (log EW = 1.17−0.73log LX,44 for and log EW = 2.14−0.39log LX,44 for ) using the relationship of Hasinger (2008), while the green dashed lines represent those attained using the relationship of Burlon et al. (2011). The intercepts obtained in the quasar regime have been modified to match those obtained at lower luminosities.

In the quasar regime, we have shown that, while the medium X-ray θOA − LX relationship of Hasinger (2008) cannot explain the observations (Fig. 6), the slope obtained by the IR θOA − LX relationship is consistent with our fit to the Chandra/HEG data in the same luminosity band. However, as for the latter relationship, because the range of values of required to explain the slope and the intercept do not overlap, it cannot be considered a likely explanation. The hard X-ray θOA − LX relationship of Burlon et al. (2011) is flat above 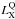, and would thus produce a constant EW of the iron Kα line and a slope of B ~ 0 for the whole range of , consistent within 1σ with the value found using Chandra/HEG data. The intercept we found using this relation is also consistent with the observational value for a large range of average equatorial column densities of the torus (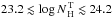). The fraction of obscured AGN is not well constrained at high luminosities, thus any trend with the luminosity between that of Burlon et al. (2011) and that of Hasinger (2008) would be able to reproduce the observed slope. Because the relation of Hasinger (2008) produces negative values of f obs for log LX ≳ 45.8, a flattening of the decline is expected below this luminosity. From Fig. 7 (left panel) in Hasinger (2008), one can see that above log LX ≃ 45 the value of f obs appears to be constant, similarly to what has been found in the hard X-ray band. A flattening of fobs in the quasar regime would also be expected when considering the large amount of accreting material needed to power the AGN at these luminosities. It must, however, be stressed that the X-ray Baldwin effect has not been well studied at high luminosities, and that the Chandra/HEG sample we used in this luminosity range is small, not allowing us to reach a firm conclusion on the variation of the iron Kα EW with the luminosity. Possible evidence of a flattening of the X-ray Baldwin effect in the quasar regime has recently been found by Krumpe et al. (2010).

4.2. The differences between X-ray and IR half-opening angle-luminosity relationships

The main difference between the different θOA − LX relationships that we used is that those obtained in the X-rays are based on direct observations of the absorbing material in the line of sight, while the relationship of Maiolino et al. (2007) is extrapolated from the ratio of the thermal infrared emission to the primary AGN continuum. The θOA − Lλ(5100 Å) relationship obtained by Maiolino et al. (2007) was converted into θOA − LX using the L 2 keV − Lλ(2500 Å) relation obtained by Steffen et al. (2006). It was then converted into the LX − Lλ(5100 Å) relation assuming the optical-UV spectral slope obtained by Vanden Berk et al. (2001). All this is likely to introduce some error in the θOA − LX obtained by their IR work. It has been argued by Maiolino et al. (2007) that the larger normalization of the θOA − LX relation they found is related to the fact that medium X-ray surveys such as that of Hasinger (2008) are likely to miss a certain fraction of heavily obscured objects, which can instead be detected in the IR. This is because most of the X-ray emission is depleted for Compton-thick AGN at energies  ≲10 keV. However, hard X-ray surveys such as that of Burlon et al. (2011), which are much less biased by absorption, have found a normalization of the θOA − LX relation consistent with that obtained at lower X-ray energies (see Fig. 1). Our results also show that the X-ray Baldwin effect can be explained by a Compton-thin torus and that larger values of fobs would imply even lower average values of . Consequently missing heavily obscured objects would not significantly affect our results. X-rays are also probably better suited to probe the material responsible for the iron Kα line emission. The line can, in fact, be emitted by both gas and dust, and while the IR can probe only the latter, X-rays are able to infer the amount of both gas and dust. We thus conclude that for the purpose of our study the X-ray θOA − LX relations are better suited than those extrapolated from IR observations.

It could be argued that the value of the hydrogen column density commonly used to determine the fraction of obscured objects (and thus as an indicator of the presence of the torus) is N H ~ 1022 cm, while the torus is believed to have larger values of , and that this obscuration might be related to the presence of dust lanes or molecular structures in the host galaxy (e.g., Matt 2000). However, Bianchi et al. (2009), using the results of Della Ceca et al. (2008), have shown that a similar decrease of fobs with the luminosity is obtained when this threshold is set to a larger value of line-of-sight column density. They found that the fraction of CT AGN decreases with the luminosity as fCT ∝ L-0.22, similarly to what is found for fobs in the X-rays (e.g., Hasinger 2008, see Eq. (1)). A similar result was obtained by Fiore et al. (2009) from a Chandra and Spitzer study of AGN in the COSMOS field. This implies that the contribution of dust lanes or galactic molecular structures to the observed N H does not significantly affect the fobs − LX relationships obtained in the X-rays.

4.3. The equatorial column density of the torus

The distribution of values of the equatorial column density of the torus in AGN is still poorly constrained. X-ray observation can in fact infer solely the obscuration in the line of sight, and only studies of the reprocessed X-ray emission performed using physical torus models like those of Ikeda et al. (2009), Brightman & Nandra (2011) and Murphy & Yaqoob (2009) can help to deduce the value of the equatorial column density of the torus. However, these kinds of studies are still very scarce (e.g., Rivers et al. 2011; Brightman & Ueda 2012), besides being largely geometry dependent. Studies of AGN in the mid-IR band performed using the clumpy torus formalism of Nenkova et al. (2008) have shown that the number of clouds along the equator is N0 ~ 5−10 (Mor et al. 2009). If, as reported by Mor et al. (2009), each cloud of the torus has an optical depth of τV ~ 30−100 (i.e., 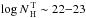), the equatorial column density of the torus is expected to be 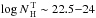, in agreement with our results. However, the value of the intercept of the X-ray Baldwin effect obtained by the simulations is strongly dependent on our assumptions on the metallicity of the torus. This implies that our constraints of the average value of are also tightly related to the choice of the metallicity: lower values of the metallicity would lead to larger values of . To study this effect, we repeated our study in the Seyfert regime using half-solar metallicities for the reflection model. We found that in this scenario one needs values of the equatorial column density of the torus about two times larger than for the solar-metallicity case (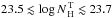) to explain the X-ray Baldwin effect. To have a Compton-thick torus, one would then need values of the metallicity of Z ≲ 0.2 Z⊙. A Compton-thick torus has often been invoked to explain the Compton hump observed in the spectrum of many unobscured AGN (e.g., Bianchi et al. 2004). It is still unclear, however, which fraction of the Compton hump is produced in the distant reflector and which in the accretion flow. From our study, we have found that in unobscured objects the X-ray Baldwin effect can be explained by a luminosity-dependent covering factor of the torus for an average value of the equatorial column density of 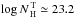. This value is lower than the line-of-sight N H of many Seyfert 2s (e.g., Ricci et al. 2011; Burlon et al. 2011) and might be related either to the geometry we adopted or to the presence of objects with sub-solar metallicities. In particular, due to the constant reflection angle relative to a local normal in any point of the reflecting surface, the spherical-toroidal geometry produces larger values of EW (and thus larger values of the intercept) with respect to a toroidal structure (Murphy & Yaqoob 2009).

It is possible that there exists a wide spread of equatorial column densities of the torus in AGN. Thus one could envisage that this, together with the different values of θ i, would introduce the scatter observed in the anti-correlation. In Fig. 7 we show the X-ray Baldwin effect obtained from our simulations using the relationship of Hasinger (2008) for 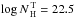and 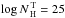in both the Seyfert and the quasar regime, together with the time-averaged Chandra/HEG data of Shu et al. (2010). From the figure it is evident that all the data are well within the range expected from our simulations, both in the Seyfert and in the quasar regime. It is not known whether there exists a relation between the equatorial column density of the torus and the AGN luminosity. However, we have shown that the variation of the covering factor of the torus with the luminosity alone can fully explain the observed trend, so that no additional luminosity-dependent physical parameter is needed.

4.4. Luminosity-dependent unification of AGN

The relation of fobs with the luminosity might be connected to the increase of the inner radius of the torus with the luminosity due to dust sublimation. Both near-IR reverberation (Suganuma et al. 2006) and mid-IR interferometric (Tristram & Schartmann 2011) studies have confirmed that the inner radius of the molecular torus increases with the luminosity as Rin ∝ L0.5. Considering the geometry of Fig. 1, the fraction of obscured objects (see Eq. (4)) would be related to the ratio of the height to the inner radius of the torus (H/R) by 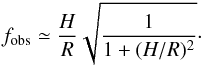(6)For values of H/R ≲ 1, fobs ∝ H/R. In the original formulation of the receding torus model (Lawrence 1991), the height H was considered to be constant. Assuming that R has the same luminosity dependence as Rin, this would lead to fobs ∝ L-0.5. This has been shown to be inconsistent with recent observations, which point towards a flatter slope (fobs ∝ L-0.25, e.g., Hasinger 2008, see Eq. (1)) and imply H ∝ L0.25. Hönig & Beckert (2007) have shown that in the frame of the radiation-limited clumpy dust torus model, one would obtain H ∝ L0.25, which is in agreement with the observations.

The decrease of the covering factor with luminosity might also have important implications on the AGN dichotomy. It has been shown that Seyfert 2 s appear to have on average lower luminosities and lower Eddington ratios (e.g., Beckmann et al. 2009; Ricci et al. 2011) than Seyfert 1 s and Seyfert 1.5 s, which suggests that they have on average a torus with a larger covering factor. This idea is also supported both by the fact that the luminosity function of type II AGN has been found to peak at lower luminosities than that of type I AGN (Della Ceca et al. 2008; Burlon et al. 2011) and by the results obtained by the recent mid-IR work of Ramos Almeida et al. (2011, see also Elitzur 2012). A difference in the torus covering factor distribution between different types of AGN would also explain why the average hard X-ray spectrum of Compton-thin Seyfert 2s shows a larger reflection component than that of Seyfert 1 s and Seyfert 1.5 s (Ricci et al. 2011). A similar result was found by Brightman & Ueda (2012): studying high-redshift AGN in the Chandra Deep Field South, they found that more obscured objects appear to have tori with larger covering factors, although they did not find a clear luminosity dependence.

5. Summary and conclusions

In this work we have studied the hypothesis that the X-ray Baldwin effect is related to the decrease of the covering factor of the torus with the luminosity. We used the physical torus models of Ikeda et al. (2009) and Brightman & Nandra (2011) to account for the reprocessed X-ray radiation, and the values of the fraction of obscured sources obtained by recent surveys in the X-rays and in the IR as a proxy of the covering factor of the torus. Our simulations show that the variation of the covering factor of the torus with the luminosity can explain the X-ray Baldwin effect. In the Seyfert regime (LX ≤ 1044.2 erg s-1), the observed EW − LX trend can be exactly (both in slope and intercept) reproduced by an average value of the equatorial column density of the torus of 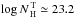, while a slope consistent with the observations is obtained for a larger range of column densities (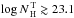). At higher luminosities (LX > 1044.2 erg s-1), the situation is less clear due to the small number of high-quality observations available. Moreover, it is not clear whether fobs still decreases with the luminosity in the quasar regime, similarly to what is found in the Seyfert regime (as shown by Hasinger 2008), or whether it is constant (as found by Burlon et al. 2011). A flattening of the θOA − LX relationship could explain the observations at high luminosities (for 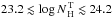), and it might naturally arise from the large amount of accreting mass needed to power these luminous quasars.

In the next few years ASTRO-H (Takahashi et al. 2010), with its high energy-resolution calorimeter SXS, will allow to constrain the origin of the narrow component of the iron Kα line, being able to separate the narrow core coming from the torus from the flux emitted closer to the central engine even better than Chandra/HEG. ASTRO-H will also be able to probe the narrow iron Kα line in the quasar regime, which will allow us to understand the behavior of the X-ray Baldwin effect at high luminosities.

Acknowledgments

We thank the anonymous referee for his/her comments that helped improve the paper. We thank XinWen Shu and Rivay Mor for providing us with useful details about their work, and Chin Shin Chang and Poshak Gandhi for their comments on the manuscript. C.R. thanks the Sherpa group and IPAG for their hospitality during his stay in Grenoble. C.R. is a Fellow of the Japan Society for the Promotion of Science (JSPS).

References

  1. Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
  2. Baldwin, J. A. 1977, ApJ, 214, 679 [NASA ADS] [CrossRef] [Google Scholar]
  3. Beckmann, V., Soldi, S., Ricci, C., et al. 2009, A&A, 505, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bianchi, S., Matt, G., Balestra, I., Guainazzi, M., & Perola, G. C. 2004, A&A, 422, 65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bianchi, S., Guainazzi, M., Matt, G., & Fonseca Bonilla, N. 2007, A&A, 467, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bianchi, S., La Franca, F., Matt, G., et al. 2008, MNRAS, 389, L52 [NASA ADS] [Google Scholar]
  7. Bianchi, S., Bonilla, N. F., Guainazzi, M., Matt, G., & Ponti, G. 2009, A&A, 501, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Brightman, M., & Nandra, K. 2011, MNRAS, 413, 1206 [CrossRef] [Google Scholar]
  9. Brightman, M., & Ueda, Y. 2012, MNRAS, 2850 [Google Scholar]
  10. Burlon, D., Ajello, M., Greiner, J., et al. 2011, ApJ, 728, 58 [NASA ADS] [CrossRef] [Google Scholar]
  11. Croom, S. M., Rhook, K., Corbett, E. A., et al. 2002, MNRAS, 337, 275 [NASA ADS] [CrossRef] [Google Scholar]
  12. de La Cal le Pérez, I., Longinotti, A. L., Guainazzi, M., et al. 2010, A&A, 524, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Della Ceca, R., Caccianiga, A., Severgnini, P., et al. 2008, A&A, 487, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Dietrich, M., Hamann, F., Shields, J. C., et al. 2002, ApJ, 581, 912 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dwelly, T., & Page, M. J. 2006, MNRAS, 372, 1755 [NASA ADS] [CrossRef] [Google Scholar]
  16. Elitzur, M. 2012, ApJ, 747, L33 [NASA ADS] [CrossRef] [Google Scholar]
  17. Elitzur, M., & Shlosman, I. 2006, ApJ, 648, L101 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fabian, A. C., Iwasawa, K., Reynolds, C. S., & Young, A. J. 2000, PASP, 112, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fiore, F., Puccetti, S., Brusa, M., et al. 2009, ApJ, 693, 447 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fukazawa, Y., Hiragi, K., Mizuno, M., et al. 2011, ApJ, 727, 19 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gandhi, P., Horst, H., Smette, A., et al. 2009, A&A, 502, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Grandi, P., Malaguti, G., & Fiocchi, M. 2006, ApJ, 642, 113 [NASA ADS] [CrossRef] [Google Scholar]
  23. Green, P. J., Forster, K., & Kuraszkiewicz, J. 2001, ApJ, 556, 727 [NASA ADS] [CrossRef] [Google Scholar]
  24. Grimes, J. A., Rawlings, S., & Willott, C. J. 2004, MNRAS, 349, 503 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hasinger, G. 2008, A&A, 490, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Hönig, S. F., & Beckert, T. 2007, MNRAS, 380, 1172 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hönig, S. F., Smette, A., Beckert, T., et al. 2008, A&A, 485, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Ikeda, S., Awaki, H., & Terashima, Y. 2009, ApJ, 692, 608 [NASA ADS] [CrossRef] [Google Scholar]
  29. Iwasawa, K., & Taniguchi, Y. 1993, ApJ, 413, L15 [NASA ADS] [CrossRef] [Google Scholar]
  30. Jiang, P., Wang, J. X., & Wang, T. G. 2006, ApJ, 644, 725 [NASA ADS] [CrossRef] [Google Scholar]
  31. Jiménez-Bailón, E., Piconcelli, E., Guainazzi, M., et al. 2005, A&A, 435, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Krolik, J. H., Madau, P., & Zycki, P. T. 1994, ApJ, 420, L57 [NASA ADS] [CrossRef] [Google Scholar]
  33. Krumpe, M., Lamer, G., Markowitz, A., & Corral, A. 2010, ApJ, 725, 2444 [NASA ADS] [CrossRef] [Google Scholar]
  34. Lawrence, A. 1991, MNRAS, 252, 586 [NASA ADS] [Google Scholar]
  35. Lawrence, A., & Elvis, M. 1982, ApJ, 256, 410 [NASA ADS] [CrossRef] [Google Scholar]
  36. Lawrence, A., & Elvis, M. 2010, ApJ, 714, 561 [NASA ADS] [CrossRef] [Google Scholar]
  37. Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
  38. Maiolino, R., Shemmer, O., Imanishi, M., et al. 2007, A&A, 468, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Matt, G. 2000, A&A, 355, L31 [NASA ADS] [Google Scholar]
  40. Matt, G., Guainazzi, M., & Maiolino, R. 2003, MNRAS, 342, 422 [NASA ADS] [CrossRef] [Google Scholar]
  41. Miyakawa, T., Ebisawa, K., & Inoue, H. 2012, PASJ, 64, 140 [NASA ADS] [Google Scholar]
  42. Mor, R., Netzer, H., & Elitzur, M. 2009, ApJ, 705, 298 [NASA ADS] [CrossRef] [Google Scholar]
  43. Murphy, K. D., & Yaqoob, T. 2009, MNRAS, 397, 1549 [NASA ADS] [CrossRef] [Google Scholar]
  44. Nandra, K. 2006, MNRAS, 368, L62 [NASA ADS] [CrossRef] [Google Scholar]
  45. Nandra, K., George, I. M., Mushotzky, R. F., Turner, T. J., & Yaqoob, T. 1997, ApJ, 488, L91 [NASA ADS] [CrossRef] [Google Scholar]
  46. Nandra, K., O’Neill, P. M., George, I. M., & Reeves, J. N. 2007, MNRAS, 382, 194 [NASA ADS] [CrossRef] [Google Scholar]
  47. Nenkova, M., Sirocky, M. M., Ivezić, Ž., & Elitzur, M. 2008, ApJ, 685, 147 [NASA ADS] [CrossRef] [Google Scholar]
  48. Netzer, H., Laor, A., & Gondhalekar, P. M. 1992, MNRAS, 254, 15 [NASA ADS] [CrossRef] [Google Scholar]
  49. Page, K. L., O’Brien, P. T., Reeves, J. N., & Turner, M. J. L. 2004, MNRAS, 347, 316 [NASA ADS] [CrossRef] [Google Scholar]
  50. Petrucci, P. O., Henri, G., Maraschi, L., et al. 2002, A&A, 388, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Ramos Almeida, C., Levenson, N. A., Alonso-Herrero, A., et al. 2011, ApJ, 731, 92 [NASA ADS] [CrossRef] [Google Scholar]
  52. Reeves, J. N., & Turner, M. J. L. 2000, MNRAS, 316, 234 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ricci, C., Walter, R., Courvoisier, T. J.-L., & Paltani, S. 2011, A&A, 532, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Rivers, E., Markowitz, A., & Rothschild, R. 2011, ApJ, 732, 36 [NASA ADS] [CrossRef] [Google Scholar]
  55. Shu, X. W., Yaqoob, T., & Wang, J. X. 2010, ApJS, 187, 581 [NASA ADS] [CrossRef] [Google Scholar]
  56. Shu, X. W., Yaqoob, T., & Wang, J. X. 2011, ApJ, 738, 147 [NASA ADS] [CrossRef] [Google Scholar]
  57. Shu, X. W., Wang, J. X., Yaqoob, T., Jiang, P., & Zhou, Y. Y. 2012, ApJ, 744, L21 [NASA ADS] [CrossRef] [Google Scholar]
  58. Simpson, C. 2005, MNRAS, 360, 565 [NASA ADS] [CrossRef] [Google Scholar]
  59. Singh, V., Shastri, P., & Risaliti, G. 2011, A&A, 532, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Steffen, A. T., Strateva, I., Brandt, W. N., et al. 2006, AJ, 131, 2826 [NASA ADS] [CrossRef] [Google Scholar]
  61. Suganuma, M., Yoshii, Y., Kobayashi, Y., et al. 2006, ApJ, 639, 46 [NASA ADS] [CrossRef] [Google Scholar]
  62. Takahashi, T., Mitsuda, K., Kelley, R., et al. 2010, in SPIE Conf. Ser., 7732 [Google Scholar]
  63. Treister, E., Krolik, J. H., & Dullemond, C. 2008, ApJ, 679, 140 [NASA ADS] [CrossRef] [Google Scholar]
  64. Tristram, K. R. W., & Schartmann, M. 2011, A&A, 531, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Turner, T. J., & Miller, L. 2009, A&ARv, 17, 47 [Google Scholar]
  66. Ueda, Y., Akiyama, M., Ohta, K., & Miyaji, T. 2003, ApJ, 598, 886 [NASA ADS] [CrossRef] [Google Scholar]
  67. Ueda, Y., Hiroi, K., Isobe, N., et al. 2011, PASJ, 63, 937 [Google Scholar]
  68. Van den Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
  69. Yaqoob, T., & Padmanabhan, U. 2004, ApJ, 604, 63 [NASA ADS] [CrossRef] [Google Scholar]
  70. Zhou, X.-L., & Wang, J.-M. 2005, ApJ, 618, L83 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Summary of the most recent studies (along with the original work of Iwasawa & Taniguchi 1993) of the X-ray Baldwin effect.

In the text

All Figures

thumbnail Fig. 1

Schematic representation of the torus geometry considered. The angle θ i is the inclination of the line of sight with respect to the torus axis, while θOA and are the half-opening angle and the equatorial column density of the molecular torus, respectively. H is the maximum height of the torus, while Rin and R are its inner and outer radius, respectively.
In the text
thumbnail Fig. 2

Variation of the fraction of obscured sources (fobs) and of the half-opening angle of the torus (θOA) with the 2–10 keV luminosity for three of the most recent medium X-ray (2–10 keV, Hasinger 2008), hard X-ray (15–55 keV, Burlon et al. 2011), and IR (Maiolino et al. 2007) studies (Eqs. (1)–(3)).

In the text
thumbnail Fig. 3

Top panel: extract in the 5.5–7.5 keV region of a spectrum simulated using the model of Ikeda et al. (2009). The model has a torus with a half-opening angle of θOA = 46.2° (equivalent to log LX = 42.7, according to the relationship of Hasinger 2008), an equatorial column density of , and an inclination angle of θ i = 1°. The continuous line represents the fit to the simulated spectrum using for the continuum the same model we used for the simulations and a Gaussian line for the iron Kα fluorescent line. Bottom panel: contribution to the chi-squared for the best fit to the simulated spectrum.
In the text
thumbnail Fig. 4

Equivalent width of the iron Kα line versus the X-ray luminosity obtained simulating a torus with an equatorial column density of and a covering factor decreasing with the luminosity. The θOA − LX relationship used here is that of Hasinger (2008; see Fig. 2). The relations of Bianchi et al. (2007, black dashed line) and Shu et al. (2012, blue line, obtained averaging different observations of the same source) are also shown for comparison (see also Table 1). The normalization of the relation of Bianchi et al. (2007) has been fixed to an arbitrary value for comparison.
In the text
thumbnail Fig. 5

Left panel: value of the slope (B) of the X-ray Baldwin effect obtained simulating the variation of the reprocessed X-ray radiation with the luminosity for tori with different values of the equatorial column density (in the range ) for the different θOA − LX relationships shown in Fig. 2 (Eqs. (1)–(3)) in the Seyfert regime (42 < log LX ≤ 44.2). The model used is that of Ikeda et al. (2009), and the simulated data were fitted with Eq. (5). The red line represents the value of the slope (B = − 0.12 ± 0.04) obtained by fitting in the Seyfert regime the data per source reported in Shu et al. (2010); the red shadowed area represents the 1σ contour of the slope. Right panel: same as left panel, but considering the intercept (A) of the X-ray Baldwin effect obtained by our simulations. The red line represents the value of the intercept (A = 1.64 ± 0.05) obtained by the fit to the Chandra/HEG data in the Seyfert regime, while the red shadowed area represents its 1σ error.
In the text
thumbnail Fig. 6

Left panel: value of the slope (B) of the X-ray Baldwin effect obtained simulating the variation of the reprocessed X-ray radiation with the luminosity for tori with different values of the equatorial column density for the different θOA − LX relationships shown in Fig. 2 (Eqs. (1)–(3)) in the quasar regime (log LX > 44.2). The model used is that of Brightman & Nandra (2011), and the simulated data were fitted with Eq. (5). The red line represents the value of the slope (B = −0.16 ± 0.22), which was obtained by fitting in the quasar regime the data per source reported in Shu et al. (2010); the red shadowed area represents the 1σ contour of the slope. Right panel: same as left panel, but considering the intercept (A) of the X-ray Baldwin effect obtained by our simulations. The red line represents the value of the intercept (A = 1.5 ± 0.3) obtained by the fit to the Chandra/HEG data in the quasar regime, while the red shadowed area represents its 1σ error.
In the text
thumbnail Fig. 7

Iron Kα EW versus X-ray luminosities and predicted trends obtained for different values of the equatorial column density of the torus. The points are the values of the EW of the iron Kα line reported by Shu et al. (2010) and obtained by averaging multiple Chandra/HEG observations of AGN. The two blue dash-dotted lines are the fits to our simulations of the X-ray Baldwin effect using the θOA − LX relationship of Hasinger (2008) for the Seyfert regime (log EW = 1.01−0.17log LX,44 for , and log EW = 2.05−0.08log LX,44 for ). The blue long-dashed lines represent the EW − LX relations obtained in the quasar regime (log EW = 1.17−0.73log LX,44 for and log EW = 2.14−0.39log LX,44 for ) using the relationship of Hasinger (2008), while the green dashed lines represent those attained using the relationship of Burlon et al. (2011). The intercepts obtained in the quasar regime have been modified to match those obtained at lower luminosities.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.