| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220756 | |
| Published online | 10 April 2013 | |
The distance to NGC 1316 (Fornax A): yet another curious case⋆,⋆⋆,⋆⋆⋆
1
INAF, Osservatorio Astronomico di Teramo, via M. Maggini snc,
64100
Teramo,
Italy
e-mail:
cantiello@oa-teramo.inaf.it
2
INAF, Osservatorio Astronomico di Capodimonte, salita
Moiariello, 80131
Napoli,
Italy
3
Dominion Astrophysical Observatory, Herzberg Institute of
Astrophysics, National Research Council of Canada, Victoria
BC V82 3H3, Canada
4
INAF, Osservatorio Astronomico di Roma, via Frascati 33, Monte
Porzio Catone, 00040
Roma,
Italy
5
European Southern Observatory, Karl–Schwarzschild–Str. 2, 85748
Garching bei München,
Germany
6
International Centre for Relativistic Astrophysics, Piazzale della
Repubblica 2, 65122
Pescara,
Italy
Received: 16 November 2012
Accepted: 14 February 2013
Aims. The distance of NGC 1316, the brightest galaxy in the Fornax cluster, provides an interesting test for the cosmological distance scale. First, because Fornax is the second largest cluster of galaxies within ≲25 Mpc after Virgo and, in contrast to Virgo, has a small line-of-sight depth; and second, because NGC 1316 is the single galaxy with the largest number of detected Type Ia supernovae (SNe Ia), giving the opportunity to test the consistency of SNe Ia distances both internally and against other distance indicators.
Methods. We measure surface brightness fluctuations (SBF) in NGC 1316 from ground- and space-based imaging data. The sample provides a homogeneous set of measurements over a wide wavelength interval. The SBF magnitudes, coupled with empirical and theoretical absolute SBF calibrations, are used to estimate the distance to the galaxy. We also present the first B-band SBF measurements of NGC 1316 and use them together with the optical and near-IR SBF data to analyze the properties of field stars in the galaxy.
Results. We obtain mag, or d = 20.8 ± 0.5(stat.) ± 1.5(sys.) Mpc. When placed in a consistent Cepheid distance scale, our result agrees with the distances from other indicators. On the other hand, our distance is ~17% larger than the most recent estimate based on SNe Ia. Possible explanations for this disagreement are the uncertain level of internal extinction, and/or calibration issues. Concerning the stellar population analysis, we confirm the results from other spectro-photometric indicators: the field stars in NGC 1316 are dominated by a component with roughly solar metallicity and intermediate age. A non-negligible mismatch exists between B-band SBF models and data. We confirm that such behavior can be accounted for by an enhanced percentage of hot horizontal branch stars.
Conclusions. Our study of the SBF distance to NGC 1316, and the comparison with distances from other indicators, raises some concern about the homogeneity between the calibrations of different indicators. If not properly placed in the same reference scale, significant differences can occur, with dramatic impact on the cosmological distance ladder. Our results on the stellar populations properties show that SBF data over a broad wavelength interval are an efficient means of studying the properties of unresolved systems in peculiar cases like NGC 1316.
Key words: galaxies: elliptical and lenticular, cD / galaxies: distances and redshifts / galaxies: clusters: individual: NGC 1316 / galaxies: photometry / galaxies: stellar content / galaxies: peculiar
Based on data obtained from the ESO Science Archive Facility, and on observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA) and the Canadian Astronomy Data Centre (CADC/NRC/CSA).
Appendices A and B are available in electronic form at http://www.aanda.org
Reduced VLT images (as FITS files) are only available at the CDS via anonymous ftp to http://cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/552/A106
© ESO, 2013
1. Introduction
The past three decades have seen remarkable progress in the study of the distance scale of the Universe (Jacoby et al. 1992; Ferrarese et al. 2000; Freedman et al. 2001; Freedman & Madore 2010), resulting in a general convergence of distances based on different indicators. Nevertheless, to resolve the lingering discrepancies (Tammann et al. 2008; Freedman & Madore 2010), there is an urgent need to (i) lower the statistical (intrinsic) and systematic (external) errors for single distance indicators; (ii) obtain distance measurements from indicators with a large range of applicability in terms of distances and of useful targets in order to minimize the error propagation over the cosmological distance scale; and (iii) improve/analyze the matching between independent indicators. A particularly promising distance indicator for addressing the three listed items is the surface brightness fluctuations technique (SBF, Tonry & Schneider 1988; Tonry et al. 1990; Blakeslee et al. 2009).
Median 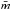 and
and 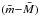 errors from the literature.
errors from the literature.
After the first two “rungs” of the cosmological distance scale, represented by geometric methods and by primary indicators (variable stars, main-sequence fitting, etc.), the SBF method is one of the most accurate indicators, with a median 0.14 mag accuracy on distance moduli, or ~7% in distance, up to ~100 Mpc (Mei et al. 2003; Biscardi et al. 2008). However, the accuracy gets considerably smaller, to a mean ~0.08 mag (~4% in distance) from space-based optical data (Table 1).
By definition, the SBF signal corresponds to the ratio of the second to the first moments of the luminosity function of stars in a galaxy. As opposed to the surface brightness that does not scale with the distance of the galaxy, the SBF signal scales inversely with the distance squared. Observationally, the SBF method relies on the measurement of the intrinsic flux variance in a galaxy, generated by the Poissonian fluctuations in the surface brightness due to the statistical variation of the stellar counts in adjacent resolution elements. The variance, normalized to the local mean surface brightness, is converted to an apparent magnitude, 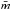 , from which the distance modulus,
, from which the distance modulus, 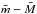 , follows once the absolute
, follows once the absolute 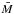 is known.
is known.
Given its definition, 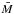 in a given bandpass is dependent on the properties of the underlying stellar populations. The analysis of large samples of early-type systems, including galaxy in groups, has made it possible to characterize the dependence of
in a given bandpass is dependent on the properties of the underlying stellar populations. The analysis of large samples of early-type systems, including galaxy in groups, has made it possible to characterize the dependence of 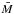 on stellar population properties using linear relations with respect to some broad-band optical colour (Tonry et al. 2001; Mei et al. 2007; Cantiello et al. 2007a).
on stellar population properties using linear relations with respect to some broad-band optical colour (Tonry et al. 2001; Mei et al. 2007; Cantiello et al. 2007a).
In Table 1 we report the median errors on SBF measurements, 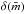 , and on the associated distance moduli,
, and on the associated distance moduli, 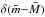 , derived from different samples. For optical SBF, the typical accuracy for ground-based measurements has been ≲0.2 mag (10% in distance). Because this is dominated by measurement errors, the superior resolution of HST leads to an improved accuracy of ~0.08 mag. For a comparison, the internal scatter of the period-luminosity (PL) relation of Cepheids ranges from 0.20 mag in the V band, to 0.09 mag in the Spitzer [3.6] μm and [4.5] μm bands (e.g., Ngeow et al. 2009). The mean uncertainties for the near-IR SBF sample quoted in Table 1 are generally larger than the optical ones, ≲0.2 mag (~10% on distances) even in the case of space-based data. This is due both to observational/technical issues (e.g. dark current patterns, “wormy” background, see Jensen et al. 1998, 2001), and to the scatter of the calibration (mostly related to the sensitivity of the SBF signal to the properties of AGB and TP-AGB stars in these bands, see Mei et al. 2001; Liu et al. 2002; Jensen et al. 2003; Raimondo et al. 2005; González-Lópezlira et al. 2010). The availability of Wide Field Camera 3 (WFC3) on board of the Hubble Space Telescope (HST) is expected to significantly improve the situation in this wavelength regime. Finally, the zero point of the calibration is typically tied to the Cepheid distance scale to an accuracy ≲0.08 mag (Tonry et al. 2000; Blakeslee et al. 2010).
, derived from different samples. For optical SBF, the typical accuracy for ground-based measurements has been ≲0.2 mag (10% in distance). Because this is dominated by measurement errors, the superior resolution of HST leads to an improved accuracy of ~0.08 mag. For a comparison, the internal scatter of the period-luminosity (PL) relation of Cepheids ranges from 0.20 mag in the V band, to 0.09 mag in the Spitzer [3.6] μm and [4.5] μm bands (e.g., Ngeow et al. 2009). The mean uncertainties for the near-IR SBF sample quoted in Table 1 are generally larger than the optical ones, ≲0.2 mag (~10% on distances) even in the case of space-based data. This is due both to observational/technical issues (e.g. dark current patterns, “wormy” background, see Jensen et al. 1998, 2001), and to the scatter of the calibration (mostly related to the sensitivity of the SBF signal to the properties of AGB and TP-AGB stars in these bands, see Mei et al. 2001; Liu et al. 2002; Jensen et al. 2003; Raimondo et al. 2005; González-Lópezlira et al. 2010). The availability of Wide Field Camera 3 (WFC3) on board of the Hubble Space Telescope (HST) is expected to significantly improve the situation in this wavelength regime. Finally, the zero point of the calibration is typically tied to the Cepheid distance scale to an accuracy ≲0.08 mag (Tonry et al. 2000; Blakeslee et al. 2010).
Main properties of NGC 1316.
Thus, SBF distances are characterized by reasonably well defined and small (especially in optical bands) internal and calibration errors (item (i) in the list above). The technique has been used to estimate distances for Local Group galaxies (even closer than that if one takes into account the work on Galactic globular clusters by Ajhar et al. 1994), out to galaxies at ≳100 Mpc (Jensen et al. 2001; Biscardi et al. 2008). With the highly improved near-IR imaging capabilities of the WFC3/IR and similar instruments, and thanks to the much brighter SBF signal in the near-IR, the upper limit on SBF distances is expected to increase significantly. Thus, SBF can encompass more than two orders of magnitude in distance, bridging local to cosmological distances with the use of a single indicator (item (ii) above).
In this paper we present measurements of SBF magnitudes for the intermediate-age merger remnant NGC 1316, also known as Fornax A (e.g., Schweizer 1980; Terlevich & Forbes 2002). This galaxy is peculiar in many ways. Although by far the brightest member of the Fornax cluster, it is not near the cluster center, being ~3.7° away from the central giant elliptical NGC 1399 (projected separation of ~1.3 Mpc at the distance of Fornax). It shows numerous dust features, a prominent dust lane, Hα filaments, loops, and tidal tails originally analyzed by Schweizer (1980). Moreover, it is a powerful radio-galaxy and, to date NGC 1316 is the single galaxy with the largest number of discovered Type Ia supernovae (SNe Ia hereafter; four events recorded). The latter property makes NGC 1316 a remarkable place to test the extragalactic distance scale, because of the role of SNe Ia for cosmological distances, and because NGC 1316 is one of the nearest massive post-merger galaxies.
We have collected data covering a large wavelength interval (from B to H band), with the specific purpose of performing a self-consistent analysis of SBF data for this galaxy in order to carry out a comprehensive study of the SBF in NGC 1316, and consequently, of the galaxy distance (item (iii) above).
Furthermore, given their dependence on the square of the stellar luminosity, SBF magnitudes are especially sensitive to the brightest stars at a particular wavelength and at a given evolutionary phase of a stellar population. As shown by various authors SBF magnitudes and, in particular, SBF colors, can be used to investigate the properties of a specific stellar component in the host stellar population, depending on the observing wavelength (Worthey 1993a; Blakeslee et al. 2001; Cantiello et al. 2003; Jensen et al. 2003; Raimondo et al. 2005). As an example, SBF colors involving bluer bands, like B, have been used to study the hot stellar component in unresolved systems (e.g., Cantiello et al. 2007b). Likewise, specific phenomena like the mass-loss rates in the AGB phase have been analyzed by taking advantage of near-IR SBF data (Raimondo 2009; González-Lópezlira et al. 2010). As a consequence of the quoted relation between the SBF signal and stellar population properties, we take advantage of the broad passband coverage to characterize the properties of field stars in the galaxy, in order also to provide new constraints on the formation history and evolution of the peculiar galaxy NGC 1316.
The organization of the paper is as follows. In Sect. 2 we present a description of the imaging data used, the data reduction and calibration procedures. Sections 3 and 4 describe the procedures for SBF measurements and the calibrations used to determine the distances. In Sect. 5 we compare the SBF distance to previous results from other indicators. We analyze the properties of the unresolved field star populations in Sect. 6, and summarize our conclusions in Sect. 7. In Appendix A a detailed comparison of SBF and PNLF distances is presented. Finally, Appendix B presents some details on the SBF versus SNe Ia comparison.
2. Observations and reductions
This work is based on data of NGC 1316 from the Very Large Telescope (VLT) and HST archives. We used i) B, V and I-band observations obtained with the FORS1 Imager at ESO’s VLT in Paranal (Program 64.H-0624(A), P.I. M. Della Valle), and from the HST; ii) ACS F475W and F850LP-band data from the ACSFCS survey (Jordán et al. 2007); iii) WFC3/IR observations in the F110W and F160W filters, plus WFC3/UVIS F336W (HST Program ID 11691, P.I. Goudfrooij).
It is useful to note, for the forthcoming discussion, that the VLT observations were part of a project aimed at discovering, monitoring and characterizing the properties of the nova population in NGC 1316, with the specific purpose of deriving the distance to the galaxy using novae (Della Valle & Gilmozzi 2002). Some relevant properties of the target are listed in Table 2.
In the remainder of this section we describe the reduction and calibration procedures adopted for the data from both telescopes. In all cases we used SExtractor (Bertin & Arnouts 1996) for the source photometry, and the IRAF/STSDAS task ELLIPSE (based on the method described by Jedrzejewski 1987) to fit the galaxy isophotes.
2.1. VLT data
2.1.1. Data reduction
The data reduction was carried out with the VST-Tube imaging pipeline (Grado et al. 2004, 2012), specifically developed by one of the co-authors of this work (A.G.) for data from the VLT Survey Telescope (Capaccioli et al. 2005; Capaccioli & Schipani 2011, VST). VST-Tube is a very versatile software for astronomical data analysis, tested against imaging data taken with different telescopes/detectors, adaptable to existing or future multi-CCD cameras (more details will be given in a dedicated forthcoming publication, Grado et al., in prep.). Further, VST-Tube offers the great advantage of fully controlling each step of the data processing.
Total and used exposure times for each band.
In Table 3 we report the total exposure times available for each VLT filter. Unfortunately, technical problems with the camera made a fraction of the total observing time unusable (55%, 60% and 44% of the total exposure time in B, V, and I band respectively). The VLT images downloaded from the archive and used for this work showed a strong degradation during the thirteen observing runs spanning nearly two months, from December 1999 to February 2000 (Fig. 1). This is partly due to moon illumination, and also to the problem of instrument contamination. A decontamination process of FORS1 was performed in November 1999, and one more in January 2000 (Cavadore et al. 1999). The effect of the last intervention is clearly visible in a ≳1.0 mag jump in the background level between observations before and after the decontamination (see Table 7). For this reason, we decided to select only images taken before 2000 January 15th and, in case of the I filter, we also included the last two exposures of 2000 February 4th (column “Used data” in Table 7). The total exposure times used after the selection for good frames are also reported in Table 3.
The images were reduced as usual removing the instrumental signatures (overscan correction, bias subtraction, flat field correction and, in the case of the I band, fringe pattern removal). The resulting co-added mosaic are approximately 6.9 × 7.0 arcmin2, a color combined image of the three mosaics is shown in Fig. 2 (upper panel).
 |
Fig. 1 Left panel: mosaic single exposure in B on 1999 December 27th (600 s total, the first observing run of the proposal). Right panel: as left, but for an exposure taken during the night of 2000 January 20th. |
 |
Fig. 2 Left panel: false colour combined VLT BVI frames. Middle panel: as left panel, but for residual frames. The location of the ACS frames is outlined in black. Right panel: ACS and WFC3/UVIS combined residual images. Colour coding is chosen to enhance the presence of dust. The sites of three over four of the SNe Ia host by the galaxy are shown. |
 |
Fig. 3 Comparison between the VLT (this work, t.w.) BVI photometry and NTT data from G01 used for calibrating FORS1 photometry. |
2.1.2. Calibration
The VLT data were calibrated adopting the Goudfrooij et al. (2001b, G01 hereafter) photometry as reference, then solving the photometric equations accordingly. G01 obtained optical photometry of the sources in the field of NGC 1316 using archival NTT/EMMI data in B, V, and I filters. Furthermore, the authors also derived JHKS photometry for eight candidate globular clusters (GCs) in the galaxy, using the IRAC2 camera mounted on the ESO/MPI 2.2 m telescope.
The panels in Fig. 3 show the B, V and I VLT photometry versus the G01 calibrating data. Note that G01 adopted Galactic extinction E(B − V) = 0.0 from Burstein & Heiles (1984), while we adopted E(B − V) = 0.021 from Schlegel et al. (1998)1.
The comparisons in Fig. 3 are obtained in the same observational conditions, prior to corrections for Galactic extinction.
2.2. HST data
HST instruments, thanks to the high resolution and the sharp PSF, provide ideal observational datasets for SBF analysis (e.g., Ajhar et al. 1997; Jensen et al. 2001; Biscardi et al. 2008; Blakeslee et al. 2010). We analyze the optical ACS data and provide the first near-IR WFC3/IR SBF analysis, with the specific purpose of deriving a consistent set of ground and space-based SBF measurements to secure a reliable distance to NGC 1316.
 |
Fig. 4 Comparison between our photometry and the ACSFCS results. Black dots and labels refer to the whole sample of ~620 matched sources, gray circles and labels to the ~40 selected sources. The median difference and the associated rms are also reported. |
2.2.1. NGC 1316 as seen by the ACS
We analyzed the ACS F475W (~SDSS g band) and F850LP (~SDSS z) observations of NGC 1316 obtained for the ACSFCS survey (see Côté et al. 2004; Jordán et al. 2007, and references therein for details on the observations and the data reduction procedures for the ACSFCS and its twin ACSVCS survey)2.
Other ACS observations in the F435W, F555W, and F814W (~BV and I, respectively) bands are also available from the HST archive. The B-band data are not suitable for SBF analysis, while the V and I band have already been analyzed by us (Cantiello et al. 2007a), providing results in good agreement with the present study (see below). Such observations will be used to improve the mapping of the dust in NGC 1316. The image processing, including cosmic-ray rejection, alignment, and final image combination, is performed with the APSIS ACS data reduction software (Blakeslee et al. 2003), also used for ACSFCS image alignment.
For sake of homogeneity with the other datasets used in this work, our photometric analysis of the ACS frames was performed independently from the ACSFCS one. Hence, it is a noteworthy result that our gF475W and zF850LP surface brightness profiles, derived as described in the following section, match within <0.05 mag the ACSFCS ones from Côté et al. (2007).
The situation is a bit more complex for the photometry of point-like sources and/or “slightly-resolved” ones. For this comparison we used the preliminary catalog of GC candidates from the ACSFCS team, derived as described in Jordán et al. (2004, 2009), and our photometric catalog obtained as described in Sect. 3. The results of the comparison are shown in Fig. 4. If the full sample of ~620 matching sources is used, the median difference between our and ACSFCS photometry overlaps with zero within the rms scatter. The large scatter between the catalogs is due to the independent analysis procedures, especially in the way slightly-resolved sources are treated. At the distance of the Fornax cluster with the resolution of ACS, the GCs hosted by NGC 1316 appear slightly resolved. The ACSFCS analysis is optimized to generate accurate photometry of GCs with different radii. The aperture correction for such sources needs to be evaluated using more refined analysis methods (Jordán et al. 2004, 2009) than the ones adopted here (see next section). The gray circles in Fig. 4 show a selection of GC candidates with i) Δm ≤ 0.05 mag and brighter than m = 24 mag in both ACS bands; ii) galactocentric radius ≥60″, to reduce the number of objects highly contaminated by dust; and iii) ACSFCS estimated radius ≤0.03″, to select only the most compact sources, for which the issue of a different treatment of the aperture correction should not complicate the comparison. For the selected sample of sources the matching is significantly improved (gray symbols in the figure). The gF475W data are statistically consistent in the two catalogs, while a small 0.01 mag offset is seen in the zF850LP band. However, for the purposes of the present work, such an offset only affects the estimate of the contribution to the fluctuation amplitude due to external sources (Tonry et al. 1990; Sodemann & Thomsen 1995; Blakeslee et al. 1999). Given the level of completeness of the GC catalog, and the amplitude of the offset, the impact on 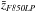 is negligible. As will be shown in Sect. 3, in fact, our SBF measurements are in very good agreement with the ACSFCS ones (Blakeslee et al. 2009)3.
is negligible. As will be shown in Sect. 3, in fact, our SBF measurements are in very good agreement with the ACSFCS ones (Blakeslee et al. 2009)3.
2.2.2. NGC 1316 as seen by the WFC3
 |
Fig. 5 Left panel: colour–colour diagram with the ACS and WFC3/IR magnitudes. Gray crosses mark the full sample of common sources, black circles show selected GC candidates (see text). Right panel: comparison between WFC3/IR photometry and the IRAC2 data from Goudfrooij et al. (2001a). In both panels the predictions from SPoT simple stellar population models with different metallicity are shown with different colour/line styles ([Fe/H] = −2.3, −1.4, −0.7, −0.4, 0.0 and +0.4 dex shown with dark-yellow, cyan, magenta, green, blue and brown, respectively). The age range is 3 to 14 Gyr. (See electronic version of the Journal for a colour version of the figure.) |
The F110W (~J) and F160W (~H) band images of NGC 1316 taken with the WFC3/IR were downloaded from the Hubble Legacy Archive together with the WFC3/UVIS F336W (~U-band) image. The near-IR images were downloaded for the specific purpose of deriving SBF magnitudes, while the UF336W has been used to improve the detection and masking of dust over the entire set of available images.
We calibrated the WFC3/IR photometry using the VEGA zero points given by Kalirai et al. (2009). To check the WFC3/IR photometric data, we made two different comparisons, both shown in Fig. 5. Figure 5 (left panel) plots the WFC3/IR color JF110W − HF160W versus the ACS gF475W − zF850LP for the combined ACS-WFC3 data set. The crosses give the full sample of sources. In order to select the best GC candidates, the black filled circles show the sources with zF850LP ≤ 23.5 mag, photometric error ΔzF850LP ≲ 0.1 mag, SExtractor class-star parameter ≥0.7, and galactocentric distance ≥45″. The simple stellar population (SSP) models from the Teramo Stellar Population Tools (SPoT, see below) group4 for the age range from 3 to 14 Gyr, and [Fe/H] from −2.3 dex to +0.4 dex, are also shown in the figure. Even though a non-negligible scatter exist between the data of selected GCs candidates and SSP models (≲0.2 mag), the match with the locus of SSP models is satisfactory for the purposes of the present work.
The right panel of Fig. 5 shows the comparison between the combined WFC3/IR and G01 near-IR samples. The SPoT models are also shown in the figure, and sources enshrouded in dust are rejected from the comparison. Notwithstanding the large error bars of ground-based observations, we find Δ [(J − H)G01 − (JF110W − HF160W) ~ 0.08] mag, in agreement with model predictions.
3. SBF measurements
To derive the photometry of sources in each of the selected VLT and HST frames, and measure the fluctuation amplitudes, we used the procedures described in our previous works (see Cantiello et al. 2011a, and references therein). The procedure is basically the same for VLT/FORS1, HST/ACS, and HST/WFC3/IR data with minor differences outlined below.
 |
Fig. 6 Upper left panel: UF336w/WFC3/UVIS, BVI/FORS1, gF475WzF850LP/ACS, and JF110WHF160W/WFC3/IR surface brightness profiles for NGC 1316. Each band is shown with a different line style/colour. A vertical shift is applied for sake of clarity as labeled. Lower left panel: as upper left panel, but in R1/6 scale. The Sersic profile fitting procedure used leaves the n-index free to vary. Here we use the median n = 6 value, which is also consistent with Côté et al. (2007). The full dots are extrapolated from Carter et al. (1983), accordingly shifted for each band (see colour image). Right panels: the difference between observed and fitted surface brightness profiles. (See electronic version of the Journal for a colour version of the figure.) |
The main steps of SBF measurement involve: sky background determination and subtraction; galaxy model and large scale residual subtraction; photometry and masking of point-like and extended sources, including dust; power spectrum analysis of the residual frame. We determined the sky background by fitting the surface brightness profile of the galaxy with a Sersic law (Sersic 1968) plus a constant term. After sky determination, a first model of the galaxy was obtained and subtracted from the sky-subtracted frame, and a mask of the bright sources was obtained. The large scale residuals, still present in the frame after subtracting the galaxy model, were removed using the background map obtained with SExtractor adopting a mesh size ~10 times the FWHM (Tonry et al. 1990; Cantiello et al. 2005). In the following we refer to the sky, galaxy-model and large scale residuals subtracted image as the residual frame.
The procedure of i) surface brightness analysis and sky determination; ii) model fitting and subtraction; iii) sources/dust masking; and iv) large scale residual subtraction was iteratively repeated until the residual frame appeared “flat” in the regions of interest for SBF measurements, i.e., until the residual did not show any (local) artifact due to the subtracted galaxy model. The middle panel of Fig. 2 show the false colour combined BVI image of the residual frames. The right panel of the figure, instead, shows a combination of the ACS and WFC3/UVIS frames, used to map the dust around the center of the galaxy. The positions of three of the four SNe Ia host in the galaxy is also indicated in the figure (the region of SN 1980D is not covered by either the HST or VLT frames; we adopted the revised SNe Ia coordinates from Stritzinger et al. 2010).
The surface brightness profiles for all bands analyzed, as well as the difference between modeled and observed profiles, are shown in Fig. 6.
The photometry of fore/background sources and of GCs was derived running SExtractor on the residual frames. As described in our previous work, we modified the input weighting image of SExtractor by adding the galaxy model (times a factor between 0.5 and 10, depending on the expected amplitude of the SBF signal; for details see Jordán et al. 2004; Cantiello et al. 2005) so that the SBFs were not detected as real objects. The aperture correction was obtained from a number of isolated point-source candidates in the frames and by making a curve of growth analysis out to large radii (Cantiello et al. 2009, 2011b). The outer radius used for FORS1 data was 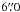 . For ACS(WFC3) we adopted
. For ACS(WFC3) we adopted 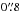 (
(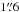 ) and then added an extra aperture correction term to infinite radius by using the instrument encircled energy tables (for ACS we used Sirianni et al. 2005, while for WFC3 we adopted the Instrument Handbook, version 4).
) and then added an extra aperture correction term to infinite radius by using the instrument encircled energy tables (for ACS we used Sirianni et al. 2005, while for WFC3 we adopted the Instrument Handbook, version 4).
Once the catalog of sources was derived, the next step was to fit the luminosity function of the sources, to be used to estimate the already mentioned background fluctuation term due to unmasked faint sources. We obtained the fit to the GC and background galaxy luminosity functions from the photometric catalog of sources, after removing the brightest/saturated point-like sources and the brightest and most extended objects. The best fit to the sum of the two luminosity functions, and the background fluctuation correction term, Pr, were derived as in Cantiello et al. (2005).
 |
Fig. 7 Power spectrum analysis of the BVIzF850LPJF110WHF160W frames. Each panel shows a different band, as labeled. For all bands, the upper panels show the logarithm of the power spectrum of the residual frame (gray dots) and the best fit P(k) curve. In the middle panels the difference between observed and fitted power spectra is shown. The flat region of log P0(kfit > k) between vertical dashed lines (lower panels) is used to evaluate the best fit parameters P0, and P1. |
To measure SBF magnitudes we estimated the azimuthal average of the residual frame power spectrum, P(k), then matched it to the power spectrum of a template PSF convolved with the mask image, E(k). The total fluctuation amplitude P0 was obtained via a robust minimization method (Press et al. 1992) as the multiplicative factor in the power spectrum representation P(k) = P0 × E(k) + P1, where P1 is the white noise constant term. We used one to five different isolated bright point sources in each residual frame for the template PSFs. Each PSF, after normalization, was singularly adopted to estimate the SBF signal of the galaxy. Finally, the SBF amplitude, Pf = P0 − Pr, was estimated within circular annuli. The results of the power spectrum analysis are summarized in Fig. 7, with one example for each band.
The results of the SBF and colour measurements for all bands considered are reported in Table 4. For each filter, in addition to the statistical error, we report the systematic uncertainty due to PSF fitting. For HF160W, since we could only find one good candidate PSF in the frame, we assumed a conservative PSF scatter of 0.2 mag5. In the case of JF110W no good PSF was found over the WFC3/IR frame, thus we used a PSF star taken from different observations associated with the same HST proposal. As for HF160W we assumed 0.2 mag PSF uncertainty.
Surface brightness fluctuations and colour measurements corrected for galactic extinction.
4. The SBF distance to NGC 1316
Distances from SBF measurements.
The estimate of distances in the SBF method relies on knowledge of the absolute SBF magnitudes. Using the measurements reported in Table 4, together with empirical and theoretical calibrations given in Table 5, we obtained the distance moduli reported in the (m − M) column of the table. In particular we obtained a mean distance modulus of 31.59 ± 0.05 mag and 31.60 ± 0.11 mag with the empirical and theoretical equations, respectively. In the following we provide some details on the calibration equations adopted.
4.1. Absolute SBF magnitudes from empirical calibrations
The empirical calibrations of SBF magnitudes in optical bands, in particular in the I band, are the most thoroughly analyzed (Tonry et al. 1990, 2001; Mei et al. 2007; Blakeslee et al. 2010). The two aforementioned HST surveys of the Virgo and Fornax clusters provided an extremely accurate calibration of 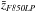 , including some degree of non-linearity in the calibration. Some debate still exists on near-IR bands calibrations (see González-Lópezlira et al. 2010, and references therein), although, as already mentioned, relevant progress will be done thanks to the installation of the WFC3/IR (Blakeslee 2012; French et al. 2012).
, including some degree of non-linearity in the calibration. Some debate still exists on near-IR bands calibrations (see González-Lópezlira et al. 2010, and references therein), although, as already mentioned, relevant progress will be done thanks to the installation of the WFC3/IR (Blakeslee 2012; French et al. 2012).
In the upper part of Table 5 we report the distance moduli obtained using the empirical calibrations taken from literature, together with the adopted calibrations.
As a first general comment on the empirical equations, we must emphasize that the numbers reported in the table are all tied to the same common zero point, i.e., to the Cepheid distances with metallicity correction to the PL relation from Freedman et al. (2001). The resulting zero points of the 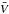 ,
, 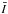 and
and 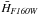 versus V − I calibrations are shifted of + 0.06, + 0.06 and − 0.10 mag with respect to the calibrations in the original papers (see Appendix A in Blakeslee et al. 2010).
versus V − I calibrations are shifted of + 0.06, + 0.06 and − 0.10 mag with respect to the calibrations in the original papers (see Appendix A in Blakeslee et al. 2010).
For the 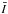 versus B − I calibration, taken from Cantiello et al. (2005), we do not make any revision since the zero point is already based on the chosen set of Cepheids. Similarly, the zF850LP-band calibration does not need any change (Blakeslee et al. 2009).
versus B − I calibration, taken from Cantiello et al. (2005), we do not make any revision since the zero point is already based on the chosen set of Cepheids. Similarly, the zF850LP-band calibration does not need any change (Blakeslee et al. 2009).
For the HF160W-band distance estimate, we used two independent calibrations. The first derived by Jensen et al. (2003) from HST/NICMOS data. We adopted the SPoT SSP models to evaluate the changes in the calibration due to the difference between the NICMOS2 and the WFC3/IR HF160W passbands. The result is that the WFC3/IR 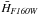 zero point is 0.2 mag fainter than the NICMOS2 HF160W one. This is partly expected because of the cut at larger/redder wavelengths of the WFC3/IR filter (1400–1700 nm passband, versus 1400–1800 nm for NICMOS2). Hence, we add a 0.2 mag to the zero point of the Jensen et al. (2003) empirical relation, assuming a default 0.1 mag uncertainty because of the model-dependent correction term. The second calibration is a preliminary result obtained by Cho et al. (2013), based on the observations of 16 early-type galaxies in Virgo and Fornax specifically obtained to empirically calibrate the SBF for the WFC3/IR passband. For the near-IR data, in contrast with the optical measurements, the distance modulus includes the systematic PSF uncertainty since it is dominant with respect to the statistical errors of the SBF measurement and of the calibration zero point.
zero point is 0.2 mag fainter than the NICMOS2 HF160W one. This is partly expected because of the cut at larger/redder wavelengths of the WFC3/IR filter (1400–1700 nm passband, versus 1400–1800 nm for NICMOS2). Hence, we add a 0.2 mag to the zero point of the Jensen et al. (2003) empirical relation, assuming a default 0.1 mag uncertainty because of the model-dependent correction term. The second calibration is a preliminary result obtained by Cho et al. (2013), based on the observations of 16 early-type galaxies in Virgo and Fornax specifically obtained to empirically calibrate the SBF for the WFC3/IR passband. For the near-IR data, in contrast with the optical measurements, the distance modulus includes the systematic PSF uncertainty since it is dominant with respect to the statistical errors of the SBF measurement and of the calibration zero point.
All distances based on the empirical calibrations reported in Table 5 agree with each other within the quoted uncertainties. The weighted mean of distance moduli is also given in the table.
4.2. Absolute SBF magnitudes from theoretical calibrations
Various authors have analyzed the possibility to calibrate absolute SBF magnitudes using stellar populations synthesis models, thereby making it a primary distance indicator, not linked to the Cepheids zero point (Buzzoni 1993; Worthey 1993b; Blakeslee et al. 2001; Biscardi et al. 2008). In this work we have taken as reference the SBF versus colour equations derived using the simple stellar population models from the Teramo SPoT group. For a detailed review of the SPoT models we refer to Raimondo et al. (2005) and Raimondo (2009), and references therein. These models have been shown to be very effective in matching the empirical SBF calibration in different bands, as well as in reproducing the resolved (colour magnitude diagrams) and unresolved (colors, magnitudes) properties of stellar populations (Brocato et al. 2000; Cantiello et al. 2007a; Cantiello 2012). We used the updated version of the SPoT models, which for the photometric bands and chemical composition used in this section confirms the results obtained from the previous Raimondo et al. (2005) models (Raimondo, priv. comm.). The grid of models used has [Fe/H] = −0.4, 0.0, +0.4 dex and ages from 3 to 14 Gyr. The choice was made based on the age and chemical composition properties of fields stars in NGC 1316 derived from various independent spectro-photometric indicators (e.g., Terlevich & Forbes 2002; Silva et al. 2008; Konami et al. 2010), and also confirmed by GC analysis (Goudfrooij et al. 2001a,b, see also Sect. 6). Under these assumptions, and using a bootstrap approach, we obtained the calibration equations reported in the lower part of Table 5. For each equation, the scatter of the 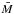 versus colour relation is also tabulated. The uncertainties on distance moduli are derived by summing in quadrature the scatter of the theoretical calibration and the uncertainty on
versus colour relation is also tabulated. The uncertainties on distance moduli are derived by summing in quadrature the scatter of the theoretical calibration and the uncertainty on 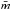 .
.
The distance moduli derived with the theoretical calibrations from the SPoT models are given in the Table 5. All reported distances agree to within the quoted uncertainties.
4.3. Combining SBF-based distance moduli (plus a fundamental note on uncertainties)
The SBF distance of NGC 1316 presented in Sects. 4.1 and 4.2 is based on a self-consistent treatment of empirical and theoretical SBF calibrations. Empirical calibrations have been tied to the same common zero point reference. On the other hand, the theoretical calibrations are based on a well defined set of SSP models ranging from V to HF160W, i.e., a wavelength interval that, in terms of SBF and colors, samples very different stellar population (sub)components.
It is noteworthy that the empirical and theoretical evaluations agree very well with each other. Taking into account that the two methods are based on independent calibration procedures, subject to different types of systematic and statistical uncertainties, this result suggests that both types of errors are reasonably well constrained.
For what concerns the systematic errors in our measurements, summing up all expected sources of uncertainty for each one of the three instruments considered – filter zero point, data reduction, calibration zero point, PSF normalization – the expected systematic uncertainty is ≲0.1 mag, with the exception of near-IR bands, where the contribution from the PSF normalization is dominant with respect to the others.
For the systematic errors in the empirical calibrations, recall that all relations are linked to the same Cepheid zero point (Freedman et al. 2001), which accounts for a further systematic ≲0.2 mag uncertainty6.
 |
Fig. 8 V, I and HF160W-band SBF versus (V − I) predictions from five independent stellar population synthesis codes: solid line (black), dotted line (red), dashed line (blue), long-dashed line (green), dot-dashed (cyan) line show the updated SPoT, Blakeslee et al. (2001), Liu et al. (2002), Marín-Franch & Aparicio (2006), and González-Lópezlira et al. (2010) best fit lines, respectively. Empty (magenta) circles show the corresponding empirical relations, also given in Table 5. (See electronic version of the Journal for a colour version of the figure.) |
Estimating the systematic uncertainty in theoretical SBF calibrations is not a simple task. One way to get such an estimate would be to change the ingredients in the SSP code (stellar tracks, initial mass function, atmosphere models, etc.), and then analyze the effects on SBF. A rough (indirect) estimation of the uncertainty on theoretical calibrations is to compare the results from independent models, obtained from different SSP codes relying on independent physical input and algorithms. A first attempt along these lines was carried out by Cantiello et al. (2003). To estimate this uncertainty for the present work, we compare SSP model predictions from Blakeslee et al. (2001), Liu et al. (2002), Marín-Franch & Aparicio (2006), González-Lópezlira et al. (2010) and the SPoT models. For all these models, we obtain linear fits to the V, I and HF160W SBF amplitudes versus (V − I) colour (Fig. 8). The empirical calibration for each band is also shown in the figure. Note the different range of colour used for each equation, depending on the range of validity of the empirical equation (Tonry et al. 2001; Blakeslee et al. 2001; Jensen et al. 2003; Cantiello et al. 2007a). We find that a scatter of ~0.2 mag provides a first approximation to the systematic uncertainty of SBF calibrations derived from SSP models. A discussion on the origin of the scatter between models is beyond the scope of this paper. We refer the interested reader to the quoted papers and references thereafter.
In conclusion, by combining the weighted mean distance moduli,
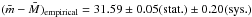 mag and
mag and 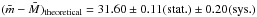 mag, we conclude that our best estimate of the distance of NGC 1316 is
mag, we conclude that our best estimate of the distance of NGC 1316 is 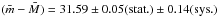 mag, or d = 20.8 ± 0.5(stat.) ± 1.5(sys.) Mpc.
mag, or d = 20.8 ± 0.5(stat.) ± 1.5(sys.) Mpc.
5. Comparison with distances from the literature
As already mentioned, the VLT observations used here were obtained to detect and study the population of novae in NGC 1316, and to use them to derive the galaxy distance. Della Valle & Gilmozzi (2002), using the data of four detected novae (the first detected beyond the Virgo cluster at the time), and the Buscombe-de Vaucouleurs relation (Buscombe & de Vaucouleurs 1955; Capaccioli et al. 1989, 1990) set an upper limit on the distance of the galaxy equal to 22.4 Mpc, and a lower limit of 16 Mpc from the data of Nova A in their sample. In spite of the difficulties (observational and statistical) in using the novae in Fornax A to estimate the galaxy distance, the range obtained by Della Valle & Gilmozzi is in excellent accord with our estimates. Moreover, the lower limit distance is also in complete accord with the SNe Ia as well as the PNLF distances (see below).
In the following sections we compare our distance estimates with others available in the literature. We consider the results obtained from three different distance indicators: Type Ia supernovae, the planetary nebula luminosity function (PNLF), and mean properties of the GC system. Other distances indicators, such as the Tully-Fisher relation or the fundamental plane, cannot be used reliably for NGC 1316 because of its irregular post-merger morphology; moreover, these indicators are normally applied to groups or clusters as a whole, rather than giving precise distances to individual galaxies.
5.1. Comparison with SNe Ia
Ajhar et al. (2001), and later Cantiello et al. (2011a), have presented a comparison of SBF and Type Ia SNe distances for a total of 15 different SNe Ia in 14 galaxies. Both studies found excellent overall agreement between the two distance indicators, including the case of NGC 1316, provided that a consistent set of Cepheid-based distances is used. Similarly, Freedman et al. (2001) and Freedman & Madore (2010) derive essentially identical values of H0 from these two methods when calibrated consistently via Cepheids.
Type Ia Supernova distances to NGC 1316 available in the literature.
NGC 1316 has been a prolific producer of Type Ia supernovae, with four recorded events: SN 1980N, SN 1981D, SN 2006dd, and the fast declining SN 2006mr. All SN Ia light-curves have been used to determine the distance of the host galaxy using several methods. Furthermore, being one of the nearest bright galaxies with well sampled SNe Ia light-curves, NGC 1316 is frequently used in calibrating samples for high-redshift SNe Ia (e.g., Jha et al. 2007; Burns et al. 2011). Based on the MLCS SN Ia distance method (Riess et al. 1998), Goudfrooij et al. (2001a) reported mag for NGC 1316 and concluded that it was therefore ~0.25 mag more distant than the rest of the Fornax cluster, for which Ferrarese et al. (2000) gave a mean distance modulus of 31.54 mag from Cepheids and other indicators. However, no details on the calibration, etc., were given by Goudfrooij et al. (2001a). Ajhar et al. (2001) reported both MLCS and Δm15 distances (Phillips 1993; Hamuy et al. 1996) for SN 1980N in NGC 1316 under different calibrations. Rescaling their results to H0 = 72 km s-1 Mpc-1 gives and from the MLCS and Δm15 methods, respectively. Interestingly, the Δm15 value coincides exactly with the mean SBF distance for the Fornax cluster by Blakeslee et al. (2009).
On the other hand, Stritzinger et al. (2010, Str10 hereafter) have recently reanalyzed the SN Ia distance to NGC 1316, and obtained (m − M) = 31.25 ± 0.03 (stat.) ±0.04 (sys.) mag, based on the analysis of the three “normal” SNe Ia (adopting H0 = 72 km s-1 Mpc-1, see Table 6). The authors also obtain values of (m − M) ~ 31.7–31.8 mag from the data of the fast declining SN 2006mr; however, they consider as doubtful the suitability of fast-declining SNe Ia for estimating distances. Thus, the best distance modulus to NGC 1316 obtained by Str10 is ~0.34 mag fainter than ours, equivalent to a 17% smaller distance. Note that the new distances derived by Str10, as pointed out by the authors, are based on a thorough analysis and discussion of the four SNe Ia, while little or no detail were given in previous studies. Hence, such a difference is very interesting, and needs further analysis, especially because of the primary role in the cosmological distance scale of both these indicators.
As a first general comment, it is useful to highlight that two of the normal SNe (SN 1980N and SN 1981D) were observed in the pre-CCD era. So, although they afford a nice opportunity to test the internal consistency of SNe Ia distances, one should not forget that the quality of the data of these objects is lower than what is currently being obtained. Bearing this in mind, we proceed to our analysis taking the SNe Ia distances, and their associated systematic/statistical errors, from the cited references.
The SNe Ia distances to NGC 1316 obtained before the study of Str10, are listed in Table 6. For consistency with our and Str10’s measurements, all distances are converted to a scale with H0 = 72 km s-1 Mpc-1. In the table we do not report the systematic errors, which are not given by all authors. Taking the weighted mean of all measurements in Table 6, except those of Str10, adopting 0.4 mag default uncertainty where no error is reported, we obtain (m − M) = 31.35 ± 0.05 mag. Although such value agrees with our estimates better than the Str10 result, we caution the reader against these “general” averages, reported here only to emphasize the relative distribution of distances with respect to a reference point. Some of the values reported in Table 6, in fact, are obtained using the same methods/objects but under different assumptions (e.g. MLCS and MLCS2k2), and/or with different calibrators, so that the reported average does not necessarily have a correct physical meaning.
Str10 derives the distance to NGC 1316 using three different methods: the EBV, the Tripp method, and the near-IR light-curves of Type Ia SNe. Each method has its own calibration, and is quantitatively independent from the others. Hence, there can be various possible causes for the difference between our and Str10 distances. First, for the EBV method, the authors adopt negligible internal extinction for all four SNe Ia, but also comment that the spectroscopic analysis provides results “totally inconsistent with the low host galaxy reddening” (Str10, Sect. 4). However, the optical and optical/near-IR colors of these objects are consistent with minimal to unreddened supernova (Fig. 13 of Str10). Second, for the near-IR method, which is intrinsically much less affected by the host internal extinction, we find that the calibration used, from Krisciunas et al. (2009), is based in part on a compilation of Cepheid and/or SBF distances that is not internally consistent (see the discussion in Appendix B).
Interestingly, Str10 obtain a SN Ia distance modulus for the Fornax cluster member NGC 1380 of mag, which is consistent with the SBF result for the same galaxy of 31.632 ± 0.075 mag (Blakeslee et al. 2009), and very similar to the SBF distance for NGC 1316. In fact, there is little significant variation in the SBF distances among the magnitude-limited sample of 43 early-type Fornax galaxies studied by Blakeslee et al. (2009), and most are consistent with the mean Fornax SBF modulus of 31.51 ± 0.03 mag7.
Finally, we must note that the Tripp, the maximum near-IR magnitudes, and the MLCS2k2 methods applied to the fast declining SN 2006mr give distance estimates in agreement with the ones presented here. In spite of this, it should also be emphasized that the debate on whether fast declining SNe Ia can be used to determine precise distances is still open (so that different authors include or not these objects in their final samples; e.g. Jha et al. 2007; Folatelli et al. 2010; Burns et al. 2011; Str10).
5.2. Distances from globular cluster system properties
Distances to NGC 1316 derived from the properties of the globular cluster system have generally been flagged as unreliable by the authors due to the peculiar properties of the galaxy and its GC system.
Gómez et al. (2001) made one of the first attempts to constrain the distance to NGC 1316 with the Globular Cluster Luminosity Function (GCLF, Harris 2001), using ESO/EFOSC2 data. The BVI weighted average distance modulus they provided is (m − M) ~ 31.4 mag, based on a calibration consistent with ours. However, the authors specifically commented on the existence of red and blue sub-populations of GCs and concluded that their catalog was not sufficiently deep to reliably constrain the galaxy distance. In an earlier study of five bright Fornax cluster galaxies, Blakeslee & Tonry (1996) had noted that overall the GCLF of NGC 1316 was not well fitted by a Gaussian (reduced χn > 3, as compared to χn ≈ 1 for the four others), and thus could not provide a reliable GCLF distance for it. Goudfrooij et al. (2004) presented a deeper analysis of the GC system based on ACS data. These authors confirmed the previous results of a blue GC sub-population, consistent with a Gaussian luminosity function, and a further component of red GCs with a power law luminosity function. More recently, Villegas et al. (2010) for the ACSFCS survey, write “NGC 1316 is [...] not included in the fits because the observed GC system in this galaxy is highly influenced by its interaction and proximity with its satellite galaxies, and therefore our GCLF fit is not reliable.”
Masters et al. (2010) use the GC-radii method (Jordán et al. 2005) to analyze the distances of Fornax Cluster galaxies. However, the authors warn that, while the method is effective for typical GC systems, it cannot be applied to NGC 1316 due to the large number of extended GCs.
In conclusion, the GC-based distances reported, for example in the NED archive, (m − M)GCLF,g = 33.55 mag, (m − M)GCLF,z = 33.68 mag, and (m − M)GC − radius = 30.59 ± 0.11 mag, are excluded from the comparison.
5.3. Planetary nebulae luminosity functions
Feldmeier et al. (2007) reported a PNLF distance modulus to NGC 1316 of 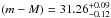 mag. This result relies on the PNLF calibration by Ciardullo et al. (2002), whose zero point is tied to the Freedman et al. (2001) sample of Cepheid’s distance moduli with no dependence on metallicity of the PL relations. As discussed above (Sect. 4.1), the SBF calibrations presented here are based on the metallicity-corrected Cepheid PL relations. Hence, to properly compare the PNLF and SBF distance, a correction is necessary. In a recent review, Ciardullo (2012) finds that if one adopts the metallicity-dependent Cepeheid PL relations, the PNLF zero point brightens by 0.07 mag, going from M∗ = −4.46 ± 0.05 to M∗ = −4.53 ± 0.04 mag (external scatter σ = 0.16 mag). Feldmeier et al. (2007) actually used M∗ = −4.47; thus their PNLF distance modulus for NGC 1316 becomes
mag. This result relies on the PNLF calibration by Ciardullo et al. (2002), whose zero point is tied to the Freedman et al. (2001) sample of Cepheid’s distance moduli with no dependence on metallicity of the PL relations. As discussed above (Sect. 4.1), the SBF calibrations presented here are based on the metallicity-corrected Cepheid PL relations. Hence, to properly compare the PNLF and SBF distance, a correction is necessary. In a recent review, Ciardullo (2012) finds that if one adopts the metallicity-dependent Cepeheid PL relations, the PNLF zero point brightens by 0.07 mag, going from M∗ = −4.46 ± 0.05 to M∗ = −4.53 ± 0.04 mag (external scatter σ = 0.16 mag). Feldmeier et al. (2007) actually used M∗ = −4.47; thus their PNLF distance modulus for NGC 1316 becomes 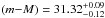 mag8.
mag8.
Both PNLF distances given above agree within quoted uncertainties with the Str10 distance. However, the SBF and the updated PNLF distances are consistent within the given statistical and systematic errors, notwithstanding that the difference between them remains non-negligible. In other words, within the given uncertainties, the SBF distance is consistent with the PNLF, and the latter with the SNe Ia, but SBF and SNe Ia are not consistent with each other. Moreover, with the revised zero point that corrects for the metallicity dependence of the Cepheids, the other PNLF distances published in the past decade for Fornax galaxies are mag for NGC 1380 (Feldmeier et al. 2007) and mag for NGC 1344 (Teodorescu et al. 2005). Thus, although the PNLF method finds systematically lower distances to both the Virgo and Fornax clusters, it is consistent with SBF in placing NGC 1316 well within the distance range of the other Fornax cluster galaxies. Further details on the SBF-PNLF comparison are given in Appendix A.
6. SBF and integrated colors to constrain stellar population properties
The comparison of model predictions with observed SBF magnitudes and SBF colors to understand the properties of the host galaxy has already been successfully used by different authors (Tonry et al. 1990; Buzzoni 1993; Jensen et al. 2003; Raimondo et al. 2005; Cantiello et al. 2007b; Buzzoni & González-Lópezlira 2008).
 |
Fig. 9 Panels a–c): SPoT standard SSP models compared with SBF measurements of NGC 1316 (full black circle). The data of NGC 4374 (filled square), and NGC 4621 (filled triangle) from Cantiello et al. (2011a) are also shown. Different line styles mark different [Fe/H] contents: dot-dashed (magenta), long-dashed (green), solid (blue) and dashed (drown) refer to [Fe/H] = −0.7, −0.4, 0.0 and + 0.4 dex, respectively. Models in the age-range 3–14 Gyr are shown. The arrow in panel a) indicates the direction of increasing age. Panels d)–n): SPoT models obtained with non-canonical assumptions. In all cases the initial (reference) population has solar metallicity, t ~ 14 Gyr, and is shown with a blue star, while the final composite population is shown with a different colour and connected with a dotted line to the reference model. The symbols for observational data are the same as in panels a)–c). Panels d)–f): A fraction equal to 50% of the total HB-stars is simulated being HHB. For these models three ages are considered (t = 10, 12 and 14 Gyr, increasing ages are marked with larger symbols). Panels g)–i): a young population of t = 30 Myr (red), or t = 100 Myr (magenta) is added to the old solar one. The fraction in mass of old to young stars is reported in the lower panel. Panels l)–n): old SSPs with various [Fe/H] are mixed to the solar one, as labeled. The mass fraction metal-poor to standard SSPs is shown in the lower panel. (See electronic version of the Journal for a colour version of the figure.) |
 |
Fig. 10 Same as in Fig. 9, but |
Quality control statistics for the exposures.
The SBF colour versus integrated B − V for NGC 1316, plus two more Virgo cluster galaxies, NGC 4374 and NGC 4621 (data from Cantiello et al. 2011a), are shown in Figs. 9 and 10. The data in the figures are compared to SPoT SSP models computed with standard assumptions for different metallicity and age (panels a–c), while the panels from d to n show the predictions for solar-metallicity standard and non-standard models: specifically, i) in panels d–f SSPs with an enhanced hot horizontal branch component (HHB, having ~50% stars in the canonical HB and ~50% HHB stars) are considered; ii) in panels g–i results obtained by adding a fraction of very young stars of 30 or 100 Myr to the old, solar [Fe/H] component (in proportion 1:1000) are plotted; and iii) in panels from l to n predictions for models with a mix of an old solar metallicity component, and a further one with [Fe/H] = −2.3, −1.3, −0.7, −0.4 and +0.4 dex (in portions 1:1) are shown.
Panel c in Fig. 9 clearly shows the well-known age-metallicity degeneracy that affects classical integrated colors (e.g., Worthey 1994). The position of galaxies in this panel overlaps nicely with SSP models, though nothing can be said about the stellar content. Because of the overlap between models, the field stellar component in NGC 1316 could be either older and more metal poor or younger and more metal rich than the other two galaxies. In contrast, the SBF colour versus B − V models shown in panels a–b are much less affected by the degeneracy, especially for the 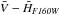 colour. The data for the three galaxies lie near the region of solar metallicity models. A possible interpretation of the relative positions of the three galaxies in the
colour. The data for the three galaxies lie near the region of solar metallicity models. A possible interpretation of the relative positions of the three galaxies in the 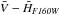 and
and 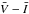 versus (B − V) colour planes, is that NGC 1316 hosts a field component that is as metal rich as in NGC 4621, with [Fe/H] ~ 0.0 dex, but significantly younger (3 ≤ t (Gyr) ≤ 10). In fact, while both the galaxies in Virgo lie near the edge of old SSP models, this is not the case for NGC 1316, for which the stellar light is polluted by an intermediate-age component. This is seen more clearly in some of the other panels of the figure.
versus (B − V) colour planes, is that NGC 1316 hosts a field component that is as metal rich as in NGC 4621, with [Fe/H] ~ 0.0 dex, but significantly younger (3 ≤ t (Gyr) ≤ 10). In fact, while both the galaxies in Virgo lie near the edge of old SSP models, this is not the case for NGC 1316, for which the stellar light is polluted by an intermediate-age component. This is seen more clearly in some of the other panels of the figure.
Inspecting panels l–n we find that, while the colour–colour panel n shows the expected age-metallicity degeneracy, the situation changes for SBF colors (panels l–m). The Virgo cluster galaxies, in fact, overlap with the region of models obtained with the mixing of old t = 14 Gyr SSPs with different [Fe/H]s. In both the l and m panels NGC 1316 lies above the line of mixed old SSPs, suggesting that a younger SSP is necessary to obtain a good match with the models. Again, this is not surprising since NGC 1316 is a known example of an intermediate-age merger remnant, and also has Mg2 ~ 0.25 mag, while the other two targets have Mg2 > 0.28 mag.
The data to models comparison is less straightforward when B-band SBF magnitudes are considered. As discussed by other authors (e.g., Worthey 1993a; Cantiello et al. 2007b), B-band SBF cannot be used to get reliable galaxy distances, both because the amplitude of the signal is 2–3 orders of magnitude fainter than in optical/near-IR bands, and because of the strong sensitivity to stellar population properties. This is depicted in Fig. 10 (panels a–c), where we plot SBF colors obtained with 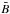 versus the B − V for the three galaxies, and the standard SPoT models. One major difference with the results in Fig. 9 is the substantial mismatch between data and models seen in panel b and, especially, in panel c. The
versus the B − V for the three galaxies, and the standard SPoT models. One major difference with the results in Fig. 9 is the substantial mismatch between data and models seen in panel b and, especially, in panel c. The 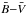 versus B − V models are clearly affected by the age-metallicity degeneracy, but in this case the data are offset by ~0.6 mag with respect to the models. The mismatch is less evident for the
versus B − V models are clearly affected by the age-metallicity degeneracy, but in this case the data are offset by ~0.6 mag with respect to the models. The mismatch is less evident for the 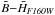 colour, due to the much larger baseline of this colour.
colour, due to the much larger baseline of this colour.
If non-standard SPoT SSP models are taken into account (panels from d to n in Fig. 10) we notice that:
-
models with an enhanced number of hot HB stars provide a good match to the data;
-
the mean metallicity of the dominant stellar component in NGC 1316 is apparently lower than that of the two Virgo galaxies. The models shown in panels d–f, in fact, are obtained assuming HHB “enhancement” for three different ages and solar metallicity. Hence, taking into account SSP models with lower [Fe/H], i.e., bluer colors, the matching with the position of NGC 1316 will improve;
-
the presence of a diffuse very young stellar component, with an age of 30 Myr, seems to reduce the mismatch with data (panels g–i). However, even in the case of the merger remnant NGC 1316, the presence of such a young diffuse stellar component is unlikely even if the presence of a relatively young stellar population is expected in strong radio-emitter galaxies (Della Valle & Panagia 2003);
-
the improved data and models matching in panel l seems to support the possibility of an old [Fe/H] mixed stellar component. However, this is ruled out by the comparison in panel n, showing a poor match to the
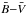 predictions for the same data set.
predictions for the same data set.
At this stage it is useful to recall that the HHB scenario is supported by other independent observations. First, we mention the results by Brown et al. (2000) and Brown et al. (2008) who found a significant fraction of HHB stars in M 32 using HST UV data. Second, the puzzling presence of a strong UV emission in some regular early-type galaxies, discovered several decades ago (Code et al. 1972; Bertola et al. 1980), is now widely interpreted as the presence of an old hot stellar component. Although the mechanisms regulating this component are not well understood (Park & Lee 1997; Kaviraj et al. 2007; Han 2008), some of these old hot stellar sources may have effects on 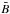 , as independently predicted by various SSP models (Worthey 1993a; Cantiello et al. 2003), or based on empirical evidence (Shopbell et al. 1993; Sodemann & Thomsen 1996; Cantiello et al. 2007b).
, as independently predicted by various SSP models (Worthey 1993a; Cantiello et al. 2003), or based on empirical evidence (Shopbell et al. 1993; Sodemann & Thomsen 1996; Cantiello et al. 2007b).
We emphasize that, when computing the SBF calibration equations using the models with HHB, we find that 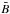 brightens by ~0.2 mag at fixed colour. The effect is ≲0.05 mag in other bands (negligible redwards of z). Such behavior, again, highlights the uselessness of
brightens by ~0.2 mag at fixed colour. The effect is ≲0.05 mag in other bands (negligible redwards of z). Such behavior, again, highlights the uselessness of 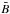 for distance determinations, and confirms the interest on SBF in blue bands for analyzing the properties of unresolved blue hot stellar components.
for distance determinations, and confirms the interest on SBF in blue bands for analyzing the properties of unresolved blue hot stellar components.
In conclusion, the present analysis of the stellar population properties for NGC 1316 seems to confirm the results of NGC 4374 and NGC 4621, i.e., that a diffuse component of hot old stars contributes to the SBF signal in the B-band. Furthermore, the relative comparison of SBF and colour data of NGC 1316 with those of the two galaxies in Virgo seems to indicate that the dominant stellar component in NGC 1316 is younger and slightly less metal rich, as expected for an intermediate-age merger remnant.
7. Summary
We have measured SBF magnitudes in NGC 1316, the brightest galaxy in the Fornax cluster, using ground-based VLT/FORS1 data in BVI-bands, and space-based gF475W and zF850LP from ACS/WFC, plus JF110W and HF160W WFC3/IR observations.
The distance of NGC 1316 is particularly interesting in the context of the cosmological distance scale. The Fornax cluster, in fact, is the second largest cluster of galaxies within ≲25 Mpc after the Virgo cluster. However, in contrast to Virgo, the line-of-sight depth of Fornax is small, enabling accurate calibration of distances without the additional scatter intrinsic to the spatial extent of the cluster. Furthermore, NGC 1316 is among the galaxies with the largest number of detected Type Ia supernovae (SN 1980N, SN 1981D, SN 2006dd and SN 2006mr). For this reason, it is a unique place to test the consistency of SNe Ia distances, both internally and against other distance indicators.
Using our SBF measurements in VIzF850LPHF160W and available empirical calibration of the absolute 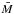 , we obtained a weighted mean distance modulus to NGC 1316
, we obtained a weighted mean distance modulus to NGC 1316 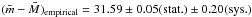 mag.
mag.
Additionally, we obtained SBF distances from VIzF850LPJF110WHF160W data based on theoretical calibrations derived from the SPoT SSP models. The resulting weighted mean distance modulus is 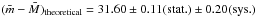 mag.
mag.
The good agreement between SBF distances obtained from empirical and theoretical calibrations is a notable result. The two classes of calibration are, in fact, completely independent of each other, one relying on the first two rungs of the cosmic distance scale, the other on the present knowledge of the various ingredients that go into stellar population synthesis (stellar evolution theory, stellar atmospheres, etc.). Furthermore, since SBF magnitudes over such a wide range of wavelengths depend on the properties of stars in different evolutionary stages, even the agreement between distance moduli obtained in different bands should be regarded as a remarkable result particularly in terms of the high degree of reliability reached by SSP models.
By combining the distance moduli from the two types of calibrations, we obtain 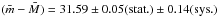 mag, or d = 20.8 ± 0.5(stat.) ± 1.5(sys.) Mpc.
mag, or d = 20.8 ± 0.5(stat.) ± 1.5(sys.) Mpc.
This distance modulus agrees generally well with estimates obtained from other indicators, and with SNe Ia light-curves analysis obtained before 2010. A non-negligible difference exists with the most recent analysis based on SNe Ia by Stritzinger et al. (2010), who obtained a best estimate for the distance ~17% smaller than ours. The possible sources of the disagreement may be related to the complex issue of the internal extinction, and to zero point calibration issues of both distance indicators.
The comparison to PNLF is also subject to the lingering problem of zero point calibration. When placed in a Cepheid distance scale consistent with ours, the PNLF distance to NGC 1316 is d = 18.4 ± 1.0(stat.) ± 1.5(sys.) Mpc and agrees within the quoted errors with our SBF distance. However, the difference between SBF and (the updated) PNLF distance remains non-negligible, and lowering the uncertainties (especially systematic; see Appendix A) would be a desirable result for both indicators.
In order to analyze the properties of the dominant stellar component in the galaxy, we compared SBF colors and integrated colors to SSP model predictions. We found that the stellar light of the galaxy seems to be dominated by a [Fe/H]≲ 0.0 dex, intermediate age stellar population. The comparison with analogous measurements for NGC 4374 and NGC 4621 also supports a scenario in which field stars in NGC 1316 have a younger age and slightly lower metallicity than the two bright Virgo cluster members.
Moreover, we found that SBF predictions from standard SSP models do not match with observations if B-band SBF data are included in the model comparison. As in the cases of NGC 4374 and NGC 4612, which showed a similar mismatch to models, we used the SPoT stellar population synthesis code to generate SSP models with non-canonical properties. In particular, we considered the following three cases: starting from an old t ~ 14 Gyr population with solar metallicity we have 1) enhanced the content of hot HB stars; 2) added a very young diffuse secondary component; and 3) added a more metal poor SSP. As in the previous case (Cantiello et al. 2011a), the simulations seem to favor the HHB component scenario. Assuming a contribution to 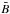 from such hot HB stars removes the discrepancy between the data and models in this band, yet has negligible effect on SBF in other bands, i.e., it does not affect the theoretical calibrations used to obtain distances.
from such hot HB stars removes the discrepancy between the data and models in this band, yet has negligible effect on SBF in other bands, i.e., it does not affect the theoretical calibrations used to obtain distances.
Our results on the distance and stellar population properties of NGC 1316 based on SBF analysis have shown that, despite the great progress in recent years, many issues remain open on both topics. Concerning distances, the calibration of distance indicators, and the treatment of error propagation in the distance scale, still need to be accurately and consistently analyzed. Concerning stellar populations, SBF colors, as a new and independent stellar population analysis technique, seem to provide useful constraints to the properties of field stars, hidden to many classical photometric indicators.
Online material
Appendix A: Some musings on PNLF and SBF distances
One of the most intriguing issues in the extragalactic distance scale is the ~+0.3 mag average offset between the PNLF and SBF distance moduli (Ciardullo 2012). Locally, there appears to be very little offset, but the discrepancy increases with distance, such that the PNLF method gives smaller mean distances for the Virgo and Fornax clusters, as well as a smaller relative distance of Fornax with respect to Virgo (see Villegas et al. 2010). Consistently, Feldmeier et al. (2007) found that the value of H0 obtained from SNe Ia was 10% higher when the SN Ia distances were calibrated via PNLF distances, as compared to the H0 obtained by calibrating the SN Ia distances by either SBF or directly from Cepheid distances.
As discussed in detail in Sects. 4 and 5, to reliably compare two or more distance indicators, it is of paramount importance to verify the consistency of the calibrations (or calibrators) used. Both PNLF and SBF calibrations are tied to the same primary indicator, the period-luminosity relation of Cepheids, and to the same dataset, i.e., the Cepheids from Freedman et al. (2001). However, the zero points of present SBF calibrations are tied to the Cepheid distances obtained with metallicity-dependent PL relations (DPLZ hereafter; Mei et al. 2007; Blakeslee et al. 2009, 2010, this paper), while the standard PNLF calibration relies on Cepheid distances with no dependence on metallicity (DPL; Ciardullo et al. 2002; Feldmeier et al. 2007; Ciardullo 2012).
In this appendix, we take the detailed discussion presented in Ciardullo et al. (2002) – who found the ~0.3 mag mismatch between the two distance indicators – and analyze the correction terms needed to homogenize the comparison.
First, as discussed above, Tonry et al. (2001) distance moduli should be revised downward by 0.06 mag when using the DPLZ. For PNLF, instead, Ciardullo (2012) reported a +0.07 mag correction to the PNLF distance moduli (0.07 mag brighter zeropoint, M∗) when the DPLZdistances are used instead of DPL. It is useful to note that the author also finds that the best-fit value to M∗ calibrated against the RGB-Tip distances, i.e., independently from Cepheid distances, is again +0.07 mag brighter than the PNLF calibration obtained from DPL.
The two corrections: a) −0.06 mag for SBF distances, and b) +0.07 mag for PNLF, both deriving from the adoption of the DPLZ, can justify ~0.13 mag of the PNLF-SBF offset.
SBF to PNLF comparison.
Figure A.1 shows the histogram of the differences between PNLF and SBF distance moduli based on various SBF and PNLF distance and/or calibration. Panel a) in the figure shows the PNLF to SBF difference, ΔPNLF − SBF, using the original sample of 28 galaxies by Ciardullo et al. (2002), with updated zero points for both distance indicators. The mean is ΔPNLF − SBF = −0.23 mag, to be compared to ΔPNLF − SBF = −0.36 mag before zero-point correction.
After the Ciardullo et al. (2002) paper, few PNLF distances have been obtained for galaxies with SBF measurements. Panel b) in Fig. A.1 shows the PNLF to SBF difference for a total of 33 galaxies, including the distances obtained after 2002. The comparison shown in panel c) is obtained using the recent SBF distances from the ACSVCS and ACSFCS surveys (when available) in place of the Tonry et al. (2001) distances. Finally, panel d) uses the same SBF and PNLF distances of panel c) except that for the galaxies with old Tonry et al. (2001) corrected distances we include the further “Q-correction” term using Eq. (A.1) from Blakeslee et al. (2010). Table A.1 presents the average and median differences for all assumptions shown in Fig. A.1.
It is worth mentioning that, according to Ciardullo et al. (2002), to properly compare PNLF and SBF, the latter distance moduli should be further reduced by 0.04 mag. If one includes this correction term, all differences reported in Table A.1 becomes smaller, with the best sample (i.e., d in the table) providing ΔPNLF − SBF = −0.14 ± 0.06 mag, and a median of − 0.22 mag.
Taking into account all the corrections described above, the offset between SBF and PNLF distances is reduced to half of the original estimate, once the proper calibrations and recent/updated distances are used for both indicators. However, even in the best case there is a non-negligible ≲0.2 mag offset between SBF and PNLF that implies ~10% larger SBF distances. Again, this difference occurs mainly beyond ~10 Mpc, and is similar to the 10% larger H0 obtained when calibrating SNe Ia via PNLF instead of Cepheids (Feldmeier et al. 2007).
Even though the data presented in Table A.1 (with the possible further +0.04 mag improvement cited above) suggest that the best average difference is statistically consistent with zero – especially taking into account the systematic uncertainties, not considered in this comparison – the scatter we find is larger, or nearly equal to the squared sum of the estimated internal scatters of both indicators. Taken at face value, this result either means that the internal scatter of one or both indicators is underestimated, or that a real systematic offset exists between the two.
As another test, to further check the latter concern, we analyzed the PNLF to SBF offset by considering late-type and early-type galaxies separately. Using sample d in Table A.1, we find the following differences: 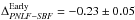 mag (median − 0.30 mag) based on the data of 24 galaxies, and
mag (median − 0.30 mag) based on the data of 24 galaxies, and 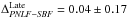 mag (median − 0.02 mag) for the remaining 9 galaxies. The result shows that for the class of galaxies used to derive SBF and PNLF zero points, i.e., the late types hosting Cepheids, there is no statistically significant offset between the two indicators. On the other hand, for early-type galaxies the offset is large, and statistically inconsistent with zero. Related to this, one fundamental difference between the two indicators is that absolute SBF magnitudes are “corrected” for galaxy stellar content, i.e., the difference between early- and late-type galaxies is taken into account with SBF, while the PNLF distances are based on the constancy of M∗ for both types of galaxy.
mag (median − 0.02 mag) for the remaining 9 galaxies. The result shows that for the class of galaxies used to derive SBF and PNLF zero points, i.e., the late types hosting Cepheids, there is no statistically significant offset between the two indicators. On the other hand, for early-type galaxies the offset is large, and statistically inconsistent with zero. Related to this, one fundamental difference between the two indicators is that absolute SBF magnitudes are “corrected” for galaxy stellar content, i.e., the difference between early- and late-type galaxies is taken into account with SBF, while the PNLF distances are based on the constancy of M∗ for both types of galaxy.
The calibration of SBF magnitudes, and its dependence on galaxy type, has been analyzed in detail over a ground-based sample of ~300 galaxies by Tonry et al. (2001), and more recently from HST data of ~150 galaxies by Blakeslee et al. (2009, 2010). The derived SBF calibrations, as is well-known, include a colour-dependent term, which, as also shown by SSP models (Worthey 1993b; Cantiello et al. 2003; Raimondo et al. 2005), is basically a metallicity correction term. In optical bands, this correction term implies fainter SBF magnitudes for redder/more metal-rich systems.
 |
Fig. A.1 Histograms of the difference between PNLF and SBF distance moduli. Each panel shows different comparison/calibration samples. Panel a) original sample of 28 galaxies with PNLF and SBF distances from Ciardullo et al. (2002) and Tonry et al. (2001) respectively, with revised Cepheids calibration. Dotted/dashed vertical lines show the mean/median of the difference. Panel b) as in a) but 5 more galaxies with PNLF measurements made after Ciardullo et al. (2002) are added to the sample. Panel c) as b), but more recent ACSFCS and ACSVCS SBF distances are used when available. Panel d) as c), but the correction from Eq. (A.1) by Blakeslee et al. (2010) is included to Tonry et al. (2001) distances. |
 |
Fig. A.2 Figure 5 from Ciardullo (2012) showing the sole data with metallicity corrected Cepheids distances. (See electronic version of the Journal for a colour version of the figure.) |
In contrast, the M∗ calibration to PNLF does not include any metallicity dependent term for bright galaxies. A dependence of the PNLF M∗ to metallicity has been found by Ciardullo et al. (2002) and Ciardullo (2012), however the authors conclude that such dependence is relevant only in small, metal-poor systems.
Inspecting the open circles in Fig. 5 of Ciardullo (2012, open circles mark the data obtained from DPLZ, reported in Fig. A.2, one can see that a) the trend of M∗ with metallicity has the opposite sign with respect to SBF, meaning that M∗ gets brighter for more metal-rich systems, and that b) some residual correlation of M∗ with metallicity also appears in the high metallicity regime.
This strongly suggests that there may be some unaccounted for residual dependence of the PNLF calibration on the metallicity, presently unquantified because of the relatively limited sample – though detectable even in present datasets (Fig. A.2). If so, one possible explanation for the irreducible ~–0.2 mag offset between PNLF and SBF is that it may be due to a bias introduced by data from early-type galaxies, which are intrinsically on average more massive and more metal-rich than late types and, therefore, would typically have larger distances with respect to the current metallicity-independent calibration of the PNLF method.
Appendix B: Some notes on Type Ia SNe distances from Stritzinger et al. (2010)
 |
Fig. B.1 Zoom in 6 × 6 arcsec2 of the residual frames centered on the positions of the four SNe Ia, as labeled. Black circles mark the position of the respective SNa. UVIS/F336W, ACS/F435W and ACS/F555W frames (left, middle and right panels, respectively) are shown for the SN 1981D, SN 2006dd and SN 2006dd. The panels showing SN 1980N are g, r, and i observations taken from the Gemini Telescope archive. |
To understand the possible causes of the difference between our and Str10 distance we must recall that, as for SBF, in order to calibrate SNe Ia light curves one must rely on sources at known distance and/or with well-known intrinsic properties, and then standardize the absolute magnitude of the SN Ia (e.g., Phillips 1993).
Str10 derives the distance to NGC 1316 using three different methods: the EBV, the Tripp method, and the near-IR light-curves. The authors also use the MLCS2k2 method on SN 2006mr, obtaining a distance that is 50% further than the average they derived from the normal events.
In the following we discuss each one of the three methods used by Str10, trying to highlight the possible causes leading to the observed difference.
Appendix B.1: The colour excess method
Str10 adopted the calibration from Burns et al. (2011, AJ in press at the time Str10 was published) to obtain the distance moduli with the “EBV” model in their fitting package SNooPy. For this model they adopt the recommended calibration from Burns et al. (2011), which uses a sub-sample of unreddened SNe Ia from Folatelli et al. (2010), excluding fast declining objects, as SN 2006mr. Folatelli et al. (2010), in turn, calibrate their dataset using 26 SNe Ia at z > 0.01, whose distances are based on Hubble’s law assuming H0 = 72 km s-1 Mpc-1, and three SNe Ia at z < 0.01 with direct distance measurements. The three nearest objects include SN 2006mr, whose host’s distance is assumed (m − M) = 31.59 ± 0.08 mag from the SBF measurements by Cantiello et al. (2007a).
The SNooPy/EBV method relies (also) on an estimate of the internal reddening around the SN Ia. Str10 find that all four SNe Ia in NGC 1316 have negligible internal extinction. The authors warn about some complications in the interpretation of the data. With respect to spectroscopic analysis of Na I D absorption in the spectra of SN 2006dd and SN 2006mr, these authors state that “the very strong Na I D absorption observed in SNe Ia 2006dd and SN 2006mr is totally inconsistent with the low host galaxy reddening we derive from the light curve observations” (Str10, Sect. 4), as the colour evolution of the two SNe Ia closely resembles that of unreddened SNe Ia. However, while there is a general observational agreement on higher color excess corresponding to higher Na I D equivalent width (EW), this correlation is tight in high-resolution spectra, but the scatter increases substantially at lower resolution (Blondin et al. 2009; Poznanski et al. 2011, 2012), with considerable confusion due to the blending of the Na I D doublet. For instance, using Fig. 5 in Blondin et al. (2009), at EW ~ 1.5 (similar to that obtained by Str10 for NGC 1316) E(B − V)host ranges from ~0.1 to ~1.5 mag. As a further complication, besides the possible line blending, the line profiles for both SNe show clear evidence for structure, interpreted by Str10 as evidence of the presence of two unresolved sodium components. Nevertheless, coupling the EW measurements from Str10 (their Table 10, obtained from the authors’ highest dispersion spectra), with Eqs. (7)–(8) from Poznanski et al. (2012), we obtain E(B − V)host > 0.45 and >0.1 mag for SN 2006dd and SN 2006mr, respectively (with mean values ~1.4 and ~0.6 mag).
Nearby galaxy sample used for near-IR calibration: original and revised distances.
Clearly, as also highlighted by Str10, the strong Na I D absorption associated with no internal reddening might also be indicative of a non-standard gas-to-dust ratio for Fornax A, which given the merger history of this galaxy does not seem unreasonable.
A 6″ × 6″ zoom of the regions around the four SNe Ia is shown in Fig. B.1. In the upper part of the figure we show the HST UVIS/F336W, ACS/F435W and ACS/F555W residual frames of the three SNe Ia located within the frames analyzed in this work (SN 1981D, SN 2006dd, SN 2006mr). For sake of completeness, we have obtained archival g, r, and i-band Gemini/GMOS-S data of the region around the SN 1980N, shown in the lower panels of Fig. B.1. As evidenced in the figure, there are undeniable patterns of dust near the position of the 2006 SNe Ia, though one cannot decide whether the SNe are behind, in front of, or within such dust lanes.
The comparison with previous estimates of internal extinction from the literature show that for SN 1980N and SN 1981D, Jha et al. (2007) find E(B − V)host values larger than Str10 (three times larger in the case of SN 1981D) but in agreement within uncertainties with the SNooPy fits. The agreement gets worse if the extinctions derived by Str10 from near-IR data are taken into account. Note, however, that Str10 corrected the optical and near-IR photometry for host galaxy contamination. Such a correction, although negligible for the case of SN 1980N, does not seem to be discussed by Jha et al.
For both the two most recent SNe Ia, 2006dd and 2006mr, Maoz & Mannucci (2008) estimate an internal extinction of ~0.08 mag. In the case of SN 2006dd, SNooPy provides E(B − V)host = 0.043 ± 0.008 mag; while, as mentioned above, SNooPy cannot be used for fitting the light-curves of the fast declining SN 2006mr.
In conclusion, the three SNe Ia used by Str10 to get the best estimate of (m − M) could be controversial in terms of internal extinction, affecting both the estimate of with the EBV method, and the associated uncertainties.
Appendix B.2: The Tripp method
The second method adopted by Str10 is based on the two-parameter model of Tripp (1998) which, differently from the EBV method, can also be applied to fast declining SNe Ia. The calibrating sample is again taken from Folatelli et al. (2010), and SN 2006mr is omitted in the re-computed calibration relations, to avoid circularity.
The distance to the three normal SNe Ia with this method is consistent with the estimates based on the SNooPy/EBV method. In contrast, the (m − M) obtained with the data of SN 2006mr is ~+0.5 mag larger than the average of the other three SNe Ia.
One interesting point to note is that if one uses a distance modulus of ~31.2 mag to NGC 1316, as derived by Str10 from the three normal SNe Ia, then the data-point of SN 2006mr placed in Fig. 16 of Folatelli et al. (2010) is more than +0.5 mag off the linear relation drawn by the authors, with a scatter to the relation much larger than the rms reported in the cited figure. Certainly, changing the distance modulus of one of the calibrating data-points in the Folatelli et al. sample implies changing the linear calibration relation shown in the cited figure, and possibly reduces the offset between data and fit. In any case, though, using (m − M) ~ 31.2 entails considerably increasing the scatter in the calibrating sample of the Canergie Supernova Project, with NGC 1316 being one of the nearest objects and also the host galaxy with the largest scatter.
Appendix B.3: The near-IR method
The last method used by Str10 is based on near-IR light-curves of SNe Ia, calibrated using Krisciunas et al. (2009) absolute near-IR peak magnitudes without NGC 1316 data. The Krisciunas et al. calibration of near-IR peak magnitudes adopts new observations of SNe Ia, and data previously published by the same team (Krisciunas et al. 2004a,b). For the nearby galaxies, the authors adopted distances based on either SBF or Cepheids. From a careful reading of the cited papers, we find that Krisciunas et al. (2004a) obtained the JHK calibration from 16 SNe Ia. For three nearby galaxies, NGC 1316, NGC 4526, and NGC 5128, the authors adopt the SBF distance from Ajhar et al. (2001, based on DPLZ, while for NGC 4536 and NGC 3368 the DPL distances from Cepheids is used. Both SBF and Cepehids distances are based on the same Freedman et al. (2001) calibrating sample.
Krisciunas et al. (2004b) extended the sample of SNe Ia with well-sampled near-IR light-curves to about 20 objects. The authors added two more supernova-host galaxies with SBF distances – NGC 4374 and NGC 3190 – to the previous list of nearby galaxies. However, in contrast with Krisciunas et al. (2004a), they adopted the Tonry et al. (2001) distance moduli, which are based on DPL; that is, they are 0.06 mag larger than the reported by Ajhar et al. (2001).
Finally, the most recent calibration of near-IR light-curves of SNe Ia by Krisciunas et al. (2009), used the distance moduli for nearby galaxies from the SBF survey by Tonry et al. (2001) with the revised Jensen et al. (2003) zero points (+0.16 mag with respect to Tonry et al. 2001). More specifically, in the new list of ~25 supernova-host galaxies, the authors added three new objects, NGC 936, NGC 1201 and NGC 1371, with SBF-based distances. In addition, Krisciunas et al. adopted a revised SBF distance to NGC 5128 from Jensen et al. (2003). However, the authors corrected the (m − M) by +0.16 mag, which is the difference between the Tonry et al. (2001) and Jensen et al. (2003) calibrations, and not by +0.10 mag, i.e., the difference between the Ajhar et al. (2001) and Jensen et al. (2003) calibrations.
Hence, the calibration of the absolute magnitudes in near-IR bands used by Str10 relies on a sample of ~25 SNe Ia, with nine nearby calibrators (after excluding NGC 1316) having distances based on non-homogeneous calibrations. In Table B.1 we summarize the distance moduli used by Krisciunas et al. to calibrate the maxima of SNe Ia light-curves, and the ones revised by us in order to be a) internally homogeneous, and b) consistent with the Cepheid distances used in this work. As shown in the table, the revised distance moduli are on average 0.06 mag larger than the ones used for the original SNe Ia near-IR calibration. If one simply takes the average of these numbers, adding a sample of 15 objects more (25 total SNe Ia minus the nine nearby objects and NGC 1316) where no shift has to be applied, the correction to the absolute magnitudes in Table 9 of Str10 is ~–0.02 mag (a correction that should be applied to the calibration by Krisciunas et al. 2009).
Although a +0.02 mag shift in Str10 distance moduli goes in the direction of reducing the mismatch between our and Str10 distances, the amplitude of the correction is negligible. However, it suggests that the uncertainties associated with the near-IR calibrations might be underestimated.
In conclusion, the analysis presented in this Appendix highlights two main issues: i) the homogeneity of the calibrators used; and ii) the estimate of internal extinctions for SNe Ia (although one should not forget that the quality of the SN 1980N and SN 1981D data is lower than others). While the first issue listed works in the direction of reducing the difference between our and Str10 distance moduli, both issues imply an increase of the present levels of statistical/systematic uncertainties on SNe Ia distances.
The new measurements of dust reddening from Schlafly & Finkbeiner (2011) provide ~0.002 mag smaller Galactic extinction, being E(B − V) = 0.019. The effect of this change is at most ~0.02, for B magnitudes, and ~0.002 mag on the colour indices used throughout the present work.
All information on both surveys are also available via web at the URL: www.astrosci.ca/users/VCSFCS
We adopt as reference the photometric VEGA zero points, while ACSFCS results use the AB ones. All ACSFCS data, including the calibration of SBF magnitudes, are transformed to the VEGA magnitude system using Sirianni et al. (2005) zero point transformations.
Previous studies indicate SBF variations <0.1 mag with PSF (e.g., Liu et al. 2002; Cantiello et al. 2005; Blakeslee et al. 2010; Cantiello et al. 2011b).
A further component to the systematic error comes from bandpass mismatch with various telescopes. Blakeslee et al. (2001) presented a discussion of this issue (see their Sect. 5.5, Fig. 15 in particular), showing that at the color of the SBF, 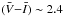 for NGC 1316, the difference in the standard Cousins I and the HST I can vary by ± 0.02 mag.
for NGC 1316, the difference in the standard Cousins I and the HST I can vary by ± 0.02 mag.
The recent Type Ia supernova SN 2012fr (Childress et al. 2012) occurred in NGC 1365, a giant barred spiral galaxy in the direction of the Fornax cluster with a measured Cepheid distance (Silbermann et al. 1999; Freedman et al. 2001). However, from a comparison of Cepheid and SNe Ia distances, Suntzeff et al. (1999) suggested that NGC 1365 is actually ~0.3 mag in front of the Fornax cluster ellipticals; Kelson et al. (2000) came to a similar conclusion based on the fundamental plane.
We have not taken into account a further −0.04 mag correction term to SBF distance moduli cited by Ciardullo et al. (2002, their Sect. 6). Including such an extra correction to our distance modulus implies 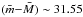 mag.
mag.
Acknowledgments
Part of this work was supported by PRIN-INAF 2010 (P.I.: Clementini), PRIN-INAF 2011 (P.I. Grado) and PRIN-INAF 2011 (P.I.: Marconi), and the FIRB-MIUR 2008 (P.I. Imbriani). We are grateful to M. Capaccioli, E. Di Carlo, and I. Biscardi for useful discussions related to this work. This research has made use of the NASA/IPAC Extragalactic Data-base (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has also made use of the SIMBAD database, operated at CDS, Strasbourg, France, and of the HyperLeda database (http://leda.univ-lyon1.fr).
References
- Ajhar, E. A., Blakeslee, J. P., & Tonry, J. L. 1994, AJ, 108, 2087 [NASA ADS] [CrossRef] [Google Scholar]
- Ajhar, E. A., Lauer, T. R., Tonry, J. L., et al. 1997, AJ, 114, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Ajhar, E. A., Tonry, J. L., Blakeslee, J. P., Riess, A. G., & Schmidt, B. P. 2001, ApJ, 559, 584 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertola, F., Capaccioli, M., Holm, A. V., & Oke, J. B. 1980, ApJ, 237, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Biscardi, I., Raimondo, G., Cantiello, M., & Brocato, E. 2008, ApJ, 678, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P. 2012, Ap&SS, 341, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., & Tonry, J. L. 1996, ApJ, 465, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Ajhar, E. A., & Tonry, J. L. 1999, in ASSL 237, Post-Hipparcos cosmic candles, 181 [Google Scholar]
- Blakeslee, J. P., Vazdekis, A., & Ajhar, E. A. 2001, MNRAS, 320, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Anderson, K. R., Meurer, G. R., Benítez, N., & Magee, D. 2003, in Astronomical Data Analysis Software and Systems XII, ASP Conf. Ser., 295 [Google Scholar]
- Blakeslee, J. P., Jordán, A., Mei, S., et al. 2009, ApJ, 694, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Cantiello, M., Mei, S., et al. 2010, ApJ, 724, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, S., Prieto, J. L., Patat, F., et al. 2009, ApJ, 693, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Brocato, E., Castellani, V., Poli, F. M., & Raimondo, G. 2000, A&AS, 146, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M., Bowers, C. W., Kimble, R. A., Sweigart, A. V., & Ferguson, H. C. 2000, ApJ, 532, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T. M., Smith, E., Ferguson, H. C., et al. 2008, ApJ, 682, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, C. R., Stritzinger, M., Phillips, M. M., et al. 2011, AJ, 141, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Burstein, D., & Heiles, C. 1984, ApJS, 54, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Buscombe, W., & de Vaucouleurs, G. 1955, The Observatory, 75, 170 [NASA ADS] [Google Scholar]
- Buzzoni, A. 1993, A&A, 275, 433 [NASA ADS] [Google Scholar]
- Buzzoni, A., & González-Lópezlira, R. A. 2008, ApJ, 686, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M. 2012, Ap&SS, 341, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Raimondo, G., Brocato, E., & Capaccioli, M. 2003, AJ, 125, 2783 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Blakeslee, J. P., Raimondo, G., et al. 2005, ApJ, 634, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Blakeslee, J., Raimondo, G., Brocato, E., & Capaccioli, M. 2007a, ApJ, 668, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Raimondo, G., Blakeslee, J. P., Brocato, E., & Capaccioli, M. 2007b, ApJ, 662, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., Brocato, E., & Blakeslee, J. P. 2009, A&A, 503, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Biscardi, I., Brocato, E., & Raimondo, G. 2011a, A&A, 532, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Brocato, E., & Capaccioli, M. 2011b, A&A, 534, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capaccioli, M., & Schipani, P. 2011, The Messenger, 146, 2 [NASA ADS] [Google Scholar]
- Capaccioli, M., Della Valle, M., Rosino, L., & D’Onofrio, M. 1989, AJ, 97, 1622 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioli, M., Della Valle, M., D’Onofrio, M., & Rosino, L. 1990, ApJ, 360, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioli, M., Mancini, D., & Sedmak, G. 2005, The Messenger, 120, 10 [NASA ADS] [Google Scholar]
- Carter, D., Jorden, P. R., Thorne, D. J., Wall, J. V., & Straede, J. C. 1983, MNRAS, 205, 377 [Google Scholar]
- Cavadore, C., Beletic, J., & Monnet, G. 1999, De-Contamination report of FORS1 CCD, Tech. rep. [Google Scholar]
- Childress, M., Zhou, G., Tucker, B., et al. 2012, Central Bureau Electronic Telegrams, 3275, 2 [NASA ADS] [Google Scholar]
- Cho, H., Jensen, J. B., Blakeslee, J. P., et al. 2013, in IAU Symp., 289, 371 [NASA ADS] [Google Scholar]
- Ciardullo, R. 2012, Ap&SS, 149 [Google Scholar]
- Ciardullo, R., Feldmeier, J. J., Jacoby, G. H., et al. 2002, ApJ, 577, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Code, A. D., Welch, G. A., & Page, T. L. 1972, in Scientific results from the orbiting astronomical observatory (OAO-2), ed. A. D. Code, NASA SP, 310, 559 [NASA ADS] [Google Scholar]
- Côté, P., Blakeslee, J. P., Ferrarese, L., et al. 2004, ApJS, 153, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Côté, P., Ferrarese, L., Jordán, A., et al. 2007, ApJ, 671, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Della Valle, M., & Gilmozzi, R. 2002, Science, 296, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Della Valle, M., & Panagia, N. 2003, ApJ, 587, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmeier, J. J., Jacoby, G. H., & Phillips, M. M. 2007, ApJ, 657, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., Mould, J. R., Kennicutt, R. C., et al. 2000, ApJ, 529, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Folatelli, G., Phillips, M. M., Burns, C. R., et al. 2010, AJ, 139, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., & Madore, B. F. 2010, ARA&A, 48, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- French, B. S., Jensen, J. B., & Blakeslee, J. P. 2012, in Am. Astron. Soc. Meet. Abstr., 220, 332.02 [Google Scholar]
- Gómez, M., Richtler, T., Infante, L., & Drenkhahn, G. 2001, A&A, 371, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Lópezlira, R. A., Bruzual-A., G., Charlot, S., Ballesteros-Paredes, J., & Loinard, L. 2010, MNRAS, 403, 1213 [NASA ADS] [CrossRef] [Google Scholar]
- Goudfrooij, P., Alonso, M. V., Maraston, C., & Minniti, D. 2001a, MNRAS, 328, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Goudfrooij, P., Mack, J., Kissler-Patig, M., Meylan, G., & Minniti, D. 2001b, MNRAS, 322, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Goudfrooij, P., Gilmore, D., Whitmore, B. C., & Schweizer, F. 2004, ApJ, 613, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Grado, A., Capaccioli, M., Silvotti, R., et al. 2004, Astron. Nachr., 325, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Grado, A., Capaccioli, M., Limatola, L., & Getman, F. 2012, Mem. Soc. Astron. It. Supp., 19, 362 [Google Scholar]
- Hamuy, M., Phillips, M. M., Maza, J., et al. 1991, AJ, 102, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996, AJ, 112, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z. 2008, A&A, 484, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 2001, in Saas-Fee Advanced Course 28: Star Clusters [Google Scholar]
- Herrmann, K. A., Ciardullo, R., Feldmeier, J. J., & Vinciguerra, M. 2008, ApJ, 683, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Jacoby, G. H., Branch, D., Ciardullo, R., et al. 1992, PASP, 104, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Jedrzejewski, R. I. 1987, MNRAS, 226, 747 [Google Scholar]
- Jensen, J. B., Tonry, J. L., & Luppino, G. A. 1998, ApJ, 505, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, J. B., Tonry, J. L., Thompson, R. I., et al. 2001, ApJ, 550, 503 [Google Scholar]
- Jensen, J. B., Tonry, J. L., Barris, B. J., et al. 2003, ApJ, 583, 712 [Google Scholar]
- Jha, S., Riess, A. G., & Kirshner, R. P. 2007, ApJ, 659, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Jordán, A., Blakeslee, J. P., Peng, E. W., et al. 2004, ApJS, 154, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Jordán, A., Côté, P., Blakeslee, J. P., et al. 2005, ApJ, 634, 1002 [NASA ADS] [CrossRef] [Google Scholar]
- Jordán, A., McLaughlin, D. E., Côté, P., et al. 2007, ApJS, 171, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Jordán, A., Peng, E. W., Blakeslee, J. P., et al. 2009, ApJS, 180, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Kalirai, J. S., MacKenty, J., Bohlin, R., et al. 2009, WFC3 SMOV Proposal 11451: The Photometric Performance and Calibration of WFC3/IR, Tech. rep. [Google Scholar]
- Kaviraj, S., Sohn, S. T., O’Connell, R. W., et al. 2007, MNRAS, 377, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Kelson, D. D., Illingworth, G. D., Tonry, J. L., et al. 2000, ApJ, 529, 768 [NASA ADS] [CrossRef] [Google Scholar]
- Konami, S., Matsushita, K., Nagino, R., et al. 2010, PASJ, 62, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Hastings, N. C., Loomis, K., et al. 2000, ApJ, 539, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Phillips, M. M., & Suntzeff, N. B. 2004a, ApJ, 602, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Suntzeff, N. B., Phillips, M. M., et al. 2004b, AJ, 128, 3034 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Marion, G. H., Suntzeff, N. B., et al. 2009, AJ, 138, 1584 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C., Graham, J. R., & Charlot, S. 2002, ApJ, 564, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Mannucci, F. 2008, MNRAS, 388, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Marín-Franch, A., & Aparicio, A. 2006, A&A, 450, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masters, K. L., Jordán, A., Côté, P., et al. 2010, ApJ, 715, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, S., Silva, D. R., & Quinn, P. J. 2001, A&A, 366, 54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mei, S., Scodeggio, M., Silva, D. R., & Quinn, P. J. 2003, A&A, 399, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mei, S., Blakeslee, J. P., Côté, P., et al. 2007, ApJ, 655, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Ngeow, C.-C., Kanbur, S. M., Neilson, H. R., Nanthakumar, A., & Buonaccorsi, J. 2009, ApJ, 693, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Park, J., & Lee, Y. 1997, ApJ, 476, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Poznanski, D., Ganeshalingam, M., Silverman, J. M., & Filippenko, A. V. 2011, MNRAS, 415, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Poznanski, D., Prochaska, J. X., & Bloom, J. S. 2012, MNRAS, 426, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing, 2nd edn. (Cambridge: University Press) [Google Scholar]
- Raimondo, G. 2009, ApJ, 700, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Raimondo, G., Brocato, E., Cantiello, M., & Capaccioli, M. 2005, AJ, 130, 2625 [NASA ADS] [CrossRef] [Google Scholar]
- Reindl, B., Tammann, G. A., Sandage, A., & Saha, A. 2005, ApJ, 624, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Sambhus, N., Gerhard, O., & Méndez, R. H. 2006, AJ, 131, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schweizer, F. 1980, ApJ, 237, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Sersic, J. L. 1968, Atlas de galaxias australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
- Shopbell, P. L., Bland-Hawthorn, J., & Malin, D. F. 1993, AJ, 106, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Silbermann, N. A., Harding, P., Ferrarese, L., et al. 1999, ApJ, 515, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, D. R., Kuntschner, H., & Lyubenova, M. 2008, ApJ, 674, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Sirianni, M., Jee, M. J., Benítez, N., et al. 2005, PASP, 117, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Sodemann, M., & Thomsen, B. 1995, AJ, 110, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Sodemann, M., & Thomsen, B. 1996, AJ, 111, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Burns, C. R., Phillips, M. M., et al. 2010, AJ, 140, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Suntzeff, N. B., Phillips, M. M., Covarrubias, R., et al. 1999, AJ, 117, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Tammann, G. A., Sandage, A., & Reindl, B. 2008, ApJ, 679, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Teodorescu, A. M., Méndez, R. H., Saglia, R. P., et al. 2005, ApJ, 635, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Teodorescu, A. M., Méndez, R. H., Bernardi, F., Riffeser, A., & Kudritzki, R. P. 2010, ApJ, 721, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Terlevich, A. I., & Forbes, D. A. 2002, MNRAS, 330, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J., & Schneider, D. P. 1988, AJ, 96, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Ajhar, E. A., & Luppino, G. A. 1990, AJ, 100, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Blakeslee, J. P., Ajhar, E. A., & Dressler, A. 2000, ApJ, 530, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Dressler, A., Blakeslee, J. P., et al. 2001, ApJ, 546, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Tripp, R. 1998, A&A, 331, 815 [NASA ADS] [Google Scholar]
- Villegas, D., Jordán, A., Peng, E. W., et al. 2010, ApJ, 717, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G. 1993a, ApJ, 415, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G. 1993b, ApJ, 409, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G. 1994, ApJS, 95, 107 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Surface brightness fluctuations and colour measurements corrected for galactic extinction.
Nearby galaxy sample used for near-IR calibration: original and revised distances.
All Figures
 |
Fig. 1 Left panel: mosaic single exposure in B on 1999 December 27th (600 s total, the first observing run of the proposal). Right panel: as left, but for an exposure taken during the night of 2000 January 20th. |
| In the text | |
 |
Fig. 2 Left panel: false colour combined VLT BVI frames. Middle panel: as left panel, but for residual frames. The location of the ACS frames is outlined in black. Right panel: ACS and WFC3/UVIS combined residual images. Colour coding is chosen to enhance the presence of dust. The sites of three over four of the SNe Ia host by the galaxy are shown. |
| In the text | |
 |
Fig. 3 Comparison between the VLT (this work, t.w.) BVI photometry and NTT data from G01 used for calibrating FORS1 photometry. |
| In the text | |
 |
Fig. 4 Comparison between our photometry and the ACSFCS results. Black dots and labels refer to the whole sample of ~620 matched sources, gray circles and labels to the ~40 selected sources. The median difference and the associated rms are also reported. |
| In the text | |
 |
Fig. 5 Left panel: colour–colour diagram with the ACS and WFC3/IR magnitudes. Gray crosses mark the full sample of common sources, black circles show selected GC candidates (see text). Right panel: comparison between WFC3/IR photometry and the IRAC2 data from Goudfrooij et al. (2001a). In both panels the predictions from SPoT simple stellar population models with different metallicity are shown with different colour/line styles ([Fe/H] = −2.3, −1.4, −0.7, −0.4, 0.0 and +0.4 dex shown with dark-yellow, cyan, magenta, green, blue and brown, respectively). The age range is 3 to 14 Gyr. (See electronic version of the Journal for a colour version of the figure.) |
| In the text | |
 |
Fig. 6 Upper left panel: UF336w/WFC3/UVIS, BVI/FORS1, gF475WzF850LP/ACS, and JF110WHF160W/WFC3/IR surface brightness profiles for NGC 1316. Each band is shown with a different line style/colour. A vertical shift is applied for sake of clarity as labeled. Lower left panel: as upper left panel, but in R1/6 scale. The Sersic profile fitting procedure used leaves the n-index free to vary. Here we use the median n = 6 value, which is also consistent with Côté et al. (2007). The full dots are extrapolated from Carter et al. (1983), accordingly shifted for each band (see colour image). Right panels: the difference between observed and fitted surface brightness profiles. (See electronic version of the Journal for a colour version of the figure.) |
| In the text | |
 |
Fig. 7 Power spectrum analysis of the BVIzF850LPJF110WHF160W frames. Each panel shows a different band, as labeled. For all bands, the upper panels show the logarithm of the power spectrum of the residual frame (gray dots) and the best fit P(k) curve. In the middle panels the difference between observed and fitted power spectra is shown. The flat region of log P0(kfit > k) between vertical dashed lines (lower panels) is used to evaluate the best fit parameters P0, and P1. |
| In the text | |
 |
Fig. 8 V, I and HF160W-band SBF versus (V − I) predictions from five independent stellar population synthesis codes: solid line (black), dotted line (red), dashed line (blue), long-dashed line (green), dot-dashed (cyan) line show the updated SPoT, Blakeslee et al. (2001), Liu et al. (2002), Marín-Franch & Aparicio (2006), and González-Lópezlira et al. (2010) best fit lines, respectively. Empty (magenta) circles show the corresponding empirical relations, also given in Table 5. (See electronic version of the Journal for a colour version of the figure.) |
| In the text | |
 |
Fig. 9 Panels a–c): SPoT standard SSP models compared with SBF measurements of NGC 1316 (full black circle). The data of NGC 4374 (filled square), and NGC 4621 (filled triangle) from Cantiello et al. (2011a) are also shown. Different line styles mark different [Fe/H] contents: dot-dashed (magenta), long-dashed (green), solid (blue) and dashed (drown) refer to [Fe/H] = −0.7, −0.4, 0.0 and + 0.4 dex, respectively. Models in the age-range 3–14 Gyr are shown. The arrow in panel a) indicates the direction of increasing age. Panels d)–n): SPoT models obtained with non-canonical assumptions. In all cases the initial (reference) population has solar metallicity, t ~ 14 Gyr, and is shown with a blue star, while the final composite population is shown with a different colour and connected with a dotted line to the reference model. The symbols for observational data are the same as in panels a)–c). Panels d)–f): A fraction equal to 50% of the total HB-stars is simulated being HHB. For these models three ages are considered (t = 10, 12 and 14 Gyr, increasing ages are marked with larger symbols). Panels g)–i): a young population of t = 30 Myr (red), or t = 100 Myr (magenta) is added to the old solar one. The fraction in mass of old to young stars is reported in the lower panel. Panels l)–n): old SSPs with various [Fe/H] are mixed to the solar one, as labeled. The mass fraction metal-poor to standard SSPs is shown in the lower panel. (See electronic version of the Journal for a colour version of the figure.) |
| In the text | |
 |
Fig. 10 Same as in Fig. 9, but |
| In the text | |
 |
Fig. A.1 Histograms of the difference between PNLF and SBF distance moduli. Each panel shows different comparison/calibration samples. Panel a) original sample of 28 galaxies with PNLF and SBF distances from Ciardullo et al. (2002) and Tonry et al. (2001) respectively, with revised Cepheids calibration. Dotted/dashed vertical lines show the mean/median of the difference. Panel b) as in a) but 5 more galaxies with PNLF measurements made after Ciardullo et al. (2002) are added to the sample. Panel c) as b), but more recent ACSFCS and ACSVCS SBF distances are used when available. Panel d) as c), but the correction from Eq. (A.1) by Blakeslee et al. (2010) is included to Tonry et al. (2001) distances. |
| In the text | |
 |
Fig. A.2 Figure 5 from Ciardullo (2012) showing the sole data with metallicity corrected Cepheids distances. (See electronic version of the Journal for a colour version of the figure.) |
| In the text | |
 |
Fig. B.1 Zoom in 6 × 6 arcsec2 of the residual frames centered on the positions of the four SNe Ia, as labeled. Black circles mark the position of the respective SNa. UVIS/F336W, ACS/F435W and ACS/F555W frames (left, middle and right panels, respectively) are shown for the SN 1981D, SN 2006dd and SN 2006dd. The panels showing SN 1980N are g, r, and i observations taken from the Gemini Telescope archive. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


