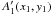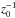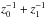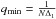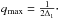| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220172 | |
| Published online | 04 April 2013 | |
Simulation of optical interstellar scintillation
1
Laboratoire de l’Accélérateur Linéaire, IN2P3 − CNRS, Université de
Paris-Sud,
BP 34,
91898
Orsay Cedex,
France
e-mail:
moniez@lal.in2p3.fr
2
School of Astronomy, Institute for Research in Fundamental
Sciences (IPM), PO Box
19395-5531, Tehran,
Iran
3
Department of Physics, Sharif University of
Technology, PO Box
11365-9161, Tehran,
Iran
4
Perimeter Institute for Theoretical Physics, 31 Caroline Street North,
Waterloo, Ontario
N2L 2y5,
Canada
Received:
6
August
2012
Accepted:
6
February
2013
Aims. Stars twinkle because their light propagates through the atmosphere. The same phenomenon is expected on a longer time scale when the light of remote stars crosses an interstellar turbulent molecular cloud, but it has never been observed at optical wavelengths. The aim of the study described in this paper is to fully simulate the scintillation process, starting from the molecular cloud description as a fractal object, ending with the simulations of fluctuating stellar light curves.
Methods. Fast Fourier transforms are first used to simulate fractal clouds. Then, the illumination pattern resulting from the crossing of background star light through these refractive clouds is calculated from a Fresnel integral that also uses fast Fourier transform techniques. Regularisation procedure and computing limitations are discussed, along with the effect of spatial and temporal coherency (source size and wavelength passband).
Results. We quantify the expected modulation index of stellar light curves as a function of the turbulence strength – characterised by the diffraction radius Rdiff – and the projected source size, introduce the timing aspects, and establish connections between the light curve observables and the refractive cloud. We extend our discussion to clouds with different structure functions from Kolmogorov-type turbulence.
Conclusions. Our study confirms that current telescopes of ~4 m with fast-readout, wide-field detectors have the capability of discovering the first interstellar optical scintillation effects. We also show that this effect should be unambiguously distinguished from any other type of variability through the observation of desynchronised light curves, simultaneously measured by two distant telescopes.
Key words: dark matter / Galaxy: disk / Galaxy: halo / Galaxy: structure / local insterstellar matter / ISM: molecules
© ESO, 2013
1. Introduction
This paper is a companion paper to the observational results published in Habibi et al. (2011), and it focusses on the simulation of the scintillation effects that were searched for. Cold transparent molecular clouds are one of the last possible candidates for the missing baryons of cosmic structures on different scales (Pfenniger & Combes 1994; Pfenniger & Revaz 2005 and McGaugh et al. 2010). Since these hypothesised clouds do not emit or absorb light, they are invisible for the terrestrial observer, so we have to investigate indirect detection techniques. Our proposal for detecting such transparent clouds is to search for the scintillation of the stars located behind the transparent medium, caused by the turbulence of the cloud (Moniez 2003 and Habibi et al. 2011). The objective of this technical paper is to describe the way we can connect observations to scintillation parameters through a realistic simulation. We used these connections in the companion paper (Habibi et al. 2011) to establish constraints both from null results (towards SMC) and from observations pointing to a possible scintillation effect (towards nebula B68). Similar studies of propagation through a stochastic medium followed by Fresnel diffraction have been made by 3 and for use in radio-astronomy by 9.
We first introduce the notations and the formalism in Sect. 2. Then we describe the different stages of the simulation pipeline up to the production of simulated light curves in Sect. 3. We study the observables that can be extracted from the light curve of a scintillating star, and in particular, we check the expected modulation amplitude properties in Sect. 4. The discussion is extended to non-Kolmogorv turbulence cases in Sect. 5. In Sect. 6 we use the results from the simulation pipeline to optimise the observational strategy for discovering scintillating stars, and indicate some perspectives in the conclusion.
Complementary information on observations made with the ESO-NTT telescope and on the analysis based on the present simulations are to be found in our companion paper (Habibi et al. 2011).
2. Basic definitions and formalism
 |
Fig. 1 Geometric configuration. The source is located in the
(x2,y2)
plane, the screen contains the refractive structure, and the observer is located in
the (x0,y0)
plane.
A1(x1,y1)
and |
The formalism described in this section has been inspired and adapted from the
radioastronomy studies (Narayan 1992). But at optical
wavelength, the scintillation is primarily due to the refraction through dense clouds of
H2 + He instead of the interaction with the ionised interstellar medium. The
origin of the stochastic phase fluctuation experienced by the electromagnetic wave when
crossing the refractive medium is the phase excess induced by the stochastic fluctuation of
the column density due to the turbulence (Moniez
2003): 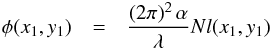 (1)where
x1 and y1 are the coordinates in
the cloud’s plane, perpendicular to the sightline (see Fig. 1). Here
φ(x1,y1)
is the phase delay induced to the wavefront after crossing the cloud,
Nl(x1,y1)
is the cloud column density of H2 molecules plus He atoms along the line of
sight, α is the medium polarisability, and λ the
wavelength. The phase delay here scales with λ-1, in contrast to
the radioastronomy where it scales with λ. Since other sources of phase
delay, such as the geometrical delay induced by scattering from cloud inhomogeneities, are
negligible, the thin screen approximation can be used, and the cloud can be considered as a
2D scattering screen whose optical properties are mapped by the phase screen
φ(x1,y1).
The statistical properties of the phase screen are described by the phase structure function
Dφ(x1,y1).
By assuming an isotropic turbulence (Narayan 1992):
(1)where
x1 and y1 are the coordinates in
the cloud’s plane, perpendicular to the sightline (see Fig. 1). Here
φ(x1,y1)
is the phase delay induced to the wavefront after crossing the cloud,
Nl(x1,y1)
is the cloud column density of H2 molecules plus He atoms along the line of
sight, α is the medium polarisability, and λ the
wavelength. The phase delay here scales with λ-1, in contrast to
the radioastronomy where it scales with λ. Since other sources of phase
delay, such as the geometrical delay induced by scattering from cloud inhomogeneities, are
negligible, the thin screen approximation can be used, and the cloud can be considered as a
2D scattering screen whose optical properties are mapped by the phase screen
φ(x1,y1).
The statistical properties of the phase screen are described by the phase structure function
Dφ(x1,y1).
By assuming an isotropic turbulence (Narayan 1992):
![\begin{eqnarray} &&D_\phi(x_1,y_1)= D_\phi(r) \nonumber \\ &&=\left\langle\left[ \phi(x_1\!+\!x_1^{\,\prime},y_1\!+\!y_1^{\,\prime})\!- \phi(x_1^{\,\prime},y_1^{\,\prime})\right]^2\right\rangle_{(x_1^{\,\prime},y_1^{\,\prime})}\!=\! \left[\frac{r}{R_{\rm diff}}\right]^{\beta-2}\!\!\!, \label{dphi} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq19.png) (2)where
the first expression is averaged over the plane positions
(2)where
the first expression is averaged over the plane positions
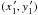 ,
,
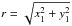 ,
β is the turbulence exponent – equals 11/3 for Kolmogorov turbulence –
and the diffraction radius, Rdiff, is the transverse distance on
the phase screen for which the root mean square of the phase variation in one radian. The
diffraction radius can be expressed in terms of the cloud parameters (Habibi et al. 2011); assuming Kolmogorov turbulence it is given by
,
β is the turbulence exponent – equals 11/3 for Kolmogorov turbulence –
and the diffraction radius, Rdiff, is the transverse distance on
the phase screen for which the root mean square of the phase variation in one radian. The
diffraction radius can be expressed in terms of the cloud parameters (Habibi et al. 2011); assuming Kolmogorov turbulence it is given by
![\begin{eqnarray} R_{\rm diff}(\lambda)\! =\! 263\,{\rm km}\left[\frac{\lambda}{1\, \mu {\rm m}}\right]^{\frac{6}{5}} \!\left[\frac{L_z}{10\,{\rm AU}}\right] ^{-\frac{3}{5}} \! \left[\frac{L_{\rm out}}{10\,{\rm AU}}\right]^{\frac{2}{5}}\! \left[\frac{\sigma_{3n}}{10^9\,\rm {cm}^{-3}}\right]^{-\frac{6}{5}}\!\!\!\! , \label{relrdiffout} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq23.png) (3)where
Lz is the cloud size along the sightline,
Lout is the turbulence outer scale, and
σ3n is the dispersion of the volumic number
density in the medium1. Here we assume the gas to be a
mixing of H2/He with 24% He by mass (corresponding to the primordial abundances)
and therefore ⟨ α ⟩ = 0.720 × 10-30 m3. In this
expression, the cloud parameters are scaled to the values given by the Pfenniger-Combes
model for the clumpuscules (the tiniest cloudlets of the molecular cloud). In the NIR band,
the diffraction radius of a typical clumpuscule is expected to be
Rdiff ~ 500 km.
(3)where
Lz is the cloud size along the sightline,
Lout is the turbulence outer scale, and
σ3n is the dispersion of the volumic number
density in the medium1. Here we assume the gas to be a
mixing of H2/He with 24% He by mass (corresponding to the primordial abundances)
and therefore ⟨ α ⟩ = 0.720 × 10-30 m3. In this
expression, the cloud parameters are scaled to the values given by the Pfenniger-Combes
model for the clumpuscules (the tiniest cloudlets of the molecular cloud). In the NIR band,
the diffraction radius of a typical clumpuscule is expected to be
Rdiff ~ 500 km.
The phase statistics of the screen can be equivalently described in Fourier space by the
phase spectral density: 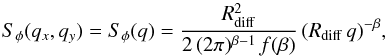 (4)where Fourier
coordinates qx and
qy have inverse length dimension,
(4)where Fourier
coordinates qx and
qy have inverse length dimension,
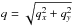 ,
and
,
and 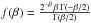 is a constant.
is a constant.
After crossing the cloud, the distorted wavefront of a point source
propagates toward the observer and produces an illumination pattern on the
observer’s plane given by 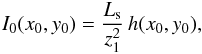 (5)where
I0(x0,y0)
is the light intensity on the observer’s plane, Ls is the source
luminosity, z1 is the source-screen distance (see Fig. 1), and
h(x0,y0)
is given by the Fresnel-Huygens diffraction integral after considering the Fresnel and the
stationary phase approximations (Born & Wolf
2002; Moniez 2003):
(5)where
I0(x0,y0)
is the light intensity on the observer’s plane, Ls is the source
luminosity, z1 is the source-screen distance (see Fig. 1), and
h(x0,y0)
is given by the Fresnel-Huygens diffraction integral after considering the Fresnel and the
stationary phase approximations (Born & Wolf
2002; Moniez 2003): 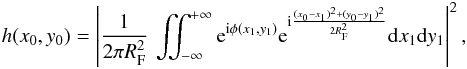 (6)where
RF =
(6)where
RF = 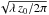 is the Fresnel radius2 and
z0 is the screen-observer distance. The Fresnel radius can be
expressed as
is the Fresnel radius2 and
z0 is the screen-observer distance. The Fresnel radius can be
expressed as ![\begin{eqnarray} R_{\rm F} = 2214 \,{\rm km} \left[\frac{\lambda}{1 ~\mu \rm m}\right]^{\frac{1}{2}} \, \left[\frac{z_0}{1~\rm kpc}\right]^{\frac{1}{2}}\cdot\label{Rfresnel} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq45.png) (7)At
the typical distance of a halo object (~10 kpc), RF ~ 7000 km
for NIR wavelengths. Because of the motion of the cloud with respect to the Earth-source
line-of-sight, the illumination pattern sweeps the observer plane, so that a terrestrial
observer receives fluctuating intensity light from the point source. This effect, the
scintillation, has two different scattering regimes (Uscinski 1977; Tatarskii & Zavorotnyi
1980), a weak regime
(Rdiff > RF)
and a strong regime
(Rdiff < RF).
In the present studies, we concentrate on the strong regime, which clearly is easier to
detect, but some realistic configurations may involve the intermediate regime studied by
Goodman & Narayan (2006). For the strong
regime, there are two different modes of flux variations (Narayan 1992; see also Rickett 1986; Rumsey 1975; Sieber
1982). The first one is the diffractive mode with length scale corresponding to the
screen’s scale of phase variations Rdiff given by Eq. (3). The resulting “speckles”, with typical size
of the order of Rdiff, are shown in Fig. 4. The corresponding time scale of the light fluctuations is
tdiff =
Rdiff/VT:
(7)At
the typical distance of a halo object (~10 kpc), RF ~ 7000 km
for NIR wavelengths. Because of the motion of the cloud with respect to the Earth-source
line-of-sight, the illumination pattern sweeps the observer plane, so that a terrestrial
observer receives fluctuating intensity light from the point source. This effect, the
scintillation, has two different scattering regimes (Uscinski 1977; Tatarskii & Zavorotnyi
1980), a weak regime
(Rdiff > RF)
and a strong regime
(Rdiff < RF).
In the present studies, we concentrate on the strong regime, which clearly is easier to
detect, but some realistic configurations may involve the intermediate regime studied by
Goodman & Narayan (2006). For the strong
regime, there are two different modes of flux variations (Narayan 1992; see also Rickett 1986; Rumsey 1975; Sieber
1982). The first one is the diffractive mode with length scale corresponding to the
screen’s scale of phase variations Rdiff given by Eq. (3). The resulting “speckles”, with typical size
of the order of Rdiff, are shown in Fig. 4. The corresponding time scale of the light fluctuations is
tdiff =
Rdiff/VT:
![\begin{eqnarray} &&t_{\rm diff}(\lambda) = 2.6{\rm s} \nonumber\\ &&\times\left[\!\frac{\lambda}{1 ~\mu \rm {m}}\!\right]^{\frac{6}{5}} \left[\!\frac{L_z}{10 ~{\rm AU}} \!\right]^{-\frac{3}{5}} \left[\!\frac{L_{\rm out}}{10\, {\rm AU}}\!\right]^{\frac{2}{5}} \left[\!\frac{\sigma_{3n}}{10^9 \,{\rm cm}^{-3}}\!\right]^{-\frac{6}{5}} \left[\!\frac{V_{\rm T}}{100\, \,{\rm km\,s^{-1}}}\!\right]^{-1}, \label{tdiff} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq51.png) (8)where
VT is the sightline relative transverse motion. Therefore fast
flux variations are expected with a typical time scale of
tdiff ~ few s. The second variation mode is the refractive mode
associated to the longer length scale called refraction radius:
(8)where
VT is the sightline relative transverse motion. Therefore fast
flux variations are expected with a typical time scale of
tdiff ~ few s. The second variation mode is the refractive mode
associated to the longer length scale called refraction radius: ![\begin{eqnarray} R_{\rm ref}(\lambda)\!=\!\frac{\lambda z_0}{R_{\rm diff}(\lambda)} \sim 30\,860\, {\rm km}\left[\frac{\lambda}{1~\mu {\rm m}}\right]\left[\frac{z_0}{1\, {\rm kpc}}\right]\left[\frac{R_{\rm diff}(\lambda)}{1000\, {\rm km}}\right]^{-1}\!\cdot \label{Rrefraction} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq54.png) (9)This
natural length scale corresponds to the size, in the observer’s plane, of the diffraction
spot from a patch of Rdiff(λ) in the screen’s
plane. This is also the size of the region in the screen where most of the scattered light
seen at a given observer’s position originates. Our convention for
Rref differs from Narayan (1992) by a factor 2π since it emerges naturally from the
Fourier transform we use for calculating the illumination pattern (see formula (14)), and it also matches the long
distance-scale flux variations visible in Fig. 4. The
corresponding time scale is given by
tref = Rref/VT:
(9)This
natural length scale corresponds to the size, in the observer’s plane, of the diffraction
spot from a patch of Rdiff(λ) in the screen’s
plane. This is also the size of the region in the screen where most of the scattered light
seen at a given observer’s position originates. Our convention for
Rref differs from Narayan (1992) by a factor 2π since it emerges naturally from the
Fourier transform we use for calculating the illumination pattern (see formula (14)), and it also matches the long
distance-scale flux variations visible in Fig. 4. The
corresponding time scale is given by
tref = Rref/VT:
![\begin{equation} t_{\rm ref}(\lambda) \!\simeq\! 5.2\, {\rm min} \left[\!\frac{\lambda}{1~\mu {\rm m}}\!\right]\left[\!\frac{z_0}{1\, {\rm kpc}}\!\right] \left[\!\frac{R_{\rm diff}(\lambda)}{1000\, {\rm km}}\!\right]^{-1}\left[\!\frac{V_{\rm T}}{100\, {\rm km\,s^{-1}}}\!\right]^{-1}\!\cdot \label{em} \end{equation}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq59.png) (10)
(10)
3. Simulation description
In this section, we describe the simulation pipeline with some numerical tricks, from the generation of the phase screen induced by turbulent gas, up to the light versus time curves expected from realistic stars seen through this gas. The steps in this pipeline are listed below:
-
The simulation of the refractive medium: inSect. 3.1 we describe the generation of a phasescreen and examine the impact of the limitations caused by thesampling and by the finite size of the screen by comparing theinitial (theoretical) and reconstructed diffraction radii.
-
The computation of the illumination pattern: in Sect. 3.2, we first describe the calculation of the illumination pattern produced on Earth by a point monochromatic source as seen through the refractive medium. We explain the technique for avoiding numerical (diffraction) artefacts caused by the borders of the simulated screen, and discuss the criterion on the maximum pixel size to avoid aliasing effects. The pattern computation is then generalised to extended polychromatic sources.
-
The light curve simulation: we describe in Sect. 3.3 the simulation of the light fluctuations with time at a given position induced by the motion of the refractive medium with respect to the line of sight.
3.1. Simulation of the phase screen
 |
Fig. 2 The phase-delay variations near the average for a simulated refractive screen with Nx × Ny = 20 000 × 20 000 pixels, Δ1 = 22.6 km, and Rdiff = 100 km. The grey scale ranges between ± 50 × 2π rad (clear regions correspond to an excess of phase with respect to the average). The zoom (inset in the lower-right corner) illustrates the self-similarity of the simulated screen (grey scale amplitude of 5 × 2π rad). |
Numerical realisations of the 2D phase screen – made of
Nx × Ny
squared pixels of size Δ1 – are randomly generated from the phase spectral
density
Sφ(qx,qy),
determined by the choice of Rdiff in relation (4). Such a phase screen – with the desired
statistical properties – is obtained from the random realisation of a Fourier transform
Fφ(qx,qy)
in a way that makes the ensemble of such realisations satisfy the relation 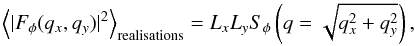 (11)where
Lx and
Ly are the screen physical size, and the
average is the ensemble averaging over the different realisations. For each
(11)where
Lx and
Ly are the screen physical size, and the
average is the ensemble averaging over the different realisations. For each
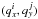 vector associated to a pixel
(i,j), we generate a random complex number
vector associated to a pixel
(i,j), we generate a random complex number
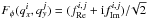 where each component
where each component 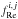 and
and
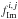 spans the
Gaussian distribution3 of zero mean, and
spans the
Gaussian distribution3 of zero mean, and
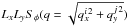 width.
In this way, relation 11 is automatically
satisfied when averaging on a large number of such realisations, since the average of
| Fφ(qx,qy)|2
for the ensemble of
(qx,qy)
vectors with the same module q equals
LxLySφ(q)
by construction. The phase screen
φ(x1,y1)
is finally obtained by numerically computing the inverse Fourier transform of this phase
spectrum
Fφ(qx,qy).
Figure 2 shows a phase screen generated by assuming
Kolmogorov turbulence (β = 11/3).
width.
In this way, relation 11 is automatically
satisfied when averaging on a large number of such realisations, since the average of
| Fφ(qx,qy)|2
for the ensemble of
(qx,qy)
vectors with the same module q equals
LxLySφ(q)
by construction. The phase screen
φ(x1,y1)
is finally obtained by numerically computing the inverse Fourier transform of this phase
spectrum
Fφ(qx,qy).
Figure 2 shows a phase screen generated by assuming
Kolmogorov turbulence (β = 11/3).
3.1.1. Preliminary checks, limitations
To check the accuracy of the numerically generated phase screen (Fig. 2), we recomputed the phase structure function
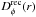 (and consequently
(and consequently
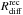 ) from the
generated phase Fourier transform
Fφ(qx,qy),
and we compared it with the theoretical phase structure function (Eq. (2)). First, the spectral density is
recomputed from the generated
Fφ(qx,qy)
using relation
) from the
generated phase Fourier transform
Fφ(qx,qy),
and we compared it with the theoretical phase structure function (Eq. (2)). First, the spectral density is
recomputed from the generated
Fφ(qx,qy)
using relation 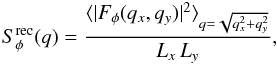 (12)where
the average is performed on the
(qx,qy)
coordinates4 spanning the circle of radius
(12)where
the average is performed on the
(qx,qy)
coordinates4 spanning the circle of radius
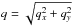 .
The corresponding phase auto-correlation function is then given by Fourier transform:
.
The corresponding phase auto-correlation function is then given by Fourier transform:
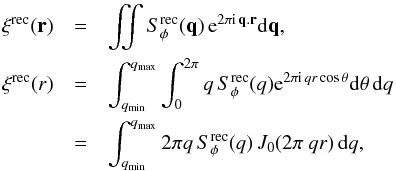 (13)where
J0 is the Bessel function. The recomputed structure
function is then given by
(13)where
J0 is the Bessel function. The recomputed structure
function is then given by 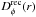 =
2(ξrec(0) − ξrec(r)),
and the value of
=
2(ξrec(0) − ξrec(r)),
and the value of 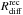 is deduced from
its definition
is deduced from
its definition 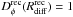 .
.
 |
Fig. 3 Phase structure functions Dφ(r) for a phase screen with Rdiff = 500 km. Blue line is the initial (theoretical) structure function. Red line is reconstructed from one of the realisations of the phase screen through simulation. The black curve is obtained from the numerical integration of the initial phase spectral density sampled as in the simulation. |
In Fig. 3, we show the theoretical phase structure
function of a turbulent medium with Rdiff = 500 km – for
which Dφ(r = 500 km) = 1
by definition –, and the recomputed (effective) structure function from one of the
realisations of the screen. From this recomputed function, we find
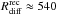 km since
km since
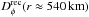 = 1. To find the origin of the
difference with the input value Rdiff = 500 km, we replaced
= 1. To find the origin of the
difference with the input value Rdiff = 500 km, we replaced
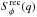 in Eq. (13) by the theoretical spectrum
Sφ(q) sampled as in the
simulation (number of pixels
Nx × Ny ~ 14 000 × 14 000
with pixel size Δ1 = 28.85 km). Then we computed the integral (13) numerically with the same integration
limits
(qmin,qmax)5 as the simulation. The integration result differs
only by a few percent from the function recomputed from the simulated screen. We showed
that the black curve approaches the blue curve when qmin → 0
and qmax → ∞. This means that the sampling is mainly
responsible for the difference between Dφ
and
in Eq. (13) by the theoretical spectrum
Sφ(q) sampled as in the
simulation (number of pixels
Nx × Ny ~ 14 000 × 14 000
with pixel size Δ1 = 28.85 km). Then we computed the integral (13) numerically with the same integration
limits
(qmin,qmax)5 as the simulation. The integration result differs
only by a few percent from the function recomputed from the simulated screen. We showed
that the black curve approaches the blue curve when qmin → 0
and qmax → ∞. This means that the sampling is mainly
responsible for the difference between Dφ
and 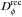 . Since
our simulation is limited by the number of pixels, we lose the contributions of the
large and small scales in the recomputed Rdiff. The only way
to push back this limitation is to generate larger screens (larger
Nx and
Ny) with higher resolutions (smaller
Δ1) to cover wider interval of spatial frequencies which in return needs
higher computational capacities (see also Sect. 3.4).
. Since
our simulation is limited by the number of pixels, we lose the contributions of the
large and small scales in the recomputed Rdiff. The only way
to push back this limitation is to generate larger screens (larger
Nx and
Ny) with higher resolutions (smaller
Δ1) to cover wider interval of spatial frequencies which in return needs
higher computational capacities (see also Sect. 3.4).
3.2. Illumination pattern
To obtain the illumination pattern on the observer plane, we numerically compute the
integral (6) which can be written as a
Fourier transform: ![\begin{eqnarray} \label{intens} h(x_{0},y_{0}) = \frac{1}{2\pi~ R_{\rm F}^{\,2}} \Big\vert FT\left[G(x_1,y_1)\right]\Big\vert ^{2}\,_{\left(f_x = \frac{x_0}{2\pi R_{\rm F}^2},\,f_y = \frac{y_0}{2\pi R_{\rm F}^2}\right)} , \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq110.png) (14)where
(14)where
![\begin{eqnarray} G(x_1,y_1) &=& \exp\left[{\rm i}\,\left(\phi(x_1,y_1)\,+\,\frac{x_1^{2}+y_1^{2}}{2~R_{\rm F}^{\,2}}\,\right)\right]\cdot \label{Gxy} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq111.png) (15)Here,
(x1,y1) and
(x0,y0) are the
screen and observer coordinates, respectively. Coordinates
(fx,fy)
are the conjugated variables in Fourier space. Before computing expression (14), a regularisation procedure for
G(x1,y1)
has been defined to avoid computational artefacts.
(15)Here,
(x1,y1) and
(x0,y0) are the
screen and observer coordinates, respectively. Coordinates
(fx,fy)
are the conjugated variables in Fourier space. Before computing expression (14), a regularisation procedure for
G(x1,y1)
has been defined to avoid computational artefacts.
3.2.1. Screen regularisation
Since integral (14) is computed
numerically, the coordinates
(x1,y1) have
discrete (integer) values describing pixel position centres on the screen, to allow
simple combinations of illumination patterns with different pixel sizes (corresponding
to different wavelengths). That the integration domain is limited is physically
equivalent to computing the Fresnel integral within a diaphragm with the size of the
screen. In this case, we face a parasitic effect: the light diffraction from the sharp
edges of the diaphragm. This causes rapid intensity variations at the borders of the
observer plane. To attenuate this effect and remove the resulting diffraction fringes,
we multiply the screen intensity transmission by a 2D smoothing function. We define the
following 1D smoothing function SF(x) (see Fig. 6): ![\begin{eqnarray*} S\!F(x) = \left\{ \begin{array}{ll} \frac{1}{2}\left[1+\sin\left(\frac{\pi x}{L_{\rm m}}-\frac{\pi}{2}\right)\right] & 0\leq x \leq L_{\rm m},\\ 1 & L_{\rm m} < x < L-L_{\rm m},\\ \frac{1}{2}\left[1+\sin\left(\frac{\pi (x-L+L_{\rm m})}{L_{\rm m}}+\frac{\pi}{2}\right)\right] & L-L_{\rm m} \leq x \leq L,\\ 0 & \mbox{{otherwise}},\\ \end{array} \right. \end{eqnarray*}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq116.png) where
Lm = 10RF is the margin length
from the borders of the screen with size L. We multiply the function
G(x1,y1)
by
SF(x1) × SF(y1)
in expression (14). Since the Fresnel
integral is dominated by the contribution of the integrand within a disk that is within
a few Fresnel radii, it is sufficient to smooth the discontinuity of
G(x1,y1)
within a distance of a few Fresnel radii (here
Lm = 10 RF). We tested the
efficiency of this regularisation procedure by checking that the simulated illumination
pattern from a point-source projected through a uniform phase screen was – as expected –
also uniform beyond our precision requirements (<1%) (Habibi 2011). To define a reliable fiducial domain in
the observer plane excluding the regions that are only partially illuminated owing to
the diaphragm, we also delimited an
Rref/2 margin from the borders of the
illumination pattern, corresponding to the typical radius (half-size) of the large-scale
luminous spots (see also Coles et al. 1995). Figure 4 shows the pattern produced by a point source through a turbulent medium with
Rdiff = 100 km located at
z1 = 160 pc from the Earth at wavelength
λ = 2.162 μm. Since the corresponding Fresnel
radius RF = 1300 km is larger than the diffraction radius,
the regime is the strong scintillation regime. The hot speckles (of typical size
Rdiff ~ 100 km) can be distinguished from the larger
dark/luminous structures that have a typical size of
where
Lm = 10RF is the margin length
from the borders of the screen with size L. We multiply the function
G(x1,y1)
by
SF(x1) × SF(y1)
in expression (14). Since the Fresnel
integral is dominated by the contribution of the integrand within a disk that is within
a few Fresnel radii, it is sufficient to smooth the discontinuity of
G(x1,y1)
within a distance of a few Fresnel radii (here
Lm = 10 RF). We tested the
efficiency of this regularisation procedure by checking that the simulated illumination
pattern from a point-source projected through a uniform phase screen was – as expected –
also uniform beyond our precision requirements (<1%) (Habibi 2011). To define a reliable fiducial domain in
the observer plane excluding the regions that are only partially illuminated owing to
the diaphragm, we also delimited an
Rref/2 margin from the borders of the
illumination pattern, corresponding to the typical radius (half-size) of the large-scale
luminous spots (see also Coles et al. 1995). Figure 4 shows the pattern produced by a point source through a turbulent medium with
Rdiff = 100 km located at
z1 = 160 pc from the Earth at wavelength
λ = 2.162 μm. Since the corresponding Fresnel
radius RF = 1300 km is larger than the diffraction radius,
the regime is the strong scintillation regime. The hot speckles (of typical size
Rdiff ~ 100 km) can be distinguished from the larger
dark/luminous structures that have a typical size of
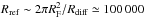 km.
km.
 |
Fig. 4 Typical illumination pattern from a point-like source. Here Rdiff = 100 km, the screen is at z0 = 160 pc, λ = 2.16 μm, then RF = 1300 km and Rref = 106 000 km. The typical length scale of the small-scale speckles is Rdiff, and the scale of the larger structures is Rref. The white square shows our fiducial zone with a margin of Lm = Rref/2 from the borders. Grey scale range from 0 to 4 times the mean intensity. The image has 20 000 × 20 000 pixels, each with a 22.6 km side. |
 |
Fig. 5 Typical illumination pattern from an extended source produced through the same screen as in Fig. 4, with source radius rs = 0.5 R⊙, located at z0 + z1 = 1 kpc + 160 pc (Rs ≃ 53 000 km). The small-scale speckles are smeared, and only the larger scale fluctuations survive. The white square shows the restricted fiducial zone with margin of Lm = Rref/2 + Rs from the borders. Grey scale ranges ± 20% around the mean intensity. |
 |
Fig. 6 The smoothing function SF(x). L is the screen size, Lm is the margin from the screen borders. |
3.2.2. Effect of sampling
Here, we discuss some limitations caused by the pixellisation. The screen should be
sampled often enough to avoid the aliasing effects. Aliasing happens when
G(x1,y1)
contains frequencies that are higher than the Nyquist frequency
fNyq = 1/(2Δ1), where
Δ1 is the pixel size. In relation (15), G contains two length scales, the diffraction and the
Fresnel radii (Rdiff and RF).
Rdiff is the characteristic length of the phase screen
variations
φ(x1,y1);
it is at least necessary that
Δ1 < Rdiff/2
in order to sample phase variations up to
1/Rdiff spatial frequency.
RF appears in the quadratic term
![\hbox{$\exp \left[{\rm i}\,\frac{x_1^{2}+y_1^{2}}{2R_{\rm F}^{\,2}}\right ]$}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq147.png) ;
the oscillation of this term accelerates as x1 and
y1 increase, and aliasing occurs as soon as the distance
between two consecutive peaks is smaller than 2Δ1. In one dimension we
therefore expect aliasing if
;
the oscillation of this term accelerates as x1 and
y1 increase, and aliasing occurs as soon as the distance
between two consecutive peaks is smaller than 2Δ1. In one dimension we
therefore expect aliasing if ![\begin{eqnarray} \frac{(x_1+2\Delta_1)^2 - x_1^2}{2 R_{\rm F}^2} > 2\pi, \nonumber \\ {\rm i.e.}\ \frac{x_1}{\Delta_1} > \pi \left[\frac{R_{\rm F}}{\Delta_1}\right]^2 - 1, \label{alias1} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq148.png) (16)where
x1/Δ1 is the distance to the
optical axis, expressed in pixels. The condition
Δ1 = RF/2 would be obviously
insufficient here to avoid aliasing, since beyond ~11 pixels only from the optical axis
(x1/Δ1 > 11 pixel),
the quadratic term would be under-sampled. In practice, for the configurations
considered in this paper, the Fresnel radius is >1000 km. When
Δ1 = 22 km in the simulation, the aliasing starts at
x1/Δ1 > 6490
pixels from the centre of the image, corresponding to more than
140RF, which is large enough to cover the sensitive domain
related to the stationary phase approximation.
(16)where
x1/Δ1 is the distance to the
optical axis, expressed in pixels. The condition
Δ1 = RF/2 would be obviously
insufficient here to avoid aliasing, since beyond ~11 pixels only from the optical axis
(x1/Δ1 > 11 pixel),
the quadratic term would be under-sampled. In practice, for the configurations
considered in this paper, the Fresnel radius is >1000 km. When
Δ1 = 22 km in the simulation, the aliasing starts at
x1/Δ1 > 6490
pixels from the centre of the image, corresponding to more than
140RF, which is large enough to cover the sensitive domain
related to the stationary phase approximation.
3.2.3. Extended source (spatial coherency)
The illumination pattern of a scintillating extended source is given by the convolution
product of the illumination pattern of the point-like source with the projected source
limb profile (Moniez 2003; & Habibi 2011), 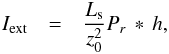 (17)where
Ls is the source luminosity, and the normalised limb
profile is described as a uniform disk:
(17)where
Ls is the source luminosity, and the normalised limb
profile is described as a uniform disk: 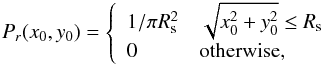 where
where
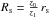 is the
projected source radius on the observer’s plane, and rs is
the source radius. Figure 5 shows the convolution
of the pattern of Fig. 4 with the projected profile
of a star with radius
rs = 0.5 R⊙, located at
z0 (160 pc) +z1 (1 kpc) =
1.16 kpc (Rs = 53 000 km). High-frequency fluctuations due
to diffractive speckle disappear, and the pattern loses contrast, but the variations on
Rref scale remain visible. As the convolution involves a
disk of radius Rs, we can perform the calculation only at a
distance greater than Rs from the borders. We therefore
define a new fiducial zone by excluding a margin of
Rref/2 + Rs
from the initial borders. Any statistical analysis will be made within this zone to be
safe from any border perturbation.
is the
projected source radius on the observer’s plane, and rs is
the source radius. Figure 5 shows the convolution
of the pattern of Fig. 4 with the projected profile
of a star with radius
rs = 0.5 R⊙, located at
z0 (160 pc) +z1 (1 kpc) =
1.16 kpc (Rs = 53 000 km). High-frequency fluctuations due
to diffractive speckle disappear, and the pattern loses contrast, but the variations on
Rref scale remain visible. As the convolution involves a
disk of radius Rs, we can perform the calculation only at a
distance greater than Rs from the borders. We therefore
define a new fiducial zone by excluding a margin of
Rref/2 + Rs
from the initial borders. Any statistical analysis will be made within this zone to be
safe from any border perturbation.
 |
Fig. 7 Simulated illumination maps (20 000 × 20 000 pixel of 22.6 km side) produced on Earth by a source located at z0 + z1 = 1.18 kpc through a refracting cloud assumed to be at z0 = 160 pc with a turbulence parameter Rdiff(2.16 μm) = 100 km. Here Rref(2.16 μm) ≃ 100 000 km. Top-left and middle: illumination produced at λ = 2.16 μm from a point-source with a zoomed detail; the contrast is 100%. The grey scale ranges from 0 to 4 times the mean intensity. Top-right: the same from a K0V star (rs = 0.85 R⊙, MV = 5.9, at 1.18 kpc V = 16.3). The circle shows the projection of the stellar disk (RS = rs × z0/z1). Here the modulation index is only 3.3%, and the grey scale ranges from ±20% around the mean intensity. The bottom maps are the illuminations in Ks wide band (λcentral = 2.162 μm, Δλ = 0.275 μm), using the same grey scales as above. The modulation index is 55% for the point-source (left and centre) and 3.3% for the extended source (right). The two parallel straight lines show the sections sampled by two observers located about 10 000 km apart, when the screen moves with the transverse velocity VT. |
3.2.4. Polychromatic source (time coherency)
The illumination patterns shown in Figs. 4 and 5 are computed for a monochromatic source (fixed λ), but observations are done through filters with finite-width passbands. To take the contributions of different wavelengths to the pattern into account, we superimpose the illumination patterns obtained with the same refractive structure (the same column density fluctuations) at different wavelengths6. We have considered the passband of the SOFI camera in Ks band and approximated it as a rectangular function over the transmitted wavelengths with a central value 2.162 μm and width 0.275 μm. Twenty-one illumination patterns were computed for 21 regularly spaced wavelengths within the [2.08, 2.28] μm interval, and were co-added to simulate the illumination pattern through the Ks passband. We checked that the spacing between successive wavelengths was small enough to produce a co-added image with a realistic residual modulation index, by studying this index as a function of the number of monochromatic components equally spaced within the full bandwidth. We found that an asymptotic value is reached with a co-added image made up of only about ten components.
Figure 7 (left and centre) shows a comparison
between monochromatic (up) and Ks passband (down)
illumination patterns of a point-like source. The speckle pattern is attenuated when the
light is not monochromatic (or equivalently when time coherency is limited). This is
caused by the small decorrelation bandwidth
δλdec of the strong diffractive
scintillation regime, which is given by
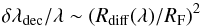 (18)(Narayan 1992; Gwinn et
al. 1998). This chromatic effect results from the high sensitivity of the
constructive interference condition with the wavelength7. In the case of Fig. 7, the
decorrelation bandwidth is
δλdec/λ ~ 1%.
Since the Ks passband is
δλ/λ ~ 0.1 ~ 10 × δλdec/λ,
a first-order estimation of the modulation index for a Ks
passband pattern is the value obtained when adding ten decorrelated patterns of speckle
i.e. one multiplied by ~
(18)(Narayan 1992; Gwinn et
al. 1998). This chromatic effect results from the high sensitivity of the
constructive interference condition with the wavelength7. In the case of Fig. 7, the
decorrelation bandwidth is
δλdec/λ ~ 1%.
Since the Ks passband is
δλ/λ ~ 0.1 ~ 10 × δλdec/λ,
a first-order estimation of the modulation index for a Ks
passband pattern is the value obtained when adding ten decorrelated patterns of speckle
i.e. one multiplied by ~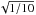 .
The modulation index found with our simulation (~55%) has the correct order of
magnitude.
.
The modulation index found with our simulation (~55%) has the correct order of
magnitude.
By contrast, structures of size of Rref are much less
sensitive to the variations in λ, according to the combination of
(3) and (9): 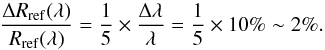 (19)As a consequence of the
large-scale smearing of the point-source pattern when considering an extended
source, there is no significant difference between monochromatic and
polychromatic patterns for such an extended source, as shown in Fig.
7 (right). Therefore, in the following we ignore
the impact of the Rdiff structures.
(19)As a consequence of the
large-scale smearing of the point-source pattern when considering an extended
source, there is no significant difference between monochromatic and
polychromatic patterns for such an extended source, as shown in Fig.
7 (right). Therefore, in the following we ignore
the impact of the Rdiff structures.
3.3. Simulation of light curves
What we observe with a single telescope is not the 2D illumination pattern but a light curve. Because of the relative motions, the telescope sweeps a 1D section of the pattern, at a constant velocity as long as parallax can be neglected. We therefore simulated light versus time curves by sampling the 2D pattern pixels along straight lines, with the relative speed of the telescope.
3.4. Computing limitations
We adopted the same number of pixels N × N and the same
pixel scale Δ1 to numerically describe both the screen’s and the observer’s
planes; indeed, the light emerging from the screen is essentially contained in its shadow,
and this choice optimises the screen filling. Since the two planes are conjugated, the
following relation arises: 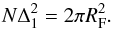 (20)Because of this
relation, N has to be as large as possible to minimize Δ1 and
also to get a wide useful area. This area is indeed restricted by the definition of the
fiducial domain, which can be heavily reduced when simulating the illumination from an
extended source. Also a large fiducial domain is essential when simulating long-duration
light curves. As a consequence, memory limitations affect the maximum size of the screen
and illumination 2D patterns. In the present paper, we were limited to patterns of
20 000 × 20 000 pixels.
(20)Because of this
relation, N has to be as large as possible to minimize Δ1 and
also to get a wide useful area. This area is indeed restricted by the definition of the
fiducial domain, which can be heavily reduced when simulating the illumination from an
extended source. Also a large fiducial domain is essential when simulating long-duration
light curves. As a consequence, memory limitations affect the maximum size of the screen
and illumination 2D patterns. In the present paper, we were limited to patterns of
20 000 × 20 000 pixels.
4. Observables
The observable parameters of the scintillation process are the modulation index and the
modulation’s characteristic time scales. The main observable we used in our data analysis
(Habibi et al. 2011) is the modulation index. It is
defined as the flux dispersion σI divided by
the mean flux 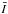 :
:
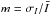 .
We first compare the effective modulation index of simulated screens with the theoretical
expectations, then examine the precision we can reach on m from a light
curve, and give a numerical example. We also show how we can connect the observed modulation
index to the geometrical parameters (Rdiff(λ),
λ, Rs, etc.) through simulation.
.
We first compare the effective modulation index of simulated screens with the theoretical
expectations, then examine the precision we can reach on m from a light
curve, and give a numerical example. We also show how we can connect the observed modulation
index to the geometrical parameters (Rdiff(λ),
λ, Rs, etc.) through simulation.
 |
Fig. 8 The effective intensity modulation index |
4.1. Modulation Index
For a point-like source in the strong scintillation regime the
modulation index m ≈ 1. For an extended source (radius
rs, projected radius
Rs = rs.z0/z1)
in the same regime, we always have m < 1, and
Narayan (1992) showed that when the small-scale
(diffractive) speckle is completely smeared,
![\begin{eqnarray} m \approx \ \left[\frac{R_{\rm diff}}{R_{\rm F}}\right]^{1/3} \left[\frac{\theta_{\rm ref}}{2\pi \theta_{\rm s}}\right]^{7/6} \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq196.png) (21)in
the case of the Kolmogorov turbulence. Here,
θref = Rref/z0
is the angular refraction radius8 and
θs the source angular radius. In this expression, Narayan (1992) assumed that
z0 ≪ z1, therefore
z0 + z1 ≈ z1.
We use the following expression, which is formally identical to the previous one for
z0 ≪ z1 but can also be used
when z0 is not negligible:
(21)in
the case of the Kolmogorov turbulence. Here,
θref = Rref/z0
is the angular refraction radius8 and
θs the source angular radius. In this expression, Narayan (1992) assumed that
z0 ≪ z1, therefore
z0 + z1 ≈ z1.
We use the following expression, which is formally identical to the previous one for
z0 ≪ z1 but can also be used
when z0 is not negligible: ![\begin{eqnarray} m &\approx& \left[\frac{R_{\rm diff}}{R_{\rm F}}\right]^{1/3} \left[\frac{R_{\rm ref}}{2\pi~ R_{\rm s}}\right]^{7/6} \\ &\approx& 0.035 \left[\frac{\lambda}{1 \,\mu\rm m}\right] \left[\frac{z_0}{1\,\rm kpc}\right]^{-\frac{1}{6}} \left[\frac{R_{\rm diff}}{1000\,\rm km}\right]^{-\frac{5}{6}} \left[\frac{r_{\rm s}/z_1}{R_\odot/10~\rm kpc}\right]^{-\frac{7}{6}}\!\!\cdot\label{xparam} \quad\quad \end{eqnarray}](/articles/aa/full_html/2013/04/aa20172-12/aa20172-12-eq201.png) This
relation can be qualitatively justified by noticing firstly that
Rdiff quantity has to be considered relatively to
RF when considering its impact on diffraction, and secondly
that the convolution of the point-source pattern (see Fig. 7-up) with the projected stellar profile (following expression (17)) makes the contrast decrease when the
number of Rref-size domains within
RS = rSz0/z1
increases. The “exotic” exponents are related to the Kolmogorov turbulence. It should be
emphasised that this relation assumes the scintillation is strong and quenched
(Rs/RF > RF/Rdiff > 1).
This
relation can be qualitatively justified by noticing firstly that
Rdiff quantity has to be considered relatively to
RF when considering its impact on diffraction, and secondly
that the convolution of the point-source pattern (see Fig. 7-up) with the projected stellar profile (following expression (17)) makes the contrast decrease when the
number of Rref-size domains within
RS = rSz0/z1
increases. The “exotic” exponents are related to the Kolmogorov turbulence. It should be
emphasised that this relation assumes the scintillation is strong and quenched
(Rs/RF > RF/Rdiff > 1).
We checked this relation by performing series of simulations with different phase screens
and stellar radii. We generated series of screens with
Rdiff = 50 km to 500 km by steps of 50 km. For each screen, we
considered different sources –at the same geometrical distances– with radii from 0.25
R⊙ to 1.5 R⊙ by steps of 0.25
R⊙ and computed corresponding illumination pattern
realisations. The modulation indices were estimated within the fiducial zone for each 2D
illumination pattern. In Fig. 8, the thus estimated
m for each generated pattern are plotted as a function of the
theoretical value expected from expression (23). We note that the modulation has relatively large scatter. This is because
the fiducial zone is not large enough, and it contains a limited number of regions with
sizes of Rref (the scale that dominates the light variations).
In some cases there are very few distinct dark/luminous regions (as in Fig. 5). The number of such regions within the fiducial domain
is 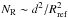 , where
d is the size of the fiducial zone. After discarding the cases with
NR < 5, we computed the mean and
root mean square of the effective m values, for each series of
configurations with the same theoretical modulation index. Figure 8 shows that relation (23) is satisfied for a modulation index smaller than 0.15. The higher values of
m are systematically underestimated in our simulation owing to the
limitation of the screen size, which has a stronger impact on the number of large
dark/luminous regions in this part of the figure. This number is indeed smaller (though it
is larger than 5), and the chances for sampling the deepest valleys and the highest peaks
are fewer, therefore biasing the modulation index towards low values.
, where
d is the size of the fiducial zone. After discarding the cases with
NR < 5, we computed the mean and
root mean square of the effective m values, for each series of
configurations with the same theoretical modulation index. Figure 8 shows that relation (23) is satisfied for a modulation index smaller than 0.15. The higher values of
m are systematically underestimated in our simulation owing to the
limitation of the screen size, which has a stronger impact on the number of large
dark/luminous regions in this part of the figure. This number is indeed smaller (though it
is larger than 5), and the chances for sampling the deepest valleys and the highest peaks
are fewer, therefore biasing the modulation index towards low values.
Therefore, by measuring the modulation index from an observed light curve and using an estimate of star type (i.e. radius) and distance z0 + z1 ≈ z1, we can constrain Rdiff(λ) from this relation (23)9, even with poor knowledge of the screen’s distance z0, considering the slow dependence with this parameter. This technique allowed us to infer constraints in Habibi et al. (2011) on the gas turbulence within galactic nebulae (z0 ~ 80−190 pc and z1 = 8 kpc), and upper limits on hidden turbulent gas within the galactic halo (assuming z0 ~ 10 kpc and z1 + z0 = 62 kpc).
 |
Fig. 9 Light curves extracted along the 3 horizontal white lines for two illumination patterns. Left column: 2D pattern from a point-like source in Ks band with Rdiff = 300 km and Rref ≈ 28 000 km. The modulation indices of the three light curves differ by less than 5% from the 2D pattern modulation index. Right column: the illumination pattern for an extended source with Rs ≈ 41 000 km, through the same refractive screen. The modulation indices fluctuate by more than 30% around the 2D pattern index, implying the necessity of longer light curves for a better statistical representativity. The distance scale is common to both patterns. The circle shows the projected star disk. The 3 light curves from the right column are not completely decorrelated, because of their common proximity to the same large positive fluctuation. |
4.2. Information from the light curves
If a light curve is long enough (or equivalently if the observation time is long enough),
its series of light measurements represents an unbiased subsample of the 2D pattern. For
instance, the left hand panels of Fig. 9 represent
the illumination pattern of a point-like source and three associated light curves. Here,
Rref ≈ 28 000 km and the modulation index
mpoint = 1.18. The light curves are extracted from three
horizontal parallel lines with lengths of ~3.5 × 105 km. The corresponding
time scale depends on the relative transverse velocity. The lines are selected far from
each other in order not to be affected by the fluctuations of the same regions. Modulation
indices along the light curves differ from the 2D’s by less than 5%. When the modulation
is characterised by both Rref and
Rdiff, a light curve that spans a few
Rref is a sample of the 2D screen, which is large enough to
provide a good approximation of the scintillation modulation index for a point-like
source. The right hand panels of Fig. 9 show the 2D
pattern for an extended source with Rs ≈ 41 000 km. Here,
Rs > Rref
and the flux fluctuations are smoothed, characterised by the unique length scale
Rref, and have a much smaller modulation index
mextended = 0.04. The light curves are extracted in the same
way as the point-like source within the corresponding restricted fiducial zone (see Fig.
5), therefore they span
~2.5 × 105 km and statistically include a little bit less than 10
Rref-scale variations. Because of this statistically short
length, the light-curve-to-light-curve estimates of mextended
typically fluctuate by ~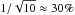 . The
fluctuations on mextended estimates can only be reduced with
longer light curves. To get a precision value of 5% on
mextended, the light curve should indeed be as long as
~400 × Rref. As an example, if we observe through a
turbulent gaseous core with Rdiff = 200 km in B68 nebula
located at z0 = 80 pc at
λ = 2.16 μm
(Rref ~ 27 000 km), and assuming
VT ~ 20 km s-1, an observing time of ~150 h is
needed to measure the modulation index with this precision of 5%. When searching for
unseen turbulent media located at unknown distances from us, the diffraction and
refraction radii are unknown, and we can only obtain a probability distribution of the
observation time for a requested precision on the modulation index.
. The
fluctuations on mextended estimates can only be reduced with
longer light curves. To get a precision value of 5% on
mextended, the light curve should indeed be as long as
~400 × Rref. As an example, if we observe through a
turbulent gaseous core with Rdiff = 200 km in B68 nebula
located at z0 = 80 pc at
λ = 2.16 μm
(Rref ~ 27 000 km), and assuming
VT ~ 20 km s-1, an observing time of ~150 h is
needed to measure the modulation index with this precision of 5%. When searching for
unseen turbulent media located at unknown distances from us, the diffraction and
refraction radii are unknown, and we can only obtain a probability distribution of the
observation time for a requested precision on the modulation index.
 |
Fig. 10 Simulation of illumination scintillation patterns with associated light curves from an extended source assuming a refractive screen with non-Kolmogorov turbulences (left β = 3.1, right β = 3.9, see text). Here Rdiff = 100 km, Rref ≈ 8 × 104 km and the projected star radius is RS ~ 0.36Rref = 28 800 km. |
 |
Fig. 11 Top: two different phase screen power laws. Bottom: the corresponding modulation indices as a function of the expected modulation index for the Kolmogorov turbulence. The 3 indices plotted at a given abscissa correspond to screens with β = 3.1 (red), 3.67 (Kolmogorov, blue, along the diagonal), and 3.9 (black) with the same Rdiff. As the power law gets steeper, a larger modulation is expected. Blue dots show the Kolmogorov turbulence case. |
The other important information carried by the light curves are the characteristic time
scale between peaks
tref = Rref/VT,
associated to the refraction radius (Fig. 7 upper
left), a correlation duration
ts = Rs/VT,
associated to the source radius (Fig. 7 upper right)
and possibly
tdiff = Rdiff/VT,
associated to the small diffractive speckle structure (Fig. 7 lower left); the latter could be detected in exceptionally favourable cases
(source with very small angular size, assuming the strong diffractive scintillation
regime) with a powerful detection setup such as LSST10. The time power spectrum of the expected stochastic light curve should show a
slope break around frequency 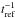 ,
and possibly around
,
and possibly around 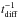 (Goodman & Narayan 1985), which should
allow one to distinguish it from purely randomly fluctuating light curves due to
photometric noise, and to extract constraints on the scintillation configuration.
Estimating ts would be challenging, since the extended source
acts as a low passband filter on the point-source pattern; therefore, the imprint of the
projected radius is essentially within the attenuation of the light curve autocorrelation
(Goodman & Narayan 2006), and more
specifically – as mentioned above – within the modulation index, that can be polluted by
many observational artefacts. These potentialities of the time studies need more
investigation and should be discussed in more detail in a forthcoming paper.
(Goodman & Narayan 1985), which should
allow one to distinguish it from purely randomly fluctuating light curves due to
photometric noise, and to extract constraints on the scintillation configuration.
Estimating ts would be challenging, since the extended source
acts as a low passband filter on the point-source pattern; therefore, the imprint of the
projected radius is essentially within the attenuation of the light curve autocorrelation
(Goodman & Narayan 2006), and more
specifically – as mentioned above – within the modulation index, that can be polluted by
many observational artefacts. These potentialities of the time studies need more
investigation and should be discussed in more detail in a forthcoming paper.
5. Probing various turbulence laws
Up to now, we have focussed on the standard Kolmogorov turbulence. In this section, we investigate a possible deviation from the Kolmogorov turbulence law11. We chose two different phase spectra with β = 3.1 and β = 3.9 in relation (4). To study the corresponding scintillation modes, we generated two series of phase screens according to the spectra and computed the illumination patterns from an extended source with Rs ~ 0.36 Rref through each of them. The patterns are represented in Fig. 10 with corresponding light curve samples. For both images, Rdiff = 100 km, RF = 1150 km, and Rref ≈ 8 × 104 km. The pattern with β = 3.1 (left) shows a small modulation index m(3.1) = 0.04, while the pattern with β = 3.9 (right) shows a much larger modulation index m(3.9) = 0.22. As can be seen from its visual aspect, the turbulence with a higher exponent produces stronger contrast on large scales compared to the other one (β = 3.1). To understand the origin of the difference, we compared the two phase spectra at the top of Fig. 11. The steeper spectrum (β = 3.9) has more power for fluctuations on large scales. Moreover, by integrating Eq. (4), we computed that the total power distributed from Rref to Rdiff is about an order of magnitude larger for β = 3.9 than for β = 3.1. Therefore, the larger the β exponent is the stronger flux fluctuations are produced. As a conclusion, the detection of scintillation should be easier for turbulences with steeper spectrum, because a larger modulation index is expected. This is illustrated at the bottom of Fig. 11 where we plot the modulation indices produced by three screens with different β values (including the Kolmogorov case), as a function of the “classical” Kolmogorov turbulence expected index. In this plot, each abscissa corresponds to a distinct Rdiff value, which is common to the three screens. By increasing β, we increase the modulation, especially for high m values.
6. Discussion: guidelines provided by the simulation
The observations analysed in (Habibi et al. 2011) were intrepreted by using our simulation pipeline. But we have used our simulation not only to establish connections between the observed light curves and the scintillation configuration, but also to define observing strategies as follows.
Firstly, a correct sensitivity to the scintillation needs the ability to sample, with <1% photometric precision at a sub-minute rate, the light curves of small distant background stars (M ~ 20−21), which have a projected radius small enough to allow for a modulation index of a few percent (typically <R⊙ at 10 kpc). Our study of the time coherency shows that the usual large passband filters can be used without significant loss of modulation index. Since the optical depth of the process is unknown, a large field of view seems necessary for the exploratory observations, either toward extragalactic stellar sources within LMC or SMC or through known gaseous nebulae. To summarise, an ideal setup for searching for scintillation with series of sub-minute exposures would be a ~4 m class telescope equipped with a fast readout wide field camera and a standard filter (optical passband to search for invisible gas towards extragalactic sources, infrared to observe stars through visible dusty nebulae).
Secondly, our work on the simulation provides us with a guideline to find an undisputable signature of scintillation. The first possibility consists in the search for chromatic effects. Subtle chromatic effects betwen the different regimes (associated to different time scales) have been shown, but will probably be hard to observe. Figure 7 (left and centre) shows the expected speckle image from a point source. The position/size of the small speckles (characterised by Rdiff(λ)) are very sensitive to the wavelength, and it is clear that a desynchronisation of the maxima would be expected when observing such an idealised point source through different (narrow) passbands. But that real sources have a much larger projected radius than the speckle size completely screens this chromatic effect. The impact of the wavelength on the position/size of the wide (refractive) spots (Fig. 7-right) is much weaker (following λ− 1/5 according to the combination of expressions (3) and (9)). Therefore, only a weak chromatic effect is expected from an extended source, even when observing with two very different passbands. For a clear signature of scintillation, it seems easier to take advantage of the rapidly varying luminosity with the observer’s position within the illumination pattern. As a consequence, simultaneous observations with two ~4 m class telescopes at a large separation (few 103 km) would sample different regions of the illumination patterns (see Fig. 7 bottom right), and therefore measure (at least partially) decorrelated light curves as shown in Fig. 9 (right). The decorrelation will be complete if the distance between the two telescopes is greater than 2 × max(Rref,Rs). A single observation of such a decorrelation will be sufficient to definitely confirm the discovery of a propagation effect that cannot be mimicked by an intrinsic variability.
7. Conclusions and perspectives
Through this work, we have simulated the phase delay induced by a turbulent refractive medium on the propagation of a wave front. We discussed the computational limitations of sampling the phase spectrum and to obtaining large enough illumination patterns. These limitations will be overriden in the near future with increasing computing capabilities. The illumination pattern on the observer’s plane has been computed for the promising strong regime of scintillation, and the effects of the source spatial and time coherencies have been included. We have established the connection between the modulation index (as an observable) of the illumination pattern with the geometrical parameters of the source and the strength of the turbulence (quantified by Rdiff). Furthermore, we showed that when the spectral index of the turbulence increases (as in the case of supersonic turbulence), the detection of scintillating light curves should be easier.
These simulation studies and, more specifically, the modulation index topic were successfully used in our companion paper (Habibi et al. 2011) to interpret our light curve test observations of stars located behind known galactic nebulae and of stars from the Small Magellanic Cloud, in the search for hypothetical cold molecular halo clouds.
Time scales, such as tref = Rref/VT and ts = Rs/VT (where VT is the relative velocity between the cloud and the line of sight), are observables that we plan to study further and in detail. Their extraction can be done through analysing the time power spectrum of the light curves, and it should give valuable information on the geometrical configuration, as well as on the turbulent medium.
The observing strategy has been refined through the use of the simulation, and we showed that observing desynchronised light curves simultaneously measured by two distant four-metre class telescopes would provide an unambiguous signature of scintillation as a propagation effect.
A cloud column of width Lz can include several turbulent structures with outer scale Lout. The direct relation of Lout with the turbulence strengh explains why Rdiff increases in conjunction with this parameter. By contrast, since the column density increases with Lz, then the refraction also increases, thus decreasing Rdiff.
For a given physical screen characterised by the column density Nl(x1,y1), Rdiff varies with λ6/5, as shown in Eq. (3).
Nevertheless, one should consider that the gaseous screen is a non-dispersive medium for optical wavelengths (dielectric medium with an index independent of λ), unlike the radioastronomy case (plasma), which may result in weaker chromaticity sensitivity. This specificity deserves more detailed studies, which are beyond the scope of this paper, considering the minor impact of the bandwidth compared to the smearing produced by the source size.
In Habibi et al. (2011), we used a simplified relation, with no significant impact on the resulting constraints.
The detection condition would be rs/z1 ≲ 10 × Rdiff/z0 (for which the projected stellar disk includes less than ~100 speckle spots), assuming a setup able to sample the target star with ≲1% photometric precision every few seconds. The scintillation of an A0 type star (R = 2.4 R⊙) in the LMC (magnitude V = 19.4) seen through a screen with Rdiff = 100 km at distance 30 pc is an example of such a favourable configuration, which could be discovered by the LSST (Abell 2009).
For the observed supersonic turbulence (with β > 11/3) see 10.
Acknowledgments
We thank J.-F. Lestrade, J.-F. Glicenstein, F. Cavalier, and P. Hello for their participation in preliminary discussions. We wish to thank our referee, Prof. B. J. Rickett, for his very careful review, which helped us to significantly improve the manuscript.
References
- Abell P. A., et al. (LSST Science Collaboration) 2009, LSST Science Book, submitted [arXiv:0912.0201] [Google Scholar]
- Born, M., & Wolf, E. 2002, Principles of Optics (Cambridge: University Press), 7th edn. [Google Scholar]
- Coles, Wm. A., Filice, J. P., Frehlich, R. G., & Yadlowsky, M. 1995, Appl. Opt., 34, 2089 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., & Narayan, R. 1985, MNRAS, 214, 519 [NASA ADS] [Google Scholar]
- Goodman, J., & Narayan, R. 2006, ApJ, 636, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Gwinn, C. R., Britton, M. C., Reynolds, J. E. et al. 1998, ApJ, 505, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Habibi, F. 2011, Ph.D. Thesis, Paris-Sud and Sharif Universities [Google Scholar]
- Habibi, F., Ansari, R., Moniez, M., & Rahvar, S. 2011, A&A, 525, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamidouche, M., & Lestrade, J.-F. 2007, A&A, 468, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E. 1970, Ph.D. Thesis, Cornell University [Google Scholar]
- Lyne, A. G., & Graham-Smith, F. 1998, Pulsar Astronomy (Cambridge University Press) [Google Scholar]
- McGaugh, S. S., Schombert De Block, W. J. G., & Zagursky, M. J. 2010, ApJ, 708, L14 [Google Scholar]
- Moniez, M. 2003, A&A, 412, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, R. 1992, Phil. Trans. Roy. Soc. Lond. A, 341, 151 [Google Scholar]
- Pfenniger, D., & Combes, F. 1994, A&A, 285, 94 [NASA ADS] [Google Scholar]
- Pfenniger, D., & Revaz, Y. 2005, A&A, 431, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rickett, B. J. 1986, ApJ, 307, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Rumsey, V. H. 1975, Radio Sci., 10, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Sieber, W. 1982, A&A, 113, 311 [NASA ADS] [Google Scholar]
- Tatarskii, V. I., & Zavorotnyi, V. U. 1980, Progr. Opt., 18, 207 [Google Scholar]
- Uscinski, B. J. 1977, The elements of wave propagation in random media (New York: McGraw-Hill) [Google Scholar]
All Figures
 |
Fig. 1 Geometric configuration. The source is located in the
(x2,y2)
plane, the screen contains the refractive structure, and the observer is located in
the (x0,y0)
plane.
A1(x1,y1)
and |
| In the text | |
 |
Fig. 2 The phase-delay variations near the average for a simulated refractive screen with Nx × Ny = 20 000 × 20 000 pixels, Δ1 = 22.6 km, and Rdiff = 100 km. The grey scale ranges between ± 50 × 2π rad (clear regions correspond to an excess of phase with respect to the average). The zoom (inset in the lower-right corner) illustrates the self-similarity of the simulated screen (grey scale amplitude of 5 × 2π rad). |
| In the text | |
 |
Fig. 3 Phase structure functions Dφ(r) for a phase screen with Rdiff = 500 km. Blue line is the initial (theoretical) structure function. Red line is reconstructed from one of the realisations of the phase screen through simulation. The black curve is obtained from the numerical integration of the initial phase spectral density sampled as in the simulation. |
| In the text | |
 |
Fig. 4 Typical illumination pattern from a point-like source. Here Rdiff = 100 km, the screen is at z0 = 160 pc, λ = 2.16 μm, then RF = 1300 km and Rref = 106 000 km. The typical length scale of the small-scale speckles is Rdiff, and the scale of the larger structures is Rref. The white square shows our fiducial zone with a margin of Lm = Rref/2 from the borders. Grey scale range from 0 to 4 times the mean intensity. The image has 20 000 × 20 000 pixels, each with a 22.6 km side. |
| In the text | |
 |
Fig. 5 Typical illumination pattern from an extended source produced through the same screen as in Fig. 4, with source radius rs = 0.5 R⊙, located at z0 + z1 = 1 kpc + 160 pc (Rs ≃ 53 000 km). The small-scale speckles are smeared, and only the larger scale fluctuations survive. The white square shows the restricted fiducial zone with margin of Lm = Rref/2 + Rs from the borders. Grey scale ranges ± 20% around the mean intensity. |
| In the text | |
 |
Fig. 6 The smoothing function SF(x). L is the screen size, Lm is the margin from the screen borders. |
| In the text | |
 |
Fig. 7 Simulated illumination maps (20 000 × 20 000 pixel of 22.6 km side) produced on Earth by a source located at z0 + z1 = 1.18 kpc through a refracting cloud assumed to be at z0 = 160 pc with a turbulence parameter Rdiff(2.16 μm) = 100 km. Here Rref(2.16 μm) ≃ 100 000 km. Top-left and middle: illumination produced at λ = 2.16 μm from a point-source with a zoomed detail; the contrast is 100%. The grey scale ranges from 0 to 4 times the mean intensity. Top-right: the same from a K0V star (rs = 0.85 R⊙, MV = 5.9, at 1.18 kpc V = 16.3). The circle shows the projection of the stellar disk (RS = rs × z0/z1). Here the modulation index is only 3.3%, and the grey scale ranges from ±20% around the mean intensity. The bottom maps are the illuminations in Ks wide band (λcentral = 2.162 μm, Δλ = 0.275 μm), using the same grey scales as above. The modulation index is 55% for the point-source (left and centre) and 3.3% for the extended source (right). The two parallel straight lines show the sections sampled by two observers located about 10 000 km apart, when the screen moves with the transverse velocity VT. |
| In the text | |
 |
Fig. 8 The effective intensity modulation index |
| In the text | |
 |
Fig. 9 Light curves extracted along the 3 horizontal white lines for two illumination patterns. Left column: 2D pattern from a point-like source in Ks band with Rdiff = 300 km and Rref ≈ 28 000 km. The modulation indices of the three light curves differ by less than 5% from the 2D pattern modulation index. Right column: the illumination pattern for an extended source with Rs ≈ 41 000 km, through the same refractive screen. The modulation indices fluctuate by more than 30% around the 2D pattern index, implying the necessity of longer light curves for a better statistical representativity. The distance scale is common to both patterns. The circle shows the projected star disk. The 3 light curves from the right column are not completely decorrelated, because of their common proximity to the same large positive fluctuation. |
| In the text | |
 |
Fig. 10 Simulation of illumination scintillation patterns with associated light curves from an extended source assuming a refractive screen with non-Kolmogorov turbulences (left β = 3.1, right β = 3.9, see text). Here Rdiff = 100 km, Rref ≈ 8 × 104 km and the projected star radius is RS ~ 0.36Rref = 28 800 km. |
| In the text | |
 |
Fig. 11 Top: two different phase screen power laws. Bottom: the corresponding modulation indices as a function of the expected modulation index for the Kolmogorov turbulence. The 3 indices plotted at a given abscissa correspond to screens with β = 3.1 (red), 3.67 (Kolmogorov, blue, along the diagonal), and 3.9 (black) with the same Rdiff. As the power law gets steeper, a larger modulation is expected. Blue dots show the Kolmogorov turbulence case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.