| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219609 | |
| Published online | 15 April 2013 | |
The filtering of interstellar dust in the solar system ⋆
1 Universität Stuttgart, IRS Pfaffenwaldring 31 70569 Stuttgart Germany
2 Max Planck Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany
e-mail: veerle.sterken@mpi-hd.mpg.de
3 IGEP, TU Braunschweig, Mendelssohnstr. 3, 38106 Braunschweig, Germany
4 ESA, PO Box 78, 28691 Villanueva de la Cañada, Madrid, Spain
5 LASP, University of Colorado, 1234 Innovation Dr., Boulder, CO 80303-7814, USA
6 MPS, Max-Planck-Strasse 2, 37191 Katlenburg-Lindau, Germany
Received: 15 May 2012
Accepted: 19 February 2013
Context. Theoretical predictions demonstrate that small (<0.1 μm) interstellar grains are mostly excluded from reaching the planetary system by electromagnetic interactions in the heliopause region and in the inner heliosphere. Bigger interstellar grains have been recorded in the planetary system by dust measurements on board Ulysses and other spacecraft. It was found that the interstellar dust flux is modulated by the interplanetary magnetic field.
Aims. The objective of this study is to analyze the heliospheric filtering of the interstellar dust flow through the solar system and throughout the solar cycle. In the heliosphere the dynamics of interstellar dust is governed by the gravitational pull of the Sun, by the repulsion of solar radiation, and by the deflection caused by the interaction of the charged interstellar dust (ISD) grains with the interplanetary magnetic field. These interactions are described by the parameters of the radiation pressure constant β and the charge-to-mass ratio Q/m, which depend on the particle’s size, physical properties, and composition. A previous paper studied the flow characteristics of ISD moving through the solar system were studied. In this follow-up paper, we focus on how the ISD size distribution varies during its passage through the solar system.
Methods. In a parametric study of 70 different β and Q/m values, we calculated interstellar dust trajectories starting at the boundary of the heliosphere with starting times spread over a complete solar cycle of 22 years.
Results. As a result we obtained the interstellar dust flux and dust speed for these times and positions and demonstrate the effects of the filtering on the dust size distributions. The size distribution of ISD observed at any time and at any position in the planetary system is strongly modified from when it entered the heliosphere. Peaks in relative flux of 10 times the original flux possibly depend on the grain size and place and time in the solar system. We did a detailed study of three cases of the flux and size distribution of interstellar grains reaching the planets Saturn, Jupiter, and the main-belt asteroid Ceres. These cases are used to get a first idea of what a dust detector or collector on a mission to these bodies might see of ISD.
Key words: ISM: general / interplanetary medium
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
In 1930 the attenuation of starlight over kpc galactic distances was recognized as caused by interstellar dust (Trumpler 1930). This wavelength-dependent attenuation – “extinction” of distant stars from UV to infrared wavelengths – has provided us with knowledge of the interstellar dust size distribution, and spectral absorption features have revealed its chemical composition. The size distribution of interstellar dust (ISD) has been modeled by Mathis et al. (1977), Draine & Lee (1984), Weingartner & Draine (2001), and Zubko et al. (2004) to fit the observations of the broad continuum absorption, as well as the spectral absorption lines of stars, which are hidden by the dust. The size distribution from Mathis et al. (1977) is the so-called MRN-distribution, and it is used as a working hypothesis throughout this paper.
The ultimate source of this dust is the continuous mass loss from asymptotic giant branch (AGB) and post-AGB stars, as well as novae and supernovae explosions. Stars that are in their late evolutionary stages lose up to 10-4 solar masses per year. In cooling, expanding gas flows from these stars and solid dust particles condense (Whittet 1989). The carbon-to-oxygen ratio in the stellar atmospheres determines whether carbon-rich particles or silicates and metal oxides form. In circumstellar envelopes, evidence of silicate dust appears in spectral bands at 10 μm and 18 μm (Dorschner 2001). Metal oxides can form in the stellar atmosphere of O-rich stars. In a carbon-rich circumstellar environment, a variety of carbon compounds can form, including amorphous carbon and polycyclic aromatic hydrocarbons (PAHs).
This stardust provides the seeds for ISD particles that grow in cool interstellar clouds via the accretion of atoms and molecules and by agglomeration (Zhukovska et al. 2008). Interstellar shock waves provide an effective destruction mechanism for ISD particles because small particles are caught in the shock and collide with bigger particles that do not follow the motion of the shock because of their higher inertia (Jones et al. 1996). In diffuse interstellar clouds, the particles lose their volatile constituents owing to ultraviolet irradiation (Greenberg et al. 1995) and thermal sputtering in interstellar shock fronts. An ISD particle can be incorporated and ultimately destroyed in a newly forming star, or it can become part of a planetary system. In this way ISD particles are repeatedly recycled through the galactic evolution process (Dorschner & Henning 1995).
Direct measurements of interstellar dust were made in situ in the solar system, using the dust instruments on spacecraft like Ulysses (Grün et al. 1994; Baguhl et al. 1996; Landgraf et al. 2000; Krüger et al. 2007), Galileo (Baguhl et al. 1996; Altobelli et al. 2005), Helios (Altobelli et al. 2006), and Cassini (Altobelli et al. 2003). Ulysses provided the most extended data set of interstellar dust in the solar system from which an ISD size distribution was derived which is valid for the Ulysses observation period and orbit (Landgraf et al. 2000). The first few years of the Ulysses ISD data were also compared to ISD trajectory simulations (Landgraf 2000). However, there is a discrepancy between the MRN distribution and the Ulysses size distribution (Fig. A.1). Smaller grains are less abundant in the Ulysses data, and although the MRN distribution has a cut-off at 0.25 micron for silicate grains and 1 micron for carbon grains, Ulysses still detected several of the large grains up to 10-14–10-13 kg (about 1–2 μm assuming compact spherical silicates). We suggest that this discrepancy in size distribution for the small grains can be explained by a filtering at the heliopause and in the inner solar system, instrumental effects, and the possibility that the LIC has an atypical grain size distribution. The discrepancy for the large grains cannot be explained yet. The filtering mechanism in the inner solar system and the resulting ISD flow characteristics have been modeled and illustrated qualitatively in a preceding paper (Sterken et al. 2012b, “Paper I”). Effects at the heliopause were not taken into account.
In this paper we give insight into the typical modulation of the ISD mass distributions resulting from dust dynamics in the inner solar system, and we focus on the methodology for deriving absolute numbers for ISD fluxes in the planetary system starting from an assumed initial ISD size distribution. We start with an extrapolation of the MRN distribution (Sect. 2) as a working hypothesis (the “reference distribution”), quantitatively discuss the role of the filtering at the heliopause (Sect. 3), and apply the previously modeled filtering (Paper I) in the planetary system to the reference distribution. The resulting size distributions depend on the location in the solar system and on the phase of the solar cycle. We first discuss in general the resulting size distributions at different locations along the flow axis of the interstellar dust (Sect. 4), and then apply the method to Saturn, Jupiter, and the asteroid belt as an illustration of the size distribution that a dust instrument on a spacecraft in these systems would record (Sect. 5). In this paper, the “size” of the grain means its radius a.
2. The interstellar dust size distribution in the LIC
The solar system is currently passing through a small cloud of low-density, weakly ionized interstellar medium in our galaxy that may have originated in the Scorpius Centaurus association (Frisch et al. 1999). This cloud, the Local Interstellar Cloud (LIC), is part of a collection of neighboring clouds of gas and dust that are located in a cavity of hot and very low density gas: the “Local Bubble”. Each one of these clouds has its own density and temperature, and it is not unthinkable that they have different dust compositions and size distributions. Our current knowledge of the LIC comes mainly from astronomical observations. The relative velocity and direction of motion of the solar system with respect to the LIC was determined from in-situ neutral helium observations by Ulysses (Witte et al. 1993). It is this relative velocity that causes the ISD grains to enter the solar system. Later, the directionality of the ISD was found to agree with the interstellar upstream direction, using the Ulysses dust measurements (Baguhl et al. 1996). Also astronomical (radial velocity) observations confirmed these results (Redfield & Linsky 2008). In this study we assume a relative velocity of 26 km s-1 and a (downstream) direction of 79° ecliptic longitude and –8° latitude (Frisch et al. 1999). McComas et al. (2012) reports a slower relative velocity of the Sun with respect to the ISM of 23 km s-1 and a directionality of 79° ecliptic longitude and –5° latitude. Such initial velocities and directions would have a small but visible influence on our final results (a slightly stronger focusing/defocusing effect) but would not alter the main outcome and conclusions of this paper.
Besides the wavelength-dependent extinction and polarization of starlight, information on interstellar dust is obtained from astronomical observations of absorption features, from UV to infrared wavelengths; light scattering in the visible and ultraviolet, small-angle scattering of X-rays, thermal emission from infrared to sub-mm wavelengths, and microwave radiation from spinning dust.
The extinction curve was reproduced very well by the two-component size distribution of Mathis, Rumpl, and Nordsieck (Mathis et al. 1977). This MRN size distribution ranges from 5 nm to about 1000 nm in size (corresponding to masses of about 10-21 to 10-14 kg, assuming a density of 2 g/cm3). The observed interstellar extinction over the UV to near-IR wavelength was fitted with a very general particle size distribution of graphite and amorphous silicates. The size distribution is a power law with an exponent of –3.5. The size distribution for graphite is about 5 nm to 1000 nm, the silicate distribution is narrower: 25 to 250 nm. The slope of the MRN distribution is determined by using the extinction measurements of distant stars, but the number of large particles is not well constrained by these measurements because they do not contribute much to the visible extinction. However, the number of large particles is constrained by cosmic abundances: an integration of the MRN mass distribution slope over masses higher than the cut-off would overshoot the mass of condensable elements derived from gas-phase abundances and elemental depletion factors, in relation to solar abundances. The nearby depletion measurements thus do not contribute to the shape of the size distribution except that the total (integral over the mass distribution) is limited by cosmic abundances.
The MRN size distribution of grains in the diffuse interstellar medium is given by a power law, 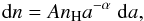 (1)with the number of grains dn within the size interval da, slope α = 3.5, and A = 7.76 × 10-26 cm-2.5 per H nucleus (Mathis et al. 1977). In the following, we assume nH = 0.3 cm-3, a typical value for the local interstellar medium (Frisch et al. 1999). The grain sizes, a, range from 5 nm to 250 nm (m = 1.7 × 10-21 kg to 2.2 × 10-16 kg). For size distributions covering a wide mass range, it is convenient to use the logarithmic differential distribution. For comparing these distributions to astronomical observations, the cross sectional size distribution is more relevant, whereas for comparison with spacecraft measurements, the mass number distribution and cumulative mass number distribuions are relevant. How they relate to the original number size distributions is explained in Appendix A.
(1)with the number of grains dn within the size interval da, slope α = 3.5, and A = 7.76 × 10-26 cm-2.5 per H nucleus (Mathis et al. 1977). In the following, we assume nH = 0.3 cm-3, a typical value for the local interstellar medium (Frisch et al. 1999). The grain sizes, a, range from 5 nm to 250 nm (m = 1.7 × 10-21 kg to 2.2 × 10-16 kg). For size distributions covering a wide mass range, it is convenient to use the logarithmic differential distribution. For comparing these distributions to astronomical observations, the cross sectional size distribution is more relevant, whereas for comparison with spacecraft measurements, the mass number distribution and cumulative mass number distribuions are relevant. How they relate to the original number size distributions is explained in Appendix A.
Kimura et al. (2003) have derived a size distribution before filtering in the inner solar system, starting from the Ulysses data by fitting a powerlaw to the data with m > 3.2 × 10-16 kg (from 1992 until 1995). The authors divided these data into four segments depending on distance to the Sun and extrapolated the powerlaw characteristics of the size distributions in each segment to obtain an “initial” power-law of the dust in the LIC after filtering at the heliopause. However, extrapolation of such mass distributions has large uncertainties due to the limited dataset, and it requires knowledge of physical processes like gravitational focusing and Lorentz forces, as is illustrated in Fig. 4, even for masses ≥3.2 × 10-16 kg. Since this paper aims at demonstrating the attenuation factors that apply to the ISD fluxes and to the methodology for predicting absolute fluxes rather than to the absolute flux predictions themselves, we assume a simple powerlaw distribution that corresponds to astronomical observations over kpc distances.
Although there are more modern and more detailed size distributions of interstellar dust in the diffuse interstellar medium (e.g. Weingartner & Draine 2001; and Zubko et al. 2004), they all have a powerlaw characteristics, and we use the MRN size distribution (extended over the range of mass of our simulations) as a basis for a simple representation of the dust in the LIC. The “reference distribution” is thus a working hypothesis, characterized by a logarithmic distribution with exponent 3.5. This reference distribution is illustrative, and is not meant to imply that the extended MRN distribution would reflect the true grain size distribution in the LIC.
3. Filtering at the heliopause
When interstellar dust grains enter the solar system, they pass several transition regions where magnetic field and plasma properties, hence grain charging and Lorentz forces, change. First, the grains “encounter” the bow shock1 at about 250 AU where the gas of the LIC slows down to subsonic speeds. After the bow shock, the magnetic field strength increases but is still governed by the magnetic field of the LIC. Then, the grains encounter the zone where the LIC gas and the solar wind stagnate: the heliopause. Inside the heliopause (probably about 120 AU from the Sun), the solar wind dominates but is still subsonic. At about 80 AU from the Sun, the solar wind becomes supersonic at the termination shock. The region between the heliopause and the termination shock is called the heliosheath. Its magnetic field is influenced by the magnetic field of the solar wind, but it is now also known to be filled with turbulent plasma (Opher et al. 2011).
The grains in the undisturbed LIC are typically charged to have an equilibrium potential of 0.5 V (Grün & Svestka 1996). When entering the transition region to the heliosphere, they get charged to equilibrium potentials of up to ten times higher (Linde & Gombosi 2000) and experience the increased magnetic field strengths. The smallest grains (highest charge-to-mass ratio) get filtered out and are carried around the heliosphere. Linde & Gombosi (2000) have modeled this filtering between the bow shock and the termination shock and found that grains get filtered between sizes of 0.1–0.2 μm, including the recharging. Slavin et al. (2010) modeled the exclusion of small grains from the heliosphere, using full magnetohydrodynamics modeling, and conclude that 0.1 μm grains are strongly filtered, but some particles can still get into the inner heliosphere, whereas 0.01 μm grains seem to be totally filtered out. For these results, the findings of (Opher et al. 2011) have not yet been included. Only silicates were assumed that get higher charges (Kimura & Mann 1998), plasma temperatures in the heliosheath are lower than expected (Richardson et al. 2008; Slavin et al. 2010), and thus charging could be milder. Both Linde & Gombosi (2000) and Slavin et al. (2010) calculated the deviation of the grains for a “defocusing” configuration of the interplanetary magnetic field in the heliosheath (positive magnetic field polarity at the north ecliptic pole). It is well possible that during other periods of the solar cycle, smaller grains get through better than presented here, due to focusing at the heliosphere boundary (Slavin et al. 2012, pers. comm.). More research is needed to get this clear. The filtering at the heliospheric boundary is hereafter referred to as “primary filtering”.
4. Filtering in the inner solar system
The ISD grains that do pass the heliopause may still be filtered out from the inner solar system by solar radiation pressure force and Lorentz forces. This kind of filtering is referred to hereafter as “secondary filtering”.
Apart from the effect of the solar radiation pressure force, Levy & Jokipii (1976) predicted the effects of the Lorentz force on the stream of interstellar grains and concluded that nanometer-sized grains are excluded from the inner solar system. The effect of focusing and defocusing (w.r.t. the solar equatorial plane) of ISD throughout the 22-year cycle of the solar magnetic field was further demonstrated and modeled by Gustafson & Misconi (1979) as well as Morfill & Grün (1979). Landgraf (2000) modeled the secondary filtering and compared the results with the measured Ulysses data from 1992–1998.
Sterken et al. (2012b) (hereafter referred to as “Paper I”) describes the mechanism quantitatively, as well as the effects of it on the flow of ISD grains in the solar system. Here, we go one step further and investigate the effect of this filtering on the size distribution of the dust. We start with the simple case of solar radiation pressure and solar gravity alone (Sect. 4.1), and then expand to include the Lorentz force (Sect. 4.2).
4.1. Gravity and radiation pressure only
Since both gravitational and solar radiation pressure forces act radially and decrease with the squared distance to the Sun, it is convenient to describe the total force F(G + rad) = (1 − β)FG, where β is the ratio of radiation pressure force to gravitational force for a specific particle, and it depends only on properties of the particle like size, density, porosity, and composition. Figure 14 of Paper I shows some examples of β-curves for different materials. Generally, β increases with decreasing particle size or mass until the size is comparable to the effective wavelength of sunlight below which β decreases again. For absorbing particles, the maximum β can exceed the value 1.
In Sect. 2.1 of Paper I the dynamics by solar gravity and radiation pressure alone of ISD grains is described. While particles with β < 1 are attracted and focused behind the Sun, particles with β > 1 are repelled by the Sun, and an exclusion zone forms around and behind the Sun (Figs. 1–3, Paper I). Particles with β < 1 are also accelerated closer to the Sun, whereas particles with β > 1 are slower when they come closer to β-cones. This different behavior of particles of different sizes (β-values) has as consequence that the size distribution of ISD inside the heliosphere varies from the size distribution outside the heliosphere just from the effect of radiation pressure alone.
To demonstrate this effect, we evaluated the ISD density (Eq. (15), Paper I) in a column along the axis of the incoming ISD flow (Fig. 1). For this we assumed a β-curve based on the “astronomical silicates” curve from Gustafson (1994) but with β-values adapted to the results of Landgraf et al. (1999) who assume densities of 2000 kg m-3. We call this the β-curve of the reference material or the “reference curve” in this paper. In the incoming portion up to about –5 AU, the relative density for all sizes is about 1, i.e. similar to the density at the heliospheric boundary. For particles with β < 1, the density increases and reaches enhancements behind the Sun of factors 100 and more. For particles with β > 1, the density increases slightly in front of the exclusion zone, but then strongly decreases and becomes zero inside the exclusion zone.
The variation in the relative mass distribution is shown in Fig. 2. Well in front of the Sun the density variation as function of particle mass is small. However, it becomes significant around and behind the Sun. Particles with β > 1 become depleted in the paraboloid-shaped exclusion zone around and behind the Sun, while particles with β < 1 are focused behind the Sun. Such a bite-out feature in the mass distribution has been observed in the Ulysses data (Landgraf et al. 1999) and was used to get information on the β-values of interstellar grains. The enhancement of particles smaller than 10-17 kg will be reduced or enhanced by electromagnetic interactions (see below).
 |
Fig. 1 Variation in the mean interstellar dust density of a given particle mass along the axis of the interstellar dust flow. The Sun is at distance 0 AU. The densities correspond to the mean densities in a 1 AU column around the flow axis. The dashed lines corresponds to density = 0. The density lines for different particle masses are offset by a factor 10. |
 |
Fig. 2 Variation in the interstellar dust density in a 1 AU column around the axis of the interstellar dust flow as a function of particle mass and distance from the Sun. Density 0 was set to the bottom of the diagram at 0.1. The blue lines denote the plane of density level of 1. The reference β-curve as introduced in Sect. 4.1 was assumed. |
4.2. Lorentz forces
In Sects. 2.2 to 2.4 of Paper I we explained in some detail the dynamical interaction of charged dust particles with the interplanetary magnetic field. Below we sketch only the most important facts of this interaction.
Interstellar dust grains in interplanetary space are electrically charged to a potential of approximately +5 V (Mukai 1981; Kimura & Mann 1998). Such a surface potential is compatible with direct measurements of interplanetary dust charges with the Cassini dust detector (Kempf et al. 2004). The outwardly streaming solar wind carries a magnetic field away from the Sun, causing the Lorentz force on the charged particle. The net effect of the Lorentz force on micron-sized particles is weak compared to gravity and radiation pressure forces. For sub-micron-sized interstellar particles, the Lorentz force becomes stronger and has a large effect on their trajectories.
The overall polarity of the solar magnetic field changes with the solar cycle of 11 years (Table 2, Paper I). For one solar cycle positive magnetic polarity prevails in the northern and negative polarity in the southern solar hemisphere. In Paper I we modeled the interplanetary magnetic field and calculated the trajectories of interstellar grains. Sub-micron-sized interstellar particles that enter the solar system are either deflected toward the solar equatorial plane that is close to the ecliptic plane or away from it depending on the overall polarity of the magnetic field. Interstellar particles entering the heliosphere from one direction at a speed of 26 km s-1 need about 20 years (approximately one complete solar cycle of 22 years) to get close to the Sun. Therefore, trajectories of small interstellar particles (≪1 micron radius) are strongly diverted: in some regions of space, their density is strongly increased, in others they are depleted.
Three parameters determine the dynamics of interstellar grains in the heliosphere: β, Q/m, and time because of the time-variable magnetic field. In Fig. 3 we show the β and Q/m parameter space covered by our simulations. Each point in this diagram represents a particle of a specific material characterized by size, composition, and structure (density or fluffiness). Particles with different sizes of a specific material are located along a β-curve through this diagram. Three β-curves are shown for specific materials: the thick solid line represents our “reference β-curve” that fits the Ulysses measurements (Landgraf et al. 1999) best. A more absorbing material (e.g. carbon) is represented by the upper curve, and the lower curve represents a denser or less absorbent material. Micron-sized particles are on the lefthand side (small Q/m values), while 0.1 micron and smaller particles are on the righthand side of the diagram (cf. Table 2).
 |
Fig. 3 Overview of the simulations in the β-Q/m-space. The seventy simulations are shown as dots in the β-Q/m diagrams. The β-curves for carbon, the “reference β-curve” (see Sect. 4.1) and β-curve for silicates from Kimura & Mann (1999) are shown as dotted, bold, and normal curves. |
In a Monte Carlo simulation, a couple of million dust trajectories starting at 50 AU were calculated for 70 different β and Q/m values with starting times spread over a complete solar cycle of 22 years. In Appendices B and C and Fig. 9 we display and discuss smoothed values of the interstellar relative dust flux (relative to the flux value at the outer boundary of the simulation) and speed for different points in space and time covering roughly the Q/m and β ranges shown in Fig. 3.
Mass, β, Q/m, and radius used for the calculations of the size distribution.
4.3. Effects along the interstellar flow axis
In this paragraph we analyze how the size distribution of our reference particles (solid thick line in Fig. 3) changes along the flow axis of interstellar dust. For all sizes given in Table 2 we obtain the relative flux values at the corresponding β and Q/m positions (cf. Figs. B.1–B.4) and multiply them with our reference size distribution. In Fig. 4 we display the resulting size distribution at different epochs during the solar cycle for each of the positions along the flow axis of the dust (–10, –5, –3, and 3 AU). For an initial reference size distribution we show the number density and the plain enhancement or reduction factor that can be applied to any size distribution we choose. The filtering at the heliopause is ignored.
The crosses in Fig. 4 are not interpolated like in Figs. B.1−B.4, but are the exact simulation results for seven different Q/m-values. The density of the grains assumed is 2 g/cm3, and the assumed interstellar density of H atoms is 0.3 cm-3.
Far upstream at –10 AU, the number density is reduced in the defocusing phase of the solar cycle for all grain sizes (year 2000: top row of Fig. 4). During the focusing phase, it is enhanced, and because of the complexity of the interplay of β-cone with Lorentz force, the enhancements occur at different sizes in the size distribution, for different positions in the solar system (compare in Fig. 4 the position of the peak of the blue line of –10 AU (top row) with the peak of the blue line of –5 AU (second row)). During the defocusing phase, the smallest grains get filtered out (e.g. the leftmost point of the red line).
Upstream (–10 to –3 AU in Fig. 4), the size distribution for the largest grains (mass = 3 × 10-15 kg) more or less follows the reference distribution. However, downstream (+3 AU in Fig. 4) these large grains are focused by gravitational focusing (low β), so the fluxes are enhanced by a factor of up to 10.
Even if reduction factors of 10 or more are present for the smallest grains, they still outnumber the largest grains in the number density!
 |
Fig. 4 Simulated size distributions for different positions upstream and downstream of the Sun on the flow axis. From top to bottom: –10 AU (upstream), –5 AU, –3 AU, +3 AU. The different colors indicate different epochs in the solar cycle. The dotted straight line is the original reference distribution for nH = 0.3 cm-3. The black straight line is the reference distribution range for which simulations were done. This reference distribution is illustrative, and is not meant to imply that the extended MRN distribution would reflect the true grain size distribution in the LIC. |
5. Application to Saturn, Jupiter, asteroid belt
We apply the size filtering to three cases: to Saturn (ca. 10 AU), to Jupiter (ca. 5 AU), and to an Asteroid (ca. 3 AU). We chose these examples in order to show the fluxes and the size distributions that can be measured by a dust instrument, such as with Cassini at Saturn (2004 to 2017-planned), Galileo (1996−2003), and the Jupiter ICy moons Explorer (JUICE, 2030–2033) at Jupiter, and missions in the neighborhood of the asteroid belt (Stardust and Rosetta like missions, or missions like Dawn, although it does not have a dust detector). In these cases we also demonstrate what variation due to the solar cycle can be expected. Again, we discuss the fluxes for the reference material in this section, whereas the whole β-Q/m-parameter space from which these are derived is discussed in Appendix C.
 |
Fig. 5 Orbit of the Earth, asteroid Ceres, Jupiter, and Saturn around the Sun, with the β-cones shown by colored dotted lines. The positions for which we show the β-Q/m plots in Appendix C and size distributions in Sects. 5.1.1, 5.2.3, and 5.3.1 are indicated as blue dots. The left plot corresponds to the defocusing phase, and the right plot corresponds to the focusing phase of the solar cycle for the asteroid and Jupiter orbits. Galileo was flying from 1996 until 2003 and was thus in large parts of its orbit in the β-cones, as well as moving in the same direction of the dust flow. |
5.1. Predictions for Saturn
We applied the method of Sect. 4 to the case of Saturn. Here, the flux variations in time and location in the solar system are correlated through the orbit of Saturn. Saturn’s orbital period (29.5 years) is longer than the 22 year full solar cycle. We looked at the size distribution at Saturn during one orbit between 1991 and 2020 and chose eight positions along its orbit relative to the ISD flux: upstream, downstream, sidestreams, and four positions in between. Figure 5 shows the orbit of Saturn in this period. The eight blue dots on the orbit show the eight positions for which the relative fluxes and size distributions are predicted (Figs. C.1–7).
The relative fluxes with respect to Saturn throughout the solar cycle are shown in Fig. 6 for seven particle sizes (Table 2) representing β and Q/m values of our nominal material (cf. solid line in Figs. C.1 and C.2). The biggest particles (0.7 μm) display a strongly enhanced flux (factor 4) around 2003 when Saturn is in the gravitational focusing region downstream of the Sun. The enhanced fluxes (factor 2) around 2010 are due to the motion of Saturn against the interstellar dust flow. Conversely the flux is reduced around 1996 when Saturn moves parallel to the interstellar flow. In 2003 Saturn is in the β-cone for smaller particles (β > 1) so no such interstellar grains can reach Saturn. The flux enhancements of smaller interstellar grains around 2010 become even more pronounced for smaller grains (0.15 μm) and reach values of factors up to 10, and the maximum flux shifts to later years (2013). For the smallest particles considered (~0.1 μm) the flux is still enhanced in the period 2007 to 2012 but no longer as much as for the somewhat bigger particles. Sharp peaks in the small particle flux appear around 2017 when Saturn is in the upstream region of the interstellar dust flow.
5.1.1. The ISD size distribution at Saturn
The enhancements or reduction of the size distributions (ignoring the heliopause filtering) again follow the solar cycle and β-cones (see Fig. 7). The modulation of the size-dependent flux ranges from total disappearance of some particle sizes to enhancements of up to factor 10. Small particles are absent when Saturn is within the respective β-cone. This is visible around the year 2002 when only the biggest particles (0.7 μm) reach Saturn at an enhanced flux (gravitational focusing). In the period from 2009 to 2013, the flux of >~0.2 μm sized particles is strongly enhanced to a large extent by the increased relative speed between Saturn and the interstellar flow but also by the focusing effect of the interplanetary magnetic field.
Except for the downstream region, the number flux is biggest for the smallest particles (~0.15 μm; if they can traverse the heliopause). At favorable times (2009 to 2013) the mass flux will be highest not for the biggest particles (as for the undisturbed reference distribution) but for the mid-sized grains around 0.2 μm. In 2017 the small grains contribute very clearly if they are not filtered out at the heliopause. Depending on that filtering, a final number for the small grains can be given. In 2013, 1991, and 1995 (later in the focusing phase, and in even in the onset of the defocusing phase), there are high fluxes for small grains, owing to mirroring and focusing upstream from the Sun.
5.2. Predictions for Jupiter
Jupiter’s orbital period (12 years) is only half of the full solar cycle period. Therefore we applied the simulated dust flux to the case of Jupiter for two orbital periods from 1994 until 2018 (Fig. 5), spanning not only the orbit of Jupiter but also both the focusing and defocusing phase of the solar cycle. We discuss the results in the framework of the ISD measurements with the Galileo mission, as well as future prospects for the JUpiter ICy moons Explorer (JUICE) mission. Jupiter is at 5 AU, meaning that “upstream” of the Sun, it reaches the β = 3 cone; i.e., no interstellar grains with β > 3 ever reach Jupiter.
Figure 8 shows the simulated time variation of the relative flux of interstellar grains of nominal composition between 1990 and 2020 at and relative to Jupiter. For β = 0.5 and Q/m = 0.125 C/kg (0.7 μm), two peaks up to four times the “unfiltered” flux are visible in 2001 and 2013. This is because Jupiter is at the gravitational focusing downstream of the Sun. For β > 1 and Q/m > 0.5 C/kg (grains <0.3 μm), two gaps in the flux are visible corresponding to the β-cones when Jupiter is downstream of the Sun (2001, 2013). Between these peaks and gaps, there is a cyclic variation that doubles or halves the relative flux depending on whether Jupiter moves with or against the stream of ISD. Also, just before entering the β-cone and just after leaving it, a very small increase in relative flux is visible as explained in Sects. 4.1. (The density increases slightly in front of the exclusion zone.) For higher Q/m-ratio (hence smaller grains), the influence of the solar cycle becomes clearer. For grains with β > 1 and very small grains (i.e., high Q/m values), the flux during the defocusing periods will become zero, whereas the flux in focusing periods, which are not in the β-gap, is enhanced (e.g. around 2007).
 |
Fig. 6 Time series of relative fluxes with respect to Saturn for different grain sizes (0.73, 0.36, 0.26, 0.21, 0.15, 0.11, and 0.07 μm). As the grain size decreases, the influence of the solar cycle becomes more dominant. Filtering at the heliopause is not taken into account. |
 |
Fig. 7 Simulated size distributions of the ISD at Saturn for the 8 positions along its orbit. The gravitational focusing in 2002 is clear for the largest particles, as is the strong influence of the solar cycle on the size distributions, especially for the smaller grains (cf. Fig. 4). The dotted straight line is the original reference distribution for nH = 0.3 cm-3. The black straight line is the reference distribution range for which simulations were done. This reference distribution is illustrative, and is not meant to imply that the extended MRN distribution would reflect the true grain size distribution in the LIC. |
 |
Fig. 8 Time series of relative fluxes with respect to Jupiter for different grain sizes (0.73, 0.36, 0.26, 0.21, 0.15, 0.11, and 0.07 μm cf. Fig. 6). As the grain size decreases, the influence of the solar cycle becomes more dominant. Filtering at the heliopause is not taken into account. |
 |
Fig. 9 Relative flux (left) and relative velocity (right) with respect to Jupiter prior to the arrival of JUICE in mid-2029. The last part of the cruise phase is perfectly suited to some add-on science: the ISD flux is high due to the focusing phase of the solar cycle, and Jupiter is moving into the stream of ISD grains. Source: Sterken et al. (2012a). |
 |
Fig. 10 Simulated size distributions of the ISD at Jupiter for the 4 positions per orbit. The gravitational focusing in 2001 and 2013 is clear for the largest particles.The influence of the solar cycle on the size distributions is visible, especially for the smaller grains (cf. Fig. 4). The dotted straight line is the original reference distribution for nH = 0.3 cm-3. The black straight line is the reference distribution range for which simulations were done. This reference distribution is illustrative, and is not meant to imply that the extended MRN distribution would reflect the true grain size distribution in the LIC. |
5.2.1. The Galileo mission
Galileo was launched in 1989 and reached Jupiter in 1996, which it orbited until 2003. During its interplanetary cruise it measured interplanetary and interstellar grains (Baguhl et al. 1995; Altobelli et al. 2005). During the orbital tour of the Galileo mission (1996–2003) the conditions for measuring interstellar dust were quite unfavorable because the solar cycle was in the defocusing condition and Jupiter moved approximately parallel with the interstellar dust flow, reducing both the relative speed and the flux of interstellar grains (Fig. 5). Also large parts of Jupiters orbit were downstream from the Sun in the β-cones. Besides, there were also pointing issues: the antenna was directed toward the earth, and the dust counter was thus pointing in the opposite direction from ISD stream, at least in the downstream part of the orbit.
5.2.2. The JUICE mission
The case of 2007 is comparable to the arrival of the planned JUICE mission at Jupiter in 2029: the spacecraft is upstream of the Sun resulting in being able to observe almost all small (high-β) grains. Besides this, the mission is planned for the focusing phase of the solar cycle, therefore JUICE is perfectly suited to doing some add-on dust science. The relative flux and velocity for the arrival phase of JUICE at Jupiter is shown in Fig. 9. The conditions are very favorable for measuring interstellar grains on top of Jupiter system dust. Sterken et al. (2012a) provides an in-depth discussion of the ISD predictions for JUICE.
5.2.3. Size distributions at Jupiter
Figure 10 shows the derived size distributions of the ISD at Jupiter, at different epochs corresponding to eight positions of Jupiter along two subsequent orbits starting in 1995 (cf. Figs. 5, C.3, and C.4). These distributions are – as in Sects. 4.3 and 5.1.1 – for our reference material introduced in Sect. 4.1. Very clear is that the mass and number density vary by large factors with the phase of the solar cycle and the orbital position of Jupiter. As was the case for Saturn, “downstream” the β-gap (for relatively small to intermediate grains) and the gravitational focusing (for large grains) is also visible here: the size distribution for 2001 shows only one point for the largest grains because the smaller ones are filtered out by the β-gap, as well as by the Lorentz forces. The size distribution for 2013 shows two points for the larger grains (0.7 μm) and one point for the very small grains (0.07 μm). This is in the focusing phase of the solar cycle, when the smallest grains may still come through since they have β < 1 and are focused by Lorentz forces (assuming they get through the heliosphere). The highest flux enhancements (> factor 5 for 0.15 and 0.21 μm particles) occur during the focusing period of the solar cycle (2007 and 2010). During the defocusing periods the fluxes are at least a factor 3 lower.
5.3. Predictions for the asteroid belt
In this section we discuss the variation in the size-dependent ISD flux in the main asteroid belt. We chose Ceres, the biggest main belt asteroid as an example. Ceres has a semimajor axis of 2.8 AU and an orbital period of 4.8 years. Figure 5 shows two orbits of Ceres in two different periods of the solar cycle (defocusing: 1999–2002; focusing: 2010–2014). Most of the asteroid’s orbit lies within the β = 3 cone, therefore, only particles with lower β values will reach the asteroid.
The fluxes onto Ceres of interstellar grains of nominal composition are shown in Fig. 11 throughout time from 1990 until 2020. In the top lefthand figure, the gravitational focusing of large (0.7 μm) grains is visible as regular sharp peaks in relative flux. There is also a modulation due to the motion of Ceres parallel to or against the stream, resulting in flux enhancements or reductions by factors of 2 and 0.5, respectively, throughout its orbit. A weak influence of the solar cycle is already visible, since the peaks of the relative fluxes are larger around 2010 and reduced around 2000.
The second plot of Fig. 11 shows the same periodicity for 0.36 μm grains. The β-cones are visible as small gaps in the flux. The entry-side of the cone has a lower relative flux than when Ceres is going out of the β-cone, because of the apparent motion of Ceres with respect to the flux direction. However, both show the slight enhancement in dust flux at the boundary of the β-cones. Also here, a slight variation in the peaks of the flux is visible, which depends on the phase of the solar cycle. For even smaller grains, the influence of the solar cycle becomes more pronounced: the gravitational focusing is counterworked partially in 2000, and is enhanced in 2010. For particles <0.2 μm with increasing Q/m, the effect of the Lorentz force gets stronger until finally the flux becomes zero between roughly 1995 and 2005. However, in 2010, even the smallest grains may be able to reach the asteroid at even enhanced fluxes.
 |
Fig. 11 Time series of relative fluxes with respect to main-belt asteroid Ceres for different grain sizes (0.73, 0.36, 0.26, 0.21, 0.15, 0.11, and 0.07 μm cf. Fig. 6). As the grain size decreases, the influence of the solar cycle becomes more dominant. Filtering at the heliopause is not taken into account. |
5.3.1. Size distributions in the asteroid belt
Figure 12 shows the derived size distributions of the ISD at four positions of Ceres during two orbits (cf. Figs. 5, C.5, and C.6). The first orbit from 1999 to 2002 is during the defocusing solar cycle and the second orbit from 2010 to 2014 is during the focusing solar cycle. These distributions are for our nominal material. Again, as in the Jupiter case the mass and number density varies by large factors with the phase of the solar cycle and the orbital position of the asteroid. During the defocusing cycle, only the biggest grains (0.7 μm) display enhanced flux in the downstream region (1999). The size distribution for 2001 shows only one point for the largest grains because the smaller ones are filtered out by the β-gap as are the Lorentz forces. The fluxes of all other (smaller) grains are strongly reduced by the combined radiation pressure and electromagnetic interactions. During the focusing cycle (around 2010), almost all particles have enhanced fluxes except in the downstream region where only the biggest particles display enhanced fluxes. The size distribution for 2012 – day 323 shows two points for the larger grains and one point for the very small grains. The highest flux enhancements (> factor 5 for 0.11 and 0.21 μm particles) occur during the focusing period of the solar cycle (2010). During the defocusing periods the fluxes are at least an order of magnitude lower.
 |
Fig. 12 Simulated size distributions of the ISD at the main-belt asteroid Ceres for the 4 positions per orbit (cf. Fig. 4). The dotted straight line is the original reference distribution for nH = 0.3 cm-3. The black straight line is the reference distribution range for which simulations were done. This reference distribution is illustrative, and is not meant to imply that the extended MRN distribution would reflect the true grain size distribution in the LIC. |
6. Summary and conclusions
The first obstacle to interstellar dust reaching the planetary region of the solar system is the bow shock region around the solar system where smallest (<0.1 μm) interstellar grains become strongly depleted. In the heliosphere the dynamics of bigger interstellar dust is governed by the gravitational pull of the Sun, by the repulsion of solar radiation, and by a deflection caused by the interaction of the charged grains with the interplanetary magnetic field. The last two effects reduce (or enhance) the number of particles reaching the inner solar system over the effect of gravity alone. The strength of these interactions is conveniently described by two parameters: the radiation pressure constant β and the charge-to-mass ratio Q/m. These parameters only depend on the particle’s size, physical properties, and composition. Particles of different sizes flow on different trajectories through the solar system. Therefore, the size distribution of interstellar grains varies with the positions in the solar system. Because the interplanetary magnetic field varies during the 22 year solar cycle, there is also a time variation of the size distribution, especially at its small end.
In the heliosphere, a major effect sculpting the interstellar dust flow is solar radiation pressure. It prevents submicron-sized particles with β > 1 to reach the vicinity of the Sun and the region downstream of it. The electromagnetic interaction of charged interstellar grains with the solar wind magnetic field has varying strength but is increasing closer to the Sun. A typical dust charge corresponding to +5 V surface potential is compatible with direct measurements of dust charge in interplanetary space. During the eleven-year focusing cycle, ISD is deflected toward the ecliptic plane leading to enhancement of the ISD flux in the planetary region. During the defocusing eleven-year period, ISD is diverted from the ecliptic plane leading to a depletion of ISD in the planetary system.
We studied in detail three cases of the flux and size distribution of interstellar grains reaching the planets Saturn and Jupiter and the main-belt asteroid Ceres. These cases are used to get a first idea of what a dust detector on a mission to these planets might see of ISD. Some typical characteristics of the dust flux and the relative speed at which ISD encounters these objects are derived:
-
The size distribution of ISD observed at any time and at anyposition in the planetary system is strongly modified from the oneat which it entered the heliosphere.
-
Downstream of the Sun, no small ISD grains with β > 1 can reach the planet. This region (β-cone) is more or less extended around the ISD flow axis, depending on the β value of the dust particles.
-
During the focusing solar cycle, the flux of ISD is strongly enhanced in the planetary region and vice versa. The contrast of fluxes during the focusing and defocusing phase of the solar cycle is strongest for particles between 0.1 and 0.3 μm in size. Bigger particles are less affected by the electromagnetic interaction relative to gravitation and radiation pressure, and smaller particles are already strongly deflected in the outer regions of the solar system, hence depleted inside 10 AU.
-
The orbital motion of the planet around the Sun has a strong effect on the speed at which interstellar grains encounter the planet, so that the dust flux is strongly modulated. When the planet moves toward the interstellar flow, both the relative speed and the flux increase. In contrast, when the planet moves parallel to the interstellar flow, both the relative speed and the flux decrease. While high relative speeds are favorable to detecting ISD by in-situ dust detectors, low relative speeds are favorable to the collection of ISD (e.g., the Stardust mission, Tsou et al. 2003). The contrast along the orbit of a planet in fluxes and relative speeds gets stronger for planets closer to the Sun.
-
Flux variations along planetary orbits are most pronounced for big ISD particles >0.3 μm in size. Electromagnetic interactions strengthen or soften the effects of radiation pressure depending on the solar cycle. Solar cycle variations dominate ISD flux variations for particles <0.2 μm.
Measurements of the ISD flux along the orbits of asteroids, Mars or Jupiter are very well suited to characterizing the ISD dynamics, size distribution, and grain composition with time. Suited space missions were proposed to ESA, such as DUNE-eXpress (Srama et al. 2006), SARIM (Srama et al. 2009), or SARIM PLUS (Srama et al. 2012). Cassini will use the opportunity to continue ISD measurements at Saturn in the remaining years of the tour.
In this paper we only discussed the effect of flux and speed variations of the interstellar flow. However, we demonstrated in Paper I that the direction of the ISD flow also varies with position in the solar system, with time in the solar cycle and with size of the particle. Because of the limited FOV of any real-life dust detector or collector, this directional variation needs to be considered when making predictions of ISD grains to be recorded or collected. This aspect will be discussed in a follow-up paper (Sterken, in prep.) for the case of the ISD collectors on the Stardust mission.
Previous analyses by Landgraf et al. (1999) have demonstrated that ISD measurements by the Galileo and Ulysses dust detectors constrain the material properties of the recorded ISD particles (cf. the discussion of the nominal ISD material, Sects. 4.2 and 2.4.1, Paper I). Since this analysis, especially
the Ulysses mission has provided much more data (Krüger et al. 2007, 2010) that can be used to characterize ISD material even better. In an upcoming study, spatially and time resolved data from the Ulysses spacecraft will be used to further constrain the material properties of interstellar grains.
Online material
Appendix A: The different faces of grain size distributions
 |
Fig. A.1 ISD distributions from Ulysses data (stars) between 1992 and 2008 and the (extrapolated) MRN distributions for a hydrogen density of 0.1, 0.2, and 0.3 cm-3 (dashed, dotted, and continuous lines) adapted from Mathis et al. (1977). The left plot shows the number density, the middle plot the mass number density, and the right plot the cross section number density. The cut-off for silicate grains in the MRN-distribution is indicated with a vertical dashed line at 0.25 μm (1.3 × 10-16 kg) and for carbon grains at 1 μm (8.4 × 10-15 kg). |
The differential number (n), mass number (nm), and cross-sectional number distributions (nA) with respect to grain size a can be calculated from Eq. (1): 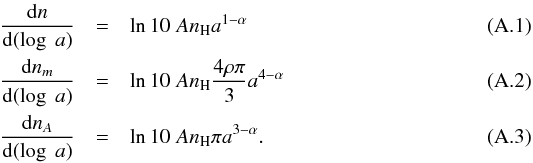 The logarithmic mass number distribution as function of mass is then given by
The logarithmic mass number distribution as function of mass is then given by 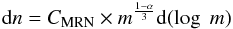 (A.4)with the constant
(A.4)with the constant 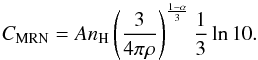 (A.5)The logarithmic differential (number) distribution shows the amount of grains per logarithmic mass interval (see Fig. A.1, left). The smaller grains are more abundant than the larger ones. In order to know how the mass is distributed among the grain sizes, we multiply the logarithmic differential number distribution with the mass of the grains to get the logarithmic differential mass distribution:
(A.5)The logarithmic differential (number) distribution shows the amount of grains per logarithmic mass interval (see Fig. A.1, left). The smaller grains are more abundant than the larger ones. In order to know how the mass is distributed among the grain sizes, we multiply the logarithmic differential number distribution with the mass of the grains to get the logarithmic differential mass distribution: 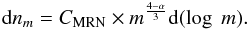 (A.6)Although the smaller ISD grains are more abundant in number, the largest part of the mass resides in larger grains (see Fig. A.1, middle). The total mass thus depends on the largest of the grains that are present. The logarithmic differential cross-section distribution is important because of emission, scattering, and absorption of light, which depends on the grain cross-section. It is derived by multiplying the differential number distribution by the cross-sectional area of the grains:
(A.6)Although the smaller ISD grains are more abundant in number, the largest part of the mass resides in larger grains (see Fig. A.1, middle). The total mass thus depends on the largest of the grains that are present. The logarithmic differential cross-section distribution is important because of emission, scattering, and absorption of light, which depends on the grain cross-section. It is derived by multiplying the differential number distribution by the cross-sectional area of the grains: 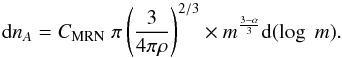 (A.7)
(A.7)
Slopes of the logarithmic differential densities.
The logarithmic differential cross-section distribution is shown in Fig. A.1 on the right, and it shows that the smallest grains dominate the total “cross-section” of the grains (thus making them dominate astronomical observations), but their slope is less steep than for the logarithmic differential number density.
In-situ dust instruments (e.g. like the Ulysses dust detector) count particles above a given mass threshold, therefore cumulative distributions are important. The slope of these cumulative distributions is the same as the corresponding differential logarithmic distribution. The cumulative distributions (number of grains above a threshold mass) can be calculated using 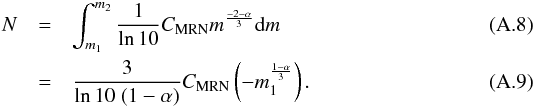
Appendix B: Detailed discussion: filtering effects along the interstellar flow axis
 |
Fig. B.1 Relative flux (left) and relative velocity (right) at –10 AU (upstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
 |
Fig. B.2 Relative flux (left) and relative velocity (right) at –5 AU (upstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
 |
Fig. B.3 Relative flux (left) and relative velocity (right) at –3 AU (upstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
 |
Fig. B.4 Relative flux (left) and relative velocity (right) at 3 AU (downstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
Here, we illustrate the combined effect of the Lorentz force, solar gravity, and solar radiation pressure force on the dust size distribution along the flow-axis of the dust toward the Sun, in analogy with Sect. 4.1. We plot the relative flux and relative velocity on color scale as a function of β and Q/m on the vertical and horizontal axes (Figs. B.1–B.4). The β-Q/m plots are constructed from a matrix of 70 simulations, as shown in Fig. 3, where the simulation results are interpolated (in 2D) to fill the whole β-Q/m space. The solid lines in Figs. B.1–B.4 show the reference β-curve. Following the simulated fluxes along the reference curve yields the results in Fig. 4 for this specific material assumption. We do this for the locations of –10 AU (upstream), –5 AU, –3 AU, and 3 AU (downstream) at a specific time. To show the effect of the solar cycle, we selected a time in the year 2000 (max. effect of the defocusing phase) and 2011 (max. effect of the focusing phase). This is about three years after the optimum focusing/defocusing field conditions (Table 2, paper 1), because interstellar grains need that time to display an enhanced density near the ecliptic plane.
At 10 AU upstream (–10 AU, Fig. B.1), the flux of big particles (Q/m < 1) is affected little by the Lorentz force. Only the flux of small particles is reduced during the defocusing phase around year 2000. Eleven years later the flux of small particles (1 < Q/m < 5) is enhanced especially for high β values. The speed of β ≤ 1 particles has increased in comparison to the speed at the heliospheric boundary, whereas the speed of β ≥ 1 particles has decreased. For the grains with Q/m > 8 C/kg in the defocusing phase, no velocity is drawn where the flux is zero. Closer to the Sun (–5 AU, Fig. B.2) these effects become more pronounced except that the flux of very small grains (Q/m > 8) is enhanced during the focusing phase because these particles are deflected from higher latitudes to the ecliptic plane.
At 3 AU upstream (–3 AU, Fig. B.3), the effect of the β-cone becomes obvious in the flux of large β (>2.5) particles, which is strongly reduced. In addition the flux of small particles (Q/m > 1) becomes strongly modulated by the electromagnetic interaction during the focusing and defocusing phases. Downstream of the Sun and close to the interstellar flow axis (3 AU, Fig. B.4), only particles with β < 1 can be found, the biggest of which (Q/m < 2) show an enhanced flux due to gravitational focusing. Again the flux of small particles (Q/m > 2) is strongly modulated by the electromagnetic interaction. The farther downstream, the more abrupt the β-cone appears in terms of enhancement (gravitational focusing) and dust depletion (β-cone).
Appendix C: Detailed discussion: application to Saturn, Jupiter, and the asteroid belt
Appendix C.1: Detailed predictions for Saturn
In analogy with Sect. 4.3, we discuss the β-Q/m graphs for the relative flux and velocity of ISD at Saturn. Figures C.1 and C.2 show these for the eight positions throughout the solar cycle and Saturn’s orbit. In 1991, between the focusing and defocusing period (Table 2 Paper I) Saturn is in the upstream portion of the interstellar flow. The flux of particles with 2 < Q/m < 4 and β-values >1.3 is still enhanced more than a factor 2, while the flux of particles with Q/m > 6 is significantly reduced (Fig. C.1). This flux enhancement shifts to lower β values in 1995. In 1999 the interstellar flux is strongly reduced for all particles except for big particles (Q/m < 0.1 and β < 1.5). In 2002, Saturn is in the downstream portion of the interstellar flow inside the β-cone for all small particles (β > 1) and in the focusing region of big particles (β < 1). However, electromagnetic interactions diffuse the focusing effect for Q/m > 1. In the whole period from 1991 to 1999, the relative speed between Saturn and interstellar grains is below the vinf (26 km s-1) because Saturn is moving parallel to the interstellar dust flow, so the relative speed is reduced by Saturn’s orbital speed (9.7 km s-1). Only in 2002 does the relative speed of big interstellar particles (β < 1) exceed vinf because the speed vector of interstellar dust and Saturn are no longer close to parallel.
The relative fluxes and velocities in 2005 to 2017 are much higher (Fig. C.2) than in the preceding period because Saturn is moving into the dust direction (increasing both flux and relative velocity), as well as because of the focusing phase of the solar cycle (2009 to 2013). By 2009, Saturn is on the edge of the β = 3 cone, is moving against the dust stream, and is in the midst of the focusing phase of the solar cycle. A very interesting era starts for finding ISD in Cassini data, for the high fluxes, and because all sizes of all materials are theoretically able to reach the Cassini spacecraft location (outside the β = 3 cone), hence the detector. We ignore in this discussion the influence of the Saturnian magnetosphere on the grain trajectories, which may be important for Cassini, although we expect this effect to be small. Furthermore, Cassini CDA will collect ISD measurements mostly outside Saturn’s magnetosphere. In 2013, Lorentz forces change the shape of the β-Q/m plot, but very high fluxes can still be found for small grains with Q/m between 3 to 6 C/kg, presuming they can traverse the heliopause. Impact velocities get reduced because of the direction of motion of Saturn. In 2017, even grains up to Q/m = 12 C/kg could reach Saturn, assuming they would get through the heliopause. Mid-sized and smaller grains (Q/m between 0.5 and 5 C/kg) experience very strong flux enhancements at different times (the larger ones of 0.5 C/kg in 2009 and the smaller ones up to 5 C/kg in 2013). This has to do with the complicated focusing mechanism upstream of the Sun for grains with higher Q/m values (cf. Fig. 38 in Paper I: the grains are reflected upstream of the Sun, which we refer to as mirroring).
 |
Fig. C.1 Relative flux (left) and relative velocity (right) with respect to Saturn for approximately the defocusing phase (1991–1992) of the solar cycle. Saturn is moving mainly in the same direction as the dust flow and is downstream of the Sun in 2002 (inside all β-cones). The reference β-curve is shown as a black line. |
 |
Fig. C.2 Relative flux (left) and relative velocity (right) with respect to Saturn for approximately the focusing phase (2005–2017) of the solar cycle. Saturn is moving mainly into the dust flow and is upstream of the Sun in 2017. The reference β-curve is shown as a black line. |
Appendix C.2: Detailed predictions for Jupiter
A first look at the β-Q/m plots (Figs. C.3 and C.4) immediately reveals that there is a strong effect on the focusing and defocusing phase of the solar cycle: fluxes are strongly reduced in Fig. C.3, whereas they are enhanced in Fig. C.4. The locations in the plots for 1995, 1998, 2001, and 2004 are equal to the locations in the plots of 2007, 2010, 2013, and 2016, but the period in the solar cycle is different (defocusing in Fig. C.3 versus focusing in Fig. C.4). From top to bottom, Jupiter is upstream, sidestream (moving with the flow of ISD), downstream, and again sidestream (against the flow of ISD).
Upstream, the relative flux is moderate for 1995 (see phase of solar cycle in Table 2 in Paper I, add 3 years latency to get the maximum effect), whereas it is high for the focusing phase (2007). The relative velocities vary from high velocities at low β, and lower velocities for higher β-values (as grains get slower near the β-cone for β > 1 and faster for lower β-values). The variation in velocities with different β is more than in the case of Saturn, because we are closer to the Sun (see also figures in Sect. 4.3) and Jupiter’s orbital speed is faster. On the sidestream side there is a very low flux in 1998 because of both the defocusing phase of the solar cycle and the relative movement of Jupiter with respect to the dust flow direction. In the focusing phase the flux is somewhat higher. Both show very low relative velocities since the orbital speed of Jupiter is about 13 km s-1, and the nominal dust speed is 26 km s-1. In 2001 and 2013, Jupiter is downstream of the Sun. The β-cone is visible through having no flux above β = 1 and the gravitational focusing is visible for low β-values through a strong enhancement of relative flux. During the focusing phase of the solar cycle (Fig. C.4), this enhancement is stronger for certain combinations of β and Q/m. During the defocusing phase (Fig. C.3), also downstream the grains are filtered out as from a certain size (Q/m > 2 C/kg). The Lorentz forces seem to slow the grains down slightly during the focusing phase (Fig. C.4). When in the sidestream position against the ISD flow, the flux in the focusing phase (2016 in Fig. C.4) is clearly higher than in the defocusing case (2004 in Fig. C.3). The defocusing flux is higher in 2004 than in 1998 (Figs. C.3) because we are further along in the solar cycle as well as moving into the stream of ISD grains. This is clearly visible in the relative velocities, which become very high.
 |
Fig. C.3 Relative flux (left) and relative velocity (right) with respect to Jupiter for approximately the defocusing phase (1995–2004) of the solar cycle for the 4 positions indicated in 5 (left). The reference β-curve is shown as a black line. |
 |
Fig. C.4 Relative flux (left) and relative velocity (right) with respect to Jupiter for approximately the focusing phase (2007–2016) of the solar cycle for the 4 positions indicated in 5 (right). The reference β-curve is shown as a black line. |
Appendix C.3: Detailed predictions for the asteroid belt
During the defocusing period only bigger particles (Q/m < 1 and β < 1) reach the asteroid at somewhat enhanced fluxes (Fig. C.5). The relative speeds of interstellar grains are generally higher than their initial speed of 26 km s-1 because of the significant orbital speed of the asteroid (18 km s-1). Only in 2002 when the asteroid moves approximately parallel with the interstellar flow does the relative speed become as low as 10 km s-1. At this and similar periods, interstellar material may be collected at the asteroid surface.
For about half of the asteroid’s orbit, no particles with β ≥ 2 will reach the asteroid (Fig. C.6). However, their fluxes are generally enhanced except for 2011 when the asteroid’s motion subtracts from the interstellar flow speed and, consequently, the fluxes are also reduced. Only the flux of particles with Q/m ~ 2 are enhanced even there. Downstream of the interstellar flow (end of 2012) the fluxes of all particles of β < 1 are strongly enhanced (gravitational focusing and Lorentz forces).
 |
Fig. C.5 Relative flux (left) and relative velocity (right) with respect to main-belt asteroid Ceres for approximately the defocusing phase (1999–2002) of the solar cycle for the 4 positions indicated in 5 (left). The variation in velocity is mainly due to the direction in which Ceres moves with respect to the ISD flow direction. The reference β-curve is shown as a black line. |
 |
Fig. C.6 Relative flux (left) and relative velocity (right) with respect to main-belt asteroid Ceres for approximately the focusing phase (2010–2013) of the solar cycle for the 4 positions indicated in 5 (right). The variation in velocity is mainly due to the direction in which Ceres moves with respect to the ISD flow direction. The reference β-curve is shown as a black line. |
McComas et al. (2012) reports a slower relative velocity of the Sun with respect to the ISM and suggest that there is therefore no bow shock ahead of the heliosphere.
References
- Altobelli, N., Kempf, S., Landgraf, M., et al. 2003, J. Geophys. Res. (Space Physics), 108, 8032 [Google Scholar]
- Altobelli, N., Kempf, S., Krüger, H., et al. 2005, J. Geophys. Res. (Space Physics), 110, 7102 [NASA ADS] [CrossRef] [Google Scholar]
- Altobelli, N., Grün, E., & Landgraf, M. 2006, A&A, 448, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baguhl, M., Grün, E., Hamilton, D. P., et al. 1995, Space Sci. Rev., 72, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Baguhl, M., Grün, E., & Landgraf, M. 1996, Space Sci. Rev., 78, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Dorschner, J. 2001, Interplanetary Dust (Springer), 727 [Google Scholar]
- Dorschner, J., & Henning, T. 1995, A&ARv., 6, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Frisch, P. C., Dorschner, J. M., Geiss, J., et al. 1999, ApJ, 525, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, J. M., Li, A., Mendoza-Gomez, C. X., et al. 1995, ApJ, 455, L177 [NASA ADS] [CrossRef] [Google Scholar]
- Grün, E., & Svestka, J. 1996, Space Sci. Rev., 78, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Grün, E., Gustafson, B., Mann, I., et al. 1994, A&A, 286, 915 [NASA ADS] [Google Scholar]
- Gustafson, B. S. 1994, Ann. Rev. Earth Planet. Sci., 22, 553 [Google Scholar]
- Gustafson, B. S., & Misconi, N. 1979, Nature, 282, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Kempf, S., Srama, R., Altobelli, N., et al. 2004, Icarus, 171, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, H., & Mann, I. 1998, ApJ, 499, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, H., & Mann, I. 1999, in Meteroids 1998, eds. W. J. Baggaley, & V. Porubcan, 283 [Google Scholar]
- Kimura, H., Mann, I., & Jessberger, E. K. 2003, ApJ, 583, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Krüger, H., Landgraf, M., Altobelli, N., & Grün, E. 2007, Space Sci. Rev., 130, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Krüger, H., Dikarev, V., Anweiler, B., et al. 2010, Planet. Space Sci., 58, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Landgraf, M. 2000, J. Geophys. Res., 105, 10303 [NASA ADS] [CrossRef] [Google Scholar]
- Landgraf, M., Augustsson, K., Grün, E., & Gustafson, B. A. S. 1999, Science, 286, 2319 [NASA ADS] [CrossRef] [Google Scholar]
- Landgraf, M., Baggaley, W. J., Grün, E., Krüger, H., & Linkert, G. 2000, J. Geophys. Res., 105, 10343 [NASA ADS] [CrossRef] [Google Scholar]
- Levy, E. H., & Jokipii, J. R. 1976, Nature, 264, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Linde, T. J., & Gombosi, T. I. 2000, J. Geophys. Res., 105, 10411 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Alexashov, D., Bzowski, M., et al. 2012, Science, 336, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Morfill, G. E., & Grün, E. 1979, Planet. Space Sci., 27, 1283 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, T. 1981, A&A, 99, 1 [NASA ADS] [Google Scholar]
- Opher, M., Drake, J. F., Swisdak, M., et al. 2011, ApJ, 734, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Redfield, S., & Linsky, J. L. 2008, The Structure of the Local Interstellar Medium. IV. Dynamics, Morphology, Physical Properties, and Implications of Cloud-Cloud Interactions [Google Scholar]
- Richardson, J. D., Kasper, J. C., Wang, C., Belcher, J. W., & Lazarus, A. J. 2008, Nature, 454, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Slavin, J. D., Frisch, P. C., Heerikhuisen, J., et al. 2010, Twelfth International Solar Wind Conference, 1216, 497 [NASA ADS] [Google Scholar]
- Slavin, J. D., Frisch, P. C., Müller, H.-R., et al. 2012, ApJ, 760, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Srama, R., Altobelli, N., de Kam, J., et al. 2006, Adv. Space Res., 38, 2093 [NASA ADS] [CrossRef] [Google Scholar]
- Srama, R., Stephan, T., Grün, E., et al. 2009, Exp. Astron., 23, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Srama, R., Krüger, H., Yamaguchi, T., et al. 2012, Exp. Astron., 33, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Sterken, V. J. 2012, Meteor. Planet. Sci., submitted [Google Scholar]
- Sterken, V. J., Altobelli, N., Kempf, S., et al. 2012a, Planet. Space Sci., 71, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Sterken, V. J., Altobelli, N., Kempf, S., et al. 2012b, A&A, 538, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trumpler, R. J. 1930, PASP, 42, 214 [Google Scholar]
- Tsou, P., Brownlee, D. E., Sandford, S. A., Hörz, F., & Zolensky, M. E. 2003, J. Geophys. Res. (Planets), 108, 8113 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. 1989, in Interstellar Dust, eds. L. J. Allamandola, & A. G. G. M. Tielens, IAU Symp., 135, 455 [Google Scholar]
- Witte, M., Rosenbauer, H., Banaszkiewicz, M., & Fahr, H. 1993, Adv. Space Res., 13, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S., Gail, H.-P., & Trieloff, M. 2008, A&A, 479, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zubko, V., Dwek, E., & Arendt, R. G. 2004, ApJS, 152, 211 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Variation in the mean interstellar dust density of a given particle mass along the axis of the interstellar dust flow. The Sun is at distance 0 AU. The densities correspond to the mean densities in a 1 AU column around the flow axis. The dashed lines corresponds to density = 0. The density lines for different particle masses are offset by a factor 10. |
| In the text | |
 |
Fig. 2 Variation in the interstellar dust density in a 1 AU column around the axis of the interstellar dust flow as a function of particle mass and distance from the Sun. Density 0 was set to the bottom of the diagram at 0.1. The blue lines denote the plane of density level of 1. The reference β-curve as introduced in Sect. 4.1 was assumed. |
| In the text | |
 |
Fig. 3 Overview of the simulations in the β-Q/m-space. The seventy simulations are shown as dots in the β-Q/m diagrams. The β-curves for carbon, the “reference β-curve” (see Sect. 4.1) and β-curve for silicates from Kimura & Mann (1999) are shown as dotted, bold, and normal curves. |
| In the text | |
 |
Fig. 4 Simulated size distributions for different positions upstream and downstream of the Sun on the flow axis. From top to bottom: –10 AU (upstream), –5 AU, –3 AU, +3 AU. The different colors indicate different epochs in the solar cycle. The dotted straight line is the original reference distribution for nH = 0.3 cm-3. The black straight line is the reference distribution range for which simulations were done. This reference distribution is illustrative, and is not meant to imply that the extended MRN distribution would reflect the true grain size distribution in the LIC. |
| In the text | |
 |
Fig. 5 Orbit of the Earth, asteroid Ceres, Jupiter, and Saturn around the Sun, with the β-cones shown by colored dotted lines. The positions for which we show the β-Q/m plots in Appendix C and size distributions in Sects. 5.1.1, 5.2.3, and 5.3.1 are indicated as blue dots. The left plot corresponds to the defocusing phase, and the right plot corresponds to the focusing phase of the solar cycle for the asteroid and Jupiter orbits. Galileo was flying from 1996 until 2003 and was thus in large parts of its orbit in the β-cones, as well as moving in the same direction of the dust flow. |
| In the text | |
 |
Fig. 6 Time series of relative fluxes with respect to Saturn for different grain sizes (0.73, 0.36, 0.26, 0.21, 0.15, 0.11, and 0.07 μm). As the grain size decreases, the influence of the solar cycle becomes more dominant. Filtering at the heliopause is not taken into account. |
| In the text | |
 |
Fig. 7 Simulated size distributions of the ISD at Saturn for the 8 positions along its orbit. The gravitational focusing in 2002 is clear for the largest particles, as is the strong influence of the solar cycle on the size distributions, especially for the smaller grains (cf. Fig. 4). The dotted straight line is the original reference distribution for nH = 0.3 cm-3. The black straight line is the reference distribution range for which simulations were done. This reference distribution is illustrative, and is not meant to imply that the extended MRN distribution would reflect the true grain size distribution in the LIC. |
| In the text | |
 |
Fig. 8 Time series of relative fluxes with respect to Jupiter for different grain sizes (0.73, 0.36, 0.26, 0.21, 0.15, 0.11, and 0.07 μm cf. Fig. 6). As the grain size decreases, the influence of the solar cycle becomes more dominant. Filtering at the heliopause is not taken into account. |
| In the text | |
 |
Fig. 9 Relative flux (left) and relative velocity (right) with respect to Jupiter prior to the arrival of JUICE in mid-2029. The last part of the cruise phase is perfectly suited to some add-on science: the ISD flux is high due to the focusing phase of the solar cycle, and Jupiter is moving into the stream of ISD grains. Source: Sterken et al. (2012a). |
| In the text | |
 |
Fig. 10 Simulated size distributions of the ISD at Jupiter for the 4 positions per orbit. The gravitational focusing in 2001 and 2013 is clear for the largest particles.The influence of the solar cycle on the size distributions is visible, especially for the smaller grains (cf. Fig. 4). The dotted straight line is the original reference distribution for nH = 0.3 cm-3. The black straight line is the reference distribution range for which simulations were done. This reference distribution is illustrative, and is not meant to imply that the extended MRN distribution would reflect the true grain size distribution in the LIC. |
| In the text | |
 |
Fig. 11 Time series of relative fluxes with respect to main-belt asteroid Ceres for different grain sizes (0.73, 0.36, 0.26, 0.21, 0.15, 0.11, and 0.07 μm cf. Fig. 6). As the grain size decreases, the influence of the solar cycle becomes more dominant. Filtering at the heliopause is not taken into account. |
| In the text | |
 |
Fig. 12 Simulated size distributions of the ISD at the main-belt asteroid Ceres for the 4 positions per orbit (cf. Fig. 4). The dotted straight line is the original reference distribution for nH = 0.3 cm-3. The black straight line is the reference distribution range for which simulations were done. This reference distribution is illustrative, and is not meant to imply that the extended MRN distribution would reflect the true grain size distribution in the LIC. |
| In the text | |
 |
Fig. A.1 ISD distributions from Ulysses data (stars) between 1992 and 2008 and the (extrapolated) MRN distributions for a hydrogen density of 0.1, 0.2, and 0.3 cm-3 (dashed, dotted, and continuous lines) adapted from Mathis et al. (1977). The left plot shows the number density, the middle plot the mass number density, and the right plot the cross section number density. The cut-off for silicate grains in the MRN-distribution is indicated with a vertical dashed line at 0.25 μm (1.3 × 10-16 kg) and for carbon grains at 1 μm (8.4 × 10-15 kg). |
| In the text | |
 |
Fig. B.1 Relative flux (left) and relative velocity (right) at –10 AU (upstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
| In the text | |
 |
Fig. B.2 Relative flux (left) and relative velocity (right) at –5 AU (upstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
| In the text | |
 |
Fig. B.3 Relative flux (left) and relative velocity (right) at –3 AU (upstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
| In the text | |
 |
Fig. B.4 Relative flux (left) and relative velocity (right) at 3 AU (downstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
| In the text | |
 |
Fig. C.1 Relative flux (left) and relative velocity (right) with respect to Saturn for approximately the defocusing phase (1991–1992) of the solar cycle. Saturn is moving mainly in the same direction as the dust flow and is downstream of the Sun in 2002 (inside all β-cones). The reference β-curve is shown as a black line. |
| In the text | |
 |
Fig. C.2 Relative flux (left) and relative velocity (right) with respect to Saturn for approximately the focusing phase (2005–2017) of the solar cycle. Saturn is moving mainly into the dust flow and is upstream of the Sun in 2017. The reference β-curve is shown as a black line. |
| In the text | |
 |
Fig. C.3 Relative flux (left) and relative velocity (right) with respect to Jupiter for approximately the defocusing phase (1995–2004) of the solar cycle for the 4 positions indicated in 5 (left). The reference β-curve is shown as a black line. |
| In the text | |
 |
Fig. C.4 Relative flux (left) and relative velocity (right) with respect to Jupiter for approximately the focusing phase (2007–2016) of the solar cycle for the 4 positions indicated in 5 (right). The reference β-curve is shown as a black line. |
| In the text | |
 |
Fig. C.5 Relative flux (left) and relative velocity (right) with respect to main-belt asteroid Ceres for approximately the defocusing phase (1999–2002) of the solar cycle for the 4 positions indicated in 5 (left). The variation in velocity is mainly due to the direction in which Ceres moves with respect to the ISD flow direction. The reference β-curve is shown as a black line. |
| In the text | |
 |
Fig. C.6 Relative flux (left) and relative velocity (right) with respect to main-belt asteroid Ceres for approximately the focusing phase (2010–2013) of the solar cycle for the 4 positions indicated in 5 (right). The variation in velocity is mainly due to the direction in which Ceres moves with respect to the ISD flow direction. The reference β-curve is shown as a black line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


