| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219609 | |
| Published online | 15 April 2013 | |
Online material
Appendix A: The different faces of grain size distributions
 |
Fig. A.1
ISD distributions from Ulysses data (stars) between 1992 and 2008 and the (extrapolated) MRN distributions for a hydrogen density of 0.1, 0.2, and 0.3 cm-3 (dashed, dotted, and continuous lines) adapted from Mathis et al. (1977). The left plot shows the number density, the middle plot the mass number density, and the right plot the cross section number density. The cut-off for silicate grains in the MRN-distribution is indicated with a vertical dashed line at 0.25 μm (1.3 × 10-16 kg) and for carbon grains at 1 μm (8.4 × 10-15 kg). |
| Open with DEXTER | |
The differential number (n), mass number (nm), and cross-sectional number distributions (nA) with respect to grain size a can be calculated from Eq. (1): 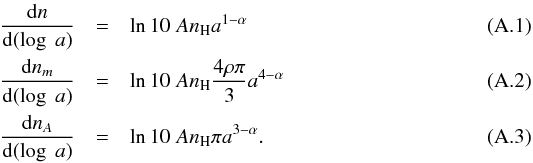 The logarithmic mass number distribution as function of mass is then given by
The logarithmic mass number distribution as function of mass is then given by 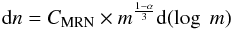 (A.4)with the constant
(A.4)with the constant 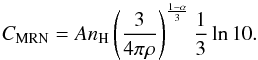 (A.5)The logarithmic differential (number) distribution shows the amount of grains per logarithmic mass interval (see Fig. A.1, left). The smaller grains are more abundant than the larger ones. In order to know how the mass is distributed among the grain sizes, we multiply the logarithmic differential number distribution with the mass of the grains to get the logarithmic differential mass distribution:
(A.5)The logarithmic differential (number) distribution shows the amount of grains per logarithmic mass interval (see Fig. A.1, left). The smaller grains are more abundant than the larger ones. In order to know how the mass is distributed among the grain sizes, we multiply the logarithmic differential number distribution with the mass of the grains to get the logarithmic differential mass distribution: 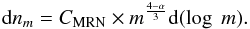 (A.6)Although the smaller ISD grains are more abundant in number, the largest part of the mass resides in larger grains (see Fig. A.1, middle). The total mass thus depends on the largest of the grains that are present. The logarithmic differential cross-section distribution is important because of emission, scattering, and absorption of light, which depends on the grain cross-section. It is derived by multiplying the differential number distribution by the cross-sectional area of the grains:
(A.6)Although the smaller ISD grains are more abundant in number, the largest part of the mass resides in larger grains (see Fig. A.1, middle). The total mass thus depends on the largest of the grains that are present. The logarithmic differential cross-section distribution is important because of emission, scattering, and absorption of light, which depends on the grain cross-section. It is derived by multiplying the differential number distribution by the cross-sectional area of the grains: 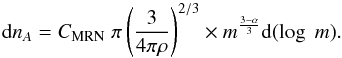 (A.7)
(A.7)
Slopes of the logarithmic differential densities.
The logarithmic differential cross-section distribution is shown in Fig. A.1 on the right, and it shows that the smallest grains dominate the total “cross-section” of the grains (thus making them dominate astronomical observations), but their slope is less steep than for the logarithmic differential number density.
In-situ dust instruments (e.g. like the Ulysses dust detector) count particles above a given mass threshold, therefore cumulative distributions are important. The slope of these cumulative distributions is the same as the corresponding differential logarithmic distribution. The cumulative distributions (number of grains above a threshold mass) can be calculated using 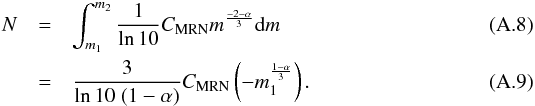
Appendix B: Detailed discussion: filtering effects along the interstellar flow axis
 |
Fig. B.1
Relative flux (left) and relative velocity (right) at –10 AU (upstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
| Open with DEXTER | |
 |
Fig. B.2
Relative flux (left) and relative velocity (right) at –5 AU (upstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
| Open with DEXTER | |
 |
Fig. B.3
Relative flux (left) and relative velocity (right) at –3 AU (upstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
| Open with DEXTER | |
 |
Fig. B.4
Relative flux (left) and relative velocity (right) at 3 AU (downstream) from the Sun for the defocusing phase (2000, day 182, top figures) and the focusing phase (2011, day 182, bottom figures). The reference β-curve is shown as a black line. |
| Open with DEXTER | |
Here, we illustrate the combined effect of the Lorentz force, solar gravity, and solar radiation pressure force on the dust size distribution along the flow-axis of the dust toward the Sun, in analogy with Sect. 4.1. We plot the relative flux and relative velocity on color scale as a function of β and Q/m on the vertical and horizontal axes (Figs. B.1–B.4). The β-Q/m plots are constructed from a matrix of 70 simulations, as shown in Fig. 3, where the simulation results are interpolated (in 2D) to fill the whole β-Q/m space. The solid lines in Figs. B.1–B.4 show the reference β-curve. Following the simulated fluxes along the reference curve yields the results in Fig. 4 for this specific material assumption. We do this for the locations of –10 AU (upstream), –5 AU, –3 AU, and 3 AU (downstream) at a specific time. To show the effect of the solar cycle, we selected a time in the year 2000 (max. effect of the defocusing phase) and 2011 (max. effect of the focusing phase). This is about three years after the optimum focusing/defocusing field conditions (Table 2, paper 1), because interstellar grains need that time to display an enhanced density near the ecliptic plane.
At 10 AU upstream (–10 AU, Fig. B.1), the flux of big particles (Q/m < 1) is affected little by the Lorentz force. Only the flux of small particles is reduced during the defocusing phase around year 2000. Eleven years later the flux of small particles (1 < Q/m < 5) is enhanced especially for high β values. The speed of β ≤ 1 particles has increased in comparison to the speed at the heliospheric boundary, whereas the speed of β ≥ 1 particles has decreased. For the grains with Q/m > 8 C/kg in the defocusing phase, no velocity is drawn where the flux is zero. Closer to the Sun (–5 AU, Fig. B.2) these effects become more pronounced except that the flux of very small grains (Q/m > 8) is enhanced during the focusing phase because these particles are deflected from higher latitudes to the ecliptic plane.
At 3 AU upstream (–3 AU, Fig. B.3), the effect of the β-cone becomes obvious in the flux of large β (>2.5) particles, which is strongly reduced. In addition the flux of small particles (Q/m > 1) becomes strongly modulated by the electromagnetic interaction during the focusing and defocusing phases. Downstream of the Sun and close to the interstellar flow axis (3 AU, Fig. B.4), only particles with β < 1 can be found, the biggest of which (Q/m < 2) show an enhanced flux due to gravitational focusing. Again the flux of small particles (Q/m > 2) is strongly modulated by the electromagnetic interaction. The farther downstream, the more abrupt the β-cone appears in terms of enhancement (gravitational focusing) and dust depletion (β-cone).
Appendix C: Detailed discussion: application to Saturn, Jupiter, and the asteroid belt
Appendix C.1: Detailed predictions for Saturn
In analogy with Sect. 4.3, we discuss the β-Q/m graphs for the relative flux and velocity of ISD at Saturn. Figures C.1 and C.2 show these for the eight positions throughout the solar cycle and Saturn’s orbit. In 1991, between the focusing and defocusing period (Table 2 Paper I) Saturn is in the upstream portion of the interstellar flow. The flux of particles with 2 < Q/m < 4 and β-values >1.3 is still enhanced more than a factor 2, while the flux of particles with Q/m > 6 is significantly reduced (Fig. C.1). This flux enhancement shifts to lower β values in 1995. In 1999 the interstellar flux is strongly reduced for all particles except for big particles (Q/m < 0.1 and β < 1.5). In 2002, Saturn is in the downstream portion of the interstellar flow inside the β-cone for all small particles (β > 1) and in the focusing region of big particles (β < 1). However, electromagnetic interactions diffuse the focusing effect for Q/m > 1. In the whole period from 1991 to 1999, the relative speed between Saturn and interstellar grains is below the vinf (26 km s-1) because Saturn is moving parallel to the interstellar dust flow, so the relative speed is reduced by Saturn’s orbital speed (9.7 km s-1). Only in 2002 does the relative speed of big interstellar particles (β < 1) exceed vinf because the speed vector of interstellar dust and Saturn are no longer close to parallel.
The relative fluxes and velocities in 2005 to 2017 are much higher (Fig. C.2) than in the preceding period because Saturn is moving into the dust direction (increasing both flux and relative velocity), as well as because of the focusing phase of the solar cycle (2009 to 2013). By 2009, Saturn is on the edge of the β = 3 cone, is moving against the dust stream, and is in the midst of the focusing phase of the solar cycle. A very interesting era starts for finding ISD in Cassini data, for the high fluxes, and because all sizes of all materials are theoretically able to reach the Cassini spacecraft location (outside the β = 3 cone), hence the detector. We ignore in this discussion the influence of the Saturnian magnetosphere on the grain trajectories, which may be important for Cassini, although we expect this effect to be small. Furthermore, Cassini CDA will collect ISD measurements mostly outside Saturn’s magnetosphere. In 2013, Lorentz forces change the shape of the β-Q/m plot, but very high fluxes can still be found for small grains with Q/m between 3 to 6 C/kg, presuming they can traverse the heliopause. Impact velocities get reduced because of the direction of motion of Saturn. In 2017, even grains up to Q/m = 12 C/kg could reach Saturn, assuming they would get through the heliopause. Mid-sized and smaller grains (Q/m between 0.5 and 5 C/kg) experience very strong flux enhancements at different times (the larger ones of 0.5 C/kg in 2009 and the smaller ones up to 5 C/kg in 2013). This has to do with the complicated focusing mechanism upstream of the Sun for grains with higher Q/m values (cf. Fig. 38 in Paper I: the grains are reflected upstream of the Sun, which we refer to as mirroring).
 |
Fig. C.1
Relative flux (left) and relative velocity (right) with respect to Saturn for approximately the defocusing phase (1991–1992) of the solar cycle. Saturn is moving mainly in the same direction as the dust flow and is downstream of the Sun in 2002 (inside all β-cones). The reference β-curve is shown as a black line. |
| Open with DEXTER | |
 |
Fig. C.2
Relative flux (left) and relative velocity (right) with respect to Saturn for approximately the focusing phase (2005–2017) of the solar cycle. Saturn is moving mainly into the dust flow and is upstream of the Sun in 2017. The reference β-curve is shown as a black line. |
| Open with DEXTER | |
Appendix C.2: Detailed predictions for Jupiter
A first look at the β-Q/m plots (Figs. C.3 and C.4) immediately reveals that there is a strong effect on the focusing and defocusing phase of the solar cycle: fluxes are strongly reduced in Fig. C.3, whereas they are enhanced in Fig. C.4. The locations in the plots for 1995, 1998, 2001, and 2004 are equal to the locations in the plots of 2007, 2010, 2013, and 2016, but the period in the solar cycle is different (defocusing in Fig. C.3 versus focusing in Fig. C.4). From top to bottom, Jupiter is upstream, sidestream (moving with the flow of ISD), downstream, and again sidestream (against the flow of ISD).
Upstream, the relative flux is moderate for 1995 (see phase of solar cycle in Table 2 in Paper I, add 3 years latency to get the maximum effect), whereas it is high for the focusing phase (2007). The relative velocities vary from high velocities at low β, and lower velocities for higher β-values (as grains get slower near the β-cone for β > 1 and faster for lower β-values). The variation in velocities with different β is more than in the case of Saturn, because we are closer to the Sun (see also figures in Sect. 4.3) and Jupiter’s orbital speed is faster. On the sidestream side there is a very low flux in 1998 because of both the defocusing phase of the solar cycle and the relative movement of Jupiter with respect to the dust flow direction. In the focusing phase the flux is somewhat higher. Both show very low relative velocities since the orbital speed of Jupiter is about 13 km s-1, and the nominal dust speed is 26 km s-1. In 2001 and 2013, Jupiter is downstream of the Sun. The β-cone is visible through having no flux above β = 1 and the gravitational focusing is visible for low β-values through a strong enhancement of relative flux. During the focusing phase of the solar cycle (Fig. C.4), this enhancement is stronger for certain combinations of β and Q/m. During the defocusing phase (Fig. C.3), also downstream the grains are filtered out as from a certain size (Q/m > 2 C/kg). The Lorentz forces seem to slow the grains down slightly during the focusing phase (Fig. C.4). When in the sidestream position against the ISD flow, the flux in the focusing phase (2016 in Fig. C.4) is clearly higher than in the defocusing case (2004 in Fig. C.3). The defocusing flux is higher in 2004 than in 1998 (Figs. C.3) because we are further along in the solar cycle as well as moving into the stream of ISD grains. This is clearly visible in the relative velocities, which become very high.
 |
Fig. C.3
Relative flux (left) and relative velocity (right) with respect to Jupiter for approximately the defocusing phase (1995–2004) of the solar cycle for the 4 positions indicated in 5 (left). The reference β-curve is shown as a black line. |
| Open with DEXTER | |
 |
Fig. C.4
Relative flux (left) and relative velocity (right) with respect to Jupiter for approximately the focusing phase (2007–2016) of the solar cycle for the 4 positions indicated in 5 (right). The reference β-curve is shown as a black line. |
| Open with DEXTER | |
Appendix C.3: Detailed predictions for the asteroid belt
During the defocusing period only bigger particles (Q/m < 1 and β < 1) reach the asteroid at somewhat enhanced fluxes (Fig. C.5). The relative speeds of interstellar grains are generally higher than their initial speed of 26 km s-1 because of the significant orbital speed of the asteroid (18 km s-1). Only in 2002 when the asteroid moves approximately parallel with the interstellar flow does the relative speed become as low as 10 km s-1. At this and similar periods, interstellar material may be collected at the asteroid surface.
For about half of the asteroid’s orbit, no particles with β ≥ 2 will reach the asteroid (Fig. C.6). However, their fluxes are generally enhanced except for 2011 when the asteroid’s motion subtracts from the interstellar flow speed and, consequently, the fluxes are also reduced. Only the flux of particles with Q/m ~ 2 are enhanced even there. Downstream of the interstellar flow (end of 2012) the fluxes of all particles of β < 1 are strongly enhanced (gravitational focusing and Lorentz forces).
 |
Fig. C.5
Relative flux (left) and relative velocity (right) with respect to main-belt asteroid Ceres for approximately the defocusing phase (1999–2002) of the solar cycle for the 4 positions indicated in 5 (left). The variation in velocity is mainly due to the direction in which Ceres moves with respect to the ISD flow direction. The reference β-curve is shown as a black line. |
| Open with DEXTER | |
 |
Fig. C.6
Relative flux (left) and relative velocity (right) with respect to main-belt asteroid Ceres for approximately the focusing phase (2010–2013) of the solar cycle for the 4 positions indicated in 5 (right). The variation in velocity is mainly due to the direction in which Ceres moves with respect to the ISD flow direction. The reference β-curve is shown as a black line. |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


