| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A59 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201220267 | |
| Published online | 22 November 2012 | |
Statistics and implications of substructure detected in a representative sample of X-ray clusters
1
Max-Planck-Institut für extraterrestrische Physik,
85748
Garching,
Germany
e-mail: gchon@mpe.mpg.de
2 School of Physics and Astronomy, University of Birmingham,
Edgbaston, Birmingham B15 2TT, England
Received: 21 August 2012
Accepted: 16 October 2012
We present a morphological study of 35 X-ray luminous galaxy clusters at 0.15 < z < 0.3, selected in a similar manner to the Local Cluster Substructure Survey (LoCuSS), for which deep XMM-Newton observations are available. We characterise the structure of the X-ray surface brightness distribution of each cluster by measuring both their power ratios and centroid shift, and thus rank the clusters by the degree of substructure. These complementary probes give a consistent description of the cluster morphologies with some well understood exceptions. We find a remarkably tight correlation of regular morphology with the occurrence of cool cores in clusters. We also compare our measurements of X-ray morphology with measurements of the luminosity gap statistics and ellipticity of the brightest cluster galaxy (BCG), to examine recent suggestions that these quantities may be efficient probes of the assembly history of and observer’s viewing angle through cluster-scale mass distributions. Our X-ray analysis confirms that cluster with large luminosity gaps form a relatively homogeneous population that appears more regular with the implication that such systems did not suffer from recent merger activity. Similarly, we find a clear correlation between the ellipticity of the BCGs and the shape of the cluster. In particular nearly circular BCGs (ϵ < 0.2) are found in undisturbed systems with regular X-ray morphologies. For these systems it has been suggested that they are intrinsically prolate and viewed along the line of sight close to the major axis. Finally, we check how our new X-ray morphological analysis maps onto cluster scaling relations, finding that (i) clusters with relatively undisturbed X-ray morphologies are on average more luminous at fixed X-ray temperature than those with disturbed morphologies, and (ii) disturbed clusters have larger X-ray masses than regular clusters for a given temperature in the MX − T relation. We also show that the scatter in the ratio of X-ray and weak lensing based cluster mass measurements is larger for disturbed clusters than for those of more regular morphology. Overall, our results demonstrate the feasibility of assembling a self-consistent picture of the physical structure of clusters from X-ray and optical data, and the potential to apply this in the measurement of cosmological cluster scaling relations.
Key words: X-rays: galaxies: clusters / galaxies: clusters: general / cosmology: observations
© ESO, 2012
1. Introduction
Galaxy clusters are ideal probes for tracing the large-scale cosmic matter distribution and for testing cosmological models (e.g. Vikhlinin et al. 2009; Böhringer 2011; Allen et al. 2011). A prerequisite for these studies is a good measure of the galaxy cluster masses. Only for small samples will the masses be determined individually while for the large cosmological samples of galaxy clusters the masses will be estimated through the application of mass-observable scaling relations, where the observable is for example the X-ray luminosity in the case of galaxy cluster samples from X-ray surveys (e.g. Pratt et al. 2009; Vikhlinin et al. 2009; for more references see Böhringer et al. 2012). This then requires the calibration of the mass-observable relation with mass determinations for a calibration sample.
X-ray observations can be used effectively to characterise the structure of galaxy clusters, which are to first order described in theory as dark matter halos (e.g. Navarro et al. 1995). The X-ray emitting gas is filling the entire dark matter halos providing an outline of their structure and a measure of their gravitational potentials. Assuming that the X-ray emitting intracluster medium (ICM) is filling the potential in a nearly hydrostatic way, the cluster mass can be determined from the intracluster plasma density and temperature distribution through the hydrostatic equation, where density and temperature profiles are determined from X-ray imaging and X-ray spectroscopy (e.g. Sarazin 1986). However, galaxy clusters are dynamically young objects, that is, their dynamical timescale is not much shorter than their age and the Hubble time. Therefore, in contrast to elliptical galaxies for example, a significant fraction of the clusters are not very close to a dynamical equilibrium. This provides a challenge to mass determination. The validity and precision of the mass determination with X-ray observations thus needs to be tested.
Observations of the gravitational lensing effect of galaxy clusters offer an alternative route to the determination of the cluster mass, which is not dependent on the assumption of hydrostatic equilibrium of the ICM. This approach has other drawbacks, however, since the mass determined refers to all the excess mass over the mean density of the Universe in the line-of-sight of the cluster. Further the gravitational lensing distortion signal statistics is limited by the number of background galaxies that can be observed, which provides a fundamental limit on the significance of the lensing analysis results. Therefore large efforts are undertaken to provide an inter-calibration of the two methods (Hoekstra 2007; Bardeau et al. 2007; Pedersen & Dahle 2007; Mahdavi et al. 2008; Leauthaud et al. 2010). The Local Cluster Substructure Survey (LoCuSS) project (Smith et al. 2005) involves one of the largest of these efforts (Zhang et al. 2008, 2010; Okabe et al. 2010a,b) concentrating on clusters at 0.15 < z < 0.3.
In this context it is very important to investigate how possible deviations in the mass measurement with the two methods depend on the dynamical state of the galaxy clusters. For example, early results from LoCuSS, based on characterising the X-ray morphology of 12 clusters using Asymmetry and Fluctuation parameters imply that “undisturbed” clusters are on average more massive than “disturbed” clusters in mass-YX relations at 2σ significance (Okabe et al. 2010b). The YX parameter is defined as the product of the gas mass and the temperature, which is believed to be a particularly good mass proxy (Kravtsov et al. 2006).
The main goal of this paper is, therefore, to measure substructure in the X-ray surface brightness distribution of clusters at 0.15 < z < 0.3 as signatures of deviations from dynamical equilibrium, and to compare with optical/near-infrared indicators of cluster structure. We apply the currently most popular substructure statistics of power ratios and centre shifts to a sample of 35 clusters which have deep X-ray observations with XMM-Newton in order to rank the clusters by their substructure in the X-ray surface brightness image. These substructure parameters are then compared to a number of physical cluster properties determined from X-ray data. We also compare the occurrence of substructure with selected optical/near-infrared properties of the clusters, including the luminosity gap between the first and second ranked cluster galaxies, and the ellipticity of the brightest cluster galaxy (BCG). We also investigate how cluster scaling relations vary as a function of the degree of substructure.
The paper is structured as follows. In Sect. 2 we give a brief description of the cluster sample, and outline the methods used in our analysis in Sect. 3. The results of the substructure analysis and correlations with other cluster physical parameters are presented in Sect. 4, and Sect. 5 provides a comparison of the substructure measures with optical cluster parameters. The influence of substructure on scaling relations is studied in Sect. 6. The conclusions and a summary are given in Sect. 7.
Throughout the paper we adopt a flat Λ-cosmological model with Ωm = 0.3 and a Hubble constant of H0 = 70 km s-1 Mpc-1 for the calculations of all distant dependent quantities.
2. Cluster sample and X-ray data reduction
We select massive clusters from the X-ray galaxy cluster catalogues, BCS (Ebeling et al. 1998, 2000) and REFLEX (Böhringer et al. 2004), based on the ROSAT All-Sky Survey (Trümper 1993) using the same selection criteria as LoCuSS: LX/E(z)2.7 > 4.1 × 1044 erg/s in the 0.1−2.4 keV band and z = 0.15−0.3 with a line-of-sight interstellar column density nH < 7 × 1020 cm2 (Smith et al., in prep.; see also Marrone et al. 2012), with no restriction on declination. After cross-comparison with the XMM-Newton archive this yields a sample of 37 clusters with deep XMM-Newton observations. This sample has previously been analysed by Zhang et al. (2008). Here we analyse 35 of the 37 clusters of this sample; the two clusters, Abell 115 and Abell 901 have not been included here, because both are a part of larger structures. Abell 115 comprises two cores (e.g. Gutierrez & Krawczynski 2005; Barrena et al. 2007), and Abell 901 is a part of a supercluster together with Abell 902 (e.g. Gray et al. 2002) where in both cases it is difficult to disentangle cluster emission from the emission of the rest of the environment.
The XMM-Newton observations for all three detectors were flare-cleaned, and out-of-time events were statistically subtracted from the pn data. Point sources and other sources unrelated to the galaxy clusters were removed and the holes were statistically filled with photons from surrounding regions. The images from all three detectors were combined and the corresponding exposure maps were added with an appropriate weighting for the MOS detectors to bring them to the level of an effective pn exposure. The substructure analysis was then applied to the exposure-corrected and background-subtracted combined images. In practice the analysis programs use the count, exposure and background maps simultaneously to reconstruct all relevant quantities related to photon noise. The XMM-Newton data and substructure analysis is described in more detail in Böhringer et al. (2010).
3. Characterising substructure
To characterise the degree of substructure of clusters in our sample, we concentrate here on two methods: centre shifts as a function of the aperture radius (e.g. Mohr et al. 1993, 1995; Poole et al. 2006; O’Hara et al. 2006) and the determination of so-called power ratios (e.g. Buote & Tsai 1995, 1996; Jeltema et al. 2005, 2008; Valdarnini 2006; Ventimiglia et al. 2008; Böhringer et al. 2010). We use the same technique as in Böhringer et al. (2010) with some modifications as outlined below.
3.1. Power ratios
The power ratio method was introduced by Buote & Tsai (1995) using the X-ray surface brightness as a representation of the projected mass distribution of a cluster. A multipole decomposition of the potential of the two-dimensional, projected mass distribution then provides moments which are identified as power ratios once they are normalised by the zeroth moment. In the analysis of Buote & Tsai, the moments, Pm are determined as follows ![\begin{eqnarray} P_0 &=& \left[ a_0 \ln (R_{\rm ap}) \right]^2 % \\ % P_m &=& { 1 \over 2 m^2 R_{\rm ap}^{2m} } \left( a_m^2 + b_m^2 \right) \end{eqnarray}](/articles/aa/full_html/2012/12/aa20267-12/aa20267-12-eq15.png) where Rap is the aperture radius. The moments am and bm are calculated by:
where Rap is the aperture radius. The moments am and bm are calculated by: 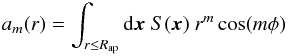 (3)and
(3)and 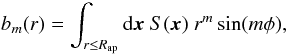 (4)where S(x) is the X-ray surface brightness image, and the integral extends over all pixels inside the aperture radius. a0 in Eq. (1) is thus the total radiation intensity inside the aperture radius.
(4)where S(x) is the X-ray surface brightness image, and the integral extends over all pixels inside the aperture radius. a0 in Eq. (1) is thus the total radiation intensity inside the aperture radius.
Since all terms, Pm, are proportional to the total intensity of the cluster X-ray emission, while only the relative contribution of the higher moments to the total emission is of interest, the moments are normalised by P0, resulting in the so-called power ratios, Pm/P0. Similarly to all previous studies, we only make use of the lowest moments from P2 to P4 (quadrupole, hexapole and octopole). Before the multipole moments are determined, the centre for the calculations is found by determining the photon count centre within the aperture used. The dipole, P1, should therefore vanish, which is checked during the calculations. P2/P0 describes the quadrupole of the surface brightness distribution, and is not necessarily a measure of substructure; a quadrupole will also be detected for a very regular elliptical cluster. In practice, low to moderate values of P2/P0 are found for regular elliptical clusters, while larger values of P2/P0 are a sign of cluster mergers. The lowest power ratio moment providing a clear substructure measure is thus P3/P0. P4/P0 describes substructure on slightly finer scales and is found to be correlated with P2/P0 here and in previous studies.
The uncertainty of the power ratio measurement and the influence of photon noise are studied by simulations in which an additional Poisson-noise is imposed on the count images with background. This “Poissonisation” is equivalent to the Poisson-noise introduced by the observation involving a finite number of detected photons. We interpret the variance of the power ratio results from the simulations as the measurement uncertainty. We also investigate how much additional signal is introduced by the artificial Poissonisation. We then make the assumption that the additional power introduced by the Poissonisation is similar to the extra power in the power ratios introduced by the photon shot noise of the observation. We therefore subtract the additional noise found in the mean of all simulations compared to the observations from the observational result.
Power ratios are routinely determined in 10 different apertures with radius r ≤ n × 0.1r500 (with n = 1, 2, ..., 10). Different to the prime approach in Böhringer et al. (2010) we are not excising the cluster core in the surface brightness distribution in our substructure analysis. A core excision has been found to have not much influence on the result except for the smallest aperture.
3.2. Modified power ratio calculation
We also introduce a couple of modifications to the calculation of power ratios motivated by the following arguments. The power ratios evaluated at r500 with the r2m weighting are predominantly influenced by the dynamical state in the outskirts of a cluster. In turn this means that disturbances near the centre of the cluster, especially if their scale is relatively small compared to r500, will be severely weighted down. To overcome this strong bias to the outer part of the cluster, we measure the averaged power ratios at ten radii defined by fractions of r500.
An alternative approach to reduce the strong weighting of the outer region uses a different weighting in r. We have chosen a linear weighting in r (instead of rm in Eqs. (3) and (4)), since for an approximate radial dependence of the surface brightness proportional to r-2 this procedure gives similar weight to linearly spaced annuli. We expect these two modified approaches to yield similar results.
3.3. Centre shifts
In most recent work the centre shift method is based on a measurement of the variance of the separation between the X-ray peak and the centroid calculated within concentric apertures with increasing aperture size. Instead of comparing the aperture centroids with the separately determined X-ray maximum, we measure the centroid shift for each aperture with respect to the mean of all centroids. We will explain the reason for this modification below. The centroid of each aperture is found by determining the “centre of mass” of the photon distribution in each aperture, which was already used for the centring prior to the power ratio determination. The resulting w is then the standard deviation of the different centre shifts (in units of r500), defined as (see also Poole et al. 2006): ![\begin{equation} w~ =~ \left[ {1 \over N-1}~ \sum \left( \Delta_i - \langle \Delta \rangle \right)^2 \right] ^{1/2} ~\times~ {1 \over r_{500} } \end{equation}](/articles/aa/full_html/2012/12/aa20267-12/aa20267-12-eq39.png) (5)where Δi is the distance between the mean centroid and the centroid of the ith aperture. We have decided to use the mean centroid value of all apertures as the reference centre. One finds that the variance, w, of the centre shift determined with Eq. (5) depends on the choice of the reference centre. Rather than using a reference centre determined in a completely different way – as in the case where the X-ray maximum is adopted for the reference centre – we prefer a reference centre obtained within our system of centre determinations. A logical choice is then to take the mean centre of all apertures as reference. Comparing this approach to the previously used X-ray maximum reference, we find that the new method yields on average slightly smaller w values. Consequently we find as described below smaller values of w for convenient boundaries between regular and disturbed clusters.
(5)where Δi is the distance between the mean centroid and the centroid of the ith aperture. We have decided to use the mean centroid value of all apertures as the reference centre. One finds that the variance, w, of the centre shift determined with Eq. (5) depends on the choice of the reference centre. Rather than using a reference centre determined in a completely different way – as in the case where the X-ray maximum is adopted for the reference centre – we prefer a reference centre obtained within our system of centre determinations. A logical choice is then to take the mean centre of all apertures as reference. Comparing this approach to the previously used X-ray maximum reference, we find that the new method yields on average slightly smaller w values. Consequently we find as described below smaller values of w for convenient boundaries between regular and disturbed clusters.
The uncertainties in the centre shifts and in the w parameter are determined with the same simulations as the uncertainties of the power ratios, i.e., by using Poissonised re-sampled cluster X-ray images. The standard deviation of the w parameter in the simulation is used as an estimate of the measurement uncertainties. We do not use the noise-bias subtracted w-parameter as in the case of the power ratios since the bias correction is mostly much smaller than the errors or the bias correction does not shift the w-parameter to alter the classification of the cluster morphology.
All error calculations for the power ratios and centre shifts properly include any correlations and systematics that may exist. This is ensured by the end-to-end Monte-Carlo simulations of the Poissonised data analysed exactly the same way as we calculate the power ratios and centre shifts with the original X-ray data.
4. Results
In the following we will use the average value of P3/P0 from all rings and the new definition for the w-parameter as our primary results for the discussion. The power ratios reported in the following are determined without core excision. All biases and errors resulted from one thousand simulations. Where power ratios fall below zero, we kept them at the left-most side of each plot truncating their lower error bars. Morphological parameters for individual clusters are listed in Table A.1 in the Appendix. Clusters are numerically labelled in descending order by the centre shift values in the legend of all figures. For convenience we abbreviate Pm/P0 as Pm for the rest of this paper except the figure axis labels. Throughout this paper we used r500 and M500 determined in Zhang et al. (2008) for the consistency.
4.1. Comparing power ratios and centre shifts
P3 is the first moment that contains information on deviations from azimuthal symmetry above a simple ellipticity. We therefore explore the w − P3 plane first, and subsequently inspect the P2 − P3 and P4 − P3 spaces to further investigate aspects of X-ray cluster morphology.
 |
Fig. 1 Centre shift and averaged P3 parameters. Clearly seen are the five most disturbed clusters in the upper right corner with the largest w and P3 values. The intermediate cases are bounded by the two vertical dashed lines below the horizontal line, and the regular clusters are located in the left lower corner. Clusters 3, 6, 7, and 10 have very low P3 values, however, they are classified as disturbed given the large centre shifts. In the same way 20, 24, 26, and 31 are disturbed due to their large P3 values. Clusters are numerically labelled by their w values in descending order. |
Figure 1 shows the w-parameter against the modified and normalised P3 for the sample as described in the previous section. The distribution of the substructure parameters is continuous as is the morphological appearance of clusters and there are no very obvious criteria to draw boundaries between different sub-classes of clusters. Indeed, detailed inspection of sensitive observations of any cluster reveals some asymmetric features, therefore it is problematic to classify a subset of clusters as (for example) completely “relaxed”. Nevertheless, to aide the discussion that follows, we sub-divide the clusters in our sample into three classes based on their locations in the w − P3 plane, as delineated by three gray dashed lines. First we draw attention to the five clusters in the upper right corner that have the largest centre shifts and P3 – these five include famous merging clusters such as the “Bullet cluster”, which is number 8 in our sample. However we use wider criteria to classify clusters as “disturbed”: w > 0.006 or P3 > 2 × 10-7, i.e. above the horizontal gray line and/or to the right of the right vertical gray line. Clusters in the lower left rectangle display the smallest centre shifts and lowest P3 – we classify clusters that satisfy w < 0.006 and P3 < 7 × 10-8 as having a “regular” X-ray morphology. Finally, we classify clusters in the lower narrow rectangle surrounded by the gray dashed lines as having an “intermediate” X-ray morphology – i.e. w < 0.006 and 7 × 10-8 < P3 < 2 × 10-7. The results on the classification are summarised in Table A.1 of the appendix. In summary we classify 8 clusters as regular, 11 clusters as intermediate, and 16 clusters as disturbed. We stress that this classification is not unique and clusters have a rather continuous distribution of morphologies. We have visually checked this classification scheme, and found it to give the most consistent picture in a comparison of the visual impression and the numerical classification compared to the studies described below.
 |
Fig. 2 Comparison of P3 calculated at r500, and averaged over the ten rings. A general linear correlation can be seen with some scatter as expected. These two ways of calculating P3 values classify a number of clusters differently, see text for details. |
To set this result using the radially averaged P3 value into perspective with previous results, we compare in Fig. 2 the average P3 result with the P3 values determined for the largest aperture, r500. We expect these values to be almost linearly correlated, except for those cases in which P3,r500 boosts a structure near the aperture radius or overlooks a structure in the central region. Indeed clusters 16, 21, 23, 29, 30, and 34 would have been identified as disturbed, and 13, 17, 24, and 27 as more regular if the traditional P3 value was adopted. On the other hand clusters 6 and 7 have much larger P3 evaluated at r500. They would have been identified as regular clusters based solely on the averaged P3, however, as seen in Fig. 1, our joint w − P3 classification identifies these clusters as disturbed systems.
 |
Fig. 3 Comparison of P3 parameters calculated with a linear weight in the radial direction to the averaged P3 over the ten rings. A similar trend is shown as in Fig. 2 with a tighter scatter. It shows that our modified P3 calculation is closer to a linear weighting in radius instead of rm. |
We also tested another approach to determine the hexapole moment P3. Assuming the surface brightness profile of a cluster falls with r-2 where the beta parameter is close to 0.5, and the area of a ring scales as Δ ∗ r, where Δ is a fixed increment such as 0.1 to 1, we find that a scaling proportional to r cancels both effects. Specifically P3 from the linear weighting in r from Eqs. (2)–(4) is shown in Fig. 3 compared to the average P3. One notes a clear linear correlation except cluster Nos. 6, 10, and 15, which, however, accompany very large uncertainties. P3 calculated by the traditional method represents mainly the asymmetries in the outskirts of clusters while the dynamical state near the core is almost ignored. A cluster with a merging event localised at the centre, for example, will not be identified as disturbed if the traditional method is used. In our new approach the averaged P3 can trace closely any distinct changes in the dynamical state in a nearly equal weight in r as seen in Fig. 3. Note that on average the absolute values of the different definitions of P3 are expected to change.
 |
Fig. 4 Comparison of the P2 and P3 parameters. Easily seen are the three disturbed clusters, 6, 7, and 10 in the top left corner flagged by large P2 values. |
 |
Fig. 5 Similarly P4 and P3 are compared. Cluster 7 is a clearly disturbed system as given by its P4 value although it has a a very low P3. |
Because the hexapole moments, P3, may not catch all forms of disturbed morphologies, as for example very elongated or bimodal merging clusters which are nearly axisymmetric, we also inspect the results of the quadrupole and octopole analysis P2 and P4. Figure 4 shows a diagram of the distribution of P2 and P3 values. While there is a good correlation of two parameters, we immediately recognise two outliers with low P3 and high P2 values, the cluster Nos. 6 and 7. Both are elongated merging clusters and both have already been flagged as disturbed by their high centre shift values, w. Cluster 10 is a similar less extreme case also flagged as disturbed by its w value.
Figure 5, which presents the distribution of P3 and P4 values shows again the clusters 6 and 7 with high P4 and low P3 values. Another cluster with a relatively high P4 value is cluster No. 3, again an object with a high w-parameter in Fig. 1.
 |
Fig. 6 Comparison of P2 and the ellipticity, ϵ, calculated from a fit of an elliptical β model to the X-ray image. The blue stars represent those classified as regular, the green diamonds the intermediate, and the disturbed clusters are marked by the red squares. This convention is carried throughout the paper. There is a positive correlation between two parameters. We note that there is a segregation effect which separates regular clusters from the intermediate and disturbed ones. |
In summary the inspection of the P2 and P4 parameters did not change our classification, rather reinforced our previous finding. To further explore the meaning of the P2 parameter, we also determined the ellipticity of the clusters in the X-ray images of the sample directly, which is defined by 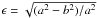 where a is the semi-major and b is the semi-minor axis of the fitted elliptical β surface brightness model. Figure 6 shows that there is a good correlation of ϵ and P2. According to the three morphological classes the clusters are colour (symbol)-coded as shown in Fig. 6. The blue stars are those classified as regular, the green diamonds represent the intermediate, and the disturbed clusters are marked by the red squares. This convention is carried through for the rest of the paper. We see a clear segregation of all regular clusters and one intermediate cluster having P2 values below ≈3 × 10-6 and the disturbed and all other intermediate clusters lying above this devision. For the ellipticity, ϵ, the trend is also there but the segregation is less strong. Figure 6 seems to give the strong implication that the quadrupole moments up to about P2 ≈ 3 × 10-6 refer mostly to nearly relaxed elliptical clusters, while larger values of P2 are caused by dynamical distortions of the clusters.
where a is the semi-major and b is the semi-minor axis of the fitted elliptical β surface brightness model. Figure 6 shows that there is a good correlation of ϵ and P2. According to the three morphological classes the clusters are colour (symbol)-coded as shown in Fig. 6. The blue stars are those classified as regular, the green diamonds represent the intermediate, and the disturbed clusters are marked by the red squares. This convention is carried through for the rest of the paper. We see a clear segregation of all regular clusters and one intermediate cluster having P2 values below ≈3 × 10-6 and the disturbed and all other intermediate clusters lying above this devision. For the ellipticity, ϵ, the trend is also there but the segregation is less strong. Figure 6 seems to give the strong implication that the quadrupole moments up to about P2 ≈ 3 × 10-6 refer mostly to nearly relaxed elliptical clusters, while larger values of P2 are caused by dynamical distortions of the clusters.
In Table 1 we list a number of the correlation coefficients for the most relevant cases in our paper with the Kendall and Spearman tests. We use the Astronomical Survival Statistics (ASURV, Isobe et al. 1986) package to calculate the correlations in the presence of censored data. The correlation for the w-P3 pair gives probabilities of 0.19 for no correlation according to Kendall’s τ, and 0.28 to Spearman’s ρ test. When we re-calculate this correlation excluding the clusters 3, 6, and 7 in Fig. 1, we obtain much smaller probabilities for no correlation, 0.006 for Kendall’s and 0.01 for Spearman’s tests giving stronger significance to the correlation. However, we emphasise that the morphological classification that we adopt in this paper relies on both w and P3 parameters as explained above, and the correlation found between these two parameters is not necessarily expected to be generalised without exceptions as demonstrated by clusters 3, 6, and 7.
The correlation coefficient for P2 and the X-ray ellipticity, ϵ is also shown in Table 1. It is one of the most tightly correlated relations confirming quantitatively our visual impression in Fig. 6. This relation gives vanishing probability for no correlation for both statistical tests.
Correlation coefficients measured for various cluster and substructure parameters.
4.2. Correlation of cluster cool-core parameters and morphology
We now compare our ranking of clusters based on measured substructure parameters with physical cluster parameters. First, we consider the existence of a cool core in the centres of clusters signified by a strong central density increase and a central temperature drop (e.g. Peterson & Fabian 2006; Hudson et al. 2010). In the X-ray surface brightness distribution a cool core shows up as a bright central cusp. Hence the ratio of the luminosity with and without the core can be used to divide the cluster sample into cool and non-cool core clusters.
We take the core-excised and core-included X-ray bolometric luminosity of the clusters from Zhang et al. (2008) where the core was defined by r < 0.2r500. Figure 7 shows the X-ray luminosity ratio against the core-excised X-ray luminosity. For the rest of the paper the luminosity ratio refers to the ratio of two luminosities determined with and without the core, 0.2r500. In addition, given the number statistics we group the regular and intermediate clusters together whenever a numerical evaluation is performed. The dashed line is the median of the luminosity ratio which divides the clusters roughly in two subsamples, the regular and disturbed systems with the intermediate in between. There is a clear trend that this division also separates regular and disturbed clusters. All regular clusters have large luminosity ratios, and the disturbed clusters have low values with two exceptions, Abell 1914 and Abell 2390. Abell 1914 falls somewhere in between intermediate and disturbed, and Abell 2390 is close to the boundary, but it is known to have a strong cool core (Böhringer et al. 1998).
 |
Fig. 7 Luminosity ratio as a function of the core-excised luminosity. A clear trend is shown with the horizontal line, which marks the median of the luminosity ratio where the regular clusters have a higher luminosity ratio compared to the disturbed. |
Figure 8 shows the correlations between the two structural parameters and the luminosity ratio. The upper panel shows the w-parameter against the luminosity ratio. Two dashed lines, which represent the median of the luminosity ratios and w values from Fig. 1, divide the clusters in two groups. Notably the regular clusters are confined in the quadrant with the largest luminosity ratios and smaller w. While the intermediate clusters are spread in between, two clusters, Abell 2390 and Abell 1914 are the exceptions to be cool-core clusters flagged as disturbed by the P3 parameter. A similar trend is shown in the lower panel of Fig. 8 for P3. Here four other clusters appear as exceptions, 3, 6, 7, and 10, which are not recognised as disturbed by P3 but are flagged as such by their w-parameters. The correlations for both cases are quantified in Table 1. w and luminosity ratio are tightly anti-correlated with zero probability of being uncorrelated. Its Kendall’s τ is 4.87, and Spearman’s ρ is −0.76. A similar anti-correlation is seen for the P3 and luminosity ratio pair with the probability of 0.01 and 0.03 to be uncorrelated. This null-probability shrinks by a factor of three if the three clusters, 3, 6, and 7 are excluded. Finally, we note that we obtain similar results if we adopt the central electron density as our measure of the cool-core strength instead of the luminosity ratio.
 |
Fig. 8 Structural parameters as a function of the luminosity ratio where a high luminosity ratio is an indicator of a cool core in the cluster. The regular clusters have the lowest w values, and the largest luminosity ratio as shown in the upper panel. This trend is repeated for P3 in the lower panel. |
5. Correlations with optical/near-infrared parameters
5.1. Comparison of luminosity gap with X-ray morphology
We now consider the so-called luminosity gap – i.e. the difference between the apparent magnitude of the BCG and the second BCG, denoted by Δm12 = m1 − m2. Smith et al. (2010) showed that clusters with dominant BCGs (Δm12 > 1) form a relatively homogeneous population of concentrated cool-core clusters with negligible substructure and an elliptical or disky BCG morphology. In contrast clusters with Δm12 < 1 form a heterogeneous population. In summary, Smith et al. interpreted their results as indicating that luminosity gap probes a combination of both the formation epoch and recent assembly history (i.e. last few Gyr – roughly one crossing timescale) of a cluster. Specifically, the homogeneity of clusters with dominant BCGs suggests that such clusters formed relatively early and have not suffered significant in-fall recently. Such clusters would be expected to have relatively undisturbed X-ray morphologies, likely residing in the regular category discussed above.
To test Smith et al.’s interpretation we compare the X-ray morphologies that we measure in this article with luminosity gap measurements for the 26 clusters in common between the respective samples. Figure 9 shows that the four clusters with the most dominant BCGs (Δm12 > 1.7) have exclusively low hexapole moments (P3 ≤ 10-7) and are classified exclusively as having regular/intermediate X-ray morphology. At less extreme luminosity gap the picture is less clear-cut, with clusters at Δm12 > 1 including a few disturbed systems, albeit at P3 ~ 10-7−4 × 10-7. Clusters with low luminosity gaps (Δm12 < 1) have the full range of hexapole moments seen in the present sample. These results are consistent with Smith et al.’s interpretation, although some of the detailed differences (e.g. the disturbed X-ray morphology of some clusters with Δm12 > 1) is likely due to the differences between the apertures within which the respective measurements are made. Specifically, the field of view of Smith et al.’s data necessitated measuring Δm12 within a fixed physical radius of 640 kpc at each cluster redshift, in contrast to the mean measurements of P3 plotted in Fig. 9. To quantify this seemingly weak correlation we calculated the correlation coefficients in Table 1. Kendall’s τ coefficient is 1.1 with the null probability of 0.26 and Spearman’s ρ test gives −0.19 with 0.35 when including all data points. The correlation becomes much tighter without those three corresponding clusters, which were excluded for other correlation calculations. The null probability for Kendall’s τ is ten times smaller, 0.02 while that for Spearman’s ρ test is 0.04. A detailed investigation of optical and X-ray cluster morphology will be presented in a separate article.
 |
Fig. 9 Luminosity gap compared to P3. In total there are 26 clusters whose luminosity gap data is available. Clusters with large luminosity gaps are a relatively homogeneous population of clusters with regular/intermediate X-ray morphology, with clusters that host less dominant BCGs presenting a wider range of X-ray morphology including the most extreme disturbed morphologies. |
5.2. Comparison of BCG ellipticity with X-ray morphology
Previous studies have shown that the orientation of most BCGs is roughly aligned with the elongation of the cluster X-ray emission, and thus with the elongation of the cluster mass distribution under the assumption that clusters are in approximate hydrostatic equilibrium (e.g. Böhringer et al. 1997; Hashimoto et al. 2008). The latter found a strong indication of an alignment between the cluster X-ray emission and BCGs, while no clear direct correlation between the ellipticity of X-ray and BCG was detected. Their sample includes a wide range of observational parameters in exposure times, redshift and fluxes, which may result in a much wider range of image quality. More recently Marrone et al. (2012) have pointed out that the interpretation of BCG ellipticity is likely more subtle, in that clusters hosting relatively circular (ϵ < 0.2) BCGs may be elongated clusters that are observed along a line of sight close to the major axis of an underlying prolate mass and gas distribution.
In our study as shown in Fig. 6 we found a close correlation of the ellipticity of the X-ray emitting gas and the power ratio parameter, P2. We therefore extend this comparison by plotting in Fig. 10 the ellipticity of the BCG to the cluster P2 parameter for a subsample of 18 clusters for which BCG ellipticity measurements are available (Marrone et al. 2012). We also show in Fig. 10 a comparison of the BCG ellipticity with the X-ray ellipticity directly.
In both comparisons we find a clear correlation with a larger scatter for the cluster ellipticity measurements than for the P2 parameter. Quantitatively we show the correlations measured for both cases in Table 1. A Kendall’s τ test gives a probability of no correlation of 0.6%, and similarly for a Spearman rank test in the case of the BCG ellipticity and P2 parameter. The correlation is slightly decreased for the BCG ellipticity and the X-ray ellipticity where the null-probability increases by a factor of 1.6 and 1.3, which still means 1% of no correlation. Therefore an inspection of the upper panel of Fig. 10 is showing two effects: BCGs with small ellipticities are living in clusters with small elongations and also in the most regular clusters. Interestingly the clusters hosting the BCGs with the largest ellipticities are classified as intermediate. These are the clusters with moderately large P3 values and small centre shifts. A closer look at the 4 clusters at the top of the BCG ellipticity distributions shows that the host clusters are not very much disturbed but rather elongated (elliptical). This raises the question what role line-of-sight projections play in this effect. As suggested by Marrone et al. (2012), BCGs and clusters with low ellipticities in projection could also imply prolate objects oriented with the major axis along the line-of-sight. In this case the BCG or cluster ellipticity could help to reveal the three-dimensional orientation. A detailed investigation of the degeneracy between cluster orientation and the underlying structure of clusters is beyond the scope of this article, and will be visited in a future publication.
Results of the fitted scaling relations.
 |
Fig. 10 Comparison of the BCG ellipticity and the P2 parameter for the clusters in the upper panel, and the cluster ellipticity in the lower panel. The cluster ellipticities were determined from the X-ray data as shown in Fig. 6, and the BCG ellipticities by Marrone et al. (2012). |
6. Influence of substructure on scaling relations
As outlined in the introduction, one of the main applications of the substructure analysis is the study of the influence of substructure on the scaling relations of X-ray observables and cluster mass. Previous studies of such scaling relations have used a variety of methods to classify clusters, including the presence/absence of a cool core, X-ray centroid shift, concentration and asymmetry parameters, and offset between X-ray centroid and BCG. Here we consider the location of our classes of regular/intermediate and disturbed clusters, as determined from our w − P3 classification in the parameter planes of the LX − T and MX − T relations, to study the power of the method by the significance with which it reveals morphological segregation effects in these relations.
We model the scaling relation between the bolometric luminosity and temperature for 35 clusters by L/L0 = B(T/T0)A where L0 = 1045 erg/s, and T0=7 keV. We assume that the LX − T relation is non-evolving (see Böhringer et al. 2012), and do not use a self-similar evolution. The luminosities used here are the values from Zhang et al. (2008) without the cool-core correction, and the temperatures used refer to the volume-averaged results. It is known that different fitting methods give very different results. We give the fitting results from BCES(Y|X) (Akritas & Bershady 1996) in Table 2. Okabe et al. (2010b) noted that their results are very close to the results from the bisector, and we give also these results by using the bisector fit in Table 2.
Our finding is shown in Fig. 11. The best-fit for all 35 clusters is shown as the black solid line. We divide the clusters into two morphological groups, the regular and the intermediate together, and the irregular clusters. The former consists of 19, and the latter 16 which divide the clusters into two groups of similar size. The blue dashed line in Fig. 11 is the best fit for regular/intermediate clusters, and the red dashed line is for the irregular clusters. In both cases we fix the slope to the best fit for 35 clusters, and only fit for the normalisations. We see a trend that the more regular clusters have a higher, and the disturbed clusters have a lower normalisation, both with 9–10σ significance. In the presence of cool cores one expects and has previously observed such a trend as cool cores boost the luminosity (e.g. Fabian et al. 1994; Chen et al. 2007; Pratt et al. 2009), and cool cores are more frequent among the more regular clusters (Fig. 8 of Böhringer et al. 2010). This is why the trend is found with a high significance since the X-ray luminosity fitted here includes the cool core. We calculated the intrinsic scatter by the quadratic difference between the scatter from the data and that expected from the statistical measurement uncertainties with results listed in Table 2. This quantity should, however, be taken with a caution since the measurement error includes systematics which can not be corrected for in this type of calculation.
 |
Fig. 11 LX − T relation with the fitted results from the BCES(Y|X) method. The black solid line is the best fit for all 35 clusters, the blue dashed line is that for the regular and the intermediate clusters, and the red dashed line for the disturbed clusters. The fitted normalisations for the two sub-groups in blue and red move to the opposite directions from the best fit found for all clusters. The numbering of the clusters follows that of Fig. 1. |
 |
Fig. 12 MX − T relation with the fitted results from the bisector method. The fitted lines follow the same notation as in Fig. 11. The two morphological groups move to the opposite sides from the best-fit of the 35 clusters. Disturbed clusters appear slightly more massive for a given temperature. |
We show the scaling relation of MX − T with the best fitting model function in Fig. 12. The cluster masses are taken from Zhang et al. (2008), which were determined from the temperature and density profiles derived from X-ray observations on the assumption of hydrostatic equilibrium and spherical symmetry. We model the relation by M/M0E(z) = B(T/T0)A where M0 = 6 × 1014 M⊙ and T0 = 7 keV, and assume self-similar evolution. The results are given in Table 1 and Fig. 12, where the notation is the same as in Fig. 11. When we fit the more regular and disturbed subsamples separately with the slope fixed to that of the total sample, we find a significantly higher normalisation of the mass for a given temperature for the disturbed clusters. The offset from the fit of the total sample is roughly 11% (− 8.5%) for the disturbed (more regular) clusters. The offset could possibly come from the fact that some of the energy in the ICM is in the form of kinetic energy of internal motions which will subsequently be converted to heat when the cluster relaxes. A substantial amount of turbulent energy is seen in post-merger clusters in, for example, the observations of the Coma cluster (Schuecker et al. 2004) and in simulations (Sunyaev et al. 2003). Thus in the relaxed phase the cluster would have a higher temperature for a given mass. Alternatively the effect could come from an overestimation of the cluster mass. The distortions of the cluster as seen in the surface brightness distribution most often lead to azimuthally averaged surface brightness and gas density profiles with an extended core and steeper outer slope, both of which yield an increase in the mass determination using spherical symmetry. To further investigate if this interpretation is likely we also studied the Mgas − T relation for these clusters. For the Mgas − T relation we find offsets of similar sign as for MX, but the offsets are less than 1%, much smaller than for MX. As Mgas is a quantity that results from an integration over the gas density profile and not just from the slope at r500 as MX, it is less prone to be affected by substructure. We therefore conclude that most likely the major part of the effect of disturbed clusters in the MX − T relation come from a mass overestimation due to the assumption of hydrostatic equilibrium and spherical symmetry.
 |
Fig. 13 Ratio of the weak-lensing and X-ray determined masses as a function of the weak-lensing mass estimates. Morphologically disturbed clusters have the largest scatter compared to more regular clusters. |
A subsample of twelve clusters was previously analysed using the weak-lensing and X-ray data by Okabe et al. (2010a,b) and Zhang et al. (2010) defined by the overlapping sample between Subaru/Suprim-Cam and XMM-Newton observations in LoCuSS. In this section we study the correlation between the X-ray morphologies presented in this article, based on w − P3, and the degree of agreement in the mass estimation in the two different wavelengths. Our analysis contains currently eleven clusters which excludes Abell 115 for the reason explained above, and all mass estimates are taken at r500. A first look at the mass estimate comparison for clusters classified in the w − P3 plane is provided in Fig. 13. We find that disturbed clusters present larger scatter in the mass comparison than regular/intermediate clusters. With a slight difference in classification for individual clusters this result is in line with Zhang et al. where the X-ray morphology was determined by concentration and asymmetry parameters given in Okabe et al. This probably reflects the fact that mass determination is more difficult for those disturbed clusters.
7. Summary and conclusions
For the XMM-Newton observations of the 35 X-ray luminous galaxy clusters we characterised the X-ray morphologies with the modified power ratio and the centre shift method. The first moment that can consistently describe the degree of departures from the symmetry is the P3, and together with the w-parameter we categorised the clusters into three groups as regular, intermediate, and disturbed after checking the consistency with other power ratio parameters. We caution readers that this division is not unique and discrete, while the distribution of parameters is rather continuous as was seen in Sect. 4.1. Nevertheless this classification also agrees with the visual impression of the X-ray images and known properties of the clusters, and helps to simplify the presentation of results.
Having a reliable description of the cluster morphology in hand, we investigated the correlations of different cluster morphologies with a number of cluster physical parameters. We took the X-ray luminosity ratio between the core-included and the core-excised cases where a high luminosity ratio is an indicator of a cool core in the cluster, and compared to our representative structural parameters, P3 and w. Consistent with the earlier results in Böhringer et al. (2010) we found that regular clusters have a larger luminosity ratio compared to the morphologically disturbed clusters. This is also confirmed by comparing the luminosity ratio to the P3 and w parameters, where larger luminosity ratios are associated to low w and P3. This result implies the known fact that cool cores are much more frequent in regular clusters, and are rarely found in very disturbed systems. This applies similarly to the central electron density, where we expect that more X-ray emitting gas is concentrated at the centre of the cool-core clusters.
Another interesting aspect studied was the comparison of the optical and X-ray morphology. The luminosity gap between the BCG and the second ranked cluster galaxy was compared with P3, and the general trend was found that the clusters with the most dominant BCGs form a relatively homogeneous population of regular/intermediate systems. In contrast, clusters with less dominant BCGs present a more heterogeneous range of X-ray morphologies including the most disturbed. These results are consistent with the picture that the BCG dominance probes a combination of cluster formation epoch and the time interval since the last episode of major hierarchical infall into the cluster potential well (Smith et al. 2010). Clusters that host dominant BCGs formed relatively early, and have suffered negligible recent infall. This allows the bright galaxies to suffer dynamical friction and to merge to form a bright BCG, and the X-ray gas to settle down into a regular morphology. On the other hand clusters with less dominant BCGs either formed more recently, or formed relatively early but have suffered more significant recent infall than their cousins that host a dominant BCG.
We also compared our X-ray morphological analysis with the surface photometry of the relevant BCGs, specifically the ellipticity of these galaxies measured in projection on the sky. In general we find a good correlation between the BCG ellipticity and the quadrupole moment of the X-ray surface brightness distribution, and a similar correlation with larger scatter between BCG ellipticity and the X-ray ellipticity. We thus find that the clusters that host relatively circular BCGs (ϵBCG < 0.2) have exclusively small quadrupole moments and X-ray ellipticity. This is consistent with the suggestion by Marrone et al. (2012) that BCG ellipticity may be a useful indicator of orientation of the underlying dark matter distribution of a cluster, with respect to the observer’s line of sight where a small ellipticity is partly the result of the line-of-sight orientation of a prolate cluster and its BCG.
Finally, we examined the dependence of cluster locations in the LX − T and MX − T planes on their X-ray morphology, as determined by our w − P3 classification, and also how well X-ray and lensing cluster mass estimates agree as a function of X-ray morphology. All three of these tests are based on previous published measurements of LX,T,MX, and MWL, and can thus serve for consistency checks between our morphological analysis and complementary methods in the literature as well as for the study of new morphological diagnostics. We find that on average regular/intermediate clusters are separated from disturbed clusters in the LX − T plane, with the former 17% more luminous than the latter at fixed temperature, at ~9−10σ significance. We stress that this result is based on LX and T measurements that do not excise the core of each cluster. This result therefore demonstrates the strong relationship between cooling timescale in cluster cores and the location of clusters in the w − P3 plane. In our study of the MX − T relation we find that disturbed clusters have a higher mass by ~11% for a given temperature than the overall average. We tentatively attribute most of this effect to an overestimation of the mass for disturbed clusters, since the corresponding Mgas − T relation does not show such a strong segregation. We also find that disturbed clusters present larger scatter than regular/intermediate clusters in the comparison on X-ray and lensing-based cluster mass estimates, although the current sample is not large enough to draw definitive conclusions.
In summary, this study together with our previous work for the REXCESS cluster sample (Böhringer et al. 2010) has shown that the morphological classification of galaxy clusters by power ratios and centre shifts provides an effective tool to analyse the influence of morphology on other properties of galaxy clusters. We have demonstrated that these techniques can be used to probe cluster morphology in a manner that correlates well with other physical cluster properties, both at X-ray and optical/near-infrared wavelengths. They therefore offer a promising route to the morphological analysis of larger, more complete samples that will form the basis of the cosmological interpretation of upcoming large cluster samples from eROSITA, and EUCLID.
Acknowledgments
H.B. acknowledge support by the cluster of excellence “Origin and Structure of the Universe” (www.universe-cluser.de). H.B. and G.C. acknowledge support from the DfG Transregio Program TR 33. G.C. acknowledges the support from Deutsches Zentrum für Luft und Raumfahrt (DLR) with the program ID 50 R 1004. G.P.S. acknowledges support from the Royal Society, and thanks his colleagues in the LoCuSS collaboration for helpful discussions.
References
- Abell, G. O. 1958, ApJS, 3, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeau, S., Soucail, G., Kneib, J.-P., et al. 2007, A&A, 470, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrena, R., Boschin, W., Girardi, M., et al. 2007, A&A, 469, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H. 2008, in The Universe in X-rays, eds. J. E. Trümper, & G. Hasinger (Springer), 395 [Google Scholar]
- Böhringer, H. 2011, AIP Conf. Proc., 1381, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Tanaka, Y., & Mushotzky, R. F. 1998, A&A, 334, 789 [NASA ADS] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2001, A&A, 369, 826 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Pratt, G. W., & Arnaud, M. 2010, A&A, 514, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Dolag, K., & Chon, G. 2012, A&A, 539, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buote, D. A., & Tsai, J. C. 1995, ApJ, 452, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A., & Tsai, J. C. 1996, ApJ, 458, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Reiprich, T. H., Böhringer, H., et al. 2007, A&A, 466, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Crawford, C. S., Edge, A. C., et al. 1994, MNRAS, 267, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, M. E., Taylor, A. N., Meisenheimer, K., et al. 2002, ApJ, 568, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Gutierrez, K. & Krawczynski, H. 2005, ApJ, 619, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Hashimoto, Y., Henry, J. P., & Böhringer, H. 2008, MNRAS, 390, 1562 [NASA ADS] [Google Scholar]
- Hoekstra, H. 2007, MNRAS, 379, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, D. S., Mittal, R., & Reiprich, T. H. 2010, A&A, 513, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isobe, T., Feigelson, E. D., & Nelson, P. I. 1986, ApJ, 306, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Jeltema, T. E., Canizares, C. R., Bautz, M. W., et al. 2005, ApJ, 624, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Jeltema, T. E., Hallman, E. J., Burns, J. O., & Motl, P. M. 2008, ApJ, 681, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Vkhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Leauthaud, A., Finoguenov, A., Kneib, J.-P., et al. 2010, ApJ, 709, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., et al. 2008, MNRAS, 384, 1567 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, D. P., Smith, G., Okabe, N., et al. 2012, ApJ, 754, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Mohr, J. J., Fabricant, D. G., & Geller, M. J. 1993, ApJ, 413, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Mohr, J. J., Evrard, A. E., Fabricant, D. G., & Geller, M. J. 1995, ApJ, 447, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J., Frenk, C. S., & White, S. D. M. 1995, MNRAS, 274, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Takada, M., Okabe, N., & Smith, G. 2010, MNRAS, 405, 2215 [NASA ADS] [Google Scholar]
- O’Hara, T. B., Mohr, J. J., Bialek, J. J., & Evrard, A. E. 2006, ApJ, 639, 64O [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., Takada, M., Umetsu, K., et al. 2010a, PASJ, 62, 811 [NASA ADS] [Google Scholar]
- Okabe, N., Zhang, Y.-Y., Finoguenov, A., et al. 2010b, ApJ, 721, 8750 [NASA ADS] [CrossRef] [Google Scholar]
- Pedersen, K., & Dahle, H. 2007, ApJ, 667, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, J. R., & Fabian, A. C. 2006, Phys. Rep., 427, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Poole, G. B., Fardal, M. A., Babul, A., et al. 2006, MNRAS, 373, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Pratt, G. W., Böhringer, H., Croston, J. H., et al. 2007, A&A, 461, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Böhringer, H. 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Schuecker, P., Böhringer, H., Reiprich, T. H., & Feretti, L. 2001, A&A, 378, 408 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuecker, P., Böhringer, H., Collins, C. A., & Guzzo, L. 2003a, A&A, 398, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuecker, P., Caldwell, R. R., Böhringer, H., et al. 2003b, A&A, 402, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuecker, P., Finoguenov, A., Böhringer, H., et al. 2004, A&A, 426, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, G. P., Kneib, J.-P., Smail, I., et al. 2005, MNRAS, 359, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G. P., Khosroshahi, H. G., Dariush, A., et al. 2010, MNRAS, 509, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., Norma, M. L., & Bryan, G. L. 2003, Astron. Lett., 29, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Trümper, J. 1993, Science, 260, 1769 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Valdarnini, R. 2006, New Astron., 12, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Ventimiglia, D. A., Voit, G. M., Donahue, M., & Ameglio, S. 2008, ApJ, 685, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y.-Y., Finoguenov, A., Böhringer, H., et al. 2008, A&A, 482, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y-Y., Okabe, N., Finoguenov, A., et al. 2010, ApJ, 711, 1033 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Morphological parameters for individual clusters
In Table A.1 we provide the results for the morphological parameters, power ratios, and centre shifts for the individual clusters in our study sample. We also indicate the morphological type from our classification based on both w and P3 as described in Sect. 4.1.
Morphological classification of the 35 clusters in our sample according to the revised centre shift and power ratios.
All Tables
Correlation coefficients measured for various cluster and substructure parameters.
Morphological classification of the 35 clusters in our sample according to the revised centre shift and power ratios.
All Figures
 |
Fig. 1 Centre shift and averaged P3 parameters. Clearly seen are the five most disturbed clusters in the upper right corner with the largest w and P3 values. The intermediate cases are bounded by the two vertical dashed lines below the horizontal line, and the regular clusters are located in the left lower corner. Clusters 3, 6, 7, and 10 have very low P3 values, however, they are classified as disturbed given the large centre shifts. In the same way 20, 24, 26, and 31 are disturbed due to their large P3 values. Clusters are numerically labelled by their w values in descending order. |
| In the text | |
 |
Fig. 2 Comparison of P3 calculated at r500, and averaged over the ten rings. A general linear correlation can be seen with some scatter as expected. These two ways of calculating P3 values classify a number of clusters differently, see text for details. |
| In the text | |
 |
Fig. 3 Comparison of P3 parameters calculated with a linear weight in the radial direction to the averaged P3 over the ten rings. A similar trend is shown as in Fig. 2 with a tighter scatter. It shows that our modified P3 calculation is closer to a linear weighting in radius instead of rm. |
| In the text | |
 |
Fig. 4 Comparison of the P2 and P3 parameters. Easily seen are the three disturbed clusters, 6, 7, and 10 in the top left corner flagged by large P2 values. |
| In the text | |
 |
Fig. 5 Similarly P4 and P3 are compared. Cluster 7 is a clearly disturbed system as given by its P4 value although it has a a very low P3. |
| In the text | |
 |
Fig. 6 Comparison of P2 and the ellipticity, ϵ, calculated from a fit of an elliptical β model to the X-ray image. The blue stars represent those classified as regular, the green diamonds the intermediate, and the disturbed clusters are marked by the red squares. This convention is carried throughout the paper. There is a positive correlation between two parameters. We note that there is a segregation effect which separates regular clusters from the intermediate and disturbed ones. |
| In the text | |
 |
Fig. 7 Luminosity ratio as a function of the core-excised luminosity. A clear trend is shown with the horizontal line, which marks the median of the luminosity ratio where the regular clusters have a higher luminosity ratio compared to the disturbed. |
| In the text | |
 |
Fig. 8 Structural parameters as a function of the luminosity ratio where a high luminosity ratio is an indicator of a cool core in the cluster. The regular clusters have the lowest w values, and the largest luminosity ratio as shown in the upper panel. This trend is repeated for P3 in the lower panel. |
| In the text | |
 |
Fig. 9 Luminosity gap compared to P3. In total there are 26 clusters whose luminosity gap data is available. Clusters with large luminosity gaps are a relatively homogeneous population of clusters with regular/intermediate X-ray morphology, with clusters that host less dominant BCGs presenting a wider range of X-ray morphology including the most extreme disturbed morphologies. |
| In the text | |
 |
Fig. 10 Comparison of the BCG ellipticity and the P2 parameter for the clusters in the upper panel, and the cluster ellipticity in the lower panel. The cluster ellipticities were determined from the X-ray data as shown in Fig. 6, and the BCG ellipticities by Marrone et al. (2012). |
| In the text | |
 |
Fig. 11 LX − T relation with the fitted results from the BCES(Y|X) method. The black solid line is the best fit for all 35 clusters, the blue dashed line is that for the regular and the intermediate clusters, and the red dashed line for the disturbed clusters. The fitted normalisations for the two sub-groups in blue and red move to the opposite directions from the best fit found for all clusters. The numbering of the clusters follows that of Fig. 1. |
| In the text | |
 |
Fig. 12 MX − T relation with the fitted results from the bisector method. The fitted lines follow the same notation as in Fig. 11. The two morphological groups move to the opposite sides from the best-fit of the 35 clusters. Disturbed clusters appear slightly more massive for a given temperature. |
| In the text | |
 |
Fig. 13 Ratio of the weak-lensing and X-ray determined masses as a function of the weak-lensing mass estimates. Morphologically disturbed clusters have the largest scatter compared to more regular clusters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


