| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 15 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201220183 | |
| Published online | 30 November 2012 | |
ArtDeco: a beam-deconvolution code for absolute cosmic microwave background measurements⋆
1
University of HelsinkiDepartment of Physics,
PO Box 64
00014,
Helsinki
Finland
e-mail: elina.keihanen@helsinki.fi
2
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741
Garching,
Germany
e-mail: martin@mpa-garching.mpg.de
Received:
7
August
2012
Accepted:
10
October
2012
We present a method for beam-deconvolving cosmic microwave background (CMB) anisotropy measurements. The code takes as input the time-ordered data along with the corresponding detector pointings and known beam shapes, and produces as output the harmonic aTlm, aElm, and aBlm coefficients of the observed sky. From these one can derive temperature and Q and U polarisation maps. The method is applicable to absolute CMB measurements with wide sky coverage, and is independent of the scanning strategy. We tested the code with extensive simulations, mimicking the resolution and data volume of Planck 30 GHz and 70 GHz channels, but with exaggerated beam asymmetry. We applied it to multipoles up to l = 1700 and examined the results in both pixel space and harmonic space. We also tested the method in presence of white noise.
Key words: cosmic background radiation / methods: data analysis / methods: numerical
The code is released under the terms of the GNU General Public License and can be obtained from http://sourceforge.net/projects/art-deco/
© ESO, 2012
1. Introduction
Removing systematic effects plays an important role in the data analysis of modern high-sensitivity cosmic microwave background (CMB) experiments, such as the WMAP and Planck missions (Jarosik et al. 2011; Tauber et al. 2010). In this work we concentrate on one source of systematic effects, the beam asymmetry. We present an efficient beam deconvolution code, called artDeco. It can be applied to any absolute CMB experiment with sufficient sky coverage.
The required input consists of the time-ordered data (TOD), the corresponding detector pointings, and known beam shapes. The primary output of the code consists of the harmonic aTlm, aElm, and aBlm coefficients of the sky. From these one can derive temperature and Q and U polarisation maps.
This is the usual deconvolution map-making problem (see, e.g., Armitage & Wandelt 2004; Armitage-Caplan & Wandelt 2009; Harrison et al. 2011). Our method differs from the earlier works by an efficient reformulation of the deconvolution problem through heavy use of Wigner functions. The formulation is general and makes no assumptions on the scanning pattern. Similar ideas have been studied by Prézeau, independently of us (priv. comm.).
In the CMB literature the concept of map-making often refers to a procedure that involves removal of correlated noise. Methods for doing this have been treated in several papers (Keihänen et al. 2005, 2010; Poutanen et al. 2006; Ashdown et al. 2007a,b; Kurki-Suonio et al. 2009; Sutton et al. 2009). The methods discussed in these works construct pixelised temperature and Q, U polarisation maps, but do not attempt to correct for an asymmetric beam shape.
Our method steps in at the point where the correlated noise has already been cleaned from the data. The input TOD is assumed to include signal and uncorrelated noise only. We are assuming here that the correlated noise component can be removed from the data to a sufficient degree prior to the beam deconvolution step. The noise removal step itself is affected by beam asymmetries because signal differences caused by beam mismatch can be falsely interpreted as noise. Fortunately, in destriping methods it is possible to strongly reduce this effect by masking out the regions with the strongest foreground contamination that generate most of the effect. Also, destriping methods produce as natural output the noise-cleaned TOD, which is the required input in deconvolution map-making. Accordingly, destriping methods are the natural counterparts of our deconvolution method.
Since the aim of this paper is to present a new deconvolution method, rather than assess the performance of any particular instrument, we tested the code with a somewhat idealised simulation. In particular, we ignored other systematic effects such as frequency response. On the other hand, we chose strongly asymmetric beam shapes to show the beam effects more clearly.
2. Beam deconvolution
2.1. Constructing the linear system
In this section we present the deconvolution problem using a formalism based on Wigner functions. We write the solution in a form that allows us to solve the problem numerically in an efficient way. Some details are left for Appendix A.
We start by writing the signal tj received
by a detector at a given time τj as
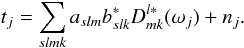 (1)The
aslm (s = 0, ± 2) are
harmonic coefficients that represent temperature and polarisation of the sky signal,
bslk are corresponding beam coefficients,
nj represents noise, and
(1)The
aslm (s = 0, ± 2) are
harmonic coefficients that represent temperature and polarisation of the sky signal,
bslk are corresponding beam coefficients,
nj represents noise, and
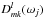 is a Wigner function that
defines a rotation of the beam from a fiducial orientation at the north pole to its actual
position and orientation. For exact definitions, see Appendix A.
is a Wigner function that
defines a rotation of the beam from a fiducial orientation at the north pole to its actual
position and orientation. For exact definitions, see Appendix A.
We have adopted a compact notation where ωj denotes a combination of three angles { φj,θj,ψj } , which define the detector’s orientation. Angles θj and φj define a point on the celestial sphere, and ψj defines the beam orientation. The angles can be interpreted as Euler rotation angles.
We perform a simple linear least-squares fit of aslm to the data up to some multipole lmax.
In general, a linear least-squares fit leads to an equation of the form
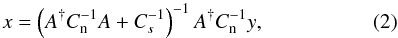 (2)where
x is the vector of unknowns, y is the data vector,
Cn is noise covariance, and
Cs represents a priori information on the
covariance of x (Wiener 1949).
Matrix A relates the unknowns to the data through
(2)where
x is the vector of unknowns, y is the data vector,
Cn is noise covariance, and
Cs represents a priori information on the
covariance of x (Wiener 1949).
Matrix A relates the unknowns to the data through
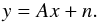 (3)In the present case
matrix A is
(3)In the present case
matrix A is 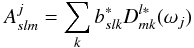 (4)and x
represents aslm.
(4)and x
represents aslm.
We made two simplifying assumptions, which are not of fundamental nature, however.
Firstly, we assume the noise is white with constant variance, and assign equal weights to
all samples j. Secondly, we use no a priori information on the sky
signal, i.e. the harmonic coefficients are assumed to be uncorrelated and can host a
signal of infinite variance. Under these assumptions the covariance matrices drop out of
the equation (Cn = const.,
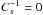 ). The least-squares solution
for aslm is obtained by solving the linear
system of equations
). The least-squares solution
for aslm is obtained by solving the linear
system of equations 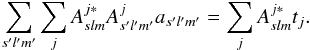 (5)In the following we
process Eq. (5) further to bring it into a
form where it can be solved in an efficient way. We treat the right- and left-hand sides
separately.
(5)In the following we
process Eq. (5) further to bring it into a
form where it can be solved in an efficient way. We treat the right- and left-hand sides
separately.
2.1.1. Right-hand side
The right-hand side yields 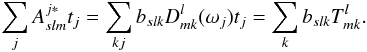 (6)Here we define
(6)Here we define
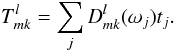 (7)The triplets
ωj = { φj,θj,ψj }
define the detector orientation and are provided as input to the code. To numerically
evaluate the transform, we replace the sum over TOD samples by a sum over a
three-dimensional (3D) grid as follows. We divide the space spanned by all possible
triplets ω = { φ,θ,ψ } into bins of equal volume and
denote by t(ω) the sum of values
tj falling into one bin. In
θ,φ we use HEALPix1 pixelisation
(Górski et al. 2005), and in ψ
we divide the space uniformly. Most elements of t(ω)
are zero, since a particular HEALPix pixel is typically observed only in a few
orientations of the beam.
(7)The triplets
ωj = { φj,θj,ψj }
define the detector orientation and are provided as input to the code. To numerically
evaluate the transform, we replace the sum over TOD samples by a sum over a
three-dimensional (3D) grid as follows. We divide the space spanned by all possible
triplets ω = { φ,θ,ψ } into bins of equal volume and
denote by t(ω) the sum of values
tj falling into one bin. In
θ,φ we use HEALPix1 pixelisation
(Górski et al. 2005), and in ψ
we divide the space uniformly. Most elements of t(ω)
are zero, since a particular HEALPix pixel is typically observed only in a few
orientations of the beam.
We call quantity t(ω) the 3D signal
map, and quantity 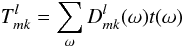 (8)the
Wigner transform of the signal map.
(8)the
Wigner transform of the signal map.
Here ∑ ω denotes a sum over all bins. Since most bins are empty, the sum needs to be carried out only over a subset of all ω values. Expansion (8)can be evaluated numerically quite efficiently using fast Fourier transforms (FFTs) and fast algorithms for the generation of Wigner functions.
Quantities t(ω) and
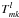 carry no
memory of the order in which the sky was scanned. They just record which pixels of the
sky were observed in which orientation of the beam.
carry no
memory of the order in which the sky was scanned. They just record which pixels of the
sky were observed in which orientation of the beam.
2.1.2. Left-hand side
Consider then the matrix on the left-hand side of Eq. (5), 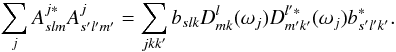 (9)The multiplier
matrix is too large to be inverted. Instead, we use the conjugate gradient (CG)
iteration method to solve Eq. (5).
(9)The multiplier
matrix is too large to be inverted. Instead, we use the conjugate gradient (CG)
iteration method to solve Eq. (5).
We pixelise the 3D pointing space in the same way we did with the signal, and denote by n(ω) the number of hits into bin ω. In line with the definition of the 3D signal map, we call n(ω) the 3D hit map.
We replace the sum over samples j by a sum over bins and write
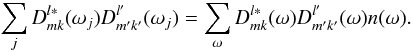 (10)As the next step, we
write the Wigner functions as
(10)As the next step, we
write the Wigner functions as 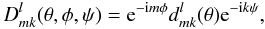 (11)where
(11)where
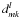 are the
reduced Wigner functions. Inserting this into (10), we obtain
are the
reduced Wigner functions. Inserting this into (10), we obtain 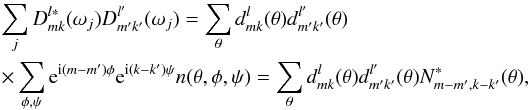 (12)where
we have defined
(12)where
we have defined 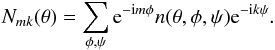 (13)The sums over
θ,φ,ψ are carried out over 3D bins. Substituting this back into
(9)and rearranging, we bring the
left-hand side of the deconvolution equation into the form
(13)The sums over
θ,φ,ψ are carried out over 3D bins. Substituting this back into
(9)and rearranging, we bring the
left-hand side of the deconvolution equation into the form 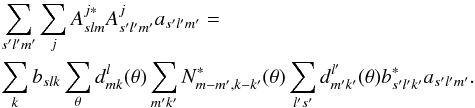 (14)This
can be evaluated much more quickly than the original formula (9), since the summation over the long TOD
vector has been replaced by an operation on the more compact N object.
Also, the convolution operations in indices k and m
can be carried out efficiently with FFTs.
(14)This
can be evaluated much more quickly than the original formula (9), since the summation over the long TOD
vector has been replaced by an operation on the more compact N object.
Also, the convolution operations in indices k and m
can be carried out efficiently with FFTs.
The terms are written in the order in which they are applied in the code.
2.2. Formulation through 3j coefficients and preconditioner
Equation (9)can be written in a yet more compact form.
The product of two Wigner functions can be expressed in terms of 3j
symbols (Appendix A.3) as
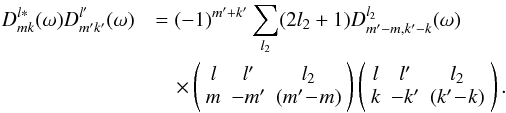 (15)Substituting
this into (10)and that into (9), we arrive at the formula
(15)Substituting
this into (10)and that into (9), we arrive at the formula 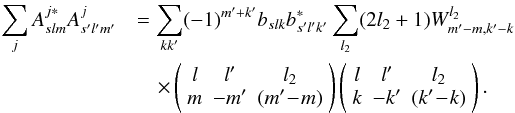 (16)Indices
l and l′ run from 0 to
lmax. The sum over l2 covers the
values for which
|l − l′| ≤ l2 ≤ l + l′.
We have defined the Wigner transform of the hit map as
(16)Indices
l and l′ run from 0 to
lmax. The sum over l2 covers the
values for which
|l − l′| ≤ l2 ≤ l + l′.
We have defined the Wigner transform of the hit map as 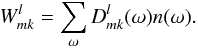 (17)We use the formula
(16)to explicitly construct the diagonal
of the matrix, which serves as a preconditioner to speed up the CG iteration.
(17)We use the formula
(16)to explicitly construct the diagonal
of the matrix, which serves as a preconditioner to speed up the CG iteration.
The formulation presented here is general, and makes no assumptions on the scanning pattern or on the sky coverage.
3. Implementation
3.1. User interface
The artDeco code takes two lists of input data objects containing the beam coefficients bslk and the so-called 3D maps for the respective detector for all detectors that are to be processed simultaneously. The beam coefficients can be read from FITS files in the format that is also being used by the HEALPix package for storing spherical harmonic coefficients.
The 3D maps contain the quantities n(ω) and
t(ω) for a given detector; they are created from time
streams of detector pointings and sky signal, respectively, by another stand-alone module
called todtobin. This module achieves the angular discretisation of the detector pointings
by sorting them into pixels of a HEALPix map with a user-defined
Nside parameter, which are in turn subdivided into
nψ bins for the discretisation in
ψ. The choice of Nside and
nψ has direct consequences on the run-time
of the deconvolver and the accuracy of its results: if high values are chosen, the 3D map
will become very large, and the deconvolver will require more memory and CPU time. On the
other hand, too low values will result in noticeable discretisation errors and inaccurate
output aXlm. As a guideline,
Nside should be chosen in such a way that the smallest
features of all beams are well resolved at the angular resolution
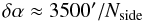 (18)associated
with this Nside. In a similar fashion,
nψ should be large enough to resolve
azimuthal features of the beams (assuming the beams are centred on a pole). For completely
axisymmetric beams, nψ = 1 is sufficient.
Generally,
nψ = 10kmax
(where kmax is the highest azimuthal multipole used to
describe the beams) is a good choice.
(18)associated
with this Nside. In a similar fashion,
nψ should be large enough to resolve
azimuthal features of the beams (assuming the beams are centred on a pole). For completely
axisymmetric beams, nψ = 1 is sufficient.
Generally,
nψ = 10kmax
(where kmax is the highest azimuthal multipole used to
describe the beams) is a good choice.
The computational complexity of todtobin is approximately
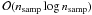 ,
where nsamp is the total number of TOD samples, since its
runtime is dominated by the sorting of the input TOD according to HEALPix pixel number and
ψ bin. Consequently, Nside and
nψ only have a significant effect on the
size of the output 3D maps. Typical execution times for todtobin with several billion
samples (as used for the experiments shown in this paper) are of the order of a few
minutes.
,
where nsamp is the total number of TOD samples, since its
runtime is dominated by the sorting of the input TOD according to HEALPix pixel number and
ψ bin. Consequently, Nside and
nψ only have a significant effect on the
size of the output 3D maps. Typical execution times for todtobin with several billion
samples (as used for the experiments shown in this paper) are of the order of a few
minutes.
ArtDeco takes several user-supplied parameters that influence its behaviour. Most important among these are lmax, which specifies the maximum multipole up to which deconvolution is carried out, and kmax ≤ lmax, which limits the maximum azimuthal multipole used for the beams. The explicit introduction of kmax is advantageous since most beams can be expressed accurately even when using a kmax ≪ lmax (even kmax = 0 if the beam has rotational symmetry and is unpolarised), and the reduction in kmax reduces CPU and memory requirements dramatically.
ArtDeco’s output consists of a set of alm in HEALPix-compatible format. Depending on whether the user requested polarisation, the file contains only aTlm or additional aElm and aBlm coefficients.
3.2. Algorithm overview
The deconvolution algorithm has been implemented in C++, making use of the MPI library for parallelisation. The quantities that depend on θ, such as d and N, are distributed to MPI tasks according to the θ angle. This allows a fairly good load balance. Summation over θ, when needed, is done efficiently through the collective MPI_Reduce() routine. The aslm coefficients are distributed according to index m. The beam coefficients bslk are fully present on all tasks.
The procedure of evaluating Eq. (14)can be summarised as follows. First we multiply the input a by the beam coefficients b. Then we perform a loop over index m′, inside which we broadcast the as′l′m′ coefficients for the current m′ to all processes, multiply by b, construct the reduced Wigner matrices for the local values of θ, and accumulate over l′. The multiplication by matrix N is a convolution operation in indices m,k and can be performed efficiently using 2D FFTs. Each MPI task performs the multiplication by N independently for the local θ. After that, we make another loop over index m, construct again the Wigner matrices, sum over θ, collect the result according to m to the owner process, and multiply by the beam coefficients.
The solution is assumed to have converged sufficiently as soon as the residual of the current aslm estimate is less than 10-12 times the residual of a vector containing all zeroes.
To generate the 3j symbols needed to construct the preconditioner, we use a C implementation of the recursive algorithm described by Schulten & Gordon (1975).
For a more detailed technical description of the algorithm, see Appendix B. CPU and memory requirements of various runs are presented and discussed in Appendix C.
4. Simulation setup
The deconvolution algorithm was tested using mock data produced by the Planck simulation package (Level-S, Reinecke et al. 2006).
4.1. Mission parameters
We assumed a scanning strategy that caused the telescope’s spin axis to perform two cycloidal excursions from the ecliptic plane per year with an amplitude of 7.5°; in azimuthal direction, the spin axis always pointed towards the Sun.
Time-ordered data were generated for a time span of 10 000 h, corresponding to slightly more than two full sky surveys; their length is of the order of 109 samples.
4.2. Detector geometry
For the first set of experiments, data were simulated for two horns, i.e. two pairs of
detectors, which were modelled roughly following Planck’s 30 GHz channel. In particular,
the detectors had an average FWHM of 32 2, the
polarisation directions in each detector pair were rotated by about (but not exactly) 90°
against each other, and the polarisation directions of the two horns were in turn shifted
by 45°. Both horns followed the same scan path on the sky, although with a little time
delay.
2, the
polarisation directions in each detector pair were rotated by about (but not exactly) 90°
against each other, and the polarisation directions of the two horns were in turn shifted
by 45°. Both horns followed the same scan path on the sky, although with a little time
delay.
The beam shapes were assumed to be elliptical, with ellipticities of 1.7 and 1.8 for each detector in a pair, respectively. These values are considerably higher than in a typical experiment and were chosen to demonstrate the performance of the method even under unfavourable conditions.
In order to show the algorithm’s performance at higher resolutions, another data set was produced using two horns sensitive at 70 GHz and with an average FWHM of 13′.
Table 1 gives an overview over the detector properties.
Overview of the detector parameters.
4.3. Input data
To generate a theoretical power spectrum for the CMB emission, we used the CAMB2 code with the cosmological parameters Ωb = 0.045, Ωcdm = 0.255 and Ωλ = 0.7. Using the HEALPix tool syn_alm_cxx, we created a random, unconstrained realisation of polarised alm from this power spectrum.
Emission maps of foreground components were generated using the Planck pre-launch Sky model3 (PSM, Delabrouille et al. 2012), version 1.6.6. We chose to include the contributions from galactic infrared emission (galactic synchrotron radiation, free-free emission, as well as thermal and spinning dust).
The signal from strong point sources was taken into account as well; to achieve this, a PSM-generated catalogue of point sources was directly expanded into spherical harmonic coefficients, using a sufficiently high cutoff value lmax that the beam response was negligible at this scale.
Polarised emission was disabled for all contributions except for the CMB, which makes it very easy to detect leakage of the strong temperature signal in the galactic plane into the polarisation signal.
We neglected bandpass effects and assumed an identical delta frequency response for all detectors.
The power spectra of the signal components at 30 GHz are plotted in Fig. 1.
 |
Fig. 1 Spectra of the 30 GHz input sky components: CMB (blue), diffuse foregrounds (purple), point sources (red), and total (black). |
4.4. Noise
In some of our simulations, detector noise was added to the idealised sky signal. Since the deconvolution method requires correlated noise to be removed from the TOD beforehand, we only added Gaussian white noise with an appropriately chosen σ to the simulated samples (see Table 1).
4.5. 3D map generation
The mock TOD were processed with the todtobin tool to generate the 3D input maps required by the deconvolver. We set Nside = 1024 for the 30 GHz case, and Nside = 2048 for 70 GHz; nψ was always set to 256.
5. Results
5.1. Constructing a sky map
The primary output of the deconvolution code consists of the aXlm (X = T, E, B) coefficients of the sky, up to lmax. From these one can construct the usual temperature and Q, U polarisation maps through harmonic expansion of the coefficients. We did this with the alm2map_cxx tool of the HEALPix package.
For comparison, we also produced binned maps directly from the TOD. A binned map is
constructed by assigning each TOD sample completely to the pixel containing the centre of
the beam. The binning operation can be formally written as
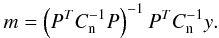 (19)Here P
is a pointing matrix, Cn is white noise covariance, and
m is a (I, Q, U) map
triplet.
(19)Here P
is a pointing matrix, Cn is white noise covariance, and
m is a (I, Q, U) map
triplet.
Binned maps are distorted by beam effects if the beam is asymmetric. In particular, the polarisation component of a binned map is contaminated by temperature leakage through beam shape mismatch. We aim at demonstrating that deconvolution can reduce these undesired effects.
Since our simulation includes point sources, the input aXlm coefficients are not band-limited. However, we can only solve the coefficients up to some limited lmax. This leads to ringing artefacts if a map is constructed directly from the raw aXlm coefficients. Ringing is particularly prominent around point sources and other sharp features.
Ringing is caused by the sharp cut-off of the spectrum at lmax, and it occurs even if the deconvolved coefficients are fully correct up to lmax. For this reason it is necessary to smooth the coefficients with a symmetric Gaussian beam prior to constructing a map. The required amount of smoothing depends on the spectrum of the underlying sky, and on lmax. The highest lmax that one can solve in turn depends on the beam width. In other words, it is not possible to recover structures significantly smaller than the beam itself. This gives the following rule of thumb: the required smoothing width is given by the smallest features of the original beam.
 |
Fig. 2 Ringing due to insufficient smoothing. A map constructed from the input aTlm coefficients with lmax = 800 with no smoothing (left) or smoothed to FWHM = 32′ (right). The cut-off of the spectrum at lmax leads to strong ringing effects around a point source. |
In Fig. 2 we demonstrate the ringing around a point source. We show an image of a point source, constructed from the input aXlm, but including only coefficients up to lmax = 800. Ringing artefacts are evident. On the right we show the same region of the sky after the map is smoothed with a FWHM = 32′ Gaussian symmetric beam. Smoothing removes the ringing, but naturally also smoothes out the smallest structures in the map.
5.2. Signal-only simulations with elliptic beam
We analyse first the noise-free 30 GHz simulation in detail. A detailed description of the simulation was given in Sect. 4. We ran the code with various combinations of parameters lmax, kmax, and analysed the results both in pixel space and in harmonic space. We included data from all four detectors and considered both temperature and polarisation.
5.2.1. Temperature map
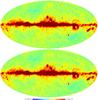 |
Fig. 3 30 GHz temperature map without noise: binned (top), and deconvolved and FWHM = 32′ smoothed (bottom). |
In Fig. 3 we show a full-sky Mollweide projection of the binned temperature map together with that of the deconvolved map. We used deconvolution parameters lmax = 800, kmax = 6.
We chose the value FWHM = 32′ as the baseline smoothing width for the 30 GHz maps. This corresponds to the mean width of the input beam. In some cases it was necessary to apply even stronger smoothing.
 |
Fig. 4 Zoom into the 30 GHz temperature map without noise: binned (left) and deconvolved (right). Shown is a 1000′ × 1000′ patch of the sky. The deconvolved map can be compared to the map constructed from the input aTlm (right panel of Fig. 2). |
The difference between the binned and the deconvolved map does not appear dramatic in the full-sky map image, but becomes evident when we zoom into a point source. Figure 4 shows a randomly selected strong point source below the galactic plane. While the source in the binned map is clearly elongated due to beam shape, it appears circular in the deconvolved map.
The deconvolved image can be compared to the right panel of Fig. 2, where we have shown the same patch of the sky constructed from the input aXlm coefficients. The maps are nearly identical.
5.2.2. Polarisation maps
 |
Fig. 5 30 GHz Q polarisation maps, in absence of noise: binned (top), and deconvolved with FWHM = 32′ (middle), or FWHM = 45′ (bottom) smoothing. The whole galactic structure is a fake polarisation signal arising from beam mismatch. |
The beam effects show up more dramatically in the polarisation maps (Fig. 5). The temperature signals recorded by two detectors differ due to the different beam shapes. The binning procedure interprets this erroneously as polarisation signal. This leads to a leakage of temperature signal into the polarisation maps. Since our simulation did not include polarised foregrounds, the whole galactic structure seen in the binned map is temperature leakage through beam mismatch.
We show deconvolved maps with two levels of smoothing below the binned map. Smoothing with a FWHM = 32′ beam is not sufficient to fully remove the galactic residual, but if we smooth the map further to FWHM = 45′, the residual disappears almost completely.
 |
Fig. 6 Zoom into the 30 GHz Q polarisation map without noise: binned (left) and deconvolved (right). The maps were smoothed to resolution FWHM = 32′ (top), or to 45′ (bottom). We show a 2500′ × 2500 ′ patch of the sky. The horizontal structure is spurious signal due to temperature leakage from the galaxy. |
In Fig. 6 we show a zoom into the Q polarisation map, just below the galactic plane. In the binned map we see a strong galactic residual, and typical “four-leaf clover” structures that arise from temperature leakage at the location of a point source. We show the deconvolved map again for two levels of smoothing: FWHM = 32′ and FWHM = 45′. The additional smoothing removes the clover structure nearly completely. To show that this is not only an effect of more aggressive smoothing, we smoothed the binned map further with a Gaussian beam of width FWHM = 32′, which, combined with the 32′ of the original beam, gives a total smoothing of 45′. This map is shown below the unsmoothed binned map. The additional smoothing has little effect on the galactic residual.
5.2.3. Harmonic space
 |
Fig. 7 Noise-free 30 GHz TT (top), EE (middle), and TE (bottom) spectra. Shown are the input (black) and the spectra constructed from the aXlm coefficients from deconvolution. Deconvolution results are shown for kmax = 4 (purple) and kmax = 6 (red), and for lmax = 400, 500, 600, 700, 800. The best-case results (lmax = 800, kmax = 6) are plotted with a thicker linetype. For comparison we show also the spectrum obtained from harmonic expansion of a naive binned map (green). The spectrum of the binned map decreases rapidly with l because the binning procedure inherently produces a beam-smoothed map. The blue line (TT and EE) is obtained by dividing the latter by the window function of a symmetric Gaussian beam with FWHM = 32′. The TE spectra have been binned over ten multipoles to reduce scatter and to make the plot more readable. |
We proceed to analyse the deconvolution results in harmonic space. We computed the TT, EE, and TE spectra of the deconvolved aXlm coefficients and compared them to the corresponding input spectra. The spectrum is constructed as
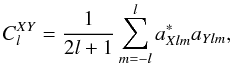 where
X and Y stand for T and
E.
where
X and Y stand for T and
E.
We ran the code for all combinations of kmax = 4, 6 and lmax = 400, 500, 600, 700, 800. Results for different combinations are shown in Fig. 7. We applied no smoothing to the coefficients.
We observe that the optimal value for kmax is coupled to lmax. Results for kmax = 4 and kmax = 6 begin to diverge only above l = 400. The results for different lmax with kmax = 6 are practically on top of each other, except for the highest multipoles near lmax, which are clearly distorted. When constructing a map, we cut out the last 20 multipoles before making the harmonic expansion.
For comparison we also show the spectrum obtained from a harmonic expansion of the binned map, which we computed using the anafast tool of the HEALPix package. This decreases rapidly as a function of l as a result of beam smoothing. To correct for the smoothing, we divided the spectrum by the window function of a symmetric Gaussian beam with FWHM = 32′. This corrects for the mean smoothing and allows one to recover the correct spectrum up to lmax = 300. Above that, the result begins to deviate from the input spectrum due to beam ellipticity, which cannot be corrected for by application of a window function only.
Deconvolution recovers the TT input spectrum well up to l = 800. At higher multipoles there is little information left in the signal, and the convergence properties of the code become poor. The weaker EE and TE spectra are recovered up to l = 400. Owing to temperature leakage, the binned map only gives the correct EE spectrum for the ten first multipoles in EE, and the TE spectrum is useless.
We did one run with parameters lmax = 600, kmax = 8 (not shown), to see if it would help to recover the EE spectrum to even higher multipoles. The results, however, did not differ significantly from the lmax = 600, kmax = 6 case.
5.2.4. Reconstruction error of harmonic coefficients
A comparison between the reconstructed spectrum and the input spectrum is not a fully reliable test of the correctness of the deconvolution result. It is possible to construct a set of harmonic coefficients that provides the correct spectrum, although the individual coefficients are incorrect.
To assess directly the accuracy of the
aXlm coefficients, we constructed a
quantity we call the error spectrum. It is computed as follows. We take the difference
between the aXlm coefficients we obtain
from deconvolution and the corresponding input coefficients
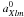 . As before,
X stands for T or E. We compute the spectrum of this difference as
. As before,
X stands for T or E. We compute the spectrum of this difference as
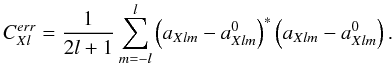 The resulting
spectrum is a measure of the error in the reconstruction of the
aXlm coefficients, as a function of
scale.
The resulting
spectrum is a measure of the error in the reconstruction of the
aXlm coefficients, as a function of
scale.
 |
Fig. 8 30 GHz error spectrum, for T (top) and E (bottom), without noise. See main text for definition. The deconvolution results are shown for the same combinations of parameters as in Fig. 7. The input spectrum is shown in black. Also shown is the error spectrum for a harmonic expansion of the binned map, corrected with a window function of a symmetric Gaussian beam (blue), or (T only) with an ideal window function (light blue). The ideal window function was defined as the ratio of the input spectrum and the spectrum of the uncorrected binned map. |
We show the error spectra of the 30 GHz runs for T and E coefficients in Fig. 8. For comparison, we show the input TT or EE spectrum in the same figure. The aXlm coefficients are recovered with good accuracy when the error spectrum is well below the input spectrum. The meaning of the blue line is the same as in Fig. 7, that is, we compute the harmonic expansion of the binned map and divide them by the window function of a symmetric Gaussian beam (FWHM = 32′).
We made another comparison with an ideal window function, which we computed as the ratio of the uncorrected spectrum of the binned map, and the input spectrum (green and black lines in the top panel of Fig. 7). The error spectrum for this is shown in light blue in Fig. 8 (TT spectrum only). By construction, applying the ideal window function to the spectrum of the binned map returns exactly the correct input spectrum. The error spectrum, however, is not improved with respect to the result obtained with Gaussian window function, which shows that the failure of the binning procedure to recover the correct spectrum above l = 300 in Fig. 7 was not just a result of a poorly chosen window function.
The error spectrum reveals that the deconvolved aXlm coefficients are more accurate than those obtained by harmonic expansion of the binned map already at the lowest multipoles.
5.3. Simulations with noise
The first simulation was quite idealised, since the data were noise-free. We made another simulation, where we added white noise to the TOD. In other aspects the simulation was identical to the first one. No correlated noise was added. We are implicitly assuming that correlated noise components, if present, were removed to sufficient accuracy prior to deconvolution.
As expected, noise made the deconvolution process more difficult, and the code did not converge for the highest values of lmax. We reached full convergence for the combinations lmax = 600, kmax = 6, and lmax = 700, kmax = 4. Case lmax = 700, kmax = 6 did not converge anymore.
 |
Fig. 9 Zoom into the 30 GHz temperature map in presence of noise: binned (left), and deconvolved (right). In the top row we show the unsmoothed binned map and the deconvolved map with FWHM = 32′ smoothing. The deconvolved map is distorted by ringing and amplification of noise. In the bottom row we show the same maps smoothed further to FWHM = 45′. The additional smoothing removes the distortion. |
Figure 9 shows a zoom into a point source, the same as in Fig. 4, in presence of white noise. The deconvolution parameters were lmax = 600, kmax = 6. The deconvolved map smoothed with the fiducial FWHM = 32′ is contaminated by distorted noise. Also, we see some ringing around the point source due to the moderately low lmax. We therefore smoothed the map further to FWHM = 45′, which was enough to remove the distortion. For comparison we also smoothed the binned map to comparable resolution by applying a smoothing by another FWHM = 32′ to it. This, combined with the original beam, gives a total resolution of roughly FWHM = 45′. These two maps are shown in the bottom row. Even after the additional smoothing, the point source in the binned map is elongated. Deconvolution restores the circular shape of the source.
 |
Fig. 10 Zoom into the 30 GHz Q polarisation map: binned (left) and deconvolved (right) in presence of noise. The maps were smoothed to FWHM = 45′. As in the noiseless case, the smoothed deconvolved map does not exhibit the spurious leakage signal in the galactic plane. |
 |
Fig. 11 30 GHz TT, EE, and TE spectra with white noise included. The TE spectra have been binned over 20 multipoles. The deconvolution results are shown for three combinations of parameters: kmax = 4 and lmax = 600, 700 (purple), and kmax = 6, lmax = 6 (red). The spectrum of a naive binned map is shown in green. The blue line shows the spectrum of the binned map corrected for a symmetric beam. The corresponding noise-free result is shown with dashed linetype in the TT plot, to indicate the region where noise begins to dominate over signal. |
Figure 10 shows a zoom into the Q polarisation map. We show the same patch of the sky as in Fig. 6. The raw binned map (not shown) is fully noise-dominated. We show maps smoothed to FWHM = 45′. Again, deconvolution removes the galactic leakage that is apparent in the binned map.
Figure 11 shows the spectra constructed from the deconvolved aXlm coefficients for the parameter combinations for which the code converged fully. Again we also show the spectrum of the binned map, and the same corrected for a symmetric Gaussian beam with FWHM = 32′. Deconvolution recovers the true TT spectrum up to nearly l = 600, after which noise begins to dominate. The spectrum of the binned map begins to deviate already below l = 400. In the case of the EE spectrum, both deconvolution and binning are unable to recover the true spectra except for the very lowest multipoles. In the case of the TE spectrum, deconvolution performs considerably better than binning, and the result follows the input spectrum up to l = 300, although it is noisy.
Finally, in Fig. 12 we show the error spectra in presence of noise. Deconvolution recovers the aTlm coefficients well up to l = 600. In the case of aElm coefficients, the error is well above the input spectrum for all but the lowest multipoles.
 |
Fig. 12 30 GHz error spectra in presence of white noise. The purple and red lines correspond to the same combinations of deconvolution parameters as in 11. The blue line shows the error spectrum for the harmonic expansion of a binned map, corrected for a symmetric beam with FWHM = 32′. |
It is a well-known and often quoted fact that deconvolution tends to amplify noise at high multipoles. We see this clearly in the upper deconvolved map in Fig. 9. The effects can, however, be suppressed by applying a sufficiently strong smoothing to the map, as we see from the lower panels of the same figure.
We can look at the amplification of noise also in harmonic space (Fig. 11). While the TT spectrum of the binned map (green line) continues to fall until it levels out at l = 900 (not seen in the plot), the deconvolution spectrum begins to rise above l = 600. Note, however, that for the whole multipole range where we have a deconvolution result, the extra power in the deconvolved map is still below that in the binned map corrected for a symmetric beam (blue line).
In the EE spectrum, the power of the deconvolved map exceeds that in the binned map corrected for a symmetric beam, around l = 300. This is in the domain where we have full noise domination in any case.
5.4. 70 GHz simulation
To test the performance of the code at higher multipoles, we generated one noise-free simulation mimicking the data voulme of the Planck 70 GHz channel. The used elliptic beams have an average FWHM of 13′; for more parameters see Table 1. We ran the deconvolution code with parameters lmax = 1700, kmax = 6.
Temperature and polarisation maps constructed from the aXlm with resolution FWHM = 13′ (T), or FWHM = 18′ (Q) are shown in Figs. 13 and 14 together with the corresponding binned maps. We show the same region of the sky as with 30 GHz simulations. Again, deconvolution has worked well, returning the circular shape of the point source, and removing the galactic leakage in the Q polarisation map.
In Fig. 15 we show the TT and EE error spectra for the 70 GHz simulation. The aTlm are recovered well nearly up to l = 1700, and the aElm coefficients well above l = 1000. Thus we have shown that, with sufficient computational resources, our deconvolution method can be applied to realistic data sets of volume and resolution of the Planck 70 GHz channel.
 |
Fig. 13 70 GHz temperature map without noise: binned (left) and deconvolved (right). The deconvolved map was smoothed to resolution FWHM = 13′, corresponding to the mean width of the actual beam. Shown is the same patch of sky as in Fig. 4. |
 |
Fig. 14 70 GHz Q polarisation map without noise: binned (left) and deconvolved (right). Both maps were smoothed to final resolution FWHM = 18′. Shown is the same patch of sky as in Fig. 6. Deconvolution removes the spurious galactic signal. |
 |
Fig. 15 70 GHz TT (top) and EE (bottom) error spectra, without noise. The blue line represents harmonic expansion of the binned map, corrected for a symmetric beam with FWHM = 13′. The fully converged deconvolution result (lmax = 1700, kmax = 6), is shown by a red line. We also show the error after 200 (purple dashed) and 500 (purple solid) iteration steps. |
5.5. Convergence
The convergence criterion we had set in our code is rather strict. We require that the square of the residual vector has fallen below a fraction of 10-12 of its initial value.
To see if a less strict criterion would help in reducing the computation time, we studied the convergence of the solution. We dumped the aXlm coefficients after every 50 steps, and computed the error spectrum with respect to the input coefficients.
We show the TT and EE spectra after 200 and 500 iteration steps in Fig. 15, along with the final results. We observe that the solution changes only very little after the first few hundred iterations, and 200 steps already give a significant improvement over the harmonic expansion of the binned map. In fact, after the first 100 iteration steps we can see no visible improvement in the reconstructed sky map. We could thus reduce the computation time by a large factor if we used a more relaxed convergence criterion and would not significantly lose accuracy.
5.6. Complicated beam shape
 |
Fig. 16 Unconventional beam pattern. |
To demonstrate the power of the deconvolution method, we made yet another simulation with an unconventional D-shaped beam (D for “deconvolution”), which is shown in Fig. 16. The linear dimension of the beam was approximately 12° squared. For demonstration purposes we included only point sources and considered temperature only. For the binning process into the 3D map, we chose Nside = 1024 and nψ = 256. Deconvolution parameters were lmax = 500, kmax = 30, and only a single full-sky survey was simulated. The comparatively high value of kmax was required to properly take into account the complicated azimuthal structure of the beam.
 |
Fig. 17 Sky seen through a D-beam: binned (left) and deconvolved (right) temperature map. The beam transforms the image of a point source into an image of the beam. Deconvolution recovers the original shapes of the sources. The size of the shown patch is 83.3° squared. The horizontal structure near the bottom of the plots is the accumulation of weak point sources in the galactic plane. |
A map binned directly from the TOD is shown in the left panel of Fig. 17. The beam transforms the image of a point source into a D-shaped pattern, resembling the beam. The deconvolved map is shown on the right; it was smoothed by a symmetric Gaussian beam with FWHM = 1° to reduce ringing. Even with this complicated beam shape we are able to recover the underlying point sources.
It is interesting that in this case it was sufficient to smooth the map with a beam of FWHM = 1° to obtain a very satisfactory map, although the full dimension of the beam is much larger.
6. Conclusions
We have presented an efficient beam deconvolution code, designed for absolute CMB experiments, and tested it on simulated data.
We looked at maps constructed from the recovered aTlm, aElm, and aBlm coefficients, and examined the coefficients directly in harmonic space. These reflect different aspects of the solution. We compared the results to a harmonic expansion of a binned map. We have also shown that with sufficient computational resources, we can extend the method to lmax = 1700, which would be sufficient for the Planck 70 GHz channel.
In absence of noise we could recover the aTlm coefficients to a high accuracy, and remove the effects of beam asymmetry. When white noise was added, we were able to reach a lower value of lmax, but the advantage of deconvolution over binning was still clear.
In the case of polarisation, deconvolution worked well in absence of noise. We were able to almost completely remove the temperature leakage due to beam mismatch. When noise was added, results were less clear. Deconvolution removed the visible galactic residual that arises from beam mismatch, but in harmonic space deconvolution did not seem to bring a clear benefit over binning. The recovered aElm coefficients were dominated by noise at nearly all multipoles, but this was true for both deconvolved and binned maps.
Our simulation used beams that were highly asymmetrical and also had a strong mismatch between them, which leads to a significant polarisation leakage. We did this to show the beam effects more clearly, but at the same time we also made the deconvolution problem very challenging. The accuracy we can expect when the code is applied to a real experiment strongly depends on the beam shapes of the particular experiment.
Some topics for future study can be mentioned. We have set a very strict convergence criterion for the CG iteration. Our convergence study indicates that a much more relaxed criterion could be sufficient for practical purposes. A future improvement would be to define a more suitable convergence criterion. This could reduce the computation time by a significant factor.
We applied the method to a simulation data set that provides full sky coverage. Our code is built on a formalism that makes no assumptions on the sky coverage. In practice, good convergence requires nearly full coverage. This is intuitively evident, since we are solving the harmonic coefficients, which necessarily represent the complete celestial sphere. If the input data only cover a part of the sky, the coefficients cannot be well constrained. A straighforward extension of the method would be to insert a prior that constrains the solution in the region which is not covered by the data, but this is beyond the scope of this paper and is a subject for future study.
Yet another topic for further study is determining the noise bias present in the TT and EE spectra at high multipoles.
Though the simulations used in this work mimic some aspects of the Planck mission, the parameters used do not reflect the properties of the actual instrument. The results presented in this paper are thus not representative of the sensitivity of the Planck experiment, and the authors do not represent the Planck collaboration in this context.
Acknowledgments
Some of the results in this paper have been derived using the HEALPix (Górski et al. 2005) package. We acknowledge the use of the Planck Sky Model, developed by the Component Separation Working Group (WG2) of the Planck Collaboration. M.R. is supported by the German Aeronautics Center and Space Agency (DLR), under program 50-OP-0901, funded by the Federal Ministry of Economics and Technology. E.K. is supported by Academy of Finland grant 253204. This work was granted access to the HPC resources of CSC made available within the Distributed European Computing Initiative by the PRACE-2IP, receiving funding from the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreement RI-283493. We thank CSC – the IT Center for Science Ltd. (Finland) – for computational resources. We thank Torsten Enßlin for constructive discussions and feedback, Valtteri Lindholm for help in using the Planck Sky Model, and Ronnie James Dio for the D-beam.
References
- Armitage, C., & Wandelt, B. D. 2004, Phys. Rev. D, 70, 123007 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage-Caplan, C., & Wandelt, B. D. 2009, ApJS, 181, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Ashdown, M. A. J., Baccigalupi, C., Balbi, A., et al. 2007a, A&A, 471, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ashdown, M. A. J., Baccigalupi, C., Balbi, A., et al. 2007b, A&A, 467, 761 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delabrouille, J., Betoule, M., Melin, J.-B., et al. 2012, A&A, submitted [arXiv:1207.3675] [Google Scholar]
- Frigo, M., & Johnson, S. G. 1998, in Proc. 1998 IEEE Intl. Conf. Acoustics Speech and Signal Processing, 3, 1381 [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, D. L., van Leeuwen, F., & Ashdown, M. A. J. 2011, A&A, 532, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarosik, N., Bennett, C. L., Dunkley, J., et al. 2011, ApJS, 192, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Keihänen, E., Kurki-Suonio, H., & Poutanen, T. 2005, MNRAS, 360, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Keihänen, E., Keskitalo, R., Kurki-Suonio, H., Poutanen, T., & Sirviö, A.-S. 2010, A&A, 510, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurki-Suonio, H., Keihänen, E., Keskitalo, R., et al. 2009, A&A, 506, 1511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
- Poutanen, T., de Gasperis, G., Hivon, E., et al. 2006, A&A, 449, 1311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prézeau, G., & Reinecke, M. 2010, ApJS, 190, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Reinecke, M., Dolag, K., Hell, R., Bartelmann, M., & Enßlin, T. A. 2006, A&A, 445, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schulten, K., & Gordon, R. G. 1975, J. Math. Phys., 16, 1961 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, D., Johnson, B. R., Brown, M. L., et al. 2009, MNRAS, 393, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J.-L., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Varshalovich, D. A., Moskalev, A. N., & Khersonskii, V. K. 1988, Quantum Theory of Angular Momentum (World Scientific Publishers) [Google Scholar]
- Wiener, N. 1949, Extrapolation, interpolation, and smoothing of stationary time series: with engineering applications, Technology press books in science and engineering (Technology Press of the Massachusetts Institute of Technology) [Google Scholar]
Appendix A: Definitions
In this appendix we present definitions and conventions used in the paper. We follow the conventions of Varshalovich et al. (1988).
A.1. Harmonic expansion of the CMB radiation field
The CMB temperature and polarisation fields can be presented by spin-weighted harmonic functions with spin s = 0, ±2. Spin s = 0 represents the temperature field, while components s = ±2 represent polarisation.
The temperature field on the celestial sphere is expanded as 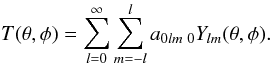 (A.1)The
Q and U Stokes fields, which describe linear
polarisation, can be written as
(A.1)The
Q and U Stokes fields, which describe linear
polarisation, can be written as 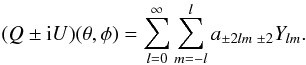 (A.2)Here
(A.2)Here
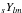 are spin-weighted
harmonic functions, and aslm are the
corresponding (complex) coefficients. The harmonic functions and coefficients obey the
symmetry relation
are spin-weighted
harmonic functions, and aslm are the
corresponding (complex) coefficients. The harmonic functions and coefficients obey the
symmetry relation 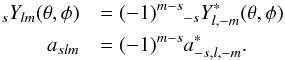 (A.3)The
harmonic functions are related to the Wigner functions
(A.3)The
harmonic functions are related to the Wigner functions
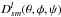 through
through 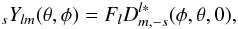 (A.4)where
(A.4)where
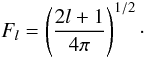 (A.5)It is convenient
to define further
(A.5)It is convenient
to define further 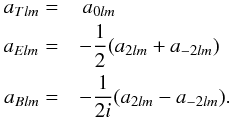 (A.6)The
CMB radiation field is expected to be a statistically isotropic Gaussian spin 0, 2
field. The statistical properties of the harmonic expansion coefficients are then fully
characterised by four spectra
(A.6)The
CMB radiation field is expected to be a statistically isotropic Gaussian spin 0, 2
field. The statistical properties of the harmonic expansion coefficients are then fully
characterised by four spectra 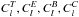 , such that
, such that
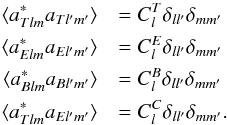 (A.7)
(A.7)
A.2. Wigner functions and rotations on a sphere
The harmonic coefficients transform under rotations as follows.
Assume we are given the coefficients aslm in one coordinate system. We then rotate the coordinate system, as described by Euler angles φ,θ,ψ:
-
1.
Rotate by angle ψ around the z-axis (in positive direction).
-
2.
Rotate by angle θ around the initial y-axis.
-
3.
Rotate by angle φ around the initial z-axis.
The rotation is equivalent to rotating first by angle φ around the
z-axis, then by angle θ around the new
y-axis, and finally by angle ψ around the
new z-axis. The harmonic coefficients in the rotated
coordinate system are given by 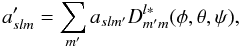 (A.8)where
(A.8)where
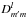 are
Wigner functions.
are
Wigner functions.
A Wigner function may be split into a product of three terms, each of which only
depends on one of the angles: 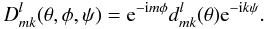 (A.9)Functions
(A.9)Functions
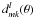 are the reduced
Wigner functions. They have the property
are the reduced
Wigner functions. They have the property 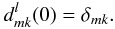 (A.10)They are
real-valued and obey the symmetry relation
(A.10)They are
real-valued and obey the symmetry relation
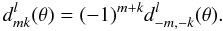 (A.11)The symmetry relation
for the full Wigner functions is
(A.11)The symmetry relation
for the full Wigner functions is
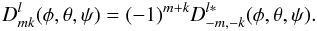 (A.12)
(A.12)
A.3. Wigner expansion
Wigner functions 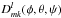 for integer values of
l,m,k are defined in domain V:
for integer values of
l,m,k are defined in domain V:
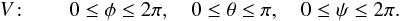 (A.13)Domain
V can be interpreted as the space of Euler angles. The volume element
in domain V is
dV = sinθdθdφdψ,
and V’s total volume is 8π2.
(A.13)Domain
V can be interpreted as the space of Euler angles. The volume element
in domain V is
dV = sinθdθdφdψ,
and V’s total volume is 8π2.
Any finite function f(φ,θ,ψ) defined in domain
V may be expanded in a series of Wigner functions as 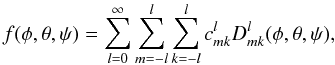 (A.14)where the coefficients
(A.14)where the coefficients
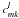 are given
by
are given
by 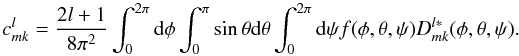 (A.15)Expansion (A.14)can be understood as the 3D equivalent
of the spherical harmonics expansion.
(A.15)Expansion (A.14)can be understood as the 3D equivalent
of the spherical harmonics expansion.
In particular, a product of two Wigner functions
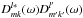 can be expanded as a
series of Wigner functions as
can be expanded as a
series of Wigner functions as 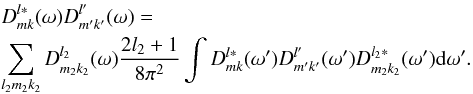 (A.16)An
integral over a product of three Wigner functions is given by Wigner 3j
symbols as
(A.16)An
integral over a product of three Wigner functions is given by Wigner 3j
symbols as 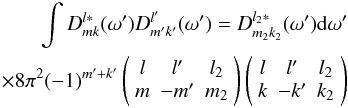 (A.17)
(A.17)
The following properties of the 3j symbols help in restricting the
range of summation. A 3j symbol is non-vanishing
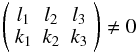 (A.18)only if the two
conditions
(A.18)only if the two
conditions 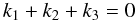 (A.19)and
(A.19)and
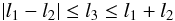 (A.20)are
fulfilled. We can thus eliminate the summation over k2 and
m2. Product (A.16)becomes
(A.20)are
fulfilled. We can thus eliminate the summation over k2 and
m2. Product (A.16)becomes 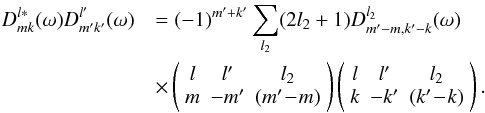 (A.21)
(A.21)
A.4. Beam
A.4.1. Detector signal and definition of beam coefficients
Consider a detector measuring CMB temperature and linear polarisation.
We assume now, very generally, that the signal recorded by a detector, apart from
noise, is proportional to the aslm
coefficients. We define the beam coefficients
bslk as follows. When the detector is
at some (predefined) fiducial position and orientation (for instance at the north
pole), the signal detected in the absence of noise is 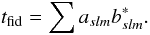 (A.22)It is clear
from the definition that the beam coefficients must contain all information not only
of the beam shape, but also of the possible polarisation sensitivity and orientation.
(A.22)It is clear
from the definition that the beam coefficients must contain all information not only
of the beam shape, but also of the possible polarisation sensitivity and orientation.
We may then rotate the beam to another position and orientation, as described in
Sect. A.2. The rotation brings the beam onto
location θ,φ in spherical coordinates, in an orientation defined by
angle ψ. The harmonic coefficients transform under
rotations according to (A.8). The
signal seen by the rotated detector is then
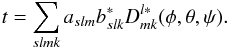 (A.23)In the following we
derive expressions for the beam coefficients in some special cases.
(A.23)In the following we
derive expressions for the beam coefficients in some special cases.
A.4.2. Non-polarised beam
Consider first a detector with an ideal beam, beam width equal to zero, and no
sensitivity to polarisation. The signal detected by the beam is directly given by
(A.1). We see readily, by comparing
(A.1)and (A.22), that if the chosen fiducial beam
position is at the north pole (θ = 0,φ = 0), the
beam coefficients must be 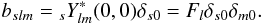 (A.24)A general
non-polarised beam with sensitivity g(θ,φ) gives for
the s = 0 components
(A.24)A general
non-polarised beam with sensitivity g(θ,φ) gives for
the s = 0 components 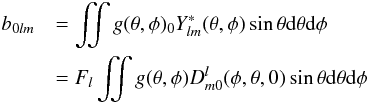 (A.25)and
bslm = 0 for s = ± 2.
(A.25)and
bslm = 0 for s = ± 2.
A.4.3. Polarisation measurements
A polarisation-sensitive detector requires careful treatment, because the Stokes parameters Q and U are not defined at the pole. The beam coefficients can still be defined in a meaningful way, as we show in the following.
Consider again a beam at a fiducial position and orientation at the north pole. A general beam may have different polarisation sensitivity at different locations. We therefore define the beam shape g(θ,φ) separately for temperature and polarisation.
The signal detected may be written in a general form as ![\appendix \setcounter{section}{1} \begin{eqnarray} \label{detected} t &&= \iint \sin\theta {\rm d}\theta {\rm d}\phi \Big\{ g_T(\theta,\phi) T(\theta,\phi) \nonumber\\ &&\quad +g_P(\theta,\phi) \left[ Q(\theta,\phi)\cos(2\psi(\theta,\phi)) +U(\theta,\phi)\sin(2\psi(\theta,\phi)) \right] \Big\}\text{.} \end{eqnarray}](/articles/aa/full_html/2012/12/aa20183-12/aa20183-12-eq190.png) (A.26)Here
ψ(θ,φ) is the local direction of
polarisation sensitivity, measured as an angle from the local meridian. Functions
gT(θ,φ),
gP(θ,φ), and
ψ(θ,φ) together define a general beam.
(A.26)Here
ψ(θ,φ) is the local direction of
polarisation sensitivity, measured as an angle from the local meridian. Functions
gT(θ,φ),
gP(θ,φ), and
ψ(θ,φ) together define a general beam.
We proceed to calculate the beam coefficients. We write the trigonometric functions
in exponential form, to obtain ![\appendix \setcounter{section}{1} \begin{eqnarray} t &&= \iint \sin\theta {\rm d}\theta {\rm d}\phi \Big\{ g_T(\theta,\phi) T(\theta,\phi) \label{detected_exponential} \nonumber \\ &&\quad +\frac{g_P(\theta,\phi)}{2} \left[ (Q-{\rm i}U)(\theta,\phi) {\rm e}^{i2\psi(\theta,\phi)} + (Q+{\rm i}U)(\theta,\phi) {\rm e}^{-{\rm i}2\psi(\theta,\phi)} \right] \Big\}\text{.} \end{eqnarray}](/articles/aa/full_html/2012/12/aa20183-12/aa20183-12-eq194.png) (A.27)We
can now insert the harmonic expansions (A.1)and (A.2)into (A.27)and read the beam coefficients
(A.27)We
can now insert the harmonic expansions (A.1)and (A.2)into (A.27)and read the beam coefficients
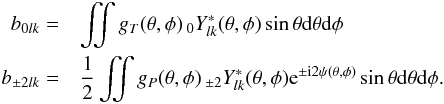 (A.28)We
then use definition (A.4)and write the
harmonic functions in terms of Wigner functions. In terms of the reduced Wigner
functions we have
(A.28)We
then use definition (A.4)and write the
harmonic functions in terms of Wigner functions. In terms of the reduced Wigner
functions we have 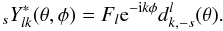 (A.29)The
ψ-term can be transferred inside the Wigner function. We may thus
write for a general polarised beam
(A.29)The
ψ-term can be transferred inside the Wigner function. We may thus
write for a general polarised beam 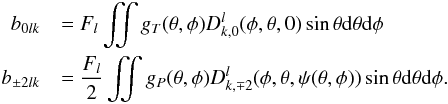 (A.30)The
above formulas for the beam coefficients are completely general as long as the beam
response is linear.
(A.30)The
above formulas for the beam coefficients are completely general as long as the beam
response is linear.
We now make the simplifying assumption that the polarisation sensitivity is “in the
same direction” everywhere on the beam. By “same direction” we mean that the direction
of polarisation sensitivity at an arbitrary location is obtained by rotating the
polarisation direction vector at the north pole to the desired location along a
meridian. The local polarisation orientation angle then becomes
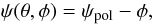 (A.31)where
ψpol is the deviation of polarisation direction from
φ = 0 at the north pole.
(A.31)where
ψpol is the deviation of polarisation direction from
φ = 0 at the north pole.
At this point it is convenient to write the Wigner functions in terms of the reduced
Wigner functions (A.9). The
coefficients for a beam with unique polarisation direction become 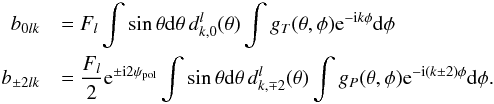 (A.32)We
readily see that for a symmetric beam the only non-vanishing coefficients are those
with k + s = 0. Especially, for a perfect beam with
zero width and perfect polarisation sensitivity
(gP = gT)
we obtain
(A.32)We
readily see that for a symmetric beam the only non-vanishing coefficients are those
with k + s = 0. Especially, for a perfect beam with
zero width and perfect polarisation sensitivity
(gP = gT)
we obtain 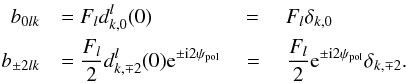 (A.33)We
have assumed normalisation
(A.33)We
have assumed normalisation 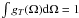 .
.
In this work we have constructed the beam coefficients according to (A.32), but the assumption of unique polarization direction is not crucial for the deconvolution method. A more general beam presentation is given by (A.30).
Appendix B: Methods used to accelerate computation
B.1. Load balancing
In an MPI-parallel code, good load balancing among the individual tasks is crucial. As was mentioned in Sect. 3.2, some quantities are distributed across tasks depending on their colatitude θ or the index m. Since the computational cost of the algorithm is not independent of θ and m, but rather an unknown, smoothly varying function of these two numbers, it is advisable not to assign sequential ranges of those indices to individual MPI tasks, because choosing index ranges that distribute the load evenly is very hard in that scenario.
To avoid this complication, we adopted a “round robin” strategy for data distribution. Assuming n MPI tasks numbered 0 to n − 1, we assign to a particular task i the θ indices θi, θi + n, θi + 2n, ..., and deal with the index m in analogous fashion. This results in near-perfect load balancing.
B.2. Convolution optimisation
A significant part of total CPU time is spent in the FFTs necessary for the convolution with the quantity N (see Sect. 3.2). Fortunately, several measures can be taken to decrease the resource requirements. First of all, we are making use of the highly optimised FFTW4 library (Frigo & Johnson 1998), which provides close to optimal performance for FFTs of specific size.
Furthermore, it is important to notice that the execution time for an FFT of length n depends sensitively on the prime factorisation of n; in general, an n composed of only small prime factors is much preferable.
Since we are performing a convolution operation, we have some freedom in the choice of array dimensions; they can be increased and zero-padded if desired. In our case, the minimal array dimensions are 4lmax + 1 and 4kmax + 1, respectively; if necessary, we increase both of them to the next larger number, which is a product of the prime factors 2, 3, and 5 only. Depending on the prime factorisation of the original array dimensions, this can decrease the run-time for this part of the code by integral factors.
Finally, the quantities that are to be convolved exhibit the symmetry
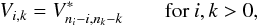 which allows us
to employ the specialised “real-valued” FFT, resulting in another substantial speedup
and a size reduction of the precomputed Fourier transform of N (see
Sect. B.5).
which allows us
to employ the specialised “real-valued” FFT, resulting in another substantial speedup
and a size reduction of the precomputed Fourier transform of N (see
Sect. B.5).
B.3. Efficient computation of the reduced Wigner functions
During code execution, the reduced Wigner functions
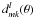 are required twice in every
conjugate gradient iteration step. Storing them in memory is prohibitively expensive, so
it is important to regenerate them efficiently whenever needed. For this purpose we used
code originally presented by Prézeau & Reinecke
(2010), which was extended to make use of the SSE2 instruction set present in
all modern Intel-compatible CPUs. We also used the symmetry properties of the
d matrix to avoid redundant computations.
are required twice in every
conjugate gradient iteration step. Storing them in memory is prohibitively expensive, so
it is important to regenerate them efficiently whenever needed. For this purpose we used
code originally presented by Prézeau & Reinecke
(2010), which was extended to make use of the SSE2 instruction set present in
all modern Intel-compatible CPUs. We also used the symmetry properties of the
d matrix to avoid redundant computations.
B.4. Shortcuts for symmetrical beams
If a beam used for deconvolution is symmetric with respect to a 180° rotation around its axis (which is true for elliptical beams, for example), all its bslm coefficients for odd m vanish by definition. This fact is used to skip unnecessary computations as well as save space by not storing any array elements that are known to be zero. It also reduces the minimum second dimension of the convolution arrays from 4kmax + 1 to 2kmax + 1, saving even more time on the FFT operations and reducing memory consumption.
B.5. Optional precomputation
The convolution step mentioned in Sect. 3.2 requires the Fourier transform of array N, which is constant throughout a run. The code permits one to precompute and store this quantity, which reduces total CPU time (because only two FFT operations are then needed for each convolution step, instead of three). However, especially for runs with high lmax and kmax this increases the total memory consumption considerably. So for situations where the available main memory is insufficient to store this precomputed array, we provide the option of recomputing the Fourier-transformed N whenever necessary, approximately halving the memory consumption of the code, but also slowing it down by 5–15 percent. For the 70 GHz runs described in this paper, we had to make use of this space-saving feature.
B.6. Supplying an initial guess
While not strictly a performance optimisation, the code allows the user to supply an initial guess from which to start the CG iteration, which is then used instead of a vector of zeroes. This is particularly helpful if one tries to compute series of deconvolutions on the same input data set, but with different parameters. For example, if a solution for a deconvolution problem with a given lmax and kmax has already been obtained, it can be used as a good starting point for other calculations with higher lmax and/or kmax. In any case, the convergence criterion will still be evaluated with respect to an all-zero aslm, not the supplied guess.
Appendix C: Resource usage
Most computations discussed in this paper were performed on a computer with 64 GB of RAM and 24 Intel Xeon E7450 cores. Since this computer is used interactively, we only ran our calculations on 16 of these cores and ensured that interactive usage did not exceed the capability of the remaining 8 cores. Nevertheless, the measured timings contain small uncertainties and should be interpreted as upper limits.
Resource usage for various deconvolution runs.
Table C.1 gives an overview of the parameters of the various runs and their impact on resource usage. Runs 30a–g are the 30 GHz calculations discussed in Sect. 5.2; runs 70a, 70x, and 70y are related to the 70 GHz high-resolution study (Sect. 5.4), and run “D” is the deconvolution with the D-shaped beam presented in Sect. 5.6. For all runs except the D-beam, the beam was assumed to be symmetrical with respect to a 180° rotation around its axis. Also, for all runs except the 70 GHz ones the FFT of array N was cached (see Sect. B.5).
For the 70 GHz run on the test machine described above (run 70a), each CG iteration step needed significantly more time than for the calculations using the 30 GHz data set; in combination with the high number of iterations, this leads to an inconveniently long computation time. As a consequence, deconvolution runs of this magnitude are better suited for execution on massively parallel computers. We therefore repeated the computation on the Louhi supercomputer of CSC (Cray XT4/XT5) on 128 and 512 processor cores, respectively. The corresponding performance figures are listed as runs 70x and 70y in Table C.1; memory consumption was not measured for these runs.
The computational power of a single CPU core is roughly the same on both computers used for our tests. Looking at the total wall clock time for the 70 GHz runs, it becomes obvious that the scaling from 16 to 128 cores is close to ideal, but becomes much worse when going from 128 to 512 cores. In this range, MPI communication and redundant computations begin to dominate. For deconvolution problems with larger lmax, we expect that this transition will occur at a higher number of MPI tasks.
The numbers of iterations required for the 70 GHz runs are not identical, as one might intuitively expect. This is because in an MPI-parallel code some computation steps – most notably summations and other reductions of quantities residing on all tasks – are not carried out in a strictly defined order, but depend on the relative timing of the tasks during such an operation, which is nondeterministic. Since floating-point algebra with finite precision is non-associative, the results of such operations can differ slightly from run to run, causing the conjugate gradient solver to take different paths towards the solution, but of course ultimately solving the same numerical problem.
Compared to earlier publications on deconvolution map-making, it is evident that both memory and CPU requirements of the presented algorithm are quite modest and allow deconvolution up to values of lmax that were prohibitively expensive up to now. Making use of massively parallel computing clusters, we expect that the algorithm can be applied to data sets with even higher resolution than those presented here.
All Tables
All Figures
 |
Fig. 1 Spectra of the 30 GHz input sky components: CMB (blue), diffuse foregrounds (purple), point sources (red), and total (black). |
| In the text | |
 |
Fig. 2 Ringing due to insufficient smoothing. A map constructed from the input aTlm coefficients with lmax = 800 with no smoothing (left) or smoothed to FWHM = 32′ (right). The cut-off of the spectrum at lmax leads to strong ringing effects around a point source. |
| In the text | |
 |
Fig. 3 30 GHz temperature map without noise: binned (top), and deconvolved and FWHM = 32′ smoothed (bottom). |
| In the text | |
 |
Fig. 4 Zoom into the 30 GHz temperature map without noise: binned (left) and deconvolved (right). Shown is a 1000′ × 1000′ patch of the sky. The deconvolved map can be compared to the map constructed from the input aTlm (right panel of Fig. 2). |
| In the text | |
 |
Fig. 5 30 GHz Q polarisation maps, in absence of noise: binned (top), and deconvolved with FWHM = 32′ (middle), or FWHM = 45′ (bottom) smoothing. The whole galactic structure is a fake polarisation signal arising from beam mismatch. |
| In the text | |
 |
Fig. 6 Zoom into the 30 GHz Q polarisation map without noise: binned (left) and deconvolved (right). The maps were smoothed to resolution FWHM = 32′ (top), or to 45′ (bottom). We show a 2500′ × 2500 ′ patch of the sky. The horizontal structure is spurious signal due to temperature leakage from the galaxy. |
| In the text | |
 |
Fig. 7 Noise-free 30 GHz TT (top), EE (middle), and TE (bottom) spectra. Shown are the input (black) and the spectra constructed from the aXlm coefficients from deconvolution. Deconvolution results are shown for kmax = 4 (purple) and kmax = 6 (red), and for lmax = 400, 500, 600, 700, 800. The best-case results (lmax = 800, kmax = 6) are plotted with a thicker linetype. For comparison we show also the spectrum obtained from harmonic expansion of a naive binned map (green). The spectrum of the binned map decreases rapidly with l because the binning procedure inherently produces a beam-smoothed map. The blue line (TT and EE) is obtained by dividing the latter by the window function of a symmetric Gaussian beam with FWHM = 32′. The TE spectra have been binned over ten multipoles to reduce scatter and to make the plot more readable. |
| In the text | |
 |
Fig. 8 30 GHz error spectrum, for T (top) and E (bottom), without noise. See main text for definition. The deconvolution results are shown for the same combinations of parameters as in Fig. 7. The input spectrum is shown in black. Also shown is the error spectrum for a harmonic expansion of the binned map, corrected with a window function of a symmetric Gaussian beam (blue), or (T only) with an ideal window function (light blue). The ideal window function was defined as the ratio of the input spectrum and the spectrum of the uncorrected binned map. |
| In the text | |
 |
Fig. 9 Zoom into the 30 GHz temperature map in presence of noise: binned (left), and deconvolved (right). In the top row we show the unsmoothed binned map and the deconvolved map with FWHM = 32′ smoothing. The deconvolved map is distorted by ringing and amplification of noise. In the bottom row we show the same maps smoothed further to FWHM = 45′. The additional smoothing removes the distortion. |
| In the text | |
 |
Fig. 10 Zoom into the 30 GHz Q polarisation map: binned (left) and deconvolved (right) in presence of noise. The maps were smoothed to FWHM = 45′. As in the noiseless case, the smoothed deconvolved map does not exhibit the spurious leakage signal in the galactic plane. |
| In the text | |
 |
Fig. 11 30 GHz TT, EE, and TE spectra with white noise included. The TE spectra have been binned over 20 multipoles. The deconvolution results are shown for three combinations of parameters: kmax = 4 and lmax = 600, 700 (purple), and kmax = 6, lmax = 6 (red). The spectrum of a naive binned map is shown in green. The blue line shows the spectrum of the binned map corrected for a symmetric beam. The corresponding noise-free result is shown with dashed linetype in the TT plot, to indicate the region where noise begins to dominate over signal. |
| In the text | |
 |
Fig. 12 30 GHz error spectra in presence of white noise. The purple and red lines correspond to the same combinations of deconvolution parameters as in 11. The blue line shows the error spectrum for the harmonic expansion of a binned map, corrected for a symmetric beam with FWHM = 32′. |
| In the text | |
 |
Fig. 13 70 GHz temperature map without noise: binned (left) and deconvolved (right). The deconvolved map was smoothed to resolution FWHM = 13′, corresponding to the mean width of the actual beam. Shown is the same patch of sky as in Fig. 4. |
| In the text | |
 |
Fig. 14 70 GHz Q polarisation map without noise: binned (left) and deconvolved (right). Both maps were smoothed to final resolution FWHM = 18′. Shown is the same patch of sky as in Fig. 6. Deconvolution removes the spurious galactic signal. |
| In the text | |
 |
Fig. 15 70 GHz TT (top) and EE (bottom) error spectra, without noise. The blue line represents harmonic expansion of the binned map, corrected for a symmetric beam with FWHM = 13′. The fully converged deconvolution result (lmax = 1700, kmax = 6), is shown by a red line. We also show the error after 200 (purple dashed) and 500 (purple solid) iteration steps. |
| In the text | |
 |
Fig. 16 Unconventional beam pattern. |
| In the text | |
 |
Fig. 17 Sky seen through a D-beam: binned (left) and deconvolved (right) temperature map. The beam transforms the image of a point source into an image of the beam. Deconvolution recovers the original shapes of the sources. The size of the shown patch is 83.3° squared. The horizontal structure near the bottom of the plots is the accumulation of weak point sources in the galactic plane. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


