| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 27 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219668 | |
| Published online | 24 October 2012 | |
A dynamical model for the Taffy galaxies UGC 12914/5⋆
1 CDS, Observatoire astronomique, UMR 7550, 11 rue de l’université, 67000 Strasbourg, France
e-mail: bvollmer@astro.u-strasbg.fr
2 Univ. Bordeaux, Laboratoire d’Astrophysique de Bordeaux, UMR 5804, 33270 Floirac, France
3 CNRS, LAB, UMR 5804, 33270 Floirac, France
4 Astronomical Observatory, Jagiellonian University, ul. Orla 171, 30-244 Kraków, Poland
Received: 24 May 2012
Accepted: 20 September 2012
The spectacular head-on collision of the two gas-rich galaxies of the Taffy system, UGC 12914/15, gives us a unique opportunity to study the consequences of a direct ISM-ISM collision. To interpret existing multi-wavelength observations, we made dynamical simulations of the Taffy system including a sticky particle component. To compare simulation snapshots to Hi and CO observations, we assume that the molecular fraction of the gas depends on the square root of the gas volume density. For the comparison of our simulations with observations of polarized radio continuum emission, we calculated the evolution of the 3D large-scale magnetic field for our simulations. The induction equations including the time-dependent gas-velocity fields from the dynamical model were solved for this purpose. Our simulations reproduce the stellar distribution of the primary galaxy, UGC 12914, the prominent Hi and CO gas bridge, the offset between the CO and Hi emission in the bridge, the bridge isovelocity vectors parallel to the bridge, the Hi double-line profiles in the bridge region, the large line-widths (~200 km s-1) in the bridge region, the high field strength of the bridge large-scale regular magnetic field, the projected magnetic field vectors parallel to the bridge and the strong total power radio continuum emission from the bridge. The stellar distribution of the secondary model galaxy is more perturbed than observed. The observed distortion of the Hi envelope of the Taffy system is not reproduced by our simulations which use initially symmetric gas disks. The model allows us to define the bridge region in three dimensions. We estimate the total bridge gas mass (Hi, warm and cold H2) to be 5 to 6 × 109 M⊙, with a molecular fraction MH2/MHI of about unity. Despite the enormous mass of molecular gas in the bridge, very little star formation is present, similar to other systems with extraplanar gas and broad CO lines. The structure of the model gas bridge is bimodal: on kpc-scales there is a dense (≳0.01 M⊙ pc-3) component with a high velocity dispersion >100 km s-1 and a less dense (~10-3 M⊙ pc-3) component with a smaller, but still high, velocity dispersion ~50 km s-1. The synchrotron lifetime of relativistic electrons is only long enough to be consistent with the existence of the radio continuum bridge for the less dense component. On the other hand, only the high-density gas undergoes a high enough mechanical energy input to produce the observed strong emission of warm H2. We propose that, despite the high local gas densities, this high input of mechanical energy drives strong turbulence and quenches star formation in the bridge gas except for the giant Hii region near UGC 12915. Our model suggests that we observe this galaxy head-on collision near the time of maximum CO and H2 emission.
Key words: galaxies: interactions / galaxies: ISM / galaxies: kinematics and dynamics
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Galactic evolution is largely due to interactions of various sorts. We can distinguish tidal encounters, which are essentially gravitational interactions, from head-on collisions in which the gaseous components actually hit each other, resulting in fantastic shocks and injection of energy into the gas. A further type of interaction is the ram-pressure stripping suffered by cluster galaxies.
We are concerned here with the head-on collisions and focus on the Taffy galaxies, UGC 12914 and UGC 12915, a spectacular bridge system first noticed by Condon et al. (1993). In these collisions, the stellar morphology is determined by the tidal interaction while the morphology of the gaseous component is determined by both gravity and hydrodynamics. While the general geometry of the system was suggested by Condon et al. (1993), no numerical simulations of the collision have been made until now.
The Taffy system attracted attention through its strong radio synchrotron bridge, a very unusual feature. The bridge is HI-rich and was subsequently found to be rich in molecular gas as well through CO observations (Gao et al. 2003; Braine et al. 2003). Dust appears to be underabundant with respect to gas in the bridge (Zink et al. 2000; Zhu et al. 2007), presumably due to grain ablation during the collision. The galaxies themselves are particularly massive, with rotation velocities of 250 km s-1 or more and some 1.5 × 1010 M⊙ of Hi and a similar quantity of molecular gas, dependent on the N(H2)/ICO conversion factor from CO emission to H2 column density. Some 10 − 20% of the gas is in the bridge, making it at least as rich in gas as the entire Milky Way. Condon et al. (1993) estimate that the galaxy disks passed through each other about 20 Myr ago with a transverse velocity of about 600 km s-1. The bridge and the counter-rotating galaxies are seen close to edge-on as the recession velocities of the two galaxies are virtually equal. Figure A.1 shows the morphology of the system.
The wealth of available data makes the Taffy system both attractive and challenging to model. We present the first simulations of the collision, attempting to simultaneously reproduce (i) the morphologies of the stellar and gaseous components; (ii) the relative bridge and galaxy gas masses; (iii) the velocity field including the presence of double peaks in the bridge spectra; (iv) the magnetic field orientation; and (v) the morphology of the polarized and unpolarized radio continuum emission. A sticky particle code is used in order to enable cloud-cloud collisions to occur.
We are most familiar with the interstellar medium (ISM) and star formation (SF) in the Milky Way, a quiescent rotating disk. At the velocities observed in the Milky Way, ISM-ISM (i.e. hydro) collisions are believed to favor star formation, the clearest example being the triggered star formation sometimes found around Hii regions (Zavagno et al. 2010). The impact velocity of the interstellar media of the UGC 12914/5 system is ≳800 km s-1, very much greater than can be observed in the Milky Way. Despite the enormous gas mass and strong CO emission in the bridge, strikingly little star formation is present (Braine et al. 2004). Numerically modeling the encounter is the first step towards understanding the effect of injecting huge amounts of kinetic energy into the gas found in the bridge.
The UGC 12914/5 system is not the only ISM-ISM collision known. The so-called Taffy2 system, UGC 813/6 (Condon et al. 2002), is very similar although the galaxies are somewhat less massive and less gas-rich. Nonetheless, the bridge is quite spectacular and the geometry quite similar. Stephan’s Quintet is similar in terms of collision velocity but the velocity is entirely along the line of sight; the collision is on-going and involves an intruder galaxy hitting the intra-group medium of this compact group with a velocity of ~1000 km s-1. The resulting large-scale shock (~40 kpc) emits in X-ray (Trinchieri et al. 2003) and radio continuum emission (van der Hulst 1981). Powerful high-velocity dispersion molecular hydrogen is associated with the intergalactic shock wave (Appleton et al. 2006; Guillard et al. 2009). About 5 × 108 M⊙ of warm H2 spread over ~480 kpc2 were found in the main shock region (Cluver et al. 2010). In addition, CO(1−0), (2−1) and (3−2) line emission have been detected in this region with complex profiles, spanning a velocity range ~1000 km s-1 (Guillard et al. 2012). The intra-group material involved has most probably been tidally stripped by a past galaxy-galaxy interaction (Renaud et al. 2010; Hwang et al. 2012). Colliding ring galaxies can also have gas and star bridges. As an example, the Hi bridge between the two galaxies in Arp 284 (NGC 7714/15) contains 2 × 109 M⊙ (Smith et al. 1997). Struck & Smith (2003) showed that a fast (~400 km s-1) off-center (~4 kpc) inclined collision is responsible for the peculiar morphology of the system. The models suggest that the gas bridge interacts with tidally stripped gas from an older component.
Head-on collisions of gas-rich galaxies are rare events in the local Universe. However, galaxy encounters of all types were more frequent, and galaxies more gas-rich, at earlier epochs. The Taffy system UGC 12914/15 can thus give insight into how mass assembled in the early Universe.
Pre-collision model galaxy parameters.
2. The model
We used the N-body code described in Vollmer et al. (2001), which consists of two components: a non-collisional component that simulates the stellar bulge/disk and the dark halo, and a collisional component that simulates the ISM. The non-collisional component of each galaxy consists of 81 920 particles, which simulate the galactic halo, bulge, and disk. The characteristics of the different galactic components are presented in Table 1. The first of the two galaxies, the primary, is 2.3 times more massive and its disk scalelength is 1.6 times larger than that of the secondary galaxy. The resulting rotation velocities are ~295 km s-1 and ~245 km s-1, respectively.
We adopted a model where the ISM is simulated as a collisional component, i.e. as discrete particles that possess a mass and a radius and can have partially inelastic collisions. Since the ISM is a turbulent and fractal medium (see e.g. Elmegreen & Falgarone 1996), it is neither continuous nor discrete. The volume filling factor of the warm and cold phases is smaller than one. The warm neutral and ionized gas fills about 30 − 50% of the volume, whereas cold neutral gas has a volume filling factor smaller than 10% (Boulares & Cox 1990). It is unclear how this fraction changes when an external pressure is applied. We thus do not identify the cloud particles with giant molecular clouds (GMC) but treat the entire ISM as a collisional medium. In contrast to smoothed particle hydrodynamics (SPH), which is a quasi-continuous approach where the particles cannot penetrate each other, our approach allows a finite penetration length, which is given by the mass-radius relation of the particles.
The 20 000 particles of the collisional component in each galaxy represent gas cloud complexes that evolve in the gravitational potential of the galaxy. The total assumed gas mass of the two galaxies is 2.4 × 1010 M⊙. The mass distribution of the cloud complexes is N(m)dm ∝ m-1.3dm for 2 × 105 M⊙ ≤ m ≤ 2 × 107 M⊙. This is close to the mass spectrum of Galactic giant molecular clouds (m-1.5; Solomon et al. 1987; Rosolowsky 2005). To each particle, a radius is attributed depending on its mass: 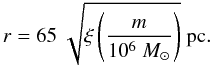 (1)We used different values for the cloud size parameter ξ, which is not known a priori.
(1)We used different values for the cloud size parameter ξ, which is not known a priori.
During the disk evolution, the cloud particles can have partially inelastic collisions, the outcome of which (coalescence, mass exchange, or fragmentation) is simplified following the geometrical prescriptions of Wiegel (1994). Figure 1 shows the overlapping mass fraction for a collision of two clouds as a function of the ratio between the cloud radius rcl and the impact parameter b. For a collision of clouds of equal mass, the ratio between the overlapping and the total cloud masses is small for b ~ 2rcl and rises steeply to ~0.5 for b = rcl. For b < rcl the mass fraction slowly rises toward unity. For a collision of clouds with a mass ratio of ten, the shape of the overlapping mass fraction with respect to r1/b is the same as in the previous case, but shifted to higher r1/b and lower mass fractions. We conclude that for r1 < b < r1 + r2 the mass fraction which is involved in the cloud-cloud collision is small. Our method which treats the cloud collisions geometrically is close to that of Olson & Kwan (1990) and Theis & Hensler (1993). All partially inelastic collisions conserve mass and momentum. The collisions result in an effective gas viscosity in the disk. Since the code has a maximum number of particles of 40 000, mass exchange between the two colliding gas clouds occurs most frequently. Colliding clouds can only fragment if cloud coalescence occurred before elsewhere. During a mass exchange the less massive cloud always gains and the more massive cloud loses mass. After a large number of collisions, this leads to steepening of the mass spectrum at the high and low-mass ends, and ultimately to a flat mass spectrum around the mean cloud mass of 6 × 105 M⊙.
 |
Fig. 1 Overlapping cloud mass which is affected by a cloud-cloud collision divided by the total cloud mass as a function of the fraction between the radius of the massive cloud r1 and the impact parameter b (from Wiegel 1994). Crosses: cloud of equal mass M1 = M2. Triangles: M1 = 10 × M2. |
The particle trajectories are integrated using an adaptive timestep for each particle. This method is described in Springel et al. (2001). The following criterion for an individual timestep is applied: 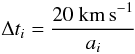 (2)where ai is the acceleration of the particle i. The minimum value of ti defines the global timestep used for the Burlisch-Stoer integrator that integrates the collisional component, and is typically a few 104 yr.
(2)where ai is the acceleration of the particle i. The minimum value of ti defines the global timestep used for the Burlisch-Stoer integrator that integrates the collisional component, and is typically a few 104 yr.
Since each cloud-cloud collision is resolved in time and space by the code, the cloud collision rate is physical and follows the classical equation 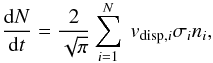 (3)where vdisp,i is the 1D velocity dispersion, σi the cross section of particle i, and ni is the local cloud density around particle i (Theis & Hensler 1993). Since we use a cloud mass spectrum, the cross section is σ = ϵπr2, with 1 ≤ ϵ ≤ 4, instead of σ = 4 πr2 that applies for particles of same size. For the comparison with the collision rate of the dynamical simulations in Sect. 3, we set ϵ = 2.
(3)where vdisp,i is the 1D velocity dispersion, σi the cross section of particle i, and ni is the local cloud density around particle i (Theis & Hensler 1993). Since we use a cloud mass spectrum, the cross section is σ = ϵπr2, with 1 ≤ ϵ ≤ 4, instead of σ = 4 πr2 that applies for particles of same size. For the comparison with the collision rate of the dynamical simulations in Sect. 3, we set ϵ = 2.
Parameters of the first set of Taffy simulations.
3. The simulations
We made two sets of simulations of head-on collisions of two gas-rich spiral galaxies: (i) a first set with a simplified collision geometry to determine the cloud size parameter ξ and the inclination angle i between the two galaxies before the collision and (ii) a second set of simulations with fixed ξ and a fixed range of inclinations, where we varied the impact parameter systematically.
3.1. Cloud size parameter and galaxy inclination
In the first set of simulations the more massive (primary) galaxy is placed in the x-y plane, the second galaxy is placed in a plane parallel to that of the first one, but offset by 12 kpc along the z-axis and by 0.5 kpc along the x-axis. The initial velocity of the less massive galaxy is 500 km s-1 along the z-axis toward the primary galaxy which is at rest. We varied the inclination angle between the two galactic disks between − 45° and 45° and the cloud size parameter between 1 ≤ ξ ≤ 16 (Table 2).
For the sky projection we used the observed position and inclination angles of UGC 12914: PA = 160°, i = 30°. The position angle and inclination of the model primary galaxy define a plane in three dimensional space. The model galaxy can then be rotated within this plane by the azimuthal viewing angle which is chosen such that the secondary galaxy is close to the observed position of UGC 12915.
 |
Fig. 2 Time evolution of a Taffy galaxy collision (simulation 10). Left panels: stellar surface density. The greyscale is logarithmic from 8 to 5600 M⊙ pc-2. Right panels: total gas surface density. The greyscale are (1,4,9,16,25,36,49,...,400) M⊙ pc-2. The timestep of interest (26 Myr) is marked by “model”. The impact parameter is ~3 kpc. |
Figure 2 shows a representative time evolution of the simulated head-on collision between two gas-rich galaxies. The galaxies collide1 at t = 0 Myr. The projected distance between the two galaxies is close to the distance between UGC 12914 and UGC 12915 at t = 26 Myr. The head-on collision produces a prominent gas bridge between the galaxies without a stellar counterpart. At t = 26 Myr the gas within the bridge forms an X-structure. The outer gas disk of the primary galaxy is not affected by the collision because of the small size of the initial gas disk of the secondary galaxy. For t ≥ 20 Myr both galaxies develop stellar and gaseous ring structures which are characteristic for head-on galaxy collisions (see, e.g., the Cartwheel galaxy; Higdon et al. 1995, 1996).
 |
Fig. 3 Snapshots at the time of interest (26 Myr) for simulations with different inclination angles between the disks and different cloud particle sizes as described in Table 2. Greyscale levels are (2,4,8,16,32,64,128,256) M⊙ pc-2. |
The gas distribution of the bridge displays an X-structure in all simulations. Since the X-structure is visible at all azimuthal viewing angles, we conclude that it stems from a 3D hourglass shape. The X-structure is symmetric for i = 0°, i.e. when the colliding disks are parallel. Increasing the inclination angle between the two disks increases the gas surface density of the upper part of the X-structure, toward the less massive galaxy leading to a higher bridge mass. An increase of the cloud size parameter ξ leads to an increase of the overall gas surface density in the bridge region without changing the gas morphology.
The time evolution of the cloud collisions in the whole system are presented in Fig. 4. The collision rate of the clouds in the two galactic disks is constant before the collision. As expected, its absolute value increases with increasing cloud size parameter ξ (from blue to red). During the collision, the cloud collision rate rises steeply within a few Myr, stays high during ~10 Myr, drops to a minimum at t ~ 40 Myr, and rises again slightly for t > 40 Myr (Fig. 4). The latter rise is due to the formation of prominent gas rings of high surface densities in both galaxies. The ratio between the maximum and initial collision rates mainly depends on the inclination angle between the disks. This fraction is ~13 for i = 0° and ~22 for i = 30° − 45°.
The quantitative relations of the influence of the inclination angle between the disks i and the cloud size parameter ξ on the cloud collision rate during the galaxy collision and the gas mass in the bridge region are shown in Fig. 5. We define the bridge region as a cylinder whose base is parallel to the disk plane of the primary galaxy with an infinite radius and extending from 3 kpc to 12 kpc perpendicular to the plane of the primary galaxy (UGC 12914). Based on Eq. (3), the collision rate of an ensemble of particles should be proportional to the cloud size parameter ξ (Eq. (1)). The situation changes if the ensemble has an evolving spectrum of particle sizes. After a large number of collisions, the mass spectrum steepens at the high end (see Sect. 2). This steepening decreases the number of massive clouds which dominate the overall collision rate because of their large cross sections. The local particle density and velocity dispersion is calculated using the 50 nearest neighbors. As expected for a slight steepening of the cloud mass spectrum with increasing collision rate, the correlation between the theoretical collision rate of the system based on Eq. (3) and the measured model collision rate of the quiet galaxy system before collision is close to linear with a slope of 0.8 (upper panel of Fig. 5). The ratio between the maximum collision rate counted in bins of 10 Myr and the collision rate of the quiet system is 5.3 ± 0.6 for all simulations. The correlation between the cloud size parameter ξ and the maximum collision rate has a slope of 0.65 (middle panel of Fig. 5), i.e. it is somewhat shallower than the correlation of the collision rate of the quiescent system. We ascribe this difference again to the cloud size spectrum.
The correlation between the bridge gas mass and the maximum collision rate is 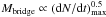 (lower panel of Fig. 5). This behavior is caused by the geometrical cloud collision scheme (Sect. 2): for a constant impact parameter b, the ratio between the mass of the colliding clouds that is affected by the collision mcoll, i.e. the mass included in the geometrical overlap between the clouds, and the initial masses of the colliding clouds mini is small for r1 < b < r1 + r2 and increases rapidly with increasing cloud radius r1. Only cloud-cloud collisions with b/r1 < 0.7 lead to significant transfer of mass and momentum. An increase of the cloud radius with increasing ξ (Eq. (1)) thus leads to an increase of the collision rate which is approximately proportional to ξ. However, many of the new cloud-cloud collisions do not lead to a significant mass and momentum transfer. Since the gas bridge is caused by momentum transfer during cloud-cloud collisions, the bridge gas mass is expected to increase more slowly than the cloud collision rate, as observed in our simulations.
(lower panel of Fig. 5). This behavior is caused by the geometrical cloud collision scheme (Sect. 2): for a constant impact parameter b, the ratio between the mass of the colliding clouds that is affected by the collision mcoll, i.e. the mass included in the geometrical overlap between the clouds, and the initial masses of the colliding clouds mini is small for r1 < b < r1 + r2 and increases rapidly with increasing cloud radius r1. Only cloud-cloud collisions with b/r1 < 0.7 lead to significant transfer of mass and momentum. An increase of the cloud radius with increasing ξ (Eq. (1)) thus leads to an increase of the collision rate which is approximately proportional to ξ. However, many of the new cloud-cloud collisions do not lead to a significant mass and momentum transfer. Since the gas bridge is caused by momentum transfer during cloud-cloud collisions, the bridge gas mass is expected to increase more slowly than the cloud collision rate, as observed in our simulations.
With (dN/dt)max ∝ ξ0.65, the correlation between the bridge gas mass and the cloud size parameter ξ is Mbridge ∝ ξ0.3. The maximum collision rate does not depend on the inclination angle between the disks. The dependence of the bridge mass on the inclination angle between the disk is weak compared to that on the cloud size parameter ξ (Fig. 5).
For ξ ≥ 8 the bridge gas mass exceeds 2.7 × 109 M⊙ (Table 2). This is at the lower end, but comparable to the observed bridge gas mass of 3 − 4 × 109 M⊙. We thus decided to fix the cloud size parameter at ξ = 8 for the second set of simulations. Since only simulations with − 30° ≤ i ≤ 0° lead to distributions of stars and gas that reproduce observations, we restricted the second set of simulations to this range of inclination angles between the two disks.
 |
Fig. 4 Cloud particle collision rate for the simulations described in Table 2. The factor of the cloud particle mass-size relation ξ increases from blue to red. |
 |
Fig. 5 Correlation for the simulations described in Table 2. Upper panel: cloud collision rate of the simulated quiet galaxies before collision as a function of the theoretical cloud collision rate based on Eq. (3). Middle panel: maximum collision rate in bins of 10 Myr as a function of the cloud particle mass-size relation ξ. Lower panel: total gas mass in the bridge region as a function of the maximum collision rate. Crosses: i = 0°; diamonds: i = 30°; triangles: i = 45°. |
3.2. Comparison with SPH simulations
The main difference between our collisional model and SPH simulations of head-on collisions (Struck 1997; Tsuchiya et al. 1998) is the finite penetration length of the collisional particles compared to the interdiction of penetration in SPH. The impact generally carves a hole in the primary disk which is filled quite rapidly (Struck 1997). Since in SPH all particles in the overlapping region collide, one expects a much higher momentum transfer in SPH than in a collisional scheme. Due to the strong momentum transfer, a less massive (~20% of the primary) companion gas disk is destroyed during the head-on collision (Struck 1997). As in our model, head-on collisions of gas-rich galaxies form prominent gas bridges in SPH. The SPH bridges also show high gas column densities, comparable to those found in our simulations. In contrast with our model, SPH simulations can include gas heating and cooling. Struck (1997) showed that the colliding gas is heated to temperatures up to 106 K at the impact. The bridge gas than cools down to ~105 K after 35 Myr and to ~104 K within less than 100 Myr2. The overall gas distributions of isothermal SPH simulations compared to SPH simulation including heating and cooling are similar. In general, the edges of the gas distributions are sharper in the isothermal simulations (Fig. 4 of Struck 1997). We expect that our model simulations are closer to isothermal SPH simulations of head-on galaxy collisions, but they involve a smaller amount of momentum transfer between the ISM of the colliding galaxies.
3.3. Realistic Taffy galaxy models
In our second set of simulations we set the cloud size parameter ξ = 8 and the inclination between the two galaxies i = −30°, 0°. To test the influence on the impact parameter, we varied the initial position of the secondary galaxy ( − 71.5,1.0, − 96.5) kpc by adding 3 kpc-long and 9 kpc-long vectors with directions pointing toward the eight corners and six sides of a cube. From these 28 simulations we chose those which best fit the observed CO gas distribution and velocity field. The initial conditions of these four simulations are presented in Table 3.
Parameters of the second set of Taffy simulations which are used for comparison with observations.
In the following, we restrict our discussion on the two “best-fit” models, simulations 19 and 20. These simulations differ in the inclination angle between the disks, the impact parameter, and the maximum relative velocity. Whereas the maximum relative velocity between the two galaxies is between 1080 and 1120 km s-1, it decreases rapidly after the impact, and is only between 660 and 690 km s-1 at the time of interest, i.e. 23 Myr after the impact. The time evolution of the stellar and gaseous components for are presented in Fig. 6 (simulation 20) and Fig. 7 (simulation 19). The main difference between these simulations is that in simulation 19 the secondary galaxy forms strong tidal tails to the east and west parallel to the secondary’s trajectory, much stronger than observed. The origin of a part of the gas mass in the bridge region is the secondary’s western tidal arm. These tails are also formed in simulation 20, but they are much shorter (3 kpc instead of 10 kpc for simulation 19).
Both simulations produce prominent gas bridges along the secondary’s trajectory whose morphologies are very similar to those of the previous set of simulations with simplified collision geometries (Fig. 2). Whereas the gas bridge of simulation 20 has the morphology of a 3D hourglass, the morphology of the gas bridge of simulation 19 is dominated by a straight filament which bifurcates toward the secondary galaxy. For both simulations the high-surface density small-scale structures disperse and disappear ~30 Myr after the galaxy collision. At the same time, the width of the gas bridge increases. As in the previous set of simulations, the outer gas disk of the primary galaxy is not affected by the interaction, because of the relatively small extent of the secondary’s gas disk. For t > 30 Myr, both galaxies develop prominent ring stellar and gaseous structures.
The total cloud collision rates of the system for simulations 18 − 21 are shown in Fig. 8. The shape of the time evolution of the cloud collision rate mainly depends on the inclination angle i between the two disks. In the case of parallel disks (i = 0°, simulations 18 and 20), the cloud collision rate abruptly increases during a few Myr. After its peak, it decreases until 10−15 Myr, rises again slightly until 20−25 Myr, and then declines slowly until 50 Myr after the impact. The collision rate shows a different behavior for inclined galactic disks ( i = −30°, simulations 19 and 21): the cloud collision rate slowly rises already 10 Myr before the impact. At the moment of impact, it rises abruptly during a few Myr. After the impact, the collision rate declines until t ~ 7 Myr, increases again to a secondary maximum at t ~ 10 Myr, and then declines monotonically until t = 50 Myr. The formation of the secondary maximum is due to the formation of the prominent tidal tail in the secondary galaxy (see timestep 10 Myr in Fig. 7). For t > 20 Myr the evolution of the collision rates are similar for all four simulations.
3.4. The time of impact
The time of interest is chosen to reproduce the main observed characteristics of the Taffy system: the projected positions of UGC 12914/15, the high gas column density of the bridge, and the double-line profile of the spectra of the total gas in the bridge region. This leads us to choose the timestep 23 Myr after impact. This timestep of interest is indicated in Figs. 6 and 7
Condon et al. (1993) estimated the time of impact under the assumption that their orbits are parabolic. Since the systemic velocities of UGC 12914 and UGC 12915 are very close (Δvr = 35 km s-1), the galaxies 3D velocity vectors are located in the plane of the sky. With the projected distance between the galaxies (~15 kpc) and galaxy masses, they derived a relative velocity of 600 km s-1. This leads to a time since impact of t ~ 24 Myr which is consistent with the time derived from spectral steepening of the radio bridge (Condon et al. 1993). We thus confirm this estimate of the collision time.
 |
Fig. 6 Time evolution of simulation 20 (i = 0°, δy = 4 kpc). Left panels: stellar surface density. The greyscale is logarithmic from 8 to 5600 M⊙ pc-2. Right panels: total gas surface density. The greyscale are (1,4,9,16,25,36,49,...,400) M⊙ pc-2. The timestep of interest (26 Myr) is marked by “model”. |
 |
Fig. 7 Time evolution of simulation 19 (i = −30°, δy = 1 kpc). Left panels: stellar surface density. The greyscale is logarithmic from 8 to 5600 M⊙ pc-2. Right panels: total gas surface density. The greyscale are (1,4,9,16,25,36,49,...,400) M⊙ pc-2. The timestep of interest (26 Myr) is marked by “model”. |
4. Comparison with observations
To test the goodness of our “best-fit” simulations 19 and 20, we compare the model results to the following observations of the Taffy galaxy system UGC 12914/15:
-
stellar distribution;
-
Hi and CO gas distributions;
-
CO velocity field;
-
Hi and CO spectra;
-
polarized radio continuum emission intensity and projected direction of the regular magnetic fields;
-
radio continuum total power emission.
For the comparison we use a unique projection with the primary (UGC 12914) seen at PA = 160°, i = 30°, and an azimuthal viewing angle (rotation around the angular momentum axis of the primary’s disk; see Fig. 9 of Vollmer et al. 2008a) az = 20°.
4.1. Stellar distribution
The Spitzer 3.6 μm map which traces the stellar mass distribution of the Taffy galaxy system UGC 12914/15 is shown in the upper panel of Fig. 9. The smaller galaxy, UGC 12915, has a prominent tidal arm toward the northwest and a faint counterarm to the southeast. The inner disk of UGC 12914 shows the well-known ring structure at a distance of ~20′′ = 6 kpc3 from the center. Two spiral arms are visible in the north and south of the galactic disk. The stellar surface density of the outer (6−10 kpc) disk is higher in the north than in the south. Moreover, UGC 12914 shows a low surface density stellar halo up to a radius of ~80′′ = 23 kpc.
 |
Fig. 8 Cloud particle collision rate for the simulations described in Table 3. Red: simulation 18; blue: simulation 19; yellow: simulation 20; green: simulation 21. |
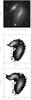 |
Fig. 9 Stellar surface density distribution. Upper panel: based on Spitzer IRAC 3.6 μm observations. Middle panel: timestep t = 23 Myr of simulation 20. Lower panel: timestep t = 23 Myr of simulation 19. Contour levels are (1,2,4,8,16,32,64,128,256,512,1024) × 5 M⊙ pc-2. Projection parameters are PA = 160°, i = 30°, and az = 20°. |
 |
Fig. 10 Stellar surface density distribution of simulation 20 with projection parameters PA = 160°, i = 20°, and az = 0°. The stellar morphology of UGC 12915 is better reproduced by the model. |
The model stellar distributions of simulation 19 and 20 are shown in the lower and middle panel of Fig. 9. There is rough agreement between simulations and observations: all secondary galaxies show a tidal distortion along the major axis. However, in both simulations the secondary galaxy is more distorted than observed. Moreover, the curvature of the northern tidal arm is stronger than that of UGC 12915 in both simulations. This is caused by the fact that the secondary galaxy is not observed exactly edge-on. A change of the inclination by 10° and the azimuthal viewing angle by 20° of simulation 20 leads to an edge-on projection of the secondary galaxy which reproduces the observed stellar distribution of UGC 12915 (Fig. 10). We keep the azimuthal viewing angle of Fig. 9, because the associated projection best reproduces the gas distribution and velocity field. As already stated in Sect. 3.1, the secondary galaxy of simulation 19 shows more prominent tidal arms than that of simulation 20 or the observations. Even in the case of an edge-on projection of the secondary galaxy in simulation 19, the curvature of its northern tidal tail is much stronger than observed.
The resemblance between simulations and observations is better for the primary galaxy, UGC 12914. Especially the higher stellar surface density in the northern outer stellar disk at (−6, 2) kpc is reproduced. This is a direct effect of the passage of UGC 12915 in this region of the disk of UGC 12914. We conclude that simulation 20 better reproduces the stellar mass distribution of the Taffy galaxy system UGC 12914/15.
4.2. Gas distribution
The model gas clouds represent the ISM as an entity. To distinguish molecular from atomic gas we use a prescription based on the total gas volume density, which has been successfully applied to the Virgo spiral galaxies NGC 4522 (Vollmer et al. 2008b) and NGC 4330 (Vollmer et al. 2012a): we assume that the molecular fraction depends linearly on the square root of the gas density 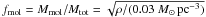 and the molecular fraction cannot exceed unity. A detailed motivation for this prescription is given in Vollmer et al. (2008b). The atomic and molecular gas surface density distributions are thus given as ΣHI = (1 − fmol) Σtot and ΣH2 = fmol Σtot. The atomic and molecular gas distributions of the model snapshots of simulation 19 and 20 are shown together with the CO (Gao et al. 2003) and Hi (Condon et al. 1993) distributions in Fig. 11.
and the molecular fraction cannot exceed unity. A detailed motivation for this prescription is given in Vollmer et al. (2008b). The atomic and molecular gas surface density distributions are thus given as ΣHI = (1 − fmol) Σtot and ΣH2 = fmol Σtot. The atomic and molecular gas distributions of the model snapshots of simulation 19 and 20 are shown together with the CO (Gao et al. 2003) and Hi (Condon et al. 1993) distributions in Fig. 11.
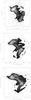 |
Fig. 11 HI (contour) on CO (greyscale) surface density. Upper panel: observations from Condon et al. (1993) and Gao et al. 2003). Contour levels are (4,8,12,16,20,24,28,32) M⊙ pc-2; greyscale levels are (55,60,65,70,75,85,100,125,150,175,200) M⊙ pc-2. Middle panel: timestep t = 23 Myr of simulation 20. Contour levels are (1,2,4,8,12,16,32,64,128) M⊙ pc-2; greyscale levels are (1,2,8,16,32,64,128,256) M⊙ pc-2. Lower panel: timestep t = 23 Myr of simulation 19. Contour and greyscale levels are the same as for the middle panel. |
The outer envelope of the Hi distribution of model primary galaxies of simulation 19 and 20 are relatively unperturbed. That of the secondary galaxy follows tidal perturbations visible in the stellar distribution (Fig. 9). The observed outer Hi envelope is different, with prominent Hi maxima to the north and south. In addition, the northern extension of UGC 12914’s gas disk is entirely missing. The surface density of the observed Hi bridge is not constant between UGC 12914 and UGC 12915. The maximum of the Hi bridge is located closer to UGC 12914 and shifted to the northwest with respect to the line connecting the two galaxy centers. Contrary to observations, the surface density distributions of the model Hi bridges are constant along lines connecting the two galaxies. As for the observed Hi distribution, the regions of maximum surface density of the model Hi bridges are shifted to the northwest with respect to the line connecting the two galaxy centers. This is a direct consequence of the impact which occurs northwest of the center of the primary galaxy.
The comparison between the model and observed H2 distributions is always limited by an uncertain conversion factor between CO surface brightness and H2 surface density. In the Taffy system, this conversion factor varies significantly between the disk and bridge regions (Braine et al. 2003; Zhu et al. 2007). Because of the uncertainty of the local conversion factor, we apply a constant Galactic CO-H2 conversion factor N(H2)/ICO = 1020 cm-2 (K km s-1)-1 to the whole Taffy system (Zhu et al. 2007). For this comparison one has to bear in mind that the CO-H2 conversion factor in the bridge might be several times lower than that in the galaxy disks (Braine et al. 2003; Zhu et al. 2007).
The maximum CO surface brightness and CO luminosity of UGC 12915 are higher than those of UGC 12914. The CO emission distributions of UGC 12914 and UGC 12915 are asymmetric along the major axis: they are more extended to the north than to the south. The maximum CO emission of the bridge is observed close to UGC 12915 and harbors a giant Hii region (Gao et al. 2003; Braine et al. 2003; Zhu et al. 2007). The projected width of the CO bridge is about half that of the Hi bridge. The CO bridge is offset toward the southeast with respect to the Hi bridge.
In the model, the H2 surface density of the two galactic disks is about the same. Whereas the H2 surface density of the primary galaxy is more extended to the south in simulation 20, that of the secondary galaxy is more extended to the northwest. In simulation 19 the H2 distribution of the primary galaxy is more symmetric, and that of the secondary is strongly distorted by the strong tidal fields. The model H2 bridges are more continuous than the observed CO bridge. Whereas there is more bridge H2 found in the northeast in simulation 20, the opposite trend is observed in simulation 19. As observed, the widths of the H2 bridges are about half that of the model Hi bridges, and they are offset to the southeast with respect to the Hi bridges.
4.3. Molecular gas velocity field
The observed CO velocity field of the Taffy system (Gao et al. 2003) is presented in Fig. 12 together with the model molecular gas velocity fields.
 |
Fig. 12 CO velocity field (colors). Contours: H2 surface density from Fig. 11. Upper panel: observations from Gao et al. (2003). Middle panel: timestep t = 23 Myr of simulation 20. Lower panel: timestep t = 23 Myr of simulation 19. |
The observed CO velocity field of the galactic disks is quite regular, i.e. the isovelocity contours are approximately parallel to the disks’ minor axes. The molecular gas of most of the bridge region has a zero velocity, i.e. that of UGC 12914. The velocities become positive (~150 km s-1) in the northwestern bridge region toward UGC 12915 and in the southern bridge region toward UGC 12914. The velocity gradient of most of the bridge is parallel to that of disk rotation.
Only simulation 20 shows undisturbed disk rotation fields which reproduce the observations. The isovelocity contours in the disks of simulation 19 are not parallel to the minor axes, but bent, as in barred spiral galaxies. In both simulations, most of the bridge gas is at zero velocity, in agreement with observations. The positive velocity of the northern receding side of the secondary galaxy and the southern receding side of the primary galaxy extend into the bridge region, giving rise to a velocity gradient which is parallel to that of disk rotation, again, in agreement with observations. The observed CO velocity structure of the bridge is better reproduced by simulation 19.
4.4. H i and CO spectra
The CO observations of Gao et al. (2003) presented in the previous Section were made with the BIMA interferometer. Due to the lack of very short baselines, the interferometer cannot detect extended structures of molecular gas. This extended molecular gas component is best detected by a single dish telescope, as the IRAM 30m telescope. In the presence of complex line shapes, the moment maps contain less information than the individual spectra. Therefore, we show in Fig. A.1 30 m CO(1−0) spectra together with VLA Hi spectra of the Taffy system (Fig. 1 of Braine et al. 2003) for the comparison with our simulations.
In the disk regions, where the lines are broad (~700 km s-1), the CO line follows the Hi line. In the bridge region the Hi spectra show a pronounced double-peaked spectrum. Both peaks have comparable widths (~200 km s-1) and intensities. They are separated by ~100−300 km s-1. Only the high-velocity part of the Hi spectra has a CO counterpart. On the western side of UGC 12914 a double-line profile is observed in Hi, with a CO counterpart only for the low velocity line. The corresponding model spectra are presented in Fig. A.2 for simulation 20 and in Fig. A.3 for simulation 19. The model Hi and CO lines of the primary galaxy have broad widths in both simulations, comparable to the observed line widths. Those of the secondary galaxy are comparable to the observed line widths only in simulation 20, because the secondary is seen less edge-on in simulation 19. In the bridge region, both simulations display double-line profiles. Both simulations thus reproduce the observed double line profiles. Moreover, only the low-velocity line has a CO counterpart in the region around (−7,10) kpc for simulation 20 and around (−3,10) kpc for simulation 19. Although the linewidths of the two components of the observed double-line profiles in the bridge region are well reproduced by simulation 20, their velocity separation is about twice the observed separation. On the other hand, simulation 19 reproduces the observed velocity separation between the lines, but the linewidth of the high-velocity line is about 1.5 times broader than observed. Both simulations reproduce the observed double-line profile west of the center of UGC 12914, with a CO line at low velocities and an Hi line at high velocities. The causes of the double-line profile will be discussed in Sect. 5.2.
4.5. Radio continuum
4.5.1. Observations
We re-reduced archival VLA 6 cm total power and polarized continuum data first published in Condon et al. (1993). Similar maps of the Taffy system are shown in Drzazga et al. (2011). Only the bridge region is detected in polarized emission (Fig. 13). The maximum of polarized intensity is located in the southern part of the gas bridge. The projected vectors of the large-scale regular magnetic field are parallel to the bridge or perpendicular to the galactic disks. The total power emission is shown in Fig. 14. As shown in Condon et al. (1993) the bridge region shows strong radio continuum emission at 6 cm. Moreover, UGC 12915 has a ~4 times higher central surface brightness than UGC 12914.
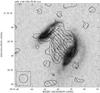 |
Fig. 13 Observed 6 cm polarized radio continuum contours and projected magnetic field vectors (from Condon et al. 1993) on a Digitized Sky survey image of the UGC 12914/5 system. Contour levels are (3,5,8,12,20,30,50,80,120,200,300,500) × 15 μJy/beam. |
 |
Fig. 14 Observed 6 cm total power radio continuum contours and projected magnetic field vectors (based on archival VLA data first published by Condon et al. 1993) on a Digitized Sky survey image of the UGC 12914/5 system. Contour levels are (3,5,8,12,20,30,50,80,120,200,300,500) × 16 μJy/beam. |
4.5.2. Model
To calculate the large-scale regular magnetic field for our simulations, we apply the same procedure as Otmianowska-Mazur & Vollmer (2003) and Vollmer et al. (2012a). We solve the induction equation: 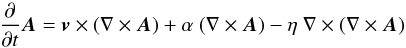 (4)where A = ∇ × B is the magnetic potential, B the magnetic induction, v the large-scale velocity of the gas, and η the coefficient of a turbulent diffusion, on a 3D grid (200 × 200 × 250). The cell size is 300 pc. Time-dependent gas-velocity fields are provided by the 3D dynamical simulations presented in Sect. 2. The induction equation is solved using a second order Godunov scheme with second order upstream partial derivatives together with a second order Runge-Kutta scheme for the time evolution. This results in less numerical diffusion than that of the ZEUS 3D MHD code (Stone & Norman 1992a,b). The 3D velocity field obtained from the N-body code has a discrete distribution. The interpolation to a regular 3D grid was done with the Kriging method (Soida et al. 2006). We assume the magnetic field to be partially coupled to the gas via the turbulent diffusion process (Elstner et al. 2000) assuming the magnetic diffusion coefficient to be η = 3 × 1025 cm2 s-1. We do not implement any dynamo process (α = 0). The initial magnetic field is purely toroidal with an exponential distribution with a scalelength of 1 kpc in the vertical direction. Because very rapidly (~1000 km s-1) evolving gas particles lead to numerical artifacts in our code, only the primary galaxy, which is kept at rest, is initially magnetized. During the galaxy-galaxy collision the magnetic field propagates into the gas bridge and is then amplified by the dynamics of the bridge gas. Due to the enormous amount of kinetic energy in the bridge gas, the final magnetic field configuration is expected to be independent of the seed field.
(4)where A = ∇ × B is the magnetic potential, B the magnetic induction, v the large-scale velocity of the gas, and η the coefficient of a turbulent diffusion, on a 3D grid (200 × 200 × 250). The cell size is 300 pc. Time-dependent gas-velocity fields are provided by the 3D dynamical simulations presented in Sect. 2. The induction equation is solved using a second order Godunov scheme with second order upstream partial derivatives together with a second order Runge-Kutta scheme for the time evolution. This results in less numerical diffusion than that of the ZEUS 3D MHD code (Stone & Norman 1992a,b). The 3D velocity field obtained from the N-body code has a discrete distribution. The interpolation to a regular 3D grid was done with the Kriging method (Soida et al. 2006). We assume the magnetic field to be partially coupled to the gas via the turbulent diffusion process (Elstner et al. 2000) assuming the magnetic diffusion coefficient to be η = 3 × 1025 cm2 s-1. We do not implement any dynamo process (α = 0). The initial magnetic field is purely toroidal with an exponential distribution with a scalelength of 1 kpc in the vertical direction. Because very rapidly (~1000 km s-1) evolving gas particles lead to numerical artifacts in our code, only the primary galaxy, which is kept at rest, is initially magnetized. During the galaxy-galaxy collision the magnetic field propagates into the gas bridge and is then amplified by the dynamics of the bridge gas. Due to the enormous amount of kinetic energy in the bridge gas, the final magnetic field configuration is expected to be independent of the seed field.
 |
Fig. 15 Model 6 cm polarized radio continuum contours and projected magnetic field vectors on the model stellar surface density distribution for two azimuthal viewing angles. Upper panels: simulation 20; lower panels: simulation 19. |
The MHD model does not contain a galactic wind. The resulting polarized emission is calculated by assuming a density of relativistic electrons that is proportional to the model gas density ρ. This rather crude approximation is motivated by (i) the fact that in quiescent galaxies, the density of relativistic electrons is approximately proportional to the star formation density which depends on ρ1−1.7; and (ii) the transport mechanism of relativistic electrons into the bridge region during the galaxy collision is unknown. During the collision, the magnetic field in the bridge region is amplified by shear and compression motions. The overall morphology of the magnetic field does not evolve significantly for timesteps around the time of interest (20−35 Myr).
Since the direction of the projected magnetic field vectors strongly depends on projection, we show the resulting model polarized emission together with the model projected B vectors for simulation 19 and 20 for two azimuthal viewing angles az = 0° and 20° in Fig. 15. In all model polarized emission maps the bridge region is prominent. The model polarized emission of the bridge is as strong as that of the two galactic disks. Its maximum is located in the northern/southern part of the bridge in simulation 19/20. The different azimuthal viewing angles do not lead to significant changes for simulation 20, but do change of the location of the maximum polarized emission near the secondary galaxy in simulation 19. The width of the bridge of polarized emission is ~7 kpc in simulation 20 and ~12 kpc in simulation 19.
The model magnetic field vectors are mostly parallel to the bridge in simulation 20. Only one region close to the primary galaxy displays an offset by ~45°. In simulation 19 the southwestern part of the bridge has magnetic field vectors parallel to the bridge, whereas the B vectors of the northeastern part show an offset of ~30°. The overall resemblance between the observed and model polarized emission is better for simulation 20 with the maximum located in the southern part of the bridge and the B vectors parallel to the bridge.
Whereas the polarized radio continuum emission depends on the large-scale (compared to the beam) regular magnetic field, the total power emission depends mainly on the small-scale turbulent magnetic field, which dominates the total magnetic field strength. Since our MHD model only includes the regular magnetic field, we have to derive the turbulent magnetic field in a different way. For this we assume equipartition between the magnetic field B and the turbulent motions of the gas: 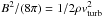 , where ρ is the ISM density and vturb its turbulent velocity dispersion. The total power emission is proportional to the density of relativistic electrons times the square of the turbulent magnetic field. During the galaxy head-on collision, cosmic ray electrons are dragged into the bridge region. Since we do not know the mechanisms of the cosmic ray drag, we approximate the total power emission by the square of the small-scale turbulent magnetic field (Fig. 16). In both simulation snapshots the total power emission of the bridge region is as strong as that of the primary galaxy. This is mainly caused by the high gas velocity dispersion of the bridge gas (Sect. 5). The model total power emission of the secondary galaxy is higher than that of the primary. The model thus qualitatively reproduces the 6 cm total power emission of the Taffy system (Fig. 14).
, where ρ is the ISM density and vturb its turbulent velocity dispersion. The total power emission is proportional to the density of relativistic electrons times the square of the turbulent magnetic field. During the galaxy head-on collision, cosmic ray electrons are dragged into the bridge region. Since we do not know the mechanisms of the cosmic ray drag, we approximate the total power emission by the square of the small-scale turbulent magnetic field (Fig. 16). In both simulation snapshots the total power emission of the bridge region is as strong as that of the primary galaxy. This is mainly caused by the high gas velocity dispersion of the bridge gas (Sect. 5). The model total power emission of the secondary galaxy is higher than that of the primary. The model thus qualitatively reproduces the 6 cm total power emission of the Taffy system (Fig. 14).
 |
Fig. 16 Model 6 cm total polarized radio continuum emission (contours) and projected magnetic field vectors on the model 6 cm total power radio continuum emission distribution (greyscale: (1,2,4,8,16,32,64,128) × an arbitrary value). Upper panel: simulation 20; lower panel: simulation 19. |
5. Discussion
5.1. How well does the model reproduce observations?
To assess the goodness of the model, we determined the main observational characteristics that a galaxy collision model should reproduce (Table 4). We then checked if these characteristics are reproduced. In summary, both simulations reproduce the primary’s stellar distribution, the prominent Hi and CO gas bridge, the offset between the CO and Hi emission in the bridge, the bridge isovelocity vectors parallel to the bridge, the Hi double-line profiles in the bridge region with CO emission only associated to the high-velocity line, the large line-widths (100 − 200 km s-1) in the bridge region (simulation 19: 100−200 km s-1, simulation 20: ~100 km s-1), the high field strength of the bridge large-scale regular magnetic field, the projected magnetic field vectors parallel to the bridge and the strong total power radio continuum emission from the bridge. The small separation (~330 km s-1) between the two Hi lines in the bridge region is only reproduced by simulation 19 (~400 km s-1), whereas the symmetric velocity field in the galactic disks and the southern maximum of polarized intensity in the bridge region are only reproduced by simulation 20. The stellar distribution of the secondary galaxy can only be approximately reproduced by simulation 20 with a somewhat different (20°) projection. The distorted Hi envelope is reproduced by either simulation. This is probably due to the collisional description of the model ISM4 In the outer parts of the galactic disks, where the particle density is low, cloud-cloud collisions become rare. In reality, the Hi gas of these regions is in form of filamentary structures with a possibly higher area filling factor than our clouds. The impact of the galaxy collision on this gas might thus be stronger than predicted by our model. For the gas in the outer galactic disks, a continuous description of the ISM (SPH or hydro) might thus be preferable.
Model ability to reproduce observational characteristics.
The present simulations thus reproduce qualitatively most of the observed multiwavelength characteristics. Simulation 20 better reproduces observations than simulation 19. Despite the calculation of 45 models, we were not able to find one single initial condition and projection that reproduces all observed characteristics. We thus decided to stop our parameter study. We are confident that the actual interaction parameters of the Taffy system UGC 12914/15 are not very far from those used for simulation 19 and 20 (Table 3).
5.2. The role of collisions
For simulation 19 where the secondary’s disk is initially inclined by 30° with respect to the primary’s disk, the disk of the secondary galaxy is strongly distorted by the tidal fields (Fig. 9). The secondary’s tidal distortion is much less strong in simulation 20, where the two disks are initially parallel.
What is the role of tidal distortions and distortions caused by the collisional nature of the modelled ISM? To investigate the role of the cloud-cloud collisions, we re-simulated simulation 19 suppressing the cloud collisions. It is surprising that there are regions in the bridge that show a double-line profile reminiscent of the observed double-line profile (Fig. A.1) with comparable linewidths and line separations. Contrary to observations, the low-velocity line of the model is most prominent in CO. Moreover, the model lines in the bridge region are much weaker than the observed ones. The double-lines in this simulation are produced by the projection of two spatially different gas flows. Tidal effects thus can create double-line profiles, but they are not the main mechanism for the creation of the observed double-line profiles in the bridge of the Taffy system UGC 12914/15.
5.3. Isolating the bridge region
There is a debate in the literature (Gao et al. 2003; Braine et al. 2003; Zhu et al. 2007) about how much gas is located in the bridge between UGC 12914 and UGC 12915. This debate has three aspects: (i) the delimitation of the bridge region; (ii) the CO–H2 conversion factor of the bridge gas; and (iii) the Hi mass belonging to the bridge. Our model can help to clarify points (i) and (iii). For this purpose we have separated the bridge region in 3D from the disk regions as described in Sect. 3: we define the bridge region as a vertical cylinder with an infinite radius extending from 3 kpc to 12 kpc with respect to the disk plane of the primary galaxy. The model spectra of simulation 19 showing only the bridge region is presented in Fig. A.4. In the region of the secondary’s stellar tidal tail a double-line profile is found with a dominant high-velocity component. The linewidth of this component is large (~200 km s-1). The 3D bridge region extends from the eastern border of the primary’s to the western border of secondary’s high surface brightness disk. Almost all lines from the bridge region are strong in CO emission. Since our model Hi/CO separation is based on gas density, this means that the bridge gas has a relatively high gas density.
We thus conclude that the bridge region delimited by Braine et al. (2003, Fig. A.1) is somewhat too small. It should extend until the border of the high surface brightness disk of UGC 12914. Within the disk, only the high-velocity component of the double-lines belongs to the bridge. Based on these conclusions we revise the bridge Hi mass to be MHIbridge ~ 3 × 109 M⊙. Applying a CO–H2 conversion factor of N(H2)/ICO = 4 × 1019 cm-2 (K km s-1)-1 (Zhu et al. 2007), the mass of the molecular gas located in the bridge is also MH2bridge ~ 2 × 109 M⊙. The recently discovered warm H2 (Peterson et al. 2012) might add up to 109 M⊙ to the molecular gas content if the H2-emitting gas is different from the CO-emitting gas5. The bridge gas thus has a molecular fraction of MH2/MHI ~ 1.
5.4. Cloud collisions in the gas bridge
The bridge gas has a high surface density (ΣHI ~ 30 M⊙ pc-2; ΣCO ~ 50 M⊙ pc-2; see Fig. 11). The bright CO emission of the disk gas implies high gas densities (~1000 cm-3) of a significant portion of the bridge gas. Our model reproduces these findings. However, there is no star formation associated with most of the bridge gas (Gao et al. 2003; Braine et al. 2003; Zhu et al. 2007). Only the bridge gas of very high surface density close to UGC 12915 is vigorously forming stars. What makes the bridge gas not form stars despite its high density? To investigate this question, we need to have a closer look at the physical properties of the bridge gas. Figure 17 shows the gas velocities in the plane of the sky. We identify large-scale colliding flows from the south of the bridge into the bridge region of highest surface density around the position ( − 3,7) kpc. These flows lead to a compression of the gas and enhances the cloud-cloud collision rate.
 |
Fig. 17 Transverse gas velocities of simulation 19 on the total gas surface density distribution. The primary galaxy is at rest. The thick arrow indicates the transverse velocity of the secondary galaxy. |
The time evolution of the local cloud-cloud collision rate of simulation 19 is presented in Fig. 18. As expected, the local cloud collision rate generally follows the gas surface density. Before the galaxy collision most cloud-cloud collisions occur in the inner galactic disks and in spiral arms where the gas density is high. This situation does not change significantly until ~10 Myr after the impact. The local cloud collision rate in the bridge region is as high as in the spiral arms of the unperturbed disks. After ~16 Myr the local collision rate in the portion of the bridge near the primary galaxy begins to increase. It reaches its maximum ~23 Myr after the impact. This corresponds exactly to the timestep of interest. For t > 23 Myr the local cloud collision rate in the bridge decreases again. The bridge region at the time of interest is thus in a phase of active compression with a high input of mechanical energy.
 |
Fig. 18 Simulation 19. Contours of the total gas surface density on the distribution of cloud-cloud collisions (greyscale). The timestep t = 0 Myr corresponds to the impact. |
For t > 23 Myr ring structures form in both galactic disk where the local cloud collision rate is enhanced.
5.5. Gas densities and velocity dispersions in the bridge
To further investigate the physical properties of the disk region, we present the time evolution of the gas density and 3D velocity dispersion of simulation 20/19 in Figs. 19 and 20. With our kpc resolution, the densities of the unperturbed disk range between 10-3 and 1 M⊙ pc-3, the velocity dispersions between (10 and 30 km s-1). Due to the galaxy collision, the velocity dispersion increases up to 400 km s-1. The velocity dispersion of most of the gas located in the bridge is between 100 and 200 km s-1. In addition, there are regions in the bridge where the velocity dispersion reaches 200 to 300 km s-1. In simulation 19 these regions are mostly close to the secondary galaxy for t > 23 Myr. In both simulations, the mean velocity dispersion of the bridge gas decreases for t > 23 Myr. In simulation 20, the velocity dispersion is about constant along the bridge. On the other hand, in simulation 19 the bridge velocity dispersion increases slowly from the primary to the secondary galaxy along the bridge. At t = 30 Myr an X-structure forms.
 |
Fig. 19 Evolution of the bridge gas properties of simulation 20. Left panels: total gas volume density as a function of distance along the bridge. Right panels: 3D velocity dispersion as a function of distance along the bridge. |
In both simulations the bridge contains a high-density filament embedded into low-density regions. The density distribution is not continuous between these extremes. The density of the high-density filament at the time of interest is of the order of 10-2 M⊙ pc-3 in both simulations. Due to the expansion of the bridge region with time, the overall gas density in the bridge decreases for t > 20 Myr in simulation 20 and for t > 26 Myr in simulation 19. Whereas the high-density gas has a velocity dispersion higher than 100 km s-1, the low-density gas has a velocity dispersion lower than 100 km s-1 in both simulations. We identify the high-density (10-2 M⊙ pc-3), high-velocity-dispersion (>100 km s-1) bridge regions with those regions emitting in the CO line. The observed large linewidth (~200 km s-1) of the CO lines in the bridge are thus consistent with a high intrinsic velocity dispersion of the bridge gas in our model.
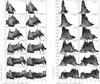 |
Fig. 20 Evolution of the bridge gas properties of simulation 19. Left panels: total gas volume density as a function of distance along the bridge. Right panels: 3D velocity dispersion as a function of distance along the bridge. |
Assuming equipartition between the kinetic and the magnetic energy density 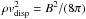 , a velocity dispersion of vdisp = 150 km s-1, and a total gas density of ρ = 0.01 M⊙ pc-3, we estimate the total magnetic field strength in the high-density bridge region to be B ~ 65 μG. The total magnetic field strength in the low-density bridge region (ρ = 10-3 M⊙ pc-3, vdisp = 50 km s-1) is B ~ 7 μG. The latter value is close to the magnetic field strength derived from the 1.4 GHz specific intensity assuming equipartition between the energy of the relativistic electrons and the magnetic field (Condon et al. 1993). The lifetime of synchrotron-emitting electrons is t ~ 1 (B/1 μG)-1.5(ν/1 GHz)-0.5 Gyr, where ν is the frequency of the observation. This lifetime is ~1 Myr for the high-density regions and ~25 Myr for the low-density regions at ν = 4.8 GHz. In the absence of newly injected relativistic electrons produced in supernova explosions, the radio continuum emission of the high-density regions drops under the detection limit after a few Myr. That of the low-density regions persists for several 10 Myr.
, a velocity dispersion of vdisp = 150 km s-1, and a total gas density of ρ = 0.01 M⊙ pc-3, we estimate the total magnetic field strength in the high-density bridge region to be B ~ 65 μG. The total magnetic field strength in the low-density bridge region (ρ = 10-3 M⊙ pc-3, vdisp = 50 km s-1) is B ~ 7 μG. The latter value is close to the magnetic field strength derived from the 1.4 GHz specific intensity assuming equipartition between the energy of the relativistic electrons and the magnetic field (Condon et al. 1993). The lifetime of synchrotron-emitting electrons is t ~ 1 (B/1 μG)-1.5(ν/1 GHz)-0.5 Gyr, where ν is the frequency of the observation. This lifetime is ~1 Myr for the high-density regions and ~25 Myr for the low-density regions at ν = 4.8 GHz. In the absence of newly injected relativistic electrons produced in supernova explosions, the radio continuum emission of the high-density regions drops under the detection limit after a few Myr. That of the low-density regions persists for several 10 Myr.
In the bridge region, star formation only occurs in the giant Hii region close to UGC 12915. Most of the bridge region is devoid of star formation and thus devoid of the injection of relativistic electrons. In this latter region, the high surface brightness 20 cm emission follows the Hi and not the CO distribution (Fig. 8 of Gao et al. 2003), i.e. it follows the low-density atomic gas. Based on our model, we thus conclude that the observed synchrotron radio continuum emission of the bridge region outside the giant Hii region near UGC 12915 mainly stems from the low-density, high-velocity-dispersion bridge gas which is observed in Hi.
The high mechanical energy input into the bridge region is consistent with the recent detection of strong, resolved emission from warm H2 in the bridge of the Taffy galaxy system UGC 12914/15 (Peterson et al. 2012). The latter authors state that “since the cooling time of warm H2 is short (~5000 yr), shocks must be permeating the molecular gas bridge region in order to continue heating the H2”. Based on our model, we identify the energy source to be the mechanical energy from compressive colliding gas flows in the bridge region. Peterson et al. (2012) estimate the mean surface brightness of warm H2 emission to be ΔE/(ΔAΔt) ~ 1.7 × 10-7 W m-2. The mechanical energy input is 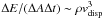 . For the high-density bridge gas (ρ = 0.01 M⊙ pc-3, vdisp = 150 km s-1) we obtain ΔE/(ΔAΔt) ~ 2.5 × 10-6 W m-2, for the low-density gas (ρ = 10-3 M⊙ pc-3, vdisp = 50 km s-1) ΔE/(ΔAΔt) ~ 10-8 W m-2. We thus conclude that only the high-density gas undergoes a high enough mechanical energy input to produce the observed emission of warm H2. Our model suggests that we observe this galaxy head-on collision near the time of maximum CO and H2 emission. The physical properties of the bridge gas are similar to those of the dense gas in the large-scale shock of Stephan’s Quintet. There, the molecular gas carries a large fraction of the gas kinetic energy involved in the collision which has not been thermalized yet (Guillard et al. 2012).
. For the high-density bridge gas (ρ = 0.01 M⊙ pc-3, vdisp = 150 km s-1) we obtain ΔE/(ΔAΔt) ~ 2.5 × 10-6 W m-2, for the low-density gas (ρ = 10-3 M⊙ pc-3, vdisp = 50 km s-1) ΔE/(ΔAΔt) ~ 10-8 W m-2. We thus conclude that only the high-density gas undergoes a high enough mechanical energy input to produce the observed emission of warm H2. Our model suggests that we observe this galaxy head-on collision near the time of maximum CO and H2 emission. The physical properties of the bridge gas are similar to those of the dense gas in the large-scale shock of Stephan’s Quintet. There, the molecular gas carries a large fraction of the gas kinetic energy involved in the collision which has not been thermalized yet (Guillard et al. 2012).
 |
Fig. 21 Star formation rate based on the FUV and 24 μm emission as a function of the molecular gas surface density. The crosses are based on X = 1020 cm-2 (K km s-1)-1, which is half of the Galactic value. The bridge region outside the giant Hii region near UGC 12915 are marked as squares with crosses. Squares without crosses correspond to a 2.5 times lower X factor as suggested by Zhu et al. (2007). Data of NGC 4438 are shown as triangles. The dashed lines correspond to constant star formation timescales of 2 and 4 Gyr. |
5.6. The low star formation efficiency in the bridge
The local star formation rate was calculated from the FUV luminosities corrected by the 24 μm IR emission following Leroy et al. (2008). This method takes into account the UV photons from young massive stars which escape the galaxy and those which are absorbed by dust and re-radiated in the far infrared: 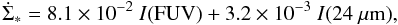 (5)where I(FUV) is the GALEX far ultraviolet and I(24 μm) the Spitzer MIPS 24 μm intensity in units of MJy sr-1.
(5)where I(FUV) is the GALEX far ultraviolet and I(24 μm) the Spitzer MIPS 24 μm intensity in units of MJy sr-1. 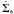 has the units of M⊙ kpc-2 yr-1. Following Helou et al. (2004), we subtracted the stellar continuum from the 24 μm surface brightnesses (in MJy sr-1) using
has the units of M⊙ kpc-2 yr-1. Following Helou et al. (2004), we subtracted the stellar continuum from the 24 μm surface brightnesses (in MJy sr-1) using 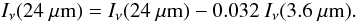 (6)The full width at half-maximum (FWHM) of the point spread functions (PSFs), as stated in the Spitzer Observer’s Manual (Spitzer Science Centre 2006), are 1.7 and 6 arcsec at 3.6 and 24 μm, respectively, that of the CO data is 10′′. First, the data are convolved with kernels that match the PSFs of the images in the 3.6 and 24 μm bands to a common PSF of 12′′. The CO data of Gao et al. (2003) were also convolved to the common resolution. Next, the data were re-binned to the common pixel size of 8.5′′.
(6)The full width at half-maximum (FWHM) of the point spread functions (PSFs), as stated in the Spitzer Observer’s Manual (Spitzer Science Centre 2006), are 1.7 and 6 arcsec at 3.6 and 24 μm, respectively, that of the CO data is 10′′. First, the data are convolved with kernels that match the PSFs of the images in the 3.6 and 24 μm bands to a common PSF of 12′′. The CO data of Gao et al. (2003) were also convolved to the common resolution. Next, the data were re-binned to the common pixel size of 8.5′′.
The resulting pixel-by-pixel star formation rate as a function of the molecular gas surface density is presented in Fig. 21. Since the CO-to-H2 conversion factor X is uncertain especially in the bridge region, we show molecular gas surface densities based on X = 1020 cm-2 (K km s-1)-1 and X = 4 × 1019 cm-2(K km s-1)-1 (Zhu et al. 2007). This should cover the expected range. The mean star formation rate timescale with respect to the molecular gas (t∗ ~ 2 Gyr; Bigiel et al. 2011) is shown as a dashed line. We also show a line with t∗ = 4 Gyr, which is still in the expected range. The star formation efficiency with respect to the molecular gas is normal in the galactic disks, but it is at least a factor of 2 to 3 lower in the bridge region. This decrease in star formation efficiency is very similar to what is observed in the extraplanar gas of the Virgo spiral galaxy NGC 4438 (Vollmer et al. 2012b) and in the interacting galaxies NGC 3226/27 (region 2 in Table 1 of Lisenfeld et al. 2008). Whereas this decrease is observed at low molecular gas surface densities (~10 M⊙) in NGC 4438 and NGC 3226/27, it occurs at a 3 to 5 times higher molecular gas surface density in the Taffy bridge. The quenching of star formation in the extraplanar gas of NGC 4438 is caused by a combined tidal and ram pressure interaction (Vollmer et al. 2005).
The detection of CO(1–0) emission from the gas bridge implies high local gas densities of the order of ≳100 cm-3 = 5 M⊙ pc-3. With an overall density of 0.01 M⊙ pc-3 on kpc-scales, this leads to a volume filling factor of ≲2 × 10-3. The CO-emitting dense gas is thus highly clumped, as the disk ISM, and the clumps have a very low volume filling factor. We suggest that star formation is quenched by the high velocity dispersion of the bridge gas caused by mechanical energy input, which prevents the gravitational collapse of the high-density gas clumps.
Obviously, this suggestion does not hold for the giant Hii region near UGC 12915, where gas clouds do collapse and form stars. We suggest that this is caused by a higher local gas density leading to a Jeans length which equals or is smaller than the extent of the gas. To illustrate this effect, we calculated the local Jeans length for the gas in our simulations. In Fig. 22 we only show gas with a Jeans length smaller than 2 kpc.
 |
Fig. 22 Potential sites of star formation. Greyscale: total gas surface density. Contours: surface density of gas with a local Jeans length smaller than 2 kpc. Upper panel: simulation 20. Lower panel: simulation 19. |
The gas in the bridges of both simulations has local Jeans lengths exceeding 2 kpc. The gas north of the primary galaxies’ centers with local Jeans lengths smaller than 2 kpc is mostly located in the disks of the primary galaxies. Only in simulation 20 is there a region of high surface density south of the secondary galaxy’s center at ( − 12,12) kpc, which has a local Jeans length smaller than 2 kpc. This region is supposed to form stars and might correspond to the giant Hii region south of UGC 12915. We do not claim to reproduce the giant Hii region but we think that Fig. 22 can be seen as a proof of concept.
6. Conclusions
The Taffy system UGC 12914/15 is a rare case of a head-on collision between two gas-rich spiral galaxies. We made dynamical simulations of this galaxy collision, in which the gas of both galaxies collide, using a model which includes a collisionless (halo and stellar particles) and a collisional (gas) component. The gaseous component is simulated by a sticky particle scheme where gas particles undergo partially inelastic collisions. The collision rate depends on the mass-radius relation of the gas particles (Eq. (1)). With a first set of simulations with a simplified collision geometry, we investigated the behavior of the collision rate as a function of cloud size parameter ξ. The collision rate increases with increasing ξ. Our collision rates are in reasonable agreement with theoretical expectation. A higher collision rate leads to more momentum transfer between the cloud particles during the galaxy collision. A higher collision rate during impact increases the gas mass of the bridge region between the two colliding galaxies. We fixed ξ to obtain a bridge gas mass exceeding 3 × 109 M⊙.
In a second step, we made a second set of parameters with fixed inclination angles between the two counter-rotating disks of 0° and − 30° where we varied systematically the position of impact. We found two simulations, that reproduce the observed main characteristic of the Taffy system. For both simulations, the relative velocity at impact is ~1000 km s-1. The transverse velocity at the present time is between 650 km s-1 and 660 km s-1. We confirm the time of impact estimated by Condon et al. (1993). Our best-fit models place the impact 23 Myr ago. For times >20 Myr all models develop ring structures characteristic for galaxy head-on collisions.
To compare simulation snapshots to Hi and CO observations (Gao et al. 2003; Braine et al. 2003), we assume that the molecular fraction of the gas depends on the square root of the gas volume density. This recipe allows us produce model Hi and CO cubes. For the comparison of our simulations with observations of polarized radio continuum emission, we calculated the evolution of the 3D large-scale magnetic field for our simulations. The induction equations including the time-dependent gas-velocity fields from the dynamical model were solved for this purpose.
Since we could not find a single simulation which reproduces all observed characteristics, we present two “best-fit” simulations. The first simulation better reproduces the Hi and CO line profiles of the bridge region (Braine et al. 2003), whereas the second simulation better reproduces the stellar distribution of UGC 12915, the symmetric gas velocity fields of the galactic disks, the projected magnetic field vectors in the bridge region, and the distribution of the 6 cm polarized radio continuum emission (Condon et al. 1993). The following observational characteristics can be reproduced by our models:
-
1.
The stellar distribution of the Taffy system. The stellardistribution of the model secondary galaxy is more distorted thanthat of UGC 12915.
-
2.
The prominent Hi and CO gas bridge.
-
3.
The offset of the CO emission to the south with respect to the Hi emission in the bridge region.
-
4.
The gas symmetric velocity fields in the galactic disks.
-
5.
The isovelocity contours of the CO velocity field which are parallel to the bridge.
-
6.
The Hi double-line profiles in the disk region.
-
7.
CO emission is only detected in the high-velocity component of the double-line.
-
8.
The large gas linewidths (100−200 km s-1) in the bridge region.
-
9.
The velocity separation between the double lines (~330 km s-1).
-
10.
The high field strength of the regular magnetic field in the bridge region.
-
11.
The projected magnetic field vectors, which are parallel to the bridge.
-
12.
The offset of the maximum of the 6 cm polarized radio continuum emission to the south of the bridge.
-
13.
The strong total power emission from the disk.
The observed distortion of the Hi envelope of the Taffy system (Condon et al. 1993) cannot be reproduced by our model. This is due to an insufficient momentum transfer between the gas particles located in the outer galactic disks. For this gas a continuous description of the ISM (SPH or hydro) might be preferable.
The model allows us to redefine the bridge region in three dimensions. We estimate the total gas mass (Hi, warm and cold H2) to be 5 to 6 × 109 M⊙. Its molecular fraction MH2/MHI is about unity. The structure of the model gas bridge is bimodal. There is a dense (~0.01 M⊙ pc-3) component with a high velocity dispersion >100 km s-1 and a less dense (~10-3 M⊙ pc-3) component with a smaller, but still high velocity dispersion ~50 km s-1. The synchrotron lifetime of relativistic electrons is only long enough to be consistent with the existence of the radio continuum bridge (Condon et al. 1993) for the less dense component. This explains why the radio continuum emission follows the Hi and not the CO emission of the bridge outside the giant Hii region near UGC 12915. On the other hand, only the high-density gas undergoes a high enough mechanical energy input to produce the observed strong emission of warm H2 (Peterson et al. 2012). We propose that, despite the high local gas densities, this high input of mechanical energy quenches star formation in the bridge gas except for the giant Hii region near UGC 12915. Our model suggests that we observe this galaxy head-on collision near the time of maximum CO and H2 emission.
Online material
Appendix A: CO and Hi observed and model spectra of the Taffy system UGC 12914/15
For a better readability of this article, we decided to show the CO and Hi observed and model spectra as an appendix.
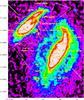 |
Fig. A.1 CO(1−0) spectra (yellow line and yellow scale, intensity in milliKelvins) overlaid with Hi spectra (black line) on a Digitized Sky survey image of the UGC 12914/5 system (from Braine et al. 2003). The center of UGC 12915 is at 00h01m41.9s, 23°29′44.9′′. The bridge region is delimited by the white polygon. |
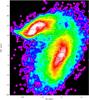 |
Fig. A.2 Simulation 20. CO(1−0) model spectra (white line) overlaid with Hi spectra (black line) on the model stellar surface density distribution. |
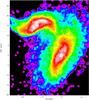 |
Fig. A.3 Simulation 19. CO(1−0) model spectra (white line) overlaid with Hi spectra (black line) on the model stellar surface density distribution. |
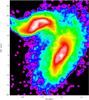 |
Fig. A.4 Simulation 19 where the disk gas has been removed. Thus only the gas located in the bridge region is visible. CO(1−0) model spectra (white line) overlaid with Hi spectra (black line) on the model stellar surface density distribution. |
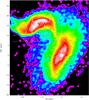 |
Fig. A.5 Simulation 19 wihout cloud-cloud collisions. CO(1−0) model spectra (white line) overlaid with Hi spectra (black line) on the model stellar surface density distribution. |
It is very likely that at least some of the gas detected in warm H2 emission by Peterson et al. (2012) is the same as what we detect in CO. While the warm H2 they detect is very different from what is seen in galactic giant molecular clouds, (i) the 13CO emission is very weak in the bridge (Braine et al. 2003), such that even the 12CO emission may be optically thin and (ii) the CO(2–1)/CO(1–0) ratio is compatible with warm optically thin emission from low-density molecular gas. It would be very useful to have observations of higher-J transitions in order to break this degeneracy.
Acknowledgments
We would like to thank Y. Gao for providing his CO data to us. This work has been supported by the Polish Ministry of Science and Higher Education grant No. 2011/03/B/ST9/01859.
References
- Appleton, P. N., Xu, K. C., Reach, W., et al. 2006, ApJ, 639, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Boulares, A., & Cox, D. P. 1990, ApJ, 365, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A. K., Walter, F., et al. 2011, ApJ, 730, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Braine, J., Davoust, E., Zhu, M., et al. 2003, A&A, 408, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braine, J., Lisenfeld, U., Duc, P.-A., et al. 2004, A&A, 418, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cluver, M. E., Appleton, P. N., Boulanger, F., et al. 2010, ApJ, 710, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Helou, G., Sanders, D. B., & Soifer, B. T. 1993, AJ, 105, 1730 [Google Scholar]
- Condon, J. J., Helou, G., & Jarrett, T. H. 2002, AJ, 123, 1881 [Google Scholar]
- Drzazga, R. T., Chyży, K. T., Jurusik, W., & Wiórkiewicz, K. 2011, A&A, 533, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, B. G., & Falgarone, E. 1996, ApJ, 471, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Elstner, D., Otmianowska-Mazur, K., von Linden, S., & Urbanik, M. 2000, A&A, 357, 129 [NASA ADS] [Google Scholar]
- Gao, Y., Zhu, M., & Seaquist, E. R. 2003, AJ, 126, 2171 [NASA ADS] [CrossRef] [Google Scholar]
- Guillard, P., Boulanger, F., Pineau des Forêts, G., et al. 2012, ApJ, 749, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Helou, G., Roussel, H., Appleton, P., et al. 2004, ApJS, 154, 253 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Higdon, J. L. 1995, ApJ, 455, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Higdon, J. L. 1996, ApJ, 467, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Hwang, J.-S., Struck, C., Renaud, F., & Appleton, P. N. 2012, MNRAS, 419, 1780 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [NASA ADS] [CrossRef] [Google Scholar]
- Lisenfeld, U., Mundell, C. G., Schinnerer, E., Appleton, P. N., & Allsopp, J. 2008, ApJ, 685, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Olson, K. M., & Kwan, J. 1990, ApJ, 349, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Otmianowska-Mazur, K., & Vollmer, B. 2003, A&A, 402, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, B. W., Appleton, P. N., Helou, G., et al. 2012, ApJ, 751, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Appleton, P. N., & Xu, C. K. 2010, ApJ, 724, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E. 2005, PASP, 117, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B. J., Struck, C., & Pogge, R. W. 1997, ApJ, 483, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Soida, M., Otmianowska-Mazur, K., Chyży, K., & Vollmer, B. 2006, A&A, 458, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Yoshida, N., & White, S. D. M. 2001, New Astron., 6, 79 [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992a, ApJS, 80, 753 [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992b, ApJS, 80, 791 [Google Scholar]
- Struck, C. 1997, ApJS, 113, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Struck, C., & Smith, B. J. 2003, ApJ, 589, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Theis, C., & Hensler, G. 1993, A&A, 280, 85 [NASA ADS] [Google Scholar]
- Trinchieri, G., Sulentic, J., Breitschwerdt, D., & Pietsch, W. 2003, A&A, 401, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trinchieri, G., Sulentic, J., Pietsch, W., & Breitschwerdt, D. 2005, A&A, 444, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsuchiya, T., Korchagin, V., & Wada, K. 1998, ApJ, 505, 607 [NASA ADS] [CrossRef] [Google Scholar]
- van der Hulst, J. M., & Rots, A. H. 1981, AJ, 86, 1775 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Cayatte, V., Balkowski, C., & Duschl, W. J. 2001, ApJ, 561, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Vollmer, B., Braine, J., Combes, F., & Sofue, Y. 2005, A&A, 441, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Chung, A., et al. 2008a, A&A, 483, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Braine, J., Pappalardo, C., & Hily-Blant, P. 2008b, A&A, 491, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Soida, M., Braine, J., et al. 2012a, A&A, 537, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vollmer, B., Wong, O. I., Braine, J., Chung, A., & Kenney, J. D. P. 2012b, A&A, 543, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegel W. 1994, Diploma Thesis, University of Heidelberg [Google Scholar]
- Zavagno, A., Anderson, L. D., Russeil, D., et al. 2010, A&A, 518, L101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhu, M., Gao, Y., Seaquist, E. R., & Dunne, L. 2007, AJ, 134, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Zink, E. C., Lester, D. F., Doppmann, G., & Harvey, P. M. 2000, ApJS, 131, 413 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameters of the second set of Taffy simulations which are used for comparison with observations.
All Figures
 |
Fig. 1 Overlapping cloud mass which is affected by a cloud-cloud collision divided by the total cloud mass as a function of the fraction between the radius of the massive cloud r1 and the impact parameter b (from Wiegel 1994). Crosses: cloud of equal mass M1 = M2. Triangles: M1 = 10 × M2. |
| In the text | |
 |
Fig. 2 Time evolution of a Taffy galaxy collision (simulation 10). Left panels: stellar surface density. The greyscale is logarithmic from 8 to 5600 M⊙ pc-2. Right panels: total gas surface density. The greyscale are (1,4,9,16,25,36,49,...,400) M⊙ pc-2. The timestep of interest (26 Myr) is marked by “model”. The impact parameter is ~3 kpc. |
| In the text | |
 |
Fig. 3 Snapshots at the time of interest (26 Myr) for simulations with different inclination angles between the disks and different cloud particle sizes as described in Table 2. Greyscale levels are (2,4,8,16,32,64,128,256) M⊙ pc-2. |
| In the text | |
 |
Fig. 4 Cloud particle collision rate for the simulations described in Table 2. The factor of the cloud particle mass-size relation ξ increases from blue to red. |
| In the text | |
 |
Fig. 5 Correlation for the simulations described in Table 2. Upper panel: cloud collision rate of the simulated quiet galaxies before collision as a function of the theoretical cloud collision rate based on Eq. (3). Middle panel: maximum collision rate in bins of 10 Myr as a function of the cloud particle mass-size relation ξ. Lower panel: total gas mass in the bridge region as a function of the maximum collision rate. Crosses: i = 0°; diamonds: i = 30°; triangles: i = 45°. |
| In the text | |
 |
Fig. 6 Time evolution of simulation 20 (i = 0°, δy = 4 kpc). Left panels: stellar surface density. The greyscale is logarithmic from 8 to 5600 M⊙ pc-2. Right panels: total gas surface density. The greyscale are (1,4,9,16,25,36,49,...,400) M⊙ pc-2. The timestep of interest (26 Myr) is marked by “model”. |
| In the text | |
 |
Fig. 7 Time evolution of simulation 19 (i = −30°, δy = 1 kpc). Left panels: stellar surface density. The greyscale is logarithmic from 8 to 5600 M⊙ pc-2. Right panels: total gas surface density. The greyscale are (1,4,9,16,25,36,49,...,400) M⊙ pc-2. The timestep of interest (26 Myr) is marked by “model”. |
| In the text | |
 |
Fig. 8 Cloud particle collision rate for the simulations described in Table 3. Red: simulation 18; blue: simulation 19; yellow: simulation 20; green: simulation 21. |
| In the text | |
 |
Fig. 9 Stellar surface density distribution. Upper panel: based on Spitzer IRAC 3.6 μm observations. Middle panel: timestep t = 23 Myr of simulation 20. Lower panel: timestep t = 23 Myr of simulation 19. Contour levels are (1,2,4,8,16,32,64,128,256,512,1024) × 5 M⊙ pc-2. Projection parameters are PA = 160°, i = 30°, and az = 20°. |
| In the text | |
 |
Fig. 10 Stellar surface density distribution of simulation 20 with projection parameters PA = 160°, i = 20°, and az = 0°. The stellar morphology of UGC 12915 is better reproduced by the model. |
| In the text | |
 |
Fig. 11 HI (contour) on CO (greyscale) surface density. Upper panel: observations from Condon et al. (1993) and Gao et al. 2003). Contour levels are (4,8,12,16,20,24,28,32) M⊙ pc-2; greyscale levels are (55,60,65,70,75,85,100,125,150,175,200) M⊙ pc-2. Middle panel: timestep t = 23 Myr of simulation 20. Contour levels are (1,2,4,8,12,16,32,64,128) M⊙ pc-2; greyscale levels are (1,2,8,16,32,64,128,256) M⊙ pc-2. Lower panel: timestep t = 23 Myr of simulation 19. Contour and greyscale levels are the same as for the middle panel. |
| In the text | |
 |
Fig. 12 CO velocity field (colors). Contours: H2 surface density from Fig. 11. Upper panel: observations from Gao et al. (2003). Middle panel: timestep t = 23 Myr of simulation 20. Lower panel: timestep t = 23 Myr of simulation 19. |
| In the text | |
 |
Fig. 13 Observed 6 cm polarized radio continuum contours and projected magnetic field vectors (from Condon et al. 1993) on a Digitized Sky survey image of the UGC 12914/5 system. Contour levels are (3,5,8,12,20,30,50,80,120,200,300,500) × 15 μJy/beam. |
| In the text | |
 |
Fig. 14 Observed 6 cm total power radio continuum contours and projected magnetic field vectors (based on archival VLA data first published by Condon et al. 1993) on a Digitized Sky survey image of the UGC 12914/5 system. Contour levels are (3,5,8,12,20,30,50,80,120,200,300,500) × 16 μJy/beam. |
| In the text | |
 |
Fig. 15 Model 6 cm polarized radio continuum contours and projected magnetic field vectors on the model stellar surface density distribution for two azimuthal viewing angles. Upper panels: simulation 20; lower panels: simulation 19. |
| In the text | |
 |
Fig. 16 Model 6 cm total polarized radio continuum emission (contours) and projected magnetic field vectors on the model 6 cm total power radio continuum emission distribution (greyscale: (1,2,4,8,16,32,64,128) × an arbitrary value). Upper panel: simulation 20; lower panel: simulation 19. |
| In the text | |
 |
Fig. 17 Transverse gas velocities of simulation 19 on the total gas surface density distribution. The primary galaxy is at rest. The thick arrow indicates the transverse velocity of the secondary galaxy. |
| In the text | |
 |
Fig. 18 Simulation 19. Contours of the total gas surface density on the distribution of cloud-cloud collisions (greyscale). The timestep t = 0 Myr corresponds to the impact. |
| In the text | |
 |
Fig. 19 Evolution of the bridge gas properties of simulation 20. Left panels: total gas volume density as a function of distance along the bridge. Right panels: 3D velocity dispersion as a function of distance along the bridge. |
| In the text | |
 |
Fig. 20 Evolution of the bridge gas properties of simulation 19. Left panels: total gas volume density as a function of distance along the bridge. Right panels: 3D velocity dispersion as a function of distance along the bridge. |
| In the text | |
 |
Fig. 21 Star formation rate based on the FUV and 24 μm emission as a function of the molecular gas surface density. The crosses are based on X = 1020 cm-2 (K km s-1)-1, which is half of the Galactic value. The bridge region outside the giant Hii region near UGC 12915 are marked as squares with crosses. Squares without crosses correspond to a 2.5 times lower X factor as suggested by Zhu et al. (2007). Data of NGC 4438 are shown as triangles. The dashed lines correspond to constant star formation timescales of 2 and 4 Gyr. |
| In the text | |
 |
Fig. 22 Potential sites of star formation. Greyscale: total gas surface density. Contours: surface density of gas with a local Jeans length smaller than 2 kpc. Upper panel: simulation 20. Lower panel: simulation 19. |
| In the text | |
 |
Fig. A.1 CO(1−0) spectra (yellow line and yellow scale, intensity in milliKelvins) overlaid with Hi spectra (black line) on a Digitized Sky survey image of the UGC 12914/5 system (from Braine et al. 2003). The center of UGC 12915 is at 00h01m41.9s, 23°29′44.9′′. The bridge region is delimited by the white polygon. |
| In the text | |
 |
Fig. A.2 Simulation 20. CO(1−0) model spectra (white line) overlaid with Hi spectra (black line) on the model stellar surface density distribution. |
| In the text | |
 |
Fig. A.3 Simulation 19. CO(1−0) model spectra (white line) overlaid with Hi spectra (black line) on the model stellar surface density distribution. |
| In the text | |
 |
Fig. A.4 Simulation 19 where the disk gas has been removed. Thus only the gas located in the bridge region is visible. CO(1−0) model spectra (white line) overlaid with Hi spectra (black line) on the model stellar surface density distribution. |
| In the text | |
 |
Fig. A.5 Simulation 19 wihout cloud-cloud collisions. CO(1−0) model spectra (white line) overlaid with Hi spectra (black line) on the model stellar surface density distribution. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


