Effects of helium enrichment in globular clusters

A. A. R. Valcarce; M. Catelan; A. V. Sweigart

doi:10.1051/0004-6361/201219510

Home

All issues

Volume 547 (November 2012)

A&A, 547 (2012) A5

Full HTML

Free Access

Issue		A&A Volume 547, November 2012


Article Number		A5
Number of page(s)		18
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/201219510
Published online		18 October 2012

A&A 547, A5 (2012)

I. Theoretical plane with PGPUC stellar evolution code^⋆

A. A. R. Valcarce¹^,2^,3^,4, M. Catelan¹^,3^,4 and A. V. Sweigart⁵

¹ Pontificia Universidad Católica de Chile, Facultad de FísicaDepartamento de Astronomía y Astrofísica, Av. Vicuña Mackena 4860, 782-0436 Macul, Santiago, Chile
e-mail: avalcarc@astro.puc.cl; mcatelan@astro.puc.cl
² Universidade Federal do Rio Grande do Norte, Departamento de Física, 59072-970 Natal, RN, Brazil
e-mail: avalcarc@dfte.ufrn.cl
³ The Milky Way Millennium Nucleus, Av. Vicuña Mackenna 4860, 782-0436, Macul, Santiago, Chile
⁴ Pontificia Universidad Católica de Chile, Centro de Astroingeniería, Av. Vicuña Mackena 4860, 782-0436 Macul, Santiago, Chile
⁵ NASA Goddard Space Flight Center, Exploration of the Universe Division, Code 667, Greenbelt, MD 20771, USA
e-mail: allen.v.sweigart@nasa.gov

Received: 30 April 2012
Accepted: 27 August 2012

Abstract

Aims. Recently, the study of globular cluster (GC) color−magnitude diagrams (CMDs) has shown that some of them harbor multiple populations with different chemical compositions and/or ages. In the first case, the most common candidate is a spread in the initial helium abundance, but this quantity is difficult to determine spectroscopically due to the fact that helium absorption lines are not present in cooler stars, whereas for hotter GC stars gravitational settling of helium becomes important. As a consequence, indirect methods to determine the initial helium abundance among populations are necessary. For that reason, in this series of papers, we investigate the effects of a helium enrichment in populations covering the range of GC metallicities.

Methods. In this first paper, we present the theoretical evolutionary tracks, isochrones, and zero-age horizontal branch (ZAHB) loci calculated with the Princeton-Goddard-PUC (PGPUC) stellar evolutionary code, which has been updated with the most recent input physics and compared with other theoretical databases. The chemical composition grid covers 9 metallicities ranging from Z = 1.60 × 10^-4 to 1.57 × 10^-2(−2.25 ≲ [Fe/H] ≲ −0.25), 7 helium abundances from Y = 0.230 to 0.370, and an alpha-element enhancement of [α/Fe] = 0.3.

Results. The effects of different helium abundances that can be observed in isochrones are: splits in the main sequence (MS), differences in the luminosity (L) and effective temperature (T_eff) of the turn off point, splits in the sub giant branch being more prominent for lower ages or higher metallicities, splits in the lower red giant branch (RGB) being more prominent for higher ages or higher metallicities, differences in L of the RGB bump (with small changes in T_eff), and differences in L at the RGB tip. At the ZAHB, when Y is increased there is an increase of L for low T_eff, which is affected in different degrees depending on the age of the GC being studied. Finally, the ZAHB morphology distribution depending on the age explains how for higher GC metallicities a population with higher helium abundance could be hidden at the red ZAHB locus.

Key words: stars: evolution / stars: general / stars: horizontal-branch / globular clusters: general

^⋆

Appendix A is available in electronic form at http://www.aanda.org

© ESO, 2012

1. Introduction

Globular clusters (GCs) are objects orbiting around the Milky Way and other galaxies and containing between ~10⁴ and ~10⁷ stars. Nowadays, ~160 GCs are known in the Milky Way, with metallicities [M/H] = log (Z/X) − log (Z/X)_⊙ between ~− 2.3 and ~− 0.25 (Harris 1996, revision 2010) and with ages ranging from ~6.5 to ~13 Gyr (Aparicio et al. 2001; Chaboyer 2001; Marín-Franch et al. 2009; Dotter et al. 2010; Moni Bidin et al. 2011a).

For several decades these objects have been considered as an excellent laboratory for the study of simple stellar populations (SSPs) because it was believed that all stars inside them were formed from a homogeneous cloud at the same time. However, it was recognized early that their horizontal branch (HB) morphologies could not be simply parametrized. While the metallicity of a GC is the first parameter defining its HB morphology (Sandage & Wallerstein 1960), empirical findings show clearly that it cannot be the only parameter at work. In fact, for many years we have been well aware of several GCs characterized by quite different HB morphologies in spite of their quite similar metallicity. For this reason, several second parameters have been invoked to solve this conundrum, where, of course, the most direct, and also the first invoked, second parameter was the age (Sandage & Wallerstein 1960; Rood & Iben 1968). This problem has been widely debated until the present date, but without reaching a consensus (e.g. Catelan & de Freitas Pacheco 1993; Lee et al. 1994; Stetson et al. 1996; Sarajedini et al. 1997; Ferraro et al. 1997; Catelan 2009a; Dotter et al. 2010; Gratton et al. 2010,and references therein).

Another early invoked candidate was the initial helium abundance (van den Bergh 1965, 1967; Sandage & Wildey 1967; Hartwick 1968), but the major difficulty with this element is its extremely difficult measurement, which requires high temperatures in order to be detected in stars. Moreover, blue HB stars hotter than ~11 500 K as well as stars on the so-called extreme HB suffer from metal levitation and helium settling (e.g., Grundahl et al. 1999; Behr 2003), leaving only a narrow band between ~11 500 and ~8000 K for detecting the initial helium abundance in HB stars. Even so, its measurement remains difficult (see Villanova et al. 2009, 2012). Even though helium was one of the first candidates, this explanation of the second-parameter effect became less popular after the Milky Way formation scenario of Searle & Zinn (1978), where the age is assumed to be the second parameter. In addition, differences in helium among GCs also seemed less likely, due to the increasing evidence that GCs have similar helium abundances (e.g., Salaris et al. 2004).

However, after the observational evidence of multiple main sequences (MSs) in GCs (Bedin et al. 2004; Norris 2004; Piotto et al. 2005; D’Antona et al. 2005; Piotto et al. 2007), the hypothesis that helium is the second parameter has regained strength, but in this case the difference in the initial helium abundance is mostly among stars inside the same GC (D’Antona et al. 2002, 2005; Norris 2004; Lee et al. 2005; Piotto et al. 2005, 2007, among several others). In fact, it seems that the combination of age as the second parameter and a helium spread among stars as the “third parameter” is a promising attempt (Gratton et al. 2010).

It is worth noting that, although the existence of a correlation between the chemical abundance anomalies (such as light-element anticorrelations) and the HB morphology has been suggested for a long time (Norris 1981; Smith & Norris 1983; Catelan & de Freitas Pacheco 1995), only recently has direct evidence of this correlation been obtained, as in the case of the GC M4 (Marino et al. 2011; Villanova et al. 2012).

As can be noted, the hypothesis that GCs are SSPs is being ruled out, due to the chemical inhomogeneities among stars of the same GC that have been (directly or indirectly) detected and associated to different star formation episodes in the same GC (Decressin et al. 2007; D’Ercole et al. 2008; Carretta et al. 2010; Conroy & Spergel 2011; Bekki 2011; Valcarce & Catelan 2011, and references therein).

In addition to the presence of multiple populations in GCs, another development makes the availability of evolutionary tracks for different helium abundances highly necessary: as pointed out by Catelan & de Freitas Pacheco (1996) and Catelan (2009b), and also emphasized recently by Nataf & Gould (2012), Nataf & Udalski (2011), and Nataf et al. (2011a,b), stellar populations with different enrichment histories may have different helium enrichment “laws” (i.e., different Y − Z relations).

In this article, we show the effects of the helium enrichment in isochrones and zero-age HB (ZAHB) loci in the theoretical Hertzsprung-Russell (HR) diagram. First in Sect. 2, we present the Princeton-Goddard-PUC (PGPUC) stellar evolution code (SEC) which we used to create a set of evolutionary tracks, isochrones and ZAHB loci for different metallicities and helium abundances (Sect. 3). Then, we show the effects of the helium enrichment (Sect. 4) and end with the conclusions (Sect. 5)¹.

2. PGPUC stellar evolution code

The PGPUC stellar evolution code (SEC) is an updated version of the code created by Schwarzschild & Härm (Schwarzschild & Härm 1965; Härm & Schwarzschild 1966), and then highly modified by Sweigart (Sweigart 1971, 1973, 1994, 1997a; Sweigart & Demarque 1972; Sweigart & Gross 1974, 1976; Sweigart & Catelan 1998,and references therein). It is focused mainly on the study of low-mass stars, defined as stars that develop a degenerate helium core before the onset of helium burning. Since almost all the stars living in present-day GCs can be considered as low-mass stars, the PGPUC SEC is ideal to be used as the basis to create isochrones and ZAHBs for studying the GC properties.

In the following subsections we first explain some of the updates to the input physics included in the PGPUC SEC and then provide a comparison with other codes. Unless otherwise noted, all physical quantities are given in cgs units.

2.1. Opacities

For high-temperature opacities the original version of our SEC (hereafter called PG) used the Rosseland mean opacity tables calculated by the OPAL team (Iglesias et al. 1987), as distributed in 1992 (Rogers & Iglesias 1992, OPAL92), where twelve metals were considered. In PGPUC, we used the most recent version of the OPAL tables (Iglesias & Rogers 1996, OPAL96), where seven new metals are considered, and some errors in the original OPAL code were fixed.

In the PG SEC, conductive opacity was calculated using the Hubbard & Lampe (1969, for log ρ < and Canuto (1970, for log ρ ≥ tables. However, these tables cover a limited mixture of elements, and their approximations are not completely valid when the matter is in a state between gas and liquid, which happens in the interior of low-mass stars in the RGB phase (Catelan et al. 1996; Catelan 2009b). In the PGPUC SEC, we used the Cassisi et al. (2007, hereafter C07) calculations for the conductive opacities, which cover the partial and high electron degeneracy regimes. These calculations include electron-ion, electron-phonon, and electron-electron scattering.

When the temperature drops below log T ~ 4.5, opacity sources that are not considered in the high-temperature regime begin to be important. These sources include: i) negative H ion, which is a large source of continuum opacity; ii) atoms that are not completely ionized; iii) molecules that are formed at low temperatures; and iv) dust grains, which are important at very low temperatures. These opacity sources are important for the outer layers of cool stars, and thus should be included for a proper description of most of the evolutionary phases of low-mass stars. In PGPUC, we used the opacity tables calculated by Ferguson et al. (2005, F05), instead of the opacity tables calculated by Bell (1994, unpublished) for the PG SEC using the SSG synthetic spectrum program (Bell & Gustafsson 1978; Gustafsson & Bell 1979). The F05 tables were obtained with a modified version of the stellar atmosphere code PHOENIX (Alexander & Ferguson 1994), which includes an improved equation of state, additional atomic and molecular lines, and dust opacity.

2.2. Boundary conditions

When a stellar model is computed, boundary conditions are required to solve the problem. In the center of a star the conditions are that mass and luminosity are zero, while in the outer layers a relation between the temperature and the optical depth (τ) is required to know the behavior of the temperature, and then to obtain the pressure.

In a simplified treatment, this relation can be obtained analytically, as Eddington (1926) did, where 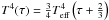$T^{4} (τ) = \frac{3}{4} T_{eff}^{4}^{(} τ + {\frac{2}{3}}^{)}$ $\hbox{$T^4(\tau) = \frac{3}{4} T^4_{\rm eff} \left( \tau + \frac{2}{3} \right)$}$ , which defines the effective temperature (T_eff) as the temperature where a photon emitted from the depth with τ = 2/3 has a probability of e^−2/3 ~ 0.5 of emerging from the surface. However, this relation uses the gray atmosphere approximation, that is not a bad approximation when: i) the opacity is dominated by H⁻; ii) local thermodynamical equilibrium is achieved (which is not appropriate for low-surface-gravity stellar atmospheres, where densities are too low); iii) hydrostatic equilibrium is valid (the pressure gradient exactly balances gravity, which is not valid for hot stars); and iv) there is radiative equilibrium (radiation is the main form of energy transport).

On the other hand, reliable photospheric boundary conditions can be determined without these approximations from actual stellar atmosphere models (e.g., VandenBerg et al. 2008; Dotter et al. 2008), but these calculations need a lot of computing time, and due to the many parameters involved, tabulated tables covering the full evolutionary track of a GC star do not yet exist. Instead of using a theoretical relation with many approximations, or one that is very time consuming, semi-analytical formulae are often used. PG SEC uses the Krishna Swamy (1966)T − τ relation, which was determined using the limb darkening of the Sun. However, Catelan (2007) has pointed out that this relation does not fit correctly the Krishna Swamy data, suggesting the following improved fit²: 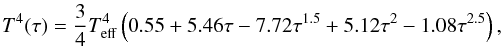$T^{4} (τ) = \frac{3}{4} T_{eff}^{4} (0.55 + 5.46 τ - 7.72 τ^{1.5} + 5.12 τ^{2} - 1.08 τ^{2.5}),$ $\begin{equation} \label{Cat07}T^4(\tau) = \frac{3}{4} T^4_{\rm eff} \left( 0.55 + 5.46\tau - 7.72 \tau^{1.5} + 5.12 \tau^{2} - 1.08 \tau^{2.5} \right), \end{equation}$ (1)which is now used in the PGPUC SEC.

2.3. Thermonuclear reaction rates

The thermonuclear reaction rates taken into account in the PG SEC are the reactions related to hydrogen and helium burning, as given by Caughlan & Fowler (1988) except for the higher rate of the ¹²C(α, γ)¹⁶O reaction advocated by Weaver & Woosley (1993). In this update, all the reaction rates were changed from the analytical formulas determined by Caughlan & Fowler (1988) to the latest available analytical formulae of the NACRE compilation (Angulo et al. 1999), where each rate is determined with an extrapolation of the measured cross section down to astrophysical energies, following theoretical approximations. However, for two important reactions, namely ¹²C(α, γ)¹⁶O and ¹⁴N(p, γ)¹⁵O, the rates used are from Kunz et al. (2002, K02) and Formicola et al. (2004, F04)³, respectively.

2.4. Equation of state

To determine the structure and evolution of a star, it is required to solve the four basic equations of structure. However, an additional equation is needed to solve this set of equations, namely the so-called equation of state (EOS), which determines the density (ρ) knowing the pressure (P), the temperature (T), and the chemical composition. In this work we changed the original EOS (Sweigart 1973) to Irwin’s EOS (FreeEOS, Irwin 2007)⁴, which takes into account non-ideal effects, mainly pressure ionization, Coulomb effects, and quantum electrodynamic corrections, which can be important even at non-relativistic temperatures and non-degenerate densities (Heckler 1994). The 20 elements considered in FreeEOS are H, He, C, N, O, Ne, Na, Mg, Al, Si, P, S, Cl, Ar, Ca, Ti, Cr, Mn, Fe, and Ni, while all molecules are ignored except for H₂ and 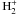$H_{2}^{+}$ $\hbox{${\rm H}_2^+$}$ . Because of the several time-consuming non-ideal effects included in FreeEOS, different approximations have been implemented to solve the equations, reducing the CPU time required. The most accurate FreeEOS option (EOS1) takes into account 295 ionization states of the 20 elements, while EOS1a considers some less abundant metals as fully ionized. EOS2, EOS3, and EOS4 use a faster (but less accurate) approximation for the pressure ionization effect; however, while EOS2 considers the 295 ionization states, EOS3 and EOS4 consider all metals fully ionized when log T > 6. The difference between EOS3 and EOS4 is that the latter uses the approximation of Pols et al. (1995, P95) to calculate the number of particles used to determine the Coulomb free energy, and it is exact when all elements are neutral or completely ionized. However, the P95 algorithm has a discontinuity problem when H₂ is dissociated, which affects mainly stars with masses below 0.1 M_⊙. In PGPUC we use the EOS4 approximation due to its lowest consuming time, and the small difference in almost all the parameters with the other approximations (see Table 1). As can be seen, the mass of the helium core (M_cHe), one of the most important parameters that defines the whole HB phase, only changes by 0.002% with respect to the calculation with EOS1.

Table 1

Properties of a 0.8 M_⊙ star (Y = 0.25, Z = 0.001, [α/Fe] = 0.0) at the RGB tip, where the complete evolution was computed using the labeled FreeEOS approximation (in case of EOS1a and EOS2, PGPUC SEC did not converge with these initial properties).

2.5. Mass loss

Historically, the mass loss rate has usually been determined by the formula of Reimers (1975, R75), which was obtained empirically. It reads 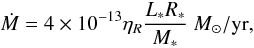$Ṁ = 4 \times 10^{-13} η_{R} \frac{L_{*} R_{*}}{M_{*}} M_{⊙} / yr,$ $\begin{equation} \dot{M} = 4\times 10^{-13} \eta_R \frac{L_* R_*}{M_*}~M_\odot/{\rm yr}, \label{Reimers} \end{equation}$ (2)where L_∗, R_∗, and M_∗ are the luminosity, radius, and mass of the star in solar units, respectively, and η_R is a free parameter whose value is usually taken as ~0.5 due to uncertainty in the numerical coefficient (e.g., in order to fit the observed HB morphology in the GC’s the numerical coefficient used is 2 × 10^-13). It is now well known that this formula does not provide a good description of the available mass loss rates for RGB stars, and several alternative prescriptions have been proposed in the literature (e.g., Catelan 2000, 2009b,and references therein). In particular, Schröder & Cuntz (2005, SC05) have recently suggested a new mass loss rate formula that more properly describes the empirical data and additional physical constraints. They obtained 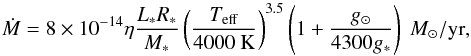$Ṁ = 8 \times 10^{-14} η \frac{L_{*} R_{*}}{M_{*}} {(\frac{T_{eff}}{4000 K})}^{3.5} (1 + \frac{g_{⊙}}{4300 g_{*}}) M_{⊙} / yr,$ $\begin{equation} \dot{M} = 8\times 10^{-14} \eta \frac{L_* R_*}{M_*} \left(\frac{T_{\rm eff}}{4000~{\rm K}}\right)^{3.5}\left( 1 + \frac{g_\odot}{4300 g_*}\right)~M_\odot/{\rm yr}, \label{SC05} \end{equation}$ (3)where L_∗, R_∗, and M_∗ have the same meaning as in Eq. (2), T_eff is the effective temperature in Kelvin, g_⊙ is the solar surface gravity, g_∗ is the stellar surface gravity, and η is a free parameter that we added to allow varying the final stellar mass, even though the value 8 × 10^-14 was calibrated to satisfy the HB morphology of two GCs (NGC 5904 = M5 and NGC 5927), suggesting that the η value added here is typically ~1 (SC05). The two new parameters (T_eff and g_∗) are related to the mechanical energy flux added to the outer layer of the star (depends on T_eff) and to the chromospheric height (depends on g_∗). This new formula has been tested using well-studied nearby stars with measured mass loss rates, reproducing them within the error bars (Schröder & Cuntz 2007). For these reasons, we used the SC05 mass loss rate formulation, instead of the R75 one.

2.6. Neutrino energy loss

When a photon is propagating in a plasma under sufficiently extreme conditions (high temperature, high density), the photon can be coupled to this plasma. When this happens, the photon can decay into a neutrino and an anti-neutrino (emitted in opposite directions), which cannot occur when a photon is not coupled to the plasma, since energy and momentum cannot simultaneously be conserved under these circumstances (e.g., Kantor & Gusakov 2007, KG07). In low-mass stars, these extreme conditions are reached in the degenerate core when the star is in the RGB and the white dwarf phases. Generally, in stellar evolution codes fitting formulae are used to take into account the energy loss by this effect, the most common ones being those proposed by Haft et al. (1994, 1995, H94) and Itoh et al. (1996, I96). However, KG07 have pointed out the ineffectiveness of these formulae to reproduce the real energy loss via neutrino emission for extreme values of ρ/μ_e while, moreover, the I96 fitting formula is only valid near the maximum of emissivity. KG07 obtained this emissivity numerically, suggesting a new fitting formula, which solves the problem for extreme values.

Figure 1 shows the fractional error of the H94 and KG07 fits, compared to the numerical neutrino emissivity from KG07. It can be seen that the H94 formula reproduces the numerical results better in the relevant conditions for low-mass stars (vertical black lines). For this reason, we continue using the H94 recipe. However, if calculations for extreme values are required, we recommend the use of an interpolation of their numerical tables.

2.7. Comparison with other codes

In this subsection we compare the PGPUC SEC with some SECs widely used in the study of low-mass stars and GCs. These SECs are: Victoria-Regina (VandenBerg et al. 2006, hereafter VIC-REG), BaSTI (Pietrinferni et al. 2004), GARSTEC (Weiss & Schlattl 2008), STAREVOL (Siess 2006), and PADOVA (Bertelli et al. 2008). Table 2 shows the input physics used in these codes, where it can be seen that BaSTI and GARSTEC include nearly the same physics used in PGPUC.

Fig. 1

Fractional error δ = (Q_fit − Q_numKG07)/Q_numKG07 for temperatures concerning low-mass RGB stars, where Q_fit is the neutrino emissivity calculated with the H94 (red lines) or KG07 (blue lines) fitting formulae, and Q_numKG07 is the neutrino emissivity calculated numerically by KG07. Vertical black lines indicate the log (ρ/μ_e) value in the center of three stars (Y = 0.245, and the labeled initial mass and metallicity) along their evolution through the RGB phase, when the center reaches the labeled temperature. In the panel for log T = 8, vertical lines indicate the density for the maximum temperature reached in the center (log T ~ 7.87). The log (ρ/μ_e) ranges are determined by the limits of the KG07 numerical values.

Table 2

Physical inputs included in compared SECs.

Fig. 2

Comparison of some evolutionary properties for a 0.8 M_⊙ star with Y = 0.250 and Z = 0.001, as predicted by some of the codes presented in Table 2: PG, dotted black lines; PGPUC, black lines; BaSTI, red lines; GARSTEC, blue lines; STAREVOL, cyan lines. The properties are luminosity (L/L_⊙), effective temperature (T_eff), radius (R), central temperature (T_c), density (ρ_c), and hydrogen abundance (X_C). Small boxes are zoom-in to show the small differences between BaSTI and PGPUC results.

Fig. 3

RGB evolutionary track comparison between PGPUC and the labeled codes (see Table 2) for a 0.8 M_⊙ star with three different helium abundances: Y = 0.250 (left), Y = 0.237 (middle) and Y = 0.230 (right). The metallicity is Z = 0.001 and the chemical composition is solar-scaled according to Grevesse & Noels (1993), except when labeled GN98, where the chemical composition is solar-scaled according to Grevesse & Sauval (1998). Each panel contains an upper left and a lower right panel with zooms to the RGB tip and RGB bump regions, respectively, with the same scales for each Y.

Fig. 4

Comparison between PGPUC and BaSTI results for non-standard chemical compositions. Left panel: evolutionary tracks with Y = 0.30 and Z = 9.2 × 10^-4. Middle panel: evolutionary tracks with Y = 0.35 and Z = 8.5 × 10^-4. Right panels: ZAHB loci for Y = 0.30 and Z = 9.2 × 10^-4 (upper panel) and Y = 0.35 and Z = 8.5 × 10^-4 (lower panel), where for comparison BaSTI ZAHB loci are moved Δlog (L/L_⊙) = −0.025. PGPUC ZAHB loci are shown for progenitor masses of M_i = 0.7 M_⊙ and M_i = 0.9 M_⊙.

In Fig. 2, we compare some stellar (internal and external) properties of the SECs that have these data available⁵. The star has a mass of 0.8 M_⊙, an initial helium abundance of Y = 0.250 (near to the primordial helium abundance Y_p = 0.245; Izotov et al. 2007, and references therein), a metal abundance of Z = 0.001, a solar scaled abundance of alpha elements ([α/Fe] = 0.0) according to Grevesse & Noels (1993), and the evolution is without mass loss. These properties are close to the mass, helium, and metallicity of turn-off (TO) stars in GCs. Moreover, only for this comparison PGPUC uses the NACRE reaction rate for ¹⁴N(p, γ)¹⁵O, which is the rate used for all codes that use NACRE as input. In that figure the good agreement of PGPUC with BaSTI and GARSTEC can be observed, the latter being the codes using FreeEOS (interpolated tables). Note that the remaining different physical inputs could produce the observed differences; e.g., if the GARSTEC SEC adopted the conductive opacities from C07 instead of Itoh et al. (1984), its predicted luminosity at the end of the RGB phase would decrease due to the earlier helium flash (C07). The differences with the PG and STAREVOL SECs must be produced by the different EOS’s which lead to a lower central density (ρ_c) and temperature (T_c) than the other three codes, and, consequently, a lower hydrogen burning rate.

The impact of these differences can also be observed in an HR diagram, where in the left panel of Fig. 3 we show the evolutionary tracks calculated with the same codes as in Fig. 2. As can be observed, PGPUC has better agreement in the MS with BaSTI, GARSTEC, and STAREVOL, but PGPUC produces the hottest MS (ΔT_eff ~ 35 K at a solar luminosity). In the sub-giant branch (SGB) these differences are reduced, but at the base of the RGB STAREVOL begins to diverge from the other three codes. At the RGB bump PGPUC is slightly brighter and cooler than predicted by BaSTI and GARSTEC (ΔT_eff ~ 18 K and Δlog (L/L_⊙) ~ 0.03 with BaSTI). Finally, at the RGB tip the PGPUC track has the lower luminosity. Although there are several other differences along the RGB evolution, they tend to be very small.

Table 3

Iron abundances [Fe/H] as a function of the metallicity value Z and the helium abundance Y for an α-element enhancement of [α/Fe] = 0.3.

For comparison with the VIC-REG model (middle panel of Fig. 3), we produced an additional evolutionary track with the same properties as used to produce the left panel of the same figure, except for the initial helium abundance that in this case is Y = 0.237. However, due to the different input physics between PGPUC and VIC-REG, the differences along the evolution are relatively large⁶. In the right panel of Fig. 3, we also compared with PADOVA evolutionary track, where the properties are: M = 0.8 M_⊙, Y = 0.230, Z = 0.001, and [α/Fe] = 0.0 according to Grevesse & Sauval (1998). It reveals some small differences similar to those in the left panel, but at the RGB bump there is a difference of Δlog (L/L_⊙) ~ 0.15 (PGPUC is brighter). Also, at the RGB tip the difference has the same magnitude, but PGPUC is instead fainter. This could be due to the differences in the conductive opacity tables and in the thermonuclear reaction rates, because both changes produced an increase of the RGB bump luminosity and a decrease of the RGB tip luminosity.

Due to the fact that this paper is focused on He-enhanced theoretical models, in Fig. 4 we compared PGPUC and BaSTI results for [Fe/H] = −1.62 with Y = 0.30 and Y = 0.35, where PGPUC results are interpolated as is described in Appendix A (see also Dotter et al. 2008; Bertelli et al. 2009; Di Criscienzo et al. 2010; Dell’Omodarme et al. 2012). In the left and middle panels, we show the comparison of evolutionary tracks with masses between 0.5 and 1.1 M_⊙ in intervals of ΔM = 0.1 M_⊙. As can be seen, there are not large differences at the MS except for 0.7 and 0.5 M_⊙, where PGPUC tracks are cooler. At high luminosities it is possible to observe that PGPUC results are also cooler and fainter than BaSTI tracks. In the right panels are shown the comparisons between the ZAHB loci of the two SECs, which are created using a progenitor mass of 0.7 M_⊙. For this comparison we have to move the BaSTI ZAHB loci by Δlog (L/L_⊙) = −0.025, since the BaSTI’s code uses the P99 conductive opacity table inducing a brighter ZAHB than the C07 ones (see C07). Apart from previous difference in luminosity, there is still a difference at the red part of the ZAHB, with the most important factor likely being the rate of the reaction ¹⁴N(p, γ)¹⁵O that is adopted in both codes. More specifically, for this comparison the PGPUC SEC uses the F04 rate, whereas BaSTI uses the NACRE one. Pietrinferni et al. (2010) pointed out that two ZAHB loci created with these rates have a difference in luminosity of the order presented here at log T_eff = 3.85, the ZAHB determined with the NACRE reaction rate being brighter (at this metallicity). As far as the predicted temperatures are concerned, we do not find any significant differences. We also show the ZAHB loci created with a progenitor mass of 0.9 M_⊙, and this case is discussed in more detail in Sect. 4.4.1. Finally, we conclude that PGPUC models are in agreement with BaSTI ones, except for ZAHB loci being fainter by Δlog (L/L_⊙) = −0.025, due to the differences in the adopted input physics.

3. PGPUC database

3.1. Evolutionary tracks

To study the effects of a helium enrichment in globular clusters, we created a database of evolutionary tracks covering the evolutionary phases from the zero-age main sequence (ZAMS) to the tip of the RGB, together with zero-age horizontal branch (ZAHB) loci. This database of evolutionary tracks includes stellar masses between 0.5 and 1.1 M_⊙ with ΔM = 0.1 M_⊙, for 7 helium abundances, 9 metallicities, an enhancement of the alpha elements by [α/Fe] = 0.3, and a mass loss rate according to Eq. (3) (with η = 1.0). The metallicity values were selected to obtain the iron abundances [Fe/H] shown in the second column of Table 3 when Y = 0.245. Since it is assumed that nearly all GCs do not undergo internal chemical enrichment due to supernova explosions, the mass fraction of Fe within a given GC (but not [Fe/H]) would be constant over the range of possible helium abundances (e.g., Valcarce & Catelan 2011). For this reason we will use the same metallicity value for each set of Y values in our analysis. Even though variations of other elements can be associated to He-enrichment and also produce some changes in the theoretical evolutionary tracks and ZAHB loci (C+N+O and/or other heavier elements; Milone et al. 2008; Cassisi et al. 2008; Pietrinferni et al. 2009; Ventura et al. 2009; Marín-Franch et al. 2009; Alves-Brito et al. 2012; VandenBerg et al. 2012), in this paper we focus exclusively on He. We leave the calculations with non-standard metal ratios for future papers, where we also plan to increase the ranges of masses, metallicities, and [α/Fe] ratios covered.

We adopted the solar chemical abundances presented by Grevesse & Sauval (1998, GS98), where Z/X = 0.0231 ± 0.005, when calibrating the models⁷. Using this solar composition, we computed a Standard Solar Model, assuming an age for the Sun of 4.6 Gyr. By fitting the present solar luminosity, radius and Z/X ratio, we obtained a mixing length parameter α = 1.896, an initial solar helium abundance Y_⊙ = 0.262 and a global solar metallicity Z_⊙ = 0.0167.

3.2. Isochrones

For studying GCs, if the canonical SSP is accepted, it can be assumed that all stars were formed at the same time with the same chemical composition. Since higher-mass stars evolve more rapidly, one cannot compare the evolutionary tracks for an SSP directly with the GC observations. Instead, it is necessary to build isochrones which connect the points at the same age along the evolutionary tracks with different masses.

Fig. 5

Set of evolutionary tracks (black lines) for stars between 1.1 (hottest track) and 0.5 M_⊙ (coolest track) with Y = 0.245, Z = 9.3 × 10^-4, and [α/Fe] = +0.3, plotted at ΔM = 0.1 M_⊙ intervals. Red points are the EEPs for each track, while green lines are isochrones, from left to right, between 7 and 15 Gyr, in steps of 1 Gyr. Inner panels are zoom-ins to the RGB tip (left) and RGB bump (right).

To construct our isochrones, we use the equivalent evolutionary points (EEP) technique first proposed by Prather (1976). These EEPs represent points with similar properties (which can be internal or external) for tracks of different masses. For low-mass stars, the EEPs are:

EEP1: this point is defined as the beginning of the MS, where wetake, as a first approximation forlow-mass stars, the age to be zero(for SECs including the pre-MS evolution, thispoint is defined when the luminosity due to gravitational collapsedecreases to 0.01 L_⊙).
EEP2: this point is defined when the helium abundance in the center reaches a value of 90%, which is near the point when low-mass MS stars have reached their maximum effective temperature.
EEP3: this point is similar to EEP2, but is determined when the central hydrogen is completely depleted.
EEP4: this is the point where the mass of the convective envelope is 25% of the total mass, which characterizes the base of the RGB.
EEP5: this point is determined when the star’s luminosity starts to decrease as the H burning shell arrives at the chemical composition discontinuity previously produced when the envelope convection zone reached its maximum depth.
EEP6: this is where the star’s luminosity starts to increase again, as the stellar structure readjusts after EEP5 to the higher H abundance outside the composition discontinuity. For the cases where the RGB bump does not exist (M ≲ 0.7 M_⊙ in Fig. 5), EEP5 and EEP6 are determined by extrapolating the RGB bump positions for lower-mass stellar tracks with well-defined RGB bumps.
EEP7: finally, the last point is defined when log (L_He/L_⊙) > 2.0 due to the beginning of the helium flash or when T_eff starts to increase due to the star’s leaving the RGB before igniting He in the core.

The definition for these points was kindly provided by S. Yi (2008, priv. comm.), except for EEP3 which was added to obtain a better resolution, and EEP7 where the original definition took into account only the luminosity via helium burning. Indeed, the original definition of EEP7 was valid only if the star could ignite helium, whereas our new definition is valid for any star (see also Bergbusch & Vandenberg 1992). Figure 5 shows an example of some isochrones between 7 and 15 Gyr, which were created using PGPUC evolutionary tracks, the technique presented before, and the Hermite interpolation algorithm for constructing reasonable analytic curves through discrete data points presented by Hill (1982).

Finally, we emphasize that the EEP technique can also be applied to tracks for different Y, Z, [α/Fe], and any other parameter (mixing length parameter, mass loss rates, overshooting, etc.). This means that one can always create new evolutionary tracks with a parameter inside the original set of tracks, maintaining the others constants. For example, instead of interpolating in mass (as was used to create an isochrone), one can interpolate in Y to create a new evolutionary track for a different helium abundance while maintaining fixed the other parameters (initial mass, Z, [α/Fe], C+N+O abundance, etc.). This procedure can be repeated for each parameter, with the end result that one can always create a new evolutionary track (and consequently isochrones) with any parameter inside the grid of original parameters. Such a procedure is implemented in the PGPUC online web page (see Appendix A).

3.3. ZAHB loci

At the moment when the helium flash and the subsequent secondary flashes have completely removed the degeneracy in the helium core, the star has arrived at the ZAHB. In this phase, the star is burning helium in the core, while in an outer shell it keeps burning hydrogen. Because stars in the HB phase spend ~50% of their life without varying their luminosity by a large fraction (≲ 5%, based on PGPUC calculations), it is useful to create ZAHB loci which represent the lower boundary of the HB loci.

Serenelli & Weiss (2005) have compared different methods to construct ZAHB models without computing the complete evolution for several stars with different masses and mass loss rates. They concluded that ZAHB loci could be well-defined if a star is evolved without mass loss from the MS to the HB (passing through the flash phase), and then stopping the temporal evolution of this star at the point when the rate of change in the internal thermal energy is smallest. At this point the carbon abundance in the center is 5%, and the core convection has reached the center. This defines the red end of the ZAHB sequence. Then mass from the envelope is removed until the minimum envelope mass is reached, which corresponds to the removal of almost all the envelope at the hottest point along the ZAHB sequence. The ZAHB locus corresponds to the line connecting all these ZAHB models, computed for different envelope masses but with the same core mass. We will therefore adopt the method suggested by Serenelli & Weiss (2005) when constructing ZAHB loci with the PGPUC SEC.

4. Effects of ΔY

As is pointed out in Sect. 1, a spread in helium abundance among stars has been suggested to explain why some GCs show multiple populations in their CMDs, which is difficult to verify because the initial abundance of this element can only be measured, in such old populations, at high resolution and with high S/N, over a small range in temperatures along the HB (Villanova et al. 2009, 2012). In this section, we show the effects of helium enrichment upon evolutionary tracks, isochrones and ZAHB loci using PGPUC models, which give us some clues of what we should observe in GC’s color−magnitude diagrams when a helium enhancement is present.

4.1. Effects of ΔY on [Fe/H]

In Table 3 we show how [Fe/H] increases with increasing Y for a constant Z. Thus if multiple populations in a GC are only formed with enriched helium and without any enrichment in metals (e.g., Valcarce & Catelan 2011), stars with different Y will show different [Fe/H] values (see also Sweigart 1997b; Bragaglia et al. 2010a). For example, if in a GC a population exists with a primordial initial helium abundance (Y_FG = 0.245) alongside another population with Y_SG = 0.345, and if both populations have the same metallicity Z = 1.6 × 10^-3 (corresponding to [Fe/H] = −1.25 when Y = 0.245), then one should observe a spread in the iron abundance by Δ[Fe/H] ~ 0.063. In fact, the analytical formula for this spread in [Fe/H] is given straightforwardly by $Δ [Fe / H] = [Fe / H]_{FG} - [Fe / H]_{SG} = \log (\frac{1 - Y_{SG} - Z}{1 - Y_{FG} - Z}),$ $\begin{equation} {\Delta \rm [Fe/H]} = {\rm [Fe/H]_{FG}-[Fe/H]_{SG}}= \log \left( \frac{1-Y_{\rm SG}-Z}{1-Y_{\rm FG}-Z} \right), \label{EqIron} \end{equation}$ (4)where the subscripts FG and SG refer to the first and second generations, respectively.

From spectroscopic observations Bragaglia et al. (2010b) have found a spread of Δ[Fe/H] = 0.070 among the RGB stars in NGC 2808 (average [Fe/H] = −1.15, Carretta et al. 2009), implying a spread in helium of ΔY ~ 0.1 from Eq. (4) for a metallicity of Z = 2.18 × 10^-3. This helium spread is close to the value suggested to reproduce the difference between the bluest and reddest MSs in this particular GC (D’Antona et al. 2005; Piotto et al. 2007).

On the other hand, in addition to the already discussed possibility of a variation in the CNO abundances, and thus different metallicity at fixed [Fe/H] for the enhanced populations, there is a small possibility that second generation stars could have higher Y and lower Z than the first generation, if there was capture of metal-poor material from outside of the GC which was then mixed with material processed inside the GC (Conroy & Spergel 2011).

4.2. Effects of ΔY on evolutionary tracks

Before comparing isochrones and ZAHB loci, we show the effects of changing the metallicity and the helium abundance on the evolutionary tracks for stars with 0.9 M_⊙ (see Fig. 6). Even though many of these effects have been known since the first evolutionary codes appeared (Simoda & Iben 1968; Aizenman et al. 1969; Iben 1974; Simoda & Iben 1970), we summarize them again using PGPUC stellar models. Although the input physical ingredients have been updated over the years, the main effects are almost the same.

Fig. 6

Evolutionary tracks for stars with 0.9 M_⊙ from the MS to the tip of the RGB. The left panel shows the effects produced by different metallicities (from left to right: Z = 1.6 × 10^-4, 1.6 × 10^-3, 5.03 × 10^-3, and 1.57 × 10^-2) with Y = 0.245. The effects produced by different helium abundances (Y = 0.245, 0.295, and 0.345) for two metallicities ([Fe/H] = −2.25, and −0.25) are shown in the right panel. In parentheses are labeled the age in Gyr at the RGB tip for each evolutionary track.

Fig. 7

Relation between age at the RGB tip and the He core mass (M_cHe) reached for stars with different initial masses, metallicities, helium abundances and different mass loss rates (solid lines: no mass loss, or η = 0; dotted line: η = 1.0). Interpolated lines connect the real values for different initial helium abundances Y, from top to bottom: 0.245 (red), 0.295 (green), and 0.345 (blue). For stars with η = 1.0 and η = 0.0, the initial masses go, from left to right, from 1.1 to 0.5 M_⊙ and from 0.9 to 0.7 M_⊙, respectively, in steps of 0.1 M_⊙. As can be seen from the monotonic behavior of the solid lines, the helium core mass increases for higher ages (or lower initial masses). In the case of stars with mass loss (dotted lines), there is a maximum value for M_cHe because, for the mass loss efficiency assumed (η = 1.0), stars lose a large fraction of their masses at higher ages, which decreases the hydrogen-burning rate and leads to a premature departure from the RGB; a hot flasher may then take place. (See text for further details.)

As is observed in the left panel of Fig. 6, stars with lower metallicities have higher luminosities and effective temperatures from the ZAMS to the tip of the RGB. This occurrence is mainly due to the decrease of the radiative opacity when the metallicity decreases, thus enhancing the outward transport of energy from the core to the surface. As a result, metal-poor stars have a denser and hotter core, which increases the H-burning nuclear rates. This is also the reason for which the core H-burning lifetime decreases with decreasing metallicity.

Moreover, the temperature of the RGB decreases faster for high metallicities due to the higher opacity and the consequent faster increase of the radius. At the RGB bump, two additional effects are observed: i) its luminosity decreases for higher metallicities due to a deeper penetration of the convective envelope into the interior during the first dredge-up and ii) its prominence also increases for higher metallicities due to the larger discontinuity in the H abundance, and hence in the radiative opacity, at the deepest point reached by the convective envelope (Thomas 1967; Iben 1968; Sweigart 1978; Sweigart & Gross 1978; Lee 1978; Yun & Lee 1979).

Finally, we note that stars with a higher metallicity reach a higher luminosity at the tip of the RGB (Iben & Faulkner 1968; Demarque & Mengel 1973). This result is a consequence of two competing effects. First, the energy output of the hydrogen-burning shell in a more metal-rich star on the RGB is greater at each value of the He core mass due to the greater abundance of the CNO elements which increases the nuclear reaction rates of the CNO cycle. As a consequence the He core then grows and heats up more rapidly, thereby causing He ignition to occur at a lower He core mass (Sweigart & Gross 1978; Cavallo et al. 1998). However, the greater hydrogen-shell luminosity more than compensates for the smaller core mass at helium ignition, leading to the increased RGB tip luminosity with metallicity shown in Fig. 6.

In the case of different helium abundances (right panel of Fig. 6), helium-rich ZAMS stars have higher luminosity and T_eff (Demarque 1967; Iben & Faulkner 1968; Simoda & Iben 1968, 1970; Demarque et al. 1971; Hartwick & VandenBerg 1973; Sweigart & Gross 1978). To maintain adequate pressure, i.e., hydrostatic equilibrium, a helium-rich star must have a higher temperature in the center to compensate for the fewer particles which have to support the same mass, with the end result that these stars are more compact, which increases the T_eff. In addition, the opacity is also lower, and then the greater energy being produced in the center can more easily flow outward when the helium abundance is increased.

Even though stars with different Y arrive on the RGB with different luminosities, the slope of the track along the RGB in a log L − log T_eff diagram is very similar. However, there are an increase of the luminosity and a decrease of the extension of the RGB bump when Y is increased, due to the fact that the convective envelope in a helium-rich star does not penetrate as deeply during the first dredge-up and therefore the composition discontinuity produced at the deepest penetration point is then both smaller and further out in mass.

Finally, the luminosity of the RGB tip decreases when Y is increased because the flash occurs at a smaller core mass (see Fig. 7). This is a consequence of the faster growth in the core mass and hence faster increase in the maximum core temperature.

4.3. Effects of ΔY on isochrones

Figure 8 shows isochrones with ages between 7.5 and 15.0 Gyr, for several Z values and helium abundances from Y = 0.245 to 0.370, whereas Fig. 9 shows in more detail the RGB bump. As can be observed in these figures, there are several effects on isochrones when Y is increased whose detailed study would be quite time-consuming. For this reason, here we summarize them qualitatively, to give us hints of what places in HR diagrams we should focus our attention to, when we tabulate these effects quantitatively; a preliminary discussion can also be found in Catelan et al. (2010). Again, we emphasize that several of the following effects were directly or indirectly found in the past (e.g. Demarque 1967; Iben & Faulkner 1968; Simoda & Iben 1968, 1970; Demarque et al. 1971; Hartwick & VandenBerg 1973; Sweigart & Gross 1978; Lee 1978; Yun & Lee 1979).

MS: as was pointed out for the case of evolutionary tracks,when Y is increased the effects on MS stars with equal masses include an increase in both L and T_eff. Then, if the difference in L between isochrones of the same age is compared for the same T_eff, this is a comparison between stars with different masses, where the more massive stars are the ones with lower Y. Finally, since low-mass stars and/or stars with low He abundance have longer evolutionary times, the size of the difference in luminosity between MS stars with different Y but the same Z almost does not depend on age in the range of ages studied here.
TO: when isochrones for the same Z are compared, the TO point is affected by the difference in Y and also by the age. While an increase in Y drives a reduction of L and an increase in T_eff, an increase in age decreases both L and T_eff. As can be seen, at the TO point the difference in log T_eff between isochrones with different Y changes with age at almost the same rate independently of the metallicity, but the difference in log (L/L_⊙) changes faster with age for higher metallicities.
SGB: here, the difference produced by an increase in Y is observed as a decrease in L. However, this difference is more prominent for low ages or high metallicities (see also Di Criscienzo et al. 2010), or in other words, when the difference in the initial masses of the stars in this zone is large, the difference in the log L − log T_eff loci is also large.
Lower RGB: in the lower RGB there are three important effects to consider when Y is increased: i) the minimum luminosity almost does not depend on Y, but depends on Z and age; ii) as in the TO point, T_eff at the base of the RGB is higher for higher helium abundances, while the difference in T_eff between isochrones with different Y increases for higher ages; iii) finally, the absolute value of the lower RGB slope is higher for lower helium abundances.
RGB bump: the effect of an increase in Y at the RGB bump is shown in Fig. 9, where an increase of L and a reduction of the extension of the RGB bump can be seen (see Sect. 4.2). However, the maximum T_eff of the RGB bump decreases for higher Y, but this effect is more evident for lower metallicities. An increase in age also increases the difference in L between Y values, while the difference in T_eff almost does not change with age. These effects may be observed as changes of the shape of the RGB bump in luminosity functions, where for large extensions of the theoretical RGB bump the shape is bimodal, while for small extensions the shape is single-peaked (Cassisi et al. 2002).
Upper RGB: above the RGB bump, as was pointed out in Sect. 4.2, the difference in Y does not induce any great difference in the RGB slope, the only observable effect being a shift in the position of the RGB tip, whose luminosity decreases for higher helium abundances. However, this reduction of the RGB tip luminosity (and the luminosity function at this position) should be very difficult to observe in color−magnitude diagrams of GCs, due to the small number of stars near this point.

4.4. Effects of ΔY on ZAHBs

Fig. 8

Isochrones for (from upper left to lower right) 7.5, 10.0, 12.5, and 15.0 Gyr with metallicities, from left to right, Z₁ = 1.60 × 10^-4, Z₂ = 1.60 × 10^-3, and Z₃ = 1.57 × 10^-2 in the log L − log T_eff plane. Different colors represent different initial helium abundances: Y = 0.245 (red), 0.270 (yellow), 0.295 (green), 0.320 (cyan), 0.345 (blue), and 0.370 (black).

Fig. 9

Isochrones for the labeled metallicities at the RGB bump. Colors represent the same Y values as in Fig. 8.

As for the isochrones, in several previous works (e.g., Faulkner & Iben 1966; Iben & Faulkner 1968; Iben & Rood 1970; Sweigart 1987) the effects of different helium abundances have been studied in ZAHB loci and HB models for different Z values. Here, we summarize the main effects for ZAHB loci.

Figure 10 shows changes in the ZAHB locus when the He abundance is increased for several metallicities. When Z is constant, it is observed that for high Y i) cooler HB stars (the more massive ones) have high ZAHB luminosities; and ii) hotter HB stars (the less massive ones) have lower ZAHB luminosities. Cooler HB stars show this effect for the same reason MS stars are brighter: high helium abundances decrease the radiative opacity, thus stars are more compressed (increasing the internal temperature and density), leading to an increase in the hydrogen burning rate, while the helium burning rate at the core decreases due to the smaller helium core mass (see Fig. 7), but the luminosity’s decrease due to the helium burning is lower than the luminosity’s increase due to the hydrogen burning, with the end result that the total luminosity increases. In the case of hotter HB stars, in view of the small He core, together with the fact that hotter HB stars have tiny envelopes and thus small hydrogen burning rates, these stars have lower luminosities when Y is higher: their luminosity comes chiefly from the helium burning rate in the (smaller) core.

Moreover, the luminosity difference between ZAHBs with different Y depends on the metallicity, where this difference between cooler HB stars is smaller for lower Z, but the difference between hotter HB stars is higher for lower Z. The higher increase in luminosity for higher metallicity when Y is increased is due to the increase of the efficiency of the CNO cycle (due to the higher Z) that makes stronger the effect of the increase of Y mentioned in the previous paragraph. In the case of hotter HB stars, the difference in luminosity is due to the difference in the helium core masses, which are greater for lower metallicities (Fig. 7).

Although Caputo & Degl’Innocenti (1995) have shown that the luminosity of the ZAHB at a fixed T_eff depends on age for low metallicities, this effect has not been (recently) studied in detail for the complete range of T_eff and for different Y. In the next section we show the effects of age upon ZAHB loci, which must be taken into account for all metallicities.

4.4.1. ZAHB dependence on age

Fig. 10

ZAHB loci for different metallicities (increasing from upper left to bottom right) and initial helium abundances. For each Y value, ZAHB loci were constructed using three RGB progenitors with different initial masses (M_i), which can be related to an age dependence of the ZAHB, which is particularly evident at low metallicities.

In this section we stress the ZAHB loci dependence on age, and how this effect is more important at low metallicity and/or high helium abundances. Although this effect has been known for a long time (e.g., Iben 1974), so far it has been largely neglected. However, nowadays, due to the high precision of the available photometric and spectroscopic data for HB stars (see, e.g., Catelan et al. 2009; Dalessandro et al. 2011; Moehler et al. 2011; Moni Bidin et al. 2011b), it is increasingly important to determine the ZAHB locus for the appropriate He core mass, which (as already discussed in Iben’s review) depends on the metallicity, initial helium abundance and the RGB progenitor mass (and thus the age). This is especially true when blue HB, extreme blue HB and blue hook stars are studied, and even more so when the bluest filters are used.

In regard to the time required for stars to reach the RGB tip (t_Tip), it depends on three main factors: i) the initial helium abundance, where t_Tip decreases with higher Y because the H burning rate increases; ii) the heavy element abundance, where t_Tip increases with higher Z because density and temperature in the stellar interior are lower in metal-rich stars, which decreases the H burning rate at the MS since the burning rate by the CNO cycle is negligible; iii) the initial mass, since more massive stars have higher internal temperatures, thus t_Tip decreases (Iben & Rood 1970; Hartwick & VandenBerg 1973). These effects are shown in Fig. 7, for different [Fe/H], Y, and initial masses.

As Fig. 10 shows, the progenitor mass used to create ZAHB loci changes the ZAHB luminosity due to the different helium core masses reached by these stars at the RGB tip. The helium core mass at the RGB tip is determined by a competition between the hydrogen burning luminosity which controls the rate at which the helium core grows and heats up and the cooling rate via thermal conduction and neutrino emission during the RGB evolution. To produce the helium flash, T ~ 10⁸ K and ρ ~ 10⁶ g/cm³ are required as condition, which is reached when some fraction of the helium core is completely supported by degenerate electron pressure.

As is shown in Fig. 7, the parameters that determine the final helium core mass are the helium abundance, initial mass, and amount of mass loss on the RGB – the latter two quantities depending on the age (for a given chemical composition). The sense of the dependence of M_cHe on Y and initial mass is that an increase in either increases the temperature at the hydrogen-burning shell, and consequently the helium flash takes place earlier and with a lower M_cHe. The dependence on mass loss becomes relevant only when the total RGB mass loss becomes quite substantial, which may lead to a decrease in efficiency of the H-burning shell, and hence to a He flash that may take place only after the star has already left the RGB, while the star is on its way to the white dwarf cooling curve, or even on the white dwarf cooling curve proper (e.g., Castellani & Castellani 1993; D’Cruz et al. 1996; Brown et al. 2001; Moehler et al. 2011). This effect explains the downward variation of M_cHe with age towards old ages that is seen in Fig. 7, particularly for Y > 0.245 and η = 1.0. The metallicity also plays an important rôle in the final M_cHe value, but an increase in metallicity induces two effects: i) a decrease in the temperature at the hydrogen-burning shell; and ii) an increase of the CNO cycle efficiency. Then, which one of these effects is more important depends on the initial mass of the star, as observed in the change of the slope of M_cHe with Z in Fig. 7. The temperature of the hydrogen burning shell is determined solely by the mass of the helium core. This is the same reason why an RGB star evolves to higher luminosities. As in a white dwarf, the higher the mass of the helium core, the smaller its radius, but the temperature of the outer layer of the core is higher, which increases the temperature of the hydrogen shell around the core with the consequent increase of the hydrogen burning rate (Renzini et al. 1992).

Fig. 11

Relation between age at the RGB tip and the initial stellar mass (M_i) depending on the initial helium abundance and the metallicity. Colors represent different helium abundances. Dots, and lines have the same meaning as in Fig. 7.

Table 4

Difference in the bolometric magnitude m_bol (four last columns) between ZAHB loci with different progenitor masses (ΔM_i), for 3 metallicities and 3 helium abundances (first column) at the labeled log T_eff.

Fig. 12

Dependence of the effective temperature of ZAHB stars on their mass for three different metallicities: Z₁ = 1.60 × 10^-4, Z₂ = 1.60 × 10^-3 and Z₃ = 1.57 × 10^-2.

Depending on the helium core mass, the luminosity of the ZAHB will change. Figure 10 shows this effect in HR diagrams, where ZAHB loci can be misrepresented if the mass used to construct them does not give the required helium core mass for the stellar population being studied. For example, ZAHB loci for a GC with [Fe/H] = −1.48 and three populations with Y = 0.245, 0.295, and 0.345 at an age of 12.5 Gyr, must be created from RGB progenitor masses of ~0.83, ~0.75, and ~0.68 M_⊙, respectively. However, if the age is 7.5 Gyr, the RGB progenitor masses for these ZAHBs must be ~0.95, ~0.87, and ~0.79 M_⊙. Then, when ZAHB loci are used together with isochrones, the initial mass used to create the ZAHB must be defined by the initial mass of the star at the RGB tip of the respective isochrone, which depends on Y and Z (see Fig. 11). This means that the whole ZAHB depends on the age of the GC. This property is more important for high helium abundance and/or lower metallicities.

In Table 4 are shown the errors in bolometric magnitude m_bol that can be induced if ZAHB loci were created with a progenitor mass of 0.9 M_⊙ instead of a progenitor mass determined according to the age of the GC. When GCs with multiple populations are studied, the mass of the progenitor mass of the ZAHB has to be defined by Fig. 11 if it is assumed that all the stellar populations were born at almost the same time. Otherwise, the mass of the progenitor of the ZAHB for the younger population has to be defined by Fig. 11 but with M_i-Age relation of the given helium abundance displaced in the time that this population required to be formed.

4.4.2. ZAHB morphology in multiple populations

The HB morphology of GCs has been studied for several decades, but without a consensus about the second parameter (together with the metallicity) to parameterize the HB morphology (see Sect. 1). Historically, multimodality on the HB has been used as an argument in favor of the importance of other second parameter candidates, besides cluster age (e.g., Norris 1981; Norris & Smith 1983; Crocker et al. 1988; Rood et al. 1993; Fusi Pecci et al. 1996, see also Catelan 2008 for a recent review on the subject of gaps and multimodality on the HB). More recently, with the discovery of multiple populations often extending down to the MS, which have largely confirmed the expectations based on those earlier HB morphology arguments, HB multimodality is once again being used as a diagnostic of the presence of multiple populations in GCs (e.g., Alonso-García et al. 2012). Here we briefly show that a GC with multiple populations could have an unimodal HB morphology, even though these populations could have a difference in their initial helium abundance, as in the possible case of 47 Tuc (e.g., Nataf et al. 2011a; Milone et al. 2012).

First, Fig. 12 shows the effective temperature of stars when they arrive at the ZAHB with a given mass (M_ZAHB) for three metallicities, where there is a range of masses that are concentrated near to the minimum T_eff of the ZAHB, and this range of masses is higher for higher metallicities. This figure also shows how the relation between T_eff and M_ZAHB changes with different progenitor masses (upper panel), and different initial helium abundances (lower panel). As can be seen, a decrease in the progenitor mass induces an increase of the minimum T_eff of the ZAHB, the effect being greater for lower metallicities. This decrease also induces a small increase of the M_ZAHB for a given T_eff. When the initial helium abundance is increased the range of masses concentrated near the minimum T_eff of the ZAHB also increases, which also induces a decrease of M_ZAHB for a given T_eff.

Fig. 13

Effective temperature of the stars arriving to the ZAHB for ages between 4 and 15 Gyr for 3 initial helium abundances Y = 0.245 (coolest continuous line), Y = 0.295 (dotted-dashed line) and Y = 0.345 (hottest continuous line), and 3 metallicities: 1.60 × 10^-4 (left panel), 1.60 × 10^-3 (middle panel), and 1.57 × 10^-2 (right panel). Dotted lines show the change in the effective temperatures when a dispersion of 0.02 M_⊙ in the total mass loss is considered. Dashed line shows an age of 13 Gyr.

For estimating the mean T_eff of a stellar population one can use the final mass of stars at the RGB tip (M_Tip) depending on the age for a given metallicity and initial helium abundance. Assuming that the difference between M_Tip and M_ZAHB is small (not a bad approximation considering the short time spent in the pre-ZAHB phase), one can estimate M_ZAHB knowing the age of the GC in study, and then estimate the mean T_eff. Figure 13 shows the change in T_eff depending on the age for two coeval initial helium abundances (Y = 0.245 and Y = 0.345) and 3 different metallicities, where continuous lines show the T_eff at M_ZAHB = M_Tip, and dotted lines represent the effect of a possible dispersion in the mass loss rate, which show the T_eff at M_ZAHB = M_Tip ± 0.02 M_⊙ (Rood & Crocker 1989; Catelan et al. 2001; Valcarce & Catelan 2008). The additional dotted-dashed line represents an initial helium abundance of Y = 0.295. As can be seen, a 13 Gyr old GC with higher metallicity (right panel) can hide populations with a ΔY = 0.10 with the initial helium abundance within a small range of temperatures of the red ZAHB, but these populations will have a great difference in their luminosity. For the same age, metal-intermediate and metal-poor GCs (middle and left panel of Fig. 13, respectively) cannot hide multiple populations with a large difference in the initial helium abundance due to the consequent differences in T_eff. However, smaller differences in Y can be indistinguishable for lower metallicities. Of course, evolutionary effects also play a rôle in the shape of the HB, but for studying these effects HB evolutionary tracks and Monte Carlo simulations are required, which is not the focus of this paper.

Finally, we have to recall that here we are using Eq. (3) with η = 1.0 to take into account the mass loss during the RGB evolution for all stars, irrespective of its chemical composition. Unfortunately, there are at present no strong constraints available on a possible dependence of η on Y. On the other hand, Ṁ in He-rich populations could in principle be constrained, in view of the strong dependence of HB morphology on the He abundance. Future work along these lines is strongly encouraged.

5. Conclusions

In this work, we studied the effects that must be observed in the theoretical log (L/L_⊙) − log (T_eff) plane for isochrones and ZAHB loci with different initial helium abundances and fixed metallicity, which is the most common hypothesis to explain the multiple populations observed in the color−magnitude diagrams in some GCs. Our study is based on stellar evolutionary calculations for different evolutionary phases in the life of a low-mass star.

First, we presented the PGPUC SEC that was updated with the most recent physical ingredients available in the literature, including opacities, both radiative and conductive (Iglesias & Rogers 1996; Ferguson et al. 2005; Cassisi et al. 2007); thermonuclear reaction rates (Angulo et al. 1999; Kunz et al. 2002; Formicola et al. 2004; Imbriani et al. 2005); equation of state (Irwin 2007); mass loss (Schröder & Cuntz 2005); and boundary conditions (Catelan 2007). Even though the neutrino energy loss rate was not updated, we recommend the use of the Kantor & Gusakov (2007) interpolated tables for extreme conditions (high densities), which however are not achieved for the stars in our study.

Comparison between PGPUC SEC and other theoretical databases shows similar results. In fact, PGPUC SEC evolutionary tracks and isochrones are in excellent agreement with those produced using the PADOVA, GARSTEC and (specially) BaSTI codes.

We create a large set of evolutionary tracks for a wide range of metallicities and helium abundances for a GS98 chemical composition and [α/Fe] = +0.3, which are available in the PGPUC Online web page. Then theoretical isochrones and ZAHB loci were used to show the effects of different helium abundances at different evolutionary phases along the HR diagram, where in isochrones:

At the MS, the separation induced by Y increases for high Z.
At the SGB, the separation induced by Y increases for high Z, but it decreases with the age.
At the base of the RGB, the difference in T_eff induced by Y increases for high Z and also increase with the age.

While at the ZAHB loci:

When Y increases, the L of the cooler HB stars increases, but the L of the hotter HB stars decreases.
When the age increases, the L of the hotter HB stars increase due to the increase of the M_cHe.
When Z increases, there is an increase in the separation in L due to a difference in Y at the cooler HB stars, but the luminosity difference induced by the age decreases.

We emphasized the importance of the age in determining the ZAHB locus (as pointed out by Caputo & Degl’Innocenti 1995, and references in Sect. 4.4.1), and also the location of stars when they arrive to the ZAHB loci depending on the age. In the next papers of this series we will study these effects in different filters for comparing with GCs data, and we will also create a new set of evolutionary tracks with different CNO ratios.

Online material

Appendix A: PGPUC online

PGPUC online (http://www2.astro.puc.cl/pgpuc) is our web page containing all the PGPUC evolutionary tracks and ZAHB loci. In this web page the Hermite interpolation algorithm for constructing reasonable analytic curves through discrete data points presented by Hill (1982) is used, which produces evolutionary tracks from the MS to the RGB tip for any mass, helium, and metallicities in the ranges 0.5 M_⊙ ≤ M ≤ 1.1 M_⊙, 0.230 ≤ Y ≤ 0.370, and 0.00016 ≤ Z ≤ 0.01570, respectively, for an [α/Fe] = 0.3 and a SC05 mass loss rate with η = 1.0. More specifically, to interpolate an evolutionary track of a given mass M_x, helium abundance Y_x, and metallicity Z_x within a range of masses ({ M_i } , with i = 1...7), helium abundances ({ Y_j } , with j = 1...7), and metallicities ({ Z_k } , with k = 1...9) we follow the next steps:

Using the first EEP of each evolutionary track with mass M = M₁, helium abundance Y = Y₁, and all the 9 metallicities Z_k, the first EEP of the track with M = M₁, Y = Y₁, and Z = Z_x is interpolated. This process is followed for each EEP of the evolutionary track with M = M₁ and Y = Y₁ with the end result that an interpolated evolutionary track with M = M₁, Y = Y₁, and Z = Z_x is created.
Following the previous process for each of the seven masses M_i, we have an interpolated set of evolutionary tracks with seven masses M_i, a helium abundance Y = Y₁, and a metallicity Z = Z_x.
Doing the previous two steps for each helium abundance Y_j, one has a set of evolutionary tracks with seven masses M_i, for each of the seven helium abundances Y_j, and with a given Z = Z_x.
Now, using the first EEP of each evolutionary track with mass M = M₁, metallicity Z_x, and all the 7 helium abundances Y_j, the first EEP of the track with Y = Y_x, that obviously has a Z = Z_x, is interpolated. This process is followed for each EEP of the evolutionary track with M = M₁ and Z = Z_x, with the end result that an interpolated evolutionary track with M = M₁, Y = Y_x, and Z = Z_x is created.
When the previous step is repeated for each mass M_i a set of evolutionary tracks with 7 masses M_i, Y = Y_x, and Z = Z_x is obtained.
Finally, using the first EEP of each mass M_i one can interpolate the first EEP of the mass M_x. Repeating this process for each EEP, one creates the final interpolated evolutionary track with M = M_x, Y = Y_x, and Z = Z_x (see Fig. A.1).

Fig. A.1

Interpolated evolutionary tracks (red lines) from the original theoretical set of evolutionary tracks (blue lines). Upper panel: metallicity interpolation (metallicity increases from left to right) with constant helium abundance Y = 0.245 and mass of 0.9 M_⊙. Middle panel: helium interpolation (helium increases from right to left) with constant metallicity Z = 0.0016 and masses of 0.9 (hotter) and 0.5 M_⊙ (cooler). Bottom panel: mass interpolation (mass increases from right to left) with constant metallicity Z = 0.0016 and helium abundance Y = 0.245.

Fig. A.2

Interpolated ZAHB loci (red lines) from the original theoretical set of ZAHB loci (blue lines). Open triangles show the locus where the convective envelope dissapears. Upper panel: Z interpolation (Z increases from top to bottom) with constant Y = 0.245 and M_i = 0.9 M_⊙. Middle panel: Y interpolation (Y increases from bottom to top at the red ZAHB and inversely at the blue ZAHB) with constant Z = 0.0016 and M_i = 0.9 M_⊙. Bottom panel: M_i (M_i increases from bottom to top at the blue ZAHB) with two constant Z (Z = 0.0016 and Z = 0.00016) and Y = 0.245. Dots are the initial points for each ZAHB locus, with the mass increasing from bottom to top.

In the case that we have the same set of evolutionary tracks, but for different α-element enhancements [α/Fe] _l, one can follow the previous procedure for each [α/Fe] _l, ending with the interpolation of the EEPs for each evolutionary track with M = M_x, Y = Y_x, Z = Z_x, and [α/Fe] _l to create ones with a given α-element enhancement. Of course, this procedure can be done for each initial property that can be parameterized (e.g., mass loss, mixing length parameter, overshooting, C+N+O abundance, etc.), which is our intention with the PGPUC online web page: that the user can select the initial property that he or she wants.

Moreover, since any evolutionary track can be created, in this web page it is also possible to create any isochrones within the previous ranges of helium and metallicity. However, due to the fact that the maximum mass for each chemical composition is 1.1 M_⊙, the minimum age limit is not constant, with a value equal to the required time for the star with 1.1 M_⊙ of the given chemical composition to evolve from the MS to the RGB tip. In the near future, we plan to increase the maximum mass value.

In the case of the ZAHB, they can also be interpolated for any chemical composition within the range of chemical compositions. This is done using the so-called equivalent ZAHB points (EZAHBPs), which are defined using two criteria, depending on whether the ZAHB star has a convective envelope or not. In Fig. A.2 the open triangles show the points which divide stars with and without a convective envelope, cooler stars being the ones with convective envelopes. For stars with a convective envelope, 34 EZAHBPs are defined depending on the percentage of convective envelope mass, from the coolest point of the ZAHB (the star with higher convective envelope mass) until the point without a convective envelope. For ZAHB stars without a convective envelope, 100 EZAHBPs are defined, depending on the percentage of envelope mass that ZAHB stars have, from the point without a convective envelope (100% of envelope mass) until the hottest point at the given ZAHB (0% of envelope mass). Using the EZAHBPs it is possible to interpolate directly in metallicity and helium abundance (see Fig. A.2). However, the method used to interpolate between progenitor masses is more complex. First, the EZAHBPs can be used only from the hottest ZAHB point until the coolest point of the minimum progenitor mass (in this case, 0.7 M_⊙). The cool part of the ZAHB is extrapolated from the ZAHB with the nearest higher progenitor mass weighted according to the difference in the stellar parameters between the three progenitor masses. As can be seen from Fig. A.2, we note that the interpolated ZAHB loci are quite satisfactory.

¹

All of the models described in this paper can be downloaded from the “PGPUC Online” dedicated website (http://www2.astro.puc.cl/pgpuc), as described in Appendix A.

²

Catelan’s published formula was misprinted.

³

The analytical formula was determined by Imbriani et al. (2005).

⁴

All FreeEOS documentation is available at http://freeeos.sourceforge.net/

⁵

GARSTEC evolutionary tracks were obtained from the Stellar Model Challenge project (http://www.mpa-garching.mpg.de/stars/SCC/Models.html), while PADOVA and VIC-REG ones were download from their respective web pages: http://www3.cadc-ccda.hia-iha.nrc-cnrc.gc.ca/community/VictoriaReginaModels and http://pleiadi.pd.astro.it/. STAREVOL evolutionary track was obtained via private communication with Ana Palacios. BaSTI evolutionary tracks were obtained from the official webpage http://albiones.oa-teramo.inaf.it/ or via private communication with Santi Cassisi.

⁶

During the publication of this paper, an updated version of VIC-REG was published by VandenBerg et al. (2012), which could reduce these differences.

⁷

Although recent analyses using 3D hydrodynamical models of the solar atmosphere (Asplund et al. 2005; Lodders et al. 2009; Caffau et al. 2011) have resulted in lower values for Z/X compared to the previous GS98 mix, we do not use these lower values because they disagree with high-precision helioseismological determinations of the solar structure (e.g., Basu & Antia 2004; Serenelli et al. 2009, 2011; Bi et al. 2011; Antia & Basu 2011,and references therein).

Acknowledgments

We thank the anonymous referee for her/his comments, which have helped improve the presentation of our results. A.A.R.V. thanks Santi Casissi for his useful comments during A.A.R.V.’s Ph.D. Thesis on this topic. Support for A.A.R.V. and M.C. is provided by the Ministry for the Economy, Development, and Tourism’s Programa Iniciativa Científica Milenio through grant P07-021-F, awarded to The Milky Way Millennium Nucleus; by Proyecto Basal PFB-06/2007; by FONDAP Centro de Astrofísica 15010003; by Proyecto FONDECYT Regular #1110326; and by Proyecto Anillo de Investigación en Ciencia y Tecnología PIA CONICYT-ACT 86. A.A.R.V. acknowledges additional support from CNPq, CAPES, from Proyecto ALMA-Conicyt 31090002, MECESUP2, and SOCHIAS.

References

Aizenman, M. L., Demarque, P., & Miller, R. H. 1969, ApJ, 155, 973 [NASA ADS] [CrossRef] [Google Scholar]
Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]
Alonso-García, J., Mateo, M., Sen, B., et al. 2012, AJ, 143, 70 [NASA ADS] [CrossRef] [Google Scholar]
Alves-Brito, A., Yong, D., Meléndez, J., Vásquez, S., & Karakas, A. I. 2012, A&A, 540, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
Antia, H. M., & Basu, S. 2011, J. Phys. Conf. Ser., 271, 012034 [NASA ADS] [CrossRef] [Google Scholar]
Aparicio, A., Rosenberg, A., Saviane, I., Piotto, G., & Zoccali, M. 2001, in Astrophysical Ages and Times Scales, eds. T. von Hippel, C. Simpson, & N. Manset, ASP Conf. Ser., 245, 182 [Google Scholar]
Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
Bahcall, J. N., & Pinsonneault, M. H. 1992, Rev. Mod. Phys., 64, 885 [NASA ADS] [CrossRef] [Google Scholar]
Basu, S., & Antia, H. M. 2004, ApJ, 606, L85 [NASA ADS] [CrossRef] [Google Scholar]
Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] [Google Scholar]
Behr, B. B. 2003, ApJS, 149, 67 [NASA ADS] [CrossRef] [Google Scholar]
Bekki, K. 2011, MNRAS, 412, 2241 [NASA ADS] [CrossRef] [Google Scholar]
Bell, R. A., & Gustafsson, B. 1978, A&AS, 34, 229 [NASA ADS] [Google Scholar]
Bergbusch, P. A., & Vandenberg, D. A. 1992, ApJS, 81, 163 [NASA ADS] [CrossRef] [Google Scholar]
Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bi, S. L., Li, T. D., Li, L. H., & Yang, W. M. 2011, ApJ, 731, L42 [NASA ADS] [CrossRef] [Google Scholar]
Bragaglia, A., Carretta, E., Gratton, R., et al. 2010a, A&A, 519, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bragaglia, A., Carretta, E., Gratton, R. G., et al. 2010b, ApJ, 720, L41 [NASA ADS] [CrossRef] [Google Scholar]
Brown, T. M., Sweigart, A. V., Lanz, T., Landsman, W. B., & Hubeny, I. 2001, ApJ, 562, 368 [NASA ADS] [CrossRef] [Google Scholar]
Caffau, E., Ludwig, H., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]
Canuto, V. 1970, ApJ, 159, 641 [NASA ADS] [CrossRef] [Google Scholar]
Caputo, F., & Degl’Innocenti, S. 1995, A&A, 298, 833 [NASA ADS] [Google Scholar]
Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cassisi, S., Salaris, M., & Bono, G. 2002, ApJ, 565, 1231 [NASA ADS] [CrossRef] [Google Scholar]
Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
Cassisi, S., Salaris, M., Pietrinferni, A., et al. 2008, ApJ, 672, L115 [NASA ADS] [CrossRef] [Google Scholar]
Castellani, M., & Castellani, V. 1993, ApJ, 407, 649 [NASA ADS] [CrossRef] [Google Scholar]
Catelan, M. 2000, ApJ, 531, 826 [NASA ADS] [CrossRef] [Google Scholar]
Catelan, M. 2007, in Graduate School in Astronomy: XI Special Courses at the National Observatory of Rio de Janeiro (XI CCE), eds. F. Roig, & D. Lopes, AIP Conf. Ser., 930, 39 [Google Scholar]
Catelan, M. 2008, Mem. Soc. Astron. Italiana, 79, 388 [NASA ADS] [Google Scholar]
Catelan, M. 2009a, in New Quests in Stellar Astrophysics II: The Ultraviolet Properties of Evolved Stellar Populations, eds. M. Chavez, E. Bertone, D. Rosa-Gonzalez, & L. H. Rodriguez-Merino (New York: Springer), 175 [Google Scholar]
Catelan, M. 2009b, Ap&SS, 320, 261 [NASA ADS] [CrossRef] [Google Scholar]
Catelan, M., & de Freitas Pacheco, J. A. 1993, AJ, 106, 1858 [NASA ADS] [CrossRef] [Google Scholar]
Catelan, M., & de Freitas Pacheco, J. A. 1995, A&A, 297, 345 [NASA ADS] [Google Scholar]
Catelan, M., & de Freitas Pacheco, J. A. 1996, PASP, 108, 166 [NASA ADS] [CrossRef] [Google Scholar]
Catelan, M., de Freitas Pacheco, J. A., & Horvath, J. E. 1996, ApJ, 461, 231 [NASA ADS] [CrossRef] [Google Scholar]
Catelan, M., Ferraro, F. R., & Rood, R. T. 2001, ApJ, 560, 970 [NASA ADS] [CrossRef] [Google Scholar]
Catelan, M., Grundahl, F., Sweigart, A. V., Valcarce, A. A. R., & Cortés, C. 2009, ApJ, 695, L97 [NASA ADS] [CrossRef] [Google Scholar]
Catelan, M., Valcarce, A. A. R., & Sweigart, A. V. 2010, in IAU Symp. 266, eds. R. de Grijs, & J. R. D. Lépine, 281 [Google Scholar]
Caughlan, G. R., & Fowler, W. A. 1988, Atom. Data Nucl. Data Tables, 40, 283 [Google Scholar]
Cavallo, R. M., Sweigart, A. V., & Bell, R. A. 1998, ApJ, 492, 575 [NASA ADS] [CrossRef] [Google Scholar]
Chaboyer, B. 2001, in Astrophysical Ages and Times Scales, eds. T. von Hippel, C. Simpson, & N. Manset, ASP Conf. Ser., 245, 162 [Google Scholar]
Conroy, C., & Spergel, D. N. 2011, ApJ, 726, 36 [NASA ADS] [CrossRef] [Google Scholar]
Crocker, D. A., Rood, R. T., & O’Connell, R. W. 1988, ApJ, 332, 236 [NASA ADS] [CrossRef] [Google Scholar]
Dalessandro, E., Salaris, M., Ferraro, F. R., et al. 2011, MNRAS, 410, 694 [NASA ADS] [CrossRef] [Google Scholar]
D’Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
D’Antona, F., Bellazzini, M., Caloi, V., et al. 2005, ApJ, 631, 868 [NASA ADS] [CrossRef] [Google Scholar]
D’Cruz, N. L., Dorman, B., Rood, R. T., & O’Connell, R. W. 1996, ApJ, 466, 359 [NASA ADS] [CrossRef] [Google Scholar]
Decressin, T., Charbonnel, C., & Meynet, G. 2007, A&A, 475, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dell’Omodarme, M., Valle, G., Degl’Innocenti, S., & Pra da Moroni, P. G. 2012, A&A, 540, 26 [Google Scholar]
Demarque, P. 1967, ApJ, 149, 117 [NASA ADS] [CrossRef] [Google Scholar]
Demarque, P., & Mengel, J. G. 1973, A&A, 22, 121 [NASA ADS] [Google Scholar]
Demarque, P., Mengel, J. G., & Aizenman, M. L. 1971, ApJ, 163, 37 [NASA ADS] [CrossRef] [Google Scholar]
D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
Di Criscienzo, M., Ventura, P., D’Antona, F., Milone, A., & Piotto, G. 2010, MNRAS, 408, 999 [NASA ADS] [CrossRef] [Google Scholar]
Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]
Dotter, A., Sarajedini, A., Anderson, J., et al. 2010, ApJ, 708, 698 [NASA ADS] [CrossRef] [Google Scholar]
Eddington, A. S. 1926, The Internal Constitution of the Stars (Cambridge University Press) [Google Scholar]
Faulkner, J., & Iben, Jr., I. 1966, ApJ, 144, 995 [NASA ADS] [CrossRef] [Google Scholar]
Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
Ferraro, F. R., Paltrinieri, B., Fusi Pecci, F., et al. 1997, ApJ, 484, L145 [NASA ADS] [CrossRef] [Google Scholar]
Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Phys. Lett. B, 591, 61 [NASA ADS] [CrossRef] [Google Scholar]
Fusi Pecci, F., Bellazzini, M., Ferraro, F. R., Buonanno, R., & Corsi, C. E. 1996, in Formation of the Galactic Halo... Inside and Out, eds. H. L. Morrison, & A. Sarajedini, ASP Conf. Ser., 92, 221 [Google Scholar]
Girardi, L., Bressan, A., Chiosi, C., Bertelli, G., & Nasi, E. 1996, A&AS, 117, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gratton, R. G., Carretta, E., Bragaglia, A., Lucatello, S., & D’Orazi, V. 2010, A&A, 517, 81 [Google Scholar]
Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]
Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
Grundahl, F., Catelan, M., Landsman, W. B., Stetson, P. B., & Andersen, M. I. 1999, ApJ, 524, 242 [NASA ADS] [CrossRef] [Google Scholar]
Gustafsson, B., & Bell, R. A. 1979, A&A, 74, 313 [NASA ADS] [Google Scholar]
Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222; Erratum: ApJ, 438, 1017 [NASA ADS] [CrossRef] [Google Scholar]
Härm, R., & Schwarzschild, M. 1966, ApJ, 145, 496 [NASA ADS] [CrossRef] [Google Scholar]
Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
Hartwick, F. D. A. 1968, ApJ, 154, 475 [NASA ADS] [CrossRef] [Google Scholar]
Hartwick, F. D. A., & VandenBerg, D. A. 1973, ApJ, 185, 887 [CrossRef] [Google Scholar]
Heckler, A. F. 1994, Phys. Rev. D, 49, 611 [Google Scholar]
Hill, G. 1982, Publications of the Dominion Astrophysical Observatory Victoria, 16, 67 [NASA ADS] [Google Scholar]
Hubbard, W. B., & Lampe, M. 1969, ApJS, 18, 297 [NASA ADS] [CrossRef] [Google Scholar]
Iben, I. 1968, Nature, 220, 143 [NASA ADS] [CrossRef] [Google Scholar]
Iben, Jr., I.1974, ARA&A, 12, 215 [NASA ADS] [CrossRef] [Google Scholar]
Iben, Jr., I., & Faulkner, J. 1968, ApJ, 153, 101 [CrossRef] [Google Scholar]
Iben, Jr., I., & Rood, R. T. 1970, ApJ, 161, 587 [NASA ADS] [CrossRef] [Google Scholar]
Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
Iglesias, C. A., Rogers, F. J., & Wilson, B. G. 1987, ApJ, 322, L45 [NASA ADS] [CrossRef] [Google Scholar]
Imbriani, G., Costantini, H., Formicola, A., et al. 2005, EPJ A, 25, 455 [Google Scholar]
Irwin, A. W. 2007, http://freeeos.sourceforge.net/ [Google Scholar]
Itoh, N., Kohyama, Y., Matsumoto, N., & Seki, M. 1984, ApJ, 285, 758 [NASA ADS] [CrossRef] [Google Scholar]
Itoh, N., Hayashi, H., Nishikawa, A., & Kohyama, Y. 1996, ApJS, 102, 411 [NASA ADS] [CrossRef] [Google Scholar]
Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
Kantor, E. M., & Gusakov, M. E. 2007, MNRAS, 381, 1702 [NASA ADS] [CrossRef] [Google Scholar]
Krishna Swamy, K. S. 1966, ApJ, 145, 174 [NASA ADS] [CrossRef] [Google Scholar]
Kunz, R., Fey, M., Jaeger, M., et al. 2002, ApJ, 567, 643 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Lee, S. 1978, J. Korean Astron. Soc., 11, 1 [NASA ADS] [Google Scholar]
Lee, Y., Demarque, P., & Zinn, R. 1994, ApJ, 423, 248 [Google Scholar]
Lee, Y., Joo, S., Han, S., et al. 2005, ApJ, 621, L57 [NASA ADS] [CrossRef] [Google Scholar]
Lodders, K., Plame, H., & Gail, H. 2009, in Landolt-Börnstein – Group VI Astronomy and Astrophysics Numerical Data and Functional Relationships in Science and Technology Volume 4B: Solar System, ed. J. E. Trümper, 4.4., 44 [Google Scholar]
Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
Marino, A. F., Villanova, S., Milone, A. P., et al. 2011, ApJ, 730, L16 [NASA ADS] [CrossRef] [Google Scholar]
Mihalas, D., Hummer, D. G., Mihalas, B. W., & Daeppen, W. 1990, ApJ, 350, 300 [NASA ADS] [CrossRef] [Google Scholar]
Milone, A. P., Bedin, L. R., Piotto, G., et al. 2008, ApJ, 673, 241 [NASA ADS] [CrossRef] [Google Scholar]
Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012, ApJ, 744, 58 [NASA ADS] [CrossRef] [Google Scholar]
Moehler, S., Dreizler, S., Lanz, T., et al. 2011, A&A, 526, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
MoniBidin, C., Mauro, F., Geisler, D., et al. 2011a, A&A, 535, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Moni Bidin, C., Villanova, S., Piotto, G., Moehler, S., & D’Antona, F. 2011b, ApJ, 738, L10 [NASA ADS] [CrossRef] [Google Scholar]
Nataf, D. M., & Gould, A. P. 2012, ApJ, 751, L39 [NASA ADS] [CrossRef] [Google Scholar]
Nataf, D. M., & Udalski, A. 2011 [arXiv:1106.0005] [Google Scholar]
Nataf, D. M., Gould, A., Pinsonneault, M. H., & Stetson, P. B. 2011a, ApJ, 736, 94 [NASA ADS] [CrossRef] [Google Scholar]
Nataf, D. M., Udalski, A., Gould, A., & Pinsonneault, M. H. 2011b, ApJ, 730, 118 [NASA ADS] [CrossRef] [Google Scholar]
Norris, J. 1981, ApJ, 248, 177 [NASA ADS] [CrossRef] [Google Scholar]
Norris, J. E. 2004, ApJ, 612, L25 [NASA ADS] [CrossRef] [Google Scholar]
Norris, J., & Smith, G. H. 1983, ApJ, 275, 120 [NASA ADS] [CrossRef] [Google Scholar]
Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
Pietrinferni, A., Cassisi, S., Salaris, M., Percival, S., & Ferguson, J. W. 2009, ApJ, 697, 275 [NASA ADS] [CrossRef] [Google Scholar]
Pietrinferni, A., Cassisi, S., & Salaris, M. 2010, A&A, 522, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] [Google Scholar]
Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]
Potekhin, A. Y. 1999, A&A, 351, 787 [NASA ADS] [Google Scholar]
Prather, M. J. 1976, Ph.D. Thesis, Yale Univ. [Google Scholar]
Reimers, D. 1975, Mem. Soc. Roy. Sci. Liege, 8, 369 [Google Scholar]
Renzini, A., Greggio, L., Ritossa, C., & Ferrario, L. 1992, ApJ, 400, 280 [NASA ADS] [CrossRef] [Google Scholar]
Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]
Rood, R., & Iben, Jr., I.1968, ApJ, 154, 215 [NASA ADS] [CrossRef] [Google Scholar]
Rood, R. T., & Crocker, D. A. 1989, in The Use of pulsating stars in fundamental problems of astronomy, ed. E. G. Schmidt, 111 [Google Scholar]
Rood, R. T., Crocker, D. A., Fusi Pecci, F., et al. 1993, 48, 218 [Google Scholar]
Salaris, M., Riello, M., Cassisi, S., & Piotto, G. 2004, A&A, 420, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sandage, A., & Wallerstein, G. 1960, ApJ, 131, 598 [NASA ADS] [CrossRef] [Google Scholar]
Sandage, A., & Wildey, R. 1967, ApJ, 150, 469 [NASA ADS] [CrossRef] [Google Scholar]
Sarajedini, A., Chaboyer, B., & Demarque, P. 1997, PASP, 109, 1321 [NASA ADS] [CrossRef] [Google Scholar]
Schröder, K., & Cuntz, M. 2005, ApJ, 630, L73 [NASA ADS] [CrossRef] [Google Scholar]
Schröder, K., & Cuntz, M. 2007, A&A, 465, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Schwarzschild, M., & Härm, R. 1965, ApJ, 142, 855 [NASA ADS] [CrossRef] [Google Scholar]
Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
Serenelli, A., & Weiss, A. 2005, A&A, 442, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Serenelli, A. M., Basu, S., Ferguson, J. W., & Asplund, M. 2009, ApJ, 705, L123 [NASA ADS] [CrossRef] [Google Scholar]
Serenelli, A. M., Haxton, W. C., & Peña-Garay, C. 2011, ApJ, 743, 24 [NASA ADS] [CrossRef] [Google Scholar]
Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Simoda, M., & Iben, Jr., I. 1968, ApJ, 152, 509 [NASA ADS] [CrossRef] [Google Scholar]
Simoda, M., & Iben, Jr., I. 1970, ApJS, 22, 81 [NASA ADS] [CrossRef] [Google Scholar]
Smith, G. H., & Norris, J. 1983, ApJ, 264, 215 [NASA ADS] [CrossRef] [Google Scholar]
Stetson, P. B., Vandenberg, D. A., & Bolte, M. 1996, PASP, 108, 560 [NASA ADS] [CrossRef] [Google Scholar]
Sweigart, A. V. 1971, ApJ, 168, 79 [NASA ADS] [CrossRef] [Google Scholar]
Sweigart, A. V. 1973, A&A, 24, 459 [NASA ADS] [Google Scholar]
Sweigart, A. V. 1978, in The HR Diagram – The 100th Anniversary of Henry Norris Russell, eds. A. G. D. Philip, & D. S. Hayes, IAU Symp., 80, 333 [Google Scholar]
Sweigart, A. V. 1987, ApJS, 65, 95 [NASA ADS] [CrossRef] [Google Scholar]
Sweigart, A. V. 1994, ApJ, 426, 612 [NASA ADS] [CrossRef] [Google Scholar]
Sweigart, A. V. 1997a, ApJ, 474, L23 [NASA ADS] [CrossRef] [Google Scholar]
Sweigart, A. V. 1997b, in The Third Conference on Faint Blue Stars, eds. A. G. D. Philip, J. Liebert, R. Saffer, & D. S. Hayes (Schenectady: L. Davis Press), 3 [Google Scholar]
Sweigart, A. V., & Catelan, M. 1998, ApJ, 501, L63 [NASA ADS] [CrossRef] [Google Scholar]
Sweigart, A. V., & Demarque, P. 1972, A&A, 20, 445 [NASA ADS] [Google Scholar]
Sweigart, A. V., & Gross, P. G. 1974, ApJ, 190, 101 [NASA ADS] [CrossRef] [Google Scholar]
Sweigart, A. V., & Gross, P. G. 1976, ApJS, 32, 367 [NASA ADS] [CrossRef] [Google Scholar]
Sweigart, A. V., & Gross, P. G. 1978, ApJS, 36, 405 [NASA ADS] [CrossRef] [Google Scholar]
Thomas, H. 1967, ZAp, 67, 420 [Google Scholar]
Valcarce, A. A. R., & Catelan, M. 2008, A&A, 487, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Valcarce, A. A. R., & Catelan, M. 2011, A&A, 533, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
van den Bergh, S. 1965, JRASC, 59, 151 [NASA ADS] [Google Scholar]
van den Bergh, S. 1967, AJ, 72, 70 [NASA ADS] [CrossRef] [Google Scholar]
VandenBerg, D. A., Swenson, F. J., Rogers, F. J., Iglesias, C. A., & Alexander, D. R. 2000, ApJ, 532, 430 [NASA ADS] [CrossRef] [Google Scholar]
VandenBerg, D. A., Bergbusch, P. A., & Dowler, P. D. 2006, ApJS, 162, 375 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
VandenBerg, D. A., Edvardsson, B., Eriksson, K., & Gustafsson, B. 2008, ApJ, 675, 746 [NASA ADS] [CrossRef] [Google Scholar]
VandenBerg, D. A., Bergbusch, P. A., Dotter, A., et al. 2012, ApJ, 755, 15 [NASA ADS] [CrossRef] [Google Scholar]
Ventura, P., Caloi, V., D’Antona, F., et al. 2009, MNRAS, 399, 934 [NASA ADS] [CrossRef] [Google Scholar]
Villanova, S., Piotto, G., & Gratton, R. G. 2009, A&A, 499, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Villanova, S., Geisler, D., Piotto, G., & Gratton, R. G. 2012, ApJ, 748, 62 [NASA ADS] [CrossRef] [Google Scholar]
Weaver, T. A., & Woosley, S. E. 1993, Phys. Rep., 227, 65 [NASA ADS] [CrossRef] [Google Scholar]
Weiss, A., & Schlattl, H. 2008, Ap&SS, 316, 99 [NASA ADS] [CrossRef] [Google Scholar]
Yun, H., & Lee, S. 1979, J. Korean Astron. Soc., 12, 17 [NASA ADS] [Google Scholar]

All Tables

Table 1

Properties of a 0.8 M_⊙ star (Y = 0.25, Z = 0.001, [α/Fe] = 0.0) at the RGB tip, where the complete evolution was computed using the labeled FreeEOS approximation (in case of EOS1a and EOS2, PGPUC SEC did not converge with these initial properties).

In the text

Table 2

Physical inputs included in compared SECs.

In the text

Table 3

Iron abundances [Fe/H] as a function of the metallicity value Z and the helium abundance Y for an α-element enhancement of [α/Fe] = 0.3.

In the text

Table 4

Difference in the bolometric magnitude m_bol (four last columns) between ZAHB loci with different progenitor masses (ΔM_i), for 3 metallicities and 3 helium abundances (first column) at the labeled log T_eff.

In the text

All Figures

Fig. 1

Fractional error δ = (Q_fit − Q_numKG07)/Q_numKG07 for temperatures concerning low-mass RGB stars, where Q_fit is the neutrino emissivity calculated with the H94 (red lines) or KG07 (blue lines) fitting formulae, and Q_numKG07 is the neutrino emissivity calculated numerically by KG07. Vertical black lines indicate the log (ρ/μ_e) value in the center of three stars (Y = 0.245, and the labeled initial mass and metallicity) along their evolution through the RGB phase, when the center reaches the labeled temperature. In the panel for log T = 8, vertical lines indicate the density for the maximum temperature reached in the center (log T ~ 7.87). The log (ρ/μ_e) ranges are determined by the limits of the KG07 numerical values.

In the text

Fig. 2

Comparison of some evolutionary properties for a 0.8 M_⊙ star with Y = 0.250 and Z = 0.001, as predicted by some of the codes presented in Table 2: PG, dotted black lines; PGPUC, black lines; BaSTI, red lines; GARSTEC, blue lines; STAREVOL, cyan lines. The properties are luminosity (L/L_⊙), effective temperature (T_eff), radius (R), central temperature (T_c), density (ρ_c), and hydrogen abundance (X_C). Small boxes are zoom-in to show the small differences between BaSTI and PGPUC results.

In the text

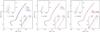Fig. 3

RGB evolutionary track comparison between PGPUC and the labeled codes (see Table 2) for a 0.8 M_⊙ star with three different helium abundances: Y = 0.250 (left), Y = 0.237 (middle) and Y = 0.230 (right). The metallicity is Z = 0.001 and the chemical composition is solar-scaled according to Grevesse & Noels (1993), except when labeled GN98, where the chemical composition is solar-scaled according to Grevesse & Sauval (1998). Each panel contains an upper left and a lower right panel with zooms to the RGB tip and RGB bump regions, respectively, with the same scales for each Y.

In the text

Fig. 4

Comparison between PGPUC and BaSTI results for non-standard chemical compositions. Left panel: evolutionary tracks with Y = 0.30 and Z = 9.2 × 10^-4. Middle panel: evolutionary tracks with Y = 0.35 and Z = 8.5 × 10^-4. Right panels: ZAHB loci for Y = 0.30 and Z = 9.2 × 10^-4 (upper panel) and Y = 0.35 and Z = 8.5 × 10^-4 (lower panel), where for comparison BaSTI ZAHB loci are moved Δlog (L/L_⊙) = −0.025. PGPUC ZAHB loci are shown for progenitor masses of M_i = 0.7 M_⊙ and M_i = 0.9 M_⊙.

In the text

Fig. 5

Set of evolutionary tracks (black lines) for stars between 1.1 (hottest track) and 0.5 M_⊙ (coolest track) with Y = 0.245, Z = 9.3 × 10^-4, and [α/Fe] = +0.3, plotted at ΔM = 0.1 M_⊙ intervals. Red points are the EEPs for each track, while green lines are isochrones, from left to right, between 7 and 15 Gyr, in steps of 1 Gyr. Inner panels are zoom-ins to the RGB tip (left) and RGB bump (right).

In the text

Fig. 6

Evolutionary tracks for stars with 0.9 M_⊙ from the MS to the tip of the RGB. The left panel shows the effects produced by different metallicities (from left to right: Z = 1.6 × 10^-4, 1.6 × 10^-3, 5.03 × 10^-3, and 1.57 × 10^-2) with Y = 0.245. The effects produced by different helium abundances (Y = 0.245, 0.295, and 0.345) for two metallicities ([Fe/H] = −2.25, and −0.25) are shown in the right panel. In parentheses are labeled the age in Gyr at the RGB tip for each evolutionary track.

In the text

Fig. 7

Relation between age at the RGB tip and the He core mass (M_cHe) reached for stars with different initial masses, metallicities, helium abundances and different mass loss rates (solid lines: no mass loss, or η = 0; dotted line: η = 1.0). Interpolated lines connect the real values for different initial helium abundances Y, from top to bottom: 0.245 (red), 0.295 (green), and 0.345 (blue). For stars with η = 1.0 and η = 0.0, the initial masses go, from left to right, from 1.1 to 0.5 M_⊙ and from 0.9 to 0.7 M_⊙, respectively, in steps of 0.1 M_⊙. As can be seen from the monotonic behavior of the solid lines, the helium core mass increases for higher ages (or lower initial masses). In the case of stars with mass loss (dotted lines), there is a maximum value for M_cHe because, for the mass loss efficiency assumed (η = 1.0), stars lose a large fraction of their masses at higher ages, which decreases the hydrogen-burning rate and leads to a premature departure from the RGB; a hot flasher may then take place. (See text for further details.)

In the text

	Fig. 8 Isochrones for (from upper left to lower right) 7.5, 10.0, 12.5, and 15.0 Gyr with metallicities, from left to right, Z₁ = 1.60 × 10^-4, Z₂ = 1.60 × 10^-3, and Z₃ = 1.57 × 10^-2 in the log L − log T_eff plane. Different colors represent different initial helium abundances: Y = 0.245 (red), 0.270 (yellow), 0.295 (green), 0.320 (cyan), 0.345 (blue), and 0.370 (black).
In the text

	Fig. 9 Isochrones for the labeled metallicities at the RGB bump. Colors represent the same Y values as in Fig. 8.
In the text

	Fig. 10 ZAHB loci for different metallicities (increasing from upper left to bottom right) and initial helium abundances. For each Y value, ZAHB loci were constructed using three RGB progenitors with different initial masses (M_i), which can be related to an age dependence of the ZAHB, which is particularly evident at low metallicities.
In the text

	Fig. 11 Relation between age at the RGB tip and the initial stellar mass (M_i) depending on the initial helium abundance and the metallicity. Colors represent different helium abundances. Dots, and lines have the same meaning as in Fig. 7.
In the text

	Fig. 12 Dependence of the effective temperature of ZAHB stars on their mass for three different metallicities: Z₁ = 1.60 × 10^-4, Z₂ = 1.60 × 10^-3 and Z₃ = 1.57 × 10^-2.
In the text

Fig. 13

Effective temperature of the stars arriving to the ZAHB for ages between 4 and 15 Gyr for 3 initial helium abundances Y = 0.245 (coolest continuous line), Y = 0.295 (dotted-dashed line) and Y = 0.345 (hottest continuous line), and 3 metallicities: 1.60 × 10^-4 (left panel), 1.60 × 10^-3 (middle panel), and 1.57 × 10^-2 (right panel). Dotted lines show the change in the effective temperatures when a dispersion of 0.02 M_⊙ in the total mass loss is considered. Dashed line shows an age of 13 Gyr.

In the text

Fig. A.1

Interpolated evolutionary tracks (red lines) from the original theoretical set of evolutionary tracks (blue lines). Upper panel: metallicity interpolation (metallicity increases from left to right) with constant helium abundance Y = 0.245 and mass of 0.9 M_⊙. Middle panel: helium interpolation (helium increases from right to left) with constant metallicity Z = 0.0016 and masses of 0.9 (hotter) and 0.5 M_⊙ (cooler). Bottom panel: mass interpolation (mass increases from right to left) with constant metallicity Z = 0.0016 and helium abundance Y = 0.245.

In the text

Fig. A.2

Interpolated ZAHB loci (red lines) from the original theoretical set of ZAHB loci (blue lines). Open triangles show the locus where the convective envelope dissapears. Upper panel: Z interpolation (Z increases from top to bottom) with constant Y = 0.245 and M_i = 0.9 M_⊙. Middle panel: Y interpolation (Y increases from bottom to top at the red ZAHB and inversely at the blue ZAHB) with constant Z = 0.0016 and M_i = 0.9 M_⊙. Bottom panel: M_i (M_i increases from bottom to top at the blue ZAHB) with two constant Z (Z = 0.0016 and Z = 0.00016) and Y = 0.245. Dots are the initial points for each ZAHB locus, with the mass increasing from bottom to top.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Aizenman, M. L., Demarque, P., & Miller, R. H. 1969, ApJ, 155, 973 [NASA ADS] [CrossRef] [Google Scholar]

[2] Alexander, D. R., & Ferguson, J. W. 1994, ApJ, 437, 879 [NASA ADS] [CrossRef] [Google Scholar]

[3] Alonso-García, J., Mateo, M., Sen, B., et al. 2012, AJ, 143, 70 [NASA ADS] [CrossRef] [Google Scholar]

[4] Alves-Brito, A., Yong, D., Meléndez, J., Vásquez, S., & Karakas, A. I. 2012, A&A, 540, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[5] Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]

[6] Antia, H. M., & Basu, S. 2011, J. Phys. Conf. Ser., 271, 012034 [NASA ADS] [CrossRef] [Google Scholar]

[7] Aparicio, A., Rosenberg, A., Saviane, I., Piotto, G., & Zoccali, M. 2001, in Astrophysical Ages and Times Scales, eds. T. von Hippel, C. Simpson, & N. Manset, ASP Conf. Ser., 245, 182 [Google Scholar]

[8] Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes III, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]

[9] Bahcall, J. N., & Pinsonneault, M. H. 1992, Rev. Mod. Phys., 64, 885 [NASA ADS] [CrossRef] [Google Scholar]

[10] Basu, S., & Antia, H. M. 2004, ApJ, 606, L85 [NASA ADS] [CrossRef] [Google Scholar]

[11] Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] [Google Scholar]

[12] Behr, B. B. 2003, ApJS, 149, 67 [NASA ADS] [CrossRef] [Google Scholar]

[13] Bekki, K. 2011, MNRAS, 412, 2241 [NASA ADS] [CrossRef] [Google Scholar]

[14] Bell, R. A., & Gustafsson, B. 1978, A&AS, 34, 229 [NASA ADS] [Google Scholar]

[15] Bergbusch, P. A., & Vandenberg, D. A. 1992, ApJS, 81, 163 [NASA ADS] [CrossRef] [Google Scholar]

[16] Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[17] Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[18] Bi, S. L., Li, T. D., Li, L. H., & Yang, W. M. 2011, ApJ, 731, L42 [NASA ADS] [CrossRef] [Google Scholar]

[19] Bragaglia, A., Carretta, E., Gratton, R., et al. 2010a, A&A, 519, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[20] Bragaglia, A., Carretta, E., Gratton, R. G., et al. 2010b, ApJ, 720, L41 [NASA ADS] [CrossRef] [Google Scholar]

[21] Brown, T. M., Sweigart, A. V., Lanz, T., Landsman, W. B., & Hubeny, I. 2001, ApJ, 562, 368 [NASA ADS] [CrossRef] [Google Scholar]

[22] Caffau, E., Ludwig, H., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [NASA ADS] [CrossRef] [Google Scholar]

[23] Canuto, V. 1970, ApJ, 159, 641 [NASA ADS] [CrossRef] [Google Scholar]

[24] Caputo, F., & Degl’Innocenti, S. 1995, A&A, 298, 833 [NASA ADS] [Google Scholar]

[25] Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[26] Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2010, A&A, 516, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[27] Cassisi, S., Salaris, M., & Bono, G. 2002, ApJ, 565, 1231 [NASA ADS] [CrossRef] [Google Scholar]

[28] Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]

[29] Cassisi, S., Salaris, M., Pietrinferni, A., et al. 2008, ApJ, 672, L115 [NASA ADS] [CrossRef] [Google Scholar]

[30] Castellani, M., & Castellani, V. 1993, ApJ, 407, 649 [NASA ADS] [CrossRef] [Google Scholar]

[31] Catelan, M. 2000, ApJ, 531, 826 [NASA ADS] [CrossRef] [Google Scholar]

[32] Catelan, M. 2007, in Graduate School in Astronomy: XI Special Courses at the National Observatory of Rio de Janeiro (XI CCE), eds. F. Roig, & D. Lopes, AIP Conf. Ser., 930, 39 [Google Scholar]

[33] Catelan, M. 2008, Mem. Soc. Astron. Italiana, 79, 388 [NASA ADS] [Google Scholar]

[34] Catelan, M. 2009a, in New Quests in Stellar Astrophysics II: The Ultraviolet Properties of Evolved Stellar Populations, eds. M. Chavez, E. Bertone, D. Rosa-Gonzalez, & L. H. Rodriguez-Merino (New York: Springer), 175 [Google Scholar]

[35] Catelan, M. 2009b, Ap&SS, 320, 261 [NASA ADS] [CrossRef] [Google Scholar]

[36] Catelan, M., & de Freitas Pacheco, J. A. 1993, AJ, 106, 1858 [NASA ADS] [CrossRef] [Google Scholar]

[37] Catelan, M., & de Freitas Pacheco, J. A. 1995, A&A, 297, 345 [NASA ADS] [Google Scholar]

[38] Catelan, M., & de Freitas Pacheco, J. A. 1996, PASP, 108, 166 [NASA ADS] [CrossRef] [Google Scholar]

[39] Catelan, M., de Freitas Pacheco, J. A., & Horvath, J. E. 1996, ApJ, 461, 231 [NASA ADS] [CrossRef] [Google Scholar]

[40] Catelan, M., Ferraro, F. R., & Rood, R. T. 2001, ApJ, 560, 970 [NASA ADS] [CrossRef] [Google Scholar]

[41] Catelan, M., Grundahl, F., Sweigart, A. V., Valcarce, A. A. R., & Cortés, C. 2009, ApJ, 695, L97 [NASA ADS] [CrossRef] [Google Scholar]

[42] Catelan, M., Valcarce, A. A. R., & Sweigart, A. V. 2010, in IAU Symp. 266, eds. R. de Grijs, & J. R. D. Lépine, 281 [Google Scholar]

[43] Caughlan, G. R., & Fowler, W. A. 1988, Atom. Data Nucl. Data Tables, 40, 283 [Google Scholar]

[44] Cavallo, R. M., Sweigart, A. V., & Bell, R. A. 1998, ApJ, 492, 575 [NASA ADS] [CrossRef] [Google Scholar]

[45] Chaboyer, B. 2001, in Astrophysical Ages and Times Scales, eds. T. von Hippel, C. Simpson, & N. Manset, ASP Conf. Ser., 245, 162 [Google Scholar]

[46] Conroy, C., & Spergel, D. N. 2011, ApJ, 726, 36 [NASA ADS] [CrossRef] [Google Scholar]

[47] Crocker, D. A., Rood, R. T., & O’Connell, R. W. 1988, ApJ, 332, 236 [NASA ADS] [CrossRef] [Google Scholar]

[48] Dalessandro, E., Salaris, M., Ferraro, F. R., et al. 2011, MNRAS, 410, 694 [NASA ADS] [CrossRef] [Google Scholar]

[49] D’Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[50] D’Antona, F., Bellazzini, M., Caloi, V., et al. 2005, ApJ, 631, 868 [NASA ADS] [CrossRef] [Google Scholar]

[51] D’Cruz, N. L., Dorman, B., Rood, R. T., & O’Connell, R. W. 1996, ApJ, 466, 359 [NASA ADS] [CrossRef] [Google Scholar]

[52] Decressin, T., Charbonnel, C., & Meynet, G. 2007, A&A, 475, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[53] Dell’Omodarme, M., Valle, G., Degl’Innocenti, S., & Pra da Moroni, P. G. 2012, A&A, 540, 26 [Google Scholar]

[54] Demarque, P. 1967, ApJ, 149, 117 [NASA ADS] [CrossRef] [Google Scholar]

[55] Demarque, P., & Mengel, J. G. 1973, A&A, 22, 121 [NASA ADS] [Google Scholar]

[56] Demarque, P., Mengel, J. G., & Aizenman, M. L. 1971, ApJ, 163, 37 [NASA ADS] [CrossRef] [Google Scholar]

[57] D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]

[58] Di Criscienzo, M., Ventura, P., D’Antona, F., Milone, A., & Piotto, G. 2010, MNRAS, 408, 999 [NASA ADS] [CrossRef] [Google Scholar]

[59] Dotter, A., Chaboyer, B., Jevremović, D., et al. 2008, ApJS, 178, 89 [NASA ADS] [CrossRef] [Google Scholar]

[60] Dotter, A., Sarajedini, A., Anderson, J., et al. 2010, ApJ, 708, 698 [NASA ADS] [CrossRef] [Google Scholar]

[61] Eddington, A. S. 1926, The Internal Constitution of the Stars (Cambridge University Press) [Google Scholar]

[62] Faulkner, J., & Iben, Jr., I. 1966, ApJ, 144, 995 [NASA ADS] [CrossRef] [Google Scholar]

[63] Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]

[64] Ferraro, F. R., Paltrinieri, B., Fusi Pecci, F., et al. 1997, ApJ, 484, L145 [NASA ADS] [CrossRef] [Google Scholar]

[65] Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Phys. Lett. B, 591, 61 [NASA ADS] [CrossRef] [Google Scholar]

[66] Fusi Pecci, F., Bellazzini, M., Ferraro, F. R., Buonanno, R., & Corsi, C. E. 1996, in Formation of the Galactic Halo... Inside and Out, eds. H. L. Morrison, & A. Sarajedini, ASP Conf. Ser., 92, 221 [Google Scholar]

[67] Girardi, L., Bressan, A., Chiosi, C., Bertelli, G., & Nasi, E. 1996, A&AS, 117, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[68] Gratton, R. G., Carretta, E., Bragaglia, A., Lucatello, S., & D’Orazi, V. 2010, A&A, 517, 81 [Google Scholar]

[69] Grevesse, N., & Noels, A. 1993, in Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]

[70] Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]

[71] Grundahl, F., Catelan, M., Landsman, W. B., Stetson, P. B., & Andersen, M. I. 1999, ApJ, 524, 242 [NASA ADS] [CrossRef] [Google Scholar]

[72] Gustafsson, B., & Bell, R. A. 1979, A&A, 74, 313 [NASA ADS] [Google Scholar]

[73] Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222; Erratum: ApJ, 438, 1017 [NASA ADS] [CrossRef] [Google Scholar]

[74] Härm, R., & Schwarzschild, M. 1966, ApJ, 145, 496 [NASA ADS] [CrossRef] [Google Scholar]

[75] Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]

[76] Hartwick, F. D. A. 1968, ApJ, 154, 475 [NASA ADS] [CrossRef] [Google Scholar]

[77] Hartwick, F. D. A., & VandenBerg, D. A. 1973, ApJ, 185, 887 [CrossRef] [Google Scholar]

[78] Heckler, A. F. 1994, Phys. Rev. D, 49, 611 [Google Scholar]

[79] Hill, G. 1982, Publications of the Dominion Astrophysical Observatory Victoria, 16, 67 [NASA ADS] [Google Scholar]

[80] Hubbard, W. B., & Lampe, M. 1969, ApJS, 18, 297 [NASA ADS] [CrossRef] [Google Scholar]

[81] Iben, I. 1968, Nature, 220, 143 [NASA ADS] [CrossRef] [Google Scholar]

[82] Iben, Jr., I.1974, ARA&A, 12, 215 [NASA ADS] [CrossRef] [Google Scholar]

[83] Iben, Jr., I., & Faulkner, J. 1968, ApJ, 153, 101 [CrossRef] [Google Scholar]

[84] Iben, Jr., I., & Rood, R. T. 1970, ApJ, 161, 587 [NASA ADS] [CrossRef] [Google Scholar]

[85] Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]

[86] Iglesias, C. A., Rogers, F. J., & Wilson, B. G. 1987, ApJ, 322, L45 [NASA ADS] [CrossRef] [Google Scholar]

[87] Imbriani, G., Costantini, H., Formicola, A., et al. 2005, EPJ A, 25, 455 [Google Scholar]

[88] Irwin, A. W. 2007, http://freeeos.sourceforge.net/ [Google Scholar]

[89] Itoh, N., Kohyama, Y., Matsumoto, N., & Seki, M. 1984, ApJ, 285, 758 [NASA ADS] [CrossRef] [Google Scholar]

[90] Itoh, N., Hayashi, H., Nishikawa, A., & Kohyama, Y. 1996, ApJS, 102, 411 [NASA ADS] [CrossRef] [Google Scholar]

[91] Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]

[92] Kantor, E. M., & Gusakov, M. E. 2007, MNRAS, 381, 1702 [NASA ADS] [CrossRef] [Google Scholar]

[93] Krishna Swamy, K. S. 1966, ApJ, 145, 174 [NASA ADS] [CrossRef] [Google Scholar]

[94] Kunz, R., Fey, M., Jaeger, M., et al. 2002, ApJ, 567, 643 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

[95] Lee, S. 1978, J. Korean Astron. Soc., 11, 1 [NASA ADS] [Google Scholar]

[96] Lee, Y., Demarque, P., & Zinn, R. 1994, ApJ, 423, 248 [Google Scholar]

[97] Lee, Y., Joo, S., Han, S., et al. 2005, ApJ, 621, L57 [NASA ADS] [CrossRef] [Google Scholar]

[98] Lodders, K., Plame, H., & Gail, H. 2009, in Landolt-Börnstein – Group VI Astronomy and Astrophysics Numerical Data and Functional Relationships in Science and Technology Volume 4B: Solar System, ed. J. E. Trümper, 4.4., 44 [Google Scholar]

[99] Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]

[100] Marino, A. F., Villanova, S., Milone, A. P., et al. 2011, ApJ, 730, L16 [NASA ADS] [CrossRef] [Google Scholar]

[101] Mihalas, D., Hummer, D. G., Mihalas, B. W., & Daeppen, W. 1990, ApJ, 350, 300 [NASA ADS] [CrossRef] [Google Scholar]

[102] Milone, A. P., Bedin, L. R., Piotto, G., et al. 2008, ApJ, 673, 241 [NASA ADS] [CrossRef] [Google Scholar]

[103] Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012, ApJ, 744, 58 [NASA ADS] [CrossRef] [Google Scholar]

[104] Moehler, S., Dreizler, S., Lanz, T., et al. 2011, A&A, 526, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[105] MoniBidin, C., Mauro, F., Geisler, D., et al. 2011a, A&A, 535, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[106] Moni Bidin, C., Villanova, S., Piotto, G., Moehler, S., & D’Antona, F. 2011b, ApJ, 738, L10 [NASA ADS] [CrossRef] [Google Scholar]

[107] Nataf, D. M., & Gould, A. P. 2012, ApJ, 751, L39 [NASA ADS] [CrossRef] [Google Scholar]

[108] Nataf, D. M., & Udalski, A. 2011 [arXiv:1106.0005] [Google Scholar]

[109] Nataf, D. M., Gould, A., Pinsonneault, M. H., & Stetson, P. B. 2011a, ApJ, 736, 94 [NASA ADS] [CrossRef] [Google Scholar]

[110] Nataf, D. M., Udalski, A., Gould, A., & Pinsonneault, M. H. 2011b, ApJ, 730, 118 [NASA ADS] [CrossRef] [Google Scholar]

[111] Norris, J. 1981, ApJ, 248, 177 [NASA ADS] [CrossRef] [Google Scholar]

[112] Norris, J. E. 2004, ApJ, 612, L25 [NASA ADS] [CrossRef] [Google Scholar]

[113] Norris, J., & Smith, G. H. 1983, ApJ, 275, 120 [NASA ADS] [CrossRef] [Google Scholar]

[114] Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]

[115] Pietrinferni, A., Cassisi, S., Salaris, M., Percival, S., & Ferguson, J. W. 2009, ApJ, 697, 275 [NASA ADS] [CrossRef] [Google Scholar]

[116] Pietrinferni, A., Cassisi, S., & Salaris, M. 2010, A&A, 522, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[117] Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [NASA ADS] [CrossRef] [Google Scholar]

[118] Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]

[119] Pols, O. R., Tout, C. A., Eggleton, P. P., & Han, Z. 1995, MNRAS, 274, 964 [NASA ADS] [CrossRef] [Google Scholar]

[120] Potekhin, A. Y. 1999, A&A, 351, 787 [NASA ADS] [Google Scholar]

[121] Prather, M. J. 1976, Ph.D. Thesis, Yale Univ. [Google Scholar]

[122] Reimers, D. 1975, Mem. Soc. Roy. Sci. Liege, 8, 369 [Google Scholar]

[123] Renzini, A., Greggio, L., Ritossa, C., & Ferrario, L. 1992, ApJ, 400, 280 [NASA ADS] [CrossRef] [Google Scholar]

[124] Rogers, F. J., & Iglesias, C. A. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]

[125] Rood, R., & Iben, Jr., I.1968, ApJ, 154, 215 [NASA ADS] [CrossRef] [Google Scholar]

[126] Rood, R. T., & Crocker, D. A. 1989, in The Use of pulsating stars in fundamental problems of astronomy, ed. E. G. Schmidt, 111 [Google Scholar]

[127] Rood, R. T., Crocker, D. A., Fusi Pecci, F., et al. 1993, 48, 218 [Google Scholar]

[128] Salaris, M., Riello, M., Cassisi, S., & Piotto, G. 2004, A&A, 420, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[129] Sandage, A., & Wallerstein, G. 1960, ApJ, 131, 598 [NASA ADS] [CrossRef] [Google Scholar]

[130] Sandage, A., & Wildey, R. 1967, ApJ, 150, 469 [NASA ADS] [CrossRef] [Google Scholar]

[131] Sarajedini, A., Chaboyer, B., & Demarque, P. 1997, PASP, 109, 1321 [NASA ADS] [CrossRef] [Google Scholar]

[132] Schröder, K., & Cuntz, M. 2005, ApJ, 630, L73 [NASA ADS] [CrossRef] [Google Scholar]

[133] Schröder, K., & Cuntz, M. 2007, A&A, 465, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[134] Schwarzschild, M., & Härm, R. 1965, ApJ, 142, 855 [NASA ADS] [CrossRef] [Google Scholar]

[135] Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]

[136] Serenelli, A., & Weiss, A. 2005, A&A, 442, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[137] Serenelli, A. M., Basu, S., Ferguson, J. W., & Asplund, M. 2009, ApJ, 705, L123 [NASA ADS] [CrossRef] [Google Scholar]

[138] Serenelli, A. M., Haxton, W. C., & Peña-Garay, C. 2011, ApJ, 743, 24 [NASA ADS] [CrossRef] [Google Scholar]

[139] Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[140] Simoda, M., & Iben, Jr., I. 1968, ApJ, 152, 509 [NASA ADS] [CrossRef] [Google Scholar]

[141] Simoda, M., & Iben, Jr., I. 1970, ApJS, 22, 81 [NASA ADS] [CrossRef] [Google Scholar]

[142] Smith, G. H., & Norris, J. 1983, ApJ, 264, 215 [NASA ADS] [CrossRef] [Google Scholar]

[143] Stetson, P. B., Vandenberg, D. A., & Bolte, M. 1996, PASP, 108, 560 [NASA ADS] [CrossRef] [Google Scholar]

[144] Sweigart, A. V. 1971, ApJ, 168, 79 [NASA ADS] [CrossRef] [Google Scholar]

[145] Sweigart, A. V. 1973, A&A, 24, 459 [NASA ADS] [Google Scholar]

[146] Sweigart, A. V. 1978, in The HR Diagram – The 100th Anniversary of Henry Norris Russell, eds. A. G. D. Philip, & D. S. Hayes, IAU Symp., 80, 333 [Google Scholar]

[147] Sweigart, A. V. 1987, ApJS, 65, 95 [NASA ADS] [CrossRef] [Google Scholar]

[148] Sweigart, A. V. 1994, ApJ, 426, 612 [NASA ADS] [CrossRef] [Google Scholar]

[149] Sweigart, A. V. 1997a, ApJ, 474, L23 [NASA ADS] [CrossRef] [Google Scholar]

[150] Sweigart, A. V. 1997b, in The Third Conference on Faint Blue Stars, eds. A. G. D. Philip, J. Liebert, R. Saffer, & D. S. Hayes (Schenectady: L. Davis Press), 3 [Google Scholar]

[151] Sweigart, A. V., & Catelan, M. 1998, ApJ, 501, L63 [NASA ADS] [CrossRef] [Google Scholar]

[152] Sweigart, A. V., & Demarque, P. 1972, A&A, 20, 445 [NASA ADS] [Google Scholar]

[153] Sweigart, A. V., & Gross, P. G. 1974, ApJ, 190, 101 [NASA ADS] [CrossRef] [Google Scholar]

[154] Sweigart, A. V., & Gross, P. G. 1976, ApJS, 32, 367 [NASA ADS] [CrossRef] [Google Scholar]

[155] Sweigart, A. V., & Gross, P. G. 1978, ApJS, 36, 405 [NASA ADS] [CrossRef] [Google Scholar]

[156] Thomas, H. 1967, ZAp, 67, 420 [Google Scholar]

[157] Valcarce, A. A. R., & Catelan, M. 2008, A&A, 487, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[158] Valcarce, A. A. R., & Catelan, M. 2011, A&A, 533, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[159] van den Bergh, S. 1965, JRASC, 59, 151 [NASA ADS] [Google Scholar]

[160] van den Bergh, S. 1967, AJ, 72, 70 [NASA ADS] [CrossRef] [Google Scholar]

[161] VandenBerg, D. A., Swenson, F. J., Rogers, F. J., Iglesias, C. A., & Alexander, D. R. 2000, ApJ, 532, 430 [NASA ADS] [CrossRef] [Google Scholar]

[162] VandenBerg, D. A., Bergbusch, P. A., & Dowler, P. D. 2006, ApJS, 162, 375 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

[163] VandenBerg, D. A., Edvardsson, B., Eriksson, K., & Gustafsson, B. 2008, ApJ, 675, 746 [NASA ADS] [CrossRef] [Google Scholar]

[164] VandenBerg, D. A., Bergbusch, P. A., Dotter, A., et al. 2012, ApJ, 755, 15 [NASA ADS] [CrossRef] [Google Scholar]

[165] Ventura, P., Caloi, V., D’Antona, F., et al. 2009, MNRAS, 399, 934 [NASA ADS] [CrossRef] [Google Scholar]

[166] Villanova, S., Piotto, G., & Gratton, R. G. 2009, A&A, 499, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]