| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220001 | |
| Published online | 08 October 2012 | |
Dissipation in planar resonant planetary systems
1
Astronomie et Systèmes Dynamiques, IMCCE-CNRS UMR8028, Observatoire de
Paris, UPMC,
77 Av. Denfert-Rochereau,
75014
Paris,
France
e-mail: delisle@imcce.fr
2
Department of Physics, I3N, University of Aveiro, Campus
Universitário de Santiago, 3810-193
Aveiro,
Portugal
3
Centro de Astrofísica, Universidade do Porto,
Rua das Estrelas, 4150-762
Porto,
Portugal
Received:
12
July
2012
Accepted:
25
August
2012
Close-in planetary systems detected by the Kepler mission present an excess of period ratios that are just slightly larger than some low order resonant values. This feature occurs naturally when resonant couples undergo dissipation that damps the eccentricities. However, the resonant angles appear to librate at the end of the migration process, which is often believed to be an evidence that the systems remain in resonance. Here we provide an analytical model for the dissipation in resonant planetary systems valid for low eccentricities. We confirm that dissipation accounts for an excess of pairs that lie just aside from the nominal period ratios, as observed by the Kepler mission. In addition, by a global analysis of the phase space of the problem, we demonstrate that these final pairs are non-resonant. Indeed, the separatrices that exist in the resonant systems disappear with the dissipation, and remains only a circulation of the orbits around a single elliptical fixed point. Furthermore, the apparent libration of the resonant angles can be explained using the classical secular averaging method. We show that this artifact is only due to the severe damping of the amplitudes of the eigenmodes in the secular motion.
Key words: celestial mechanics / planets and satellites: general / planetary systems
© ESO, 2012
1. Introduction
Dissipation due to tidal interactions is a possible mechanism that explains the abundance of planetary systems that lie near but not at exact mean-motion commensurability. Papaloizou & Terquem (2010) (in the case of three planets Laplace resonances) and Papaloizou (2011) (for two planets resonances) showed that planets that have been temporarily locked in resonance due to differential migration could have their period ratios to depart from strict commensurability due to the circularization of their orbits by tidal interactions with the star. More recently, Batygin & Morbidelli (2012) and Lithwick & Wu (2012) use similar effects to explain the excess of systems of two planets that lie near resonances but with planets slightly farther from each other than the nominal mean-motion commensurability ratio.
One of the most intriguing features that is common in these different studies is the observation that resonant angles continue to librate far from exact commensurability and the authors leave unanswered the question of determining if these systems are in resonance or not. It seems important to clarify this point and to understand why resonant angles can librate so far from exact commensurability.
Our analysis is based on the study of the phase space of two planets in mean-motion resonance (MMR) in the conservative case (without any dissipation). This is the object of Sect. 2. We pay a particular attention to apsidal corotation resonances (ACR) which play a major role in the dynamics of these systems and in the understanding of the topology of the phase space. ACR have been extensively studied both in the asteroidal restricted problem (e.g. Ferraz-Mello et al. 1993) and the planetary problem (e.g. Hadjidemetriou 2002; Michtchenko et al. 2006).
Most of the studies on the subject have been made using numerical (or semi-analytical) models that remain valid for arbitrary values of the eccentricities but which do not always provide a global picture of the dynamics. In the present study we are only concerned in the dynamics at low eccentricities since our aim is to understand the motion at the end of the circularization process. A completely analytical model is thus well suited in this case. Analytical studies of planetary MMR have already be done up to degree two in eccentricities in the cases of the 2:1 (Callegari et al. 2004) and the 3:2 (Callegari et al. 2006) MMR.
The dissipative case (studied in Sect. 3) is modeled using the conservative case as a basis and very simple and general prescriptions for the dissipation. Our study is mainly aimed at understanding the impact of tides on the dynamics of resonant planets pairs and, in this case, we follow the prescriptions introduced by Papaloizou (2011). However we show that the differential migration process that allows a resonant locking of both planets can also be accounted for in our model. This process has already been widely studied (e.g. Lee & Peale 2002; Ferraz-Mello et al. 2003; Lee 2004; Beaugé et al. 2006), and is also considered in Papaloizou & Terquem (2010); Papaloizou (2011). Eventually, we treat this perturbation of the conservative case by following the lines of Laskar et al. (2012).
In Sect. 4 we show that the final state of the resonant systems that undergo a circularization process is very well characterized by the secular normal form. We explain, with the secular problem, why resonant angles appear to librate even far from resonances.
Finally, we present in Sect. 5 the results of two numerical simulations that confirm and illustrate the different mechanisms that we highlight with our analytical model.
2. Dynamics of two resonant planets in the conservative case
2.1. Model
We study in this section the case of two planets orbiting a star in the same plane and
without any dissipative force. This problem is usually referred to as the planar planetary
three body problem. We note with a subscript 1 the internal planet and 2 the external one.
The star is referred to as body 0. Masses are noted
mi. For both planets we define:
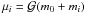 ,
and
βi = m0mi/(m0 + mi),
where
,
and
βi = m0mi/(m0 + mi),
where 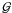 is the gravitational constant. We note ai the
semi-major axis of planet i, and
ei its eccentricity.
is the gravitational constant. We note ai the
semi-major axis of planet i, and
ei its eccentricity.
We use Delaunay canonical pairs of astrocentric coordinates for both planets. The actions
are the circular angular momentum and the angular momentum of both planets:
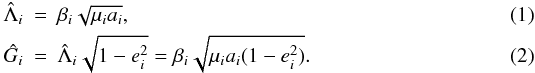 The
associated angles are the mean anomalies (Mi)
and the arguments of periastron (ωi) of both
planets.
The
associated angles are the mean anomalies (Mi)
and the arguments of periastron (ωi) of both
planets.
The Hamiltonian of the system reads, in these coordinates:
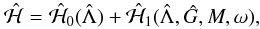 (3)where
(3)where
 is the Keplerian part and
is the Keplerian part and  is the perturbative part due to planet-planet interactions taking into account both direct
and indirect effects. The Keplerian part depends only on
is the perturbative part due to planet-planet interactions taking into account both direct
and indirect effects. The Keplerian part depends only on
 (i = 1,2):
(i = 1,2): 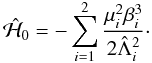 (4)Whereas the perturbative
part depends on all eight Delaunay coordinates. We do not need to express the explicit
form of
(4)Whereas the perturbative
part depends on all eight Delaunay coordinates. We do not need to express the explicit
form of 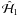 at this point but it could be seen as a Fourier series of all four angles (with
coefficients depending on actions).
at this point but it could be seen as a Fourier series of all four angles (with
coefficients depending on actions).
At first sight, we have to deal with a four degrees of freedom differential system. However, we will now introduce two well-known transformations which will reduce this problem to two degrees of freedom. The first reduction makes use of the total angular momentum conservation and is always valid. The second one corresponds to an averaging of the equations of motion and is only valid near a specified MMR. More precisely, it is only valid far from all other MMR.
2.1.1. Conservation of the total angular momentum
In the Delaunay coordinates system, the total angular momentum conservation
(Ĝ = Ĝ1 + Ĝ2)
is equivalent to the fact that the Hamiltonian depends only on the value of the
difference of arguments of periastron:
Δω = ω1 − ω2
and not on individual values of both angles. The reduction resulting from the
conservation of the angular momentum is performed by using the coordinates
Δω, ω2 instead of
ω1, ω2. These two new angles
are respectively canonically conjugated to the actions Ĝ1,
Ĝ. Therefore, the system of coordinates
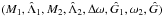 is canonical and with these coordinates, ω2 does not appear
anymore in the expression of the Hamiltonian. Ĝ is a first integral of
the equations of motion. We can thus study the three degrees of freedom system
constituted of
is canonical and with these coordinates, ω2 does not appear
anymore in the expression of the Hamiltonian. Ĝ is a first integral of
the equations of motion. We can thus study the three degrees of freedom system
constituted of 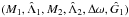 and consider Ĝ as a parameter of this system.
and consider Ĝ as a parameter of this system.
2.1.2. Averaging the Hamiltonian near a MMR
We now suppose that the system is near a mean-motion commensurability of the form
(p + q):p, that is:
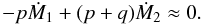 (5)We may then introduce
the argument of the (p + q):p MMR:
(5)We may then introduce
the argument of the (p + q):p MMR:
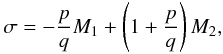 (6)such as
(6)such as
 .
.
We then construct the resonant normal form to the first order of the planets masses
(with respect to the stellar mass) by averaging over all rapid angles, i.e. all
combinations of the mean anomalies that are not harmonics of σ. By
doing this averaging we need to introduce a new set of variables which corresponds to
the averaged problem. The change of coordinates is close to identity so we can identify
both sets of coordinates in first approximation. Strictly speaking the transformation to
the initial set of coordinates reintroduces high frequencies (e.g. Morbidelli 2002). Before constructing the normal form, we introduce
the change of variables:  and
we consider the canonical set of coordinates:
(σ,Î,M2,Γ,Δω,Ĝ1).
With this set of coordinates, the resonant normal form is obtained by averaging over
M2. Thus, by definition, M2
does not appear anymore in the averaged Hamiltonian, and Γ is a first integral of the
averaged motion. Therefore, the system is reduced to a two degrees of freedom problem
with four canonical coordinates:
(σ,Î,Δω,Ĝ1)
and two parameters: Ĝ and Γ. However this set of coordinates is not
very well suited for the study of low-eccentricities systems and it is a lot more
convenient to introduce rectangular canonically conjugated variables similar to Poincaré
variables.
and
we consider the canonical set of coordinates:
(σ,Î,M2,Γ,Δω,Ĝ1).
With this set of coordinates, the resonant normal form is obtained by averaging over
M2. Thus, by definition, M2
does not appear anymore in the averaged Hamiltonian, and Γ is a first integral of the
averaged motion. Therefore, the system is reduced to a two degrees of freedom problem
with four canonical coordinates:
(σ,Î,Δω,Ĝ1)
and two parameters: Ĝ and Γ. However this set of coordinates is not
very well suited for the study of low-eccentricities systems and it is a lot more
convenient to introduce rectangular canonically conjugated variables similar to Poincaré
variables.
2.1.3. Rectangular coordinates
We first introduce the two resonant angles which correspond to both planets (e.g. Ferraz-Mello et al. 1993):
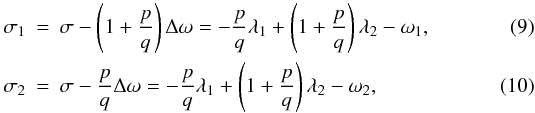 where
λi = Mi + ωi
is the mean longitude of planet i. We complete this change of variables
with the canonically conjugated actions:
where
λi = Mi + ωi
is the mean longitude of planet i. We complete this change of variables
with the canonically conjugated actions: 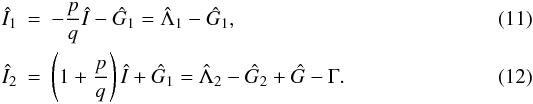 Note
that, since Ĝ and Γ are constants of the motion, we can redefine the
action Î2 as:
Note
that, since Ĝ and Γ are constants of the motion, we can redefine the
action Î2 as:
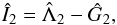 (13)without any
change for Î1, σ1 and
σ2.
(13)without any
change for Î1, σ1 and
σ2.
The associated rectangular coordinates are then: 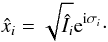 (14)
(14)
2.1.4. Elimination of the first integral Γ
The dynamics of our two degrees of freedom system should depend on the value of both
first integrals: Γ and Ĝ. However, it is possible to eliminate the
dependency in Γ by dividing all actions by its value:
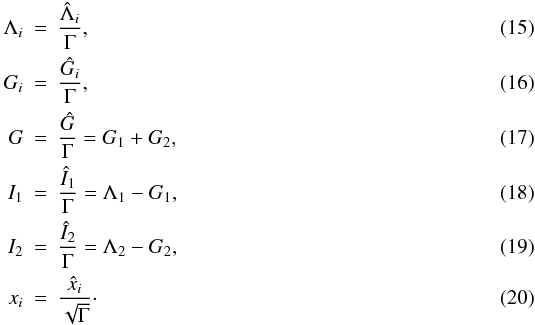 With
these renormalized variables, Hamilton equations are still valid if the Hamiltonian is
also divided by Γ:
With
these renormalized variables, Hamilton equations are still valid if the Hamiltonian is
also divided by Γ: 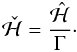 (21)However, the
Hamiltonian
(21)However, the
Hamiltonian 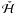 ,
and thus the dynamics, still depends on the value of Γ. The complete elimination of Γ is
achieved by renormalizing both energy and time scales:
,
and thus the dynamics, still depends on the value of Γ. The complete elimination of Γ is
achieved by renormalizing both energy and time scales:
 It
can be verified that ℋ does not depend anymore on Γ and Hamilton’s equations now reads:
It
can be verified that ℋ does not depend anymore on Γ and Hamilton’s equations now reads:
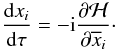 (24)This means that the
value of Γ does not influence the dynamics of the system except by changing the scales
of distance, time and energy (respectively by a factor of Γ2, Γ3
and 1/Γ2). With this renormalization, we reduced the
number of parameters of our system from two (Ĝ, Γ) to one
(G = Ĝ/Γ).
(24)This means that the
value of Γ does not influence the dynamics of the system except by changing the scales
of distance, time and energy (respectively by a factor of Γ2, Γ3
and 1/Γ2). With this renormalization, we reduced the
number of parameters of our system from two (Ĝ, Γ) to one
(G = Ĝ/Γ).
2.1.5. Explicit form of the Hamiltonian
We need to express the Hamiltonian ℋ as a function of
xi
(i = 1,2) and G. Let us start with
the Keplerian part. The renormalized Keplerian part (ℋ0) has the same form as
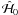 (see Eq. (4)) if we replace
(see Eq. (4)) if we replace
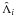 with Λi. Moreover, Λi are simple
functions of xi and G:
with Λi. Moreover, Λi are simple
functions of xi and G:
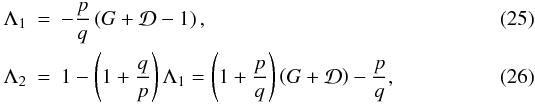 where
where
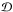 is the (renormalized) angular momentum deficit (AMD, e.g. Laskar 2000) defined by:
is the (renormalized) angular momentum deficit (AMD, e.g. Laskar 2000) defined by:
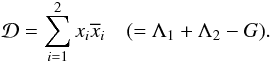 (27)Therefore, the
Keplerian part is obtained by substituting Λi values in the
expression of ℋ0. This expression is then expanded to a given degree in
eccentricities (i.e. to a given power in xi
variables). Note that the Keplerian part is now expressed as a power series of
eccentricities even if it only depends on semi-major axes in Delaunay coordinates
system. It should be remarked that xi
variables only appear in the Keplerian part with
(27)Therefore, the
Keplerian part is obtained by substituting Λi values in the
expression of ℋ0. This expression is then expanded to a given degree in
eccentricities (i.e. to a given power in xi
variables). Note that the Keplerian part is now expressed as a power series of
eccentricities even if it only depends on semi-major axes in Delaunay coordinates
system. It should be remarked that xi
variables only appear in the Keplerian part with 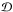 (which is of degree two and symmetrical for both planets). As a consequence the
Keplerian part only contains terms of even degree in eccentricities.
(which is of degree two and symmetrical for both planets). As a consequence the
Keplerian part only contains terms of even degree in eccentricities.
For the perturbative part, we use the expansion method presented in Laskar & Robutel (1995) and implemented in
the algebraic manipulator TRIP (Gastineau &
Laskar 2011). The Poincaré coordinates used in Laskar & Robutel (1995), noted x, and
x′, are related to our rectangular coordinates with the
relations:  with:
with:
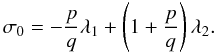 (30)Laskar & Robutel (1995) method is aimed at
computing the perturbative part of the Hamiltonian in power series of
x, x′, and in Fourier series of the mean
longitudes λ1, λ2 (with
coefficients depending on
(30)Laskar & Robutel (1995) method is aimed at
computing the perturbative part of the Hamiltonian in power series of
x, x′, and in Fourier series of the mean
longitudes λ1, λ2 (with
coefficients depending on 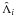 ).
The averaging method described in Sect. 2.1.2
consists in selecting in this expansion the terms that do not depend upon combinations
of the mean longitudes other than σ0 (and its harmonics).
).
The averaging method described in Sect. 2.1.2
consists in selecting in this expansion the terms that do not depend upon combinations
of the mean longitudes other than σ0 (and its harmonics).
Then it is straightforward to express ℋ1 as a function of
xi and G, by
substituting x, x′ and
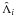 by their values and renormalizing by Γ. We obtain a power series of
xi with coefficients depending
on G.
by their values and renormalizing by Γ. We obtain a power series of
xi with coefficients depending
on G.
The ratio between the perturbative and the Keplerian parts is of the order of the mass ratio between the planets and the star. To be consistent, the Keplerian part must be expanded to a higher degree in eccentricities than the perturbative part.
As an example, for a first order resonance (of the form
(p + 1):p), the Hamiltonian expanded to the fourth
degree in eccentricities for the Keplerian part and to the second degree for the
perturbation (noted degree 4-2) has the form: 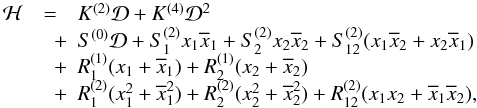 (31)where
all coefficients (K, S, R) depends
on G and on the masses, and K stands for Keplerian
terms, S for secular terms and R for resonant terms
(see Appendix A for a description of their
computation). For a resonance of order two (or more), the expression would be similar
but there would not be resonant terms of the degree one. These terms are very important
in the dynamics since they introduce constant terms (non-zero right-hand side) in
Hamilton’s equations (Eq. (24)). When
there are no first degree terms (resonance of order two or more),
xi = 0
(i = 1,2) is always a fixed point. On the contrary,
for first order resonances, this fixed point does not exist and an initially circular
system will not stay circular. Note that since the Hamiltonian is expanded as series of
eccentricities, this model is only valid for low eccentricities.
(31)where
all coefficients (K, S, R) depends
on G and on the masses, and K stands for Keplerian
terms, S for secular terms and R for resonant terms
(see Appendix A for a description of their
computation). For a resonance of order two (or more), the expression would be similar
but there would not be resonant terms of the degree one. These terms are very important
in the dynamics since they introduce constant terms (non-zero right-hand side) in
Hamilton’s equations (Eq. (24)). When
there are no first degree terms (resonance of order two or more),
xi = 0
(i = 1,2) is always a fixed point. On the contrary,
for first order resonances, this fixed point does not exist and an initially circular
system will not stay circular. Note that since the Hamiltonian is expanded as series of
eccentricities, this model is only valid for low eccentricities.
2.2. Study of the dynamics
2.2.1. Energy levels
We consider a first order resonance and construct the resonant normal form developed up
to degree 4 for the Keplerian part and to first degree for the perturbation (noted
degree 4-1). For given values of the masses of the three bodies, a given mean-motion
commensurability (p + q):p, and a
given value of G, we are able to compute the needed coefficients
K, S and R. We can then look at the
energy levels of this Hamiltonian. Since our problem has two degrees of freedom and four
dimensions, we cannot have a global view of these energy levels but we can represent
them on section planes. Figure 1 shows the energy
levels, represented in different section planes (see the legend), in the case of the
2:1 MMR with a star mass of
m0 = m⊙ (solar mass),
planets masses of
m1 = m2 = m ⊕
(Earth’s mass), and with
G = G0(1−10-4).
G0 is the value of the total circular angular momentum at
nominal resonance. At nominal resonance, the exact commensurability of mean-motions
induces the relation: 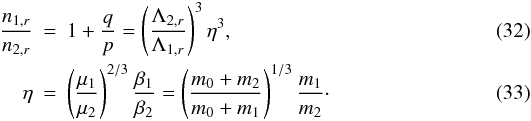 Together
with the relation
Together
with the relation 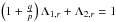 (see Eq. (25)), this imposes the values
Λ1,r and Λ2,r at nominal
resonance:
(see Eq. (25)), this imposes the values
Λ1,r and Λ2,r at nominal
resonance: ![\begin{eqnarray} \Lambda_{1,r} & = & \left[ \left(1+\frac{q}{p}\right) + \left(1+\frac{q}{p}\right)^{1/3} \eta^{-1} \right]^{-1},\\ \Lambda_{2,r} & = & \left[ 1 + \left(1+\frac{q}{p}\right)^{2/3} \eta \right]^{-1}, \end{eqnarray}](/articles/aa/full_html/2012/10/aa20001-12/aa20001-12-eq88.png) G0
is then given by:
G0
is then given by: ![\begin{equation} G_0 = \Lambda_{1,r} + \Lambda_{2,r} = \left\{ 1 + \frac{q}{p} \left[ 1 + \left( 1 + \frac{q}{p}\right)^{1/3} \eta^{-1} \right]^{-1} \right\}^{-1}. \end{equation}](/articles/aa/full_html/2012/10/aa20001-12/aa20001-12-eq89.png) (36)In Fig. 1, we distinguish three areas in the different section
planes (except in the plane
(sinσ1,sinσ2)
on the top right of the graph). There are two zones of circulation: internal circulation
for low eccentricities and external circulation for high eccentricities. Between these
two circulation areas, we observe a libration zone (banana-shaped level curves)
separated from both circulation areas by two separatrices. Fixed points of the system
(see next section) are marked with colored dots (for stable ones) and crosses (for
unstable ones). The red dot corresponds to the libration center in Fig. 1, bottom-left.
(36)In Fig. 1, we distinguish three areas in the different section
planes (except in the plane
(sinσ1,sinσ2)
on the top right of the graph). There are two zones of circulation: internal circulation
for low eccentricities and external circulation for high eccentricities. Between these
two circulation areas, we observe a libration zone (banana-shaped level curves)
separated from both circulation areas by two separatrices. Fixed points of the system
(see next section) are marked with colored dots (for stable ones) and crosses (for
unstable ones). The red dot corresponds to the libration center in Fig. 1, bottom-left.
 |
Fig. 1 2:1 resonance energy levels in section planes defined by: e2 = 0 (top left), cosσ1 = cosσ2 = 0 (top right), sinσ1 = sinσ2 = 0 (bottom left), and e1 = 0 (bottom right). Stable ACR solutions are highlighted with colored dots (red and green). Unstable ones are highlighted with colored crosses (blue). The star mass is given by m0 = m⊙ and planets masses by m1 = m2 = m ⊕ . The constant G is set to G = G0(1−10-4). The Hamiltonian is developed up to degree 4-1. |
 |
Fig. 2 Energy levels sections in the plane defined by sinσ1 = sinσ2 = 0 for the 2:1 resonance (A1 to F1), and the 3:2 resonance (A2 to F2). The constant G/G0 − 1 is set to −10-3 (A1, A2), −5 × 10-4 (B1, B2), −10-4 (C1, C2), −3.2 × 10-5 (D1, D2), −3 × 10-5 (E1, E2), and + 10-3 (F1, F2). Stable ACR solutions are highlighted with colored dots (red and green). Unstable ones are highlighted with colored crosses (blue). The star mass is given by m0 = m⊙ and planets masses by m1 = m2 = m ⊕ . The Hamiltonian is developed up to degree 4-1. Note that the scales are different for graphs A1, A2, B1, and B2 than for other graphs. |
Figure 2 shows the energy levels on the section plane defined by sinσ1 = sinσ2 = 0 for increasing values of the parameter G and for the 2:1 and the 3:2 MMR. The masses are the same as for Fig. 1 (m0 = m⊙, m1 = m2 = m ⊕ ). Figure 2, C1 is the same as Fig. 1, bottom-left. When G decreases (Figs. 2, A1, B1), the libration area moves to higher eccentricities and the internal circulation area takes more space. On the contrary, for higher values of G (Figs. 2, D1 to F1), the internal circulation and the libration areas tend to shrink and eventually completely disappear leaving only the external circulation area.
We observe the same evolution for the 3:2 MMR (Figs. 2, A2 to F2) and it seems that this behavior is common to all first order MMR.
Even if these section planes give an insight on the nature of the motion, it is important to keep in mind that the real motion occurs on the total four dimensional phase space and that these sections cannot provide a global picture of the dynamics. The easiest way to have a good insight on the global structure of the phase space is to look at the positions and natures of the fixed points of the system. These fixed points are commonly referred to as apsidal corotation resonances or ACR (e.g. Ferraz-Mello et al. 1993).
2.2.2. Fixed points
The positions of the fixed points are obtained solving Hamilton’s equations (Eq. (24)). For instance, at degree 4-2
(Eq. (31)): 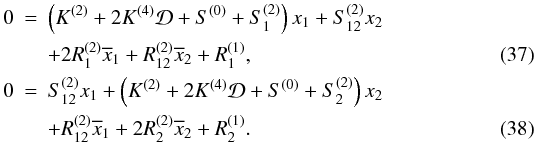 This
imply to solve a system of four polynomial real equations (real and imaginary parts of
Eqs. (37), (38)) with four real unknowns (real and imaginary parts of
x1, x2). We solve it using the
Maple RootFinding[Isolate] function (see Rouillier 1999). Then, for each solution, we linearize the equations
of motion around the fixed point in order to compute the eigenvalues and to distinguish
between elliptic (purely imaginary eigenvalues) and hyperbolic (nonzero real parts)
fixed points.
This
imply to solve a system of four polynomial real equations (real and imaginary parts of
Eqs. (37), (38)) with four real unknowns (real and imaginary parts of
x1, x2). We solve it using the
Maple RootFinding[Isolate] function (see Rouillier 1999). Then, for each solution, we linearize the equations
of motion around the fixed point in order to compute the eigenvalues and to distinguish
between elliptic (purely imaginary eigenvalues) and hyperbolic (nonzero real parts)
fixed points.
Degree 4-1
Figure 3 shows the positions and nature of ACR solutions as functions of G, in case of the 2:1 MMR with the same masses than before. The Hamiltonian is still developed up to degree 4-1. In this figure, continuous lines represent stable fixed points and dashed lines represent unstable ones. The choice of colors is consistent with Figs. 1 and 2. We gave the positions of ACR only in the directions e1cosσ1 and e2cosσ2 because all ACR solutions that we found have sinσ1 = sinσ2 = 0. On the left of Fig. 3 (lowest values of G), there are two elliptic and one hyperbolic ACR. This corresponds to the situation of Figs. 1 and 2, A1 to D1. The red elliptic ACR corresponds to the center of the libration area. The green one corresponds to the center of the internal circulation area. The blue hyperbolic ACR corresponds to the crossing of internal and external separatrices.
 |
Fig. 3 2:1 ACR positions as functions of G. The star mass is given by m0 = m⊙ and planets masses by m1 = m2 = m ⊕ . The Hamiltonian is developed up to degree 4-1. Elliptic (stable) ACR are plotted using continuous lines whereas hyperbolic (unstable) ACR are plotted using dashed lines. At this degree of development, all ACR have sinσ1 = sinσ2 = 0. |
Around G = G0, we observe a bifurcation and the green and the blue ACR disappear whereas the red one remains the only one to survive and it stay stable. This corresponds to the situation observed in Fig. 2, E1, F1 and which cannot be considered as a resonant situation.
In order to have a better view of the spatial positions of these ACR we plotted in Fig. 4 the semi-major axes ratio of ACR solutions as functions of G. We observe that the center of libration corresponds to values of α lower than the nominal resonant value. This is equivalent to values of P2/P1 greater than the nominal resonant value (2). It means that planets are farther away from each other than the nominal resonance distance. On the contrary, the hyperbolic ACR and the center of the internal resonant area correspond to higher values of α, thus two planets closer to each other than the nominal resonance distance.
Note that when the system moves away from the semi-major axes nominal resonant ratio, both elliptic ACR solutions tend to zero eccentricities (Figs. 3 and 4).
Higher degrees of development
In order to evaluate the upper bound of the eccentricities for which the situation that we described is realistic we compare the results obtained for increasing degree of development of the Hamitonian. If the global structure of the phase space remains the same for higher degrees and the number, natures and positions of ACR seem to converge we can consider that our model is realistic.
We realized different tests in order to compare the structure of the phase space for different degrees. It seems that the degree of development of the Keplerian part is not significantly affecting the structure of the phase space as long as we keep the first four degrees terms. The main effect of the subsequent terms is to slightly shift the structures. However, the degree of development of the perturbative part is more important.
Figures 5, and 6 show the ACR positions of the 2:1 MMR as functions of G in the same case than before but with a resonant Hamiltonian developed up to degree 4-2, 4-3, and 4-4. Figure 5 show the ACR positions in the directions of cosσi, and Fig. 6 show them in the directions of sinσi. We only plot the degree 4-2 in Fig. 6 because at degrees 4-3, and 4-4, all ACR solutions have sinσi = 0.
 |
Fig. 5 2:1 ACR positions in the directions of cosσi as functions of G. The conditions are the same as for Fig. 3 but the Hamiltonian is developed up to degree 4-2 (left), 4-3 (center), 4-4 (right). At degrees 4-3 and 4-4, all ACR have sinσ1 = sinσ2 = 0. For the degree 4-2, the positions of ACR in the directions of sinσi are plotted in Fig. 6. |
We see that around G = G0 the structure of the phase space remains the same as for degree 4-1. However, the presence of degree two terms induces a significant change in the position of the libration center in the direction e2cosσ2. This shift is also observed at degrees 4-3 and 4-4. For G < G0(1−2 × 10-3) a more complex structure appears at degree 4-2 with two new fixed points that diverge from the libration center in the direction of sinσi. Note that this structure disappears at degrees 4-3 and 4-4. We thus interpret this structure as an artifact due to a too low degree of development. Between degree 4-3 and degree 4-4 there are no significant changes in the structure of the phase space but the degree 4-4 brings small corrections to the positions of ACR solutions. We thus conclude that for the small eccentricities considered here, the structure would no change qualitatively if we consider higher degrees of development.
 |
Fig. 6 2:1 ACR positions in the directions of sinσi as functions of G. The conditions are the same as for Fig. 3 but the Hamiltonian is developed up to degree 4-2. |
Moreover, the structure of the phase space at higher eccentricities is not important for the following discussion since we are interested in the very end of a tidal circularization process of a resonant system when planets have low eccentricities.
The same analysis can be done for any first order MMR. For instance, Figs. 7, and 8 show the ACR positions of the 3:2 MMR in the same conditions (masses, etc.) as previously and with a Hamiltonian developed up to degree 4-1 (Fig. 7), 4-2, 4-3, and 4-4 (Fig. 8). The structure of the phase space is very similar at low eccentricities. As for the 2:1 resonance, at degree 4-2, some complex structures appear for low values of the parameter G. However these structures are completely different between degrees 4-2, 4-3, and 4-4 so they should also be consider as artifacts. For G > G0(1−1.5 × 10-3) the structure of the phase space is the same between degrees 4-3 and 4-4, and is very similar to the structure observed for the 2:1 MMR. This should not change much if we consider higher degrees of development and this structure seems to be common to all first order MMR.
 |
Fig. 7 3:2 ACR positions as functions of G. The star mass is given by m0 = m⊙ and planets masses by m1 = m2 = m ⊕ . The Hamiltonian is developed up to degree 4-1. Elliptic (stable) ACR are plotted using continuous lines whereas hyperbolic (unstable) ACR are plotted using dashed lines. At this degree of development, all ACR have sinσ1 = sinσ2 = 0. |
3. Dynamics of two resonant planets with dissipation
 |
Fig. 8 3:2 ACR positions as functions of G in the same conditions as for Fig. 7 but the Hamiltonian is developed up to degree 4-2 (left), 4-3 (center), 4-4 (right). |
In this section we consider the case of two planets in resonance in the presence of a dissipative force (tidal effect with the star, planet-disk interactions, etc.). In this case, Ĝ and Γ are no longer constants of the motion. However, if the dissipative force is sufficiently weak, their evolution is slow and we can apply the adiabatic invariant theory (see Henrard 1982; Henrard & Lemaitre 1983). This means that the short term evolution of the system is still close to the one observed in the conservative case. On the long term, the dissipation affects the constants Ĝ and Γ and thus the parameter G. When G evolves, the phase space of the system evolves as presented in the previous section.
Depending on the type of dissipation, G can either increase or decrease.
Its evolution depends on how the dissipation affects the eccentricities and the semi-major
axes of both planets. More precisely, the derivative of G is given by:
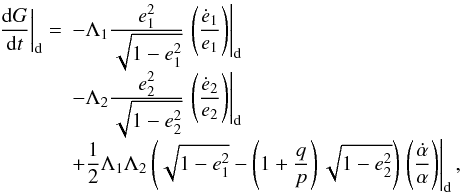 (39)where
(39)where
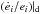 ,
,
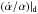 are given by the
dissipation model and Λi are the renormalized (by Γ) actions.
are given by the
dissipation model and Λi are the renormalized (by Γ) actions.
3.1. Migration
In the case of a strong migration of the planets and with low eccentricities, the
dominant term in Eq. (39) is the third one
which depend on the semi-major axes ratio evolution. For low eccentricities we have:
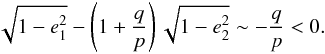 (40)Thus, if the planets
undergo convergent migration
(40)Thus, if the planets
undergo convergent migration 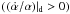 ,
G should decrease and if the migration is divergent, G
should increase. As it is already known (see Henrard
& Lemaitre 1983), a resonant capture can occur only if the migration is
convergent and the resonance is crossed with a decreasing parameter G.
,
G should decrease and if the migration is divergent, G
should increase. As it is already known (see Henrard
& Lemaitre 1983), a resonant capture can occur only if the migration is
convergent and the resonance is crossed with a decreasing parameter G.
3.2. Tidal circularization
3.2.1. Evolution of the parameter G
In the case of circularization of the orbits due to tides raised on the planets by the
star, the angular momentum of each planet is almost conserved and the dissipation in
eccentricities reads to lower order in eccentricities (see Papaloizou 2011): 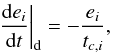 (41)where
tc,i is a damping constant (see
Eq. (82)). Since the angular momentum
of each planet remains unaffected by the dissipation, the semi-major axes compensate the
eccentricities decreases. The evolution of semi-major axes then reads to lowest order in
eccentricities:
(41)where
tc,i is a damping constant (see
Eq. (82)). Since the angular momentum
of each planet remains unaffected by the dissipation, the semi-major axes compensate the
eccentricities decreases. The evolution of semi-major axes then reads to lowest order in
eccentricities: 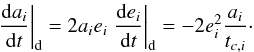 (42)In this case,
the easiest way to compute how the dissipation affects the constant G
is not to use Eq. (39) but to go back to
the definition of G. Since
G = Ĝ/Γ and Ĝ is
conserved, we have:
(42)In this case,
the easiest way to compute how the dissipation affects the constant G
is not to use Eq. (39) but to go back to
the definition of G. Since
G = Ĝ/Γ and Ĝ is
conserved, we have: 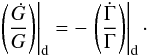 (43)From Eq. (42) we deduce the impact of the
circularization process on
(43)From Eq. (42) we deduce the impact of the
circularization process on 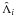 (to lowest order in eccentricities):
(to lowest order in eccentricities):
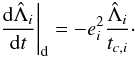 (44)Therefore, the
evolution of Γ is given by:
(44)Therefore, the
evolution of Γ is given by: 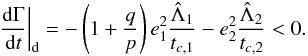 (45)And the
evolution of G is governed by:
(45)And the
evolution of G is governed by: 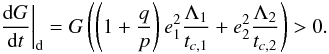 (46)It results that,
in the case of tidal circularization of the orbits, G slowly increases
with time (dominant term of order 2 in eccentricities). Looking at Figs. 3 to 8, the
position of the system on these graphs will slowly migrate from the left to the right,
and eventually, the system will pass through the bifurcation (around
G = G0). The only remaining ACR solution
is the one that corresponds to the libration center but the separatrix of the resonance
and the resonant area disappear. The motion around the only remaining fixed point is
elliptic and this fixed point is quickly decreasing to zero eccentricities. Thus, the
motion should be very well approximated by the secular problem (using a complete
averaging instead of the partial one introduced to obtain the resonant normal form).
Looking at Fig. 4, we see that the remaining ACR
depart from exact commensurability with a lower value of α (and higher
value of
P2/P1) than
the nominal resonance value. This corresponds to planets farther away from each other
than the nominal resonant distance. Therefore, as noticed by Papaloizou & Terquem (2010) the long-term effect of the tidal
circularization is a repulsion of both planets. This is why Batygin & Morbidelli (2012) and Lithwick & Wu (2012) invoke this process to explain the
excess of Kepler systems whose planets are just slightly further away
from each other than nominal resonances.
(46)It results that,
in the case of tidal circularization of the orbits, G slowly increases
with time (dominant term of order 2 in eccentricities). Looking at Figs. 3 to 8, the
position of the system on these graphs will slowly migrate from the left to the right,
and eventually, the system will pass through the bifurcation (around
G = G0). The only remaining ACR solution
is the one that corresponds to the libration center but the separatrix of the resonance
and the resonant area disappear. The motion around the only remaining fixed point is
elliptic and this fixed point is quickly decreasing to zero eccentricities. Thus, the
motion should be very well approximated by the secular problem (using a complete
averaging instead of the partial one introduced to obtain the resonant normal form).
Looking at Fig. 4, we see that the remaining ACR
depart from exact commensurability with a lower value of α (and higher
value of
P2/P1) than
the nominal resonance value. This corresponds to planets farther away from each other
than the nominal resonant distance. Therefore, as noticed by Papaloizou & Terquem (2010) the long-term effect of the tidal
circularization is a repulsion of both planets. This is why Batygin & Morbidelli (2012) and Lithwick & Wu (2012) invoke this process to explain the
excess of Kepler systems whose planets are just slightly further away
from each other than nominal resonances.
3.2.2. Motion around the libration center
The dissipation strongly affects the eccentricities (dominant terms of order one in
Eq. (41)) whereas the constants Γ
(or G) are only slightly affected (dominant terms of order two in
Eqs. (45), (46)). Thus, we can consider that the damping
of eccentricities happens on a shorter time scale than the evolution of Γ
and G. These quantities can thus still be considered as constants (in
first approximation) when we take into account the damping of eccentricities in the
equations of motion (adiabatic invariant theory). From Eq. (41), we deduce: 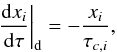 (47)with
(47)with
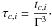
Now, suppose that the system lie in the vicinity of the libration center of a first
order MMR whose position is noted 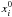 (i = 1,2). Let us define the vector
x as:
(i = 1,2). Let us define the vector
x as:
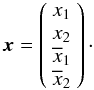 (48)We can linearize the
equations of motion (of the conservative case) around the fixed elliptic point
x0:
(48)We can linearize the
equations of motion (of the conservative case) around the fixed elliptic point
x0:
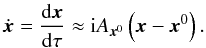 (49)Equations of
motion of the dissipative problem are thus simply given (to first order in
eccentricities) by:
(49)Equations of
motion of the dissipative problem are thus simply given (to first order in
eccentricities) by: 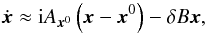 (50)with
(Eq. (47)):
(50)with
(Eq. (47)):
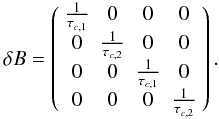 (51)Thus:
(51)Thus: 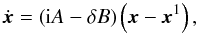 (52)with
(52)with
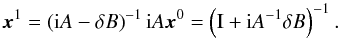 (53)Since
δB is a pertubation of iA, we can make the
approximation (to first order):
(53)Since
δB is a pertubation of iA, we can make the
approximation (to first order): 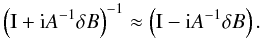 (54)Hence:
(54)Hence: 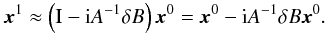 (55)The dynamics around the
libration center is thus modified by the dissipation in two different ways. First, the
position of the fixed point is slightly changed by the offset
A-1δBx0
in the imaginary directions (see Eq. (55)). Secondly, the matrix giving the motion around the fixed point is modified
(see Eq. (52)).
(55)The dynamics around the
libration center is thus modified by the dissipation in two different ways. First, the
position of the fixed point is slightly changed by the offset
A-1δBx0
in the imaginary directions (see Eq. (55)). Secondly, the matrix giving the motion around the fixed point is modified
(see Eq. (52)).
Noting
y = x−x1,
we can apply directly the method described in Laskar
et al. (2012) to y. This method highlights the
effects of the pertubation on the eigenvectors (i.e. the diagonalizing linear
transformation) and on the eigenvalues of the system. If we note
S0 the diagonalizing matrix and
D0 = diag(g1,g2, −g1, −g2)
the diagonalized matrix of the conservative case such as:  where
u is the vector of eigenmodes and
g1, g2 are the eigenvalues.
The diagonalizing matrix and the diagonalized matrix in the dissipative case are given
by:
where
u is the vector of eigenmodes and
g1, g2 are the eigenvalues.
The diagonalizing matrix and the diagonalized matrix in the dissipative case are given
by:  The
small change δS1 of the eigenvectors (see
Laskar et al. 2012) does not introduce a major
change in the dynamics but can be seen as a corrective term as well as the correction on
the position of the fixed point. However, the pertubation
δD1 of the eigenvalues is much more
important. Noting
δD1 = diag(γ1,γ2,γ1,γ2),
we have:
The
small change δS1 of the eigenvectors (see
Laskar et al. 2012) does not introduce a major
change in the dynamics but can be seen as a corrective term as well as the correction on
the position of the fixed point. However, the pertubation
δD1 of the eigenvalues is much more
important. Noting
δD1 = diag(γ1,γ2,γ1,γ2),
we have: 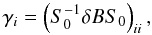 (61)and these
coefficients are real and positive. Finally the diagonalized equations of motion now
read:
(61)and these
coefficients are real and positive. Finally the diagonalized equations of motion now
read: 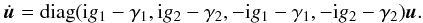 (62)Thus, the
dissipation introduces negative real parts
(–γi) in the eigenvalues of the system.
Therefore, all the eigenmodes will be damped on time scales given by these coefficients
and the fixed point is no more elliptic but attractive. The main short-term effect of
the dissipation is to induce an attraction of the system toward the libration center.
(62)Thus, the
dissipation introduces negative real parts
(–γi) in the eigenvalues of the system.
Therefore, all the eigenmodes will be damped on time scales given by these coefficients
and the fixed point is no more elliptic but attractive. The main short-term effect of
the dissipation is to induce an attraction of the system toward the libration center.
To sum up, the tidal circularization process induce two main effects for planets that are initially resonant. On the short-term, planets tend to reach the stable ACR solution corresponding to the libration center and whose position is slightly modified by the dissipative terms. On the long-term, planets tend to leave the resonance by moving away from each other (the parameter G increases and the planets follow the stable ACR outside of the resonance).
Note that, even outside of the resonance, the attractive ACR solution continues to exist and is not exactly at zero eccentricities. We will focus in the next section on the behavior of the resonant angles outside the resonances.
4. Secular motion at very low eccentricities
In this section we consider a conservative system of two planets around a star (on the same
plane) that are far from any resonance and which have very low eccentricities. More
precisely, we suppose that eccentricities have already been damped by the dissipation and we
study the dynamics of the system after the dissipation process. We are in the field of
application of the secular normal form. We start our study with the Poincaré rectangular
astrocentric coordinates: 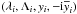 for each planet
(i = 1,2) (e.g. Laskar
& Robutel 1995). Note that, for the simplicity of notations, we omit the
hats even if these variables are not renormalized anymore by Γ.
y1, y2 are the usual Poincaré
rectangular coordinates that are noted x, x′ in
Laskar & Robutel (1995):
for each planet
(i = 1,2) (e.g. Laskar
& Robutel 1995). Note that, for the simplicity of notations, we omit the
hats even if these variables are not renormalized anymore by Γ.
y1, y2 are the usual Poincaré
rectangular coordinates that are noted x, x′ in
Laskar & Robutel (1995): 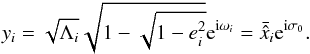 (63)The Hamiltonian can
be developed in power series of yi,
(63)The Hamiltonian can
be developed in power series of yi,
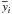 and in Fourier
series of the mean longitudes λi:
and in Fourier
series of the mean longitudes λi:
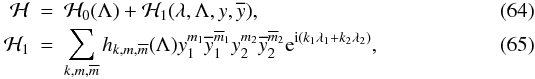 where
the D’Alembert rule reads:
where
the D’Alembert rule reads: 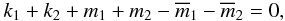 (66)and the coefficients
(66)and the coefficients
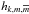 are functions of Λ1, Λ2 which can be expressed in terms of Laplace
coefficients (see Laskar & Robutel 1995).
are functions of Λ1, Λ2 which can be expressed in terms of Laplace
coefficients (see Laskar & Robutel 1995).
To first order of the planets masses, the secular normal form is obtained by averaging the
perturbative part of the Hamiltonian over the mean longitudes. This is performed by
introducing a change of coordinates close to the identity. Let us note
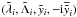 the new coordinates,
the new coordinates,
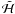 the
new Hamiltonian, and W1 the generating Hamiltonian of the
transformation. By definition, if we note
the
new Hamiltonian, and W1 the generating Hamiltonian of the
transformation. By definition, if we note 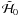 and
and 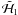 the Keplerian part and the first order part (in planets masses) of the new Hamiltonian, the
transformation reads (to first order in planets masses):
the Keplerian part and the first order part (in planets masses) of the new Hamiltonian, the
transformation reads (to first order in planets masses):
 where
the Poisson brackets are noted with braces. The secular normal form (at the first order) is
obtained by imposing:
where
the Poisson brackets are noted with braces. The secular normal form (at the first order) is
obtained by imposing: 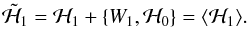 (69)Equation (69) is commonly called the homological equation
and its solution is given by:
(69)Equation (69) is commonly called the homological equation
and its solution is given by: 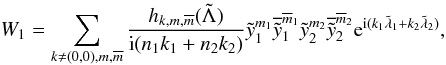 (70)where
n1, n2 are the unperturbed
Keplerian mean-motions of the planets.
(70)where
n1, n2 are the unperturbed
Keplerian mean-motions of the planets.
By construction the secular Hamiltonian reads to first order of the masses:
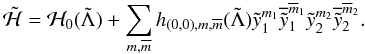 (71)
(71)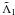 and
and
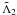 are constants of the motion (first integrals) and
are constants of the motion (first integrals) and 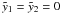 is a stable fixed point around
which the equations of motion can be linearized (Lagrange-Laplace theory). The change of
variables is constructed to be close to the identity, but the reversion to the initial set
of coordinates reintroduces short period terms. This reversion reads up to the first order
in planets masses:
is a stable fixed point around
which the equations of motion can be linearized (Lagrange-Laplace theory). The change of
variables is constructed to be close to the identity, but the reversion to the initial set
of coordinates reintroduces short period terms. This reversion reads up to the first order
in planets masses: 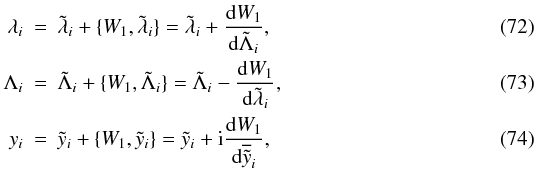 In
general, this reversion to the original set of variables only introduces small corrections
to the dominant secular terms. But if secular eigenmodes are totally damped (i.e.
In
general, this reversion to the original set of variables only introduces small corrections
to the dominant secular terms. But if secular eigenmodes are totally damped (i.e.
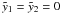 ), the only terms that are nonzero
in the expressions of y1, y2 are
those corresponding to first order mean-motion commensurabilities:
), the only terms that are nonzero
in the expressions of y1, y2 are
those corresponding to first order mean-motion commensurabilities:
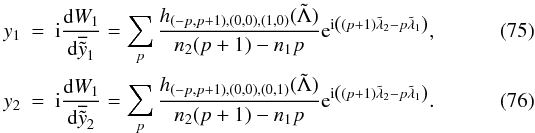 Now,
if we consider a system which is near a first order mean-motion commensurability
(p + 1):p but still outside it, the divisor
(p + 1)n2 − pn1
is smaller than the others (but not considerably small) and the corresponding term dominates
the evolution of y1 and y2. Thus
y1 and y2 are of the form:
Now,
if we consider a system which is near a first order mean-motion commensurability
(p + 1):p but still outside it, the divisor
(p + 1)n2 − pn1
is smaller than the others (but not considerably small) and the corresponding term dominates
the evolution of y1 and y2. Thus
y1 and y2 are of the form:
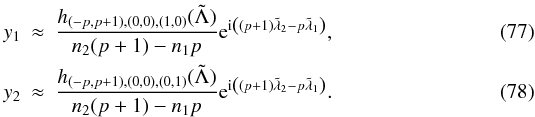 In
terms of arguments of periastron (see Eq. (63)), this means that:
In
terms of arguments of periastron (see Eq. (63)), this means that: 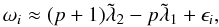 (79)where
ϵi = 0 or π, depending on
the sign of the amplitudes in Eqs. (77),
(78). Of course, in this situation the
resonant angles
σ1 = (p + 1)λ2 − pλ1 − ω1
and
σ2 = (p + 1)λ2 − pλ1 − ω2
will librate (around 0 or π). Figure 9
illustrates this phenomenon of artificial libration. It is important to notice that contrary
to the resonant case,
(p + 1)λ2 − pλ1
and ωi are dominated by short periods (high
frequencies). In the resonant case, we always have
(p + 1)n2 − pn1 ≈ 0,
thus
(p + 1)λ2 − pλ1
has a long period and ωi are dominated by
secular eigenmodes, which also have long periods. This is the reason why the classical
secular averaging is valid in this case.
(79)where
ϵi = 0 or π, depending on
the sign of the amplitudes in Eqs. (77),
(78). Of course, in this situation the
resonant angles
σ1 = (p + 1)λ2 − pλ1 − ω1
and
σ2 = (p + 1)λ2 − pλ1 − ω2
will librate (around 0 or π). Figure 9
illustrates this phenomenon of artificial libration. It is important to notice that contrary
to the resonant case,
(p + 1)λ2 − pλ1
and ωi are dominated by short periods (high
frequencies). In the resonant case, we always have
(p + 1)n2 − pn1 ≈ 0,
thus
(p + 1)λ2 − pλ1
has a long period and ωi are dominated by
secular eigenmodes, which also have long periods. This is the reason why the classical
secular averaging is valid in this case.
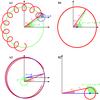 |
Fig. 9 Illustration of the artificial libration of the resonant angles. We plot the evolution of the complex variables e1eiω1 (A1, A2) and e1eiσ1 (B1, B2) in the case of a strong secular eigenmode (A1, B1) and in the case of a severely damped one (A2, B2). For the sake of simplicity, we suppose that there is only one secular eigenmode (of frequency g), but the reasoning would be the same with more. We also suppose that there is only one high frequency term, corresponding to the nearest first order resonance, and whose frequency is ν = (p + 1)n2 − pn1. The secular contribution is plotted in green in all graphs whereas the high frequency term contribution is plotted in blue. The red curves correspond to the sums of both contributions. When there is a strong secular eigenmode, the high frequency term only brings small perturbations around the secular evolution of the argument of periastron ω1 (A1) and the resonant angle σ1 (B1) which circulates. When the eigenmode is damped, the evolution of ω1 (A2) and σ1 (B2) are dominated by the high frequency ν. The amplitude corresponding to ν does not change between A1, B1 and A2, B2 (the scale changes) but in B2 σ1 appears to librate because the circulation center (marked with a blue dot in B1, B2) is not at zero. |
Thus, in the case of very low eccentricities, when eigenmodes are almost completely damped by dissipation (Fig. 9, A2, B2), the fact that the resonant angles are librating (Fig. 9, B2) does not mean that the system is resonant. It is just a geometrical effect due to the fact that the circulation center is not at zero. More precisely, the amplitude of the considered argument (Eqs. (77), (78)) is larger than the amplitude of the proper mode.
5. Numerical simulation
In order to confirm the different behaviors of resonant systems with dissipation that we highlighted in Sect. 3, we ran two numerical simulations, one in the case of the 3:2 MMR and the other for the 2:1 MMR.
5.1. Simulation S1, 3:2 MMR
The first numerical simulation concerns the two innermost planets of the GJ581 system which are near the 3:2 MMR (e.g. Papaloizou 2011). Our simulation is comparable to the
one presented in Papaloizou (2011). The star mass
is m0 = 0.31 m⊙, and planets
masses are set to m1 = 1.94 m ⊕
and m2 = 15.64m ⊕ . The initial
semi-major axes are set to a1 = 0.11 AU and
a2 = 0.15 AU. Initial eccentricities are set to
e1 = 0.01, and e2 = 0.001. At
the beginning of the simulation both planets undergo a migration process due to
interactions with a disk. We adopted the same migration time scale as Papaloizou (2011):
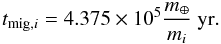 (80)Because the outer
planet is more massive, its migration is more efficient and the system undergo a
convergent migration. During this migration phase the time scale of the circularization is
set to be 100 times shorter than the migration time scale (see Lee & Peale 2002):
(80)Because the outer
planet is more massive, its migration is more efficient and the system undergo a
convergent migration. During this migration phase the time scale of the circularization is
set to be 100 times shorter than the migration time scale (see Lee & Peale 2002):
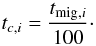 (81)At
t = 10 kyr, the migration stops (the disk is gone) and the only
dissipative force that remains is the tidal interaction with the star. The timescale of
this circularization process is given by (still following Papaloizou 2011):
(81)At
t = 10 kyr, the migration stops (the disk is gone) and the only
dissipative force that remains is the tidal interaction with the star. The timescale of
this circularization process is given by (still following Papaloizou 2011): 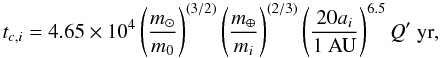 (82)where
Q′ is a parameter of the tidal dissipation model.
Q′ is set to 1.5 in this simulation in order to reduce the
computation time required to see the effect of the circularization (see Papaloizou 2011). A realistic value would be several
order of magnitude greater. This means that the time scale of the evolution of the system
during the circularization process in our simulation is much shorter than the realistic
one. We perform a direct n-body integration of the system using the ODEX integrator (see
Hairer et al. 2010), with the dissipative force
acting on each planet given by:
(82)where
Q′ is a parameter of the tidal dissipation model.
Q′ is set to 1.5 in this simulation in order to reduce the
computation time required to see the effect of the circularization (see Papaloizou 2011). A realistic value would be several
order of magnitude greater. This means that the time scale of the evolution of the system
during the circularization process in our simulation is much shorter than the realistic
one. We perform a direct n-body integration of the system using the ODEX integrator (see
Hairer et al. 2010), with the dissipative force
acting on each planet given by: 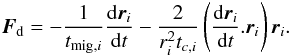 (83)Figure 10 shows the evolution of semi-major axes, and
eccentricities of both planets as well as the evolution of the
parameter G at the beginning of the simulation (up to 20 kyr). During
the first 10 kyr of the simulation, the planets undergo convergent migration
and G decreases (Fig. 10, bottom
in gray). The system enters very quickly in the 3:2 resonance and we can see in Fig. 10, middle, that the semi-major axes stay locked in the
resonant ratio. As explained by Lee & Peale
(2002), the eccentricities are excited by the resonance until they reach an
equilibrium state that depends on the strength of the circularization process which comes
with the migration (Fig. 10, top).
(83)Figure 10 shows the evolution of semi-major axes, and
eccentricities of both planets as well as the evolution of the
parameter G at the beginning of the simulation (up to 20 kyr). During
the first 10 kyr of the simulation, the planets undergo convergent migration
and G decreases (Fig. 10, bottom
in gray). The system enters very quickly in the 3:2 resonance and we can see in Fig. 10, middle, that the semi-major axes stay locked in the
resonant ratio. As explained by Lee & Peale
(2002), the eccentricities are excited by the resonance until they reach an
equilibrium state that depends on the strength of the circularization process which comes
with the migration (Fig. 10, top).
At t = 10 kyr, the migration stops and the only remaining dissipative force is the tidal circularization of the orbits. The long term evolution of G is shown in Fig. 11. As expected, we see in Fig. 11 that the effect of the tidal circularization is an increase of G that eventually exceed G0. The increase is slower and slower, and at the end of the simulation G is almost constant.
 |
Fig. 10 Evolution of eccentricities (top), semi-major axes (middle), and the parameter G (bottom) during the first 20 kyr of simulation S1. The red curves correspond to planet 1. The green curves correspond to planet 2. The gray part of the G curve (bottom) corresponds to the migration phase whereas the black part corresponds to the tidal circularization phase. |
We can follow the evolution of the system on graphs similar to those of Sect. 2. Figure 12 gives the positions of 3:2 ACR solutions for the system considered in the simulation (masses), superimposed over the successive positions of the system on these graphs. The colors of the fixed points are the same as in Sect. 2. In particular, the center of libration of the resonant area is plotted in red. The gray dots corresponds to positions of the system during the first 10 kyr (migration phase), whereas the black dots corresponds to the circularization phase. Since G decreases during the migration phase (in gray) the system goes from the right to the left of the graphs. On the contrary, during the tidal circularization phase (in black) G increases and the system goes from the left to the right of the graphs.
 |
Fig. 11 Long term evolution of the parameter G during simulation S1. |
 |
Fig. 12 Superposition of the successive positions of the system in simulation S1 over the 3:2 ACR positions as functions of G. ACR positions are computed using our model with the parameters of the considered system (masses). The colors of ACR are consistent with graphs of Sect. 2 but we inverted continuous and dashed lines in order to improve the visibility of the simulation dots. The gray dots correspond to the migration phase and go from the right to the left of the graph whereas the black ones correspond to the tidal circularization phase and go from the left to the right. |
At the very beginning of the simulation, the system is not yet in the resonance. In Fig. 12, the system lies at the right of the bifurcation and there is only one fixed point. The phase space is similar to the one of Figs. 2, E2, F2. Then, due to the convergent migration (gray dots) the system passes through the bifurcation and the phase space looks like the one of Figs. 2, A2 to D2. The system undergo oscillations around the libration center (red dot). Finally, due to the circularization process (black dots), the system passes a second time through the bifurcation. Thus, the system leaves the resonance and the phase space is again similar to Figs. 2, E2, F2.
We see in Fig. 12 that the system follows very well the ACR solution corresponding to the libration center both during the migration and the circularization phases. We also see that the tidal dissipation induces a decrease of the amplitude of oscillations around this fixed point. This corresponds to the expected damping of eigenmodes around the libration center (Sect. 3).
Figure 13 shows the evolution of the semi-major axes ratio (and period ratios) as a function of G for the simulation and for the fixed points of our model. We see that during the migration process (in gray), the semi-major axes ratio (α) increases until it reaches the resonant ratio. During this migration phase, α does not oscillate much, but when the system enter the resonance, α begins to oscillate around the libration center position. During the circularization process (in black), the system follows the libration center position, the oscillations are damped and the semi-major axes ratio decreases (the period ratios increases). Thus the system quits the resonance with a period ratios larger than the resonant one, as expected.
Note that when G increases, the eccentricities quickly tend to zero (Fig. 12) and the circularization process is less and less effective. This is why G increases slower and slower (Fig. 11). This means that the system cannot depart very far away from the MMR on a finite time (see Appendix B for an estimation of the asymptotic evolution of G). This is even more true for a real system, since in this simulation the circularization process is several order of magnitude more efficient than in reality. This mechanism explains why Kepler systems lie just slightly farther away from the MMR.
Figure 14 shows the evolution of the resonant angle σ1 (in red) and the difference of periastrons Δω = σ2 − σ1 (in green). We see that both resonant angles and Δω librate during the whole simulation even if the system is outside the resonance at the end of the simulation (see Figs. 12 and 13). σ1 librates around 0, while σ2 and Δω librate around π. This could have also been deduced from Fig. 12.
5.2. Simulation S2, 2:1 MMR
 |
Fig. 13 Superposition of the successive positions of the system in simulation S1 over the 3:2 ACR positions in the plane (G,α). ACR positions are computed using our model with the parameters of the considered system (masses). The colors of ACR are consistent with graphs of Sect. 2 but we inverted continuous and dashed lines in order to improve the visibility of the simulation dots. The gray dots correspond to the migration phase and go from the right to the left of the graph whereas the black ones correspond to the tidal circularization phase and go from the left to the right. |
 |
Fig. 14 Evolution of the resonant angle σ1 (red) and the difference of periastrons Δω = σ2 − σ1 (green) in simulation S1. |
We also ran a simulation of the same system but in the case of the 2:1 MMR. The masses of the star and the planets are the same but initial semi-major axes are set to a1 = 0.11 AU, and a2 = 0.18 AU. Initial eccentricities are set to e1 = 0.002, and e2 = 0. All other parameters are the same as for the first simulation.
 |
Fig. 15 Evolution of the eccentricities (top) the semi-major axes (middle) and the parameter G (bottom) during the first 20 kyr of simulation S2. The red curves correspond to planet 1. The green curves correspond to planet 2. The gray part of the G curve (bottom) corresponds to the migration phase whereas the black part corresponds to the tidal circularization phase. |
 |
Fig. 16 Long term evolution of the parameter G during simulation S2. |
 |
Fig. 17 Superposition of the successive positions of the system in simulation S2 over the 2:1 ACR positions as functions of G. ACR positions are computed using our model with the parameters of the considered system (masses). The colors of ACR are consistent with graphs of Sect. 2 but we inverted continuous and dashed lines in order to improve the visibility of the simulation dots. The gray dots correspond to the migration phase and go from the right to the left of the graph whereas the black ones correspond to the tidal circularization phase and go from the left to the right. |
 |
Fig. 18 Superposition of the successive positions of the system in simulation S2 over the 2:1 ACR positions in the plane (G,α). ACR positions are computed using our model with the parameters of the considered system (masses). The colors of ACR are consistent with graphs of Sect. 2 but we inverted continuous and dashed lines in order to improve the visibility of the simulation dots. The gray dots correspond to the migration phase and go from the right to the left of the graph whereas the black ones correspond to the tidal circularization phase and go from the left to the right. |
 |
Fig. 19 Evolution of the resonant angle σ1 (red) and the difference of periastrons Δω = σ2 − σ1 (green) during the first 10 Myr of simulation S2. |
Figure 15 shows the evolution of eccentricities, semi-major axes and G during the first 20 kyr of the simulation. Their behaviors are very similar to those of the simulation S1 (Fig. 10). Note that as for the resonance 3:2, G decreases during the migration phase (in gray). We plot in Fig. 16 the long term evolution of G which increases due to the circularization process. Figures 17 and 18 show the superposition of the fixed points of our model with the successive positions of the system. Figure 17 gives the eccentricities as functions of G and Fig. 18 gives the semi-major axes ratio (as well as the period ratios) as a function of G. As for the 3:2 resonance, in the case of the 2:1 resonance, the system begins outside the resonance (on the right of the graphs) and the phase space corresponds to the situation of Figs. 2, E1, F1. Due to the convergent migration of planets the system goes from the right to the left (gray dots) and passes through the bifurcation following the red ACR solution. At this point the phase space is similar to those of Figs. 2, A1 to D1. During the circularization phase, the system goes from the left to the right in Figs. 17, 18 (black dots). The system passes again at the bifurcation and leaves the resonance (phase space of Figs. 2, E1, F1). Shortly after the system quited the resonance, the amplitude of oscillations around the fixed point suddendly increases in the direction of e2. This is due to the crossing of a 2:1 resonance between the two proper modes of the motion around the fixed point (see Appendix C for more details). However the dissipation damps again the oscillations after this event and the system keeps following the ACR solution.
We observe in Fig. 19 that the first resonant angle σ1 keeps librating around 0 during the whole simulation whereas Δω and σ2 circulate almost all the time. More precisely, during the first 0.5 Myr of the simulation, Δω and σ2 librate around 0. Then, these angles circulate during a short laps of time around t = 0.5 Myr. After this event, they begin to librate around π. Actually, the system is still in resonance and oscillates around the libration center but the position of this fixed point crosses the value e2 = 0 for G/G0 − 1 = 5 × 10-4 (see Fig. 17) around t = 0.5 Myr. The dynamics does not change and this event is only geometrical. Thus, even if the system is clearly in the resonance area, very close the the libration center, we observe a circulation of σ2. Around t = 1.4 Myr, Δω and σ2 begin to circulate (Fig. 19). This corresponds to the crossing of the resonance (see Appendix C) that we observe in Fig. 17. This event increases the amplitude of oscillations around the fixed point and due to this higher amplitude the system passes through e2 = 0 at each oscillation. This is why we observe a circulation of Δω and σ2.
Note that both simulations show that it is possible to observe an oscillation of the resonant angles outside of resonances (σ1 and σ2 for S1, and only σ1 for S2). On the opposite, in simulation S2 we observe a circulation of σ2 when the libration center position crosses the axis e2 = 0 while the system is clearly inside the resonance and oscillates very close to the libration center. Therefore, it appears that resonant angles have to be considered with great caution and cannot always be used to distinguish between truly dynamical effects and simple geometrical effects.
6. Conclusion
In this work, we presented a study of planar resonant planetary systems in the conservative case and in presence of a dissipative force. Our main interest was to understand the dynamics at the end of a circularization process in resonant systems. We used a completely analytical model developed in power series of eccentricities which is well suited for the study of these low eccentricity systems. Before introducing the dissipative force in the model we characterized the dynamics in the conservative case. In particular, we highlighted the fact that apsidal corotation resonances (ACR) are a powerful tool to understand the global dynamics of a system. Then, we showed that the introduction of a dissipative force1 in a resonant system has two main effects. On the short-term, the system is attracted toward the libration center if it initially relies in its vicinity. On the long-term, the system tends to follow this ACR solution outside the resonance and both planets tend to move away from each other. These two mechanisms are well illustrated and confirmed by the results of two simulations (one for the 2:1 MMR and the other for the 3:2 MMR) of the innermost planets of the GJ581 (see Sect. 5). Since the ACR solution do not correspond to zero eccentricities even far from the resonance, it is possible to have resonant angles to oscillate outside of resonances. However, we showed that in this case the motion is completely characterized by the secular problem and that the fact that resonant angles appear to librate only means that the secular eigenmodes are (almost) totally damped. The important fact is that the nature of the motion is the same as when the eigenmodes are not damped and the separatrix of the resonance does not exist anymore in this region of the phase space. Thus, it is inappropriate to consider such systems as resonant ones.
Acknowledgments
We thank Philippe Robutel for helpful discussions. This work has been supported by PNP-CNRS, CS of Paris Observatory, PICS05998 France-Portugal program, the European Research Council/European Community under the FP7 through a Starting Grant, and Fundação para a Ciênca e a Tecnologia, Portugal (grants PTDC/CTE-AST/098528/2008 and PEst-C/CTM/LA0025/2011).
References
- Batygin, K., & Morbidelli, A. 2012, ApJ, accepted [arXiv:1204.2791] [Google Scholar]
- Beaugé, C., Michtchenko, T. A., & Ferraz-Mello, S. 2006, MNRAS, 365, 1160 [Google Scholar]
- Callegari, N., Michtchenko, T. A., & Ferraz-Mello, S. 2004, Celest. Mech. Dyn. Astron., 89, 201 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Callegari, N., Ferraz-Mello, S., & Michtchenko, T. A. 2006, Celest. Mech. Dyn. Astron., 94, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraz-Mello, S., Tsuchida, M., & Klafke, J. C. 1993, Celest. Mech. Dyn. Astron., 55, 25 [Google Scholar]
- Ferraz-Mello, S., Beaugé, C., & Michtchenko, T. A. 2003, Celest. Mech. Dyn. Astron., 87, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Gastineau, M., & Laskar, J. 2011, trip 1.1.12, TRIP reference manual, IMCCE, Paris Observatory, http://www.imcce.fr/trip/ [Google Scholar]
- Hadjidemetriou, J. D. 2002, Celest. Mech. Dyn. Astron., 83, 141 [Google Scholar]
- Hairer, E., Nørsett, S. P., & Wanner, G. 2010, Solving Ordinary Differential Equations I: Nonstiff Problems (Springer) [Google Scholar]
- Henrard, J. 1982, in NATO ASIC Proc. 82: Applications of Modern Dynamics to Celestial Mechanics and Astrodynamics, ed. V. Szebehely, 153 [Google Scholar]
- Henrard, J., & Lemaitre, A. 1983, Celest. Mech., 30, 197 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Laskar, J. 2000, Phys. Rev. Lett., 84, 3240 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Laskar, J., & Robutel, P. 1995, Celest. Mech. Dyn. Astron., 62, 193 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Laskar, J., Boué, G., & Correia, A. C. M. 2012, A&A, 538, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. H. 2004, ApJ, 611, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. H., & Peale, S. J. 2002, ApJ, 567, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Lithwick, Y., & Wu, Y. 2012, ApJ, 756, 11 [Google Scholar]
- Michtchenko, T. A., Beaugé, C., & Ferraz-Mello, S. 2006, Celest. Mech. Dyn. Astron., 94, 411 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Morbidelli, A. 2002, Modern celestial mechanics: aspects of solar system dynamics [Google Scholar]
- Papaloizou, J. C. B. 2011, Celest. Mech. Dyn. Astron., 111, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Terquem, C. 2010, MNRAS, 405, 573 [NASA ADS] [Google Scholar]
- Rouillier, F. 1999, Applicable Algebra in Engineering, Communication and Computing, 9, 433 [Google Scholar]
Appendix A: Computation of the Hamiltonian coefficients
In this section we explain in more details the computations of coefficients K, S, and R of the resonant normal form (Eq. (31)) up to any order.
The Keplerian part is given by:
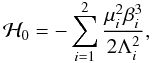 (A.1)with:
(A.1)with:
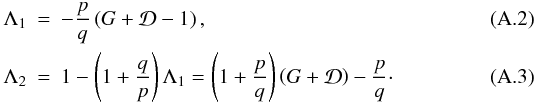 Kcoefficients
are thus simply given by the Taylor series of
1/(1 + x)2 where
Kcoefficients
are thus simply given by the Taylor series of
1/(1 + x)2 where
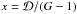 for the inner planet and
for the inner planet and 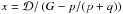 for the outer one.
for the outer one.
For the pertubation, the first step is to determine which inequalities
k1λ1 + k2λ2
have to be computed. The secular part is given by the inequality
k1 = k2 = 0. The resonant terms
are given by inequalities k1 = −kp,
k2 = k(p + q),
with
−d/q ≤ k ≤ d/q
where d is the chosen degree of development. Each inequality is computed
as a power series of x1, x2 by
using the algorithm presented in Laskar & Robutel
(1995). For instance, in the case of the 2:1 resonance, the perturbative part of
the Hamiltonian reads: 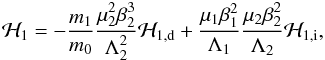 (A.4)where
ℋ1,d is the direct part of the development,
and ℋ1,i is the indirect part. The direct part is
given by:
(A.4)where
ℋ1,d is the direct part of the development,
and ℋ1,i is the indirect part. The direct part is
given by: 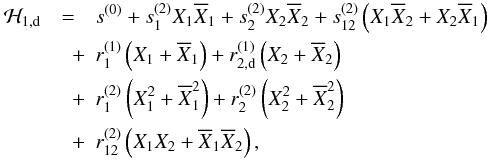 (A.5)and
the indirect part reads:
(A.5)and
the indirect part reads: 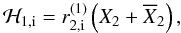 (A.6)where we note
(A.6)where we note
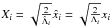 (see Laskar & Robutel 1995). The coefficients
S, R of Eq. (31) correspond to coefficients s, r appearing
in Eqs. (A.5), (A.6) but with a renormalization due to the use
of x1, x2 instead of
X1, X2 and the factors in front
of the direct and indirect parts in Eq. (A.4). s, r coefficients can be expressed as
functions of α and Laplace coefficients
(see Laskar & Robutel 1995). The coefficients
S, R of Eq. (31) correspond to coefficients s, r appearing
in Eqs. (A.5), (A.6) but with a renormalization due to the use
of x1, x2 instead of
X1, X2 and the factors in front
of the direct and indirect parts in Eq. (A.4). s, r coefficients can be expressed as
functions of α and Laplace coefficients
 :
:
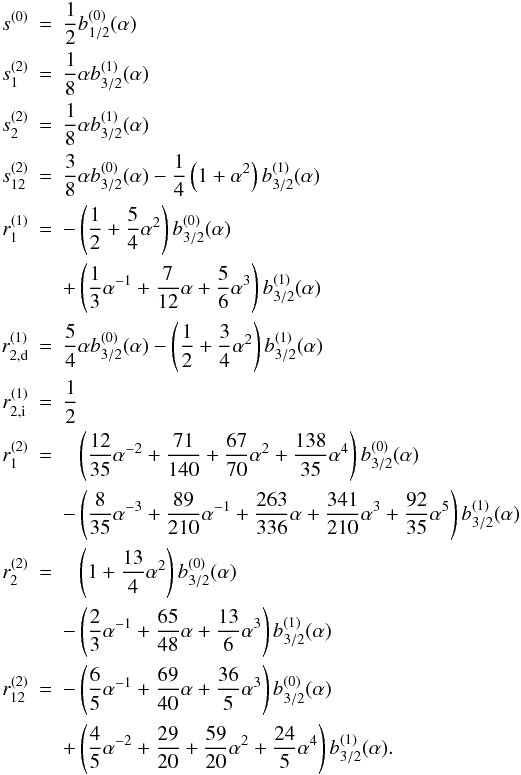 (A.7)As
for the Keplerian part, we substitute Λ1 and Λ2 by their power
series in
(A.7)As
for the Keplerian part, we substitute Λ1 and Λ2 by their power
series in 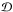 each time they appear in the expression of ℋ1. For the Laplace coefficients we
first need to develop them in power series around the nominal resonant semi-major axes
ratio which is defined by:
each time they appear in the expression of ℋ1. For the Laplace coefficients we
first need to develop them in power series around the nominal resonant semi-major axes
ratio which is defined by: 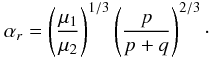 (A.8)Then the deviation
δα = α − αr
to the nominal value is substituted by its power series in
(A.8)Then the deviation
δα = α − αr
to the nominal value is substituted by its power series in
 .
Of course the degrees of development of all these series are adjusted in order to be
consistent with the desired degree in eccentricities (d).
.
Of course the degrees of development of all these series are adjusted in order to be
consistent with the desired degree in eccentricities (d).
Appendix B: Asymptotic evolution of G
In this section we show how to estimate the asymptotic evolution of G. This allows to determine the position of the system in our graphs as a function of time. We have seen that the evolution of G during the tidal circularization phase is slower and slower. Moreover, the escape from the resonance is very quick and the evolution of the system after this escape is very slow. Thus, the initial position of the system in the resonance does not influence much its final position (outside the resonance) after a long time.
The evolution of G during the circularization phase is governed by
Eq. (46). Since G
remains very close to G0, and Λi
stay very close to Λi,r, we can substitute these values in the
expression of Ġ. However, ei
cannot be considered as constants since the ACR solution tends to zero eccentricities
when G increases. Thus we have to compute
ei as functions of
δG = G − G0 with the help
of Eqs. (37), (38). In the asymptotic evolution, eccentricities are very low and the ACR position
can be well approximated with lowest order terms :  Thus
the ACR solution is simply given by:
Thus
the ACR solution is simply given by:  and
ei are given by:
and
ei are given by:
 (B.5)K(2),
(B.5)K(2),
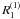 ,
and
,
and  are functions of G but
are functions of G but 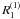 ,
and
,
and  are almost constants and can be approximated with their values for
G = G0 (see Appendix A):
are almost constants and can be approximated with their values for
G = G0 (see Appendix A): 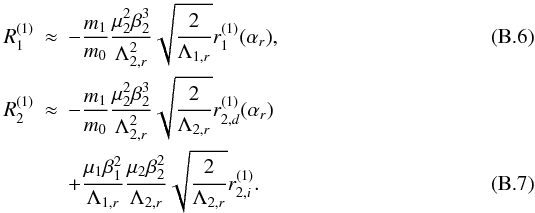 On
the contrary, in first approximation K(2) is proportional to
δG:
On
the contrary, in first approximation K(2) is proportional to
δG: ![\appendix \setcounter{section}{2} \begin{equation} K^{(2)} \approx -3 \left[ \left(\frac{p}{q}\right)^2 \frac{\mu_1^2 \beta_1^3}{\Lambda_{1,r}^4} + \left(1+\frac{p}{q}\right)^2 \frac{\mu_2^2 \beta_2^3}{\Lambda_{2,r}^4} \right] \delta G. \end{equation}](/articles/aa/full_html/2012/10/aa20001-12/aa20001-12-eq272.png) (B.8)Finally, this means
that:
(B.8)Finally, this means
that: 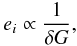 (B.9)and
(B.9)and
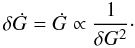 (B.10)The asymptotic evolution
of G is thus given by:
(B.10)The asymptotic evolution
of G is thus given by:
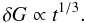 (B.11)The eccentricities
evolve as:
(B.11)The eccentricities
evolve as: 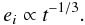 (B.12)The semi-major axes ratio
asymptotic evolution is governed by:
(B.12)The semi-major axes ratio
asymptotic evolution is governed by:
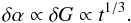 (B.13)We thus find the
same asymptotic law (t1/3) as Papaloizou (2011), and Lithwick & Wu (2012).
(B.13)We thus find the
same asymptotic law (t1/3) as Papaloizou (2011), and Lithwick & Wu (2012).
Appendix C: 2:1 resonance between proper modes around the ACR solution in S2
In this section we present a brief analysis of the event happening in S2
around t = 1.4 Myr (Fig. 17). We
interpret the increase of the amplitude of oscillations in the direction of
e2 as a consequence of the crossing of the 2:1 resonance
between both proper modes around the ACR solution. The linear equations of motion around
the fixed point (see Eq. (58)) correspond
to degree two terms in the diagonalized Hamiltonian:
 (C.1)The resonance appears
in this Hamiltonian at degree three with the term of the form:
(C.1)The resonance appears
in this Hamiltonian at degree three with the term of the form:
 (C.2)where
ρ is a constant depending on the parameters and initial conditions. Let
us note
(C.2)where
ρ is a constant depending on the parameters and initial conditions. Let
us note 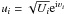 .
We can average over all other angles than the resonant one
(υ1 − 2υ2) with a similar
procedure than the one used in Sect. 2. The system is
then reduced to one degree of freedom and we have a new constant of the (averaged) motion:
.
We can average over all other angles than the resonant one
(υ1 − 2υ2) with a similar
procedure than the one used in Sect. 2. The system is
then reduced to one degree of freedom and we have a new constant of the (averaged) motion:
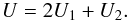 (C.3)The energy levels
curves for the values of the constants G and U taken by
the system of simulation S2 at the moment of the event (around
t = 1.4 Myr) are shown in Fig. C.1 superimposed with the trajectory of the system. We see that before the
event, the proper mode 2 is almost totally damped compared to proper mode 1 (red dots in
Fig. C.1), whereas just after the event, this
proper mode gained some amplitude (green dots in Fig. C.1) and the system follows very well the expected motion.
(C.3)The energy levels
curves for the values of the constants G and U taken by
the system of simulation S2 at the moment of the event (around
t = 1.4 Myr) are shown in Fig. C.1 superimposed with the trajectory of the system. We see that before the
event, the proper mode 2 is almost totally damped compared to proper mode 1 (red dots in
Fig. C.1), whereas just after the event, this
proper mode gained some amplitude (green dots in Fig. C.1) and the system follows very well the expected motion.
 |
Fig. C.1 Superposition of the trajectory of the system S2 during the event (around t = 1.4 Myr) with the energy levels curves of the 2:1 resonance between both proper modes around the ACR solution. The successive positions of the system just before the event are marked with red dots while the positions of the system just after the event are marked with green dots. |
The resonant angle υ1 − 2υ2 does not enter in libration in the simuation S2 but this may be due to the very strong dissipation present in this simulation and which induces an evolution of the constant G quicker than expected for a real system. Thus the frequencies g1, g2 and the phase space evolve very quickly and the system crosses the resonance before it has time to enter in the libration area. The important
fact is that due to the crossing of the resonance, the proper mode 2 increases its amplitude while the proper mode 1 amplitude’s decreases (U = 2U1 + U2 stays constant). However, since the proper mode 1 has initially a much higher amplitude, this decrease is imperceptible. Moreover, since the diagonalizing matrix is dominated by diagonal terms, the evolution of e1 is dominated by the proper mode 1 and the evolution of e2 by the proper mode 2. Thus, e1 is only weakly affected by the event while e2 is strongly affected.
All Figures
 |
Fig. 1 2:1 resonance energy levels in section planes defined by: e2 = 0 (top left), cosσ1 = cosσ2 = 0 (top right), sinσ1 = sinσ2 = 0 (bottom left), and e1 = 0 (bottom right). Stable ACR solutions are highlighted with colored dots (red and green). Unstable ones are highlighted with colored crosses (blue). The star mass is given by m0 = m⊙ and planets masses by m1 = m2 = m ⊕ . The constant G is set to G = G0(1−10-4). The Hamiltonian is developed up to degree 4-1. |
| In the text | |
 |
Fig. 2 Energy levels sections in the plane defined by sinσ1 = sinσ2 = 0 for the 2:1 resonance (A1 to F1), and the 3:2 resonance (A2 to F2). The constant G/G0 − 1 is set to −10-3 (A1, A2), −5 × 10-4 (B1, B2), −10-4 (C1, C2), −3.2 × 10-5 (D1, D2), −3 × 10-5 (E1, E2), and + 10-3 (F1, F2). Stable ACR solutions are highlighted with colored dots (red and green). Unstable ones are highlighted with colored crosses (blue). The star mass is given by m0 = m⊙ and planets masses by m1 = m2 = m ⊕ . The Hamiltonian is developed up to degree 4-1. Note that the scales are different for graphs A1, A2, B1, and B2 than for other graphs. |
| In the text | |
 |
Fig. 3 2:1 ACR positions as functions of G. The star mass is given by m0 = m⊙ and planets masses by m1 = m2 = m ⊕ . The Hamiltonian is developed up to degree 4-1. Elliptic (stable) ACR are plotted using continuous lines whereas hyperbolic (unstable) ACR are plotted using dashed lines. At this degree of development, all ACR have sinσ1 = sinσ2 = 0. |
| In the text | |
 |
Fig. 4 2:1 ACR positions in the plane (G,α) in the same conditions as for Fig. 3. |
| In the text | |
 |
Fig. 5 2:1 ACR positions in the directions of cosσi as functions of G. The conditions are the same as for Fig. 3 but the Hamiltonian is developed up to degree 4-2 (left), 4-3 (center), 4-4 (right). At degrees 4-3 and 4-4, all ACR have sinσ1 = sinσ2 = 0. For the degree 4-2, the positions of ACR in the directions of sinσi are plotted in Fig. 6. |
| In the text | |
 |
Fig. 6 2:1 ACR positions in the directions of sinσi as functions of G. The conditions are the same as for Fig. 3 but the Hamiltonian is developed up to degree 4-2. |
| In the text | |
 |
Fig. 7 3:2 ACR positions as functions of G. The star mass is given by m0 = m⊙ and planets masses by m1 = m2 = m ⊕ . The Hamiltonian is developed up to degree 4-1. Elliptic (stable) ACR are plotted using continuous lines whereas hyperbolic (unstable) ACR are plotted using dashed lines. At this degree of development, all ACR have sinσ1 = sinσ2 = 0. |
| In the text | |
 |
Fig. 8 3:2 ACR positions as functions of G in the same conditions as for Fig. 7 but the Hamiltonian is developed up to degree 4-2 (left), 4-3 (center), 4-4 (right). |
| In the text | |
 |
Fig. 9 Illustration of the artificial libration of the resonant angles. We plot the evolution of the complex variables e1eiω1 (A1, A2) and e1eiσ1 (B1, B2) in the case of a strong secular eigenmode (A1, B1) and in the case of a severely damped one (A2, B2). For the sake of simplicity, we suppose that there is only one secular eigenmode (of frequency g), but the reasoning would be the same with more. We also suppose that there is only one high frequency term, corresponding to the nearest first order resonance, and whose frequency is ν = (p + 1)n2 − pn1. The secular contribution is plotted in green in all graphs whereas the high frequency term contribution is plotted in blue. The red curves correspond to the sums of both contributions. When there is a strong secular eigenmode, the high frequency term only brings small perturbations around the secular evolution of the argument of periastron ω1 (A1) and the resonant angle σ1 (B1) which circulates. When the eigenmode is damped, the evolution of ω1 (A2) and σ1 (B2) are dominated by the high frequency ν. The amplitude corresponding to ν does not change between A1, B1 and A2, B2 (the scale changes) but in B2 σ1 appears to librate because the circulation center (marked with a blue dot in B1, B2) is not at zero. |
| In the text | |
 |
Fig. 10 Evolution of eccentricities (top), semi-major axes (middle), and the parameter G (bottom) during the first 20 kyr of simulation S1. The red curves correspond to planet 1. The green curves correspond to planet 2. The gray part of the G curve (bottom) corresponds to the migration phase whereas the black part corresponds to the tidal circularization phase. |
| In the text | |
 |
Fig. 11 Long term evolution of the parameter G during simulation S1. |
| In the text | |
 |
Fig. 12 Superposition of the successive positions of the system in simulation S1 over the 3:2 ACR positions as functions of G. ACR positions are computed using our model with the parameters of the considered system (masses). The colors of ACR are consistent with graphs of Sect. 2 but we inverted continuous and dashed lines in order to improve the visibility of the simulation dots. The gray dots correspond to the migration phase and go from the right to the left of the graph whereas the black ones correspond to the tidal circularization phase and go from the left to the right. |
| In the text | |
 |
Fig. 13 Superposition of the successive positions of the system in simulation S1 over the 3:2 ACR positions in the plane (G,α). ACR positions are computed using our model with the parameters of the considered system (masses). The colors of ACR are consistent with graphs of Sect. 2 but we inverted continuous and dashed lines in order to improve the visibility of the simulation dots. The gray dots correspond to the migration phase and go from the right to the left of the graph whereas the black ones correspond to the tidal circularization phase and go from the left to the right. |
| In the text | |
 |
Fig. 14 Evolution of the resonant angle σ1 (red) and the difference of periastrons Δω = σ2 − σ1 (green) in simulation S1. |
| In the text | |
 |
Fig. 15 Evolution of the eccentricities (top) the semi-major axes (middle) and the parameter G (bottom) during the first 20 kyr of simulation S2. The red curves correspond to planet 1. The green curves correspond to planet 2. The gray part of the G curve (bottom) corresponds to the migration phase whereas the black part corresponds to the tidal circularization phase. |
| In the text | |
 |
Fig. 16 Long term evolution of the parameter G during simulation S2. |
| In the text | |
 |
Fig. 17 Superposition of the successive positions of the system in simulation S2 over the 2:1 ACR positions as functions of G. ACR positions are computed using our model with the parameters of the considered system (masses). The colors of ACR are consistent with graphs of Sect. 2 but we inverted continuous and dashed lines in order to improve the visibility of the simulation dots. The gray dots correspond to the migration phase and go from the right to the left of the graph whereas the black ones correspond to the tidal circularization phase and go from the left to the right. |
| In the text | |
 |
Fig. 18 Superposition of the successive positions of the system in simulation S2 over the 2:1 ACR positions in the plane (G,α). ACR positions are computed using our model with the parameters of the considered system (masses). The colors of ACR are consistent with graphs of Sect. 2 but we inverted continuous and dashed lines in order to improve the visibility of the simulation dots. The gray dots correspond to the migration phase and go from the right to the left of the graph whereas the black ones correspond to the tidal circularization phase and go from the left to the right. |
| In the text | |
 |
Fig. 19 Evolution of the resonant angle σ1 (red) and the difference of periastrons Δω = σ2 − σ1 (green) during the first 10 Myr of simulation S2. |
| In the text | |
 |
Fig. C.1 Superposition of the trajectory of the system S2 during the event (around t = 1.4 Myr) with the energy levels curves of the 2:1 resonance between both proper modes around the ACR solution. The successive positions of the system just before the event are marked with red dots while the positions of the system just after the event are marked with green dots. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


