| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 17 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201219788 | |
| Published online | 13 September 2012 | |
On the formation of C iii 4647-50-51 and C iii 5696 in O star atmospheres⋆
1
LUPM–UMR 5299, CNRS & Université Montpellier II,
Place Eugène Bataillon,
34095
Montpellier Cedex 05,
France
e-mail: fabrice.martins@univ-montp2.fr
2
Department of Physics and Astronomy, University of
Pittsburgh, 3941 O’Hara
Street, Pittsburgh,
PA
15260,
USA
Received: 11 June 2012
Accepted: 30 July 2012
Context. Surface abundances of OB stars provide important information on mixing processes in stellar interiors and on evolutionary status. Performing abundance determination from selected C, N and O lines in the optical spectra of OB stars is thus necessary to understand the evolution of massive stars.
Aims. In this study, we investigate the formation of C iii 4647–51–50 and C iii 5696 in the atmosphere of O stars to see if they can be reliably used for abundance determinations.
Methods. We used atmosphere models computed with the code CMFGEN. The key physical ingredients explaining the formation of the C iii lines were extracted from comparisons of models with different stellar parameters and through examining rates controlling the level populations.
Results. The strength of C iii 5696 critically depends on UV C iii lines at 386, 574 and 884 Å. These lines control the C iii 5696 upper and lower level population. C iii 884 plays a key role in late O stars where it drains the lower level of C iii 5696. C iii 386 and C iii 574 are more important at early spectral types. The overlap of these UV lines with Fe iv 386.262, Fe iv 574.232 and S v 884.531 influences the radiative transfer at 386, 574 and 884 Å, and consequently affects the strength of C iii 5696. C iii 4650 is mainly controlled by the C iii 538 line, which acts as a drain on its lower level. Fe iv 538.057 interacts with C iii 538 and has an impact on the C iii 4650 profile. Low temperature dielectronic recombinations have a negligible effect on the line profiles. The main effect of the wind on the C iii lines is an increase of the emission as mass loss rate increases, due to a shift of the formation region toward high velocity. Such a shift also implies desaturation of C iii 386, C iii 538, C iii 574 and C iii 884, which in turn modify the C iii 4650 and C iii 5696 line profiles. Metallicity effects are complex and result from an interplay between ionization, metallic line interaction with UV C iii lines, and wind effects.
Conclusions. Given our current understanding of the stellar and wind properties of O stars, and in view of the present results, the determination of accurate carbon abundances from C iii 4647–51–50 and C iii 5696 is an extremely challenging task. Uncertainties lower than a factor of two on C/H determinations based only on these two sets of lines should be regarder as highly doubtful. Our results provide a possible explanation of the variability of C iii 4650 in Of?p stars.
Key words: stars: abundances / stars: massive / stars: atmospheres / stars: fundamental parameters
Appendices are only available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Massive stars turn hydrogen into helium through the CNO cycle in their core. In this process, nitrogen is produced at the expense of carbon and oxygen. Mixing processes subsequently transport the products of nucleosynthesis from the core to the outer layers and surface of the star. The spectrum of a massive star thus contains the imprints of nuclear reactions taking place in the interior of the star. The older a star, the larger its nitrogen content and the lower its carbon abundance (provided the star is of type O and not yet an evolved object such as Wolf-Rayet (W-R), red supergiant or luminous blue variable). The surface chemical composition depends on the star’s rotation rate, metallicity, and mass. A fast rotation, for example, favors the transport of chemical species and thus quicker enrichment of the photosphere by material synthesized in the core (Maeder & Meynet 2000). Low metallicity stars burn hydrogen more efficiently, as does a 60 M⊙ stars compared to a 20 M⊙ star. Chemical surface abundances are thus a key to understand the physical processes controlling the evolution of massive stars. It was surface abundances that provided key clues that W-R stars were evolved (e.g., Smith 1973; Smith & Willis 1982). Recent results (Hunter et al. 2008; Przybilla et al. 2010; Brott et al. 2011; Martins et al. 2012) have shown that strong constraints on the physics of massive stars could be obtained by spectroscopic analysis and abundance studies.
Nevertheless, the determination of surface abundances of O stars is challenging. Non-LTE atmosphere models including line-blanketing and winds are required, and there is a rarity of metallic lines in O star spectra. The UV range contains a few strong resonance lines (C iii 1176, N v 1240, C iv 1550, N iv 1720) but they are mainly formed in the wind part of the atmosphere where numerous effects (X-rays, clumping) render their modelling difficult. Photospheric lines are found in the optical range, but, here again, only a few lines are available.
Rivero Gonzalez et al. (2011) have revisited the formation mechanism of N iii 4634–4640 and have used several N ii, N iii and N IV lines to derive abundances of O stars in the Magellanic Clouds. Martins et al. (2012) studied the effect of magnetism on the surface abundance of O stars, and based their nitrogen abundance measurements on N ii, N iii and N iv optical lines. Nitrogen is a crucial indicator of chemical enrichment. But more precise constraints can be brought to stellar evolution if the ratio N/C can be derived because N/C is less sensitive to the initial metal content than N/H. For instance the ratio of N/C in the Galaxy to N/C in the SMC is less that 3, while N/H in the Galaxy is 13 times larger than N/H in the SMC. Thus N/C, especially when combined to the N/O ratio (e.g. Przybilla et al. 2010), provides stronger constraints on the enrichment and mixing history of CNO material at a given metallicity.
Unfortunately, carbon lines are even less numerous than nitrogen lines in O stars spectra. In the optical range, the strongest lines are C iii 4647–50–51 (hereafter C iii 4650), C iii 5696, and C iv 5801–12. C iii 4650 is observed in absorption in most O stars. It shows emission only in the earliest O supergiants. In early O dwarfs, it is almost absent. A peculiar class of objects – the Ofc stars (Walborn et al. 2010) – displays always C iii 4650 emission. Stars of the Ofc class encompass Of?p stars which, among other characteristics, have a strong but varying C iii 4650 emission. Many of them are magnetic (Donati et al. 2006; Hubrig et al. 2008; Martins et al. 2010; Wade et al. 2012). Ofc stars are found mainly at spectral type O5 but at all luminosity classes (Walborn et al. 2010). So far, no explanation has been given for the appearance of such C iii 4650 emission. Its analysis is rendered difficult by the presence of the neighbouring strong N iii 4634–4640 lines. C iv 5801–12 is present in most O stars, but is often not observed. In late-type stars it is in absorption, while in early type stars it can exhibit a complex profile with broad emission wings and absorption (Conti 1974; Bouret et al. 2012).
C iii 5696 is present in most O stars except the earliest ones (Walborn 1980). It is in emission in giants and supergiants, and in most dwarfs. The emission is on average stronger in supergiants than in dwarfs (Conti 1974). Contrary to C iii 4650, C iii 5696 is located in a spectral region free of other lines and hence its profile is well defined. Spectroscopic analysis have generally not considered this line for carbon abundance determination – atmosphere models often have difficulties reproducing the observed profiles, even if the H, He i, He ii and UV CNO lines are well fitted. This indicates that the formation of that line is complex and probably depends on missing or improperly accounted for physics. Nussbaumer (1971) found that the C iii 5696 emission was due to a depopulation of the lower level by C iii 884. Hence, a correct description of the radiative transfer close to 884 Å is required. Since the models used by Nussbaumer (1971) did not include a proper line-blanketing and non-LTE treatment, we revisit the formation of C iii 5696. We also investigate the formation of C iii 4650.
In Sect. 2 we present the method and models we have used. Section 3 describes the formation mechanism of C iii 5696 and Sect. 4 focuses on C iii 4650. The wind effects are gathered in Sect. 5. We summarize our results in Sect. 6.
2. Model description
 |
Fig. 1 Spectra of C iii 5696 illustrating the dramatic dependence of the line profile on surface gravity and effective temperature. The left panel is for Teff = 30 500 K while the right panel is for Teff = 42 000 K. Particularly striking is the strong dependance of the profile on log g, and that this dependance is of opposite sign in models of different effective temperature. |
Our investigation of the formation mechanisms of C iii 4650 and C iii 5696 relied on the computation of model atmosphere and the analysis of the processes populating the levels involved in the C iii transitions. We have used the code CMFGEN (Hillier & Miller 1998) to compute atmosphere models. CMFGEN produces non-LTE models including winds and line-blanketing. The radiative transfer is solved in the comoving frame and the geometry is spherical. The rate equation and the radiative transfer equation are solved simultaneously and iteratively until convergence of the level populations. A super-level formalism is used to reduce the number of levels involved in the computations (to reduce the amount of memory required). Table A.1 provides the number of levels used in our computations. Our models include H, He, C, N, O, Ne, Si, S, Ar, Ca, Fe, Ni. The reference solar abundances of Grevesse et al. (2007) were adopted. The radiative equilibrium condition sets the temperature structure and the density structure in the inner atmosphere is obtained by iteration. Once the level populations are (roughly) converged, the radiative force is computed and the momentum equation is solved to yield the density structure; the radiative field and level populations are then re-computed until full convergence of the model is achieved. A couple of these hydrodynamical iterations are performed. In the outer atmosphere, the velocity law is given by a classical β law (e.g. Kudritzki et al. 1989). The density and velocity distributions are related via the mass conservation equation.
The emergent spectrum is computed using CMF_FLUX (Busche & Hillier 2005), and results from a formal solution of the radiative transfer equation using the atmosphere model provided by CMFGEN. A depth dependent microturbulent velocity, varying from 10 km s-1 in the photosphere to 200 km s-1 in the upper wind, is used. Proper pressure and Stark broadening is included for H, He i, He ii and CNO resonance lines. Other lines are treated by Gaussian profiles.
For our purpose, we selected two sets of model: one with Teff = 30 500 K and one with 42 000 K. They correspond to late and early O stars respectively (Martins et al. 2005). The atomic data for carbon were taken from various sources: the photoionization rates are from the opacity project (Seaton 1987)1, oscillator strengths and the low-temperature dielectronic transition data were kindly computed by Peter Storey (priv. comm.). For collisional excitation we write the collisional excitation rate (in cgs units) as 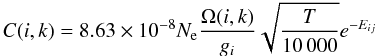 where Ne is the electron density, gi the statistical weight of the lower level, Eij the excitation energy, T the temperature, and Ω(i,k) the dimensionless collision strength. The collisional data for the six lowest levels (singlet and triplet states) are from Berrington et al. (1985); for other collisional data we use the approximation of van Regemorter (1962) who writes the collision strength for a transition between two levels in-terms of the oscillator strength (for optically allowed transitions).
where Ne is the electron density, gi the statistical weight of the lower level, Eij the excitation energy, T the temperature, and Ω(i,k) the dimensionless collision strength. The collisional data for the six lowest levels (singlet and triplet states) are from Berrington et al. (1985); for other collisional data we use the approximation of van Regemorter (1962) who writes the collision strength for a transition between two levels in-terms of the oscillator strength (for optically allowed transitions).
3. C iii 5696
C iii 5696 (2s3p 1Po-2s3d 1D) can either be in absorption or emission, and exhibits a complex variation with Teff and log g. To illustrate these dependencies, we show the C iii 5696 profile for Teff = 30 500 K and log g =3.25 and 3.75 in Fig. 1 (left panel). In the low log g model C iii 5696 is in emission, while in the high log g model it is in absorption. The opposite behavior is observed in a much hotter model with Teff = 42 000 K – C iii 5696 is in absorption for log g = 3.5 but in emission for log g = 4.0.
As C iii 5696 is primarily photospheric a key quantity controlling the line strength (and whether the line is in emission or absorption) is the line source function. An increase in the line source function will weaken an absorption line, possibly driving the line into emission. Conversely, a decrease in the line source function will enhance (weaken) the absorption (emission) profile. The line source function can be increased by decreasing the population of the lower level, and/or by increasing the population of the upper level. Thus, to understand the origin of C iii 5696, we need to understand the transitions populating and depopulating its lower and upper level.
 |
Fig. 2 Simplified Grotrian diagram for the singlet system of C iii. The C iii 5696 transition is indicated in red. |
 |
Fig. 3 Effect of the C iii UV lines on the formation of C iii 5696. Left: initial C iii 5696 spectrum (solid) and spectra from models in which several C iii UV lines have been artificially removed. Right: departure coefficient of the C iii 5696 lower and upper levels in the initial model (solid lines), the model without C iii 884 Å (dashed lines) and the model without C iii 574 Å (dotted lines). Departure coefficients are plotted as a function of Rosseland opacity. The dot-dashed line at the bottom indicates the C iii 5696 formation region expressed in terms of the contribution function as a function of τRosseland. |
Figure 2 presents a simplified Grotrian diagram of the singlet system of C iii. We see that the lower and upper levels of C iii 5696 (2s3p 1Po and 2s3d 1D respectively) are connected to lower levels by several extreme UV transitions, and to upper levels by far UV/UV transitions. Level 2s3p 1Po is also connected to the ground level by a transition at 386 Å.
To illustrate which transitions control the lower and upper level populations of C iii 5696 we computed different models (all with Teff = 30 500 K, log g = 3.25, Ṁ = 2.0 × 10-6M⊙ and v∞ = 2000 km s-1) in which we selectively removed specific C iii transitions by reducing their oscillator strength by a factor 10 000. The results are displayed in Fig. 3 (left panel). As an example, the dotted green line is the model in which C iii 884 was removed. This figure highlights the key role of C iii 884. Its effect is dramatic: C iii 5696 switches from emission to absorption when it is removed from the model. Several other C iii lines (e.g., C iii 386 and C iii 574) also have a significant impact on C iii 5696, although with a reduced effect compared with C iii 884.
The right panel of Fig. 3 shows the departure coefficients of levels 2s3d 1D and 2s3p 1Po (upper and lower levels of C iii 5696) in the initial model and the models without C iii 884 and C iii 574 (i.e., the lines leading to the strongest changes). We see that in the absence of the C iii 884 Å transition, the departure coefficients are close to 1.0, while in the initial model, the lower level is depopulated compared to the upper level, leading to emission. The total radiative rate2 in C iii 884 is positive in the initial model (see left panel of Fig. 5). Thus, C iii 884 acts as a drain for level 2s3p 1Po. When we remove it, the drain is suppressed and the 2s3p 1Po population is higher, as seen in Fig. 3 (right panel).
Similarly, the total radiative rate in C iii 574 is also positive (see right panel of Fig. 5), draining the population of 2s3d 1D. When C iii 574 is removed, 2s3d 1D is less depopulated, its departure coefficient is higher than in the initial model (Fig. 3) and C iii 5696 emission is strengthened.
In the model with Teff = 42 000 K3 the physical conditions are different and the reaction of C iii 5696 to the removal of UV lines is slightly different. Figure 4 shows the effect of different C iii UV lines on C iii 5696 for the model with Teff = 42 000 K and log g = 3.5. Compared to the left panel of Fig. 3 (Teff = 30 500 K, log g = 3.25), lines have qualitatively similar effects. Removing C iii 574 leads to a stronger emission than the initial model; removing C iii 386 also leads to a stronger emission, but not as strong as in the case of C iii 574; and removing C iii 884 leads to more absorption. But at 42 000 K, it is the removal of C iii 386 and C iii 574 (and not C iii 884), which leads to the switch between absorption and emission. Thus depending on the temperature the C iii 5696 emission is driven by different C iii UV lines. In Appendix B we present the effect of these lines on the appearance of C iii 8500 (its upper level is the lower level of C iii 5696) relevant for future Gaia observations.
 |
Fig. 5 Effect of log g on the formation of C iii 5696 for Teff = 30 500 K. Left: total radiative rates out of level 2s3p 1Po at log g = 3.25 (upper panel) and log g = 3.75 (lower panel) as a function of Rosseland opacity. Notice how the largest rate is for λ 884, and that this rate shows a qualitatively different behavior in the two models. The dotted lines indicate the C iii 5696 line formation region. Right: total radiative rates out of level 2s3d 1D at log g = 3.25 (upper panel) and log g = 3.75 (lower panel). |
 |
Fig. 6 Effect of log g on departure coefficients. Departure coefficients are plotted as a function of Rosseland opacity for the levels on C iii 5696 (upper panel) and for the fundamental level (2s2 1S) and the lower level of C iii 884 (2p2 1D). The dotted line shows the C iii 5696 line formation region. |
3.1. Explanation of log g effect
Earlier we saw that the C iii 5696 profile varies dramatically with both Teff and log g. We can now use our understanding of the key role of C iii 386, C iii 574 and C iii 884 in controlling the strength of C iii 5696 to explain this behavior.
In the left panel of Fig. 5 we show the total radiative rates from level 2s3p 1Po (i.e. the lower lower level of C iii 5696) for log g = 3.25 and 3.75 at 30 500 K. Focusing on the low gravity case, we see that over the C iii 5696 formation region the highest rate is observed for the C iii 884 Å transition. In addition, this rate is positive, indicating a depopulation of the 2s3p 1Po level as seen previously. Turning to the log g = 3.75 model, we see that the C iii 884 Å radiative rate has a qualitatively different behavior – in most of the C iii 5696 formation region it is negative, and hence it does not act as a significant drain on the population of the lower level of C iii 5696. Consequently, C iii 5696 switches to absorption.
We can understand the differences as follows. A decrease of log g translates into a smaller Lyman jump and to a higher ionizing flux (e.g. Abbott & Hummer 1985). This also follows from density arguments – at a given Teff, a low log g model is less dense, hence there are less recombinations and the atmosphere is more highly ionized than a higher log g model. Consequently, the ionization is stronger in the log g = 3.25 model atmosphere. C iv is the most abundant ion while at log g = 3.75, it is C iii. In addition, the ground state and 2p2 1D (the lower level of C iii 884) are collisionally coupled.
The switch from absorption to emission for C iii 5696 when log g decreases is due to the following chain of events: the ground state and 2p2p 1D are depopulated due to the higher ionization and consequently the downward radiative rate in C iii 884 has increased; the C iii 884 drain on the 2s3p 1Po (lower level of C iii 5696) population increases, which leads to emission in C iii 5696. Figure 6 confirms that when log g decreases, the ground state and 2p2p 1D are depopulated, leading to a strong depopulation of 2s3p 1Po through C iii 884.
At Teff = 42 000 K, the effect of log g on C iii 5696 is opposite (Fig. 1). The total radiative rates of the low and high log g models at 42 000 K are shown in Fig. 7. C iii 884 always acts as drain, and drives C iii 5696 into emission. However, the resonance line C iii 386 switches from near radiative equilibrium at log g = 4.0 to a net negative rate at log g = 3.5 (left panel of Fig. 7), implying that it populates the 2s3p 1Po level. This compensates for the C iii 884 drain, and C iii 5696 is in weak absorption.
In conclusion, the reaction of C iii 5696 to changes in log g is directly related to the line formation mechanism and the key role of the C iii UV lines. As the temperature increases, the peak of the spectral energy distrubution shifts to shorter wavelengths and consequently higher energy C iii UV lines become more and more important at the expense of lower energy transitions.
3.2. Dielectronic recombinations
 |
Fig. 8 Effect of low temperature dielectronic recombination (LTDR) on C iii 5696 in the models with Teff = 30 500 K (upper panel) and 42 000 K (lower panel). The red solid curve shows the standard model profile, while the blue dashed profile shows the effect of “double counting” the influence of LTDR. The green dot-dashed line is the standard model in which the LTDR from levels forbidden to autoionize in LS coupling have been omitted. |
So far we have focused on detailed non-LTE radiative transfer effects to explain the morphology of C iii 5696. Dielectronic recombination is another mechanism, which might have an influence on the appearance of C iii 5696. As low temperature dielectronic recombination (LTDR) for levels permitted to autoionize in LS-coupling is handled via resonances in the photoionization cross-sections they cannot be easily omitted from the calculations. Instead, we run a model in which we utilize the Einstein A values computed using intermediate coupling by Peter Storey (priv. comm.) to add important LTDR transitions into the photoionization cross-sections. Although this means that we are exaggerating their influence (since we are double counting) we can still use the change in line profile to infer whether LTDR is important. Figure 8 shows the effect of low temperature dielectronic recombinations on the appearance of C iii 5696 at high and low effective temperature. The additional dielectronic recombinations, when included, lead to a slight increase of the emission line, but quantitatively, the effect is smaller than that of UV lines (see Figs. 3 and 4). We also run a test model in which we switch off LTDR for transitions not permitted to autoionize in LS coupling. These were also found to have only a small effect on C iii 5696. Thus LTDR is not a viable mechanism to explain the observed behavior of C iii 5696 in O stars. Similar results are found for N iii 4634–4640 by Rivero Gonzalez et al. (2011).
3.3. Line blanketing effects
3.3.1. Microturbulence and metallic line interactions
In Fig. 9 we show the effect of a change of the microturbulent velocity in the atmosphere model (and not in the calculation of the spectrum) on the C iii 5696 line. A reduction of vturb translates into a stronger emission. Modifying vturb affects the efficiency of line-blocking and thus the temperature structure and EUV radiation field. But different microturbulent velocities also imply different metallic line width and thus different line overlap, which can affect radiative transfer in UV C iii lines.
We have seen in Sect. 3 that the C iii 386, C iii 574 and C iii 884 lines significantly influence the strength of C iii 5696. Depending on the microturbulent velocity the lines have a typical width between 15 and 30 km s-1, and hence will interact with other lines whose separations are less than 15−30 km s-1. To test the effect of metallic lines on the C iii UV features and thus on C iii 5696, we have run test models with Teff = 30 500 K. We selectively removed metallic features (Fe vi 386.186, Fe iv 386.211, Fe v 386.262, Fe iv 574.229, Fe vi 574.230, Fe iv 574.232, Ar iv 574.243, Ni iv 574.291, N iii 574.298, N iii 884.466, Fe iv 884.497, Fe iv 884.520, S v 884.530, and Fe v 884.578) in the model atmosphere and computed the resulting C iii 5696 line profile. Atomic data for the transitions found to influence C iii 5696 and C iii are discussed in Appendix A.
 |
Fig. 9 Effect of the microturbulent velocity on the C iii 5696 emission strength in three CMFGEN models. The microturbulent velocity has been changed only in the atmosphere computation. The spectra have all been computed with vturb increasing from 10 to 200 km s-1 throughout the wind. |
 |
Fig. 10 Effect of metallic lines on C iii 5696. The solid line is the initial spectrum. The dashed line is a model in which the oscillator strength of Fe v 386.262 Å is artificially reduced by a factor 10 000. The dot-dashed (dotted) line is the initial model in which Fe iv 574.232 Å (S V 884.531 Å) is reduced by the same factor. |
In all but three cases, which are shown in Fig. 10, the C iii 5696 feature is basically unchanged. The model with Fe iv 574.232 removed (dot-dashed) has a stronger C iii 5696 than the initial model (solid). The explanation for this emission increase can be inferred from Figs. 11 and 12. In Fig. 11, the departure coefficients of the upper and lower levels of C iii 5696 are shown for both the initial model and the model without Fe iv 574.232. Initially, the lower level is more depopulated than the upper level, explaining the emission. When Fe iv 574.231 is removed, the upper level becomes more populated while the departure coefficient of the lower level is barely changed. This translates into the stronger emission seen in Fig. 10.
The reason for the enhanced emission can be understood from Fig. 12, which shows the total radiative rates in C iii 574.281, C iii 5696 and Fe iv 574.231. The total rate in C iii 574.281 is positive in the initial model while the rate in the iron transition is negative. Consequently the Fe iv 574.232 transition removes photons from the C iii 574.281 line. These photons are not available for re-absorption in the C iii 574.281 and hence the population of 2s3d 1D, the upper level of C iii 5696, is reduced. When the Fe iv 574.232 line is artificially removed, it does not “steal” photons any more from the C iii 574.281 transition, resulting in a smaller depopulation of 2s3d 1D, as seen in Fig. 11, and the emission in C iii 5696 is stronger.
The scenario presented above also partly4 explains why a lower microturbulent velocity results in a stronger C iii 5696 emission. In the case of a large vturb, the line overlap between C iii 574.281 and Fe iv 574.232 is wider, favoring the drain effect described above. When vturb is reduced, the reduction of the overlap translates in a less efficient drain of the 2s3d 1D level population, implying a stronger C iii 5696 emission.
 |
Fig. 11 Effect of a change in the oscillator strength of Fe iv 574.232 Å on the departure coefficient (plotted as a function of Rosseland opacity) of the levels of the C iii 5696 transition. The red curves correspond to the upper level and the blue ones to the lower level. The solid lines are for the initial model. The dashed lines are the level populations in the model with a reduced Fe iv 574.232 line. The dotted line is the C iii 5696 formation region. |
 |
Fig. 12 Effect of the Fe iv 574.232 Å line on the total radiative rates of several transitions. The solid lines are for the initial model, the dashed lines for the model in which the iron transition has been removed in the atmosphere calculation. The dotted line indicates the C iii 5696 line formation region in the initial model. |
In Fig. 10, we have also plotted the spectrum resulting from a model in which Fe v 386.262 Å was reduced artificially. As for the Fe iv 574.232 line, the result is a stronger emission. This Fe v line can interact with C iii 386 (Fig. 2). The total radiative rates in the initial model are negative for both lines (Fe v 386.262 and C iii 386). This means that the iron line absorbs photons that could in principle be absorbed by the carbon line. When the iron line is removed, the photons are effectively absorbed by the carbon line. This excess of absorption could in principle overpopulate the 2s3p 1Po level and lead to a weaker emission. But in practice, the 2s3p 1Po population is reduced. This is explained by the need to maintain the ground level population constant, as indicated by our models (the ground level population being controlled by ionization/recombination processes). Since in the absence of Fe v 386.262 the absorption in C iii 386 is stronger and since the ground level population is unchanged, an increase of the downward transition is needed to maintain the ground level rate equation equilibrium. Consequently, the 2s3p 1Po is depopulated, leading to a stronger emission. Here again, this mechanism explains that a smaller microturbulent velocity leads to less absorption by Fe v 386.262 and thus to a stronger C iii 5696 emission.
Finally, Fig. 10 also shows the effect of the S V 884.531 line on C iii 5696. Removing this feature translates into a reduction of the C iii 5696 emission. The explanation comes from the Grotrian diagram in Fig. 2 and the effect of the C iii 884 transition on C iii 5696 (at Teff = 30 500 K). The total radiative rate in the S V line is negative throughout the C iii 5696 line formation region, while the C iii 884 Å line rate is positive. Thus the sulfur line enhances the drain of 2s3p 1Po through C iii 884. By removing the sulfur line, we reduce the drain, thus re-populate the 2s3p 1Po level, and consequently reduce the C iii 5696 emission.
3.3.2. Metallicity effects
 |
Fig. 13 Effect of the metallicity Z on the formation of C iii 5696 at Teff = 30 500 K. Left: spectra of C iii 5696 at Z⊙ (solid), 1/5th Z⊙ (dashed) and 1/5th Z⊙ but with C/H at the solar value (dotted). Right: departure coefficient of the C iii 5696 lower and upper levels at Z⊙ (solid lines), 1/5th Z⊙ (dashed lines) and 1/5th Z⊙ with C/H at the solar value (dotted). The dot-dashed line indicates the line formation region. |
We have seen in Sect. 3.1 that C iii 5696 was indirectly sensitive to the ionizing flux. We thus expect that any reduction of the Lyman continuum flux will affect the C iii 5696 morphology. Since an increase of the metal content severely reduces the ionizing fluxes (e.g. Schaerer & de Koter 1997), and thus the ionization structure, we expect metallicity to have a significant impact on the appearance of C iii 5696.
Figure 13 shows the influence of the metallicity Z on the C iii 5696 line profile and departure coefficients at Teff = 30 500 K. We have computed models with a global metallicity reduced by a factor five compared to the initial, solar metallicity model. We have also computed a model with a global metallicity of 1/5th the solar metallicity, but with the carbon abundance fixed to the solar value. As expected, at low metallicity the ground state level is depopulated (see right panel of Fig. 13). The collisional coupling with the 2p2p 1D level leads to a strong drain through C iii 884 Å and to a depopulation of 2s3p 1Po. But at the same time, we observe a strong depopulation of 2s3d 1D as well, so that the net outcome of a reduction of Z is a decrease of the C iii 5696 emission. This is not just an effect of the scaling of the emission strength with the carbon abundance, since in the model with a solar C/H but reduced metallicity we also observe a reduction of the line intensity. The reason is the depopulation of 2s3d 1D. It is due to a stronger radiative rate in the C iii 574 line at low metallicity. This is explained by the reduced strength of the Fe iv 574.232 line and consequently its reduced interaction with C iii 574 as described in Sect. 3.3.1.
Appendix C shows how C iii 5696 reacts to a change of metallicity for Teff = 42 000 K. A combination of lower ionizing flux and reduced metallic line interaction explains the observed behavior. This highlights the complexity in predicting the shape of C iii 5696. Metallicity can also affect the line formation by its influence on the wind strength (see Sect. 5).
3.3.3. Influence of N iv λ322
Gauzit (1966) argued that C iii 5696 emission could be due to the interplay between N iv 322 and C iii 322 between levels 2s2 1S and 2p3s 1Po5, the latter being connected to 2s3d 1D (the upper level of C iii 5696) by a transition at 2982 Å (see discussion in Nussbaumer 1971). We have tested this possibility by removing C iii 2982. The result, shown in Fig. 3, indicates that the 2982 Å feature plays little role in populating 2s3d 1D. Hence, inducing the C iii 322 transition and decay through C iii 2982 by N iv 322 is not responsible for the appearance of C iii 5696 emission.
In conclusion, we have identified a general mechanism responsible for the morphology of C iii 5696. It is the influence of UV C iii transitions on the population of the upper and lower levels of C iii 5696 that play a key role. The main lines are C iii 386, C iii 574, and C iii 884. At low Teff, C iii 884 is crucial for determining the lower level population, while at high Teff, C iii 386 is more important. Subtle line-blanketing effects modify the strength of the C iii 5696 emission. Obtaining an excellent fit to C iii 5696 is an extremely challenging task since it requires the knowledge of several stellar parameters including the microturbulent velocity, the metallicity, as well as accurate wavelengths and oscillator strength of several weak metal lines.
4. C iii 4647–50–51
We now turn to the study of C iii 4650. We follow the same method as that used to identify the formation mechanism of C iii 5696.
4.1. Line formation mechanism
The C iii 4650 lines are produced by the triplet system of C iii. They are the triplet equivalent of the C iii 8500 transition in the singlet system (i.e., a transition between levels 3s and 3p). The triplet equivalent of C iii 5696 is C iii 9710. Figure 14 shows the simplified Grotrian diagram for this system.
 |
Fig. 14 Simplified Grotrian diagram for the triplet system of C iii. The C iii 4647-50-51 transitions are shown in red. The star symbols indicate multiplets. |
4.1.1. Effects of UV lines
 |
Fig. 15 Effect of C iii UV lines on C iii 4647–50–51 in the model with Teff = 30 500 K (upper panel) and 42 000 K (lower panel). The solid line is the initial model. The other lines are models in which a given C iii UV line has been removed by reducing its oscillator strength by a factor 10 000. |
To understand the formation of C iii 4650, we proceeded as for C iii 5696, looking for key transitions that control the upper and lower level populations. Figure 15 shows the C iii 4647-50-51 profiles in the low (upper panel) and high (lower panel) Teff case. The solid line is the initial model, while the other lines correspond to models in which specific C iii UV lines connected to either the upper or the lower level of C iii 4650 have been removed (by reducing their oscillator strength by a factor 10 000). Only the models with the largest changes are shown. The following lines were tested: C iii 538, C iii 818, C iii 981, C iii 1175, C iii 1256, C iii 1428, C iii 1578, C iii 1620, C iii 1908, C iii 2009.
The C iii 538 Å transition is found to play a crucial in the formation of the C iii 4647-50-51 line, since removing it leads to a strong increase of the absorption. The C iii 2009 line also has a non negligible role on the shape of C iii 4650, but its impact is much weaker than that of C iii 538. The same results are obtained in the model with Teff = 42 000 K – all models have C iii 4650 in emission, except the model in which C iii 538 is removed and where absorption is observed. From the Grotrian diagram (Fig. 14) we can suspect C iii 538 to be a drain for level 2s3s 3S. Inspection of the departure coefficient of 2s3s 3S in the initial model, and the model without C iii 538 (not shown), confirm that 2s3s 3S is more populated when C iii 538 is absent.
4.1.2. Effect of log g
This mechanism (depopulation of 2s3s 3S by C iii 538) explains the behavior seen in Fig. 16. The effect of log g on C iii 4647-50-51 in a model at 42 000 K is shown. The reduction of the gravity turns the weak emission in the log g = 4.0 model into a strong emission in the log g = 3.5 model. The departure coefficients are shown in the right panel of Fig. 16. While the upper level has bi close to 1 in both models, the lower level has a departure coefficient much lower than 1 in the low gravity model. This increases the line source function, leading to strong emission in the low gravity model.
Given the Grotrian diagram seen in Fig. 14 one can conclude that the mechanism is similar to that of C iii 884 for C iii 5696. The higher ionization of the low log g model leads to a depopulation of the ground level (2s21S) and the 2s2p 3Po to which it is collisional coupled. The lower population of 2s2p 3Po enhances the C iii 538 drain (the total radiative rate is positive) depopulating 2s3s 3S and driving C iii 4647-50-51 into emission. Hence, C iii 538 controls the population of the lower level of C iii 4650 and its morphology (absorption or emission) at both high and low effective temperature. The situation for C iii 4650 is clearer than for C iii 5696, since the only line affecting significantly its morphology is C iii 538. In particular, C iii 818, connected to 2s3p 3Po (upper level of C iii 4650), has no impact on the appearance of C iii 4650 (Fig. 15). The reason is related to a quirk of the atomic physics: the Einstein coefficient A for the 818 transition is only 2.3 × 106 compared with 7.2 × 107 for C iii 4650 and 4.1 × 108 for C iii 538.
 |
Fig. 16 Effect of log g on C iii 4647–50–51. Left panel: the red line is a model with log g = 3.5; the blue line is the same model with log g = 4.0. The effective temperature is 42 000 K. Right panel: departure coefficient of the upper and lower levels of C iii 4647–50–51 (upper panel) and of levels 2s2 1S (n = 1), 2s2p 3Po (n = 2,3,4), 2p2p 3D (n = 6,7,8) (lower panel) for log g = 3.5 (solid line) and log g = 4.0 (dashed line), plotted as a function of Rosseland opacity. The dotted line is the C iii 4650 formation region. |
As for C iii 5696, we also tested the effect of low temperature dielectronic recombination and found out that its role was marginal. The line profiles show slightly more emission (or less absorption) when LTDR is included, but the changes are minor compared to the effects of UV lines highlighted above. In O stars, LTDR is not responsible for the strength of C iii 4650.
4.2. Line blanketing effects
4.2.1. Microturbulence and metallic lines
As for C iii 5696 we find that microturbulence and line blanketing effects influence the morphology of C iii 4650. In particular, an increase of vturb lead to a significant strengthening of the absorption. Inspection of our line list also indicates that several metallic lines are located near the C iii 538 transition – the only UV line that significantly influences the strength of C iii 4650.
We tested the influence of the following lines on the strength of C iii 4650: Fe iv 538.044, Fe iv 538.057, Fe vi 538.097, Fe vi 538.112, Fe iv 538.176, Fe iv 538.265, Fe vi 538.285, O iii 538.320, Ar iii 538.348. Only Fe iv 538.057 leads to a change of the C iii 4650 profile – its absence translates into a “small” increase in the absorption (Fig. 17). While the effect of Fe iv 538.057 is important C iii 538 has a much larger impact. The Fe iv 538.057 has a negative total radiative rate and consequently assists in the depopulation of the 2s3s 3S state, like Fe iv 574.232 for the upper level of C iii 5696.
4.2.2. Metallicity effects
Figure 18 shows the effect of metallicity on C iii 4650 at Teff = 30 500 K (left) and 42 000 K (right). At low effective temperature, a global reduction of the metallicity translates into a stronger absorption. If the carbon content is kept at the solar value, the absorption is further strengthened, simply because there is more carbon and thus more C iii in the atmosphere. The increase of the absorption due the reduction of Z can be understood as follows. We have seen in Fig. 17 that removing C iii 538 and Fe iv 538.057 lead to an increase of the C iii 4650 absorption. A reduction of Z corresponds to a reduction of the strength of C iii 538 and Fe iv 538.057. Consequently, a lower Z implies a stronger C iii 4650 absorption.
For Teff = 42 000 K, the behavior of C iii 4650 is the same as that of C iii 5696 (see Appendix C). Reducing Z produces a weaker emission. But keeping C/H at the solar value and reducing the abundance of all other elements lead to a C iii 4650 emission stronger than at solar metallicity. The reason is that the condition for emission are more favorable at low Z. In particular, the ionization is higher, draining the population of 2s3s 3S significantly even if C iii 538 is weaker at low metallicity.
 |
Fig. 17 Synthetic spectra around the C iii 4650 triplet in models with Teff = 30 500 K. The red line is the initial model. The blue line is the same model in which we have removed the C iii 538 Å line. The green model is the same as the initial model in which the Fe iv 538.057 Å line has been removed. |
As highlighted in the introduction, C iii 4650 and C iii 5696 are usually the strongest C iii lines in O stars optical spectra. It is tempting to use them to perform carbon abundance determinations. However, we have seen that both lines critically depends on metallic lines the characteristics of which are not accurately known. We illustrate in Fig. 19 how such uncertainties can affect carbon abundance determinations. Removing Fe iv 574.232 in a model with C/H = 1/2 C/H⊙ leads to a C iii 5696 profile almost as strong as in the solar C/H model (left panel). For C iii 4650, the effect of removing Fe iv 538.057 is even larger since the absorption in the C/H = 1/2 C/H⊙ model without this iron line is stronger than the absorption in the solar C/H model. In conclusion, using C iii 4650 and C iii 5696 to determine the carbon content of O stars is very risky, and quoting an uncertainty of less than a factor of two in the derived C/H using these lines is unrealistic.
 |
Fig. 18 Effect of metallicity on the C iii 4650 triplet at 30 500 K (left) and 42 000 K (right). The solid line is a solar metallicity model. The dashed line is a model with Z = 1/5th Z⊙. The dotted line is the same model as the dashed line model but with a solar C/H. |
 |
Fig. 19 Effect of C/H on the intensity of C iii 4650 (left) and C iii 5696 (right) at Teff = 30 500 K. In both panels, the solid line is a solar metallicity model. The dashed (dotted) line is a model with C/H = 1/2 (1/5) C/H⊙, all other elements having the solar abundances. In the left (right) panel, the dot-dashed line is the C/H = 1/2 C/H⊙ model in which the Fe iv 538.057 (574.232) line has been removed. |
5. Wind effects
We devote a special section to the effects of winds on the morphology of the C iii optical lines. Details are also given in Appendix D. In Fig. 20, we show the effects of changes in the mass loss-rate at 30 500 K and 42 000 K. The effects are complex, sometimes counter–intuitive, and do not change monotonically with mass-loss rate. The changes show that the optical lines cannot be modeled without modeling the wind, and that an accurate estimate of the mass-loss is required. Because of clumping, obtaining an accurate estimate of the mass-loss rate is not easy. Because mass-loss rates strongly correlate with luminosity, we expect the C iii optical lines (at fixed Teff and log g) to correlate with luminosity.
Let us first examine C iii 5696. At Teff = 30 500 K, starting from the low mass loss rate model (3 × 10-9 M⊙ yr-1), we see that the emission line profile first strengthens when Ṁ increases. A further increase of Ṁ from 10-8 to 3 × 10-8 M⊙ yr-1 translates into a change from emission to weak absorption. Above 3 × 10-8 M⊙ yr-1, the increase of Ṁ resumes to produce stronger emission. Thus, the behavior of the C iii 5696 line strength/morphology with increasing mass loss rate is not monotonic. At higher effective temperature, there is a clear anti-correlation of strength of C iii 5696 emission with mass loss rate above 10-7 M⊙ yr-1. Below that value, the emission stregnth is almost at the level of the 10-7 M⊙ yr-1 model.
For C iii 4650 at low Teff, an increase of the mass loss rate is associated with a decrease of the absorption and/or an increase of the emission is seen. This is what is commonly observed in wind sensitive lines such as Hα. In the 42 000 K model, below 10-7 M⊙ yr-1, C iii 4650 has a rather constant emission level, with slight fluctuations. Above 10-7 M⊙ yr-1, the emission increases with mass loss rate.
A detailed explanation of the observed behavior is provided in Appendix D. Basically, it is related to the influence of UV lines on the populations of the upper levels. As we increase the mass-loss rate we increase the velocity at a fixed Rosseland optical depth, and this alters the radiation transfer in the UV lines. For example, at higher velocities the lines desaturate earlier, which can enhance both photon escape and photon pumping. Which of the two processes dominates depends on both the radiation field in the lines neighborhood and the line under consideration. These two processes have opposite effects on the strength of an optical line – photon escape in the UV line enhances optical emission (weakens absorption) while photon pumping enhances absorption (weakens emission) when the UV line’s upper state is the lower level of the optical transition. The converse occurs when the UV lines is connected to the upper state of the optical transition. The behavior of C iii 5696 at low mass loss rates is complex and not straightforward.
 |
Fig. 20 Effects of a change in the mass loss rate on C iii 4650 and C iii 5696 in models with Teff = 30 500 K (left) and Teff = 42 000 K (right). The mass loss rates (in M⊙ yr-1) are indicated in the C iii 5696 panels. |
6. Concluding remarks
We have investigated the formation processes of C iii 5696 and C iii 4650 in the atmosphere of O stars. We have used the non-LTE atmosphere code CMFGEN to perform simulations at two effective temperatures (30 500 K and 42 000 K) corresponding to late and early spectral types. Our results can be summarized as follows:
-
For wind densities typical of O stars, the formation of C iii 5696 is controlled by several UV transitions: C iii 386, C iii 574 and C iii 884. The latter is crucial at low Teff: when it is removed from models, C iii 5696 switches from emission to absorption. C iii 574 and C iii 386 play the same role at high Teff.
-
C iii 884 acts as a drain on the 2s3p 1Po population (lower level of C iii 5696). When it is removed, 2s3p 1Po is more populated and emission is reduced/suppressed. C iii 574 drains the 2s3d 1D population and C iii 386 populates 2s3p 1Po. When they are removed, 2s3d 1D is more populated and 2s3p 1Po is depopulated, favoring emission.
-
Lower gravity models have larger ionizing flux. As a consequence, the lower level of C iii 884 (2p2p 1D), which is collisionally coupled to the ground level, is depopulated at low log g. The drain of 2s3p 1Po by C iii 884 is thus increased. This leads to an increase of C iii 5696 emission when log g decreases at 30 500 K. At Teff = 42 000 K, the effect of log g is opposite and is due to the role of C iii 386 in populating the lower level of C iii 5696.
-
The strength of C iii 5696 is very sensitive to the action of a few metallic lines on the radiative transfer near 386, 574 and 884 Å. In particular, Fe iv 386.262 and Fe iv 574.232, when removed from models, lead to a stronger C iii 5696 emission. If S v 884.531 is removed, the C iii 5696 emission is reduced. The reason is the overlap of these features with the key C iii lines controlling the shape of C iii 5696. As an example, Fe iv 574.232 extracts photons from C iii 574 leading to a lower population of 2s3d 1D. Consequently, Fe iv 574.232 limits the C iii 5696 emission. When it is removed, 2s3d 1D is more populated and the C iii 5696 emission is stronger.
-
The formation of C iii 4650 is controlled by radiative transfer at 538 Å. The C iii 538 line drains the population of 2s3s 3S, the lower level of C iii 4650. When C iii 538 is removed, 2s3s 3S is more populated and C iii 4650 switches from emission to absorption, or shows a stronger absorption.
-
Fe iv 538.057 enhances photon escape in the C iii 538 line, which helps to reduce the population of 2s3s 3S, and thus weakens the C iii 4650 absorption (or enhances the emission).
-
Low temperature dielectronic recombinations have a limited effect on the appearance of C iii 5696 and C iii 4650 in O stars.
-
When the mass loss rate increases, a growing fraction of the C iii 4650 and C iii 5696 lines is formed in the wind, leading to a larger emission. In addition, as Ṁ gets higher, the formation region of the C iii lines (UV and optical) shifts to higher velocities. The associated Doppler shifts lead to desaturation of the key C iii UV lines. This affects the level populations and consequently the intrinsic C iii 4650 and C iii 5696 line profiles. At low mass-loss rates, the change in line profile with a change in the mass-loss rate is not monotonic.
-
Metallicity effects are a complex interplay between C iii UV lines, metallic Fe iv and S v lines, ionization, winds and abundance effects. There is no simple way of predicting how C iii 4650 and C iii 5696 will react to a change of metallicity or abundance of specific elements.
In view of our results, it seems highly risky to derive accurate carbon abundances from C iii 4650 and C iii 5696 in O star atmospheres. Uncertainties of at least a factor of two on C/H are expected just because of the uncertainty on atomic data and wavelengths of metallic lines. Priority should be given to other carbon lines, such as the C iii 2s4f 3Fo-2s5g 3G multiplet at 4070 Å, or even UV lines (C iv 1164 and C iii 1176) provided the wind is not too strong and they are mainly photospheric.
The current results can be used to try to understand the behavior of C iii 4650 in Of?p stars, many (all?) of which are magnetic (Donati et al. 2006; Hubrig et al. 2008; Martins et al. 2010; Wade et al. 2012, 2011). Of?p stars show periodic variability, especially in C iii 4650 emission, which can be as strong as in the neighbouring N iii lines before almost vanishing. Hα shows the same variability and is strongest when C iii is at its maximum emission strength. Sundqvist et al. (2012) demonstrated that the changes in Hα emission of HD 191612 could be understood as a result of viewing the dynamic magnetosphere from different angles.
Due to wind confinement by the magnetic field, an overdense region is created in the magnetic equator. If the star is seen from the magnetic pole, a large surface of the overdense region is observed and the Hα emission is stronger than if the star is seen from the magnetic equator. In the present study, we have seen that C iii 4650 can show emission if the wind contribution becomes dominant, and/or if for some reason the drain effect of C iii 538 is increased so that 2s3s 3S is depopulated. If we observe HD 191612 from the magnetic pole, the wind velocity at a given radius is larger than in the magnetic equator, due to confinement (see Fig. 2 of Sundqvist et al. 2012). The role of the wind is thus stronger, favoring C iii 4650 emission. In addition, since the atmosphere density is lower in the magnetic pole direction, we can expect a larger ionizing flux due to reduced opacity. As seen in our study, this favors the drain of 2s3s 3S through C iii 538, and thus C iii 4650 emission. Hence, the existence of an equatorial overdensity could lead to the observed C iii 4650: more emission when the star is seen pole-on, less emission when it is seen equator-on, just as Hα. Of course, this needs to be tested by detailed 2D radiative transfer calculation, but the present results provide a good working frame.
Online material
Appendix A: Metal line atomic data
Elements and number of levels (super-levels) included in the CMFGEN models.
Table A.1 provides the number of levels and super-levels used in our computations. Basic atomic data for the important transitions that influence C iii 5696 and 4650 are listed in Table A.2. There is some uncertainty in the oscillator strengths, and this must be regarded as a source of uncertainty when modeling the C iii lines. For a comparison we provide an alternative f values that is available in the literature for each transition. Fortunately, for the transitions which significantly influence C iii 5696 and 4650, the wavelengths and/or energy levels for the relevant transition are known. The wavelengths of most of the other transitions tested are (very) uncertain, but potentially could have influenced the modeling because of line overlap. A more worrisome concern is there may be some other important transition which overlaps with one of the key UV transitions, and which has a wrong wavelength (because it has not been measured in the laboratory) or was omitted from the model atoms used in the model atmosphere. The work presented in the current paper, and that of Najarro et al. (2006), highlights the need for accurate Fe wavelengths and oscillator strengths for modeling O star spectra.
Basic line data for the important overlapping transitions.
Appendix B: Effect of metallic lines on C iii 8500
The Grotrian diagram for the C iii singlets (Fig. 2) shows that the C iii 8500 transition should also strongly depend on the efficiency of the C iii 884 and C iii 386 drains since 2s3p 1Po is the upper level of all three transitions. Consequently, any modification of the 2s3p 1Po population will change the C iii 8500 morphology.
In Fig. B.1 we show how this line reacts to the C iii UV lines at Teff = 30 500 K (upper panel) and Teff = 42 000 K (lower panel). As expected, removing the drain from C iii 884 translates into a weaker absorption at low Teff and to emission at high Teff. C iii 386 populates 2s3p 1Po at high Teff and thus removing it leads to absorption in C iii 8500. C iii 690 has also a strong drain effect on 2s3s 1S since removing it leads to a strong absorption. The C iii 8500 transition is of special interest in the context of future observations of O stars by Gaia, since it is basically the only non H/He line in the spectral window of the Radial Velocity Spectrometer onboard the satellite. Understanding its properties is thus important to classify O stars observed by Gaia.
 |
Fig. B.1 Effect of C iii UV lines on the appearance of C iii 8500 for Teff = 30 500 K (top panel) and 42 000 K (lower panel). |
Appendix C: Effect of metallicity on C iii 5696 for Teff = 42 000 K
 |
Fig. C.1 Effect of metallicity on C iii 5696 in the model with Teff = 42 000 K. |
Figure C.1 presents the effect of a change of metallicity on C iii 5696 in the model with Teff = 42 000 K. We show a model with a global reduction of Z by a factor 5 (dashed line) and a model with the same reduction, but in which C/H is kept at the solar value (dotted line). The solid line is the solar metallicity model. A global reduction of Z (including a reduction of C/H) by a factor 5 leads to a significant reduction of the emission in C iii 5696. But a model with Z = 1/5th Z⊙ and a solar carbon content has a C iii 5696 line slightly stronger than the solar metallicity model. The higher ionizing flux at low Z implies a depopulation of 2s3p 1Po and thus more emission. In addition, the reduced effect of Fe iv 574.232, Fe v 386.262 and S v 884.531 tend to increase emission (see Fig. 10). All in all, the conditions are more favorable at low Z, explaining that for a similar C/H, the emission is stronger than at solar metallicity.
Appendix D: An explanation for the influence of the wind on optical C iii 5696 lines
In this section we provide an investigation of the mechanisms responsible for the trend observed in Fig. 20 which shows the effect of mass loss on C iii 4650 and C iii 5696.
We first focus on C iii 5696. Its behavior in the 42 000 K model can be understood as follows. Figure D.1 shows the departure coefficients of the lower and upper levels of C iii 5696 in a model with Ṁ = 4 × 10-7 M⊙ yr-1 (dashed line) and 2 × 10-6 M⊙ yr-1 (solid line). In the low Ṁ model, 88% of the line is formed at log τRosseland > −1.8, corresponding to velocities smaller than 10 km s-1. In that region, the lower level is always less populated than the upper level, a favorable condition for emission. In the high Ṁ model, a significant fraction of C iii 5696 (41%) is formed at velocities higher than 10 km s-1(log τRosseland < −1.2). In the low velocity part of the formation region, the lower level is less populated than the upper level, but above 10 km s-1, the lower level is much more populated. As a result, the global C iii 5696 emission is weaker than in the low Ṁ model. The behavior of C iii 5696 with mass loss observed in the left panel of Fig. 20 is thus a direct consequence of the strengthening of the wind.
 |
Fig. D.1 Effects of mass loss rate on 2s3p 1Po (blue) and 2s3d 1D (red) departure coefficients in a model with Teff = 42 000 K. The dashed (solid) lines corresponds to a model with Ṁ = 4 × 10-7 (2 × 10-6) M⊙ yr-1. The dot-dashed (short dash – long dashed) line is the line formation region in the low (high) Ṁ model. |
 |
Fig. D.2 Effect of mass loss rate on total radiative rates for lines from level 2s3p 1Po (left) and level 2s3d1D (right). The models have Teff = 42 000 K. The upper panels correspond to the model with Ṁ = 2 × 10-6 M⊙ yr-1, the lower panel to models with Ṁ = 4 × 10-7 M⊙ yr-1. |
The behavior of 2s3p 1Po and 2s3d 1D when the wind sets in is explained as follows. Figure D.2 shows the total radiative rates in lines connecting the upper and lower levels of C iii 5696. The rates are shown for two mass loss rates discussed above (4 × 10-7 and 2 × 10-6 M⊙ yr-1). When Ṁ is increased, we see 1) that the rate in the C iii 574 line increases slightly (compared to the rate in C iii 5696) and 2) the rate in C iii 386 shows a slightly more negative excursion at the end of the C iii 5696 line formation region. The net effect is to re-populate 2s3p 1Po and to depopulate 2s3d 1D, leading to a reduced emission. The higher rates in C iii 386 and C iii 574 can be understood as a desaturation effect. Due to the higher mass loss rate, the formation region is shifted toward larger velocities. The associated Doppler shift allows C iii 386 and C iii 574 to absorb more photons from the adjacent continuum, and consequently the radiative rates in those lines are increased. As we have seen in Sect. 4.1, C iii 884 does not play an important role in the formation of C iii 4650 in the high temperature model.
In the 30 500 K model, the increase of the emission when Ṁ strengthens from 3 × 10-8 to 2 × 10-6 M⊙ yr-1 is mainly due to a growing contribution of the wind to the line profile, as at higher temperature. The fraction of the line formed above 10 km s-1 grows from 0.6% for Ṁ = 3 × 10-8 M⊙ yr-1 to 23.5% for Ṁ = 2 × 10-6 M⊙ yr-1. Consequently, the contribution of the wind (emission6) is larger for higher mass loss rates. In addition to this dominant effect, there is also a higher radiative rate in the C iii 884 line in the photosphere (below 10 km s-1). In the same time, the rates in the C iii 386 and C iii 574 lines are not significantly modified compared to the other rates. Desaturation is responsible for the enhanced rate in C iii 884. A lower 2s3p 1Po population results from this, with the consequence of stronger C iii 5696 emission. All in all, a higher mass loss rate leads to a stronger C iii 5696 emission at low Teff.
Wind effects can also explain the behavior of the C iii 4650 triplet in Fig. 20. The higher the mass loss rate, the larger the fraction of the line formed at velocities higher than 10 km s-1. The wind contribution to the line profile increases, implying more emission at high effective temperature and less absorption at low temperature. In addition, at high Teff, the UV lines populating the upper and lower level of C iii 4650 are formed at velocities larger in the high Ṁ model than in the low Ṁ model. They all have positive radiative rates over the line formation region. As a result C iii 538 depopulates 2s3s 3S as soon as Doppler shifts allow the line to absorb more continuum photons. In the same time, C iii 1256, C iii 1428, C iii 1578, C iii 2009 populate 2s3p 3Po. The effect is an increase of the C iii 4650 emission, as observed in Fig. 20.
Data for the opacity project can be obtained from http://cdsweb.u-strasbg.fr/topbase/testop/TheOP.html
The total radiative rate is the difference between the number of radiative transitions from the upper level toward the lower level and the number of radiative transitions from the lower level toward the upper level. It is positive when there is a net decay of electrons from the upper state and negative when there is a net excitation of electrons into the upper state.
For clarity and given the conclusion of our test, we have not shown these transitions in Fig. 2.
Acknowledgments
We thank our referee, Joachim Puls, for a careful reading of the manuscript. F.M. acknowledges support from the Agence Nationale de la Recherche. D.J.H. acknowledges support from STScI theory grants HST-AR-11756.01.A and HST-AR-12640.01. S.T.S.c.I. is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555.
References
- Abbott, D. C., & Hummer, D. G. 1985, ApJ, 294, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, S. R., & Butler, K. 1992, A&A, 265, 647 [NASA ADS] [Google Scholar]
- Becker, S. R., & Butler, K. 1995a, A&A, 294, 215 [NASA ADS] [Google Scholar]
- Becker, S. R., & Butler, K. 1995b, A&A, 301, 187 [NASA ADS] [Google Scholar]
- Berrington, K. A., Burke, P. G., Dufton, P. L., & Kingston, A. E. 1985, Atom. Data Nucl. Data Tables, 33, 195 [Google Scholar]
- Bouret, J.-C., Hillier, D. J., Lanz, T., & Fullerton, A. W. 2012, A&A, 544, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busche, J. R., & Hillier, D. J. 2005, AJ, 129, 454 [NASA ADS] [CrossRef] [Google Scholar]
- Conti, P. S. 1974, ApJ, 187, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Howarth, I. D., Bouret, J.-C., et al. 2006, MNRAS, 365, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Gauzit, J. 1966, C.R., 258, 1309 [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, Space Sci. Rev., 130, 105 [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Schöller, M., Schnerr, R. S., et al. 2008, A&A, 490, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R. P., Pauldrach, A., Puls, J., & Abbott, D. C. 1989, A&A, 219, 205 [NASA ADS] [Google Scholar]
- Kurucz, R. L. 2009, in AIP Conf. Ser. 1171, eds. I. Hubeny, J. M. Stone, K. MacGregor, & K. Werner, 43 [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Donati, J., Marcolino, W. L. F., et al. 2010, MNRAS, 407, 1423 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Escolano, C., Wade, G. A., et al. 2012, A&A, 538, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Najarro, F., Hillier, D. J., Puls, J., Lanz, T., & Martins, F. 2006, A&A, 456, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nussbaumer, H. 1971, ApJ, 170, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Przybilla, N., Firnstein, M., Nieva, M. F., Meynet, G., & Maeder, A. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ralchenko, Y., Kramida, A. E., Reader, I., & NIST ASD Team 2012, version 4, NIST Atomic Spectra Database, version 3.1.5 [Google Scholar]
- Rivero Gonzalez, J. G., Puls, J., & Najarro, F. 2011, A&A, 536, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., & de Koter, A. 1997, A&A, 322, 598 [NASA ADS] [Google Scholar]
- Seaton, M. J. 1987, J. Phys. B Atom. Molecul. Phys., 20, 6363 [Google Scholar]
- Smith, L. F. 1973, in Wolf-Rayet and High-Temperature Stars, eds. M. K. V. Bappu, & J. Sahade, IAU Symp., 49, 15 [Google Scholar]
- Smith, L. J., & Willis, A. J. 1982, MNRAS, 201, 451 [NASA ADS] [Google Scholar]
- Sundqvist, J. O., ud-Doula, A., Owocki, S. P., et al. 2012, MNRAS, 423, L2 [NASA ADS] [CrossRef] [Google Scholar]
- van Regemorter, H. 1962, ApJ, 136, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Howarth, I. D., Townsend, R. H. D., et al. 2011, MNRAS, 416, 3160 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, G. A., Grunhut, J., Gräfener, G., et al. 2012, MNRAS, 419, 2459 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1980, ApJS, 44, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Sota, A., Maíz Apellániz, J., et al. 2010, ApJ, 711, L143 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spectra of C iii 5696 illustrating the dramatic dependence of the line profile on surface gravity and effective temperature. The left panel is for Teff = 30 500 K while the right panel is for Teff = 42 000 K. Particularly striking is the strong dependance of the profile on log g, and that this dependance is of opposite sign in models of different effective temperature. |
| In the text | |
 |
Fig. 2 Simplified Grotrian diagram for the singlet system of C iii. The C iii 5696 transition is indicated in red. |
| In the text | |
 |
Fig. 3 Effect of the C iii UV lines on the formation of C iii 5696. Left: initial C iii 5696 spectrum (solid) and spectra from models in which several C iii UV lines have been artificially removed. Right: departure coefficient of the C iii 5696 lower and upper levels in the initial model (solid lines), the model without C iii 884 Å (dashed lines) and the model without C iii 574 Å (dotted lines). Departure coefficients are plotted as a function of Rosseland opacity. The dot-dashed line at the bottom indicates the C iii 5696 formation region expressed in terms of the contribution function as a function of τRosseland. |
| In the text | |
 |
Fig. 4 Same as left panel of Fig. 3 for the model with Teff = 42 000 K. |
| In the text | |
 |
Fig. 5 Effect of log g on the formation of C iii 5696 for Teff = 30 500 K. Left: total radiative rates out of level 2s3p 1Po at log g = 3.25 (upper panel) and log g = 3.75 (lower panel) as a function of Rosseland opacity. Notice how the largest rate is for λ 884, and that this rate shows a qualitatively different behavior in the two models. The dotted lines indicate the C iii 5696 line formation region. Right: total radiative rates out of level 2s3d 1D at log g = 3.25 (upper panel) and log g = 3.75 (lower panel). |
| In the text | |
 |
Fig. 6 Effect of log g on departure coefficients. Departure coefficients are plotted as a function of Rosseland opacity for the levels on C iii 5696 (upper panel) and for the fundamental level (2s2 1S) and the lower level of C iii 884 (2p2 1D). The dotted line shows the C iii 5696 line formation region. |
| In the text | |
 |
Fig. 7 Same as Fig. 5 but for a model with Teff = 42 000 K and log g = 3.5 and 4.0. |
| In the text | |
 |
Fig. 8 Effect of low temperature dielectronic recombination (LTDR) on C iii 5696 in the models with Teff = 30 500 K (upper panel) and 42 000 K (lower panel). The red solid curve shows the standard model profile, while the blue dashed profile shows the effect of “double counting” the influence of LTDR. The green dot-dashed line is the standard model in which the LTDR from levels forbidden to autoionize in LS coupling have been omitted. |
| In the text | |
 |
Fig. 9 Effect of the microturbulent velocity on the C iii 5696 emission strength in three CMFGEN models. The microturbulent velocity has been changed only in the atmosphere computation. The spectra have all been computed with vturb increasing from 10 to 200 km s-1 throughout the wind. |
| In the text | |
 |
Fig. 10 Effect of metallic lines on C iii 5696. The solid line is the initial spectrum. The dashed line is a model in which the oscillator strength of Fe v 386.262 Å is artificially reduced by a factor 10 000. The dot-dashed (dotted) line is the initial model in which Fe iv 574.232 Å (S V 884.531 Å) is reduced by the same factor. |
| In the text | |
 |
Fig. 11 Effect of a change in the oscillator strength of Fe iv 574.232 Å on the departure coefficient (plotted as a function of Rosseland opacity) of the levels of the C iii 5696 transition. The red curves correspond to the upper level and the blue ones to the lower level. The solid lines are for the initial model. The dashed lines are the level populations in the model with a reduced Fe iv 574.232 line. The dotted line is the C iii 5696 formation region. |
| In the text | |
 |
Fig. 12 Effect of the Fe iv 574.232 Å line on the total radiative rates of several transitions. The solid lines are for the initial model, the dashed lines for the model in which the iron transition has been removed in the atmosphere calculation. The dotted line indicates the C iii 5696 line formation region in the initial model. |
| In the text | |
 |
Fig. 13 Effect of the metallicity Z on the formation of C iii 5696 at Teff = 30 500 K. Left: spectra of C iii 5696 at Z⊙ (solid), 1/5th Z⊙ (dashed) and 1/5th Z⊙ but with C/H at the solar value (dotted). Right: departure coefficient of the C iii 5696 lower and upper levels at Z⊙ (solid lines), 1/5th Z⊙ (dashed lines) and 1/5th Z⊙ with C/H at the solar value (dotted). The dot-dashed line indicates the line formation region. |
| In the text | |
 |
Fig. 14 Simplified Grotrian diagram for the triplet system of C iii. The C iii 4647-50-51 transitions are shown in red. The star symbols indicate multiplets. |
| In the text | |
 |
Fig. 15 Effect of C iii UV lines on C iii 4647–50–51 in the model with Teff = 30 500 K (upper panel) and 42 000 K (lower panel). The solid line is the initial model. The other lines are models in which a given C iii UV line has been removed by reducing its oscillator strength by a factor 10 000. |
| In the text | |
 |
Fig. 16 Effect of log g on C iii 4647–50–51. Left panel: the red line is a model with log g = 3.5; the blue line is the same model with log g = 4.0. The effective temperature is 42 000 K. Right panel: departure coefficient of the upper and lower levels of C iii 4647–50–51 (upper panel) and of levels 2s2 1S (n = 1), 2s2p 3Po (n = 2,3,4), 2p2p 3D (n = 6,7,8) (lower panel) for log g = 3.5 (solid line) and log g = 4.0 (dashed line), plotted as a function of Rosseland opacity. The dotted line is the C iii 4650 formation region. |
| In the text | |
 |
Fig. 17 Synthetic spectra around the C iii 4650 triplet in models with Teff = 30 500 K. The red line is the initial model. The blue line is the same model in which we have removed the C iii 538 Å line. The green model is the same as the initial model in which the Fe iv 538.057 Å line has been removed. |
| In the text | |
 |
Fig. 18 Effect of metallicity on the C iii 4650 triplet at 30 500 K (left) and 42 000 K (right). The solid line is a solar metallicity model. The dashed line is a model with Z = 1/5th Z⊙. The dotted line is the same model as the dashed line model but with a solar C/H. |
| In the text | |
 |
Fig. 19 Effect of C/H on the intensity of C iii 4650 (left) and C iii 5696 (right) at Teff = 30 500 K. In both panels, the solid line is a solar metallicity model. The dashed (dotted) line is a model with C/H = 1/2 (1/5) C/H⊙, all other elements having the solar abundances. In the left (right) panel, the dot-dashed line is the C/H = 1/2 C/H⊙ model in which the Fe iv 538.057 (574.232) line has been removed. |
| In the text | |
 |
Fig. 20 Effects of a change in the mass loss rate on C iii 4650 and C iii 5696 in models with Teff = 30 500 K (left) and Teff = 42 000 K (right). The mass loss rates (in M⊙ yr-1) are indicated in the C iii 5696 panels. |
| In the text | |
 |
Fig. B.1 Effect of C iii UV lines on the appearance of C iii 8500 for Teff = 30 500 K (top panel) and 42 000 K (lower panel). |
| In the text | |
 |
Fig. C.1 Effect of metallicity on C iii 5696 in the model with Teff = 42 000 K. |
| In the text | |
 |
Fig. D.1 Effects of mass loss rate on 2s3p 1Po (blue) and 2s3d 1D (red) departure coefficients in a model with Teff = 42 000 K. The dashed (solid) lines corresponds to a model with Ṁ = 4 × 10-7 (2 × 10-6) M⊙ yr-1. The dot-dashed (short dash – long dashed) line is the line formation region in the low (high) Ṁ model. |
| In the text | |
 |
Fig. D.2 Effect of mass loss rate on total radiative rates for lines from level 2s3p 1Po (left) and level 2s3d1D (right). The models have Teff = 42 000 K. The upper panels correspond to the model with Ṁ = 2 × 10-6 M⊙ yr-1, the lower panel to models with Ṁ = 4 × 10-7 M⊙ yr-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


