| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 11 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201219349 | |
| Published online | 23 July 2012 | |
The Australia Telescope Large Area Survey: 2.3 GHz observations of ELAIS-S1 and CDF-S
Spectral index properties of the faint radio sky⋆
1 Astronomical Institute of Ruhr-University Bochum, Universitätsstraße 150, 44801 Bochum Germany
e-mail: zinn@astro.rub.de
2 CSIRO Astronomy & Space Science, PO Box 76, Epping, NSW 1710, Australia
3 Sydney Institute for Astronomy, School of Physics, The University of Sydney, NSW 2006, Australia
4 Australian Astronomical Observatory, PO Box 296, Epping, NSW 1710, Australia
5 School of Mathematics & Physics, University of Tasmania, Private Bag 37, 7001 Hobart, Australia
Received: 5 April 2012
Accepted: 22 June 2012
Context. The Australia Telescope Large Area Survey (ATLAS) aims to image a 7 deg2 region centred on the European Large Area ISO Survey – South 1 (ELAIS-S1) field and the Chandra Deep Field South (CDF-S) at 1.4 GHz with high sensitivity (up to σ ~ 10 μJy) to study the evolution of star-forming galaxies (SFGs) and Active Galactic Nuclei (AGN) over a wide range of cosmic time.
Aims. We present here ancillary radio observations at a frequency of 2.3 GHz obtained with the Australia Telescope Compact Array (ATCA). The main goal of this is to study the radio spectra of an unprecedented large sample of sources (~2000 observed, ~600 detected in both frequencies).
Methods. With this paper, we provide 2.3 GHz source catalogues for both ATLAS fields, with a detection limit of 300 μJy (equivalent to 4.5σ in the ELAIS-S1 field and 4.0σ in the CDF-S). We compute spectral indices between 1.4 GHz and 2.3 GHz using matched-resolution images and investigate various properties of our source sample in dependence of their spectral indices.
Results. We find the entire source sample to have a median spectral index αmed = −0.74, in good agreement with both the canonical value of −0.7 for optically thin synchrotron radiation and other spectral index studies conducted by various groups. Regarding the radio spectral index as indicator for source type, we find only marginal correlations so that flat or inverted spectrum sources are usually powered by AGN and hence conclude that at least for the faint population the spectral index is not a strong discriminator. We investigate the z–α relation for our source sample and find no such correlation between spectral index and redshift at all. We do find a significant correlation between redshift and radio to near-infrared flux ratio, making this a much stronger tracer of high-z radio sources. We also find no evidence for a dependence of the radio-IR correlation on spectral index.
Key words: galaxies: active / catalogs / galaxies: evolution / radio continuum: galaxies / surveys
Full Table 2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/544/A38
© ESO, 2012
1. Introduction
Large-scale radio surveys are the primary instrument in the toolbox of contemporary astronomy to investigate demography and evolution of active galaxies across cosmic time. Consequently, there have been numerous attempts to use this tool, whether in a wide, shallow layout (e.g. the National Radio Astronomy Observatory Very Large Array Sky Survey, Condon et al. 1998) or in a deep, but more pencil beam-like layout such as for the Cosmic Evolution Survey (COSMOS, Schinnerer et al. 2010) or even the Lockman Hole survey by Owen & Morrison (2008), the most sensitive radio observation to date.
The Australia Telescope Large Area Survey (ATLAS, Norris et al. 2006; Middelberg et al. 2008) attempts to break this dichotomy by obtaining deep images (σ ~ 10 μJy in the final data release 3) over an unprecedented large area of sky. Distributed over the well-studied Chandra Deep Field South (CDF-S) and the European Large Area ISO Survey – South 1 (ELAIS-S1) field, the total area covered by ATLAS is approximately seven square degrees. This allowsus to study the faint radio sky without being affected by cosmic variance (Moster et al. 2011). Furthermore, the wealth of ancillary photometric data ranging across the entire electromagnetic spectrum (e.g. from SWIRE, COMBO-17 or GEMS Lonsdale et al. 2003; Wolf et al. 2003; Rix et al. 2004) as well as numerous spectroscopic campaigns (Sacchi et al. 2009; Popesso et al. 2009; Balestra et al. 2010; Mao et al. 2012) enables one to conduct detailed studies of radio-detected objects.
In this paper, we focus on radio spectral properties of the ATLAS source sample. The main ATLAS data releases are DR 1 by Norris et al. (2006) and Middelberg et al. (2008), DR 2 by Hales et al. (in prep.), and DR 3 by Banfield et al. (in prep.). These data consistof 1.4 GHz observations as for most contemporary radio surveys, and we here supplement these data with observations at 2.3 GHz. The main goal of this is to calculate spectral indices 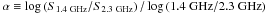 for all sources detected at both wavelength and so to characterise their radio emission mechanism, source type and dependence on other spectral quantities. Even though many blind surveys of extragalactic radio sources are available already, only few studies have been carried out which characterise the radio spectra of a large source population by means of their spectral index. For example, Bondi et al. (2007) and Ibar et al. (2009) use supplementary 610 MHz data to calculate spectral indices at frequencies below 1.4 GHz with the main aim to identify steep spectrum sources which are regarded as good candidates for being high-redshift objects (see Sect. 4.3). The most comprehensive study of spectral indices between 1.4 GHz and a higher frequency was conducted by Prandoni et al. (2006) using 5 GHz Very Large Array (VLA) data in the Australia Telescope ESO Slice Project survey field. With a sensitivity of ~70 μJy over an area of one square degree, their source sample consists of approximately 100 objects which are detected at both frequencies, so our sample exceeds this by a factor of six.
for all sources detected at both wavelength and so to characterise their radio emission mechanism, source type and dependence on other spectral quantities. Even though many blind surveys of extragalactic radio sources are available already, only few studies have been carried out which characterise the radio spectra of a large source population by means of their spectral index. For example, Bondi et al. (2007) and Ibar et al. (2009) use supplementary 610 MHz data to calculate spectral indices at frequencies below 1.4 GHz with the main aim to identify steep spectrum sources which are regarded as good candidates for being high-redshift objects (see Sect. 4.3). The most comprehensive study of spectral indices between 1.4 GHz and a higher frequency was conducted by Prandoni et al. (2006) using 5 GHz Very Large Array (VLA) data in the Australia Telescope ESO Slice Project survey field. With a sensitivity of ~70 μJy over an area of one square degree, their source sample consists of approximately 100 objects which are detected at both frequencies, so our sample exceeds this by a factor of six.
According to Komatsu et al. (2011), we adopt a flat ΛCDM cosmology with H0 = 70.2 km s-1 Mpc-1 and ΩΛ = 0.725 throughout this paper.
2. Observations and imaging
In the following description, we give the actual numbers for all things concerning the ELAIS-S1 field first, followed by the numbers for the CDF-S in parentheses. If there is only a single number given, it is approximately equal for both fields. Observations at 2.3 GHz for the ATLAS fields were carried out between December 2006 and March 2007 on 52 separate days where the ATCA was only in its 750B and 750C configurations. This resulted in a substantially lower resolution than at 1.4 GHz since the longest baselines used for imaging at 2.3 GHz was 750 m, or 5.7 kλ, resulting in an angular resolution of 33″ (57″), compared to 30 kλ at 1.4 GHz. The ATCA primary beam at a frequency of 2.3 GHz has a FWHM of 21 arcmin, therefore 76 (88) overlapping pointings were observed in a hexagonal lattice with an average integration time of 6.17 h (4.13 h) per pointing (compared to approx. 12 h per pointing for the 1.4 GHz image) to cover the entire area of the 1.4 GHz maps.
For phase calibration, which was done approximately every 45 min, PKS 0022-423 (PKS 0237-233) was observed as secondary calibrator. Flux calibration was done for both fields using PKS 1943-638 which was observed at least once a day for 10 min. As for 1.4 GHz, the ATCA provides two independent frequency bands with a bandwidth of 128 MHz divided into 33 channels. During the first two days of observations for the ELAIS-S1 field, the two bands were centred at 2.368 GHz and 2.560 GHz in an attempt to reduce local Radio Frequency Interference (RFI). The fluxes density of the primary calibrator, PKS 1934-638, was assumed to be 11.589 Jy and 10.932 Jy, respectively. Because using a higher frequency for the upper band did not significantly decrease the RFI, the remaining time was observed with the standard band configuration, meaning that the upper band was lowered in central frequency to 2.496 GHz. There, the primary calibrator was assigned to have a flux density of 11.138 Jy. We note that the final images were made with the entire data set.
The calibration of the data were carried out using standard Miriad (Sault et al. 1995) tasks. ATLOD was used to convert the raw data from RPFITS format to the native Miriad format. For the further calibration, both channels at the end of the bands were discarded due to a significant lack of sensitivity, hence a data set containing two times 13 channels with 8 MHz bandwidth each was obtained, yielding a net bandwidth of 208 MHz. Fortunately, our data do not suffer from self-interference typical for the ATCA. These so-called “birdies” occur within the samplers at integer multiples of 128 MHz. The 19th harmonic at 2.432 GHz fortunately lies exactly between our two bands and therefore does not affect our data. After bandpass-calibration, RFI was removed using Pieflag (Middelberg 2006), a tool that compares statistics from channels with no or little RFI contamination to the other channels in the data and looks for outliers and sections with high noise. Bandpass calibration was carried out using the observations of PKS 1934-638. Phase calibration was done using the regular scans of the secondary calibrators, and then amplitude calibration was carried out using PKS 1934-638. The data were split into the individual pointings which were imaged separately using uniform weighting. This provides a higher resolution at the cost of lower sensitivity than natural weighting. The cell size was set to 6″ (3″). Because of the low fractional bandwidth (<10%), a normal CLEAN procedure was used (in contrast to the Miriad multi-frequency clean implementation MFCLEAN for the 1.4 GHz data) for deconvolution. Also the dynamic range in the pointings was sufficiently low as to not require any special deconvolution procedures. Cleaning was carried out using 2000 iterations, after which only marginal sidelobes around the two strongest sources remained, and the effects of clean bias should be negligible. After cleaning, the models were convolved with a restoring beam of 33.56″ × 19.90″ (57.15″ × 22.68″) at a position angle of − 1.32 deg ( − 1.90 deg). The final mosaics were produced using Miriad’s LINMOS task to account for primary beam attenuation and overlapping regions of the individual pointings. As a result, the edges of the final images exhibit a significantly higher noise level than the central regions (see Fig. 1).
 |
Fig. 1 2.3 GHz noise maps of both ATLAS fields: CDF-S (left) and ELAIS-S1 (right). Contours start at 70 μJy beam-1 (dark blue contour line) and increase by a constant value of 40 μJy beam-1. |
3. The source catalogue
Source extraction from the final 2.3 GHz images was performed in two steps: first, all known 1.4 GHz sources from ATLAS DR 2 (Hales et al., in prep.) were used as an input catalogue to search for 2.3 GHz counterparts. This catalogue contains a total of 2240 individual 1.4 GHz sources across both the ELAIS-S1 and the CDF-S of which 631 could be reliably detected at 2.3 GHz. To identify these counterparts, the 2.3 GHz image was inspected by eye at the location of every individual 1.4 GHz source. This was done by half-automatically browsing through an input catalogue, simultaneously displaying the corresponding regions in the 1.4 GHz and 2.3 GHz images and, if a 2.3 GHz counterpart was found, fitting a Gaussian to it and recording all fit parameters in an output catalogue. Thus, no blind search was conducted at 2.3 GHz, allowing the inclusion of sources fainter than the typical 5σ cutoff in the catalogue. The lowest signal-to-noise ratio among the 2.3 GHz sources is 3.9.
In a second step, we checked for “2.3 GHz-only” sources. Those sources are unlikely to occur because of the noise levels of the 1.4 GHz and 2.3 GHz images. Since the faintest 1.4 GHz sources in the DR 2 catalogue are as faint as 100 μJy, whereas the faintest sources in 2.3 GHz are three times brighter, a 2.3 GHz-only source would have a highly inverted spectral index of α ≥ 2.4. Also, we note that, due to the temporal offsets between the 1.4 GHz and 2.3 GHz observations, possible variability of some radio sources may lead to flawed spectral indices. Nevertheless, we used MIRIAD’s SAD task to automatically produce a 2.3 GHz catalogue with a detection threshold of 5σ and matched the sources obtained that way to the 2.3 GHz catalogue obtained by cross-matching to 1.4 GHz sources. All sources identified by SAD could be matched to sources previously found as 1.4 GHz counterparts, hence not a single 2.3 GHz-only source was found.
Parameters of the observations.
To compute spectral indices, the flux densities in 1.4 GHz had to be re-measured because the resolutions of the 1.4 GHz and 2.3 GHz images differ significantly. Whilst the 1.4 GHz observations included long baseline configurations of the ATCA (e.g. the 6A and 6B configurations), the 2.3 GHz observations were obtained with the ATCA in 750B and 750C configurations only. This leads to a resolution three to five times lower at 2.3 GHz compared to the ~10″ resolution of the 1.4 GHz observations, despite the shorter wavelength. Therefore, in order to avoid resolution effects, we convolved the original 1.4 GHz images with a Gaussian kernel to match the resolution of the 2.3 GHz images as given in Table 1. We then used the ATLAS DR 2 catalogue again as input to re-measure the 1.4 GHz flux densities in the low-resolution images. Because the image sensitivity was reduced by a factor of ~2 by this convolution (which is equal to tapering the data in the uv-plane, so in fact weighting down long baselines), all sources in the low-resolution image should be a true subset of the hi-res sources and, therefore, all low-resolution sources should be detected when using the high-resolution catalogue as input sample.
During the re-measurement of the 1.4 GHz flux densities using convolved images, a problem surfaced with the ELAIS-S1 image. Unlike with the CDF-S convolved 1.4 GHz image, where the procedure outlined above went well, the MIRIAD task imfit overestimated the flux densities by a significant amount (up to 50%). This became obvious by inspecting residual images for sources with various flux densities and degrees of compactness. While the residuals looked good in the CDF-S, they showed bowls of negative flux in the ELAIS-S1 image. The cause of the effect remains unclear. The fitting routines in the software package CASA (Jaeger 2008) yielded similarly overestimated flux densities, so it appears that the effect is not caused by the fitting software, but is inherent in the images, and we had to work around this issue. This was done by iteratively fitting Gaussians to every individual source. The first Gaussian fit (which was always overestimating the flux density) was used as prior. The resulting residual image was then examined in terms of total flux and rms noise. If the total flux in the residual image (trimmed to a size twice as large as the restoring beam) was negative and the rms noise was deviating from the median rms in the region of the source by more than 10%, the fit was discarded and replaced by a fit with a peak flux density 2% lower than in the previous fit. The residual image was again examined in a similar way. This procedure was iteratively repeated until the criteria (non-negative total flux and rms noise consistent with the rms in this region) were entirely met. As a last step, all final residual images were inspected by eye to assure the quality of the fit.
A further problem in calculating spectral indices for every 1.4 GHz was introduced by the very different resolutions of the 1.4 GHz and 2.3 GHz observations. Because the resolutions differ by a large factor, as explained above, numerous sources which are clearly separated in the high-res images are blended together in the low-res images. Therefore, we chose to completely exclude such blended sources from our final catalogue if they could not be separated by simultaneously fitting two or more Gaussians. We note that this may bias our sample towards fainter sources since classic radio doubles (which are mainly excluded by the blending) are generally brighter than single, isolated sources.
The final catalogue was then constructed by merging the individual catalogues from ELAIS-S1 and CDF-S. This resulted in a final catalogue comprising 631 radio sources with clear detections and well-measured flux densities in both 1.4 GHz and 2.3 GHz. A portion of the catalogue is shown in Table 2 for illustration.
A representative portion of the ATLAS 2.3 GHz source catalogue of the ELAIS-S1 field for illustration purposes. The CDF-S catalogue contains the same information.
We give an identifier for each source, the position, the original 1.4 GHz flux density as measured by Hales et al. (in prep.), the re-measured 1.4 GHz flux density using the convolved image, the 2.3 GHz flux density as measured during the cross-matching process and finally the spectral index calculated from the matched-resolution 1.4 GHz and 2.3 GHz flux densities. All flux densities are integrated quantities.
Errors for the flux densities were either taken from Hales et al. (in prep.) in case of the original 1.4 GHz flux densities or calculated following Hopkins et al. (2003) for the low-resolution 1.4 GHz flux densities and the 2.3 GHz flux densities, taking into account both the local rms noise at the source position as well as the quality of the Gaussian fit:  (1)where μimage quantifies the uncertainty in flux density due to the image noise and μfit represents uncertainties due to the fitting of a Gaussian. These two quantities can be calculated following Windhorst et al. (1984),
(1)where μimage quantifies the uncertainty in flux density due to the image noise and μfit represents uncertainties due to the fitting of a Gaussian. These two quantities can be calculated following Windhorst et al. (1984), 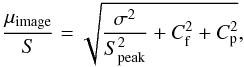 (2)where σ is the local rms noise, Cf the error in absolute flux calibration and Cp the error in flux due to eventual pointing errors. We here adopt a conservative value of
(2)where σ is the local rms noise, Cf the error in absolute flux calibration and Cp the error in flux due to eventual pointing errors. We here adopt a conservative value of 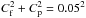 . The fitting error is calculated following Condon (1997),
. The fitting error is calculated following Condon (1997), 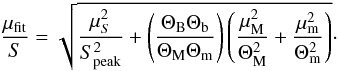 (3)Here, ΘBΘb are the restoring beam’s major and minor axes, whereas ΘMΘm represent the major and minor axes of the fitted Gaussian. The errors μS,μM and μm stand for the errors of the fitted Gaussian’s peak flux, major and minor axes. The error of the spectral index was finally calculated using simple Gaussian error propagation,
(3)Here, ΘBΘb are the restoring beam’s major and minor axes, whereas ΘMΘm represent the major and minor axes of the fitted Gaussian. The errors μS,μM and μm stand for the errors of the fitted Gaussian’s peak flux, major and minor axes. The error of the spectral index was finally calculated using simple Gaussian error propagation,  (4)where the factor of 2 ≈ | [ log (1.4 GHz/2.3 GHz)·ln(10)] -1 | arises from deriving the spectral index as defined in Sect. 1 with respect to the flux densities, which are the only quantities with uncertainties in this equation (the error in frequency is neglected).
(4)where the factor of 2 ≈ | [ log (1.4 GHz/2.3 GHz)·ln(10)] -1 | arises from deriving the spectral index as defined in Sect. 1 with respect to the flux densities, which are the only quantities with uncertainties in this equation (the error in frequency is neglected).
Histograms illustrating the distribution of flux densities in the final catalogues are shown in Fig. 2, the relative flux density errors as a function of flux density are presented in Fig. 3. Further spectral index properties are investigated in the next section.
 |
Fig. 2 Distribution of 1.4 GHz (hi-res) and 2.3 GHz flux densities in the final catalogue. AGN classifications of the sources are from Mao et al. (2012). |
 |
Fig. 3 The fractional flux density errors for all ELAIS-S1 and CDF-S sources as function of their flux density. The solid red line indictates how the fractional error should decrease with increasing flux density in an image with an overall rms noise of 70 μJy according to Eq. (2). A calibration error of 5% is assumed. |
4. Spectral index properties
The distribution of spectral indices for our sample of 631 1.4 GHz sources with unambiguously identified 2.3 GHz counterpart is shown in Fig. 4.
 |
Fig. 4 Distribution of 1.4 GHz to 2.3 GHz spectral indices in the final catalogue for all sourceswith unambiguously detected 2.3 GHz counterpart and both the 1.4 GHz and 2.3 GHz flux densities exceeding 0.3 mJy. AGN classifications of the sources are from Mao et al. (2012). |
With a median spectral index of −0.74 our sample matches the canonical value for synchrotron radiation of −0.7 very well. However, we note that the distribution is broad with a median absolute deviation of 0.35. We here use the median absolute deviation defined as MAD ≡ mediani(|xi − medianj(xj) | ) as a measure for the spread of a distribution since it is more robust against outliers than, for instance, the normal standard deviation, σ. In case of a perfect Gaussian distribution, σ and MAD are related via σ ≈ 1.4826 MAD. This also compares nicely to other studies such as Prandoni et al. (2006) whose sample has MAD = 0.33. The spread of the Ibar et al. (2009) sample is slightly smaller with MAD = 0.27. This difference is due to the larger number of sources with flat or inverted spectra in our sample. We repeated the analysis including upper limits (following the survival analysis techniques developed in Feigelson & Nelson 1985) for all 1.4 GHz sources which do not have a 2.3 GHz counterpart and are not affected by resolution effects (see Sect. 3). These sources do have a 2.3 GHz flux density less than three times the rms noise at the respective position. The median spectral index then becomes slightly steeper with −0.81 and a MAD of 0.38. The main reason for only having this slight change is the large difference between the 1.4 GHz sensitivity (about 30 μJy) and the 2.3 GHz sensitivity (70−80 μJy). The number of sources detected at both 1.4 GHz and 2.3 GHz is 631 whereas there are 552 sources with an unambiguous upper limit at 2.3 GHz. We note that the errors of our spectral indices become quite large for low flux densities. This is because currently available radio data and the flux densities extracted from them have typical uncertainties at the 10% level. This is mostly due to either inhomogeneous data processing and calibration strategies as well as the widely adopted method of fitting 2-dimensional Gaussians to extract flux densities (see e.g. Condon 1997). Future large-scale continuum surveys, such as ASKAP/EMU, are attempting to reach flux density errors of only 1% by developing both novel, fully automated calibration as well as source extraction techniques (Norris et al. 2011b).
4.1. Spectral index vs. flux density
A plot of the spectral index of our sources against their flux density is shown in Fig. 5. We point out that the sensitivities of our 1.4 GHz and 2.3 GHz data differ by a factor of about 3. Therefore, progressively negative spectral indices cannot be measured anymore towards fainter 1.4 GHz fluxes (as indicated by the black dashed line in Fig. 5). For instance, a source with S1.4 GHz = 200 μJy can only have a 2.3 GHz counterpart when exhibiting a spectral index ≳0.5 since the 3σ detection level of our 2.3 GHz data is about 250 μJy (see Sect. 2). To account for this fact, we also included upper limits on spectral index for all 1.4 GHz sources that unambiguously show no 2.3 GHz counterpart (the upper limits were calculated using S2.3 GHz < 3σ where σ is the local rms noise for a point source) and are not affected by resolution issues (see Sect. 3, e.g. a close double in 1.4 GHz that would be inseparable at the 2.3 GHz resolution). With these upper limits, we calculated median spectral indices for different flux density bins to investigate a potential flattening of the mean spectral index towards fainter flux densities. As expected, the median spectral indices for only the detected sample (so the 631 sources with 2.3 GHz counterparts) show a clear trend of flatter spectral indices with lower flux density (Fig. 5, blue circles). Including the upper limits into the median calculation, this trend vanishes immediately (Fig. 5, blue diamonds): the lowest flux density bin (about 300 − 600 μJy) is completely dominated by the upper limits and can hence not be included in further analysis whereas the two flux density bins at 700 μJy and 1 mJy are now a even a little steeper than the ones at higher flux densities. Hence, we find no evidence for a flattening of the spectral index towards the lowest flux densities. This is consistent with the findings by Randall et al. (2012) who used three frequencies (840 MHz, 1.4 GHz and 2.3 GHz) for their spectral index calculation and extend their findings to fainter flux limits. Ibar et al. (2009) come to the same conclusion, too.
 |
Fig. 5 Spectral index vs. flux density. The grey 2D histogram shows our sample of 631 sources with 1.4 GHz and 2.3 GHz detections. Since the sensitivity of the 2.3 GHz observations is ~3 times lower than that of the 1.4 GHz data, the black dashed line indicates the minimum spectral index that could be measured with our data. Therefore, the median spectral indices (blue circles, x-error bars indicate the flux density bin size, y-error bars correspond to the MAD) for just the 2.3 GHz detected sample show significantly flatter values towards lower flux densities. When including also upper limits from the 2.3 GHz non-detected sources, this trend completely vanishes (blue diamonds). Hence we conclude that there is no evidence for a flattening of the mean spectral index with lower flux density. |
A flattening of the spectral index with lower flux density levels, as e.g. seen by Zhang et al. (2003), was initially suspected by Windhorst et al. (1993). A major line of argument is that, at sub-mJy levels, a change in population takes place: at mJy levels, the radio sky is completely dominated by AGN (see e.g. Padovani et al. 2011), so the dominant emission mechanism is non-thermal synchrotron radiation. An intrinsically flatter spectrum would e.g. be produced by dominating emission due to thermal bremsstrahlung, but this makes up only a marginal fraction even in starburst galaxies (see Condon 1992). In addition, recent work by several authors indicate that the transition from AGN-dominated to SF-dominated radio sources takes place below a flux density of 100 μJy. For instance, Padovani et al. (2011) argue that AGN still dominate the source population down to 100 μJy and Smolčić et al. (2008) claim that the fraction of SF-powered radio sources has a nearly constant value of about 40% for flux levels between 50 μJy and 700 μJy. A similar result is obtained by Seymour et al. (2008) investigating the differential number counts in the 13 Hour XMM-Newton/Chandra Deep Field Survey. Hence, this change in the faint radio population cannot account for our findings since we do not reach such faint flux density levels.
With our catalogue of 631 sources with spectral indices, we now focus on the application of the spectral index in terms of its predictive quality. Since it is a quantity which is relatively easy to measure, the spectral index would be a useful tool to characterise sources in large-scale surveys, if a dependence on other properties of interest such as source type, redshift or other scaling relations can be established.
4.2. Spectral indices as object type discriminator
The radio spectral index is commonly regarded as a possible tool for discriminating different radio source types, hence emission mechanisms. For instance, Huynh et al. (2007) select AGN basedon the assumption that, at low frequencies, only AGN can produce flat or inverted spectral indices because of self-absorption in an optically thick medium. Hence they propose a cut between α = −0.3 and α = 0 to classify sources as AGN.
With our source sample, we can examine this classification scheme. We cross-matched all our sources with and without unambiguous 2.3 GHz counterpart to the spectral classifications for ATLAS sources by Mao et al. (2012). This cross-match lead to 132 resultant sources of which we can identify 22 SF galaxies and 98 AGN among our sample with measured spectral indices. The remainder 12 sources could either not be reliably classified by means of their optical spectrum (4 sources), or they only have spectral index upper limits (5 AGN, 3 SF galaxies). We suspect that the reason for most spectroscopically classified sources having actual spectral index measurements is due to the fact that the target sources for spectroscopy were chosen such that stronger radio sources were favoured against weaker ones. Therefore, the spectroscopically classified sample shows a significantly higher mean flux density at 1.4 GHz so that most of these sources are detected at 2.3 GHz, too. Hence, since the vast majority of cross-identifications both have reliable spectral classifications and accurately measured spectral indices, we chose to omit the few sources that miss some information and proceed with these 120 sources. A histogram showing the distribution of spectral indices among those 120 sources is presented in Fig. 6.
 |
Fig. 6 Histogram illustrating the distribution of spectral indices of spectroscopically classified AGN and SF galaxies. |
As one can clearly see, the AGN population shows significantly flatter spectral indices than the SF galaxies with median values of −0.63 for AGN and − 0.85 for SF galaxies. Note that there are only two SF galaxy exhibiting a spectral index greater than −0.5. Therefore, flat or inverted spectral indices can reliably be associated with dominant AGN activity. On the other hand, steep spectral indices (i.e. α < −1.0) are not associated with any source type as the histogram clearly shows. Therefore, uniquely steep spectra cannot be used as discriminator for source type.
Because the vast majority of (radio) sources detected in contemporary and forthcoming surveys will not have any spectroscopic information, we also searched for correlations between the spectral index and other photometric object type indicators. A popular way of photometrically selecting AGN without being biased by extinction is the use of an infrared colour–colour diagram based on the four channels of the IRAC instrument (Fazio et al. 2004) aboard the Spitzer Space Telescope. Originally proposed by Lacy et al. (2004) and therefore often referred to as the “Lacy diagram”, this plot has been further investigated (for an overview see Soifer et al. 2008) so that there are currently reliable template spectral energy distributions (SEDs) available covering the entire optical to MIR regime (e.g. Assef et al. 2010). To construct a “Lacy diagram” for our source sample, we cross-matched the radio sources with the SWIRE catalogue, data release 3, to obtain IRAC flux densities. We found 265 secure identifications where all four IRAC fluxes are available. The corresponding plot is presented in Fig. 7. For comparison, we also plotted all SWIRE-detected sources in the CDF-S and the ELAIS-S1 field as colour-coded, 2-dimensional histogram. The locus of potential AGN in this diagram with respect to various contaminating effects, predominantly line emission by polycyclic aromatic Hydrocarbons (PAHs), was determined by Dasyra et al. (2009) and is indicated in Fig. 7 with a dashed line. We split our source sample in three sub-samples based on their spectral index: steep spectrum sources are classified as having α < median(α) − MAD, normal spectrum sources satisfy median(α) − MAD < α < median(α) + MAD and flat/inverted spectrum sources show α > median(α) + MAD. One can see that flat or inverted spectrum sources are more frequent on the “AGN branch” of the diagram whereas the location of star-forming galaxies (the branch that goes straight up) is more or less avoided by these sources. This “star formation branch” (log (S5.8 μm/S3.6 μm) < 0) is dominated by normal and steep spectrum objects with only a very few flat/inverted spectrum sources.
 |
Fig. 7 “Lacy diagram” of our source sample. For comparison, all sources detected in all four IRAC bands within the SWIRE survey of ELAIS-S1 and CDF-S are plotted as 2-dimensional histogram. The black dashed line indicates the locus of AGN in this diagram as proposed by Dasyra et al. (2009). |
 |
Fig. 8 “Lacy diagram” of our source sample with spectroscopic classification from Mao et al. (2012). As in Fig. 7, all sources detected in all four IRAC bands within the SWIRE survey of ELAIS-S1 and CDF-S are plotted as 2-dimensional histogram. The black dashed line indicates the locus of AGN in this diagram as proposed by Dasyra et al. (2009). |
To summarise, the radio spectral index can at least be used to identify a fraction AGN, namely those with optically thick media that cause their radio emission to flatten because of self-absorption energy losses. However, spectral indices are not a strong discriminator for the source type because (i) outliers from this general trend are frequent and (ii) optically thin AGN cannot be separated from SF galaxies with spectral indices. This is further highlighted in Fig. 8 where we plotted the “Lacy diagram” for all ATLAS sources with spectroscopic classification (Mao et al. 2012). It becomes obvious that the “AGN branch” in this plot is really occupied by AGN only whereas the “star formation branch” both hosts SF galaxies and AGN. Hence, also a selection based on MIR colour criteria leads to the result that a AGN can be reliably selected without contamination by star forming objects. The other way round, selecting SF galaxies only without AGN contamination, is not possible by means of MIR colour selection, similar to a selection based on radio spectral indices.
4.3. The z–α relation
The z–α relation is an empirical relation seen between the spectral index of radio sources in a flux-limited sample and their redshifts. It states that higher-redshift radio sources tend to exhibit steeper spectral indices, typically with α < −1. It was found by various authors using different large-scale radio surveys at the Jy and mJy level, see e.g. Athreya & Kapahi (1998), De Breuck et al. (2000, 2001, 2006), Klamer et al. (2006), Afonso et al. (2011), and Ker et al. (2012). The first quantitative formulation of this relation was given by Verkhodanov & Khabibullina (2010) using a large sample (~2500) of distant radio galaxies selected from various surveys across the entire sky. Above a redshift of 1, they find clear evidence for such a correlation and quantify it by a linear fit α = (−0.70 ± 0.02) + (−0.15 ± 0.01)z out to z ~ 5. The currently favoured explanation for this effect is based on cosmic expansion (Klamer et al. 2006): at higher redshifts, when the universe was denser on average than at present, the radio jets of high-z AGN had to penetrate into a denser intergalactic medium where they are compressed, similar to the jets of radio galaxies located in the cores of dense clusters in the nearby universe. This compression then leads to the characteristic steepening of the spectral index due to synchrotron and inverse-Compton energy losses of the relativistic electrons.
With the spectroscopic information from Mao et al. (2012), we have investigated the z–α relation in our sub-mJy sample. From our initial 631 sources with measured spectral index, 169 (27%) have spectroscopic redshifts. In addition, we have 236 sources with spectroscopic redshift and an upper limit on α only. A plot of these redshifts versus the spectral index or the upper limits, respectively, is shown in Fig. 9. We again note that the 169 sources with spectroscopic redshifts and actual spectral index measurements are not affected by sensitivity bias (see Sect. 4) since they all have 1.4 GHz flux densities in excess of 0.8 mJy and hence spectral indices of at least − 2.0 can be measured for them, given our 2.3 GHz sensitivity.
 |
Fig. 9 Redshift versus spectral index plot for all sources with spectroscopic redshift in our sample.Sources with an actual measurement of α are split in spectroscopic classes (AGN: black square, SF: black star, unknown: black diamond). Sources with an upper limit on α only (black dots) were not split up. Note that R2 = 0.09 for the fit to our data points (black symbols) indicates highly uncorrelated quantities. A slight correlation is usually assumed when R2 > 0.5 with good correlation for R2 > 0.85. |
Surprisingly, in this diagram, there is no obvious correlation between spectral index and redshift. Note that this result is also independent of the spectroscopic classification of the objects. But since radio sources with significant redshift are, due to the sensitivity limits of currently available telescopes, all AGN-powered (even a galaxy forming stars at a very high rate of 1000 M⊙ yr-1 would be undetectable within ATLAS for any redshift z > 1.2), the z–α relation is yet only investigated for AGN.
This finding (the absence ofa z–α relation) contradicts the contemporary literature, and we offer two potential explanations: First, our sample of sources is very small (only 9 sources) for the redshift range z > 1 were the z–α relation becomes important (see Verkhodanov & Khabibullina 2010). Hence, our findings rely on small number statistics and have therefore to be treated with care. Second, there could be a change in the radio source population between our sub-mJy sample and the samples used in other work which are mainly much more luminous sources with flux densities of several tens to hundreds of mJy (despite their significant redshifts, so these sources are very luminous). We also point out that Ker et al. (2012) found only a slight correlation between spectral index and redshift. They argue that the relation becomes fully applicable only for resolved sources, if the explanation is correct that the z–α relation arises from high-redshift radio lobes working against the denser intergalactic medium. This reasoning is supported by our findings because nearly all of our sources are compact. In order to effectively select potential high-z radio sources, Ker et al. (2012) suggest to use the relation between K-band flux density (or also Spitzer 3.6 μm IRAC channel) and redshift which is much tighter than the traditional z–α relation, see also Norris et al. (2011a). This relation was also investigated by Middelberg et al. (2011) to select a certain class of objects which is suspected to be located at very high redshifts (z > 2), the so-called Infrared-Faint Radio Sources (IFRS).
According to Zinn et al. (2011), a source is deemed an IFRS if its measured ratio between radio (20 cm) and near-infrared (NIR, mostly Spitzer IRAC 3.6 μm) flux density exceeds a cutoff-value of 500 and, at the same time, its NIR flux density is less than 30 μJy. Those extreme sources (often exhibiting no 3.6 μm counterpart at all, even in ultra-deep or stacked NIR images with noise levels reaching the 100 nJy level) are very difficult to investigate, in particular regarding their redshift, since optical spectroscopy can only be done for such IFRS that at least have moderately bright optical counterparts. Therefore, we only have very few sources in our sample with spectroscopic redshifts that meet at least the first IFRS criterion. A real IFRS meeting both criteria is not in our sample. A plot illustrating the S20 cm/S3.6 μm flux ratios of our source sample with respect to redshift is shown in Fig. 10. Contrary to the z–α relation in Fig. 9, there is a clear trend of increasing redshift with increasing S20 cm/S3.6 μm flux ratio. Although the scatter in the relation is fairly large, in particular for high flux ratios, this relation seems to be a much better estimator for the redshift of a source than the classical z–α relation. This is in very good agreement with the findings of Ker et al. (2012) who also see only a marginal correlation of the spectral index with redshift but state that by far the most efficient selection criterion for high-z sources in complete samples is based on K-band magnitude.
We conclude that our data do not confirm the z–α relation, at least for faint radio sources. This may have several explanations: On the one hand, the popular belief that the z–α relation is caused by the denser intergalactic medium (IGM) at higher redshifts against which the radio jets of powerful sources have to work and thereby lose energy (Klamer et al. 2006), may not be applicable to faint sources since they are mostly compact. For instance, the simulations used by Raccanelli et al. (2012) predict that compact Fanaroff-Riley type I (FR I) sources are more frequent at any redshift greater than 1 by several orders of magnitude compared to extended FR II sources. Therefore, the overall radio population, at least at the sub-mJy level, should mainly consist of such compact FR I sources for which the Klamer et al. (2006) explanation is less suitable. Furthermore, the z–α relation may only be an apparent correlation. Nearly all radio spectra of the highest-z (z > 4) radio sources known to date are significantly curved or even peaked at observed-frame frequencies of ≲ 500 MHz (Ker et al. 2012,their Fig. 5), a behaviour that is indicative for either young sources or sources with recent merger activity (e.g. O’Dea 1998; Randall et al. 2011). Hence, spectral indices calculated between 1.4 GHz and another radio frequency commonly in use today, e.g. 610 MHz or 5 GHz, measure the high-frequency flank of such a peaked spectrum which yields increasingly steep spectral indices the more the radio spectrum is curved or peaked. Therefore, sources selected by a steep spectral index are predominantly of these two types (either young or merger). Because those sources are more frequent at higher redshifts when the universe was denser (more merger) and younger (more young sources), it only appears that a selection based on steep spectral indices yields high-redshift objects despite the real astrophysical phenomenon that is selected is completely different, namely young or merger sources.
 |
Fig. 10 S20 cm/S3.6 μm flux ratios for our spectral index source sample. Note the clear but not very tight trend of increasing redshift with increasing S20 cm/S3.6 μm. The limiting value for IFRS is shown as red dashed line. |
4.4. Spectral indices and the radio-IR correlation
The radio-IR correlation is deemed to be one of the tightest correlations in astrophysics. It states that the radio emission of a galaxy is positively correlated with its mid- and far-infrared emission due to recent star-formation activity. The IR emission in this scenario is produced directly by the star-formation processes whereas the radio emission comes from supernova remnants related to the star-formation event. After its discovery in the late 1980s (e.g. de Jong et al. 1985; Condon et al. 1991), it was subjected to intensive studies while the technology of infrared telescopes advanced (Appleton et al. 2004) and is nowadays proven to hold over a wide range in both flux density (Boyle et al. 2007; Garn & Alexander 2009) and redshift (Huynh et al. 2010; Mao et al. 2011).
We here use co-located Spitzer observations at 24 μm from the SWIRE survey (Lonsdale et al. 2003) to investigate the dependence of the correlation parameter, q24 ≡ log (S24 μm/S20 cm) on the radio spectral index. Matching our initial sample of 631 radio sources to the SWIRE IR catalogue with a match radius of 5″, 145 counterparts were identified. Because the radio-IR correlation should only hold for star-forming objects, we excluded all known AGN among these sources based on the spectral classifications by Mao et al. (2012) and other AGN indicators like morphology which was done in Norris et al. (2006) and Middelberg et al. (2008). After this rejection procedure, we were left with a total of 86 sources with secure 24 μm detection and no signs of AGN activity. A plot showing S24 μm versus S20 cm for these objects is presented in Fig. 11.
 |
Fig. 11 Diagram illustrating the correlation between the flux densities at 24 μm and 20 cm (1.4 GHz). The sources are divided in three spectral index bins according to α < median(α) − MAD, median(α) − MAD < α < median(α) + MAD and α > median(α) + MAD where MAD is the median absolute deviation of the spectral index of the entire 24 μm-detected sample. |
The correlation in our source sample is, at least for their slope, well described by the fit of Appleton et al. (2004) which was obtained using SWIRE data but over many fields, not just ELAIS-S1 and CDF-S. The few sources that lie at the top-left corner of the diagram, exhibiting an excess of radio emission, are leftover AGN which were not removed from the sample during the AGN rejection step.
Calculating the correlation parameter q24 for our sample, we find a median value of 0.68 with a fairly large spread of MAD = 0.36. When plotting the individual values of q24 against the spectral indices of the sample (Fig. 12), we see no clear correlation between the two quantities.
 |
Fig. 12 q24 values of our source sample plotted against spectral index. The solid red lines indicate the median of the two quantities while the dashed lines indicate the spread in terms of (median ± MAD). |
Nevertheless, a general trend could be found that sources with a spectral index steeper than the median value show a much larger spread in q24 values than sources with a spectral index flatter than the median. This is increasingly surprising with the results of Sect. 4.2 where we found that flat or inverted spectral indices are indicative for AGN-powered sources. Since AGN should not obey the radio-IR correlation, this tightening of the scatter in q24 with increasing spectral index is still to be investigated. One possible explanation could arise from the findings of Padovani et al. (2011) who investigated star forming galaxies, radio-loud and radio quiet AGNs in the CDF-S. They found that regarding their luminosity function and its evolution, radio-quiet AGN are pretty much similar to star forming galaxies and not to their radio-loud siblings. Although we aimed to exclude AGN from the sample discussed in this section based on indicators such as radio morphology or spectroscopy, we predominantly eliminated radio-loud AGN and several radio-quiet AGN may still contaminating the sample (as suggested by the few flat and inverted spectrum sources in Fig. 12). That these radio-quiet AGN do obey the radio-IR correlation is a natural consequence of the findings of Padovani et al. (2011) and already discussed in their work.
In summary, we conclude that the radio-IR correlation is not affected by the radio spectral indices of sources in a flux-limited sample. This is yet another proof for their remarkable universality which has been shown for redshift, flux density levels and now also for radio spectral properties.
5. Summary and outlook
We have conducted deep (σ = 70−80 μJy) radio observations of the ELAIS-S1 and CDF-S regions at 2.3 GHz using the ATCA to supplement the sources detected at 1.4 GHz within ATLAS with spectral index information. Our final catalogue with sources well detected at both frequencies and therefore with high quality spectral indices comprise a total of 631 sources and is available at the CDS. The median spectral index of our distribution is − 0.73 with a median absolute deviation (MAD) of 0.35. We have investigated the properties of the population with respect to spectral index and tested correlations between the spectral index and various other quantities. Our main findings are as follows:
-
1.
We do not find evidence for a flattening of the spectral index towards fainter (several 100 μJy) flux densities. This is in good agreement with the majority of previous work by other authors (e.g. Randall et al. 2012; Ibar et al. 2009). Since we also find that star-forming galaxies tend to have steeper radio spectra compared to AGN, we can support the current notion that star-forming galaxies become the dominant type of radio sources only at flux densities below 100 μJy since our sample does not reach such low flux densities.
-
2.
Considering the spectral index as discriminator for the object type, we find that flat- or inverted-spectrum sources are mostly AGN while SF galaxies show significantly steeper spectra with a median spectral index of − 0.85 (AGN median spectral index is − 0.68). This flattening is caused by self-absorption losses within optically thick AGN under physical conditions which are not in general met in SF galaxies. However, there is a significant number of outliers which affects the selection of AGN based on spectral indices. Furthermore, optically thin AGN exhibiting the canonical spectral index of − 0.7 for synchrotron radiation can not be separated from SF galaxies. Therefore, we conclude that the spectral index is not a strong discriminator for the source type but can be helpful if there are no other, more sophisticated diagnostics.
-
3.
We investigate the z–α relation which states that high-redshift radio galaxies show steeper spectral indices. The relation cannot be confirmed with our data. We suspect that this is explained either by the fact that the currently favoured explanation for the z–α relation (Klamer et al. 2006) is not applicable to the sub-mJy population or because of the complete failure of the z–α relation which may only be an apparent correlation. Since most high-z radio galaxies show curved or even peaked radio spectra, indicative for young or merger sources, a selection based on steep spectral indices may predominantly select those sources. But because both young and merger sources are more frequent at high redshifts when the universe was denser and younger, it appears to select high-z sources.
-
4.
We find no evidence for a dependence of the radio-IR correlation on radio spectral index. This therefore widens the universality of this correlation which is already known to hold over a wide range of flux densities and redshifts. However, we do see a trend for the scatter of q24 which is larger for sources with steep spectral indices and becomes smaller while going to positive spectral indices.
Acknowledgments
We thank our anonymous referee for many insightful comments and suggestions which improved the scientific validity of this paper a lot. P.C.Z. acknowledges funding by the Ruhr-University Research School.
References
- Afonso, J., Bizzocchi, L., Ibar, E., et al. 2011, ApJ, 743, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Appleton, P. N., Fadda, D. T., Marleau, F. R., et al. 2004, ApJS, 154, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaboldi, M., Neeser, M. J., Parker, L. C., et al. 2007, The Messenger, 127, 28 [NASA ADS] [Google Scholar]
- Assef, R. J., Kochanek, C. S., Brodwin, M., et al. 2010, ApJ, 713, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Athreya, R. M., & Kapahi, V. K. 1998, J. Astrophys. Astron., 19, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Balestra, I., Mainieri, V., Popesso, P., et al. 2010, A&A, 512, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bondi, M., Ciliegi, P., Venturi, T., et al. 2007, A&A, 463, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyle, B. J., Cornwell, T. J., Middelberg, E., et al. 2007, MNRAS, 376, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Condon, J. J. 1997, PASP, 109, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Anderson, M. L., & Helou, G. 1991, ApJ, 376, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Dasyra, K. M., Yan, L., Helou, G., et al. 2009, ApJ, 701, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- De Breuck, C., van Breugel, W., Röttgering, H. J. A., & Miley, G. 2000, A&AS, 143, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Breuck, C., van Breugel, W., Röttgering, H., et al. 2001, AJ, 121, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- De Breuck, C., Klamer, I., Johnston, H., et al. 2006, MNRAS, 366, 58 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, T., Klein, U., Wielebinski, R., & Wunderlich, E. 1985, A&A, 147, L6 [NASA ADS] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Garn, T., & Alexander, P. 2009, MNRAS, 394, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., Afonso, J., Chan, B., et al. 2003, AJ, 125, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Huynh, M. T., Jackson, C. A., & Norris, R. P. 2007, AJ, 133, 1331 [NASA ADS] [CrossRef] [Google Scholar]
- Huynh, M. T., Gawiser, E., Marchesini, D., Brammer, G., & Guaita, L. 2010, ApJ, 723, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Ibar, E., Ivison, R. J., Biggs, A. D., et al. 2009, MNRAS, 397, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezic, Z., Axelrod, T., Brandt, W. N., et al. 2008, Serbian Astron. J., 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Jaeger, S. 2008, in Astronomical Data Analysis Software and Systems XVII, eds. R. W. Argyle, P. S. Bunclark, & J. R. Lewis, ASP Conf. Ser., 394, 623 [Google Scholar]
- Kaiser, N., Burgett, W., Chambers, K., et al. 2010, in SPIE Conf. Ser., 7733 [Google Scholar]
- Keller, S. C., Schmidt, B. P., Bessell, M. S., et al. 2007, PASA, 24, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ker, L. M., Best, P. N., Rigby, E. E., Röttgering, H. J. A., & Gendre, M. A. 2012, MNRAS, 2178 [Google Scholar]
- Klamer, I. J., Ekers, R. D., Bryant, J. J., et al. 2006, MNRAS, 371, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, M., Storrie-Lombardi, L. J., Sajina, A., et al. 2004, ApJS, 154, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Smith, H. E., Rowan-Robinson, M., et al. 2003, PASP, 115, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, M. Y., Huynh, M. T., Norris, R. P., et al. 2011, ApJ, 731, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, M. Y., Norris, R. P., Sharp, R. G., & Middelberg, E. 2012, MNRAS, accepted [Google Scholar]
- Middelberg, E. 2006, PASA, 23, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Middelberg, E., Norris, R. P., Cornwell, T. J., et al. 2008, AJ, 135, 1276 [NASA ADS] [CrossRef] [Google Scholar]
- Middelberg, E., Norris, R. P., Hales, C. A., et al. 2011, A&A, 526, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morganti, R., Rottgering, H., Snellen, I., et al. 2010 [arXiv:1001.2384] [Google Scholar]
- Moster, B. P., Somerville, R. S., Newman, J. A., & Rix, H.-W. 2011, ApJ, 731, 113 [Google Scholar]
- Norris, R. P., Afonso, J., Appleton, P. N., et al. 2006, AJ, 132, 2409 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Afonso, J., Cava, A., et al. 2011a, ApJ, 736, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Hopkins, A. M., Afonso, J., et al. 2011b, PASA, 28, 215 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P. 1998, PASP, 110, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, F. N., & Morrison, G. E. 2008, AJ, 136, 1889 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Miller, N., Kellermann, K. I., et al. 2011, ApJ, 740, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Popesso, P., Dickinson, M., Nonino, M., et al. 2009, A&A, 494, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prandoni, I., Parma, P., Wieringa, M. H., et al. 2006, A&A, 457, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raccanelli, A., Zhao, G.-B., Bacon, D. J., et al. 2012, MNRAS, 424, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Randall, K. E., Hopkins, A. M., Norris, R. P., & Edwards, P. G. 2011, MNRAS, 416, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Randall, K., Hopkins, A., Norris, R., et al. 2012, MNRAS, 421, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., Barden, M., Beckwith, S. V. W., et al. 2004, ApJS, 152, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Rottgering, H., Afonso, J., Barthel, P., et al. 2011, J. Astrophys. Astron., 32, 557 [Google Scholar]
- Sacchi, N., La Franca, F., Feruglio, C., et al. 2009, ApJ, 703, 1778 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 [Google Scholar]
- Schinnerer, E., Sargent, M. T., Bondi, M., et al. 2010, ApJS, 188, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Seymour, N., Dwelly, T., Moss, D., et al. 2008, MNRAS, 386, 1695 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Schinnerer, E., Scodeggio, M., et al. 2008, ApJS, 177, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Soifer, B. T., Helou, G., & Werner, M. 2008, ARA&A, 46, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Verkhodanov, O. V., & Khabibullina, M. L. 2010, Astron. Lett., 36, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Windhorst, R. A., van Heerde, G. M., & Katgert, P. 1984, A&AS, 58, 1 [NASA ADS] [Google Scholar]
- Windhorst, R. A., Fomalont, E. B., Partridge, R. B., & Lowenthal, J. D. 1993, ApJ, 405, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Meisenheimer, K., Rix, H.-W., et al. 2003, A&A, 401, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X.-Z., Reich, W., Reich, P., & Wielebinski, R. 2003, Chin. J. Astron. Astrophys., 3, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, P.-C., Middelberg, E., & Ibar, E. 2011, A&A, 531, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
A representative portion of the ATLAS 2.3 GHz source catalogue of the ELAIS-S1 field for illustration purposes. The CDF-S catalogue contains the same information.
All Figures
 |
Fig. 1 2.3 GHz noise maps of both ATLAS fields: CDF-S (left) and ELAIS-S1 (right). Contours start at 70 μJy beam-1 (dark blue contour line) and increase by a constant value of 40 μJy beam-1. |
| In the text | |
 |
Fig. 2 Distribution of 1.4 GHz (hi-res) and 2.3 GHz flux densities in the final catalogue. AGN classifications of the sources are from Mao et al. (2012). |
| In the text | |
 |
Fig. 3 The fractional flux density errors for all ELAIS-S1 and CDF-S sources as function of their flux density. The solid red line indictates how the fractional error should decrease with increasing flux density in an image with an overall rms noise of 70 μJy according to Eq. (2). A calibration error of 5% is assumed. |
| In the text | |
 |
Fig. 4 Distribution of 1.4 GHz to 2.3 GHz spectral indices in the final catalogue for all sourceswith unambiguously detected 2.3 GHz counterpart and both the 1.4 GHz and 2.3 GHz flux densities exceeding 0.3 mJy. AGN classifications of the sources are from Mao et al. (2012). |
| In the text | |
 |
Fig. 5 Spectral index vs. flux density. The grey 2D histogram shows our sample of 631 sources with 1.4 GHz and 2.3 GHz detections. Since the sensitivity of the 2.3 GHz observations is ~3 times lower than that of the 1.4 GHz data, the black dashed line indicates the minimum spectral index that could be measured with our data. Therefore, the median spectral indices (blue circles, x-error bars indicate the flux density bin size, y-error bars correspond to the MAD) for just the 2.3 GHz detected sample show significantly flatter values towards lower flux densities. When including also upper limits from the 2.3 GHz non-detected sources, this trend completely vanishes (blue diamonds). Hence we conclude that there is no evidence for a flattening of the mean spectral index with lower flux density. |
| In the text | |
 |
Fig. 6 Histogram illustrating the distribution of spectral indices of spectroscopically classified AGN and SF galaxies. |
| In the text | |
 |
Fig. 7 “Lacy diagram” of our source sample. For comparison, all sources detected in all four IRAC bands within the SWIRE survey of ELAIS-S1 and CDF-S are plotted as 2-dimensional histogram. The black dashed line indicates the locus of AGN in this diagram as proposed by Dasyra et al. (2009). |
| In the text | |
 |
Fig. 8 “Lacy diagram” of our source sample with spectroscopic classification from Mao et al. (2012). As in Fig. 7, all sources detected in all four IRAC bands within the SWIRE survey of ELAIS-S1 and CDF-S are plotted as 2-dimensional histogram. The black dashed line indicates the locus of AGN in this diagram as proposed by Dasyra et al. (2009). |
| In the text | |
 |
Fig. 9 Redshift versus spectral index plot for all sources with spectroscopic redshift in our sample.Sources with an actual measurement of α are split in spectroscopic classes (AGN: black square, SF: black star, unknown: black diamond). Sources with an upper limit on α only (black dots) were not split up. Note that R2 = 0.09 for the fit to our data points (black symbols) indicates highly uncorrelated quantities. A slight correlation is usually assumed when R2 > 0.5 with good correlation for R2 > 0.85. |
| In the text | |
 |
Fig. 10 S20 cm/S3.6 μm flux ratios for our spectral index source sample. Note the clear but not very tight trend of increasing redshift with increasing S20 cm/S3.6 μm. The limiting value for IFRS is shown as red dashed line. |
| In the text | |
 |
Fig. 11 Diagram illustrating the correlation between the flux densities at 24 μm and 20 cm (1.4 GHz). The sources are divided in three spectral index bins according to α < median(α) − MAD, median(α) − MAD < α < median(α) + MAD and α > median(α) + MAD where MAD is the median absolute deviation of the spectral index of the entire 24 μm-detected sample. |
| In the text | |
 |
Fig. 12 q24 values of our source sample plotted against spectral index. The solid red lines indicate the median of the two quantities while the dashed lines indicate the spread in terms of (median ± MAD). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


