| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 18 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201219205 | |
| Published online | 21 June 2012 | |
On the origin of LS 5039 and PSR J1825−1446
1 Departament d’Astronomia i Meteorologia, Institut de Ciències del Cosmos (ICC), Universitat de Barcelona (IEEC-UB), Martí i Franquès 1, 08028 Barcelona, Spain
e-mail: jmoldon@am.ub.es
2 National Radio Astronomy Observatory, PO Box 0, Socorro, NM 87801, USA
3 Max Planck Institut für Radioastronomie, Auf dem Huegel 69, 53121 Bonn, Germany
4 Jodrell Bank Centre for Astrophysics, School of Physics and Astronomy, University of Manchester, Manchester M13 9PL, UK
Received: 9 March 2012
Accepted: 16 April 2012
Context. The gamma-ray binary LS 5039 and the isolated pulsar PSR J1825−1446 were proposed to have been formed in the supernova remnant (SNR) G016.8−01.1.
Aims. We aim to obtain the Galactic trajectory of LS 5039 and PSR J1825−1446 to find their origin in the Galaxy, and in particular to check their association with SNR G016.8−01.1 to restrict their age.
Methods. By means of radio and optical observations we obtained the proper motion and the space velocity of the sources.
Results. The proper motion of PSR J1825−1446 corresponds to a transverse space velocity of 690 km s-1 at a distance of 5 kpc. Its Galactic velocity at different distances is not compatible with the expected Galactic rotation. The velocity and characteristic age of PSR J1825−1446 make it incompatible with SNR G016.8−01.1. There are no clear OB associations or SNRs crossing the past trajectory of PSR J1825−1446. We estimate the age of the pulsar to be 80–245 kyr, which is compatible with its characteristic age. The proper motion of LS 5039 is μαcosδ = 7.09 and μδ = −8.82 mas yr-1. The association of LS 5039 with SNR G016.8−01.1 is unlikely, although we cannot discard it. The system would have had to be formed in the association Ser OB2 (at 2.0 kpc) if the age of the system is 1.0–1.2 Myr, or in the association Sct OB3 (distance 1.5–2 kpc) for an age of 0.1–0.2 Myr. If the system were not formed close to Ser OB2, the pseudo-synchronization of the orbit would be unlikely.
Conclusions. PSR J1825−1446 is a high-velocity isolated pulsar ejected from the Galaxy. The distance to LS 5039, which needs to be constrained by future astrometric missions such as Gaia, is a key parameter for restricting its origin and age.
Key words: stars: individual: LS 5039 / pulsars: individual: PSR J1825-1446 / radio continuum: stars / proper motions / X-rays: binaries / gamma rays: stars
© ESO, 2012
1. Introduction
During a core-collapse supernova explosion of a massive star, the remaining compact object, either isolated or in a binary system, can receive a natal kick and obtain a high peculiar velocity (Hills 1983; van den Heuvel et al. 2000). A binary system can obtain a moderate velocity from a symmetric Blaauw kick (Blaauw 1961), whereas the compact object can acquire additional momentum from an asymmetric supernova kick (Stone 1982). If the system remains bound after the explosion, the parameters of the binary system before and after the supernova explosion can be related by measuring the high peculiar velocity of the system, in particular for X-ray binaries (see e.g. Brandt & Podsiadlowski 1995; and the particular cases in Tauris et al. 1999; Martin et al. 2009). On the other hand, the space velocity of a binary system can be used to determine its past Galactic trajectory (see e.g. Ribó et al. 2002; Dhawan et al. 2007; Miller-Jones et al. 2009a). Of particular interest are the runaway systems, which have acquired very high peculiar velocities (Mirabel et al. 2001, 2002). With enough information, a complete evolutionary history of the binary system can be obtained with constraints on the progenitor and the formation of the compact object, (see e.g. Willems et al. 2005; Fragos et al. 2009). Among the binary systems receiving natal kicks we can find the special case of gamma-ray binaries, which usually form eccentric binary systems (Casares et al. 2010).
Only a few binary systems have been associated with gamma-ray sources, and therefore it is important to understand how they formed, and how they are distributed in the Galaxy. However, the origin of most of the binaries with gamma-ray emission is still unknown. Mirabel et al. (2004) studied the origin of the gamma-ray binary LS I +61 303, and Dhawan et al. (2006) measured a precise proper motion that allowed the authors to obtain the space velocity of the source and constrain the mass lost in the supernova event that formed the compact object of the system to ~1 M⊙. The natal kick of the supernova that produced the pulsar in the system PSR B1259−63/LS 2883 was discussed in Hughes & Bailes (1999) and Wang et al. (2006), although no proper motion has been measured for this system. The Galactic motion of LS 5039 was extensively discussed in Ribó et al. (2002) (see details in Sect. 2.1). Mirabel & Rodrigues (2003) and Reid et al. (2011) used high-accuracy radio astrometry to compute the Galactic velocity of Cygnus X-1, which allowed them to obtain the mass of the progenitor of the black hole, and its association with the Cyg OB2 association. They also determined that the black hole was formed without a supernova explosion. For Cygnus X-3, Miller-Jones et al. (2009b) obtained an accurate proper motion of the source that was used to better identify the position of the X-ray binary core, although the origin of the system is still unknown. Moldón et al. (2011b) determined for HESS J0632+057 that its total proper motion is below 4 mas yr-1. Other recent gamma-ray binary candidates are 1FGL J1018.6 − 5856 (Corbet et al. 2011; Pavlov et al. 2011; Ackermann et al. 2012) and AGL J2241+4454 (Williams et al. 2010; Casares et al. 2010). However, the proper motion of these sources is still unknown. These examples show the potential of a good determination of the proper motion of a system, and also the need for better astrometry in this peculiar binary population.
On the other hand, accurate astrometry of isolated pulsars opens a wide field of scientific research including fundamental reference frame ties, physics in the core-collapse supernovae and imparted momentum kicks, association with supernova remnants (SNRs) and determination of the age of pulsars, model-independent estimates of distances through parallax measurements, or determination of the distribution of electron density in the interstellar medium (see for example Chatterjee et al. 2009; Brisken et al. 2002, and references therein). It is common that pulsars acquire high velocities at birth, becoming the fastest population in the Galaxy, with a mean transverse velocity of ~450 km s-1, and up to above 103 km s-1 (Lyne & Lorimer 1994; Hobbs et al. 2005; Chatterjee et al. 2005). The pulsar velocity distribution provides information about the supernova symmetry and the binary population synthesis (Brisken et al. 2003).
Here we present the results from two high-resolution astrometric projects to determine the proper motion of LS 5039, and the nearby pulsar PSR J1825−1446, the only known compact objects in the field of the SNR G016.8 − 01.1. In Sect. 2 we describe the gamma-ray binary LS 5039, its possible association with SNR G016.8−01.1, and the motivation to obtain the proper motion of the pulsar PSR J1825−1446. In Sect. 3 we describe the VLBA astrometric project on PSR J1825−1446, and we obtain the proper motion of the source. In Sect. 4 we present three sets of radio observations of LS 5039, as well as the available radio and optical astrometry of the source, and we compute the proper motion and discuss the uncertainties of the fit. In Sect. 5 we compute the Galactic velocity of both sources. In Sect. 6 we analyse the past trajectories of the sources and discuss their possible birth location. Finally, we summarise the obtained results in Sect. 7.
2. Compact objects in the field of SNR G016.8 − 01.1
2.1. The gamma-ray binary LS 5039
LS 5039 is a gamma-ray binary system that displays non-thermal persistent and variable emission from radio frequencies to high-energy (HE; E > 100 MeV) and very-high-energy (VHE; E > 100 GeV) gamma rays. The system contains a bright ON6.5 V((f)) star (Clark et al. 2001; McSwain et al. 2004) and a compact object of unknown nature. This degenerate companion has a mass greater than ~1.5 M⊙, which depends on the binary system inclination, which is an unknown parameter (Casares et al. 2005). The orbit of the system has a period of 3.9 days and an eccentricity around 0.35 (Casares et al. 2005; Aragona et al. 2009; Sarty et al. 2011). The distance to the source has recently been updated to 2.9 ± 0.8 kpc (Casares et al., in prep.). The persistent synchrotron radio emission (Martí et al. 1998; Ribó et al. 1999; Godambe et al. 2008; Bhattacharyya et al. 2012) appears extended when observed Baseline Interferometry (VLBI), at scales of 5–300 milliarcsecond (mas) (Paredes et al. 2000, 2002; Ribó et al. 2008). The X-ray spectrum of the system (Reig et al. 2003; Martocchia et al. 2005) is well fitted by a simple power law, and it is clearly periodic, as shown by RXTE and Suzaku (Bosch-Ramon et al. 2005; Takahashi et al. 2009). Durant et al. (2011) discovered a large-scale extended component in X-rays up to 1′ from LS 5039. The system has also been detected by INTEGRAL up to 200 keV (Goldoni et al. 2007; Hoffmann et al. 2009), and with BATSE up to 1 MeV (Harmon et al. 2004). LS 5039 was first associated with an EGRET source in Paredes et al. (2000), and variability was detected by Fermi between 100 and 300 GeV with a 3.9-d period (Abdo et al. 2009). The system is also a TeV emitter, with persistent, variable, and periodic emission, as detected by H.E.S.S. (Aharonian et al. 2005, 2006). No short-period pulsations were found that could demonstrate the presence of a pulsar either in radio (McSwain et al. 2011) or X-rays (Rea et al. 2011). We note that traditionally the name of the optical star, LS 5039, has also been used to refer to the binary system, and so we will do in this paper.
In all gamma-ray binaries, the nature of the compact object is fundamental for understanding the physical processes involved in the particle acceleration that is responsible for the multi-wavelength emission. If the compact object is a black hole, the accelerated particles would be powered by accretion, and produced in the jets of a microquasar (Paredes et al. 2006; Bosch-Ramon et al. 2006; and the review in Bosch-Ramon & Khangulyan 2009). On the other hand, if the compact object is a young non-accreting pulsar, the particle acceleration would be produced in the shock between the relativistic wind of the pulsar and the stellar wind of the massive companion star. This scenario was described in Maraschi & Treves (1981), Tavani & Arons (1997), Kirk et al. (1999), Dubus (2006), Khangulyan et al. (2007), and Bogovalov et al. (2008, 2012). Dedicated discussions on the wind-wind collision scenario for LS 5039 can be found in Khangulyan et al. (2007), Sierpowska-Bartosik & Torres (2007), Dubus et al. (2008), and Khangulyan et al. (2008). Considerations on the spectral signature of the pulsar wind are provided in Cerutti et al. (2008), on secondary cascading in Bosch-Ramon et al. (2008) and Cerutti et al. (2010), while X-ray absorption and occultation are discussed in Szostek & Dubus (2011), and limits on the spin-down luminosity of the putative pulsar in Zabalza et al. (2011).
The orbital parameters of LS 5039 such as the eccentricity, masses, and orbit inclination are not well constrained or are still under discussion (Casares et al. 2005; Aragona et al. 2009; Sarty et al. 2011). The proper motion and the space velocity of the source were first determined in Ribó et al. (2002). These authors found that LS 5039 is escaping from its own regional standard of rest with a total systemic velocity of 150 km s-1. The past trajectory of LS 5039 for the last 105 yr computed in Ribó et al. (2002) marginally suggests an association with SNR G016.8−01.1. These authors also discovered an H i cavity in the ISM, and argued that it may have been caused by the stellar wind of LS 5039 or by the progenitor of the compact object in the system. An in-depth discussion on the supernova process that produced the compact object in the system LS 5039 can be found in McSwain & Gies (2002), Ribó et al. (2002), McSwain et al. (2004), and Casares et al. (2005). The authors discussed the expected mass loss during the supernova explosion that produced the compact object, obtained from the orbital parameters and the mass of the system. This allowed them to estimate some orbital parameters of the pre-supernova system. We note that the main limitation for obtaining accurate pre-supernova properties of LS 5039 is the determination of the orbital parameters, which can be improved by means of optical observations.
 |
Fig. 1 Wide field map around SNR G016.8−01.1. The grey scale corresponds to the Parkes-MIT-NRAO survey at 5 GHz (Tasker et al. 1994), and the contours, with higher resolution, to the NRAO VLA Sky Survey (NVSS) at 1.4 GHz (Condon et al. 1998). The dashed line outlines the area covered by the diffuse emission at 4.75 GHz in Reich et al. (1986), and the dotted line the polarised emission in the same image. These two components trace the morphology of SNR G016.8 − 01.1. The more relevant sources in the field are indicated. |
The region around LS 5039, shown in Fig. 1, contains a complex radio structure that has initially been described in Reich et al. (1986). By means of observations with the Effelsberg 100-m telescope at 1.4, 4.8, and 10 GHz, these authors identified the complex as a composition of different objects. The brightest source corresponds to the H ii region RCW 164, which coincides with the optical 8′ × 6′ counterpart in Rodgers et al. (1960). It appears to be an optically thick thermal component that produces the inverted integrated radio emission of the global structure. Other sources within the structure are a source with 0.11 Jy at 4.8 GHz coincident with the Wolf-Rayet star WR 115 (IC14 − 19 in Reich et al. 1986), and an unidentified source with 0.13 Jy at 4.8 GHz, also detected with the VLA as NVSS J182535 − 145555 (Condon et al. 1998). Finally, diffuse emission with a size of ~30′ surrounds all the sources. The source is also visible at 2.7 GHz in the Effelsberg 11 cm radio continuum survey of the Galactic plane (Reich et al. 1990). This emission was identified as a supernova remnant because it is highly polarised (up to 40% at 4.8 GHz, Reich et al. 1986). The dashed and dotted contours in Fig. 1 delimit the diffuse and polarised emission, respectively, and should trace the shape of the supernova. Unfortunately, the high contamination of the bright RCW 164 prevents the determination of the SNR parameters, and consequently its age, distance, centre, and surface brightness are unknown. The lack of polarization in the direction of RCW 164 indicates that the SNR is located behind RCW 164, which is located at ~1.8 kpc (Ribó et al. 2002). Therefore ~2 kpc is the lower limit for the SNR distance. The size of the polarised structure is ~30′ and it is approximately centred at 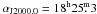 and δJ2000.0 = −14°46′ (Reich et al. 1986; Green 2009).
and δJ2000.0 = −14°46′ (Reich et al. 1986; Green 2009).
2.2. The nearby isolated pulsar PSR J1825−1446
As part of our project to unveil the origin of the binary LS 5039, we searched for other possible sources, such as fossil neutron stars, that may be related to SNR G016.8−01.1. The aim was to obtain the proper motion by means of VLBI of the best candidates to check any possible relation with the SNR. The most obvious candidate is PSR J1825−1446, which, in projection, lies within the SNR itself. To explore other possible candidates we used the ATNF Pulsar Catalogue, PSRCAT1 (Manchester et al. 2005), which is the most complete and updated pulsar database, and accepts searches based on pulsar parameters. We restricted the search to those angular distances for which the pulsars proper motion and age make their past trajectory compatible with the location of the SNR. We note that this selection is not complete because, among the known pulsars many do not have good determinations of the proper motion and/or the age, and their trajectories are compatible only because of their large uncertainties. We discarded pulsars with distances below 1.9 kpc and above 9.0 kpc. We found no other candidate with enough constraints to justify a long-term VLBI project, and therefore we restricted our observations to PSR J1825 − 1446.
Parameters of the isolated pulsar PSR J1825-1446.
PSR J1825−1446 (B1822 − 14) is an isolated pulsar with a period of 0.28 s discovered in a high radio frequency survey conducted at Jodrell Bank by Clifton & Lyne (1986). The main properties of the pulsar are described in Table 1. The radio spectrum of PSR J1825−1446 can be found in Kijak et al. (2007), and it presents a turnover at 1.4 GHz. The spectral index is −1.4 ± 0.7 above this frequency, and it is inverted at lower frequencies. The proper motion in Table 1 was obtained by means of pulsar timing. The pulse profile obtained by Gould & Lyne (1998) shows a single component at 1.4 and 1.6 GHz. We computed the distance to PSR J1825−1446 using the pulsar dispersion measure, although it is not a direct measurement because it depends on the model of the electron distribution in the Galaxy. We used the dispersion measure quoted in Table 1 and the electron density model NE 2001, described in Cordes & Lazio (2002), and obtained a distance of 5.0 ± 0.6 kpc. The distance uncertainty is 10%, although it could be overestimated if the medium along the line of sight of the pulsar is denser than given by the model.
The possible association between SNR G016.8−01.1 and PSR J1825−1446 has been discussed in the literature. Clifton & Lyne (1986) already suggested a possible association based only on a positional coincidence. Clifton et al. (1992) mentioned the possible relation between them, and the proximity with the intense H ii region RCW 164 (see Fig. 1). However, they already found that this H ii region appears to be much closer to the Sun than the pulsar, thus contributing to the DM of the pulsar. The authors also argued that the probability of having a pulsar in a randomly selected area of the size of SNR G016.8 − 01.1 at this Galactic longitude is about 1 in 18, and therefore the positional proximity may only be by chance. Some notes on associations between old (τ ≳ 105 yr) pulsars and supernova remnants can be found in Gaensler & Johnston (1995).
3. Astrometry and proper motion of PSR J1825−1446
The previously known proper motion of the pulsar, shown in Table 1, has large uncertainties and did not allow us to study the origin of this pulsar. The astrometry in the literature, detailed in Sect. 3.2, is scarce. Therefore, we conducted a dedicated 2-yr VLBI astrometric project to measure the proper motion of the pulsar.
3.1. Radio VLBI observations
Before starting the VLBI project, we conducted a short VLA observation at 8.6 GHz to obtain the initial position required for the correlation of the VLBA data. The VLA observation was conducted on November 14, 2008, in the A configuration of the VLA, and lasted 30 min. At that epoch the VLA was performing the upgrade to the EVLA. Seventeen antennas used the new EVLA feeds, eight used the old VLA feeds, and four antennas were not available. We observed the source during three scans of 3.6 min, bracketed by 1.6-minute scans on the phase calibrator J1832−1035 (1832−105). The correlation position of the reference source J1832 − 1035 was 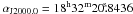 and
and 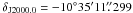 . Standard data reduction in AIPS2 was performed, including standard normalization of the flux density between EVLA and non-EVLA antennas. The data were imaged with an intermediate robust parameter of 0 within AIPS, as a compromise between angular resolution and sensitivity, providing a synthesized beam of 460 × 210 mas at a position angle (PA) of 37°. We used a cell size of 10 mas. The image shows a point-like source with a peak flux density of 0.76 ± 0.07 mJy beam-1, and a total flux density of 0.8 ± 0.1 mJy. The pulsar position was measured with the AIPS task JMFIT.
. Standard data reduction in AIPS2 was performed, including standard normalization of the flux density between EVLA and non-EVLA antennas. The data were imaged with an intermediate robust parameter of 0 within AIPS, as a compromise between angular resolution and sensitivity, providing a synthesized beam of 460 × 210 mas at a position angle (PA) of 37°. We used a cell size of 10 mas. The image shows a point-like source with a peak flux density of 0.76 ± 0.07 mJy beam-1, and a total flux density of 0.8 ± 0.1 mJy. The pulsar position was measured with the AIPS task JMFIT.
The VLBI campaign consisted of three observations with the Very Long Baseline Array (VLBA) at 5 GHz separated by one year. The observations were conducted on the same day (May 4) in 2009, 2010, and 2011, during six hours between UTC 07:40 and 13:40. Observations separated by one year prevent any annual parallax displacement, which is expected to have a maximum amplitude of ~0.2 mas for a source at 5 kpc. Additionally, identical schedules were chosen to minimise any observational difference between epochs (e.g. source elevation, scan structure). The observations were conducted at a frequency of 5.0 GHz (6 cm wavelength), which was chosen as a compromise between angular resolution, spectral index of the pulsar (α ~ −1.4), and the quality of the best VLBI calibrator next to the source, J1825−1718, which is partially resolved at long baselines due to interstellar scattering. The first epoch was recorded with a total data rate of 256 Mbps per station distributed in four dual polarisation subbands, each of them with a bandwidth of 8 MHz, and recorded using 16 frequency channels, two-bit sampling, and 2 s of integration time. The correlation of this first epoch was performed in the hardware VLBA correlator at Socorro. The second and third epochs, observed and correlated in 2010 and 2011, respectively, were recorded at the available bit rate of 512 MHz, and eight subbands were used, which improved the sensitivity of the observation. The 2010 and 2011 correlations were performed with the DiFX (Deller et al. 2007) software correlator at Socorro. The data from the three observations of PSR J1825 − 1446 were also correlated using pulsar gating (see Appendix A).
The observations were performed using phase-referencing on the nearby phase calibrator J1825 − 1718, located at 2.5° from the pulsar, switching between them with a cycling time of four minutes, which is compatible with the expected coherence time. The phase calibrator was correlated at 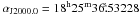 and
and 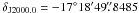 . However, for the final fit result we used the last available position of the source in the frame of ICRF (see Sect. 3.3). As an astrometric check source we observed the quasar J1844 − 1324, which is separated 5° from the pulsar and 6° from the phase calibrator. The source has a flux density of 65 mJy, which, in natural weighted images, is dominated by a compact core that accounts for 94% of the total emission, and displays slightly extended emission eastwards. Only the compact core is seen in the uniformly weighted images used to measure its position. Two scans of the fringe finder J1733−1304 were observed at each epoch.
. However, for the final fit result we used the last available position of the source in the frame of ICRF (see Sect. 3.3). As an astrometric check source we observed the quasar J1844 − 1324, which is separated 5° from the pulsar and 6° from the phase calibrator. The source has a flux density of 65 mJy, which, in natural weighted images, is dominated by a compact core that accounts for 94% of the total emission, and displays slightly extended emission eastwards. Only the compact core is seen in the uniformly weighted images used to measure its position. Two scans of the fringe finder J1733−1304 were observed at each epoch.
Ionospheric correction applied to the VLBA data on PSR J1825 − 1446. Units are mas.
The data reduction was performed in AIPS. Flagging based on predicted off-source times, owing to slewing or failures, was applied using UVFLG. A priori visibility amplitude calibration used the antenna gains and the system temperatures measured at each station. We used ionospheric total electron content (TEC) models based on GPS data obtained from the CDDIS data archive3 to correct the data from the sparse ionospheric variations. Several ionospheric models are produced each day by different groups (i.e. the Jet Propulsion Laboratory (JPL), the Center for Orbit Determination in Europe (CODE), the Geodetic Survey Division of Natural resources Canada (EMR), the ESOC Ionosphere Monitoring Facility (ESA), and the Universitat Politècnica de Catalunya (UPC), among others). We applied the corrections from all available models to the data to check the consistency between models. There are currently 12 models available for the data obtained in 2009, 16 for 2010, and 19 for 2011. In Table 2 we show the offset position between the uncorrected data and the corrected data (average value considering all models) for right ascension and declination, respectively. We also show the standard deviation of the positions measured with the different models, and the model that provides a position closer to the mean value, which was used for the final data reduction.
Standard instrumental corrections were applied (parallactic angle, instrumental offsets, and bandpass corrections). Fringe-fitting on the phase calibrator was performed with the AIPS task FRING. The amplitude and phase calibration, flags, and bandpass correction tables were applied to the target pulsar and the astrometric check source data, which were averaged in frequency, and clean images were produced with IMAGR. A cell size of 0.1 mas was used for cleaning all images, which were produced using a weighting scheme with robust parameter − 2 within AIPS. A tapering of 60 Mλ was applied to avoid the use of phases where the correlated flux density of the calibrator was below ~ 40–10 mJy. No self-calibration of the data was possible because of the low flux density of the target source.
Parameters of the observations of PSR J1825 − 1446, and the resulting images.
The source has a declination of −15°, and the maximum elevation for most of the VLBA antennas is 40°. Some phase decoherence was present when using the data from the beginning and the end of the observations, presumably as a consequence of the atmospheric effects caused by the low elevation of the source and the phase calibrator. To reduce the astrometric errors, we flagged all visibilities with elevations below 20°, and only used the data closer to the culmination of the source, discarding about 1.5 h at the beginning and at the end of the observations. To reduce the effects of the extended emission of the astrometric check source, visibilities with uv-distances below 10 Mλ were not used. The positions of PSR J1825−1446 and the astrometric check source were measured by fitting a Gaussian component with JMFIT within AIPS. In Table 3 we show some parameters of the observation, the resolution, and a comparison of the obtained signal-to-noise ratio with and without pulsar gating (see Appendix A for the details). The position errors of PSR J1825 − 1446 were finally computed as the standard deviation of the three positions of the astrometric check source. The final positions measured in the images from the data correlated with pulsar gating are shown in Table 4.
Astrometry and fit residuals of PSR J1825 − 1446.
3.2. Archival astrometry of PSR J1825 − 1446
To measure the proper motion of PSR J1825−1446 we searched all currently available astrometry of this isolated pulsar. Frail & Scharringhausen (1997) imaged the field around several pulsars with the VLA. They observed PSR J1825−1446 (B1822−14) on March 14, 1993 at 8.4 GHz for two scans of 10 min each. The observations were conducted with the VLA in its B configuration. The phase calibrator was J1832−1035 (J1832−105, 1829−106). We have re-analysed the data to measure the position of the pulsar. Although the scan duration is longer than optimal for astrometry, the pulsar is detected as a point-like source with a peak flux density of 0.78 ± 0.10 mJy beam-1 when using uniform weighting, which yields a synthesized beam size of 1.0 × 0.6 arcsec2. We transformed the positions of the observation from B1950 to J2000, and we updated the position of the phase calibrator to the best currently known position, quoted in Sect. 3.1. We fitted the position using JMFIT within AIPS, and the errors correspond to formal errors of a Gaussian fit. The fitted position can be found in Table 4.
The position of PSR J1825 − 1446 found in Hobbs et al. (2004), obtained by means of pulsar timing, is also shown in Table 4. The position is in the solar system centre of mass, or barycentric, frame, and it was obtained by fitting the pulsar period and period derivative, the ecliptic position and proper motion, among other variables, to the time of arrival (TOA) of the pulses during several years. However, we can see in Table 4 that the timing position differs from the expected position by 245 mas (3-σ) in right ascension, which appears to indicate that the uncertainty may be underestimated (see also Fig. 2 and the difference with the declination error). The difference between the errors in right ascension and declination can be understood considering the pulsar position. The pulsar is located near the ecliptic plane (with ecliptic latitude 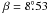 ), which has two consequences in the errors of the ecliptic coordinates (λ, β). In particular, the uncertainty in λ and β are inversely proportional to cosβ, and sinβ, respectively4. For PSR J1825 − 1446 we have that (cosβ)-1 ~ 1.0, and (sinβ)-1 ~ 6.7, which intrinsically yields larger errors in the determination of the ecliptic latitude by means of pulsar timing. Large errors in the ecliptic latitude β produce the large error in declination, which is indeed a factor 6.7 larger than the uncertainty in right ascension. Another possible source of error is the pulsar timing fit solution. Hobbs et al. (2004) fitted 197 time of arrival (TOA) data points spanning 17.4 years and obtained a proper motion of μαcosδ = 10 ± 18 and μδ = 19 ± 115 mas yr-1. The fitting time residuals were 7.539 ms. If this value were understimated, this would explain the small error in right ascension. Another possible source of error is the uncertainty in the link between the barycentric celestial reference system (BCRS) and the ICRF. However, it should be well below the 245 mas difference found between the timing position and the expected position at that epoch; for example Chatterjee et al. (2009) found differences between both reference frames below 1 mas. We have not found any clear explanation to justify the discrepancy between the right ascension position given by pulsar timing and the expected one. Given the large difference, and the intrinsic difference between an interferometric measurement and a timing fit, we have not included the timing position in our final determination of the proper motion of PSR J1825 − 1446, although we have included the position in Table 4 and Fig. 2 for reference.
), which has two consequences in the errors of the ecliptic coordinates (λ, β). In particular, the uncertainty in λ and β are inversely proportional to cosβ, and sinβ, respectively4. For PSR J1825 − 1446 we have that (cosβ)-1 ~ 1.0, and (sinβ)-1 ~ 6.7, which intrinsically yields larger errors in the determination of the ecliptic latitude by means of pulsar timing. Large errors in the ecliptic latitude β produce the large error in declination, which is indeed a factor 6.7 larger than the uncertainty in right ascension. Another possible source of error is the pulsar timing fit solution. Hobbs et al. (2004) fitted 197 time of arrival (TOA) data points spanning 17.4 years and obtained a proper motion of μαcosδ = 10 ± 18 and μδ = 19 ± 115 mas yr-1. The fitting time residuals were 7.539 ms. If this value were understimated, this would explain the small error in right ascension. Another possible source of error is the uncertainty in the link between the barycentric celestial reference system (BCRS) and the ICRF. However, it should be well below the 245 mas difference found between the timing position and the expected position at that epoch; for example Chatterjee et al. (2009) found differences between both reference frames below 1 mas. We have not found any clear explanation to justify the discrepancy between the right ascension position given by pulsar timing and the expected one. Given the large difference, and the intrinsic difference between an interferometric measurement and a timing fit, we have not included the timing position in our final determination of the proper motion of PSR J1825 − 1446, although we have included the position in Table 4 and Fig. 2 for reference.
 |
Fig. 2 Position of PSR J1825 − 1446 with respect to time (MJD in lower axis and year in top axis) in right ascension (left) and declination (right). The solid black lines represent the fitted proper motion, and the grey area the uncertainty of the fit at 3-σ level. The black squares represent the VLA positions, the black circles indicate the VLBA positions, and the grey circle the position from pulsar timing (not used in the fit). The inset shows the position residuals from the fitted model for the 2008–2012 period. The source positions are plotted with uncertainties at 1-σ level. |
3.3. Proper motion of PSR J1825−1446
To obtain the proper motion, we used the two VLA and the three VLBA observations presented in Sect. 3. The reference position of the phase calibrator for the VLA observations was updated to the currently known position of the phase calibrator, quoted in Sect. 3.1. All VLBA positions were updated according to the most recent available position5 of J1825 − 1718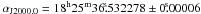 (or ± 0.9 mas) and
(or ± 0.9 mas) and 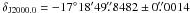 (or ± 1.4 mas). This global uncertainty of the reference source position should be included when working in the ICRF. However, in this case it is only a common offset shared by all VLBA observations. We have computed the proper motion fit using the position of J1825−1718 as a reference. This means that the 0.9 and 1.4 mas uncertainties have been included in all the non-VLBA (but not in the VLBA ones), to compute the proper motion, and it has been added afterwards to the final fitted position. All positions and uncertainties are shown in Table 4. We fitted the proper motion of the source as a linear model of position as a function of time for right ascension and declination separately. We fitted the data using a Levenberg-Marquardt nonlinear least-squares fit (Marquardt 1963). The solution is highly dominated by the three VLBA observations, which were performed in the same scheduled conditions (see Sect. 3.1). The reference epoch is computed as the weighted mean MJD, which is MJD 55291.525. The obtained astrometric parameters for PSR J1825−1446 are
(or ± 1.4 mas). This global uncertainty of the reference source position should be included when working in the ICRF. However, in this case it is only a common offset shared by all VLBA observations. We have computed the proper motion fit using the position of J1825−1718 as a reference. This means that the 0.9 and 1.4 mas uncertainties have been included in all the non-VLBA (but not in the VLBA ones), to compute the proper motion, and it has been added afterwards to the final fitted position. All positions and uncertainties are shown in Table 4. We fitted the proper motion of the source as a linear model of position as a function of time for right ascension and declination separately. We fitted the data using a Levenberg-Marquardt nonlinear least-squares fit (Marquardt 1963). The solution is highly dominated by the three VLBA observations, which were performed in the same scheduled conditions (see Sect. 3.1). The reference epoch is computed as the weighted mean MJD, which is MJD 55291.525. The obtained astrometric parameters for PSR J1825−1446 are 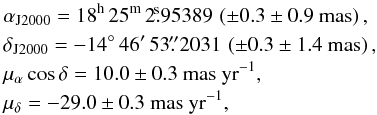 where the first set of errors in the positions corresponds to statistical uncertainties, and the second set corresponds to the uncertainty in the phase reference position. The degrees of freedom of the fit are 4, and the reduced χ2 is 0.95 and 0.98 in right ascension and declination, respectively.
where the first set of errors in the positions corresponds to statistical uncertainties, and the second set corresponds to the uncertainty in the phase reference position. The degrees of freedom of the fit are 4, and the reduced χ2 is 0.95 and 0.98 in right ascension and declination, respectively.
4. Astrometry and proper motion of LS 5039
To fit the proper motion of LS 5039 we used new interferometric radio data together with archival radio and optical data. In this section we will only describe in detail the data reduction of three radio projects. The description of the other data used is already published, or will be published elsewhere. In particular we will describe a VLA+PT observation conducted in 2003, three VLBA observations conducted between 2004 and 2006, and a short EVN observation conducted in 2011. The parameters of these observations are summarised in Table 5.
4.1. VLA-PT observation
We observed LS 5039 with the VLA plus the VLBA antenna in Pie Town (PT) at 15.0 GHz on August 05, 2003. We used the VLA in its A configuration plus PT, which is located at a distance of 52 km from the VLA site, and provides longer baselines with all the VLA antennas. The observation spanned from 01:00 to 08:40 UTC, and was centred at MJD 52856.2. The phase reference calibrator was J1832−1035 (1832−105), located at 4.5° from LS 5039. Two IFs of 50 MHz were used. The cycle time including the phase calibrator and the target source was 3 min. The ICRF source J1911−2006 (1911−201) was observed regularly during the observations. The flux calibrator was 3C 286 (1331+305). The orbital phase of the binary system at the time of the observation was 0.92, using the ephemeris from Casares et al. (in prep.).
Standard reduction procedures were applied to the data, and a precise position of the source was obtained when using a uniform weighting scheme (robust −5 within AIPS), and a cellsize parameter of 5 mas. The source position, fitted with JMFIT within AIPS, has an uncertainty of 1 and 2 mas in right ascension and declination, respectively. The observational details, the obtained synthesized beam size, and the fitted components are shown in Table 5.
4.2. VLBA astrometric project
The VLBA projects BD087 and BD105 are part of a long-term astrometric project to measure the proper motion and parallax of several X-ray binaries. The segment BD087G, and the continuations BD105A and BD105G observed LS 5039 at a frequency of ~8.5 GHz. The observations took place on June 11, 2004, June 11, 2005, and January 29, 2006, and lasted 6, 6, and 5 h, respectively. The three observations were recorded with a total data bit rate of 128 Mbps. In the first epoch, the data rate was distributed in 8 IF channels with a bandwidth of 4 MHz each, with one single polarisation (right circular polarisation) and two-bit sampling, while the latter two used two IF channels with 8 MHz bandwidth and dual circular polarisation, also recorded with two-bit sampling.
The phase reference source was J1825−1718, which is slightly resolved also at 8.4 GHz (although it is much more compact than at 5 GHz), and is located at 2.47° from LS 5039. The cycling time of the phase-referenced observations was three minutes. Several check sources were observed during the three epochs. In particular, the sources N1834 − 1433, N1819−1419, and N1818−1108 were observed in all epochs and were used to estimate the astrometric uncertainties. The fringe finder was J1733−1304. The data reduction is analogous to the one described in Sect. 3.1. In this case, an statistical approach to determine the best ionospheric correction was not applied, because the effect is smaller at this frequency. We note that the correction of the Earth orientation parameters was not applied to the data because it did not affect the position measurement, and therefore we preferred not to apply this additional correction to the datasets.
Owing to the lower flux density of LS 5039 at 8.4 GHz, the three epochs were imaged using a weighting scheme with robust parameter 0 within AIPS, as a compromise between spatial resolution and signal-to-noise ratio (S/N). To reduce the effect of the source extended emission (see Sect. 4.5) we omitted the baselines with shortest uv-distances. We found a compromise between significance of the detection, and the uv-distance reduction by cutting the baselines below 20, 30, and 40 Mλ for the three epochs. For the first epoch a lower threshold was required because the data quality was worse. On the other hand, the longest baselines had to be softened because of the poor quality of the partially resolved phase reference source. We reduced the weight of baselines longer than a certain value. For the first epoch we used a tapering parameter of 60 Mλ. For the latter two projects, the tapering was at 120 Mλ. The resulting resolution and fitted components are shown in Table 5.
Astrometry and fit residuals of LS 5039 for optical and radio projects.
4.3. EVN observations
The most recent VLBI observation of LS 5039 was performed with the European VLBI Network (EVN). We observed several sources around LS 5039 to search for possible phase calibrators and in-beam calibrators, and test the longest EVN baselines to check the viability of an astrometric project. Among other sources, we observed the phase calibrator J1825−1718, also used in the previously described VLBI observations. The observations were conducted on March 15, 2011, between UTC 02:00 and 05:00. We only observed 11 scans on LS 5039, bracketed by scans on the phase calibrator with a cycling time of 3.4 min and distributed along the observation. The total time on-source was approximately 20 min. The antennas included in the observation were Effelsberg, Westerbork, Onsala, Medicina, Yebes, Svetloe, Badary, Zelenchukskaya, Nanshan (Urumqi), Sheshan (Shanghai), and Hartebeesthoek. The data were recorded with a total data bit rate of 1024 Mbps, providing a high-sensitivity array. The correlated parameters are eight IF channels with both circular polarisations, each of them with 16 MHz bandwidth (provided by 32 frequency channels of 500 kHz), and two-bit sampling.
The data reduction is analogous to the one described in Sects. 3.1 and 4.2. No useful FRING solutions were found between Hartebeesthoek and the rest of the antennas, which considerably reduced the North-South array extend, and therefore the resolution in declination on the final image. After the phase calibration from J1825−1718, the North-South maximum baseline was of about 20–40 Mλ, while in the East-West direction it was of 160–180 Mλ, although large gaps were present in the uv-plane due to the short observation time. We note that large phase instabilities appeared due to the low declination of the source. We finally imaged the source with robust parameter 0, minimum uv-distance set to 15 Mλ, and uv-taper set to 120 Mλ. Even with the long maximum baselines, the final synthesized beam size is 5.6 × 1.3 mas2 in PA of −15°. The resolution of the images and the fitted components are shown in Table 5.
4.4. Archival data of LS 5039
Astrometry of LS 5039 can be obtained from two types of observations. On one hand we have positions from optical observations of the main star of the system. This observations, coming from large (and global) astrometric projects, cover a long time, of the order of decades, although they provide limited astrometric accuracy of about 10–300 mas. On the other hand, radio interferometric observations provide observations of the radio nebula around the binary system. These observations have been obtained in the last ~10 years, but their uncertainties are between 1 and 10 mas. The time span of the optical observations can be combined with the precise radio positions to fit an accurate position and proper motion of the source. However, combining datasets with considerable different properties brings important caveats that have to be taken into account. These will be described in Sect. 4.6. The astrometry described here is summarized in Table 6. The corresponding orbital phases were computed using the ephemerides in Casares et al. (in prep.).
4.4.1. Archival optical astrometry of LS 5039
Optical observations of LS 5039 are available from historical photographic catalogues since 1905. Updated global solutions have been obtained for the historical photographic plates by using more recent reference catalogues. The updated versions of the classical catalogues provide improved systematic uncertainties on the star position. However, some newer versions combine catalogues from different epochs to fit a global solution that considers the proper motion of the stars. Therefore, they are not suitable for our proper motion determination because they are not independent, and they include a proper motion estimation in their own position fitting. This is the case, for example, of the Palomar Observatory Sky Survey plates used to produce the USNO-A2.0 catalogue (Monet 1998), which uses only the blue and red original plates, while the new version of the catalogue, USNO-B1.0 (Monet et al. 2003), with better uncertainties, uses data from 1949 to 2002, combined using a proper motion of 4, and −14 mas yr-1 in right ascension and declination, respectively. It is also the case of GSC 1.2 compared to the newer versions (GSC 2.2 and GSC 2.3.2), or UCAC1 when compared to UCAC2 and UCAC3, which have improved references and systematic error treatment. Therefore, although new catalogues are currently available, we have used only the versions that are not compilation catalogues. This means that most of the optical values used here were already available at the time of writing of Ribó et al. (2002).
In particular, for the proper motion determination we used the following catalogues. AC2000.2 is the second version of the Astrographic Catalog 2000 and provides accurate optical positions of LS 5039 on 1906 in Hipparcos Celestial Reference System (HCRS, coincident with J2000.0). USNO-A2.0 contains a global reduction of the data in the Palomar Observatory Sky Survey plates obtained around 1950. The Twin Astrographic Catalog version 2 (TAC 2.0) provides a position based on four observations (the plates were compiled between 1977 and 1986). Following Ribó et al. (2002), we included an additional uncertainty of 15 mas in each coordinate, as suggested in Zacharias et al. (1999). We also used the Guide Star Catalog (GSC) version 1.2, which consists of a single-epoch collection of 6.4° × 6.4° Schmidt plates (the newer versions of the catalog are compiled, and proper motions are fitted using Tycho positions). The GSC position is less relevant for the fit because of the relatively large errors (300 mas) for a position obtained in 1986. The Tycho-2 Catalog was obtained from the Tycho star mapper observations of the ESA Hipparcos satellite (Høg et al. 2000). It provides the mean position at epoch J2000, corrected from proper motion, as well as the observed position, which is the one used in our analysis. Following Ribó et al. (2002), we have used the conservative error estimate of σαcosδ = 149 mas and σδ = 120 mas. Skrutskie et al. (2006) detected LS 5039 at near-infrared bands with the all-sky Two Micron All–Sky Survey (2MASS), and a very precise position was obtained. The three observed bands (J, H, and Ks) were tied with the Tycho-2 Reference Catalog, so it is in the ICRS frame. Finally, accurate astrometry of LS 5039 can be found in the latest versions of the US Naval Observatory CCD Astrograph Catalog (Zacharias et al. 2010). However, we can only use the position from the UCAC1 version (Zacharias et al. 2000). All these optical positions and their uncertainties are quoted in Table 6.
4.4.2. Archival radio astrometry of LS 5039
The binary system LS 5039 is a known radio emitter discovered by Martí et al. (1998). Since then, several radio interferometric observations have been conducted to study its morphological and spectral properties at different orbital phases. Here we list the radio projects in which the system has been observed with sufficient resolution to provide an accurate position of the source. In particular, it has been observed with the VLA, the VLBA and the EVN at frequencies between 5 and 15 GHz. Observations at lower frequencies with the VLA are excluded because they provide positions with uncertainties above 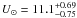 for relatively recent epochs, and do not contribute to the proper motion fit when compared to the 1–10 mas accuracy of the other radio observations.
for relatively recent epochs, and do not contribute to the proper motion fit when compared to the 1–10 mas accuracy of the other radio observations.
We briefly summarise the observations included in the fit. Martí et al. (1998) conducted a multi-epoch and multi-frequency project of the system with the VLA at four frequencies between 1 and 15 GHz. They provided a single position derived from the 15 GHz data obtained with the highest resolution configuration (A) of the VLA. The reference source was the ICRF source J1911-2006 (1911-201), and their error estimate is 10 mas. The source was next observed with the VLBA and the VLA for two epochs in June 2000 at 5 GHz (Ribó et al. 2008). Only one of the two epochs provides good astrometry. The source was also observed with the EVN within project EF018 in March 2007. The project consists of three observations at 5 GHz, observed every two days. The low elevation of LS 5039 during the observations affects the phase calibration of the data and therefore the astrometry. To obtain a reliable position, we removed the data with the lowest elevations and then averaged the three measurements. The uncertainty of this position was computed as the standard deviation of the three runs. We conducted a similar project, observing the source with the VLBA during five consecutive days in July 2007 at 5 GHz (see details in Moldón et al. 2012). A similar procedure was used in this case, computing the average position of the source from the five images produced with uniform weighting. Finally, we used a recent position obtained within the VLBA large project BC1966 (PI: J. Condon), whose solutions are available online. The positions, uncertainties (see the overview in Condon et al. 2011), and residuals with respect to the final proper motion fit are shown in Table 6.
4.5. Uncertainties in the position of LS 5039
LS 5039 is known to be extended at mas scales, and a bipolar jet-like structure is present in all VLBI (VLBA and EVN) radio observations of the source (Paredes et al. 2000, 2002; Ribó et al. 2008; Moldón et al. 2011c, 2012). Although the source displays a bright core, we do not know the offset between the peak of the radio core and the position of the binary system. There are two main reasons. First, the particles accelerated in the system travel distances much longer than the system orbit, and the location of the peak of the emission at any moment depends on the physical conditions (basically the electron distribution, and the synchrotron cooling time). Second, for each observed frequency, each interferometer array is sensitive to different ranges of spatial scales, therefore inter-comparison is not straightforward because we are seeing different regions of the particle flow. In summary, the unknown position of the system within the radio outflow is variable (at time scales of 1 or more days), and depends on the observed frequency and array. We tried to minimise this effect by measuring positions derived from the uniformly weighted images, which trace the most compact emission from the core component of the source.
 |
Fig. 3 Offsets in right ascension (left) and declination (right) of LS 5039 with respect to time in MJD and year. The solid black lines in each panel represent the fitted proper motion, and the grey area the uncertainty of the fit at 3-σ level. The upper panels include all data points used for the fit, and the lower panels are the zoom of the last 16 years (marked by the small rectangles), and include the residuals with respect to the fitted model. The empty blue triangles represent the optical data, the green squares show the VLA data, the red triangles correspond to the VLBI observations at 5 GHz, and the black circles are the VLBI data at 8.6 GHz. The source positions are plotted with uncertainties at 1-σ level. |
Preliminary fits of the position and proper motion of LS 5039 using the formal astrometric errors of the radio positions yielded reduced χ2 of 4.1 and 2.3 in right ascension and declination, respectively, which indicated that a linear model did not completely describe the source positions. This means that the formal astrometric errors for the radio observations underestimate our real knowledge of the position of the binary system within the radio emission. A shift on the peak of the emission was observed in LS I +61 303, PSR B1259−63, and HESS J0632+057 (Dhawan et al. 2006; Moldón et al. 2011a,b). Based on these observations, and the estimations in Dubus (2006) and Bosch-Ramon & Khangulyan (2011), we expect the peak of the emission to follow an ellipse with semimajor axis of about ~1 mas, although the size should depend on the frequency, and should be larger at low frequencies. It is not possible to measure this unknown deviation with the current resolution and data sampling, especially when observing at different frequencies and resolutions. Therefore, we increased the position uncertainty of the radio positions to compensate our ignorance of this time-dependent offset. In particular, we added in quadrature an ad-hoc uncertainty of 1.0 mas to all radio positions before performing the fit. This uncertainty is already included in Table 6.
Another source of uncertainty is the systematic errors on the position of the phase calibrators, which are the reference of the measured positions. Fortunately, the phase reference calibrator for all VLBI observations was J1825−1718. Although the calibrator was correlated at different positions, we have shifted all measurements to the common reference position quoted in Sect. 3.3. We followed the same procedure as with PSR J1825−1446, and these uncertainties were not included in the proper motion determination, but were added afterwards to the final fitted position.
We also included the effect of the annual parallax of LS 5039, assuming a distance of 2.9 kpc, which corresponds to a deviation of 0.3 mas. The equations governing the parallax displacements can be found, for example, in Brisken et al. (2002) and Loinard et al. (2007). The additional displacements were added to the data before performing the fit, and are not included in Table 6.
4.6. Proper motion of LS 5039
We fitted the reference position and the proper motion to the data in right ascension and declination independently for the 16 positions available, using the Levenberg-Marquardt nonlinear least-squares fit. The reference epoch for the fit, computed as the weighted mean of the dates of observations, is MJD 53797.064. The resulting astrometric parameters for LS 5039 are 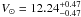 where the first set of errors in the positions corresponds to statistical uncertainties, and the second set corresponds to the uncertainty in the phase reference position. The reduced χ2 of the right ascension and declination fits were 0.75 and 1.35, respectively. The positions, fit, and uncertainties are shown in Fig. 3. The solution is dominated by the radio observations, but the optical observations provide better stability to the fit. We note that the effect of the parallax correction on the data is small. If the correction is not included, the reduced χ2 in right ascension increases by 0.02, and does not change in declination. We also tried to fit the parallax to the data, with and without the ad hoc 1 mas uncertainty, but the parallax is too small to be measured with the current data.
where the first set of errors in the positions corresponds to statistical uncertainties, and the second set corresponds to the uncertainty in the phase reference position. The reduced χ2 of the right ascension and declination fits were 0.75 and 1.35, respectively. The positions, fit, and uncertainties are shown in Fig. 3. The solution is dominated by the radio observations, but the optical observations provide better stability to the fit. We note that the effect of the parallax correction on the data is small. If the correction is not included, the reduced χ2 in right ascension increases by 0.02, and does not change in declination. We also tried to fit the parallax to the data, with and without the ad hoc 1 mas uncertainty, but the parallax is too small to be measured with the current data.
To better understand the systematic fit uncertainties, we analysed the distribution of fit solutions following a procedure similar to the one discussed in Chatterjee et al. (2009). The bootstrap method used consists of fitting the proper motion and reference position from different samples of the available positions. For each iteration we randomly selected 16 positions, with replacement, and produced a proper motion fit. By repeating the fit for different combinations of positions, we obtained a probability distribution of proper motions obtained with all possible combinations of the data. The probability distribution functions (PDF) and the cumulative distribution functions (CDF) of these PDFs are plotted in Fig. 4. The distributions were computed with a bin width of 0.01 mas yr-1. The number of iterations (different combinations with replacement) is 2 × 107, which is more than necessary to smoothly cover the one-dimensional range of values, but it is required for the 2D distribution (see below). The shaded grey areas in Fig. 4 indicate the minimum regions containing the 68.2, 95.4 and 99.7% of the samples, from darker to lighter, respectively. The best-fit value of the proper motion can be computed in two ways: as the mode of the distribution (value that occurs most frequently), which is marked as the vertical line in the top panels, or as the value that accumulates the 50% of the events (the median), which is marked as the vertical line in the bottom panels of Fig. 4. These two values are not identical, but the difference is well below the 1-σ uncertainty of the proper motion estimation. We can clearly see that the distribution is approximately Gaussian at the central region, but it shows considerable asymmetric wings. The mode and the confidence intervals are 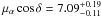 mas yr-1 and
mas yr-1 and 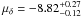 mas yr-1.
mas yr-1.
Owing to the asymmetry in the distributions of Fig. 4 we computed the 2D distribution of proper motions obtained with the bootstrap method in right ascension and declination simultaneously to better identify any other correlation or asymmetry between the confidence regions. The simulated fit results were gridded with a bin size of 0.01 mas yr-1 in both directions. The minimum regions covering the 68.2, 95.4 and 99.7% of the events were obtained, and they were smoothed with a Gaussian filter with a size of 18 bins. The corresponding confidence regions are shown in Fig. 5. We can see that the distribution is clearly skewed towards lower values of μδ and more moderately to lower values of μαcosδ.
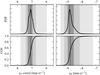 |
Fig. 4 Top: distribution of proper motion fit results for LS 5039 estimated with the bootstrap method, which is equivalent to an un-normalised probability distribution function (PDF) for right ascension and declination independently. Bottom: corresponding cumulative distribution functions (CDF). For all panels, the grey shaded areas correspond to the minimum region that includes the 68.2, 95.4 and 99.7% of the events, from dark grey to light grey. The vertical line marks the most common value (the mode) for the PDF distributions, and the value covering the 50% of the events for the CDF. |
 |
Fig. 5 Distribution of proper motion fits for LS 5039 computed with the bootstrap method. The central contours represent, from inside to outside, the minimum smoothed regions containing 68.2, 95.4, and 99.7% of the events. The two histograms are the projected 1D distributions shown in Fig. 4. |
5. Galactic space velocity
We can now study the Galactic space velocity of LS 5039 and PSR J1825−1446, following the work in Ribó et al. (2002), Dhawan et al. (2007), and Miller-Jones et al. (2009a). The space velocity of each source can be obtained by combining the proper motion and the radial velocity of the source (optical systemic velocity, γ, in velocity lightcurves) to form a space velocity vector (μαcosδ,μδ,γ). This velocity can be rotated to the cartesian coordinates U, V, W, defined as U positive towards the Galactic Centre, V positive towards l = 90° (sense of the Galactic rotation), and W positive towards the North Galactic Pole (NGC). The rotation is described in Johnson & Soderblom (1987), although we used the updated definition of the North Galactic Pole direction from Reid & Brunthaler (2004) (the direction of the NGP is 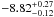 and
and 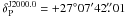 , with the zero longitude at
, with the zero longitude at 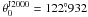 ). We computed the heliocentric Galactic space velocity by subtracting the peculiar velocity of the Sun with respect to the local standard of rest (LSR). We used the recent determination from Schönrich et al. (2010) of
). We computed the heliocentric Galactic space velocity by subtracting the peculiar velocity of the Sun with respect to the local standard of rest (LSR). We used the recent determination from Schönrich et al. (2010) of 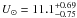 ,
, 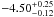 ,
, 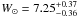 km s-1. We note that V⊙ is significantly larger than in previous estimations. The obtained heliocentric Galactic velocities (U,V,W)LSR for LS 5039 and PSR J1825−1446 are shown in Table 7.
km s-1. We note that V⊙ is significantly larger than in previous estimations. The obtained heliocentric Galactic velocities (U,V,W)LSR for LS 5039 and PSR J1825−1446 are shown in Table 7.
Galactic coordinates and Galactic space velocities of LS 5039, and PSR J1825−1446.
We note that the distance to the source is the highest source of error when converting from angular to linear velocities. We used the most recent determination of the distance to LS 5039, 2.9 ± 0.8 kpc (Casares et al., in prep.). The distance to PSR J1825−1446 is 5.0 ± 0.6 kpc. The first set of errors in the Galactic velocities in Table 7 corresponds to the proper motion uncertainty, and the second set of errors corresponds to the contribution of the distance uncertainty.
We can now compute the Galactic space velocity as measured from the Galactic Centre (GC). We need to transform the velocity vector to the reference frame of an observer situated at the position of the source that participates in the Galactic rotation. This reference frame is the regional standard of rest (RSR). The transformation from the LSR to the RSR takes into account the distance from the Sun to the GC, 8.0 ± 0.5 kpc (Reid 1993), and the circular rotation about the GC, 236 km s-1 (Reid & Brunthaler 2004), which we consider constant. From the Galactic velocity (U,V,W)RSR, we directly obtain the Galactocentric velocity of a source, with the radial velocity vrad away from the GC, vcir, in the direction of the Galactic rotation at each point, and vz, perpendicular to the Galactic Plane, and positive towards the NGP. The expected velocity of a system following the Galactic rotation is zero for vrad and vz, whereas vcir is expected to be 236 km s-1. The deviation from the expected circular rotation is the peculiar velocity ![\hbox{$v_{\rm pec}= [v^{2}_{\rm rad} + (v_{\rm cir}-236{\rm ~km~s}^{-1}) ^{2} + v^{2}_{z} ]^{1/2}$}](/articles/aa/full_html/2012/07/aa19205-12/aa19205-12-eq173.png) . The Galactic velocities from the GC for LS 5039 and PSR J1825 − 1446 are shown in Table 7.
. The Galactic velocities from the GC for LS 5039 and PSR J1825 − 1446 are shown in Table 7.
The large error in the distance of the sources limits the determination of their space velocity. In this case it is convenient to plot the Galactic velocities as a function of the distance from the Sun. In Figs. 6 and 7 we show the computed velocities (black lines) and their uncertainties (dark grey areas) for a range of distances. The horizontal dashed lines mark the expected velocity when following the Galactic rotation. The grey areas indicate the cosmic velocity dispersion of the Galactic young disc stars, which depends on the age of the stellar system. LS 5039 is an O-type star and its companion could have been more massive. The progenitor of PSR J1825 − 1446 is unknown, but collapse to form a neutron star usually occurs for stars with total mass between 8 and 15 M⊙ (Lyne & Graham-Smith 2005). Therefore, we assumed that the progenitor was a young star formed in the Galactic thin disc. The measured velocity dispersion of young OB stars is biased towards local values because the stars with known 3D velocities and radial distances are predominantly located in the solar neighbourhood. However, the velocity dispersion of young stars should follow the velocity dispersion of the gas in the Galactic disc. This dispersion is of about 4–5 km s-1 in the plane (σU,σV), and can be as low as 1–2 km s-1 in the direction perpendicular to the plane (σW), although spiral shocks can induce higher in-plane velocities of about ~7–10 km s-1 (Kim et al. 2006). This agrees with values measured in Torra et al. (2000) for stars of 0–30 Myr of (σU,σV,σW) = (7.9,7.2,4.3) km s-1. We assume that the expected velocity dispersion of young stars is (σU,σV,σW) = (10,10,5) km s-1.
 |
Fig. 6 Components of the Galactic and peculiar velocity of LS 5039 (solid black lines) and their uncertainties at 3-σ level (dark grey areas). The horizontal dashed lines and light grey areas mark the expected Galactic velocity, and the velocity dispersion expected for young stars, respectively. The vertical dotted lines indicate the measured distance to the source. |
 |
Fig. 7 Same as Fig. 6 for PSR J1825−1446. The solid black line in each panel indicates the Galactic velocity assuming a radial velocity of 0 km s-1. The velocity uncertainties at 3-σ level are smaller than the black lines. The red thin line corresponds to an hypothetical radial velocity from the Sun of +500 km s-1 (away from the Sun) and the blue thin line to −500 km s-1 (towards the Sun). |
We can see in Fig. 6 that LS 5039 has a high peculiar velocity, mainly perpendicular to the Galactic plane, and it is not compatible with the expected velocity dispersion for any of the considered distances. This reaffirms the runaway nature of the system, which was originally discussed in Ribó et al. (2002). On the other hand, PSR J1825−1446 shows a much higher space velocity. This is an isolated pulsar, and therefore it is not possible to measure any radial velocity from the Sun. In Fig. 7 we show the Galactic velocities assuming a radial velocity of 0, +500, and −500 km s-1 (black, red, and blue lines, respectively). This covers a generous range of possible radial velocities. We note that this contribution is less notorious in the direction perpendicular to the Galactic Plane because both the pulsar and the Sun are at a similar distance from the Galactic plane. For PSR J1825−1446 we plot a wide range of distances, considering that the distance estimate could be overestimated by the DM determination. The pulsar space velocity is not compatible with the expected rotation of the Galaxy. Remarkably, the pulsar has a velocity perpendicular to the Galactic Plane of ~550 km s-1 and away from it. Therefore, PSR J1825−1446 is clearly a runaway pulsar that has been ejected from the Galatic disc at a very high speed. The peculiar velocity for the nominal distance of 5.0 kpc is 690 ± 7 km s-1. This transverse velocity is high even for a runaway isolated pulsar, because it lays in the tail of the transverse velocity distribution of young pulsars shown in Hobbs et al. (2005). The peculiar velocity would be lower if the distance is overestimated, and would be 500 ± 5 km s-1 for a distance of 3.6 kpc.
6. The origin of LS 5039 and PSR J1825−1446
LS 5039 is a young O6.5 main sequence star, which has a total lifetime of a few million years. This sets an upper limit to the age of the binary system LS 5039/compact object, which allows us to constrain the possible locations where the supernova took place, and therefore where the system originated. We have explored possible origins of LS 5039 in the last 1–10 Myr, even though for ages older than 1–2 Myr the source birthplace lies well outside the Galactic plane, which is unlikely. Therefore, we only consider the projected past trajectory of LS 5039 during the last ~106 yr, and discuss possible associations that cross this trajectory. We know that the characteristic age of PSR J1825−1446 is 1.95 × 105 yr. This value is computed as the ratio between the period and the period derivative of the pulsar, and it is valid under certain assumptions: the initial spin period of the pulsar was much shorter than that observed today (P0 ≪ P), there is no magnetic field decay (PṖ is constant), and the energy loss corresponds to a spinning dipolar magnet in perfect vacuum. The slowdown model of a pulsar is generally parametrised by the braking index, which is usually considered close to 3, although it can take a range of values (see Faucher-Giguère & Kaspi 2006). The uncertainty on this parameter prevents the characteristic age from being a faithful estimate. It has been shown that the characteristic age of a pulsar can be significantly lower than the true age of the pulsar (e.g. Gaensler & Frail 2000) or even higher than the real age of the pulsar (e.g. Kramer et al. 2003). Therefore, a wide range of ages, and consequently possible angular distances from the current location of the pulsar, should be explored.
 |
Fig. 8 Area around LS 5039 and PSR J1825−1446 in Galactic coordinates. The lines mark the past trajectory in the last 106 yr for LS 5039, and 1.95 × 105 yr for PSR J1825−1446. The green circles are supernova remnants from the catalogue compiled in Green (2009). The red circles are open clusters from the WEBDA database, and the blue ellipses mark the position of the known OB associations (Mel’Nik & Efremov 1995). The OB stars (Reed 2003) and the star-forming regions (Avedisova 2002) are marked with blue and grey dots, respectively, and provide a general view of the young system distribution in this region of the Galaxy. The red crosses mark the H ii regions (Lockman 1989). The objects in regions #1, #2, and #3 are described in the text. |
In Fig. 8 we show the region around the current position of LS 5039 and PSR J1825−1446 (green and red crosses, respectively) in Galactic coordinates. We also plot different objects related with young stars. The ellipses in green, red, and blue mark the positions of the supernova remnants, the open clusters and the OB associations, respectively. To have a better context of the distribution of young systems, we include the O and B stars, the star-forming regions, and the H ii regions close in this part of the Galactic plane. The past trajectories in the last 106 yr for LS 5039, and 1.95 × 105 yr for PSR J1825−1446 are indicated by the green and red continuous lines, respectively. The plotted trajectories are linear, and therefore not affected by the Galactic potential. We checked the validity of this assumption using the software package galpy7 to compute the trajectories under a standard Milky Way potential (combination of a Miyamoto-Nagai disc, a Navarro-Frenk-White halo, and a Hernquist bulge potentials, see the documentation for details). For all aspects discussed in this paper the slight difference between the integrated orbit in the Galactic potential and the free (linear) trajectory are irrelevant. Therefore, we do not use the orbit integration to avoid using additional parameters to describe the Galaxy. We used the software to check that the space velocity of PSR J1825−1446 is above the escape velocity, and therefore it will be ejected from the Galaxy.
As can be seen in Fig. 8, the past trajectory of LS 5039 and PSR J1825−1446 crosses three interesting regions, marked with numbers from #1 to #3. The first region (#1) is composed of the objects at short angular distances from the systems. In the WEBDA database8 we can see that LS 5039 and PSR J1825−1446 are within the open cluster Dolidze 28 (C 1822−146), whose central star is WR 115. Manchanda et al. (1996) determined the distance to the cluster to be 2.2 kpc (note that the cluster is wrongly named Do 78 instead of Do 28 in Table 1 of Manchanda et al. 1996). We used the 2MASS photometric magnitude of WR 115 (Wolf-Rayet of type WN6) from Table A1 in Crowther et al. (2006), MKs = −5.10, and colours for a nominal subtype WN6 star (J − K)0 = 0.17 and (H − K)0 = 0.15. The absorption estimate of the source is AK = 0.59, which yields a distance of 2.0 kpc, compatible with the distance quoted above. In the same field we find the OB association Sct OB3 (see Mel’Nik & Efremov 1995), with ten members in a region of 25.8 × 33.6 pc2, and an estimated distance of 1.5 kpc. This distance is compatible with the estimate in Dambis et al. (2001), obtained from a parallax measurement, of 1.4 kpc. They also provide an age of Sct OB3 of 4–5 Myr. The closest H ii ionised region is RCW 164, already discussed in Sect. 2.1.
In Fig. 9 we show the most relevant objects of region #1 together with the past trajectories of LS 5039 and PSR J1825−1446. We can see that although PSR J1825−1446 is currently very close to RCW 164, it comes from the opposite direction at high speed. The trajectory is not compatible with the central region of SNR G016.8−01.1 either. Although it is not possible to determine the kinematic centre of the SNR precisely, the projected past trajectory of LS 5039 seems to be far away from the central region of the remnant (see Fig. 1), although an association cannot be discarded. We note that the 1-σ accuracy in the position of LS 5039 105 yr ago is approximately 18 arcsec, although the uncertainties do not follow a Gaussian distribution, as shown by the contours in Fig. 9.
 |
Fig. 9 Wide-field map around SNR G016.8−01.1. The grey scale corresponds to the Parkes-MIT-NRAO survey at 5 GHz (Tasker et al. 1994). The green and red lines mark the past trajectory of LS 5039 and PSR J1825−1446, respectively. The arrows mark the proper motion sense. Circles are plotted in the trajectories every 104 yr. The contours represent the 68.2, 95.4 and 99.7% confidence levels on the position that LS 5039 had 105 and 5 × 104 years ago (see uncertainties in the proper motion shown in Fig. 5). The grey dotted lines show the Galactic coordinates. |
The past trajectory of LS 5039 shown in Fig. 9 suggests an interesting possibility, namely that the binary system LS 5039 and WR 115 come from the same point on the sky, and that they might have been a triple system, from which WR 115 was ejected in the opposite direction after the supernova explosion. This would tightly restrict the age of the triple system. However, we have computed a proper motion of WR 115 using positions from optical catalogues, in particular from AC2000.2, GSC 1.2, Hipparcos, UCAC3, and 2MASS, see Sect. 4.4.1. The proper motion obtained is 4.5 ± 0.6 and − 5 ± 4 mas yr-1 in right ascension and declination, respectively. The proper motion in right ascension discards the possibility of a triple system with WR 115 because the linear momentum conservation would require that the system pre-supernova already had a runaway velocity much higher than expected from Galactic diffusion.
Region #2 is found at an angular distance of ~3° from both sources, and harbours an active site of star formation and young stars. The OB association shown in region #2 is Ser OB2 (Mel’Nik & Efremov 1995), with a size of 22.8 and 33.0 pc in Galactic longitude and latitude, respectively, an average radial velocity relative to the Sun of −2.4 ± 3.9 km s-1, and an average distance of 1.45 kpc. Forbes (2000) provides a distance to the association of 1.9 ± 0.3 kpc, and an average age of 5 ± 1 Myr. Tetzlaff et al. (2010) provide a parallax measurement based on Hipparcos stars of 0.63 mas, which correspond to a distance from the Sun of 1.6 kpc and sets an age of the association of 4–5 Myr. On the other hand, the open cluster in the centre of region #2 is NGC 6604, which can be found in the WEBDA catalogue, with a distance of 1.7 kpc, and an age of ~6 Myr. Loktin & Beshenov (2003) measured an average proper motion of this cluster, formed by ~97 stars, and obtained −0.66 ± 0.19 and −0.88 ± 0.17 mas yr-1 in right ascension and declination, respectively, as well as the distance quoted in the WEBDA database. Recently, Dambis et al. (2001) set a parallax of 0.59 mas, corresponding to a distance from the Sun of 1.7 kpc, and an age of 4–5 Myr. There is also an interesting H ii region that might be associated with this complex, SH 2-54, from the catalogue of H ii regions in Sharpless (1959). Its radial velocity was measured by Blitz et al. (1982) to be 27.6 ± 0.5 km s-1, much higher than the average velocity of Ser OB2 quoted above, and the distance from the Sun is 2.0 ± 0.2 kpc, which is compatible within errors with the structures discussed above. In summary, region #2, which harbours many young stars and star-forming regions, is undergoing intense formation of new stars, it is at a distance of 1.5–2.0 kpc from the Sun, and has an age of 4–5 Myr. The age of the complex is enough to allow LS 5039 to have travelled from that region of the sky to its current position. Considering the large uncertainties in the distance to the system, this is a plausible birth region for LS 5039 provided that it is located between 1.5 and 2.0 kpc from the Sun. For this distance range, Fig. 6 shows that LS 5039 would have a lower peculiar Galactic velocity of about 70–95 km s-1. In this case, LS 5039 would have an age between 1.0 and 1.2 Myr.
Finally, region #3 in Fig. 8 marks the position of SNR G017.4−00.1, which has a diameter of 6′, a flux density of 0.4 Jy, and a spectral index of +0.7 (Brogan et al. 2006; Green 2009). This partial shell remnant is of class II, which corresponds to a gravitational collapse supernova explosion. The minimum projected distance between the past trajectory of LS 5039 and this SNR took place 4 × 105 yr ago, and for PSR J1825−1446 it took place 0.13 × 105 yr ago. For these high ages we do not expect to still detect the SNR, consequently it is unlikely that PSR J1825−1446 and SNR G017.4−00.1 are related, whereas it is not possible that LS 5039 and SNR G017.4−00.1 are related. On the other hand, Bochow (2011) used the Σ − D relationship to estimate the distance to SNR G017.4−00.1, and obtained 12 kpc. The distance to the SNR seems considerably larger than the distance to the sources, although we note that this estimate can be very uncertain.
Besides the specific regions on the sky in the past trajectory of both systems, we can constrain the lifetime of the systems considering that the systems had contained young massive stars, which are generally formed in a specific region of the Galactic plane, the thin disc. The stellar space density decays exponentially as a function of the distance above or below the Galactic plane, and each stellar population has a particular scale height h. For young OB stars hOB = 45 pc (Reed 2000), while Maíz-Apellániz (2001) found that the O–B5 stellar population is distributed with a scale height of 34.2 ± 0.8 ± 2.5 pc. No good determination for the O-type population alone has been found, basically due to the lack of good statistics with this population, and therefore we used the more conservative value of 45 pc both for LS 5039 and PSR J1825−1446. From the Galactic latitudes quoted in Table 7, the current height with respect to the Galactic plane is −65 and − 96 pc for LS 5039 and PSR J1825−1446, respectively. With the proper motion of the systems, we compute for different distances from the Sun the time when they were crossing the Galactic plane at a height within ±45 pc. The expected ages are quoted in Table 8.
Crossing times of LS 5039 and PSR J1825−1446 through the Galactic thin disc, with a scale height for OB stars of ±45 pc, for different distances from the Sun.
7. Discussion and conclusions
We have obtained a set of accurate positions of the isolated pulsar PSR J1825 − 1446 by means of VLBI observations. We used the pulsar gating technique to enhance the detected pulsar flux density to improve the astrometry. We fitted a linear proper motion to new and archival astrometry and obtained a proper motion of μαcosδ = 10.0 ± 0.3 mas yr-1, and μδ = −29.0 ± 0.3 mas yr-1. For a distance from the Sun of 5.0 kpc, the proper motion of PSR J1825−1446 corresponds to a projected transverse velocity of 690 ± 7 km -1, which makes it a high-velocity pulsar ejected from the Galactic plane.
We note that the high space velocity of PSR J1825−1446 suggests that it is possible that a bow-shock has formed in front of the pulsar. For example, the pulsar wind nebula G359.230.82 is the bow shock produced by the young pulsar J1747−2958, which has a spin-down luminosity of 2.5 × 1036 erg s-1, and a transverse velocity of 300 km s-1 in a medium with hydrogen number density of 1.0 cm-3 (Hales et al. 2009). However, the spin-down luminosity of PSR J1825−1446 is only 4.1 × 1034 erg s-1, and therefore such a structure would only be visible if the medium surrounding PSR J1825−1446 were much denser than in the case of J1747−2958.
The space velocity of the source has allowed us to investigate possible origins of PSR J1825−1446. The characteristic age of PSR J1825−1446 is approximately 0.2 Myr. The velocity and age of PSR J1825−1446 make it incompatible with SNR G016.8−01.1. There are no clear OB associations or SNRs crossing the past trajectory of the pulsar. Our estimate of the age of the pulsar, assuming that its progenitor died in the Galactic disc, is 80–245 kyr, compatible with its characteristic age. We have seen that the space velocity of this pulsar is high enough to escape from the Galactic potential.
We compiled all radio interferometric observations of LS 5039 with accurate astrometry, and reduced all data in a consistent way. Combining the radio positions with archival optical astrometry from global catalogues we obtained a proper motion of the source of 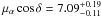 mas yr-1, and
mas yr-1, and 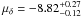 mas yr-1. We have reduced the uncertainty on the proper motion by approximately one order of magnitude with respect to the one obtained in Ribó et al. (2002), which is compatible at 2-σ level. The data were collected from very heterogeneous observations (completely different instruments, conditions, frequencies, and reference calibrators), and the fit is affected by systematic errors. We investigated the effects of these unknown uncertainties using a bootstrap method, which provides realistic uncertainties of our measurement. We confirmed the runaway nature of the system, which has a peculiar space velocity of
mas yr-1. We have reduced the uncertainty on the proper motion by approximately one order of magnitude with respect to the one obtained in Ribó et al. (2002), which is compatible at 2-σ level. The data were collected from very heterogeneous observations (completely different instruments, conditions, frequencies, and reference calibrators), and the fit is affected by systematic errors. We investigated the effects of these unknown uncertainties using a bootstrap method, which provides realistic uncertainties of our measurement. We confirmed the runaway nature of the system, which has a peculiar space velocity of 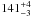 km s-1, with a main component of
km s-1, with a main component of 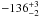 km s-1 perpendicular to the Galactic plane, for a distance to the source of 2.9 kpc.
km s-1 perpendicular to the Galactic plane, for a distance to the source of 2.9 kpc.
We were unable to identify a secure origin for LS 5039. We restricted the proper motion of the system, and the past trajectory is not far from the putative centre of SNR G016.8−01.1, which is very uncertain. However, this association would imply an age of 105 yr for the SNR, which is above the expected lifetime for such a bright SNR (Frail et al. 1994). The age of the SNR depends on the ambient density and its distance, which are unknown parameters (see Ribó et al. 2002). However, even if SNR G016.8−01.1 is not related to LS 5039, the entire region shown in Fig. 9 is an active region of stellar formation, with the open cluster Dolidze 28, WR 115, and the H ii region RCW 164. It is possible that the compact object was formed within this complex. In this case, LS 5039 should be at a distance of around 2 kpc, and the age of the binary would be below 0.1–0.2 Myr. On the other hand, the region of Ser OB2 lies within the past trajectory of LS 5039, at a distance from the Sun of 1.5–2.0 kpc, which is still compatible at 2-σ level with the distance to LS 5039, 2.9 ± 0.8 kpc. In this case the age of the system would be 1.0–1.2 Myr, and the peculiar Galactic velocity would be 70–95 km s-1. A third possibility is that the system LS 5039 was formed in the Galactic plane, but it was not associated with any known young stellar association. In this case the age of the system would be between 0.1 and 0.8 Myr, assuming a distance of 2.9 kpc.
The age of LS 5039 has consequences on the nature of the compact object. When the compact object was formed, the system received a powerful kick, and therefore the orbit could not be pseudo-synchronised after the explosion. Pseudo-synchronous rotation is reached through tidal forces in an eccentric binary, when the rotation of the massive star and the motion of the compact object at periastron are synchronised (Hall 1986). Casares et al. (2005) determined that the compact object should be a black hole (low system inclination and high compact object mass) if the orbit of the system is pseudo-synchronised. They estimated the time for this system to reach orbital pseudo-synchronism to be ~1 Myr, although it is highly uncertain. If the system was formed in Sct OB3 region, its age would be below 0.2 Myr, and the hypothesis in Casares et al. (2005) would be unlikely. Only if the source was formed close to Ser OB2 region, 1–2 Myr ago, would it be possible to reach orbital pseudo-synchronism. Based on the proper motion of the source, it is not expected that the system age is greater than 1–2 Myr if the system was born in the Galactic disc.
We have seen that any determination of the age and origin of LS 5039 is limited by the uncertainty in its distance to the Sun. This distance cannot be obtained by means of parallax VLBI measurements with the current resolution, and the effects of the source structure and variability. An accurate distance will be obtained by the Gaia satellite (see de Bruijne 2012, and references therein) through measurements of the parallax of the massive companion. The satellite will also determine the distance to the OB associations with high accuracy, and therefore any identification or association should be much more straightforward, and will help to clarify the origin of the system. On the other hand, the distance to PSR J1825 − 1446 could be obtained by means of a challenging long-term VLBI project. This would provide a model-independent distance that can be compared to the estimated one from the dispersion measure. Finally, there is no obvious approach to accurately determine the distance to SNR G016.8 − 01.1, whose radio structure is severely contaminated by the H ii region RCW 164.
Sun et al. (2011), based on polarisation studies, note that the object G16.8 − 1.1 appears to be a misidentification and is likely an H ii region. This changes the initial motivation of our study but not the results and conclusions.
The NRAO Astronomical Image Processing System. http://www.aips.nrao.edu/
The Crustal Dynamics Data Information System. http://cddis.nasa.gov/
Acknowledgments
We are grateful to J. Casares for allowing us to mention several new parameters of LS 5039 prior to publication. The NRAO is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. The European VLBI Network (http://www.evlbi.org/) is a joint facility of European, Chinese, South African, and other radio astronomy institutes funded by their national research councils. This work made use of the Swinburne University of Technology software correlator, developed as part of the Australian Major National Research Facilities Programme and operated under licence. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. We acknowledge support by the Spanish Ministerio de Ciencia e Innovación (MICINN) under grants AYA2010-21782-C03-01 and FPA2010-22056-C06-02. J.M. acknowledges support by MICINN under grant BES-2008-004564. M.R. acknowledges financial support from MICINN and European Social Funds through a Ramón y Cajal fellowship. J.M.P. acknowledges financial support from ICREA Academia.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 706, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Ballet, J., et al. 2012, Science, 335, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005, Science, 309, 746 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 460, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aragona, C., McSwain, M. V., Grundstrom, E. D., et al. 2009, ApJ, 698, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Avedisova, V. S. 2002, Astron. Rep., 46, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharyya, S., Godambe, S., Bhatt, N., Mitra, A., & Choudhury, M. 2012, MNRAS, 421, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Blaauw, A. 1961, Bull. Astron. Inst. Netherlands, 15, 265 [NASA ADS] [Google Scholar]
- Blitz, L., Fich, M., & Stark, A. A. 1982, ApJS, 49, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Bochow, A. 2011, Ph.D. Thesis. Max-Planck-Institut für Kernphysik [Google Scholar]
- Bogovalov, S. V., Khangulyan, D. V., Koldoba, A. V., Ustyugova, G. V., & Aharonian, F. A. 2008, MNRAS, 387, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bogovalov, S. V., Khangulyan, D., Koldoba, A. V., Ustyugova, G. V., & Aharonian, F. A. 2012, MNRAS, 419, 3426 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., & Khangulyan, D. 2009, Int. J. Mod. Phys. D, 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., & Khangulyan, D. 2011, PASJ, 63, 1023 [NASA ADS] [Google Scholar]
- Bosch-Ramon, V., Paredes, J. M., Ribó, M., et al. 2005, ApJ, 628, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., Romero, G. E., & Paredes, J. M. 2006, A&A, 447, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., Khangulyan, D., & Aharonian, F. A. 2008, A&A, 482, 397 [Google Scholar]
- Brandt, N., & Podsiadlowski, P. 1995, MNRAS, 274, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Brisken, W. F., Benson, J. M., Goss, W. M., & Thorsett, S. E. 2002, ApJ, 571, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Brisken, W. F., Fruchter, A. S., Goss, W. M., Herrnstein, R. M., & Thorsett, S. E. 2003, AJ, 126, 3090 [NASA ADS] [CrossRef] [Google Scholar]
- Brogan, C. L., Gelfand, J. D., Gaensler, B. M., Kassim, N. E., & Lazio, T. J. W. 2006, ApJ, 639, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Casares, J., Ribó, M., Ribas, I., et al. 2005, MNRAS, 364, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Casares, J., Ribó, M., Ribas, I., et al. 2010, MNRAS, 421, 1103 [Google Scholar]
- Cerutti, B., Dubus, G., & Henri, G. 2008, A&A, 488, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerutti, B., Malzac, J., Dubus, G., & Henri, G. 2010, A&A, 519, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chatterjee, S., Vlemmings, W. H. T., Brisken, W. F., et al. 2005, ApJ, 630, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Chatterjee, S., Brisken, W. F., Vlemmings, W. H. T., et al. 2009, ApJ, 698, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, J. S., Reig, P., Goodwin, S. P., et al. 2001, A&A, 376, 476 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clifton, T. R., & Lyne, A. G. 1986, Nature, 320, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Clifton, T. R., Lyne, A. G., Jones, A. W., McKenna, J., & Ashworth, M. 1992, MNRAS, 254, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J., Darling, J., Kovalev, Y. Y., & Petrov, L. 2011 [arXiv:1110.6252] [Google Scholar]
- Corbet, R. H. D., Cheung, C. C., Kerr, M., et al. 2011, ATel, 3221 [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002 [arXiv:astroph/0207156] [Google Scholar]
- Crowther, P. A., Hadfield, L. J., Clark, J. S., Negueruela, I., & Vacca, W. D. 2006, MNRAS, 372, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Dambis, A. K., Mel’nik, A. M., & Rastorguev, A. S. 2001, Astron. Lett., 27, 58 [NASA ADS] [CrossRef] [Google Scholar]
- de Bruijne, J. H. J. 2012, Ap&SS, in press [arXiv:1201.3238] [Google Scholar]
- Deller, A. T., Tingay, S. J., Bailes, M., & West, C. 2007, PASP, 119, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Dhawan, V., Mioduszewski, A., & Rupen, M. 2006, in Proc. VI Microquasar Workshop: Microquasars and Beyond, 52, 1 [Google Scholar]
- Dhawan, V., Mirabel, I. F., Ribó, M., & Rodrigues, I. 2007, ApJ, 668, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G. 2006, A&A, 456, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubus, G., Cerutti, B., & Henri, G. 2008, A&A, 477, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Durant, M., Kargaltsev, O., Pavlov, G. G., Chang, C., & Garmire, G. P. 2011, ApJ, 735, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C.-A., & Kaspi, V. M. 2006, ApJ, 643, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. 2000, AJ, 120, 2594 [NASA ADS] [CrossRef] [Google Scholar]
- Fragos, T., Willems, B., Kalogera, V., et al. 2009, ApJ, 697, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., & Scharringhausen, B. R. 1997, ApJ, 480, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Frail, D. A., Goss, W. M., & Whiteoak, J. B. Z. 1994, ApJ, 437, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Gaensler, B. M., & Frail, D. A. 2000, Nature, 406, 158 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gaensler, B. M., & Johnston, S. 1995, MNRAS, 275, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Godambe, S., Bhattacharyya, S., Bhatt, N., & Choudhury, M. 2008, MNRAS, 390, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Goldoni, P., Ribó, M., di Salvo, T., et al. 2007, Ap&SS, 309, 293 [Google Scholar]
- Gould, D. M., & Lyne, A. G. 1998, MNRAS, 301, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 2009, VizieR Online Data Catalog, 7253 [Google Scholar]
- Hales, C. A., Gaensler, B. M., Chatterjee, S., van der Swaluw, E., & Camilo, F. 2009, ApJ, 706, 1316 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, D. S. 1986, ApJ, 309, L83 [Google Scholar]
- Harmon, B. A., Wilson, C. A., Fishman, G. J., et al. 2004, ApJS, 154, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1983, ApJ, 267, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lyne, A. G., Kramer, M., Martin, C. E., & Jordan, C. 2004, MNRAS, 353, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffmann, A. D., Klochkov, D., Santangelo, A., et al. 2009, A&A, 494, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Hughes, A., & Bailes, M. 1999, ApJ, 522, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, D. R. H., & Soderblom, D. R. 1987, AJ, 93, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Hnatic, S., Aharonian, F., & Bogovalov, S. 2007, MNRAS, 380, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Aharonian, F., & Bosch-Ramon, V. 2008, MNRAS, 383, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Kijak, J., Gupta, Y., & Krzeszowski, K. 2007, A&A, 462, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, C.-G., Kim, W.-T., & Ostriker, E. C. 2006, ApJ, 649, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Ball, L., & Skjaeraasen, O. 1999, Astropart. Phys., 10, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, M., Lyne, A. G., Hobbs, G., et al. 2003, ApJ, 593, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J. 1989, ApJS, 71, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Torres, R. M., Mioduszewski, A. J., et al. 2007, ApJ, 671, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Loktin, A. V., & Beshenov, G. V. 2003, Astron. Rep., 47, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Lorimer, D. R., Yates, J. A., Lyne, A. G., & Gould, D. M. 1995, MNRAS, 273, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., & Graham-Smith, F. 2005, Pulsar Astronomy (Cambridge Astrophysics) [Google Scholar]
- Lyne, A. G., & Lorimer, D. R. 1994, Nature, 369, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Maíz-Apellániz, J. 2001, AJ, 121, 2737 [Google Scholar]
- Manchanda, R. K., Polcaro, V. F., Norci, L., et al. 1996, A&A, 305, 457 [NASA ADS] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., & Treves, A. 1981, MNRAS, 194, 1 [Google Scholar]
- Marquardt, D. 1963, SIAM J. Appl. Math., 11, 431 [Google Scholar]
- Martí, J., Paredes, J. M., & Ribó, M. 1998, A&A, 338, L71 [NASA ADS] [Google Scholar]
- Martin, R. G., Tout, C. A., & Pringle, J. E. 2009, MNRAS, 397, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Martocchia, A., Motch, C., & Negueruela, I. 2005, A&A, 430, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McSwain, M. V., & Gies, D. R. 2002, ApJ, 568, L27 [NASA ADS] [CrossRef] [Google Scholar]
- McSwain, M. V., Gies, D. R., Huang, W., et al. 2004, ApJ, 600, 927 [NASA ADS] [CrossRef] [Google Scholar]
- McSwain, M. V., Ray, P. S., Ransom, S. M., et al. 2011, ApJ, 738, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Mel’Nik, A. M., & Efremov, Y. N. 1995, Astron. Lett., 21, 10 [NASA ADS] [Google Scholar]
- Miller-Jones, J. C. A., Jonker, P. G., Nelemans, G., et al. 2009a, MNRAS, 394, 1440 [NASA ADS] [CrossRef] [Google Scholar]
- Miller-Jones, J. C. A., Sakari, C. M., Dhawan, V., et al. 2009b, in Proc. 8th International e-VLBI Workshop, ed. J. Conwy, et al. [Google Scholar]
- Mirabel, I. F., & Rodrigues, I. 2003, Science, 300, 1119 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mirabel, I. F., Dhawan, V., Mignani, R. P., Rodrigues, I., & Guglielmetti, F. 2001, Nature, 413, 139 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mirabel, I. F., Mignani, R., Rodrigues, I., et al. 2002, A&A, 395, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mirabel, I. F., Rodrigues, I., & Liu, Q. Z. 2004, A&A, 422, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moldón, J., Johnston, S., Ribó, M., Paredes, J. M., & Deller, A. T. 2011a, ApJ, 732, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Moldón, J., Ribó, M., & Paredes, J. M. 2011b, A&A, 533, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moldón, J., Ribó, M., & Paredes, J. M. 2011c, in High-Energy Emission from Pulsars and their Systems, ed. D. F. Torres, & N. Rea, 1 [Google Scholar]
- Moldón, J., Ribó, M., & Paredes, J. M. 2012, A&A, submitted [Google Scholar]
- Monet, D. G. 1998, BAAS, 30, 120 [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Paredes, J. M., Martí, J., Ribó, M., & Massi, M. 2000, Science, 288, 2340 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Paredes, J. M., Ribó, M., Ros, E., Martí, J., & Massi, M. 2002, A&A, 393, L99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paredes, J. M., Bosch-Ramon, V., & Romero, G. E. 2006, A&A, 451, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlov, G. G., Misanovic, Z., Kargaltsev, O., & Garmire, G. P. 2011, ATel, 3228 [Google Scholar]
- Rea, N., Torres, D. F., Caliandro, G. A., et al. 2011, MNRAS, 416, 1514 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, B. C. 2000, AJ, 120, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, B. C. 2003, AJ, 125, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Reich, W., Fuerst, E., Reich, P., Sofue, Y., & Handa, T. 1986, A&A, 155, 185 [NASA ADS] [Google Scholar]
- Reich, W., Fuerst, E., Reich, P., & Reif, K. 1990, A&AS, 85, 633 [NASA ADS] [Google Scholar]
- Reid, M. J. 1993, ARA&A, 31, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., McClintock, J. E., Narayan, R., et al. 2011, ApJ, 742, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P., Ribó, M., Paredes, J. M., & Martí, J. 2003, A&A, 405, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribó, M., Reig, P., Martí, J., & Paredes, J. M. 1999, A&A, 347, 518 [NASA ADS] [Google Scholar]
- Ribó, M., Paredes, J. M., Romero, G. E., et al. 2002, A&A, 384, 954 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribó, M., Paredes, J. M., Moldón, J., Martí, J., & Massi, M. 2008, A&A, 481, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodgers, A. W., Campbell, C. T., & Whiteoak, J. B. 1960, MNRAS, 121, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Sarty, G. E., Szalai, T., Kiss, L. L., et al. 2011, MNRAS, 411, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Sharpless, S. 1959, ApJS, 4, 257 [Google Scholar]
- Sierpowska-Bartosik, A., & Torres, D. F. 2007, ApJ, 671, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, R. C. 1982, AJ, 87, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X. H., Reich, P., Reich, W., et al. 2011, A&A, 536, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szostek, A., & Dubus, G. 2011, MNRAS, 411, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, T., Kishishita, T., Uchiyama, Y., et al. 2009, ApJ, 697, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Tasker, N. J., Condon, J. J., Wright, A. E., & Griffith, M. R. 1994, AJ, 107, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., Fender, R. P., van den Heuvel, E. P. J., Johnston, H. M., & Wu, K. 1999, MNRAS, 310, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Tavani, M., & Arons, J. 1997, ApJ, 477, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Tetzlaff, N., Neuhäuser, R., Hohle, M. M., & Maciejewski, G. 2010, MNRAS, 402, 2369 [NASA ADS] [CrossRef] [Google Scholar]
- Torra, J., Fernández, D., & Figueras, F. 2000, A&A, 359, 82 [NASA ADS] [Google Scholar]
- van den Heuvel, E. P. J., Portegies Zwart, S. F., Bhattacharya, D., & Kaper, L. 2000, A&A, 364, 563 [NASA ADS] [Google Scholar]
- Von Hoensbroech, A. 1998, Mem. Soc. Astron. It., 69, 1055 [NASA ADS] [Google Scholar]
- Wang, C., Lai, D., & Han, J. L. 2006, ApJ, 639, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Willems, B., Henninger, M., Levin, T., et al. 2005, ApJ, 625, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, S. J., Gies, D. R., Matson, R. A., et al. 2010, ApJ, 723, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V., Bosch-Ramon, V., & Paredes, J. M. 2011, ApJ, 743, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Zacharias, M. I., & de Vegt, C. 1999, AJ, 117, 2895 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Urban, S. E., Zacharias, M. I., et al. 2000, AJ, 120, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C., Girard, T., et al. 2010, AJ, 139, 2184 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Pulsar gating on PSR J1825−1446
To improve the sensitivity of the detections, and thus the astrometry, we correlated the three VLBA observations using pulsar gating (Brisken et al. 2002; Chatterjee et al. 2009). In normal VLBI observations, with integration times of a few seconds, one measures the period-averaged flux density of the observed pulsar, although most of the time the pulsar is not emitting. The instantaneous flux density during the pulsation is usually tens of times higher than the period-averaged value, because the duty cycle (the ratio of the pulse width to the pulse period) is usually below 10%. To optimise radio observations of pulsars one can take advantage of this fact by only correlating the data during on-pulse, and disabling correlation during off-pulse. The total correlated on-source time is considerably reduced (a few minutes for every observed hour), which increases the final image noise (rms) by a factor proportional to one over the square root of the duty cycle (Δτν) at a certain frequency ν. However, the flux (Sν) increase is approximately proportional to one over the duty cycle, yielding a final S/N gain: 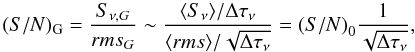 (A.1)where the subindex G stands for the gated values. This provides a theoretical S/N increase proportional to one over the square root of the duty cycle of the pulsar. Typically, the real signal-to-noise improves by a factor between 2 and 6 (Brisken et al. 2002), which can make the difference between a non-detection and accurate astrometry. The duty cycle of PSR J1825−1446 is 2.5% (6.8 ms) at 4.8 GHz, yielding a maximum theoretical signal-to-noise gain of 6.3. For the three VLBA correlations, updated ephemeris of the pulse time of arrivals were obtained to configure the opening and closing time “gates” of the correlator. The timing was obtained thanks to the regular pulsar monitoring conducted in the Jodrell Bank Observatory. Two sets of data were obtained for each observation, one from a normal correlation and one using pulsar gating. This allowed us to compare the results obtained with and without the pulsar gating correlation. The three VLBA observations were correlated with a gate covering pulsar phases from 0.99056 to 0.01389, integrating 6.5 ms of each pulsar cycle.
(A.1)where the subindex G stands for the gated values. This provides a theoretical S/N increase proportional to one over the square root of the duty cycle of the pulsar. Typically, the real signal-to-noise improves by a factor between 2 and 6 (Brisken et al. 2002), which can make the difference between a non-detection and accurate astrometry. The duty cycle of PSR J1825−1446 is 2.5% (6.8 ms) at 4.8 GHz, yielding a maximum theoretical signal-to-noise gain of 6.3. For the three VLBA correlations, updated ephemeris of the pulse time of arrivals were obtained to configure the opening and closing time “gates” of the correlator. The timing was obtained thanks to the regular pulsar monitoring conducted in the Jodrell Bank Observatory. Two sets of data were obtained for each observation, one from a normal correlation and one using pulsar gating. This allowed us to compare the results obtained with and without the pulsar gating correlation. The three VLBA observations were correlated with a gate covering pulsar phases from 0.99056 to 0.01389, integrating 6.5 ms of each pulsar cycle.
The same calibration tables applied to the normal data were also applied to the data correlated with pulsar gating. We produced images of PSR J1825−1446 using the same parameters, and we compared the astrometry obtained with and without pulsar gating. The obtained signal-to-noise ratio and the corresponding gain factor improvement are shown in Table 3. On average, the obtained gain of 2 is relatively small. This can be explained by an asymmetric pulse profile, or an inaccurate determination of the pulsar gate.
All Tables
Ionospheric correction applied to the VLBA data on PSR J1825 − 1446. Units are mas.
Galactic coordinates and Galactic space velocities of LS 5039, and PSR J1825−1446.
Crossing times of LS 5039 and PSR J1825−1446 through the Galactic thin disc, with a scale height for OB stars of ±45 pc, for different distances from the Sun.
All Figures
 |
Fig. 1 Wide field map around SNR G016.8−01.1. The grey scale corresponds to the Parkes-MIT-NRAO survey at 5 GHz (Tasker et al. 1994), and the contours, with higher resolution, to the NRAO VLA Sky Survey (NVSS) at 1.4 GHz (Condon et al. 1998). The dashed line outlines the area covered by the diffuse emission at 4.75 GHz in Reich et al. (1986), and the dotted line the polarised emission in the same image. These two components trace the morphology of SNR G016.8 − 01.1. The more relevant sources in the field are indicated. |
| In the text | |
 |
Fig. 2 Position of PSR J1825 − 1446 with respect to time (MJD in lower axis and year in top axis) in right ascension (left) and declination (right). The solid black lines represent the fitted proper motion, and the grey area the uncertainty of the fit at 3-σ level. The black squares represent the VLA positions, the black circles indicate the VLBA positions, and the grey circle the position from pulsar timing (not used in the fit). The inset shows the position residuals from the fitted model for the 2008–2012 period. The source positions are plotted with uncertainties at 1-σ level. |
| In the text | |
 |
Fig. 3 Offsets in right ascension (left) and declination (right) of LS 5039 with respect to time in MJD and year. The solid black lines in each panel represent the fitted proper motion, and the grey area the uncertainty of the fit at 3-σ level. The upper panels include all data points used for the fit, and the lower panels are the zoom of the last 16 years (marked by the small rectangles), and include the residuals with respect to the fitted model. The empty blue triangles represent the optical data, the green squares show the VLA data, the red triangles correspond to the VLBI observations at 5 GHz, and the black circles are the VLBI data at 8.6 GHz. The source positions are plotted with uncertainties at 1-σ level. |
| In the text | |
 |
Fig. 4 Top: distribution of proper motion fit results for LS 5039 estimated with the bootstrap method, which is equivalent to an un-normalised probability distribution function (PDF) for right ascension and declination independently. Bottom: corresponding cumulative distribution functions (CDF). For all panels, the grey shaded areas correspond to the minimum region that includes the 68.2, 95.4 and 99.7% of the events, from dark grey to light grey. The vertical line marks the most common value (the mode) for the PDF distributions, and the value covering the 50% of the events for the CDF. |
| In the text | |
 |
Fig. 5 Distribution of proper motion fits for LS 5039 computed with the bootstrap method. The central contours represent, from inside to outside, the minimum smoothed regions containing 68.2, 95.4, and 99.7% of the events. The two histograms are the projected 1D distributions shown in Fig. 4. |
| In the text | |
 |
Fig. 6 Components of the Galactic and peculiar velocity of LS 5039 (solid black lines) and their uncertainties at 3-σ level (dark grey areas). The horizontal dashed lines and light grey areas mark the expected Galactic velocity, and the velocity dispersion expected for young stars, respectively. The vertical dotted lines indicate the measured distance to the source. |
| In the text | |
 |
Fig. 7 Same as Fig. 6 for PSR J1825−1446. The solid black line in each panel indicates the Galactic velocity assuming a radial velocity of 0 km s-1. The velocity uncertainties at 3-σ level are smaller than the black lines. The red thin line corresponds to an hypothetical radial velocity from the Sun of +500 km s-1 (away from the Sun) and the blue thin line to −500 km s-1 (towards the Sun). |
| In the text | |
 |
Fig. 8 Area around LS 5039 and PSR J1825−1446 in Galactic coordinates. The lines mark the past trajectory in the last 106 yr for LS 5039, and 1.95 × 105 yr for PSR J1825−1446. The green circles are supernova remnants from the catalogue compiled in Green (2009). The red circles are open clusters from the WEBDA database, and the blue ellipses mark the position of the known OB associations (Mel’Nik & Efremov 1995). The OB stars (Reed 2003) and the star-forming regions (Avedisova 2002) are marked with blue and grey dots, respectively, and provide a general view of the young system distribution in this region of the Galaxy. The red crosses mark the H ii regions (Lockman 1989). The objects in regions #1, #2, and #3 are described in the text. |
| In the text | |
 |
Fig. 9 Wide-field map around SNR G016.8−01.1. The grey scale corresponds to the Parkes-MIT-NRAO survey at 5 GHz (Tasker et al. 1994). The green and red lines mark the past trajectory of LS 5039 and PSR J1825−1446, respectively. The arrows mark the proper motion sense. Circles are plotted in the trajectories every 104 yr. The contours represent the 68.2, 95.4 and 99.7% confidence levels on the position that LS 5039 had 105 and 5 × 104 years ago (see uncertainties in the proper motion shown in Fig. 5). The grey dotted lines show the Galactic coordinates. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


