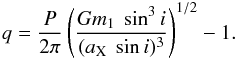| Issue |
A&A
Volume 539, March 2012
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201118397 | |
| Published online | 27 February 2012 | |
Tidal effects on the radial velocity curve of HD 77581 (Vela X-1)
1 Instituto de Ciencias Físicas, Universidad Nacional Autónoma de México, Cuernavaca, Mor. 62210, Mexico
e-mail: gloria@astro.unam.mx
2 Instituto de Astronomía, Universidad Nacional Autónoma de México, 04510, Mexico
e-mail: edmundo@astro.unam.mx
3 Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI, 96822 USA
e-mail: dmh@ifa.hawaii.edu
Received: 3 November 2011
Accepted: 9 January 2012
Context. The mass of the neutron star in Vela X-1 has been found to be larger than the canonical 1.5 M⊙. This result relies on the assumption that the amplitude of the optical component’s measured radial velocity curve is not seriously affected by the interactions in the system.
Aims. Our aim is to explore the effect on the radial velocity curve caused by surface motions excited by tidal interactions.
Methods. We use a calculation from first principles that involves solving the equations of motion of a Lagrangian grid of surface elements. The velocities on the visible surface of the star are projected along the line-of-sight to the observer to obtain the Doppler shifts which are applied to the local line-profiles, which are then combined to obtain the absorption-line profile in the observer’s reference frame. The centroid of the line-profiles for different orbital phases is then measured and a simulated RV curve constructed. Models are run for the “standard” (v sini = 116 km s-1) and “slow” (56 km s-1) supergiant rotation velocities.
Results. The surface velocity field is complex and includes fast, small-spatial scale structures. It leads to strong variability in the photospheric line profiles which, in turn, causes significant deviations from a Keplerian RV curve. The peak-to-peak amplitudes of model RV curves are in all cases larger than the amplitude of the orbital motion. Keplerian fits to RV curves obtained with the “standard” rotation velocity imply mns ≥ 1.7 M⊙. However, a similar analysis of the “slow” rotational velocity models allows for mns ~ 1.5 M⊙. Thus, the stellar rotation plays an important role in determining the characteristics of the perturbed RV curve.
Conclusions. Given the observational uncertainty in GP Vel’s projected rotation velocity and the strong perturbations seen in the published and the model RV curves, we are unable to rule out a small (~1.5 M⊙) mass for the neutron star companion.
Key words: stars: neutron / binaries: spectroscopic / stars: rotation / stars: individual: HD 77581
© ESO, 2012
1. Introduction
The high mass X-ray binary system Vela X-1 (4U 0900-40) consists of a pulsar (Ppulse = 283 s) in an eccentric (e = 0.09, Porb = 8.96 d) orbit around the B0.5-supergiant star HD 77581 = GP Vel. Particular interest in this system is sparked by the mass derived for the neutron star, Mns ~ 1.8 M⊙, since this is significantly larger than the canonical 1.5 M⊙ upper limit that is predicted by the standard neutron star equation of state as well as that which is predicted from supernova models for the newly formed neutron stars.
The maximum possible mass of a neutron star depends on the equation of state of the ultradense matter in its interior (Lattimer & Prakash 2007; Page & Reddy 2006). For nuclear densities ~3 × 1014 g cm-3, the equation of state is a “soft” one, and the maximum mass is ~1.5 M⊙. For larger densities, the equation of state is a “stiff” one, and depending on the adopted equation of state, the upper mass limit may be as high as 2.9 M⊙ (Kalogera & Baym 1996). The majority of neutron stars in binary systems do indeed have mns ≤ 1.5 M⊙ (Thorsett & Chakrabarty 1999; Schwab et al. 2010; Lattimer & Prakash 2010). On the other hand, the existence of mns ~ 2 M⊙ neutron stars is now fairly well established (Demorest et al. 2010), although it is not clear whether such high-mass neutron stars are created at birth in the supernova event or are the consequence of subsequent accretion processes (Woosley & Heger 2007; Timmes et al. 1996). Van den Heuvel (2004) has argued that the GP Vel system provides direct evidence that there is at least one group of neutron stars that are indeed born with such a large mass.
The procedure for determining the neutron star mass in binary systems such as GP Vel is based on the radial velocity (RV) curve which is derived from photospheric absorption lines observed in the spectrum of the optical companion. Implied in this approach is the assumption that the RV variations truly represent the orbital motion of the star. In the case of GP Vel, the validity of this assumption is highly questionable because it has long been known that the photospheric absorptions of GP Vel undergo prominent line profile variability. Specifically, the lines develop asymmetries over the orbital cycle which lead to systematic deviations of the measured RV data points from a Keplerian RV curve. It is believed that the line-profile variability is associated with tidal forcing, non-radial pulsations and other interaction effects in the binary system (van Paradijs et al. 1977b; van Kerkwijk et al. 1995; Barziv et al. 2001; Quaintrell et al. 2003). This raises the question of whether these systematic deviations may not lead to an artificially large RV curve amplitude and, hence, an overestimate of the neutron star mass.
The tidal effects are clearly present, as shown by the optical light curve which displays ellipsoidal variations with a full amplitude ~0.1 mag indicating that the star is strongly distorted by the neutron star’s gravitational field (Jones & Liller 1973; Zuiderwijk et al. 1977; Tjemkes et al. 1986). Van Paradijs et al. (1977b) explored the effects of the deformation of the star on the RV curves. They assumed a circular orbit and synchronous rotation and computed the shape of photospheric absorption lines assuming a non-uniform temperature distribution. However, the rotation of GP Vel is clearly slower than synchronous, and it cannot be assumed to have a simple Roche geometry. Indeed, Tjemkes et al. (1986) showed that a model for the ellipsoidal variations based on the assumption of an “equilibrium tide” does not adequately reproduce the shape of the observed light curve. They suggested that non-linear effects might be important, but full non-linear calculations for tidally interacting stars are only now becoming available (Weinberg et al. 2011).
We have developed a 2D calculation, the TIDES1 code, that provides the time-dependent shape of the stellar surface and its surface velocity field for the general case of an elliptic orbit and asynchronous rotation. Using the derived velocity field, the line-profile variability is computed (Moreno & Koenigsberger 1999; Moreno et al. 2005). The method, though limited to the analysis of the surface layer, provides insight into the non-linear effects that appear in binary stars that are not in an equilibrium configuration. In particular, it allows the analysis of highly eccentric and asynchronous systems. Here, tidal flows are present in forcing regimes that are far from equilibrium configurations, and linear approximations are inapplicable. In this paper we use this model to explore the effects on the absorption line-profiles produced by the tidal flows on the B-supergiant’s surface, and the resulting deformation of the RV curve.
In Sect. 2 of this paper we summarize the method for calculating the tidally-perturbed RV curves; Sect. 3 describes the method for chosing the stellar and binary parameters; Sect. 4 contains the results; and Sect. 5 lists the conclusions.
2. Calculation of tidally-perturbed RV curves
2.1. The TIDES code calculations
Our method consists of computing the motion of a Lagrangian grid of surface elements distributed along a series of co-latitudes covering the surface of the star with mass m1 as it is perturbed by its companion of mass m2, which is assumed to be a point source. The main stellar body below the perturbed layer is assumed to have uniform rotation. The equations of motion that are solved for the set of surface elements include the gravitational fields of m1 and m2, the Coriolis force, the centrifugal force, and gas pressure. The motions of all surface elements are coupled through the viscous stresses included in the equations of motion. The surface layer is coupled to the interior body of the star also through the viscosity. The simultaneous solution of the equations of motion for all surface elements yields values of the radial and azimuthal velocity fields over the stellar surface, vr and vϕ, respectively.
The calculated velocity field is then projected along the line-of-sight to the observer to obtain the Doppler shifts required to produce the integrated photospheric absorption line profiles. We assume a Gaussian shape for the local profiles2 and a limb-darkening law of the form s(θ) = (1 − u + ucosθ), with u = 0.6 as in the Milne-Eddington approximation. Full details of the model are given in Moreno & Koenigsberger (1999), Toledano et al. (2007) and Moreno et al. (2005, 2011). An application of the model to the B-type binary α Vir (Spica) may be found in Harrington et al. (2009).
It is worth noting that the TIDES model computes the surface motions of the optical component from first principles and allowing for non-linear effects. However, there are currently two simplifications in the method. The first simplification is that the equations of motion are solved only for a thin surface layer, instead of for the entire star, which has the disadvantage that the perturbations from deeper layers in the star are neglected. This includes the excitation of non-radial pulsation modes which have been shown to cause oscillations in the RV curve (Willems & Aerts 2002). On the other hand, its response is representative of the effects that are produced on the outer stellar layer, which is the one that is most strongly affected by the tidal forces (see, for example, Dolginov & Smel’chakova 1992). The second simplification is that motions in the polar direction are suppressed, allowing only motions in the radial and azimuthal directions. In addition, we neglect the effects of possible temperature variations across the stellar surface.
The benefits of the model are: 1) we make no a priori assumption regarding the mathematical formulation of the tidal flow structure since we derive the velocity field from first principles; 2) the method is not limited to slow stellar rotation rates nor to small orbital eccentricities; and 3) it is computationally inexpensive.
The parameters that are needed for the calculation are: the orbital period, P, eccentricity, e, inclination, i, and argument of periastron, ωper; the stellar masses, m1 and m2, the radius of the primary star, R1, its equatorial rotation speed, vrot, the polytropic index3, n, and kinematical viscosity of its material, ν. In addition, the code requires the depth of the surface layer, dR/R1 and the number surface elements for which the equations of motion are to be solved. The latter is specified by the number of longitudes into which the equator is divided and the number of latitudes between the equator and the polar region. We have done a thorough investigation of the TIDES code behavior (Harrington et al., in prep.) and find that 500 partitions in the azimuthal direction at the equator and 20 latitudes is sufficient to resolve the small-scale structure. This implies approximately 6800 surface elements4 in the semi-hemisphere above and including the equator. Since the axis of stellar rotation is assumed to be parallel to that of the orbital motion, the perturbations on the northern and southern hemispheres are assumed to be symmetric. Table 1 gives a description of the input parameters and lists the values for those parameters which were held constant throughout all the calculations in this paper.
The line-profile calculation is performed after the initial transitory phase of the calculation has damped down. In the case of GP Vel, the steady state is attained after ~ 20 orbital cycles, and the line-profile calculation is performed after 30 orbital cycles.
Description of input parameters for the TIDES code.
2.2. RV measurements
For each given set of input parameters, the output of the TIDES code yields two line-profile files, one containing the line-profiles arising in the tidally perturbed surface and the second containing the profiles arising from the unperturbed, rigidly-rotating surface. The lines are measured to obtain their centroid. The centroid was computed through the weighted sum over all wavelengths, λi, as follows: 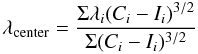 (1)where the summation is carried out between the two limits within which the absorption line lies. In practice, the limits are the points where the absorption meets the continuum level. Ii and Ci are the line and continuum intensities, respectively. This definition of the centroid is the same as that used by the “e” function in the IRAF5 subroutine splot.
(1)where the summation is carried out between the two limits within which the absorption line lies. In practice, the limits are the points where the absorption meets the continuum level. Ii and Ci are the line and continuum intensities, respectively. This definition of the centroid is the same as that used by the “e” function in the IRAF5 subroutine splot.
The RVs were also measured through a Gaussian fit to the line profiles, using the IDL routine GAUSSFIT. Although a Gaussian fit is a very poor approximation to the actual shape of the lines, the derived RV’s were in general very similar to those obtained with the flux-weighted centroid method. In the remainder of this paper we use the flux-weighted centroids.
2.3. Semi-amplitude of the RV curve
The radial velocities that were obtained from the model line profiles were used to construct the RV curves. These curves were fit with the function that characterizes the orbital motion; i.e., the function describing the Keplerian orbit6: ![\begin{equation} V_r=V_0 + K_1[e~\cos~\omega_{\rm per} + \cos(\theta+\omega_{\rm per})] \end{equation}](/articles/aa/full_html/2012/03/aa18397-11/aa18397-11-eq46.png) (2)where
(2)where 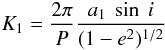 (3)is the semi-amplitude of the RV curve, a1 is the semi-major axis of m1’s orbit, V0 is a constant vertical offset (the “gamma” velocity), and θ is the true anomaly.
(3)is the semi-amplitude of the RV curve, a1 is the semi-major axis of m1’s orbit, V0 is a constant vertical offset (the “gamma” velocity), and θ is the true anomaly.
The fit was performed using the Powell minimization method in an IDL script7. The free parameters for the fit were a1sini and V0. The fitted value of K1 was then computed using Eq. (3).
2.4. A note on orbital phases
In order to be able to compare the theoretical models with the observational data, the conventions for setting orbital phase φ = 0 need to be specified. In this paper, we define φ = 0 at periastron passage. In most observational investigations φobs = 0 is defined at the orbital latitude 90° from the line of nodes. This definition is such that φobs = 0 at the midpoint of the X-ray eclipse (Bildsten et al. 1997; van Kerkwijk et al. 1995; Barziv et al. 2001), and periastron passage occurs at φobs = 0.17. Hence, φobs = φ + 0.17.
3. Observationally constrained parameters of GP Vel
The spectral type and class of the optical component in GP Vel is given by Morgan et al. (1955) as B0.5Ib. Howarth et al. (1997) assign the same spectral type but a more luminous class, B0.5Iae. Estimates of m1’s mass lie in the range 21.7 M⊙ (van Paradijs et al. 1977a, assuming i = 78.8°) to 24.0 M⊙ (Rawls et al. 2011). Van Kerkwijk et al. (1995) derive a value for the stellar radius, R1 = 29.9–30.2 R⊙, under the assumption that the supergiant star fills its effective Roche lobe at periastron. Rawls et al. (2011) derived R1 = 31.82, under the same assumption. These values are consistent with the radii of B0.5Ia (26–38 R⊙) stars listed in the catalogue of Passinetti-Fracassini et al. (2001), but not with those of B0.5Ib (18–26 R⊙) stars. Hence, GP Vel’s radius is quite uncertain but most likely lies in the range 26–32 R⊙. Its effective temperature, Teff = 25 000 ± 1000 K was determined by Sadakane et al. (1985) from the equivalent width of UV Fe IV and Fe III lines, and a comparison with other B0-B1 Ib stars. Fraser et al. (2010) determined log(g/cm s-2) = 2.90 and Teff = 26 500 K from a model atmosphere fit to the spectrum.
The orbital inclination angle depends on GP Vel’s assumed radius. Given the large range of possible values for the radius, it is, hence, rather uncertain. It also depends on the observed duration of the X-ray eclipse, θc, which, however, is time variable and energy dependent (Quaintrell et al. 2003). With these considerations in mind, most authors agree that i ≥ 78°. A recent analysis by Rawls et al. (2011) yields as most probable values i = 85.9° and i = 78.8°8.
Table 2 summarizes the ranges in the parameters that are generally adopted for the GP Vel system. The most reliable of its parameters are those that have been determined from the X-ray pulsar’s delay times; specifically, Porb, e, the projected semi-major axis of the neutron star orbit, aXsini, and argument of periastron, ωper. We adopt these as the basic known parameters and keep them fixed throughout this paper.
Given the considerable uncertainties that are associated with the remaining parameters, we opted to construct sets of self-consistent parameters for conducting the numerical simulations. The method for deriving the self-consistent parameter sets is described in Sects. 3.1–3.3. A sample of self-consistent parameters is listed in Table 3. The TIDES code was run first for a selection of these parameters. We then constructed a second block of parameters with small variations of one or more of the self-consistent parameters and the TIDES code was run for these as well.
Published stellar and orbital parameters.
3.1. Stellar masses
The mass ratio, q = m2/m1, is constrained by the known value of aX sin i and Kepler’s third law 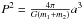 . Using q = m2/m1 = a1/a2, and and a = a1 + a2 = a2(1 + q), with a1 and a2 = aX the semimajor axes of the two stars’ orbits,
. Using q = m2/m1 = a1/a2, and and a = a1 + a2 = a2(1 + q), with a1 and a2 = aX the semimajor axes of the two stars’ orbits,
Adopting P = 8.964368, axsini = 113.89 light-seconds (Bildsten et al. 1997), and writing m1 in solar units, 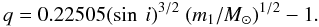 (5)Thus, for a fixed value of i, each value of m1 defines a unique value of m2. The range in m1 = 22.5–24.5 M⊙ leads to a range m2 = 1.427–2.04 M⊙ for the cases analyzed for i = 78.8°.
(5)Thus, for a fixed value of i, each value of m1 defines a unique value of m2. The range in m1 = 22.5–24.5 M⊙ leads to a range m2 = 1.427–2.04 M⊙ for the cases analyzed for i = 78.8°.
3.2. Primary Radius, R1
The value of the B-supergiant’s radius, R1, is particularly relevant since the tidal forces scale as 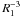 . There are three constraints on its value. The first relies on the assumption that it is close to filling its Roche Lobe, an assumption that requires knowledge of its rotation velocity and the neutron star’s mass, mns. The second relies on: 1) the duration of the X-ray eclipse; 2) the orbital separation; a, and 3) the orbital inclination, i. The third constraint on R1 relies on a stellar atmosphere model fit to its spectrum which yields log g, from which R1 can be derived given knowledge of m1. We have chosen the latter constraint to fix R1 values for the calculations. With the observational constraint on log g, the value of R1 follows from the choice of m1 using
. There are three constraints on its value. The first relies on the assumption that it is close to filling its Roche Lobe, an assumption that requires knowledge of its rotation velocity and the neutron star’s mass, mns. The second relies on: 1) the duration of the X-ray eclipse; 2) the orbital separation; a, and 3) the orbital inclination, i. The third constraint on R1 relies on a stellar atmosphere model fit to its spectrum which yields log g, from which R1 can be derived given knowledge of m1. We have chosen the latter constraint to fix R1 values for the calculations. With the observational constraint on log g, the value of R1 follows from the choice of m1 using 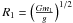 , where g is the value of the surface gravity. With log g = 2.90 cm s-2 from Fraser et al. (2010),
, where g is the value of the surface gravity. With log g = 2.90 cm s-2 from Fraser et al. (2010), 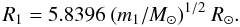 (6)For the range in m1 that was analyzed, the above expression leads to a range R1 = 27.7–28.9 R⊙. It is important to note that R1 is the equilibrium radius of m1 in the absence of m2 and assuming no rotational deformation. These two effects lead to an aspherical shape and a unique value of the stellar radius cannot be defined.
(6)For the range in m1 that was analyzed, the above expression leads to a range R1 = 27.7–28.9 R⊙. It is important to note that R1 is the equilibrium radius of m1 in the absence of m2 and assuming no rotational deformation. These two effects lead to an aspherical shape and a unique value of the stellar radius cannot be defined.
Sets of self-consistent input parameters.
Model input parameters and RV curve amplitudes.
3.3. RV curve semi-amplitude, K1
The orbital velocity semi-amplitude is given by Binnendijk (1960, p. 151): 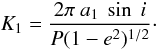 (7)Writing
(7)Writing 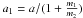 , and again using Kepler’s third law,
, and again using Kepler’s third law, 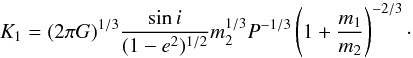 (8)Determinations of K1 since 1976 lie in the range ~17–28 km s-1 (see Table 1 of Quaintrell et al. 2003, for a summary). More stringent limits have been given by Quaintrell et al. (22.6 ± 1.5 km s-1) and Barziv et al. (21.7 ± 1.6 km s-1). These limits are derived from fits of Keplerian RV curves to the observational data.
(8)Determinations of K1 since 1976 lie in the range ~17–28 km s-1 (see Table 1 of Quaintrell et al. 2003, for a summary). More stringent limits have been given by Quaintrell et al. (22.6 ± 1.5 km s-1) and Barziv et al. (21.7 ± 1.6 km s-1). These limits are derived from fits of Keplerian RV curves to the observational data.
3.4. Equatorial rotation velocity
There are two widely different determinations of the projected equatorial rotation velocity, vsini. Zuiderwijk (1995) obtained vsini = 116 ± 6 km s-1 by fitting synthetic profiles to the observations. This is consistent with the 114 km s-1 obtained by Howarth et al. (1997). Recently, however, Fraser et al. (2010) applied the Fourier transform method (Gray 2008) to the spectrum and obtained vsini = 56 km s-1. They attribute the additional broadening observed in the spectral lines to “macroturbulence”.
It is important to note that, in general, the stellar rotation velocity plays a very important role in determining the behavior of the stellar surface. For example, faster rotation leads to a larger deformation of the star. In addition, the ratio of stellar angular rotation velocity, ω, to orbital angular velocity, Ω, plays a critical role in the time dependence and amplitude of the tidal forcing. Thus, the synchronicity parameter β = ω/Ω, which describes the degree of departure from an equilibrium configuration, is of importance in the calculation. Note that when β = 1, the system is in synchronous rotation, which is one of the conditions for equilibrium. In an eccentric binary, Ω changes with orbital phase and thus, β is a function of orbital phase.
In our model, the stellar rotation velocity is specified as an input parameter through β0 = ω/Ω0, where Ω0 is the orbital angular velocity at periastron. It can be conveniently expressed as, 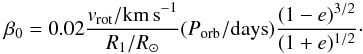 (9)The two different values of v sin i imply β0 ~ 0.3 or 0.6 (for R1 ~ 28–29 R⊙ and i > 78°). We shall refer to the case β0 ~ 0.6 as the “standard” case and the β0 ~ 0.3 as the “slow” rotation case.
(9)The two different values of v sin i imply β0 ~ 0.3 or 0.6 (for R1 ~ 28–29 R⊙ and i > 78°). We shall refer to the case β0 ~ 0.6 as the “standard” case and the β0 ~ 0.3 as the “slow” rotation case.
4. Results
Table 4 lists the input parameters of the model runs performed for this paper. The first block of models (cases 61a–72d) are run with self-consistent sets of parameters, derived as is described in the previous section. The parameters of the second block (list starting with case 72e) are not fully self-consistent. Columns 2–5, and 7 list, respectively, m1, m2, i, β0 and R1; Col. 6 contains the depth of the surface layer, dR/R1, used in the model. Columnn 8 lists the value of the kinematical viscosity, ν (in units of 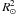 /day).
/day).
4.1. The equilibrium case
It is illustrative to first analyze an equilibrium case having parameters similar to those of the GP Vel system, but in which e = 0 and β = 1. We chose the case with m1 = 24.2 M⊙, m2 = 1.83 M⊙, R1 = 28.721 R⊙ and vrot = 118 km s-1, the latter corresponding to the “standard” rotation speed and an orbital inclination i = 78.8°. In order for this system to be in equilibrium (i.e., β = 1), we had to set the orbital period to 12.2 days. We prefered modifying P instead of vrot because in order to make β = 1 using GP Vel’s orbital period, we would need to set vrot ~ 160 km s-1, significantly larger than its actual rotation speed. This leads to a stronger deformation of the star. The main difference of using a larger orbital period instead of the actual period is that the tidal force is weaker, so the tidal deformation is smaller.
The start of the TIDES calculation is characterized by a transitory phase during which the star adjusts from its initially spherical shape to the new equilibrium shape. During this transitory phase, the star undergoes initially large amplitude (~0.03 R⊙ in the present case) oscillations that rapidly damp out, reaching an amplitude < 0.002 R⊙ by 20 cycles after the start of the calculation. At this time, the star has
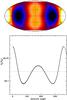 |
Fig. 1 Top: shape of the stellar surface in the equilibrium configuration (case 065); black/white color coding corresponds to the minimum/maximum radius; the map is centered on 180° longitude. The asymmetry in the tidal bulges stems from the fact that the orbital separation is small compared to the radius of m1. Bottom: the radius as a function of longitude at the equator. All the 40 orbital phases for which it was computed are plotted, showing that no surface perturbations are present in this calculation. |
attained its equilibrium shape, which consists of two tidal bulges. Figure 1 shows a color-coded Mollweide representation of the stellar radius at each surface element. The left edge of the map corresponds to azimuth angle 0° (i.e., the sub-binary longitude, defined as the longitude that intersects the line connecting the centers of the two stars) and the right edge is at 360°. The plot below the map illustrates the magnitude of the radius at the equatorial latitude as a function of azimuth. Note that the size of the two tidal bulges is not the same due to the fact that the orbital separation is relatively small compared to the stellar radius. The height of the primary bulge above the equilibrium radius in this calculation is δR = 0.06 R⊙. This corresponds to δR/R1 = 0.002, which is significantly smaller than the depth of the surface layer used in the TIDES calculation, dR/R1 = 0.06. Also, note that the primary bulge points directly towards the companion, another indication that the system is in the equilibrium configuration. In non-equilibrium configurations, the bulge either “lags” behind or is advanced with respect to the line connecting the centers of the stars, a phenomenon that leads to the tidal torques in the system.
Once the equilibrium configuration is attained, there are no significant surface motions. Figure 1 (bottom) is actually a plot of the equatorial latitude of the star at the 40 orbital phases for which it was computed. The width of the curve is an indication of the stability over time of the configuration. As a consequence, no significant variability in the photospheric absorption-line profiles is observed in our calculations9.
 |
Fig. 2 Top: shape of the stellar surface for “standard” cases (model 65c) at periastron. Color coding and orientation are the same as in Fig. 1. Bottom: the crosses represent the radius at each azimuth angle along the equator. The dotted line is the equilibrium shape shown in Fig. 1, rescaled by a factor of 3. The strong departures from the equilibrim configuration when β0 = 0.6 are evident. The detailed pattern changes as a function of orbital phase, causing the line-profile variations. |
4.2. The “standard” case
The situation is very different when the system departs from the equilibrium configuration. The fact that β0 ≠ 1 implies that the star rotates asynchronously, and this introduces perturbations on the stellar surface. We illustrate this case with a model for m1 = 24.2 M⊙, m2 = 1.83 M⊙, R1 = 28.721 R⊙ (case 65c). Contrary to the equilibrium case, the stellar surface does not attain a simple shape with two tidal bulges. The map in Fig. 2 shows a color-coded representation of the stellar radius at each surface element, with white/black indicating maximum/minimum extent. The map corresponds to the time of periastron passage. The Mollweide representation and orientation are the same as in Fig. 1. The primary tidal bulge can be seen to lie between 320° and 360°, “lagging” behind the line connecting the centers of the two stars (which lies at azumuth 0°). This is as expected for a sub-synchronously rotating star. Furthermore, the bulge shape is not smooth, but consists of smaller-scale structures. These can be most easily visualized in the plot shown below the map, which shows the radius at the equator plotted as a function of azimuth. A similar configuration obtains for all other orbital phases as well. The comparison between Fig. 2 and the equilibrium configuration shown in Fig. 1 shows that an “equilibrium tide” representation for GP Vel is a poor approximation.
The non-equilibrium configuration leads to large-scale flows on the stellar surface (see Tassoul 1987; and Eggleton et al. 1998, for a good description of this phenomenon). These are referred to as “tidal flows”. The tidal flows are motions of localized regions of the stellar surface relative to the underlying, (assumed) rigidly-rotating stellar interior. The changing flow patterns lead to variable line-profiles. A sample of the type of variability predicted by the TIDES code is illustrated in Fig. 3, where the perturbed line profiles are compared to their corresponding non-perturbed line profiles. Note the appearance of “bumps” and “wiggles” in the profiles, as well as the occassional blue or red extended wing. In calculations performed with significantly smaller “turbulent” speeds (for example, 10 km s-1 instead of the 30 km s-1 used here), the “bumps” are narrower, and the profiles give the appearance of having narrow discrete absorption features that generally travel from “blue” to “red” along the line profile (see Harrington et al. 2009, for an example of this type of behavior). In the case shown in Fig. 3 the discrete absorptions are significantly smoothed out due to the large “turbulent” speed.
 |
Fig. 3 Predicted line profiles at different orbital phases for case 65c. The dotted profiles correspond to the non-perturbed, rigidly-rotating surface. The asymmetries in the perturbed line-profiles are responsible for the departures from a Keplerian RV curve. |
 |
Fig. 4 Radial velocity curves from the tidally perturbed line profiles (squares) compared to the actual projected orbital motion (dotted curve) and best-fit curve (dash curve). Δ RV is the difference between the perturbed and non-perturbed RV values. Top: mns = 1.830 M⊙, β0 = 0.614 (the “standard” case; case65c); Bottom: mns = 1.468 M⊙, β0 = 0.300 (case 61a). |
The RV curve derived from these line profiles, using the flux-weighted mean method, is plotted in Fig. 4 (top)10. Also plotted in this figure is the RV curve corresponding to the actual orbital motion (dots), and the best-fit Keplerian curve derived from the analysis that is described in Sect. 2.3 (dashes). The deviations of the perturbed RV curve with respect to that of the actual orbital motion are shown below the RV curve. They are as large as ± 5 km s-1 in the phase intervals φ = 0.1–0.3 and φ = 0.9–1.0. Despite the large deformations on the perturbed RV curve, the best-fit Keplerian is very similar to the curve which describes the actual orbital motion. Thus, although the peak-to-peak amplitude of the perturbed RV curve is significantly larger than the actual orbital motion, the “excursions” of the RV curve are such that they nearly cancel out in the fitting algorithm. This indicates that Keplerian curve fits to the tidally-perturbed RV curves yield reasonable results as long as the entire set of data is fit; i.e., without excluding portions of the RV curve.
The general characteristics described above appear in all of the model runs listed in Table 4 for which β0 ~ 0.6. The semi-amplitudes of the corresponding RV curves derived from the fits (Klsq) are plotted as filled symbols in Fig. 5 with m2 = mns on the abscissa. Also plotted in this figure are the values of K1 for the Keplerian orbit (crosses). The observational limits are drawn with horizontal dotted lines. Only models with mns = m2 > 1.7 M⊙ have values of Klsq that lie within the observational limits. Hence, we conclude that for the β0 ~ 0.6 group of models, the systematic shifts in RV caused by tidal flows produce only small departures from the actual orbital RV curve, and the derived neutron star mass is not severely affected by the tidal flows.
 |
Fig. 5 Predicted semi-amplitude of the GP Vel RV curves for different assumed neutron star masses and model input parameters: open symbols: β0 ~ 0.3; filled symbols: β0 ~ 0.6. All models were run with dR/R1 = 0.06. The dotted lines indicate the observed range of semi-amplitudes from Barziv et al. (2001) and Quaintrell et al. (2003). The Keplerian semi-amplitudes (crosses) are generally smaller than those predicted by the model calculations. Note that for the slow-rotation (β0 ~ 0.3) models, masses as low as mns = 1.55 M⊙ yield K1 values within the observed range. |
4.3. The “slow” rotation case
The slow rotation models also show significant line-profile variability. The deformation of the RV curves leads to systematically larger values of Klsq. To illustrate this case we use a model with m1 = 23.6 M⊙, m2 = 1.468 M⊙, and R1 = 28.363 R⊙ (case 61a). Figure 4 (bottom) shows that the perturbed RV curve departs significantly more from its Keplerian motion than the β0 ~ 0.6 case. There are ~5 km s-1 excesses around φ = 0.1 and 0.65, phases which lie close to the extrema in the actual orbital RV curve. This causes the best-fit RV curve (dashes) to have a significantly larger amplitude than the curve describing the orbital motion (dots).
The summary of Keplerian fit semi-amplitudes, Klsq, for the β0 ~ 0.3 cases is shown in Fig. 5 with open symbols. For models in which the layer depth is dR/R1 = 0.06, we see that masses as low as mns = 1.55 yield values of Klsq (marginally) consistent with the observations.
Thus, for the β ~ 0.3 group of models, the systematic shifts in RV caused by tidal flows produce significant deviations from the actual orbital RV curve.
The basic conclusion of this section is that different rotation speeds lead to tidal flows with different characteristics and amplitudes and, thus, it is crucial to have a well-established value for this parameter in order to properly estimate the magnitude of the RV curve perturbations.
4.4. Dependence on layer depth
Calculations performed with different layer depths in the “standard” rotation case yield similar results. However, significant differences are present in the “slow” rotation cases where the dR/R1 = 0.10 layer depths lead to larger RV curve amplitudes than those for dR/R1 = 0.06. Figure 6 illustrates the radial velocities obtained from calculations with these two layer depths. Also plotted are the corresponding best-fit Keplerian curves and the curve that describes the actual orbital motion (continuous curve).
The largest amplitudes occur for β0 ~ 0.3 and dR/R1 = 0.10, as illustrated in Fig. 7 where we plot Klsq as a function of mns. These model calculations indicate that the β0 ~ 0.3 systems with mns as low as 1.47 M⊙ are consistent with the observations.
 |
Fig. 6 Radial velocities obtained from calculations with different layer depths for the “standard” rotation velocity (top; cases 61c,d) and the “slow” velocity (bottom; cases 61a,b). Also plotted are the corresponding best-fit Keplerian curves and the curve that describes the actual orbital motion (continuous curve). Crosses and the dotted curve correspond to dR/R1 = 0.06; and triangles and the dash curve correspond to dR/R1 = 0.10. The perturbations due to tidal flows are more significant for the “slow” rotation velocity cases. |
4.5. The “blue dip” and a structured wind
A prominent feature in our model RV curves is a “blue dip” that appears at φ ~ 0.3, shortly after the maximum in the curve. It is a persistent feature in all our computations, and it is caused by the asymmetrical shape of the line profiles. Figure 8 displays the line profiles over the phase interval 0.12–0.36 for model 65c, illustrating the source of this feature. Between phases 0.14–0.22, the line develops an excess blue absorption wing while at the same time the red wing becomes less extended. The combination of these two effects moves the centroid of the line towards shorter wavelengths. A natural question is what causes this asymmetry in the line profiles?
A map of the azimuthal velocity perturbations over the visible surface of the B-supergiant at orbital phase φ = 0.2 is presented in Fig. 9. The light color indicates motion of the surface elements that is faster than the underlying rigid-body rotation rate. Hence, the large white area on the left side of the map indicates that the surface elements that lie near the limb of the star are approaching the observer faster than the stellar rotation velocity. This leads to the more extended blue wing in the line profiles. Also evident in Fig. 9 is the dark area in the map, which corresponds to surface elements whose azimuthal velocity is slower than that of the stellar rotation. When this region reaches the right limb of the visible disk, it leads to a less extended red wing in the absorption line profile.
An extensive analysis of GP Vel’s observational RV curve has been made by Barziv et al. (2001) and Quaintrell et al. (2003), using independent data sets. Barziv et al. (2001) report the presence of a “blue excursion” in the Hδ data that produces a local minimum in the RV curve at φ ~ 0.37. They interpret the “blue excursion” in terms of a photoionization wake. Figure 10 is a plot of the Hδ 4102 Å line RV values (crosses) from Barziv et al. (2001) showing that the “blue excursion” initiates at φ ~ 0.25. This coincides with the “blue dip” in our models, but its duration is far longer than that of the “blue dip”. An alternative explanation for the “blue excursion” is the presence of enhanced mass outflow after periastron passage and it is tempting to speculate that it could be triggered by the strong tidal effects that appear after periastron passage.
It is also interesting to note that Kreykenbohm et al. (2008) detected flaring activity and temporary quasi-periodic oscillations in INTEGRAL X-ray observations. In particular, the two largest flares observed in these data occur around orbital phase 0.4 (with respect to periastron) in two different orbital cycles. This is significant because this is just ~0.03 in phase later than the minimum in the “blue excursion” in Barziv et al.’s data. Assuming a mean wind velocity of 1105 km s-1 (Howarth et al. 1997), a gas stream that originates near the B-supergiant surface would travel ~3 × 1012 cm during this time interval, which is on the order of magnitude of the distance to the neutron star. Hence, the picture which emerges is one in which tidal flows may cause instabilities that produce time-dependent ouflows leading to a structured wind. When high-density wind regions reach the neutron star, the larger accretion rates lead to an increase in the X-ray emission, as described by Kreykenbohm et al. (2008). These authors also found temporary quasi-periodic oscillations with a timescale of ~ 2 h which they attribute to alternating high and low density regions within GP Vel’s stellar wind. A similarly structured wind has been suggested to exist in the Be/X-ray binary system 2S0114+650 and to possibly be produced by tidally induced pulsations (Koenigsberger et al. 2006).
 |
Fig. 8 Montage of line profiles at orbital phases φ = 0.12–0.36, showing that the “dip” in the RV curve is largely a consequence of the more extended blue wing and less extended red wing. Dotted curves are the unperturbed line profiles. Phases with respect to periastron passage are listed. |
 |
Fig. 9 Map depicting the azimuthal (“horizontal”) velocity field at orbital phase φ = 0.2 for case65c. Velocities that are larger than the rigid-body rotation rate are coded in light color, while those that are slower are coded in dark. The “blue dip” in the theoretical RV curve is caused by the extended blue wing in the photospheric absorption lines, and this is produced by the large white area near the approaching (left) limb of the star. The bottom panel is a plot of the azimuthal velocity perturbations along the equatorial latitude. |
 |
Fig. 10 Theoretical RV curves for a neutron-star mass mns = 1.83 M⊙ for β0 = 0.614 (continuous curve; case 65c) and mns = 1.468 M⊙ for β0 = 0.300 (dash curve; case 61b). Data points are the RV measurements from Barziv et al. (2001): the average of several lines (triangles) and the values for Hδ (crosses). The vertical dash lines indicate the phase of X-ray eclipse, the approximate location of the blue “dip” in the RV curve and the “blue excursion”. The latter may be due to outflows from the B-supergiant. We suggest these outflows may be associated with activity induced by the tidal flows. |
5. Discussion and conclusions
In this paper, we explored the manner in which surface motions that are induced by the tidal interactions affect the shape of the RV curve. The objective was to analyze the manner in which these motions affect the neutron star mass determination. We performed a calculation from first principles which involves solving the equations of motions of a Lagrangian grid of surface elements to determine the surface velocity field on the B-supergiant. The velocities on the visible surface of the star were then projected along the line-of-sight to the observer and the local line-profile at each surface element was Doppler-shifted correspondingly. The Doppler-shifted local line-profiles were combined to obtain the absorption-line profile that would be detected by an observer at each orbital phase. For each set of model binary parameters, the centroids of the resulting line-profiles were measured and a theoretical RV curve constructed.
In all our models, the peak-to-peak amplitude of the model RV curve is larger than the corresponding Keplerian RV curve. However, the fit using Keplerian curves yields semi-amplitudes that may have only small departures from the true orbital motion, depending on the assumed stellar rotation rate. In the “standard” rotation case, the deformations of the RV curve are such that they nearly cancel out in the Keplerian fit. Thus, the derived semi-amplitude of the RV curve in this case is only slightly larger than that of the actual orbital motion. If GP Vel rotates at the “standard” rotation rate, then the neutron star mass may indeed be ≥ 1.7 M⊙. However, in the “slow” rotation velocity cases, the deformations of the RV curve are significantly more pronounced and the Keplerian fits to the RV curves yield significanlty larger amplitudes than that of the orbital motion. In this case, mns ~ 1.5 M⊙ is feasible.
Model input parameters and RV curve amplitudes.
Thus, the assumed rotation speed clearly plays a very important role in determining the effect of the tidal flows on the amplitude of the RV curve. The “standard” and “slow” speeds we have adopted here are the two values cited in the literature. However, because of the prominent line-profile variability, it is not clear whether either of these two values accurately represents the rotation velocity of the B-supergiant. This is an issue that requires further study.
The analysis of the RV curve is further complicated by the observed variations that occur from one orbit to the next. Trial calculations do show small differences in the predicted shape of the star for different orbital cycles, and the maximum extent of the primary tidal bulge varies from one periastron passage to the next. However, these do not lead to significant differences in the predicted line-profiles at the same orbital phase for different cycles, and thus the theoretical RV curves are virtually the same from one orbital cycle to the next.
A final question to address is the following: if the distortions in the RV curve introduced by tidal flows on the surface of GP Vel lead to an artificially large neutron star mass, shouldn’t this same effect be present in other binary systems? The answer is that, indeed, the effect should be present in binary systems in which the stellar rotation departs from synchronous rotation. In this context, it is interesting to consider the set of neutron star binary systems with optical counterparts which is listed in Table 5. These are the 7 known neutron stars with optical counterparts for which stellar parameters have been well determined. Five of these have OB-type spectral types, while the remainder have A–K spectral types. The orbital periods range from ~1 day to ~10 days. Figure 11 is a plot of the derived neutron star mass vs. (1. − β0), which tells us whether there is a dependence of mns on the degree of departure of the optical component from synchronous rotation. A possible trend for larger mns with larger departures from synchronicity is apparent in Fig. 11, although more data points are clearly required before we can conclude that a correlation exists. However, this result is consistent with the idea that asynchronous rotation leads to significant line-profile variability which, in turn, distorts the RV curve, potentially leading to an error in the stellar masses. Furthermore, this hypothesis applies to all types of binary systems.
 |
Fig. 11 The neutron star mass plotted vs. the asynchronicity factor 1 − β0 for the 7 binary systems listed in Table 5. Synchronously-rotating optical components lie at 1 − β0 = 0. Error bars are the uncertainties quoted by the authors listed in Table 5. A trend for more massive neutron stars with larger departures from synchronicity is observed. Whether this indicates a systematic error in the mass determination due to tidal effects is an open question that requires a larger sample of systems before a firm conclusion may be drawn. |
In conclusion, we find that: 1) the assumption of an “equilibrium tide” configuration for the B-supergiant shape is a poor approximation; 2) the tidal effects produce orbital phase-dependent variations in the line profiles leading to asymmetries such as extended blue or red wings; 3) the line-profile variability causes the shape of the RV curve to depart significantly from that of a Keplerian RV curve, artificially enhancing the semi-amplitude; 4) the characteristics of the RV curve depend on the assumed rotation velocity of the B-supergiant.
Our analysis neglects the effects of a non-uniform temperature distribution over the stellar surface, those of non-radial pulsations and the possible presence of enhanced mass-outflows after periastron passage. These effects are expected to contribute even further towards deforming the line profiles. Hence, we conclude that given these uncertainties and the results of our calculations, a low-mass neutron star (mns ~ 1.5 M⊙) cannot as yet be excluded for the Vela X-1 system.
The polytropic index of a radiative supergiant star is n ≥ 3, Schwarzschild (1958, p. 258).
Binnendijk (1960, pp. 149–151).
The POWELL algorithm as described in Press et al. (1992), Sect. 10.5.
This is the value given in their Table 4, although in the text the value quoted is 77.8°.
Note that our model does not take into account a variable temperature structure across the observable stellar disk. In the case of a more complete calculation in which a model stellar atmosphere is used, a phase-dependent variation in the line-profiles is expected due to gravity darkening effects, see Zuiderwijk et al. (1977); and Palate & Rauw (2012).
Acknowledgments
The authors would like to acknowledge Matthieu Palate and the anonymous referee for helpful comments, Alfredo Diaz and Ulises Amaya for computing assistance, and UNAM/PAPIIT project 107711-2 for financial support.
References
- Barziv, O., Kaper, L., van Kerkwijk, M. H., Telting, J. H., & van Paradijs, J. 2001, A&A, 377, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Binnendijk, L. 1960, Properties of Double Stars, University of Pennsylvania Press, Philadelphia, Library of Congress #58-8011 [Google Scholar]
- Casares, J., Charles, P., & Kuulkers, E. 1998, ApJ, 493, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, G. W. 2000, ApJ, 542, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dolginov, A. Z., & Smel’chakova, E. V., 1992, A&A, 257, 783 [NASA ADS] [Google Scholar]
- Eggleton, P. P., Kiseleva, L. G., & Hut, P. 1998, ApJ, 499, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, M., Dufton, P. L., Hunter, I., & Ryans, R. S. I. 2010, MNRAS, 404, 1306 [NASA ADS] [Google Scholar]
- Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres, 3rd edition (Cambridge: Cambridge University Press) [Google Scholar]
- Harrington, D. M., Koenigsberger, G., Moreno, E., & Kuhn, J. 2009, ApJ, 704, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., Siebert, K. W., Hussain, G. A. J., & Prinja, R. K. 1997, MNRAS, 284, 265. [NASA ADS] [CrossRef] [Google Scholar]
- Jones, C., & Liller, W. 1973, ApJ, 184, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Kalogera, V., & Baym, G. 1996, ApJ, 470, 61 [Google Scholar]
- Koenigsberger, G., Georgiev, L., Moreno, E., et al. 2006, A&A, 458, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreykenbohm, I., Wilms, J., Kretschmar, P., et al. 2008, A&A, 492, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landstreet, J. D., Kupka, F., Ford, H. A., et al. 2009, A&A, 503, 973 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2007, Phys. Rep., 442, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, & Prakash 2010, in Gerry Brown’s Festschrift, ed. S. Lee, in press [arXiv:1012.3208] [Google Scholar]
- Moreno, E., & Koenigsberger, G. 1999, RMA&A, 35, 157 [Google Scholar]
- Moreno, E., Koenigsberger, G., & Toledano, O. 2005, A&A, 437, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moreno, E., Koenigsberger, G., & Harrington, D. 2011, A&A, 528, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morgan, W. W., Code, A. D., & Whitford, A. E. 1955, ApJS, 2, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Mukherjee, U., Raichur, H., Paul, B., Naik, S., & Bhatt, N. 2006, JApA, 27, 411 [Google Scholar]
- Page, D., & Reddy, S. 2006, Annu. Rev. Nucl. Part. Sci., 56, 327 [Google Scholar]
- Palate, M., & Rauw, G. 2012, A&A, 537, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasinetti-Fracassini, L. E., Pastori, L., Covino, S., & Pozzi, A. 2001, A&A, 367, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Podsiadlowski, Ph., & Rappaport, S. 2000, ApJ, 529, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., et al. 1992, Numerical Recipes in C: The Art of Scientific Computing, second edition (Cambridge University Press) [Google Scholar]
- Quaintrell, H., Norton, A. J., Ash, T. D. C., et al. 2003, A&A, 401, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rawls, M. L., Orosz, J. A., McClintock, J. E., et al. 2011, ApJ, 730, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Sadakane, K., Hirata, R., Jugaku, J., et al. 1985, ApJ, 288, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Schwab, J., Podsiadlowski, Ph., & Rappaport, S. 2010, ApJ, 719, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzschild, M. 1958, Structure and Evolution of the Stars (Dover Publ.) [Google Scholar]
- Tassoul, J. L. 1987, ApJ, 322, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Thorsett, S. E., & Chakrabarty, D. 1999, ApJ, 512, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1996, ApJ, 457, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Tjemkes, S. A., Zuiderwijk, B. J., & van Paradijs, J. 1986, A&A, 154, 77 [NASA ADS] [Google Scholar]
- Toledano, O., Moreno, E., Koenigsberger, G., Detmers, R., & Langer, N. 2007, A&A, 461, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Heuvel, E. P. J. 2004, in ESA SP 552, 5th INTEGRAL Workshop on the INTEGRAL Universe, ed. V. Schoenfelder, G., Lichti, & C. Winkler (Noordwijk: ESA), 185 [Google Scholar]
- van der Meer, A., Kaper, L., van Kerkwijk, M. H., Heemskerk, M. H. M., & van den Heuvel, E. P. J. 2007, A&A, 473, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Kerkwijk, M. H., van Paradijs, J., Zuiderwijk, E. J., et al. 1995, A&A, 303, 483 [NASA ADS] [Google Scholar]
- van Paradijs, J. A., Hammerschlag-Hensberge, G., van den Heuvel, E. P. J., et al. 1976, Nature, 259, 247 [Google Scholar]
- van Paradijs, J. A., Zuiderwijk, E. J., Takens, R. J., et al. 1977a, A&AS, 30, 195 [NASA ADS] [Google Scholar]
- Weinberg, N. N., Arras, P., Quataert, E., & Burkart, J. 2011, ApJ, submitted [arXiv:1107.0946W] [Google Scholar]
- Willems, B., & Aerts, C. 2002, A&A, 384, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., & Heger, A. 2007, PhR, 442, 269 [Google Scholar]
- Zuiderwijk, E. J. 1995, A&A, 299, 79 [NASA ADS] [Google Scholar]
- Zuiderwijk, E. J., Hammerschlag-Hensberge, G., van Paradijs, J., Sterken, C., & Henseberge, H. 1977, A&AS, 27, 433 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top: shape of the stellar surface in the equilibrium configuration (case 065); black/white color coding corresponds to the minimum/maximum radius; the map is centered on 180° longitude. The asymmetry in the tidal bulges stems from the fact that the orbital separation is small compared to the radius of m1. Bottom: the radius as a function of longitude at the equator. All the 40 orbital phases for which it was computed are plotted, showing that no surface perturbations are present in this calculation. |
| In the text | |
 |
Fig. 2 Top: shape of the stellar surface for “standard” cases (model 65c) at periastron. Color coding and orientation are the same as in Fig. 1. Bottom: the crosses represent the radius at each azimuth angle along the equator. The dotted line is the equilibrium shape shown in Fig. 1, rescaled by a factor of 3. The strong departures from the equilibrim configuration when β0 = 0.6 are evident. The detailed pattern changes as a function of orbital phase, causing the line-profile variations. |
| In the text | |
 |
Fig. 3 Predicted line profiles at different orbital phases for case 65c. The dotted profiles correspond to the non-perturbed, rigidly-rotating surface. The asymmetries in the perturbed line-profiles are responsible for the departures from a Keplerian RV curve. |
| In the text | |
 |
Fig. 4 Radial velocity curves from the tidally perturbed line profiles (squares) compared to the actual projected orbital motion (dotted curve) and best-fit curve (dash curve). Δ RV is the difference between the perturbed and non-perturbed RV values. Top: mns = 1.830 M⊙, β0 = 0.614 (the “standard” case; case65c); Bottom: mns = 1.468 M⊙, β0 = 0.300 (case 61a). |
| In the text | |
 |
Fig. 5 Predicted semi-amplitude of the GP Vel RV curves for different assumed neutron star masses and model input parameters: open symbols: β0 ~ 0.3; filled symbols: β0 ~ 0.6. All models were run with dR/R1 = 0.06. The dotted lines indicate the observed range of semi-amplitudes from Barziv et al. (2001) and Quaintrell et al. (2003). The Keplerian semi-amplitudes (crosses) are generally smaller than those predicted by the model calculations. Note that for the slow-rotation (β0 ~ 0.3) models, masses as low as mns = 1.55 M⊙ yield K1 values within the observed range. |
| In the text | |
 |
Fig. 6 Radial velocities obtained from calculations with different layer depths for the “standard” rotation velocity (top; cases 61c,d) and the “slow” velocity (bottom; cases 61a,b). Also plotted are the corresponding best-fit Keplerian curves and the curve that describes the actual orbital motion (continuous curve). Crosses and the dotted curve correspond to dR/R1 = 0.06; and triangles and the dash curve correspond to dR/R1 = 0.10. The perturbations due to tidal flows are more significant for the “slow” rotation velocity cases. |
| In the text | |
 |
Fig. 7 Same as in Fig. 5, but from calculations performed with a layer depth dR/R1 = 0.10. |
| In the text | |
 |
Fig. 8 Montage of line profiles at orbital phases φ = 0.12–0.36, showing that the “dip” in the RV curve is largely a consequence of the more extended blue wing and less extended red wing. Dotted curves are the unperturbed line profiles. Phases with respect to periastron passage are listed. |
| In the text | |
 |
Fig. 9 Map depicting the azimuthal (“horizontal”) velocity field at orbital phase φ = 0.2 for case65c. Velocities that are larger than the rigid-body rotation rate are coded in light color, while those that are slower are coded in dark. The “blue dip” in the theoretical RV curve is caused by the extended blue wing in the photospheric absorption lines, and this is produced by the large white area near the approaching (left) limb of the star. The bottom panel is a plot of the azimuthal velocity perturbations along the equatorial latitude. |
| In the text | |
 |
Fig. 10 Theoretical RV curves for a neutron-star mass mns = 1.83 M⊙ for β0 = 0.614 (continuous curve; case 65c) and mns = 1.468 M⊙ for β0 = 0.300 (dash curve; case 61b). Data points are the RV measurements from Barziv et al. (2001): the average of several lines (triangles) and the values for Hδ (crosses). The vertical dash lines indicate the phase of X-ray eclipse, the approximate location of the blue “dip” in the RV curve and the “blue excursion”. The latter may be due to outflows from the B-supergiant. We suggest these outflows may be associated with activity induced by the tidal flows. |
| In the text | |
 |
Fig. 11 The neutron star mass plotted vs. the asynchronicity factor 1 − β0 for the 7 binary systems listed in Table 5. Synchronously-rotating optical components lie at 1 − β0 = 0. Error bars are the uncertainties quoted by the authors listed in Table 5. A trend for more massive neutron stars with larger departures from synchronicity is observed. Whether this indicates a systematic error in the mass determination due to tidal effects is an open question that requires a larger sample of systems before a firm conclusion may be drawn. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.