| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201117983 | |
| Published online | 20 January 2012 | |
Angular correlation functions of X-ray point-like sources in the full exposure XMM-LSS field⋆
1 Institut d’Astrophysique et de Géophysique, Université de Liège, 4000 Liège, Belgium
e-mail: elyiv@astro.ulg.ac.be
2 Main Astronomical Observatory, Academy of Sciences of Ukraine, 27 Akademika Zabolotnoho St., 03680 Kyiv, Ukraine
3 DSM/Irfu/SAp, CEA/Saclay, 91191 Gif-sur-Yvette Cedex, France
4 Institute of Astronomy & Astrophysics, National Observatory of Athens, Thessio 11810, Athens, Greece
5 Instituto Nacional de Astrofísica, Óptica y Electrónica, 72000 Puebla, Mexico
6 Academy of Athens, Research Center for Astronomy and Applied Mathematics, Soranou Efesiou 4, 11527 Athens, Greece
7 High Energy Physics Group, Dept. ECM, Universitat de Barcelona, Av. Diagonal 647, 08028 Barcelona, Spain
8 INAF-IASF Milano, via Bassini 15, 20133 Milano, Italy
9 Institute of Space and Astronautical Science (ISAS), Japan Aerospace Exploration Agency, 3-1-1 Yoshinodai, Chuo-ku, Sagamihara, Kanagawa 252-5210, Japan
10 Astronomical Observatory, Kyiv National University, 3 Observatorna St., 04053 Kyiv, Ukraine
11 Argelander Institut für Astronomie, Universität Bonn, Germany
Received: 31 August 2011
Accepted: 13 November 2011
Aims. Our aim is to study the large-scale structure of different types of AGN using the medium-deep XMM-LSS survey.
Methods. We measure the two-point angular correlation function of ~5700 and 2500 X-ray point-like sources over the ~11 sq. deg. XMM-LSS field in the soft (0.5–2 keV) and hard (2–10 keV) bands. For the conversion from the angular to the spatial correlation function we used the Limber integral equation and the luminosity-dependent density evolution model of the AGN X-ray luminosity function.
Results. We have found significant angular correlations with the power-law parameters γ = 1.81 ± 0.02, θ0 = 1.3′′ ± 0.2′′ for the soft, and γ = 2.00 ± 0.04, θ0 = 7.3′′ ± 1.0′′ for the hard bands. The amplitude of the correlation function w(θ) is higher in the hard than in the soft band for fx ≲ 10-14 erg s-1 cm-2 and lower above this flux limit. We confirm that the clustering strength θ0 grows with the flux limit of the sample, a trend which is also present in the amplitude of the spatial correlation function, but only for the soft band. In the hard band, it remains almost constant with r0 ≃ 10h-1 Mpc, irrespective of the flux limit. Our analysis of AGN subsamples with different hardness ratios shows that the sources with a hard-spectrum are more clustered than soft-spectrum ones. This result may be a hint that the two main types of AGN populate different environments. Finally, we find that our clustering results correspond to an X-ray selected AGN bias factor of ~2.5 for the soft band sources (at a median 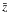 ≃ 1.1) and ~3.3 for the hard band sources (at a median
≃ 1.1) and ~3.3 for the hard band sources (at a median 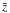 ≃ 1), which translates into a host dark matter halo mass of ~1013h-1M⊙ and ~1013.7h-1M⊙ for the soft and hard bands, respectively.
≃ 1), which translates into a host dark matter halo mass of ~1013h-1M⊙ and ~1013.7h-1M⊙ for the soft and hard bands, respectively.
Key words: X-rays: galaxies / galaxies: active / surveys
© ESO, 2012
1. Introduction
The study of the large-scale structure for the universe and of structure formation processes makes it necessary to carry out wide-field surveys of extragalactic objects. These surveys are performed in almost all accessible wavelength bands. X-ray surveys constitute an important part of these surveys because of the weak absorption at such high energies. The most recent and prominent observational X-ray results have been obtained with the XMM-Newton and Chandra space observatories (Brandt & Hasinger 2005). More than 95% of all detected objects in X-ray surveys away from the galactic plane are point-like and predominantly active galactic nuclei (AGN), the rest are mostly extended sources (groups and clusters of galaxies and relatively nearby galaxies). Owing to their high X-ray luminosity, AGN can be detected over a wide range of redshifts in contrast to normal galaxies (Hartwick & Schade 1989), and therefore these objects are excellent tracers of the cosmic web and a convenient tool for studying evolutionary phenomena in the Universe. It is known that the optical and X-ray classification of type 2 (obscured) AGN agree quite well, see for example Garcet et al. (2007) and references therein. X-ray selected AGN also provide a relatively unbiased census of the AGN phenomenon because obscured AGN, which are largely missed in optical surveys, are included in X-ray surveys.
The clustering pattern of the AGN population can provide important information regarding the cosmography of matter density fluctuations at different scales and the cosmological parameters (e.g., Hickox et al. 2007; Engels et al. 1999; Plionis et al. 2010; Ebrero et al. 2009; Basilakos & Plionis 2009, 2010), the evolution of the AGN phenomenon (e.g., Comastri & Brusa 2008; Koulouridis et al. 2011; Allevato et al. 2011), the relation between AGN activity and their dark matter halo hosts, supermassive black hole formation (e.g., Mandelbaum et al. 2009; Miyaji et al. 2011; Allevato et al. 2011), and so on. The most common approach to quantify AGN clustering, without redshift information is to measure the AGN two-point angular correlation function (ACF; Akylas et al. 2000; Yang et al. 2003; Manners et al. 2003; Basilakos et al. 2005; Gandhi et al. 2006; Puccetti et al. 2006; Miyaji et al. 2007; Carrera et al. 2007; Garcet et al. 2007; Ebrero et al. 2009), which provides an estimate of how significant the excess of AGN pairs is, within some projected angular separation over that of a random distribution. Once the angular correlation function is measured, it is possible to reconstruct the spatial clustering, under some specific assumptions, using the Limber integral equation (Limber 1953; Peebles 1980). However, spectroscopic follow-up as well as multiwavelength photometric observations in a number of different bands allow us to measure or estimate redshifts for a large number of AGN and to apply the direct spatial correlation analysis (e.g., Gilli et al. 2005; Yang et al. 2006; Gilli et al. 2009; Coil et al. 2009; Cappelluti et al. 2010; Miyaji et al. 2011).
Clustering analyses of the various surveys of X-ray selected AGN in the soft and hard bands have provided a wide range of angular and spatial clustering lengths. Strong indications for a flux-limit clustering dependence appear to reconcile most of the diverse results, however (Plionis et al. 2008; Ebrero et al. 2009; Krumpe et al. 2010).
Another important question is whether the clustering of X-ray selected AGN evolves with time. Gilli et al. (2009) did not find any significant difference between the X-ray AGN clustering below and above z = 1. Even so, the X-ray AGN bias factor should evolve with time, and indeed Yang et al. (2006) found a rapid increase of the bias factor with redshift with b(z = 0.45) = 0.95 ± 0.15 and b(z = 2.07) = 3.03 ± 0.83. Similarly, Allevato et al. (2011) estimated the average bias in the COSMOS AGN survey and found a redshift evolution of the bias factor with b(z = 0.92) = 2.30 ± 0.11 and b(z = 1.94) = 4.37 ± 0.27.
The AGN clustering pattern can also be used for the verification of the unification model, because both obscured and unobscured AGN should have identical correlation function, if the orientation of the torus is the only determining factor of the AGN phenomenology. Gilli et al. (2009) used the 2 sq. deg. XMM-COSMOS field and did not find any significant difference in the spatial distribution of the broad and narrow line AGN. Similarly, Ebrero et al. (2009), studying 1063 XMM-Newton observations, found consistent correlation properties for sources with high and low hardness ratios, which mostly correspond to obscured and unobscured AGN, respectively. These results postulate that obscured and unobscured objects populate similar environments, which agrees with the unified model of AGN.
However, the analysis of the 9 sq. deg. Bootes multiwavelength survey showed slightly different clustering properties for the two types of AGN (Hickox et al. 2011). Similarly, Puccetti et al. (2006) investigated the central 0.6 sq. deg. region of the ELAIS-S1 field and found that the correlation amplitude in the hard band (θ0 = 12.8′′ ± 7.8′′) is 2.5 times higher than that in the soft band (5.2′′ ± 3.8′′), but with a weak significance (~1σ). Gandhi et al. (2006) used the hardness ratio (HR) and divided the point-like sources in mainly obscured (HR > −0.2) and unobscured (HR < −0.2) subsamples, finding a positive clustering signal only for the obscured sources in the hard band.
In this work we will revisit these questions by presenting the final results of the point-like source distribution of the XMM-Newton Large Scale Structure (XMM-LSS) survey of Pierre et al. (2004). In Gandhi et al. (2006) we presented the AGN clustering results based on the previous release of 4.2 sq. deg. of this survey. A weak positive correlation signal was found in the soft band (angular scale θ0 = 6.3′′ ± 3′′ with a slope γ = 2.2 ± 0.2). At present the full XMM-LSS field is one of the widest (~11 sq. deg.) medium-deep surveys. It is part of an even larger project, the XXL, observations of which are currently being implemented (Pierre et al. 2011).
In the following sections we present the description of the XMM-LSS survey (Sect. 2). Results of the numerical simulations of the X-ray point-like sources are presented in Sect. 3. Basic properties of the XMM-LSS field, like its source distribution on the sky and the point-source log N–log S relation, are shown in Sect. 4. Section 5 includes the method used to produce the random catalogs and the ACF analysis for the different samples. Inverting from angular to spatial clustering and the derived bias of AGN are presented in Sects. 6 and 7, respectively, while the main conclusions are listed in Sect. 8.
2. The sample of X-ray point-like sources
In the present correlation function analysis, we have used point-like X-ray sources from the XMM-LSS field, which consists of 87 pointings with maximum available exposures from 10 to 28 ks. Also we used 7 pointings of the independent deeper Subaru/XMM-Newton Deep Survey (SXDS) (Ueda et al. 2008) whose data we reanalyzed with our pipeline because it is fully enclosed in the XMM-LSS area, although with a different spacing pattern. For S01 pointing of SXDS we kept only 40 ks chunk to prevent possible source confusion.
Altogether, the XMM-LSS field is contiguous and contains ~5700 sources in the soft (0.5–2 keV) band and ~2500 in the hard (2–10 keV) band, out of which ~180 are extended (mainly galaxy clusters). Although all extended sources were removed from our analysis, it is interesting to note that they were categorized according to their extension likelihood1 (EXTlike) and core radius (EXT) into two classes: “C1” which are the true extended sources with EXTlike > 33 and EXT > 5′′, containing 54 objects, and “C2” which is a class with almost 50 per cent contamination at 15 < EXTlike < 33 and EXT > 5′′, containing 129 objects (see Pacaud et al. 2006 for details).
Separately, we have made use of a more uniform XMM-LSS survey for our analysis which consists of 10 ks chunks. This catalog will be published soon (Chiappetti et al., in prep.)
We considered all point-like sources as AGN, although we do expect a ~3% stellar contamination (Salvato et al. 2009). More details about the source classification will be given in Melnyk et al. (in prep.). The sensitivity limits of the joined sample are near 10-15 and 3 × 10-15 erg s-1 cm-2 for the soft and hard bands, respectively.
The average distances between the centers of adjacent pointings were substantially shorter than the FoV diameter of the EPIC cameras to gain a more homogeneous coverage. This caused overlaps between adjacent pointings. Because each pointing was processed individually, the final merged catalog was produced a posteriori (Pierre et al. 2007; Chiappetti et al., in prep.). As a first possibility, we only considered sources with an off-axis distance <10′. In this way, we did not have to consider boundary sources that are often detected with large errors. The total effective area of the fields was 8.3 sq. deg. The distribution of the corresponding 4066 X-ray sources located within the borders is shown in Fig. 1. As an alternative merging possibility we applied a Voronoi boundary delimitation (Matsuda & Shima 1984) without imposing an off-axis cutoff and using sources across the full exposure XMM-LSS field. In other words, in any overlap region among two pointings we only kept those detections in our final catalog that had the shortest off-axis distance. In this way, we were able to use the widest possible area 10.9 sq. deg. of the investigated field. The distribution of the 5093 point-like X-ray sources is shown in Fig. 2. The basic ACF results were checked considering both approaches and it was found that apart from larger uncertainties in the case of the <10′ delimitation method, the results were statistically identical.
 |
Fig. 1 Distribution of the X-ray point-like sources observed in the soft band within the whole XMM-LSS field with an off-axis distance less than 10′. The red circles represent the borders between the different pointings. Note that even when using the 10′ limitation, we may have some overlapping regions. We discarded these minor overlaps using the Voronoi tessellation method. |
 |
Fig. 2 Distribution of the X-ray point-like sources observed in the soft band within the whole XMM-LSS field with the Voronoi tessellation method. Note that using the Voronoi tessellation we did not exceed the 13′ off-axis distance for any pointing. |
3. Simulations of XMM-LSS AGN
For a proper correlation function analysis we need to know the values of the detection probability for each registered source. Therefore we performed extensive simulations of each individual XMM pointing. We briefly describe our procedure and the set of simulations that were used for the representation of the XMM-LSS field.
3.1. Description of the XMM-Newton point-source simulation
The principle of the simulations is similar to the one presented in Pacaud et al. (2006) and Gandhi et al. (2006). The main steps of the procedure consist in i) generating an input source list drawn from a fiducial flux distribution that is randomly distributed across the pointing field of view; ii) simulating images of the field as it would be seen by XMM-Newton by reproducing the main instrumental effects (vignetting, PSF distortion, detector masks, background and Poisson noise); iii) detecting sources with the XMM-LSS pipeline (Pacaud et al. 2006) and obtaining their likelihoods and measured count-rates2; iv) correlating the detected source list with the input catalog using a 6′′ radius and deriving the rates of true and false detections as well as the detection probabilities.
The simulations were performed in the soft and the hard bands. The original source distribution was taken from Moretti et al. (2003) using either their soft or hard band fitting formulae, down to a flux which approximately corresponds to 2 photons on-axis (i.e. below XMM-Newton detection limit). This value depends on the exposure time chosen for each particular simulation. Non-resolved AGN photon background was added following Read & Ponman (2003), then we subtracted the contribution of the AGN resolved by our detection algorithm. The constant conversion factor cf between the total count-rates and the physical fluxes S was calculated on the basis of the MOS and PN camera factors provided by Pierre et al. (2007).
Particle background was also added according to values quoted in Read & Ponman (2003) and was subsequently modified by multiplying these values by an arbitrary factor between 0.1 and 8 to allow for pointing-to-pointing background variations. In any case, this component was not vignetted. We summarize our typical background values in Table 1. The PSF model was taken from the XMM-Newton medium model calibration files. The vignetting was modeled through its off-axis variation onto each detector.
The detection algorithm provides for each source an estimate of its count-rate on each detector as well as the local background value at the source position. A key parameter is the source detection likelihood. Following Pacaud et al. (2006), this quantity was computed using the C-statistic. Its value is the difference between the likelihood of the best-fitting point-source model and the likelihood of a pure background fluctuation. As such, the source likelihood LH represents the significance of the detection. A value of 15 provides a good balance between contamination and completeness (see Pacaud et al. 2006 and paragraph 3.2 for a discussion of the stability of this criterion).
 |
Fig. 3 Examples of simulated XMM-Newton pointings in the soft band. The large blue circle indicates the region in which the source detection is performed (13 arcmin maximal off-axis angle). Green boxes indicate the positions of sources detected with a likelihood ML > 15. Left: Texp = 10 ks, background ratio = 1; Middle: Texp = 10 ks, background ratio = 4; Right: Texp = 40 ks, background ratio = 1. |
Typical background values for the pointing simulations.
3.2. Set of simulations
To fully account for the variations of the detection efficiency across the XMM-LSS fields, we simulated 18 900 and 6480 pointings in the soft and the hard bands, respectively. Table 2 details the simulation set. Figure 3 illustrates the influence of exposure time and background ratio value for three pointings from our simulation set at 10 and 40 ks and for background ratios 1 and 4.
Summary of the soft and hard band simulation sets.
Thanks to the high number of simulated fields, we were able to bin our results by source off-axis angle. We have chosen six annuli of equal area to obtain approximately the same level of significance in each bin. Values defining the bin bounds are 0, 5.3, 7.5, 9.2, 10.6, 11.9 and 13.0 arcmin.
3.2.1. Completeness/contamination balance
The source selection was based on the detection likelihood value (ML) all detected sources with ML > 15 were included in the final sample of point-like sources. A fraction of these sources comes from false detections. Figure 4 shows the distribution of the recovered sources for three configurations in the innermost off-axis bin (0–5.3 arcmin). We see little dependence of the contamination rate on the background level and exposure time, and the ML = 15 threshold appears as the best choice for homogeneous balance between completeness of the sample and contamination by spurious sources.
We numerically computed the rate of false detections as a function of the off-axis angle, background level and exposure time and in any configuration. The average rate of spurious detections is between 2 and 5 per pointing (up to 13 arcmin off-axis angle). A typical pointing (Texp = 10 ks, background ratio = 1) gives from 40 to 50 detections in the [0−10] arcmin off-axis, which leads to a contamination rate of about 5%.
 |
Fig. 4 Examples of likelihood versus count-rate plots for three combinations of pointing exposures and background ratios from our soft band simulation set. Green symbols show detections with a real input counterpart while red points indicate spurious (false) detections. All sources within 5 arcmin from the pointing center are shown here. Left: 540 pointings with Texp = 10 ks, background ratio = 1; Middle: 540 pointings with Texp = 10 ks, background ratio = 4; Right: 540 pointings with Texp = 40 ks, background ratio = 1. The horizontal line corresponds to ML = 15, the threshold above which detected sources are included in the catalog. The separation between false and real detections is relatively independent of the pointing quality. |
3.2.2. Detection efficiency as a function of pointing characteristics
We show in Figs. 5–7 the probability curves derived from our simulations. These curves were computed by dividing the number of detected (ML > 15) sources by the number of input sources in a given input count-rate bin and for a given exposure time, background ratio and off-axis bin. The detection efficiency is close to the flux-limited efficiency, whose limit depends on the local pointing characteristics. A strong dependence on the off-axis position is noticeable in Fig. 7 because the effect of vignetting and PSF distortions are growing with off-axis distance. The exposure time dependence (Fig. 5) is compatible with a ∝ 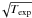 improvement factor over the signal-to-noise ratio, while the background level has a milder influence on the detection efficiency. In a typical pointing (Texp = 10 ks, background ratio = 1) the flux limit is 2.5 × 10-15 (4 × 10-15) erg s-1 cm-2 at 50% (90%) completeness.
improvement factor over the signal-to-noise ratio, while the background level has a milder influence on the detection efficiency. In a typical pointing (Texp = 10 ks, background ratio = 1) the flux limit is 2.5 × 10-15 (4 × 10-15) erg s-1 cm-2 at 50% (90%) completeness.
 |
Fig. 5 Efficiency of our source detection algorithm in the innermost annulus (0–5 arcmin) of the simulated soft band XMM observations, as a function of the input source count-rate (or equivalently, flux for a typical AGN spectrum and a galactic hydrogen column density fixed to 2.6 × 1020 cm-2). The exposure time differs from one curve to the other, but not the background rate. |
 |
Fig. 6 Same as Fig. 5 for various background rates in the soft band (defined by a multiplicative factor times the values quoted in the 2nd column of Table 1). Exposure time is held at 10 ks in all cases. |
 |
Fig. 7 Same as Fig. 5 for the six off-axis bins in the soft band (see text). Exposure time is held at 10 ks in all cases, and the particle background ratio is set to 1. |
3.2.3. Relating real data to simulations
Sensitivity maps across the entire XMM-LSS field can be derived through interpolation between simulated pointings. The exposure time of a given pointing is a straightforward quantity, as is the off-axis angle at the position of a source. To relate the background ratio quantity to real data, we used estimates of the local background fitted by our detection algorithm at each detected source position (see Pacaud et al. 2006 for a description of the fitting procedure). Estimated numbers of background counts per pixel are put out as two quantities PNT_BG_MAP_MOS and PNT_BG_MAP_PN. Figure 8 shows the relationship between the input background ratio and these quantities as derived from simulations. As expected, local background estimates computed by the detection algorithm are well correlated with the background ratio values introduced in the simulations. We fitted the local background values by PNT_BG_MAP_MOS(PN) using the least-squares method separately for each pointing. With this we determined the background ratio level B, which corresponds to the best parameter of the fitting.
 |
Fig. 8 Pipeline-estimated background values on MOS (left) and PN (right) detectors, in the soft band, as seen in the simulations. Curves from bottom to top stand for background ratios B equal to 0.1, 0.25, 0.5, 1, 2, 4 and 8. This plot shows how the local background estimate output of the detection algorithm can be related to the background ratio parameter introduced in the simulations. The error bars represent 1-σ standard variation computed from the source sample. The vertical lines correspond to bounds of our equal-area off-axis bins. Only the results for 10 ks are displayed and similar relations are extracted for 7, 20, 40 and 80 ks pointings. |
4. Sky coverages and log -log distributions
An important characteristic of an X-ray survey is the sky coverage or, in other words, the effective area curve. This indicates the maximum effective area over which we can detect sources brighter than some given flux limit. We have constructed the area curves using the numerically calculated probabilities p to detect sources with a certain flux S, an off-axis distance R in a pointing with some effective exposure T and particle background level B. The effective area A(S) is calculated while integrating over the whole field area Ω: 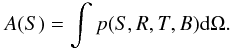 (1)Figure 9 shows the effective area curves for the investigated samples in the soft and hard bands, with a minimum flux 10-15 for the soft and 3 × 10-15 erg s-1 cm-2 for the hard bands. For the construction of the illustrated area curves we used the Voronoi tessellation delimitation method.
(1)Figure 9 shows the effective area curves for the investigated samples in the soft and hard bands, with a minimum flux 10-15 for the soft and 3 × 10-15 erg s-1 cm-2 for the hard bands. For the construction of the illustrated area curves we used the Voronoi tessellation delimitation method.
 |
Fig. 9 Effective area curves for the whole XMM-LSS field in the soft (0.5–2 keV) and hard (2–10 keV) bands. |
 |
Fig. 10 Comparison of the normalized effective area curves in the soft band for the full exposure XMM-LSS field, the 10 ks version (see Sect. 5.1), the XMM-LSS 4.2 sq. deg. (Gandhi et al. 2006), the XMM Medium Deep Survey (XMDS Chiappetti et al. 2005), the 2XMM (Ebrero et al. 2009) and the COSMOS (Miyaji et al. 2007; Cappelluti et al. 2007). |
Figure 10 shows a comparison between the normalized effective area curves of various recent X-ray surveys. The effective area curve as a function of flux depends mainly on the depth of the source detection (indicated by the signal-to-noise ratio or likelihood thresholds). It also depends on the distributions of the pointing exposures, particle background level and the procedure of handling the pointing overlaps. Evidently, the COSMOS field has the lowest flux limit and the steepest area curve among the considerable surveys with the likelihood limit for the source detection being equal to 6 (Cappelluti et al. 2007). Our full exposure XMM-LSS survey, having a significant fraction of the contributing pointings with exposures between 10 and 15 ks and a source detection threshold of ML = 15, has the next lowest flux-limit after the COSMOS survey, and a quite steeply increasing area-curve. The corresponding 10 ks XMM-LSS field has its area curve shifted to the right and its flux limit increased by a factor of ~1.2.
Using those area curves and the differential distributions of the sources as a function of their flux, we constructed the log N − log S relation. Note that it is important to take into account the flux boosting. This phenomenon especially affects faint objects with a low detection probability. Owing to Poisson noise, we may detect objects fainter than the flux limit in successful cases and sometimes not detect sources brighter than the flux limit in unsuccessful cases. This may cause the creation of an artificial bump in the log N − log S distribution.
 |
Fig. 11 Example of the dependence between input and output count-rates for the hard band, T = 20 ks, b = 1. The red line corresponds to CRin = CRout. |
 |
Fig. 12 Distributions of CRin for three detected CRout created on the basis of the simulated distribution in Fig. 11. |
To take this effect into account, we used the numerically simulated dependencies between the input CRin and the output CRout count rates individually for each pointing (see Fig. 11 for example). Clearly, when we detect some flux CRout, it corresponds to a real input CRin distributed over a wide range. For each CRout bin we constructed the density probability distribution as a function of CRin. Figure 12 represents the normalized distributions of CRin for three detected CRout. At low flux, we may see an asymmetric shape in the distribution that is shifted toward smaller CRin because of an artificial flux boosting. Therefore, we randomly chose some CRin for each detected source with CRout according to the density probability function. In this way, we carried out Monte-Carlo simulations with the deconvolution of the output into the input rates and constructed log N − log S curves for various considered samples (Figs. 13, 14).
The currently estimated log N − log S are lower for both bands than those of the 2XMM (Ebrero et al. 2009) and COSMOS (Cappelluti et al. 2007) surveys, with deviations not exceeding the 2–3σ Poisson level. However, they excellently agree with those derived by Gandhi et al. (2006) and Chiappetti et al. (2005), based on previous releases of XMM-LSS fields. Moreover, the XMDS (Chiappetti et al. 2005) was based on a totally different pipeline used for extracting the X-ray point-like sources. This suggests that the observed deficiency could be an intrinsic characteristic of the XMM-LSS field.
 |
Fig. 13 Log N − log S distributions in the soft band for the whole XMM-LSS sample and for the two different procedures of handling the pointing overlaps. The results of the XMM Medium Deep Survey (XMDS (Chiappetti et al. 2005), 2XMM (Ebrero et al. 2009), XMM-LSS 4.2 sq. deg. (Gandhi et al. 2006) and COSMOS (Miyaji et al. 2007; Cappelluti et al. 2007) are shown for comparison. The vertical bars denote 1σ uncertainties. |
 |
Fig. 14 Log N − log S distributions in the hard band for the whole sample and for the two different procedures of handling the pointing overlaps. For comparison we present the log N − log S distributions for the same samples as in Fig. 13. |
5. The angular correlation function analysis
To determine the ACF, we generated random catalogs in the following way. Firstly, we distributed the fiducial point-like sources with random coordinates over the whole investigated field. Secondly, we chose for each random source a flux according to the log N − log S distribution and calculated the probability p of detecting the corresponding point-like source in the relevant pointing, taking into account the exposure time, the particle background level (B) of the pointing and the off-axis distance of the corresponding source. Then, we chose a random number ρ for each random point-like source that is uniformly distributed between 0 and 1. If the ρ value was less than p, we kept the source, if it was higher, we discarded the source. If a random source was closer than 10 arcsec to another one, we removed it because the extension of the EPIC PSF (~6′′ minimum, on axis) prevents one from detecting such close pairs and blends them into a single source. We generated random catalogs in this way that contain 100 times the number of point-like sources in the real source catalog, that was used in the present analysis. The larger the point population of the random catalog, the more accurate the ACF measurement because it suppresses random fluctuations caused by small numbers.
To calculate the ACF, we used two estimators, the Hamilton estimator (Hamilton 1993), as in Gandhi et al. (2006): 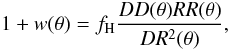 (2)and the Landy & Szalay estimator (Landy & Szalay 1993):
(2)and the Landy & Szalay estimator (Landy & Szalay 1993): 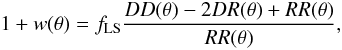 (3)where DD, RR and DR represent the numbers of data-data, random-random and data-random pairs with a separation θ, while fH and fLS are the corresponding normalization factors of the two estimators. In general the two estimators provide consistent results but in any case we will present the results based on both estimators in the correlation function plots.
(3)where DD, RR and DR represent the numbers of data-data, random-random and data-random pairs with a separation θ, while fH and fLS are the corresponding normalization factors of the two estimators. In general the two estimators provide consistent results but in any case we will present the results based on both estimators in the correlation function plots.
To speed-up our calculations, we divided the random catalog of those samples with more than 2000 X-ray sources into a maximum of 10 random subcatalogs, and we averaged w(θ) for each θ bin over the whole random catalogs. Note that we verified by investigating one such sample that the above procedure provides stable correlation results. The w(θ) uncertainty in each θ-bin is given by 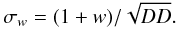 (4)The ACF calculations were performed for angular scales in the range: 20′′ < θ < θmax, where θmax = 12 000′′. We used 20′′ as our lowest angular-separation limit because of the large size of the XMM-Newton PSF near the FoV borders. We verified that pairs, constituted by sources belonging to adjacent pointings, are real only for pair separations ≳ 20′′. We then fitted the resulting ACF with the power-law in the angular range where it was possible, i.e., using only the positive w values:
(4)The ACF calculations were performed for angular scales in the range: 20′′ < θ < θmax, where θmax = 12 000′′. We used 20′′ as our lowest angular-separation limit because of the large size of the XMM-Newton PSF near the FoV borders. We verified that pairs, constituted by sources belonging to adjacent pointings, are real only for pair separations ≳ 20′′. We then fitted the resulting ACF with the power-law in the angular range where it was possible, i.e., using only the positive w values: 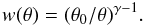 (5)We analyze here the ACF of the full exposure XMM-LSS field. However, because there are strong indications for a flux-limit dependence of the correlation function amplitude (e.g., Plionis et al. 2008), we also analyzed a homogeneous sample of an effective 10 ks exposure over the whole XMM-LSS region. To this end we cut the event list of the pointings into 10 ks chunks and repeated the source detection procedure from the beginning. We also separately estimated the ACF of samples based on the hardness ratio (HR).
(5)We analyze here the ACF of the full exposure XMM-LSS field. However, because there are strong indications for a flux-limit dependence of the correlation function amplitude (e.g., Plionis et al. 2008), we also analyzed a homogeneous sample of an effective 10 ks exposure over the whole XMM-LSS region. To this end we cut the event list of the pointings into 10 ks chunks and repeated the source detection procedure from the beginning. We also separately estimated the ACF of samples based on the hardness ratio (HR).
 |
Fig. 15 Soft band ACF for the whole sample: Voronoi delimitation (top panel); off-axis angle < 10′ (lower panel). The filled (black) points correspond to the Hamilton estimator while the open (red) squares to the Landy & Szalay estimator. The error bars represent 1σ standard deviation. The dashed line represents the best power-law fit, while the continuous line corresponds to the constant γ = 1.8 fit. The inset plot presents the 1, 2 and 3σ contours in the fitted (θ0,γ) parameter space. |
 |
Fig. 16 Hard band ACF for the whole sample: Voronoi delimitation (upper panel); off-axis angle < 10′ (lower panel). |
5.1. The whole XMM-LSS field
We first present in Figs. 15 and 16 the ACF results of the full exposure XMM-LSS region for both the soft and hard bands and for the Voronoi delimitation and off-axis angle < 10′ overlap approaches. In the inset panels we present the 1, 2 and 3σ contours of the fitted parameters in the (θ0,γ) plane, while in Table 3 we present the corresponding best fit θ0 and γ parameters and their standard deviation, as well as the value of θ0 for a fixed slope γ = 1.8 and the integral ACF signal within separations of 3.3 arcmin, w(<3.3′). Evidently, that there are no significant differences between the results based on the correlation function estimators (as seen in Figs. 15, 16) or on the two delimitation methods. Therefore we used for the remaining study only the samples based on the space-filling Voronoi delimitation method and the Landy & Szalay ACF estimator (see also Kerscher et al. (2000) for a detailed comparison of different estimators).
Furthermore, we find that the hard band correlation function is slightly but clearly stronger than the corresponding soft band, as can be also verified by comparing the corresponding inset contour plots, which agree with the results of Basilakos et al. (2005), Puccetti et al. (2006) but disagree with those of Ebrero et al. (2009).
Soft and hard band correlation functions for the whole XMM-LSS field, as well as for the two possible overlap approaches.
As discussed above, to provide a “clean” ACF, that is unaffected by the convolution of (a) the variable flux-limit in the different parts of the survey and (b) the flux-limit clustering dependence, we considered a sample with a homogeneous 10 ks exposure time across the whole XMM-LSS area. Table 4 and Fig. 17 show the parameters of the ACFs for both bands. The main variation with respect to the previous analysis is that the ACF difference between the soft and hard bands is now even more prominent.
Correlation function for the 10 ks chunk samples.
 |
Fig. 17 ACF for the 10 ks sample in the soft band (upper panel) and for the hard band (lower panel). |
 |
Fig. 18 Best-fit correlation length θ0 for γ = 1.8 as a function of the flux limit of the homogeneous 10 ks sample in the soft (filled circles) and the hard bands (open circles). |
We also investigated the flux-limit dependence of clustering with our homogeneous 10 ks sample. To this end we estimated the angular clustering length, θ0 for various flux-limited subsamples by keeping the slope of the ACF fixed to its nominal value of γ = 1.8. Figure 18 shows the corresponding results for the soft and hard bands. Evidently the known dependence is clearly reproduced with our data, and it will be interesting to investigate whether this dependence is present in the spatial correlation length, via Limber’s inversion (see further below). Another interesting result is that the amplitude of the hard band ACF is larger than that of the soft band only in the lowest flux-limits. At flux limits ≥ 10-14 erg s-1 cm-2 the trend is reversed and the soft band is stronger than the hard band clustering.
How do our results compare with those of other XMM surveys? With respect to our previous release of the 4.2 sq. deg. XMM-LSS survey (Gandhi et al. 2006), our new catalog introduces many improvements. Among them is the wider (by ~2.6 times) sampled area, and the inclusion of a deeper SXDS field. Furthermore, we updated the point-like source detection procedure and introduced a novel definition of the selection function and random-catalog generation procedure.
Our current XMM-LSS area curve is substantially different from that of Gandhi et al. (2006) (see Fig. 10). To investigate the reasons of this difference in detail, we used the 44 pointings common to both studies to compare the corresponding point-like source catalogs in the soft band. The current XMM-LSS catalog contains 2106 objects with off-axis distances less than 10′ and the Gandhi et al. (2006) catalogue contains 1093 such sources, while the common sources are 1048. Figure 19 shows the dependence between flux and ML for both catalogs. Obviously, the chosen ML limit of the Gandhi et al. (2006) catalog is substantially higher than the current limit of ML = 15 and it is equal to ML ~ 40. It is also evident, inspecting Fig. 19, that a value of ML ~ 40 is associated with a significantly higher flux-limit with respect to that of ML = 15, causing the observed difference of the corresponding area curves (see Fig. 10).
 |
Fig. 19 Dependence between flux and ML in the soft band for the point like sources of 44 pointings from the present XMM-LSS survey (black open circles) and from Gandhi et al. (2006) (red filled circles). |
The above mentioned changes and improvements, particularly the lower ML detection limit, have resulted in a variation of some of our results with respect to those of Gandhi et al. (2006). Specifically, we found a slightly different clustering signal in the soft band; θ0 = 1.3′′ ± 0.2′′ for γ = 1.81 vs. 6.3′′ ± 3′′ for γ = 2.2 in Gandhi et al. (2006). However, at the fixed canonical value of the exponent (γ = 1.8), the Gandhi et al. (2006) soft band analysis provides a clustering amplitude of θ0 = 1.7′′ ± 0.9′′ versus 1.2′′ ± 0.2′′ for the current XMM-LSS survey. The lower correlation signal of our current XMM-LSS survey should be attributed to the lower ML limit, which introduces a significantly higher fraction of faint sources with respect to the higher ML limit of the Gandhi et al. (2006) catalog. Also, we found a significant clustering signal in the hard band, in contrast to the absence of any significance in Gandhi et al. (2006).
With respect to the COSMOS (Miyaji et al. 2007) and 2XMM (Ebrero et al. 2009) surveys, we find (at fixed canonical γ = 1.8) a lower soft band correlation function amplitude, θ0 = 1.2′′ ± 0.2′′, compared to 1.9′′ ± 0.3′′ and to 7.7′′ ± 0.1′′ for the COSMOS and the 2XMM surveys, respectively. Our hard band (2–10 keV) XMM-LSS correlation amplitude of 3.6′′ ± 0.7′′ is also lower than the corresponding 2XMM value of 5.9′′ ± 0.3′′, while the COSMOS hard band correlation results are not very significant, probably because they are divided into two sub-bands (2–4.5 and 4.5–10 keV).
Note, however, that the wide contiguous area of the XMM-LSS survey implies that we should have a better estimation of w(θ) on large angular scales (i.e., 1000′′ ≲ θ ≲ 10 000′′), while COSMOS and 2XMM are limited to ~6000′′ and ~1000′′, respectively.
In Fig. 20 we compare the soft band w(θ) of our XMM-LSS and the 2XMM surveys. The large 2XMM w(θ) amplitude at small angular scales is evident, although at ~1000′′ the two correlation functions appear to be consistent. The higher 2XMM correlation amplitude should be attributed to the considerably different mix of faint and bright sources in the two surveys, as shown by their respective area curves (see Fig. 10). The larger part of faint sources in the current XMM-LSS survey causes the lower amplitude of the source angular correlation function with respect to the 2XMM, as expected from the known dependence between clustering and flux-limit (Plionis et al. 2008; Ebrero et al. 2009), a fact which has also been verified by our analysis (Fig. 18).
 |
Fig. 20 Soft band ACF comparison between our XMM-LSS survey (filled points) and that of the 2XMM survey (crosses) of Ebrero et al. (2009). |
5.2. Subsamples of sources with soft and hard spectra
An interesting question, that relates to the unification paradigm of AGN, is whether the clustering pattern, among others, of hard and soft-spectrum AGN is comparable. According to the unification paradigm, what determines the appearance of an AGN as obscured or unobscured (type II or I) is its orientation with respect to the observer’s line-of-sight. Therefore, there should be no intrinsic difference in their clustering pattern. On this question there have been conflicting results in the literature and we here re-address this with our data.
To this end we compared the correlation function of the hard and soft-spectrum sources by separating them, within each band, using the hardness ratio, HR, indicator defined as 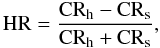 (6)where CRs and CRh represent the total count rates in the soft and the hard band, respectively. It is known that most of the sources with HR > −0.2 are likely to be obscured (hard-spectrum) AGN; conversely, the sources with HR < −0.2 are mostly (soft-spectrum) unobscured (see Gandhi et al. 2004 for details). Using this criterion, we split the whole sample and derived the log N − log S distributions for each of them in the soft and the hard bands (Fig. 21). Table 5 and Figs. 22, 23 show the parameters and ACFs for the obtained subsamples.
(6)where CRs and CRh represent the total count rates in the soft and the hard band, respectively. It is known that most of the sources with HR > −0.2 are likely to be obscured (hard-spectrum) AGN; conversely, the sources with HR < −0.2 are mostly (soft-spectrum) unobscured (see Gandhi et al. 2004 for details). Using this criterion, we split the whole sample and derived the log N − log S distributions for each of them in the soft and the hard bands (Fig. 21). Table 5 and Figs. 22, 23 show the parameters and ACFs for the obtained subsamples.
 |
Fig. 21 Log N − log S distributions in the soft and the hard bands for sources with different hardness ratios. |
 |
Fig. 22 ACF for the whole XMM-LSS sample in the soft band for sources with HR > −0.2 (filled circles, hard-spectrum AGN), and for sources with HR < −0.2 (open circles; soft-spectrum AGN). Note that for clarity reasons we do not plot the w(θ) uncertainties of the later sources. The solid line represents the γ = 1.8 fit to the HR > −0.2 w(θ), while the dashed line corresponds to the HR < −0.2 w(θ) fit. |
Correlation function for the subsamples characterized by their hardness ratio above and below −0.2.
The main result of this analysis is that there is a distinct clustering difference between the sources with hard and soft spectra in the soft band, with the former sources being significantly more clustered. In the hard band the corresponding comparison shows a much weaker difference, in the same direction, but not that significant. However, one also observes that the integrated signal within separations ≲ 3 arcmin indicates that at least on these small scales the hard-spectrum sources show a stronger clustering signal than the corresponding soft-spectrum ones. Similar results were found in Gandhi et al. (2006). Therefore, one may conclude that indeed there are indications for a different clustering pattern between hard-spectrum and soft-spectrum sources, which cannot be attributed to their different flux-limits, since we verified that this result is valid for brighter flux-limits as well. We believe that this result suggests a possible environmental component in the determination of the different types of AGN, beyond their orientation with respect to the observer’s line-of-sight. An environmental dependence of the AGN type has also been found in local optical AGN samples (e.g., Koulouridis et al. 2006a,b, 2011,and references therein).
6. Inverting from angular to spatial clustering
We now derive the spatial correlation length that corresponds to the measured angular clustering. To this end we used the usual Limber inversion (Peebles 1980). The main steps are sketched below.
In a spatially flat universe, the ACF w(θ) can be obtained from the spatial one, ξ(r), by ![\begin{equation} w(\theta)=2\frac{\int_{0}^{\infty} \int_{0}^{\infty} x^{4} \phi^{2}(x) \xi(r,z) {\rm d}x {\rm d}u} {[\int_{0}^{\infty} x^{2} \phi(x){\rm d}x]^{2}} , \end{equation}](/articles/aa/full_html/2012/01/aa17983-11/aa17983-11-eq201.png) (7)where the physical separation between any two sources that are separated by an angle θ and considering the small angle approximation, is given by
(7)where the physical separation between any two sources that are separated by an angle θ and considering the small angle approximation, is given by 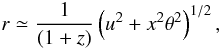 (8)while φ(x) is the selection function (the probability that a source at a distance x is detected in the survey) given by
(8)while φ(x) is the selection function (the probability that a source at a distance x is detected in the survey) given by 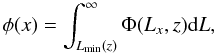 (9)where Φ(Lx,z) is the redshift-dependent luminosity function of the X-ray selected AGN. A variety of X-ray source luminosity functions are available in the literature, and to investigate the uncertainty that their differences can introduce in the derived value of r0, we will present results for a number of Φ(Lx,z). Although the most recent soft/hard band luminosity functions are those of Ebrero et al. (2009), we will also use those of Hasinger et al. (2005) for the soft band, while for the hard band we used those of Ueda et al. (2008) and of La Franca et al. (2005). In all cases we used of course the luminosity-dependent density evolution model of the luminosity function.
(9)where Φ(Lx,z) is the redshift-dependent luminosity function of the X-ray selected AGN. A variety of X-ray source luminosity functions are available in the literature, and to investigate the uncertainty that their differences can introduce in the derived value of r0, we will present results for a number of Φ(Lx,z). Although the most recent soft/hard band luminosity functions are those of Ebrero et al. (2009), we will also use those of Hasinger et al. (2005) for the soft band, while for the hard band we used those of Ueda et al. (2008) and of La Franca et al. (2005). In all cases we used of course the luminosity-dependent density evolution model of the luminosity function.
The proper distance x(z) is related to the redshift through 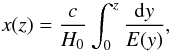 (10)with
(10)with ![\begin{equation} E(z)=[\Omega_{\rm m}(1+z)^{3}+\Omega_{\Lambda}]^{1/2} \;\;\; \Omega_{\rm m}=1-\Omega_{\Lambda}. \end{equation}](/articles/aa/full_html/2012/01/aa17983-11/aa17983-11-eq210.png) (11)In this context, the spatial correlation function can be modeled as in de Zotti et al. (1990)
(11)In this context, the spatial correlation function can be modeled as in de Zotti et al. (1990)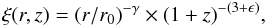 (12)where r0 is the correlation length in three dimensions and ϵ( ≡ γ − 3) parameterizes the type of clustering evolution. A value of ϵ = −1.2 for γ = 1.8, indicates a constant clustering in comoving coordinates, while ϵ = −3 indicates a constant clustering in physical coordinates (e.g., de Zotti et al. 1990).
(12)where r0 is the correlation length in three dimensions and ϵ( ≡ γ − 3) parameterizes the type of clustering evolution. A value of ϵ = −1.2 for γ = 1.8, indicates a constant clustering in comoving coordinates, while ϵ = −3 indicates a constant clustering in physical coordinates (e.g., de Zotti et al. 1990).
Combining the above system of equations, we obtained the following integral equation for w(θ) 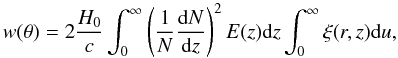 (13)where dN/dz denotes the number of objects in the given survey within a solid angle Ωs and in the shell (z,z + dz). It takes the following form:
(13)where dN/dz denotes the number of objects in the given survey within a solid angle Ωs and in the shell (z,z + dz). It takes the following form: 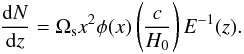 (14)Using Eqs. (12), (8) and (13), we find that the amplitude θ0 in two dimensions is related to the correlation length r0 in three dimensions through the equation (see Basilakos et al. 2005):
(14)Using Eqs. (12), (8) and (13), we find that the amplitude θ0 in two dimensions is related to the correlation length r0 in three dimensions through the equation (see Basilakos et al. 2005): 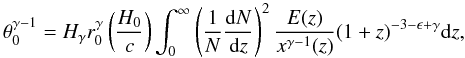 (15)where
(15)where 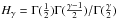 .
.
Spatial correlation length r0 (in h-1 Mpc), provided by Limber’s inversion of the ACF and using different AGN X-ray luminosity functions, for the homogeneous 10 ks sample and for the lowest flux-limit available.
Following the previous steps, we derived the spatial clustering length scale for fixed γ = 1.8 and for both values of clustering evolution parameter (ϵ = −1.2 and −3). The results are presented in Table 6. Evidently that all three hard band luminosity functions provide the same r0 value, while for ϵ = −1.2 there is a difference in the soft band with the Hasinger et al. (2005) Φx(L), providing an r0 value that is 16% higher than that provided by Ebrero et al. (2009) Φx(L). As we will see, this difference increases proportionally to the flux-limit of the subsample used. In Fig. 24 we present the inverted r0 values as a function of the different flux limits, as they appear in Fig. 18. We see that for the soft band the two luminosity functions used in the inversion provide r0 values that diverge with increasing flux-limit.
The dashed lines in Fig. 24 correspond to fits of the data, using for each band results based on all different luminosity functions, of the form: 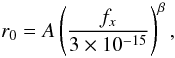 (16)with (A,β) ≃ (6.5,0.54) for the soft band and (A,β) ≃ (9.4,0.1) for the hard band. Evidently, the flux dependence of clustering, once one inverts from angular to 3D space, is preserved mostly in the soft band. In the hard band we see at most a weak dependence and only for fluxes ≳ 2 × 10-14 erg s-1 cm-2, while a constant hard band value of r0 ≃ 10h-1 Mpc, irrespective of the flux limit, appears also to be consistent with the data. These hard band results agree with those of Ebrero et al. (2009), who found that the weak dependence of θ0 on the flux-limit translates into a roughly constant r0 as a function of flux-limit, or equivalently as a function of median redshift or median X-ray luminosity of the sample. However, a relatively strong dependence of the soft band r0 with respect to the flux-limit disagree with Ebrero et al. (2009), but agrees with Plionis et al. (2008).
(16)with (A,β) ≃ (6.5,0.54) for the soft band and (A,β) ≃ (9.4,0.1) for the hard band. Evidently, the flux dependence of clustering, once one inverts from angular to 3D space, is preserved mostly in the soft band. In the hard band we see at most a weak dependence and only for fluxes ≳ 2 × 10-14 erg s-1 cm-2, while a constant hard band value of r0 ≃ 10h-1 Mpc, irrespective of the flux limit, appears also to be consistent with the data. These hard band results agree with those of Ebrero et al. (2009), who found that the weak dependence of θ0 on the flux-limit translates into a roughly constant r0 as a function of flux-limit, or equivalently as a function of median redshift or median X-ray luminosity of the sample. However, a relatively strong dependence of the soft band r0 with respect to the flux-limit disagree with Ebrero et al. (2009), but agrees with Plionis et al. (2008).
 |
Fig. 24 Spatial correlation length r0 for γ = 1.8 and ϵ = −1.2 considering the homogeneous 10 ks based observations as a function of the flux limit of the sample in the soft band (filled and empty circles correspond to the Ebrero and Hasinger Φx(L), respectively) and in the hard band (filled square, open squares and open hexagons correspond to the Ebrero, Ueda and La Franca Φx(L), respectively). |
7. Bias of the X-ray selected AGN
The concept of biasing between different classes of extragalactic objects and the background matter distribution was introduced by Kaiser (1984) and Bardeen et al. (1986) to explain the higher amplitude of the two-point correlation function of clusters of galaxies with respect to that of galaxies themselves. In our case and within the framework of linear biasing (cf. Kaiser 1984; Benson et al. 2000), the evolution of the bias parameter is usually defined as ![\begin{equation} \label{eq:biasdef} b^2(z)=\frac{\xi_{\rm AGN}(8,z)}{\xi_{\rm DM}(8,z)}=\left[\frac{r_{0}(z)}{8}\right]^{\gamma} \frac{1}{\xi_{\rm DM}(8,z)}, \end{equation}](/articles/aa/full_html/2012/01/aa17983-11/aa17983-11-eq245.png) (17)where ξAGN(8,z) = (r0(z)/8)γ and ξDM(8,z) are the spatial correlation functions of AGN and dark matter halos evaluated at 8 h-1 Mpc, respectively. Notice that the correlation lengths in 3D are presented in Table 6. The correlation function of the DM halos is given by Peebles (1980)
(17)where ξAGN(8,z) = (r0(z)/8)γ and ξDM(8,z) are the spatial correlation functions of AGN and dark matter halos evaluated at 8 h-1 Mpc, respectively. Notice that the correlation lengths in 3D are presented in Table 6. The correlation function of the DM halos is given by Peebles (1980)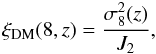 (18)where J2 = 72/[(3 − γ)(4 − γ)(6 − γ)2γ] and
(18)where J2 = 72/[(3 − γ)(4 − γ)(6 − γ)2γ] and 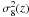 is the dark matter density variance in a sphere with a comoving radius of 8 h-1 Mpc, which evolves as
is the dark matter density variance in a sphere with a comoving radius of 8 h-1 Mpc, which evolves as 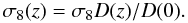 (19)Note that D(z) is the linear growth factor scaled to unity at the present time. For the concordance Λ cosmology3 the growth factor becomes (see Peebles 1993)
(19)Note that D(z) is the linear growth factor scaled to unity at the present time. For the concordance Λ cosmology3 the growth factor becomes (see Peebles 1993) 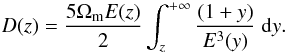 (20)Finally, inserting Eqs. (19) and (18) into Eq. (17), we obtain the evolution of biasing with epoch as a function of the clustering properties
(20)Finally, inserting Eqs. (19) and (18) into Eq. (17), we obtain the evolution of biasing with epoch as a function of the clustering properties ![\begin{equation} \label{obsbias24} b(z)=\left[ \frac{r_{0}(z)}{8}\right]^{\gamma/2} \frac{J_{2}^{1/2}}{\sigma_{8} D(z)/D(0)} \cdot \end{equation}](/articles/aa/full_html/2012/01/aa17983-11/aa17983-11-eq255.png) (21)For angular clustering we may identify the dominant redshift of the sample under study as that predicted by the luminosity function of the sources used and the flux limit of the sample, which predicts the redshift distribution of the sources. We can then obtain from the last equation an estimate of the bias of our X-ray sources (see Table 7). Of course one has to keep in mind that this is a quite crude estimate since we implicitly assume that all detected sources obey the same luminosity function, while in effect luminosity functions are derived from subsamples of all the detected X-ray sources for which optical counterparts are identified.
(21)For angular clustering we may identify the dominant redshift of the sample under study as that predicted by the luminosity function of the sources used and the flux limit of the sample, which predicts the redshift distribution of the sources. We can then obtain from the last equation an estimate of the bias of our X-ray sources (see Table 7). Of course one has to keep in mind that this is a quite crude estimate since we implicitly assume that all detected sources obey the same luminosity function, while in effect luminosity functions are derived from subsamples of all the detected X-ray sources for which optical counterparts are identified.
Linear bias factor for the lowest flux-limit results of the homogeneous 10 ks XMM-LSS data (and for the same X-ray luminosity functions as in Table 6).
We see again that although our hard band results roughly agree with those of Ebrero et al. (2009), our soft band results are significantly different, because we found a significantly weaker clustering amplitude than the aforementioned authors.
We can now use a bias evolution model (e.g., Sheth et al. 2001; Basilakos et al. 2008, and references therein) to estimate the halo mass that corresponds to the above estimated bias factors (for ϵ = −1.2), assuming that each halo hosts one AGN source. Using the latter model (see details in Papageorgiou et al., in prep.), we obtain that for the soft band and the Ebrero et al. luminosity function the corresponding halo mass is Mh ≃ 1012.9 ± 0.3h-1 M⊙, while using the Hasinger luminosity function the corresponding value is Mh ≃ 1013.2 ± 0.3h-1M⊙. For the hard band we find that Mh ≃ 1013.7 ± 0.3h-1M⊙. Note that using the Sheth et al. bias model, we find very similar Mh values (for example, for the hard band results we find Mh ≃ 1013.6h-1M⊙).
8. Main conclusions
We have performed a two-point correlation function analysis of the XMM-LSS sample of point sources that contains in total 94 XMM-Newton pointings (more than five thousand point-like sources). The observations were made near the celestial equator at high galactic latitudes over ~ 11 sq. deg. in the soft (0.5–2 keV) and hard (2–10 keV) bands with effective exposures ranging from 8.1 to 47.3 ks. The minimum flux limits are almost 10-15 and 3 × 10-15 erg s-1 cm-2 for the soft and hard bands, respectively. For the definition of the detection probabilities for each source and for the proper generation of the mock catalogs we performed a series of numerical Monte-Carlo simulations of the XMM-Newton observations. The most important points and results of our work are listed below.
To deal with the pointing overlap question, we considered two approaches: that of a 10′ off-axis limitation, and the Voronoi delimitation. No major differences were observed in the derived point-source correlation function between these two approaches. We consequently followed the statistically richer Voronoi delimitation approach, which produces a contiguous field.
The log N–log S distributions for the soft and hard bands were found to agree well with the results from the previously released XMM-LSS catalog (Gandhi et al. 2006). Using the whole exposure XMM-LSS data, we extended the log N − log S to lower fluxes, ie., 10-15 and 3 × 10-15 erg s-1 cm-2 for the soft and hard bands, respectively.
The amplitude of the correlation function w(θ) is significantly higher in the hard band than in the soft band at the lowest fluxes. When analyzing a homogeneous 10 ks extracted sample from the full exposure data, this difference becomes more prominent. At higher fluxes (fx ≳ 10-14 erg s-1 cm-2) the amplitude of the correlation function becomes higher in the soft band. These results provide a bias factor at a median redshift 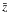 of ~ 2.5 for the soft band when inverted to 3D (and for ϵ = −1.2), and at
of ~ 2.5 for the soft band when inverted to 3D (and for ϵ = −1.2), and at 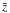 of ~3.3 for the hard band sources. These bias values correspond to a mass of the halos hosting the AGN sources of Mh ~ 1013 ± 0.3h-1 M⊙ for the soft band and Mh ~ 1013.7 ± 0.3h-1 M⊙ for the hard band.
of ~3.3 for the hard band sources. These bias values correspond to a mass of the halos hosting the AGN sources of Mh ~ 1013 ± 0.3h-1 M⊙ for the soft band and Mh ~ 1013.7 ± 0.3h-1 M⊙ for the hard band.
The correlation at degree-scale ( ≳ 3000′′) nicely extends that observed on an arcmin scale (100–1000′′), a result which is obtained thanks to the wide contiguous area covered by the survey.
The hard-spectrum sources show a stronger clustering than the soft-spectrum ones, especially in the soft band. This hints at an environmental dependence of the AGN type.
The amplitude of the spatial correlation function grows with flux limit, but mostly in the soft band. In the hard band there is at most a weak dependence, with a constant value of r0 ≃ 10h-1 Mpc, which is consistent with the data.
Acknowledgments
The simulations were performed at the CNRS “Centre de Calcul de l’IN2P3” located in Lyon, France. The authors would like to thank Pierrick Micout for his help regarding the use of the CC-IN2P3. A.E., O.M., E.G. and J.S. acknowledge support from the ESA PRODEX Programme “XMM-LSS”, from the “Belgian Federal Science Policy Office” and from the “Communauté française de Belgique – Actions de recherche concertées – Académie universitaire Wallonie-Europe”.
References
- Akylas, A., Georgantopoulos, I., & Plionis, M. 2000, MNRAS, 318, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Allevato, V., Finoguenov, A., Cappelluti, N., et al. 2011, ApJ, 736, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., & Plionis, M. 2009, MNRAS, 400, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., & Plionis, M. 2010, ApJ, 714, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., Plionis, M., Georgakakis, A., & Georgantopoulos, I. 2005, MNRAS, 356, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., Plionis, M., & Ragone-Figueroa, C., 2008, ApJ, 678, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, A. J., Cole, S., Frenk, C. S., Baugh, C. M., & Lacey, C. G. 2000, MNRAS, 311, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, W. N., & Hasinger, G. 2005, ARA&A, 43, 827 [Google Scholar]
- Cappelluti, N., Hasinger, G., Brusa, M., et al. 2007, ApJS, 172, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Cappelluti, N., Ajello, M., Burlon, D., et al. 2010, ApJ, 716, L209 [NASA ADS] [CrossRef] [Google Scholar]
- Carrera, F. J., Ebrero, J., Mateos, S., et al. 2007, A&A, 469, 27 [Google Scholar]
- Chiappetti, L., Tajer, M., Trinchieri, G., et al. 2005, A&A, 439, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coil, A. L., Georgakakis, A., Newman, J. A., et al. 2009, ApJ, 701, 1484 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., & Brusa, M. 2008, Astron. Nachr., 329, 122 [NASA ADS] [CrossRef] [Google Scholar]
- de Zotti, G., Persic, M., Franceschini, A., et al. 1990, ApJ, 351, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Ebrero, J., Mateos, S., Stewart, G. C., Carrera, F. J., & Watson, M. G. 2009, A&A, 500, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engels, D., Tesch, F., & Ledoux, C. 1999, Proceedings of the Conference, Highlights in X-ray Astronomy, ed. B. Aschenbach, & M. Freyberg, MPE-Report 272, 218 [Google Scholar]
- Gandhi, P., Crawford, C. S., Fabian, A. C., & Johnstone, R. M. 2004, MNRAS, 348, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Gandhi, P., Garcet, O., Disseau, L., et al. 2006, A&A, 457, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garcet, O., Gandhi, P., Gosset, E., et al. 2007, A&A, 474, 473 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilli, R., Daddi, E., Zamorani, G., et al. 2005, A&A, 430, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilli, R., Zamorani, G., Miyaji, T., et al. 2009, A&A, 494, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamilton, A. J. S. 1993, ApJ, 417, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hartwick, F. D. A., & Schade, D. 1990, ARA&A, 28, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., Miyaji, T., & Schmidt, M. 2005, A&A, 441, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hickox, R. C., Jones, C., Forman, W. R., et al. 2007, Cosmic Frontiers, ASP Conf. Ser., 379, 181 [NASA ADS] [Google Scholar]
- Hickox, R. C., Myers, A. D., Brodwin, M., et al. 2011, ApJ, 731, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N. 1984, ApJ. 284, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kerscher, M., Szapudi, I., & Szalay, A. S. 2000, ApJ, 535, L13 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Koulouridis, E., Plionis, M., Chavushyan, V., et al. 2006a, ApJ, 639, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koulouridis, E., Chavushyan, V., Plionis, M., Krongold, Y., & Dultzin-Hacyan, D. 2006b, ApJ, 651, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Koulouridis, E., Plionis, M., et al. 2011, ApJ, submitted [arXiv:1111.4084] [Google Scholar]
- Krumpe, M., Miyaji, T., & Coil, A. L. 2010, ApJ, 713, 558 [NASA ADS] [CrossRef] [Google Scholar]
- LaFranca, F., Fiore, F., Comastri, A., et al. 2005, ApJ, 635, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Landy, S. D., & Szalay, A. S. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Limber, D. N. 1953, ApJ, 117, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Manners, J. C., Johnson, O., Almaini, O., et al. 2003, MNRAS, 343, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Li, C., Kauffmann, G., & White, S. D. M. 2009, MNRAS, 393, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuda, T., & Shima, E. 1984, Progr. Theoret. Phys., 71, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Miyaji, T., Zamorani, G., Cappelluti, N., et al. 2007, ApJS, 172, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Miyaji, T., Krumpe, M., Coil, A. L., & Aceves, H. 2011, ApJ, 726, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Campana, S., Lazzati, D., & Tagliaferri, G. 2003, ApJ, 588, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Pacaud, F., Pierre, M., Refregier, A., et al. 2006, MNRAS, 372, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The large-scale structure of the universe (Princeton, N.J.: Princeton University Press), 435 [Google Scholar]
- Peebles, P. J. E. 1993, Principles of Physical Cosmology (Princeton New Jersey: Princeton University Press) [Google Scholar]
- Pierre, M., Valtchanov, I., Altieri, B., et al. 2004, J. Cosm. Astropart. Phys., 9, 11 [Google Scholar]
- Pierre, M., Chiappetti, L., Pacaud, F., et al. 2007, MNRAS, 382, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Pierre, M., Pacaud, F., Juin, J. B., et al. 2011, MNRAS, 414, 1732 [NASA ADS] [CrossRef] [Google Scholar]
- Plionis, M., Rovilos, M., Basilakos, S., Georgantopoulos, I., & Bauer, F. 2008, ApJ, 674, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Plionis, M., Terlevich, R., Basilakos, S., et al. 2010, Invisible Universe: Proceedings of the Conference, AIP Conf. Proc., 1241, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Puccetti, S., Fiore, F., D’Elia, V., et al. 2006, A&A, 457, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Read, A. M., & Ponman, T. J. 2003, A&A, 409, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvato, M., Hasinger, G., & Ilbert, O. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
- Sheth, R. K., Mo, H. J., & Tormen, G. 2001, MNRAS, 323, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Watson, M. G., Stewart, I. M., et al. 2008, ApJS, 179, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Mushotzky, R. F., Barger, A. J., et al. 2003, ApJ, 585, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y., Mushotzky, R. F., Barger, A. J., & Cowie, L. L. 2006, ApJ, 645, 68 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Soft and hard band correlation functions for the whole XMM-LSS field, as well as for the two possible overlap approaches.
Correlation function for the subsamples characterized by their hardness ratio above and below −0.2.
Spatial correlation length r0 (in h-1 Mpc), provided by Limber’s inversion of the ACF and using different AGN X-ray luminosity functions, for the homogeneous 10 ks sample and for the lowest flux-limit available.
Linear bias factor for the lowest flux-limit results of the homogeneous 10 ks XMM-LSS data (and for the same X-ray luminosity functions as in Table 6).
All Figures
 |
Fig. 1 Distribution of the X-ray point-like sources observed in the soft band within the whole XMM-LSS field with an off-axis distance less than 10′. The red circles represent the borders between the different pointings. Note that even when using the 10′ limitation, we may have some overlapping regions. We discarded these minor overlaps using the Voronoi tessellation method. |
| In the text | |
 |
Fig. 2 Distribution of the X-ray point-like sources observed in the soft band within the whole XMM-LSS field with the Voronoi tessellation method. Note that using the Voronoi tessellation we did not exceed the 13′ off-axis distance for any pointing. |
| In the text | |
 |
Fig. 3 Examples of simulated XMM-Newton pointings in the soft band. The large blue circle indicates the region in which the source detection is performed (13 arcmin maximal off-axis angle). Green boxes indicate the positions of sources detected with a likelihood ML > 15. Left: Texp = 10 ks, background ratio = 1; Middle: Texp = 10 ks, background ratio = 4; Right: Texp = 40 ks, background ratio = 1. |
| In the text | |
 |
Fig. 4 Examples of likelihood versus count-rate plots for three combinations of pointing exposures and background ratios from our soft band simulation set. Green symbols show detections with a real input counterpart while red points indicate spurious (false) detections. All sources within 5 arcmin from the pointing center are shown here. Left: 540 pointings with Texp = 10 ks, background ratio = 1; Middle: 540 pointings with Texp = 10 ks, background ratio = 4; Right: 540 pointings with Texp = 40 ks, background ratio = 1. The horizontal line corresponds to ML = 15, the threshold above which detected sources are included in the catalog. The separation between false and real detections is relatively independent of the pointing quality. |
| In the text | |
 |
Fig. 5 Efficiency of our source detection algorithm in the innermost annulus (0–5 arcmin) of the simulated soft band XMM observations, as a function of the input source count-rate (or equivalently, flux for a typical AGN spectrum and a galactic hydrogen column density fixed to 2.6 × 1020 cm-2). The exposure time differs from one curve to the other, but not the background rate. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 for various background rates in the soft band (defined by a multiplicative factor times the values quoted in the 2nd column of Table 1). Exposure time is held at 10 ks in all cases. |
| In the text | |
 |
Fig. 7 Same as Fig. 5 for the six off-axis bins in the soft band (see text). Exposure time is held at 10 ks in all cases, and the particle background ratio is set to 1. |
| In the text | |
 |
Fig. 8 Pipeline-estimated background values on MOS (left) and PN (right) detectors, in the soft band, as seen in the simulations. Curves from bottom to top stand for background ratios B equal to 0.1, 0.25, 0.5, 1, 2, 4 and 8. This plot shows how the local background estimate output of the detection algorithm can be related to the background ratio parameter introduced in the simulations. The error bars represent 1-σ standard variation computed from the source sample. The vertical lines correspond to bounds of our equal-area off-axis bins. Only the results for 10 ks are displayed and similar relations are extracted for 7, 20, 40 and 80 ks pointings. |
| In the text | |
 |
Fig. 9 Effective area curves for the whole XMM-LSS field in the soft (0.5–2 keV) and hard (2–10 keV) bands. |
| In the text | |
 |
Fig. 10 Comparison of the normalized effective area curves in the soft band for the full exposure XMM-LSS field, the 10 ks version (see Sect. 5.1), the XMM-LSS 4.2 sq. deg. (Gandhi et al. 2006), the XMM Medium Deep Survey (XMDS Chiappetti et al. 2005), the 2XMM (Ebrero et al. 2009) and the COSMOS (Miyaji et al. 2007; Cappelluti et al. 2007). |
| In the text | |
 |
Fig. 11 Example of the dependence between input and output count-rates for the hard band, T = 20 ks, b = 1. The red line corresponds to CRin = CRout. |
| In the text | |
 |
Fig. 12 Distributions of CRin for three detected CRout created on the basis of the simulated distribution in Fig. 11. |
| In the text | |
 |
Fig. 13 Log N − log S distributions in the soft band for the whole XMM-LSS sample and for the two different procedures of handling the pointing overlaps. The results of the XMM Medium Deep Survey (XMDS (Chiappetti et al. 2005), 2XMM (Ebrero et al. 2009), XMM-LSS 4.2 sq. deg. (Gandhi et al. 2006) and COSMOS (Miyaji et al. 2007; Cappelluti et al. 2007) are shown for comparison. The vertical bars denote 1σ uncertainties. |
| In the text | |
 |
Fig. 14 Log N − log S distributions in the hard band for the whole sample and for the two different procedures of handling the pointing overlaps. For comparison we present the log N − log S distributions for the same samples as in Fig. 13. |
| In the text | |
 |
Fig. 15 Soft band ACF for the whole sample: Voronoi delimitation (top panel); off-axis angle < 10′ (lower panel). The filled (black) points correspond to the Hamilton estimator while the open (red) squares to the Landy & Szalay estimator. The error bars represent 1σ standard deviation. The dashed line represents the best power-law fit, while the continuous line corresponds to the constant γ = 1.8 fit. The inset plot presents the 1, 2 and 3σ contours in the fitted (θ0,γ) parameter space. |
| In the text | |
 |
Fig. 16 Hard band ACF for the whole sample: Voronoi delimitation (upper panel); off-axis angle < 10′ (lower panel). |
| In the text | |
 |
Fig. 17 ACF for the 10 ks sample in the soft band (upper panel) and for the hard band (lower panel). |
| In the text | |
 |
Fig. 18 Best-fit correlation length θ0 for γ = 1.8 as a function of the flux limit of the homogeneous 10 ks sample in the soft (filled circles) and the hard bands (open circles). |
| In the text | |
 |
Fig. 19 Dependence between flux and ML in the soft band for the point like sources of 44 pointings from the present XMM-LSS survey (black open circles) and from Gandhi et al. (2006) (red filled circles). |
| In the text | |
 |
Fig. 20 Soft band ACF comparison between our XMM-LSS survey (filled points) and that of the 2XMM survey (crosses) of Ebrero et al. (2009). |
| In the text | |
 |
Fig. 21 Log N − log S distributions in the soft and the hard bands for sources with different hardness ratios. |
| In the text | |
 |
Fig. 22 ACF for the whole XMM-LSS sample in the soft band for sources with HR > −0.2 (filled circles, hard-spectrum AGN), and for sources with HR < −0.2 (open circles; soft-spectrum AGN). Note that for clarity reasons we do not plot the w(θ) uncertainties of the later sources. The solid line represents the γ = 1.8 fit to the HR > −0.2 w(θ), while the dashed line corresponds to the HR < −0.2 w(θ) fit. |
| In the text | |
 |
Fig. 23 As in Fig. 22 but for the hard band. |
| In the text | |
 |
Fig. 24 Spatial correlation length r0 for γ = 1.8 and ϵ = −1.2 considering the homogeneous 10 ks based observations as a function of the flux limit of the sample in the soft band (filled and empty circles correspond to the Ebrero and Hasinger Φx(L), respectively) and in the hard band (filled square, open squares and open hexagons correspond to the Ebrero, Ueda and La Franca Φx(L), respectively). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


