| Issue |
A&A
Volume 537, January 2012
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201116886 | |
| Published online | 17 January 2012 | |
Deconstructing blazars: A different scheme for jet kinematics in flat-spectrum AGN
1 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
2 Reimar-Lüst Fellow of the Max Planck Society
e-mail: mkarouzos@astro.snu.ac.kr
3 I. Physikalisches Institut, Universität zu Köln, Zülpicher Str. 77, 50937 Köln, Germany
Received: 14 March 2011
Accepted: 21 October 2011
Context. Recent VLBI studies of the morphology and kinematics of individual BL Lac objects (S5 1803+784, PKS 0735+178, etc.) have revealed a new paradigm for the pc-scale jet kinematics of these sources. Unlike the apparent superluminal outward motions usually observed in blazars, most, if not all, jet components in these sources appear to be stationary with respect to the core, while exhibiting strong changes in their position angles. As a result, the jet ridge lines of these sources evolve substantially, at times forming a wide channel-flow.
Aims. We investigate the Caltech-Jodrell Bank flat-spectrum (CJF) sample of radio-loud active galaxies to study this new kinematic scenario for flat-spectrum AGN. Comparing BL Lac objects and quasars in the CJF, we look for differences in the kinematics and morphologies of their jet ridge lines. The large number of sources in the CJF sample, together with the excellent kinematical data available, allow us to perform a robust statistical analysis in this context.
Methods. We develop a number of tools to extract information about the apparent linear and angular evolution of the CJF jet ridge lines, as well as their morphology. We study both the radial and non-radial apparent motions in the CJF jets. A statistical analysis of the extracted information allows us to test this new kinematic scenario and assess the importances of the radial and non-radial motions in flat-spectrum AGN jets in general and especially in BL Lacs compared to quasars. We also use these tools to check the kinematics for (multi-wavelength) variable AGN.
Results. We find that approximately half of the sample display appreciable apparent jet widths (>10 degrees), with BL Lac jet ridge lines showing significantly larger apparent widths than those of both quasars and radio galaxies. In addition, BL Lac jet ridge lines are found to change their apparent width more strongly. Finally, BL Lac jet ridge lines show the least apparent linear evolution, which translates into the smallest apparent expansion speeds for their components. We find compelling evidence supporting a substantially different kinematic scenario for flat-spectrum radio-AGN jets and in particular for BL Lac objects. In addition, we find that variability is closely related to the properties of a source’s jet ridge line. Variable quasars are found to have “BL Lac like” behavior, relative to their non-variable counterparts.
Key words: galaxies: statistics / galaxies: active / galaxies: nuclei / galaxies: jets / BL Lacertae objects: general
© ESO, 2012
1. Introduction
Although observed in the minority of active galaxies (~5–15%; Kellermann et al. 1989; Padovani 1993; Jiang et al. 2007), extragalactic jets are some of the most pronounced morphological features in AGN research. Their presumably direct connection to the active core and the supermassive black hole (SMBH) residing there, makes them invaluable tools in the effort to characterize the properties and the underlying physics of activity in galaxies. VLBI observations enable the direct imaging of AGN jets and thus the study of their properties on parsec scales. One of the most prominent discoveries, related to jet kinematics, was that of the apparent superluminal motion of jet components (e.g., Whitney et al. 1971; Pearson & Readhead 1981), a combination of relativistic expansion speeds (close to the speed of light) and the projected geometry onto the plane of the sky (e.g., Rees 1966).
Jet kinematics, as studied through the investigation of distinct components, is usually explained in terms of the shock-in-jet model (e.g., Marscher & Gear 1985), where the observed jet knots are manifestations of shocks propagating down the jet at relativistic speeds. Beaming and projection effects regulate the observed properties of the jets. There have been continuous efforts to distinguish whether the different types of active galaxies (e.g., quasars, BL Lacs, Fanarrof-Riley, etc.) are just a result of orientation effects, or if additionally these objects have intrinsically different properties. The current paradigm is that indeed different jet properties can be attributed to geometrical effects combined with factors such as the black hole mass or the accretion rate. For example, Ghisellini et al. (1993) for a sample of 39 superluminal sources find no appreciable difference between the distribution of Doppler factors between BL Lacs and flat-spectrum radio-quasars (FSRQs), with RGs having smaller values. Some indications to the contrary also exist (e.g., Gabuzda 1995; Gabuzda et al. 2000). Analysis of statistically important samples (large number of sources and/or stringent selection criteria) of active galaxies have been of fundamental importance to this end (e.g., Ghisellini 1993; Vermeulen & Cohen 1994; Vermeulen 1995; Taylor et al. 1996; Hough et al. 2002; Lister & Homan 2005; Britzen et al. 2007b).
Although it is crucial to pursue a statistical approach to the open problem of AGN jet kinematics, the study of individual sources is indispensable. It has helped to elucidate particular mechanisms or effects that might be smoothed by the poor temporal or spatial resolution usually available in large statistical samples. Such a case of a detailed study of an individual object is that of S5 1803+784.
1.1. S5 1803+784: A case study
The active galaxy S5 1803+784 is at a moderate redshift of z = 0.68 (Hewitt & Burbidge 1989). It has been classified as a BL Lac object. Being a member of the complete S5 sample (Witzel 1987), it has been extensively studied in the radio, at different wavelengths and with different instruments (see Britzen et al. 2010a for a detailed review of the source’s radio observation history). Typical of its class of objects, 1803+784 has been found to be variable in the radio and the optical on both long and short timescales (e.g., Wagner & Witzel 1995; Heidt & Wagner 1996; Nesci et al. 2002; Fan et al. 2007).
Britzen et al. (2010a), by (re-)analyzing more than 90 epochs of global VLBI and VLBA data, revealed a new kinematic scheme for 1803+784. All components in the inner part of the jet (out to 12 mas) appear stationary with respect to the core. This behavior is seen at all frequencies studied by the authors (1.6–15 GHz). In contrast to this, the components show strong changes in their position angles, implying a prevailing movement perpendicular to the jet axis.
Britzen et al. (2010a) also studied the jet ridge line morphology and evolution of S5 1803+784. A jet ridge line at a given epoch is defined as the line that linearly connects all component positions at that epoch. The authors find that the jet ridge line changes in an almost periodic manner, starting by resembling a straight line, evolving into a sinusoid-like pattern, and finally returning to its original linear pattern, although slightly displaced from its original position. A period of ~8.5 years is calculated for the evolution of the jet ridge line.
Finally, the authors find that the jet changes its apparent width (across a range of between a few and a few tens of degrees) in an almost periodic way with a timescale similar to the one found from the evolution of the jet ridge line. All of the above properties support a new kinematic scheme for 1803+784, whose components have oscillatory-like trajectories, where their movement is predominantly perpendicular to the jet axis rather than along it. Moreover, the jet appears at times to form a wide channel of flow, while changing its width considerably across time.
1.2. Motivation
S5 1803+784 is one of several BL objects that have the behavior described above. 0716+714 has been shown to behave in a similar way (Britzen et al. 2009), with most of its components being stationary with respect to the core, while their position angles change considerably. PKS 0735+178 is another example of a source with similar, but rather more complicated, kinematic properties (Gómez et al. 2001; Agudo et al. 2006; Britzen et al. 2010b). Under the unification scheme of active galaxies (e.g., Antonucci 1993; Urry & Padovani 1995), both BL Lac objects and FSRQs are believed to be active galaxies for which the viewing angle to their jets is very small, leading to strong relativistic effects. Given the similar viewing angle distributions, in the last several years the general classification of blazar has often been used to describe members of either class, also in terms of their jet properties. However, this phenomenological unification of FSRQs and BL Lacs has been questioned by investigations of sources such as S5 1803+784, PKS 0735+178, and 0716+714. Is the peculiar kinematic behavior seen in these objects revealed owing to the unprecedented richness of the datasets available, and possibly relevant to all flat-spectrum radio-AGN, or are BL Lacs characterized by a genuinely different set of kinematic properties?
This paper focuses on the relevance of this new kinematic scheme to flat-spectrum radio-AGN, while investigating the apparent distinction between BL Lac and FSRQ jet kinematics. As valuable as single source studies are to an in-depth understanding of particular phenomena, there are a number of biases or unaccounted-for factors that alter and ultimately hinder a universal application of their results. In this context, we use the CJF sample to statistically investigate and assess the similarity, or divergence, of the kinematic and morphological properties between the two distinct sub-samples of FSRQs and BL Lac objects in the CJF. We wish to test whether the jet components of BL Lac objects indeed have slower apparent speeds with respect to their cores, than FSRQs. Furthermore, we are interested in the phenomenon exhibited in S5 1803+784 of, at times, very wide jet, as well as a strong evolution of that width. For this investigation, we use tools that extract information from the jet ridge line of the sources, instead of focusing on individual components. This allows us to perform an investigation that is mostly independent of component modeling and cross-identification.
The paper is organized as follows: in Sect. 1.1, we introduce the new kinematic scheme for BL Lac objects, as shown for the case of the source 1803+784, and discuss the motivation of this work, in Sect. 2 we describe the CJF sample, in Sect. 3 we describe the data used, in Sect. 4 we present the analysis of our data and the results, and in Sect. 5 we discuss our results and present our conclusions. Throughout the paper, we assume the cosmological parameters H0 = 71 km s-1 Mpc -1, ΩM = 0.27, and ΩΛ = 0.73 (from the first-year WMAP observations; Spergel et al. 2003).
2. The CJF sample
The CJF sample (Taylor et al. 1996) consists of 293 radio-loud active galaxies selected (see Table 1) from three different samples (for details, see Britzen et al. 2007b). The sources span a large redshift range (see Fig. 1), the farthest object being at a redshift z = 3.889 (1745+624; Hook et al. 1995) and the closest at z = 0.0108 (1146+596; de Vaucouleurs 1991). The average redshift of the sample is zavg = 1.254, 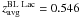 ,
, 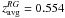 , and
, and 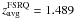 for BL Lacs, radio galaxies, and FSRQs, respectively. All the objects have been observed with the VLBA and/or the global VLBI network. Each source has at least three epochs of observations (with a maximum of five epochs) and has been imaged and studied kinematically (Britzen et al. 1999; Britzen et al. 2007b; Britzen et al. 2008). The X-ray properties have been studied and correlated with their VLBI properties (Britzen et al. 2007a). The evolution of active galaxies, in the context of the merger-driven evolution scheme (e.g., Hopkins et al. 2006), was also investigated with the help of the CJF, identifying candidate CJF sources in different evolutionary stages, including new binary black hole candidates (Karouzos et al. 2010).
for BL Lacs, radio galaxies, and FSRQs, respectively. All the objects have been observed with the VLBA and/or the global VLBI network. Each source has at least three epochs of observations (with a maximum of five epochs) and has been imaged and studied kinematically (Britzen et al. 1999; Britzen et al. 2007b; Britzen et al. 2008). The X-ray properties have been studied and correlated with their VLBI properties (Britzen et al. 2007a). The evolution of active galaxies, in the context of the merger-driven evolution scheme (e.g., Hopkins et al. 2006), was also investigated with the help of the CJF, identifying candidate CJF sources in different evolutionary stages, including new binary black hole candidates (Karouzos et al. 2010).
 |
Fig. 1 Redshift distribution of radio galaxies (grey blocks), BL Lacs (dashed line), and FSRQs (solid line) in the CJF sample. |
CJF sample and its properties.
2.1. Radio emission
The CJF is a flux-limited radio-selected sample of flat-spectrum radio-loud AGN. The sample was originally created to study, among other things, the kinematics of pc-scale jets and the phenomenon of apparent superluminal motion (see Taylor et al. 1996 for more details).
The CJF sample (Table 1) has been most extensively studied in the radio regime (e.g., Taylor et al. 1996; Pearson et al. 1998; Britzen et al. 1999; Vermeulen et al. 2003; Pollack et al. 2003; Lowe et al. 2007; Britzen et al. 2007b; Britzen et al. 2008). Britzen et al. (2008) developed a localized method for calculating the bending of the jet associated with individual components. The maximum of the distribution of local angles is at zero degrees, although a substantial fraction of the sample show some bending (0–40 degrees). A few sources exhibit sharp bends of the order of > 50 degrees (see Fig. 13 in Britzen et al. 2008).
Although the CJF sample consists mostly of core-dominated AGN, presumably highly beamed sources, the kinematical study of the sample identifies a large number of sources with stationary, subluminal, or, at best, mildly superluminal outward velocities (e.g., see Fig. 15 in Britzen et al. 2008). Combined with a number of sources with inwardly moving components (e.g., 0600+422, 1751+441, 1543+517, Britzen et al. 2007b), these sources do not fit into the regular paradigm of outward, superluminally moving components in blazar jets. One explanation of these peculiar kinematic behaviors is that of a precessing, or helical jet (e.g., Conway & Murphy 1993) possibly as a result of a SMBH binary system. Other interpretations include trailing shocks produced in the wake of a single perturbation propagating down the jet (e.g., Agudo et al. 2001; but see also Mimica et al. 2009), or standing re-collimation shocks (e.g., Gomez et al. 1995).
 |
Fig. 2 Radio maps at 5 GHz of 1928+738 (left) and 0700+470 (right), with jet ridge lines superimposed. Two examples of a sinusoid-like jet morphology (left) and a single-bent one (right). The VLBI maps are taken from Britzen et al. (2007b). |
Karouzos et al. (2010) compiled a list of all the CJF sources found to display a long timescale variability in the radio (as well as in other wavelength regimes). This list comprises in total of 40 CJF sources, 27 of which have been argued to possibly have periodically variable fluxes. The authors do not take into account intra-day variability.
3. Data
The work presented here is heavily based on the kinematic analysis of the CJF sample (Britzen et al. 2007b; Britzen et al. 2008). An extensive observing campaign of all 293 CJF sources was undertaken using both the VLBA and the global VLBI array at 5 GHz (see Britzen et al. 2007b for details). We note that five CJF sources were initially excluded from any further analysis owing to problematic observations (0256+424, 0344+405, 0424+670, 0945+664, 1545+497) hence are also omitted here. In total, 288 sources are considered and analyzed in the following sections. Among these sources, according to the optical classification from Britzen et al. (2007b), 196 are classified as quasars, 49 as radio galaxies, 33 as BL Lac objects , and 10 are not classified.
Owing to the scope of the CJF program, the identification and analysis of pc-scale jet component kinematics has focused on the part of the jet that is beamed towards us. For a number of sources, several components belonging to the counter-jet have been identified. However, for these sources the cross-identification of the counter-jet components over different epochs has not yet been carried out. For this reason, and given the nature of the analysis that we undertook (see below), we excluded all counter-jet components in the investigation that we now present. In a total number of 2468 components identified, 82 (3.32%) counter-jet components were identified and excluded from our analysis. Britzen et al. (2007b) reported that on average radio galaxies have 3.6 components identified per jet, 2.7 components are identified per quasar jet, and 2.9 components per BL Lac jet. This reflects the relative difference of projected jet length for the different types of object classes. This shall be discussed more thoroughly in Sect. 5.
In the following, the tools that we use for the analysis of the CJF jet ridge lines, in the context described in Sect. 1.1, are described. In short, we used the following measures:
-
monotonicity index, M.I;
-
apparent jet width, dP;
-
apparent jet width evolution, ΔP;
-
apparent jet linear evolution, Δℓ.
We note that all the above measures, as their names imply, refer strictly to values projected onto the plane of the sky. Although it is possible to constrain, or in some cases have a specific estimate of the viewing angle of each source and therefore attempt to calculate intrinsic jet properties, this is outside the scope of this paper. For the following sections, we adopt the basic assumption described by the AGN unification scheme (e.g., Antonucci 1993; Urry & Padovani 1995) that BL Lacs and FSRQs are seen at the smallest viewing angles, while radio galaxies have jet axes that are further away from our line of sight. As we are mainly interested in the comparison between FSRQs and BL Lacs, the deprojection of the jet properties investigated here is not critical. For the sake of brevity, we shall drop the characterization of “apparent” when referring to these values in the text, although this is implied throughout unless otherwise stated.
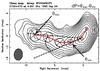 |
Fig. 3 Radio map of 0700+470 at 5 GHz, exhibiting the calculation of the jet ridge line width. The two arrows denote the components with the maximum and minimum position angles, while the area in-between is defined as the opening, or apparent width, of the jet ridge line. The VLBI core is found at (0,0) coordinates. The VLBI map is taken from Britzen et al. (2007b). |
3.1. Monotonicity Index, M.I.
It is known that a large number of active galaxies exhibit bent or otherwise non-linear jet morphologies on various scales. Individual sources such as S5 1803+784 and PKS 0735+178 (see references above), as well as others (e.g. 3C 345; Lobanov & Zensus 1999; B0605-085; Kudryavtseva et al. 2011), have been extensively studied to understand the origin of these bends. Britzen et al. (2008) calculate the “bends” between successive components of the pc-scale jet for all CJF sources, finding large local variations in the position angles of the sources. In this context, we are interested in quantifying the bending of the whole jet ridge line. Moreover, we wish to differentiate between a “monotonically bent” jet, i.e., a jet that is bent in only one direction (see Fig. 2, right), as opposed to a more sinusoid-like morphology (similar to what is seen for some epochs of S5 1803+784, see Fig. 2, left). This analysis is performed by means of the monotonicity index, M.I..
We quantify a sinusoid-like morphology of a jet by identifying the local extrema in a given jet ridge line, in the core separation – position angle plane. For an epoch i, a component m exhibits a local extremum under the definition
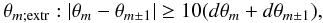 where θm and dθm denote the position angle of components and its uncertainty, and θm is calculated as
where θm and dθm denote the position angle of components and its uncertainty, and θm is calculated as
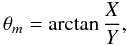 where X and Y are cartesian coordinates on the plane of the sky. After calculating the number of extrema for a given jet ridge line at an epoch i, we define the M.I. as
where X and Y are cartesian coordinates on the plane of the sky. After calculating the number of extrema for a given jet ridge line at an epoch i, we define the M.I. as
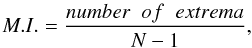 where N is the total number of components at that given epoch. This is a crude calculation, but can provide us with information about how the bending of the jet behaves along the jet. For M.I. values close to one, the jet more closely resembles a sinusoid. An M.I. value close to zero reveals a monotonic, single-bend, jet morphology. We normalize for the number of components N to account for longer, or shorter, jets and to enable a comparison between different sources. As an example, for the sources shown in Fig. 2, 1928+738 is found to have an M.I. value of 0.4, compared to 0700+470, which has an M.I. value of 0.
where N is the total number of components at that given epoch. This is a crude calculation, but can provide us with information about how the bending of the jet behaves along the jet. For M.I. values close to one, the jet more closely resembles a sinusoid. An M.I. value close to zero reveals a monotonic, single-bend, jet morphology. We normalize for the number of components N to account for longer, or shorter, jets and to enable a comparison between different sources. As an example, for the sources shown in Fig. 2, 1928+738 is found to have an M.I. value of 0.4, compared to 0700+470, which has an M.I. value of 0.
As in the case of most of the tools described in this section, the value of M.I. depends strongly on the resolution of the observations. Given that the resolution is not the same across all epochs and sources, an uncertainty is introduced when comparing the M.I. values of two different sources. A final remark pertains to the definition of an extremum. We use a 10σ1 value as the lower limit to flagging an extremum. A different level of significance (e.g., 5σ) would result in different values of M.I. The choice of the 10σ significance is a conservative approach to the identification of extrema in the jet ridge line. In the following, the M.I. is used as more of a qualitative tool rather than a quantitative measure of the actual jet morphology.
3.2. Apparent jet width, dP
For an epoch i and a jet consisting of N components characterized by their core separation and position angle (ri,θi), we identify the components with the maximum and the minimum position angles. The apparent width of the jet dP, measured in degrees, is then calculated to be (see Fig. 3)
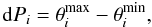 while the error is calculated by the propagation of errors formula. There is a number of factors that should be considered at this point. The most obvious drawback of the above definition is the non-localized nature of this measure. Using two different components, at different core separations, gives us only an approximate notion of the width of the flow. Higher resolution investigations might resolve the structure of the jet perpendicular to the jet axis and provide us with a more real estimate of the local width of the jet. Alternatively, one can calculate a localized value of the jet width by using the FWHM of the fitted Gaussian components (e.g., Pushkarev et al. 2009). In this case however, the width depends strongly on the beam size and therefore on the resolution. By using the definition above, we seek instead to quantify the opening of the jet flow and identify the effect of a channel-like jet, as seen in the case of S5 1803+784. In the context of the localization problem, we implemented in our calculations a constraint on the maximum allowed distance between the two components identified with the minimum and maximum position angles. The value of this limit depends on the jet length and is discussed in Sect. 4.
while the error is calculated by the propagation of errors formula. There is a number of factors that should be considered at this point. The most obvious drawback of the above definition is the non-localized nature of this measure. Using two different components, at different core separations, gives us only an approximate notion of the width of the flow. Higher resolution investigations might resolve the structure of the jet perpendicular to the jet axis and provide us with a more real estimate of the local width of the jet. Alternatively, one can calculate a localized value of the jet width by using the FWHM of the fitted Gaussian components (e.g., Pushkarev et al. 2009). In this case however, the width depends strongly on the beam size and therefore on the resolution. By using the definition above, we seek instead to quantify the opening of the jet flow and identify the effect of a channel-like jet, as seen in the case of S5 1803+784. In the context of the localization problem, we implemented in our calculations a constraint on the maximum allowed distance between the two components identified with the minimum and maximum position angles. The value of this limit depends on the jet length and is discussed in Sect. 4.
In the case of a narrow but highly bent jet, it is clear that dP would then measure the amplitude of the bending rather than the width of the flow itself. In the context of this study, this effect does not present a problem as we are, to first order, interested in the final result, i.e., an apparently wide jet ridge line opening, rather than whether this effect is due to a genuinely wide jet flow or a high-amplitude bending.
3.3. Apparent jet width evolution, ΔP
The jet width evolution ΔP, measured in degrees per unit time, is measured between two successive epochs i and (i–1). It is calculated as
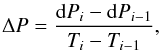 where Ti denotes the time at epoch i, measured in years. We can also define the maximum jet width evolution as
where Ti denotes the time at epoch i, measured in years. We can also define the maximum jet width evolution as
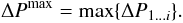 This value is characteristic of each source and reflects the maximum potential width change of the jet flow for that source. We note that the jet width evolution does not reflect an angular speed (as implied by the units of degrees per unit time). Instead the per unit time reflects a normalization for time that ensures a comparison between sources that have been observed during different time spans. The currently available data are too sparse to allow us to calculate a real angular speed for how the jet width (and orientation) changes with time.
This value is characteristic of each source and reflects the maximum potential width change of the jet flow for that source. We note that the jet width evolution does not reflect an angular speed (as implied by the units of degrees per unit time). Instead the per unit time reflects a normalization for time that ensures a comparison between sources that have been observed during different time spans. The currently available data are too sparse to allow us to calculate a real angular speed for how the jet width (and orientation) changes with time.
For both the width dP and the width evolution ΔP, the sensitivity and dynamic range of our observations play a regulating role. Given that we need at least two components to define the width, a dimming of one of these components across epochs can result to a false or altered value for both the calculated width and width evolution. A more detailed discussion of this can be found in Sect. 5.
3.4. Apparent jet linear evolution, Δℓ
We calculate the linear evolution across all available epochs and for all components, ultimately acquiring a value reflecting the total linear displacement of the whole jet ridge line. We use plane-of-the-sky coordinates (Xi,Yi) to calculate the linear displacement of component m between epochs i and (i+1)
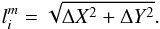 To calculate the total displacement of the whole jet ridge line, we then need to sum up over all components and all available observing epochs
To calculate the total displacement of the whole jet ridge line, we then need to sum up over all components and all available observing epochs
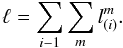 We need to account for both the different time span of observations, as well as the different number of components. Therefore, we define the jet linear evolution Δℓ, measured in parsecs per unit time and per component, as
We need to account for both the different time span of observations, as well as the different number of components. Therefore, we define the jet linear evolution Δℓ, measured in parsecs per unit time and per component, as
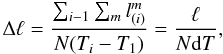 where N here is the total number of components used across all the available epochs. We need to underline a fundamental difference between the way in which the jet linear evolution, Δℓ, is calculated, compared to the measures described previously. For the calculation of the displacement of an individual component ℓ between two consecutive epochs, and consequently of Δℓ, the cross-identification of components across epochs is necessary. Therefore, for Δℓ, unlike the previously discussed jet ridge line characteristic values, the actual identification of components is important.
where N here is the total number of components used across all the available epochs. We need to underline a fundamental difference between the way in which the jet linear evolution, Δℓ, is calculated, compared to the measures described previously. For the calculation of the displacement of an individual component ℓ between two consecutive epochs, and consequently of Δℓ, the cross-identification of components across epochs is necessary. Therefore, for Δℓ, unlike the previously discussed jet ridge line characteristic values, the actual identification of components is important.
The reason for normalizing this value over the time span of observations is the same as for the jet width evolution. In this case however we also need to account for the number of components for each individual jet. We therefore divide the total displacement of the whole jet ridge line by the actual number of components used for the calculation (hence the number of components cross-identified across each pair of observation epochs).
The parameter Δℓ essentially reflects the apparent speed distribution of all cross-identified components of the jet and therefore represents a value characteristic of the whole jet, rather than for any individual component. By summing up all components and epochs, we therefore exchanged temporal and positional resolution for a universal treatment of the entire jet. In this way, we can test whether the kinematics of BL Lac objects differ fundamentally from those of FSRQs while averaging out the localized properties of individual components. The parameter Δℓ can be considered as a mean jet component speed, with the difference that it is acquired through averaging not only over all components, but additionally over all available epochs. Although it certainly reflects a measure of the outward motion in BL Lac jets, the calculation of Δℓ is done in such a way, that the potential curvature of the components’ trajectories is taken into account. This separates Δℓ from a simple linear regression fit to the core-separation versus time diagrams usually employed to calculate outward velocities, making it sensitive to non-radial motions, that are otherwise missed.
Lastly, given the large span of redshifts that the CJF sources cover, we must account for the different linear scales probed for sources at different distances from us. By comparing sources at different redshifts, one implicitly studies a different part of their jet. To counter this effect, we explicitly define a maximum apparent core separation limit, above which components are not included in our investigation. There are however additional arguments that indicate the necessity of such a limit, both technical as well as physical. It is known that AGN jets appear to be most curved closer to the core, with bending effects becoming dumped at larger distances (e.g., Krichbaum et al. 1994; Britzen et al. 2000). We also note that at larger separations from the reference center of a map (the core), the uncertainties involved in the identification and fitting of jet components increase. By constraining our analysis to the inner structure of the jets, we partly compensate for this effect. In this way, we ensure that we probe the same linear scales for all CJF sources, albeit with different resolutions. The latter effect can be counteracted by using redshift bins throughout. Additionally, by using redshift bins, we can probe the possible evolution of the studied properties with redshift, if any. Given that the separation limit used is an apparent one, a level of uncertainty that depends on the scatter in the viewing angle distribution within a certain object class, is expected.
4. Analysis and results
The apparent jet length, which is expressed by the maximum distance of the outermost jet component identified in each source across all available epochs, and the jet morphology, which is expressed by the M.I., are used as a basis for the further analysis and are hence discussed first.
4.1. Apparent jet length and morphology
We found that BL Lacs have shorter jets on parsec scales in median values, than both quasars and radio galaxies (17.3 ± 2.7 pc compared to 27.1 ± 2.4 pc and 43 ± 7 pc; ~3σ level), with their average values however not being statistically significantly different (34 ± 5 pc, compared to 31 ± 4 pc and 50 ± 6 pc, respectively; < 3σ)2. Having calculated the average and median apparent jet lengths for the CJF objects, we are able to define a maximum apparent core separation limit (for the reasons discussed in Sect. 3). As we are interested in the behavior of BL Lacs, we use them as the basis of our decision. For 1803+784, peculiar kinematics of the components is observed for the inner-most part of its jet (up to 12 mas), with most robust effects out to 6 mas. For this source’s redshift (z = 0.68), this translates roughly to (82 pc) 41 pc. Similarly to 1803+784, 0735+178 and 0716+714 also show the most prominent evolution of their jet ridge line out to ~6 mas (39.6 pc and 33 pc, for their respective redshifts). Given that most of the BL Lacs in our sample are at z < 1, the length scale implied by the three sources mentioned above (the only objects whose jet ridge line has been investigated in detail) ensures that the inner-jet of sources at z < 1 is covered. We adopt therefore an apparent core separation limit of 40 parsecs. All components at separations larger than 40 parsecs with respect to the core are not included in the following analysis. For a limit of 40 pc we probe the whole jet for 60% of the CJF sources (72% for BL Lacs, 60% for radio galaxies, and 56% for FSRQs), while for approximately 17% of the CJF sources more than half of the jet is excluded from further analysis.
Adopting a core distance limit somewhat reduces the available number of components and therefore possibly increases the scatter in the following statistical analysis. Moreover, this limit implicitly gives a higher weight to more strongly beamed sources. This bias however applies equally to both BL Lacs and FSRQs, and should therefore not influence the comparison between the two classes. The higher number of components “missed” for the FSRQs because of this limit is mainly due to their redshift distribution and therefore using redshift bins should minimize the bias to our results.
We investigate how, if at all, a jet resembles a sinusoid (as in the case of S5 1803+784). To do this, we calculate the M.I. from the jet ridge lines of our sources. The M.I. is calculated for the whole jet (we do not apply the core separation limit of 40 pc), as we are interested in the morphology of the entire jet ridge line, rather than a localized property. Additionally, a large number of components are needed to help us achieve a robust interpretation of the M.I., we therefore take into account only epochs with at least three identified components. Finally, we define the maximum M.I. value for each source across the available epochs. The fluctuations in the M.I. of a source between epochs are small.
Under the above constraints, we found that there are in total 46 sources with M.I. 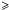 0.5. This translates in 37% of the total number of sources used here. The BL Lacs have jets more often with sinusoid-like morphologies, than both FSRQs and RGs. More than half of the FSRQs (~51%) have an M.I. value of 0, while two thirds (~66%) have an M.I. value lower than 0.5. For RGs, the respective percentages are ~41% and ~66%. In contrast to this, only one third of the BL Lacs (~33%) have M.I. = 0 and fewer than half (~44%) of them have M.I. < 0.5. Figure 4 shows the histogram of the M.I. for the different types of objects. The BL Lacs display their maximum in the [0.4, 0.6) bin. In contrast, both FSRQs and RGs have their maxima in the [0, 0.2) bin. In Table 2, we provide the statistical properties of the different types of objects. It can be seen that the average M.I. values for BL Lacs and FSRQs agree to within the 1σ errors. When considering the median values for the three classes of objects, the difference becomes more apparent, with BL Lacs and FSRQs differing at >3σ level. We note that a robust quantitative treatment of the M.I. is problematic, given the severe restrictions imposed by the small number of components per jet, as well as the limited temporal resolution of the observations used here.
0.5. This translates in 37% of the total number of sources used here. The BL Lacs have jets more often with sinusoid-like morphologies, than both FSRQs and RGs. More than half of the FSRQs (~51%) have an M.I. value of 0, while two thirds (~66%) have an M.I. value lower than 0.5. For RGs, the respective percentages are ~41% and ~66%. In contrast to this, only one third of the BL Lacs (~33%) have M.I. = 0 and fewer than half (~44%) of them have M.I. < 0.5. Figure 4 shows the histogram of the M.I. for the different types of objects. The BL Lacs display their maximum in the [0.4, 0.6) bin. In contrast, both FSRQs and RGs have their maxima in the [0, 0.2) bin. In Table 2, we provide the statistical properties of the different types of objects. It can be seen that the average M.I. values for BL Lacs and FSRQs agree to within the 1σ errors. When considering the median values for the three classes of objects, the difference becomes more apparent, with BL Lacs and FSRQs differing at >3σ level. We note that a robust quantitative treatment of the M.I. is problematic, given the severe restrictions imposed by the small number of components per jet, as well as the limited temporal resolution of the observations used here.
 |
Fig. 4 Monotonicity index (M.I.) distribution for BL Lacs (dashed line), FSRQs (solid line), and RGs (grey blocks). The histogram has been normalized to area unity. |
Statistical properties of the monotonicity index (M.I.) distribution for FSRQs, BL Lacs, and RGs.
In this somewhat qualitative context, BL Lacs appear to more often show sinusoid-like curved jets, as seen for S5 1803+784 and 0716+714.
4.2. Apparent jet width, P, statistics
In Sect. 3, we briefly discussed the concept of localized width and how this relates to what we investigate here. To help us understand this relation more clearly, we study how the distribution of the widths of the CJF jet ridge lines relates to the maximum distance between the two components used to calculate this width. For one epoch of the source S5 1803+784 and one epoch of the source 2200+420, a width of ~180 degrees is found. This is probably due to a problem in the original component fitting and we therefore exclude these two epochs in this analysis.
We calculate the non-zero jet widths for a total of 557 epochs (multiple epochs per source). Of these, 277 are larger than 10 degrees, while 125 are larger than 20 degrees. This translates in 22.4% of the sample possessing jets with widths exceeding 20 degrees.
We calculated the average jet ridge line width of our sources. Without imposing any constraints on the maximum distance between the θmax and θmin components used, we found that BL Lacs have significantly wider jet ridge lines (average value of 19.3 ± 1.8°), than FSRQs (12.0 ± 0.4°; 4σ difference). The RGs do not appear to have significant differences in their mean width from BL Lacs. A Student’s t-test gives a significance of > 99.99% that BL Lacs and FSRQs have different mean values. After imposing a constraint of 20 pc on the maximum distance between the θmax and θmin components, the BL Lacs still have statistically wider jet ridge lines. Small-number statistics does not allow us to draw a robust conclusion for more localized widths (at ~5 pc linear scales) of our CJF jet ridge lines.
We also investigated sources in the redshift bin [0, 1]. Although the redshifts of the CJF sources extend to almost 4, for the 32 BL Lacs included among the CJF, only 23 have redshift information. Of these, 20 are below redshift 1. Therefore in the following, we focus our investigation on sources up to redshift 1. In Table 3, we show the characteristic statistical parameters for the CJF jet ridge line widths for all sources with available redshifts, as well as sources in the redshift bin [0, 1]. Given the above analysis of the distance constraints, in Table 3 we also provide values for the case where a 20 pc constraint on the maximum distance between the θmax and θmin components is assumed.
Characteristic statistical values concerning the width of the jet ridge line of sources with measured redshifts.
The jet-ridge-line width appears to be independent of redshift. To test this further, we use the sub-sample of CJF FSRQs to calculate average and median width values for different redshift bins (Fig. 5). Out to z = 2.5, the jet ridge line width remains fairly stable, with the median values showing larger changes than the average ones. The number of sources contained in the last two bins is drastically lower than the low-redshift bins (as reflected by the much larger error bars) hence it is difficult to conclude whether the strong increase in both average and median values is either a true or a spurious effect. We note that this sharp increase coincides with the epoch of maximum nuclear and star-formation activity in the Universe (at z ~ 2−3, e.g., Hasinger 1998; Madau et al. 1996). Focusing on the redshift bin [0, 1], from Table 3 we see that BL Lac jet ridge lines appear to be significantly wider than their FSRQ counterparts (20.4 ± 2.0°, compared to 11.1 ± 0.8°; > 4σ). The same behavior is seen when looking at the median values (albeit at the 2σ level). Considering the values when the maximum distance limit between the θmax and θmin components is assumed, the jets of the BL Lacs remain substantially (at a ~4σ difference level) wider. Radio galaxies have similar jet widths to BL Lacs within the 1σ uncertainties.
In Fig. 6 (left), we show the distribution of jet-ridge-line widths for BL Lacs, FSRQs, and RGs, in the redshift bin [0, 1]. It can be seen that all three classes have similar distributions, with their maxima situated at around ten degrees. The distribution of BL Lac appears to be wider and to extend to larger widths, than the FSRQs, which have a rather more compact distribution at smaller width values than BL Lacs. For the 125 epochs where CJF sources have apparent jet widths >20 degrees, we found 14 BL Lacs, 27 FSRQs, and 13 RGs. When taking into account the total number of each type of object, we calculate that 47.3% of BL Lacs have jets wider than 20 degrees, as opposed to only 13.6% and 25% for FSRQs and RGs, respectively.
We apply the two-sample Kolmogorov-Smirnoff (K-S) test to our data to see whether the three classes of AGN, BL Lacs, FSRQs, and RGs, differ indeed in terms of their jet ridge line widths. Comparing the jet ridge line widths of BL Lacs and FSRQs (no redshift binning), the K-S test gives a 0.7 × 10-3% probability that these two sub-samples originate from the same parent distribution. Comparing FSRQs with RGs, we get a probability of 0.7%. The K-S test does not reject the null hypothesis (22.1% probability) for the comparison between BL Lacs and RGs. We also compare the sub-samples of BL Lacs, FSRQs, and RGs in the redshift bin [0, 1]. In this case, the K-S test gives a probability of 1% that BL Lacs and FSRQs are drawn from the same parent sample. For BL Lacs and RGs, the test again does not reject the null hypothesis. Finally, we also apply the K-S test after we assume the 20 pc distance constraint between the θmax/θmin components. In this case, we get a 4.4% probability for BL Lacs and FSRQs, while for BL Lacs and RGs the test once again does not reject the null hypothesis. The latter comparison is affected by small-number statistics. We can conclude that BL Lacs display a significantly different distribution of jet ridge line widths than FSRQs. In both average and median values, BL Lacs have substantially wider jets than both FSRQs and RGs.
4.3. Apparent jet width evolution, ΔP, statistics
As mentioned before, component identification is unimportant when working with jet ridge lines. While this is true, the actual detection of the same number of components across different epochs does bear some importance for our results. The effect of a vanishing component (either because of a diminishing flux, poor observing conditions, or otherwise flawed data) will induce a spurious width change, affecting the overall statistics of the sample. Although in the case of diminishing flux, one could argue that this change is indeed intrinsic and therefore important, usually the latter two effects dominate. Moreover, as we mentioned in Sect. 3, the given sensitivity and dynamic range of the observations define our results. For far more sensitive observations, jets would probably appear wider and have a more complex structure than those we found here.
To take this effect into account, we flag our data accordingly. The highest quality data (“OK”) are those for which a width change is calculated between epochs with the same number of components identified per source. As moderate quality data (“!”), we flag those for which the width change is calculated between epochs with ± 1 number of components identified per source. If the number of components varies by 2 or more, the data are flagged as bad (“NO”). In this way, we can still take into account the ejection of new components. Within the time spans between most epochs (~2 years), the appearance of more than one new component is unexpected. In Table 4, the number of epochs for each class of object with each of the corresponding flags is shown. As can be seen, FSRQs and RGs have the highest quality data, with only a 24% and 27%, respectively, of the data flagged as not “OK” (“!” and “NO” flag). In contrast, BL Lacs have almost half their data (47%) flagged accordingly. This reflects the difficulty of a consistent component model-fitting of BL Lac jets across epochs. This is a result of (1) the variable nature of these objects; (2) the intrinsically fainter nature of BL Lacs; and (3) the possible shorter length of their jets that leads to confusion between components (compared for example to FSRQ jets).
 |
Fig. 5 Jet width for CJF FSRQs, as a function of redshift. We use a 0.5 redshift binning to calculate averages (continuous line) and median values (dashed line). Number of sources per bin are: 38 (0–0.5), 53 (0.5–1), 106 (1–1.5), 61 (1.5–2), 55 (2–2.5), 18 (2.5–3), and 12 (3–4). |
 |
Fig. 6 Jet ridge line width (left) and width evolution (right) distributions for BL Lacs (dashed line), FSRQs (solid line), and RGs (grey blocks). For this histogram, sources with redshifts in the [0, 1] bin are used. Sources flagged as “NO” are excluded. |
Three different types of flagging for our data, along with their definition.
We calculate a non-zero maximum apparent width evolution for 180 sources (sources flagged as “NO” are not counted here). Among these, 51 undergo an evolution in their width larger than 4 deg/yr, while 17 have a ΔPmax > 8. We thus find that 28.3% of the sources display significant evolution in their apparent jet width.
We compare the maximum values of the jet-ridge-line width evolution per source between BL Lacs, quasars, and radio galaxies, using no maximum distance limit between the θmax and θmin components for the width calculation and excluding data flagged as “NO”. The differences in the average and median values for the different classes are not found to be statistically significant (<3σ). BL Lacs do however display somewhat stronger width evolution than the other two classes. When checking the maximum and minimum values of each sub-sample, it becomes obvious that FSRQs and BL Lacs have far more extended distributions than RGs.
In Fig. 6 (right), we show the distributions of the maximum jet-ridge-line width evolution for FSRQs, BL Lacs, and RGs. We use a redshift bin of [0, 1] and exclude all data flagged as “NO” (this corresponds to the last three columns of the left part of Table 5). The BL Lac objects have a wide distribution of jet width evolution values, with a primary maximum at 3 degrees/yr that extends to 18 deg/yr. Radio galaxies follow a somewhat similar trend with a plateau between 2 and 4 degrees/yr. In contrast, quasars have a confined distribution with a strong maximum around 3 degrees/yr and all values contained between 0 and 10 degrees/yr. We apply the K-S test to see whether these distributions differ significantly. Concentrating on the comparison in the [0, 1] redshift bin, the K-S test does not reject the null hypothesis (33.8% probability). Calculating the relative occurrences of the different classes, we find that for 12.5% of the CJF BL Lacs ΔPmax > 8, as opposed to 4% and 5.7% for FSRQs and RGs, respectively.
4.4. Apparent jet linear evolution, Δℓ, statistics
Focusing on the final measure of the jet ridge line kinematics that is studied in this paper, we investigate whether the stationarity of components, as observed in the case of S5 1803+784, is commonplace among other BL Lacs. We use the linear evolution measure, as described in Sect. 3, to do this. We follow the same procedure as previously, to check the statistics of the individual classes.
In Table 5 (right), we give the statistical properties of the total linear evolution of the jet ridge line (measured in parsecs per unit time and component) distributions for FSRQs, BL Lacs, and RGs. On average, both BL Lacs and RGs display weaker evolution of their jet ridge lines than FSRQs (~2σ difference). Looking at the median values, BL Lacs and RGs experience a smaller amount of evolution than FSRQs (0.24 ± 0.06, 0.28 ± 0.04, and 0.414 ± 0.020 pc/yr/comp respectively; ~3σ difference). We also study the statistics of the sub-sample of CJF sources in the [0, 1] redshift bin (also in Table 5). The behavior remains the same as before, with differences between BL Lacs and FSRQs becoming more pronounced (with a ~4σ difference in median values).
Statistical properties of the maximum jet width evolution (left) and jet linear evolution (right) distributions for FSRQs, BL Lacs, and RGs.
We now turn to the actual distribution of the total jet linear evolution for the three types of objects, shown in Fig. 7. We once again only take into account sources in the redshift bin [0, 1]. Quasars show a pronounced maximum around 0.63 pc/yr/comp, extending to 2 pc/yr/comp. In contrast, both BL Lacs and RGs have their distribution maxima around 0.25 pc/yr/comp. Quasars appear to have a wider distribution of total linear evolution values, also showing the highest maximum values among all three types (see Table 5). Interestingly, RGs and BL Lacs, in total, have very similar distributions. Once again, we employ the K-S test to compare the distributions. For the whole sample (independent of redshift constraints), the K-S test gives a probability of 4.3% that BL Lacs and FSRQs are drawn from the same parent population. For BL Lacs and RGs, the test does not reject the null hypothesis. Focusing on the 0 < z < 1 sub-sample, we get a marginal 5.4% probability that BL Lacs and FSRQs stem from the same parent sample. These results give a positive answer as to whether BL Lacs display less absolute linear evolution of their jets than their FSRQ counterparts. A somewhat surprising result concerns the comparison between BL Lacs and RGs.
 |
Fig. 7 Distribution of the total linear evolution of the CJF jet ridge lines for FSRQs (solid line), BL Lacs (dashed line), and RGs (grey blocks). We use sources with redshift lower than 1. |
4.5. Jet ridge line properties and variability
Karouzos et al. (2010) gathered variability information from the literature for the CJF sources, focusing on the long timescale (~1−101 years) variability, which is often linked to a helical jet structure and/or a binary AGN core. We use this information to define a subsample of 40 CJF variable sources and study their properties in terms of the measures discussed in Sect. 3. Given the small number of sources/epochs for this investigation, we impose no additional constraints on our sub-sample (e.g., redshift bins).
The sub-sample of variable sources exhibits both higher average (18.3 ± 1.3°, compared to 14.4 ± 0.4°; ~3σ difference) and median (15.7 ± 0.9°, compared to 9.70 ± 0.26°; 6σ difference) width values. In Fig. 8 (left), we plot the jet-ridge-line width distribution for the sub-sample of variable sources, as well as for the rest of the CJF. We see that the parent (non-variable3) CJF sample shows strong maximum in the lowest bin [0°,8°] with a decreasing trend. In contrast, the sub-sample of variable sources have two maxima in bins [0°,8°] (main) and [16°,24°] (secondary), with a secondary to primary ratio of ~0.9. Variable CJF sources indeed show a more extended distribution of jet ridge line widths, shifted towards higher values than the parent CJF sample. A K-S test gives a very low (0.3%) probability that the two sub-samples are drawn from the same parent population.
Statistical properties of the jet width, maximum jet width evolution, and jet linear evolution for the sub-sample of variable CJF sources (see text for definition of variability).
 |
Fig. 8 Jet ridge line width (left) and linear evolution (right) distributions for the sub-sample of variable sources from Karouzos et al. (2010) (black line) and for the remainder (non-variable) of the CJF sample (grey blocks). Owing to the large difference in absolute numbers for the two samples, we have normalized to unity surface area. No redshift or distance constraints are assumed. |
The BL Lacs appear to maintain the same average and median width as their parent sample (within errors). However, FSRQs appear to have both much higher average (22.0 ± 2.7°, compared to 10.8 ± 0.5°; 4σ difference) and median values than their parent sample (17.8 ± 1.6°, compared to 7.00 ± 0.28°; 4σ difference). Variable RGs show marginal evidence of a lower average (12.9 ± 2.1°, compared to 16.5 ± 1.2°) but similar median value.
For ΔP, compared to the parent sample, the sub-sample of variable sources exhibits both higher average (5.5 ± 0.9°/yr, compared to 3.51 ± 0.18°/yr) and median values (3.1 ± 0.4°/yr, compared to 2.37 ± 0.11°/yr), albeit at a low (2σ) significance level. Variable BL Lacs appear to maintain both the same average width as their parent sample (within errors), as well as the same median value (2.5 ± 0.5°/yr, compared to 2.3 ± 0.3°/yr). FSRQs appear to have both higher average (8.4 ± 2.3°/yr, compared to 3.44 ± 0.22°/yr; 2σ difference) and median values (5.0 ± 1.0°/yr, compared to 2.26 ± 0.13°/yr; 2.5σ) than their parent sample. Variable RGs show lower average (1.9 ± 0.6°/yr, compared to 3.3 ± 0.3°/yr) but similar median values (1.6 ± 1.0°/yr, compared to 2.48 ± 0.20°/yr).
For Δℓ, relative to the parent sample, the sub-sample of variable sources does not exhibit significantly different average and median values. For both samples, the total maximum of the distribution occurs in the [0.2,0.4] bin, where the variable CJF sources however display a weaker maximum than the non-variable sample (see Fig. 8, right). In contrast to the non-variable sources, the variable sample has a secondary maximum in the bin [0.8,1] pc/yr/comp implying that the distribution of Δℓ is broader for variable sources. The K-S test does not reject the null hypothesis (23.8% probability). The BL Lac objects appear to have the same average and median linear evolution as their parent sample (within errors). Variable quasars appear to have both higher average (0.615 ± 0.063, compared to 0.470 ± 0.016; > 4σ difference) and median values (0.53 ± 0.04 pc/yr/comp, compared to 0.414 ± 0.020 pc/yr/comp) than their parent sample. Variable RGs have similar average (within the errors) but lower median values (0.135 ± 0.003 pc/yr/comp, compared to 0.28 ± 0.04 pc/yr/comp).
There seems to be a strong link between the kinematic properties studied here and the variability observed in these sources. For all three measures, BL Lacs appear to maintain their statistical behavior between the variable and parent samples, whereas variable quasars tend to have more of a “BL Lac-like” behavior. We note however that, especially for RGs, this comparison is problematic owing to the small number of sources (three RGs).
4.6. Jet kinematics and source luminosity
In addition to the above, we also search for a possible correlation between the kinematic and morphological measures described in Sect. 3 and the radio luminosity of the sources, a value probably less strongly dependent on the jet structure/morphology.
 |
Fig. 9 Total linear evolution of the jet ridge lines for the BL Lac and RG sub-samples (up; left and right, respectively) and the FSRQ sub-sample (down) as a function of the total source luminosity at 5 GHz. Quasars are shown with squares, BL Lacs with circles, and RGs with triangles. We use a color gradient to denote different redshifts. |
In Fig. 9, we show the total linear evolution of the CJF jet ridge lines as a function of the core luminosity of the source at 5 GHz (from VLA observations). It can be immediately seen that a correlation exists between radio luminosity and total linear evolution of the jet ridge line. This is seen as an upper envelope, above which no sources are found. More strongly evolving jets inhabit brighter sources. Conversely, low luminosity sources appear to display the smallest linear displacement of their jets. A similar correlation has been reported between maximum apparent jet-component speed and radio luminosity (Cohen et al. 2007; Britzen et al. 2008; Lister et al. 2009). Britzen et al. (2008) discussed this correlation in terms of a redshift-induced effect. As can be seen in Fig. 9, there is an indication that this is not an effect caused by redshift (e.g., CJF sources at the highest redshifts (>3), albeit only being a few, all appear to have rather weak linear evolution of their jet ridge lines). Further arguments against a redshift-induced effect dominating this correlation can be found in Britzen et al. (2008). It should be noted that small-number statistics might affect our results. For low luminosity sources, as well as high redshift sources, we have a small number of available objects. That hinders the global validity of what is seen in Fig. 9.
Concerning differences between FSRQs, BL Lacs, and RGs, no strong effects can be seen in this context. The low-luminosity tail of the distribution is populated predominantly by RGs and BL Lacs, with FSRQs mainly dominating the higher luminosities. Cohen et al. (2007) use Monte Carlo simulations to show that such an envelope can be explained in terms of “aspect curves”, essentially supporting the beaming model of relativistic jets as an explanation of this effect. In Fig. 9 (right), we plot the same correlation but only for the RGs in our sample. They form the same upper envelope, with more strongly evolving jets appearing in more luminous RGs. In the context of the unification scheme, where RGs are believed to be observed at large angles to their jet axes, Fig. 9 indicates that the correlation between total linear evolution of the jet ridge line and the luminosity cannot be attributed only to geometric effects.
5. Discussion
Given the flux-limited nature of the CJF sample, we are interested in investigating the possible factors influencing the results presented in this paper, which can be briefly summarized in the following:
-
the relative number of FSRQs and BL Lacs;
-
the CJF redshift range;
-
jet component identification;
-
projection effects.
We address each of these points separately.
5.0.1. Total and absolute source numbers
Compared to other samples of a similar nature (e.g., MOJAVE), the CJF contains a larger number of sources, enabling the study of individual populations or sub-groups of sources (i.e., FSRQs, BL Lacs, etc.). We note that, given the selection criteria of the sample and of course the relative cosmic abundance of these sources, quasars dominate the sample, with there being only a few BL Lacs and radio galaxies in comparison. This introduces a certain degree of small-number statistics uncertainties for some of the comparisons in this paper. Future radio surveys with next-generation instruments will surely allow the definition of much larger samples that will address this problem.
5.0.2. Redshift distribution
The large redshift span of the CJF, as well as the uneven sampling of that range with respect to the three types of AGN influence our results. BL Lac objects are over-represented in the redshift range 0 to 2. Radio galaxies have a similar behavior, where most sources are in the redshift range [0, 1], but a few are at higher redshifts. In contrast to that, FSRQs are over-represented in the redshift bin [1, 2] and extend to the highest redshift values of the sample.
As we briefly discussed before, the fixed sensitivity and resolution of the arrays used allow us to make a direct comparison between the different CJF sources. At the same time however, it also essentially leads us to observe different scales of the jet for objects at different redshifts. It is expected that the properties, kinematics, and morphology of a jet are strong functions of the distance to the core. We therefore adopt redshift bins for all of the comparisons we do. Given the distribution of redshifts for the CJF, the only bin we can use without losing most of the BL Lacs is the [0, 1] one4.
5.0.3. Component identification
The way that we study the width and width evolution of the jet is completely independent of the component identification. However an exception to this is the linear evolution of the jet ridge line. For this measure, we are forced to follow the given identification of components (from Britzen et al. 2007b) as we need some reference point to calculate the absolute displacements. Despite the inevitable coupling of prior component identification to our Δℓ measure, that we include in this measure all components and all epochs ensures a treatment of the jet as a whole, evening out peculiarities or possible misidentifications of individual components.
Our measures are however sensitive to the number of components identified at a certain epoch. This is especially relevant to BL Lacs, given the nature of their jets. As we have already discussed, BL Lacs are extremely variable sources. This is in part caused by the presumably small angle to our line of sight, which results in beaming effects that change the flux of both the core and the jet. Secondly, we have shown that BL Lacs have somewhat shorter jets than both FSRQs and RGs. This translates into a greater difficulty in consistently model-fitting the jets of BL Lacs, as blending effects become more prominent as the viewing angle decreases. Moreover, given the strong variability of both the core and jet, these components might simply vanish as a result of diminishing luminosity or insufficient dynamic range of the observations. A further way to demonstrate this is by using the quality classification of jet components used by Britzen et al. (2008). Jet component proper motions are classified as Q1 for the highest quality data, and Q2 and Q3 for data of lower quality. The ratio N(Q1)/(N(Q2) + N(Q3)), where N(x) is the number of x quality components of that type of source, is 0.63 for FSRQs, 0.80 for RGs, and 0.41 for BL Lacs. Returning to our original point, we see therefore that the number of components across epochs in BL Lacs jets is more variable than both FSRQs and RGs. This introduces some uncertainty into our results.
5.0.4. Projection effects
That the values calculated here are all projected onto the plane of the sky introduces some uncertainty and consequently a scatter in this statistical investigation. Although for this analysis and the following discussion, we have adopted the general AGN unification scheme, where BL Lacs and FSRQs are at the smallest viewing angles and radio galaxies are at larger viewing angles, the dispersion in the actual angles within each class introduces the aforementioned scatter in our statistics.
An alternative path would be to try and deproject the jet values calculated here. Although certainly possible for a number of the CJF sources where a Doppler factor has been calculated (e.g., Britzen et al. 2007a), it would introduce additional degrees of uncertainty into our analysis that are not so easily constrained. As we are mainly interested in the comparison between FSRQs and BL Lacs rather than the calculation of intrinsic jet properties, the deprojection is not essential to the results of this paper.
5.1. Possible explanations
It is of great interest to try and explain the kinematic behavior seen in a large number of the CJF. Combining the percentages calculated from both apparent width and apparent width evolution, we indeed find that approximately 30% of the sample have wide jets that change their width strongly. In a similar way, BL Lacs appear to display this behavior more often than FSRQs. One obvious factor that should play a deciding role for the kinematics of jet components is the viewing angle under which a source is observed. It is known that BL Lacs and FSRQs are seen jet-on, at the smallest viewing angles, with steeper-spectrum quasars and radio galaxies being sources observed at progressively larger viewing angles (e.g., Antonucci 1993; Urry & Padovani 1995). Could a viewing angle difference explain the kinematic differences seen in some of the CJF sources and in particular observed between BL Lacs and FSRQs? Assuming that jet components follow ballistic, linear paths, one can expect that viewed at smaller viewing angles (smaller than the critical angle 1/γ, with γ being the Lorentz factor of the flow), the components are observed to cover smaller distances, than if seen edge-on. Therefore, the slower speeds, and hence smaller total linear evolution of their jet ridge lines, observed for BL Lacs could be explained in terms of a systematically smaller viewing angle for BL Lacs, compared to FSRQs.
However, Hovatta et al. (2009) (based on an investigation initiated by Lähteenmäki & Valtaoja 1999) used the long-timescale variability of AGN, together with jet kinematics, to derive Doppler factors and consequently viewing angles of a sample of 87 AGN. They found that FSRQs actually have smaller mean viewing angles than BL Lacs (a result also found by Lähteenmäki & Valtaoja 1999). Although there are certain limitations to the method used by the authors, their results are difficult to reconcile with a viewing-angle-dependent explanation of our results.
Our results would therefore indicate the need for an additional, potentially geometric, effect in play. This would be in agreement with Cohen et al. (2007), who postulate that low-speed components in FSRQ and BL Lac jets appear so because their pattern Lorentz factor is lower than the bulk Lorentz factor of the jet. Alternatively, it should be considered whether there is some systematic bias in the way Doppler factors are estimated, that would lead to an over- or underestimation of the viewing angles of BL Lacs and FSRQs, respectively.
The large jet widths and jet widths changes are more difficult to explain. An additional mechanism or effect must be introduced to produce a wide jet. The precession of the jet axis, or the assumption that the components follow non-ballistic and non-linear paths, can lead to such jet properties (e.g., Steffen et al. 1995; Gong 2008; Roland et al. 2008; Gong et al. 2011). In these models, jet components follow highly curved trajectories, which, viewed face-on, would give the impression of a wider distribution of jet component position angles. A precessing jet, or rather a precessing jet nozzle, would imply that different components follow different trajectories. That would result in a changing jet component position angle distribution, that is more pronounced at smaller viewing angles. That more BL Lacs have a value of M.I. closer to one than FSRQs, implying a highly curved, sinusoid-like ridge-line, lends additional support to this scenario. Following this train of thought would then lead us to the conclusion that either (1) there is a sub-set of FSRQs and BL Lacs (~30% in our sample) for which non-ballistic and/or precession effects play an important role, or more generally that (2) for these sources the viewing angles are below some critical angle θc that allow us to witness and thus characterize the helical or “non-ballistic” structure common in all radio-AGN jets, but which would otherwise be blended out by the projection effects at viewing angles > θc.
In a following paper, we shall use an expanded version of the helical jet model of Steffen et al. (1995) to evaluate the statistical results presented here, in terms of the viewing angle (and hence beaming) effect, as well as a possible helical geometry of the jet.
A final scenario that needs to be discussed is whether there is a systematic difference between the Lorentz factors γ between FSRQs and BL Lacs could produce the effects observed here. It has been argued that BL Lacs have smaller Lorentz factors than FSRQs (e.g., Morganti et al. 1995; Urry & Padovani 1995; Hovatta et al. 2009). If this is true (and not a selection bias in the samples used) then that would naturally explain the slower components in BL Lacs. The above in turn can be related to the currently accepted unification scheme (e.g., Urry & Padovani 1995). In that paradigm, BL Lacs and FSRQs are drawn from two, presumably different, parent samples of Fanaroff-Riley I (low luminosity) and II (high luminosity) galaxies (FR; Fanaroff & Riley 1974; Padovani & Urry 1991; Capetti & Celotti 1999; Xu et al. 2009), respectively. If this were true, then the differences seen in the jet ridge line properties of BL Lacs and FSRQs should then translate into differences between FRI and FRII jet kinematics. Interestingly, studies of FRI and FRII kinematics have shown that both types have similar parcec-scale jet Lorentz factors (e.g., Giovannini et al. 2001), contradictory to what we find here, as well as in other studies mentioned above, concerning the parsec-scale jet speeds in BL Lacs and FSRQs.
We note however that FRI sources show disrupted jets much earlier (i.e., closer to the core) than FRIIs (e.g., see Laing 1996 and references therein). Perucho et al. (2010) explain this in terms of decollimation through the growth of non-linear Kelvin-Helmholtz instability modes in FRI jets. In this context, the wider jets seen in BL Lacs could indicate that there are larger amplitude instabilities (closer to the non-linear regime) in the jet that, given the lower-speed flows observed in these objects, would lead to an earlier disruption of the jet on kpc scales (as expected for FRIs).
It is difficult to offer a single interpretation of our results. It is very likely that both viewing angle and Lorentz factor effects, as well as flow instabilities depending on the latter, influence the appearance of BL Lac and FSRQ jets. A comparison between the jet ridge lines of FRIs and FRIIs to BL Lacs and FSRQs, respectively, would offer additional insight into the problem. A much larger sample than the CJF would be required for such a study.
5.2. Comparison with previous studies
It should be noted that this is the first time the jet ridge lines of a sample of AGN this size have been explicitly and exclusively studied in a statistical manner. While the ridge line of a jet is not a new concept, so far only the jet ridge lines of individual sources (both galactic and stellar) have been studied (e.g., Condon & Mitchell 1984; Steffen et al. 1995; Lister et al. 2003; Lobanov et al. 2006; Britzen et al. 2009; Perucho et al. 2009; Lister et al. 2009; Britzen et al. 2010a). The definition of the jet ridge line can differ from study to study. We define the ridge line of a jet at a certain epoch as the line that linearly connects the projected positions of all components at that epoch. Alternatively, one can use an algorithm to more directly extract the jet ridge line from the VLBI map of each epoch (e.g., Pushkarev et al. 2009). One should however be careful about over-sampling any given map, in effect extracting information that is not actually there. In this sense, the method followed here, although perhaps simpler, is more robust in the quality of information used.
The one obvious direct comparison that can be drawn is to the MOJAVE/2 cm sample (Lister & Homan 2005; Paper I of a series of 6 papers). As the work presented here is a prototype in its conception, it is difficult to make direct comparisons with the MOJAVE sample. It is of interest to compare the apparent velocity distributions for the MOJAVE and the CJF, as the apparent velocities are in a sense reflected in our measure of the total jet ridge line linear evolution. The CJF sources appear to be significantly slower than what is seen in the MOJAVE sample (e.g., compare Fig. 7 from Britzen et al. 2008 and Fig. 7 from Lister et al. 2009). In the distribution of apparent speeds, for the CJF there is a maximum at around 4c and then a turn down, with very few sources above 15c. In contrast, the distribution for the MOJAVE sources shows a maximum at 10c with a fair number of sources showing speeds greater than 20c. This can be explained in terms of the higher temporal resolution of the MOJAVE sample (owing to the larger number of epochs per source) that might allow the detection of these more rapid motions. We note that no clear distinction has been made in the MOJAVE sample between BL Lacs and FSRQs, probably owing to the relatively small number of BL Lacs. However, Lister et al. (2009) do mention that BL Lacs are more often found to exhibit “low-pattern speeds”, i.e., components with slow motions, that are significantly lower than others in the same jet. Similar evidence has been previously found in different VLBI samples (e.g., Jorstad et al. 2001; Kellermann et al. 2004). Combined with the argument that BL Lac jets exhibit lower Lorentz factors, as a result of a possible correlation between intrinsic AGN luminosity and jet Lorentz factor (e.g., Morganti et al. 1995), the above results agree with those for CJF BL Lacs showing on average weaker linear evolution than FSRQs. It should be noted that the agreement with previous studies in terms of the outward motions of BL Lacs objects supports the robustness and reliability of our method.
As was previously mentioned, a correlation between apparent speeds and luminosity has also been studied for the MOJAVE sample (Cohen et al. 2007; Lister et al. 2009). A similar correlation was also observed for the CJF sample, as shown in Britzen et al. (2008). It should be noted that for both samples, these correlations were between luminosity and either the maximum apparent speed per source (in the case of MOJAVE), or only the highest quality (Q1) data (for the CJF). In this paper, we have presented a similar correlation between 5 GHz core luminosity (as derived from VLA measurements) and the total linear evolution of the jet ridge line. In this sense, we have included speed information for all components identified across epochs and therefore considered the jet as a whole, rather than distinguishing the fastest component. The result is however remarkably similar to what was previously found. Cohen et al. (2007) and Lister et al. (2009) discussed possible interpretations of the upper-envelope that is observed in this correlation, in terms of the beaming model. They concluded that there is no apparent argument as to why such an envelope should exist. They instead offered an alternative interpretation in terms of a link between the energy output of the AGN and the intrinsic Lorentz factor of a jet. They concluded however that the shallow flux limit of the MOJAVE sample does not allow a robust conclusion to be made. The deeper flux-limit of the CJF (and the resulting more than double the number of sources) allows us to re-address the same issue. That this correlation remains in the CJF sample, both in the sense of a maximum apparent jet speed, as well as that of the linear evolution measure (in essence a mean jet speed), argues in favor of a link between the intrinsic luminosity and Lorentz factor. A definite answer would come from the inclusion of low-luminosity sources in such an investigation. It would then become obvious whether this envelope holds and can distinguish between a beaming model signature and that of an intrinsic relation between the energy output and the jet kinematics.
A final note concerning the comparison between our results and these of the MOJAVE sample pertains to the observation frequency of each sample. Unlike the CJF, the MOJAVE uses VLBI observations at 15 GHz, meaning that a potentially different regime of the jet is probed, compared to what is studied in the CJF. Two-zone models, such as the “two-fluid” model (e.g., Sol et al. 1989; Pelletier & Roland 1989), predict a fast jet spine, embedded in a slower moving sheath. This would imply that the MOJAVE potentially probes deeper, thus faster, jet layers compared to what is seen in the CJF sample. Moreover, higher observation frequency also corresponds to higher angular resolution and therefore to probing effects closer to the core and also enabling the detection of faster moving components. In this case, it would be interesting to apply the methods used in this paper to the MOJAVE dataset, as it is expected that the curvature of the jet (and therefore potentially the angular properties and evolution of the jet ridge line) should play an increasingly important role at closer core separations.
6. Conclusions
We have developed a number of tools to investigate both the morphology and kinematics of the CJF jet ridge lines and in particular the quantities:
-
monotonicity index;
-
apparent jet width;
-
apparent jet width evolution;
-
apparent jet linear evolution.
Using these tools, we have found that:
-
BL Lacs jet ridge lines more closely resemble asinusoidal curve than those of both FSRQs and RGs. In contrast,two-thirds of the FSRQs have an M.I. lower than 0.5 (indicatingfairly monotonic jets);
-
22.4% of the CJF sources have apparent jet widths larger than 20 degrees. In addition, 47.3% of BL Lacs, compared to 13.6% and 25% of FSRQs and RGs, respectively, have dP > 20 degrees;
-
BL Lacs exhibit substantially apparently wider jets. This effect persists under several constraints (e.g., redshift bins, core separation limits). Quasars have the least wide jets of the three classes. This supports the effects seen in individual BL Lac objects (i.e., 1803+784, 0716+714, etc.);
-
there is no indication of a change in the apparent jet width with redshift, at least out to z ~ 2;
-
the distribution of apparent jet ridge line widths for BL Lacs appears to extend towards higher values, with FSRQs mainly contained at lower values. Radio galaxies have a somewhat wider distribution of widths than FSRQs. A K-S test indicates a 0.7 × 10-3% probability that FSRQs and BL Lacs are drawn from a single parent population;
-
28.3% of the CJF sources exhibit an apparent jet width evolution that is greater than 4 deg/yr, and that 12.5% of BL Lacs have ΔPmax > 4, compared to 4% and 5.7% for FSRQs and RGs, respectively;
-
when taking into account the maximum values of the apparent width evolution for the CJF sources, BL Lacs are found to experience a marginally stronger evolution of their apparent jet widths, with FSRQs and RGs showing similar values (within errors). This behavior holds for a narrower redshift bin;
-
BL Lac objects, on average, show weaker apparent linear evolution of their jet ridge lines than FSRQs. Interestingly, RGs display even weaker linear evolution. Both BL Lac objects and radio galaxies display apparently slower moving jets than quasars;
-
variable CJF source are, on average, found to exhibit apparently wider jets than the non-variable ones. A K-S test gives a 1% probability that these two sub-samples stem from the same parent distribution.
-
variable sources in the CJF show, on average, a stronger apparent angular evolution than the non-variable ones. This is reflected in the wider distribution of the apparent jet width evolution angles than the parent (non-variable) sample;
-
variable sources exhibit stronger apparent linear evolution, as seen also in the distributions of the two sub-samples.
-
variable FSRQs show more “BL Lac like” behavior with wider jets that also change their width more strongly;
-
a correlation, in the form of an upper envelope, exists between the total apparent linear evolution of the CJF jet ridge lines and their radio (VLA, 5 GHz) core luminosities. Although partly attributed to relativistic effects, there are indications of an intrinsic effect in addition to the geometric one.
By statistically analyzing the CJF sample, we have been able to provide detailed insight into the morphology and evolution of AGN jet ridge lines. The statistical investigation of the CJF sources lends independent support to the different kinematical scenario proposed for a number of BL Lac objects (1803+784, Britzen et al. 2010a; 0735+178, Britzen et al. 2010b; etc.). We have found that 25%–30% of the CJF sample appear to have considerably wide jets and undergo a strong width evolution (in projection). The BL Lac objects appear to deviate the strongest from the kinematic paradigm that is widely accepted for blazars, of outward superluminally moving jet components. BL Lacs appear to evolve their jet ridge lines (with respect to the core) less than the other source classes, hence indicating that there is a slower apparent flow in their jets. However, they appear to have, in projection, significantly wider jets that change their widths more strongly with time, than both FSRQs and RGs. All of these three effects have been previously observed in the jets of 1803+784, 0716+714, and 0735+178. Viewing BL Lacs at small angles to their jet axis possibly allows us to uncover this peculiar kinematic behavior that would otherwise be inaccessible at larger viewing angles. However, the picture does not remain “simple”. By studying a sub-sample of CJF sources identified as variable, we have found that these sources actually display wider, more strongly evolving jet ridge lines with time. We also have found that variable FSRQs exhibit a more “BL Lac like” behavior. All the aforementioned results, combined with the significant number of CJF sources that show properties consistent with a different kinematic scheme (independent of their classification), imply that such a scheme applies universally, rather than uniquely to BL Lacs.
It should therefore be noted that the above results underline that the notion of linear, ballistic trajectories usually employed for AGN jet components is a very crude approximation and, more often than not, deviates grossly from the reality. It is of great interest to uncover the process that leads to the properties of AGN jet ridge lines studied in this paper. In an upcoming paper, we shall use a simple jet model to address this point.
Here σ is defined as the sum of the position angle errors for θm and θm ± 1. The choice of this σ reflects an original underestimation (in Britzen et al. 2007b) of the position angle errors during the component fitting.
We underline that the number of variable sources is explicitly regulated by the availability, or lack thereof, of the appropriate observations (long-timescale variability can be uncovered only by means of extensive monitoring of a source). Some of the sources labeled here as “non-variable” are probably variable but not observed as such.
Acknowledgments
M. Karouzos was supported for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics. M.K. acknowledges the support from the Creative Research Initiative program, No. 2010-0000712, of the National Research Foundation of Korea (NRFK) funded by the Korea government(MEST). M.K. wishes to thank Lars Fuhrmann and Mar Mezcua, as well as an anonymous referee for insightful discussions and comments that greatly improved this manuscript. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. The Very Long Baseline Array is operated by the USA National Radio Astronomy Observatory, which is a facility of the USA National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
References
- Agudo, I., Gómez, J., Martí, J., et al. 2001, ApJ, 549, L183 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Gómez, J. L., Gabuzda, D. C., et al. 2006, A&A, 453, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Britzen, S., Vermeulen, R. C., Taylor, G. B., et al. 1999, in BL Lac Phenomenon, ed. L. O. Takalo, & A. Sillanpää, ASP Conf. Ser., 159, 431 [Google Scholar]
- Britzen, S., Witzel, A., Krichbaum, T. P., et al. 2000, A&A, 360, 65 [NASA ADS] [Google Scholar]
- Britzen, S., Brinkmann, W., Campbell, R. M., et al. 2007a, A&A, 476, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Britzen, S., Vermeulen, R. C., Taylor, G. B., et al. 2007b, A&A, 472, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Britzen, S., Vermeulen, R. C., Campbell, R. M., et al. 2008, A&A, 484, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Britzen, S., Kam, V. A., Witzel, A., et al. 2009, A&A, 508, 1205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Britzen, S., Kudryavtseva, N. A., Witzel, A., et al. 2010a, A&A, 511, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Britzen, S., Witzel, A., Gong, B. P., et al. 2010b, A&A, 515, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capetti, A., & Celotti, A. 1999, MNRAS, 304, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M. H., Lister, M. L., Homan, D. C., et al. 2007, ApJ, 658, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., & Mitchell, K. J. 1984, ApJ, 276, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Conway, J. E., & Murphy, D. W. 1993, ApJ, 411, 89 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1991, Science, 254, 1667 [NASA ADS] [Google Scholar]
- Fan, J. H., Liu, Y., Yuan, Y. H., et al. 2007, A&A, 462, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Gabuzda, D. C. 1995, Proc. National Academy of Science, 92, 11393 [Google Scholar]
- Gabuzda, D. C., Pushkarev, A. B., & Cawthorne, T. V. 2000, MNRAS, 319, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G. 1993, Adv. Space Res., 13, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Padovani, P., Celotti, A., & Maraschi, L. 1993, ApJ, 407, 65 [Google Scholar]
- Giovannini, G., Cotton, W. D., Feretti, L., Lara, L., & Venturi, T. 2001, ApJ, 552, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, J. L., Guirado, J. C., Agudo, I., et al. 2001, MNRAS, 328, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, J. L., Marti, J. M. A., Marscher, A. P., Ibanez, J. M. A., & Marcaide, J. M. 1995, ApJ, 449, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, B. 2008, MNRAS, 389, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, B., Kong, S. W., Xue, F., Li, Y., & Huang, Y. F. 2011, MNRAS, 418, 2451 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G. 1998, Astron. Nachr., 319, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Heidt, J., & Wagner, S. J. 1996, A&A, 305, 42 [NASA ADS] [Google Scholar]
- Hewitt, A., & Burbidge, G. 1989, in A new optical catalog of QSO [Google Scholar]
- Hook, I. M., McMahon, R. G., Patnaik, A. R., et al. 1995, MNRAS, 273, L63 [NASA ADS] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hough, D. H., Vermeulen, R. C., Readhead, A. C. S., et al. 2002, AJ, 123, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Hovatta, T., Valtaoja, E., Tornikoski, M., & Lähteenmäki, A. 2009, A&A, 494, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, L., Fan, X., Ivezić, Ž., et al. 2007, ApJ, 656, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Mattox, J. R., et al. 2001, ApJ, 556, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Karouzos, M., Britzen, S., Eckart, A., Witzel, A., & Zensus, A. 2010, A&A, 519, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kellermann, K. I., Sramek, R., Schmidt, M., Shaffer, D. B., & Green, R. 1989, AJ, 98, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Lister, M. L., Homan, D. C., et al. 2004, ApJ, 609, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Krichbaum, T. P., Witzel, A., Standke, K. J., et al. 1994, in Compact Extragalactic Radio Sources, ed. J. A. Zensus, & K. I. Kellermann, 39 [Google Scholar]
- Kudryavtseva, N., Britzen, S., Witzel, A., et al. 2011, A&A, 526, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lähteenmäki, A., & Valtaoja, E. 1999, ApJ, 521, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A. 1996, in Extragalactic Radio Sources, ed. R. D. Ekers, C. Fanti, & L. Padrielli, IAU Symp., 175, 147 [Google Scholar]
- Lister, M. L., & Homan, D. C. 2005, AJ, 130, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Kellermann, K. I., Vermeulen, R. C., et al. 2003, ApJ, 584, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P., & Zensus, J. A. 1999, ApJ, 521, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P., Krichbaum, T. P., Witzel, A., & Zensus, J. A. 2006, PASJ, 58, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Lowe, S. R., Gawroński, M. P., Wilkinson, P. N., et al. 2007, A&A, 474, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madau, P., Ferguson, H. C., Dickinson, M. E., et al. 1996, MNRAS, 283, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Mimica, P., Aloy, M., Agudo, I., et al. 2009, ApJ, 696, 1142 [NASA ADS] [CrossRef] [Google Scholar]
- Morganti, R., Oosterloo, T. A., Fosbury, R. A. E., & Tadhunter, C. N. 1995, MNRAS, 274, 393 [NASA ADS] [Google Scholar]
- Nesci, R., Massaro, E., Maesano, M., et al. 2002, AJ, 124, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P. 1993, MNRAS, 263, 461 [NASA ADS] [Google Scholar]
- Padovani, P., & Urry, C. M. 1991, ApJ, 368, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, T. J., & Readhead, A. C. S. 1981, ApJ, 248, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, T. J., Browne, I. W. A., Henstock, D. R., et al. 1998, in IAU Colloq. 164: Radio Emission from Galactic and Extragalactic Compact Sources, ed. J. A. Zensus, G. B. Taylor, & J. M. Wrobel, ASP Conf. Ser., 144, 17 [Google Scholar]
- Pelletier, G., & Roland, J. 1989, A&A, 224, 24 [NASA ADS] [Google Scholar]
- Perucho, M., Lobanov, A. P., & Kovalev, Y. Y. 2009, in ASP Conf. Ser., 402, ed. Y. Hagiwara, E. Fomalont, M. Tsuboi, & M. Yasuhiro, 349 [Google Scholar]
- Perucho, M., Martí, J. M., Cela, J. M., et al. 2010, A&A, 519, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, L. K., Taylor, G. B., & Zavala, R. T. 2003, ApJ, 589, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Pushkarev, A. B., Kovalev, Y. Y., Lister, M. L., & Savolainen, T. 2009, A&A, 507, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rees, M. J. 1966, Nature, 211, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Roland, J., Britzen, S., Kudryavtseva, N. A., Witzel, A., & Karouzos, M. 2008, A&A, 483, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sol, H., Pelletier, G., & Asseo, E. 1989, MNRAS, 237, 411 [NASA ADS] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, W., Zensus, J. A., Krichbaum, T. P., Witzel, A., & Qian, S. J. 1995, A&A, 302, 335 [Google Scholar]
- Taylor, G. B., Vermeulen, R. C., Readhead, A. C. S., et al. 1996, ApJS, 107, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vermeulen, R. C. 1995, Proc. Nat. Acad. Sci., 92, 11385 [Google Scholar]
- Vermeulen, R. C., & Cohen, M. H. 1994, ApJ, 430, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Vermeulen, R. C., Britzen, S., Taylor, G. B., et al. 2003, in Radio Astronomy at the Fringe, ed. J. A. Zensus, M. H. Cohen, & E. Ros, ASP Conf. Ser., 300, 43 [Google Scholar]
- Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Whitney, A. R., Shapiro, I. I., Rogers, A. E. E., et al. 1971, Science, 173, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Witzel, A. 1987, in Superluminal Radio Sources, ed. J. A. Zensus, & T. J. Pearson, 83 [Google Scholar]
- Xu, Y.-D., Cao, X., & Wu, Q. 2009, ApJ, 694, L107 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Statistical properties of the monotonicity index (M.I.) distribution for FSRQs, BL Lacs, and RGs.
Characteristic statistical values concerning the width of the jet ridge line of sources with measured redshifts.
Statistical properties of the maximum jet width evolution (left) and jet linear evolution (right) distributions for FSRQs, BL Lacs, and RGs.
Statistical properties of the jet width, maximum jet width evolution, and jet linear evolution for the sub-sample of variable CJF sources (see text for definition of variability).
All Figures
 |
Fig. 1 Redshift distribution of radio galaxies (grey blocks), BL Lacs (dashed line), and FSRQs (solid line) in the CJF sample. |
| In the text | |
 |
Fig. 2 Radio maps at 5 GHz of 1928+738 (left) and 0700+470 (right), with jet ridge lines superimposed. Two examples of a sinusoid-like jet morphology (left) and a single-bent one (right). The VLBI maps are taken from Britzen et al. (2007b). |
| In the text | |
 |
Fig. 3 Radio map of 0700+470 at 5 GHz, exhibiting the calculation of the jet ridge line width. The two arrows denote the components with the maximum and minimum position angles, while the area in-between is defined as the opening, or apparent width, of the jet ridge line. The VLBI core is found at (0,0) coordinates. The VLBI map is taken from Britzen et al. (2007b). |
| In the text | |
 |
Fig. 4 Monotonicity index (M.I.) distribution for BL Lacs (dashed line), FSRQs (solid line), and RGs (grey blocks). The histogram has been normalized to area unity. |
| In the text | |
 |
Fig. 5 Jet width for CJF FSRQs, as a function of redshift. We use a 0.5 redshift binning to calculate averages (continuous line) and median values (dashed line). Number of sources per bin are: 38 (0–0.5), 53 (0.5–1), 106 (1–1.5), 61 (1.5–2), 55 (2–2.5), 18 (2.5–3), and 12 (3–4). |
| In the text | |
 |
Fig. 6 Jet ridge line width (left) and width evolution (right) distributions for BL Lacs (dashed line), FSRQs (solid line), and RGs (grey blocks). For this histogram, sources with redshifts in the [0, 1] bin are used. Sources flagged as “NO” are excluded. |
| In the text | |
 |
Fig. 7 Distribution of the total linear evolution of the CJF jet ridge lines for FSRQs (solid line), BL Lacs (dashed line), and RGs (grey blocks). We use sources with redshift lower than 1. |
| In the text | |
 |
Fig. 8 Jet ridge line width (left) and linear evolution (right) distributions for the sub-sample of variable sources from Karouzos et al. (2010) (black line) and for the remainder (non-variable) of the CJF sample (grey blocks). Owing to the large difference in absolute numbers for the two samples, we have normalized to unity surface area. No redshift or distance constraints are assumed. |
| In the text | |
 |
Fig. 9 Total linear evolution of the jet ridge lines for the BL Lac and RG sub-samples (up; left and right, respectively) and the FSRQ sub-sample (down) as a function of the total source luminosity at 5 GHz. Quasars are shown with squares, BL Lacs with circles, and RGs with triangles. We use a color gradient to denote different redshifts. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.