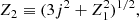| Issue |
A&A
Volume 697, May 2025
|
|
|---|---|---|
| Article Number | A176 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202453260 | |
| Published online | 16 May 2025 | |
Accretion properties and jet mechanisms for the low-excitation radio galaxies
1
Dipartimento di Fisica e Astronomia “G. Galilei”, Università di Padova, Via F. Marzolo, 8, I-35131 Padova, Italy
2
Istituto Nazionale di Fisica Nucleare, Sezione di Padova, I-35131 Padova, Italy
3
Centre for Astrophysics, Guangzhou University, Guangzhou 510006, People’s Republic of China
4
INAF – Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna, Italy
5
College of Physics and Electronic Engineering, Qujing Normal University, Qujing 655011, People’s Republic of China
6
Astronomy Science and Technology Research Laboratory of Department of Education of Guangdong Province, Guangzhou 510006, People’s Republic of China
⋆ Corresponding authors: denis.bastieri@unipd.it, fjh@gzhu.edu.cn
Received:
2
December
2024
Accepted:
23
March
2025
Context. Radio galaxies (RGs) are a subclass of active galactic nuclei, which are suggested to be the parent populations of blazars. Based on morphologies and radio powers, RGs can be classified as Fanaroff-Riley type 0 (FR 0s), I (FR Is), and II (FR IIs) RGs. According to the accretion-ejection paragram, RGs can be classified as low-excitation or high-excitation radio galaxies (LERGs or HERGs).
Aims. We aim to compile a distance-limited (z < 0.15) sample of 431 LERGs (FR 0s, FR Is, and FR IIs) in order to discuss their jet-formation mechanism with the advection-dominated accretion-flow (ADAF) scenario, and compare their accretion properties with Fermi BL Lacertae objects (BL Lacs).
Methods. We explored different jet mechanisms (Blandford-Znajek [BZ] model and a mixture of the BZ and Blandford-Payne hybrid model) within the framework of ADAF-type disc around a Kerr black hole for both LERGs and Fermi BL Lacs.
Results. Based on standard assumptions on the accretion-ejection coupling in RGs, the maximum kinetic jet and accretion power for FR 0s, FR Is, and FR IIs can be explained by an ADAF with the pure BZ mechanism or hybrid jet mechanism. In addition, for one-third of the FR IIs, to account for their kinetic jet power that is higher than what is expected of the hybrid jet mechanism, the magnetic field could play an important role, for example as in the form of magnetisation-driven outflows or stronger magnetic structures observed in some BL Lacs with high jet powers.
Conlcusions. Similarities between BL Lacs and LERGs (e.g. accretion-ejection and clustering properties) suggest that high-synchrotron-peaked BL Lacs could be the beamed counterparts of FR 0s, and a potential general unification between LERGs and BL Lacs populations is discussed. However, a complete sample of BL Lacs is needed to robustly compare the jet and accretion properties with those of LERGs in the future.
Key words: accretion / accretion disks / galaxies: active / BL Lacertae objects: general / galaxies: jets
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Radio galaxies (RGs), a subclass of radio-loud active galactic nuclei (AGNs), are classified as Fanaroff-Riley type I (FR Is) or type II (FR IIs) RGs based on morphologies and radio powers (Fanaroff & Riley 1974). However, the FR dichotomy for RGs is not strictly separated by a typical value of the extended radio power (Lext; Owen & Ledlow 1994; Zirbel & Baum 1995); FR Is have lower radio powers (Lext < 1024.5 W/Hz), while FR IIs have higher radio powers (Lext > 1026 W/Hz). An intermediary region (1024.5 < Lext < 1026 W/Hz) is occupied by both FR Is and FR IIs. Besides the radio sources extended up to megaparsec scales, the compact radio sources have also been studied for decades (e.g. Condon & Dressel 1978; Kellermann & Pauliny-Toth 1981; Falcke et al. 2004). The population of compact radio sources dominates the local Universe (e.g. O’Dea & Saikia 2021). A large fraction of these compact RGs lack a kiloparsec extended structure, and they are not interpreted as young RGs: these have been named as Fanaroff-Riley type 0 RGs (FR 0s; Baldi et al. 2015; Baldi 2023). The FR 0s share similar nuclear and host properties to FR Is, but they show total luminosities lower than those of classical FR Is and FR IIs by a factor of 100-1000 (Baldi et al. 2015), hence not fitting into the traditional FR I-II classification.
Best & Heckman (2012) suggested a fundamental classification for RGs using the accretion-ejection paradigm, where different structures and different environments surrounding the black hole lead to different accretion mechanisms. Radio galaxies with a ‘standard’ geometrically thin and optically thick disc (Shakura & Sunyaev 1973), showing a higher accretion rate (ṁ, typically 1–10% of their Eddington rate) onto the supermassive black holes (BHs), are classified as high-excitation radio galaxies (HERGs); in contrast, RGs with low accretion rates, dominated by a radiatively inefficient disc, are named as low-excitation radio galaxies (LERGs; Heckman & Best 2014). At the centre of LERGs, the thin accretion disc is replaced by an advection-dominated accretion flow (ADAF; Narayan & Yi 1995; Heckman & Best 2014). Most FR 0s and FR Is are LERGs, whereas FR IIs exhibit varying accretion properties (Balmaverde et al. 2008; Heckman & Best 2014; Capetti et al. 2017a; Torresi et al. 2018). Some FR IIs have high accretion rates, known as FR II HERGs, while others display low accretion disc properties called FR II LERGs (Hardcastle et al. 2009; Mingo et al. 2022). In general, HERGs are homogeneous with FR IIs, while LERGs are heterogeneous with both FR Is and FR IIs (Buttiglione et al. 2010).
Blazars are a subclass of radio-loud AGNs showing extreme observation properties with the relativistic jets closely aligned to the line of sight; these include rapid variabilities, high polarisations, high luminosities, superluminal motions, radio core-dominance morphologies, and highly energetic radiations (Urry & Padovani 1995; Xiao et al. 2019; Pei et al. 2020; Fan et al. 2016, 2021; Homan et al. 2021; Ajello et al. 2022; Liodakis et al. 2022; Yuan et al. 2022; Liang et al. 2023; Zhang et al. 2023). There are two subclasses of blazars: BL Lacertae objects (BL Lacs) with weak equivalent emission-line widths (EW < 5 Å) and flat-spectrum radio quasars (FSRQs) with significant equivalent emission-line widths (EW > 5 Å; Stickel et al. 1991). The classification schemes for (misaligned) RGs and (aligned) blazars are still inconsistent. Radio galaxies are typically classified based on their radio morphology and radio power (Fanaroff & Riley 1974), whereas classes of blazars are classified by the strengths of the emission lines (Stickel et al. 1991). The classical picture was that FR Is and FR IIs are the parental populations of BL Lacs and FSRQs, respectively.
Radio-loud AGNs are characterised by a non-thermal synchrotron spectrum, generated from accretion-ejection physical processes from the central engine, which has a typical luminosity peak at a specific radio-band peak frequency where the emission moves from an optically thick regime to an optically-thin one. Based on the synchrotron peak of the spectral energy distribution (SED), blazars are classified as low-synchrotron-peaked blazars (log νpeak < 13.7 Hz), intermediate-synchrotron-peaked blazars (13.7 < log νpeak < 14.9 Hz), and high-synchrotron-peaked blazars (log νpeak > 14.9 Hz; Yang et al. 2022a). Most FSRQs are low synchrotron peaked sources, while BL Lacs can be classified into low-, intermediate-, and high-synchrotron-peaked BL Lacs, as is noted for LBLs, IBLs, and HBLs (Ajello et al. 2022). In the plane of the synchrotron peak frequency-peak luminosity (νpeak − Lpeak), an anti-correlation between them for blazars (so-called blazar sequence) was first discussed in Fossati et al. (1998). The blazar sequence is explained by the Compton cooling effect (Ghisellini et al. 1998; Prandini & Ghisellini 2022), selection effects (Giommi et al. 2012), or beaming effects (Nieppola et al. 2008; Yang et al. 2022b). However, Keenan et al. (2021) found little evidence of the anti-correlation for the blazar sequence, but they found a dichotomy: stronger jets and more efficient discs in HERGs, FSRQs, and most LBLs than LERGs and blazars with νpeak > 1015 Hz.
For radio-loud AGNs, there are two main scenarios explaining the jet formation within the accretion disc and/or spinning BH (Blandford & Znajek 1977; Blandford & Payne 1982). If jets extract the rotational energy of BHs, the jet formation mechanism follows the Blandford-Znajek (BZ) mechanism (Blandford & Znajek 1977). If the jets extract the rotational energy from the accretion disc, it follows the Blandford-Payne (BP) mechanism (Blandford & Payne 1982). The jet power difference between the pure BZ and BP models is primarily determined by the BH spin and the self-similar index, which describes how the poloidal magnetic field varies with the cylindrical radius of the jet. Nevertheless, at a given magnetic field, for a rapid BH spin (e.g. j > 0.9), the jet power of the BZ model is larger than that of the BP model for any magnetic-field configuration (Li et al. 2008). Both BZ and BP models contribute to the physics of the disc, leading to an expected relationship between the disc luminosity and jet power (Ghisellini et al. 2011; Sbarrato et al. 2012). If the rotational energy of the jet is from both accretion discs and BHs, the jet formation mechanism could be a mixture (hybrid model) of BP and BZ mechanisms (Meier 2001; Nemmen et al. 2007). In this work, we compiled a nearby sample (z < 0.15) of 431 LERGs (FR 0s, FR Is, and FR IIs) to discuss their jet mechanisms in the case of ADAFs and compared their accretion properties with those of the Fermi BL Lacs. A Λ-CMD cosmology with ΩΛ ∼ 0.7, ΩM ∼ 0.3, and H0 = 70 km s−1 Mpc−1 is applied throughout the paper.
2. Sample
Best & Heckman (2012) compiled a sample of 18 286 radio-loud AGNs by cross-checking several datasets from the Sloan Digital Sky Survey (SDSS), the National Radio Astronomy Observatory (NRAO) Very Large Array (VLA) Sky Survey (NVSS), and the Faint Images of the Radio Sky at Twenty centimetres (FIRST) survey, and classified the sources as LERGs or HERGs based on their emission-line properties, applying multiple classification criteria (e.g. Kewley et al. 2006; Buttiglione et al. 2010; Cid Fernandes et al. 2010). Within this sample, Capetti et al. (2017a,b) searched for low-power FR Is (FRICAT) and FR IIs (FRIICAT) by using the morphological classifications of the FIRST radio images. They visually inspected the FIRST images of each radio source with a flux density larger than 5 mJy and limited the sample with a redshift of z < 0.15. All sources with radio emissions extending at least 30 kpc are preserved. The 30 kpc radius corresponds to 11″.4 for the distant sources and ensures that all the FRICAT/FRIICAT sources are well resolved with the 5″ resolution of the FIRST images, enabling a detailed exploration of their morphologies. FRICAT sources have one- or two-sided jets that fade in brightness along their length without brightening at the ends, while FRIICAT sources show edge-brightened morphology peaking at least 30 kpc from the optical host centre. They obtained a sample of 327 RGs, including 219 FR I LERGs and 108 FR II LERGs, which we considered in this work.
Baldi et al. (2018) followed the same procedures outlined by Capetti et al. (2017a,b), selecting the sources with z < 0.05, a minimum flux density of 5 mJy, and a maximum offset of 2″ from the optical centre. They visually inspected the FIRST images and eliminated the sources with clearly extended radio emissions to select only the compact radio sources. Sources with an observed major axis smaller than 6″.7 were preserved, corresponding to a size of 5 kpc at z = 0.05. Finally, Baldi et al. (2018) compiled a sample of 108 FR 0 LERGs, of which four FR 0 LERGs were discarded based on the images of high-resolution radio observations by Baldi et al. (2019a).
In summary, we compiled a total of 431 LERGs, of which 104 were FR 0s, 219 FR Is, and 108 FR IIs. This sample consists of low-power, radio-loud AGNs (> 5 mJy at 1.4 GHz) that are weaker than the classical 3CR (Third Cambridge Revised Catalogue) RGs (e.g. Bennett 1962; Spinrad et al. 1985, selected at > 9 Jy at 178 MHz), and their hosts have r-band magnitudes in the range of 15.5 < r < 13, covering a redshift completeness of ∼90% of the SDSS optical main galaxies sample (Strauss et al. 2002). The 431 LERGs with available redshifts, 1.4 GHz NVSS radio luminosities, emission-line luminosities, jet powers, and BH masses are presented in Table 1.
The parameters for 431 nearby low-excitation radio galaxies and 75 Fermi BL Lacertae objects.
2.1. Redshift
The redshift range for FR 0s is from z = 0.011 to z = 0.05, with an average redshift of ⟨z0⟩ = 0.037 ± 0.001. In comparison, FR Is and FR IIs have higher redshift ranges: FR Is range from z = 0.024 to z = 0.15, with an average redshift of ⟨zI⟩ = 0.114 ± 0.002, and FR IIs range from z = 0.045 to z = 0.148, with an average redshift of ⟨zII⟩ = 0.115 ± 0.003. The redshifts for the 431 LERGs are presented in Fig. 1 and Table 1.
 |
Fig. 1. Cumulative distributions of redshifts for 431 low-excitation radio galaxies. The solid black line is for FR 0s, the dashed red line is for FR Is, and the dash-dotted blue line is for FR IIs. The average redshift for FR 0s is ⟨z0⟩ = 0.037 ± 0.001, whereas that of FR Is is ⟨zI⟩ = 0.114 ± 0.002, and that of FR IIs is ⟨zII⟩ = 0.115 ± 0.003. |
The Kolmogorov-Smirnov (K-S) test results suggest that FR Is and FR IIs have similar redshift distributions (K-S test p = 0.09). However, both of these distributions are significantly larger than the redshift distribution of FR 0s (both p < 0.05).
2.2. Kinetic jet power
For large-scale radio sources, a portion of the total jet power is either converted into kinetic energy or dissipated through expansion of the lobes (Scheuer 1974; Willott et al. 1999). The jets push the relativistic plasma to interact with the surrounding thermal gas, appearing as bubbles or cavities in X-ray observations (e.g. Boehringer et al. 1993). Willott et al. (1999) estimated the kinetic (mechanical) jet power for FR IIs from the 151 MHz radio luminosity, assuming that the lobes store the minimum energy required to produce the observed synchrotron emission over an age of 107 years. Cao & Rawlings (2004) suggested that this estimation is also applicable for FR Is, with an acceptable accuracy of an order of magnitude compared to other methods (e.g. M87; Bicknell & Begelman 1999; Young et al. 2002). The extension of this estimation from FR IIs to sources in gas-rich environments, primarily FR Is, became feasible after the launch of the Chandra satellite. Bîrzan et al. (2004) presented an analysis of 16 galaxy clusters to estimate radio jet powers by assessing the jet to inflate pV energy in cavities. They adopted a buoyancy timescale to estimate cavity ages and found a strong correlation between cavity powers and 1.4 GHz radio luminosities. Cavagnolo et al. (2010) expanded the sample (mainly FR Is) in Bîrzan et al. (2004) based on the Chandra X-ray and VLA radio data, deriving a mean scaling relation between the kinetic jet power and the radio luminosity. The scaling relation is in line with the model proposed by Willott et al. (1999). Later, Heckman & Best (2014) recast these kinetic jet power methods, presenting a best-fitting linear relation between the kinetic jet power and the large-scale NVSS 1.4 GHz radio emissions with the sample of Cavagnolo et al. (2010):
The L1.4 is the NVSS 1.4 GHz radio luminosity. The fcav includes the uncertainties on the physical state of lobes and is suggested to be fcav = 4 from the best linear relation of the data (Heckman & Best 2014). There is evidence that FR 0s also show the presence of compact jets based on LOFAR (LOw-Frequency ARray), VLA, and VLBI observations (Cheng & An 2018; Baldi et al. 2019a; Capetti et al. 2020; Cheng et al. 2021; Giovannini et al. 2023), and their multi-band nuclear luminosities are comparable with those of low-power FR Is: these results support that the Lkin − L1.4 relation is also valid for low-power RGs consistent with an FR 0 classification (Heckman & Best 2014). Here, we followed the line of interpretation of Baldi (2023) and Heckman & Best (2014) for FR 0s and low-power RGs, and we computed the kinetic jet powers for our sample by assuming fcav = 4 as a broad balance between AGN heating and radiative cooling in massive clusters for all LERGs. Based on the data scatter of the relation, we assumed an uncertainty on the Lkin estimate of ∼0.7 dex (Rafferty et al. 2006; Bîrzan et al. 2008; Cavagnolo et al. 2010).
The radio luminosity is obtained by the corresponding K-corrected radio flux [Sν(1 + z)α − 1] and the luminosity distance (dL): νLν = 4πdL2νSν(1 + z)α − 1, in which α is the radio spectral index (Sν ∼ ν−α) and the luminosity distance dL is determined by the redshift (z):
The radio spectral index is assumed to be 0.7 (Jackson & Wall 2001) in an optically thin synchrotron regime.
2.3. Supermassive BH
In this paper, the BH mass for nearby LERGs was estimated using the MBH − σ* relation (Tremaine et al. 2002). The stellar velocity dispersions (σ*; see Capetti et al. 2017a,b; Baldi et al. 2018) were obtained from the MPA-JHU SDSS DR7 release of optical spectrum measurements (Abazajian et al. 2009). The BH mass was calculated using the formula log(M/M⊙) = (8.13 ± 0.06)+(4.02 ± 0.32)log(σ*/σ0), where σ0 = 200 km/s (Tremaine et al. 2002). This M − σ* relation has an intrinsic spread in log MBH (BH mass in the unit of solar mass) that is no more than 0.25–0.3 dex (Tremaine et al. 2002). The three FRCAT samples have comparable BH masses (≳107.5 M⊙)1.
The BH masses and kinetic jet powers are presented in Table 1 and are both subject to uncertainties arising from the data scatter of their defining relations (0.25 and 0.7 dex, respectively; e.g. Tremaine et al. 2002; Cavagnolo et al. 2010). Here, we used these uncertainties to broadly evaluate the consistency of the relations studied in Figs. 4 and 5 with the observed data points.
3. Jet formation mechanism
The central jet formation of AGNs is related to the spin of a BH (BZ model; Blandford & Znajek 1977) or related to the accretion disc (BP model; Blandford & Payne 1982). Some authors also suggested that a hybrid (BP-BZ) jet model could be adopted for the explanation of the jet formations (Meier 2001; Nemmen et al. 2007). Here, we calculated the kinetic jet power, and we now discuss the possible jet model mechanism for the 431 LERGs based on the self-similar solution of ADAF around a Kerr BH as follows.
(1) The Blandford-Znajek jet model
According to the BZ model, the jet power is calculated in consideration of the following formula (Nemmen et al. 2007; Wu & Cao 2008):
The ωF is a factor determined by the relation between the angular velocity of the flux (ΩF) threading the horizon and the angular velocity of the BHs (ΩH): ωF = ΩF(ΩH − ΩF)/ΩH2. The ωF = 1/2 is for the maximum power outputs (MacDonald & Thorne 1982). The c is the speed of light. The B⊥ represents the strength of the magnetic field perpendicular to the horizon and is assumed to be approximated to the poloidal component of the magnetic field (Livio 1999; Nemmen et al. 2007): B⊥ ≈ Bp(Rms)≈g(Rms)B(Rms). g is the field-enhancing shear expressed as g = Ω/Ω′. The Rms is the radius at the marginally stable orbit of the accretion disc, which is related to the BH mass and spin (Eq. (A.12)). The observer at infinity will see an angular velocity Ω = Ω′+ω with the Boyer-Lindquist coordinate system (Bardeen et al. 1972), where ω is the local space-time rotation enforced by the Kerr BH under the same system, determined as shown in Appendix A. 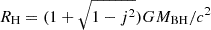 is the horizon radius (Nemmen et al. 2007), where G is the gravitational constant and j is the spin of the BH.
is the horizon radius (Nemmen et al. 2007), where G is the gravitational constant and j is the spin of the BH.
(2) The hybrid jet model
The numerical simulations of both the accretion flow and magnetic fields are the essential elements for jet productions (Meier 2001). Therefore, the jet formation mechanism can be formed via a mix of BP and BZ mechanisms. In the case of the hybrid (BP-BZ) jet model, the jet power is estimated by (Meier 2001; Nemmen et al. 2007)
in which the azimuthal component of the magnetic field is Bϕ = g(Rms)B(Rms) and the vertical half-thickness of the disc is similar to the radii in the self-similar ADAF model (Nemmen et al. 2007), H ≈ R. The relevant parameters for the above model with the self-similar solution of the ADAF model are shown in Appendix A. The radius is evaluated at the marginally stable orbit of the accretion disc: R = Rms.
4. Discussion
4.1. Jet power
In the ADAF scenario, most of the total jet power is converted into the kinetic power with the minimal radiative power (Nemmen et al. 2012; Heckman & Best 2014). In the ADAF-dominated galaxies, the total radio luminosity is used as a proxy for estimating the kinetic jet power. We estimated the kinetic jet power within the NVSS 1.4 GHz flux density by following the computations of Heckman & Best (2014) [Eq. (1)]. The cumulative distributions of jet powers for the whole 431 LERGs is shown in Fig. 2. The average kinetic jet power for FR 0s is ⟨log L0, kin⟩ = 42.93 ± 0.02 erg/s, while for FR Is it is ⟨log LI, kin⟩ = 43.86 ± 0.02 erg/s and for FR IIs, it is ⟨log LII, kin⟩ = 44.14 ± 0.03 erg/s, and they are all statistically different.
 |
Fig. 2. Cumulative distributions of the kinetic jet power for 431 low-excitation radio galaxies. The labels are the same as in Fig. 1. The kinetic jet power is derived from the NVSS 1.4 GHz kiloparsec-scale radio emissions. The average kinetic jet power for FR 0s is ⟨log L0, kin⟩ = 42.93 ± 0.02 erg/s, while for FR Is, it is ⟨log LI, kin⟩ = 43.86 ± 0.02 erg/s, and for FR IIs, it is ⟨log LII, kin⟩ = 44.14 ± 0.03 erg/s. |
4.2. Accretion rate
The division between FR Is and FR IIs is explained by the differences in host properties or accretion processes. Ledlow & Owen (1996) analysed a statistically complete sample of 188 RGs and demonstrated that FR Is and FR IIs are distinctly separated by a dividing line (Ledlow-Owen line) between the host mass and the total radio luminosity. Ghisellini & Celotti (2001) suggested that variations in central engines and accretion rates could explain this FR I-FR II dichotomy. Later, Wu & Cao (2008) used the hybrid jet model developed by Meier (2001), based on ADAFs around Kerr BHs, to calculate the maximum jet power. They found that the relationship between the jet power and BH mass predicted by the hybrid jet model (e.g. the dashed red line of the hybrid jet model in Fig. 4) is distributed similarly to the Ledlow-Owen line, assuming a standard conversion from host mass to BH mass (McLure & Dunlop 2001; Ghisellini & Celotti 2001).
To evaluate the disc properties, Wang et al. (2002) defined a line accretion rate between the total line luminosity and the Eddington luminosity:
where LEdd is the Eddington luminosity [LEdd = 1.38 × 1038(M/M⊙) erg/s]. The total line luminosity is determined by the fractional contribution of the observed line (e.g. Lyman-alpha line) to the overall line emission (Celotti et al. 1997), ⟨Lline⟩ = 5.56⟨LLyα⟩. The fractional line-emission ratio ⟨LLyα⟩:⟨L[O III]⟩ = 100 : 3.4 is presented by Francis et al. (1991) from a high signal-to-noise composite quasar spectrum. We collected the BH mass and [O III] (λ5007Å) emission for 431 LERGs (Capetti et al. 2017a,b; Baldi et al. 2018) to compute their line accretion rate (λ) and study disc properties.
The cumulative distributions of the line accretion rates (in log scale) for the 431 LERGs are presented in the upper panel of Fig. 3. The average line accretion rate for FR 0s is ⟨log λ0⟩= − 4.73 ± 0.05; for FR Is it is ⟨log λI⟩= − 4.89 ± 0.03, and that for FR IIs it is ⟨log λII⟩= − 4.64 ± 0.06. Radiatively inefficient discs, such as ADAF-type ones, are characterised by the low accretion rates (ṁ < 0.2).
 |
Fig. 3. Cumulative distributions of line accretion rate [λ = Lline/LEdd]. The line accretion rate distributions are divided into four regions that correspond to different accretion discs: (1) λ < λ1 is the pure advection-dominated accretion flows (ADAFs); (2) λ1 < λ < λ2 is the coexistence of the ADAFs and the optically thick and geometrically thin disc; (3) λ2 < λ < λ3 is the standard thin disc; (4) λ > λ3 is the super-Eddington accretion. The upper panel covers 431 low-excitation radio galaxies. The labels are the same as in Fig. 1. The lower panel is for the 75 Fermi BL Lacertae objects. The solid yellow line is for high-synchrotron-peaked BL Lacs (HBLs); the dashed purple line is for intermediate-synchrotron-peaked BL Lacs (IBLs), and the dash-dotted orange line is for low-synchrotron-peaked BL Lacs (LBLs). |
It is assumed that the narrow-line region (where the lines are measured from) is photoionised by the accretion disc2, Lline = ξLdisc, where ξ ≈ 0.1 (Netzer 1990; Ghisellini et al. 2014). In Mahadevan (1997), the total disc luminosity from an ADAF is given by 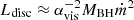 , and the dimensionless accretion rate
, and the dimensionless accretion rate 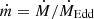 ,
, 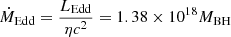 (g s−1), η = 0.1 represents the accretion efficiency (Quataert et al. 1999). Considering the relation between the disc and total emission-line luminosities (Lline = ξLdisc), the relation between the line accretion rate (λ) and the dimensionless accretion rate (ṁ) for the optically thin ADAFs can be expressed as follows (Wang et al. 2002):
(g s−1), η = 0.1 represents the accretion efficiency (Quataert et al. 1999). Considering the relation between the disc and total emission-line luminosities (Lline = ξLdisc), the relation between the line accretion rate (λ) and the dimensionless accretion rate (ṁ) for the optically thin ADAFs can be expressed as follows (Wang et al. 2002):
where α0.3 = αvis/0.3, αvis is the viscosity parameter, λ−4 = λ/10−4, and ξ−1 = ξ/0.1.
The ADAFs are thought to follow 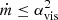 (Quataert et al. 1999). Therefore, λ1 could be rewritten as
(Quataert et al. 1999). Therefore, λ1 could be rewritten as
Optically thin ADAFs require λ < λ1. The optically thick, geometrically thin disc (SS) obeys (Wang et al. 2003)
and the condition 1 > ṁ ≥ α2 gives
A standard thin disc satisfies λ ≥ λ2 (Wang et al. 2003). When the dimensionless accretion rate reaches 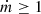 , we have
, we have
A slim disc requires λ ≥ λ3 (Wang et al. 2003), namely super-Eddington accretion. The region between λ1 and λ2 is considered a transition zone where both ADAFs and thin discs can coexist (Quataert et al. 1999; Ho et al. 2000).
The corresponding boundaries are strongly influenced by the viscosity parameter αvis. Advection models have been successful in explaining BH candidates with αvis values in the 0.1 − 0.3 range (Narayan et al. 1995); the ADAF model for X-ray binaries with BH candidates requires αvis ≈ 0.25 to match observations (Quataert et al. 1999). Following Narayan & Yi (1995), Mahadevan (1997), Wang et al. (2002), and Nemmen et al. (2007), we adopted αvis = 0.3 to analyse the accretion scenarios. The boundaries for λ are marked by the green dashed lines in Fig. 3. All LERGs but one (SDSS J122640.22+253855.5 – z = 0.134 – falls between the λ1 and λ2 boundaries) lie below the λ1 boundary, suggesting that pure ADAFs dominate their central regions. The K-S tests reveal differences in accretion distributions among FR 0s, FR Is, and FR IIs, which each pair with p < 0.09.
4.3. Accretion-ejection paradigm
Considering the distributions of line accretion rates, most LERGs fall into the pure ADAF region where ṁ < λ1. Based on this, we explored the BZ and BP-BZ hybrid jet mechanisms for LERGs within the framework of ADAFs around the Kerr BH. The BP model is generally associated with an AGN with a bright disc (Rawlings & Saunders 1991); however, the only BP model is not considered because there is no evidence of luminous disc emissions in the LERG population in general (Hardcastle et al. 2009; Baldi et al. 2010; Best & Heckman 2012).
We adopted αvis = 0.3 for the hybrid jet power calculation, as this value aligns with magnetohydrodynamic simulations in the Kerr metric (Wu & Cao 2008). In fact, two different values of the viscosity parameter, αvis = 0.1 and 0.3, would have a negligible effect on the jet powers estimated from both the BZ and hybrid jet models (Δlog Lkin ∼ 0.1 erg/s) for a given BH mass (log MBH = 8) and accretion rate (ṁ = 0.01; Wu & Cao 2008). A maximal BH spin of 0.998 (Thorne 1974) and ṁ = 0.01 were adopted to compute the maximum jet powers (see Appendix A). Additionally, in the ADAF-dominated sources, the estimated magnetic-field strength (Bp ≈ B⊥) near the BH is of the order of kGauss for BH masses (log MBH) between 8 and 9 (see Appendix A.2), which is consistent with estimated values for FR Is (Blandford et al. 2019; Kino et al. 2022, 2024).
The jet powers are expected to depend on both the spin of the BH, the magnetic field, and the structure of the accretion disc. If the radio jet is powered by a rotating BH accreting from a magnetised plasma, this mechanism extracts rotational energy from the magnetic-field lines threading the spinning BH, in which the relation between the BZ jet power and the strength of the magnetic field perpendicular to the horizon (B⊥) satisfies that 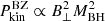 (Frank et al. 1992). This implies that more massive and highly magnetised BHs can generate stronger jets, with the efficiency mainly depending on the spin of the BH. On the other hand, when the radio jet power is contributed by both a rotating accretion disc and BH via magnetic fields anchored inside and outside the ergosphere, the jet power is related to the azimuthal component of the magnetic field (Bϕ) and BH mass, following the relation
(Frank et al. 1992). This implies that more massive and highly magnetised BHs can generate stronger jets, with the efficiency mainly depending on the spin of the BH. On the other hand, when the radio jet power is contributed by both a rotating accretion disc and BH via magnetic fields anchored inside and outside the ergosphere, the jet power is related to the azimuthal component of the magnetic field (Bϕ) and BH mass, following the relation 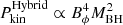 , in which H ∼ R for ADAF-dominated sources.
, in which H ∼ R for ADAF-dominated sources.
The relationship between the jet power and BH mass is presented in the upper panel of Fig. 4. The solid black line is for the maximum output of BZ jet model, while the dashed red line is for the maximum output of BP-BZ hybrid model. Around 99% (103/104) of FR 0s lie below the pure BZ line, suggesting that the jet powers of FR 0s are most likely explained by the BZ mechanism, although an explanation from the BP-BZ hybrid mechanism cannot be entirely excluded (e.g. spine-sheath jet structure; see Baldi 2023 and references therein). Notably, we disfavour the BP mechanism for FR 0s because there are no signatures of bright, standard, thin discs in FR 0s based on the X-ray properties (Torresi et al. 2018). Therefore, conservatively, the BZ-based jet coupled with an ADAF-type disc is more in agreement with the general radio and X-ray characteristics of FR 0s.
 |
Fig. 4. Kinetic jet power versus black holes. (1) Upper panel: 431 low-excitation radio galaxies. The black triangle is for FR 0s, the red circle is for FR Is, and the blue diamond is for FR IIs. (2) Lower panel: 75 Fermi BL Lacertae objects. The yellow triangle is for LBLs, the purple square is for IBLs, and the green pentagon is for HBLs. Their intrinsic kinetic jet power is obtained assuming a Doppler factor of δ ∼ 10 within the continuous jet model (p = 2 + α) and the flat spectral index (α = 0). The solid black line is for the maximum jet power in the Blandford-Znajek (BZ) jet model; the dashed red line is the mixture (hybrid) of the BZ and Blandford-Payne jet models; the average uncertainty for BH mass is 0.25 dex, and the average jet power uncertainty is 0.7 dex. |
Compelling, multi-band, observational evidence points to the presence of an ADAF disc at the centre of FR Is (e.g. Chiaberge et al. 1999; Balmaverde et al. 2006; Hardcastle et al. 2007; He et al. 2024). Cao & Rawlings (2004) proposed that the BZ mechanism alone does not provide enough power to explain the high radio jet power for at least a third of the FR Is in their sample. In this work, we found that ∼99% FR Is (218/219) fall below the BP-BZ hybrid line, with 146 of these 218 FR Is also falling below the BZ line. This suggests that the BZ mechanism by itself cannot explain the all FR I sample and that a mix of pure BZ and BP-BZ jet mechanisms and/or higher magnetic intensity could reduce the tension with the results, as seen by Cao & Rawlings (2004).
However, only 23 of 108 FR IIs fall below the BZ jet model line, indicating that the jet power of the majority of FR IIs cannot be explained by the pure BZ model; almost half of the sample of FR IIs (58/108) are located between the BZ and hybrid lines; their accretion disc may contribute to supporting their jets and explain their kinetic jet power. Additionally, 27 out of 108 FR IIs lie above the BP-BZ hybrid jet power line. The BP-BZ hybrid jet mechanism and the ADAF scenario are not able to explain the higher jet power for at least a third of the FR II sample. The higher jet power may be explained by the magnetisation-driven outflows from the accretion disc (Cao & Spruit 2013). Cao (2018) compared the jet powers of blazars with the BZ and BP jet mechanisms and stated that the maximal jet powers from both BZ and BP models are always insufficient to explain the strong jets in some blazars. Therefore, the author proposed that large magnetic fields dragged inwards by the accretion disc with magnetized outflows may support and accelerate the jets and explain their high kinetic powers. Analogously, this mechanism may account for the high jet luminosities observed in some BL Lacs (Chen et al. 2023), as well as in this subset of FR IIs.
Even though the higher jet power in some FR Is and FR IIs could be explained by the hybrid BP-BZ mechanisms and/or the magnetisation-driven outflows; however, the observed spread of the jet powers among FR 0s, FR Is, and FR IIs could also be explained by the differences in either BH spins or magnetic-field intensities under the framework of the BZ jet mechanism (Grandi et al. 2021). Both the BZ and the hybrid BP-BZ jet power are proportional to the BH mass, BH spin, and magnetic field, but the dynamic range of BH spin values (0-1) is much smaller than the observed range of magnetic fields involved in the jet (some orders of magnitudes3). Therefore, since BH masses among the various FR classes are similar, it is natural to expect that the magnetic field might be the main ingredient supporting the most powerful jets (Nemmen et al. 2007). Unfortunately, accurately estimating the magnetic field is challenging, and how the magnetic fields evolve in the jet base among FR 0s, FR Is, and FR IIs is unclear. Figure 4 shows the maximum BZ (solid black line) jet power for a jet with maximised BH spin (j = 0.998) by considering the magnetic field at the marginally stable orbit of the accretion disc. If we assume that FR 0s, FR Is, and FR II LERGs consist of a single population of RGs with a continuous distribution of properties, which share the same BZ jet mechanism (Baldi 2023), a gradual increase of the magnetic field of the jet base could lead to a gradual increase of the jet power across the FR 0-FR I-FR II LERG population. In fact, the lower magnetic-field intensity in FR 0s compared to FR Is has been invoked to justify the failure to develop a powerful jet for the former (Grandi et al. 2021; Baldi 2023), and the stronger magnetic field in FR IIs compared to FR Is has instead been invoked to account for different SED fitting with a synchrotron self-Compton model (Xue et al. 2017) or different accretion-ejection efficiencies (Grandi et al. 2021).
4.4. Unification scenario
The unified scheme for blazars and RGs has been studied for decades (e.g. Urry & Padovani 1995). BL Lacs are suggested to be the beamed populations of FR Is, and FSRQs are the beamed populations of FR IIs (Padovani 1992; Ghisellini et al. 1993; Xie et al. 1993; Urry & Padovani 1995; Chiaberge et al. 2000). The accretion-rate separations for blazars are discussed in Ghisellini et al. (2011) and Sbarrato et al. (2012). BL Lacs exhibit lower jet powers and accretion rates, clearly separating them from FSRQs. An accretion-based unification of blazars and RGs is discussed in the works (Xu et al. 2009; Sbarrato et al. 2014; Chen et al. 2015a). If blazars are RGs viewed from a small jet viewing angle, they should share similar accretion discs and jet formation mechanisms.
Thanks to the Fermi Large Area Telescope (LAT), 3814 AGNs were observed in the latest LAT 12-year source catalogue (4FGL-DR3; Ajello et al. 2022). Yang et al. (2022a) compiled a large sample of 2709 Fermi-LAT blazars with multi-band data and fitted the first peak of the SED with a parabolic equation to discuss their jet properties and acceleration mechanisms. Based on the Bayesian classification of the synchrotron peak frequencies, they classified the BL Lacs into low-, intermediate-, and high-synchrotron-peaked BL Lacs (analogously to blazar classifications, see Sect. 1). Because some BL Lacs exhibited broad emission lines, akin to FSRQs (Ghisellini et al. 2011), Paliya et al. (2021) divided a Fermi sample of 1077 blazars into emission- and absorption-line blazars based on the optical spectroscopic information. They presented a negative tendency of Fermi blazars between the disc accretion rate (Ldisc/LEdd) and synchrotron peak frequency (νpeak). The majority of emission-line blazars are predominantly low-synchrotron-peaked sources (e.g. FSRQs and LBLs) and are characterised by broad emission lines and high disc accretion rates, whereas absorption-line blazars, are predominantly intermediate- or high-synchrotron-peaked sources (e.g. IBLs and HBLs) exhibiting prominent absorption lines and low disc accretion rates (Paliya et al. 2021).
For a consistent comparison to LERGs, we compiled a redshift-limited (z < 0.15) sample of 75 Fermi absorption-line BL Lacs (61 HBLs, 11 IBLs, and 3 LBLs) with observed 1.4 GHz radio luminosities and synchrotron-peak classifications from Yang et al. (2022a) and disc luminosities4 and BH mass estimations (from the stellar velocity dispersion5) from Paliya et al. (2021). Given the Doppler-beaming effect in radio jets, the intrinsic radio luminosity for BL Lacs follows – log Lin = log Lob − plog δ – where p = 2 + α is for a continuous jet model, and p = 3 + α is for a spherical jet model (Urry & Padovani 1995). The kinetic jet power for BL Lacs was calculated using Eq. (1), with the intrinsic radio luminosity based on an average Doppler factor of δ ≈ 10 (Liodakis et al. 2018; Homan et al. 2021) in the case of a continuous jet model (p = 2 + α) with a flat spectral index (α = 0; see e.g. Capetti et al. 2002a). All the parameters are presented in Table 1.
Figure 5 depicts the kinetic jet powers for our LERG sample and 75 Fermi BL Lacs, which all fall below the line of Lkin = 0.01LEdd; this is in agreement with the results of Ghisellini & Celotti (2001) and Xu et al. (2009). LERGs and BL Lacs are both expected to have low-accretion sources. Therefore, we computed the line accretion rate (λ) for BL Lacs [Eq. (5)]. The cumulative distributions of λ for our BL Lac sample are shown in the lower panel of Fig. 3. The line accretion rates for 75 BL Lacs are smaller than the boundary of λ1, suggesting that the central discs for the absorption-line BL Lacs (mostly HBLs) are dominated by ADAFs.
 |
Fig. 5. Kinetic jet powers versus black holes with the lines of the Lkin = LEdd (black solid line) and Lkin = 0.01LEdd (red dotted line). (1) Upper panel: is for 431 low-excitation radio galaxies; (2) the lower panel is for 75 Fermi BL Lacertae objects. The labels are the same as in Fig. 4. |
Our results agree with previous studies on BL Lacs. i) Chen et al. (2023), studying the accretion properties of the BL Lac sample from Paliya et al. (2021), found that IBLs and HBLs are in the optically thin ADAF state. ii) Zhao et al. (2024), studying the energy budget in the jets of a sample of 348 Fermi HBLs, concluded that HBLs may have optically thin ADAFs in their centres due to their very low radiation efficiency. A larger and more complete sample of IBLs and LBLs is needed to robustly compare the accretion properties with LERGs.
When discussing the relationship between kinetic jet powers and BH mass, and considering the jet mechanism for BL Lacs, the intrinsic jet power for 75 BL Lacs (mostly HBLs) can be explained by the BZ mechanisms (Fig. 4). Based on our results, the BZ model appears sufficient to justify the kinetic jet power for the absorption-line BL Lacs (mostly HBLs). However, due to the limited number of LBLs and IBLs in the sample, a solid conclusion cannot be drawn for these sub-classes. In summary, our results and previous results indicate a possible affinity between HBLs and low-ṁ RGs.
4.4.1. FR 0 LERGs and BL Lacs
On one hand, compact radio sources hosted in red, massive, early-type galaxies have been named as FR 0 RGs (Sadler et al. 2014; Baldi et al. 2016). The nuclei of these FR 0s show evidence of an ADAF-dominated disc and are classified as LERGs (Torresi et al. 2018; Baldi et al. 2019b; Baldi 2023). On the other hand, LERGs and HERGs are proposed to be the parent populations for BL Lacs and FSRQs, respectively (Laing et al. 1994; Giommi et al. 2012). As a sub-class of LERGs, FR 0s are expected to align with the unified scheme for BL Lacs.
In line with this scenario, Massaro et al. (2020), studying the cluster richness difference between BL Lacs and RGs, noted that the large-scale environmental properties of 14 nearby BL Lacs are statistically consistent with those of FR 0s, suggesting that FR 0s could be the parent population of the BL Lacs. In addition, both FR 0s and BL Lacs share similar intrinsically low jet powers that weaker than those of their relative RG ’cousins’, FR I-IIs and FSRQs.
Furthermore, we cross-checked the 14 nearby BL Lacs of Massaro et al. (2020) with the synchrotron classification of Yang et al. (2022a), and 11 of 14 are matched within the name and the redshift. The synchrotron classification and the synchrotron peak value for the 11 BL Lacs are listed in (4) and (5) of Table 2. 10/11 BL Lacs are classified as HBLs with the frequency range of log νpeak = 15.5 − 17.3 Hz. Meanwhile, one BL Lac (5BZBJ1203+6031) falls into the classification of IBL with a synchrotron peak of log νpeak = 14.8 Hz, which is close to the high-synchrotron-peaked boundary (log νpeak = 14.9 Hz, Yang et al. 2022a). These results support that the HBLs may reasonably be regarded as the beamed counterparts of nearby FR 0s: both of their centres are dominated by the ADAFs (low-ṁ in general) hosted in early-type galaxies, their jet powers can be explained by the BZ mechanism, and they share the similar large-scale environments (Massaro et al. 2020).
Physical parameters for 14 nearby (z < 0.15) BL Lacertae objects from Massaro et al. (2020).
4.4.2. FR I-II LERGs and BL Lacs
Concerning the FR I LERGs, the classical unification between FR Is and BL Lacs has been discussed for decades (Padovani 1992; Xie et al. 1993; Urry & Padovani 1995; Capetti & Celotti 1999; Chen et al. 2015b). However, the beamed counterparts of FR Is may not belong to a single sub-class of BL Lacs (Meyer et al. 2011). Giroletti et al. (2004) found that BL Lacs, particularly HBLs, have intrinsic core radio powers similar to those of FR Is. In a study of a large sample of radio-loud AGNs, Meyer et al. (2011) explored the blazar sequence envelope and its unification. They identified two populations on the νpeak − Lpeak plane: a strong-jet population, consisting of FSRQs and high-power LBLs, which will evolve into FR IIs as the jet viewing angle increases; and a weak-jet population, including IBLs, HBLs, and low-power LBLs, which are expected to evolve into the FR I population as the jet viewing angle increases (e.g. the Fig. 4 and Table 4 of Meyer et al. 2011). In this unification scheme, a stratified jet structure (fast jet spine and a slower layer, Ghisellini et al. 2005; Boughelilba et al. 2023) common to FR Is and BL Lacs would explain their different observed multi-band properties (Chiaberge et al. 2000; Capetti et al. 2002b); a mix of HBLs and LBLs could be the parental population of FR I LERGs (Bai & Lee 2001).
For FR II LERGs, unfortunately, the attempts for a unification with BL Lacs remains in uncharted territory because of the limitation of the data, sample completeness, and homogeneity (or clustering properties, e.g. Pesce et al. 1993; Falomo et al. 1993; Muriel 2016). Some studies showed that the LBLs with intrinsic jet power (log Lkin > 44.6 erg/s), comparable to those of FSRQs, and weak lines could be the beamed counterpart of the FR II LERG population (Giommi et al. 2012; Fan & Wu 2019). These LBLs (assuming the BH mass, log MBH, ranges from 8 to 9.5) cannot be completely explained by the hybrid jet model with the minimum required magnetic field (e.g. red dashed line in Fig. 4), but a magnetisation-driven outflow may account for their intrinsic jet power, as observed in some BL Lacs with high jet power (Cao 2018; Chen et al. 2023), which is similar to our study of one-third of the FR II LERG sub-sample.
The common characteristics that may point to a kinship between the LERG and BL Lac populations in general can be summarised as follows: a similar low-accretion mode (ADAF type) and lack of evidence of a luminous standard accretion disc (e.g. no broad emission lines), low intrinsic jet power explained by a BZ model, and generally rich megaparsec-scale environment (e.g. Gendre et al. 2013; Massaro et al. 2019, 2020). In line with this commonality, Mooney et al. (2021) found that the size and luminosity distribution of the extended radio emission at 144 MHz of BL Lacs are consistent with expectations based on the AGN unification paradigm, as they are the aligned counterparts of LERGs. However, a more statistically robust multi-band analysis on flux-limited samples of FR I-FR II LERGs and BL Lacs is needed to draw a solid conclusion on their affinity. This tentative unification, however, does not consider the life cycle of RG populations (e.g. FR II LERGs might evolve from HERGs, Tadhunter 2016; Macconi et al. 2020), which complicates this scenario further.
This proposed unifying scenario would reconcile with the cooling model as an explanation for the blazar sequence, in which the blazars with the stronger (intrinsic) jet power would display the lower synchrotron peak spectrum because of the strong cooling effect (Ghisellini et al. 1998; Prandini & Ghisellini 2022). While for the higher (intrinsic) jet power in FR IIs the stronger cooling effect will make the jet particles lose more energy and make their synchrotron peak frequencies of the beamed counterparts of FR IIs fall in the lower frequency part, which, ideally, is expected to be more populated by LBLs (Capetti et al. 2002b).
5. Conclusions
We compiled a sample of 431 LERGs with available 1.4 GHz radio and emission-line luminosities and BH masses to investigate their accretion discs and jet formation mechanisms. We also compared the accretion properties of 75 Fermi BL Lacs with those of the 431 LERGs. We come to the following conclusions:
-
There is a sequence of kinetic jet powers from FR 0s to FR Is and FR IIs, with FR 0s having an order of magnitude smaller kinetic jet power than FR Is and FR IIs.
-
Almost all the line accretion rates for LERGs are below the pure ADAF disc boundary (λ < λ1), supporting the idea that LERGs have ADAF-dominated flows.
-
Considering ADAFs surrounding Kerr BHs, we computed the maximum jet power for the BZ and the BP-BZ hybrid jet models and found that the kinetic jet power of FR 0s can be explained by the pure BZ model. The kinetic jet power of FR Is can be explained by both the BZ model and the BP-BZ hybrid jet models, whereas the kinetic jet power for about one third of FR IIs could not be explained by the BP-BZ hybrid model. The possible explanations are that the high jet power for this third of the FR II sub-sample could be explained by a magnetisation-driven outflow from the accretion disc, or it could be covered by the BZ jet model if we considered a more intense magnetic field, as indicated in Grandi et al. (2021).
-
Both BL Lacs (predominantly HBLs) and LERGs are below the
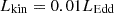 , and their centres are likely dominated by ADAFs. By cross-checking the BL Lac sample of Massaro et al. (2020) and SED classification (Yang et al. 2022a), 11 out of 14 BL Lacs are confirmed as high-synchrotron-peaked BL Lacs. Several arguments support the notion that the high-frequency-peaked BL Lacs (i.e. HBLs) could be the beamed counterparts of FR 0s, reinforcing the cooling model as an explanation for the blazar sequence.
, and their centres are likely dominated by ADAFs. By cross-checking the BL Lac sample of Massaro et al. (2020) and SED classification (Yang et al. 2022a), 11 out of 14 BL Lacs are confirmed as high-synchrotron-peaked BL Lacs. Several arguments support the notion that the high-frequency-peaked BL Lacs (i.e. HBLs) could be the beamed counterparts of FR 0s, reinforcing the cooling model as an explanation for the blazar sequence. -
We tentatively propose a possible unification between the LERG population and BL Lacs, based on currently available partial results; HBLs, IBLs, high-power LBLs could be the beamed counterparts of the whole LERG population, embracing different radio morphological classes FR 0, FR I, and FR II.
On one hand, the LERG population (FR 0s, FR Is, and FR IIs) show observational evidence of establishing a single continuous population, with similar BH masses, galaxy types, accretion properties, and environments, regardless of their different jet morphologies (Baldi 2023). On the other hand, BL Lacs show more affinity with the LERG population rather than with HERG, which we highlight with this work. However, a comprehensive study with a more complete BL Lac sample would provide more robust results regarding the accretion-based unification between BL Lacs and LERGs.
Data availability
Full Table 1 is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/697/A176
Apart from three FR II LERGs with MBH< 107.5 M⊙ that could represent a non-negligible radio-quiet AGN contamination in the sample (Chiaberge & Marconi 2011).
Although a possible jet contribution photoionising the medium is not negligible (e.g. Capetti et al. 2005).
A wide range of magnetic-field intensities are observed in RGs ranging (as B ∼ r−1) from the central engine to the jet, from kGauss to tens of μGauss (e.g. Dallacasa et al. 2002; Croston et al. 2005; Stawarz et al. 2005; Stawarz & Kataoka 2005; Bruni et al. 2013; Orienti et al. 2020; Kino et al. 2022, 2024).
log(M/M⊙) = (8.12 ± 0.08)+(4.24 ± 0.41)×log(σ*/200 km s−1), Gültekin et al. (2009).
Acknowledgments
We greatly appreciate the comments from the anonymous referee, which have helped us improve the manuscript. The work is partially supported by the National Natural Science Foundation of China (NSFC 12433004, U2031201, NSFC 11733001), the Eighteenth Regular Meeting Exchange Project of The Scientific and Technological Cooperation Committee between the People’s Republic of China and the Republic of Bulgaria (Series No. 1802). We also acknowledge the science research grants from the China Manned Space Project with NO. CMS-CSST-2021-A06, and the support for Astrophysics Key Subjects of Guangdong Province. R.D.B. acknowledges financial support from INAF mini-grant “FR0 radio galaxies” (Bando Ricerca Fondamentale INAF 2022). This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. X. H. Ye acknowledges the support (NO.202208440164) from the Chinese Scholarship Council.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [Google Scholar]
- Ajello, M., Baldini, L., Ballet, J., et al. 2022, ApJS, 263, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, J. M., & Lee, M. G. 2001, ApJ, 548, 244 [Google Scholar]
- Baldi, R. D. 2023, A&A Rev., 31, 3 [Google Scholar]
- Baldi, R. D., Chiaberge, M., Capetti, A., et al. 2010, ApJ, 725, 2426 [NASA ADS] [CrossRef] [Google Scholar]
- Baldi, R. D., Capetti, A., & Giovannini, G. 2015, A&A, 576, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldi, R. D., Capetti, A., & Giovannini, G. 2016, AN, 337, 114 [Google Scholar]
- Baldi, R. D., Capetti, A., & Massaro, F. 2018, A&A, 609, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldi, R. D., Capetti, A., & Giovannini, G. 2019a, MNRAS, 482, 2294 [NASA ADS] [CrossRef] [Google Scholar]
- Baldi, R. D., Torresi, E., Migliori, G., & Balmaverde, B. 2019b, Galaxies, 7, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Balmaverde, B., Capetti, A., & Grandi, P. 2006, A&A, 451, 35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balmaverde, B., Baldi, R. D., & Capetti, A. 2008, A&A, 486, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [Google Scholar]
- Bennett, A. S. 1962, MmRAS, 68, 163 [NASA ADS] [Google Scholar]
- Best, P. N., & Heckman, T. M. 2012, MNRAS, 421, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Bicknell, G. V., & Begelman, M. C. 1999, in The Radio Galaxy Messier 87, eds. H. J. Röser, & K. Meisenheimer (New York: Springer), 530, 235 [Google Scholar]
- Bîrzan, L., Rafferty, D. A., McNamara, B. R., Wise, M. W., & Nulsen, P. E. J. 2004, ApJ, 607, 800 [Google Scholar]
- Bîrzan, L., McNamara, B. R., Nulsen, P. E. J., Carilli, C. L., & Wise, M. W. 2008, ApJ, 686, 859 [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Boehringer, H., Voges, W., Fabian, A. C., Edge, A. C., & Neumann, D. M. 1993, MNRAS, 264, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Boughelilba, M., Reimer, A., Merten, L., & Lundquist, J. P. 2023, arXiv e-prints [arXiv:2308.10596] [Google Scholar]
- Bruni, G., Dallacasa, D., Mack, K. H., et al. 2013, A&A, 554, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buttiglione, S., Capetti, A., Celotti, A., et al. 2010, A&A, 509, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, X. 2018, MNRAS, 473, 4268 [Google Scholar]
- Cao, X., & Rawlings, S. 2004, MNRAS, 349, 1419 [Google Scholar]
- Cao, X., & Spruit, H. C. 2013, ApJ, 765, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Capetti, A., & Celotti, A. 1999, MNRAS, 304, 434 [Google Scholar]
- Capetti, A., Celotti, A., Chiaberge, M., et al. 2002a, A&A, 383, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capetti, A., Trussoni, E., Celotti, A., Feretti, L., & Chiaberge, M. 2002b, New A Rev., 46, 335 [Google Scholar]
- Capetti, A., Verdoes Kleijn, G., & Chiaberge, M. 2005, A&A, 439, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capetti, A., Massaro, F., & Baldi, R. D. 2017a, A&A, 598, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capetti, A., Massaro, F., & Baldi, R. D. 2017b, A&A, 601, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capetti, A., Brienza, M., Baldi, R. D., et al. 2020, A&A, 642, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavagnolo, K. W., McNamara, B. R., Nulsen, P. E. J., et al. 2010, ApJ, 720, 1066 [Google Scholar]
- Celotti, A., Padovani, P., & Ghisellini, G. 1997, MNRAS, 286, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Zhang, X., Zhang, H., et al. 2015a, Ap&SS, 357, 100 [Google Scholar]
- Chen, Y.-Y., Zhang, X., Xiong, D., & Yu, X. 2015b, AJ, 150, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y., Gu, Q., Fan, J., et al. 2023, MNRAS, 526, 4079 [Google Scholar]
- Cheng, X. P., & An, T. 2018, ApJ, 863, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, X., An, T., Sohn, B. W., Hong, X., & Wang, A. 2021, MNRAS, 506, 1609 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., & Marconi, A. 2011, MNRAS, 416, 917 [Google Scholar]
- Chiaberge, M., Capetti, A., & Celotti, A. 1999, A&A, 349, 77 [NASA ADS] [Google Scholar]
- Chiaberge, M., Celotti, A., Capetti, A., & Ghisellini, G. 2000, A&A, 358, 104 [NASA ADS] [Google Scholar]
- Cid Fernandes, R., Stasińska, G., Schlickmann, M. S., et al. 2010, MNRAS, 403, 1036 [Google Scholar]
- Condon, J. J., & Dressel, L. L. 1978, ApJ, 221, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Hardcastle, M. J., Harris, D. E., et al. 2005, ApJ, 626, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Dallacasa, D., Tinti, S., Fanti, C., et al. 2002, A&A, 389, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falcke, H., Körding, E., & Nagar, N. M. 2004, New Astron. Rev., 48, 1157 [Google Scholar]
- Falomo, R., Pesce, J. E., & Treves, A. 1993, ApJ, 411, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X.-L., & Wu, Q. 2019, ApJ, 879, 107 [Google Scholar]
- Fan, J. H., Yang, J. H., Liu, Y., et al. 2016, ApJS, 226, 20 [CrossRef] [Google Scholar]
- Fan, J. H., Kurtanidze, S. O., Liu, Y., et al. 2021, ApJS, 253, 10 [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Fossati, G., Maraschi, L., Celotti, A., Comastri, A., & Ghisellini, G. 1998, MNRAS, 299, 433 [Google Scholar]
- Francis, P. J., Hewett, P. C., Foltz, C. B., et al. 1991, ApJ, 373, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. 1992, in Accretion power in astrophysics, Camb. Astrophys. Ser., 21 [Google Scholar]
- Gendre, M. A., Best, P. N., Wall, J. V., & Ker, L. M. 2013, MNRAS, 430, 3086 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., & Celotti, A. 2001, A&A, 379, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Padovani, P., Celotti, A., & Maraschi, L. 1993, ApJ, 407, 65 [Google Scholar]
- Ghisellini, G., Celotti, A., Fossati, G., Maraschi, L., & Comastri, A. 1998, MNRAS, 301, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401 [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., & Ghirlanda, G. 2011, MNRAS, 414, 2674 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Maraschi, L., Celotti, A., & Sbarrato, T. 2014, Nature, 515, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Giommi, P., Padovani, P., Polenta, G., et al. 2012, MNRAS, 420, 2899 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannini, G., Baldi, R. D., Capetti, A., Giroletti, M., & Lico, R. 2023, A&A, 672, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giroletti, M., Giovannini, G., Taylor, G. B., & Falomo, R. 2004, ApJ, 613, 752 [Google Scholar]
- Grandi, P., Torresi, E., Macconi, D., Boccardi, B., & Capetti, A. 2021, ApJ, 911, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [Google Scholar]
- Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2009, MNRAS, 396, 1929 [NASA ADS] [CrossRef] [Google Scholar]
- He, H., You, B., Jiang, N., et al. 2024, MNRAS, 530, 530 [Google Scholar]
- Heckman, T. M., & Best, P. N. 2014, ARA&A, 52, 589 [Google Scholar]
- Ho, L. C., Rudnick, G., Rix, H.-W., et al. 2000, ApJ, 541, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Cohen, M. H., Hovatta, T., et al. 2021, ApJ, 923, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, C. A., & Wall, J. V. 2001, ASP Conf. Ser., 250, 400 [Google Scholar]
- Keenan, M., Meyer, E. T., Georganopoulos, M., Reddy, K., & French, O. J. 2021, MNRAS, 505, 4726 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., & Pauliny-Toth, I. I. K. 1981, ARA&A, 19, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [Google Scholar]
- Kino, M., Takahashi, M., Kawashima, T., et al. 2022, ApJ, 939, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kino, M., Ro, H., Takahashi, M., et al. 2024, ApJ, 973, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Laing, R. A., Jenkins, C. R., Wall, J. V., & Unger, S. W. 1994, ASP Conf. Ser., 54, 201 [NASA ADS] [Google Scholar]
- Ledlow, M. J., & Owen, F. N. 1996, AJ, 112, 9 [Google Scholar]
- Li, Y., Wang, D. X., & Gan, Z. M. 2008, A&A, 482, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, J., Zeng, X., Chen, G., et al. 2023, PASP, 135, 084103 [Google Scholar]
- Liodakis, I., Hovatta, T., Huppenkothen, D., et al. 2018, ApJ, 866, 137 [Google Scholar]
- Liodakis, I., Marscher, A. P., Agudo, I., et al. 2022, Nature, 611, 677 [CrossRef] [Google Scholar]
- Livio, M. 1999, Phys. Rep., 311, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Macconi, D., Torresi, E., Grandi, P., Boccardi, B., & Vignali, C. 2020, MNRAS, 493, 4355 [NASA ADS] [CrossRef] [Google Scholar]
- MacDonald, D., & Thorne, K. S. 1982, MNRAS, 198, 345 [Google Scholar]
- Mahadevan, R. 1997, ApJ, 477, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, F., Álvarez-Crespo, N., Capetti, A., et al. 2019, ApJS, 240, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, F., Capetti, A., Paggi, A., et al. 2020, ApJ, 900, L34 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Dunlop, J. S. 2001, MNRAS, 327, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Meier, D. L. 2001, ApJ, 548, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, E. T., Fossati, G., Georganopoulos, M., & Lister, M. L. 2011, ApJ, 740, 98 [Google Scholar]
- Mingo, B., Croston, J. H., Best, P. N., et al. 2022, MNRAS, 511, 3250 [NASA ADS] [CrossRef] [Google Scholar]
- Mooney, S., Massaro, F., Quinn, J., et al. 2021, ApJS, 257, 30 [Google Scholar]
- Muriel, H. 2016, A&A, 591, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Yi, I., & Mahadevan, R. 1995, Nature, 374, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Nemmen, R. S., Bower, R. G., Babul, A., & Storchi-Bergmann, T. 2007, MNRAS, 377, 1652 [Google Scholar]
- Nemmen, R. S., Georganopoulos, M., Guiriec, S., et al. 2012, Science, 338, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 1990, in Active Galactic Nuclei, eds. R. D. Blandford, H. Netzer, L. Woltjer, T. J. L. Courvoisier, & M. Mayor, 57 [Google Scholar]
- Nieppola, E., Valtaoja, E., Tornikoski, M., Hovatta, T., & Kotiranta, M. 2008, A&A, 488, 867 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Dea, C. P., & Saikia, D. J. 2021, A&A Rev., 29, 3 [CrossRef] [Google Scholar]
- Orienti, M., Migliori, G., Brunetti, G., et al. 2020, MNRAS, 494, 2244 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, F. N., & Ledlow, M. J. 1994, ASP Conf. Ser., 54, 319 [NASA ADS] [Google Scholar]
- Padovani, P. 1992, A&A, 256, 399 [NASA ADS] [Google Scholar]
- Paliya, V. S., Domínguez, A., Ajello, M., Olmo-García, A., & Hartmann, D. 2021, ApJS, 253, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Z., Fan, J., Bastieri, D., Yang, J., & Xiao, H. 2020, SCPMA, 63, 259511 [Google Scholar]
- Pesce, J. E., Falomo, R., & Treves, A. 1993, Am. Astron. Soc. Meeting Abstr., 183, 107.01 [Google Scholar]
- Prandini, E., & Ghisellini, G. 2022, Galaxies, 10, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Quataert, E., Di Matteo, T., Narayan, R., & Ho, L. C. 1999, ApJ, 525, L89 [CrossRef] [Google Scholar]
- Rafferty, D. A., McNamara, B. R., Nulsen, P. E. J., & Wise, M. W. 2006, ApJ, 652, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Rawlings, S., & Saunders, R. 1991, Nature, 349, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Sadler, E. M., Ekers, R. D., Mahony, E. K., Mauch, T., & Murphy, T. 2014, MNRAS, 438, 796 [Google Scholar]
- Sbarrato, T., Ghisellini, G., Maraschi, L., & Colpi, M. 2012, MNRAS, 421, 1764 [Google Scholar]
- Sbarrato, T., Padovani, P., & Ghisellini, G. 2014, MNRAS, 445, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Scheuer, P. A. G. 1974, MNRAS, 166, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Spinrad, H., Djorgovski, S., Marr, J., & Aguilar, L. 1985, PASP, 97, 932 [CrossRef] [Google Scholar]
- Stawarz, Ł., & Kataoka, J. 2005, in 22nd Texas Symposium on Relativistic Astrophysics, eds. P. Chen, E. Bloom, G. Madejski, & V. Patrosian, 471 [Google Scholar]
- Stawarz, Ł., Siemiginowska, A., Ostrowski, M., & Sikora, M. 2005, ApJ, 626, 120 [Google Scholar]
- Stickel, M., Padovani, P., Urry, C. M., Fried, J. W., & Kuehr, H. 1991, ApJ, 374, 431 [Google Scholar]
- Strauss, M. A., Weinberg, D. H., Lupton, R. H., et al. 2002, AJ, 124, 1810 [Google Scholar]
- Tadhunter, C. 2016, A&A Rev., 24, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Thorne, K. S. 1974, ApJ, 191, 507 [Google Scholar]
- Torresi, E., Grandi, P., Capetti, A., Baldi, R. D., & Giovannini, G. 2018, MNRAS, 476, 5535 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.-M., Staubert, R., & Ho, L. C. 2002, ApJ, 579, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J. M., Ho, L. C., & Staubert, R. 2003, A&A, 409, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willott, C. J., Rawlings, S., Blundell, K. M., & Lacy, M. 1999, MNRAS, 309, 1017 [Google Scholar]
- Wu, Q., & Cao, X. 2008, ApJ, 687, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, H., Fan, J., Yang, J., et al. 2019, SCPMA, 62, 129811 [Google Scholar]
- Xie, G. Z., Zhang, Y. H., Fan, J. H., & Liu, F. K. 1993, A&A, 278, 6 [Google Scholar]
- Xu, Y.-D., Cao, X., & Wu, Q. 2009, ApJ, 694, L107 [Google Scholar]
- Xue, Z.-W., Zhang, J., Cui, W., Liang, E.-W., & Zhang, S.-N. 2017, RAA, 17, 090 [Google Scholar]
- Yang, J. H., Fan, J. H., Liu, Y., et al. 2022a, ApJS, 262, 18 [Google Scholar]
- Yang, W. X., Wang, H. G., Liu, Y., et al. 2022b, ApJ, 925, 120 [Google Scholar]
- Young, A. J., Wilson, A. S., & Mundell, C. G. 2002, ApJ, 579, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Y. H., Wang, G. G., Xiao, H. B., et al. 2022, ApJS, 262, 43 [Google Scholar]
- Zhang, L., Yang, J., Liu, Y., & Fan, J. 2023, SCPMA, 66, 109511 [Google Scholar]
- Zhao, X. Z., Yang, H. Y., Zheng, Y. G., & Kang, S. J. 2024, ApJ, 967, 104 [Google Scholar]
- Zirbel, E. L., & Baum, S. A. 1995, ApJ, 448, 521 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Derivation of the jet power
The self-similar ADAF structure is described by Narayan & Yi (1995). In this paper, we followed the idea of self-similar solution ADAFs structure from Narayan & Yi (1995) to quantify the BZ and hybrid BP-BZ mechanism for both LERGs and BL Lacs. The parameters of self-similar ADAF structure as discussed below:
where the Ω′ is the angular velocity of the disc; MBH is the BH mass in solar mass unit (MBH = M/M⊙); r is the radii in Schwarzschild units (r = R/(2GM/c2)), where c is the speed of light, and G is the gravitational constant. B is the magnetic field; ṁ is the dimensionless accretion rate; H is the vertical half-thickness of the disc.
The constants for c1, c2, c3 are (Bardeen et al. 1972)
in which both the g′(αvis, ϵ′) and ϵ′ are the variable replacement expressions:
here f is the advection parameter that represents the fraction of viscously dissipated energy (Narayan & Yi 1995; Nemmen et al. 2007), and γ is the ratio of specific heats (Narayan & Yi 1995).
The relationships among αvis, β, and γ are defined as follows,
Where αvis is the viscosity parameter, and β is the ratio of gas to magnetic pressure.
The angular velocity of the field seen by an outside observer at infinity in the Boyer-Lindquist frame is Ω = Ω′+ω: where ω is determined by (Bardeen et al. 1972):
with the geometrized units (G = c = 1). The j is the spin of the black hole.
Within the consideration of ADAF-dominated flows, the H ∼ R, and Bp ≈ H/RBϕ ≈ Bϕ. The azimuthal component of the magnetic field is determined by Bϕ = g(R)B(R). The all the quantities defined in the equations at the marginally stable orbit of the accretion disc R = Rms.
A maximal BH spin of 0.998 (Thorne 1974), αvis = 0.3 (Nemmen et al. 2007), f = 1 (Nemmen et al. 2007), and ṁ = 0.01 (Wu & Cao 2008; Chen et al. 2023) were adopted to compute the maximum jet powers.
All Tables
The parameters for 431 nearby low-excitation radio galaxies and 75 Fermi BL Lacertae objects.
Physical parameters for 14 nearby (z < 0.15) BL Lacertae objects from Massaro et al. (2020).
All Figures
 |
Fig. 1. Cumulative distributions of redshifts for 431 low-excitation radio galaxies. The solid black line is for FR 0s, the dashed red line is for FR Is, and the dash-dotted blue line is for FR IIs. The average redshift for FR 0s is ⟨z0⟩ = 0.037 ± 0.001, whereas that of FR Is is ⟨zI⟩ = 0.114 ± 0.002, and that of FR IIs is ⟨zII⟩ = 0.115 ± 0.003. |
| In the text | |
 |
Fig. 2. Cumulative distributions of the kinetic jet power for 431 low-excitation radio galaxies. The labels are the same as in Fig. 1. The kinetic jet power is derived from the NVSS 1.4 GHz kiloparsec-scale radio emissions. The average kinetic jet power for FR 0s is ⟨log L0, kin⟩ = 42.93 ± 0.02 erg/s, while for FR Is, it is ⟨log LI, kin⟩ = 43.86 ± 0.02 erg/s, and for FR IIs, it is ⟨log LII, kin⟩ = 44.14 ± 0.03 erg/s. |
| In the text | |
 |
Fig. 3. Cumulative distributions of line accretion rate [λ = Lline/LEdd]. The line accretion rate distributions are divided into four regions that correspond to different accretion discs: (1) λ < λ1 is the pure advection-dominated accretion flows (ADAFs); (2) λ1 < λ < λ2 is the coexistence of the ADAFs and the optically thick and geometrically thin disc; (3) λ2 < λ < λ3 is the standard thin disc; (4) λ > λ3 is the super-Eddington accretion. The upper panel covers 431 low-excitation radio galaxies. The labels are the same as in Fig. 1. The lower panel is for the 75 Fermi BL Lacertae objects. The solid yellow line is for high-synchrotron-peaked BL Lacs (HBLs); the dashed purple line is for intermediate-synchrotron-peaked BL Lacs (IBLs), and the dash-dotted orange line is for low-synchrotron-peaked BL Lacs (LBLs). |
| In the text | |
 |
Fig. 4. Kinetic jet power versus black holes. (1) Upper panel: 431 low-excitation radio galaxies. The black triangle is for FR 0s, the red circle is for FR Is, and the blue diamond is for FR IIs. (2) Lower panel: 75 Fermi BL Lacertae objects. The yellow triangle is for LBLs, the purple square is for IBLs, and the green pentagon is for HBLs. Their intrinsic kinetic jet power is obtained assuming a Doppler factor of δ ∼ 10 within the continuous jet model (p = 2 + α) and the flat spectral index (α = 0). The solid black line is for the maximum jet power in the Blandford-Znajek (BZ) jet model; the dashed red line is the mixture (hybrid) of the BZ and Blandford-Payne jet models; the average uncertainty for BH mass is 0.25 dex, and the average jet power uncertainty is 0.7 dex. |
| In the text | |
 |
Fig. 5. Kinetic jet powers versus black holes with the lines of the Lkin = LEdd (black solid line) and Lkin = 0.01LEdd (red dotted line). (1) Upper panel: is for 431 low-excitation radio galaxies; (2) the lower panel is for 75 Fermi BL Lacertae objects. The labels are the same as in Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



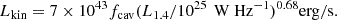
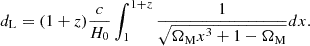
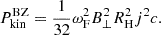
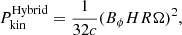
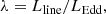
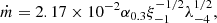
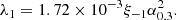
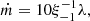
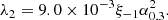
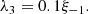
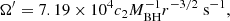
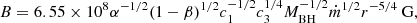
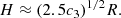
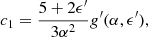
![$$ \begin{aligned} c_2=[\frac{2\epsilon (5+2\epsilon ^{\prime })}{9\alpha ^2} g^{\prime }(\alpha , \epsilon ^{\prime }) ]^{1/2}, \end{aligned} $$](/articles/aa/full_html/2025/05/aa53260-24/aa53260-24-eq24.gif)
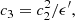
![$$ \begin{aligned} g^{\prime }(\alpha _{\rm {vis}}, \epsilon ^{\prime }) \equiv [1+\frac{18\alpha _{\rm {vis}}^2}{(5+2\epsilon ^{\prime })^2}]^{1/2} -1, \end{aligned} $$](/articles/aa/full_html/2025/05/aa53260-24/aa53260-24-eq26.gif)
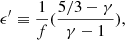
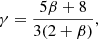
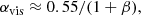
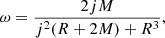
![$$ \begin{aligned} R_{\rm {ms}}=GM/c^2 \{3+Z_2-[(3-Z_1)(3+Z_1+2Z_2)]^{1/2}\}, \end{aligned} $$](/articles/aa/full_html/2025/05/aa53260-24/aa53260-24-eq31.gif)
![$$ \begin{aligned} Z_1 \equiv 1+(1-j^2)^{1/3}[(1+j)^{1/3}+(1-j)^{1/3}], \end{aligned} $$](/articles/aa/full_html/2025/05/aa53260-24/aa53260-24-eq32.gif)