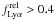| Issue |
A&A
Volume 536, December 2011
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201117685 | |
| Published online | 09 December 2011 | |
On Lyα emission in z ~ 3–6 UV-selected galaxies
1
Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
e-mail: daniel.schaerer@unige.ch
2
CNRS, IRAP, 14 Avenue E. Belin, 31400 Toulouse, France
3
Kavli Institute of Cosmology and Institute of Astronomy, University of Cambridge, Madingley Road Cambridge CB30HA, UK
Received: 12 July 2011
Accepted: 19 October 2011
Context. Determining Lyα properties of distant galaxies is of great interest for various astrophysical studies.
Aims. We examine how the strength of Lyα emission can be constrained from broad-band SED fits instead of relying on spectroscopy.
Methods. We use our SED-fitting tool, which includes the effects of nebular emission and considers in particular Lyα emission as a free parameter, and we demonstrate our method with simulations of mock galaxies. With this tool we analyse a large sample of U, B, V, and i dropout galaxies with multi-band photometry.
Results. We find significant trends in the fraction of galaxies with Lyα emission increasing both with redshift z and towards fainter magnitude (at fixed z), and similar trends for the Lyα equivalent width. Our inferred Lyα properties are in good agreement with the available spectroscopic observations and other data.
Conclusions. These results demonstrate that the strength of Lyα emission in distant star-forming galaxies can be inferred quantitatively from broad-band SED fits, at least statistically for sufficiently large samples with good photometric coverage.
Key words: galaxies: high-redshift / ultraviolet: galaxies / galaxies: starburst
© ESO, 2011
1. Introduction
For various reasons, observations of the Lyα line in high-redshift galaxies are of great interest. For example, Lyα together with other observations can provide useful information on the physical properties of distant galaxies, such as their outflows, dust content, Hi column density, and age (e.g. Shapley et al. 2003; Verhamme et al. 2008; Atek et al. 2008; Pentericci et al. 2009; Hayes et al. 2010, 2011). It may also be used as a signature to distinguish “normal” stellar populations from extremely metal-poor ones, or even to find Population III stars (e.g. Schaerer 2003; Nagao et al. 2008). Understanding the behaviour of Lyα also allows us to clarify the overlap between different galaxy types such as Lyman break galaxies (LBGs) and Lyman alpha emitters (LAEs) (Verhamme et al. 2008) and the influence of this line on selection functions (Stanway et al. 2008; Reddy & Steidel 2009). Finally, Lyα observations of distant galaxies are also being used to study questions of more cosmological nature, such as galaxy clustering and dark energy, and to probe cosmic reionisation beyond z > 6 (Hamana et al. 2004; Malhotra & Rhoads 2004; Hill et al. 2008).
Generally, the Lyα properties of distant galaxies have been determined from spectroscopic observations (follow-up or blind) or via narrow-band observations targetted to specific redshifts. Cooke (2009) has shown that LBGs at z ~ 3 dominated by Lyα absorption or emission can be distinguished based on broad-band photometry. Using SED modelling techniques taking emission lines into account (cf. Schaerer & de Barros 2009, 2010), we take this one step further, thereby demonstrating quantitatively that the properties of Lyα emission can also be inferred from broad-band observations, at least statistically for large samples with sufficient photometric bands. This allows us, for example, to determine trends of Lyα with redshift and other parameters, without resort to spectroscopy.
Our paper is structured as follows. The observational data and the method used for SED modelling are described in Sect. 2. The results are presented and discussed in Sect. 3. Section 4 summarises our main conclusions. We adopt a Λ-CDM cosmological model with H0 = 70 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7.
 |
Fig. 1 Example of an SED fit for B-drop galaxy best fit with strong Lyα. Black solid line: best-fit SED including nebular emission. Red crosses: flux in the photometric bands derived from the SED including nebular emission. Blue symbols show the observed fluxes or 1σ upper limits. Green dashed lines show the positions/shape of all the availabe photometric bands. Left: full SED showing all the available photometric data. Right: zoom on the SED showing the spectral range up to 2.4 μm only (restframe UV to Balmer break). |
2. Observational data and SED modelling
De Barros et al. (in prep., hereafter dB11) have analysed a large sample of z ~ 3−6 dropout-selected galaxies in depth using an up-to-date photometric redshift and SED-fitting tool that treats the effects of nebular emission on the SEDs of galaxies. In their homogeneous analysis they determine the main physical properties, such as the star formation rate (SFR), stellar mass, age, and reddening. They assess carefully their uncertainties, and discuss the evolution of these properties with redshift. We here extend these simulations to perform SED fits with variable strengths of Lyα for the same set of galaxies, to examine whether the available photometry allows us to distinguish any trends in Lyα with redshift and/or other properties.
2.1. Photometric data and sample selection
We have used the GOODS-MUSIC catalogue of Santini et al. (2009), which provide photometry in the U, B435, V606, i776, z850LP, J, H, and K bands mostly from the VLT and HST, and the 3.6, 4.5, 5.8, and 8.0 μm bands from the IRAC camera onboard Spitzer. Using standard criteria as in Stark et al. (2009), we then selected U, B, V, and i-drop galaxies. To reduce the contamination rate (typically ~ 10−20%) we only retained the objects whose median photometric redshifts agree with the targetted redshift range. This leaves us with a sample of 389, 705, 199, and 60 galaxies with median photometric redshifts of zphot = 3.3, 3.9, 4.9, and 6.0. See dB11 for more details.
2.2. SED models
Our SED-fitting tool, described in Schaerer & de Barros (2009) and Schaerer & de Barros (2010), is based on a version of the Hyperz photometric redshift code of Bolzonella et al. (2000), modified to take nebular emission into account. In dB11 we considered a large set of spectral templates based on the GALAXEV synthesis models of Bruzual & Charlot (2003) and covering different metallicities and a wide range of star formation histories. A Salpeter IMF was adopted. Nebular emission from continuum processes and numerous emission lines was added to the spectra predicted from the GALAXEV models as described in Schaerer & de Barros (2009), proportionally to the Lyman continuum photon production. The intergalactic medium (IGM) was treated with the prescription of Madau (1995).
The free parameters of our SED fits are: redshift z, metallicity Z (of stars and gas), star formation history described by the timescale τ (i.e. SFR ∝ exp( − t/τ)), the age t ⋆ defined since the onset of star-formation, and attenuation AV described by the Calzetti law (Calzetti et al. 2000). In addition, we here introduce a variable Lyα strength described by the relative Lyα escape fraction 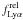 ∈ [0,1] , defined by
∈ [0,1] , defined by  (1)where LB(Lyα) is the intrinsic Lyα luminosity of the spectral template given by its Lyman continuum flux and the case B assumption, and L(Lyα) is the adopted Lyα luminosity for the spectral template (before any additional attenuation with the Calzetti law, assumed to affect stars and gas in the same manner). Values
(1)where LB(Lyα) is the intrinsic Lyα luminosity of the spectral template given by its Lyman continuum flux and the case B assumption, and L(Lyα) is the adopted Lyα luminosity for the spectral template (before any additional attenuation with the Calzetti law, assumed to affect stars and gas in the same manner). Values 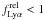 therefore describe an additional reduction of Lyα beyond the attenuation suffered by the UV continuum.
therefore describe an additional reduction of Lyα beyond the attenuation suffered by the UV continuum.
In practice we compute SED fits for all combinations of z ∈ [0, 10] in steps of 0.1, Z = (0.02 = Z⊙, 0.004, 0.001), τ = (10, 30, 50, 70, 100, 300, 500, 700, 1000, 3000, ∞) Myr, 51 age steps from 0 to the age of the Universe (see Bolzonella et al. 2000), AV ∈ [0, 4] mag in steps of 0.1, and 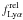 = (0, 0.25, 0.5, 0.75, 1.0). Minimisation over the entire parameter space yields the best-fit parameters, along with other properties such as the predicted Lyα equivalent width and UV magnitude. To determine the uncertainties of the physical parameters, we used Monte-Carlo simulations by running typically 1000 realisations of each object. From this we derived the probability distribution function for each parameter/quantity, either for each individual object or for (sub)samples.
= (0, 0.25, 0.5, 0.75, 1.0). Minimisation over the entire parameter space yields the best-fit parameters, along with other properties such as the predicted Lyα equivalent width and UV magnitude. To determine the uncertainties of the physical parameters, we used Monte-Carlo simulations by running typically 1000 realisations of each object. From this we derived the probability distribution function for each parameter/quantity, either for each individual object or for (sub)samples.
Examples of best-fit SEDs of two B-drop galaxies where a high (low) Lyα equivalent width was inferred from the data are shown in Figs. 1, 2 for illustration. The position and shape of the availabe photometric bands are also shown. Several issues can be seen from these figures. First, we see that two to three bands, unaffected by Lyα, are available to constrain the restframe UV domain, i.e. the UV slope. This is also true for our higher redshift samples, where e.g. the JHK bands probe the UV restframe for I-drops. Of course, the photometry is not necessarily available and deep enough for all objects. Second, the contribution of nebular emission to the broad-band filters can in general vary strongly from case to case. Figure 1 shows an object best fit with a strong lines and a strong nebular continuum, whereas for the object shown in Fig. 2 nebular emission is negligible. The first object shows a clear excess at 3.6 μm relative to 4.5 μm, which is naturally explained by the strong lines (Hα and others) in the first filter and a few lines in the second for galaxies in this redshift range (z ~ 3.8−5, cf. Shim et al. 2011; de Barros et al., in prep.). In this case strong intrinsic Lyα emission is also expected, and our fitting method yields a median (mean) Lyα escape fraction fLyα = 0.75 (0.57) and a corresponding Lyα equivalent width EW(Lyα) = 93 (71) Å. Finally, strong Lyα emission does not necessarily imply a strong excess in the filter encompassing this line compared to the next redward filter, since intrinsically EW(Lyα) is not very large, and since the continuum flux starts to be reduced by the IGM at z ≳ 3.
Typically Lyα contributes to ~ 25−30% of the broad-band flux for U- to I-drops if we assume EWrest(Lyα) = 60 Å and compare this value to the filter width. However, this contribution is higher if we take into account the fact that the continuum flux decreases blueward of Lyα. Therefore, depending on the source redshift and on the exact IGM attenuation, the relative contribution of Lyα to the photometric signal can exceed the above estimate significantly. In either case, when enough filters are available, the Lyα signal can be determined (albeit with considerable uncertainty), as we show below.
3. Results
3.1. Evolution of the Lyα fraction with redshift and UV magnitude
 |
Fig. 3 Fraction rLya of galaxies with Lyα emission (defined by |
We have examined the probability distribution function (pdf) of the relative Lyα escape fraction 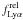 of our samples. Overall it turns out that
of our samples. Overall it turns out that 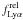 is not well constrained for individual objects. For each sample, however, the pdf shows two relative maxima close to
is not well constrained for individual objects. For each sample, however, the pdf shows two relative maxima close to 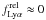 and 1, whose relative importance varies between the samples. To quantify this behaviour further, regardless of the detailed shape of the pdf, we count the number of objects with a relative escape fraction above 40%, and define the corresponding fraction of Lyα objects as
and 1, whose relative importance varies between the samples. To quantify this behaviour further, regardless of the detailed shape of the pdf, we count the number of objects with a relative escape fraction above 40%, and define the corresponding fraction of Lyα objects as  . This number should provide a simple estimate of the fraction of objects with Lyα emission among the total dropout samples.
. This number should provide a simple estimate of the fraction of objects with Lyα emission among the total dropout samples.
In Fig. 3 we plot rLya as a function of the absolute UV magnitude for the samples of z ~ 3 − 6 galaxies. Two main results emerge from this figure. First, we find that the fraction of objects showing Lyα emission increases with redshift (both on average and within each magnitude bin). Second, at each redshift we find that Lyα emission is more common in galaxies with fainter UV magnitudes. Except at the brightest and faintest magnitudes, where the number of galaxies is relatively small, our trends are significant. The same trend is also found when using cuts in equivalent width instead of rLya, as shown below.
 |
Fig. 4 Same as Fig. 3 for galaxies with a large Lyα equivalent width (EW(Lyα) > 50 Å) compared to the observed fraction derived from follow-up spectroscopy of z ~ 4 (blue points) and 5 (black points) LBGs (data for B and V drops by from Stark et al. 2010). |
Interestingly, our derived Lyα fraction shows the same behaviour with redshift and UV magnitude as obtained from and hinted at by several other studies, mostly based on spectroscopic observations of z ≳ 3 galaxies. For example, using photometric criteria derived from spectroscopy, Cooke (2009) shows an increasing fraction of objects with strong Lyα emission among faint z ~ 3 LBGs. The most direct comparison can be made with the work of Stark et al. (2010), who determined the Lyα fraction of LBGs from spectroscopy of ~400 B, V, I, and z dropout galaxies. These authors indeed found the same trends just described both with UV magnitude and with redshift. To compare our Lyα with that derived by Stark et al. (2010), we applied the same criterion on the Lyα restframe equivalent width (EW(Lyα) > 50 Å) on our samples. The result, shown in Fig. 4, is very encouraging, although some discrepancy seems to remain at intermediate magnitudes. The same holds when we compare our data with those of Stark et al. (2011). For our U-drop sample we find ≈10 ± 5% of objects with EW(Lyα) > 20 Å at MUV < −20.5, comparable to ~20−25% of LBGs in the sample of Shapley et al. (2003) at similar UV magnitudes. Among z ~ 5 LBGs, Douglas et al. (2010) find ~55% with EW(Lyα) > 20 Å or 22 ± 4% after correction for spectroscopically unconfirmed galaxies. Our values for the same EW(Lyα) cut are between ~15−60% for magnitudes brighter than MUV ~ −20. We conclude that the Lyα trends derived with our method are in reasonable agreement with the available spectroscopic data.
Other data also support the trend toward a higher Lyα fraction at high redshift. For example, a convergence of the luminosity functions and number densities of LBGs and LAEs has been noticed by various studies (e.g. Ouchi et al. 2008; Cassata et al. 2011). Using such surveys, Hayes et al. (2011) and Blanc et al. (2011) show that, on average, the absolute Lyα escape fraction1 increases with redshift from z ~ 0 to 6.5 in UV selected, star-forming galaxies. Our analysis shows that this also holds for LBGs.
3.2. The distribution of EW(Lyα) with magnitude and other comparisons
The “recovered” best-fit values of EW(Lyα) for all ~1300 galaxies from z ~ 3−5 are plotted in Fig. 5 as a function of the UV magnitude. Our models show clearly – at each redshift – an absence of UV bright objects with large Lyα equivalent widths, whereas for fainter objects EW(Lyα) occupies a wide range. This behaviour is well known, as it has been found in virtually all samples of LAE and LBGs at z ≳ 2 (or above 3) (see e.g. Shapley et al. 2003; Ando et al. 2006; Tapken et al. 2006; Shimasaku et al. 2006; Ouchi et al. 2008; Pentericci et al. 2009; Stark et al. 2010), although Nilsson et al. (2009) question the statistical robustness of this trend. Our analysis of a large sample of LBGs therefore provides an independent confirmation for the deficit of large Lyα equivalent widths at bright UV continuum luminosities and for an increasing maximum of EW(Lyα) toward fainter magnitudes found from spectroscopic and narrow-band surveys of LBGs and LAEs. The statistical significance of our result has already been shown in Fig. 3.
 |
Fig. 5 Predicted best-fit values of the restframe Lyα equivalent width EW(Lyα) as a function of MUV for the U, B, and V dropout galaxies studied here. Same colour symbols as in previous figures. To illustrate the typical uncertainties for the individual objects, we show errorbars randomly for every fifth B-drop. |
 |
Fig. 6 Comparison of the predicted Lyα (rest-frame) equivalent width with the observed one for the 36 objects in common with spectroscopic measurements of Stark et al. (2010). Observational errorbars of ~25%, typical for the brighter objects, are adopted. A logarithmic x-axis is chosen to optimise the readability of the plot. Red symbols indicate the i-drops, black V-drops, and blue B-drops. |
The Lyα equivalent widths predicted from our SED fits span a reasonable range of values, comparable to those observed in various LBG samples (cf. e.g. Stark et al. 2010; Pentericci et al. 2009; Shapley et al. 2003), with most values between 0 and ~60 Å (the typical value for constant star-formation with 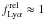 ). A good agreement is found between the EW distribution of Shapley et al. (2003) and our results for the U-drop sample.
). A good agreement is found between the EW distribution of Shapley et al. (2003) and our results for the U-drop sample.
Finally we have examined all individual objects for which spectroscopic measurements of Lyα were available. From the data of Stark et al. (2010) we find 36 objects in common with our sample. The predicted and observed Lyα equivalent widths of these objects is shown in Fig. 6. Overall we find an agreement within a 68% confidence interval for ~60% of the objects. The main outliers are three i-drop galaxies for which our model predicts equivalent widths that are too large (possibly related to uncertainties with the IGM treatment, cf. below), and several B-drops where the model underestimates EW(Lyα). Although encouraging, further comparisons with larger samples may be helpful.
We conclude that our SED-fitting method relying purely on broad-band photometry allows us to derive statistically meaningful trends of Lyα with redshift and UV magnitude. Furthermore, the trends and the predicted Lyα strength appears both qualitatively and quantitatively in good or, at least, reasonable agreement with the existing observations.
3.3. Test of our method using mock simulations
The above comparison of our results with 36 galaxies with available Lyα measurements can be improved by mock simulations that allow a more complete assessment of our method. To do this we constructed a set of synthetic galaxy spectra with known physical properties including EW(Lyα), from which we then derive the synthetic photometry including typical observational errors. The photometry of these mock galaxies is then fitted with our SED-fitting tool, and the derived EW(Lyα) compared to the intrinsic (input) one. In practice we chose to simulate a sample of 500 B-drop galaxies. To construct their synthetic spectra, we randomly drew their physical parameters, i.e. varying age from 0 to ~0.5 Gyr, star-formation histories with variable τ (taking the same values as for the SED fits, cf. above), variable ![\hbox{$\frellya \in [0,1]$}](/articles/aa/full_html/2011/12/aa17685-11/aa17685-11-eq75.png) , AV ∈ [0,1] , and z ∈ [3.8,4.5] . We chose the intermediate metallicity (Z = 0.004), since our fits are very degenerate in Z (cf. dB11). Finally we added noise to the synthetic photometry taking the median photometric uncertainty of the observed B-drop sample in each band. Our artificial sample of galaxies should therefore be representative of typical B-drop galaxies.
, AV ∈ [0,1] , and z ∈ [3.8,4.5] . We chose the intermediate metallicity (Z = 0.004), since our fits are very degenerate in Z (cf. dB11). Finally we added noise to the synthetic photometry taking the median photometric uncertainty of the observed B-drop sample in each band. Our artificial sample of galaxies should therefore be representative of typical B-drop galaxies.
The mock sample generated in this manner is then fitted using the same procedure as adopted for the observed LBGs, allowing us to verify the accuracy of our fitting procedure. The result for the Lyα equivalent width is shown in Fig. 7. Good agreement is found between the derived (output) and input equivalent widths, albeit with a relatively large uncertainty. Examing the full probability distribution function of the derived equivalent widths we find (EW(Lyα) − 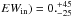 Å (within 68% confidence), which demonstrates that our method is statistically able to recover the input value with no systematic offset. As expected the dispersion between the input and output equivalent widths increases with decreasing input EW(Lyα). This dispersion has been obtained for a sample with a relatively low median EWin = 20 Å.
Å (within 68% confidence), which demonstrates that our method is statistically able to recover the input value with no systematic offset. As expected the dispersion between the input and output equivalent widths increases with decreasing input EW(Lyα). This dispersion has been obtained for a sample with a relatively low median EWin = 20 Å.
One may wonder whether the accuracy of recovering the strength of the Lyα line depends on the UV slope of the galaxy. If this was the case, the trends found above with UV magnitude could be biased, since the observed UV slope appears to correlate with this quantity (e.g. Bouwens et al. 2009). In Fig. 8 we show the relative difference (“error”) between the output (derived) and input Lyα equivalent width for our mock sample as a function of the UV slope β determined in a standard fashion from the (i776 − z850LP) colour (Bouwens et al. 2009). For clarity we separate galaxies according to their input equivalent width EWin in this plot. We find no trend of the relative “error” with β for objects with EWin > 50 Å. For objects with faint Lyα emission, the errors become larger, as expected, but show no clear trend with UV slope, at least over the range of typical slopes observed at z ~ 4 (β ~ −3 to −1). We therefore conclude that our multi-band SED-fitting method is able to recover the strength of Lyα emission with an uncertainty that is independent of the intrinsic UV slope of the galaxy.
 |
Fig. 7 Derived median Lyα equivalent width (restframe) versus input Lyα equivalent width for our mock sample of 500 B-drop galaxies. The errorbar indicates the median 68% confidence limit on the derived EW(Lyα); no offset between the derived median and the input value is obtained, which demonstrates that our method works, at least statistically. A small fraction of objects is found at higher EW(Lyα), outside the plot. Good agreement is obtained for all of them. |
 |
Fig. 8 Relative difference between the output (derived) and input restframe Lyα equivalent width for our mock sample as a function of the UV slope β determined from the (i776-z850LP) colour. Blue: objects with EWin > 50 Å, green: 50 ≥ EWin > 20, black: EWin < 20 Å. |
3.4. Possible biases
Could the main results obtained with our method, i.e. the increasing fraction of Lyα emission towards fainter UV magnitudes and the increase in Lyα with redshift among LBGs, be due to biases and not intrinsic to the galaxy population? We think that this is not the case for the following reasons.
First, our method is not biased by a possible trend of the UV slope towards fainter magnitudes, at least for the objects with strong enough Lyα emission (e.g. EW(Lyα) > 50 Å). Furthermore, our photometric method yields the same behaviour as spectroscopic measurements, which should be subject to different biases and which generally do not reach the same depths. To avoid biases due to the difficulty of detecting faint Lyα emission from objects faint in the continuum, Stark et al. (2010) measured the fraction of LBGs at z ~ 4−6 with EW(Lyα) above an appropriate threshold, and we applied the same cuts here (Fig. 4). Recent, deeper observations of z ~ 2−3 LBGs by N. Reddy (Priv. comm.) also show a persistent increase in the Lyα fraction towards faint objects once corrected for this bias.
Finally, these trends could also be biased by the LBG selection, which can be affected by the strength of Lyα emission (cf. Stanway et al. 2007, 2008; Reddy et al. 2008; Reddy & Steidel 2009). As pointed out by Stark et al. (2010) this bias is minimised by simultaneously targetting “adjacent” drop-out populations, e.g. U, B, V, and I-drops as done here. In this way objects with strong Lyα emission scattered out from one selection window will be recovered by the selection of the adjacent drop-out. Therefore biases related to Lyα affecting the colours used for the LBG selection should only influence the approximate redshift distribution of galaxies, but should not bias the overall sample with respect to the strength of Lyα.
We conclude that the derived trends of Lyα with magnitude and redshift must be an intrinsic property of UV selected star-forming galaxies at high redshift.
3.5. Discussion
What explains the observed trends of Lyα with UV magnitude and redshift? Based on radiation transfer models and on comparisons with observations Verhamme et al. (2008) and Schaerer & Verhamme (2008) show that absorption by dust is the main process responsible for the observed diversity of Lyα line profiles and strengths among LBGs and LAEs. From this they suggest that variations in the dust content with galaxy mass, UV magnitude, and redshift should explain the increasing fraction of Lyα emission both with z and with decreasing brightness of the objects. Findings of a correlation between extinction and the Lyα escape fraction (cf. Atek et al. 2009; Hayes et al. 2010), and the observed decrease of the average UV attenuation with increasing redshift go to support this picture, even quantitatively (Hayes et al. 2011). To examine this further, we checked whether our SED models reveal any correlation between 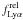 and AV (or other physical properties). Beyond the one shown above with MUV, we have not found any clear additional correlations, beacuse the uncertainties/degeneracies are too large. We can speculate that future studies of large galaxy samples with additional observational constraints, e.g. from deep surveys with large sets of filters, should be able to detect such correlations.
and AV (or other physical properties). Beyond the one shown above with MUV, we have not found any clear additional correlations, beacuse the uncertainties/degeneracies are too large. We can speculate that future studies of large galaxy samples with additional observational constraints, e.g. from deep surveys with large sets of filters, should be able to detect such correlations.
Can our method be used to constrain cosmic reionisation? In principle, yes, since as shown above, we are able to determine the strength of Lyα in a similar way to spectroscopic observations, at least for a large sample of galaxies. From this we are then in principle able to determine the fraction of Lyα emitters, the Lyα luminosity function, or other related quantities, which can in turn be used to probe the evolution of the neutral hydrogen fraction with redshift (see e.g. Malhotra & Rhoads 2004; Dijkstra et al. 2007). However, we should be aware of the following possible limitations. At high-z (z ≫ 5) the IGM significantly alters the SED shortward of Lyα. To correctly predict the Lyα strength from broad-band SED fits, one therefore also needs the most accurate treatment of the Lyα forest (in principle of stochastic nature) possible. At the same time there are some degeneracies between Lyα strength, IGM, and also redshift that can all modify the flux in the broad-band filter encompassing Lyα. It is therefore clear that our method should become less accurate at very high redshift. Future applications to larger samples of high-z galaxies observed in as many photometric bands as possible, and careful examination of the above-mentioned degeneracies will show whether our SED-fitting method can also provide useful constraints on Lyα during the epoch of reionisation.
4. Summary and conclusions
Using an updated version of the Hyperz photometric redshift code of Bolzonella et al. (2000) adding nebular emission to the spectral templates (see Schaerer & de Barros 2009, 2010), we have analysed a large sample of Lyman-break selected galaxies at z ~ 3−6 in the GOODS-S field, for which deep multi-band photometry from the U-band to 8 μm is available. We have added a variable Lyα strength, described by a relative Lyα escape fraction 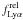 , to our extensive exploration of the parameter space covering redshift, metallicity, star-formation history, age, and attenuation whose results are discussed in detail in de Barros et al. (in prep.). We show that significant trends of Lyα strength with redshift and with UV magnitude can be inferred from broad-band photometric observations of large samples of galaxies using our method. The validity of our method is also demonstrated by our simulations of mock galaxies. Our method relies on fitting all the photometric bands constraining the UV and optical rest-frame SED. However, even with just three bands some Lyα trends may be detectable, as shown already by e.g. Cooke (2009) for z ~ 3 galaxies.
, to our extensive exploration of the parameter space covering redshift, metallicity, star-formation history, age, and attenuation whose results are discussed in detail in de Barros et al. (in prep.). We show that significant trends of Lyα strength with redshift and with UV magnitude can be inferred from broad-band photometric observations of large samples of galaxies using our method. The validity of our method is also demonstrated by our simulations of mock galaxies. Our method relies on fitting all the photometric bands constraining the UV and optical rest-frame SED. However, even with just three bands some Lyα trends may be detectable, as shown already by e.g. Cooke (2009) for z ~ 3 galaxies.
We find an increase in the fraction of LBGs showing Lyα emission both with redshift and towards fainter UV-restframe magnitudes at each redshift. Furthermore, we also infer a decrease in the average and the maximum Lyα equivalent width toward bright objects. Our results are fully compatible with the trends found from spectroscopic observations of individual LBGs and LAEs (e.g. Ando et al. 2006; Ouchi et al. 2008; Stark et al. 2010) and with other more global trends in the Lyα escape fraction with redshift (Hayes et al. 2011).
In principle our method should also be applicable to derive the Lyα properties of z > 6 galaxies, of particular interest for studies of the history of cosmic reionisation and in other contexts. At least we did show that even broad-band photometric observations can reveal some information about Lyα emission in high-redshift galaxies.
Acknowledgments
We have appreciated stimulating discussions with Matthew Hayes, Naveen Reddy, and other colleagues during the spring-summer of 2011. The work of D.S. and S.d.B. is supported by the Swiss National Science Foundation. D.P.S. is supported by an STFC postdoctoral research fellowship.
References
- Ando, M., Ohta, K., Iwata, I., et al. 2006, ApJ, 645, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Atek, H., Kunth, D., Hayes, M., Östlin, G., & Mas-Hesse, J. M. 2008, A&A, 488, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atek, H., Kunth, D., Schaerer, D., et al. 2009, A&A, 506, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanc, G. A., Adams, J. J., Gebhardt, K., et al. 2011, ApJ, 736, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Miralles, J., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2009, ApJ, 705, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Le Fèvre, O., Garilli, B., et al. 2011, A&A, 525, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooke, J. 2009, ApJ, 704, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Dijkstra, M., Wyithe, J. S. B., & Haiman, Z. 2007, MNRAS, 379, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, L. S., Bremer, M. N., Lehnert, M. D., Stanway, E. R., & Milvang-Jensen, B. 2010, MNRAS, 409, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Hamana, T., Ouchi, M., Shimasaku, K., Kayo, I., & Suto, Y. 2004, MNRAS, 347, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Östlin, G., Schaerer, D., et al. 2010, Nature, 464, 562 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hayes, M., Schaerer, D., Ostlin, G., et al. 2011, ApJ, 730, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, G. J., Gebhardt, K., Komatsu, E., et al. 2008, in Panoramic Views of Galaxy Formation and Evolution, ed. T. Kodama, T. Yamada, & K. Aoki, ASP Conf. Ser., 399, 115 [Google Scholar]
- Madau, P. 1995, ApJ, 441, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, S., & Rhoads, J. E. 2004, ApJ, 617, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Sasaki, S. S., Maiolino, R., et al. 2008, ApJ, 680, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, K. K., Möller-Nilsson, O., Møller, P., Fynbo, J. P. U., & Shapley, A. E. 2009, MNRAS, 400, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Shimasaku, K., Akiyama, M., et al. 2008, ApJS, 176, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Pentericci, L., Grazian, A., Fontana, A., et al. 2009, A&A, 494, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reddy, N. A., & Steidel, C. C. 2009, ApJ, 692, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Steidel, C. C., Pettini, M., et al. 2008, ApJS, 175, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Santini, P., Fontana, A., Grazian, A., et al. 2009, A&A, 504, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D. 2003, A&A, 397, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., & de Barros, S. 2009, A&A, 502, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., & de Barros, S. 2010, A&A, 515, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaerer, D., & Verhamme, A. 2008, A&A, 480, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Shim, H., Chary, R.-R., Dickinson, M., et al. 2011, ApJ, 738, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Shimasaku, K., Kashikawa, N., Doi, M., et al. 2006, PASJ, 58, 313 [NASA ADS] [Google Scholar]
- Stanway, E. R., Bunker, A. J., Glazebrook, K., et al. 2007, MNRAS, 376, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., Bremer, M. N., & Lehnert, M. D. 2008, MNRAS, 385, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Bunker, A., et al. 2009, ApJ, 697, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., Chiu, K., Ouchi, M., & Bunker, A. 2010, MNRAS, 408, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S., & Ouchi, M. 2011, ApJ, 728, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Tapken, C., Appenzeller, I., Gabasch, A., et al. 2006, A&A, 455, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhamme, A., Schaerer, D., Atek, H., & Tapken, C. 2008, A&A, 491, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Example of an SED fit for B-drop galaxy best fit with strong Lyα. Black solid line: best-fit SED including nebular emission. Red crosses: flux in the photometric bands derived from the SED including nebular emission. Blue symbols show the observed fluxes or 1σ upper limits. Green dashed lines show the positions/shape of all the availabe photometric bands. Left: full SED showing all the available photometric data. Right: zoom on the SED showing the spectral range up to 2.4 μm only (restframe UV to Balmer break). |
| In the text | |
 |
Fig. 2 Same as Fig. 1 for an object best-fit with a low EW(Lyα). |
| In the text | |
 |
Fig. 3 Fraction rLya of galaxies with Lyα emission (defined by |
| In the text | |
 |
Fig. 4 Same as Fig. 3 for galaxies with a large Lyα equivalent width (EW(Lyα) > 50 Å) compared to the observed fraction derived from follow-up spectroscopy of z ~ 4 (blue points) and 5 (black points) LBGs (data for B and V drops by from Stark et al. 2010). |
| In the text | |
 |
Fig. 5 Predicted best-fit values of the restframe Lyα equivalent width EW(Lyα) as a function of MUV for the U, B, and V dropout galaxies studied here. Same colour symbols as in previous figures. To illustrate the typical uncertainties for the individual objects, we show errorbars randomly for every fifth B-drop. |
| In the text | |
 |
Fig. 6 Comparison of the predicted Lyα (rest-frame) equivalent width with the observed one for the 36 objects in common with spectroscopic measurements of Stark et al. (2010). Observational errorbars of ~25%, typical for the brighter objects, are adopted. A logarithmic x-axis is chosen to optimise the readability of the plot. Red symbols indicate the i-drops, black V-drops, and blue B-drops. |
| In the text | |
 |
Fig. 7 Derived median Lyα equivalent width (restframe) versus input Lyα equivalent width for our mock sample of 500 B-drop galaxies. The errorbar indicates the median 68% confidence limit on the derived EW(Lyα); no offset between the derived median and the input value is obtained, which demonstrates that our method works, at least statistically. A small fraction of objects is found at higher EW(Lyα), outside the plot. Good agreement is obtained for all of them. |
| In the text | |
 |
Fig. 8 Relative difference between the output (derived) and input restframe Lyα equivalent width for our mock sample as a function of the UV slope β determined from the (i776-z850LP) colour. Blue: objects with EWin > 50 Å, green: 50 ≥ EWin > 20, black: EWin < 20 Å. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.