| Issue |
A&A
Volume 536, December 2011
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201015857 | |
| Published online | 06 December 2011 | |
Solar turbulent magnetic fields: Non-LTE modeling of the Hanle effect in the C2 molecule
1 Institute of Astronomy, ETH Zurich, 8093 Zurich, Switzerland
e-mail: kleint@astro.phys.ethz.ch
2 Istituto Ricerche Solari Locarno (IRSOL), 6605 Locarno Monti, Switzerland
3 Physikalisch-Meteorologisches Observatorium Davos, World Radiation Center, Dorfstrasse 33, 7260 Davos Dorf, Switzerland
4 Kiepenheuer-Institut für Sonnenphysik, Schöneckstrasse 6, 79104 Freiburg, Germany
Received: 2 October 2010
Accepted: 3 October 2011
Context. Scattering polarization measurements contain a wealth of information that needs a thorough interpretation. This often requires accounting for the non-local origin of photons with different frequencies and at different limb positions. Currently, modeling scattering polarization in several molecular C2 lines simultaneously is only successful for lines with similar quantum numbers. More sophisticated models are needed to understand the dependence on quantum numbers and to reliably derive the strength of the turbulent magnetic fields using the differential Hanle effect.
Aims. We have developed a non-LTE analyzing technique for the C2 lines to determine the strength of turbulent magnetic fields and have applied it to observations obtained during our synoptic program at the Istituto Ricerche SOlari Locarno (IRSOL).
Methods. The influence of magnetic fields on scattering polarization can be interpreted differentially, i.e., by comparing several spectral lines within one spectral region. Through the application of the differential Hanle effect and non-LTE 1D radiative transfer, we are able to infer a magnetic field strength from the photospheric C2 lines around 5141 Å. Compared to previous models we include the effect of collisions and investigate their dependence on the total angular momentum number J.
Results. We carry out a detailed parameter study to investigate the influence of model parameters on the resulting scattering polarization. A good fit can now be obtained for spectral lines from different C2 triplets. For the 78 measurements obtained during the solar minimum in 2007–2009 we infer a mean magnetic field strength of 7.41 G with a standard deviation of 0.76 G.
Key words: radiative transfer / polarization / magnetic fields / Sun: photosphere / scattering / molecular processes
© ESO, 2011
1. Introduction
Coherent scattering processes in the solar atmosphere produce a linearly polarized spectrum, which is called second solar spectrum (Ivanov 1991; Stenflo & Keller 1997) and poses a challenge to current modeling. Different physical processes for the continuum and line polarization, including magnetic fields and collisions, have to be taken into account to model this spectrum. Turbulent magnetic fields can modify scattering polarization via the Hanle effect (e.g., Stenflo 1994). Therefore, the second solar spectrum is a very important diagnostic of weak fields, which fill most of the solar atmosphere. Their properties and evolution are important for understanding the solar magnetism. However, determining their field strength is not straightforward and may be influenced by other processes in the atmosphere. By analyzing the Q/I amplitude ratios of several spectral lines with a similar formation height and different quantum mechanical parameters such as Landé factors, it is possible to eliminate many unknown parameters and derive the magnetic field strength. This differential approach is very useful for the Hanle effect in molecular lines because molecules are often observed in bands and the Landé factors within multiplets or branches of molecules can differ significantly (see e.g., Berdyugina et al. 2002; Trujillo Bueno 2003; Berdyugina & Fluri 2004).
In our first paper (Kleint et al. 2010, hereafter Paper I) we applied this approach to the molecular C2 lines of the Swan system (d3Π − a3Π) around 5141 Å and constrained the magnetic field strength to be at least 4.7 ± 0.2 G. This spectral region shows six prominent C2 lines in two triplets, each with a different sensitivity to the magnetic field and similar other parameters. The R-triplet including R1(14), R2(13) and R3(12) is resolved and unblended. The adjacent P-triplet with P1(42), P2(41) and P3(40) is also unblended but unresolved. Three amplitude ratios are sufficient for a unique determination of the magnetic field from these lines (Berdyugina & Fluri 2004). In Paper I we used the ratios R1/R2, R3/R2 and R2/P (P = P1 + P2), as well as P/P3 to exclude magnetic fields stronger than 80 G. We found that the magnetic field strength can be evaluated only from lines with similar quantum numbers, while the observed amplitude ratios between two different C2 triplets cannot be reproduced. We concluded that this could be because of neglected differences between the triplets, e.g. collision rates. Therefore, the resulting field strength was only a lower limit.
Here we present a more detailed radiative transfer modeling. We use 1D NLTE radiative transfer (see Sect. 2) to synthesize C2 spectra and fit the data from Paper I. All synoptic data were taken at IRSOL with the ZIMPOL2 system in intervals of 2 to 3 weeks, starting in December 2007 and until the end of 2009. For the current paper, we use a selection of the synoptic data set, excluding all measurements outside of a range of heliocentric angles 0.07 < μ < 0.13. As described in Paper I, μ is accurately determined through a calibration using the amplitude of a magnetically less sensitive C2 line.
The use of radiative transfer allows us to include the previously neglected influence of collisions and the depolarization of the continuum and to investigate their effects on amplitude ratios. Earlier modeling of various spectral lines (e.g., Faurobert & Arnaud 2003; Trujillo Bueno et al. 2006) have resulted in different magnetic field strengths, ranging from a few Gauss to hundreds of Gauss for the turbulent magnetic field. While we were able to exclude the presence of stronger fields (above 80 G) for the C2 lines with the simple line-ratio model and set a lower limit of 4.7 G, our goal is to obtain a more accurate field strength when taking into account more radiative transfer effects.
We explain the model in Sect. 2 and carry out a parameter study in Sect. 3. The data are compared with the model in Sect. 4. The average magnetic field strength calculated from the 78 measurements obtained during the solar minimum is found to be 7.41 G with a standard deviation of 0.76 G.
2. Radiative transfer model
2.1. Basic assumptions
In Paper I we employed a simple model expressing the C2 polarization amplitudes via a number of line parameters, including the intrinsic line polarizability W2 and the depolarization factors due to the Hanle effect WH and collisions Wc (Berdyugina & Fluri 2004). This model was further simplified by assuming that Wc = 1 for all C2 lines. We found however that this model cannot produce a sufficiently good fit to our current data sets for the R- and P-triplets with very different total angular momentum numbers. To investigate the possibility to fit both triplets simultaneously, we now apply a more consistent approach using radiative transfer, similar to the one employed by Holzreuter et al. (2005) and Shapiro et al. (2011a) who applied it to the first and second solar spectrum in strong chromospheric lines and the CN violet system, respectively. While a detailed description of the code can be found in those papers, we will emphasize the differences and required changes for our modeling.
The scattering process is a radiative excitation followed by an emission of a photon. Each photon can be produced through different excitation processes. For each C2 line, we take into account nine radiative excitation processes as shown in Fig. 1, each corresponding to absorption. Transitions with the same initial and final states are called Rayleigh scattering, the others are Raman scattering. In principle, all these transitions have to be calculated and treated separately and the line source function has contributions from all of them. Also, contributions from other vibrational states should be included, but we verified them to be negligible. In addition to the scattering processes, thermal absorption and emission take place as well.
Thus, the line source function consists of two terms: scattering and thermal part. For the ith line it is 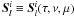 and within the CRD approximation it can be written as
and within the CRD approximation it can be written as 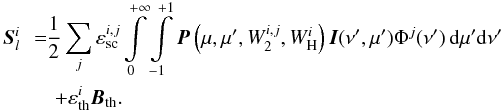 (1)The variables μ and μ′ indicate the outgoing and incoming directions of photons, respectively, and ν and ν′ the outgoing and incoming frequencies of the photons. Each of the integrals in Eq. (1) corresponds to one excitation possibility with the index j denoting the set of quantum numbers of the initial level. There are nine integrals for each C2 line. The term with i = j is Rayleigh scattering and terms with i ≠ j describe Raman scattering. P is the phase matrix describing the scattering process, I is the Stokes vector and Φj is the line profile. The values for the intrinsic line polarizabilities
(1)The variables μ and μ′ indicate the outgoing and incoming directions of photons, respectively, and ν and ν′ the outgoing and incoming frequencies of the photons. Each of the integrals in Eq. (1) corresponds to one excitation possibility with the index j denoting the set of quantum numbers of the initial level. There are nine integrals for each C2 line. The term with i = j is Rayleigh scattering and terms with i ≠ j describe Raman scattering. P is the phase matrix describing the scattering process, I is the Stokes vector and Φj is the line profile. The values for the intrinsic line polarizabilities 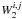 were calculated from formulas (15)–(17) in Berdyugina et al. (2002). The vector Bth = (Bν,0) is the thermal source term, which is given by the Planck function. The parameters
were calculated from formulas (15)–(17) in Berdyugina et al. (2002). The vector Bth = (Bν,0) is the thermal source term, which is given by the Planck function. The parameters 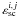 and
and 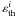 (which are depth dependent) define the branching between scattering and thermal parts of the source function, as follows
(which are depth dependent) define the branching between scattering and thermal parts of the source function, as follows 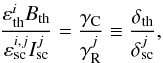 (2)where
(2)where 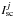 is the intensity part of the jth scattering integral, γC is the total collisional exciting rate,
is the intensity part of the jth scattering integral, γC is the total collisional exciting rate, 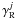 is the radiative exciting rate from the lower level j. The total collisional rate is defined as the sum of rates of all possible collisional excitation processes. The coefficients δth and
is the radiative exciting rate from the lower level j. The total collisional rate is defined as the sum of rates of all possible collisional excitation processes. The coefficients δth and 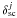 define the parts of the thermal and scattered photons
define the parts of the thermal and scattered photons 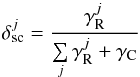 (3)and
(3)and 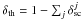 . To simplify the calculations, we substituted the total exciting collision rates by the total decay rates. Both rates are equal in LTE, and we have verified that they are so close to each other in our case that no significant error is introduced.
. To simplify the calculations, we substituted the total exciting collision rates by the total decay rates. Both rates are equal in LTE, and we have verified that they are so close to each other in our case that no significant error is introduced.
 |
Fig. 1 Diagram showing the nine considered transitions for the R2(13) line. The diagrams for all other C2 lines are similar. The energy differences of the levels are not to scale. Primed (′) variables correspond to upper levels and double-primed (′′) variables to lower levels. Dotted lines represent Q-branch transitions, which are significantly weaker than the other transitions. Transitions from satellite branches are not shown because they are even weaker than the Q-branch. |
The considered C2 lines are optically thin in the solar atmosphere. Using the second solar spectrum atlas (Gandorfer 2000) we verified that none of the absorption lines, which excite the upper level of our lines of interest, are blended with other strong lines (I/Ic is always larger than 0.85). Hence, the values of the scattering integrals in Eq. (1) differ only by the intrinsic polarizability factors W2 and Einstein coefficients, which both depend on the line quantum numbers (see Berdyugina et al. 2002). In particular, the main contribution is owing to P- and R-branch transitions (ΔJ = ± 1) since the Q-branch (ΔJ = 0) is much weaker. To simplify the matter, we considered only the Rayleigh scattering integral but with the effective scattering polarizability that is calculated as a weighted mean of the nine polarizabilities with the Einstein coefficients for absorption being the weights. A similar approach was used by Landi Degl’Innocenti (2006, 2007) who analytically calculated the polarizability factors for diatomic molecules in an intermediate Hund’s case (a–b). We calculated the level structure and the Einstein coefficients numerically, using matrix elements for the effective Hamiltonian listed by Brown & Merer (1979) and Brazier et al. (1986). The level structure includes shifts due to orbit-rotation coupling, which normally for levels with a non-zero orbital momentum results in the Λ-doubling effect. In the case of C2, rotational levels shift up or down in energy depending on the parity. The normalization of Einstein coefficients was according to Whiting & Nicholls (1974), but without the Λ-doubling perturbation, which is consistent with Trujillo Bueno et al. (2006) and differs by factor of two from Berdyugina & Fluri (2004). Using numerical values was easier with our approach but the result of both methods would be similar. We evaluated that the error induced by our effective polarizabilities is not larger than 5% and does not affect our conclusions. This is in contrast to e.g. the CN violet system where Raman scattering plays an important role because those lines are optically thick (Shapiro et al. 2011a). Some of the parameters that were used for the calculations are given in tables in Paper I and in Berdyugina & Fluri (2004). The full line list containing main and satellite branch transitions in several vibrational bands is available upon request. The band oscillator strengths were taken from Curtis et al. (1976), while the molecular constants were obtained from Prasad & Bernath (1994).
The actual calculation was done in two steps, analogous to the approach by Holzreuter et al. (2005). First, Stokes I and opacities were calculated. The statistical equilibrium in the C2 lines is solved with the 1D version of the NLTE radiative transfer code (hereafter RH-code) written by Uitenbroek (2001). The code is employing the multilevel accelerated lambda iterations (MALI) method by Rybicki & Hummer (1991, 1992). To make the calculations less time-consuming, the statistical equilibrium equations were solved only for electronic-vibrational states, while populations of rotational levels within one vibrational state were assumed to obey the Boltzmann law. The molecular number densities were calculated by solving the chemical equilibrium equations, using the solar abundances by Grevesse & Anders (1991). The CNO abundances that are important for the C2 equilibrium are C = 8.6, N = 8.0 and O = 8.93 with respect to hydrogen H = 12 in the logarithmic scale. Molecular partition functions and equilibrium constants were calculated with the polynomial approximation by Sauval & Tatum (1984).
In the second step, the intensity and opacities calculated by the RH-code were used as input for the second code POLY by Fluri & Stenflo (2003). This code iteratively solves the polarized radiative transfer equation for Stokes Q/I, assuming that polarization does not affect the opacity. This is a valid assumption for our case because of the low polarization degrees (<1%). The continuum polarization is calculated according to Stenflo (2005).
2.2. Model parameters
1D radiative transfer with standard solar model atmospheres is not able to reproduce Stokes I/Ic and Q/I simultaneously. Models that give a reasonable intensity fit, produce very small Q/I signals owing to a lack of radiation anisotropy (Holzreuter & Stenflo 2007). To overcome this problem we follow the approach of Shapiro et al. (2011a) and introduce a free parameter f, which allows us to account for the missing anisotropy at higher layers of 1D model atmospheres (see Sect. 3.4).
We assume a turbulent, isotropic, single-valued magnetic field, constant over the formation heights of our C2 lines. The magnetic field strength B is a free parameter, and determining its value is our main goal.
The collision rates for the C2 transitions were never measured in the laboratory for conditions similar to those on the Sun. Therefore, there are big uncertainties in their values as well as dependence on temperature and pressure. Following a theoretical development by Derouich (2006), we assumed that C2 collision rates vary with temperature T and the hydrogen concentration NH as γC ∝ T0.3NH. Then, we chose the branching coefficient δth at the height of 220 km above τ5000 = 1 as a free parameter ρC = δth(220 km). This height corresponds to the maximum of the Stokes I contribution function for the selected lines at the limb distance μ = 0.1. Because of the high pressure gradient over the formation region of the C2 lines, δth is changing quickly.
Using these free parameters, a good fit can be found for either the R-triplet with lower J numbers or the P-triplet with higher Js, but not for both simultaneously. These triplets have a somewhat different absorption depth, but they are both still optically thin. For μ = 0.1 the continuum is depolarized to 87% of its value in the line cores of the R-triplet lines and to 68% for the line core of P1 and P2. Our calculations show that the larger absorption in the P-triplet cannot account for the observed difference in Q/I.
Also, the triplets form at about the same height in the solar atmosphere, which is seen from their contribution functions. A possible explanation for their difference might be that collisions affect the triplets differently. For instance, Derouich (2006) predicted that collision rates should decrease with increasing J. Since J of our P lines (40 ≤ J ≤ 42) are significantly higher than those of the R lines (12 ≤ J ≤ 14), one can expect higher collision rates for the R-triplet. To account for this behavior we introduced a free parameter ρJ describing the ratio between collision rates for different J numbers. In our case, ρJ = γC(12 ≤ J ≤ 14) / γC(40 ≤ J ≤ 42), which corresponds to the ratio of the collision rates of the two triplets.
These four parameters, namely B, f, ρC and ρJ, allow us to obtain a good fit to the observed spectra using a χ2-minimization.
3. Parameter study
The radiative transfer approach allows us to investigate the dependence of calculated spectra and line amplitude ratios on model parameters. Our parameter study is described in the following sections.
3.1. Atmosphere model
We simulated spectra using the standard atmospheres from Fontenla et al. (1993): FAL-C for the averaged quiet Sun, FAL-A for the faint supergranule cell interior and FAL-P for a plage. The polarization amplitude ratios were found similar for all atmospheres for a fixed set of other free parameters. The absolute value of the polarization was significantly lower for the FAL-P model, which can be explained by the different temperature structure of this atmosphere. For our final calculations we used FAL-C and adjusted its radiation anisotropy. This model, combined with our molecular constants and the element abundances from Grevesse & Anders (1991), results in C2 intensity profiles that agree well with the measurements, as can be seen in Fig. 2.
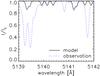 |
Fig. 2 Measured intensity spectrum (dotted) and model calculation (solid). Only C2 lines were taken into account for the calculation, which explains the differences to the observed, deep atomic absorption lines. Some small differences in the C2 lines may be caused by vignetting effects, which could not be fully removed because flatfields were not available for the observations. |
3.2. Collisions
In all previous models for C2 lines, the effect of collisions was considered in a simplified way. Our NLTE radiative transfer model allows us to consistently take collisions into account and investigate their influence on polarization. In the POLY code, depolarization because of the Hanle effect is calculated using the equation 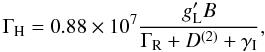 (4)where
(4)where 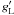 is the upper level Landé factor, ΓR the radiative decay rate, γI the inelastic collision rate, and D(2) the rate of depolarizing elastic collisions.
is the upper level Landé factor, ΓR the radiative decay rate, γI the inelastic collision rate, and D(2) the rate of depolarizing elastic collisions.
The elastic and inelastic collisions enter into Eq. (4) in the same way, therefore we cannot distinguish between them. Thus, we treat the sum D(2) + γI as one height-dependent variable. Zero value of the ρC parameter corresponds to calculations without collisions (D(2) + γI = 0). The collisional term goes to infinity for ρC → 1 which yields ΓH → 0. For the comparison without collisions, this collisional term was set to zero for all heights.
The collision rates also enter via the branching factors εi in the source function given by Eq. (1). For the comparison without collisions, we have set the thermal part of the source function to zero, i.e. 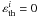 . These branching factors are determined from ρC via δth (see Eq. (2)). For example, if ρC is close to 1, then collisions dominate and the source function is close to the Planck function (pure LTE). For ρC = 0 we have the opposite case where the source function is given by its scattering part without any contribution from the Planck function (
. These branching factors are determined from ρC via δth (see Eq. (2)). For example, if ρC is close to 1, then collisions dominate and the source function is close to the Planck function (pure LTE). For ρC = 0 we have the opposite case where the source function is given by its scattering part without any contribution from the Planck function (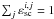 and
and 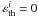 ).
).
Figure 3 shows a comparison between line ratios including collisions (top panels, ρC = 0.05) and without collisions (bottom panels, D(2) + γI = 0 and 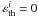 ). The left panels are magnifications of the plots on the right with a smaller range of magnetic field values. The effective W2 values were used, as defined in Sect. 2.1, which explains the small differences to the plots of Berdyugina & Fluri (2004) for the case without collisions. It is visible that the R2/P ratio is rather high because the J-dependent collisions were neglected in this plot (ρJ = 1), making it impossible to fit our new observations (see Paper I). The comparison shows that the ratios change significantly when the effect of collisions is included. The collisions mainly influence how fast the ratios increase or decrease with magnetic field but the shape of the curves is very similar for both cases. Basically, the main difference is the scaling of the B-axis because of the collisional term in the denominator of Eq. (4).
). The left panels are magnifications of the plots on the right with a smaller range of magnetic field values. The effective W2 values were used, as defined in Sect. 2.1, which explains the small differences to the plots of Berdyugina & Fluri (2004) for the case without collisions. It is visible that the R2/P ratio is rather high because the J-dependent collisions were neglected in this plot (ρJ = 1), making it impossible to fit our new observations (see Paper I). The comparison shows that the ratios change significantly when the effect of collisions is included. The collisions mainly influence how fast the ratios increase or decrease with magnetic field but the shape of the curves is very similar for both cases. Basically, the main difference is the scaling of the B-axis because of the collisional term in the denominator of Eq. (4).
3.3. Magnetic field strength
The different sensitivities of the C2 lines to the magnetic field strength is the key to our differential Hanle interpretation. The decrease of the amplitudes from 0 G to 300 G is presented in Fig. 4. The simulation was performed for realistic parameters: μ = 0.11, ρJ = 1.5 and ρC = 0.05. The left panel shows the fast decrease of the amplitudes of R1 (solid) and R3 (dash-dotted) which have the lowest critical field of our observed lines, i.e. depolarize the fastest. Their amplitude is nearly constant above 100 G. The amplitudes of R2 (dashed) and P (dotted) decrease slower. P is a combination of P1 and P2 where the first line has a rather low critical field strength (58 G) and the second line has the highest critical field strength of our sample (1622 G). These values of the critical field strength correspond to 75% line depolarization (Paper I). In the right panel, the region from 0 G to 100 G is shown. The curves show the decrease of the amplitudes in percent with respect to the zero magnetic field case. The amplitudes of R2 and P are less affected by the magnetic field than R1 and R3. This was already used for the calibration of our observed limb distances in Paper I.
 |
Fig. 3 Amplitude ratios vs. B for the calculations including collisions (top, ρC = 0.05) and without collisions (bottom). The left panels show a magnified part of the right plots with a smaller range of values for the magnetic field. It is clearly visible that collisions influence the amplitude ratios significantly. |
 |
Fig. 4 Variation of the absolute Q/I including the continuum polarization with magnetic field. The parameters used for the simulation are: ρC = 0.05, ρJ = 1.5 and μ = 0.11. Left panel: the amplitudes of R1 (solid) and R3 (dash-dotted) decrease very fast and are nearly fully depolarized above 100 G. The critical field strengths of R2 (dashed) and P (dotted) are higher. Right panel: magnification of the region from 0 G to 100 G. The y-axis is scaled with the zero magnetic field Q/I value, i.e. shows the amplitude decrease in percent. Because the continuum polarization is included and not only the line polarization is shown, the ratio does not necessarily decrease to 20% for high B. |
3.4. Radiation anisotropy
Model atmospheres are empirically constructed to fit the solar intensity spectrum. The scattering polarization scales with the anisotropy, which is mainly given by the temperature gradient of the atmosphere. An average temperature structure that may produce a good fit to Stokes I will almost always underestimate the actual, local anisotropy of the radiation field and result in a too low polarization for Stokes Q. The solar atmosphere is highly inhomogeneous, especially in its higher layers (Ayres & Testerman 1981), but this anisotropy is averaged out in 1D atmosphere models (Uitenbroek & Criscuoli 2011). A first approach may include adjusting the temperature structure of the model atmosphere to fit Q/I but this will result in a bad fit for the center-to-limb variation of Stokes I. Even when two or more atmospheric components are used for fits, it is not possible to simultaneously fit Stokes I and Q/I for different heliocentric angles. This is a well-known problem in 1D radiative transfer modeling and may be solved by adding additional anisotropy, which only influences Stokes Q (Holzreuter & Stenflo 2007; Shapiro et al. 2011a). Similarly to Shapiro et al. (2011a), we introduce an additional factor f in the Q component of the source function. The exact formulae for f can be found in that paper.
The additional radiation anisotropy f can be constrained through additional observations and therefore does not have to be treated equally to the other free parameters. We have repeatedly measured the center-to-limb variation of the Q/I amplitude of the lines and, in case of THEMIS measurements, also the center-to-limb variation of the continuum polarization. We therefore adjust the effective polarizability of the continuum (see Stenflo 2005) and the additional anisotropy factor to fit the observations using the FAL-C atmosphere model. The additional anisotropy is correlated with the collisions ρC, and corrections to the unknown height-dependence of δsc may be induced through f. Therefore, it can not be excluded that a slightly different f with accordingly different collisions ρC may lead to the same spectra, but as shown in Fig. 9, the determination of the magnetic field is independent.
Figure 5 is similar to Fig. 6 of Paper I and shows the P polarization amplitude with limb distance (left panel) for different additional anisotropy functions f (right panel). It can demonstrate how the final f was found. Without any additional anisotropy (triangles, left panel), the calculated Q/I amplitudes are significantly below the measured levels (dashed line, left panel). A constant f, as used by Shapiro et al. (2011a), cannot reproduce the measured μ dependence in our case. The physical mechanisms that influence the additional anisotropy could be different for the optically thick CN lines and the optically thin C2 lines. For example, the scattering polarization of CN and C2 may originate from different regions on the solar surface. The figure shows that the largest correction in anisotropy was required for measurements that were taken close to the limb. A linearly increasing f (solid line, right panel and diamonds, left panel) can reproduce the observed amplitudes very well. Because the differences in formation height at different limb distances are quite small (less than 100 km), f needs to be steeply increasing. Only the P amplitude is shown in our figure for clarity, but to find the final f, the slope of f was varied until the calculated R2 and P amplitudes agreed with the observations for a non-zero value of ρC. The result was well-defined for a given choice of ρC and did not change when the magnetic field was changed. The R2 and P amplitudes were chosen because they are least affected by the magnetic field.
 |
Fig. 5 Left panel: the dashed line represents the P amplitude fit to the center-to-limb THEMIS and IRSOL measurements from Paper I. Calculations with a constant anisotropy factor f cannot reproduce these amplitudes (asterisks for f = 5 and triangles for f = 0). The right panel shows the corresponding height dependence of f (dash-dotted line for f = 5 and dotted line for f = 0). It was varied linearly (solid line, right panel), which created a good fit to the measured P amplitudes (diamonds, left panel). |
3.5. J-dependence of the collisions
Figure 6 shows the effect of J-dependent collision rates for the observed P and R triplets. The code was modified for our desired R triplet around 5141 Å only, while other R triplets, partly visible in the figure, are not affected. The numbers ρJ denote the factor between the collision rates. While Derouich (2006) predicted a factor of ~5.5, we found that a lower factor is needed (see Table 1). Because we cannot distinguish between elastic and inelastic collisions in the code and the prediction was for elastic collisions only, this difference is well possible.
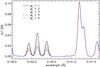 |
Fig. 6 When the collision rates of the R triplet are enhanced by a factor of ρJ compared to the P triplet, the R lines show additional depolarization. These J-dependent collisions were predicted by Derouich (2006) and were necessary to obtain good fits to the observed spectra. The parameters used to produce this figure are ρC = 0.05, B = 7 and μ = 0.11. |
4. Fitting the observations
We calculate the χ2-minimization comparing the simulations with the observations, and obtain the collision rates, the J-dependent collisions and the value of B from the best fit. In this section we calculate the model fits to the 78 synoptic observations with limb distance 0.07 < μ < 0.13 from Paper I including the peculiar measurement ms080509 and to the atlas of the second solar spectrum (Gandorfer 2000). The minimization was calculated using three wavelength points of each of the C2 peaks, giving a total of 18 data points per observation. In this way the P and R triplets are weighted equally and since the wavelength points are chosen close to the maximum values of each peak, the amplitude ratios of each best fit agree well with the amplitude ratios of the respective observation. We minimize the χ2-value defined as 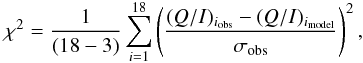 (5)where σobs denotes the noise of the observed Q/I spectrum. The filling factor α of the turbulent magnetic field was assumed to be α = 1 in agreement with the results of Paper I.
(5)where σobs denotes the noise of the observed Q/I spectrum. The filling factor α of the turbulent magnetic field was assumed to be α = 1 in agreement with the results of Paper I.
The best fits (smallest χ2) are shown in Fig. 7 for an average synoptic observation, the atlas and ms080509 (from top to bottom). The observations (dotted), always averaged over the slit, and the calculations (solid) were shifted so that the continuum is at the zero level. The parameters for each best fit are given in Table 1.
The limb distance (μ) was a fixed parameter, determined for each observation separately as described in Paper I. The model was calculated for steps of Δμ = 0.01 and linearly interpolated for each observation. It was verified that within these small steps of μ, a linear interpolation results in a relative error of less than 1% that is lower than the noise level of our observations.
The parameters, especially the magnetic field, are well constrained. Of all measurement, the lowest obtained magnetic field is 6.0 G and the highest amounts to 9.7 G. The deviations in the collision factor and ρJ are slightly larger because they are both coupled with our additional anisotropy. As mentioned before, we chose an additional anisotropy linearly increasing with height. Our simplification may not be entirely correct and therefore, for measurements with different μ and thus line formation heights, one may need different collision rates to depolarize the lines to their “best fit”. This is indeed the case, as all of the lowest occurring collision rates (0.03) are for μ < 0.08. The magnetic field however will not be affected because of the differential Hanle effect.
 |
Fig. 7 Best fits for Q/I (solid), as determined by the χ2-minimization, to an example synoptic observation, the atlas and ms080509 (dotted, from top to bottom). Blend lines (Fe i and Cr i) were not included for the calculations which explains the large differences below 5139.8 Å. |
The J-dependent collision factor is coupled in a similar way: the difference in the formation heights of the P and R lines gets larger for measurements taken closer to the solar limb. Therefore, P and R then each get a different amount of additional anisotropy and collisions. Thus, ρJ is correlated with the limb distance of the observations.
 |
Fig. 8 Contours of constant χ2-values (confidence levels {68.3%, 95.4%, 99.7%}, solid lines; two degrees of freedom) for fits to the atlas observation. ρJ was fixed and the contours were calculated for the μ-value of the observation. The dotted ellipse represents a confidence interval of 68.3% for one degree of freedom. It is used to derive the errors of the single parameters by projections onto one dimensional intervals (see Press et al. 2002). |
The errors for the single measurements, which were determined from χ2-contours, are comparably large, because similar amplitude ratios can be reached with different combinations of B, ρJ and ρC. Figure 8 shows the contours of constant χ2-values for the atlas observation for a fixed ρJ = 1.2. Contours for the synoptic measurements are similar, although generally smaller because their noise level is lower. In Paper I, the derived error bars were smaller because they were determined directly from the measurement noise and collisions were neglected. Here, the collisions can compensate for variations in magnetic fields (see Fig. 8) and therefore, we cannot conclude on any variability between the synoptic measurements and the atlas. The measurement noise, σobs, was taken from the observations as the standard deviation of Q/I of a region without spectral lines. If σobs was overestimated, then the errors of the single measurements would be smaller. Deriving the error bars from levels of constant χ2-values assumes that the errors are distributed normally. However, systematic errors may be present and in that case, the current error bars may be underestimated. Because the actual collisions rates on the Sun are unknown, it is not possible to restrict the field strength more exactly. The error bars get smaller with better statistics. Therefore, it certainly is worthwhile to continue the synoptic program and compare the atlas measurement with future measurements taken during more active phases. The errors given in Table 1, namely the standard deviation and the error of the mean, both assume that the errors are distributed normally, which we cannot reliably determine with the current number of measurements because statistical tests are inconclusive. If the errors follow a normal distribution, then the error of the mean may be calculated as 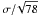 , which would equal to 0.09 G. In this case, increasing the number of measurements and thus the statistics, would lower the value of the error bars.
, which would equal to 0.09 G. In this case, increasing the number of measurements and thus the statistics, would lower the value of the error bars.
Parameters for best fits.
 |
Fig. 9 Scatter plots of the magnetic field B vs. ρC, μ and ρJ (from left to right). No correlation can be seen and therefore B is independent. |
Even though a good fit is found for ms080509, it does not reproduce the observed R1/R2 ratio. It is 0.56 in the model but 0.47 in the observation. We cannot provide a definitive explanation for ms080509. It is unlikely that the collision rates were different on one specific date at one specific place in the Sun. What may be possible is a change in the anisotropy. Even though our slit subtends 180′′ there could be a small chance to place it over a region with anomalous anisotropy. The anisotropy in our model was fixed using (average) polarization amplitudes and because anisotropy, collision rates and magnetic field are linked, it could explain the result of the fit. Also, the iron lines are more depolarized for this specific measurement and the broad wing of the line next to R1 could influence the ratio. In conclusion, we cannot absolutely rule out any of the possibilities and can only speculate about this measurement.
While some of the other variables are correlated with each other (like ρJ and μ, for example), the magnetic field is independent when comparing the different measurements of our dataset. The scatter plots in Fig. 9 show the lack of correlation for the magnetic field B and the collision factor ρC, μ and ρJ (from left to right) for the 78 best fits. It indicates that even if the collision rates or the anisotropy are slightly off, the determination of the magnetic field does not depend on it.
5. Conclusions
We adapted a 1D NLTE radiative transfer model to be able to calculate C2 lines around 5141 Å. It was found that an implementation of collisions, and especially J-dependent collisions, is necessary for a proper modeling of C2. Using the differential Hanle effect, we calculated the average turbulent magnetic field strength to be 7.41 G for our fits to 78 measurements spanning two years. The standard deviation of 0.76 G is either because of statistical noise or possible fluctuations of the magnetic field. The value of the magnetic field strength is in agreement with Paper I, where only a lower limit of 4.7 ± 0.2 G could be determined.
Our value for the turbulent magnetic field agrees well with strengths inferred from previous measurements of optically thin molecular lines. The values of different authors and different molecular lines range from a few G to 30 G using the least model-dependent interpretation, the differential Hanle effect. While some authors considered the effect of collisions (e.g., Faurobert et al. 2001; Derouich et al. 2006; Bommier et al. 2006), others neglected them (e.g., Faurobert & Arnaud 2003; Berdyugina & Fluri 2004) and thus the latter results should be compared to the magnetic field value from Paper I, where depolarization because of collisions was also neglected. For example, Trujillo Bueno et al. (2006) analyzed different C2 lines and found a value of 7 G assuming a single-value, isotropic, turbulent magnetic field but neglecting collisions. Measurements involving atomic lines, for example Sr i, usually result in higher magnetic field strengths (Trujillo Bueno et al. 2006). One proposed explanation suggests that the scattering polarization of molecular lines may be formed in upflowing regions where the magnetic field is weaker (Trujillo Bueno 2003). Another possibility for the discrepancy may be the different methods employed for the interpretation of the polarization in molecular and atomic lines. For instance, atomic depolarization is always compared to a model dependent non-magnetic level of scattering polarization, while molecular lines allow for a differential Hanle effect.
Measurements of optically thick molecular lines, such as CN, suggest a field strength closer to the atomic values. Shapiro et al. (2011a) deduced a magnetic field strength of 82 G from the observations in the region of the CN (0–0) bandhead and 45 G from the observations in the region of the CN (1–1) bandhead. This result is compatible with the explanation proposed by Trujillo Bueno (2003). For the optically thick lines, the scattering polarization may not only form in the center of granules as in the optically thin case, but also in intergranular areas that may contain a higher magnetic field. The optical thickness of lines in the (1–1) bandhead region is generally smaller than of those in the (0–0) bandhead region. Therefore, one can expect that the relative contribution of intergranular areas to the overall signal in the (1–1) bandhead region is smaller than in the (0–0) bandhead region. This could explain the differences in the deduced values of the magnetic field from various molecular lines. Whether the optical thickness plays a role in the sensitivity of atomic lines to turbulent magnetic fields needs to be clarified. It appears that the higher temperature sensitivity of molecular lines makes them more sensitive to the granular structure of the photosphere.
A remarkable property of our measurements is that the magnetic field was homogeneous across all solar latitudes during the past solar minimum. The accuracy of our measurements does not allow us to unambiguously state that there is a variation of the magnetic field between the solar maximum and minimum. This is mainly because of the low accuracy of the single atlas measurement taken close to the solar maximum. Additionally, more exact collision rates would be needed to restrict the error bars of the magnetic field for single measurements. The continuation of our program will help clarifying the variability and testing the present models of the origin of the quiet Sun magnetism. If the homogeneous distribution of the magnetic field persists over the solar cycle, this could be considered as a hint that the local dynamo plays a significant role in the formation of the quiet Sun magnetism. On the other hand, the modulation of the turbulent magnetic field with the solar cycle (if confirmed) could indicate that the debris from decaying active regions may also have an important contribution. Moreover, as the evolution of the quiet Sun magnetism could influence the long-term trend in the solar irradiance, the synoptic program may also provide important information for the modeling of the long-term solar variability and clarification of its role in the natural climate change (cf. Shapiro et al. 2011b). Our results help characterizing the turbulent magnetic field on the Sun and it would be most interesting to obtain measurements with a higher spatial resolution in order to look for variations on granular scales.
Acknowledgments
We thank Han Uitenbroek for providing his RH code and Dominique Fluri for his POLY code. We gratefully acknowledge the technical support provided by Daniel Gisler, Peter Steiner and Renzo Ramelli. THEMIS is operated by the CNRS. This work has been funded by the SNSF, grants 200020-117821 and 200020-127329. SVB acknowledges the EURYI (European Young Investigator) Award provided by the ESF (see www.esf.org/euryi) and the SNSF grant PE002-104552. AIS was funded by the SNSF under grant CRSI122-130642 (FUPSOL).
References
- Ayres, T. R., & Testerman, L. 1981, ApJ, 245, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., & Fluri, D. M. 2004, A&A, 417, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Stenflo, J. O., & Gandorfer, A. 2002, A&A, 388, 1062 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bommier, V., Landi Degl’Innocenti, E., Feautrier, N., & Molodij, G. 2006, A&A, 458, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brazier, C. R., Ram, R. S., & Bernath, P. F. 1986, J. Molec. Spectrosc., 120, 381 [Google Scholar]
- Brown, J. M., & Merer, A. J. 1979, J. Molec. Spectrosc., 74, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Curtis, L., Engman, B., & Erman, P. 1976, Phys. Scr., 13, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Derouich, M. 2006, A&A, 449, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Bommier, V., Malherbe, J. M., & Landi Degl’Innocenti, E. 2006, A&A, 457, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faurobert, M., & Arnaud, J. 2003, A&A, 412, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faurobert, M., Arnaud, J., Vigneau, J., & Frisch, H. 2001, A&A, 378, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fluri, D. M., & Stenflo, J. O. 2003, A&A, 398, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontenla, J. M., Avrett, E. H., & Loeser, R. 1993, ApJ, 406, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Gandorfer, A. 2000, The Second Solar Spectrum, Vol I: 4625 Å to 6995 Å (Zurich: VdF) [Google Scholar]
- Grevesse, N., & Anders, E. 1991, Solar element abundances, 1227–1234 [Google Scholar]
- Holzreuter, R., & Stenflo, J. O. 2007, A&A, 467, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holzreuter, R., Fluri, D. M., & Stenflo, J. O. 2005, A&A, 434, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivanov, V. V. 1991, in Stellar Atmospheres: Beyond Classical Models, NATO ASI Series C 341, ed. L. Crivellari, I. Hubeny & D. G. Hummer (Dordrecht: Kluwer), 81 [Google Scholar]
- Kleint, L., Berdyugina, S. V., Shapiro, A. I., & Bianda, M. 2010, A&A, 524, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landi Degl’Innocenti, E. 2006, in ASP Conf. Ser. 358, ed. R. Casini & B. W. Lites, 293 [Google Scholar]
- Landi Degl’Innocenti, E. 2007, A&A, 461, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prasad, C. V. V., & Bernath, P. F. 1994, ApJ, 426, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical recipes in C++: the art of scientific computing, ed. W. H. Press, S. A. Teukolsky, W. T. Vetterling & B. P. Flannery, [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] [Google Scholar]
- Sauval, A. J., & Tatum, J. B. 1984, ApJS, 56, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, A. I., Fluri, D. M., Berdyugina, S. V., Bianda, M., & Ramelli, R. 2011a, A&A, 529, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, A. I., Schmutz, W., Rozanov, E., et al. 2011b, A&A, 529, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O. 1994, Solar Magnetic Fields (Dordrecht: Kluwer) [Google Scholar]
- Stenflo, J. O. 2005, A&A, 429, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O., & Keller, C. U. 1997, A&A, 321, 927 [NASA ADS] [Google Scholar]
- Trujillo Bueno, J. 2003, in Solar Polarization 3, ed. J. Trujillo Bueno & J. Sánchez Almeida, ASP Conf. Ser., 307, 407 [Google Scholar]
- Trujillo Bueno, J., Asensio Ramos, A., & Shchukina, N. 2006, in Solar Polarization 4, ed. R. Casini & B. W. Lites, ASP Conf. Ser., 358, 269 [Google Scholar]
- Uitenbroek, H. 2001, ApJ, 557, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H., & Criscuoli, S. 2011, ApJ, 736, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Whiting, E. E., & Nicholls, R. W. 1974, ApJS, 27, 1 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Diagram showing the nine considered transitions for the R2(13) line. The diagrams for all other C2 lines are similar. The energy differences of the levels are not to scale. Primed (′) variables correspond to upper levels and double-primed (′′) variables to lower levels. Dotted lines represent Q-branch transitions, which are significantly weaker than the other transitions. Transitions from satellite branches are not shown because they are even weaker than the Q-branch. |
| In the text | |
 |
Fig. 2 Measured intensity spectrum (dotted) and model calculation (solid). Only C2 lines were taken into account for the calculation, which explains the differences to the observed, deep atomic absorption lines. Some small differences in the C2 lines may be caused by vignetting effects, which could not be fully removed because flatfields were not available for the observations. |
| In the text | |
 |
Fig. 3 Amplitude ratios vs. B for the calculations including collisions (top, ρC = 0.05) and without collisions (bottom). The left panels show a magnified part of the right plots with a smaller range of values for the magnetic field. It is clearly visible that collisions influence the amplitude ratios significantly. |
| In the text | |
 |
Fig. 4 Variation of the absolute Q/I including the continuum polarization with magnetic field. The parameters used for the simulation are: ρC = 0.05, ρJ = 1.5 and μ = 0.11. Left panel: the amplitudes of R1 (solid) and R3 (dash-dotted) decrease very fast and are nearly fully depolarized above 100 G. The critical field strengths of R2 (dashed) and P (dotted) are higher. Right panel: magnification of the region from 0 G to 100 G. The y-axis is scaled with the zero magnetic field Q/I value, i.e. shows the amplitude decrease in percent. Because the continuum polarization is included and not only the line polarization is shown, the ratio does not necessarily decrease to 20% for high B. |
| In the text | |
 |
Fig. 5 Left panel: the dashed line represents the P amplitude fit to the center-to-limb THEMIS and IRSOL measurements from Paper I. Calculations with a constant anisotropy factor f cannot reproduce these amplitudes (asterisks for f = 5 and triangles for f = 0). The right panel shows the corresponding height dependence of f (dash-dotted line for f = 5 and dotted line for f = 0). It was varied linearly (solid line, right panel), which created a good fit to the measured P amplitudes (diamonds, left panel). |
| In the text | |
 |
Fig. 6 When the collision rates of the R triplet are enhanced by a factor of ρJ compared to the P triplet, the R lines show additional depolarization. These J-dependent collisions were predicted by Derouich (2006) and were necessary to obtain good fits to the observed spectra. The parameters used to produce this figure are ρC = 0.05, B = 7 and μ = 0.11. |
| In the text | |
 |
Fig. 7 Best fits for Q/I (solid), as determined by the χ2-minimization, to an example synoptic observation, the atlas and ms080509 (dotted, from top to bottom). Blend lines (Fe i and Cr i) were not included for the calculations which explains the large differences below 5139.8 Å. |
| In the text | |
 |
Fig. 8 Contours of constant χ2-values (confidence levels {68.3%, 95.4%, 99.7%}, solid lines; two degrees of freedom) for fits to the atlas observation. ρJ was fixed and the contours were calculated for the μ-value of the observation. The dotted ellipse represents a confidence interval of 68.3% for one degree of freedom. It is used to derive the errors of the single parameters by projections onto one dimensional intervals (see Press et al. 2002). |
| In the text | |
 |
Fig. 9 Scatter plots of the magnetic field B vs. ρC, μ and ρJ (from left to right). No correlation can be seen and therefore B is independent. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


