| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201117812 | |
| Published online | 12 October 2011 | |
The population of young stellar clusters throughout the disk of M 33⋆
1
INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
e-mail: saurabh@arcetri.astro.it; edvige@arcetri.astro.it; giova@arcetri.astro.it; hunt@arcetri.astro.it; palla@arcetri.astro.it;
2
Aryabhatta Research Institute of Observational Sciences (ARIES), Manora Peak, 263 129 Nainital, India
e-mail: saurabh@aries.res.in
Received: 2 August 2011
Accepted: 29 August 2011
Aims. The properties of young stellar clusters (YSCs) in M 33, identified from the center out to about twice the size of the bright star-forming disk, are investigated to determine possible spatial and time variations of the star formation process in this Local Group blue galaxy.
Methods. 915 MIR sources have been extracted from the Spitzer 24 μm image. Upon inspection of Hα and GALEX images and exclusion of evolved AGB stars, a sample of 648 objects is selected as candidate YSCs and their luminosity function is examined. The spectral energy distribution of each object, based on aperture photometry, is compared with Starburst99 models to derive age, mass and AV of individual clusters. In the analysis we allow for different values of the upper mass cutoff of the stellar initial mass function (IMF), the porosity of the ISM, and the dustiness of HII regions. We also examine the influence of different dust models and include corrections for incompleteness of the IMF.
Results. We find discrete MIR sources as far as the extent of the warped HI disk, i.e. 16 kpc from the galaxy center. Their surface density has a steep radial decline beyond 4.5 kpc, and flattens out beyond the optical radius at 8.5 kpc. We are able to identify YSCs out to 12 kpc. At large galactocentric radii, the paucity of luminous clusters and the relevance of hot dust emission become evident from the analysis of the bolometric and MIR luminosity functions. The YSC mass and size are correlated with a log-log slope of 2.09 ± 0.01, similar to that measured for giant molecular clouds in M 33 and the Milky Way, which represent the protocluster environment. Most of the YSCs in our sample have AV ~ 0−1 mag and ages between 3 and 10 Myr. In the inner regions of M 33 the clusters span a wide range of mass (102 < M < 3 × 105 M⊙) and luminosity (1038 < Lbol < 3 × 1041 erg s-1), while at galactocentric radii larger than ~4 kpc we find a deficiency of massive clusters. Beyond 7 kpc, where the Hα surface brightness drops significantly, the dominant YSC population has M < 103 M⊙ and a slightly older age (10 Myr). This implies the occurrence of star formation events about 10 Myr ago as far as 10−12 kpc from the center of M 33. The cluster LFUV vs. LHα relation is non-linear for LFUV < 1039 erg s-1, in agreement with randomly sampled models of the IMF which, furthermore, shows no appreciable variation throughout the M 33 disk.
Key words: galaxies: individual: M 33 / galaxies: ISM / galaxies: star clusters: general / galaxies: star formation
Full Tables 1 and 2 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/534/A96
© ESO, 2011
1. Introduction
Young stellar clusters (YSCs) are important tools for the study of the star formation (SF) process in galaxies. Having just formed from gravitationally bound molecular clouds and often still embedded in the parent nebular regions, they are a unique laboratory for understanding the early dynamical evolution of the associated stellar population, the properties of the initial mass function (IMF), and the interaction between young massive stars and the interstellar medium. Massive YSCs and complexes contain hot massive stars which play an important role in galaxy evolution, by ionizing, heating and enriching the ISM of heavy elements. They power the hot infrared (IR) radiation of dust and, at the end of their lives, they eventually trigger further SF events (Grossi et al. 2010). The IMF is a probabilistic function describing the distribution in mass of stars at their birth; its logarithmic slope above ~1 M⊙ has been often found close to the original value of −2.3 (Salpeter 1955). Given the rarity of massive stars predicted by the IMF, a statistically meaningful ensemble of YSCs is needed to test the IMF at its upper end.
External galaxies offer large numbers and a variety of SF sites but, except for the Milky Way satellite galaxies, YSCs are too compact for individual stars to be resolved. Even though the physical scales which can be spatially resolved will never be as small as in Galactic surveys, some global properties of the YSCs can be investigated using their integrated spectral energy distribution, from the UV to long enough wavelengths to overcome extinction (Grossi et al. 2010). Tracers of SF such as IR, Hα, far-ultraviolet (FUV), and near-ultraviolet (NUV) emission make a good combination to study the properties of YSCs. For example, Corbelli et al. (2009) have probed the stochasticity of the IMF using multiwavelength photometry of a few tens of infrared selected YSCs in the inner disk of M 33. In addition to the much reduced distance ambiguities, the advantage of studying YSCs in external galaxies is that large samples can be easily selected to probe different environments across the disk, such as spiral arms and inter-arms, central areas versus outskirts, and to compare star-forming sites in galaxies of different morphological types in a quiescent or dynamical stage.
The Local Group galaxy M 33 is a quiescent blue galaxy at a moderate inclination showing no sign of recent mergers or interaction. Located at a distance D = 840 kpc, it is currently forming stars at a rate of 0.45 M⊙ yr-1. The star formation rate (SFR) inferred from the FUV emission is slightly higher (0.55 M⊙ yr-1) than that deduced by Hα emission (0.35 M⊙ yr-1), but the difference could be simply due to the uncertain correction for extinction. When traced by the Hα emission (Kennicutt 1989; Verley et al. 2009), the SFR is found to decline radially with a scale length of about 2 kpc and then it drops sharply at galactocentric distances of about 7 kpc. This location is often referred to as the star formation edge of the disk. This sharp drop is less evident at other wavelengths, such as the mid-IR. In the far-UV the contribution of discrete sources drops at the SF edge but the diffuse emission has no apparent truncation or steeper decline out to the extent of the GALEX maps (Thilker et al. 2005). The difference in the behavior traced by these indicators can be explained in terms of a SFR which has substantially decreased during the last 100 − 200 Myr, or by the lack of massive stars at large galactocentric radii. The former possibility has received some support by the recent deep optical surveys (Grossi et al. 2011; Davidge & Puzia 2011) of regions beyond the optical radius where the average gas column density is only 2 × 1020 cm-2 (Corbelli 2003). These studies have revealed the presence of a population of relatively young main sequence stars with ages of about 100 − 200 Myr, indicating the existence of a more extended star forming disk in the recent past. Concentrations of ultraviolet light seen at large radii in some nearby spiral and dwarf galaxies are often sign of in situ star-formation (Hunter et al. 2011; Gil de Paz et al. 2008; Thilker et al. 2007). Localized density enhancements beyong the bright star-forming disk may occur and give birth to a population of low-mass clusters. Clustering on sub-kiloparsec scale seen among stars with ages 10 Myr close to the optical edge of M 33 has given evidence of recent star-formation (Davidge et al. 2011).
Inside the SF edge, the distribution of the ISM in the disk of M 33 is not at all uniform. The flocculent spiral arms fade away around 4 kpc and this dramatic change might be responsible for the variation in the properties of the interstellar clouds. Full imaging of the molecular cloud complexes in M 33 (Engargiola et al. 2003; Heyer et al. 2004; Gratier et al. 2010) has shown that those with masses above 105 M⊙ are very rare beyond 4 kpc. Bastian et al. (2007) also find that the number of young stellar groups also drops suddenly at radii > 4 kpc. However, a population of small mass molecular clouds exists at larger distances and it becomes dominant. This is also shown by the positive results of deep CO searches around dim IR sources close to the SF edge (see also Corbelli et al. 2011).
Mid-IR maps are generally very helpful to select stellar clusters in their early evolutionary phase due to the presence of hot dust in the surrounding parent gas. The resolution (6 arcmin) and extent (16 kpc) of the 24 μm Spitzer map of Verley et al. (2007) is ideal for selecting YSC candidates throughout the whole disk of M 33. The presence of UV or Hα emission is quite valuable to confirm the nature of mid-IR sources as YSC candidates since infrared emission alone cannot distinguish between YSCs and evolved stars, such as AGBs, that also contribute to the source counts in a galaxy (Corbelli et al. 2011). The spatial extent of UV and Hα maps will confine our YSC analysis to somewhat smaller radii.
Previous studies of infrared selected YSCs in M 33 have been restricted to a few tens of them located in the inner disk. A more complete study of the properties of the whole YSC population throughout the star-forming disk and possibly beyond it, still need to be done. Finding YSCs in the outermost regions of M 33 will definitively prove the in situ origin of the pervasive stellar population of ages 100 Myr recently discovered. The main aim of this paper is to investigate the properties of YSC population in M 33 identified on the basis of their mid-IR, UV and Hα emission from the galaxy center out to about 12 kpc. By comparing the emission of YSCs in the mid-IR, Hα, FUV and NUV bands with that predicted by theoretical models, we investigate possible differences in the distribution of mass, age, IMF and extinction throughout the M 33 disk. This will help set further constraints on the spatial and time variation of the star formation process in this nearby blue galaxy.
The paper is organized as follows. In Sect. 2 we present the sample and the multiwavelength dataset. In Sect. 3 we analyze the properties of the infrared and bolometric luminosity functions. The fitting method to the spectral energy distribution (SED) of YSCs is described in Sect. 4. In Sect. 5 we discuss the implications of the YSCs analysis on the IMF throughout the M 33 disk. The cluster properties are summarized in Sects. 6 and 7 lists our main conclusions.
2. Multiwavelength data and the 24 μm catalog
We select the young stellar cluster candidates of M 33 using the 24 μm images from Spitzer satellite data assembled by Verley et al. (2007). These authors cataloged 515 mid-infrared sources spanning over 4 orders of magnitude in luminosity and reaching, on the faint side, values equivalent to a single B2V star. However, this catalog is confined to the inner disk M 33 with only few sources extending as far as 7 kpc from the center. In order to extend the census of YSCs in the outermost regions of M 33, we have used the largest available 24 μm map and the SExtractor software (Bertin & Arnouts 1996) to identify discrete sources following the same method of Verley et al. (2007) .
The sources were extracted above the 8σ level and their photometry computed using the parameter “flux iso” in SExtractor, which uses isophotal photometry (sum of all pixels above threshold within the 8σ isophote); the background for the SExtractor photometry was the local median in a 32 × 32 pixel box centered on the source. We found 400 additional sources, so that our final list of 24 μm selected sources amounts to 915 objects (515 + 400), whose spatial distribution is shown in Fig. 1 overlaid on the 24 μm mosaic. It is evident that most of the Verley et al. (2007) sources (blue circles) lie in the inner region, whereas those identified by us (red circles) occupy mainly the outer regions, extending as far as 50 arcmin from the center. Table 1 gives the position and size of the sources in Verley et al. (2007) identified as YSCs. To the information already present in Verley et al. (2007) we add the source size and its galactocentric radius. Table 2 refers to the newly added 400 sources; the reported size is the semi-major axis of the ellipse fitted to the 8σ isophote.
 |
Fig. 1 The spatial distribution of 915 mid-IR sources (circles) and 648 young stellar clusters (squares) overlaid on the 24 μm Spitzer image. The light-blue and red circles in the on-line version represent IR sources from the Verley et al. (2007) catalogue and from the present study, respectively. |
In order to identify YSC candidates from the selected mid-IR sources, we complement the Spitzer 24 μm data with observations in other bandpasses:
i): mid (8 μm) and far-infrared (70 and 160 μm) data provided by the Spitzer InfraRed Camera (IRAC) and by the Multiband Imaging Photometer for Spitzer, as described in Verley et al. (2007);
ii): FUV and NUV maps obtained from the Galaxy Evolution Explorer (GALEX) satellite (Gil de Paz et al. (2007), using the GALEX-UV images at their original sampling of 1.5 arcsec/pixel;
iii): the narrow-band Hα map of Greenawalt et al. (1998), described in detail by Hoopes & Walterbos (2000).
We perform photometry in these other bandpasses using the position and size of the sources included in the 24 μm catalogue with the IRAF aperture photometry DAOPHOT package. Since the position of the source center and the extension of the emission may change with wavelength, we have chosen a slightly larger photometric aperture, namely 1.5 times the 24 μm size as determined by SExtractor. We estimated the background (using the “mode” function) in a 5-pixel wide circular annulus. Pixels 7σ below the background were rejected and the measurements were corrected for foreground Galactic extinction following Schlegel et al. (1998).2.1. The sample of young stellar clusters
 |
Fig. 2 (Top left) Sky area covered by various maps along with the position of all the 24 μm sources (915, dot symbols) and the sample of YSCs (648, open circles). Coordinates are for the J2000 epoch. (Top right) Histogram of the number of clusters N as a function of the galactocentric distance RG for Mid-IR sources (white) and YSCs (grey). (Bottom left & right panels) Profiles of the number density of clusters per unit area in kpc2 in linear and log scale, respectively, as a function of galactocentric distance for the same samples. See text for details on the disk deprojection model. |
Position, size and galactocentric distances “RG” for sources in Verley et al. (2007) classified as young stellar clusters and included in the analysis of YSC properties presented in this paper.
The catalogue of YSCs of M 33 includes all the Spitzer 24 μm sources with reliable photometry in the FUV, NUV, and Hα. We are limited by the smaller extent of the GALEX and Hα maps, compared to the mid-IR Spitzer maps, for the identification of 24 μm sources as YSCs. In the upper left panel of Fig. 2 we have marked the area covered by the GALEX maps together with the 24 μm mosaic and all the 915 sample objects. The 24 μm map is larger than that covered by GALEX and 53 of the 24 μm sources lie outside of the latter. We were able to obtain reliable (error < 0.5 mag) photometry for 789 sources in FUV, and 774 in NUV. A few other sources are too weak in the maps for an estimate of the UV fluxes. The adopted zero-points in the AB system (Oke 1990) are 18.82 (FUV) and 20.08 (NUV). We added, in quadrature, to the formal error provided by DAOPHOT an uncertainty of 0.10 mag to allow for zero-point calibration errors ( ≃ 0.05 mag) and large-scale background variance.
The total field of view of the Hα map is 1.75 × 1.75 deg2 with a scale of 2 arcsec/pixel. The Hα map is also smaller than the 24 μm mosaic (see Fig. 2 upper left panel) and 55 of the 24 μm sources fall outside its borders. We obtained reliable photometry (error < 0.5 mag) for 772 sources. We added in quadrature an error of 5% in flux and corrected the Hα flux assuming a 5% contamination by NII emission, as suggested by Hoopes & Walterbos (2000).
Additional 24 μm source catalogue (added to the catalogue of Verley et al. 2007).
IR sources with no, or weak, Hα counterpart are generally faint and their nature is not obvious. A possibility is that they might be AGBs which are quite luminous in the mid IR. Alternatively, they could be small sites of star formation lacking massive stars, or deeply embedded clusters, or background objects. McQuinn et al. (2007) have assembled a catalog of AGBs in M 33 based on Spitzer data. We have cross-checked our list with this catalog by searching for AGBs within the SExtractor 24 μm outer isophot.
In conclusion, out of the original 915 24 μm sources, our final list of YSCs is made of 648 objects, 407 from the catalogue of Verley et al. (2007) listed in Table 1, and 241 from the newly selected sources given in Table 2. The lack of the YSC label in the last column of Table 2 implies that either the MIR source is outside one of map boundary (Hα, FUV or NUV) or it is a bona fide AGB (being associated to a MIR variable), or that it has unreliable photometry in Hα, or FUV- or NUV-band. We retain as YSCs the few sources associated to MIR selected AGBs which have a non-negligible number of ionizing photons, log Hα > 36.8 erg s-1: these are large HII regions with an AGB star from a previous generation-star or close by in projection.
The YSCs selected at 24 μm have a wide range in size and luminosity and they are found in a variety of environments: from fully isolated, mainly in the galaxy outskirts, to crowded groups, especially in the inner spiral arms. Sources in Table 2 are mostly in the outer regions and isolated. In order to clearly assess the presence of UV and Hα counterparts and the reliability of the extraction process, we made up and inspected an atlas where, for each source, we assembled the images of the surrounding field in Hα, FUV, 8 and 24 μm. This allowed us to select also a sample of 24 μm sources with insignificant FUV and Hα brightness as candidate embedded star forming regions which will be examined in a forthcoming paper. An insight on their nature could come from a possible association with a molecular cloud or clump (Corbelli et al. 2011) but we have to wait for deep enough CO maps with sufficiently high spatial resolution to help in this regard.
3. Radial densities and luminosity functions of IR selected sources
Throughout the paper we assume a distance D to M 33 of 840 kpc (Freedman et al. 1991) to convert fluxes into luminosities or to compute galactocentric distances. Assuming that the sources lie in the disk and adopting the geometry and warp model of Corbelli & Schneider (1997), described in detail in Corbelli & Salucci (2000), we derive the distance RG from the center of our sample objects. The radial distribution of the 24 μm sources and the selected YSCs are plotted in the top right panel of Fig. 2. We can see that the MIR sources are found up to the largest distances, while YSCs are distributed over the whole area of overlap of the various maps.
In Fig. 2 the bottom panels display the radial density distribution in linear and log scale, respectively. The densities of the 24 μm sources and of the YSCs behave similarly with an overall exponential decay with radius. In particular, we note i) a shallow slope in the inner disk, 0−4.5 kpc; ii) a steep decrease between 4.5 and 8.5 kpc; and iii) a flattening in the outer disk. Past studies have found evidence for systematic radial variations in the star formation history of the M 33 disk. Bastian et al. (2007) showed that the number of young stellar groups drops suddenly at radii > 4 kpc and attributed this result to a change in the properties of the star forming sites. To study the inner and outer region clusters separately, we divide the 24 μm sources in “inner clusters” with RG < 4 kpc and “outer clusters” at larger distances. In this way, the size of the two groups is about the same.
3.1. Estimate of the bolometric luminosity
The bolometric luminosity of YSCs can be computed as the sum of the FUV and NUV luminosities uncorrected for absorption, the Hα luminosity corrected for extinction, 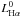 , and the total infrared luminosity LTIR:
, and the total infrared luminosity LTIR: 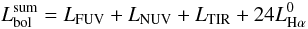 (1)where the terms Hα account for the ionizing radiation (Leitherer et al. 1999) and LTIR for the UV radiation absorbed by grains and re-emitted in the IR. We have not considered the radiation longward of 2800 A which becomes important only for young clusters with luminosities lower than 1038 erg s-1. The luminosity in the FUV and NUV has been derived from
(1)where the terms Hα account for the ionizing radiation (Leitherer et al. 1999) and LTIR for the UV radiation absorbed by grains and re-emitted in the IR. We have not considered the radiation longward of 2800 A which becomes important only for young clusters with luminosities lower than 1038 erg s-1. The luminosity in the FUV and NUV has been derived from 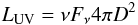 (2)with D the distance to M 33, ν = 1.95 × 1015 Hz for the FUV and ν = 1.3 × 1015 Hz for the NUV, and
(2)with D the distance to M 33, ν = 1.95 × 1015 Hz for the FUV and ν = 1.3 × 1015 Hz for the NUV, and 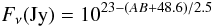 (3)AB indicates the corresponding magnitude in the FUV or NUV band.
(3)AB indicates the corresponding magnitude in the FUV or NUV band.
The total IR flux (FTIR) and LTIR are computed from the expressions: 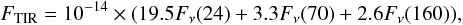 (4)
(4)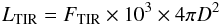 (5)where FTIR is in Wm-2 and Fν in Jy (Dale & Helou 2002). The size of a large fraction of sources in our YSC sample is below the Spitzer telescope resolution limit at 70 and 160 μm. Hence, we cannot use the above expression to compute LTIR except for a limited sample of extended resolved sources. We can estimate LTIR from the emission at 8 and 24 μm if we find a good correlation between these and LTIR. For the sample of resolved sources at 70 and 160 μm we derive LTIR and its relationship to the emission at 8 and 24 μm using the IRAC 8.0 μm photometry. This relation has been inferred previously but it might depend on the properties of the galaxy considered and on the scale examined (e.g. Engelbracht et al. 2005; Pérez-González et al. 2006). To find a relation between the 8 and 24 μm emission and LTIR, Verley et al. (2009) plotted the L24/LTIR ratio as a function of the 8/24 μm flux ratio for their sample of stellar complexes in the inner disk and derived a linear fit:
(5)where FTIR is in Wm-2 and Fν in Jy (Dale & Helou 2002). The size of a large fraction of sources in our YSC sample is below the Spitzer telescope resolution limit at 70 and 160 μm. Hence, we cannot use the above expression to compute LTIR except for a limited sample of extended resolved sources. We can estimate LTIR from the emission at 8 and 24 μm if we find a good correlation between these and LTIR. For the sample of resolved sources at 70 and 160 μm we derive LTIR and its relationship to the emission at 8 and 24 μm using the IRAC 8.0 μm photometry. This relation has been inferred previously but it might depend on the properties of the galaxy considered and on the scale examined (e.g. Engelbracht et al. 2005; Pérez-González et al. 2006). To find a relation between the 8 and 24 μm emission and LTIR, Verley et al. (2009) plotted the L24/LTIR ratio as a function of the 8/24 μm flux ratio for their sample of stellar complexes in the inner disk and derived a linear fit: 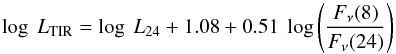 (6)where L24 is νFν × 4πD2. We have checked that the above relation also holds in the outer disk i.e. that the numerical coefficients of the above relation for sources in the outer disk are, within the errors, compatible with those relative to sources in the inner disk. Thus, in this study we adopt the relation of Verley et al. (2009) to compute LTIR from the 8 and 24 μm fluxes. An error of 0.10 mag is added in quadrature to the photometric error to compute the uncertainties in the 8 μm flux. The IRAC 8 μm map is smaller than the 24 μm mosaic (see Fig. 2 upper left panel) and 57 of the 915 sources fall outside it. For these sources and for the few (25) without a reliable 8.0 μm photometry (error < 0.5 mag) we use the relation
(6)where L24 is νFν × 4πD2. We have checked that the above relation also holds in the outer disk i.e. that the numerical coefficients of the above relation for sources in the outer disk are, within the errors, compatible with those relative to sources in the inner disk. Thus, in this study we adopt the relation of Verley et al. (2009) to compute LTIR from the 8 and 24 μm fluxes. An error of 0.10 mag is added in quadrature to the photometric error to compute the uncertainties in the 8 μm flux. The IRAC 8 μm map is smaller than the 24 μm mosaic (see Fig. 2 upper left panel) and 57 of the 915 sources fall outside it. For these sources and for the few (25) without a reliable 8.0 μm photometry (error < 0.5 mag) we use the relation 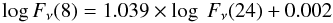 (7)to derive the flux at 8 μm which is needed to calculate LTIR. These coefficients are derived from a least square fit to the sources detected in both bands.
(7)to derive the flux at 8 μm which is needed to calculate LTIR. These coefficients are derived from a least square fit to the sources detected in both bands.
Extinction corrections to the Hα flux can be estimated using AHα = 0.83AV with AV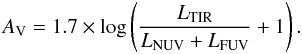 (8)This is similar to the visual extinction formula used by Calzetti (2001) if the “fudge factor” used to infer the luminosity outside the FUV band is replaced with the luminosity in the NUV.
(8)This is similar to the visual extinction formula used by Calzetti (2001) if the “fudge factor” used to infer the luminosity outside the FUV band is replaced with the luminosity in the NUV.
 |
Fig. 3 The cumulative luminosity functions of: a) the 24 μm sources (915), b) the 8 μm sources (833) shown as a function of LTIR, c) the selected YSCs (648) as a function of Lbol and d) the selected YSCs (648), as a function of the 24 μm flux. Filled and open circles represent counts in the inner and outer regions, respectively. Linear fits for different flux ranges are shown as solid lines for the inner sample, and dashed for the outer one. |
3.2. Luminosity functions
The luminosity function (LF) of YSCs is a fundamental probe of the star formation process of a galaxy. The cumulative LFs for the case of the inner and outer YSCs of M 33 are shown in Fig. 3. We plot separately the cumulative function for the 24 μm flux for all the 915 24 μm sources (Fig. 3a), and the cumulative function for the TIR luminosity relative only to sources with an 8 μm counterpart (Fig. 3b). We see that the shape of the two LFs is similar; their slopes are given in Table 3. In the same figure we also plot the cumulative LFs of the selected 648 YSCs as a function of Lbol (Fig. 3c) and of the 24 μm flux (Fig. 3d). The values of the slope of the best least square fit to the data points between Fν(24 μm) = 0.4 to 70 mJy are listed in Table 3 as 1st fit, while the 2nd fit includes points with higher values of Fν(24 μm). Since the values are lower than unity, the differential distribution N(L)dL ∝ L − γdL has γ lower than 2.
Overall, the main features of the LFs are the following:
(a): the slope of the cumulative function flattens at the faint end dueto incompleteness. Crowding in the inner disk implies asomewhat higher completeness limit;
(b): the LF of the inner disk shows a definite change of slope for a TIR or Bolometric luminosity of order of 1040 erg s-1. The bright end slope is similar to that found for bright HII regions in M 33 (Wyder et al. 1997) and in late-type spirals (Caldwell et al. 1991);
(c): the LF of the inner and outer YSCs differ markedly: there are very few bright outer sources and the outer LF is steeper at the faint end. The presence of a break is not evident and, if present, it occurs at a lower luminosity. The distribution can be well described by a single power law.
From the flattening of the distribution at the faint end, we estimate the completeness limit of the catalog around 0.4 mJy or LTIR ~ 5 × 1037 erg s-1. This corresponds to the bolometric luminosity of a single B1.5V star (Cox 2000), indicating that our sample is close to being complete even for faint obscured HII regions. The difference in the slopes of the inner and outer LFs between Fν(24 μm) = 0.4 to 70 mJy can be explained by a difference in the population of the star clusters. Namely, the inner regions have more massive clusters with the IMF fully populated up to the upper mass end. Conversely, the outer regions form predominantly clusters of lower mass and hence the presence of massive stars is rare and stochastic, as we shall discuss in Sect. 5. Owing to the similarity between the LFs for the infrared and bolometric luminosity, we can exclude the possibility that YSCs in the outer regions are fainter in the IR due to the formation in an environment with a lower dust-to-gas mass ratio. As we will see below, the estimated YSC extinctions show no radial variation. In fact, beyond the edge of active star formation the MIR-to-FUV or to-Hα ratios increase. YSCs in the outer regions are intrinsically of lower luminosity: we will discuss in the next Section whether this is due to an aging effect or to a different distribution in mass.As for the inner clusters, the distribution from the faint to the bright end can be broadly divided into two regimes with different slopes. The steep slope at high luminosity is often observed in the LF of HII regions, open clusters and associations (McKee & Williams 1997). In the simple scenario, the change of slope represents the transition from poor to rich clusters, where the latter are populous enough to reproduce the high-mass IMF (Oey & Clarke 1998). In this case, the transition point between the two regimes marks the luminosity of the single brightest star: below this value, the observed statistics is modified by the sampling variance. We find that the transition occurs around Fν(24 μm) ~ 60 mJy, i.e. 1040 erg s-1, close to the luminosity of an O3V star (Vacca et al. 1996). This implies that most of the bright MIR sources are in fact luminous YSCs.
Slope of best least-square fit to the cumulative distribution of the clusters of inner and outer region of M 33 galaxy.
4. SED fitting
Using the photometry in the FUV, NUV, Hα and MIR, we have constructed the SED of each YSC. By a comparison with model SEDs from Starburst99 (Leitherer et al. 1999; Vázquez & Leitherer 2005; SB99), we can then derive the individual age, extinction, and mass; in addition, we provide some estimate of the average properties of the whole YSC population with implications on the IMF and on the ambient ISM. Below, we illustrate the procedure.
 |
Fig. 4 Data (filled dots) and best fit model (open squares) SEDs for four YSCs with small errorbars but different χ2. Models in the bottom panels give good fits to the data. Models with a χ2 of order 100, as in the top-left panel, are of lower quality, but still yield acceptable fits. The few sources whose best fit model has χ2 ≫ 100 have a SED inconsistent with YSC models used in this paper. |
4.1. Stellar population modeling
We model the YSC SEDs with the SB99 single-age stellar population synthesis. We consider that YSCs formed in an instantaneous burst and assume a sub-solar metallicity of Z = 0.004 (Magrini et al. 2010). The IMF is chosen to be the default Kroupa IMF, that is a broken power law (φ(M) ∝ M − α) with a slope α = 1.3 for 0.1 M⊙ < M < 0.5 M⊙ and α = 2.3 for 0.5 M⊙ < M < Mmax (Kroupa 2001). Two sets of models were generated for different upper mass cutoffs: Mmax = 40 M⊙ and Mmax = 100 M⊙, respectively. We use the Padova evolutionary tracks with full AGB evolution to account for their non negligible contribution to MIR fluxes. However, we did not consider the contribution of thermally pulsating AGB stars that should be minimal for associations younger than 1 Gyr (Maraston et al. 2006). The time evolution is followed with logarithmic sampling (30 steps) from 1 to 100 Myr.
The SB99 calculations refer to a total stellar mass of 106 M⊙, and no allowance is made for dust extinction or emission. The main output of the simulation is the emerging spectrum at each sampled age which we then convolve with the GALEX and Spitzer filter bandpasses to generate the synthetic photometry. The model spectrum we use is the one taking into account both stellar and nebular emission, the latter being computed for the case of ionization-bounded regions; under this hypothesis, SB99 also provides the Hα luminosity.
First, in order to include the effect of extinction and dust emission in the SB99 photometry, we select a dust model among 3 cases made available by Weingartner & Draine (2001)1: Milky Way with RV = 3.1 (MW31), LMC “average” distribution (LMCAV), and LMC “2” distribution (LMC2). For our purposes, the difference among them is mainly in the relative extinction between FUV and NUV. We first assume that AV is mainly produced in the neutral ISM (screen geometry). Second, we choose a leakage factor Flkg as the fraction of the stellar radiation that escapes unimpeded by interaction with the ISM, that is without any extinction and re-emission in the IR and also without ionization and Hα production. We consider two values of the leakage factor of 0 and 1/3. Third, we allow the possibility that a fraction Kdust of the dust optical depth is contributed within the ionized phase (dusty HII regions): in this case, an important part of the ionizing flux is absorbed and reprocessed by dust, again without Hα emission. Again, we explore the influence of Kdust for only two values, 0% and 30%, of the extinction within the HII region.
In conclusion, given a dust model, a value of AV, the leakage fraction Flkg, and the fractional extinction in the HII region Kdust, we integrate the SB99 spectra and determine, apart from a multiplicative factor, the corrected FUV, NUV, Hα, and TIR luminosities, where TIR corresponds to the total amount of radiation absorbed by dust.
Sum of the χ2 obtained for different set of model parameters for inner and outer disk clusters.
4.2. χ2 minimization: reddening, age and mass fitting
As outlined above, the corrected FUV, NUV, Hα and TIR model luminosities depend on 3 cluster variables (age T, extinction AV, and mass M) and 4 population variables (upper mass cutoff, dust model, leakage, and HII region dustiness). For a given set of values of the population variables, we used a χ2-minimization on each YSC and derived the best-fit values of the cluster variables (T,AV,M) ![\begin{equation} \chi^2(T,A_{\rm V},M) = \sum_N { [\log(L_{\rm obs}) - \log(L_{\rm model}) -A]^2\over \sigma^2_{\rm obs}} \end{equation}](/articles/aa/full_html/2011/10/aa17812-11/aa17812-11-eq111.png) (9)where N is the number of bandpasses (4), Lobs is the observed luminosity, Lmodel is the model luminosity, and
(9)where N is the number of bandpasses (4), Lobs is the observed luminosity, Lmodel is the model luminosity, and 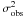 is the estimated photometric error. In practice, the age and extinction of each cluster are determined by comparing the shape of the SED to that of the SB99 models, while the mass is the scale factor required to best match the absolute values of the measured fluxes. Finally, A = log (M/106 M⊙). As an illustration of the method, we display in Fig. 4 the SED best fits to four YSCs with different χ2 values.
is the estimated photometric error. In practice, the age and extinction of each cluster are determined by comparing the shape of the SED to that of the SB99 models, while the mass is the scale factor required to best match the absolute values of the measured fluxes. Finally, A = log (M/106 M⊙). As an illustration of the method, we display in Fig. 4 the SED best fits to four YSCs with different χ2 values.
The average ⟨ χ2 ⟩ over the whole ensemble of YSCs of the minimized χ2’s is then used to discriminate among the different combinations of population variables. Such comparison is also performed separately for inner and outer clusters. Table 4 lists the mean ⟨ χ2 ⟩ for all the combinations of cluster variables. For the inner clusters we find that ⟨ χ2 ⟩ has a minimum for Mmax = 100,MW31,Flkg = 0, and Kdust = 0, while for outer clusters the minimum is obtained for Mmax = 100,LMC2,Flkg = 0, and Kdust = 0. The distribution of the χ2 for such combinations is shown in Fig. 5.
We conclude that the possibility of large-scale variations of the IMF, of radiation leakage, and of dusty HII regions do not appear to be supported by these models that, however, favor a systematic variation in the dust model. The best fitting extinction curve for the inner and outer disk in fact differs, varying from Milky Way-type for the inner disk to LMC2-type for the outer disk. The best ⟨ χ2 ⟩ is 14.8 for YSCs in the inner disk and 42.6 for those in the outer disk. These values are rather large, despite the general goodness of the fit, because of our conservative uncertainty estimate. Models with ⟨ χ2 ⟩ values lower than 17.1 and 50.2 for the inner and outer disk, respectively, are within the 2σ probability level, if we normalize the χ2 values to ⟨ χ2 ⟩ = 14.8. Thus, they cannot be ruled out. This implies that some dust absorption inside the HII region is still a possibility, but a 30% or higher fraction of leakage of radiation is unlikely.
 |
Fig. 5 Distribution of the χ2 for the sample of inner and outer YSCs. |
For each YSC, we can then compare the estimates of AV and Lbol from the available photometry (see Eqs. (1) and (8)) to the values obtained with the χ2 minimization method. This is illustrated in Fig. 6. While the Lbol values are in excellent agreement, the estimated AVs using Eq. (8) are consistently higher than those inferred by the SED fits. The relation between the two quantities has a slope of 0.54. Since Eq. (8) is purely empirical and does not take into account the evolutionary state of the cluster and the dust model, we consider the fitted value as more reliable.
 |
Fig. 6 (Left panel) Comparison of the AV values for the YSC sample derived from two different methods: AV as given in Eq. (8) using the TIR luminosity ( |
The age, mass and extinction distribution of the inner and outer YSCs as derived from the best-fit SED models are shown in Figs. 7 − 9 respectively.
 |
Fig. 7 Histogram showing the distribution of YSC ages in the inner and outer disk of M 33. On the x-axis the age “T” is in a log scale; on the y-axis the number of clusters for each age bin is normalized to the total number of clusters in the inner (left panel) and outer (right panel) disk. |
 |
Fig. 8 Distribution of the cluster mass in the inner and outer disk of M 33. We plot the log of mass (in solar units) and of N + 1 (where N is the number of clusters in each mass bin), respectively. The grey and white histograms are for the masses computed with or without incompletness corrections (see Sect. 5), respectively. |
 |
Fig. 9 Distribution of the visual extinction in the inner and outer disk of M 33. AV is in magnitudes, while the number of clusters per bin is shown normalized to the total number in each sample. |
5. The massive stellar population of YSCs
Among all the models employed in the fitting, we find that the lowest average χ2 corresponds to a solution with the IMF populated up to 100 M⊙, with negligible leakage of radiation and dust absorption inside the Strömgren sphere. From the ⟨ χ2 ⟩ values given in Table 4 we can see that an IMF with a maximum mass lower than 100 M⊙ has a lower probability but it cannot be ruled out. Models with an IMF fully populated only up to 40 M⊙ have been used also to fit the SED of clusters with Lbol < 2 × 1039 erg s-1 only, or the sample of clusters beyond 7 kpc (the nominal edge of the star-forming disk). However, this choice did not provide an improvement in the average ⟨ χ2 ⟩ . Therefore, we consider models with the upper mass cutoff at 100 M⊙ as the best representation of the stellar population of YSCs throughout the M 33 disk.
There is a clear difference between the mass distribution of clusters which form in the inner disk with respect to those forming at large radii: beyond 4 kpc clusters more massive than 104 M⊙ are very rare. Similarly, beyond the Hα edge at 7 kpc, most YSCs have masses smaller than 1000 M⊙. If clusters form with total mass below 104 M⊙, the number of stars is not high enough for the IMF to be fully populated up to 100 M⊙. It is well known that the most massive stars in a cluster tend to have a mass that increases with the cluster mass (Larson 1982). This correlation leads to the question of whether the upper limit to the stellar mass in a particular cluster depends on the cluster mass because of some physically limiting process, or it is simply the result of random sampling of the IMF. In the first case, low-mass clusters cannot produce high-mass stars (Weidner & Kroupa 2004, 2006). In the second case they could as long as there is enough gas, and intermediate-mass clusters should occasionally be found with unusually massive stars – “outliers” in the IMF (Elmegreen 2006; Cerviño & Luridiana 2006). A consequence of this model, often referred to as stochastic or randomly sampled IMF model, is that the summed IMF from many small mass YSCs should be the same as the IMF of a massive YSC. Considering the case for M 33, the higher ⟨ χ2 ⟩ shown by the IMF model with a mass cutoff lower than 100 M⊙, even considering only the low-luminosity cluster sample or clusters beyond a certain radius, does not favor models which relate the maximum stellar mass to the cluster mass. We recall that the results on the cluster birthline of M 33 support the stochastic model (Corbelli et al. 2009), which also appears favoured by the analysis of the IMF in more distant galaxies (Calzetti et al. 2010; Fumagalli et al. 2011). Hence, in what follows we will compare our data to the predictions of the stochastic IMF.
We simulate the cluster light and mass distributions considering a stochastic IMF from 0.1 to 100 M⊙ with slope α = −2.3 for stellar masses greater than 0.1 M⊙ and α = −1.3 for lower masses. We simulate 40,000 clusters that are distributed in number according to their mass between 20 and 104 M⊙ as 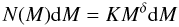 (10)where K is a constant, and δ is the spectral index of the Initial Cluster Mass Function, which we assume to be δ = −2. This is in close agreement with the mass distribution of our IR selected YSCs (see also next section) and with previous findings (e.g. de Grijs & Parmentier 2007, and references therein), even though the results of the simulations are not very sensitive to the value of δ. We populate each cluster with stars randomly selected from the stellar IMF. More details on the numerical simulation are given in Corbelli et al. (2009).
(10)where K is a constant, and δ is the spectral index of the Initial Cluster Mass Function, which we assume to be δ = −2. This is in close agreement with the mass distribution of our IR selected YSCs (see also next section) and with previous findings (e.g. de Grijs & Parmentier 2007, and references therein), even though the results of the simulations are not very sensitive to the value of δ. We populate each cluster with stars randomly selected from the stellar IMF. More details on the numerical simulation are given in Corbelli et al. (2009).
Assuming the mean value ⟨ χ2 ⟩ = 14.8 of the best fit model for the inner disk YSC distribution as the peak of the parent distribution, we consider YSCs whose best fit model has ⟨ χ2 ⟩ ≤ 100 well fitted by the SED models. This is shown also by Fig. 4. Leaving out clusters with χ2 > 100, with large photometric errors (greater than 2 in log) and clusters older than 25 Myr, we now compare the relation between the FUV and Hα luminosities with that obtained by simulating a distribution of clusters at birth. We correct the observed FUV and Hα luminosities for extinction using the extinction value of the best fitting SED model.
In the bottom panel of Fig. 10 we show the distribution of Hα luminosities as a function of the FUV luminosities corrected for extinction according to the best fitting SED model. The dashed line shows the linear relation which is consistent with the distribution of the bright clusters. Clearly, the distribution deviates from the linear trend as LFUV drops below 1039 erg s-1. The sensitivity of our survey is good enough to trace the non-linear relation for LFUV > 5 × 1037 erg s-1. In the upper panel of the figure the same data are shown together with the average value of log LHα (filled squares) in 0.4 wide bins of log LFUV. The filled circles show the same expected values as derived from the simulation of the stochastic IMF for clusters at birth (i.e. younger than 3 Myr). The most relevant result is that the expected deviations from the linear scaling for a random sampled IMF model agree with the data. The measured Hα luminosities for bright clusters are about 0.2 dex lower than those predicted by the stochastic model. This is because our sample does not contain very young massive stellar clusters, and aging for massive clusters lowers the expected Hα luminosity even if T < 10 Myr. From the figure we also see that stochasticity implies a large spread in the Hα luminosities for LFUV < 1039 erg s-1.
 |
Fig. 10 (Bottom panel) Distribution of Hα luminosities as a function of FUV luminosities corrected for extinction according to the best fitting SED model. Units are erg s-1. The dashed line shows the linear relation consistent with the distribution for bright clusters. Filled triangles and open circles are for inner and outer disk YSCs, respectively. (Top panel) The same data are shown using small dots together with the average value of log LHα (filled squares) in 0.4 wide bins of log LFUV. The filled circles show the expected values as derived from the simulation of the stochastic IMF for clusters at birth. |
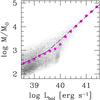 |
Fig. 11 Simulated distribution of cluster mass as a function of the cluster bolometric luminosities at birth. The large filled circles show the average cluster mass in each bolometric luminosity bin. The broken dashed line is a fit to the average log M − log Lbol relation: at high luminosities it follows the linear relation between mass and luminosity expected for a fully populated IMF, while for log Lbol < 3 × 1039 erg s-1 it approximates well the simulation results. |
 |
Fig. 12 (Left panel) Distribution of cluster mass as a function of size. The best fit for clusters with size > 10 pc is shown by a solid line. Masses have been corrected for incompleteness. (Right panel) Relation between cluster mass and the Hα luminosity. |
The presence of outliers in low-mass clusters populated according to a stochastic IMF implies that the relation between the cluster luminosity and its mass is no longer linear, or uniquely determined. We show in Fig. 11 the distribution of cluster masses as a function of the cluster bolometric luminosity at birth. We have simulated the mass distribution using for massive clusters a M − Lbol relation consistent with that given by the SED models for objects younger than 3 Myr. The filled dots in Fig. 11 are the average values of log M, in solar units, for different values of log Lbol. For low-mass clusters, stochastic sampling of the IMF implies a mass higher, on average, than that obtained from the extrapolation of a fully populated IMF. Deviations from a linear scaling are evident as Lbol approaches 1040 erg s-1 and become relevant for the average mass when Lbol ≤ 1039 erg s-1. A cluster of given luminosity can be of smaller mass when some bright outlier dominates its integrated light, or can have a larger mass if no outliers are present. The dashed line in Fig. 11 shows the linear approximation to the log M − log Lbol relation for clusters at birth. We use this relation to derive the cluster mass from the fitted bolometric luminosity. Given a cluster age T, we define a critical luminosity 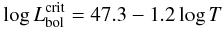 (11)and, when
(11)and, when 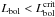 , we correct for incompleteness using the expression:
, we correct for incompleteness using the expression: 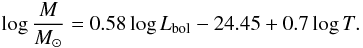 (12)In the above formulae Lbol is in erg s-1, T is the cluster age in yr for clusters older than 3 Myr and is T = 106 yr for younger clusters for which the time evolution of Lbol is negligible. For
(12)In the above formulae Lbol is in erg s-1, T is the cluster age in yr for clusters older than 3 Myr and is T = 106 yr for younger clusters for which the time evolution of Lbol is negligible. For 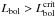 the SED models show that the cluster mass is well approximated by the relation log M/M⊙ = log Lbol − 44.3 + 1.2log T.
the SED models show that the cluster mass is well approximated by the relation log M/M⊙ = log Lbol − 44.3 + 1.2log T.
Our main conclusion of the analysis of YSCs in M 33 is that a stochastically sampled IMF with a maximum mass of 100 M⊙ well describes many properties of their integrated light distribution throughout the whole disk.
6. YSC properties
We have corrected the mass of the less luminous clusters inferred by the SED model fits for incompleteness of the IMF according to the results of the previous section. The average mass of low luminosity clusters is underestimated if no correction is applied.
The mass-radius relation of the YSCs of our sample is illustrated in the left panel of Fig. 12. Here, the size is the 24 μm semi-major axis from SExtractor. The distribution shows a large scatter for sizes less than 10 pc, as already noted for our Galaxy by Zepf et al. (1991) and Larsen (2004) who found a poor mass-radius correlation for compact star clusters (radius < 10 pc) with ages between a few tens to hundreds of Myr. In nearby spiral galaxies, Larsen (2004) obtains M ∝ R2.1 in relatively young compact clusters with age < 1 Gyr and R < 10 pc (confirmed by Grossi et al. 2010, for YSC in M 33). In our sample YSCs larger than 10 pc show a good correlation with a log-log slope of 2.09 ± 0.01 (least square fit). In M 33 Blitz & Rosolowsky (2005) obtain a similar slope considering giant molecular clouds (Mcl ∝ R2.2), similar to other nearby galaxies such as M51 (Bastian et al. 2005) for GMCs with similar ages than the YSCs in M 33 but larger sizes. We may thus arrive at the conclusion that the YSCs display average characteristics reminiscent of the protocluster environment from which they were born. A similar conclusion was also drawn by Grossi et al. (2010) from the analysis of stellar clusters and complexes.
 |
Fig. 13 The radial distribution of mass and age of YSCs as a function of the galactocentric distance RG. Circles indicate YSCs with unreliable fits (χ2 > 100). |
 |
Fig. 14 Iso-density contours showing the age-mass-reddening relationship for the YSCs in our sample. |
The relation between mass and Hα luminosity is shown in the right panel of Fig. 12. We observe a good correlation for cluster masses in excess of ~500 M⊙, although the spread is significant at the faint end, as expected for the stochastic IMF model (see previous section).
The age distribution of the inner and outer YSCs is displayed in Fig. 7. The distribution of the former is narrower than the latter and indicate that clusters tend to be younger in the inner regions of M 33. On the other hand, the cluster mass distribution for the two subsamples shown in Fig. 8 reveals a broader spread for the inner sample, while the outer regions peak at ~ 102 M⊙ and are devoid of massive objects (>104 M⊙). The distribution of cluster masses, corrected for incompleteness of the IMF, is compatible with a differential distribution of index − 2. This is consistent with the value found in the MW and in M 33 (van den Bergh & Lafontaine 1984; Christian & Schommer 1988; de Grijs & Parmentier 2007).
For the large majority of the YSCs selected in the mid-IR with a UV and Hα counterpart we find ages between 3 and 10 Myr. Given the sample selection criteria, we are unable to trace the very early phases of the cluster formation process. Beyond the Hα edge, at about 7 kpc, we do not find clusters younger than 6 Myr and the average age is of order 10 Myr (see Fig. 13). There is no clear evidence that this result is due to a selection bias as if, for example, outer YSCs, being of smaller mass (and luminosity), would be more difficult to detect in their early stages, especially due to the requirement of an Hα and UV counterpart. The lack of younger clusters in the outer regions is not ameliorated if the IMF is truncated at 40 M⊙, while this IMF model increases slightly the number of clusters with T < 3 Myr in the inner regions.
Figure 9 shows the AV distributions. Most of the YSCs in our selected sample have AV between 0.2 and 1. We do not find evidence that the outer clusters suffer from lower extinction, although there is evidence for a different extinction curve. The radial variation of age and cluster mass for our sample of YSCs is shown in Fig. 13. We can clearly see that, with increasing galactocentric radii, the clusters become less massive and older. The SEDs of clusters at very large radii are characterized by a higher IR-to-UV and IR-to-Hα light ratios. This property is well fitted by the synthesis models of older clusters. However, the presence of low-mass clusters as young as ~10 Myr beyond the SF edge of the disk, where the average HI column disk is only a few times 1020 cm-2, is remarkable. Localized density enhancements are evidently present with the consequent formation of small H2 clouds, birthplaces of low mass YSCs. The molecular gas dispersal time is comparable to the YSC ages that we find (Leisawitz 1990). Hence only some residual gas is present in the YSC environment, similar to that detected around MIR sources with Hα counterparts close to the SF disk edge (Corbelli et al. 2011). Hence, the low extinction values found are due to our selection criteria: we have included in our sample only MIR sources with FUV and Hα counterparts.
Finally, in Fig. 14 the relations between age, mass and AV are displayed as density images to overcome the crowding of points. Again, we can see that the distributions are rather tight with most YSCs having AV = 0 − 1 mag, log (T) = 6.5 − 7.1 Myr and log (M/M⊙) = 2 − 4. The peak of the density maps corresponds to AV = 0.3 mag, log (T) = 6.7 Myr, and log (M/M⊙) = 2.5.
7. Summary and conclusions
In this study we have selected 915 mid-IR sources in M 33 from the largest available 24 μm Spitzer map. Complementing the mid and far-infrared Spitzer data with UV data from the GALEX satellite and with Hα data, we have investigated the properties of 648 mid-IR sources which are YSC candidates distributed from small to large galactocentric radii. The observed SED for each YSC is compared with theoretical synthesis models to derive the cluster age, mass and extinction. SED models with different leakage fractions, IMF upper mass cutoffs, extinction curves and dust absorption fraction in HII regions have been tested separately for the inner (RG < 4 kpc) and outer cluster sample. This allows us to constrain the IMF and ISM properties of the inner and outer disk of M 33. The main results can be summarized as follows.
-
We find IR sources as far as 16 kpc from the center, corresponding to the boundary of the 24 μm mosaic and to the extent of the warped HI disk. The completeness of the MIR source catalogue presented here is about 0.4 mJy, equivalent to the luminosity of a single B1.5V star. The radial decline of the IR source density becomes steeper at galactocentric distances RG = 4−5 kpc and flattens out beyond the optical radius (8.5 kpc). YSCs selected in the mid-IR with Hα and UV counterpart follow a similar radial distribution.
-
The luminosity distribution of 24 μm sources as a function of the infrared or bolometric luminosity is steeper at the faint end in the outer regions, which are devoid of very bright sources. The LF in the inner disk displays a double slope, steepening at the high luminosity end where the slope is similar to that observed for HII regions in M 33.
-
The average extinction of the YSCs is modest, since most of them have AV < 1. The similarity between the bolometric and infrared LFs throughout the M 33 disk and the lack of radial trends in AV imply that the dusty environment does not vary appreciably between star forming sites at small and large galactocentric radii. However, a Milky Way-type extinction curve is preferred in the inner disk while for the outer disk an LMC2-type gives the best fitting SED models.
-
The mass-radius relation of YSCs shows a linear correlation with slope 2.09 ± 0.01, in close agreement with the GMC mass-size relation. Hence, the stellar densities of the YSCs in our sample are representative of the protocluster environment.
-
Low luminosity clusters (M < 103 M⊙) become the dominant population at large galactocentric radii. We find YSCs with age of about 10 Myr as far out as 12 kpc, corresponding to the extent of the Hα map used for the identification of YSC candidates. Previous surveys have uncovered a population of ∼ 100 Myr old stars in the outskirts of M 33, but our finding implies a more recent episode of star formation in the outer galaxy.
-
The YSCs in the inner disk show a broad mass and age range, extending in mass up to 105 M⊙, and with ages between 3 and 10 Myr. The peak of the YSC distribution lies at AV = 0.3 mag, age = 5 Myr and mass = 300 M⊙.
-
The best fit synthesis models to the SED favour an IMF with an invariant upper mass cutoff at 100 M⊙ throughout the M 33 disk. Taking into account the stochasticity of the IMF, relevant for low-mass clusters which cannot populate the IMF up to the upper mass end, we are able to reproduce the deviations from linearity of the UV-continuum–Hα relation that we observe for YSCs.
Acknowledgments
This work is based on observations made with the NASA Galaxy Evolution Explorer and with the Spitzer Space Telescope. GALEX is operated for NASA by the California Institute of Technology under NASA contract NAS5-98034. The Spitzer Space Telescope is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. We thank René Walterbos for providing us the Hα image of M 33.
References
- Bastian, N., Gieles, M., Efremov, Y. N., & Lamers, H. J. G. L. M. 2005, A&A, 443, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bastian, N., Ercolano, B., Gieles, M., et al. 2007, MNRAS, 379, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blitz, L., & Rosolowsky, E. 2005, in The Initial Mass Function 50 Years Later, ed. E. Corbelli, F. Palla, & H. Zinnecker, Astrophys. Space Sci. Lib., 327, 287 [Google Scholar]
- Caldwell, N., Kennicutt, R., Phillips, A. C., & Schommer, R. A. 1991, ApJ, 370, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 2001, PASP, 113, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Chandar, R., Lee, J. C., et al. 2010, ApJ, 719, L158 [NASA ADS] [CrossRef] [Google Scholar]
- Cerviño, M., & Luridiana, V. 2006, A&A, 451, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christian, C. A., & Schommer, R. A. 1988, AJ, 95, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Corbelli, E. 2003, MNRAS, 342, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Corbelli, E., & Salucci, P. 2000, MNRAS, 311, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Corbelli, E., & Schneider, S. E. 1997, ApJ, 479, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Corbelli, E., Verley, S., Elmegreen, B. G., & Giovanardi, C. 2009, A&A, 495, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbelli, E., Giovanardi, C., Palla, F., & Verley, S. 2011, A&A, 528, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, A. N. 2000, Allen’s astrophysical quantities, ed. A. N. Cox [Google Scholar]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Davidge, T. J., & Puzia, T. H. 2011, ApJ, 738, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Davidge, T. J., Puzia, T. H., & McConnachie, A. W. 2011, ApJ, 728, L23 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., & Parmentier, G. 2007, Chinese J. Astron. Astrophys., 7, 155 [Google Scholar]
- Elmegreen, B. G. 2006, ApJ, 648, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Engargiola, G., Plambeck, R. L., Rosolowsky, E., & Blitz, L. 2003, ApJS, 149, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Gordon, K. D., Rieke, G. H., et al. 2005, ApJ, 628, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Wilson, C. D., & Madore, B. F. 1991, ApJ, 372, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Fumagalli, M., da Silva, R. L., & Krumholz, M. R. 2011, ApJ, in press [arXiv:1105.6101] [Google Scholar]
- Gil de Paz, A., Boissier, S., Madore, B. F., et al. 2007, ApJS, 173, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Thilker, D. A., Bianchi, L., et al. 2008, in Formation and Evolution of Galaxy Disks, ed. J. G. Funes, & E. M. Corsini, ASP Conf. Ser., 396, 197 [Google Scholar]
- Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., et al. 2010, A&A, 522, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greenawalt, B., Walterbos, R. A. M., Thilker, D., & Hoopes, C. G. 1998, ApJ, 506, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Grossi, M., Corbelli, E., Giovanardi, C., & Magrini, L. 2010, A&A, 521, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grossi, M., Hwang, N., Corbelli, E., et al. 2011, A&A, 533, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyer, M. H., Corbelli, E., Schneider, S. E., & Young, J. S. 2004, ApJ, 602, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Hoopes, C. G., & Walterbos, R. A. M. 2000, ApJ, 541, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, D. A., Elmegreen, B. G., Oh, S.-H., et al. 2011, AJ, 142, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Larsen, S. S. 2004, in The Formation and Evolution of Massive Young Star Clusters, ed. H. J. G. L. M. Lamers, L. J. Smith, & A. Nota, ASP Conf. Ser., 322, 19 [Google Scholar]
- Larson, R. B. 1982, MNRAS, 200, 159 [NASA ADS] [Google Scholar]
- Leisawitz, D. 1990, ApJ, 359, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Magrini, L., Stanghellini, L., Corbelli, E., Galli, D., & Villaver, E. 2010, A&A, 512, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maraston, C., Daddi, E., Renzini, A., et al. 2006, ApJ, 652, 85 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Williams, J. P. 1997, ApJ, 476, 144 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, K. B. W., Woodward, C. E., Willner, S. P., et al. 2007, ApJ, 664, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S., & Clarke, C. J. 1998, AJ, 115, 1543 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B. 1990, AJ, 99, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Kennicutt, Jr., R. C.,Gordon, K. D., et al. 2006, ApJ, 648, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Hoopes, C. G., Bianchi, L., et al. 2005, ApJ, 619, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Bianchi, L., Meurer, G., et al. 2007, ApJS, 173, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, W. D., Garmany, C. D., & Shull, J. M. 1996, ApJ, 460, 914 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S., & Lafontaine, A. 1984, AJ, 89, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez, G. A., & Leitherer, C. 2005, ApJ, 621, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Verley, S., Hunt, L. K., Corbelli, E., & Giovanardi, C. 2007, A&A, 476, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verley, S., Corbelli, E., Giovanardi, C., & Hunt, L. K. 2009, A&A, 493, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidner, C., & Kroupa, P. 2004, MNRAS, 348, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., & Kroupa, P. 2006, MNRAS, 365, 1333 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wyder, T. K., Hodge, P. W., & Skelton, B. P. 1997, PASP, 109, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Zepf, S. E., Whitmore, B. C., & Levison, H. F. 1991, ApJ, 383, 524 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Position, size and galactocentric distances “RG” for sources in Verley et al. (2007) classified as young stellar clusters and included in the analysis of YSC properties presented in this paper.
Additional 24 μm source catalogue (added to the catalogue of Verley et al. 2007).
Slope of best least-square fit to the cumulative distribution of the clusters of inner and outer region of M 33 galaxy.
Sum of the χ2 obtained for different set of model parameters for inner and outer disk clusters.
All Figures
 |
Fig. 1 The spatial distribution of 915 mid-IR sources (circles) and 648 young stellar clusters (squares) overlaid on the 24 μm Spitzer image. The light-blue and red circles in the on-line version represent IR sources from the Verley et al. (2007) catalogue and from the present study, respectively. |
| In the text | |
 |
Fig. 2 (Top left) Sky area covered by various maps along with the position of all the 24 μm sources (915, dot symbols) and the sample of YSCs (648, open circles). Coordinates are for the J2000 epoch. (Top right) Histogram of the number of clusters N as a function of the galactocentric distance RG for Mid-IR sources (white) and YSCs (grey). (Bottom left & right panels) Profiles of the number density of clusters per unit area in kpc2 in linear and log scale, respectively, as a function of galactocentric distance for the same samples. See text for details on the disk deprojection model. |
| In the text | |
 |
Fig. 3 The cumulative luminosity functions of: a) the 24 μm sources (915), b) the 8 μm sources (833) shown as a function of LTIR, c) the selected YSCs (648) as a function of Lbol and d) the selected YSCs (648), as a function of the 24 μm flux. Filled and open circles represent counts in the inner and outer regions, respectively. Linear fits for different flux ranges are shown as solid lines for the inner sample, and dashed for the outer one. |
| In the text | |
 |
Fig. 4 Data (filled dots) and best fit model (open squares) SEDs for four YSCs with small errorbars but different χ2. Models in the bottom panels give good fits to the data. Models with a χ2 of order 100, as in the top-left panel, are of lower quality, but still yield acceptable fits. The few sources whose best fit model has χ2 ≫ 100 have a SED inconsistent with YSC models used in this paper. |
| In the text | |
 |
Fig. 5 Distribution of the χ2 for the sample of inner and outer YSCs. |
| In the text | |
 |
Fig. 6 (Left panel) Comparison of the AV values for the YSC sample derived from two different methods: AV as given in Eq. (8) using the TIR luminosity ( |
| In the text | |
 |
Fig. 7 Histogram showing the distribution of YSC ages in the inner and outer disk of M 33. On the x-axis the age “T” is in a log scale; on the y-axis the number of clusters for each age bin is normalized to the total number of clusters in the inner (left panel) and outer (right panel) disk. |
| In the text | |
 |
Fig. 8 Distribution of the cluster mass in the inner and outer disk of M 33. We plot the log of mass (in solar units) and of N + 1 (where N is the number of clusters in each mass bin), respectively. The grey and white histograms are for the masses computed with or without incompletness corrections (see Sect. 5), respectively. |
| In the text | |
 |
Fig. 9 Distribution of the visual extinction in the inner and outer disk of M 33. AV is in magnitudes, while the number of clusters per bin is shown normalized to the total number in each sample. |
| In the text | |
 |
Fig. 10 (Bottom panel) Distribution of Hα luminosities as a function of FUV luminosities corrected for extinction according to the best fitting SED model. Units are erg s-1. The dashed line shows the linear relation consistent with the distribution for bright clusters. Filled triangles and open circles are for inner and outer disk YSCs, respectively. (Top panel) The same data are shown using small dots together with the average value of log LHα (filled squares) in 0.4 wide bins of log LFUV. The filled circles show the expected values as derived from the simulation of the stochastic IMF for clusters at birth. |
| In the text | |
 |
Fig. 11 Simulated distribution of cluster mass as a function of the cluster bolometric luminosities at birth. The large filled circles show the average cluster mass in each bolometric luminosity bin. The broken dashed line is a fit to the average log M − log Lbol relation: at high luminosities it follows the linear relation between mass and luminosity expected for a fully populated IMF, while for log Lbol < 3 × 1039 erg s-1 it approximates well the simulation results. |
| In the text | |
 |
Fig. 12 (Left panel) Distribution of cluster mass as a function of size. The best fit for clusters with size > 10 pc is shown by a solid line. Masses have been corrected for incompleteness. (Right panel) Relation between cluster mass and the Hα luminosity. |
| In the text | |
 |
Fig. 13 The radial distribution of mass and age of YSCs as a function of the galactocentric distance RG. Circles indicate YSCs with unreliable fits (χ2 > 100). |
| In the text | |
 |
Fig. 14 Iso-density contours showing the age-mass-reddening relationship for the YSCs in our sample. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.