| Issue |
A&A
Volume 534, October 2011
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 18 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201015377 | |
| Published online | 17 October 2011 | |
The MCXC: a meta-catalogue of x-ray detected clusters of galaxies⋆
1
Laboratoire AIM, IRFU/Service d’Astrophysique – CEA/DSM – CNRS – Université
Paris Diderot, Bât. 709, CEA-Saclay,
91191
Gif-sur-Yvette Cedex
France
e-mail: rocco.piffaretti@cea.fr
2
Université de Toulouse, CNRS, CESR, 9 av. du colonel Roche, BP 44346, 31028
Toulouse Cedex 04,
France
3
DSM/Irfu/SPP, CEA/Saclay, 91191
Gif-sur-Yvette Cedex,
France
Received:
12
July
2010
Accepted:
4
May
2011
We present the compilation and properties of a meta-catalogue of X-ray detected clusters of galaxies, the MCXC. This very large catalogue is based on publicly available ROSAT All Sky Survey-based (NORAS, REFLEX, BCS, SGP, NEP, MACS, and CIZA) and serendipitous (160SD, 400SD, SHARC, WARPS, and EMSS) cluster catalogues. Data have been systematically homogenised to an overdensity of 500, and duplicate entries from overlaps between the survey areas of the individual input catalogues are carefully handled. The MCXC comprises 1743 clusters with virtually no duplicate entries. For each cluster the MCXC provides three identifiers, a redshift, coordinates, membership in the original catalogue, and standardised 0.1−2.4 keV band luminosity L500, total mass M500, and radius R500. The meta-catalogue additionally furnishes information on overlaps between the input catalogues and the luminosity ratios when measurements from different surveys are available, and gives notes on individual objects. The MCXC is available in electronic format for maximum usefulness in X-ray, SZ, and other multiwavelength studies.
Key words: X-rays: galaxies: clusters / cosmology: observations / large-scale structure of Universe / galaxies: clusters: general / catalogs
The catalog is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/534/A109
© ESO, 2011
1. Introduction
Clusters of galaxies provide cosmological constraints through the number density and evolution of objects, through the power spectrum of their three-dimensional distribution, and through their baryon fraction and its evolution. Moreover, the physical properties of clusters provide a test of the structure formation scenario, giving vital information for understanding the gravitational collapse of the dark matter and of the evolution of baryons in the dark matter potential (see Voit 2005, for a review).
X-ray observations are ideal for these studies since the density squared dependence of the X-ray emission implies that clusters can be found efficiently over a wide redshift range. Cluster sources were evident in the first all-sky X-ray survey with Uhuru, and more objects were found by HEAO-1 and Ariel-V; subsequent follow-up observations with Einstein and EXOSAT allowed more accurate characterisation of their physical properties (see Rosati et al. 2002, for a review).
In this context, the ROSAT satellite has played a central role. The 1990–1991 ROSAT All-Sky Survey (RASS, Voges et al. 1999) and later deep pointed observations have led to the discovery of hundreds of clusters. Subsequent follow-up observations, in particular those conducted with the current generation of X-ray satellites XMM-Newton, Chandra, and Suzaku, have provided statistical samples for cosmological studies (e.g., Vikhlinin et al. 2009; Mantz et al. 2010b) and detailed information on the structural properties of the cluster population (e.g., Vikhlinin et al. 2006; Pratt et al. 2010; Arnaud et al. 2010). Other X-ray observations have allowed in-depth study of the hierarchical assembly process through merging (e.g., Markevitch & Vikhlinin 2007, and references therein) and the physical mechanisms associated with feedback and its impact on structure formation (e.g., McNamara & Nulsen 2007, and references therein). However, while several XMM-Newton and Chandra X-ray surveys are ongoing (e.g., Romer et al. 2001; Barkhouse et al. 2006; Pacaud et al. 2007; Fassbender 2007)1, the associated cluster catalogues are either not yet published or only partially available.
Outside of the X-ray domain, the redshift-independent thermal Sunyaev-Zel’dovich effect (Sunyaev & Zel’dovich 1972, hereafter SZ) is emerging as an efficient way to detect distant, massive clusters that fall below the flux limits of X-ray surveys. Several SZ surveys, including those being undertaken with the South Pole Telescope (SPT, Carlstrom et al. 2011) survey, the Atacama Cosmology Telescope (ACT, Fowler et al. 2007), and Planck (Tauber et al. 2010), are actively ongoing and have started to provide the first SZ-selected cluster samples (e.g., Vanderlinde et al. 2010; Menanteau et al. 2010; Planck Collaboration 2011d). X-ray observations of SZ-detected clusters are important in many respects. The X-ray properties allow a better characterisation of the SZ signal (e.g., Melin et al. 2006; Andersson et al. 2011; Planck Collaboration 2011g) and yield the calibration of the scaling relations needed for cosmological studies with SZ-selected cluster samples (e.g., Majumdar & Mohr 2003). In addition, X-ray observations allow testing of the selection function of SZ surveys and verification of new SZ cluster candidates (e.g., Šuhada et al. 2010; Planck Collaboration 2011e). Moreover, they are essential for statistical analyses of the SZ data (e.g., Melin et al. 2011; Komatsu et al. 2010; Planck Collaboration 2011f,g,h, and references therein).
Cosmological tests that rely on knowledge of the evolution of the mass function or baryon fraction require an estimate of the cluster mass. Surveys provide only an observable (typically luminosity, temperature or SZ y-parameter) that is then linked to the cluster mass via scaling relations. While simultaneous constraints on cosmological parameters and scaling relations have recently been derived (Mantz et al. 2010a), the mass proxy relations are typically separately calibrated using deep observations of well-understood and if possible representative samples (e.g., Arnaud et al. 2007; Maughan 2007; Vikhlinin et al. 2009; Pratt et al. 2009). Although their redshift evolution is at present poorly known, a consensus on the type of scaling relations to be calibrated and their precise definition has been reached. For example, the bias introduced by cool core clusters in luminosity and temperature measurements is taken into account, low scatter mass proxies such as YX (Kravtsov et al. 2006) or the gas mass Mgas are widely used, and all quantities are measured up to a standard characteristic radius R500, the radius within which the mean over-density of the cluster is 500 times the critical density at the cluster redshift. Substantial progress has also been made in understanding the systematics affecting X-ray mass estimates via simulations (e.g., Rasia et al. 2006; Nagai et al. 2007a; Piffaretti & Valdarnini 2008) and via combination with gravitational lensing (e.g., Mahdavi et al. 2008; Zhang et al. 2010; Meneghetti et al. 2010).
ROSAT-derived catalogues still play a major role in providing targets for deeper observation with the current generation of X-ray instruments (e.g., Böhringer et al. 2007; Vikhlinin et al. 2009), and for identification of existing clusters in new surveys in other wavelength bands (e.g., Popesso et al. 2004). These catalogues have been derived from a number of surveys based on RASS data or ROSAT pointed observations (see Sect. 2). Even though these catalogues are public, their large sizes and the different conventions employed (e.g., cosmology, integration radius etc.) mean that no attempt has yet been made to merge them and to homogenise the data contained within. The time is thus ripe for a major effort to standardise the information available in these catalogues.
Our aim in this paper is to provide such a service to the community by collecting the disparate measurements available in the major publicly-available X-ray cluster catalogues and regularising them to the same cosmology and integration radius. In particular, our approach is based on the use of the [0.1−2.4] keV X-ray luminosity as a mass proxy. Used together with a luminosity profile and the X-ray luminosity-mass scaling laws recently derived from the representative sample of X-ray clusters REXCESS, we standardise all measurements to an integration radius of R500. The latter is chosen since it encloses a substantial fraction of the total virialised mass of the system, while being the largest radius probed in current high resolution X-ray observations of moderately large samples. Furthermore, use of the REXCESS luminosity profile and scaling laws ensures the best possible description of the average properties of the X-ray cluster population, and allows maximum self-consistency in our approach.
The basic characteristics of the resulting meta-catalogue of X-ray detected clusters of galaxies (hereafter MCXC) are its large number of objects (1743 unique systems), its homogeneously estimated [0.1−2.4] keV band luminosities (L500) and total masses (M500), its use of a uniform format for all provided quantities, and its careful control of duplicate entries originating from overlaps between the input catalogues. In order to be easily manipulated, the MCXC is provided in electronic format. The final catalogue gives a first overview of the published, publicly-available X-ray survey selected cluster population.
Here it is worth clarifying what we envisage the MCXC is useful for. One purpose as a large, homogeneous catalogue is for cross correlation with existing or future surveys in various wavelengths. Such an approach will be extremely useful for studies based on ongoing SZ surveys such as Planck, SPT, and ACT, and upcoming optical surveys such as PanSTARRS2 and DES3. In addition, as the MCXC provides a self-consistently estimated measure of the total mass M500, it can be used to predict various global quantities of the clusters contained within. For example, combination with the appropriate scaling laws allows prediction of the integrated SZ flux YSZ,500, or total optical light. In this context, the meta-catalogue will be useful for the defintion of subsamples for deeper analysis, including archival investigations and follow-up observations with SZ and optical/IR instruments, and for a first characterisation of known objects detected in new surveys. However, while the MCXC comprises virtually all known X-ray clusters, its selection function is impossible to reconstruct as the individual selection functions of the subsamples used in its construction are extremely complex and, in most cases, are not known or not available. Use of the MCXC for e.g., X-ray scaling relation studies is thus possible only via the definition of subsamples for which the selection function is known or can be characterised.
The paper is organised as follows. In Sect. 2 we describe the basic properties of the catalogues used to construct the MCXC. In Sect. 3 we explain how the information is homogenised and detail the quantities provided by the MCXC. The handling of duplicate entries is presented in Sect. 4 and in Sect. 5 we discuss various aspects of the final catalogue. In Sect. 6 we summarise our results and present our conclusions.
As a cosmological model we adopt a ΛCDM cosmology with H0 = 70 km s-1 Mpc-1, ΩM = 0.3 and ΩΛ = 0.7 throughout the paper. The quantity h(z) is the ratio of the Hubble constant at redshift z to its present value, H0, i.e., h(z)2 = Ωm(1 + z)3 + ΩΛ. All quantities related to the MCXC electronic Table are given in typewriter typeface.
2. Input X-ray catalogues
In the following we describe the input catalogues used to construct the MCXC. We recall the basic characteristics of the X-ray surveys used to construct each catalogue and how the X-ray quantities adopted in our work are measured. We discuss only X-ray information essential to the MCXC and focus on the quantities that allow us to compute the luminosities, L500. For more details on the individual surveys, and in particular the associated optical observations/follow-up, we refer the reader to the cited papers and references therein.
Generally speaking, two types of X-ray survey can be distinguished: contiguous area surveys, which use data from the ROSAT All-Sky Survey (RASS, Voges et al. 1999), and serendipitous cluster surveys, which are based on data from deeper pointed X-ray observations. In the following, we therefore distinguish between RASS-based and serendipitous catalogues. In addition to handling duplicate entries and removing particular clusters as discussed below, we exclude clusters with non measured redshifts or luminosities. Table 1 summarises the contributions of the various input catalogues to the MCXC.
The bulk of the X-ray data used to construct the MCXC are derived from ROSAT observations. Exceptions are EMSS and some physical quantities for MACS, as described in more detail below. Future work will include incorporation of as-yet unpublished catalogues such as RDCS (the ROSAT Deep Cluster Survey, Rosati et al. 1998), XCS (the XMM Cluster Survey, Romer et al. 2001), XDCP (the XMM-Newton Distant Cluster Project, Fassbender 2007), and the complete MACS catalogue (Ebeling et al. 2001).
2.1. RASS-based catalogues
We compiled data from nine RASS-based contiguous area surveys, as described below.
2.1.1. REFLEX and NORAS
REFLEX (ROSAT-ESO Flux Limited X-ray Galaxy Cluster Survey, Böhringer et al. 2004a) is based on RASS data for a survey area covering the southern sky up to a declination δ = 2.5 deg with the galactic plane (| b| ≤ 20 deg) and the regions of the Magellanic clouds excluded. The total survey area is 13 924 deg2 and the survey is flux-limited (0.1−2.4 keV band flux ≥3 × 10-12 erg s-1 cm-2).
NORAS (Northern ROSAT All-Sky galaxy cluster survey Böhringer et al. 2000a) is also based on RASS data excluding the same region around the galactic plane, but covers the northern sky. This survey catalogue is not flux-limited and selection is based on minimum count rate (0.06 cts / s in the 0.1−2.4 keV band) and a source extent likelihood.
The data analysis and catalogue production for both NORAS and REFLEX are performed by essentially the same authors and, although REFLEX has been more extensively studied and characterised than NORAS, the information provided is extremely similar. A growth curve analysis is adopted to determine source fluxes (the typical flux measurement accuracy is 10−20 per cent) and luminosities. The REFLEX catalogue provides aperture luminosities Lap as well as total luminosities. The latter are computed by estimating the missing flux outside the detection aperture by assuming a β-model with β = 2 / 3, a core radius rc which scales with mass, and a cluster extent of 12 × rc. For the NORAS clusters a similar procedure is performed, but the resulting total luminosities are not reported. Therefore the NORAS catalogue provides only aperture luminosities.
For both catalogues data (Böhringer et al. 2000b, 2004b) are retrieved from VizieR4. Because of the homogeneity of these two catalogues we merge them into a single NORAS/REFLEX catalogue. The names NORAS and REFLEX are kept as sub-catalogue labels. Because of the overlap of the NORAS and REFLEX survey areas, there are ten duplicate entries. For these ten clusters the information provided by NORAS and REFLEX is almost identical and we exclude, for each of the duplicates, the cluster with the larger flux uncertainty.
Since the number of clusters in the combined NORAS/REFLEX catalogue is large (889 objects, see Table 1) and because the information provided by the authors is homogeneous and detailed, it is the cornerstone of the MCXC.
2.1.2. ROSAT BCS and eBCS
The ROSAT BCS (The ROSAT Brightest Cluster Sample, Ebeling et al. 1998) comprises the brighter sources of the NORAS survey. We use data for the 90 per cent complete BCS, a flux-limited sample (0.1−2.4 keV band flux ≥4.4 × 10-12 erg s-1 cm-2) of z ≤ 0.3 clusters. The eBCS (The extended ROSAT Brightest Cluster Sample, Ebeling et al. 2000a) is the low flux extension of the BCS (0.1−2.4 keV band flux ≥2.8 × 10-12 erg s-1 cm-2).
The type of information provided is the same for both samples. In both cases detection and cluster emission characterisation are based upon the Voronoi tesselation and percolation (VTP) algorithm. The emission outside the detection region is computed by correcting the detected count rate. For clusters this is undertaken by assuming a β-model profile with β = 2 / 3 and a core radius estimated from the source profile, taking into account the telescope PSF. The resulting total luminosities, the corrected and uncorrected count rates, and the VTP aperture radius are provided. This implies that the luminosity within the VTP aperture radius can be computed for all the clusters in the sample.
Data (Ebeling et al. 2000b,c) are retrieved from VizieR and merged into a single BCS catalogue where the names BCS and eBCS are kept as sub-catalogue labels (see Table 1). There is only one cluster, A1758a, that is listed in both BCS and eBCS. The two luminosities are almost identical and we remove it from the BCS sub-catalogue. In addition, for the Virgo cluster we adopt the luminosity estimate of Böhringer et al. (1994).
2.1.3. SGP
The SGP (A Catalog of Clusters of Galaxies in a Region of 1 Steradian around the South Galactic Pole, Cruddace et al. 2002a) covers a region of 1.013 sr centred on the south Galactic pole and is based on the same X-ray source detection and characterisation procedures as REFLEX. The lowest detected flux is 1.5 × 10-12 erg s-1 cm-2 in the 0.1−2.4 keV band, and a complete subsample can be obtained by imposing a flux limit of 3 × 10-12 erg s-1 cm-2.
Luminosities are computed within a cutoff radius provided by the growth curve analysis. Since the cutoff radius is not given in the catalogue, we treat the quoted luminosity as the total luminosity.
Data for the entire non-flux-limited, SGP sample (Cruddace et al. 2002b, 2003) were retrieved from VizieR.
2.1.4. NEP
The NEP (The ROSAT North Ecliptic Pole survey, Henry et al. 2006) surrounds the north ecliptic pole in a survey area of 80.6 deg2, and has the deepest exposure in the northern RASS (exposure times from 2000 to over 40 000 s). Source detection is based on Voges et al. (1999) and the selection is performed by adopting thresholds for the source extent likelihood and signal-to-noise ratio.
The quoted total luminosities are computed from size corrected fluxes. The latter are computed from detected fluxes within apertures of radius 5′ (6.5′ for RXJ1834.1+7057) by assuming a PSF-corrected β-profile with β = 2 / 3 and a fixed core radius of 180 kpc. The profile is integrated up to R200, which is estimated from the size-temperature relation of Evrard et al. (1996). Size correction factors are provided so that aperture luminosities can be computed.
Data for the whole flux-limited sample (0.5−2 keV band flux ≥2. × 10-14 erg s-1 cm-2, Henry et al. 2006) were retrieved from VizieR, and only sources identified as clusters were selected (see Table 1).
2.1.5. MACS
The MACS (Massive Cluster Survey, Ebeling et al. 2001) is based on the ROSAT Bright Source Catalogue with the aim of increasing the number of known very luminous, z ≥ 0.3 clusters. A MACS catalogue has not yet been published in its entirety and we therefore collected data from different publications as detailed below. We would like to point out that the data reported in these publications are based on Chandra follow-up observations and that these publications yield all publicly-available MACS clusters with coordinates, redshifts, and luminosities (i.e., the minimal set of quantities required for the MCXC).
Number of clusters in the catalogues used to construct the MCXC before and after handling of multiple entries.
Properties of a complete subsample of z > 0.5 MACS clusters (the MACS_DIST sub-catalogue, twelve objects) are listed in Ebeling et al. (2007). A further complete subsample of bright objects in the 0.3 < z < 0.5 redshift range (the MACS_BRIGHT sub-catalogue, 34 clusters) are given in Ebeling et al. (2010). All MACS_BRIGHT clusters are analysed in more detail in Mantz et al. (2010b), where quantities such as L500, M500, etc., are provided. This information is also merged into the MACS_BRIGHT sub-catalogue.
Further MACS clusters are analysed in Maughan et al. (2008, the MACS_MJFV , who provide very complete information on the physical properties of these objects. Of the MACS_MJFV sample there are six clusters in common with the MACS_DIST sub-catalogue and twelve clusters in common with the MACS_BRIGHT sub-catalogue. We construct a unique MACS catalogue by merging the three sub-catalogues and keeping only measurements given by Maughan et al. (2008) for the eighteen duplicate clusters (see Table 1). Apart from the six MACS_DIST luminosity measurements in Ebeling et al. (2007), the luminosities L500 are directly available for all MACS clusters.
2.1.6. CIZA
The CIZA (Clusters in the Zone of Avoidance, Ebeling et al. 2002; and Kocevski et al. 2007, respectively CIZAI and CIZAII) catalogues are based on the ROSAT Bright Source Catalogue and focus on the region around the galactic plane (|b| ≤ 20 deg). Candidate selection is based on limits on the detected fluxes and spectral hardness ratios. CIZAI comprises the X-ray brightest objects (flux ≥5. × 10-12 erg s-1 cm-2), while CIZAII is its low-flux extension (flux ≥3. × 10-12 erg s-1 cm-2).
Quoted luminosities are computed from raw RASS data using very large apertures and can be therefore safely interpreted as total luminosities.
The type of data available for the two catalogues is identical, and after retrieving data (Ebeling et al. 2002; Kocevski et al. 2007) from VizieR, we merged them into a single CIZA catalogue where the names CIZAI and CIZAII define the sub-catalogues (see Table 1).
2.2. Serendipitous catalogues
We compiled data from a further seven serendipitous surveys as described below.
2.2.1. 160SD
The 160SD (The 160 Square Degree ROSAT Survey, Mullis et al. 2003) is based on the serendipitous detection of extended X-ray emission in 647 archival ROSAT PSPC observations. With the galactic plane (| b| ≤ 30 deg) and the regions of the Magellanic clouds excluded, the resulting sky coverage at high fluxes is 160 deg2.
A wavelet algorithm is used to detect galaxy clusters and the quoted total luminosities are computed from the detected fluxes by assuming a β-profile with β = 2 / 3 and a fitted core radius.
We retrieved the full dataset (Mullis et al. 2003) from VizieR and selected only sources identified as galaxy clusters.
2.2.2. 400SD
The 400SD (The 400 Square Degree ROSAT PSPC Galaxy Cluster Survey, Burenin et al. 2007) extends the 160SD methodology to additional PSPC observations by adopting less restrictive selection criteria (e.g., galactic latitude and absorption, exposure times). A total of 1610 fields, corresponding to a total survey area of 397 deg2, are analysed to yield a large flux-limited (0.5−2 keV band flux ≥1.4 × 10-13 erg s-1 cm-2) cluster catalogue. 400SD data is available for serendipitously and not entirely serendipitously detected clusters (clusters at redshift very close to the target redshift).
We retrieved data (Burenin et al. 2009) from VizieR, and merged the information into a unique 400SD catalogue, introducing the sub-catalogue labels 400SD_SER and 400SD_NONSER to distinguish between the two classes of objects (see Table 1).
2.2.3. SHARC Bright and SHARC Southern
The SHARC survey is based on archival ROSAT PSPC observations. The SHARC Bright (Bright Serendipitous High-Redshift Archival ROSAT Cluster survey, Romer et al. 2000a) is a wide area shallow survey covering a total area of 178.6 deg2 with a flux limit of 1.63 × 10-13 erg s-1 cm-2. The SHARC Southern (The Southern Serendipitous High-Redshift Archival ROSAT Cluster survey, Burke et al. 2003a) is a narrow area deep survey covering 17.7 deg2 with a flux limit of 4.66 × 10-14 erg s-1 cm-2. Cluster detection is based on a wavelet and sliding-box techniques, respectively.
For both catalogues a β-profile with fixed β = 2 / 3 and rc is used to determine the total luminosity and a circular aperture of radius r80, which contains 80 per cent of the total flux. This implies that in addition to the extrapolated total luminosities, the aperture luminosities Lap ≡ L(<r80) are available.
Data (Burke et al. 2003b; Romer et al. 2000b) are retrieved from VizieR and merged into a single SHARC catalogue (only sources identified as clusters are selected from Romer et al. 2000b) with sub-catalogues labelled SHARC_SOUTH and SHARC_BRIGHT (see Table 1).
2.2.4. WARPS and WARPSII
The WARPS survey is also based on ROSAT PSPC observations. WARPS (Wide Angle ROSAT Pointed Survey, Perlman et al. 2002a), covers 16.2 deg2 in 86 PSPC fields, while its extension WARPSII (Wide Angle ROSAT Pointed Survey II, Horner et al. 2008) covers 56.7 deg2 in 301 PSPC fields. The WARPS survey uses the VTP algorithm for cluster detection and characterization.
The quoted total luminosities are computed as in Ebeling et al. (1998), but no information which allows the computation of aperture luminosities is reported.
Data (Perlman et al. 2002b; Horner et al. 2009) are retrieved from VizieR. For both catalogues we include clusters below the nominal flux limit that defines the statistically complete sample. The two catalogues are merged into a single WARPS catalogue and WARPSI and WARPSII are adopted as sub-catalogue labels (see Table 1).
2.2.5. EMSS
The EMSS (Einstein Observatory Extended Medium Sensitivity Survey, Gioia et al. 1990) cluster catalogue is constructed from a flux-limited sample of sources serendipitously detected in Einstein IPC (Imaging Proportional Counter) fields at high galactic latitudes.
Data are compiled from the Tables published in Gioia
& Luppino (1994) and Henry
(2004). While the sample presented in Gioia
& Luppino (1994) is the most complete and up-to-date work on the entire
EMSS cluster catalogue, Henry (2004) provides
more reliable ASCA measurements for the z ≥ 0.3 EMSS clusters. The
Einstein luminosities reported in Gioia & Luppino (1994) are computed from the flux measured in a
2 4
× 2
4
× 2 4
detection cell by adopting a β-model with fixed
β = 2 / 3. The information provided is not
sufficient to compute aperture luminosities from the quoted total luminosities. The ASCA
luminosities in Henry (2004) are total
luminosities. Since distant clusters are not resolved by ASCA, these luminosities were
derived by assuming that the clusters are point sources. Hence in this case only total
luminosities are available.
4
detection cell by adopting a β-model with fixed
β = 2 / 3. The information provided is not
sufficient to compute aperture luminosities from the quoted total luminosities. The ASCA
luminosities in Henry (2004) are total
luminosities. Since distant clusters are not resolved by ASCA, these luminosities were
derived by assuming that the clusters are point sources. Hence in this case only total
luminosities are available.
Clusters in the Henry (2004) sample are removed from Gioia & Luppino (1994)5. We remove MS1209.0+3917, MS1333.3+1725, and MS1610.4+6616 for the reasons mentioned in Henry (2004). The data are then merged into a single EMSS catalogue where the names EMSS_1994 and EMSS_2004 denote the sub-catalogue labels (see Table 1).
 |
Fig. 1 Redshift histograms of the input catalogues used to construct the MCXC and of the MCXC after handling of multiple entries. Different area shadings are used for RASS-based, serendipitous, and MCXC catalogues. |
3. Data extraction and homogenisation
The data provided by the different input catalogues (positions, redshifts, names, luminosities, etc.) are rather similar. However some data homogenisation is needed, in particular for quantities such as luminosity and mass.
As detailed above, in many cases the luminosity is measured within some small aperture Rap, where Lap ≡ L(<Rap) is the corresponding aperture luminosity, and then extrapolated to some larger radius using a reasonable model of the surface brightness profile. Extrapolation might be performed at a very large radius, implying that the derived luminosity is basically equal to the total luminosity Ltot = L(<∞). With the present generation of X-ray observations, the standard choice is R500 (L500 ≡ L(<R500)), and we have chosen this radius for the MCXC data homogenisation procedure.
The assumed cosmological model is of course at the basis of our homogenisation procedure. In the following all luminosities and other cluster parameters which depend on the distance scale are converted to our reference cosmology (i.e. ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km s-1 Mpc-1).
Below we list all the quantities that are provided by the MCXC and explain in detail how they are derived from the original information in the input catalogues. The names of the quantities as given in the associated electronic Table are given in typewriter typeface. MCXC clusters are ordered by right ascension. As an example we list the first 40 entries in Table 2.
3.1. Coordinates and redshifts
The cluster coordinates given in the input catalogues are those of the cluster centroid determined from X-ray data (apart from those in the sub-catalogue EMSS_1994 which are the coordinates of the cluster optical position). For the MCXC, all coordinates are converted to right ascension and declination for the epoch J2000 in hours (degrees), minutes, and seconds (RAJ2000 and DEJ2000) and in units of decimal degrees (_RAJ2000 and _DEJ2000). We also provide the cluster positions in galactic coordinates – GLON and GLAT are galactic longitude and latitude, respectively, in degrees (see Table 2).
No manipulation is needed for the cluster redshifts z. As stated above, only clusters with measured redshift are retained in the MCXC (see Table 2). In Fig. 1, we show the redshift histograms of the individual input catalogues used to construct the MCXC, and of the MCXC after handling of multiple entries (see Sect. 4). The histograms highlight the different redshift ranges typically probed by serendipitous and RASS-based surveys, with the latter generally being confined to local and medium redshift clusters.
3.2. Names
Two types of cluster name are usually listed in the input catalogues: the name assigned by the authors NAME, and the alternative name NAME_ALT (see Table 2). NAME is usually constructed from the cluster coordinates (e.g., RXJ0041.1-2339 in 160SD, MS0007.2-3532 in EMSS, MACSJ0011.7-1523 in MACS, RXC J0000.1+0816 in NORAS/REFLEX, CIZA, and SGP, RX J1716.6+6410 in NEP and SHARC, J0022.0+0422 in WARPS). Exceptions to this format are BCS and 400SD. BCS names are listed as they appear in optical catalogues (e.g. ZwCl1432, A602), while in the 400SD, names are not assigned. We therefore assigned a NAME to 400SD_SER clusters according to the standard SIMBAD6 format acronym “BVH2007 NNN” (Burenin+Vikhlinin+Hornstrup+, 2007, e.g., BVH2007 193), and for the 400SD_NONSER we created a new acronym “BVH2007 NS NNN” (e.g., BVH2007 NS 12). For all but the 400SD clusters we retain the original names as listed in the input catalogues.
The first 40 entries of the MCXC catalogue. The full MCXC is available at the CDS.
Alternative names in the input catalogues are mostly based on catalogued optical counterparts to the X-ray sources: Abell and Zwicky Cluster names, names of NGC and UGC central dominant galaxies, etc. (e.g., A2894, ZwCl 0104.9+5350, UGC 12890). Thus in some cases alternative names refer to objects that are not clusters of galaxies. In other cases alternative names are given as notes or comments, and we also use this information to construct NAME_ALT in the MCXC by extracting the suitable piece of information. Alternative names are homogenised so as to match both SIMBAD and NED7 standards. When this is not possible we choose the SIMBAD acronym conventions. Moreover, when multiple alternative names are available, they are listed separated with a comma. For BCS clusters we set NAME_ALT equal to NAME. For 160SD and 400SD clusters alternative names are extracted from the notes. For 160SD clusters the identifier “VMF98 NNN” is also used. In most of the input catalogues alternative names end with letters for double systems (e.g., A2384 (A), A3574E, etc.). Such information is important because it indicates whether the measured luminosity refers to the whole system to only a part of it.
Our choice of formats for NAME and NAME_ALT in the MCXC is made in order to facilitate queries in the SIMBAD and NED databases. Both NAME and NAME_ALT also facilitate the handling of duplicate entries as discussed extensively below in Sect. 4.
As NAME and NAME_ALT are heterogeneous and do not always exist in the original catalogues, a homoegenous designation of the clusters, which follows the IAU designation rules, is added in the first column (NAME_MCXC in Table 2). This internal designation allows a fully unambiguous cluster identification within the MCXC catalogue. We would like to point out that NAME and NAME_ALT often contain information on how the cluster was discovered (Abell, Zwicky, EMSS, MACS, etc. clusters). This kind of information is not contained in NAME_MCXC.
3.3. Catalogue and sub-catalogue
As explained above in Sect. 2 and listed in Table 1, for each cluster the input catalogue and sub-catalogue names are given in CATALOGUE and SUB_CATALOGUE (see Table 2). If no sub-catalogue exists the sub-catalogue name is equal to the catalogue name.
 |
Fig. 2 Relation between input quantities Rap and Lap = L(<Rap) and the iteratively estimated R500 and L500 = L(<R500) for the NORAS/REFLEX clusters. The luminosity ratio as a function of aperture radius ratio is shown in the left panel, while the luminosity ratio histogram is shown in the right panel. |
3.4. Luminosities
3.4.1. Luminosity calculation
The luminosities are homogenised according to the following procedure:
-
1.
When necessary, we first convert the input luminosity (e.g., 0.5−2 keV band in NEP, bolometric in MACS_MJFV, 0.3−3.5 keV band in EMSS_1994) to the 0.1−2.4 keV energy band using the MEKAL plasma code (Mewe et al. 1985; Liedahl et al. 1995). The temperature dependence of this conversion is taken into account either by using measured temperatures when available in the input catalogue, or by iteration about the non-core-excised luminosity-temperature relation of Pratt et al. (2009), assuming an abundance of 0.3. In the following all the quoted luminosities are therefore as measured in the 0.1−2.4 keV energy band for our reference cosmology.
-
2.
The resulting luminosities are then converted to L500. We adopt two different procedures, depending on the type of luminosity measurement available in the input catalogue.
-
(a)
If only the total luminosityLtot (i.e., extrapolated up to large distances) is available, we adopt L500 = a × Ltot, where a is the ratio L500 / Ltot for a luminosity profile model based in the average gas density profile derived from the representative X-ray cluster sample REXCESS (Croston et al. 2008). More precisely, from the individual scaled density profiles (see Arnaud et al. 2010, left panel of Fig. 3), we computed the average profile and fitted it with the AB-model given by Eq. (2) of Pratt & Arnaud (2002):
![\begin{equation} \rho_{\rm gas} \propto \left( \frac{x}{x_{\rm c}} \right)^{-\alpha} \times \left[1+ \left( \frac{x}{x_{\rm c}} \right)^{2} \right]^{-3 \beta /2 + \alpha/2} , \label{nmean:eq} \end{equation}](/articles/aa/full_html/2011/10/aa15377-10/aa15377-10-eq71.png) (1)for
x = r / R500,
finding xc = 0.303, α = 0.525,
and β = 0.768. As the [0.1−2.4] keV band luminosity is
only weakly temperature-dependent (e.g., Mewe et al. 1985), and temperature profiles of clusters vary only
by a factor of ~2−3 with radius (e.g., Piffaretti et al. 2005; Pratt et al. 2007), a three-dimensional average luminosity profile
is obtained by simply taking the square of the density profile given in
Eq. (1). Since only
recently observational progress has shown that the AB-model (Eq. (1)) yields a more accurate
description than the traditional β-model (see Croston et al. 2008, and references
therein), most of the analyses listed in Sect. 2 adopted the latter when extrapolating luminosities to large
radii. For the sake of clarity, in Appendix A we illustrate the differences between luminosities computed
adopting the AB-model or the β-model. We notice that the
mean REXCESS density profile was defined from a sample with mass
M500 ≳ 1014 M⊙.
The recent analysis of the pressure profiles of galaxy groups with masses as
small as
M500 ~ 1013 M⊙
by Sun et al. (2011) shows perfect
agreement with REXCESS results. Taken together with the good agreement
between temperature profiles in group and cluster scale objects (e.g., Rasmussen & Ponman 2007), and the
weak dependence of temperature on radius, this result supports our use of
the REXCESS density profile for lower luminosity systems. As the observed
luminosities are derived from integration of surface brightness profiles
within circular apertures, the three dimensional average luminosity profile
is cylindrically integrated up to aperture radii of 1 and
5 × R500 to compute
L500 and Ltot,
respectively. The cluster boundary is also assumed to be equal to
5 × R500. We find a ratio
a = L500 / Ltot = 0.91
and that the exact choice of the aperture enclosing the total luminosity is
not relevant. This constant ~10 per cent correction is therefore
applied to all the 160SD, 400SD, SGP, WARPS, CIZA, MACS_DIST, and EMSS
clusters for which only total luminosities are available (see Sect. 2). For the MACS_MJFV and MACS_BRIGHT
clusters no conversion is needed since the quoted luminosities are
L500.
(1)for
x = r / R500,
finding xc = 0.303, α = 0.525,
and β = 0.768. As the [0.1−2.4] keV band luminosity is
only weakly temperature-dependent (e.g., Mewe et al. 1985), and temperature profiles of clusters vary only
by a factor of ~2−3 with radius (e.g., Piffaretti et al. 2005; Pratt et al. 2007), a three-dimensional average luminosity profile
is obtained by simply taking the square of the density profile given in
Eq. (1). Since only
recently observational progress has shown that the AB-model (Eq. (1)) yields a more accurate
description than the traditional β-model (see Croston et al. 2008, and references
therein), most of the analyses listed in Sect. 2 adopted the latter when extrapolating luminosities to large
radii. For the sake of clarity, in Appendix A we illustrate the differences between luminosities computed
adopting the AB-model or the β-model. We notice that the
mean REXCESS density profile was defined from a sample with mass
M500 ≳ 1014 M⊙.
The recent analysis of the pressure profiles of galaxy groups with masses as
small as
M500 ~ 1013 M⊙
by Sun et al. (2011) shows perfect
agreement with REXCESS results. Taken together with the good agreement
between temperature profiles in group and cluster scale objects (e.g., Rasmussen & Ponman 2007), and the
weak dependence of temperature on radius, this result supports our use of
the REXCESS density profile for lower luminosity systems. As the observed
luminosities are derived from integration of surface brightness profiles
within circular apertures, the three dimensional average luminosity profile
is cylindrically integrated up to aperture radii of 1 and
5 × R500 to compute
L500 and Ltot,
respectively. The cluster boundary is also assumed to be equal to
5 × R500. We find a ratio
a = L500 / Ltot = 0.91
and that the exact choice of the aperture enclosing the total luminosity is
not relevant. This constant ~10 per cent correction is therefore
applied to all the 160SD, 400SD, SGP, WARPS, CIZA, MACS_DIST, and EMSS
clusters for which only total luminosities are available (see Sect. 2). For the MACS_MJFV and MACS_BRIGHT
clusters no conversion is needed since the quoted luminosities are
L500. -
(b)
For the remaining clusters, i.e. those with available aperture luminosities Lap (1333 objects in total), we compute L500 iteratively as follows. The basic ingredients of this iterative procedure are the three dimensional luminosity profile model computed from Eq. (1) as detailed above and the luminosity-mass relation (L − M relation, hereafter):
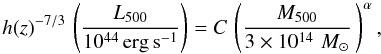 (2)with
log (C) = 0.274 and α = 1.64 (see Table
1 in Arnaud et al. 2010). These values
are slightly different from those given in Pratt et al. (2009) due to Arnaud
et al.’s use of an updated
M500 − YX
relation. Specifically, we use the relation in Eq. (2) of Arnaud et al. (2010), i.e. we adopt a
non-self-similar slope for the
M500 − YX
relation. The adopted C and α values are
derived from REXCESS luminosity data uncorrected for the Malmquist bias. The
effect of these choices is further discussed below. For a given
M500 estimated using Eq. (2), the characteristic radius
R500 entering into Eq. (1) is computed using:
(2)with
log (C) = 0.274 and α = 1.64 (see Table
1 in Arnaud et al. 2010). These values
are slightly different from those given in Pratt et al. (2009) due to Arnaud
et al.’s use of an updated
M500 − YX
relation. Specifically, we use the relation in Eq. (2) of Arnaud et al. (2010), i.e. we adopt a
non-self-similar slope for the
M500 − YX
relation. The adopted C and α values are
derived from REXCESS luminosity data uncorrected for the Malmquist bias. The
effect of these choices is further discussed below. For a given
M500 estimated using Eq. (2), the characteristic radius
R500 entering into Eq. (1) is computed using:
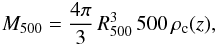 (3)where
the critical density is
ρc(z) = 3H(z)2 / 8πG.
For a given cluster with measured luminosity
L500, the set of Eqs. (1)–(3) allow us to fully model the observed radial luminosity
profile. Cylindrical integration is needed to relate the three dimensional
luminosity profile to the observed one. In practice, the equations are used
to iteratively compute L500 from
Rap and
Lap = L(<Rap)
(the circular aperture radius and the aperture luminosity, respectively).
The latter are either directly available from the input catalogues or can be
computed as explained in Sect. 2 for
the NORAS/REFLEX, BCS, SHARC, and NEP catalogues. The iteration adopts an
arbitrary starting value for the luminosity L500
in Eq. (2), which yields an
estimated R500 through Eq. (3), and thus an observed
luminosity profile which is then normalised such that
Lap = L(<Rap).
The resulting profile is used to compute
L500 = L(<R500),
which is subsequently adopted as a new value for the luminosity
L500 in Eq. (2). The iteration converges rapidly and obviously the
final value of L500 does not depend on the
adopted starting luminosity. In Fig. 2
we illustrate the relation between the input luminosity
Lap and L500 for
the NORAS/REFLEX clusters. As expected, small/large apertures yield final
luminosities L500 which are higher/lower than
the input aperture luminosities (left panel). While on average the
difference between Lap and
L500 is ~5 per cent, it is very
relevant for a significant portion of the sample (right panel).
(3)where
the critical density is
ρc(z) = 3H(z)2 / 8πG.
For a given cluster with measured luminosity
L500, the set of Eqs. (1)–(3) allow us to fully model the observed radial luminosity
profile. Cylindrical integration is needed to relate the three dimensional
luminosity profile to the observed one. In practice, the equations are used
to iteratively compute L500 from
Rap and
Lap = L(<Rap)
(the circular aperture radius and the aperture luminosity, respectively).
The latter are either directly available from the input catalogues or can be
computed as explained in Sect. 2 for
the NORAS/REFLEX, BCS, SHARC, and NEP catalogues. The iteration adopts an
arbitrary starting value for the luminosity L500
in Eq. (2), which yields an
estimated R500 through Eq. (3), and thus an observed
luminosity profile which is then normalised such that
Lap = L(<Rap).
The resulting profile is used to compute
L500 = L(<R500),
which is subsequently adopted as a new value for the luminosity
L500 in Eq. (2). The iteration converges rapidly and obviously the
final value of L500 does not depend on the
adopted starting luminosity. In Fig. 2
we illustrate the relation between the input luminosity
Lap and L500 for
the NORAS/REFLEX clusters. As expected, small/large apertures yield final
luminosities L500 which are higher/lower than
the input aperture luminosities (left panel). While on average the
difference between Lap and
L500 is ~5 per cent, it is very
relevant for a significant portion of the sample (right panel).
-
(a)
In the literature the luminosity is sometimes extrapolated within R200. We compute the ratio L500 / L200 in the same way as we compute the ratio L500 / Ltot when aperture luminosities are not available (i.e., assuming AB-model Eq. (1) in procedure (a) above), adopting R200 / R500 = 1.52. The latter value is computed assuming an NFW profile with concentration c200 = 4.61, the mean concentration measured for a morphologically relaxed cluster sample by Pointecouteau et al. (2005). We find L500 / L200 = 0.96. A fair estimate of the luminosity L200 = L(<R200) can thus be obtained from the listed L500 by assuming this average luminosity ratio.
3.4.2. Effect of underlying model assumption on L500
In order to explore the effect of our choice of M500 − YX relation, we iteratively estimated L500 by instead adopting the Malmquist bias uncorrected L − M relation derived from the M500 − YX relation with self-similar slope, as given in Eq. (3) of Arnaud et al. (2010). We find that for ~96 (91) per cent of the clusters the difference is less than 5 (2) per cent, with the largest differences found for low luminosity objects. Considering only clusters with L500 ≥ 1043 erg s-1, we find that for ~99 (95) per cent of objects the difference is less than 5 (2) per cent.
To examine the reliability of our assumption concerning the Malmquist bias correction of the L − M relation, we repeated our iterative procedure by using the Malmquist bias corrected relation of Pratt et al. (2009), finding essentially the same L500 (relative differences are ~1 per cent). This is expected, because the steep drop of the typical cluster luminosity profile with radius makes L500 rather insensitive to the exact choice of R500.
For the same reason we find negligible changes in the iteratively estimated L500 if L − M relations derived from samples other than that of REXCESS are adopted. We performed our computations using the L − M relations reported in Reiprich & Böhringer (2002) and Vikhlinin et al. (2009), finding that for clusters with L500 ≥ 1043 erg s-1 the difference is at most 3 per cent, and for lower luminosity systems it is always less than 10 per cent.
3.4.3. Uncertainties on L500
There are two main sources of uncertainty on a given value of L500. The first is due to uncertainties in the underlying model used in the homogenisation procedure; the second is due to the measurement uncertainty in the original input catalogue.
As discussed above, the choice of L − M relation has a negligible effect on the final value of L500 due to the steep drop of the luminosity profile model with radius. For the same reason, intrinsic scatter in the adopted L − M relation (Pratt et al. 2009) propagates into negligible uncertainties on L500 (≤ 1 per cent). The effect of the assumed luminosity profile model is more difficult to quantify. Firstly, the deviation of the luminosity profiles in individual objects from the average is linked to cluster dynamical state (Pratt et al. 2009; Arnaud et al. 2010), and this information is not available for most of the MCXC clusters. Secondly, uncertainties due to the assumed profile propagate differently depending on the procedure adopted to compute L500 (procedures (a) and (b) detailed above). These uncertainties are also linked to the ratio between R500 and the aperture in which the luminosity is originally measured in a non-trivial way. However, as we argue above, the AB-model derived from the REXCESS observations is a more accurate description of the luminosity profile of X-ray clusters than the β-model that is conventionally used.
Most importantly, the measurement uncertainties in the original input catalogues were estimated in a number of very different ways. Some input catalogues assume simple counting errors; some take into account assumptions on the source extent; some have no uncertainties at all. On average the measurement uncertainties given in the input catalogues range from around 15 to 20 per cent, but can vary strongly from object to object.
For all of these reasons, we conclude that the L500 uncertainties are impossible to evaluate in the self-consistent way required for a homogeneous meta-catalogue, and thus the MCXC does not include this information.
3.5. Total masses
Total masses M500, estimated for the same cosmology adopted here, are directly available only for MACS_MJFV and MACS_BRIGHT clusters. For almost all the clusters we therefore rely on luminosity as a mass proxy and estimate M500 (M_500 in Table 2) using Eq. (2). The uncertainty on M500 is dominated by the intrinsic dispersion in the L − M relation (Pratt et al. 2009). While our computation of L500 does not depend on the details of the adopted L − M relation (see discussion above), the estimated M500 obviously does. In particular, the M500 values provided by the MCXC rely on the assumption that on average the Malmquist bias for the samples used to construct the MCXC is the same as that of the REXCESS sample. Since the selection functions of the samples we use are complex (and indeed, in most cases are not known or available), our mass estimates must rely on this assumption. In addition, while our choice ensures maximal self-consistency in our modelling, other calibrations of the L − M relation could be adopted. Nevertheless, given our estimated L500, the computation of total masses from a different L − M relation is straightforward. Finally, from the mass M500 we estimate the characteristic radii R500 (R_500 in Table 2) using Eq. (3).
3.6. Notes
We gather together useful information concerning individual objects and add it to the MCXC as notes (NOTES in Table 2). In the input catalogues this information is usually provided as notes and comments and because it is different in type and size from catalogue to catalogue its homogenisation is not straightforward. In general, we choose not to include detailed and extended information and we therefore refer the reader to the cited papers for more information, e.g., the notes to Table 1 in Gioia & Luppino (1994) or in Table 2 of Romer et al. (2000a). In the following we describe the type of information we included in NOTES. For the meaning of abbreviations we refer the reader to the cited papers of each sub-catalogue.
For BCS, SGP, SHARC, NEP, MACS, CIZA, and EMSS no information is provided or is too detailed to be added in concisely. For NORAS we take information from column ID in Table 1 of Böhringer et al. (2000a) (information on source identification). For REFLEX, (Böhringer et al. 2004a), where the provided information is fairly detailed, we merge the following: (i) information in column Cm of Table 1 (information on source identification); (ii) the information concerning groupings as given in Table 10 with the simple note GR1, GR2, ..., GR10 if the cluster is listed in one of the 10 groupings listed in the table; (iii) multipeak information as given in Table 11 (columns Morphology and Orientation are merged, as e.g., two maxima/NE-SW); and (iv) information on whether the cluster is part of a line of sight structure as given in Table 12 (we simply add losStr if the cluster appears in the table). For 400SD clusters we take the information given in the column Notes in Table 4 of Burenin et al. (2007, information on alternative names is not used). For 160SD clusters we take the information given in the column Notes in Table 4 of Mullis et al. (2003, information on alternative names is not used).
3.7. Scale
In order to facilitate the conversion between angular and physical sizes (e.g., for R500) we provide the angular scale factor SCALE in kpc/arcsec (see Table 2).
4. Duplicate clusters
The overlap between the survey areas of the input catalogues induces duplicate (and in some cases triplicate, quadruplicate, etc.) entries in the MCXC catalogue. Here we explain how multiple entries are identified and which entry is retained in the MCXC. For a given cluster, according to criteria based on the type of data and the size of the input catalogue, we retain only one entry in the MCXC. Quantities from different input catalogues are not mixed or merged: for multiple input entries we retain all physical quantities (coordinates, redshift, luminosity, etc.) as given in the selected input catalogue. The full list of 2397 clusters without removal of multiple entries can be requested from the authors.
The most important criterion that we use to decide which duplicate cluster is preserved in the MCXC is the size of the input catalogue. In addition we give higher priority to catalogues that provide aperture luminosities because they ensure the most reliable and self-consistent computation of L500. These two criteria allow us to rank the input catalogues from highest to lowest priority as in Table 1. Obviously, because of its size and the type of information it provides, NORAS/REFLEX is the catalogue with the highest priority. It is followed by other large and well-defined catalogues such as the 400SD, 160SD, BCS, etc. Hence, when a cluster is listed in more than one catalogue its MCXC entry corresponds to that from the higher priority catalogue. This catalogue ranking is not crucial for CIZA because the overlap of its survey area with other surveys is minimal.
Our procedure therefore reduces to the identification of multiple entries. This identification is based mainly on centroid coordinate differences, and to a lesser extent on redshift differences. Given the large number of entries, cluster identification is performed in three steps in order to progressively reduce the number of candidate multiple entries.
-
1.
In a first step if two clusters in different catalogues have centroid offsets of less than 1′ and their relative redshift difference is less than 10 per cent they are identified as being the same cluster. Although this step removes a large number of duplicate entries, we compare their names and alternative names to make sure that we do not remove single entries. In the case of a doubtful association we do not remove any entry.
-
2.
In a second step the resulting catalogue is inspected once more by carefully identifying clusters with centroid offsets of less than 5, 10, or even 20′, and by varying the relative redshift difference. This time consuming procedure is needed because different source analysis techniques can yield rather different centroid positions, in particular for nearby clusters. Redshift differences can be very large and we use them only as indicators and not as stringent constraints. Each multiple entry candidate is checked, with names and alternative names used to facilitate the procedure. Again in this step we are rather conservative and do not remove any cluster if the identification is not certain.
-
3.
In a third step the cleaned catalogue is inspected once more with large allowances for centroid offsets, and any overlaps are checked by visually inspecting RASS and PSPC maps. The associations inspected in this last step are either multiple systems or entries where very different redshifts are given for the same X-ray cluster.
In each of the three steps we make some exceptions to the general rules explained above. First, when the redshift difference is large we keep the cluster with more reliable redshift measurement. This explains why, although it has the highest priority, the NORAS/REFLEX catalogue finally contains 11 clusters less than before our handling of duplicates. We choose the most reliable redshift measurement by taking into account the information given in the input catalogues and related papers (notes in Tables, discussion of individual objects, redshift references, etc.). If no specific note is available, we assume that the most recent measurement is the most reliable. A second exception to the general selection criteria concerns double or multiple systems, for which we retain measurements for each of the components instead of measurements of the whole system. If possible, we compared our duplicates identifications with those in other work (e.g., Mullis et al. 2003) and find perfect agreement.
A total of 558 MCXC entries list the properties of a cluster that is a member of more than one input catalogue, and for which the information from only one input catalogue has been retained. For these entries there are therefore N measurements of each of the cluster quantities (one provided by the MCXC and N − 1 unused overlaps). There are 5 clusters with N = 5, 8 with N = 4, 59 with N = 3, and 486 with N = 2.
We find that the distribution of the ratio between the redshift given in the discarded input catalogue entry and that given in the MCXC has a median equal to 1 and is very narrow (the robust standard deviation computed using the IDL routine ROBUST_SIGMA is 0.2 per cent8), but there are some large outliers. In Appendix B we discuss these outliers individually. We focus on the 25 duplicates with redshifts differing by more than an extreme factor of 1.1, and illustrate in detail how the input catalogue providing the most reliable redshift measurement was selected.
We find that positional differences between duplicates are always less than 0.2 (0.5) × R500 in 91 (99) per cent of the cases, i.e. they typically lie well within a cluster core radius. Duplicates are further discussed in Sect. 5.3, where they are used to investigate the robustness of the L500 estimates.
In order to retain useful information, when an entry with no available alternative name is kept in the MCXC catalogue while the one we discard provides it, we copy this information into the retained entry.
The MCXC provides information concerning multiple entries in the input catalogues though the label CAT_OV (see Table 2) which contains the name of the sub-catalogue from which the removed cluster entry is a member.
5. Discussion
5.1. Global catalogue characteristics
The final MCXC is constructed from the input catalogues discussed in Sect. 2 with information homogenised as explained in Sect. 3. Multiple entries in the resulting catalogue are handled as described in Sect. 4. This procedure yields the final MCXC catalogue, which comprises in total 1743 clusters (2397 initially, see Table 1) and contains virtually no multiple entries. In the following we illustrate some basic properties of the MCXC. Because of the priorities we assign to the input catalogues, NORAS/REFLEX clusters constitute a large fraction of the MCXC (see Table 1).
The MCXC redshift histogram is illustrated in the bottom right hand panel of Fig. 1: 282, 77, and 18 clusters (~16, 4, 1 per cent, respectively) have redshifts higher than 0.3, 0.5 and 0.7. In Fig. 3 we show the number of clusters as a function of luminosity: 846, 64 (~49, 4 per cent, respectively) of the clusters have 0.1−2.4 keV band luminosities L500 larger than 1,10 × 1044 erg s-1.
 |
Fig. 3 Luminosity distribution of MCXC clusters. |
In Fig. 4 we show the 0.1−2.4 keV band luminosities L500 of the 1743 MCXC clusters as a function of redshift in log-log (top panel) and the more conventional lin-log scale (bottom panel). These figures highlight both the different nature of RASS-based and serendipitous surveys and their complementarity. For a given redshift, serendipitously discovered clusters are less luminous than those from RASS-based catalogues because the deeper exposures allow lower flux limits to be adopted. This implies that the fraction of high redshift clusters in serendipitous surveys is much higher than that of RASS-based surveys.
 |
Fig. 4 Top: the 0.1−2.4 keV band luminosities L500 of the 1743 MCXC clusters as a function of redshift. Diamonds and triangles indicate clusters from RASS-based and serendipitous catalogues, respectively. Bottom: same, but in lin-log scale. |
In addition to redshift and luminosity (and total mass), a fundamental quantity provided by the MCXC is the cluster position in the sky, both in equatorial and galactic coordinates. In Fig. 5 we show the distribution on the sky of the 1743 MCXC clusters in galactic coordinates. Some distinctive features are: NORAS/REFLEX, BCS and MACS clusters are fairly homogeneously distributed; the only clusters at low galactic latitude are from the CIZA survey; the RASS-based clusters of SGP and NEP are localised in narrow regions; serendipitous clusters are sparsely distributed across the sky.
 |
Fig. 5 Sky map of the 1743 MCXC clusters in galactic coordinates. Symbols and colors are the same as in Fig. 4. |
5.2. Robustness of luminosity measurements
As the luminosity L500 the most relevant physical quantity provided by the MCXC, we focus on its discussion in the remainder of this section.
Since the modelling adopted in Sect. 3 is based on results from the REXCESS sample, and that the latter is a subsample of REFLEX, the comparison of the L500 values derived in this work and those given in Pratt et al. (2009) for the 31 REXCESS clusters provides a useful test for our procedure. We remind the reader that for all the REFLEX clusters we computed the luminosities L500 from aperture luminosities by means of the iterative procedure explained in Sect. 3. We find that our derived R500 is larger than Rap for only seven REXCESS clusters, and at most only by ~20 per cent. In Fig. 6 we show the ratio between our estimate of L500 and the XMM-Newton measurements given in Pratt et al. (2009), . Uncertainties on the luminosity ratios are computed from quadratic sum of the errors given in Pratt et al. (2009) and propagation of the aperture luminosity errors provided in Böhringer et al. (2004a). For one cluster the redshift adopted in our work differs from the one used in . Although we correct for this difference, this has no impact on our results. Symbols in Fig. 6 are as in Pratt et al. (2009), i.e. blue stars for cool core clusters and red squares for morphologically disturbed clusters. We compute error weighted means and standard deviations of the luminosity ratio and find: 0.965 ± 0.141 for all 31 clusters, 0.932 ± 0.078 for the cool core clusters, and 0.951 ± 0.193 for the disturbed clusters. Our comparison indicates a good agreement between the two measurements. Notice the fairly large scatter at low luminosity, the large scatter for disturbed clusters with respect to cool core clusters, and that there is an indication that our luminosity estimates are on average biased low in cool core systems (a 1σ effect). The lower luminosity ratio for cool core clusters is expected because they are modeled using the AB-model derived from the mean of the REXCESS sample (Eq. (1)), although their emission is more centrally peaked. We find no trend of luminosity ratio with the ratio Rap / R500 and no redshift dependence as the REXCESS sample redshift leverage is too small.
5.3. Intercomparison of original luminosity measurements
The procedure adopted to handle multiple entries (detailed in Sect. 4 ) allows us to compare L500 estimates derived from different input luminosity measurements. For each of the 558 MCXC clusters that are member of more than one input catalogue we compute the ratio L500 / L500,MCXC where L500,MCXC is the luminosity given in the MCXC and L500 is the luminosity of the same cluster, but derived from a different input catalogue (i.e., the overlap luminosity). As explained in Sect. 4, in some cases the redshifts provided by the input catalogues can be fairly different. We therefore correct the luminosities of the overlaps by multiplying them with the squared ratio of the luminosity distances at the two different redshifts. This is equivalent to comparing the 0.1−2.4 keV band fluxes within R500. The MCXC provides these luminosity ratios though the quantity L_500_RAT (see Table 2) where they are ordered in the same way as the sub-catalogue names in CAT_OV.
In Fig. 7 we show the luminosity L500 of the overlaps (top panel) and the ratio L500 / L500,MCXC (bottom panel, in dex units) as a function of L500,MCXC. Both a direct fit to the data (which is shown in the top panel of the figure and basically indistinguishable from equality) and the mean value of the luminosity ratios indicate that the different luminosity determinations are in excellent agreement. The error weighted mean and standard deviation of the luminosity ratio L500 / L500,MCXC are adopted to quantify the agreement between the different luminosity estimates. Errors are computed from the uncertainties quoted in the input catalogues, assuming that the relative error on the luminosities L500 is the same as that of the input luminosities. We find 1.03 and 0.27 for the error weighted mean and standard deviation, respectively.
In Fig. 8 we show the ratio L500 / L500,MCXC as a function of z, the cluster redshift given in the MCXC. A visual inspection of the Figure indicates that there is no significant trend between the two quantities. We performed a linear fit to the data shown in the bottom panel of Fig. 7 and in Fig. 8 and, in both cases, we find a slope consistent with zero, i.e. find no statistically significant trend of the luminosity ratio with either luminosity or redshift. We performed the same analysis by taking into account whether the compared luminosities are derived from RASS or pointed observations, and whether they are computed iteratively or just by adopting a constant conversion factor (see Sect. 3), and find no significant trend.
The luminosity comparison therefore shows that on average the agreement between different L500 measurements is excellent. However, the clear outliers in Fig. 7 indicate that for some clusters there are large discrepancies.
Although a discussion on individual objects, and thus on the difference between specific survey measurements, is beyond the scope of our work, we briefly discuss very discrepant luminosity estimates by focussing on strong outliers with luminosity ratios larger than 2 or smaller 0.5 in Fig. 7 (i.e., differences larger than a factor of 2). There is a total of twenty objects (~4 per cent of those with more than one luminosity measurement) of such discrepant estimates. For six of these clusters, three luminosity estimates are available. Interestingly, of these, we always find that only one of the three is very different from the others, and that the two remaining estimates agree within a few per cent. For the other fourteen clusters only two estimates of L500 are available. Of these, five involve measurements from the EMSS and seven are faint objects at low redshift, where extrapolation might strongly affect the luminosity estimates. For the remaining two clusters (A2507 and RXC J1003.0+3254) we find no obvious explanation.
 |
Fig. 6 Ratio between our estimate of the 0.1−2.4 keV band luminosities L500 and the XMM-Newton measurements of Pratt et al. (2009) as a function of L500. Blue stars indicate cool core clusters while red squares morphologically disturbed clusters. Solid lines indicate error weighted means and dashed lines represent the error weighted means ± error weighted standard deviations (black for all clusters, blue for cool core clusters, and red for morphologically disturbed clusters as defined in Pratt et al. 2009). |
 |
Fig. 7 Luminosity L500 of the overlaps (top panel) and the ratio L500 / L500,MCXC in dex (bottom panel) as a function of L500,MCXC, the luminosity measurements retained in the MCXC. Symbols and colors are the same as in Fig. 4, but refer to the overlaps only. The solid line in the top panel indicates the best fit to the data. The solid line in the bottom panel indicates the error weighted mean of the luminosity ratio, while the dashed horizontal lines indicates the luminosity ratios equal to 2 and 0.5. |
 |
Fig. 8 Ratio L500 / L500,MCXC in dex as a function of redshift. Symbols, colors, and lines are the same as in Fig. 7. |
6. Summary and conclusions
Motivated by the strong need for a large, homogeneous compilation in the framework of X-ray, SZ and other multiwavelength studies, we have presented the construction and properties of the MCXC, a Meta-Catalogue of X-ray detected Clusters of galaxies. The MCXC is constructed from publicly-available RASS-based (NORAS, REFLEX, BCS, SGP, NEP, MACS, and CIZA) and serendipitous (160SD, 400SD, SHARC, WARPS, and EMSS) cluster catalogues (see Sect. 2). The information from these input catalogues is systematically homogenised using the most up to date knowledge of the structural properties and scaling relations of X-ray clusters, and is undertaken in a self-consistent way (see Sect. 3). More specifically, in addition to the fairly straightforward standardisation of quantities such as coordinates and redshifts (RAJ2000, DEJ2000, etc., and Z in Table 2, we converted the available luminosities to 0.1−2.4 keV band luminosities L500(L_500 in Table 2) by adopting the average gas density profile (Croston et al. 2008) and L − M relation (Pratt et al. 2009) derived from the representative X-ray cluster sample REXCESS. The computation is performed directly from aperture luminosities when available (~76 per cent of the MCXC clusters) and we verify that the derived luminosities do not depend on the details of the adopted L − M relation.
Total masses M500 and radii R500 can be computed from the luminosities L500 by adopting an L − M relation. The MCXC provides these quantities computed self-consistently using the L − M relation adopted in this work (M_500 and R_500 in Table 2). The MCXC further provides three cluster identifiers: the MCXC name, the original name as given in the input catalogues, and an alternative name (NAME_MCXC, NAME, and NAME_ALT in Table 2, respectively). The latter has been homogenised to match both SIMBAD and NED standards. In addition, we collated important information usually provided as notes and comments in the input catalogues (NOTES in Table 2).
Multiple entries originating from overlaps between the survey areas of the input catalogues are very carefully handled (see Sect. 4). The result of this procedure is provided by the MCXC (CAT_OV in Table 2). We compare luminosity measurements from different catalogues, finding that on average the agreement is excellent, and discuss the most discrepant measurements (see Sect. 5). We find good agreement with the precisely measured REXCESS luminosities given in Pratt et al. (2009). These comparisons strongly support the validity of our approach. The MCXC provides the luminosity ratios for clusters that appear in multiple input catalogues (see L_500_RAT in Table 2).
The MCXC comprises 1743 clusters ordered by right ascension, and contains virtually no multiple entries. The full MCXC is available at CDS9 and contains the information given in Cols. (1)–(19) in Table 2, where the first 40 entries are given as an example.
The work by Melin et al. (2011) is one example of how the information provided by the MCXC can be used for SZ studies. In particular, their work illustrates that given the MCXC luminosities, the universal pressure profile and the associated SZ scaling relations provided by Arnaud et al. (2010) can be used to yield the X-ray predicted SZ signal from individual objects, which can be then compared to that observed with WMAP. A further, more extensive, example of the MCXC in use is provided by the recent papers released by the Planck Collaboration (Planck Collaboration 2011c,d,e,f,g,h). In particular, in Planck Collaboration (2011d), Planck SZ candidate sources are cross-correlated with the MCXC to find known X-ray clusters. In Planck Collaboration (2011g), the MCXC is cross-correlated with the XMM-Newton archive to yield a list of observed X-ray clusters detected at high signal to noise in the Planck survey. Finally, in Planck Collaboration (2011f), the Planck SZ signal at the position of all objects in the MCXC is bin-averaged in X-ray luminosity and compared to X-ray model predictions.
The MCXC is an ongoing project and will be extended to include available data for individual clusters at high redshift (the most relevant for cosmological studies), and cluster catalogues derived from ongoing X-ray surveys, when they are publicly available.
See http://cxc.harvard.edu/xraysurveys/surveys.html for a complete list of ongoing XMM-Newton and Chandra surveys.
For a comparison between EMSS and ASCA flux measurements see Henry (2004).
Acknowledgments
We thank Isabella Gioia, Patrick Henry, and Donald Horner for helpful discussions and Nabila Aghanim for strongly supporting the project. This research has made use of the VizieR database, operated at CDS, Strasbourg. E.P. acknowledges the support of grant ANR-06-JCJC-0141.
References
- Abazajian, K., Adelmam McCarthy, J. K., Agüeros, M. C., et al. 2005, AJ, 129, 1755 [Google Scholar]
- Andersson, K., Benson, B. A., Ade, P. A. R., et al. 2011, ApJ, 738, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2007, A&A, 474, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2009, A&A, 517, A92 [Google Scholar]
- Barkhouse, W. A., Green, P. J., Vikhlinin, A., et al. 2006, ApJ, 645, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Barr, J., Davies, R., Jørgensen, I., Bergmann, M., & Crampton, D. 2005, AJ, 130, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Briel, U. G., Schwarz, R. A., et al. 1994, Nature, 368, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000a, ApJS, 129, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000b, VizieR Online Data Catalog, 212, 90435 [NASA ADS] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004a, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004b, VizieR Online Data Catalog, 342, 50367 [NASA ADS] [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burenin, R. A., Vikhlinin, A., Hornstrup, A., et al. 2007, ApJS, 172, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Burenin, R. A., Vikhlinin, A., Hornstrup, A., et al. 2009, VizieR Online Data Catalog, 217, 20561 [NASA ADS] [Google Scholar]
- Burke, D. J., Collins, C. A., Sharples, R. M., Romer, A. K., & Nichol, R. C. 2003a, MNRAS, 341, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, D. J., Collins, C. A., Sharples, R. M., Romer, A. K., & Nichol, R. C. 2003b, VizieR Online Data Catalog, 734, 11093 [NASA ADS] [Google Scholar]
- Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2011, PASP, 123, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Pratt, G. W., Böhringer, H., et al. 2008, A&A, 487, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cruddace, R., Voges, W., Böhringer, H., et al. 2002a, ApJS, 140, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Cruddace, R., Voges, W., Böhringer, H., et al. 2002b, VizieR Online Data Catalog, 214, 239 [Google Scholar]
- Cruddace, R., Voges, W., Böhringer, H., et al. 2003, ApJS, 144, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Bohringer, H., et al. 1998, MNRAS, 301, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Allen, S. W., et al. 2000a, MNRAS, 318, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Boehringer, H., et al. 2000b, VizieR Online Data Catalog, 730, 10881 [NASA ADS] [Google Scholar]
- Ebeling, H., Edge, A. C., Allen, S. W., et al. 2000c, VizieR Online Data Catalog, 731, 80333 [NASA ADS] [Google Scholar]
- Ebeling, H., Edge, A. C., & Henry, J. P. 2001, ApJ, 553, 668 [Google Scholar]
- Ebeling, H., Mullis, C. R., & Tully, R. B. 2002, ApJ, 580, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Barrett, E., Donovan, D., et al. 2007, ApJ, 661, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Mantz, A., et al. 2010, MNRAS, 407, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Evrard, A. E., Metzler, C. A., & Navarro, J. F. 1996, ApJ, 469, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Fassbender, R., 2007, Ph.D. Thesis [astro-ph/0806.0861v1] [Google Scholar]
- Fowler, J. W., Niemack, M. D., Dicker, S. R., et al. 2007, Appl. Opt., 46, 3444 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gioia, I. M., Maccacaro, T., Schild, R. E., et al. 1990, ApJS, 72, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Gioia, I. M., & Luppino, G. A. 1994, ApJS, 94, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Gioia, I. M., Henry, J. P., Mullis, C. R., et al. 2003, ApJS, 149, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, J. P. 2000, ApJ, 534, 565 [Google Scholar]
- Henry, J. P. 2004, ApJ, 609, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, J. P., Mullis, C. R., Voges, W., et al. 2006, ApJS, 162, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, D. J., Perlman, E. S., Ebeling, H., et al. 2008, ApJS, 176, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, D. J., Perlman, E. S., Ebeling, H., et al. 2009, VizieR Online Data Catalog, 217, 60374 [NASA ADS] [Google Scholar]
- Huchra, J. P., Henry, J. P., Postman, M., & Geller, M. J. 1990, ApJ, 365, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., Geller, M. J., Clemens, C. M., Tokarz, S. P., & Michel, A. 1992, Bulletin d’Information du Centre de Donnees Stellaires, 41, 31 [Google Scholar]
- Kocevski, D. D., Ebeling, H., Mullis, C. R., & Tully, R. B. 2007, ApJ, 662, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2010, ApJSS, 192, 18 [Google Scholar]
- Kravtsov, A. V., Vikhlinin, A., & Nagai, D. 2006, ApJ, 650, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., & Henry, J. P. 2008, MNRAS, 384, 1567 [NASA ADS] [CrossRef] [Google Scholar]
- Majumdar, S., & Mohr, J. J. 2003, ApJ, 585, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A., Allen, S. W., Rapetti, D., & Ebeling, H. 2010a, MNRAS, 406, 1759 [NASA ADS] [Google Scholar]
- Mantz, A., Allen, S. W., Ebeling, H., Rapetti, D., & Drlica-Wagner, A. 2010b, MNRAS, 406, 1773 [NASA ADS] [Google Scholar]
- Markevitch, M., & Vikhlinin, A. 2007, Phys. Rep., 443, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maughan, B. J. 2007, ApJ, 668, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Maughan, B. J., Jones, C., Forman, W., & Van Speybroeck, L. 2008, ApJS, 174, 117 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Melin, J.-B., Bartlett, J. G., & Delabrouille, J. 2006, A&A, 459, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melin, J.-B., Bartlett, J. G., Delabrouille, J., et al. 2010, A&A, 525, A139 [Google Scholar]
- Menanteau, F., Gonzalez, J., Juin, J.-B., et al. 2010, ApJ, 723, 1523 [NASA ADS] [CrossRef] [Google Scholar]
- Meneghetti, M., Rasia, E., Merten, J., et al. 2010, A&A, 514, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [NASA ADS] [Google Scholar]
- Mullis, C. R., McNamara, B. R., Quintana, H., et al. 2003, ApJ, 594, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Pacaud, F., Pierre, M., Refregier, A., et al. 2007, MNRAS, 382, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Horner, D. J., Jones, L. R., et al. 2002a, ApJS, 140, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Horner, D. J., Jones, L. R., et al. 2002b, VizieR Online Data Catalog, 214, 265 [Google Scholar]
- Piffaretti, R., Jetzer, P., Kaastra, J. S., & Tamura, T. 2005, A&A, 433, 101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piffaretti, R., & Valdarnini, R. 2008, A&A, 491, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011c, A&A, 536, A7 DOI: 10.1051/0004-6361/201116474 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011d, A&A, 536, A8 DOI: 10.1051/0004-6361/201116459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011e, A&A, 536, A9 DOI: 10.1051/0004-6361/201116460 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011f, A&A, 536, A10 DOI: 10.1051/0004-6361/201116457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011g, A&A, 536, A11 DOI: 10.1051/0004-6361/201116458 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011h, A&A, 536, A12 DOI: 10.1051/0004-6361/201116489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pointecouteau, E., Arnaud, M., & Pratt, G. W. 2005, A&A, 435, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Böhringer, H., Brinkmann, J., Voges, W., & York, D. G. 2004, A&A, 423, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., & Arnaud, M. 2002, A&A, 394, 375 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Böhringer, H., Croston, J. H., et al. 2007, A&A, 461, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Bohringer, H. 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Arnaud, M., Piffaretti, R., et al. 2010, A&A, 511, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasia, E., Ettori, S., Moscardini, L., et al. 2006, MNRAS, 369, 2013 [NASA ADS] [CrossRef] [Google Scholar]
- Rasmussen, J., & Ponman, T.J. 2007, MNRAS, 380, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Romer, A. K., Nichol, R. C., Holden, B. P., et al. 2000a, ApJS, 126, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Romer, A. K., Nichol, R. C., Holden, B. P., et al. 2000b, VizieR Online Data Catalog, 212, 60209 [NASA ADS] [Google Scholar]
- Romer, A. K., Viana, P. T. P., Liddle, A. R., & Mann, R. G. 2001, ApJ, 547, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., della Ceca, R., Norman, C., & Giacconi, R. 1998, ApJ, 492, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., Borgani, S., & Norman, C. 2002, ARA&A, 40, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Struble, M. F., & Rood, H. J. 1991, ApJS, 77, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Šuhada, R., Song, J., Böhringer, H., et al. 2010, A&A, 514, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sun, M., Sehgal, N., Voit, G. M., et al. 2011, ApJ, 727, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1972, Comments on Astrophysics and Space Physics, 4, 173 [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J.-L., et al. 2010, 520, A1 [Google Scholar]
- Vanderlinde, K., Crawford, T. M., de Haan, T., et al. 2010, ApJ, 772, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., van Speybroeck, L., Markevitch, M., Forman, W. R., & Grego, L. 2002, ApJ, 578, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., & Forman, W. R. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phy., 77, 207 [Google Scholar]
- Zhang, Y.-Y., Okabe, N., Finoguenov, A., et al. 2010, ApJ, 711, 1033 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: AB-model versus β-model luminosity profiles
In the following we illustrate the difference between predictions based on the AB-model and a “typical” β-model. In particular we focus on L500 and total luminosities Ltot estimated from a given aperture luminosity.
 |
Fig. A.1 Luminosity radial profile normalised at Rap = 0.5 × R500 for the AB-model (black line) and β-models with different core radii (color lines). |
 |
Fig. A.2 The β-model to AB-model ratio of the normalised luminosity profile L / Lap evaluated at R500 (solid lines) and 5 × R500 (dashed lines) as a function of Rap. |
The AB-model adopted in this work is given by Eq. (1) with x = r / R500, xc = 0.303, α = 0.525, and β = 0.768 (see Sect. 3) and we investigate β-models given by Eq. (1) with α = 0, β = 2 / 3, and xc = 0.05,0.1,0.2,0.3, and 0.4 (xc = rc / R500, where rc is the usual β-model core radius).
For all models we compute luminosity profiles (spherically symmetric) which are then cylindrically integrated to obtain “projected” luminosities as a function of cluster-centric distance. Finally these are normalised at Rap where L(<Rap) = Lap and shown in Fig. A.1 for Rap = 0.5 × R500. The Figure shows that, with respect to the AB-model, β-models with small core radii yield centrally concentrated luminosity profiles, which in turn are shallow at large radii. The opposite is true for β-models with large core radii, which predict very extended profiles. With respect to the AB-model, a β-model with xc = 0.05 underestimates L500 by ~20 per cent while for xc = 0.4 it yields a factor of 2 larger value.
We investigate the effect of modelling on global luminosities by computing L500 and Ltot = L(<5 × R500) as a function of Rap. In Fig. A.2 we show the β-model to AB-model ratio of L / Lap (the normalised luminosity profile) evaluated at R500 (i.e. L = L500, solid lines) and 5 × R500 (i.e. L = Ltot, dashed lines) as a function of Rap. With respect to the AB-model, β-models with small/large core radii underestimate/overestimate L500 for apertures smaller than R500, while for Rap > R500 this behavior is reversed. Total luminosities Ltot are always higher/lower than the AB-model estimates for β-models with small/large core radii and the difference increases with decreasing Rap.
Appendix B: Duplicate clusters with discrepant redshift measurements
The 1743 object MCXC described in this paper is available at CDS. As described in Sect. 4, construction of the MCXC includes the identification and removal of multiple entries from the full list of clusters resulting from combination of all input catalogues. The full compilation of 2397 clusters without removal of multiple entries can be requested from the authors.
Here, we discuss in detail duplicate clusters for which the redshift given in the discarded input catalogue entry and that given in the MCXC differ by more than 10 per cent. As discussed in Sect. 4, the overall agreement in redshift between duplicates is excellent, and there are only 25 objects fulfilling this criterion in the MCXC. In Table B.1 we list cluster name, sub-catalogue, coordinates, and redshift as given in the MCXC, together with cluster name, sub-catalogue, and redshift of the discarded overlap. The last column of the Table gives the angular separation between the duplicates. We notice that BVH2007 132 is a triplicate (rows 4 and 5 in Table B.1 ). In the following we provide information on redshift estimates of these duplicate clusters individually and justify our selection of the reliable redshift measurement.
-
1.
The WARPS redshift estimate is uncertain (see note inTable 5 in Perlmanet al. 2002a).
-
2.
The discrepancy between 160SD and WARPS redshifts is discussed in Mullis et al. (2003).
-
3.
The 400SD redshift estimates are based on higher quality data (Abazajian et al. 2005) than those used in the EMSS (Gioia & Luppino 1994). In addition, this object is discussed in the notes to Table 1 in Gioia & Luppino (1994).
-
4.
The discrepancy between 400SD and SHARC redshifts is discussed in Sect. 4.1 of Burenin et al. (2007).
-
5.
The WARPSII redshift for this cluster is not secure (see Sect. 3.2 in Horner et al. 2008).
-
6.
The 400SD redshift estimates are based on higher quality data (Abazajian et al. 2005) than those used in the 160SD (Huchra et al. 1990).
-
7.
Same as for 6 (BVH2007 184).
-
8.
The average temperature of 5.1 keV measured by Vikhlinin et al. (2002) rules out the low redshift estimate. The redshift quoted in the 400SD is in excellent agreement with the one given in 160SD and WARPSII.
-
9.
Redshifts in the 400SD (see Table 4 in Burenin et al. 2007) and NEP (Gioia et al. 2003) were obtained from a dedicated follow-up programmes. The 400SD is the more recent.
-
10.
The BCS redshift reference (Huchra et al. 1992) is more recent than the NORAS one (Struble & Rood 1991).
-
11.
Same as for 10 (A1185).
-
12.
Both eBCS and NORAS quote redshift measurements obtained from their optical follow-up programmes. The eBCS measurement is the most recent and has subsequently been confirmed by Barr et al. (2005).
-
13.
Same as for 12 (RXJ0142.0+2131). In this case the eBCS redshift measurement is in excellent agreement with the one given in NEP.
-
14.
The eBCS redshift was obtained from a dedicated follow-up programme (see Table 1 in Ebeling et al. 2000a) and is more recent than the redshift references adopted for NORAS (see Table 1 in Böhringer et al. 2000a).
-
15.
Redshifts of MACS clusters are obtained from recent, dedicated follow-up observations (Ebeling et al. 2010).
-
16.
Same as for 15 (MACSJ0358.8-2955).
-
17.
Same as for 15.
-
18.
The NORAS redshift was obtained from a dedicated follow-up programme (see Table 1 in Böhringer et al. 2000a) and is more recent than the redshift references adopted for BCS (see Table 3 in Ebeling et al. 1998).
-
19.
The NORAS redshift reference (year 2000; see Table 1 in Böhringer et al. 2000a) is more recent than the one adopted for the eBCS (year 1991; see Table 1 in Ebeling et al. 2000a).
-
20.
The NORAS redshift was obtained from a dedicated follow-up programme (see Table 1 in Böhringer et al. 2000a) and is more recent than the redshift references adopted for eBCS (see Table 1 in Ebeling et al. 2000a).
-
21.
Same as for 20 (RXC J1715.2+0309).
-
22.
The REFLEX redshift reference (year 2002; see Table 6 in Böhringer et al. 2004a) is more recent than the one adopted for the SGP (year 1991; see Table 3 in Cruddace et al. 2002a).
-
23.
The REFLEX redshift reference (Böhringer et al. 2004a) is more recent than the one in the EMSS (Gioia & Luppino 1994).
-
24.
The REFLEX redshift was obtained from a dedicated follow-up programme (see Table 6 in Böhringer et al. 2004a) and is more recent than the redshift references adopted for SGP (see Table 3 in Cruddace et al. 2002a).
-
25.
The REFLEX redshift reference (year 2002; see Table 6 in Böhringer et al. 2004a) is more recent than the redshift references adopted for SGP (year 1991; see Table 3 in Cruddace et al. 2002a).
All Tables
Number of clusters in the catalogues used to construct the MCXC before and after handling of multiple entries.
The first 40 entries of the MCXC catalogue. The full MCXC is available at the CDS.
All Figures
 |
Fig. 1 Redshift histograms of the input catalogues used to construct the MCXC and of the MCXC after handling of multiple entries. Different area shadings are used for RASS-based, serendipitous, and MCXC catalogues. |
| In the text | |
 |
Fig. 2 Relation between input quantities Rap and Lap = L(<Rap) and the iteratively estimated R500 and L500 = L(<R500) for the NORAS/REFLEX clusters. The luminosity ratio as a function of aperture radius ratio is shown in the left panel, while the luminosity ratio histogram is shown in the right panel. |
| In the text | |
 |
Fig. 3 Luminosity distribution of MCXC clusters. |
| In the text | |
 |
Fig. 4 Top: the 0.1−2.4 keV band luminosities L500 of the 1743 MCXC clusters as a function of redshift. Diamonds and triangles indicate clusters from RASS-based and serendipitous catalogues, respectively. Bottom: same, but in lin-log scale. |
| In the text | |
 |
Fig. 5 Sky map of the 1743 MCXC clusters in galactic coordinates. Symbols and colors are the same as in Fig. 4. |
| In the text | |
 |
Fig. 6 Ratio between our estimate of the 0.1−2.4 keV band luminosities L500 and the XMM-Newton measurements of Pratt et al. (2009) as a function of L500. Blue stars indicate cool core clusters while red squares morphologically disturbed clusters. Solid lines indicate error weighted means and dashed lines represent the error weighted means ± error weighted standard deviations (black for all clusters, blue for cool core clusters, and red for morphologically disturbed clusters as defined in Pratt et al. 2009). |
| In the text | |
 |
Fig. 7 Luminosity L500 of the overlaps (top panel) and the ratio L500 / L500,MCXC in dex (bottom panel) as a function of L500,MCXC, the luminosity measurements retained in the MCXC. Symbols and colors are the same as in Fig. 4, but refer to the overlaps only. The solid line in the top panel indicates the best fit to the data. The solid line in the bottom panel indicates the error weighted mean of the luminosity ratio, while the dashed horizontal lines indicates the luminosity ratios equal to 2 and 0.5. |
| In the text | |
 |
Fig. 8 Ratio L500 / L500,MCXC in dex as a function of redshift. Symbols, colors, and lines are the same as in Fig. 7. |
| In the text | |
 |
Fig. A.1 Luminosity radial profile normalised at Rap = 0.5 × R500 for the AB-model (black line) and β-models with different core radii (color lines). |
| In the text | |
 |
Fig. A.2 The β-model to AB-model ratio of the normalised luminosity profile L / Lap evaluated at R500 (solid lines) and 5 × R500 (dashed lines) as a function of Rap. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


