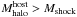| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015780 | |
| Published online | 11 August 2011 | |
How do galaxies acquire their mass?
1
Laboratoire d’Astrophysique de Marseille, UMR 6110 CNRS - Univ. de Provence, 38 rue Frédréric Joliot-Curie, 13388 Marseille Cedex 13, France
e-mail: Andrea.Cattaneo@oamp.fr
2
Centre de Recherche Astrophysique de Lyon, UMR 5574 CNRS - Univ. Claude Bernard - ENS Lyon, 9 av. Charles André, 69561 Saint Genis Laval Cedex, France
3
Astrophysikalisches Institut Potsdam, an der Sternwarte 16, 14482 Potsdam, Germany
4
Institut d’Astrophysique de Paris, UMR 7095 CNRS - UPMC, 98bis boulevard Arago, 75014 Paris, France
5
Astrophysics and BIPAC, Department of Physics, University of Oxford, Keble Rd, Oxford OX1 3RH, UK
6
Departamento de Fisica Teorica, Modulo C-XI, Universidad Autonoma de Madrid, 28049 Cantoblanco, Madrid, Spain
Received: 17 September 2010
Accepted: 9 June 2011
We study the growth of galaxy masses, via gas accretion and galaxy mergers. We introduce a toy model that describes (in a single equation) how much baryonic mass is accreted and retained into galaxies as a function of halo mass and redshift. In our model, the evolution of the baryons differs from that of the dark matter because 1) gravitational shock heating and AGN jets suppress gas accretion mainly above a critical halo mass of Mshock ~ 1012 M⊙; 2) the intergalactic medium after reionisation is too hot for accretion onto haloes with circular velocities vcirc ≲ 40 km s-1; 3) stellar feedback drives gas out of haloes, mainly those with vcirc ≲ 120 km s-1. We run our model on the merger trees of the haloes and sub-haloes of a high-resolution dark matter cosmological simulation. The galaxy mass is taken as the maximum between the mass given by the toy model and the sum of the masses of its progenitors (reduced by tidal stripping). Designed to reproduce the present-day stellar mass function of galaxies, our model matches fairly well the evolution of the cosmic stellar density. It leads to the same z = 0 relation between central galaxy stellar and halo mass as the one found by abundance matching and also as that previously measured at high mass on SDSS centrals. Our model also predicts a bimodal distribution (centrals and satellites) of stellar masses for given halo mass, in very good agreement with SDSS observations. The relative importance of mergers depends strongly on stellar mass (more than on halo mass). Massive galaxies with mstars > mcrit ~ Ωb/ΩmMshock ~ 1011 M⊙ acquire most of their final mass through mergers (mostly major and gas-poor), as expected from our model’s shutdown of gas accretion at high halo masses. However, although our mass resolution should see the effects of mergers down to mstars ≃ 1010.6 h-1 M⊙, we find that mergers are rare for mstars ≲ 1011 h-1 M⊙. This is a consequence of the curvature of the stellar vs. halo mass relation set by the physical processes of our toy model and found with abundance matching. So gas accretion must be the dominant growth mechanism for intermediate and low mass galaxies, including dwarf ellipticals in clusters. The contribution of galaxy mergers terminating in haloes with mass Mhalo < Mshock (thus presumably gas-rich) to the mass buildup of galaxies is small at all masses, but accounts for the bulk of the growth of ellipticals of intermediate mass (~1010.5 h-1 M⊙), which we predict must be the typical mass of ULIRGs.
Key words: galaxies: formation / galaxies: evolution / galaxies: luminosity function, mass function / galaxies: interactions / galaxies: elliptical and lenticular, cD / galaxies: halos
© ESO, 2011
1. Introduction
In the standard theory (White & Rees 1978; Blumenthal et al. 1984; White & Frenk 1991), galaxy formation is a two-stage process. The gravitational instability of primordial density fluctuations forms dark matter haloes that merge hierarchically into larger and larger structures. Galaxies grow within these haloes (i) by accreting gas that dissipates and falls to the centre of the gravitational potential wells of the dark matter; and (ii) by merging with other galaxies after their haloes have become part of larger structures. These two paths explain why there are two galaxy morphological types: in the standard theory, gas accretion is the mechanism that builds up disc galaxies (i.e. spirals; Fall & Efstathiou 1980), while galaxy merging is the mechanism by which elliptical galaxies acquire the bulk of their mass (Toomre 1977; Mamon 1992).
In the present article, we wish to revisit the question of how galaxies acquired their present-day stellar mass. Was it mainly through mergers or through smooth gas accretion? Were the galaxies merging together mainly gas-rich (often called “wet” mergers) or gas-poor (“dry” mergers)? How important are major mergers involving galaxies of similar mass, compared to more minor ones involving very different mass galaxies? What are the respective roles of feedback mechanisms such as reionisation of the IGM (Rees 1986), supernova explosions (Dekel & Silk 1986), jets from active galactic nuclei (AGN, Silk & Rees 1998), and the absence or presence of shock fronts between the infalling and virialised gas, depending on the mass of the halo (Birnboim & Dekel 2003)? How do the relative impacts of these physical processes depend on the final (observable) stellar mass of the galaxy?
To answer these questions, one must first estimate the build-up of dark matter haloes, either through Monte-Carlo merger-trees (Lacey & Cole 1993; Somerville & Kolatt 1999; Neistein & Dekel 2008) or through cosmological N-body simulations, which also provide spatial information. If we assume that the position of a galaxy is tracked by the centre of mass of its halo, then the halo merger rate will also give us the rate at which galaxies merge (assuming the knowledge of the evolution of haloes once they become sub-haloes of larger ones). It is more difficult to compute the stellar masses of galaxies prior to merging, which determine the contribution from gas accretion, because they depend not only on the gas mass that accretes onto galaxies but also on feedback processes that eject gas from galaxies.
There are two approaches to deal with this complexity. Semi-analytic models (SAMs, Kauffmann et al. 1993; Cole et al. 1994; also Cattaneo et al. 2006; Bower et al. 2006; Croton et al. 2006; Somerville et al. 2008; Lo Faro et al. 2009, and references therein) use simple recipes to describe the various physical processes affecting the baryons within haloes, and predict many observables. However, even the simplest SAMs quickly reach considerable complexity and involve a large number of free parameters.
The halo occupation distribution (HOD) approach (Berlind & Weinberg 2002; Conroy et al. 2006; Yang et al. 2009) does not make any assumption about the physics that govern the number (Berlind & Weinberg 2002), the luminosity (Yang et al. 2003) or the stellar mass (Yang et al. 2009) of galaxies within haloes. Instead, in the HOD approach, one computes either the mean (abundance matching, see Marinoni & Hudson 2002; Conroy et al. 2006) or the statistical distributions that these properties must have as a function of halo mass and redshift to reproduce the observational data (assuming that the properties of dark matter haloes, i.e. the mass function and clustering, are modelled correctly). However, HOD models cannot tell us how much of this mass comes from gas accretion and how much comes from mergers.
Our approach is intermediate between the two. We parameterise, in a single equation, the mass of stars formed after gas accretion as a function of halo mass and redshift, ![\hbox{$m_{\rm stars} = \widetilde m_{\rm stars}[M_{\rm halo},v_{\rm circ}(M_{\rm halo},z)]$}](/articles/aa/full_html/2011/09/aa15780-10/aa15780-10-eq12.png) , where
, where 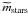 takes into account various feedback effects that quench gas accretion and subsequent star formation. We compute galaxy mergers by following dark matter substructures. When the latter are no longer resolved, we merge the galaxies on a dynamical friction timescale using a formula calibrated on cosmological hydrodynamic simulations (Jiang et al. 2008), thus allowing the formation of galaxies with
takes into account various feedback effects that quench gas accretion and subsequent star formation. We compute galaxy mergers by following dark matter substructures. When the latter are no longer resolved, we merge the galaxies on a dynamical friction timescale using a formula calibrated on cosmological hydrodynamic simulations (Jiang et al. 2008), thus allowing the formation of galaxies with ![\hbox{$m_{\rm stars} > \widetilde m_{\rm stars}[M_{\rm halo},v_{\rm circ}(M_{\rm halo},z)]$}](/articles/aa/full_html/2011/09/aa15780-10/aa15780-10-eq14.png) .
.
Not only is our approach much simpler than fully fledged SAMs (we shall see that it contains only four parameters), it is also simpler than “lighter” models such as the one recently proposed by Neistein & Weinmann (2010), who parameterised the dependence of the time derivatives of the masses of the stellar, cold and hot gas components of galaxies as a function of halo mass and redshift. Admittedly, the simplicity of our approach limits its scope. But we believe that it makes robust predictions on the mass growth of galaxies, which provide a stepping stone to more complex analyses. At the same time, differently from HOD, our model allow us to follow mergers and thus to separate growth via gas accretion and growth via mergers.
The structure of the article is as follows. In Sect. 2, we present the N-body simulation used to follow the gravitational evolution of the dark matter, and two simple formulae, one that expresses the timescale for orbital decay of unresolved sub-haloes, and the other that expresses the stellar mass at the centre of each halo if galaxies grew only by gas accretion. In Sect. 3, we present our results for the relative importance of gas accretion and mergers as a function of galaxy mass. Section 4 discusses our results and summarises our conclusions.
2. The galaxy formation model
2.1. Gravitational evolution of the dark matter
The hierarchical formation and clustering of dark matter haloes is followed by means of a cosmological N-body simulation. The computational volume of the simulation presented here is a cube with side length L = 50 h-1 Mpc and periodic boundary conditions. The values of the cosmological parameters used to generate the initial conditions at redshift z = 50 by means of the Zel’dovich approximation (Efstathiou et al. 1985) and to run the simulation are those from the Wilkinson Microwave Anisotropy Probe’s 5th-year analysis (WMAP5) combined with results from type Ia supernovae and baryonic acoustic oscillations (Komatsu et al. 2009): Ωm = 0.279, ΩΛ = 0.721, Ωb = 0.046, h = 0.70, σ8 = 0.817 and ns = 0.96. The simulation was run with the tree-PM code GADGET2 (Springel 2005) at a resolution of 5123 particles. We saved the outputs at 101 timesteps equally spaced in time (Δt = 92 h-1 Myr) from z = 10 to z = 0. The number of timesteps was chosen so that Δt is smaller than any merging timescale. The particle mass is 7.3 × 107 h-1 M⊙ and the force softening is 2 h-1 kpc.
The MPI version of the AMIGA1 halo finder, AHF (Knollmann & Knebe 2009)2, was used to identify haloes and sub-haloes in each of the saved outputs3. AHF is an improvement of the MHF halo finder (Gill et al. 2004), which locates peaks in an adaptively smoothed density field as prospective halo centres. For each of these density peaks, we determined the particle with the lowest gravitational potential and considered the surrounding particles sorted in distance to iteratively find the largest collection of bound particles encompassing the density peak, using their mean velocity as the kinetic reference. Only peaks with at least 20 bound particles are considered as haloes and retained for further analysis. Therefore, the minimum halo mass is 1.5 × 109 h-1 M⊙ (corresponding to vcirc = 15 km s-1). Our halo finding algorithm automatically identifies haloes, sub-haloes, sub-sub-haloes, and so on (see Knollmann & Knebe 2009, for the details of the algorithm).
For each halo at epoch z, we compute the virial radius rvir, which is the radius where the mean density drops below Δ(z) times the critical density of the Universe at redshift z. The threshold Δ(z) is computed using the spherical top-hat collapse model and is a function of both cosmological model and time (Nakamura 1996, cited in Kitayama & Suto 1996; Gross 1997; Bryan & Norman 1998). For the cosmology that we are using, Δ = 98 at z = 0, i.e. the overdensity at the virial radius is 352 times the present-day mean density of the Universe.
After each halo has been identified by AHF in this manner, we define sub-haloes to be haloes (defined with the same overdensity Δ) that lie within the virial region of a more massive halo, the so-called host halo, of mass 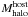 . As sub-haloes are embedded within their host halo, their own density profile usually shows a characteristic upturn at the radius rt ≲ rvir where the density profile becomes dominated by the surrounding host halo4. We use this truncation radius as the outer edge of the sub-halo. Halo and sub-halo properties (i.e. mass, density profile, velocity dispersion, rotation curve) are calculated using the gravitationally bound particles inside either the virial radius rvir for a host halo or the truncation radius rt for a sub-halo.
. As sub-haloes are embedded within their host halo, their own density profile usually shows a characteristic upturn at the radius rt ≲ rvir where the density profile becomes dominated by the surrounding host halo4. We use this truncation radius as the outer edge of the sub-halo. Halo and sub-halo properties (i.e. mass, density profile, velocity dispersion, rotation curve) are calculated using the gravitationally bound particles inside either the virial radius rvir for a host halo or the truncation radius rt for a sub-halo.
We build merger trees by cross-correlating haloes in consecutive simulation outputs. For this purpose, we use a tool that comes with the AHF package, called MergerTree. As the name suggests, it serves the purpose of identifying corresponding objects in a same simulation at different redshifts. We follow each halo (either host or sub-halo) identified at redshift z = 0 backwards in time. The direct progenitor at the previous redshift is the one that shares the greatest number of particles with the present halo and is closest to it in mass. The latter criterion is important for sub-haloes as all their particles are also part of the host halo, but there is normally a large gap between sub-halo and host halo masses.
In the study presented here, we walk along the tree starting at redshift z = 10 and moving toward z = 0. Sub-haloes are followed within the environment of their respective hosts until the point where AHF can no longer resolve them either because they have been tidally disrupted or because they have merged with their host (of course, many sub-haloes survive until z = 0). Section 2.2 below describes how we follow sub-haloes when we can no longer resolve them numerically.
2.2. Growth via galaxy mergers
We associate galaxies to the smallest resolved dark matter substructures. We say that two haloes have merged at the cosmic time 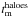 when a sub-halo is no longer resolved in the N-body simulation (Fig. 1). With this definition, the merging of two dark matter haloes is a necessary but non-sufficient condition for the merging of their central galaxies because generally a sub-halo ceases to be resolved before reaching the centre of its host halo. Let tdf be the time the sub-halo takes to reach the centre after it is no longer resolved. The galaxy at the centre of the sub-halo has merged with the galaxy at the centre of the host halo by cosmic time t if
when a sub-halo is no longer resolved in the N-body simulation (Fig. 1). With this definition, the merging of two dark matter haloes is a necessary but non-sufficient condition for the merging of their central galaxies because generally a sub-halo ceases to be resolved before reaching the centre of its host halo. Let tdf be the time the sub-halo takes to reach the centre after it is no longer resolved. The galaxy at the centre of the sub-halo has merged with the galaxy at the centre of the host halo by cosmic time t if 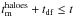 . If this condition is satisfied, then the sub-halo’s central galaxy is merged with that of the host halo at the first timestep for which
. If this condition is satisfied, then the sub-halo’s central galaxy is merged with that of the host halo at the first timestep for which 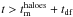 . Otherwise, the galaxy properties are frozen after
. Otherwise, the galaxy properties are frozen after  .
.
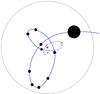 |
Fig. 1 Sketch illustrating the merger of two haloes. Once the smaller halo penetrates the larger one (whose central galaxy is denoted by a red circle), it becomes a sub-halo. Its orbit (adapted from an N-body simulation by Colpi et al. 1999), shown by the blue curve (with positions shown for equal timesteps), decays by dynamical friction and its size, shown by the circles, is reduced by tidal stripping from the larger halo’s potential. The solid part of the blue curve is followed directly by the N-body simulation, while the dashed part shows the trajectory that the sub-halo is expected to take after it (open circles) is no longer resolved in the simulation. In our analysis, the duration of the motion along the dashed stretch of the blue curve is computed analytically from Eqs. (1–3). |
To compute the time for the satellite’s orbit to decay to the centre, we use Chandrasekhar’s (1943) dynamical friction time, which can be written as 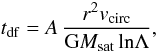 (1)(e.g. Binney & Tremaine 2008), where r is the sub-halo’s orbital radius at the time
(1)(e.g. Binney & Tremaine 2008), where r is the sub-halo’s orbital radius at the time 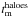 when it ceases to be resolved, vcirc is the circular velocity at radius r, lnΛ is the so-called Coulomb logarithm, and A is a factor of order unity that depends on orbital eccentricity (Colpi et al. 1999, and see below). In the following two paragraphs, we explain our choice for lnΛ and A.
when it ceases to be resolved, vcirc is the circular velocity at radius r, lnΛ is the so-called Coulomb logarithm, and A is a factor of order unity that depends on orbital eccentricity (Colpi et al. 1999, and see below). In the following two paragraphs, we explain our choice for lnΛ and A.
Jiang et al. (2008) used high-resolution cosmological hydrodynamical simulations to show that, once a halo of mass Msat penetrates the virial sphere of a larger one, of mass Mhalo (and thus becomes a sub-halo, i.e. satellite), the time it takes to fall to the centre of its parent halo is given by Eq. (1), where r and vcirc are measured at the virial radius rvir of the host halo and where the Coulomb logarithm is lnΛ = ln(1 + Mhalo/Msat). We thus assume that for r < rvir, the appropriate Coulomb logarithm is the one computed using 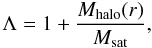 (2)where Mhalo(r) is the halo mass enclosed within the sphere of radius r.
(2)where Mhalo(r) is the halo mass enclosed within the sphere of radius r.
The normalisation A of the dynamical friction time is often chosen to be independent of the shape of the satellite’s orbit (e.g. 1.17 according to Binney & Tremaine 2008). But for given orbit apocentre, the time of orbital decay is expected to be shorter for satellites on radial orbits, which feel more dynamical friction as they reach the high density region near the centre of their halo. Jiang et al. calibrated this effect and found 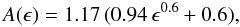 (3)where ϵ = J/Jcirc(E) is the orbital circularity, that is, the ratio of angular momentum to that of a circular orbit of the same energy (ϵ = 0 for a radial orbit and ϵ = 1 for a circular orbit). Jiang et al.’s parametrisation of the Coulomb logarithm and normalisation of the orbital decay time, based upon hdyrodynamical cosmological N-body simulations, implicitly takes into account the greater concentration of baryons with respect to the dark matter as well as the effects of tidal stripping on the dynamical friction time.
(3)where ϵ = J/Jcirc(E) is the orbital circularity, that is, the ratio of angular momentum to that of a circular orbit of the same energy (ϵ = 0 for a radial orbit and ϵ = 1 for a circular orbit). Jiang et al.’s parametrisation of the Coulomb logarithm and normalisation of the orbital decay time, based upon hdyrodynamical cosmological N-body simulations, implicitly takes into account the greater concentration of baryons with respect to the dark matter as well as the effects of tidal stripping on the dynamical friction time.
We now explain how we compute in our model the value of ϵ that we insert into Eq. (3). The radial coordinate r, the orbital speed v, and the radial and tangential velocities vr and 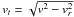 of the sub-halo with respect to the centre of mass of the host halo are extracted from the N-body simulation at the last timestep when the sub-halo is resolved. We compute the sub-halo’s angular momentum and energy per unit mass. They are, respectively, J = r vt and E = 1/2 v2 + φ(r), where φ(r) is the gravitational potential of the host halo that we compute assuming an NFW model (Navarro et al. 1996). This requires to know the halo concentration. The latter could be evaluated directly from the particle distribution but this may lead to noise, particularly in low-mass haloes, which contain fewer particles. Instead, we use the most recent determination of the concentration-mass relation for regular haloes in ΛCDM simulations with WMAP-5th year cosmological parameters (Macciò et al. 2008): c = 6.1 (Mhalo/1014h M⊙)-0.094. With this assumption we compute Jcirc(E) by solving the equation
of the sub-halo with respect to the centre of mass of the host halo are extracted from the N-body simulation at the last timestep when the sub-halo is resolved. We compute the sub-halo’s angular momentum and energy per unit mass. They are, respectively, J = r vt and E = 1/2 v2 + φ(r), where φ(r) is the gravitational potential of the host halo that we compute assuming an NFW model (Navarro et al. 1996). This requires to know the halo concentration. The latter could be evaluated directly from the particle distribution but this may lead to noise, particularly in low-mass haloes, which contain fewer particles. Instead, we use the most recent determination of the concentration-mass relation for regular haloes in ΛCDM simulations with WMAP-5th year cosmological parameters (Macciò et al. 2008): c = 6.1 (Mhalo/1014h M⊙)-0.094. With this assumption we compute Jcirc(E) by solving the equation 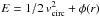 for r where the squared circular velocity is
for r where the squared circular velocity is 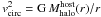 , and where
, and where 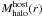 is also computed with the NFW model. This equation has a solution for E < 0. When E ≥ 0, the sub-structure is not gravitationally bound to the host, so the satellite and the central galaxy do not merge.
is also computed with the NFW model. This equation has a solution for E < 0. When E ≥ 0, the sub-structure is not gravitationally bound to the host, so the satellite and the central galaxy do not merge.
In our analysis, the galaxy merging history is determined fully and solely by the underlying evolution of the dark matter component. It does not depend on the efficiency with which gas dissipates, sinks to the centre and makes stars. This is why we have discussed galaxy mergers immediately after presenting the N-body simulation. The processes that determine the growth of luminous galaxies via accretion within dark matter haloes are considered in the following subsection.
2.3. Growth via gas accretion
We compute the stellar mass of a galaxy, mstars, as a function of Mhalo using a model that is an improvement over the one introduced by Cattaneo (2001). Despite its simplicity, that model was shown to be in reasonable agreement with the galaxy luminosity function and the cosmic evolution of the star formation rate (SFR) density.
The key assumption is that, in the absence of mergers, the mass of the stars in a dark matter halo is basically a function of two quantities only: the halo mass Mhalo and the halo circular velocity vcirc(Mhalo,z).
The effects of shock heating and feedback enter our model through the form of this function. Cosmic reionisation suppresses gas accretion and star formation in haloes below a minimum circular velocity vreion, stellar feedback mitigates star formation in haloes below a characteristic circular velocity vSN, and gravitational shock heating coupled to black hole feedback suppresses gas accretion and star formation above a critical halo mass of Mshock.
The stellar mass of a galaxy at any given time is assumed to be given by ![\begin{equation} \label{M1new} m_{\rm stars} = {\rm max}\left\{ \widetilde m_{\rm stars}[M_{\rm halo},v_{\rm circ}(M_{\rm halo},z)],\, \sum_{\rm prog} m_{\rm stars}^{\rm (prog)}s_{\rm prog}\right\}, \end{equation}](/articles/aa/full_html/2011/09/aa15780-10/aa15780-10-eq82.png) (4)where
(4)where 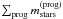 is the sum of the stellar masses of all progenitors and 0 < sprog ≤ 1 is a factor that accounts for the tidal stripping of the mass of a satellite progenitor prior to merging. For the main progenitor, sprog = 1. The way in which sprog is computed for the other progenitors is discussed in Sect. 2.4.
is the sum of the stellar masses of all progenitors and 0 < sprog ≤ 1 is a factor that accounts for the tidal stripping of the mass of a satellite progenitor prior to merging. For the main progenitor, sprog = 1. The way in which sprog is computed for the other progenitors is discussed in Sect. 2.4.
Our model does not contain any rate and does not integrate any differential equations. However, Eq. (4) implies that the stellar mass at timestep i can be larger than the value computed from the function 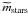 at timestep i if the stellar mass at timestep i − 1 is larger than the mass computed from the function
at timestep i if the stellar mass at timestep i − 1 is larger than the mass computed from the function 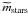 at timestep i. This has a simple physical reason: besides the effects of stellar evolution (neglected in our model), the mass of the stars that have already formed and are already in a galaxy cannot decrease, even if the potential well becomes shallower.
at timestep i. This has a simple physical reason: besides the effects of stellar evolution (neglected in our model), the mass of the stars that have already formed and are already in a galaxy cannot decrease, even if the potential well becomes shallower.
While Eq. (4) suggests that the final halo mass is independent of the mass accretion history (MAH) of its halo, our prevention of any decrease in stellar mass implies some dependence on the halo MAH: A galaxy with a low-mass present-day halo might have never formed stars if its halo circular velocity was always below the threshold for galaxy (star) formation (see Sect. 2.3.2 below). Another galaxy with the same halo mass at z = 0 may have acquired stars if its halo mass had grown fast enough for its circular velocity to break the threshold for galaxy formation, and in our model it would keep its stellar mass. The implications for the results of our model will be discussed in Sect. 3.
 |
Fig. 2 Star formation efficiency versus halo circular velocity and mass at two different epochs in our toy model (Eq. (8)). This figure has been plotted for the parameters of Table 1 that produce the best fit to the stellar mass function at z = 0 (see Sect. 3.1). The upper (black) mass scale is for z = 0, while the lower (red) mass scale is for z = 5. The gold shaded region shows the relation predicted by abundance matching by Guo et al. (2010). |
We now describe how we choose the functional form of 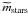 (the rest of this section) and sprog (Sect. 2.4).
(the rest of this section) and sprog (Sect. 2.4).
2.3.1. Shock heating and AGN feedback
The accretion of gas onto low mass haloes is understood to proceed in the form of cold filaments (Kereš et al. 2005) that fall onto the disc, where the new material is shock heated, but cools very rapidly thanks to the very high gas density of the disc. However, as shown by Birnboim & Dekel (2003), above a critical halo mass Mshock ~ 1012 M⊙ (roughly independent in time, see Fig. 2 of Dekel & Birnboim 2006), the condition for the propagation of a stable shock is satisfied, and the post-shock gas builds up a hot atmosphere that cools inefficiently (see also Oser et al. 2010). Moreover, AGN couple to the hot gas preventing it from cooling down again (see the review of Cattaneo et al. 2009, and references therein, in particular Croton et al. 2006, for the first explicit implementation in a SAM). Following Cattaneo (2001), we model these two effects by assuming that the mass accreted by the galaxy from the start of the simulation to the timestep under consideration is, to first order, 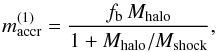 (5)for vcirc ≫ vreion, where fb = Ωb/Ωm is the mean baryonic fraction of the Universe. In other words,
(5)for vcirc ≫ vreion, where fb = Ωb/Ωm is the mean baryonic fraction of the Universe. In other words, 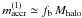 when Mhalo ≪ Mshock, while
when Mhalo ≪ Mshock, while 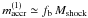 when Mhalo ≫ Mshock. In the latter case, the galaxy mass grows very slowly with increasing halo mass (except for the effects of mergers, which are not considered in the calculation of the accreted mass)5.
when Mhalo ≫ Mshock. In the latter case, the galaxy mass grows very slowly with increasing halo mass (except for the effects of mergers, which are not considered in the calculation of the accreted mass)5.
2.3.2. Reionisation
Heating by the photoionising UV background raises the entropy of the gas and suppresses the concentration of baryons in shallow potential wells (Ikeuchi 1986; Rees 1986; Blanchard et al. 1992 – for Compton heating –, Efstathiou 1992; Gnedin 2000; Kravtsov et al. 2004). Here we take a phenomenological approach and model the effects of photoionisation heating by introducing a lower circular velocity cut-off at vcirc ~ vreion that mimics the shutoff of gas infall when Tvir < TIGM (Blanchard et al. 1992; Thoul & Weinberg 1996). Cosmological hydrodynamical simulations give conflicting answers on the temperature of the intergalactic medium (IGM) in the intermediate density regions outside the virial radius, from which gas should fall in (McQuinn et al. 2009, and references therein). We assume that this IGM temperature does not vary with redshift at z ≲ zreion > 10 (z ≃ 10 is where our calculations start), which is in rough agreement with hydrodynamical simulations (McQuinn et al. 2009, and references therein). We also suppose that the mass maccr that can flow to the centre in a halo of mass Mhalo is suppressed with respect to the first-order accreted mass by a factor of 1 − (vreion/vcirc)2 at vcirc ≥ vreion, so that: ![\begin{equation} m_{\rm accr} = \left [1-\left ({v_{\rm reion}\over v_{\rm circ}}\right)^2\right]\,m_{\rm accr}^{(1)}. \label{mreion} \end{equation}](/articles/aa/full_html/2011/09/aa15780-10/aa15780-10-eq104.png) (6)At vcirc < vreion the suppression is total (maccr = 0). This extreme approximation is ad hoc, but it is not unreasonable given the high mass-to-light ratios measured in low-mass objects and is in agreement with hydrodynamical simulations (Thoul & Weinberg 1996)6.
(6)At vcirc < vreion the suppression is total (maccr = 0). This extreme approximation is ad hoc, but it is not unreasonable given the high mass-to-light ratios measured in low-mass objects and is in agreement with hydrodynamical simulations (Thoul & Weinberg 1996)6.
2.3.3. Supernovae
When the circular velocity becomes larger than vreion, the gas starts flowing to the centre and making stars, which feed energy back to the interstellar medium mainly via type II supernova explosions. The energy fed back to the interstellar medium is proportional to the stellar mass of the galaxy, 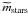 . A fraction of this energy is used to drive an outflow. Let mwind be the total mass ejected from a galaxy from the start of the simulation to the timestep under consideration. For a given wind kinetic energy,
. A fraction of this energy is used to drive an outflow. Let mwind be the total mass ejected from a galaxy from the start of the simulation to the timestep under consideration. For a given wind kinetic energy, 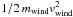 , mwind is maximum when the wind speed, vwind, is minimum. However, the wind speed cannot be lower than the escape velocity, which is proportional to the circular velocity vcirc, because otherwise the gas would not flow out. The maximum outflow condition thus implies that
, mwind is maximum when the wind speed, vwind, is minimum. However, the wind speed cannot be lower than the escape velocity, which is proportional to the circular velocity vcirc, because otherwise the gas would not flow out. The maximum outflow condition thus implies that 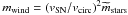 (Dekel & Silk 1986), where
(Dekel & Silk 1986), where 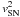 is a proportionality constant, the value of which is to be determined by fitting the galaxy mass function and is physically related to the supernova energy that goes into wind kinetic energy. We also require mass conservation:
is a proportionality constant, the value of which is to be determined by fitting the galaxy mass function and is physically related to the supernova energy that goes into wind kinetic energy. We also require mass conservation: 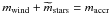 . In other words, all the gas accreted onto a galaxy is either ejected or forms stars. This assumption is crude because galaxies do not turn all the accreted gas instantaneously into stars. However, even in spiral galaxies, typical gas fractions (cold gas divided by cold gas plus stars) rarely exceed ~10−20% (except for dwarf irregulars and blue compact dwarfs, see e.g., McGaugh et al. 2010). Therefore, the error on the galaxy stellar mass that one makes by assuming that the entire galaxy mass is in stars is consistent with the other uncertainties of our model at all but the lowest masses. When we substitute
. In other words, all the gas accreted onto a galaxy is either ejected or forms stars. This assumption is crude because galaxies do not turn all the accreted gas instantaneously into stars. However, even in spiral galaxies, typical gas fractions (cold gas divided by cold gas plus stars) rarely exceed ~10−20% (except for dwarf irregulars and blue compact dwarfs, see e.g., McGaugh et al. 2010). Therefore, the error on the galaxy stellar mass that one makes by assuming that the entire galaxy mass is in stars is consistent with the other uncertainties of our model at all but the lowest masses. When we substitute 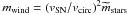 into
into 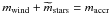 , we find
, we find 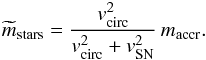 (7)
(7)
2.3.4. Synthesis
By putting together Eqs. (5)–(7), we can write a simple but physically motivated equation for the model stellar mass (in the absence of mergers) of the central galaxy of a halo of mass Mhalo in the absence of merging: 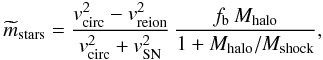 (8)where
(8)where ![\begin{eqnarray} v_{\rm circ}&\equiv&v_{\rm circ}(M_{\rm halo},z) \nonumber \\ &=& \left [{\Delta(z)\over 2}\right]^{1/6} [G\,H(z)]^{1/3}\,M_{\rm halo}^{1/3}. \label{vcirc} \end{eqnarray}](/articles/aa/full_html/2011/09/aa15780-10/aa15780-10-eq117.png) (9)Had we taken into account that some gas is neither blown away by the supernovae nor converted into stars, then mass conservation would have given
(9)Had we taken into account that some gas is neither blown away by the supernovae nor converted into stars, then mass conservation would have given 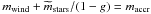 , where g is the fraction of galaxy baryons in the form of remaining gas. Hence, Eq. (8) would become
, where g is the fraction of galaxy baryons in the form of remaining gas. Hence, Eq. (8) would become 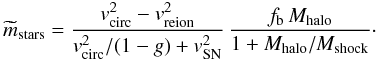 (10)At each timestep, the galaxy stellar mass is assigned according to Eqs. (8) and (9), unless this produces a lower stellar mass than at the previous timestep.
(10)At each timestep, the galaxy stellar mass is assigned according to Eqs. (8) and (9), unless this produces a lower stellar mass than at the previous timestep.
Equation (8) should be seen more as an empirical fitting formula than as a physical model, although the arguments that we have presented above provide some physical justification for it. We are neglecting a host of other physical processes such as the conditions for the formation of clumpy molecular clouds from cold atomic gas, and mechanisms operating inside halos such as ram pressure stripping, conduction, magnetic fields, cosmic rays, etc., because we wish to build the simplest model that provides an adequate fit to the galaxy mass function of galaxies and thus allows the study of the mass buildup of galaxies.
The key point of this article is not to present a new model for processes such as shock heating, cooling, star formation, and feedback (SAMs do that more satisfactorily), but rather to estimate the role of mergers in the galaxy growth. For this we need a prescription to associate a galaxy mass to a halo mass at each redshift and this is what Eq. (8) does. What is more important is that we compute galaxy mergers accurately and this is where our model is state-of-the-art (Sect. 2.2).
Best-fit parameters corresponding to the full model in Fig. 4.
Figure 2 illustrates how, in our toy model (Eq. (8)), the efficiency with which halo mass growth results in stellar mass growth depends on halo mass. This efficiency has been plotted, at two different redshifts, for the parameter set that gives the best fit to the z = 0 galaxy mass function (see Sect. 3.1 and Table 1 above). The star formation efficiency is maximum at Mhalo ~ 1011 − 1012 h-1 M⊙, decreasing sharply at lower masses and more mildly at higher masses. Figure 2 shows that in a z = 0 halo, <20% of the baryonic mass is expected to be in stars. The fraction of baryons that may be locked up in stars can reach 50% at high redshift, where feedback is less important because the circular velocity thresholds of Eq. (8) correspond to lower mass thresholds (Eq. (9), noting that Δ(z) and especially H(z) increase with z). Our model produces a z = 0 stellar mass vs. halo mass relation very similar to that obtained by Guo et al. (2010) with the abundance matching technique, except that our toy model (Eq. (8)) underestimates the stellar mass at large halo masses relative to the abundance matching solution. This will be compensated by the effects of galaxy mergers (see Eq. (4)) as we shall see in Sect. 3 (Fig. 6) below.
Figure 3 shows how these processes quench star formation during the growth of a dark matter halo. The contours show mstars/(fb Mhalo) as a function of halo mass and redshift (for the best-fit parameters used for Fig. 2, see Sect. 3.1 and Table 1). The term in vcirc in Eq. (8) suppresses galaxy formation in low-mass haloes, while the cut-off at Mshock suppresses galaxy formation in high-mass haloes. The result is a galaxy formation zone at 1010 M⊙ ≲ Mhaloh ≲ 1012.5M⊙. Galaxy formation begins and ends when a halo moves in and out of the galaxy formation zone, respectively. The four red curves in Fig. 3 show the mass growth with redshift of four haloes whose final masses at z = 0 are roughly 1011, 1012, 1013 and 1014 h-1 M⊙. The haloes that are more massive enter and exit the galaxy formation zone at an earlier epoch. Since the most massive haloes contain the most massive galaxies, this explains why the most massive galaxies contain the oldest stellar populations (archaeological downsizing, Cattaneo et al. 2008).
The dashed curve in Fig. 3 shows the characteristic mass Mnl of density fluctuations that become non-linear at redshift z, i.e. the characteristic mass scale on which the cosmic variance of linearly extrapolated primordial density fluctuations is equal to δc ≃ 1.68 at redshift z. Here δc is the density contrast of a top hat fluctuation that the linear theory predicts at the time when the fluctuation actually collapses. The value of δc depends very weakly on Ωm and ΩΛ. The redshifts at which Mnl comes in and out of the galaxy formation zone mark the beginning and the end of the main epoch of galaxy formation in the Universe.
 |
Fig. 3 Growth of halo mass and efficiency of star formation. The contours show the efficiency of star formation, |
Similar simple toy models were independently constructed by Croton (priv. commun.) and by Bouché et al. (2010), although in their models the low-mass cut-off does not depend on redshift, while in our model it is the circular velocity that is fixed, so the minimum mass decreases with increasing redshift (see Fig. 3).
2.4. Tidal stripping
The dynamical friction time given by Eqs. (1)–(3), which was calibrated by Jiang et al. (2008) on hydrodynamical cosmological simulations, implicitly incorporates the effects of tides, which strip the secondaries to lower masses as they orbit through the primary, on the dynamical friction time. However, knowledge of the stellar mass at a given time is necessary to compare to the observed galaxy mass function, so we need to estimate the time evolution of the stellar mass caused by tidal stripping.
Tidal forces are known to strip galaxy haloes very efficiently once they penetrate larger ones (e.g., Ghigna et al. 1998), and each pericentric passage generates more mass loss (Hayashi et al. 2003). But tides also affect, to a lesser extent, the more bound stellar material. For example, Klimentowski et al. (2009) ran simulations of a low-mass high-resolution spiral galaxy around the fixed potential of the Milky Way and found that over 5 orbits, while the dark matter mass was reduced by a factor 100, the stellar mass was reduced by a factor 10, meaning that a fraction of ηstrip = 1 − (1/10)1/5 = 0.37 of the stellar mass was lost at every pericentric passage. This tidally stripped stellar mass should form what is known as the stellar halo in the case of a galaxy and the intracluster light in the case of a cluster.
According to the simulations of Klimentowski et al., the mean mass loss ηstrip is roughly constant for every pericentric passage, so the importance of tidal stripping depends on the number of orbital revolutions that a galaxy makes from when its orbit starts decaying to when either the galaxy merges with the central galaxy of its parent halo or the simulation ends. In the former case, the total time span during which a galaxy is stripped is given by the time it takes to decay by dynamical friction from the virial radius to the centre (Eq. (1) with r and vcirc taken at the virial radius). Taking torb ~ 2πr/vcirc for the orbital time, we find 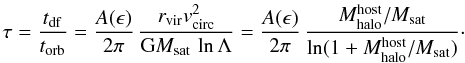 (11)The normalisation, A(ϵ), of the dynamical friction time is computed using the formula in Jiang et al. (2008), which fits the results of SPH simulations and accounts for the tidal stripping of sub-structures. Equation (11) implies that, for a fixed value of ηstrip, the importance of tidal stripping increases with
(11)The normalisation, A(ϵ), of the dynamical friction time is computed using the formula in Jiang et al. (2008), which fits the results of SPH simulations and accounts for the tidal stripping of sub-structures. Equation (11) implies that, for a fixed value of ηstrip, the importance of tidal stripping increases with  .
.
2.5. Summary
In summary, the final equation for the galaxy stellar at any given time is ![\begin{equation} m_{\rm stars} = {\rm max}\left\{ \begin{array}{l} \displaystyle \widetilde m_{\rm stars}[M_{\rm halo},v_{\rm circ}(M_{\rm halo},z)]\ ,\\[4mm] \displaystyle\sum_{\rm prog} m_{\rm stars}^{\rm (prog)}(1-\eta_{\rm strip})^\tau , \end{array}\right. \label{updatemass} \end{equation}](/articles/aa/full_html/2011/09/aa15780-10/aa15780-10-eq149.png) (12)where
(12)where 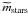 and τ are given in Eqs. (8) and (11), respectively, with τ = 0 for the main progenitor. Equation (12) contains four free parameters (vreion, vSN, Mshock, and ηstrip), the first three of which enter the model through the function
and τ are given in Eqs. (8) and (11), respectively, with τ = 0 for the main progenitor. Equation (12) contains four free parameters (vreion, vSN, Mshock, and ηstrip), the first three of which enter the model through the function 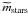 of Eqs. (8) and (9). The fourth parameter ηstrip affects the final galaxy masses by controlling the efficiency of tidal stripping, but, as we shall see, ηstrip has comparatively little bearing on our results. There are no free parameters in the calculation of the halo and thus galaxy merger rate.
of Eqs. (8) and (9). The fourth parameter ηstrip affects the final galaxy masses by controlling the efficiency of tidal stripping, but, as we shall see, ηstrip has comparatively little bearing on our results. There are no free parameters in the calculation of the halo and thus galaxy merger rate.
3. Results
3.1. Best-fit model and effects of physical processes
We start with the set of our 4 parameters, vreion, vSN, Mshock, and ηstrip, that provide a best-fit to the galaxy stellar mass function deduced by Bell et al. (2003) from the SDSS observations, and then consider how the predictions vary when the assumptions are changed.
The stellar masses of galaxies derived by Bell et al. (2003) to compute the SDSS mass function depend on the Hubble constant used to compute galaxy luminosities and on the stellar initial mass function (IMF). The masses inferred from observed luminosities scale as h-2 while simulated masses scale as h-1. As it is not possible to make the comparison between model and observations completely independent of h, we convert the observationally determined masses in units of h-1 M⊙ by assuming h = 0.7. Bell et al. (2003) compute the stellar mass function using a diet Salpeter IMF (Bell & de Jong 2001). To convert to a Salpeter (1955) or a Kroupa (2002) IMF, one should add a correction of + 0.15 and –0.1 dex, respectively (see Bell et al. 2003).
 |
Fig. 4 Stellar mass function of galaxies at z = 0. The filled squares show the galaxy mass function determined observationally by Bell et al. (2003). The solid line shows our best-fit model (the “full” model, with parameter values listed in Table 1). The fit assumes h = 0.7 because observationally inferred masses scale as h-2. a) Variations of the stellar mass function for different assumptions on merging and stripping: best-fit full model (black solid line), no tidal stripping (ηstrip = 0, red dotted line), no mergers at all (green dashed line), and maximum merging (blue dash-dotted line); b) variations of the stellar mass function for different assumptions on the baryonic physics: best-fit full model (black solid line, same as in panel a), baryons trace dark matter (mstars = fb Mhalo, red dotted line), no high-mass cutoff (Mshock → ∞, green dashed line), and no low circular velocity cutoff (vSN = vreion = 0, blue dash-dotted line). In both panels, all variations start from the best-fit parameters of the full model except for the fact that we use ηstrip = 0 in all models apart from the full one. |
The solid lines in the two panels of Fig. 4 indicate that our best-fit model (Table 1) matches well the Bell et al. (2003) mass function at 108.7 M⊙ < h mstars < 1011.6 M⊙. Different determinations of the stellar mass function of galaxies (e.g. Baldry et al. 2008; Yang et al. 2009) would lead to slightly different best-fit parameters. Reasonable modifications to the IMF will also yield slightly different best-fit parameters. However, the conclusions of our article are robust to these uncertainties, as they do not depend on the precise values of the model parameters. We also note that vSN = 120 km s-1 is close to the value of 100 km s-1 derived by Dekel & Silk (1986). It implies a supernova efficiency of ~ 1% if there is one 1052 erg supernova every 100 M⊙ of star formation and the escape speed is 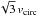 , that is, the required wind kinetic energy is ~ 1% of the supernova energy.
, that is, the required wind kinetic energy is ~ 1% of the supernova energy.
With vreion = 40 km s-1 our model cannot form galaxies below this halo circular velocity. One may argue that galaxies are known with lower maximum rotation velocities. Indeed, since our model starts at roughly the epoch of reionisation, we will be missing the galaxies of lower mass that form before reionisation (see, e.g., Mamon et al. 2010b). It turns out that the precise value of vreion has little effect on the conclusions of our paper, because of our finite galaxy mass resolution. Moreover, relative to their halo masses, their stellar masses are extremely low, hence they contribute little to the growth of more massive galaxies.
The incorporation of ηstrip reduces the stellar masses of satellite galaxies at each timestep. Comparison with the case ηstrip = 0 (Fig. 4a, dotted line) shows that this effect is negligible at mstars ≲ 1011 h-1 M⊙. Tidal stripping is, however, important at higher masses, where the galaxy mass function is predicted to be shifted toward high masses by ~ 0.2 dex in mass compared to the Bell et al. (2003) mass function if satellites are not stripped of part of their mass before they merge into the galaxies that populate this part of the mass function. This discrepancy may also be due to systematic measurement errors in the data, since many massive ellipticals extend outside the photometric aperture used to measure their luminosities. Lauer et al. (2007) find errors of up to a magnitude in the SDSS luminosities of such galaxies and these are the same data that anchor the high end of the Bell et al. mass function in Fig. 4. We shall elaborate on this in the Discussion (Sect. 4.1).
Assuming that every halo merger immediately results in a galaxy merger causes the most massive galaxies to grow even larger (dash-dotted line in Fig. 4a) but the difference between the dash-dotted line and the dotted line is fairly minor suggesting that most halo mergers do result in galaxy mergers. The difference between the two curves in the highest mass bin disappears if the dash-dotted line is computed not for all halo mergers, but for those of bound halo-satellite systems.
The dashed line in Fig. 4a corresponds to the extreme opposite assumption that whenever a new halo appears a new galaxy is created but there are no galaxy mergers at all. This assumption predicts too many low-mass galaxies and too few high-mass galaxies with respect to the observations.
Both the dotted line and the dash-dotted line in Fig. 4a assume models without tidal stripping (so does the dashed line). In both cases the cosmic stellar mass density obtained by integrating the galaxy stellar mass function over all masses exceeds the observational value inferred from the Bell et al. (2003) mass function. This suggests that stripping is necessary, since, in our model, changing the merging rate does not affect the cosmic stellar mass density.
Having seen how the mass function depends on the capture and the probable stripping of satellites, we now examine how it depends on our assumptions on the quiescent growth of galaxies in isolated haloes (Fig. 4b). We compare the full model with three unrealistic simpler models, which are, however, useful for illustrative purposes. They are: i) a model in which the stellar mass grows proportionally to the mass of the dark matter (mstars = fb Mhalo; dotted line); ii) a model with the term in vcirc but without the cutoff at high masses (dashed line); and iii) a model with the cutoff at high masses but not the term in vcirc (dash-dotted line).
Figure 4b illustrates the well known fact that supernova and reionisation feedback processes are essential to reconcile the observed galaxy mass function with the halo mass function of a cold dark matter Universe (compare the solid line and the dash-dotted line). The suppression of star formation at Mhalo > Mshock is necessary to reproduce the break in the galaxy stellar mass function at ~ 1011 M⊙ (compare the solid line and the dashed line). It is the combination of these low and high mass cut-offs that allows the best-fit model to reproduce the normalisation and the characteristic break of the galaxy stellar mass function. Figure 4b shows that the low vcirc cut-off is important, not only for the low-mass end, but also for the high-mass end of the galaxy mass function, because the high-mass cut-off alone is not enough if the building blocks of giant ellipticals have been allowed to grow in an uncontrolled fashion before crossing the critical mass7. We also find that the quenching of high mass galaxies by shock heating is much more effective than the reduction of their masses by tidal stripping, as can be seen by comparing Figs. 4a (red dotted curve) and 4b (green dashed curve).
 |
Fig. 5 The evolution of the cosmic SFR density with redshift in the observed Universe (points with error bars and hatched region) and in our model (thick black solid line; the dotted and dotted-dashed lines correspond to the two models where baryons trace dark matter and without a low circular velocity cutoff, respectively, see Fig. 4b). The blue squares are UV data Giavalisco et al. (2004); Wilson et al. (2002); Massarotti et al. (2001); Sullivan et al. (2000); Steidel et al. (1999); Cowie et al. (1999); Treyer et al. (1998); Connolly et al. (1997); Baldry et al. (2005); Schiminovich et al. (2005); Wolf et al. (2003); Arnouts et al. (2005); Bouwens et al. (2003); Bouwens (2006); Bunker et al. (2004); Ouchi et al. (2004). The blue pentagons are Hubble Ultra Deep Field estimates (Thompson et al. 2006). The red squares are Hα, Hβ and OII data (Hanish et al. 2006; Pérez-González et al. 2003; Tresse et al. 2002; Hopkins et al. 2000; Moorwood et al. 2000; Sullivan et al. 2000; Glazebrook et al. 1999; Yan et al. 1999; Tresse & Maddox 1998; Gallego et al. 1995; Pettini et al. 1998; Teplitz et al. 2003; Gallego et al. 2002; Hogg et al. 1998; Hammer et al. 1997). The orange squares are 1.4 GHz data (Mauch & Sadler 2007; Condon et al. 2002; Sadler et al. 2002; Serjeant et al. 2002; Machalski & Godlowski 2000; Haarsma et al. 2000; Condon 1989). The orange pentagon at z ≃ 0.24 is X-ray data (Georgakakis et al. 2003). The green squares are infrared (Pérez-González et al. 2005; Flores et al. 1999) and sub-mm (Barger et al. 2000) data. The green hatched region is the far infrared (24 μm) SFR history from Le Floc’h et al. (2005). Most of them were taken from the compilations in Hopkins (2004) and Hopkins & Beacom (2006). The red curve, |
 |
Fig. 6 Galaxy stellar mass vs. host halo mass at z = 0 for the set of parameters (Table 1) that fit best the galaxy stellar mass function. Each point is one of our simulated galaxies. The symbol sizes and colours vary with the fraction fmerg of mass acquired in mergers, and the fraction gcold of this mass acquired by cold-mode mergers (where the sum of the masses of the haloes of the merging galaxies is below Mshock), respectively, according to the legend. The vertical green line corresponds to Mhalo = Mshock, while the oblique magenta line indicates mstars = fb Mhalo. The green curves show the stellar masses of galaxies acquired through the accretion channel (Eq. (8) with best-fit parameters from Table 1) at z = 0 (lower) and z = 3 (upper curve). The shaded cyan and gold regions correspond to the observations from the SDSS (Yang et al. 2009), and the halo-galaxy abundance matching of Guo et al. (2010). For the latter, the halo masses were shifted by log 10h to conform to our units. Also, the stellar masses were shifted by − log 10h and log 10h for Yang et al. and Guo et al., respectively, to take into account the different units with h. We also shifted the stellar masses by an additional factor of +0.1 and + 0.15 dex to pass from the Kroupa and Chabrier IMFs, respectively assumed by Yang et al. and Guo et al. to the diet Salpeter IMF assumed by Bell et al. (2003), on whose mass function we have calibrated our model. |
Figure 5 shows the evolution of the cosmic SFR density. There are two ways to compute the cosmic SFR density: by observations (or SAM simulations) of the total rate of star formation, or by taking the time derivative of the total mass integrated over the galaxy stellar mass function. Since our model does not incorporate the concept of SFR, we adopt the latter method, which we show as the black lines (solid for our best-fit model). The agreement between our best-fit model and the data (especially those derived with the second method, e.g. Wilkins et al. 2008, red curve) is reasonable given how simple our model is8.
3.2. Central and satellite galaxies: the role of the environment
Figure 6 provides a deeper insight of what happens inside our model. We have plotted all our simulated galaxies, at z = 0, in an mstars vs. 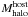 diagram, where
diagram, where 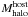 is the mass of the largest halo in which a galaxy is contained (so that if a small galaxy is located near a larger one, itself within a group of galaxies, the host halo is that of the group and not that of the larger galaxy). In other words, Fig. 6 constitutes a representation of the Tully-Fisher (1977) scaling relation between stellar mass in galaxies and their halo properties (where the halo is quantified here by the mass at the virial radius instead of the maximum circular velocity). The symbol with which a galaxy is plotted has been sized and colour-coded according to the values of the fraction fmerg of present-day mass acquired via mergers (symbol size) and the fraction gcold of the mass acquired by mergers that was acquired in “cold-mode” mergers (symbol colour), where “cold-mode” and “hot-mode” mergers are defined as follows. A merger that takes place between the two N-body snapshots s and s + 1 is classified as being “cold-mode” if the mass of the host halo of the merger remnant at s + 1 is
is the mass of the largest halo in which a galaxy is contained (so that if a small galaxy is located near a larger one, itself within a group of galaxies, the host halo is that of the group and not that of the larger galaxy). In other words, Fig. 6 constitutes a representation of the Tully-Fisher (1977) scaling relation between stellar mass in galaxies and their halo properties (where the halo is quantified here by the mass at the virial radius instead of the maximum circular velocity). The symbol with which a galaxy is plotted has been sized and colour-coded according to the values of the fraction fmerg of present-day mass acquired via mergers (symbol size) and the fraction gcold of the mass acquired by mergers that was acquired in “cold-mode” mergers (symbol colour), where “cold-mode” and “hot-mode” mergers are defined as follows. A merger that takes place between the two N-body snapshots s and s + 1 is classified as being “cold-mode” if the mass of the host halo of the merger remnant at s + 1 is 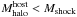 . Figure 6 only shows the best-fit model, corresponding to the solid line in Fig. 4.
. Figure 6 only shows the best-fit model, corresponding to the solid line in Fig. 4.
We clearly see two galaxy populations separated by an empty zone: a population of central galaxies (galaxies for which 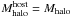 ), which follows a narrow curved band in the mstars –
), which follows a narrow curved band in the mstars – 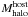 plane, roughly following the stellar masses predicted from the accretion channel (Eq. (8)) and a population of satellite galaxies (
plane, roughly following the stellar masses predicted from the accretion channel (Eq. (8)) and a population of satellite galaxies (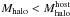 ), which are scattered over a broad area of the diagram lying below the central galaxy relation.
), which are scattered over a broad area of the diagram lying below the central galaxy relation.
It is important to note that the masses in the y-axis of Fig. 6 are stellar masses. Neglecting the mass in cold gas is reasonable for massive galaxies, but not at low stellar masses (log h mstars < 8.7, e.g. Zhang et al. 2009), where the HI mass dominates the stellar mass. The inclusion of gas in our toy model (Eq. (10)) with gas-to-star ratios given in Baldry et al. (2008, and references therein) leads to baryonic masses of low-mass galaxies that are nearly twice as large as inferred from the stellar masses in Fig. 6.
Central galaxies with fmerg ≲ 0.1 tend to accumulate in a narrow zone of the mstars – 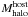 diagram, which appears as a black curve of points, and corresponds to the present-day
diagram, which appears as a black curve of points, and corresponds to the present-day 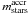 – Mhalo relation (lower green curve) given by Eq. (8). Its broadness is due to the higher value, for given
– Mhalo relation (lower green curve) given by Eq. (8). Its broadness is due to the higher value, for given 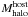 , of vcirc and therefore mstars at higher redshifts, as can be seen from the two green curves in Fig. 6. Galaxies that lie well above the critical z = 0 curve either live in haloes that have lost mass due to tidal stripping (dots and triangles) or are galaxies that have grown above the relation by mergers (filled circles). Galaxies lying below the critical z = 0 curve are the centrals of hosts containing a non-negligible fraction of their mass in satellites, so that the host halo mass is larger than the mass of the halo directly associated with the galaxy.
, of vcirc and therefore mstars at higher redshifts, as can be seen from the two green curves in Fig. 6. Galaxies that lie well above the critical z = 0 curve either live in haloes that have lost mass due to tidal stripping (dots and triangles) or are galaxies that have grown above the relation by mergers (filled circles). Galaxies lying below the critical z = 0 curve are the centrals of hosts containing a non-negligible fraction of their mass in satellites, so that the host halo mass is larger than the mass of the halo directly associated with the galaxy.
Our general mstars – 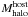 relation predicted for the central galaxies of groups and clusters in Fig. 6 is highly consistent with that found in the SDSS shown in Fig. 4 of Yang et al. (2009) (shaded cyan region in Fig. 6). At lower masses, it is also highly consistent with the relation that Guo et al. (2010) deduced (shaded gold region in Fig. 6) by matching the halo and sub-halo mass function measured in the Millennium-II cosmological simulation to the galaxy mass function deduced by Li & White (2009). This gives us some confidence that our model of Eq. (8) provides a reasonable approximation of the true stellar – halo mass relation.
relation predicted for the central galaxies of groups and clusters in Fig. 6 is highly consistent with that found in the SDSS shown in Fig. 4 of Yang et al. (2009) (shaded cyan region in Fig. 6). At lower masses, it is also highly consistent with the relation that Guo et al. (2010) deduced (shaded gold region in Fig. 6) by matching the halo and sub-halo mass function measured in the Millennium-II cosmological simulation to the galaxy mass function deduced by Li & White (2009). This gives us some confidence that our model of Eq. (8) provides a reasonable approximation of the true stellar – halo mass relation.
 |
Fig. 7 The galaxy stellar mass function at z = 0 split by environment, defined by host halo mass (top) or group richness (number of companions with mstars > 1010 M⊙/h in the same host halo, bottom). The dashed curves in the top panel show the conditional mass function fits to the SDSS data by Yang et al. (2009). The same h and IMF corrections as in Fig. 6 apply. |
Figure 7a shows how different environments contribute to the galaxy stellar mass function at z = 0. The galaxy mass function in haloes with 1012 M⊙ < h Mhalo < 1012.3 M⊙ contains a strong peak at mstars ~ 1010.7 h-1 M⊙, the characteristic mass of the central galaxy of a halo in that mass range (Fig. 7a, black curve). The contribution of satellites to the galaxy mass function is at least an order of magnitude smaller than that of the central galaxies. In a halo with 1012.9 M⊙ < h Mhalo < 1013.2 M⊙, the relative contribution of satellite galaxies is higher but we still see a clear valley between central and satellite galaxies at mstars ~ 1010.4 h-1 M⊙, while the central galaxy peak has moved up to mstars ~ 1011.1 h-1 M⊙ (blue curve). The peak of the green curve is at a lower number density than the peak of the blue curve, because there are less central galaxies of haloes with 1012.9 M⊙ < h Mhalo < 1013.2 M⊙ than there are central galaxies of haloes with 1012 M⊙ < h Mhalo < 1012.3 M⊙. At 1013.5 M⊙ < h Mhalo < 1013.8 M⊙, the satellite population has become so numerous and the central galaxy peak has moved down so much that the valley is no longer visible (green curve). Thus, the more massive the halo, the greater is the relative importance of the satellite population.
Similar bimodal (wide satellite + peaked central) galaxy stellar mass functions at given halo mass are also seen in the analysis of SDSS galaxies by Yang et al. (2008) (their Fig. 2) and Yang et al. (2009) (their Fig. 4), with peaks and troughs occurring at very similar values of mstars (dashed and solid curves in Fig. 7a, respectively for the SDSS and our model, where we used the same narrow bins of halo mass as they did for better comparison). The lack of galaxies with stellar masses just below those of central galaxies (Fig. 6) thus appears to be consistent with the two population (centrals + satellites) model (e.g., Yang et al.).
For observers, it is easier to define the environment of a galaxy in terms of the number of companions above a luminosity limit than by its halo mass. For this reason, we show in Fig. 7b how the galaxy stellar mass function differs between rich and poor systems, where rich and poor are defined by having respectively less than four or at least four companions with mstars > 1010 h-1 M⊙. Since we use two wide bins of richness in Fig. 7b, we cannot see peaks as we did in Fig. 7a. However, there is an important difference between the mass functions of poor and rich systems: poor systems display a strong lack in massive galaxies relative to richer systems. In contrast, the low-end slopes of the mass function is the same for poor and rich haloes. In other words, if one used the Schechter (1976) parametrisation, f(m) ∝ mαexp(−m/m∗), the exponential cutoff of the mass function, m∗, would be much lower for the poor systems, while the faint-end slope, α would be independent of richness.
3.3. The importance of mergers
Figure 8 shows the median value of the mass fraction, fmerg, acquired by mergers (instead of by gas accretion) in different mass bins for the five models plotted in Fig. 4a. This median hides a large scatter, as one can see from the distribution of fmerg at constant mstars in Fig. 6, but several statistically significant trends emerge, as we shall now see.
Our standard model (black solid curve) shows that, for final galaxy masses above 1011 h-1 M⊙, typical galaxies have acquired the bulk of their mass by galaxy mergers, whereas at lower masses, typical galaxies grow mainly by gas accretion.
Could the lack of mergers at low mass be a consequence of our limited mass resolution? One can compare our standard model to one where galaxies follow the haloes: mstars = fb Mhalo (red dotted curve). The median fraction of mass acquired by mergers in the model where baryons trace the dark matter decreases with decreasing final galaxy mass for mstars ≳ 1010.8 h-1 M⊙, which suggests possible effects of mass resolution at lower final galaxy masses. However, for mstars > 1010.6 h-1 M⊙, this decrease is much sharper in our standard model. In other words, as one goes from the highest galaxy masses down to mstars > 1010.6 h-1 M⊙, the median mass fraction acquired by mergers decreases much faster in our standard model than in our model where baryons trace the dark matter. We thus conclude that the decreasing importance of galaxy mergers from mstars = 1011.0 h-1 M⊙ to mstars = 1010.6 h-1 M⊙ is robust to the effects of our limited mass resolution.
 |
Fig. 8 Median fraction of the z = 0 galaxy mass acquired via mergers rather than via gas accretion for various models: best-fit full model (black solid line), baryons trace dark matter (mstars = fb Mhalo, red dotted line), no high-mass cutoff (Mshock → ∞, green short-dashed line), no low circular velocity cutoff (vSN = vreion = 0, blue dash-dotted line), and no tidal stripping (ηstrip = 0, black long-dashed line). |
Note that the host haloes of galaxies with mstars ~ 1010.5 h-1 M⊙ are well resolved. It is their merging histories that are not. Neglecting all mergers with sub-resolution haloes (Mhalo < 1.5 × 109 h-1 M⊙) does not affect the value of fmerg for a cluster galaxy, but the effects of neglecting mergers with sub-resolution haloes propagate to galaxies with masses up to nearly the critical mass, mcrit = fb Mshock = 1.3 × 1011 h-1 M⊙.
Reionisation and supernova feedback (the terms in vcirc in Eq. (8)) produce an effect analogous to that of mass resolution by suppressing galaxy formation in all haloes below vcirc = 40 km s-1 and by considerably lowering the masses of galaxies in haloes just above this threshold. Therefore, mergers with small haloes make no or a very small contribution to the growth of the galaxy stellar mass, which results in a strong suppression of fmerg at all masses (Fig. 8, green dashed line vs. red dotted line).
The suppression of star formation at halo masses greater than Mshock has a small effect on the merging histories of galaxies with Mhalo ≲ Mshock (blue dash-dotted line vs. red dotted line in Fig. 8), but it means that mergers provide the only mechanism for galaxies to grow above the limit mass mstars = mcrit. Therefore, including the cut-off at Mshock increases the fractional importance of mergers in the growth of galaxies with mstars > mcrit (dash-dotted line relative to dotted line), not by affecting the merger rate but by decreasing the importance of gas accretion. Combining the terms in vcirc and Mshock in Eq. (8) causes: i) a strong suppression of the importance of mergers at mstars < mcrit; and ii) a strong increase in the importance of mergers at mstars > mcrit, both with respect to a simple model where the baryons follow the dark matter (dotted line). This explains the presence of two growth regimes, one dominated by gas accretion, the other dominated by mergers, respectively below and above mstars = mcrit. Adding tidal stripping (solid line) has a minor effect on the median value fmerg, which may not be statistically significant.
 |
Fig. 9 Top: median mass fraction at z = 0 acquired via gas accretion (black line), “cold mode” galaxy mergers within haloes with |
Figure 6 shows that fmerg increases with mstars along the relation for central galaxies. The top panel of Fig. 9 splits the mass accretion history of galaxies into three channels: 1) gas accretion; 2) cold-mode mergers; and 3) hot-mode mergers (see Sect. 3.2 for a precise definition of cold/hot-mode mergers). In turns out that half of the galaxies with mstars > 1011 h-1 M⊙ have acquired at least half of their mass via merging, and this merging involves almost always a primary halo more massive than Mshock. On the other hand, most galaxies with mstars < 1011 h-1 M⊙ have acquired most of their mass through gas accretion. This figure is virtually unchanged when we restrict ourselves to the central galaxies.
The top panel of Fig. 9 shows that cold-mode mergers appear to contribute little to the growth of galaxies. In no mass bin is their median contribution to the final stellar mass more than ~ 5%. This minor channel of galaxy mass growth reaches its maximum relative significance at a galaxy stellar mass of order mstars = fb Mshock. In particular, among the satellites in groups and clusters with 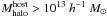 , only 2% have acquired over half their mass by mergers (6% of the more massive ones with mstars > 1010 h-1 M⊙ and 1% of the ones with 109 M⊙ < h mstars < 1010 M⊙).
, only 2% have acquired over half their mass by mergers (6% of the more massive ones with mstars > 1010 h-1 M⊙ and 1% of the ones with 109 M⊙ < h mstars < 1010 M⊙).
 |
Fig. 10 Distribution of fraction of the z = 0 mass acquired by mergers for galaxies in different bins of stellar mass. |
Still, some low-mass galaxies do acquire most of their their stellar mass via mergers. Figure 6 shows nearly one hundred central galaxies with host halo masses below Mshock that have acquired most of their stellar mass by mergers, more precisely by cold-mode mergers9. Figure 10 shows the distribution of the fractional contribution of mergers to the final stellar mass for galaxies in four stellar mass intervals. A few galaxies that have accreted a significant fraction of their mass via mergers are present even in the lowest mass bin. In other words, by assuming that a large mass fraction acquired by mergers implies elliptical galaxy morphology (either through single major mergers or through repeated minor mergers, as suggested by Bournaud et al. 2007), our model can accommodate the presence of 1010.5 M⊙ galaxies with early type morphologies. However, the probability that a galaxy has an early type morphology (high fmerg) is much higher at mstars > 1011 h-1 M⊙ than it is at 1010 M⊙ < h mstars < 1010.5 M⊙. As seen in the middle panel of Fig. 9, cold-mode mergers thus do play an important role in the formation of those intermediate-mass galaxies that mainly grow by mergers, and which may be compared to intermediate-mass ellipticals.
Finally, the bottom panel of Fig. 9 shows that the fraction of galaxies where the mass fraction acquired via mergers is 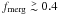 matches reasonably well the observed fraction of ellipticals for galaxy masses above 1010 h-1 M⊙10. At 109 h-1 M⊙ < mstars < 1010 h-1 M⊙, our model seems to predict less ellipticals than observed in the SDSS. Our interpretation (based also on the structural properties of dwarf ellipticals and dwarf spheroidals) is that these objects were not formed by mergers, but this occurs below our estimated mass resolution limit. We defer further discussion of this point to the conclusion.
matches reasonably well the observed fraction of ellipticals for galaxy masses above 1010 h-1 M⊙10. At 109 h-1 M⊙ < mstars < 1010 h-1 M⊙, our model seems to predict less ellipticals than observed in the SDSS. Our interpretation (based also on the structural properties of dwarf ellipticals and dwarf spheroidals) is that these objects were not formed by mergers, but this occurs below our estimated mass resolution limit. We defer further discussion of this point to the conclusion.
 |
Fig. 11 Top: fraction of galaxies with over 40% of their z = 0 mass acquired by mergers versus stellar mass in bins of halo mass (labelled by log h M). The errors are binomial. Bottom: same versus halo mass in bins of stellar mass (labelled by log h mstars). |
The top panel of Fig. 11 shows the fraction of galaxies with over 40% of the mass acquired by mergers (as the dotted line of the bottom panel of Fig. 9), split in bins of halo mass. It is clear the halo mass plays only a minor role in determining the fraction of galaxies with at least 40% of their mass acquired by mergers. In contrast, the bottom panel of Fig. 11 shows how the fraction of galaxies with over 40% of the mass acquired by mergers varies with halo mass in bins of stellar mass. If fmerg > 0.4 is a proxy for elliptical galaxies (as can be inferred from the bottom panel of Fig. 9), we predict that the fraction of ellipticals should depend more on the stellar mass of a galaxy than on its global environment.
 |
Fig. 12 Top: median fraction of the mass at z = 0 acquired by mergers due to major mergers for galaxies with fmerg > 0.4. The red and blue lines use stellar mass ratios between 1:1 and respectively 1:3 and 1:5 to define major mergers. The error bars are bootstrap estimates of the uncertainties of the mean fractions. Bottom: geometric mean mass ratio of mergers for galaxies with fmerg > 0.4 at z = 0. The error bars are bootstrap estimates of the uncertainties of the geometric mean ratios. The red and blue horizontal lines respectively represent the 1:3 and 1:5 limits of major mergers. |
The top panel of Fig. 12 shows the contribution of major mergers to the total mass fraction at z = 0 acquired via mergers for galaxies with fmerg > 0.4 (hereafter, candidate elliptical galaxies, following the bottom panel of Fig. 9). Defining major mergers as those with stellar mass ratios between 1:1 and 1:3 (red lines in Fig. 12), we find that at mstars < 1010.7 h-1 M⊙ major mergers account for little of the mass growth of candidate ellipticals occurring through mergers. But in galaxies with 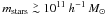 , major mergers contribute half of the mass growth by mergers of candidate ellipticals. If we relax our definition of major mergers to include mergers with stellar mass ratios between 1:1 and 1:5 (blue lines in Fig. 12), 80% of the merger mass growth of massive candidate ellipticals (m > 1011 h-1 M⊙) occurs through major mergers, while at lower masses (10 < log h m < 11), major mergers account for at least one-third of the mass growth via mergers.
, major mergers contribute half of the mass growth by mergers of candidate ellipticals. If we relax our definition of major mergers to include mergers with stellar mass ratios between 1:1 and 1:5 (blue lines in Fig. 12), 80% of the merger mass growth of massive candidate ellipticals (m > 1011 h-1 M⊙) occurs through major mergers, while at lower masses (10 < log h m < 11), major mergers account for at least one-third of the mass growth via mergers.
The bottom panel of Fig. 12 shows the geometric mean of the mass ratios of the merging galaxies involved in the mass growth of candidate ellipticals. Again one sees that the merger mass growth of candidate ellipticals is mainly through minor mergers at low mass ( < 1010.5 h-1 M⊙) and major mergers at high mass ( > 1011 h-1 M⊙). The importance of major mergers peaks around mstars = 1011.3 h-1 M⊙.
4. Discussion and conclusion
Our goal is to understand how galaxies grow in mass, i.e. what are the respective roles of gas accretion and galaxy mergers, as well as that of feedback mechanisms in the growth of galaxies.
We have developed a toy model of galaxy formation, using a very simple hybrid SAM/HOD approach to parameterise, as a function of halo mass and redshift, the stellar mass present in galaxies after gas accretion and quenching of gas infall by virial shocks and AGN and of star formation by reionisation and supernovae. We also include galaxy mergers, as measured from our high-resolution cosmological N-body simulation. The stellar mass acquired via gas accretion is modelled with a simple equation involving only three parameters, while we added a fourth parameter to describe the stellar mass loss caused by tidal stripping. We fined-tuned our four parameters to the observed z = 0 stellar mass function of galaxies.
In contrast with SAMs, our toy model does not incorporate structural or morphological properties of galaxies, has no time derivatives built-in (for the transfer of mass between galaxy components), and does not incorporate luminosity, hence our galaxies have no colours.
Our choice to model the stellar mass as a unique function of halo mass and redshift may seem oversimplified in view of the complexity of galaxy formation, as exemplified by the very complex semi-analytical codes of galaxy formation. However, at log h Mhalo > 12.15 (where it can be measured) the SDSS observations also appear to show a very small scatter of mstars vs. Mhalo for central galaxies (Yang et al. 2009 and the cyan region of our Fig. 6). Moreover, both semi-analytical and hydrodynamical models of galaxy formation indicate that central galaxies in halos show a very small scatter between the stellar and halo masses (see Fig. 2 of Cattaneo et al. 2007), at z = 0 and at z = 3.
The main worry with our model is that our prescription for mstars of Eq. (8) may not be correct at z > 0. However, our mstars − Mhalo relation at z = 5 (Fig. 2) is not dramatically different from that of Behroozi et al. (2010). Moreover, we have reasons to believe that the cutoffs at low and high mass should be of the right order, so the worry is on the maximum efficiency (e.g. the maximum height of the top (red) curve of Fig. 2). Furthermore, our approximate match of the evolution of the cosmic star formation rate density (Fig. 5) suggests that, at z > 0, our model of Eq. (8) is of the right order of magnitude.
While we do not claim to have explored all possible parameter combinations, any model that suppresses star formation even further will worsen our agreement with the normalisation of the cosmic SFR density (Fig. 5). We also note that the tendency to be at the lower limit of the observational range for the cosmic SFR density is not specific to our model, since it is also found in state-of-the-art semianalytic models that are based on the same fundamental assumptions (see Fig. 8 in Cattaneo et al. 2006).
4.1. Tidal stripping
Without tidal stripping, we find that, even after correcting for overmerging, we still have an excess of massive galaxies compared to the Bell et al. (2003) mass function (dotted line in Fig. 4a). This remains true for other observed determinations of the galaxy stellar mass function (Baldry et al. 2008; Yang et al. 2009). One could argue that, although the semianalytic model that we use for the merger time is a good match to what is seen in hydrodynamic simulations (Jiang et al. 2008), we may still overestimate the galaxy merger rate, which is still somewhat uncertain. However, it is difficult to lower the merger rate without overproducing low-mass galaxies (see the dashed line in Fig. 4a). One could imagine compensating for this effect by increasing feedback at low masses, but we could not find a plausible parameter set that does this and fits the galaxy mass function as well as the full model in Fig. 4 does.
We believe that tidal stripping and observational errors in the SDSS magnitudes that anchor the high end of the Bell et al. (2003) mass function (which according to Lauer et al. 2007 can run up to a magnitude) can easily reconcile our model with the high end of the galaxy stellar mass function. The fundamental reason why the magnitudes of bright ellipticals are difficult to measure is that their shallow light profiles do not converge. So it is hard to estimate the total light, let alone distinguish galaxy light from intracluster light (see the discussion in the Appendix A of Cattaneo et al. 2008). Since the extended envelopes of massive ellipticals are probably the products of interactions, the distinction between the full model and the full model without stripping may be one more of name than of substance. If we decide that the envelopes belong to the galaxies, then we should conclude that the full model without stripping is correct and that the problem lies with the data, which are likely to underestimate the real masses. If instead we decide that the envelopes are intracluster light, then we should conclude that the model that includes tidal stripping is the most physical one.
Our best-fit stripped fraction per orbit, ηstrip = 0.4, matches well the value determined in a recent dissipationless simulation of a dwarf irregular galaxy orbiting the Milky Way with a fixed potential (Klimentowski et al. 2009)11. For ηstrip = 0.4, the stripped mass in haloes with Mhalo ~ 1013 − 1014 h-1 M⊙ is in the range of ~ 0.05 − 0.1fbMhalo. This value is consistent with a number of independent measurements: Castro-Rodriguéz et al. (2009) find 7% of diffuse intracluster light (ICL) in the Virgo cluster, while Feldmeier et al. (2004) find 15% in Virgo; but Lin & Mohr (2004) find as much as 50% in clusters, suggesting that ηstrip might be even higher than we found.
4.2. The role of feedback
In agreement with previous studies, we find that in all haloes, but more so in low (Mhalo ≪ Mshock) and high (Mhalo > Mshock) mass haloes, mstars/Mhalo must be much smaller than the universal cosmic baryon fraction if the halo mass function predicted by the CDM model is to be reconciled with the observed galaxy mass function.
The mechanism that suppresses star formation in haloes with Mhalo > Mshock is clear. The post-shock gas is hot enough to maintain a stable shock, while in lower mass halos, the post-shock gas radiates efficiently and can no longer provide the thermal pressure to support the shock and collapses instead. The question is why can’t the gas around massive haloes cool down again. Growing evidence suggests that this is due to heating from the central AGN (see Cattaneo et al. 2009, and references therein).
Reionisation and supernova feedback are widely invoked to explain the very small mstars/Mhalo ratios of the low mass galaxies observed e.g., McGaugh et al. (2010). The trouble is that attempts to simulate these processes have difficulty to produce outflows as large as those that are required by this study because the energy that is available is used inefficiently (Dubois & Teyssier 2008; Ceverino & Klypin 2009). However, unless the CDM model is wrong, whatever other process may be relevant must behave analogously to the reionisation and supernova feedback model described in the article, if it is to fit the observed stellar mass function (Bell et al. 2003) that we have used.
The fact that mstars/Mhalo drops at halo masses below and above Mshock introduces a characteristic scale for galaxy masses that makes them deviate from the dark matter’s self-similar evolution (Marinoni & Hudson 2002; Baldry et al. 2008; Li & White 2009). If the evolution of baryons followed that of the dark matter, then galaxies of all masses would have similar merging histories (to the extent that dark matter halos evolve self-similarly, which is true to first order, e.g. van den Bosch 2002). Instead, it is clear that the baryonic physics, whatever they are, break the dark matter’s scale-invariant behaviour by suppressing star formation in low and high-mass haloes. It is only within haloes in a narrow mass-range around Mhalo ~ Mshock ~ 1012 h-1 M⊙ that baryons can form stars efficiently (the galaxy formation zone in Fig. 3).
This conclusion is similar to that of Bouché et al. (2010), who developed a toy model similar to ours in that it also incorporates minimum and maximum halo masses for efficient galaxy formation, although their emphasis is different. They argue that a fixed halo mass floor of 1011 M⊙ for galaxy formation appears to be required to reproduce the observations of specific star formation rate as a function of stellar mass, the evolution of the cosmic star formation rate and the Tully-Fisher relation. Our model is more focussed on the accurate treatment of the role of galaxy mergers in the growth of galaxies, than on the modeling of star formation rates. However, our model also allows for lower galaxy masses at high redshift, which may help explain the lowest mass dwarf galaxies.
4.3. Mergers vs. gas accretion
The shutdown of gas accretion above the critical mass Mshock ~ 1012 M⊙ is the reason why, in our model, mergers are the only opportunity for galaxies to grow above the limiting mass mcrit ≡ fb Mshock. Therefore, galaxies with mgal ≫ mcrit must have acquired a significant fraction of their mass via mergers. This conclusion appears quite robust because without this shutdown massive galaxies would be too frequent and too blue (Bower et al. 2006; Cattaneo et al. 2006; Croton et al. 2006).
Where does the dearth of mergers at galaxy masses lower than 1011 h-1 M⊙ come from? It cannot be a resolution effect (though finite resolution makes it more pronounced) because even at mstars > 1010.6 h-1 M⊙ the mass fraction acquired via mergers rises faster with galaxy mass in our best-fit model than when we force the baryons to trace the dark matter. There is, instead, a simple explanation why the importance of mergers decreases at low masses. The steeper slope of stellar versus halo mass at low mass (Fig. 6) naturally reduces the relative abundance of major partners relative to minor ones, and therefore the mass contribution that any merger can make. Hopkins et al. (2010) have made a similar kind of argument.
The present work reinforces the new picture in which most galaxies grow through gas accretion and form stars along the Blue Cloud until the critical halo mass for shock and AGN heating is reached. Then, gas accretion is shut off, star formation is quenched and they migrate to the Red Sequence, where gas-poor mergers represent their only opportunity for growth (Bower et al. 2006; Cattaneo et al. 2006; Croton et al. 2006; Faber et al. 2007; Cattaneo et al. 2008).
We refer to mergers that take place in host haloes above Mshock as hot-mode mergers, and to mergers that take place in host haloes below Mshock as cold-mode mergers. The former usually contain little cold gas, while the latter involve galaxies containing large masses of cold gas supplied by cold accretion. It is thus tempting to identify hot-mode and cold-mode mergers with gas-poor (dissipationless) and gas-rich mergers, respectively. The latter are mainly confined to galaxies below the critical stellar mass fb Mshock (Fig. 6) and are most frequent just below fb Mshock (top panel of Fig. 9). This points to a characteristic mass of ~ 1010.5h-1 M⊙ for ultraluminous infrared galaxies (ULIRGs, e.g. Colina et al. 2001) and quasar hosts (e.g. Bonoli et al. 2009), of which gas-rich mergers are the supposed triggering mechanism (top panel of Fig. 9).
Our model, therefore, predicts three regimes of galaxy formation (see top panel of Fig. 9): Galaxies with mstars ≲ 1010 M⊙ were effectively built up by gas accretion only. At 1010 M⊙ ≲ mstars ≲ 1011 M⊙ gas accretion remains the dominant mechanism, but we also see a population that was built by gas-rich mergers. Galaxies with 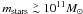 were mainly built by gas-poor mergers, in agreement with the analysis of SDSS galaxies by Bernardi et al. (2011), who explain the high-mass trends of color, elongation and color gradient of SDSS ellipticals with gas-poor mergers, by invoking a transition at the same stellar mass. Galaxies built by gas-rich mergers are rare at all masses. However, as expected from our model (middle panel of Fig. 9), cold-mode mergers dominate the growth of those galaxies with mstars < 1011 ⊙ that are mainly built by mergers.
were mainly built by gas-poor mergers, in agreement with the analysis of SDSS galaxies by Bernardi et al. (2011), who explain the high-mass trends of color, elongation and color gradient of SDSS ellipticals with gas-poor mergers, by invoking a transition at the same stellar mass. Galaxies built by gas-rich mergers are rare at all masses. However, as expected from our model (middle panel of Fig. 9), cold-mode mergers dominate the growth of those galaxies with mstars < 1011 ⊙ that are mainly built by mergers.
Running a semi-analytical model on top of the Millennium Simulation, De Lucia et al. (2006) find that the “effective” number of progenitors (a proxy for the number of major progenitors) of galaxies increases sharply beyond 1011 M⊙, which appears to be consistent with our conclusion that high-mass galaxies are built by major mergers.
Analyzing the same Millennium Simulation (which has 11 times worse mass resolution than our simulation), Guo & White (2008) measured the rate of growth of galaxies in the channels of gas accretion (which they denote “star formation”), and major and minor mergers. They also found that while major mergers dominate the growth of the most massive present-day galaxies, mergers contribute negligibly to the growth of low present-mass galaxies. Moreover, they noticed, as we did (our Fig. 8) that the importance of mergers increases with final galaxy mass in a stronger way than do mergers of the dark matter haloes.
Hopkins et al. (2010) followed an alternative approach to analyse the role of mergers in the growth of galaxies, in particular the relative importance of major and minor mergers. They used the halo merger rate function that Fakhouri & Ma (2009) derived from N-body simulations together with abundance matching to associate stellar masses to the merging haloes. The delay between halo mergers and galaxy mergers was calculated with the fitting formula by Boylan-Kolchin et al. (2008), which is analogous to the Jiang et al. (2008) formula that we use here. Their results for the relative importance of major mergers are, to first order, similar to ours: 1) major mergers dominate the formation and assembly of mstars ~ mcrit ellipticals, but the contribution of minor mergers is non-negligible ~ 30%; 2) the formation of elliptical galaxies becomes dominated by minor mergers at lower masses; But Hopkins et al. find that the relative importance of major mergers rapidly decreases again at high galaxy masses mstars > 1011 M⊙, while we find a small and not statistically significant drop in the importance of major mergers at very high galaxy masses (log h mstars > 11.5). When we consider the geometric mean mass ratio as a function of stellar mass, which is more comparable to the median mass ratio of bulges considered by Hopkins et al., we obtain (bottom panel of Fig. 12) a globally similar trend as Hopkins et al., although again with two differences: 1) their peak for for major mergers occurs at 3 times lower galaxy mass (after correcting for h); 2) the drop in merger mass ratio is much more pronounced in their model than in ours.
It is difficult to say which result is more correct in quantitative detail. The approach followed by Hopkins et al. is certainly more accurate in its capacity to predict the galaxy merger rate at a given time, since the halo occupation distribution is directly derived from abundance matching. However, our approach follows more consistently the merger history across the Hubble time of each halo inside the N-body simulation.
Maller et al. (2006) analysed the problem directly with hydrodynamic cosmological simulations. They concluded that mergers are more important at high galaxy masses. However, their simulations lack effective feedback and substantially overestimate the observed galaxy mass function. Therefore, they overestimated the role of gas accretion. Nevertheless, they determined that the average number of both minor and major mergers increases with mstars. They found that their high mass galaxies have typically undergone one major (1:1 to 1:4) merger through their lifetime. We note that the threshold they use to define high-mass galaxies is low (log h mstars = 10.6), so we expect that the dominance of mergers in their high mass bin is diluted by the importance of accretion near this mass threshold. Not only do we find that mergers are common among the most massive galaxies. We also find that the masses of these galaxies were mainly built by mergers.
Naab et al. (2007) also used hydrodynamic simulations to address the importance of mergers. However, in contrast with Maller et al. (2006), who simulated a cosmic volume at low resolution, they used very high resolution to zoom into the formation of three individual ellipticals. They found that their galaxies have grown by mergers from z = 1 to z = 0 by 25% in mass on average. They, therefore, concluded that intermediate-mass elliptical galaxies were not built by major mergers. We note, however, that their three ellipticals accreted over half of their mass by mergers since z = 5. Moreover, at z = 0, these galaxies live in haloes with virial masses in the range of 1.6 − 2.3 × 1012 M⊙. For central galaxies, this halo mass range corresponds to mstars ≃ 1011.0 − 1011.2 h-1 M⊙, which is about the galaxy mass for the transition in mass acquisition 1) by gas accretion and by mergers (Fig. 9), and 2) by minor and major mergers (Fig. 12). We therefore find the agreement between our results and those by Naab et al. (2007) quite encouraging.
The increasing importance of mergers on one hand and the importance of major mergers on the other are confirmed through two analytical developments that are deferred to a forthcoming article.
Finally, we remark that the delay of galaxy mergers with respect to halo mergers, which we compute with the the dynamical friction formula in the Jiang et al. (2008) version, turns out to play a very modest role in our conclusions: the galaxies that have not yet merged with the central galaxies of their direct hosts, even though their galactic haloes have merged with their immediate host haloes (or have become unresolved because of tidal stripping of most of their mass), account for ≲ 1% of the total galaxy population and ~ 10% of the satellite galaxy population at mstars > 109 h-1 M⊙ (satellites make up ~ 10 − 15% of all galaxies).
4.4. The dichotomy between central and satellite galaxies
Our very simple toy model of galaxy formation shows very distinct properties for central and satellite galaxies (see Fig. 6). Central galaxy mass increases slightly with halo mass, while the galaxy mass function, when measured within a narrow range of halo mass, clearly separates the central population and the satellite population, with a sharp peak at high-masses that corresponds to central galaxies (top panel of Fig. 7). This feature was first predicted by Benson et al. (2003) and Zheng et al. (2005) and first clearly observed by Yang et al. (2009) in the SDSS survey, who also modelled it with the conditional stellar mass function formalism. As we wrote these lines, we learnt that Liu et al. (2010) were also able to reproduce this behaviour with a semi-analytical model.
Over three-quarters12 of the galaxies in clusters, the huge majority of which are satellites, are observed to lie on the Red Sequence (Yang et al. 2008), which is visible to very low luminosities (e.g. Boué et al. 2008) and is mainly composed of galaxies with early-type morphologies, the great majority of which are classified as dwarf ellipticals (dEs).
Since mergers are found to be unimportant for the growth of most satellites (Fig. 6), including those in groups and clusters (Sect. 3.3), one is led to the conclusion that dEs must also acquire their mass by gas accretion. Therefore, the morphological properties and the shutdown of star formation in dEs (and by extension in dwarf spheroidals) must be due to processes unrelated to mergers and not included in our model (which does not describe the conversion of gas into stars), such as ram-pressure stripping (Gunn & Gott 1972), starvation (Larson et al. 1980) and harassment by repeated fast encounters (Moore et al. 1998; Mastropietro et al. 2005).
Therefore, we conclude that the mass-growth of elliptical galaxies is a function of their present-day mass: the most massive ones (mstars > 1011 h-1 M⊙) have mainly grown by gas-poor mergers, intermediate-mass ellipticals (1010 h-1 M⊙ < mstars < 1011h-1 M⊙) by gas-rich mergers, and the low-mass ones (mstars < 1010 h-1 M⊙) by gas accretion and later transformed by non-merging processes such as ram pressure stripping or galaxy harassment. This is similar to the picture for all galaxies, except that intermediate-mass ellipticals grow by gas-rich mergers while intermediate-mass spirals are built by gas accretion.
4.5. Caveats
An important caveat to our analysis is that our model does not describe star formation rates, as we are only interested in the total mass of a galaxy and the fraction of this mass that comes from mergers. This paper is not concerned with the fraction of the mass that is in gas and the fraction of the mass that is in stars. The SFRs that we show (Fig. 5) are simply mass accretion rates that are estimated assuming that all the accreted gas is instantaneously turned into stars. Therefore, it is not surprising that our model anticipates the peak of the star formation rate in comparison with observations (Fig. 5). In practice, at redshift z ~ 0, where we compare our model with the data (Figs. 4a and 6), the gas is usually a small fraction of the galaxy mass for intermediate and high-mass galaxies (see, e.g., McGaugh et al. 2010 and references therein). Therefore, the error that we make by identifying the stellar mass with the total galaxy mass (stars plus cold gas) is at most ~10−20%, which is compatible with the level of accuracy that we expect from our model. We note that even observationally, the cosmic SFR density derived from dust-corrected measured SFRs deviates at z > 1 from the time derivative of the cosmic stellar mass density (Wilkins et al. 2008; Fig. 5). The origin of this discrepancy is an open problem. Our model matches the observed time derivative of the comic stellar mass density much better than it matches the measured star formation rate density.
Much higher mass resolution on our side would certainly be desirable to properly follow substructures until they have merged with their hosts. However, this problem has been partly handled with the incorporation of delayed merging on a dynamical friction timescale (Sect. 2.2). Moreover, we are confident that our finite mass resolution is sufficient to indicate the strong drop in the importance of mergers at masses below 1011 h-1M⊙ (Fig. 8). Also, our low vcirc cut-off implies that there is not much advantage at resolving haloes with masses that are much lower than the mass at which vcirc = vreion, because there is no formation of galaxies in those haloes after the epoch of reionisation.
Of course, the details of our toy galaxy formation model are most probably oversimplified. The trend seen in the relation of galaxy mass to halo mass (Fig. 6) might be incorrect at low masses (although there is good agreement with the relation that Guo et al. 2010 derived from abundance matching, see Fig. 6). Nevertheless, none of our conclusions seem to depend on the accuracy of the model at low masses.
4.6. Open questions
Mergers are a reality and we have tried to present a careful and robust estimate of their importance. Our work suggests that present-day giant ellipticals can only be built by gas-poor mergers, as gas accretion must be quenched at high halo mass to avoid over-massive galaxies. Moreover, intermediate-mass ellipticals have probably grown by gas-rich mergers, while mergers appear unimportant for dwarf ellipticals. These conclusions are consistent with the structural properties of ellipticals: the surface brightness profiles of massive ellipticals tend to display inner cores, while those of less massive ellipticals tend to be cuspy (Kormendy et al. 2009).
Still many questions remain. Can the well-defined relation between the masses of central supermassive black holes and the spheroids of their hosts (Magorrian et al. 1998) be understood with both gas-poor mergers at the high mass end and gas-rich mergers at intermediate masses? Can this relation be extended from ellipticals to spiral galaxies? How do mergers fit in the growth of galaxies viewed at much higher redshift? Are other mechanisms responsible for the growth of proto-ellipticals at high redshift (e.g. Dekel et al. 2009)?
AHF can be downloaded from http://popia.ft.uam.es/AMIGA.
The actual density profile of sub-haloes after the removal of the host’s background drops faster than for isolated haloes (e.g. Kazantzidis et al. 2004). Only when measured within the background still present shall we find the characteristic upturn used here to define the truncation radius rt.
Gnedin (2000) have used more refined hydrodynamical simulations to find that the suppression by reionisation scales as 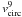 (see also Okamoto et al. 2008), but this should produce negligible differences in the mass range of galaxies studied here.
(see also Okamoto et al. 2008), but this should produce negligible differences in the mass range of galaxies studied here.
The discrepancy in Fig. 5 between the directly measured SFR densities (symbols with error bars) and the evolution of the SFR density computed from the time derivative of the integrated galaxy stellar mass function (red curve and shaded area) is an open observational problem.
In a sequel with a live Milky Way potential, Łokas et al. (2010) find an even stronger decrease in stellar mass, that amounts to 0.65 per orbit among the particles within 1 kpc. Note, however, that the secondary galaxy is 4 times more massive and with half the apocenter as the respective values in the simulations of Klimentowski et al. (2009).
The 22% of non-Red Sequence cluster galaxies found by Yang et al. (2008) matches perfectly the fraction of interlopers projected along the virial sphere, i.e. the average fraction of particles in the virial cone that are outside the virial sphere (Mamon et al. 2010a). Hence, the fraction of non-Red Sequence galaxies within the virial sphere is probably much lower than one-quarter. Indeed, the observed increase of the fraction of recent star forming galaxies (RSBGs) with projected radius has been deprojected by Mahajan et al. (2011) to yield a fraction of 13 ± 1% of RSBGs within the virial spheres in comparison with 18 ± 1% within the virial cones.
Acknowledgments
A.C. thanks the IAP for its hospitality during numerous visits. A.C. and G.A.M. acknowledge stimulating conversations with M. Bernardi, D. Ceverino, I. Chilingarian, A. Dekel, S.M. Faber, J.P. Ostriker, J. Silk, D. Tweed, F. van den Bosch, and D. Weinberg. We acknowledge anonymous referees for numerous useful comments. We also thank C. Wagner for running our simulation, as well as A. Hopkins and M. Bernardi for providing the observational data for Figs. 5 and 9, respectively. A.K. is supported by the MICINN through the Ramon y Cajal programme. K.W. acknowledges support through the DFG grant KN 755/1.
References
- Arnouts, S., Schiminovich, D., Ilbert, O., et al. 2005, ApJ, 619, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Glazebrook, K., Budavári, T., et al. 2005, MNRAS, 358, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Glazebrook, K., & Driver, S. P. 2008, MNRAS, 388, 945 [NASA ADS] [Google Scholar]
- Barger, A. J., Cowie, L. L., & Richards, E. A. 2000, AJ, 119, 2092 [Google Scholar]
- Behroozi, P. S., Conroy, C., & Wechsler, R. H. 2010, ApJ, 717, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, A. J., Frenk, C. S., Baugh, C. M., Cole, S., & Lacey, C. G. 2003, MNRAS, 343, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Berlind, A. A., & Weinberg, D. H. 2002, ApJ, 575, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Shankar, F., Hyde, J. B., et al. 2010, MNRAS, 404, 2087 [NASA ADS] [Google Scholar]
- Bernardi, M., Roche, N., Shankar, F., & Sheth, R. K. 2011, MNRAS, 412, 684 [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton, NJ USA: Princeton University Press), Chap. 8.1 [Google Scholar]
- Birnboim, Y., & Dekel, A. 2003, MNRAS, 345, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchard, A., Valls-Gabaud, D., & Mamon, G. A. 1992, A&A, 264, 365 [NASA ADS] [Google Scholar]
- Blumenthal, G. R., Faber, S. M., Primack, J. R., & Rees, M. J. 1984, Nature, 311, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Bonoli, S., Marulli, F., Springel, V., et al. 2009, MNRAS, 396, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Bouché, N., Dekel, A., Genzel, R., et al. 2010, ApJ, 718, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Boué, G., Adami, C., Durret, F., Mamon, G. A., & Cayatte, V. 2008, A&A, 479, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bournaud, F., Jog, C. J., & Combes, F. 2007, A&A, 476, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. 2006, in The Fabulous Destiny of Galaxies: Bridging Past and Present, ed. V. Le Brun, A. Mazure, S. Arnouts, & D. Burgarella, 373 [Google Scholar]
- Bouwens, R., Broadhurst, T., & Illingworth, G. 2003, ApJ, 593, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Boylan-Kolchin, M., Ma, C.-P., & Quataert, E. 2008, MNRAS, 383, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, G. L., & Norman, M. L. 1998, ApJ, 495, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Stanway, E. R., Ellis, R. S., & McMahon, R. G. 2004, MNRAS, 355, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Castro-Rodriguéz, N., Arnaboldi, M., Aguerri, J. A. L., et al. 2009, A&A, 507, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cattaneo, A. 2001, MNRAS, 324, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Dekel, A., Devriendt, J., Guiderdoni, B., & Blaizot, J. 2006, MNRAS, 370, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Blaizot, J., Weinberg, D. H., et al. 2007, MNRAS, 377, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Dekel, A., Faber, S. M., & Guiderdoni, B. 2008, MNRAS, 389, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Faber, S. M., Binney, J., et al. 2009, Nature, 460, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ceverino, D., & Klypin, A. 2009, ApJ, 695, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1943, ApJ, 97, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Aragon-Salamanca, A., Frenk, C. S., Navarro, J. F., & Zepf, S. E. 1994, MNRAS, 271, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Colina, L., Borne, K., Bushouse, H., et al. 2001, ApJ, 563, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi, M., Mayer, L., & Governato, F. 1999, ApJ, 525, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1989, ApJ, 338, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., & Broderick, J. J. 2002, AJ, 124, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Connolly, A. J., Szalay, A. S., Dickinson, M., Subbarao, M. U., & Brunner, R. J. 1997, ApJ, 486, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Wechsler, R. H., & Kravtsov, A. V. 2006, ApJ, 647, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Songaila, A., & Barger, A. J. 1999, AJ, 118, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Springel, V., White, S. D. M., Croton, D., & Kauffmann, G. 2006, MNRAS, 366, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Silk, J. 1986, ApJ, 303, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dubois, Y., & Teyssier, R. 2008, A&A, 477, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efstathiou, G. 1992, MNRAS, 256, 43P [Google Scholar]
- Efstathiou, G., Davis, M., White, S. D. M., & Frenk, C. S. 1985, ApJS, 57, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., Willmer, C. N. A., Wolf, C., et al. 2007, ApJ, 665, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Fakhouri, O., & Ma, C.-P. 2009, MNRAS, 394, 1825 [NASA ADS] [CrossRef] [Google Scholar]
- Fall, S. M., & Efstathiou, G. 1980, MNRAS, 193, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmeier, J. J., Ciardullo, R., Jacoby, G. H., & Durrell, P. R. 2004, ApJ, 615, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Flores, H., Hammer, F., Thuan, T. X., et al. 1999, ApJ, 517, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Nakamura, O., Okamura, S., et al. 2007, AJ, 134, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Gallego, J., Zamorano, J., Aragon-Salamanca, A., & Rego, M. 1995, ApJ, 455, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Gallego, J., García-Dabó, C. E., Zamorano, J., Aragón-Salamanca, A., & Rego, M. 2002, ApJ, 570, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakakis, A., Hopkins, A. M., Sullivan, M., et al. 2003, MNRAS, 345, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Ghigna, S., Moore, B., Governato, F., et al. 1998, MNRAS, 300, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Dickinson, M., Ferguson, H. C., et al. 2004, ApJ, 600, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, S. P. D., Knebe, A., & Gibson, B. K. 2004, MNRAS, 351, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Glazebrook, K., Blake, C., Economou, F., Lilly, S., & Colless, M. 1999, MNRAS, 306, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Gnedin, N. Y. 2000, ApJ, 542, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Gross, M. A. K. 1997, Ph.D. Thesis, University of California, Santa Cruz [Google Scholar]
- Gunn, J. E., & Gott, J. R. 1972, ApJ, 176, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., & White, S. D. M. 2008, MNRAS, 384, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Q., White, S., Li, C., & Boylan-Kolchin, M. 2010, MNRAS, 404, 1111 [NASA ADS] [Google Scholar]
- Haarsma, D. B., Partridge, R. B., Windhorst, R. A., & Richards, E. A. 2000, ApJ, 544, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, F., Flores, H., Lilly, S. J., et al. 1997, ApJ, 481, 49 [CrossRef] [Google Scholar]
- Hanish, D. J., Meurer, G. R., Ferguson, H. C., et al. 2006, ApJ, 649, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, E., Navarro, J. F., Taylor, J. E., Stadel, J., & Quinn, T. 2003, ApJ, 584, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Cohen, J. G., Blandford, R., & Pahre, M. A. 1998, ApJ, 504, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M. 2004, ApJ, 615, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hopkins, A. M., Connolly, A. J., & Szalay, A. S. 2000, AJ, 120, 2843 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Ikeuchi, S. 1986, Ap&SS, 118, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, C. Y., Jing, Y. P., Faltenbacher, A., Lin, W. P., & Li, C. 2008, ApJ, 675, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., White, S. D. M., & Guiderdoni, B. 1993, MNRAS, 264, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Kazantzidis, S., Mayer, L., Mastropietro, C., et al. 2004, ApJ, 608, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kitayama, T., & Suto, Y. 1996, ApJ, 469, 480 [CrossRef] [Google Scholar]
- Klimentowski, J., Łokas, E. L., Kazantzidis, S., Mayer, L., & Mamon, G. A. 2009, MNRAS, 397, 2015 [NASA ADS] [CrossRef] [Google Scholar]
- Knollmann, S. R., & Knebe, A. 2009, ApJS, 182, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Gnedin, O. Y., & Klypin, A. A. 2004, ApJ, 609, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lacey, C., & Cole, S. 1993, MNRAS, 262, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., Tinsley, B. M., & Caldwell, C. N. 1980, ApJ, 237, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Gebhardt, K., Faber, S. M., et al. 2007, ApJ, 664, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Le Floc’h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., & White, S. D. M. 2009, MNRAS, 398, 2177 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., & Mohr, J. J. 2004, ApJ, 617, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, L., Yang, X., Mo, H. J., van den Bosch, F. C., & Springel, V. 2010, ApJ, 712, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Faro, B., Monaco, P., Vanzella, E., et al. 2009, MNRAS, 399, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Łokas, E. L., Kazantzidis, S., Majewski, S. R., et al. 2010, ApJ, 725, 1516 [NASA ADS] [CrossRef] [Google Scholar]
- Macciò, A. V., Dutton, A. A., & van den Bosch, F. C. 2008, MNRAS, 391, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Machalski, J., & Godlowski, W. 2000, A&A, 360, 463 [NASA ADS] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Mahajan, S., Mamon, G. A., & Raychaudhury, S. 2011, MNRAS, in press [arXiv:1106.3062] [Google Scholar]
- Maller, A. H., Katz, N., Kereš, D., Davé, R., & Weinberg, D. H. 2006, ApJ, 647, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A. 1992, ApJ, 401, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A., Biviano, A., & Murante, G. 2010a, A&A, 520, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamon, G. A., Tweed, D., Cattaneo, A., & Thuan, T. X. 2010b, in A Universe of Dwarf Galaxies: Observations, Theories, Simulations, ed. M. Koleva, P. Prugniel, & I. Vauglin, EAS Publ. Ser., 48, 435 [Google Scholar]
- Marinoni, C., & Hudson, M. J. 2002, ApJ, 569, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Massarotti, M., Iovino, A., & Buzzoni, A. 2001, ApJ, 559, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Mastropietro, C., Moore, B., Mayer, L., et al. 2005, MNRAS, 364, 607 [Google Scholar]
- Mauch, T., & Sadler, E. M. 2007, MNRAS, 375, 931 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Schombert, J. M., de Blok, W. J. G., & Zagursky, M. J. 2010, ApJ, 708, L14 [Google Scholar]
- McQuinn, M., Lidz, A., Zaldarriaga, M., et al. 2009, ApJ, 694, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Lake, G., & Katz, N. 1998, ApJ, 495, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Moorwood, A. F. M., van der Werf, P. P., Cuby, J. G., & Oliva, E. 2000, A&A, 362, 9 [NASA ADS] [Google Scholar]
- Naab, T., Johansson, P. H., Ostriker, J. P., & Efstathiou, G. 2007, ApJ, 658, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, T. T. 1996, Master’s thesis, Univ. of Tokyo [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Neistein, E., & Dekel, A. 2008, MNRAS, 383, 615 [Google Scholar]
- Neistein, E., & Weinmann, S. M. 2010, MNRAS, 405, 2717 [NASA ADS] [Google Scholar]
- Okamoto, T., Gao, L., & Theuns, T. 2008, MNRAS, 390, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Oser, L., Ostriker, J. P., Naab, T., Johansson, P. H., & Burkert, A. 2010, ApJ, 725, 2312 [NASA ADS] [CrossRef] [Google Scholar]
- Ouchi, M., Shimasaku, K., Okamura, S., et al. 2004, ApJ, 611, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Gallego, J., Zamorano, J., et al. 2003, ApJ, 587, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-González, P. G., Rieke, G. H., Egami, E., et al. 2005, ApJ, 630, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., Kellogg, M., Steidel, C. C., et al. 1998, ApJ, 508, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J. 1986, MNRAS, 218, 25P [Google Scholar]
- Sadler, E. M., Jackson, C. A., Cannon, R. D., et al. 2002, MNRAS, 329, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schiminovich, D., Ilbert, O., Arnouts, S., et al. 2005, ApJ, 619, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Serjeant, S., Gruppioni, C., & Oliver, S. 2002, MNRAS, 330, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J., & Rees, M. J. 1998, A&A, 331, L1 [NASA ADS] [Google Scholar]
- Somerville, R. S., & Kolatt, T. S. 1999, MNRAS, 305, 1 [Google Scholar]
- Somerville, R. S., Hopkins, P. F., Cox, T. J., Robertson, B. E., & Hernquist, L. 2008, MNRAS, 391, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Giavalisco, M., Dickinson, M., & Pettini, M. 1999, ApJ, 519, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Treyer, M. A., Ellis, R. S., et al. 2000, MNRAS, 312, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Teplitz, H. I., Collins, N. R., Gardner, J. P., Hill, R. S., & Rhodes, J. 2003, ApJ, 589, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, R. I., Eisenstein, D., Fan, X., et al. 2006, ApJ, 647, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Thoul, A. A., & Weinberg, D. H. 1996, ApJ, 465, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1977, in The Evolution of Galaxies and Stellar Populations, ed. B. M. Tinsley, & R. B. Larson (New Haven: Yale University Press), 401 [Google Scholar]
- Tresse, L., & Maddox, S. J. 1998, ApJ, 495, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Tresse, L., Maddox, S. J., Le Fèvre, O., & Cuby, J.-G. 2002, MNRAS, 337, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Treyer, M. A., Ellis, R. S., Milliard, B., Donas, J., & Bridges, T. J. 1998, MNRAS, 300, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- van den Bosch, F. C. 2002, MNRAS, 331, 98 [Google Scholar]
- White, S. D. M., & Frenk, C. S. 1991, ApJ, 379, 52 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkins, S. M., Trentham, N., & Hopkins, A. M. 2008, MNRAS, 385, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, G., Cowie, L. L., Barger, A. J., & Burke, D. J. 2002, AJ, 124, 1258 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Wisotzki, L., Borch, A., et al. 2003, A&A, 408, 499 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, L., McCarthy, P. J., Freudling, W., et al. 1999, ApJ, 519, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., & van den Bosch, F. C. 2003, MNRAS, 339, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., & van den Bosch, F. C. 2008, ApJ, 676, 248 [Google Scholar]
- Yang, X., Mo, H. J., & van den Bosch, F. C. 2009, ApJ, 695, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, W., Li, C., Kauffmann, G., et al. 2009, MNRAS, 397, 1243 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Berlind, A. A., Weinberg, D. H., et al. 2005, ApJ, 633, 791 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Sketch illustrating the merger of two haloes. Once the smaller halo penetrates the larger one (whose central galaxy is denoted by a red circle), it becomes a sub-halo. Its orbit (adapted from an N-body simulation by Colpi et al. 1999), shown by the blue curve (with positions shown for equal timesteps), decays by dynamical friction and its size, shown by the circles, is reduced by tidal stripping from the larger halo’s potential. The solid part of the blue curve is followed directly by the N-body simulation, while the dashed part shows the trajectory that the sub-halo is expected to take after it (open circles) is no longer resolved in the simulation. In our analysis, the duration of the motion along the dashed stretch of the blue curve is computed analytically from Eqs. (1–3). |
| In the text | |
 |
Fig. 2 Star formation efficiency versus halo circular velocity and mass at two different epochs in our toy model (Eq. (8)). This figure has been plotted for the parameters of Table 1 that produce the best fit to the stellar mass function at z = 0 (see Sect. 3.1). The upper (black) mass scale is for z = 0, while the lower (red) mass scale is for z = 5. The gold shaded region shows the relation predicted by abundance matching by Guo et al. (2010). |
| In the text | |
 |
Fig. 3 Growth of halo mass and efficiency of star formation. The contours show the efficiency of star formation, |
| In the text | |
 |
Fig. 4 Stellar mass function of galaxies at z = 0. The filled squares show the galaxy mass function determined observationally by Bell et al. (2003). The solid line shows our best-fit model (the “full” model, with parameter values listed in Table 1). The fit assumes h = 0.7 because observationally inferred masses scale as h-2. a) Variations of the stellar mass function for different assumptions on merging and stripping: best-fit full model (black solid line), no tidal stripping (ηstrip = 0, red dotted line), no mergers at all (green dashed line), and maximum merging (blue dash-dotted line); b) variations of the stellar mass function for different assumptions on the baryonic physics: best-fit full model (black solid line, same as in panel a), baryons trace dark matter (mstars = fb Mhalo, red dotted line), no high-mass cutoff (Mshock → ∞, green dashed line), and no low circular velocity cutoff (vSN = vreion = 0, blue dash-dotted line). In both panels, all variations start from the best-fit parameters of the full model except for the fact that we use ηstrip = 0 in all models apart from the full one. |
| In the text | |
 |
Fig. 5 The evolution of the cosmic SFR density with redshift in the observed Universe (points with error bars and hatched region) and in our model (thick black solid line; the dotted and dotted-dashed lines correspond to the two models where baryons trace dark matter and without a low circular velocity cutoff, respectively, see Fig. 4b). The blue squares are UV data Giavalisco et al. (2004); Wilson et al. (2002); Massarotti et al. (2001); Sullivan et al. (2000); Steidel et al. (1999); Cowie et al. (1999); Treyer et al. (1998); Connolly et al. (1997); Baldry et al. (2005); Schiminovich et al. (2005); Wolf et al. (2003); Arnouts et al. (2005); Bouwens et al. (2003); Bouwens (2006); Bunker et al. (2004); Ouchi et al. (2004). The blue pentagons are Hubble Ultra Deep Field estimates (Thompson et al. 2006). The red squares are Hα, Hβ and OII data (Hanish et al. 2006; Pérez-González et al. 2003; Tresse et al. 2002; Hopkins et al. 2000; Moorwood et al. 2000; Sullivan et al. 2000; Glazebrook et al. 1999; Yan et al. 1999; Tresse & Maddox 1998; Gallego et al. 1995; Pettini et al. 1998; Teplitz et al. 2003; Gallego et al. 2002; Hogg et al. 1998; Hammer et al. 1997). The orange squares are 1.4 GHz data (Mauch & Sadler 2007; Condon et al. 2002; Sadler et al. 2002; Serjeant et al. 2002; Machalski & Godlowski 2000; Haarsma et al. 2000; Condon 1989). The orange pentagon at z ≃ 0.24 is X-ray data (Georgakakis et al. 2003). The green squares are infrared (Pérez-González et al. 2005; Flores et al. 1999) and sub-mm (Barger et al. 2000) data. The green hatched region is the far infrared (24 μm) SFR history from Le Floc’h et al. (2005). Most of them were taken from the compilations in Hopkins (2004) and Hopkins & Beacom (2006). The red curve, |
| In the text | |
 |
Fig. 6 Galaxy stellar mass vs. host halo mass at z = 0 for the set of parameters (Table 1) that fit best the galaxy stellar mass function. Each point is one of our simulated galaxies. The symbol sizes and colours vary with the fraction fmerg of mass acquired in mergers, and the fraction gcold of this mass acquired by cold-mode mergers (where the sum of the masses of the haloes of the merging galaxies is below Mshock), respectively, according to the legend. The vertical green line corresponds to Mhalo = Mshock, while the oblique magenta line indicates mstars = fb Mhalo. The green curves show the stellar masses of galaxies acquired through the accretion channel (Eq. (8) with best-fit parameters from Table 1) at z = 0 (lower) and z = 3 (upper curve). The shaded cyan and gold regions correspond to the observations from the SDSS (Yang et al. 2009), and the halo-galaxy abundance matching of Guo et al. (2010). For the latter, the halo masses were shifted by log 10h to conform to our units. Also, the stellar masses were shifted by − log 10h and log 10h for Yang et al. and Guo et al., respectively, to take into account the different units with h. We also shifted the stellar masses by an additional factor of +0.1 and + 0.15 dex to pass from the Kroupa and Chabrier IMFs, respectively assumed by Yang et al. and Guo et al. to the diet Salpeter IMF assumed by Bell et al. (2003), on whose mass function we have calibrated our model. |
| In the text | |
 |
Fig. 7 The galaxy stellar mass function at z = 0 split by environment, defined by host halo mass (top) or group richness (number of companions with mstars > 1010 M⊙/h in the same host halo, bottom). The dashed curves in the top panel show the conditional mass function fits to the SDSS data by Yang et al. (2009). The same h and IMF corrections as in Fig. 6 apply. |
| In the text | |
 |
Fig. 8 Median fraction of the z = 0 galaxy mass acquired via mergers rather than via gas accretion for various models: best-fit full model (black solid line), baryons trace dark matter (mstars = fb Mhalo, red dotted line), no high-mass cutoff (Mshock → ∞, green short-dashed line), no low circular velocity cutoff (vSN = vreion = 0, blue dash-dotted line), and no tidal stripping (ηstrip = 0, black long-dashed line). |
| In the text | |
 |
Fig. 9 Top: median mass fraction at z = 0 acquired via gas accretion (black line), “cold mode” galaxy mergers within haloes with |
| In the text | |
 |
Fig. 10 Distribution of fraction of the z = 0 mass acquired by mergers for galaxies in different bins of stellar mass. |
| In the text | |
 |
Fig. 11 Top: fraction of galaxies with over 40% of their z = 0 mass acquired by mergers versus stellar mass in bins of halo mass (labelled by log h M). The errors are binomial. Bottom: same versus halo mass in bins of stellar mass (labelled by log h mstars). |
| In the text | |
 |
Fig. 12 Top: median fraction of the mass at z = 0 acquired by mergers due to major mergers for galaxies with fmerg > 0.4. The red and blue lines use stellar mass ratios between 1:1 and respectively 1:3 and 1:5 to define major mergers. The error bars are bootstrap estimates of the uncertainties of the mean fractions. Bottom: geometric mean mass ratio of mergers for galaxies with fmerg > 0.4 at z = 0. The error bars are bootstrap estimates of the uncertainties of the geometric mean ratios. The red and blue horizontal lines respectively represent the 1:3 and 1:5 limits of major mergers. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



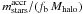
~M_\odot~{\rm Mpc}^{-3}$}](/articles/aa/full_html/2011/09/aa15780-10/aa15780-10-eq177.png)