| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201016399 | |
| Published online | 27 July 2011 | |
Continuum and line modelling of discs around young stars
II. Line diagnostics for GASPS from the DENT grid
1
Kapteyn Astronomical Institute, Postbus 800, 9700 AV Groningen, The Netherlands
e-mail: kamp@astro.rug.nl
2
UK Astronomy Technology Centre, Royal Observatory, Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
3
UJF-Grenoble 1/CNRS-INSU, Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) UMR 5274, 38041 Grenoble Cedex 9, France
4
School of Physics & Astronomy, University of St. Andrews, North Haugh, St. Andrews KY16 9SS, UK
5
SUPA, Institute for Astronomy, Royal Observatory, Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
6
Astronomy Department, University of California, Berkeley, CA 94720-3411, USA
Received: 23 December 2010
Accepted: 16 March 2011
Aims. We want to understand the chemistry and physics of discs on the basis of a large unbiased and statistically relevant grid of disc models. One of the main goals is to explore the diagnostic power of various gas emission lines and line ratios for deriving main disc parameters such as the gas mass.
Methods. We explored the results of the DENT grid (Disk Evolution with Neat Theory) that consists of 300 000 disc models with 11 free parameters. Through a statistical analysis, we searched for correlations and trends in an effort to find tools for disc diagnostic.
Results. All calculated quantities like species masses, temperatures, continuum, and line fluxes differ by several orders of magnitude across the entire parameter space. The broad distribution of these quantities as a function of input parameters shows the limitation of using a prototype T Tauri or Herbig Ae/Be disc model. The statistical analysis of the DENT grid shows that CO gas is rarely the dominant carbon reservoir in discs. Models with large inner radii (10 times the dust condensation radius) and/or shallow surface density gradients lack massive gas-phase water reservoirs. Also, 60% of the discs have gas temperatures averaged over the oxygen mass in the range between 15 and 70 K; the average gas temperatures for CO and O differ by less than a factor two. Our study of the observational diagnostics shows that the [C ii] 158 μm fine structure line flux is very sensitive to the stellar UV flux and presence of a UV excess, and that it traces the outer disc radius (Rout). In the submm, the CO low J rotational lines also trace Rout. Low [O i] 63/145 line ratios (<a few) can be explained with cool atomic O gas in the uppermost surface layers leading to self-absorption in the 63 μm line. This occurs mostly for massive non-flaring, settled disc models without UV excess. A combination of the [O i] 63 line and low J CO lines correlates with several disc properties, such as the average O i gas temperature in discs, the outer disc radius, and the UV excess.
Conclusions. The [O i] 63/CO 2−1 line ratio is a powerful diagnostic for breaking disc modelling degeneracies. A combination of the [O i] 63 μm flux and the [O i] 63/CO 2−1 line ratio can be used for Mgas ≤ 10-3 M⊙ to obtain an order of magnitude estimate for the disc gas mass purely from gas observations. The previously used conversion of a CO submm line flux alone generally leads to larger uncertainties.
Key words: astrochemistry / circumstellar matter / stars: formation / radiative transfer / methods: numerical / line: formation
© ESO, 2011
1. Introduction
In the recent decade, modelling of the gas chemistry and physics in protoplanetary discs has become a field of its own, following the lead of the dust SED modelling with multi-dimensional continuum radiative transfer (e.g. Chiang & Goldreich 1997; D’Alessio et al. 1998; Dullemond et al. 2002). The impact of the gas chemistry and energy balance is greatest in the disc surface layers where most of the infrared and sub-mm line emission arises (e.g. Kamp & Dullemond 2004; Jonkheid et al. 2004; Gorti & Hollenbach 2004; Nomura & Millar 2005). The complexity of the gas chemistry and individual heating/cooling processes, as well as their mutual dependence, makes gas structure modelling more complicated, physically more demanding, and computationally more time consuming. As a result, most modelling has so far concentrated on either single selected objects (e.g. Qi et al. 2003; Semenov et al. 2005; Qi et al. 2008; Gorti & Hollenbach 2008; Henning et al. 2010), prototypes (e.g. Aikawa et al. 2002; Meijerink et al. 2008; Goicoechea et al. 2009), or small model series studying the dependencies of specific parameters on the gas emission from discs (e.g. Aikawa & Nomura 2006; Jonkheid et al. 2007; Nomura et al. 2007; Glassgold et al. 2009; Kamp et al. 2010).
Current and upcoming observing facilities such as Herschel, ALMA, JWST/MIRI, SPICA/SAFARI are excellent tools for studying the gas in large samples of protoplanetary discs. There is therefore a clear need for a simultaneous and consistent modelling of dust and gas in protoplanetary discs, with the aim to identify the diagnostic power of certain continuum and line observations for the physical, chemical and temperature structure in the discs. These identifications must be based on a wide variety of disc models covering a wide spread in stellar, disc, dust, and gas parameters.
We jointly produced a grid of 300 000 disc models (Disc Evolution with Neat Theory – DENT) to study the predictive power of individual gas lines, line ratios, and continuum tracers (Woitke et al. 2010). The line emission studies concentrate on a series of fine structure (O i and C ii) and molecular lines (high J CO and H2O) that are observable with Herschel, as well as on a number of CO sub-mm lines accessible from the ground. A first analysis of the grid has shown that, for example, the [O i] 63 μm emission strongly depends on the amount of UV excess coming from the star (Woitke et al. 2010). Subsequent application to the first findings from the Herschel open time key program GASPS (Pinte et al. 2010) has revealed that the measured [O i] fluxes for a sample of 30 discs indicate that discs around T Tauri stars indeed require extra heating of the disc surface – either through a UV excess and/or X-ray irradiation – while the emission from discs around Herbig Ae stars can generally be matched by photospheric heating alone. This paper now presents a more systematic and complete study of the gas properties and diagnostics from the DENT grid. The dust diagnostics will be discussed in a separate paper.
In the following, we briefly summarize the DENT grid approach (Sect. 2) as presented in Woitke et al. (2010) before we discuss the statistics of gas chemistry and thermal structure of the 300 000 models in Sect. 3 and the line diagnostics in Sect. 4. We present our current best strategies for deriving disc gas parameters in the final conclusions (Sect. 6).
2. The DENT grid
The DENT grid has been described for the first time in Woitke et al. (2010) and we summarize here only a few key aspects. More details can be found in the Appendix.
The grid is computed using the 3D Monte Carlo radiative transfer code MCFOST (Pinte et al. 2006, 2009) and the gas chemistry and physics modules of ProDiMo (Woitke et al. 2009a; Kamp et al. 2010). The column densities, flaring, dust size distribution and settling are parametrized with power laws, assuming a prescribed global gas-to-dust ratio. Mie theory is used to compute the dust optical properties assuming an astronomical silicate composition. The central star is parametrized by its mass and age, as well as strength of the UV excess. Dust and gas temperatures are calculated separately from Monte Carlo continuum radiative transfer and a detailed heating/cooling network, respectively (see Sects. 2.1 and 2.2).
We have chosen 11 free model parameters for the grid, leading to a total of 322 030 disc models. The range of parameter values explored in DENT is discussed further in the Appendix. The total computing time of the grid is 200 000 CPU hours, an average of 40 CPU minutes per model. The total grid took 3 weeks on 400 processors and generated 1.8 TB of data.
The grid is very coarse in nature, e.g. stepping through gas mass in factors of ten. Hence, we cannot expect any method that we develop to measure disc properties such as the disc gas mass from gas line emission or line ratios to be more accurate than that step size, in this case an order of magnitude. The same holds for other quantities such as the outer disc radius, the flaring index, the dust-to-gas mass ratio etc.
For the following analysis, it is also important to keep in mind that the grid of disc models is not constructed to reflect the statistics with which discs occur in nature, e.g. the fact that some objects are rarer than others. There could be some disc types that we missed in our approach, or others that simply do not occur in nature. We take the latter into account by excluding certain parameter combinations in the analysis of the grid. Models with a flaring index of β = 0.8 are for example more appropriate for late stages of disc evolution such as debris discs and so they are excluded from the study of line diagnostics in younger discs (noted in the figure captions whenever appropriate). A global disc analysis using the Toomre criterium shows that 94% of the disc models in the DENT grid are gravitationally stable (see Appendix A.3).
We chose parametrized density structures to avoid imposing the complex gas structure that is based on presumptions mainly derived from disc modelling approaches such as those of Gorti & Hollenbach (2004), Nomura & Millar (2005) or Woitke et al. (2009a). While it is true that the more consistent vertical disc structure models need less assumptions than the simple parametrized models used in DENT, even a full ProDiMo including the vertical structure calculation (Woitke et al. 2009a) is not guaranteed to capture all relevant physics. Using parametrized disc structures enables us to explore a wide unbiased parameter space. From these simplified disc structures, we can still assess the relative influence of several of the key parameters on line and continuum fluxes. Even though the modeled fluxes are not absolute, we can still test fundamental aspects of our disc understanding, such as uncertainties in various observational techniques to derive disc dust and gas masses.
2.1. MCFOST
MCFOST is a 3D Monte Carlo continuum and line radiative transfer code. The details of the numerical schemes are presented in Pinte et al. (2006) and Pinte et al. (2009). In short, the code stochastically propagates photon packets in 3D through the disc. The transport of packets is governed by successive scattering, absorption and re-emission events, which are determined by the local dust properties (opacity, albedo, scattering matrix) and temperature. MCFOST uses the immediate re-emission concept (Bjorkman & Wood 2001) with a continuous deposition of energy to estimate the mean intensity (Lucy 1999). In the optically thick regions of the disc, the code uses a diffusion approximation method to converge the temperature structure. Emerging SEDs are generated by a ray-tracing run from the temperature and radiation field estimated by the Monte Carlo run.
For the DENT grid, 106 packets were used to compute the temperature structure. The radiation field was converged using 104 packets per wavelength bin at wavelength greater than 0.5 μm. As a reliable estimate of the UV field is critical for the chemistry module in ProDiMo, we used 105 packets per wavelength bin for wavelengths shorter than 0.5 μm. This ensures that the UV radiation field is well converged, even in the deep regions of the disc.
MCFOST also includes a NLTE line transfer module which is not fully used here, but whose ray-tracing module is used instead to compute the emerging spectral lines from the level populations estimated by ProDiMo.
2.2. ProDiMo
ProDiMo calculates radiation thermo-chemical models of protoplanetary discs. It is described in detail in Woitke et al. (2009a) and Kamp et al. (2010) and we summarize here the most salient features. Most noticable, the code is not used in its full capacity, because the self-consistent computation of the vertical hydrostatic equilibrium structure is omitted.
The code takes as input the dust density and temperature, ndust(r,z), Tdust(r,z) and dust properties as provided by MCFOST. In addition, the mean radiation field Jν(r,z) from MCFOST is passed on to ProDiMo. There are two grid parameters that apply only to the gas part of the model: the gas mass Mgas, and hence the dust-to-gas mass ratio δ, and the fractional UV luminosity defined as fUV = LUV/L ∗ in the wavelength range between 91 and 250 nm.
The chemical network consists of 9 elements, 71 species connected through 950 reactions (neutral-neutral, ion-molecule, photoreactions, cosmic ray reactions and adsorption & desorption of CO, CO2, H2O, NH3, CH4). The background radiation field Jν enters the computation of the gas chemical and energy balance at several points, namely in the detailed frequency dependent integration of the UV ionization and dissociation cross sections, in the radiative pumping rates involved in the non-LTE modelling of atoms and molecules (O i, C i, C ii, Mg ii, Fe ii, Si ii, S ii, CO rotational & ro-vibrational, o-H2 & p-H2 ro-vibrational, o-H2O & p-H2O rotational), and in the photoelectric heating rates. The atomic and molecular data used in the statistical equilibrium calculation is described in detail in Sect. 6.1.5 of Woitke et al. (2009a).
3. Gas physics and chemistry
As a first step in the statistical analysis of the DENT grid, we discuss here how the masses and average temperatures of a number of key species (O, CO, C+ and H2O) depend on the grid parameters (see Appendix A.4). With this method, we can obtain a first understanding of the disc chemistry (atomic versus molecular), the relevance of ices (how much CO or H2O is bound in ice form) and the thermal disc structure (gas dust de-coupling and cool surface layers).
3.1. Oxygen and CO masses
Oxygen is the third most abundant element in the interstellar medium. In dense molecular clouds or protoplanetary discs, oxygen can be either in the gas or ice phase (both are included in our chemical model); in the gas phase, it can be atomic (O) or molecular (CO, O2, H2O). By measuring all possible phases, we can constrain the total oxygen mass in a disc.
Maximum possible fraction of total disc mass for selected species Xsp assuming all carbon or oxygen are locked into that species.
 |
Fig. 1 The atomic oxygen mass fraction X(O) = M(O)/Mgas for all disc models with Mgas ≥ 10-7 M⊙. Colour coded is the total disc gas mass. Note that the y-axis is logarithmic. |
 |
Fig. 2 The CO gas mass fraction X(CO) = M(CO)/Mgas for all disc models with Mgas ≥ 10-7 M⊙. Colour coded is the total disc gas mass. |
 |
Fig. 3 The CO gas mass fraction X(CO) = M(CO)/Mgas for all disc models. Colour coded is the dust-to-gas mass ratio. |
Figure 1 shows the statistical distribution of atomic oxygen masses. Low mass disc models have almost no CO, H2O or ices (X(CO) ≲ 10-3, X(H2O) ≲ 10-4) and hence their atomic oxygen mass fraction is close to maximum. Assuming all oxygen is atomic, we obtain a mass fraction of X(O) = 2.3 × 10-3. Higher mass disc models show a wider distribution of atomic oxygen mass fractions in Fig. 1. This is due to a higher molecular fraction (dust shielding and gas self-shielding), e.g. CO, CH4, and H2O. Studying the CO mass fraction distribution (Fig. 2), the number of discs with masses greater than 10-5 M⊙ that have a particular CO mass fraction is rising all the way towards the maximum possible CO mass fraction. The lowest mass discs (10-6 ≤ Mgas ≤ 10-7 M⊙) show instead a broader and flatter distribution; ice formation and photodissociation for those models are extremely model dependent. Also, none of those models ever shows all carbon being bound in CO. The dust-to-gas mass ratio lowers for example the peak of the CO mass fraction by a factor 5 going from 0.001 to 1 (Fig. 3). This is due to the average dust temperature being lower in the high dust-to-gas models and hence more CO freezing out.
3.2. Water masses
 |
Fig. 4 The H2O mass fraction X(H2O) = M(H2O)/Mgas for disc models with an inner radius equal the sublimation radius. Colour coded is the surface density power law index ϵ. |
The mass fraction of gas phase water depends strongly on the surface density power law index, i.e. on the distribution of mass within the disc. Massive disc models that concentrate the mass in the inner dense disc (ϵ = 1.5), convert a substantial amount of their oxygen into water (Fig. 4). For shallower density gradients, the outer disc contains more mass than the inner disc; here temperatures are low so that water is predominantly frozen on the grain surfaces. What remains is a low abundance of gas phase water above the ice layer. Models that have an inner gap, i.e. Rin = 10 or 100 times the sublimation radius tend to have lower mass fractions of gas phase water. Those models lack the big inner gas phase water reservoir (Woitke et al. 2009b).
3.3. Oxygen gas temperatures
We calculate average gas temperatures for various species from the models following  (1)where nsp is the species density and msp its mass. Msp is the total mass of a species in the disc model. The oxygen gas temperature distribution peaks at 20 K and the median gas temperature is 40 K. The distribution shows that ~ 60% of the models stay between 15 and 70 K. The temperature distributions for specific subsamples of parameters, such as the the stellar luminosity and disc gas mass, are shown in Figs. 5 and 6. If we split the sample by luminosity, the higher luminosity models show on average higher gas temperatures. This can be directly attributed to the higher energy deposition rate which leads to an increased gas heating. Looking at low mass disc models (Fig. 6), we note that their average gas temperature is almost a factor three higher than that of high mass disc models. This is explained by optical depth effects: in models with moderate optical depth, a higher fraction of the total mass can be heated by irradiation. Hence, models with lower disc mass tend to have on average higher gas temperatures. These general trends are based on a huge number of disc models and the actual distribution of gas temperatures is fairly wide with a long shallow tail towards very high gas temperatures (Fig. 6).
(1)where nsp is the species density and msp its mass. Msp is the total mass of a species in the disc model. The oxygen gas temperature distribution peaks at 20 K and the median gas temperature is 40 K. The distribution shows that ~ 60% of the models stay between 15 and 70 K. The temperature distributions for specific subsamples of parameters, such as the the stellar luminosity and disc gas mass, are shown in Figs. 5 and 6. If we split the sample by luminosity, the higher luminosity models show on average higher gas temperatures. This can be directly attributed to the higher energy deposition rate which leads to an increased gas heating. Looking at low mass disc models (Fig. 6), we note that their average gas temperature is almost a factor three higher than that of high mass disc models. This is explained by optical depth effects: in models with moderate optical depth, a higher fraction of the total mass can be heated by irradiation. Hence, models with lower disc mass tend to have on average higher gas temperatures. These general trends are based on a huge number of disc models and the actual distribution of gas temperatures is fairly wide with a long shallow tail towards very high gas temperatures (Fig. 6).
The O i gas temperature statistics (and emerging line fluxes) have already been used in Pinte et al. (2010) to identify the need for an extra heating mechanism from the [O i] line fluxes of T Tauri stars. In that particular case, the stellar luminosity of the low mass stars does not provide enough energy to explain the observed flux levels. Our models show that a UV excess (fUV = 0.1), which can originate either from a chromosphere or from ongoing accretion, can provide this extra energy and reproduce the observed fluxes. X-ray heating is an alternative process for T Tauri discs (Nomura et al. 2007; Gorti & Hollenbach 2008; Aresu et al. 2011).
 |
Fig. 5 Mean gas temperature of oxygen (see Eq. (1)) for all models. Colour coded is the stellar luminosity. |
 |
Fig. 6 Mean gas temperature of oxygen (see Eq. (1)) for all models. Colour coded is the disc gas mass in three bins representing optically thin disc models, disc models in the transition from thin to thick, and optically thick disc models. |
 |
Fig. 7 Ratio of gas and dust temperatures of neutral oxygen as a function of the dust settling parameter (s = 0 – without settling, s = 0.5 – with settling). This ratio is a measure of the temperature de-coupling in the disc surface. |
Figure 7 shows the impact of dust settling on the coupling of gas and dust temperature for the regions in which atomic oxygen dominates. Since atomic oxygen is widely distributed in the disc, we can take this to first order as an estimate of the amount of thermal gas-dust de-coupling. Well mixed models, s = 0, show a fairly narrow peak around Tg = Td and a tendency to have gas temperatures higher than dust temperatures (often in the form of a hot surface gas layer). The settled models, s = 0.5, show on average gas temperatures that are lower than those of the dust. This is not due to the presence of cool surface layers in settled models (see Sect. 3.6); the mass averaged O i gas temperature is hardly affected and so the reason lies in the average dust temperature. In settled models, only the small grains stay behind in the disc surface, while the larger ones settle towards the midplane (see Table A.1). Hence, the effective grain size in the surface of settled models is smaller compared to non-settled models, thereby decreasing the dust emissivity at long wavelength. This leads to slightly warmer dust.
3.4. CO gas temperatures
 |
Fig. 8 Mean gas temperature of CO (see Eq. (1)) for all models. Colour coded is the outer radius Rout. |
 |
Fig. 9 Mean gas temperature of CO (see Eq. (1)) for all models. Colour coded is the surface density power law exponent ϵ. |
Figures 8 and 9 show the distribution of CO mass averaged gas temperatures in the disc models as a function of the outer radius and the surface density power law index. Given our choice of surface density power laws, it is evident that the CO mass is dominated by the material close to the outer radius. Since the gas temperature is also a clear function of distance, models with larger outer radius show on average lower CO gas temperatures. Figure 8 also illustrates the limitations of the concept of a single canonical CO temperature TCO to convert submm line fluxes into disc gas masses. We will get back to this point when looking for possibilities to estimate disc gas masses from line fluxes in Sects. 5.2 and 5.3. The surface density power law exponent also impacts the distribution of mass in the disc. Hence, models with a low ϵ put more mass in the outer disc compared to the inner disc; hence, they show on average lower CO gas temperatures. In addition, the trends with luminosity and disc mass found for oxygen, hold also for CO.
 |
Fig. 10 Difference between average gas temperatures of atomic oxygen and CO for all models. Colour coded is the dust-to-gas mass ratio. |
For a high percentage of models, the average gas temperatures for atomic oxygen and CO are very similar. Except for the lowest mass discs, both temperatures are within a factor two of each other. This also holds across all gas-to-dust mass ratios as can be seen from Fig. 10.
3.5. Ionized carbon in discs
Ionized carbon forms a thin skin on the disc surface with a typical column density of 1017−18 cm-2. Very low mass disc models, Mgas ≤ 10-5 M⊙, are so optically thin that carbon is fully ionized throughout the disc resulting in a constant M(C + )/Mgas fraction of ~1.2 × 10-3. This is only weakly dependent on detailed disc parameters.
As soon as the ionizing UV radiation is blocked by sufficient dust opacity, carbon turns atomic and subsequently molecular. The higher mass models show thus a decreasing fractional C+ mass, with the total M(C+) levelling off at ~10-8 M⊙. The variation between models can be an order of magnitude mostly depending on the choice of disc extension and stellar luminosity (Fig. 11): the C+ mass is higher for larger outer disc radii and higher luminosity stars. The gas residing in the outer disc is generally more optically thin – also to interstellar UV radiation – than the gas in the inner disc regions.
 |
Fig. 11 Mass of ionized carbon as a function of total disc gas mass. Colour coded is the outer disc radius. |
 |
Fig. 12 Mean gas temperature of ionized carbon (see Eq. (1)) for all models. Color coded is the stellar luminosity. |
The dependency of the C+ gas temperatures on stellar luminosity is less pronounced than for atomic oxygen. The distribution has a strong peak at low temperatures around 20 K except for luminosities L∗ > 3.6 L⊙ (Fig. 12). There is a clear dependency on the outer radius similar to CO, with large models (Rout = 300,500 AU) having an average C+ gas temperature of  K. The small models (Rout = 100 AU) show a much broader flat distribution between 25 and 100 K. The reason is that the C+ mass averaged temperature is dominated by the outermost regions – just as for CO – since it is evenly distributed over the entire disc surface. Hence, the inner radius plays no significant role here.
K. The small models (Rout = 100 AU) show a much broader flat distribution between 25 and 100 K. The reason is that the C+ mass averaged temperature is dominated by the outermost regions – just as for CO – since it is evenly distributed over the entire disc surface. Hence, the inner radius plays no significant role here.
3.6. Cool surface layers
A subset of DENT grid models shows very cool surface layers on top of warmer midplanes, i.e. models with a positive gas temperature gradient (as seen from the surface). These are very flat, massive discs in which the grains have started to settle. Typical models in this category show Mgas ≥ 0.01 M⊙, no UV excess, settled dust (s = 0.5) and are non-flaring (β = 0.8,1.0). These models appear here for the first time because of the wide unbiased parameter study.
A related effect has been seen earlier in models by Aikawa & Nomura (2006) who studied grain growth in disc models that do solve iteratively for the vertical hydrostatic equilibrium. For well mixed models with a large maximum grain size amax, those authors find a similar effect. Photoelectric heating is diminished in those models resulting in lower gas temperatures in the disc atmosphere. On the other hand, optical depth is reduced as well allowing stellar UV photons to penetrate deeper and heat the gas and dust at intermediate heights. The authors also find that discs with larger amax flare less than those with small molecular cloud like grain size distributions. This is an immediate result of the lower gas temperatures in the surface layers. For their largest maximum grain size amax = 10 cm, they find that the gas in the disc atmosphere becomes cooler than the dust. In a subsequent paper Nomura et al. (2007) included the effect of grain settling and X-ray heating and show that – compared to the standard well-mixed model with molecular cloud like grains – this indeed lowers the gas temperature in the surface and increases the gas and dust temperatures close to the midplane. The gas temperature gradient becomes much flatter, but there is no pronounced positive temperature gradient. Unfortunately we cannot disentangle from their published model the effect of additional gas heating by X-rays and decrease in gas photoelectric heating due to dust growth and settling.
Jonkheid et al. (2007) have studied a series of four Herbig discs with an increasing gas-to-dust mass ratio due to grain growth and settling. The basic dust disc models are taken from Dullemond & Dominik (2004), who use the dust midplane temperature to set the scale height of the disc. Jonkheid et al. (2007) do not iterate the vertical structure based on the gas temperature and so their approach is somewhat similar to our choice of parametrized disc models. They find that a large amount of the disc gas mass is indeed cooler than the dust and that the highest gas-to-dust mass ratios lead indeed to a positive gradient in the vertical gas temperature.
In nature, we do not expect such flat, massive discs, with strong settling to be very common. However, the presence of such cool surface layers would have implications for the disc surface chemical composition and line emission. At cold temperatures, neutral-neutral chemistry becomes inefficient and the formation of warm water in the disc surface could be affected. Self-absorption in the dominant cooling line [O i] 63 μm (see Sect. 4.3) and temperature gradients as measured from various 12CO and 13CO lines could reveal such cool surfaces.
 |
Fig. 13 Statistical distribution of [C ii] 158 μm emission as a function of disc gas mass. Color codes is the logarithmic disc gas mass. |
4. Line diagnostics
In the following sections, we explore the diagnostic power of individual emission lines from the DENT grid. We check especially for clean dependencies on disc input parameters such as outer radius, disc mass, dust-to-gas mass ratio, surface density power law exponent etc.
4.1. The C+ fine structure line at 158 μm
Since ionized carbon originates from a thin skin around the discs, its mass (column densities) tends to be constant until the disc gas mass itself becomes so low that the disc is transparent to UV photons. The total [C ii] 158 μm flux correlates well with the mass in C+ indicating that the line is mostly optically thin.
Figure 13 illustrates this effect nicely through the statistical distribution of [C ii] 158 μm fluxes as a function of disc mass. Down to disc masses of 10-4 M⊙, the discs stay optically thick and the C+ mass fraction and hence its emission stays constant around ~3 × 10-18 W/m2. The large width of the flux distribution for these models reflects the spread in stellar luminosity, UV excess, outer disc radius, flaring angle; the higher fluxes results from models with high luminosities (stellar and/or UV – see Fig. 14), large outer radii, and flaring geometry. The [C ii] line flux depends only weakly on the disc surface density gradient, the gas-to-dust mass ratio, settling, the minimum grain radius amin, and the inner disc radius. For lower gas masses, the peak of the [C ii] distribution shifts towards lower fluxes and the distribution becomes much narrower.
 |
Fig. 14 [C ii] 158 μm fluxes as a function of stellar luminosity for disc models with Mgas > 10-5 M⊙. Color coded is the UV excess fUV. |
The DENT grid was generated using only two values of UV excess, 10% and 0.1% of the total stellar luminosity. While these values bracket the UV excess observed for young T Tauri stars, it can lead to an overestimate of the UV radiation for Herbig Ae/Be stars that do not possess an excess in the first place. Figure 14 shows that the [C ii] emission increases by an order of magnitude for the high UV models. The Herbig Ae/Be models with pure photospheric UV fluxes would fall even below the red points in Fig. 14.
 |
Fig. 15 Unusual behaviour of the [O i] lines in some disc models. For massive discs with settled dust distribution, the fundamental [O i] 63 μm line may go into central absorption (l.h.s.) whereas the [O i] 145 μm line stays in emission (r.h.s.), which complicates the data interpretation. Model parameters M ⋆ = 2 M⊙, age = 3 Myr, (Teff = 4960 K, L ⋆ = 3.66 L⊙), fUV = 0.001, Mgas = 0.1 M⊙, dust/gas = 0.01, Rin = 17.8 AU, Rout = 500 AU, ϵ = 0.5, β = 1.0, s = 0.5, amin = 1 μm. |
In practice, the [C ii] 158 μm line is easily contaminated by the low density surrounding gas, even with Herschel/PACS. Although the line is potentially a good tracer as shown above, it requires a very careful observational procedure and data reduction to ensure that the flux measured is indeed purely from the disc.
4.2. Oxygen fine structure lines at 63 and 145 μm
In the DENT grid, 80% of the disc models show a 145 μm line that is a factor 10 − 100 weaker than the 63 μm line. Given that the Herschel sensitivity limits for both lines are very similar, this clearly favors the detection of the 63 μm line.
Woitke et al. (2010) have shown that the 63 μm fine structure line could be promising as an order of magnitude disc gas mass estimator. Their Fig. 4 illustrates that if we can estimate the average excitation temperature of neutral oxygen, the measurement of the 63 μm line can be used to derive gas masses in the context of a statistical analysis of a large sample of discs such as the GASPS sample.
4.3. The [O i] 63/145 line ratio
In PDRs, low [O i] line ratios ( < 10) are expected if both lines are optically thick (Tielens & Hollenbach 1985) and the gas is cooler than ~200 K. Liseau et al. (2006) argue that confusion with cool envelope gas might explain ratios of a few in observations of YSO’s. Lorenzetti et al. (2002) suggested that high optical depths in the [O i] 63 and 145 μm lines can explain the [O i] 63/145 ratios of 2 − 10 observed by ISO/LWS in massive discs around early-type HerbigAeBe stars.
The grid results presented here confirm that the [O i] 63/145 ratios for massive (>10-2 M⊙) discs is of the order of 1 − 10. In our models, we observe that [O i] 63/145 < 10 can be produced by the discs themselves, when [O i] 63 μm is about to go into absorption, whereas [O i] 145 μm is still in emission. As a fundamental line, [O i] 63 μm can go into central absorption if the emitted light has to pass through another cold neutral oxygen layer above, whereas the [O i] 145 μm line practically never goes into absorption. These effects happen for massive discs only, in particular for settled dust distributions, and are strongly dependent on inclination, see Fig. 15 and also Sect. 3.6. The hypothesis that such models exist is a unique testcase for the SOFIA/GREAT instrument that can observe the [O i] 63 μm line with high spectral resolution and thus check for self-absorption within the line profile.
The median [O i] line ratio for the entire DENT grid is 25. Contrary to PDRs, the [O i] 63/145 line ratio of disc models is not sensitive to the average oxygen gas temperature over a wide range of temperatures between 50 and 500 K. The line ratio correlates instead with e.g. the dust-to-gas mass ratio (Fig. 16).
 |
Fig. 16 Statistical distribution of [O i] 63/145 line ratios as a function of the dust-to-gas mass ratio. |
4.4. The CO low J rotational lines
The low J12CO rotational lines are optically thick and arise mainly from the outer disc surfaces. Hence they form an excellent tracer of the outer disc radius. The larger the disc, the larger the emitting surface. The oxygen fine structure line at 63 μm is not affected by the disc outer radius for Rout ≥ 100 AU (Kamp et al. 2010). Figure 17 shows the mean [O i] line flux plotted against the CO 2 − 1 flux with the outer disc radius coded in colour. In this diagram, the disc models clearly separate into small ones with Rout = 100 AU and ones that are larger than 300 AU. This indicates that a combination of the oxygen and CO line can help to remove the outer disc radius degeneracy in measuring disc masses.
Detection limits with current radio telescopes such as APEX or SMA are a few times 10-20 W/m2. With ALMA coming along soon, we will be able to detect much fainter discs down to ~10-22 W/m2. Figure 18 shows the CO 2 − 1 line flux versus the dust continuum at 1.2 mm with the respective ALMA band 6 detection limits. These grid results suggest that ALMA is sensitive enough to detect disc masses of the order of 10-6 M⊙.
 |
Fig. 17 [O i] 63 μm versus 12CO J = 2 − 1 line emission. Colour coded is the outer disc radius with values of 100, 300, and 500 AU. |
 |
Fig. 18 12CO J = 2 − 1 line emission versus continuum flux at 1.2 mm. For discrete intervals in CO line flux and 1.2 mm flux, mean disc masses are calculated from the ensemble of grid models within that bin. The coloured contours show the distribution of these mean disc gas masses. Overplotted are the line and continuum sensitivity limits of ALMA band 6. |
4.5. The [O i] 63/CO 2–1 line ratio
Figure 19 illustrates that the [O i] 63/CO 2 − 1 line ratio correlates with the average oxygen gas temperature in the range 15 − 70 K. If the [O i] 63 μm line is optically thin, it depends on disc gas mass and average oxygen gas temperature (Woitke et al. 2010). The CO 2 − 1 line is always optically thick (down to Mgas ~ 10-4 M⊙) and is therefore a function of the CO gas temperature and disc surface area, i.e. Rout. Using the two lines [O i] 63 μm and CO 2 − 1, we also get a handle of the amount of extra UV radiation irradiating the disc (see Fig. 20).
From Figs. 17, 19 and 20, it becomes clear that this [O i]/CO line ratio captures in a complex way a number of disc properties such as the average gas temperature, the disc outer radius, the flaring index, and the amount of extra UV irradiation (fUV). Thus this line ratio is a powerful means to break the modelling degeneracy and find a suitable method to estimate gas masses even in the case of very few observational constraints. This is especially relevant for large surveys such as GASPS (Dent et al. 2011, in prep.) that contains many objects where only the [O i] 63 μm fine structure line is detected and ancillary data is mostly restricted to SED’s and CO submm lines.
 |
Fig. 19 Histogram of the [O i] 63/CO 2 − 1 line ratio in models with 15 < ⟨ Tg(O) ⟩ < 70 K (60% of all models, see Sect. 3.3). Colour coded is the mass average oxygen gas temperature ⟨ Tg(O) ⟩ . |
 |
Fig. 20 [O i] 63 μm versus 12CO J = 2 − 1 line emission. Color coded is the amount of UV excess, fUV. |
4.6. Water lines
Due to the molecular structure, water emission lines are not only difficult to calculate (non-LTE, population inversion, optical depth effects), but also difficult to interpret in terms of global disc parameters such as gas mass or surface density profiles (Cernicharo et al. 2009). Woitke et al. (2009b) traced the origin of water lines in the discs around Herbig Ae stars back to three main water reservoirs: (1) a main water reservoir in the central midplane out to ~10 AU (containing most of the water mass); (2) a cold water belt at r ≈ 10−100 AU and z/r ≈ 0.05 (originating from desorption of water ice mantles); and (3) a hot water surface layer at distances of 2−25 AU (originating from an active neutral-neutral chemistry at T > 200 K). Water lines that originate deeper in the disc suffer from the problem that gas and dust temperature couple at some fiducial depth, making it potentially impossible to see the line emission above the strong dust continuum (Woitke et al. 2009b; Pontoppidan et al. 2010).
Figure 21 shows that for massive discs (Mgas ≥ 0.01 M⊙), the water lines are generally stronger in the settled models. The effect of dust settling on the water chemistry and line emission is very complex as it affects the available dust surface area, the temperature gradients and the continuum optical depth. Disentangling those effects simply from the grid observables is impossible. Hence, we discuss here two exemplary models to illustrate the general trend displayed in Fig. 21. Picking a settled and non-settled flaring disc model with amin = 1.0 μm (M ∗ = 2 M⊙, Teff = 4960 K, 3.7 L⊙, Rin,out = 17,500 AU, Mgas = 0.1 M⊙, δ = 0.01, ϵ = 0.5, β = 1.0), we find that the dust in the surface layers of the settled model is warmer on average, while the gas temperature barely changes (using Eq. (1) for oxygen, it changes from 13 to 16 K). This was already discussed in Sect. 3.3.
Even though the temperatures are low, there is very little grain surface area available for e.g. H2 or ice formation. The H2 formation on grain surfaces is thus inefficient and atomic hydrogen abundances are high in these settled models. As a consequence of the lack of grain surfaces in the settled model, molecular hydrogen forms via the H− route and the atomic hydrogen abundance stays a factor 100 higher than in the non-settled models. This leads to an efficient cold water formation route driven by radiative association  The relevance of radiative association for cool atomic H regions was already pointed out by Glassgold et al. (2009), but found to be irrelevant for the inner disc structures that they studied. These reactions have low rate coefficients1, but with atomic hydrogen being a factor 100 more abundant in settled models, they dominate the formation route of water. The surface layers (z/r > 0.2) of the settled model show water abundances that are several orders of magnitude higher than those of the unsettled model.
The relevance of radiative association for cool atomic H regions was already pointed out by Glassgold et al. (2009), but found to be irrelevant for the inner disc structures that they studied. These reactions have low rate coefficients1, but with atomic hydrogen being a factor 100 more abundant in settled models, they dominate the formation route of water. The surface layers (z/r > 0.2) of the settled model show water abundances that are several orders of magnitude higher than those of the unsettled model.
 |
Fig. 21 Ortho-H2O 179 μm line flux versus continuum 160 μm flux for massive disc models with Mgas ≥ 0.01 M⊙. Colour coded is the settling parameter: s = 0 denotes homogeneously mixed models, s = 0.5 denotes models in which the dust grains have settled to a smaller scale height |
5. Diagnostic tools
In the following, we discuss a few methods to measure the disc gas masses from gas line observations. It is evident by the way how we set up the parameter space that the DENT grid does not reflect a proper distribution of disc properties, e.g. number of T Tauri versus Herbig discs, distribution of disc masses reflecting disc lifetimes etc. Hence, our aim is not to decide which method is better, but to put the various methods into the context of disc modelling and discuss some of the limitations and uncertainties that become evident if one confronts the simple methods with a wide variety of disc appearances (sizes, flaring indices, gas-to-dust mass ratios, etc.).
The most common technique to estimate disc gas masses has been the use of the mm dust continuum flux. At those wavelengths, the disc is assumed to be optically thin. Hence, the mm-flux should reflect the entire dust mass contained in large grains. The main uncertainties in converting the mm-flux into a total dust and subsequently gas mass are the dust opacities κν ~ κ0(ν/ν0) − β and the dust-to-gas mass ratio δ. An average opacity index β ~ 0.46 has been recently found for the discs in the ρ Ophiuchus star forming region (Ricci et al. 2010); these low values of β (compared to 1.7 for the dust in the interstellar medium) are generally interpreted in terms of grain growth, see also Draine (2006). However, recent interferometric data suggests that β varies with location in the disc (e.g. Isella et al. 2010). The dust-to-gas mass ratio is generally assumed to be the canonical value of δ = 0.01 found for the interstellar medium neglecting potential differences in dust and gas evolutionary timescales. Even if the dust mass could be estimated very precisely, this method would still leave us with large uncertainties on Mgas because of the unknown conversion factor. Hence, the intrinsic uncertainties of this method are much greater than an order of magnitude.
Very few direct estimates of the gas-to-dust mass ratio exist for discs. An example is the study by (Glauser et al. 2008) that estimates dust and gas mass on the same disc line-of-sight in a disc. The derived ratio of  is compatible with the canonical value of 100.
is compatible with the canonical value of 100.
The following three sections discuss potential methods only based on gas emission line fluxes, their limitations, and uncertainties.
5.1. [O i] and [C ii] fine structure line ratios
Figure 22 shows a two-colour line flux diagram suggesting a method how to determine the disc gas mass purely from three line flux observations. As was argued by Kamp et al. (2010), the [O i] 63/145 line ratio shows a clear correlation with gas mass. This plot includes the results for all types of central stars, low and high excess UV, flared and non-flared discs, continuous discs as well as discs with big inner holes, and varying dust parameters and outer disc radii. Despite this variety of disc types, all models with a certain disc gas mass fall into certain regions in this two-colour diagram. Apparently, the main dependencies on fUV and β tend to cancel out here, because these parameters shift all line fluxes up and down equally.
 |
Fig. 22 Two colour line flux diagram, [O i] 63/145 versus [O i] 63/[C ii] 158, of a sub-selection of 10 740 DENT models with ρd/ρg = 0.01, ϵ = 0.5, s = 0.5, inclination angle 41°. Colour coded is the disc gas mass. |
However, the diagram looks different for other sub-selections of models as the one stated in the caption of Fig. 22. A steeper surface density power law (higher ϵ) weakens in particular the [C ii] 158 μm flux and hence shifts the points rightward in the figure.
Selecting only settled models has shifted the location of massive models (Mgas ≥ 0.01 M⊙) downward in Fig. 22 compared to a similar plot for unsettled models. The reason for this is mainly [O i] 63 μm self-absorption in the cool surface layers as discussed in Sect. 3.6.
In addition, there are other parameters such as the outer disc radius Rout and the dust size parameters, which introduce additional non-trivial dependencies and also a large scatter in the various mass bins. Thus a mass determination exclusively based on these three line ratios would implicate large errors especially for the higher mass disc models.
5.2. Low J CO lines
For many objects, the [O i] 145 and [C ii] 158 μm lines will not be available as they are often at least a factor 10 fainter than the [O i] 63 μm line. Therefore, we study in the following also the CO low J lines that are accessible from the ground. Especially with ALMA coming up, these lines will be detectable for a large number of discs (see Sect. 4.4).
The low J12CO lines are often optically thick and can hence provide at most a lower limit to the total gas mass. Dent et al. (2005) present a formula to convert the CO 3−2 line flux ICO 3−2 into a gas mass assuming LTE and a constant 12CO/H2 conversion factor of 5 × 10-5. We adopt here their approach and derive a relation between gas mass and intensity  (4)where ICO 3 − 2 is the integrated CO 3 − 2 line intensity in K km s-1. Since most of the CO mass will reside in the outer disc, the line flux will be dominated by cold gas. Hence, an average gas excitation temperature of Tex = 50 K is assumed in the following estimates. To apply Eq. (4) to our grid data, we need to convert the modeled integrated line fluxes in W/m2 to K km s-1 (formula adapted from Thi et al. 2004)
(4)where ICO 3 − 2 is the integrated CO 3 − 2 line intensity in K km s-1. Since most of the CO mass will reside in the outer disc, the line flux will be dominated by cold gas. Hence, an average gas excitation temperature of Tex = 50 K is assumed in the following estimates. To apply Eq. (4) to our grid data, we need to convert the modeled integrated line fluxes in W/m2 to K km s-1 (formula adapted from Thi et al. 2004)  (5)Here, λ = 8.6696 × 10-2 cm and k is the Boltzman constant in erg/K. The solid angle is assumed to be Ω = π(HPBW/2)2, with HPBW = 13.7′′ the half power beamwidth of the JCMT at 345 GHz. The formulas for the CO 2−1 line look similar; however, the line is generally a factor 2.6 weaker than the CO 3−2 line reflecting the difference in the Planck function (ν3−2/ν2 − 1)3.
(5)Here, λ = 8.6696 × 10-2 cm and k is the Boltzman constant in erg/K. The solid angle is assumed to be Ω = π(HPBW/2)2, with HPBW = 13.7′′ the half power beamwidth of the JCMT at 345 GHz. The formulas for the CO 2−1 line look similar; however, the line is generally a factor 2.6 weaker than the CO 3−2 line reflecting the difference in the Planck function (ν3−2/ν2 − 1)3.
We insert our modeled fluxes first into Eq. (5) and then the converted intensities into Eq. (4) to derive a gas mass estimate. These derived values underestimate the actual gas mass, especially at the high mass end, where the CO 3−2 line is optically thick. Figure 23 shows that the behaviour is much more complex and that there is a regime, where the simple formula even overestimates the disc gas mass, most likely due to the simplified assumption of a uniform excitation temperature of 50 K for all models. Most notably, the standard deviation across all disc parameters for this method to measure disc gas mass is large, generally more than two orders of magnitude.
 |
Fig. 23 Correlation between the gas mass estimated from the modeled CO 3 − 2 line fluxes (Eqs. (4) and (5)) and the original input gas mass of the models. The blue dots are the mean estimated gas masses and the error bar denotes the standard deviation. The red solid line is the expected correlation together with the dashed lines that denote an uncertainty of one order of magnitude. |
5.3. The [O i] 63/CO 2–1 line ratio
We proceed thus to suggest here an alternative approach using the insight on the diagnostic power of the [O i] 63/CO 2−1 line ratio from the previous sections. Figure 24 shows for each bin of [O i] 63/CO 2−1 line ratios the resulting fit using a 3rd order polynomial. The coefficients for these polynomial fits are presented in Table 2. In the following, we check how accurate the disc masses derived from a combination of these two lines are.
 |
Fig. 24 Correlation between the gas mass in the disc and the [O i] 63 μm line. The second relevant parameter, the average gas temperature, is colour coded through the [O i] 63/CO 2 − 1 line ratio. A selection is made for CO 2 − 1 fluxes greater than 10-23 W m-2. The coloured lines are polynomial fits of 3rd order to the data. |
Coefficients for the polynomial fit of Mgas as a function of [O i] 63 μm flux F [O I] and the [O i] 63/CO 2 − 1 line ratio: ![\hbox{$M_{\rm gas} = a_0 + a_1 F_{\rm [O\,I]} + a_2 F^2_{\rm [O\,I]} + a_3 F^3_{\rm [O\,I]}$}](/articles/aa/full_html/2011/08/aa16399-10/aa16399-10-eq159.png) .
.
For every model, we calculate the [O i] 63/CO 2−1 line ratio and then select the corresponding curve from Fig. 24. This curve in combination with the calculated [O i] 63 μm flux results in a “measured” disc gas mass. This value is then compared to the actual gas mass in the models (Fig. 25). The standard deviation indicates that this method can provide an order of magnitude estimate of the disc gas mass. The method does frequently overestimate the disc gas mass by a factor two. Figure 25 also shows that the relation levels off at disc masses beyond 10-3 M⊙ where the [O i] 63 μm line becomes optically thick.
 |
Fig. 25 Correlation between the gas mass estimated (or “measured”) from a combination of the [O i] 63 μm line flux and the [O i] 63/CO 2−1 line ratio and the input gas mass of the disc. The blue dots are the mean “measured” gas masses and the error bar denotes the standard deviation. The red solid line is the expected correlation together with the dashed lines that denote an uncertainty of one order of magnitude. |
For a large statistical sample in which individual disc parameters are less well known, this method can indeed help to assess gas evolution in discs and to measure the gas dispersal timescale. The errors of this method are much smaller than the ones from the CO 3−2 line alone. Of course, more observational constraints on any object should naturally lead to more accurate measurements.
6. Conclusions
We have calculated a grid of 300 000 disc models using the dust Monte Carlo radiative transfer code MCFOST and the gas chemistry and heating/cooling balance code ProDiMo. These models span an 11-dimensional parameter space and enable us to study disc properties such as temperatures, species masses, gas line fluxes, and dust continuum fluxes in a statistical manner. The goal is to find suitable gas diagnostics that allow us to characterize the main disc parameters such as radial extent, gas mass, and flaring from observational quantities.
The main results found from an extensive statistical analysis of the entire DENT model grid are:
-
The[O i] 63 μm traces disc mass but for massive non-flaring, settled disc models without UV excess, the line is optically thick and often suffers from self-absorption in upper cool disc layers.
-
The [C ii] 158 μm fine structure line flux is very sensitive to the stellar UV flux and presence of a UV excess.
-
The CO low rotational lines trace the outer disc radius.
-
Dust settling enhances the water abundance in the surface layers through an efficient radiative association channel. The initial step of H2 formation proceeds in the gas phase via H−.
-
Low [O i] 63/145 line ratios (<a few) can be explained with cool gas in the uppermost surface layers instead of 63 μm absorption by cool envelope remnant gas as suggested by Liseau et al. (2006).
-
The [O i] 63/CO 2−1 line ratio correlates with several disc properties such as the average O i gas temperature in discs, the outer disc radius, and the UV excess. As such it is a powerful diagnostic to break disc modelling degeneracies.
-
A combination of the [O i] 63 μm flux and the [O i] 63/CO 2−1 line ratio can be used for Mgas ≤ 10-3 M⊙ to obtain an order of magnitude estimate for the disc gas mass purely from gas observations. The previously used conversion of a CO submm line flux alone generally leads to larger uncertainties.
The UMIST rates are k(H + O) = 9.90 × 10-19(T/ 300 K)-0.38 cm3 s-1, and k(H + OH) = 5.26 × 10-18(T/ 300 K)-5.22exp(90/T) cm3 s-1 (Field et al. 1980).
Acknowledgments
F.M., C.P., W.F.T., and J.C.A. acknowledge PNPS, CNES and ANR (contract ANR-07-BLAN-0221) for financial support. C.P. acknowledges funding from the European Comission seventh Framework Program (contracts PIEF-GA-2008-220891 and PERG06-GA-2009-256513). I.K. acknowledges funding from an NWO MEERVOUD grant.
References
- Aikawa, Y., & Nomura, H. 2006, ApJ, 642, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Aikawa, Y., van Zadelhoff, G. J., van Dishoeck, E. F., & Herbst, E. 2002, A&A, 386, 622 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aresu, G., Kamp, I., Meijerink, R., et al. 2011, A&A, 526, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, K. L., Berrington, K. A., & Thomas, M. R. J. 1998, MNRAS, 293, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Bjorkman, J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Brott, I., & Hauschildt, P. H. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 565 [Google Scholar]
- Cernicharo, J., Ceccarelli, C., Ménard, F., Pinte, C., & Fuente, A. 2009, ApJ, 703, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Chambaud, G., Levy, B., Millie, P., et al. 1980, J. Phys. B At. Mol. Phys., 13, 4205 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- D’Alessio, P., Canto, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Dent, W. R. F., Greaves, J. S., & Coulson, I. M. 2005, MNRAS, 359, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2006, ApJ, 636, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Dubernet, M., & Grosjean, A. 2002, A&A, 390, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2004, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., van Zadelhoff, G. J., & Natta, A. 2002, A&A, 389, 464 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faure, A., Crimier, N., Ceccarelli, C., et al. 2007, A&A, 472, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Field, D., Adams, N. G., & Smith, D. 1980, MNRAS, 192, 1 [NASA ADS] [Google Scholar]
- Flower, D. R. 2001, J. Phys. B, 34, 2731 [Google Scholar]
- Flower, D. R., & Launay, J. M. 1977, J. Phys. B At. Mol. Phys., 10, 3673 [Google Scholar]
- Glassgold, A. E., Meijerink, R., & Najita, J. R. 2009, ApJ, 701, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Glauser, A. M., Ménard, F., Pinte, C., et al. 2008, A&A, 485, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., Swinyard, B., & Spica/Safari Science Team 2009, in SPICA joint European/Japanese Workshop, held 6 − 8 July, at Oxford, United Kingdom, ed. A. M. Heras, B. M. Swinyard, K. G. Isaak, & J. R. Goicoechea, EDP Sciences, 02002 [Google Scholar]
- Gorti, U., & Hollenbach, D. 2004, ApJ, 613, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2008, ApJ, 683, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Green, S., Maluendes, S., & McLean, A. D. 1993, ApJS, 85, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., Semenov, D., Guilloteau, S., et al. 2010, ApJ, 714, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Carpenter, J. M., & Sargent, A. I. 2010, ApJ, 714, 1746 [NASA ADS] [CrossRef] [Google Scholar]
- Jankowski, P., & Szalewicz, K. 2005, JChPh 123, 10, 104301 [Google Scholar]
- Jaquet, R., Staemmler, V., Smith, M. D., & Flower, D. R. 1992, J. Phys. B At. Mol. Phys., 25, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Jonkheid, B., Faas, F. G. A., van Zadelhoff, G.-J., & van Dishoeck, E. F. 2004, A&A, 428, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jonkheid, B., Dullemond, C. P., Hogerheijde, M. R., & van Dishoeck, E. F. 2007, A&A, 463, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamp, I., & Dullemond, C. P. 2004, ApJ, 615, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Kamp, I., Tilling, I., Woitke, P., Thi, W., & Hogerheijde, M. 2010, A&A, 510, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Launay, J. M., & Roueff, E. 1977, A&A, 56, 289 [NASA ADS] [Google Scholar]
- Liseau, R., Justtanont, K., & Tielens, A. G. G. M. 2006, A&A, 446, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lorenzetti, D., Giannini, T., Nisini, B., et al. 2002, A&A, 395, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 1999, A&A, 345, 211 [NASA ADS] [Google Scholar]
- Meijerink, R., Glassgold, A. E., & Najita, J. R. 2008, ApJ, 676, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Nomura, H., & Millar, T. J. 2005, A&A, 438, 923 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Nomura, H., Aikawa, Y., Tsujimoto, M., Nakagawa, Y., & Millar, T. J. 2007, ApJ, 661, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Pinte, C., Ménard, F., Duchêne, G., & Bastien, P. 2006, A&A, 459, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Harries, T. J., Min, M., et al. 2009, A&A, 498, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinte, C., Woitke, P., Ménard, F., et al. 2010, A&A, 518, L126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Blake, G. A., et al. 2010, ApJ, 720, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Kessler, J. E., Koerner, D. W., Sargent, A. I., & Blake, G. A. 2003, ApJ, 597, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Wilner, D. J., Aikawa, Y., Blake, G. A., & Hogerheijde, M. R. 2008, ApJ, 681, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., & Brooks, K. J. 2010, A&A, 521, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semenov, D., Pavlyuchenkov, Y., Schreyer, K., et al. 2005, ApJ, 621, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] [Google Scholar]
- Thi, W.-F., van Zadelhoff, G.-J., & van Dishoeck, E. F. 2004, A&A, 425, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Tuthill, P. G., Monnier, J. D., & Danchi, W. C. 2001, Nature, 409, 1012 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Plas, G., van den Ancker, M. E., Waters, L. B. F. M., & Dominik, C. 2011, A&A, submitted [Google Scholar]
- Wernli, M., Valiron, P., Faure, A., et al. 2006, A&A, 446, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, N. J., & Bell, K. L. 2002, MNRAS, 337, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W.-F. 2009a, A&A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Thi, W.-F., Kamp, I., & Hogerheijde, M. R. 2009b, A&A, 501, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Pinte, C., Tilling, I., et al. 2010, MNRAS, 405, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., Riaz, B., Duchene, G., et al. 2011, A&A, in press [arXiv:1103.5309] [Google Scholar]
- Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The DENT grid
The general outline of our numerical pipeline is described in Woitke et al. (2010) (see their Fig. 1). In the first step, MCFOST is used to compute the dust temperature Tdust(r,z) and frequency dependent radiation field Jν(r,z) from radiative transfer. This information is passed on in the second step to ProDiMo to compute the detailed gas chemistry nmol(r,z) and temperature Tgas(r,z). The resulting gas structure together with the non-LTE level population numbers of the relevant species is inserted back into MCFOST to do the line radiative transfer and calculate the line profiles and integrated fluxes (step 3). In a second radiative transfer step, dust spectral energy distributions (SED) are calculated for all models (step 4).
Parameters for the model grid and values assumed.
A.1. Parametrized disc models
For the shape and mass distribtion of the gas in the disc, we use the following parametric description  (A.1)between an inner and outer disc radius, Rin and Rout, respectively, with sharp edges. ρ(r,z) is the local gas mass density. The constant ρ0 is adjusted such that the integrated disc mass 2π ! ρ(x,z) dz r dr equals Mdisc. H(r) is the vertical scale height of the disc, assuming to vary with radius as
(A.1)between an inner and outer disc radius, Rin and Rout, respectively, with sharp edges. ρ(r,z) is the local gas mass density. The constant ρ0 is adjusted such that the integrated disc mass 2π ! ρ(x,z) dz r dr equals Mdisc. H(r) is the vertical scale height of the disc, assuming to vary with radius as  (A.2)H0 is the reference scale height at reference radius r0. ϵ is the column density powerlaw index and β the flaring power.
(A.2)H0 is the reference scale height at reference radius r0. ϵ is the column density powerlaw index and β the flaring power.
Stellar parameters of the model grid interpolated from Siess et al. (2000) for solar metallictities.
The dust grains are assumed have a unique powerlaw size distribution  (A.3)between minimum grain radius amin and maximum grain radius amax. The free constant in Eq. (A.3) is adjusted to result in the specified dust/gas mass ratio ρd/ρ (see Sect. 4.6 in Woitke et al. 2009a), which is assumed to be constant throughout the model volume (e.g. no dust settling). The dust absorption and scattering opacities are calculated by applying Mie theory with optical constants for astronomical silicate from Draine & Lee (1984). The DENT grid comprises also models with dust setlling, although that particular parameter is only sampled by the two extremes of non-settled models and models in which grains larger than 0.05 μm have settled to a smaller scale height than the gas, H(r,a) ≈ H(r)(a/0.05 μm)-0.25 (for s = 0.5).
(A.3)between minimum grain radius amin and maximum grain radius amax. The free constant in Eq. (A.3) is adjusted to result in the specified dust/gas mass ratio ρd/ρ (see Sect. 4.6 in Woitke et al. 2009a), which is assumed to be constant throughout the model volume (e.g. no dust settling). The dust absorption and scattering opacities are calculated by applying Mie theory with optical constants for astronomical silicate from Draine & Lee (1984). The DENT grid comprises also models with dust setlling, although that particular parameter is only sampled by the two extremes of non-settled models and models in which grains larger than 0.05 μm have settled to a smaller scale height than the gas, H(r,a) ≈ H(r)(a/0.05 μm)-0.25 (for s = 0.5).
Table A.1 summarizes the free parameters in the DENT grid. For completeness, it also contains the fixed parameters r0, H0, χISM, ζCR, fPAH, α, amax, ρgr, and vturb.
Effective temperature and luminosity are related parameters and are consistently chosen from the evolutionary tracks of pre-main sequence stars (Siess et al. 2000) for solar metallicities. Table A.2 lists the parameter combinations chosen for the representative five stellar masses 0.5, 1.0, 1.5, 2.0, and 2.5 M⊙. Disc models are calculated at four stellar evolutionary times, 1, 3, 10, and 100 Myr. The stellar input spectra are interpolated from Phoenix stellar atmosphere models (Brott & Hauschildt 2005) with solar metallicities.
At UV wavelengths, however, where stellar activity and mass accretion create an UV excess with respect to the classical stellar atmosphere models, we switch to a powerlaw UV input spectrum with spectral intensity [erg/cm2/s/Å/sr]  (A.4)The flux is scaled to yield the prescribed fractional UV luminosity of fUV = LUV/L ⋆ = 0.1 (high UV) or 0.001 (low UV) with the UV luminosity LUV being integrated from 912 Å to 2500 Å as introduced by Woitke et al. (2010). Very few stars have a well known fUV (given the wavelength range defined above and the gaps in observational data of e.g. STIS and FUSE). One of the few stars is ET Cha, which has a value of 0.02 (Woitke et al. 2011).
(A.4)The flux is scaled to yield the prescribed fractional UV luminosity of fUV = LUV/L ⋆ = 0.1 (high UV) or 0.001 (low UV) with the UV luminosity LUV being integrated from 912 Å to 2500 Å as introduced by Woitke et al. (2010). Very few stars have a well known fUV (given the wavelength range defined above and the gaps in observational data of e.g. STIS and FUSE). One of the few stars is ET Cha, which has a value of 0.02 (Woitke et al. 2011).
A.2. The observables
The quantities that can be compared to observations such as the gas line emission and dust SED are computed in step 3 and 4 of the grid modelling procedure (see introduction to Sect. 2). All quantities are computed for 5 different inclinations that are uniformly distributed, 0o, 41.41o, 60o, 75.52o, and 90o (edge-on).
The dust SED is computed at 57 wavelength points between 0.1 and 3500 μm. The line profiles and integrated fluxes of four species are computed: C ii, O i, CO, and H2O (ortho and para). Table A.3 provides an overview of the respective atomic/molecular line data.
Atomic and molecular data for lines calculated in the DENT grid.
A.3. Disc stability
We choose here the Toomre criterium to check our disc models against gravitational instabilities. The Toomre Q parameter is defined as 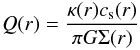 (A.5)where cs is the sound speed, Σ the surface density, G the gravitational constant and the epicyclic frequency κ is defined as
(A.5)where cs is the sound speed, Σ the surface density, G the gravitational constant and the epicyclic frequency κ is defined as  (A.6)with Ω the orbital frequency. The disc is unstable at a certain distance r from the star if Q(r) < 1. In the following, we derive an expression that provides a simple analytical way of checking “global” disc instability. For that, we make a few simplifying assumptions
(A.6)with Ω the orbital frequency. The disc is unstable at a certain distance r from the star if Q(r) < 1. In the following, we derive an expression that provides a simple analytical way of checking “global” disc instability. For that, we make a few simplifying assumptions
-
1.
The discs rotate with keplerian frequency
 , hence κ(r) = Ωkep(r).
, hence κ(r) = Ωkep(r). -
2.
The midplane gas temperature can be approximated by a radial power law T = T0(r/Rin)-0.5.
We will discuss the impact of these simplifications further below.
Inserting the power laws for temperature and surface density into Eq. (A.5), we obtain  (A.7)Here T0 and Σ0 denote the gas temperature and surface density at the inner radius of the disc Rin. Since for our values of ϵ (0.5, 1.0, 1.5) Q(r) decreases with radius, disc models that obey Q > 1 at the outer radius are also stable at smaller radii. Hence, in the following, we derive an expression for Q at r = Rout, which can be used to determine the global stability of a disc model.
(A.7)Here T0 and Σ0 denote the gas temperature and surface density at the inner radius of the disc Rin. Since for our values of ϵ (0.5, 1.0, 1.5) Q(r) decreases with radius, disc models that obey Q > 1 at the outer radius are also stable at smaller radii. Hence, in the following, we derive an expression for Q at r = Rout, which can be used to determine the global stability of a disc model.
The surface density and temperature at the inner radius can be derived from the total disc gas mass Mdisc and the luminosity and effective temperature of the central star L ∗ , Teff (Tuthill et al. 2001; van der Plas et al. 2011) 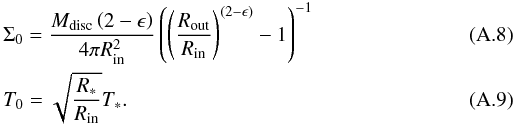 Using these, we can rewrite Eq. (A.7) entirely in terms of the input parameters of the DENT grid
Using these, we can rewrite Eq. (A.7) entirely in terms of the input parameters of the DENT grid  (A.10)We apply this criterium to all 322 030 disc models and find that only 16 422 of them are unstable according to the above derived criterium. Hence, 94% of all models are not affected by gravitational instabilities. This percentage changes by less than 1% if we (a) choose a more realistic temperature profile for optically thick discs T ~ (r/Rin)-0.25 or (b) change T0 by a factor 2. The fact that Q(r) decreases with r still holds for T ~ (r/Rin)-0.25. Overall, we find that models with high gas disc masses – as expected – are more subject to instabilities. However, even in our highest mass bin the percentage of unstable models is only ~ 30%. The plots and conclusions of the analysis of the DENT grid are not affected by the small number of models that could become unstable.
(A.10)We apply this criterium to all 322 030 disc models and find that only 16 422 of them are unstable according to the above derived criterium. Hence, 94% of all models are not affected by gravitational instabilities. This percentage changes by less than 1% if we (a) choose a more realistic temperature profile for optically thick discs T ~ (r/Rin)-0.25 or (b) change T0 by a factor 2. The fact that Q(r) decreases with r still holds for T ~ (r/Rin)-0.25. Overall, we find that models with high gas disc masses – as expected – are more subject to instabilities. However, even in our highest mass bin the percentage of unstable models is only ~ 30%. The plots and conclusions of the analysis of the DENT grid are not affected by the small number of models that could become unstable.
A.4. Methodology
The high number of disc models makes it impossible to carry out an individual study of their chemical and thermal structure. Hence in the following, we study the statistics of species gas temperatures and masses and how they depend on certain grid parameters such as the surface density distribution and settling.
For the statistical analysis, we define a scalar quantity Xi of any model i. It can be a parameter, or can be a measured value like the total mass of atomic oxygen M(O) of model i. Next, we select an interval on which we perform the statistics [Xk − dx/2,Xk + dx/2], where Xk are sampling points for X. The total number of models (selected i) in that selected range are Nsel. The expected value and standard deviation of the distribution are then defined as 
All Tables
Maximum possible fraction of total disc mass for selected species Xsp assuming all carbon or oxygen are locked into that species.
Coefficients for the polynomial fit of Mgas as a function of [O i] 63 μm flux F [O I] and the [O i] 63/CO 2 − 1 line ratio: ![\hbox{$M_{\rm gas} = a_0 + a_1 F_{\rm [O\,I]} + a_2 F^2_{\rm [O\,I]} + a_3 F^3_{\rm [O\,I]}$}](/articles/aa/full_html/2011/08/aa16399-10/aa16399-10-eq159.png) .
.
Stellar parameters of the model grid interpolated from Siess et al. (2000) for solar metallictities.
All Figures
 |
Fig. 1 The atomic oxygen mass fraction X(O) = M(O)/Mgas for all disc models with Mgas ≥ 10-7 M⊙. Colour coded is the total disc gas mass. Note that the y-axis is logarithmic. |
| In the text | |
 |
Fig. 2 The CO gas mass fraction X(CO) = M(CO)/Mgas for all disc models with Mgas ≥ 10-7 M⊙. Colour coded is the total disc gas mass. |
| In the text | |
 |
Fig. 3 The CO gas mass fraction X(CO) = M(CO)/Mgas for all disc models. Colour coded is the dust-to-gas mass ratio. |
| In the text | |
 |
Fig. 4 The H2O mass fraction X(H2O) = M(H2O)/Mgas for disc models with an inner radius equal the sublimation radius. Colour coded is the surface density power law index ϵ. |
| In the text | |
 |
Fig. 5 Mean gas temperature of oxygen (see Eq. (1)) for all models. Colour coded is the stellar luminosity. |
| In the text | |
 |
Fig. 6 Mean gas temperature of oxygen (see Eq. (1)) for all models. Colour coded is the disc gas mass in three bins representing optically thin disc models, disc models in the transition from thin to thick, and optically thick disc models. |
| In the text | |
 |
Fig. 7 Ratio of gas and dust temperatures of neutral oxygen as a function of the dust settling parameter (s = 0 – without settling, s = 0.5 – with settling). This ratio is a measure of the temperature de-coupling in the disc surface. |
| In the text | |
 |
Fig. 8 Mean gas temperature of CO (see Eq. (1)) for all models. Colour coded is the outer radius Rout. |
| In the text | |
 |
Fig. 9 Mean gas temperature of CO (see Eq. (1)) for all models. Colour coded is the surface density power law exponent ϵ. |
| In the text | |
 |
Fig. 10 Difference between average gas temperatures of atomic oxygen and CO for all models. Colour coded is the dust-to-gas mass ratio. |
| In the text | |
 |
Fig. 11 Mass of ionized carbon as a function of total disc gas mass. Colour coded is the outer disc radius. |
| In the text | |
 |
Fig. 12 Mean gas temperature of ionized carbon (see Eq. (1)) for all models. Color coded is the stellar luminosity. |
| In the text | |
 |
Fig. 13 Statistical distribution of [C ii] 158 μm emission as a function of disc gas mass. Color codes is the logarithmic disc gas mass. |
| In the text | |
 |
Fig. 14 [C ii] 158 μm fluxes as a function of stellar luminosity for disc models with Mgas > 10-5 M⊙. Color coded is the UV excess fUV. |
| In the text | |
 |
Fig. 15 Unusual behaviour of the [O i] lines in some disc models. For massive discs with settled dust distribution, the fundamental [O i] 63 μm line may go into central absorption (l.h.s.) whereas the [O i] 145 μm line stays in emission (r.h.s.), which complicates the data interpretation. Model parameters M ⋆ = 2 M⊙, age = 3 Myr, (Teff = 4960 K, L ⋆ = 3.66 L⊙), fUV = 0.001, Mgas = 0.1 M⊙, dust/gas = 0.01, Rin = 17.8 AU, Rout = 500 AU, ϵ = 0.5, β = 1.0, s = 0.5, amin = 1 μm. |
| In the text | |
 |
Fig. 16 Statistical distribution of [O i] 63/145 line ratios as a function of the dust-to-gas mass ratio. |
| In the text | |
 |
Fig. 17 [O i] 63 μm versus 12CO J = 2 − 1 line emission. Colour coded is the outer disc radius with values of 100, 300, and 500 AU. |
| In the text | |
 |
Fig. 18 12CO J = 2 − 1 line emission versus continuum flux at 1.2 mm. For discrete intervals in CO line flux and 1.2 mm flux, mean disc masses are calculated from the ensemble of grid models within that bin. The coloured contours show the distribution of these mean disc gas masses. Overplotted are the line and continuum sensitivity limits of ALMA band 6. |
| In the text | |
 |
Fig. 19 Histogram of the [O i] 63/CO 2 − 1 line ratio in models with 15 < ⟨ Tg(O) ⟩ < 70 K (60% of all models, see Sect. 3.3). Colour coded is the mass average oxygen gas temperature ⟨ Tg(O) ⟩ . |
| In the text | |
 |
Fig. 20 [O i] 63 μm versus 12CO J = 2 − 1 line emission. Color coded is the amount of UV excess, fUV. |
| In the text | |
 |
Fig. 21 Ortho-H2O 179 μm line flux versus continuum 160 μm flux for massive disc models with Mgas ≥ 0.01 M⊙. Colour coded is the settling parameter: s = 0 denotes homogeneously mixed models, s = 0.5 denotes models in which the dust grains have settled to a smaller scale height |
| In the text | |
 |
Fig. 22 Two colour line flux diagram, [O i] 63/145 versus [O i] 63/[C ii] 158, of a sub-selection of 10 740 DENT models with ρd/ρg = 0.01, ϵ = 0.5, s = 0.5, inclination angle 41°. Colour coded is the disc gas mass. |
| In the text | |
 |
Fig. 23 Correlation between the gas mass estimated from the modeled CO 3 − 2 line fluxes (Eqs. (4) and (5)) and the original input gas mass of the models. The blue dots are the mean estimated gas masses and the error bar denotes the standard deviation. The red solid line is the expected correlation together with the dashed lines that denote an uncertainty of one order of magnitude. |
| In the text | |
 |
Fig. 24 Correlation between the gas mass in the disc and the [O i] 63 μm line. The second relevant parameter, the average gas temperature, is colour coded through the [O i] 63/CO 2 − 1 line ratio. A selection is made for CO 2 − 1 fluxes greater than 10-23 W m-2. The coloured lines are polynomial fits of 3rd order to the data. |
| In the text | |
 |
Fig. 25 Correlation between the gas mass estimated (or “measured”) from a combination of the [O i] 63 μm line flux and the [O i] 63/CO 2−1 line ratio and the input gas mass of the disc. The blue dots are the mean “measured” gas masses and the error bar denotes the standard deviation. The red solid line is the expected correlation together with the dashed lines that denote an uncertainty of one order of magnitude. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



