| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201016052 | |
| Published online | 03 March 2011 | |
Collapse, outflows and fragmentation of massive, turbulent and magnetized prestellar barotropic cores
1 Laboratoire de radioastronomie, UMR
8112 du CNRS, École normale supérieure et Observatoire de
Paris, 24 rue
Lhomond, 75231 Paris Cedex
05, France
e-mail: patrick.hennebelle@ens.fr
2 Max Planck Institute for Astronomy,
Königsthul 17,
69117
Heidelberg,
Germany
3 Zentrum für Astronomie der
Universität Heidelberg, Institut für Theoretische Astrophysik,
Albert-Ueberle-Str.
2, 69120
Heidelberg,
Germany
4 Department of Astronomy and
Astrophysics, University of California, Santa Cruz, CA
95064,
USA
5 Department of Astronomy, University
of Florida, Gainesville, FL
32611,
USA
6 Laboratoire AIM, Paris-Saclay,
CEA/IRFU/SAp - CNRS - Université Paris Diderot, 91191
Gif-sur-Yvette Cedex,
France
7 Institute for theoretical Physics,
University of Zürich, 8057
Zürich,
Switzerland
Received: 3 November 2010
Accepted: 28 December 2010
Context. Stars, and more particularly massive stars, have a drastic impact on galaxy evolution. Yet the conditions in which they form and collapse are still not fully understood.
Aims. In particular, the influence of the magnetic field on the collapse of massive clumps is relatively unexplored, it is therefore of great relevance in the context of the formation of massive stars to investigate its impact.
Methods. We perform high resolution, MHD simulations of the collapse of one hundred solar masses, turbulent and magnetized clouds, with the adaptive mesh refinement code RAMSES. We compute various quantities such as mass distribution, magnetic field, and angular momentum within the collapsing core and study the episodic outflows and the fragmentation that occurs during the collapse.
Results. The magnetic field has a drastic impact on the cloud evolution. We find that magnetic braking is able to substantially reduce the angular momentum in the inner part of the collapsing cloud. Fast and episodic outflows are being launched with typical velocities of the order of 1−3 km s-1, although the highest velocities can be as high as 20−40 km s-1. The fragmentation in several objects is reduced in substantially magnetized clouds with respect to hydrodynamical ones by a factor of the order of 1.5−2.
Conclusions. We conclude that magnetic fields have a significant impact on the evolution of massive clumps. In combination with radiation, magnetic fields largely determine the outcome of massive core collapse. We stress that numerical convergence of MHD collapse is a challenging issue. In particular, numerical diffusion appears to be important at high density and therefore could possibly lead to an overestimation of the number of fragments.
Key words: magnetohydrodynamics (MHD) / instabilities / ISM: kinematics and dynamics / ISM: clouds / stars: formation
© ESO, 2011
1. Introduction
It is believed that stars form during the collapse of prestellar cores inside molecular clouds. Understanding this process is of great relevance as it determines the initial conditions of the protostars as well as the properties of accretion disks which form in their vicinity. It is also during this process that the fragmentation, that is the formation of binaries and clusters rather than a single object, may occur. During the last decades, many studies have been investigating the fragmentation of dense cores using either smooth particles hydrodynamic (SPH) based codes or grid codes (see e.g. Matsumoto & Hanawa 2003; Commerçon et al. 2008; or Goodwin et al. 2007, for a review). Until recently, most works have been neglecting the magnetic field and assume an isothermal equation of state until the gas becomes optically thick. Under these conditions, various studies infer that the massive cores fragment into several objects. Simulations like the ones performed by Bonnell et al. (2004), Klessen & Burkert (2000, 2001) and Dobbs et al. (2005) generally find that the number of fragments is comparable with or even exceeds the number of initial Jeans masses within the clouds, which implies that a massive core may result in a cluster that contains tens objects or even more.
Observationally the question as to whether massive cores are fragmented is difficult to investigate because of the large distances at which these objects are located. Preliminary investigations do not appear to show such high levels of fragmentation. For example, Bontemps et al. (2010) report 1700 AU-resolution observations using PdBI of IR-quiet massive cores in Cygnus X, and find that although one of them does break up to some degree when observed at high resolution, most of them do not have most of their collapsed mass in low mass objects. Some of them do not break up at all, and remain single compact objects even at 1700 AU resolution. Recent submillimeter array observations by Longmore et al. (2010) reach similar conclusions: there is some fragmentation in massive cores, but the number of objects remains limited. Although higher resolution observations need to be performed before definite conclusions can be reached, it is important to investigate which physical processes could reduce fragmentation substantially.
Although it has early been recognized that the magnetic field and the stellar feedback, e.g. the heating or even ionization of the gas caused by the radiation emanating from the protostars should both play an active role in the cloud evolution in particular regarding the fragmentation, it is only recently that the progresses of numerical algorithms and the increase of the computing power have permitted this problem to be addressed numerically. The impact of radiative feedback on fragmentation has been investigated analytically by Krumholz (2006) and Krumholz & McKee (2008), and numerically by Krumholz et al. (2007, 2010), Bate (2009), Offner et al. (2009), Urban et al. (2010), Kuiper et al. (2010) and Peters et al. (2010a,b,c, 2011). All authors agree that the radiative heating increases the Jeans mass and changes the effective equation of state, reducing the degree of fragmentation and leads to the formation of higher-mass stars. The quantitative effect on the stellar cluster formation, however, differs substantially among the simulations. It is unclear to what extent these differences result from differences in the numerical schemes used to treat the radiation and to what extent it reflects differing initial conditions (Girichidis et al. 2010). For low mass stars, while Offner et al. (2009) conclude that the protostellar feedback is still sufficient to heat the gas substantially and therefore stabilizing the disk efficiently, Stamatellos et al. (2009) conclude that the disks are fragmenting. The differences of these studies are not clear yet and could be owing to the initial conditions or the absence of feedback in Stamatellos et al. (2009), as recently suggested by Offner et al. (2010).
The effect of the magnetic field on the low mass core fragmentation, assuming ideal MHD, has been considered by Hosking & Whitworth (2004), Machida et al. (2005), Price & Bate (2007), Hennebelle & Teyssier (2008) and Duffin & Pudritz (2009). They generally conclude that even modest values of the magnetic field corresponding to high values of the mass-to-flux over critical mass-to-flux ratio, μ, can deeply impact the fragmentation and even suppress it when density perturbation of modest amplitude are initially seeded in the core. This is because in typical hydrodynamical simulations of low mass cores, the dominant modes of fragmentation are rotationally driven, i.e. induced by the formation of massive strongly gravitationally unstable disks. The magnetic field can efficiently suppress this mode of fragmentation because i) magnetic braking extracts the angular momentum possibly suppressing the disk formation ii) when the field is too weak to prevent disk formation, the azimuthal component of the magnetic field is quickly amplified by the differential rotation, which stabilizes the disk. Few studies have explored the influence of non ideal MHD effects. Machida et al. (2008) include ohmic dissipation and find that binaries may form during the second collapse, while Duffin & Pudritz (2009) consider ambipolar diffusion and find that in a highly rotating case, two fragments instead of one form when ambipolar diffusion is included.
In the context of massive cores (Beuther et al. 2002a; Motte et al. 2007; Wu et al. 2010; Csengeri et al. 2011), the influence of the magnetic field is not extensively explored yet because only few studies have been performed (e.g. Banerjee & Pudritz 2007) in spite of the measurement which suggest that it reaches substantial values (Crutcher 1999; Falgarone et al. 2008; Girart et al. 2009). Studying the impact that in particular magnetic fields may have in this context is important as well because the massive cores present differences with regard to the low mass ones. First, massive cores are expected to contain initially more Jeans masses because the thermal over gravitational energy ratio is lower in these objects. Second, massive cores are expected to be much more turbulent (e.g. McKee & Tan 2003; Wu et al. 2010) than low mass cores in which usually sonic or subsonic motions are observed. We also stress that no one has yet been investigating in detail the influence that magnetic braking may have in a turbulent core. Note nevertheless that Matsumoto & Hanawa (2011) recently investigated the collapse of low mass, magnetized, and turbulent cores. The purpose of this paper is to address these issues for massive cores assuming a simple barotropic equation of state. While there is little doubt that radiative transfer is playing a major role in the evolution of massive cores (although the exact influence of an outflow cavity along which the radiation may escape remains to be understood e.g. Krumholz et al. 2005), it seems necessary to consider the various effects separately before treating them altogether. We note that recently Commerçon et al. (2010), Tomida et al. (2010) and Peters et al. (2011d) have performed the first simulations of collapsing low mass cores at small scales with grid techniques, which simultaneously consider the magnetic field and the radiative transfer, while Price & Bate (2009) have been performing these simulations on larger scales with SPH.
The plan of the paper is as follows. In the second section we describe the initial conditions and the numerical method we use. In the third section we discuss the evolution of the various core properties, such as density, angular momentum, and magnetic field during collapse. The fourth section is devoted to the study of the outflows, which are spontaneously launched in our calculations, while in the fifth section we investigate the fragmentation, which occurs in the cores. In the sixth section, we discuss the various restrictions of this work that we will need to improve. The seventh section concludes the paper.
2. Initial conditions and numerical setup
2.1. Initial conditions
We investigate the collapse of hundred solar masses cores. The initial conditions consist of a sphere whose profile resembles the observed cores and is given by ρ(r) = ρc/(1 + (r/r0)2). We impose a density contrast of 10 between the central density and the edge density, ρe. Outside the cloud, a warm and diffuse medium of density ρe/10 in pressure equilibrium with the cloud edge is set up. The peak density is initially equal to 6.6 × 103 cm-3 or 1.4 × 10-20 g cm-3, corresponding to a freefall time of about 0.43 Myr. The size of the core is initially equal to 1.35 pc while the central plateau has a radius of r0 ≃ 0.22 pc. The temperature within the dense core is initially equal to T0 = 10 K, leading to a thermal over gravitational energy ratio, αth, equal to about 0.12. At high density, a barotropic equation of state is used to mimic the optically thick regime, and the temperature is then given by T = T0(1 + (ρ/ρc)Γ), where Γ is equal to 7/5. The critical density is equal to 10-13 g cm-3 or about 3 × 1010 cm-3.
The cloud is initially threaded by a magnetic field along the x-axis, whose intensity is proportional to the column density through the cloud. The initial degree of magnetization is determined by the parameter μ, the mass-to-flux over critical mass-to-flux ratio equal to μ = (M/φ)/(Mcrit/φ) where Mcrit/φ = c1/(3π)(5/G)1/2 (Mouschovias & Spitzer 1976). While Mouschovias & Spitzer (1976) infer c1 ≃ 0.53, we estimate in our case, which corresponds to a different magnetic configuration, that c1 ≃ 1. Three degrees of magnetization are investigated, μ = 120, corresponding to a weak magnetic field, μ = 5 and μ = 2 close to the values of the order of 1 − 4, which have been observationally inferred (Crutcher 1999; Falgarone et al. 2008). Finally, an internal turbulent velocity dispersion is initially given to the cores. The velocity field is obtained by imposing a Kolmogorov power spectrum while the phases are randomly determined. Only one realization is explored at this stage. The turbulent energy is initially equal to about 20% of the gravitational one.
It is worth at this stage to express the amount of support that is initially provided to the clouds. Neglecting the surface terms, the virial theorem is 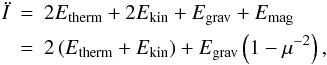 (1)since the magnetic energy, Emag can be written as − Egrav × μ-2 (Lequeux 2005). The conditions for virial equilibrium is that
(1)since the magnetic energy, Emag can be written as − Egrav × μ-2 (Lequeux 2005). The conditions for virial equilibrium is that 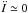 , thus:
, thus: 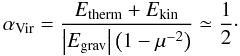 (2)In the hydrodynamical case, αvir ≃ 0.3 and the cloud is therefore out of virial equilibrium by a factor of almost 2. In the μ = 2 case, αvir ≃ 0.4, which implies that the cloud is closer to equilibrium because of the magnetic field, which dilutes gravity.
(2)In the hydrodynamical case, αvir ≃ 0.3 and the cloud is therefore out of virial equilibrium by a factor of almost 2. In the μ = 2 case, αvir ≃ 0.4, which implies that the cloud is closer to equilibrium because of the magnetic field, which dilutes gravity.
Observationally, it is inferred that massive cores present motions, which are apparently not far from virial equilibrium (Bontemps et al. 2010; Wu et al. 2010). The values chosen here are close to but slightly below virial equilibrium. We stress however that these values correspond to the initial conditions and evolve rapidly. In particular, gravity triggers large infall motions and tends to increase the ratio of kinetic over gravitational energy ratio (see e.g. Peretto et al. 2007). Indeed it is observationally difficult to separate the contributions of the systematic infall motions and the turbulent ones (Csengeri et al. 2011), in particular because massive cores are located at large distances. It is therefore likely the case that the motions observed in dense massive cores should not be entirely attributed to turbulent support. Finally, we note that higher values of the initial turbulent energy induce the formation of several collapsing regions within the clouds, which can be described as large scale fragmentation and could be seen as an ensemble of cores, rather than a single one. By contrast with the value adopted in this work, the cloud is undergoing a global contraction at large scale.
To characterize the initial state of the cloud, it is also worth estimating the thermal and magnetic Jeans masses. To calculate the former, we rely on the expression 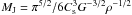 , obtained by defining the thermal Jeans mass as the mass contained within a sphere of radius λJ/2, λJ being the Jeans length. This leads to
, obtained by defining the thermal Jeans mass as the mass contained within a sphere of radius λJ/2, λJ being the Jeans length. This leads to 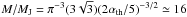 . Note that because the contrast between the central and edge densities is ten, the Jeans mass is about 3 times smaller in the centre than near the cloud boundary. To estimate the initial magnetic Jeans mass, we follow Li et al. (2010). The smallest pieces of gas, which are initially not supported by the magnetic field, are typically critical. Let lcrit be the characteristic size, we have M/φ ≃ ρclcrit/Bc ≃ (M/φ)crit. Because for the cloud Mc/φc ≃ ρclc/Bc ≃ μ(M/φ)crit holds, we have M/Mc = (lcrit/lc)3 = μ-3 = 8. Thus, when μ = 2, there are initially about twice as many thermal Jeans masses than magnetic Jeans masses in the cloud.
. Note that because the contrast between the central and edge densities is ten, the Jeans mass is about 3 times smaller in the centre than near the cloud boundary. To estimate the initial magnetic Jeans mass, we follow Li et al. (2010). The smallest pieces of gas, which are initially not supported by the magnetic field, are typically critical. Let lcrit be the characteristic size, we have M/φ ≃ ρclcrit/Bc ≃ (M/φ)crit. Because for the cloud Mc/φc ≃ ρclc/Bc ≃ μ(M/φ)crit holds, we have M/Mc = (lcrit/lc)3 = μ-3 = 8. Thus, when μ = 2, there are initially about twice as many thermal Jeans masses than magnetic Jeans masses in the cloud.
2.2. Numerical setup
To carry out our numerical simulations, we employed RAMSES (Teyssier 2002; Fromang et al. 2006), an adaptive mesh refinement code that uses Godunov schemes to solve the MHD equations and the constrained transport method to ensure that divB is maintained at zero within machine accuracy. Initially the simulations start with an uniform grid of 2563 cells corresponding to level 8 in RAMSES. Throughout the simulations the Jeans length is resolved with at least 10 cells up to the AMR level 16 for the low resolution calculations and 18 for the high resolution ones. This corresponds to a minimum resolution of about 8 AU in the first case and 2 AU in the second case. No other level is introduced because this leads to timesteps so small that advancing the simulations sufficiently becomes too prohibitive. For this reason the low resolution runs were performed for longer times than the high resolution ones. Because the minimum Jeans mass in the simulation, which is obtained for the density at which the gas becomes adiabatic, has a Jeans length which is about 20 AU, a reasonable numerical resolution is ensured regarding gravity. It is however worth stressing that turbulence and magnetic field may require the resolution of smaller spatial scales. Another difference between the two types of runs is that for the high resolution runs, the HLLD solver (Miyoshi & Kuzano 2005) is employed, while for the lower resolution runs we use the HLL solver, which is more diffusive but permits bigger timesteps.
The combination of lower resolution runs and higher ones allows us to test the numerical convergence in terms of the smaller scale solved in the simulations and at the same time to obtain results for longer physical times. Below, we display the properties of the high resolution calculations and where necessary, we also display the properties for the two types of runs. Note that at this stage we did not explore the influence of increasing the initial resolution or the number of cells per Jeans length.
We did not use sink particles at this stage meaning that the dense gas is prevented from collapsing by the barotropic equation of state, which ensures that the thermal support stops the gravitational contraction.
The lower resolution simulations were performed on 32 CPU while the higher resolution ones use 128 CPU. Typically each low resolution simulation required about 25 000 CPU hours while the high resolution ones took about 80 000 − 100 000 CPU hours. The high resolution calculations have about 107 computing cells in total while the low resolution one have about three times less.
3. Core evolution during collapse
In this section we discuss various properties of the cores that are important to characterize their evolution and interpret the trends regarding the outflows and the core fragmentation that will be discussed in the next section.
 |
Fig. 1 Total mass above various density thresholds in the simulations as a function of time. Solid lines correspond to a density threshold of 103 cm-3, dotted lines to 105 cm-3, dashed to 107 cm-3, dot-dashed to 109 cm-3, triple dot-dashed to 1011 cm-3 and long-dashed to 1013 cm-3. The left column shows the high resolution simulations, while the right column shows the lower resolution. Top panels display the μ = 2 case, middle panels the μ = 5 ones, while bottom panels display the μ = 120 case. |
3.1. Mass evolution and density distribution
Figure 1 displays the total mass above various density thresholds as a function of time. As expected, the collapse time (estimated to be equal to about 0.52 Myr in the μ = 120 case) increases with the magnetic intensity, which is a simple consequence of the magnetic support. The simulations are run up to about 0.1−0.2 freefall time after the formation of the first protostar for the high resolution simulations and 0.4−0.5 freefall time for the low resolution calculations. By the end of the simulations, about 5−10 solar masses of gas, corresponding to 5−10% of the gas within the massive core, is typically at densities higher than 1011 cm-3 for the low resolution runs, while for the high resolution runs about 3 solar masses of gas have reached this density. This gas would have further collapsed up to stellar densities if the simulations could follow the second collapse phase. Note that as will be discussed later, the disk fragments and therefore the accretion rate is the total accretion rate occurring on all fragments. Interestingly, the accretion obviously does not proceed in the same way for the three simulations. In particular the fraction of dense gas is smaller for the μ = 2 case than for the two less magnetized ones, which clearly is a consequence of the magnetic support.
For μ = 120 and μ = 5 the accretion rate is initially of the order of ≃ 10-4 M⊙ yr-1 and then drops to values of the order of ≃ 10-5 M⊙ yr-1 while it stays close to this latter value when μ = 2. These values correspond to accretion rate 10 to 100 times higher than the canonical (Shu 1977) 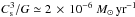 as already noted by Banerjee & Pudritz (2007) in closer agreement with the accretion rate inferred by Larson (1969) and Penston (1969). Our accretion rates are at least one order of magnitude lower than those considered in the fiducial case of McKee & Tan (2003) of the collapse of a core with a mean mass surface density of ≃ 1 g cm-2. This is mostly because our core has an initial mass surface density, which is significantly smaller, ≃10-2 g cm-2 (the exact value depends on the time and the radius on which it is estimated) as shown in Fig. 2, which displays the column density through the core. We note that recent mid-IR extinction mapping studies have derived observed core mass surface densities in the range of several 10-2 to several 10-1 g cm-2 (Butler & Tan 2009).
as already noted by Banerjee & Pudritz (2007) in closer agreement with the accretion rate inferred by Larson (1969) and Penston (1969). Our accretion rates are at least one order of magnitude lower than those considered in the fiducial case of McKee & Tan (2003) of the collapse of a core with a mean mass surface density of ≃ 1 g cm-2. This is mostly because our core has an initial mass surface density, which is significantly smaller, ≃10-2 g cm-2 (the exact value depends on the time and the radius on which it is estimated) as shown in Fig. 2, which displays the column density through the core. We note that recent mid-IR extinction mapping studies have derived observed core mass surface densities in the range of several 10-2 to several 10-1 g cm-2 (Butler & Tan 2009).
 |
Fig. 2 Core column density for μ = 120 (bottom panel), μ = 5 (middle panel) and μ = 2 (top panel) along the z-axis. |
Figure 3 shows the mean gas density within a sphere of radius, r, centred at the cloud density maximum, as a function of r. The first timesteps, which correspond to the thick solid line are before the formation of the first protostar. The thin solid lines show the density of the singular isothermal sphere 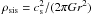 . Interestingly the density is about ten times higher than ρsis. As shown analytically by Shu (1977), densities significantly higher than ρsis are typical signatures of a very dynamical collapse in which the infall velocity is several times the sound speed. Indeed the higher the infall velocity, the denser the envelope. A density equal to about 10 times ρsis has also been found in numerical simulations of a highly dynamical collapse in which the infall is 2 − 3 times the sound speed (Hennebelle et al. 2003), which agrees well with observations of fast collapsing cores (Belloche et al. 2006). In the inner part of the cloud, the density is as high as ≃ 10 − 20 × ρsis. While the density profile in the outer part is very close to r-2, it is slightly stiffer in the inner part, where it is about ≃ r-2.3 below 1000 AU and even stiffer below 300 AU. This is because of the support provided by rotation and turbulence and can be qualitatively understood as follows. In the inner part, systematic infall motions are weak, meaning that the cloud is on average not far from an equilibrium, which implies that:
. Interestingly the density is about ten times higher than ρsis. As shown analytically by Shu (1977), densities significantly higher than ρsis are typical signatures of a very dynamical collapse in which the infall velocity is several times the sound speed. Indeed the higher the infall velocity, the denser the envelope. A density equal to about 10 times ρsis has also been found in numerical simulations of a highly dynamical collapse in which the infall is 2 − 3 times the sound speed (Hennebelle et al. 2003), which agrees well with observations of fast collapsing cores (Belloche et al. 2006). In the inner part of the cloud, the density is as high as ≃ 10 − 20 × ρsis. While the density profile in the outer part is very close to r-2, it is slightly stiffer in the inner part, where it is about ≃ r-2.3 below 1000 AU and even stiffer below 300 AU. This is because of the support provided by rotation and turbulence and can be qualitatively understood as follows. In the inner part, systematic infall motions are weak, meaning that the cloud is on average not far from an equilibrium, which implies that: 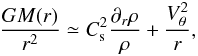 (3)where Vθ is the rotational support provided by systematic rotation, but also by the local rotation that can be provided by turbulence. In the simplest case of rotation, it is generally found that because of angular momentum conservation, Vθ ∝ r − η with typically η ≃ 0.2 − 0.5. This is the case because as angular momentum is conserved (in the hydrodynamical axisymetrical case), one gets
(3)where Vθ is the rotational support provided by systematic rotation, but also by the local rotation that can be provided by turbulence. In the simplest case of rotation, it is generally found that because of angular momentum conservation, Vθ ∝ r − η with typically η ≃ 0.2 − 0.5. This is the case because as angular momentum is conserved (in the hydrodynamical axisymetrical case), one gets 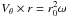 , where r0 is the initial position of the fluid particle, while r is its position along time. The mass enclosed within the radius r, M(r) is typically equal to a few times 4πρsisr3, but mass conservation gives
, where r0 is the initial position of the fluid particle, while r is its position along time. The mass enclosed within the radius r, M(r) is typically equal to a few times 4πρsisr3, but mass conservation gives 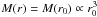 (assuming spherical contraction). Thus
(assuming spherical contraction). Thus 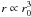 and consequently Vθ(r) ≃ r − 1/3.
and consequently Vθ(r) ≃ r − 1/3.
In the inner part, the thermal support can be neglected and one finds that ρ ∝ r − 2(1 + η) ≃ r-2.66 close to the exponent obtained below 300 AU.
 |
Fig. 3 Mean gas density within a sphere of radius r as a function of r for three different timesteps of the high resolution runs. The solid line is before the protostar formation while dotted and dashed lines correspond to later times. The straight line corresponds to the density of the singular isothermal sphere. The times are in Myr. |
3.2. Infall velocity
Infall velocity is another important quantity to characterize the collapsing clouds. Figure 4 shows the mean radial component of the velocity, ⟨ vr ⟩ = ( ∑ ρvrdV)/(∑ ρdV), as a function of radius. In the outer part of the cloud, it monotonically decreases to reach about 0.8 km s-1 ≃ 4Cs, Cs being the sound speed, in the μ = 120 case and about half this value for μ = 2. These high values are typical of very dynamical collapse as described analytically by the Larson-Penston solution (Larson 1969; Penston 1969) and have been observed in some prestellar condensations (e.g. di Francesco et al. 2001; Belloche et al. 2006).
In the inner part, r < 10-2 pc, however, the picture is very different. Instead of a coherent velocity field, strong fluctuations are dominating. This is a consequence of the initial turbulence, which in particular leads to a non vanishing angular momentum that is amplified as the collapse proceeds. Their amplitude is comparable to the infall velocity which clearly indicates that the collapse proceeds in a complex, non-axisymmetric manner.
3.3. Angular momentum evolution
Although no angular momentum is explicitly set up initially, the turbulent velocity field, which is initially given to the cores, possesses local and even global angular momentum. This angular momentum plays an important role in the cloud evolution and is therefore an important quantity to study. One difficulty however resides in the choice of the origin with respect to which the angular momentum is defined. A natural choice, which we adopted in this study, is the cloud density peak. Another possible choice would be the cloud mass centre. However, this point is not necessarily corresponding to the point where the first protostars or group of protostars collapse.
To compute the specific angular momentum, J, we simply calculate its three components and then take its norm. For example the x-component of J is given by Jx = ( ∑ ρ(yvz − zvy)dV)/( ∑ ρdV) while 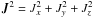 .
.
Figure 5 displays the evolution of the total specific angular momentum, | J | , above the various density thresholds specified previously in the μ = 120 (bottom panels), μ = 5 (middle panels) and μ = 2 (top panels) cases. The left column is for high resolution simulations while right column is for the low resolution calculations.
As expected | J | is almost always increasing with time and is larger for smaller density thresholds. This is simply because the angular momentum is larger in the outer part of the clouds, consequently as the collapse proceeds the material with larger angular momentum is continuously added to the dense material.
While the specific angular momentum does not vary significantly for the density threshold 103 cm-3, for all density thresholds higher than 107 cm-3, the angular momentum decreases when the magnetic intensity increases. This is a consequence of the magnetic braking, which transports angular momentum from the inner dense part of the cloud towards the envelope. The dotted lines (corresponding to a density threshold of 105 cm-3) are particularly interesting. While the specific angular momentum increases with time in the μ = 120 case (bottom panel), it is almost flat in the μ = 5 case (middle panel), and even decreases in the μ = 2 case after t ≃ 0.65 Myr, which nicely illustrates the strong braking that occurs when the magnetic intensity is high.
While we found for the μ = 120 simulation a good agreement between the left and right panels, this is not the case for the more magnetized clouds (μ = 5 and μ = 2) for which the angular momentum of the high density gas (ρ > 107 cm-3) is lower by a factor of about 3 (for example at t = 0.61 Myr) for μ = 5 and by an even larger factor for μ = 2 (e.g. t ≃ 0.70 Myr). Note that the sudden increase at 0.71 Myr is caused by the formation of a new fragment far from the density peak (see top panel of Fig. 2), implying that our simple definition of angular momentum ceases to be valid. The difference between the high and low resolution calculations, indicates that the lower resolution simulations underestimate the amount of magnetic braking as already discussed in Commerçon et al. (2010). Thus the results from the low resolution magnetized simulations must be considered with care.
Overall the specific angular momentum is about 1.5 − 2 times smaller in the μ = 2 case than in the μ = 120 case for the low resolution simulations and larger than a factor 3 for the high resolution cases. Recalling that the centrifugal force is proportional to J2, this constitutes a very substantial difference.
Note however, that the angular momentum left appears nevertheless sufficient to lead to the formation of a centrifugally supported disk because the centrifugal radius is proportional to J2. This is at variance with the conclusion that even low values of the magnetic field could entirely suppress the formation of a disk, as previously inferred by Allen et al. (2003), Galli et al. (2006), Price & Bate (2007), Hennebelle & Fromang (2008), and Mellon & Li (2008, 2009). Indeed, Hennebelle & Ciardi (2009) show that when the magnetic field is misaligned with the rotation axis, the magnetic braking is less efficient. This is because in the aligned case, the radial and azimuthal magnetic field components vanish in the equatorial plane, which produces a strong magnetic compression, that in turn decreases the thickness of the pseudo-disk and produces stiff gradients. When the magnetic field and the rotation axis are not aligned, the magnetic compression is less important because the radial and azimuthal magnetic components do not vanish any more in the equatorial plan. This is obviously the case in this study because the initial velocity field is turbulent. Along the same line, the velocity dispersion likely contributes to make the pseudo-disk thicker, which may also decrease the efficiency of the magnetic braking. Finally we note that it cannot be excluded at this stage that because of numerical diffusivity the braking may be underestimated (see Sect. 5.3) and the amount of specific angular momentum could therefore be overestimated.
3.4. Magnetic field evolution
The average magnetic intensity as a function of time is displayed in Fig. 6 for various density thresholds. As expected, the magnetic intensity increases with the density. Although for μ = 2 the magnetic intensity is about twice as high as for μ = 5, at low density (solid line corresponding to a threshold of 103 cm-3), the magnetic intensity at higher density thresholds is nearly comparable for both cases. Similarly, while the magnetic intensity is extremely low for the density threshold 105 cm-3 in the case μ = 120, it is much closer to the values obtained for μ = 5 and 2 at higher densities, although it is still weaker by a factor of a few.
 |
Fig. 8 Alfvén velocity in the xy plane. Top panel: μ = 2. Bottom panel: μ = 120. The arrows represent the direction of the magnetic field. |
This is because the magnetic field is less amplified when it is stronger because the gas tends to flow preferentially along the field lines. Indeed, in the weak field case, one expects a nearly spherical contraction that leads to B ∝ ρ2/3, while when the field is stronger, B ∝ ρ1/2 (e.g. Basu 1997). Consequently, the magnetic intensity increases more rapidly when it is low than when it is high and tends to take a narrower range of values at higher density.
This is more clearly visible in Fig. 7, which shows the mean Alfvén velocity, 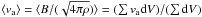 , as a function of the radius. The mean Alfvén speed rapidly decreases toward the edge of the cloud in the outer part, in particular for μ = 120, and then reaches a maximum after which it tends to form a plateau, implying that B ∝ ρ1/2. For μ = 2 while the Alfvén speed is initially of the order of 0.7 km s-1, its value in the inner part is about 2 − 3 km s-1 up to r ≃ 10-4 pc, below which the magnetic intensity steeply drops. This latter behavior is caused by the numerical diffusion, which becomes significant below ten computing cells and clearly shows the limit of these simulations. As the sound speed is about 0.2 km s-1, in the inner part of the collapsing cloud the magnetic support both in the μ = 5 and μ = 2 cases is largely dominating over the thermal one.
, as a function of the radius. The mean Alfvén speed rapidly decreases toward the edge of the cloud in the outer part, in particular for μ = 120, and then reaches a maximum after which it tends to form a plateau, implying that B ∝ ρ1/2. For μ = 2 while the Alfvén speed is initially of the order of 0.7 km s-1, its value in the inner part is about 2 − 3 km s-1 up to r ≃ 10-4 pc, below which the magnetic intensity steeply drops. This latter behavior is caused by the numerical diffusion, which becomes significant below ten computing cells and clearly shows the limit of these simulations. As the sound speed is about 0.2 km s-1, in the inner part of the collapsing cloud the magnetic support both in the μ = 5 and μ = 2 cases is largely dominating over the thermal one.
The mean values displayed in Fig. 7 do not reflect the complexity of the magnetic field behaviour, however. This is well illustrated by Fig. 8 which shows the Alfvén velocity in the xy plane for μ = 120 and μ = 2. In the first case, the Alfvén speed is, as expected very low while at smaller scales, r < 500 AU, it dominates over the sound speed. Overall, it presents large fluctuations at all scales, which is a consequence of the weakness of the field. For μ = 2, the Alfvén velocity almost always dominates over the sound speed. Interestingly, there is a layer extending along the y-axis where the Alfvén velocity is lower by a factor of about 3 than in the surrounding medium. This layer, which is the pseudo-disk, and extends nearly perpendicular to the initial direction of the magnetic field, is denser because of the magnetic compression in the x-direction induced by the pinching of the field lines (e.g. Li & Shu 1996; Hennebelle & Fromang 2008). This density enhancement is responsible for the slightly lower Alfvén velocity. At smaller scales, r < 500 AU, the Alfvén velocity fluctuates significantly and the structure of the magnetic field is clearly much less ordered. As is the case for uniformly rotating cloud, and even though the angular momentum is not well conserved, the rotation motions become dominant in the inner part of the cloud.
 |
Fig. 9 μ = 120. Column density and projected velocity field. |
4. Outflows
The purpose of this section is to study the outflows that are launched in the numerical simulations. Indeed, outflows spontaneously form in all simulations we run.
4.1. Morphology and scales
Figures 9 and 10 show three snapshots for μ = 120 and μ = 5. They display the column density along the x-axis integrated over a length equal to the length of the map whose center is the density peak of the cloud. The arrows represent the velocity field obtained by taking along the line of sight the highest projected velocity (i.e. we select the velocity that has the largest module in the yz-plane). In the top row the size of the snapshots is about 8000 AU, while it is about 32 000 AU for the bottom one except for the third column of Fig. 10, for which the size of the snapshots is four times these values.
 |
Fig. 10 μ = 5. Column density and projected velocity field. |
While the first snapshot (t = 0.5741 Myr) of Fig. 9 shows no sign of outflows, in the second snapshot a relatively fast outflow is clearly evident in the upper part of the map (z = 0 − 4000 AU). It has a broad angle of almost 90° (top panel) at 4000 AU and 45° at 1.5 × 104 AU. The outflow is not bipolar because it is almost entirely propagating towards the north with only a weak component propagating toward the south. The highest velocity which is as high as 47 km s-1 in the second snapshot, decreases with time and has dropped to about 13 km s-1 by the time of the third panel, suggesting that the high speed is associated to a transient phase rather than a stationary stage. Although outflows and jets are a common feature of MHD collapse calculations (e.g. Machida et al. 2005; Banerjee & Pudritz 2006; Mellon & Li 2008; Hennebelle & Fromang 2008; Ciardi & Hennebelle 2010), which are thought to be caused by the magneto-centrifugal mechanism (e.g. Blandford & Payne 1982; Pelletier & Pudritz 1992; Ferreira 1997; and also Spruit 1996, for a discussion about the various interpretations of the launching mechanism), it may sound surprising to see outflows being launched in a cloud that has such a small initial magnetic field. However, as already discussed, the magnetic field is strongly amplified during the collapse (see Figs. 6 and 7). In a sense it is similar to the result of Machida et al. (2008), who treated the ohmic dissipation during the second collapse, and observed in their simulation the launching of a strong jet induced by the rotation of the young protostar even though most of the magnetic flux has been lost by diffusion. In this case, the weak magnetic field is rapidly twisted by the rotation and the toroidal magnetic pressure gradient efficiently accelerates the flow (e.g. Spruit 1996). The weak collimation and the strong asymmetry are probably consequences of the weakness of the initial magnetic intensity though.
The situation is different for μ = 5. The first column reveals that the velocities are lower ( ≃ 3 − 4 km s-1) and that while the outflows tend to be more collimated, they tend to be more symmetrical with respect to the centre. Interestingly, we observe four thin flows instead of two. This is even clearer in the second snapshot, where the outflow is almost quadrupolar. These directions are significantly different from the outflow directions at time 0.563 Myr. The velocities are also about 4 − 5 times higher. The last snapshot shows that this outflow propagates through the cloud (at time 0.62 Myr it reaches about 0.3 pc) and slows down.
 |
Fig. 11 Mass in the outflows as a function of time for various velocity thresholds (see text). The left column shows the high resolution simulations, while the right column shows the lower resolution. Top panels display the μ = 2 case, middle panels the μ = 5 ones, while the bottom panel displays μ = 120. |
For μ = 2, outflows are also observed but their velocities are much lower and rarely exceed 3 km s-1. For this reason they are not displayed here although they can easily be seen in Fig. 14 (first column, bottom panel).
It seems therefore that the outflows produced in the simulations are relatively fast for low and intermediate magnetic intensities, slower for stronger fields, while in general intermittent and not bipolar. The exact reason of this is not entirely clear but it may be that for stronger fields, because there is less angular momentum left in the cloud inner part because of the efficient braking, the twisting of the field lines is weaker and therefore the pressure gradient should be less steep.
Before turning to a quantitative description, we find it useful to comment on the expected order of magnitude of the outflow velocity. In the context of stationary, axisymmetric configurations, it has been established that (e.g. Pudritz et al. 2007) 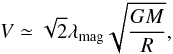 (4)where M is the mass of the central object, R is the radius from which the outflow is launched and λmag is the magnetic lever arm, which typically is found to be of the order of 2 − 3. This leads to
(4)where M is the mass of the central object, R is the radius from which the outflow is launched and λmag is the magnetic lever arm, which typically is found to be of the order of 2 − 3. This leads to 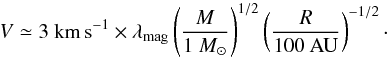 (5)The launching radius is not easily determined given the complexity of the flow. Visual inspection of Figs. 9 and 10 suggests that R ≃ 1000 AU is a reasonable order of magnitude. This is corroborated by Fig. 4, where it is shown that the radius of the inner region at which the velocity field is not dominated by systematic collapse is of the order of 1000 AU. The mass enclosed within this radius is of the order of 10 M⊙, thus a typical velocity for the outflows is of the order of 6−10 km s-1. It is worth stressing that the velocities fluctuate by orders of a few around this simple estimate. This dispersion is easily accounted for given the uncertainties on the lever arm λmag, the mass M, and the launching radius, R. One should also keep in mind that Eq. (5) is inferred in the context of stationary and axisymmetric solutions, which is obviously not the case in our simulations.
(5)The launching radius is not easily determined given the complexity of the flow. Visual inspection of Figs. 9 and 10 suggests that R ≃ 1000 AU is a reasonable order of magnitude. This is corroborated by Fig. 4, where it is shown that the radius of the inner region at which the velocity field is not dominated by systematic collapse is of the order of 1000 AU. The mass enclosed within this radius is of the order of 10 M⊙, thus a typical velocity for the outflows is of the order of 6−10 km s-1. It is worth stressing that the velocities fluctuate by orders of a few around this simple estimate. This dispersion is easily accounted for given the uncertainties on the lever arm λmag, the mass M, and the launching radius, R. One should also keep in mind that Eq. (5) is inferred in the context of stationary and axisymmetric solutions, which is obviously not the case in our simulations.
4.2. Masses and velocities
To quantify the outflows more precisely, we computed the mass within the outflows as a function of time. As a criterion to identify the mass they contain, we select the computational cells with a positive radial velocity that is higher than a given threshold. To avoid confusion with cells close to the density peak where high velocities can also be achieved, we select cells whose distance from the density peak exceeds 1000 AU. We adopt six thresholds of 1, 3, 5, 7, 10 and 20 km s-1 (shown as solid, dotted, dashed, dot-dashed, triple dot-dashed, long dashed respectively). Figure 11 shows the different masses as a function of time of the three cases μ = 120,5,2 and for the two resolutions (left column displays the high resolution runs).
At least two distinct episodes of ejection occur, for the three magnetic intensities, the second leading to faster velocities. While in μ = 2 case, only a small mass is launched at velocities higher than 3 km s-1, for μ = 5 almost 1 solar mass of gas is ejected at a speed higher than 3 km s-1 and at time 0.61 Myr, more than 0.1 solar masses possess a velocity higher than 10 km s-1. Interestingly enough for μ = 120, the low resolution calculations reveal that at later times the mass in the outflows is typically larger by a factor of a few while for μ = 2, the mass at the end of the calculation is about one orders of magnitude larger and seem to be still increasing with time. For μ = 120 and μ = 5, the ejected mass does not seem to increase with time.
A comparison between the accreted mass (at density higher than 109 − 11 cm-3) indicates that the fraction of ejected mass over accreted mass, is of the order of one third in the high resolution models (except for μ = 2) and about one tenth in the low resolution one. These numbers are close to what Ciardi & Hennebelle (2010) have been inferring for low mass cores.
Altogether, the outflows are clearly not stationary and episodic. It is important to stress that while the general trends are similar for the low and the high resolution runs, the velocities, compared at the same physical time, are larger in the high resolution case and that the outflows are more massive. This clearly means that numerical resolution plays an important role here. It is not excluded, and indeed even likely, that numerical convergence has not been reached yet and a better resolution may lead to even faster and more massive flows.
Although a detailed comparison does not seem to be possible at this stage, it is worth mentioning that observationally outflows in massive cores have been studied in details (e.g. Arce et al. 2007). In general, a broad variety of flows have been observed and we restrict our attention to the study of Beuther et al. (2002b), which present similarities with our results. They find multiples outflows, well collimated, containing about 10 M⊙ and with velocities of the order of a few 10 km s-1. Our outflows contained about ten times less mass and are less rapid on average, though velocities of that orders are reached. It should be the case that a better agreement could be obtained at later stage (as suggested by the low resolution calculations) since both the mass and the velocities increase as the collapse proceed. Another related issue is the fact that the regions they observe has stars more massive (≃10 M⊙) than the stars present in our simulations. That may indicate again that we have to wait for longer time or that the core in the simulations are less massive than the regions observed by Beuther et al. (2002b). It is particularly interesting to note that in the μ = 5 case, the outflows are well collimated and nearly quadrupolar, a feature also mentioned by Beuther et al. (2002b).
 |
Fig. 12 μ = 120. Column density. |
Finally, it should be made clear that, as we do not treat the second collapse and the formation of the protostar itself, we do not form the jets as is the case for example in the study of Banerjee & Pudritz (2006) and Machida et al. (2008). The jets have much faster velocities than the outflows and would therefore trigger further outwards motions in the cloud. The question as to whether the jets are driving the observed outflows and constitute the primary source for the outflows is not settled yet. Would this be the case, then the outflows produced in this way should dominate over the outflows obtained in this work which are directly launched at large scales through the magneto-centrifugal mechanism.
5. Fragmentation
In this section, we discuss the fragmentation which occurs in the simulations. As we do not have sink particles at this stage, we identify the dense clumps using a simple density threshold of 1011 cm-3. To construct the clumps we use a friend of friend algorithm, that is all cells above the density threshold, which are spatially connected are assigned to belong to the same entity. The mass of the clumps can then be obtained by summing over the constituting cells. One of the drawback of this method is the fact that the clumps can merge while the stars, that would have formed if the collapse would have been properly followed up to the formation of the protostars, may have not. This problem could partially be solved if sink particles were used (Bate & Burkert 1997; Krumholz et al. 2004; Federrath et al. 2010). However, sinks may alter significantly the evolution of the calculations in particular in the presence of magnetic field and we do not use them at this stage.
 |
Fig. 13 μ = 5. Column density. |
5.1. Qualitative description
Figures 12 (μ = 120 case), 13 (μ = 5) and 14 (μ = 2) show 3 snapshots of the cloud column density, around the density peak, integrated along the z-axis (top row) and along the x-axis. Each image represents a length of 2000 AU. The first time displayed is close to the formation of the first protostars (typically 104 years) and the third corresponds to the last timesteps of the simulations (these panels are zoom of Fig. 2), which is about 6 − 7 × 104 years after the formation of the first protostar while the second is intermediate.
In the three cases, it is seen that many objects form and that their numbers increase with time as accretion proceeds. This is relatively unsurprising giving that the thermal over gravitational energy ratio is initially equal to about 0.12 implying that the cloud contains about 16 Jeans masses at the beginning.
In the μ = 120 case, the objects are relatively distant from each other and the distance of the more distant objects is of the order of 1000 AU. This length roughly corresponds to the radius below which the infall velocity is smaller or comparable to the velocity fluctuations as shown by Fig. 4. This implies that fragmentation occurs when some sort of dynamical equilibrium, or at least non-uniformly collapsing region, is reached as it is the case in the inner region of radius 1000 − 2000 AU. By comparison it is seen that the fragments are significantly closer in the magnetized cases as suggested by Fig. 4, which shows that the size of the central region where the velocity is essentially random, is typically 3 to nearly 10 times smaller. As discussed previously, this is a consequence of the magnetic braking which extracts angular momentum from the inner region as shown by Fig. 5.
The comparison between the three cases also reveals that the μ = 120 case fragments more and earlier than the magnetized cases, in particular the μ = 2 case fragments significantly less than the μ = 120 case. Although a quantitative analytical estimate is mandatory here, it is qualitatively not surprising. First as revealed by Fig. 7, the magnetic field is higher in the central part for the μ = 5 and μ = 2 cases than for the μ = 120 case by a factor of about 3. As the magnetic support dominates the thermal one, this implies that the total support is indeed few times larger. Second, as mentioned above the angular momentum is smaller in the magnetized cases while large angular momentum tends to favor fragmentation (e.g. Miyama 1992; Machida et al. 2005).
 |
Fig. 14 μ = 2. Column density. |
We stress nevertheless that even if reduced, the magnetic field is, for the case explored here, not suppressing fragmentation. This is expected since, as mentioned earlier, the cloud contains about 20 Jeans masses initially and the large turbulence present in the cloud triggers large density perturbations (remembering that the rms Mach number is of the order of 2 initially). Indeed, previous authors have concluded that while a magnetic field can easily quench rotationally driven fragmentation (Price & Bate 2007; Hennebelle & Teyssier 2008), that is the fragmentation of massive self-gravitating disks, large perturbations can lead to fragmentation even when the magnetic field is relatively strong. This is because while the magnetic field is strongly amplified by the differential rotation, this is not the case when isolated Jeans masses collapse individually.
Finally, we note that for μ = 2, fragments at much larger distances form (see top panel of Fig. 2) than in the less magnetized cases. This is because the μ = 2 case is closer to an equilibrium and collapses less rapidly, leaving time for the fluctuations induced by turbulence to develop. We note that this behavior is reminiscent of the recent observations by Bontemps et al. (2010), who find that massive core are fragmented at scales of a few thousands of AU in a few (≃1−3) objects.
5.2. Quantitative estimate
We now present a more quantitative analysis of the fragment distribution.
Figure 15 displays the number of fragments more massive than 10-2 solar masses as a function of the total mass, Mf, within the fragments, that is Mf is equal to the sum of all the fragment masses. Several interesting trends can be inferred. First, as expected, the number of fragments clearly tends to increase with Mf. There are fluctuations that are caused by clump merging and also by our algorithm that is based on a simple density threshold, which is used to identify the clumps. Second, at the end of the high resolution runs, the number of fragments is about 2.5 times less for μ = 2 than for μ = 120. As both simulations have been run for about the same physical time after the formation of the first protostar, this implies that the more magnetized case fragments later. Third, in terms of mass, obviously for the same value of Mf, the number of fragments is lower for μ = 2 and μ = 5 than for μ = 120 by a factor of about ≃1.5−2. This indicates that for the same amount of mass, there are less fragments when the magnetic field is significant. The same trends are also seen in the low resolution calculations although slightly less clear. Because the number of fragments is slightly larger in the high resolution case (although only fragments more massive than 10-2 solar masses are shown) and as already shown by Fig. 5, numerical resolution clearly appears to be an issue here. It is therefore possible that higher resolution calculations could show a stronger difference between low magnetized and highly magnetized calculations.
 |
Fig. 15 Number of fragments more massive than 10-2 M⊙ versus total mass within fragments. The left column shows the high resolution simulations, while the right column shows the lower resolution. Top panels display the μ = 2 case, middle panels the μ = 5 ones, while bottom panels display the μ = 120 case. |
 |
Fig. 16 Total mass of fragments per interval of mass for various time steps. The left column shows the high resolution simulations, while the right column shows the lower resolution. Top panels display the μ = 2 case, middle panels the μ = 5 ones, while the bottom panels display the μ = 120 case. Times are given in Myr. |
Figure 16 shows the mass spectrum, more precisely the mass per interval of mass, for the six simulations and for four different times. The later time corresponds to the last timesteps calculated, the first is close to the moment when protostar formation begins and the two others are intermediate. The fragment masses are distributed between 3 × 10-3 M⊙ and 3 M⊙. For both set of simulations, high and low resolution, the trends are the same. The number of fragments is larger for μ = 120 and decreases as magnetic intensity increases (see also Fig. 15 where the number of fragments can be seen). The mass is slightly more concentrated on the more massive fragments in the MHD cases.
Although performing a quantitative analysis of the fragment distribution (e.g. Hennebelle & Chabrier 2008, 2009) seems difficult at this stage, the decrease of the fragmentation with magnetic intensity seems to be attributable to two different processes, as already discussed. First the angular momentum is larger for μ = 120 and second the magnetic support is obviously stronger for μ = 5 and μ = 2. This latter effect can be understood in the following way. As discussed in Mouschovias & Spitzer (1976), the highest external pressure for which a cloud of mass M and temperature T can be supported is given by 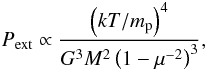 (6)mp being the mean mass per gas particle. Above this pressure, a cloud of mass M collapses. Thus, the pressure needed to produce fragments of mass M increases when μ decreases. For μ = 2, one finds that the pressure must typically be about 2.4 times higher. This value is, however a lower limit because as μ is the mass-to-flux ratio of the fragment of mass M and not the mass-to-flux of the whole cloud, μ must be lower than 21. This means that the external pressure required to form a fragment of mass M must be even higher. If, for example 3/4 of the mass within the flux tube has contracted and is available to form a new fragment, the mass-to-flux ratio of the material is about 1.5 and the external pressure would be of the order of 6 times its value in the hydrodynamical case. Note that Eq. (6) stems from the virial theorem as shown on Eq. (1), which in particular does not distinguish between the magnetic tension and the magnetic pressure. More detailed analyse by Li & Shu (1997) and more recently by Lizano et al. (2010) while finding the rescaling of the gravitational term by a factor (1 − μ2) as well, infer that the sound speed should also be modified,
(6)mp being the mean mass per gas particle. Above this pressure, a cloud of mass M collapses. Thus, the pressure needed to produce fragments of mass M increases when μ decreases. For μ = 2, one finds that the pressure must typically be about 2.4 times higher. This value is, however a lower limit because as μ is the mass-to-flux ratio of the fragment of mass M and not the mass-to-flux of the whole cloud, μ must be lower than 21. This means that the external pressure required to form a fragment of mass M must be even higher. If, for example 3/4 of the mass within the flux tube has contracted and is available to form a new fragment, the mass-to-flux ratio of the material is about 1.5 and the external pressure would be of the order of 6 times its value in the hydrodynamical case. Note that Eq. (6) stems from the virial theorem as shown on Eq. (1), which in particular does not distinguish between the magnetic tension and the magnetic pressure. More detailed analyse by Li & Shu (1997) and more recently by Lizano et al. (2010) while finding the rescaling of the gravitational term by a factor (1 − μ2) as well, infer that the sound speed should also be modified, 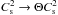 . Li & Shu (1997) infer that Θ depends on μ as well as on the ratio of the horizontal over vertical components of the gravitational field, but always remains below 2 (and would be smaller in our case as μ = 2), while Lizano et al. (2010) infer that
. Li & Shu (1997) infer that Θ depends on μ as well as on the ratio of the horizontal over vertical components of the gravitational field, but always remains below 2 (and would be smaller in our case as μ = 2), while Lizano et al. (2010) infer that 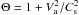 . The differences seem to arise from different assumptions linked to the thin disk approximation. In the present calculation, the Alfvén speed in the inner fragmenting region is typically a few times (up to 10) higher than the sound speed. As the Jeans mass is proportional to
. The differences seem to arise from different assumptions linked to the thin disk approximation. In the present calculation, the Alfvén speed in the inner fragmenting region is typically a few times (up to 10) higher than the sound speed. As the Jeans mass is proportional to 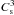 , this would have a very significant impact on the effective Jeans mass that should be multiplied by a factor ≃ 103, which does not seem to be the case in the simulation, while following the Li & Shu (1997) approach, we would get an increase of the Jeans mass, due to the effective sound speed being larger, by less than a factor 23/2 ≃ 3. Because the geometry adopted in these works (thin disk geometry) is different from the complex turbulent case that is characteristic of our simulations, and given that the coefficient renormalising the sound speed is uncertain, we adopt the simplest prescription stated by Eq. (6), keeping in mind that this is presumably a lower value.
, this would have a very significant impact on the effective Jeans mass that should be multiplied by a factor ≃ 103, which does not seem to be the case in the simulation, while following the Li & Shu (1997) approach, we would get an increase of the Jeans mass, due to the effective sound speed being larger, by less than a factor 23/2 ≃ 3. Because the geometry adopted in these works (thin disk geometry) is different from the complex turbulent case that is characteristic of our simulations, and given that the coefficient renormalising the sound speed is uncertain, we adopt the simplest prescription stated by Eq. (6), keeping in mind that this is presumably a lower value.
As shown in Fig. 3, the mean density roughly scales as r-2 and is comparable in the three cases explored here. This implies that fragments of mass M should form at radii a few times smaller for μ = 2 than for μ = 120, a reasonable estimate being (1 − μ-2)3/2 with μ < 2, which suggests a factor of the order ≃ 1.5−2.5. Since, as already mentioned, the density is roughly proportional to r-2, the mass contained within a given radius, r, is roughly scaling as r. This implies that the mass available for forming fragments of mass M is also 1.5−2.5 times smaller for μ = 2 than for μ = 120. Thus a factor of the order of 2 on the number of fragments. Note that taking into account a factor, Θ, of the order of the one proposed by Li & Shu (1997), we may expect that the pressure in Eq. (6) is multiplied by a factor Θ4 and consequently that the radius at which fragments of mass M could form is divided by a factor Θ2 implying that the available mass is also decreased by the same factor. In this case, the number of fragments should be additionally reduced by a factor of less than 4 (which corresponds to the highest value of Θ = 2 inferred by Li & Shu 1997). Altogether, this suggests that the number of fragments that we observe is higher than what is theoretically expected. As discussed below, significant flux leakage is probably reducing the effect of the magnetic field.
It is worth mentioning that the number of initial magnetic Jeans masses is about half the number of thermal one, which could offer an alternative explanation. However, the masses of the objects formed during the collapse are much smaller than the initial value of the Jeans mass, and it is unclear to which extent they can be related.
 |
Fig. 17 Mass-to-flux over initial mass-to-flux ratio of the fragments as a function of mass for μ = 2 at time t = 0.7301 Myr in the high resolution run calculations. Three density thresholds are considered. For a threshold of 107 cm-3, the mass-to-flux of the fragments is very close to the initial value, while it is typically 10 to 30 times higher for a threshold equal to 1011 cm-3, indicating that most of the magnetic flux was lost by numerical diffusion. |
5.3. Magnetic flux within fragments and numerical diffusion
To further characterize the fragments, we need to estimate the magnetic flux, which threads them. To calculate the magnetic flux, we proceed as follows. For each fragment, we calculate the magnetic flux of all the surface parallel to the x = 0, y = 0, z = 0, x = y, x = z and y = z planes intersecting the volume of the fragment. The magnetic flux is then defined as the maximum of all these fluxes.
Figure 17 shows the values of the mass-to-flux ratio over the initial mass-to-flux ratio in the fragments for three different density thresholds, 107, 109, and 1011 cm-3. Obviously, it is typically close to 1 for 107, which indicates good field freezing but about 10 − 30 for 1011 cm-3, which shows that most of the magnetic flux has been lost. Indeed, as already mentioned, the mass-to-flux ratio of any fluid particle could not be higher than 2 if magnetic flux was conserved. This implies that as already shown in Fig. 7, the numerical diffusion leads to strong magnetic flux losses at scales smaller than ≃ 20 AU. Clearly, this raises the question as to whether the formation of most of the fragments would not have been prevented if the magnetic flux had been conserved. In particular, the second panel indicates that at densities of about 109 cm-3, that is to say more than an order of magnitude in density before the gas becomes adiabatic, about two-thirds of the initial magnetic flux have been lost. As it is typically at these densities that fragmentation occurs (see for example the difference between the second and third panels of Fig. 17), this may indicate that the fragmentation is indeed overestimated in the μ = 2 case. On the other hand, the reasonable similarity between the high and low resolution calculations suggests that this may not be too severe a problem but this question should be solved when it will be possible to performed higher resolution calculations. Note that the lower resolution calculations show very similar trends regarding the mass-to-flux values. However, it is worth recalling that in this work we have not varied the number of cells per Jeans length from the first amr levels, but simply allowed for two more amr levels for the high resolution runs. Thus the possible dependence of magnetic diffusivity with numerical resolution during the first stage of collapse remains to be investigated.
In reality, it is expected that significant flux leakages either induced by ambipolar diffusion and/or ohmic dissipation (Nakano et al. 2002; Tassis & Mouschovias 2005; Kunz & Mouschovias 2010) possibly enhanced by turbulence (Santos-Lima et al. 2010), occur. However, the question as to whether the numerical diffusion captures these effects accurately enough is open. In particular, it may be the case that significant flux leakage is indeed occurring, but at higher densities. The amount and the efficiency of these processes should be thoroughly quantified in future studies.
6. Discussion
Here we provide some discussion about the aspects of the work that should be improved in future studies. We also speculate on the consequences this may have.
The choice of the initial conditions is obviously crucial in this problem. Given the large amount of CPU necessary to run each case, it was impossible to explore the influence of initial thermal energy, turbulent energy, and rotation. Varying the mass would also be necessary in the future. Different realizations of the turbulent velocity field should ideally be tested as well as different realizations of the initial magnetic field. We also stress that in our initial conditions, magnetic, velocity, and density fields are set up independently, i.e. in reality fluctuations of magnetic and density fields should be correlated with the velocity fluctuations. We did not consider any well organized rotation field, which could lead to a systematic growth of a magnetic toroidal component and could possibly modify our conclusion. Finally, fragmentation strongly depends on the initial density profile (see e.g. Girichidis et al. 2010).
An important aspect that we did not attempt to address here is the statistics of the binary systems, that will form. As is evident from Figs. 12 − 14, the size of the regions where fragments form as well as the available angular momentum are quite different for the three values of the magnetic intensity. What consequences this may have on the binary properties is an open question. This could however constitute an interesting test to know whether there is a preferred magnetization for high mass cores. This, as already discussed, requires the use of sink particles. Before introducing them, it should however be investigated how sink particles behave in the presence of a magnetic field.
Perhaps the most important restriction of the present study is the lack of radiative transfer, which has been demonstrated to play an important role during the collapse of massive cores (Yorke & Sonnhalter 2002; Krumholz et al. 2007; Bate 2009) and even low mass cores (Offner et al. 2009; Hennebelle et al. 2010; Tomida et al. 2010). As discussed in the introduction, the role of the radiative transfer has been investigated by Krumholz (2007, 2010), Bate (2009), Kuiper et al. (2010), Peters et al. (2010a,b,c, 2011), and they conclude that it has an impact on the gas temperature because of the heating induced by the accretion luminosity. The exact importance of this effect remains a matter of debate and could indeed vary with initial conditions. When magnetic field and radiation are taken into account, Commerçon et al. (2010) have suggested that the impact of the radiative feedback may be even larger, because as the magnetic braking removes angular momentum, the accretion rate is higher. That is, the trend inferred in this work regarding the reduced fragmentation may possibly be amplified because the stronger accretion onto fewer objects will trigger a stronger radiation field that may consequently tend to reduce the fragmentation even more. Another interesting effect may be caused by the magnetic outflows. As investigated by Krumholz et al. (2005), the outflows may channel the radiation and possibly modify its effect on the surrounding gas. The thermal and the radiative pressure should in principle add up to the Lorenz force and produce faster outflows.
We would like to reiterate that as only the first collapse is treated in this work, the outflows produced in our simulations are directly launched at large scales and are not the consequence of the entrainment from a fast wind generated at small scales. It is possible that the flows produced that way are too slow, but one should also keep in mind, as pointed out in this study, that numerical resolution may be an important factor in getting higher velocities.
Finally, we stress that performing integration over a longer timescale is an important issue as already discussed. Because high numerical resolution is really needed here, this constitutes a severe problem.
7. Conclusion
We performed high resolution numerical simulations of collapsing magnetized and turbulent hundred solar masses cores assuming a barotropic equation of state using the RAMSES code. Three different magnetic intensities corresponding to mass-to-flux ratio, μ equal to 120, 5, and 2 were explored. The simulations were repeated with two different resolutions to investigate the impact of the numerical method and the issue of numerical convergence. These simulations confirm the strong impact that the magnetic field has, in particular regarding the byproduct of the collapse.
The main effects of the magnetic field are i) to significantly reduce the angular momentum in the inner part of the cloud; ii) to launch episodic and relatively fast outflows, even when the value of the magnetic intensity is initially weak; iii) to reduce the fragmentation of the cloud in several objects (by about a factor 2 when μ, the mass-to-flux ratio is equal to 2).
While the collapse is relatively well organized in the outer part of the cloud and exhibites a classical r-2 density profile, the inner part is very turbulent and the infall is dominated by high velocity fluctuations. In this region, the density profile is steeper and typically goes as r − ≃2.5. The magnetic field is amplified by gravitational contraction that leads to roughly  , which in turn implies that the Alfvén velocity is nearly constant on average although it significantly fluctuates at all scales. When the magnetic field is very weak (μ = 120), the amplification is stronger which makes in the cloud inner part the Alfvén speed of the order of the sound speed.
, which in turn implies that the Alfvén velocity is nearly constant on average although it significantly fluctuates at all scales. When the magnetic field is very weak (μ = 120), the amplification is stronger which makes in the cloud inner part the Alfvén speed of the order of the sound speed.
The outflows appear to be episodic and are usually non-bipolar. Not only their velocities evolve with time, but there are events of intense ejections followed by periods without significant outflow motions. The typical velocity of these flows is of the order of 1 − 3 km s-1 but much higher velocities (5 to 10 times higher) can be reached for a small fraction of the mass, in particular when the field is weak. The total mass they carry is of the order of a tenth to a few solar masses, depending on the time and the resolution. There is a clear influence of the numerical resolution, implying that these numbers are probably underestimated.
The strongly magnetized clouds tend to fragment less (factor 1.5 − 2) than the weakly magnetized ones, implying that the mass is more concentrated in the more massive stars. The region in which fragmentation occurs is also more compact when the magnetic intensity is stronger. We stress however that numerical diffusion is clearly reducing the magnetic flux in the dense part of the clouds, which makes it possible that the fragmentation is indeed overestimated for μ = 5 and 2.
Acknowledgments
We thank the anonymous referee for comments, which helped to improve the original version of this work. P.H. thanks Daniele Galli for enlighting discussions about the role of the magnetic field in the collapse of prestellar cores. R.S.K. thanks Robi Banerjee, Rainer Beck, Florian Bürzle, Paul Clark, Christoph Federrath, Simon Glover, Dominik Schleicher, Kandaswamy Subramanian, and Sharanya Sur for stimulating discussions on magnetized collapse and the small-scale dynamo. This work was granted access to HPC resources of CINES under the allocation x2009042036 made by GENCI (Grand Equipement National de Calcul Intensif). P.H., M.J., and R.S.K. acknowledge financial support from the Institut des sciences de l’univers (CNRS) and the German Bundesministerium für Bildung und Forschung via the ASTRONET project STAR FORMAT. R.S.K. acknowledges financial support from the Baden-Württemberg Stiftung via their programme International Collaboration II (grant P-LS-SPII/18). R.S.K. furthermore gives thanks for subsidies from the Deutsche Forschungsgemeinschaft (DFG) under grants No. KL 1358/1, KL 1358/4, KL 1359/5, KL 1358/10, and KL 1358/11, as well as from a Frontier grant of Heidelberg University sponsored by the German Excellence Initiative. M.R.K. acknowledges support from an Alfred P. Sloan Fellowship; the US National Science Foundation through grants AST-0807739 and CAREER-0955300; and NASA through Astrophysics Theory and Fundamental Physics grant NNX09AK31G and through a Spitzer Space Telescope Theoretical Research Program grant. The research of B.C. is supported by the postdoctoral fellowships from Max-Planck-Institut für Astronomie. J.C.T. acknowledges support from NSF CAREER grant AST-0645412 and NASA Astrophysics Theory and Fundamental Physics grant ATP09-0094.
References
- Allen, A., Li, Z.-Y., & Shu, F. 2003, ApJ, 599, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Arce, H., Shepherd, D., Gueth, F., et al. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 9, 245 [Google Scholar]
- Banerjee, R., & Pudritz, R. 2006, ApJ, 641, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, R., & Pudritz, R. 2007, ApJ, 660, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S. 1997, ApJ, 485, 240 [CrossRef] [Google Scholar]
- Bate, M. 2009, MNRAS, 392, 1363 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M., & Burkert, A. 1997, MNRAS, 288, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Hennebelle, P., & André, P. 2006, A&A, 453, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K., et al. 2002a, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Schilke, P., Gueth, F., et al. 2002b, A&A, 387, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bontemps, S., Motte, F., Csengeri, T., & Schneider, N. 2010, A&A, 524, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R., & Payne, D. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I., Vine, S., & Bate, M. 2004, MNRAS, 349, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, M., & Tan, J. 2009, ApJ, 696, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardi, A., & Hennebelle, P. 2010, MNRAS, 409, L39 [NASA ADS] [Google Scholar]
- Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., & Teyssier, R. 2008, A&A, 482, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crutcher, R. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Csengeri, T., Bontemps, S., Schneider, N., Motte, F., & Dib, S. 2011, A&A, 527, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- di Francesco, J., Myers, P., Wilner, D., Ohashi, N., & Mardones, D. 2001, ApJ, 562, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C., Bonnell, I., & Clark, P. 2005, MNRAS, 360, 2 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Duffin, D., & Pudritz, R. 2009, ApJ, 706L, 46 [Google Scholar]
- Federrath, C., Banerjee, R., Clark, P., & Klessen, R. 2010, ApJ, 713, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J. 1997, A&A, 319, 340 [NASA ADS] [Google Scholar]
- Falgarone, E., Troland, T., Crutcher, R., & Paubert, G. 2008, A&A, 487, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galli, D., Lizano, S., Shu, F., & Allen, A. 2006, ApJ, 647, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Goodwin, S., Whitworth, A., & Ward-Thompson, D. 2004, A&A, 423, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girart, J., Beltrán, M., Zhang, Q., Rao, R., & Estalella, R. 2009, Science, 324, 1408 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Girichidis, P., Federrath, C., Banerjee, R., & Klessen, R. 2010, [arXiv:1008.5255] [Google Scholar]
- Goodwin, S., Kroupa, P., Goodman, A., & Burkert, A. 2007, prpl.conf [Google Scholar]
- Hennebelle, P., Whitworth, A., Gladwin, P., & André, P. 2003, MNRAS, 340, 870 [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2008, ApJ, 684, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Teyssier, R. 2008, A&A, 477, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2009, ApJ, 702, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Ciardi, A. 2009, A&A, 506, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., Audit, E., Chabrier, G., Teyssier, R., & Commerçon, B., 2010, A&A, 510, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hosking, G., & Whitworth, A. 2004, MNRAS, 347, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. 2006, ApJ, 641, 45 [Google Scholar]
- Krumholz, M., & McKee, C. 2008, Nature, 451, 1082 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krumholz, M., McKee, C., & Klein, R. 2004, ApJ, 611, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M., McKee, C., & Klein, R. 2005, ApJ, 654, 304 [Google Scholar]
- Krumholz, M., Klein, R., & McKee, C. 2007, ApJ, 656, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M., Cunningham, A., Klein, R., & McKee, C. 2010, ApJ, 713, 1120 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., Klahr, B., Beuther, H., & Henning, T. 2010, ApJ, 722, 1556 [CrossRef] [Google Scholar]
- Kunz, M., & Mouschovias, T. 2010, MNRAS, 408, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J. 2005, ism..book [Google Scholar]
- Li, Z.-Y., & Shu, F. 1996, ApJ, 472, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z.-Y., & Shu, F., 1997, ApJ, 475, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z.-Y., Wang, P., Abel, T., & Nakamura, F. 2010, ApJ, 720, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Lizano, S., Galli, D., Cai, J., & Adams, F. 2010, ApJ, 724, 1561 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R., & Burkert, A. 2000, ApJS, 128, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R., & Burkert, A. 2001, ApJ, 549, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M., Matsumoto, T., Tomisaka, K., & Hanawa, T. 2005, MNRAS, 362, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M., Tomisaka, K., Matsumoto, T., & Inutsuka, S.-I. 2008, ApJ, 677, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, T., & Hanawa, T. 2003, ApJ, 595, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, T., & Hanawa, T. 2011, ApJ, 728, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Miyama, S. 1992, PASP, 44, 193 [Google Scholar]
- Miyoshi, T., & Kusano, K. 2005, JCoPh, 208, 315 [Google Scholar]
- McKee, C.F., & Tan T. 2003, ApJ, 585, 850 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mellon, R., & Li, Z.-Y. 2008, ApJ, 681, 1356 [NASA ADS] [CrossRef] [Google Scholar]
- Mellon, R., & Li, Z.-Y. 2009, ApJ, 698, 922 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Bontemps, S., Schilke, P., et al. 2007, A&A, 476, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mouschovias, T., & Spitzer, L. 1976, ApJ, 210, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Nakano, T., Nishi, R., & Umebayashi, T. 2002, ApJ, 573, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S., Klein, R., McKee, C., & Krumholz, M. 2009, ApJ, 703, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Offner, S., Kratter, K., Matzner, C., Krumholz, M., & Klein, R. 2010, ApJ, 725, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Pelletier, G., & Pudritz, R. 1992, ApJ, 394, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Penston, M. 1969, MNRAS, 145, 457 [Google Scholar]
- Peretto, N., Hennebelle, P., & André, P. 2007, A&A, 464, 983 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R., et al. 2010a, ApJ, 711, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Klessen, R., MacLow, M.-M., & Banerjee, R. 2010b, ApJ, 725, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., MacLow, M.-M., Banerjee, R., Klessen, R., & Dullemond, C. 2010c, ApJ, 719, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R., & MacLow, M.-M. 2011, ApJ, 729, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D., & Bate, M. 2007, MNRAS, 377, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D., & Bate, M. 2009, MNRAS, 398, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Pudritz, R., Ouyed, R., Fendt, C., & Brandenburg, A. 2007, pprl.conf. [Google Scholar]
- Santos-Lima, R., Lazarian, A., Gouveia Dal Pino, E.-M., & Cho, J. 2010, ApJ, 714, 442 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. 1996, NATO ASI Series C., 477, 249 (Kluwer academic publishers) [Google Scholar]
- Stamatellos, D., & Whitworth, A. 2009, MNRAS, 392, 413 [Google Scholar]
- Tassis, K., & Mouschovias, T. 2005, ApJ, 618, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomida, K., Tomisaka, K., Matsumoto, T., et al. 2010, ApJ, 714, 58 [Google Scholar]
- Urban, A., Martel, H., & Evans, N. 2010, ApJ, 710, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H., & Sonnhalter, C. 2002, ApJ, 569, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., Evans, N., Shirley, N., Shirley, Y., & Knez, C. 2010, ApJS, 188, 313 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Total mass above various density thresholds in the simulations as a function of time. Solid lines correspond to a density threshold of 103 cm-3, dotted lines to 105 cm-3, dashed to 107 cm-3, dot-dashed to 109 cm-3, triple dot-dashed to 1011 cm-3 and long-dashed to 1013 cm-3. The left column shows the high resolution simulations, while the right column shows the lower resolution. Top panels display the μ = 2 case, middle panels the μ = 5 ones, while bottom panels display the μ = 120 case. |
| In the text | |
 |
Fig. 2 Core column density for μ = 120 (bottom panel), μ = 5 (middle panel) and μ = 2 (top panel) along the z-axis. |
| In the text | |
 |
Fig. 3 Mean gas density within a sphere of radius r as a function of r for three different timesteps of the high resolution runs. The solid line is before the protostar formation while dotted and dashed lines correspond to later times. The straight line corresponds to the density of the singular isothermal sphere. The times are in Myr. |
| In the text | |
 |
Fig. 4 Same as Fig. 3, except that the radial velocity is displayed. |
| In the text | |
 |
Fig. 5 Same as Fig. 1, except that the specific angular momentum is displayed. |
| In the text | |
 |
Fig. 6 Same as Fig. 1, except that the mean magnetic intensity is displayed. |
| In the text | |
 |
Fig. 7 Same as Fig. 3 except that the volume weighted mean Alfvén velocity is displayed. |
| In the text | |
 |
Fig. 8 Alfvén velocity in the xy plane. Top panel: μ = 2. Bottom panel: μ = 120. The arrows represent the direction of the magnetic field. |
| In the text | |
 |
Fig. 9 μ = 120. Column density and projected velocity field. |
| In the text | |
 |
Fig. 10 μ = 5. Column density and projected velocity field. |
| In the text | |
 |
Fig. 11 Mass in the outflows as a function of time for various velocity thresholds (see text). The left column shows the high resolution simulations, while the right column shows the lower resolution. Top panels display the μ = 2 case, middle panels the μ = 5 ones, while the bottom panel displays μ = 120. |
| In the text | |
 |
Fig. 12 μ = 120. Column density. |
| In the text | |
 |
Fig. 13 μ = 5. Column density. |
| In the text | |
 |
Fig. 14 μ = 2. Column density. |
| In the text | |
 |
Fig. 15 Number of fragments more massive than 10-2 M⊙ versus total mass within fragments. The left column shows the high resolution simulations, while the right column shows the lower resolution. Top panels display the μ = 2 case, middle panels the μ = 5 ones, while bottom panels display the μ = 120 case. |
| In the text | |
 |
Fig. 16 Total mass of fragments per interval of mass for various time steps. The left column shows the high resolution simulations, while the right column shows the lower resolution. Top panels display the μ = 2 case, middle panels the μ = 5 ones, while the bottom panels display the μ = 120 case. Times are given in Myr. |
| In the text | |
 |
Fig. 17 Mass-to-flux over initial mass-to-flux ratio of the fragments as a function of mass for μ = 2 at time t = 0.7301 Myr in the high resolution run calculations. Three density thresholds are considered. For a threshold of 107 cm-3, the mass-to-flux of the fragments is very close to the initial value, while it is typically 10 to 30 times higher for a threshold equal to 1011 cm-3, indicating that most of the magnetic flux was lost by numerical diffusion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


