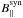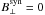| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201015634 | |
| Published online | 21 January 2011 | |
Inferring the magnetic field vector in the quiet Sun
I. Photon noise and selection criteria
1
Kiepenheuer-Institut für Sonnenphysik,
Schöneckstr. 6,
79110
Freiburg,
Germany
e-mail: borrero@kis.uni-freiburg.de
2
Max-Planck Institut für Sonnensystemforschung,
Max-Planck Str. 2,
37191
Katlenburg-Lindau,
Germany
e-mail: kobel@mps.mpg.de
Received: 24 August 2010
Accepted: 23 November 2010
In the past, spectropolarimetric data from Hinode/SP were employed to infer the distribution of the magnetic field vector in the quiet Sun. While some authors found predominantly horizontal magnetic fields, others favor an isotropic distribution. We investigate whether it is actually possible to accurately retrieve the magnetic field vector in regions with very low polarization signals (e.g. internetwork), employing the FeI line pair at 6300 Å. We first perform inversions of the Stokes vector observed with Hinode/SP in the quiet Sun at disk center in order to confirm the distributions retrieved by other authors. We then carry out several Monte-Carlo simulations with synthetic data, with which we show that the observed distribution of the magnetic field vector can be explained in terms of purely vertical (γ = 0°) and weak fields (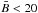 G), which are misinterpreted by the analysis technique (Stokes inversion code) as being horizontal (γ ≈ 90°) and stronger (
G), which are misinterpreted by the analysis technique (Stokes inversion code) as being horizontal (γ ≈ 90°) and stronger (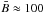 G), owing to the effect of the photon noise. This challenges the correctness of previous results, which presented the distributions for the magnetic field vector peaking at γ = 90° and
G), owing to the effect of the photon noise. This challenges the correctness of previous results, which presented the distributions for the magnetic field vector peaking at γ = 90° and 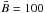 G. We propose that an accurate determination of the magnetic field vector can be achieved by decreasing the photon noise to a point where most of the observed profiles posses Stokes Q or U profiles that are above the noise level. Unfortunately, for noise levels as low as 2.8 × 10-4, only 30 % of the observed region with Hinode/SP have sufficiently strong Q or U signals, implying that the magnetic field vector remains unknown in the rest of the internetwork.
G. We propose that an accurate determination of the magnetic field vector can be achieved by decreasing the photon noise to a point where most of the observed profiles posses Stokes Q or U profiles that are above the noise level. Unfortunately, for noise levels as low as 2.8 × 10-4, only 30 % of the observed region with Hinode/SP have sufficiently strong Q or U signals, implying that the magnetic field vector remains unknown in the rest of the internetwork.
Key words: magnetic fields / Sun: photosphere / Sun: surface magnetism
© ESO, 2011
1. Introduction
The magnetic field in the quiet Sun internetwork has been subject to an intense debate over the years. Its study is motivated by the fact that much of solar magnetic flux could be contained in this region (Sánchez Almeida 2004), which has important consequences for our understanding of the solar activity cycle (Spruit 2003; Solanki et al. 2006). In addition, quiet Sun magnetic fields are subject to the strong influence of the granular convection, producing a rich variety of phenomena such as magnetic flux emergence (Centeno et al. 2007; Martínez González & Bellot Rubio 2009; Danilovic et al. 2010), convective collapse (Bellot Rubio et al. 2001; Nagata et al. 2008; Fischer et al. 2009), supersonic velocities (Socas-Navarro & Manso-Sainz 2005; Shimizu et al. 2007; Bellot Rubio 2009; Borrero et al. 2010a) and so forth, which play an important role in the heating of the upper layers of the solar atmosphere (Schrijver et al. 1997, 1998; Schrijver & Title 2003).
These studies have triggered the development of instruments with ever-increasing spatial resolution, observations in different spectral windows (Khomenko et al. 2003; Domínguez Cerdeña et al. 2006; Socas-Navarro et al. 2008), and using spectral lines that are subject to the Zeeman and Hanle effect (Manso Sainz et al. 2004; Trujillo Bueno et al. 2004; Sánchez Almeida 2005). A major step was accomplished with the deployment of the Japanese spacecraft Hinode. The spectropolarimeter (SP) attached to the Solar Optical Telescope (SOT; Tsuneta et al. 2008) onboard Hinode allows us to achieve continuous observations of the solar atmosphere with an extremely high spatial resolution. This advantage has favored the use of data from this instrument (Ichimoto et al. 2008) in the investigations of the quiet Sun magnetism over the last few years. The analysis of these data has revealed that a large portion of the magnetic flux in the internetwork presents itself in the form of horizontal magnetic fields (Orozco Suárez et al. 2007a; Lites et al. 2008). Other works, also analyzing Hinode/SP data, favor an isotropic (e.g: turbulent) distribution of the magnetic field vector (Asensio Ramos 2009; Stenflo 2010). Motivated by this controversy we revisited these results in the hope of offering possible solutions. In Sect. 2 we describe our observations and data-sets from the Hinode/SP instrument. Section 3 describes the analysis method and how we infer the magnetic field vector from spectropolarimetric observations. Section 4 presents our results and compares them with previous works, whereas Sects. 5 and 6 are fully devoted to study the effects that photon noise and the different selection criteria applied to the data have in the inferred distribution of the magnetic field. Finally, Sect. 7 summarizes our findings.
 |
Fig. 1 Observed continuum intensity (upper panel) and mean magnetic field strength at each pixel inferred from the inversion of the Stokes profiles (lower panel). This region is only a subsection of the full field of view. It was chosen to approximately match Fig. 2 in OS07a. See Sect. 2.1 for details. |
2. Observations
The data used in this work correspond to spectropolarimetric observations (full Stokes vector: I, Q, U, V) around the FeI line pair at 6301.5 Å and 6302.5 Å, recorded with the spectropolarimeter onboard the Japanese satellite Hinode (Lites et al. 2001; Kosugi et al. 2007; Tsuneta et al. 2008; Suematsu et al. 2008; Ichimoto et al. 2008). These two lines have Landé factors of geff = 1.67 and g = 2.5. The image stabilization system in Hinode (Shimizu et al. 2008) allows the slit spectropolarimeter to achieve a spatial resolution of 0.32′′. Here we analyze several data sets corresponding to quiet Sun observations. The maps employed are the same as the ones already analyzed by Orozco Suárez et al. (2007a,b) and Lites et al. (2008). Hereafter these three papers will be referred to as OS07a, OS07b and LIT08. Further analysis of some subsections of the same dataset were also carried out by Asensio Ramos (2009), Martínez González et al. (2010), and Stenflo (2010). In the following subsections we briefly describe each selected map. A summary of the their main properties can also be found in Table 1.
2.1. Normal Hinode/SP map
This map contains 2047 × 1024 pixels with a pixel size of 0.15′′ and 0.16′′ in the horizontal and vertical directions, respectively. The field of view is centered at ( − 53.1′′,7.9′′) from disk center (μ = 0.998). The exposure time at each slit position is 4.8 s, yielding a noise level of σs ≈ 10-3 (in units of the average quiet Sun intensity). Here, the index s refers to any of the four components of the Stokes vector. Hereafter we will refer to this map as Map A. The data were recorded on March 10, 2007, from 11:37 UT to 14:36 UT. A map of the continuum intensity and magnetic field strength (retrieved by the inversion; Sect. 4) in a subfield of this map is displayed in Fig. 1. The subfield has been chosen to coincide with Fig. 2 in OS07a.
 |
Fig. 2 Observed continuum intensity (upper panel) and mean magnetic field strength at each pixel inferred from the inversion of the Stokes profiles (lower panel). Note that the spectrograph’s slit was always located at the same position on the Sun, therefore the horizontal axis refers to time. See Sect. 2.2 for details. |
2.2. Deep Hinode/SP map
This map contains 727 × 1024 pixels with a pixel size of 0.15′′ and 0.16′′ in the horizontal and vertical directions, respectively. In this case, the slit did not scan across the solar surface, but instead was kept at the same location (−22.4′′, 7.8′′) on the Sun from 00:20 UT to 02:19 UT on February 27, 2007. The exposure time at each slit position is 9.6 s, yielding a noise level of σs ≈ 7.5 × 10-4 (in units of the average quiet Sun intensity). Hereafter we will refer to this map as Map B. Figure 2 shows a map of the continuum intensity and magnetic field strength.
2.3. Low-noise Hinode/SP map
In order to further decrease the noise level we averaged bundles of 7 slit exposures in Map B producing a new map (referred to as Map C) that contains 103 × 1024 pixels, with an effective exposure time of 67.2 s. The increased integration time yields a noise of level σs ≈ 2.75 × 10-4 in units of the continuum intensity.
Summary of employed datasets.
3. Inversion of Stokes profiles and magnetic field vector retrieval
The magnetic field vector was retrieved from the Stokes vector with the VFISV (Very Fast Inversion of the Stokes Vector; Borrero et al. 2010b) inversion code1. We employ a parametrized atmospheric model that contains a magnetic and a non-magnetic atmosphere side by side. The magnetic atmosphere is characterized by the following parameters: magnetic field strength B, inclination of the magnetic field with respect to the observer γ, azimuthal angle of the magnetic field in the plane perpendicular to the observer φ, line-of-sight velocity VLOS, damping parameter a, ratio of the absorption coefficient between the line core and the line continuum η0, Doppler-width ΔλDop, source function at the observer’s location S0, and the gradient of the source function with optical depth S1. The non-magnetic atmosphere has one single parameter: fractional area of the pixel filled with non-magnetic plasma (aka non-magnetic nm filling factor) αnm. Using initial values for these parameters, VFISV obtains the theoretical Stokes vector Itot = (I,Q,U,V) as 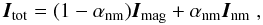 (1)where Imag is the polarized contribution of the magnetized atmosphere, which is obtained by solving the radiative transfer equation under the assumptions of the Milne-Eddington (M-E) approximation. Inm corresponds to the non-magnetic contribution, which is thus unpolarized (Qnm = Unm = Vnm = 0: see Sect. 3.1). The total theoretical Stokes vector Itot is then compared with the observed one using a merit function χ2, and by means of a non-linear least-squares-fitting algorithm (Levenberg-Marquardt method; Press et al. 1986) we iterate our initial 10 free parameters until a minimum in χ2 is reached. As an example, Figs. 1 and 2 show the resulting magnetic field strength (from the inversion) for Maps A and B.
(1)where Imag is the polarized contribution of the magnetized atmosphere, which is obtained by solving the radiative transfer equation under the assumptions of the Milne-Eddington (M-E) approximation. Inm corresponds to the non-magnetic contribution, which is thus unpolarized (Qnm = Unm = Vnm = 0: see Sect. 3.1). The total theoretical Stokes vector Itot is then compared with the observed one using a merit function χ2, and by means of a non-linear least-squares-fitting algorithm (Levenberg-Marquardt method; Press et al. 1986) we iterate our initial 10 free parameters until a minimum in χ2 is reached. As an example, Figs. 1 and 2 show the resulting magnetic field strength (from the inversion) for Maps A and B.
3.1. Treatatment of the non-magnetic atmosphere
In order to facilitate a comparison with OS07b, we adopted for our inversions a treatment of the non-magnetic atmosphere that is similar to theirs: a different Inm profile is used in the inversion of each pixel in the map2. Inm is obtained for each pixel by averaging only the intensity profiles I (polarization not included) from the neighboring pixels in a 1′′ square around the inverted one. This method attempts to mimic a narrow spectrograph’s point spread function. Orozco-Suárez et al. (2007b) interprets the need for a non-magnetic component as the reduction in the amplitude of the polarization signals (reduction ∝ [1−αnm]) caused by diffraction. Danilovic et al. (2008) ascribes it as being caused by a small defocus in the SP instrument.
Another feature of our inversions is that we do not consider the free parameter αnm (Eq. (1)), but instead use a different variable βnm, where 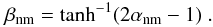 (2)Since αnm varies from 0 (pixel fully filled with the magnetic atmosphere) to 1 (pixel fully filled with non-magnetized plasma), βnm varies (through Eq. (2)) between ( − ∞, + ∞). The reason for employing βnm instead of αnm is to prevent the inversion from reaching a local minimum in the χ2-hypersurface where αnm is either 0 or 1, resulting in an unrealistic number of pixels harboring these two values. The use of βnm is supported by the fact that χ2 improves on average by about 10% when using it instead of αnm (see 5th and 6th columns in Table 1).
(2)Since αnm varies from 0 (pixel fully filled with the magnetic atmosphere) to 1 (pixel fully filled with non-magnetized plasma), βnm varies (through Eq. (2)) between ( − ∞, + ∞). The reason for employing βnm instead of αnm is to prevent the inversion from reaching a local minimum in the χ2-hypersurface where αnm is either 0 or 1, resulting in an unrealistic number of pixels harboring these two values. The use of βnm is supported by the fact that χ2 improves on average by about 10% when using it instead of αnm (see 5th and 6th columns in Table 1).
Because of our treatment of the non-magnetic atmosphere some caution should be exercised when speaking about field strengths in this work. In our modeling of the Stokes parameters (Eq. (1)) we assume that the light we observe at each pixel has a polarized contribution from the pixel itself, plus a non-polarized contribution from the surrounding pixels. From this point of view we cannot talk about intrinsic field strengths but rather about the mean field strength inside the resolution element.
An alternative interpretation of Eq. (1) assumes that inside the resolution element there are two kinds of atmospheres: a magnetized one and an non-magnetized one, where the magnetized one possesses only one magnetic field. From this point of view it is possible to refer to B as the intrinsic field strength. However, Hinode/SP’s resolution is not sufficient to fully resolve all magnetic structures in the quiet Sun. Therefore our treatment oversimplifies the problem, because we are assuming that the magnetic field is constant inside the magnetized atmosphere. In this respect, B should be interpreted as the mean field strength in the magnetized atmosphere. This implies that both interpretations of Eq. (1), although they are different from a physical point of view, are indistinguishable from each other. Because of this, we will refer below to the magnetic field as 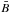 to indicate its averaged nature.
to indicate its averaged nature.
It is important to mention that the results presented here, in particular those in Sect. 5, do not depend on the scheme employed to characterize the straylight. Indeed, the same results are obtained if we consder a global3 stray-light profile, or even if it is completely neglected.
 |
Fig. 3 Panel a) histogram for the number of pixels as a function of the signal-to-noise ratio in the polarization profiles. Circular polarization (Stokes V) is indicated by the solid line, while the linear polarization ( |
3.2. One-line vs two-line inversion
One limitation of the VFISV inversion code is that it only allows us to analyze the data from one spectral line at a time. Hinode/SP records the full Stokes vector for the Fe i line pair at 6301.5 Å and 6302.5 Å across 112 spectral positions. From these two lines the obvious choice is Fe i 6302.5, because of its higher sensitivity to magnetic fields (larger Landé factor; see Sect. 2). Therefore VFISV only makes use of 50 spectral points around the second spectral line. This results in an obvious loss of information, which will yield slightly larger errors in the determination of our model parameters (Sect. 3; see also Orozco Suárez et al. 2010).
In order to make sure that this shortcoming is not critical for our study we repeated the inversions of map A with the HELIX++ inversion code (Lagg et al. 2004, 2009), which allows us to consider both spectral lines simultaneously. The resulting histograms for velocity VLOS, magnetic field strength 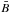 , inclination γ, etc, are very similar to those obtained from the one-line inversions using VFISV (see Fig. 3). This makes us confident that our results are not affected because only one spectral line is being employed, or at least not to the point of invalidating our results. We will return to this point in Sect. 5.
, inclination γ, etc, are very similar to those obtained from the one-line inversions using VFISV (see Fig. 3). This makes us confident that our results are not affected because only one spectral line is being employed, or at least not to the point of invalidating our results. We will return to this point in Sect. 5.
4. Results
In Figs. 3a, 4a, and 5a we present histograms for the number of pixels whose unsigned polarization signals ( | V | or 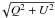 ) have peak values N times higher than or equal to the noise level in each map. This is will be referred to as SNR: signal-to-noise ratio. The vertical lines in these figures indicate the different SNR-thresholds that we considered in our analysis: 3, 4.5, and 6. For instance, the vertical dashed-dotted line in Fig. 3a corresponds to SNR = 3. This means that all pixels in map A, where at least one of the polarization profiles (Stokes Q, U or V) possesses a SNR ≥ 3, are included in the histograms of the remaining panels and represented also by the dashed-dotted line. Likewise for SNR ≥ 4.5 (solid lines) and SNR ≥ 6 (dashed lines). The rest of the panels in Figs. 3–5 show the normalized histograms for the magnetic field strength
) have peak values N times higher than or equal to the noise level in each map. This is will be referred to as SNR: signal-to-noise ratio. The vertical lines in these figures indicate the different SNR-thresholds that we considered in our analysis: 3, 4.5, and 6. For instance, the vertical dashed-dotted line in Fig. 3a corresponds to SNR = 3. This means that all pixels in map A, where at least one of the polarization profiles (Stokes Q, U or V) possesses a SNR ≥ 3, are included in the histograms of the remaining panels and represented also by the dashed-dotted line. Likewise for SNR ≥ 4.5 (solid lines) and SNR ≥ 6 (dashed lines). The rest of the panels in Figs. 3–5 show the normalized histograms for the magnetic field strength 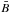 (b-panels), magnetic field inclination with respect to the observer γ (c-panels), and the magnetic filling factor αmag = 1 − αnm (d-panels), which is interpreted as the fractional area of the pixel filled with magnetized plasma. The normalization is done to ensure that the total area below each histogram equals 1. In all these histograms we avoided network regions by excluding from the analysis those pixels where the mean field strength in the resolution element exceeds 750 Gauss.
(b-panels), magnetic field inclination with respect to the observer γ (c-panels), and the magnetic filling factor αmag = 1 − αnm (d-panels), which is interpreted as the fractional area of the pixel filled with magnetized plasma. The normalization is done to ensure that the total area below each histogram equals 1. In all these histograms we avoided network regions by excluding from the analysis those pixels where the mean field strength in the resolution element exceeds 750 Gauss.
Note that in all a-panels in Figs. 3–5 the histograms for the circular and linear polarization peak at SNR ≈ 3. This is because of photon noise. The probability that photon noise produces a signal above 3σs, at a given wavelength position, is only 0.3%. However, we must take into account that we are taking the peak value for all 112 (in circular polarization or Stokes V) or 224 (in linear polarization or Stokes Q and U; see Sect. 3.2), and therefore it is almost guaranteed that at every observed spatial pixel photon noise will yield a polarization signal that is higher than or equal to 3σs.
Since all considered maps are close to disk center, we can interpret the retrieved inclination with respect to the observer, γ, as the inclination with respect to the normal direction to the solar surface. A value of γ = 0°,180° indicates a vertical magnetic field (pointing upward or downward, respectively), whereas a value of γ = 90° indicates a magnetic field that is contained in the solar surface.
The resulting histograms are quite similar in all three (A, B, and C) maps. For all SNR-thresholds considered, the distributions of the average magnetic field strength 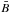 , the magnetic field inclination γ, and the magnetic filling factor αmag, peak at around 50 − 100 Gauss, 80 − 100 degrees and 20 − 30 %, respectively. These results involve the existence of fairly weak and horizontal fields in the internetwork, occupying about 20% of the resolution element at every pixel. This is in excellent agreement with the results presented in OS07a and OS07b. In particular, our retrieved histograms for Map A (Fig. 3) using a SNR-threshold of 4.5 are very similar to those in Figs. 3 and 4 in OS07a and Fig. 7 in OS07b.
, the magnetic field inclination γ, and the magnetic filling factor αmag, peak at around 50 − 100 Gauss, 80 − 100 degrees and 20 − 30 %, respectively. These results involve the existence of fairly weak and horizontal fields in the internetwork, occupying about 20% of the resolution element at every pixel. This is in excellent agreement with the results presented in OS07a and OS07b. In particular, our retrieved histograms for Map A (Fig. 3) using a SNR-threshold of 4.5 are very similar to those in Figs. 3 and 4 in OS07a and Fig. 7 in OS07b.
A closer look at Figs. 3–5 reveals several trends. The first one involves histograms for the same map (noise-level σs fixed) obtained with different signal-to-noise thresholds. Here we observe that increasing the SNR-threshold yields histograms for the magnetic field strength and magnetic filling-factor that shift toward higher values. In addition, the central peak at γ = 90° in the histogram for the inclination becomes less pronounced and almost disappears. Still, the magnetic field remains quite horizontal: γ ∈ [60,120]°. One can interpret this trend in terms of the Zeeman effect in the weak-field regime, through which the amplitude of the polarization signals is proportional to the strength of the magnetic field. From this point of view, imposing higher SNR-thresholds in the polarization immediately selects stronger fields. The histograms for γ (inclination) and αmag (magnetic filling-factor) indicate that these stronger magnetic fields tend to be more vertical and to occupy a larger fraction of the resolution element.
The second observed trend in the retrieved histograms is related to the map-to-map differences or, equivalently, to the noise level σrms in the four components of the Stokes vector. Comparing Figs. 3–5 reveals that the histogram of the magnetic field strength shifts towards lower values from Map A (σs = 10-3) to Map C (σs = 2.8 × 10-4). Again, this behavior can be explained as a consequence of being able to detect smaller polarization signals, hence weaker magnetic fields, when the noise is reduced. In addition, the disappearance of the peak at γ = 90° for large SNR-thresholds is much less pronounced in map C than in maps A or B. An explanation for this will be offered in Sect. 6.
Figure 6 shows histograms for the longitudinal component of the magnetic field 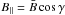 , and the transverse component of the magnetic field
, and the transverse component of the magnetic field 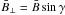 for the three analyzed maps: A (top panels), B (middle panels) and C (bottom panels). B∥ and B ⊥ can be identified with the projection of the magnetic field vector on the vertical direction to the solar surface and the projection of the magnetic field over the solar surface, respectively. Because the retrieved magnetic fields are very inclined (γ → 90°), the horizontal component of the magnetic field B ⊥ is larger than the vertical component B∥.
for the three analyzed maps: A (top panels), B (middle panels) and C (bottom panels). B∥ and B ⊥ can be identified with the projection of the magnetic field vector on the vertical direction to the solar surface and the projection of the magnetic field over the solar surface, respectively. Because the retrieved magnetic fields are very inclined (γ → 90°), the horizontal component of the magnetic field B ⊥ is larger than the vertical component B∥.
We calculated the center-of-gravity (CoG) of the histograms for B∥ and B ⊥ in Fig. 6 and plotted them as a function of the signal-to-noise ratio in Fig. 7. If we take as a reference the results obtained from considering only those pixels whose polarization levels are 4.5 times above the noise level: SNR = 4.5, we see that the CoG of B ⊥ (dashed lines) is located at around 122.0 Gauss for the Map A (σs = 10-3; crosses), and it decreases to 87.4 Gauss when the noise level is 2.8 × 10-4 (Map C; diamonds). Differences are even larger if we consider the peak-value (instead of the CoG) in the histograms: 90.6 Gauss in map A, and 57.1 Gauss in map C. Meanwhile, the CoG values in the histogram of B∥ (solid lines) only decreases from 21.6 (Map A; crosses) to 11.9 Gauss (Map C; diamonds). Similar trends are observed for other signal-to-noise thresholds. This indicates that both B∥ and B ⊥ are responsible for the decrease in the CoG and peak value of 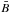 when the noise level is reduced (Figs .3b–5b), with B ⊥ as the main contributor.
when the noise level is reduced (Figs .3b–5b), with B ⊥ as the main contributor.
 |
Fig. 6 Histograms for the longitudinal component of the magnetic field B∥ (left panels) and the transverse component of the magnetic field B ⊥ (right panels). The first row corresponds to map A, while the second corresponds to map B, and the third represents map C. Dashed-dotted, solid and dashed lines correspond to a SNR-threshold of 3, 4.5, and 6, respectively. |
 |
Fig. 7 CoG (center of gravity) of the histograms for B∥ (solid) and B ⊥ (dashed) retrieved from the inversion of the profiles in map A (crosses; σs = 10-3), B (squares; σs = 7.5 × 10-4) and C (diamonds; σs = 2.8 × 10-4), as a function of the SNR-threshold. |
Figures 6 and 7 indicate that the CoG and peak values in the histograms for B∥ and B ⊥ become lower as the noise level decreases. In the light of this result, is it possible that the current noise levels in the polarization signals (in all three maps considered) is responsible for the high values of B ⊥ , and therefore for the peak at γ = 90° in the histograms for the inclinations? And if so: is it conceivable that given a sufficiently low level of noise in the polarization signals, the detection thresholds for B∥ and B ⊥ would be similar, thereby opening the possibility for the detection of non-horizontal magnetic fields? Below we will address these two questions.
5. Effect of the photon noise
In order to study the effect that the photon noise has on the retrieval of the inclination of the magnetic field vector in the quiet Sun, we performed the following Monte-Carlo-like test: we first produce a large number of synthetic profiles (1024 × 2047) where we assume that the magnetic field is always vertical. Half of the synthetic profiles posses γsyn = 0°, while the other half have γsyn = 180°. The rest of the Milne-Eddington parameters needed for the synthesis: ΔDop, VLOS, η0, αnm etc (see Sect. 3) are taken from the results of the inversion of map A. This is done in order to employ kinematic and thermodynamic parameters that are representative of the quiet Sun. The only exception is the magnetic field strength 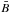 : for the synthesis we assume
: for the synthesis we assume 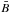 to be equal to the vertical component of the field as obtained from the inversion of map A:
to be equal to the vertical component of the field as obtained from the inversion of map A: 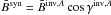 . Note that because γsyn = 0,180° this ensures that the vertical component of the magnetic field in this test is equal to the vertical component of the magnetic field from map A:
. Note that because γsyn = 0,180° this ensures that the vertical component of the magnetic field in this test is equal to the vertical component of the magnetic field from map A: 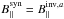 .
.
We then proceed to add noise at different levels4 and employ the VFISV code (see Sect. 3) to invert the Stokes profiles of FeI 6302.5 Å, allowing all atmospheric parameters to vary freely, including the inclination γ. Finally, we compare the original distributions for γsyn, 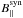 and
and 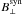 , with the retrieved ones. In our tests we employed four different levels of noise: σs = 10-3 (as in map A), 7.5 × 10-4 (as in map B), 2.8 × 10-4 (as in map C) and finally, as an example of extremely high signal-to-noise observations, σs = 10-5. All numbers are expressed in units of the continuum intensity in the quiet Sun. As in Sect. 4, our analysis considers only those profiles where the signal-to-noise ratio in at least one of the polarization profiles (Stokes Q, U or V) is equal to or higher than 3, 4.5, and 6.
, with the retrieved ones. In our tests we employed four different levels of noise: σs = 10-3 (as in map A), 7.5 × 10-4 (as in map B), 2.8 × 10-4 (as in map C) and finally, as an example of extremely high signal-to-noise observations, σs = 10-5. All numbers are expressed in units of the continuum intensity in the quiet Sun. As in Sect. 4, our analysis considers only those profiles where the signal-to-noise ratio in at least one of the polarization profiles (Stokes Q, U or V) is equal to or higher than 3, 4.5, and 6.
 |
Fig. 8 Histograms for the original longitudinal component of the magnetic field |
The results for the vertical component of the magnetic field B∥ are presented in Fig. 8. Each of the four panels in this figure displays the results for the one of the four levels of noise under consideration. The original distribution of vertical magnetic fields 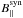 is indicated by the black lines. The retrieved distributions, corresponding to the analysis of pixels where the SNR in at least one of the polarization signal is higher than or equal to 3, 4.5, and 6, are represented by the red, green and blue lines respectively. Note that a more realistic estimation of the original B∥ is obtained by taking a lower SNR-threshold because, as already mentioned in Sect. 4, high SNR-thresholds tend to retain only the stronger magnetic fields. This explains why the blue curves fail to obtain the correct distribution of vertical magnetic fields. Only for the extreme case of σs = 10-5 choosing different SNR-thresholds yields the correct distribution of B∥. It is important to notice that the behavior of the curves in Fig. 8 closely resembles that in Fig. 6 for different SNR-thresholds obtained form the inversion of Hinode/SP data at different noise levels.
is indicated by the black lines. The retrieved distributions, corresponding to the analysis of pixels where the SNR in at least one of the polarization signal is higher than or equal to 3, 4.5, and 6, are represented by the red, green and blue lines respectively. Note that a more realistic estimation of the original B∥ is obtained by taking a lower SNR-threshold because, as already mentioned in Sect. 4, high SNR-thresholds tend to retain only the stronger magnetic fields. This explains why the blue curves fail to obtain the correct distribution of vertical magnetic fields. Only for the extreme case of σs = 10-5 choosing different SNR-thresholds yields the correct distribution of B∥. It is important to notice that the behavior of the curves in Fig. 8 closely resembles that in Fig. 6 for different SNR-thresholds obtained form the inversion of Hinode/SP data at different noise levels.
 |
Fig. 9 Same as Fig. 8 but for the transverse component of the magnetic field B ⊥ . The vertical black arrow indicates the original distribution employed to produce the synthetic Stokes profiles: it is a δ-Dirac centered at 0, because the synthetic profiles were obtained assuming that the magnetic field is longitudinal/vertical (γ = 0) and therefore |
 |
Fig. 10 Same as Fig. 8 but for the inclination of the magnetic field vector γ. The vertical black arrows indicate the original distribution employed to produce the synthetic Stokes profiles: it is a double δ-Dirac centered at 0° and 180°, because the synthetic profiles were obtained assuming that the magnetic field is longitudinal/vertical. Note however that the effect of the noise induces the inversion code to retrieve highly inclined magnetic fields (color lines). |
Figure 9 displays a similar plot to Fig. 8, but for the horizontal component of the magnetic field B ⊥ . The original distribution, now a δ-Dirac at B ⊥ = 0, is indicated by the vertical black arrow. Here it can be seen that, although we started with an original distribution of magnetic fields that was purely vertical, the retrieved horizontal component of the magnetic field B ⊥ is much larger than the vertical component of the magnetic field B∥ (see Fig. 8). The only exception to this is the case where σs = 10-5, in which case the values of B ⊥ and B∥ are on the same order.
An important feature of Figs. 8 and 9, which shows a strong resemblance with what we have seen in the real data (see Fig. 7), is that the CoG of the histograms (indicated by the vertical-dashed color lines) shifts toward lower values when the noise decreases. This happens for both B∥ and B ⊥ .
As can be expected from these results, the retrieved inclination is mostly horizontal. This is demonstrated in Fig. 10, where the histograms for the inclination of the magnetic field peak at around γ ≈ 90°. This happens in spite of having started with vertical fields, whose distribution is represented in Fig. 10 by the two vertical black arrows at γ = 0,180°. That we have obtained horizontal fields out of purely vertical ones is due to the sole effect of the photon noise. This is also true for noise levels as low as 2.8 × 10-4, which corresponds to the the highest signal-to-noise data analyzed in OS07a, OS07b and LIT08. Even at noise levels as low as 10-5 (lower-right panel in Fig. 10) the correct distribution of inclinations is not properly recovered, although at least in this case some amount of vertical fields remain after the inversion.
Another interesting feature of our Monte-Carlo simulation is that it also reproduces the drop in the central peak at γ = 90° when using a SNR-threshold of 4.5 and 6 or, in order words, when only considering pixels where the polarization signal is 6 times or more above the noise level. This was already seenn from the inversions of real data: Figs. 3c–5c. However, this simulation fails the observed drop at γ ≈ 90°, which is less pronounced for lower noise levels.
The tests presented in this section demonstrate that it is possible to deduce the existence of horizontal fields from purely vertical ones due to the sole effect of photon noise. Photon noise is also responsible for an overestimate in B ⊥ and therefore also in 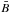 . These effects occur for noise levels as low as σs = 10-5. Therefore, results from these simulations challenge whether it is possible to correctly retrieve the distribution of the magnetic field vector in the quiet Sun internetwork. This will be addressed in the next section.
. These effects occur for noise levels as low as σs = 10-5. Therefore, results from these simulations challenge whether it is possible to correctly retrieve the distribution of the magnetic field vector in the quiet Sun internetwork. This will be addressed in the next section.
Finally it is important to mention a couple of consistency checks that were carried out. The first one was performed in order to study if our results are biased as a consequence of the inability of the VFISV inversion code to invert both the Fe i 6301.5 Å and Fe i 6302.5 Å spectral lines (see Sect. 3.2). We have repeated our Monte-Carlo experiments with the SIR inversion code (Ruiz Cobo & del Toro Iniesta 1992) and inverted both spectral lines simultaneously. Because of SIR’s limited speed we ran the experiment with only 5000 profiles, but this is sufficient to confirm the results presented throughout this section. The second consistency check is to repeat these experiments without photon noise. With this test we confirmed that vertical magnetic fields are actually retrieved (initial δ-Dirac distributions), and to test the convergence algorithm of the inversion code.
6. Selection effects
In the inversion of observed Hinode/SP data (Sect. 4) we applied a selection criterion that considers in the analysis all those pixels where any of the polarization signals (Q, U or V) are above a certain signal-to-noise ratio. This is the same criterion applied in the analysis of simulated data in Sect. 5 and also in OS07a and OS07b.
A very important consequence to be drawn from Sect. 5 is that the distributions for the magnetic field vector obtained from the inversion of the simulated data are not reliable as long as Stokes Q and U are dominated by noise. This was clearly the case in the inversion of the simulated data in that section, because there it had been assumed that the magnetic field was vertical.
It is therefore mandatory to study whether the aforementioned criteria, when applied to Hinode/SP data, select pixels where the linear polarization profiles (Q and U) are above the noise or, on the contrary, where V is the only Stokes parameter above the noise. For the simulated data in Sect. 5, the latter was certainly the case because the signals in Q and U were due only to photon noise. What about the observations from Hinode/SP employed in Sect. 4?
In Fig. 11 we show the percentage of pixels (with respect to the total number of pixels in each Hinode/SP map) as a function of the SNR-threshold applied. The three maps with different noise levels considered in Sect. 4 are indicated by the different symbols: crosses (map A: σs = 10-3), squares (map B: σs = 7.5 × 10-4), and diamonds (map C: σs = 2.8 × 10-4). Here we applied two different criterion. The first one is the same as in Sects. 4 and 5: a pixel is taken into account if any of three polarization profiles (Q, U or V) has a given signal-to-noise ratio (solid lines). The second one considers only those pixels were either Q or U posses a certain signal-to-noise ratio (dashed lines).
Taking as a reference a SNR-threshold of 4.5 (same as in OS07a) we find that 30.2% of the pixels contained in map A posses at least one of polarization signal that is above this threshold. However, if we restrict our analysis to Q or U only, we realize that only 3.4% of the pixels fulfill this criteria. This implies that the vast majority of the pixels analyzed have linear polarization profiles that are dominated by noise and thus, as demonstrated in Sect. 5, this automatically results in horizontal fields (see Fig. 10). Consequently, the peak at 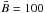 G and γ = 90° in Fig. 3 in this work and also in Fig. 3 in OS07a is not real, but due to noise.
G and γ = 90° in Fig. 3 in this work and also in Fig. 3 in OS07a is not real, but due to noise.
In map C, with a much lower noise level than map A, up to 80.0% of the pixels posses signals where at least one of the polarization profiles is above 4.5 times the noise level. However, the number drops to 31.6% if we consider only Q or U. As a consequence, only ≈ 1/3 of the peaks at 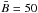 G and γ = 90° in Fig. 5 is real, with the remaining ≈ 2/3 being due to noise. This explains why in map A the peak at γ ≈ 90° disappears for large SNR-thresholds: it is mostly noise (Fig. 3c), while remaining in map C (Fig. 5c): part of the peak there is actually real.
G and γ = 90° in Fig. 5 is real, with the remaining ≈ 2/3 being due to noise. This explains why in map A the peak at γ ≈ 90° disappears for large SNR-thresholds: it is mostly noise (Fig. 3c), while remaining in map C (Fig. 5c): part of the peak there is actually real.
What then is the inclination and strength of the magnetic field vector in the pixels where Q and U are not above the noise level? This represents 97% of all pixels included in the analysis of Fig. 3 (map A) and about 70% of all pixels included in the analysis of Fig. 5 (map C). As demonstrated in Sect. 5, it is possible that they are vertical γ ≈ 0° with a field strength of 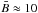 G. However, as long as B ⊥ remains below our detection threshold, this is only speculation.
G. However, as long as B ⊥ remains below our detection threshold, this is only speculation.
In order to improve the reliability of the histograms for the magnetic field vector it is possible to repeat the analysis in Sect. 4, but employing only those pixels where the linear polarization signals (Stokes Q or U) are 4.5 times above the noise level. In this case we still obtain the central peak at γ = 90° and B = 60 − 120 G in all three maps considered. This was to be expected because Q and U signals sufficiently above the noise implies the existence of highly inclined magnetic fields (γ → 90°). This is so because in the weak-field regime, the linear polarization is a second order effect (Landi Degl’Innocenti 1992) in the magnetic field as compared to the circular polarization.
However, it is important to clarify that histograms obtained applying the selection criteria to the linear polarization would only contain a minority of internetwork pixels, leaving out many of them (up to 90% of internetwork pixels in map A or up to 70% of pixels in map C) whose inclination is unknown. Our tests show that in order to correctly infer the inclination of those pixels where only Stokes V is above the signal, a noise level better than × 10-5 (see Fig. 10) is needed.
According to Fig. 11 one might think that even though only 3.4% of the pixels in map A and 31.6% in map C posses a signal-to-noise higher than or equal to 4.5, these numbers grow up to 69.6% and 85.9% respectively if a SNR-threshold of 3 is considered. However, as explained in Sect. 4, SNR ≥ 3 is not sufficient to reliably infer the magnetic field vector because photon noise produces signals that exceed 3 times the noise level in most of the pixels.
7. Conclusions
We have studied the distribution of the magnetic field vector (strength 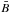 and inclination with respect to the vertical direction γ) in internetwork regions with data from the spectropolarimeter (SP) onboard the Japanese satellite Hinode. We selected three different maps recorded at disk center with different integration times and therefore different noise levels. In all three cases, the retrieved inclination of the magnetic field peaks at γ = 90°, in agreement with previous results (Orozco Suárez et al. 2007a,b).
and inclination with respect to the vertical direction γ) in internetwork regions with data from the spectropolarimeter (SP) onboard the Japanese satellite Hinode. We selected three different maps recorded at disk center with different integration times and therefore different noise levels. In all three cases, the retrieved inclination of the magnetic field peaks at γ = 90°, in agreement with previous results (Orozco Suárez et al. 2007a,b).
In addition, we found that the distribution of vertical/longitudinal fields (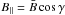 ) and horizontal/transverse fields (
) and horizontal/transverse fields (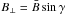 ) shift toward lower values when we analyze data with lower levels of photon noise. In spite of this decrease, the relation B ⊥ ≫ B∥ holds, which explains why all analyzed maps yield histograms for the inclination with a clear peak at γ = 90°.
) shift toward lower values when we analyze data with lower levels of photon noise. In spite of this decrease, the relation B ⊥ ≫ B∥ holds, which explains why all analyzed maps yield histograms for the inclination with a clear peak at γ = 90°.
 |
Fig. 11 Number of pixels (with respect to the total amount of pixels in each map) as a function of their signal-to-noise ratio. In solid lines we show the number of pixels when considering any of the polarization profiles (Stokes Q, U or V), whereas in dashed lines we plot the number of pixels when considering only the linear polarization (Stokes Q or U). Symbols indicate each of the three maps employed: crosses (map A; σs = 10-3), squares (map B; σs = 7.5 × 10-4) , and diamonds (map C; σs = 2.8 × 10-4.) |
To understand this result we carried out a Monte-Carlo-like simulation in which we produced a large number of synthetic profiles assuming vertical fields (γ = 0,180°) and, after adding photon noise at different levels, we inverted the synthetic Stokes profiles to investigate whether the original distributions (δ-Dirac functions) can be recovered. These tests show that peaks at γ = 90° (horizontal fields) are obtained for noise levels as low as σs = 2.8 × 10-4 even though in the synthesis we had used only vertical ones. This means that the histograms for the inclination obtained with real data are contaminated to a large extent by the effect of the photon noise, which makes vertical and horizontal fields indistinguishable.
To what extent the histograms are contaminated depends on the selection criteria employed to select pixels that enter in the analysis. If we select pixels where the signal-to-noise ratio in any of the polarization profiles (Stokes Q, U or V) is above 4.5, the contamination can be as high as 70−95% (depending on the noise level). This renders the inferred distributions for the magnetic field inclination and transverse component of the magnetic field meaningless. This is the approach followed in Orozco Suárez et al. (2007a,b). Other authors such as Lites et al. (2007) and Kobel (2009) impose a larger threshold for Stokes V (SNR ≥ 6) than for Stokes Q and U (SNR ≥ 2), which can partially avoid the contamination.
A better approach is to analyze only those pixels where the linear polarization profiles (Stokes Q and U) have a signal-to-noise ratio higher than or equal to 4.5. This strategy has the advantage that the inclination of the magnetic field can be properly retrieved by the inversion of the radiative transfer equation applied to the observed Stokes profiles. A similar conclusion is reached by Asensio Ramos (2009). The main shortcoming of this selection procedure is that it considers only small regions within the internetwork: 5 − 30% (depending on the noise level), leaving out large portions where the inclinations is not determined. We conclude therefore that the real distribution of inclinations in the quiet Sun internetwork remains unknown. A proper inference can only be carried out with noise levels that are beyond the current capabilities of modern spectropolarimeters. Workarounds can be found by introducing temporal averages, but the required integration time exceeds the lifetime of granulation. It is therefore not clear what is represented by histograms obtained with averages spanning several minutes.
The importance of the photon noise has been already acknowledged by Asensio Ramos (2009) and Stenflo (2010). In the latter work, results are interpreted in terms of an isotropic distribution of magnetic fields. However, these works do not analyze low-noise data, thus missing the contribution from pixels with strong Q and U signals: up to 30% of the total amount of pixels. The question is therefore whether an isotropic distribution of fields can explain these regions of truly horizontal fields.
Asensio Ramos (2009) and Martínez González et al. (2008) also conclude that the distribution of magnetic fields is quasi-isotropic, however, whereas the latter refers to pixels where the polarization signal is above the noise level, the former infers a quasi-isotropic distribution only for those pixels whose polarization signal is below the noise. Our work differs from those because we can explain many features of the resulting histograms for the inclination, employing only vertical fields. In the future we intend to adress the possibility of isotropism in more detail.
This inversion code is freely available for download at the Community Spectro-Polarimetric Analysis Center (CSAC; Lites et al. 2007), which is an initiative at the High Altitude Observatory and National Center for Atmospheric Research (NCAR): http://www.csac.hao.ucar.edu/
We employ the random number generator algorithm for normally distributed variables by Leva (1992).
Acknowledgments
We would like to thank Dr. Bruce W. Lites, Dr. Luis Bellot Rubio and Dr. David Orozco Suárez for fruitful discussions in the subject. We are also grateful to Dr. Andreas Lagg for comparing inversion results using the HELIX++ code with the results from the VFSIV code. This work analyzes data from the Hinode spacecraft. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway). This work has also made use of the NASA ADS database.
References
- Asensio Ramos, A. 2009, ApJ, 701, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Bellot Rubio, L. R. 2009, ApJ, 700, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Bellot Rubio, L. R., Rodríguez Hidalgo, I., Collados, M., Khomenko, E., & Ruiz Cobo, B., 2001, ApJ, 560, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., Martínez-Pillet, V., Schlichenmaier, R., et al. 2010a, ApJ, 723, L144 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., Tomczyk, S., Kubo, M., et al. 2010b, Sol. Phys., 35 [Google Scholar]
- Centeno Elliot, R., Socas-Navarro, H., Lites, B. W., et al. 2007, ApJ, 666, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Beeck, B., Pietarila, A., et al. 2010, ApJ, 723, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez Cerdeña I., Sánchez Almeida, J., & Kneer, F. 2006, ApJ, 646, 1421 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, C. E., de Wijn, A. G., Centeno, R., Lites, B. W., & Keller, C. U, 2009, A&A, 504, 583 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ichimoto, K., Lites, B. W., & Elmore, D. 2008, Solar Physics, 249, 233 [Google Scholar]
- Khomenko, E., Collados, M., Solanki, S. K., et al. 2003, A&A, 408, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobel, P. 2009, PhD Thesis, Göttingen University, Germany [Google Scholar]
- Kosugi, T., Matsuzaki, K., & Sakao, T. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lagg, A., Woch, J., Krupp, N., & Solanki, S. K. 2004, A&A, 414, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Ishikawa, R., Merenda, L., et al. 2009, in Second Hinode Science Meeting: Beyond Discovery- Towards Understanding, ed. B. Lites, M. Cheung, T. Magara, J. Mariska & K. Reeves, ASP Conf. Ser., 415, 327 [Google Scholar]
- Landi Degl’Innocenti, E. 1992, in Solar Observations: techniques and interpretation, ed. F. Sánchez, M. Collados & M. Vázquez (Cambridge: Cambridge University Press), Sect. 4–8. [Google Scholar]
- Leva, J. L. 1992, ACM Trans. Math. Software, 18, 454 [Google Scholar]
- Lites, B. W., Elmore, D., & Streander, K. V. 2001, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Proc., 236, 33 [NASA ADS] [Google Scholar]
- Lites, B. W., Casini, R., García, J., & Socas-Navarro, H. 2007, Mem. Soc. Astron. Ital., 78, 148 [Google Scholar]
- Lites, B. W., Kubo, M., Socas-Navarro, H., et al. 2008, ApJ, 672, 1237, LIT08 [NASA ADS] [CrossRef] [Google Scholar]
- Manso Sainz, R., Landi Degl’Innocenti, E., & Trujillo Bueno, J. 2004, ApJ, 614, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, M., & Bellot Rubio, L. R. 2009, ApJ, 700, 1391 [CrossRef] [Google Scholar]
- Martínez González, M., Asensio Ramos, A., López Ariste, A., & Manso-Sainz, R. 2008, A&A, 479, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez González, M., Manso-Sainz, R., Asensio Ramos, A., et al. 2010, ApJ, 711, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Nagata, S., Tsuneta, S., Suematsu, Y., et al. 2008, ApJ, 677, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C. et al. 2007a, ApJ, 670, L61 (OS07a) [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C., et al. 2007b, PASJ, 59, 837 (OS07b) [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., & del Toro Iniesta, J. C. 2010, A&A, 518, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W. H., Flannery, B. P., & Teukolsky, S. A. 1986, Numerical recipes. The art of scientific computing (Cambridge: Cambridge University Press) [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J. 2005, A&A, 438, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez Almeida, J. 2004, in The Solar-B Mission and the Forefront of Solar Physics, ed. T. Sakurai, & T. Sekii, ASP Conf. Ser., 325, 115 [Google Scholar]
- Shimizu, T., Nagata, S., & Tsuneta, S. 2008, Sol. Phys., 249, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Shimizu, T., Martinez-Pillet, V., & Collados, M. 2007, in New Solar Physics with Solar-B Mission, ed. K. Shibata, S. Nagata, & T. Sakurai, ASP Conf. Ser., 369, 113. [Google Scholar]
- Schrijver, C. J., & Title, A. M. 2003, ApJ, 597, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Title, A. M., van Ballegooijen, A. A., et al. 1997, ApJ, 487, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Title, A. M., Harvey, K. L., et al. 1998, Nature, 394, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 2010, A&A, 517, 37 [Google Scholar]
- Socas-Navarro, H., & Manso-Sainz, R. 2005, ApJ, 620, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., Borrero, J. M., Asensio Ramos, A., et al. 2008, ApJ, 674, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Inhester, B., & Schüssler, M. 2006, RPPh, 3, 563 [Google Scholar]
- Spruit, H. 2003, Sol. Phys., 213, 1 [Google Scholar]
- Suematsu, Y., Tsuneta, S., & Ichimoto, K. 2008, Sol. Phys., 249, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
- Tsuneta, S., Suetmatsu, Y., & Ichimoto, K. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Observed continuum intensity (upper panel) and mean magnetic field strength at each pixel inferred from the inversion of the Stokes profiles (lower panel). This region is only a subsection of the full field of view. It was chosen to approximately match Fig. 2 in OS07a. See Sect. 2.1 for details. |
| In the text | |
 |
Fig. 2 Observed continuum intensity (upper panel) and mean magnetic field strength at each pixel inferred from the inversion of the Stokes profiles (lower panel). Note that the spectrograph’s slit was always located at the same position on the Sun, therefore the horizontal axis refers to time. See Sect. 2.2 for details. |
| In the text | |
 |
Fig. 3 Panel a) histogram for the number of pixels as a function of the signal-to-noise ratio in the polarization profiles. Circular polarization (Stokes V) is indicated by the solid line, while the linear polarization ( |
| In the text | |
 |
Fig. 4 Same as Fig. 3 but for map B, with a characteristic noise level of σs = 7.5 × 10-4. |
| In the text | |
 |
Fig. 5 Same as Fig. 3 but for map C, with a characteristic noise level of σs = 2.8 × 10-4. |
| In the text | |
 |
Fig. 6 Histograms for the longitudinal component of the magnetic field B∥ (left panels) and the transverse component of the magnetic field B ⊥ (right panels). The first row corresponds to map A, while the second corresponds to map B, and the third represents map C. Dashed-dotted, solid and dashed lines correspond to a SNR-threshold of 3, 4.5, and 6, respectively. |
| In the text | |
 |
Fig. 7 CoG (center of gravity) of the histograms for B∥ (solid) and B ⊥ (dashed) retrieved from the inversion of the profiles in map A (crosses; σs = 10-3), B (squares; σs = 7.5 × 10-4) and C (diamonds; σs = 2.8 × 10-4), as a function of the SNR-threshold. |
| In the text | |
 |
Fig. 8 Histograms for the original longitudinal component of the magnetic field |
| In the text | |
 |
Fig. 9 Same as Fig. 8 but for the transverse component of the magnetic field B ⊥ . The vertical black arrow indicates the original distribution employed to produce the synthetic Stokes profiles: it is a δ-Dirac centered at 0, because the synthetic profiles were obtained assuming that the magnetic field is longitudinal/vertical (γ = 0) and therefore |
| In the text | |
 |
Fig. 10 Same as Fig. 8 but for the inclination of the magnetic field vector γ. The vertical black arrows indicate the original distribution employed to produce the synthetic Stokes profiles: it is a double δ-Dirac centered at 0° and 180°, because the synthetic profiles were obtained assuming that the magnetic field is longitudinal/vertical. Note however that the effect of the noise induces the inversion code to retrieve highly inclined magnetic fields (color lines). |
| In the text | |
 |
Fig. 11 Number of pixels (with respect to the total amount of pixels in each map) as a function of their signal-to-noise ratio. In solid lines we show the number of pixels when considering any of the polarization profiles (Stokes Q, U or V), whereas in dashed lines we plot the number of pixels when considering only the linear polarization (Stokes Q or U). Symbols indicate each of the three maps employed: crosses (map A; σs = 10-3), squares (map B; σs = 7.5 × 10-4) , and diamonds (map C; σs = 2.8 × 10-4.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.