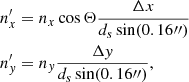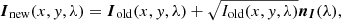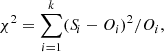| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A176 | |
| Number of page(s) | 12 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202451079 | |
| Published online | 13 November 2024 | |
Solar internetwork magnetic fields: Statistical comparison between observations and MHD simulations
Institute for Solar Physics (KIS), Georges-Köhler-Allee 401A, 79110 Freiburg, Germany
⋆ Corresponding author; ebert@leibniz-kis.de
Received:
12
June
2024
Accepted:
8
September
2024
Context. Although the magnetic fields in the quiet Sun account for the majority of the magnetic energy in the solar photosphere, inferring their exact spatial distribution, origin, and evolution poses an important challenge because the signals lie at the limit of today’s instrumental precision. This severely hinders and biases our interpretations, which are mostly made through nonlinear model-fitting approaches.
Aims. Our goal is to directly compare simulated and observed polarization signals in the Fe I 6301 Å and 6302 Å spectral lines in the very quiet Sun, the so-called solar internetwork (IN). This way, we aim to constrain the mechanism responsible for the generation of the quiet Sun magnetism while avoiding the biases that plague other diagnostic methods.
Methods. We used three different three-dimensional radiative magneto-hydrodynamic simulations representing different scenarios of magnetic field generation in the internetwork: small-scale dynamo, decay of active regions, and horizontal flux emergence. We synthesized Stokes profiles at different viewing angles and degraded them according to the instrumental specifications of the spectro-polarimeter (SP) on board the Hinode satellite. Finally, we statistically compared the simulated spectra to the Hinode/SOT/SP observations at the appropriate viewing angles.
Results. Of the three simulations, the small-scale dynamo best reproduced the statistical properties of the observed polarization signals. This is especially prominent for the disk center viewing geometry, where the agreement is excellent. Moving toward more inclined lines of sight, the agreement worsens slightly.
Conclusions The agreement between the small-scale dynamo simulation and observations at the disk center suggests that small-scale dynamo action plays an important role in the generation of quiet Sun magnetism. However, the magnetic field around 50 km above the continuum layer in this simulation does not reproduce observations as well as at the very base of the photosphere.
Key words: dynamo / magnetic fields / polarization / techniques: polarimetric / Sun: magnetic fields / Sun: photosphere
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Magnetic fields in the solar internetwork (IN) have an average magnitude of ≈100 G (Lites et al. 2008; Trujillo Bueno et al. 2004). Although much weaker than in active regions, once it is integrated over the entire solar surface, the IN makes up the majority of the solar magnetic energy. Variation of the IN fields with solar cycle has been a topic of intensive observational study (Lites et al. 2014; Faurobert & Ricort 2015; Trelles Arjona et al. 2023). Other studies have focused on the inference of the orientation of the IN fields, as this also has important implications for the origins of quiet Sun magnetism (Steiner et al. 2008; Schüssler & Vögler 2008). This particular aspect has been investigated in recent years with a myriad of methods and data, with many different outcomes. Orozco Suárez et al. (2007) and Lites et al. (2008) applied Milne-Eddington Stokes inversions to spectropolarimetric data from Hinode/SOT/SP of the Fe I line pair at 630 nm recorded at the disk center and found a preference for horizontal fields. Jafarzadeh et al. (2014) analyzed Sunrise/IMAX data (Martínez Pillet et al. 2011) and found mostly vertical fields in the internetwork using geometrical considerations on magnetic bright spots in different layers of the atmosphere. Martínez González et al. (2008) found an isotropic distribution when analyzing the two spectral lines of Fe I at 1565 nm. These lines are more sensitive to the horizontal component of the field and thus reduce the bias that arises from the very different sensitivities exhibited by the linear and circular polarization to the perpendicular and parallel components of the magnetic field1. An isotropic distribution was also favored by Asensio Ramos (2009) who carried out a Bayesian analysis of Hinode/SOT/SP data. Finally, Danilovic et al. (2016), using spatially coupled inversions of Hinode/SOT/SP data, found a quasi-isotropic distribution of the magnetic field but emphasized that the distribution cannot be constrained in detail. A more detailed summary of these results can be found in Borrero et al. (2017).
The main reason for these discrepancies is the fact that spectropolarimetric observations of the quiet Sun lie at, or even below, the noise limit of today’s instruments. The photon noise limits our sensitivity to the magnetic field and its orientation (Borrero & Kobel 2011), and cannot be increased arbitrarily without losing the temporal or spatial resolution needed to resolve the changing atmosphere. Furthermore, even in the best-case scenario, the spatial resolution of our telescopes sets a lower limit on the magnetic concentrations we can resolve using the Zeeman effect. On scales much smaller than the resolution element, where the magnetic field is tangled, opposite polarities in the same pixel cause the circular polarization to cancel out, as shown by Emonet & Cattaneo (2001), making us blind to the existence of the magnetic field. This drawback can be partially mitigated by using Hanle diagnostics (e.g., Trujillo Bueno et al. 2004; del Pino Alemán et al. 2018), but these again require specific observations and knowledge of the so-called zero-level polarization.
To mitigate or circumvent some of the aforementioned shortcomings, we propose a statistical comparison of the observed signals in Hinode’s Fe I line pair at 630 nm at several heliocentric viewing angles Θ (i.e., the angle between the line of sight and the surface normal) to synthetic Stokes profiles calculated from three different three-dimensional radiative magnetohydrodynamic (RMHD) simulations of the solar surface convection. Before comparing with the observations, the synthetic profiles are degraded to match Hinode’s spatial and spectral resolution as well as sampling. Finally, photon noise is added at the same level as in the observations. After that, histograms of the polarization signals of the observations and simulations are compared.
On the one hand, the advantage of this approach is that we do not perform any Stokes inversions and therefore our results are not affected by the inherent issues and biases introduced by those analysis techniques (Borrero & Kobel 2011, 2012, 2013). On the other hand, due to the limited number of simulations employed in this work, all we can aim for is to discriminate between different physical scenarios described by these simulations.
Each of the three employed simulations uses different initial conditions: small-scale dynamo, constant vertical field, and horizontal flux emergence. Our goal is to decipher which of these scenarios best reproduces the observations. These initial conditions are meant to represent the most plausible origins for the IN magnetic fields (Bellot Rubio & Orozco Suárez 2019): magnetic fields amplified locally in the solar photosphere by a small-scale local dynamo mechanism (Vögler & Schüssler 2007), decay or recycling of the magnetic fields of active regions (Spruit et al. 1987), and emergence of horizontal magnetic fields from the convection zone by the global solar dynamo (Stein & Nordlund 2002).
2. Observational data
2.1. Observations
The observations used in this work were recorded by the spectropolarimeter (SP) (Lites et al. 2013) attached to the optical telescope (Tsuneta et al. 2008) on board the Hinode spacecraft (Kosugi et al. 2007). These observations comprise the so-called Stokes vector I = (I, Q, U, V), where I is the total intensity, Q and U refer to the linear polarization, and V is the circular polarization. The spectral coverage of Hinode/SOT/SP goes from 6300.8 to 6303.2 Å, covering the magnetically sensitive spectral lines of neutral iron: Fe I 6301.5 Å and Fe I 6302.5 Å. This spectral region is covered by 112 wavelength points, with a wavelength sampling of 21.5 mÅ.
We chose eight maps with different heliocentric positions, which are listed in Table 1. Maps B to H are a part of the observational table compiled by Lites et al. (2017). Figure 1 shows the locations of the maps on the solar disk. The field of view along the slit in the north–south direction is 164″, which is sampled in steps of 0.16″ (i.e., equal to the width of the slit). This sampling results from the angular diffraction limit  , where D = 0.5 m is the diameter of the Hinode telescope. This results in a pixel size, at disk center, of ds ⋅ sin0.16″ = 116.4 km, where ds is the average Earth–Sun distance. The reason for choosing these specific maps is that the observations were all performed within one week, and so we can neglect changes in the solar atmosphere on longer timescales. In this period, no significant degradation of the instrumentation is expected. All the maps have the same total integration time per slit scan position of ΔT = 9.6 s resulting in a similar noise level.
, where D = 0.5 m is the diameter of the Hinode telescope. This results in a pixel size, at disk center, of ds ⋅ sin0.16″ = 116.4 km, where ds is the average Earth–Sun distance. The reason for choosing these specific maps is that the observations were all performed within one week, and so we can neglect changes in the solar atmosphere on longer timescales. In this period, no significant degradation of the instrumentation is expected. All the maps have the same total integration time per slit scan position of ΔT = 9.6 s resulting in a similar noise level.
Observational maps used for the comparison.
 |
Fig. 1. Position of each map on the solar disk in Table 1 as observed by the Hinode satellite. Shaded areas indicate the regions where ΔΘ = ±2° around the selected Θ values of [0° ,10° ,20° ,30° ,40° ,50° ,60° ] (see text for details). |
2.2. Preprocess
The value of the heliocentric angle Θ for the central position of each map was determined by extracting the heliocentric (xc, yc) coordinates from the header of each FITS file and applying:
We note that, according to Fouhey et al. (2023), the pointing information of Hinode is inaccurate by Δxc ≈ Δyc ≈ ±30″. This means that the value of Θ determined by Eq. (1) is subject to an error, referred to as σΘ, and given by:
Equation (2) results in an error of σΘ ≈ 1.8° at Θ = 0° and this increases to σΘ ≈ 3.6° at Θ = 60°. This is important because for Map H, which contains the solar limb, the xc value provided by the headers had to be corrected by +3″ such that the limb was at 959″. For map G, also containing the limb, the xc value provided by the headers had to be corrected by +7″.
Now, each of the selected maps spans a significant portion of the solar disk and therefore has a different viewing angle Θ for different pixels. The difference between the maximum and minimum value of Θ for a given map is larger for the observations closer to the solar limb. Therefore, to avoid mixing observations from pixels with very different viewing angles contained in the same map, we restrict our analysis to those pixels within each map where the viewing angle is within ±2° of the following nominal values: Θ ∈ [0°, 10°, 20°, 30°, 40°, 50°, 60°]. These restricted regions are shown as shaded areas in Fig. 1 for each of the eight selected maps.
Every quiet Sun map was normalized to its local continuum intensity (using only the selected pixels within ±2°) by dividing all four Stokes components for all wavelengths by the mean of the local continuum intensity. The noise in the measurement of the polarization signals (Q, U, V) is assumed to have a Gaussian distribution as they are obtained from the difference between two simultaneous intensity measurements. This cancels out any systematic error in the intensity measurement that might have come from imperfect flat-field correction, dark current, and so on. The level of photon noise is different for different Stokes components (see Table 1), with the linear polarization signals (Q, U) having slightly larger values than the circular polarization signals (V).
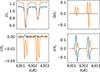 |
Fig. 2. Stokes profiles of a pixel at Θ = 0° (blue) and 60° (orange). They are normalized to the mean continuum intensity at the respective heliocentric angle. |
At continuum wavelengths, one expects no signal in the polarization, and so we infer the noise by taking the standard deviation of the continuum polarization of all selected spatial pixels. For this, the wavelength region ∈[6300.907, 6301.121] Å was chosen, which is expected to only contain the continuum. The inferred noise, in units of local quiet Sun continuum, is listed in Table 1 as 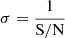 . The signal-to-noise ratio (S/N) decreases with Θ because of the limb darkening. Namely, the noise scales with the number of photons as
. The signal-to-noise ratio (S/N) decreases with Θ because of the limb darkening. Namely, the noise scales with the number of photons as 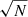 , where N is the number of detected photons, and thus, S/N also scales with the intensity as
, where N is the number of detected photons, and thus, S/N also scales with the intensity as 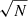 .
.
In Fig. 2 we show example profiles at Θ = 0° in blue and Θ = 60° in orange. As opposed to randomly choosing two pixels, which would likely feature mostly noise, the specific pixels were chosen because of their strong polarization signals. The pixel at Θ = 60° has also a strong signal in both linear polarizations to highlight the fact that the linear polarization is stronger when viewing from a higher inclination to the solar surface. Both pixels have such a high circular polarization that they will be excluded from the analysis as they will be considered to be part of the solar magnetic network (as explained in Sect. 3.4).
For completeness, we provide the height of the optical depth τ = 1 along the line of sight for different viewing angles in Fig. 3 (blue). As we can see, z(τ = 1) increases as we observe closer to the limb. This increase is accompanied by a decrease in the average temperature at the observed τ = 1 surface and a decrease in the observed intensity (i.e., limb darkening).
 |
Fig. 3. Average geometrical height and average temperature at τ = 1 along the line of sight for simulation #2 (see Sect. 3) as a function of heliocentric angle Θ. |
3. Synthesis of simulations and degradation
3.1. Description of simulations
The first two simulations used in this paper were performed using the MURaM radiative MHD code (Vögler et al. 2005). These simulations have a spatial domain of 24.576 × 24.576 × 7.680 Mm3. The top boundary is located at about 1.5 Mm above the average τ = 1 layer. This leaves a depth for the convective part of about 6.2 Mm. For the synthesis, only the upper 2.048 Mm are used, as lower depths do not contribute to the emergent intensity and a lot of computing time can be saved. These simulations have a sampling of Δx = Δy = Δz = 16 km in all spatial dimensions, with a total number of nx = ny = 1536 and nz = 480 grid cells.
Simulation #1 is a snapshot directly taken from Z16M in Rempel (2014). This simulation uses boundary conditions that are antisymmetric in inflow regions (B is set to zero) and symmetric in outflow regions. Here, the magnetic field arises from the small-scale dynamo, meaning that the simulation starts from a thermally relaxed convection simulation with no magnetic field to which a weak “seed field” of 0.005 G is added. Then the simulation evolves in time while the dynamo enhances the magnetic field until it reaches a saturated phase. This simulation represents a scenario where the small-scale local dynamo (SSD) is the sole origin of the IN fields (Vögler & Schüssler 2007).
Simulation #2 was obtained by taking a snapshot from a similar small-scale dynamo simulation (referred to as O16bM in Rempel 2014) and then adding a constant Bz = 30 G throughout the entire box and letting it evolve for 6 additional hours of solar time. Here the boundary conditions prescribe a symmetric behavior for all physical parameters including the magnetic field along the bottom. Simulation #2 is designed to represent a scenario where the IN fields originate from decaying fields of active regions (Spruit et al. 1987).
Simulation #3 was carried out by Calvo (2018) – where it is referred to as d3gt57g44h50mfc – using the magneto-hydrodynamic CO5BOLD Code (Freytag et al. 2012). It covers a horizontal section of 9.6 × 9.6 Mm2 of the solar atmosphere and extends from the top of the convection zone to beyond the top of the photosphere over a height range of 2.8 Mm, which is about 1240 km below and 1560 km above the solar surface (τ = 1). It has a sampling of Δx = Δy = Δz = 10 km in all spatial dimensions, with a total number of nx = ny = 960 and nz = 280 grid cells. The initial magnetic field is zero everywhere and a horizontal magnetic field with an absolute flux density of 50 G is advected through the bottom boundary. At the top boundary, the magnetic field is forced to be vertical in downflow regions and is constantly extrapolated in upflow regions. The simulation runs for 4.1 h, after which we choose the snapshot for the present analysis. This simulation represents a scenario where the IN magnetism originates from the appearance of magnetic fields – initially located in the convection zone – at the solar surface, as part of the global dynamo (Stein & Nordlund 2002).
The mean unsigned and mean signed vertical magnetic field, and the mean total magnetic field, in the simulations at τ = 1 of the selected snapshots of each simulation are shown in Table 2. We note that the mean signed vertical magnetic field is not exactly 0 G for simulations #1 and #3, nor is it exactly 30 G for simulation #2, because the values in this table correspond to a constant optical depth τ rather than to a constant height z.
Magnetic field in the three simulations.
Owing to our interest in investigating mainly the angular distribution of the magnetic field in the IN (see Sect. 1), we compare, in Fig. 4, the distribution of the inclination of the magnetic field with respect to the observer’s line of sight (γ) at τ = 1 from all three simulations. One can see that they all favor horizontal fields because there is an excess of pixels with respect to the isotropic distribution (gray line), with an inclination of between ∈[60° ,120° ]. As demonstrated by Borrero & Kobel (2013), an isotropic distribution follows a sinusoidal function that comes from the Jacobian when transforming to spherical coordinates. For simulation #2, the vertical magnetic field imposed as an initial condition can be seen at the τ = 1 level as an overabundance of pixels with an inclination of γ ∈ [0° ,30°] (blue line).
 |
Fig. 4. Histogram of the inclination of the magnetic field at τ = 1, where sin γ (gray line) corresponds to an isotropic distribution. |
3.2. Synthesis
To compare the predictions from the three simulations with observations, the emergent polarized spectra (i.e., the Stokes profiles) were synthesized from the simulation snapshots (i.e., MHD cubes) using the code FIRTEZ-dz (Pastor Yabar et al. 2019). We solve the radiative transfer equation for polarized light under the Zeeman effect, assuming local thermodynamic equilibrium (LTE) to solve the equation of state and find the populations of the atomic levels of the two lines observed by Hinode/SOT/SP (see Sect. 2.1). The parameters of the spectral lines are shown in Table 3. The data were synthesized with the same sampling as the observations of 21.5 mÅ.
Atomic parameters of the neutral iron lines used for this study.
To calculate the spectra for viewing angles Θ > 0, FIRTEZ-dz rotates the simulated atmosphere by a given angle and uses trilinear interpolation to determine the physical parameters along the inclined ray (i.e., on a new 3D grid). The essential aspect of this rotation is the assumption of periodic boundary conditions (also used in all three simulations), as it allows us to preserve the spatial extent of our boxes when doing the rotation.
3.3. Degradation
To make the simulated data comparable to the observed data, they need to be degraded to fit the spectral and spatial resolution of the Hinode/SOT/SP instrument. We used a spectral transmission profile (provided courtesy of Lites B.W. and shown in the right panel of Fig. 5) to spectrally convolve the synthetic data, thus effectively degrading its spectral resolution to ≈30 mÅ. In addition, we used the spatial point-spread function (PSF) taken from Danilovic et al. (2008) to degrade the spatial resolution to 0.16″. The spatial PSF at the disk center (Θ = 0°) is also shown in Fig. 5 (left panel). For other Θ values, the spatial PSF is modified to account for the larger pixel size along one spatial dimension. Finally, we resampled the data in x and y directions to fit the Hinode/SOT/SP pixel size using Eq. (3), which gives the new number of grid cells, nx′ and ny′, along each of the horizontal dimensions:
 |
Fig. 5. Spatial and spectral degradation of the simulated Stokes profiles. Left panel: Spatial PSF of the Hinode/SOT/SP instrument (at disk center). Right panel: Hinode/SOT/SP spectral transmission curve. |
where the foreshortening according to the viewing angle Θ is only done along one of the spatial dimensions. For instance, the above equations indicate that the simulation #1, which originally had nx = ny = 1536, has to be resampled into nx′=ny′ = 212 grid cells at Θ = 0°, but into nx′ = 183 and ny′ = 212 grid cells at Θ = 30°. The last step before comparing the simulated data with the observed data is to add the same noise level as was obtained for the observations in Sect. 2.2. The noise vector nI was created by drawing from a Gaussian distribution with standard deviations σQ, σU, or σV (see Table 1). We used wavelength-dependent noise so that the new polarization signals with noise added are given as:
where Iold(x, y, λ) is the normalized intensity profile. This ensures that less noise is added closer to the line core than in the continuum because the number of detected photons is lower. Equation (4) applies to both the intensity (Inew) and the polarization (Qnew, Unew, and Vnew) because the noise in the polarization profiles is the same as in the intensity, including its wavelength dependence. This happens because the latter is obtained from the linear combination of intensity measurements (i.e., modulation; del Toro Iniesta & Collados 2000).
3.4. Removal of network
Our work focuses on the IN fields, and so it is necessary to remove the network regions, both from the observed and synthetic data. The network is assumed to contain strong magnetic fields (> 500 G), which are observed at the disk center as mostly vertical. They are also found mostly in between supergranules, at scales of 30 Mm (Rieutord & Rincon 2010). One possibility to identify the network pixels in the observations would be to perform an inversion of the Stokes profiles and look for regions where the magnetic field features these network-like properties. However, our study avoids Stokes inversions to circumvent the biases described by Borrero & Kobel (2013). Thus, we need to identify network pixels directly from the observed Stokes vector instead of using magnetic field values from the inversion. Although the horizontal size in our simulations is smaller than the spatial scales of the network (i.e., 9.6−24.576 Mm vs. 30 Mm; Rieutord & Rincon 2010), they do contain a few network-like patches that can be seen in the vertical magnetic field (see the rightmost panel in Fig. 6). These patches of strong vertical magnetic field were then considered to be part of the network.
 |
Fig. 6. Comparison of max∥V(λ)∥ in units of continuum intensity for Θ = 0° (left panel) and Θ = 60° (middle panel) with Bz [G] of simulation #1 (right panel). |
As the magnetic field of the network is mostly vertical at disk center, there is a large signal in Stokes V. To identify the network in circular polarization, we compared in Fig. 6 the maximum of ∥V(λ)∥ at Θ = 0° (left) with Bz(x, y) at τ = 1 (right). We determined a threshold of max∥V(λ∥) = 0.05, above which a pixel is ascribed to the network and thus removed from our analysis.
Finding a threshold to identify the network off-disk center (Θ > 0) requires additional considerations. Although the network is not completely homogeneous and is known for having internal structure (Martínez González et al. 2012), we surmise that, at disk center, the network is mostly vertical. Under this assumption, the observed circular polarization or Stokes V in the network should scale as VcosΘ. To test this hypothesis, we took several patches in the simulations at disk center Θ = 0° (see left panel in Fig. 6) that were identified as network and plotted the average over those selected pixels of max∥V(λ)∥ as a function of μ = cosΘ. These patches include about 500 pixels. Results are presented in Fig. 7. Here we can see that the circular polarization signals in the simulated network roughly scale linearly with cosΘ (see orange curve), thereby justifying our initial assumption that network fields are mostly vertical. With this, we can now find a threshold with which to detect network patches in the simulations with Θ > 0 as those pixels where max∥V(λ)∥ > 0.05cosΘ. As already mentioned, pixels identified as such are masked out from our analysis. Two examples of the masked pixels in simulation #1 are presented in red in Fig. 6 (Θ = 0° and Θ = 60° in the left and middle panels, respectively).
 |
Fig. 7. Empirical relationship between the max(|V(λ)|) and μ = cosΘ for the several network patches in Fig. 6. Vertical blue bars indicate the standard deviation for the sample of about 500 pixels included in these patches. |
4. Results
To compare the observed Stokes profiles with those synthesized from the simulations, we took a statistical approach. For each spatial pixel (x, y), the maximum of the absolute value of [Q(λ),U(λ)] and V(λ) was used to make a histogram. Q and U are combined to form an approximate total linear polarization L for each pixel by taking whichever is the largest of the two. As an example, in Figs. 8 and 9 we display these histograms (in black lines) for the observed signals at Θ = 10° (map B; see Table 1). Circular and linear polarization signals are presented in the left and right panels of these two figures, respectively.
 |
Fig. 8. Histograms of the polarization signals at Θ = 10°. Left panel: max∥V(λ)∥. Right panel: max[∥Q(λ)∥, ∥U(λ)∥. Observed values are shown in black, whereas predicted histograms from simulation #2 are shown in colors for two different values of ⟨B(τ = 1)⟩: 149 G (red; original value) and 105 G (blue; 70% of the original value). |
 |
Fig. 9. Histograms of the polarization signals at Θ = 10°. Left panel: max∥V(λ)∥. Right panel: max[∥Q(λ)∥, ∥U(λ)∥. Observed values are shown in black, whereas predicted histograms from simulation #3 are shown in colors for two different values of ⟨B(τ = 1)⟩: 125 G (red; original value) and 113 G (green; 90% of the original value). |
For most of the pixels, the polarization signal is below the noise level. This can be seen in the peak of the histograms at ≈2.6 ⋅ σ ≈ 2.3 × 10−3. As there are 112 wavelength pixels (see Sect. 2.1), one expects the peak of these histograms to be at 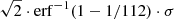 (where erf−1 is the inverse error function) if there is no signal in addition to the noise. Hereafter, we refer to this peak produced by photon noise simply as the noise-peak. Signals with a level above the noise peak until the drop above 0.05 are considered to be representative of the IN. The drop above the 0.05 level is caused by the removal of the network described in Sect. 3.4.
(where erf−1 is the inverse error function) if there is no signal in addition to the noise. Hereafter, we refer to this peak produced by photon noise simply as the noise-peak. Signals with a level above the noise peak until the drop above 0.05 are considered to be representative of the IN. The drop above the 0.05 level is caused by the removal of the network described in Sect. 3.4.
For a quantitative comparison between the observed and simulated histograms, we performed a χ2 analysis, where the merit function χ2 is defined as:
where Si and Oi are the fractions of pixels in the simulation and observations, respectively, falling in between two logarithmically spaced Stokes signals as shown in Figs. 8 through A.2. This merit function was chosen to sample in k = 125 histogram bins. A smaller χ2 value indicates a better fit between observations and simulations, but we emphasize that the values of χ2 can be influenced by slightly different positions of the noise peak in the observations and simulations, as well as by the existence of outliers in the simulations in bins where Oi → 0. Consequently, we only draw conclusions when find agreement between a quantitative analysis in terms of χ2 and a qualitative analysis based on our visual perception of the similarities between simulations and observations. The specific values of χ2 for both the circular and linear polarization, as well as the percentage of network pixels removed, are provided in the legend of Figs. A.1 and A.2.
4.1. Field strength reduction in simulations #2 and #3
Along with the histograms of the observed signals, Fig. 8 also displays the histograms of the polarization signals predicted at Θ = 10° by simulation #2 (red curves), where the average value of the magnetic field is ⟨B(τ = 1)⟩ = 149 G (see Sect. 3). Likewise, Fig. 9 shows (also in red) the predicted histograms for the polarization signals at Θ = 10°, but for simulation #3 where the average value of the magnetic field is ⟨B(τ = 1)⟩ = 125 G.
As it can be seen, simulations #2 and #3 with these mean magnetic field strengths both predict excessively strong polarization signals compared to the observations. Therefore, we tried to reduce the magnetic field by a constant factor to see if this would result in histograms closer to the observed ones. The idea is that a reduction of the magnetic field by a constant factor will not have a large effect on how the thermodynamic and kinematic parameters of the simulation behave, and therefore we can keep those to calculate the synthetic profiles without having to run new MHD simulations. This is supported by the fact that the magnetic field is, in all cases, dynamically weak (i.e., below the equipartition value: 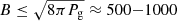 G, where Pg is the gas pressure). The magnetic field in simulations #2 and #3 was reduced from its original values of ⟨B⟩ = 149 G and ⟨B⟩ = 125 G, respectively (see Table 2), to the values shown in Table 4. We note that we reduced the total magnetic field instead of only one of its components (i.e., Bz) in order to keep the distribution of the inclination of the magnetic field the same as in the original simulation (see Fig. 4). Figures 8 and 9 include, in blue color, the predicted histograms for one of those reduction factors, namely a factor 0.7, meaning that ⟨B(τ = 1)⟩ = 105 G in simulation #2, and a factor 0.9 in simulation #3, meaning that ⟨B(τ = 1)⟩ = 113 G.
G, where Pg is the gas pressure). The magnetic field in simulations #2 and #3 was reduced from its original values of ⟨B⟩ = 149 G and ⟨B⟩ = 125 G, respectively (see Table 2), to the values shown in Table 4. We note that we reduced the total magnetic field instead of only one of its components (i.e., Bz) in order to keep the distribution of the inclination of the magnetic field the same as in the original simulation (see Fig. 4). Figures 8 and 9 include, in blue color, the predicted histograms for one of those reduction factors, namely a factor 0.7, meaning that ⟨B(τ = 1)⟩ = 105 G in simulation #2, and a factor 0.9 in simulation #3, meaning that ⟨B(τ = 1)⟩ = 113 G.
4.2. Simulation #1
Figure A.1 shows that at Θ = 0°, simulation #1 (orange lines) yields histograms for the polarization signals that are relatively close to the observations. There is still a slight excess in circular polarization at values of max∥V(λ)∥ ≥ 10−2. This suggests that simulation #1 features too many pixels with vertical magnetic fields. This is also supported by the fact that there seems to be a lack of linear polarization signal in the range [3 × 10−3, 8 × 10−3]. Therefore, despite being already rather horizontal (see green curve in Fig. 4), the magnetic field should be even more inclined (γ → 90°) in order to produce a better fit to the observed histograms. However, overall, it seems as if the magnetic field of this simulation is close to the real magnetic field in the IN regions of the Sun.
At larger heliocentric angles (see Figs. A.1 and A.2), the mismatch between the observed and simulated circular polarization increases, with simulation #1 overestimating the amplitude of the observed V signals by an increasing amount as Θ rises. Meanwhile, the simulated linear polarization gets closer to the observed one up to Θ = 40° but shows an excess in the predicted [Q, U] signals at Θ = 50° and Θ = 60°.
This might be explained by the fact that, in the observations, some pixels harboring mostly vertical fields (and thus appearing in the circular polarization when looking from lower Θ) appear in linear polarization when looking at higher Θ, thereby increasing the number of signals in the latter while lowering the signals in the former. While this effect can be seen mostly in the observations, simulation #1 also features this decrease in circular polarization for higher viewing angles, albeit in a less pronounced fashion. As the τ = 1 layer is higher in the atmosphere for higher viewing angles (see Fig. 3), one can conclude that at this height there is too much magnetic field parallel to the observer’s line of sight (B∥), while there is seemingly enough magnetic field perpendicular to the observer’s line of sight (B⊥). Relating this back to the nonrotated point of reference, this can be interpreted as the magnetic field in simulation #1 possessing too many pixels with mostly horizontal fields when sampling higher atmospheric layers.
This suggests that, in the real IN, the B⊥/B∥ ratio increases more slowly with height, similarly to that predicted by the local dynamo simulations (see Fig. 1 in Steiner et al. 2008 and Fig. 3 in Schüssler & Vögler 2008). However, this conclusion can only be made for a very limited range of heights of about 40−50 km, which corresponds to the height difference being sampled at Θ = 0° and at Θ = 60°.
4.3. Simulation #2
In Fig. 8, we see that reducing the magnetic field by a factor of 0.7 moves the histogram (right of the noise-peak) down without changing the slope, meaning that the power law in the predicted polarization signals remains the same regardless of the mean field strength. It is therefore difficult to assess at which ⟨B⟩ the simulation best fits the observations, as it depends on the polarization level at which one wants the histograms to agree. Overall, out of all values in Table 4, we choose ⟨B⟩ = 105 G (blue curves), as it seems to produce the lowest χ2 value in the circular polarization. However, even after the reduction of the magnetic field, simulation #2 does not produce similar histograms to the observations at Θ = 0°. Also, when looking at Θ > 0° (see Figs. A.1 and A.2), the slope of the circular polarization still does not come close to the observations, meaning that at those heights the power law of the distributions is still not the same. The linear polarization also seems to follow a different power law than the observations at Θ = 0° to Θ = 20° (blue curve in Fig. A.1), while the overall linear polarization beyond the noise peak is underestimated in the simulation (with reduced magnetic field) until Θ = 30° and is overestimated afterward.
Factors used to reduce the average magnetic field in the simulations.
4.4. Simulation #3
The simulation with horizontal fields, for a reduction factor of 0.9 and thus ⟨B(τ = 1)⟩ = 113 G, fits the observed histograms at Θ = 0° reasonably well: compare black and green curves in Fig. 9 (even though the χ2 for the circular polarization would still decrease for a lower factor, this factor was chosen to mitigate the increase in χ2 in the linear polarization). In Fig. A.1, we see that, at Θ = 0° (top right panel), the predicted linear polarization (green curve) has a similar distribution to the observed signals (black curve) at this heliocentric angle, while the circular polarization (top left panel) has a surplus between 4 × 10−3 and 0.01. At the same time, the observations show a greater number of pixels with strong polarizations, that is of ≥0.03. The trend of the surplus of circular polarization keeps increasing with higher viewing angles (see also Fig. A.2). At the same time, the strong circular polarization signals sometimes seem to match those of the observations (Θ = 50°; the green curve in the middle row in Fig. A.2), whereas at other times, there seems to be a shortage (i.e. Θ = 30°; the green curve in bottom row in Fig. A.1). The linear polarization shows a shortage after 30° compared to the observations.
It is important to note that part of the disagreement between observations and simulated histograms for large circular polarization signals above 0.03 and also for the linear polarization signals after the noise-peak for viewing angles of larger than Θ = 30° can be caused by the low statistics in the simulations, which becomes particularly pressing after degradation and resampling (see Sect. 3.3). This is particularly the case in CO5BOLD simulations (simulation #3), because it features a significantly smaller domain than MURaM, and where only ∼3400 pixels remain after the resampling (Sect. 3.3) for the creation of the histograms that are compared to the observations. However, in the case of the weaker circular polarization signal, it is clear that simulation #3 predicts too much of it. In conclusion, although we cannot really distinguish exactly what simulation #3 is missing that would enable it to better fit the observations, we can state that at least two factors play an important role: not only is a lower field strength needed, but it probably also requires a different distribution of inclinations of the magnetic field (γ; see Fig. 4).
4.5. Effect of adding 30 G vertical field to SSD
As described in Sect. 3, simulation #1 is an SSD simulation, whereas simulation #2 was evolved for 6 hours starting from a similar SSD simulation where a vertical field of Bz = 30 G was added over the entire domain. It is therefore interesting to study the effect of adding this vertical field on the predicted histograms for the polarization signals. This effect is visualized in Fig. 10, where we present the predicted circular (left panel) and linear (right panel) polarization signals for: simulation #1 (orange) and #2 (blue). We note that, in these histograms, the original values of the magnetic field have been used (see Table 2) and the network has not been removed, allowing us to see both low and high polarization signals.
 |
Fig. 10. Comparison of the circular and linear polarization between the small-scale dynamo simulation (simulation #1) and a small-scale dynamo simulation (simulation #2) where a 30 G vertical field is added. |
As demonstrated by Fig. 10 adding 30 Gauss of vertical field modifies the histograms both in the region of high (≥5 × 10−2) and low (∈[2 × 10−3, 5 × 10−2]) polarization signals. This suggests that the vertical field evolves in such a way that its affects both the network and the IN. The latter can indeed be affected by the inclusion of a vertical field, as this suppresses convection and thus also the feedback mechanism from the velocity field into the magnetic field via induction (i.e., the so-called dynamo).
5. Conclusions
We confronted synthesized polarimetric spectra of three simulations, each representing a different scenario for the origin of the magnetic field in the solar internetwork (IN), to Hinode observations of the quiet sun by statistically comparing the circular and linear polarization signals. Simulation #1 has a small seed magnetic field that the local dynamo amplifies until saturation, while simulation #2 has an initial vertical magnetic field imposed on top of another local dynamo simulation. Finally, simulation #3 features horizontal fields advected from the bottom boundary. From these simulation snapshots, we synthesized the Stokes vector for different viewing angles Θ (Sect. 3.2). We then degraded the synthesized spectra with the spectral and spatial PSF of Hinode and resampled the grid size to match the Hinode data (Sect. 3.3). Finally, we added photon noise to the simulated data to make the synthesized spectra comparable to the observations. The last step consisted of removing the pixels that belong to the network (Sect. 3.4) from both Hinode observations and synthesized spectra.
For simulations #2 and #3, we found that the polarization signals were too strong compared to the observations (see Figs. 8 and 9), and so we lowered the magnetic field in the simulation snapshots by multiplying it by a constant factor and synthesized the spectra again. Once these corrections are performed, we find that simulation #2, which features an initial vertical field, yields χ2 values with the observations that are a factor of 2−10 larger than in the other simulations. We conclude therefore that simulation #2 does not correctly represent the physical conditions in the solar IN, either in terms of the total field strength or in the inclination of the magnetic field. We can also conclude that our results do not support the scenario where these vertical fields originate from the decay or recycling of active regions (Spruit et al. 1987). Simulation #3, with initial horizontal fields at the bottom boundary, produces histograms of linear polarization (max[∥Q(λ)∥, ∥U(λ)∥]) that most closely resemble those derived from the observations, with χ2 values of 20 to 50% lower than the other simulations. However, in the circular polarization, the χ2 values are higher by a factor of 2 to 3 than those found for the first simulation. This suggests that the emergence of horizontal fields from the convection zone, as suggested by the global dynamo (Stein & Nordlund 2002), is unlikely to be the origin of the magnetic fields in the solar IN.
Simulation #1, representing a small-scale dynamo occurring locally in the photosphere, produces the best fits overall to the observed histograms. Although χ2 values in the linear polarization are slightly higher than in simulation #3, χ2 values in the circular polarization are significantly smaller at all studied heliocentric angles. This leads us to conclude that, of all three possible scenarios studied in this work, this one is the most likely to explain the origin of the IN. Similar conclusions were reached by Danilovic et al. (2010) and Lagg et al. (2016), who performed comparisons between small-scale dynamo simulations and quiet Sun observations using Hinode/SOT/SP or the GRIS instrument on the GREGOR solar telescope. However, the agreement with the observations is still not excellent for the circular polarization at large heliocentric angles. We surmise that this simulation would produce an even better agreement with the observations if the ratio between the horizontal and vertical components of the magnetic field in simulation #1 were not to grow so quickly with height.
As our work is mostly limited by the fact that only three different simulations were used, it would be desirable to improve our analysis by looking at more simulations with different initial conditions. Another possibility would be to employ other spectral lines to see deeper or higher in the solar atmosphere so as to better constrain how the magnetic field changes with height.
Acknowledgments
We gratefully acknowledge Ostar Steiner, Flavio Calvo, Sanja Danilovic, and Matthias Rempel for their help with CO5BOLD and MURaM MHD simulations and useful comments on the paper. Many thanks also to Bruce W. Lites for many useful discussions throughout the years about the internetwork magnetic fields. This research has made use of NASA’s Astrophysics Data System. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, and NASA and STFC (UK) as international partners. Scientific operation of the Hinode mission is conducted by the Hinode science team organized at ISAS/JAXA. This team mainly consists of scientists from institutes in the partner countries. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (U.K.), NASA, ESA, and NSC (Norway).
References
- Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [Google Scholar]
- Asensio Ramos, A. 2009, ApJ, 701, 1032 [Google Scholar]
- Bellot Rubio, L., & Orozco Suárez, D. 2019, Liv. Rev. Sol. Phys., 16, 1 [Google Scholar]
- Borrero, J. M., & Kobel, P. 2011, A&A, 527, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., & Kobel, P. 2012, A&A, 547, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., & Kobel, P. 2013, A&A, 550, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Lites, B. W., Lagg, A., Rezaei, R., & Rempel, M. 2014, A&A, 572, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Jafarzadeh, S., Schüssler, M., & Solanki, S. K. 2017, Space Sci. Rev., 210, 275 [Google Scholar]
- Calvo, F. 2018, Ph.D. Thesis, University of Geneva, Switzerland [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Schüssler, M., & Solanki, S. K. 2010, A&A, 513, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., van Noort, M., & Rempel, M. 2016, A&A, 593, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- del Pino Alemán, T., Trujillo Bueno, J., Štěpán, J., & Shchukina, N. 2018, ApJ, 863, 164 [CrossRef] [Google Scholar]
- del Toro Iniesta, J. C., & Collados, M. 2000, Appl. Opt., 39, 1637 [CrossRef] [Google Scholar]
- Emonet, T., & Cattaneo, F. 2001, ASP Conf. Ser., 236, 355 [NASA ADS] [Google Scholar]
- Faurobert, M., & Ricort, G. 2015, A&A, 582, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fouhey, D. F., Higgins, R. E. L., Antiochos, S. K., et al. 2023, ApJS, 264, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H. G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Jafarzadeh, S., Solanki, S. K., Lagg, A., et al. 2014, A&A, 569, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [Google Scholar]
- Lagg, A., Solanki, S. K., Doerr, H. P., et al. 2016, A&A, 596, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lites, B. W., Kubo, M., Socas-Navarro, H., et al. 2008, ApJ, 672, 1237 [Google Scholar]
- Lites, B. W., Akin, D. L., Card, G., et al. 2013, Sol. Phys., 283, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Centeno, R., & McIntosh, S. W. 2014, PASJ, 66, S4 [Google Scholar]
- Lites, B. W., Rempel, M., Borrero, J. M., & Danilovic, S. 2017, ApJ, 835, 14 [Google Scholar]
- Martínez González, M. J., Asensio Ramos, A., López Ariste, A., & Manso Sainz, R. 2008, A&A, 479, 229 [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez González, M. J., Bellot Rubio, L. R., Solanki, S. K., et al. 2012, ApJ, 758, L40 [CrossRef] [Google Scholar]
- Martínez Pillet, V., del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [CrossRef] [Google Scholar]
- Orozco Suárez, D., Bellot Rubio, L. R., del Toro Iniesta, J. C., et al. 2007, ApJ, 670, L61 [CrossRef] [Google Scholar]
- Pastor Yabar, A., Borrero, J. M., & Ruiz Cobo, B. 2019, A&A, 629, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rempel, M. 2014, ApJ, 789, 132 [Google Scholar]
- Rieutord, M., & Rincon, F. 2010, Liv. Rev. Sol. Phys., 7, 2 [Google Scholar]
- Schüssler, M., & Vögler, A. 2008, A&A, 481, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spruit, H. C., Title, A. M., & van Ballegooijen, A. A. 1987, Sol. Phys., 110, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2002, ESA Spec. Publ., 505, 83 [NASA ADS] [Google Scholar]
- Steiner, O., Rezaei, R., Schaffenberger, W., & Wedemeyer-Böhm, S. 2008, ApJ, 680, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Trelles Arjona, J. C., Martínez González, M. J., & Ruiz Cobo, B. 2023, ApJ, 944, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [Google Scholar]
- Vögler, A., & Schüssler, M. 2007, A&A, 465, L43 [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [Google Scholar]
Appendix A: Additional figures
 |
Fig. A.1. Histogram of the number of pixels as a function of the maximum value in their polarization signals – circular polarization (left) and linear polarization (right) – normalized to the average continuum intensity for viewing angles of Θ = 0° (top), Θ = 10° (middle), and Θ = 20° (bottom). The legend shows the χ2 between the simulation and observations for each polarization. It also shows the fraction, f, of pixels that are removed from the analysis for being considered part of the network. |
 |
Fig. A.2. Same as Fig. A.1 but for viewing angles of Θ = 30° (top), Θ = 40° (middle top), Θ = 50° (middle bottom), and Θ = 60° (bottom). |
All Tables
All Figures
 |
Fig. 1. Position of each map on the solar disk in Table 1 as observed by the Hinode satellite. Shaded areas indicate the regions where ΔΘ = ±2° around the selected Θ values of [0° ,10° ,20° ,30° ,40° ,50° ,60° ] (see text for details). |
| In the text | |
 |
Fig. 2. Stokes profiles of a pixel at Θ = 0° (blue) and 60° (orange). They are normalized to the mean continuum intensity at the respective heliocentric angle. |
| In the text | |
 |
Fig. 3. Average geometrical height and average temperature at τ = 1 along the line of sight for simulation #2 (see Sect. 3) as a function of heliocentric angle Θ. |
| In the text | |
 |
Fig. 4. Histogram of the inclination of the magnetic field at τ = 1, where sin γ (gray line) corresponds to an isotropic distribution. |
| In the text | |
 |
Fig. 5. Spatial and spectral degradation of the simulated Stokes profiles. Left panel: Spatial PSF of the Hinode/SOT/SP instrument (at disk center). Right panel: Hinode/SOT/SP spectral transmission curve. |
| In the text | |
 |
Fig. 6. Comparison of max∥V(λ)∥ in units of continuum intensity for Θ = 0° (left panel) and Θ = 60° (middle panel) with Bz [G] of simulation #1 (right panel). |
| In the text | |
 |
Fig. 7. Empirical relationship between the max(|V(λ)|) and μ = cosΘ for the several network patches in Fig. 6. Vertical blue bars indicate the standard deviation for the sample of about 500 pixels included in these patches. |
| In the text | |
 |
Fig. 8. Histograms of the polarization signals at Θ = 10°. Left panel: max∥V(λ)∥. Right panel: max[∥Q(λ)∥, ∥U(λ)∥. Observed values are shown in black, whereas predicted histograms from simulation #2 are shown in colors for two different values of ⟨B(τ = 1)⟩: 149 G (red; original value) and 105 G (blue; 70% of the original value). |
| In the text | |
 |
Fig. 9. Histograms of the polarization signals at Θ = 10°. Left panel: max∥V(λ)∥. Right panel: max[∥Q(λ)∥, ∥U(λ)∥. Observed values are shown in black, whereas predicted histograms from simulation #3 are shown in colors for two different values of ⟨B(τ = 1)⟩: 125 G (red; original value) and 113 G (green; 90% of the original value). |
| In the text | |
 |
Fig. 10. Comparison of the circular and linear polarization between the small-scale dynamo simulation (simulation #1) and a small-scale dynamo simulation (simulation #2) where a 30 G vertical field is added. |
| In the text | |
 |
Fig. A.1. Histogram of the number of pixels as a function of the maximum value in their polarization signals – circular polarization (left) and linear polarization (right) – normalized to the average continuum intensity for viewing angles of Θ = 0° (top), Θ = 10° (middle), and Θ = 20° (bottom). The legend shows the χ2 between the simulation and observations for each polarization. It also shows the fraction, f, of pixels that are removed from the analysis for being considered part of the network. |
| In the text | |
 |
Fig. A.2. Same as Fig. A.1 but for viewing angles of Θ = 30° (top), Θ = 40° (middle top), Θ = 50° (middle bottom), and Θ = 60° (bottom). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



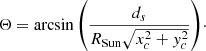
![$$ \begin{aligned} \sigma _\Theta \approx \Delta x_c \frac{d_{s}}{\sqrt{R_{\rm Sun}^2-d_s^2[x_c^2+y_c^2]}}\cdot \end{aligned} $$](/articles/aa/full_html/2024/11/aa51079-24/aa51079-24-eq3.gif)