| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015012 | |
| Published online | 21 January 2011 | |
Deuterated formaldehyde in ρ Ophiuchi A⋆,⋆⋆
1
Onsala Space Observatory, Chalmers University of Technology,
439 92
Onsala,
Sweden
e-mail: per.bergman@chalmers.se
2
Max Planck Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
3
Department of Earth and Space Sciences, Chalmers University of
Technology, 439
92
Onsala,
Sweden
4
Department of Astronomy, Stockholm University,
AlbaNova, 10691
Stockholm,
Sweden
Received:
18
May
2010
Accepted:
25
October
2010
Context. Formaldehyde is an organic molecule that is abundant in the interstellar medium. High deuterium fractionation is a common feature in low-mass star-forming regions. Observing several isotopologues of molecules is an excellent tool for understanding the formation paths of the molecules.
Aims. We seek an understanding of how the various deuterated isotopologues of formaldehyde are formed in the dense regions of low-mass star formation. More specifically, we adress the question of how the very high deuteration levels (several orders of magnitude above the cosmic D/H ratio) can occur using H2CO data of the nearby ρ Oph A molecular cloud.
Methods. From mapping observations of H2CO, HDCO, and D2CO, we have determined how the degree of deuterium fractionation changes over the central 3′ × 3′ region of ρ Oph A. The multi-transition data of the various H2CO isotopologues, as well as from other molecules (e.g., CH3OH and N2D + ) present in the observed bands, were analysed using both the standard type rotation diagram analysis and, in selected cases, a more elaborate method of solving the radiative transfer for optically thick emission. In addition to molecular column densities, the analysis also estimates the kinetic temperature and H2 density.
Results. Toward the SM1 core in ρ Oph A, the H2CO deuterium fractionation is very high. In fact, the observed D2CO/HDCO ratio is 1.34 ± 0.19, while the HDCO/H2CO ratio is 0.107 ± 0.015. This is the first time, to our knowledge, that the D2CO/HDCO abundance ratio is observed to be greater than 1. The kinetic temperature is in the range 20−30 K in the cores of ρ Oph A, and the H2 density is (6−10) × 105 cm-3. We estimate that the total H2 column density toward the deuterium peak is (1−4) × 1023 cm-2. As depleted gas-phase chemistry is not adequate, we suggest that grain chemistry, possibly due to abstraction and exchange reactions along the reaction chain H2CO → HDCO → D2CO, is at work to produce the very high deuterium levels observed.
Key words: astrochemistry / ISM: abundances / ISM: clouds / ISM: individual objects:ρ Ophiuchi A / ISM: molecules
Based on observations with the Atacama Pathfinder EXperiment (APEX) telescope. APEX is a collaboration between the Max-Planck-Institut für Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory
Figures 4, 5 and 8 are only available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
The study of deuterated molecules in the interstellar medium (ISM) has been intensified over the past decade ever since it was discovered that singly and multiply deuterated species (like the D-containing versions of H2CO, CH3OH, NH3) occurred at abundances that were orders of magnitude higher than would be expected from the local ISM D/H ratio of about 1.5 × 10-5 (Linsky 2003). The regions that show these elevated D-abundances are mainly associated with low-mass protostars. For instance, around IRAS 16293−2422, Ceccarelli et al. (1998) and later Loinard et al. (2000) detected lines from doubly-deuterated formaldehyde (D2CO) which previously had only been seen in the Orion KL ridge (Turner 1990). Later, Loinard et al. (2002) extended the study to a larger set of protostars arriving at D2CO/H2CO abundance ratios as high as 0.05−0.4. Likewise, high degrees of deuterium fractionation in CH3OH (Parise et al. 2002, 2004, 2006) and NH3 (Roueff et al. 2000; Loinard et al. 2001; Lis et al. 2002) were subsequently discovered.
These studies are all related to single telescope pointings. To our knowledge, only one effort to delineate the D2CO/H2CO abundance variation within a single source (IRAS 16293−2422) has been made (Ceccarelli et al. 2001). The D2CO/H2CO ratio peaks some 20′′ away from the protostar. Further out, the degree of deuteration seems to be lower in the quiscent gas (Ceccarelli et al. 2002). In the case of deuterated ammonia, the mapping study by Roueff et al. (2005) revealed that the deuterium peak is typically offset from the positions of the embedded protostars. These authors argued that the observed scenario could be explained by the formation of deuterium-enriched ices during the cold pre-collapse phase. At a later stage, a newly formed protostar evaporates the ices.
In their extensive study of deuterated H2CO and CH3OH, Parise et al. (2006) concluded that formation of CH3OH on grain surfaces was a likely explanation for the high degrees of deuterium fractionation seen in the various isotopologues. For H2CO, the situation was less clear and a formation path involving gas-phase reactions could not be ruled out. In fact, for the warmer Orion Bar PDR region, Parise et al. (2009) very recently advocated that gas-phase chemistry is entirely responsible for the deuterium fractionation seen for some singly deuterated species (including HDCO). It should be noted that singly-deuterated species have been detected in dark and translucent clouds (Turner 2001) where the deuteration occurs only in the dense parts.
In interstellar clouds, deuterium is mostly molecular in the form of HD. Deuterium can be
transferred from this main molecular reservoir to other molecules via exothermic reactions
with the molecular ions 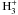 ,
,
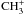 ,
and
,
and 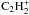 . These
basic reactions are followed by efficient ion-neutral reactions and, in some cases,
by reactions on grain surfaces. The exothermicity of the reactions involving these three
molecular ions are in the range 230−550 K (Gerlich et al.
2002; Asvany et al. 2004; Herbst et al. 1987). As a result, deuterium fractionation
is efficient in cold environments. It is also well established that a high degree of
depletion on the grains of CO, O, and other heavy species, which would otherwise destroy
efficiently H
. These
basic reactions are followed by efficient ion-neutral reactions and, in some cases,
by reactions on grain surfaces. The exothermicity of the reactions involving these three
molecular ions are in the range 230−550 K (Gerlich et al.
2002; Asvany et al. 2004; Herbst et al. 1987). As a result, deuterium fractionation
is efficient in cold environments. It is also well established that a high degree of
depletion on the grains of CO, O, and other heavy species, which would otherwise destroy
efficiently H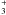 (and its deuterated analogues), is another important condition for deuterium fractionations
taking place. Correlations between CO depletion and fractionation have been observed towards
prestellar cores by, e.g., Bacmann et al. (2003) and
Crapsi et al. (2005), and in the envelope of
Class 0 protostars by Emprechtinger et al. (2009).
Because of these two conditions (low temperature and high CO depletion), deuterium
fractionation is particularly efficient during the early stages of star formation. The
surface reactions on cold grains important for deuterium fractionation of H2CO
have recently been investigated through laboratory experiments (Hidaka et al. 2009).
(and its deuterated analogues), is another important condition for deuterium fractionations
taking place. Correlations between CO depletion and fractionation have been observed towards
prestellar cores by, e.g., Bacmann et al. (2003) and
Crapsi et al. (2005), and in the envelope of
Class 0 protostars by Emprechtinger et al. (2009).
Because of these two conditions (low temperature and high CO depletion), deuterium
fractionation is particularly efficient during the early stages of star formation. The
surface reactions on cold grains important for deuterium fractionation of H2CO
have recently been investigated through laboratory experiments (Hidaka et al. 2009).
The aforementioned low-mass protostar IRAS 16293−2422 is located in the eastern part of the ρ Ophiuchi cloud complex. To the west in the same complex, more than 1 degree away, lies the ρ Oph A cloud (Loren et al. 1990) at a distance of about 120 pc (Lombardi et al. 2008; Loinard et al. 2008; Snow et al. 2008). This cloud core is well-studied by infrared, submillimeter, and millimeter continuum observations (Ward-Thompson et al. 1989; André et al. 1993; Motte et al. 1998). It hosts a well-collimated molecular outflow (André et al. 1990) and its driving source VLA 1623 (André et al. 1993). Moreover, it was in the direction of this cloud core that Larsson et al. (2007), using the Odin satellite, detected the 119 GHz line from molecular oxygen as well as the ammonia ground state line at 572 GHz (Liseau et al. 2003). More recently, while searching for the 234 GHz O18O line Liseau et al. (2010) detected several lines due to D2CO toward the millimeter continuum peaks. This study also includes C18O(3 − 2) mapping observations. Earlier, Loinard et al. (2002) reported a high D2CO/H2CO ratio toward the VLA 1623 source. The existence of D2CO in several positions of this 2′ × 3′ cloud core formed the incentive of the present study as an excellent source to delineate the distribution of H2CO, HDCO, and D2CO as we know the distribution of the dust (Motte et al. 1998) and the gas in terms of C18O (Liseau et al. 2010). Here we report on mapping observations of the ρ Oph A cloud core in several frequency settings that cover most of the low-energy H2CO, HDCO, and D2CO lines in the 1.3 millimeter band using the 12 m APEX telescope (Güsten et al. 2006). In addition, lines from many other species were observed simultaneously (e.g. CH3OH, SO, and N2D + ). Here the CH3OH results are of importance because CH3OH is directly involved in the H2CO chemistry and the N2D + results are, of course, of interest for the deuteration. Although the sulphur chemistry is not of immediate interest here we chose to include the SO and SO2 observational and analysis results since they are of importance as a complementary tool for determining the physical conditions. This paper is organized as follows. In Sect. 2 we describe the observations and then, in Sect. 3, we present the observational results. In Sect. 4 we obtain the physical conditions. Before concluding, in Sect. 6, we discuss our results in Sect. 5.
2. Observations
The APEX telescope at Chajnantor (Chile) was used to map the 3′ × 3′ (with a spacing of 30″) area centred on the coordinates α(J2000) = 16h26m27.2s and δ(J2000) = -24°23′34″ which is very close to the SM1N position in the ρ Oph A cloud core as designated by André et al. (1993) in their submillimeter continuum maps. We used the single-sideband tuned APEX-1 receiver which is part of the Swedish heterodyne facility instrument (Vassilev et al. 2008). It has a sideband rejection ratio more than 10 dB. The image band is 12 GHz above or below the observing frequency depending on whether the tuning is optimized for operation in the upper or lower sidebands, respectively. For two frequency settings, the strong CO(2 − 1) and C18O(2 − 1) lines entered via the image band and from the strength we could estimate the sideband rejection ratio to be about 15 dB in both cases. As backend we used two 1 GHz modules of the FFTS (Klein et al. 2006). Each FFTS 1 GHz module has 8192 effective channels and the modules can be placed independently within the IF band width of 4−8 GHz. At 230 GHz this channel spacing corresponds to 0.16 km s-1 and the telescope beamsize (HPBW) is 27″.
The telescope control software APECS (Muders et al. 2006) was used to control the raster mapping. All observations were performed in position-switching mode using a reference position offset by 300″ east and 200″ north of the map center. The pointing of the telescope was maintained and checked regularly by means of small CO(2 − 1) cross maps of the relatively nearby carbon stars IRAS 15194 − 5115 and RAFGL1922. The determined pointing offsets were generally consistent from day to day and we believe we have an absolute pointing uncertainty better than 5″. To optimize the antenna focussing we used continuum observations on Jupiter and Saturn.
The observations took place in two blocks and one additional day during 2009:
April 24−May 1, May 21, and July 4−July 9. The column of precipitable water vapour was
typically around 0.7 mm (varied between 0.3−2.9 mm). Typical system temperatures for the
frequencies in question (218−252 GHz) were 200−220 K. The telescope main beam efficiency
is ηmb = 0.73 at 345 GHz (Güsten
et al. 2006). Hence, using the antenna surface accuracy of 18 μm
we estimate that (using the Ruze formula) that the APEX main beam efficiency around 230 GHz
is just slightly higher than at 345 GHz, about 0.75 which we adopt when converting the
observed intensities from the 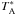 scale to the
Tmb intensity scale. The heterodyne calibration procedure at
APEX is more elaborate than the standard chopper wheel calibration scheme and involves three
measurements by apart from the normal sky observation it also measures the receiver
temperature by observing a hot and cold loads. Moreover, the atmospheric contribution is
based on the model (Pardo et al. 2001) that has been
adapted to the atmospheric characteristics at the Chajnantor site. The absolute calibration
uncertainty is estimated to be 10% in the 1 mm band.
scale to the
Tmb intensity scale. The heterodyne calibration procedure at
APEX is more elaborate than the standard chopper wheel calibration scheme and involves three
measurements by apart from the normal sky observation it also measures the receiver
temperature by observing a hot and cold loads. Moreover, the atmospheric contribution is
based on the model (Pardo et al. 2001) that has been
adapted to the atmospheric characteristics at the Chajnantor site. The absolute calibration
uncertainty is estimated to be 10% in the 1 mm band.
In Table 1 we summarize the targeted formaldehyde
lines. The additional lines are summarized in Table 2. In the tables we include the line parameters: the transition frequency (typical
uncertainty is 0.05 MHz or better), energy of lower level, and Einstein
A-coefficient. These have been compiled from the Cologne Database of
Molecular Spectroscopy (Müller et al. 2001, 2005). We here also indicate the symmetry due to the
nuclear spin direction of the H (or D) nuclei, which for H2CO,
 and D2CO
can be ortho (parallel spins) or para (anti-parallel spins). The statistical weight ratio of
the symmetries is also noted if applicable. In the case of CH3OH, the internal
rotation of the methyl group results in the symmetry species A and E. Note that radiative or
non-reactive collisional transitions are forbidden between levels of different symmetry.
and D2CO
can be ortho (parallel spins) or para (anti-parallel spins). The statistical weight ratio of
the symmetries is also noted if applicable. In the case of CH3OH, the internal
rotation of the methyl group results in the symmetry species A and E. Note that radiative or
non-reactive collisional transitions are forbidden between levels of different symmetry.
Observed H2CO,  , HDCO,
and D2CO lines.
, HDCO,
and D2CO lines.
Additional lines.
3. Results
In this section we will first display the formaldehyde mapping results of the ρ Oph A cloud core, both as spectra, integrated intensity maps or velocity position diagrams where appropriate. After that, the mapping results for the other molecules are presented. Comparisons will be made with the existing APEX C18O(3−2) data at 329 GHz of Liseau et al. (2010) and the IRAM 30 m continuum map at 1.3 mm of Motte et al. (1998). The angular resolution of the two data sets is similar; the C18O data have an HPBW of 19″ while the 1.3 mm continuum map has an angular resolution of 15″. Both these maps are shown in Fig. 1 where the 1.3 mm continuum map is shown in contours on top of a grey-scale image of the C18O(3−2) integrated intensity. The 3′ × 3′ region shown in Fig. 1 corresponds to the area that has been mapped here in formaldehyde.
 |
Fig. 1 Colour image: the C18O(3−2) integrated intensity map of ρ Oph A cloud core from Liseau et al. (2010). The intensity scale is shown to the right. Contours: the 1.3 mm continuum data by Motte et al. (1998). The contours start at 0.15 Jy with subsequent contours at every increment of 0.15 Jy. The flux densities are given in a 15″ beam. We show the positions of the mm peaks from Motte et al. (1998) and the C18O peaks of Liseau et al. (2010). The map offsets are given relative the position α(J2000) = 16h26m27.2s and δ(J2000) = -24°23′34″. |
3.1. Formaldehyde results
All lines listed in Table 1 were detected except the 11,1−00,0 transition of HDCO at 227 GHz. This transition has a much lower spontaneous rate coefficient than the other transitions. Two of the D2CO lines were not mapped and were only observed in the (0″, −30″) position. The typical rms in a map spectrum is in the range 0.06 − 0.1 K.
In Fig. 2 we plot the H2CO(30,3−20,2) and D2CO(40,4−30,3) spectra. They consist of 49 spectra separated by 30″ on a 7 × 7 grid. The H2CO lines posess a relatively complicated structure as compared to the D2CO lines. The latter line shows only one velocity component around 3.8 km s-1 with full width at half maximum (FWHM) of 0.7 km s-1 and it is peaking strongly at the (0″, −30″) position which, within the positional uncertainties, coincides with the SM1 or P3 position (cf. Fig. 1). We will hereafter refer to this position as the D-peak. The D-peak is also clearly seen in the integrated intensity maps of the three different H2CO isotopologues (Fig. 3).
 |
Fig. 2 H2CO(30,3−20,2) and D2CO(40,4−30,3) map spectra toward the ρ Oph A cloud. The (0″,0″) position is the same as in Fig. 1. The vertical scale in each spectrum represents Tmb scale in K and the horizontal scale is velocity vLSR with respect to local standard of rest in km s-1 as shown in the upper rightmost panel. |
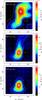 |
Fig. 3 Maps of the H2CO(30,3−20,2), HDCO(41,4−31,3), and D2CO(40,4−30,3) integrated line intensity over the range 3.0 − 4.5 km s-1. |
Maret et al. (2004) present a
H2CO(30,3−20,2) IRAM 30 m spectrum toward the
position of VLA 1623. The nearest position to VLA 1623 in our map is at (0″, −60″). The
shape of our spectrum at this position is similar to the one presented by Maret et al. (2004) and our
Tmb peak temperature of 3.8 K is slightly higher than
theirs 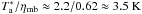 despite the higher
resolution of 11″ in the IRAM 30 m spectrum. This would be expected for a relatively
extended source which shows little variation on the scale of 11″ − 27″. Also, from the
distribution of the H2CO emission we do not see any strong component that can
be attributed to VLA 16231.
despite the higher
resolution of 11″ in the IRAM 30 m spectrum. This would be expected for a relatively
extended source which shows little variation on the scale of 11″ − 27″. Also, from the
distribution of the H2CO emission we do not see any strong component that can
be attributed to VLA 16231.
The velocity as obtained from the N2H + (1−0) observations by Di Francesco et al. (2004, 2009) (see also André et al. 2007) toward SM1 is 3.7 km s-1 with an FWHM of 0.6 km s-1, i.e. very similar to our values determined from the D2CO lines at the D-peak. The peak intensity of the D2CO line is about half that of H2CO. The size of D2CO 40,4−30,3 emission region (see Fig. 3), is found, by fitting a 2-dimensional gaussian, to be 33″ × 61″. This size corresponds to a deconvolved source size of about S = 19″ × 55″ for a beam size of B = 27″. The filling factor when pointing the 27″ beam toward the center of the source, is then S2/(S2 + B2) = (19″ × 55″)/(33″ × 61″) ≈ 0.5. This filling factor is merely an upper limit because any unresolved small-scale clumpiness may decrease the filling factor further.
In order to investigate the H2CO line distribution over the ρ Oph A cloud core we plot four velocity position diagrams (Fig. 4) between Δδ = ± 90″ at Δα = 0″. Here we also see that HDCO is peaking at the D-peak at Δδ = −30″. Looking at the HDCO emission, there appears to be a velocity gradient over the D-peak source of about 0.2 km s-1 when going from Δδ = 0″ to Δδ = −60″. It is also close to the D-peak where the C18O(3 − 2) emission has its maximum. The secondary C18O(3−2) peak (P1 in Fig. 1) is at Δδ = + 30″ and with a lower velocity of ≈3.1 km s-1 as compared to the velocity of + 3.7 km s-1 at the D-peak position and it is also here where the low-energy H2CO line intensities reach their maximum value at vLSR = 3.3 km s-1. We denote this peak P1 from now on. There is also weak emission emanating from both HDCO and D2CO at the Δδ = + 30″ position.
Interestingly, there is a third H2CO peak at Δδ = 0″ and
vLSR ≈ + 2.9 km s-1 which has no obvious
counterpart in the C18O velocity position map. This peak makes the
H2CO(30,3−20,2) spectrum at (0″,0″) to look doubly
peaked (Fig. 2). However, these are two different
cloud components and the dip is not an effect of self-absorption. This is evident from the
velocity position diagrams in Fig. 4, but is also
clear when comparing the  (31,2−21,1)
and H2CO(31,2−21,1) spectra. In Fig. 5 the central three spectra from the ortho lines
H2CO(31,2−21,1)
and
(31,2−21,1)
and H2CO(31,2−21,1) spectra. In Fig. 5 the central three spectra from the ortho lines
H2CO(31,2−21,1)
and  (31,2−21,1)
are displayed. Toward the (0″,0″) position we see the doubly peaked line profile also for
this H2CO line, however there is no hint that the
(31,2−21,1)
are displayed. Toward the (0″,0″) position we see the doubly peaked line profile also for
this H2CO line, however there is no hint that the
 line is peaking
at the velocity of the dip for H2CO. If anything, the emission from the rarer
species seems to follow that of the main species. We will return to the low-velocity
component seen in the (0″,0″) position below when we present the CH3OH results.
line is peaking
at the velocity of the dip for H2CO. If anything, the emission from the rarer
species seems to follow that of the main species. We will return to the low-velocity
component seen in the (0″,0″) position below when we present the CH3OH results.
3.2. CH3OH results
In Fig. 6 we show a map of the integrated intensity for the CH3OH 51,5−41,4 and 42,2−31,2 E-lines. The latter line comes from levels of higher energy (Table 1). The distribution of CH3OH is quite different from that of H2CO (see Fig. 3). It should be noted that the CH3OH 42,2−31,2 line and the H2CO lines at 218 GHz were observed simultaneously so the different distributions cannot be a result of large pointing offsets. The CH3OH emission has its maximum at (−30″,0) and in Fig. 7 all observed 5 − 4 lines in this position are shown. Here the peak emission velocity is lower, around vLSR ≈ 2.8 km s-1. The cloud component at (−30″,0″) extends into adjacent positions. The low-velocity feature seen for H2CO (Fig. 4) is very likely associated with the CH3OH-peak. The higher energy H2CO lines 32,2/1−22,1/0 peak near this position. In addition, there is little CH3OH at the D-peak position (Fig. 6).
 |
Fig. 6 Integrated intensity maps of the CH3OH 51,5−41,4 and 42,2−31,2 E-lines. First contour is at 0.3 K km s-1 and the increment is 0.6 K km s-1. |
 |
Fig. 7 CH3OH 5−4 lines around 241 GHz toward the (−30″,0″) position. Note that the 52,4−42,3 and 52,3−42,2 E-lines are blended. |
3.3. Results from other molecules
Two lines from SO(56−45) and
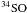 (65−54)
were covered during the observations. The map spectra are shown in Fig. 8. There is a single strong peak in the
(65−54)
were covered during the observations. The map spectra are shown in Fig. 8. There is a single strong peak in the
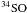 line intensity
toward the position (−60″, + 60″) which we will call the S-peak. Here the
line intensity
toward the position (−60″, + 60″) which we will call the S-peak. Here the
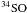 and
SO2 lines are very narrow, only about 0.4 km s-1. This is
about twice the width one would expect from thermal broadening only
(at Tkin = 20 K). Further west, at (−90″, + 30″),
the
and
SO2 lines are very narrow, only about 0.4 km s-1. This is
about twice the width one would expect from thermal broadening only
(at Tkin = 20 K). Further west, at (−90″, + 30″),
the 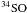 line is broader,
about 1.1 km s-1. The profile of SO shows line wings here which could be
related to outflow activity. However, it is at the very border of our map and a clear
delineation into red and blue wings are impossible. It should be pointed out that the
S-peak has no structural counterpart in the C18O(3 − 2) map nor the 1.3 mm
continuum map (cf. Fig. 1). Toward the D-peak,
the SO lines exhibit a similar emission velocity
(vLSR ≈ 3.7 km s-1) and line width
(Δv ≈ 0.83 km s-1) as the other molecules. The covered
SO2 and
line is broader,
about 1.1 km s-1. The profile of SO shows line wings here which could be
related to outflow activity. However, it is at the very border of our map and a clear
delineation into red and blue wings are impossible. It should be pointed out that the
S-peak has no structural counterpart in the C18O(3 − 2) map nor the 1.3 mm
continuum map (cf. Fig. 1). Toward the D-peak,
the SO lines exhibit a similar emission velocity
(vLSR ≈ 3.7 km s-1) and line width
(Δv ≈ 0.83 km s-1) as the other molecules. The covered
SO2 and 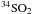 lines
(Table 2) show a distribution similar to that of
SO and
lines
(Table 2) show a distribution similar to that of
SO and 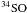 . At the
P1-position the SO and SO2 emission velocity of
about ≈ 2.9 km s-1 is lower than the velocity
of ≈ 3.3 km s-1 for the formaldehyde isotopologues and CH3OH.
. At the
P1-position the SO and SO2 emission velocity of
about ≈ 2.9 km s-1 is lower than the velocity
of ≈ 3.3 km s-1 for the formaldehyde isotopologues and CH3OH.
The deuterated version of N2H + (observed by Di Francesco et al. 2004, 2009; André et al. 2007), N2D + (3 − 2) at 231 GHz was also covered during the formaldehyde observations. The integrated intensity map of N2D + (3 − 2) is shown in Fig. 9. The peak intensity of the N2D + emission is clearly associated with the D-peak, with a secondary weaker source to the south-east. This secondary peak is not coincident with SM2 (see Fig. 1) but is located in the direction where the dust emission extends. Moreover, it shows up in the N2H + map of Di Francesco et al. (2004) and is designated N6 by them. The emission velocity of N2D + (3 − 2) at the D-peak is 3.7 km s-1 and the FWHM is 0.85 km s-1 in agreement with what is found for the other species.
 |
Fig. 9 Integrated intensity map of the N2D + 3 − 2 line toward ρ Oph A. First contour is at 0.2 K km s-1 and the increment is 0.4 K km s-1. |
3.4. Result summary
After presenting the results of the distribution of the different molecules toward the ρ Oph A cloud above we will now make a summary of the results which will be used in the analysis below. For H2CO and CH3OH we have identified three positions of interest which seem to represent distinctive sources; the D-peak at (0″, −30″), the P1 peak at (0″, + 30″), and the CH3OH peak at (−30″,0″). In addition to these three peaks, the sulphur containing molecules are localized to (−60″, + 60″) (the S-peak). The emission velocities and FWHMs as obtained for the different species in these sources are summarized in Table 3 (from gaussian fits of the lowest energy lines in those cases where we have mapped multiple lines). Integrated line intensities for the relevant positions are tabulated in Tables 4−6. In these tables the 1σ uncertainties of the integrated intensities due to noise have been entered.
Properties of the H2CO, CH3OH, SO, and SO2 emission in selected cloud positions from gaussian fits.
H2CO,  , HDCO, and
D2CO integrated line intensities in three positions of the
ρ Oph A cloud.
, HDCO, and
D2CO integrated line intensities in three positions of the
ρ Oph A cloud.
CH3OH integrated line intensities in three positions of the ρ Oph A cloud.
Integrated line intensities for other molecules in four positions of the ρ Oph A cloud.
4. Analysis
For several of the detected species (Table 4) we have multiple transitions that have significantly different energy levels. In such cases the so-called rotation diagram analysis (e.g. Goldsmith & Langer 1999) can be employed to determine the rotation temperature, Trot, and the molecular column density, Nmol. If all lines are optically thin, the rotation diagram method often is adequate to analyse multi-transition data. However, here it is likely that we have a mixture of optically thin and thick lines and therefore we adopt the modified approach to the rotation diagram method described by Nummelin et al. (2000). The modification involves the inclusion of the peak optical depth and thus, in addition to Trot and Nmol, also the beam filling factor, ηbf, can be determined by minimization of a χ2-value. For a gaussian source distribution, ηbf is given by ηbf = S2/(S2 + B2), where S is the FWHM source size and B is the FWHM beam size. If all transitions included in the analysis are optically thin and ηbf is set to 1 (B ≪ S), the method is very similar2 to the rotation diagram analysis with Nmol then representing a beam averaged column density.
In selected cases we will also check the results and refine the models obtained with the modified rotation diagram analysis by employing a more accurate treatment of the line excitation and radiative transfer. We have here adopted the accelerated lambda iteration (ALI) technique outlined by Rybicki & Hummer (1991, 1992). The ALI model cloud consists of spherically concentric shells and allows only for radial gradients of the physical parameters (kinetic temperature, molecular hydrogen density, molecular abundance, and radial velocity field). Moreover, and in contrast to the rotation diagram method, collisional excitation is included in the analysis, so the collision partner (here H2) density is a physical input parameter. The code used in the present work has been tested by Maercker et al. (2008) and it allows the inclusion of dust as a source of continuum emission in the shells. When the radiative transfer has been iteratively solved using the ALI approach, a model spectrum is produced by convolving the velocity dependent intensity distribution of the model cloud with a gaussian beam.
4.1. Analysis of the formaldehyde lines
As can be seen in Table 4 all four H2CO lines are clearly detected in the three sources (D-peak, P1, and CH3OH-peak). The three para lines at 218 GHz have all been observed simultaneously so their relative strengths are not affected by any pointing or calibration uncertainties. The only ortho transition, the 31,2−21,1 line at 225 GHz, was observed in a separate frequency setting. In our rotation diagram analysis we treat the ortho and para H2CO lines together by assuming that the population distribution is determined by Trot also between the states of different symmetry (through some exchange reaction or formation mechanism). For H2CO the lowest ortho level (11,1) is about 15 K above the lowest para level (00,0). For D2CO the reverse situation is in effect and it is the lowest level 00,0 that is an ortho state while the lowest para level 11,1 is 8 K higher up in energy. For a very low Trot (during molecule formation) most of the molecules will be in the lowest energy state (para for H2CO and ortho for D2CO). On the other hand, if Trot is much greater than the energy difference of the symmetry states, the ortho to para population ratio will be governed by the statistical weight ratio which is o/p = 3 for H2CO and o/p = 2 for D2CO.
In Table 7 the results of the modified rotation diagram analysis are shown. Here the number of lines used in the analysis for each molecule is tabulated together with best fit values of Trot, Nmol, and ηbf. In the last column, we list the minimum and maximum optical depths of the used transitions in the analysis. If there are not enough of lines or all lines are optically thin, one or two of the parameters have been set to a result obtained by another molecule in a previous fit. For instance, in the D-peak source, all three parameters could be determined in the analysis of H2CO, while for the optically thin D2CO lines, ηbf had to be set to the value found for H2CO. Using the same ηbf for all formaldehyde isotopologues will also make the determined column densities directly comparable with each other. Interestingly, the Trot obtained for D2CO, 17.4 K toward the D-peak is lower than that found for H2CO (Trot = 22.5 K). We assume this is an effect of subthermal excitation and difference in optical depths, where the higher optical depths for H2CO make the excitation more efficient via photon trapping as compared to D2CO. A lower rotation temperature of the less abundant formaldehyde isotopologues was also seen in IRAS16293 − 2422 by Loinard et al. (2000) and in several other sources by Parise et al. (2006). For the other two sources (the P1 and CH3OH peaks) the number of detected D2CO transitions is not sufficient to allow for a Trot determination and we assume that the ratio of Trot(D2CO)/Trot(H2CO) is the same in these two sources as in the D-peak source. The deduced Trot is higher in the P1 and CH3OH peaks than in the D-peak. This could be expected because the ratio of the 30,3−22,0 and 32,2−22,1 H2CO lines is a good measure of kinetic temperature (Mangum & Wootten 1993) and this ratio is highest toward the CH3OH-peak. Of course, from the models we can also estimate the intensity of lines not included in the analysis. In particular, we find for the HDCO 11,1−00,0 line that for the determined model parameters toward the D-peak its expected intensity is about 5 times below the noise level, consistent with our non-detection.
Analysis results for H2CO,  , HDCO,
D2CO, CH3OH, SO, and SO2 from using the modified
rotation diagram technique.
, HDCO,
D2CO, CH3OH, SO, and SO2 from using the modified
rotation diagram technique.
The derived H2CO rotation temperatures for the three cores are quite similar to the ones obtained by Parise et al. (2006) for other low-mass protostar sources. Likewise, the derived H2CO column densities are just slightly higher than the corresponding rotation diagram values of Parise et al. (2006). The filling factor ηbf = 0.446 determined toward the D-peak is in agreement with the filling of ~0.5 determined from the D2CO 40,4−30,3 source size in Sect. 3.1.
4.2. Analysis of the methanol lines
The CH3OH analysis using the modified rotation diagram technique is based on the integrated line intensities listed in Table 5. In all sources 6 CH3OH lines with lower state energies ranging from 23 to 46 K, have been used. In the D-peak source a couple of lines are just marginally detected but are included in the best fit analysis since they are weighted with the uncertainty and do not affect the fit significantly. The line feature at 241904 MHz is a blend of two CH3OH lines of about the same energy and A-coefficient and we have not been able to clearly resolve them into individual components. All lines at 241 GHz were observed simultaneously. The only CH3OH line not belonging to the 241 GHz 5 − 4 line forest is the 42,2−31,2 E-line which is located in the 218 GHz H2CO-band.
Only one line from the methanol A-species has been observed and included in the analysis. Just like in the case of ortho and para formaldehyde, the A- and E-species of methanol are treated together. The energy difference between the lowest A and E-methanol states is 8 K with the A-species having the lowest energy. Furthermore, we only consider methanol to be in its lowest torsional state.
The best fit results in the CH3OH analysis have been entered in Table 7. In all three sources we find a low Trot of 7 to 9 K. Also the ηbf is found to be very close to 1. The much lower rotation temperatures found in the CH3OH analysis as compared to the H2CO and D2CO results suggest that the excitation of CH3OH is quite sub-thermal and a more elaborate treatment of the excitation and radiative transfer is needed (as was demonstrated by Bachiller et al. (1998) in their Fig. 9a). This is also supported by the fact that none of the CH3OH fits are good since several of the modelled line intensities deviate substantially from the observed line intensities.
4.3. ALI modelling
Our aim with the non-LTE modelling using the ALI code is to construct a homogeneous (in
terms of physical parameters but not in terms of excitation which may vary radially)
spherical model cloud, for each of the source positions (D-, P1, and
CH3OH-peaks), that produces the observed H2CO and CH3OH
spectra. The results from the modifed rotation diagram analysis above are used as a guide
when adopting the model cloud parameters. The ALI setup for the statistical equilibrium
equations includes collisional excitation rates and for formaldehyde we use the
He-H2CO collisional coefficients calculated by Green (1991). The coefficients have been multiplied by 2.2 to
approximate the H2-H2CO collision system. For the
H2-CH3OH collision coefficients we adopt those of Pottage et al. (2004). For both species only levels
below 200 K are included and we divide the model cloud into 29 shells. We do not include
any radial velocity field in the source and instead we simply use a microturbulent
velocity width, vturb, that reproduces the observed line
widths. For an optically thin line, the FWHM line width is
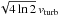 .
.
The results of the three ALI models have been summarized in Table 8. The listed cloud radii R (in the first column) are based on the corresponding H2CO beam filling results (Table 7) and a distance to ρ Oph A of 120 pc. The tabulated column densities are the source-averaged values 2 Npeak/3, where Npeak is the column density through the center of the spherical model cloud. It should be noted that the derived n(H2) (and hence N(H2)) is a compromise value since, for all three models, a 20% lower value yields better fits for CH3OH while a similarly higher value is optimum for H2CO. However, as the differences are less than about 50% any real difference in n(H2) is within the uncertainties of the adopted collisional coefficients. The ortho-to-para ratio is about 2 for all three models but since the ortho results are based on a single optically thick line (τ ~ 4) only and not observed simultaneously with the three para lines, we cannot really exclude ortho-to-para ratios in the range 1-3. The derived H2CO column densities are about 30% lower than those derived from the modified rotation diagram analysis. In contrast to N(H2CO) and N(H2) which do not vary much among the three cores, the CH3OH column densities vary from 5 × 1013 cm-2 in the D-peak to 4 × 1014 cm-2 at the CH3OH-peak position. In addition, the E/A CH3OH ratios seem to be close to 1 and since the A-line is observed simultaneously with the E-lines the determined A/E-ratio of 1 is less uncertain than the estimated ortho/para ratios for formaldehyde. The optical depth for the strongest of the CH3OH lines are about 0.5–0.6 toward the CH3OH-peak. The total H2 mass of a core is about 0.1–0.2 M⊙.
Model cloud properties and results for the ALI analysis.
To our knowledge, there are no collision coefficients available for the collision system H2-D2CO, so we cannot use our ALI model for D2CO. However, using the H2-H2CO collision rates we check what happens to the excitation temperatures when adopting a factor of 7 lower column density (the ratio of N(H2CO) and N(D2CO) in Table 7 is close to 7). We then find that the excitation temperatures of the 31,2−21,1 transition drop between 20–30% at different radii. This drop in excitation temperature is in line with the 20% lower Trot = 17.4 K found for D2CO as compared to H2CO value of Trot = 22.5 K found toward the D-peak. Hence, it is quite plausible that the lower rotation temperature found for D2CO as compared to H2CO can be explained by less efficient photon trapping in the excitation of D2CO. We also checked the influence on our results by continuum emission of dust, and the inclusion of a dust component with standard dust parameters (Td = 22 K, gas-to-dust mass ratio of 100) had negligible impact on our modelling results.
Liseau et al. (2003) report results from a large velocity gradient (LVG) analysis of the ρ Oph A using CH3OH 2 − 1 and 3 − 2 line forest data, at 96 and 145 GHz, obtained by SEST at an angular resolution larger (52′′ and 35′′) than for the present study. The analysed data were averaged from spectra spaced by 30″ in the north-south direction around the P2 position (see Fig. 1) and their spectra is thus a partial blend of the contribution of the three cores. This is especially the case for their 2–1 observations. However, their LVG results (Tkin = 20 K, n(H2) = 4.5 × 105 cm-3, X [CH3OH] = 2.7 × 10-9) are in good agreement with those reported here.
4.4. Analysis of other molecules
In the S-peak position we have detected three SO2 lines and a modified
rotation diagram analysis gave best-fit results for ηbf very
close to 1. For SO2 we find a rotation temperature of about 20 K and a column
density of N(SO2) = 7.6 × 1014 cm-2.
The same analysis was made for two of the three detected
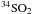 lines and we get
N(34SO2) = 5.6 × 1013 cm-2
when using the rotation temperature of the more common variant. The
111,11−100,10
lines and we get
N(34SO2) = 5.6 × 1013 cm-2
when using the rotation temperature of the more common variant. The
111,11−100,10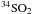 line was excluded in the fit since its observed strength is incompatible (too strong by
about a factor of 2) with the rotation temperature found for SO2, cf.
Table 6. The reason for this is unclear but could
be due to an unknown blend or a non-LTE effect involving
Ka = 0 states. Likewise, the two SO lines
detected toward the D-peak position result in a rotation temperature of 18 K and a column
density of 2.4 × 1014 cm-2 (again assuming
ηbf = 1). In the P1 position, the two detected
SO2 lines give Trot = 23 K and a beam averaged
column density of 9.9 × 1013 cm-2. Furthermore, assuming
Trot = 20 K we arrive at a beam averaged SO2
column density of 8.3 × 1012 cm-2 toward the
CH3OH-peak. The SO and SO2 results have been entered in Table 7.
line was excluded in the fit since its observed strength is incompatible (too strong by
about a factor of 2) with the rotation temperature found for SO2, cf.
Table 6. The reason for this is unclear but could
be due to an unknown blend or a non-LTE effect involving
Ka = 0 states. Likewise, the two SO lines
detected toward the D-peak position result in a rotation temperature of 18 K and a column
density of 2.4 × 1014 cm-2 (again assuming
ηbf = 1). In the P1 position, the two detected
SO2 lines give Trot = 23 K and a beam averaged
column density of 9.9 × 1013 cm-2. Furthermore, assuming
Trot = 20 K we arrive at a beam averaged SO2
column density of 8.3 × 1012 cm-2 toward the
CH3OH-peak. The SO and SO2 results have been entered in Table 7.
The analysis results of the other molecules are summarized in Table 9. The column densities listed here are all calculated
under the assumption of optically thin emission. The C18O(3-2) column densities
are based on the data from Liseau et al. (2010) and
have been derived using the kinetic temperatures derived from the ALI analysis as
excitation temperature as the lower C18O transitions are expected to be
thermalized at the high densities of the cores. For the S-peak, the SO2
rotation temperature of 20 K was used as excitation temperature for all molecules. Also
tabulated is the N(H2) column density deduced from
N(C18O) and assuming a C18O abundance of
X [C18O] = 2 × 10-7 (standard value of
undepleted gas interstellar gas, Frerking et al.
(1982), but see also Wouterloot et al.
(2005) for a discussion applicable to the ρ Oph cloud). In this
context it is enlightning to estimate how much the cores contribute to the observed
C18O(3-2) integrated line intensity. Adopting the physical parameters
(Table 8) and assuming
X [C18O] = 2 × 10-7 we find, using the ALI
code for C18O, that the cores make up 31%, 37%, and 67% of the observed
C18O(3-2) emission in the D-, P1-, and CH3OH-cores, respectively.
Firstly, this tells us that the C18O abundance in the cores cannot be much
higher than 2 × 10-7 as they then would produce too much C18O(3-2)
emission. Secondly, an appreciable part of the observed C18O(3-2) emission is
likely to arise in a lower H2 density ( ≲ 105 cm-3)
environment. This would explain the higher N(H2) column
densities deduced from optically thin C18O (Table 9) as compared to the ALI results (Table 8). A similar finding was made by Wouterloot
et al. (2005) in their CO study of other regions in the ρ Oph
cloud where the cold (~10 K) and dense (≳105 cm-3)
cores were surrounded by a warmer (~30 K) and less dense
(~104 cm-3) envelope. Also, given the observed ratio
of C18O(3-2) and 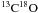 (3-2) of about 23
toward the D-peak (Liseau et al. 2010), it is
likely that the C18O(3-2) emission is somewhat optically thick
(τ ≈ 2) and hence the listed N(C18O) and
N(H2) (Table 9) would
be about a factor
τ/(1 − e − τ) ≈ 2.3
higher. The full H2 column density toward the D-peak would then be
N(H2) = 1.5 × 1023 cm-2. Likewise,
the SO column density in the D-peak position of 1.1 × 1014 cm-2 is
lower than the corresponding value of 2.3 × 1014 cm-2 (Table 7) where the latter value includes compensation by
optical depth. Using the ALI model for the D-peak core (Table 8) we find that adopting an abundance of
X [SO] = 1.6 × 10-8 results in integrated line intensites
for the SO 56−45 and 65−54 transitions
that are close to the observed values (Table 6).
Hence, using the previously derived physical properties of the D-peak we can also explain
the observed SO emission. We assume that the bulk of SO emission originates in the D-peak
core itself and not from the low-density envelope. With the same assumption for the
optically thin SO2 lines toward the D-peak, we find an SO2 abundance
of
X [SO2] = N [SO2] /N [H2] ≈ (4.23 × 1013/0.446)/3 × 1022 ≈ 3 × 10-9
using the beam averaged SO2 column density of
4.23 × 1013 cm-2, D-peak filling factor of 0.446 (Table 7) and the D-peak core H2 column density
(Table 8). Similarly, for the P1 and
CH3OH peak positions we obtain
X [SO2] = 7 × 10-9 and 6 × 10-10,
respectively. Here the value for the P1 position is uncertain since it is likely that the
SO2 emission do not originate in the same source as H2CO since
they exhibit different emission velocities (cf. Table 3). Using the P1 H2 column density from C18O(3-2)
(Table 9) instead will lower the abundance by
about a factor of five. Taken together, the SO2 abundances in the D-peak, P1,
and CH3OH cores seem to fall in the range (0.6 − 3) × 10-9. However,
these SO2 abundances are all lower than the S-peak abundance, which can be
estimated to X [SO2] = 2 × 10-8.
(3-2) of about 23
toward the D-peak (Liseau et al. 2010), it is
likely that the C18O(3-2) emission is somewhat optically thick
(τ ≈ 2) and hence the listed N(C18O) and
N(H2) (Table 9) would
be about a factor
τ/(1 − e − τ) ≈ 2.3
higher. The full H2 column density toward the D-peak would then be
N(H2) = 1.5 × 1023 cm-2. Likewise,
the SO column density in the D-peak position of 1.1 × 1014 cm-2 is
lower than the corresponding value of 2.3 × 1014 cm-2 (Table 7) where the latter value includes compensation by
optical depth. Using the ALI model for the D-peak core (Table 8) we find that adopting an abundance of
X [SO] = 1.6 × 10-8 results in integrated line intensites
for the SO 56−45 and 65−54 transitions
that are close to the observed values (Table 6).
Hence, using the previously derived physical properties of the D-peak we can also explain
the observed SO emission. We assume that the bulk of SO emission originates in the D-peak
core itself and not from the low-density envelope. With the same assumption for the
optically thin SO2 lines toward the D-peak, we find an SO2 abundance
of
X [SO2] = N [SO2] /N [H2] ≈ (4.23 × 1013/0.446)/3 × 1022 ≈ 3 × 10-9
using the beam averaged SO2 column density of
4.23 × 1013 cm-2, D-peak filling factor of 0.446 (Table 7) and the D-peak core H2 column density
(Table 8). Similarly, for the P1 and
CH3OH peak positions we obtain
X [SO2] = 7 × 10-9 and 6 × 10-10,
respectively. Here the value for the P1 position is uncertain since it is likely that the
SO2 emission do not originate in the same source as H2CO since
they exhibit different emission velocities (cf. Table 3). Using the P1 H2 column density from C18O(3-2)
(Table 9) instead will lower the abundance by
about a factor of five. Taken together, the SO2 abundances in the D-peak, P1,
and CH3OH cores seem to fall in the range (0.6 − 3) × 10-9. However,
these SO2 abundances are all lower than the S-peak abundance, which can be
estimated to X [SO2] = 2 × 10-8.
Analysis results for other molecules assuming optically thin emission.
4.5. Column density ratios
To estimate the ratios of different formaldehyde isotopologues we use the results
obtained by the modified rotation diagram technique (Table 7). Even for the main isotopic species we use the rotation diagram analysis
results and not the ALI results, since effects like adopting a spherical source will
affect the results and we rather be consequent in as many aspects as possible when
estimating column density ratios. The four column density ratios; HDCO/H2CO,
D2CO/HDCO, D2CO/H2CO,
H2CO/ have been
calculated for each source position and entered into Table 10. The listed ratio uncertainties have been estimated by including an
absolute calibration uncertainty of 10% together with the 1σ uncertainty
due to noise, where the latter is the most prominent source of error for the weak lines.
The HDCO/H2CO ratio of 0.107 ± 0.015 toward the D-peak is similar to the values
found by Parise et al. (2006) for low-mass
protostars. The D2CO/HDCO ratio of 1.34 ± 0.19 is higher than the Parise et al. (2006) values which all fall in the range
0.3–0.9. In fact, it is the only reported D2CO/HDCO ratio that is significantly
greater than 1.
have been
calculated for each source position and entered into Table 10. The listed ratio uncertainties have been estimated by including an
absolute calibration uncertainty of 10% together with the 1σ uncertainty
due to noise, where the latter is the most prominent source of error for the weak lines.
The HDCO/H2CO ratio of 0.107 ± 0.015 toward the D-peak is similar to the values
found by Parise et al. (2006) for low-mass
protostars. The D2CO/HDCO ratio of 1.34 ± 0.19 is higher than the Parise et al. (2006) values which all fall in the range
0.3–0.9. In fact, it is the only reported D2CO/HDCO ratio that is significantly
greater than 1.
Formaldehyde column density ratios.
The quantity 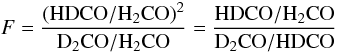 (1)is
also tabulated in Table 10. This quantity was
introduced by Rodgers & Charnley (2002) to
discern between gas phase and grain surface formation mechanisms of deuterated
formaldehyde. Our D-peak F-value of 0.08 is similar to the values
0.03–0.2 found by Roberts & Millar (2007).
In the last column of Table 10 we also list the
H2CO/CH3OH column density ratios based on the ALI model results.
(1)is
also tabulated in Table 10. This quantity was
introduced by Rodgers & Charnley (2002) to
discern between gas phase and grain surface formation mechanisms of deuterated
formaldehyde. Our D-peak F-value of 0.08 is similar to the values
0.03–0.2 found by Roberts & Millar (2007).
In the last column of Table 10 we also list the
H2CO/CH3OH column density ratios based on the ALI model results.
Bensch et al. (2001) used observations of rare CO
isotopologues to determine the 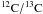 ratio toward
ρ Oph C to 65 ± 11. Although the ρ Oph C cloud core is
quite far from the ρ Oph A position they belong to the same nearby cloud
complex and our H2CO/
ratio toward
ρ Oph C to 65 ± 11. Although the ρ Oph C cloud core is
quite far from the ρ Oph A position they belong to the same nearby cloud
complex and our H2CO/ ratios
(Table 10) are in good agreement with their
value. Consequently, we will adopt this
ratios
(Table 10) are in good agreement with their
value. Consequently, we will adopt this 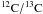 ratio of 65
also for ρ Oph A and the opacity for the C18O(3-2) line toward
the D-peak can be estimated from the optical depth of the
ratio of 65
also for ρ Oph A and the opacity for the C18O(3-2) line toward
the D-peak can be estimated from the optical depth of the
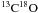 (3-2) line of
0.03 (Liseau et al. 2010) as
τ [C18O(3−2)] ≈ 65 × 0.03 ≈ 2. This is then consistent
with the discussion in the previous section on the C18O(3-2) opacity
corrections toward the D-peak.
(3-2) line of
0.03 (Liseau et al. 2010) as
τ [C18O(3−2)] ≈ 65 × 0.03 ≈ 2. This is then consistent
with the discussion in the previous section on the C18O(3-2) opacity
corrections toward the D-peak.
In Table 11 the
SO/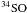 and
SO2/
and
SO2/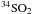 column density ratios have been listed. As noted in the table, some of the ratios are
affected by opacity in the main isotopologue and should be regarded as lower limits. The
interstellar 32S/34S ratio (Lucas
& Liszt 1998) appears to be close to its solar value of 22 (Asplund et al. 2009). We can use this isotopologue ratio
to estimate the SO abundances from the expression
22 N [34SO] /N [H2] .
For the D-peak we already have an abundance estimate, made in the previous section, of
X [SO] = 1.6 × 10-8. In the P1 and CH3OH peaks
we then get 2 × 10-8 and 3 × 10-9, respectively. The P1 value is
quite uncertain, as the SO emission velocities differ here from that of H2CO
(cf. the case of SO2 in the previous section), will be lower by a factor 5 when
using beam averaged column densities. Using the values in Table 9 for the S-peak we find that the SO abundance is
X [SO] = 22 × 5.5 × 1013/4 × 1022 ≈ 3 × 10-8.
column density ratios have been listed. As noted in the table, some of the ratios are
affected by opacity in the main isotopologue and should be regarded as lower limits. The
interstellar 32S/34S ratio (Lucas
& Liszt 1998) appears to be close to its solar value of 22 (Asplund et al. 2009). We can use this isotopologue ratio
to estimate the SO abundances from the expression
22 N [34SO] /N [H2] .
For the D-peak we already have an abundance estimate, made in the previous section, of
X [SO] = 1.6 × 10-8. In the P1 and CH3OH peaks
we then get 2 × 10-8 and 3 × 10-9, respectively. The P1 value is
quite uncertain, as the SO emission velocities differ here from that of H2CO
(cf. the case of SO2 in the previous section), will be lower by a factor 5 when
using beam averaged column densities. Using the values in Table 9 for the S-peak we find that the SO abundance is
X [SO] = 22 × 5.5 × 1013/4 × 1022 ≈ 3 × 10-8.
Other column density ratios.
The ratio N2D + /N2H + is also tabulated in Table 11 and here we use the N2H + (1-0) integrated intensity data from André et al. (2007) which have a beam size of 26″, i.e. almost identical to the resolution of our N2D + (3-2) data. The listed N(N2D + )/N(N2H + ) ratios have not been compensated for optical depth of the N2H + lines.
5. Discussion
5.1. Interaction with the molecular outflow?
As described in Sect. 3.3, the observed line profiles for SO and SO2 show broader wings in the north-western corner of our map (Fig. 8). Also the H2CO spectra exhibit line wings in this region (Fig. 2). The CO red wing emission from the prominent outflow emanating from VLA 1623 extends in this direction while the blue wing emission is extended both in the NW and SE directions (André et al. 1990). The SO and SO2 emission peaks very close to the IR reflection nebula GSS30 (Castelaz et al. 1985) which is at offsets (−79″, + 28″) in our maps. The SO and SO2 abundances (3 × 10-8 and 2 × 10-8, respectively) are here clearly higher than in other positions. The SO and SO2 line wings could very well be associated with GSS30 rather than the VLA 1623 CO outflow. The CH3OH-peak at (−30″,0″), on the other hand, could be a result of an interaction with the outflow and a dense clump (cf. Jørgensen et al. 2004). The methanol abundance is about 5 times higher here compared to its abundance in the D-peak and P1 cores. It appears also to be somewhat warmer (~30 K) than the other cores.
5.2. Depletion
The D-peak position where the deuterium fractionation is highest coincides with the emission peak (SM1) in the 1.3 mm continuum map of Motte et al. (1998). The 1.3 mm flux density, S1.3mm, can be converted into an H2 column density using N(H2) = 4 × 1020 cm-2 (S1.3mm/mJy beam-1) assuming Tdust = 20 K, a dust mass opacity of κ1.3mm = 0.5 cm2 g-1, and a gas-to-dust mass ratio of 100 (e.g. Andre et al. 1996) over the entire map (see Eq. (1′) in Motte et al. 1998). This can be compared to the H2 column density derived from the C18O(3-2) map of Liseau et al. (2010). Following the discussion in Sect. 4.4 we here assume X [C18O] = 2 × 10-7 and an excitation temperature of 20 K in all positions. The ratio, N(H2)gas/N(H2)dust, of these two estimates of N(H2) are displayed in Fig. 10. The lowest values of this ratio are around 0.15 and they are found in the central part of the cloud. Opacity corrections for C18O in this central part are of the order 2 (which will increase the ratio to 0.3), see Sect. 4.4 and probably less (closer to 1) further out. This would still mean that the N(H2)gas estimate is a factor of 3 lower than that from dust in the central portions of ρ Oph A. Here the major uncertainty is likely to be related to the adopted C18O abundance and dust mass opacity, κ1.3 mm, while influences from temperature changes are smaller. The low ratios seen could be due to depletion of CO and would then correspond to a CO depletion factor of 2–3. Given the uncertainty of the adopted dust parameters and degree of depletion (i.e. C18O abundance) we estimate that the full H2 column density toward the D-peak, cf. Sect. 4.4, is in the range (1 − 4) × 1023 cm-2.
 |
Fig. 10 Gas-to-dust ratio map of ρ Oph A calculated as the H2 column density from C18O relative to the H2 column density from dust. The gas column data are based on the C18O(3 − 2) map of Liseau et al. (2010) and the dust continuum data are from Motte et al. (1998). The gas column data have not been corrected for opacity. |
The freeze-out of CO on grains (together with low temperatures) is thought to increase the deuterium fractionation. Although the D-peak at (0″, −30″) is located in the part where the N(H2)gas/N(H2)dust opacity corrected ratio is low ~0.3−0.4, we do not see any signs that CO depletion is in effect more at (0″, −30″) than in any of the other central positions. Hence, the amount of CO depletion (at least as measured by the C18O emission and the 1.3 mm continuum data) is not directly responsible to the elevated deuterium fractionation seen in formaldehyde toward the D-peak. However, the D-peak is located within a larger region that is likely to be depleted and this may have been important in an earlier stage of the evolution of the D-peak source.
Interestingly, there is a minimum in the N(H2)gas/N(H2)dust ratio in the SE part of the map (Fig. 10). This minimum coincides with the secondary N2D + peak (N6). This would be in line with the findings that the amount of CO depletion and the N2D + /N2H + ratio are correlated in starless cores (Crapsi et al. 2005). Moreover, the Class 0 source VLA 1623 is also associated with a minimum in the N(H2)gas/N(H2)dust ratio and possibly also with a higher N2D + /N2H + ratio, compare Fig. 9 and Fig. 10. A correlation between CO depletion and N2D + /N2H + ratio has been found by Emprechtinger et al. (2009) toward several Class 0 objects.
5.3. Gas-phase chemistry models
Pure gas-phase chemistry can lead to elevated deuterium fractionations for H2CO. We have here adopted the low-metalicity (or depleted) model of Roueff et al. (2007) as their warm-core (and un-depleted) model shows low deuterium fractionations. The steady-state model work presented here includes the updates and modifications of Parise et al. (2009), and we have used it to predict relevant D/H ratios for H2CO and N2H + . The models are shown in Fig. 11. The different steady-state D/H model ratios are shown as a function of temperature and have been calculated for two different H2 densities; 5 × 105 cm-3 and 1 × 106 cm-3. The modelled ratios show little variation due to the used H2 density. The observed column density ratios (taken from Table 10 and Table 11) are represented as coloured boxes with size according to estimated uncertainty. The dashed rectangle indicates the N2D + /N2H + ratio toward the D-peak with an opacity correction.
It is noteworthy that the gas-phase depleted models yield F-values, see Eq. (1), very close to 0.5 for T ≲ 30 K for formaldehyde which are significantly higher than the observed values F ≈ 0.1, cf. Table 10. The absolute H2CO abundances, (3−6) × 10-11, for these models are much lower than the observed H2CO abundances ~5 × 10-9.
 |
Fig. 11 Gas-phase steady-state models based on the reaction network by Roueff et al. (2007). Shown are the D/H predicted ratios; HDCO/H2CO (top), D2CO/HDCO (middle), and N2D + /N2H + (bottom) as function of temperature and for two different H2 densities (5 × 105 cm-3 and 1 × 106 cm-3). The coloured boxes correspond to the observed ratios for the three cores as indicated in the top panel. The size of the rectangles represents the estimated uncertainties. |
5.4. Grain chemistry models
Our observations point to the fact that D2CO is more abundant than HDCO toward the D-peak. This is, to our knowledge, the first source where such case is observed. We note that HDCO and H2CO showed a similar anomaly towards L1527 (Parise et al. 2006), but even in that case, D2CO was less abundant than HDCO. This anomaly is difficult to explain in terms of pure gas-phase chemistry, as discussed above.
We discuss here the possibility that this anomaly stems from grain chemistry. Simple grain models which only account for H and D additions to CO to form formaldehyde and methanol cannot account for enrichment of D2CO compared to the statistically expected value. However, including the abstraction or exchange reactions of the type HDCO + H → DCO + H2, Rodgers & Charnley (2002) argue that the enrichment is anyway limited to HDCO/H2CO > D2CO/HDCO (or F > 1, see Eq. (1)). Our observational results (with F ≈ 0.1), as well as those of Parise et al. (2006) and Roberts & Millar (2007), are contradictory to this model prediction, showing that even this detailed model may be lacking some processes.
Some laboratory experiments have aimed in the last years to explain the large fractionations of formaldehyde and methanol observed towards low-mass protostars. Different types of experiments have been done (see Watanabe & Kouchi 2008, for an overview). Nagaoka et al. (2005) have exposed CO ices with H and D atoms (with D/H of 0.1) and have shown that H2CO and CH3OH (as well as their deuterated counterparts) are formed. In this experiment, they can reproduce the fractionation of all deuterated methanol molecules observed towards IRAS16293 − 2442 (Parise et al. 2004). However, they never observe an enrichment of D2CO higher than HDCO (Naoki Watanabe, priv. comm.). In a second type of experiment, Hidaka et al. (2009) aimed at clarifying the different formation routes by exposing an H2CO ice sample with D atoms. Exchanges are observed, showing that deuterium fractionation occurs very efficiently along the reaction path H2CO → HDCO → D2CO. In this case, the observed D2CO can become more abundant than HDCO (see their Fig. 3). Although a direct extrapolation from these experiments is difficult, our observations may be the definitive evidence that abstraction and exchange reactions are playing an important role in grain chemistry. It is not clear if reproducing our observations will require an increased atomic D/H ratio (from the 0.1 value used by Nagaoka et al. 2005) incoming on the grains, or if the longer timescales involved in the ISM chemistry compared to the laboratory experiments also can play a role. Detailed modelling of the complex processes taking place on the grains would be needed to definitely settle this question.
There is no known central source towards the D-peak. So, unlike the case of IRAS16293 − 2422, there is no protostar that can be responsible for releasing the deuterated material into the gas. We therefore need to invoke heating of the grains by cosmic rays (e.g. Herbst & Cuppen 2006) or through the release of the formation energy of the newly formed species (Garrod et al. 2006). Both these mechanisms can be of importance for desorption of grain mantles in starless cores. However, even if these mechanisms are responsible of releasing the deuterated material into the gas, there is no obvious reason why they would be more effective in the SM1 core as compared to the other cores. Hence, the underlying question why the D-peak shows such a high deuterium fractionation remains unanswered.
6. Conclusions
We have observed a very high degree of deuteration of formaldehyde towards a core (SM1) in ρ Oph A. In this D-peak, the deuterium fractionation manifests itself by a very high D2CO/HDCO ratio of 1.34 ± 0.19 while the ratio HDCO/H2CO is 0.107 ± 0.015. In the other parts of this cloud core the degree of deuteration in formaldehyde is much lower (although still very high compared to the ISM D/H ratio). For instance, at the P1 position, about 1′ (or 0.035 pc) north of the D-peak, the corresponding ratios are 0.27 ± 0.08 and 0.033 ± 0.006, respectively. A similar decrease in deuterium fractionation between the two positions is also seen for N2D + /N2H + . The H2CO abundance relative to H2 is estimated to be around 5 × 10-9 over the central core.
The CH3OH distribution is clearly different from that of H2CO and it has its maximum about 45′′ to the northwest of the deuterium peak. The elevated methanol abundance (by about a factor of 5 relative to the D-peak) here could be due to an interaction of the outflow with a dense clump. It would be interesting to study how the deuterated versions of CH3OH are distributed in this source (cf. Parise et al. 2006).
In order to understand the reason of the very high deuteration level observed toward the D-peak we have performed gas-phase chemistry modelling (for a depleted source). By looking at the ratio (HDCO/H2CO)/(D2CO/HDCO) (the F-value, see Eq. (1)) we find that the models result in values around 0.5 while the observed values are always around 0.1. Also, the absolute H2CO abundances obtained in these models are too low by a factor of 100. Hence, the gas-phase chemistry scheme cannot account for the observed H2CO abundances and deuterium ratios. Instead, we advocate that grain chemistry, in terms of abstraction and exchange reactions in the reaction chain H2CO → HDCO → D2CO (Hidaka et al. 2009), can be responsible for the very high deuterium fractionations observed in ρ Oph A. However, before being too conclusive about, e.g., the required atomic D/H ratio, these grain chemistry model results need to be expressed in observable quantities like the H2CO F-value. Again, observations of multiply deuterated methanol isotopologues toward the D-peak in ρ Oph A will provide additional insight as they are key ingredients in the grain chemistry scheme.
Online material
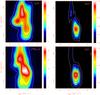 |
Fig. 4 Velocity position diagrams of the H2CO(30,3−20,2), HDCO(41,4−31,3), D2CO(40,4−30,3), and C18O(3 − 2) lines along the declination axis at Δα = 0′′. The molecule is indicated in each panel. The C18O(3 − 2) data are from Liseau et al. (2010). The vertical scale in each panel indicates the declination offset and the horizontal scale is the vLSR velocity. The intensity scale in all four panels is Tmb. |
 |
Fig. 5 Ortho H2CO(31,2−21,1) and
|
 |
Fig. 8 SO(56−45) and |
Based on the radial intensity distributions of the sub-millimeter continuum, Jayawardhana et al. (2001) suggested that the infall zone around VLA 1623 is surrounded by a constant-density region which is the dominating contribution to the radial intensity profiles at scales ≳ 10″.
The only difference is that in the normal rotation diagram analysis a straight line is least-square fitted to quantities proportional to the logarithm of the line intensities but here the fit is performed directly by minimizing the sum of the squared and error-weighted differences of observed and modelled line intensities.
Acknowledgments
We are very grateful to Frédérique Motte for sending us her continuum data of ρ Oph and to Naoki Watanabe for sending us unpublished laboratory results. Excellent support from the APEX staff during the observations is also greatly appreciated. B.P. is funded by the Deutsche Forschungsgemeinschaft (DFG) under the Emmy Noether project number PA1692/1-1.
References
- André, P., Martin-Pintado, J., Despois, D., & Montmerle, T. 1990, A&A, 236, 180 [NASA ADS] [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Andre, P., Ward-Thompson, D., & Motte, F. 1996, A&A, 314, 625 [NASA ADS] [Google Scholar]
- André, P., Belloche, A., Motte, F., & Peretto, N. 2007, A&A, 472, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Asvany, O., Schlemmer, S., & Gerlich, D. 2004, ApJ, 617, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Bachiller, R., Codella, C., Colomer, F., Liechti, S., & Walmsley, C. M. 1998, A&A, 335, 266 [Google Scholar]
- Bacmann, A., Lefloch, B., Ceccarelli, C., et al. 2003, ApJ, 585, L55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensch, F., Pak, I., Wouterloot, J. G. A., Klapper, G., & Winnewisser, G. 2001, ApJ, 562, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Castelaz, M. W., Hackwell, J. A., Grasdalen, G. L., Gehrz, R. D., & Gullixson, C. 1985, ApJ, 290, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Castets, A., Loinard, L., Caux, E., & Tielens, A. G. G. M. 1998, A&A, 338, L43 [NASA ADS] [Google Scholar]
- Ceccarelli, C., Loinard, L., Castets, A., et al. 2001, A&A, 372, 998 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceccarelli, C., Vastel, C., Tielens, A. G. G. M., et al. 2002, A&A, 381, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Di Francesco, J., André, P., & Myers, P. C. 2004, ApJ, 617, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Di Francesco, J., André, P., & Myers, P. C. 2009, ApJ, 700, 1994 [NASA ADS] [CrossRef] [Google Scholar]
- Emprechtinger, M., Caselli, P., Volgenau, N. H., Stutzki, J., & Wiedner, M. C. 2009, A&A, 493, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R., Park, I. H., Caselli, P., & Herbst, E. 2006, Chemical Evolution of the Universe, Faraday Discussions, 133, 51 [Google Scholar]
- Gerlich, D., Herbst, E., & Roueff, E. 2002, Planet. Space Sci., 50, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Green, S. 1991, ApJS, 76, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E., & Cuppen, H. M. 2006, Proceedings of the National Academy of Science, 103, 12257 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., Adams, N. G., Smith, D., & Defrees, D. J. 1987, ApJ, 312, 351 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hidaka, H., Watanabe, M., Kouchi, A., & Watanabe, N. 2009, ApJ, 702, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Jayawardhana, R., Hartmann, L., & Calvet, N. 2001, ApJ, 548, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Jørgensen, J. K., Hogerheijde, M. R., Blake, G. A., et al. 2004, A&A, 415, 1021 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, B., Philipp, S. D., Krämer, I., et al. 2006, A&A, 454, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsson, B., Liseau, R., Pagani, L., et al. 2007, A&A, 466, 999 [Google Scholar]
- Linsky, J. L. 2003, Space Sci. Rev., 106, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., Roueff, E., Gerin, M., et al. 2002, ApJ, 571, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Liseau, R., Larsson, B., Brandeker, A., et al. 2003, A&A, 402, L73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liseau, R., Larsson, B., Bergman, P., et al. 2010, A&A, 510, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loinard, L., Castets, A., Ceccarelli, C., et al. 2000, A&A, 359, 1169 [NASA ADS] [Google Scholar]
- Loinard, L., Castets, A., Ceccarelli, C., Caux, E., & Tielens, A. G. G. M. 2001, ApJ, 552, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Castets, A., Ceccarelli, C., et al. 2002, Planet. Space Sci., 50, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Loinard, L., Torres, R. M., Mioduszewski, A. J., & Rodríguez, L. F. 2008, ApJ, 675, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2008, A&A, 480, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loren, R. B., Wootten, A., & Wilking, B. A. 1990, ApJ, 365, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, R., & Liszt, H. 1998, A&A, 337, 246 [NASA ADS] [Google Scholar]
- Maercker, M., Schöier, F. L., Olofsson, H., Bergman, P., & Ramstedt, S. 2008, A&A, 479, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mangum, J. G., & Wootten, A. 1993, ApJS, 89, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Ceccarelli, C., Caux, E., et al. 2004, A&A, 416, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., André, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Muders, D., Hafok, H., Wyrowski, F., et al. 2006, A&A, 454, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nagaoka, A., Watanabe, N., & Kouchi, A. 2005, ApJ, 624, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Nummelin, A., Bergman, P., Hjalmarson, Å., et al. 2000, ApJS, 128, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001, IEEE Transactions on Antennas and Propagation, 49, 1683 [NASA ADS] [CrossRef] [Google Scholar]
- Parise, B., Ceccarelli, C., Tielens, A. G. G. M., et al. 2002, A&A, 393, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Castets, A., Herbst, E., et al. 2004, A&A, 416, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Ceccarelli, C., Tielens, A. G. G. M., et al. 2006, A&A, 453, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parise, B., Leurini, S., Schilke, P., et al. 2009, A&A, 508, 737 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottage, J. T., Flower, D. R., & Davis, S. L. 2004, MNRAS, 352, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, H., & Millar, T. J. 2007, A&A, 471, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodgers, S. D., & Charnley, S. B. 2002, Planet. Space Sci., 50, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Tiné, S., Coudert, L. H., et al. 2000, A&A, 354, L63 [NASA ADS] [Google Scholar]
- Roueff, E., Lis, D. C., van der Tak, F. F. S., Gerin, M., & Goldsmith, P. F. 2005, A&A, 438, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roueff, E., Parise, B., & Herbst, E. 2007, A&A, 464, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1992, A&A, 262, 209 [NASA ADS] [Google Scholar]
- Snow, T. P., Destree, J. D., & Welty, D. E. 2008, ApJ, 679, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E. 1990, ApJ, 362, L29 [Google Scholar]
- Turner, B. E. 2001, ApJS, 136, 579 [Google Scholar]
- Vassilev, V., Meledin, D., Lapkin, I., et al. 2008, A&A, 490, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ward-Thompson, D., Robson, E. I., Whittet, D. C. B., et al. 1989, MNRAS, 241, 119 [NASA ADS] [Google Scholar]
- Watanabe, N., & Kouchi, A. 2008, Progress In Surface Science, 83, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Wouterloot, J. G. A., Brand, J., & Henkel, C. 2005, A&A, 430, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Properties of the H2CO, CH3OH, SO, and SO2 emission in selected cloud positions from gaussian fits.
H2CO,  , HDCO, and
D2CO integrated line intensities in three positions of the
ρ Oph A cloud.
, HDCO, and
D2CO integrated line intensities in three positions of the
ρ Oph A cloud.
Integrated line intensities for other molecules in four positions of the ρ Oph A cloud.
Analysis results for H2CO,  , HDCO,
D2CO, CH3OH, SO, and SO2 from using the modified
rotation diagram technique.
, HDCO,
D2CO, CH3OH, SO, and SO2 from using the modified
rotation diagram technique.
All Figures
 |
Fig. 1 Colour image: the C18O(3−2) integrated intensity map of ρ Oph A cloud core from Liseau et al. (2010). The intensity scale is shown to the right. Contours: the 1.3 mm continuum data by Motte et al. (1998). The contours start at 0.15 Jy with subsequent contours at every increment of 0.15 Jy. The flux densities are given in a 15″ beam. We show the positions of the mm peaks from Motte et al. (1998) and the C18O peaks of Liseau et al. (2010). The map offsets are given relative the position α(J2000) = 16h26m27.2s and δ(J2000) = -24°23′34″. |
| In the text | |
 |
Fig. 2 H2CO(30,3−20,2) and D2CO(40,4−30,3) map spectra toward the ρ Oph A cloud. The (0″,0″) position is the same as in Fig. 1. The vertical scale in each spectrum represents Tmb scale in K and the horizontal scale is velocity vLSR with respect to local standard of rest in km s-1 as shown in the upper rightmost panel. |
| In the text | |
 |
Fig. 3 Maps of the H2CO(30,3−20,2), HDCO(41,4−31,3), and D2CO(40,4−30,3) integrated line intensity over the range 3.0 − 4.5 km s-1. |
| In the text | |
 |
Fig. 6 Integrated intensity maps of the CH3OH 51,5−41,4 and 42,2−31,2 E-lines. First contour is at 0.3 K km s-1 and the increment is 0.6 K km s-1. |
| In the text | |
 |
Fig. 7 CH3OH 5−4 lines around 241 GHz toward the (−30″,0″) position. Note that the 52,4−42,3 and 52,3−42,2 E-lines are blended. |
| In the text | |
 |
Fig. 9 Integrated intensity map of the N2D + 3 − 2 line toward ρ Oph A. First contour is at 0.2 K km s-1 and the increment is 0.4 K km s-1. |
| In the text | |
 |
Fig. 10 Gas-to-dust ratio map of ρ Oph A calculated as the H2 column density from C18O relative to the H2 column density from dust. The gas column data are based on the C18O(3 − 2) map of Liseau et al. (2010) and the dust continuum data are from Motte et al. (1998). The gas column data have not been corrected for opacity. |
| In the text | |
 |
Fig. 11 Gas-phase steady-state models based on the reaction network by Roueff et al. (2007). Shown are the D/H predicted ratios; HDCO/H2CO (top), D2CO/HDCO (middle), and N2D + /N2H + (bottom) as function of temperature and for two different H2 densities (5 × 105 cm-3 and 1 × 106 cm-3). The coloured boxes correspond to the observed ratios for the three cores as indicated in the top panel. The size of the rectangles represents the estimated uncertainties. |
| In the text | |
 |
Fig. 4 Velocity position diagrams of the H2CO(30,3−20,2), HDCO(41,4−31,3), D2CO(40,4−30,3), and C18O(3 − 2) lines along the declination axis at Δα = 0′′. The molecule is indicated in each panel. The C18O(3 − 2) data are from Liseau et al. (2010). The vertical scale in each panel indicates the declination offset and the horizontal scale is the vLSR velocity. The intensity scale in all four panels is Tmb. |
| In the text | |
 |
Fig. 5 Ortho H2CO(31,2−21,1) and
|
| In the text | |
 |
Fig. 8 SO(56−45) and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


