EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 524 (December 2010) A&A, 524 (2010) A44 Full HTML
Free Access
Issue
A&A
Volume 524, December 2010
Article Number A44
Number of page(s) 18
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/201014383
Published online 22 November 2010

© ESO, 2010

1. Introduction

Recent work revealed that several Galactic globular clusters (hereafter GGC) had a much more complex star-formation history than previously thought. This has implications for their use as simple stellar population (SSP) templates to study more complex and distant stellar systems and galaxies, and therefore requires careful study.

Based on deep and accurate photometric studies, GGC were found to contain different stellar populations, in the form of multiple evolutionary sequences in their color − magnitude diagrams (CMD). The first cluster found to host multiple stellar populations was ω Cen (Lee et al. 1999; Pancino et al. 2000; Bedin et al. 2004; Sollima et al. 2005; Villanova et al. 2007). Lately NGC 2808 (Piotto et al. 2007), NGC 1851 (Milone et al. 2008; Ventura et al. 2009; Han et al. 2009), NGC 6388 (Moretti et al. 2009), M 22 (Piotto 2009), and 47 Tuc (Anderson et al. 2009) joined the rapidly growing group of complex stellar population GGC.

But even before the multiple photometric sequences were detected, anti-correlations between the strength of the CN and CH bands around 3880, 4200, and 4300 Å were found, starting with the pioneering work of Osborn (1971), in all properly observed clusters. These anti-correlations are sometimes bimodal in nature (see Sect. 4.1 for references), with two separate groups of CN-strong and CN-weak stars. The first detections were of course limited to the red giant branch (RGB) stars (see Smith 1987; Kraft 1994, for early reviews), because of the instrumental limitations at that time, but later they were also found among sub giant branch (SGB) stars and even among main sequence (MS) stars (Cannon et al. 1998; Cohen 1999; Harbeck et al. 2003; Carretta et al. 2005). Anti-correlations were found among other light elements such as Na, O, Al, Mg (see the reviews by Kraft 1994; Gratton et al. 2004) and F (Cunha et al. 2003; Smith et al. 2005).

No sample of Milky Way field stars observed so far showed any sign of anti-correlations (but they do show signs of dredged up CNO processing, see Hanson et al. 1998; Gratton et al. 2000; Mishenina et al. 2006)1. Also, no chemical anomalies were found in open clusters (see references in de Silva et al. 2009; Pancino et al. 2010) or in the field stars belonging to dwarf galaxies in the Local Group. Only recently, Na-O anti-correlations were detected in extragalactic GC (globular clusters) of the Fornax dwarf galaxy and of the Large Magellanic Clouds (Letarte et al. 2006; Johnson et al. 2006; Mucciarelli et al. 2009). This suggests that environment plays a fundamental rôle in the occurrence of these anomalies.

The presence of CH-CN anti-correlations was soon interpreted as a signature of CN(O) cycle processing, which tends to deplete C and to enhance N, and of mixing that can bring CN(O) processed material to the stellar surface, during the first dredge-up that happens at the base of the RGB. To reach this conclusion, it is assumed that CN traces the N abundace and CH the C abundance (Smith et al. 1996). This is well supported by abundance analysis work based on spectral synthesis, which revealed [C/Fe] and [N/Fe] spreads of up to more than 1 dex (see e.g., Briley et al. 2004a,b; Cohen et al. 2005). However, this intrinsic scenario, often referred to as the stellar evolution scenario, was soon put into trouble by two observational facts: (i) CH and CN anti-correlations in MS stars cannot be produced by the stars themselves, because they have low mass (M ≃ 0.8   M⊙) in GGC and do not burn hydrogen through the CNO cycle; (ii) the presence of Na, Al, Mg, and O (anti-)correlations points towards the NeNa and MgAl chains that take place at much higher temperatures (Denisenkov & Denisenkova 1990; Langer et al. 1993; Prantzos et al. 2007), which are not reached in the MS or RGB phases of GGC stars. The addition of internal pollution mechanisms such as rotation-induced mixing (e.g. Sweigart & Mengel 1979; Charbonnel 1995) or the so-called canonical extra-mixing (e.g. Denissenkov & VandenBerg 2003) did not solve the problem because they still could not explain the Na-O and Al-Mg anti-correlations. Of course, mixing does occur among red giants above the base of the RGB (Smith et al. 1996; Gratton et al. 2000; Smith & Martell 2003), and this is the reason why it is better to focus on stars on the MS and SGB, which still have not undergone any mixing episode, to have a clean perspective on chemical anomalies, independent from stellar evolution effects.

A natural alternative was then some sort of extrinsic scenario, where the chemical anomalies are produced outside the GGC stars. An example is the primordial scenario proposed by Cannon et al. (1998), which foresaw the presence of two clouds with different chemical composition, merging in the formation phase of GGC. Another example is the stellar pollution scenario (D’Antona et al. 1983; Thoul et al. 2002), where only the stellar surfaces are polluted by CN(O) processed winds. These and other extrinsic scenarios are extensively discussed by Harbeck et al. (2003), and Kayser et al. (2008).

The most promising of the extrinsic scenarios remains the so-called self-enrichment scenario, first proposed by Cottrell & Da Costa (1981), which assumes the presence of two (or more) subsequent stellar generations, the first polluting the intra-cluster medium from which the second one forms. A very important constraint to this scenario is that most GGC show a remarkably homogeneous composition as far as heavier elements (e.g., Ca, Fe) are concerned. In the past five years, the chase has thus moved from finding the most promising scenario to seeking for the first generation stars responsible for polluting the intra-cluster medium. Three proposals have been made so far: (i) intermediate mass (M > 3−5   M⊙) asymptotic giant branch (AGB) stars (e.g. Ventura et al. 2001; Denissenkov & Herwig 2003; Ventura & D’Antona 2009), which naturally explain chemical anomalies, but also provide clear links to the helium problem, proposed to explain the multiple populations found in some clusters (see above) and their horizontal branch (HB) morphologies (see the series of papers by Carretta et al., the last ones being Carretta et al. 2009a,b); (ii) fast rotating massive stars (Maeder & Meynet 2006; Prantzos & Charbonnel 2006; Decressin et al. 2007), which suffer from meridional circulation, able to bring CN(O) processed material to the surface, and to release it through slow winds, through their accretion disc and, finally, through explosion; this scenario helps also in solving the helium and multiple population problems; and (iii) the very recently proposed massive interactive binaries (de Mink et al. 2009), which are known to lose mass and could indeed explain the observed anomalies. Moreover, the slow winds of all these types of polluters are prone to different degrees of stripping depending on the cluster and its environment. This can explain why different clusters show different behaviours of their multiple populations and chemical anomalies, as described in detail in Sect. 6.

The aim of this paper is to look for CH and CN band strength variations and bimodalities in a sample of unevolved stars in 12 GGC with different properties. Those clusters that show clear variations and bimodalities will be further studied in a following paper dedicated to abundance determinations, to investigate the extent of the [C/Fe] and [N/Fe] variations. Main sequence stars have not undergone any dredge-up phenomenon yet, so they are free from any evolutionary effect that, superposed to the CH and CN extrinsic variations, could confuse the picture. We will also correlate the CH and CN strength variations with GGC parameters, in order to provide additional observational constraints to the self-enrichment scenario.

The plan of the paper is the following: in Sect. 2 we discuss the observations and data reductions; in Sect. 3 we define the indices passbands and their measurement; in Sect. 4 we present our results; in Sect. 5 we discuss the results on a cluster by cluster basis; in Sect. 6 we correlate the CH and CN strengths with cluster parameters, and in Sect. 7 we summarize our findings and draw our conclusions.

2. Observations and data reduction

We selected a sample of eight GGC with different properties to test the correlations of their CH and CN strengths with cluster parameters and environmental conditions: 47 Tuc (from the ESO archive), NGC 1851, NGC 288, NGC 5927, NGC 6352, NGC 6388, NGC 6752, and Palomar 12. We also tried to select stars covering a large area in each cluster, to be free from biasses due to possible radial trends. Measurements for four more GGC were added from Kayser et al. (2008): M 15, M 22, M 55, and NGC 362, plus measurements for additional stars in NGC 288 (see Sect. 3.3). A more detailed discussion of each cluster’s properties and results can be found in Sect. 5.

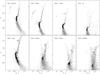thumbnail Fig. 1

Colour − magnitude diagrams for the newly observed GGC in our sample. Grey dots show our pre-imaging V, V − I photometry, calibrated with literature data (see text). For 47 Tuc, which was not part of our original observations, we used the photometry by Rosenberg et al. (2000). A selection on the photometric parameters from DAOPHOT II is applied to show only the best measured stars. Black dots mark spectroscopic targets. Clusters are ordered as a function of their metallicity from the most metal-poor (top left) to the most metal-rich (bottom right).

2.1. Observations

Table 1

Observing logs (see Sects. 2 and 5 for details).

Observations were carried out mostly in service mode in two different runs and two pre-imaging runs at the ESO VLT/UT2 telescope in Cerro Paranal, Chile, with the FORS2 multi-object spectrograph (Appenzeller et al. 1998) in MXU mode. The observing logs can be found in Table 1. The first run was dedicated to the three metal-poor clusters (NGC 6752, NGC 288, and NGC 1851) and to Pal 12, and was carried out between September and October 2001, with relatively good conditions for the pre-imaging (sky mostly clear and seeing  ≃ 1′′) and less favorable conditions for the spectroscopy observations (sky mostly veiled and seeing ranging from 0.5′′ to 2′′). The second run was dedicated to the metal-rich clusters (NGC 6352, NGC 5927, and NGC 6388) and was carried out between April and July 2002. The conditions for both pre-imaging and spectroscopy observations where less fortunate than the in the first run, with the sky often veiled or cloudy, and seeing between 1.5′′−2′′. This explains in part why the colour-magnitude diagrams (CMD) of these clusters are of a much worse quality (Fig. 1) and why the S/N ratios of their spectra tend to be quite low as well (Table 1).

Although we used the same grism, GRIS_600B, the old 2 k  ×  2 k SITE detector (24 μm/pix) was replaced by a mosaic composed by two 2 k  ×  4 k MIT CCDs (15 μm/pix) between the two runs. This implies that the covered wavelength ranges were not exactly the same in the two runs; also, the red sensitivity of the CCD was improved, but this had no effect on our measurements. The typical resolution of our spectra in both runs is R = λ/δλ ≃ 800.

2.2. Pre-imaging reductions

We obtained a set of images for one or more fields within each cluster, generally consisting of a short exposure (a few seconds) and a longer one (a few tens of seconds) for each of the Johnson V and the Cousins I filters. All images were bias-subtracted and flat-fielded with the ESO FORS pipeline. Point spread function (PSF) fitting photometry was carried out with the DAOPHOT II, ALLSTAR and ALLFRAME packages (Stetson 1987, 1994) using a constant model PSF across the field, which experience showed to yield the best results.

The photometric calibration was done using stars in common with photometry from the literature: we used the V, I catalogue published by Bellazzini et al. (2001) for NGC 1851; the B, V catalogue by Dalessandro et al. (2008b) supplemented by I magnitudes (Dalessandro, priv. comm.) for NGC 6388; and the V, I catalogue by Rosenberg et al. (2000) for 47 Tuc (NGC 104). For all remaining clusters we used the HST photometries by Piotto et al. (2002). The resulting calibrated colour-magnitude diagrams and programme stars are shown in Fig. 1.

2.3. Spectroscopy reductions

The spectroscopic target stars were selected from the pre-imaging data as the most isolated stars located around the turn-off (TO) and SGB regions of the CMD (Fig. 1). In most cases, more than one exposure was taken with a single mask, to reach a higher S/N ratio. With each mask, we were able to observe 20−30 stars with 1′′ wide, 10′′ long slitlets. The average S/N for each cluster (after the frame pre-reductions) in the CN 3880 Å region, together with the total number of good stars analysed in each cluster (see Sect. 2.5), is indicated in the last two columns of Table 1.

For the data pre-reduction, we used IRAF2 for overscan correction and bias-subtraction. We removed cosmic ray hits with the IRAF Laplacian edge-detection routine (van Dokkun 2001). The frames were subsequently flat-fielded and reduced to one-dimension spectra with the IRAF task apall. The sky background was subtracted using the information on both sides of the stellar spectrum. Finally, for those fields that were observed more than once, we co-added all spectra together on a star by star basis. We checked that the shift between the different spectra (≤ 10 km s-1) was negligible compared to our wavelength calibration uncertainty (≃ 40 km s-1) before coadding.

The shape of the final spectra is affected by the different response of the instrument at different wavelengths. There are two ways to remove this effect: flux calibration and continuum normalization. The first needs observations of standard stars, which were not available in our case. The alternative is to fit a polynomial to the pseudo-continuum and use it to normalize the spectrum. However, the CN 3880 Å band region contains many atomic lines and molecular bands, and the response of the instrument is quite low in this ultraviolet region. Therefore, no attempt was made to normalize the spectra, as many other authors skip this step for the same reason (e.g. Cohen et al. 2002; Harbeck et al. 2003; Kayser et al. 2008, among others).

2.4. Radial velocity and shifts

Finally, radial velocities were calculated by cross-correlation (with fxcor in IRAF), choosing the highest S/N star on each MXU plate as a template. The templates Vr were computed using the laboratory positions of the strongest lines (e.g. Hβ, Hδ, Ca H and K) in our wavelength region with the IRAF task rvidlines.

The three dominant sources of uncertainty for the final Vr of our spectra are: (i) uncertainty in the wavelength calibration; (ii) small shifts in the star centering within each slitlet; and (iii) variations across the field of view owing to instrument flexures. The uncertainties in the wavelength calibration are generally removed using the positions of strong emission sky lines, which could also be used to evaluate the influence of the instrument flexures (e.g. Gallart et al. 2001). Unfortunately, in the wavelength region observed here, there are no strong sky lines that can be used. The uncertainty due to small misalignment of stars in the slitlets could be estimated with the through-slit images (see Carrera et al. 2007), and we found it negligible (< 10 km s-1) in comparison with the Vr errors (~ 20−40 km s-1, see below).

thumbnail Fig. 2

Influence of telescope and/or instrument flexures on the derived radial velocities. Each point represents one star, with its radial velocity and the X and Y coordinates of the corresponding slitlet center. The solid lines represent a bilineal fit to the data (see text).

Table 2

Index measurements and radial velocities for the sample stars.

Significant variations of Vr across the field of view, most probably due to flexures, are clearly observed as shown in Fig. 2. The estimated radial velocity varies systematically with the position of each slitlet along the Y CCD axis (and on the X axis as well), by as much as  ~ 80 km s-1, i.e., larger than the the velocity uncentainty (~ 20−40 km s-1) and of the scatter expected within each cluster (of the order of a few km s-1). The example in Fig. 2 shows a typical difference of about  ≃ 60 km s-1. To correct for these variations, we computed a bilineal fit for each observed plate, in the form Vr = a + bX + cY (see Fig. 2). Stars near the centre of each MXU mask, which have the smallest shifts, were used to roughly report all the mask velocities to the GGC systemic velocity (from Harris 1996). The final velocities corrected for the above variations are reported in Table 2.

2.5. Quality control and sample selection

Given the huge amount of spectra (see Table 1) and the sometimes low S/N achieved during observations, we applied the following selection criteria:

  • spectra with S/N < 8 (per pixel) in the CN3880 Å band regionwere rejected;

  • spectra with significant defects (spikes, holes) in the measurement windows were rejected;

  • stars with discrepant radial velocity by more than 2.5σ from the cluster average were rejected;

  • stars with discrepant Ca(H+K) index measurement were rejected (see Sect. 3 for details);

  • stars with discrepant Hβ index measurements were rejected (see Sect. 3 for details).

The criterion that had the highest impact on star rejections was by far the first one. The final sample contains 356 stars (out of an initial set of  ~ 600) belonging to eight clusters, as indicated in the third column of Table 1 and also reported in Table 2.

thumbnail Fig. 3

Two spectra of CN-weak, CH-strong stars with different S/N ratio are shown as examples of our best and worst data: the upper spectrum in all panels has S/N ≃ 25 (on the S3839(CN) band) and belongs to NGC 1851; the lower spectrum has S/H ≃ 10 and belongs to NGC 6388. Both are shifted on an arbitrary flux scale for sake of clarity. The top panel illustrates the chosen windows used for the CN and CH indices (magenta hatched regions) along with their respective continuum windows (grey hatched regions); while the bottom panels show the windows adopted for the H and K Calcium index (bottom left) and the Hβ index (bottom right).

3. Index definition and measurement

The strength of a spectral feature can be evaluated with a spectral index, which is defined through one window centred on the atomic line or molecular band that we will evaluate, and one or more windows around it, used to define the continuum level. In the literature we can find many definitions of the spectral indices used to measure the strength of the CN and CH molecular bands. In most cases, these definitions are optimized for red giant stars, observed at a specific spectral resolution. In our case, because we observe subgiants and dwarfs, and we aim to compare our results with others in the literature, we chose to adopt the indices defined by Harbeck et al. (2003): 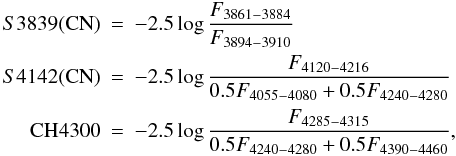where F3861−3884, for example, is the summed spectral flux in ADU counts from 3861 to 3884 Å. The related uncertainties have been obtained with the expression derived by Vollmann & Eversberg (2006), assuming pure photon (Poisson) noise statistics in the flux measurements3. Figure 3 (top panel) shows the adopted indices windows; examples of our best and worst S/N spectra are overplotted.

We also measured two additional indices, centred around the calcium H and K lines and the Hβ line (see also Fig. 3, bottom panels): 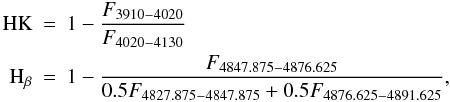The H and K line strengths depend mostly on temperature and on the calcium abundance, while the Hβ line strength depends on temperature and of course on the hydrogen abundance. We used these two indices to reject a few remaining 3σ outliers (at most 2–3 stars per cluster). Since we used the indices only in a relative sense, we did not need to compare our measurements with the literature, therefore we defined our own narrow and conservative windows (see Fig. 3, lower panels) in order to minimize the spread due to disturbing features containing other elements and to maximize our ability to pinpoint outliers.

3.1. CN-band choice

In our wavelength region, we measured two different CN band indices, S3839 for the CN band around 3880 Å and S4142 for the much weaker one around 4200 Å (Harbeck et al. 2003). Figure 4 shows a comparison between the two. The correlation appears weak for the metal-poor clusters (NGC 6752, NGC 288, NGC 1851), in spite of the higher S/N of the spectra, because these double-metal molecular bands are weaker. A clear correlation appears for the most metal-rich clusters (47 Tuc, NGC 6352, NGC 5927, and NGC 6388), although it is not as striking for NGC 6388, given the low S/N and paucity of stars. The slope of the relation between S4142 and S3839 appears to be roughly the same for all clusters (dotted line in Fig. 4), while the zeropoint varies slightly from cluster to cluster.

thumbnail Fig. 4

Comparison between the CN S3839 and the S4142 indices. Each panel shows measurements for the indicated cluster, and the median errobar is also shown in the lower right corner. Clusters are sorted by metallicity, from the most metal-poor (top-left) to the most metal-rich (bottom-right). Dotted lines are linear fits with a fixed slope (that of the whole sample) and rougly adjusted zeropoints.

As expected, Fig. 4 clearly shows that S4142 is less sensitive to the CN variations, because generally its spread is just slightly larger than the median errorbar shown in the lower-right corner of each panel. This is especially true for the metal-poor clusters. On the other hand, the spread of S3839 is always larger than its median errobar, even for the metal-poor clusters. For this reason, we will be relying on S3839 measurements for CN, and we will set aside the less reliable S4142 ones (as done also by, e.g., Cannon et al. 1998; Harbeck et al. 2003).

3.2. Dependency on temperature and gravity

At a fixed overall abundance, it is well known that the CN-band and CH-band are stronger in stars with lower temperature and gravity. To eliminate this dependency, different authors use different proxies for temperature and gravity, such as colours (e.g. Harbeck et al. 2003) or magnitudes (e.g. Norris et al. 1981) or some combination of the Balmer indices (e.g. Kayser et al. 2006). The indices are then corrected by fitting the lower envelope of the distribution in the chosen plane, and the new indices are generally indicated as δS3839(CN) and δCH4300. Most of the cited authors find generally no significant trend for S3839(CN), but they do always correct the CH4300 index, usually with a second-order polynomial. Given the diversity of shapes and slopes, we prefer to use median ridge lines4 to correct for the curvature induced by both temperature and gravity effects. We show an example of the computed median ridge lines, with NGC 1851 in Fig. 5.

Generally, we confirm that the curvature of S3839(CN) as a function of V magnitude is much smaller than the curvature of CH4300. We define our rectified δS3839(CN) and δCH4300 indices as the difference between the original S3839(CN) and CH4300 indices and their respective median ridge lines. The rectified indices will be used throughout the rest of this paper.

thumbnail Fig. 5

Example of the removal of temperature and gravity dependencies from the CH and CN indices, using median ridge lines on NGC 1851. Large black dots represent the target stars, while small grey dots represent the calibrated pre-maging photometry of NGC 1851. The median ridge lines of CH and CN as functions of V magnitude are marked as dotted lines.

3.3. Additional data from the literature and archives

To increase our observed sample, we re-reduced the 47 Tuc data we found in the ESO archive with our procedure, which is very similar to the one adopted by the original team that made the observations (Harbeck et al. 2003). This way, a direct comparison of the results was possible, showing excellent agreement and therefore providing a useful validation of our adopted procedure. We also added index measurements for the four clusters in Kayser et al. (2008) that had MS and SGB stars faint enough to have pristine surface composition, not altered by the first dredge-up mixing episode, which happens at the base of the RGB. We therefore selected from their measurements (their Table A.1) those stars in NGC 362 with V < 18.5, in M 55 with V < 17.5, in M 15 with V < 18.5, and in M 22 with V < 17 (see Fig. 2 by Kayser et al. 2008). Their definition of indices is exactly the same as ours (Sect. 3). We applied a more strict selection in radial velocity, at 2.5σ (as in Sect. 2.5). We then removed the temperature and gravity dependency from their measurements (their Table A.1), using the same procedure described in Sect. 3.2. Kayser et al. (2008) do not give the S/N of their spectra, but judging from their errobars (see their Table A.1), they should be of the order of S/N ≃ 15−20 for M 15, M 22, and M 55, and S/N ≃ 10−15 for NGC 362 anf NGC 288. In the following sections, we analyse and discuss these data together with ours.

4. Results

4.1. CH and CN bimodalities

The presence of CH and CN bimodalities, i.e., two well separated groups of stars with a different strength of these bands, was apparent almost as soon as CH and CN anomalies were discovered in red giants in the 1970s and 1980s. Some clusters showed clear bimodalities in CN (or in [N/Fe]) and weaker or missing bimodalities in CH (or in [C/Fe]), while some other clusters instead showed a continuous spread in CN strength. Various studies identified CN bimodalities among red giants of M 3 and M 13 (Suntzeff 1981; Briley et al. 2004b), NGC 6752 (Norris et al. 1981), ω Cen (Cohen & Bell 1986), NGC 6934 (Smith & Bell 1986), NGC 6171 (Smith 1988), M 71 (Smith & Penny 1989; Lee 2005), M 2 (Smith & Mateo 1990), M 5 (Ramírez & Cohen 2002), NGC 288 and NGC 362 (Kayser et al. 2008), NGC 6121 (Marino et al. 2008), NGC 6356, and NGC 6528 (Martell & Smith 2009), among others. Bimodalities among MS and sub-giant branch stars have also been found in M 71 (Cohen 1999), 47 Tuc (Cannon et al. 1998; Harbeck et al. 2003; Briley et al. 2004a; Carretta et al. 2005), and NGC 6752 (Carretta et al. 2005).

The interest related to the presence of a bimodal distribution – rather than a continuous spread – is clear in the light of the latest theories of self-enrichment for GGC (see also Sect. 1). First generation stars should have a “normal” surface composition, rich in C and poor in N, while the second generation ones, formed from CN(O) cycle processing polluted gas, should have higher N and lower C (Smith & Norris 1982). If we find a clear bimodality in the data, this supports the idea of two stellar generations5. If a bimodal distribution is found measuring the CH and CN band strengths, we expect that the underlying [C/Fe] and [N/Fe] distributions will turn out to be bimodal as well, since each cluster has the same overall metallicity and all stars in each cluster have roughly the same atmospheric parameters. This of course requires confirmation via spectrum synthesis calculations. These calculations will be the subject of a future paper. Indeed, such a bimodality in C and N enhancements has been found e.g., by Briley et al. (2004b) in RGB stars in M 13, or by Briley et al. (2004a) in MS stars in 47 Tuc. That such bimodalities have rarely been found among red giants when the Na-O anti-correlations are considered deserves further studies. We point out two possible reasons in advance: (i) the Na and especially the O abundances in giants are difficult to measure, and indeed we often see only upper limits for [O/Fe] (Carretta et al. 2009a,b) or (ii) C, N, O, and Na are not directly comparable, because they are not produced exactly at the same temperature: C and N are altered within the CN bi-cycle, O is depleted in the complete CNO cycle and Na is produced in the NeNa cycle, each dominating at progressively higher temperatures; in this second hypothesis much care should be taken with the comparison of Na-O and C-N anti-correlations with each other. Finally we note that if such a C-N bimodality is present, it should be easier to see in MS stars than in RGB stars, where it could be attenuated by internal mixing (Sect. 1).

thumbnail Fig. 6

Histograms of the δS3839(CN) (top panels) and δCH4300 (bottom panels) index strengths. The bin sizes are larger for clusters with lower S/N and/or fewer stars. Typical (median) errorbars are plotted below each histogram. Vertical dotted lines mark δS3839(CN) = 0 and δCH4300 = 0, i.e. the median ridge line of the rectified index and the border between CN or CH strong and CN or CH weak stars. Clusters are sorted by increasing metallicity, from left to right and from top to bottom.

thumbnail Fig. 7

Anti-correlation plots for the CH and CN band strengths. Each panel shows the measurements for stars (grey dots) in each cluster. CH strong and weak stars are separted by the horizontal dotted line, and their centroids are marked as large white dots, while CN strong and weak stars are separated by the vertical dotted line and their centroids are marked as large black dots. The S/N ratio in the CN band region is indicated in the lower left corners.
We studied the presence of bimodal distributions for the CN and CH rectified band strengths by means of histograms (Fig. 6) and – more importantly – by plotting our measurements in the CH-CN plane (Fig. 7, see also next Sect.). We consider a distribution to be “bimodal” when the centroids of the CN-strong (CH-weak) and CN-weak (CH-strong) stars are clearly separated6 in the CH-CN plane and – as a supporting evidence – when the histograms also show signs of bimodality. Detailed studies of the statistical significance of such bimodalities are deferred to a following paper, dealing with the [C/Fe] and [N/Fe] distributions. First, we note that all the most metal-rich clusters (Pal 12, 47 Tuc, NGC 6352, and NGC 5927), with the only exception of NGC 6388 (which has low S/N and few stars), show a clear bimodality not only in δS3839(CN), but also in δCH4300. Among the metal-poor clusters, the situation is less clear. There is a bimodality only in M 15, even if it is the most metal-poor of the sample and has a relatively low S/N ratio. For the remaining clusters we only see vague hints of possible bimodalities (see Sect. 5 for more details) in Fig. 6, but not in Figs. 7 or 8. We will discuss individual clusters in Sect. 5.

4.2. CN and CH anticorrelations

While the S/N of our metal-poor clusters spectra (NGC 362, NGC 6752, NGC 288, NGC 1851, M 22, M 55) is comparable to that of other authors (i.e., Harbeck et al. 2003; Kayser et al. 2008), the double molecule bands of CN are really weak at those low metallicities, for MS stars. On the contrary, even if the S/N of our remaining metal-rich clusters is lower due to bad weather conditions, CH and CN bands are much stronger. For the MS stars extracted from the Kayser et al. (2008) sample, the S/N is relatively low because they focussed their analysis on brighter RGB and SGB stars.

Because our S/N is sometimes at the limit of detection in the CN band region, at least for the most metal-poor clusters, we used the δCH4300 index, which has the highest S/N, to separate target stars in a CH-strong (δCH4300  >  0) and a CH-weak (δCH4300  <  0) group for each cluster. A weighted average was used to compute the centroids of the CH-strong and CH-weak groups in the CN-CH plane. The resulting centroids with their 1σ errors are reported in Fig. 7 as large white dots along with measurements for each star. For completeness we also divided the stars in CN-strong (δS3839(CN)  >  0) and CN-weak (δS3839(CN)  <  0) groups, and their centroids are marked as large black dots with their errobars. A zoom-in for those clusters with small spreads on the scale of Fig. 7 is presented in Fig. 8.

Table 3

Clusters sample intrinsic properties and structural parameters.

We see clear anti-correlations (Fig. 7) only for those clusters that showed a clear bimodality in both indices, i.e., M 15, Pal 12, 47 Tuc, NGC 6352, and NGC 5927. We would be tempted to say that where our data are good enough to show an anticorrelation, this anticorrelation is always clearly bimodal. The case of NGC 288 seems to be an exception, and it is further discussed in Sect. 5. In most of the other cases, anti-correlations and/or bimodalities were found by other authors, as discussed in detail in Sect. 5, so we suspect that in general the present data do not have high enough S/N to be conclusive on these clusters.

5. Cluster by cluster discussion

5.1. NCG 104 (47 Tucanae)

The cluster NGC 104 or 47 Tuc is one of the most massive and metal-rich GGC (Table 3). It is considered to be part of the thick disc (Dinescu et al. 1999), with a low eccentricity and relatively high inclination orbit. Currently it is located  ≃ 3 kpc below the Galactic plane in projection on the sky close to the Small Magellanic Cloud. Pritzl et al. (2005) place it in the group of thick-disc clusters, while Mackey & Gilmore (2004) classify it as bulge/disc cluster.

It is one of the most studied GGC thanks to its vicinity and its relatively high [Fe/H]. While the abundance determinations on red giants are too many to mention here (the most recent being Carretta et al. 2009c), the abundance analysis of turn-off and early subgiant stars resulted in [Fe/H]  = −0.67 ± 0.01(± 0.04) dex (Carretta et al. 2004), while James et al. (2004) derive −0.69 ± 0.06 dex for SGB stars and −0.68 ± 0.01 dex from three turnoff stars. It was one of the first GGC in which CN-CH variations were detected among MS stars (Cannon et al. 1998; Briley et al. 1994). The star-to-star scatter has been clearly detected for light elements; while the Na-O anticorrelation is not very strong, it has nevertheless been detected by Carretta et al. (2004).

The CN-CH molecular abundances of turn-off and sub-giant stars in this cluster were also topic of a detailed study by Harbeck et al. (2003) and Briley et al. (2004a), resulting in a clear bimodality in band strengths and also in [N/Fe], with abundance differences of up to 1 dex. We use here their archive data to test the homogeneity of reductions. A clearly bimodal anti-correlation is detected here (Fig. 7), which confirms the results by Harbeck et al. (2003) and Briley et al. (2004a) and which, together with the double SGB and wide MS found by Anderson et al. (2009), demonstrates the presence of two distinct populations in this cluster.

5.2. NGC 288

thumbnail Fig. 8

Zoomed version of those clusters that show a small spread on the scale of Fig. 7.

The source NGC 288 is a low concentration, low central density cluster located close to the South Galactic Pole, in a very low interstellar extinction region. Its retrograde motion and relatively low velocity components place it among the inner old halo (OH) globular clusters (Dinescu et al. 1997). Tidal shocks due to bulge and disc for this cluster are estimated to be strong compared to the usually more predominant internal relaxation and evaporation (Dinescu et al. 1999).

Its horizontal branch is composed almost entirely of stars bluer than the instability strip. It is often studied together with NGC 362, which has the same metallicity, but very different HB morphology: they represent one of the classical second parameter pairs. Bolte (1989) was one of the first to propose helium, CNO, or age differences as possible explanations for the second parameter problem. Shetrone & Keane (2000) made a comparative spectroscopic study of red giants in the second-parameter GC pair NGC 288 and NGC 362. The [Fe/H] they derived for NGC 288 is −1.39 ± 0.01 dex. These authors also remark on the Na-O and Al-O anti-correlations, which were found in both clusters. Figure 7 by Carretta et al. (2009b) shows even a hint of bimodality in the Na-O anti-correlation. A clear bimodality in the CH and CN index strength has been detected among red giants by Kayser et al. (2008) and Smith & Langland-Shula (2009).

Our data are the ones by Kayser et al. (2008), of which we selected only unevolved stars, and we do not see any clear anti-correlation. There is no reason why unevolved stars in a GGC should have a uniform composition while the evolved ones show a bimodality, because no known mixing mechanism would be able to create a bimodality from a homogeneous population. Therefore we must conclude that our data do not have a sufficient S/N to reveal a bimodality in these metal-poor MS stars. Spectral synthesis calculation will be able to quantify the sensitivity of our spectra to C and N abundances, while more higher quality data are most probably needed anyway to settle the question. We note here that as we will see in Sect. 6, NGC 288 falls perfectly in line with other clusters in all correlations with cluster parameters.

5.3. NGC 362

As mentioned before, NGC 288 and NGC 362 are one of the second-parameters pairs, with similar metallicity and different HB morphology. Bolte (1989) proposed CNO, among others, as one of the second parameters. NGC 362 has a metallicity of −1.33 ± 0.01 dex (Shetrone & Keane 2000), it is more concentrated than NGC 288 (Table 3) and slightly closer to the Galactic centre. The anomalies in the CH and CN band strengths among its giants were studied more than in NGC 288 (McClure & Norris 1974; Frogel et al. 1983; Smith & Norris 1983; Smith 1984). Kayser et al. (2008) extensively studied both NGC 288 and NGC 362, finding a clear anti-correlation among RGB and SGB stars in both clusters, and a clear bimodality among red giants in both clusters. This suggests that anti-correlations or chemical anomalies cannot be the predominant source of the different HB morphology in these two clusters.

As for NGC 288, bimodalities and an anti-correlation were found in the CH and CN band strengths of RGB stars, while our data for the MS stars reveal none. We suspect that here also this is simply owing to the low S/N of the spectra (lower than for NGC 288), and it must be worsened by the smaller sample. A study with higher quality spectra would be even more interesting than for NGC 288, because NGC 362 does not behave like the other GGC in the correlations with cluster parameters (Sect. 6) and it is not clear whether NGC 362 is a real outlier or if the present data are simply inconclusive.

5.4. NGC 1851

The cluster NGC 1851 has a very eccentric and highly inclined orbit, with a large excursion into the outer parts of the Galaxy (Dinescu et al. 1997, 1999). The iron abundance measurements from high-resolution spectra report [Fe/H]  = −1.22 ± 0.03 dex (Yong et al. 2009) and −1.27 ± 0.09 (Yong & Grundahl 2008). The bimodal HB in this cluster already hinted towards multiple stellar populations, but only recently Milone et al. (2008) detected two parallel SGB sequences, thanks to exquisite ACS@HST photometry, and Han et al. (2009) found that the use of U, U − I photometry reveals a striking bimodality in the RGB. A possible different radial distribution of the two SGB (Zoccali et al. 2009) would support some predictions of the self-enrichment scenario (D’Ercole et al. 2008), but Milone et al. (2009) do not confirm this finding.

A possible explanation for the double SGB is a CNO enriched stellar component (Cassisi et al. 2008; Salaris et al. 2008), possibly – but not necessarily – combined with some age difference of the order of 1 Gyr at most. This is expected to produce a strong effect on CN and CH molecules. Indeed, among the RGB stars some extremely CN strong stars have been detected (Hesser et al. 1982). Another study reporting a large CNO abundance spread in giant stars is that by Yong et al. (2009). The HB morphology of NGC 1851 seems to rule out a large He difference between the two populations (Salaris et al. 2008).

Unfortunately, as for NGC 288 and NGC 362, at this metallicity our S/N ratio is probably not sufficient to reveal anti-correlations and bimodalities. We only see some bimodality in the δCH4300 index (the one with the highest S/N), but not in δS3839(CN), and only in Fig. 6, but not in Figs. 7 or 8. Moreover, our targets do not fall in the ACS field, so we cannot attempt any experiment on their position on the two different SGB found by Milone et al. (2008) at this stage. More studies including higher S/N spectra and a careful target selection could help in clarifying the nature of these substructures. As for NGC 288, NGC 1851 behaves like all other clusters of similar metallicity when trends with GGC parameters are considered (Sect. 6).

5.5. NGC 5927

The source NGC 5927 belongs to the metal-rich globular clusters. It suffers from relatively high reddening and thus was not well studied spectroscopically with high-resolution data: according to Zinn & West (1984), it is one of the most metal-rich disc clusters ([Fe/H]  = −0.3 dex); Cohen (1983) found this cluster to be +0.59 dex more metal rich than 47 Tuc; Kraft & Ivans (2003) derive from low-resolution spectra [Fe/H]II = −0.67 dex; Francois (1991) derived [Fe/H] −1.08 dex based on the high-resolution study of one star only. Given the large spread in literature determinations, we adopt the Kraft & Ivans (2003) estimate, keeping in mind that NGC 5927 could well be more metal-rich than that. To the best of our knowledge, the present study is the first one dedicated to light element anti-correlations in this cluster.

We find a quite clear and bimodal anti-correlation of the CH and CN band strength, in spite of the low S/N ratio of our spectra and of the relatively high reddening in the cluster field. Clearly, at this metallicity the CN and CH bands are so strong that it is quite easy to reveal these variations. Finding a bimodal anti-correlation in such a metal-rich cluster is interesting, since for example no open cluster revealed these variations up to now (see de Silva et al. 2009; Pancino et al. 2010; Martell & Smith 2009, and references therein). Obviously, high-resolution spectroscopy of stars in this neglected cluster would be of enormous interest.

5.6. NGC 6352

NGC 6352 is a sparsely populated metal-rich cluster with disc kinematics. Pritzl et al. (2005) place it in the group of thin disc clusters, while Mackey & Gilmore (2004) classify it as a bulge/disc GGC. Based on high-resolution spectra of eight stars, Cohen (1983) found this cluster to be +0.38 dex more metal rich than 47 Tuc. Carretta & Gratton (1997) re-analysed equivalent width measurements of Gratton (1987) for three stars finding an average [Fe/H]  = −0.64 ± 0.06, and recently Carretta et al. (2009c) re-adjusted it to [Fe/H]  = −0.62 ± 0.05. A recent high-resolution study by Feltzing et al. (2009), based on nine horizontal branch stars, found [Fe/H]  = −0.55 ± 0.03 and suggested that on the HB there is a correlated trend in Al and Na abundances, similarly to what was found for stars on the RGB in other globular clusters.

No study dedicated to light elements was carried out to our knowledge, so the hint by Feltzing et al. (2009) is our only comparison. We do find a clear and bimodal CH and CN anti-correlation, which is even more striking if one considers the low number of stars observed and the relatively low S/N around 3900 Å. As for NGC 5927, the high metallicity helps in revealing CH and CN band strength variations, and the study of these metal-rich GGC would be interesting for the same reasons. An HST photometric study – seeking for multiple sequences – coupled with high-resolution spectroscopy for deriving the chemical patterns of NGC 6352 could be one of the next steps in the study of chemical abundance anomalies in GGC.

5.7. NGC 6388

The cluster NGC 6388 is one of 10 most massive in the Milky Way, it is a bulge cluster, located about 3 kpc from the Galactic centre. It is very centrally concentrated and tightly bound, and has among the highest predicted escape velocity at the cluster center (McLaughlin & van der Marel 2005). Based on high-resolution FLAMES-UVES spectra, Carretta et al. (2007a) measured [Fe/H]  = −0.44 ± 0.01(±0.03). These authors also detected the presence of Na-O and Mg-Al anti-correlations, and of a Na-Al correlation among RGB stars. A clear bimodality in CH and CN was also detected on the RGB by Smith & Langland-Shula (2009).

NGC 6388 is sometimes referred to as being unusual (e.g. Dalessandro et al. 2008b): in contrast to expectations for its high metallicity, the cluster harbours an extended blue horizontal branch (Rich et al. 1993), and RR Lyr stars with periods much longer than expected for their metallicity. In addition, the horizontal branch presents a slope, so that in the V-band its blue tail lies about 0.5 mag brighter than the red HB clump (Raimondo et al. 2002). These features are not reproducible by stellar evolutionary models with an SSP of standard GGC abundance ratios, but could be explained with the presence of more than one stellar population and some self-enrichment with CNO processed material (Yoon et al. 2008). The evidence for multiple stellar populations came from the most recent deep near-IR photometry of Moretti et al. (2009), who detected two distinct sub-giant branches in this cluster.

Unfortunately, the strong differential reddening and the insufficient S/N of our data prevent us from reaching any conclusion about the CH and CN correlation at the MS level. But given its high metallicity and total mass, this is one of the most interesting clusters for further investigations. In spite of the poor data for this cluster, NGC 6388 follows all the trends of other GGC with clusters parameters (Sect. 6).

5.8. M 22 (NGC 6656)

Besides ω Centauri, M 22 is one of the first GGC that were suspected to host multiple stellar populations and chemical anomalies (Hesser et al. 1977). Unfortunately, strong differential reddening has complicated its study (Richter et al. 1999), therefore spectroscopic studies initially gave conflicting results: while a spread in the CH and CN abundances of RGB stars appeared unquestionable (Norris & Freeman 1983), some studies reported on abundance variations of 0.3 ± 0.5 dex in Ca and/or Fe, often correlated with the CH and CN variations (Peterson 1980; Pilachowski et al. 1982; Lehnert et al. 1991; Brown & Wallerstein 1992), while other studies found no significant variation in the heavy element content (Manduca & Bell 1978; Cohen 1981; Gratton 1982; Laird et al. 1991). This was probably because the reported variations were of the order of the quoted uncertainties (see also Monaco et al. 2004). Recently, Marino et al. (2009) found that two groups of stars exist in M 22, where [Fe/H] appears correlated with the s-process elements and with [Ca/Fe], and the usual Na, O, Al anti-correlations were found. Da Costa et al. (2009) confirm that the Ca distribution shows a large spread with a possible bimodality.

Our data, belonging to the unevolved stars from the sample by Kayser et al. (2008) do not have sufficient S/N to reveal CH and CN anti-correlations or bimodalities. No clear bimodality was found by Kayser et al. (2008) among RGB stars, either. If really different metallicities co-exist in the cluster, this could further complicate the detection of anti-correlations and of their bimodalities, if they are present. Most probably spectral synthesis and the determination of [C/Fe] and [N/Fe] would help in clarifying the picture.

5.9. NGC 6752

The cluster NGC 6752 is one of the best studied regarding its chemical properties, given its relative proximity to us (Table 1). It has an intermediate metallicity and a blue HB. Its orbit is remarkably similar to that of 47 Tuc (Dinescu et al. 2000), and it is therefore associated with the thick disc by some authors. Many high-resolution spectroscopic studies of this cluster provide the following iron abundance measurements: [Fe/H]  = −1.48 ± 0.01 ± 0.06 dex by (Gratton et al. 2005) based on FLAMES-UVES spectra of 7 giants near the RGB bump, [Fe/H]  = −1.42 based on UVES spectra of MS and sub-giant stars (Gratton et al. 2001), [Fe/H]  = −1.49 ± 0.07 for 9 SGB stars, and [Fe/H]  = −1.48 ± 0.07 for 9 turnoff stars based on FLAMES-UVES spectra (James et al. 2004), [Fe/H]  = −1.61 based on 38 RGB stars observed at very high resolution (Yong et al. 2005), and [Fe/H] I = −1.56, [Fe/H]II = −1.48 based on FLAMES GIRAFFE spectra of 137 RGB stars (Carretta et al. 2007a, 2009c).

The O-Na anticorrelation is well established in NGC 6752 from observations of both MS and SGB (Gratton et al. 2001; Carretta et al. 2005), as well as of RGB (Norris & Da Costa 1995; Yong et al. 2003). Data from Grundahl et al. (2002) and Yong et al. (2003) show Na-O and Al-Mg anticorrelations in stars that are both brighter and fainter than the RGB bump. Pasquini et al. (2008) detected very strong N abundance variations in the MS Turn-off stars. Furhtermore, Yong & Grundahl (2008) detected for the first time correlations of light elements with Si and heavier elements among red giants. Recently, Villanova et al. (2009) have obtained a direct He measurement from the 5875 Å line in HB stars and found a homogeneous abundance of Y = 0.245 ± 0.012, thus putting in doubt He as the origin of multiple populations, at least in this GGC.

Unfortunately, our data have certainly too low a S/N to clearly detect anti-correlations. The histograms in Fig. 6 are suggestive of a possible bimodality, but we know already that the anti-correlations are bimodal in this cluster because Norris et al. (1981) found a clear bimodality among RGB stars and Carretta et al. (2005) among MS stars.

5.10. M 55 (NGC 6809)

The source M 55 is a moderately sized cluster (Table 3), with an unusually low central concentration, which makes it relatively easy to collect stellar samples even within the cluster core. The cluster lies in front of the southern tail of the Sagittarius dwarf galaxy (Lane et al. 2009). There are few spectroscopic measurements of metallicity for M 55 stars, yielding [Fe/H]  = −1.65 (Caldwell & Dickens 1988), [Fe/H]  = −1.95 (Minniti et al. 1993), and recently [Fe/H]  = −1.93 ± 0.02(±0.07) dex from 14 stars observed with UVES@VLT (Carretta et al. 2009c), who also found a Na-O anti-correlation and some indication of possible Al variations. Marín-Franch et al. (2009) assign M 55 to the old group of GGC, based on their relative ages scale. The blue straggler stars (BSS) of M 55 suggest an unusually high primordial population of binaries compared to other GGC (Lanzoni et al. 2007), although this contrasts with the conclusions of Sollima et al. (2007). Another interesting result concerns the abundance of helium, measured with the R-method by Vargas Álvarez & Sandquist (2007), which appears to be the highest recorded for a massive GGC: Y = 0.274 ± 0.016.

Our results on this cluster are somewhat unclear, with a possible secondary peak in the CH band histograms, but not in the CN ones (Fig. 6). This is most probably owing to the insufficient S/N ratio for MS stars in this metal-poor cluster. However, Kayser et al. (2008) found no clear sign of anti-correlation, even considering the higher S/N red giants spectra, and an early paper by Briley et al. (1993) suggests that the CN spread might be unusually low in this cluster. So the question of CH and CN anti-correlations and of their bimodalitiy in M 55 remains open.

5.11. M 15 (NGC 7078)

The most metal-poor cluster in our sample is M 15, with [Fe/H]  = −2.34 (Carretta et al. 2009c), it has a blue HB and it is a core-collapsed GGC, which is suspected to harbour a black hole in its centre (see Ho et al. 2003; McNamara et al. 2003; van den Bosch et al. 2006; Chakrabarty 2006; Kiselev et al. 2008, and references therein). It is at present quite far away from the Galactic center (Table 4).

Anti-correlations were detected among all usual light elements in M 15 (see Sneden et al. 1997, and references therein), with hints that there could be a spread also in the heavy elements (see also Sneden et al. 2000; Otsuki et al. 2006). On the low-resolution spectroscopy front, Cohen et al. (2005) obtained a beautiful C-N anti-correlation among stars on the lower RGB, with impressive abundance variations of 1−2 dex. However, neither their [C/Fe] nor [N/Fe] distributions show any evidence of bimodality. Also, Lee (2000) found an anti-correlation among bright giants. The Na-O anti-correlation was also found by Carretta et al. (2009b), although their measurements were mostly upper limits.

We selected our targets among the unevolved stars measured by Kayser et al. (2008), who found some bimodality among both evolved and unevolved stars. With our median ridge line correction of the temperature and gravity effect (Sect. 3.2) we were able to reveal a clearly bimodal CH and CN anti-correlation. This is really striking if one considers the very low metallicity and the S/N ratio of these spectra, lower than that of NGC 1851 and comparable to that of NGC 288. Indeed, the index strengths measured in this paper are – as expected – a function of global metallicity, represented by [Fe/H] in Fig. 97. A roughly linear trend appears when the distance between the centroids of the CH-weak and CN-strong stars is plotted against [Fe/H], with some sign of “saturation” at the metal-poor end, where the indices become weak. The behaviour of M 15 clearly stands out of this simple relation, and a prediction of the present work is that its [C/Fe] vs. [N/Fe] anti-correlation should be significantly more extended than those of other clusters in the sample.

thumbnail Fig. 9

Relation between the CN-strong and CN-weak centroids geometrical distance in the CN-CH plane and [Fe/H] from Table 3. The white dot represents M 15, which is excluded from the linear fit (dotted line) of the remaining clusters (black dots).

5.12. Palomar 12

A very interesting cluster to include in our sample is Pal 12, because it is one of the GGC traditionally associated with the Sagittarius dwarf spheroidal galaxy (Sgr), which is at present disrupting under the strain of the Milky Way tidal field (Ibata et al. 1995; Majewski et al. 2003). Its lower  [α/Fe]  ratio (Brown et al. 1997; Cohen 2004) and younger age than typical GGC (Rosenberg et al. 1998; Marín-Franch et al. 2009), its location close in Galactic longitude to Sgr, and towards the southern extension of Sgr, its motion towards the Sgr, and its orbital parameters indicate that it may have been captured by Sgr some 1.7 Gyr ago (Dinescu et al. 1997).

From the chemical abundance point of view, a few [Fe/H] estimates place it in the moderately metal-poor regime (Brown et al. 1997; Cohen 2004, see also Table 3). In particular, Cohen (2004) noticed not only the lack of α-enhancement in Pal 12, but also remarked on the abundance of heavy elements, which is more similar to Sgr dwarf stars (Bonifacio et al. 2000; Smecker-Hane & McWilliam 2002). The four stars she studied showed identical abundance pattern, with no evidence of star-to-star variations. Also Kayser et al. (2008) found no sign of CH and CN anti-correlation among evolved stars.

With our data, a bimodal anti-correlation of CH and CN band strengths is apparent. The group of CH-strong and CN-weak stars appears truncated and reduced in size, probably owing to our selection (Sect. 2.5), which excluded all stars with S/N < 8 in the CN spectral region. A higher S/N sample could shed some light on this peculiar effect, which makes the CN-strong to CN-weak stars ratio appear quite higher than in other clusters (see also Sect. 6).

6. Trends with cluster parameters

When trying to connect the GGC properties with the presence and extension of the anti-correlations, two parameters are usually defined: (i) the “low-resolution community”, studying the strength of molecular indices, usually builds the ratio of CN-strong to CN-weak stars rCN (e.g. Norris 1987; Smith & Mateo 1990; Smith 2002; Kayser et al. 2008); (ii) the “high-resolution community” (namely Carretta 2006; Carretta et al. 2007b) measures the extension of the Na-O and Mg-Al anti-correlations with interquartile ranges. The two parameters measure two different physical quantities, and both give clues to the understanding of the anti-correlation phenomenon. In this paper we will concentrate on the first approach, deferring the second one to a following paper, in which we will attempt to derive [C/Fe] and [N/Fe] ratios through spectral synthesis of the best S/N clusters.

To compare with rCN, we selected several cluster intrinsic (Table 3) and orbital parameters (Table 4) from the literature. Because we were looking for trends and were not particularly interested in zeropoints and absolute quantities, we preferred papers reporting homogeneous data, trying to avoid mixing of different sources whenever possible.

Table 4

Clusters sample positional and orbital parameters.

thumbnail Fig. 10

Run of the ratio rCN = nCNstrong/nCNweak for our sample clusters. In each panel, NGC 362 ans Pal 12 (grey dots) are excluded from the relations. Dotted lines mark linear fits to the remaining clusters (black dots) and the correlation coefficients are reported on top of each panel: rS stands for the Spearman and rP for the Pearson coefficient. For the meaning of X labels, see Tables 3 and 4.

Table 5

Ratio of CN-strong and CN-weak stars and centroids distance.

6.1. Ratio of CN-strong to CN-weak stars

The ratio between CN-strong and CN-weak stars tells us the relative importance of stellar groups with different chemical composition. In the framework of the self-enrichment scenario, for example, it becomes a fundamental constraint to model the chemical evolution of a GGC. A correlation between rCN and cluster ellipticity, defined as ε = 1−(b/a), was initially found (Norris 1987; Smith & Mateo 1990; Smith 2002), but later studies (Kayser et al. 2008) did not confirm it. Smith & Mateo (1990) and Kayser et al. (2008) found that clusters with a higher fraction of CN-strong stars are also more luminous and therefore more massive. This finding is supported by the trend found by Smith & Mateo (1990) with the central velocity dispersion σ0. While Kayser et al. (2008), in their compilation of literature estimates of rCN, found all possible values of rCN between 0 and 2, Carretta et al. (2009a) and Carretta et al. (2009b), using more homogeneus data, found that the second – or I as intermediate – generation stars (i.e., the CN-strong stars) are between 50% and 70% of the total.

We computed our rCN ratio by selecting stars with δS3839(CN) > 0 for our CN-strong group and stars with δS3839(CN) < 0 for our CN-weak group. The final errors on rCN were propagated by assuming Poissonian errors (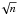) in the CN-strong and CN-weak counts8 and are reported in Table 5. We found that even if the CH4300 region has a much higher S/N in our spectra, the spread of a corresponding rCH ratio is too large to identify any correlation. We interpret this as a consequence of the fact that CN, being a double-metal band, is more sensitive to abundance variations and therefore rCN is the best indicator (see also Norris 1987).

The average ratio we find between the two populations,  ⟨ rCN ⟩  = 0.82 ± 0.29, implies that the CN-strong stars – the second generation – tend to constitute the minority of the total population, in contrast with the results by Carretta et al. (2009a,b). In both studies there are ample uncertainties, with our estimated fraction of second generation stars varying from roughly 25% to 50% of the total, and the same fraction estimated by Carretta et al. (2009a,b) varying from about 50% to 70% of the total. While the discrepancy is only marginal, and indeed the data appear consistent within the uncertainties, it is nevertheless puzzling that these two indicators – the CH-CN and the Na-O anti-correlations – give somewhat different answers (see also the discussion in Sect. 4.1).

6.2. Comparison with cluster parameters

Our results are reported in Fig. 10, where we also report on the Spearman (rS) and Pearson (rP) correlation coefficients9. As a first note, we observe that our rCN values all range between 0.5 and 1.0 (⟨ rCN ⟩  = 0.82 ± 0.29), with the only exceptions of Pal 12 and NGC 362, which have much higher uncertainties than the rest of the clusters. Indeed, our strict selection of spectra with S/N > 8 could have biased our results for Pal 12 against CN-weak stars, while for NGC 362 the S/N ratio and the low number of stars prevent us from measuring rCN properly (see also the errorbars in Fig. 6). Therefore, we have decided to leave out NGC 362 and Pal 12 from the present attempt to look for linear correlations of rCN and cluster parameters.

We do not find any highly significant correlation of cluster parameters with rCN. The only correlations that have significance slightly above 1σ, are the ones of rCN with cluster age (83%, or  ≃1.2σ), concentration c (88%, or  ≃1.3σ), total luminosity MV (82%, or  ≃1.2σ), total present-day mass in units of log (M/M⊙) (81%, or  ≃1.2σ), orbital inclination Ψ (95%, or  ≃2σ), and orbital period P (78%, or  ≃1.1σ). However weak, these relations broadly agree with past findings, except for the correlation between rCN and ellipticity. In the framework of the self-enrichment scenario, this might mean that the relative size of the two stellar generations (or the efficiency of the second star formation episode) is only marginally influenced by the cluster total mass and orbital parameters. The correlation with cluster age is detected here for the first time and if confirmed, it could mean that older clusters are more efficient in when converting gas into the second generation of stars (but see Sect. 7).

7. Discussion and conclusions

We can summarize the results of this paper as follows:

  • for the metal-rich clusters (Pal 12,47 Tuc, NGC 5927,NGC 6352) where the S/N of our spectra was goodenough, we could detect clear anti-correlations between the CNand CH band strengths, which were always clearly bimodal;

  • for the metal-poor clusters we could detect no clear anti-correlation or bimodality, even in those cases where we knew from past studies that variations should be present; we ascribe that to the fact that we were unfortunately not able to gather sufficient S/N (although higher than for the metal-rich clusters) to study CH and CN bands in these metal-poor MS stars;

  • the only exception was M 15, the most metal-poor of the entire sample; which shows an abnormally large difference in band strengths for its metallicity;

  • we computed rCN, the ratio between the CN-strong and CN-weak stars, which turned out to be on average  ⟨ rCN ⟩  = 0.82 ± 0.29;

  • no strongly significant correlation was found between rCN and 15 clusters parameters deduced from literature compilations;

  • weak correlations (slightly above 1σ) were found with cluster total present-day mass and luminosity;

  • similarly weak correlations were found with orbital parameters, with cluster concentration and with cluster age.

Now, as reviewed in Sect. 1, the so-called intrinsic scenarios involving various kinds of extra-mixing are not sufficient to explain the observed chemical anomalies in GGC, although of course mixing does occur in GGC stars (Gratton et al. 2000). This is especially true if one considers, as we did, only unevolved stars that still have not undergone the so-called first dredge-up episode. We will therefore focus on the extrinsic scenarios, and in particular on the self-enrichment scenario.

Our first result is that in all the studied clusters, those which have sufficiently good data to show CH and CN anti-correlations among MS stars are clearly bimodal in both the CN and CH band strengths. This gives a very strong support to the above scenario, especially when it predicts two (or more) subsequent stellar generations, each polluting the gas from which the following one forms. In this respect we can say that within our sample, we always find two distinct groups of stars and not more. So, while exceptions are always possible (let us not forget about, e.g., ω Cen and possibly NGC 2808), the general tendency seems to have at most two major stellar generations in each GGC10.

Our second result is that M 15 appears to possess exceptionally large variations of the CH and CN band strengths, for its metallicity. If this, as expected, will lead to an exceptionally extended [C/Fe] vs. [N/Fe] anti-correlation, it would certainly be worthwhile to follow-up on M 15 with large samples of high-resolution spectra, to better study the presence of multiple populations also in the Na-O plane. Given its peculiar properties (Sect. 5.11), M 15 could even belong to the group of massive clusters that have undergone more self-enrichment than usual, either because of their special properties or because they could be the remnants of accreted dwarf galaxies (such as ω Cen). Therefore, also further searches for variations in heavier species such as Ca, Fe, or Ba should be extremely interesting.

Our third result is that the ratio of CN-strong to CN-weak stars is on average  ⟨ rCN ⟩  = 0.82 ± 0.29. This challenges to some extent results by Carretta et al. (2009a,b), who find that the first or primordial (P) generation accounts for approximately 1/3 of the total cluster population, leaving space for a 50–70% fraction for the second or intermediate (I) population. On the one hand the discrepancy is – at best – marginal, as discussed in Sect. 6 and given the ample uncertainties involved; on the other hand, the discrepancy could be caused by the Na-O and the CH-CN anti-correlations sampling two sligthly different phenomena (as discussed in Sect. 4.1). Certaintly more studies are required to shed more light on this issue, because these kind of discrepancies – if confirmed – could turn out into further clues on the formation and evolution of GGC.

Our fourth result is that no strong correlation was found between rCN and 15 different cluster parameters compiled from the literature. While we must stress that the present study is limited to 12 clusters with spectra of modest S/N, the absence of strong corelations has one major implication in the self-enrichment scenario: it would imply that the population ratio of the two (or more) stellar generations is only mildly (if at all) influenced by the cluster properties. In particular, clusters with larger present-day total masses (and therefore luminosities) could be able to form only sligthly higher fractions of second generation stars with respect to less massive clusters. Similarly, the relations with cluster orbital parameters could hint that environment has some (minor) rôle in determining the size of the second stellar generation.

In summary, the use of low-resolution spectra to study CH and CN bands in GGC stars provides a useful complement to the high-resolution studies, needing less observing time and data analysis effort. In particular, the use of strictly unevolved stars. i.e., stars that have not undergone first dredge-up mixing, and of two elements such as C and N that (unlikely Na and O) are strictly produced in the same nuclear reaction chains and at the same temperature, can give additional constraints to studies based on red giants only.

1

Some CN-strong stars were found in the SEGUE dataset by Martell & Grebel (2010), but according to the authors they are most probably they formed in globular clusters and were transferred to the halo through tidal interactions with the Galaxy or two-body interactions inside the cluster.

2

IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.

3

We could neglect here the readout noise, always between 3 and 5 ADU, compared to our 300−3000 ADU gathered in the CN band region; the error in the sky subtraction, with tens of pixels on each side of the spectrum for sky estimation, and an order of 100 ADU sky level for the worst cases; and the spectrum tracing errors, because we always had a peak signal – in the central pixel – of at least 70 ADU, and a total 300−3000 ADU level, even in the CN region that had the lowest S/N.

4

A rough estimate of the uncertainty in the placement of the median ridge line can be obtained by using the first interquartile range of the rectified indices, divided by the square root of the total number of points. We find a typical uncertainty ranging approximately from 0.01 to 0.02 in the CN index, and from 0.005 to 0.01 in the CH index, depending on the cluster. These uncertainties are negligible for all applications in the present work.

5

The opposite is not necessarily true, in the sense that self-enrichment could also produce a continuous spread in the CH and CN band strengths, depending on the details of the chemical enrichment history, such as duration and intensity of star-formation episodes.

6

This generally implies a significant centroids separation of at least 1σ, but this separation of centroids does not grant a bimodality per se, as for NGC 6388.

7

ΔCN is the geometrical centroids distance of the CN-strong and CN-weak groups in the CH-CN plane. The geometrical distance is 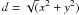, where x is the difference between the average δS3839(CN) of the δS3839(CN) > 0 and δS3839(CN) < 0 groups, while y is the difference between the average δCH4300 of the δS3839(CN) > 0 and δS3839(CN) < 0 groups. The two centroids in the CN-CH plane are represented by the two lage dots in each panel of Fig. 7. ΔCN is reported along with its uncertainty in the last two columns of Table 5.

8

As noted in Sect. 3.2, the very small uncertainty in the placement of the sparation line between CN-strong and CN-weak stars can have an impact on rCN in the sense of moving a few stars from one group to the other. This uncertainty ranges from the order of 1% to a maximum of 10%. In any case, it is always small compared to the uncertainties quoted in Table 5.

9

To compute the Spearman and Pearson coefficients and their associated probabilities, we used the algorithms described by Press et al. (1992) in their “Numerical recipes”.

10

Of course, we cannot eclude with our study the existence of small populations totalling less than  ≃ 10−20% of the respective cluster populations. Therefore, the existance of an extreme (E in the notation by Carretta et al. 2009a,b) population is by no means excluded by our data.

Acknowledgments

We warmly thank Michael Hilker for providing the data for M 55 in electronic form and Harald Kuntschner for an interesting discussion on index measurements. We are grateful to Elena Valenti and Emanuele Dalessandro for their help with photometric catalogues. We also thank Michele Bellazzini for advice on the dynamical properties of GGC and Angela Bragaglia for interesting discussions on chemical anomalies in GGC. E.P. acknowledges support by the ESO Visitorship programme both in Germany and in Chile. R.C. acknowledges the funds by the Spanish Ministry of Science and Technology under the MEC/Fullbright postdoctoral fellowship program. M.Z. acknowledges support by the FONDAP Center for Astrophysics 15010003, BASAL CATA PFB-06, Fondecyt Regular 1085278 and MIDEPLAN’s Milky Way Millennium Nucleus P07-021-F.

References

  1. Alcaino, G., Liller, W., Alvarado, F., & Wenderoth, E. 1992, AJ, 104, 190 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alcaino, G., Liller, W., & Alvarado, F. 1997, AJ, 114, 2626 [NASA ADS] [CrossRef] [Google Scholar]
  3. Anderson, J., Piotto, G., King, I. R., Bedin, L. R., & Guhathakurta, P. 2009, ApJ, 697, L58 [NASA ADS] [CrossRef] [Google Scholar]
  4. Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
  5. Baumgardt, H., Parmentier, G., Gieles, M., & Vesperini, E. 2010, MNRAS, 401, 1832 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bekki, K., Campbell, S. W., Lattanzio, J. C., & Norris, J. E. 2007, MNRAS, 377, 335 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bellazzini, M., Pecci, F. F., Ferraro, F. R., et al. 2001, AJ, 122, 2569 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bellazzini, M., Ferraro, F. R., & Ibata, R. 2003, AJ, 125, 188 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bolte, M. 1989, AJ, 97, 1688 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bonifacio, P., Hill, V., Molaro, P., et al. 2000, A&A, 359, 663 [NASA ADS] [Google Scholar]
  12. Briley, M. M., Bell, R. A., Smith, G. H., & Hesser, J. E. 1989, ApJ, 341, 800 [NASA ADS] [CrossRef] [Google Scholar]
  13. Briley, M. M., Smith, G. H., Hesser, J. E., & Bell, R. A. 1993, AJ, 106, 142 [NASA ADS] [CrossRef] [Google Scholar]
  14. Briley, M. M., Hesser, J. E., Bell, R. A., Bolte, M., & Smith, G. H., 1994, AJ, 108, 2183 [NASA ADS] [CrossRef] [Google Scholar]
  15. Briley, M. M. 1997, AJ, 114, 1051 [NASA ADS] [CrossRef] [Google Scholar]
  16. Briley, M. M., Harbeck, D., Smith, G. H., & Grebel, E. K. 2004a, AJ, 127, 1588 [NASA ADS] [CrossRef] [Google Scholar]
  17. Briley, M. M., Cohen, J. G., & Stetson, P. B. 2004b, AJ, 127, 1579 [NASA ADS] [CrossRef] [Google Scholar]
  18. Brown, J. A., & Wallerstein, G. 1992, AJ, 104, 1818 [NASA ADS] [CrossRef] [Google Scholar]
  19. Brown, J. A., Wallerstein, G., & Zucker, D. 1997, AJ, 114, 180 [NASA ADS] [CrossRef] [Google Scholar]
  20. Buonanno, R., Corsi, C. E., Pulone, L., et al. 1995, AJ, 109, 663 [NASA ADS] [CrossRef] [Google Scholar]
  21. Buonanno, R., Corsi, C. E., Pulone, L., Fusi Pecci, F., & Bellazzini, M. 1998, A&A, 333, 505 [NASA ADS] [Google Scholar]
  22. Caldwell, S. P., & Dickens, R. J. 1988, MNRAS, 234, 87 [NASA ADS] [Google Scholar]
  23. Cannon, R. 1996, J. A&A, 17, 1 [NASA ADS] [Google Scholar]
  24. Cannon, R. D., Croke, B. F. W., Bell, R. A., Hesser, J. E. & Stathakis, R. A. 1998, MNRAS, 298, 601 [NASA ADS] [CrossRef] [Google Scholar]
  25. Carrera, R., Gallart, C., Pancino, E., & Zinn, R. 2007, AJ, 134, 1298 [NASA ADS] [CrossRef] [Google Scholar]
  26. Carretta, E. 2006, AJ, 131, 1766 [NASA ADS] [CrossRef] [Google Scholar]
  27. Carretta, E., & Gratton, R. G. 1997, A&AS, 121, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Carretta, E., Gratton, R. G., Bragaglia, A., Bonifacio, P., & Pasquini, L. 2004, A&A, 416, 925 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Carretta, E., Gratton, R. G., Lucatello, S., Bragaglia, A., & Bonifacio, P. 2005, A&A, 433, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2007a, A&A, 464, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Carretta, E., Recio-Blanco, A., Gratton, R. G., Piotto, G., & Bragaglia, A. 2007b, ApJ, 671, L125 [NASA ADS] [CrossRef] [Google Scholar]
  32. Carretta, E., Bragaglia, A., Gratton, R., & Lucatello, S. 2009a, A&A, 505, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009b, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Carretta, E., Bragaglia, A., Gratton, R., D’Orazi, V., & Lucatello, S. 2009c, A&A, 508, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Casetti-Dinescu, D. I., Girard, T. M., Herrera, D., et al. 2007, AJ, 134, 195 [NASA ADS] [CrossRef] [Google Scholar]
  36. Cassisi, S., Salaris, M., Pietrinferni, A., et al. 2008, ApJ, 672, L115 [NASA ADS] [CrossRef] [Google Scholar]
  37. Catelan, M. 2009, Ap&SS, 320, 261 [NASA ADS] [CrossRef] [Google Scholar]
  38. Chakrabarty, D. 2006, AJ, 131, 2561 [NASA ADS] [CrossRef] [Google Scholar]
  39. Charbonnel, C. 1995, ApJ, 453, L41 [NASA ADS] [CrossRef] [Google Scholar]
  40. Cohen, J. G. 1978, ApJ, 223, 487 [NASA ADS] [CrossRef] [Google Scholar]
  41. Cohen, J. G. 1981, ApJ, 247, 869 [NASA ADS] [CrossRef] [Google Scholar]
  42. Cohen, J. G. 1983, ApJ, 270, 654 [NASA ADS] [CrossRef] [Google Scholar]
  43. Cohen, J. G., & Bell, R. A. 1986, ApJ, 305, 698 [NASA ADS] [CrossRef] [Google Scholar]
  44. Cohen, J. G. 1999, AJ, 117, 2434 [NASA ADS] [CrossRef] [Google Scholar]
  45. Cohen, J. G., Briley, M. M., & Stetson, P. B. 2002, AJ, 123, 2525 [NASA ADS] [CrossRef] [Google Scholar]
  46. Cohen, J. G. 2004, AJ, 127, 1545 [NASA ADS] [CrossRef] [Google Scholar]
  47. Cohen, J. G., Briley, M. M., & Stetson, P. B. 2005, AJ, 130, 1177 [NASA ADS] [CrossRef] [Google Scholar]
  48. Cottrell, P. L., & Da Costa, G. S. 1981, ApJ, 245, L79 [NASA ADS] [CrossRef] [Google Scholar]
  49. Cunha, K., Smith, V. V., Lambert, D. L., & Hinkle, K. H. 2003, AJ, 126, 1305 [NASA ADS] [CrossRef] [Google Scholar]
  50. Da Costa, G. S., & Cottrell, P. L. 1980, ApJ, 236, 83 [Google Scholar]
  51. Da Costa, G. S., Held, E. V., Saviane, I., & Gullieuszik, M. 2009, ApJ, 705, 1481 [NASA ADS] [CrossRef] [Google Scholar]
  52. Dalessandro, E., Lanzoni, B., Ferraro, F. R., et al. 2008, ApJ, 677, 1069 [NASA ADS] [CrossRef] [Google Scholar]
  53. D’Antona, F., Gratton, R., & Chieffi, A. 1983, Mem. Soc. Astron. Ital., 54, 173 [Google Scholar]
  54. D’Antona, F., Caloi, V., Montalbán, J., Ventura, P., & Gratton, R. 2002, A&A, 395, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. D’Antona, F., Bellazzini, M., Caloi, V., et al. 2005, ApJ, 631, 868 [NASA ADS] [CrossRef] [Google Scholar]
  56. Decressin, T., Meynet, G., Charbonnel, C., Prantzos, N., & Ekström, S. 2007, A&A, 464, 1029 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. de Mink, S. E., Pols, O. R., Langer, N., & Izzard, R. G. 2009, A&A, 507, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Denissenkov, P. A., & VandenBerg, D. A. 2003, ApJ, 593, 509 [NASA ADS] [CrossRef] [Google Scholar]
  59. Denisenkov, P. A., & Denisenkova, S. N. 1990, SvA Lett., 16, 275 [Google Scholar]
  60. Denissenkov, P. A., & Herwig, F. 2003, ApJ, 590, L99 [NASA ADS] [CrossRef] [Google Scholar]
  61. D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
  62. de Silva, G. M., Gibson, B. K., Lattanzio, J., & Asplund, M. 2009, A&A, 500, L25 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  63. Dinescu, D. I., Girard, T. M., van Altena, W. F., Mendez, R. A., & Lopez, C. E. 1997, AJ, 114, 1014 [NASA ADS] [CrossRef] [Google Scholar]
  64. Dinescu, D. I., Girard, T. M., & van Altena, W. F. 1999, AJ, 117, 1792 [NASA ADS] [CrossRef] [Google Scholar]
  65. Dinescu, D. I., Majewski, S. R., Girard, T. M., & Cudworth, K. M. 2000, AJ, 120, 1892 [NASA ADS] [CrossRef] [Google Scholar]
  66. Durrell, P. R., & Harris, W. E. 1993, AJ, 105, 1420 [NASA ADS] [CrossRef] [Google Scholar]
  67. Feltzing, S., Primas, F., & Johnson, R. A. 2009, A&A, 493, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Francois, P. 1991, A&A, 247, 56 [NASA ADS] [Google Scholar]
  69. Frenk, C. S., & Fall, S. M. 1982, MNRAS, 199, 565 [NASA ADS] [Google Scholar]
  70. Frogel, J. A., Persson, S. E., & Cohen, J. G. 1983, ApJS, 53, 713 [NASA ADS] [CrossRef] [Google Scholar]
  71. Fulbright, J. P. 2002, AJ, 123, 404 [NASA ADS] [CrossRef] [Google Scholar]
  72. Gallart, C., Martínez-Delgado, D., Gómez-Flechoso, M. A., & Mateo, M. 2001, AJ, 121, 2572 [NASA ADS] [CrossRef] [Google Scholar]
  73. Gnedin, O. Y., Zhao, H., Pringle, J. E., et al. 2002, ApJ, 568, L23 [NASA ADS] [CrossRef] [Google Scholar]
  74. Gratton, R. G. 1982, A&A, 115, 171 [NASA ADS] [Google Scholar]
  75. Gratton, R. G. 1987, A&A, 179, 181 [NASA ADS] [Google Scholar]
  76. Gratton, R. G., Fusi Pecci, F., Carretta, E., et al. 1997, Hipparcos - Venice ’97, 402, 651 [NASA ADS] [Google Scholar]
  77. Gratton, R. G., Sneden, C., Carretta, E., & Bragaglia, A. 2000, A&A, 354, 169 [NASA ADS] [Google Scholar]
  78. Gratton, R. G., Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Gratton, R., Sneden, C. & Carretta, E. 2004, ARA&A, 42, 385 [NASA ADS] [CrossRef] [Google Scholar]
  80. Gratton, R. G., Bragaglia, A., Carretta, E., et al. 2005, A&A, 440, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Grundahl, F., Briley, M., Nissen, P. E., & Feltzing, S. 2002, A&A 385, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Han, S.-I., Lee, Y.-W., Joo, S.-J., et al. 2009, ApJ, 707, L190 [NASA ADS] [CrossRef] [Google Scholar]
  83. Hanson, R. B., Sneden, C., Kraft, R. P., & Fulbright, J. 1998, AJ, 116, 1286 [NASA ADS] [CrossRef] [Google Scholar]
  84. Harbeck, D., Smith, G. H., & Grebel, E. K. 2003, AJ, 125, 197 [NASA ADS] [CrossRef] [Google Scholar]
  85. Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  86. Hesser, J. E., Hartwick, F. D. A., & McClure, R. D. 1977, ApJS, 33, 471 [NASA ADS] [CrossRef] [Google Scholar]
  87. Hesser, J. E., Bell, R. A., Harris, G. L. H., & Cannon, R. D. 1982, AJ, 87, 1470 [NASA ADS] [CrossRef] [Google Scholar]
  88. Hilker, M., Kayser, A., Richtler, T., & Willemsen, P. 2004, A&A, 422, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Ho, L. C., Terashima, Y., & Okajima, T. 2003, ApJ, 587, L35 [NASA ADS] [CrossRef] [Google Scholar]
  90. Ibata, R. A., Gilmore, G., & Irwin, M. J. 1995, MNRAS, 277, 781 [NASA ADS] [CrossRef] [Google Scholar]
  91. Iben, I., Jr. 1968, Nature, 220, 143 [NASA ADS] [CrossRef] [Google Scholar]
  92. Irwin, M. 1999, The Stellar Content of Local Group Galaxies, 192, 409 [Google Scholar]
  93. James, G., Francois, P., Bonifacio, P., et al. 2004, A&A, 427, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Johnson, J. A., Ivans, I. I., & Stetson, P. B. 2006, ApJ, 640, 801 [NASA ADS] [CrossRef] [Google Scholar]
  95. Kayser, A., Hilker, M., Richtler, T., & Willemsen, P. G. 2006, A&A, 458, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Kayser, A., Hilker, M., Grebel, E. K., & Willemsen, P. G. 2008, A&A, 486, 437 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Kiselev, A. A., Gnedin, Y. N., Shakht, N. A., et al. 2008, Astron. Lett., 34, 529 [NASA ADS] [CrossRef] [Google Scholar]
  98. Kraft, R. P. 1994, PASP, 106, 553 [NASA ADS] [CrossRef] [Google Scholar]
  99. Kraft, R. P., & Ivans, I. I. 2003, PASP, 115, 143 [NASA ADS] [CrossRef] [Google Scholar]
  100. Laird, J. B., Wilhelm, R. J., & Peterson, R. C. 1991, The Formation and Evolution of Star Clusters, 13, 578 [NASA ADS] [Google Scholar]
  101. Lane, R. R., Kiss, L. L., Lewis, G. F., et al. 2009, MNRAS, 400, 917 [NASA ADS] [CrossRef] [Google Scholar]
  102. Langer, G. E., Hoffman, R., & Sneden, C. 1993, PASP, 105, 301 [NASA ADS] [CrossRef] [Google Scholar]
  103. Lanzoni, B., Dalessandro, E., Perina, S., et al. 2007, ApJ, 670, 1065 [NASA ADS] [CrossRef] [Google Scholar]
  104. Lee, Y.-W., Joo, J.-M., Sohn, Y.-J., et al. 1999, Nature, 402, 55 [NASA ADS] [CrossRef] [Google Scholar]
  105. Lee, S. G. 2000, J. Korean Astron. Soc., 33, 137 [NASA ADS] [Google Scholar]
  106. Lee, S.-G. 2005, J. Korean Astron. Soc., 38, 23 [Google Scholar]
  107. Lehnert, M. D., Bell, R. A., & Cohen, J. G. 1991, ApJ, 367, 514 [NASA ADS] [CrossRef] [Google Scholar]
  108. Letarte, B., Hill, V., Jablonka, P., et al. 2006, A&A, 453, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Mackey, A. D., & Gilmore, G. F. 2004, MNRAS, 355, 504 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  110. Mackey, A. D., & van den Bergh, S. 2005, MNRAS, 360, 631 [NASA ADS] [CrossRef] [Google Scholar]
  111. McNamara, B. J., Harrison, T. E., & Anderson, J. 2003, ApJ, 595, 187 [NASA ADS] [CrossRef] [Google Scholar]
  112. Maeder, A., & Meynet, G. 2006, A&A, 448, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
  114. Manduca, A., & Bell, R. A. 1978, ApJ, 225, 908 [NASA ADS] [CrossRef] [Google Scholar]
  115. Mandushev, G., Staneva, A., & Spasova, N. 1991, A&A, 252, 94 [NASA ADS] [Google Scholar]
  116. Marino, A. F., Villanova, S., Piotto, G., et al. 2008, A&A, 490, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  117. Marino, A. F., Milone, A. P., Piotto, G., et al. 2009, A&A, 505, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  118. Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
  119. Martell, S. L., & Smith, G. H. 2009, PASP, 121, 577 [NASA ADS] [CrossRef] [Google Scholar]
  120. McClure, R. D., & Norris, J. 1974, ApJ, 193, 139 [NASA ADS] [CrossRef] [Google Scholar]
  121. McLaughlin, D. E., & van der Marel, R. P. 2005, ApJS, 161, 304 [NASA ADS] [CrossRef] [Google Scholar]
  122. Martell, S. L., & Grebel, E. K. 2010, 519, A14 [Google Scholar]
  123. Milone, A. P., Bedin, L. R., Piotto, G., et al. 2008, ApJ, 673, 241 [NASA ADS] [CrossRef] [Google Scholar]
  124. Milone, A. P., Stetson, P. B., Piotto, G., et al. 2009, A&A, 503, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  125. Minniti, D., Geisler, D., Peterson, R. C., & Claria, J. J. 1993, ApJ, 413, 548 [NASA ADS] [CrossRef] [Google Scholar]
  126. Mishenina, T. V., Bienaymé, O., Gorbaneva, T. I., et al. 2006, A&A, 456, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  127. Monaco, L., Pancino, E., Ferraro, F. R., & Bellazzini, M. 2004, MNRAS, 349, 1278 [NASA ADS] [CrossRef] [Google Scholar]
  128. Moretti, A., Piotto, G., Arcidiacono, C., et al. 2009, A&A, 493, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  129. Mucciarelli, A., Origlia, L., Ferraro, F. R., & Pancino, E. 2009, ApJ, 695, L134 [NASA ADS] [CrossRef] [Google Scholar]
  130. Norris, J., Cottrell, P. L., Freeman, K. C., & Da Costa, G. S. 1981, ApJ, 244, 205 [NASA ADS] [CrossRef] [Google Scholar]
  131. Norris, J., & Freeman, K. C. 1983, ApJ, 266, 130 [NASA ADS] [CrossRef] [Google Scholar]
  132. Norris, J. 1987, ApJ, 313, L65 [NASA ADS] [CrossRef] [Google Scholar]
  133. Norris, J. E., & Da Costa, G. S. 1995, ApJ, 447, 680 [NASA ADS] [CrossRef] [Google Scholar]
  134. Norris, J. E. 2004, ApJ, 612, L25 [NASA ADS] [CrossRef] [Google Scholar]
  135. Osborn, W. 1971, The Observatory, 91, 223 [NASA ADS] [Google Scholar]
  136. Otsuki, K., Honda, S., Aoki, W., et al. 2006, International Symposium on Nuclear Astrophysics - Nuclei in the Cosmos [Google Scholar]
  137. Pancino, E., Ferraro, F. R., Bellazzini, M., Piotto, G., & Zoccali, M. 2000, ApJL, 534, 83 [Google Scholar]
  138. Pancino, E., Pasquini, L., Hill, V., Ferraro, F. R., & Bellazzini, M. 2002, ApJ, 568, 101 [Google Scholar]
  139. Pancino, E., Carrera, R., Rossetti, E., & Gallart, C. 2010, A&A, 511, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  140. Pasquini, L., Ecuvillon, A., Bonifacio, P., & Wolff, B. 2008, A&A, 315, 489 [Google Scholar]
  141. Penny, A. J., Smith, G. H., & Churchill, C. W. 1992, MNRAS, 257, 89 [NASA ADS] [Google Scholar]
  142. Peterson, R. C. 1980, Star Formation, 85, 461 [NASA ADS] [Google Scholar]
  143. Pilachowski, C., Leep, E. M., Wallerstein, G., & Peterson, R. C. 1982, ApJ, 263, 187 [Google Scholar]
  144. Piotto, G., King, I. R., Djorgovski, S. G., et al. 2002, A&A, 391, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  145. Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
  146. Piotto, G. 2009, IAU Symp., 258, 233 [NASA ADS] [Google Scholar]
  147. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992 (Cambridge: University Press), 2nd edn. [Google Scholar]
  148. Prantzos, N., & Charbonnel, C. 2006, A&A, 458, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  149. Prantzos, N., Charbonnel, C., & Iliadis, C. 2007, A&A, 470, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  150. Pritzl, B. J., Venn, K. A., & Irwin, M. 2005, AJ, 130, 2140 [NASA ADS] [CrossRef] [Google Scholar]
  151. Pryor, C., & Meylan, G. 1993, Structure and Dynamics of Globular Clusters, 50, 357 [NASA ADS] [Google Scholar]
  152. Raimondo, G., Castellani, V., Cassisi, S., Brocato, E., & Piotto, G., ApJ, 569, 975 [Google Scholar]
  153. Ramírez, S. V., & Cohen, J. G. 2002, AJ, 123, 3277 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  154. Recio-Blanco, A., Apariacio, A., Piotto, G., de Angeli, F., & Djorgovski, S. G. 2006, A&A, 452, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  155. Renzini, A. 2008, MNRAS, 391, 354 [NASA ADS] [CrossRef] [Google Scholar]
  156. Rich, R. M., Minnit, D., & Liebert, J., 1993, ApJ, 406, 489 [NASA ADS] [CrossRef] [Google Scholar]
  157. Richter, P., Hilker, M., & Richtler, T. 1999, A&A, 350, 476 [NASA ADS] [Google Scholar]
  158. Rosenberg, A., Saviane, I., Piotto, G., & Held, E. V. 1998, A&A, 339, 61 [NASA ADS] [Google Scholar]
  159. Rosenberg, A., Saviane, I., Piotto, G., & Aparicio, A. 1999, AJ, 118, 2306 [NASA ADS] [CrossRef] [Google Scholar]
  160. Rosenberg, A., Piotto, G., Saviane, I., & Aparicio, A. 1999a, A&AS, 144, 5 [Google Scholar]
  161. Rosenberg, A., Aparicio, A., Saviane, I., & Piotto, G. 2000, A&AS, 145, 451 [Google Scholar]
  162. Rutledge, G. A., Hesser, J. E., & Stetson, P. B. 1997, PASP, 109, 907 [NASA ADS] [CrossRef] [Google Scholar]
  163. Salaris, M., Cassisi, S., & Pietrinferni, A. 2008, ApJ, 678, L25 [NASA ADS] [CrossRef] [Google Scholar]
  164. Samus, N., Ipatov, A., Smirnov, O., et al. 1995, A&AS, 112, 439 [Google Scholar]
  165. Samus, N., Kravtsov, V., Pavlov, M., Alcaino, G., & Liller, W. 1995, A&AS, 109, 487 [Google Scholar]
  166. Sbordone, L., Bonifacio, P., Marconi, G., Buonanno, R., & Zaggia, S. 2005, A&A, 437, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  167. Sbordone, L., Bonifacio, P., Buonanno, R., et al. 2007, A&A, 465, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  168. Shetrone, M. D., & Keane, M. J. 2000, AJ, 119, 840 [NASA ADS] [CrossRef] [Google Scholar]
  169. Shetrone, M. D., Côté, P., & Sargent, W. L. W. 2001, ApJ, 548, 592 [NASA ADS] [CrossRef] [Google Scholar]
  170. Smecker-Hane, T. A., & McWilliam, A. 2002, unpublished [arXiv:astro-ph/0205411] [Google Scholar]
  171. Smith, G. H., & Norris, J. 1983, ApJ, 264, 215 [NASA ADS] [CrossRef] [Google Scholar]
  172. Smith, G. H., & Norris, J. 1982, ApJ, 254, 149 [NASA ADS] [CrossRef] [Google Scholar]
  173. Smith, G. H. 1984, AJ, 89, 1545 [NASA ADS] [CrossRef] [Google Scholar]
  174. Smith, G. H., & Bell, R. A. 1986, AJ, 91, 1121 [NASA ADS] [CrossRef] [Google Scholar]
  175. Smith, G. H. 1987, PASP, 99, 67 [NASA ADS] [CrossRef] [Google Scholar]
  176. Smith, G. H. 1988, AJ, 95, 755 [NASA ADS] [CrossRef] [Google Scholar]
  177. Smith, G. H., & Penny, A. J. 1989, AJ, 97, 1397 [NASA ADS] [CrossRef] [Google Scholar]
  178. Smith, G. H., & Mateo, M. 1990, ApJ, 353, 533 [NASA ADS] [CrossRef] [Google Scholar]
  179. Smith, G. H., Shetrone, M. D., Bell, R. A., Churchill, C. W., & Briley, M. M. 1996, AJ, 112, 1511 [NASA ADS] [CrossRef] [Google Scholar]
  180. Smith, V. V., Suntzeff, N. B., Cunha, K., et al. 2000, AJ, 119, 1239 [NASA ADS] [CrossRef] [Google Scholar]
  181. Smith, G. H. 2002, PASP, 114, 1215 [NASA ADS] [CrossRef] [Google Scholar]
  182. Smith, G. H., & Martell, S. L. 2003, PASP, 115, 1211 [NASA ADS] [CrossRef] [Google Scholar]
  183. Smith, V. V., Cunha, K., Ivans, I. I., et al. 2005, ApJ, 633, 392 [NASA ADS] [CrossRef] [Google Scholar]
  184. Smith, G. H., & Langland-Shula, L. E. 2009, PASP, 121, 1054 [NASA ADS] [CrossRef] [Google Scholar]
  185. Sneden, C., Kraft, R. P., Shetrone, M. D., et al. 1997, AJ, 114, 1964 [NASA ADS] [CrossRef] [Google Scholar]
  186. Sneden, C., Johnson, J., Kraft, R. P., et al. 2000, ApJ, 536, L85 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  187. Sollima, A., Ferraro, F. R., Pancino, E., & Bellazzini, M. 2005, MNRAS, 357, 265 [NASA ADS] [CrossRef] [Google Scholar]
  188. Sollima, A., Beccari, G., Ferraro, F. R., Fusi Pecci, F., & Sarajedini, A. 2007, MNRAS, 380, 781 [NASA ADS] [CrossRef] [Google Scholar]
  189. Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
  190. Stetson, P. B., Hesser, J. E., Smith, G. H., Vandenberg, D. A., & Bolte, M. 1989, AJ, 97, 1360 [NASA ADS] [CrossRef] [Google Scholar]
  191. Stetson, P. B. 1994, PASP, 106, 250 [NASA ADS] [CrossRef] [Google Scholar]
  192. Suntzeff, N. B. 1981, ApJS, 47, 1 [NASA ADS] [CrossRef] [Google Scholar]
  193. Suntzeff, N. B., & Smith, V. V. 1911, ApJ, 381, 160 [Google Scholar]
  194. Sweigart, A. V., & Mengel, J. G. 1979, The Observatory, 91, 223 [Google Scholar]
  195. Thoul, A., Jorissen, A., Goriely, S., et al. 2002, A&A, 383, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  196. van den Bosch, R., de Zeeuw, T., Gebhardt, K., Noyola, E., & van de Ven, G. 2006, ApJ, 641, 852 [NASA ADS] [CrossRef] [Google Scholar]
  197. van Dokkun, P. G. 2001, PASP, 113, 1420 [NASA ADS] [CrossRef] [Google Scholar]
  198. Vargas Álvarez, C. A., & Sandquist, E. L. 2007, AJ, 134, 825 [NASA ADS] [CrossRef] [Google Scholar]
  199. Ventura, P., D’Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
  200. Ventura, P., & D’Antona, F. 2009, A&A, 499, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  201. Ventura, P., Caloi, V., D’Antona, F., et al. 2009, MNRAS, 399, 934 [NASA ADS] [CrossRef] [Google Scholar]
  202. Villanova, S., Piotto, G., King, I. R., et al. 2007, ApJ, 663, 296 [NASA ADS] [CrossRef] [Google Scholar]
  203. Villanova, S., Piotto, G., & Gratton, R. G. 2009, A&A, 499, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  204. Vollmann, K., & Eversberg, T. 2006, Astron. Nachr., 327, 862 [NASA ADS] [CrossRef] [Google Scholar]
  205. Willemsen, P. G., Hilker, M., Kayser, A., & Bailer-Jones, C. A. L. 2005, A&A, 436, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  206. Yong, D., Grundahl, F., Lambert, D. L., Niessen, P. E., & Shetrone M. D. 2003, A&A, 402, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  207. Yong, D., Grundahl, F., Nissen, P. E., Jensen, H. R., & Lambert, D. L. 2005, A&A, 438, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  208. Yong, D., & Grundahl, F. 2008, ApJ, 672, L29 [NASA ADS] [CrossRef] [Google Scholar]
  209. Yong, D., Grundahl, F., D’Antona, F., et al. 2009, ApJ, 695, L62 [NASA ADS] [CrossRef] [Google Scholar]
  210. Yoon, S.-J., Joo, S-J., Ree, C. H., et al. 2008, ApJ, 677, 1080 [NASA ADS] [CrossRef] [Google Scholar]
  211. Zinn, R., & West, M. J. 1984, ApJS, 55, 45 [NASA ADS] [CrossRef] [Google Scholar]
  212. Zinn, R. 1985, ApJ, 293, 424 [Google Scholar]
  213. Zinn, R. 1993, The Globular Cluster-Galaxy Connection, 48, 38 [Google Scholar]
  214. Zoccali, M., Pancino, E., Catelan, M., et al. 2009, ApJ, 697, L22 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Observing logs (see Sects. 2 and 5 for details).

In the text
Table 2

Index measurements and radial velocities for the sample stars.

In the text
Table 3

Clusters sample intrinsic properties and structural parameters.

In the text
Table 4

Clusters sample positional and orbital parameters.

In the text
Table 5

Ratio of CN-strong and CN-weak stars and centroids distance.

In the text

All Figures

thumbnail Fig. 1

Colour − magnitude diagrams for the newly observed GGC in our sample. Grey dots show our pre-imaging V, V − I photometry, calibrated with literature data (see text). For 47 Tuc, which was not part of our original observations, we used the photometry by Rosenberg et al. (2000). A selection on the photometric parameters from DAOPHOT II is applied to show only the best measured stars. Black dots mark spectroscopic targets. Clusters are ordered as a function of their metallicity from the most metal-poor (top left) to the most metal-rich (bottom right).
In the text
thumbnail Fig. 2

Influence of telescope and/or instrument flexures on the derived radial velocities. Each point represents one star, with its radial velocity and the X and Y coordinates of the corresponding slitlet center. The solid lines represent a bilineal fit to the data (see text).
In the text
thumbnail Fig. 3

Two spectra of CN-weak, CH-strong stars with different S/N ratio are shown as examples of our best and worst data: the upper spectrum in all panels has S/N ≃ 25 (on the S3839(CN) band) and belongs to NGC 1851; the lower spectrum has S/H ≃ 10 and belongs to NGC 6388. Both are shifted on an arbitrary flux scale for sake of clarity. The top panel illustrates the chosen windows used for the CN and CH indices (magenta hatched regions) along with their respective continuum windows (grey hatched regions); while the bottom panels show the windows adopted for the H and K Calcium index (bottom left) and the Hβ index (bottom right).
In the text
thumbnail Fig. 4

Comparison between the CN S3839 and the S4142 indices. Each panel shows measurements for the indicated cluster, and the median errobar is also shown in the lower right corner. Clusters are sorted by metallicity, from the most metal-poor (top-left) to the most metal-rich (bottom-right). Dotted lines are linear fits with a fixed slope (that of the whole sample) and rougly adjusted zeropoints.
In the text
thumbnail Fig. 5

Example of the removal of temperature and gravity dependencies from the CH and CN indices, using median ridge lines on NGC 1851. Large black dots represent the target stars, while small grey dots represent the calibrated pre-maging photometry of NGC 1851. The median ridge lines of CH and CN as functions of V magnitude are marked as dotted lines.
In the text
thumbnail Fig. 6

Histograms of the δS3839(CN) (top panels) and δCH4300 (bottom panels) index strengths. The bin sizes are larger for clusters with lower S/N and/or fewer stars. Typical (median) errorbars are plotted below each histogram. Vertical dotted lines mark δS3839(CN) = 0 and δCH4300 = 0, i.e. the median ridge line of the rectified index and the border between CN or CH strong and CN or CH weak stars. Clusters are sorted by increasing metallicity, from left to right and from top to bottom.
In the text
thumbnail Fig. 7

Anti-correlation plots for the CH and CN band strengths. Each panel shows the measurements for stars (grey dots) in each cluster. CH strong and weak stars are separted by the horizontal dotted line, and their centroids are marked as large white dots, while CN strong and weak stars are separated by the vertical dotted line and their centroids are marked as large black dots. The S/N ratio in the CN band region is indicated in the lower left corners.
In the text
thumbnail Fig. 8

Zoomed version of those clusters that show a small spread on the scale of Fig. 7.
In the text
thumbnail Fig. 9

Relation between the CN-strong and CN-weak centroids geometrical distance in the CN-CH plane and [Fe/H] from Table 3. The white dot represents M 15, which is excluded from the linear fit (dotted line) of the remaining clusters (black dots).
In the text
thumbnail Fig. 10

Run of the ratio rCN = nCNstrong/nCNweak for our sample clusters. In each panel, NGC 362 ans Pal 12 (grey dots) are excluded from the relations. Dotted lines mark linear fits to the remaining clusters (black dots) and the correlation coefficients are reported on top of each panel: rS stands for the Spearman and rP for the Pearson coefficient. For the meaning of X labels, see Tables 3 and 4.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.