| Issue |
A&A
Volume 523, November-December 2010
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 34 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201014468 | |
| Published online | 10 November 2010 | |
The Supernova Legacy Survey 3-year sample: Type Ia supernovae photometric distances and cosmological constraints⋆,⋆⋆
1
LPNHE, CNRS/IN2P3, Université Pierre et Marie Curie Paris 6, Université
Denis Diderot Paris 7, 4 place
Jussieu, 75252
Paris Cedex 05,
France
e-mail: guy@in2p3.fr
2
Department of Physics (Astrophysics), University of
Oxford, DWB, Keble
Road, Oxford
OX1 3RH,
UK
3
Department of Astrophysical and Planetary Sciences, University of
Colorado, Boulder,
CO
80309-0391,
USA
4
Department of Astronomy and Astrophysics, University of
Toronto, 50 St. George
Street, Toronto ON
M5S 3H4,
Canada
5
Université Paris 11, 91405
Orsay,
France
6
LAM, CNRS, BP8, Traverse du
Siphon, 13376
Marseille Cedex 12,
France
7
CPPM, CNRS-IN2P3 and Université Aix-Marseille II,
Case 907, 13288
Marseille Cedex 9,
France
8
INAF – Osservatorio Astronomico di Roma,
via Frascati 33, 00040
Monteporzio (RM),
Italy
9
Las Cumbres Observatory Global Telescope Network,
6740 Cortona Dr., Suite
102, Goleta,
CA
93117,
USA
10
Department of Physics, University of California,
Santa Barbara, Broida Hall, Mail Code
9530, Santa
Barbara, CA
93106-9530,
USA
11
CEA, Centre de Saclay, Irfu/SPP,
91191
Gif-sur-Yvette,
France
12
Network Information Operations, DRDC-Ottawa,
3701 Carling Avenue,
Ottawa, ON, K1A
0Z4, Canada
13
Department of Physics and Astronomy, University of
Victoria, PO Box 3055 STN
CSC, Victoria BC
V8T 1M8,
Canada
14
LPSC, CNRS-IN2P3, 53 rue des Martyrs, 38026
Grenoble Cedex,
France
15
Department of Astrophysics, California Institute of
Technology, MS
105-24, Pasadena,
CA
91125,
USA
16
CENTRA-Centro M. de Astrofisica and Department of Physics,
IST, Lisbon,
Portugal
17
LBNL, 1 Cyclotron Rd, Berkeley, CA
94720,
USA
18
Anglo-Australian Observatory, PO Box 296, Epping, NSW
1710,
Australia
19
Scuola Normale Superiore, Piazza dei Cavalieri 7, 56126
Pisa,
Italy
Received:
19
March
2010
Accepted:
24
June
2010
Aims. We present photometric properties and distance measurements of 252high redshift Type Ia supernovae (0.15 < z < 1.1) discovered during the first three years of the Supernova Legacy Survey (SNLS). These events were detected and their multi-colour light curves measured using the MegaPrime/MegaCam instrument at the Canada-France-Hawaii Telescope (CFHT), by repeatedly imaging four one-square degree fields in four bands. Follow-up spectroscopy was performed at the VLT, Gemini and Keck telescopes to confirm the nature of the supernovae and to measure their redshifts.
Methods. Systematic uncertainties arising from light curve modeling are studied, making use of two techniques to derive the peak magnitude, shape and colour of the supernovae, and taking advantage of a precise calibration of the SNLS fields.
Results. A flat ΛCDM cosmological fit to 231SNLS high redshift type Ia supernovae alone gives ΩM = 0.211 ± 0.034(stat) ± 0.069(sys). The dominant systematic uncertainty comes from uncertainties in the photometric calibration. Systematic uncertainties from light curve fitters come next with a total contribution of ± 0.026 on ΩM. No clear evidence is found for a possible evolution of the slope (β) of the colour-luminosity relation with redshift.
Key words: supernovae: general / cosmology: observations
Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. Based on observations obtained at the European Southern Observatory using the Very Large Telescope on the Cerro Paranal (ESO Large Programme 171.A-0486 & 176.A-0589). Based on observations (programs GS-2003B-Q-8, GN-2003B-Q-9, GS-2004A-Q-11, GN-2004A-Q-19, GS-2004B-Q-31, GN-2004B-Q-16, GS-2005A-Q-11, GN-2005A-Q-11, GS-2005B-Q-6, GN-2005B-Q-7, GN-2006A-Q-7, GN-2006B-Q-10) obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the Particle Physics and Astronomy Research Council (United Kingdom), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), CNPq (Brazil) and CONICET (Argentina). Based on observations obtained at the W.M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W.M. Keck Foundation. Mark Sullivan acknowledges support from the Royal Society.
Table 9 is available in electronic form at http://aanda.org and at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/523/A7. Tables 10 and 11 are only available in electronic form at the CDS
© ESO, 2010
1. Introduction
Since 1998 (Riess et al. 1998; Perlmutter et al. 1999), surveys of cosmologically distant type Ia supernovae (SNe Ia) have shown that the expansion of the Universe is accelerating, distant SNe Ia being fainter than expected in a decelerating Universe. With the assumption that the Universe can be described on average as isotropic and homogeneous, this acceleration implies either the existence of a fluid with negative pressure, usually called dark energy, a cosmological constant, or modifications of gravity on cosmological scales. Several other cosmological probes such as cosmic microwave background (CMB) anisotropies and baryon acoustic oscillations (BAO) confirm this result, but SNe Ia observations are currently the most sensitive technique to study dark energy or its alternatives, since they can be used to directly measure the history of the expansion of the Universe.
Recent results from high redshift SNe Ia surveys (Astier et al. 2006; Riess et al. 2007; Wood-Vasey et al. 2007; Freedman et al. 2009) and combinations of SNe Ia samples (Kowalski et al. 2008; Hicken et al. 2009b) give consistent measurements of the effective equation of state parameter of dark energy (w, the ratio of pressure over density) in the redshift range accessible with SNe data. Values consistent with w = −1 are found, as expected for a cosmological constant, with uncertainties of order of 10%, including systematics. In contrast with those analyses, Kessler et al. (2009) report a much larger systematic uncertainty on w. They obtain a discrepancy δw = 0.2 when using two different techniques to estimate SNe distances. We discuss this issue in Sect. 4.2.
This paper is the first of a set of three papers which present the cosmological analysis of the Supernova Legacy Survey (SNLS) after three years of operation. The SN Ia sample is about four times as large as the first year sample presented in Astier et al. (2006,hereafter A06). Since systematic uncertainties are close to the statistical limits, large efforts on all aspects of the analysis have been made to identify, reduce and propagate them to the final cosmological result. A key feature of the work presented in this set of papers is that the full analysis has been performed twice with significantly different techniques, including for photometry, detection of candidates, spectroscopic identification, calibration, and distance estimate. The step by step comparison of the results obtained with these different techniques made it possible to pin down systematics often ignored in previous works. This first paper describes the photometric data reduction and the estimation of light curve fit parameters for this sample. It also reports on cosmological constraints that can be obtained from SNLS supernovae alone. The second paper (Conley et al. 2010, hereafter C10) presents cosmological constraints obtained by combining the SNLS 3-yr sample with lower and higher redshift SN Ia data and the 3rd paper presents cosmological constraints when combining SN data with other cosmological probes (Sullivan et al., in prep.).
After an overview of the survey in Sect. 2, the photometric data reduction is described in Sect. 3 together with the photometric techniques used. The two light curve fitting techniques used in this analysis, SiFTO (Conley et al. 2008) and SALT2 (Guy et al. 2007), are presented in Sect. 4. Their results are compared and combined in Sect. 5 to constrain ΩM for a flat ΛCDM cosmological model. We conclude in Sect. 6.
2. Overview of the Supernova Legacy Survey
The Supernova Legacy Survey (SNLS) uses data taken as part of the deep component of the five-year Canada-France-Hawaii Telescope Legacy Survey (CFHT-LS). CFHT-LS is an optical imaging survey using the one square degree MegaCam camera (Boulade et al. 2003) on the CFHT. The deep component conducted repeat imaging of 4 low Galactic-extinction fields (see A06 for the field coordinates). The survey ended in August 2008. A detailed description of the telescope and camera is given in Regnault et al. (2009, hereafter R09). The data are time-sequenced with observations conducted every 3–4 nights in dark time. Four filters were used (denoted gMrMiMzM)1 similar to those of the Sloan Digital Sky Survey (SDSS). This data allows us to obtain high-quality multi-colour SN light curves. Since the first year analysis in A06 the cadence and exposure time of the zM observations were increased to improve the signal-to-noise in the light curves of the most distant SNe.
For the “real-time” SN searches (see Perrett et al., in prep. for details) the SNLS data was reduced by the CFHT-developed Elixir data reduction system (Magnier & Cuillandre 2004) and processed through two independent search pipelines, from which combined candidate lists were generated2. Both pipelines generated difference images, subtracting from the search images deep references constructed from previous observations, leaving only sources which had varied since the reference epoch. The subtracted images were searched using various automated techniques, with all likely candidates visually inspected by human eye. SN candidates were prioritised for spectroscopic follow up using a photometric identification technique (Sullivan et al. 2006) which identifies likely SNe Ia from 2–3 epochs of real-time photometry, predicting redshifts, phases, and temporal evolution in magnitude. New candidates were checked against a database of existing variable sources to exclude previously known AGN or variable stars.
Spectroscopic follow-up was used to confirm SN types and measure redshifts. The survey was allocated 60 h per semester on the Gemini North and South telescopes using the GMOS instruments (Hook et al. 2004) and 120 h per year at the European Southern Observatory Very Large Telescopes (VLT) using the FORS-1/2 instruments (Appenzeller et al. 1998). Spectroscopic time was also obtained at the Keck telescopes using the LRIS (Oke et al. 1995) and DEIMOS (Faber et al. 2003) instruments (PI: Perlmutter). Some additional types and redshifts were obtained as part of a separate detailed studies program also undertaken using Keck-I/LRIS (Ellis et al. 2008).
Data from the first year of the Gemini program were presented in Howell et al. (2005), from the second and third years in Bronder et al. (2008) and data from May 2006 to July 2006 in Walker et al. (in prep.). Spectra obtained at VLT are published in Balland et al. (2009) (see Baumont et al. 2008, for the reduction technique used), and Keck spectra from the detailed studies program are in Ellis et al. (2008). All spectra were analysed and uniformly typed. Two sub-classes are considered in this work according to the confidence level of the spectroscopic identification: certain SN Ia are denoted “SN Ia” (corresponding to the confidence indices CI 5 and 4 in the classification scheme of Howell et al. 2005), and probable SN Ia (CI 3) are labeled “SN Ia ⋆ ”. For most SNe, two identification techniques were used and their results cross-checked (based on the analysis presented in Howell et al. 2005; and Balland et al. 2009).
3. Photometry measurement
Elixir pre-processed images were retrieved from the Canadian Astronomy Data Centre (CADC)3. This process performs basic image “de-trending” (bias subtraction, flat-field correction and fringe removal in iM and zM bands). The flat-fields and fringe maps are more precise than the ones used for the real-time SN search as they are constructed from an entire queue run of data (including non CFHT-LS data), from median stacks of twilight and science exposures for the flat-field and fringe maps respectively. The Elixir pipeline also attempts to produce images with photometric uniformity (i.e. a constant zero point across the mosaic) by constructing photometric correction frames from dithered observations of dense stellar fields. However, this process is not perfect and some radial trends in the photometric zero point remain. This is shown in detail in R09, who found a centre to edge variation of ≃0.02 mag, and derived refined photometric correction frames.
The subsequent treatment of images including sky background subtraction, astrometry, and photometric correction has been performed in two independent pipelines. The first one follows A06. SExtractor (Bertin & Arnouts 1996) is used to produce an image catalog and a sky background map that is subtracted from the image. Second order moments of the objects are derived (using an iterative Gaussian-weighted fit), and point-like sources are identified to estimate the image quality (hereafter IQ, given by the FWHM of the point spread function). A weight map is derived using the spatial sky variance, the bad pixel map provided by Elixir, and a map of cosmic rays hits and satellite trails identified with dedicated algorithms. The astrometry of each CCD image is obtained using a match of the image catalog to an astrometric catalog derived from observations of Stone et al. (1999) astrometric calibration regions and USNO-B (Monet et al. 2003) or SDSS (Adelman-McCarthy et al. 2007) star catalogs. The photometric corrections (more precisely the ratio of the ones derived in R09 to those applied to Elixir images) are not applied to the images but to the fluxes of objects in the catalogs. The other pipeline performs the same reduction steps but uses different software (for instance the Image Reduction and Analysis Facility package4).
3.1. Measurement of the supernova fluxes
Two photometry techniques are considered. We present both and compare their outcome. The goal of this study is to cross-check the methods, and evaluate photometric systematic uncertainties from the level of agreement reached in this comparison. This also allows us to select the best technique for deriving light curve parameters of the SNe.
3.1.1. Simultaneous fit of galaxy and supernova fluxes
This first method (hereafter method A) was described in A06. It consists first in resampling all the images of a field in each pass-band to the pixel grid of the best IQ image (hereafter called reference image) for which a PSF (point spread function) model is derived. Convolution kernels of the reference image to each aligned image are then derived for subsequent use. The photometric ratio of the two images is simply given by the integral of the kernel. The photometric fit then consists in fitting simultaneously an image of the host galaxy (at the sampling and the image quality of the reference image) together with the position of the supernova and its fluxes in all images, convolving both the galaxy and PSF models using the kernels obtained previously. The supernova flux is forced to zero in images where its flux is negligible. When we calculate the pixel uncertainties, we deliberately ignore the contribution of the supernova and host galaxy fluxes, so that PSF inaccuracies affect the flux of bright and faint sources in the same way (this is further discussed in Sect. 3.2). Note that the supernovae considered here are faint enough for the departure from statistical optimality to be negligible.
Whereas DAOPHOT (Stetson 1987) was used in A06 to model the PSF, we have since then developed an independent PSF modeling code for this analysis. Also, some improvements have been made in the selection of images for alignment. The reference frame is larger than the actual reference CCD image to cover gaps between CCDs in the MegaCam focal plane. For large dithers, images from other CCDs overlapping the reference image are included so that different fractions of the same image can be aligned on different reference frames. This allows us to measure fluxes for all SNe in the field, including those that sometimes fall in the gaps between CCDs (depending on the actual pointing).
Some cuts are applied to the images: an IQ better than 1.5″ is required, the χ2 per degree of freedom of the convolution kernel fit has to be better than 1.5, and the image correlation coefficient5 at a 50 pixel lag has to be lower than 0.08. This latter cut allows us to get rid of images with large fringe residuals (in iM and zM bands) or background subtraction problems.
The ratio of images that pass the cuts, the number of exposures and total exposure time for each field and band for this dataset is shown in Table 1, along with the average IQ of the selected images. The relatively low efficiencies of about 80% in iM band for the fields D2 and D3 are due to issues with fringe subtractions for some MegaCam runs.
Total exposure time and average IQ of the SNLS 3 year data set.
For a known fixed position of the SN in the images, the photometry fit is linear and we
do not expect any bias for a perfect PSF model. However, when the position of the SN is
fit simultaneously with the fluxes, we have (for a Gaussian PSF, see Appendix B for a proof) the following fractional bias in flux:
![\begin{equation} \frac{\delta f}{f} \equiv \frac{E[\hat f] -f}{f} = - \frac{{\rm Var}(f)}{f^2} \end{equation}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq21.png) (1)where
Var(f) is the variance of the light curve amplitude
f, obtained from a fit combining observations at different epochs.
(1)where
Var(f) is the variance of the light curve amplitude
f, obtained from a fit combining observations at different epochs.
Figure 1 shows the expected bias of the observed SNe as a function of redshift in gMrMiMzM bands. For the rM and iM bands, the biases are respectively of 1 mmag and 0.6 mmag at z = 0.8, and 5 mmag and 2 mmag at z = 1. The gM and zM light curves have a low signal to noise ratio (S/N) at high redshift so we do not fit the position for those bands and use instead the weighted average of the ones obtained in the rM and iM band fits. With an astrometric precision better than 10 milliarcsec for the transformation of coordinates from one image to another (estimated from the rms of the residual match of the catalogs), and an average IQ of 0.9′′, we do not expect a bias due to the transformation of coordinates larger than 0.3 mmag (see Eq. (B.2)). As a consequence, this effect can be ignored, and the total bias is given by that obtained in iM which has the highest S/N (reaching a maximum value of 2 mmag at z = 1). Those biases are an order of magnitude smaller than calibration uncertainties for redshifts z < 0.8, and other sources of uncertainties at higher z (see Sect. 5.4), so we do not correct for them and ignore their negligible contribution to uncertainties in the following. The correlation introduced in this process between the magnitudes in different bands will also be neglected.
 |
Fig. 1 Statistical uncertainty on magnitudes (left panel) and expected bias on PSF photometry with a simultaneous fit of the position (right panel) as a function of supernova redshift. The different gMrMiMzM MegaCam bands are shown respectively with green solid, red dashed, black dotted, and blue dashed-dotted curves. |
As in A06, the photometry fit provides us with flux estimates for all exposures in a given night. Since we do not expect significant variation of the SN luminosity on this time scale, we average these measurements and use the additional scatter between measurements to account for the imperfect kernel evaluation and under-estimated statistical uncertainties due to pixel correlations (introduced by the resampling of images). A few outliers (about 1% of the data) are rejected at this level, some of which may be due to unidentified cosmic ray hits. Since the measurements on the light curve are correlated since they share the uncertainty on the host galaxy flux and SN position (in rM and iM bands), their covariance matrix is recorded for a subsequent usage in the light curve fits. The quality of the photometry fit and the fraction of outliers rejected at this level are the same as in A06.
3.1.2. PSF photometry on image subtractions
We now describe the second photometric method (method B). The PSF and IQ are measured for each image from a list of isolated stellar objects with 35–50 objects used for each CCD. Photometric alignment is performed using a multiplicative scaling factor from a comparison to the set of tertiary calibrating stars, discussed in Sect. 3.2. Aperture photometry with a radius of 4″ is used for this alignment, and the average offset to PSF photometry is recorded at the same time.
SN flux measurement are performed on a CCD-by-CCD basis; even though the telescope is dithered during observations on a given night, we measure the flux on each observation independently. A series of deep reference images are constructed for each season by combining the data from every other season in bins of IQ. The calibrated images (and their weight-maps) entering a given reference frame are geometrically re-sampled to a common pixel coordinate system using a kernel conserving flux. They are then combined using a weighted mean with 5-σ outlier rejection, generating a deep reference and associated weight-map. Each field/filter/season combination typically has five or more statistically independent references each with a different mean IQ and each at least 6 times deeper (or 36 times the integration) than the individual exposures from which the SN measurements are made.
For each calibrated image containing SN light, the reference with the closest (but superior) IQ is geometrically re-sampled to the same pixel coordinate system, and the PSFs of the two images matched by degrading the reference image to match the image containing the SN light. This adjusted reference image is then subtracted from the science image. This process avoids any geometric re-sampling of SN pixels and introduces only a minimum correlated noise in the subtraction of the deep reference. Flux measurement is then performed on the difference images using a custom-written PSF-fitting program using PSFs measured on the unsubtracted images, weighting the fit using the appropriate weight map.
3.1.3. Flux measurement uncertainties
The SNe data set considered consists of a sub-sample of all the SNe Ia detected and spectroscopically confirmed by the SNLS up to July 2006. They are listed Table 9. For those labeled “Ia∗”, one can not completely exclude Ib/c core collapse SNe. Light curves from 4SNe out of 285could not be obtained for the following reasons: lack of observations (beginning or end of an observing run, bad weather conditions, instrument failures), another variable object at the position of the SN (active host galaxy, or another SN in the same host), vicinity of a very bright star, or a specific location on the edge of the focal plane.
The calibration of light curves on tertiary standard stars obtained with method A is detailed in Sect. 3.2. Light curves obtained with method B were calibrated in two steps, first with a 4″ radius aperture photometry, then with an aperture to PSF photometry correction. We checked that both methods were equivalent, so that we can safely assume for this comparison that both light curve sets have identical calibration.
In order to compare the flux scale of each individual light curve obtained with the two methods, both light curve sets were fitted with a fiducial light curve model and the resulting light curve amplitudes were compared. In this process, only the photometric points present in both reductions were considered to minimise the statistical noise of the comparison (a residual statistical noise is expected since different cuts for the selection of images within a night were applied and references for image subtractions vary from night to night for method B).
From this comparison, a systematic over-subtraction of the galaxy was identified in the data set obtained with PSF photometry on image subtractions (method B; about 2% of the galaxy flux at the SN location, estimated with the PSF of the image with best IQ). This bias was traced to a systematic normalisation offset of the convolution kernel: its integral was forced to unity after the current and reference images were photometrically aligned using 4″ aperture photometry of field stars. This approach turned out to be incorrect. As the impact on SN fluxes is a linear function of the host galaxy flux at the location of the SN, we resorted to pursue the comparison, focusing on SNe in faint hosts, and correcting approximately for the identified bias. We account for this effect (for comparison purposes only) by fitting a linear relation between the difference of peak magnitudes obtained with both pipelines and the galaxy to SN flux ratio (fgal): mA − mB = Δm + ϵ × fgal.
We exclude from this fit noisy light curves (S/N < 50 in gMrMiM and 20 in zM, where the S/N is given by the uncertainty on the fitted light curve amplitude) and assign a 20% uncertainty on fgal which is not well defined (in addition to the statistical uncertainty on the SN flux that enters in the ratio). The results are listed in Table 2. For gMrMiM bands, the residual dispersion of order of 0.025 mag can be attributed to imperfect PSF/kernel modeling in the pipelines. The larger dispersion in zM-band of 0.05 mag is due to a much lower signal to noise ratio and fringe residuals in the images (note that we do not use exactly the same images in both pipelines so that the Poisson photon noise impacts the comparison). The average offsets from 0.002 or 0.009 mag depending on the pass-band are marginally significant, the correction for the host galaxy over-subtraction of the order of 0.01 mag on average for all bands being only approximate.
Average difference of the fitted peak magnitudes obtained with methods A and B after the correction for the host galaxy over-subtraction (Δ), slope of the correlation with fgal (ϵ), and rms for high S/N SNe in faint galaxies (see text for details).
Ratio of measured flux before 22 restframe days (before maximum) to the fitted lightcurve amplitude, averaged over events, for method A.
Light curves obtained with the simultaneous fit (method A) are respectively 13%, 13%, 3% and 16% less scattered in gMrMiM and zM bands than those obtained with photometry on subtractions (method B) with an uncertainty of 2% for all bands. Those numbers are based on the standard deviation of residuals to a light curve fit per pass-band with a free amplitude, width and date of maximum light. About half of this difference can be attributed to the relative shallowness of the reference images used for the subtractions.
In order to assess the accuracy of the host subtraction technique of method A, we compute the average measured flux before 22 rest frame days before maximum light (fzero) for each supernova and band, when available. Table 3 reports the average ratio of fzero to the fitted light curve amplitude for method A, and does not display any significant bias.
To summarise the comparison of photometric methods: Method B over-subtracts host galaxies by ~2%, which we later traced to the photometric alignment method prior to subtraction. Both methods agree on the amplitude of light curves (including the calibration transfer from field stars to supernovae) if one concentrates on supernovae hosted in faint galaxies. Method A is free from host subtraction biases at 1 to 3 mmag accuracy, depending on band.
We therefore choose to use the light curve photometry from the simultaneous fit method (method A) in the subsequent analysis.
3.2. Photometric calibration uncertainties
A catalog of calibrated tertiary stars has been obtained for each of the four CFHT-LS deep fields by R09 (those stars were calibrated against the Landolt 1992 catalog of secondary UBVRI standard stars).
It consists of a set of gMrMiMzM magnitudes for each star in a local natural system (average airmass of the observations, transmission function at the average position of the star in the focal plane). The photometric calibration consists in transfering the raw SN light curves to this system. For this purpose, a zero point (ZP ≡ mag + 2.5log 10(flux)) has to be associated with each light curve. It is simply obtained by the flux measurements of tertiary stars using the same photometry technique on the same set of images as the ones used to derive the SN light curve.
The light curves obtained with the simultaneous photometric fit (Sect. 3.1.1) are calibrated as follows. The fluxes of tertiary stars on the same CCD as the SN are measured with the same PSF photometry technique as the one used for SNe, the only difference being that a galaxy model is not considered. Least squares optimality dictates that the pixel uncertainties used for the fit include the contribution of the star itself, but we do not do so: we do not want the relative weights of pixels to change between supernovae (faint objects) and tertiary stars (mostly bright objects) such that PSF innaccuracies affect both in the same way. So, the pixel weighting we adopt for bright stars is the one that is optimal for faint objects, and this choice does not adversly affect the statistical uncertainty of the flux ratio of SN to tertiary stars, since the later are brighter and more numerous.
Since we obtain a flux measurement for each observation, this allows us to check for the photometric alignment, and discard variable stars. Before assigning a zero point to the SN using the average fluxes of stars and their associated magnitudes, the photometric corrections for the reference image, provided by R09, are applied to the stars and SN measurements, depending on their location on the focal plane. At this level, the zero point uniformity within each reference CCD frame is checked.
As an example, residuals from the calibration of a central CCD in field D1 for rM band are shown in Fig. 2. The rms of the differences between the PSF magnitudes and the aperture magnitudes (used in R09) for the tertiary stars are shown in Fig. 3, they are typically of 0.008 mag. With about 30 stars per CCD on average, the typical statistical uncertainty on the zero point determination of a light curve is of order of 0.002 mag. Since this number is averaged out when combining SNe observed on different fields on different CCDs, it adds a negligible uncertainty to the cosmological analysis.
 |
Fig. 2 Residuals from the calibration fit ( PSF magnitude minus aperture magnitude of the catalog) for CCD #13, band rM in field D1. Each point is a tertiary star. Those marked with open symbols were excluded from the fit based on cuts on rms, magnitude, and number of observations. The fit is performed iteratively with a 2.5σ outlier rejection. |
 |
Fig. 3 Rms of the differences between PSF and aperture magnitude of the tertiary stars for the gMrMiMzM bands. In each histogram, there are 36 × 4 entries, each corresponding to a CCD/field combination, for which a zero point is determined. |
 |
Fig. 4 Differences between PSF and aperture magnitudes of the tertiary stars in the gMrMiMzM bands as a function of the colour of stars (gray dots). The black points with error bars represent the average deviation and its uncertainty in bins of colour. Typical SNe colours at maximum light are marked with red dotted vertical lines. The blue curve on the top panel shows the effect of the PSF wavelength dependent correction on synthetic magnitudes obtained with PHOENIX stellar models. The colours of BD+17 4708 are marked by the black vertical lines. |
Chromatic systematic effects were identified in the residual differences between PSF and aperture magnitude as shown in Fig. 4. These are expected because of the PSF variation with wavelength which induces a colour term in the comparison of PSF and aperture magnitudes (for an achromatic PSF model per pass-band). At level of a few millimagnitudes, one cannot exclude some chromatic effects in the aperture photometry, which is contaminated by light reflected in the MegaPrime optical system, forming haloes around stars in the images.
In the rMiMzM bands, the colour dependent offset is of order of 0.002 mag. For such a small effect, we cannot separate it from the residual offset as a function of magnitude (see below) since there is a correlation between the magnitudes and colours of the tertiary stars. We will hence treat this offset as an additional source of systematic uncertainty, rather than try and correct for it. In gM band, the effect is however much larger. It is clearly related to the colours of stars. It induces a relative change of calibration of 0.015 mag for SNe at redshifts 0.2 and 0.6 (at higher redshifts, gM-band light curves are not used to derive distances, since they correspond to observations at rest-frame wavelengths shorter than 3000 Å, see Sect. 4).
 |
Fig. 5 Average differences between PSF and aperture magnitude of the tertiary stars in gMrMiMzM bands as a function of the star magnitude (once corrected for the colour dependent terms). The back error bars represent the statistical uncertainty on the average. The shaded areas represent the uncertainty on aperture magnitudes due to a systematic uncertainty on the residual background in the images used for calibration (0.1 ADU per pixel for gMrMzM, 0.2 ADU for the iM-band). |
In order to account for this PSF variation with wavelength, we have modified the effective transmission of the instrument in gM-band with a multiplicative correction depending linearly with wavelength: corr(λ) = 1 + 0.048(λ − 4979 Å)/(1000 Å). This correction was adjusted on the residuals of Fig. 4 using synthetic magnitudes of stellar spectra obtained with the Phoenix model (Hauschildt et al. 1997; Baron & Hauschildt 1998; Hauschildt & Baron 1999,and references therein)6. The resulting colour dependent effect is shown as a blue curve in Fig. 4 (for gM-band only).
As a last check of the calibration to tertiary stars, Fig. 5 presents the average differences between PSF and aperture magnitudes as a function of the magnitudes of the tertiary stars, where PSF magnitudes were corrected for the colour dependent terms. The brightest stars which are saturated on a fraction of the images (depending on image IQ, exposure time, sky transparency and Poisson fluctuation) were excluded from this analysis because of the potential biases introduced by the selection of unsaturated observations (excluding positive statistical fluctuations reaching the saturation level results in a bias on the average). The dimmest stars were also discarded to avoid biases due to the preferential detection of positive Poisson fluctuations of the signal. The range of magnitude considered was obtained by selecting stars on the plateau of Fig. 16 in R09 which presents the number of observations of the tertiary stars as a function of magnitude. Discrepancies for the dimmest stars are visible: those are consistent with a residual background in the aperture of the tertiary stars. In R09 Sect. 4.2, a residual background of order of +0.06, −0.03, −0.23, and −0.04 Analog Digital Units (hereafter ADU) per pixel is found for the gMrMiMzM bands. Assigning a systematic uncertainty of 0.1 ADU per pixel on this background for gMrMzM, and 0.2 ADU for the iM-band, leads to the shaded error bars shown in Fig. 5. Accounting for this, we assign a 0.002 mag systematic uncertainty on the photometric calibration transfer.
In this section, we have presented the photometry and calibration of the SNLS third year SN sample. One of the two techniques developed in the collaboration has been selected based on a comparison of their performances. We use this light curve data set in Sect. 5.1 to determine for each supernova the parameters needed to estimate its distance.
3.3. Interpretation of the photometric calibration
The calibrated data are formally the ratio of the target flux FSN as measured by the detector to that of a reference star Fref that would have been observed in the exact same conditions. In practice, we have determined a flux Fmeas in ADU and a zero point ZPmeas which provides a normalisation coefficient.
As we will see in the next section, the supernova light curves are fit with a spectral sequence model MSN(λ,t,...) in order to extract from the light curves a flux intensity and additional parameters that characterise the diversity of SNe Ia. For this purpose, one has to be equipped with a model of the instrument response as a function of wavelength T(λ) for each pass-band in order to compare the model to the observations.
The light curve fit consists in comparing the measured quantity 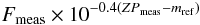 (2)to
the model
(2)to
the model 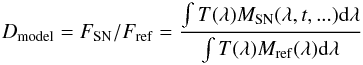 (3)where
Mref(λ) is the spectrum of the reference
star and mref its magnitude. The integrals in Eq. (3) have the dimension of counts in the detector
per unit time (i.e. in units of ADUs-1), as they model the actual
observations7. However, Eq. (3) tells us we do not need to know the
normalisation of the instrumental response function, even from pass-band to pass-band, as
it cancels in the ratio.
(3)where
Mref(λ) is the spectrum of the reference
star and mref its magnitude. The integrals in Eq. (3) have the dimension of counts in the detector
per unit time (i.e. in units of ADUs-1), as they model the actual
observations7. However, Eq. (3) tells us we do not need to know the
normalisation of the instrumental response function, even from pass-band to pass-band, as
it cancels in the ratio.
For SNLS, the magnitude system defined in R09 has been anchored to the star BD+174708 with a prescription for its magnitudes in this system. As we have photometrically aligned the SN light curves to the catalog of stars defining this system, we use BD+174708 as our reference star and consider for its magnitudes those provided by R09: gM = 9.6906, rM = 9.2183, iM = 8.9142, and zM = 8.7736. Note that those magnitudes are conventional, one could have changed them in the definition of the magnitude system as long as the magnitudes of the tertiary stars and hence the values of ZPmeas in Eq. (2) are modified accordingly. We use for Mref(λ) the spectrum of BD+174708 as measured on HST by Bohlin & Gilliland (2004); we retrieved the latest version of this spectrum on the CALSPEC database8.
Concerning the instrumental model (T(λ)), a complication arises from the fact that the transmission of MegaCam filters varies across the focal plane, following a radial pattern, with a typical variation of the central wavelength up to 5 nm from the centre to the edge. The magnitude system has been designed so that no colour transformations are required to translate our SN measurements to this system; the small residual airmass-dependent colour corrections cancel out on average and do not contribute significantly to the uncertainty of the measurements, and the variation of the effective pass-bands within the dithering pattern of the DEEP field observations are negligible. But the magnitude system has to be interpreted using a model of the response function of the instrument that follows this radial pattern. We use the transmissions provided by R09 to integrate the spectral model of supernovae, using the average position of the SNe observations on the focal plane. Note also that the magnitudes of BD+174708 have been chosen to be the same everywhere in the MegaPrime focal plane despite the fact that the filter transmissions vary.
The SNe Ia light curves of the SNLS 3-year sample are available on-line at the Centre de Données astronomiques de Strasbourg (CDS). An example of the published data is given in Table 10.
4. Modeling the supernova light curves
4.1. General considerations
The only two light curve parameters that have been found so far to correlate with the luminosity of SNe Ia are the width of their light curves (first measured in Johnson B-band, see e.g. Phillips 1993, and then extended to other bands) and their colour as measured, e.g., by the difference of magnitudes (or ratio of fluxes) in rest-frame B and V bands. Once corrected for those, the absolute maximum luminosity has a dispersion of the order of 15%. All recent high-redshift cosmological analyses use those parameters (luminosity, light curve shape and colour) in a more or less obvious way to derive distances (Riess et al. 2004, 2007; Astier et al. 2006; Wood-Vasey et al. 2007) with the notable exception of the CMAGIC technique which relies on a colour-magnitude diagram of SNe Ia (Wang et al. 2003b; Conley et al. 2006). The challenge of a cosmological application is to derive those parameters with a minimal redshift dependent bias.
4.1.1. An empirical modeling
The goal of the light curve fitting is then to evaluate for each SN those parameters from observations performed with a limited set of observer-frame filters and a limited cadence of observations. This requires a model of the spectral sequence of the SN in order to interpolate among observations. Despite the fact that there is a broad consensus as to the basic physical picture of the explosion mechanism, it is extremely difficult currently to make quantitative predictions for the observed signal based on a physical model. Indeed extremely precise 3D modeling is required in order to simulate the flame propagation in the SN progenitor. As a consequence, an empirical modeling of the observables is needed. Historically, light curve templates were built in a limited set of filters from a sample of nearby SNe (see for instance Goldhaber et al. 2001). This required a correction of the observations for redshifted supernovae, usually called K-correction (Nugent et al. 2002). Those were performed using an average spectral sequence based on a set of spectra obtained at different phases (days after maximum light) of the SN. This method is applied for the MLCS2k2 light curve fitter (Jha et al. 2007), with tabulated K-corrections as a function of phase, redshift and colour. More recently, techniques based on an explicit modeling of the spectral sequence have been developed. The data are not corrected to rest-frame filters but directly compared to the integral of the spectra in a model of the instrumental response (SALT(2): Guy et al. 2005, 2007, hereafter G07; SiFTO: Conley et al. 2008, hereafter C08). The advantage of this approach is to keep track of the correlations between the light curve shape, colours and the spectral properties in the fitting process.
4.1.2. Impact of a limited training sample: using high-z SNe
This light curve fitting technique is a fundamental ingredient of the cosmological analysis. Especially, the assumed broad-band colour relations (i.e. the relative amplitude of the SN spectral model at a wavelength scale of order of 1000 Å, beyond a simple colour tilt, in other words the curvature of the spectra) in the wavelength range of validity of the model have a direct impact on the derived distances. In order to illustrate this, let us consider two SNe observed in rM and iM band at redshifts of 0.5 and 0.8. Since those rM and iM observations correspond to the rest-frame B and V, and U and B bands respectively, the ratio of distances derived for those two SNe is directly a function of the (U−B) − (B−V) colour9 difference of the model. Since all light curve models are empirically derived from a limited training set, this latter colour has an uncertainty which introduces a redshift-dependent correlation among the derived supernova distances (see for instance Knop et al. 2003). Since many more SNe have been observed at high-redshift than at low redshift, high-z SNe must be considered in the training of the light curve models in order to overcome the statistical limitations of the nearby sample. This has been done with the SALT2 and SiFTO models; it was possible since both techniques do not make use of distances in their training process.
4.1.3. Modeling of the near UV emission
High-z SNe allow the observation of the rest-frame near UV emission from the ground without the need of space telescopes. The near UV is modelled in SALT2 and SiFTO using SNLS photometric (in gM and rM bands up to a redshift of 1) and spectroscopic observations (see references in Table 9). Using near UV data allows for a drastic improvement of the colour and hence distance estimate for SNe at redshifts of order of unity, where the sensitivity of the rest-frame B and V is limited by the quantum efficiency drop of MegaCam CCDs in the zM band. However, we still lack spectroscopic observations at early and late phases (the primary goal of the SNLS spectroscopic program was to provide an identification of the SNe which is easier at maximum brightness).
4.1.4. Diversity of SNe Ia colours: intrinsic variation or absorption by dust
There is still much debate about the treatment of the SN colour parameter (generally anchored to B−V at maximum light). Whereas all cosmological analyses based on SNe perform a linear correction of distance moduli (i.e. logarithm of distances) with the measured colour, the value of the coefficient used and its interpretation differ significantly from one analysis to another. In A06, this coefficient β is marginalised over in the cosmological fit, without any attempt to separate the reddening effect of dust absorption or a potential intrinsic variation. On the contrary, the MLCS2k2 technique used in ESSENCE (Wood-Vasey et al. 2007), GOODS (Riess et al. 2004, 2007) and SDSS surveys (Kessler et al. 2009), assumes that the derived (B−V) colour offset primarily comes from extinction by dust, and therefore that the β parameter should be identified with the RB value of the Cardelli et al. (1989) extinction law. When β is fit at the same time as cosmology, values ranging from about 2 to 3 are found depending on the technique used to derive it. Those values are systematically smaller than the value of 4.1 in the Cardelli et al. (1989) extinction law.
The large range of values obtained for β is likely to be a consequence of different assumptions on the uncertainties of the (B−V) colour estimates (and to a lesser extent the colour range of the SNe sample considered). For a given data set, the larger the assumed uncertainties on (B−V), the larger the fitted β value. This issue is raised by Freedman et al. (2009); we come back to it in Sect. 5.5. Whereas in previous papers (including papers from the SNLS collaboration: A06, G07, C08), low values of β ≃ 2 were found, we get larger values when accounting for an intrinsic scatter in SNe colour relations in this paper (see Sects. 4.4 and 5.5). Fitting for β or not has some consequences. For instance, Conley et al. (2007) have shown that either we live at the centre of an under-dense region of the Universe as proposed by Jha et al. (2007), or the relation between SN colours and luminosity does not follow the one expected for the Galactic extinction and β < RB.
 |
Fig. 6 SALT2 colour variation law for |
This low value of β points to either an unusual extinction law in host galaxies of SNe Ia or an intrinsic colour variation that dominates the effect of extinction. One hint is that the colour variation law (which describes how the SN flux varies with colour as a function of wavelength) can be derived from the SN data themselves, and differs significantly from the Cardelli et al. (1989) extinction law in the near UV and U-band, even for extreme values of RB (see Guy et al. 2005, 2007, and Fig. 6). In SiFTO, the derived relation between the (U−B) and (B−V) colours of SNe can not be explained with an extinction law either. While there is not yet a definitive proof that the colour variation we observe is intrinsic to the SN, we still have to relax the assumption that it is purely due to dust extinction as modelled by Cardelli et al. (1989). This has some consequences for the cosmological analysis. Indeed, applying an incorrect correction to luminosity introduces a redshift dependent bias since the average colour of SNe varies with redshift because of Malmquist bias (bluer SNe are brighter and hence dominant near the detection limit of a survey). This occurs at the highest redshifts of all surveys but also for nearby SNe that were observed by other means (see e.g. Conley et al. 2007).
In the MLCS2k2 approach, a colour excess E(B−V) is measured as the difference between the observed colour and that of the model. In this model, the intrinsic variability of SNe is addressed with a single parameter (Δ), and any possible additional intrinsic variation is unaccounted for. As a consequence, one expects that, at some level, the E(B−V) estimate resulting from the light-curve fit combines both dust reddening and a possible residual intrinsic colour variation. There are several examples of SNe Ia being clearly extinguished by dust. In contrast, there is no proof that part of the (B−V) colour variation is driven by intrinsic SNe properties. The only hints come from observations which point to a value of β < RB and a colour variation law incompatible with a standard dust extinction law. Nevertheless, as the physical mechanism responsible for the SN Ia explosions obviously involves more than a single parameter (composition of the progenitor, ignition conditions, ...), it is very possible that some properties of the SN impact on the observed (B−V) colour beyond that addressed by Δ. As an example, Kasen et al. (2009) present a class of supernovae simulations with various ignition conditions, deflagration to detonation transition (DDT), and viewing angles, which exhibit intrinsic variations of colour. The models with the same DDT criterion present a range of (B−V) colours (at maximum light) that are not fully correlated with the decline rate10. Such an effect, which is present in those simulations, has not been ruled out on real data.
It is further possible that the slope of the colour-luminosity relation evolves as a function of redshift. A larger range of dust opacities is expected at higher redshifts where galaxies host younger stellar populations, so that the relative weight of dust extinction and intrinsic variation in the colour-luminosity relation should evolve with redshift. Kessler et al. (2009) found an evolution of the β parameter with redshift using SALT2, but with an opposite trend with respect to the expectations (they found a lower β at higher z). We study this issue in Sect. 5.5.
4.2. Comparison of light curve fitters and distance estimate
Using different light curve fitters to estimate distances allows us to quantify the systematic uncertainties associated with this step of the analysis. As shown in C10 and to a lesser extent in Sect. 5.6 of this paper, the combined uncertainties on cosmological parameters are dominated by systematics, so the statistical precision of light curve fitters do not play a major role in their selection. For a cosmology application, the most crucial aspects are those that may lead to a redshift-dependent bias: i) K-corrections uncertainties; ii) any bias that could arise when fitting low signal to noise light curves; iii) biases associated with selection effects.
Several authors have already performed this comparison of light curve fitters. The largest systematic effects were found by Kessler et al. (2009, hereafter K09), who applied MLCS2k2 and SALT2 to a sample combining low redshift SNe, HST data and the first release of SDSS-II, ESSENCE and SNLS data. They found a difference on w of 0.2 when using MLCS2k2 or SALT2. This difference is larger that any other source of uncertainty. The authors have looked for the sources of the observed discrepancy (see Sect. 11 in K09 for a detailed discussion). For this purpose, light curves were fit with modified versions of MLCS2k2 designed to replicate some elements of the SALT2 model. They explain the discrepancies by two main differences between the light curve fitters: differences in the light curve templates, and the use of colour priors. We now review these two effects, and discuss afterwards the differences in the treatment of colour. We eventually summarise this comparison section.
4.2.1. Systematic differences in the light curve templates
Kessler et al. (2009) provide evidence that SALT2 and MLCS2k2 predict differently the rest-frame U-band. Excluding rest-frame U-band light curves from the fit of SDSS SNe at z > 0.21 changes the MLCS2k2 and SALT2 distance moduli by ≃0.13 and ≃ 0.07 mag respectively11. Note that the offset found for SALT2 is marginally consistent (at the 2σ level) with the calibration systematic uncertainties of order of 0.01 mag for all bands reported both for the SDSS-II and SNLS first year releases (the SALT2 version used in K09 was trained on SNLS first year data).
The SALT2 and SiFTO light curve fitters are more reliable than MLCS2k2 in rest-frame U-band because they were calibrated using high z supernovae. They benefit from the SNLS precise calibration and are not sensitive to the systematic uncertainties that are known to affect the observer-frame U-band calibration of low redshift SNe. In particular, the effective U-band response function is poorly known for many SNe observations because of important variations of the atmospheric transmission at wavelengths shorter than 350 nm. Also, when fitting with SALT2 or SiFTO (see Sects. 4.4 and A.2), we find a larger dispersion of residuals in the U-band for low redshift SNe (0.1 mag, rms) than in the gM band at z ≃ 0.4 where gM roughly corresponds to rest-frame U (0.05 mag). The systematic offset found by K09 could possibly be affected by some evolution of SNe properties in the UV. There is no evidence for such an effect, but even in this case, using SNe at z ≃ 0.4 to calibrate the model rest-frame U-band is more reliable than using SNe at lower z. Indeed, the model rest-frame U-band is primarily used to estimate distances of SNe at high redshift, and since a monotonous change of the average SNe UV emission with redshift is expected due to an evolution of metallicity or age of the progenitor population, U-band measurements done at the highest possible redshift should therefore be used.
4.2.2. Using priors on SNe colours.
In the MLCS2k2 approach, a prior is used that forces the extinction AV to be positive. This is equivalent to applying a prior on colour excess. However, since there is no evidence that the observed variation of SNe Ia colours is entirely and solely due to extinction by dust, applying such a prior is not justified.
Furthermore, even if the model was qualitatively correct, applying a prior is non optimal since any bias on this prior will produce a bias on cosmology and hence artificially large systematic uncertainties. For instance, more than half of the difference on w between the analysis of Wood-Vasey et al. (2007) and that of K09 is due to the choice of prior (see Sect. 10.1.4 in K09). Alternatively, not using a prior on colours does not bias the estimate; one only obtains larger and reliable statistical uncertainties.
4.2.3. Estimating distances
SALT2 and SiFTO use the colour in their distance modulus whereas MLCS2k2 uses a colour excess. This might be regarded as conceptually different, but, as shown below, the distance moduli used in the two approaches are mathematically equivalent, as long as the slopes of the brighter-slower and colour-luminosity relations are fit to the Hubble diagram.
MLCS2k2 defines the colour excess as
E(B−V) = (B−V)obs − (B−V)model.
At first order in Δ, the shape parameter,
(B−V)model = a + b × Δ
and the distance modulus can then be written (at first order in shape and colour
parameters): 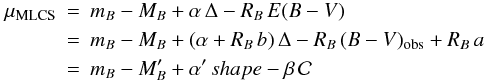 where
shape is any shape parameter and
where
shape is any shape parameter and 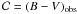 or any affine function of it.
This last expression is exactly the one used in A06 and in this paper (Eq. (5)). As a consequence, choosing to use a
colour excess or directly the observed colour to parametrise the distance modulus only
modifies the meaning and values of MB and α
coefficients, and does not change distances.
or any affine function of it.
This last expression is exactly the one used in A06 and in this paper (Eq. (5)). As a consequence, choosing to use a
colour excess or directly the observed colour to parametrise the distance modulus only
modifies the meaning and values of MB and α
coefficients, and does not change distances.
So at first order, when no prior is used on colour and RB is treated as a free parameter (β), the MLCS2k2 approach is contained in the SALT2/SiFTO as both the colour variation law (or colour relations, see Sect. 4.3.2) and the slope of the colour-luminosity relation of SALT2/SiFTO are parametrised in a way that allows the model to match a standard dust extinction law. Disentangling the contribution of intrinsic colour variation and dust extinction requires adding parameters beyond the simple one-parameter description of the SN intrinsic variation implemented in MLCS2k2, SiFTO and SALT2 (Δ, stretch, X1). As a consequence, when using these fitters, the observed colour luminosity relation could evolve with redshift as it combines two effects whose relative weight is expected to change with redshift. We investigate this in Sect. 5.5.
4.2.4. Summary of the light curve fitter comparison
We have shown above that using a colour or colour excess in the distance estimator is not the source of the differences between SALT2/SiFTO and the MLCS2k2-like approaches. MLCS2k2-like parametrisations assume a Cardelli-like colour variation law and in some cases a colour-luminosity relation, while the SALT2 or SiFTO approach allows one to derive these quantities from the data itself. The values obtained for these quantities differ significantly from the assumptions made in MLCS2k2. In addition, colour priors are used in the MLCS2k2 approach, which we think are unnecessary and subject to additional systematics.
To estimate systematic uncertainties arising for the light curve fitting process, we therefore chose to fit all SN light curves using both SALT2 and SiFTO models as described in the following section.
4.3. Fitting with SALT and SIFTO models
We use SALT2 and SiFTO to fit light curves and derive three parameters for each SN: an
amplitude conventionally described by the peak rest-frame B-band
magnitude 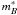 , a shape parameter, and a
colour labeled “𝒞” that roughly corresponds to the
rest-frame B−V colour at maximum light. The two models
that were fit on low-z and SNLS data minimise the modeling statistical uncertainty and
cover a large wavelength range (300–700 nm) well suited for the SNLS data set. For both
fitters, the light curves are obtained by integrating a spectral energy density (SED)
varying with phase in a model of the instrumental response function. The effective colour
parameter that is derived is due to a combination of extinction and intrinsic variation,
and this has to be kept in mind in the subsequent usage of those parameters to derive
distances. Those two techniques differ substantially in their detailed parametrisation of
observables and in the procedures considered for training and light curve fitting. As a
consequence, in the following, we use both in order to estimate the impact on cosmology of
the modeling choices that were made. Before comparing the result of the fits obtained on
the SNLS sample, we present both approaches, along with the minor modifications that were
applied since the publication of the methods in G07 and C08. The two approaches are
compared and combined in Sect. 5.1.
, a shape parameter, and a
colour labeled “𝒞” that roughly corresponds to the
rest-frame B−V colour at maximum light. The two models
that were fit on low-z and SNLS data minimise the modeling statistical uncertainty and
cover a large wavelength range (300–700 nm) well suited for the SNLS data set. For both
fitters, the light curves are obtained by integrating a spectral energy density (SED)
varying with phase in a model of the instrumental response function. The effective colour
parameter that is derived is due to a combination of extinction and intrinsic variation,
and this has to be kept in mind in the subsequent usage of those parameters to derive
distances. Those two techniques differ substantially in their detailed parametrisation of
observables and in the procedures considered for training and light curve fitting. As a
consequence, in the following, we use both in order to estimate the impact on cosmology of
the modeling choices that were made. Before comparing the result of the fits obtained on
the SNLS sample, we present both approaches, along with the minor modifications that were
applied since the publication of the methods in G07 and C08. The two approaches are
compared and combined in Sect. 5.1.
4.3.1. SALT2
The SALT2 method consists in modeling the SNe Ia spectral energy density (SED)
variation with time and its diversity using a linear combination of several principal
components multiplied by the exponential of a colour dependent function of wavelength
(which we will call “colour variation law”, although it can model a pure extinction
law). This model is trained on a large sample of nearby SNe listed in Table 12 and a sub-samble of the SNLS SNe Ia listed in
Table 9. We use only SNLS SNe with redshifts z ≤ 0.7, with an
unambiguous spectroscopic identification (excluding the
Ia ⋆ ) and a good light curve sampling (see
Sect. 4.5). Both light curves and spectra are
used in the fit. Since significant calibration uncertainties are expected for most
spectra (due for instance to slit losses), wavelength dependent corrections for each
spectrum are included in the model. The model parameters, the calibration correction
coefficients of the spectra, and the SNe parameters are fitted simultaneously. Only two
principal components have been considered; one that represents the average SN Ia, and
one which can be identified as the shape variation of light curves of SiFTO. This
training sample is larger than the one considered in G07. A few technical modifications,
detailed in Appendix A, have been applied to the
training procedure: higher resolution for the components and the colour variation law, a
new regularisation scheme, improved handling of the residual scatter about the model,
and propagation of the model statistical uncertainties. The colour variation law is
shown in Fig. 6 for  (i.e. for a
B−V colour excess of 0.1). It differs
significantly from the Cardelli et al. (1989)
extinction law for wavelengths λ < 370 nm even
when extreme values of RV are considered.
Adding more parameters to the colour law with respect to G07 has resulted in a steeper
variation at short wavelength.
(i.e. for a
B−V colour excess of 0.1). It differs
significantly from the Cardelli et al. (1989)
extinction law for wavelengths λ < 370 nm even
when extreme values of RV are considered.
Adding more parameters to the colour law with respect to G07 has resulted in a steeper
variation at short wavelength.
For the fit of SNe entering the Hubble diagram, all light curves for which the effective wavelength of the associated response function lies in the model validity range (300–700 nm rest-frame) are fit simultaneously. The actual fit is a simple least square minimisation taking into account both the covariance matrix of the flux measurements and a model uncertainty (described in Sect. A.2). Since the uncertainty on the model depends on the parameters that are fitted, the fit is performed iteratively with updates of the model uncertainties at each step until convergence is reached. The model parameters and the code to use them are public; see Sect. A.4 for details.
4.3.2. SiFTO
The SiFTO model consists of a SED sequence whose time evolution has been calibrated on
a large SNe Ia sample combining low-z and SNLS data, starting from the
spectral sequence derived by Hsiao et al. (2007).
The light curve shape variability is modelled with a time-stretching of the SED sequence
about the date of maximum light in rest-frame B-band, with a
wavelength-dependent stretch factor (s) indexed by its value in
B-band. The broad-band wavelength dependent calibration of the SED
sequence is not performed at this stage of the model building. Indeed, the derivation of
the amplitude and colour parameters is obtained in two steps: i) contrary to SALT2, the
amplitude of each light curve is a fit parameter, leading to an observer-frame peak
magnitude for each pass band; ii) these peak magnitudes are then used to adjust the SED
at maximum-light with a smooth multiplicative function of wavelength so that the flux
integrated in any rest-frame filter can be evaluated. Up to 5 rest-frame filters are
used – U02UBVR12 – resulting in 4 colour combinations of
(U02 − B),
(U−B), (B−V)
and (V−R), with the limitation that only the
rest-frame filters within 450 Å of an observer-frame filter are considered. The second
step consists in converting these colours into an estimate of
(B−V), denoted
(B−V)pred, using equations of the form
![\begin{equation} \label{eq:colrelation} \bmv_{\mathrm{UBpred}}=a\left[\umb + 0.5\right] + b\left(s-1\right) + c \end{equation}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq124.png) (4)with similar
equations relating (B−V) with
(U02 − B) and
(V−R). The data used to derive the linear relation
of the (B−V) vs.
(U−B) relation is shown in Fig. 7. The estimation of the a,b,c
parameters entering in these relations depends on the assumed intrinsic scatter of the
SNe colours, this is discussed in Sect. 4.4.
(4)with similar
equations relating (B−V) with
(U02 − B) and
(V−R). The data used to derive the linear relation
of the (B−V) vs.
(U−B) relation is shown in Fig. 7. The estimation of the a,b,c
parameters entering in these relations depends on the assumed intrinsic scatter of the
SNe colours, this is discussed in Sect. 4.4.
 |
Fig. 7 (B−V) corrected for stretch as a function of (U−B) for a selected sample of SNLS SNe as measured by SiFTO (open circles) along with the linear relations of Eq. (4) and Table 5 (a and c terms, solid lines) and the synthetised ones of SALT2 (dashed line) for the two colour scatter hypothesis. SALT2 does not contain explicitly colour relations as SiFTO, but the a,b and c coefficients can still be derived from the model. |
The final SiFTO colour parameter 𝒞 is determined by a weighted combination of each (B−V)pred together with any actual measurement of (B−V), degrading each (B−V)pred by the dispersion measured for each relation. The uncertainties in the derived colour relations introduce correlations between SNe that are propagated in the analysis.
Since C08, SiFTO has been retrained with a much larger sample of SNe including a sub-sample of the SNLS light curves presented in this paper (with stringent requirements on the time sampling) and many more at low redshift. It also uses an updated version of the SED sequence from Hsiao et al. (2007) that has been extended in the near infra-red.
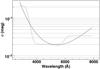 |
Fig. 8 SALT2 training sample broad-band colour dispersion as a function of wavelength for two different functional forms (solid curve: EXPPOL, dashed curve: SIGMOID). |
As a conclusion to the description of the techniques, SiFTO does not contain an explicit colour variation law as a function of wavelength, nor a broad-band colour calibration of the SED sequence as in SALT2. These two pieces of information, which are essential for distance estimate, are coded into the linear colour relations of Eq. (4). Also, the light curve stretching behaviour is a prior of the SiFTO parametrisation, whereas it is only approximately realised as an outcome of the SALT2 training. Indeed the second principal component of SALT2 turns out to be close to a derivative of the first one with respect to a stretch factor, hence mimicking a time stretching at the first order. As a consequence, based on these differences, we do not expect to get exactly the same light curve shapes so that the peak magnitudes and colours obtained with both fitters may have small systematic offsets and a stretch dependence. Some additional dispersion due to the differences in the data weighting in the least square minimisation is also anticipated.
4.4. Residual scatter
The SALT2 and SiFTO empirical models do not fully account for the diversity of SNe Ia. As a consequence, some intrinsic scatter about the best fit model is expected on top of the measurement uncertainties. The wavelength dependence of this residual scatter has to be evaluated as it affects the determination of some of the model parameters. As an example, for SiFTO, the fitted slope of the relation between (U−B) and (B−V) depends on whether the scatter about the linear relation is attributed to the estimate of (U−B) or (B−V). The same effect applies to the determination of the SALT2 colour variation law. Since a bias on this slope (for SALT2, this slope is encoded in the second derivative of the colour variation law in the UBV wavelength range) leads to bias on the average colour of SNe at high redshift where blue SNe are preferentially selected, we have to determine the amplitude of this scatter as a function of wavelength.
This cannot be obtained in the SiFTO framework where only two colours are compared at a time to derive the model parameters. On the contrary, it is possible with SALT2 since it assumes a single relation between all the peak magnitudes of a given supernova (up to five for low redshift SNe: UBVRI). Note however that with the SiFTO method, this unique relation between all observations is restored in the final colour estimate when the various (B−V)pred are combined. The technical details of the determination of the residual scatter are given in Sect. A.2. Using two parametrisations of the scatter as a function of wavelength (the exponential of a polynomial, or a combination of sigmoids, labeled respectively hereafter “EXPPOL” and “SIGMOID”, see Eq. (A.2)), one obtains the two estimates of the residual scatter shown in Fig. 8. This scatter model is translated into scatter in the reference bands used for SiFTO colour relations in Table 4. The values of the SALT2 residual scatter at the central wavelength of the U02BVR filters is used. The assumption that this scatter on magnitudes is uncorrelated between bands translates into correlated uncertainties in the colours used for the SiFTO colour relations. When accounted for in the determination of the colour relations, this leads to two sets of a,b,c parameters for each colour relation that are listed in Table 5.
In this determination of the residual scatter, we identified an additional scatter of 0.1 mag in observer U-band for low redshift SNe (see also C10 for a discussion about this issue). This is significantly larger than the dispersion obtained in the same rest-frame wavelength range with SNLS data (given by gM band observations at z ≃ 0.35, see Table 4). We hence attribute this additional dispersion to calibration uncertainties or varying effective filter transmissions from one U-band light curve to another. We de-weighted those light curves accordingly in the training of SALT2, and subsequently in the light curve fits. As for SiFTO, they were discarded for the fit of the (U−B) (B−V) colour relation and were not used for the determination of the colour parameters.
Figure 7 presents the difference between SiFTO and SALT2 colour relation between (U−B) and (B−V). Part of the differences of slopes can be explained by the use of different samples to derive those relations, and part can be attributed to the intrinsic differences in the methods used to derive those relations. Still, one can see that they have the same average estimate of (B−V) given (U−B), so we do not expect this to have a significant impact on cosmology, as we will see in the next section.
4.5. Light curve sampling
We investigate in this section the reliability of the light curve parameters determined on poorly sampled light curves, in particular those which lack photometric measurements before the date of maximum light (hereafter Tmax). Any bias on Tmax induces a bias on the parameters needed to estimate a distance (magnitude, shape and colour), and such a bias may arise if the modeling of the decline of the light curves is not sufficiently accurate. This is not really an issue for the SNLS sample presented in this paper as only 2% of the SNe lack photometry in the rising part of the light curves (between − 10 and − 1 days with respect to Tmax, rest-frame), but it has to be studied for the selection of external samples (see C10) for which this fraction is much larger (especially at low redshift because of a follow-up triggered by the spectroscopic identification).
For the purpose of this study we select well sampled SNe data with high
S/N from SNLS (using only those at
z < 0.4) and from external samples: SNe at
z < 0.1 from various surveys (see references in
C10) and SNe at
0.06 < z < 0.3 from the
SDSS (Holtzman et al. 2008). We compare the light
curve parameters 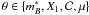 derived from the full light curve fits – hereafter θF – to
those resulting from fits ignoring a fraction of the data points. For each SN, we derive
several estimates of θ removing sequencially an increasing number of
early points, and index each of those estimates by
τf = (Tfirst − Tmax)/(1 + z)
the phase of the first remaining data point. Of course for real data
τf is not directly observable and we have to rely on
derived from the full light curve fits – hereafter θF – to
those resulting from fits ignoring a fraction of the data points. For each SN, we derive
several estimates of θ removing sequencially an increasing number of
early points, and index each of those estimates by
τf = (Tfirst − Tmax)/(1 + z)
the phase of the first remaining data point. Of course for real data
τf is not directly observable and we have to rely on
 , an
estimate of τf which results from the fitted value of
Tmax. We study the average offsets
Δθ = θ(τf) − θF
as a function of
, an
estimate of τf which results from the fitted value of
Tmax. We study the average offsets
Δθ = θ(τf) − θF
as a function of  . One
first has to correct for a trivial bias (showing up even for an unbiased estimator) that
is due to the finite width of the τf distribution. For
instance, if we consider an input distribution with
τf > 0, we will find biased
Δθ for negative values of
. One
first has to correct for a trivial bias (showing up even for an unbiased estimator) that
is due to the finite width of the τf distribution. For
instance, if we consider an input distribution with
τf > 0, we will find biased
Δθ for negative values of  simply
because we are looking at events for which
simply
because we are looking at events for which  is
systematically underestimated (and hence Tmax over-estimated).
Within each bin around a given value of
is
systematically underestimated (and hence Tmax over-estimated).
Within each bin around a given value of  , we
have an average bias on a parameter θ given by
, we
have an average bias on a parameter θ given by
![\begin{eqnarray*} \Delta_{\rm t} \theta (\widetilde{\tau_{\rm f}}) &=& \frac{ \int_{u=\widetilde{\tau_{\rm f}}-\epsilon}^{\widetilde{\tau_{\rm f}}+\epsilon} \frac{1}{n} \sum_{i=1}^n \left[ u-\tau_{\rm f}^i \right ] \, \partial_\tau \theta \, p(u|\tau_{\rm f}^i) {\rm d} u }{\int_{u=\widetilde{\tau_{\rm f}}-\epsilon}^{\widetilde{\tau_{\rm f}}+\epsilon} \frac{1}{n} \sum_{i=1}^n p(u|\tau_{\rm f}^i) {\rm d} u } \nonumber \\ &\simeq& \frac{ \sum_{i} \left[ \widetilde{\tau_{\rm f}}-\tau_{\rm f}^i \right] \, \partial_\tau \theta \, p(\widetilde{\tau_{\rm f}}|\tau_{\rm f}^i) } { \sum_{i} p(\widetilde{\tau_{\rm f}}|\tau_{\rm f}^i) } \nonumber \end{eqnarray*}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq169.png) where
the sum is on the number of tests performed (indexed by
where
the sum is on the number of tests performed (indexed by 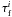 ), and
), and
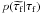 the likelihood of the estimator
the likelihood of the estimator
 knowing the true value τf (ϵ is half the bin
size).
∂τθ = − (1 + z)∂θ/∂Tmax
is the derivative of θ with respect to τf.
Such a bias can be estimated for each value of
knowing the true value τf (ϵ is half the bin
size).
∂τθ = − (1 + z)∂θ/∂Tmax
is the derivative of θ with respect to τf.
Such a bias can be estimated for each value of  and
corrected for assuming a Gaussian likelihood (with a σ given by the
redshift corrected measurement uncertainty on Tmax). We will
consider in the following
Δ′θ = Δθ − Δtθ
to study potential biases.
and
corrected for assuming a Gaussian likelihood (with a σ given by the
redshift corrected measurement uncertainty on Tmax). We will
consider in the following
Δ′θ = Δθ − Δtθ
to study potential biases.
The results for the rest-frame peak magnitude in B-band, the peak
(B−V) colour and shape parameter are shown in
Fig. 9. The potential bias on the distance modulus
μ is also shown (using best fit values for α and
β, see Eq. (5) and
Sect. 5.2). For light curves without premax data
but with 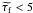 days, we do not find significant biases on
days, we do not find significant biases on
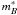 and
(B−V) but a small bias on
X1. The uncertainties on those biases are difficult to
estimate, as the de-biasing is only approximate.
and
(B−V) but a small bias on
X1. The uncertainties on those biases are difficult to
estimate, as the de-biasing is only approximate.
 |
Fig. 9 From top left to bottom right, |
For subsequent analyses, we will select SNe according to the following minimum requirements (based on the available phases τ = (Tobs − Tmax)/(1 + z) of photometric observations):
-
(i)
measurements at four different epochs or more in the range −10 < τ < +35 days. Three are mandatory to estimate both the date of maximum light and the shape parameter, one more is needed to get at least one degree of freedom;
-
(ii)
at least one measurement in the range −10 < τ < +5 days (equivalent to τf < 5 days);
-
(ii)
at least one measurement in the range +5 < τ < +20 days for a reasonable evaluation of the shape;
-
(iii)
at least two bands with one measurement or more in the range −8 < τ < +10 days in order to evaluate the SN peak luminosity and colour with confidence.
5. Light curve parameters of SNLS SNe Ia and measurement of ΩM
We present in this section a fit of the SNLS Hubble diagram based on the results obtained with the two light curve fitters described above. The goals of this study are: i) to compare the SALT2 and SiFTO light curve parameters; ii) see how their differences impact distance estimates and cosmological fits; iii) propagate the uncertainties of the whole analysis chain to the cosmological results; iv) present the constraints on cosmology provided by a single survey of high redshift supernovae.
5.1. Light curve parameters of SNLS SNe Ia
We apply in this section the two techniques described above to determine the peak magnitudes, colours and light curve shapes of the SNLS SNe Ia. Those are the basic ingredients to determine distances, they are used in C10, along with external SNe data samples, to build a Hubble diagram and constrain cosmological models. Here we focus on consistency tests and comparisons of the outcome of the two light curve fitters, any difference being considered as a systematic uncertainty that will add to the photometry and calibration uncertainties discussed in Sect. 3.
In order to get reliable estimates of magnitude, colour and light curve shape for each SN, we apply the selection described in Sect. 4.5. This set of sampling cuts discards 25SNe so that we are left with 252SNe Ia/Ia ⋆ , excluding the peculiar SNe 03D1cm, 03D3bb, 05D1by and 05D3gy. The discarded SNe are identified by the label “(s)” in Table 9.
5.1.1. Internal consistency check of the light curve fitters
In this section we try to quantify one of the primary virtues of the light curve fitters, which consists of deriving redshift-independent parameters (magnitude, shape and colour), from observations in a limited set of filters. This is possible in SNLS thanks to the high quality light curves obtained in gMrM and iM bands. For supernovae in the redshift range [ 0.2,0.7 ] , this corresponds to observations spanning the rest-frame wavelength range 2900–6400 Å.
The fitters should on average give the same estimates of the parameters for fits based on either gM + rM or rM + iM light curves. The results of such a test are shown in Fig. 10 for the difference Δ(B−V) of the estimates of rest-frame (B−V) colour, dispersed as a function of redshift. The average values of Δ(B−V) in redshift bins are compatible with zero (the maximum deviations are respectively of 0.024 ± 0.02 and 0.020 ± 0.012 for SALT2 and SiFTO). This tells us that we can reliably use rest-frame U and B observations to estimate the (B−V) colour at high-redshift where we do not have rest-frame V-band observations. Note however that the statistical uncertainties on the colour relations are accounted for: uncertainty on the c parameter of the colour relation for SiFTO (of order of 0.01 for (U−B)), and covariance matrix of the training for SALT2 propagated to the distance moduli as detailed in Sect. A.3.
 |
Fig. 10 Differences of estimated (B−V) colour at maximum from the fit of rMiM or gMrM light curves for both fitters (top: SALT2, bottom: SiFTO). |
 |
Fig. 11 Comparison of SALT2 and SiFTO parameters for a selected sub-sample of SNe of Table 11. Linear transformations of Eq. (6) and Table 6 were applied to SALT2 parameters. Each dot is a SN, the light grey areas represent the rms of the distribution in redshift bins, and the dark areas the uncertainty on the average values. The red curve on the top panel for the rest-frame B band peak magnitude is the expected discrepancy due to the differences of the SALT2 and SiFTO spectral sequences. |
5.1.2. Comparison of the SALT2 and SiFTO light curve parameters
We compare in this section the output of the two light curve fitters. The results
obtained with SALT2 and SiFTO are listed in Table 11. Since those empirical models were primarily designed for distance
estimates, it is important to briefly review how the three resulting parameters
(rest-frame magnitude, shape and colour) are combined for this purpose. As in A06, a
distance modulus is defined by the following linear combination of the parameters:
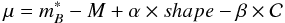 (5)where
(5)where
 is a rest-frame
B magnitude, the shape parameter is
(s − 1) for SiFTO (where s is the stretch factor),
X1 for SALT2, and 𝒞 is the colour
parameter. The absolute magnitude M, and the linear coefficients
α and β are fitted simultaneously with the
cosmological parameters (and also marginalised over for the cosmological constraints).
This approach will be applied and discussed in detail in C10. We simply note here that
any constant systematic offset between SiFTO and SALT2 parameters will have no effect on
cosmology as they will be absorbed in the absolute magnitude, that any multiplicative
factor between the SiFTO and SALT2 estimates of the shape and
C parameters will be compensated for by the α and
β coefficients, and finally that a shape dependence
of the differences of
is a rest-frame
B magnitude, the shape parameter is
(s − 1) for SiFTO (where s is the stretch factor),
X1 for SALT2, and 𝒞 is the colour
parameter. The absolute magnitude M, and the linear coefficients
α and β are fitted simultaneously with the
cosmological parameters (and also marginalised over for the cosmological constraints).
This approach will be applied and discussed in detail in C10. We simply note here that
any constant systematic offset between SiFTO and SALT2 parameters will have no effect on
cosmology as they will be absorbed in the absolute magnitude, that any multiplicative
factor between the SiFTO and SALT2 estimates of the shape and
C parameters will be compensated for by the α and
β coefficients, and finally that a shape dependence
of the differences of  and C
estimates with SiFTO and SALT2 are also accounted for by the α term.
and C
estimates with SiFTO and SALT2 are also accounted for by the α term.
As a consequence, in order to compare of the outcome of the two fitters, we will first
transform the SALT2 parameters to match those of SiFTO with the following equations:
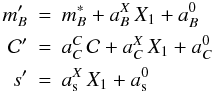 (6)
(6)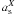 and
and
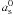 are inevitable because of
the fundamentally different modeling of the variability of light curve shapes.
are inevitable because of
the fundamentally different modeling of the variability of light curve shapes.
 and
and
 are due to the fact that
for SALT2, 𝒞 is an internal parameter of the
model that only approximately correspond to a (B−V)
colour at maximum, with a constant term so that the average value of
𝒞 on the training sample is zero,
whereas for SiFTO C is exactly the
(B−V) colour at maximum.
are due to the fact that
for SALT2, 𝒞 is an internal parameter of the
model that only approximately correspond to a (B−V)
colour at maximum, with a constant term so that the average value of
𝒞 on the training sample is zero,
whereas for SiFTO C is exactly the
(B−V) colour at maximum. 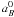 ,
, 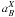 and
and
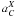 can be different from zero
since the shape of the B and V bands light curves are
not exactly the same for SALT2 and SiFTO. The values of the coefficients obtained by the
comparison of the data of Table 11 are listed in
Table 6. We apply this transformation of SALT2
parameters to focus on differences between the two light curve fitters that lead to
biases on distance moduli (Eq. (5)). The
values of the transformation coefficients themselves are simply related to differences
in the definition of the parameters in both models and do not contain any meaningful
information.
can be different from zero
since the shape of the B and V bands light curves are
not exactly the same for SALT2 and SiFTO. The values of the coefficients obtained by the
comparison of the data of Table 11 are listed in
Table 6. We apply this transformation of SALT2
parameters to focus on differences between the two light curve fitters that lead to
biases on distance moduli (Eq. (5)). The
values of the transformation coefficients themselves are simply related to differences
in the definition of the parameters in both models and do not contain any meaningful
information.
The differences of those transformed magnitude, shape and colour parameters of SALT2 with those obtained with SiFTO are dispersed as a function of redshift in Fig. 11.
Whereas the shape and colour parameters do not show any significant deviation from zero when averaged in redshift bins, there is a systematic difference on mB for some redshifts (−0.02 ± 0.005 at z ≃ 0.7 and +0.02 ± 0.005 at z ≃ 0.9). This points to different effective K-corrections between SiFTO and SALT2. Those differences can be attributed to some discrepancies in the spectral sequences used (that of SALT2 and the one derived by Hsiao et al. 2007), as the spectral distortions performed in SiFTO do not compensate for differences of fluxes on a wavelength range much shorter than the gaps between pass-bands (see the red curve in Fig. 11 top panel). However the choice of the empirical modeling of the SN diversity (global stretching or linear additive components) can also play a role, as the differences in the training sample and technical details of the training procedures. We will hence treat those differences as an additional source of systematic uncertainty.
5.2. SALT2 and SIFTO based Hubble diagrams
We present in this section fits of the Hubble diagram based on SALT2 and SiFTO
parameters. SALT2 parameters are transformed to match those of SiFTO (see Eq. (6) and Table 6). We use the distance modulus μ given in Eq. (5) with the shape and
C parameters matching the SiFTO stretch parameter and the
(B−V) colour at maximum. We consider here a ΛCDM
model, composed of unrelativistic matter and a cosmological constant, and further assume a
spatial flatness, so that we are left with a single cosmological parameter to fit:
ΩM (or alternatively ΩΛ ≡ 1 − ΩM). We apply the same
procedure as the one described in A06. The estimation consists of minimising 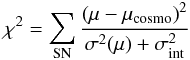 (7)where
μcosmo = 5log 10[dL(ΩM,z)/10pc],
dL being the luminosity distance, and
σint is an additional dispersion which value is chosen in
order to obtain a reduced χ2 = 1. This additional dispersion
accounts for all the sources of variability of SNe luminosities beyond their first-order
correlation to the shape of light curves and the colours of SNe. The measurement
uncertainties σ(μ) are a function of the parameters
α and β. We use
H0 = 70 km s-1 Mpc-1. This is purely
conventional as it only alters the value of the absolute magnitude M in
Eq. (5) through the normalisation of
dL, and M is fitted simultaneously with the
cosmological parameters.
(7)where
μcosmo = 5log 10[dL(ΩM,z)/10pc],
dL being the luminosity distance, and
σint is an additional dispersion which value is chosen in
order to obtain a reduced χ2 = 1. This additional dispersion
accounts for all the sources of variability of SNe luminosities beyond their first-order
correlation to the shape of light curves and the colours of SNe. The measurement
uncertainties σ(μ) are a function of the parameters
α and β. We use
H0 = 70 km s-1 Mpc-1. This is purely
conventional as it only alters the value of the absolute magnitude M in
Eq. (5) through the normalisation of
dL, and M is fitted simultaneously with the
cosmological parameters.
In addition to the sampling cuts listed in Sect. 4.5, we discard SNe with a peak rest-frame (B−V) > 0.2. Those red SNe are found only at z < 0.6 in our sample because they are fainter than the average, and hence undetected (or unidentified spectroscopically) at higher redshifts. Discarding them minimises the potential bias on distance moduli due to an inadequate colour correction. Indeed the average colour correction coefficient (β) we derive from the bulk of the SNe may not apply to those red SNe that are more likely to be extinguished by dust in their host galaxy than the bluer ones. This cut, applied to both SALT2 and SiFTO samples, discards 14SNe13. We mention in Sect. 5.4.3 the impact of a change of this colour cut on the cosmological fit. In addition to this, the peak magnitudes of 3SNe could not be obtained with SiFTO because of a lack of observations in gM and zM bands. Finally, a 3σ clipping to both SALT2 and SiFTO Hubble diagram residuals was applied, which removes 7more SNe (4 for SiFTO and 4 for SALT2 with only one in common, the others being consistent with a statistical fluctuation).
A Malmquist bias correction is applied to the distance moduli. This correction is based on a detailed study of the survey detection and spectroscopic identification efficiency using fake SNe included in the images entering the detection pipeline. This analysis is described in Perrett et al. (in prep.). The correction is equal to zero for z < 0.4 and rises at higher z reaching a value of ≃ 0.025 mag at z = 1.
The results obtained with both light curve fitters are listed in Table 7. The differences in the light curve fitters lead to a systematic difference of 0.020 on ΩM that corresponds to about two thirds of the statistical uncertainty. The rms of the Hubble residuals are similar, SiFTO residuals being slightly less scattered than the SALT2 ones. The Hubble diagram residuals from the corresponding best fit models are shown in Fig. 12. The correlation of the residuals from the Hubble diagram obtained with both fitters is shown in Fig. 13. The value of the correlation coefficient of 0.82 shows that most of the residual scatter is due to variability beyond that addressed by a single shape coefficient and a colour, irrespective of the way those parameters were derived.
 |
Fig. 12 Residuals from the Hubble diagram of the best fit ΛCDM cosmological model obtained with the two light curve fitters SALT2 (top) and SiFTO (bottom). |
ΩM and the nuisance parameters with their statistical uncertainties derived from the Hubble diagram fits using either SALT2 or SiFTO.
 |
Fig. 13 Correlations of residuals from the Hubble diagram obtained with SiFTO and SALT2. The outlier is 04D2cc for which data in the rising part of light curves is missing; the statistical uncertainty on its distance modulus μ is large with both light curve fitters (0.47 with SiFTO and 0.28 with SALT2, the difference being due to differences in the model uncertainties, or “error snake”). |
5.3. Combination of SALT2 and SiFTO results
The aim of using two light curve fitters is to evaluate the uncertainties on distances associated with the choices made in the development of those empirical models. In the following, as we do not have any physical justification for choosing one or the other, we use as a central value the average of the two, and propagate the systematic differences of the two fitters to the uncertainties on cosmological parameters.
We use for this purpose the method described in C10. In a few words, all systematic
uncertainties are accounted for in the covariance of the distance moduli. The distance
modulus of Eq. (5) can be rewritten as
μ = θTη − M
where θ = { 1,α, − β } is the vector
of the nuisance parameters, and  is the vector of the SNe parameters. With
Hi the Jacobian matrix of the derivative of
ηi with respect to the systematic
uncertainties, and Csys the covariance matrix of those
uncertainties, the covariance of the distance moduli of two supernovae is given by
is the vector of the SNe parameters. With
Hi the Jacobian matrix of the derivative of
ηi with respect to the systematic
uncertainties, and Csys the covariance matrix of those
uncertainties, the covariance of the distance moduli of two supernovae is given by
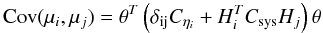 (8)where
Cηi is the
covariance matrix of the measurements ηi
(average of SALT2 and SiFTO results, including the intrinsic
σint obtained in Sect. 5.2 with each fitter independently) assuming that the SALT2 and SiFTO results
are fully correlated.
(8)where
Cηi is the
covariance matrix of the measurements ηi
(average of SALT2 and SiFTO results, including the intrinsic
σint obtained in Sect. 5.2 with each fitter independently) assuming that the SALT2 and SiFTO results
are fully correlated.
For the systematic uncertainty addressed here, we assign to H the difference of SALT2 and SiFTO parameters, averaged over a redshift range about each SN14, and consider a variance of one for this uncertainty in the covariance matrix Csys.
When fitting for a flat ΛCDM cosmological model, we obtain with this procedure ΩM = 0.201 ± 0.043, where the uncertainty includes a statistical uncertainty of ≃ 0.034 and an uncertainty due to the difference of the fitters of ≃ 0.026. If we now release the flatness prior, we obtain the confidence contours in the ΩM ΩΛ plane shown in Fig. 14. The combined confidence contour contains the ones obtained with SiFTO or SALT2 only. Those results do not include the full sources of systematic uncertainties, which will be detailed in Sects. 5.4 and 5.5 and final results will be presented in Sect. 5.6.
 |
Fig. 14 Contours at 68.3% confidence level (accounting only for statistical uncertainties) for the fit of ΛCDM cosmology to the SNLS third year sample (without additional SNe samples) for SALT2 (thin red curve), SiFTO (thin blue) and the combination of the two (thick black), on the light curve parameters. The dotted inclined ellipse represents the 68.3% confidence level from Astier et al. (2006) which includes 44 low redshift SNe along with the 71 SNe from the SNLS first year sample. |
Calibration systematic uncertainties.
5.4. Systematic uncertainties from light curve fits
We review here the list of systematic uncertainties that affect the determination of the light curve parameters and enter the covariance matrix Csys.
5.4.1. Calibration systematic uncertainties
The calibration systematics have been identified and evaluated in R09, they are listed in Table 8. All of them affect the light curve parameters. They can be divided in two sets: covariant magnitude uncertainties for each of the gMrMiMzM bands and uncertainties on the modeling of filters. The former magnitude uncertainties comprise uncertainties on the calibration transfer from Landolt stars to tertiary stars, from tertiary stars to supernova light curves, and uncertainties on the magnitude to flux transformation given by the uncertainties of our flux standard BD+17 4708 magnitudes and its spectrum. Additional uncertainties come from the calibration of the PSF photometry as discussed in Sect. 3.2.
The uncertainties on the transmission function of the instrument are approximated by uncertainties on the central wavelength of each effective filter (an effective filter combines quantum efficiency of the CCDs, transmission of the MegaPrime optics and filters, reflectivity of the primary mirror, and a model of the atmospheric transmission at the average airmass of the observations, see R09); any higher order uncertainty on the effective transmission has a negligible impact on the total uncertainty budget.
In order to propagate these uncertainties, the derivative of the peak magnitude, colour and stretch (or X1 for SALT2) with respect to each of these systematics (H matrices in Eq. (8)) have to be evaluated for each SN. For SALT2, this requires a full retraining of the model and new light curve fits for each kind of uncertainty. For the SiFTO model, calibration uncertainties only impact the linear colour relations.
As an example, the impact of the calibration uncertainties on the values of
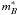 are shown in Fig. 15 for SALT2; they are similar for SiFTO. The
sensitivity of
are shown in Fig. 15 for SALT2; they are similar for SiFTO. The
sensitivity of 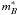 to calibration offsets
depend on the weight of each band in the fit which in turn depends on the assumed model
uncertainties.
to calibration offsets
depend on the weight of each band in the fit which in turn depends on the assumed model
uncertainties.
 |
Fig. 15 Impact of the calibration uncertainties of Table 8 on the SALT2 values of |
5.4.2. Light curve fitter systematic differences
There are three sources of uncertainties associated with the light curve fitters. First, there are the intrinsic differences of modeling given by the differences of SALT2 and SiFTO outcomes as discussed previously.
 |
Fig. 16 Uncertainties on the average distance modulus μ in redshift bins of 0.2: impact of the statistical uncertainty of the training (for SALT2, thin solid curve), calibration uncertainties (dotted curve), residual scatter model (dotted short dashed curve), systematic uncertainty due to SALT2 regularisation (dotted long dashed curve) and differences between results obtained with the two light curve fitters (thick solid curve). Values of α and β that minimise residuals from the Hubble diagram were used. |
Second, due to finite training samples, there is some statistical uncertainty associated with the determination of the parameters of the light curve fitters. For SALT2, those uncertainties are provided by the covariance matrix of the model that results from the training fit (taking into account the residual scatter). The transformation to a covariance matrix of distance moduli is detailed in Sect. A.3, as is the computation of the uncertainty on the average distance modulus in a given redshift bin. As for SiFTO, only the uncertainties on the a,b,c parameters of the colour relations are considered. The uncertainties of the spectral sequence (and especially its evolution with time) are ignored, because they induce negligible correlations of parameters derived for different supernovae: an “error snake” is used to fit light curves, but the covariance between different SNe is ignored.
Finally, as discussed in Sect. 4.4, there is some uncertainty on the wavelength dependence of the residual scatter about the best fit model. We have considered two functional forms for this dependence which provide us with an estimate of the associated systematic uncertainty.
An additional systematic uncertainty specific to the SALT2 technique is the regularisation weight. Regularisation is required to train the model because of the lack of spectra in the near UV for some SN phases. Its weight should be minimal to prevent biases, but a weight that is too low generates unphysical high frequency wiggles in the resulting spectral sequence (this is a typical feature of all deconvolution processes). So the choice of the regularisation scale is partly arbitrary. Its impact on distance moduli is evaluated by the difference of results obtained with two sets of SALT2 trainings, one with the nominal weight and the other one with a weight five times smaller. However as shown in Fig. 16, the differences obtained are typically of order of 0.005 and hence can be neglected.
Photometry of the SNLS 3-year SNe Ia.
5.4.3. Resulting uncertainties on distance moduli
Figure 16 presents the impact of light curve fitter and calibration uncertainties on distance moduli. The uncertainty induced by the choice of light curve fitter is estimated by the differences of distance moduli obtained with SiFTO and SALT2 averaged over redshift bins of size 0.2. The values of M, α and β obtained in Sect. 5.2 have been used. Because of a finite supernova sample, the uncertainty induced by the differences of the light curve fitters cannot be precisely estimated. We can however see that they are of the same order as the calibration uncertainties, with Δμ ≲ 0.03.
The statistical uncertainty of the light curve model and the choice of parametrisation of the residual scatter only play a significant role at the high redshift end of the survey. This is due to the combination of Malmquist bias and a limited wavelength coverage of the imaging survey. Because of Malmquist bias and the colour-luminosity relation, only the bluest supernovae are measured with enough signal to noise at high redshift, which results in an average colour decrease with increasing redshift. In addition to this, the rest-frame (B−V) colour is not directly measured, it is rather given by measurements in rest-frame wavelength shorter than that of the V-band so that one has to rely on the colour relations. As a consequence, any uncertainty on the colour relations will impact distance moduli, and especially a change of slope of the (U−B) or (U02−B) colour relation due to a modification of the residual scatter model will modify the average colour and impact distance moduli.
Along with the uncertainties related to the light curve parameters, several other systematic uncertainties alter the precision of the cosmological constraints resulting from the Hubble diagram fit. They are studied in detail in C10. Among those, we only consider the most relevant one for the present analysis (based on SNLS SN sample only): a 39% uncertainty on the Malmquist bias correction (see C10 for details). The other systematic uncertainties presented in C10 are negligible for this analysis. As an example, C10 found that the bias on distance moduli due to a contamination of the SN Ia sample by core collapse supernovae reaches a value of 0.005 mag at z ≃ 1. This is much smaller than the other uncertainties we consider in this paper (see Fig. 16).
The choice of the colour cut value of 0.2 applied to the SN sample is partly arbitrary. Choosing instead a cut of 0.3 for instance adds four SNe to the sample. With those additional supernovae the best fit Ωm value is shifted by 0.01. The statistical fluctuation of this difference of Ωm is ± 0.005 (based on a jackknife analysis), so the shift we obtain is marginally consistent with a statistical fluctuation.
 |
Fig. 17 α and β estimates in redshift bins of 0.2 using SALT2 (filled circles), SiFTO (open circles) and the combined light curve parameters (gray triangles, see Sect. 5.3). |
SNLS type Ia supernovae parameters.
5.5. Evolution of the colour-luminosity relation with redshift
Recently, Kessler et al. (2009, hereafter K09) found an evolution of the β parameter with redshift, based on light curve parameters resulting from SALT2 fits of the SNLS first year SNe data set (A06). Before presenting the final estimate of ΩM (including all previously listed systematic uncertainties), we have to address this issue as our cosmological constraints are based on the assumption that β is constant.
The measurement of the colour-luminosity relation at high redshift is difficult because of three combined effects:
-
i)
the fitted value of β depends on the assumed uncertainties of (B−V) (known as a total least-squares problem, see Markovsky & Huffel 2007, for a review);
-
ii)
because of a limited detection/selection efficiency, we miss red SNe at high z, and hence the range of colours to fit for the relation is reduced. This makes the determination of β both more uncertain and more sensitive to the assumed uncertainties;
-
iii)
SNe rest-frame (B−V) colour is not directly measured at high z. We measure a colour at shorter rest-frame wavelength, and rely on colour relations to estimate (B−V). Incorrect colour relations cause the apparent β to change with redshift. Furthermore the (B−V) estimate depends on assumed uncertainties of the SN model and intrinsic scatter of SN colours, which are difficult to evaluate (see Sect. 4.4).
With the improved modeling of the residual scatter presented in this paper with respect to the first version of SALT2 used by K09, we obtain larger uncertainties on the colour parameter and hence larger β at high z than those presented in K09. We repeat their analysis which consists of fitting for M, α and β in redshift bins assuming a fixed cosmological model. The results are shown in Fig. 17 using both SALT2 and SiFTO parameters. Although our redshift–β relation is much shallower than that obtained by K09, we still see a β evolution with the SALT2 parameters, β being smaller at higher z.
This change in the estimate of β at high redshift between this analysis and that of K09 comes from the combination of two effects.
-
i)
The SALT2 colour variation law used in this paper is steeper than that of G07 for λ < 3600 Å mostly because of a higher number of parameters in the model training (see Fig. 6). At z ≃ 0.8, a change of the observed (rM − iM) colour translates into a change of the colour parameter
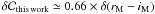 with the version of SALT2 used in this
paper whereas, using that of G07, one obtains
with the version of SALT2 used in this
paper whereas, using that of G07, one obtains 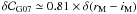 15. Hence,
15. Hence,  and because of
this, we expect
βthiswork/βG07(z = 0.8) ≃ 1.24.
and because of
this, we expect
βthiswork/βG07(z = 0.8) ≃ 1.24.
-
ii)
For supernovae at z > 0.7, which correspond to an average redshift z ≃ 0.8, we obtain an average uncertainty on SNe colours of
 in this paper whereas one obtain an
uncertainty of 0.05 when fitting the same data with the SALT2 version presented in
G07 and used in K09. If we apply the scaling factor on the colours of 0.8 coming
from the change of the colour variation law, the uncertainty on colours reduces to
in this paper whereas one obtain an
uncertainty of 0.05 when fitting the same data with the SALT2 version presented in
G07 and used in K09. If we apply the scaling factor on the colours of 0.8 coming
from the change of the colour variation law, the uncertainty on colours reduces to
 . This difference of colour
uncertainties (0.06 versus 0.04) comes from differences in the model uncertainties
that are shown in Fig. 8 in this paper and Fig.
7 in G07. Using a Monte Carlo simulation of a linear fit of the colour-luminosity
relation for SNe at z > 0.7, where we consider in the fit
that
. This difference of colour
uncertainties (0.06 versus 0.04) comes from differences in the model uncertainties
that are shown in Fig. 8 in this paper and Fig.
7 in G07. Using a Monte Carlo simulation of a linear fit of the colour-luminosity
relation for SNe at z > 0.7, where we consider in the fit
that 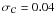 when the value is set to 0.06 in the
simulation, we find a bias
βfit − βtrue ≃ − 1 16.
when the value is set to 0.06 in the
simulation, we find a bias
βfit − βtrue ≃ − 1 16.
 )
results in a change of β of
βthiswork − βG07(z = 0.8) ≃ 1.6.
At lower z, where we measure directly the rest-frame
(B−V) colour and benefit from a larger range of SNe
colours to fit the slope of the correlation with luminosity, we do not expect any
significant difference.
)
results in a change of β of
βthiswork − βG07(z = 0.8) ≃ 1.6.
At lower z, where we measure directly the rest-frame
(B−V) colour and benefit from a larger range of SNe
colours to fit the slope of the correlation with luminosity, we do not expect any
significant difference.
Using SiFTO parameters, we see in Fig. 17 the opposite trend than that obtained with SALT2: larger β at higher z (at a 3σ significance based on a linear fit, but again, the statistical uncertainties are not meaningful), which illustrates how sensitive this measurement is to the light curve fitter modeling and error propagation.
As a consequence, given the current uncertainties in the empirical light curve models, we are not able to conclude on an evolution of β with redshift. To account for this, we have added a systematic uncertainty on the evolution of β parametrised by its first derivative with redshift, for which we assume σ(∂β/∂z) = 1.
5.6. Measurement of ΩM
We propagate the sources of uncertainties listed above with the technique described in C10 and summarised in Sect. 5.3. Except for the uncertainty associated with the difference of the two light curve fitters, the derivatives in the matrix H are the average of those obtained with SALT2 and SiFTO. For instance, the two sets of parameters ηa(b) result from fits with different weighting of the gMrMiMzM light curves, so that they have different dependences on the calibration systematics.
Recently Sullivan et al. (submitted) found with a 4σ evidence that the distance moduli (rest-frame magnitude corrected for the correlation with stretch and colour) of SNe in massive host galaxies are smaller than those of SNe in faint galaxies. In order to account for this effect in the cosmology fits, a second normalisation parameter MB is introduced in order to treat independently SNe in low or high mass galaxies (with a split value at a galaxy mass of 1010 M⊙). When we apply this procedure to the SNLS sample, the retrieved value of ΩM is shifted by 0.0035. So this effect is negligible for the present analysis based on SNLS data only.
The SALT2 low-z training sample of type Ia supernovae light curves and spectra
 |
Fig. 18 Contours at 68.3% confidence level for the fit to a ΛCDM cosmology from the SNLS third year sample (without additional SNe samples) accounting for: Hubble diagram statistical uncertainties and the difference between SALT2 and SiFTO results (dotted curve), photometric calibration (dashed curve), model training statistical uncertainties and Malmquist bias uncertainties (thin solid), and finally the potential β evolution (thick solid curve). |
The contours in the ΩM,ΩΛ plane are presented in Fig. 18. With a flatness prior (ΩM + ΩΛ = 1), we obtain ΩM = 0.211 ± 0.077, the uncertainty of which can be approximately decomposed as
| Hubble diagram statistical uncertainty | ±0.034 |
| Choice of empirical model (SALT2 vs. SiFTO) | ±0.026 |
| Model training statistical uncertainty | ±0.034 |
| Photometric calibration | ±0.048 |
| Uncertainty on Malmquist bias correction (40%) | ±0.004 |
| Uncertainty on the residual scatter (see Sect. 4.4) | ±0.010 |
| Potential β evolution (σ(∂β/∂z) = 1) | ±0.022 |
when the potential β evolution is accounted for, the best fit (ΩM,ΩΛ) is shifted. This is due to a modification of the covariances of the distance moduli and not their values. Modifying the covariances alters the weight of SNe as a function of redshift and hence the best fit cosmological parameters.
Of course, when SNe samples at lower redshifts are added to the cosmological fit, both the statistical and systematic uncertainties are significantly reduced (though other systematics have to be included), and the relative impact of each uncertainty changes. This is studied in detail in C10.
6. Conclusion
We have presented photometric properties and distances measurements of SNe discovered during the first 3-year of the SNLS project. This paper is the first of a series of three: the two others present the cosmological constraints obtained by combining this data set with other SNe Ia samples (C10) and taking into account constraints from other cosmological probes (Sullivan et al., in prep.). The various steps of the analysis were cross-checked using significantly different techniques, in order to identify and minimise systematic uncertainties. The photometric reduction was done using two independent pipelines. The calibration transfer from tertiary stars to supernovae light curves was performed with systematic uncertainties of 0.002 mag. Two light curve fitters were considered in this paper. Both are intended to estimate three parameters (magnitude, shape and colour) that can be subsequently linearly combined to determine the luminosity distances of the SNe Ia. Despite a common goal, the two methods are significantly different in their implementation, allowing us to estimate, through the comparison of their outcome, the uncertainties associated with the choice of modeling. Whereas SALT2 accounts for the SNe variability with a principal component estimation altered by a colour variation law, SiFTO assumes a pure time stretching of an average spectral sequence, and relies on a limited set of linear relations between rest-frame colours of SNe Ia. The two techniques lead to systematically different results (up to 0.02–0.03 on distance moduli), at a level comparable to other sources of uncertainties such as calibration. The quantitative impact of systematic uncertainties, and their relative weight with respect to the purely statistical uncertainty on distance moduli, depends on the subsequent usage of the distance estimates to constrain cosmological parameters, as they introduce large correlations from supernova to supernova.
In contrast to Kessler et al. (2009), we find no convincing evidence for an evolution of the colour-luminosity relation with redshift (i.e. evolution of β). This is traced to improvements made in the empirical modeling of the SNe Ia spectral sequence and to a more precise estimate of their remaining variability beyond that addressed by the models. Nevertheless, we account for a possible evolution of β in the evaluation of systematic uncertainties.
We obtain ΩM = 0.211 ± 0.034(stat) ± 0.069(sys) when fitting a flat ΛCDM cosmology to the SNLS data set only. The uncertainty is dominated by the calibration uncertainties (0.048) despite a large improvement in the precision of this calibration with respect to previous supernovae surveys. However, the impact of systematic uncertainties depends on the data set considered. In C10, we add external supernova samples to this one, and constrains further the cosmological models while accounting for other sources of systematic uncertainties.
Online material
List of SNLS 3 years type Ia supernova sample.
Candidate lists are available from http://legacy.astro.utoronto.ca/
As a consequence, if MSN and
Mref are spectral energy densities (in
ergcm-2s for instance), then T(λ) is the product of an effective
collection area (accounting for all the transmission and reflection efficiencies in the
optical path), a dimensionless quantum efficiency, the CCD gain, and the inverse of the
photon energy (in Å erg-1).
for instance), then T(λ) is the product of an effective
collection area (accounting for all the transmission and reflection efficiencies in the
optical path), a dimensionless quantum efficiency, the CCD gain, and the inverse of the
photon energy (in Å erg-1).
We selected models with the DDT criterion 3 in Table 2 of Kasen et al. (2009) (supplementary material) and found a residual (B−V) dispersion of 0.03 after correcting for a marginal correlation with decline rate. The model spectra were kindly provided to us by the author.
We consider in the Monte Carlo simulations a value β = 3, 96 SNe, an intrinsic dispersion of distance moduli of 0.87, and a dispersion of the true SNe colours of 0.05 (the rms of the observed colour distribution is of 0.08, so that one expects an rms of the true colours of order of 0.05 after subtracting the contribution of uncertainties).
Acknowledgments
We thank the anonymous referee for helping clarify and improve some sections this paper. We gratefully acknowledge the assistance of the CFHT Queued Service Observing Team. We heavily relied on the dedication of the CFHT staff and particularly J.-C. Cuillandre for continuous improvement of the instrument performance. The real-time pipelines for supernovae detection ran on computers integrated in the CFHT computing system, and were very efficiently installed, maintained and monitored by K. Withington (CFHT). We also heavily relied on the real-time Elixir pipeline which is operated and monitored by J.-C. Cuillandre, E. Magnier and K. Withington. The French collaboration members carry out the data reductions using the CCIN2P3. Canadian collaboration members acknowledge support from NSERC and CIAR; French collaboration members from CNRS/IN2P3, CNRS/INSU, PNC and CEA. This work was supported in part by the Director, Office of Science, Office of High Energy and Nuclear Physics, of the US Department of Energy. The France-Berkeley Fund provided additional collaboration support. CENTRA members were supported by Fundação para a Ciência e Tecnologia (FCT), Portugal under POCTI/FNU/43423. S. Fabbro and C. Gonçalves acknowledge support from FCT under grants No. SFRH/BPD/14682/2003 and SFRH/BPD/11641/2002 respectively.
References
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2007, ApJS, 172, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Altavilla, G., Fiorentino, G., Marconi, M., et al. 2004, MNRAS, 349, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Anupama, G. C., Sahu, D. K., & Jose, J. 2005, A&A, 429, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balland, C., Baumont, S., Basa, S., et al. 2009, A&A, 507, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barbon, R., Buondí, V., Cappellaro, E., & Turatto, M. 1999, A&AS, 139, 531 [Google Scholar]
- Baron, E., & Hauschildt, P. H. 1998, ApJ, 495, 370 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baumont, S., Balland, C., Astier, P., et al. 2008, A&A, 491, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benetti, S., Meikle, P., Stehle, M., et al. 2004, MNRAS, 348, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., & Gilliland, R. L. 2004, AJ, 128, 3053 [NASA ADS] [CrossRef] [Google Scholar]
- Boulade, O., Charlot, X., Abbon, P., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, ed. M. Iye, A. F. M. Moorwood, Proc. SPIE, 4841, 72 [Google Scholar]
- Branch, D., Lacy, C. H., McCall, M. L., et al. 1983, ApJ, 270, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Bronder, T. J., Hook, I. M., Astier, P., et al. 2008, A&A, 477, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buta, R. J., & Turner, A. 1983, PASP, 95, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, APJ, 345, 245 [Google Scholar]
- Conley, A., Goldhaber, G., Wang, L., et al. 2006, ApJ, 644, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Conley, A., Carlberg, R. G., Guy, J., et al. 2007, ApJ, 664, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Conley, A., Sullivan, M., Hsiao, E. Y., et al. 2008, ApJ, 681, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Conley, A., Guy, J., Sullivan, M., et al. 2010, ApJ, submitted [Google Scholar]
- Ellis, R. S., Sullivan, M., Nugent, P. E., et al. 2008, ApJ, 674, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., Phillips, A. C., Kibrick, R. I., et al. 2003, in SPIE Conf. Ser., ed. M. Iye, & A. F. M. Moorwood, 4841, 1657 [Google Scholar]
- Filippenko, A. V., Richmond, M. W., Matheson, T., et al. 1992, ApJ, 384, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Burns, C. R., Phillips, M. M., et al. 2009, ApJ, 704, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Garavini, G., Folatelli, G., Goobar, A., et al. 2004, AJ, 128, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Goldhaber, G., Groom, D. E., Kim, A., et al. 2001, ApJ, 558, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Guy, J., Astier, P., Baumont, S., et al. 2007, A&A, 466, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guy, J., Astier, P., Nobili, S., Regnault, N., & Pain, R. 2005, A&A, 443, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamuy, M., Phillips, M. M., Maza, J., et al. 1991, AJ, 102, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996, AJ, 112, 2408 [Google Scholar]
- Hamuy, M., Maza, J., Pinto, P. A., et al. 2002, AJ, 124, 2339 [NASA ADS] [CrossRef] [Google Scholar]
- Harville, D. A. 1977, JASA, 358, 320 [Google Scholar]
- Hauschildt, P. H., & Baron, E. 1999, J. Comp. Appl. Math., 109, 41 [Google Scholar]
- Hauschildt, P. H., Baron, E., & Allard, F. 1997, ApJ, 483, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Challis, P., Jha, S., et al. 2009a, ApJ, 700, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Wood-Vasey, W. M., Blondin, S., et al. 2009b, ApJ, 700, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Holtzman, J. A., Marriner, J., Kessler, R., et al. 2008, AJ, 136, 2306 [NASA ADS] [CrossRef] [Google Scholar]
- Hook, I. M., Jørgensen, I., Allington-Smith, J. R., et al. 2004, PASP, 116, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A., Sullivan, M., Perrett, K., et al. 2005, ApJ, 634, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A., Sullivan, M., Nugent, P. E., et al. 2006, Nature, 443, 308 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hsiao, E. Y., Conley, A., Howell, D. A., et al. 2007, ApJ, 663, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- INES. 2006, IUE Newly Extracted Spectra, Website, http://ines.vilspa.esa.es/ines/ [Google Scholar]
- Jha, S., Kirshner, R. P., Challis, P., et al. 2006, AJ, 131, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Jha, S., Riess, A. G., & Kirshner, R. P. 2007, ApJ, 659, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Röpke, F. K., & Woosley, S. E. 2009, Nature, 460, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, R., Becker, A. C., Cinabro, D., et al. 2009, ApJS, 185, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Knop, R. A., Aldering, G., Amanullah, R., et al. 2003, ApJ, 598, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Kowalski, M., Rubin, D., Aldering, G., et al. 2008, ApJ, 686, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Hastings, N. C., Loomis, K., et al. 2000, ApJ, 539, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Phillips, M. M., Stubbs, C., et al. 2001, AJ, 122, 1616 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Suntzeff, N. B., Candia, P., et al. 2003, AJ, 125, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Phillips, M. M., Suntzeff, N. B., et al. 2004a, AJ, 127, 1664 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Suntzeff, N. B., Phillips, M. M., et al. 2004b, AJ, 128, 3034 [NASA ADS] [CrossRef] [Google Scholar]
- Krisciunas, K., Prieto, J. L., Garnavich, P. M., et al. 2006, AJ, 131, 1639 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Leibundgut, B., Kirshner, R. P., Filippenko, A. V., et al. 1991, ApJ, 371, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Lira, P., Suntzeff, N. B., Phillips, M. M., et al. 1998, AJ, 116, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Magnier, E. A., & Cuillandre, J.-C. 2004, PASP, 116, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Markovsky, I., & Huffel, S. V. 2007, Signal Processing, 87, 2283, special Section: Total Least Squares and Errors-in-Variables Modeling [Google Scholar]
- Matheson, T., Kirshner, R. P., Challis, P., et al. 2008, AJ, 135, 1598 [NASA ADS] [CrossRef] [Google Scholar]
- Meikle, W. P. S., Cumming, R. J., Geballe, T. R., et al. 1996, MNRAS, 281, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, P., Kim, A., & Perlmutter, S. 2002, PASP, 114, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Oke, J. B., Cohen, J. G., Carr, M., et al. 1995, PASP, 107, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Pastorello, A., Mazzali, P. A., Pignata, G., et al. 2007, MNRAS, 377, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Benetti, S., Cappellaro, E., et al. 1996, MNRAS, 278, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Phillips, A. C., Heathcote, S. R., et al. 1987, PASP, 99, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Pignata, G., Patat, F., Benetti, S., et al. 2004, MNRAS, 355, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Regnault, N., Conley, A., Guy, J., et al. 2009, A&A, 506, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richmond, M. W., Treffers, R. R., Filippenko, A. V., et al. 1995, AJ, 109, 2121 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Kirshner, R. P., Schmidt, B. P., et al. 1999, AJ, 117, 707 [Google Scholar]
- Riess, A. G., Strolger, L., Tonry, J., et al. 2004, ApJ, 607, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Li, W., Stetson, P. B., et al. 2005, ApJ, 627, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, R. C., Pier, J. R., & Monet, D. G. 1999, AJ, 118, 2488 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M., Hamuy, M., Suntzeff, N. B., et al. 2002, AJ, 124, 2100 [NASA ADS] [CrossRef] [Google Scholar]
- Strolger, L.-G., Smith, R. C., Suntzeff, N. B., et al. 2002, AJ, 124, 2905 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Howell, D. A., Perrett, K., et al. 2006, AJ, 131, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Conley, A., Howell, D. A., et al. 2010, MNRAS, submitted [Google Scholar]
- Suntzeff, N. 1992, IAU Colloq., ed. R. McCray (Cambridge: Cambridge University Press), 145 [Google Scholar]
- Suntzeff, N. B., Phillips, M. M., Covarrubias, R., et al. 1999, AJ, 117, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Tsvetkov, D. Y. 2006, [arXiv:astro-ph/0606051] [Google Scholar]
- Valentini, G., Di Carlo, E., Massi, F., et al. 2003, ApJ, 595, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Vinkó, J., Bíró, I. B., Csák, B., et al. 2003, A&A, 397, 115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, L., Baade, D., Höflich, P., et al. 2003a, ApJ, 591, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Goldhaber, G., Aldering, G., & Perlmutter, S. 2003b, ApJ, 590, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Wells, L. A., Phillips, M. M., Suntzeff, B., et al. 1994, AJ, 108, 2233 [NASA ADS] [CrossRef] [Google Scholar]
- Wood-Vasey, W. M., Miknaitis, G., Stubbs, C. W., et al. 2007, ApJ, 666, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Zapata, A. A., Candia, P., Krisciunas, K., Phillips, M. M., & Suntzeff, N. B. 2003, Am. Astron. Soc. Meet. Abstr., 203, [Google Scholar]
Appendix A: Technicals details on the training of SALT2
A.1. Parameters and regularisation
The SALT2 SED sequence is evaluated for phases between −20 and +50 days, in the
wavelength range from 200 to 920 nm. The model is addressed using a basis of third order
b-splines for which the phase and wavelength axis have been distorted in order to allow
higher resolution in some areas of the parameter space. Those distortions have been
tuned to minimise residuals from the training data set for a given number of spline
nodes. For wavelength, the distortion is almost equivalent to a constant resolution in
log space, except in the UV range where we lack spectroscopic constraints. For this
paper, the number of parameters in phase × wavelength is 14 × 100 both for the average
SED sequence and the first component that is correlated to stretch. The magnitude of the
colour variation law is modelled as 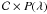 where
where
 is the colour
parameter and P(λ) is a polynomial with linear
extrapolations for wavelength smaller than 280 nm or larger than 700 nm, with four free
coefficients, the two others being fixed so that
P(λB) = 0 and
P(λV) = 1.
is the colour
parameter and P(λ) is a polynomial with linear
extrapolations for wavelength smaller than 280 nm or larger than 700 nm, with four free
coefficients, the two others being fixed so that
P(λB) = 0 and
P(λV) = 1.
The choice of the number of parameters is a trade off between the statistical noise of the model, and the minimisation of biases introduced by a forced smoothness of the model. For instance, SALT2 has many more parameters than SiFTO which assumes a pure stretching of the light curves. Also, in some areas of the parameter space, we lack data to train the model. For instance in the UV range, we have a lot of photometric information from the SNLS dataset at all phases but are missing early- and late-time spectroscopy. In this situation, the training fit is trying to deconvolve the SN SED from broad-band integrated flux measurements, which introduces high frequency noise as for any deconvolution procedure. As a consequence, when integrated in filters other than those used for the training, the model light curves in the UV are quite noisy. This is only a cosmetic issue when the statistical uncertainty of the model is propagated to the estimates of the light curve parameters (amplitude, shape and colour, see Sect. A.3). Still, we can apply priors on the properties of the SED sequence to cure part of the deconvolution noise in order to improve the statistical accuracy of the model. This however systematically introduces biases that have to be controlled and minimised.
A regularisation term for each of the two components (SED sequences) is added to the standard χ2 to be minimised of the following form:
![\appendix \setcounter{section}{1} $$ \sum_{i,j,l}\! w(i,j,l) \left[ m_{i,j+l}\! - \! m_{i,j}\right]^2 \! \!+ \! \!\sum_{i,j,k,l}\! w(i,j,l) \left[ m_{i+k,j+l} m_{i,j} \!- \!m_{i+k,j} m_{i,j+l}\right]^2 $$](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq349.png) where
mi,j is the flux value of the SED
sequence on a grid of phase and wavelength indexed by i and
j respectively (similarly k and l
index offsets in phase and wavelength). w(i,j,l) is a
weighting function whose value is inversely proportional to the amount of spectroscopic
data at the phase and wavelength position (i,j); it also decreases for
increasing l (wavelength difference) so that the regularisation has no
effect on the relative values of the SED for wavelength distant by 100 nm or more (in
order to limit the biases on colours). The first term minimises the gradient as a
function of wavelength when there is no spectroscopic information, and the second is
null if the model can be factorised as a dyadic product
mi,j = ai × bj.
Hence, the effect of the regularisation is to force the model into a simple
interpolation of spectra at different phases when there is no spectroscopic information
at intermediate phases, with a minimal impact on regions that are well constrained by
data and a small effect on broad-band colours. The strength of this regularisation is
adjusted via the normalisation of w(i,j,l) so that the
value of the colour difference
(U−B) − (B−V)
at maximum luminosity is altered by less than 0.01. The impact of this regularisation on
distance moduli obtained with SALT2 is however controlled (see Sect. 5.4.2).
where
mi,j is the flux value of the SED
sequence on a grid of phase and wavelength indexed by i and
j respectively (similarly k and l
index offsets in phase and wavelength). w(i,j,l) is a
weighting function whose value is inversely proportional to the amount of spectroscopic
data at the phase and wavelength position (i,j); it also decreases for
increasing l (wavelength difference) so that the regularisation has no
effect on the relative values of the SED for wavelength distant by 100 nm or more (in
order to limit the biases on colours). The first term minimises the gradient as a
function of wavelength when there is no spectroscopic information, and the second is
null if the model can be factorised as a dyadic product
mi,j = ai × bj.
Hence, the effect of the regularisation is to force the model into a simple
interpolation of spectra at different phases when there is no spectroscopic information
at intermediate phases, with a minimal impact on regions that are well constrained by
data and a small effect on broad-band colours. The strength of this regularisation is
adjusted via the normalisation of w(i,j,l) so that the
value of the colour difference
(U−B) − (B−V)
at maximum luminosity is altered by less than 0.01. The impact of this regularisation on
distance moduli obtained with SALT2 is however controlled (see Sect. 5.4.2).
A.2. Error modeling
For an optimal light curve fit, we need to evaluate the intrinsic SNe Ia scatter about the model in order to weight data accordingly. A perfect evaluation of the covariance of this remaining variability as a function of phase and wavelength would be equivalent to a complete modeling of SNe Ia. This is of course beyond reach so some approximations have to be made. As in G07, we evaluated the intrinsic scatter of a light curve assuming that the residuals were not correlated as a function of phase, and independently broad-band colour uncertainties defined by the scatter of light curve amplitudes as a function of the effective rest-frame wavelength of the observation pass-bands.
The intrinsic scatter of light curves as a function of phase, effective wavelength and X1, is evaluated using the covariance matrix of the best fit model as described in G07 Sect. 6.1.
The broad-band colour uncertainties (K-correction uncertainties is
G07) can be evaluated by minimising the following restricted log likelihood (see
e.g. Harville 1977): 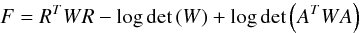 (A.1)where
the first term is the usual χ2 (W being the
inverse of the covariance matrix of the data, and R is the vector of
residuals), and A is the matrix of derivatives of the model with
respect to all parameters for each measurement
(ATWA is the inverse
of the covariance matrix of the best fit parameters). The second term is expected for a
standard log-likelihood, the last one accounts for the correlation among residuals
introduced by the fitted model.
(A.1)where
the first term is the usual χ2 (W being the
inverse of the covariance matrix of the data, and R is the vector of
residuals), and A is the matrix of derivatives of the model with
respect to all parameters for each measurement
(ATWA is the inverse
of the covariance matrix of the best fit parameters). The second term is expected for a
standard log-likelihood, the last one accounts for the correlation among residuals
introduced by the fitted model.
In practice, we have to assume a functional form for the broad-band colour
uncertainties as a function of wavelength since only a limited number of parameters can
be fit. The following two functional forms which exhibit different asymptotic behaviour
have been considered (exponential of polynomial and combination of sigmoids):
![\appendix \setcounter{section}{1} \begin{eqnarray} k_1(\lambda) &=& \exp \left( \sum_{i=0}^4 a_i \lambda^i \right) \nonumber \\ k_2(\lambda) &=& \frac{a_0-a_1}{1+ \exp \left[ ( \lambda - \lambda_0 )/ \Delta \lambda_0 \right]} + a_1 \nonumber \\ \label{eq:colorscatterfunction} && + \frac{a_2-a_1}{1+ \exp \left[( - \lambda + \lambda_2 )/ \Delta \lambda_2\right] }\cdot \end{eqnarray}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq366.png) (A.2)An
additional scatter for the observed U-band data is evaluated at the
same time, since it suffers from sizable calibration systematic uncertainties.
(A.2)An
additional scatter for the observed U-band data is evaluated at the
same time, since it suffers from sizable calibration systematic uncertainties.
Instead of minimising the restricted log likelihood of Eq. (A.1) on the full training set of SALT2, which comprises light curves and spectra, we apply the minimisation to a compressed data set. For each light curve of the SALT2 training, a flux scale is fitted to improve the match to the best fit model. An effective wavelength of the corresponding rest-frame filter is also computed (accounting for the spectrum of the SN in the filter integration window). Those flux scales with their associated uncertainties and the effective wavelength provide us the data needed for an estimate of the broad-band colour uncertainties. In this process, we fit simultaneously corrections to the colour variation law and the colours of the average SED.
This technique has been successfully tested on Monte Carlo simulations. The corrections
to the SED and colour variation law turn out to be negligible at the end of the
minimisation: about one milli-magnitude for the colours of the SED and 4% of the colour
variation amplitude in the U-band (or 0.005 mag difference in
U-band for  ), with the caveat that the
U-band dispersion σU has
been accounted for in the training of SALT217.
), with the caveat that the
U-band dispersion σU has
been accounted for in the training of SALT217.
The remaining scatter as a function of wavelength for the two parameterizations of Eq. (A.2) is shown in Fig. 8. We also obtain σU = 0.11 ± 0.02.
A.3. Propagation of the model statistical uncertainties
As discussed in Sect. 4.1, the statistical uncertainties of the SED sequence model have to be propagated to the estimates of luminosity, shape and colour of the SNe. Indeed, they introduce redshift-dependent uncertainties on distances that do not cancel with an infinite number of SNe.
For SALT2, we use the covariance matrix of the training, including the residual scatter
evaluated in the previous section. This latter is accounted for by adding to the
covariance matrix of each light curve a term
k(λ)MMT,
where M is a vector containing the model values corresponding to each
photometric point, and λ is the effective rest-frame wavelength of the
filter used for the observations. Let θ be the parameters of the model,
Cθ their covariance matrix, and
ηi the parameters
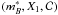 of a given SN, we may
write the χ2 as:
of a given SN, we may
write the χ2 as: ![\appendix \setcounter{section}{1} \begin{equation} \chi^2 = \sum_{i=1,N} \left[ f_i - m_i(\theta, \eta_i) \right]^T W_i \left[ f_i - m_i(\theta, \eta_i) \right] \label{eq:annexe:chi2_glob} \end{equation}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq378.png) (A.3)where
(A.3)where
-
f i are the flux measurements of SN i;
-
m i is the model;
-
W i incorporates both the measurement uncertainties and the error model discussed previously.
![\appendix \setcounter{section}{1} \begin{equation} \label{eq:eta-theta} \eta_i = (B_i W_i B_i^T)^{-1} \left[ B_i W_i (r_i - A_i^T \delta \theta) \right] \end{equation}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq386.png) (A.4)where
ri = fi − mi(θ0,ηi,0),
Ai = dmi/dθ
and
Bi = dmi/dηi.
This can be inserted into the “global” normal equation:
(A.4)where
ri = fi − mi(θ0,ηi,0),
Ai = dmi/dθ
and
Bi = dmi/dηi.
This can be inserted into the “global” normal equation: ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:theta-sol} \left[ \sum_{i=1,N} \!\! A_i W_i A_i^T\! - \!D_i^T E_i^{-1} D_i\! \right] \delta \theta\! =\! \!\!\!\sum_{i=1,N}\! \left[\! A_iW_i \!-\!D_i^TE_i^{-1}D_i B_i W_i \right] r_i \end{equation}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq390.png) (A.5)with:
(A.5)with:
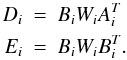 This
defines δθ, and the parameters
δηi are obtained from
Eq. (A.4). The covariance matrix
blocks can be computed:
This
defines δθ, and the parameters
δηi are obtained from
Eq. (A.4). The covariance matrix
blocks can be computed: 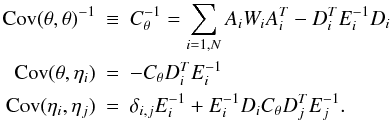 (A.6)In
the expression (A.6) for
Cov(ηi,ηj),
the first term accounts for the photometric noise, the second accounts for the model
noise. Note that when considering
Cov(ηi,ηi),
the second term does not vanish when the photometric data of this SN becomes infinitely
precise, i.e. Wi → ∞.
(A.6)In
the expression (A.6) for
Cov(ηi,ηj),
the first term accounts for the photometric noise, the second accounts for the model
noise. Note that when considering
Cov(ηi,ηi),
the second term does not vanish when the photometric data of this SN becomes infinitely
precise, i.e. Wi → ∞.
These expressions are valid for SNe in the training sample. We can as well compute the contribution of model uncertainty to the fit of a single SN which is not in the training sample. The χ2 is the same as above, but θ is fixed (and δθ = 0). Using the same notations as above, the normal equation for δηi now reads:
 and the
uncertainty of the model affects the ηi
estimator
and the
uncertainty of the model affects the ηi
estimator  by offsetting ri:
by offsetting ri:
![\appendix \setcounter{section}{1} $$ \frac{{\rm d} \hat{\eta_i}}{{\rm d} \theta} = \frac {{\rm d} \hat\eta_i}{ {\rm d} r_i} \frac{{\rm d} r_i}{{\rm d} \theta} = \left [ (B_i W_i B_i^T)^{-1} B_i W_i \right] \left [ A_i^T \right ] = E_i^{-1} D_i. $$](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq400.png) So the covariance
of SN parameters due to model uncertainties reads:
So the covariance
of SN parameters due to model uncertainties reads:
 which
is identical to the second term in expression (A.6) above. So the expression of the covariance of SN parameters’ estimators
does not depend on their belonging to the training sample. Note however that when the
training sample increases, this covariance decreases, as we expect.
which
is identical to the second term in expression (A.6) above. So the expression of the covariance of SN parameters’ estimators
does not depend on their belonging to the training sample. Note however that when the
training sample increases, this covariance decreases, as we expect.
We can now compute a covariance matrix of distance moduli (μi) of the whole sample due to light curve model statistical uncertainties. This covariance matrix is added to other noise sources and used in the cosmological fit. It reads:
 where
V is defined by
μi = VTηi
(V = {1,α, − β} from Eq. (5)).
where
V is defined by
μi = VTηi
(V = {1,α, − β} from Eq. (5)).
The uncertainty of the difference between the average distance modulus in a redshift bin [z1,z2] and the average on the whole sample (see Fig. 16) is given by
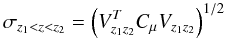 where
Vz1z2(i) = (1/Nz1z2 − 1/N)
if
z1 < zi < z2,
and − 1/N if not,
zi being the redshift of the SN number
i,
Nz1z2
the number of SNe in the bin, and N the total number of supernovae in
the sample.
where
Vz1z2(i) = (1/Nz1z2 − 1/N)
if
z1 < zi < z2,
and − 1/N if not,
zi being the redshift of the SN number
i,
Nz1z2
the number of SNe in the bin, and N the total number of supernovae in
the sample.
A.4. Public release of the light curve fitter
The SALT2 model parameters used in this paper, the code to fit light curves, the calibration files and models of the instrument responses are public. They can be found at http://supernovae.in2p3.fr/~guy/salt/ along with some documentation. Note however that the usage of this package requires some care, in particular the rest-frame wavelength validity range of the model is limited. Also, the photometric calibration of the SNe light curves of the training sample is imprinted in the spectral model broadband colours. Hence it is better suited to retrain the model when more precise calibrations of those samples become available, or when new data sets that may improve the model can be used. SALT2 is indeed more a method than a final spectral model. Finally, as described in detail in this paper, the uncertainties of the model parameters have to be taken into account (training sample statistics, calibration uncertainties, residual scatter model), and the codes to propagate those are not easy to distribute. For all these reasons, users are welcome to discuss with the author of their usage of the light curve fitter.
Appendix B: Flux bias on PSF photometry
We consider the standard PSF photometry when flux and position are fitted simultaneously,
using a PSF P(x,y), normalised to 1. We call the flux
and position parameters
(f,δx,δy).
Assuming the noise is stationary and the object faint, the weight matrix of their
estimators reads:
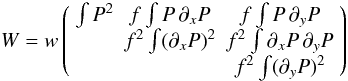 (B.1)where
w is the inverse of the noise variance per unit area.
(B.1)where
w is the inverse of the noise variance per unit area.
Assuming that the PSF is symmetric in x and y, the non-diagonal terms vanish, and the flux and position estimates are thus independent. The sums over pixels have been replaced by integrals which is adequate for our well sampled images. The flux estimator reads:
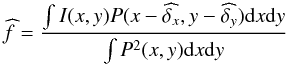 where
both sums run over pixels, the true position is assumed to be (0,0), the
fitted position is
where
both sums run over pixels, the true position is assumed to be (0,0), the
fitted position is  , and I is the sky-subtracted image. Assuming
that the image reads:
, and I is the sky-subtracted image. Assuming
that the image reads:
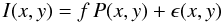 (with ϵ
representing the measurement noise: E [ ϵ ] = 0, and
its variance reads w-1 per unit area), the flux estimator
expectation value can be written as:
(with ϵ
representing the measurement noise: E [ ϵ ] = 0, and
its variance reads w-1 per unit area), the flux estimator
expectation value can be written as: ![\appendix \setcounter{section}{2} \begin{eqnarray} E\left[\widehat{f}\right] &= & f \frac {E\left[\int P(x,y)P\left(x-\widehat{\delta_x},y-\widehat{\delta_y}\right){\rm d}x{\rm d}y\right] }{\int P^2(x,y){\rm d}x{\rm d}y} \nonumber \\ & = & f \left\{ 1 + \frac{1}{2}\frac{E[\widehat{\delta_x}^2]\int P\partial^2_xP+E[\widehat{\delta_y}^2]\int P\partial^2_yP }{\int P^2(x,y){\rm d}x{\rm d}y} +{\mathcal O}(\delta^4) \right\}. \nonumber \end{eqnarray}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq428.png) The
flux and position variances read:
The
flux and position variances read: ![\appendix \setcounter{section}{2} \begin{eqnarray*} {\rm Var}\left[\widehat{f}\right] &=& \left( w \int P^2 \right) ^{-1}\nonumber \\ {\rm Var}\left[\widehat{\delta_x}\right] &=& E\left[\widehat{\delta_x^2}\right] = \left( w f^2 \int (\partial_x P)^2 \right) ^{-1}= \left(- w f^2 \int P \partial^2_x P \right) ^{-1} \nonumber \end{eqnarray*}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq429.png) hence,
hence,
![\appendix \setcounter{section}{2} \begin{equation} E[\widehat{f}] \simeq f \left\{ 1 - \frac{{\rm Var}\left[\widehat{f}\right]}{f^2} \right\} \cdot \label{eq:bias_var_flux} \end{equation}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq430.png) (B.2)So, the PSF flux is
underestimated at low S/N, due to the inaccuracy of the position, because position shifts
yield on average smaller PSF fluxes. Note that expression (B.1) assumes that flux and position are measured from the same data,
and also assumes a stationary noise and a faint object. The neglected higher order terms
may become important below S/N of a few. For S/N above 1, the bias is smaller than the
uncertainty, but should anyway be studied if averages of faint fluxes are used in the
analysis, such as at the high redshift end of a Hubble diagram.
(B.2)So, the PSF flux is
underestimated at low S/N, due to the inaccuracy of the position, because position shifts
yield on average smaller PSF fluxes. Note that expression (B.1) assumes that flux and position are measured from the same data,
and also assumes a stationary noise and a faint object. The neglected higher order terms
may become important below S/N of a few. For S/N above 1, the bias is smaller than the
uncertainty, but should anyway be studied if averages of faint fluxes are used in the
analysis, such as at the high redshift end of a Hubble diagram.
For a Gaussian PSF, we have: ![\appendix \setcounter{section}{2} \begin{eqnarray*} {\rm Var}[\widehat{f}] &=& w^{-1} 4 \pi \sigma^2 \nonumber \\ {\rm Var}[\widehat{\delta_x}] &=& w^{-1} 8 \pi \sigma^4 / f^2 \nonumber \end{eqnarray*}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq431.png) where
σ stands for the Gaussian rms. This, combined with Eq. (B.1), gives
where
σ stands for the Gaussian rms. This, combined with Eq. (B.1), gives
![\appendix \setcounter{section}{2} \begin{equation} E[\widehat{f}] = f \left\{ 1 - \frac{E[\widehat{\delta_x}^2+\widehat{\delta_y}^2]}{4 \sigma^2} \right\}\cdot \label{eq:bias_var_pos} \end{equation}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq433.png) (B.3)Schematically, the
measurement of a supernova light curve consists of a fit of a common position and varying
fluxes to an image series. As for a single image, the flux estimators are biased:
(B.3)Schematically, the
measurement of a supernova light curve consists of a fit of a common position and varying
fluxes to an image series. As for a single image, the flux estimators are biased:
![\appendix \setcounter{section}{2} $$ E[\widehat{f_i}] = f_i \left\{ 1 - \frac{E[\widehat{\delta_x}^2+\widehat{\delta_y}^2]}{4 \sigma_i^2} \right\} \label{eq:bias_var_pos2} $$](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq434.png) where
fi is the supernovae flux at epoch
i and σi is the rms of the
PSF (assumed Gaussian) at the same epoch. One may note that the images with the poorest
seeing are the less affected. We assume the position to be measured from the images
series. Its variance reads:
where
fi is the supernovae flux at epoch
i and σi is the rms of the
PSF (assumed Gaussian) at the same epoch. One may note that the images with the poorest
seeing are the less affected. We assume the position to be measured from the images
series. Its variance reads:
![\appendix \setcounter{section}{2} $$ E[\widehat{\delta_x}^2+\widehat{\delta_y}^2] = 2 {\rm Var}[\widehat{\delta_x}] = \left( \sum_i \frac {f_i^2}{4 \sigma_i^2 {\rm Var}[\widehat{f_i}]} \right)^{-1} $$](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq438.png) where
the sum runs over images. The amplitude of the light curve will be fitted to the
individual image measurements
where
the sum runs over images. The amplitude of the light curve will be fitted to the
individual image measurements  , and
is a linear combination of those. The least squares estimator of the amplitude A of the
light curve reads:
, and
is a linear combination of those. The least squares estimator of the amplitude A of the
light curve reads:
![\appendix \setcounter{section}{2} $$ \widehat{A} = k \sum_i a_i \widehat{f_i}, {\rm with} \,\,\, a_i = \frac{f_i}{{\rm Var}[\widehat{f_i}]} $$](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq440.png) where
k is a global constant depending on the chosen definition of A. We now
propagate the flux bias at individual epochs into the lightcurve amplitude:
where
k is a global constant depending on the chosen definition of A. We now
propagate the flux bias at individual epochs into the lightcurve amplitude:
![\appendix \setcounter{section}{2} \begin{eqnarray*} \widehat{A} &=& k \sum_i \frac{f_i^2}{{\rm Var}[\widehat{f_i}]} \left\{ 1 - \frac{E[\widehat{\delta}^2]}{4\sigma_i^2}\right\} \nonumber \\ &=& k \left\{ \sum_i \frac{f_i^2}{{\rm Var}[\widehat{f_i}]} - {E[\widehat{\delta}^2]} \left(\sum_i \frac{f_i^2}{4 {\rm Var}[\widehat{f_i}] \sigma_i^2} \right) \right \} \nonumber \\ &=& k \left\{ \sum_i \frac{f_i^2}{{\rm Var}[\widehat{f_i}]} - 1 \right\}. \nonumber \end{eqnarray*}](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq442.png) Using
that:
Using
that:
![\appendix \setcounter{section}{2} $$ E[\widehat{A}] = A \left( 1 - \frac{{\rm Var}[\widehat{A}]}{A^2} \right) $$](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq444.png) and
we can hence use the relative uncertainty of the lightcurve amplitude as an indicator of
its own bias, when position and amplitude are measured from the same data.
and
we can hence use the relative uncertainty of the lightcurve amplitude as an indicator of
its own bias, when position and amplitude are measured from the same data.
All Tables
Average difference of the fitted peak magnitudes obtained with methods A and B after the correction for the host galaxy over-subtraction (Δ), slope of the correlation with fgal (ϵ), and rms for high S/N SNe in faint galaxies (see text for details).
Ratio of measured flux before 22 restframe days (before maximum) to the fitted lightcurve amplitude, averaged over events, for method A.
ΩM and the nuisance parameters with their statistical uncertainties derived from the Hubble diagram fits using either SALT2 or SiFTO.
All Figures
 |
Fig. 1 Statistical uncertainty on magnitudes (left panel) and expected bias on PSF photometry with a simultaneous fit of the position (right panel) as a function of supernova redshift. The different gMrMiMzM MegaCam bands are shown respectively with green solid, red dashed, black dotted, and blue dashed-dotted curves. |
| In the text | |
 |
Fig. 2 Residuals from the calibration fit ( PSF magnitude minus aperture magnitude of the catalog) for CCD #13, band rM in field D1. Each point is a tertiary star. Those marked with open symbols were excluded from the fit based on cuts on rms, magnitude, and number of observations. The fit is performed iteratively with a 2.5σ outlier rejection. |
| In the text | |
 |
Fig. 3 Rms of the differences between PSF and aperture magnitude of the tertiary stars for the gMrMiMzM bands. In each histogram, there are 36 × 4 entries, each corresponding to a CCD/field combination, for which a zero point is determined. |
| In the text | |
 |
Fig. 4 Differences between PSF and aperture magnitudes of the tertiary stars in the gMrMiMzM bands as a function of the colour of stars (gray dots). The black points with error bars represent the average deviation and its uncertainty in bins of colour. Typical SNe colours at maximum light are marked with red dotted vertical lines. The blue curve on the top panel shows the effect of the PSF wavelength dependent correction on synthetic magnitudes obtained with PHOENIX stellar models. The colours of BD+17 4708 are marked by the black vertical lines. |
| In the text | |
 |
Fig. 5 Average differences between PSF and aperture magnitude of the tertiary stars in gMrMiMzM bands as a function of the star magnitude (once corrected for the colour dependent terms). The back error bars represent the statistical uncertainty on the average. The shaded areas represent the uncertainty on aperture magnitudes due to a systematic uncertainty on the residual background in the images used for calibration (0.1 ADU per pixel for gMrMzM, 0.2 ADU for the iM-band). |
| In the text | |
 |
Fig. 6 SALT2 colour variation law for |
| In the text | |
 |
Fig. 7 (B−V) corrected for stretch as a function of (U−B) for a selected sample of SNLS SNe as measured by SiFTO (open circles) along with the linear relations of Eq. (4) and Table 5 (a and c terms, solid lines) and the synthetised ones of SALT2 (dashed line) for the two colour scatter hypothesis. SALT2 does not contain explicitly colour relations as SiFTO, but the a,b and c coefficients can still be derived from the model. |
| In the text | |
 |
Fig. 8 SALT2 training sample broad-band colour dispersion as a function of wavelength for two different functional forms (solid curve: EXPPOL, dashed curve: SIGMOID). |
| In the text | |
 |
Fig. 9 From top left to bottom right, |
| In the text | |
 |
Fig. 10 Differences of estimated (B−V) colour at maximum from the fit of rMiM or gMrM light curves for both fitters (top: SALT2, bottom: SiFTO). |
| In the text | |
 |
Fig. 11 Comparison of SALT2 and SiFTO parameters for a selected sub-sample of SNe of Table 11. Linear transformations of Eq. (6) and Table 6 were applied to SALT2 parameters. Each dot is a SN, the light grey areas represent the rms of the distribution in redshift bins, and the dark areas the uncertainty on the average values. The red curve on the top panel for the rest-frame B band peak magnitude is the expected discrepancy due to the differences of the SALT2 and SiFTO spectral sequences. |
| In the text | |
 |
Fig. 12 Residuals from the Hubble diagram of the best fit ΛCDM cosmological model obtained with the two light curve fitters SALT2 (top) and SiFTO (bottom). |
| In the text | |
 |
Fig. 13 Correlations of residuals from the Hubble diagram obtained with SiFTO and SALT2. The outlier is 04D2cc for which data in the rising part of light curves is missing; the statistical uncertainty on its distance modulus μ is large with both light curve fitters (0.47 with SiFTO and 0.28 with SALT2, the difference being due to differences in the model uncertainties, or “error snake”). |
| In the text | |
 |
Fig. 14 Contours at 68.3% confidence level (accounting only for statistical uncertainties) for the fit of ΛCDM cosmology to the SNLS third year sample (without additional SNe samples) for SALT2 (thin red curve), SiFTO (thin blue) and the combination of the two (thick black), on the light curve parameters. The dotted inclined ellipse represents the 68.3% confidence level from Astier et al. (2006) which includes 44 low redshift SNe along with the 71 SNe from the SNLS first year sample. |
| In the text | |
 |
Fig. 15 Impact of the calibration uncertainties of Table 8 on the SALT2 values of |
| In the text | |
 |
Fig. 16 Uncertainties on the average distance modulus μ in redshift bins of 0.2: impact of the statistical uncertainty of the training (for SALT2, thin solid curve), calibration uncertainties (dotted curve), residual scatter model (dotted short dashed curve), systematic uncertainty due to SALT2 regularisation (dotted long dashed curve) and differences between results obtained with the two light curve fitters (thick solid curve). Values of α and β that minimise residuals from the Hubble diagram were used. |
| In the text | |
 |
Fig. 17 α and β estimates in redshift bins of 0.2 using SALT2 (filled circles), SiFTO (open circles) and the combined light curve parameters (gray triangles, see Sect. 5.3). |
| In the text | |
 |
Fig. 18 Contours at 68.3% confidence level for the fit to a ΛCDM cosmology from the SNLS third year sample (without additional SNe samples) accounting for: Hubble diagram statistical uncertainties and the difference between SALT2 and SiFTO results (dotted curve), photometric calibration (dashed curve), model training statistical uncertainties and Malmquist bias uncertainties (thin solid), and finally the potential β evolution (thick solid curve). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



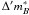
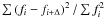
![\appendix \setcounter{section}{2} $$ \frac{{\rm Var}[\widehat{A}]}{A^2} = \left( \sum_i \frac{f_i^2}{{\rm Var}[\widehat{f_i}]} \right)^{-1}\cdot $$](/articles/aa/full_html/2010/15/aa14468-10/aa14468-10-eq443.png)