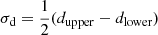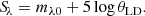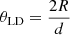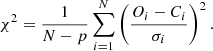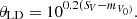| Issue |
A&A
Volume 697, May 2025
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202553815 | |
| Published online | 01 May 2025 | |
Surface brightness-color relations for red giant branch stars using asteroseismic radii and Gaia distances (the ARD method)
1
Yunnan Observatories, Chinese Academy of Sciences, 396 YangFangWang, Guandu District, Kunming 650216, PR China
2
Key Laboratory for Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, PO Box 110, Kunming 650216, PR China
3
International Centre of Supernovae, Yunnan Key Laboratory, Kunming 650216, PR China
4
CAS Key Laboratory of Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China
5
School of Astronomy and Space Science, University of the Chinese Academy of Sciences, Beijing 101408, China
6
Department of Astronomy, China West Normal University, Nanchong, China
⋆ Corresponding authors: xiongjianping@ynao.ac.cn, cxf@ynao.ac.cn
Received:
20
January
2025
Accepted:
13
March
2025
Context. Surface brightness-color relations (SBCRs) are essential for estimating distances and stellar properties. Previously, SBCRs were based on a limited number of red clump giant (RCG) stars, and red giant branch (RGB) stars with infrared interferometric measurements or eclipsing binaries with high-precision radii measurements, resulting in discrepancies in precision and accuracy. Recently, the large number of RGB stars with asteroseismic parameters and precise Gaia distance measurements has enabled the development of more accurate and robust SBCRs.
Aims. The asteroseismic radius and Gaia distance (ARD) method has been proposed to establish the SBCRs for late-type stars.
Methods. We selected Kepler RGB stars with high-precision asteroseismic radii (uncertainties < 1%) and crossmatched them with 2MASS, APASS, and Gaia to obtain Johnson-B, Johnson-V, G, J, H, and Ks-band photometric data. After applying selection criteria, we obtained 626 RGB stars to build the SBCR. Among these, 100 RGBs were used as independent validation for the distance, and the remaining samples were used to fit the SBCR.
Results. First, using 526 targets with asteroseismic radii and Gaia distances, nine SBCRs were proposed based on 2MASS (J, H, Ks), APASS (Johnson-B, Johnson-V), and Gaia (G) photometry. The average rms scatter in these relations is 0.075 mag, which corresponds to an uncertainty of approximately 3.5% in distance. These relations were further validated using 100 independent samples with Gaia distances, showing no bias, with a dispersion of approximately 3%. Compared to interferometric measurements, a systematic underestimation of 2.3% was observed, and the discrepancy decreases as the angular diameter increases. Additionally, the distances of eclipsing binaries in the Large Magellanic Cloud and Small Magellanic Cloud obtained using our SBCRs are generally consistent with the ones measured in the literature, with a dispersion of 1% and a slight overestimation of 1% to 2.5%.
Conclusions. The ARD method capitalizes on two key advantages for precise stellar distance determination: a statistically robust sample of homogeneous RGB stars with low observational costs, and independent distance verification through Gaia data. Such SBCRs can be further calibrated and expanded more efficiently and effectively.
Key words: asteroseismology / parallaxes / stars: distances / stars: fundamental parameters / stars: late-type
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Accurate distance measurement is a cornerstone of astrophysics, underpinning our understanding of the structure, scale, and expansion of the Universe. Determining precise distances to celestial objects enables us to derive fundamental properties such as luminosity and size, which are essential for testing theoretical models and exploring cosmic phenomena (Freedman & Madore 2010). Among the various distance determination methods, surface brightness-color relations (SBCRs) have emerged as powerful tools for estimating stellar angular diameters from photometric data (Barnes et al. 1976; van Belle 1999; Kervella et al. 2004; Di Benedetto 2005), thereby facilitating accurate distance measurements to stars and their host galaxies (Wesselink 1969; Lacy 1977; Pietrzyński et al. 2013, 2019; Graczyk et al. 2020). With the angular diameters derived from SBCR, when the distance is known, applying the SBCR can directly yield the stellar radius. Conversely, if the radius is known, a reliable distance can be calculated.
As a successful application, Pietrzyński et al. (2019) calibrated the SBCR using 41 nearby red clump giant stars (RCGs) within the V − K color range of 2.1 to 2.8. These RCGs were observed with precise near-infrared photometry at the South African Astronomical Observatory (Laney et al. 2012), and their angular diameters were measured using the ESO VLTI and PIONIER instruments (Gallenne et al. 2018) with a precision of 1%. Combined with 20 eclipsing binaries with radii determination, this relation was further used to measure the distance to the Large Magellanic Cloud (LMC) with a precision of 1%. Additionally, the same SBCR was employed to estimate the distance to the Small Magellanic Cloud (SMC), achieving a precision of 2% (Graczyk et al. 2020).
To calibrate the SBCRs, the angular diameters obtained through long-baseline interferometry (LBI) are usually required. Besides the SBCR presented by Pietrzyński et al. (2019), Nardetto et al. (2020) calibrated the SBCR for red giant stars in the 2.1 ≤ V − K ≤ 2.5 color range using eight G/K-type giants with the homogeneous VEGA/CHARA interferometric data. This demonstrated that the average precision on the limb-darkened angular diameters was 2.4%. Moreover, Salsi et al. (2020, 2021) collected approximately 70 F5/K7 type giants with measured angular diameters from the JMMC Measured Stellar Diameters Catalog (JMDC) (Duvert 2016) to develop the SBCR within the V − K color range of 1.8 to 3.8. Additionally, they established SBCRs for F5/K7 type dwarfs and subgiants, M dwarfs and subgiants, and M giants. The precision of the angular diameter measurements was estimated to be approximately 1% to 2.7%.
The advent of space missions such as Gaia has provided unprecedented parallax data. The SBCRs were also established by detached eclipsing binaries. As we all know, accurate stellar radii can be determined through the combination of time-domain spectroscopic and photometric observations of eclipsing binaries (Xiong et al. 2023; Torres et al. 2010), in conjunction with the distance (or trigonometric parallax), facilitating the calibration of the SBCRs. For example, Graczyk et al. (2021) used 28 eclipsing binaries with accurately determined radii and Gaia EDR3 parallaxes to construct the SBCRs, except for V − K color. They also established the SBCRs combining the Johnson B, Gaia G and 2MASS JHKs bands. However, these relations only cover dwarf and subgiant stars. The precision of angular diameters prediction for A-, F-, and G-type dwarf and subgiant starswas ∼1%.
Recent advancements aim to address these challenges by expanding SBCR calibrations to larger and more diverse samples of stars with high-precision measurements. To date, SBCRs have been proposed for various spectral types, covering both dwarfs and giants, and more than 20 distinct SBCRs have been developed (Salsi et al. 2020; Valle et al. 2024a), most of which are consistent within the V − K range of 1.5 to 2.5 (Nardetto et al. 2023). Beyond this range, these SBCRs exhibit significant discrepancies. The precision and robustness of the SBCR are highly dependent on the quality and quantity of the samples. However, the observational costs of LBI are relatively high, and there is a scarcity of detached eclipsing binary samples with high-precision time-domain spectroscopic and photometric data. Consequently, the establishment of SBCRs has been limited by the small number of available samples. Even among giants of the same spectral type, their V − K color ranges are often truncated. This limitation adversely affects the uncertainty of SBCRs.
Fortunately, thanks to the high-precision time-domain photometric data provided by the space missions Kepler (Borucki et al. 2010) and Transiting Exoplanet Survey Satellite (TESS, Ricker et al. 2015), numerous studies have produced large samples of red giant branch (RGB) and RCG stars (exceeding several thousand) with parameters such as stellar radii, ages, and masses determined using high-precision asteroseismic methods (Li et al. 2022; Wang et al. 2023; Schonhut-Stasik et al. 2024). The typical precision of radius is 4% (Pinsonneault et al. 2014; Martig et al. 2015; Valle et al. 2024b). Among these, Wang et al. (2023) have presented a catalog of 1153 Kepler RGB stars, with the radii, masses, and ages of these stars having been determined using the asteroseismic model. They combined radial-mode oscillation frequencies, gravity-mode period spacings, Gaia luminosities, and spectroscopic data from LAMOST (Large Sky Area Multi-Object fiber Spectroscopic Telescope, Cui et al. 2012; Liu et al. 2020) and APOGEE (Apache Point Observatory Galactic Evolution Experiment, Majewski et al. 2017) to characterize these stars, and the precision of radius measurements reached around 1%. Moreover, Gaia DR3 observed nearly 1.5 billion targets, providing high-precision trigonometric parallaxes and distances (Bailer-Jones et al. 2021; Gaia Collaboration 2023). This extensive data will significantly enhance our calibration of SBCRs for RGB stars.
Therefore, in this paper, we aim to establish the SBCR for RGB stars based on their asteroseismic radii and Gaia DR3 distances. The structure of the paper is as follows. Section 2 describes the sample selection and the reduction of observational data. In Sect. 3, we present the establishment of the SBCR. Section 4 presents the validation of the SBCR in this paper. Finally, Sect. 5 discusses the results and provides a summary of our findings.
2. Data
In this paper, we obtained our initial samples from Wang et al. (2023). We first compiled a sample of 1153 RGB stars, each with a radius measurement precision of 1%. Next, we acquired their distances and multiband photometry. In this section, we detail the selection criteria used to refine our samples.
2.1. Gaia distance
Gaia DR3 has provided 1.5 billion stars with parallax measurements, However, due to the nonlinear inverse relationship between parallax and distance and the significant measurement uncertainties (especially for distant stars), directly converting parallax values into distances can result in large errors and unphysical negative distances. Bailer-Jones et al. (2021) transferred the parallaxes to distances using a Bayesian approach based on a prior Galactic spatial distribution. We crossmatched the initial sample of 1153 stars with the geometric distances from Bailer-Jones et al. (2021) and obtained G-band photometry by crossmatching with Gaia DR3 data. After crossmatching, we excluded samples with RUWE > 1.4 and ones with distance uncertainties exceeding 10%. Our estimates of distance uncertainties (σd) are as follows:
where dlower and dupper are the 16th and 84th percentiles of the distances presented by Bailer-Jones et al. (2021).
2.2. Photometric selection
2.2.1. Visible photometry
The American Association of Variable Star Observers (AAVSO) Photometric All-Sky Survey (APASS) project aims to bridge the observational gap left by the shallow two-bandpass Tycho-2 photometric catalog. APASS covers a magnitude range from 10.5 mag to mag. In APASS DR91, the project has provided Johnson-B, V and Sloan g, r, i band observations for a total of 61 176 401 stars, achieving a photometric accuracy of 0.02 mag (Henden et al. 2015, 2016). In Gaia DR3, magnitudes in the G, BP, and RP bands are provided for 1.5 billion stars. The high-precision magnitudes in the G band are measured through the image parameter determination process, which employs a complex model that incorporates extensive calibrations and a shape-based point spread function (PSF). In contrast, magnitudes in the BP and RP bands are extracted from low-resolution spectra (Riello et al. 2021). Therefore, in this paper, we only include the Gaia G-band magnitudes.
2.2.2. Infrared photometry
For the infrared magnitudes, obtaining accurate infrared K magnitudes is a challenge, therefore, in previous studies, such as Salsi et al. (2020), both K and Ks photometries were utilized to calibrate SBCRs. These examinations demonstrated that SBCRs can reliably incorporate both 2MASS K and Johnson K photometries without introducing significant biases (within 2%) in angular diameter measurements. Currently, the Two Micron All Sky Survey (2MASS) remains the most comprehensive all-sky infrared photometric survey, conducting near-infrared observations in the J (1.25 μm), H (1.65 μm), and Ks (2.16 μm) bands. The 2MASS Point Source Catalog (PSC) (Skrutskie et al. 2006) includes 471 million stars. This can provide us with a complete set of infrared magnitude measurements. Consequently, in this paper, we have employed the infrared magnitudes in the Ks band of 2MASS to construct the SBCRs.
To ensure the reliability of our data, we included only photometric measurements with errors below 0.1 mag. Additionally, we performed a 1 arcsec cone search to match magnitudes in the Johnson-B, V, J, H, and Ks bands from APASS DR9 and 2MASS. For selected RGB samples, the mean measurement errors are 0.027 mag and 0.026 mag in the Johnson-B and V bands, 0.022 mag, 0.021 mag, and 0.017 mag in the J, H, and Ks bands, respectively, and 0.003 mag in the G band.
3. Establishment of SBCRs
3.1. Surface brightness calculation
The surface brightness of a star is defined as the flux density emitted per unit angular area. It is related to its intrinsic reddening-free visual magnitude and its limb-darkened angular diameter. This surface brightness can be calculated using the equation presented in Wesselink (1969), as the followingshows:
In Eq. (2), Sλ represents the surface brightness in a specific band, in this paper, λ = (B, V, and G). mλ0 is the reddening-free visual magnitude in B, V, and G bands. θLD is the limb-darkened angular diameter measured from infrared interferometry. In this paper, θLD is calculated by:
where R is the asteroseismic radius of a star and d is the distance obtained from Gaia provided by Bailer-Jones et al. (2021).
To obtain the reddening-free visual magnitude, we measured the color excess E(B − V) using the 3D dust map provided by dustmaps bayestar 2019 (Green et al. 2019). During this process, distance was used as a prior to calculate E(B − V). The visual extinction, AV, was then derived using the total-to-selective extinction ratio, RV = 3.1. Extinctions in other bands were subsequently determined using the extinction coefficients from Table 3 in Wang & Chen (2019), specifically: AB = 1.317 AV, AG = 0.789 AV, AJ = 0.243 AV, AH = 0.131 AV, and AKs = 0.078 AV.
We then calculated the surface brightness by combining the asteroseismic radii with Gaia distances using Eqs. (2) and (3). The Gaussian distributions were constructed based on the magnitudes, distances, radii, and extinction values, incorporating their respective uncertainties. To propagate these uncertainties, we performed 2000 Monte Carlo simulations using these Gaussian distributions. This approach allowed us to calculate the surface brightness in the B, V, and G bands, as well as the extinction-free magnitudes for each band. The uncertainties in these parameters were quantified by the standard deviations of the resulting distributions, which were derived from the Monte Carlo simulations. Finally, we excluded samples with surface brightness errors exceeding 0.1 mag, resulting in a total of 626 RGB samples. The mean errors of surface brightness in the B, V, and G bands are σSB = 0.055 mag, σSV = 0.056 mag and σSG = 0.044 mag respectively. We randomly selected 100 RGB samples for internal validation of the SBCRs and used the remaining 526 RGB samples to fit the SBCRs.
Fig. 1 illustrates the distribution of distances and their associated uncertainties (σd, which is estimated by Eq. 1), indicating that distance uncertainties increase with larger distances. It reveals that the selected samples cover a distance range of 0.5 kpc to 2.8 kpc, with the average distance error of 1.5%.
 |
Fig. 1. Relationship between distance and distance error for our sample. The distance uncertainties (σd) were calculated by Eq. (1). The average distance error of 1.5%. |
3.2. SBCRs fitting
In this paper, we constructed SBCRs in the Johnson-B and V bands and the Gaia G band for RGB stars. We fit these relations using a linear model, y = ax + b. Our fitting procedure employed the orthogonal distance regression (ODR) fitting (scipy.odr). The ODR method was selected because it simultaneously accounts for uncertainties in both the independent (x) and dependent (y) variables. This approach minimizes the overall perpendicular distances from the data points to the fitting line, resulting in a more accurate and reliable regression curve compared to traditional least squares methods that only consider errors in the dependent variable.
In Fig. 2, we compare our SBCR in V − K (SV = (1.230 ± 0.021)(V − Ks)0 + (2.845 ± 0.048)) with ones from the literature. The dashed magenta line, the solid sky blue line, the dotted green line, and the dashed orange line represent SBCRs proposed by Pietrzyński et al. (2019) (SV = (1.330 ± 0.017)[(V − K)0 − 2.405]+(5.869 ± 0.003)), Nardetto et al. (2020) (SV = (1.338 ± 0.160)[(V − K)0 − 2.405]+(5.849 ± 0.027)), Salsi et al. (2021) (SV = 1.22(V − K)0 + 2.864), and Graczyk et al. (2021) (SV = 1.708(V − K)−0.705(V − K)2 + 0.623(V − K)3 − 0.239(V − K)4 + 0.0313(V − K)5 + 2.521), respectively. Black points indicate our fitting samples, while open blue squares represent the RGB and RCG samples compiled from the literature (Pietrzyński et al. 2019; Salsi et al. 2020, 2021). The surface brightness of the literature samples was measured using angular diameters obtained from infrared interferometry and high-precision photometric measurements. Consequently, their dispersion is smaller compared to our samples. Moreover, these samples still fall within the range of our data. The solid red line shows the SBCR fitted in this study, and the dashed red lines represent the uncertainties (1σ) of this fitted curve. The residuals between the surface brightness predicted by the fitted line (C) and the observed surface brightness (O) are shown in the bottom panel.
 |
Fig. 2. Surface brightness-color relations in V − K. Black points represent the 526 RGB stars used in this study to fit the SBCR, with their surface brightness estimates derived from asteroseismic radii and Gaia distances. Open blue squares denote the RGB and RCG samples from the literature (Pietrzyński et al. 2019; Salsi et al. 2020, 2021) used to calibrate the SBCR, with their surface brightness estimates based on angular diameters measured via infrared interferometry. The solid red line illustrates the SBCR fitted in this work, with dashed lines indicating the associated uncertainties (1σ). The dashed magenta line, the solid sky blue line, the dotted green line, and the dashed orange line represent SBCRs proposed by Pietrzyński et al. (2019), Nardetto et al. (2020), Salsi et al. (2021), and Graczyk et al. (2021), respectively. The lower panel displays the residuals of the fit. |
As is shown in Fig. 2, the rms scatter (1σ) of SBCR for V − K in this study is unbiased 0.075 mag. The rms scatters for the relation proposed by Pietrzyński et al. (2019), Nardetto et al. (2020), and Salsi et al. (2021) are 0.018 mag, 0.039 mag, and 0.022 mag, respectively. It can also be seen that our relation generally aligns with the ones in the literature in the V − K range of 2.0 to 2.5. For example, for a specific color such as V − K = 2.3, the SV values obtained using the relations from Pietrzyński et al. (2019), Nardetto et al. (2020), and Salsi et al. (2021) are 5.729 ± 0.018 mag, 5.708 ± 0.039 mag, and 5.670 ± 0.022 mag, respectively. Using our relation, SV = 5.674 ± 0.075 mag. Furthermore, our relation agrees well with the samples from the literature, even for larger V − K values.
To assess the goodness of fit, we used the normalized chi-square (χ2), calculated as Eq. (4). Additionally, the SBCR we derived exhibits good agreement with the high-precision samples provided in the literature.
In Eq. (4), N is the number of data points, p represents the number of fitting parameters (with p = 2 in this study), Oi is the observed surface brightness and Ci corresponds to the predicted surface brightness. σi denotes the observational errors.
The SBCRs in the V − K color index, as well as colors B − J, B − H, B − Ks, V − J, V − H, G − J, G − H, and G − Ks were also derived for RGB stars. Their fitting coefficients (a, b) are presented in Table 1. The corresponding errors of the fitting parameters and rms scatters are also shown in the Table 1. An overview of the nine SBCRs is shown in Fig. 3. In Fig. 3, the solid red lines represent our fitted SBCRs, and the dashed red lines indicate the uncertainties (1σ) of the SBCRs. The bottom panels in each subplot display the residuals between the fitted values and the observations. Black points denote our RGB samples. In the G − Ks color index, the dashed blue line corresponds to the G − Ks SBCR derived by Salsi et al. (2021) (from Table 4 for F5/K7-II/III). It can be seen that the G − Ks relation obtained by Salsi et al. (2021) falls within the uncertainty range of our fit.
 |
Fig. 3. Fitting results of the surface brightness, Sλ, in the Johnson B and V bands and Gaia G band for RGB stars. Black points represent the 526 observed RGB stars. Solid red lines depict the fitting relations, while dashed red lines denote the associated uncertainties. The bottom panel displays the residuals of the fit. |
Fitting coefficients (a and b) of the surface brightness, Sλ, in the Johnson B and V and Gaia G bands for RGB stars.
Fig. 4 presents a comparison of distance predictions calculated by our SBCRs for the fitting samples. In Fig. 4, the x axis represents the geometric distances derived by from Gaia trigonometric parallaxes (Bailer-Jones et al. 2021), while the y axis shows the distances calculated using our SBCRs. The bottom panel displays the distribution of relative residuals between the predicted and observed distances. The relative residuals (Δd/dGaia) were derived by (dSBCR − dGaia)/dGaia, where dSBCR is the distance calculated by SBCR. As is shown in Fig. 4, the distances predicted using SBCRs align well with Gaia’s geometric distances, exhibiting no bias and an average dispersion of approximately 3%–4%. Dispersion increases for more distant targets, but for sources within 1 kpc, the distances we obtain are largely consistent with Gaia’s measurements. Some outliers with larger discrepancies may be attributed to observational limitations. Compared to the Ks band, the dispersion in the J and H bands is slightly larger. The likely reason is the precision of the 2MASS photometry. For the Ks band, the precision is 1%, and in the J and H bands, the precision is only 2%. In our fitting, the overall reliability of the SBCR calibration is shown and the results validate the accuracy of our fitting.
 |
Fig. 4. Validation results of the fitting samples. The x axis represents distances measured by Gaia (Bailer-Jones et al. 2021), while the y axis shows distances estimated using the SBCRs in the Johnson B and V bands and the Gaia G band. The shaded blue area indicates a deviation range of ±3%. The lower subplot displays the distribution of relative errors (Δd/dGaia, Δd was calculated by dSBCR − dGaia). |
4. Validation of SBCRs
We established the SBCRs based on APASS Johnson-B and V, Gaia G, and 2MASS J, H, Ks photometric data. To further assess the accuracy of these relations, we validated them using both internal and external datasets.
4.1. Internal validation
Fig. 5 shows the results of the independent distance calibration performed using the 100 testing samples. These 100 samples are independent of the fitting samples and were not involved in the calibration of the SBCRs. Similar to Fig. 4, the x and y axes represent the geometric distances obtained from Gaia and the distances calculated using our SBCRs, respectively. The bottom panel shows the distribution of relative residuals between the predicted and Gaia distances.
As is shown in Fig. 5, for the 100 independent testing samples, it can be seen that for all nine color indices used, the relative differences between the SBCR-derived distances and Gaia’s geometric distances are much smaller than their standard deviations, and their weighted mean is −0.004. This indicates that there is no systematic bias between the SBCR-derived distances and Gaia’s geometric distances. The average dispersion is around 3%, which corresponds to Gaia’s distance uncertainties. In summary, the overall consistency between the SBCR-predicted distances and Gaia’s geometric distances validates the accuracy scalability of our relations.
 |
Fig. 5. Validation results of the testing samples. Similar to Fig. 4, the x axis represents distances measured by Gaia (Bailer-Jones et al. 2021), while the y axis shows distances estimated using the SBCRs in the Johnson B and V bands and the Gaia G band. The shaded blue area indicates a deviation range of ±3%. The lower subplot displays the distribution of relative errors (Δd/dGaia, Δd was calculated by dSBCR − dGaia). |
4.2. External validation
4.2.1. Comparison of angular diameters
For the external validation, we compiled a sample of 109 RGB and RCG stars from the literature (Pietrzyński et al. 2019; Salsi et al. 2020) (the open squares shown in Fig. 2), all of which have angular diameters measured through infrared interferometry. These angular diameters were obtained using the ESO VLTI and PIONIER instruments, or compiled from the JMDC, achieving a precision of 1%. The JMDC is the most comprehensive and up-to-date catalog listing all interferometric measurements. We used angular diameters (θLD) compiled from the literature as reference measurements. Using the SBCR in V − K color, from Eq. (2), the θLD can be derived by Eq. (5):
Here, SV was derived from the SBCR of V − K color. The magnitudes in the V, K bands and the corresponding extinctions were also sourced from Pietrzyński et al. (2019) and Salsi et al. (2020).
Fig. 6 shows a comparison of angular diameters, where the horizontal axis represents the angular diameters obtained through infrared interferometry as reported in the literature, and the vertical axis represents the angular diameters estimated using our SBCR, and the blue-shaded area indicates a deviation range of ±3%. The bottom panel illustrates the relative differences between the SBCR-derived angular diameters and the directly observed angular diameters. It is evident that, compared to direct infrared interferometry measurements, angular diameters derived by our SBCR exhibit a systematic bias of approximately −2.3%. The uncertainties and slight systematic bias arise from a complex interplay of factors, including asteroseismology, astrometry, and interferometry.
 |
Fig. 6. Comparison of angular diameters (ΘLD). The x axis represents ΘLD directly measured using LBI (Pietrzyński et al. 2019; Salsi et al. 2020, 2021), while the y axis shows angular diameters estimated using the relation proposed in this study (SV = (1.230 ± 0.021)(V − Ks)0 + (2.845 ± 0.048)). The shaded blue area indicates a deviation range of ±3%. The bottom panel displays the relative differences between the SBCR-derived angular diameters and the interferometric angular diameters. The colors of the squares represent the distances of target (derived from parallaxes of HIPPARCOS; van Leeuwen 2007). Darker colors correspond to the larger distances. |
As is demonstrated in Eq. (3), the angular diameter is associated with both the radius and the distance. Consequently, we first obtained the distances of these targets, which are shown by color in Fig. 6, with darker colors representing greater distances. The distances depicted in Fig. 6 have been derived from the parallaxes of HIPPARCOS (van Leeuwen 2007). Although Gaia provides more precise parallaxes, but for sources with G < 6 mag (these targets are very bright (G ∼ 5 mag)), it is evident that the uncalibrated CCD saturation might lead to unreliable astrometric solutions (Lindegren et al. 2018), and in this case, HIPPARCOS might be more reliable (de Burgos et al. 2020). A comparison of the parallaxes of these sources from Gaia (RUWE < 1.4, 40 stars) and HIPPARCOS was also conducted. The results indicate that HIPPARCOS parallaxes tend to overestimate the parallaxes by approximately 0.244 mas in comparison to Gaia. As is shown in Fig. 6, all of these interferometric targets are within 200 pc. Furthermore, it also indicates that the relative difference in angular diameters is getting smaller when the angular diameter is getting larger. Here, due to the lack of interferometric data for more targets, we are unable to quantitatively confirm the discrepancies caused by distance.
In addition to the distance, the radius should also be discussed. In this paper, we adopt the radius provided by Wang et al. (2023). They used a grid-based asteroseismic modeling approach (the grid was calculated by Li et al. 2022) and incorporated two additional observed constraints (e.g. the gravity-mode period spacing and luminosity) to measure the radii, which significantly improved the accuracy of the radii. However, the inclusion of these constraints may introduce systematic bias (see Table 2 in Wang et al. 2023). Additionally, the accuracy here only refers to the measurement uncertainties of the parameters compared to the model. Finding out whether there are systematic biases requires more external data to analyze.
Moreover, combining with Gaia DR3 parallaxes, Valle et al. (2024a) compared asteroseismic radii with the ones estimated using two SBCRs presented by Pietrzyński et al. (2019) and Salsi et al. (2021). These two SBCRs were established by the samples with interferometric angular diameters. They found that, compared to the asteroseismic radii, the stellar radii estimated using the SBCR from Pietrzyński et al. (2019) were overestimated by 1.2%, whereas the ones estimated using the SBCR from Salsi et al. (2021) were underestimated by 2.5%. They also indicated that the deviations are related to the parallax and [α/Fe], and that different deviations are observed in the RCG stars and RGB stars, as well as in the K2 and Kepler data. In addition, discussions in the measurement of radii obtained from asteroseismology and interferometric measurements have been reported by various authors (see, e.g., Hekker 2020; Thomsen et al. 2022). This suggests that there are small but non-negligible differences between the radii measured by asteroseismology and the ones measured by infrared interferometry. However, the sample size and homogeneity of the data limit our understanding of the systematics in asteroseismic radii.
4.2.2. Comparison of distances
Based on eclipsing binary systems with precise radius measurements in the LMC and SMC, SBCRs were used to measure the distances for the LMC and SMC (Pietrzyński et al. 2019; Graczyk et al. 2020). Therefore, similar to Pietrzyński et al. (2019) and Graczyk et al. (2020), we applied our SBCR (SV = (1.230 ± 0.021)(V − Ks)0 + (2.845 ± 0.048)) to measure the distances of the eclipsing binaries in LMC and SMC. In these two works, the distances were estimated by the SBCR in Pietrzyński et al. (2019) (SV = (1.330 ± 0.017)[(V − K)0 − 2.405]+(5.869 ± 0.003)).
Fig. 7 presents a comparison between the distances of the detached eclipsing binary samples in the LMC (left panel) and the SMC (right panel). In Fig. 7, the x axis represents the distances derived from the literature (dr). The y axis shows the distances derived using our relation (dSBCR). The bottom panel illustrates the distribution of relative residuals (Δd/dr = (dSBCR − dr)/dr) between the distances we measured and the ones obtained from the literature. These binaries are the same sources as the ones used by Pietrzyński et al. (2019) and Graczyk et al. (2020). From their samples, we extracted the radii, (V − K)0 values, and V0 magnitudes for the eclipsing binaries. For each eclipsing binary, we obtained the mean value of the distances for two components as the final distance of each binary.
 |
Fig. 7. Comparison of distance (d) estimates for eclipsing binaries in the LMC (left panel) and the SMC (right panel). The x axis represents distances (dr) of eclipsing binaries derived from the literature (dr). The y axis shows distances (dSBCR) estimated using the SBCR developed in this study (SV = (1.230 ± 0.021)(V − Ks)0 + (2.845 ± 0.048)). The shaded blue area indicates a deviation range of ±3%. The bottom panel illustrates the distribution of relative errors (Δd/dr = (dSBCR − dr)/dr). |
As is shown in Fig. 7, for the binaries in the LMC and SMC, the distances predicted using our SBCR are in good agreement with the ones reported in the literature (dispersion ∼1%). Slight overestimations of 2.5% and 1.1% are shown. These overestimations may arise from the systematic underestimation of the angular diameters obtained using our SBCR compared to infrared interferometric measurements. In this paper, we have not applied any corrections for this deviation.
5. Discussion and conclusions
In this paper, we have established the SBCR relation by using 626 RGB stars with high-precision asteroseismic radii and Gaia photometry, and validated this relation using Gaia-independent distances. Additionally, we have further tested the relation through the eclipsing binary distance measurements in the LMC and SMC. Based on the 526 RGB stars with high-precision asteroseismic radii (precision ∼1%) and Gaia’s distances (uncertainties < 3.5%), we developed nine SBCRs for giants in the Johnson B, Johnson V, and Gaia G bands, in combination with 2MASS J, H, and K bands. Graczyk et al. (2021) previously established SBCRs for dwarfs and subgiants within these same bands. Theoretical analysis have demonstrated that SBCRs are influenced by different spectral types and luminosity classes (Salsi et al. 2022). Our work uniquely focuses on giant stars, thereby filling a critical gap in the existing literature. This expansion not only broadens the applicability of SBCRs but also facilitates more accurate distance measurements across a wider variety of stellar types.
Analysis of the test data indicates that the distances derived from the SBCRs across various color indices are consistent with Gaia’s distances, exhibiting a dispersion that increases with distance and averages around 3% to 4%. Compared to the angular diameters measured by infrared interferometry, the angular diameters derived from our SBCRs were underestimated by approximately 2.3%. Moreover, the relative difference in angular diameter decreases with increasing angular diameter. These biases may arise from asteroseismic radii, astrometric measurements and interferometric data. Additionally, distances of eclipsing binaries in the LMC and SMC obtained using our SBCRs are generally consistent with those measured through other relations, showing a dispersion of approximately 1%, but with a slight overestimation of 1%–2.5%. The consistency between the two methods requires further verification with additional data.
The key strength of our study lies in the large and homogeneous samples used to construct the SBCRs, as well as the use of more distant samples observed by Gaia for independent distance validation. In previous studies, the number of samples used to establish and validate the SBCR based on direct measurements was small (approximately 109 RGB and RCG stars, as is summarized by Pietrzyński et al. 2019; Salsi et al. 2020) and these samples were nearby targets (within ∼200 pc). In this study, we used Gaia-independent distances to demonstrate the effectiveness of SBCR for more distant targets. Compared to the observations of infrared interferometry and time-domain spectroscopic and photometric data, we utilized a substantially larger sample, required lower observational costs to obtain sample parameters, and employed a unified methodology to measure angular diameters.
For further calibration, the advancement of comprehensive photometric surveys enables the effective extension of target samples with high-quality radius and distance measurements. The integration of data from missions such as TESS and Gaia will provide comprehensive coverage and consistency of photometric measurements, thereby reducing uncertainties and improving the robustness of SBCRs across different stellar populations.
Acknowledgments
We wish to thank the referee for his/her valuable comments and suggestions, which have helped us further improve this work. This work is supported by the National Natural Science Foundation of China (NSFC) with grant Nos. 12288102, 12125303, 12090040/3, the National Key R&D Program of China (grant No. 2021YFA1600401/2021YFA1600403), the NFSC (grant Nos. 12303106, 12473034, 12103086, 12373037, 12173047), the Postdoctoral Fellowship Program of CPSF (No. GZC20232976), Yunnan Fundamental Research Projects (grant Nos. 202401AT070139, 202101AU070276), the International Centre of Supernovae, Yunnan Key Laboratory (No. 202302AN360001) and the Yunnan Revitalization Talent Support Program–Science & Technology Champion Project (No. 202305AB350003). This work is also supported by the China Manned Space Project of No. CMS-CSST-2021-A10. We thank the Gaia Data Processing and Analysis Consortium (DPAC) for their substantial contributions in producing and releasing high-quality data.
References
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Barnes, T. G., Evans, D. S., & Parsons, S. B. 1976, MNRAS, 174, 503 [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, RAA, 12, 1197 [NASA ADS] [Google Scholar]
- de Burgos, A., Simon-Díaz, S., Lennon, D. J., et al. 2020, A&A, 643, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Benedetto, G. P. 2005, MNRAS, 357, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Duvert, G. 2016, VizieR Online Data Catalog: II/345 [Google Scholar]
- Freedman, W. L., & Madore, B. F. 2010, ARA&A, 48, 673 [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallenne, A., Pietrzyński, G., Graczyk, D., et al. 2018, A&A, 616, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graczyk, D., Pietrzyński, G., Thompson, I. B., et al. 2020, ApJ, 904, 13 [Google Scholar]
- Graczyk, D., Pietrzyński, G., Galan, C., et al. 2021, A&A, 649, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Hekker, S. 2020, Front. Astron. Space Sci., 7, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Henden, A. A., Levine, S., Terrell, D., & Welch, D. L. 2015, American Astronomical Society Meeting Abstracts, 225, 336.16 [NASA ADS] [Google Scholar]
- Henden, A. A., Templeton, M., Terrell, D., et al. 2016, VizieR Online Data Catalog: II/336 [Google Scholar]
- Kervella, P., Thévenin, F., Di Folco, E., & Ségransan, D. 2004, A&A, 426, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacy, C. H. 1977, ApJ, 213, 458 [Google Scholar]
- Laney, C. D., Joner, M. D., & Pietrzyński, G. 2012, MNRAS, 419, 1637 [Google Scholar]
- Li, T., Li, Y., Bi, S., et al. 2022, ApJ, 927, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, C., Fu, J., Shi, J., et al. 2020, ArXiv e-prints [arXiv:2005.07210] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Rix, H.-W., Silva Aguirre, V., et al. 2015, MNRAS, 451, 2230 [NASA ADS] [CrossRef] [Google Scholar]
- Nardetto, N., Salsi, A., Mourard, D., et al. 2020, A&A, 639, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Gieren, W., Storm, J., et al. 2023, A&A, 671, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gieren, W., et al. 2013, Nature, 495, 76 [Google Scholar]
- Pietrzyński, G., Graczyk, D., Gallenne, A., et al. 2019, Nature, 567, 200 [Google Scholar]
- Pinsonneault, M. H., Elsworth, Y., Epstein, C., et al. 2014, ApJS, 215, 19 [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salsi, A., Nardetto, N., Mourard, D., et al. 2020, A&A, 640, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salsi, A., Nardetto, N., Mourard, D., et al. 2021, A&A, 652, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salsi, A., Nardetto, N., Plez, B., & Mourard, D. 2022, A&A, 662, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schonhut-Stasik, J., Zinn, J. C., Stassun, K. G., et al. 2024, AJ, 167, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Thomsen, J. S., Brogaard, K., Arentoft, T., et al. 2022, MNRAS, 517, 4187 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Valle, G., Dell’Omodarme, M., Prada Moroni, P. G., & Degl’Innocenti, S. 2024a, A&A, 690, A327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valle, G., Dell’Omodarme, M., Prada Moroni, P. G., & Degl’Innocenti, S. 2024b, A&A, 685, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Belle, G. T. 1999, PASP, 111, 1515 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, S., & Chen, X. 2019, ApJ, 877, 116 [Google Scholar]
- Wang, Y., Li, T., Bi, S., Bedding, T. R., & Li, Y. 2023, ApJ, 953, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Wesselink, A. J. 1969, MNRAS, 144, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Xiong, J., Liu, C., Li, J., et al. 2023, AJ, 165, 30 [CrossRef] [Google Scholar]
All Tables
Fitting coefficients (a and b) of the surface brightness, Sλ, in the Johnson B and V and Gaia G bands for RGB stars.
All Figures
 |
Fig. 1. Relationship between distance and distance error for our sample. The distance uncertainties (σd) were calculated by Eq. (1). The average distance error of 1.5%. |
| In the text | |
 |
Fig. 2. Surface brightness-color relations in V − K. Black points represent the 526 RGB stars used in this study to fit the SBCR, with their surface brightness estimates derived from asteroseismic radii and Gaia distances. Open blue squares denote the RGB and RCG samples from the literature (Pietrzyński et al. 2019; Salsi et al. 2020, 2021) used to calibrate the SBCR, with their surface brightness estimates based on angular diameters measured via infrared interferometry. The solid red line illustrates the SBCR fitted in this work, with dashed lines indicating the associated uncertainties (1σ). The dashed magenta line, the solid sky blue line, the dotted green line, and the dashed orange line represent SBCRs proposed by Pietrzyński et al. (2019), Nardetto et al. (2020), Salsi et al. (2021), and Graczyk et al. (2021), respectively. The lower panel displays the residuals of the fit. |
| In the text | |
 |
Fig. 3. Fitting results of the surface brightness, Sλ, in the Johnson B and V bands and Gaia G band for RGB stars. Black points represent the 526 observed RGB stars. Solid red lines depict the fitting relations, while dashed red lines denote the associated uncertainties. The bottom panel displays the residuals of the fit. |
| In the text | |
 |
Fig. 4. Validation results of the fitting samples. The x axis represents distances measured by Gaia (Bailer-Jones et al. 2021), while the y axis shows distances estimated using the SBCRs in the Johnson B and V bands and the Gaia G band. The shaded blue area indicates a deviation range of ±3%. The lower subplot displays the distribution of relative errors (Δd/dGaia, Δd was calculated by dSBCR − dGaia). |
| In the text | |
 |
Fig. 5. Validation results of the testing samples. Similar to Fig. 4, the x axis represents distances measured by Gaia (Bailer-Jones et al. 2021), while the y axis shows distances estimated using the SBCRs in the Johnson B and V bands and the Gaia G band. The shaded blue area indicates a deviation range of ±3%. The lower subplot displays the distribution of relative errors (Δd/dGaia, Δd was calculated by dSBCR − dGaia). |
| In the text | |
 |
Fig. 6. Comparison of angular diameters (ΘLD). The x axis represents ΘLD directly measured using LBI (Pietrzyński et al. 2019; Salsi et al. 2020, 2021), while the y axis shows angular diameters estimated using the relation proposed in this study (SV = (1.230 ± 0.021)(V − Ks)0 + (2.845 ± 0.048)). The shaded blue area indicates a deviation range of ±3%. The bottom panel displays the relative differences between the SBCR-derived angular diameters and the interferometric angular diameters. The colors of the squares represent the distances of target (derived from parallaxes of HIPPARCOS; van Leeuwen 2007). Darker colors correspond to the larger distances. |
| In the text | |
 |
Fig. 7. Comparison of distance (d) estimates for eclipsing binaries in the LMC (left panel) and the SMC (right panel). The x axis represents distances (dr) of eclipsing binaries derived from the literature (dr). The y axis shows distances (dSBCR) estimated using the SBCR developed in this study (SV = (1.230 ± 0.021)(V − Ks)0 + (2.845 ± 0.048)). The shaded blue area indicates a deviation range of ±3%. The bottom panel illustrates the distribution of relative errors (Δd/dr = (dSBCR − dr)/dr). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.