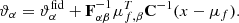| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A154 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202450259 | |
| Published online | 04 October 2024 | |
Parameter estimation from the Lyα forest in the Fourier space using an information-maximizing neural network
1
Istituto Nazionale di Astrofisica-Osservatorio Astronomico di Trieste, Via Tiepolo 11, Trieste, Italy
2
SISSA International School for Advanced Studies, Via Bonomea 265, 34136 Trieste, Italy
3
INFN – Sezione di Trieste, Via Valerio 2, 34127 Trieste, Italy
4
IFPU, Institute for Fundamental Physics of the Universe, Via Beirut 2, 34014 Trieste, Italy
5
Imperial College London, Astrophysics Group, Physics Department, Blackett Lab, Prince Consort Road, London SW7 2AZ, UK
Received:
5
April
2024
Accepted:
11
June
2024
Aims. Our aim is to present a robust parameter estimation with simulated Lyα forest spectra from Sherwood-Relics simulations suite by using an information-maximizing neural network (IMNN) to extract maximal information from Lyα 1D-transmitted flux in the Fourier space.
Methods. We performed 1D estimations using IMNN for intergalactic medium (IGM) thermal parameters T0 and γ at z = 2 − 4, and cosmological parameters σ8 and ns at z = 3 − 4. We compared our results with estimates from the power spectrum using the posterior distribution from a Markov chain Monte Carlo (MCMC). We then checked the robustness of IMNN estimates against deviation in spectral noise levels, continuum uncertainties, and instrumental smoothing effects. Using mock Lyα forest sightlines from the publicly available CAMELS project, we also checked the robustness of the trained IMNN on a different simulation. As a proof of concept, we demonstrated a 2D-parameter estimation for T0 and H I photoionization rates, ΓHI.
Results. We obtain improved estimates of T0 and γ using IMNN over the standard MCMC approach. These estimates are also more robust against signal-to-noise deviations at z = 2 and 3. At z = 4, the sensitivity to noise deviations is on par with MCMC estimates. The IMNN also provides T0 and γ estimates that are robust against continuum uncertainties by extracting small-scale continuum-independent information from the Fourier domain. In the cases of σ8 and ns, the IMNN performs on par with MCMC but still offers a significant speed boost in estimating parameters from a new dataset. The improved estimates with IMNN are seen for high instrumental resolution (FWHM = 6 km s−1). At medium or low resolutions, the IMNN performs similarly to MCMC, suggesting an improved extraction of small-scale information with IMNN. We also find that IMNN estimates are robust against the choice of simulation. By performing a 2D-parameter estimation for T0 and ΓHI, we also demonstrate how to take forward this approach observationally in the future.
Key words: intergalactic medium / quasars: absorption lines / cosmological parameters / diffuse radiation / large-scale structure of Universe
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Lyα forest absorption spectra consist of numerous absorption lines created by the 1s → 2p Lyα transition of the intervening neutral hydrogen gas along the lines of sight to distant quasars. These absorption features trace the underlying distribution of matter in the universe, and thus reveal the cosmic web’s intricate filamentary structure (Finley et al. 2014; Lee et al. 2018). The large-scale structure traced by the Lyα forest is sensitive to the nature of dark matter and dark energy and allows us to test structure formation processes down to small scales. By studying the clustering and distribution of matter on cosmic scales, one can place constraints on the density fluctuations of dark matter (Croft et al. 1998, 1999, 2002; McDonald et al. 2000; McDonald 2003; Viel et al. 2004a) and the equation of state of dark energy (Viel et al. 2003; Coughlin et al. 2019), along with cosmological parameters (Viel et al. 2004b; McDonald et al. 2000; Viel 2006), warm dark matter models (Viel et al. 2013; Iršič et al. 2017), neutrino mass (Palanque-Delabrouille et al. 2015a,b, 2020; Yèche et al. 2017), and so on governing the constitution of the Universe. In the astrophysical context, the Lyα forest is also useful in constraining the intergalactic medium (IGM) temperature, T0, at the cosmic mean density and slope, γ, of the temperature (T)-density (Δ) relation (T = T0(Δ)γ − 1) (Schaye et al. 1999, 2000; Theuns & Zaroubi 2000; McDonald et al. 2001; Becker et al. 2011; Boera et al. 2014; Gaikwad et al. 2021), cosmic reionization (Fan et al. 2006; Worseck et al. 2018), and the impact of various feedback processes (such as supernova (SN) and active galactic nucleus (AGN)-driven outflows) on the IGM that operate during the formation and evolution of galaxies over cosmic time (Aguirre et al. 2001; Oppenheimer & Davé 2006).
The Lyα forest can also act as a complementary source of information to other cosmological probes like the cosmic microwave background (CMB) and galaxy surveys. Combining data from various sources, including the Lyman forest, allows for more robust and precise cosmological parameter estimation, reducing potential biases and uncertainties (Viel et al. 2004c; Viel 2006; Lesgourgues et al. 2007). In order to extract critical information about the large-scale structure, BAO, redshift space distortions, and the nature of cosmic density fluctuations, astrophysicists have investigated the clustering of the Lyα forest, customarily adopting as a summary statistics the power spectrum of the transmitted flux (McDonald et al. 2000, 2006; Croft et al. 2002; Seljak et al. 2006). The advent of high-fidelity spectra also allows one to perform higher-order clustering studies with the Lyα forest (Viel et al. 2004b; Tie et al. 2019; Maitra et al. 2019, 2022a,b).
Moving forward, machine-learning approaches and neural networks (NNs) can enhance the precision and accuracy of parameter estimates from relevant observables, potentially leading to more reliable astrophysical and cosmological models (Gupta et al. 2018; Charnock et al. 2018; Ribli et al. 2019; Nayak et al. 2024). Additionally, a trained NN also offers a substantial boost in computational efficiency when dealing with new datasets (Nygaard et al. 2023), particularly when using the so-called “amortized” method (e.g., Karchev et al. 2022). This feature becomes especially important when estimating parameters from the current age of large astrophysical and cosmological datasets. Parameter estimation using NNs on the real space field information can offer significant constraints on the estimated parameters. However, since NNs are exceptional at picking up nonlinear features in the training data, this makes them susceptible to simulation-specific features in the training data (see Gluck et al. 2023, for example). Thus, robustness against learning unwanted features in the training data can become an issue for inference approaches from the real space field.
An alternative approach is to work in the Fourier domain to filter out such simulation-specific nonlinearities in real space and draw only relevant information from the Fourier space using NNs. In the past, NN approaches have been used to estimate parameters from the Fourier space that were more accurate and robust in comparison to traditional maximum likelihood approaches from the power spectrum (see Villaescusa-Navarro et al. 2022, for example). Some of these applications have also focused on the Lyα forest to extract thermal parameters (Alsing et al. 2018) or detect large-scale power enhancement in the power spectrum due to patchy reionization (Molaro et al. 2022, 2023). Here, we work on extracting maximal information out of the data in the Fourier space using NNs and then compare this approach with traditional likelihood-based approaches using the power spectrum. In particular, we use information-maximizing neural networks (IMNNs, Charnock et al. 2018) to extract maximal information from the Fourier space data and enhance the parameter estimation. The ability of an IMNN to extract almost lossless information for parameter inferences has been demonstrated in Makinen et al. (2021) for correlated normal and lognormal fields with cosmological power spectra. Working in Fourier space, while reducing data dimensionality, also retains relevant information regarding the clustering of the Lyα forest.
In this work, we mainly focus on 1D parameter estimation and its robustness for the thermal parameters, T0 and γ, and cosmological parameters, σ8 and nS, individually. This is because training the NNs for joint parameter estimation in many dimensions requires simulations to have simultaneous parameter variations (similar to Nayak et al. 2024) that we do not have access to at the present time. As a proof of concept, we perform a 2D joint parameter estimation for T0 and the H I photoionization rate, ΓHI, which can be varied simply as a post-processing step during the forward modeling of mock Lyα forest spectra without the need to run a new simulation. This is done to demonstrate how to take forward the IMNN approach in the future observationally for a full N-D parameter estimation. While such endeavors will require a vast array of simulations for training the NN, one can draw inspiration from recent works related to generating significantly efficient simulated training examples. For example, one way to provide the necessary training examples would be to use fast emulators, like the recently released 21cmEMU (Breitman et al. 2023), which is able to produce summary statistics from a full run of 21cmFAST with a speed-up factor of ∼104. Other promising approaches to producing cheap simulations rely on Lagrangian deep learning (Dai & Seljak 2021) and its successors (Rigo et al., in prep.).
2. Simulations and mock sightlines
For this work, we used the Sherwood-Relics suite of hydrodynamical simulations with a box size of 40 h−1 cMpc3 and 2 × 10243 particles (Puchwein et al. 2023; Bolton et al. 2017) to generate mock Lyα forest sightlines to train the NN for parameter estimation. The fiducial simulation used for this work was run with a standard ΛCDM cosmology with cosmological parameters based on Planck Collaboration XVI (2014) ({Ωm, Ωb, ΩΛ, σ8, ns, and h} = {0.308, 0.0482, 0.692, 0.829, 0.961, and 0.678}). We then used simulations with varied cosmological and astrophysical parameters to train the NN to learn from the associated variations in the Lyα forest and perform parameter estimation. We performed parameter estimation for the cosmological parameters, σ8 and ns, and the astrophysical parameters, T0 and γ, individually. T0 is the IGM temperature at mean cosmic density and γ is the slope of the IGM temperature, T, and density, Δ, relation (T = T0Δγ − 1). The fiducial simulation has σ8 and ns values of 0.829 and 0.961, as was mentioned earlier, and a redshift-independent γ of 1.3. The temperature evolves with redshift. In the case of σ8, simulations were used with variation in the parameter as σ8 = 0.829 ± 0.075. For ns, the parameter variations used were ns = 0.961 ± 0.04. In the case of T0, we used simulations that had temperatures 1.5 times higher and lower than the fiducial simulation. For γ, simulations that had γ = 1.3 ± 0.3 were used. In total, we used nine simulations to train the NN to learn parameter estimation for all these parameters individually. All these simulations with variations in parameters were run with the same initial seed density fields. We also used four other simulations that had σ8 = 0.804, 0.854, and ns = 0.941, 0.981. These simulations were used to test the ability of the NN to predict parameter values different from what it has been trained on. Additionally, we also used three other simulations run with fiducial parameters, but with different initial seed density fields on which we performed the testing of the parameter estimation. This was done to check how robust the trained NN is against new unseen data. All the above simulations were run with spatially homogenous photoionization rates and photo-heating rates from the fiducial UV background model presented in Puchwein et al. (2019) (see Table D.1). For the 2D parameter estimation of T0 and the H I photoionization rate, ΓHI, we varied ΓHI by 25% as a post-processing step on the Lyα forest spectra by uniformly scaling the optical depth field, τ. The list of all the simulations used in this work is given in Table A.1.
The snapshots for all these simulations are stored at redshift intervals of Δz = 0.1. We created mock Lyα forest transmitted flux sightlines from these simulations of length 40 h−1 cMpc at redshifts z = 2.0, 3.0, and 4.0. This was done to test parameter estimation and the constraining power of the Lyα forest at different redshifts. We generated the sightlines by first gridding 40 h−1 cMpc (the length of each sightline) into 2048 grids in wavelength. For the sake of simplicity and the fact that we are not comparing the simulated spectra with observations in this work, we retained the uniform gridding in Δx = 40/2048 h−1 cMpc (corresponding to Δz ≈ 1.96 × 10−5) inherent in the simulations. We also adjusted the photoionizing background for each of the varied simulations so that their mean flux matches the fiducial one. To check the effect of instrumental smoothing on the estimation, we also generated sightlines convolved with Gaussian profiles with FWHM = 6, 50, and 150 km s−1. However, unless otherwise mentioned, we used the transmitted flux without any Gaussian convolution. Additionally, we added random Gaussian noise to the transmitted flux. We used uniform signal-to-noise (S/N) along a single sightline but varied the S/N levels between different sightlines. The S/N values corresponding to each sightline were drawn uniformly in the logarithmic space in S/N, in the range logS/N ∈ [log20, log100]. This ensures that our sample has a larger number of low-S/N sightlines, similar to the observed spectra. We refer to this S/N distribution as S/NFid (for “fiducial”) from now on. We also generated sightlines that have 0.85 × S/NFid to evaluate the sensitivity of the parameter estimation to deviations (in this case, systematic suppression of S/N) in noise levels.
3. Parameter estimation with Markov chain Monte Carlo from the power spectrum
For the traditional approach, we used the 1D flux power spectrum, PF(k), computed over mock Lyα forest spectra of length 40 h−1 cMpc to estimate T0, γ, and σ8 using the maximum likelihood approach. To compute the 1D flux power spectrum, we first Fourier-transformed the 1D flux deviation field, 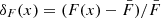 , to δF(k). The power spectrum was then simply proportional to |δF(k)|2. The 1D flux power spectrum was then normalized as
, to δF(k). The power spectrum was then simply proportional to |δF(k)|2. The 1D flux power spectrum was then normalized as
where σF2 is the variance of the field, δF(k). We then binned the power spectra in ten equally spaced logarithmic bins in k ranging from 0.314 to 31.4 h−1 cKpc. The smallest scales here correspond to 100 h−1 ckpc and the largest scale corresponds to 10 h−1 cMpc. We intentionally went to very small scales to allow the NN described in the following section to extract maximal information from such scales, which are known to be sensitive to noise.
We computed the PF(k)s corresponding to the simulation at fiducial parameter values and also for the simulations with parameter variation. The PF(k)s corresponding to the fiducial and varied astrophysical parameters (T0 and γ) are shown in the top panels of Fig. 1. The error bars shown in the figure are bootstrap error bars computed over 5000 sightlines for a sample size of 50 sightlines with 10 000 bootstrap realizations. In Fig. 2, we plot the difference in PF(k) with respect to the fiducial PF(k) for variations in the cosmological parameters (σ8 and nS). This was done to highlight the differences better since the variations in the cosmological parameters do not cause appreciable changes in the power spectrum with respect to the error bars shown. Now, to obtain a model for PF(k) and its variation with the parameters, we approximated the power spectrum by a Taylor expansion to the first order around the fiducial parameter value, ϑ0, and then modeled PF(k) for the varied parameter, ϑ, about the fiducial parameter as (check Sect. 4.1 of Viel & Haehnelt 2006, for description)
 |
Fig. 1. Plots showing the modeling of the variation of Lyα forest flux power spectrum with astrophysical parameters, T0 and γ at z = 3. The top panels show the plots of the Lyα forest flux power spectrum corresponding to fiducial and varied T0 and γ. We added Gaussian noise to the sightlines with an S/N distribution ranging from 20 to 100 (S/N distribution is uniform in the log scale, making the distribution have more low S/N sightlines). We plot the power spectrum corresponding to the fiducial simulation (red) and the varied parameters (blue and green) corresponding to mock Lyα with this S/N distribution. The error bars correspond to bootstrapping errors computed over 5000 sightlines for a sample size of 50 sightlines with 10 000 bootstrap realizations. The power spectra corresponding to the simulation runs (with similar S/N distribution) with fiducial parameters but different initial seed density fields are plotted with colored hollow points in the middle panels. We modeled the power spectrum based on the curves in the top panels. We then used the posterior distribution by running an MCMC with flat priors (see Eq. 4) to estimate the parameter values (see Sect. 3). In the middle panels, hollow blue, green, and red points correspond to the fiducial simulations with different seeds, and the posterior estimates of the parameters (and the posterior standard deviation) are given in the plots. In the bottom panels, we show the sensitivity of the parameter estimates based on power spectrum to noise levels when we lower the S/N distribution (0.85 × S/NFid) of the sightlines and use the same power spectrum modeling to estimate the parameters. |
 |
Fig. 2. Same as Fig. 1 but with cosmological parameters σ8 and ns. In the top panels, however, we plot the difference between the power spectrum at a certain parameter value to the one at the fiducial parameter. This was done for a better visualization, since the variations in σ8 and nS do not cause an appreciable change in the power spectrum within the error bars shown. |
Using this, we developed a model to capture the linear variation in PF(k) with parameters T0, γ, σ8, and nS individually. This modeling was done corresponding to sightlines that have noise levels drawn from S/NFid. We then defined a log-likelihood function of the form
where d0 = PF(k, ϑ0) are the power spectrum values for the fiducial parameters, arranged in a 10-dimensional vector binned over k-values in the range of 0.314 to 31.4 h cKpc−1, and C is the covariance matrix obtained from 10 000 bootstrap realizations of the power spectrum with a sample size of 50 sightlines, as was mentioned before. Using this log-likelihood function, we then used a Markov Chain Monte Carlo (MCMC) with uniform priors of the form
(where Δϑ is the variation in the model parameters for the simulations with varied parameters) to estimate the parameter values from a new set of three simulations run with different initial random seeds at the fiducial parameter values. We used the python package EMCEE (Foreman-Mackey et al. 2013) to run the MCMC. In the middle panels of Figs. 1 and 2, we show the estimated parameter values from these three simulations. This was done using sightlines whose noise levels were drawn from S/NFid. To check the sensitivity of the parameter estimation to the noise levels, we then used the PF(k) modeling done using S/NFid sightlines to estimate parameters for 0.85 × S/NFid sightlines. We show the estimated parameters in the bottom panels in Fig. 1. We subsequently compare these results with the NN approach in Sect. 6. It is to be noted that we used Eq. (2) to model individual parameter variations for 1D parameter estimations. In Sect. 8, where we demonstrate a 2D parameter estimation for T0 and ΓHI, we model the power spectrum for parameter variations by following a linear interpolation scheme between different simulations.
4. Information-maximizing neural network
Summarizing large datasets in a collection of sufficient summary statistics (e.g., mean flux, power spectrum, etc.) is becoming a necessary approach to deal with current cosmological and astronomical data. The aim is to reduce the data into the smallest number of summary statistics with minimum loss of information. Massively optimized parameter estimation and data (MOPED; Heavens et al. 2000) is a popular approach to summarizing the data, wherein the summaries are linear combinations of the data, reducing the number of data points down to the number of model parameters describing the data. MOPED is entirely lossless, under the assumption that the noise is independent of the model parameter and the likelihood, at least up to the first approximation, is Gaussian. However, using a linear combination of the data for the compression might not be the most optimal approach. Using machine-learning, the IMNN provides a more convenient and informative way of compressing the data into nonlinear summaries (check Prelogović & Mesinger 2024, for a recent work showing the constraining power of several 21 cm summary statistics using IMNN).
Drawing motivation from the MOPED algorithm, IMNN aims to find some transformation, f : d → x, which maps the data (d) to the compressed summary (xα, for the model parameter α) (check Charnock et al. 2018, for reference).
It transforms the original likelihood into the form
where
is the mean of ns summaries. ϑ is the set of model parameters and Cf is the covariance matrix. The modified Fisher information matrix can be expressed as
where μf, α is the partial derivative of μf with respect to the model parameter. Since the model parameters appear only in simulations, numerical differentiation was done to compute this. The numerical differentiation was performed using three different simulations, one at the fiducial parameter value and the other two at some small deviations from the fiducial parameter. We then used a neural network to find this mapping function with the Fisher information as the reward function (which maximizes the Fisher information). This ensured a mapping that preserves maximal information. After this mapping, one can then get model parameter estimates, ϑα, for the compressed testing data using score-compression,
In this work, we used the IMNN approach to extract maximal information out of Lyα forest transmitted flux in the Fourier domain and performed 1D model parameter estimation on astrophysical parameters, T0 and γ, and cosmological parameters, σ8 and nS. We did this individually for each parameter, using three simulations for each of them, since training the IMNN for an N-D parameter estimation requires training sets in which the parameters are varied simultaneously and we currently do not have access to such simulations (in Sect. 8, we demonstrate a 2D parameter estimation case for T0 and ΓHI, where ΓHI has been varied for all T0 values as a post-processing step without the need to run new simulations). Using IMNN, we first compressed the training set to a summary statistic and then used it to get parameter estimates from the testing data set using Eq. (8).
5. Training the neural network
For 1D parameter estimation of T0, γ, σ8, and nS, we used the NumericalGradientIMNN1 subclass of IMNN, which uses the derivatives of the network outputs with respect to the physical model parameters necessary to fit an IMNN. The simulations at parameter values above and below the fiducial values were used for this. To train the IMNN, we generated 5000 sightlines in total. We used 3000 of these as the training set for the NN. The remaining 2000 sightlines were used as the validation set for the training. The validation set was used at each training epoch to validate the NN trained on the training set and then adjust the network hyperparameters accordingly. As an input to the IMNN, we used the 1D field 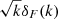 , where δF(k) is the Fourier-transformed flux deviation field and k is the corresponding wave number, ranging linearly from 0.314 to 31.4 h ckpc−1 (the same range as for the power spectrum analysis using MCMC) and containing 197 entries.
, where δF(k) is the Fourier-transformed flux deviation field and k is the corresponding wave number, ranging linearly from 0.314 to 31.4 h ckpc−1 (the same range as for the power spectrum analysis using MCMC) and containing 197 entries.
We used three different simulations, one at the fiducial parameter value, ϑ0, and the other two at ±Δϑ, with ϑ corresponding to each of the parameters {T0, γ, σ8, ns}, to compute the variation in the mean summary statistic with respect to the model parameters essential for calculating the Fisher information (Eq. 7) and for model parameter estimation (Eq. 8). We did this separately for each of the redshifts (z = 2, 3 and 4 for T0 and γ). In the case of σ8 and ns, the effect of varying the parameters on the Fourier space grows weaker with decreasing redshift. We find that the training doesn’t converge with the amount of training data at hand for z = 2 and that it requires a larger simulated volume to train properly. So, for σ8 and ns, we stuck to z = 3, and 4 only. The IMNN was then trained over 3000 sightlines for each parameter value at each redshift value separately. For each of these sightlines, the Gaussian noise added to the transmitted flux was derived from the S/NFid distribution mentioned earlier. Since the Fourier-transformed Lyα spectra are quite noisy individually, we performed a running mean over 5 pixels in the Fourier profile. We find that this makes the training much more stable without the loss of significant information. We trained a separate network for each parameter and each redshift.
Various training parameters, such as learning rates and the structure of the network, are mentioned in Table B.1. The choice of the training parameters was based on trial and run. We also ran the training with different initial random seeds (30 in total) for the NN to make the exercise more robust and then used all the trained neural estimates on our testing set to estimate the parameters. We find that 30 random seeds for the training is sufficient enough to sample the variance in the network outputs for different random initializations. The parameter estimation was done using the combined results of all the trained NNs. Examples of a single training instance at z = 3.0 and the evolution of Fisher information with the number of iterations in training are shown in Fig. 3. Currently, we have been running the training on a CPU, and each training instance takes under 1 CPU-hour. We will eventually utilize GPUs to train the IMNN over a multiple-parameter space, in which we expect it to be dramatically faster.
 |
Fig. 3. IMNN training example (using NumericalGradientIMNN subclass of IMNN) corresponding to the astrophysical parameters, T0 and γ (top panels), and cosmological parameters, σ8 and ns (bottom panels), for z = 3.0. The plots show the evolution of Fisher information during training with the training epoch. The solid lines correspond to the training sample and the dotted lines correspond to the validation sample. The training was stopped at the maximum iteration values shown in the x axis of the above plots. This choice was based on the training epoch when the Fisher information extracted from the validation sample reaches a saturation value and shows no further improvement with additional training epochs. |
6. Parameter estimation with the information-maximizing neural network
As a testing set for the parameter estimation, we used three different simulations run with the same fiducial parameter values used for training, but with different initial random seeds, and therefore showing the network sightlines that it never saw in training. Currently, we do the testing at the fiducial values of parameters since we only have access to simulations that have different initial seeds from the ones we trained the NN on. In the left panels of Fig. 4, we show the distribution of the estimated parameters at z = 3.0 computed using Eq. (8) for the testing set of sightlines with S/N values derived from the S/NFid distribution. Each realization in the distribution of the estimated parameters is a bootstrap realization of a sample size of 50 mock spectra over the entire validation set. The distributions of the parameters were generated with 10 000 bootstrap realizations for each parameter. The mean and the associated standard deviation of the estimated parameters are shown in Table 1 for all three simulations. The mean and associated error estimates over all three simulations (taking into account the effect of cosmic variance on the error estimates) are also quoted in the plots, along with Table 1. Comparing these estimates with those from the MCMC approach using the power spectrum, we find that the error estimates with IMNN are 1.52 times smaller in the case of log T0 and 1.27 times in the case of γ. However, we do not see any significant improvements in the σ8 and ns estimates with IMNN. The reason is that varying σ8 primarily changes the total power in the Fourier space, and thus the overall amplitude of the power spectrum. In this case, the MCMC approach with the power spectrum only performs well enough to extract nearly maximal information from the Fourier space. In Fig. 5, we have also shown that the IMNN works well in estimating σ8 and nS parameter values which is different than the ones that it has been trained on.
Estimation of parameters (for different redshift ranges).
 |
Fig. 4. Estimation of T0, γ, σ8, and ns using score-compression from IMNN on the Fourier-transformed Lyα forest transmitted flux for three simulations run at fiducial parameter values with different initial random seeds. Each realization in the distribution of the estimated parameters is a bootstrap realization of a sample size of 50 mock spectra over the entire testing set. The distribution of the parameters was generated with 10 000 bootstrap realizations for each parameter. On the left panels, we plot the estimation for simulated sightlines that have the S/N distribution S/NFid with IMNN trained with sightlines that have S/NFid. On the right panels, we plot the estimation for 0.85 × S/NFid with IMNN trained with S/NFid sightlines. This shows the sensitivity of the trained NNs to noise level deviations in the data. |
 |
Fig. 5. Estimation of σ8 and ns at z = 4 for parameter values (two dashed black lines) different from the parameter values with which the IMNN has been trained (dashed blue, red, and green lines). The black curves show the PDF of the estimated parameter values (at two different values). Each realization in the distribution of the estimated parameters is a bootstrap realization of a sample size of 50 mock spectra over the entire testing set. The distributions of the parameters were generated with 10 000 bootstrap realizations for each parameter. |
However, it is worth noting that even in the cases in which IMNN performs on par with the standard MCMC approach, it offers a significant boost in speed. Once trained, summarizing a new dataset and estimating the model parameters from it is almost an instantaneous process in comparison to MCMC. For instance, in estimating the model parameter σ8, generating a power spectrum from 5000 sightlines takes about 30 CPU-seconds, and then subsequently estimating the parameter using MCMC takes about 35 CPU-seconds. In comparison, estimating parameters using a trained NN on 5000 sightlines takes only about 0.1 CPU-seconds, corresponding to a speed-up factor of (30 + 35)/0.1 = 650 with respect to the MCMC approach. Thus, using an NN-based approach provides a substantial advantage in dealing with large astrophysical or cosmological datasets.
6.1. Effect of noise levels
Next, we checked the robustness of our method against variations in noise levels. Similar to what we did for the MCMC approach with the power spectrum, we used the NN trained on sightlines with noise levels derived from the S/NFid distribution and then tested it on sightlines with 0.85 × S/NFid. The corresponding estimated parameter values are shown in the right panels of Fig. 4 and also quoted in Table 1. Comparing the deviations with those from the MCMC approach, we find that IMNN estimates are 6.25 and 10.0 times (ratio of the amount of deviation in parameter estimates at 0.85 × S/NFid in comparison to S/NFid) less sensitive to variations in noise levels for log T0 and γ at z = 2, respectively. At z = 3, the IMNN estimates are less sensitive to noise variations by a factor of 4.17, 2.86, 1.41, and 2.2 times in the case of log T0, γ, σ8, and ns, respectively. At z = 4, the dependence on noise variations is almost similar for the MCMC and IMNN approaches. In the case of ns, though it might seem like there is an improvement (with an S/N deviation ratio of 1.5), it might be worth noting that there is not much variation seen in the ns estimate itself with noise. In short, we can conclude that the IMNN estimates are more robust against noise variations in comparison to the MCMC approach at z = 2 and 3, with the approach being more robust at lower redshifts.
6.2. Effects of instrumental smoothing
We investigated the effects of instrumental smoothing in the parameter estimation procedure by training the NNs with sightlines convolved with a Gaussian profile. We used Gaussian profiles that have FWHM = 6, 50, and 150 km s−1 to simulate the usual convolutional scales of high-, medium-, and low-resolution Lyα forest spectra. In Table 2, we present the results of the effects of instrumental smoothing on the estimation of parameters with the IMNN approach and compare it with the results from the MCMC approach. For the parameters T0 and γ, we find that the estimation with IMNN is better with high-resolution spectra that have FWHM = 6 km s−1. The estimates with FWHM = 6 km s−1 are roughly similar to what we obtained with unsmoothed sightlines. In the case of FWHM = 50 and 150 km s−1, we do not see any improvements in the parameter estimates using IMNN over MCMC with power spectrum. In fact, the parameter estimation fails for T0 and γ at FWHM = 150 km s−1, as can be seen from the large error bars. This was expected as the thermal effects on Lyα forest are small-scale effects that alter the broadening of Lyα absorption lines. Large-scale smoothing introduced by low-resolution spectrographs washes away this small-scale information. In conclusion, the improvements that we observed with IMNN over MCMC with the power spectrum come from enhanced extraction of small-scale information by the IMNN, which can only be realized with high-resolution spectra.
Estimation of parameters for different instrumental smoothing in both training and testing set (Gaussian; z = 3.0).
On the other hand, σ8 and ns primarily affect the global amplitude of the power spectrum, as was mentioned earlier. So, we do not find any appreciable change in the parameter estimates by introducing a Gaussian convolution with FWHM = 6, 50, and 150 km s−1. The IMNN approach works on par with the MCMC using the power spectrum in all cases.
6.3. Effect of continuum uncertainty
In this section, we check the effectiveness of IMNN in extracting continuum-independent information from the Fourier space for parameter estimation. For this, we first generated a training set of mock Lyα sightlines with their continuum levels altered. We generated random continuum levels for each sightline from a Gaussian distribution of mean μ = 1 and standard deviation σ = 0.2, and then normalized the transmitted flux for each sightline to these random continuum levels. The validation set was also treated in the same way. The NN was then trained on these continuum-altered Lyα transmitted flux sightlines. We then estimated the parameters using these trained NNs for sightlines that have continuum levels of (μ = 1, σ = 0) and (μ = 0.9, σ = 0.1). The estimated astrophysical parameters, log T0 and γ, are presented in Table 3 at z = 3. We also compare our results with the standard MCMC approach for parameter estimation using the power spectrum. We find that training the IMNN on sightlines that have varying continuum levels makes it able to extract continuum-independent information. The estimated log T0 values for (μ = 1, σ = 0) and (μ = 0.9, σ = 0.1) sightlines using IMNN are 4.224 ± 0.009 and 4.224 ± 0.010, respectively, as opposed to 4.223 ± 0.013 and 4.204 ± 0.014 using the standard MCMC approach. In the case of γ, the estimated parameters using IMNN are 1.300 ± 0.015 and 1.301 ± 0.015 as opposed to 1.295 ± 0.019 and 1.265 ± 0.021 using the MCMC approach. So, IMNN clearly outperforms the MCMC approach when considering robustness against continuum uncertainties in estimating T0 and γ.
Effects of continuum variation on the estimation of astrophysical parameters, log T0 and γ, at z = 3.0. In the case of cosmological parameters, σ8 and nS, IMNN fails to extract continuum-independent information out of the Fourier space.
The situation is different in the case of the cosmological parameters, σ8 and nS, which are known to be sensitive to the global amplitude of the power spectrum, as opposed to the astrophysical parameters, T0 and γ, which are more sensitive to the small-scale information. As was expected, the IMNN trained on (μ = 1.0, σ = 0.2) sightlines doesn’t estimate the parameters accurately for sightlines that have (μ = 1.0, σ = 0.0) and (μ = 0.9, σ = 0.1). In the case of σ8, the estimated parameters for these two cases are 0.891 ± 0.090 and 0.887 ± 0.097, respectively. In the case of nS, the estimated parameters are 0.995 ± 0.050 and 0.991 ± 0.062.
7. Robustness check with a different simulation
To check the robustness of parameter estimation using IMNN on Lyα forest spectra in the Fourier domain, we used alternate simulations to estimate parameters based on the neural trained with the Sherwood-Relics simulations. For this, we used mock Lyα forest spectra from the CAMELS project (Villaescusa-Navarro et al. 2021), generated using a (25 h−1 cMpc)3 IllustrisTNG simulation box at z = 2. We did not perform this exercise at z = 3 since IGM temperatures are elevated in the case of Sherwood-Relics simulations due to He II reionization, which makes the trained NNs unfit for testing on IllustrisTNG simulations that do not incorporate this. The cosmological parameters used in this simulation are ({Ωm, Ωb, ΩΛ, σ8, ns, h} = {0.30, 0.049, 0.70, 0.84, 0.9624, 0.6711}). We first linearly interpolated the spectra to the grid size of our simulation and then added random Gaussian noise with S/N levels drawn from the S/NFid distribution mentioned before. We then matched the mean flux of the sightlines to the mean flux of our fiducial simulation. We simultaneously checked the parameter estimation for log T0 using the standard MCMC approach from the power spectrum with the IMNN approach.
In Fig. 6, we have shown the IMNN estimates of log T0 and γ for the CAMELS simulations with the IMNN that have been trained with Sherwood-Relics simulations. The expected values of log T0 and γ in the CAMELS simulations are approximately 3.97 and 1.26, respectively. In the case of the MCMC with the power spectrum, the log T0 predicted is 3.997 ± 0.036. With IMNN, the value predicted is 3.9898 ± 0.0154. We see that the estimated values are consistent with each other as well as the expected values from CAMELS within 1σ error bars, with the IMNN predicting it with ≈2.34 times better accuracy in the case of log T0 and ≈1.73 times better accuracy in the case of γ. We thus conclude that this NN approach is relatively robust and does not learn simulation-specific features from the Fourier-transformed Lyα forest spectra.
 |
Fig. 6. Estimation of T0 and γ using MCMC with power spectrum and IMNN on the Fourier-transformed Lyα forest transmitted flux for CAMELS simulation at z = 2. The expected parameter values are log T0 = 3.97 and γ = 1.26. The power spectrum modeling for the MCMC approach and the training for the IMNN approach were done with previous Sherwood-Relics simulations. We checked the robustness of both approaches by testing them on a different simulation. |
8. Parameter inference in two dimensions
In the previous sections, we used the IMNN approach to estimate thermal and cosmological parameters individually. However, in realistic scenarios, such estimations would be performed jointly over several parameters, and then individual parameter estimates would be obtained by marginalizing over the other parameters. In this section, we demonstrate a 2D parameter estimation. Ideally, we would have liked to do this for the thermal parameters, T0 and γ. However, we find that IMNN doesn’t properly learn to perform 2D parameter inference and lift the degeneracy between these two degenerate parameters, due to the lack of training samples in which both T0 and γ are varied simultaneously. Since we currently lack such simulations in the SHERWOOD suite, as a proof of concept we demonstrate 2D parameter inference for the two parameters, T0 and the H I photoionization rate, ΓH I. The 2D parameter inferences, T0 and γ, using several parameter variation instances, similar to Nayak et al. (2024), will be addressed in a future work.
For this work, we used our original three simulations at z = 3 with log T0 = 4.225 ± 0.176 and simply generated sightlines corresponding to ΓHI = ΓHI/1.25, ΓHI and 1.25 × ΓHI to generate nine simulations in total with varied T0 and ΓHI. We used the SimulatorIMNN2 subclass for 2D parameter inference as we find that it is more suited to simultaneous parameter variations. It is also suited to future exercises in which we shall train the NN over simulations with different parameters in several dimensions. Unlike the NumericalGradientIMNN used in the previous sections – which uses the numerical gradient between the training samples corresponding to the varied parameter values – SimulatorIMNN requires a function to generate the training samples based on input parameter values. We did this by defining a function that linearly interpolates the Fourier-transformed field between the nine simulations with varied T0 and ΓHI. Such an interpolation scheme becomes possible in our case since we used simulations that have the same initial density fields and differ only in the parameters T0 and ΓHI. This means that we can easily interpolate in the parameter space between sightlines, since they essentially trace similar density fields that differ only in T0 and ΓHI. Currently, to keep the exercise simple, we avoid modeling the noise effects on the Fourier-transformed fields. We used sightlines that have a uniform noise distribution with S/N = 50. In order to compare the IMNN approach with the standard MCMC approach using power spectra, we adopted the same interpolation scheme to model the power spectrum as a function of T0 and ΓHI, which we used subsequently in the likelihood of the MCMC analysis.
For the training of IMNN, we used 5000 sightlines corresponding to each parameter value shot from the nine simulation boxes. For SimulatorIMNN, the training does not require a validation set. The network architecture and training hyperparameters used are mentioned in Table B.1. We tested the trained NN on 5000 sightlines, each corresponding to the three simulation boxes run with fiducial parameters but with different initial seed density fields. The training was done at z = 3 and the evolution of the Fisher information with the number of iterations in training is shown in the left panel of Fig. 7. In the right panel of Fig. 7, we show the 68% contour enclosing 68% of the highest-density estimates for the 2D histogram of the log T0 and logΓHI/ΓHI, Fid estimates based on the IMNN approach, compared with the equivalent posterior from the standard MCMC approach. Similar to the previous exercises, each estimate corresponds to bootstrap realizations over 50 sightlines for both the IMNN and MCMC approaches. For the 2D estimation, the distribution of the parameter values was obtained with 50 000 bootstrap realizations. We also plot the distribution functions for both these parameters individually by marginalizing over the other parameters. The average estimates along with the associated error (computed as the width of 68% interval of the distribution function) are quoted along with the plots. We find that both approaches predict the fiducial parameters (log T0 = 4.225 and logΓHI/ΓHI, Fid = 0.0) well within the error bars. For logΓHI/ΓHI, Fid, the errors are similar between the two approaches, with the MCMC error bars being about 13% smaller than the IMNN error bars. This was expected, as IMNN gives similar estimates as MCMC when the associated parameter has a more global effect (such as ΓHI, which uniformly alters the photoionizing background at all scales). The IMNN estimates get significantly better for log T0, whose effect is on small scales, with MCMC error bars being 95% larger than the IMNN error bars. This exercise here demonstrates a case for 2D parameter estimation using IMNN, which outperforms the standard MCMC approach in extracting small-scale information from the Lyα forest in Fourier space. This also sets a pathway for performing a full N-D parameter estimation for Lyα forest using IMNN. The scalability of the method to a larger number of dimensions will be the subject of future work. For starters, one needs a sufficiently large number of simulations over which to train the network, which isn’t trivial to achieve unless one resorts to semi-analytical approximations or fast emulators for the purposes. Makinen et al. (2021) only addresses a 2-dimensional parameter space, and addresses scalability only in the sense of the large numerosity of data points, rather than the number of dimensions of the underlying parameter space. Prelogović & Mesinger (2024) do investigate a larger number of parameters in the context of the 21 cm signal, and train their IMNN with about 11 000 simulations of lightcones obtained with 21cmFAST, at a computational cost of 20 k GPUh. This is only achievable thanks to the fast nature of the simulator. In the near future, we expect to be able to take advantage of similarly accelerated simulators based on the Lagrangian Deep learning framework (Rigo et al., in prep.).
 |
Fig. 7. 2D parameter estimation of T0 and ΓHI using IMNN. Top: IMNN training plot (using SimulatorIMNN subclass of IMNN) corresponding to thermal parameter, T0, and H I photoionization rate, ΓHI, for z = 3. The plot shows the evolution of Fisher information during training with the training epoch. Bottom: Contour plots showing the 68% credible region for log T0 and logΓHI/ΓHI, Fid estimates based on the IMNN approach and with MCMC. It is to be noted that in the case of MCMC, the contour plot corresponds to a posterior distribution drawn from running MCMC using a flat prior (see Eq. 4), while in the case of IMNN it corresponds to the distribution of the estimates. Accompanying this are the plots for the distribution functions (for MCMC and IMNN, respectively) for both the parameters log T0 and logΓHI/ΓHI, Fid individually by marginalizing over the other parameters. |
9. Summary and discussion
With the current advent of large astrophysical and cosmological data, reducing data dimensionality is now of the utmost importance. Reducing the entire dataset to a set of summary statistics relevant to the problem at hand with minimum loss of information is one way of achieving that. One popular approach of summarizing large datasets is MOPED (Heavens et al. 2000), which reduces the entire dataset to the number of model parameters describing the data. One can also use NNs to obtain a mapping function that maps the dataset to a set of nonlinear summaries with minimal loss of information.
In this work, we primarily performed 1D parameter estimation for model parameters T0 (IGM temperature at mean cosmic density), γ (slope IGM temperature density, Δ, relation T = T0Δγ − 1), σ8, and nS using the IMNN (Charnock et al. 2018). We performed a 1D estimation since we find that training the NN to do N-D parameter estimation requires the training set to have simulations in which the parameters are varied simultaneously. We currently do not have access to such simulations for the model parameters mentioned, but we did perform a 2D parameter estimation for T0 and the H I photoionization rate, ΓHI, to demonstrate how one will be able to use IMNN to perform N-D parameter estimation in the future. For the 1D parameter estimation, we used IMNN to summarize the Lyα forest data in the Fourier space as a single summary value with minimal loss of information. We obtained these summary values individually. One can then use the summary values to obtain the model parameter estimates. We then compared this approach with a standard technique of maximum likelihood estimation (MCMC) from the Fourier space using the power spectrum. We find that the IMNN approach leads to a significant enhancement in the parameter estimation for T0 and γ. For log T0, the enhancements are by a factor of 1.89, 1.52, and 1.21 times at z = 2, 3, and 4, respectively. For γ, the enhancements are by a factor of 1.5, 1.27, and 1.32. Besides enhancing the estimation of these parameters, we also find that the NNs are more robust against variation in noise levels in the spectra. We confirmed this by performing an exercise in which we estimated the parameters using a test set of spectra that have an S/N distribution that is 0.85 times lower than the fiducial distribution of S/N. At z = 2 and 3, the NNs were less sensitive to this variation in noise levels than the standard MCMC approach by a factor of 6.25 and 4.17 times in the case of log T0 and by a factor of 10.0 and 2.86 times for γ. However, at z = 4, the sensitivity to noise variations was more or less on par with the MCMC approach. We also performed the parameter estimation using IMNN with the cosmological parameters σ8 and nS. We find that the estimates and their sensitivity to noise variations were on par with the MCMC estimates. We think that this might be because varying σ8 or nS primarily varies the total power in the Fourier space, and thus the global amplitude of the power spectrum. Hence, the MCMC approach with the power spectrum is good enough to extract maximal information present in the Fourier space. However, it is worth emphasizing here that even in cases in which a standard MCMC approach with power spectrum works well enough, a trained NN can offer a significant boost in speed in summarizing a new dataset and estimating the model parameters from that. This becomes especially important in the current era of large astrophysical and cosmological datasets.
We also find that IMNN can provide parameter estimates for T0 and γ that are more robust against continuum uncertainties in comparison to the standard MCMC estimates. It does this by extracting small-scale continuum-independent information from the Fourier domain for these parameters. It fails, however, to do this for the cosmological parameters σ8 and nS, which are more sensitive to the global amplitude of the power spectrum.
Additionally, we also checked the parameter estimation process with different instrumental smoothing scales with FWHM = 6, 50, and 150 km s−1, corresponding to typical high-, moderate-, and low-resolution spectra. Interestingly, we find that the improvements seen in estimating T0 and γ are also seen for FWHM = 6 km s−1, but not for 50 and 150 km s−1. In fact, they perform on par with the MCMC estimates. Based on this, we can infer that the improvement we see in the case of IMNN comes mostly from additional small-scale information. In conclusion, IMNN works efficiently in extracting the maximal small-scale information in comparison to the MCMC approach. In doing so, it not only does not compromise robustness against noise level variations but rather improves it.
We also demonstrated a 2D parameter estimation for model parameters T0 and ΓHI using IMNN. In doing so, we find that the IMNN estimation works on par with the MCMC approach using the power spectrum for ΓHI (with the MCMC estimates having errors about 13% smaller), but we see significant improvements in log T0 estimates, wherein the errors are about 84% smaller. This behavior is similar to what we have seen before. Varying ΓHI uniformly rescales the optical depth field of Lyα forest, and hence induces a global effect. For such parameters, the MCMC approach with the power spectrum can extract maximal information. The IMNN approach outperforms the MCMC approach for T0 (which induces small-scale effects on the Lyα forest) by extracting additional small-scale information.
In our upcoming work, we shall implement this on observational data comprising high-resolution Lyα forest spectra obtained from publicly available surveys like KODIAQ (O’Meara et al. 2017) based on the KECK/HIRES spectrograph and the SQUAD survey (Murphy et al. 2019) based on VLT/UVES. This will also be complemented with high-resolution spectra from ESPRESSO to improve upon the current estimates of the thermal evolution of the IGM.
Acknowledgments
SM, SC, and GC acknowledge financial support of the Italian Ministry of University and Research with PRIN 201278X4FL, PRIN INAF 2019 “New Light on the Intergalactic Medium” and the ‘Progetti Premiali’ funding scheme. MV, SC, RT are supported by INDARK INFN PD51 grant. RT acknowledges co-funding from Next Generation EU, in the context of the National Recovery and Resilience Plan, Investment PE1 – Project FAIR Future Artificial Intelligence Research”. This resource was co-financed by the Next Generation EU [DM 1555 del 11.10.22]. RT is partially supported by the Fondazione ICSC, Spoke 3 “Astrophysics and Cosmos Observations”, Piano Nazionale di Ripresa e Resilienza Project ID CN00000013 “Italian Research Center on High-Performance Computing, Big Data and Quantum Computing” funded by MUR Missione 4 Componente 2 Investimento 1.4: Potenziamento strutture di ricerca e creazione di “campioni nazionali di R&S (M4C2-19 )” – Next Generation EU (NGEU). SM would also like to acknowledge Valentina D’Odorico and Prakash Gaikwad for valuable discussions, insights, and feedback regarding the topic at hand.
References
- Aguirre, A., Hernquist, L., Schaye, J., et al. 2001, ApJ, 561, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Alsing, J., Wandelt, B., & Feeney, S. 2018, MNRAS, 477, 2874 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, G. D., Bolton, J. S., Haehnelt, M. G., & Sargent, W. L. W. 2011, MNRAS, 410, 1096 [NASA ADS] [CrossRef] [Google Scholar]
- Boera, E., Murphy, M. T., Becker, G. D., & Bolton, J. S. 2014, MNRAS, 441, 1916 [CrossRef] [Google Scholar]
- Bolton, J. S., Puchwein, E., Sijacki, D., et al. 2017, MNRAS, 464, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Breitman, D., Mesinger, A., Murray, S., et al. 2023, ArXiv e-prints [arXiv:2309.05697] [Google Scholar]
- Charnock, T., Lavaux, G., & Wandelt, B. D. 2018, Phys. Rev. D, 97, 083004 [NASA ADS] [CrossRef] [Google Scholar]
- Coughlin, J. W., Mathews, G. J., Arielle Phillips, L., Snedden, A. P., & Suh, I.-S. 2019, ApJ, 874, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Croft, R. A. C., Weinberg, D. H., Katz, N., & Hernquist, L. 1998, ApJ, 495, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Croft, R. A. C., Weinberg, D. H., Pettini, M., Hernquist, L., & Katz, N. 1999, ApJ, 520, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Croft, R. A. C., Weinberg, D. H., Bolte, M., et al. 2002, ApJ, 581, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, B., & Seljak, U. 2021, Proc. Natl. Acad. Sci., 118 [Google Scholar]
- Fan, X., Strauss, M. A., Becker, R. H., et al. 2006, AJ, 132, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Finley, H., Petitjean, P., Noterdaeme, P., & Pâris, I. 2014, A&A, 572, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Gaikwad, P., Srianand, R., Haehnelt, M. G., & Choudhury, T. R. 2021, MNRAS, 506, 4389 [NASA ADS] [CrossRef] [Google Scholar]
- Gluck, N., Oppenheimer, B. D., Nagai, D., Villaescusa-Navarro, F., & Anglés-Alcázar, D. 2023, ArXiv e-prints [arXiv:2309.07912] [Google Scholar]
- Gupta, A., Zorrilla Matilla, J. M., Hsu, D., & Haiman, Z. 2018, Phys. Rev. D, 97, 103515 [NASA ADS] [CrossRef] [Google Scholar]
- Heavens, A. F., Jimenez, R., & Lahav, O. 2000, MNRAS, 317, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Iršič, V., Viel, M., Haehnelt, M. G., et al. 2017, Phys. Rev. D, 96, 023522 [CrossRef] [Google Scholar]
- Karchev, K., Trotta, R., & Weniger, C. 2022, MNRAS, 520, 1056 [Google Scholar]
- Lee, K.-G., Krolewski, A., White, M., et al. 2018, ApJS, 237, 31 [Google Scholar]
- Lesgourgues, J., Viel, M., Haehnelt, M. G., & Massey, R. 2007, JCAP, 2007, 008 [CrossRef] [Google Scholar]
- Maitra, S., Srianand, R., Petitjean, P., et al. 2019, MNRAS, 490, 3633 [NASA ADS] [CrossRef] [Google Scholar]
- Maitra, S., Srianand, R., Gaikwad, P., & Khandai, N. 2022a, MNRAS, 509, 4585 [Google Scholar]
- Maitra, S., Srianand, R., & Gaikwad, P. 2022b, MNRAS, 509, 1536 [Google Scholar]
- Makinen, T. L., Charnock, T., Alsing, J., & Wandelt, B. D. 2021, JCAP, 2021, 049 [CrossRef] [Google Scholar]
- McDonald, P. 2003, ApJ, 585, 34 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., Miralda-Escudé, J., Rauch, M., et al. 2000, ApJ, 543, 1 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., Miralda-Escudé, J., Rauch, M., et al. 2001, ApJ, 562, 52 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, P., Seljak, U., Burles, S., et al. 2006, ApJS, 163, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, M., Iršič, V., Bolton, J. S., et al. 2022, MNRAS, 509, 6119 [Google Scholar]
- Molaro, M., Iršič, V., Bolton, J. S., et al. 2023, MNRAS, 521, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, M. T., Kacprzak, G. G., Savorgnan, G. A. D., & Carswell, R. F. 2019, MNRAS, 482, 3458 [NASA ADS] [CrossRef] [Google Scholar]
- Nayak, P., Walther, M., Gruen, D., & Adiraju, S. 2024, A&A, 689, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nygaard, A., Holm, E. B., Hannestad, S., & Tram, T. 2023, JCAP, 2023, 025 [CrossRef] [Google Scholar]
- O’Meara, J. M., Lehner, N., Howk, J. C., et al. 2017, AJ, 154, 114 [CrossRef] [Google Scholar]
- Oppenheimer, B. D., & Davé, R. 2006, MNRAS, 373, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Palanque-Delabrouille, N., Yèche, C., Lesgourgues, J., et al. 2015a, JCAP, 2, 045 [CrossRef] [Google Scholar]
- Palanque-Delabrouille, N., Yèche, C., Baur, J., et al. 2015b, JCAP, 11, 011 [CrossRef] [Google Scholar]
- Palanque-Delabrouille, N., Yèche, C., Schöneberg, N., et al. 2020, JCAP, 2020, 038 [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prelogović, D., & Mesinger, A. 2024, A&A, 688, A199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puchwein, E., Haardt, F., Haehnelt, M. G., & Madau, P. 2019, MNRAS, 485, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Puchwein, E., Bolton, J. S., Keating, L. C., et al. 2023, MNRAS, 519, 6162 [NASA ADS] [CrossRef] [Google Scholar]
- Ribli, D., Pataki, B. Á., & Csabai, I. 2019, Nat. Astron., 3, 93 [Google Scholar]
- Schaye, J., Theuns, T., Leonard, A., & Efstathiou, G. 1999, MNRAS, 310, 57 [CrossRef] [Google Scholar]
- Schaye, J., Theuns, T., Rauch, M., Efstathiou, G., & Sargent, W. L. W. 2000, MNRAS, 318, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U., Slosar, A., & McDonald, P. 2006, JCAP, 10, 014 [CrossRef] [Google Scholar]
- Theuns, T., & Zaroubi, S. 2000, MNRAS, 317, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Tie, S. S., Weinberg, D. H., Martini, P., et al. 2019, MNRAS, 487, 5346 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M. 2006, ASP Conf. Ser., 352, 191 [NASA ADS] [Google Scholar]
- Viel, M., & Haehnelt, M. G. 2006, MNRAS, 365, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M., Matarrese, S., Theuns, T., Munshi, D., & Wang, Y. 2003, MNRAS, 340, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M., Haehnelt, M. G., & Springel, V. 2004a, MNRAS, 354, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M., Matarrese, S., Heavens, A., et al. 2004b, MNRAS, 347, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M., Weller, J., & Haehnelt, M. G. 2004c, MNRAS, 355, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Viel, M., Schaye, J., & Booth, C. M. 2013, MNRAS, 429, 1734 [NASA ADS] [CrossRef] [Google Scholar]
- Villaescusa-Navarro, F., Anglés-Alcázar, D., Genel, S., et al. 2021, ApJ, 915, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Villaescusa-Navarro, F., Wandelt, B. D., Anglés-Alcázar, D., et al. 2022, ApJ, 928, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Worseck, G., Davies, F. B., Hennawi, J. F., & Prochaska, J. X. 2018, ArXiv e-prints [arXiv:1808.05247] [Google Scholar]
- Yèche, C., Palanque-Delabrouille, N., Baur, J., & du Mas des Bourboux, H. 2017, JCAP, 6, 047 [CrossRef] [Google Scholar]
Appendix A: Sherwood-Relics simulations used
Table A.1 shows the list of all Sherwood-Relics simulations used in this work with varied astrophysical and cosmological parameters for training the neural network, as well as simulations having fiducial parameters but with different initial seed density fields for testing the trained neural network.
Sherwood-Relics simulations used.
Appendix B: Network architecture
The details of the network parameters including the number of layers and nodes in each layer, the learning rate and regularization parameters (λ and ϵ) are given in Table B.1. We have used an additional layer in case of log T0 using which we input the log of the 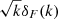 . We find that this gives a better estimation of T0. Also, we consider the summary covariances over a batch of 2000 sightlines in case of log T0 and γ and 3000 in case of σ8. As a stopping criterion of the training, we choose a patience value of 20, which is the number of iterations where there is no increase in the value of the determinant of the Fisher information matrix.
. We find that this gives a better estimation of T0. Also, we consider the summary covariances over a batch of 2000 sightlines in case of log T0 and γ and 3000 in case of σ8. As a stopping criterion of the training, we choose a patience value of 20, which is the number of iterations where there is no increase in the value of the determinant of the Fisher information matrix.
Training parameters used for each network.
All Tables
Estimation of parameters for different instrumental smoothing in both training and testing set (Gaussian; z = 3.0).
Effects of continuum variation on the estimation of astrophysical parameters, log T0 and γ, at z = 3.0. In the case of cosmological parameters, σ8 and nS, IMNN fails to extract continuum-independent information out of the Fourier space.
All Figures
 |
Fig. 1. Plots showing the modeling of the variation of Lyα forest flux power spectrum with astrophysical parameters, T0 and γ at z = 3. The top panels show the plots of the Lyα forest flux power spectrum corresponding to fiducial and varied T0 and γ. We added Gaussian noise to the sightlines with an S/N distribution ranging from 20 to 100 (S/N distribution is uniform in the log scale, making the distribution have more low S/N sightlines). We plot the power spectrum corresponding to the fiducial simulation (red) and the varied parameters (blue and green) corresponding to mock Lyα with this S/N distribution. The error bars correspond to bootstrapping errors computed over 5000 sightlines for a sample size of 50 sightlines with 10 000 bootstrap realizations. The power spectra corresponding to the simulation runs (with similar S/N distribution) with fiducial parameters but different initial seed density fields are plotted with colored hollow points in the middle panels. We modeled the power spectrum based on the curves in the top panels. We then used the posterior distribution by running an MCMC with flat priors (see Eq. 4) to estimate the parameter values (see Sect. 3). In the middle panels, hollow blue, green, and red points correspond to the fiducial simulations with different seeds, and the posterior estimates of the parameters (and the posterior standard deviation) are given in the plots. In the bottom panels, we show the sensitivity of the parameter estimates based on power spectrum to noise levels when we lower the S/N distribution (0.85 × S/NFid) of the sightlines and use the same power spectrum modeling to estimate the parameters. |
| In the text | |
 |
Fig. 2. Same as Fig. 1 but with cosmological parameters σ8 and ns. In the top panels, however, we plot the difference between the power spectrum at a certain parameter value to the one at the fiducial parameter. This was done for a better visualization, since the variations in σ8 and nS do not cause an appreciable change in the power spectrum within the error bars shown. |
| In the text | |
 |
Fig. 3. IMNN training example (using NumericalGradientIMNN subclass of IMNN) corresponding to the astrophysical parameters, T0 and γ (top panels), and cosmological parameters, σ8 and ns (bottom panels), for z = 3.0. The plots show the evolution of Fisher information during training with the training epoch. The solid lines correspond to the training sample and the dotted lines correspond to the validation sample. The training was stopped at the maximum iteration values shown in the x axis of the above plots. This choice was based on the training epoch when the Fisher information extracted from the validation sample reaches a saturation value and shows no further improvement with additional training epochs. |
| In the text | |
 |
Fig. 4. Estimation of T0, γ, σ8, and ns using score-compression from IMNN on the Fourier-transformed Lyα forest transmitted flux for three simulations run at fiducial parameter values with different initial random seeds. Each realization in the distribution of the estimated parameters is a bootstrap realization of a sample size of 50 mock spectra over the entire testing set. The distribution of the parameters was generated with 10 000 bootstrap realizations for each parameter. On the left panels, we plot the estimation for simulated sightlines that have the S/N distribution S/NFid with IMNN trained with sightlines that have S/NFid. On the right panels, we plot the estimation for 0.85 × S/NFid with IMNN trained with S/NFid sightlines. This shows the sensitivity of the trained NNs to noise level deviations in the data. |
| In the text | |
 |
Fig. 5. Estimation of σ8 and ns at z = 4 for parameter values (two dashed black lines) different from the parameter values with which the IMNN has been trained (dashed blue, red, and green lines). The black curves show the PDF of the estimated parameter values (at two different values). Each realization in the distribution of the estimated parameters is a bootstrap realization of a sample size of 50 mock spectra over the entire testing set. The distributions of the parameters were generated with 10 000 bootstrap realizations for each parameter. |
| In the text | |
 |
Fig. 6. Estimation of T0 and γ using MCMC with power spectrum and IMNN on the Fourier-transformed Lyα forest transmitted flux for CAMELS simulation at z = 2. The expected parameter values are log T0 = 3.97 and γ = 1.26. The power spectrum modeling for the MCMC approach and the training for the IMNN approach were done with previous Sherwood-Relics simulations. We checked the robustness of both approaches by testing them on a different simulation. |
| In the text | |
 |
Fig. 7. 2D parameter estimation of T0 and ΓHI using IMNN. Top: IMNN training plot (using SimulatorIMNN subclass of IMNN) corresponding to thermal parameter, T0, and H I photoionization rate, ΓHI, for z = 3. The plot shows the evolution of Fisher information during training with the training epoch. Bottom: Contour plots showing the 68% credible region for log T0 and logΓHI/ΓHI, Fid estimates based on the IMNN approach and with MCMC. It is to be noted that in the case of MCMC, the contour plot corresponds to a posterior distribution drawn from running MCMC using a flat prior (see Eq. 4), while in the case of IMNN it corresponds to the distribution of the estimates. Accompanying this are the plots for the distribution functions (for MCMC and IMNN, respectively) for both the parameters log T0 and logΓHI/ΓHI, Fid individually by marginalizing over the other parameters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



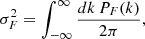
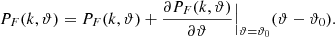
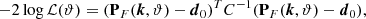
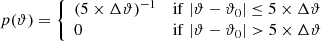
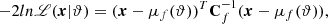
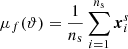
![$$ \begin{aligned} \mathbf{F }_{\alpha \beta }= \mathrm{Tr}[\mu _{f,\alpha }^T \mathbf{C }_f^{-1}\mu _{f,\beta }], \end{aligned} $$](/articles/aa/full_html/2024/10/aa50259-24/aa50259-24-eq8.gif)