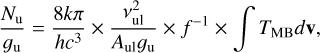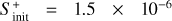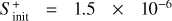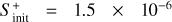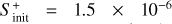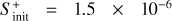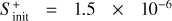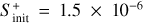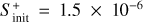| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A199 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202346721 | |
| Published online | 27 October 2023 | |
Evolution of Chemistry in the envelope of HOt corinoS (ECHOS)
I. Extremely young sulphur chemistry in the isolated Class 0 object B 335
1 Observatorio Astronómico Nacional (OAN), Alfonso XII 3, 28014 Madrid, Spain
e-mail: g.esplugues@oan.es
2 Centro de Astrobiología (CAB), INTA-CSIC, Carretera de Ajalvir Km. 4, Torrejón de Ardoz, 28850 Madrid, Spain
3 Département d’Astrophysique (DAp), Commissariat à l’Énergie Atomique et aux Énergies Alternatives (CEA), Orme des Merisiers, Bât. 709, 91191 Gif-sur-Yvette, Paris-Saclay, France
4 Institut de Ciències de l’Espai (ICE, CSIC), Can Magrans s/n, 08193, Bellaterra, Barcelona, Spain
5 Institut d’Estudis Espacials de Catalunya (IEEC), Barcelona, Spain
6 Center for Space and Habitability, Universität Bern, Gesellschaftsstrasse 6, 3012 Bern, Switzerland
7 Max-Planck-Institut für extraterrestrische Physik, 85748 Garching, Germany
Received:
21
April
2023
Accepted:
30
August
2023
Context. Within the project Evolution of Chemistry in the envelope of HOt corinoS (ECHOS), we present a study of sulphur chemistry in the envelope of the Class 0 source B 335 through observations in the spectral range λ = 7, 3, and 2 mm.
Aims. Our goal is to characterise the sulphur chemistry in this isolated protostellar source and compare it with other Class 0 objects to determine the environmental and evolutionary effects on the sulphur chemistry in these young sources.
Methods. We have modelled observations and computed column densities assuming local thermodynamic equilibrium and large velocity gradient approximation. We have also used the code Nautilus to study the time evolution of sulphur species, as well as of several sulphur molecular ratios.
Results. We have detected 20 sulphur species in B 335 with a total gas-phase S abundance similar to that found in the envelopes of other Class 0 objects, but with significant differences in the abundances between sulphur carbon chains and sulphur molecules containing oxygen and nitrogen. Our results highlight the nature of B 335 as a source especially rich in sulphur carbon chains unlike other Class 0 sources. The low presence or absence of some molecules, such as SO and SO+, suggests a chemistry not particularly influenced by shocks. We, however, detect a large presence of HCS+ that, together with the low rotational temperatures obtained for all the S species (<15 K), reveals the moderate or low density of the envelope of B 335. Model results also show the large influence of the cosmic ray ionisation rate and density variations on the abundances of some S species (e.g. SO, SO2, CCS, and CCCS) with differences of up to ~4 orders of magnitude. We also find that observations are better reproduced by models with a sulphur depletion factor of 10 with respect to the sulphur cosmic elemental abundance.
Conclusions. The comparison between our model and observational results for B 335 reveals an age of 104 < t < 105 yr, which high-lights the particularly early evolutionary stage of this source. B 335 presents a different chemistry compared to other young protostars that have formed in dense molecular clouds, which could be the result of accretion of surrounding material from the diffuse cloud onto the protostellar envelope of B 335. In addition, the theoretical analysis and comparison with observations of the SO2/C2S, SO/CS, and HCS+/CS ratios within a sample of prestellar cores and Class 0 objects show that they could be used as good chemical evolutionary indicators of the prestellar to protostellar transition.
Key words: astrochemistry / ISM: abundances / ISM: molecules / ISM: clouds / stars: formation
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Hot corinos are regions that arise during the formation of solar-type protostars. The progressive collapse of a prestellar core leads to the heating of the infalling envelope of dust and gas to temperatures of hundreds of Kelvin, while the densities increase up to ~108–109 cm−3 in the inner ~100 au around the central protostar. These are also the scales at which protoplanetary disks are expected to arise owing to the conservation of angular momentum. As the temperatures increase, the water-rich ice mantles sublimate, injecting molecules into the gas phase. Hot corinos are therefore chemically rich regions in Solar-like young protostars (Ceccarelli 2004; Ceccarelli et al. 2007b). In particular, these regions are relatively rich in interstellar complex organic molecules (Herbst & van Dishoeck 2009). Studying, therefore, the inventory and abundances of molecules in the earliest stages of star formation, that is in hot corinos, is essential to probe the initial conditions of planet and star formation processes. In spite of the detection of various hot corinos in the last decades (e.g. Cazaux et al. 2003; Okoda et al. 2023), just a few of them (such as IRAS 16293-2422, NGC 1333, and IRAS4A van Dishoeck et al. 1995; Ceccarelli et al. 2007a; Jaber et al. 2014; Caselli & Ceccarelli 2012; Jørgensen et al. 2016) have been investigated in detail until now. Many questions, therefore, still remain open about their nature and molecular composition: for instance, chemical differences between the earliest stages of star formation (Class 0 versus Class I objects), the role of the chemical characteristics inherited from the parent cloud, as well as the environmental effect on the chemical composition of hot corinos.
One way to understand the dynamics and evolution of the earliest stages of star formation is through molecular depletion. At temperatures of roughly 10 K and densities above 104 cm−3, several molecules, such as CO and CS, condense out onto dust grain surfaces (e.g. Caselli et al. 1999; Crapsi et al. 2005), and depletion increases with time (e.g. Bergin & Langer 1997; Aikawa et al. 2003). Therefore, depletion can be used as a clock, since evolved cores should be more depleted of certain species than younger cores. Regarding depletion, sulphur plays a fundamental role since, although sulphur is one of the most abundant species in the Universe and plays a crucial role in biological systems on Earth (e.g. Leustek 2002; Francioso et al. 2020), S-bearing molecules are not as abundant as expected in the interstellar medium (ISM). In particular, unlike the diffuse ISM and photon-dominated regions where the observed gaseous sulphur accounts (e.g. Goicoechea et al. 2006; Howk et al. 2006) for its total solar abundance (S/H ~ 1.5 × 10−5; Asplund et al. 2009), sulphur is strongly depleted in more dense molecular gas, since the sum of the detectable S-bearing molecules only accounts for a very small fraction of the elemental S abundance (Tieftrunk et al. 1994). In fact, to reproduce observations in hot corinos and hot cores, one needs to assume a significant sulphur depletion of at least one order of magnitude lower than the solar elemental sulphur abundance (e.g. Wakelam et al. 2004; Esplugues et al. 2014, 2022; Crockett et al. 2014; Vastel et al. 2018; Bulut et al. 2021; Navarro-Almaida et al. 2021; Hily-Blant et al. 2022; Fuente et al. 2023). Most of the sulphur seems to be locked on the icy grain mantles (e.g. Millar & Herbst 1990; Ruffle et al. 1999; Vidal et al. 2017; Laas & Caselli 2019) in the form of organo-sulphur molecules, also present in the comet 67P (Calmonte et al. 2016) and in meteoritic material (e.g. Naraoka et al. 2022; Ruf et al. 2021). However, OCS and SO2 are the only S-bearing molecules unambiguously detected in ice mantles to date (Geballe et al. 1985; Palumbo et al. 1995; McClure et al. 2023), while H2S has not been detected (Yang et al. 2022; McClure et al. 2023). Theoretical models also suggest that sulphur could be locked into pure allotropes of sulphur, especially S8 (Shingledecker et al. 2020). In any case, sulphur reservoirs in dense regions remain as an open question, as well as the time at which sulphur depletion occurs.
Given the low number of discovered hot corinos and, there-fore, the limited knowledge about them, the project Evolution of Chemistry in the envelope of HOt corinoS (ECHOS) aims to provide a complete inventory of the chemistry of hot corinos (with a sample including IRAS16293-2422, NGC 1333 IRAS 4A, HH 212, and B 335). ECHOS is carried out through homogeneous and systematic spectral surveys between 30 and 200 GHz using the Yebes-40 m and IRAM-30 m telescopes. In this paper, we focus on the analysis of B 335 and present a study of sulphur- bearing molecules in this region. Observations and a description of the source are presented in Sects. 2 and 3. In Sect. 4, we present the data and calculate column densities and abundances using different methods, depending on the number of detected transitions for each species, and also depending on the availability of collisional coefficients. A discussion of the results (including a comparison with other similar objects, as well as the use of a chemical code to study the fractional abundance evolution of sulphur species) is presented in Sect. 5. We finally summarise our conclusions in Sect. 6.
2 Observations
The observations were carried out with the Yebes-40 m and IRAM-30 m telescopes pointing to the position with coordinates αJ2000.0 = 19h37m0.93s, δJ2000.0 = +07°34′09.9″. For both telescopes, data were reduced and processed by using the CLASS and GREG packages provided within the GILDAS software1, developed by the IRAM institute.
2.1 Yebes-40 m telescope
The observations from the Yebes-40 m radiotelescope located in Yebes (Guadalajara, Spain) were obtained using a receiver that consists of two cold high electron mobility transistor amplifiers covering the 31.0–50.3 GHz Q-band with horizontal and vertical polarisations. The backends are 2 × 8 × 2.5 GHz fast Fourier transform spectrometers with a spectral resolution of 38.15 kHz, providing the whole coverage of the Q-band in both polarisations. The observations were performed in the positionswitching mode with (−400″, 0″) as the reference position. The main beam efficiency varies from 0.6 at 32 GHz to 0.43 at 50 GHz. Pointing corrections were derived from nearby quasars and SiO masers, and errors remained within 2–3″.
2.2 IRAM-30 m telescope
The observations from the IRAM-30 m radio telescope located in Pico Veleta (Granada, Spain) cover the 73–118 GHz and 130–175 GHz spectral ranges. These observations were carried out in one session in July 2021 with the Wobbler-Switching mode (±120″), using the broad-band EMIR (E090 and E150) receivers and the fast Fourier transform spectrometer in its 200 kHz of spectral resolution. The intensity scale in antenna temperature (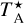 , which is corrected for atmospheric absorption and for antenna ohmic and spillover losses) was calibrated using two absorbers at different temperatures and the atmospheric transmission model (ATM; Cernicharo et al. 1985; Pardo et al. 2001). Calibration uncertainties were adopted to be 10%.
, which is corrected for atmospheric absorption and for antenna ohmic and spillover losses) was calibrated using two absorbers at different temperatures and the atmospheric transmission model (ATM; Cernicharo et al. 1985; Pardo et al. 2001). Calibration uncertainties were adopted to be 10%.
To convert to main beam brightness temperature (TMB), we used the expression
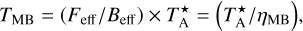 (1)
(1)
where Feff is the telescope forward efficiency and Beff is the main beam efficiency2,3. See Table 1 for a summary of the telescope beam sizes depending on frequency.
3 The source
B 335 is an isolated dense globule associated with the embedded far-infrared source IRAS 19347+0727 (Keene et al. 1980, 1983), located at a distance of ~100 pc (Olofsson & Olofsson 2009). The central source is a Class 0 source with a luminosity of 0.72 L⊙ (Evans et al. 2015), whose mass is estimated to be 0.08 M⊙ (Yen et al. 2015). Complex organic molecules (COMs), such as acetaldehyde (CH3CHO), methyl formate (HCOOCH3), and formamide (NH2CHO), have been detected (Imai et al. 2016; Okoda et al. 2022) in the vicinity of the protostar (r ~ 10 au). It reveals that B 335 harbors a hot corino (Cazaux et al. 2003; Herbst & van Dishoeck 2009), which warms up the surrounding regions leading to the sublimation of grain mantles and injecting complex organic molecules into the gas-phase (e.g. Ceccarelli 2004; Caselli & Ceccarelli 2012). Emission of CCH and c-C3H2 has also been detected around the protostar, which indicates the presence of carbon-chain molecules in this source (Sakai et al. 2008; Sakai & Yamamoto 2013). This carbon-chain molecules could suggest the presence of a so-called warm carbon-chain chemistry (WCCC; Sakai et al. 2008), characterised by various carbon-chain molecules being produced by reactions of CH4 (evaporated from grain mantles in a lukewarm region) and where the formation of HCnN is slower than that of CnHm molecules (Sakai et al. 2008, 2009; Oya et al. 2017).
Particularly interesting are the single-dish observations of CS and H2CO in B 335 (Zhou et al. 1993; Choi et al. 1995), since their optically thick lines show asymmetric profiles. This implies the presence of infalling motions in the envelope around B 335. A more detailed analysis with C18O, SO, HCN, and HCO+ ALMA observations (Evans et al. 2015, 2023; Yen et al. 2015) confirms an infalling gas motion of the inner part of the protostellar core, but rotation motion has not been detected at a spatial resolution of 0.3″ (~30 au). A rotation structure is only found at a scale of about 10 au from CH3OH and HCOOH emission (Imai et al. 2019). Single-dish and interferometric 12CO (1–0) and 13CO (1–0) observations (e.g. Hirano et al. 1988, 1992; Stutz et al. 2008; Bjerkeli et al. 2019) show also the presence of an east-west molecular outflow on ~0.2 pc (Cabrit et al. 1988; Moriarty-Schieven & Snell 1989) with an inclination between 3°–10° on the plane of the sky and an outflow opening angle of 45° (Hirano et al. 1988, 1992; Stutz et al. 2008; Yen et al. 2010). A dynamical analysis of the outflow molecular structure (Yıldız et al. 2015) implies that dynamical timescales for the CO emitting gas are of the order of 104 yr. This result, along with the absence of a rotationally supported disk on scales greater than ~ 10 au in size (Evans et al. 2015; Yen et al. 2015), suggest that the B 335 system is a particularly young source compared to other Class 0 objects, such as L 1527 which contains an embedded IRAS source and has a dynamical age of 2 × 104–105 yr (Tamura et al. 1996; André et al. 2000; Agúndez et al. 2019). The detection of abundant CCS (see Sect. 4.3) and other carbon-chain molecules in B 335 also confirms the early stage of this source since it is generally recognised that CCS and other carbon-chain molecules are abundant in the early stage of chemical evolution and become deficient at the advanced stage (Sakai et al. 2008).
So far, B 335 is one of the few hot corinos identified in a Bok globule, isolated from a large molecular cloud complex. This is therefore an ideal source for the study of the earliest stages of star formation with a chemical composition that could be regarded as a standard template for isolated protostellar cores.
Yebes-40 m and IRAM-30 m telescope efficiency data along the covered frequency range.
4 Data analysis and results
We have detected 81 emission lines from 21 different sulphur- bearing species (including isotopologs) in B 335. In particular, we have detected three transitions of CS, three of 13CS, three of C34S, three of C33S, nineteen of CCS, three of CC34S, seven of CCCS, three of CCC34S, five of OCS, three of HCS+, two of HC34S+, seven of SO, one of SO2, one of 34SO, one of H2S, one of H234S, ten of H2CS, one of HSCN, one of HNCS, and six of NS (see Table A.1 and Figs. A.1–A.21). These transitions span an energy range of Eup = 2.0–65.3 K.
4.1 Line profiles
All the lines are observed in emission. We first fitted the observed lines with Gaussian profiles using the CLASS software to derive the radial velocity (νLSR), the line width, and the intensity for each line. Results are given in Table A.1. We observed that most of the detected molecules show narrow line profiles (Δv ≲ 1.5 km s−1) that can be adjusted by a single velocity component.
It is well known that the gravitational collapse of a molecular cloud when a new star is formed is accompanied by the development of highly supersonic outflows (e.g. Bachiller & Pérez Gutiérrez 1997; Holdship et al. 2019). The material ejected through these jets collides with the surrounding cloud, compressing and heating the gas, which leads to a drastic alteration of the chemistry as endothermic reactions become efficient and dust grains are partially destroyed. Many observations have shown that several sulphur-bearing species are enhanced in the shocked regions with respect to other areas of the cloud (e.g. Pineau des Forets et al. 1993; Bachiller & Pérez Gutiérrez 1997; Codella & Bachiller 1999; Wakelam et al. 2004, 2005; Esplugues et al. 2013). However, the sulphur lines observed in B 335 present very narrow line widths (Figs. A.1–A.21), which is more consistent with the emission arising from the ambient quiescent cloud. Only for H2S, formed through the hydrogenation of sticked atomic sulphur on grains (Hatchell et al. 1998; Garrod et al. 2007; Esplugues et al. 2014; Oba et al. 2019) and thought to be the main sulphur reservoir in ices (Vidal et al. 2017; Navarro-Almaida et al. 2020), it is necessary to also consider a wider component (with Δv = 2.5 km s−1) to fit its only detected line, since the line profile shows the presence of faint wings. This could indicate that part of the H2S emission arises from the outflow, however, the line width of this component is much smaller (~2.5km s−1) than the ones observed for 12CO (~ 10–20 km s−1) in the outflow (Yen et al. 2010). Therefore, the wider H2S emission may be likely related to infall motions.
On the other hand, there are some species (CCS, CCCS, and H2CS) whose low transition lines present a double peak emission. The peak with the lowest intensity is located for all the cases at lower velocity (vLSR = 7.39–8.1 km s−1, blue peak) than for the more intense peak (vLSR = 8.80–8.97 km s−1, red peak). Line widths are slightly larger (Δv ≲ 0.83–1.63 km s−1) in the blue peaks than in the red ones (Δv ≲ 0.55–0.83 km s−1). The comparison of these profiles with those from the less abundant isotopologues shows that these two-peak profiles are due to self-absorption due to the large optical depths. All the detected lines present 0.005 < TMB < 1.5 K.
4.2 Rotational diagrams
For each molecule, we have computed a representative rotational temperature (Trot) and a column density (N) by constructing a rotational diagram, assuming a single rotational temperature for all energy levels (Goldsmith & Langer 1999). Rotational diagrams represent a technique to analyse cloud properties from molecular line emission assuming local thermodynamic equilibrium (LTE). The standard relation for the rotational diagram analysis is
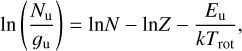 (2)
(2)
where Nu is the column density of the upper level in the optically thin limit, N is the total column density, gu is the statistical weight of the upper state of each level, Z is the partition function evaluated at a rotational temperature Trot, Eu/k is the energy of the upper level of the transition, vul is the frequency of the u→l transition, ∫ TMB dv is the velocity-integrated line intensity corrected from beam efficiency, and f is the beam filling factor. Assuming that the emission source has a 2D Gaussian shape, f is equal to 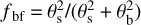 being θb the HPBW of the telescope in arcsec and θs the diameter of the Gaussian source in arcsec. In order to derive the values of f in each case, we have used the HPBW values listed in Table 1, and we have assumed a source size of 10″ according to interferometric maps of C17O emission in B 335 (Cabedo et al. 2021).
being θb the HPBW of the telescope in arcsec and θs the diameter of the Gaussian source in arcsec. In order to derive the values of f in each case, we have used the HPBW values listed in Table 1, and we have assumed a source size of 10″ according to interferometric maps of C17O emission in B 335 (Cabedo et al. 2021).
The resulting rotational diagrams are shown in Fig. 1, while the column densities and rotational temperatures obtained are listed in Table 2. The uncertainties shown in Table 2 indicate the uncertainty obtained in the least squares fit of the rotational diagrams. These uncertainties include the 10% error in the observed line intensities due to calibration. The uncertainty obtained in the determination of the line parameters with the Gaussian fitting programme is included within the error bars at each point of the rotational diagram. We did not applied the rotational diagram method to NS since its four observed lines are close to the detection limit and/or blended with other species, which would introduce a high uncertainty in the results. The analysis of NS and others molecules with only one emission line detected (e.g. SO2) has been done only with a LVG code (see next section) instead.
The obtained rotational temperatures are ≲ 15 K. In the case of CCS, the molecule with the largest number of detected transitions, we observe a trend variation (Fig. 1) between the low and the high transition energies. In particular, the transitions with Eu < 40 K are well adjusted for a Trot ~ 5 K, while transitions with Eu > 40 K are better adjusted for a Trot ~ 15 K. This suggests that CCS arises from different regions characterised by distinct excitation temperatures. The rotational temperatures for the rest of molecules with several detected transitions (e.g. C3S, OCS, SO, H2CS) have 4.5 ≲ Trot ≲ 7.4 K. These low temperatures together with their narrow line widths are consistent with emission arising from a cold and extended part of the dense core. Gas density at these scales is probably not too high as also indicated by the low Trot obtained for most of the S-molecules. All this suggests that the gas is sub-thermally excited with a moderate or low (< 105 cm−3) density, in agreement with Frerking et al. (1987). In addition, the low number of transitions detected for several species (CS, 13CS, C34S, C33S, HCS+, and HC34S+) and the optically thick emission of some transitions of CCS, CCCS, and H2CS, also indicate that the rotational diagram method not suitable to derive column densities.
Column densities (N), rotational temperatures, and abundances (X) relative to H2 of the sulphur-bearing molecules detected in B 335.
4.3 Column densities and abundances
We have therefore calculated molecular column densities for the detected S-species using a large velocity gradient (LVG) approximation. In particular, we have derived them by fitting the emission line profiles using the LVG code MADEX (Cernicharo 2012), which assumes that the radiative coupling between two relatively close points is negligible, and the excitation problem is local. The LVG models are based on the Goldreich & Kwan (1974) formalism. MADEX also includes corrections for the beam dilution of each line, depending on the different beam sizes at different frequencies. The final considered fit is the one that reproduces more line profiles better from all the observed transitions. To carry out the fits, we assume uniform physical conditions (kinetic temperature, density, line width, radial velocity). In particular, we have assumed a gas density of 5 × 104 cm−3 according to results from Sect. 4.2 and to results from Cabedo et al. (2023), who deduced a density of ~104 cm−3 for the outer regions of B 335 based on interferometric observations. We have also assumed a source size of 10″ according to interferometric maps (Cabedo et al. 2021), and a kinetic temperature of the gas TK ~ 15 K estimated by Shirley et al. (2011) from the formula for dust temperature considering only central heating by the B 335 protostar, and that dust and gas are coupled.
In the case of H2CS and H2S, we have used the code RADEX (van der Tak et al. 2007) since there are not available collisional rates in MADEX for these two molecules. The results are shown in Table 2. For those species for which one transition is observed (34SO, SO2, H2S, H234S, HSCN, and HNCS), we have derived their column densities using only the LVG approximation and not the rotational diagram technique described in Sect. 4.2. For NS, since there are not available collisional rates, we have considered LTE approximation.
Column densities derived using the rotational diagram technique and LVG calculations agree within a factor ≲3. Sources of uncertainty are the low angular resolution of the used telescopes (with beam sizes between ~36″ and ~54″ for the 40 m-Yebes telescope, and ~14″ and ~29″ for the 30 m-IRAM telescope depending on frequency), which implies that the emission from the inner region of the B 335 is blended with the outer envelope, the possible overlap with the emission from other species (e.g. the case of H234S), the limited number of detected transitions (one transition in many cases, such as for H2S, H234S, SO2, HSCN, HNCS, and 34SO), the lack of collisional rates for some species (e.g. NS), and the assumed source size derived from C17O interferometric observations. This is one of the most important uncertainties due to the lack of interferometric observations of S-species in B 335, since the emission from the different S-molecules may arise from distinct regions with slightly different sizes leading to a significant impact on the fits. In order to derive the uncertainty associated with the LVG results, we have run the LVG code varying the considered values for density, temperature, and source size. In particular, we have run models with density 5 × 104 cm−3 and 2.5 × 104 cm−3 (variation of a factor 2), temperatures of 15 K and 12 K, and source sizes of 10″ and 8″ (reduction of 20%). We found variations in the S-column densities ≲10% between these two TK which is comparable to the calibration errors, while the variations when changing the density and the source size were ≲20% and ~30%, respectively. Taking all this into account, we estimate the uncertainties in the column densities derived with LVG approximation to be of the order of ~50%.
The total column density of the sulphur-bearing species observed in B 335 is 6.2 × 1014 cm−2, with the highest contribution coming from CS (calculated from C34 S considering 32S/34S = 24.4 since CS is optically thick, Mauersberger et al. 2004), H2S, SO, and CCS. The lowest values are found for NS and HSCN. We have also observed several isotopologues relative to 13C, 34S, and 33S. In particular, from CS, we obtain 34S/33S = 10.7 (which is slightly higher than the solar abundance value 34S/33S = 5.6 − 6.3, Anders & Grevesse 1989; Mauersberger et al. 2004), and 12C/13C = 46.8, which is similar to that found in dark clouds by Cernicharo & Guelin (1987).
Table 2 also shows the fractional abundances relative to H2 (with 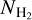 , obtained from Cabedo et al. 2021) of the sulphur molecules detected in the range λ = 2, 3, and 7 mm. Considering the detected S-molecules, we have obtained a total molecular sulphur abundance of 2.0 × 10−8, which is alike to the one found in similar sources, such as L 1544 (1.1 × 10−8, Vastel et al. 2018), L 483 (9.1 × 10−9, Agúndez et al. 2019), and B1-b (1.2 × 10−8, Fuente et al. 2016). The highest S-abundances are >10−9 (CS, H2S, CCS, and SO), with also several relatively abundant (>10−10) species, such as OCS and H2CS. In general, B 335 presents a great variety of S-bearing molecules, but less than other similar sources. In particular, although the total sulphur abundance in B 335 is similar to other sources, such as L 483, we detect a significant lower number of sulphur molecules in B 335 than in L 483. We are also missing some other S-species already reported towards L 483, including SO+, HCS, and CH3SH, for which we have derived upper limits for their column densities of N(SO+) < 1.5 × 1011 cm−2, N(HCS) < 3 × 1012 cm−2, and N(CH3SH) < 2 × 1012 cm−2. To derive these upper limits, once the physical parameters are fixed, we vary (for each species) the column density until the model fit reaches the observed intensity peak of any of the observed lines. We do not allow the model fit to be greater than any observed line.
, obtained from Cabedo et al. 2021) of the sulphur molecules detected in the range λ = 2, 3, and 7 mm. Considering the detected S-molecules, we have obtained a total molecular sulphur abundance of 2.0 × 10−8, which is alike to the one found in similar sources, such as L 1544 (1.1 × 10−8, Vastel et al. 2018), L 483 (9.1 × 10−9, Agúndez et al. 2019), and B1-b (1.2 × 10−8, Fuente et al. 2016). The highest S-abundances are >10−9 (CS, H2S, CCS, and SO), with also several relatively abundant (>10−10) species, such as OCS and H2CS. In general, B 335 presents a great variety of S-bearing molecules, but less than other similar sources. In particular, although the total sulphur abundance in B 335 is similar to other sources, such as L 483, we detect a significant lower number of sulphur molecules in B 335 than in L 483. We are also missing some other S-species already reported towards L 483, including SO+, HCS, and CH3SH, for which we have derived upper limits for their column densities of N(SO+) < 1.5 × 1011 cm−2, N(HCS) < 3 × 1012 cm−2, and N(CH3SH) < 2 × 1012 cm−2. To derive these upper limits, once the physical parameters are fixed, we vary (for each species) the column density until the model fit reaches the observed intensity peak of any of the observed lines. We do not allow the model fit to be greater than any observed line.
 |
Fig. 1 Rotational diagrams of the detected sulphur-bearing molecules in B 335. Fitted values of the rotational temperature, Trot, column density, N, and their respective uncertainties are also indicated for each molecule. |
 |
Fig. 2 Comparison of fractional abundances of sulphur-bearing species between three Class 0 objects B 335 (this work), L 483 (Agúndez et al. 2019), and B1-b (Fuente et al. 2016). |
5 Discussion
5.1 Chemical comparison
Even though the total sulphur abundance in B 335 is similar to that from other Class 0 sources, the abundances of some specific molecules significantly vary among them. Figure 2 shows a comparison between abundances of different sulphur species in three Class 0 sources, B 335, L 483, and B1-b. The first thing that stands out is that sulphur carbon chains (CS, CCS, and CCCS) in B 335 are about one order of magnitude higher than the ones observed in L 483 and B1-b. Although high abundances of carbon-chain molecules have already been found in other cold clouds, such as TMC1 (Agúndez & Wakelam 2013), it is not a universal characteristic of this type of early regions, since many of them present different degrees of carbon chain richness (e.g. Suzuki et al. 1992; Hirota et al. 2009). This therefore high-lights the nature of B 335 as a source especially rich in sulphur carbon chains.
Unlike carbon chains, sulphur molecules containing oxygen in B 335 have a similar (OCS) or even lower (SO and SO2) abundance by up to one order of magnitude than those found in L 483 and B1-b (see also Fig. 3). These oxygen-sulphur molecules are usually detected in cold dense regions with abundances between 10−10–10−8, while in hot cores and hot corinos they are significantly enhanced (e.g. Tercero et al. 2010; Esplugues et al. 2013). In particular, SO2 is a better tracer of warm gas than SO (Esplugues et al. 2013), while SO is a well-known outflow tracer (e.g. Codella & Scappini 2003; Lee et al. 2010; Tafalla et al. 2010). SO seems to be more enhanced than SO2 in shocks for timescales ~104 yr (e.g. Codella & Bachiller 1999; Viti et al. 2004; Jiménez-Serra et al. 2005). The low SO abundance found in B 335 with respect to the other two sources L 483 and B1-b suggests that its chemistry may not be significantly affected by shocks associated with the bipolar outflow (e.g. Hirano et al. 1988, 1992; Stutz et al. 2008; Bjerkeli et al. 2019).
Other sulphur molecules detected in B 335 with low abundances (Fig. 3) are those containing nitrogen, that is NS and HSCN (4 × 10−11 and 3 × 10−11, respectively). HSCN, unlike HNCS which is the most stable isomer, is metastable and only detected on Earth under specific conditions (through UV- photolysis of HNCS Wierzejewska & Mielke 2001 or through a low-pressure discharge Brünken et al. 2009). In contrast, HSCN is more easily observed in the interstellar medium. For instance, in Sgr B2 (where HSCN was first time detected) the ratio HNCS/HSCN~3 (Halfen et al. 2009) and in TMC1 this ratio is ~1 (Adande et al. 2010), while in L 1544 Vastel et al. (2018) only detect HSCN, but not HNCS. This shows the important role of non-equilibrium chemistry in dense clouds. In B 335, we only detect one transition of HNCS with a signal to noise ratio σ ~ 3.1, so we have considered its column density (NHNCS ≤ 4.7 × 1012 cm−2) as an upper limit. This leads to a ratio HNCS/HSCN < 4.7 consistent with the one found in Sgr B2.
 |
Fig. 3 Fractional abundance (X) ratios between B 335 and L 483, and B 335 and B1-b for all the detected sulphur-bearing species in B 335. |
5.2 Sulphur ions
Apart from neutral sulphur species, we have also observed the presence of some ions in B 335. Molecular ions are commonly observed in dense prestellar or protostellar regions (e.g. Caselli et al. 1998, 2002; Hogerheijde et al. 1998; van der Tak et al. 2005). To a lesser extent, ions (such as HCO+ and N2H+) have also been observed in protostellar shocks (e.g. Bachiller & Pérez Gutiérrez 1997; Hogerheijde et al. 1998; Caselli et al. 2002; van der Tak et al. 2005). The presence of ions in shocked regions is a balance between their enhancement by the sputtering of dust grain mantles, which ejects molecules into the gas phase that undergo reactions forming ions, and their destruction by electronic recombination (e.g. Neufeld & Dalgarno 1989; Viti et al. 2002). For this reason, those ions that usually decrease in shocks (such as N2H+) may indicate the presence of a pre-shock chemistry (Codella et al. 2013), while the ions that are enhanced by shock chemistry will be effective tracers of shocked gas. This is the case of HOCO+ and SO+ (Podio et al. 2014) since their abundances are predicted to be very low in the quiescent gas, but significantly enhanced in shocks following the release of CO2 and S-species from dust grain mantles (Minh et al. 1991; Turner 1992, 1994; Deguchi et al. 2006).
Among the sulphur ions, in B 335 we do not detect SO+ (strong tracer of shocked gas which forms from S+ and OH Neufeld & Dalgarno 1989), but we detect HCS+ and HC34S+ with abundances of 4.7 × 10−10 and 1.9 × 10−11, respectively. The value we have obtained for HCS+ is similar to the one observed in the bow shock L 1157-B1 (Podio et al. 2014) and one order of magnitude higher than the ones obtained by Agúndez et al. (2019) and Fuente et al. (2016) in the Class 0 objects L 483 and B1-b, respectively, as also found for CS. The abundances of HCS+ and CS are strongly related, since this ion forms through the reaction of CS with HCO+, H3+, H3O+ (Millar et al. 1985). In addition, large abundances of CS and HCS+ may also indicate that OCS is one of the main sulphur carriers on dust grains upon sputtering from the grain mantles according to previous theoretical (Podio et al. 2014) and observational (Wakelam et al. 2005; Codella et al. 2005) results.
Regarding the ratio R = HCS+/CS, we obtain from observations a value of 0.043. Thaddeus et al. (1981) determined an abundance ratio R~0.01–0.03 in ten molecular sources located in Sgr B2 and Ori A, while Millar (1983) found that R could be as large as 0.1 in cold dark clouds. This result was also verified by Irvine et al. (1983). A similar R value to that from B 335 is found as well in the pre-stellar core L 1544 (0.03, Vastel et al. 2018), while in the protostellar sources L 483 and B1-b the HCS+/CS ratio is 0.017 and 0.008, respectively (Agúndez et al. 2019; Fuente et al. 2016). According to Clary et al. (1985), rate coefficients for ion-CS reactions rapidly increase at low temperatures suggesting that the sources B 335 and L 1544 are characterised by lower temperatures than L 483 and B1-b, which can be due to an earlier evolutionary stage of B 335 and L 1544 compared to L 483 and B1-b.
5.3 Time evolution of fractional abundances
Figures 4–7 show the evolution of several S-bearing species along 10 Myr for different physical conditions of the cosmic-ray (CR) ionisation rate (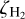 ), gas temperature (Tg), hydrogen number density (nH), and initial sulphur abundance (
), gas temperature (Tg), hydrogen number density (nH), and initial sulphur abundance (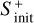 ). Given that the CR ionisation rate is still uncertain and spreads over a range of values (van der Tak & van Dishoeck 2000) determined as
). Given that the CR ionisation rate is still uncertain and spreads over a range of values (van der Tak & van Dishoeck 2000) determined as 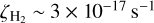 in dense clouds, Indriolo & McCall (2012) obtained a range (1.7–10.6) ×−16 s−1 in a sample of diffuse clouds, and Neufeld & Wolfire (2017) derived a
in dense clouds, Indriolo & McCall (2012) obtained a range (1.7–10.6) ×−16 s−1 in a sample of diffuse clouds, and Neufeld & Wolfire (2017) derived a 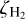 of the order of a few 10−16 s−1 in the Galactic disk), we have considered two values for the cosmic ionisation rate
of the order of a few 10−16 s−1 in the Galactic disk), we have considered two values for the cosmic ionisation rate 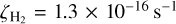 and 1.3 × 10−17 s−1. For the gas temperature and density, given the results obtained in Sects. 4.2 and 4.3, we have run models considering Tg = 7 K and 15 K, and nH =2 × 104 cm−3 and 2 × 105 cm−3. For the case of the initial sulphur abundance, we have considered the solar elemental sulphur fractional abundance (
and 1.3 × 10−17 s−1. For the gas temperature and density, given the results obtained in Sects. 4.2 and 4.3, we have run models considering Tg = 7 K and 15 K, and nH =2 × 104 cm−3 and 2 × 105 cm−3. For the case of the initial sulphur abundance, we have considered the solar elemental sulphur fractional abundance (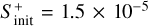 ) and also one factor of S depletion (1.5 × 10−6) since to reproduce observations in hot corinos one needs to assume a significant sulphur depletion of at least one order of magnitude lower than the solar elemental sulphur abundance as previously stated in Sect. 1.
) and also one factor of S depletion (1.5 × 10−6) since to reproduce observations in hot corinos one needs to assume a significant sulphur depletion of at least one order of magnitude lower than the solar elemental sulphur abundance as previously stated in Sect. 1.
We have obtained these models using the Nautilus time-dependent chemical code (Ruaud et al. 2016). Nautilus is a three-phase model in which gas, surface icy mantle, bulk icy mantle, and their interactions are considered. Nautilus solves the kinetic equations for both the gas phase species and the surface species of interstellar dust grains and computes the evolution with time of chemical abundances for a given physical structure. The chemical network is based on the KInetic Database for Astrochemistry (KIDA4). The used version here is detailed in Wakelam et al. (2021). In particular, this Nautilus version considers gas-phase processes including neutral-neutral and ion-neutral reactions, direct cosmic ray ionisation or dissociation, ionisation or dissociation by UV photons, ionisation or dissociation produced by photons induced by cosmic-ray interactions with the medium (Prasad & Tarafdar 1983), and electronic recombinations. For species on the surfaces, there is a distinction between species in the most external layers (surface species) and species below these layers (mantle species). The species are adsorbed on the surface and become the mantle during the construction of the ices. Similarly, when the species desorb, only the species from the surface can desorb, but surface species are gradually replaced by the mantle species. Regarding surface reactions, the model includes thermal desorption, photo-desorption, chemical desorption, and cosmic-ray heating. See Wakelam et al. (2021) for extensive details about the surface parameters considered in each surface reaction. In all models, we have adopted the initial abundances shown in Table 3 and a visual extinction Av = 15 mag5.
In general, we observe that the abundances of all the species considered in Figs. 4–7 increase with time up to t ~ 5 × 105 yr, moment at which the abundances of various species decrease abruptly. This is the case of CS, SO, and SO2, whose abundances decrease by about 2×4 orders of magnitude between t ~ 5 × 105 yr and t ~ 5 × 106 yr since they react with other species to form more complex molecules. In particular, for t > 105 yr, CS SO, and SO2 are mainly destroyed by reacting with 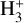 and forming HCS+, HSO+, and
and forming HCS+, HSO+, and 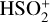 , respectively. For the abundances of the rest of sulphur species, this decrease after reaching the maximum value is lower and not greater than two orders of magnitude. From these figures, we also deduce the formation time scales of S-species. In particular, we have observed that CS is one of the molecules reaching first its maximum abundance value in all the models at t ~ 5 × 104 yr, followed by HCS+ with its maximum abundance reached at t ~ 105 yr. Other molecules, such as H2CS, can be considered as late molecules, since their maximum abundance values are found when the chemical evolution exceeds one million years.
, respectively. For the abundances of the rest of sulphur species, this decrease after reaching the maximum value is lower and not greater than two orders of magnitude. From these figures, we also deduce the formation time scales of S-species. In particular, we have observed that CS is one of the molecules reaching first its maximum abundance value in all the models at t ~ 5 × 104 yr, followed by HCS+ with its maximum abundance reached at t ~ 105 yr. Other molecules, such as H2CS, can be considered as late molecules, since their maximum abundance values are found when the chemical evolution exceeds one million years.
Regarding the influence of the physical conditions (cosmic- ray ionisation rate, temperature, density, and initial sulphur abundance) on the S-abundances, the parameter with the highest impact is the hydrogen nuclei number density, nH, since varying nH by one order of magnitude leads to abundance variations of up to three orders of magnitude for CS, CCS, OCS, HCS+, SO, and SO2 given a specific evolutionary time (see Fig. 6). In general terms, we observe in Fig. 6 that the chemical evolution of each considered species is accelerated when the density increases since collisions are more frequent than in a low density regime. This results in the abundance peak of the species being reached at earlier times for larger densities, although the chemical behaviour along time is roughly maintained. In particular, for t ~ 104 yr, we obtain that SO2 is mainly formed by the reaction O+SO for nH =2 × 104 and 2 × 105 cm−3, while for t ~ 105 yr (when the SO2 peak is reached) this molecule mainly forms by the reaction O+SO for nH =2 × 104 cm−3 and by OH+SO for nH =2 × 105 cm−3. The most responsible species of destroying SO2 for both densities is C for t ~ 104 yr, and 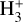 for t≥105 yr. Regarding CS, for t ~ 104 yr, it is mainly formed by the reaction HCS++e− for the low density value, while CS is mainly formed through the reaction between atomic S and C4 for nH =2 × 105 cm−3. For t ~ 105 yr (when the CS abundance decreases for any model), CS is mainly destroyed by its reaction with
for t≥105 yr. Regarding CS, for t ~ 104 yr, it is mainly formed by the reaction HCS++e− for the low density value, while CS is mainly formed through the reaction between atomic S and C4 for nH =2 × 105 cm−3. For t ~ 105 yr (when the CS abundance decreases for any model), CS is mainly destroyed by its reaction with 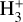 and with HCO+.
and with HCO+.
Another parameter with a big impact on S-abundances is the cosmic-ray ionisation rate, ζ, since the variation from ζ =1.3 × 10−17 to 1.3 × 10−16 s−1 changes by about two orders of magnitude the abundances of all the sulphur species considered in the sample (Fig. 4). For the case of carbon-chains (CCS, C3S), we observe that the larger ζ, the larger the S-abundances for t ≲ 105 yr. Similar results are found for the species SO, SO2, NS, H2CS, and OCS. For t ~ 104 yr, we find that CCS is mainly formed by C+HCS for the low ζ model, while it is mainly formed through HC3S++e− in a more efficient way for a model with larger ζ (1.3 × 10−16 s−1). In the case of SO (one of the most affected molecules by ζ between 104 ≲ t ≲ 106 yr), it is mostly formed by the reaction O+HS in a model with low ζ, while the reaction between S+OH becomes more important to form SO2 when increasing ζ by one order of magnitude.
On the other hand, changing the temperature (from Tgas = 7 K to 15 K) and especially the initial sulphur abundance (from 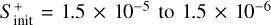 ) in the models leads to abundance variations smaller than two orders of magnitude for t > 104 yr. In particular, we have found that an increase of the
) in the models leads to abundance variations smaller than two orders of magnitude for t > 104 yr. In particular, we have found that an increase of the 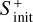 value by one order of magnitude also enhances the S-abundances by one order of magnitude during the entire duration of core evolution.
value by one order of magnitude also enhances the S-abundances by one order of magnitude during the entire duration of core evolution.
For the particular case of HCS+ and CS, the main physical parameters significantly influencing their abundances are the density (the lower density, the higher the HCS+ and CS abundances for t > 104 yr) and the cosmic-ray ionisation rate (the higher the ζ, the higher the HCS+ and CS abundances for t > 5 × 105 yr). By contrast, other physical parameters, such as the gas temperature, barely affect the HCS+ and CS abundances for t < 106 yr.
 |
Fig. 4 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
 |
Fig. 5 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
 |
Fig. 6 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
 |
Fig. 7 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
Abundances with respect to total hydrogen nuclei considered in the chemical code Nautilus.
5.4 Comparison with observations
We now compare the different models considered in the previous section with observational results to derive the current evolutionary stage of B 335. Figures A.22–A.25 show the ratio between the abundances obtained from the models (Xmodel) and from the observations (Xobs) for several sulphur-bearing species. In particular, we have considered those S-species for which we observe more than one emission line and those that are not close to the limit of detection. The results are shown for five specific evolution times (t = 104, 5 × 104, 105, 5 × 105, and 106 yr). In order to find the cases with the closest values between the theoretical and observational results, we have considered for each model the largest number of S-species for which −0.5 ≤ log(Xmodel/Xobs) ≤ 0.5 in order to only consider discrepancies between model and observational results smaller than a factor of ~3. Results show that the evolutionary stages that better reproduce the observed abundances of the largest number of S-species in B 335 are those between t = 104–105 yr. This result obtained from a chemical approach agrees with the results obtained from Evans et al. (2015) who derived an age of ~5 × 104 yr for B 335 through a dynamical perspective, by applying an inside-out collapse model that is compared with ALMA observations. Altogether this reveals, therefore, the particularly early evolutionary stage of B 335, which is comparable to the ages of pre-stellar condensations (e.g. Caselli & Ceccarelli 2012). As B 335 is an isolated globule, this may be due to the fact that the condensation has formed from very little dense gas (~103 cm−3) without a dense pre-phase between the formation of the globule and the beginning of the collapse. This gives B 335 a different chemistry compared to other young protostars that have form in dense molecular clouds, such as L 483 and B1-b. Another plausible scenario is that material from the diffuse cloud surrounding B 335 may currently be accreting onto the protostellar envelope, thus rejuvinating its chemistry. This accretion has been found (e.g. Pineda et al. 2020) in another Class 0 source embedded in the Perseus Molecular Cloud Complex. Interferometric observations are requested to distinguish between both scenarios.
From Figs. A.22–A.25, we have also deduced that chemical models with values of nH = 2 × 104 cm−3, Tg = 15 K, 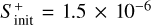 , and ζ =1.3 × 10−17 s−1 best reproduce the observations of the largest number of S-species for t = 104–105 yr. This value of ζ agrees with results from Cabedo et al. (2023) who found a cosmic-ray ionisation rate ≲10−16 s−1 in the outer regions of B 335, especially for an envelope radii > 500 au. A sulphur depletion factor of 10 with respect to the sulphur cosmic elemental abundance is also consistent with results from Fuente et al. (2023) in low-mass star-forming regions, such as Taurus and Perseus.
, and ζ =1.3 × 10−17 s−1 best reproduce the observations of the largest number of S-species for t = 104–105 yr. This value of ζ agrees with results from Cabedo et al. (2023) who found a cosmic-ray ionisation rate ≲10−16 s−1 in the outer regions of B 335, especially for an envelope radii > 500 au. A sulphur depletion factor of 10 with respect to the sulphur cosmic elemental abundance is also consistent with results from Fuente et al. (2023) in low-mass star-forming regions, such as Taurus and Perseus.
 |
Fig. 8 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
 |
Fig. 9 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
 |
Fig. 10 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
5.5 Sulphur chemical ratios
We have considered several sulphur-bearing molecular ratios and have also analysed their evolution with time. Model results obtained with the Nautilus code are shown in Figs. 8–11. We have also changed some of the physical conditions (cosmic-ray ionisation rate, temperature, density, and initial sulphur abundance) in order to study their impact on the evolution of these ratios. We first notice that while there are some ratios, such as HCS+/CS, that present small variations of up 1 order of magnitude between t = 104–106 yr, there are other ratios that significantly change with time. In particular, the SO2/C2S, SO/CS, SO2/CS, NS/CS, H2S/CS, and H2CS/CS ratios show variations of up to ~5 orders of magnitude in that time range (104–106 yr). The physical parameter affecting sulphur ratios the most is the density, leading to differences of up to ~4–5 orders of magnitude especially between 5 × 104 and 106 yr. The cosmic-ray ionisation rate is the next physical parameter with the greatest effect on the sulphur ratios with differences of about one order of magnitude in their values. In particular, the SO2/CS, SO/CS, SO2/C2S, and C2S/CS ratios are among those mostly influenced by ζ, while the SO/SO2 ratio is one of the least affected. The SO/SO2 ratio is, however, more sensitive to the density variation. We also observe a large density impact on the NS/CS ratio, finding that the higher the density, the larger the NS/CS for t ~ 105–106 yr, with NS being mostly formed during that time range through the neutral-neutral reaction N+HS and, to a lesser extent, through the dissociative recombination of HNS+. On the other hand, varying the gas temperature from 7 to 15 K (Fig. 9) mostly affects the H2S/SO ratio between 104 and 106 yr, and the SO/CS, SO2/CS, and H2S/CS ratios at late times (t ≳ 106 yr). Regarding the only ion detected in B 335, its HCS+/CS ratio slightly increases when the initial sulphur abundance is decreased, and also when the cosmic-ray ionisation rate or the density increase.
The use of molecular ratios as indicators of chemical evolution of young stellar sources has been previously approached from both observational and theoretical perspectives (e.g. Pineau des Forets et al. 1993; Charnley 1997; Hatchell et al. 1998; Codella & Bachiller 1999; Gibb et al. 2000; Boogert et al. 2000; Wakelam et al. 2004). Our models (Figs. 4–7) show that SO and SO2 constantly increase with time reaching both their peaks at t ≳ 5 × 105 yr, which prevents the use of their ratio as a chemical clock. Nevertheless, Figs. 8–11 show that there are other sulphur ratios that could be used as evolutionary tracers since they maintain a constant trend over time. This is for instance the case of the SO2/C2S and SO/CS ratios, whose values constantly increase during the first ~2 × 105 yr. In order to compare these theoretical results with observations, we have considered a sample of sources that includes starless cores (TMC1 and L 1544 considered as starless and prestellar cores, respectively, see for example Crapsi et al. 2005; Schnee et al. 2007; Lefloch et al. 2018; Agúndez et al. 2019; Cernicharo et al. 2021) and Class 0 objects (B 335, L 483, and B1-b). Observational results are shown in Fig. 12, where we have indeed found a clear trend where the SO2/C2 S and SO/CS ratios increase with the age of the objects, suggesting that these sulphur ratios could be used as chemical clocks. We have also included in Fig. 12 observational results for the HCS+/CS ratio. In this case, we have obtained a negative trend in which the value of HCS+/CS decreases with the age of the objects.
Comparing the observational HCS+/CS, SO2/C2S, and CO/CS ratios for B 335 with the theoretical results (Figs. 8–11), we observe that, for the temperature and density values used in Sect. 4.3 to derive observational results, the three ratios would be reproduced at 5 × 104 ≲ t ≲ 105 yr when considering a high cosmic-ray ionisation rate (ζ = 1.3 × 10−16 s−1) and a S depletion of at least a factor 10 with respect to the solar elemental sulphur abundance. This depletion is also found by many authors (e.g. Wakelam et al. 2004; Crockett et al. 2014; Vastel et al. 2018; Bulut et al. 2021; Navarro-Almaida et al. 2021; Esplugues et al. 2022; Hily-Blant et al. 2022; Fuente et al. 2023) in other star-forming regions.
 |
Fig. 11 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
6 Summary and conclusions
We have carried out a comprehensive observational and theoretical study of sulphur in the Class 0 object B 335. This source is an isolated dense Bok globule located at a distance of ~100 pc. We have detected 20 different sulphur-bearing species (including isotopologues) using Yebes-40 m and IRAM-30 m telescope observations. In order to derive column densities, we have applied the method of rotational diagrams. For this purpose, we have also used non-LTE radiative transfer codes given the low number of transitions detected for some species and the optically thick emission of some lines. Our results show low rotational temperatures (≲ 15 K), suggesting that the gas is sub-thermally excited, and thus revealing a relatively low (< 105 cm−3) gas density. These low temperatures, the narrow line widths, and the relatively low density are also consistent with emission arising from a cold and extended region, suggesting that the detected S-emission does not trace the hot corino, but its cold envelope.
From the column densities of all the observed sulphur species, we have derived a total molecular sulphur abundance of 2.0 × 10−8, which is similar to that found in the envelopes of other Class 0 objects. Nevertheless, we have also found that the abundances of some specific S-molecules vary significantly across the sample of Class 0 objects (B 335, L 483, and B1-b) considered in this paper. In particular, we have derived high abundances of sulphur carbon-chain molecules in B 335 compared to those found in other Class 0 objects, and also compared with those abundances of S-molecules containing oxygen or nitrogen. This points out the nature of B 335 as a source especially rich in sulphur carbon chains, which could be due to the fact that B 335 is an isolated source compared to other young protostars that have formed in dense molecular clouds, such as L 483 and B1-b, or to accretion of material from the diffuse cloud surrounding B 335 onto the protostellar envelope, thus rejuvenating its chemistry. The comparison between envelopes of different Class 0 objects has also allowed to deduce a low SO abundance in B 335 with respect to L 483 and B1-b. SO is a well- known outflow tracer, which is thought to be enhanced in shocks. Its low abundance in B 335 together with the non-detection of other shock tracers, such SO+, suggests that its chemistry in B 335 is not particularly influenced by shocks.
In this work, we have also used the time-dependent chemical code Nautilus to study the time evolution of fractional S-abundances, as well as the influence of several physical and chemical parameters (cosmic-ray ionisation rate, density, gas temperature, and initial sulphur abundance) on these abundances. The comparison between chemical model results and observations shows that the evolutionary stages that better reproduce the observed abundances of the largest number of S-species in B 335 correspond to t = 104–105 yr, in agreement with previous age estimations obtained by applying theoretical methods with the use of a dynamical model. The results from Nautilus have also revealed that the physical parameters with the highest influence on the S-abundances are the density and the cosmic-ray ionisation rate whose variations by one order of magnitude lead to abundance variations of several orders of magnitude for different sulphur-bearing species such as SO, SO2, CS, and CCCS. We have also used Nautilus to explore the behaviour of different S-molecular ratios with time, finding that there are some sulphur ratios that could be used as chemical evolution tracers since they maintain a constant trend over time. A comparison of the observational results of S-ratios in a sample of objects (including starless and prestellar cores, and Class 0 objects) characterised by different evolutionary stages confirms a clear trend where the SO2/C2S and SO/CS ratios increase with the age of the objects, while HCS+/CS decreases with the evolutionary stage. We, therefore, conclude that these S-ratios could be used as good chemical evolutionary indicators tracing the prestellar to protostellar transition.
 |
Fig. 12 Observational sulphur molecular ratios of potentially good chemical evolution tracers of the prestellar to protostellar transition for different objects (TMC1, L 1544, B 335, L 483, and B1-b). Data for TMC1 were taken from Marcelino et al. (2007), Cernicharo (2012), Cernicharo et al. (2021), and Rodríguez-Baras et al. (2021). Data for L 1544 were taken from Vastel et al. (2018). L 483 and B1-b data were gathered from Agúndez et al. (2019) and Fuente et al. (2016), respectively. |
Acknowledgements
We thank the Spanish MICINN for funding support from PID2019-106235GB-I00. This project has been carried out with observations from the 30-m radio telescope of the Institut de radioastronomie millimétrique (IRAM) and from the 40-m radio telescope of the National Geographic Institute of Spain (IGN) at Yebes Observatory. Yebes Observatory thanks the ERC for funding support under grant ERC-2013-Syg-610256-NANOCOSMOS. A.F. is grateful to the European Research Council (ERC) for funding under the Advanced Grant project SUL4LIFE, grant agreement No101096293. D.N.A. acknowledges funding support from Fundación Ramón Areces through their international postdoc grant program. Á.S.M. acknowledges support from the RyC2021-032892-I grant funded by MCIN/AEI/10.13039/501100011033 and by the European Union ‘Next GenerationEU’/PRTR, as well as the program Unidad de Excelencia María de Maeztu CEX2020-001058-M. M.N.D. acknowledges the support by the Swiss National Science Foundation (SNSF) Ambizione grant no. 180079, the Center for Space and Habitability (CSH) Fellowship, and the IAU Gruber Foundation Fellowship. We also thank the anonymous referee for valuable comments that improved the manuscript.
Appendix A Tables and figures
Line parameters of sulphur-bearing molecules detected in B 335.
 |
Fig. A.1 Observed lines of CS in B 335 (black) with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.2 Observed lines of 13CS in B 335 (black) with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.3 Observed lines of C34S in B 335 (black) with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.4 Observed lines of C33S in B 335 (black) with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.5 Observed lines of CCS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.6 Observed lines of CC34S in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.7 Observed lines of CCCS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.8 Observed lines of CCC34S in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.9 Observed lines of OCS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.10 Observed lines of HCS+ in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.11 Observed lines of HC34S+ in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.12 Observed lines of SO in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.13 Observed lines of 34SO in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.14 Observed lines of o-H2CS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.15 Observed lines of p-H2CS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.16 Observed lines of NS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
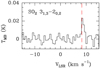 |
Fig. A.17 Observed line of SO2 in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
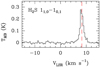 |
Fig. A.18 Observed line of H2S in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.19 Observed line of H234S in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.20 Observed line of HSCN in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.21 Observed line of HNCS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
 |
Fig. A.22 Ratios between the abundances obtained from the models, Xmodel, and the observations, Xobs, for different sulphur species at specific evolution times (t=104, 5×104, 105, 5×105, and 106 yr), when varying the cosmic-ray rate (ζ). |
 |
Fig. A.23 Ratios between the abundances obtained from the models, Xmodel, and the observations, Xobs, for different sulphur species at specific evolution times (t=104, 5×104, 105, 5×105, and 106 yr), when varying the gas temperature. |
 |
Fig. A.24 Ratios between the abundances obtained from the models, Xmodel, and the observations, Xobs, for different sulphur species at specific evolution times (t=104, 5×104, 105, 5×105, and 106 yr), when varying the hydrogen number density (nH). |
 |
Fig. A.25 Ratios between the abundances obtained from the models, Xmodel, and the observations, Xobs, for different sulphur species at specific evolution times (t=104, 5×104, 105, 5×105, and 106 yr), when varying the initial sulphur abundance ( |
References
- Adande, G. R., Halfen, D. T., Ziurys, L. M., Quan, D., & Herbst, E. 2010, ApJ, 725, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., & Wakelam, V. 2013, Chem. Rev., 113, 8710 [Google Scholar]
- Agúndez, M., Marcelino, N., Cernicharo, J., Roueff, E., & Tafalla, M. 2019, A&A, 625, A147 [Google Scholar]
- Aikawa, Y., Ohashi, N., & Herbst, E. 2003, ApJ, 593, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 2000, in Protostars and Planets IV, eds. V. Mannings, A. P. Boss, & S. S. Russell, 59 [Google Scholar]
- Asplund, M., Grevesse, N., Sauvai, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bachiller, R., & Pérez Gutiérrez, M. 1997, ApJ, 487, L93 [Google Scholar]
- Bergin, E. A., & Langer, W. D. 1997, ApJ, 486, 316 [Google Scholar]
- Bjerkeli, P., Ramsey, J. P., Harsono, D., et al. 2019, A&A, 631, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [Google Scholar]
- Boogert, A. C. A., Tielens, A. G. G. M., Ceccarelli, C., et al. 2000, A&A, 360, 683 [NASA ADS] [Google Scholar]
- Brünken, S., Yu, Z., Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2009, ApJ, 706, 1588 [CrossRef] [Google Scholar]
- Bulut, N., Roncero, O., Aguado, A., et al. 2021, A&A, 646, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabedo, V., Maury, A., Girart, J. M., & Padovani, M. 2021, A&A, 653, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabedo, V., Maury, A., Girart, J. M., et al. 2023, A&A, 669, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabrit, S., Goldsmith, P. F., & Snell, R. L. 1988, ApJ, 334, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Calmonte, U., Altwegg, K., Balsiger, H., et al. 2016, MNRAS, 462, S253 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., & Ceccarelli, C. 2012, A&ARv, 20, 56 [Google Scholar]
- Caselli, P., Walmsley, C. M., Terzieva, R., & Herbst, E. 1998, ApJ, 499, 234 [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [Google Scholar]
- Caselli, P., Walmsley, C. M., Zucconi, A., et al. 2002, ApJ, 565, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [CrossRef] [Google Scholar]
- Ceccarelli, C. 2004, in ASP Conf. Ser., 323, Star Formation in the Interstellar Medium: In Honor of David Hollenbach, eds. D. Johnstone, F. C. Adams, D. N. C. Lin, D. A. Neufeeld, & E. C. Ostriker, 195 [Google Scholar]
- Ceccarelli, C., Caselli, P., Herbst, E., Tielens, A. G. G. M., & Caux, E. 2007a, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil, 47 [Google Scholar]
- Ceccarelli, L., Valotto, C., Lambas, D. G., & Padilla, N. 2007b, in ASP Conf.Ser., 379, Cosmic Frontiers, eds. N. Metcalfe, & T. Shanks, 287 [NASA ADS] [Google Scholar]
- Cernicharo, J. 2012, in EAS Pub. Ser., 58, 251 [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., & Guelin, M. 1987, A&A, 176, 299 [NASA ADS] [Google Scholar]
- Cernicharo, J., Bachiller, R., & Duvert, G. 1985, A&A, 149, 273 [NASA ADS] [Google Scholar]
- Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021, A&A, 648, A3 [Google Scholar]
- Charnley, S. B. 1997, ApJ, 481, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, M., Evans, I. Neal, J., Gregersen, E. M., & Wang, Y. 1995, ApJ, 448, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Clary, D. C., Smith, D., & Adams, N. G. 1985, Chem. Phys. Lett., 119, 320 [CrossRef] [Google Scholar]
- Codella, C., & Bachiller, R. 1999, A&A, 350, 659 [NASA ADS] [Google Scholar]
- Codella, C., & Scappini, F. 2003, MNRAS, 344, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Codella, C., Bachiller, R., Benedettini, M., et al. 2005, MNRAS, 361, 244 [Google Scholar]
- Codella, C., Viti, S., Ceccarelli, C., et al. 2013, ApJ, 776, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Crockett, N. R., Bergin, E. A., Neill, J. L., et al. 2014, ApJ, 781, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Deguchi, S., Miyazaki, A., & Minh, Y. C. 2006, PASJ, 58, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Esplugues, G. B., Tercero, B., Cernicharo, J., et al. 2013, A&A, 556, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esplugues, G. B., Viti, S., Goicoechea, J. R., & Cernicharo, J. 2014, A&A, 567, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esplugues, G., Fuente, A., Navarro-Almaida, D., et al. 2022, A&A, 662, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, I., Neal, J., Di Francesco, J., Lee, J.-E., et al. 2015, ApJ, 814, 22 [CrossRef] [Google Scholar]
- Evans, I., Neal, J., Yang, Y.-L., Green, J. D., et al. 2023, ApJ, 943, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Francioso, A., Baseggio Conrado, A., Mosca, L., & Fontana, M. 2020, OxidativeMedicine and Cellular Longevity, 2020, 8294158 [Google Scholar]
- Frerking, M. A., Langer, W. D., & Wilson, R. W. 1987, ApJ, 313, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Cernicharo, J., Roueff, E., et al. 2016, A&A, 593, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuente, A., Rivière-Marichalar, P., Beitia-Antero, L., et al. 2023, A&A, 670, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geballe, T. R., Baas, F., Greenberg, J. M., & Schutte, W. 1985, A&A, 146, L6 [NASA ADS] [Google Scholar]
- Gibb, E. L., Whittet, D. C. B., Schutte, W. A., et al. 2000, ApJ, 536, 347 [Google Scholar]
- Goicoechea, J. R., Pety, J., Gerin, M., et al. 2006, A&A, 456, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Kwan, J. 1974, ApJ, 191, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [Google Scholar]
- Graedel, T. E., Langer, W. D., & Frerking, M. A. 1982, ApJS, 48, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Halfen, D. T., Ziurys, L. M., Brünken, S., et al. 2009, ApJ, 702, L124 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchell, J., Thompson, M. A., Millar, T. J., & MacDonald, G. H. 1998, A&AS, 133, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herbst, E., & van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Pineau des Forêts, G., Faure, A., & Lique, F. 2022, A&A, 658, A168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hincelin, U., Wakelam, V., Hersant, F., et al. 2011, A&A, 530, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirano, N., Kameya, O., Nakayama, M., & Takakubo, K. 1988, ApJ, 327, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Hirano, N., Kameya, O., Kasuga, T., & Umemoto, T. 1992, ApJ, 390, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Hirota, T., Ohishi, M., & Yamamoto, S. 2009, ApJ, 699, 585 [Google Scholar]
- Hogerheijde, M. R., van Dishoeck, E. F., Blake, G. A., & van Langevelde, H. J. 1998, ApJ, 502, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Holdship, J., Jimenez-Serra, I., Viti, S., et al. 2019, ApJ, 878, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Howk, J. C., Sembach, K. R., & Savage, B. D. 2006, ApJ, 637, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Imai, M., Sakai, N., Oya, Y., et al. 2016, ApJ, 830, L37 [CrossRef] [Google Scholar]
- Imai, M., Oya, Y., Sakai, N., et al. 2019, ApJ, 873, L21 [Google Scholar]
- Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Irvine, W. M., Good, J. C., & Schloerb, F. P. 1983, A&A, 127, L10 [NASA ADS] [Google Scholar]
- Jaber, A. A., Ceccarelli, C., Kahane, C., & Caux, E. 2014, ApJ, 791, 29 [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [Google Scholar]
- Jiménez-Serra, I., Martín-Pintado, J., Rodríguez-Franco, A., & Martín, S. 2005, ApJ, 627, L121 [Google Scholar]
- Jørgensen, J. K., van der Wiel, M. H. D., Coutens, A., et al. 2016, A&A, 595, A117 [Google Scholar]
- Keene, J., Hildebrand, R. H., Whitcomb, S. E., & Harper, D. A. 1980, ApJ, 240, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Keene, J., Davidson, J. A., Harper, D. A., et al. 1983, ApJ, 274, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Laas, J. C., & Caselli, P. 2019, A&A, 624, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, C.-F., Hasegawa, T. I., Hirano, N., et al. 2010, ApJ, 713, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Lefloch, B., Bachiller, R., Ceccarelli, C., et al. 2018, MNRAS, 477, 4792 [Google Scholar]
- Leustek, T. 2002, Arabidopsis Book, 1, e0017 [CrossRef] [Google Scholar]
- Marcelino, N., Cernicharo, J., Agúndez, M., et al. 2007, ApJ, 665, L127 [Google Scholar]
- Mauersberger, R., Ott, U., Henkel, C., Cernicharo, J., & Gallino, R. 2004, A&A, 426, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClure, M. K., Rocha, W. R. M., Pontoppidan, K. M., et al. 2023, Nat. Astron., 7, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J. 1983, MNRAS, 202, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J., & Herbst, E. 1990, A&A, 231, 466 [NASA ADS] [Google Scholar]
- Millar, T. J., Adams, N. G., Smith, D., & Clary, D. C. 1985, MNRAS, 216, 1025 [NASA ADS] [Google Scholar]
- Minh, Y. C., Brewer, M. K., Irvine, W. M., Friberg, P., & Johansson, L. E. B. 1991, A&A, 244, 470 [NASA ADS] [Google Scholar]
- Moriarty-Schieven, G. H., & Snell, R. L. 1989, ApJ, 338, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Naraoka, H., Takano, Y., Dworkin, J. P., Hayabusa2-Initial-Analysis SOM Team, & Hayabusa2-Initial-Analysis Core 2022, in LPI Contributions, 2678, 53rd Lunar and Planetary Science Conference, 1781 [Google Scholar]
- Navarro-Almaida, D., Le Gal, R., Fuente, A., et al. 2020, A&A, 637, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro-Almaida, D., Fuente, A., Majumdar, L., et al. 2021, A&A, 653, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A., & Dalgarno, A. 1989, ApJ, 340, 869 [Google Scholar]
- Neufeld, D. A., & Wolfire, M. G. 2017, ApJ, 845, 163 [Google Scholar]
- Neufeld, D. A., Wolfire, M. G., & Schilke, P. 2005, ApJ, 628, 260 [Google Scholar]
- Oba, Y., Tomaru, T., Kouchi, A., & Watanabe, N. 2019, ApJ, 874, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Okoda, Y., Oya, Y., Imai, M., et al. 2022, ApJ, 935, 136 [CrossRef] [Google Scholar]
- Okoda, Y., Oya, Y., Francis, L., et al. 2023, ApJ, 948, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, S., & Olofsson, G. 2009, A&A, 498, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oya, Y., Sakai, N., Watanabe, Y., et al. 2017, ApJ, 837, 174 [Google Scholar]
- Palumbo, M. E., Tielens, A. G. G. M., & Tokunaga, A. T. 1995, ApJ, 449, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001, IEEE Trans. Antennas Propag., 49, 1683 [Google Scholar]
- Pineau des Forets, G., Roueff, E., Schilke, P., & Flower, D. R. 1993, MNRAS, 262, 915 [CrossRef] [Google Scholar]
- Pineda, J. E., Segura-Cox, D., Caselli, P., et al. 2020, Nat. Astron., 4, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Podio, L., Lefloch, B., Ceccarelli, C., Codella, C., & Bachiller, R. 2014, A&A, 565, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [Google Scholar]
- Rodríguez-Baras, M., Fuente, A., Riviére-Marichalar, P., et al. 2021, A&A, 648, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruaud, M., Wakelam, V., & Hersant, F. 2016, MNRAS, 459, 3756 [Google Scholar]
- Ruf, A., Bouquet, A., Schmitt-Kopplin, P., et al. 2021, A&A, 655, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruffle, D. P., Hartquist, T. W., Caselli, P., & Williams, D. A. 1999, MNRAS, 306, 691 [Google Scholar]
- Sakai, N., & Yamamoto, S. 2013, Chem. Rev., 113, 8981 [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2008, ApJ, 672, 371 [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., Burton, M., & Yamamoto, S. 2009, ApJ, 697, 769 [Google Scholar]
- Schnee, S., Caselli, P., Goodman, A., et al. 2007, ApJ, 671, 1839 [NASA ADS] [CrossRef] [Google Scholar]
- Shingledecker, C. N., Lamberts, T., Laas, J. C., et al. 2020, ApJ, 888, 52 [Google Scholar]
- Shirley, Y. L., Mason, B. S., Mangum, J. G., et al. 2011, AJ, 141, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Stutz, A. M., Rubin, M., Werner, M. W., et al. 2008, ApJ, 687, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, H., Yamamoto, S., Ohishi, M., et al. 1992, ApJ, 392, 551 [Google Scholar]
- Tafalla, M., Santiago-García, J., Hacar, A., & Bachiller, R. 2010, A&A, 522, A91 [CrossRef] [EDP Sciences] [Google Scholar]
- Tamura, M., Ohashi, N., Hirano, N., Itoh, Y., & Moriarty-Schieven, G. H. 1996, AJ, 112, 2076 [NASA ADS] [CrossRef] [Google Scholar]
- Tercero, B., Cernicharo, J., Pardo, J. R., & Goicoechea, J. R. 2010, A&A, 517, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thaddeus, P., Guelin, M., & Linke, R. A. 1981, ApJ, 246, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Tieftrunk, A., Pineau des Forets, G., Schilke, P., & Walmsley, C. M. 1994, A&A, 289, 579 [Google Scholar]
- Turner, B. E. 1992, ApJ, 396, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E. 1994, ApJ, 430, 727 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., & van Dishoeck, E. F. 2000, A&A, 358, L79 [NASA ADS] [Google Scholar]
- van der Tak, F. F. S., Caselli, P., & Ceccarelli, C. 2005, A&A, 439, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Blake, G. A., Jansen, D. J., & Groesbeck, T. D. 1995, ApJ, 447, 760 [Google Scholar]
- Vastel, C., Quénard, D., Le Gal, R., et al. 2018, MNRAS, 478, 5514 [Google Scholar]
- Vidal, T. H. G., Loison, J.-C., Jaziri, A. Y., et al. 2017, MNRAS, 469, 435 [Google Scholar]
- Viti, S., Natarajan, S., & Williams, D. A. 2002, MNRAS, 336, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., Collings, M. P., Dever, J. W., McCoustra, M. R. S., & Williams, D. A. 2004, MNRAS, 354, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., & Herbst, E. 2008, ApJ, 680, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Castets, A., Ceccarelli, C., et al. 2004, A&A, 413, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Ceccarelli, C., Castets, A., et al. 2005, A&A, 437, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Dartois, E., Chabot, M., et al. 2021, A&A, 652, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wierzejewska, M., & Mielke, Z. 2001, Chem. Phys. Lett., 349, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y.-L., Green, J. D., Pontoppidan, K. M., et al. 2022, ApJ, 941, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Yen, H.-W., Takakuwa, S., & Ohashi, N. 2010, ApJ, 710, 1786 [NASA ADS] [CrossRef] [Google Scholar]
- Yen, H.-W., Takakuwa, S., Koch, P. M., et al. 2015, ApJ, 812, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Yıldız, U. A., Kristensen, L. E., van Dishoeck, E. F., et al. 2015, A&A, 576, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, S., Evans, I. Neal, J., Koempe, C., & Walmsley, C. M. 1993, ApJ, 404, 232 [NASA ADS] [CrossRef] [Google Scholar]
Derived from results in Table 2 and the expression
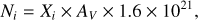 (4)
(4)
where Ni is the column density of the species i, Xi its abundance, Av the visual extinction, and 1.6 × 1021 the hydrogen column density at 1 mag of extinction (Bohlin et al. 1978).
All Tables
Yebes-40 m and IRAM-30 m telescope efficiency data along the covered frequency range.
Column densities (N), rotational temperatures, and abundances (X) relative to H2 of the sulphur-bearing molecules detected in B 335.
Abundances with respect to total hydrogen nuclei considered in the chemical code Nautilus.
All Figures
 |
Fig. 1 Rotational diagrams of the detected sulphur-bearing molecules in B 335. Fitted values of the rotational temperature, Trot, column density, N, and their respective uncertainties are also indicated for each molecule. |
| In the text | |
 |
Fig. 2 Comparison of fractional abundances of sulphur-bearing species between three Class 0 objects B 335 (this work), L 483 (Agúndez et al. 2019), and B1-b (Fuente et al. 2016). |
| In the text | |
 |
Fig. 3 Fractional abundance (X) ratios between B 335 and L 483, and B 335 and B1-b for all the detected sulphur-bearing species in B 335. |
| In the text | |
 |
Fig. 4 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
| In the text | |
 |
Fig. 5 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
| In the text | |
 |
Fig. 6 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
| In the text | |
 |
Fig. 7 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
| In the text | |
 |
Fig. 8 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
| In the text | |
 |
Fig. 9 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
| In the text | |
 |
Fig. 10 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
| In the text | |
 |
Fig. 11 Evolution of fractional abundances of CS, CCS, C3S, OCS, SO, SO2, HCS+, H2CS, and NS as a function of time for an initial sulphur abundance |
| In the text | |
 |
Fig. 12 Observational sulphur molecular ratios of potentially good chemical evolution tracers of the prestellar to protostellar transition for different objects (TMC1, L 1544, B 335, L 483, and B1-b). Data for TMC1 were taken from Marcelino et al. (2007), Cernicharo (2012), Cernicharo et al. (2021), and Rodríguez-Baras et al. (2021). Data for L 1544 were taken from Vastel et al. (2018). L 483 and B1-b data were gathered from Agúndez et al. (2019) and Fuente et al. (2016), respectively. |
| In the text | |
 |
Fig. A.1 Observed lines of CS in B 335 (black) with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.2 Observed lines of 13CS in B 335 (black) with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.3 Observed lines of C34S in B 335 (black) with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.4 Observed lines of C33S in B 335 (black) with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.5 Observed lines of CCS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.6 Observed lines of CC34S in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.7 Observed lines of CCCS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.8 Observed lines of CCC34S in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.9 Observed lines of OCS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.10 Observed lines of HCS+ in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.11 Observed lines of HC34S+ in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.12 Observed lines of SO in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.13 Observed lines of 34SO in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.14 Observed lines of o-H2CS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.15 Observed lines of p-H2CS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.16 Observed lines of NS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.17 Observed line of SO2 in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.18 Observed line of H2S in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.19 Observed line of H234S in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.20 Observed line of HSCN in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.21 Observed line of HNCS in B 335 with rms>3σ. The red dashed line indicates the systemic velocity of the source vLSR=8.3 km s−1. |
| In the text | |
 |
Fig. A.22 Ratios between the abundances obtained from the models, Xmodel, and the observations, Xobs, for different sulphur species at specific evolution times (t=104, 5×104, 105, 5×105, and 106 yr), when varying the cosmic-ray rate (ζ). |
| In the text | |
 |
Fig. A.23 Ratios between the abundances obtained from the models, Xmodel, and the observations, Xobs, for different sulphur species at specific evolution times (t=104, 5×104, 105, 5×105, and 106 yr), when varying the gas temperature. |
| In the text | |
 |
Fig. A.24 Ratios between the abundances obtained from the models, Xmodel, and the observations, Xobs, for different sulphur species at specific evolution times (t=104, 5×104, 105, 5×105, and 106 yr), when varying the hydrogen number density (nH). |
| In the text | |
 |
Fig. A.25 Ratios between the abundances obtained from the models, Xmodel, and the observations, Xobs, for different sulphur species at specific evolution times (t=104, 5×104, 105, 5×105, and 106 yr), when varying the initial sulphur abundance ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.